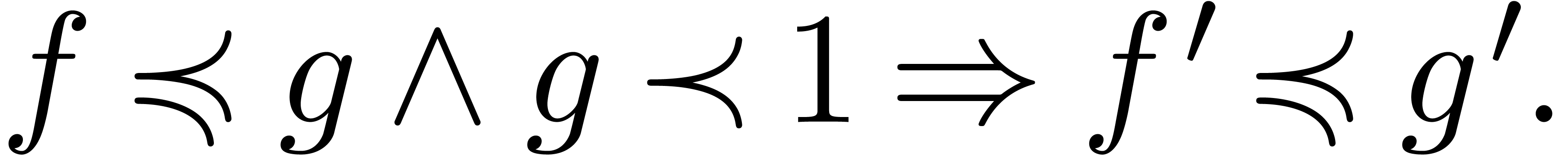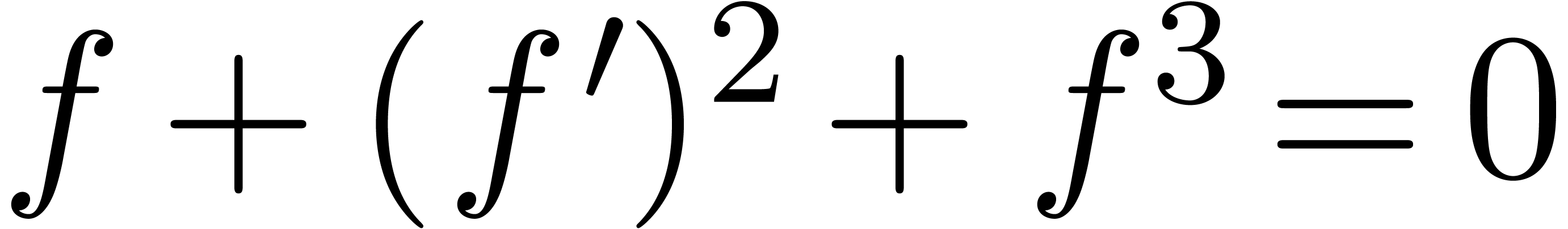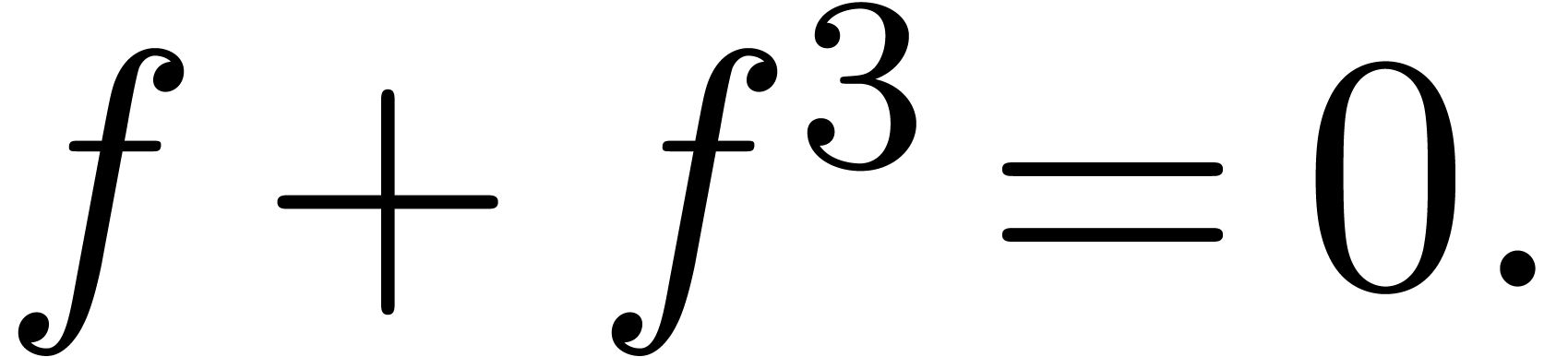| A differential intermediate value
theorem |
|
Département de Mathématiques
(Bât. 425)
Université
Paris-Sud
91405 Orsay Cedex
France
|
|
|
1Introduction
In this survey paper, we will outline the proof of a recent differential
intermediate value theorem for transseries [vdH00] (with a
few corrections in [vdH01]). A transseries is a
generalization of a formal power series, in which one allows the
recursive intrusion of exponentials and logarithms. In this paper we
will only deal with real transseries at infinity ( ). Some examples of such transseries are
). Some examples of such transseries are
The transseries 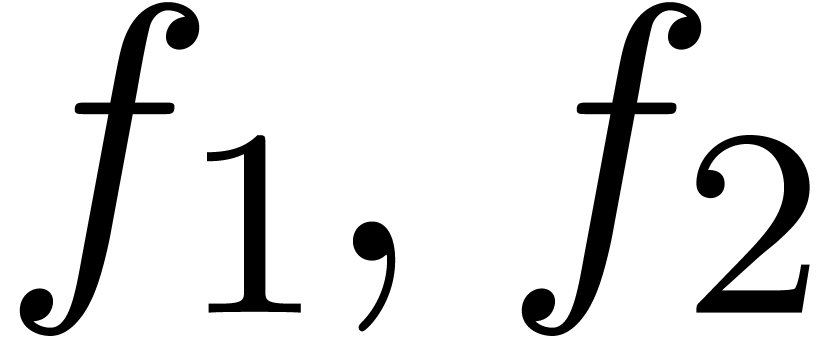 and
and 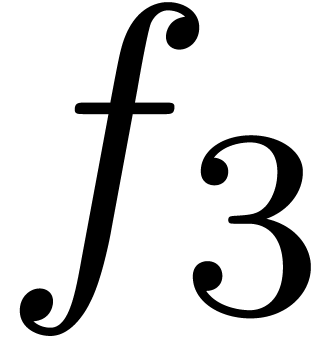 are
examples of grid-based transseries, the first two being
convergent and the last one divergent. In section 2 we will
construct the field of grid-based transseries
are
examples of grid-based transseries, the first two being
convergent and the last one divergent. In section 2 we will
construct the field of grid-based transseries  , which will be our main object of study in the
sequel. More exotic, well-ordered transseries are
, which will be our main object of study in the
sequel. More exotic, well-ordered transseries are 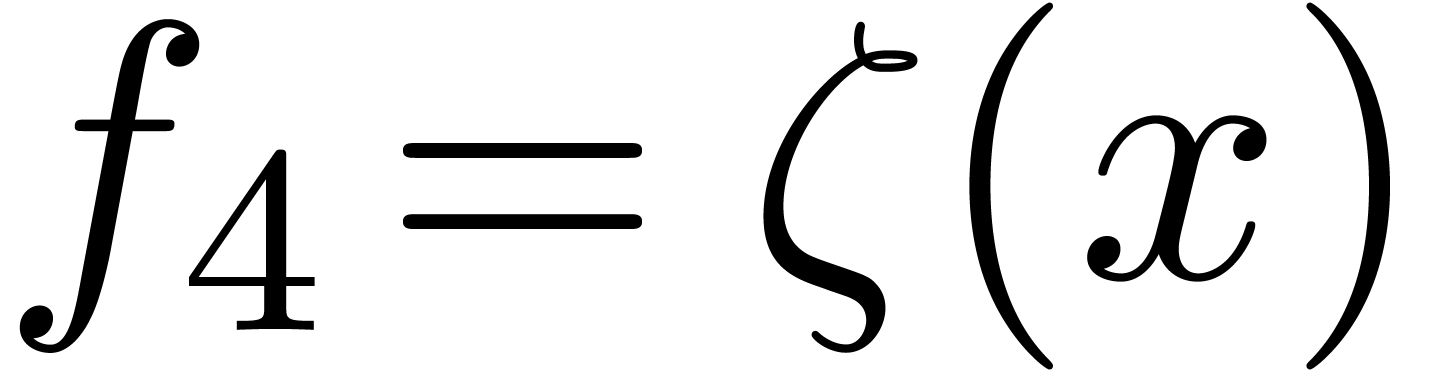 and
and 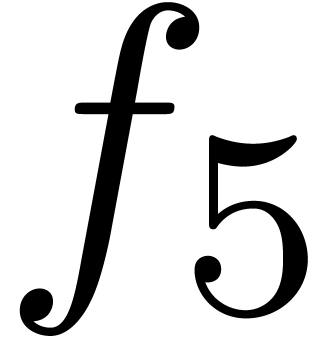 . Notice
that
. Notice
that 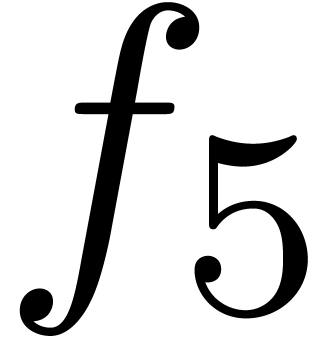 satisfies the functional equation
satisfies the functional equation
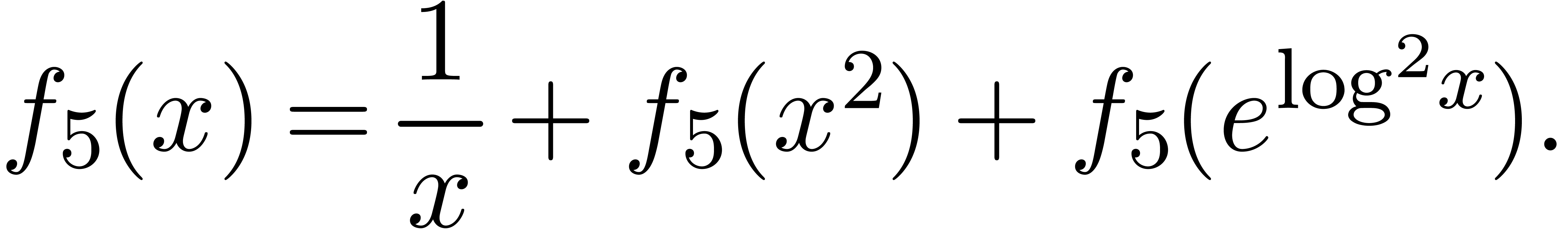
Historically speaking, transseries appeared independently in at least
three different contexts:
-
Model theory
-
The first construction of the field of transseries goes back to
Dahn and Göring [DG86], who were interested in
non standard models for the theory of real numbers with
exponentiation. Much recent progress on this subject has been made
through works by Wilkie, van den Dries, Macintyre and others. The
theory of transseries also bears many similarities with Conway's
theory of surreal numbers.
-
Analyzable functions
-
The main current application of transseries is in the proof of
Dulac's conjecture by Écalle [É92].
More precisely, Écalle proved that a planar real analytic
vector field can only have a finite number of limit cycles.
Essentially, he shows that the Poincaré return map near a
limit cycle can be represented by an analyzable function
 . Formally, such a
function is a transseries, but through a complicated process of
accelero-summation, this formal transseries can be given an
analytic meaning. Since the real transseries form a
totally ordered field, one must have
. Formally, such a
function is a transseries, but through a complicated process of
accelero-summation, this formal transseries can be given an
analytic meaning. Since the real transseries form a
totally ordered field, one must have  ,
,
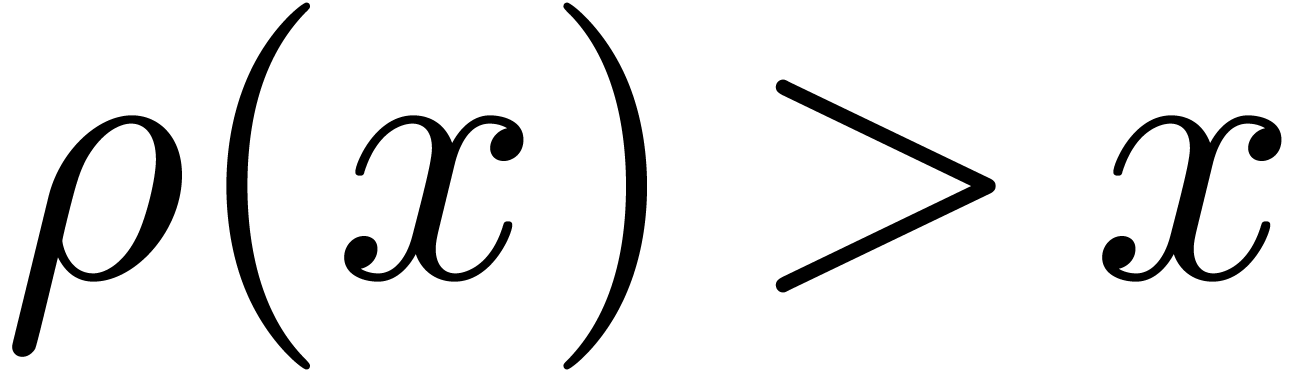 or
or 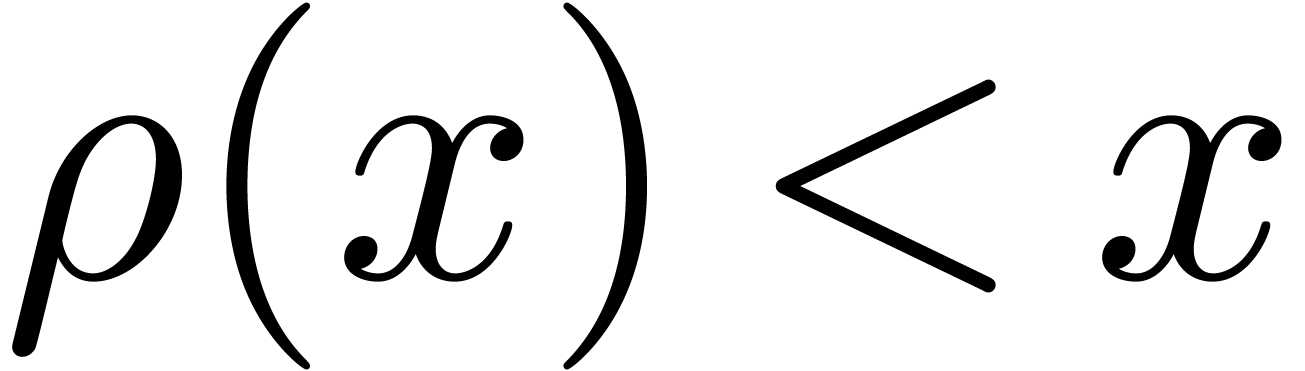 in a small
neighbourhood of the limit cycle. In other words, either all or no
orbits are periodic in this neighbourhood.
in a small
neighbourhood of the limit cycle. In other words, either all or no
orbits are periodic in this neighbourhood.
-
Effective asymptotic analysis
-
Transseries also implicitly appeared during the research of
algorithms for doing asymptotic analysis [Sha90, Sal91, GG92]. In the formal context of
transseries, we were able to do such effective computations in a
more systematic way [vdH97].
There is no doubt that the combination of the techniques from these
three different areas will lead to an extremely powerful theory, whose
development is far from finished. A nice feature of such a theory will
be that it will both have theoretical and practical aspects (we expect
effective numerical accelero-summation to have many applications in
numerical analysis, for instance).
Before dealing with all these aspects of the theory of transseries, it
is interesting to study which kind of asymptotic problems might a
priori be adequately modelled by transseries (at least from the
formal point of view). For instance, it is well known that linear
differential equations with power series coefficients in 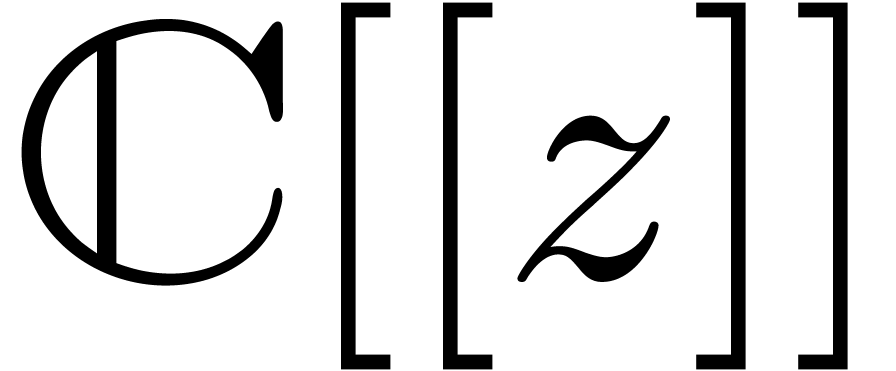 always have a full basis of solutions of the form
always have a full basis of solutions of the form
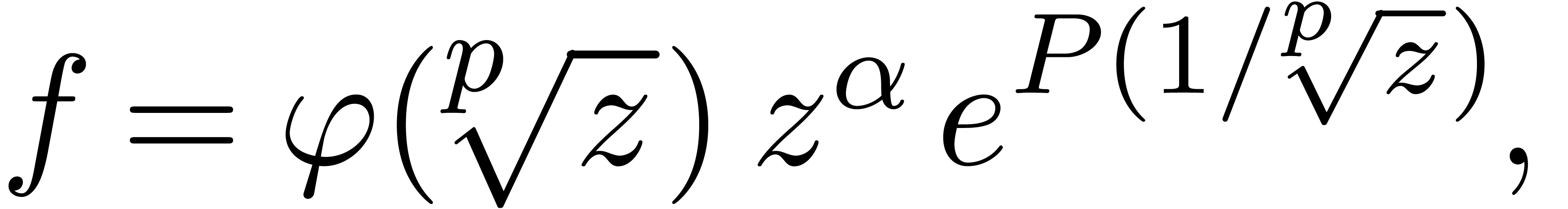
where  is a polynomial,
is a polynomial,  and
and 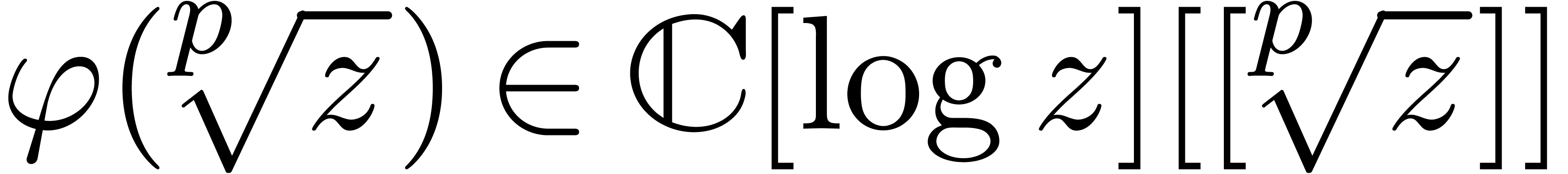 a power series whose coefficients are
polynomials in
a power series whose coefficients are
polynomials in  of uniformly bounded degree. It
is tempting to generalize this result to non-linear differential
equations and even to more general functional equations.
of uniformly bounded degree. It
is tempting to generalize this result to non-linear differential
equations and even to more general functional equations.
When considering non-linear equations, say algebraic ones, the first
difficulty one has to face is that the set of solutions to such
equations is closed under composition. For instance, given an infinitely
large indeterminate  , we have
to incorporate iterated exponentials
, we have
to incorporate iterated exponentials  of
arbitrarily high orders into our theory. This is problematic if
of
arbitrarily high orders into our theory. This is problematic if  is complex, because
is complex, because 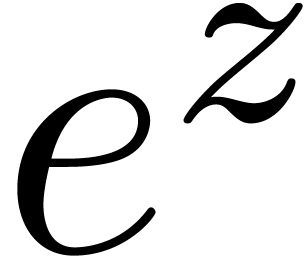 behaves
very differently in the positive and negative halfplanes.
behaves
very differently in the positive and negative halfplanes.
In order to do asymptotics, a reasonable next step is therefore to
reduce one's attention to real functions without oscillatory behavior.
Of course, this is a very strong restriction, since we will no longer be
able to solve simple equations like
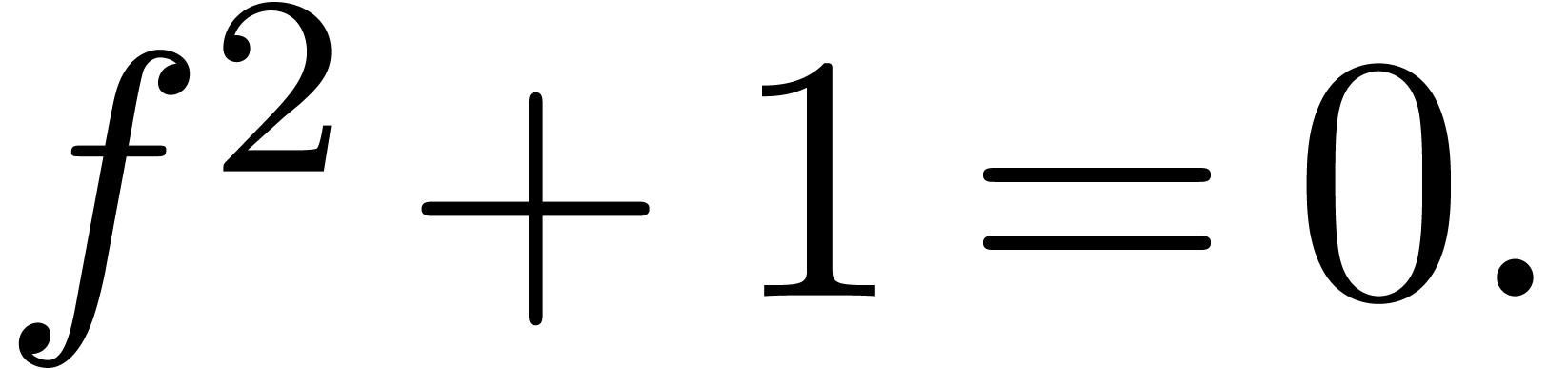 |
(1) |
Nevertheless, this restriction does allow us to construct a clean,
totally ordered field of formal grid-based transseries  in an infinitely large real variable
in an infinitely large real variable  (see
section 2). In this field, we will have asymptotic
relations
(see
section 2). In this field, we will have asymptotic
relations  and
and  (using the
notation of Hardy:
(using the
notation of Hardy: 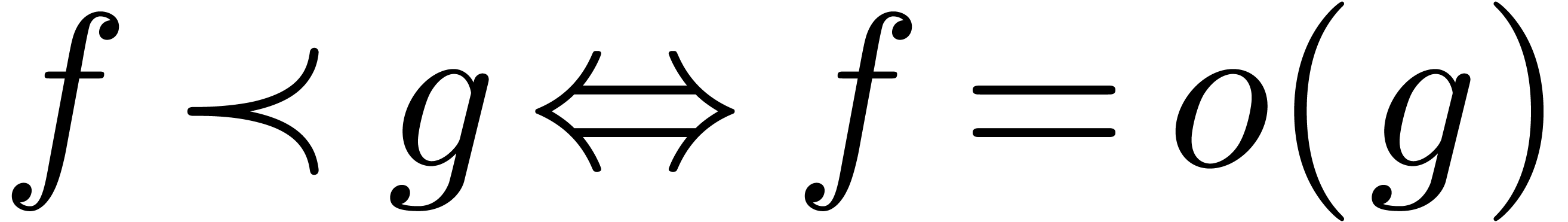 and
and 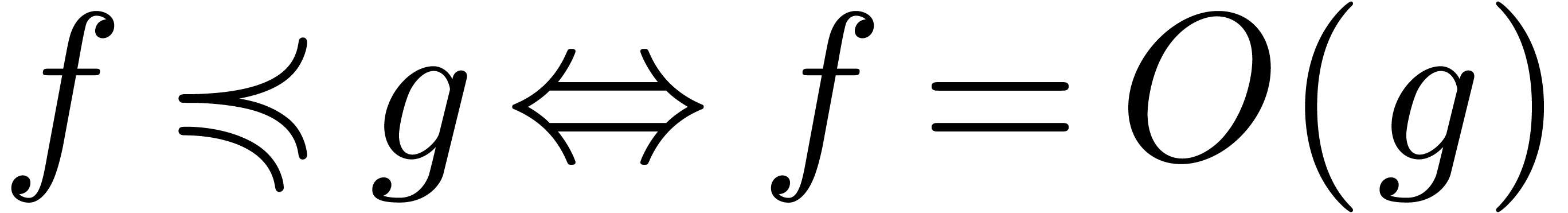 ). Furthermore,
). Furthermore,  is closed
under differentiation, composition and functional inversion. So what
about solving differential equations? Since even simple equations such
as (1) do not always have solutions, we have to search for
existence theorems of solutions which take into account the realness of
the context. In this paper, we outline a proof of the following such
theorem:
is closed
under differentiation, composition and functional inversion. So what
about solving differential equations? Since even simple equations such
as (1) do not always have solutions, we have to search for
existence theorems of solutions which take into account the realness of
the context. In this paper, we outline a proof of the following such
theorem:
Theorem 1. (Differential
intermediate value theorem) Let 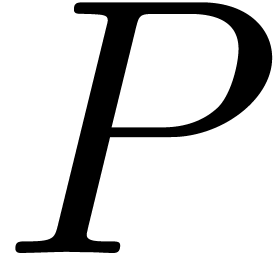 be
an algebraic differential polynomial with coefficients in
be
an algebraic differential polynomial with coefficients in  . Given
. Given 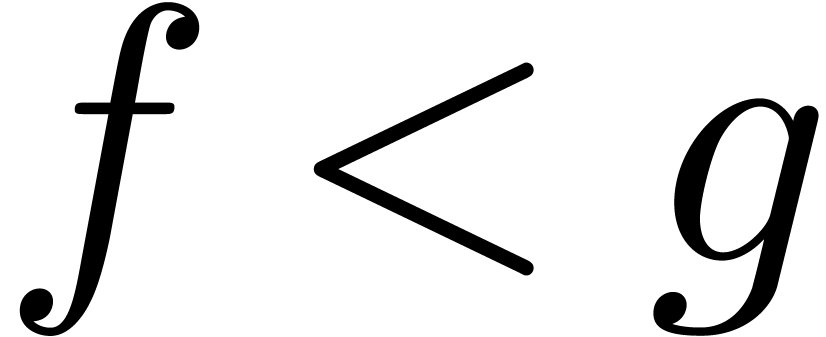 in
in  , such that
, such that 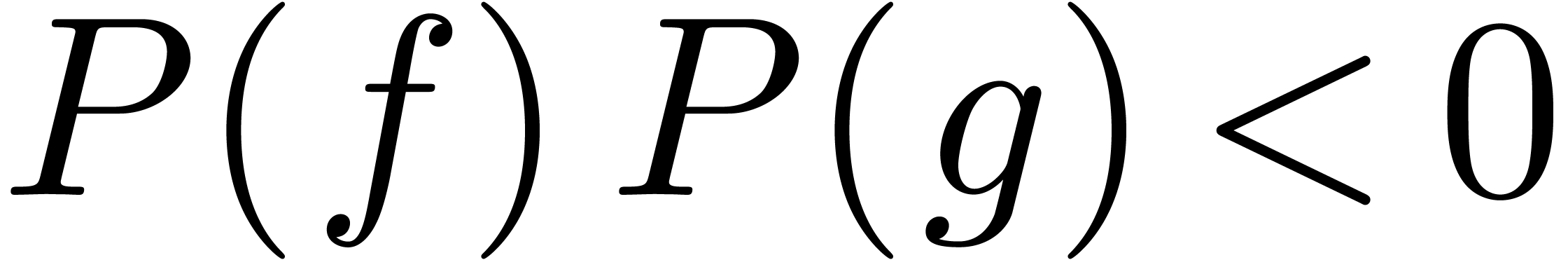 ,
there exists a solution
,
there exists a solution  of
of 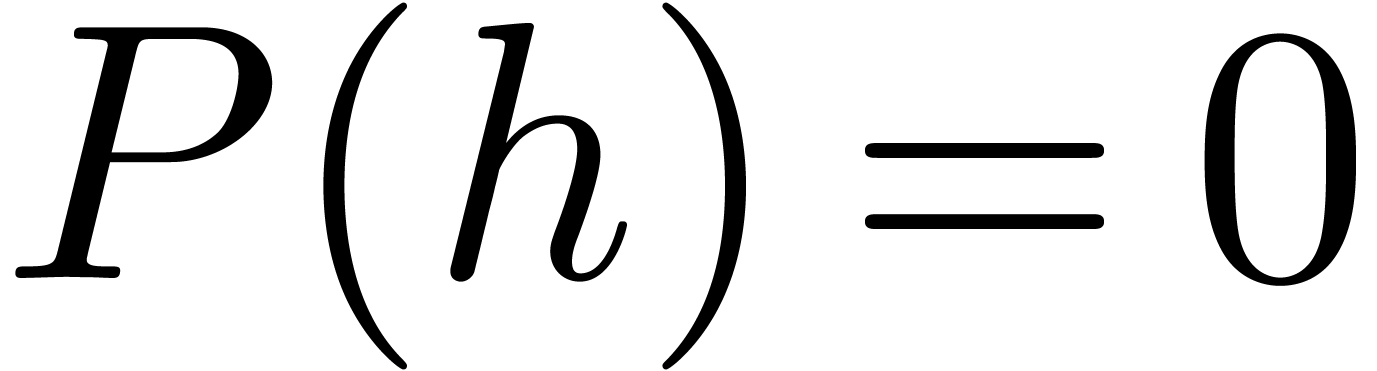 with
with 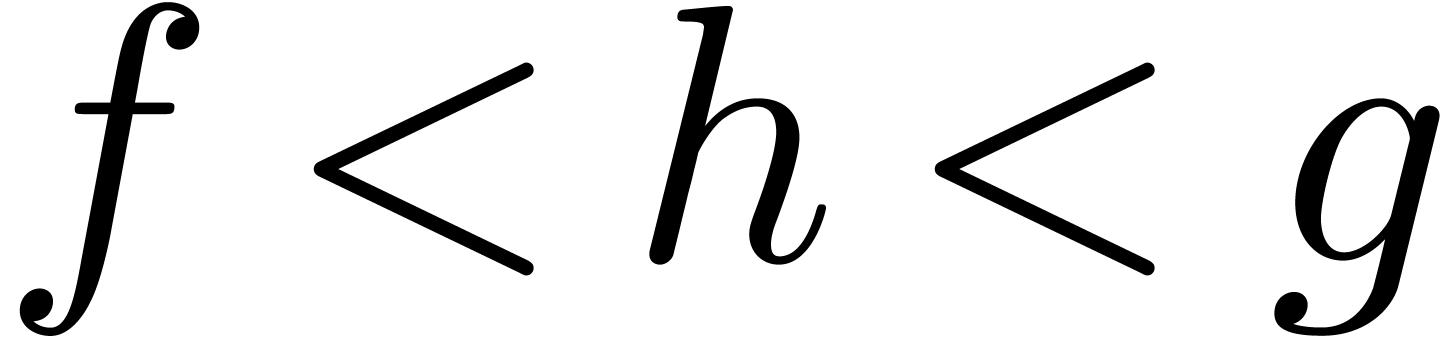 .
.
In particular, the theorem implies that an algebraic differential
equation of odd degree like
always has a solution in  .
Our proof is based on a differential version of the Newton polygon
method, which will be sketched in section 3. Using a
variant of Stevin's dichotomic method to find roots of continuous
functions, we next indicate (section 4) how to find a solution
.
Our proof is based on a differential version of the Newton polygon
method, which will be sketched in section 3. Using a
variant of Stevin's dichotomic method to find roots of continuous
functions, we next indicate (section 4) how to find a solution  of
of 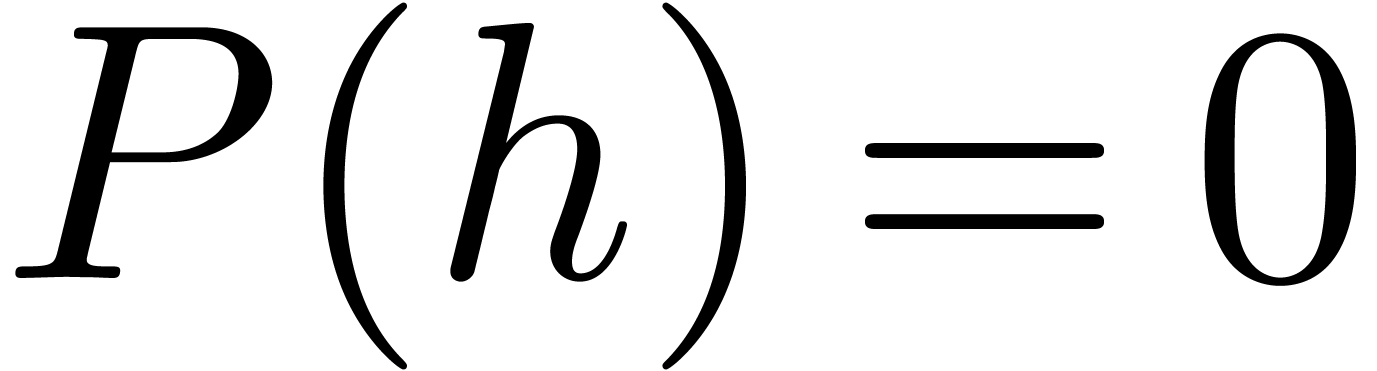 . For full
proofs, we refer to [vdH97, vdH00, vdH01].
In section 5, we will finally discuss some perspectives for
the resolution of more general algebraic differential equations using
complex transseries.
. For full
proofs, we refer to [vdH97, vdH00, vdH01].
In section 5, we will finally discuss some perspectives for
the resolution of more general algebraic differential equations using
complex transseries.
2The field of real, grid-based
transseries
2.1Generalized power series
Let  be a constant field and
be a constant field and  a totally ordered, multiplicative, commutative group of
monomials. For instance, the monomial group
a totally ordered, multiplicative, commutative group of
monomials. For instance, the monomial group 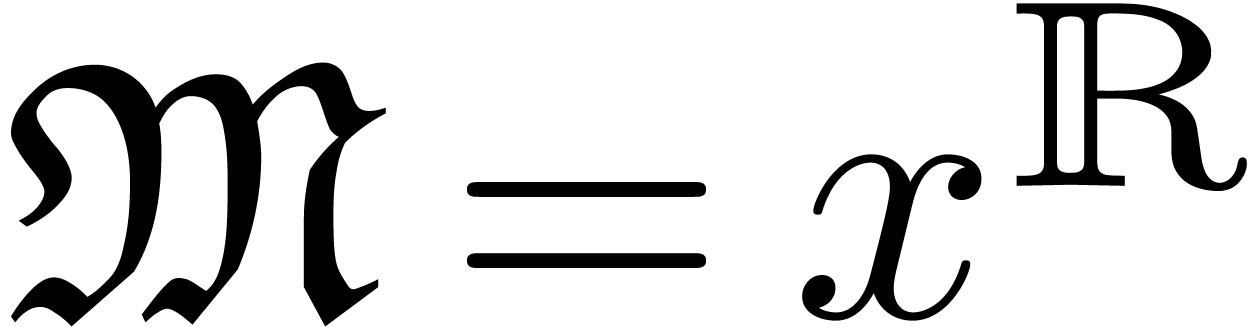 of real powers of an infinitely large
of real powers of an infinitely large  is a
monomial group with
is a
monomial group with  . The
relation
. The
relation  corresponds to Landau's
corresponds to Landau's  -symbol and
-symbol and  to the
to the
 -symbol. We write
-symbol. We write  if
if  and
and  .
.
A generalized power series is a mapping 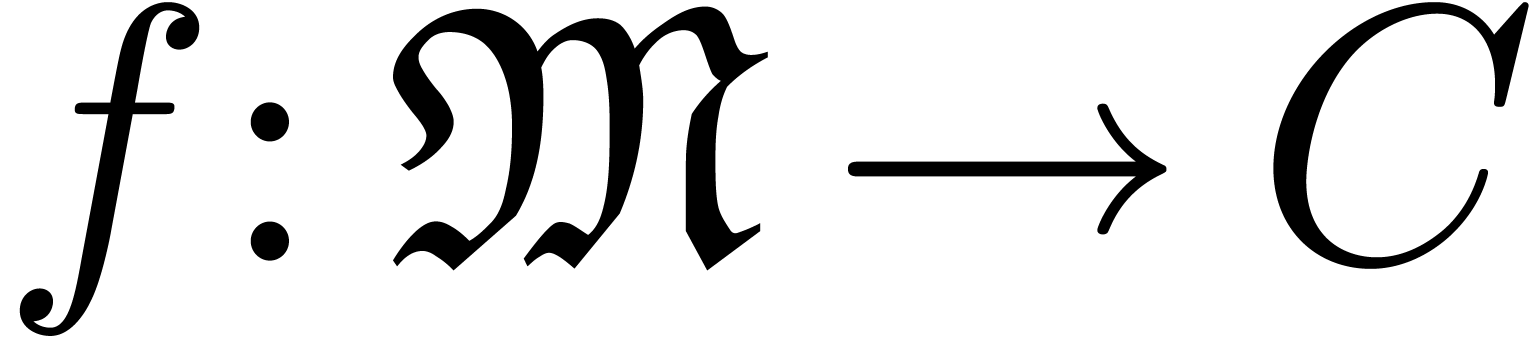 with well-ordered support. We usually write
with well-ordered support. We usually write 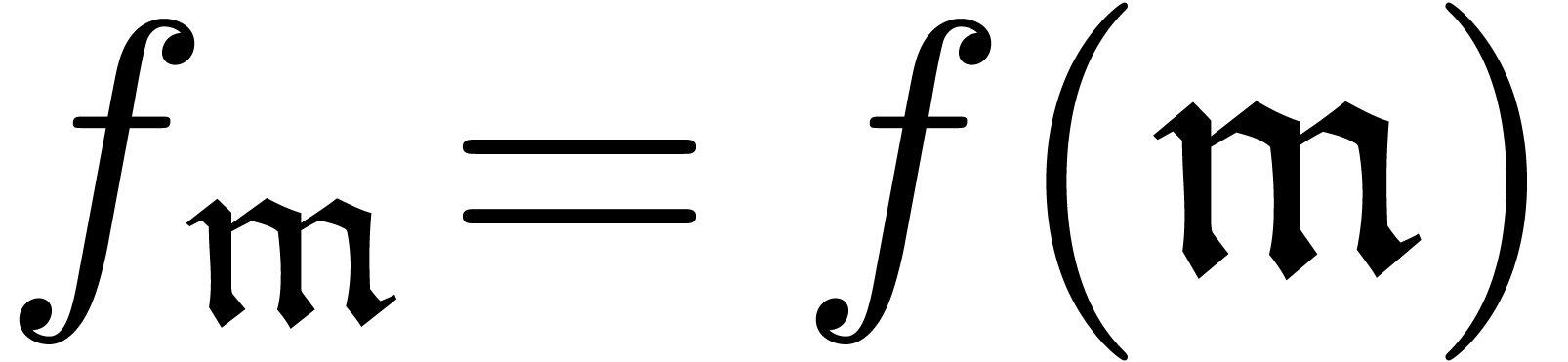 and
and
 and the support
and the support  of
of  is the set of
is the set of 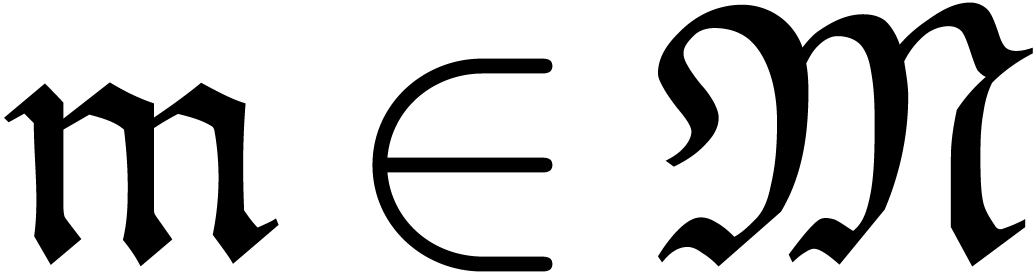 with
with  . The condition on the support of
. The condition on the support of
 means that there does not exist an infinite
sequence
means that there does not exist an infinite
sequence  of monomials with
of monomials with 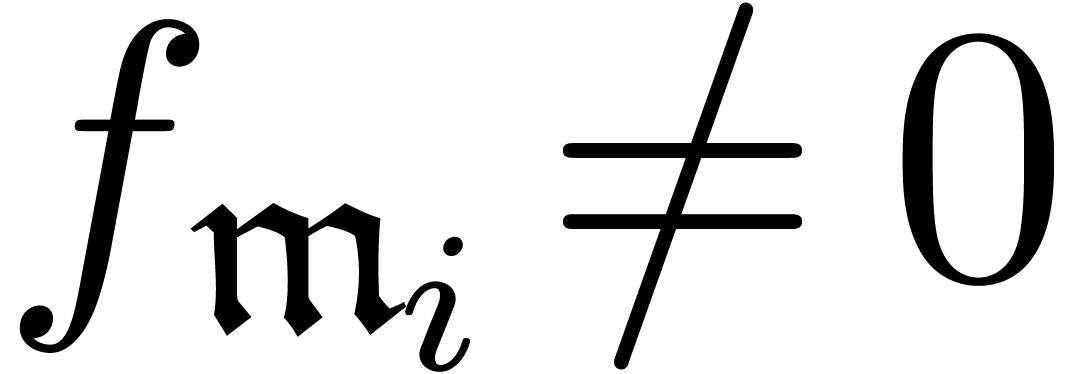 for all
for all 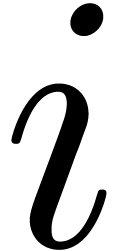 . We write
. We write 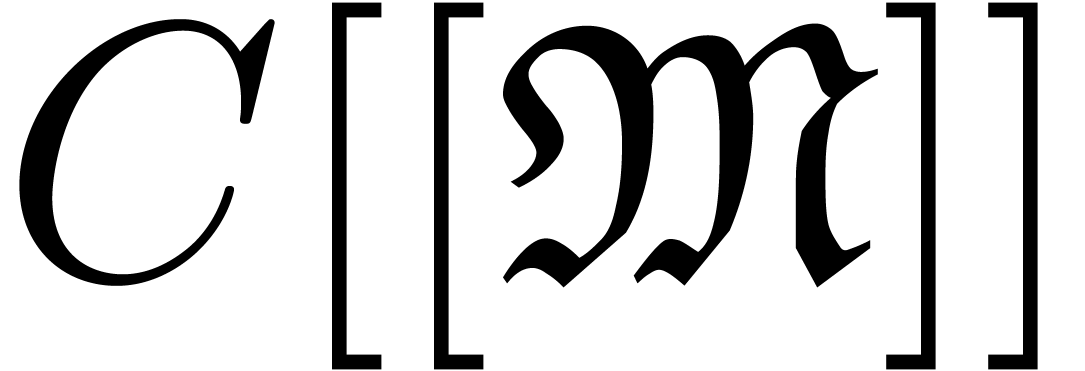 for the set of generalized (or well-ordered) power series.
for the set of generalized (or well-ordered) power series.
It is known since long [Hah07] that the well-ordering
condition allows us to define a natural multiplication on 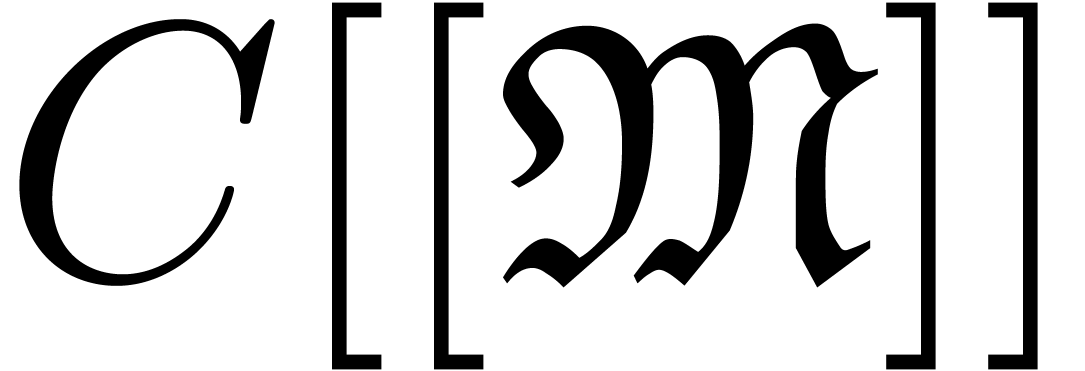 by
by
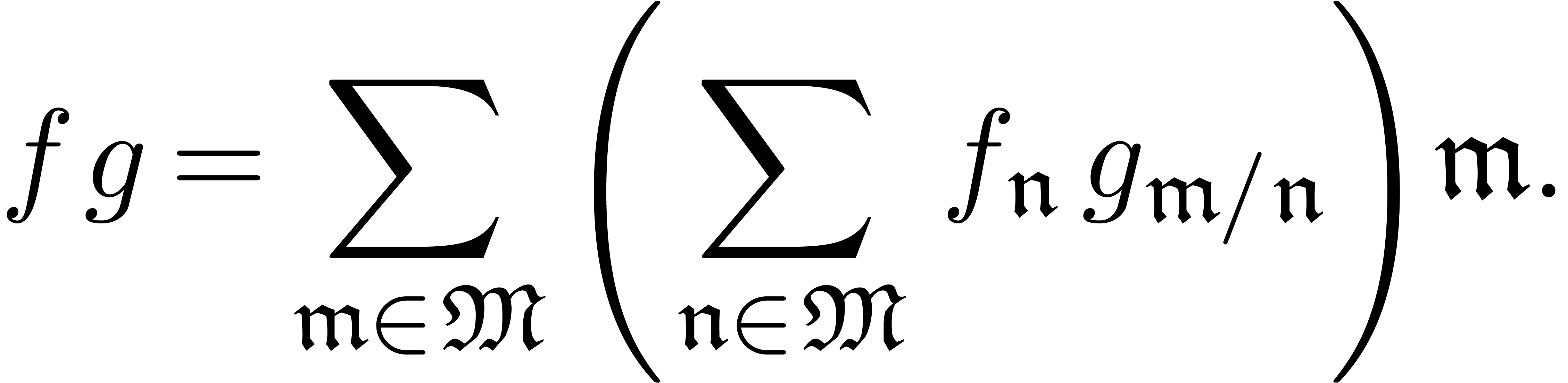
This multiplication actually gives 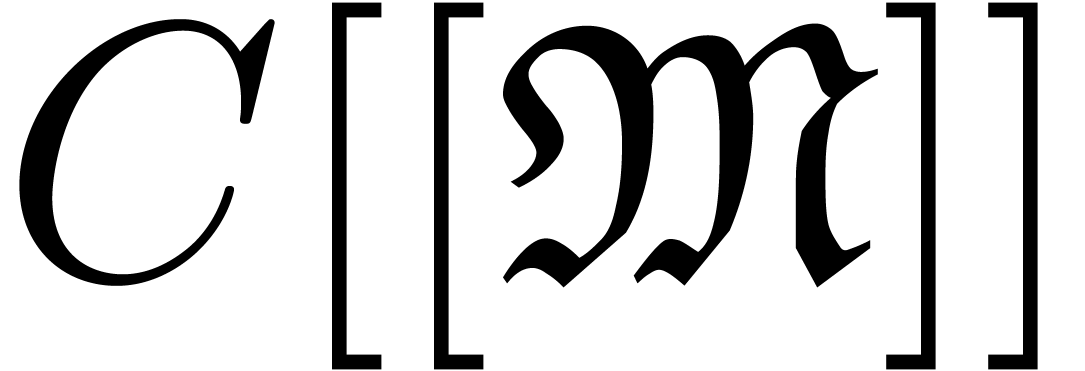 the structure
of a field. Examples of well-ordered series in
the structure
of a field. Examples of well-ordered series in 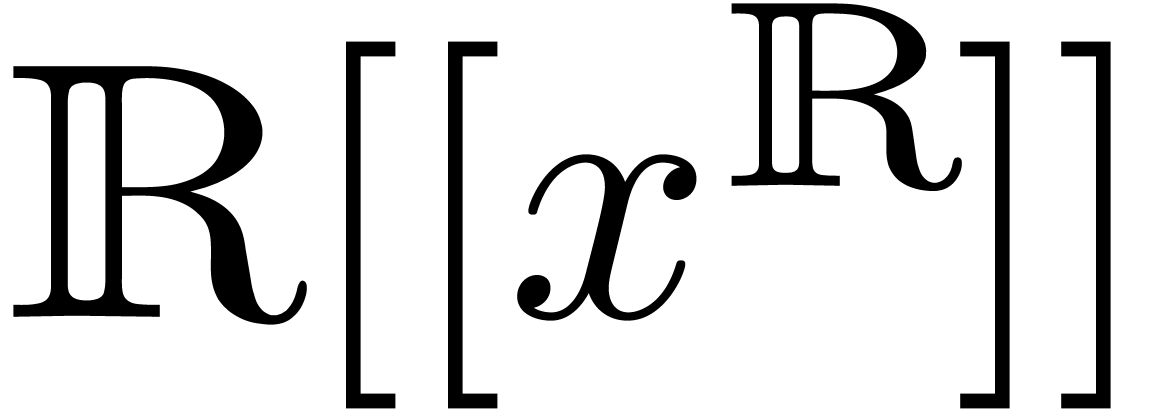 are
are
Notice that the order type of 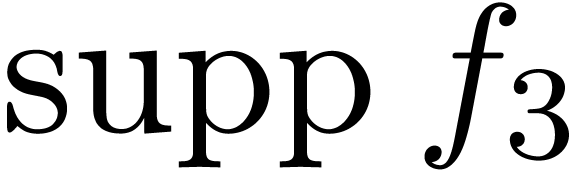 is transfinite
(namely
is transfinite
(namely 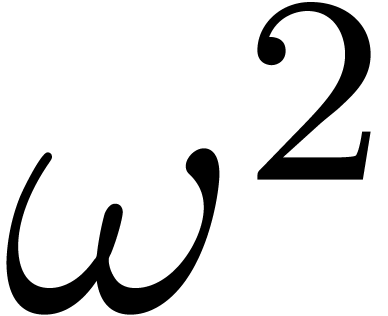 ) and that
) and that 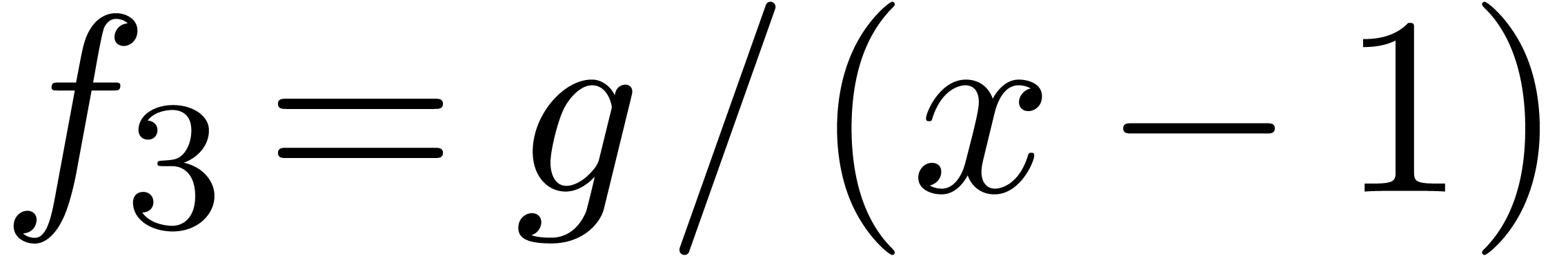 , where
, where
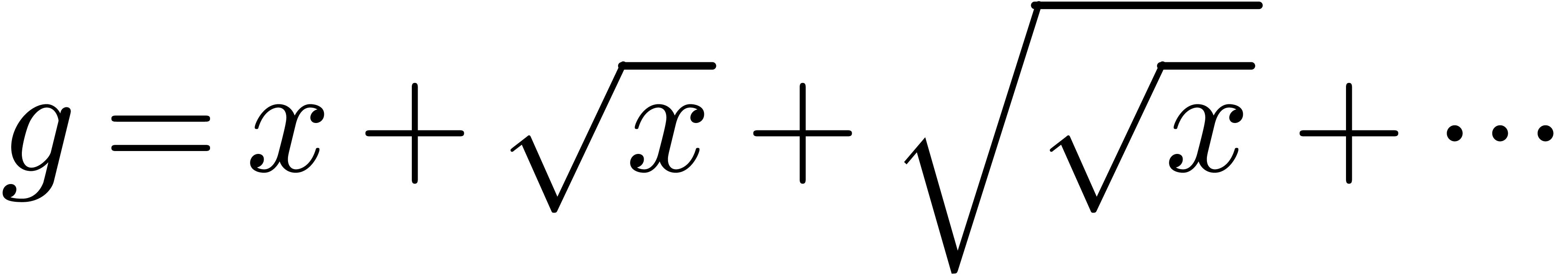
satisfies the functional equation 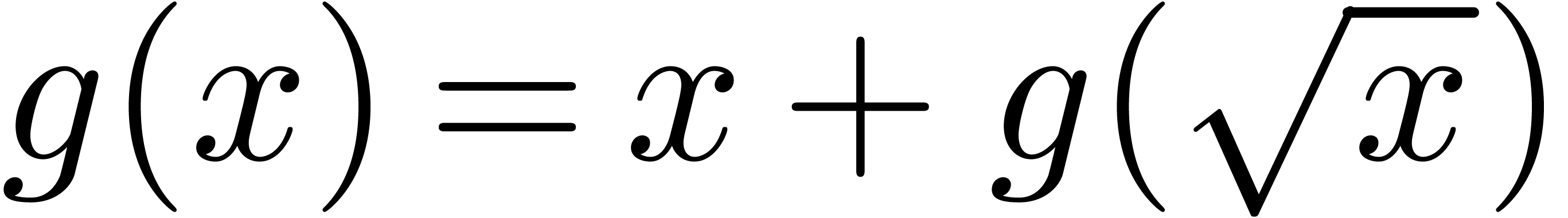 .
.
The more exotic types of well-ordered series like 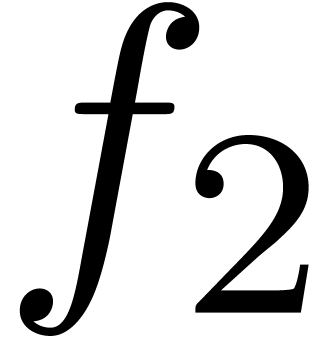 and
and 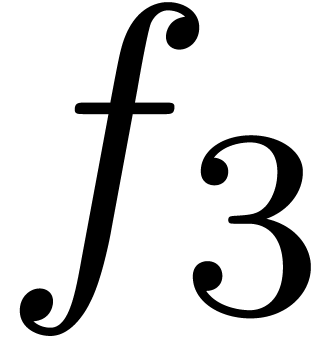 usually do not occur when studying
differential equations. We say that a subset
usually do not occur when studying
differential equations. We say that a subset  of
of
 is grid-based if there exists a
monomial
is grid-based if there exists a
monomial 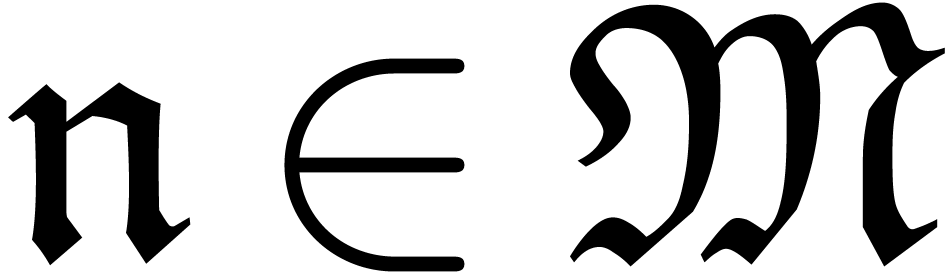 and a finite number of infinitesimal
monomials
and a finite number of infinitesimal
monomials  in
in  ,
such that
,
such that

In other words, for each  ,
there exist
,
there exist 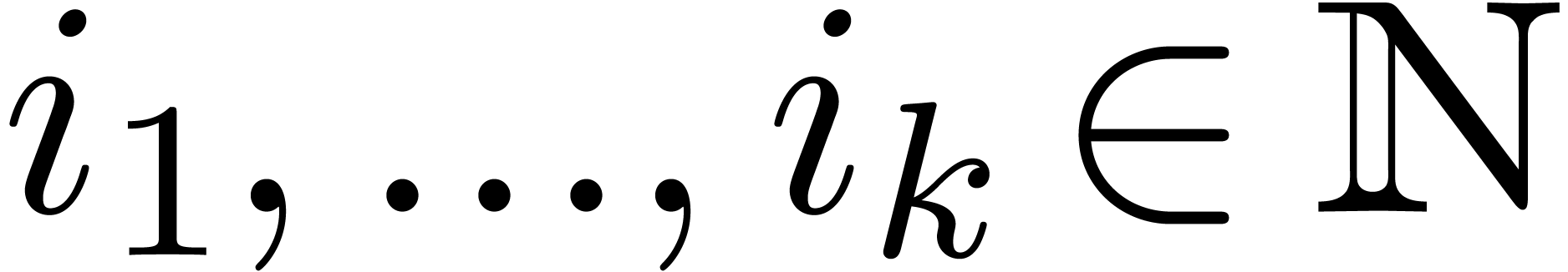 with
with 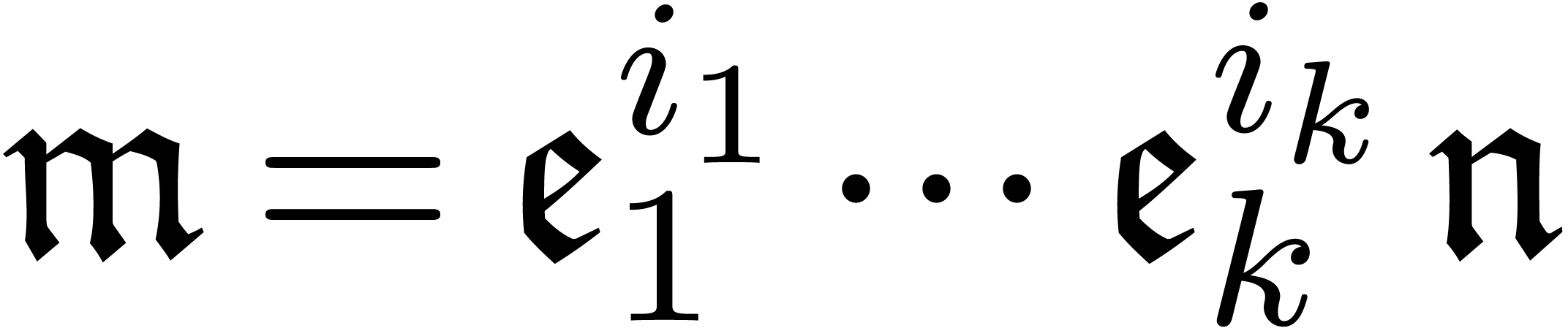 .
We say that a series
.
We say that a series  is grid-based if
its support is grid-based. It can be shown that the set
is grid-based if
its support is grid-based. It can be shown that the set  of grid-based series forms a subfield of
of grid-based series forms a subfield of 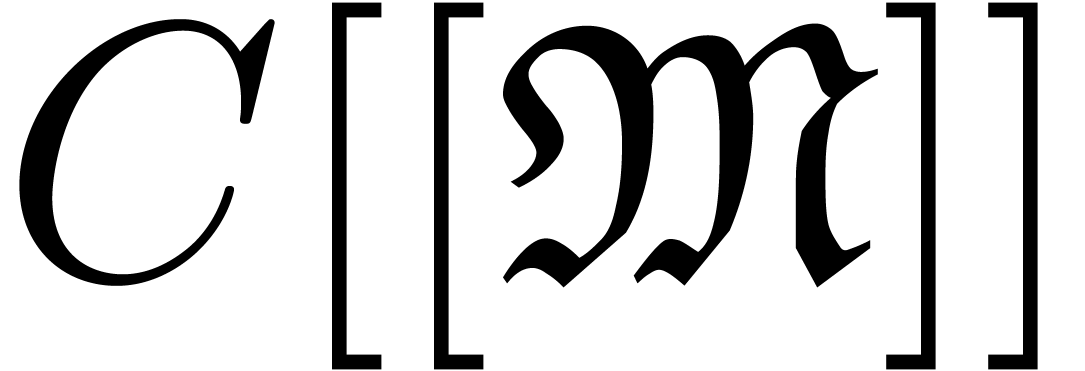 .
Notice that the support of a grid-based series can still be transfinite
when
.
Notice that the support of a grid-based series can still be transfinite
when  is a non-archimedian monomial group.
Indeed, the order type of
is a non-archimedian monomial group.
Indeed, the order type of 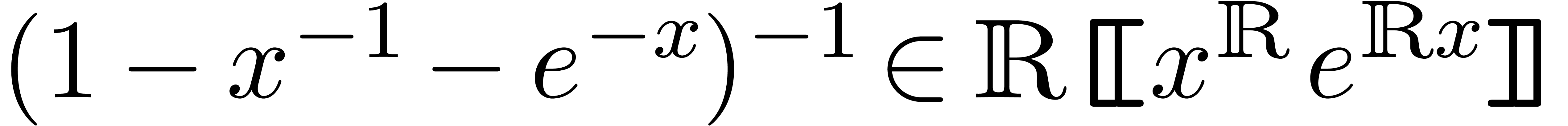 is again
is again 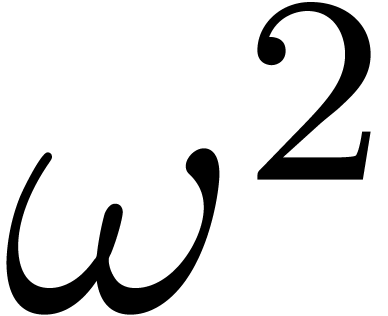 , where
, where 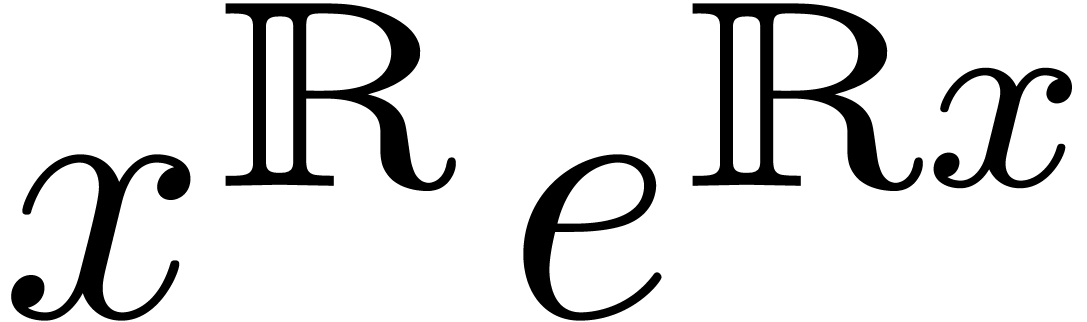 is ordered by
is ordered by
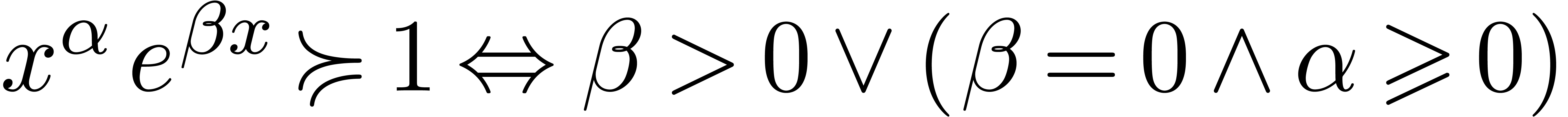 .
.
The fields 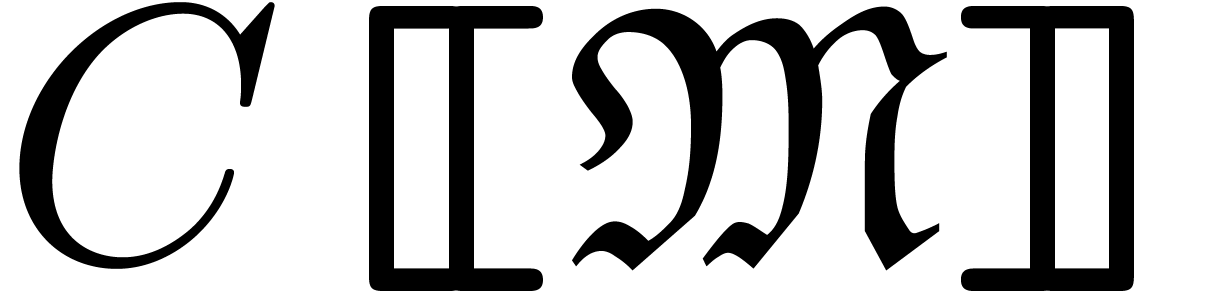 (resp.
(resp. 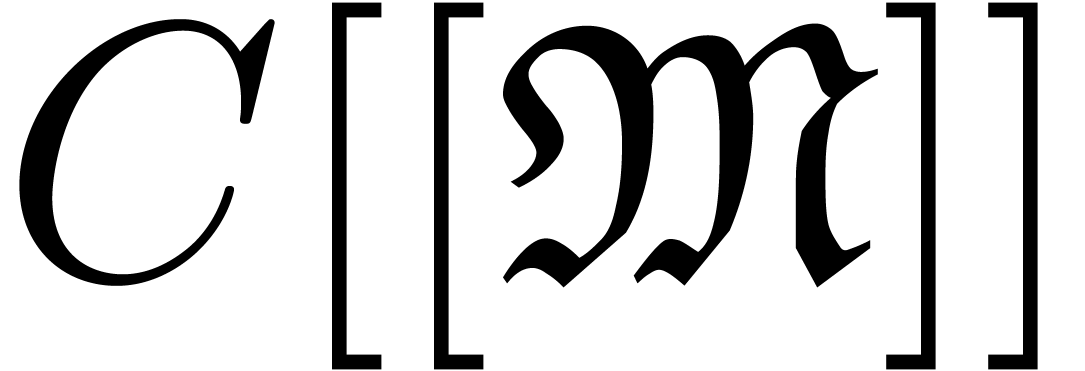 ) can be given further structure. Given
) can be given further structure. Given 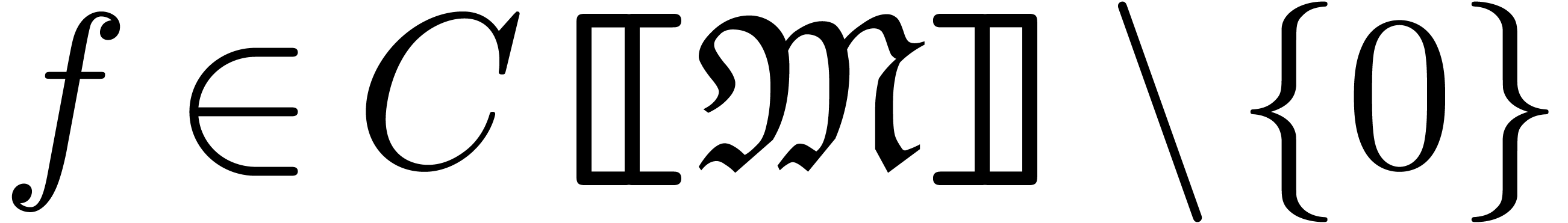 , we define its dominant
monomial
, we define its dominant
monomial  to be the
to be the  -maximal element in
-maximal element in  .
The dominant coefficient
.
The dominant coefficient  of
of  is the corresponding coefficient
is the corresponding coefficient  .
We extend
.
We extend  to
to 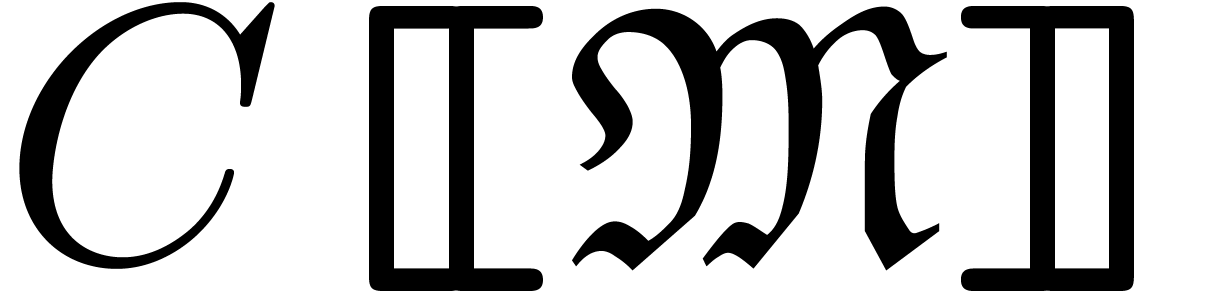 by
by  (here we assume
(here we assume 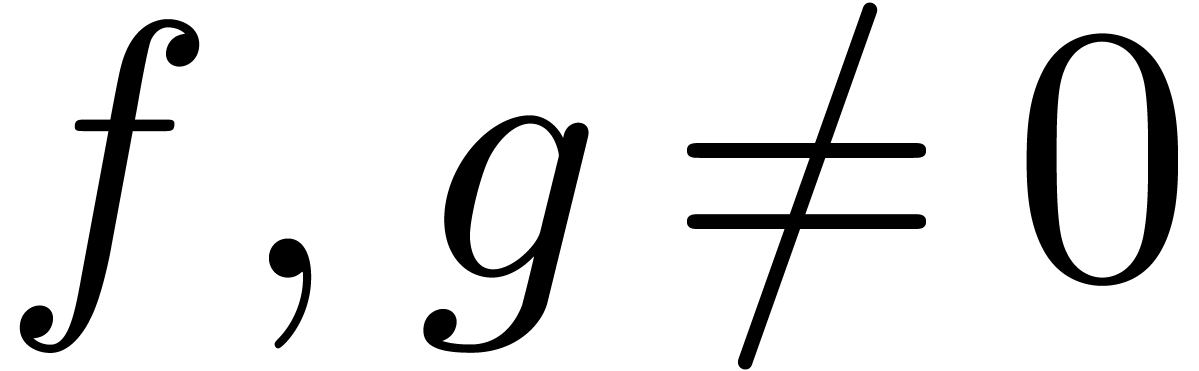 ;
we take
;
we take  for all
for all  and
and  whenever
whenever 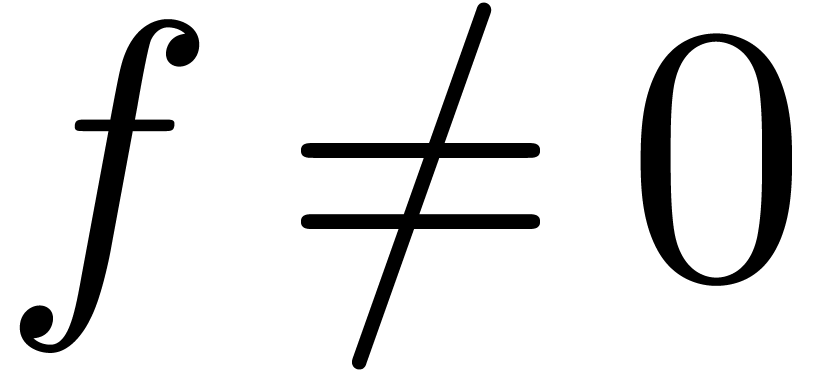 ).
Each series
).
Each series 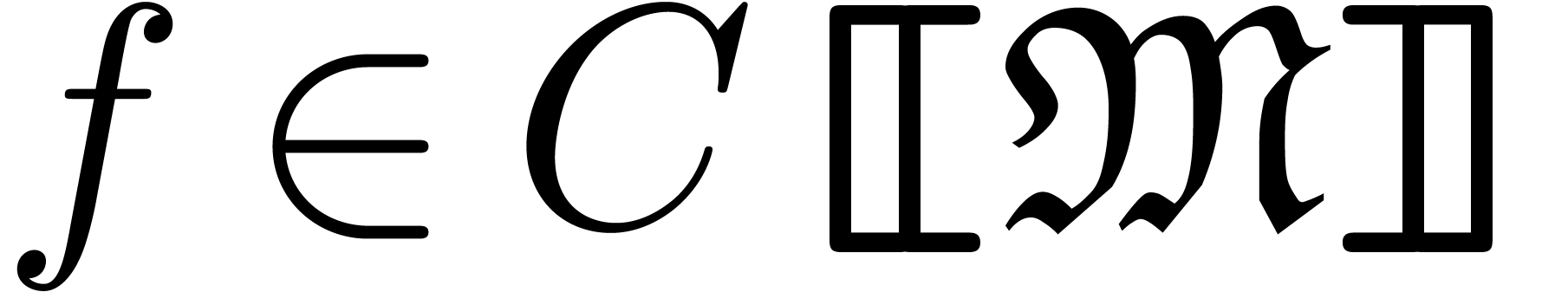 also admits a canonical
decomposition into a purely infinite, a constant,
and an infinitesimal part:
also admits a canonical
decomposition into a purely infinite, a constant,
and an infinitesimal part:
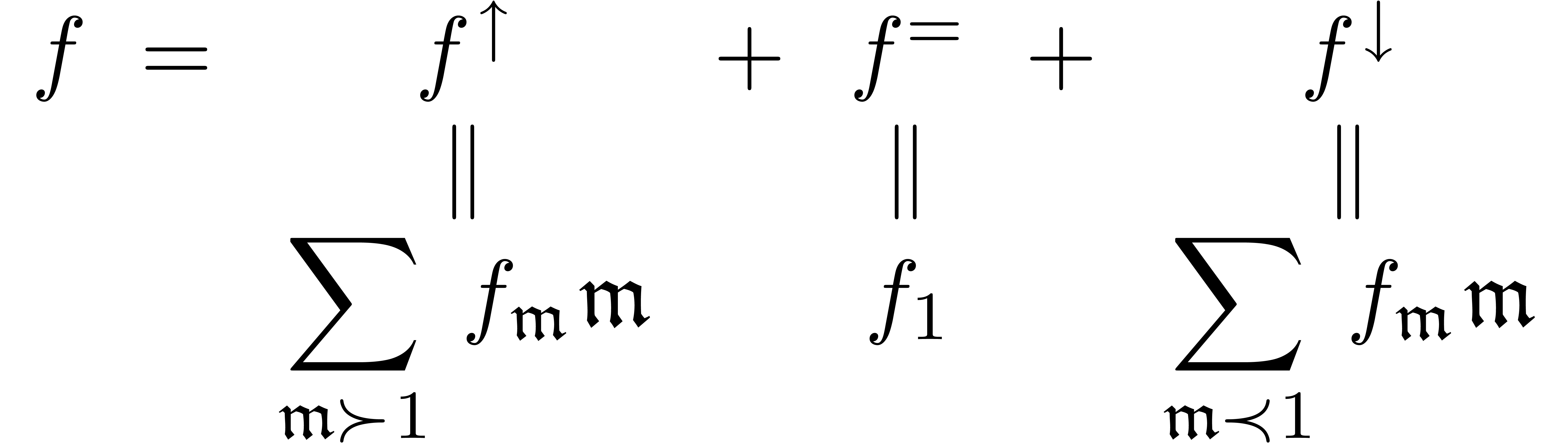
Finally, if  is a totally ordered field, like
is a totally ordered field, like
 , then we define a total
ordering on
, then we define a total
ordering on  by
by  .
.
Another important operation on  (resp.
(resp. 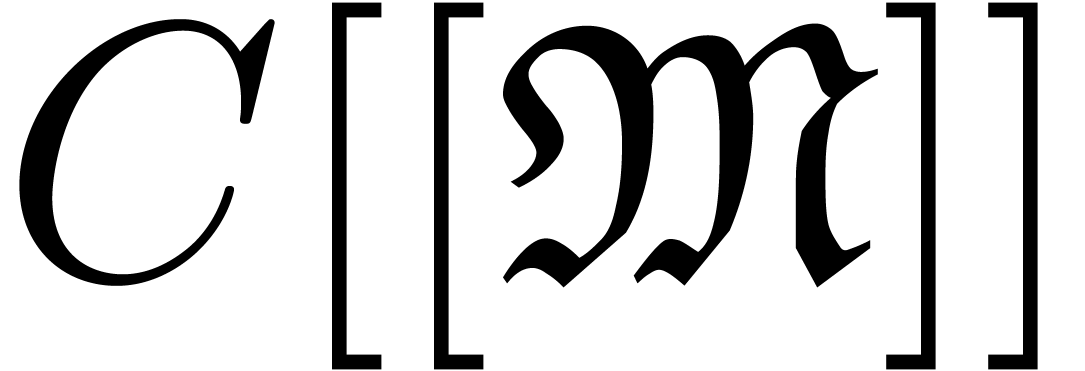 ) is
strong summation. A family
) is
strong summation. A family 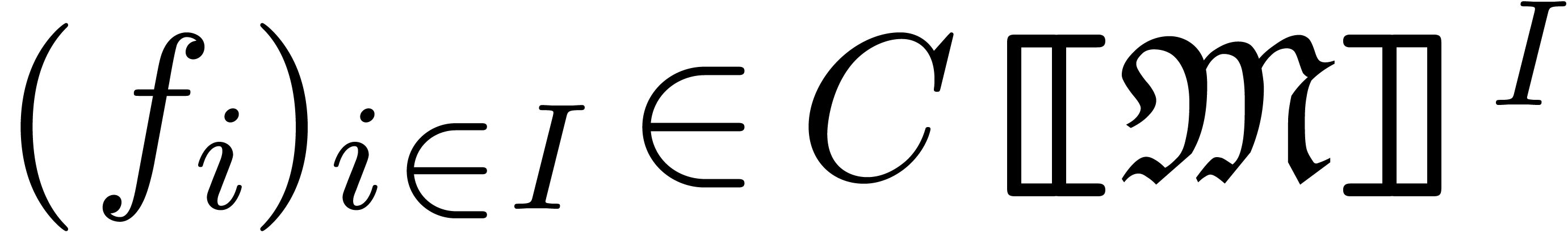 is said to
be grid-based (or strongly summable), if
is said to
be grid-based (or strongly summable), if
-
GBF1
-
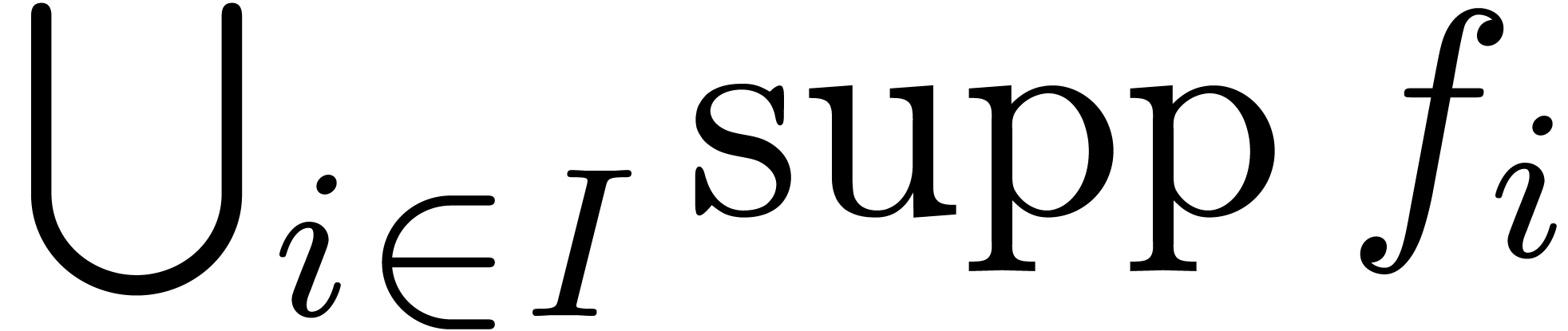 is a grid-based subset of
is a grid-based subset of  .
.
-
GBF2
-
For each  , the set
, the set  is finite.
is finite.
Given such a family, we may define its sum 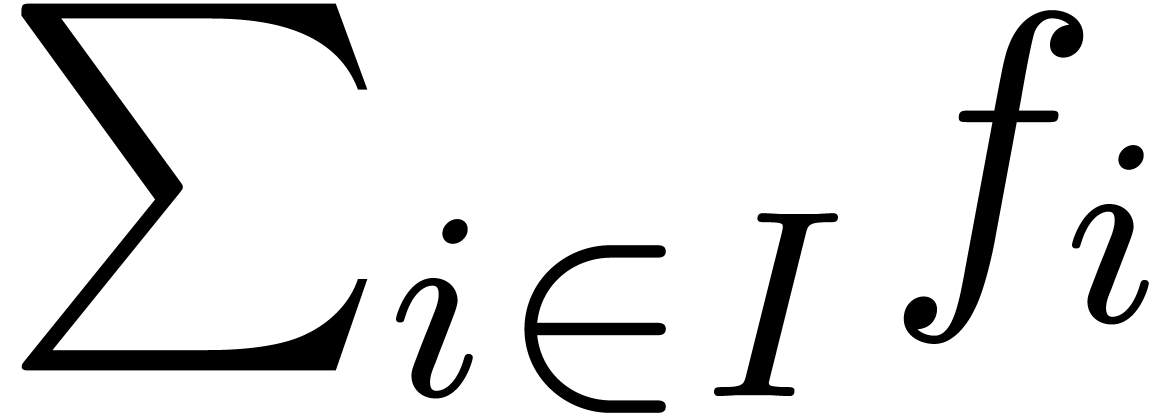 by
by
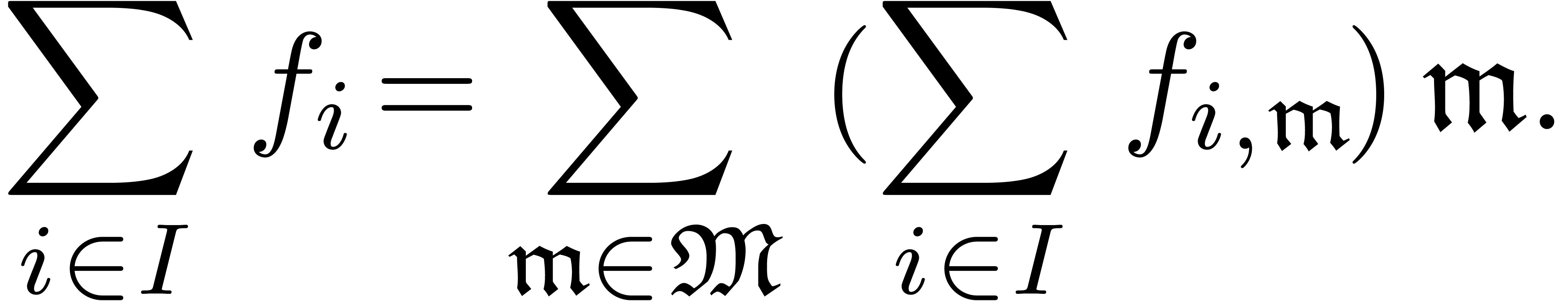
Given a classical power series 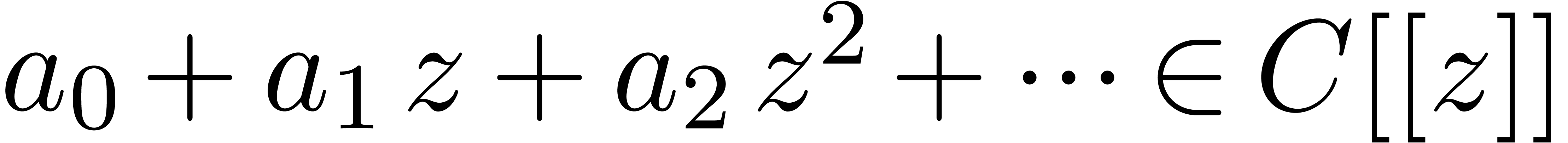 and an
infinitesimal
and an
infinitesimal  , it can for
instance be shown that
, it can for
instance be shown that 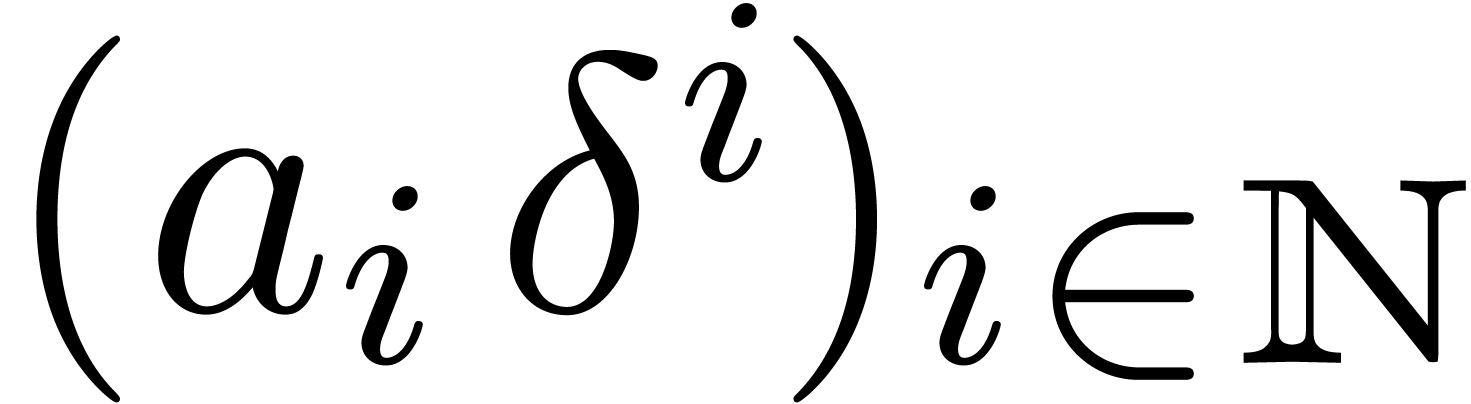 is a grid-based family.
Consequently,
is a grid-based family.
Consequently, 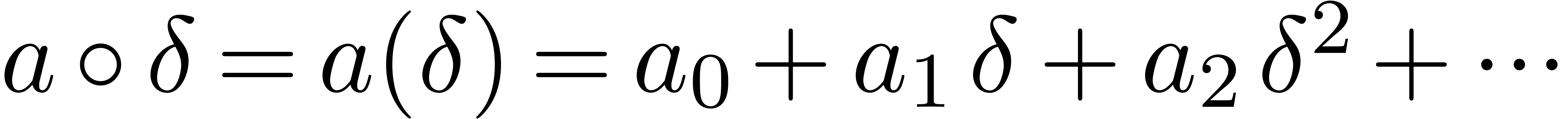 is well-defined.
is well-defined.
2.2Grid-based transseries in 
We now want to define a field of grid-based series  with additional functions
with additional functions 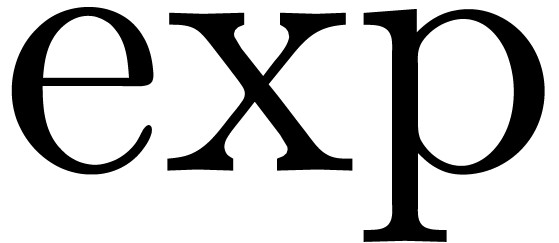 and
and 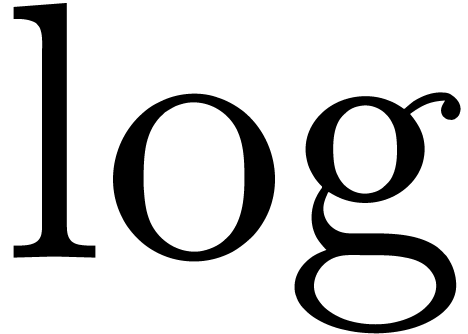 , such that
, such that 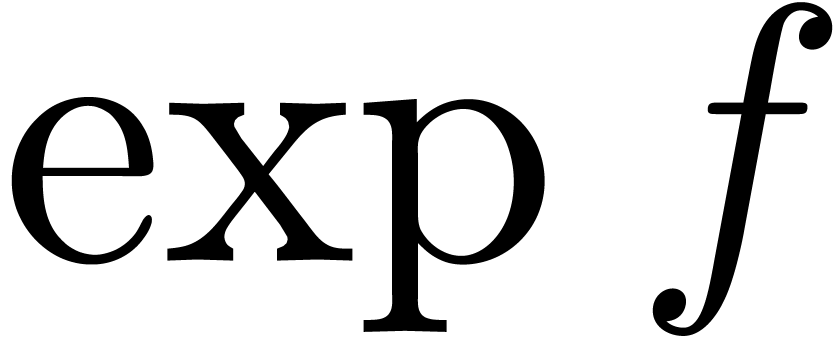 is defined
for all
is defined
for all 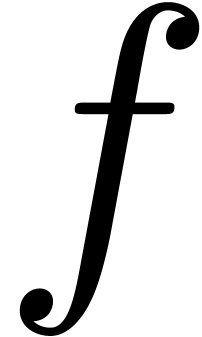 and
and 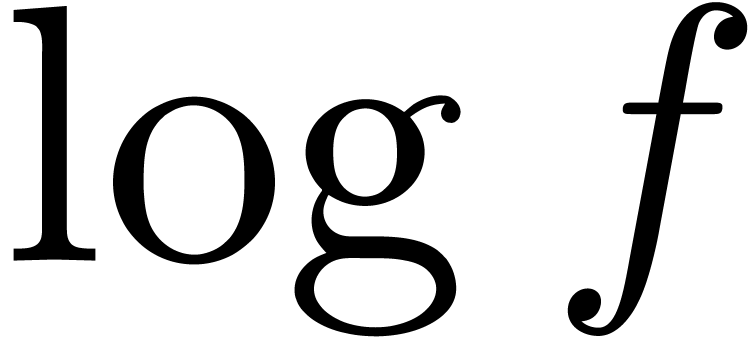 for all
for all
 . Classically [DG86,
É92], one starts with the field
. Classically [DG86,
É92], one starts with the field 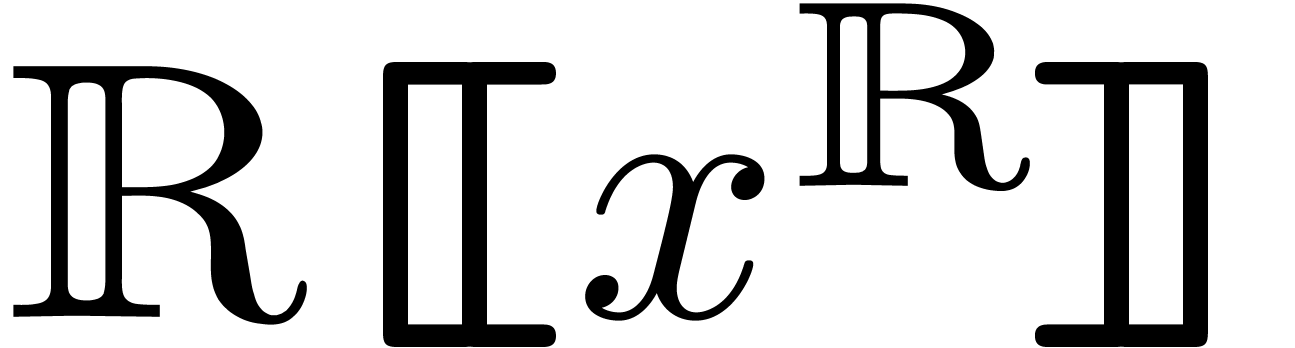 and successively closes it under exponentiation and logarithm. We will
follow the inverse strategy: we start with the field of logarithmic
transseries
and successively closes it under exponentiation and logarithm. We will
follow the inverse strategy: we start with the field of logarithmic
transseries  and close it under exponentiation.
Both constructions turn out to be equivalent in the grid-based setting.
and close it under exponentiation.
Both constructions turn out to be equivalent in the grid-based setting.
2.2.1Logarithmic transseries
Consider the monomial group

where 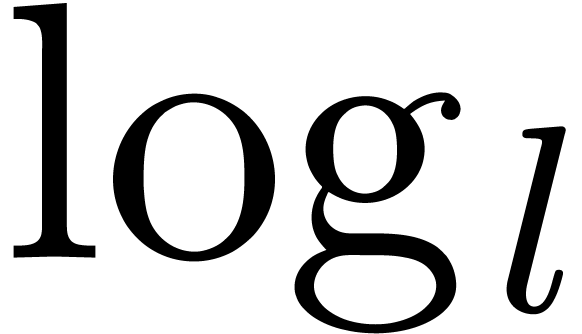 stands for the
stands for the  iterated
iterated  times. The infinitesimal monomials of
times. The infinitesimal monomials of
 are of the form
are of the form

with  ,
,  and
and 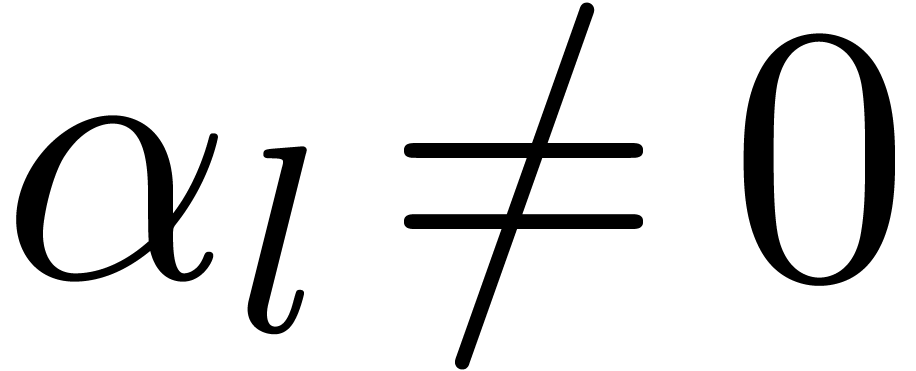 . Elements of
. Elements of 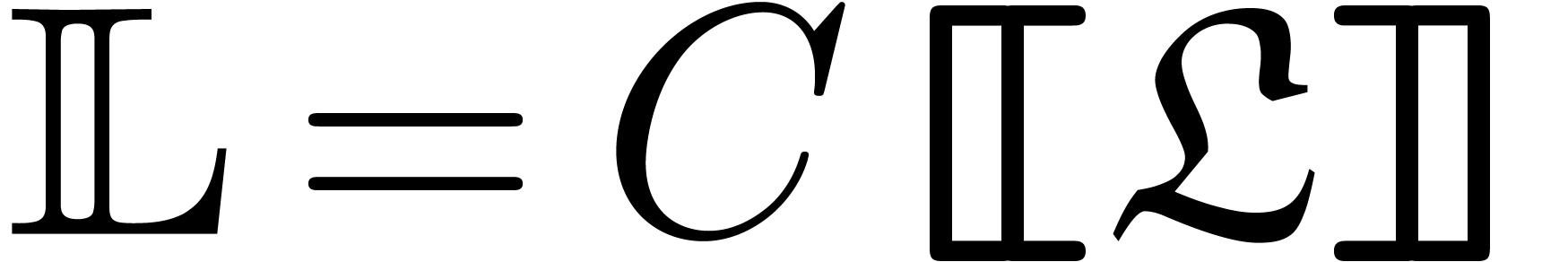 are called logarithmic transseries.
are called logarithmic transseries.
We now have to define a logarithm on 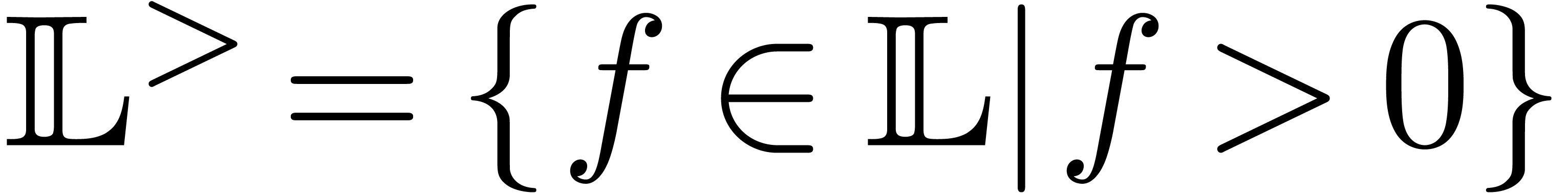 .
Given
.
Given  , we may write
, we may write
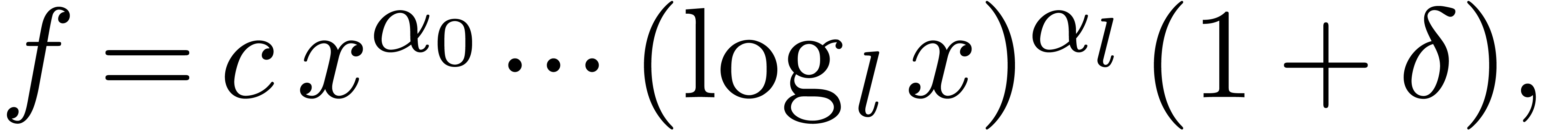
where  ,
, 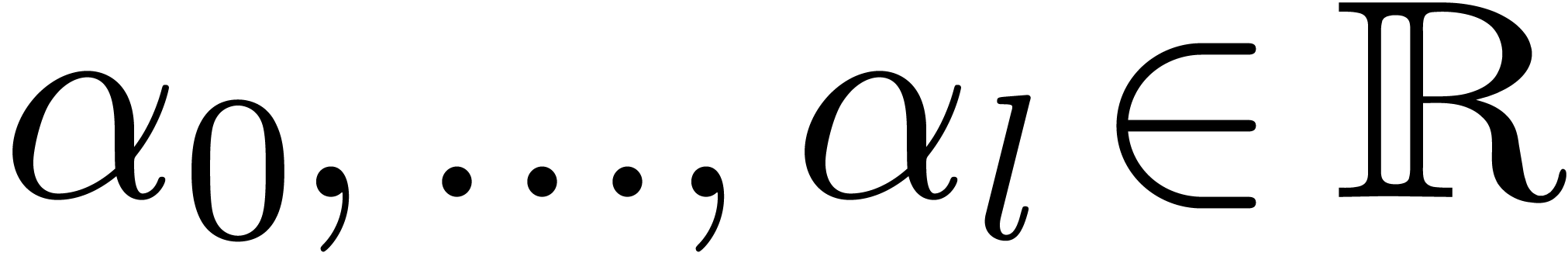 and
and  . Then we define
. Then we define

Here we remind that 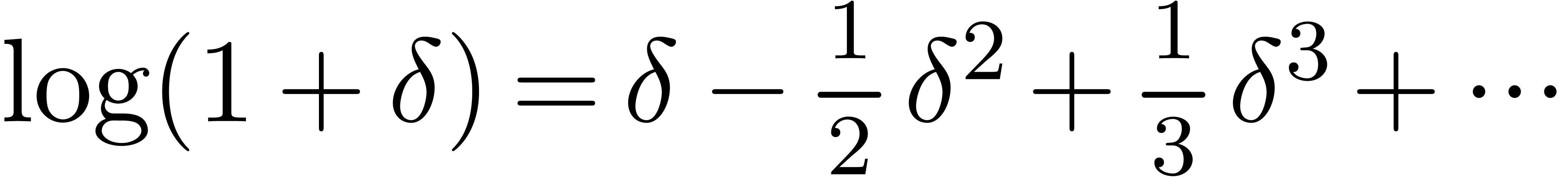 is well defined as the sum
of a grid-based family.
is well defined as the sum
of a grid-based family.
2.2.2Exponential extensions
We next have to show how new exponentials can be added to  . The main point here is to decide which
exponentials give rise to new monomials. In
. The main point here is to decide which
exponentials give rise to new monomials. In  , we observe that
, we observe that 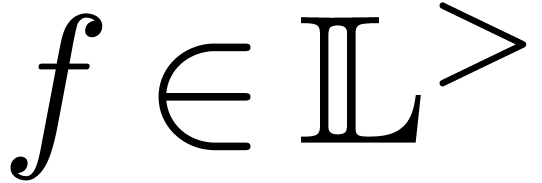 is a
monomial if and only if
is a
monomial if and only if 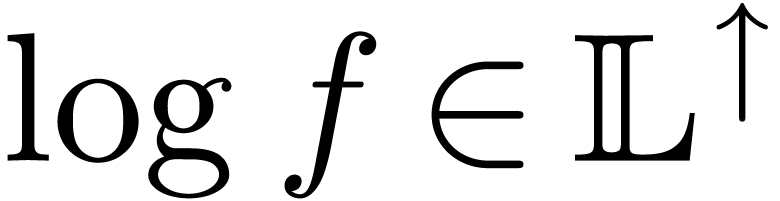 (in which case we say
that
(in which case we say
that 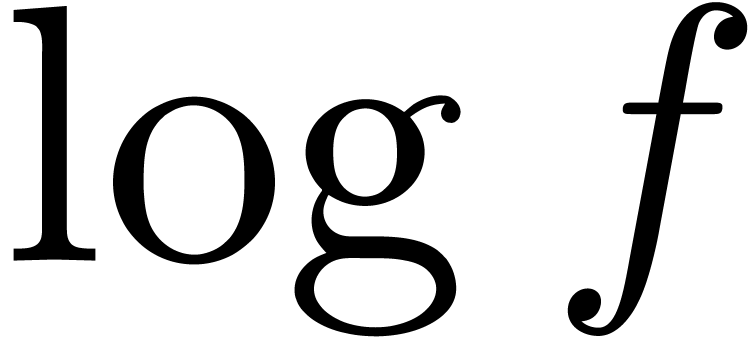 is purely infinite). We will use
this observation as a criterion for extensions by exponentials.
is purely infinite). We will use
this observation as a criterion for extensions by exponentials.
So assume that we have constructed the field  of
transseries of exponential depth
of
transseries of exponential depth  .
The case
.
The case  has been dealt with above. Then we take
has been dealt with above. Then we take
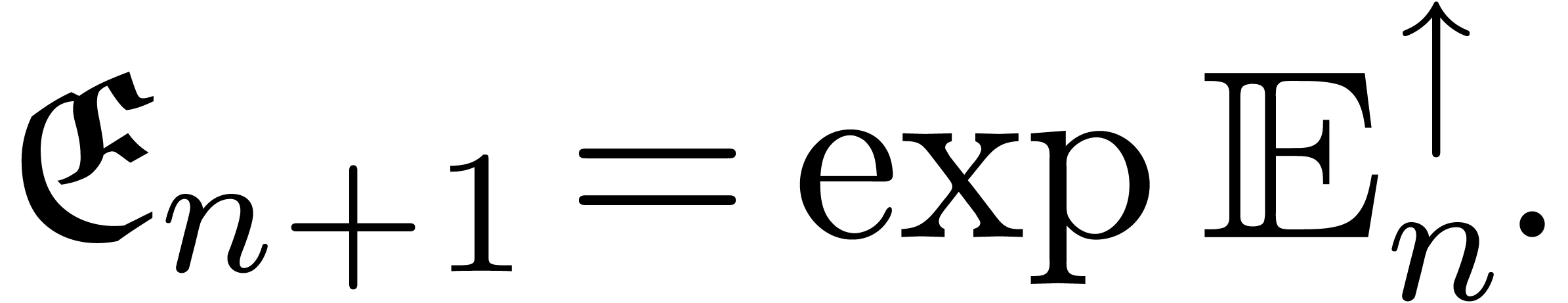
In other words, each monomial in  is the formal
exponential of an element in
is the formal
exponential of an element in  .
The asymptotic ordering on
.
The asymptotic ordering on  is inherited from the
usual ordering on
is inherited from the
usual ordering on  :
:

for all  . Finally, the
exponential of an arbitrary element
. Finally, the
exponential of an arbitrary element  exists in
exists in
 and is given by
and is given by
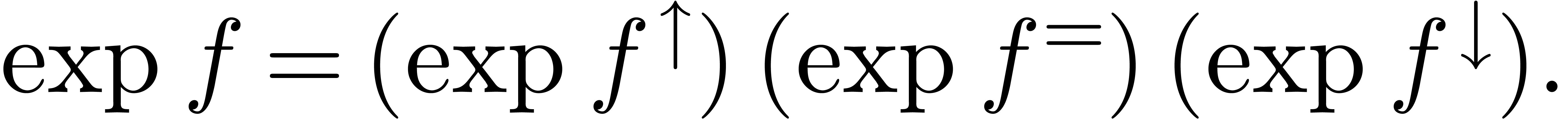
The logarithm remains totally defined as an inverse function of  on
on  , which
guarantees that
, which
guarantees that  at each step.
at each step.
Example 2. 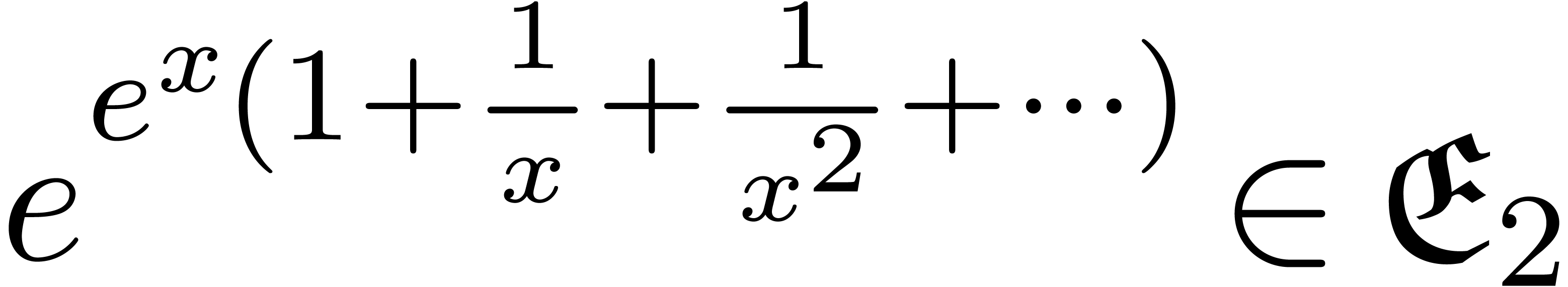 , but
, but 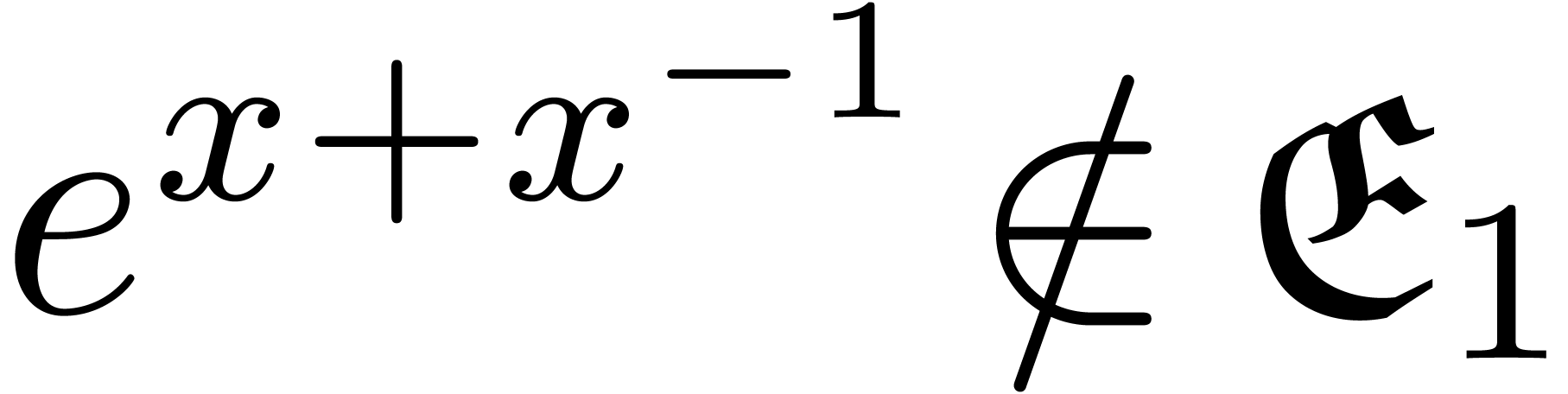 .
.
2.2.3The field of grid-based transseries in

The field
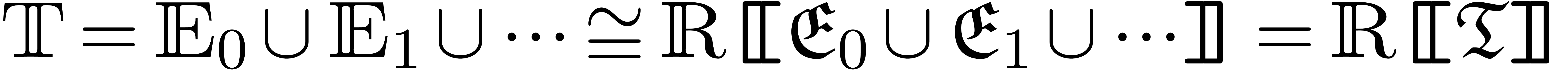
is called the field of grid-based transseries in  . The exponentiation and logarithm are totally
defined on
. The exponentiation and logarithm are totally
defined on  resp.
resp.  .
.
It can be shown that the usual axioms 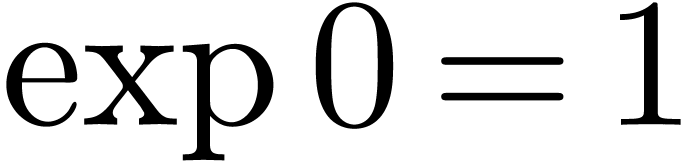 and
and 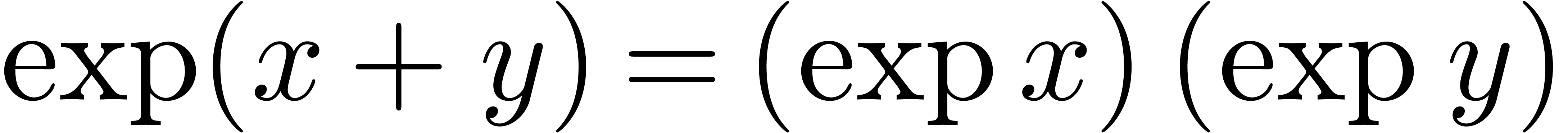 for exponentiation are satisfied in
for exponentiation are satisfied in  . The exponentiation also satisfies the
following more interesting properties
. The exponentiation also satisfies the
following more interesting properties
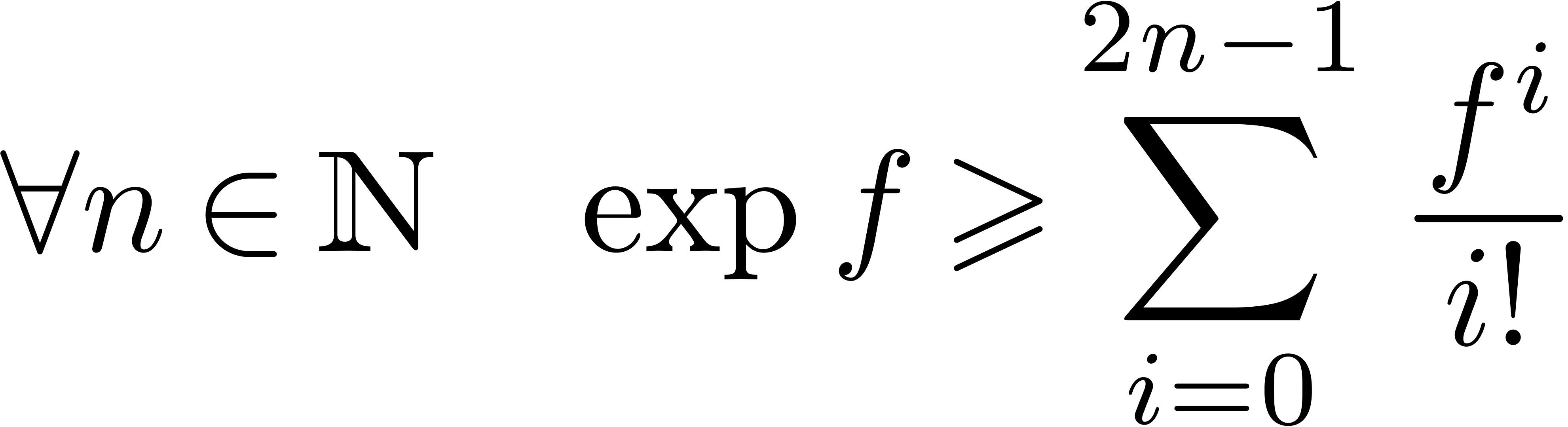
in relation to the ordering. These properties imply in particular that
 is increasing and that
is increasing and that 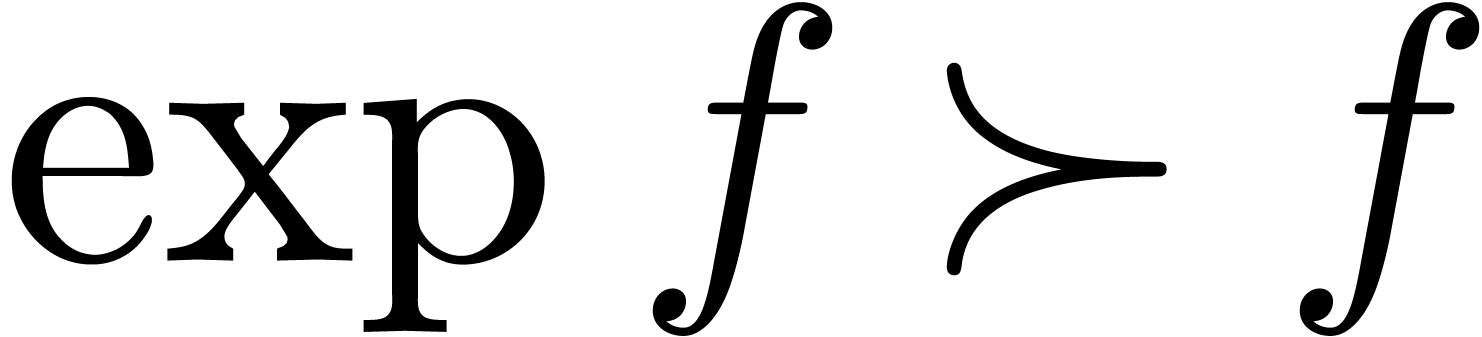 for all
for all  .
.
2.3Computations with transseries
We will now present some techniques for doing effective computations
with transseries. Although these techniques will not essentially be used
in the sequel, they will allow the reader to get a better understanding
of the nested structure of transseries and the transfinite and
non-archimedian nature of their supports.
2.3.1Asymptotic bases
The transmonomial group  can actually be seen as
an ordered
can actually be seen as
an ordered  -vector space,
where addition is replaced by multiplication and scalar multiplication
by raising to real powers. As a consequence, we also have
-vector space,
where addition is replaced by multiplication and scalar multiplication
by raising to real powers. As a consequence, we also have  and
and  -like
relations on this vector space: we say that
-like
relations on this vector space: we say that  is
flatter than
is
flatter than  , and
write
, and
write  , if and only if
, if and only if 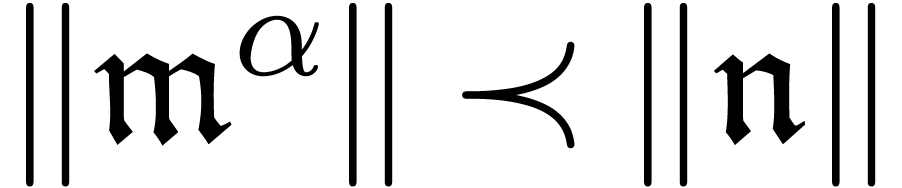 for all
for all  .
Here
.
Here 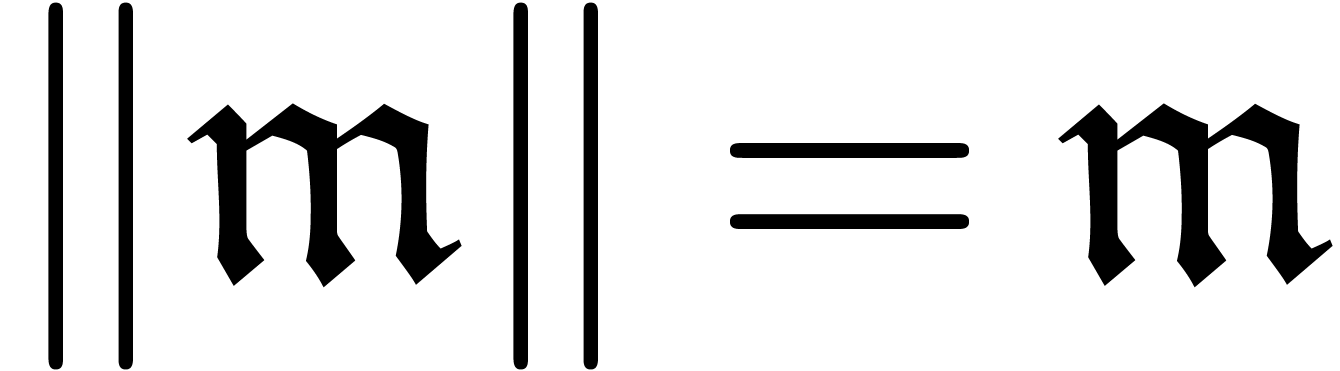 if
if  and
and 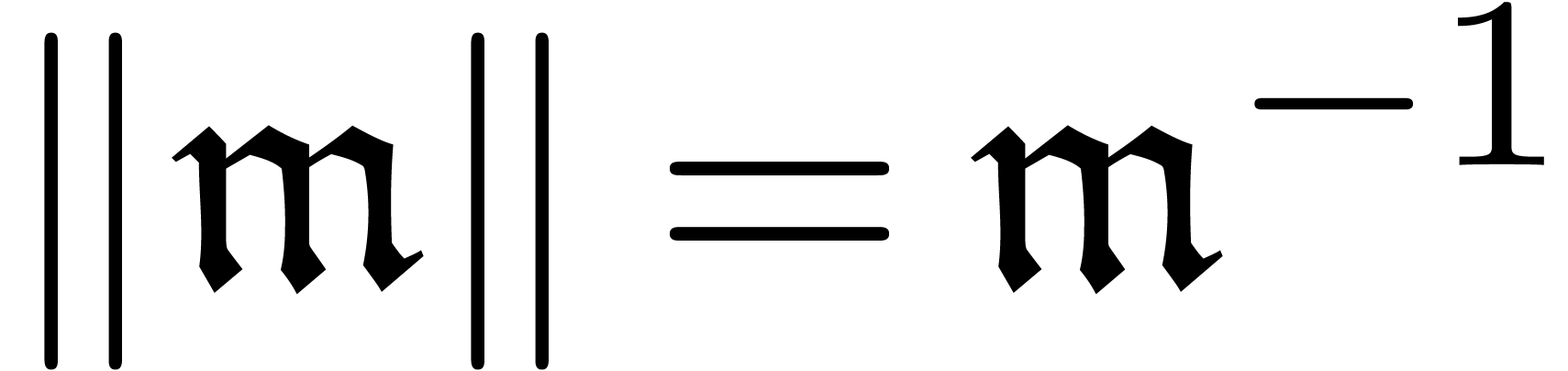 otherwise. The flatness relation can be extended to
otherwise. The flatness relation can be extended to  itself: given
itself: given  ,
we define
,
we define
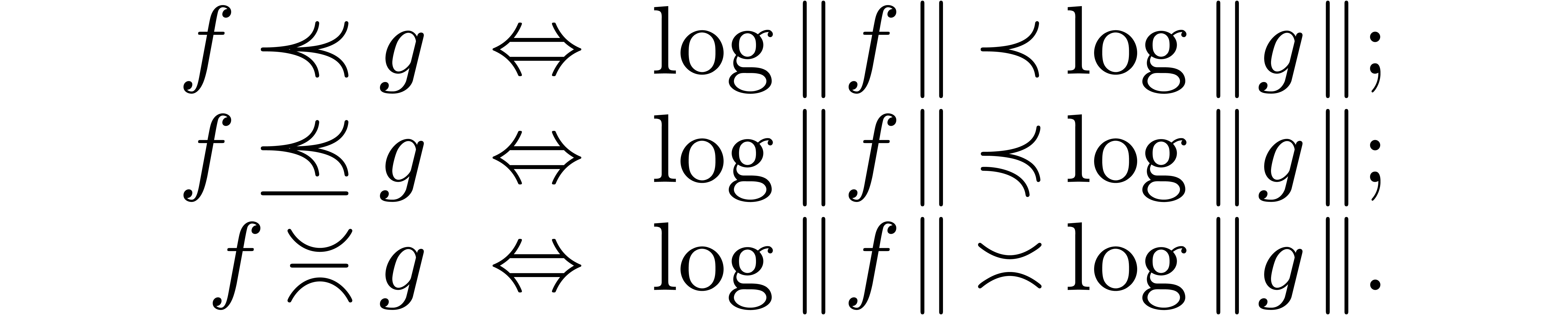
Here we understand that  if
if  and
and  otherwise. For instance,
otherwise. For instance, 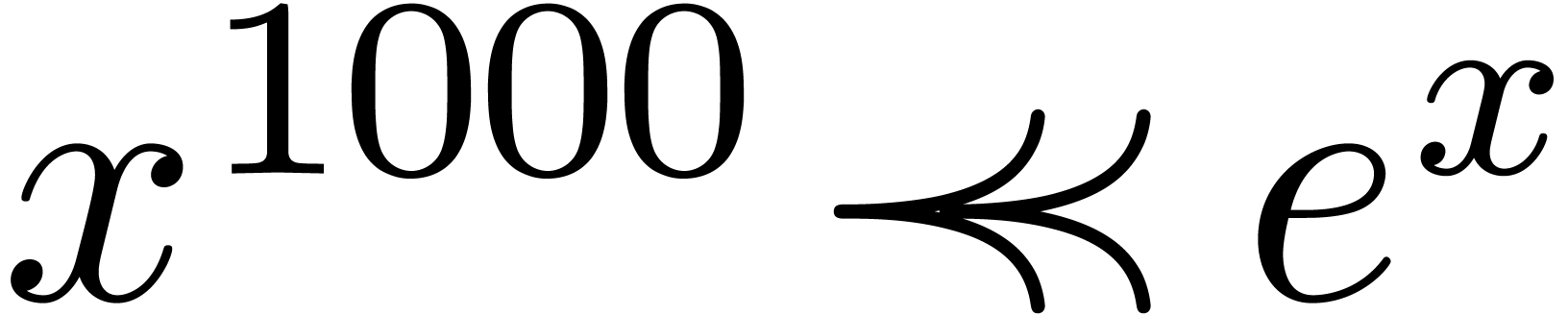 , but
, but 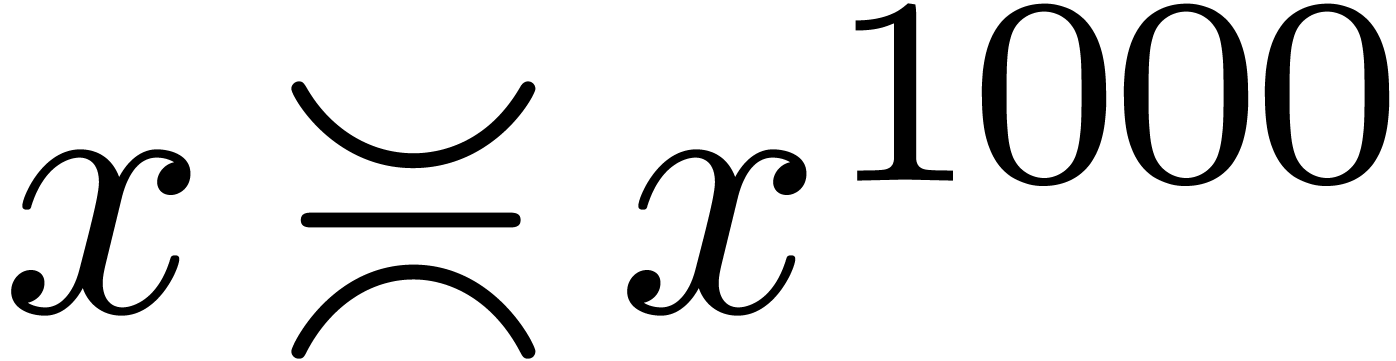 .
Also,
.
Also,  .
.
An asymptotic basis is a tuple 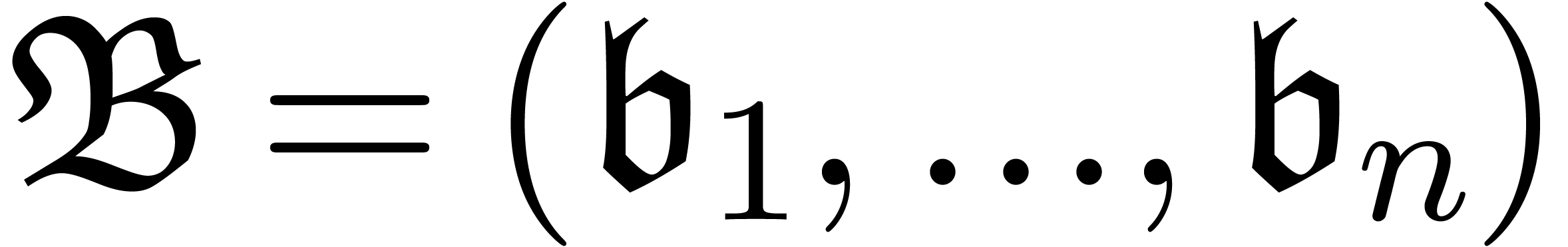 ,
with
,
with 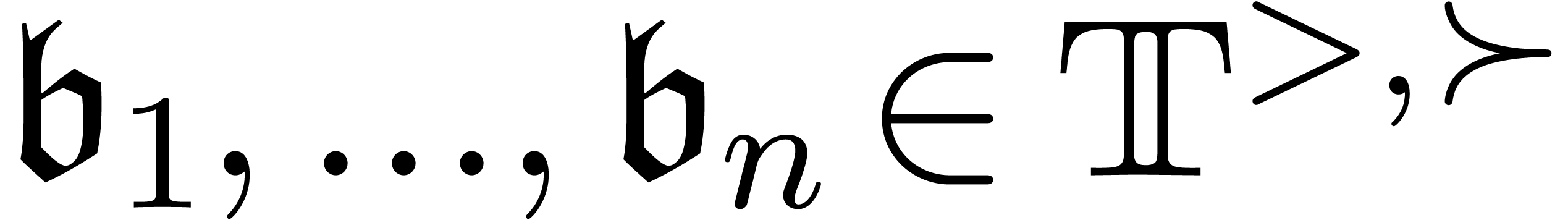 and
and  .
Such a basis generates an asymptotic scale
.
Such a basis generates an asymptotic scale  . The field of grid-based series
. The field of grid-based series 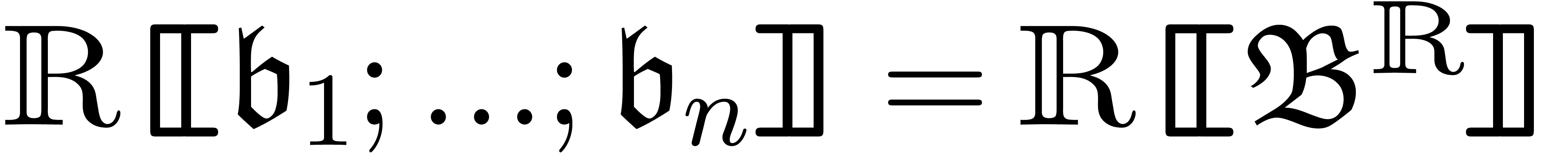 is naturally included in
is naturally included in  and
elements of
and
elements of  may be expanded recursively
w.r.t.
may be expanded recursively
w.r.t.  :
:
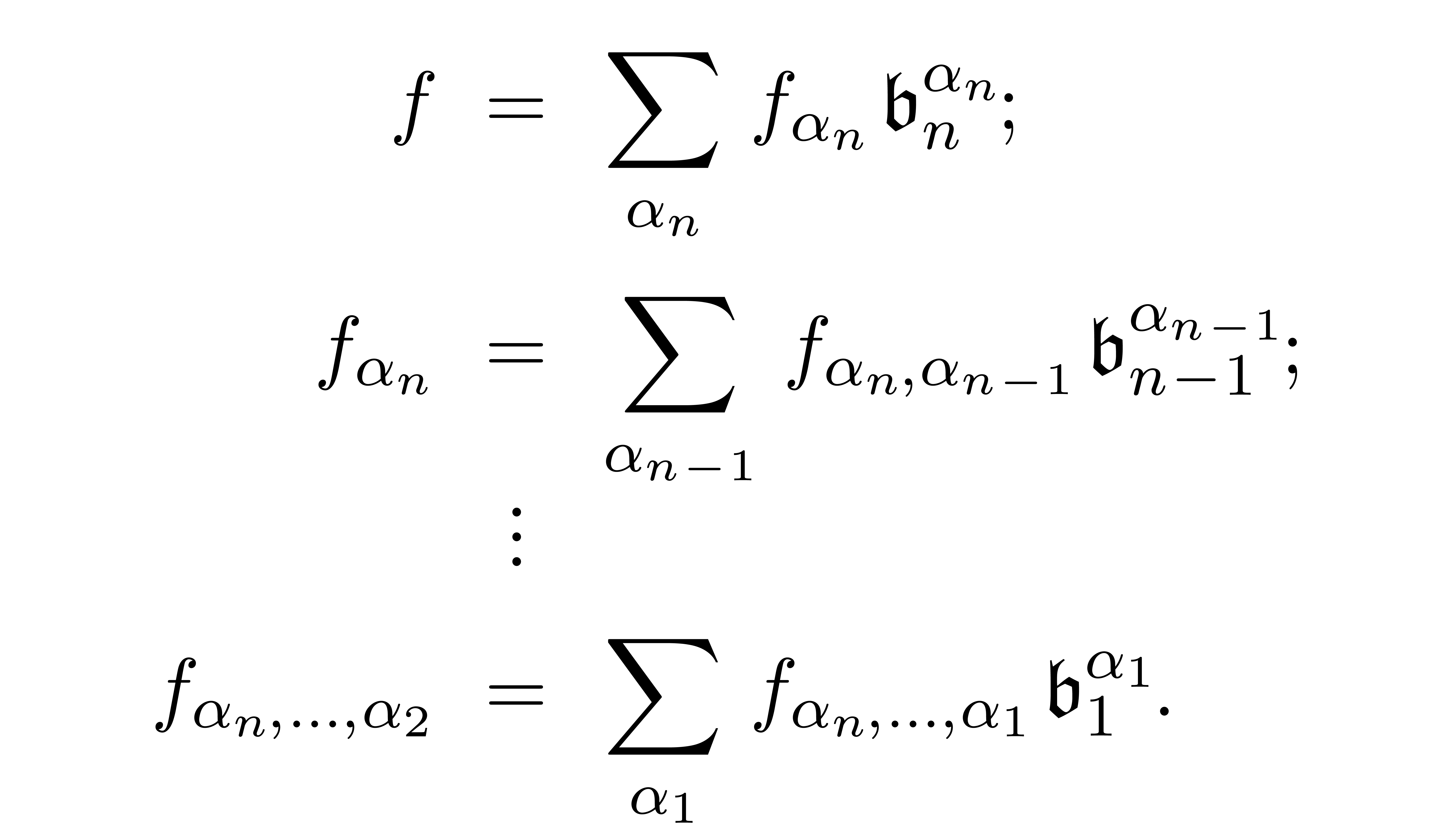
Conversely, for any transseries  in
in  there exists an asymptotic basis
there exists an asymptotic basis  with
with 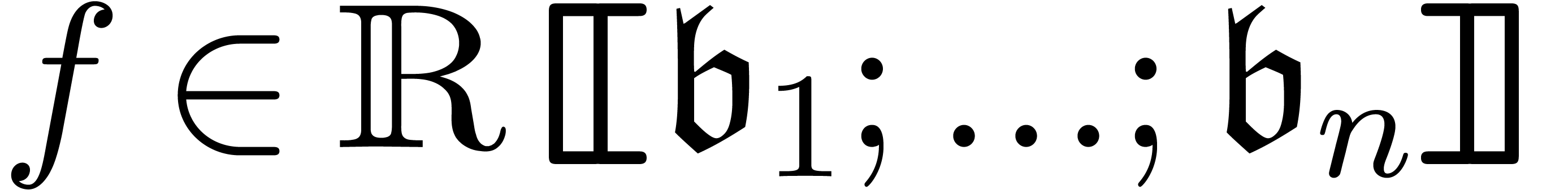 . In fact, we may always
choose
. In fact, we may always
choose  to be transmonomials, although this is
not always the most convenient choice. For instance, from a
computational point, it is more efficient to see
to be transmonomials, although this is
not always the most convenient choice. For instance, from a
computational point, it is more efficient to see
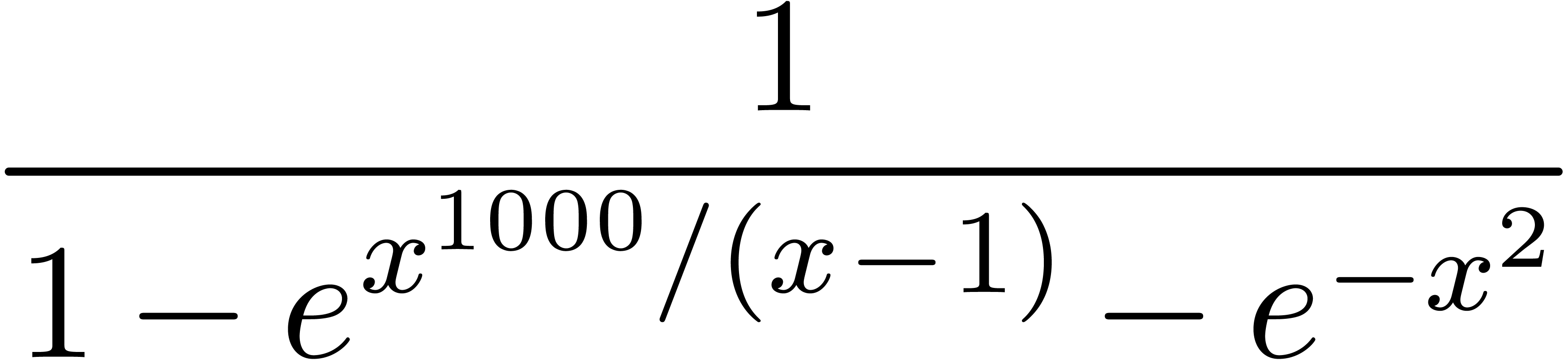
as an element of 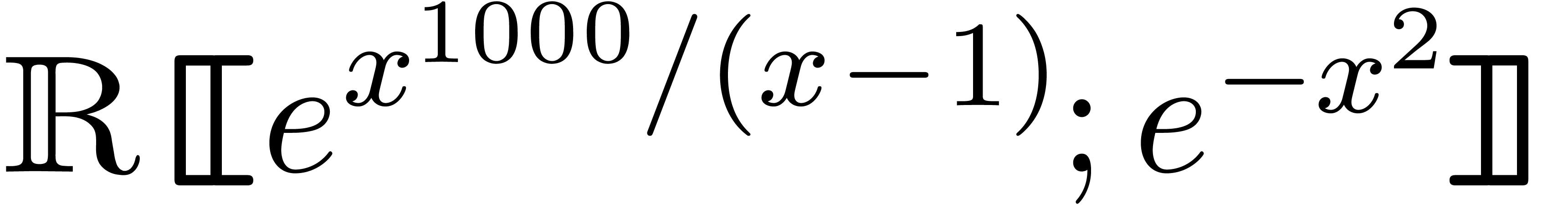 rather than
rather than 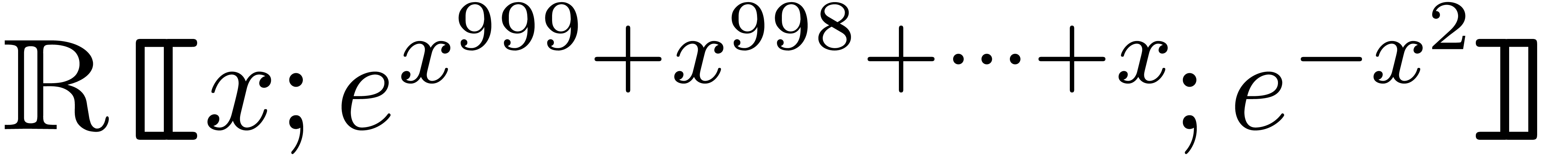 .
.
In the grid-based context, the fact that  is
archimedian implies that the types of the supports of the infinite sums
in recursive expansions are at most
is
archimedian implies that the types of the supports of the infinite sums
in recursive expansions are at most  .
Consequently, the type of the support of a series in
.
Consequently, the type of the support of a series in 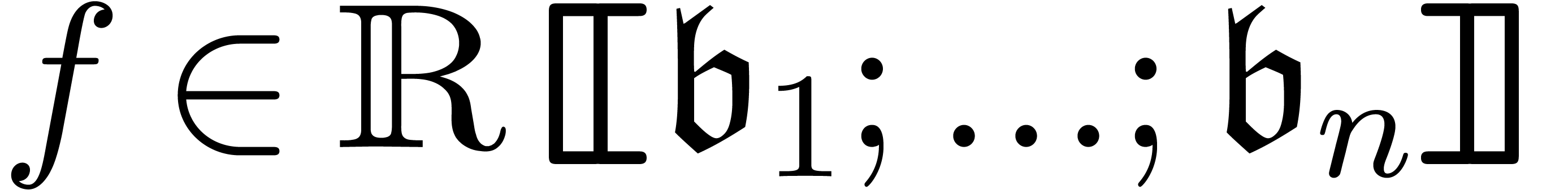 is at most
is at most 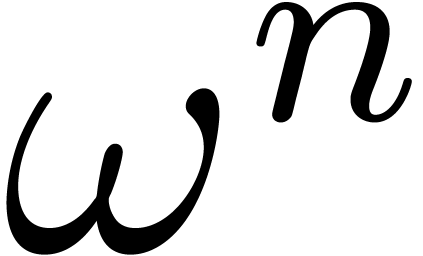 . For instance,
the type of the support of
. For instance,
the type of the support of
is 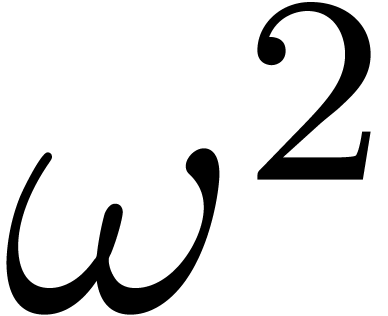 . In fact, this
transseries may also be interpreted as a multivariate Laurent series
. In fact, this
transseries may also be interpreted as a multivariate Laurent series
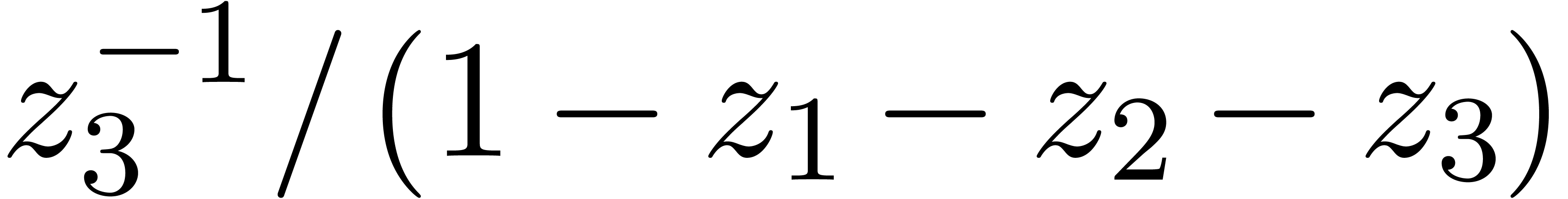 in which we substituted
in which we substituted 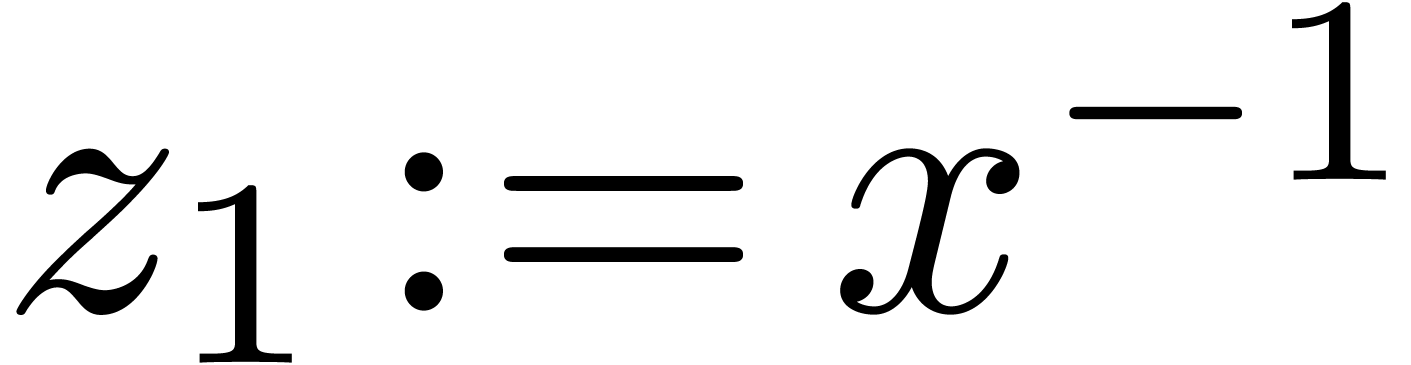 ,
, 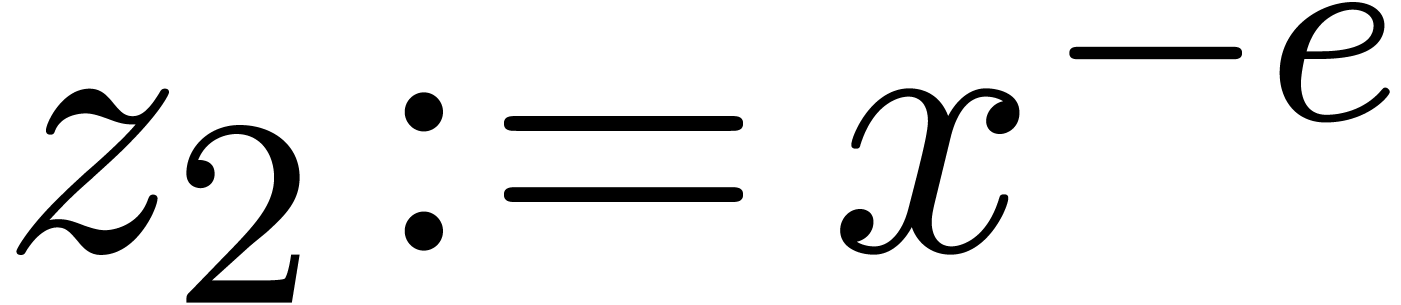 ,
, 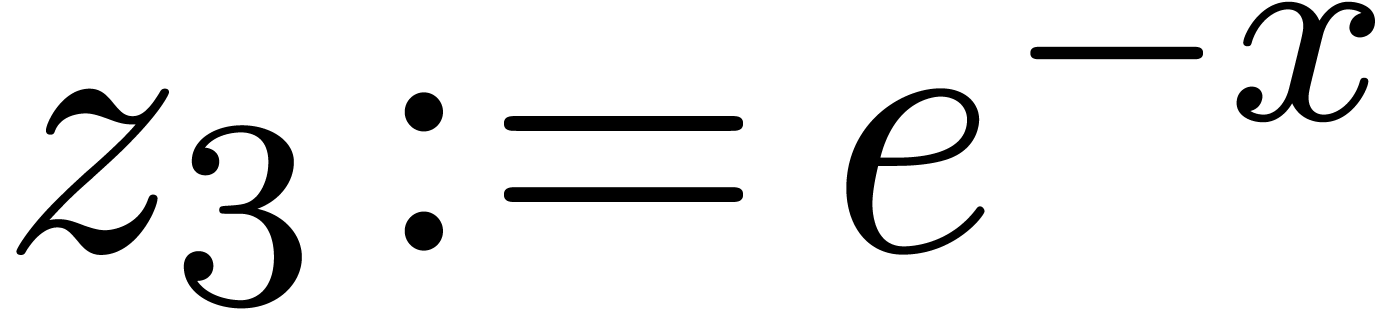 . We call this a Cartesian
representation of the transseries. Cartesian representations exist
in general and they are best suited for doing effective computations on
transseries [vdH97].
. We call this a Cartesian
representation of the transseries. Cartesian representations exist
in general and they are best suited for doing effective computations on
transseries [vdH97].
2.3.2Transbases
For computations which involve exponentiation and differentiation,
asymptotic bases do not necessarily carry sufficient structure. A
transbasis is a tuple 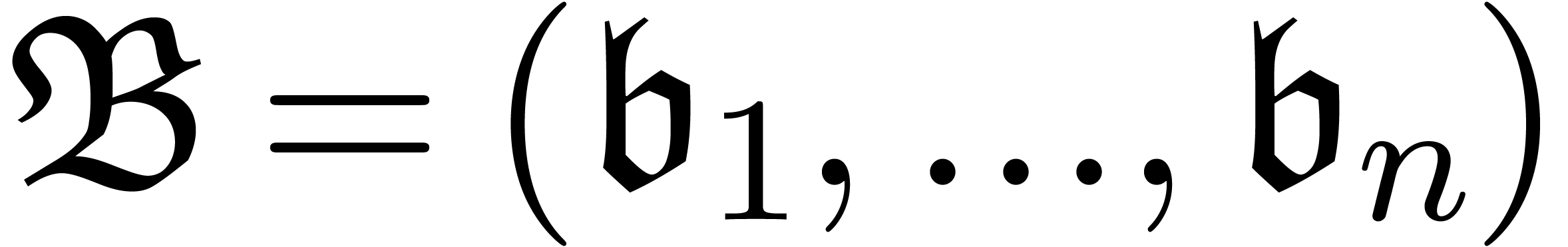 with
with
-
TB0
-
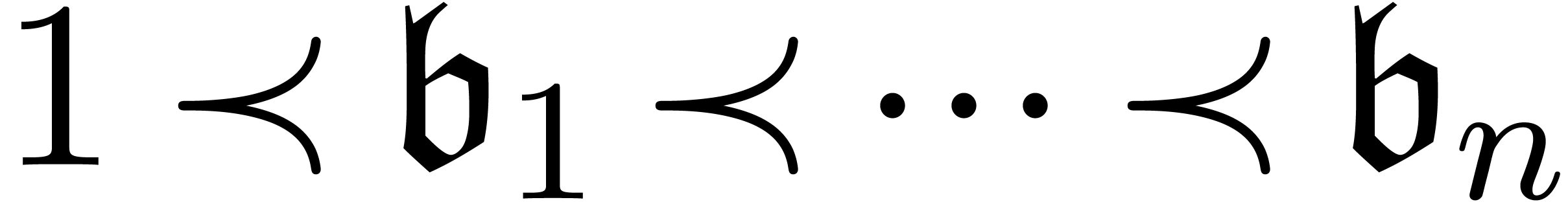 .
.
-
TB1
-
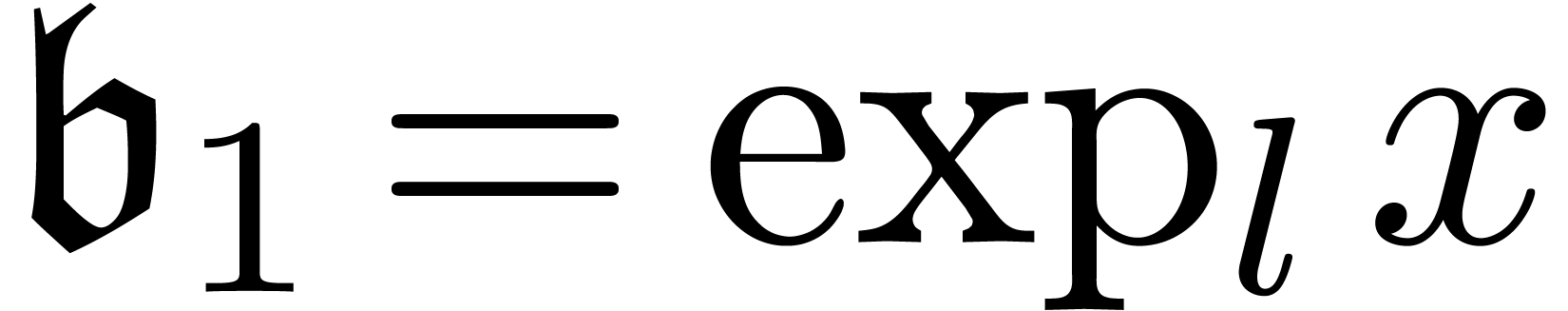 , with
, with 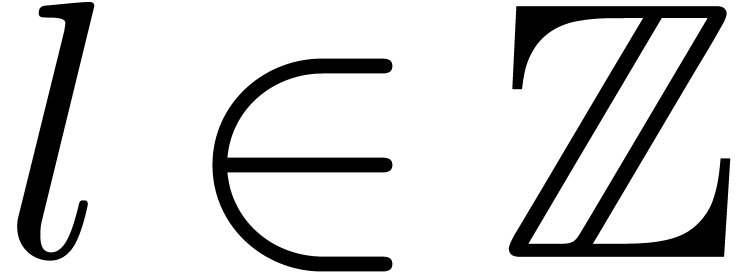 .
.
-
TB2
-
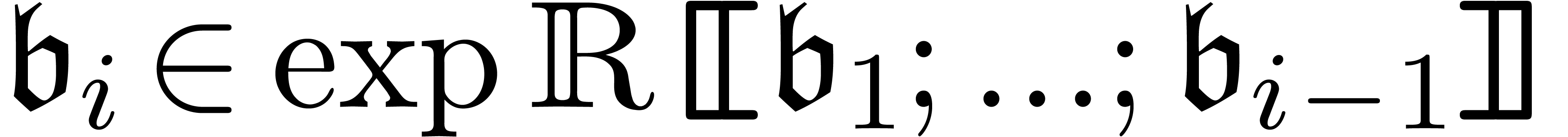 for
for 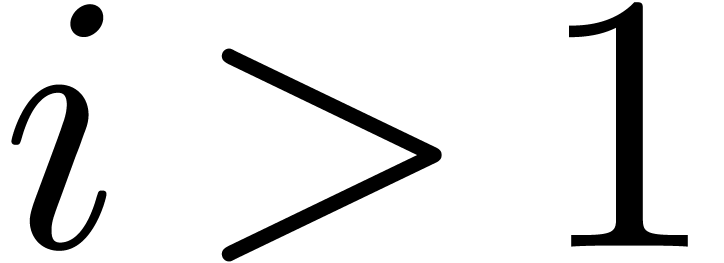 .
.
A transbasis is necessarily an asymptotic basis and any transseries may
be expanded w.r.t. a suitable transbasis. In fact, the
following incomplete transbasis theorem holds.
Theorem 3. Let 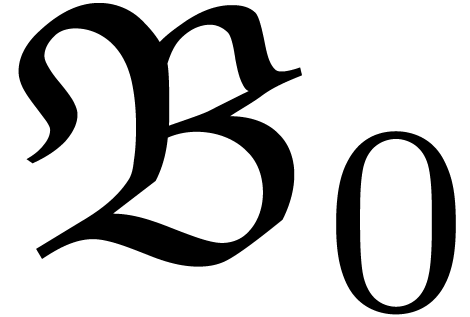 be a transbasis and
be a transbasis and 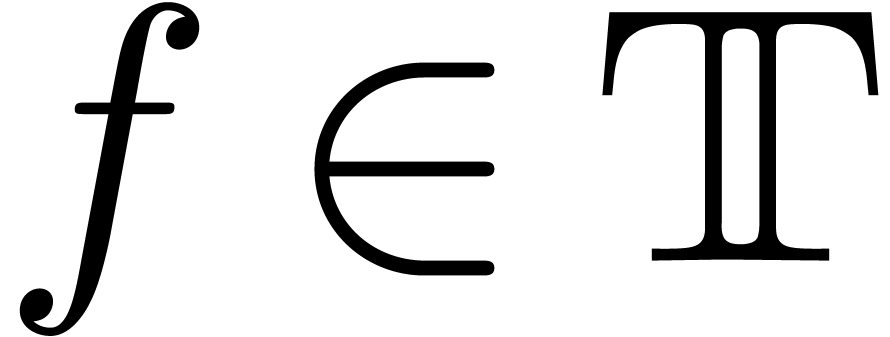 a transseries.
Then there exists a supertransbasis
a transseries.
Then there exists a supertransbasis  ,
such that
,
such that 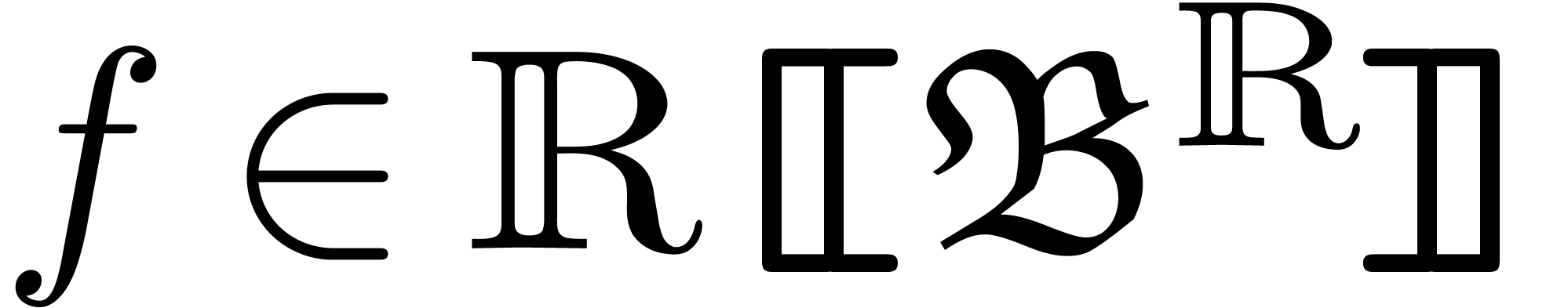 .
.
Example 4. 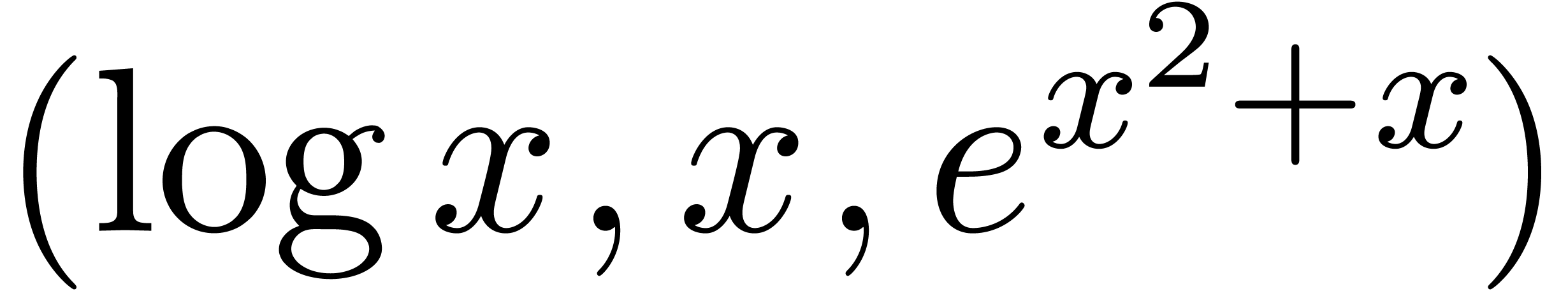 is a transbasis and
is a transbasis and  . The
tuple
. The
tuple 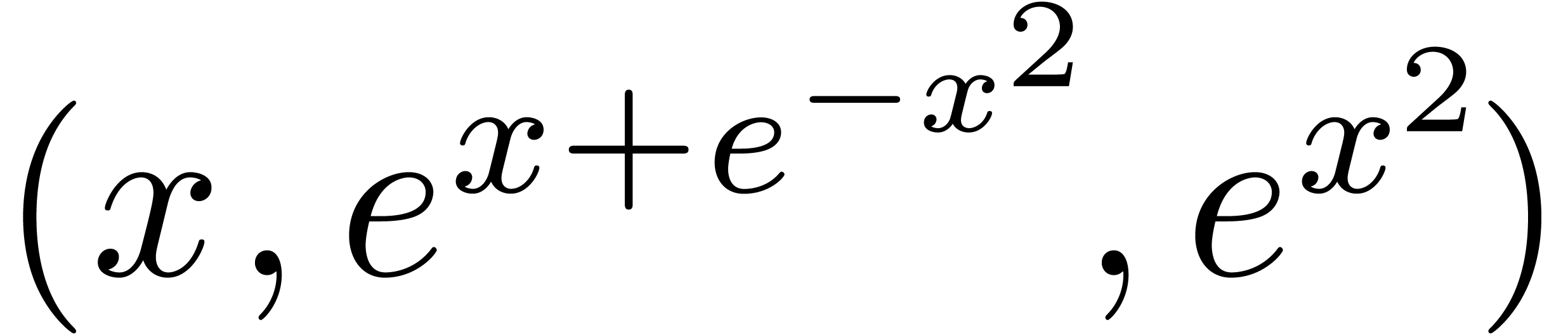 is not a transbasis.
is not a transbasis.
2.4Differentiation and composition
2.4.1Differentiation
Differentiation may be defined inductively on all  as follows. We start by defining the differentiation on the monomial
group
as follows. We start by defining the differentiation on the monomial
group  . If
. If 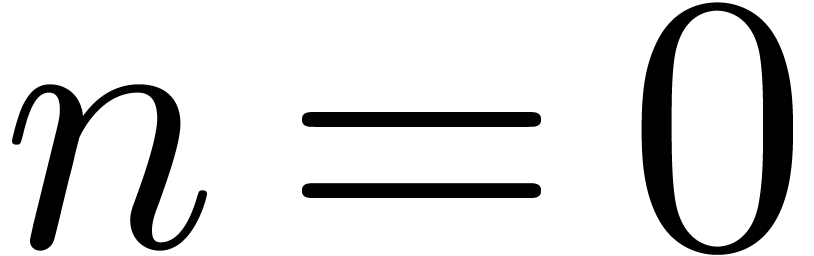 , then we set
, then we set
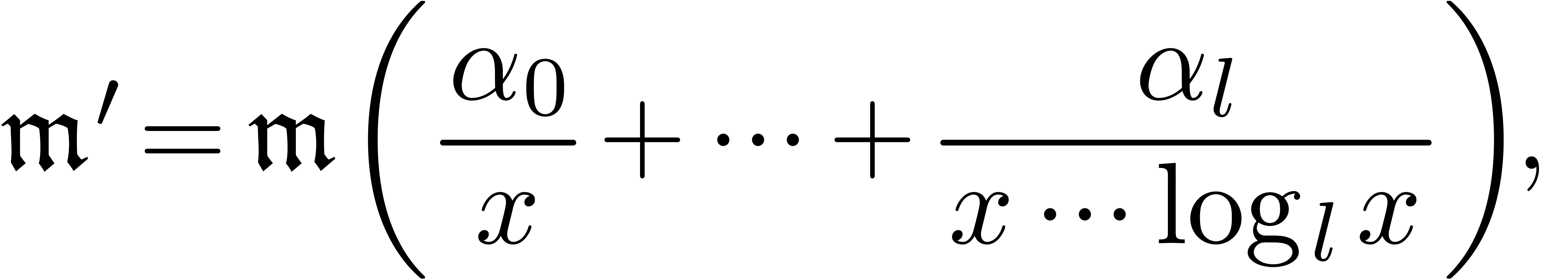
for each monomial 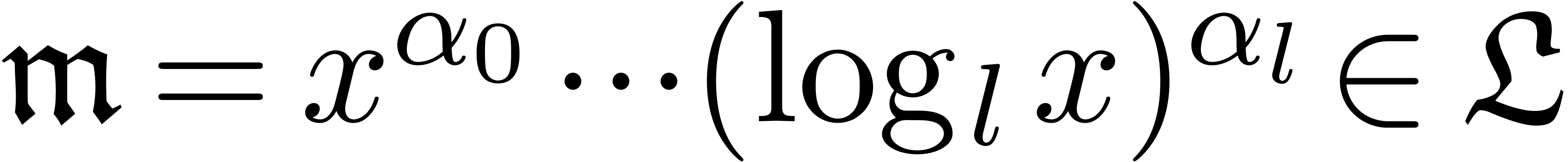 . If
. If 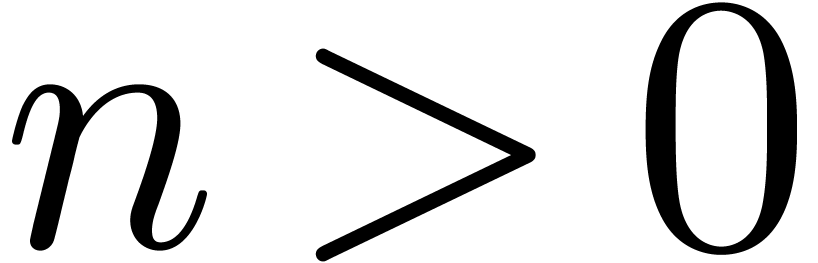 , then each monomial in
, then each monomial in  has the form
has the form  for some
for some  and we define
and we define
where  has already been defined by the induction
hypothesis. Having defined the derivative of each monomial in
has already been defined by the induction
hypothesis. Having defined the derivative of each monomial in  , we “extend the derivation
to
, we “extend the derivation
to  by strong linearity”:
by strong linearity”:
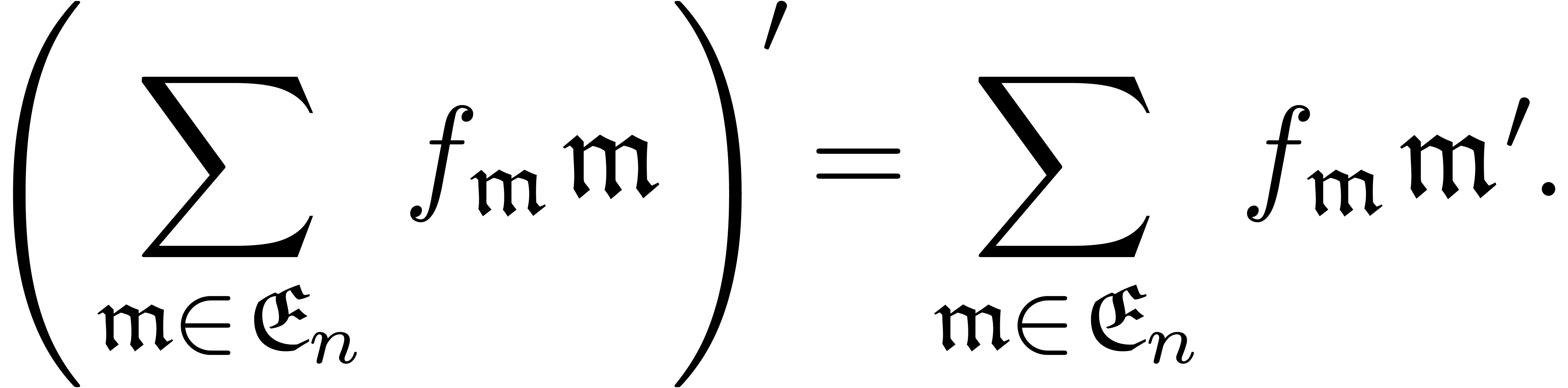
In order for this to work, we have to check that for each grid-based
subset  of
of  ,
the set
,
the set 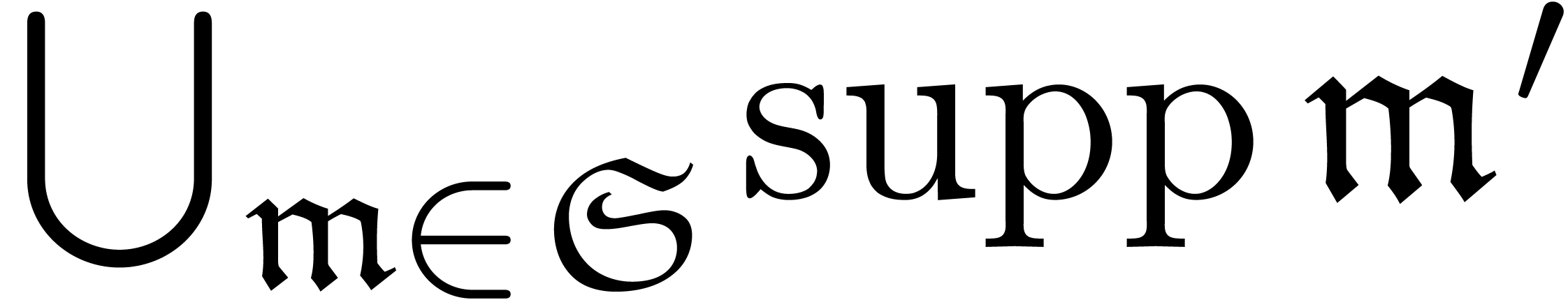 is again grid-based. Now if
is again grid-based. Now if  and
and  are such that
are such that  , then
, then
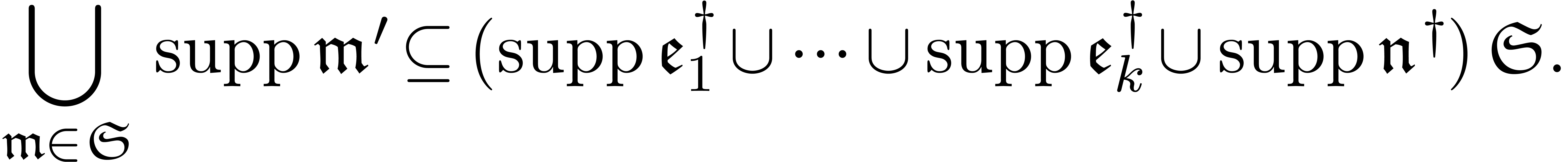
Here 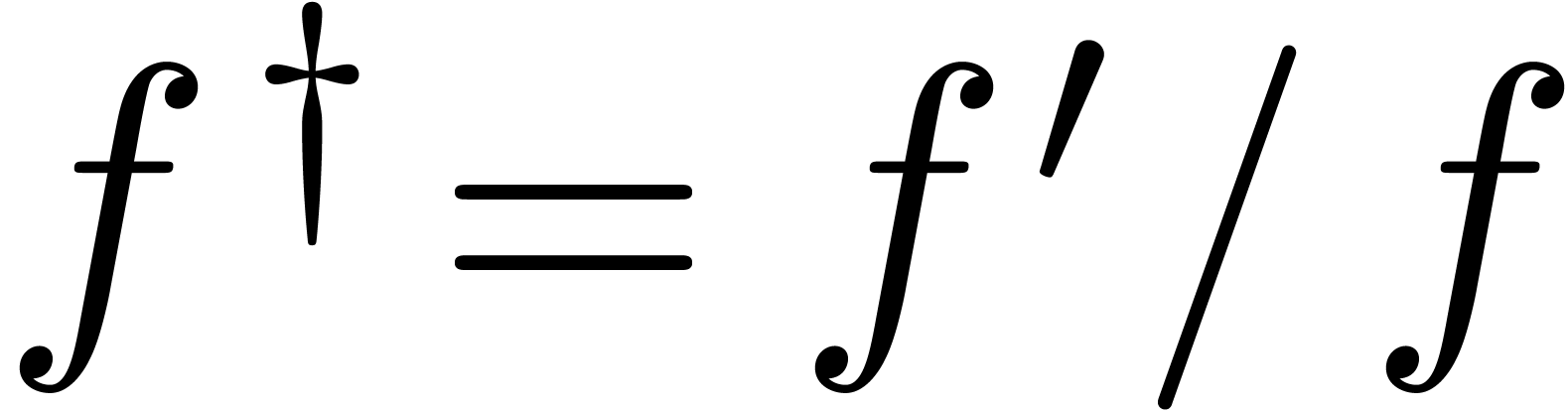 denotes the logarithmic derivative of
denotes the logarithmic derivative of 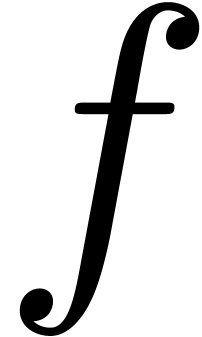 .
.
2.4.2Composition
For the definition of general composition, we refer to [É92,
vdH97]. In what follows we will only use right compositions
with 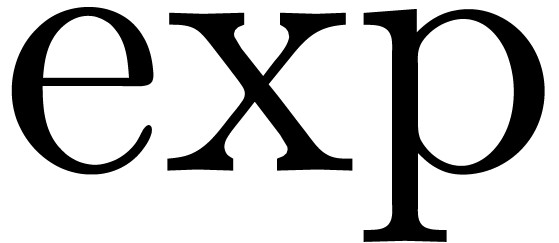 and
and 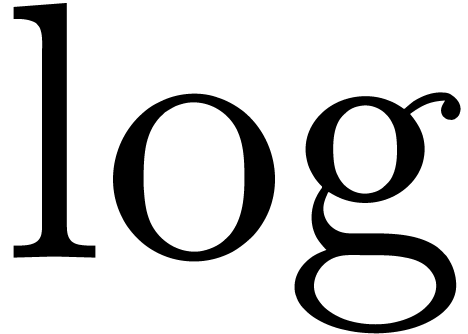 ,
which are defined in a straightforward way using the systematic
substitution of
,
which are defined in a straightforward way using the systematic
substitution of  resp.
resp.  for
for  in a transseries (in
particular, transmonomials map to transmonomials). In the sequel, we
will denote
in a transseries (in
particular, transmonomials map to transmonomials). In the sequel, we
will denote 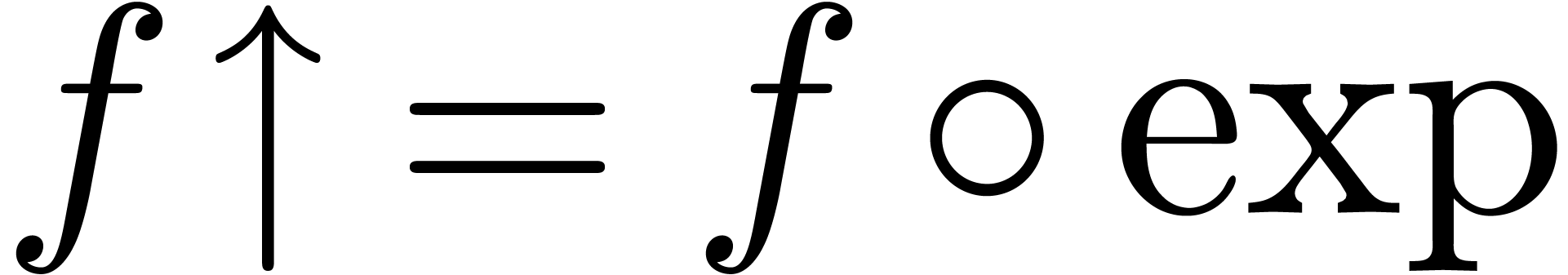 for the upward shifting of
a transseries
for the upward shifting of
a transseries  and
and 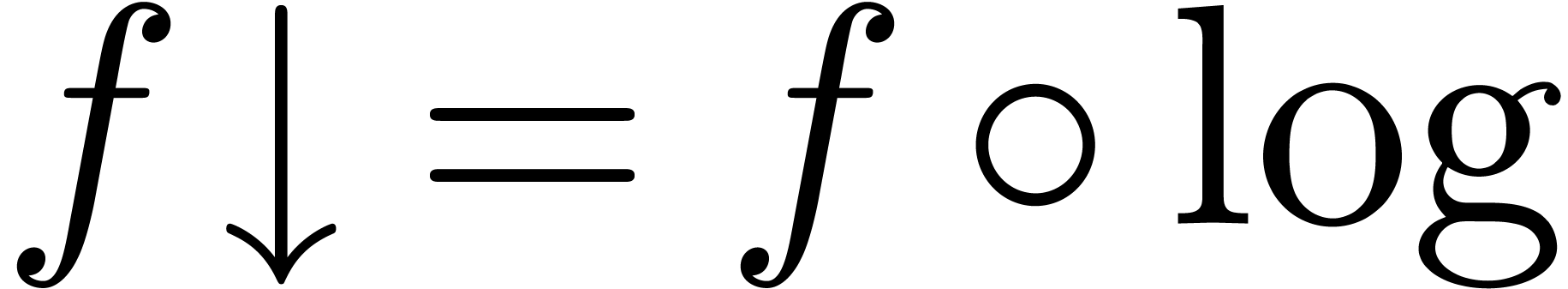 for
its downward shifting.
for
its downward shifting.
3The differential Newton polygon
method
In this section, we will show how to generalize the Newton polygon
method in order to solve asymptotic algebraic differential
equations like
 |
(2) |
Here 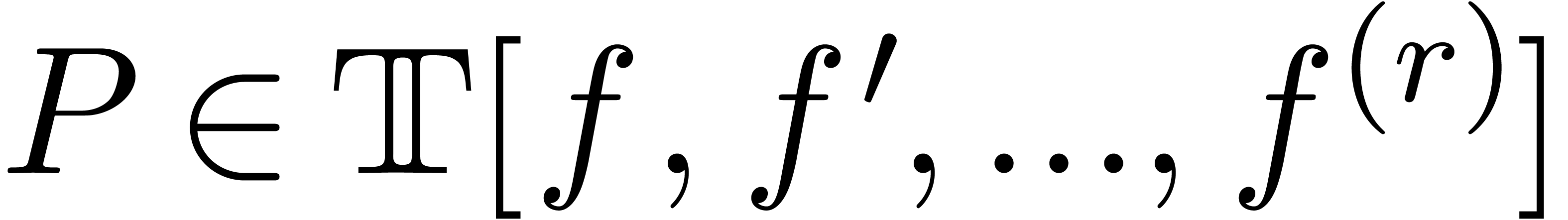 is a differential polynomial with
transseries coefficients and
is a differential polynomial with
transseries coefficients and  a transmonomial. We
also allow
a transmonomial. We
also allow  to be a formal monomial with
to be a formal monomial with  (i.e.
(i.e.  for all
for all
 ) in order to cover the case
of usual algebraic equations. The fact that we consider
asymptotic differential equations (i.e. with the
asymptotic side condition
) in order to cover the case
of usual algebraic equations. The fact that we consider
asymptotic differential equations (i.e. with the
asymptotic side condition  ),
enables us to associate invariants to the equation (21),
which prove to be very useful when applying the Newton polygon method.
),
enables us to associate invariants to the equation (21),
which prove to be very useful when applying the Newton polygon method.
3.1Notations
3.1.1Natural decomposition of 
The differential polynomial  is most naturally
decomposed as
is most naturally
decomposed as
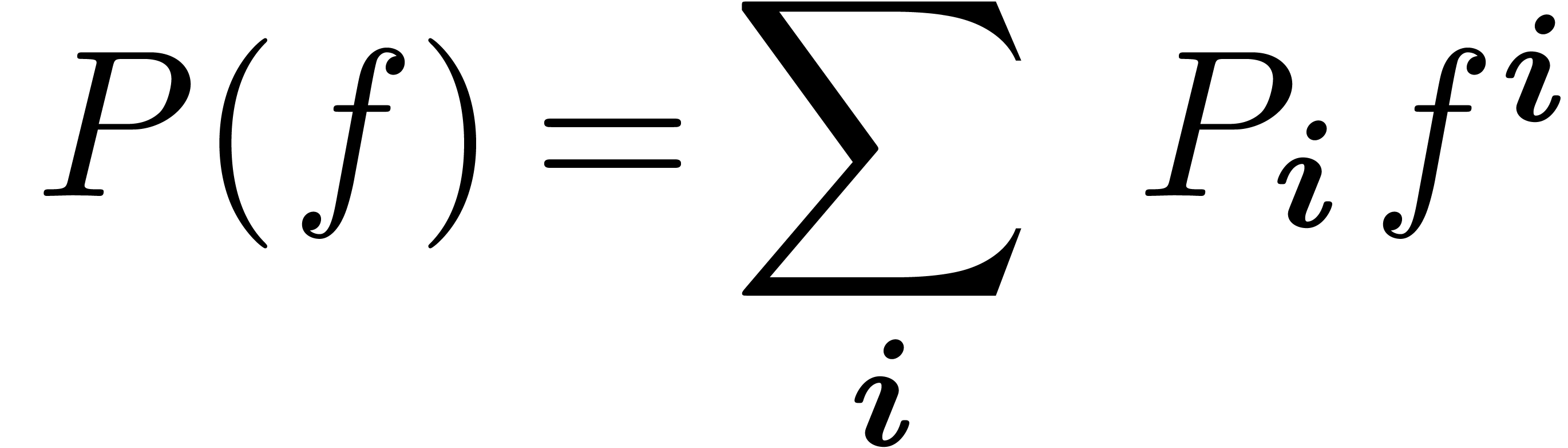 |
(3) |
Here we use vector notation for tuples 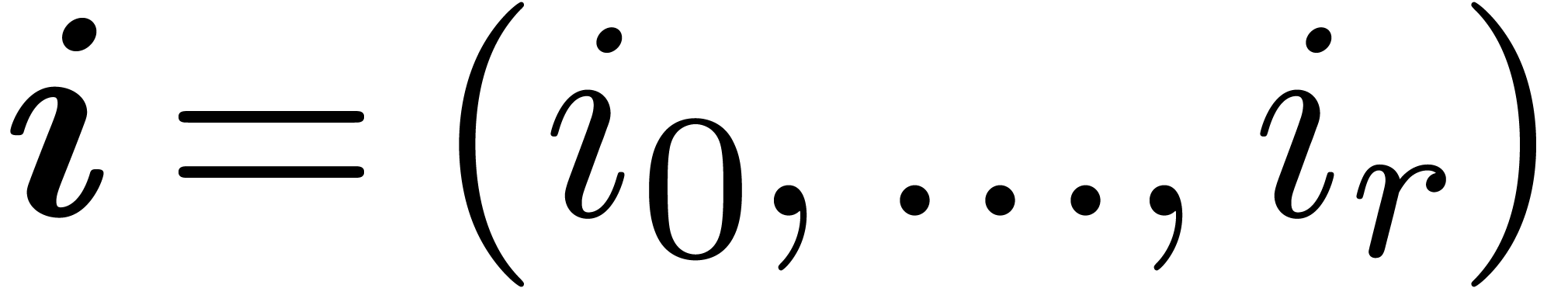 and
and 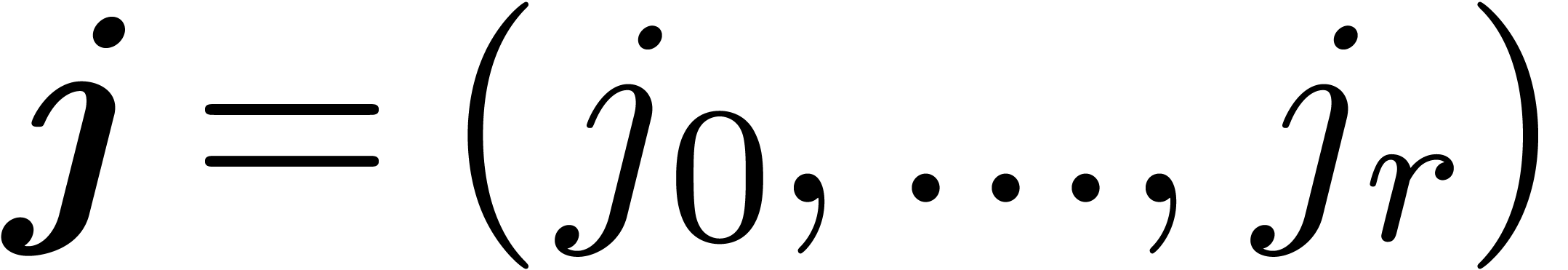 of non-negative integers:
of non-negative integers:
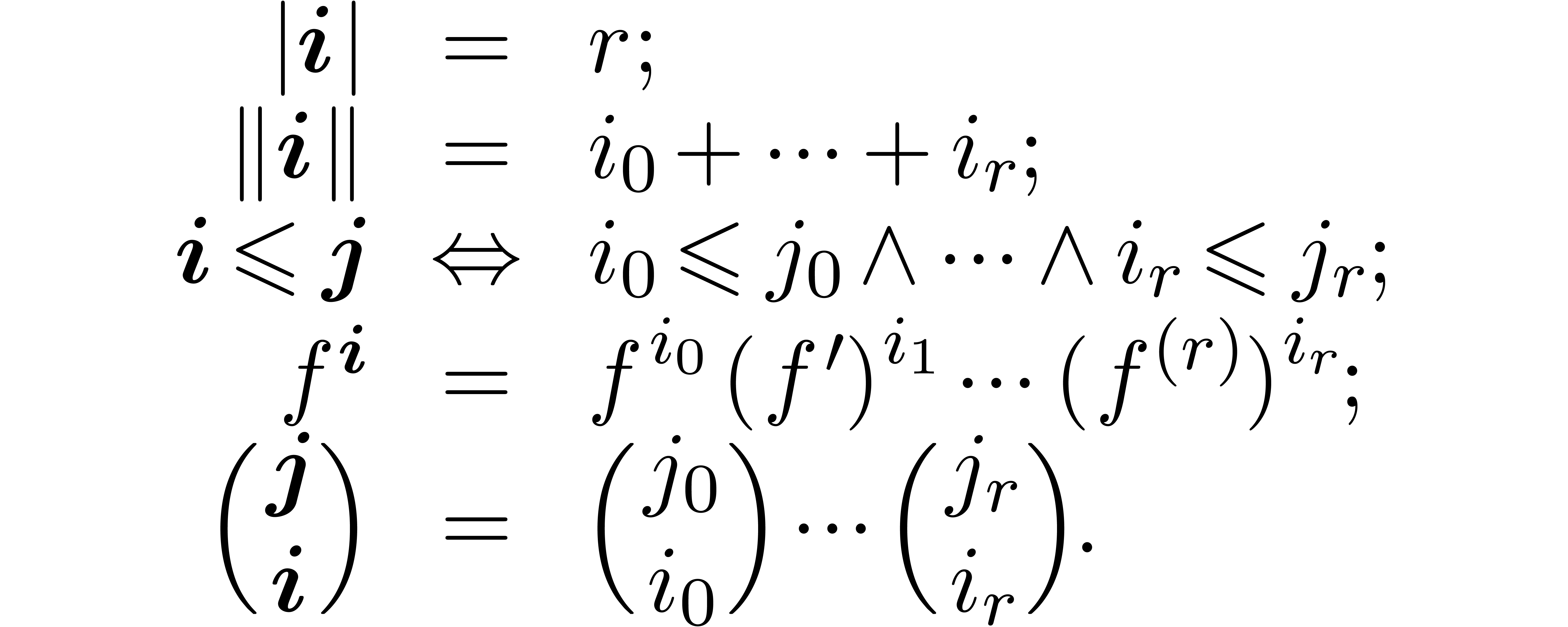
The  -th homogeneous
part of
-th homogeneous
part of  is defined by
is defined by
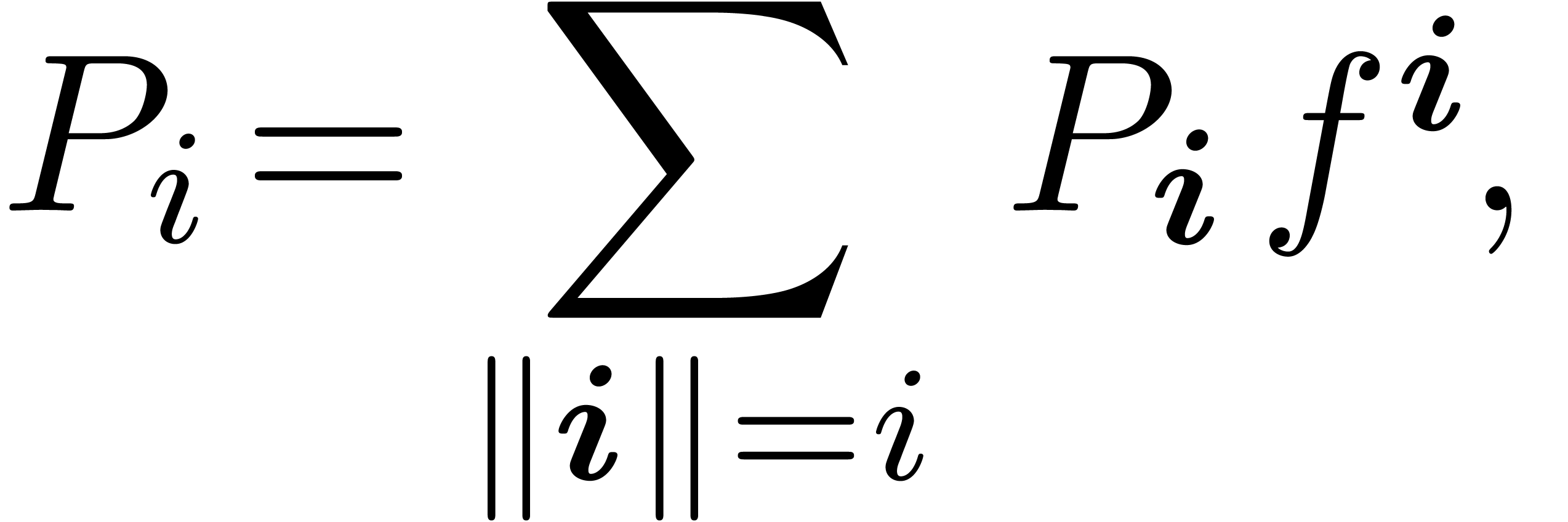
so that
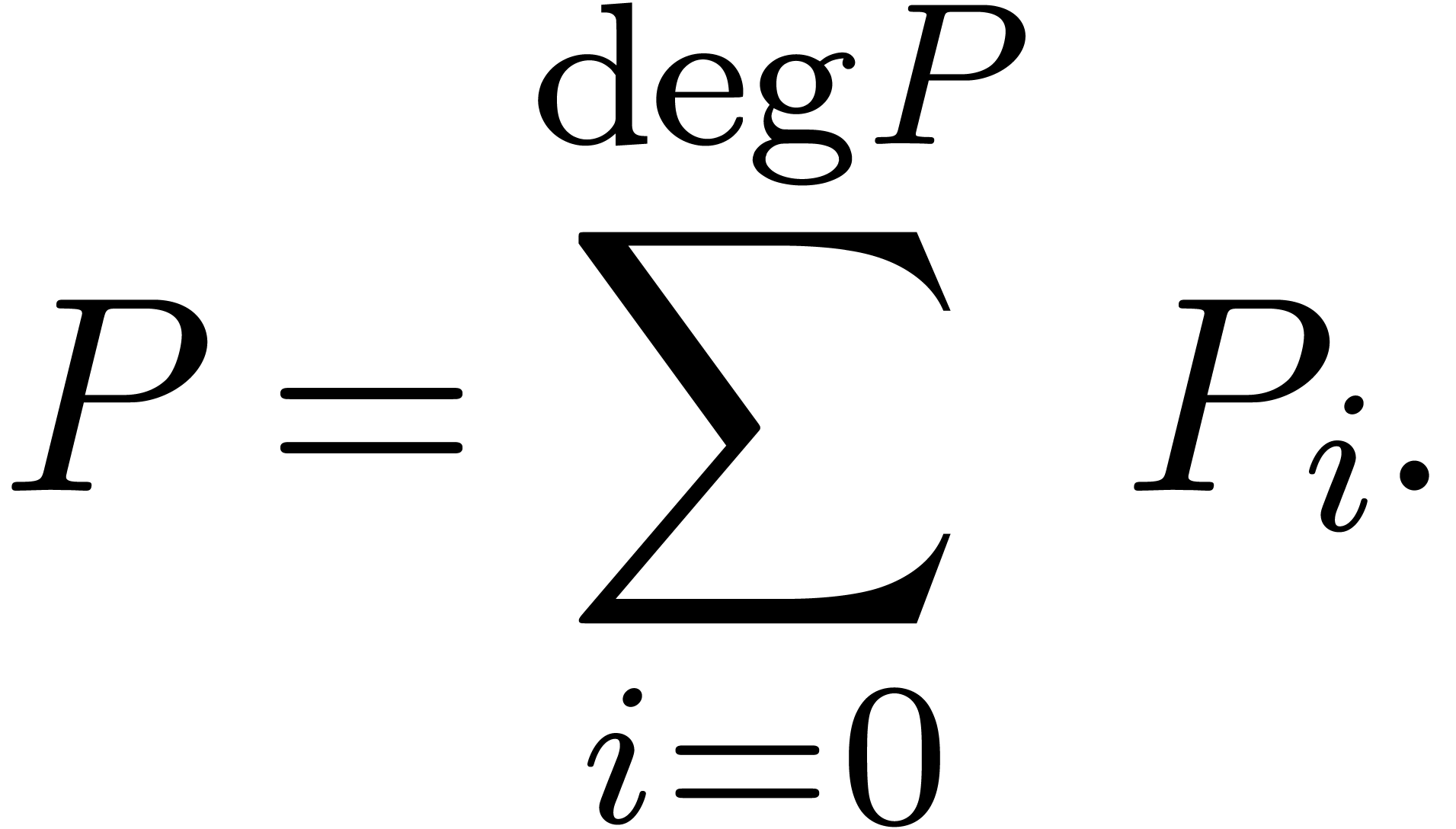
3.1.2Decomposition of  along orders
along orders
Another very useful decomposition of  is its
decomposition along orders:
is its
decomposition along orders:
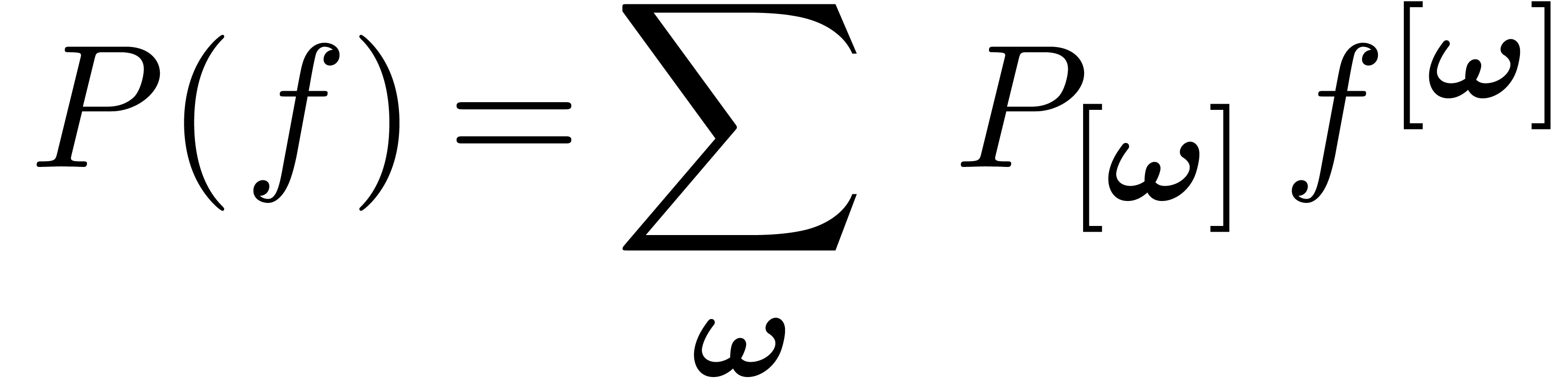 |
(4) |
In this notation,  runs through tuples
runs through tuples 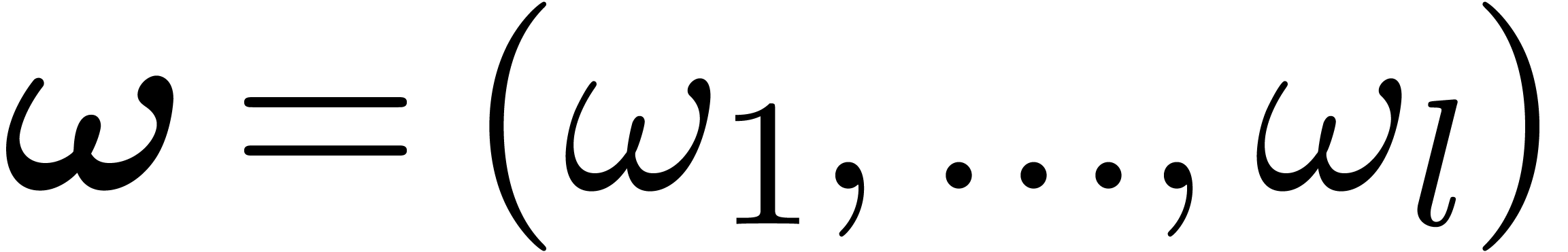 of integers in
of integers in  of length
of length  , and
, and 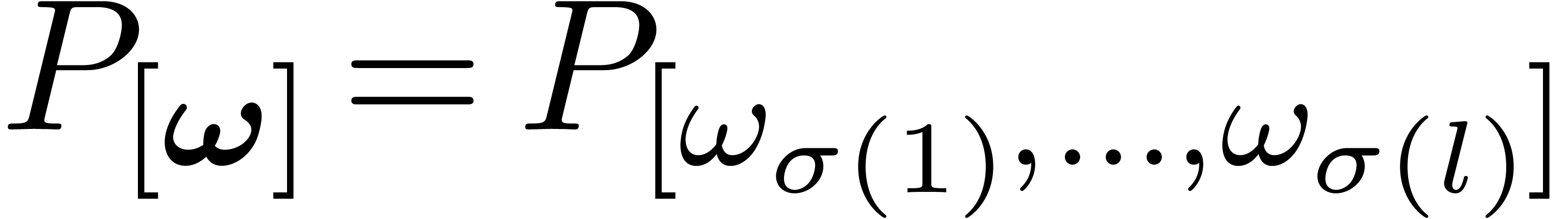 for
all permutations of integers. We again use vector notation for such
tuples
for
all permutations of integers. We again use vector notation for such
tuples
We call  the weight of
the weight of  and
and
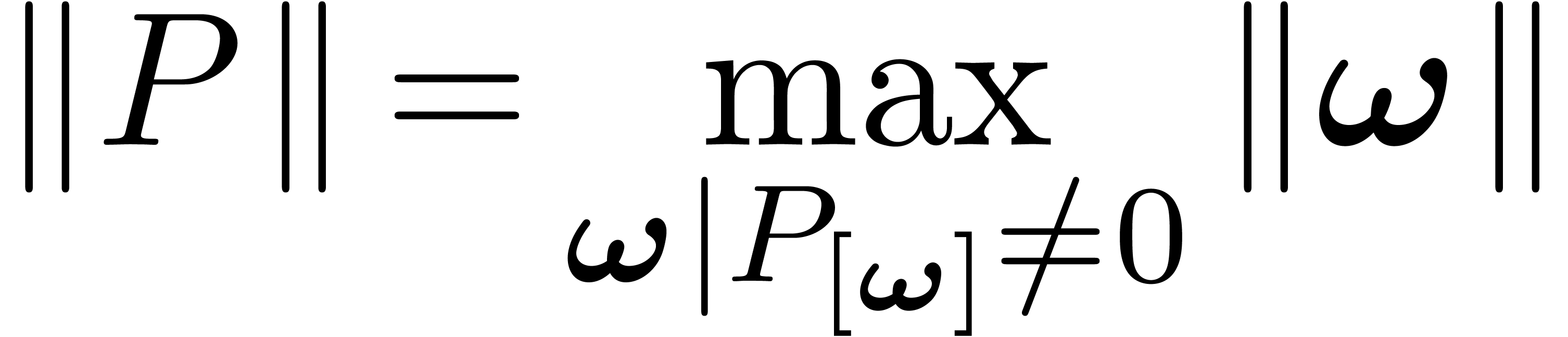
the weight of  .
.
3.1.3Logarithmic decomposition of 
It is convenient to denote the successive logarithmic derivatives of
 by
by
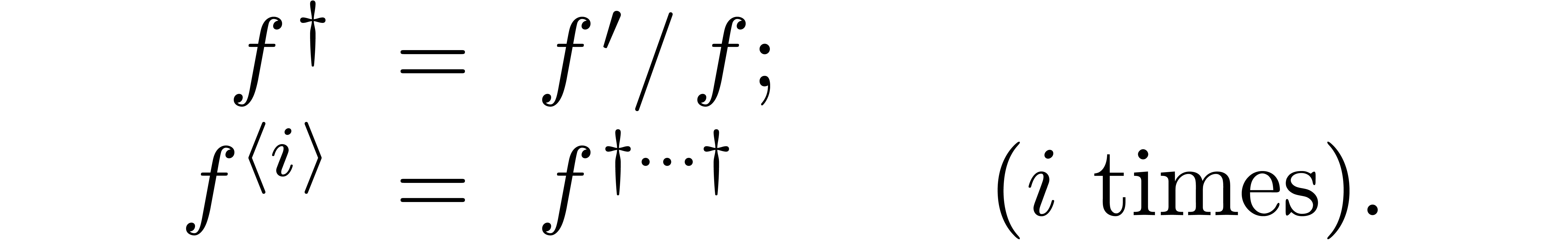
Then each  can be rewritten as a polynomial in
terms of
can be rewritten as a polynomial in
terms of  :
:
We define the logarithmic decomposition of  by
by
 |
(5) |
where
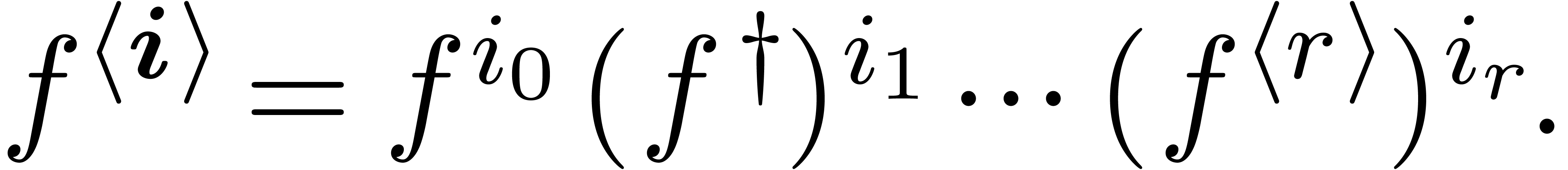
Now consider the lexicographical ordering 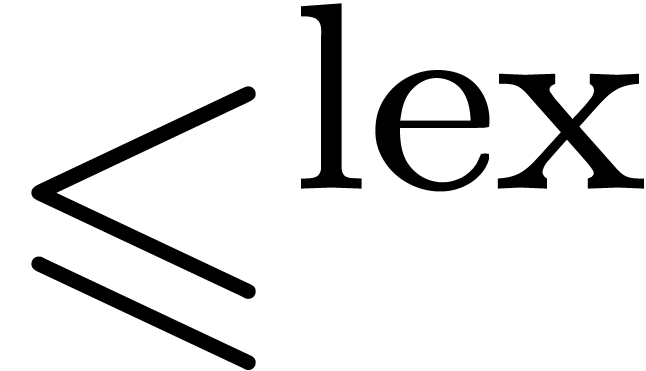 on
on
 , defined by
, defined by
This ordering is total, so there exists a maximal  for
for 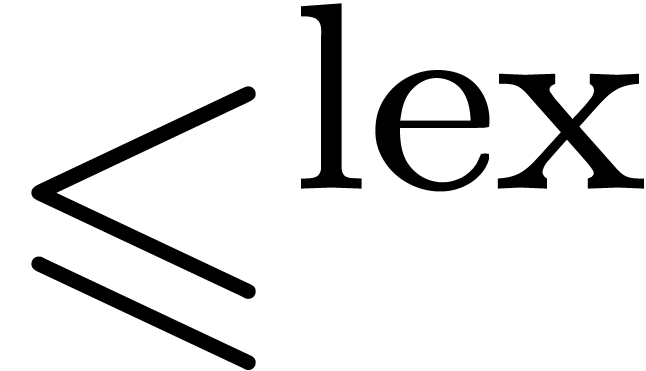 with
with  ,
assuming that
,
assuming that  . For this
. For this
 , we have
, we have
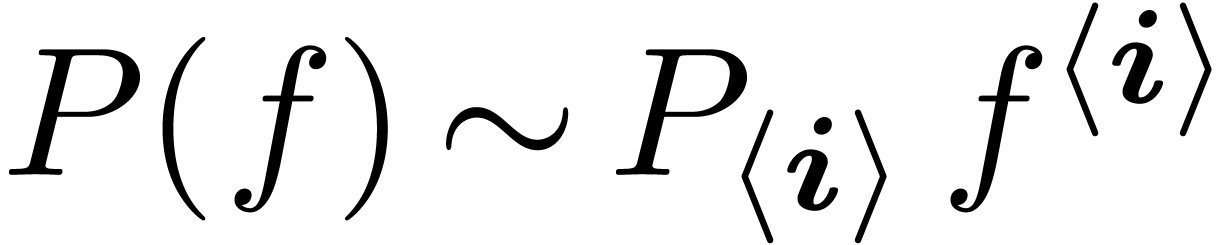 |
(6) |
for all  , whose dominant
monomial is sufficiently large.
, whose dominant
monomial is sufficiently large.
3.1.4Additive and multiplicative conjugations
and upward shifting.
Given a differential polynomial  and a
transseries
and a
transseries  it is useful to define the
additive and multiplicative conjugates
it is useful to define the
additive and multiplicative conjugates 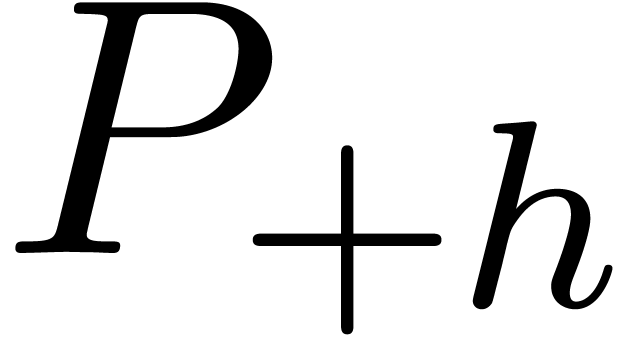 and
and 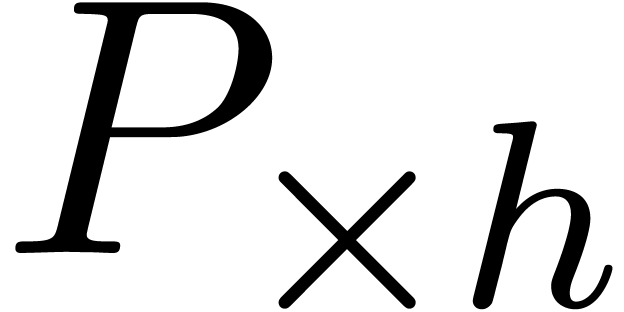 of
of  w.r.t.
w.r.t. 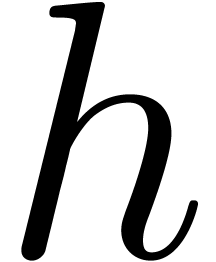 and the upward shifting
and the upward shifting 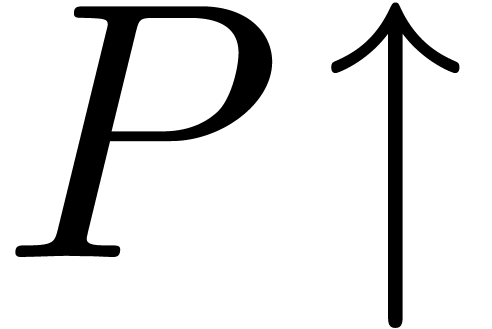 of
of
 as being the unique differential polynomials,
such that for all
as being the unique differential polynomials,
such that for all  , we have
, we have
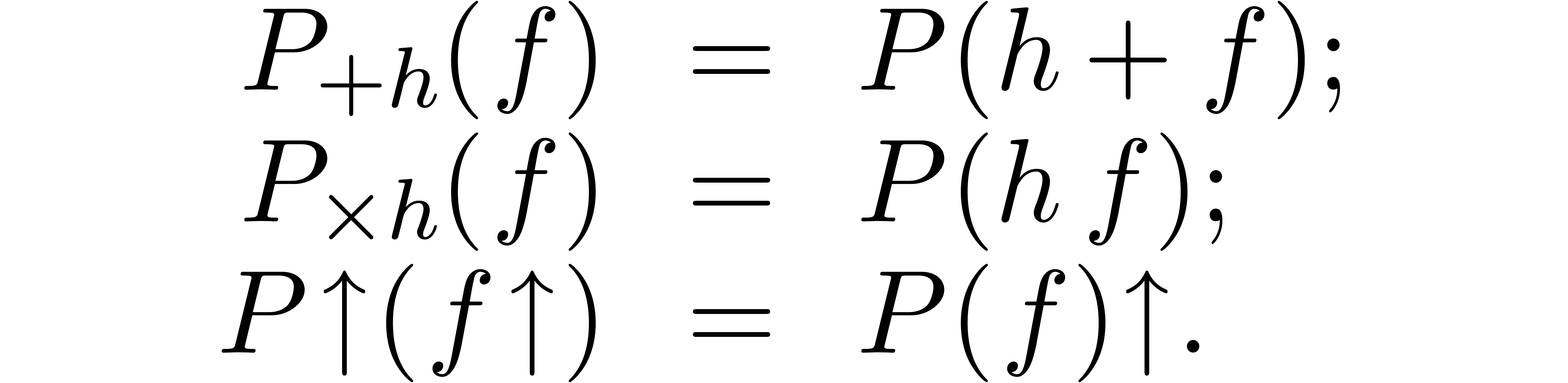
The coefficients of 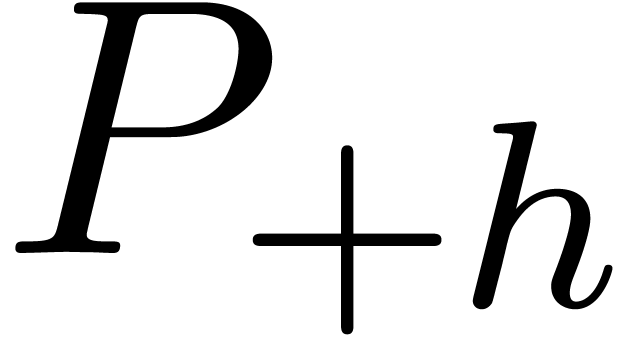 are explicitly given by
are explicitly given by
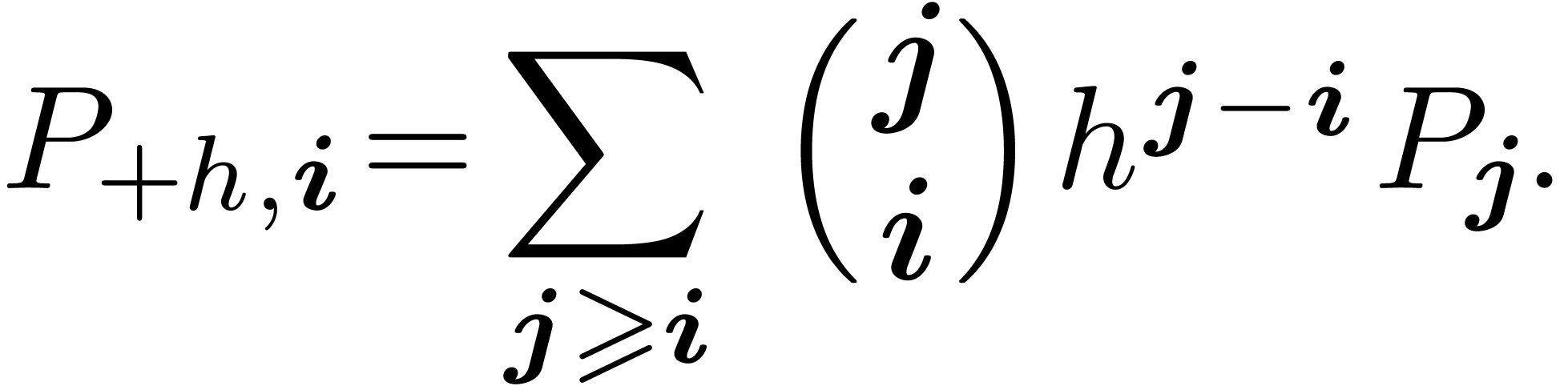 |
(7) |
The coefficients of 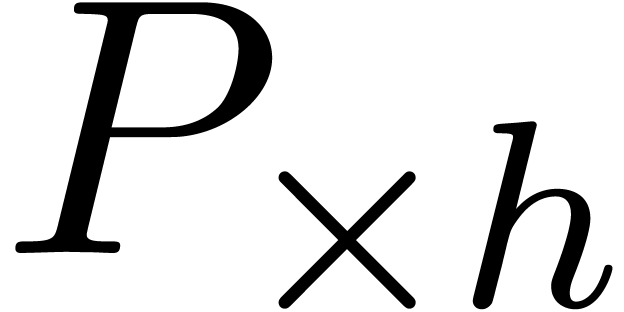 are more easily expressed
using decompositions along orders:
are more easily expressed
using decompositions along orders:
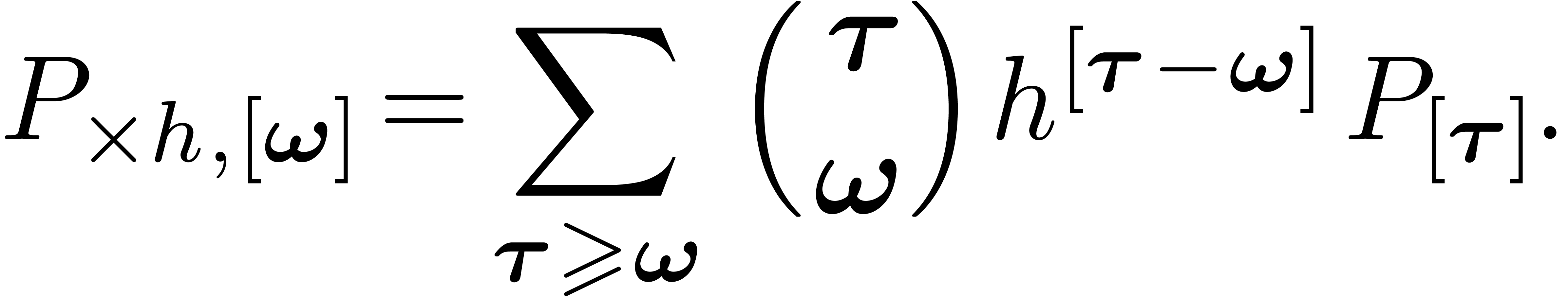 |
(8) |
The coefficients of the upward shifting (or compositional conjugation by
 ) are given by
) are given by
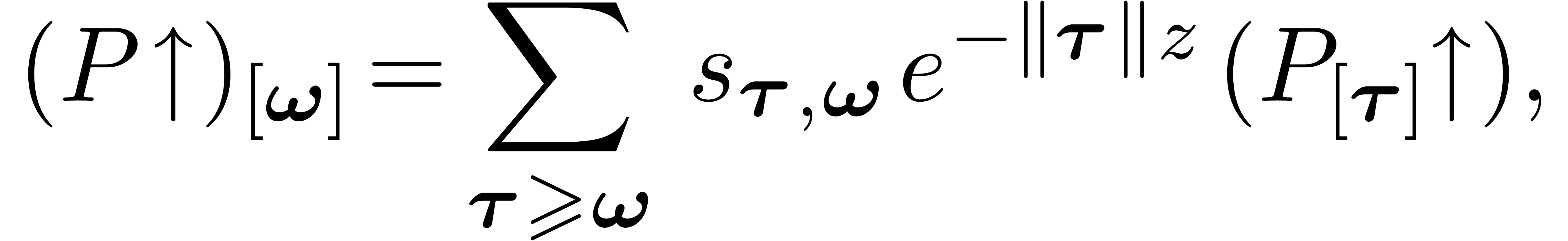 |
(9) |
where the 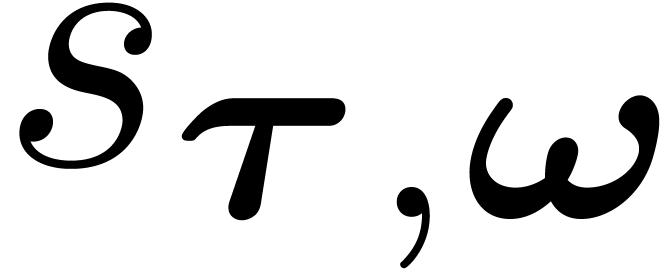 are generalized Stirling numbers of
the first kind:
are generalized Stirling numbers of
the first kind:
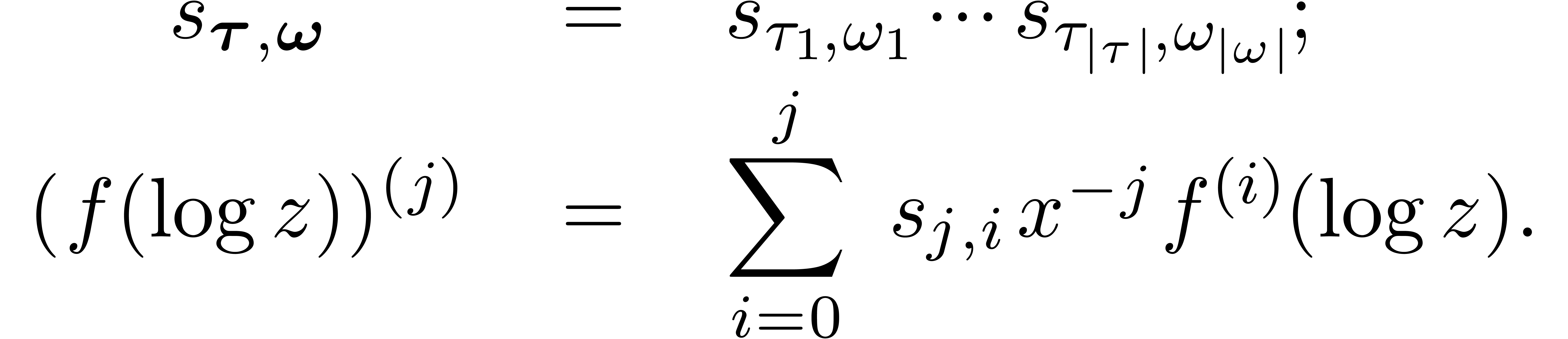
3.2Potential dominant terms and Newton
degree
3.2.1Introduction
In order to solve (21), the first step is to find all
possible dominant monomials of solutions, together with their
coefficients. In the classical setting of algebraic equations, such
potential dominant monomials can be read off graphically from the slopes
of the Newton polygon and the corresponding coefficients are roots of
the Newton polynomials associated to these slopes.
In the differential setting, several phenomena make it more difficult to
find the potential dominant terms in such a direct way. First of all, in
the algebraic setting, potential dominant monomials always correspond to
the cancellation of two terms in  of different
degrees. In the differential setting, cancellations may also arise in a
single homogeneous component. For instance, the differential equation
of different
degrees. In the differential setting, cancellations may also arise in a
single homogeneous component. For instance, the differential equation
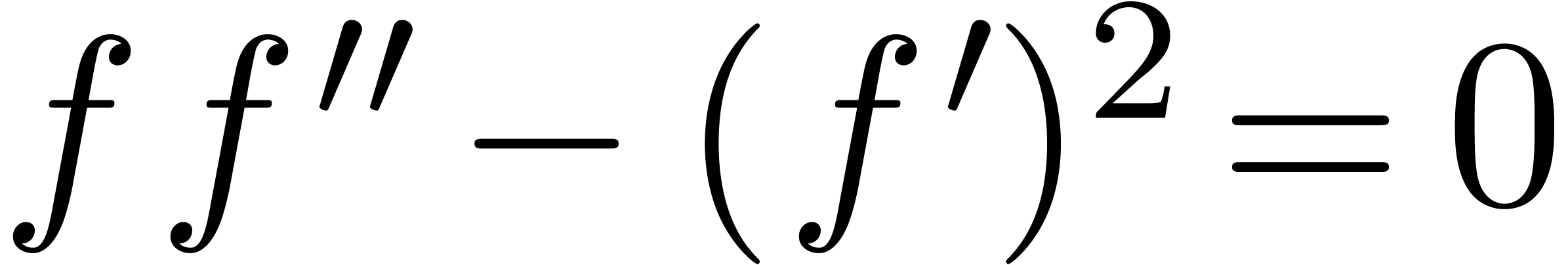
has  as its general solution. Another difficulty
is that differentiation does not preserve valuation: we usually do not
have
as its general solution. Another difficulty
is that differentiation does not preserve valuation: we usually do not
have 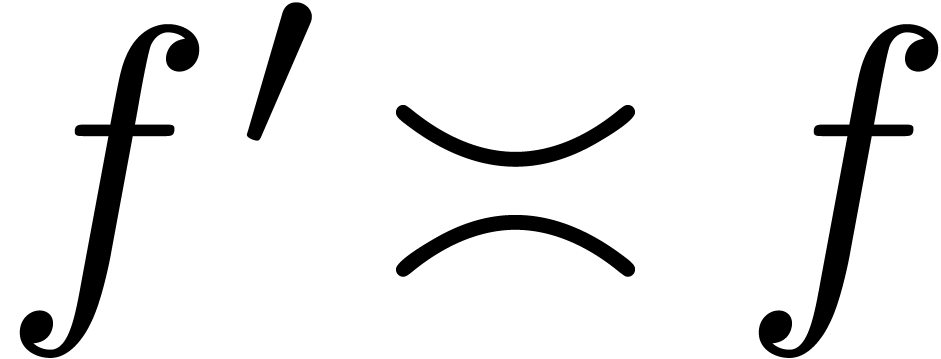 for transseries
for transseries 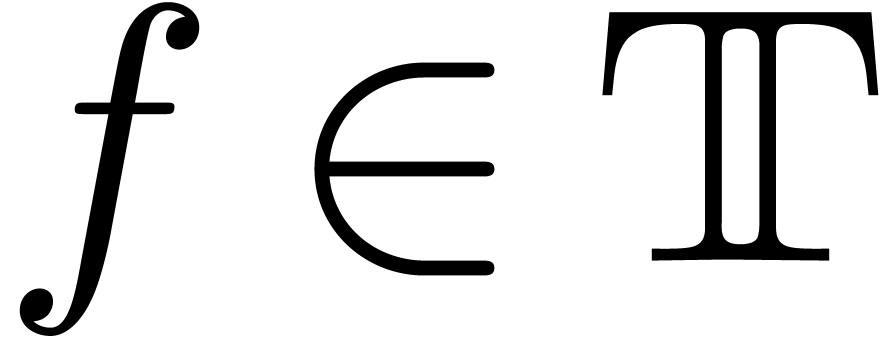 . Consequently, even if we know that the dominant
monomial corresponds to the cancellation of two single terms in
. Consequently, even if we know that the dominant
monomial corresponds to the cancellation of two single terms in  of different degrees, then the potential dominant
monomial can not be read off directly from the dominant monomials of
these terms. For instance, in the equation
of different degrees, then the potential dominant
monomial can not be read off directly from the dominant monomials of
these terms. For instance, in the equation
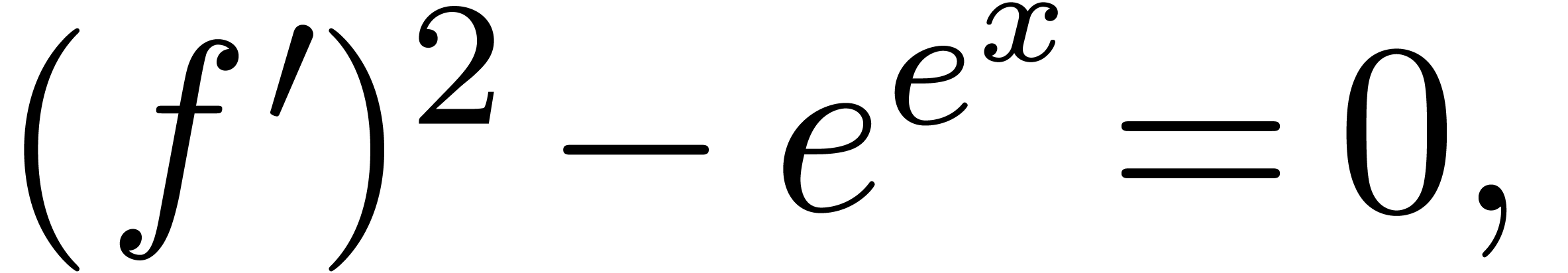
the only potential dominant monomial is  .
However
.
However  is not the square root
is not the square root 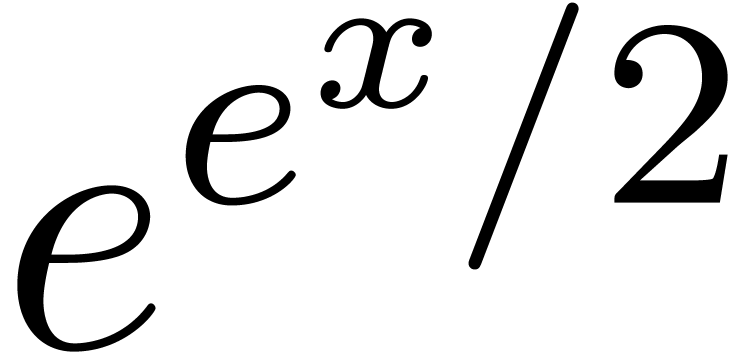 of the quotient of the dominant monomials
of the quotient of the dominant monomials 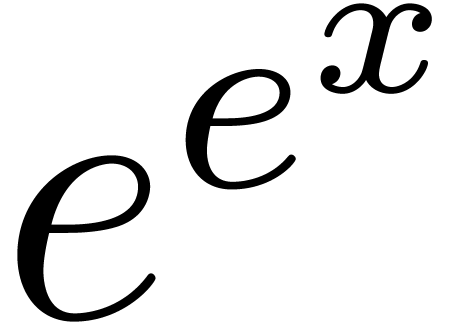 and
and
 of the coefficients of
of the coefficients of  and
and 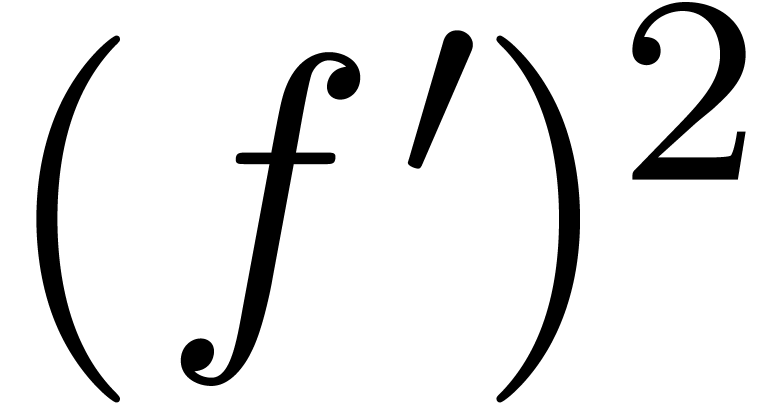 in
in  .
.
In order to solve these problems, we use the combination of several
ideas. First of all, we will no longer seek to read off potential
dominant monomials directly from the Newton polygon. Instead, we will
characterize when  is a potential dominant
monomial, so we will only have to consider horizontal slopes. Then
is a potential dominant
monomial, so we will only have to consider horizontal slopes. Then  will be a potential dominant monomial for the
equation (21) if and only if
will be a potential dominant monomial for the
equation (21) if and only if 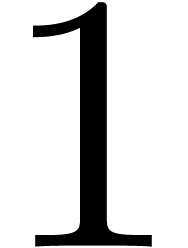 is a
potential dominant monomial for the equation
is a
potential dominant monomial for the equation

A second important tool is upward shifting. Although we do not always
have 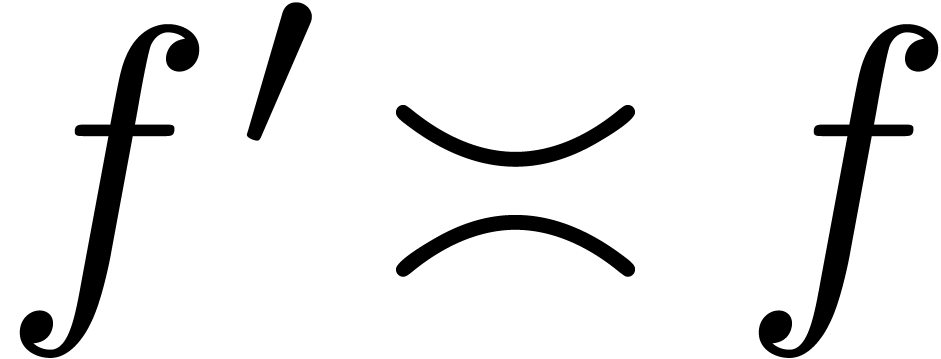 , we do have
, we do have  for all purely exponential transseries
for all purely exponential transseries 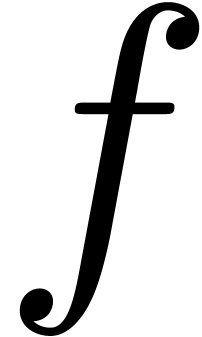 with
with  . Here a purely
exponential transseries is a transseries which can be expanded with
respect to transbases
. Here a purely
exponential transseries is a transseries which can be expanded with
respect to transbases  with
with  . For instance,
. For instance,  is
purely exponential, but
is
purely exponential, but 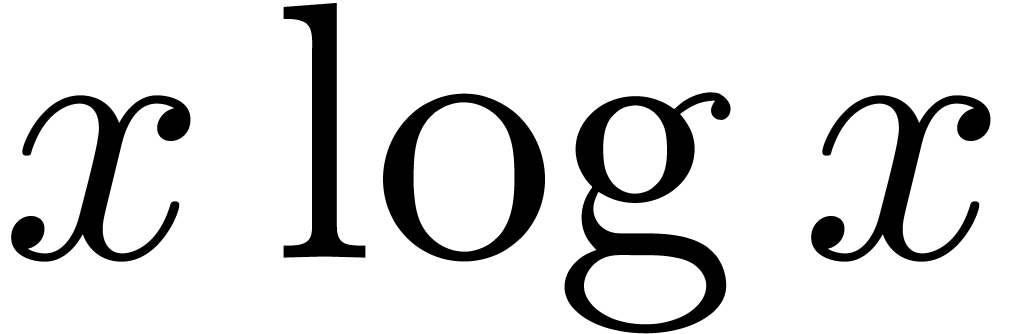 and
and  are not. Any transseries becomes purely exponential after a sufficient
number of upward shiftings.
are not. Any transseries becomes purely exponential after a sufficient
number of upward shiftings.
3.2.2Potential dominant terms and Newton
degree
In order to decide whether  is a potential
dominant monomial for (21), it is interesting to study the
nature of the dominant part of
is a potential
dominant monomial for (21), it is interesting to study the
nature of the dominant part of  after a
sufficient number of upward shiftings. Setting
after a
sufficient number of upward shiftings. Setting  , we define this dominant part of
, we define this dominant part of  to be the differential polynomial
to be the differential polynomial
with coefficients in  .
Denoting by
.
Denoting by 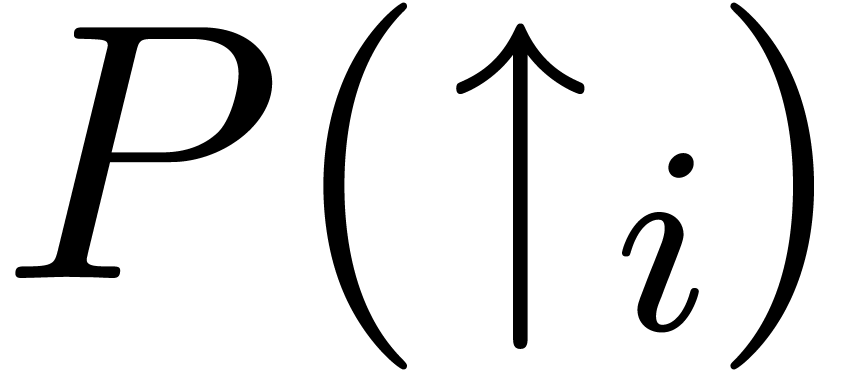 the
the 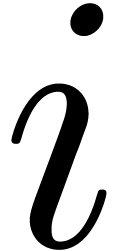 -th
upward shifting of the differential polynomial
-th
upward shifting of the differential polynomial  , the following result can be proved [vdH00,
vdH01]:
, the following result can be proved [vdH00,
vdH01]:
Proposition 5. Let
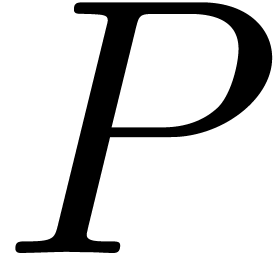 be a differential polynomial with purely
exponential coefficients. Then there exists a polynomial
be a differential polynomial with purely
exponential coefficients. Then there exists a polynomial 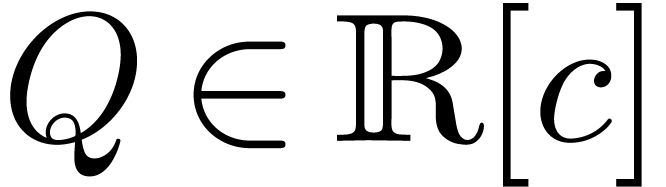 and an integer
and an integer 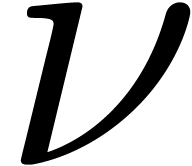 ,
such that for all
,
such that for all 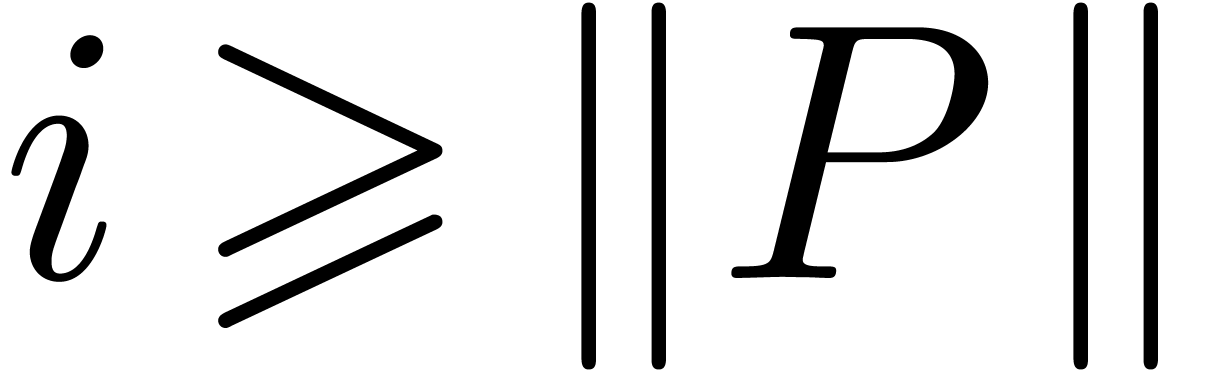 , we have
, we have
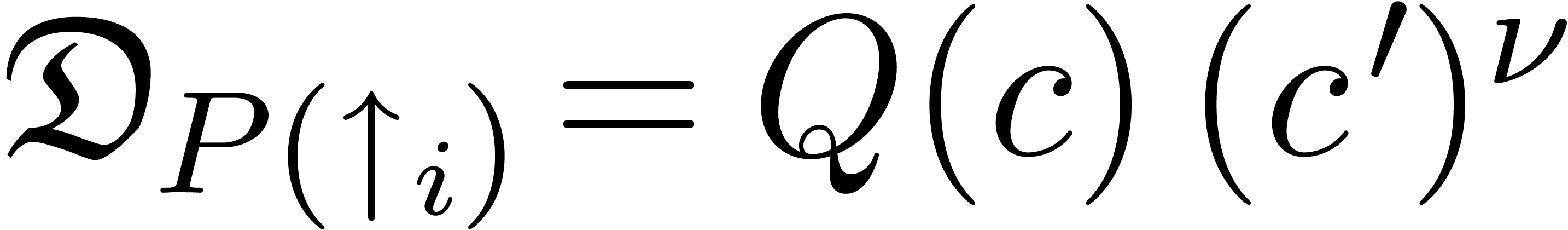 .
.
Example 6. For 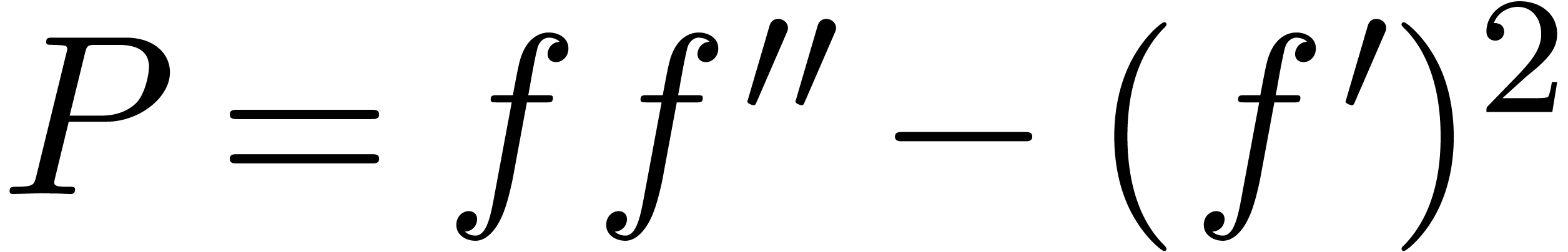 , we have
, we have
and
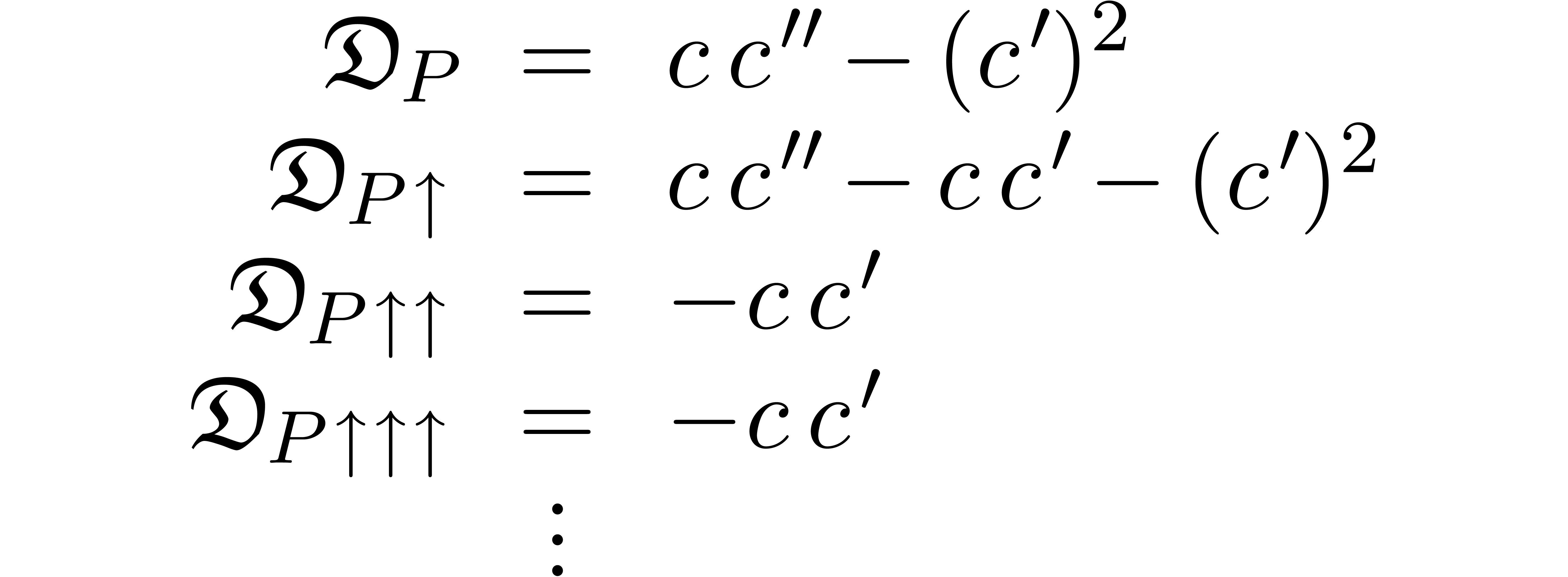
In particular, we see that 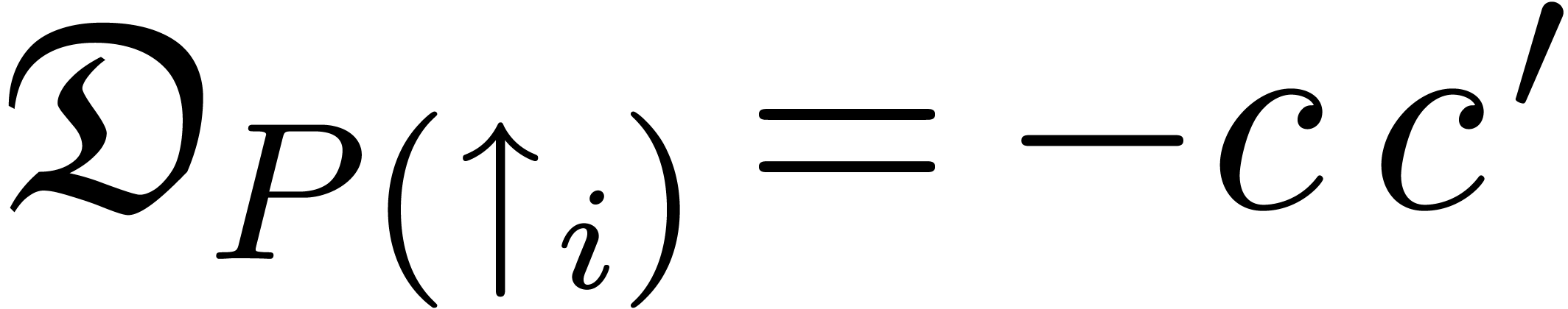 for all
for all  (whence
(whence 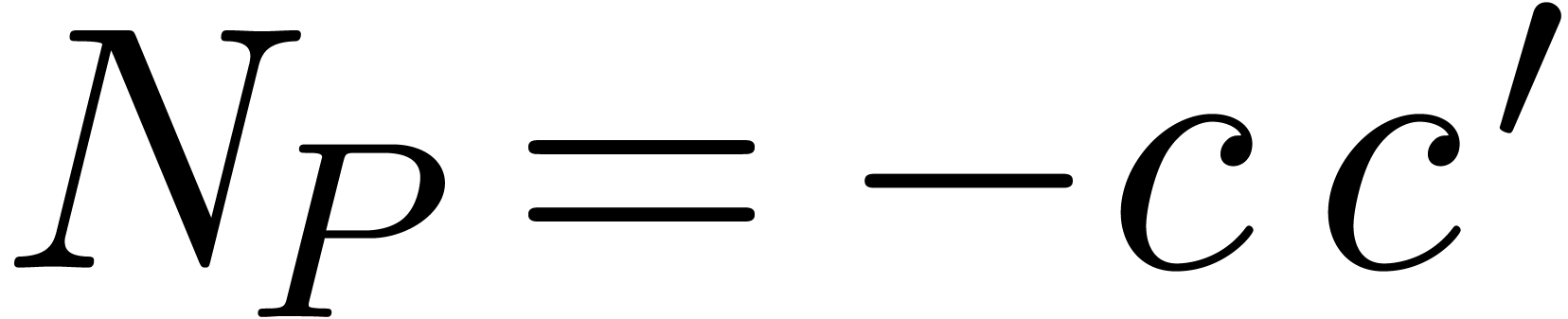 ; see
below).
; see
below).
The polynomial  in proposition 5 is
called the differential Newton polynomial associated to
in proposition 5 is
called the differential Newton polynomial associated to  , and we denote it by
, and we denote it by 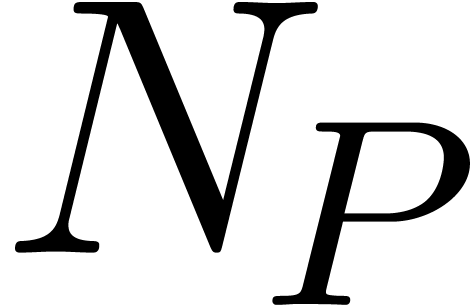 .
More generally, the differential Newton polynomial associated to a
transmonomial
.
More generally, the differential Newton polynomial associated to a
transmonomial 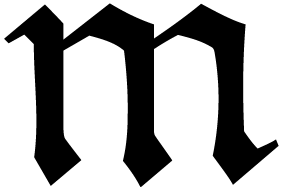 is
is 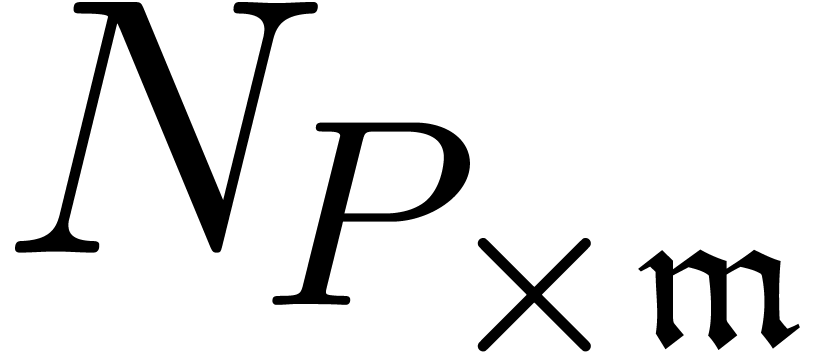 .
We say that
.
We say that  is a potential dominant
monomial for (21), if and only if
is a potential dominant
monomial for (21), if and only if  and
and 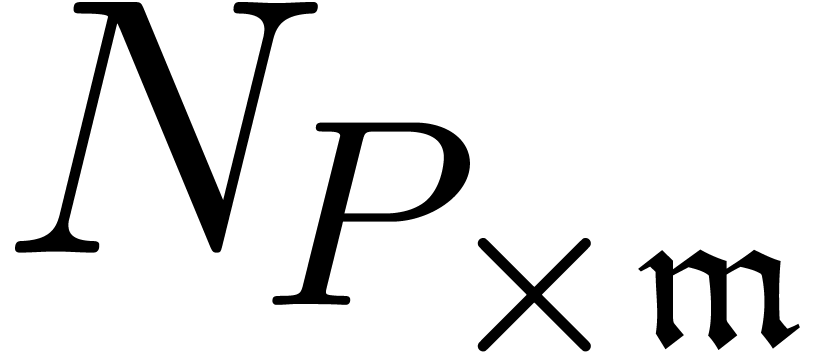 has a non trivial root
has a non trivial root  . Given such a root
. Given such a root  , we call
, we call  a potential
dominant term for (21). It should be noticed that
potential dominant monomials are not always dominant monomials of
solutions in the context of real transseries. Indeed, an
equation like
a potential
dominant term for (21). It should be noticed that
potential dominant monomials are not always dominant monomials of
solutions in the context of real transseries. Indeed, an
equation like
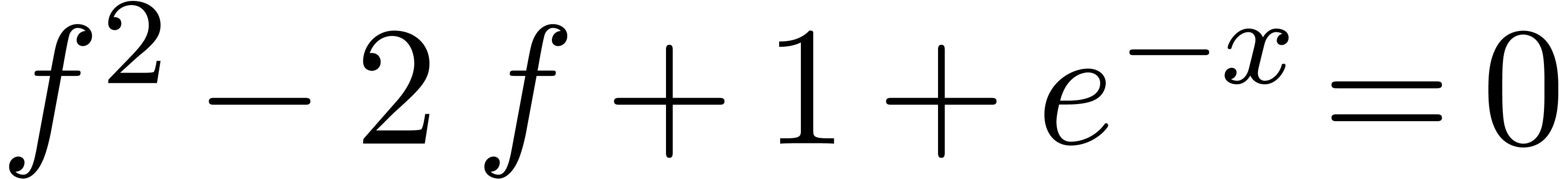
has no transseries solution, although it does admit 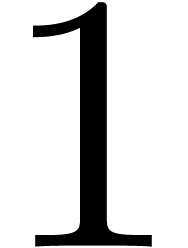 as a potential dominant monomial.
as a potential dominant monomial.
An important invariant of (21) is its Newton
degree, which is by definition the highest possible degree of the
Newton polynomial  associated to a transmonomial
associated to a transmonomial
 . In the algebraic setting,
the Newton degree gives a bound to the number of solutions to (21),
when counting with multiplicities (if the constant field is
algebraically closed, it actually gives the exact number of solutions).
In the differential setting, the Newton degree must be non-zero if we
want the equation to admit solutions.
. In the algebraic setting,
the Newton degree gives a bound to the number of solutions to (21),
when counting with multiplicities (if the constant field is
algebraically closed, it actually gives the exact number of solutions).
In the differential setting, the Newton degree must be non-zero if we
want the equation to admit solutions.
3.2.3Algebraic and mixed potential dominant
monomials
Now that we know how to define potential dominant monomials, the next
question is how to find them. In fact, there are three types of
potential dominant monomials  ,
depending on the form of
,
depending on the form of  . If
. If
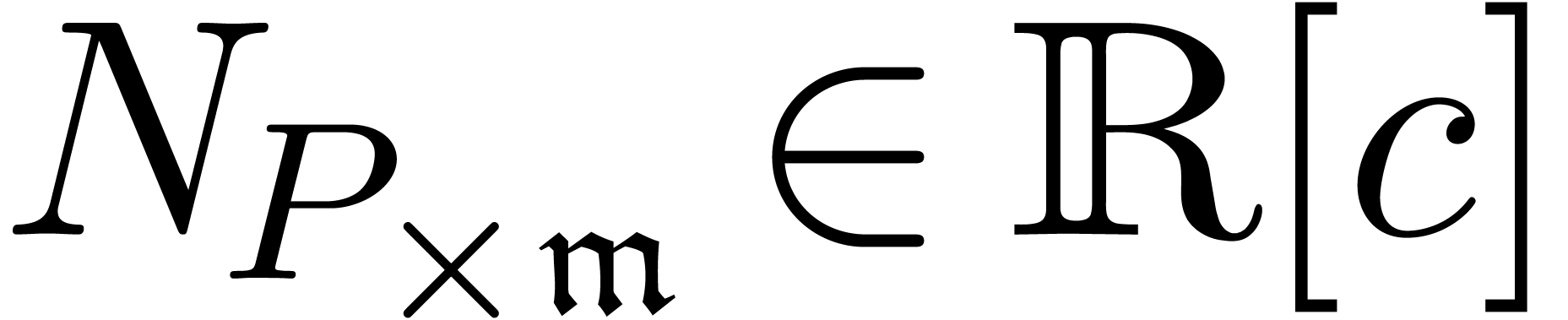 , then we say that
, then we say that  is algebraic. If
is algebraic. If 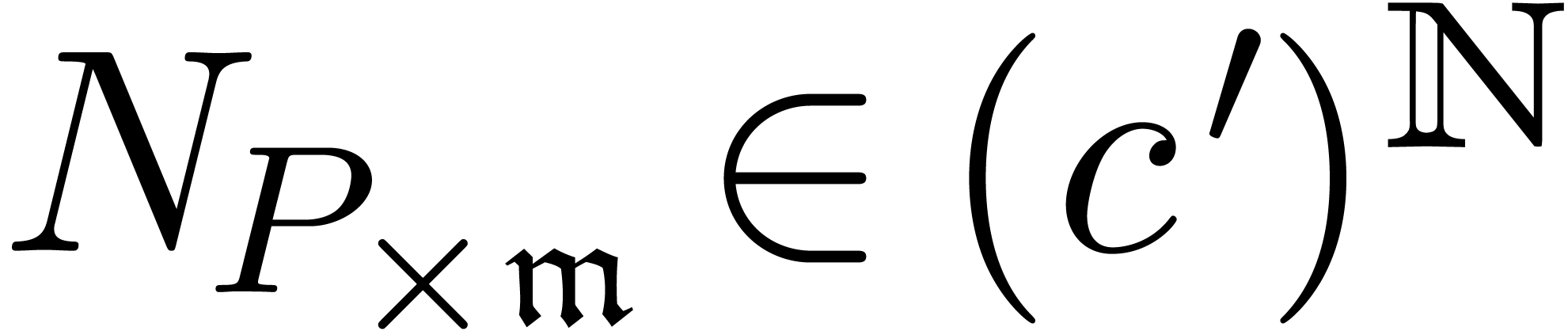 ,
then we say that
,
then we say that  is differential. In
the remaining case, when
is differential. In
the remaining case, when 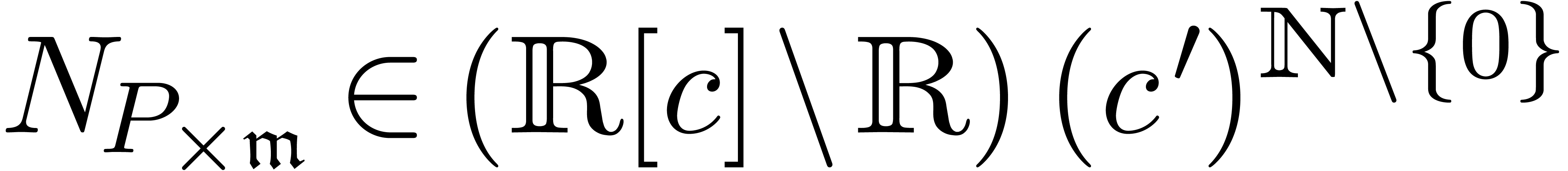 , we
say that
, we
say that  is mixed. The algebraic and
mixed potential dominant monomials correspond to the slopes of
“what would have been the differential Newton polygon”.
Differential and mixed potential dominant monomials correspond to the
introduction of integration constants in the general solution to (21).
is mixed. The algebraic and
mixed potential dominant monomials correspond to the slopes of
“what would have been the differential Newton polygon”.
Differential and mixed potential dominant monomials correspond to the
introduction of integration constants in the general solution to (21).
The algebraic and mixed potential dominant monomials can all be found by
“equalizing” the dominant monomials 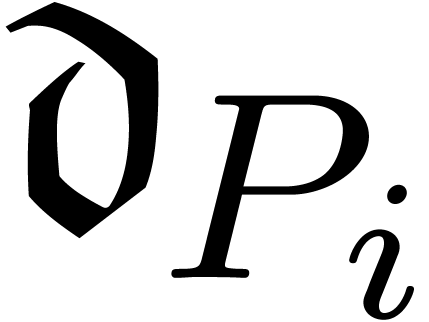 and
and 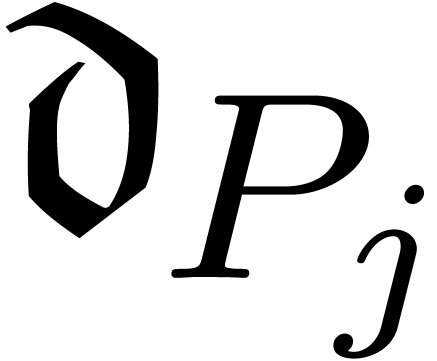 of two different homogeneous components of
of two different homogeneous components of
 via a multiplicative conjugation. This is always
possible [vdH97, vdH01]:
via a multiplicative conjugation. This is always
possible [vdH97, vdH01]:
Proposition 7. Let
 be such that
be such that 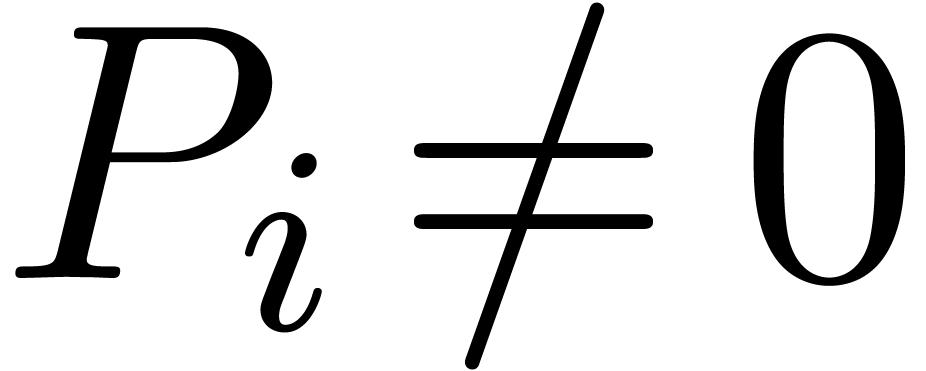 and
and 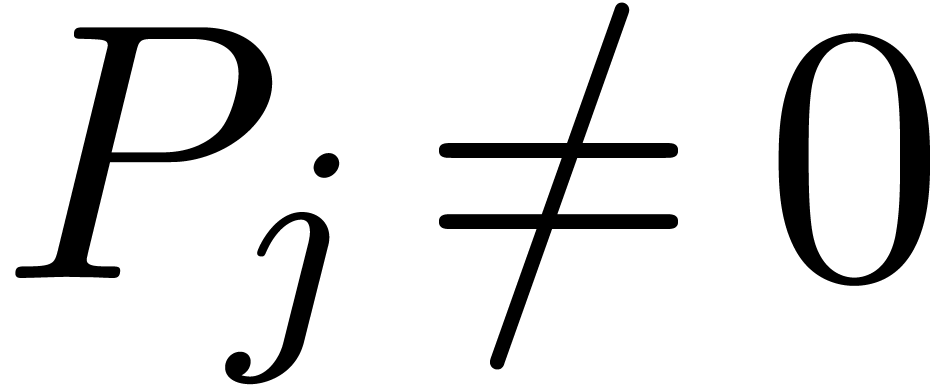 . Then there exists a unique
transmonomial
. Then there exists a unique
transmonomial 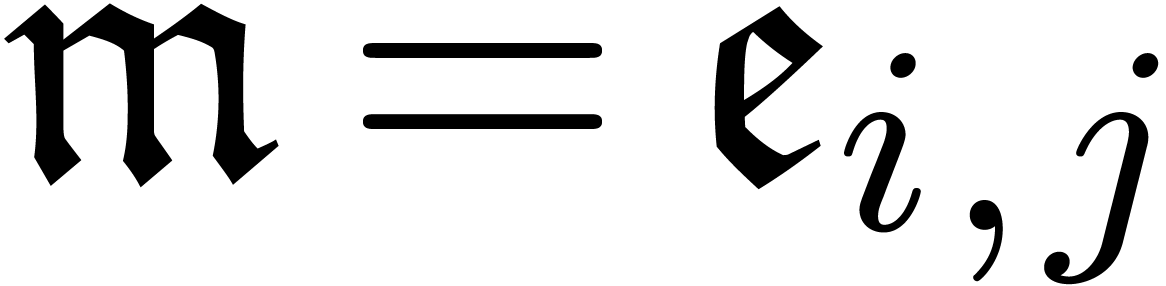 , such that
, such that
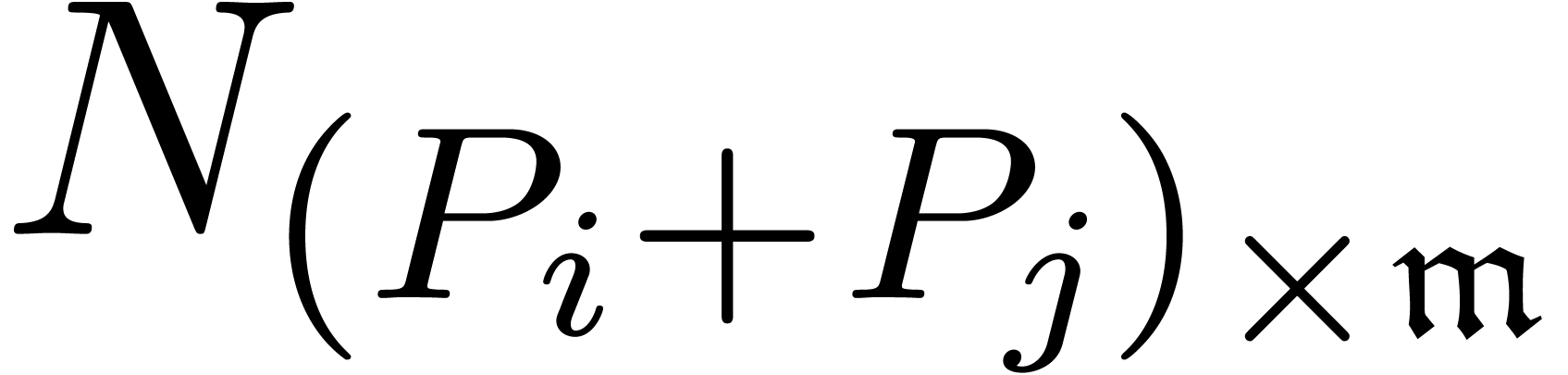 is not homogeneous.
is not homogeneous.
We call 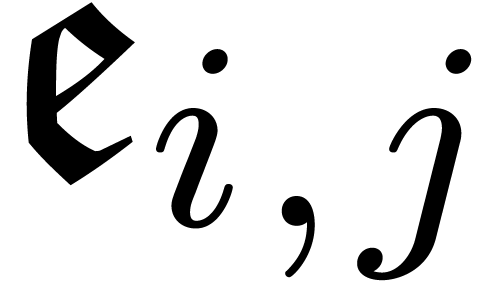 an equalizer for
an equalizer for  and there are clearly at most a finite number of them. All
algebraic and mixed potential dominant monomials for (21)
are necessarily equalizers, although not all equalizers are potential
dominant monomials. Under the assumption that we made sufficiently many
upward shiftings so that all
and there are clearly at most a finite number of them. All
algebraic and mixed potential dominant monomials for (21)
are necessarily equalizers, although not all equalizers are potential
dominant monomials. Under the assumption that we made sufficiently many
upward shiftings so that all 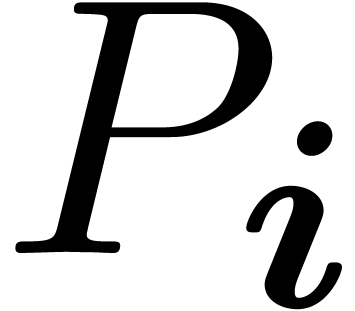 can be expanded
with respect to a transbasis
can be expanded
with respect to a transbasis  with
with  , the equalizers can be computed recursively,
using the fact that
, the equalizers can be computed recursively,
using the fact that  for all purely exponential
for all purely exponential
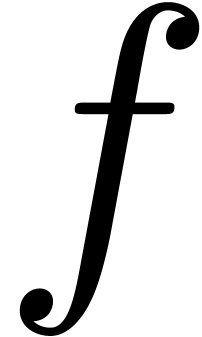 with
with  .
.
Example 8. Let us compute 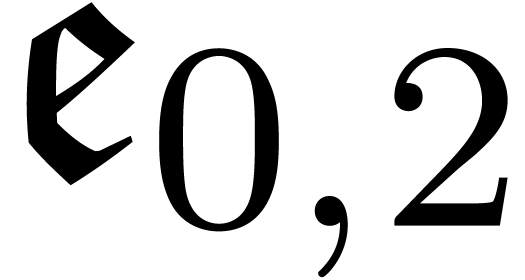 for
for
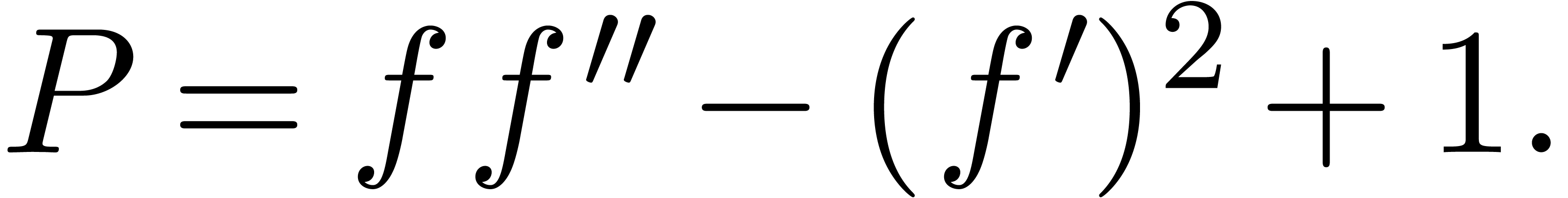
Since 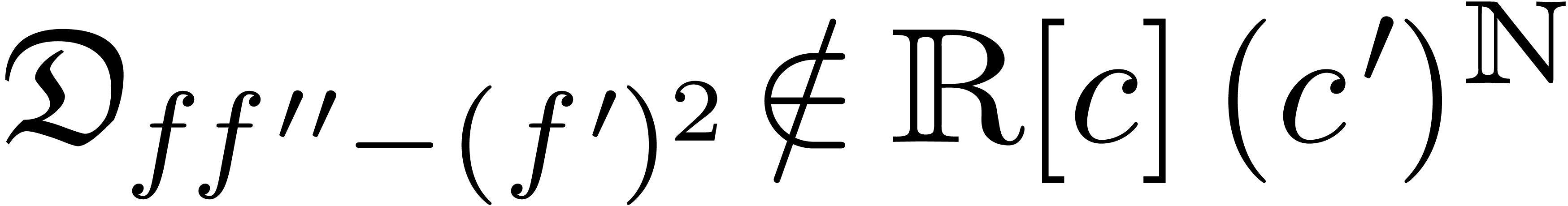 , we first shift
upwards:
, we first shift
upwards:
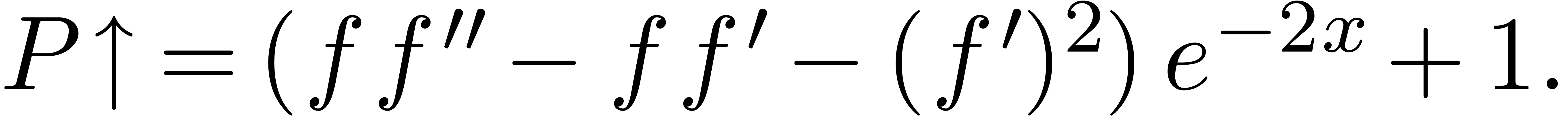
We now have to equalize  and
and  via a multiplicative conjugation with
via a multiplicative conjugation with  :
:
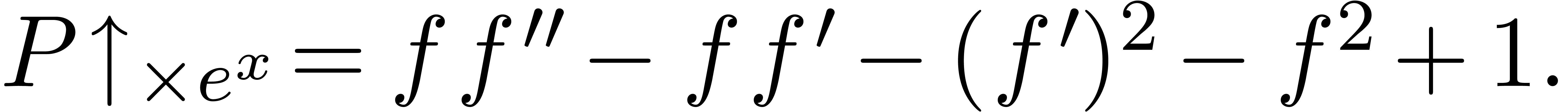
We still do not have  , so we
shift upwards once more:
, so we
shift upwards once more:
At this point, we both have 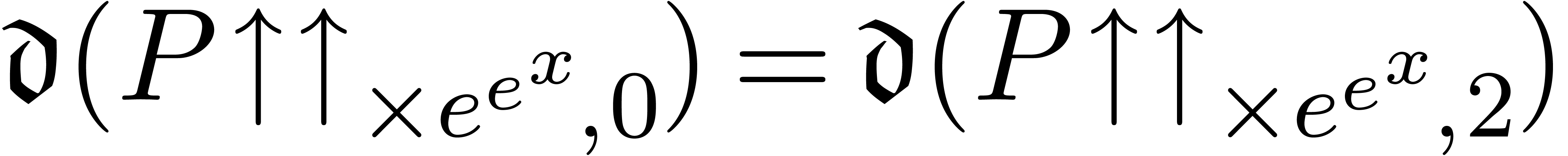 and
and 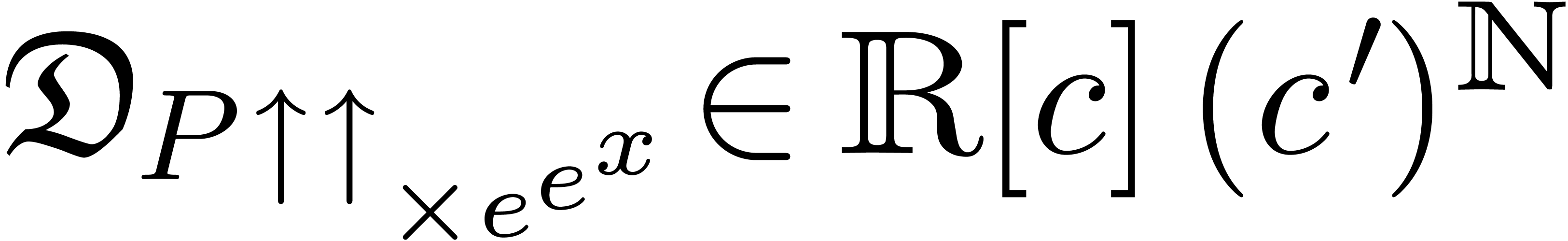 . In other words,
. In other words, 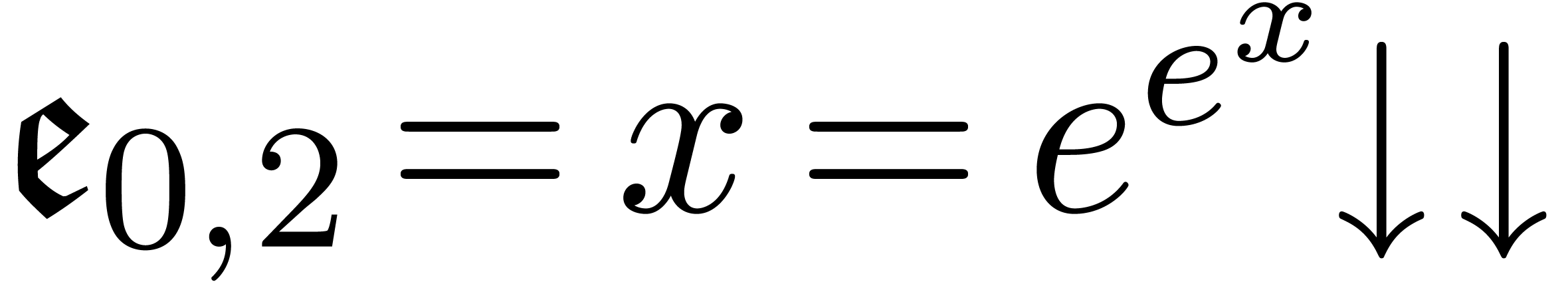 is
the desired equalizer.
is
the desired equalizer.
3.2.4Differential potential dominant
monomials
The remaining type of potential dominant monomials, viz.
the differential potential dominant monomials, corresponds to
cancellations inside homogeneous parts of  .
Now in order to solve a homogeneous equation
.
Now in order to solve a homogeneous equation  , one usually rewrites
, one usually rewrites 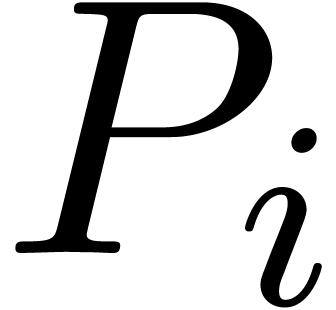 in
terms of the
in
terms of the 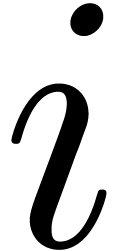 -th
differential Riccati polynomial
-th
differential Riccati polynomial 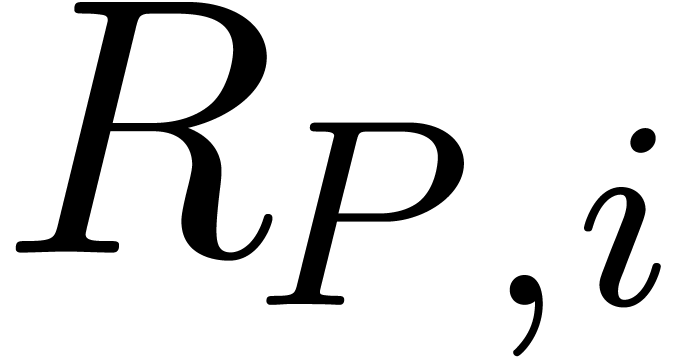 :
:
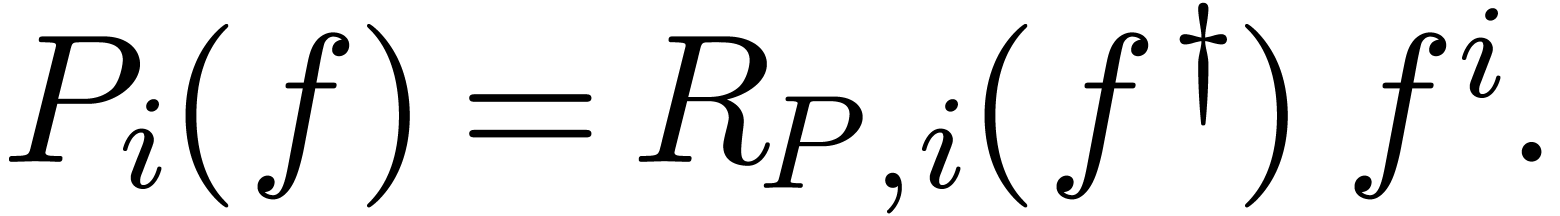
For instance,
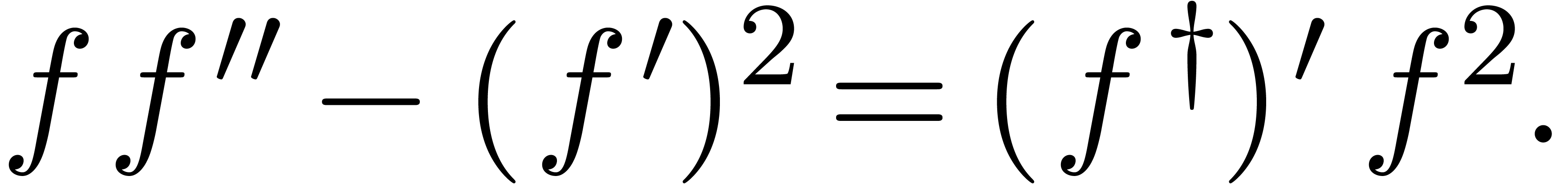
In order to find the differential potential dominant monomials that
correspond to cancellations inside 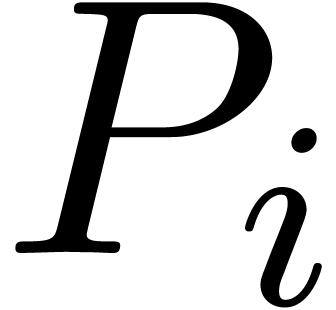 ,
we now need to “solve
,
we now need to “solve 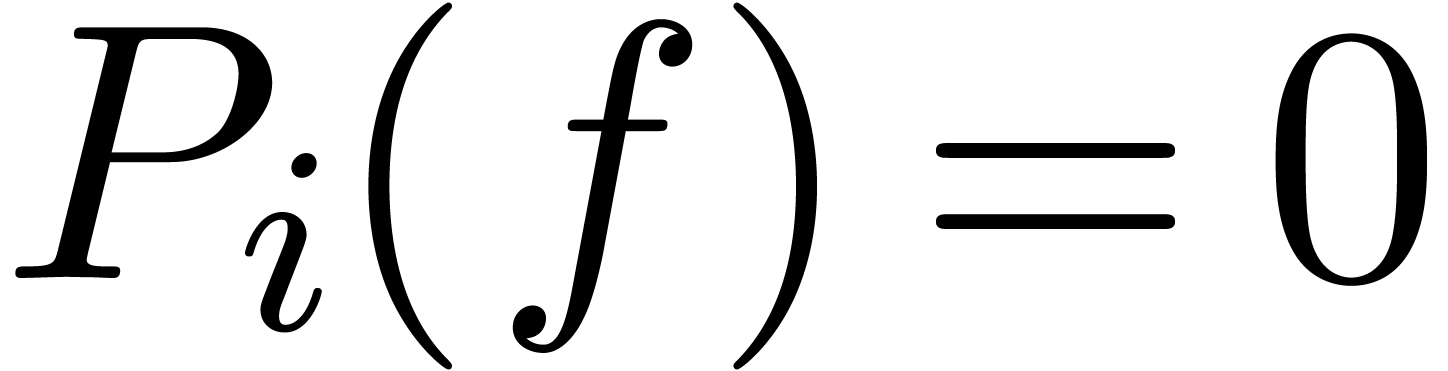 up to
up to 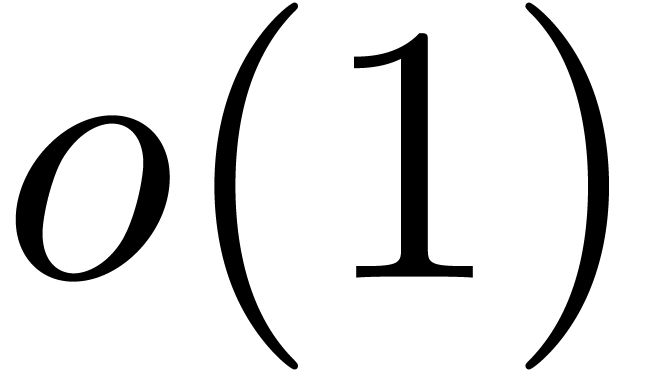 ”, which is equivalent to “solving
”, which is equivalent to “solving
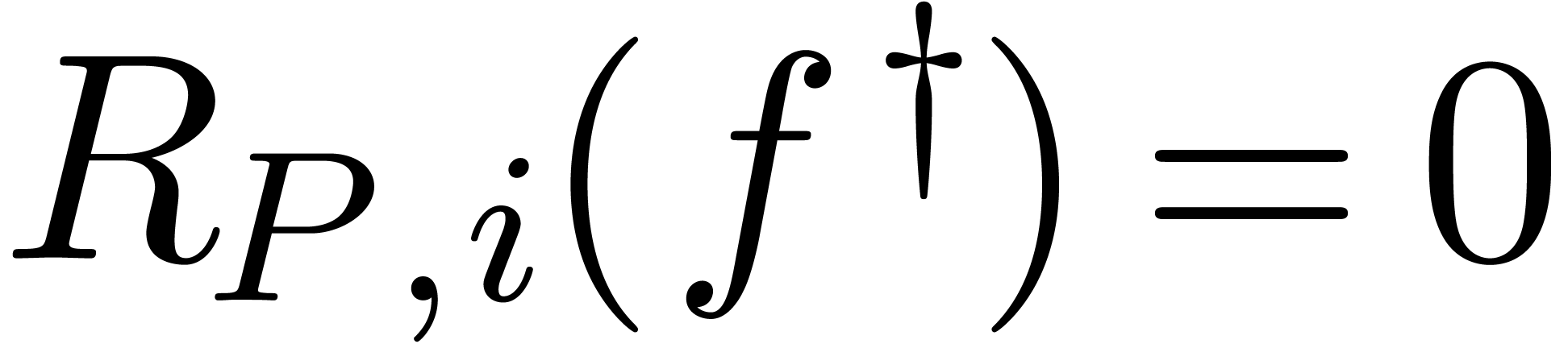 up to
up to  ”.
The border
”.
The border  is special in the sense that
is special in the sense that  whenever
whenever  and
and  whenever
whenever  . More precisely, we
have [vdH97, vdH01]:
. More precisely, we
have [vdH97, vdH01]:
Proposition 9. The
monomial  is a potential dominant monomial of
is a potential dominant monomial of
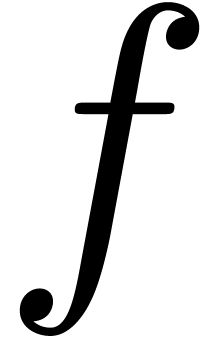 w.r.t.
w.r.t.
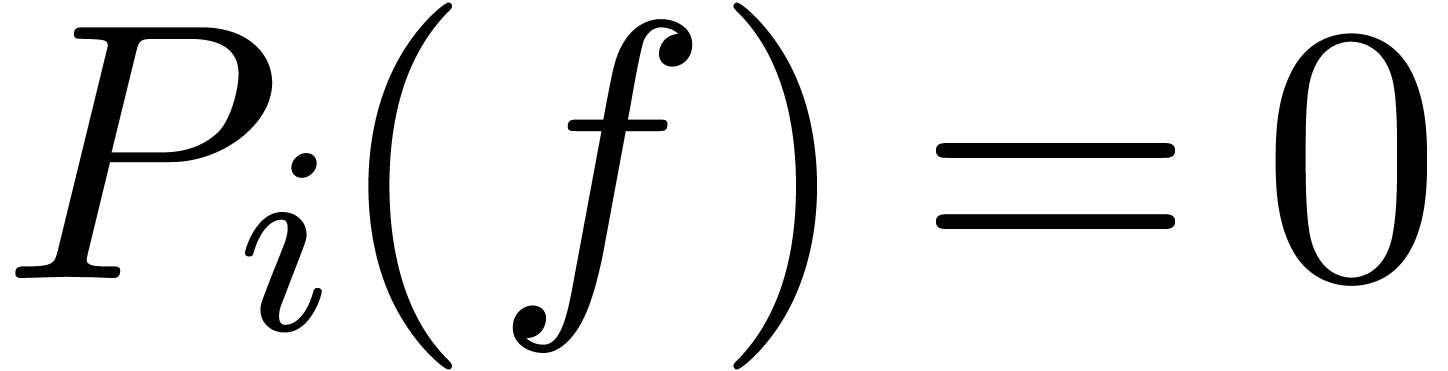 |
(10) |
if and only if the equation
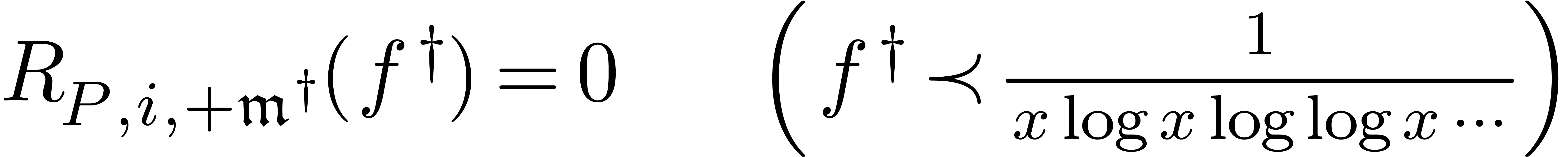 |
(11) |
has strictly positive Newton degree.
Remark 10. We committed a small
abuse of notation by treating 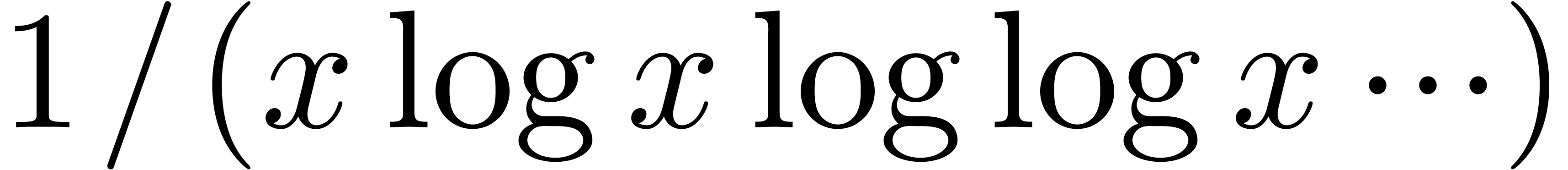 as a
transmonomial. In order to be painstakingly correct, we should replace
as a
transmonomial. In order to be painstakingly correct, we should replace
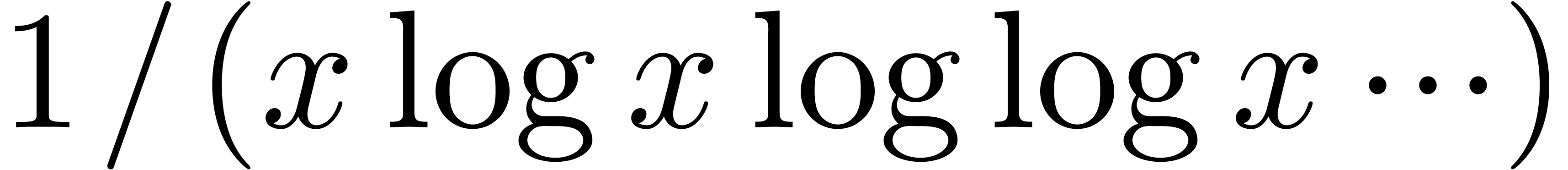 by
by 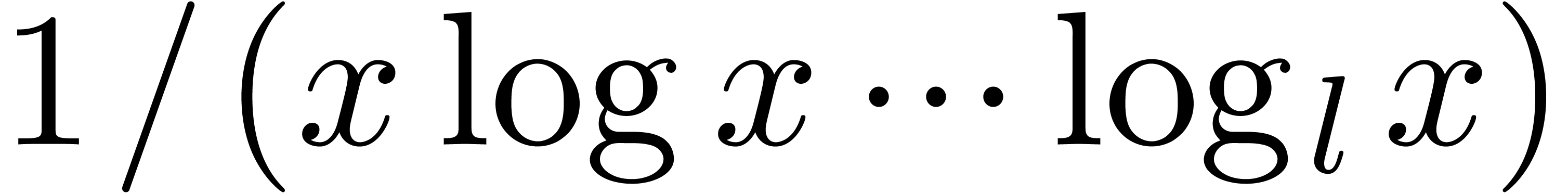 ,
where
,
where 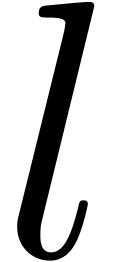 is a strict bound for the logarithmic
depths of
is a strict bound for the logarithmic
depths of  and all coefficients of
and all coefficients of  .
.
3.3Refinements
3.3.1Reducing the Newton degree through
refinements
Assuming that we have found a potential dominant term  for (21), we next have to show how to find the remaining
terms of a solution (or a “solution up to
for (21), we next have to show how to find the remaining
terms of a solution (or a “solution up to  ”). This is done through a finite
process of refinements. A refinement is a change of variables
with an asymptotic constraint
”). This is done through a finite
process of refinements. A refinement is a change of variables
with an asymptotic constraint
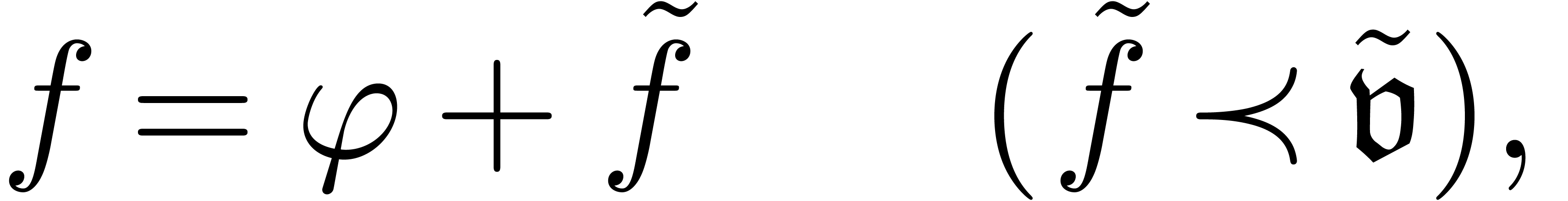 |
(12) |
where  is an arbitrary transseries (and not
necessarily a term in
is an arbitrary transseries (and not
necessarily a term in  ; we
will soon see the importance of this) and
; we
will soon see the importance of this) and  a
transmonomial. Such a refinement transforms (21) into
a
transmonomial. Such a refinement transforms (21) into
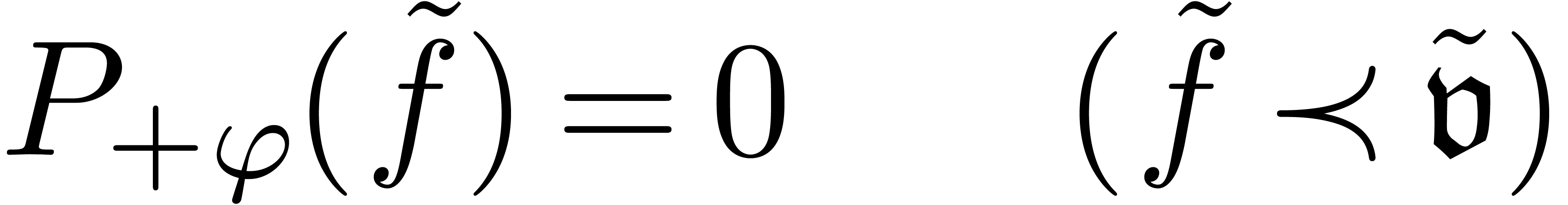 |
(13) |
and we call it admissible, if (13) has strictly
positive Newton degree. The important property of refinements is that
they bring us closer to solutions [vdH97, vdH01]:
Proposition 11. Let
 be the dominant term of
be the dominant term of  and assume that
and assume that 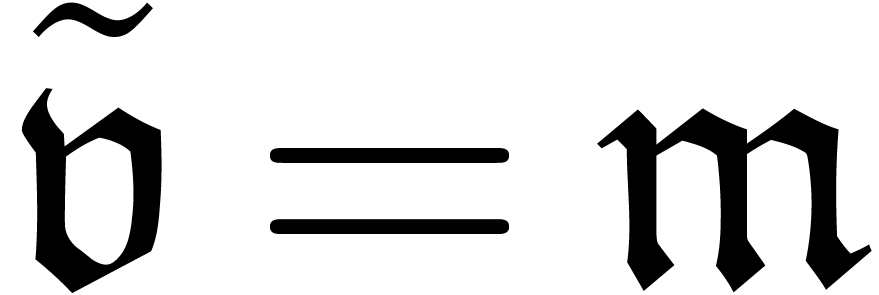 . Then the
Newton degree of (13) is equal to the
multiplicity
. Then the
Newton degree of (13) is equal to the
multiplicity  of
of  as a
root of
as a
root of  . In particular,
. In particular,  is bounded by the Newton degree of (21).
is bounded by the Newton degree of (21).
In the proposition, the multiplicity of  as a
root of
as a
root of  is understood to be the least
is understood to be the least  , such that there exists an
, such that there exists an  with
with  and
and 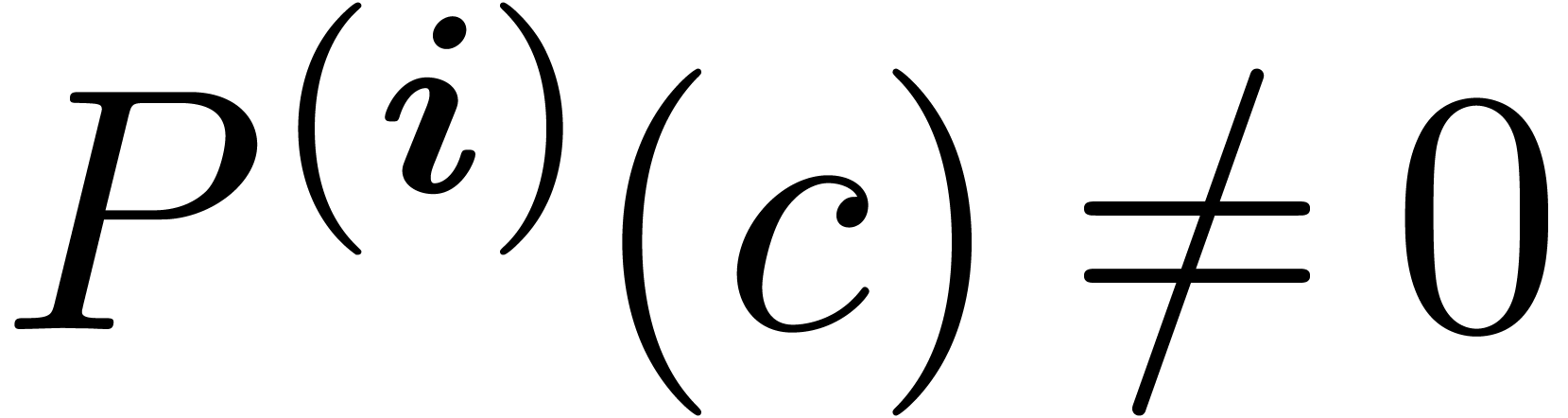 . Here
. Here 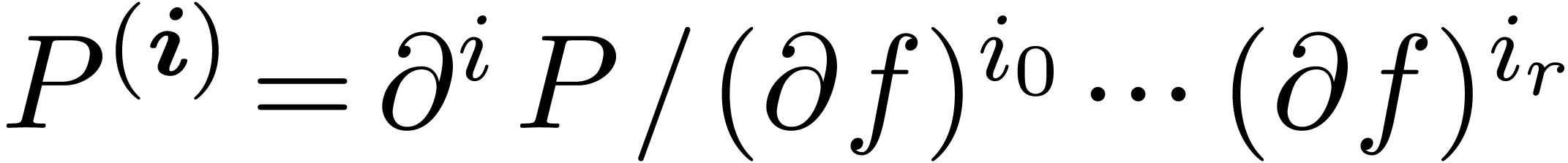 .
In favorable cases, the Newton degree strictly decreases until it
becomes equal to
.
In favorable cases, the Newton degree strictly decreases until it
becomes equal to 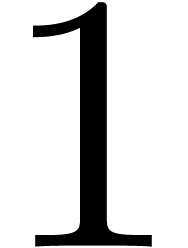 . At this
point, we call the new equation quasi-linear, and it has at
least one solution [vdH97, vdH01]:
. At this
point, we call the new equation quasi-linear, and it has at
least one solution [vdH97, vdH01]:
Proposition 12. Assume
that the equation (21) is
quasi-linear. Then it admits at least one transseries solution.
In fact, we proved that there exists a very special,
“distinguished” solution, which has some nice additional
properties. Given such a distinguished transseries solution  to a quasi-linear equation, all other solutions can be
seen found by solving the homogeneous quasi-linear equation
to a quasi-linear equation, all other solutions can be
seen found by solving the homogeneous quasi-linear equation 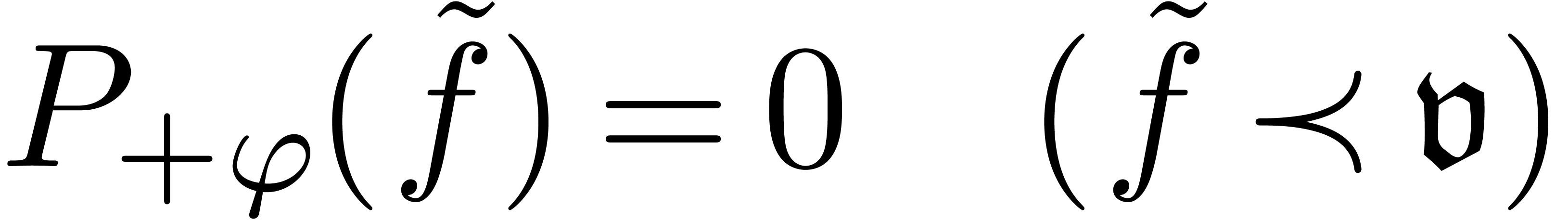 . A homogeneous quasi-linear equation should
really be seen as a twisted homogeneous linear differential equation.
For instance, we have [vdH97]:
. A homogeneous quasi-linear equation should
really be seen as a twisted homogeneous linear differential equation.
For instance, we have [vdH97]:
Proposition 13. Let  be solutions to a quasi-linear differential equation
(21) with
be solutions to a quasi-linear differential equation
(21) with 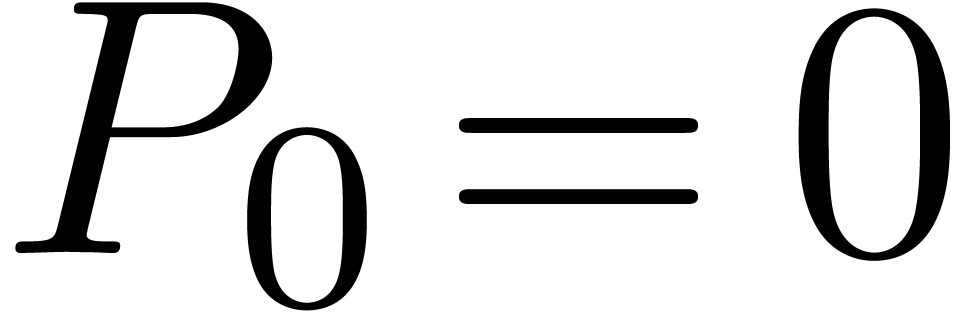 . Then
. Then 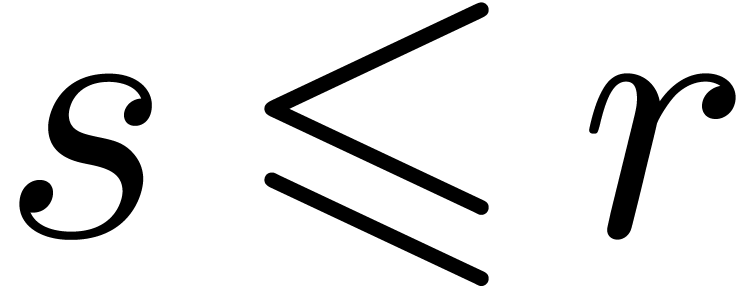 .
.
3.3.2Unravelling almost multiple
solutions
A more complicated situation is when the Newton degree does not descend
to one after a finite number of termwise refinements (12)
with 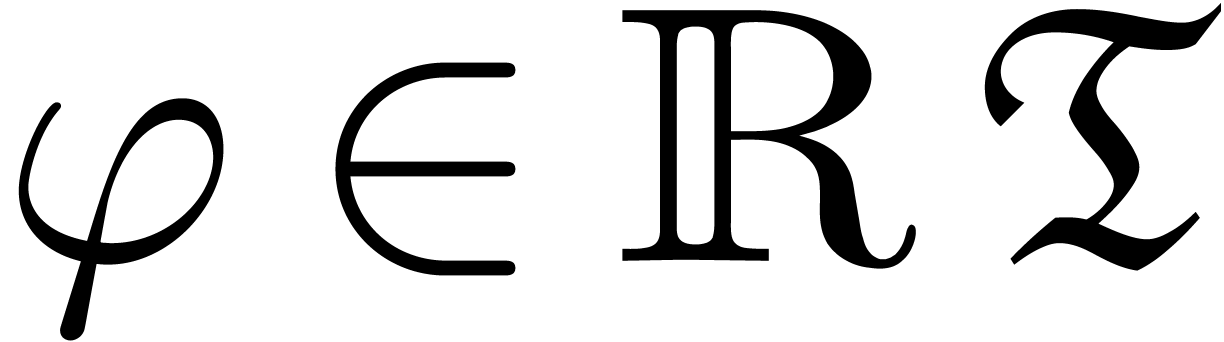 . This typically occurs
in presence of almost double solutions, like in the example
. This typically occurs
in presence of almost double solutions, like in the example
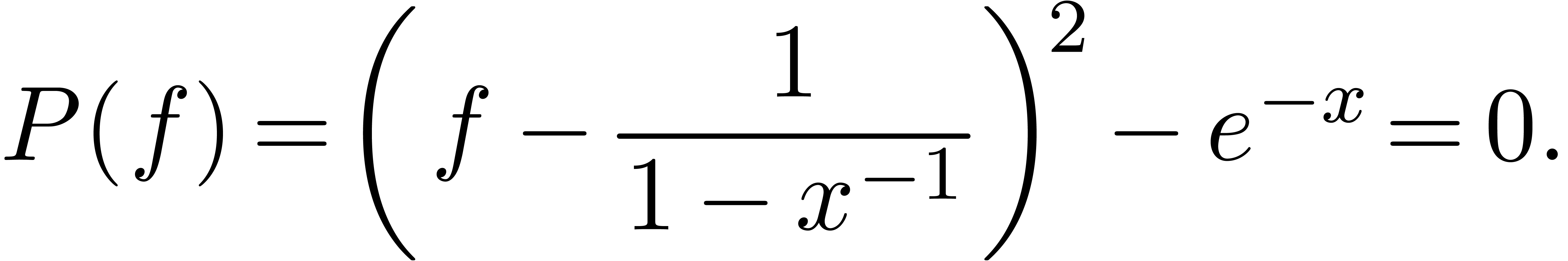 |
(14) |
When applying the naive, termwise refinement procedure, we would obtain
an infinite chain of refinements:
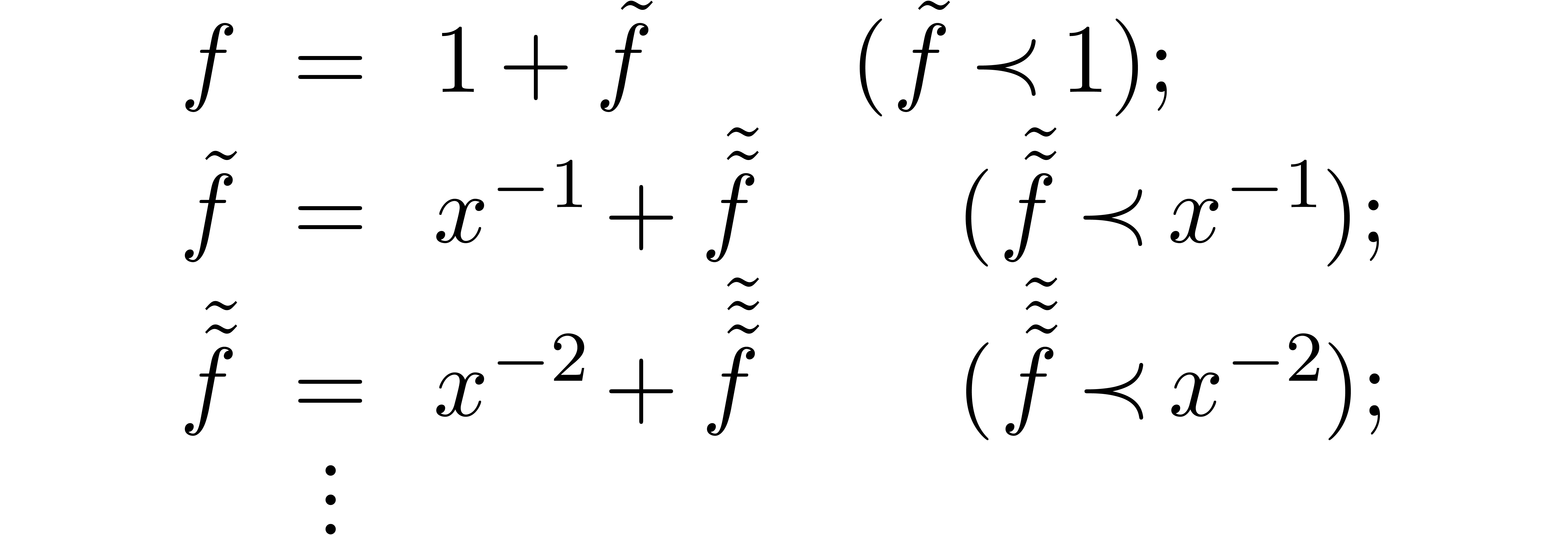
Now a classical way to find multiple solutions is to differentiate the
equation, which yields
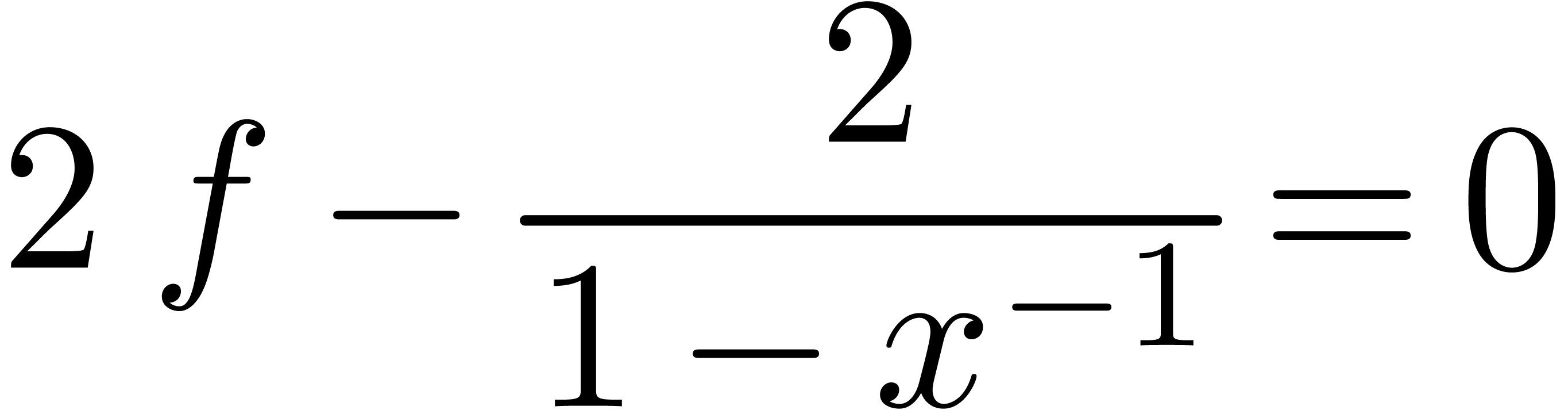 |
(15) |
in our example (14). In order to find the almost double
solutions, we now replace the above infinite chain of refinements by a
single one
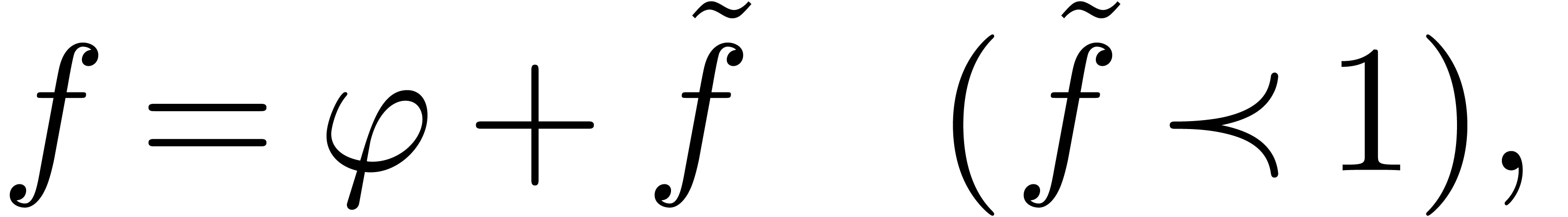
where  is a solution to the quasi-linear equation
(15).
is a solution to the quasi-linear equation
(15).
More generally, the objective is to force a strict decrease in the
Newton degree after a finite number of refinements, while solving
partial derivatives of the equation w.r.t.  . More precisely, denoting by
. More precisely, denoting by 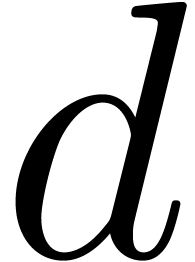 the Newton degree of (21), an unravelling is a
refinement
the Newton degree of (21), an unravelling is a
refinement
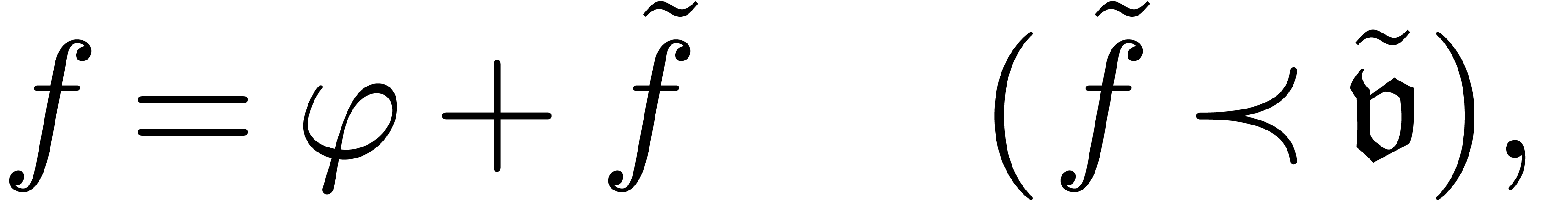
such that
-
U1
-
The Newton degree of 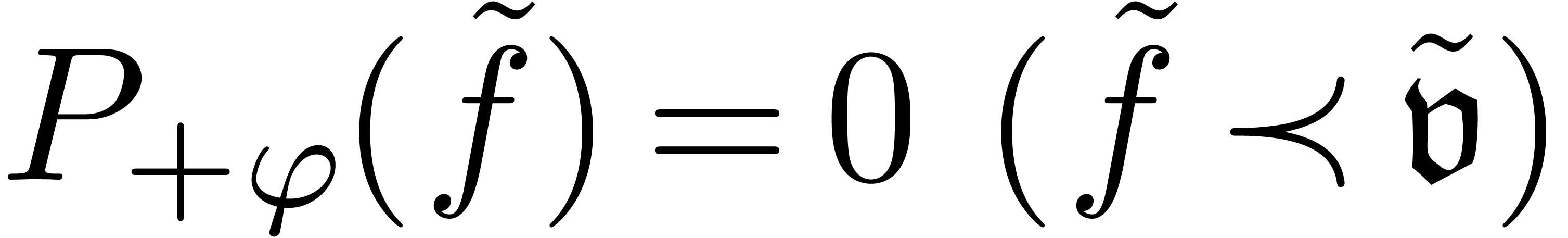 equals
equals  .
.
-
U2
-
For any  , the Newton
degree of
, the Newton
degree of 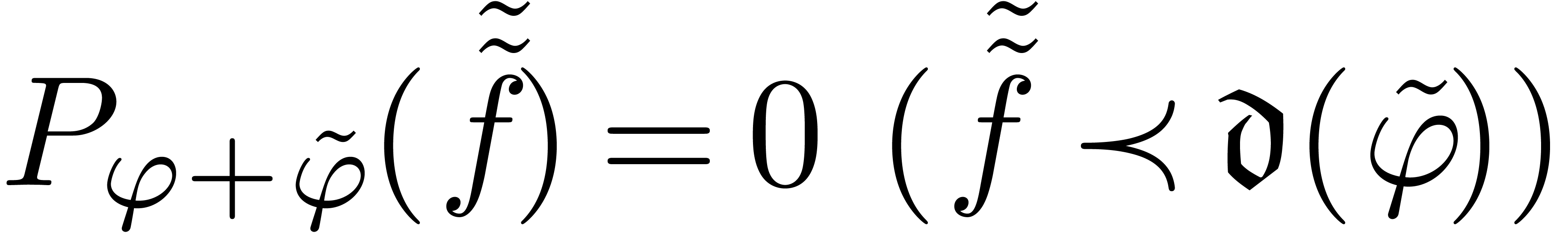 is
is  .
.
In [vdH01], we proved that we may achieve an unravelling
through a finite number of well-understood refinements:
Proposition 14. Let
 be a potential dominant term for (21) of multiplicity
be a potential dominant term for (21) of multiplicity 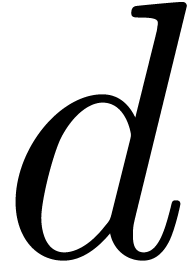 (i.e. (13) has Newton
degree
(i.e. (13) has Newton
degree 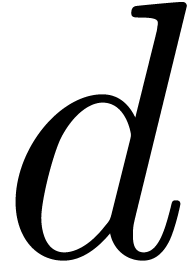 ). Then there exists a
finite sequence of refinements
). Then there exists a
finite sequence of refinements
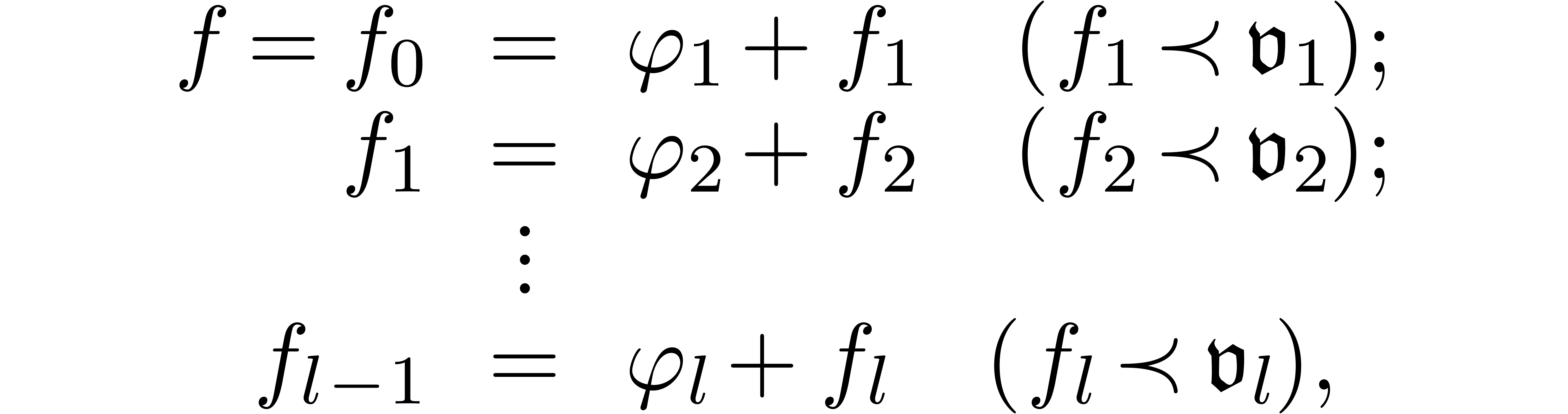
such that each 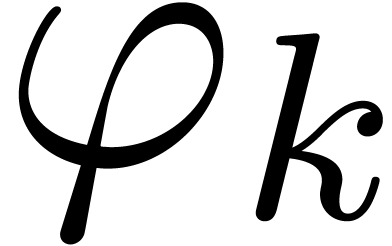 is either a term in
is either a term in  or a solution to an equation of the form
or a solution to an equation of the form
where 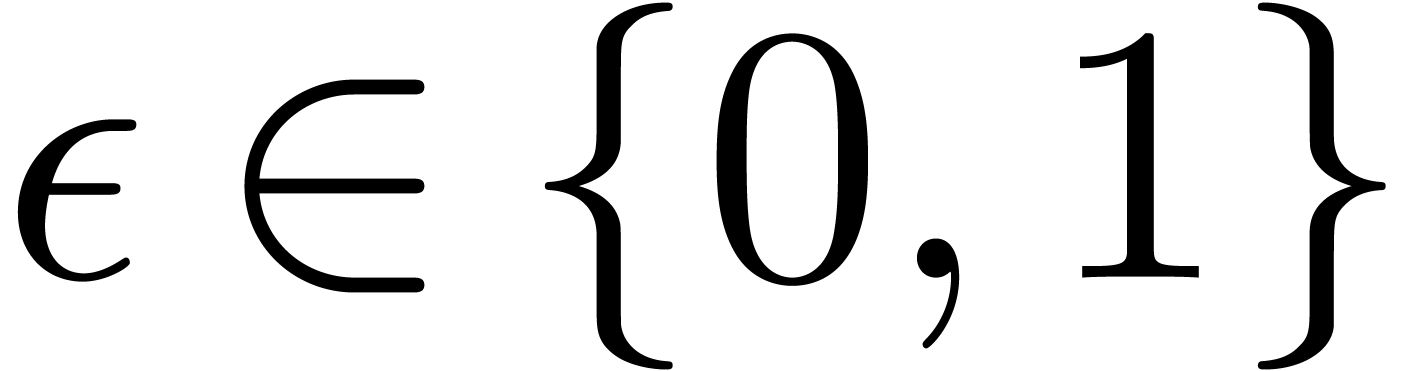 and
and  is a
transmonomial, and such that
is a
transmonomial, and such that
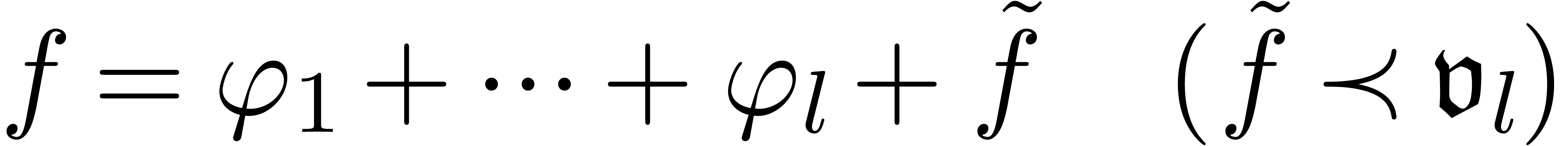
is an unravelling, and 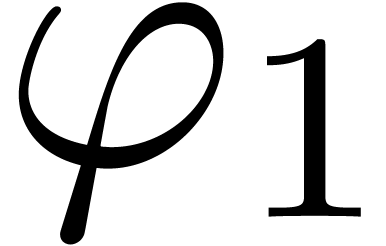 has
has  as its dominant term.
as its dominant term.
3.3.3The structure of solutions to algebraic
differential equations
Putting together all techniques described so far, we obtain a theoretic
way to compute all solutions to asymptotic algebraic differential
equations. In fact, we have shown [vdH97, vdH01]
how to compute the generic solution of such an equation (which involves
a finite number of integration constants) in a fully effective way. As a
side effect, we also obtained bounds for the logarithmic depths of
solutions to (21) and the fact that such solutions are
necessarily grid-based if the coefficients of (21) are.
Theorem 15. Consider an
asymptotic algebraic differential equation (21)
with transseries coefficients in  of logarithmic
depths
of logarithmic
depths 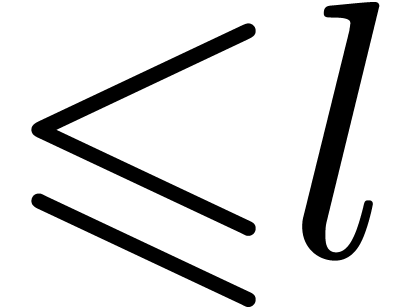 , and let
, and let 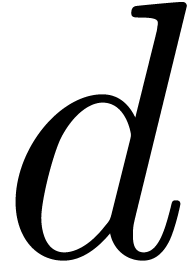 ,
,  and
and  denote its Newton degree, order resp. weight. Then any
transseries (whether grid-based or not) solution to (21) lies in
denote its Newton degree, order resp. weight. Then any
transseries (whether grid-based or not) solution to (21) lies in  and its
logarithmic depth is bounded by
and its
logarithmic depth is bounded by 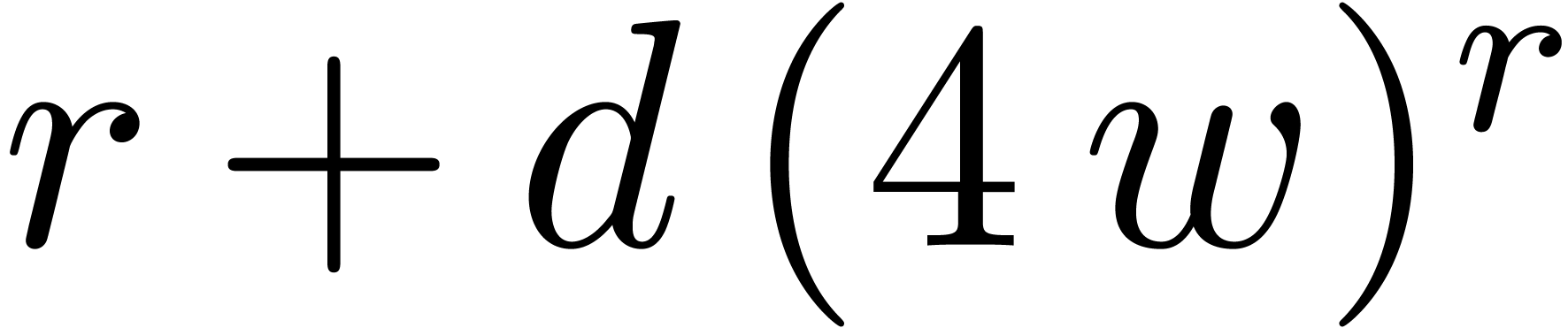 .
.
This theorem has a certain number of remarkable consequences. It proves
for instance that the Riemann  -function
does not satisfy any algebraic differential equation over
-function
does not satisfy any algebraic differential equation over  (nor over
(nor over  or
or  ). Similarly, solutions like
). Similarly, solutions like
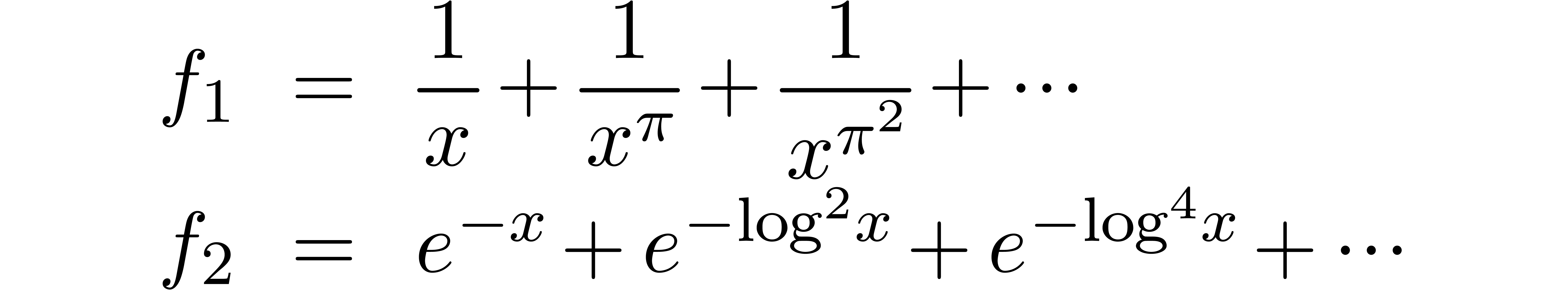
to functional equations
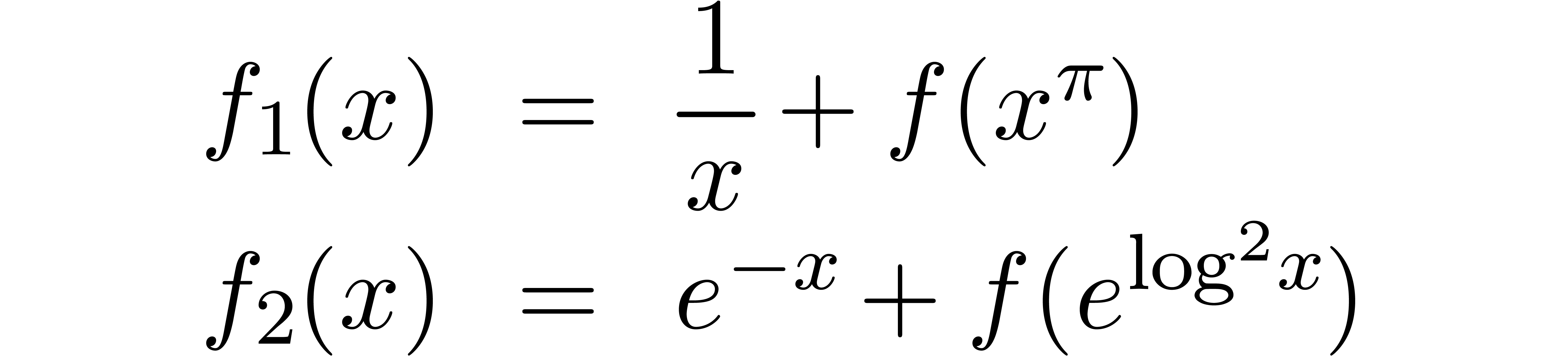
do not satisfy any algebraic differential equations over  .
.
4The intermediate value
theorem
4.1Introduction
Using the methods from the previous section to find all transseries
solutions to asymptotic algebraic differential equations, the
intermediate value theorem should now be a mere application. Indeed, we
will mimic the classical dichotomic method for finding roots of
continuous functions on an interval where a sign change occurs. In our
case, the “transline”  is very non
archimedian, so we will have to consider non-standard intervals. The
Newton polygon method will be used to restrict the interval where we
search more and more by maintaining the sign change property.
is very non
archimedian, so we will have to consider non-standard intervals. The
Newton polygon method will be used to restrict the interval where we
search more and more by maintaining the sign change property.
In section 2.6 of [vdH97], we have shown that
(non-standard) transseries intervals are always of the form 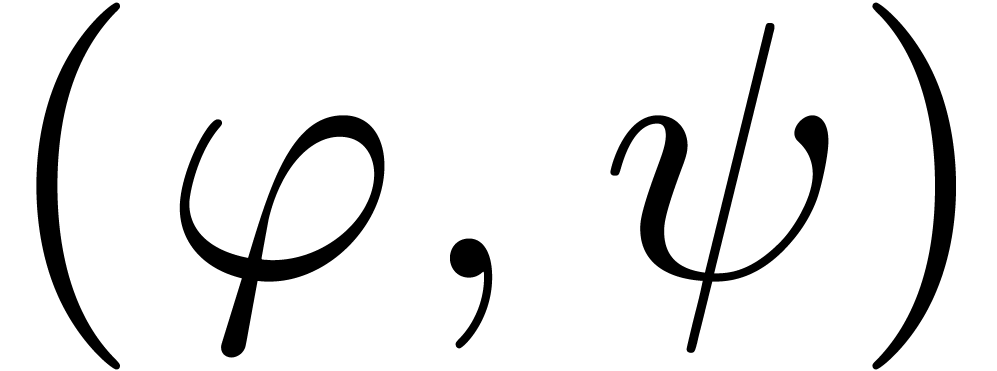 ,
, 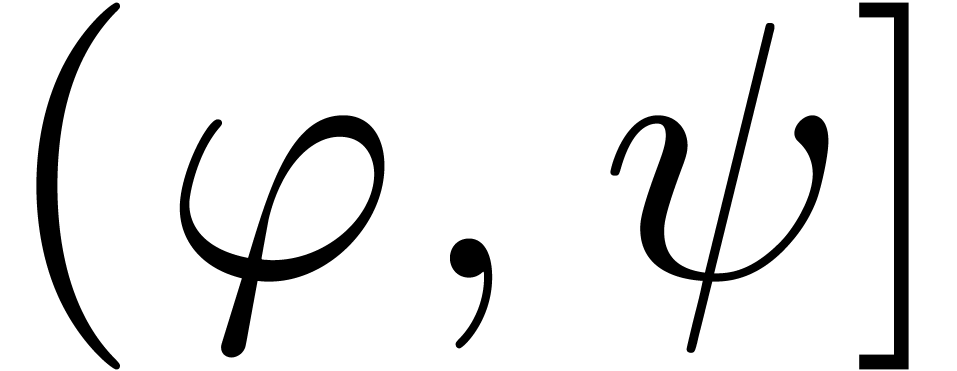 ,
,
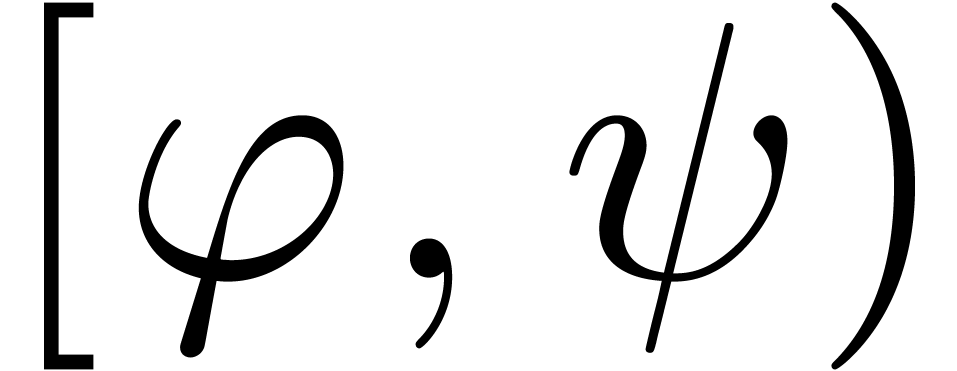 or
or 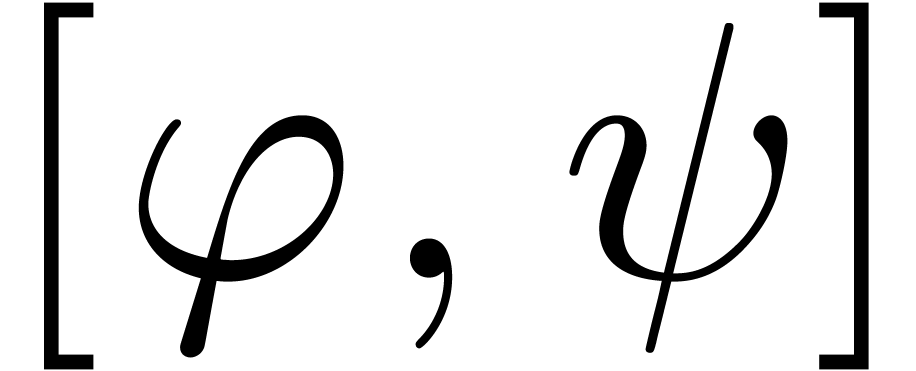 ,
where
,
where  and
and  are in the
“compactification” of
are in the
“compactification” of  .
In the sequel, we will only need to consider intervals
.
In the sequel, we will only need to consider intervals 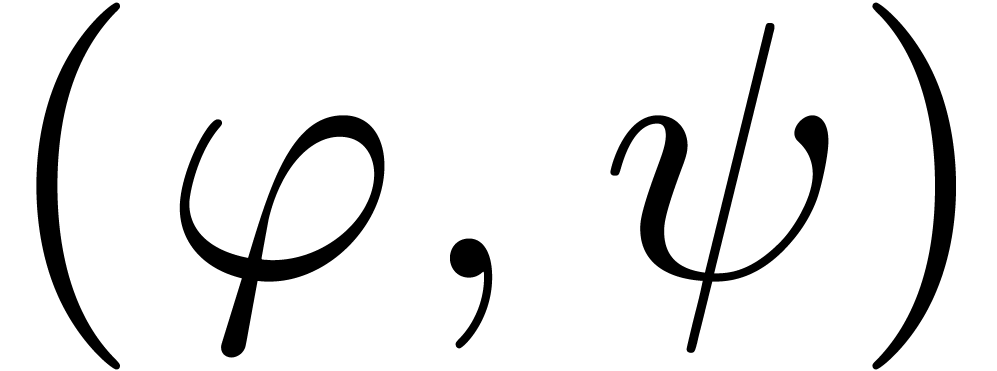 , with non-standard
, with non-standard  (and
(and  ) of the following
forms:
) of the following
forms:
Here  and
and  respectively
designate formal infinitely small and large constants
respectively
designate formal infinitely small and large constants 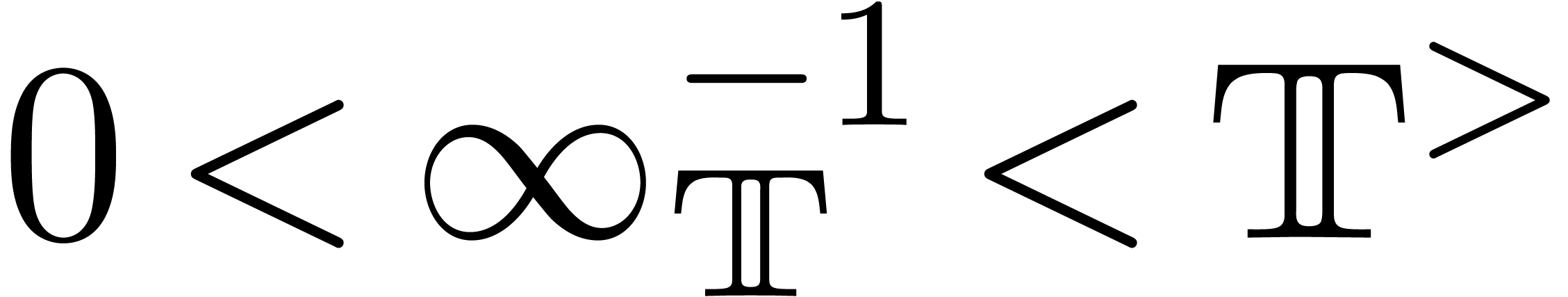 and
and 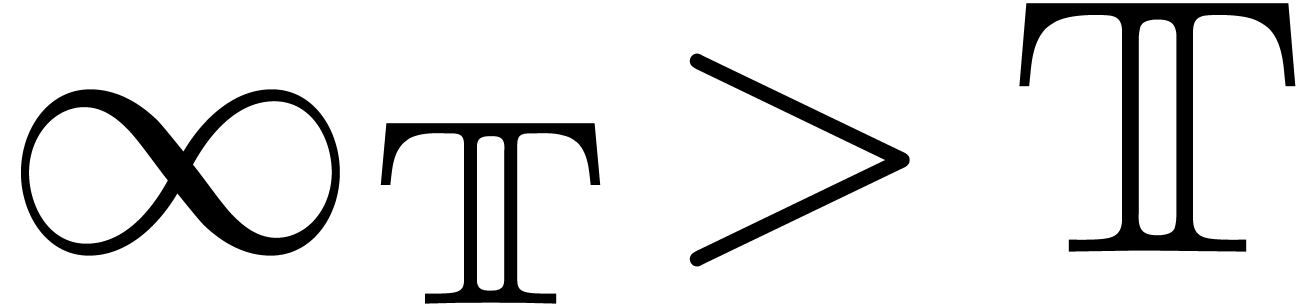 . Similarly,
. Similarly,  and
and  designate the infinitely small
and large constants
designate the infinitely small
and large constants  and
and  . We may interpret
. We may interpret  as a
cut of the transline
as a
cut of the transline  into two pieces
into two pieces
 . Notice that
. Notice that
For instance, 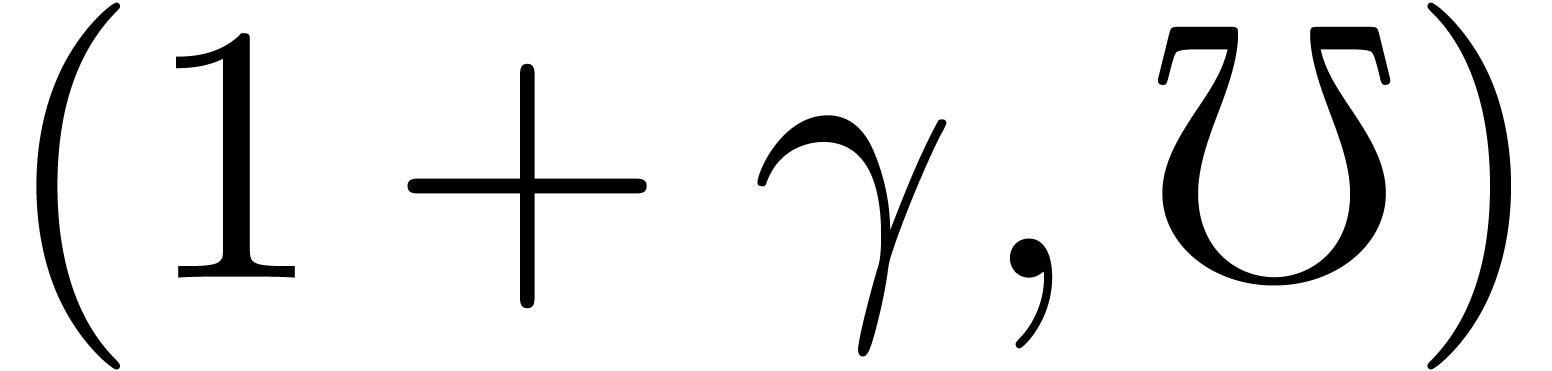 contains all transseries which are
larger than
contains all transseries which are
larger than 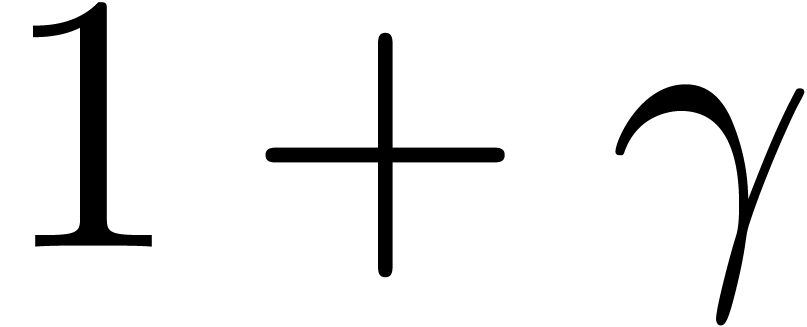 , like
, like 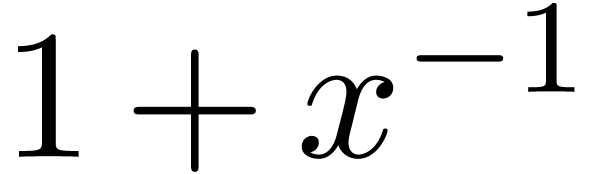 and
and 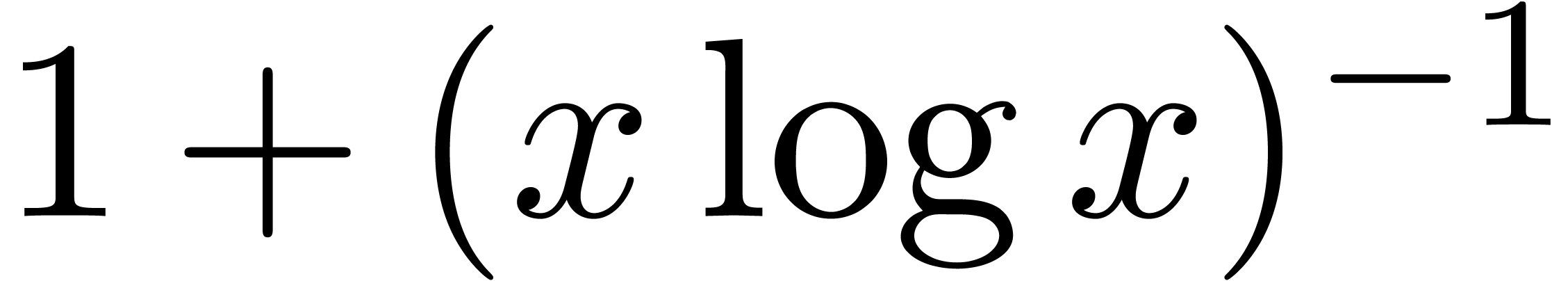 , but not
, but not
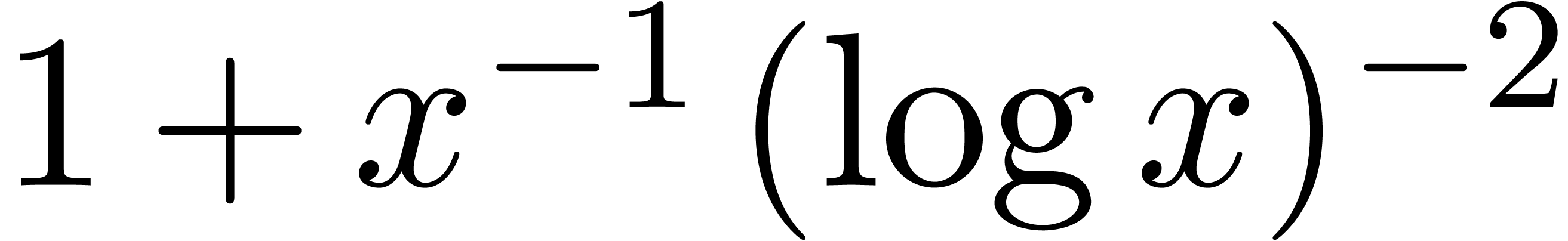 .
.
Now instead of directly proving the intermediate value theorem, it is
more convenient to prove a generalization of it for non-standard
intervals. Before doing this, we first have to extend the notion of the
sign of 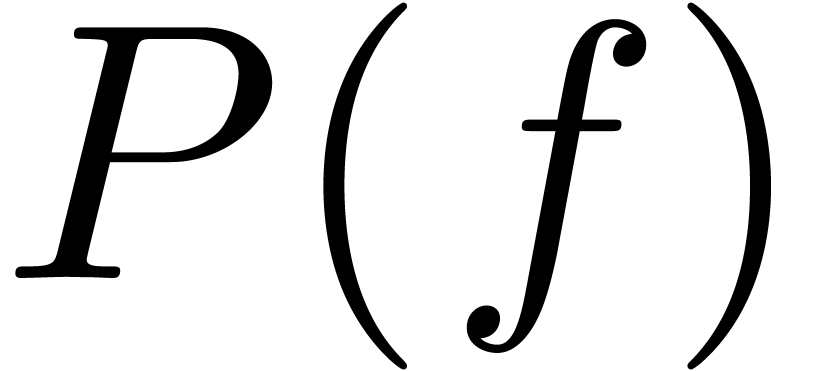 to the end-points of non-standard
intervals. After that, we will be able to state the more general
intermediate value theorem and prove it using the Newton polygon method.
to the end-points of non-standard
intervals. After that, we will be able to state the more general
intermediate value theorem and prove it using the Newton polygon method.
4.2Extending the sign function at non-standard
points
We will show that, given a cut  of one of the
above types, the function
of one of the
above types, the function 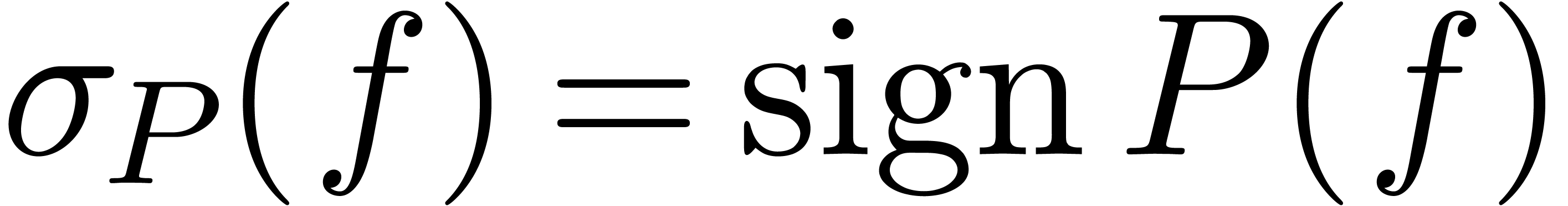 may be extended by
continuity into
may be extended by
continuity into  from at least one direction:
from at least one direction:
(In the cases  ,
,  and so on, one has to interchange left and right
continuity in the above list.) Modulo additive and multiplicative
conjugations, it suffices to deal with the cases when
and so on, one has to interchange left and right
continuity in the above list.) Modulo additive and multiplicative
conjugations, it suffices to deal with the cases when  and
and 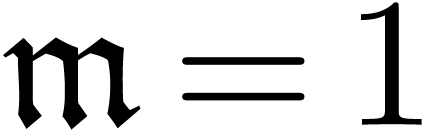 . We may also assume
without loss of generality that we have made sufficiently many upward
shiftings, so that the coefficients of
. We may also assume
without loss of generality that we have made sufficiently many upward
shiftings, so that the coefficients of  are
purely exponential. The next two lemmas deal with the first two cases.
are
purely exponential. The next two lemmas deal with the first two cases.
Lemma 16. Let  be a differential polynomial with coefficients in
be a differential polynomial with coefficients in
 . Then
. Then 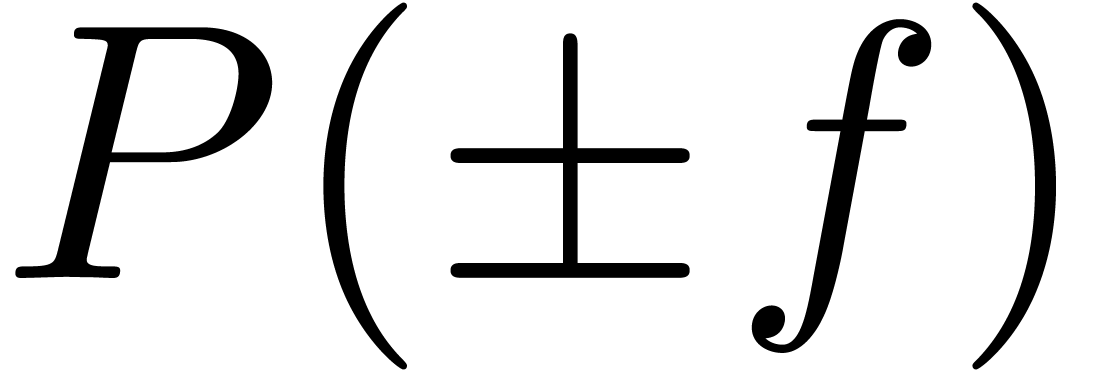 has constant sign
has constant sign  for all sufficiently large
for all sufficiently large
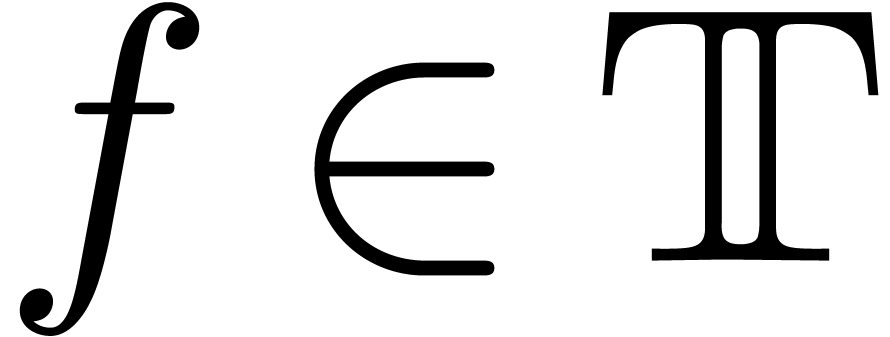 .
.
Proof. This follows from (6).
Lemma 17. Let  be a differential polynomial with coefficients in
be a differential polynomial with coefficients in
 . Then
. Then  has constant sign
has constant sign  for all sufficiently small
for all sufficiently small
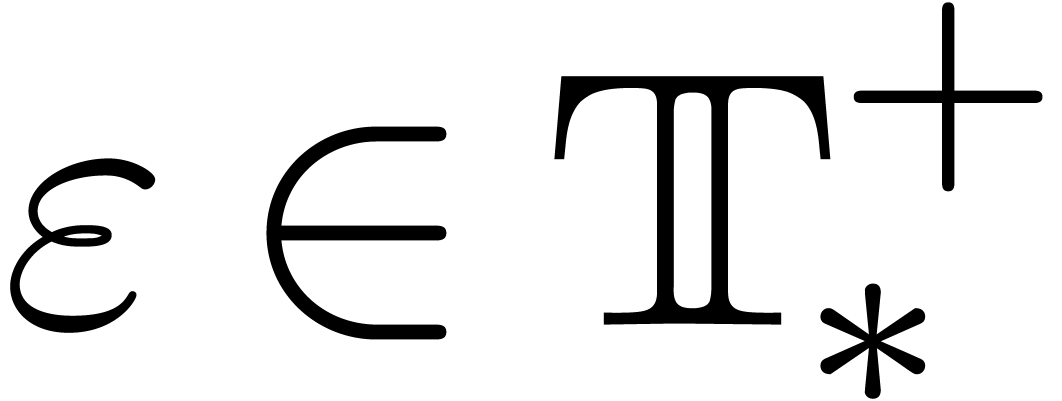 .
.
Proof. This is proved in a similar way as lemma 16.
In order to deal with the remaining three cases, we may assume without
loss of generality that
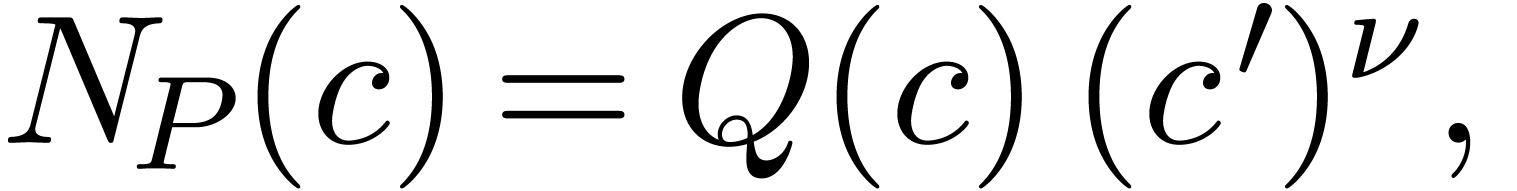 |
(16) |
with 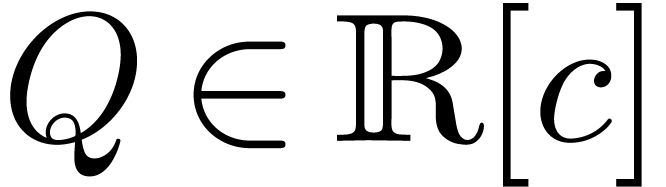 and
and 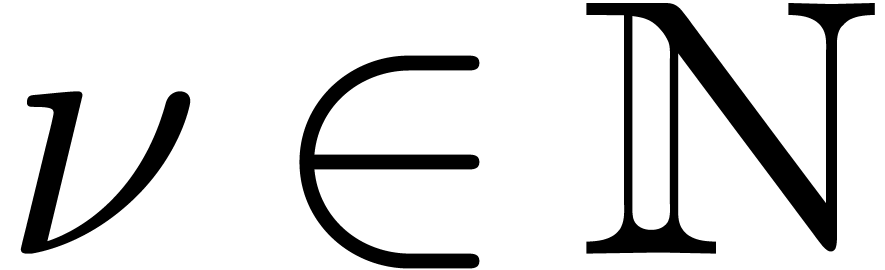 (by theorem 5 and modulo at most
(by theorem 5 and modulo at most  upward
shiftings). We will denote the multiplicity of
upward
shiftings). We will denote the multiplicity of  as a root of
as a root of  by
by  .
.
Lemma 18. For all
 with
with  ,
the signs of
,
the signs of 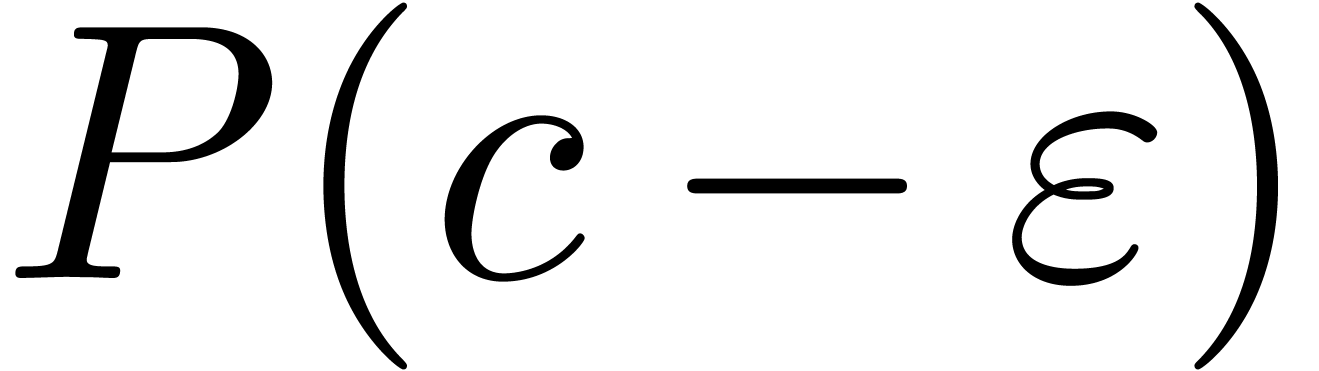 and
and 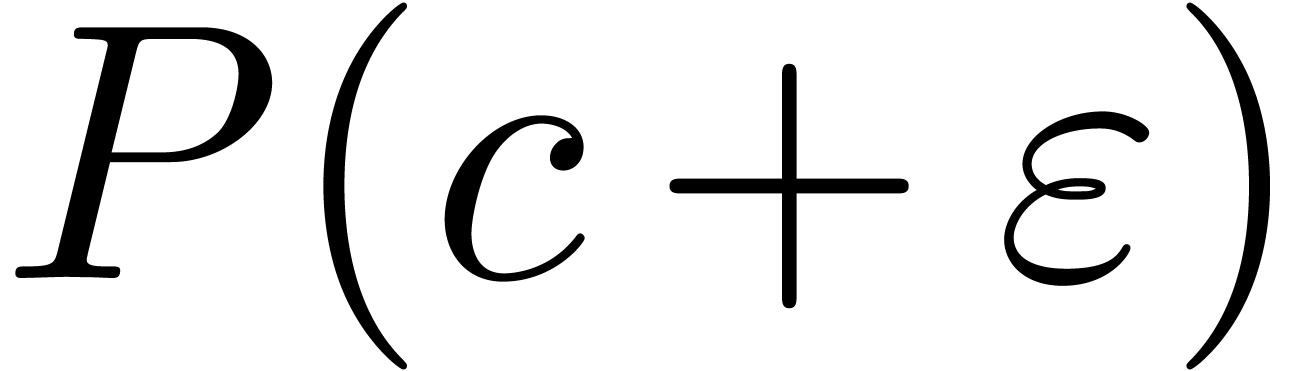 are
independent of
are
independent of  and given by
and given by
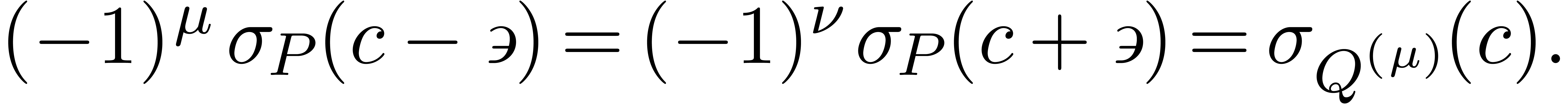 |
(17) |
Proof. This follows from (16), (17)
and the fact that
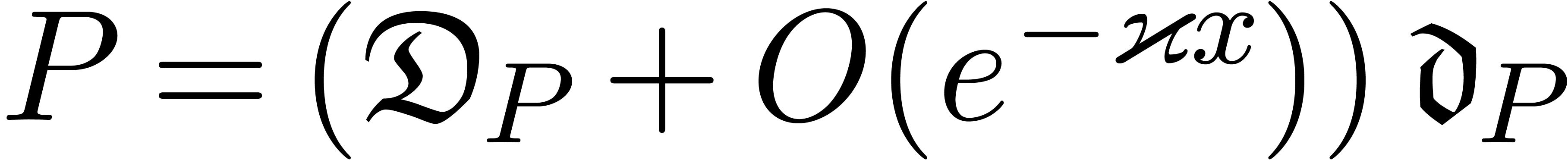
for some 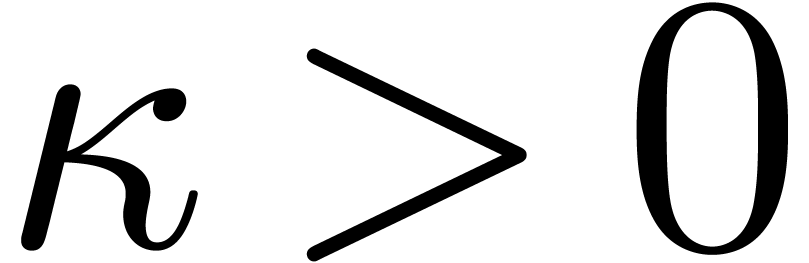 , because the
coefficients of
, because the
coefficients of  are pure exponential [vdH01].
are pure exponential [vdH01].
Corollary 19. If  is homogeneous of degree
is homogeneous of degree  ,
then
,
then
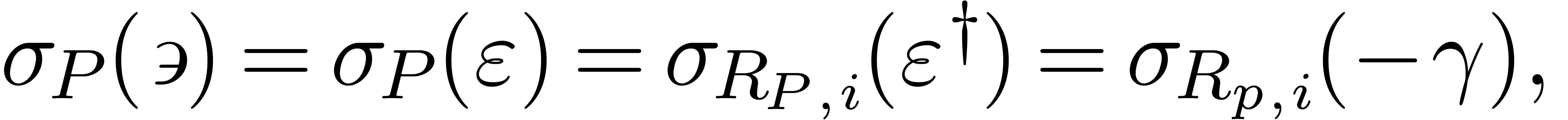 |
(18) |
for all  with
with  .
.
Corollary 20. Let
 be constants such that
be constants such that 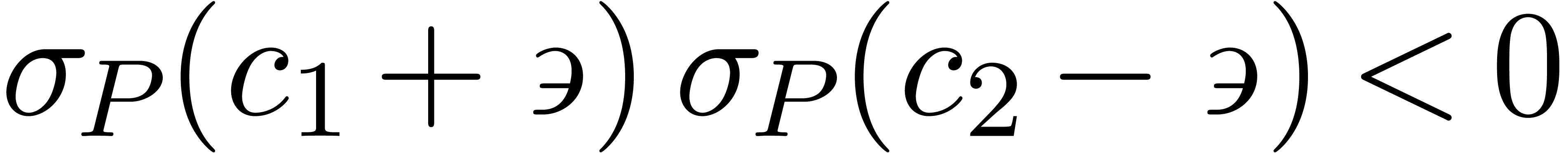 . Then there exists a constant
. Then there exists a constant 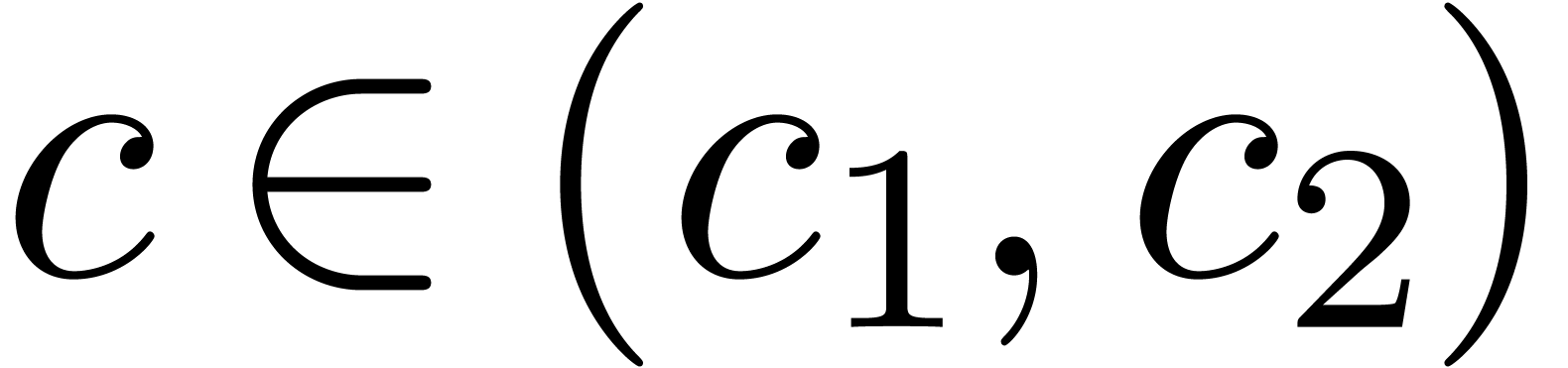 with
with 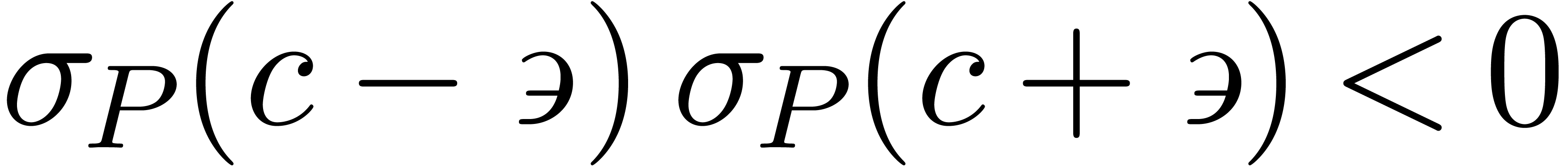 .
.
Lemma 21. For all
 with
with  ,
the signs of
,
the signs of 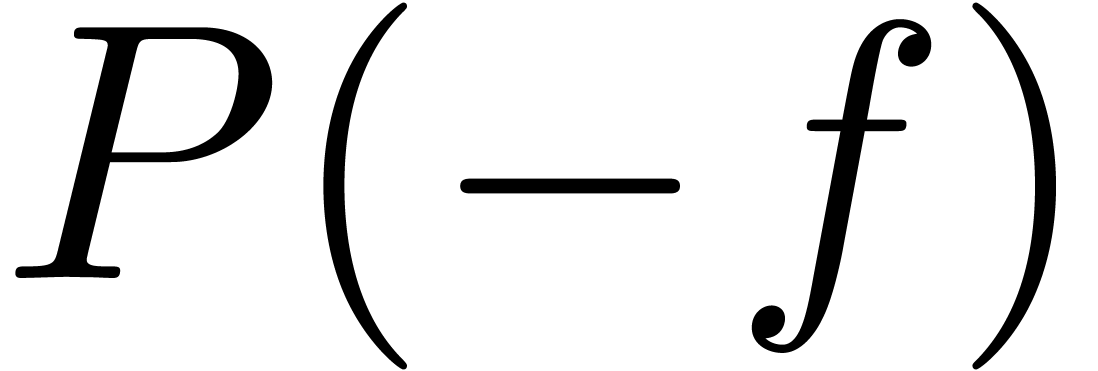 and
and 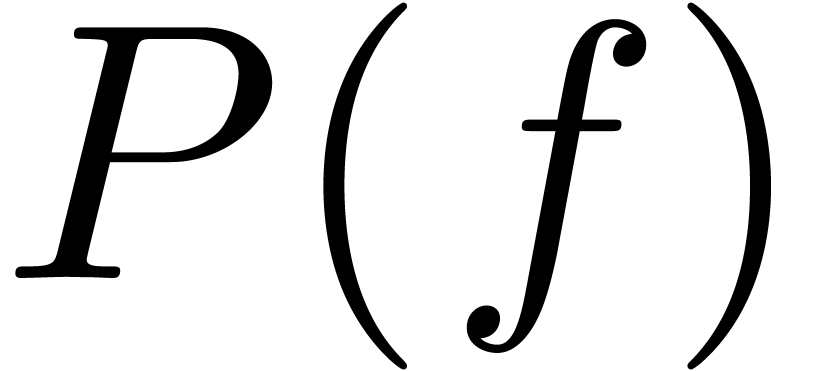 are
independent of
are
independent of 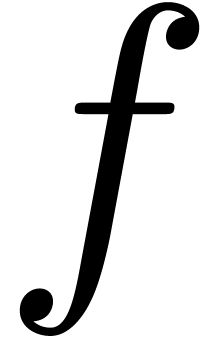 and given by
and given by
 |
(19) |
Proof. This is proved in a similar way as lemma 18.
Corollary 22. If  is homogeneous of degree
is homogeneous of degree  ,
then
,
then
 |
(20) |
for all  with
with  .
.
Corollary 23. Let
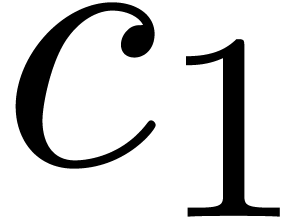 be a constant such that
be a constant such that 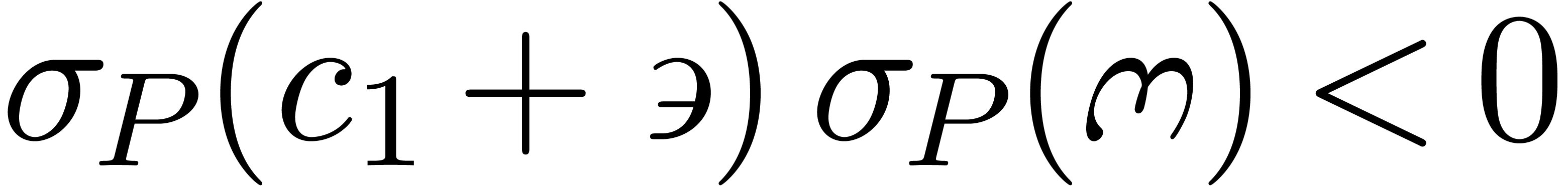 . Then there exists a constant
. Then there exists a constant 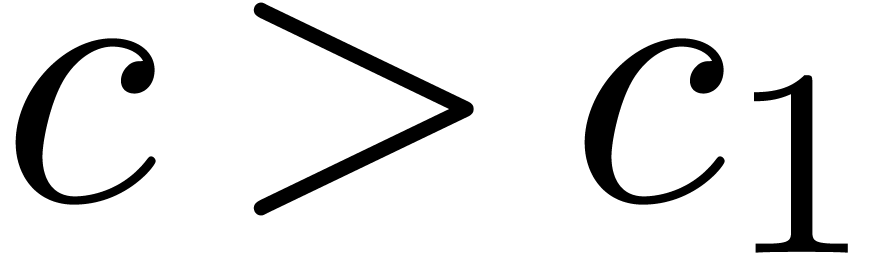 with
with 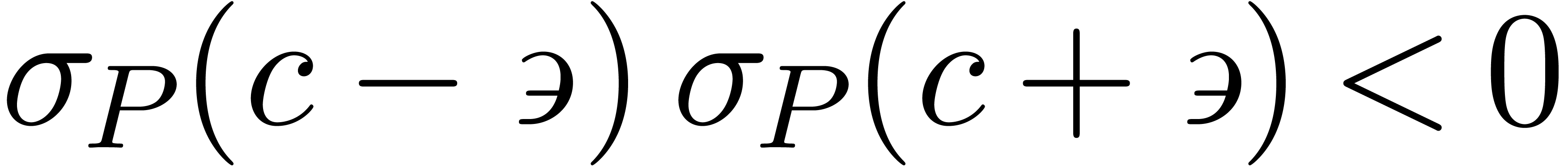 .
.
4.3Proof of the intermediate value theorem on
generalized intervals
We can now state and sketch the proofs of the differential intermediate
value theorem for generalized intervals. In fact, we simultaneously
proved two theorems [vdH01]: the intermediate value theorem
itself and a variant “modulo 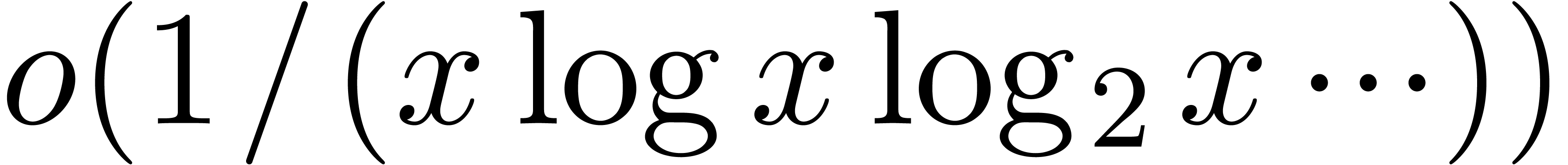 ”.
”.
Theorem 24. Let
 and
and  be a transseries
resp. a transmonomial in
be a transseries
resp. a transmonomial in  .
Assume that
.
Assume that  changes sign on an open interval
changes sign on an open interval
 of one of the following forms:
of one of the following forms:
-
 , for some
, for some 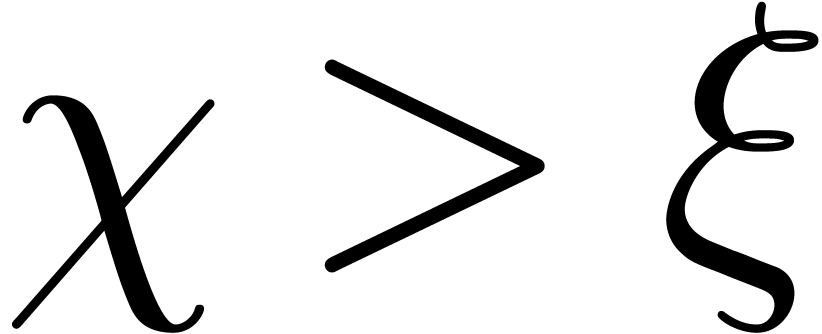 with
with 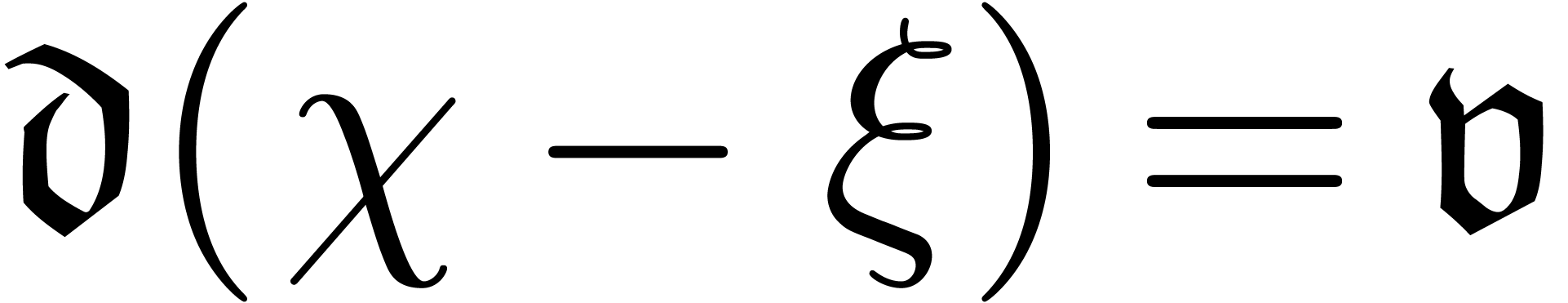 .
.
-
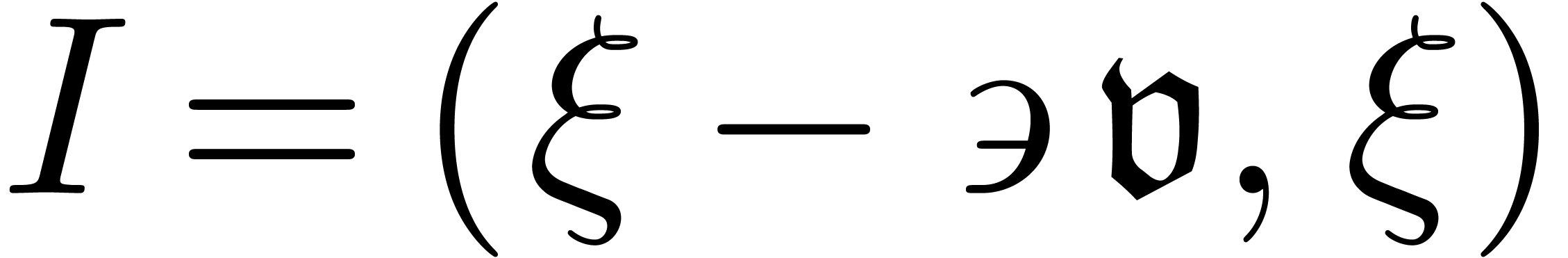 .
.
-
 .
.
-
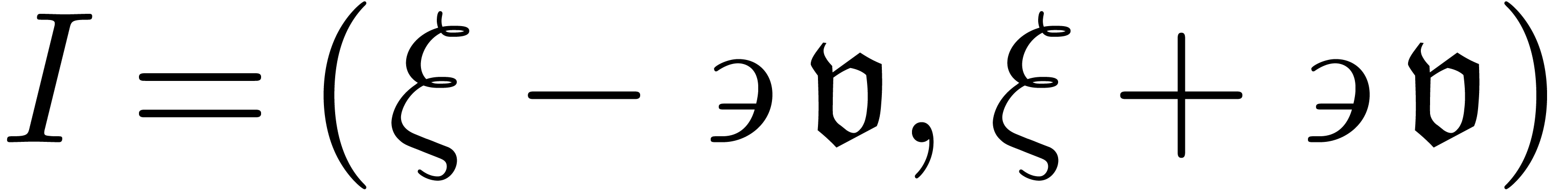 .
.
Then 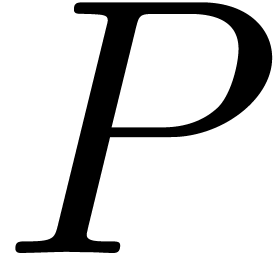 changes sign at some
changes sign at some  .
.
Theorem 25. Let
 and
and  be a transseries
resp. a transmonomial in
be a transseries
resp. a transmonomial in  .
Assume that
.
Assume that 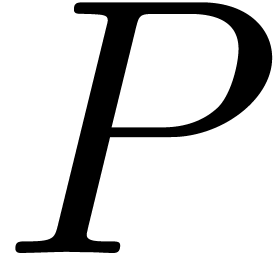 changes sign on an open interval
changes sign on an open interval
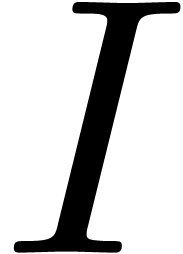 of one of the following forms:
of one of the following forms:
-
 , for some
, for some  with
with  .
.
-
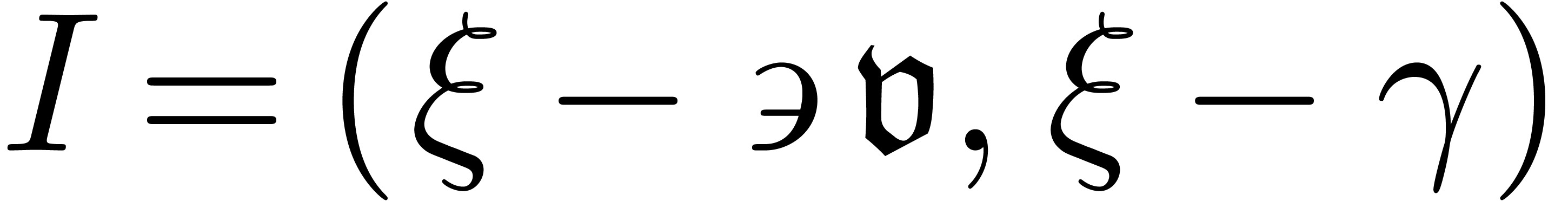 .
.
-
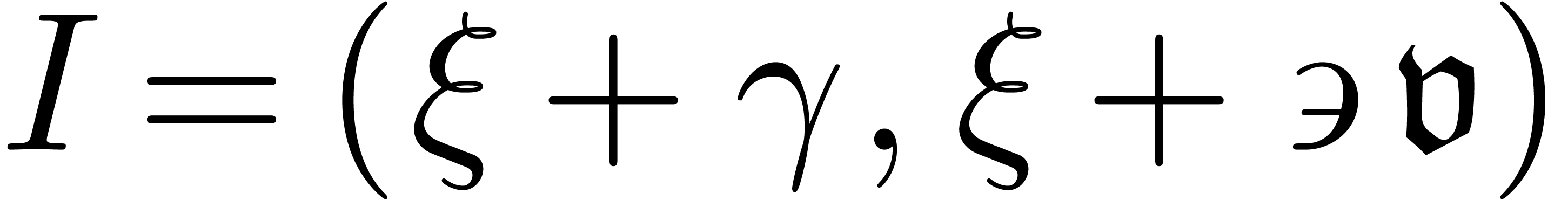 .
.
-
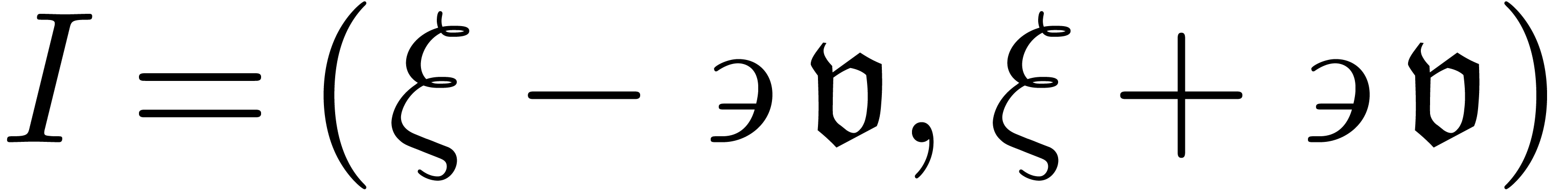 .
.
Then  changes sign on
changes sign on 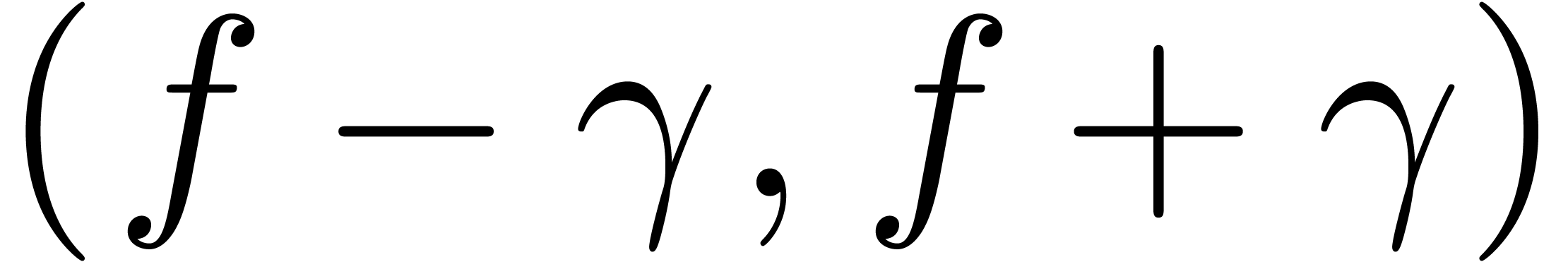 for some
for some  with
with 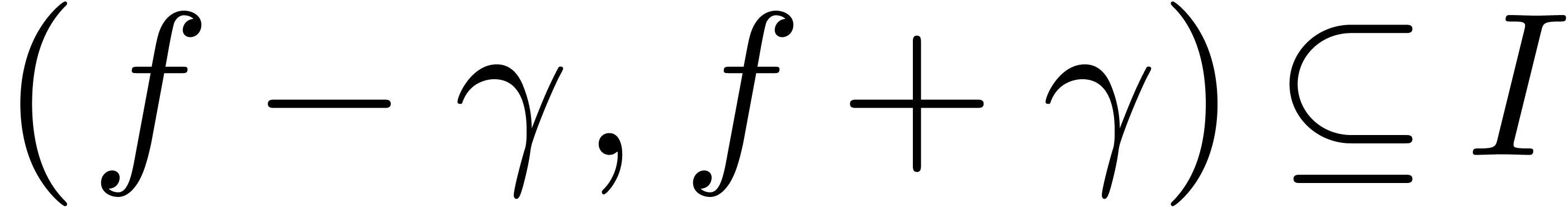 .
.
Proof. Using symmetry considerations and splitting up
the interval in smaller parts, it is first shown that it suffices to
consider case (b). Then we may assume without loss of generality
that 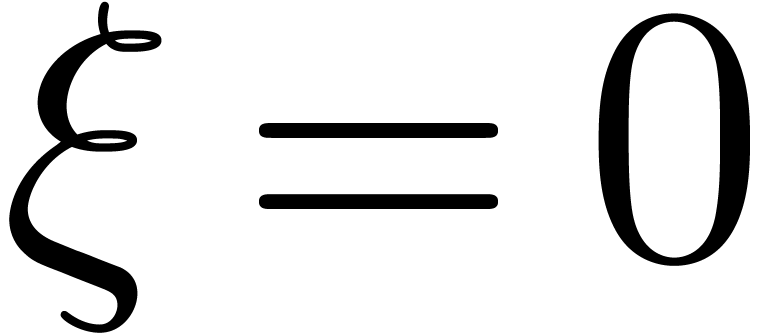 (modulo an additive conjugation of
(modulo an additive conjugation of  by
by  ) and
the theorem is proved by a triple induction over the order
) and
the theorem is proved by a triple induction over the order 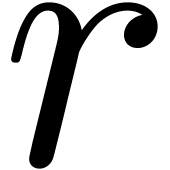 of
of 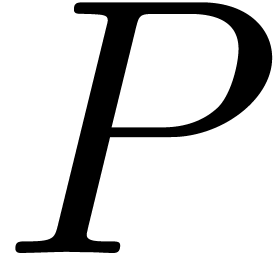 , the Newton
degree
, the Newton
degree 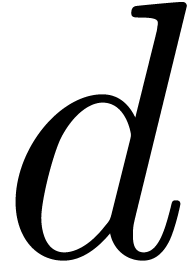 of the asymptotic algebraic differential
equation
of the asymptotic algebraic differential
equation
 |
(21) |
and the maximal length 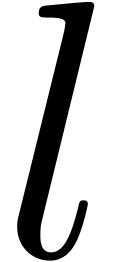 of a shortest sequence of
refinements like in proposition 14. If
of a shortest sequence of
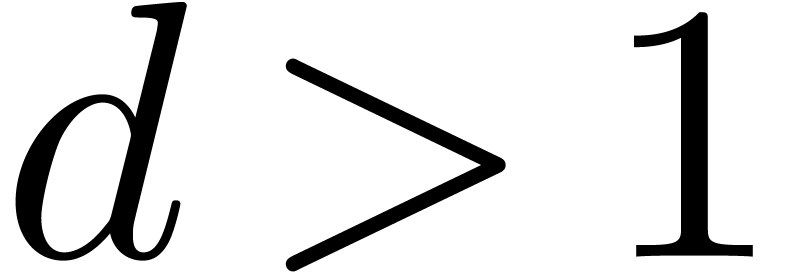
refinements like in proposition 14. If  , it is not hard to improve proposition 12 so that it yields a solution where a sign change occurs. If
, it is not hard to improve proposition 12 so that it yields a solution where a sign change occurs. If
 , the lemmas and their
corollaries from the previous section may be used in order to reduce the
interval
, the lemmas and their
corollaries from the previous section may be used in order to reduce the
interval 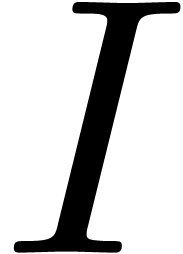 together with
together with 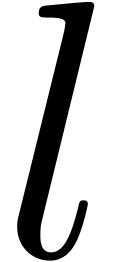 ,
, 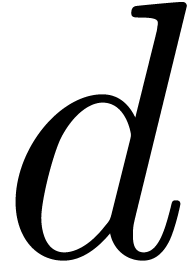 or
or 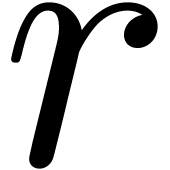 , so that we may conclude by induction.
, so that we may conclude by induction.
5Perspectives
In the introduction, we mentioned the question of finding out which
solutions of differential (or more general) equations may be modelled
adequately using transseries. We know for instance (although we still
have to write this down in detail) that the intermediate value theorem
also holds for algebraic differential-difference equations, where the
difference operators are post-compositions with transseries  of exponentiality
of exponentiality 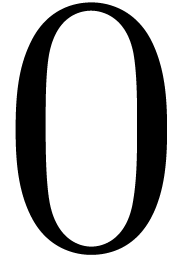 (this means that
(this means that
 for all sufficiently large
for all sufficiently large 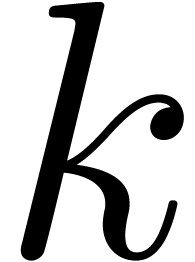 ; for instance,
; for instance, 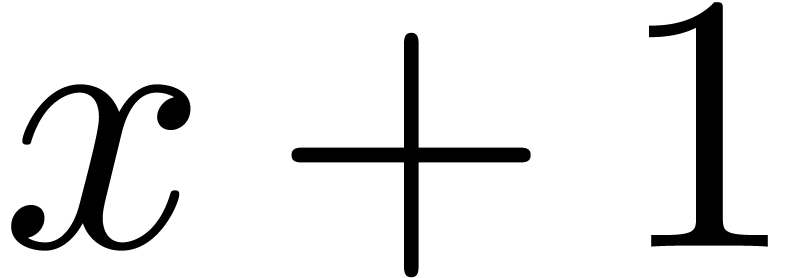 ,
,
 ,
,  and
and
 have exponentiality
have exponentiality  , but not
, but not 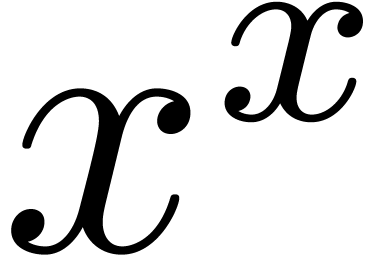 ).
Of course, one has to allow well-ordered transseries in this case, but
the exponential and logarithmic depths remain bounded.
).
Of course, one has to allow well-ordered transseries in this case, but
the exponential and logarithmic depths remain bounded.
It would be interesting to know whether more general intermediate value
theorems would follow from similar theorems for surreal numbers. Indeed,
such theorems might be easier to prove for surreal numbers, because of
the concept of the simplest surreal number which satisfies a certain
property. In order to make this work, one would have to define a
canonical derivation and composition for the surreal numbers,
where  plays the role of
plays the role of  . From an effective point of view, proofs using
surreal numbers would be less satisfying though. Also such proofs would
not provide us with a method for finding generic solutions to
differential equations in terms of integration constants.
. From an effective point of view, proofs using
surreal numbers would be less satisfying though. Also such proofs would
not provide us with a method for finding generic solutions to
differential equations in terms of integration constants.
Yet another interesting setting for proving intermediate value theorems
is model theory. The field of transseries satisfies some interesting
axioms involving the ordered field operations, differentiation and the
asymptotic relation  . For
instance,
. For
instance,
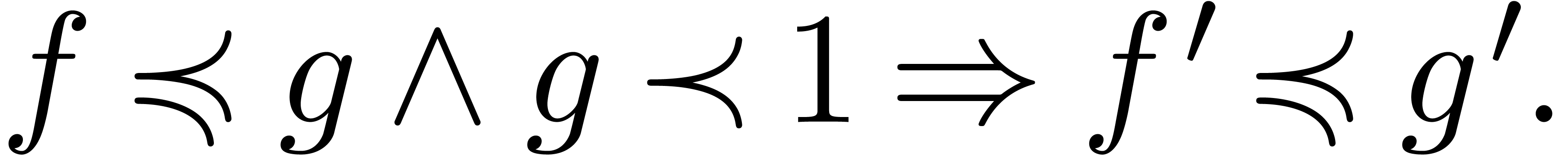
What differential Henselian property would be needed in order to prove
intermediate value theorems in more general models of theories that
contain axioms like the above one? Is it always possible to embed models
of such theories into suitable generalizations of fields of transseries?
We recently made some progress on this topic with Aschenbrenner and van
den Dries.
Another interesting problem is to prove the analytic counterparts of the
intermediate value theorem and its generalizations in Écalle's
setting of analyzable functions. We are confident that there should not
be any major problems here, although the details still need to be worked
out.
So far, we have been working in the real setting, in absence of any
oscillation. Another major problem is to generalize the theory to the
complex setting. Some progress has been made in [vdH01] on
this question: we showed how to construct fields of complex transseries
on “non degenerate regions” and proved that any algebraic
differential equation over such a field admits a solution. We also
proved that linear differential equations admit a full system of
solutions. In other words, the Picard-Vessiot extension of a field of
complex transseries is isomorphic to the field itself. Unfortunately,
the current fields of complex transseries are not differentially
algebraically closed, since the only solutions to the elliptic equation
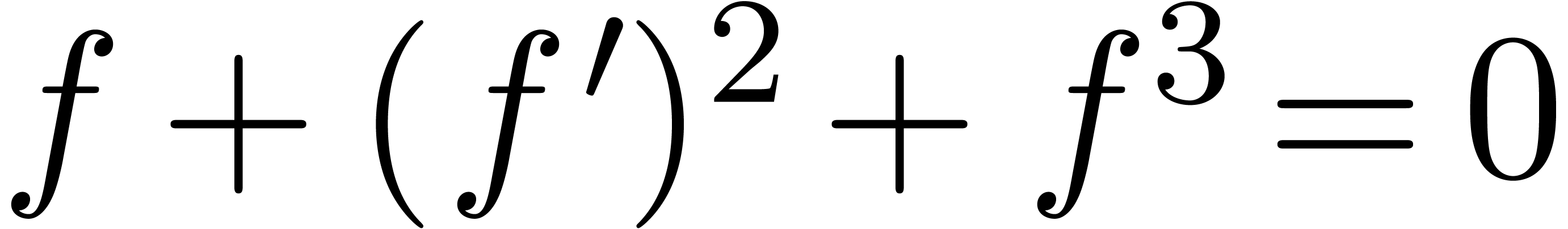
are the solutions to
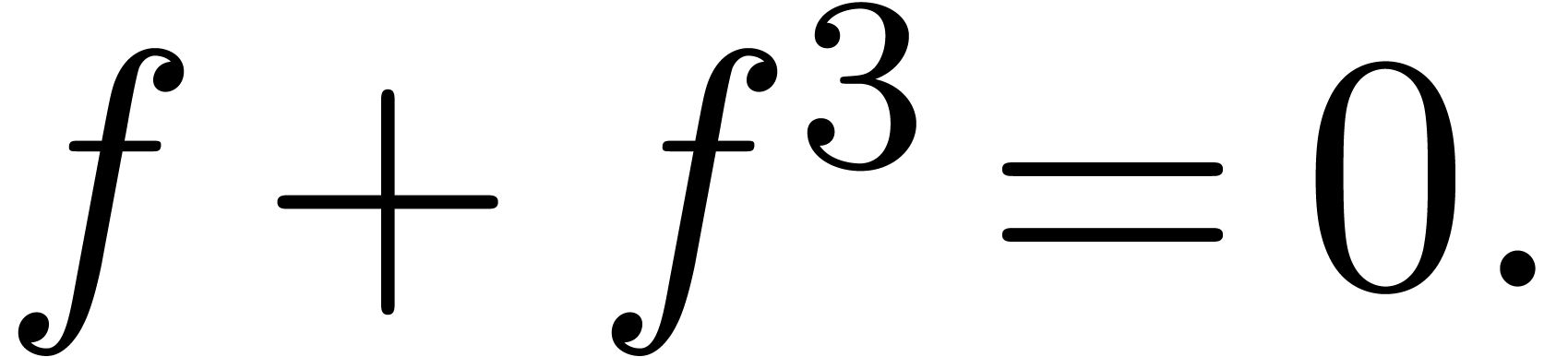
The question of constructing a differentially algebraically closed
field, which reflects the asymptotic behavior of solutions to algebraic
differential equations, still remains open…
Bibliography
-
[DG86]
-
B. I. Dahn and P. Göring. Notes on
exponential-logarithmic terms. Fundamenta Mathematicae,
127:45–50, 1986.
-
[É92]
-
J. Écalle. Introduction aux fonctions
analysables et preuve constructive de la conjecture de
Dulac. Hermann, collection: Actualités
mathématiques, 1992.
-
[GG92]
-
G.H. Gonnet and D. Gruntz. Limit computation in
computer algebra. Technical Report 187, ETH, Zürich, 1992.
-
[Hah07]
-
H. Hahn. Über die nichtarchimedischen
Größensysteme. Sitz. Akad. Wiss. Wien,
116:601–655, 1907.
-
[Sal91]
-
B. Salvy. Asymptotique automatique et fonctions
génératrices. PhD thesis, École
Polytechnique, France, 1991.
-
[Sha90]
-
J. Shackell. Growth estimates for exp-log functions.
Journal of symbolic computation, 10:611–632, 1990.
-
[vdH97]
-
J. van der Hoeven. Automatic asymptotics. PhD
thesis, École polytechnique, France, 1997.
-
[vdH00]
-
Joris van der Hoeven. A differential intermediate
value theorem. Technical Report 2000-50, Univ. d'Orsay, 2000.
-
[vdH01]
-
Joris van der Hoeven. Complex transseries solutions
to algebraic differential equations. Technical Report 2001-34,
Univ. d'Orsay, 2001.
 the field of transseries, the
intermediate value theorem states that for any differential
polynomials
the field of transseries, the
intermediate value theorem states that for any differential
polynomials  with coefficients in
with coefficients in  and
and  in
in  with
with 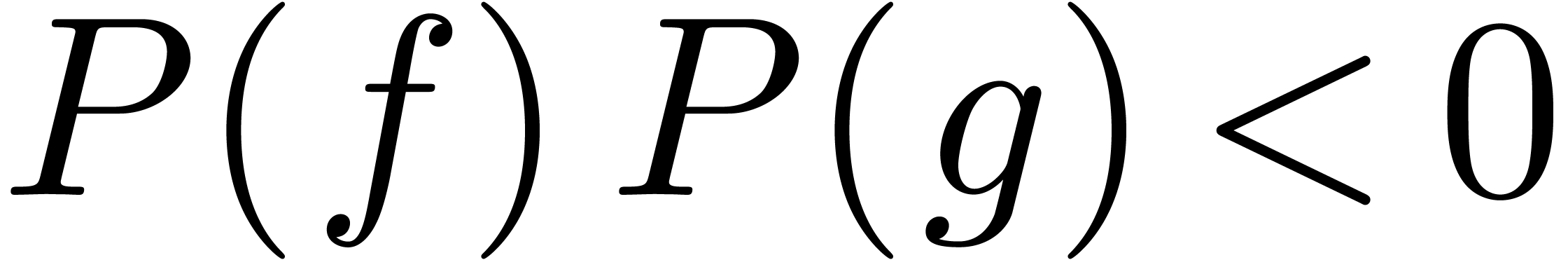 , there exists a
solution
, there exists a
solution 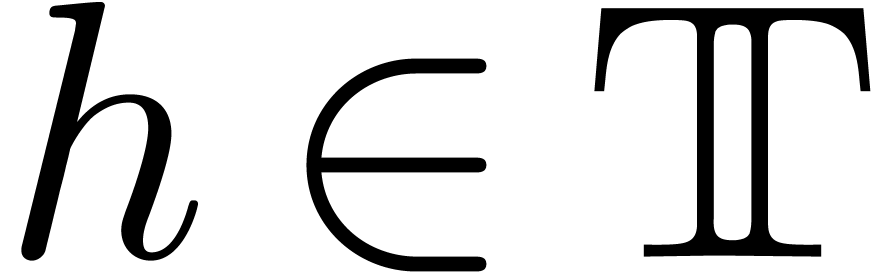 to
to 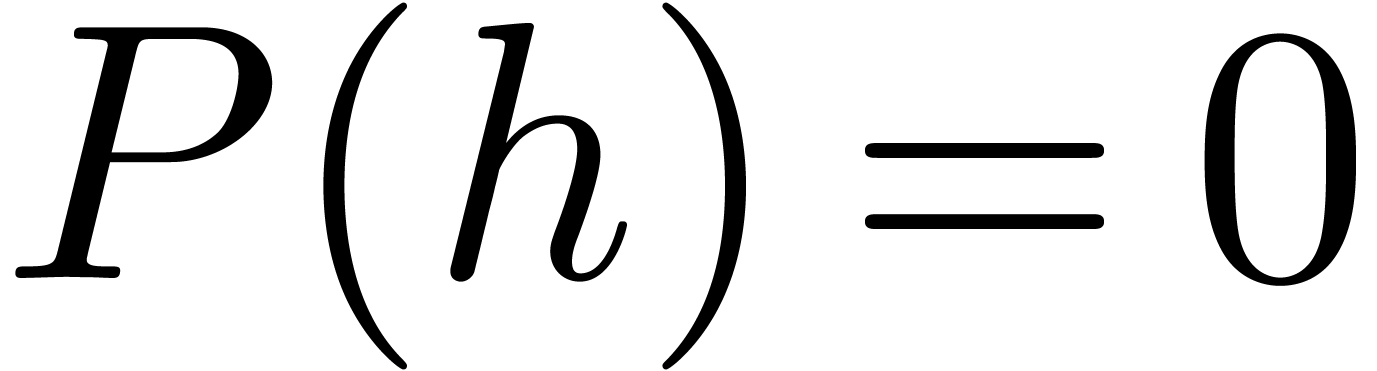 with
with 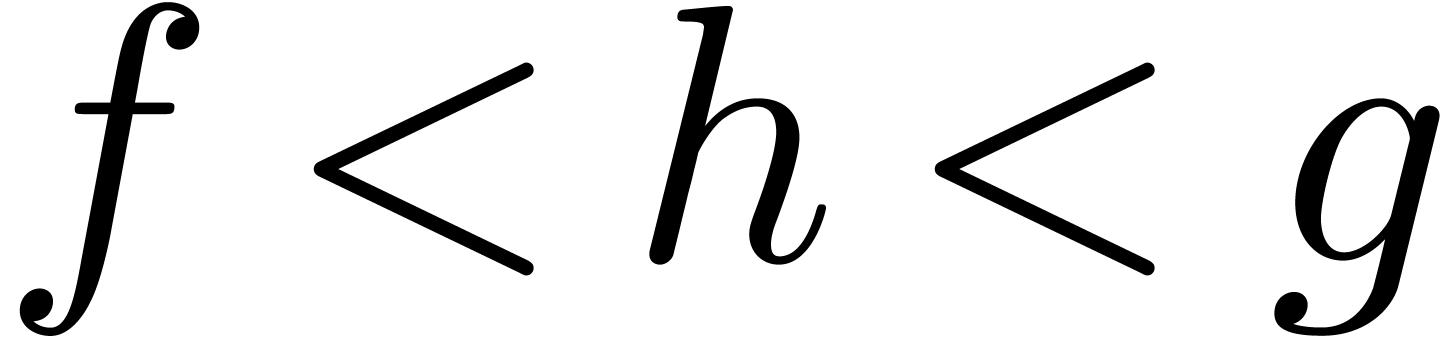 .
.
 ).
).
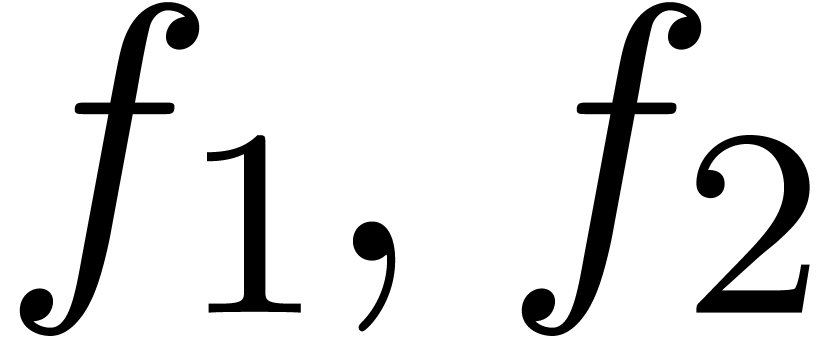 and
and 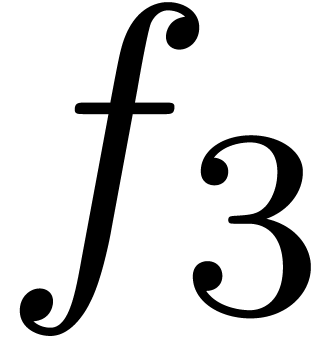 are
examples of grid-based transseries, the first two being
convergent and the last one divergent. In section
are
examples of grid-based transseries, the first two being
convergent and the last one divergent. In section  ,
,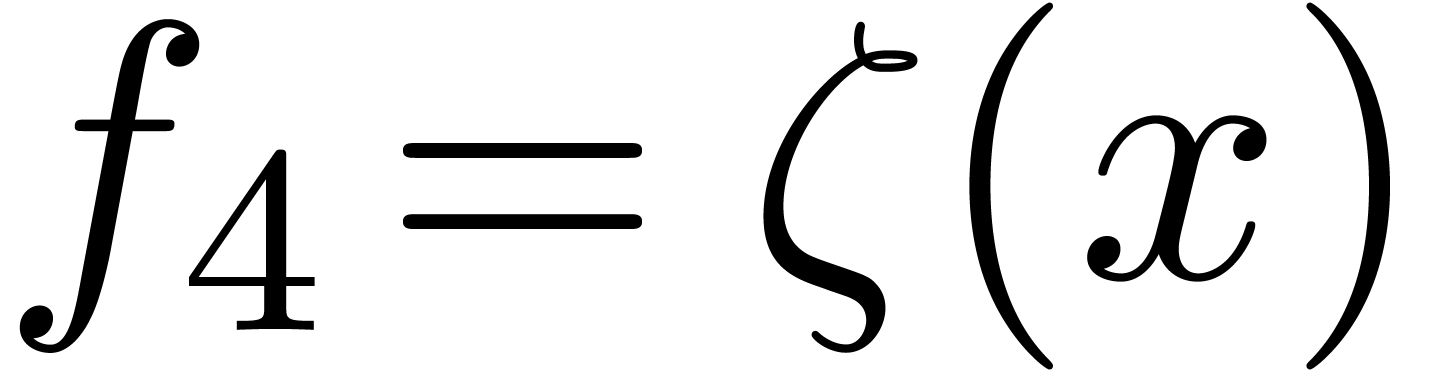 and
and  .
.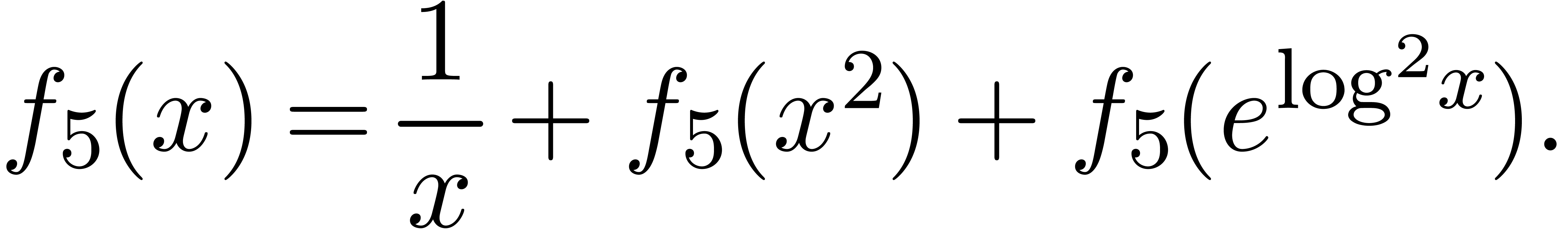
 .
.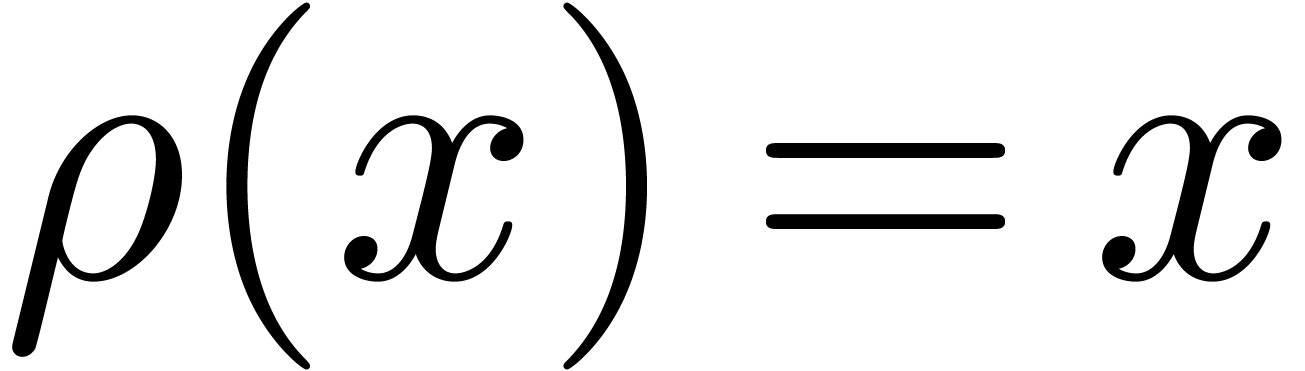 ,
,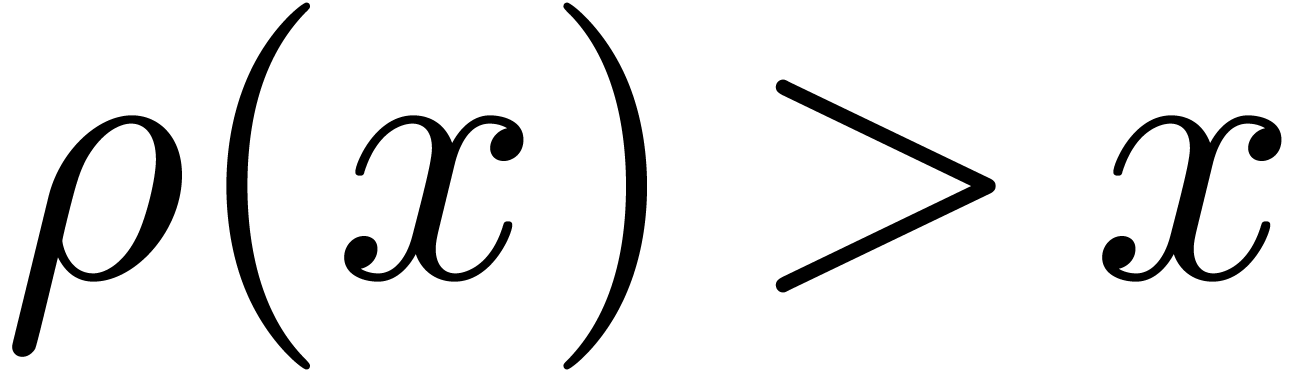 or
or 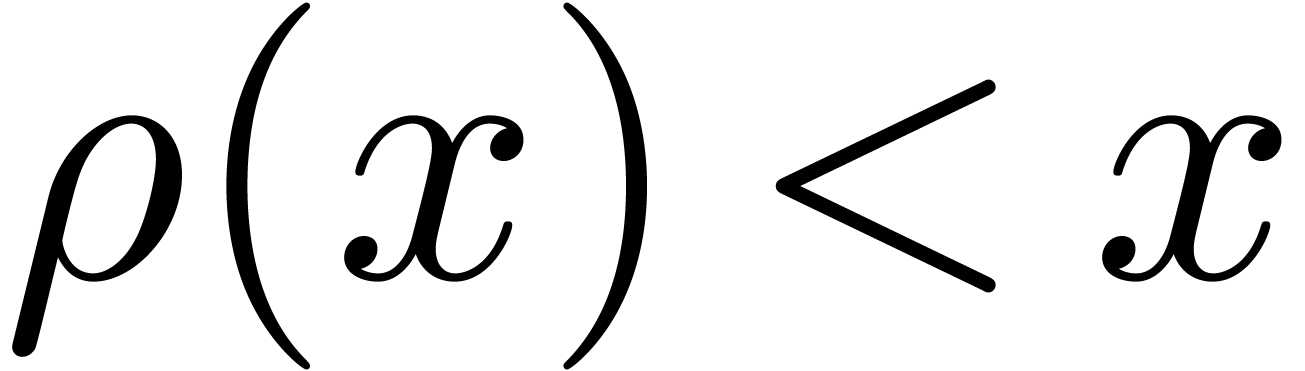 in a small
neighbourhood of the limit cycle. In other words, either all or no
orbits are periodic in this neighbourhood.
in a small
neighbourhood of the limit cycle. In other words, either all or no
orbits are periodic in this neighbourhood.
 always have a full basis of solutions of the form
always have a full basis of solutions of the form
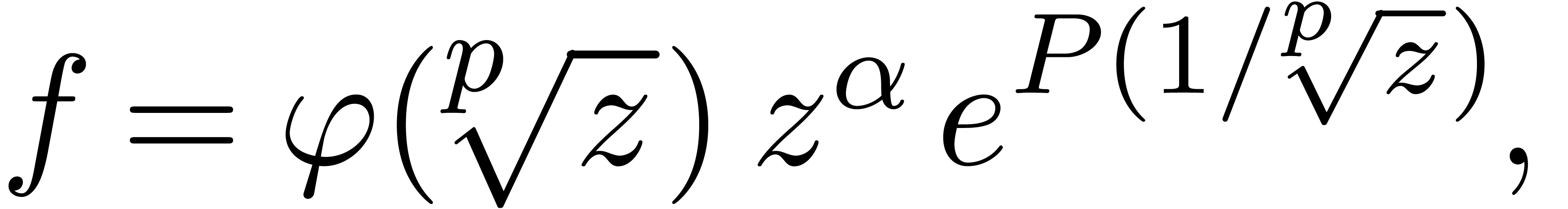
 is a polynomial,
is a polynomial,  and
and 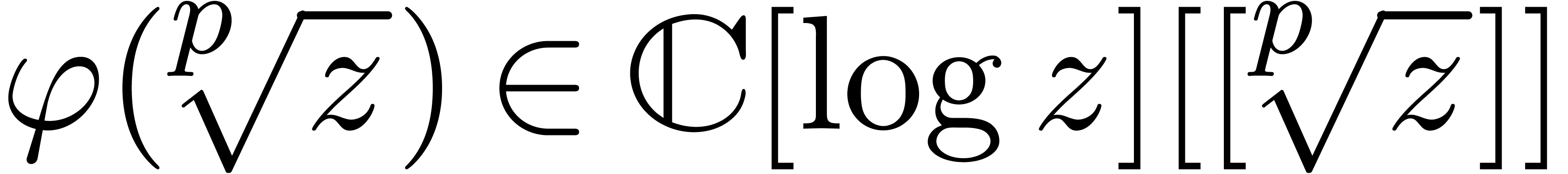 a power series whose coefficients are
polynomials in
a power series whose coefficients are
polynomials in  of uniformly bounded degree. It
is tempting to generalize this result to non-linear differential
equations and even to more general functional equations.
of uniformly bounded degree. It
is tempting to generalize this result to non-linear differential
equations and even to more general functional equations.
 ,
,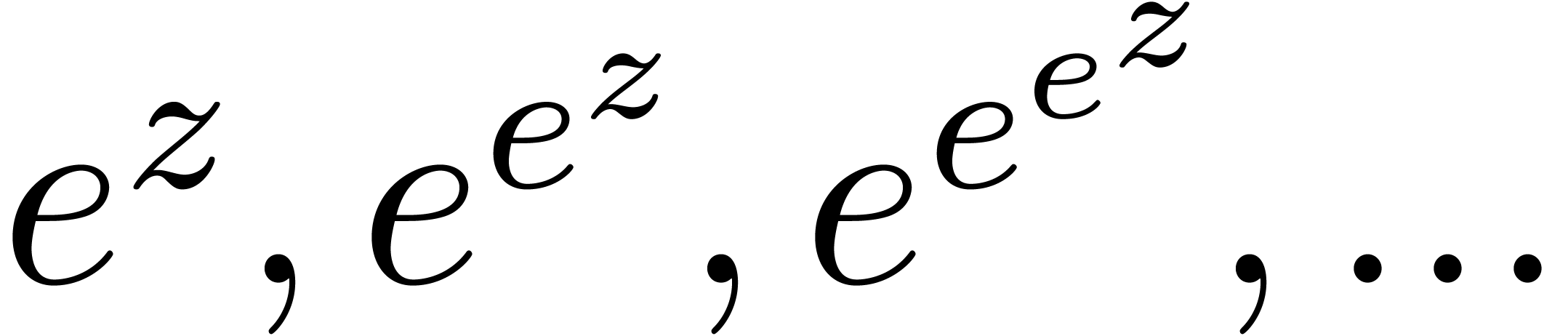 of
arbitrarily high orders into our theory. This is problematic if
of
arbitrarily high orders into our theory. This is problematic if 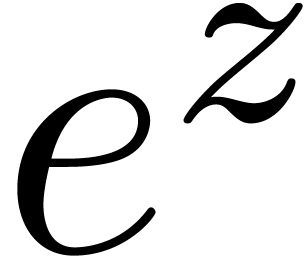 behaves
very differently in the positive and negative halfplanes.
behaves
very differently in the positive and negative halfplanes.
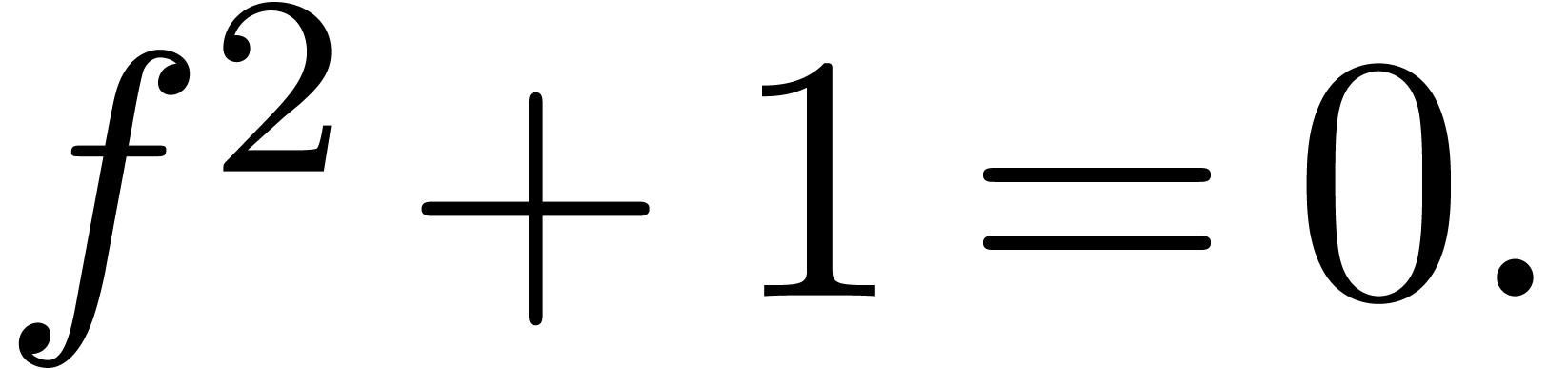
 (see
section
(see
section  and
and  (using the
notation of Hardy:
(using the
notation of Hardy: 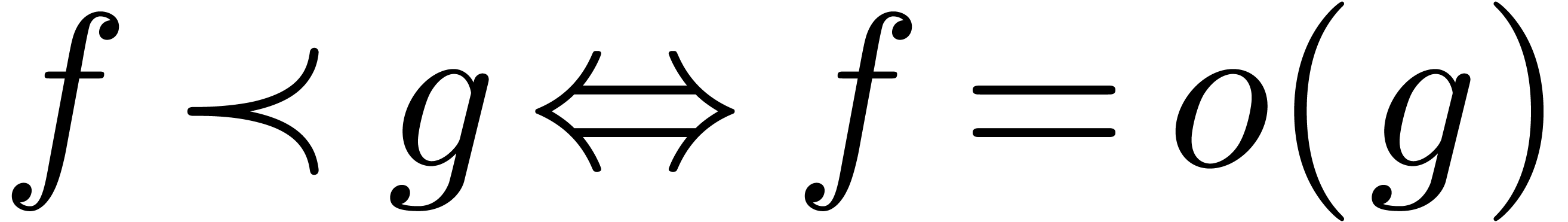 and
and 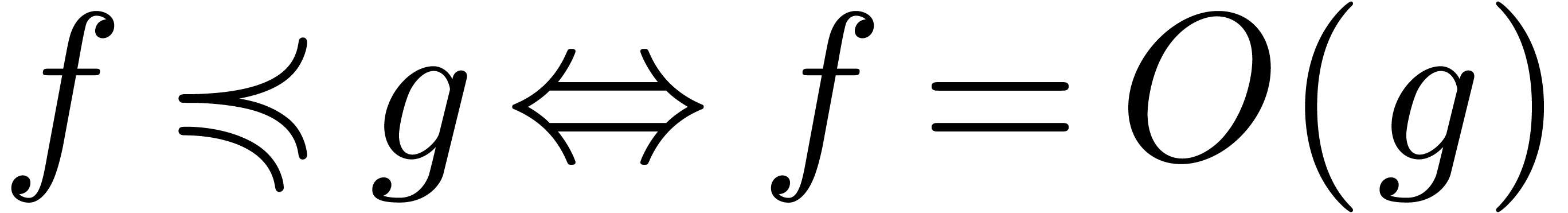 ).
).
 of
of  be a constant field and
be a constant field and  a totally ordered, multiplicative, commutative group of
monomials. For instance, the monomial group
a totally ordered, multiplicative, commutative group of
monomials. For instance, the monomial group 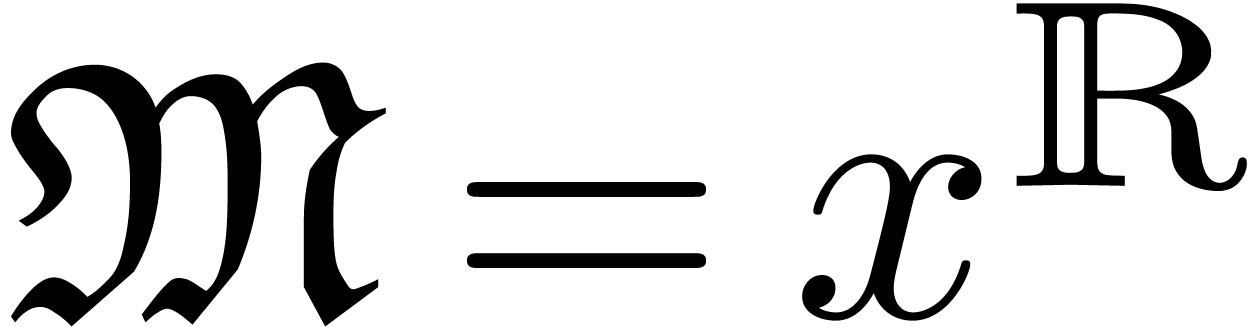 of real powers of an infinitely large
of real powers of an infinitely large 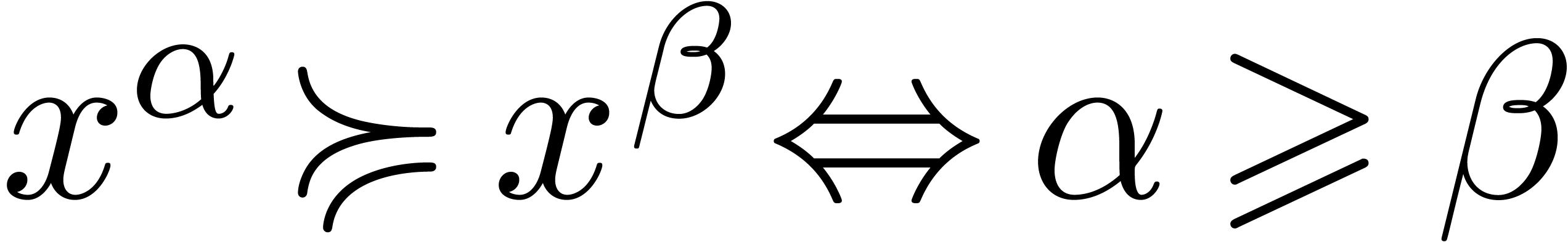 .
. corresponds to Landau's
corresponds to Landau's  -symbol
-symbol to the
to the
 -symbol.
-symbol. if
if  and
and  .
.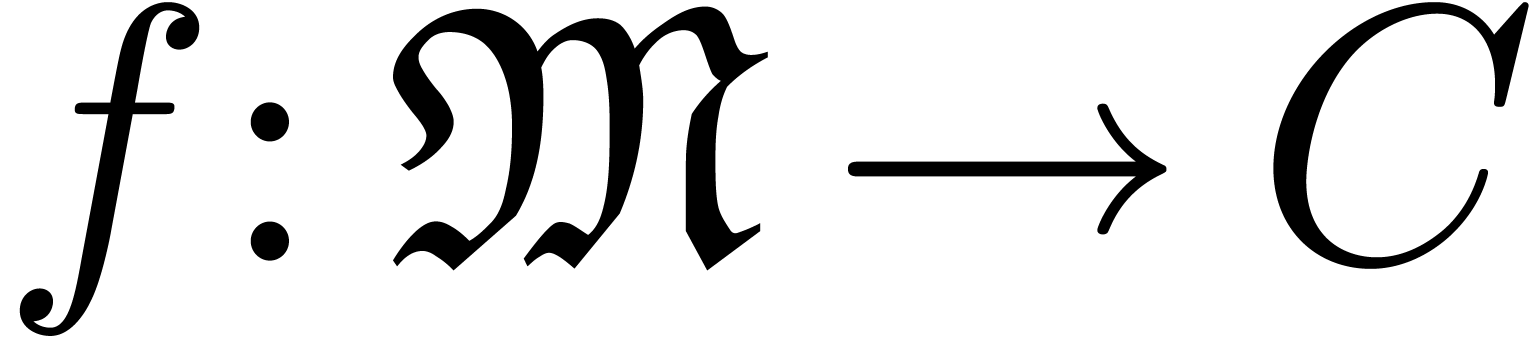 with well-ordered support. We usually write
with well-ordered support. We usually write  and
and
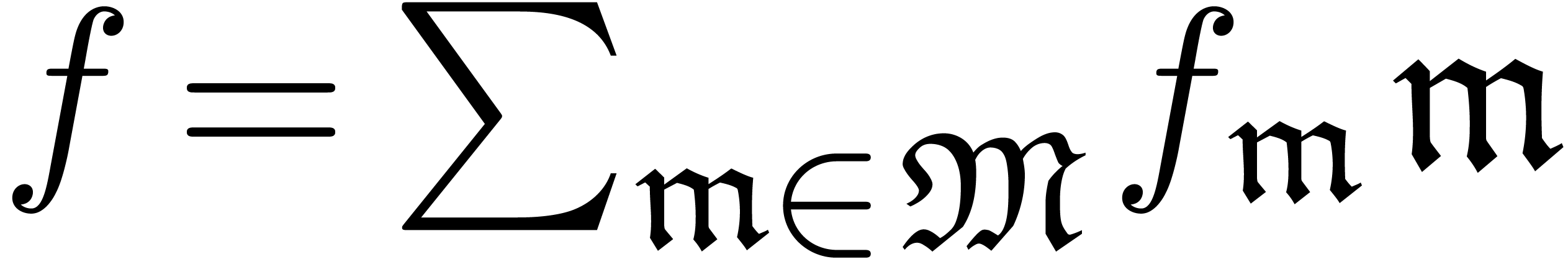 and the support
and the support  of
of  is the set of
is the set of  with
with 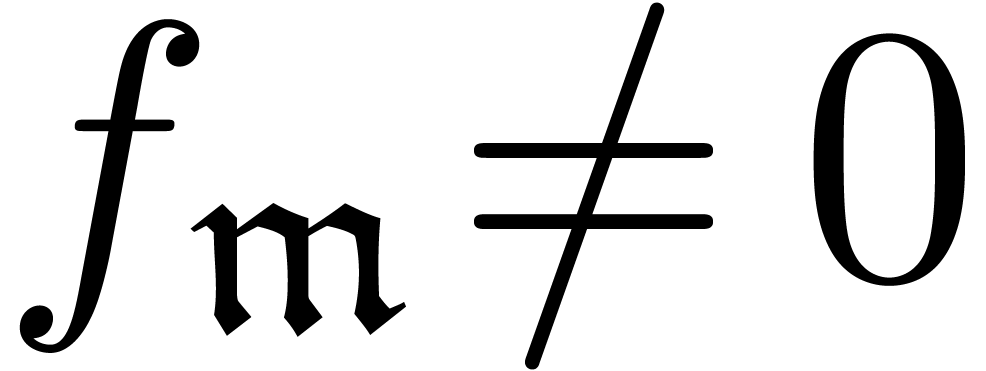 .
. of monomials with
of monomials with 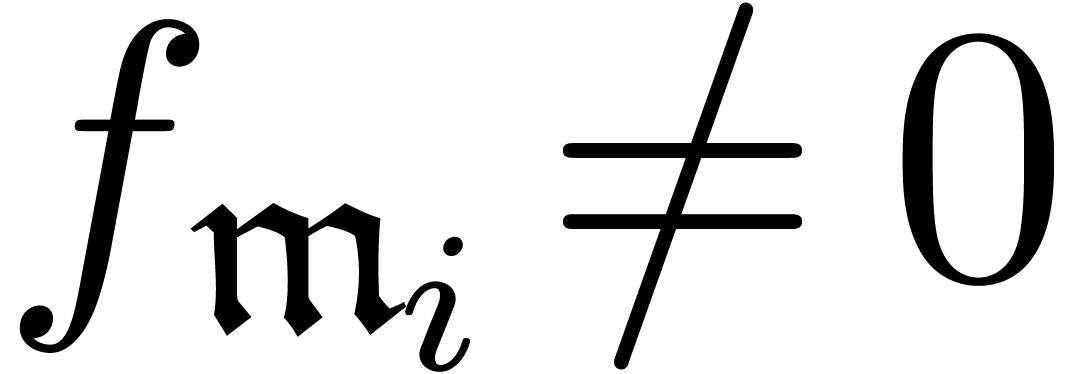 for all
for all  .
. for the set of generalized (or well-ordered) power series.
for the set of generalized (or well-ordered) power series.
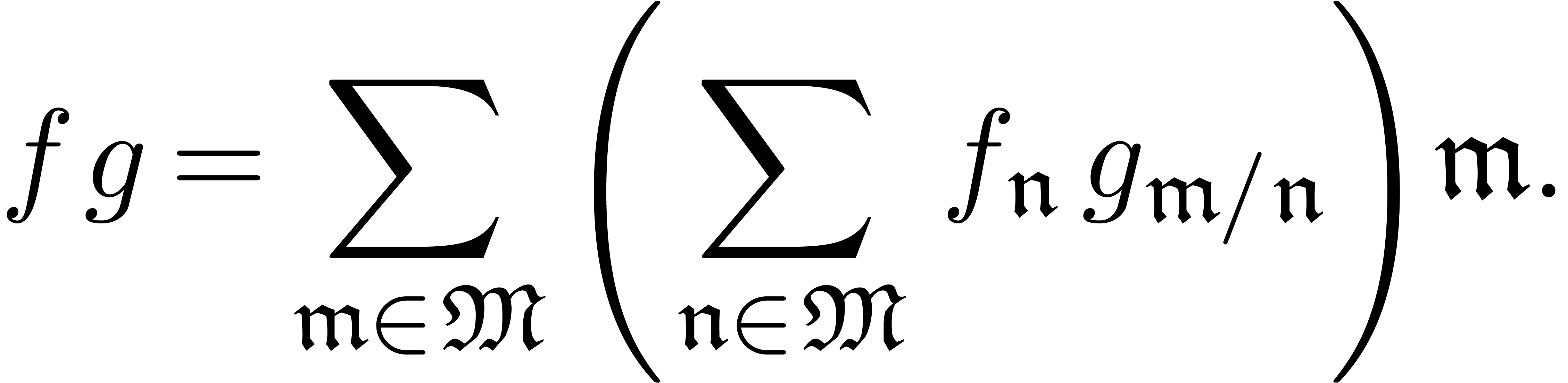
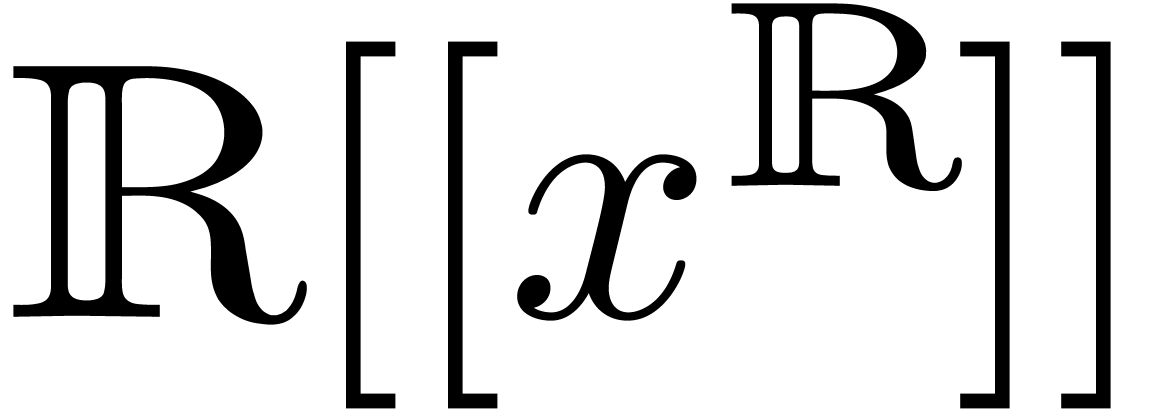 are
are
 is transfinite
(namely
is transfinite
(namely 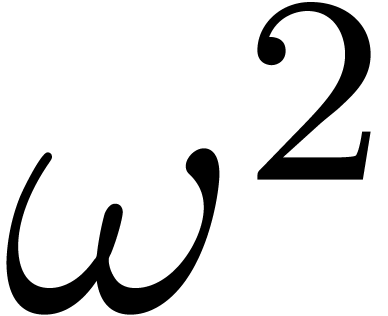 )
) ,
,
 .
. and
and  of
of
 is grid-based if there exists a
monomial
is grid-based if there exists a
monomial  and a finite number of infinitesimal
monomials
and a finite number of infinitesimal
monomials  in
in 
 ,
,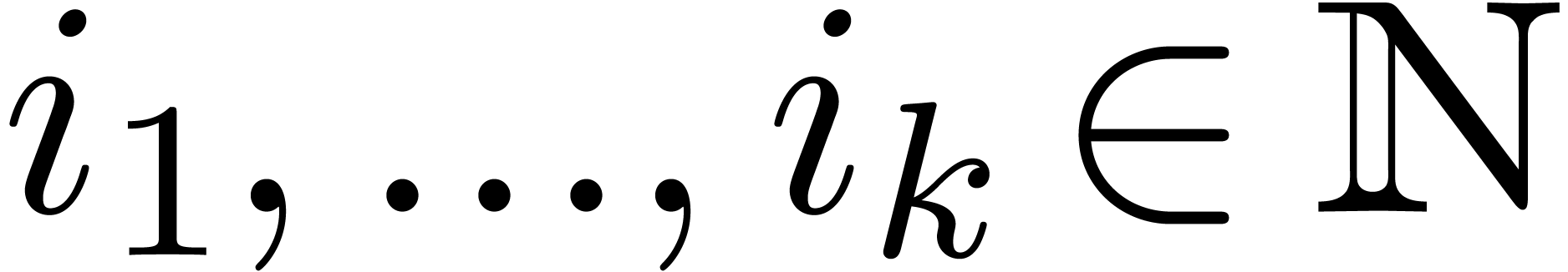 with
with 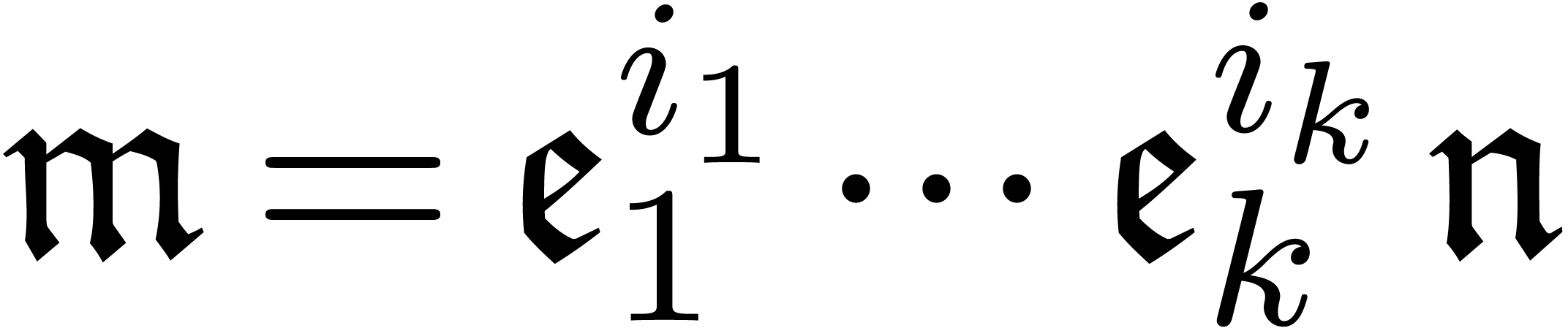 .
. of grid-based series forms a subfield of
of grid-based series forms a subfield of 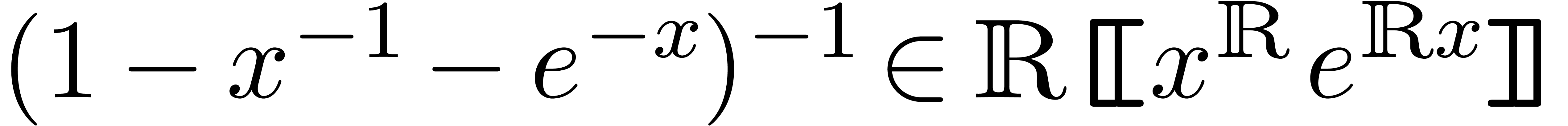 is again
is again 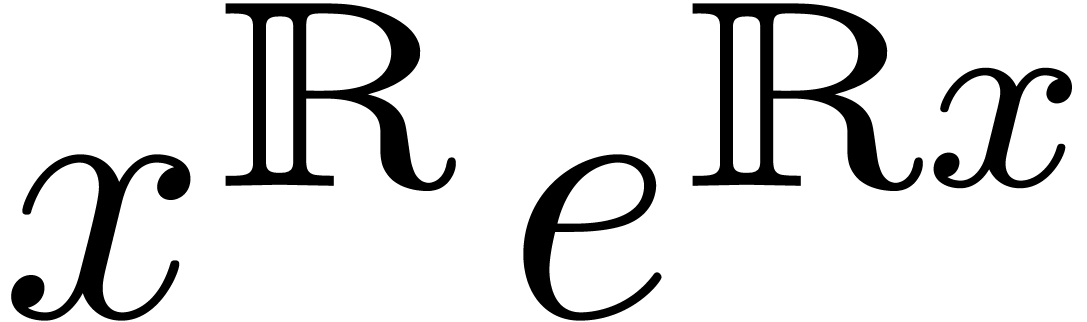 is ordered by
is ordered by
 .
.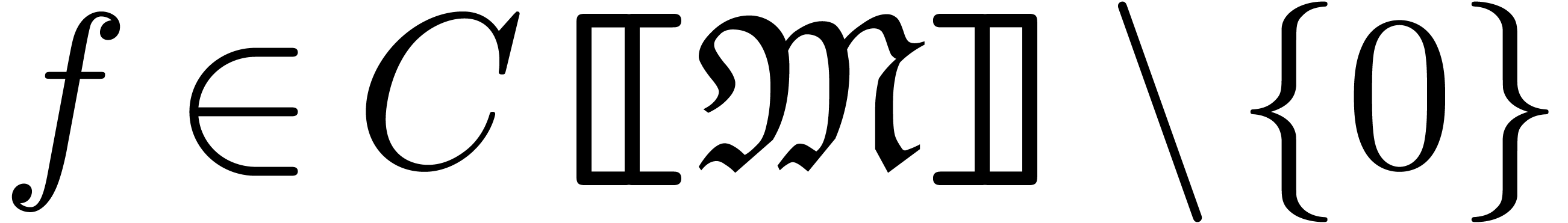 ,
, to be the
to be the  of
of  .
. (here we assume
(here we assume  ;
; for all
for all  and
and  whenever
whenever 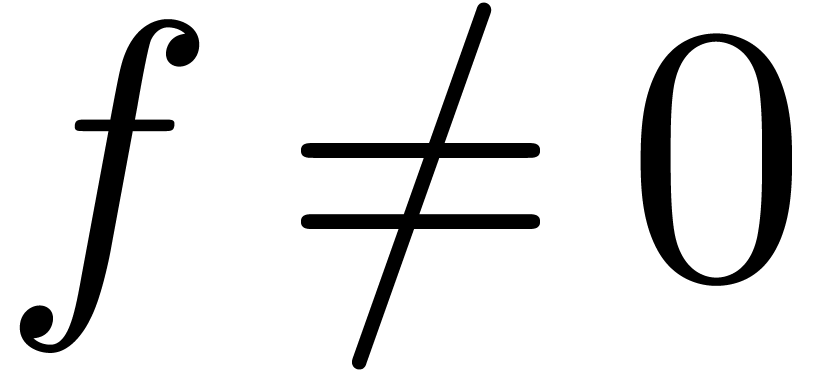 ).
). also admits a canonical
decomposition into a purely infinite, a constant,
and an infinitesimal part:
also admits a canonical
decomposition into a purely infinite, a constant,
and an infinitesimal part:
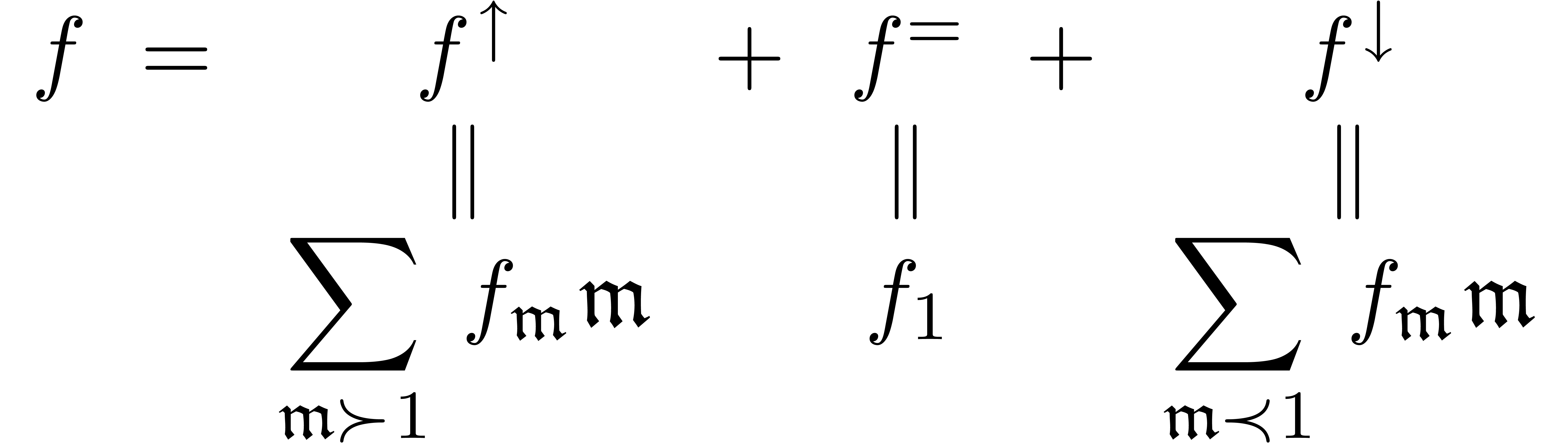
 ,
, .
.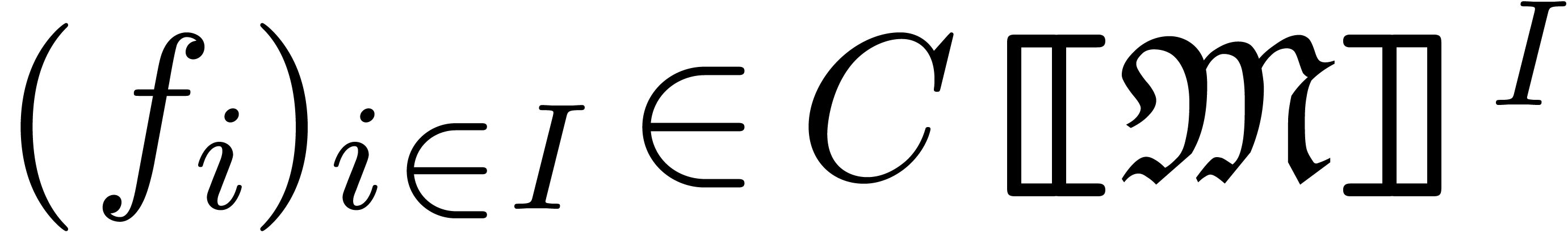 is said to
be grid-based (or strongly summable), if
is said to
be grid-based (or strongly summable), if
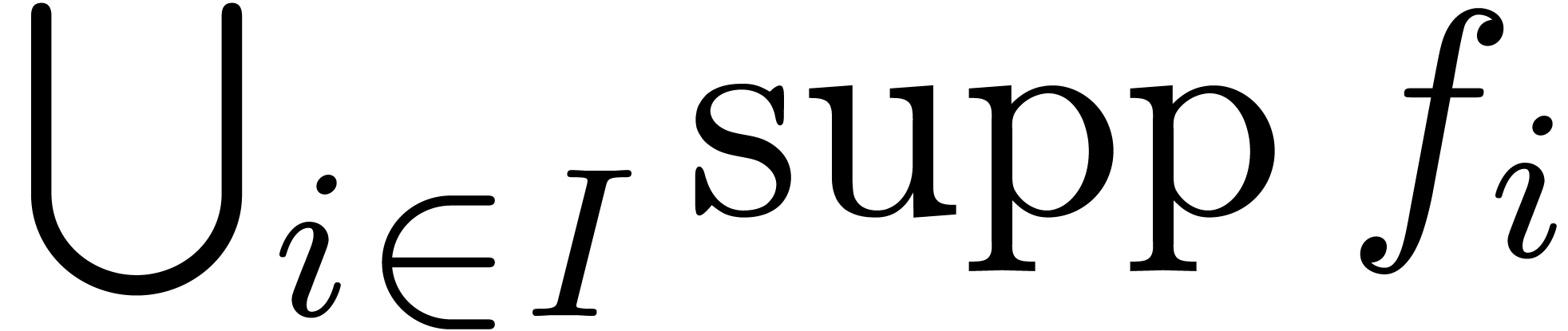 is a grid-based subset of
is a grid-based subset of  is finite.
is finite.
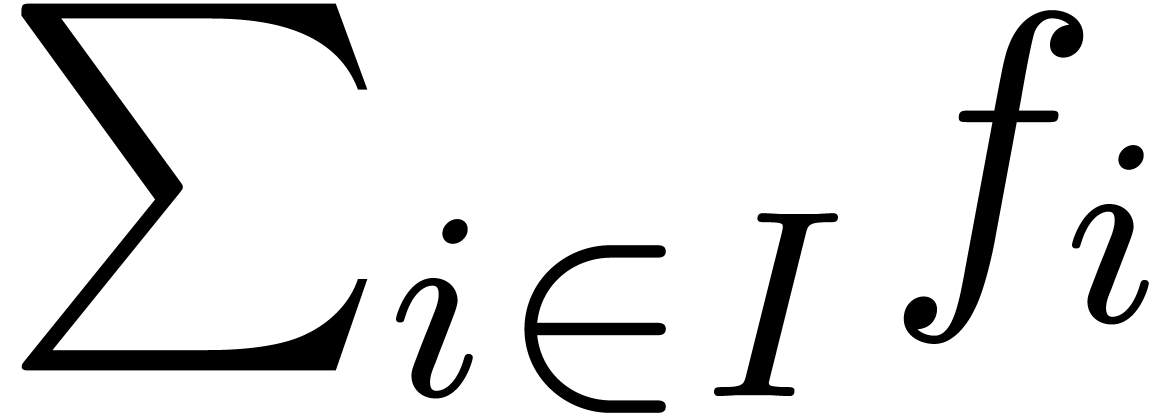 by
by
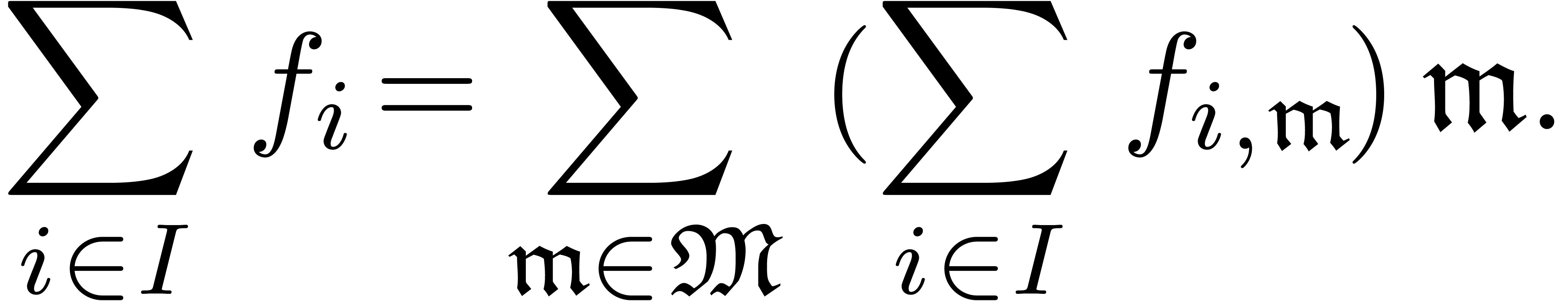
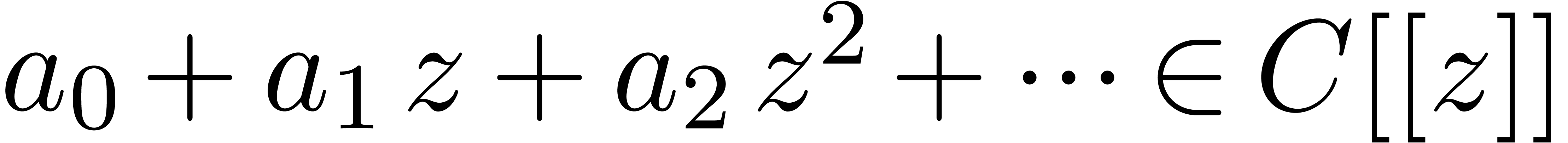 and an
infinitesimal
and an
infinitesimal  ,
,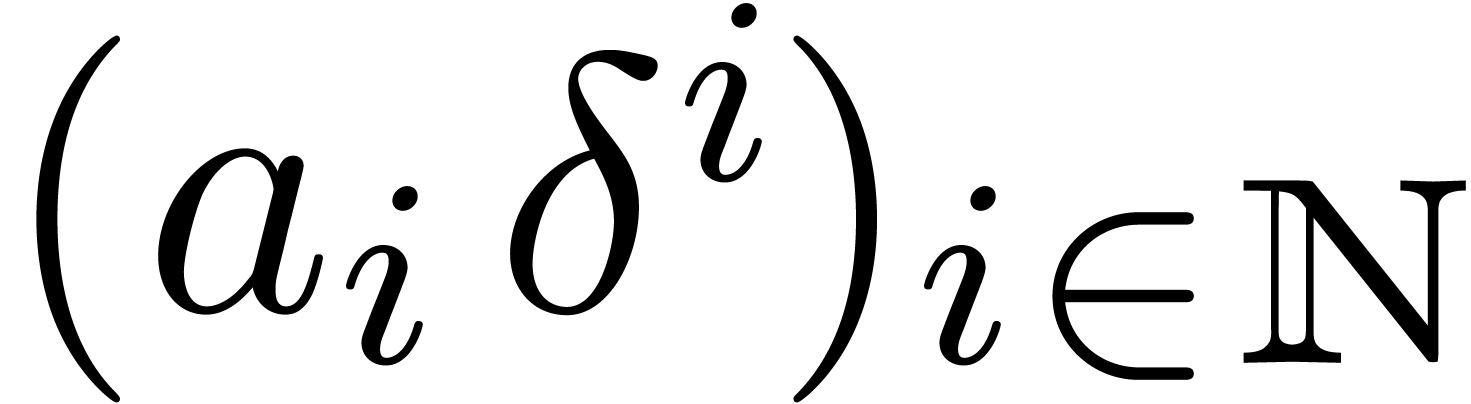 is a grid-based family.
Consequently,
is a grid-based family.
Consequently, 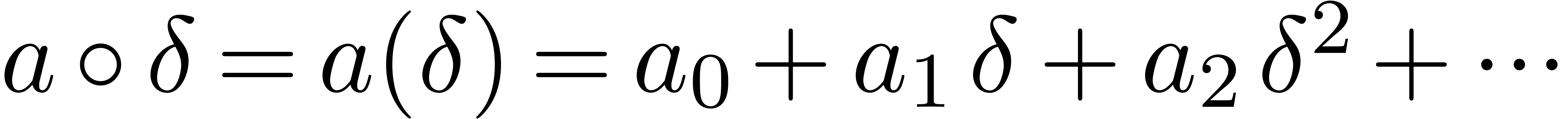 is well-defined.
is well-defined.
 with additional functions
with additional functions  and
and 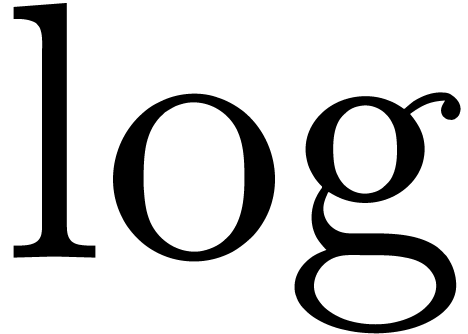 ,
,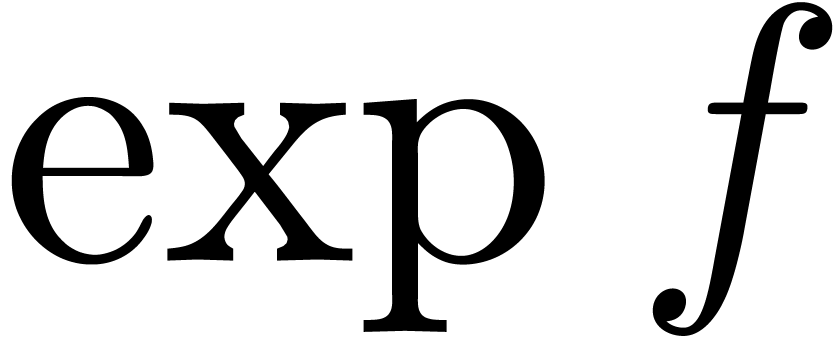 is defined
for all
is defined
for all 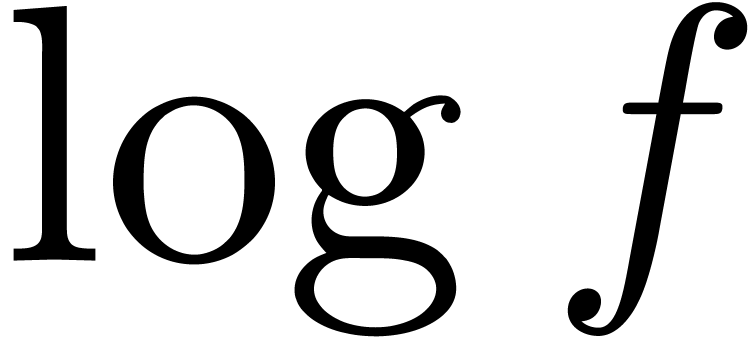 for all
for all
 .
. and successively closes it under exponentiation and logarithm. We will
follow the inverse strategy: we start with the field of logarithmic
transseries
and successively closes it under exponentiation and logarithm. We will
follow the inverse strategy: we start with the field of logarithmic
transseries  and close it under exponentiation.
Both constructions turn out to be equivalent in the grid-based setting.
and close it under exponentiation.
Both constructions turn out to be equivalent in the grid-based setting.

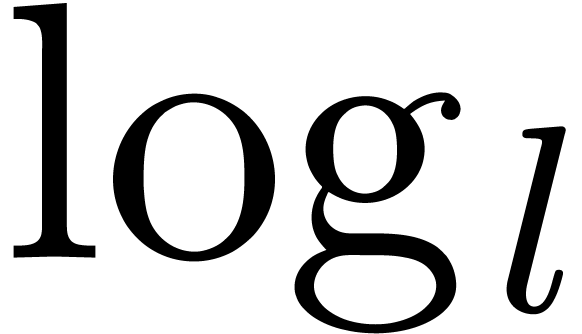 stands for the
stands for the 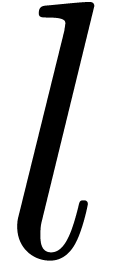 times. The infinitesimal monomials of
times. The infinitesimal monomials of
 are of the form
are of the form

 ,
, and
and  .
.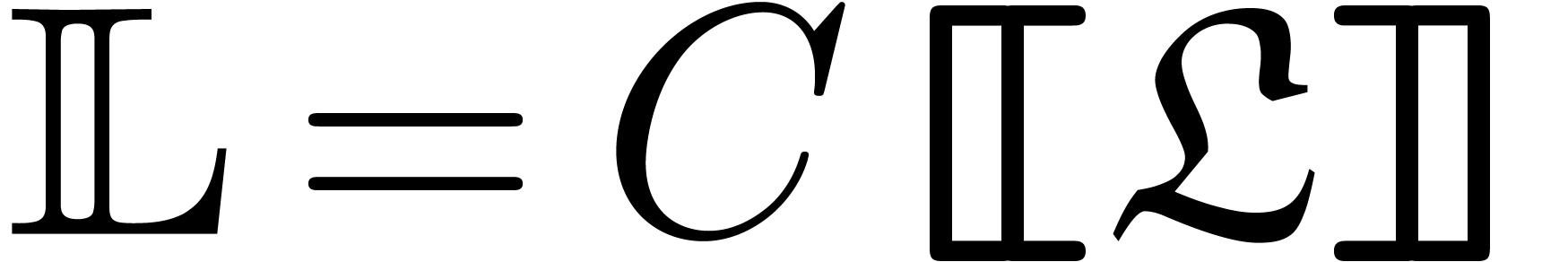 are called logarithmic transseries.
are called logarithmic transseries.
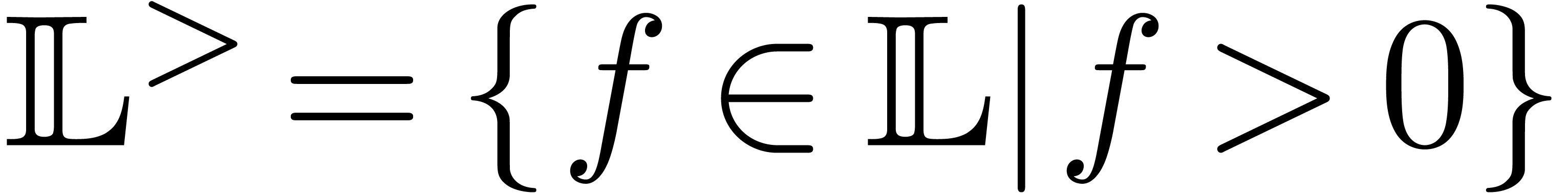 .
.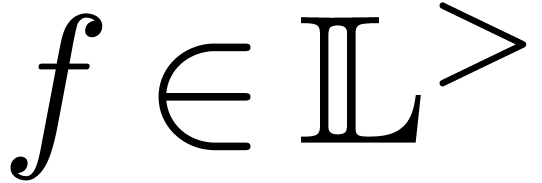 ,
,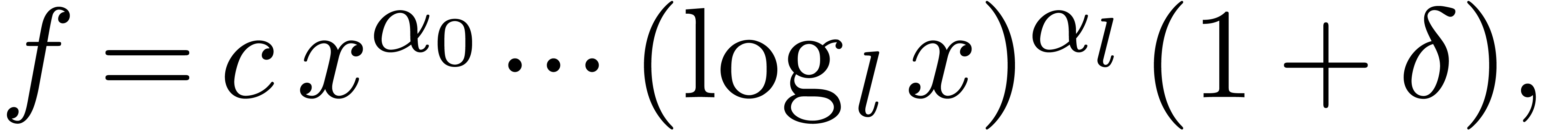
 ,
,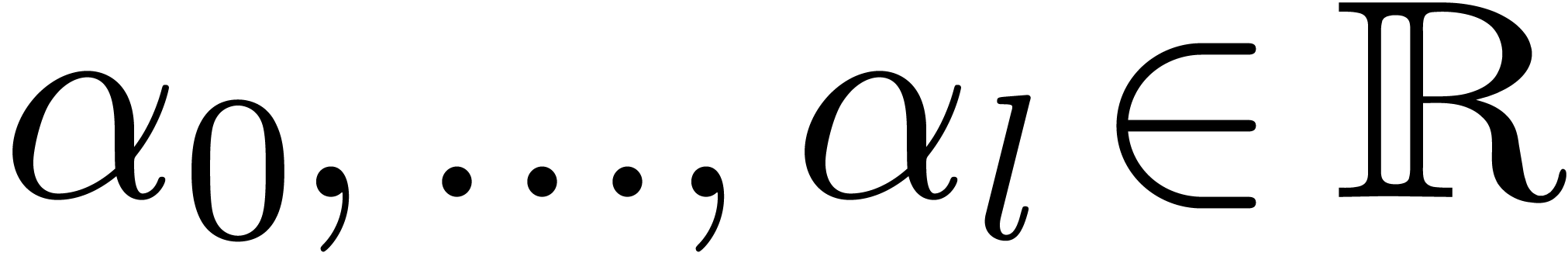 and
and  .
.
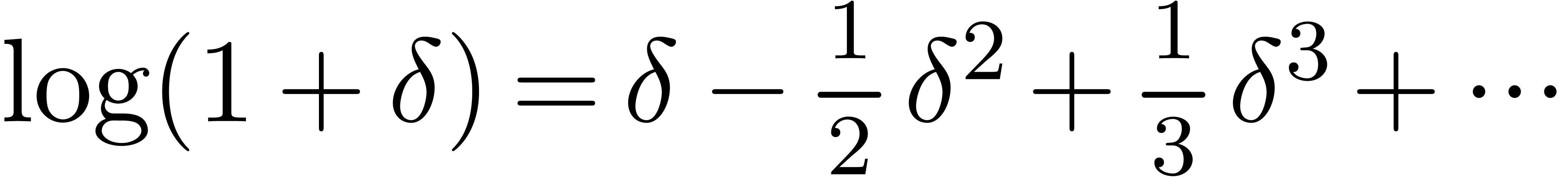 is well defined as the sum
of a grid-based family.
is well defined as the sum
of a grid-based family.
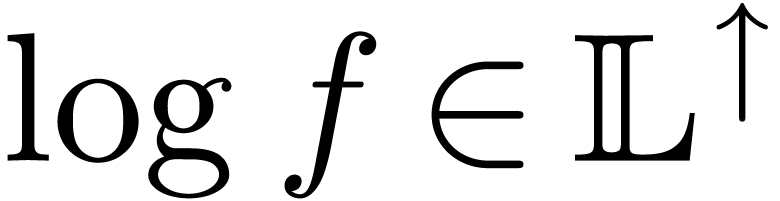 (in which case we say
that
(in which case we say
that  of
transseries of exponential depth
of
transseries of exponential depth 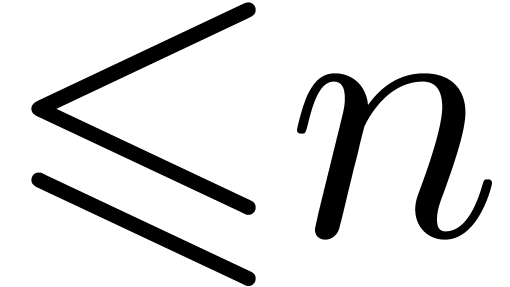 .
.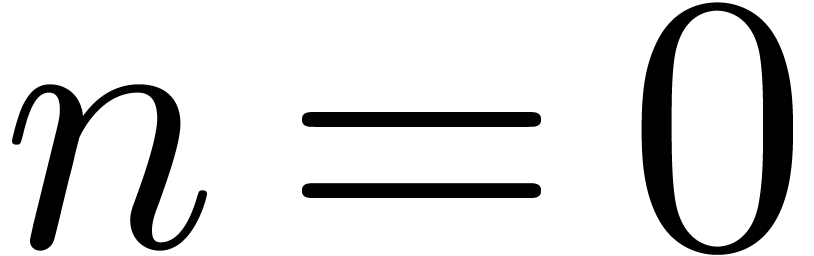 has been dealt with above. Then we take
has been dealt with above. Then we take
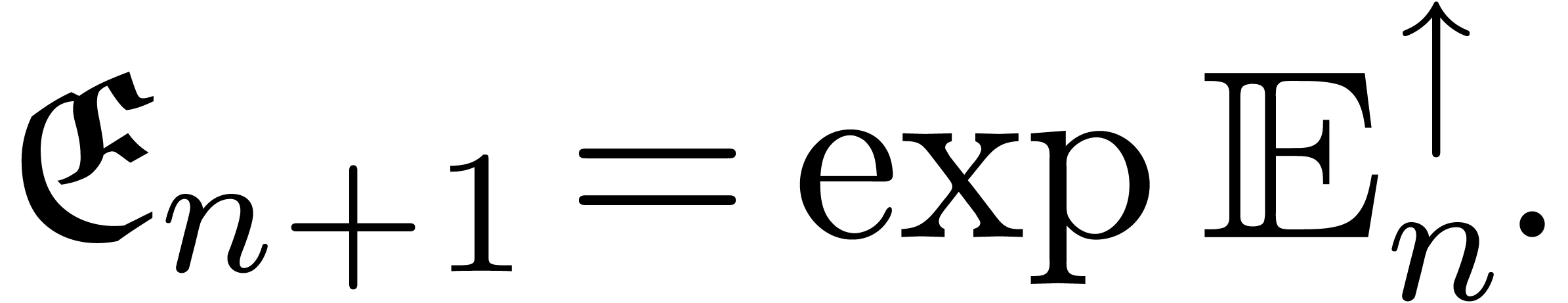
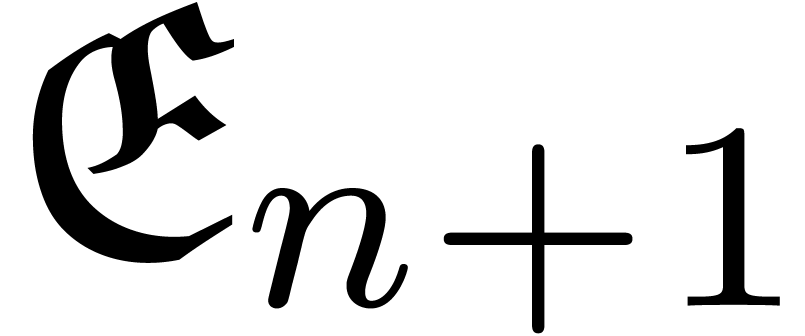 is the formal
exponential of an element in
is the formal
exponential of an element in 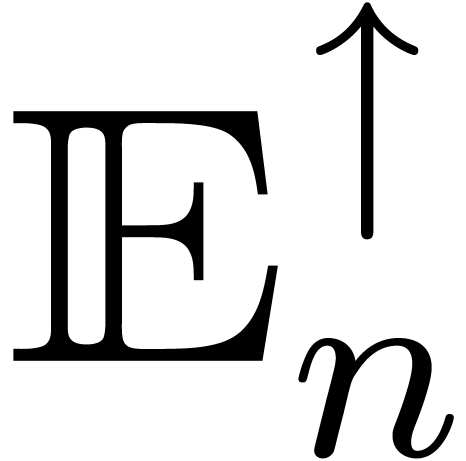 .
.
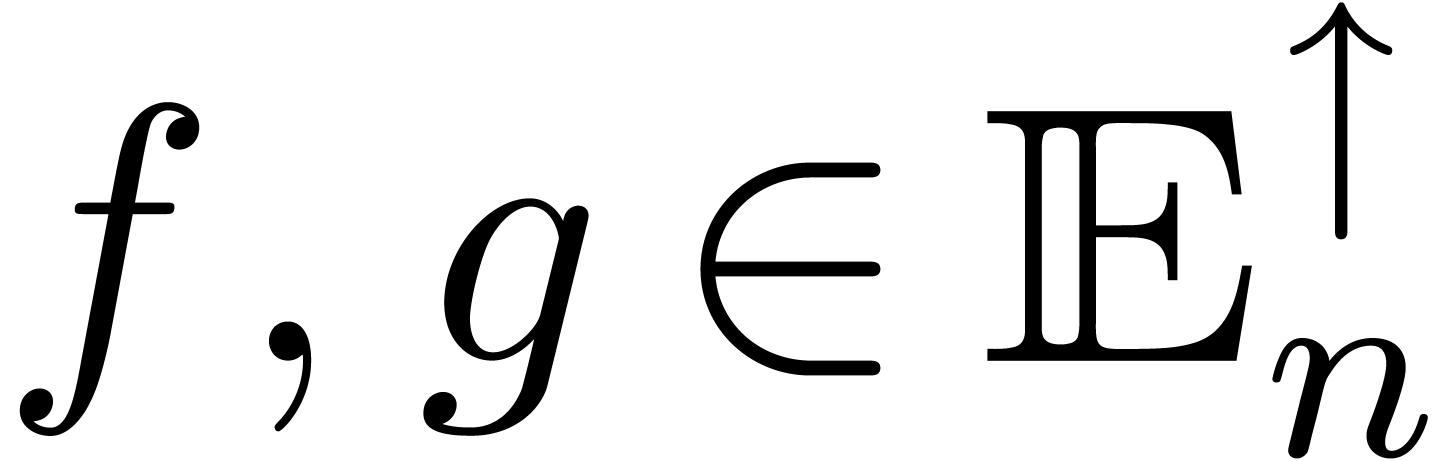 .
.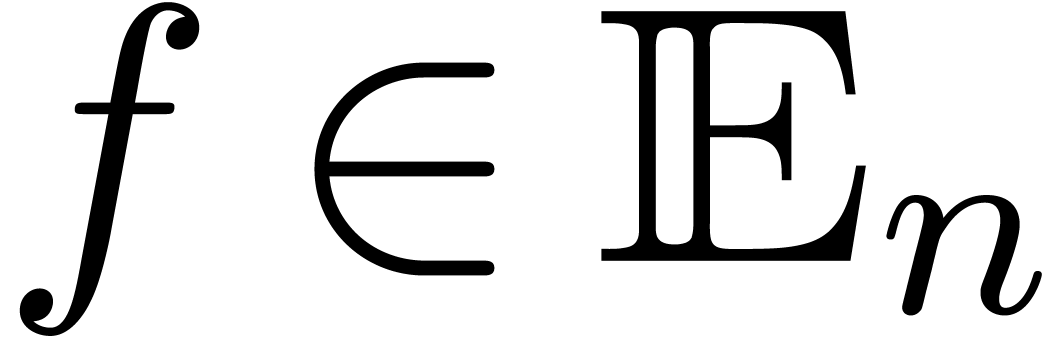 exists in
exists in
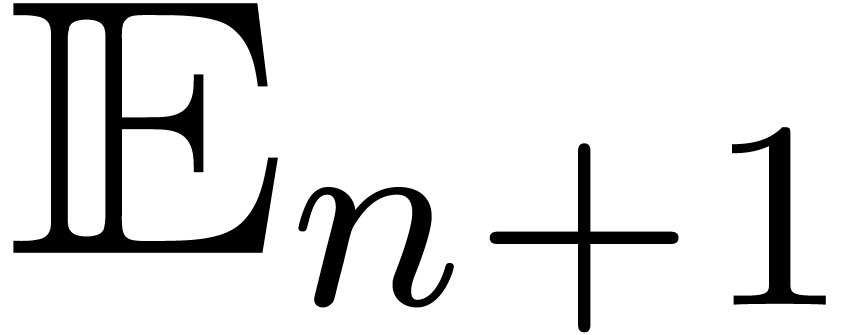 and is given by
and is given by
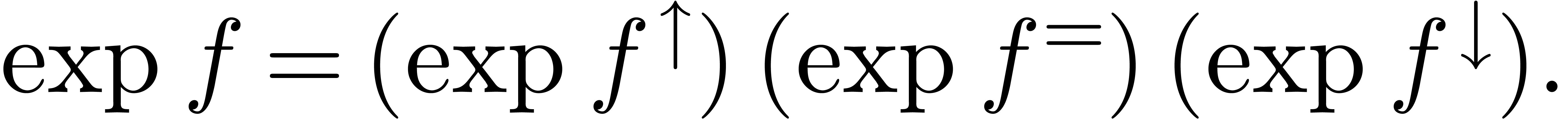
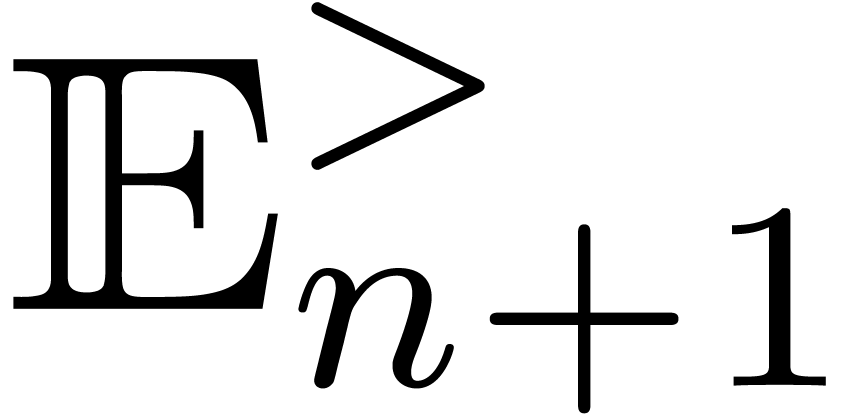 ,
,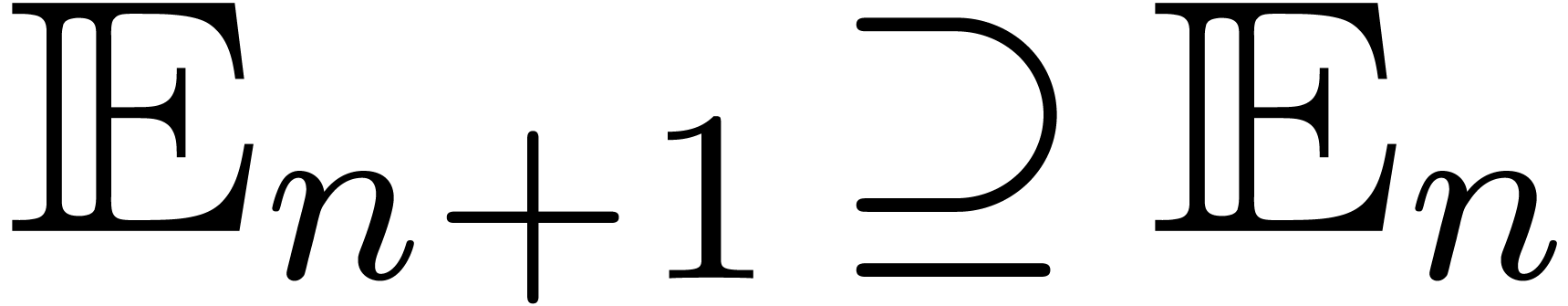 at each step.
at each step.
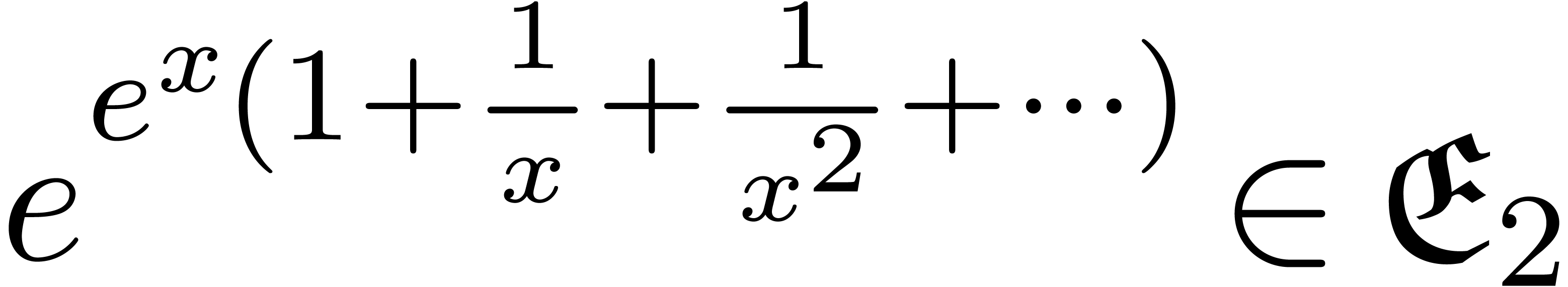 ,
,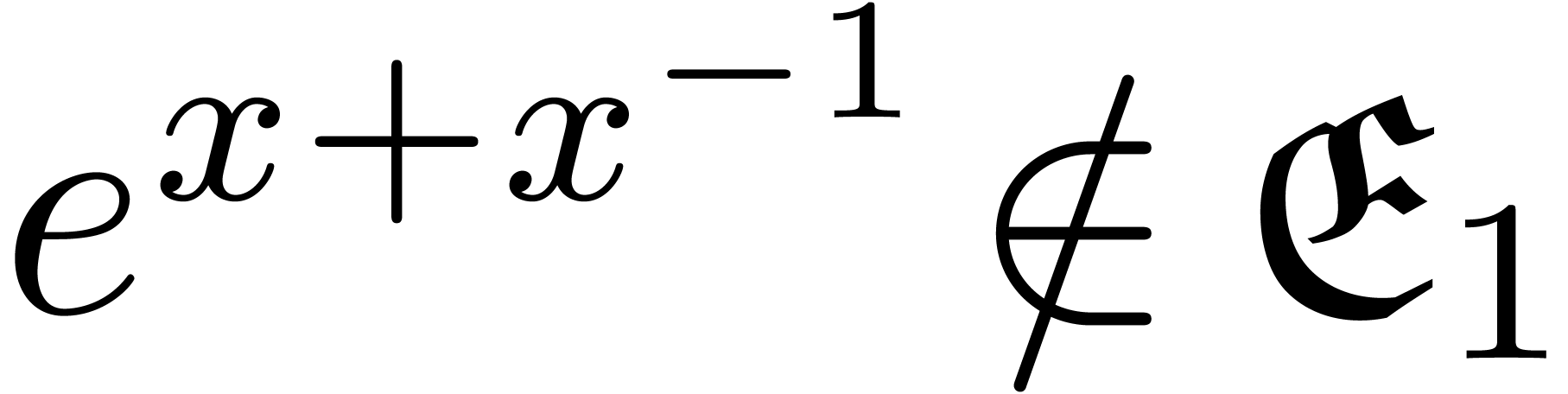 .
.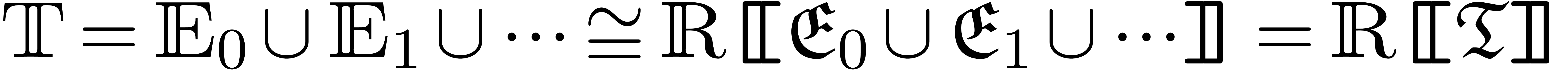
 .
.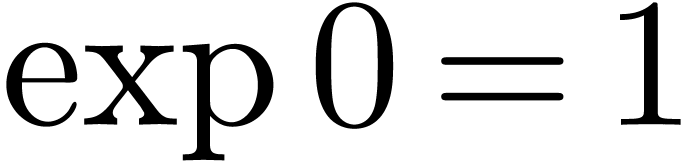 and
and 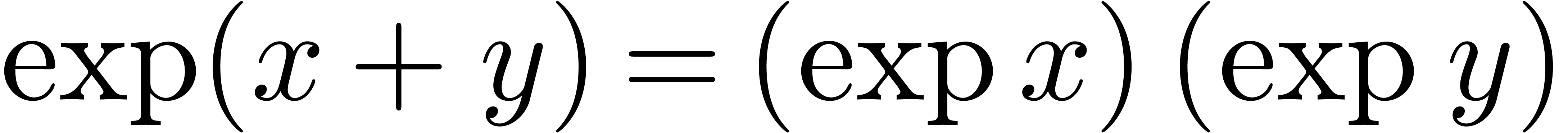 for exponentiation are satisfied in
for exponentiation are satisfied in 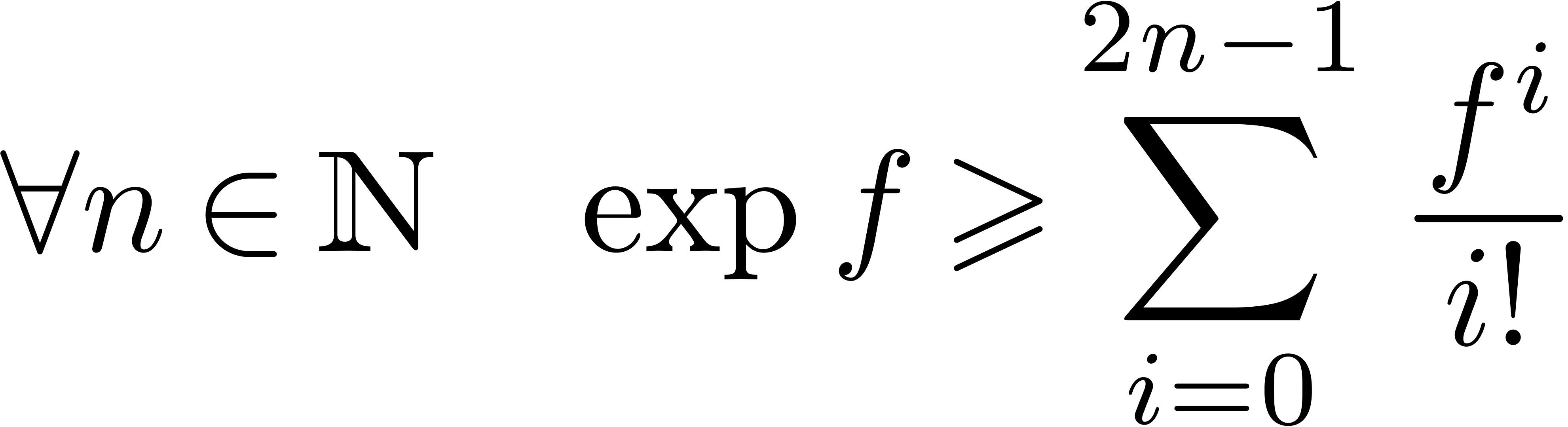
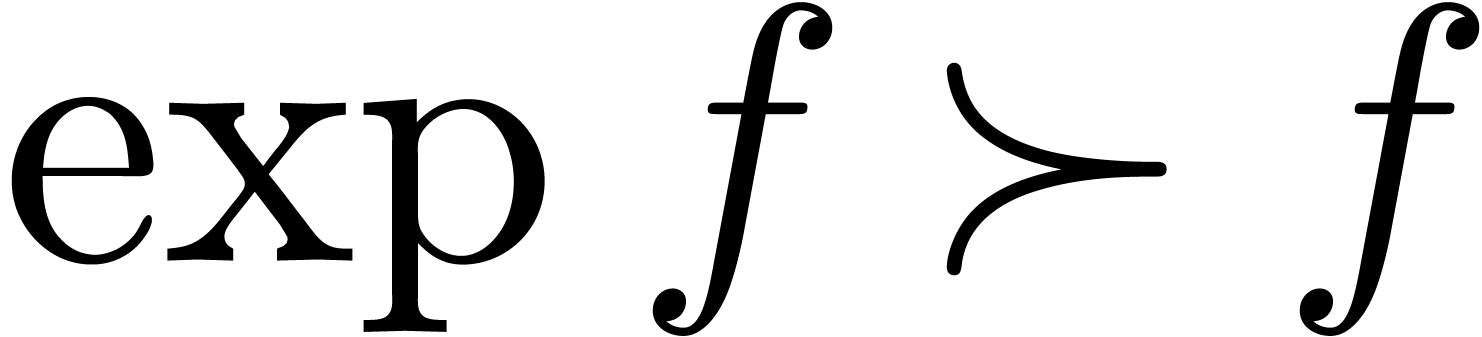 for all
for all  .
. can actually be seen as
an ordered
can actually be seen as
an ordered  is
flatter than
is
flatter than  ,
, ,
, for all
for all  .
.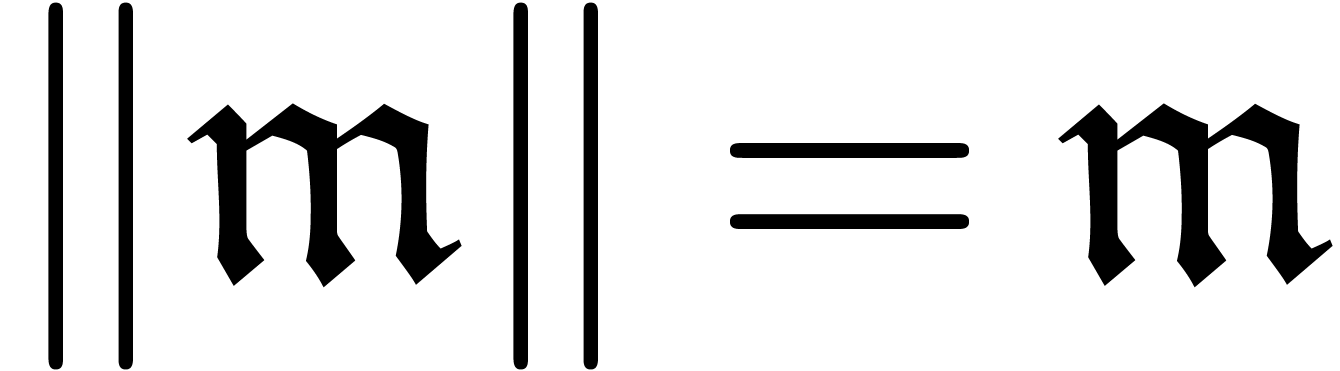 if
if  and
and 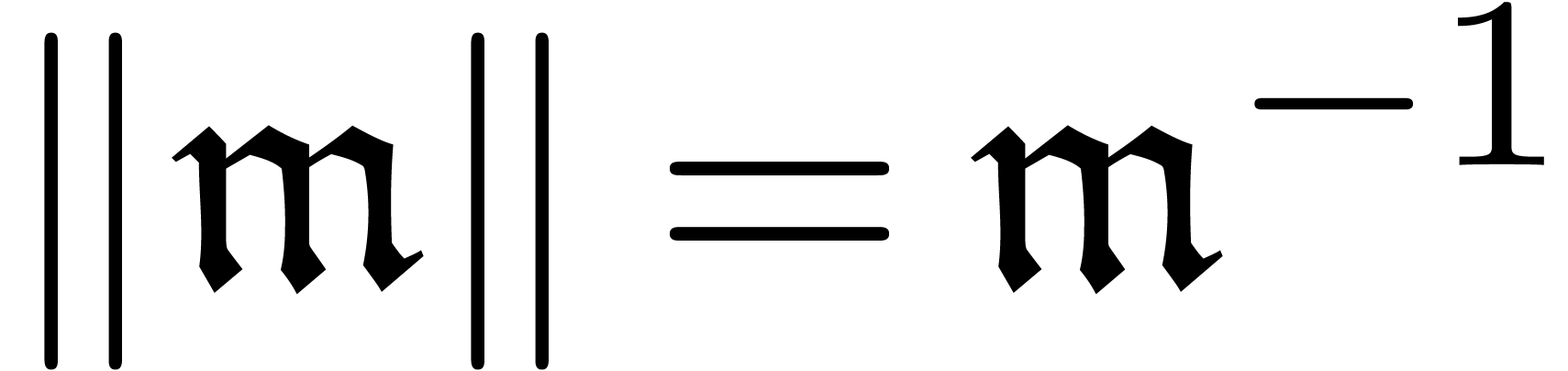 otherwise. The flatness relation can be extended to
otherwise. The flatness relation can be extended to  itself: given
itself: given  ,
,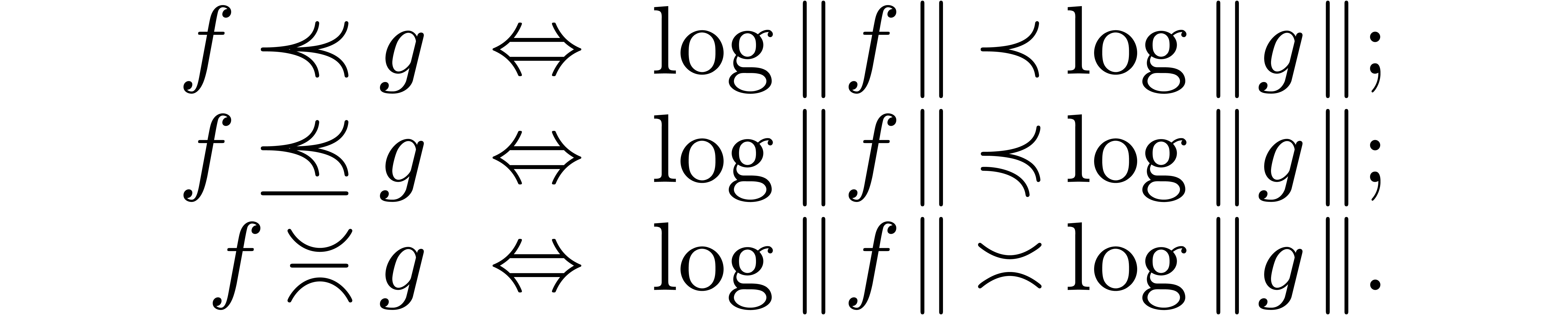
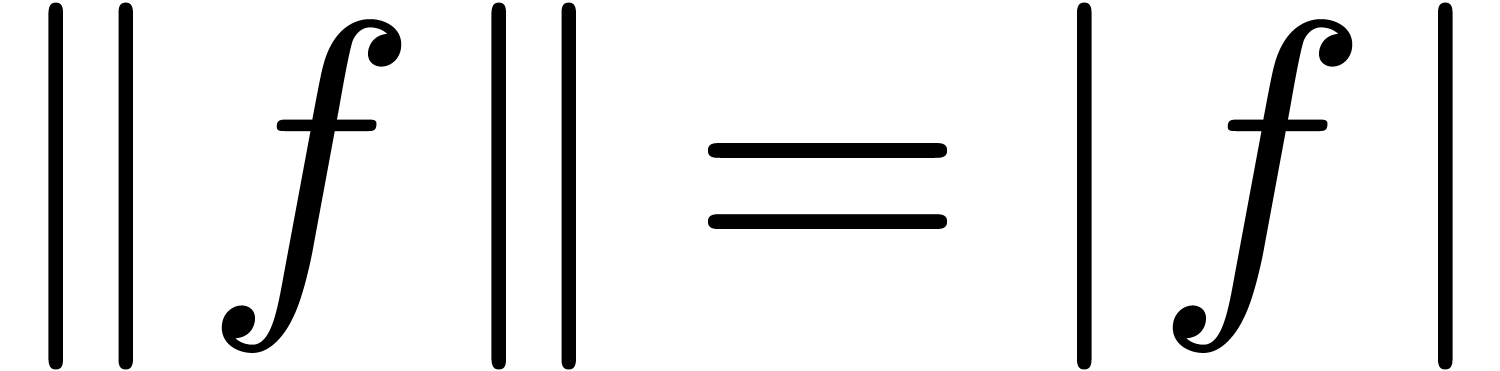 if
if  and
and 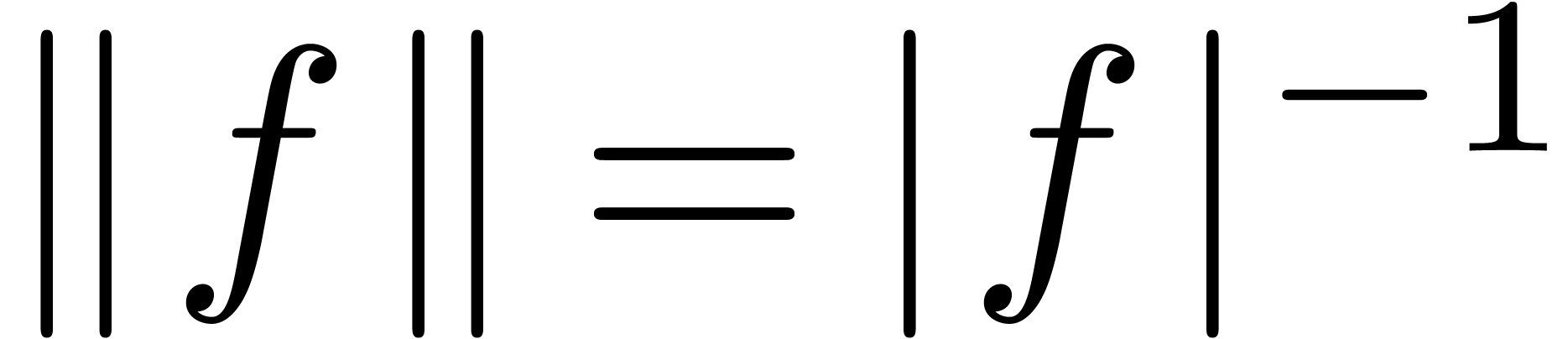 otherwise. For instance,
otherwise. For instance,  ,
, .
.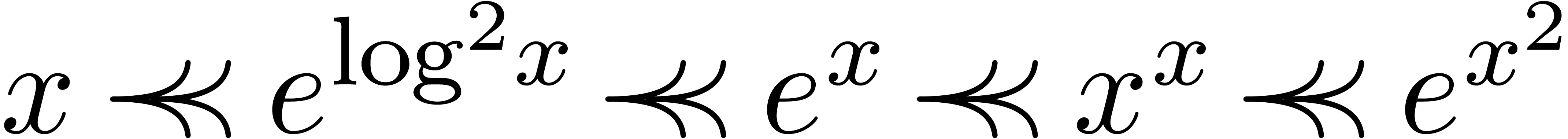 .
. ,
, and
and  .
. .
. is naturally included in
is naturally included in  may be expanded recursively
w.r.t.
may be expanded recursively
w.r.t.  :
: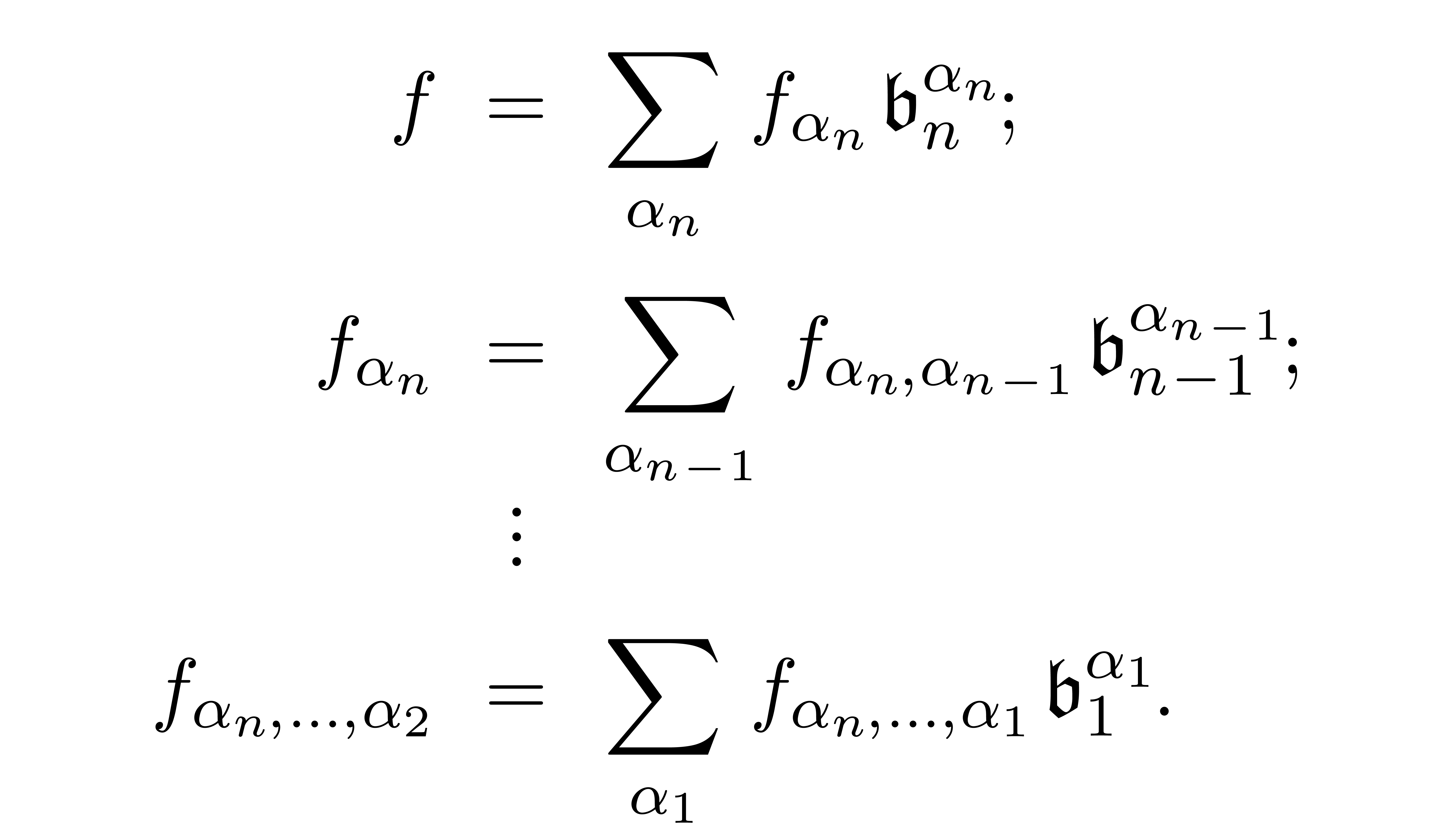
 with
with 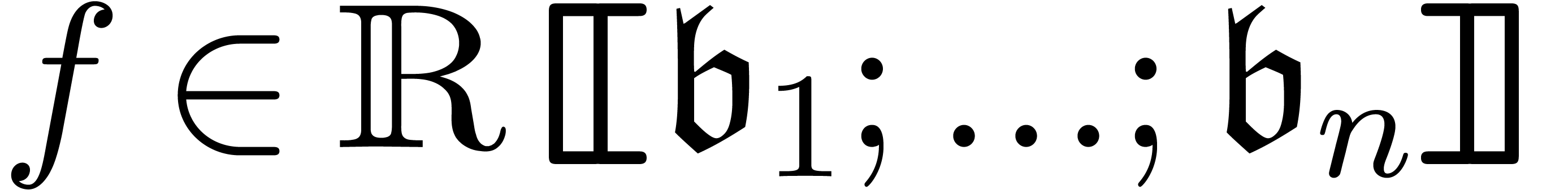 .
. to be transmonomials, although this is
not always the most convenient choice. For instance, from a
computational point, it is more efficient to see
to be transmonomials, although this is
not always the most convenient choice. For instance, from a
computational point, it is more efficient to see
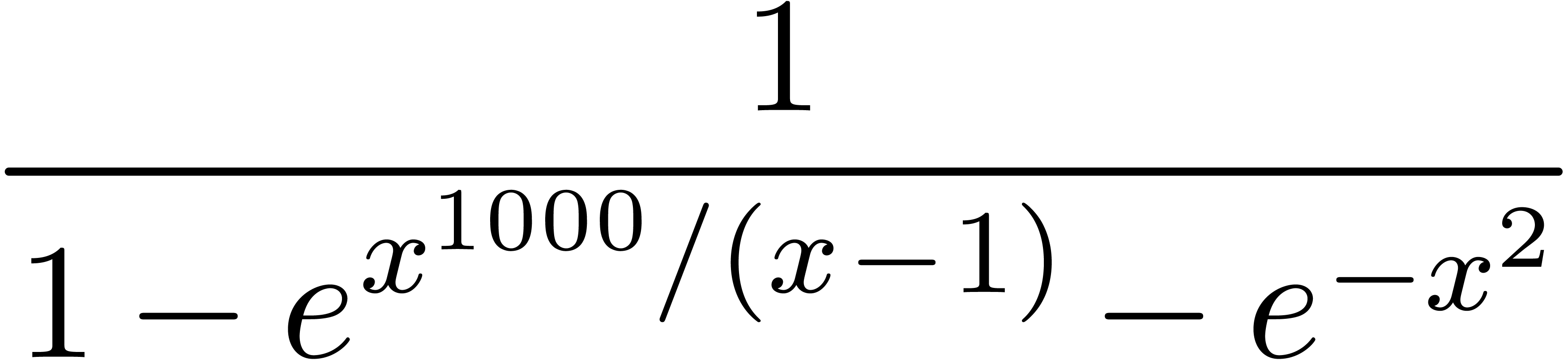
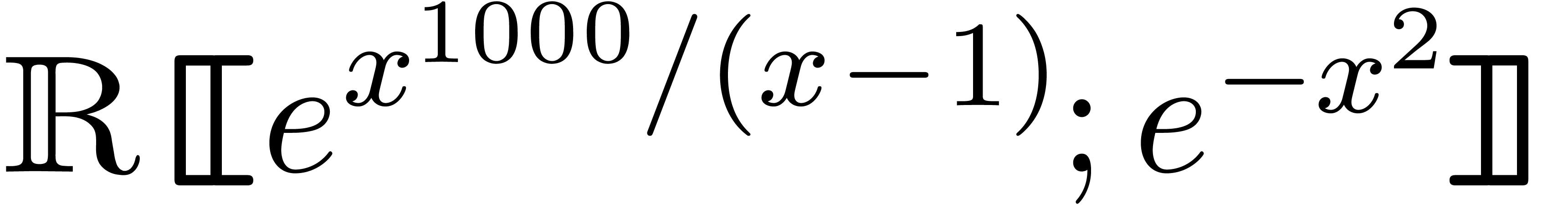 rather than
rather than 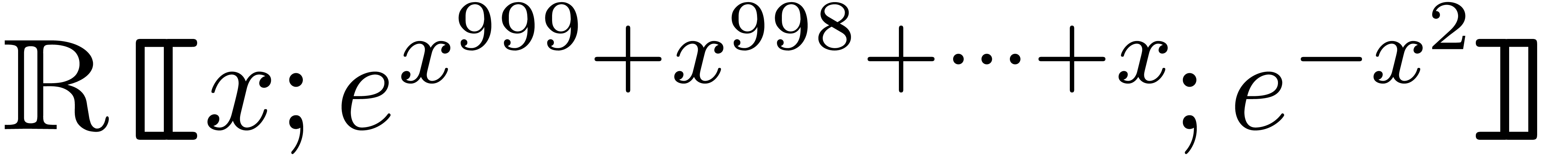 .
. .
.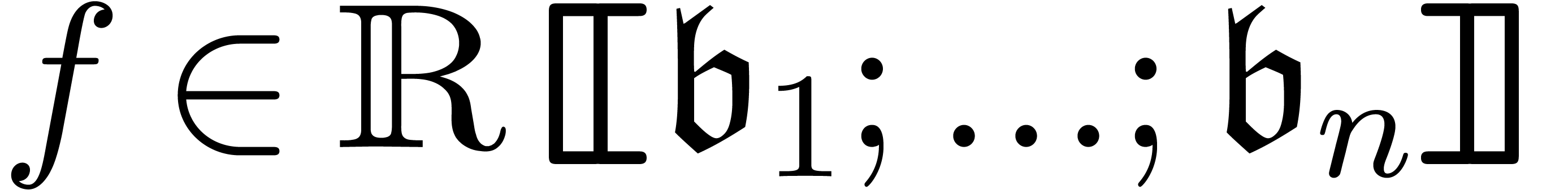 is at most
is at most  .
.
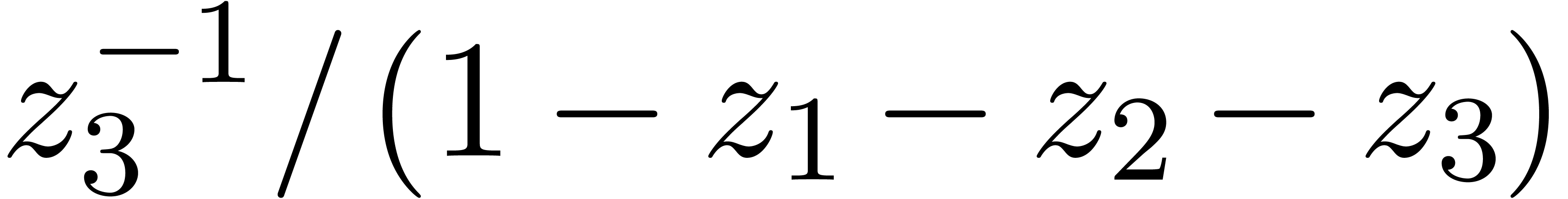 in which we substituted
in which we substituted 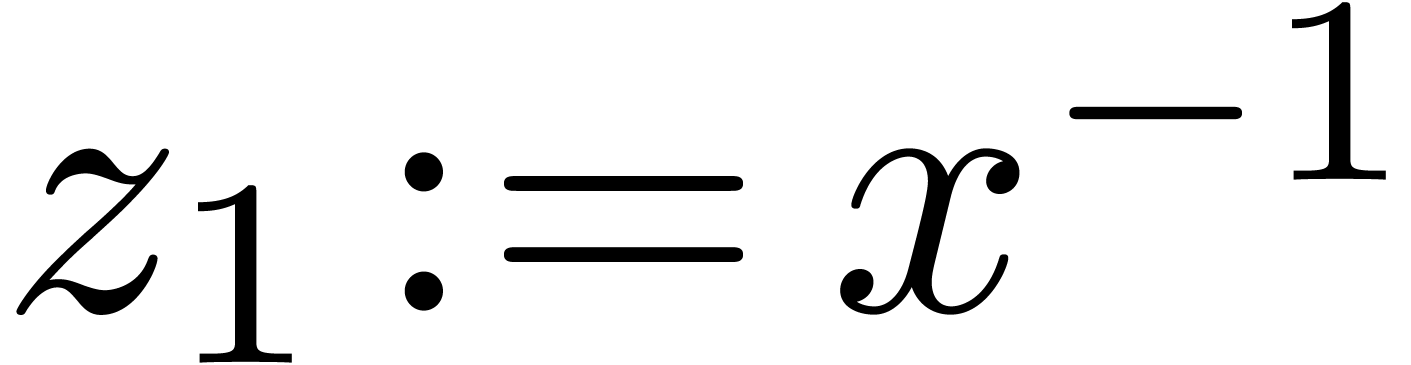 ,
,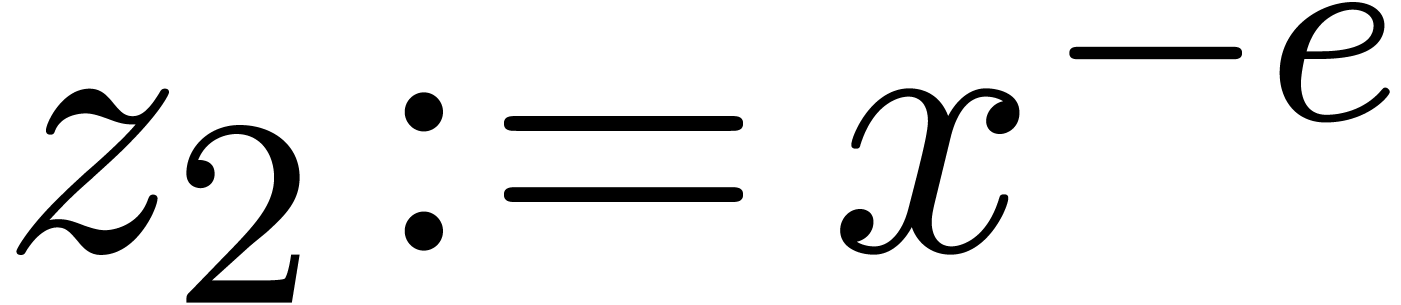 ,
,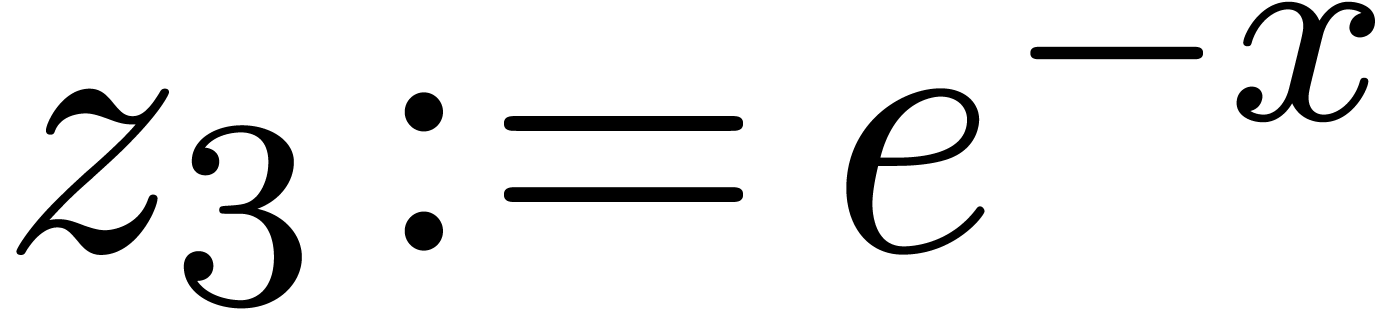 .
.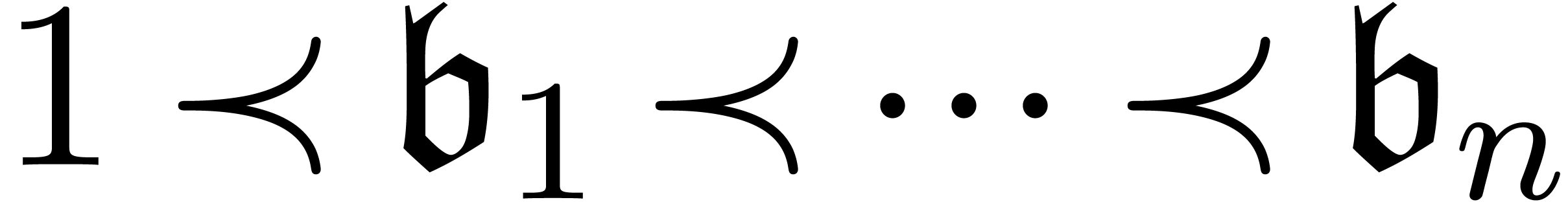 .
.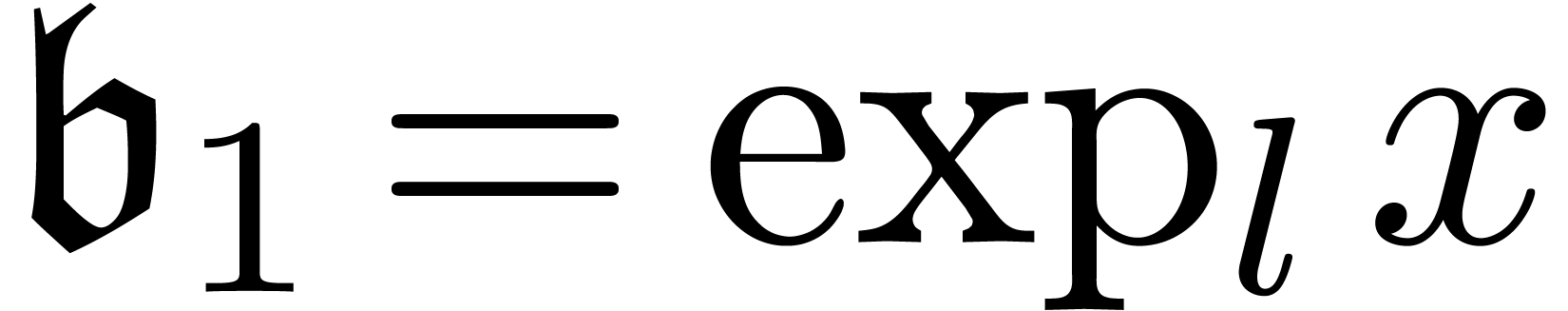 ,
, .
.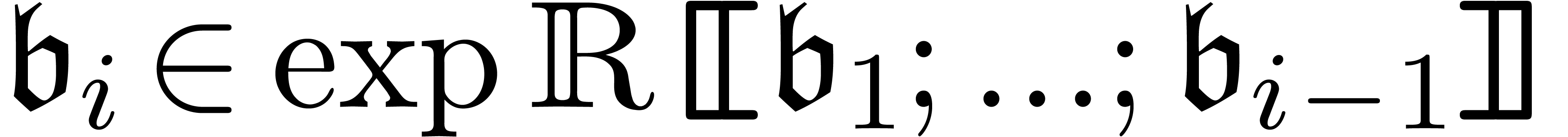 for
for  .
. be a transbasis and
be a transbasis and 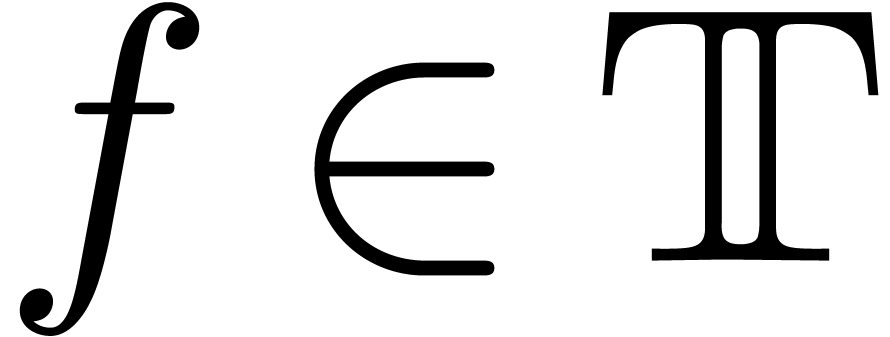 a transseries.
Then there exists a supertransbasis
a transseries.
Then there exists a supertransbasis  ,
, .
.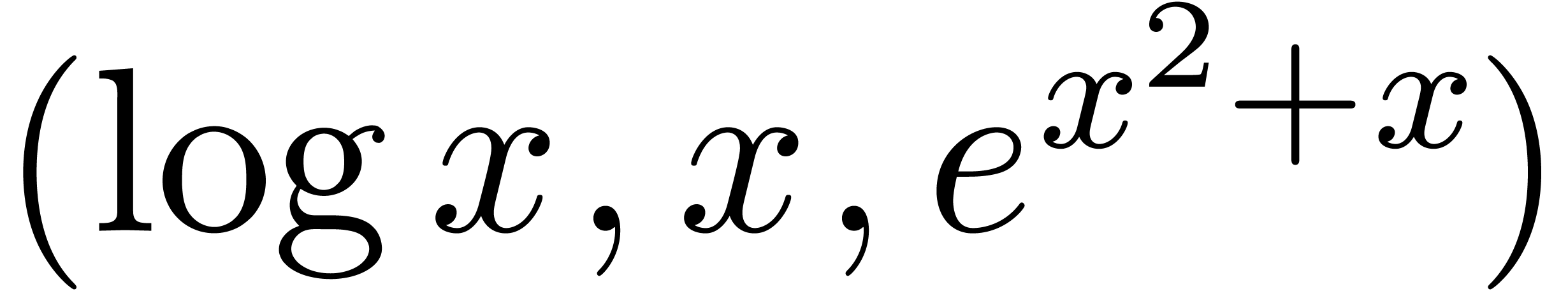 is a transbasis and
is a transbasis and 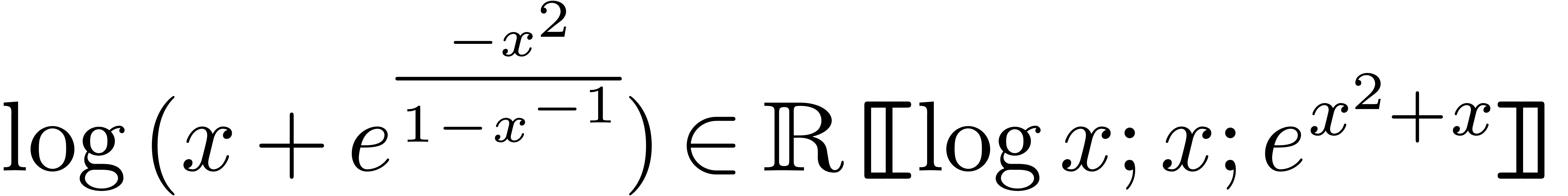 .
.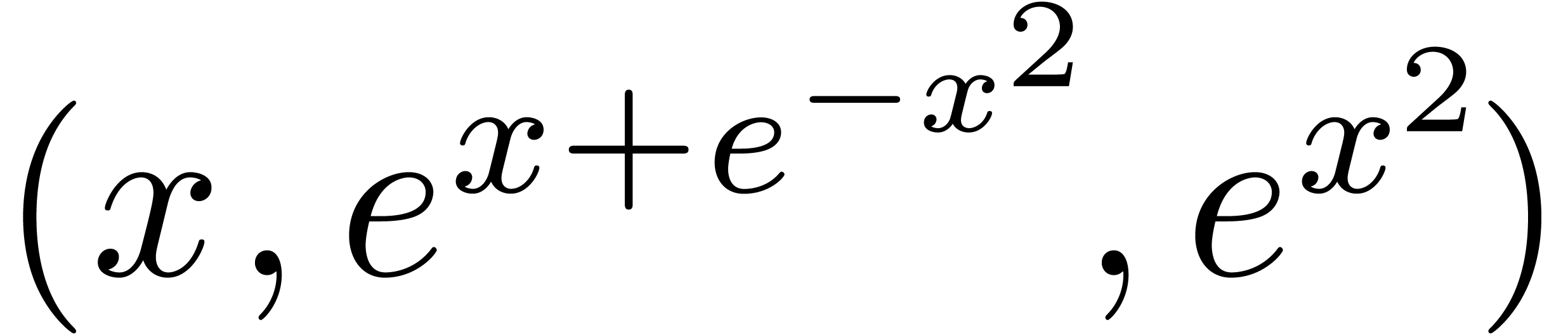 is not a transbasis.
is not a transbasis.
 as follows. We start by defining the differentiation on the monomial
group
as follows. We start by defining the differentiation on the monomial
group  .
.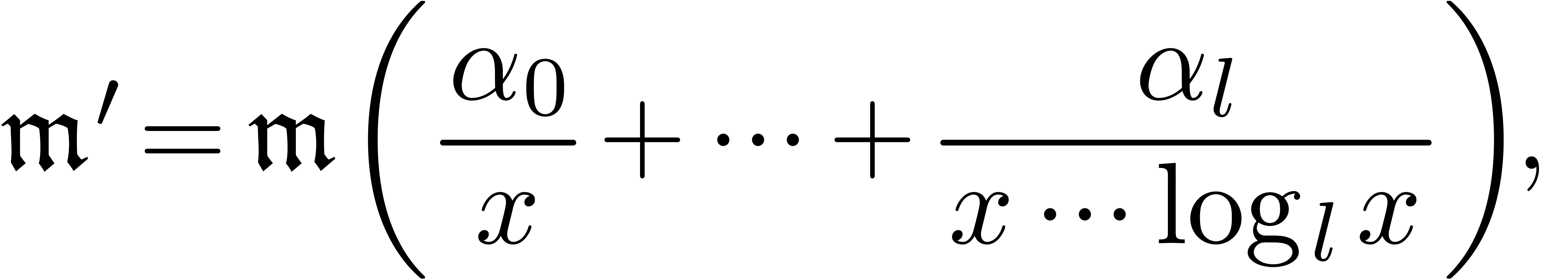
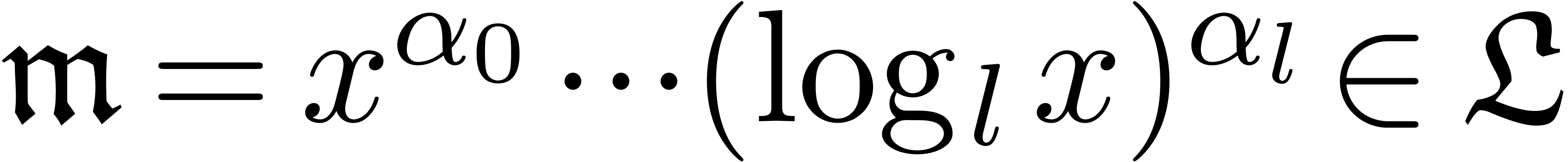 .
. ,
,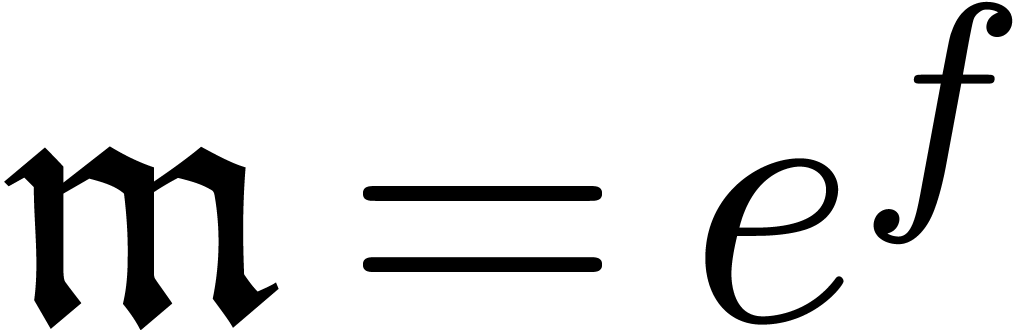 for some
for some 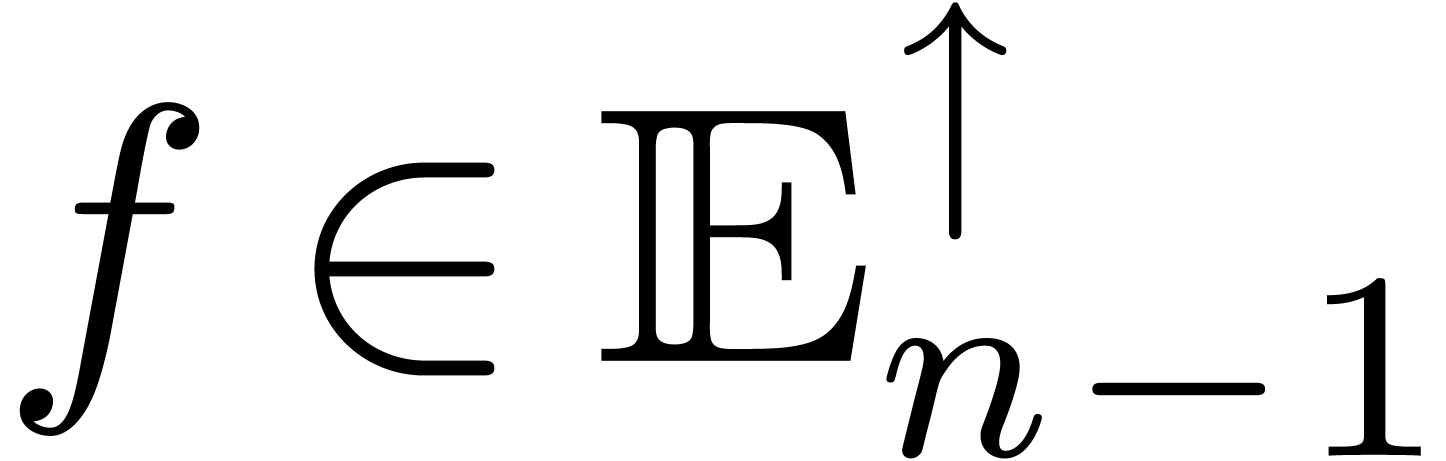 and we define
and we define
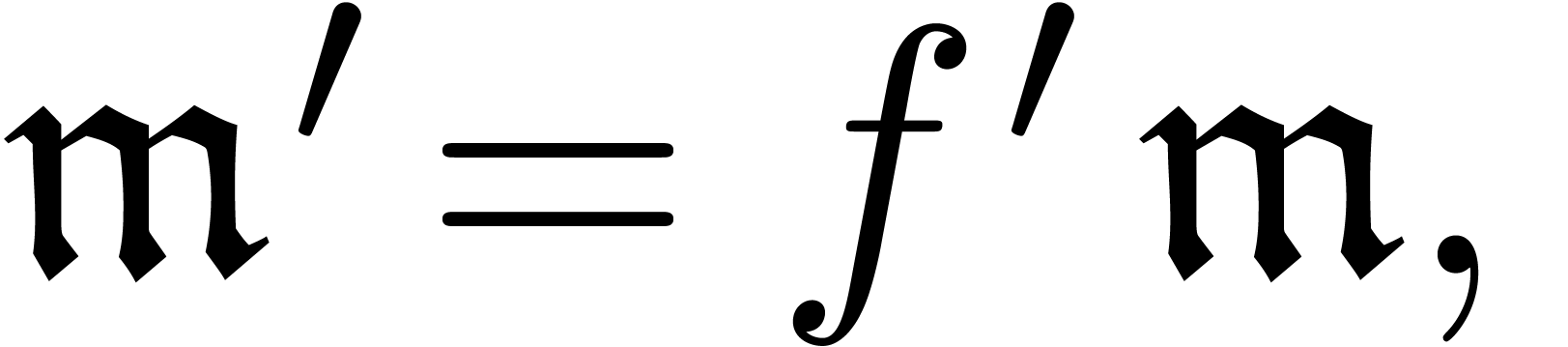
 has already been defined by the induction
hypothesis. Having defined the derivative of each monomial in
has already been defined by the induction
hypothesis. Having defined the derivative of each monomial in 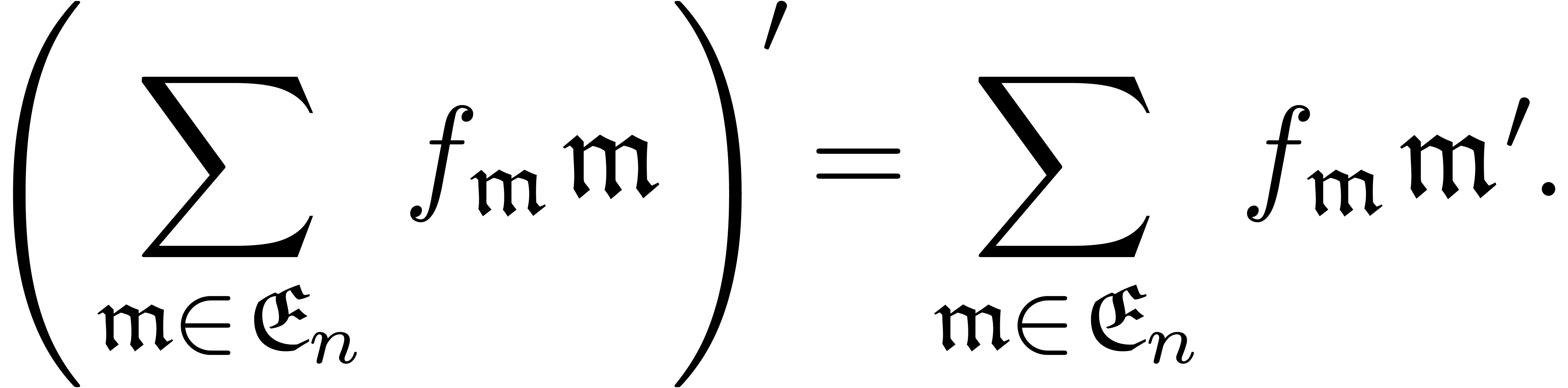
 of
of 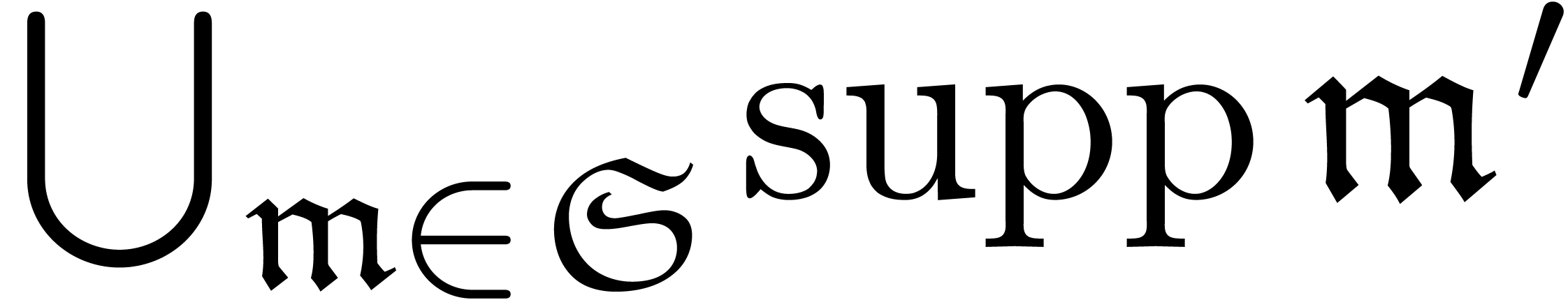 is again grid-based. Now if
is again grid-based. Now if  and
and  are such that
are such that  ,
,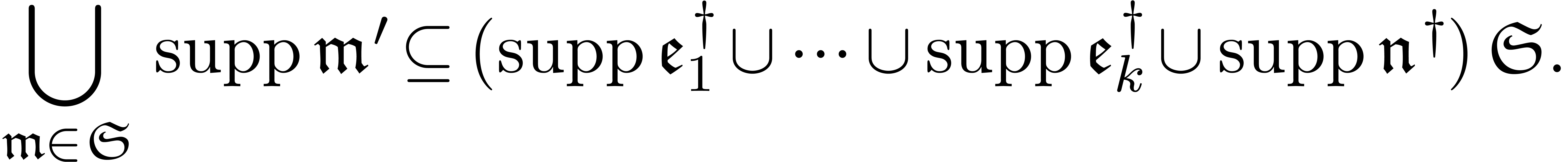
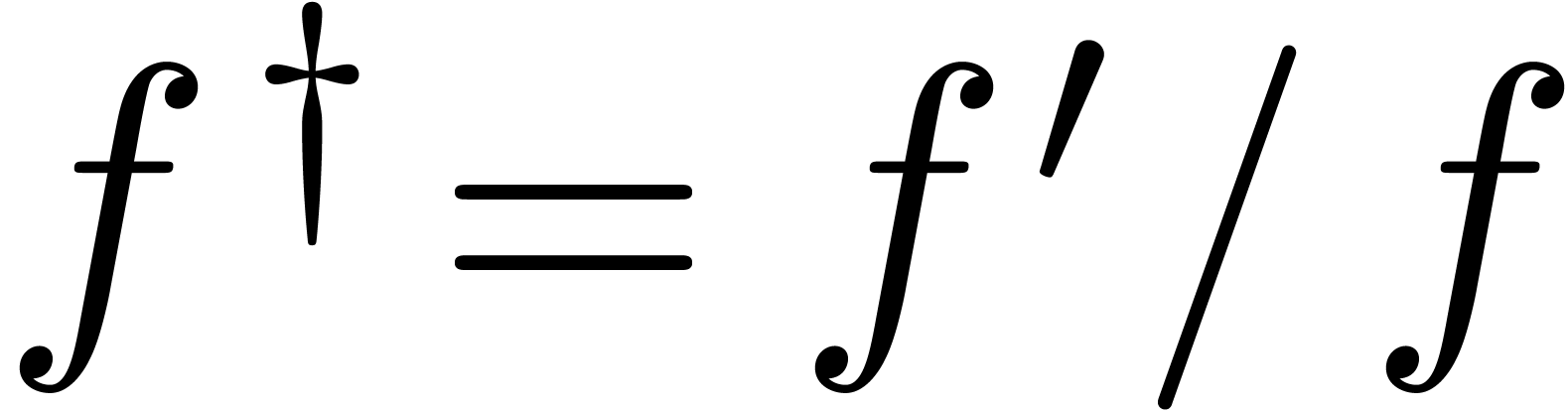 denotes the logarithmic derivative of
denotes the logarithmic derivative of 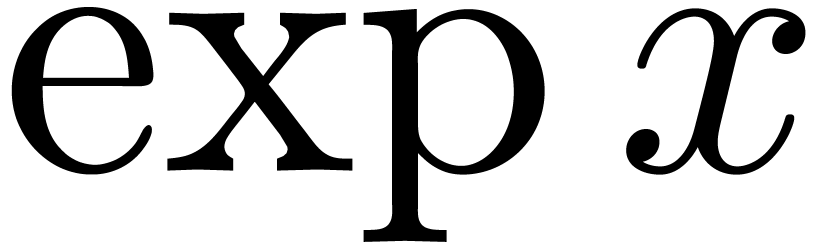 resp.
resp. 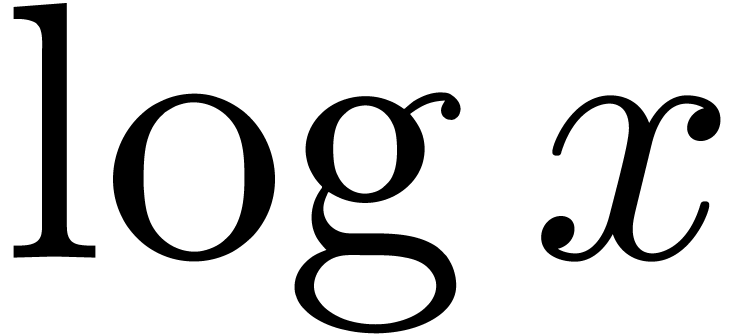 for
for 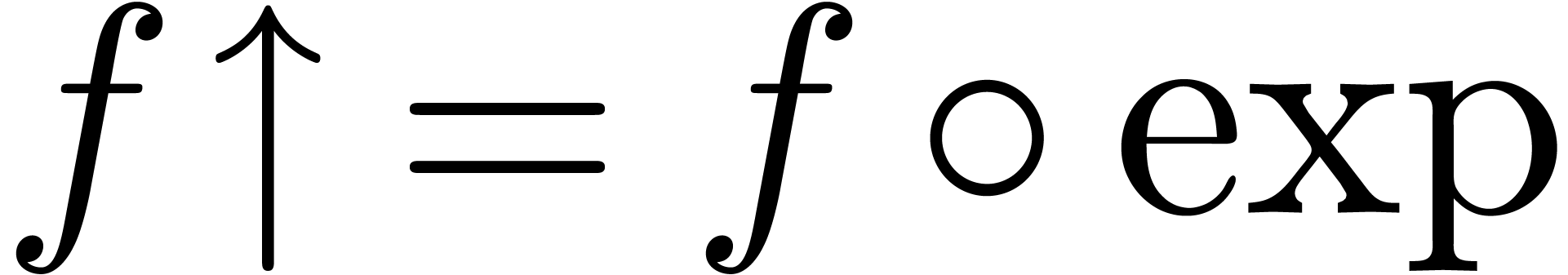 for the upward shifting of
a transseries
for the upward shifting of
a transseries 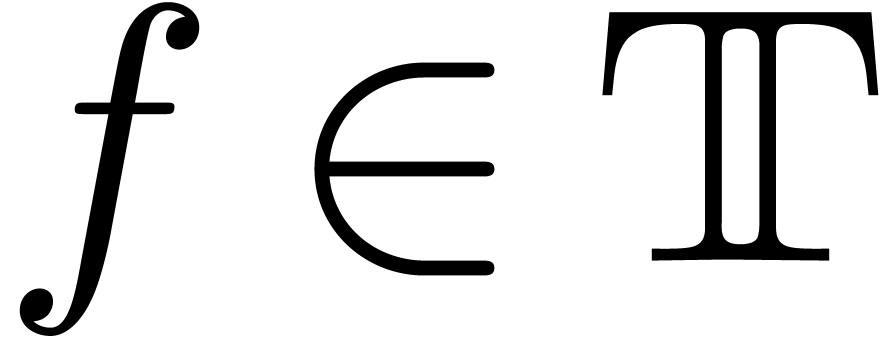 and
and 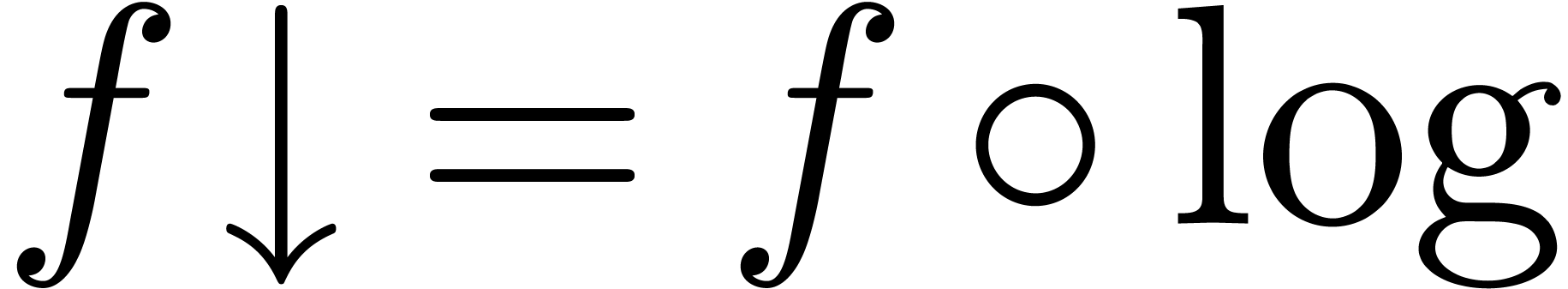 for
its downward shifting.
for
its downward shifting.

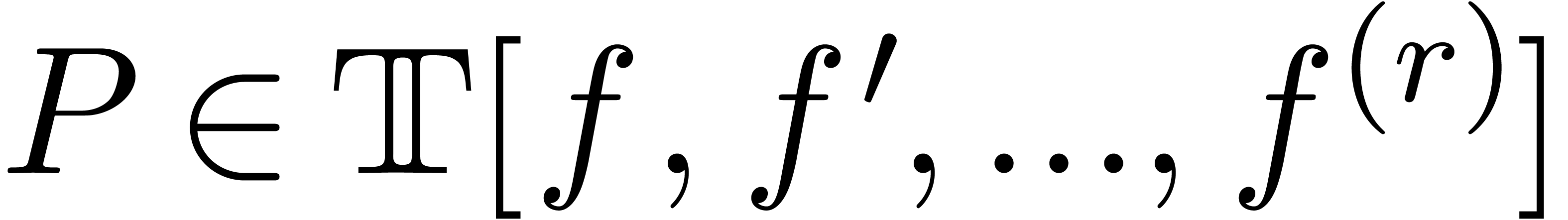 is a differential polynomial with
transseries coefficients and
is a differential polynomial with
transseries coefficients and  a transmonomial. We
also allow
a transmonomial. We
also allow  to be a formal monomial with
to be a formal monomial with  (i.e.
(i.e.  for all
for all
 ),
),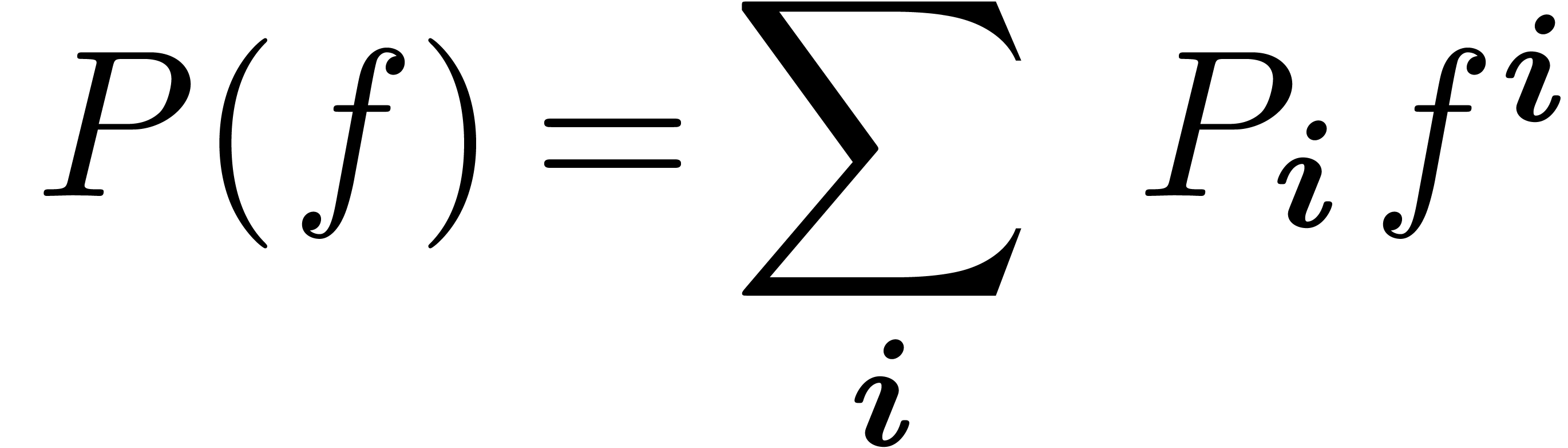
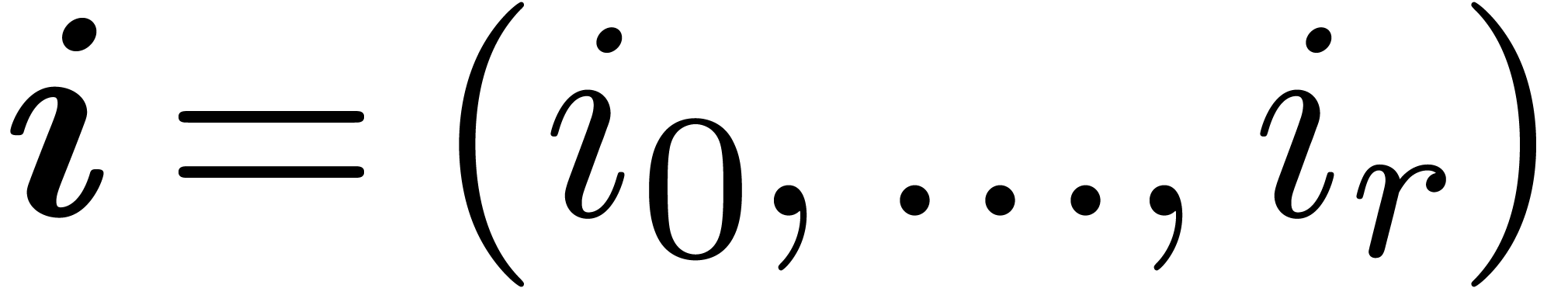 and
and 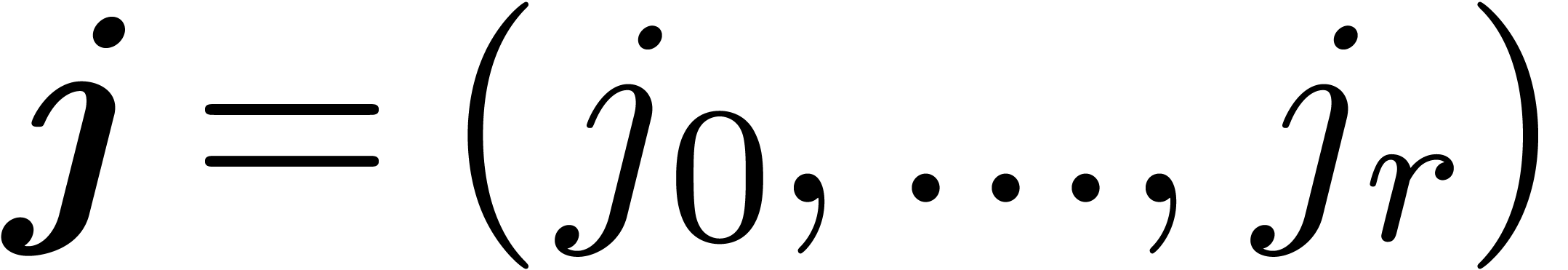 of non-negative integers:
of non-negative integers:
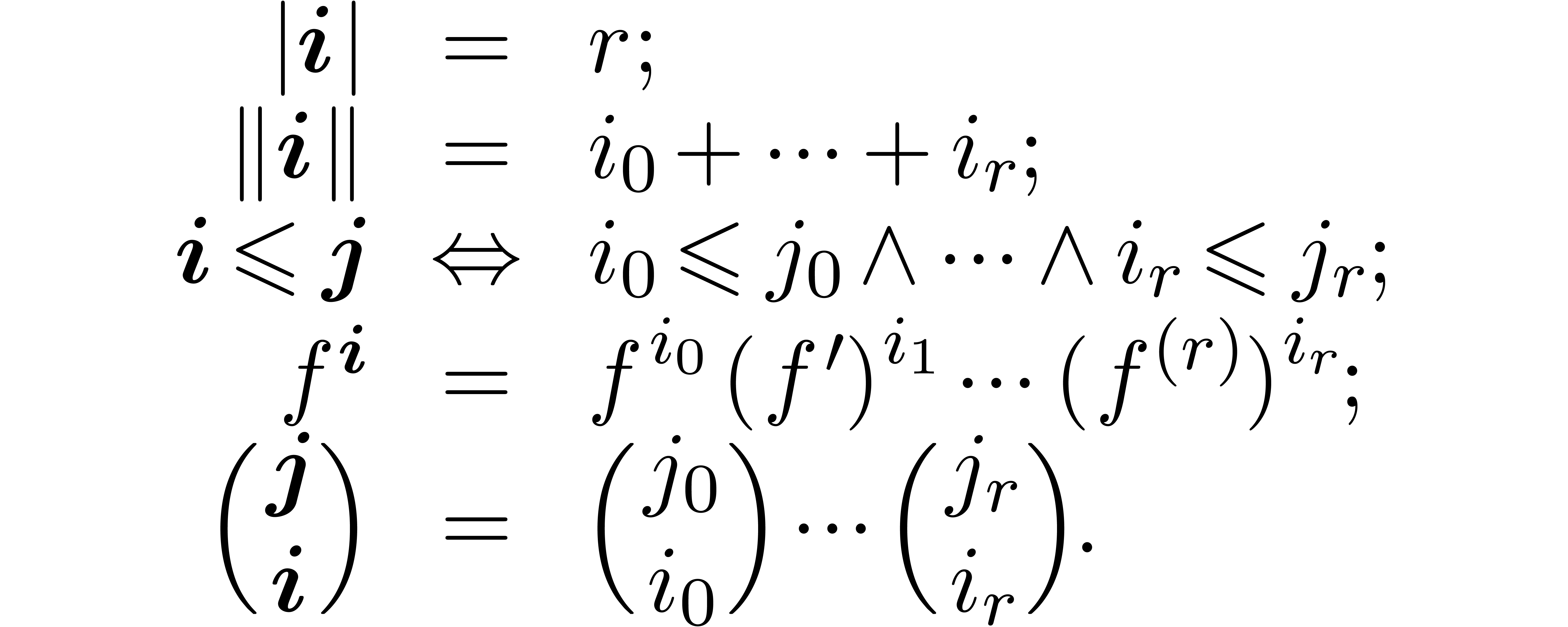
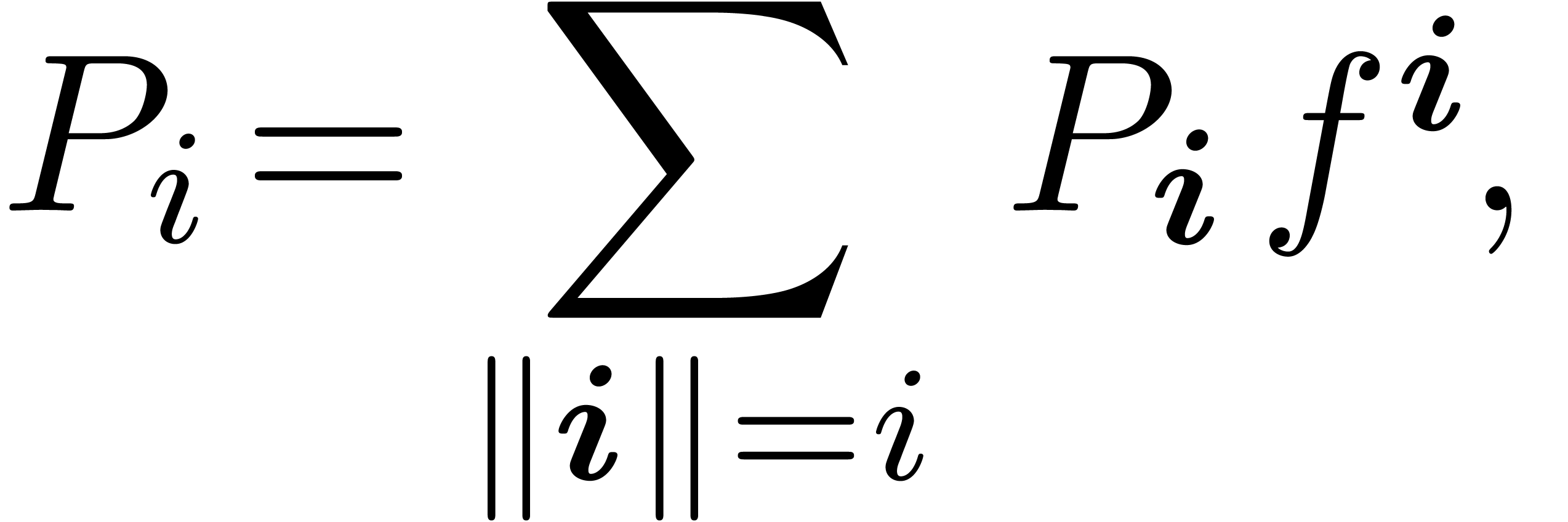
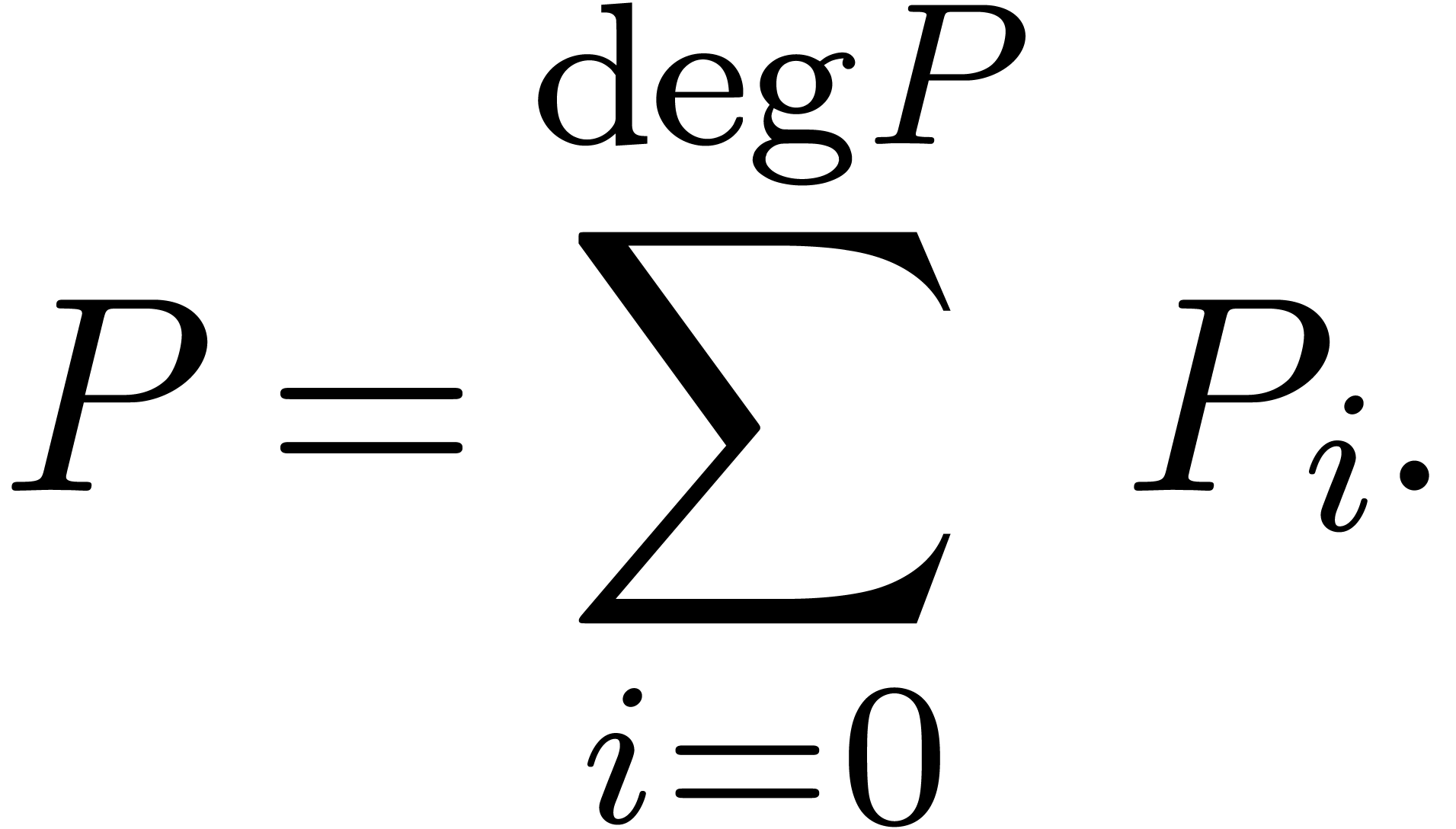
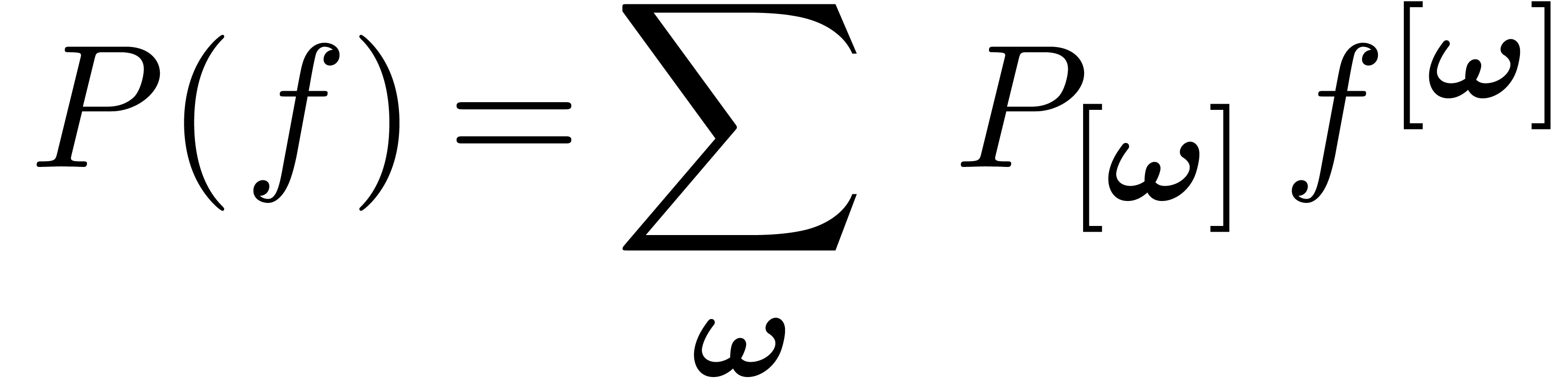
 runs through tuples
runs through tuples 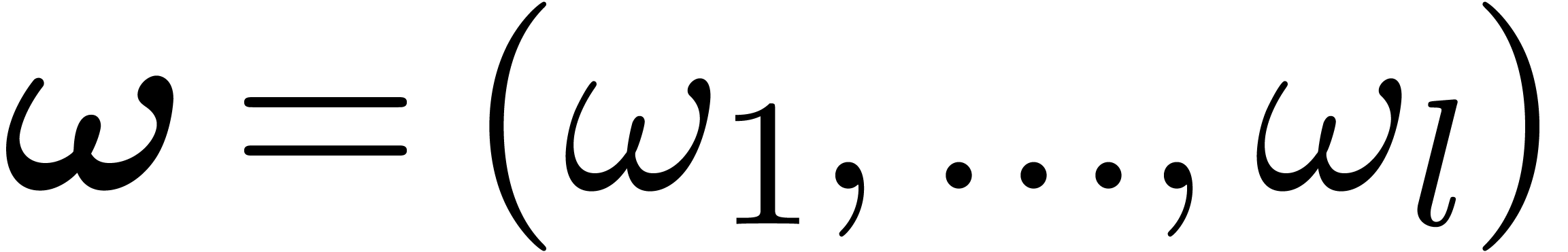 of integers in
of integers in  of length
of length  ,
,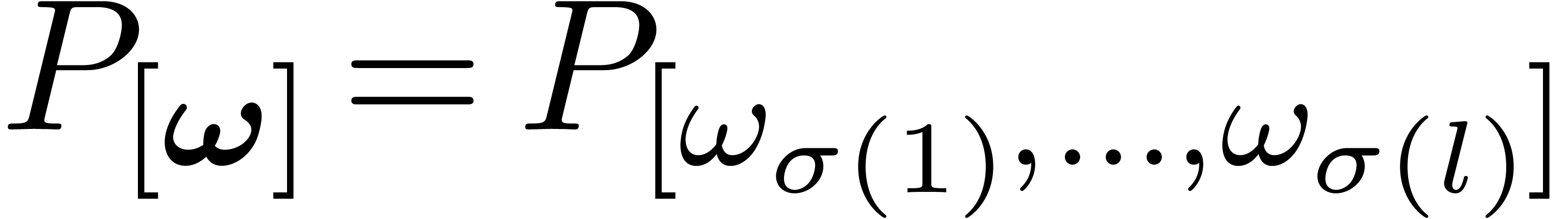 for
all permutations of integers. We again use vector notation for such
tuples
for
all permutations of integers. We again use vector notation for such
tuples
 the weight of
the weight of 
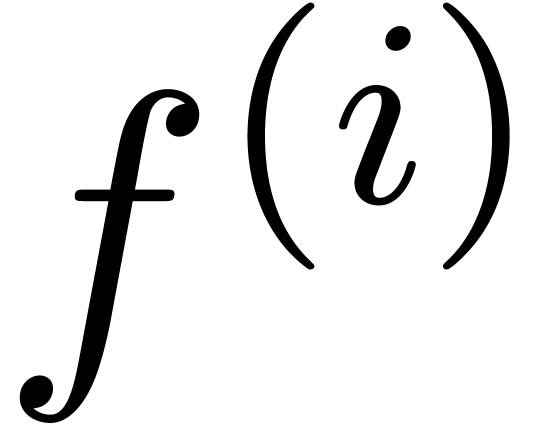 can be rewritten as a polynomial in
terms of
can be rewritten as a polynomial in
terms of 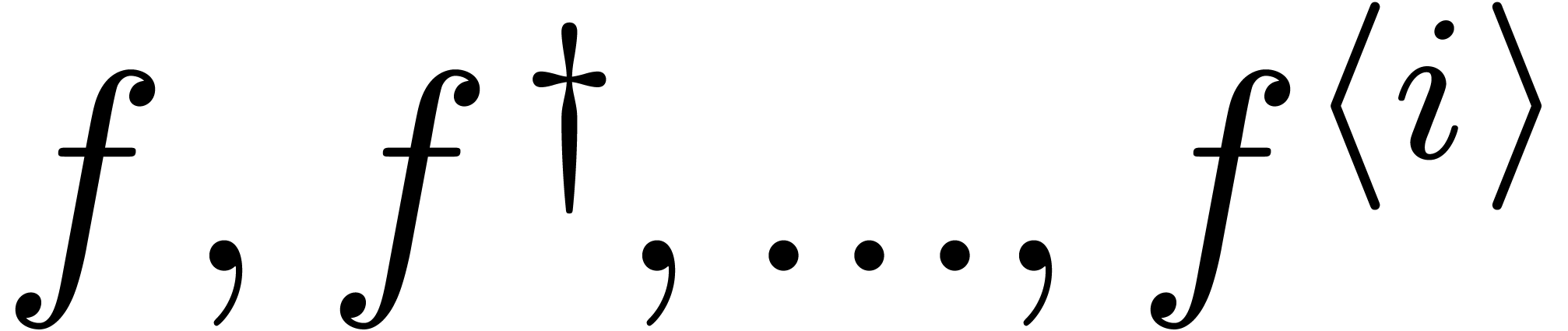 :
:
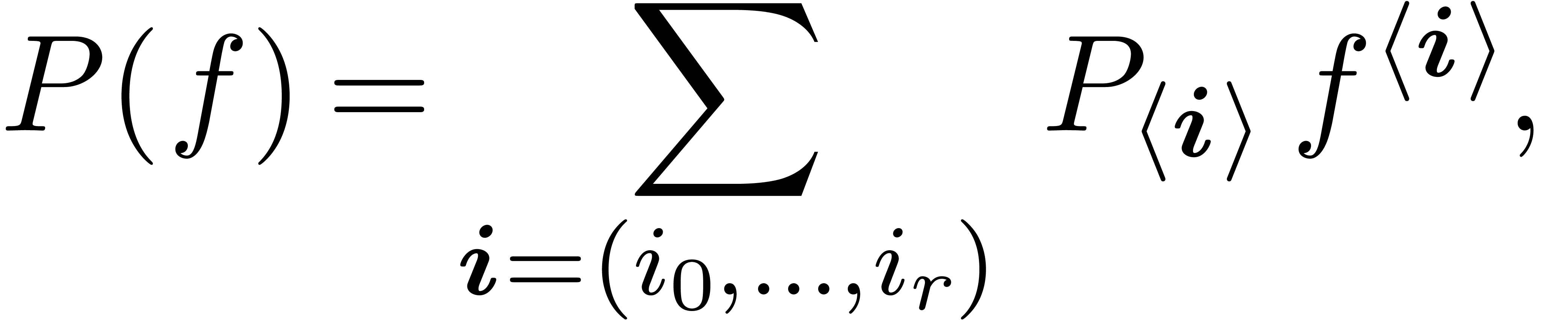
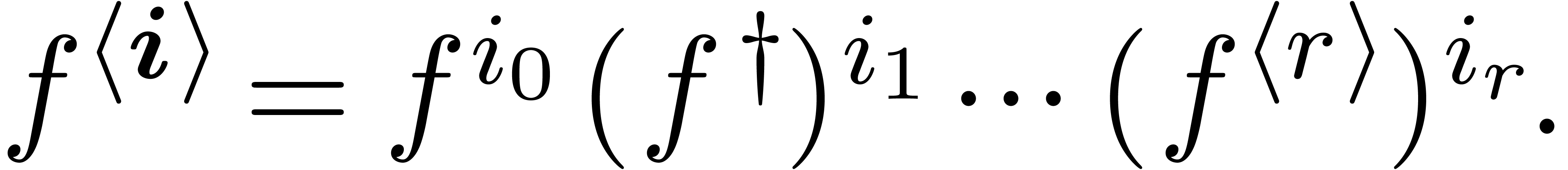
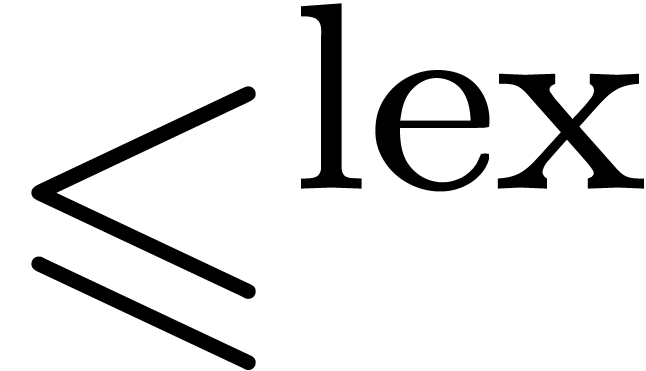 on
on
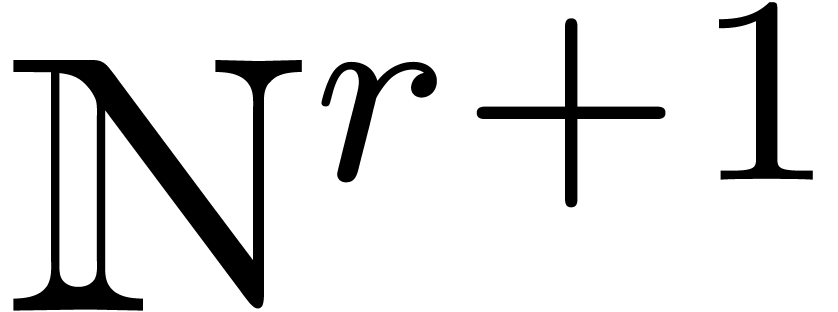 ,
,
 for
for 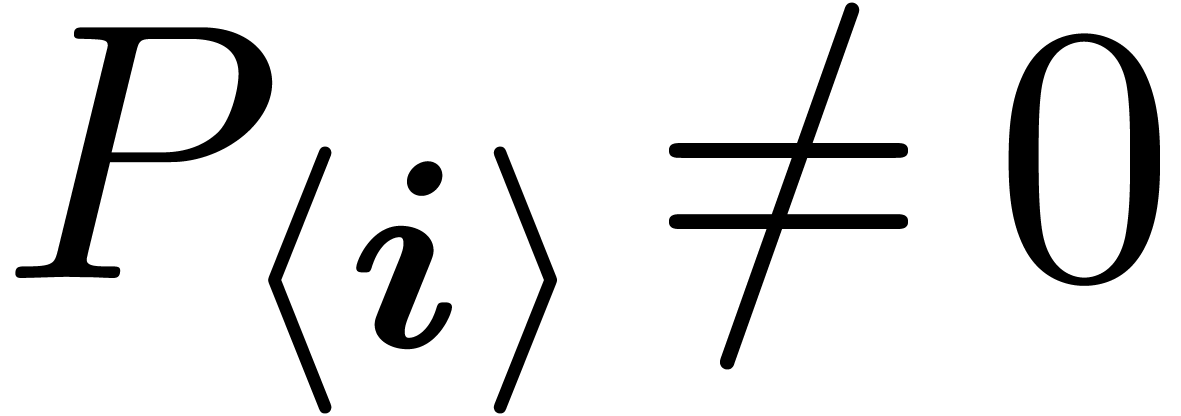 ,
,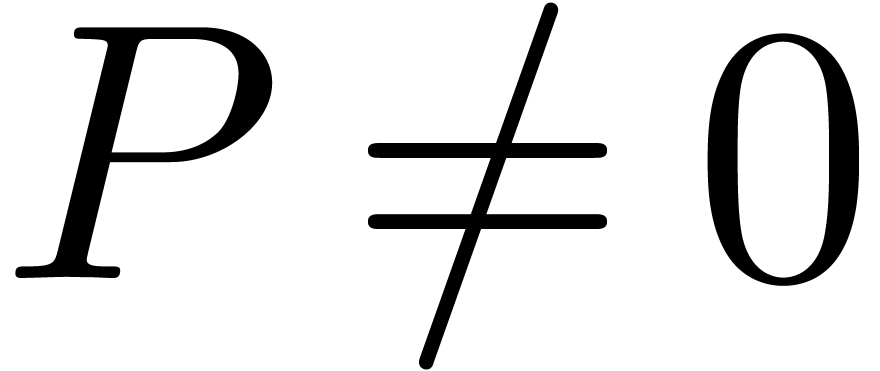 .
.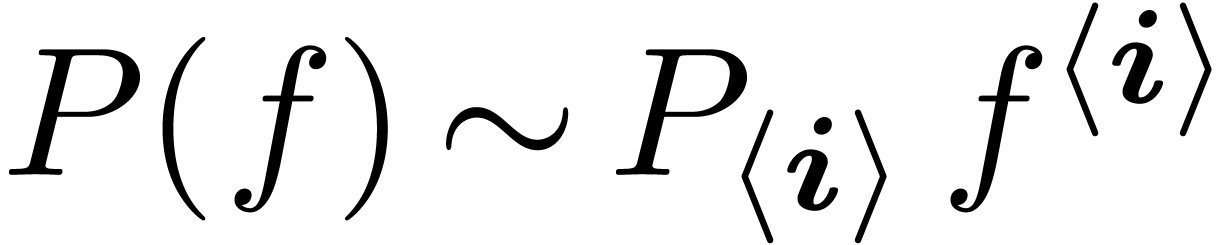
 and
and 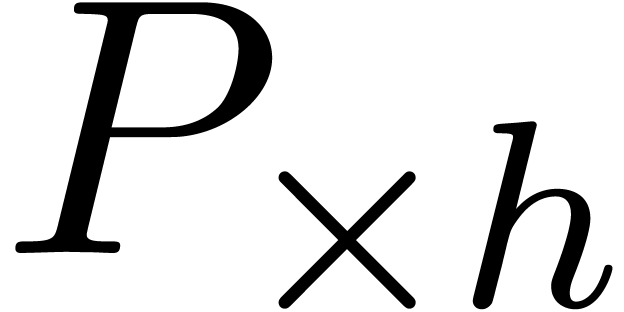 of
of 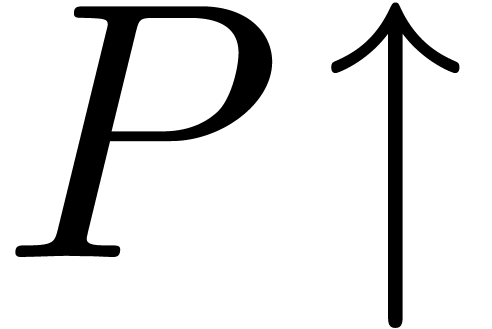 of
of
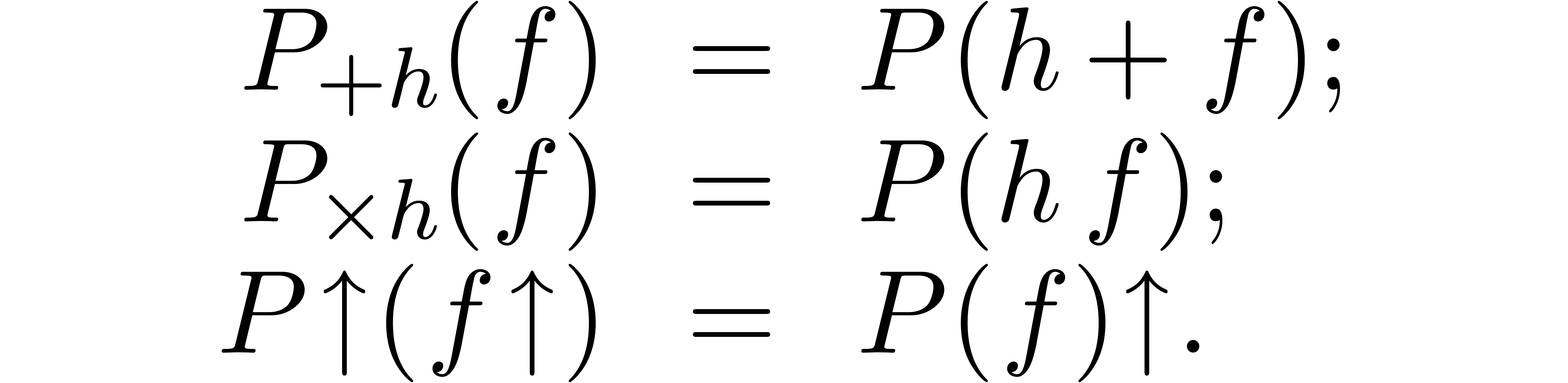
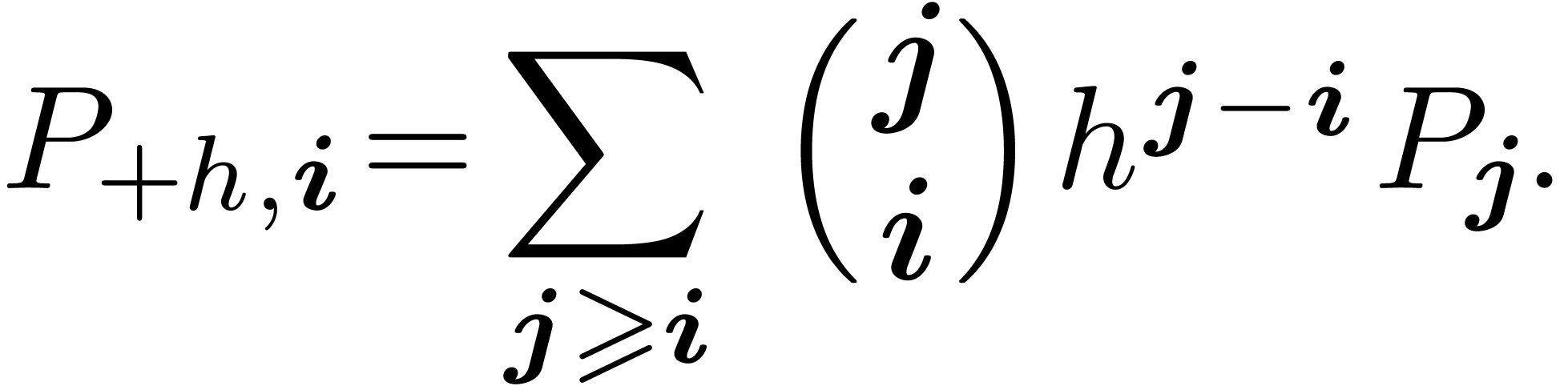
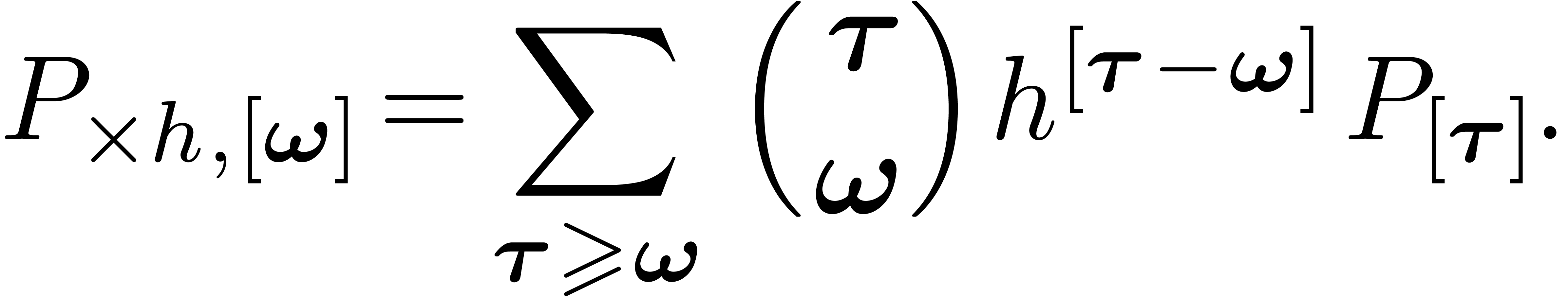
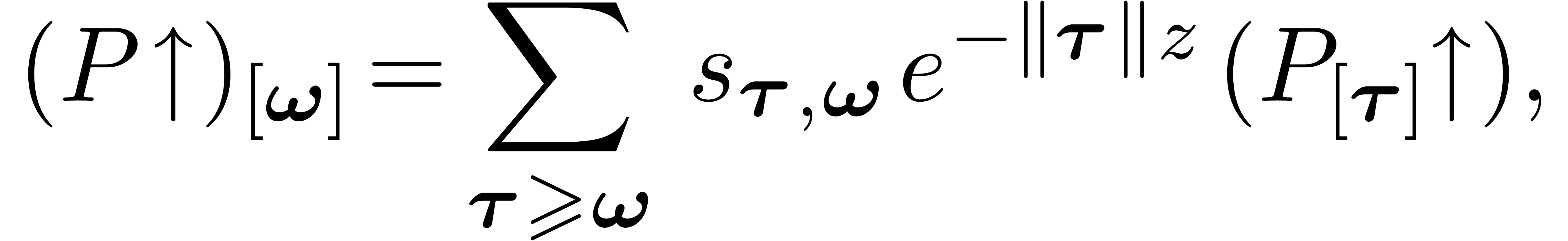
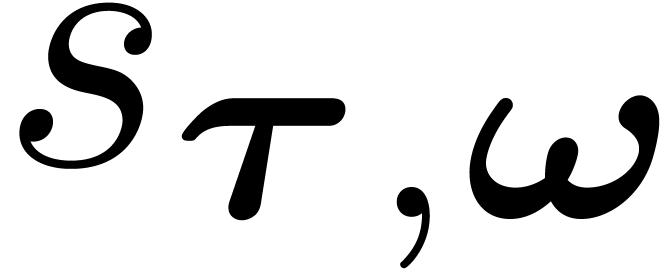 are generalized Stirling numbers of
the first kind:
are generalized Stirling numbers of
the first kind:
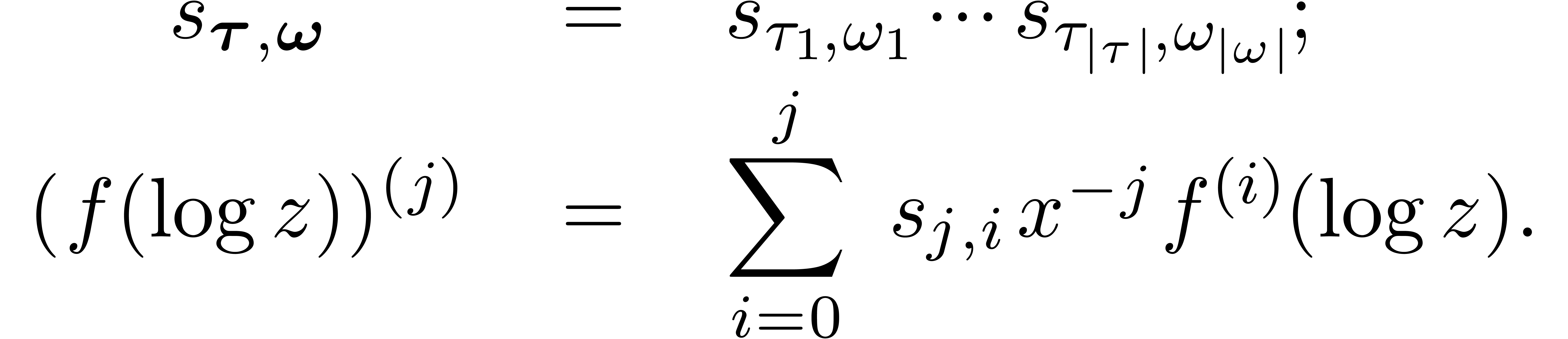
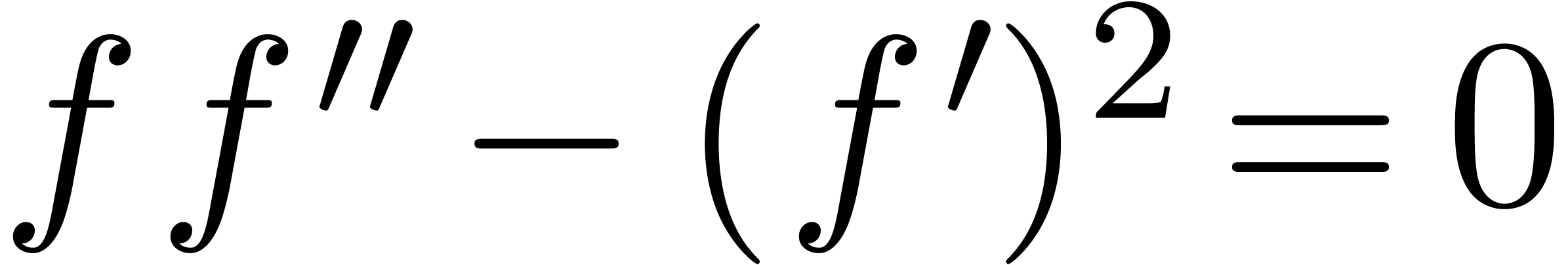
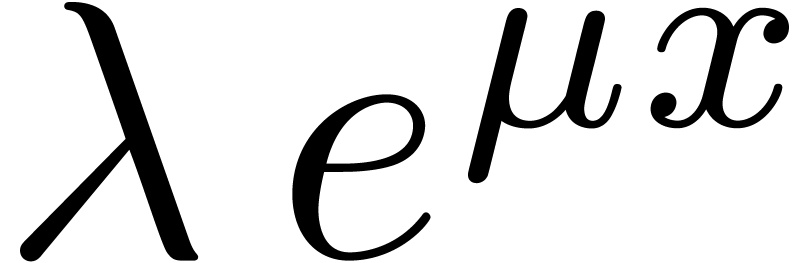 as its general solution. Another difficulty
is that differentiation does not preserve valuation: we usually do not
have
as its general solution. Another difficulty
is that differentiation does not preserve valuation: we usually do not
have 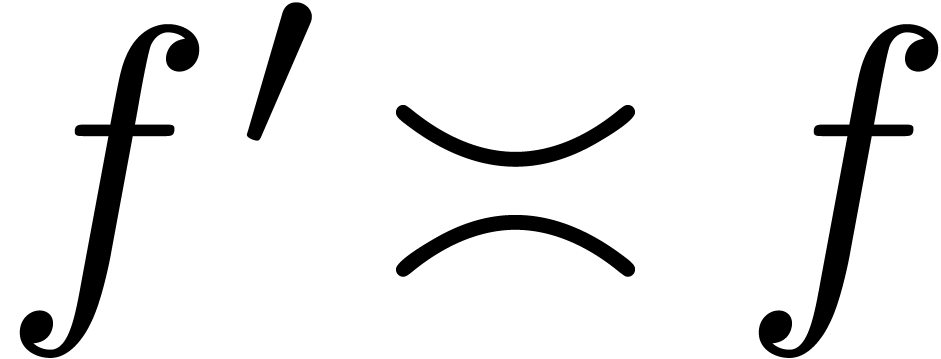 for transseries
for transseries 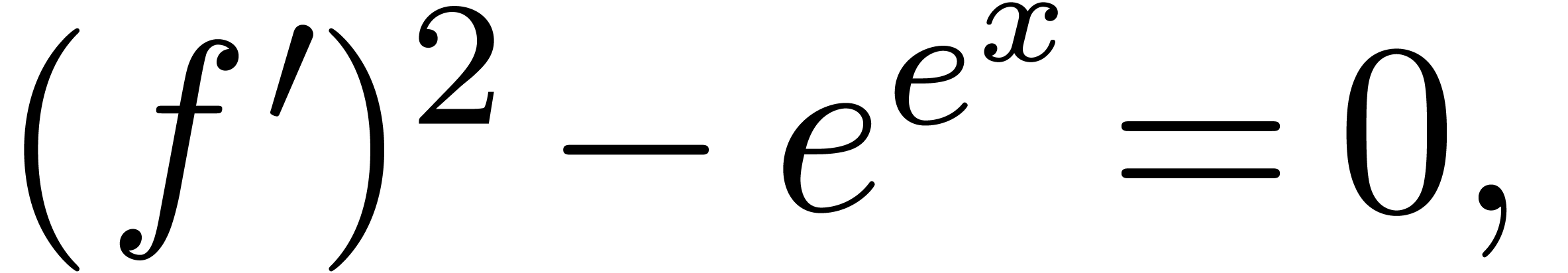
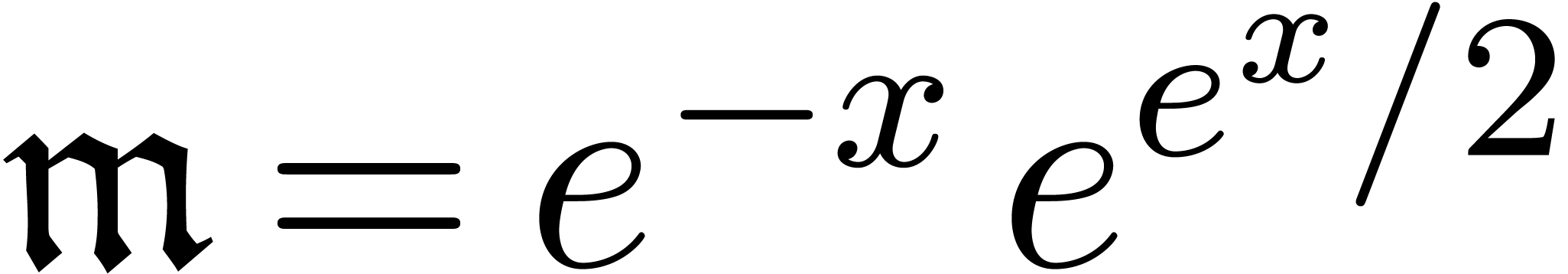 .
. is not the square root
is not the square root 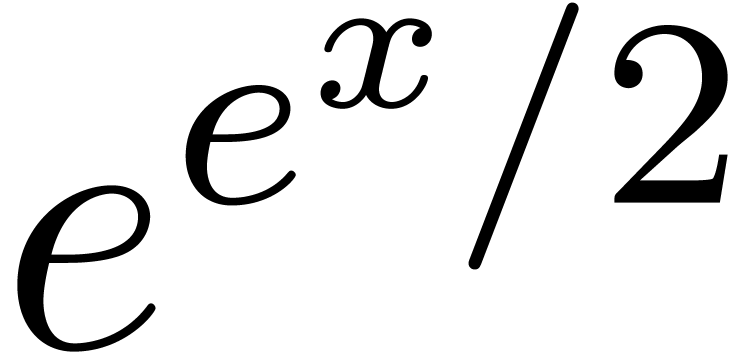 of the quotient of the dominant monomials
of the quotient of the dominant monomials 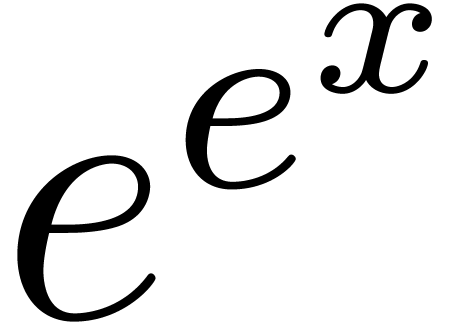 and
and
 of the coefficients of
of the coefficients of 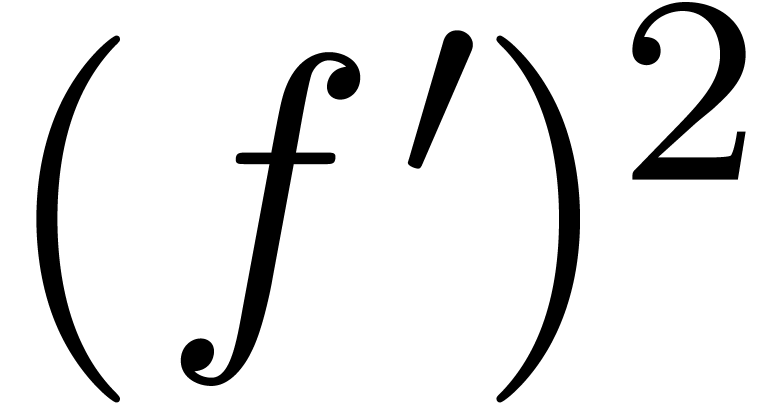 in
in 
 for all purely exponential transseries
for all purely exponential transseries  .
. .
. is
purely exponential, but
is
purely exponential, but  and
and 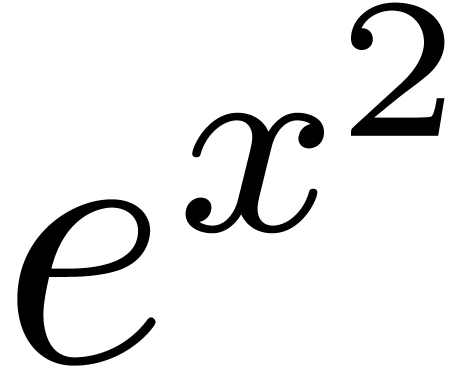 are not. Any transseries becomes purely exponential after a sufficient
number of upward shiftings.
are not. Any transseries becomes purely exponential after a sufficient
number of upward shiftings.
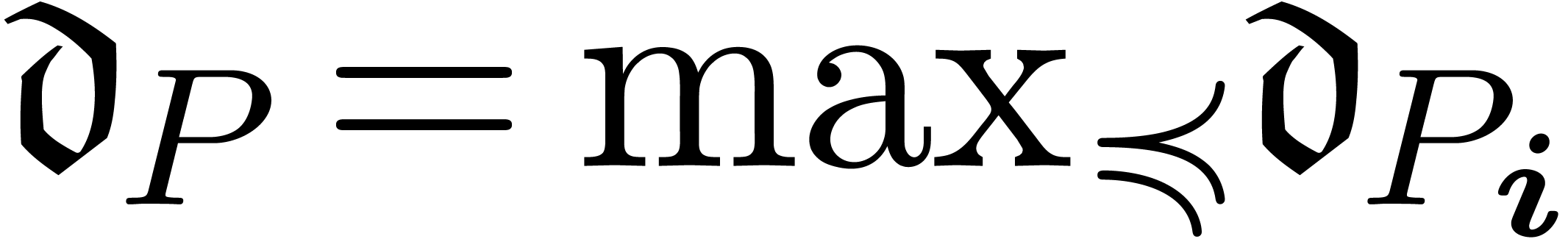 ,
,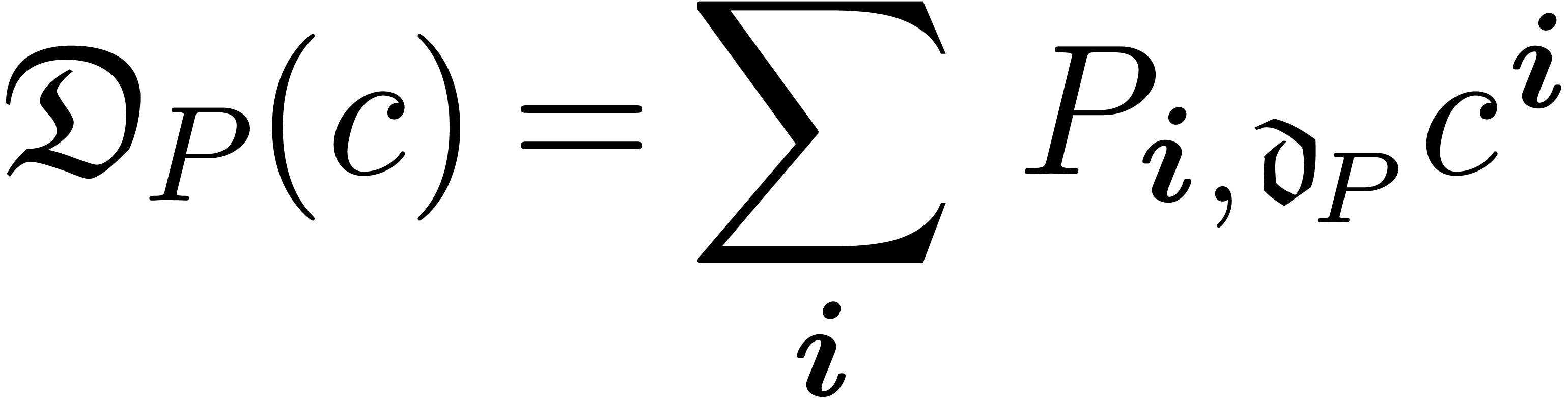
 the
the 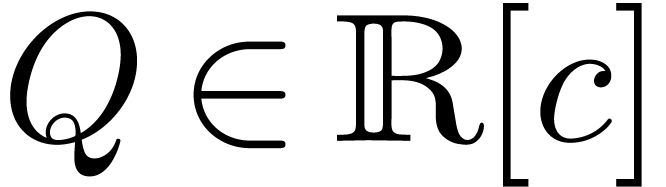 and an integer
and an integer  ,
,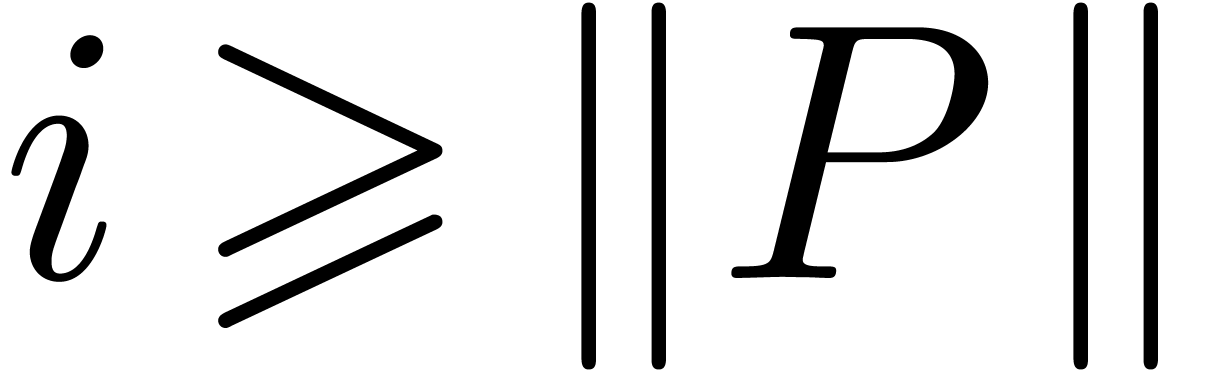 ,
,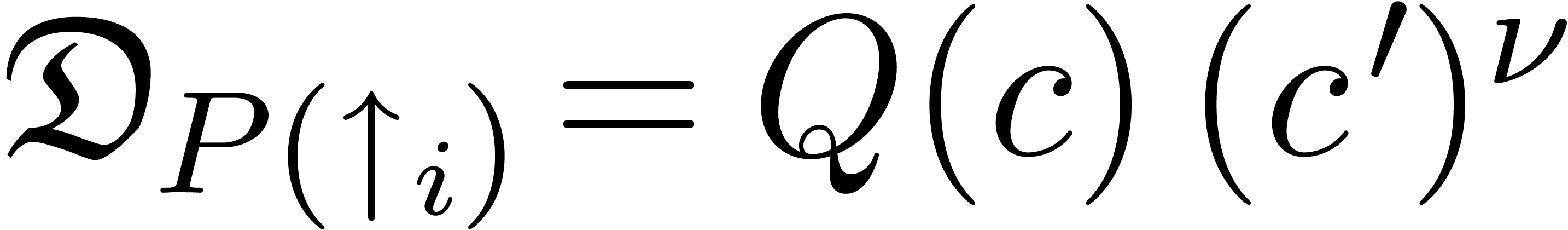 .
.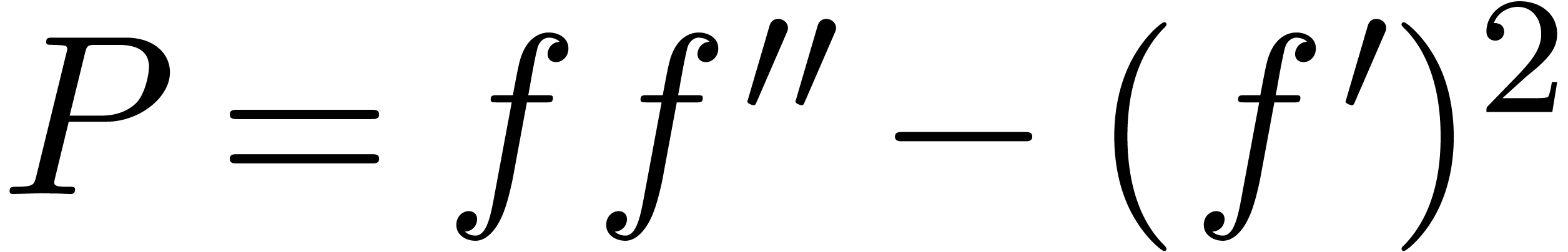 ,
,
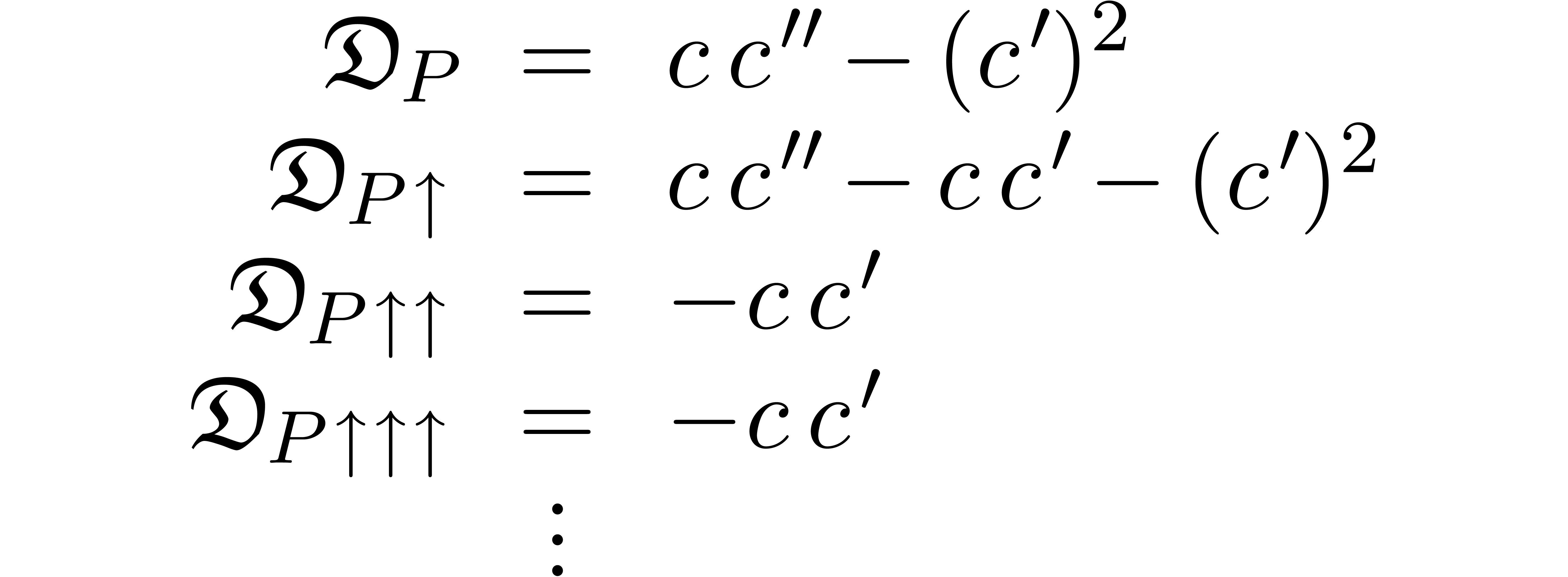
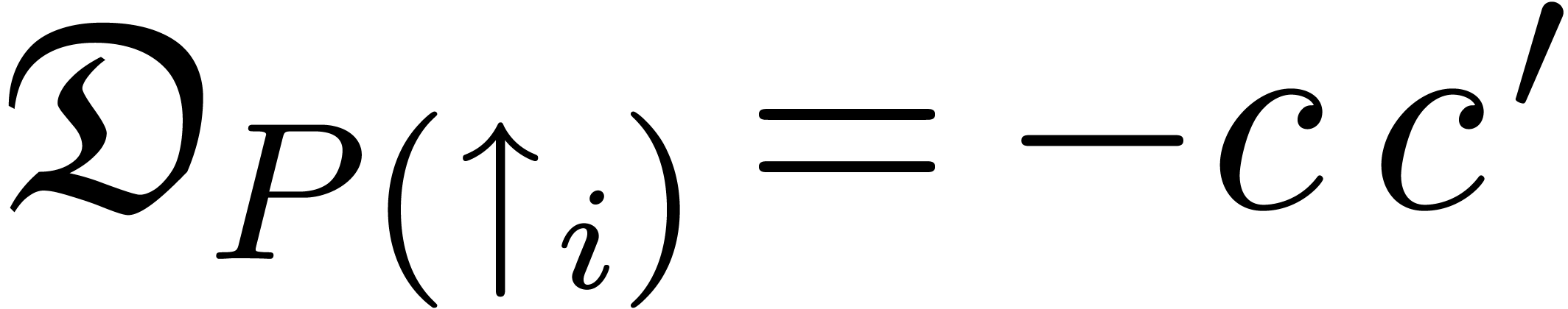 for all
for all  (whence
(whence 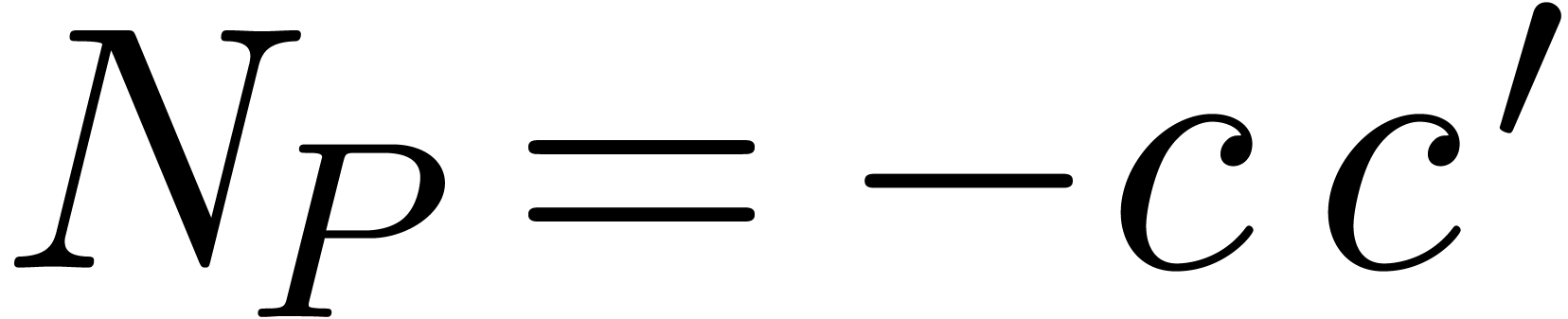 ;
; in proposition
in proposition  .
.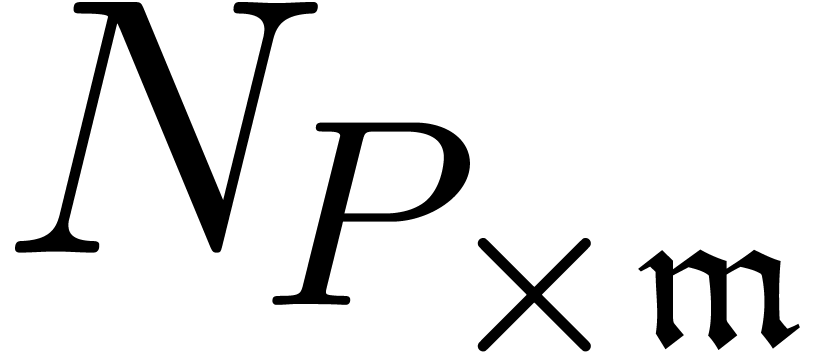 .
. and
and 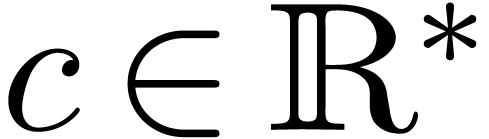 .
. ,
, a potential
dominant term for (
a potential
dominant term for (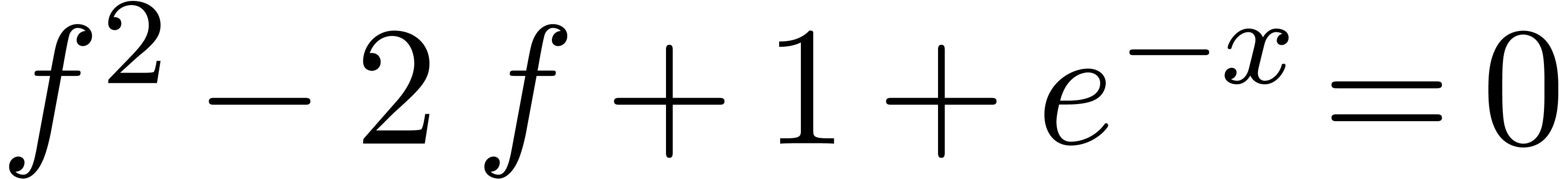
 associated to a transmonomial
associated to a transmonomial
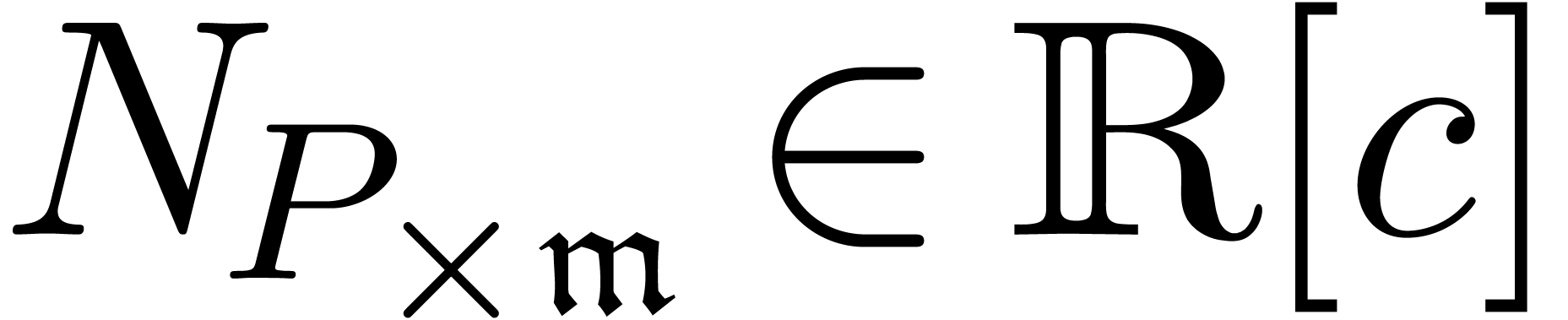 ,
,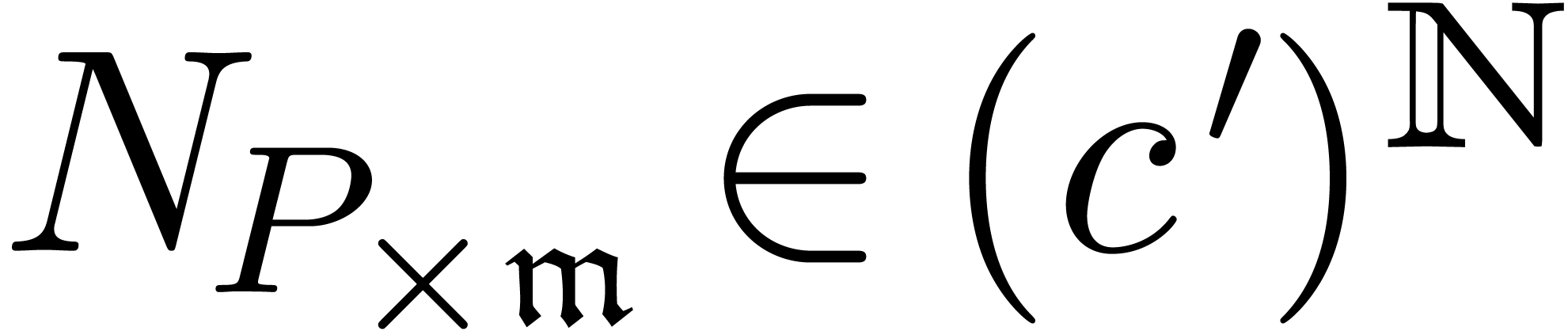 ,
,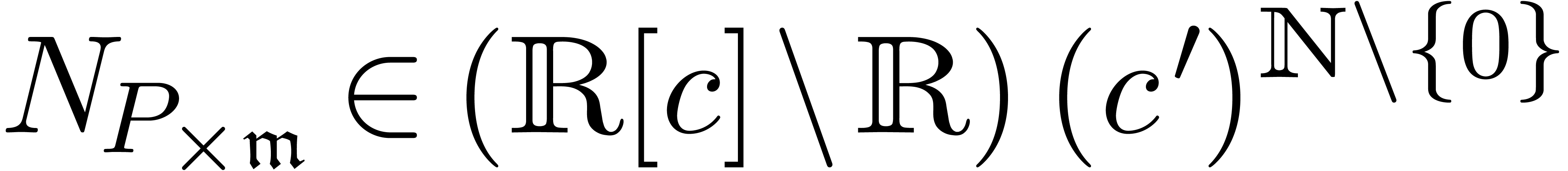 ,
,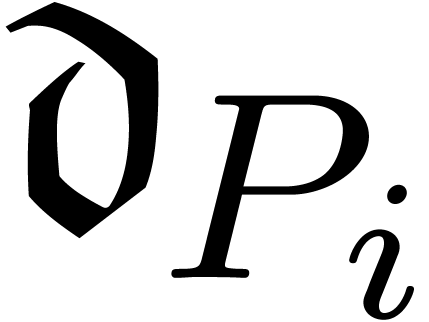 and
and 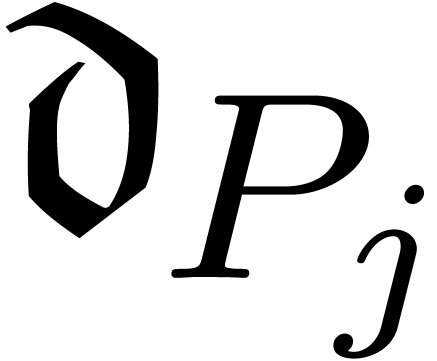 of two different homogeneous components of
of two different homogeneous components of
 be such that
be such that 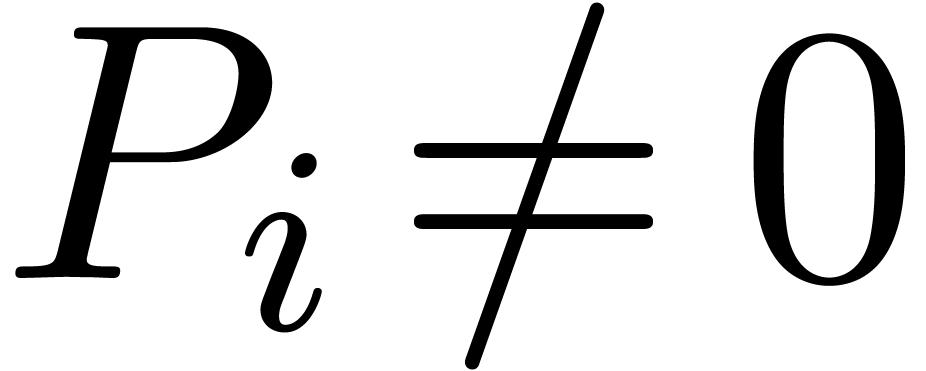 and
and 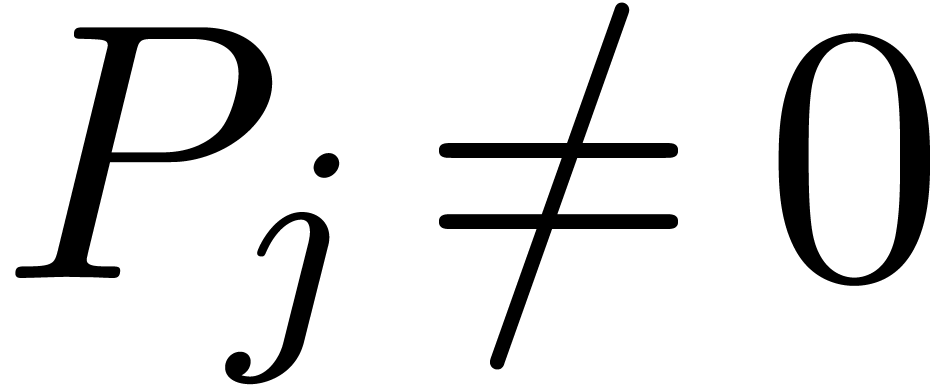 .
.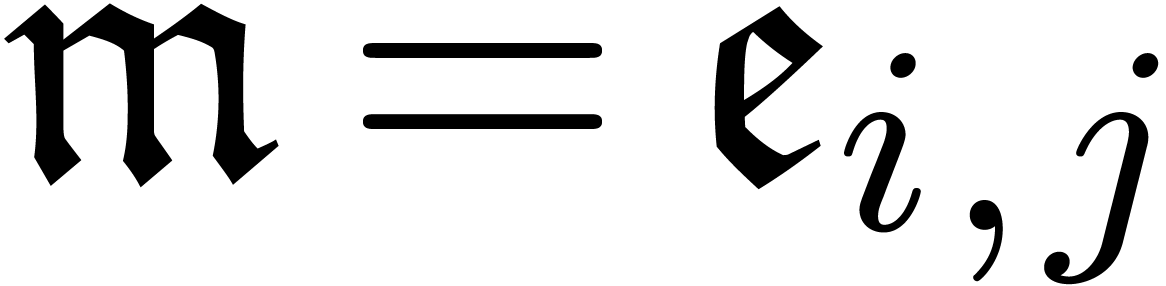 ,
,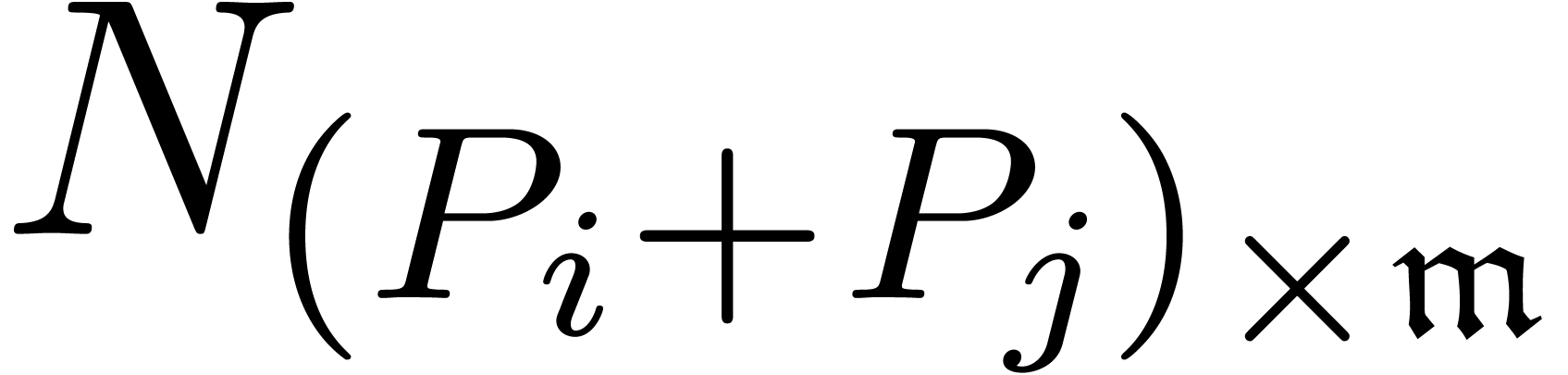 is not homogeneous.
is not homogeneous.
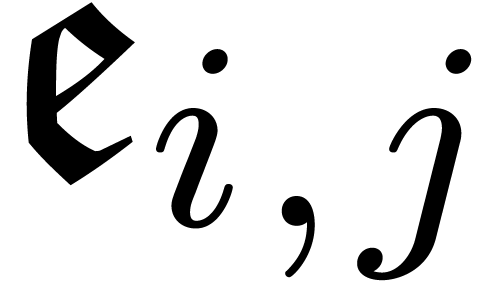 an equalizer for
an equalizer for 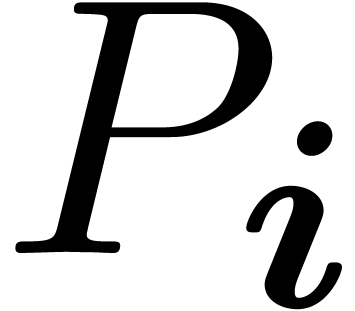 can be expanded
with respect to a transbasis
can be expanded
with respect to a transbasis  with
with 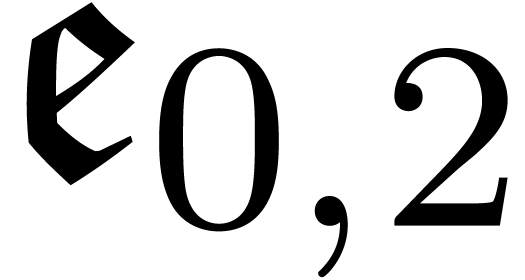 for
for
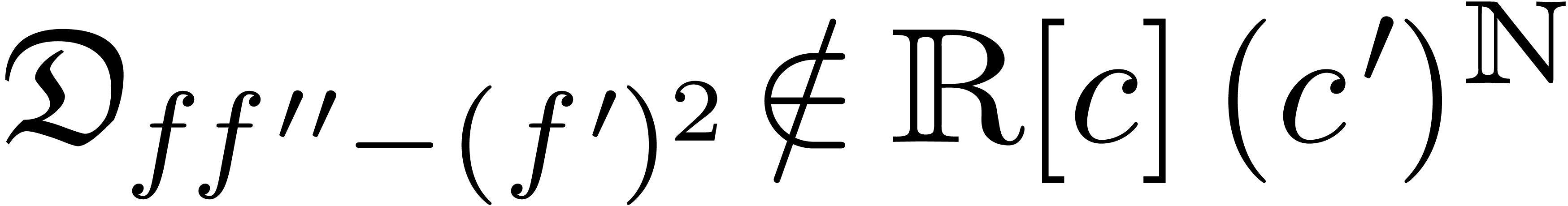 ,
,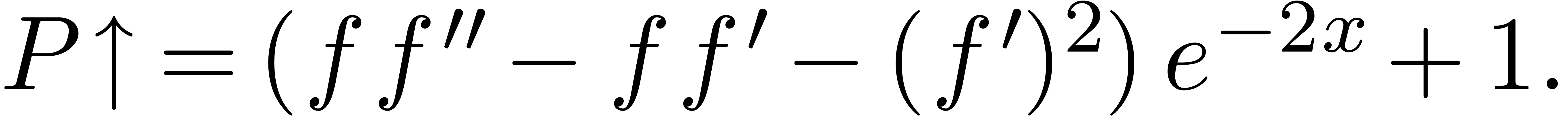
 and
and  via a multiplicative conjugation with
via a multiplicative conjugation with  :
: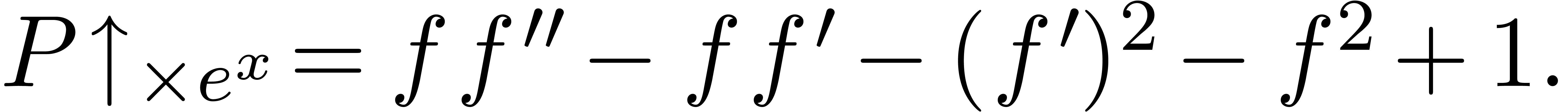
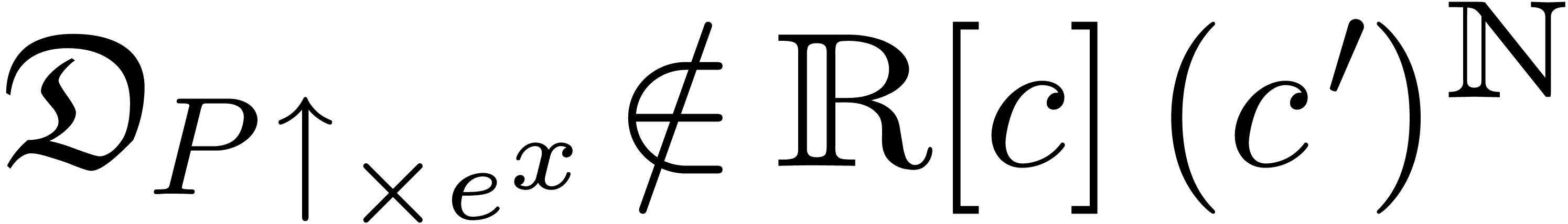 ,
,
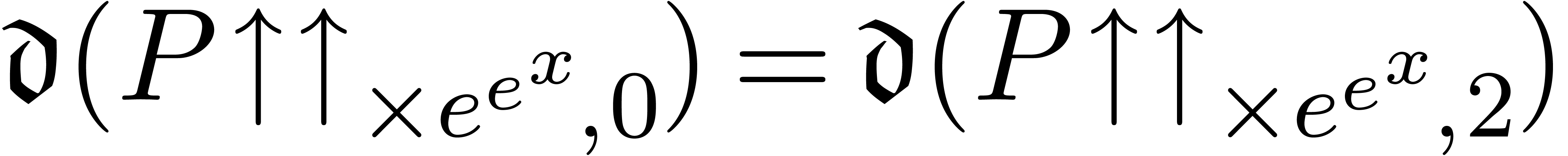 and
and 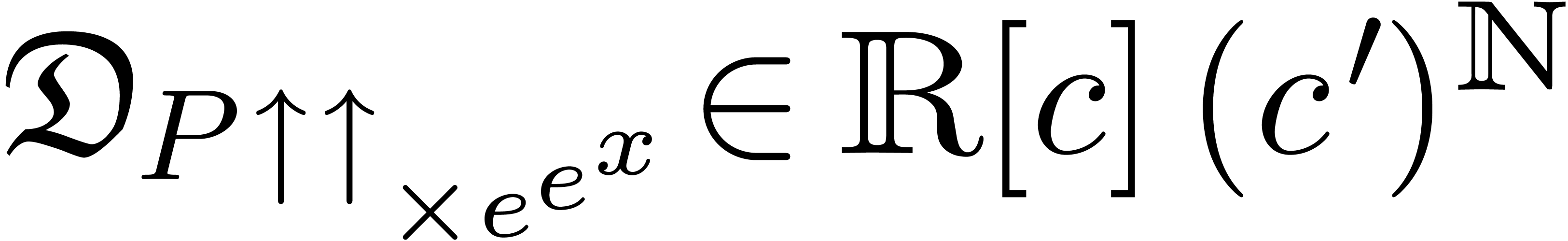 .
.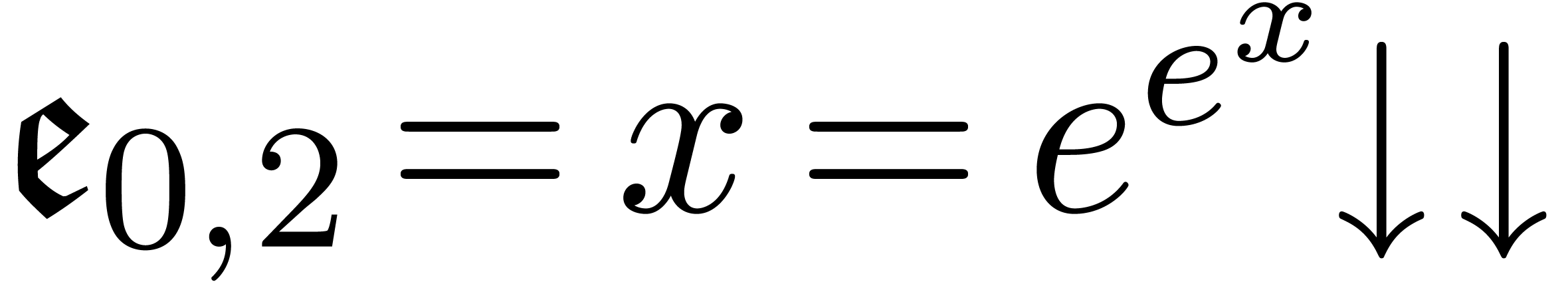 is
the desired equalizer.
is
the desired equalizer.
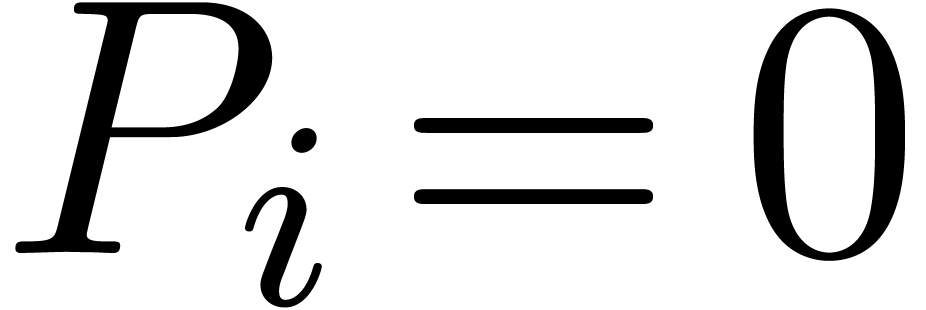 ,
,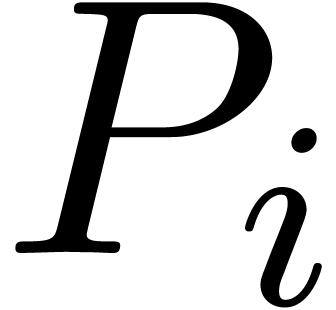 in
terms of the
in
terms of the 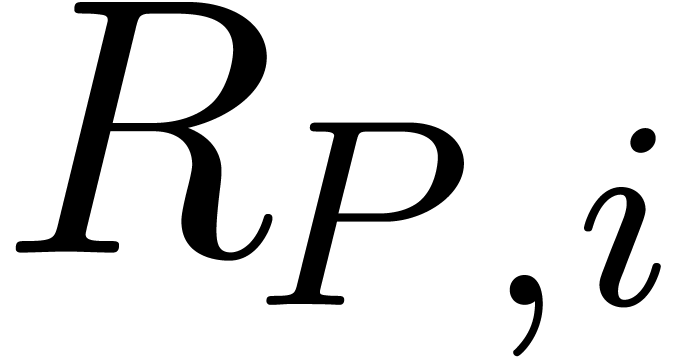 :
: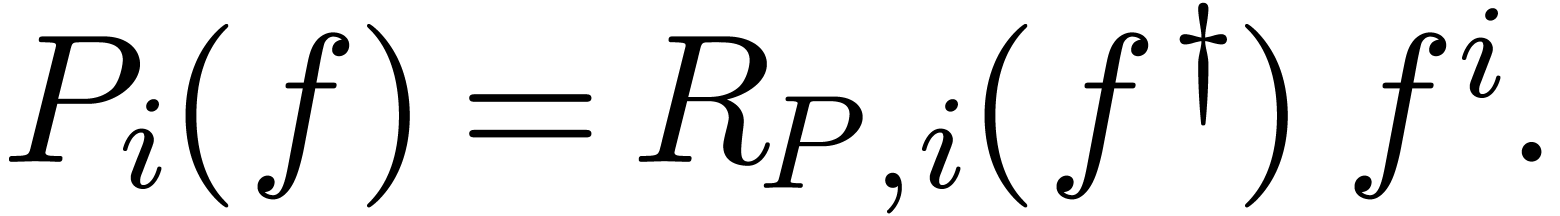
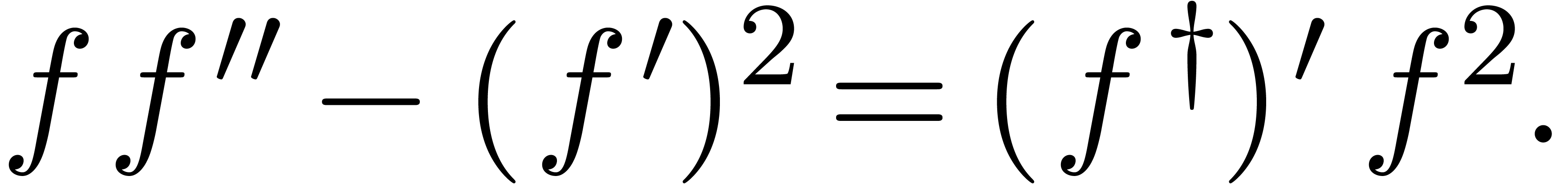
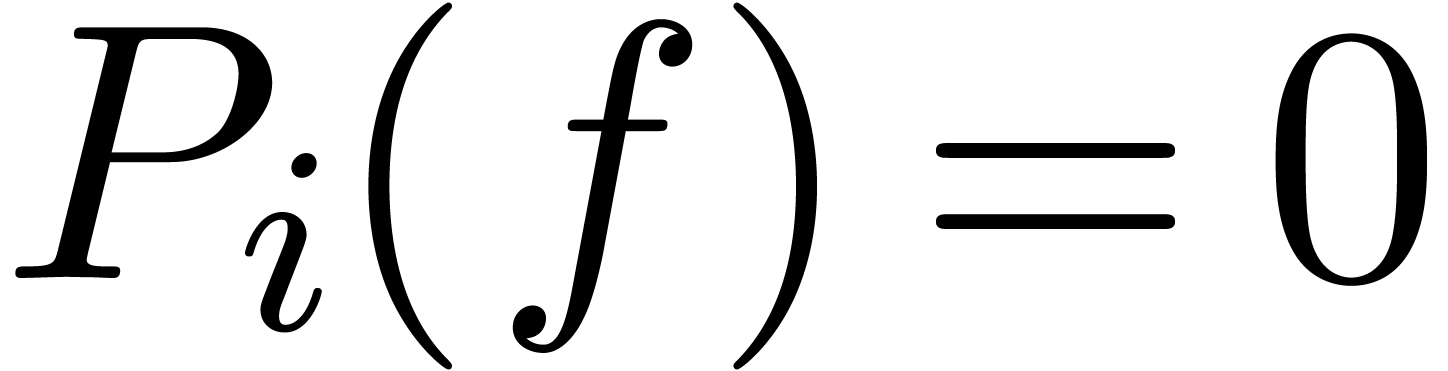 up to
up to 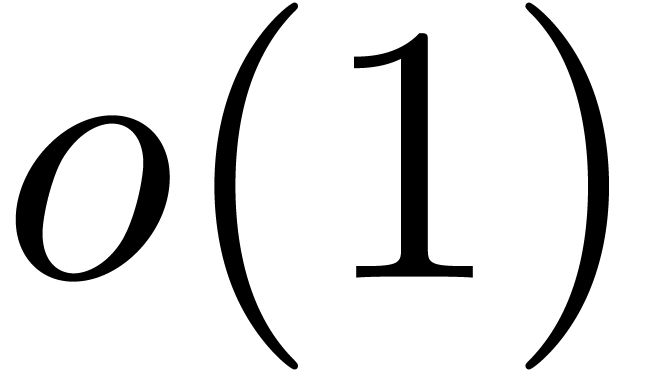 ”,
”,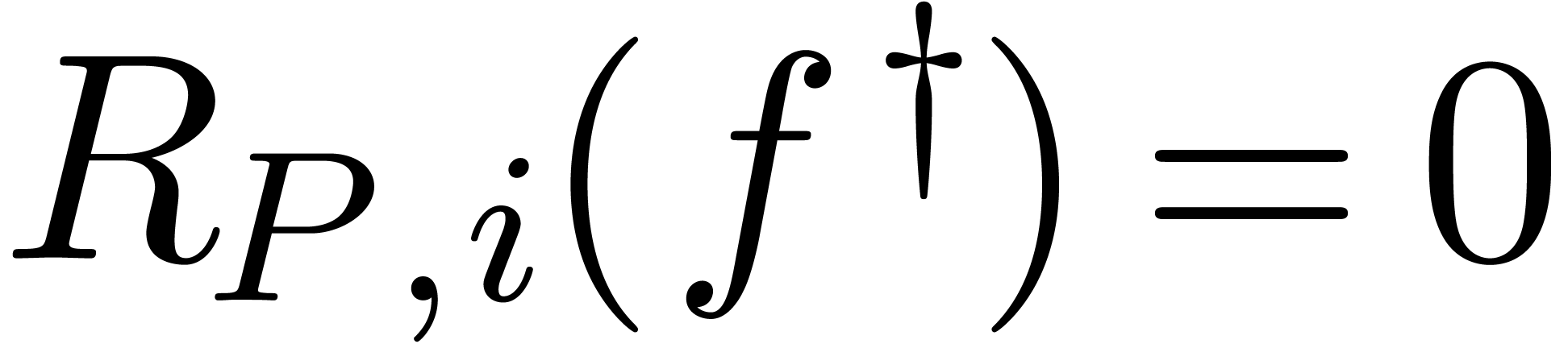 up to
up to  ”.
”. is special in the sense that
is special in the sense that  whenever
whenever  and
and  whenever
whenever  .
. is a potential dominant monomial of
is a potential dominant monomial of
 w.r.t.
w.r.t.
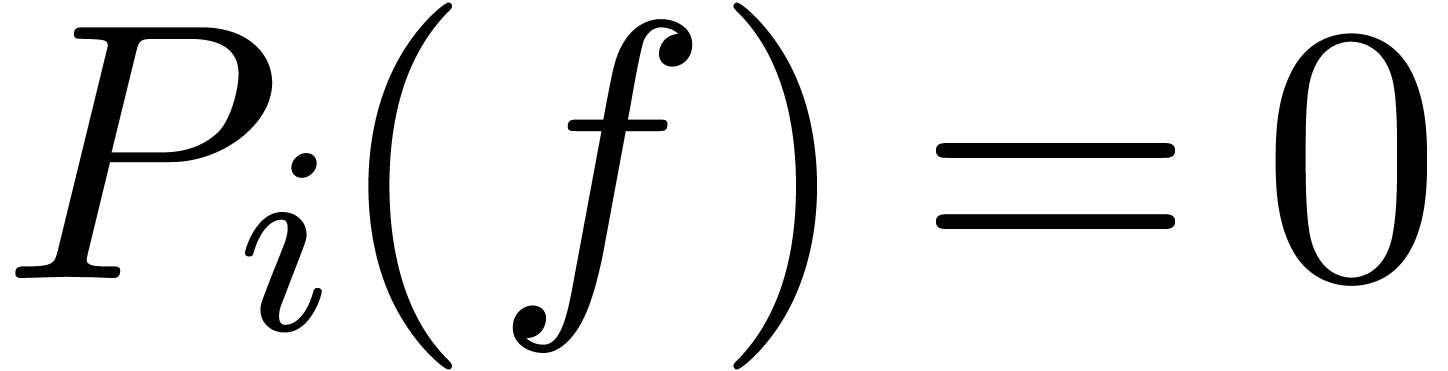
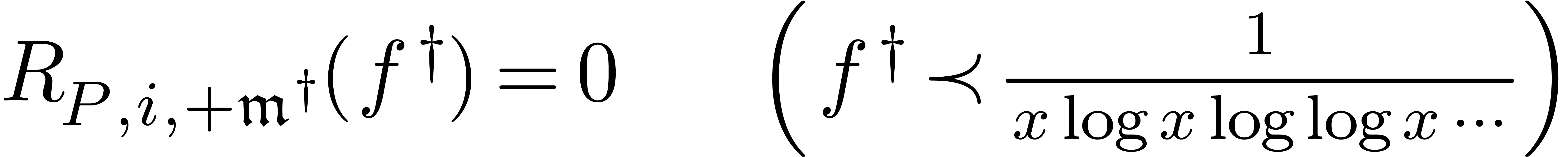
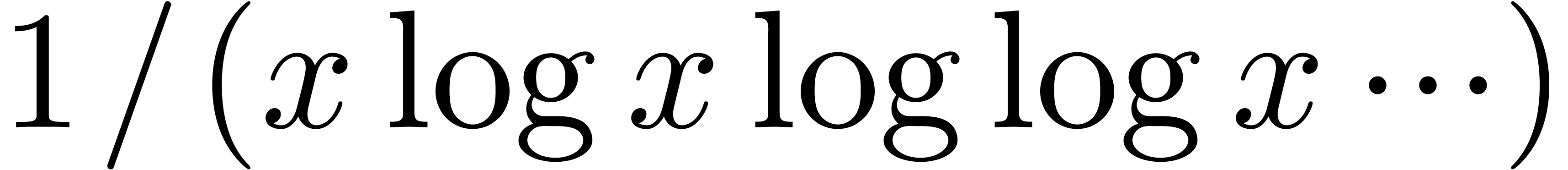 as a
transmonomial. In order to be painstakingly correct, we should replace
as a
transmonomial. In order to be painstakingly correct, we should replace
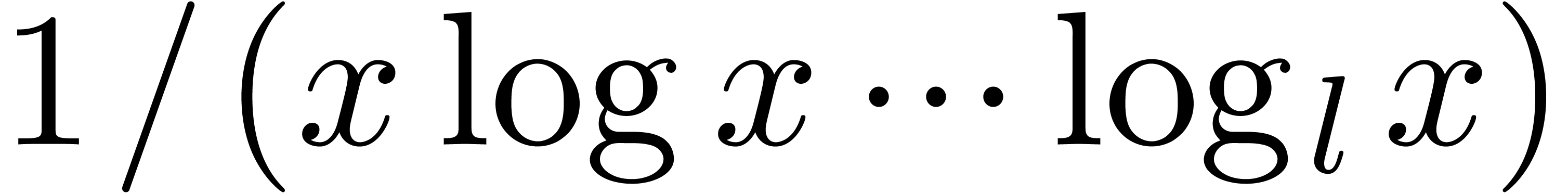 ,
, is a strict bound for the logarithmic
depths of
is a strict bound for the logarithmic
depths of  and all coefficients of
and all coefficients of  for (
for ( ”).
”).
 is an arbitrary transseries (and not
necessarily a term in
is an arbitrary transseries (and not
necessarily a term in  ;
; a
transmonomial. Such a refinement transforms (
a
transmonomial. Such a refinement transforms (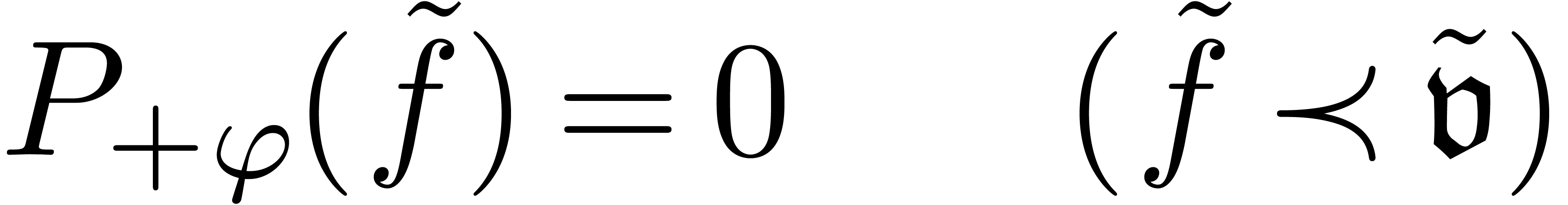
 be the dominant term of
be the dominant term of  and assume that
and assume that  .
. of
of  as a
root of
as a
root of  with
with 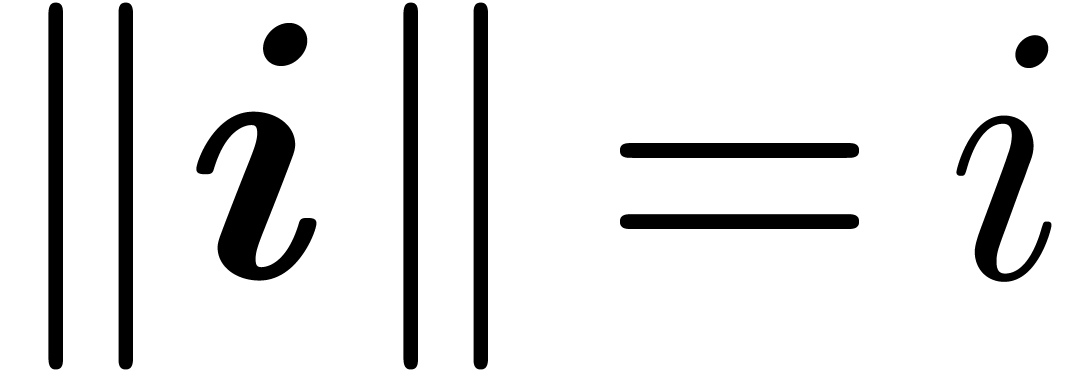 and
and 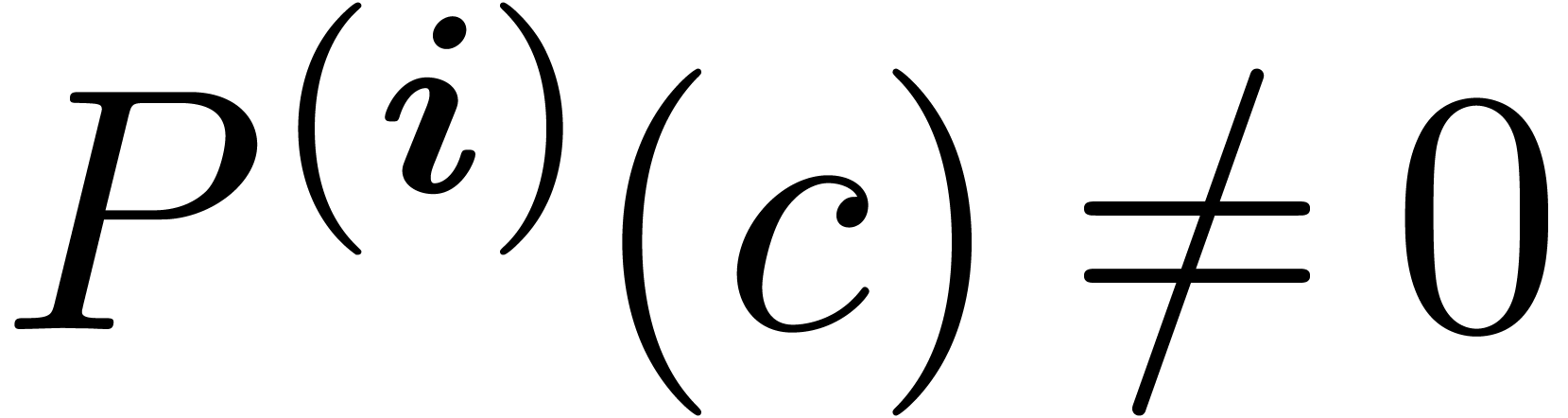 .
.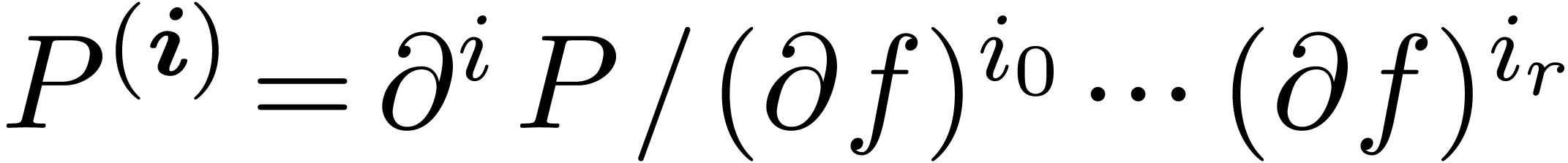 .
. to a quasi-linear equation, all other solutions can be
seen found by solving the homogeneous quasi-linear equation
to a quasi-linear equation, all other solutions can be
seen found by solving the homogeneous quasi-linear equation  .
. be solutions to a quasi-linear differential equation
be solutions to a quasi-linear differential equation
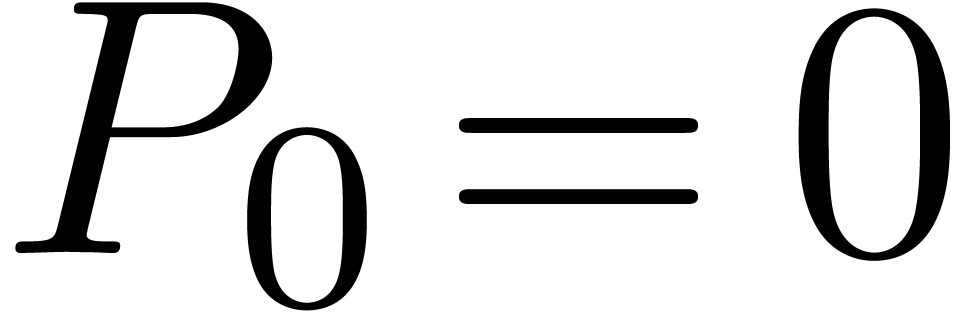 .
. .
. .
.
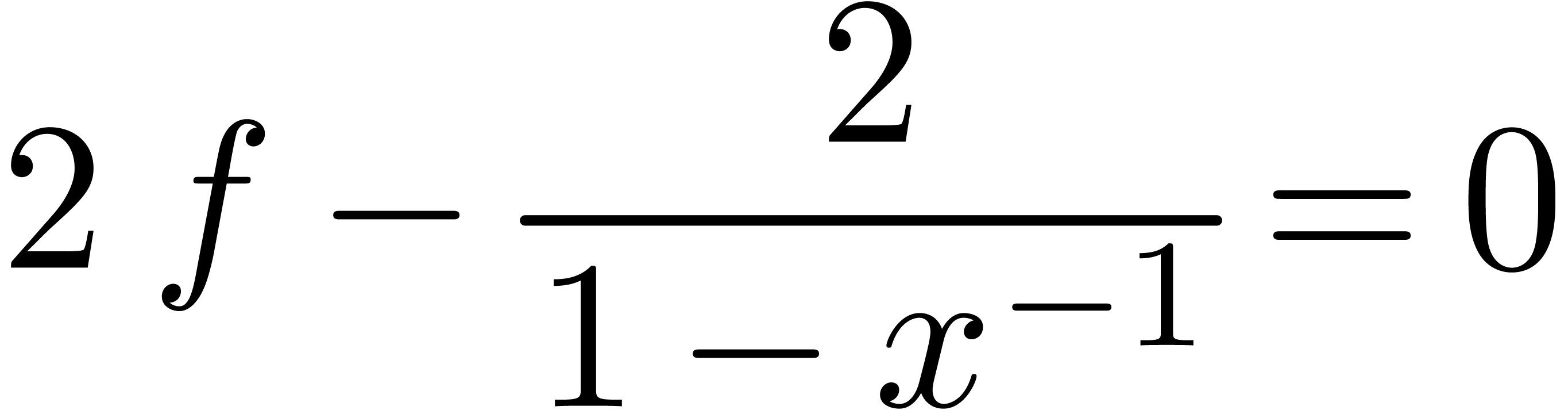
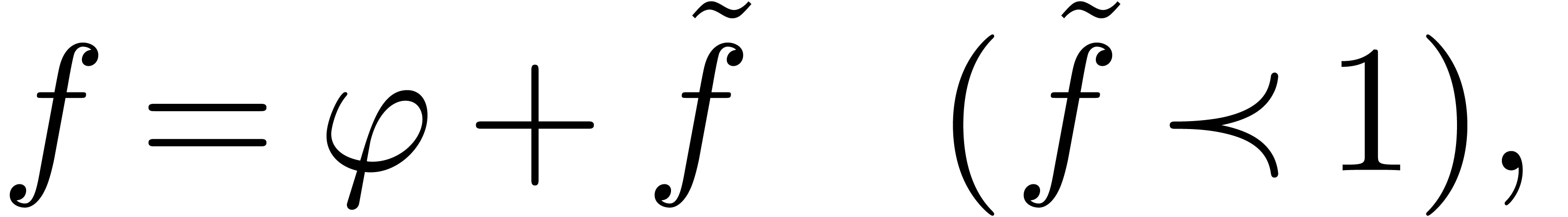
 .
. the Newton degree of (
the Newton degree of (
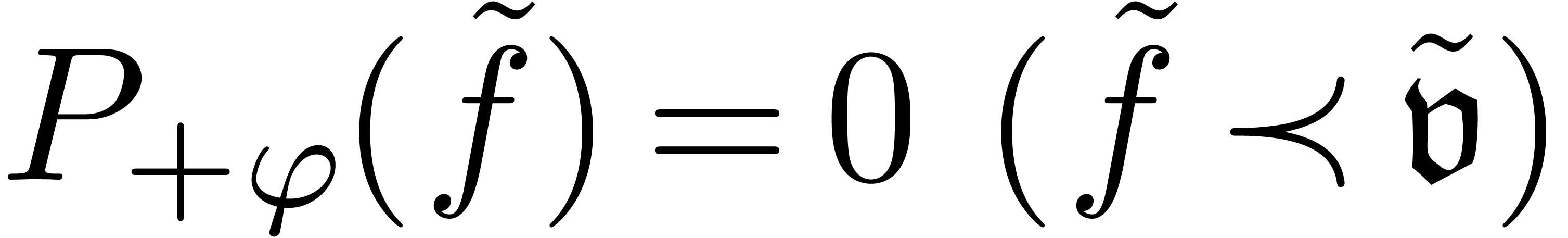 equals
equals  ,
,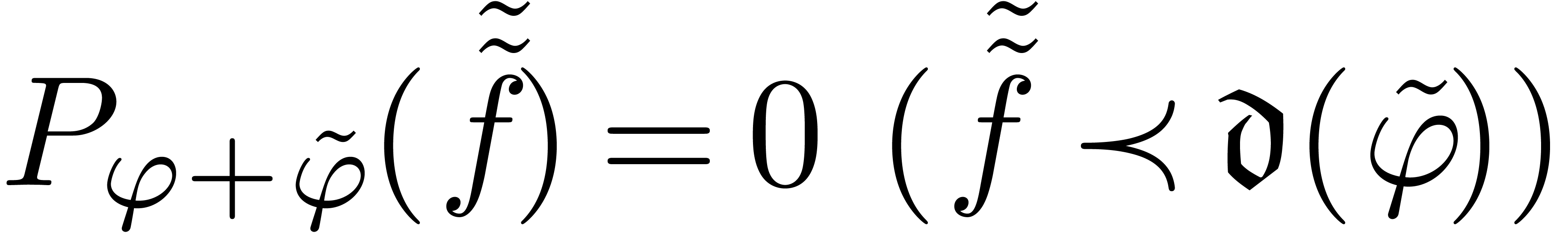 is
is 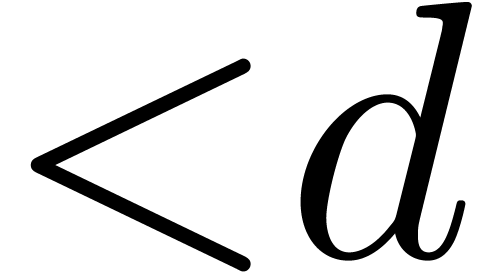 .
.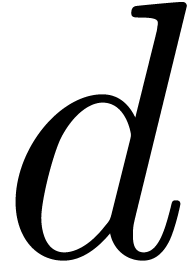 (i.e.
(i.e. 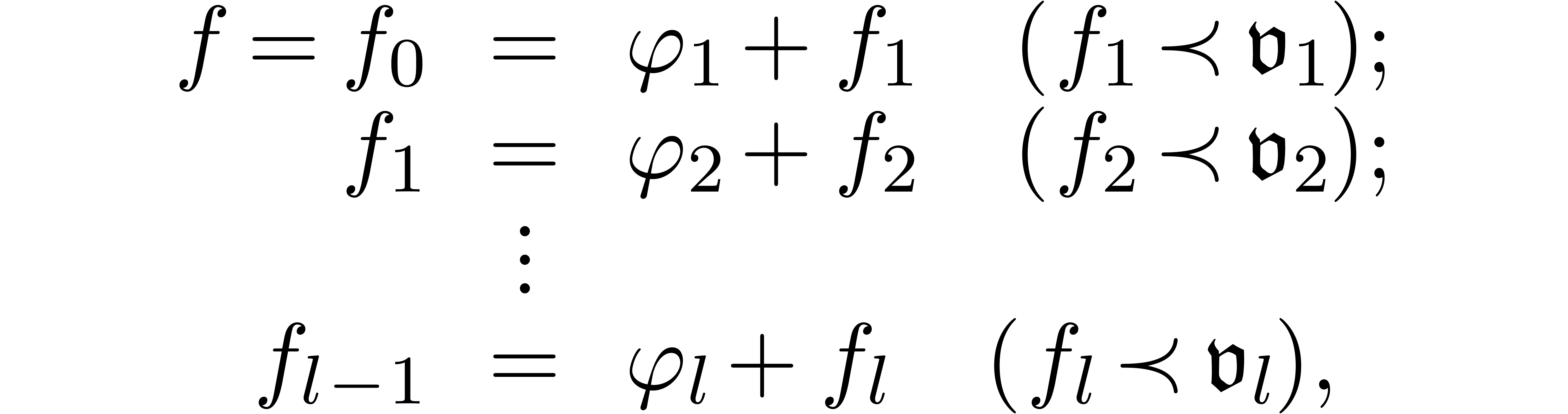
 is either a term in
is either a term in  or a solution to an equation of the form
or a solution to an equation of the form
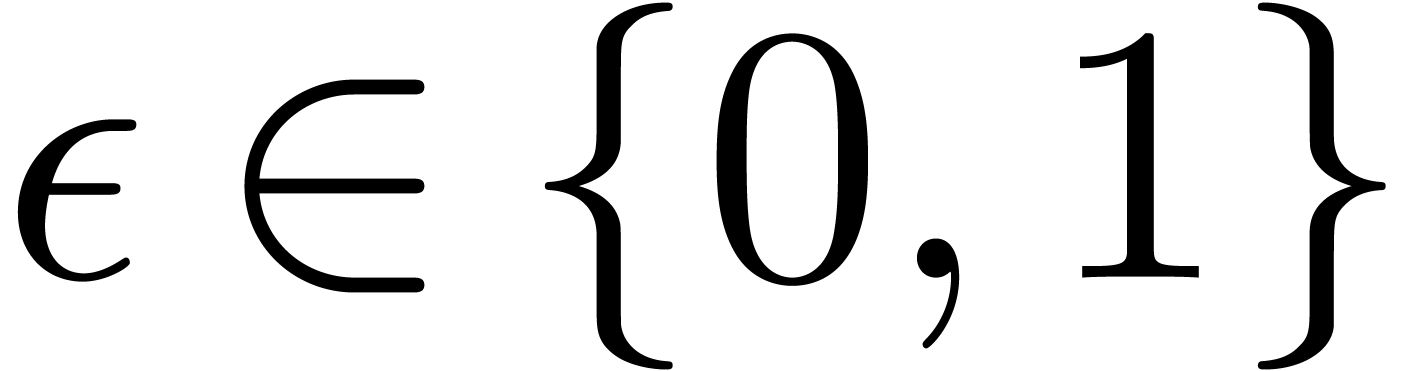 and
and 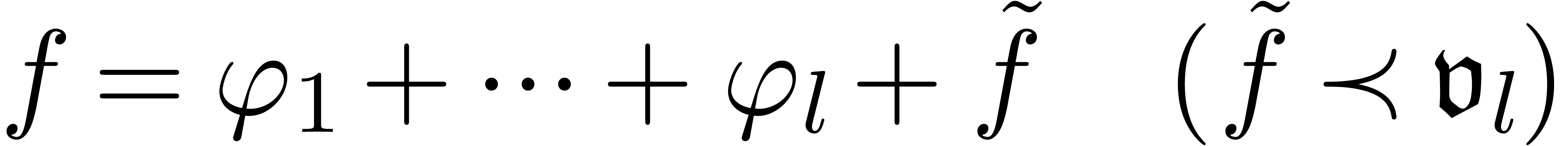
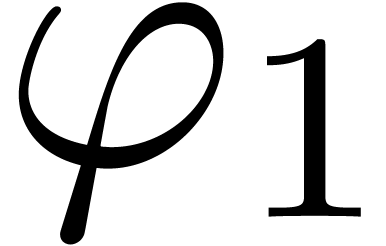 has
has 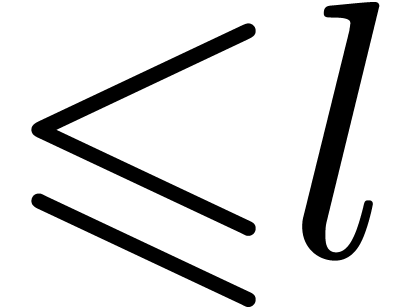 ,
, and
and  denote its Newton degree, order resp. weight. Then any
transseries (whether grid-based or not) solution to
denote its Newton degree, order resp. weight. Then any
transseries (whether grid-based or not) solution to  .
. -function
-function or
or 
 ,
, ,
, or
or  ,
, are in the
“compactification” of
are in the
“compactification” of  .
. ,
, ;
; ,
, ,
, ,
, ,
,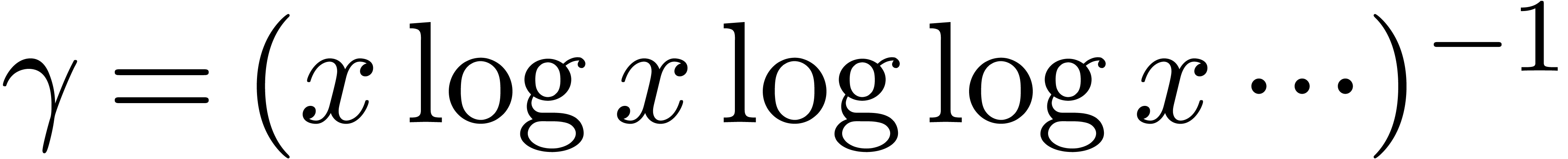 .
. and
and  respectively
designate formal infinitely small and large constants
respectively
designate formal infinitely small and large constants 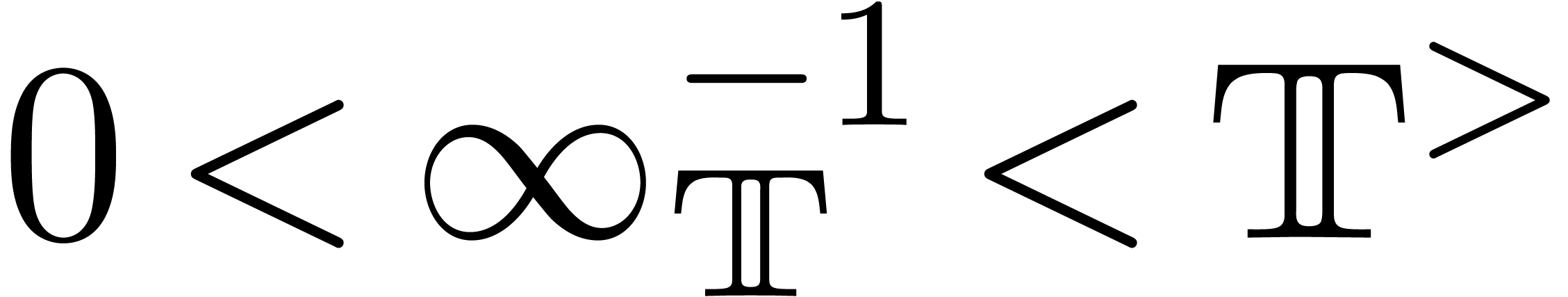 and
and 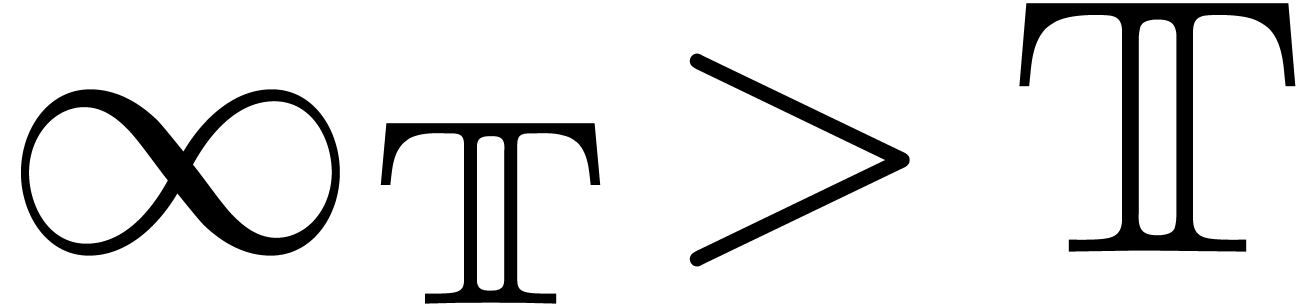 .
. and
and  designate the infinitely small
and large constants
designate the infinitely small
and large constants  and
and  .
. .
.
 contains all transseries which are
larger than
contains all transseries which are
larger than  ,
,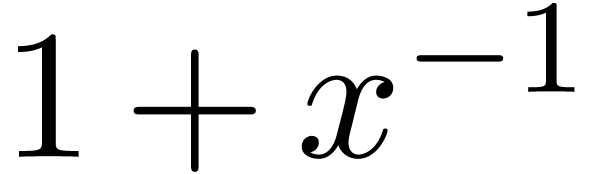 and
and 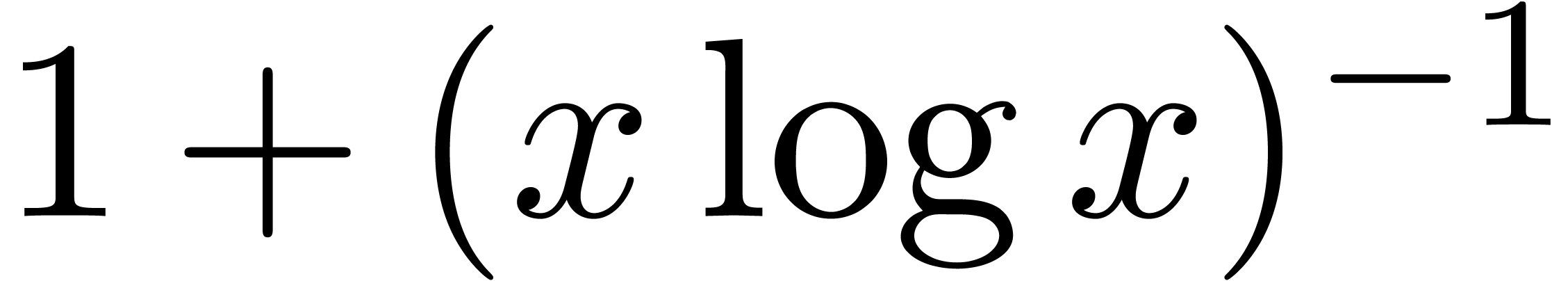 ,
,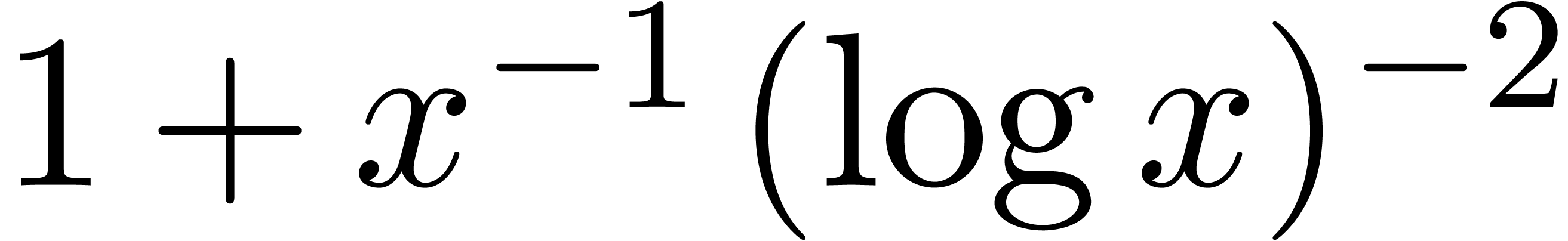 .
. to the end-points of non-standard
intervals. After that, we will be able to state the more general
intermediate value theorem and prove it using the Newton polygon method.
to the end-points of non-standard
intervals. After that, we will be able to state the more general
intermediate value theorem and prove it using the Newton polygon method.
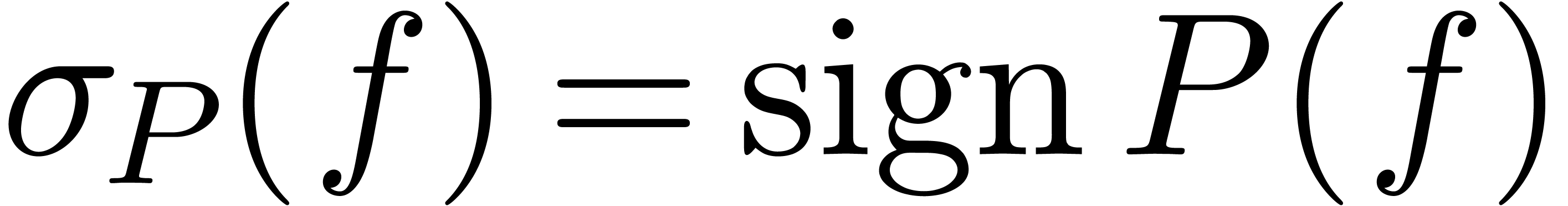 may be extended by
continuity into
may be extended by
continuity into  ,
, is constant on
is constant on  for some
for some  .
. ,
, for some
for some 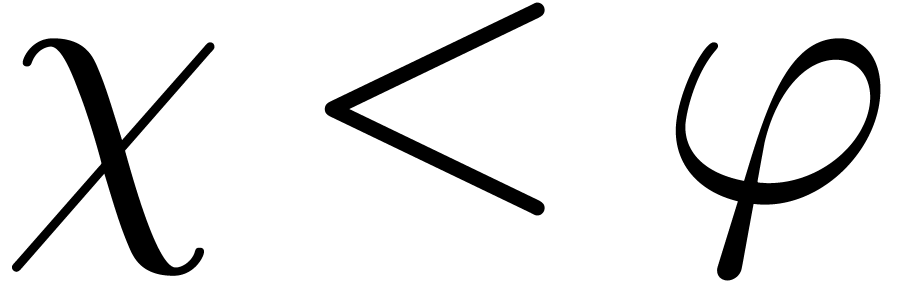 .
. ,
, ,
, for some
for some  ,
, ,
,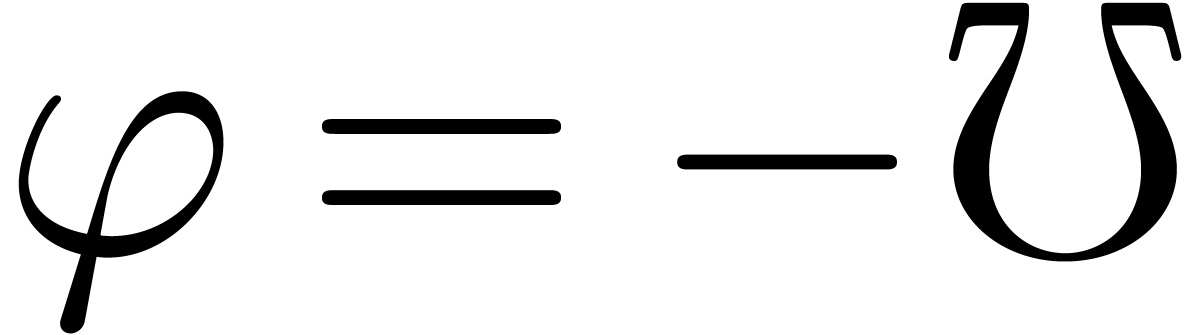 and so on, one has to interchange left and right
continuity in the above list.) Modulo additive and multiplicative
conjugations, it suffices to deal with the cases when
and so on, one has to interchange left and right
continuity in the above list.) Modulo additive and multiplicative
conjugations, it suffices to deal with the cases when 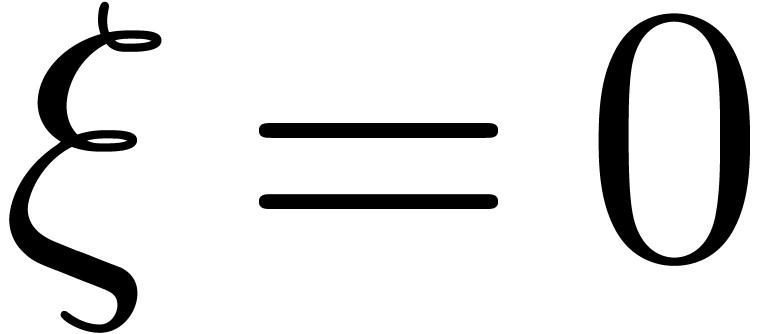 and
and  .
. .
. has constant sign
has constant sign  for all sufficiently large
for all sufficiently large

 has constant sign
has constant sign 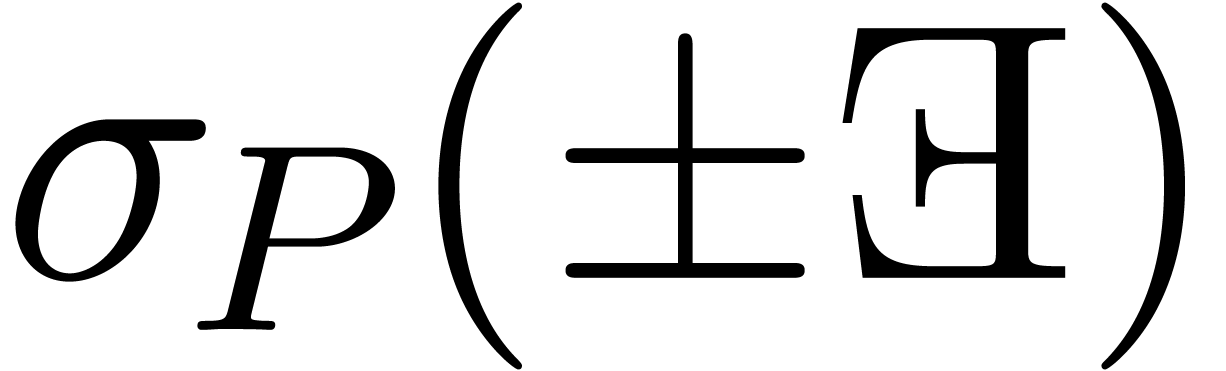 for all sufficiently small
for all sufficiently small
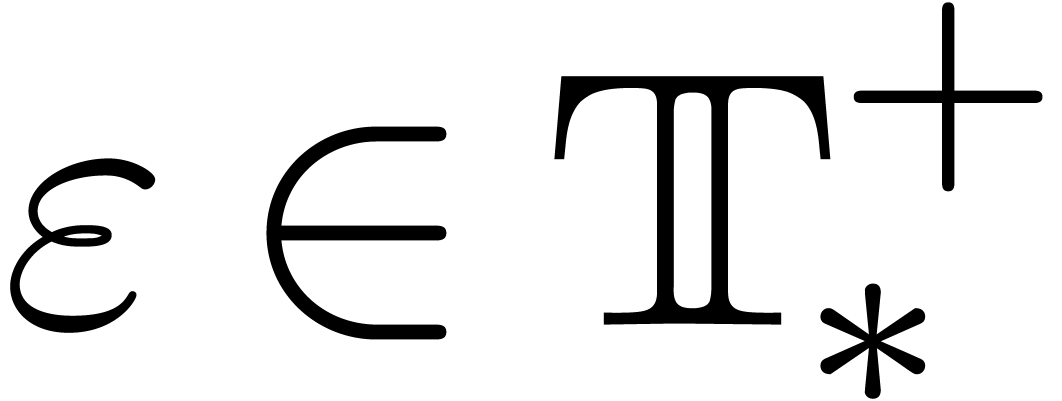 .
.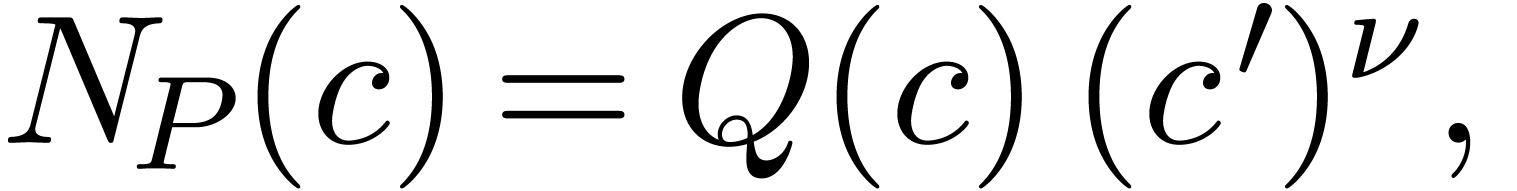
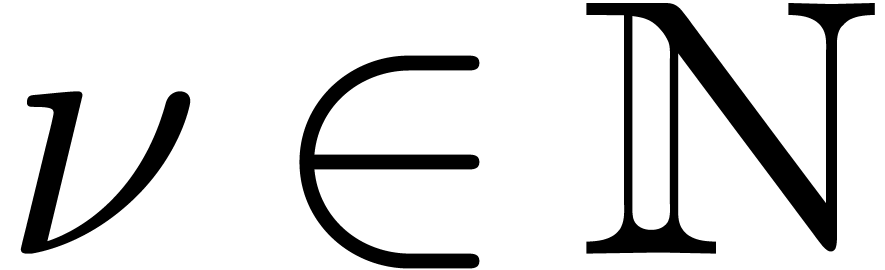 (by theorem
(by theorem  upward
shiftings). We will denote the multiplicity of
upward
shiftings). We will denote the multiplicity of  by
by  .
. with
with  ,
, and
and  are
independent of
are
independent of  and given by
and given by
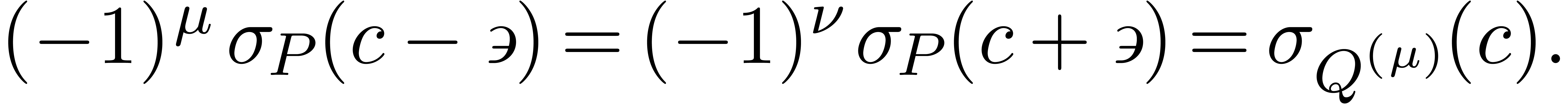
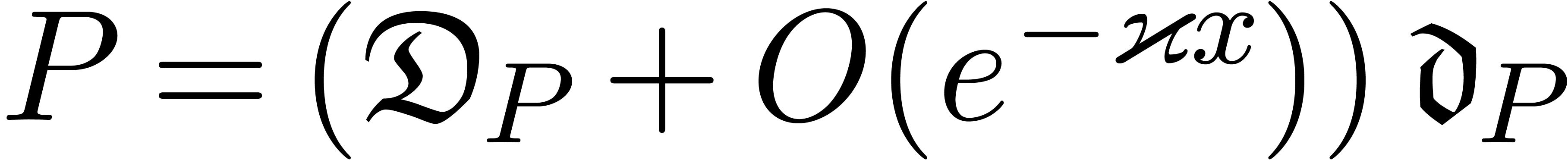
 ,
, ,
,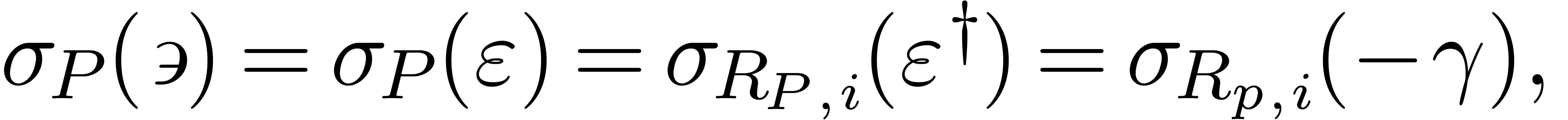
 be constants such that
be constants such that 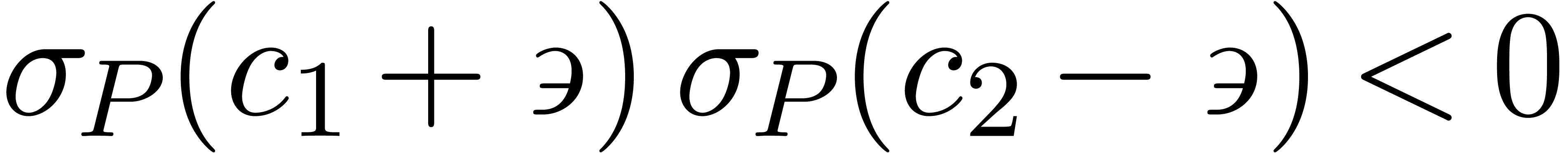 .
.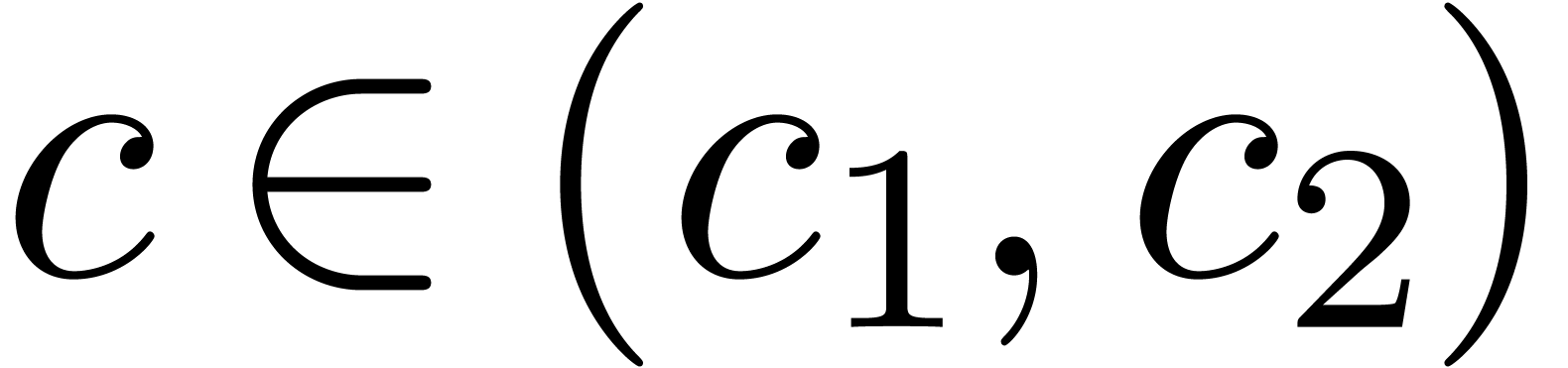 with
with 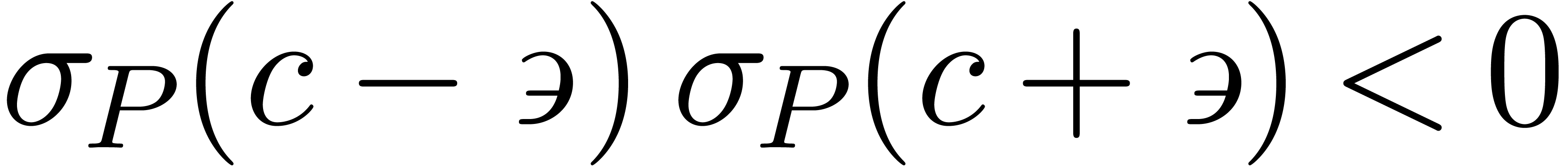 .
. with
with  ,
,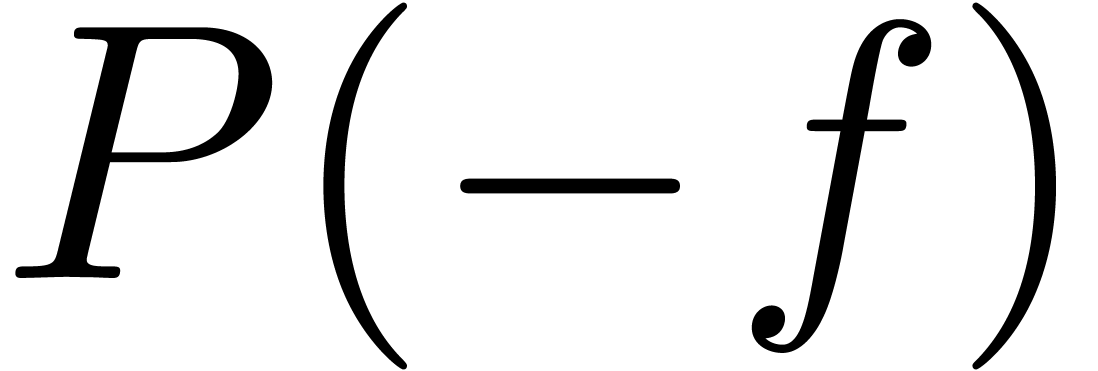 and
and 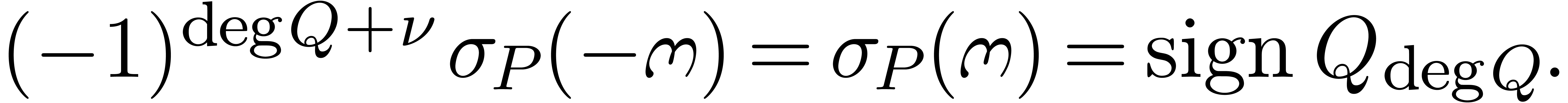
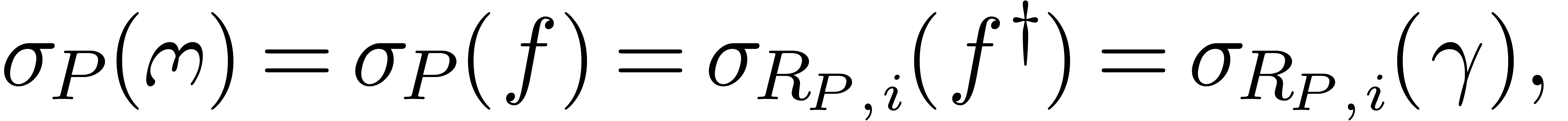
 be a constant such that
be a constant such that 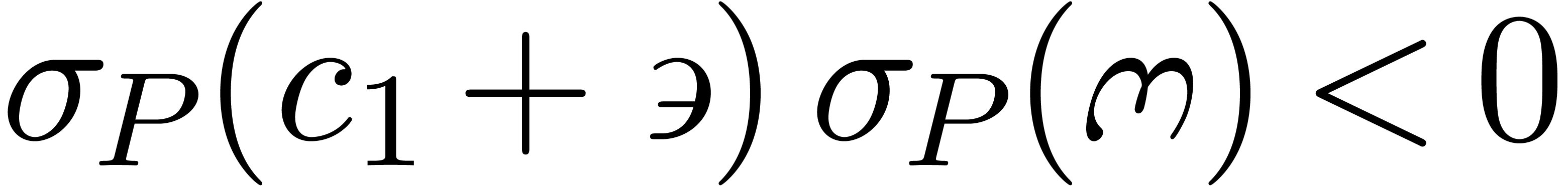 .
. with
with  ”.
”. and
and  be a transseries
resp. a transmonomial in
be a transseries
resp. a transmonomial in  of one of the following forms:
of one of the following forms:
 ,
, with
with  .
.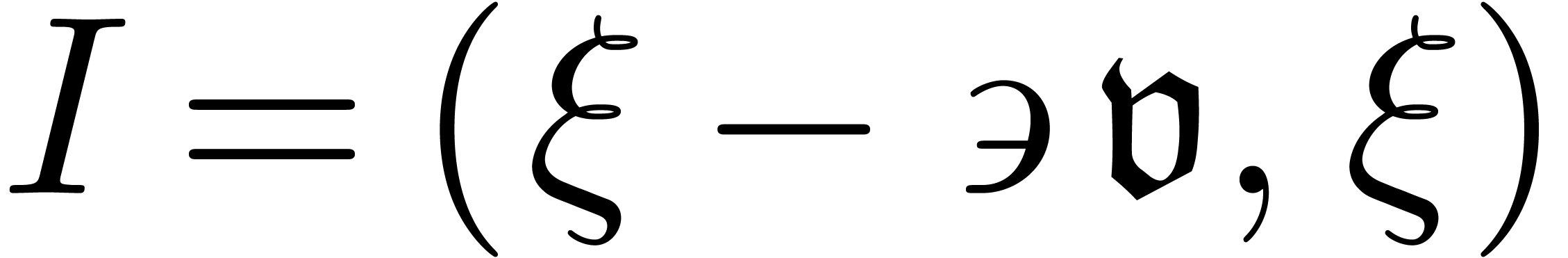 .
. .
.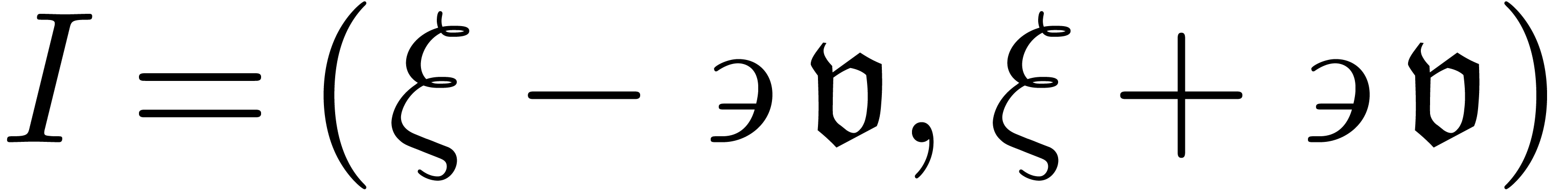 .
. .
. be a transseries
resp. a transmonomial in
be a transseries
resp. a transmonomial in 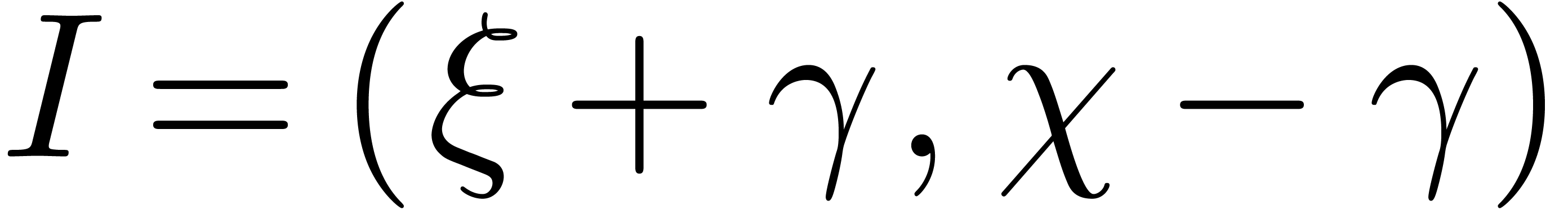 ,
,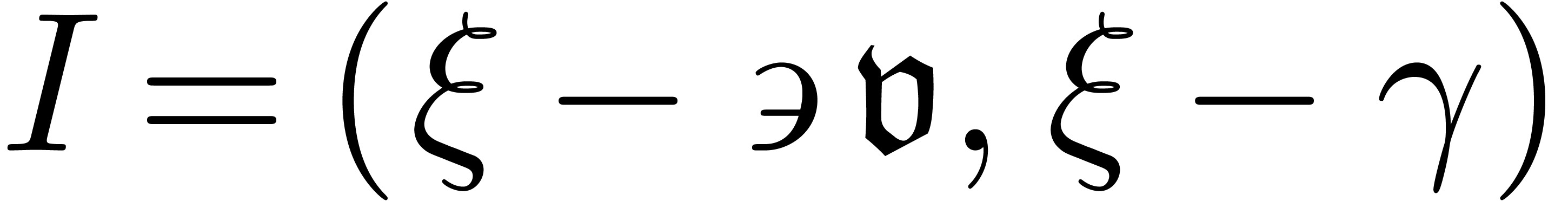 .
.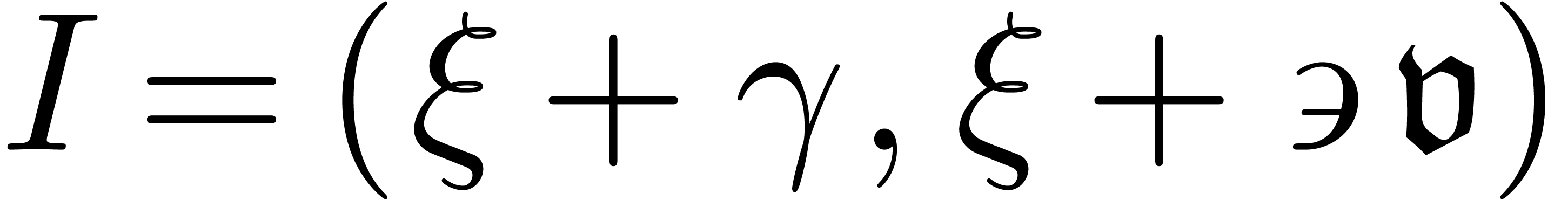 .
.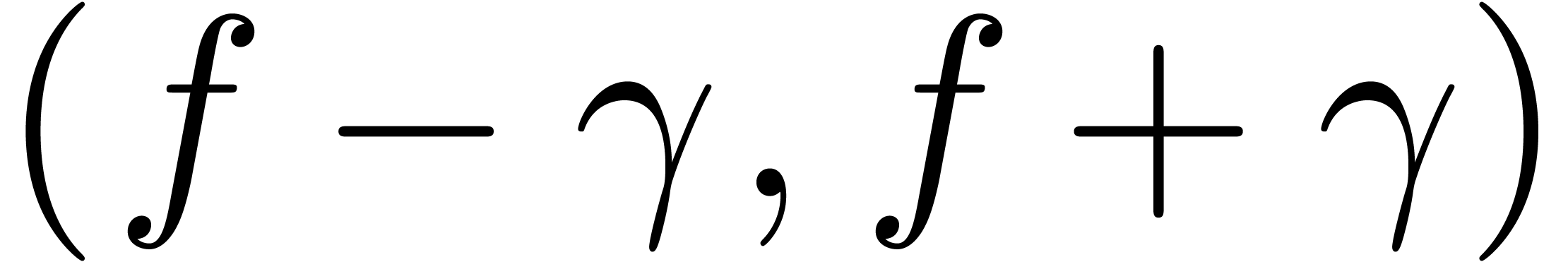 for some
for some 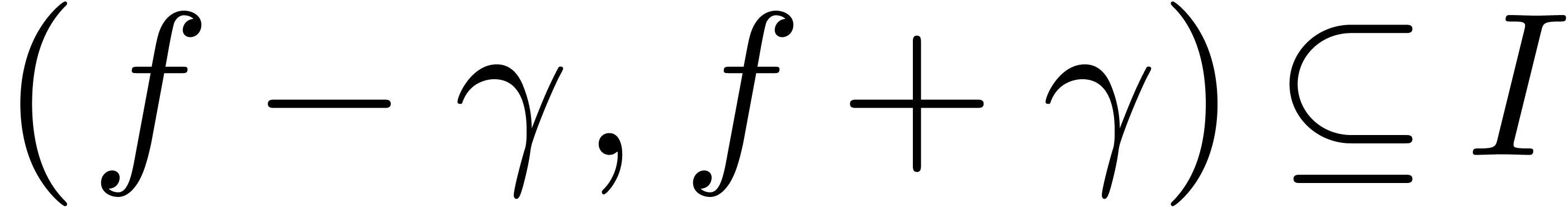 .
.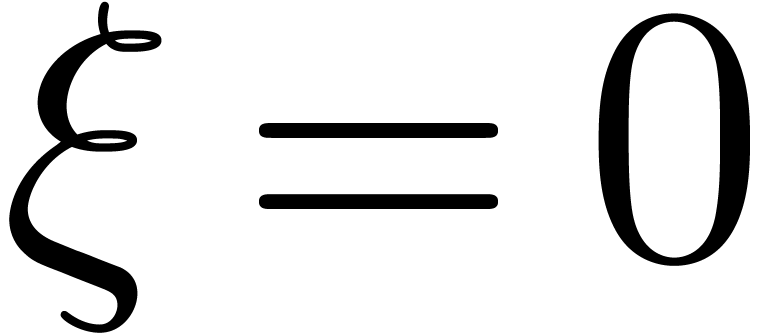 (modulo an additive conjugation of
(modulo an additive conjugation of 
 ,
, ,
, (this means that
(this means that
 for all sufficiently large
for all sufficiently large  ;
; ,
, ,
, and
and
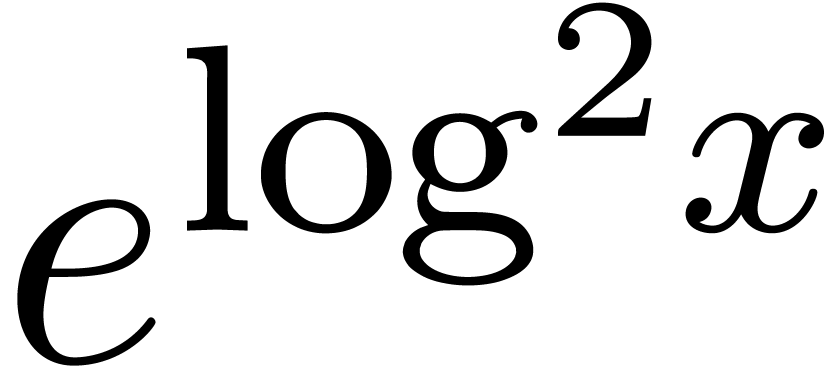 have exponentiality
have exponentiality 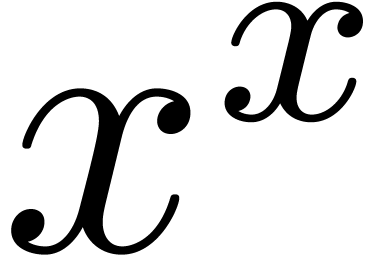 ).
). .
.