| On the computation of limsups |
|
| February 26, 1996 |
|
In the last years, several asymptotic expansion algorithms have appeared, which have the property that they can deal with very general types of singularities, such as singularities arising in the study of algebraic differential equations. However, attention has been restricted so far to functions with “strongly monotonic” asymptotic behaviour: formally speaking, the functions lie in a common Hardy field, or, alternatively, they are determined by transseries.
In this article, we make a first step towards the treatment of
functions involving oscillatory behaviour. More precisely, let
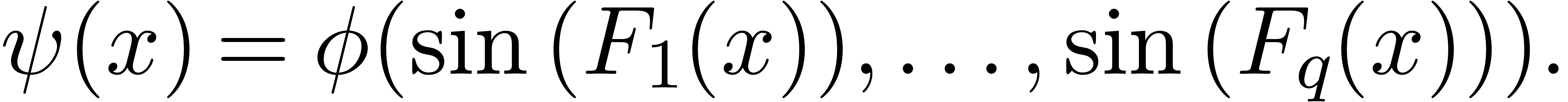
We give a method to compute
|
In the last years, several asymptotic expansion algorithms have appeared [Sha90, Sha91, GG92, RSSH96, Hoe96a]. These algorithms are have the property that they can deal with very general types of singularities, such as singularities arising in the study of certain algebraic differential equations. However, attention has been restricted so far to functions with “strongly monotonic” asymptotic behaviour. This means that the functions lie in a common Hardy field, or, alternatively, that they are determined by transseries. In this article, we make a first step to the treatment of functions involving oscillatory behaviour. We also notice that Grigoriev obtained some very interesting related results in [Gri94, Gri95] although his more probabilistic point of view is different (even complementary) from ours.
The structure of this paper is as follows: in section 2, we
recall a classical density theorem for linear curves on the 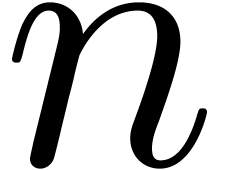 -dimensional torus (see for example [Kok36,
KN74]). In section 3, this theorem is
generalized to more general classes of curves on the torus.
-dimensional torus (see for example [Kok36,
KN74]). In section 3, this theorem is
generalized to more general classes of curves on the torus.
In section 4, we study exp-log functions at infinity: an
exp-log function is a function which is built up from the rationals  and
and  ,
using the field operations, exponentiation and logarithm. An exp-log
function at infinity is an exp-log function which is defined in a
neighbourhood of infinity. We present a more compact version of an
expansion algorithm of exp-log functions at infinity, originally due to
Shackell [Sha91] (see also [RSSH96]). For
this, we assume the existence of an oracle for deciding whether an
exp-log function is zero in a neighbourhood of infinity. This problem
has been reduced to the corresponding problem for exp-log constants in
[Hoe96b, Hoe96a]. A solution to the constant
problem was given by Richardson in [Ric94], modulo
Schanuel's conjecture:
,
using the field operations, exponentiation and logarithm. An exp-log
function at infinity is an exp-log function which is defined in a
neighbourhood of infinity. We present a more compact version of an
expansion algorithm of exp-log functions at infinity, originally due to
Shackell [Sha91] (see also [RSSH96]). For
this, we assume the existence of an oracle for deciding whether an
exp-log function is zero in a neighbourhood of infinity. This problem
has been reduced to the corresponding problem for exp-log constants in
[Hoe96b, Hoe96a]. A solution to the constant
problem was given by Richardson in [Ric94], modulo
Schanuel's conjecture:
 are
are  -linearly
independent complex numbers, then the transcendence degree of
-linearly
independent complex numbers, then the transcendence degree of 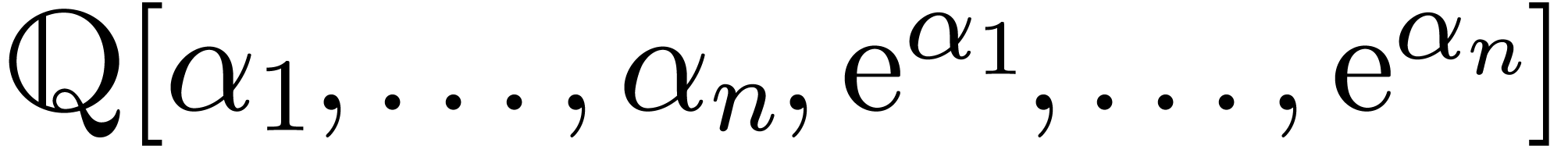 over
over  is at least
is at least 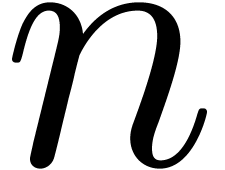 .
.
In section 5, we are given an algebraic function 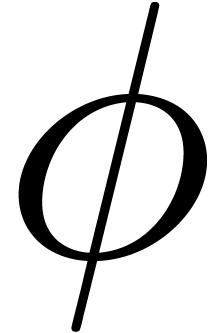 defined on
defined on 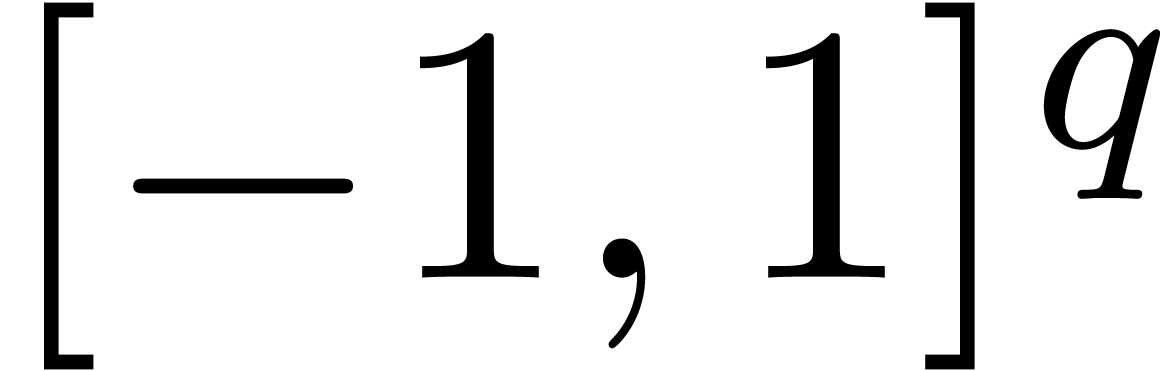 ,
and exp-log functions at infinity
,
and exp-log functions at infinity  in
in  . We show how to compute
. We show how to compute
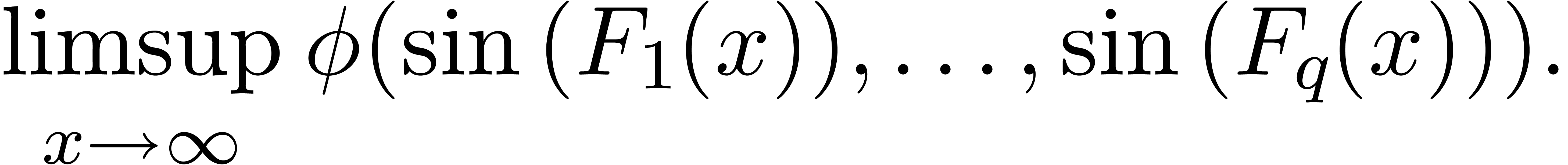
In section 5, we will assume the existence of an oracle for
checking the  -linear
dependence of exp-log constants. Actually, Richardson's algorithm can
easily be adapted to yield an algorithm for doing this modulo Schanuel's
conjecture.
-linear
dependence of exp-log constants. Actually, Richardson's algorithm can
easily be adapted to yield an algorithm for doing this modulo Schanuel's
conjecture.
 -dimensional torus
-dimensional torus
Let  be
be  -linearly
independent numbers: we will use vector notation, and denote the vector
-linearly
independent numbers: we will use vector notation, and denote the vector
 by
by  .
In this section, we prove that the image of
.
In this section, we prove that the image of 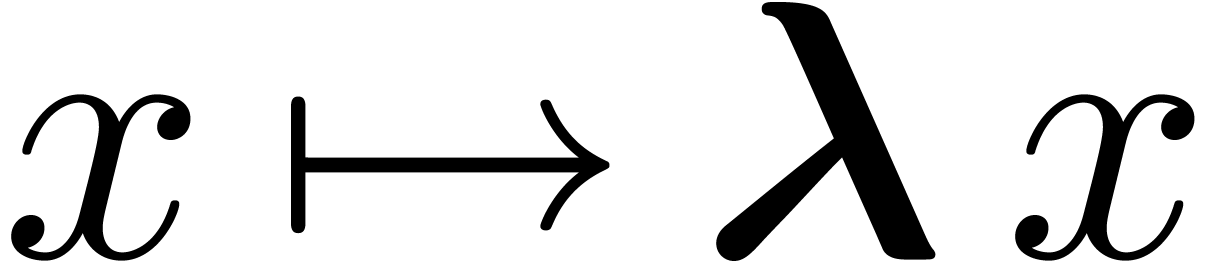 , from
, from  in the
in the 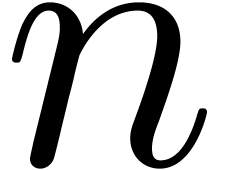 -dimensional torus
-dimensional torus  is
dense. Notice that we use the same notation for
is
dense. Notice that we use the same notation for  and its class modulo
and its class modulo  .
Moreover, we show that the “density” of the image is uniform
is a sense that will be made precise. The following theorem is
classical:
.
Moreover, we show that the “density” of the image is uniform
is a sense that will be made precise. The following theorem is
classical:
 be
be  -linearly
independent real numbers. Let
-linearly
independent real numbers. Let  be the canonical
base of
be the canonical
base of 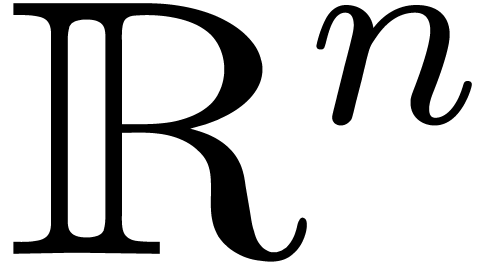 . Then
. Then 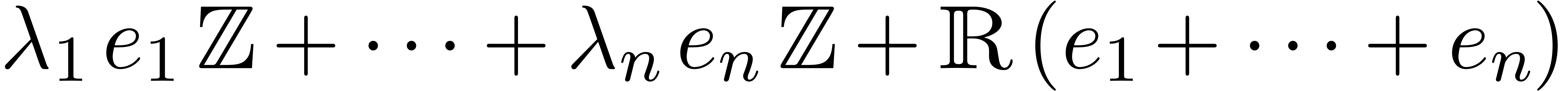 is dense in
is dense in 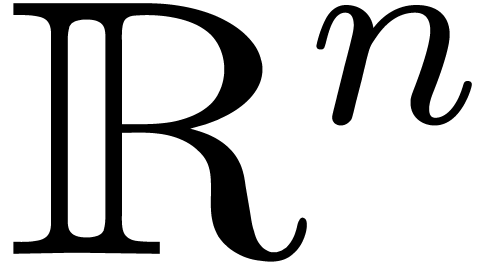 .
.
Now let 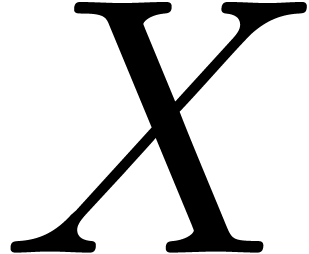 be a measurable subset of
be a measurable subset of 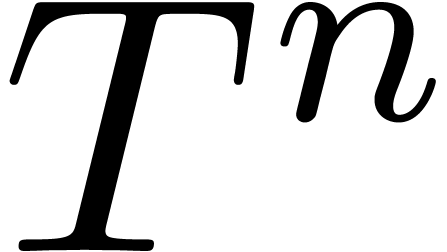 , and let
, and let 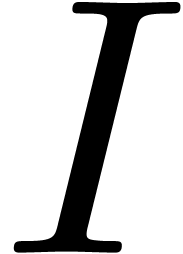 be some
interval of
be some
interval of  . Denoting the
Lebesgue measure by
. Denoting the
Lebesgue measure by 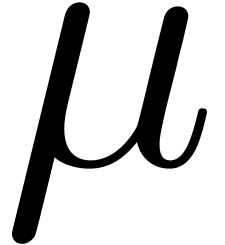 , we
define
, we
define
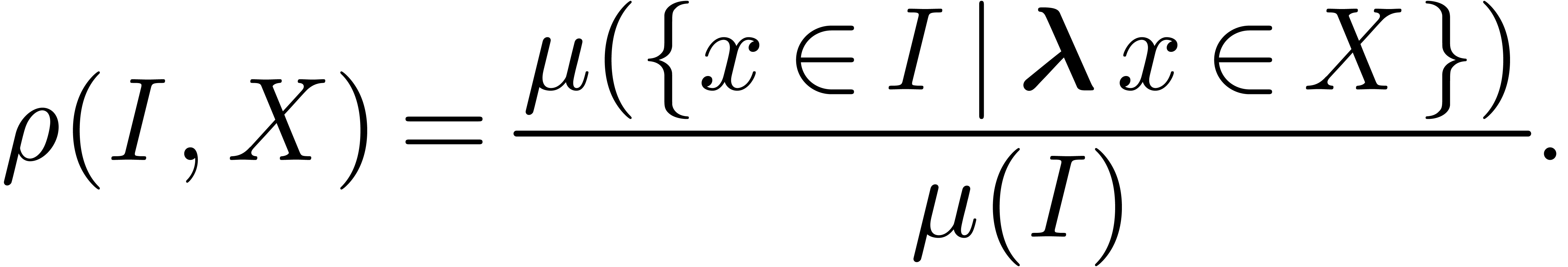 |
(1) |
Let us also denote by  the Euclidean distance on
the Euclidean distance on
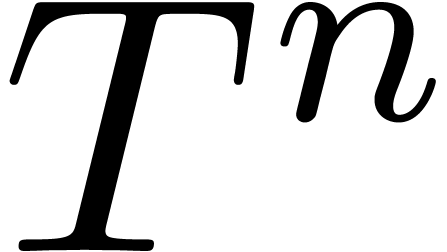 . Let
. Let 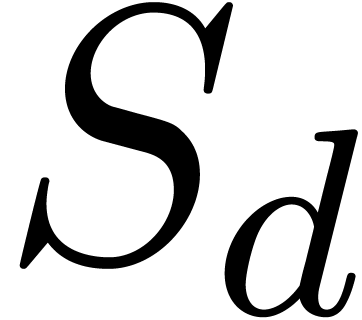 , resp.
, resp. 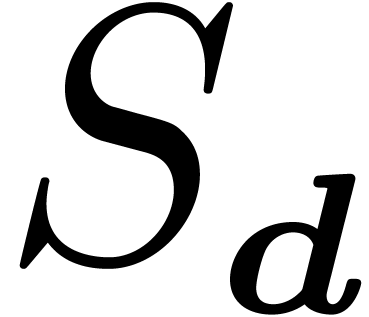 denote the shift
operator on
denote the shift
operator on  (resp.
(resp.  or
or
 ):
): 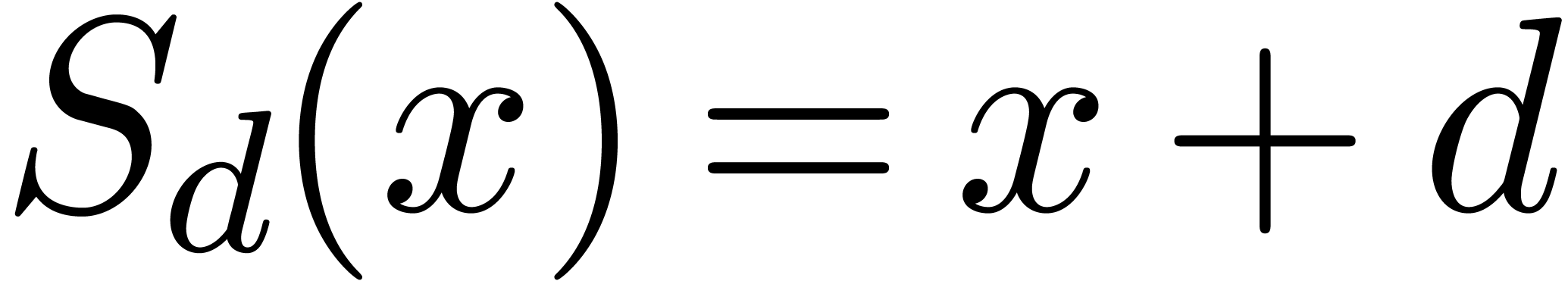 and
and  . The following are
immediate consequences of the definition of
. The following are
immediate consequences of the definition of 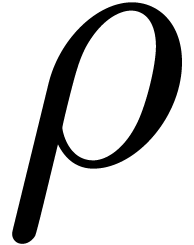 :
:
It will be convenient to adopt some conventions for intervals 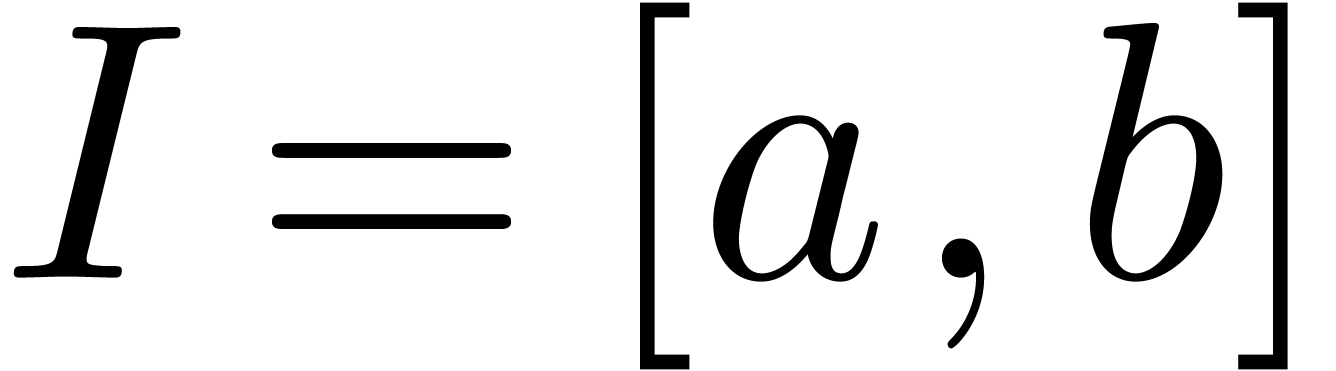 (resp.
(resp. 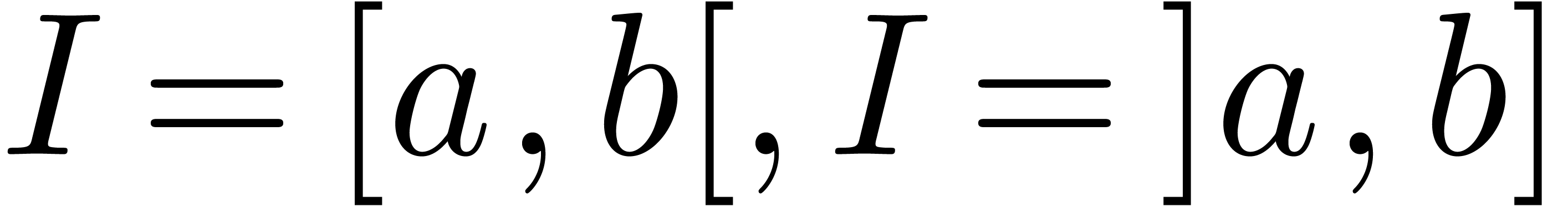 or
or 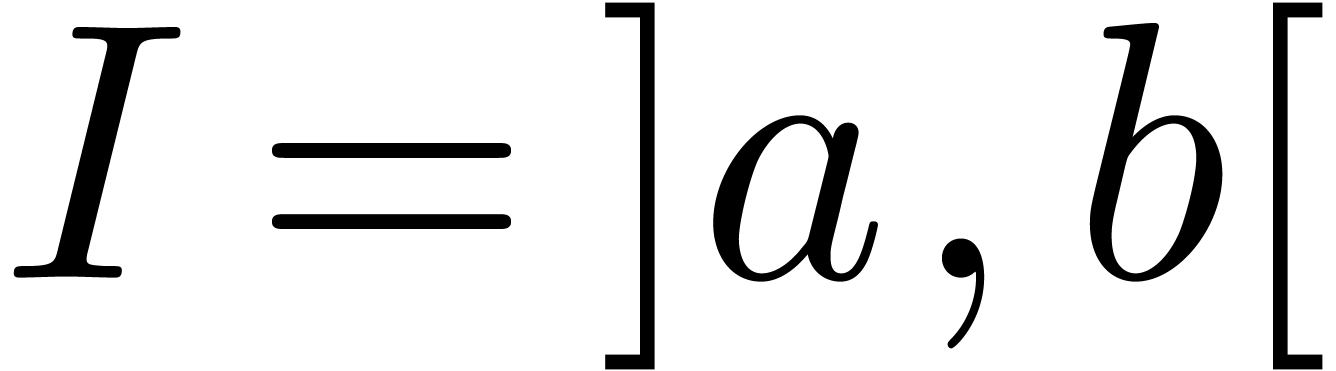 ) whose lengths
) whose lengths  tend to
infinity: we say that a property
tend to
infinity: we say that a property  holds uniformly
in
holds uniformly
in  , if the property holds
uniformly in
, if the property holds
uniformly in  :
:
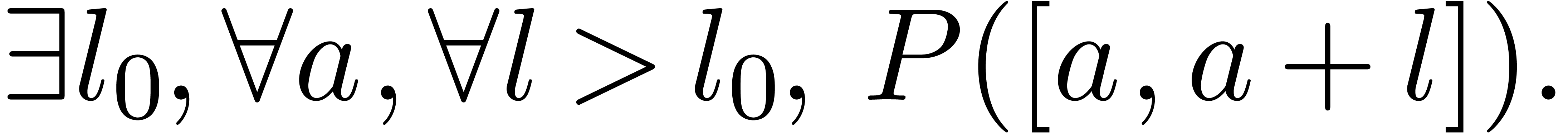
We say that 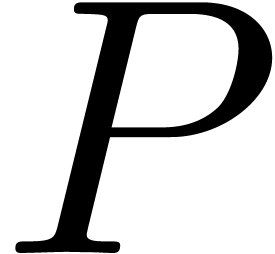 holds for all
holds for all 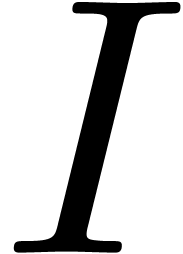 sufficiently close to infinity, if
sufficiently close to infinity, if 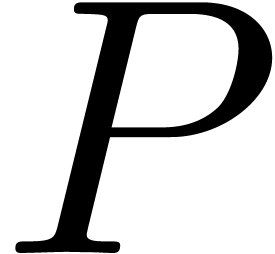 holds for all
sufficiently large
holds for all
sufficiently large  .
.
The next theorem is also classical, but for convenience of the reader we present a proof, since similar techniques will be used in the next section:
 be
be  -linearly independent real numbers and let
-linearly independent real numbers and let
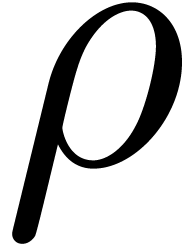 be given by
be given by

be an 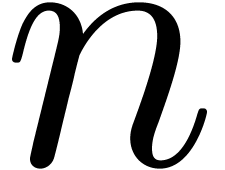 -dimensional
block, with
-dimensional
block, with  for all
for all 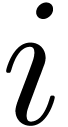 . Then
. Then
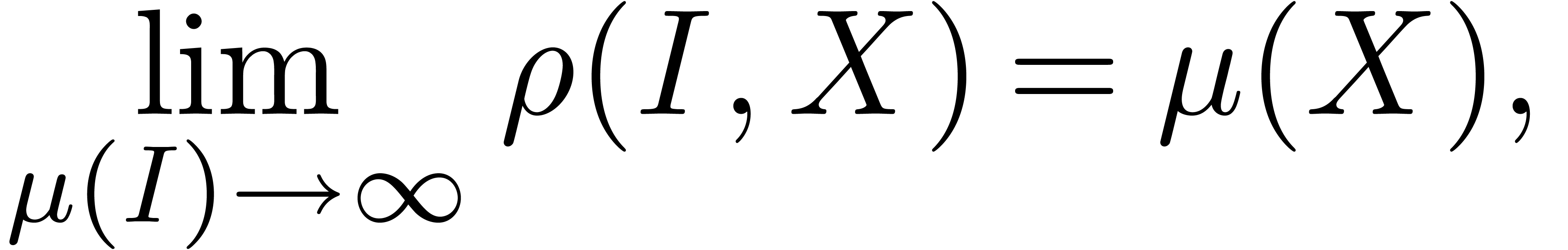
uniformly in 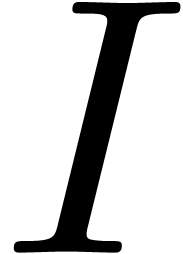 .
.
Proof. The theorem trivially holds if 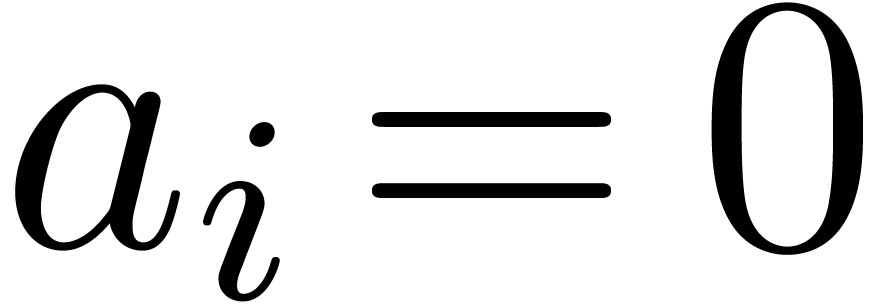 and
and 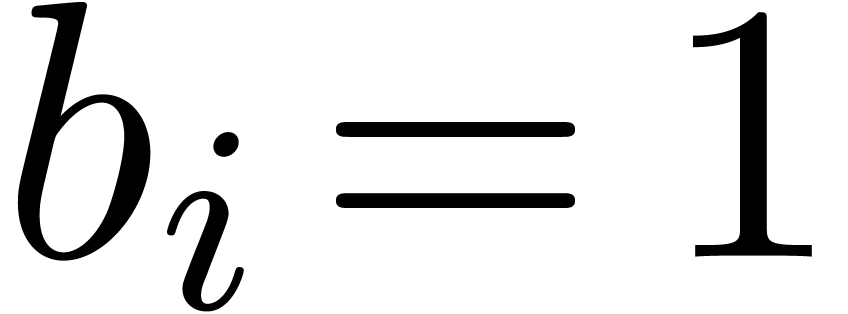 for all but one
for all but one 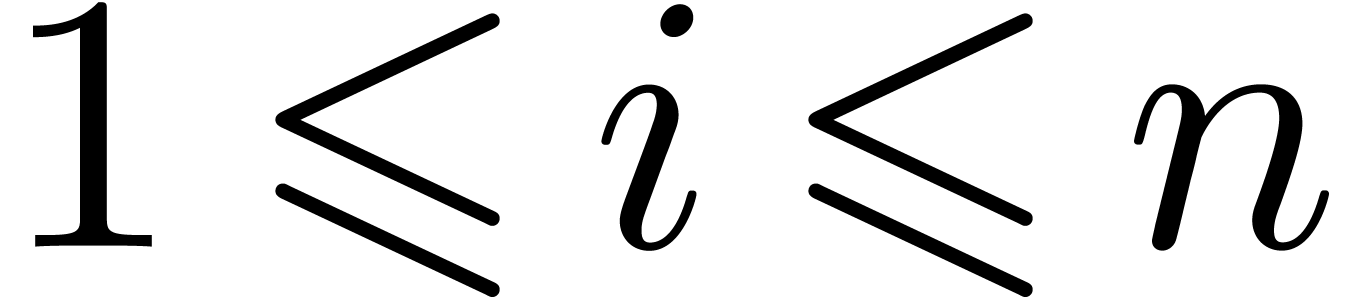 . Hence, it suffices to prove the theorem when
the
. Hence, it suffices to prove the theorem when
the 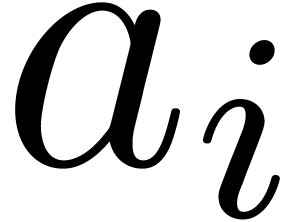 's and the
's and the 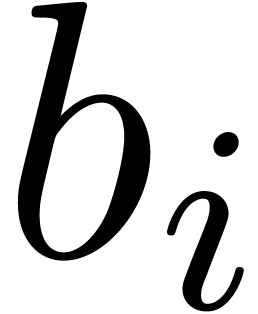 's are rational numbers. Indeed, let
's are rational numbers. Indeed, let  be rational numbers with
be rational numbers with 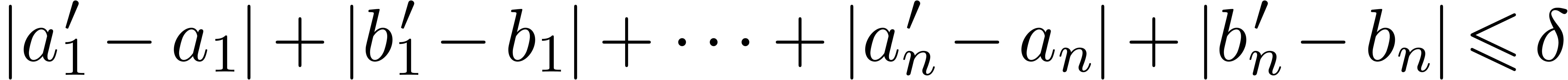 ,
and denote
,
and denote  . Then
. Then 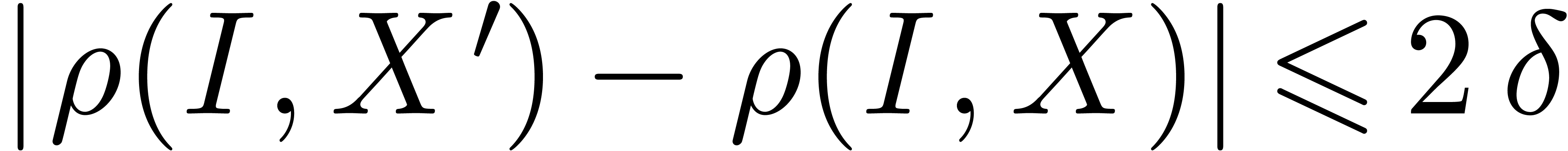 for
for 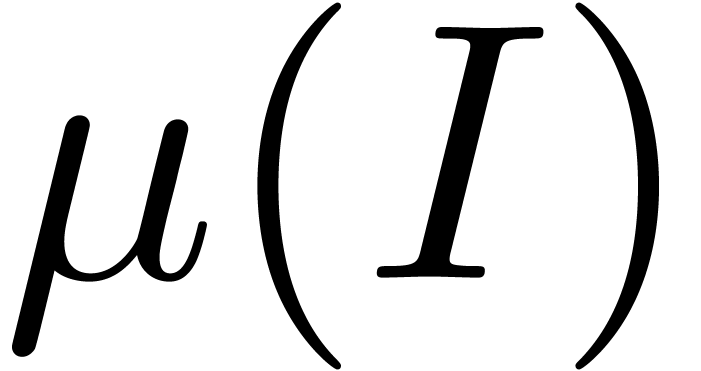 sufficiently large, uniformly
in
sufficiently large, uniformly
in 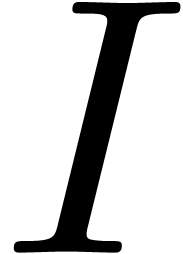 .
.
Because of Proposition 3(a) and (b), it suffices to prove
the theorem for fixed 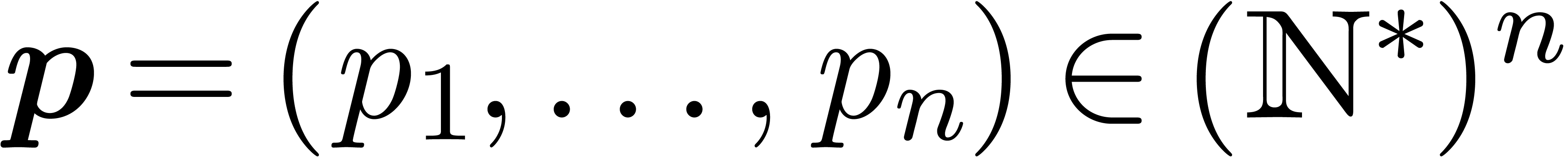 and for all
and for all
with  . We remark that
. We remark that 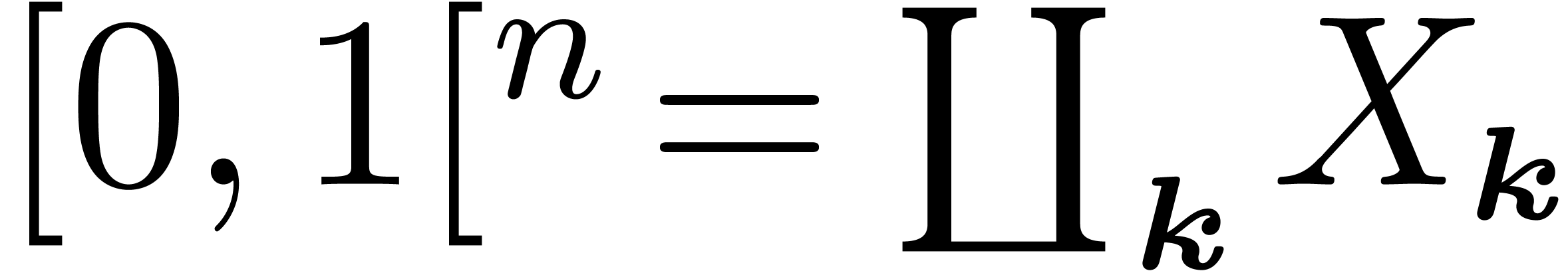 , so that
, so that 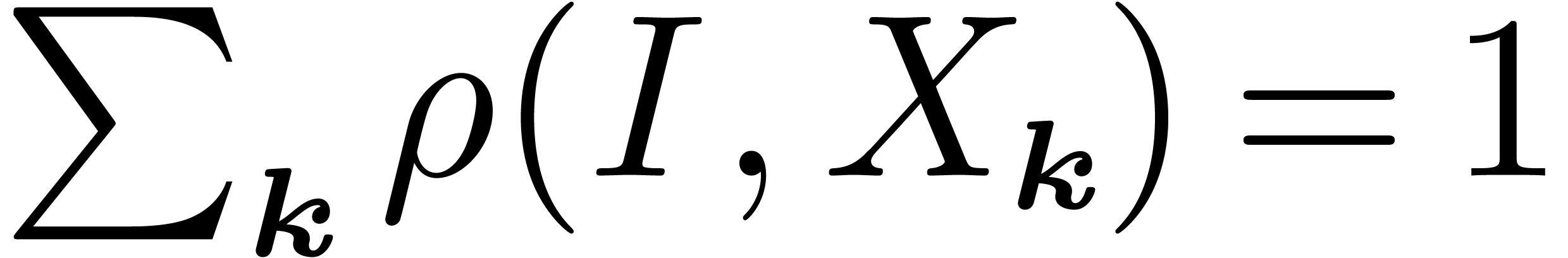 .
.
Now let  . For each
. For each 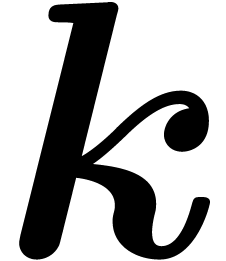 , we can find
, we can find 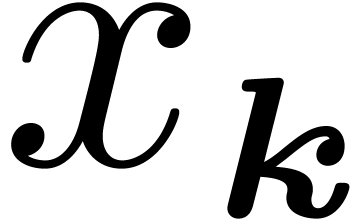 , with
, with 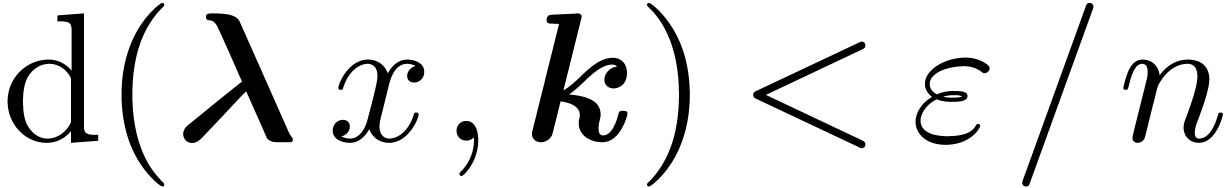 ,
by Proposition 2. Consequently, we have
,
by Proposition 2. Consequently, we have 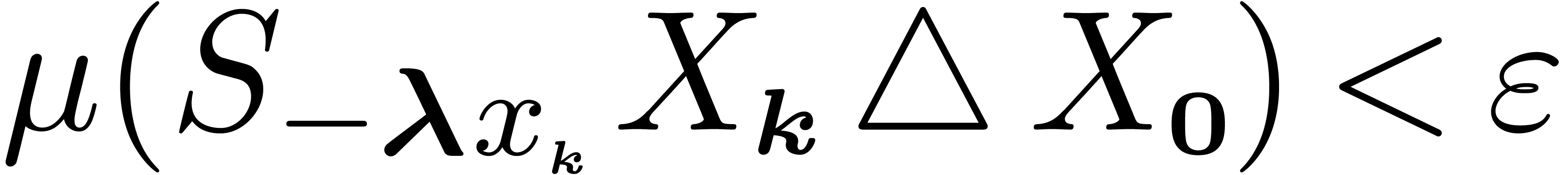 , where
, where  denotes the
symmetric difference of
denotes the
symmetric difference of  and
and  . Hence,
. Hence, 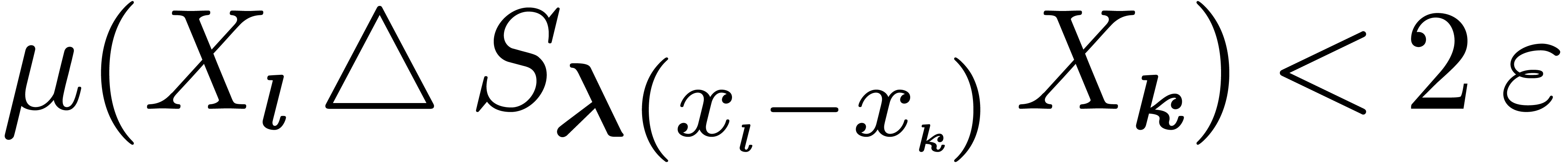 ,
for each
,
for each  with
with  .
Using Proposition 3, we can now estimate
.
Using Proposition 3, we can now estimate
Taking 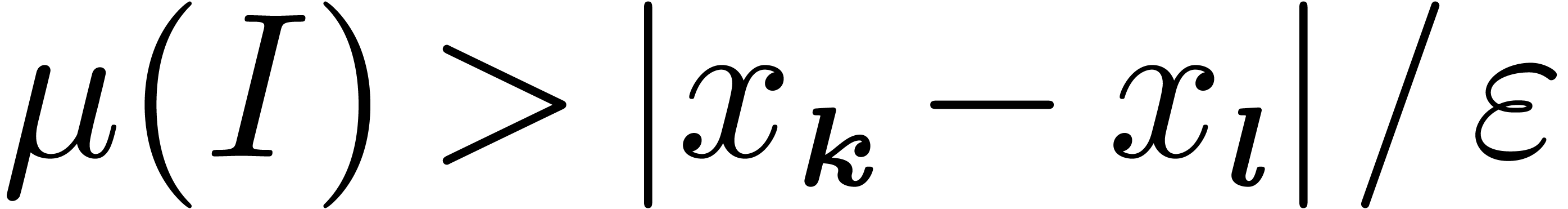 , for any
, for any 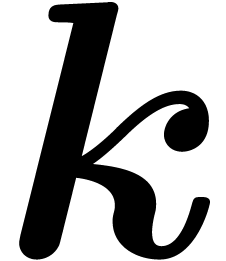 and
and 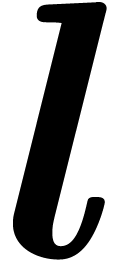 , we get
, we get
Hence 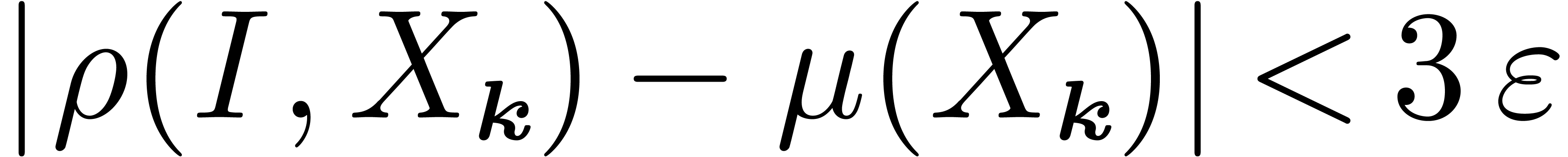 , for sufficiently
large
, for sufficiently
large 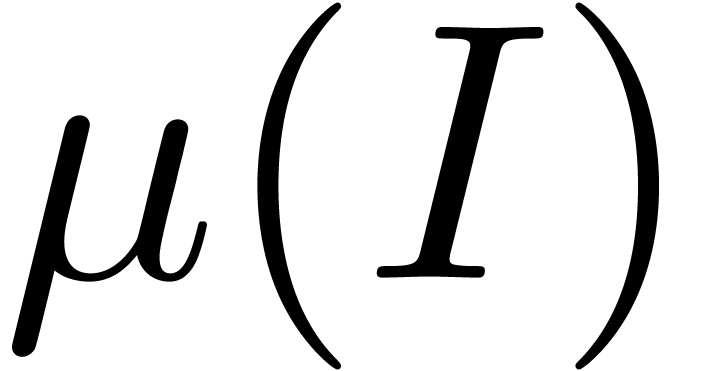 , uniformly in
, uniformly in 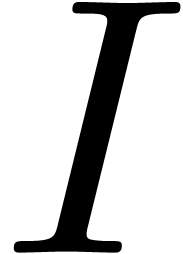 . This completes our proof.
. This completes our proof.
In this section we will obtain a more general uniform density theorem on
the torus, when the application  from section 2 is replaced by a non linear mapping, which satisfies
suitable regularity conditions. Before coming to this generalization, we
will need some definitions and lemmas. We say that a function
from section 2 is replaced by a non linear mapping, which satisfies
suitable regularity conditions. Before coming to this generalization, we
will need some definitions and lemmas. We say that a function 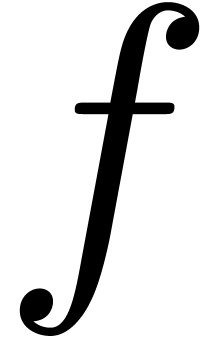 defined in a neighbourhood of infinity is steadily
dominated by
defined in a neighbourhood of infinity is steadily
dominated by  ,
if
,
if 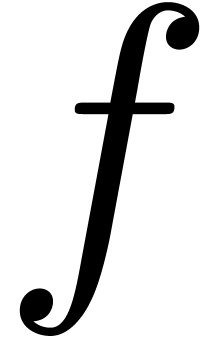 has a continuous second derivative,
has a continuous second derivative, 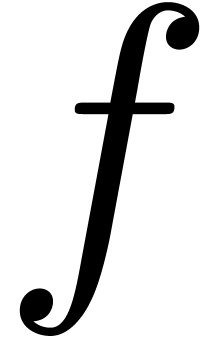 tends to infinity,
tends to infinity, 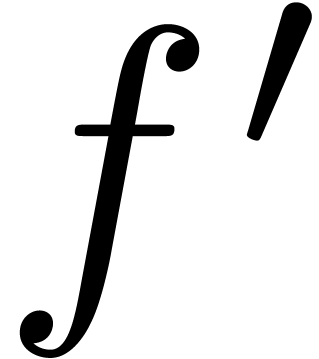 decreases
strictly towards zero, and
decreases
strictly towards zero, and 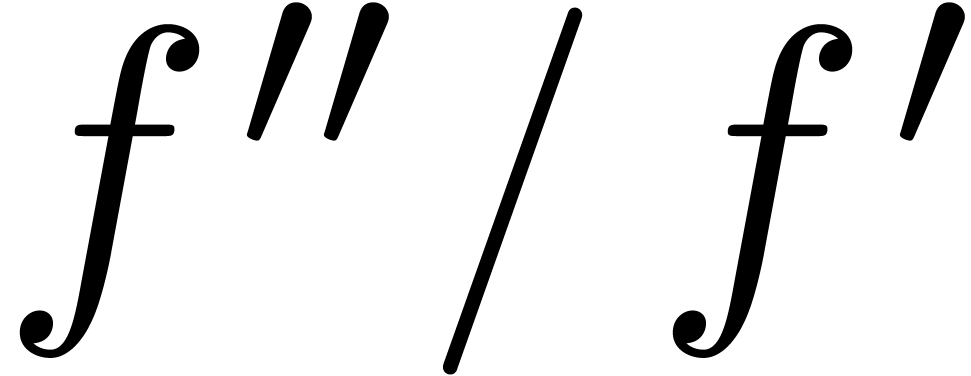 tends to zero. We
remark that such functions admit functional inverses in a neighbourhood
of infinity.
tends to zero. We
remark that such functions admit functional inverses in a neighbourhood
of infinity.
More generally, we say that if 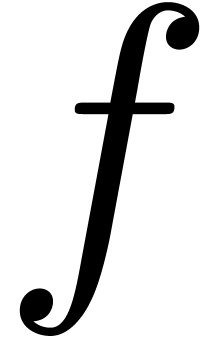 and
and 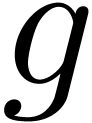 are functions in a neighbourhood of infinity, such that
are functions in a neighbourhood of infinity, such that
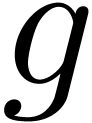 is invertible, then
is invertible, then 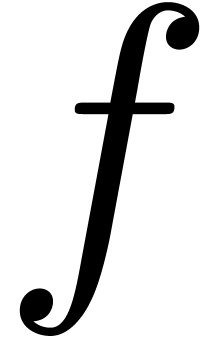 is
steadily dominated by
is
steadily dominated by 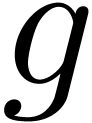 , if
, if
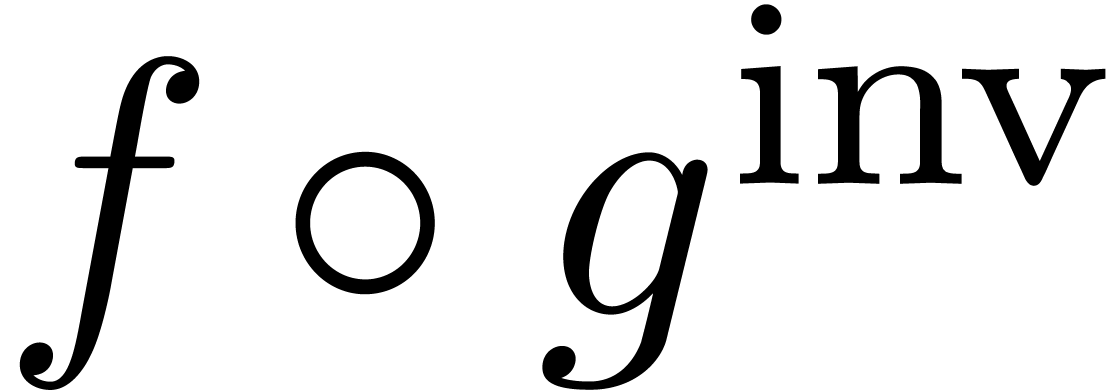 is steadily dominated by
is steadily dominated by  . In this case, we write
. In this case, we write  . It is easily verified that if
. It is easily verified that if  and
and  , then
, then 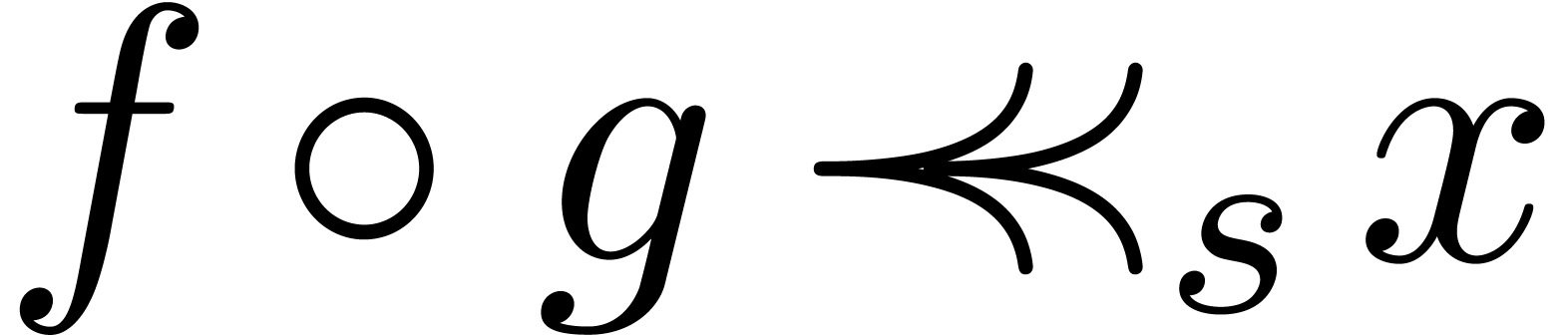 , so that
, so that  is
transitive. We also remark that if
is
transitive. We also remark that if  and if
and if 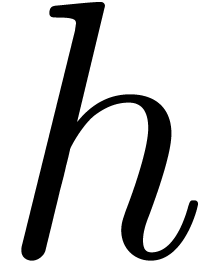 is a function, which has a continuous second
derivative and tends to infinity, then
is a function, which has a continuous second
derivative and tends to infinity, then  .
We finally have the following property of steady domination:
.
We finally have the following property of steady domination:
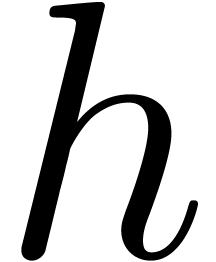 be steadily dominated by
be steadily dominated by  and let
and let 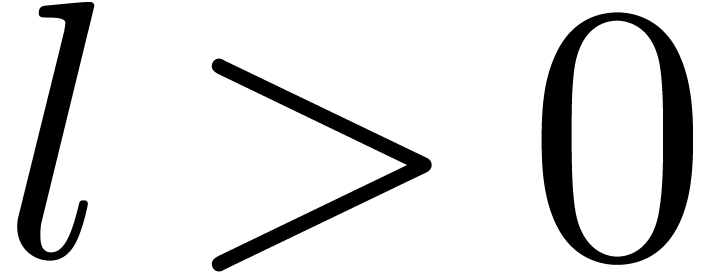 and
and  be given.
Then for all sufficiently large
be given.
Then for all sufficiently large  we have
we have 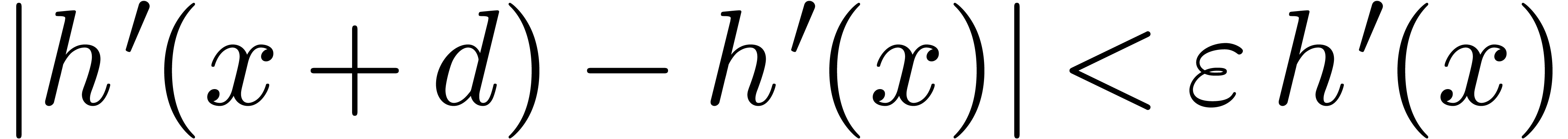 , for all
, for all 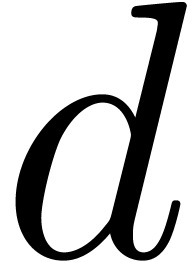 with
with 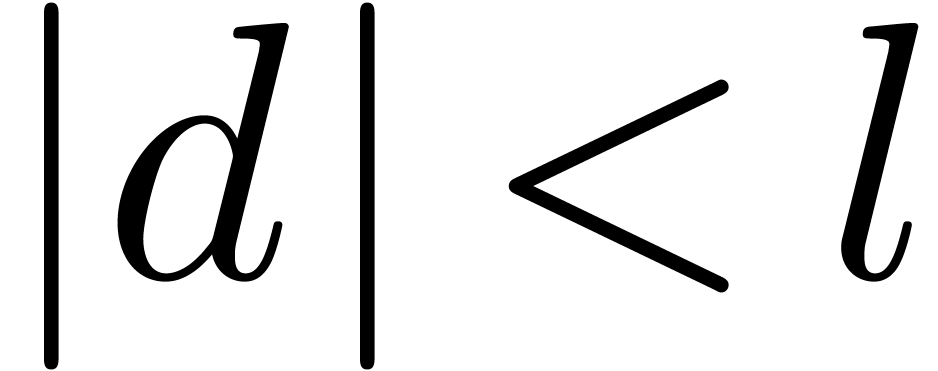 .
.
Proof. Let  be such that
be such that
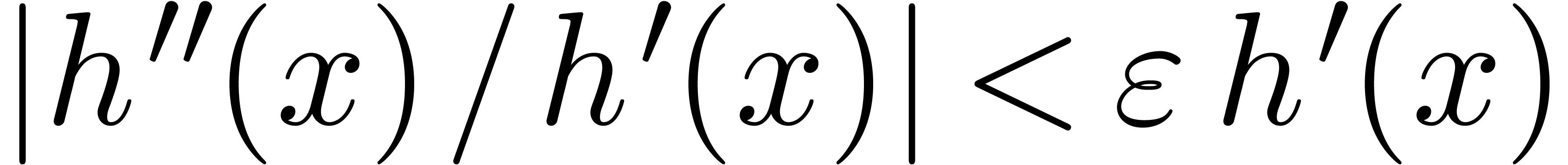 , for all
, for all 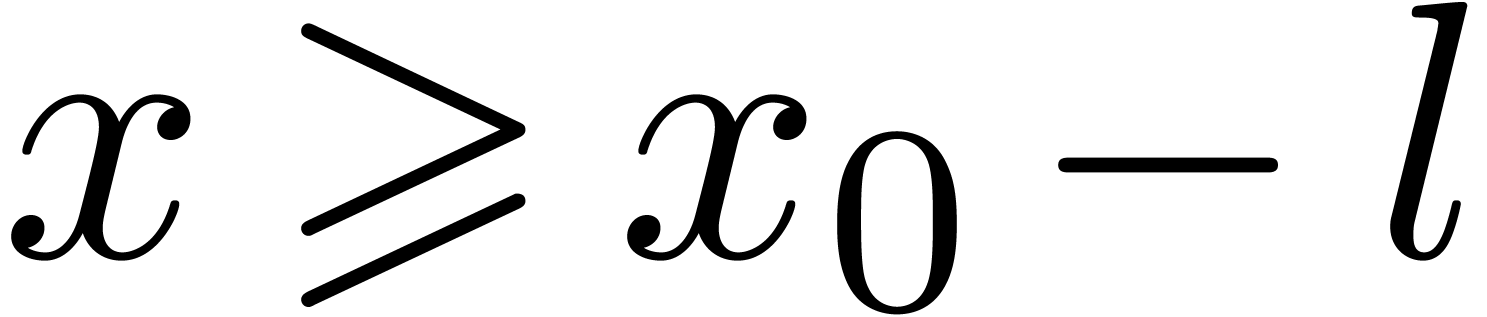 . We have
. We have  ,
for some
,
for some  between
between  and
and
 . If
. If 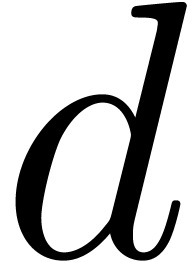 is positive, then
is positive, then  , and we
are done. In the other case, we have
, and we
are done. In the other case, we have 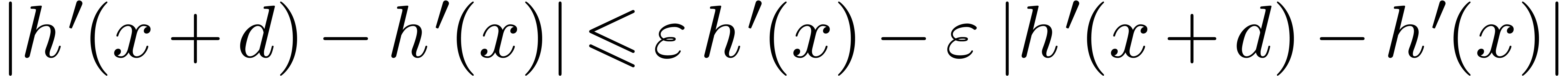 ,
whence
,
whence  .
.
Now let 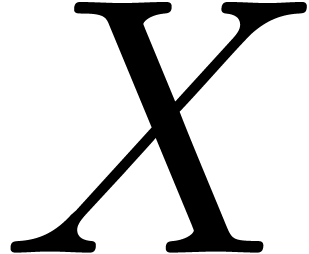 be a measurable subset of
be a measurable subset of  . For each interval
. For each interval 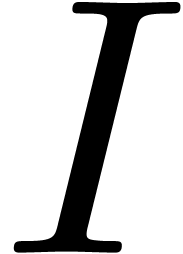 , we define:
, we define:
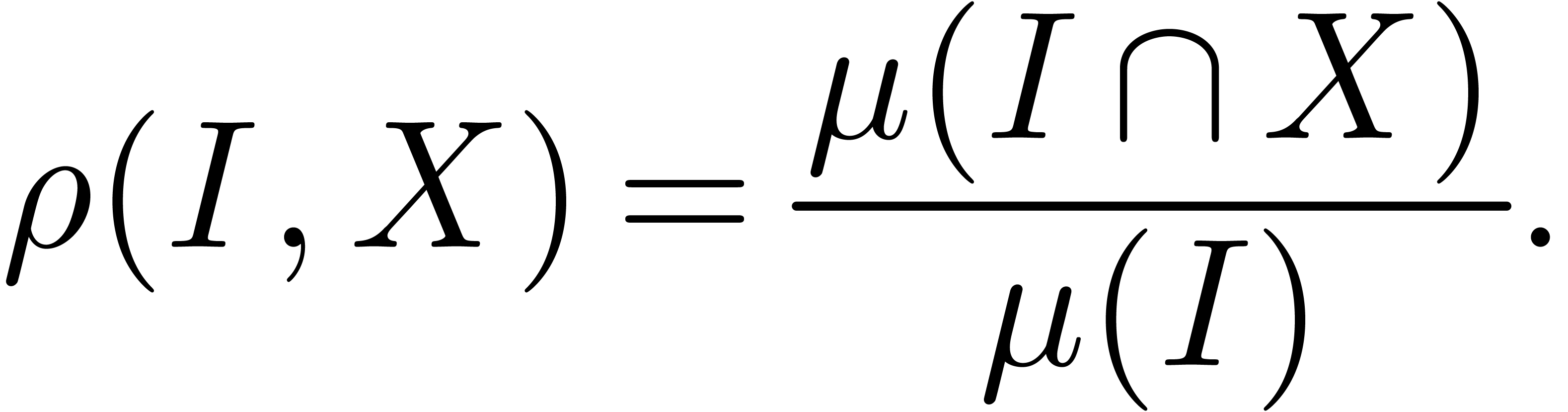
We say that 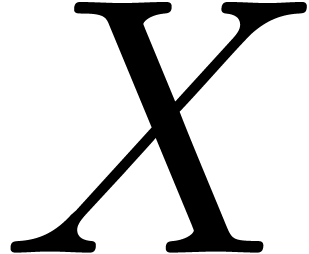 admits an asymptotic
density
admits an asymptotic
density 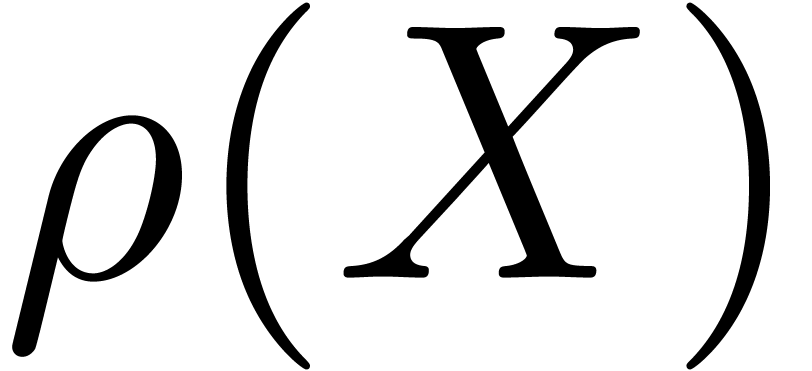 if
if
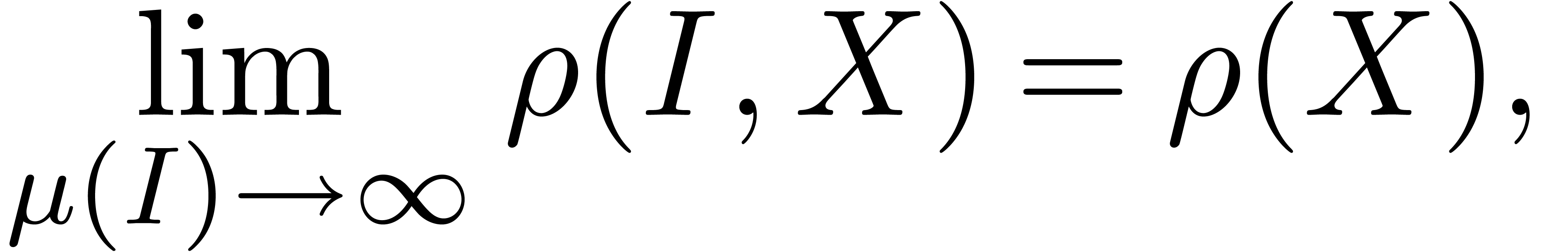
uniformly in 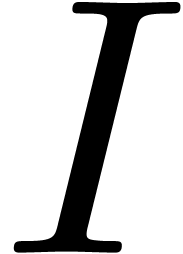 , for
, for 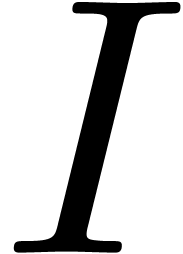 sufficiently close to infinity. More generally, if
sufficiently close to infinity. More generally, if 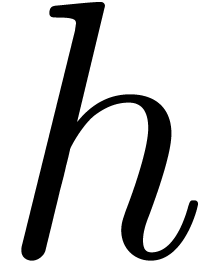 is steadily dominated by
is steadily dominated by  , then we say that
, then we say that  admits
admits
 -asymptotic density
-asymptotic density 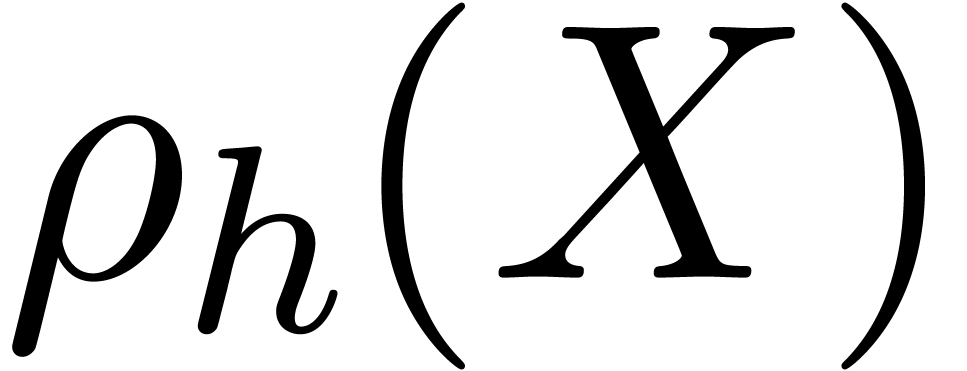 if
if
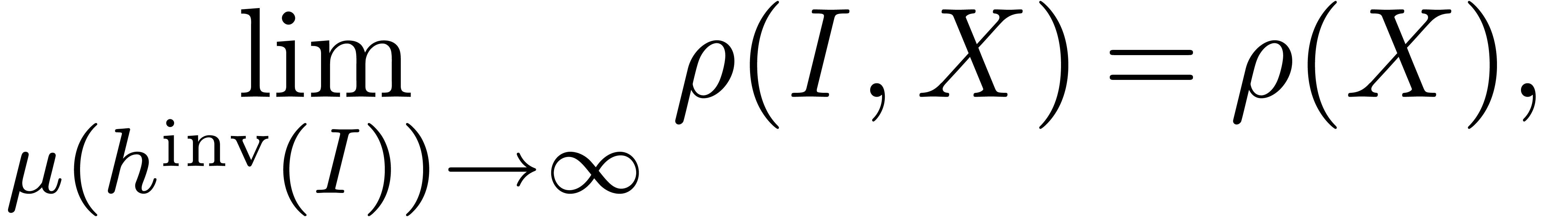
uniformly in 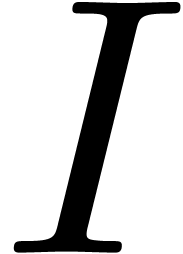 , for
, for 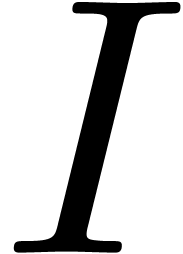 sufficiently close to infinity.
sufficiently close to infinity.
 be a measurable subset of
be a measurable subset of  and let
and let  be steadily dominated by
be steadily dominated by  . If
. If 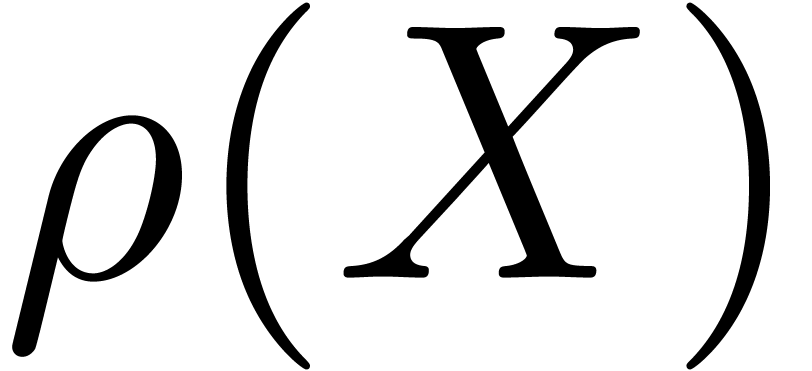 exists, then so
does
exists, then so
does  and we have
and we have  .
.
Proof. Let  .
Let
.
Let  be such that
be such that 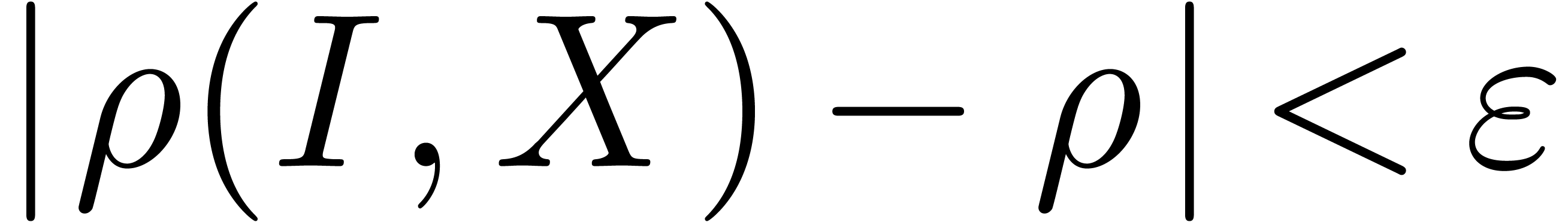 ,
whenever
,
whenever 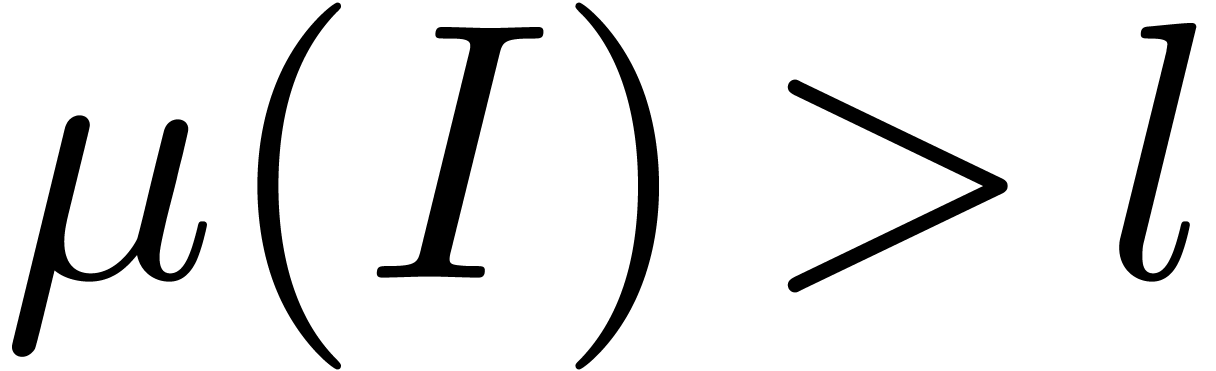 . Let
. Let 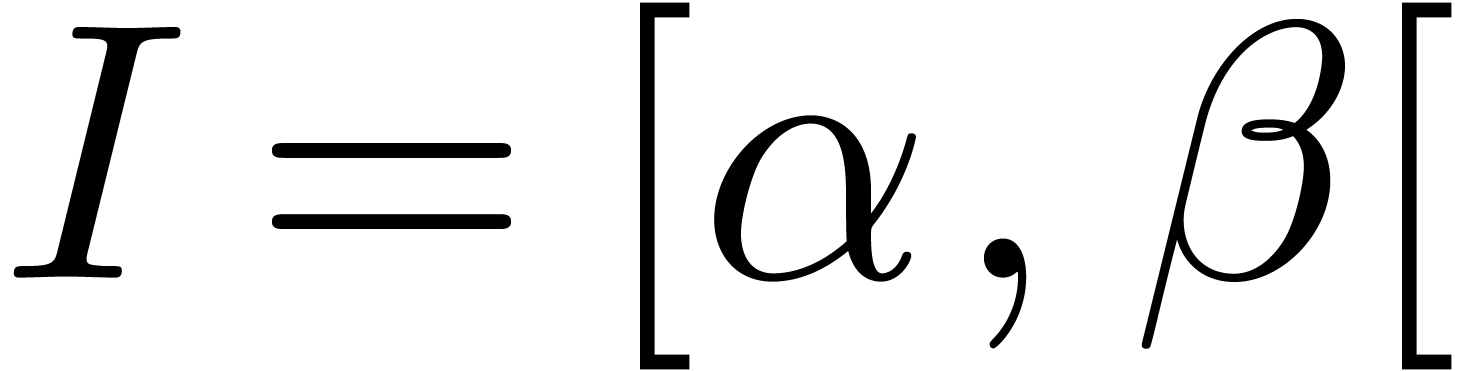 with
with 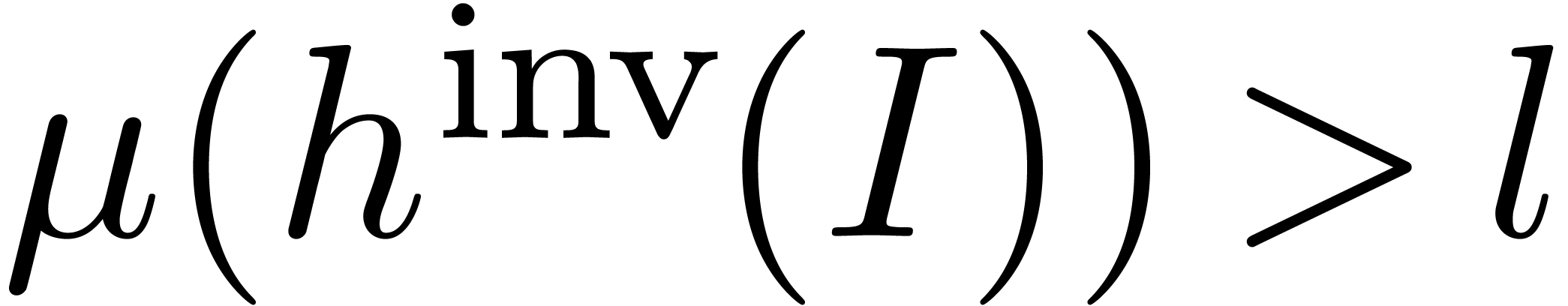 and subdivide
and subdivide 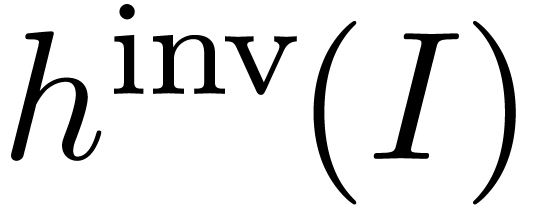 in
in 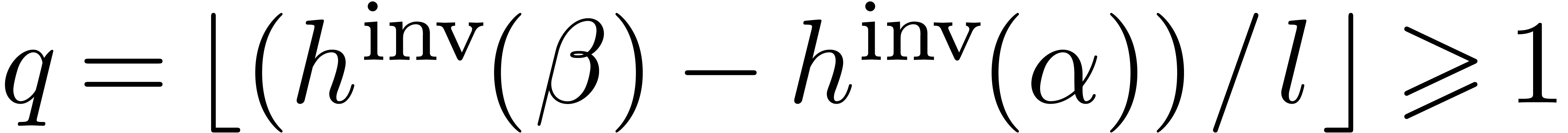 parts of equal length
parts of equal length 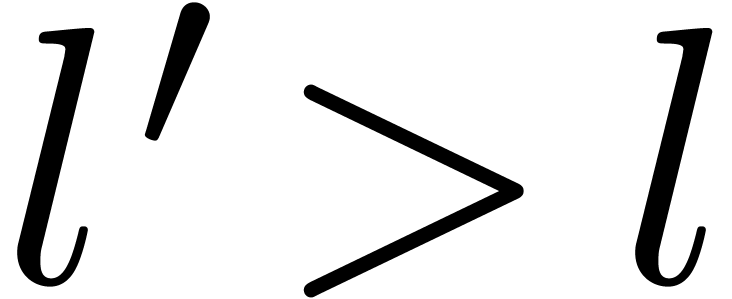 :
:
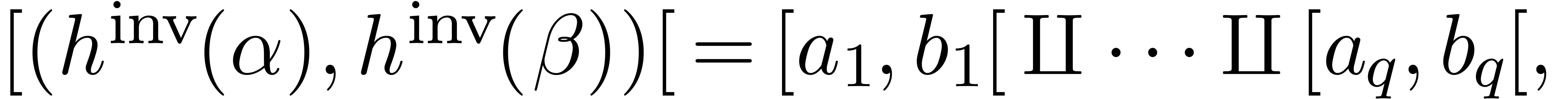
with 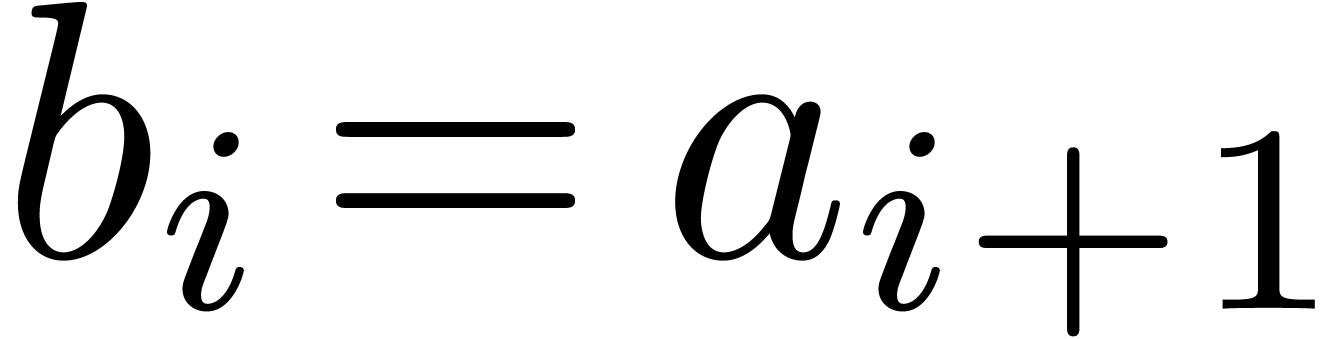 for
for 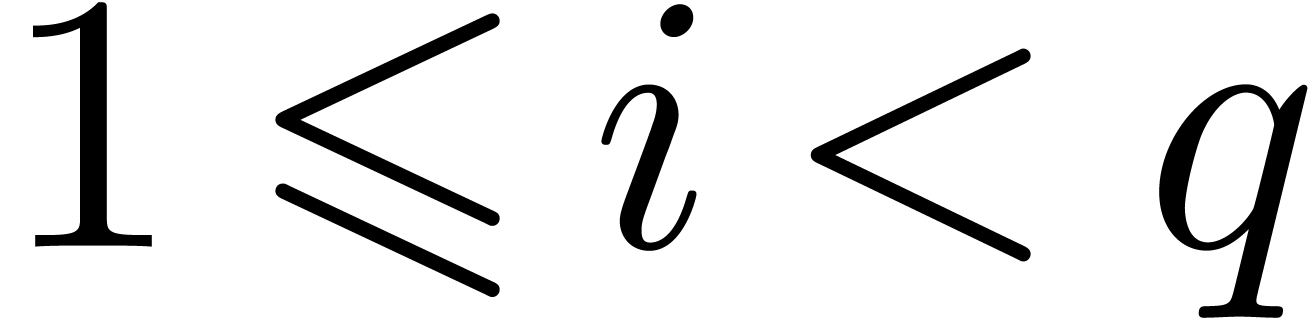 .
Then we have
.
Then we have
By Lemma 5, for all sufficiently large  , we have
, we have 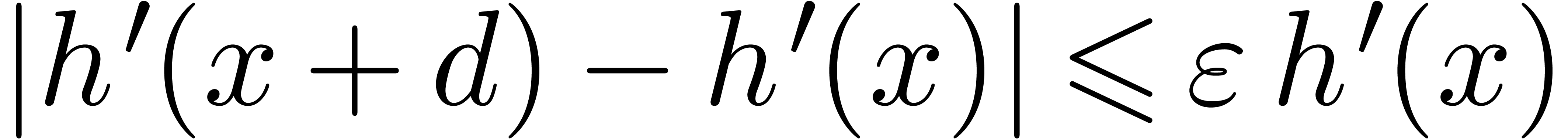 ,
for all
,
for all 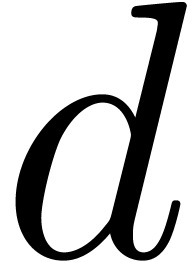 with
with 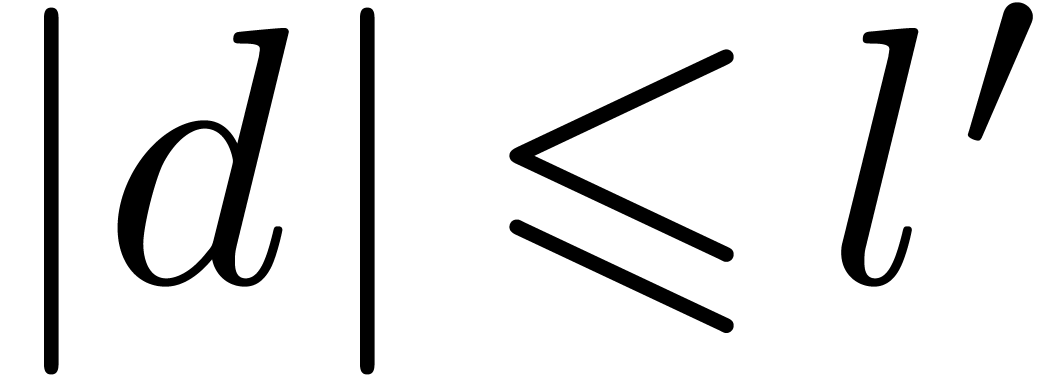 .
Hence,
.
Hence,
and we have a similar estimation, when replacing 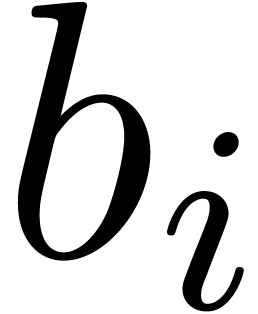 by
by 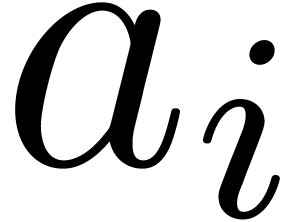 . Consequently,
. Consequently,
This completes our proof.
Let  be continuous functions defined in a
neighbourhood of infinity, which strictly increase towards infinity. Let
be continuous functions defined in a
neighbourhood of infinity, which strictly increase towards infinity. Let
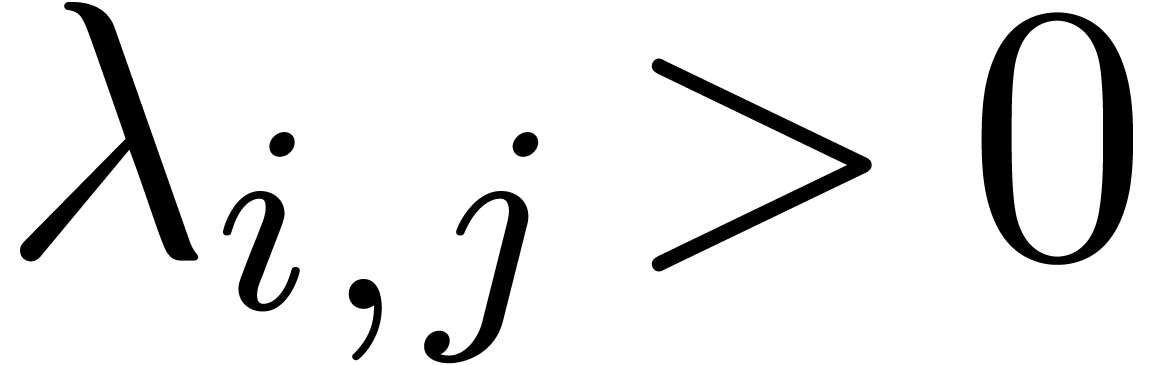 (
(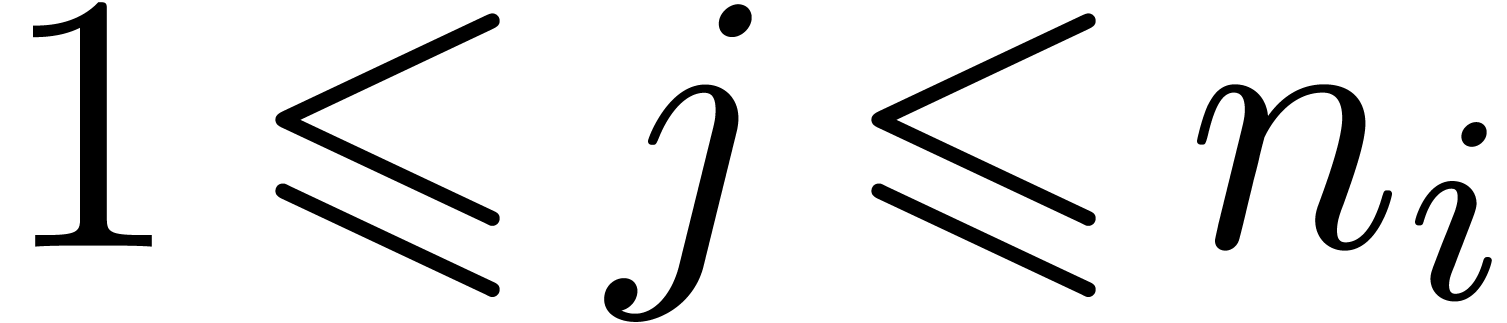 ) be
such that
) be
such that  are
are  -linearly
independent for each
-linearly
independent for each 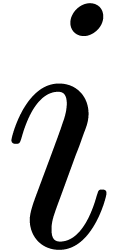 . Now
consider the curve
. Now
consider the curve
on 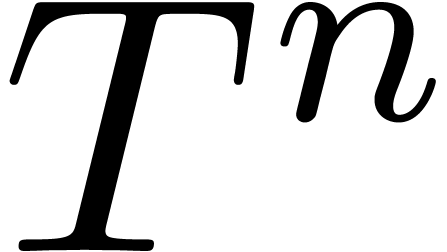 (
(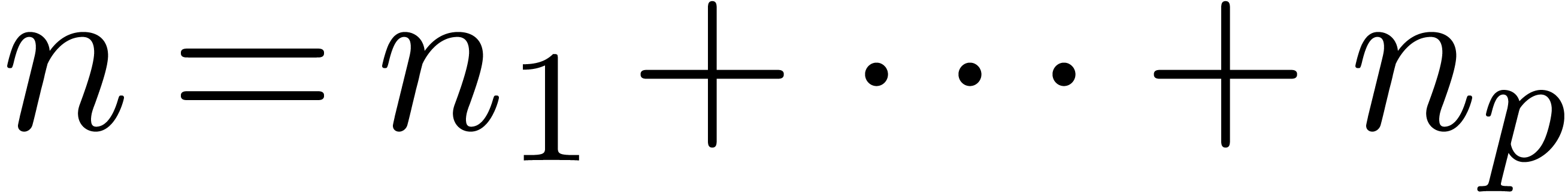 ),
which is defined for sufficiently large
),
which is defined for sufficiently large  .
By analogy with the preceding section, we define
.
By analogy with the preceding section, we define
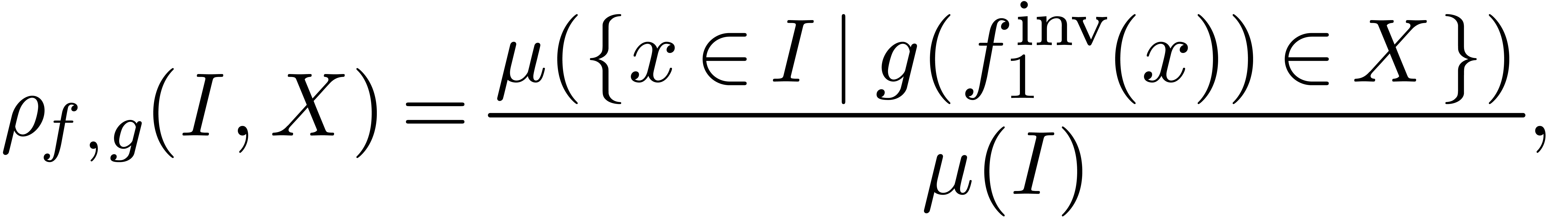 |
(2) |
for intervals 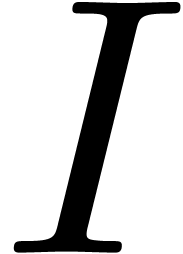 sufficiently close to infinity,
and measurable subsets
sufficiently close to infinity,
and measurable subsets 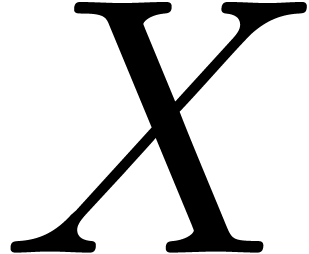 of
of 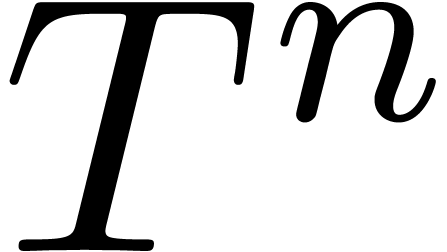 .
.
 and
and 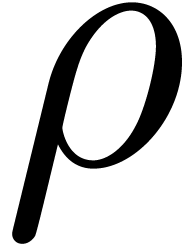 be
given as above and let
be
given as above and let

be an 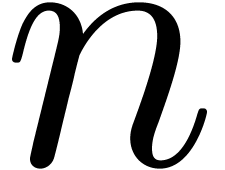 -dimensional
block. Then
-dimensional
block. Then
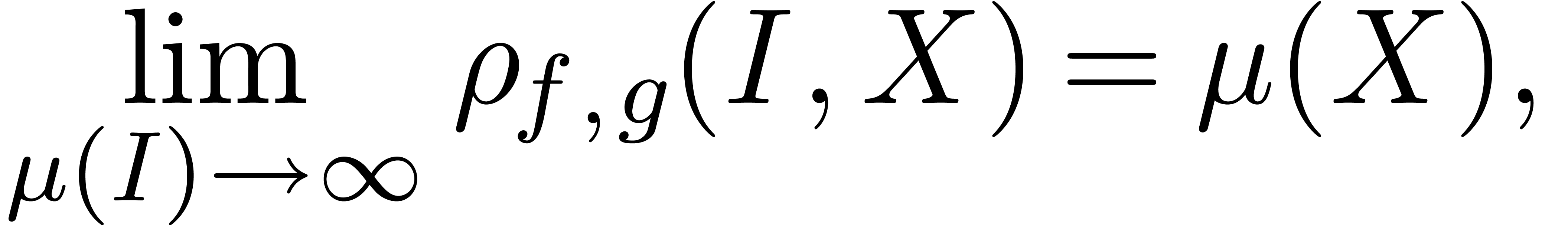
uniformly, for intervals sufficiently close to infinity.
Proof. We proceed by induction over 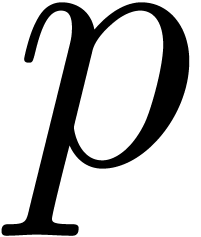 . If
. If 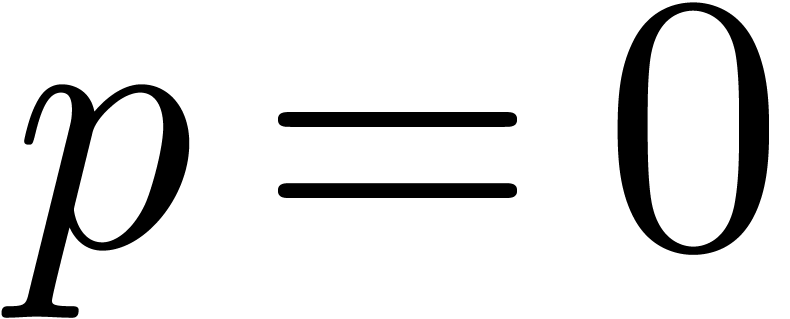 ,
we have nothing to prove. As before, it suffices to prove the theorem
for multidimensional blocks
,
we have nothing to prove. As before, it suffices to prove the theorem
for multidimensional blocks 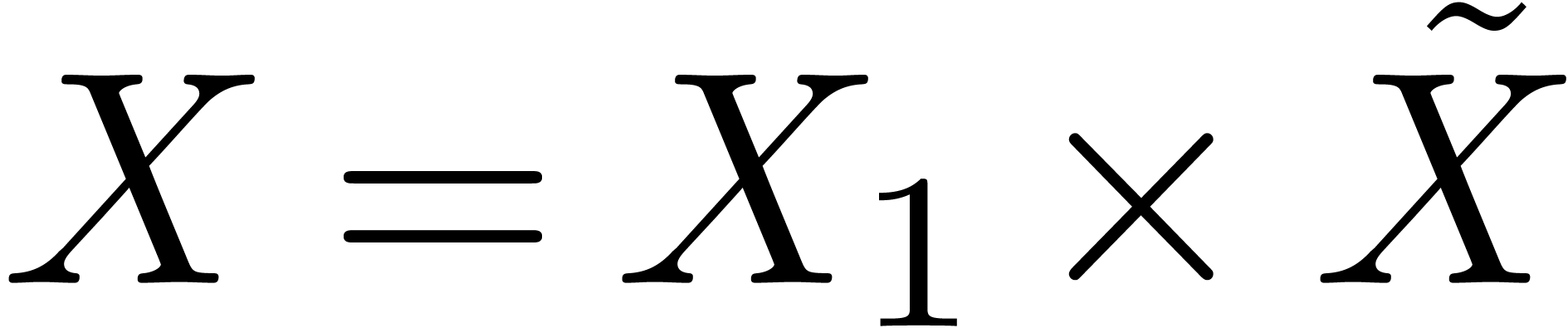 ,
with
,
with 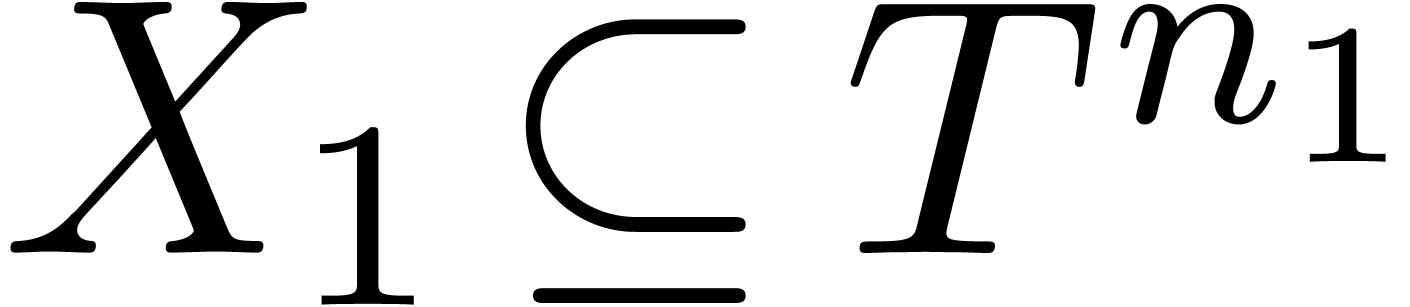 and
and 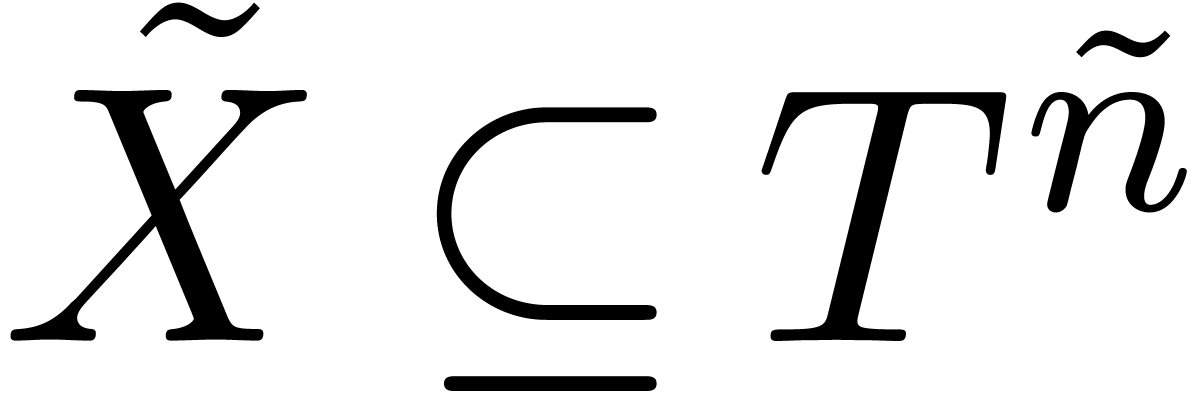 ,
where
,
where 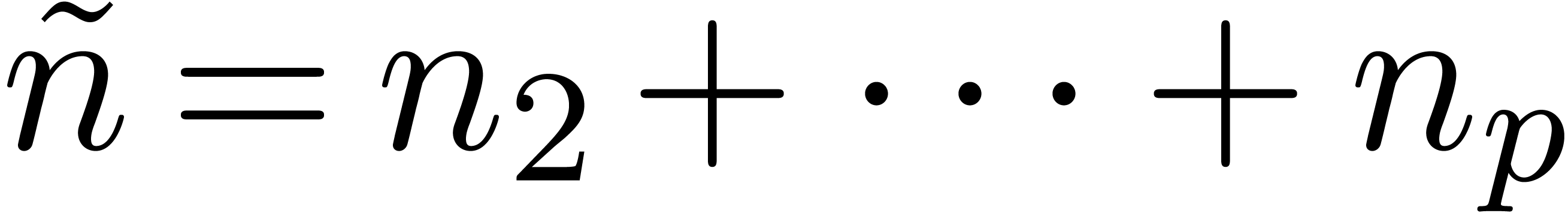 . We denote by
. We denote by 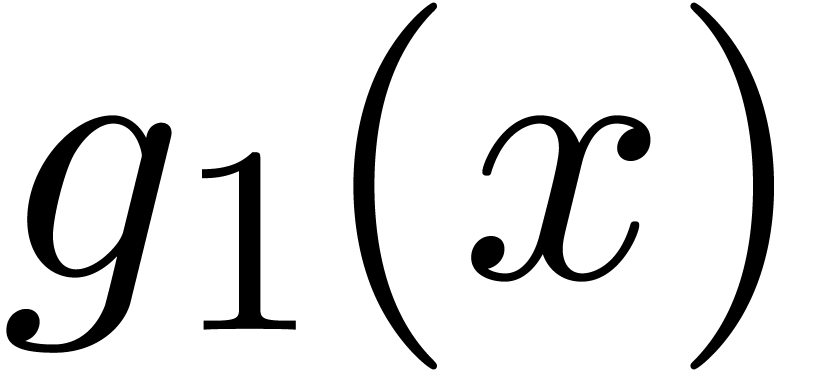 resp.
resp. 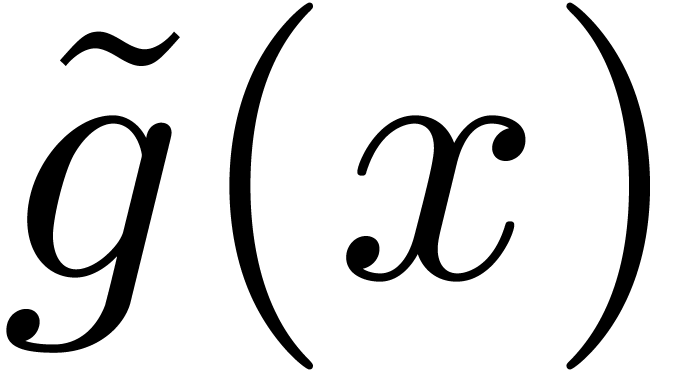 the projections of
the projections of 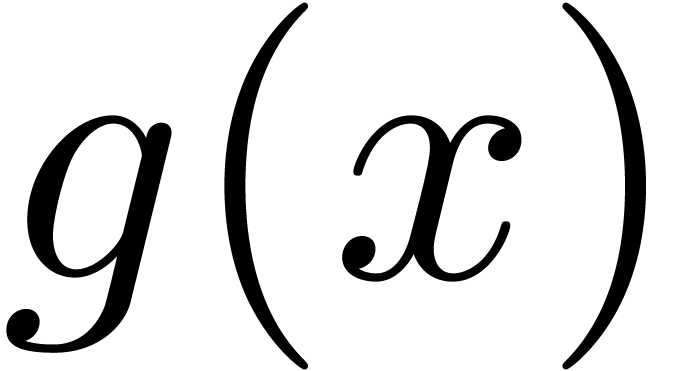 on
on 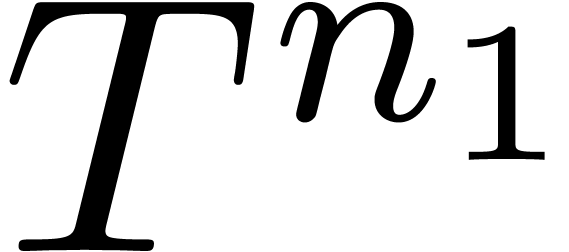 resp.
resp. 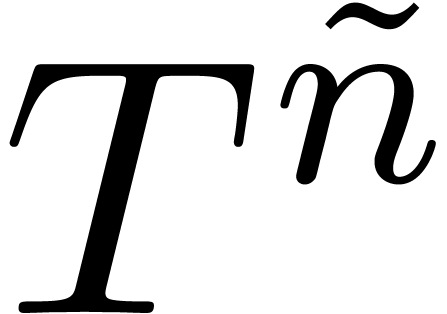 , when considering
, when considering 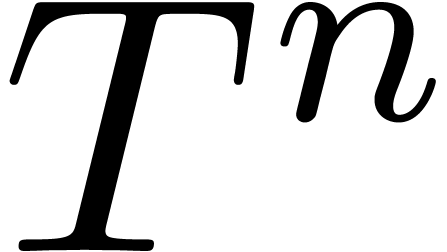 as
the product of
as
the product of 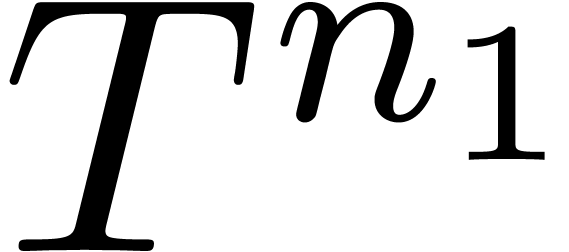 and
and 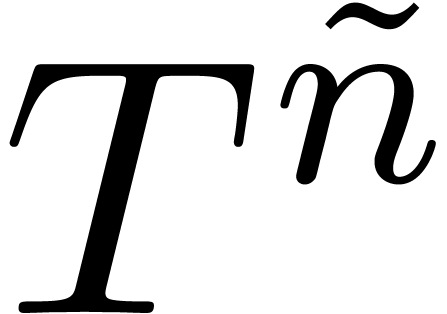 .
Without loss of generality, we may assume that
.
Without loss of generality, we may assume that 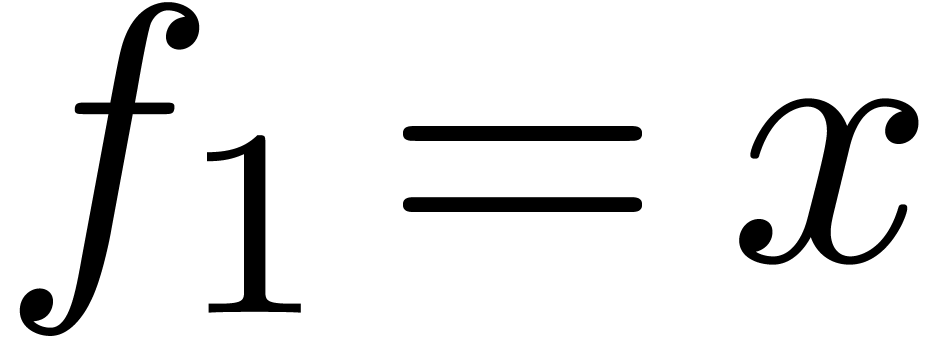 .
.
Given a subset  of
of  or
or
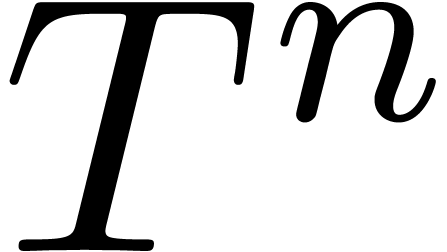 and its frontier
and its frontier  ,
we denote for any
,
we denote for any 
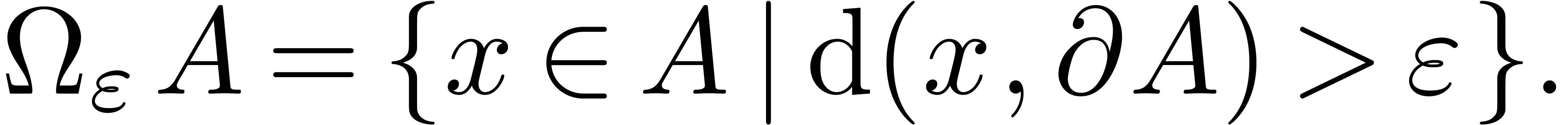
Let  . If
. If 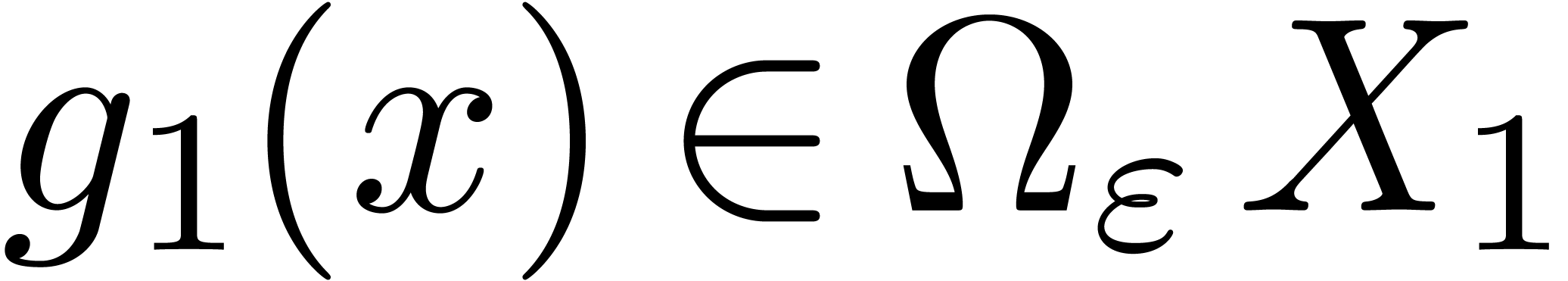 , then
, then 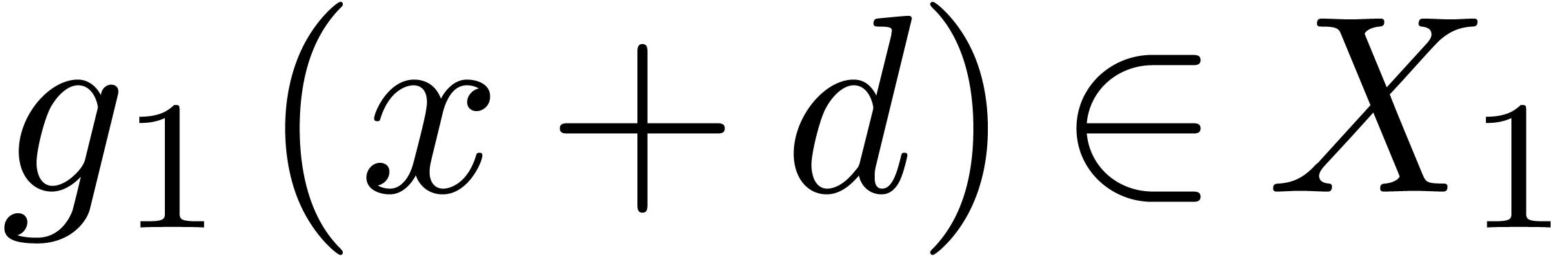 for all
for all 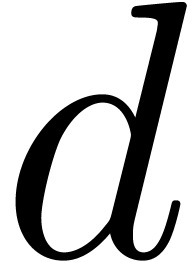 with
with  ,
where
,
where 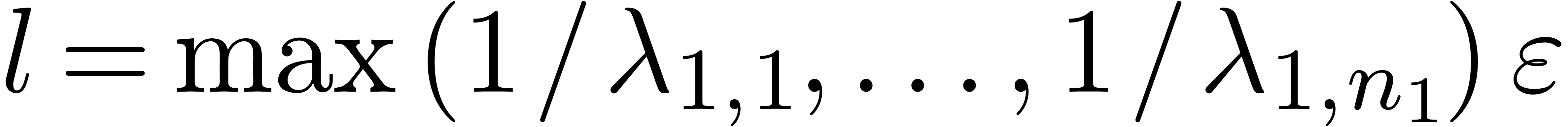 . Hence, for
. Hence, for 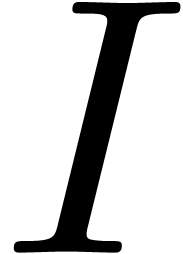 sufficiently close to infinity,
sufficiently close to infinity,
Therefore, Theorem 4 implies that for 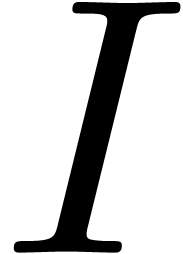 sufficiently close to infinity
sufficiently close to infinity
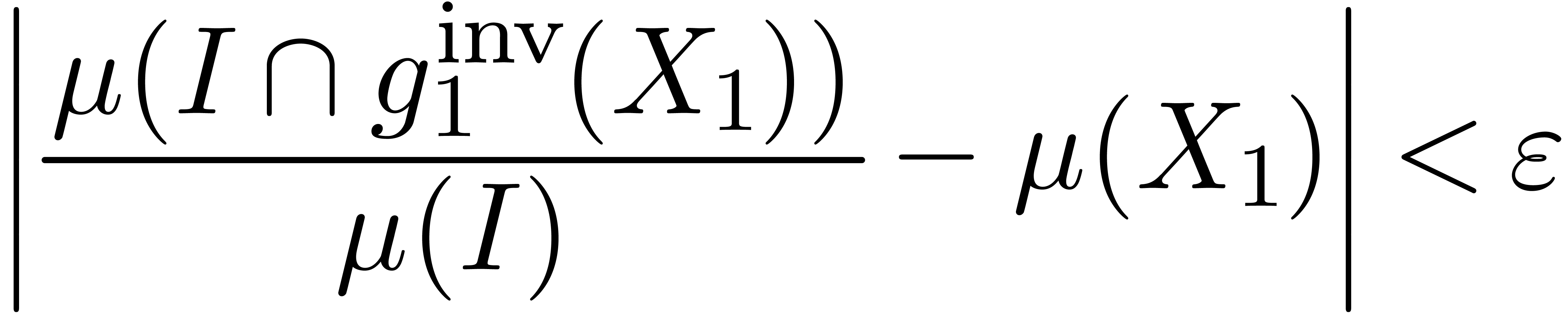 |
(3) |
and (using that 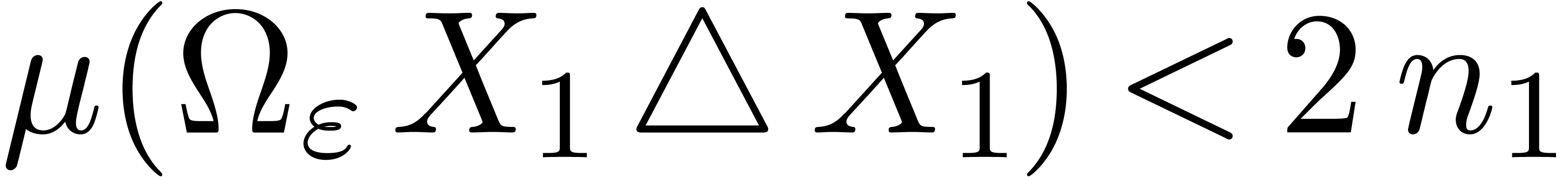 )
)
 |
(4) |
Now 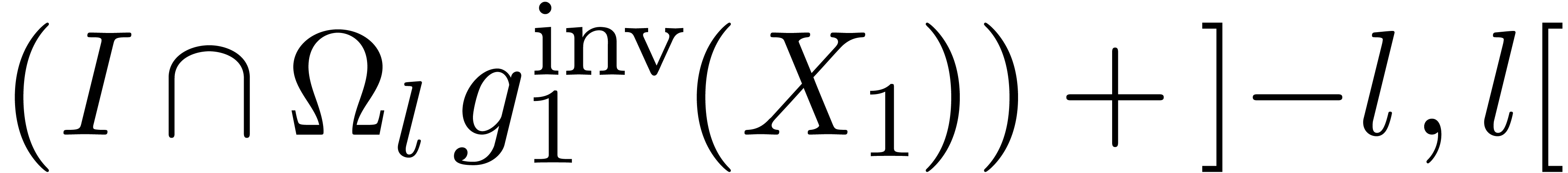 is a finite union of intervals, say
is a finite union of intervals, say
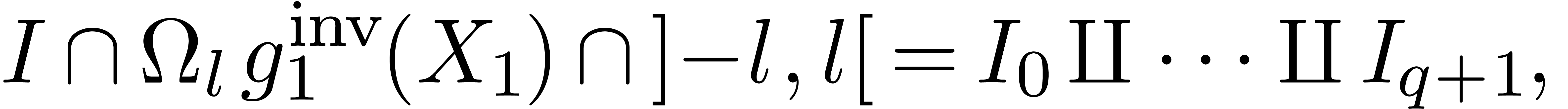
where  have length at least
have length at least 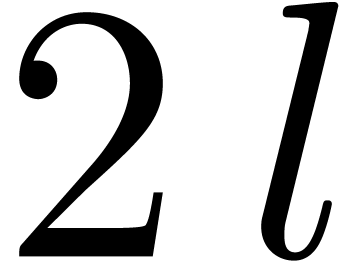 , and where
, and where 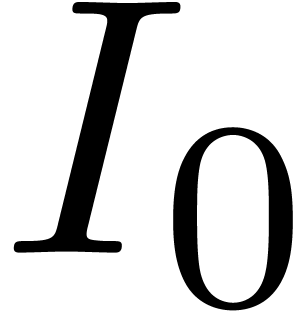 and
and 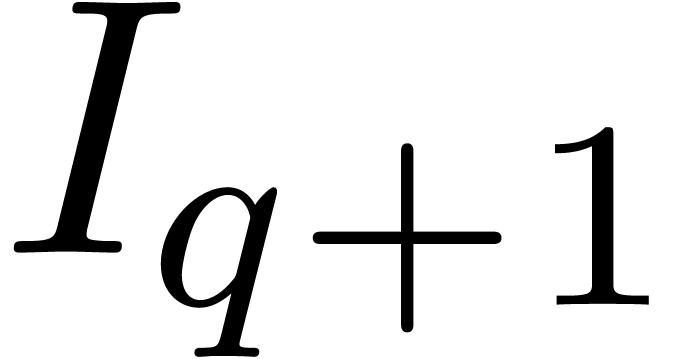 have length at most
have length at most 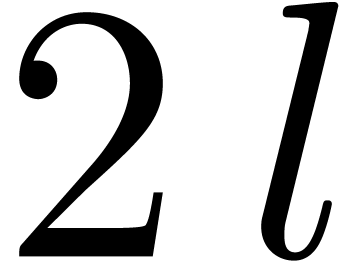 .
.
By the induction hypothesis, we have
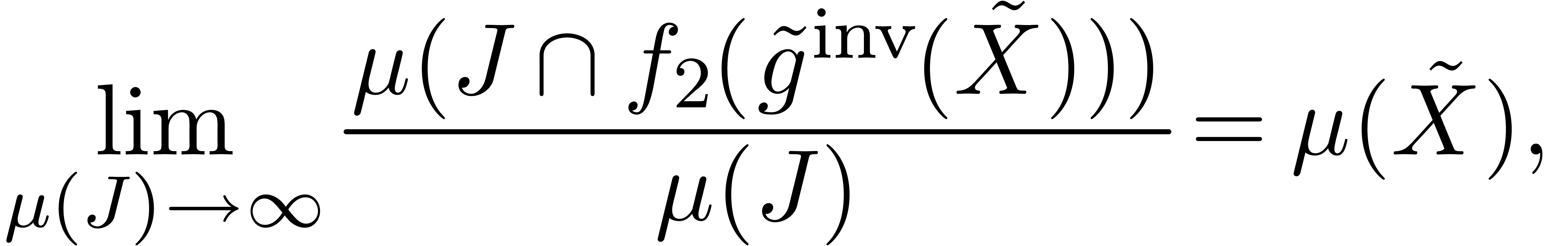
uniformly, for 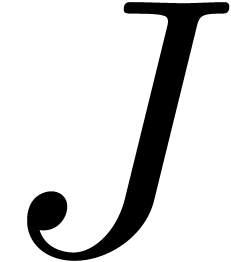 sufficiently close to infinity.
Using Lemma 6 for
sufficiently close to infinity.
Using Lemma 6 for 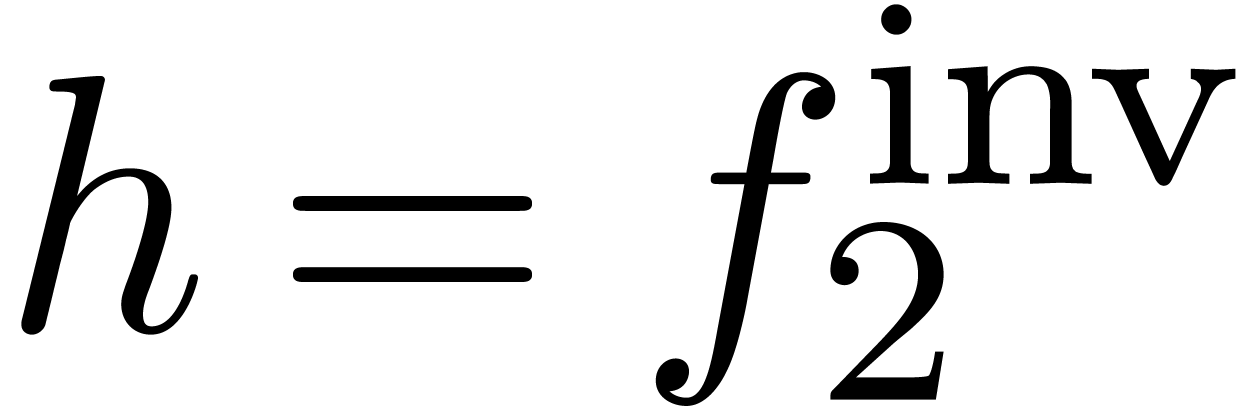 ,
this gives us
,
this gives us
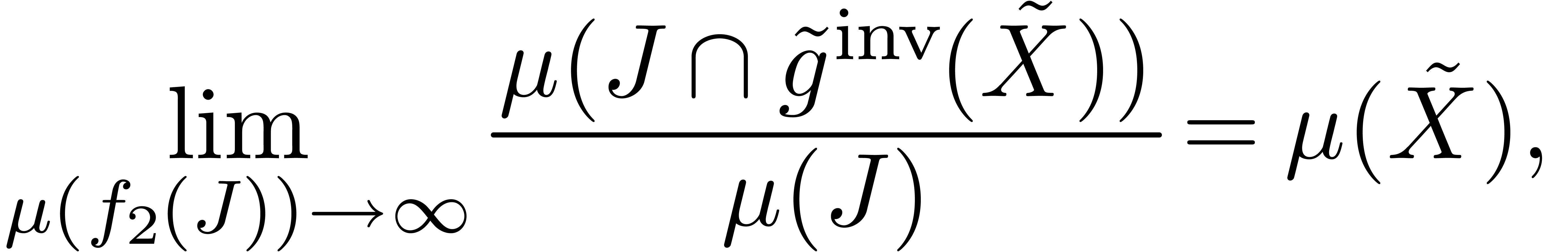
uniformly, for 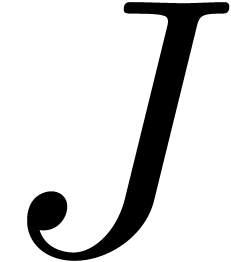 sufficiently close to infinity.
In particular, we have
sufficiently close to infinity.
In particular, we have
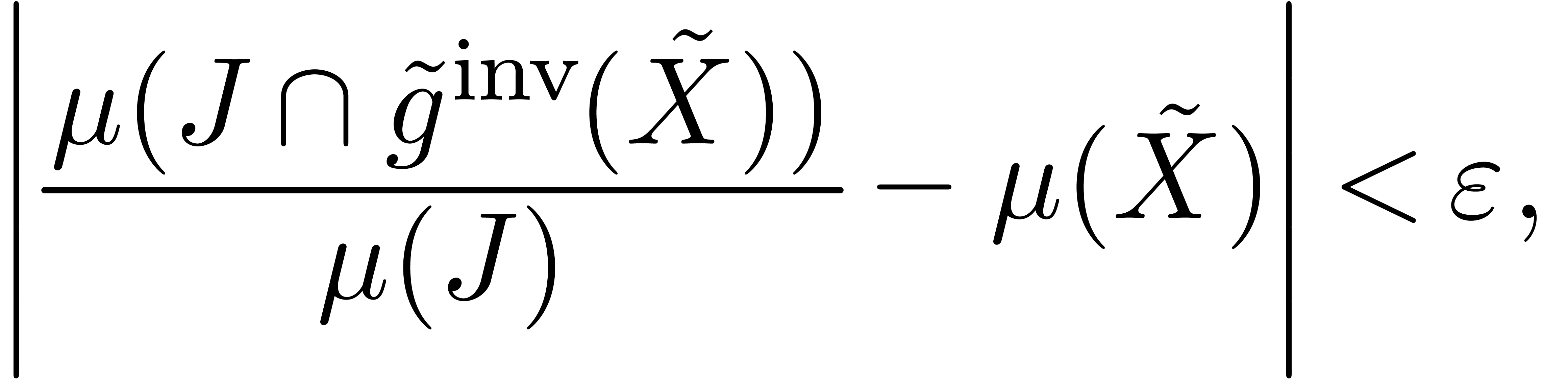
for all 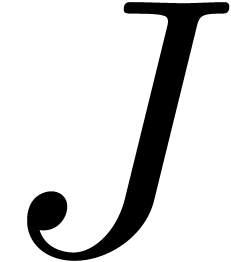 sufficiently close to infinity, with
sufficiently close to infinity, with
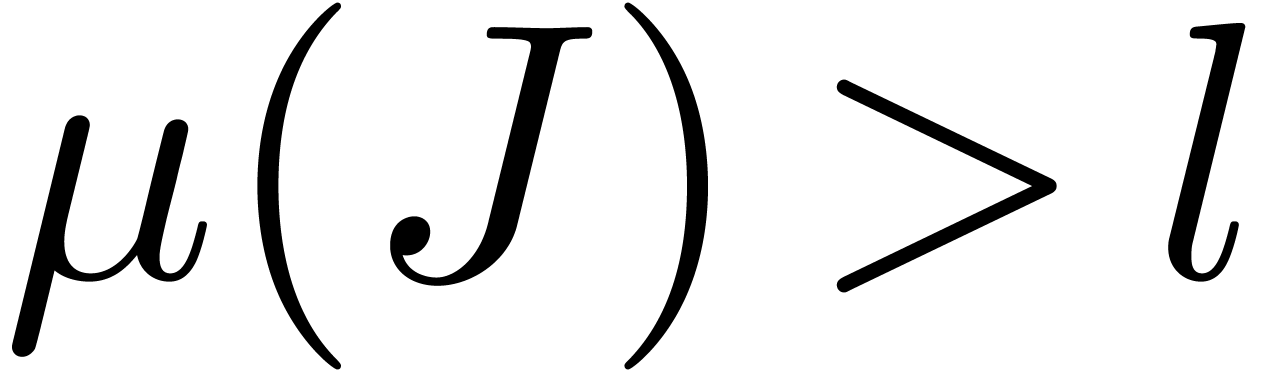 . Thus, choosing
. Thus, choosing 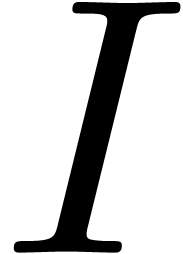 sufficiently close to infinity, we have
sufficiently close to infinity, we have
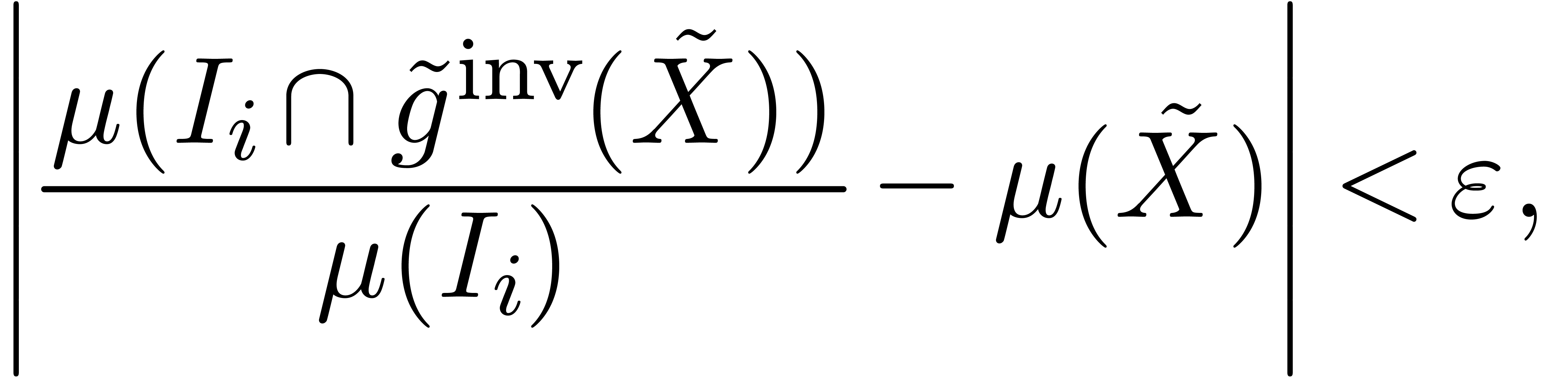
for all 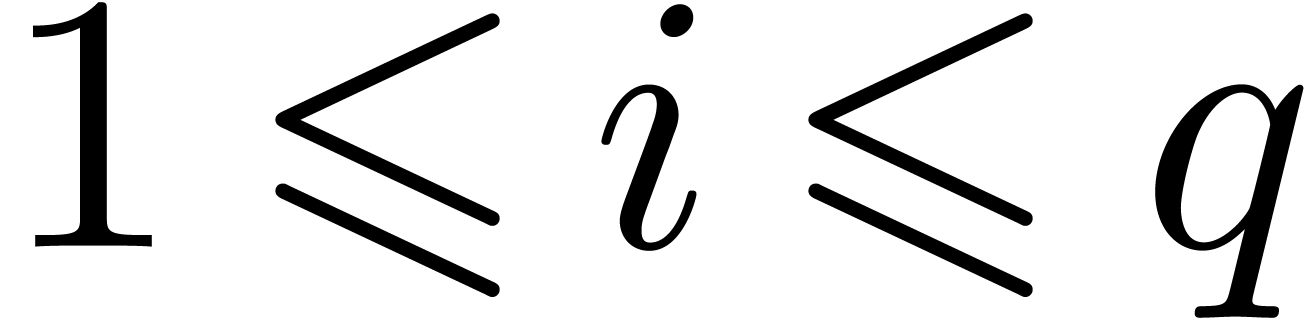 .
.
Taking 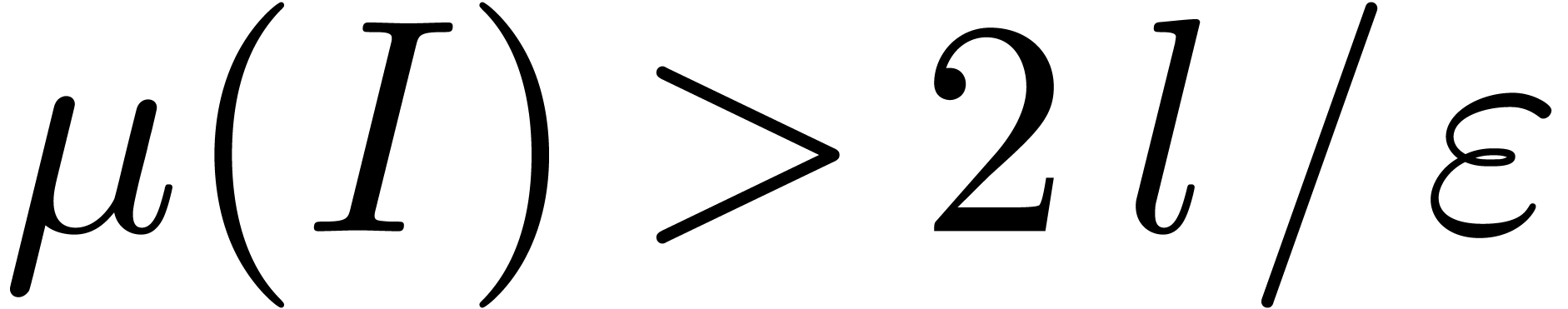 , and using (3)
and (4), this gives us
, and using (3)
and (4), this gives us
This completes the proof.
Let  denote the field of germs at infinity of
exp-log functions and
denote the field of germs at infinity of
exp-log functions and  the subfield of exp-log
constants. Elements of
the subfield of exp-log
constants. Elements of  can be represented by
exp-log expressions — i.e. finite trees whose internal nodes are
labeled by
can be represented by
exp-log expressions — i.e. finite trees whose internal nodes are
labeled by 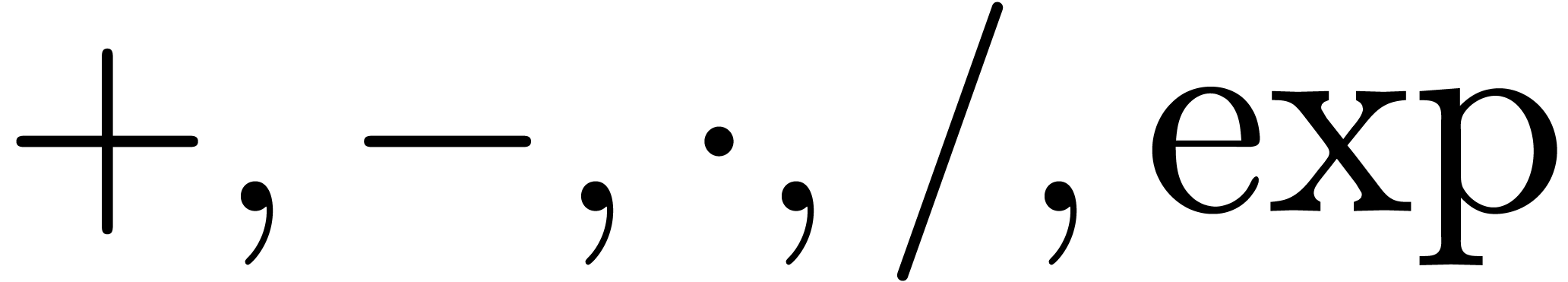 or
or 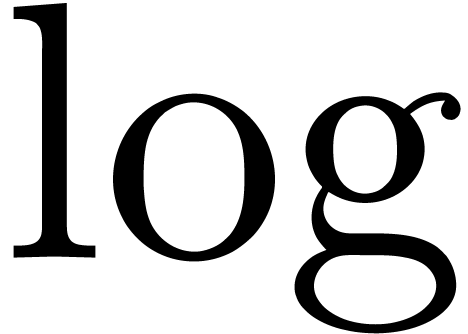 ,
and whose leaves are labeled by
,
and whose leaves are labeled by  or rational
numbers. The set of exp-log expressions which can be evaluated in a
neighbourhood of infinity is denoted by
or rational
numbers. The set of exp-log expressions which can be evaluated in a
neighbourhood of infinity is denoted by 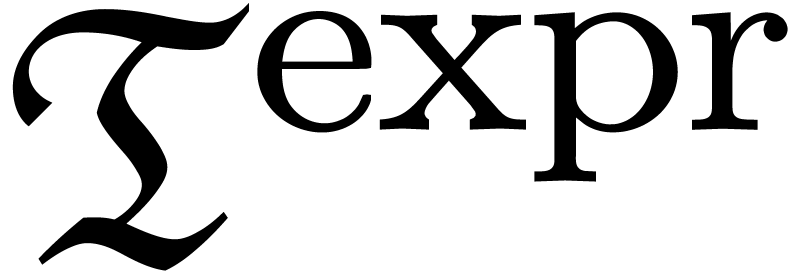 .
We have a natural projection
.
We have a natural projection 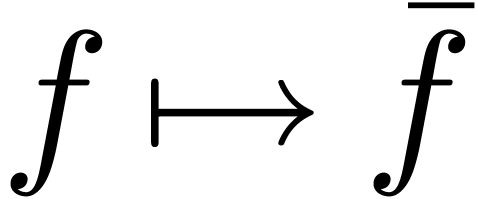 from
from  onto
onto  . We make
the assumption that we have at our disposal an oracle which can decide
whether a given exp-log expression in
. We make
the assumption that we have at our disposal an oracle which can decide
whether a given exp-log expression in  is zero in
a neighbourhood of infinity. In view of [Hoe96b, Hoe96a]
it actually suffices to assume the existence of an oracle to decide
whether a given exp-log constant is zero.
is zero in
a neighbourhood of infinity. In view of [Hoe96b, Hoe96a]
it actually suffices to assume the existence of an oracle to decide
whether a given exp-log constant is zero.
Let us first recall some basic concepts. An effective asymptotic
basis is an ordered finite set  of positive infinitesimal exp-log expressions in
of positive infinitesimal exp-log expressions in
 , such that
, such that 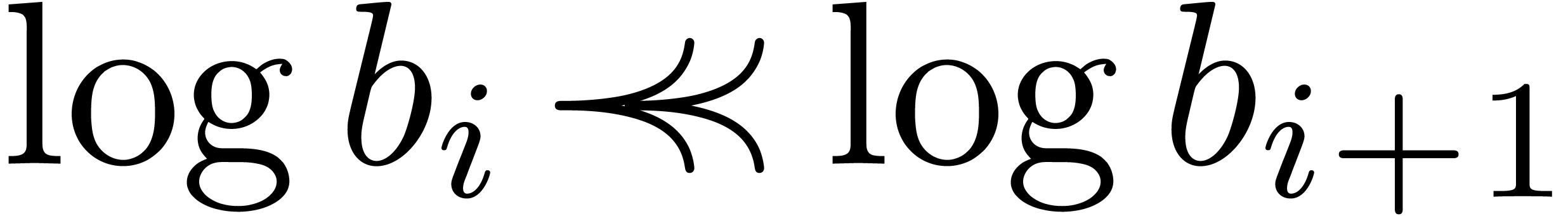 (i.e.
(i.e. 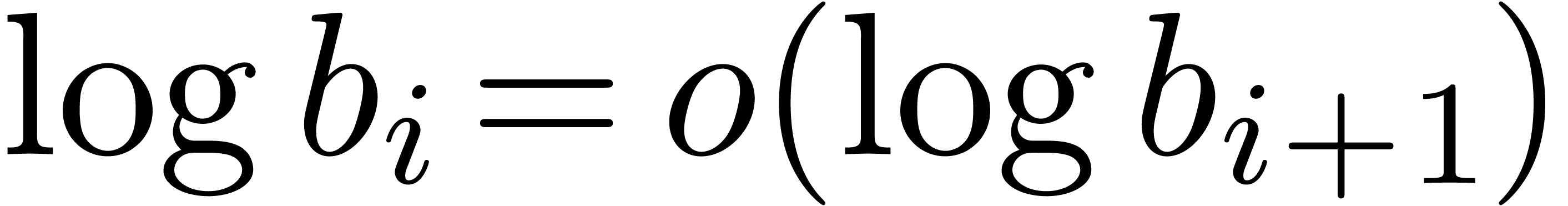 ) for
) for  . For instance, the set
. For instance, the set 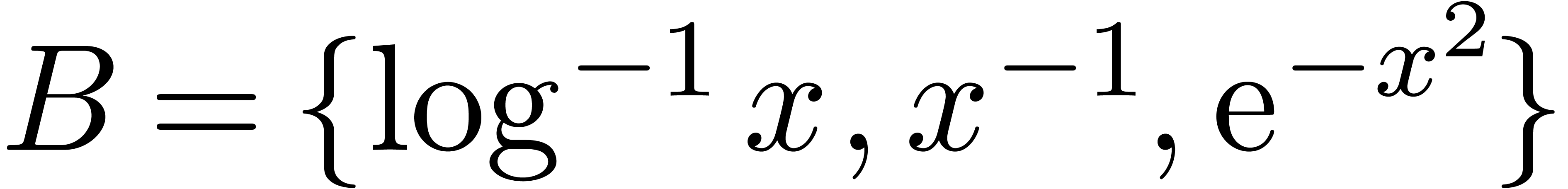 is an effective asymptotic basis. An effective asymptotic basis
is an effective asymptotic basis. An effective asymptotic basis  generates an effective asymptotic scale, namely the set
generates an effective asymptotic scale, namely the set 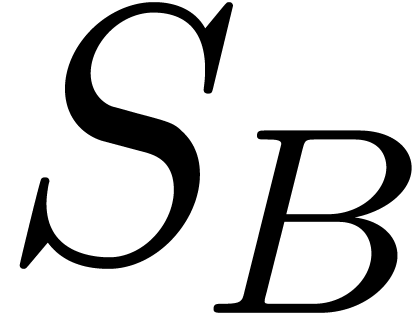 of all
products
of all
products  of powers of the
of powers of the 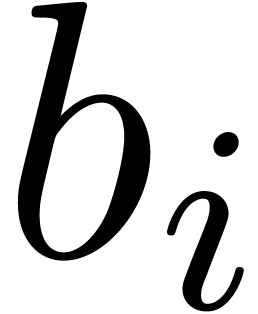 's, with the
's, with the 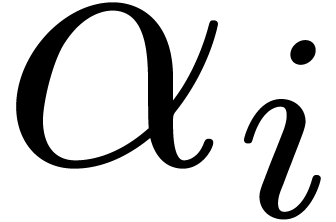 's
in
's
in  . Elements of
. Elements of  are also called monomials.
are also called monomials.
Given an effective asymptotic basis  ,
let
,
let  denote the set of expressions which are
built up from
denote the set of expressions which are
built up from 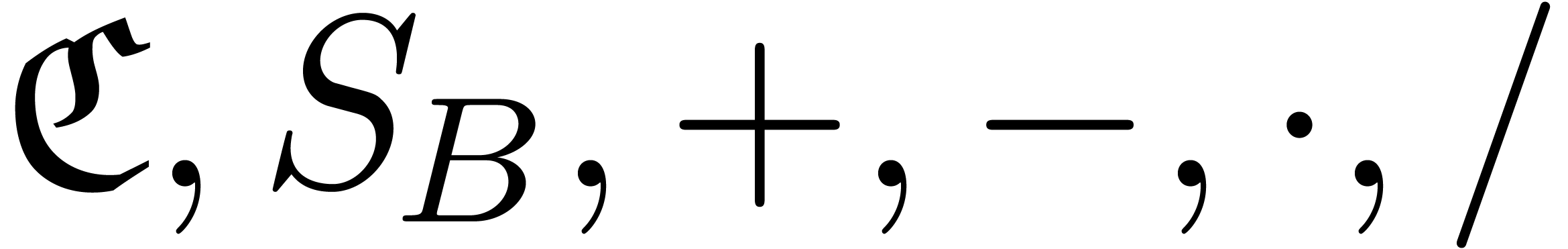 and the operations
and the operations  , resp.
, resp.  ,
for infinitesimal
,
for infinitesimal  . We
observe that
. We
observe that 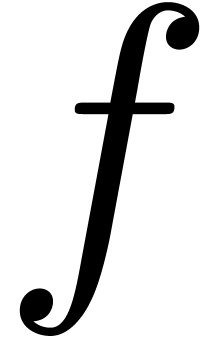 can be expanded as a series in
can be expanded as a series in 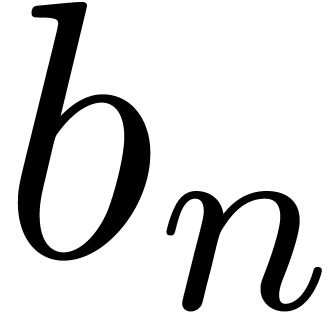 with coefficients in
with coefficients in 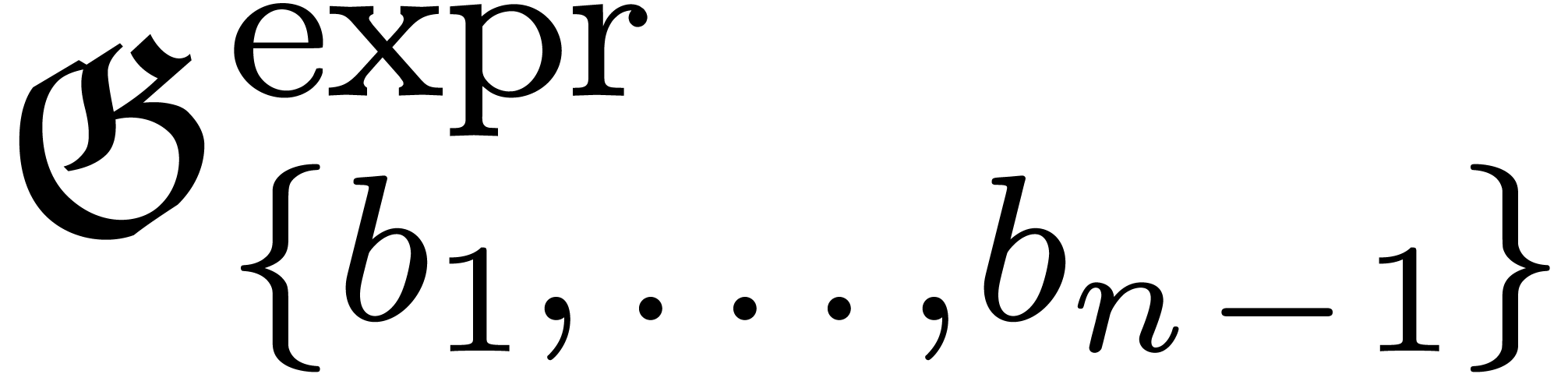 .
Moreover, these coefficients can recursively be expanded in
.
Moreover, these coefficients can recursively be expanded in  :
:
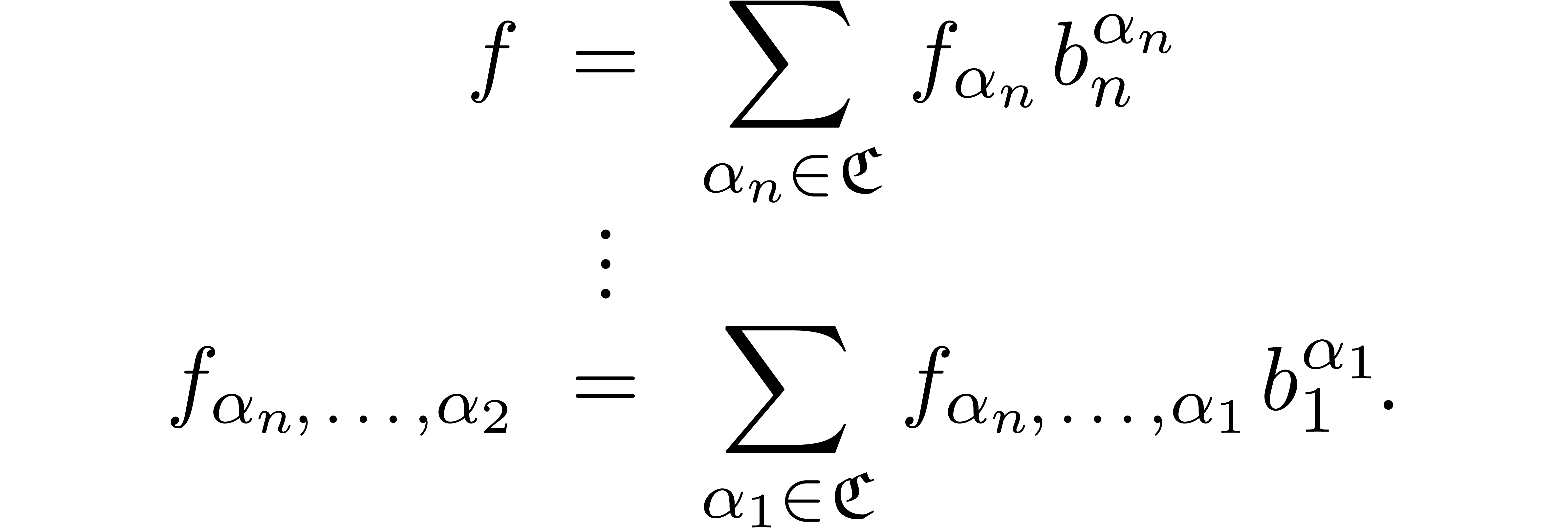
The exp-log expressions of the form 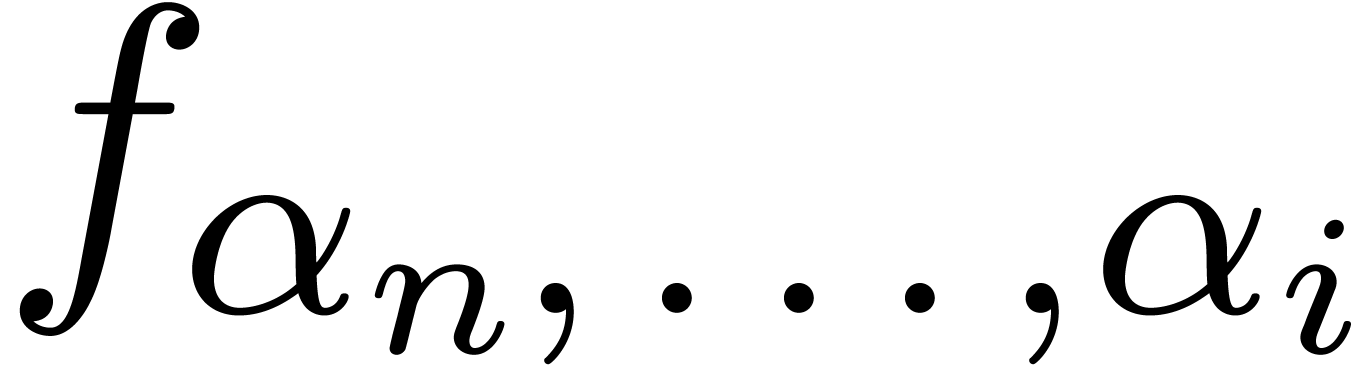 are called
iterated coefficients of
are called
iterated coefficients of  . In particular, the iterated coefficients of
the form
. In particular, the iterated coefficients of
the form  are exp-log constants.
are exp-log constants.
The above expansions of  have an important
property [Hoe96a]: the support of
have an important
property [Hoe96a]: the support of  as a series in
as a series in  is included in a set of the form
is included in a set of the form
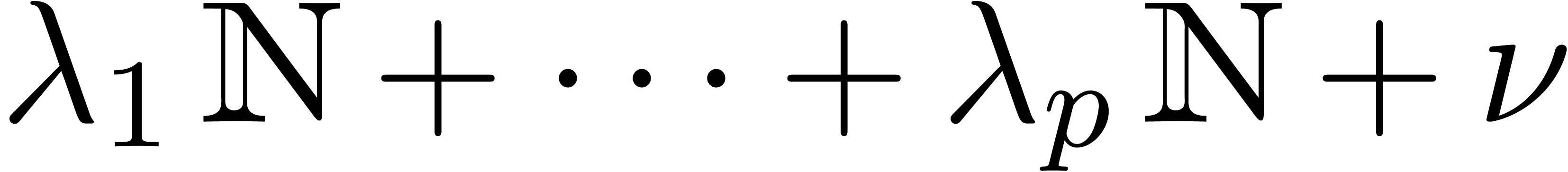 , where the
, where the 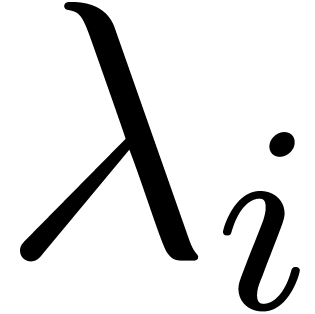 's and
's and  are constants in
are constants in
 — we say that
— we say that 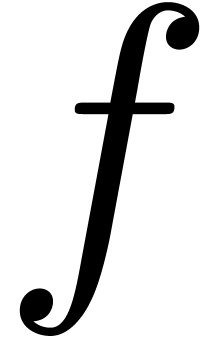 is a
grid-based series. From this property, it
follows that the support of
is a
grid-based series. From this property, it
follows that the support of 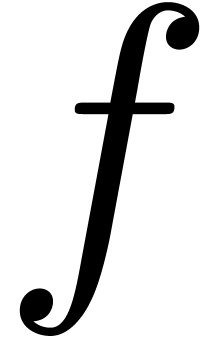 is well-ordered.
is well-ordered.
Another important property of the expansion of 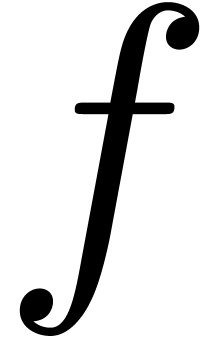 in
in 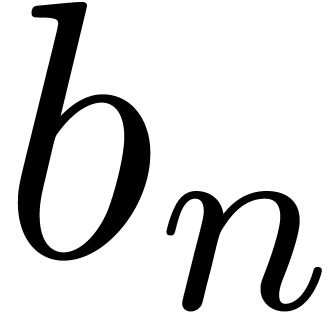 and the expansions of its iterated
coefficients is that they can be computed automatically. By this we mean
that for each integer
and the expansions of its iterated
coefficients is that they can be computed automatically. By this we mean
that for each integer 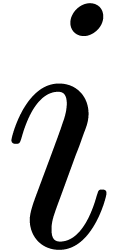 , we
can compute the first
, we
can compute the first 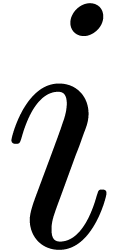 terms of the expansion of
terms of the expansion of
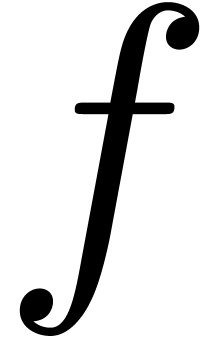 and so can we for its iterated coefficients. In
particular, we can compute the sign of
and so can we for its iterated coefficients. In
particular, we can compute the sign of 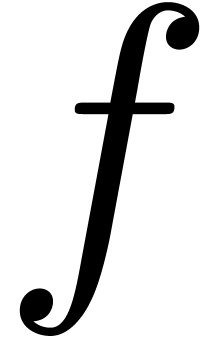 ,
test whether
,
test whether 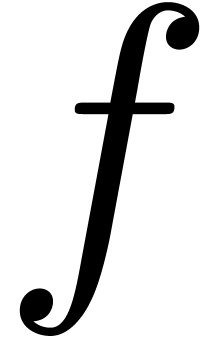 is infinitesimal, etc.
is infinitesimal, etc.
For the computation of the expansions of 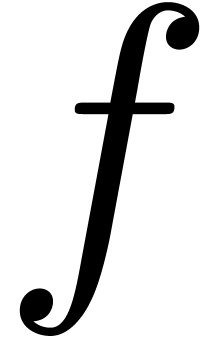 in
in
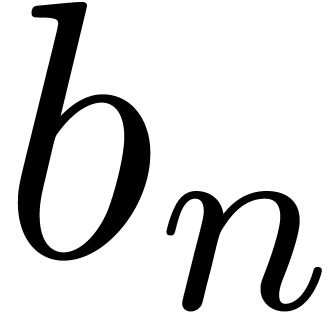 , we use the usual Taylor
series formulas. In the case of division
, we use the usual Taylor
series formulas. In the case of division 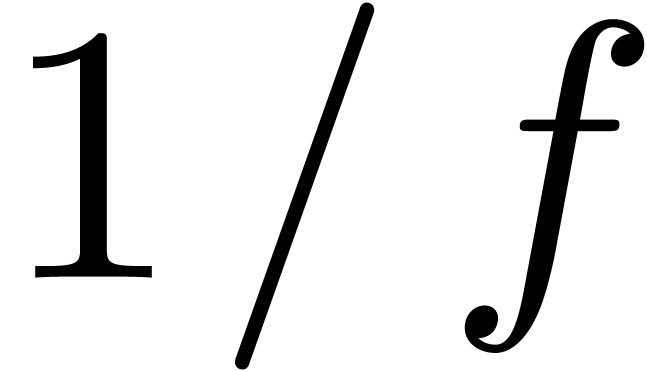 ,
we compute the first term
,
we compute the first term  of
of  and then use the formula
and then use the formula 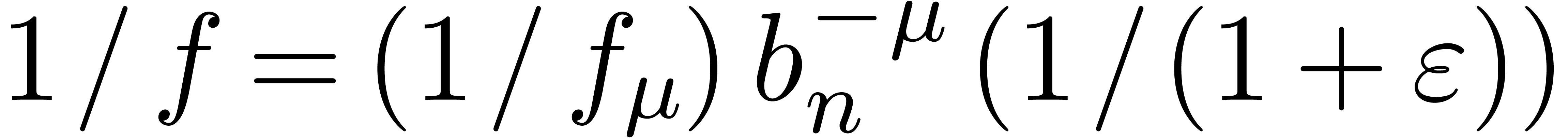 ,
where
,
where 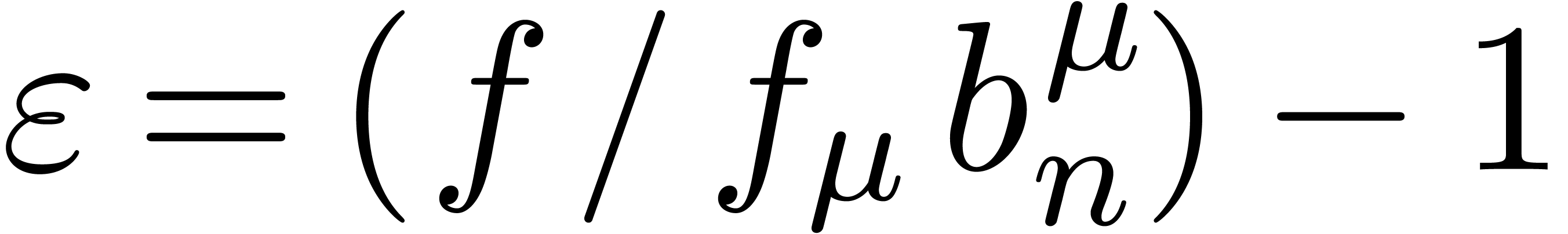 . The only problem when
applying these formulas is that we have to avoid indefinite cancelation:
note that indefinite cancelation only occurs if after having computed
the first
. The only problem when
applying these formulas is that we have to avoid indefinite cancelation:
note that indefinite cancelation only occurs if after having computed
the first 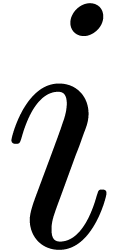 terms of the expansion,
terms of the expansion,  is actually equal to the sum of these terms. But this can
be tested using the oracle, and we stop the expansion in this case.
is actually equal to the sum of these terms. But this can
be tested using the oracle, and we stop the expansion in this case.
The asymptotic expansion algorithm takes an exp-log expression  on input, computes a suitable effective asymptotic basis
on input, computes a suitable effective asymptotic basis
 and rewrites
and rewrites  into an
element of
into an
element of 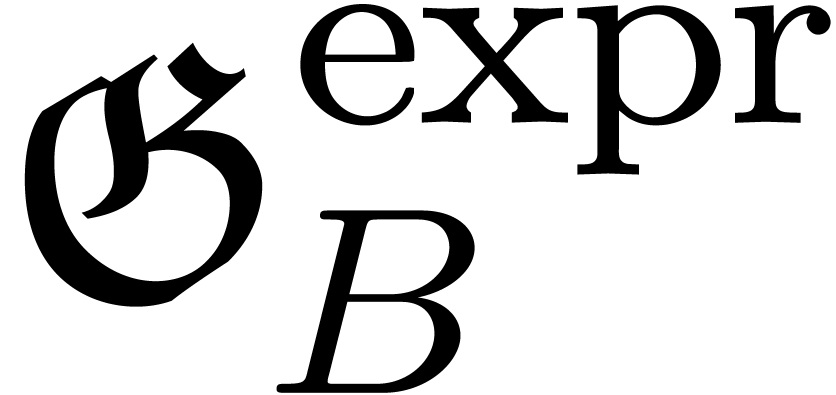 . The main idea of
the algorithm lies in imposing some suitable conditions on
. The main idea of
the algorithm lies in imposing some suitable conditions on  : we say that a linearly ordered set
: we say that a linearly ordered set  is an effective normal basis if
is an effective normal basis if
 is an effective asymptotic basis.
is an effective asymptotic basis.
 for all
for all 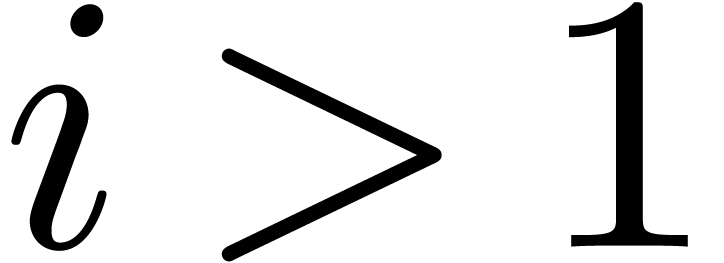 ,
where
,
where 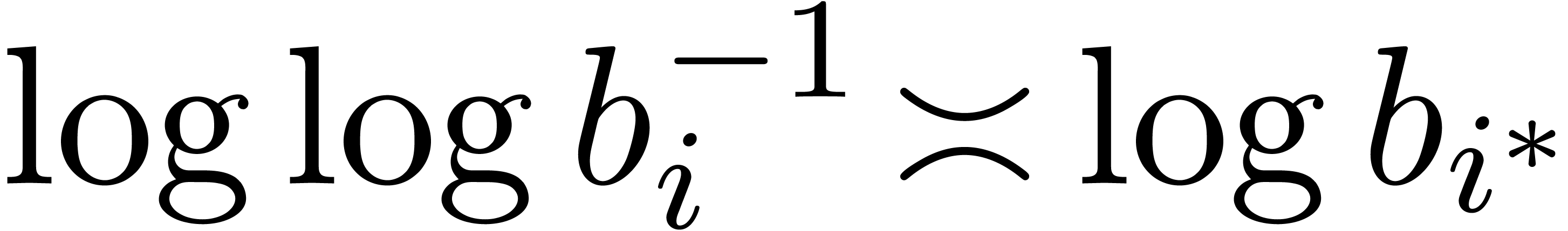 .
.
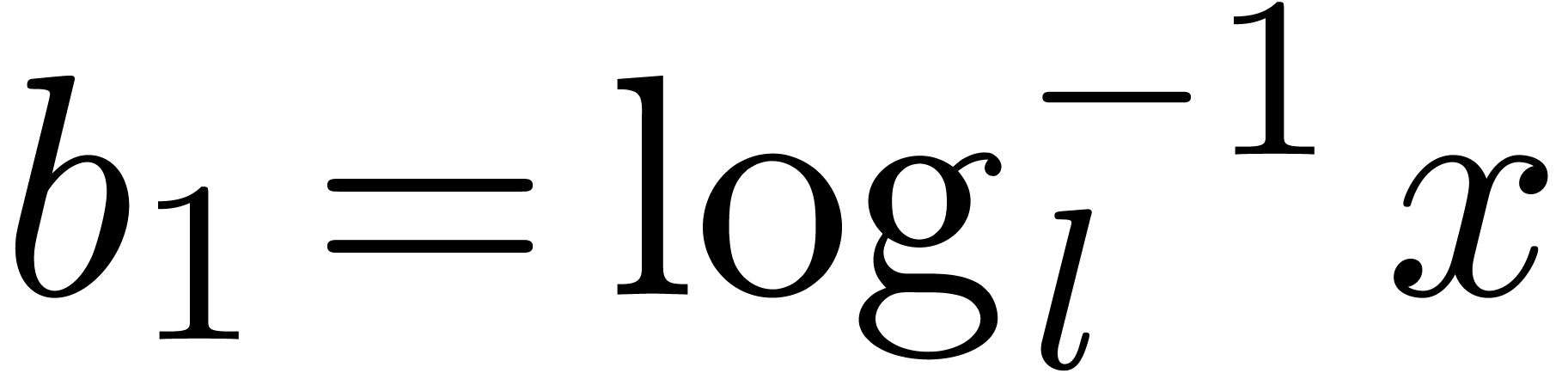 for some
for some  ,
where
,
where 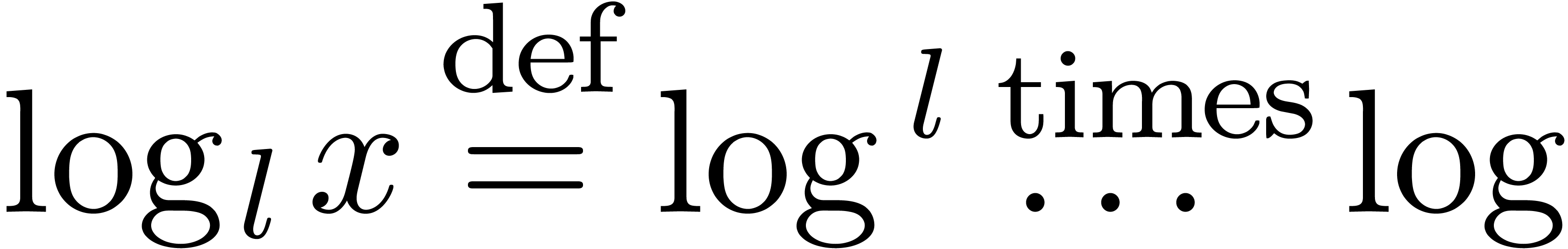 .
.
Such a basis is constructed gradually during the algorithm
— i.e.  is a global variable in which we
insert new elements during the execution of the algorithm, while
maintaining the property that
is a global variable in which we
insert new elements during the execution of the algorithm, while
maintaining the property that  is an effective
normal basis. We also say that
is an effective
normal basis. We also say that  is a dynamic
effective normal basis. Let us now explicitly give the
algorithm, using a PASCAL-like notation:
is a dynamic
effective normal basis. Let us now explicitly give the
algorithm, using a PASCAL-like notation:
Algorithm  . The
algorithm takes an exp-log expression
. The
algorithm takes an exp-log expression  on input
and rewrites it into a grid-based series in
on input
and rewrites it into a grid-based series in 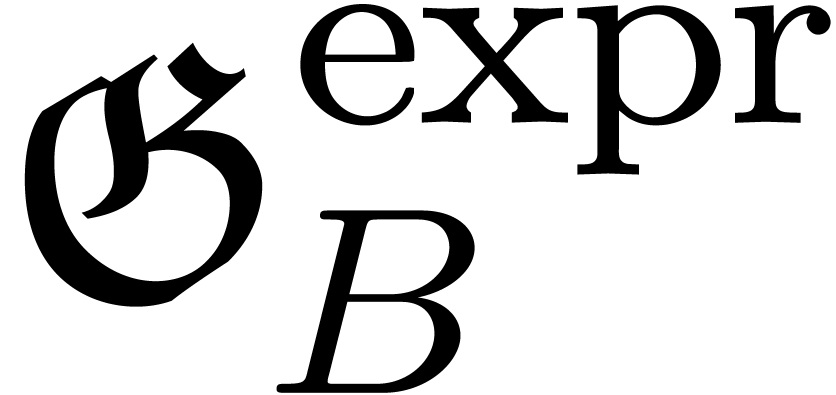 , where the global variable
, where the global variable  contains an effective normal basis which is initialized by
contains an effective normal basis which is initialized by 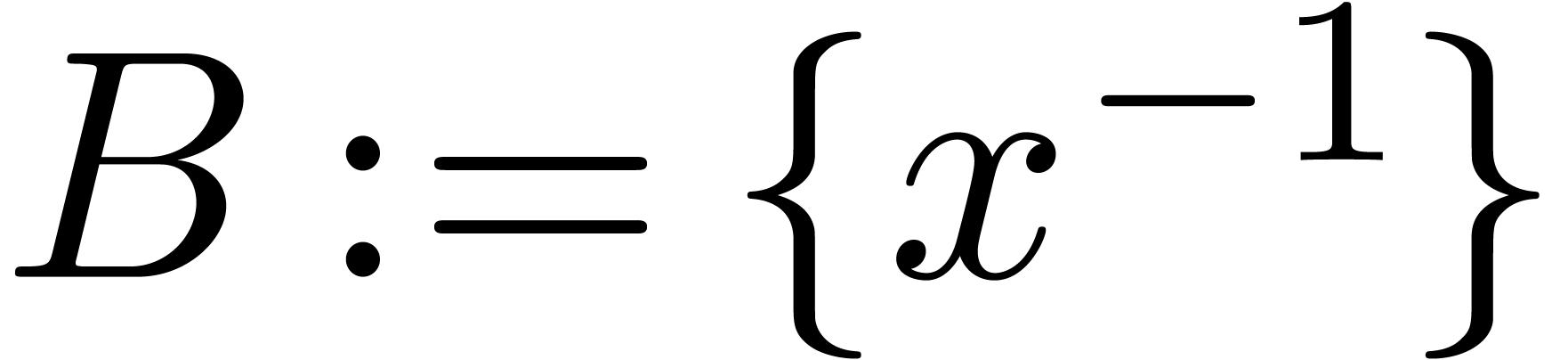 .
.
case 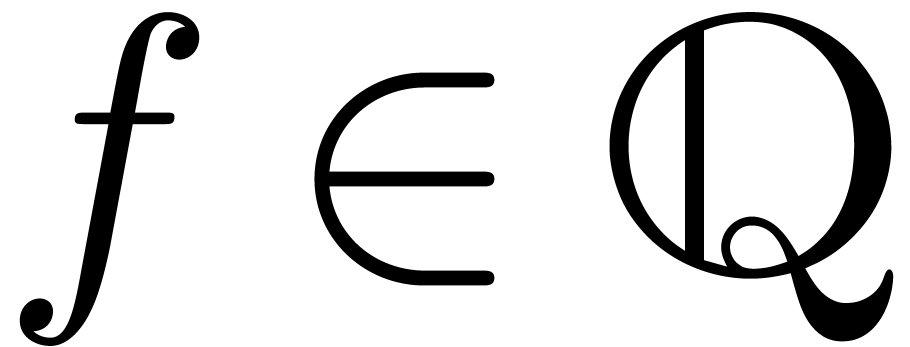 : return
: return
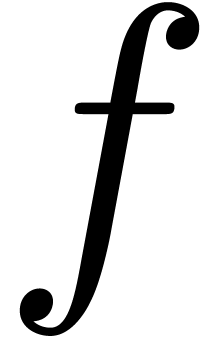
case 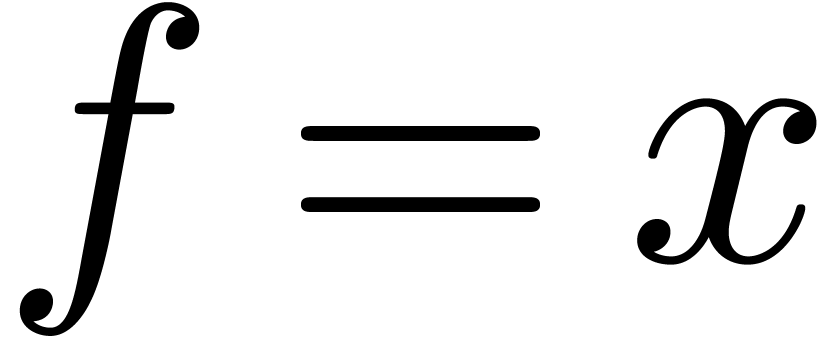 : return
: return
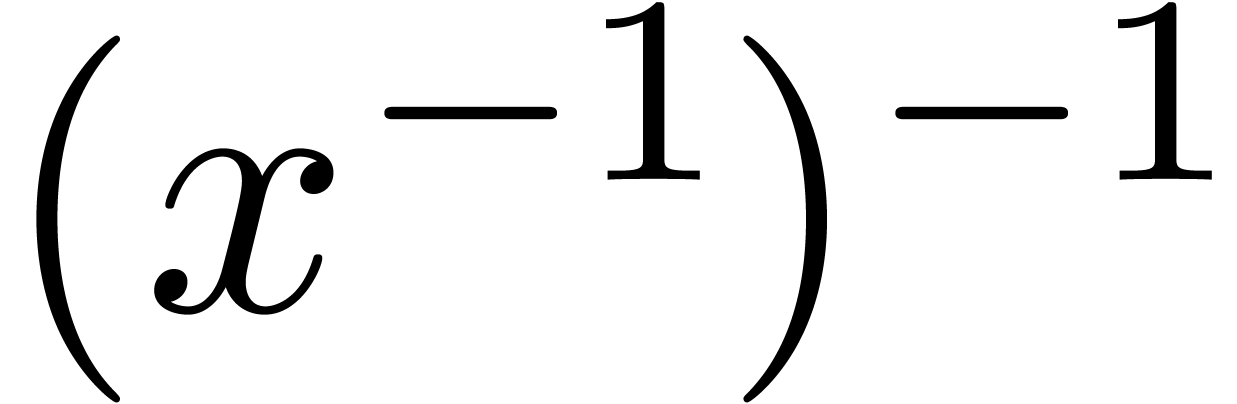
case 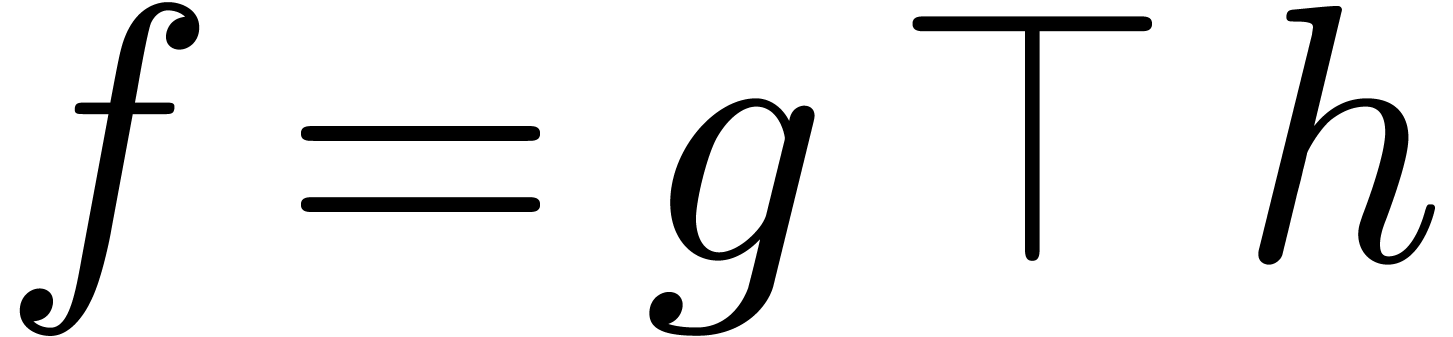 , where
, where 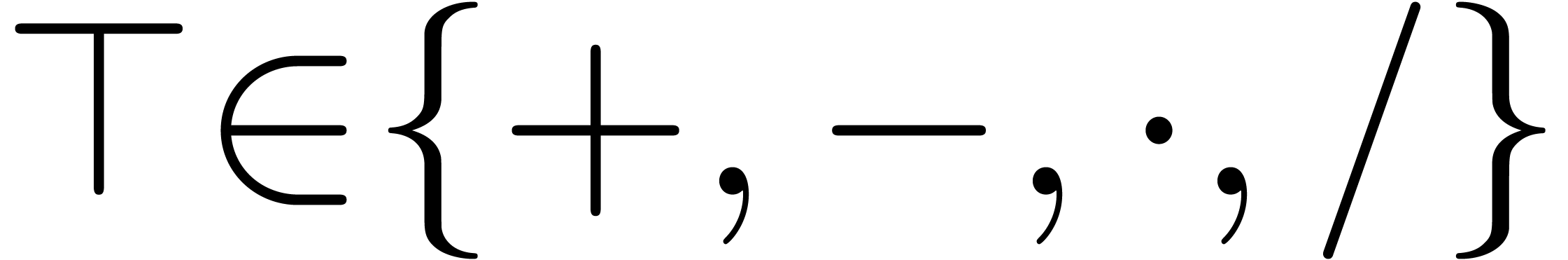 :
:
if 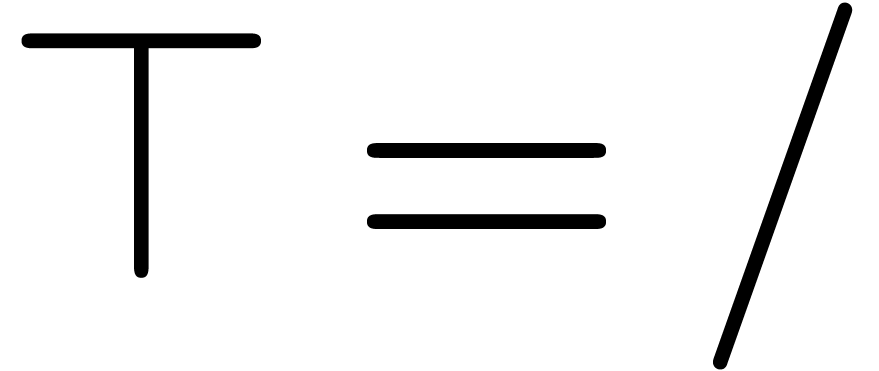 and
and 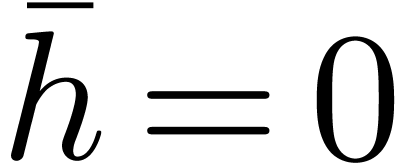 then error “division by zero”
then error “division by zero”
return 
case 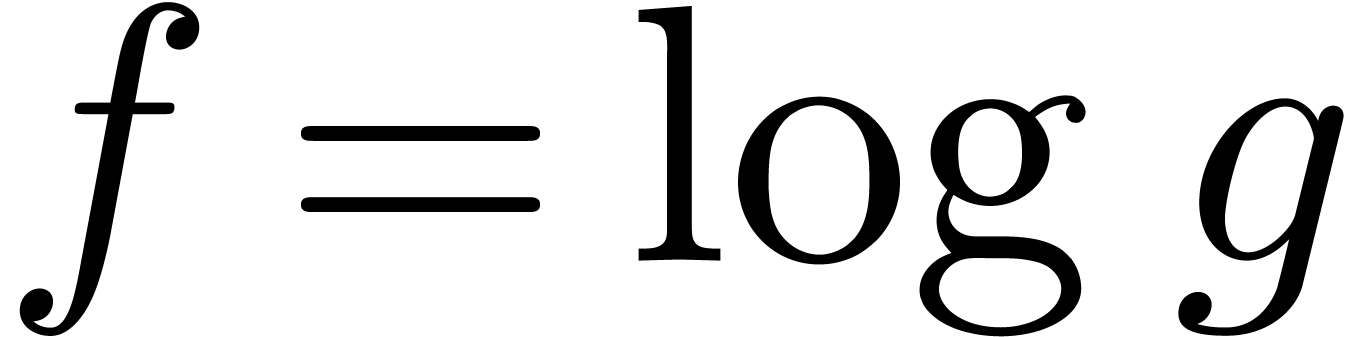 :
:
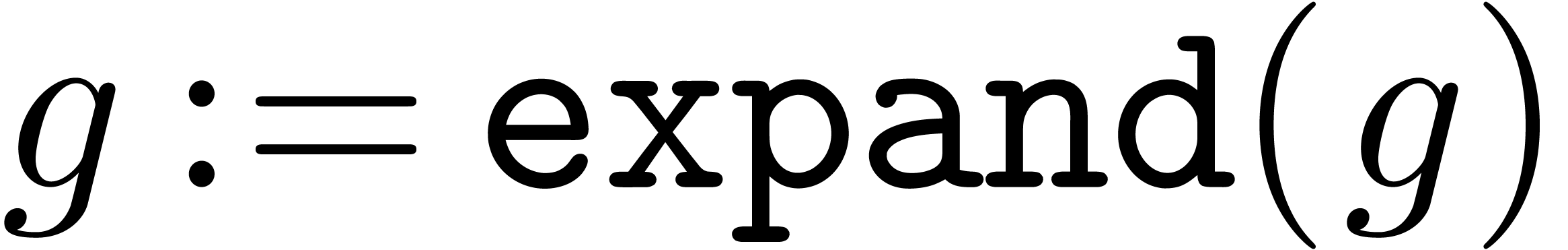
 Denote
Denote 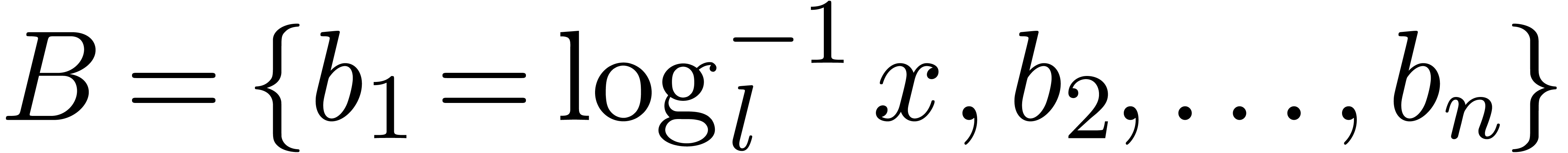 .
.
if 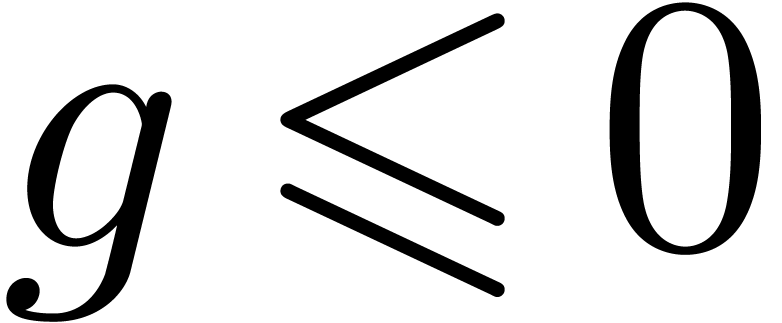 then error
“invalid logarithm”
then error
“invalid logarithm”
 Rewrite
Rewrite 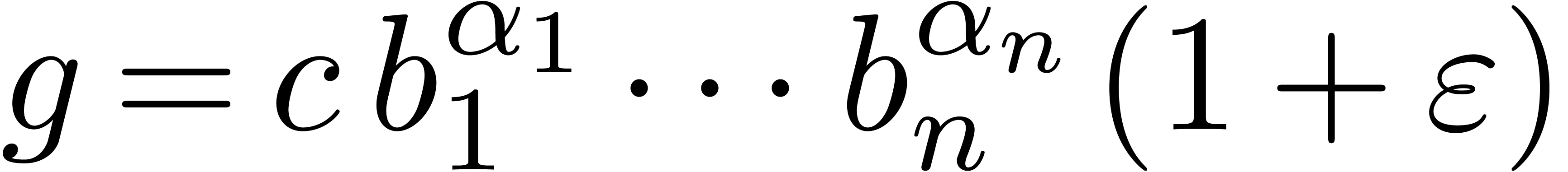 ,
with infinitesimal
,
with infinitesimal  in
in  and
and 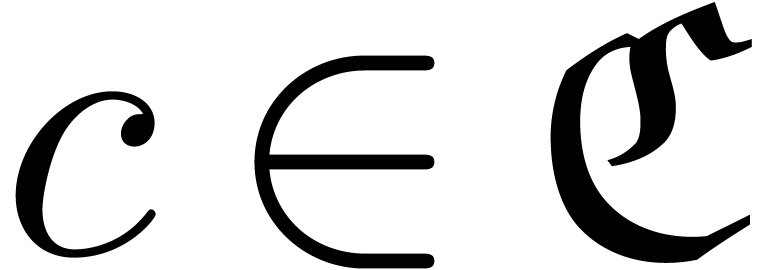 .
.
if 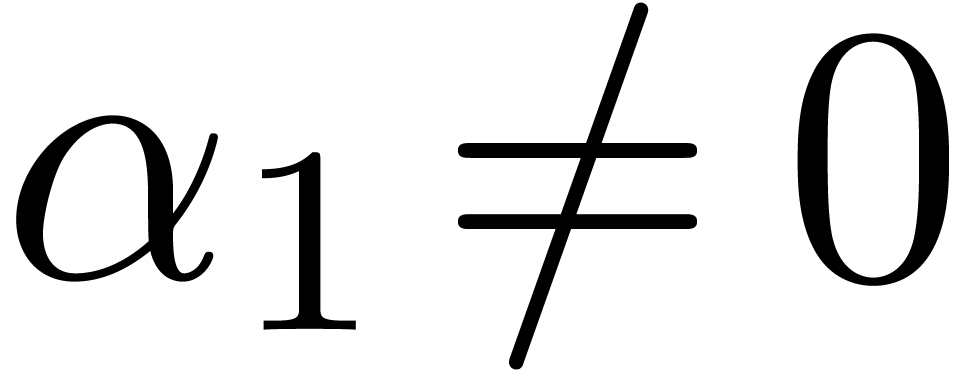 then
then 
return 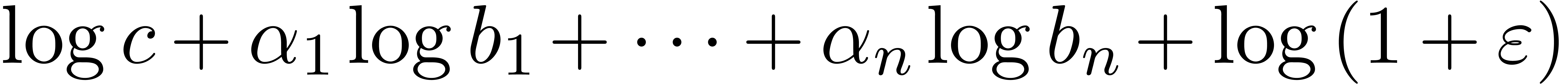
case 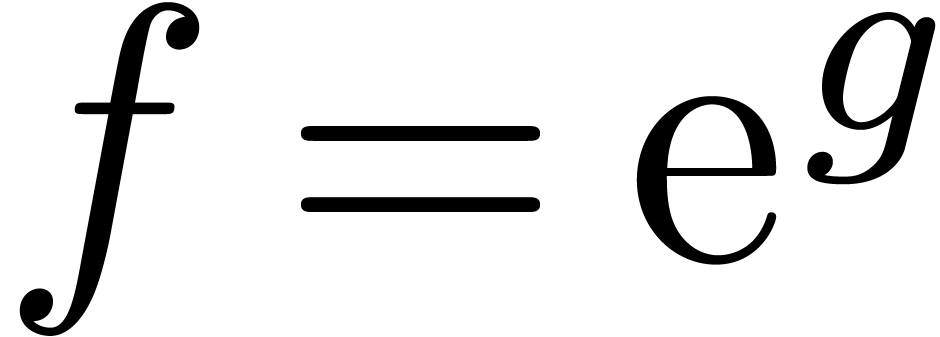 :
:
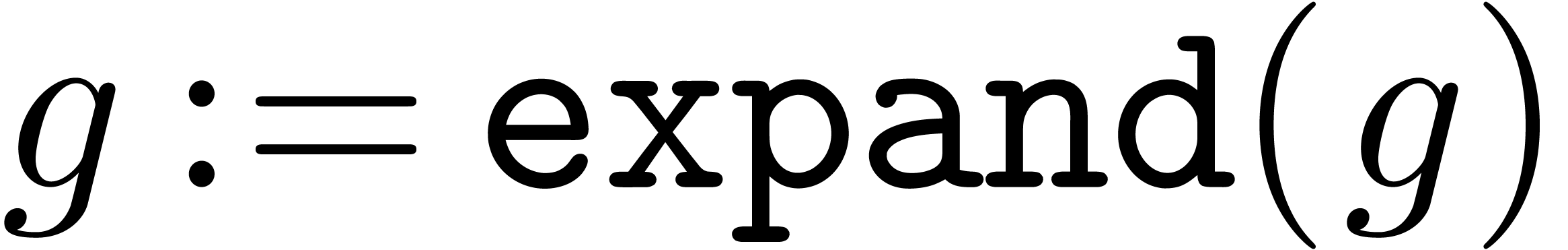
 Denote
Denote 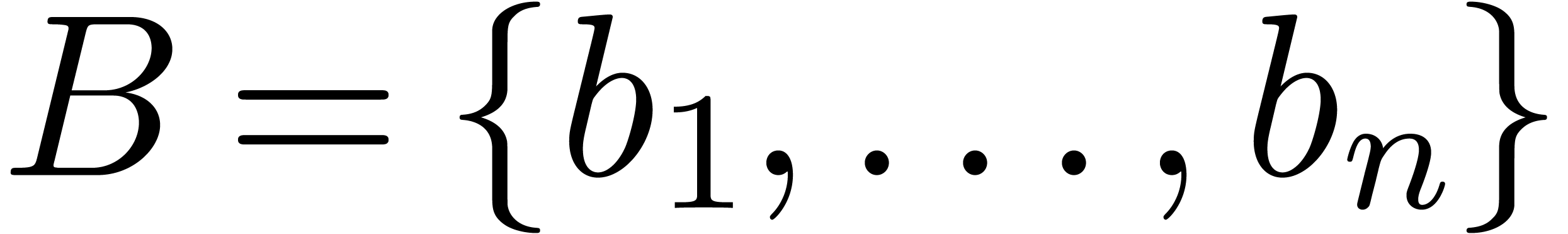 .
.
if 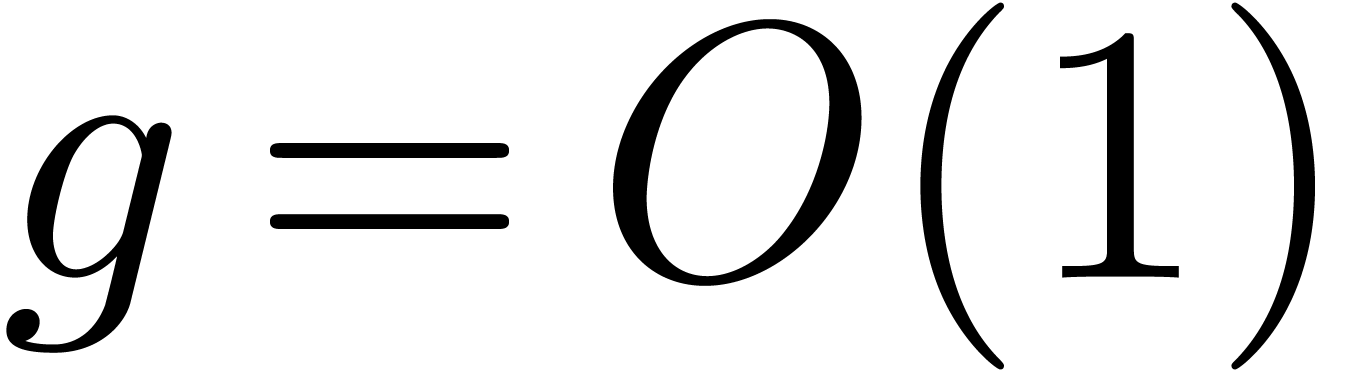 then return
then return 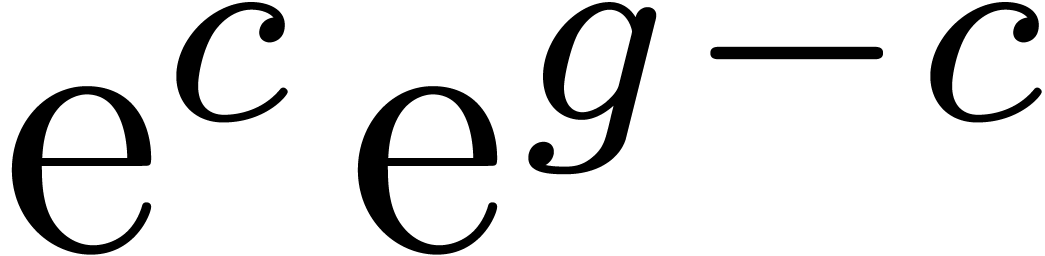 , where
, where 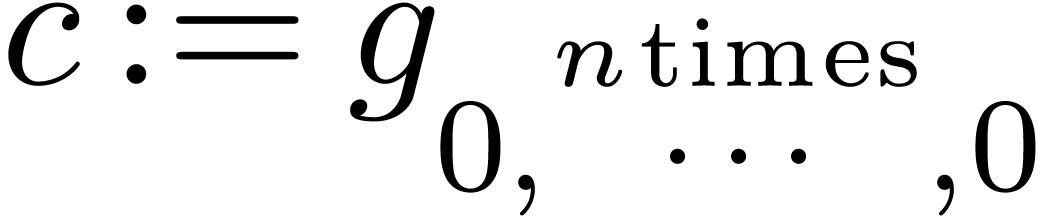
if 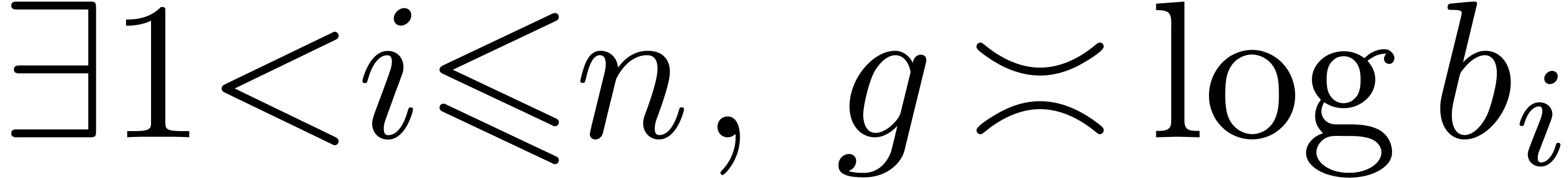 then
then
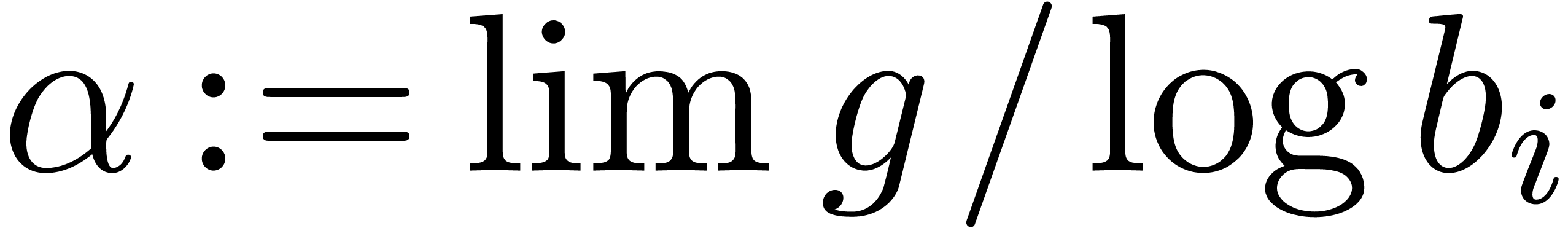
return 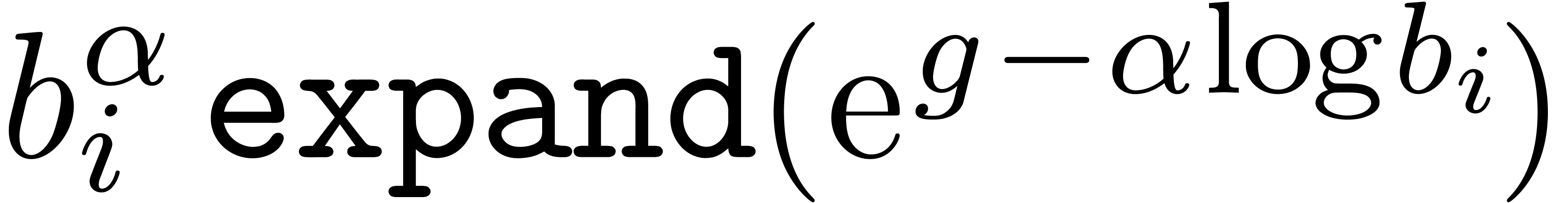
 Let
Let  be such that
be such that  .
.
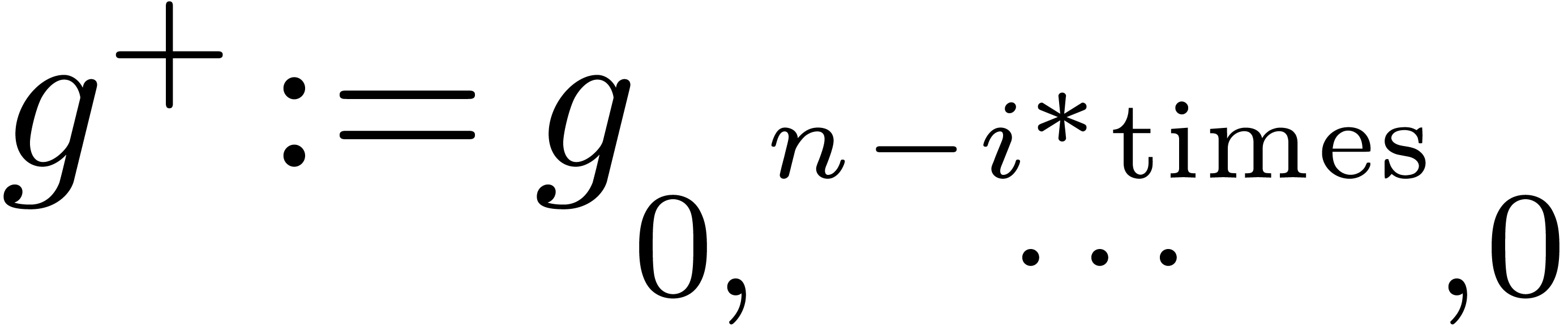
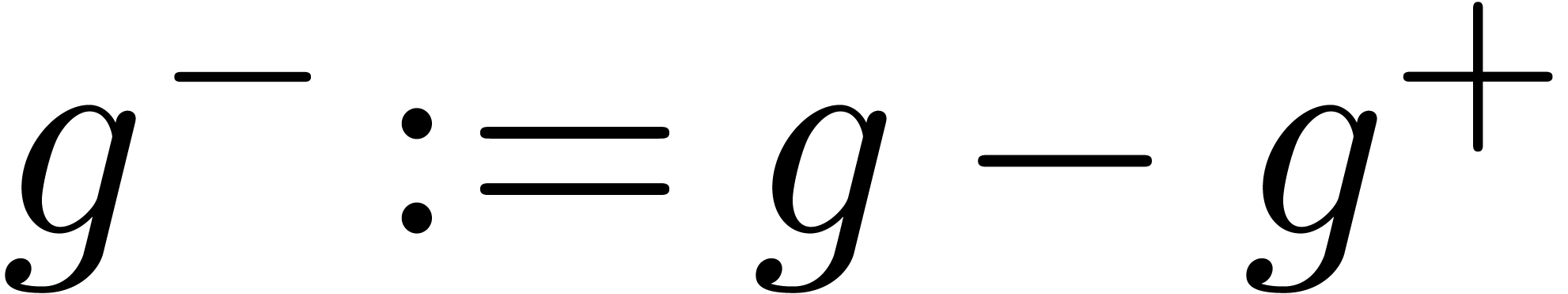
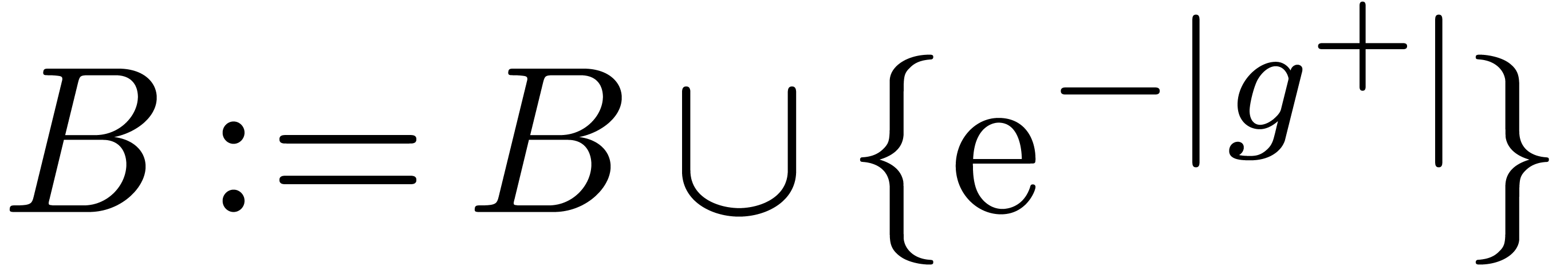
return 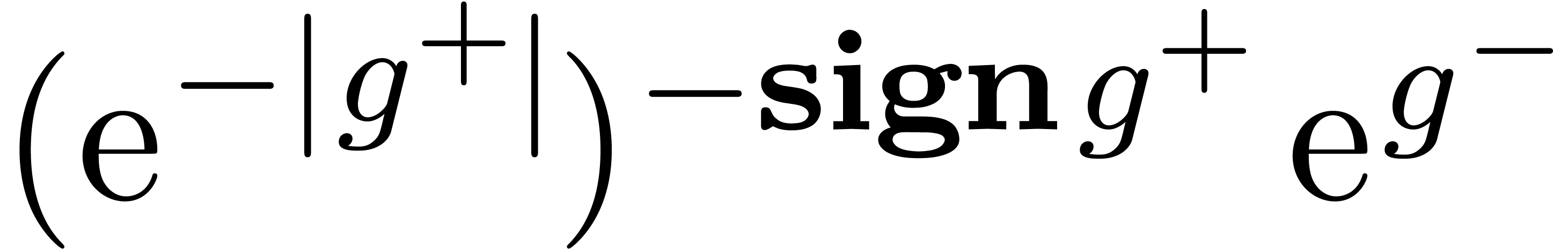
Let us comment the algorithm. The first three cases do not need
explanation. In the case 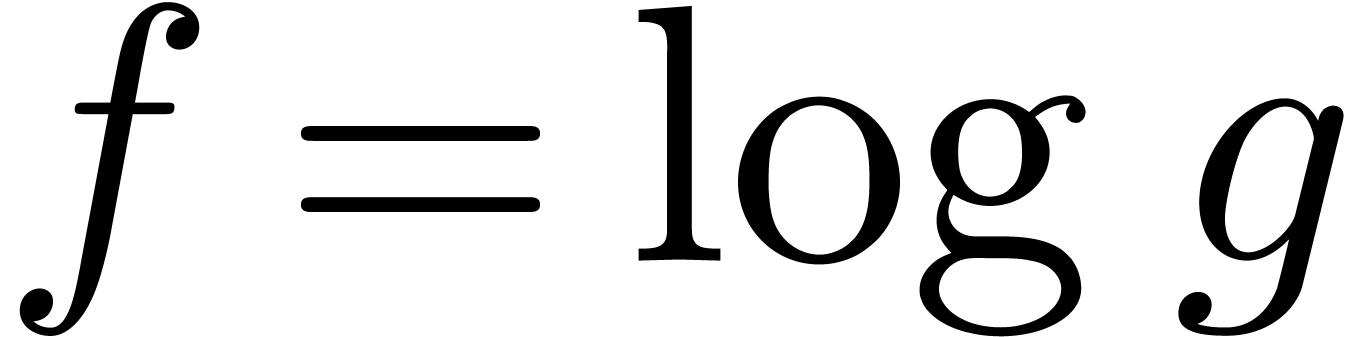 ,
the fact that
,
the fact that  is an effective normal basis is
used at the end:
is an effective normal basis is
used at the end:  is indeed an expression in
is indeed an expression in
 . The expansion of the
exponential of a bounded series
. The expansion of the
exponential of a bounded series 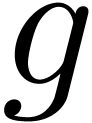 is done by a
straightforward Taylor series expansion. If
is done by a
straightforward Taylor series expansion. If 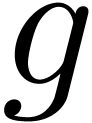 is
unbounded, then we test whether
is
unbounded, then we test whether 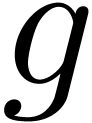 is asymptotic to
the logarithm of an element in
is asymptotic to
the logarithm of an element in  — i.e. we
test whether
— i.e. we
test whether 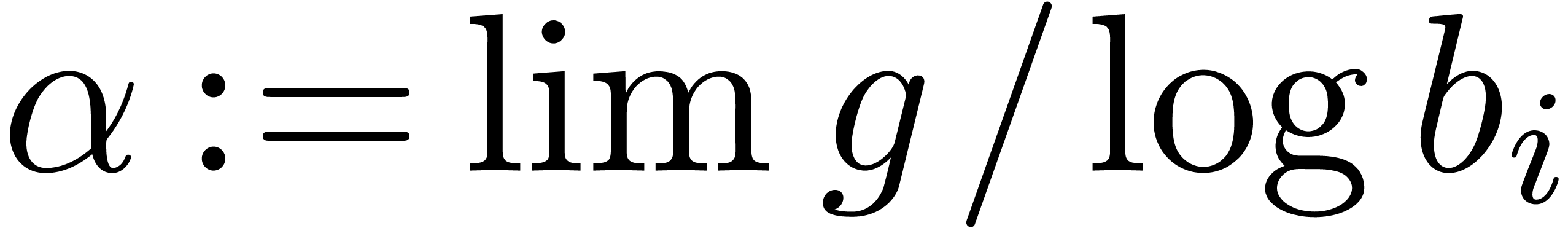 is a non zero finite number for
some
is a non zero finite number for
some 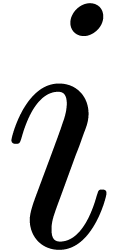 . If this is so, then
. If this is so, then
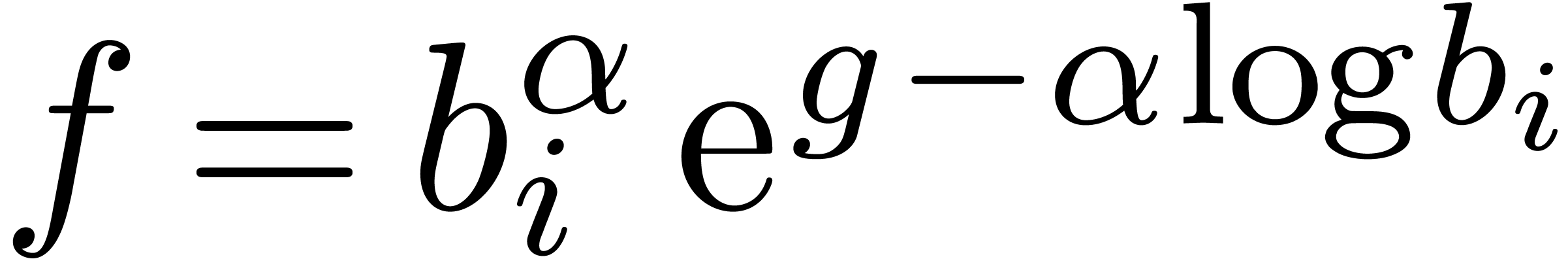 and
and 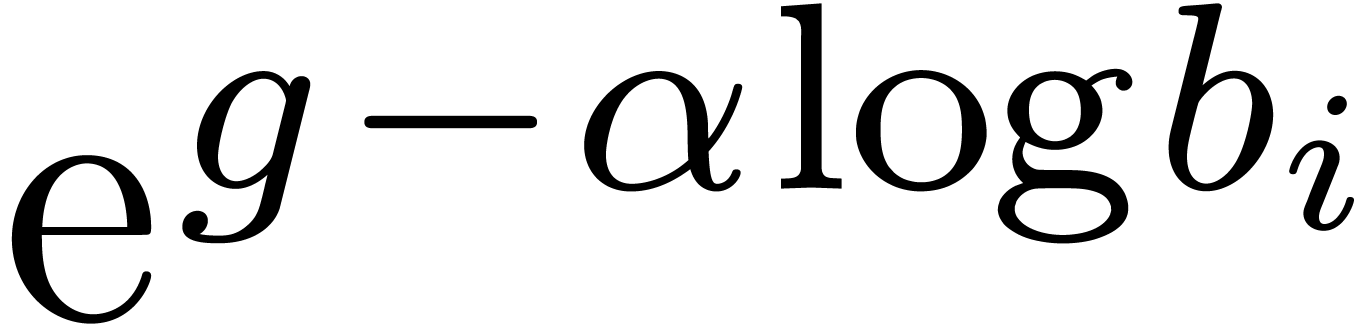 is expanded
recursively. We remark that no infinite loop can arise from this,
because successive values of
is expanded
recursively. We remark that no infinite loop can arise from this,
because successive values of 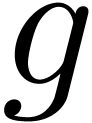 in such a loop
would be asymptotic to the logarithms of smaller and smaller elements of
in such a loop
would be asymptotic to the logarithms of smaller and smaller elements of
 , while
, while  remains unchanged. Finally, if
remains unchanged. Finally, if 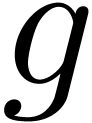 is not asymptotic
to the logarithm of an element in
is not asymptotic
to the logarithm of an element in  ,
then
,
then  has to be extended with an element of the
order of growth of
has to be extended with an element of the
order of growth of 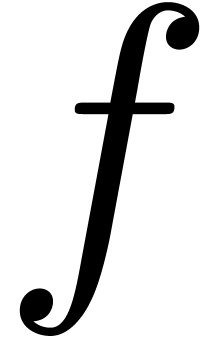 . The
decomposition
. The
decomposition 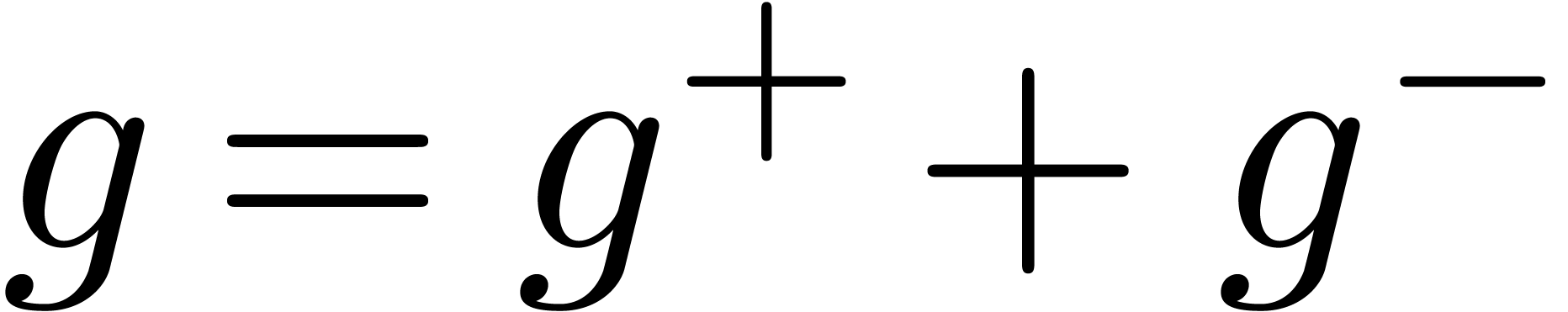 is computed in order to ensure
that
is computed in order to ensure
that  remains an effective normal basis.
remains an effective normal basis.
In this section we show how Theorem 7 can be applied to compute limsups (or liminfs) of certain bounded functions, involving trigonometric functions. The idea is based on the following consequence of Theorem 7.
 be exp-log functions at infinity.
Let
be exp-log functions at infinity.
Let 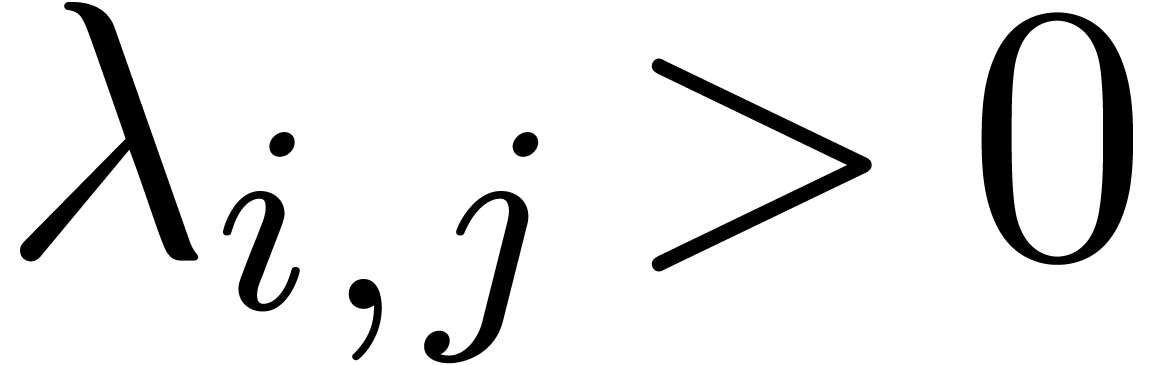 (
(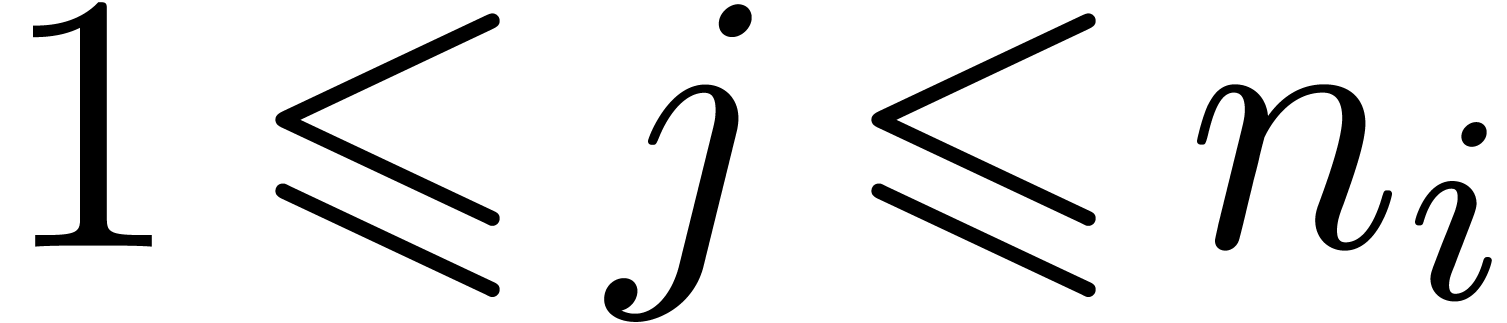 )
be such that
)
be such that  are
are  -linearly
independent for each
-linearly
independent for each 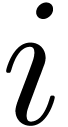 .
Denote
.
Denote 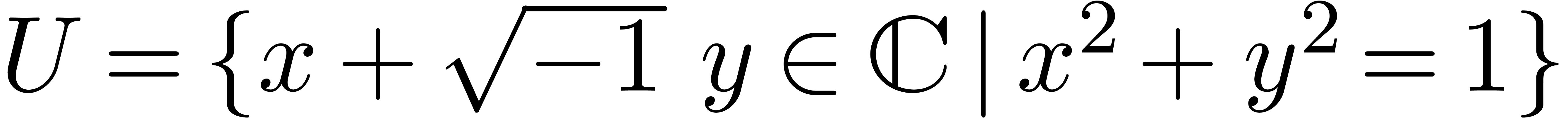 and
and 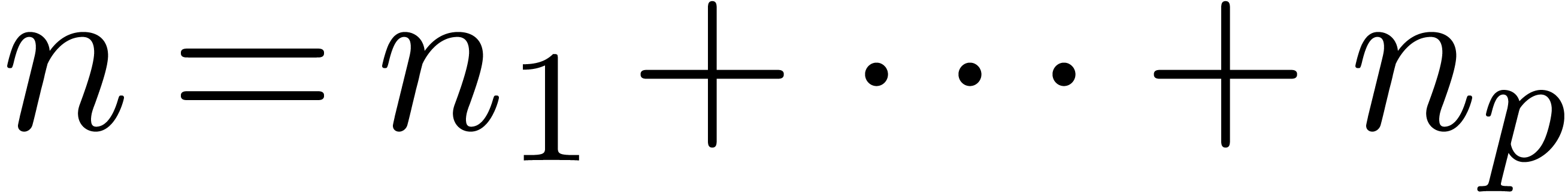 .
Let
.
Let 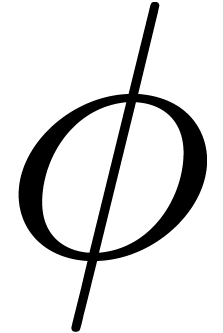 be a continuous function from
be a continuous function from  into
into  and let
and let
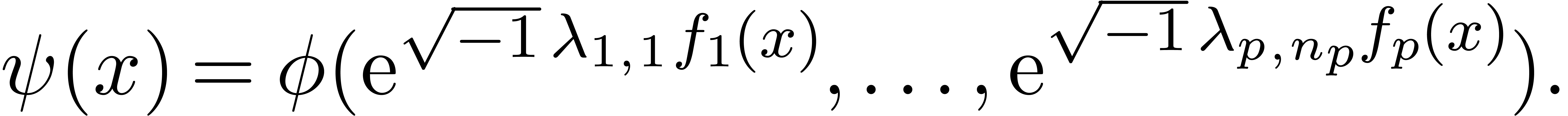
Then
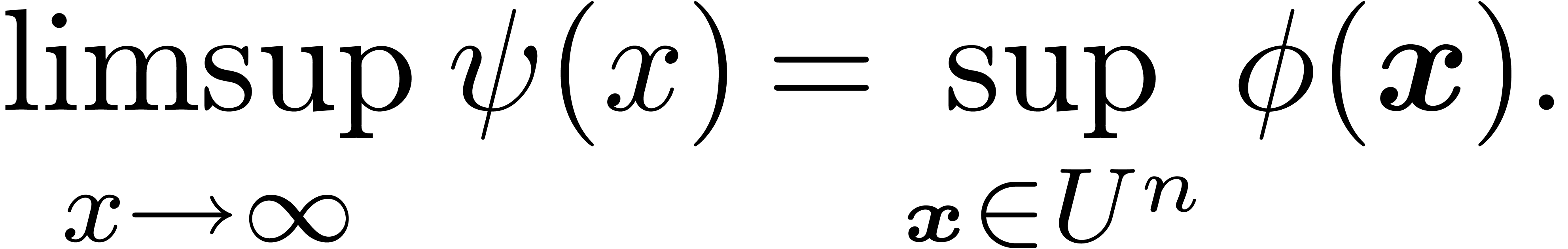
Proof. We first notice that we will be able to
apply Theorem 7 on our input data: by a well known theorem,
which goes back to Hardy [Har11], the germs at infinity of
 lie in a common Hardy field. Consequently,
lie in a common Hardy field. Consequently,  , and
, and  are
strictly increasing in a suitable neighbourhood of infinity.
are
strictly increasing in a suitable neighbourhood of infinity.
The mapping 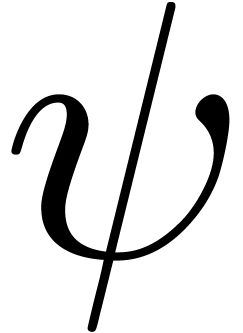 is defined in a neighbourhood
is defined in a neighbourhood  of infinity, and can be factored
of infinity, and can be factored 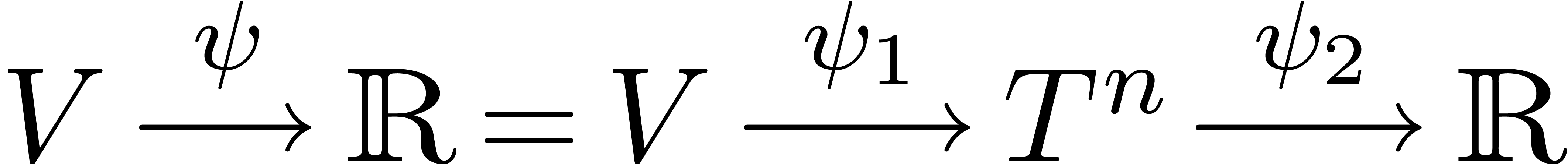 , with
, with
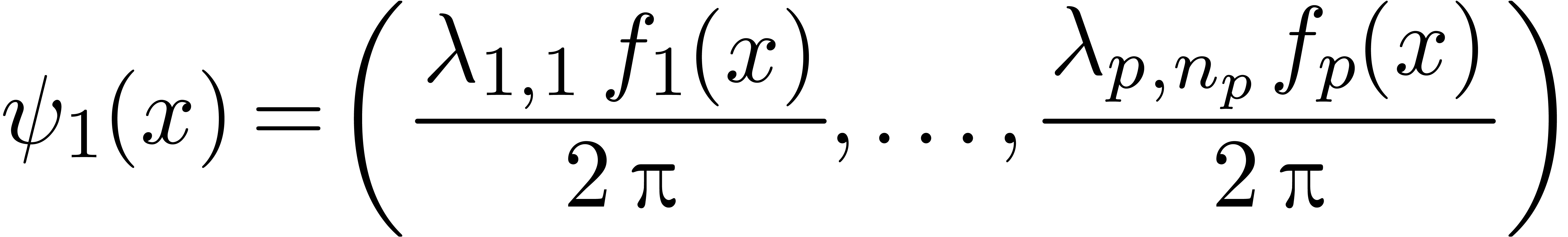
and
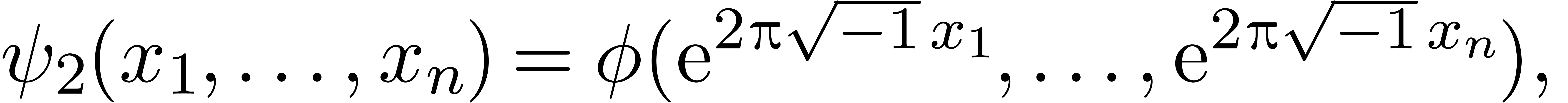
where 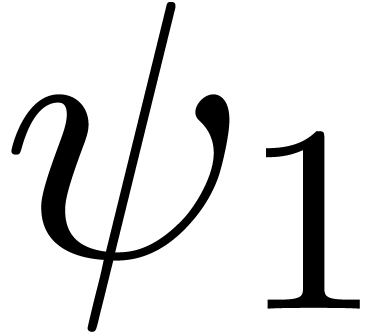 and
and 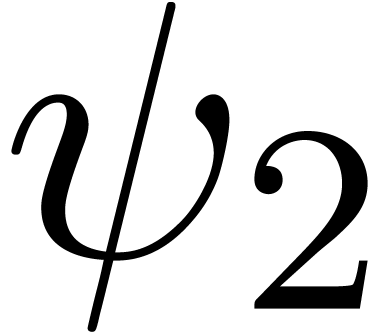 are both
continuous. Since
are both
continuous. Since  is compact, there exists a
point
is compact, there exists a
point  in which
in which 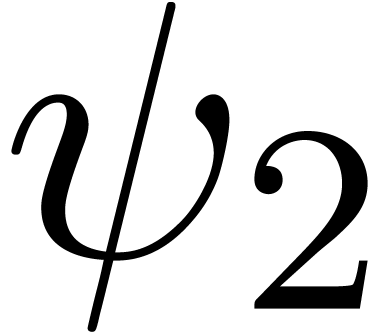 attains
its maximum. Let
attains
its maximum. Let  . There
exists a neighbourhood
. There
exists a neighbourhood  of
of  , such that
, such that 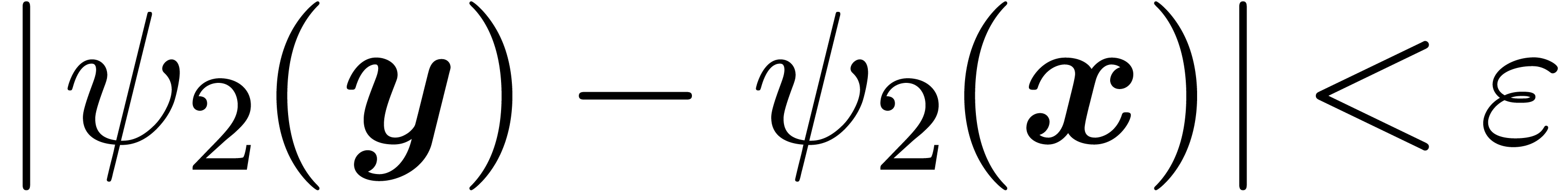 ,
for any
,
for any  in
in  .
By Theorem 7, there exist
.
By Theorem 7, there exist  ,
with
,
with 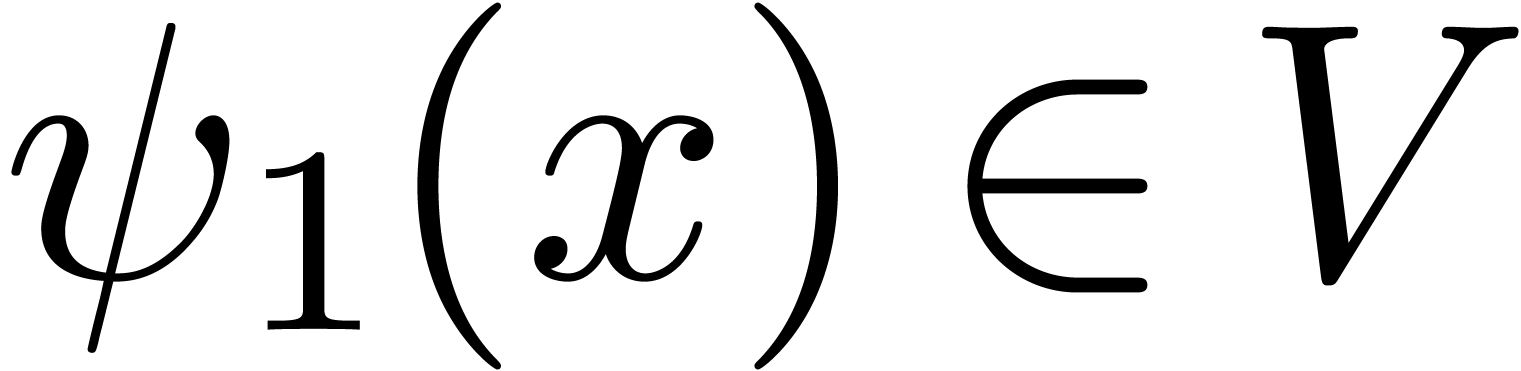 as close to infinity as we wish. For such
as close to infinity as we wish. For such
 , we have
, we have 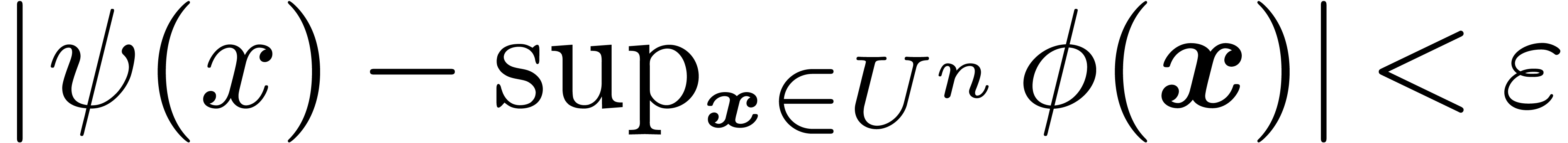 .
.
We now turn to the computation of this limit.
 be exp-log functions at infinity.
Let
be exp-log functions at infinity.
Let 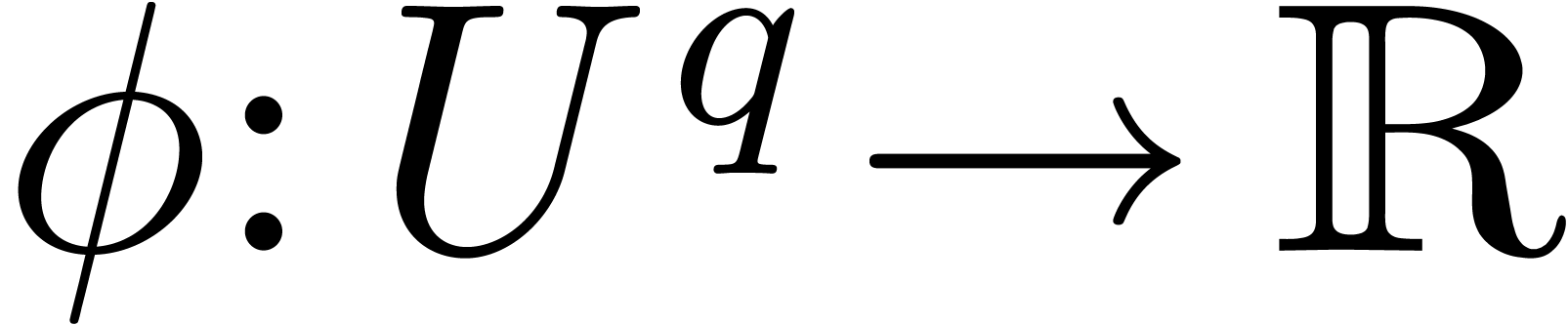 a real algebraic function, where we
consider
a real algebraic function, where we
consider  as a real algebraic variety. Assume
that we have an oracle to test the
as a real algebraic variety. Assume
that we have an oracle to test the  -linear
dependence of exp-log constants. Then there exists an algorithm to
compute the limsup of
-linear
dependence of exp-log constants. Then there exists an algorithm to
compute the limsup of 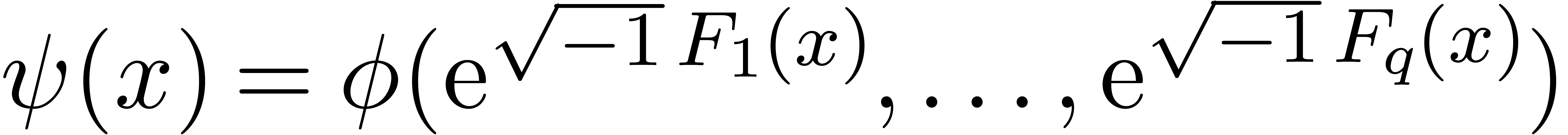 .
.
Proof. Using the identity 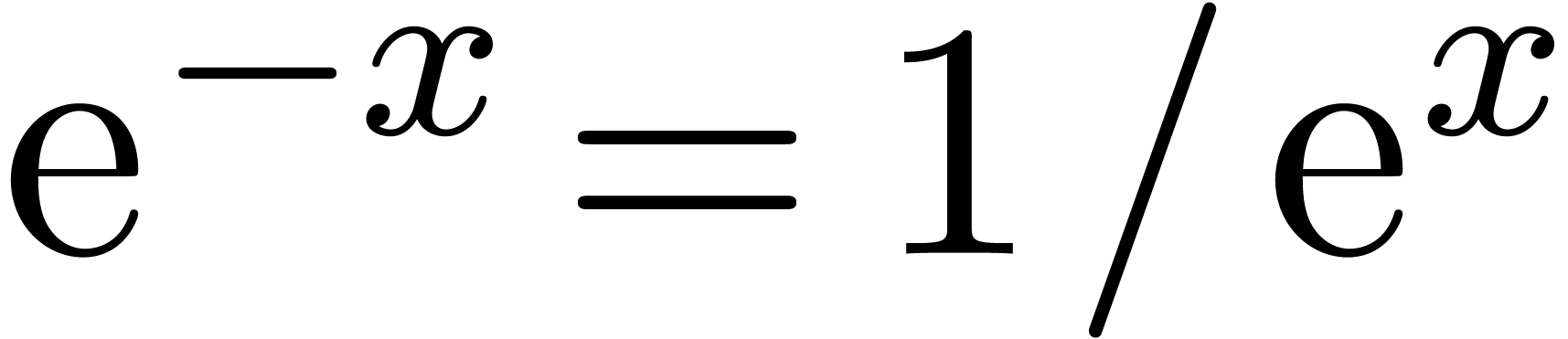 , we may always assume without loss of generality,
that the
, we may always assume without loss of generality,
that the 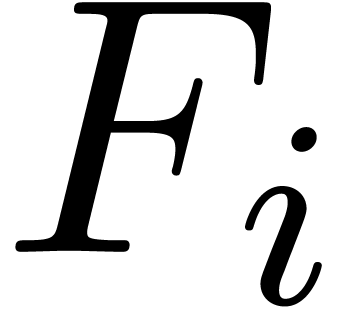 's are all positive.
Now the algorithm consists of the following steps:
's are all positive.
Now the algorithm consists of the following steps:
Step 1. Compute a common effective normal basis for  , using the algorithm from section 4.
Order the
, using the algorithm from section 4.
Order the 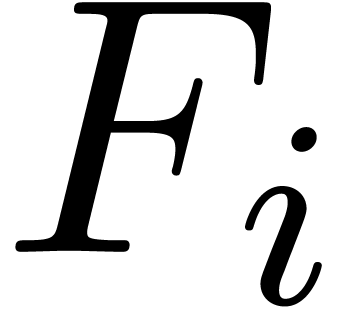 's
w.r.t.
's
w.r.t.  ; that
is,
; that
is,  or
or  ,
whenever
,
whenever 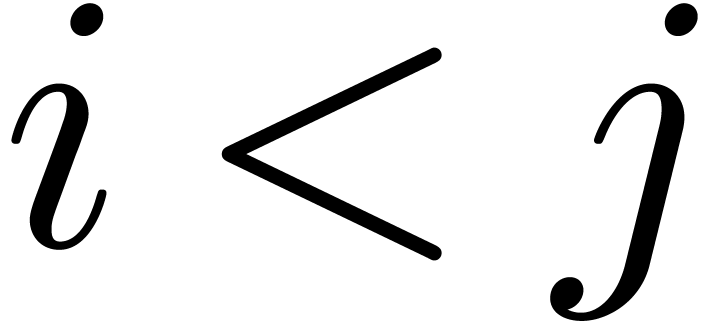 .
.
Step 2. Simultaneously modify the 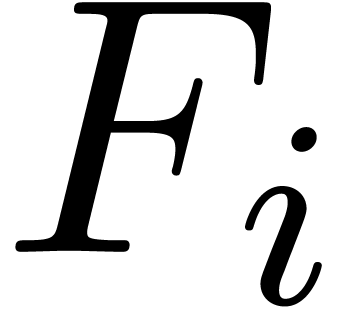 's
and the algebraic function
's
and the algebraic function  in the
in the 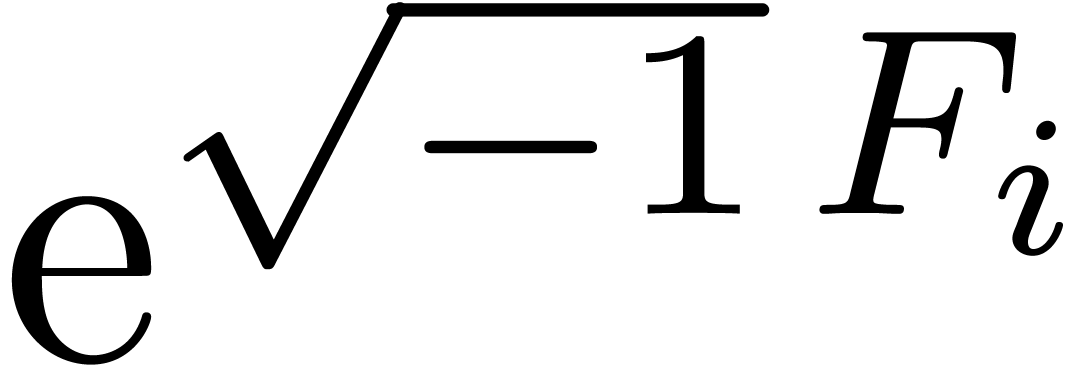 's, until we either have
's, until we either have  , or
, or 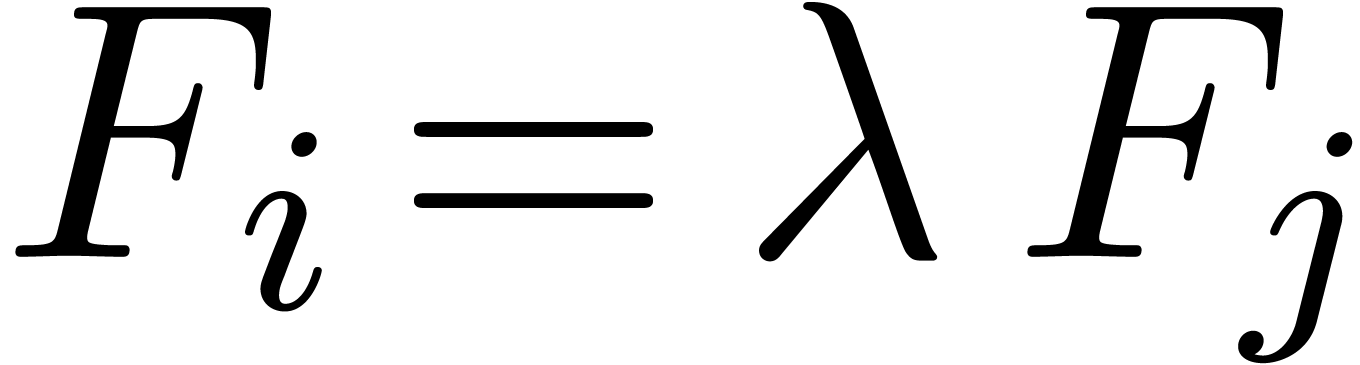 ,
for some
,
for some 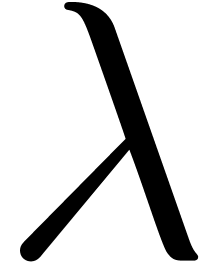 , whenever
, whenever  . As long as this is not the case,
we take
. As long as this is not the case,
we take  maximal, such that the above does not
hold, and do the following:
maximal, such that the above does not
hold, and do the following:
First compute the limit 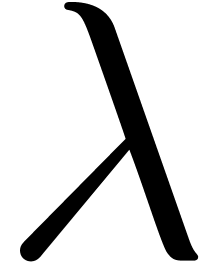 of
of 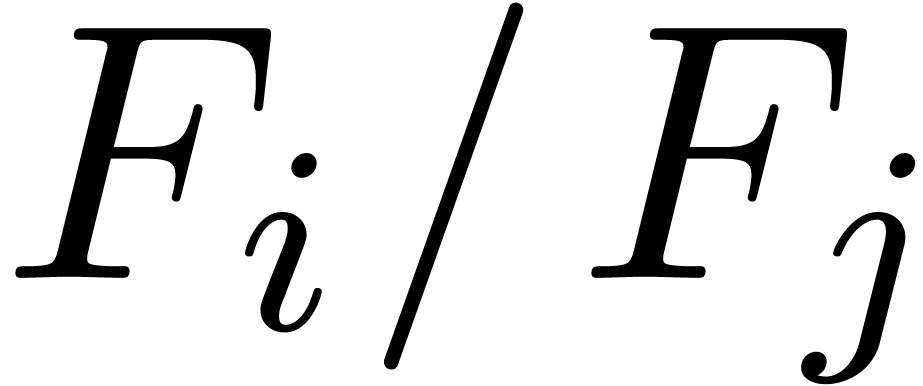 . Next insert
. Next insert 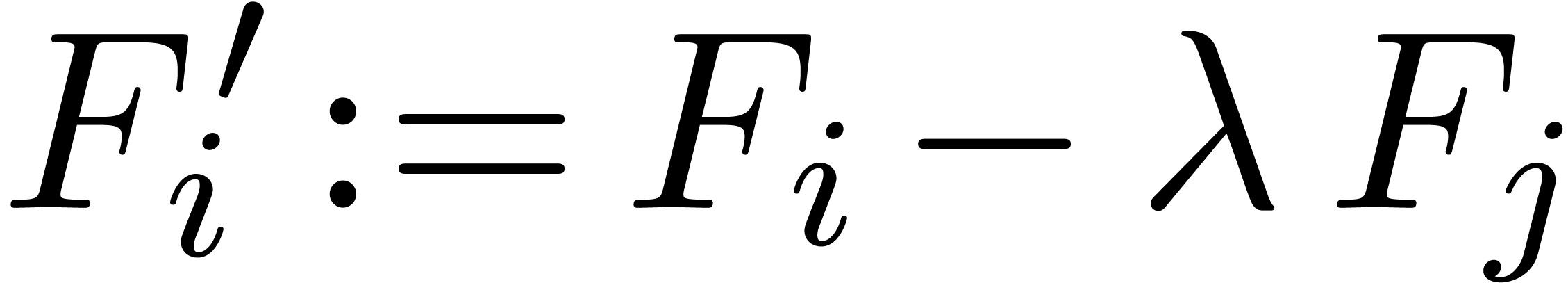 and
and 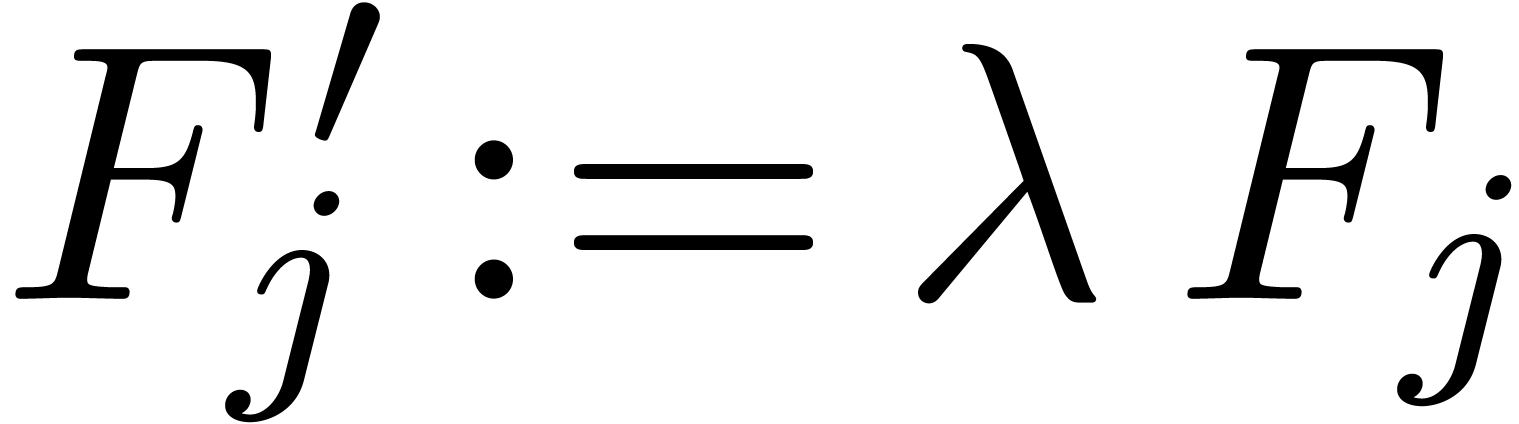 into the set of
into the set of 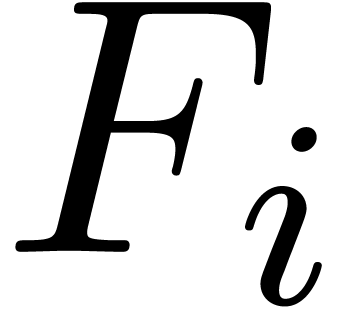 's
and remove
's
and remove 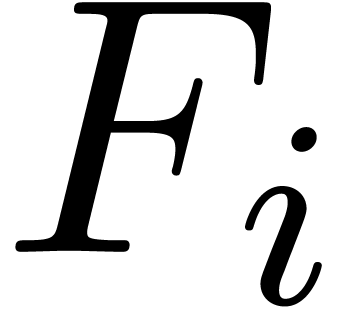 . The new
expression for
. The new
expression for  is obtained by replacing each
is obtained by replacing each
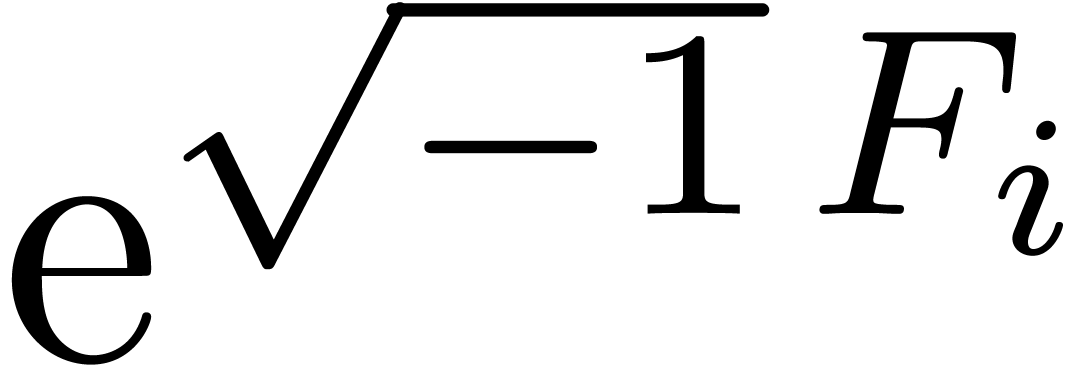 by
by 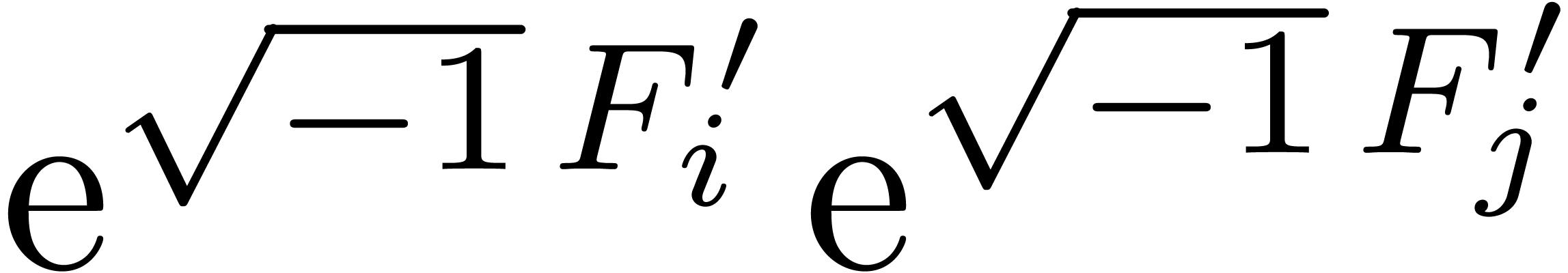 .
.
Step 3. Compute exp-log functions  ,
and constants
,
and constants 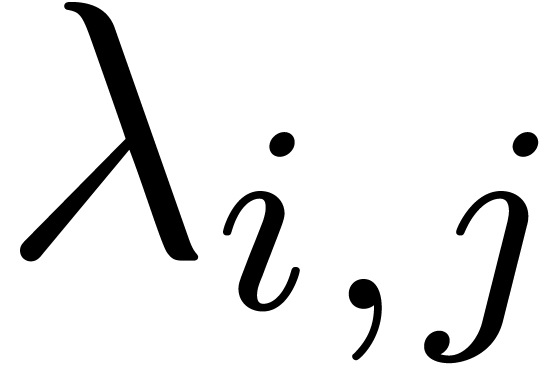 (
(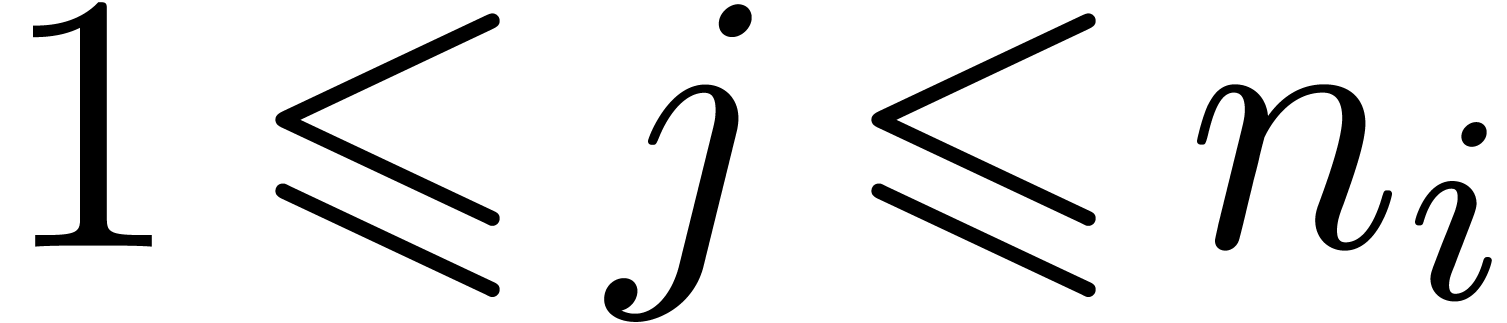 ),
such that each
),
such that each 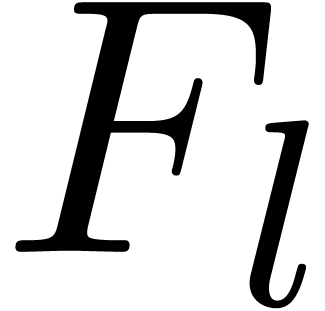 can be written as
can be written as 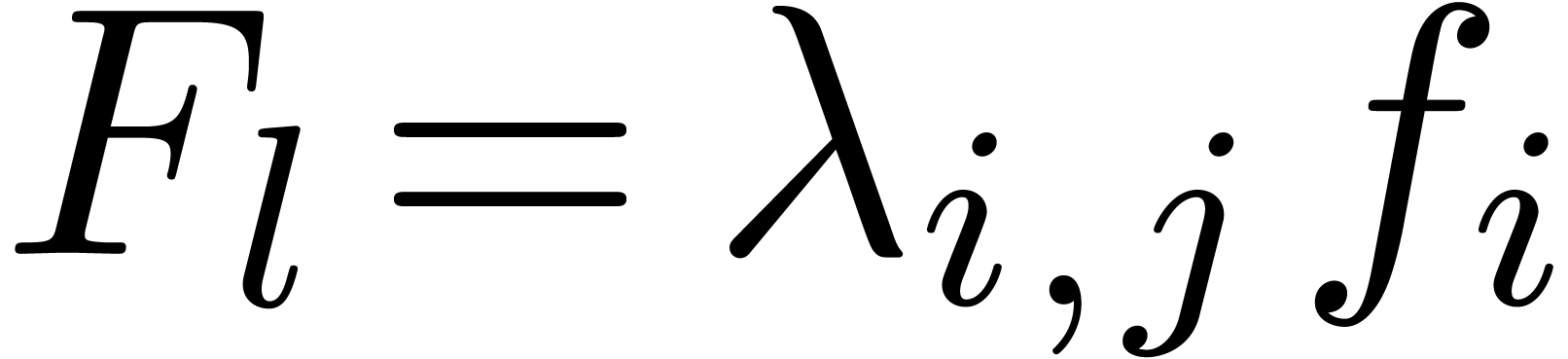 , for some
, for some 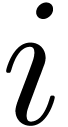 and
and  . Replacing
. Replacing 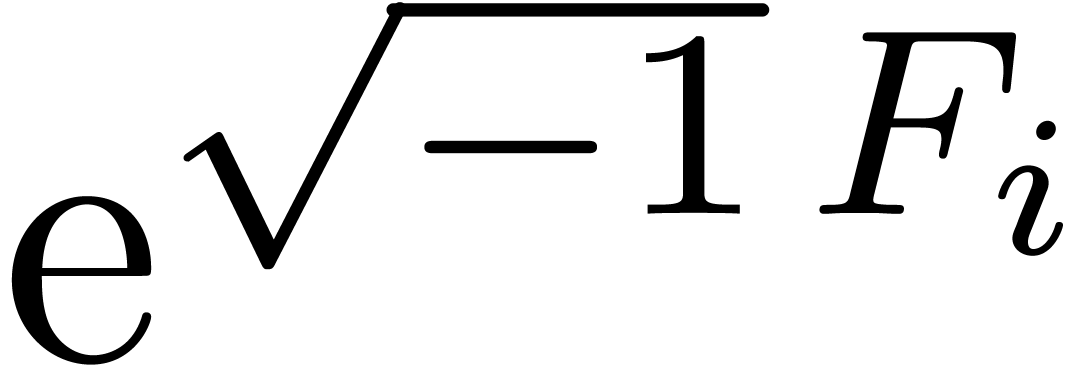 by its limit for each bounded
by its limit for each bounded 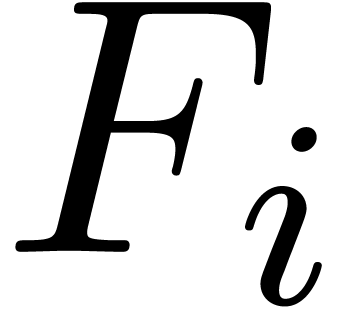 ,
we reduce the general case to the case when
,
we reduce the general case to the case when  .
.
Step 4. This step consists in making the 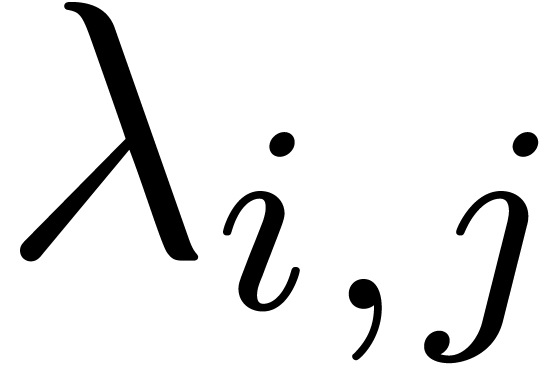 's
's  -linearly
independent for each fixed
-linearly
independent for each fixed 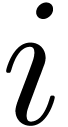 .
Whenever there exists a non trivial
.
Whenever there exists a non trivial  -linear
relation between the
-linear
relation between the 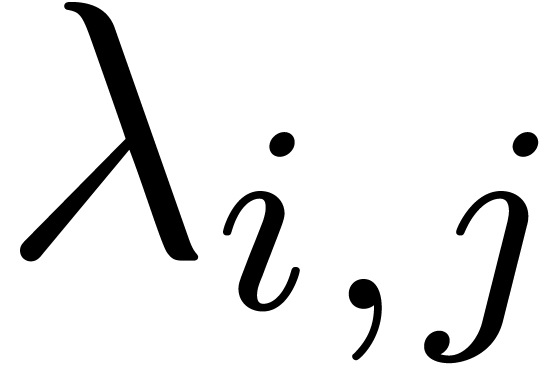 's (for
fixed
's (for
fixed 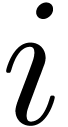 ), we may assume
without loss of generality that this relation is given by
), we may assume
without loss of generality that this relation is given by
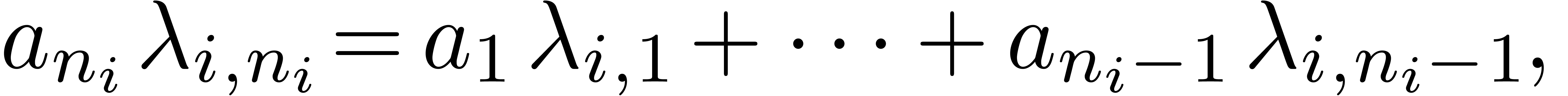
for  in
in  and
and 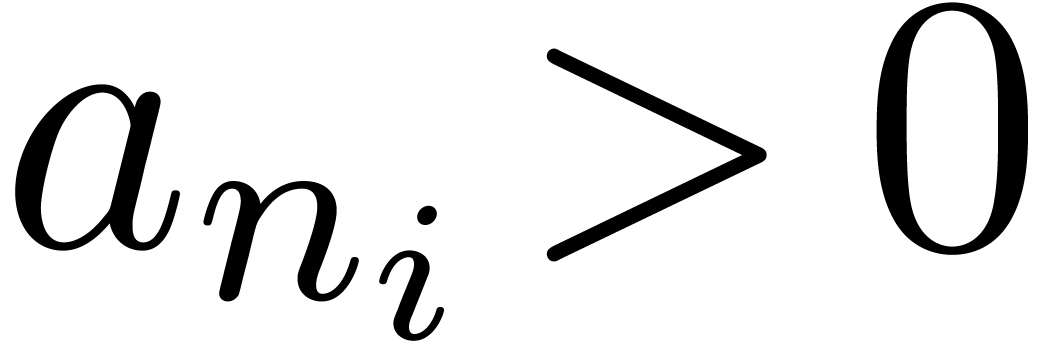 . As long as we can find such a relation, we do
the following:
. As long as we can find such a relation, we do
the following:
For all 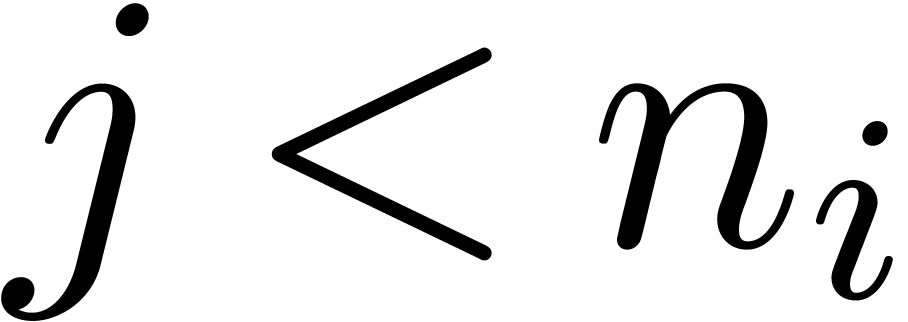 , replace
, replace  by
by 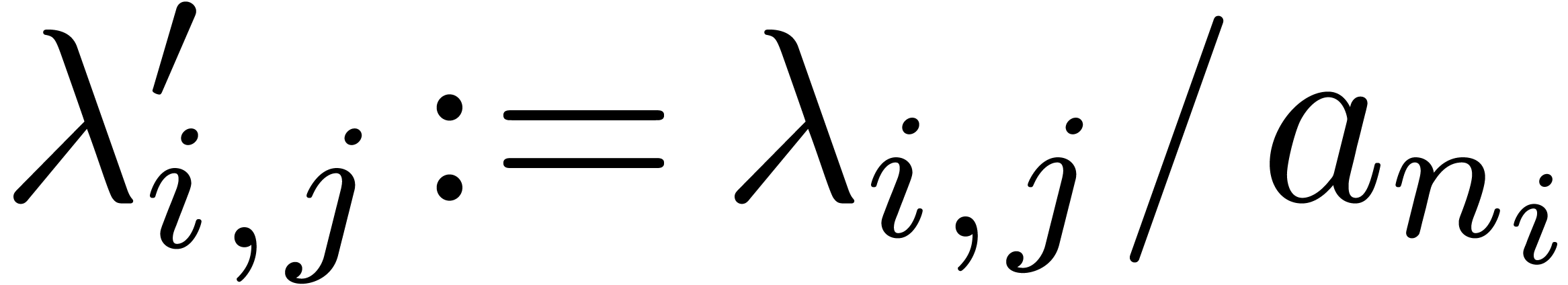 and
and 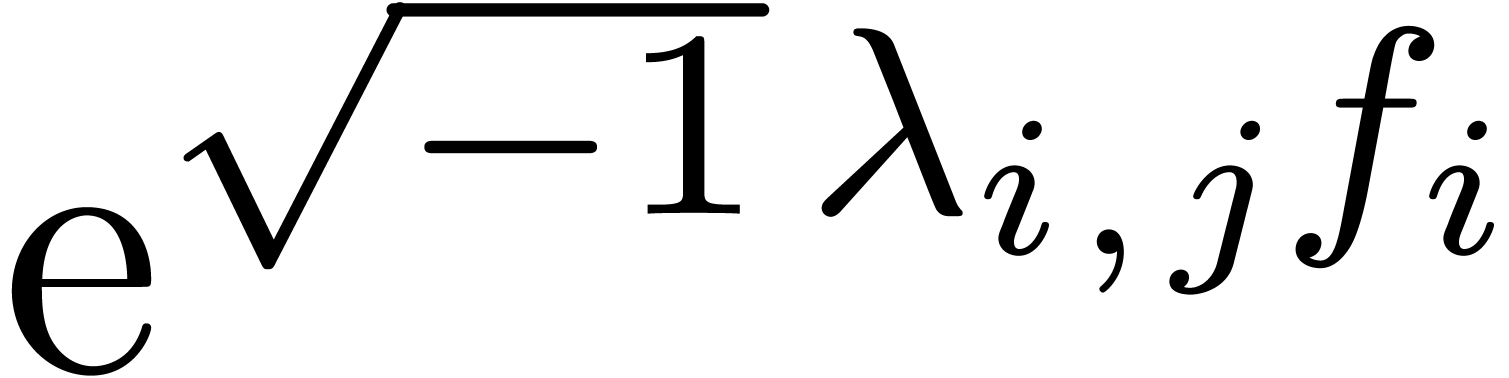 by
by
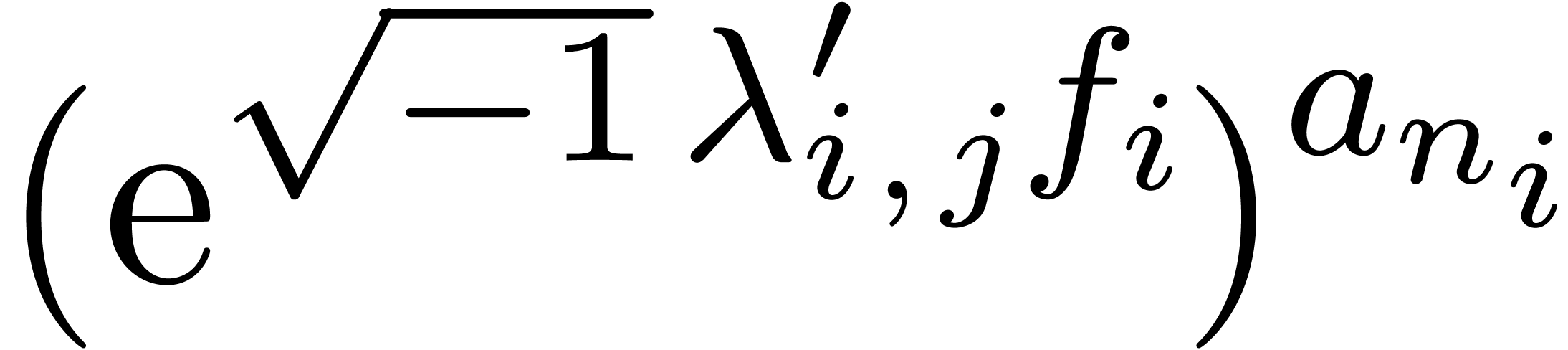 in the expression for
in the expression for  . Next, replace
. Next, replace 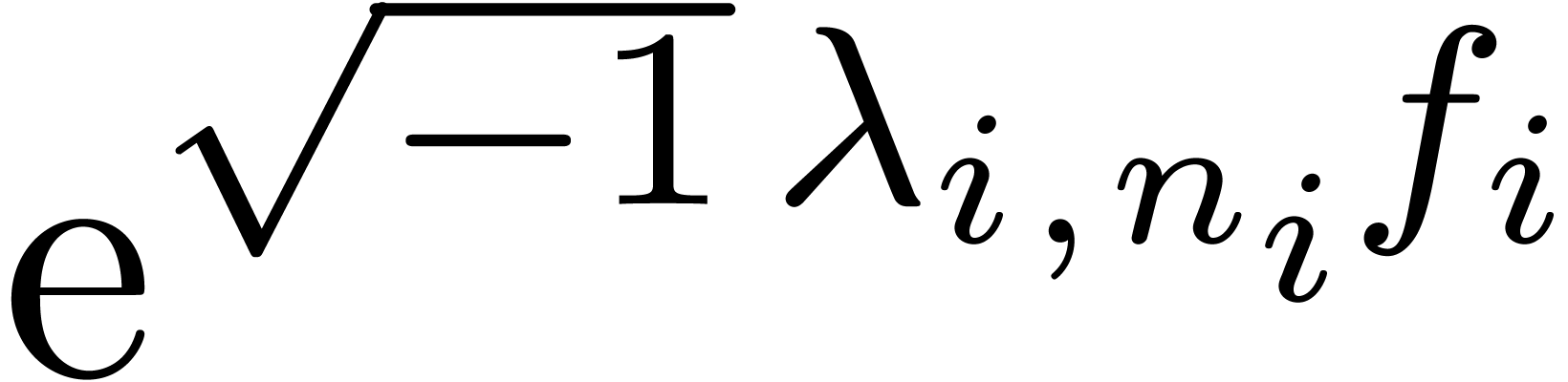 by
by 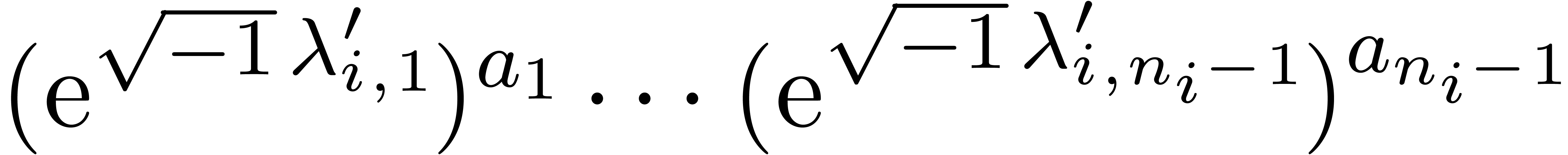 in the expression for
in the expression for  .
.
Step 5. By Theorem 8, the limsup of  is the maximum of
is the maximum of  on
on  , where
, where  .
To compute this maximum, we determine the set of zeros of the gradient
of
.
To compute this maximum, we determine the set of zeros of the gradient
of  on
on  .
Then
.
Then  is constant on each connected component and
the maximum of these constant values yields
is constant on each connected component and
the maximum of these constant values yields 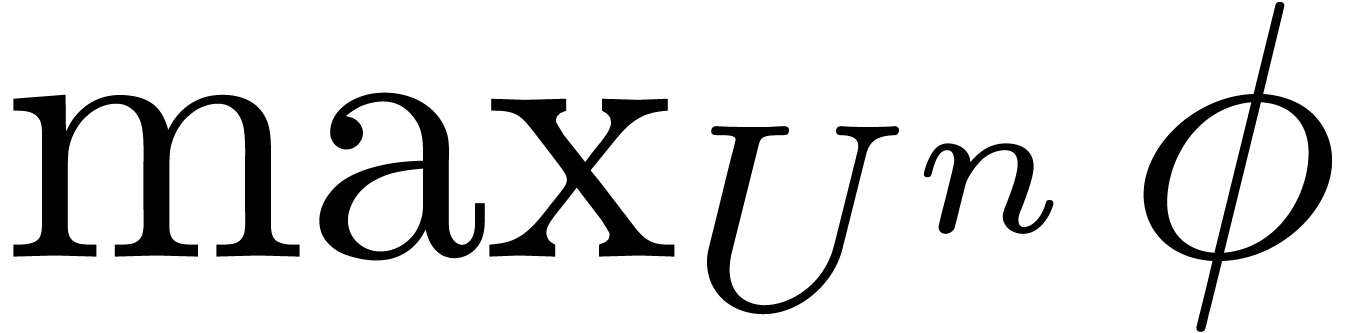 . To compute the zero set of the gradient of
. To compute the zero set of the gradient of  and its connected components, one may for instance
use cylindrical decomposition (see [Col75]). Of course,
other algorithms from effective real algebraic geometry can be used
instead.
and its connected components, one may for instance
use cylindrical decomposition (see [Col75]). Of course,
other algorithms from effective real algebraic geometry can be used
instead.
The correctness of our algorithm is clear. The termination of the loop
in step 2 follows from the fact that the new 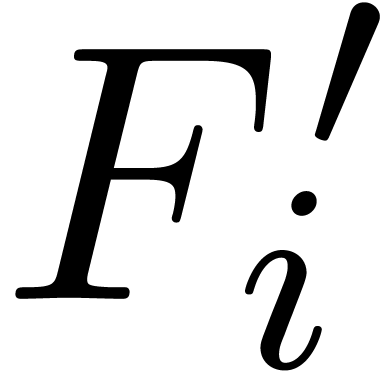 is
asymptotically smaller then
is
asymptotically smaller then 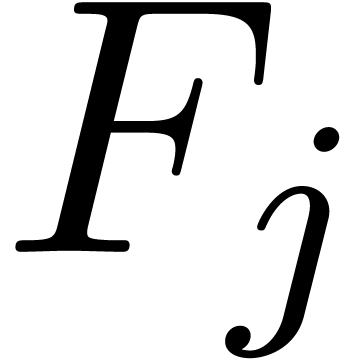 ,
so that either the
,
so that either the  -class of
-class of
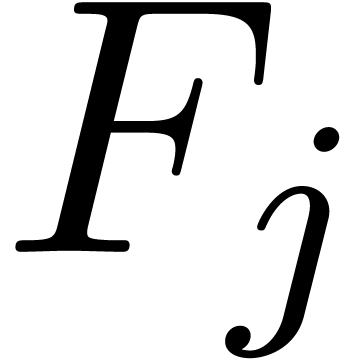 strictly decreases, or the number of
strictly decreases, or the number of 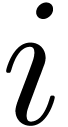 's with
's with  , but not
, but not 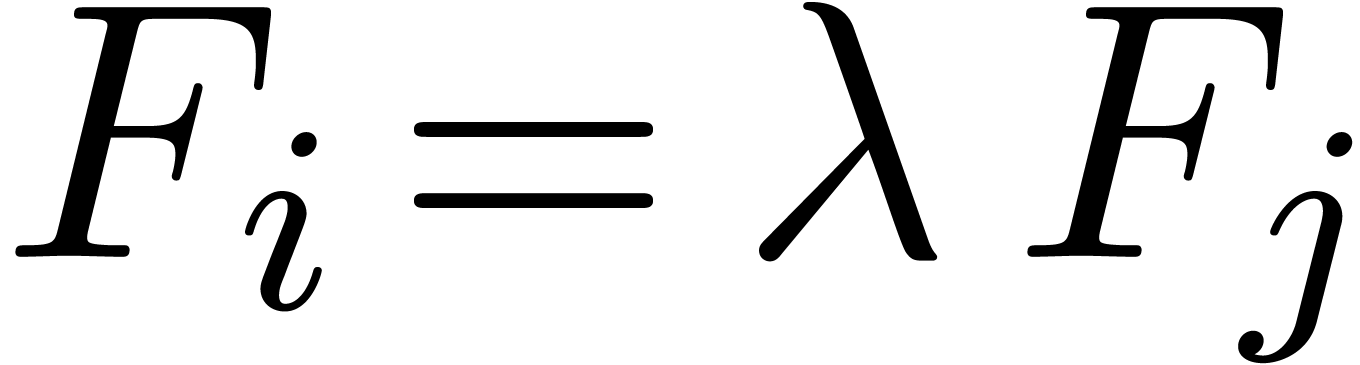 for some
for some 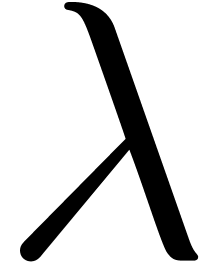 . The number of
. The number of  -classes which can be attained is bounded by
the initial value of
-classes which can be attained is bounded by
the initial value of  .
.
 be exp-log functions at infinity and
be exp-log functions at infinity and
 be an algebraic function in
be an algebraic function in  variables, defined on
variables, defined on 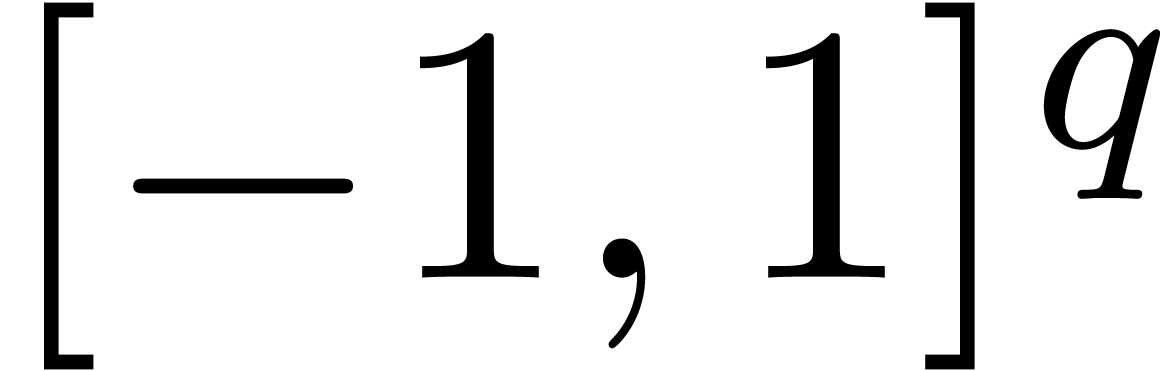 .
Assume that we have an oracle to test the
.
Assume that we have an oracle to test the  -linear dependence of exp-log constants. Then
there exists an algorithm to compute the limsup of
-linear dependence of exp-log constants. Then
there exists an algorithm to compute the limsup of 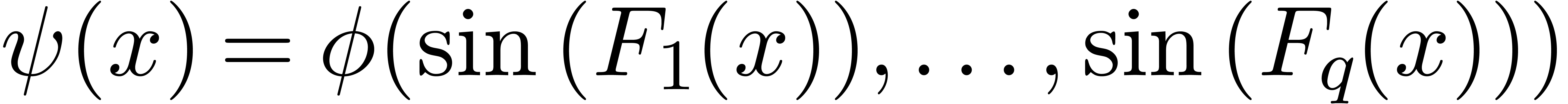 .
.

Example
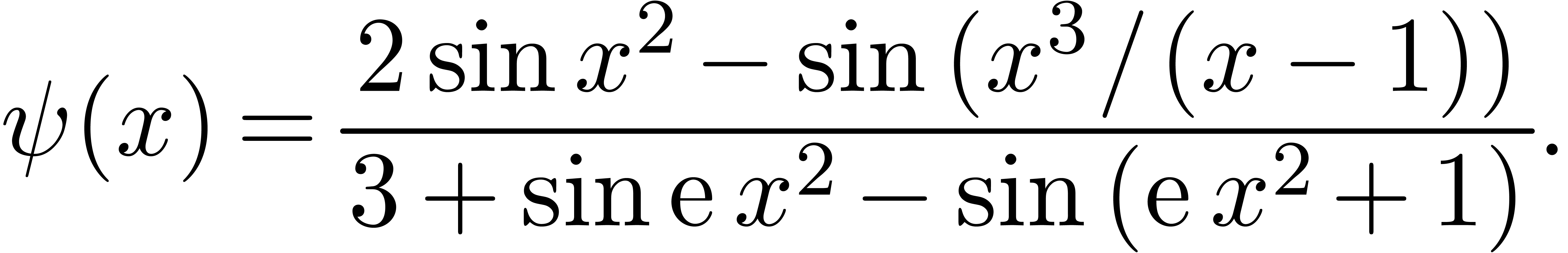
The first step consists in expanding  ,
,
 ,
, 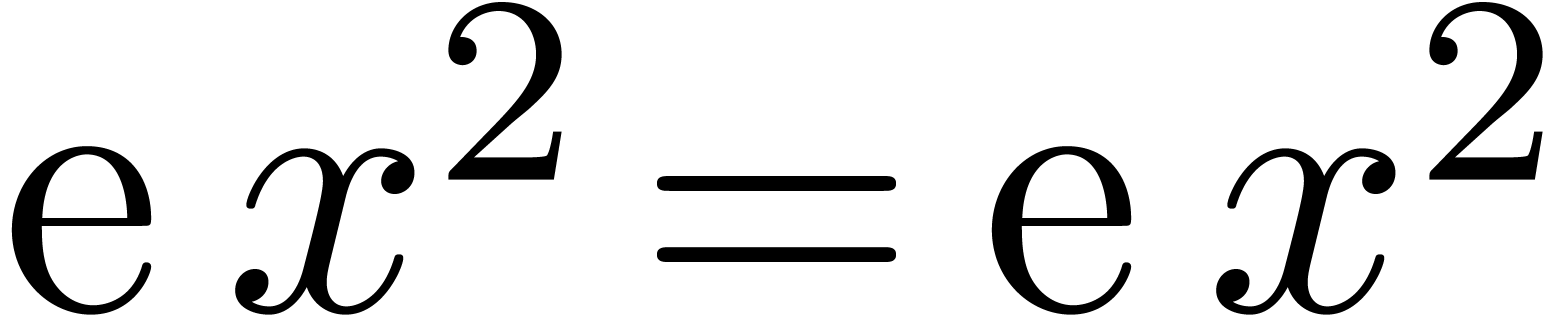 and
and
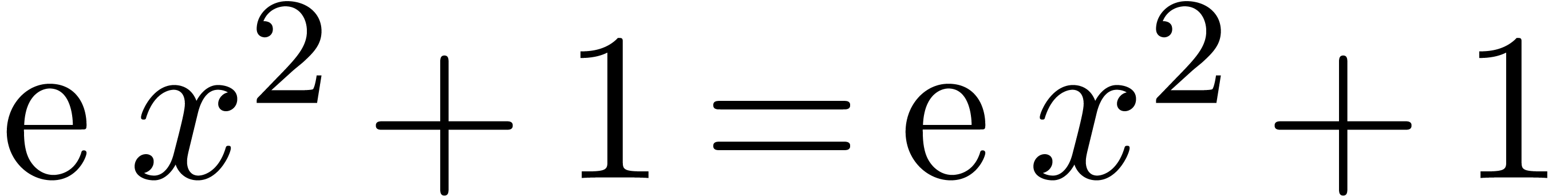 . All these functions have
the same
. All these functions have
the same  -class, but they are
not all homothetic. Therefore, some rewriting needs to be done. First,
-class, but they are
not all homothetic. Therefore, some rewriting needs to be done. First,
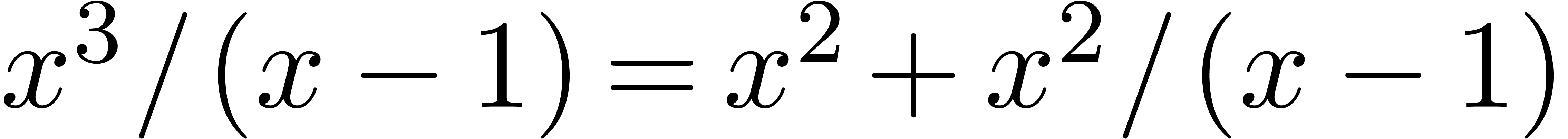 , and we rewrite
, and we rewrite
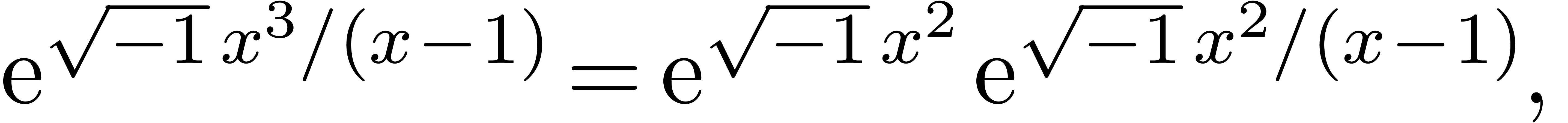
which corresponds to the rewriting
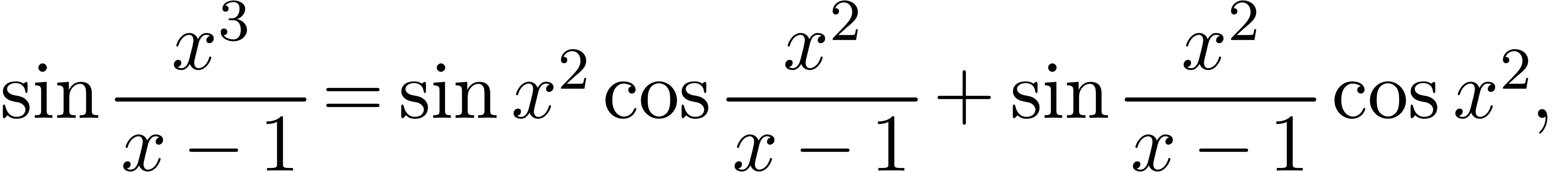
if we consider real and imaginary parts. Similarly, we rewrite
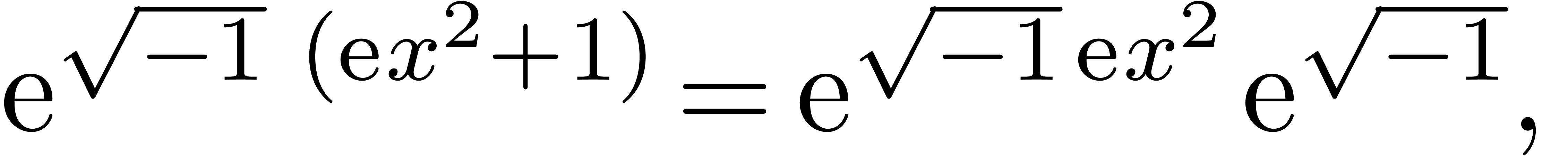
which corresponds to the rewriting
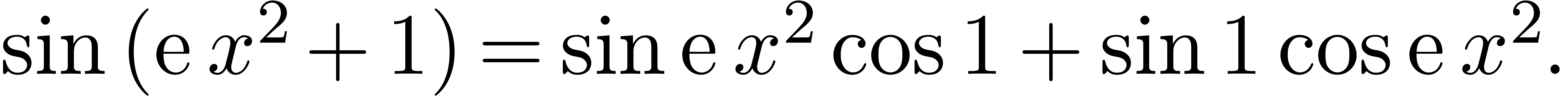
In step 4, no  -linear
relations are found, so that we have to determine the maximal value of
-linear
relations are found, so that we have to determine the maximal value of
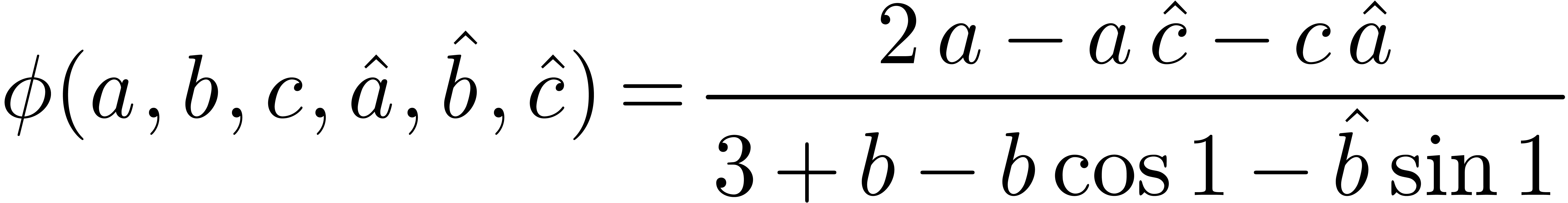 |
(5) |
on 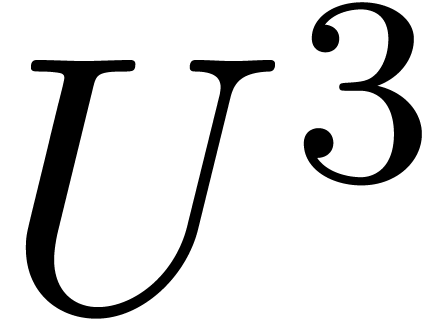 . Here we have abbreviated
. Here we have abbreviated
 (hence
(hence 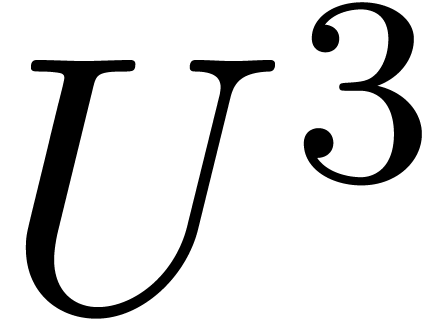 is the set of
points with
is the set of
points with 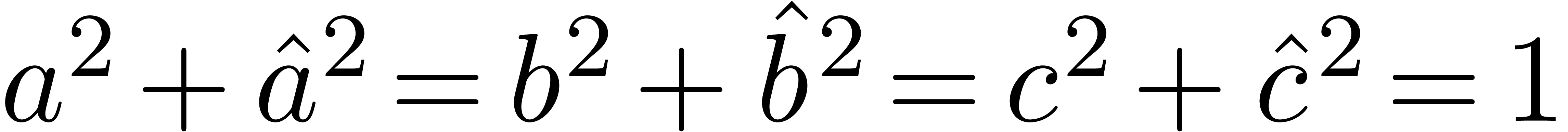 ). The maximum of
). The maximum of
 is attained for
is attained for 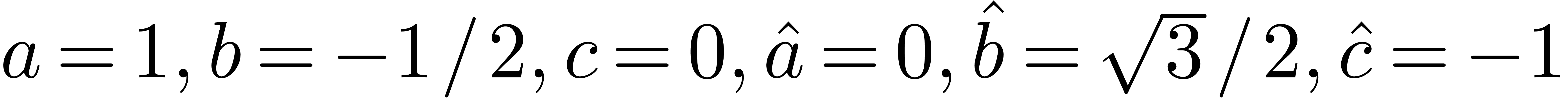 .
We deduce that
.
We deduce that
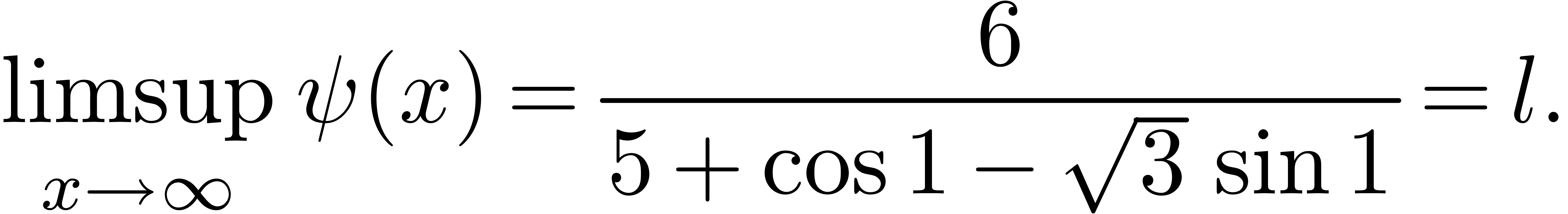
Similarly, exploiting the symmetry of (5), we have
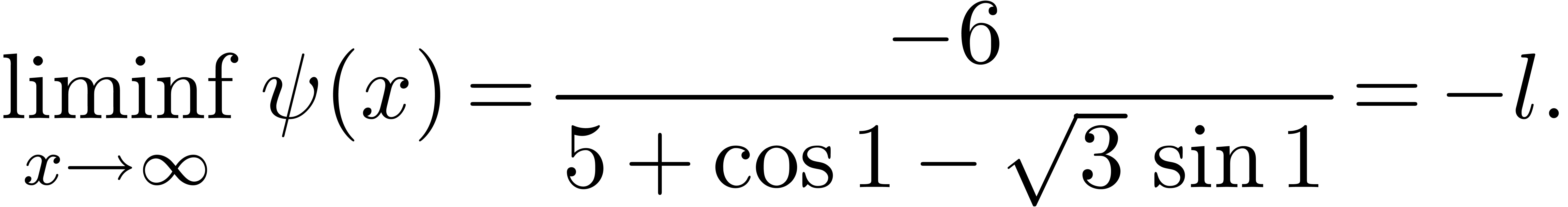
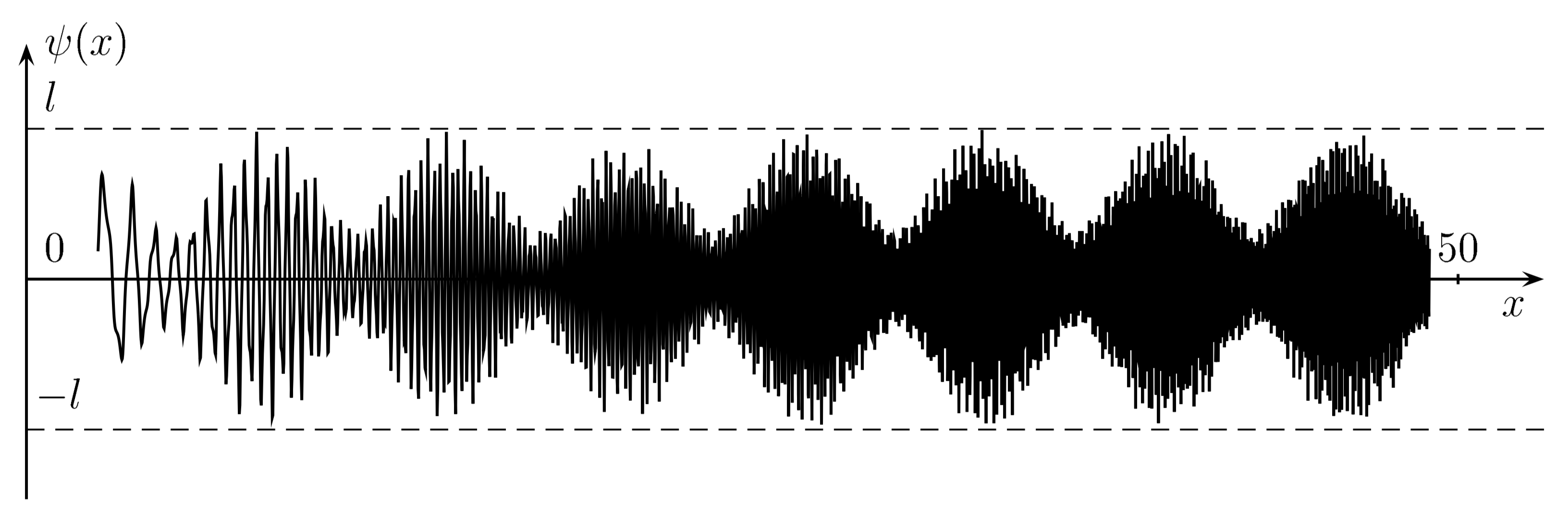 |
Figure 1. Plot of the function |
We have shown how to compute limsups of certain functions involving trigonometric functions, exponentiation and logarithm. Actually, the techniques we have used are far more general than Theorem 9 might suggest. Let us now briefly mention some generalizations. For more details, we refer to [Hoe96a].
In Theorem 9, the crucial property of the functions  is that they are strongly monotonic and that we have
an asymptotic expansion algorithm for them. Consequently, more general
functions than exp-log functions can be taken instead, like Liouvillian
functions, functions which are determined by systems of real exp-log
equations in several variables, etc.
is that they are strongly monotonic and that we have
an asymptotic expansion algorithm for them. Consequently, more general
functions than exp-log functions can be taken instead, like Liouvillian
functions, functions which are determined by systems of real exp-log
equations in several variables, etc.
The crucial property of the function  is that it
belongs to a class for which a cylindrical decomposition algorithm
exists. Again, more general classes of functions can be considered. In
particular, modulo suitable oracles, one can consider the class of
solutions to real exp-log systems in several variables.
is that it
belongs to a class for which a cylindrical decomposition algorithm
exists. Again, more general classes of functions can be considered. In
particular, modulo suitable oracles, one can consider the class of
solutions to real exp-log systems in several variables.
Our techniques can also be used to compute automatic asymptotic expansions of sin-exp-log functions at infinity of trigonometric depth one (i.e. without nested sines). However, some difficult number theoretical phenomena may occur in this case, as the following example illustrates:
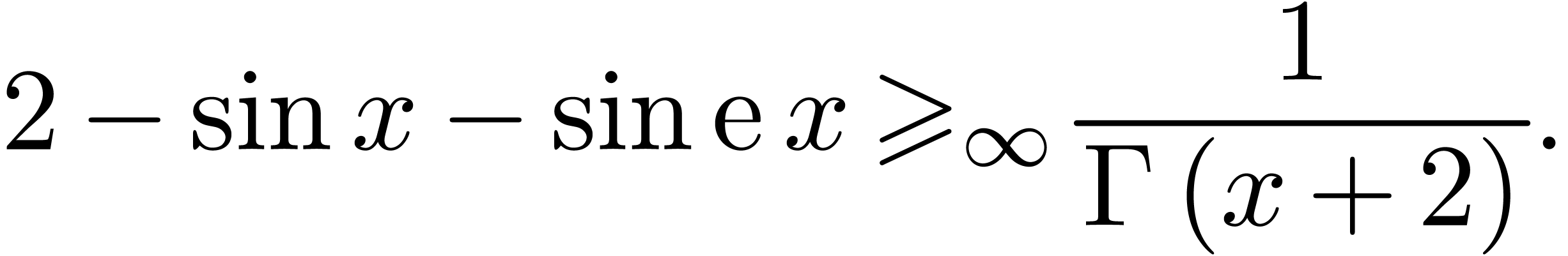
This asymptotic inequality follows from the number theoretical
properties of  . In general,
such inequalities are very hard to obtain (if decidable at all!): a
systematic way to obtain them would in particular yield solutions to
deep unsolved problems in the field of Diophantine approximation (for a
nice survey, see [Lan71]).
. In general,
such inequalities are very hard to obtain (if decidable at all!): a
systematic way to obtain them would in particular yield solutions to
deep unsolved problems in the field of Diophantine approximation (for a
nice survey, see [Lan71]).
Nevertheless, we notice that the above example is
“degenerate” in the sense that  is
precisely equal to the limsup of
is
precisely equal to the limsup of 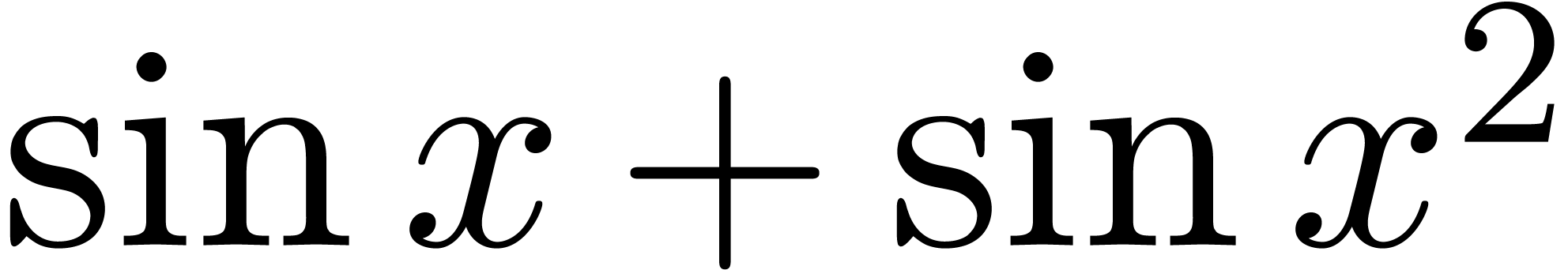 .
In the generic case, a complete asymptotic expansion for sin-exp-log
functions at infinity of trigonometric depth one does exist. In the
degenerate case, we need assume the existence of a suitable oracle for
Diophantine questions.
.
In the generic case, a complete asymptotic expansion for sin-exp-log
functions at infinity of trigonometric depth one does exist. In the
degenerate case, we need assume the existence of a suitable oracle for
Diophantine questions.
G. E. Collins. Quantifier elimination for real closed fields by cylindrical algebraic decomposition. In Proc. 2-nd conf. on automata theory and formal languages, volume 33 of Lect. Notes in Comp. Science, pages 134–183. Springer, 1975.
J. Écalle. Introduction aux fonctions analysables et preuve constructive de la conjecture de Dulac. Hermann, collection: Actualités mathématiques, 1992.
G. H. Gonnet and D. Gruntz. Limit computation in computer algebra. Technical Report 187, ETH, Zürich, 1992.
D. Y. Grigoriev. Deviation theorems for solutions to differential equations and applications to lower bounds on parallel complexity of sigmoids. Th. Comp. Sc., 133(1):23–33, 1994.
D. Y. Grigoriev. Deviation theorems for solutions to linear ordinary differential equations and applications to lower bounds on parallel complexity of sigmoids. St. Petersburg Math. J., 6(1):89–106, 1995.
G. H. Hardy. Properties of logarithmico-exponential functions. Proceedings of the London Mathematical Society, 10(2):54–90, 1911.
J. van der Hoeven. Automatic asymptotics. PhD thesis, École polytechnique, Palaiseau, France, 1996. In preparation.
J. van der Hoeven. Generic asymptotic expansions. In A. Carrière and L. R. Oudin, editors, Proc. of the fifth Rhine workshop on computer algebra, pages 17–1. 1996.
G. H. Hardy and E. M. Wright. An introduction to the theory of numbers, chapter XXIII. Oxford science publications, 1938.
L. Kuipers and H. Niederreiter. Uniform distribution sequences. Wiley, New York, 1974.
J. F. Koksma. Diophantische approximationen, volume 4 of Ergebnisse der Mathematik. Springer, 1936.
S. Lang. Transcendental numbers and diophantine approximation. Bull. Amer. Math. Soc., 77/5:635–677, 1971.
D. Richardson. How to recognise zero. Technical Report, Univ. of Bath, 1994.
D. Richardson, B. Salvy, J. Shackell, and J. van der Hoeven. Expansions of exp-log functions. In Y. N. Lakhsman, editor, Proc. ISSAC '96, pages 309–313. Zürich, Switzerland, July 1996.
B. Salvy. Asymptotique automatique et fonctions génératrices. PhD thesis, École Polytechnique, France, 1991.
J. Shackell. Growth estimates for exp-log functions. JSC, 10:611–632, 1990.
J. Shackell. Limits of Liouvillian functions. Technical Report, Univ. of Kent, Canterbury, 1991.