Static bounds for straight-line
programs |
|
| Preliminary version of June 10, 2025 |
|
 . Grégoire
Lecerf and Arnaud Minondo have been supported by the French ANR-22-CE48-0016 NODE project. Joris van der Hoeven
has been supported by an ERC-2023-ADG grant for the ODELIX
project (number 101142171).
. Grégoire
Lecerf and Arnaud Minondo have been supported by the French ANR-22-CE48-0016 NODE project. Joris van der Hoeven
has been supported by an ERC-2023-ADG grant for the ODELIX
project (number 101142171).
Funded by the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. |
 |
How to automatically determine reliable error bounds for a numerical computation? One traditional approach is to systematically replace floating point approximations by intervals or balls that are guaranteed to contain the exact numbers one is interested in. However, operations on intervals or balls are more expensive than operations on floating point numbers, so this approach involves a non-trivial overhead.
In this paper, we present several approaches to remove this
overhead, under the assumption that the function
|
Interval arithmetic is a popular technique to calculate guaranteed error bounds for approximate results of numerical computations [2, 13, 16–21]. The idea is to systematically replace floating point approximations by small intervals around the exact numbers that we are interested in. Basic arithmetic operations on floating point numbers are replaced accordingly with the corresponding operations on intervals. When computing with complex numbers or when working with multiple precision, it is more convenient to use balls instead of intervals. In this paper, we will always do so and this variant of interval arithmetic is called ball arithmetic [8, 14].
Unfortunately, ball arithmetic suffers from a non-trivial overhead:
floating point balls take twice the space of floating point numbers and
basic arithmetic operations are between two and approximately ten times
more expensive. For certain applications, it may therefore be preferable
to avoid the systematic use of balls for individual operations. Instead,
one may analyze the error for larger groups of operations. For instance,
when naively multiplying two double precision  matrices whose coefficients are all bounded by
matrices whose coefficients are all bounded by 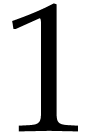 in norm (say), then it is guaranteed that the maximum error of an entry
of the result is bounded by
in norm (say), then it is guaranteed that the maximum error of an entry
of the result is bounded by 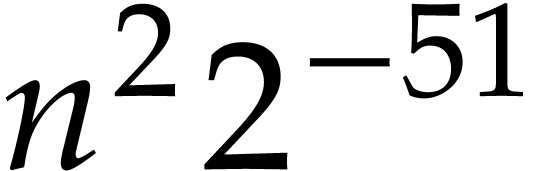 ,
without having to do any individual operations on balls.
,
without having to do any individual operations on balls.
The goal of this paper is to compute reliable error bounds in a
systematic fashion, while avoiding the overhead of ball arithmetic. We
will focus on the case when the function 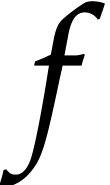 that we
wish to evaluate is given by a straight-line program (SLP).
Such a program is essentially a sequence of basic arithmetic
instructions like additions, subtractions, multiplications, and possibly
divisions [5]. For instance,
that we
wish to evaluate is given by a straight-line program (SLP).
Such a program is essentially a sequence of basic arithmetic
instructions like additions, subtractions, multiplications, and possibly
divisions [5]. For instance,  matrix
multiplication can be computed using an SLP. The SLP framework is
actually surprisingly general: at least conceptually, the trace of the
execution of a more general program that involves loops or subroutines
can often be regarded as an SLP [11, section 3].
matrix
multiplication can be computed using an SLP. The SLP framework is
actually surprisingly general: at least conceptually, the trace of the
execution of a more general program that involves loops or subroutines
can often be regarded as an SLP [11, section 3].
So consider a function 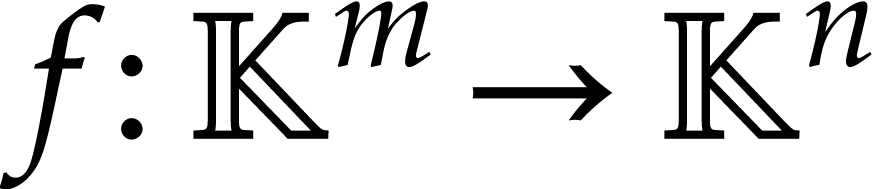 that can be computed
using an SLP, where
that can be computed
using an SLP, where 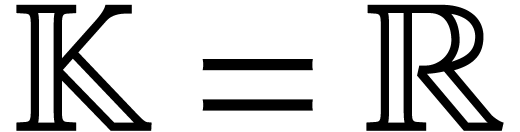 or
or 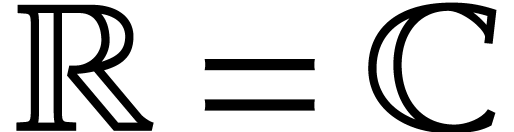 . Given
. Given 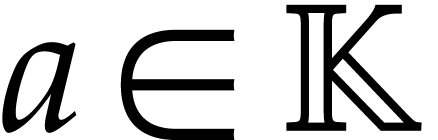 and
and 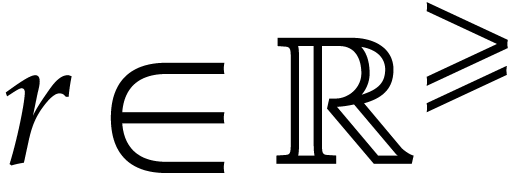 , let
, let 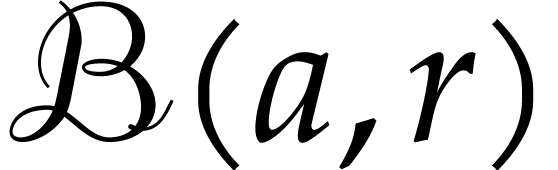 denote the ball
with center
denote the ball
with center  and radius
and radius 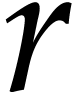 . We will consider several problems:
. We will consider several problems:
Given an approximate evaluation 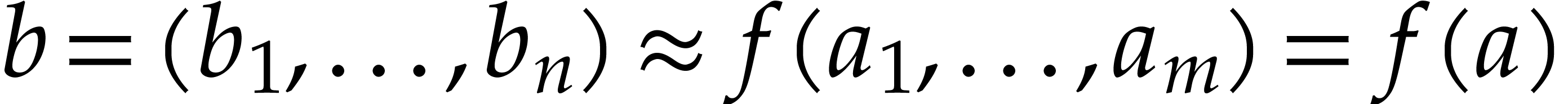 using
floating point arithmetic, can we efficiently compute a bound for
the error?
using
floating point arithmetic, can we efficiently compute a bound for
the error?
Given 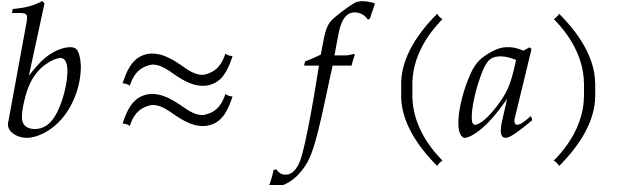 and
and 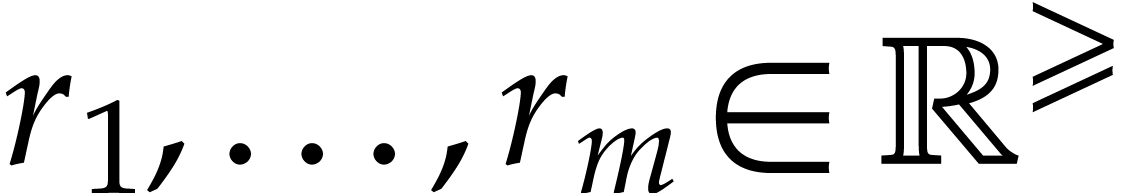 ,
can we efficiently compute
,
can we efficiently compute 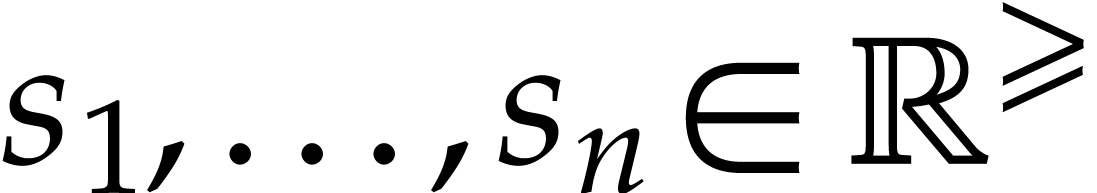 such that
such that 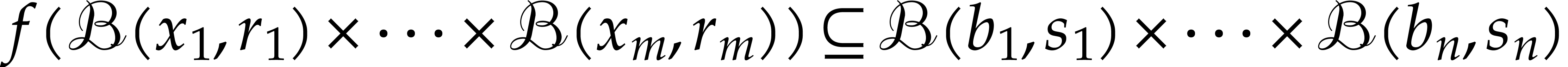 ?
?
Given balls 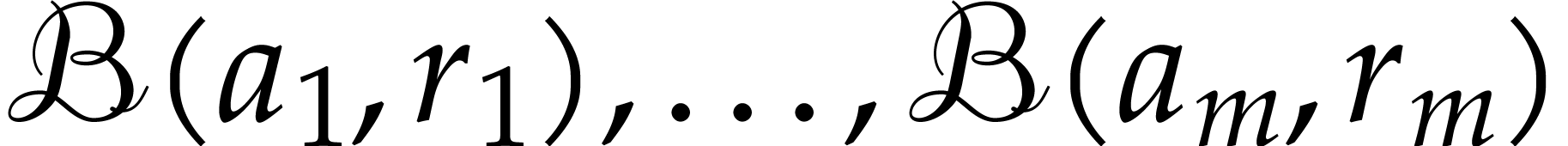 , an index
, an index
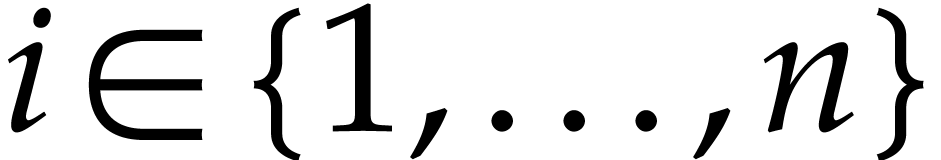 , and
, and 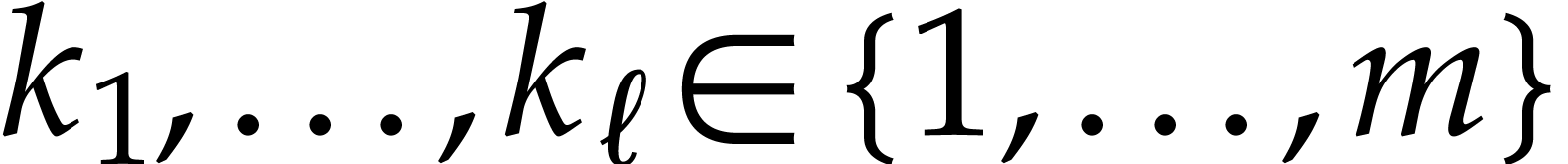 , can we efficiently compute a bound for
, can we efficiently compute a bound for
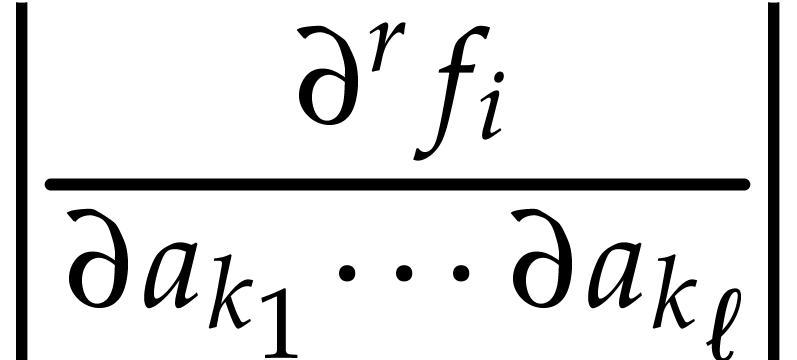 on
on  ?
?
Here “efficiently” means that the cost of the bound
computation should not exceed 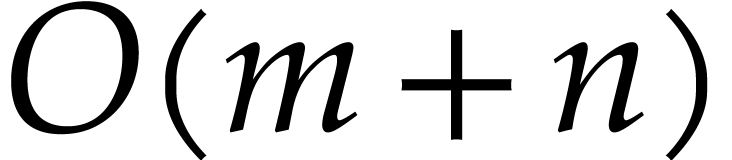 ,
ideally speaking. In particular, the cost should not depend on the
length of the SLP, but we do allow ourselves to perform precomputations
with such a higher cost. We may regard Q1 as a special
case of Q2 by taking
,
ideally speaking. In particular, the cost should not depend on the
length of the SLP, but we do allow ourselves to perform precomputations
with such a higher cost. We may regard Q1 as a special
case of Q2 by taking 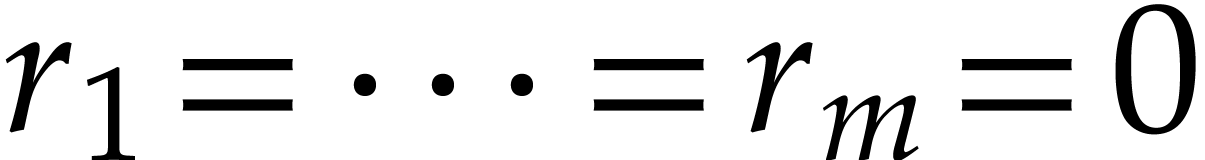 .
If
.
If 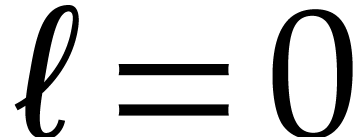 , then Q3
becomes essentially a special case of Q2, since we may
use
, then Q3
becomes essentially a special case of Q2, since we may
use 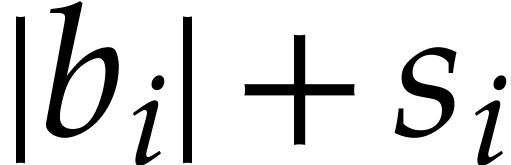 as the required bound.
as the required bound.
Of course, there is a trade-off between the cost of bound computations and the sharpness of the obtained bounds. We will allow our bounds to be less sharp than those obtained using traditional ball arithmetic. But we still wish them to be as tight as possible under the constraint that the cost of the bound computations should remain small.
We start with the special case when the centers  lie in some fixed balls
lie in some fixed balls  . For
this purpose we introduce a special variant of ball arithmetic, called
matryoshka arithmetic: see section 2. A matryoshka
is a ball whose center is itself a ball and its radius is a number in
. For
this purpose we introduce a special variant of ball arithmetic, called
matryoshka arithmetic: see section 2. A matryoshka
is a ball whose center is itself a ball and its radius is a number in
 . Intuitively speaking, a
matryoshka allows us to compute enclosures for “balls inside
balls”. By evaluating
. Intuitively speaking, a
matryoshka allows us to compute enclosures for “balls inside
balls”. By evaluating 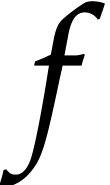 at matryoshki with
centers
at matryoshki with
centers  and zero radii, we will be able to
answer question Q1: see section 3. Using
this to compute bounds for the gradient of
and zero radii, we will be able to
answer question Q1: see section 3. Using
this to compute bounds for the gradient of 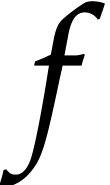 on
on
 , we will also be able to
answer question Q2 in the case when
, we will also be able to
answer question Q2 in the case when 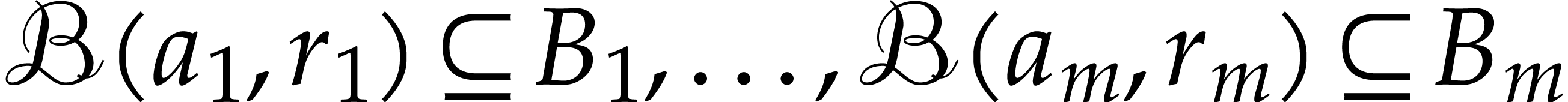 .
.
In section 3, we will actually describe a particularly efficient way to evaluate SLPs at matryoshki. For this, we will adapt transient ball arithmetic from [10]. This variant of ball arithmetic has the advantage that, during the computations of error bounds for individual operations, no adjustments are necessary to take rounding errors into account. We originally developed this technique for SLPs that only use ring operations. In section 4, we will extend it to SLPs that may also involve divisions.
For polynomial SLPs that do not involve any divisions, we will show in
section 5 that it is actually possible to release the
condition that  must be contained in fixed balls
must be contained in fixed balls
 . The idea is to first reduce
to the case when the components
. The idea is to first reduce
to the case when the components 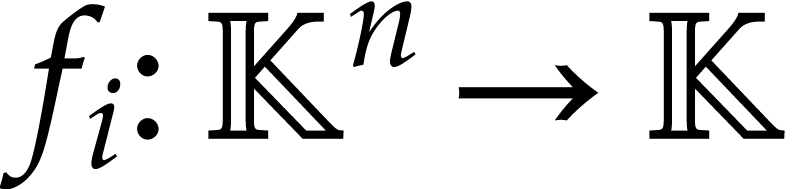 with
with 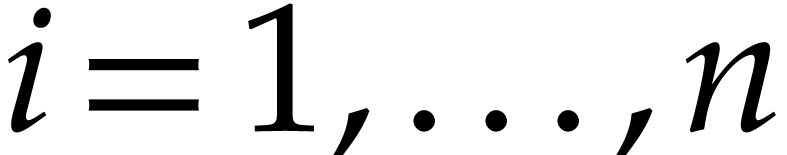 are homogeneous. Then
are homogeneous. Then 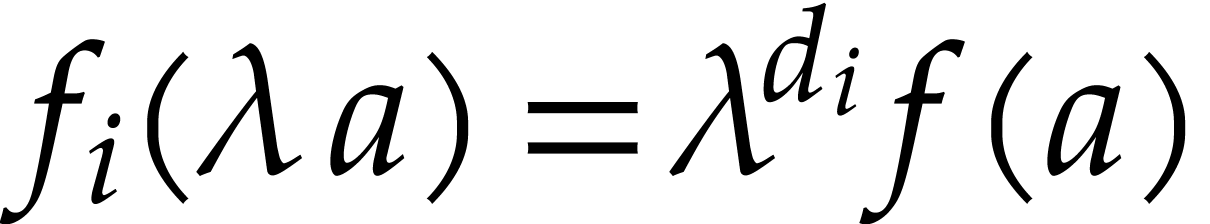 for some
for some
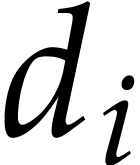 , so we may always rescale
, so we may always rescale
 such that it fits into the unit poly-ball
such that it fits into the unit poly-ball 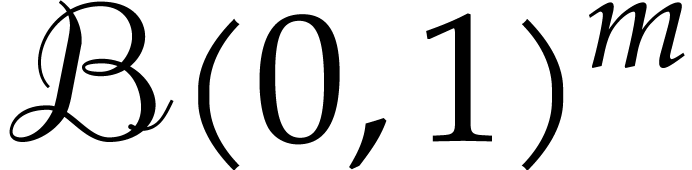 . We may then apply the theory from
sections 2 and 3. Reliable numeric homotopy
continuation [4, 6, 7, 9,
15] is a typical application for which it is important to
efficiently evaluate polynomial SLPs at arbitrary balls.
. We may then apply the theory from
sections 2 and 3. Reliable numeric homotopy
continuation [4, 6, 7, 9,
15] is a typical application for which it is important to
efficiently evaluate polynomial SLPs at arbitrary balls.
Our final section 6 is devoted to question
Q3. The main idea is to compute bounds for the 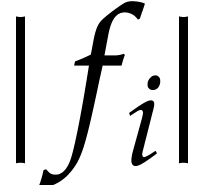 on balls
on balls 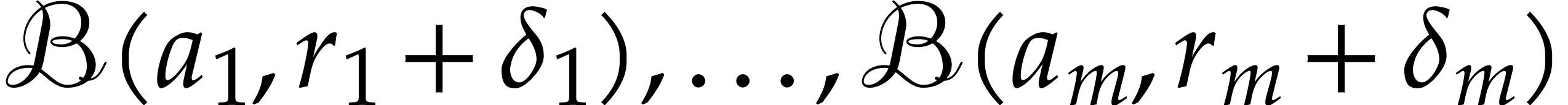 with the same
centers but larger radii. We will then use Cauchy's formula to obtain
bounds for the derivatives of
with the same
centers but larger radii. We will then use Cauchy's formula to obtain
bounds for the derivatives of 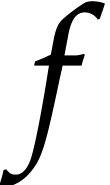 without having to
explicitly compute these derivatives. Bounds for the derivatives of
without having to
explicitly compute these derivatives. Bounds for the derivatives of 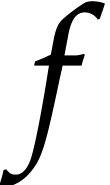 are in particular useful when developing reliable
counterparts of Runge–Kutta methods for the integration of systems
of ordinary differential equations. We intend to provide more details
about this application in an upcoming paper.
are in particular useful when developing reliable
counterparts of Runge–Kutta methods for the integration of systems
of ordinary differential equations. We intend to provide more details
about this application in an upcoming paper.
Throughout this paper, we assume that we work with a fixed floating
point format that conforms to the IEEE 754 standard. We write 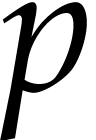 for the bit precision, i.e. the number of
fractional bits of the mantissa plus one. We also denote the minimal and
maximal allowed exponents by
for the bit precision, i.e. the number of
fractional bits of the mantissa plus one. We also denote the minimal and
maximal allowed exponents by  and
and 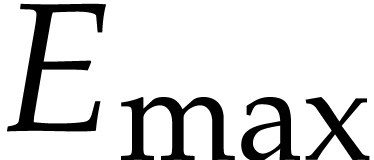 . For IEEE 754 double precision
numbers, this means that
. For IEEE 754 double precision
numbers, this means that 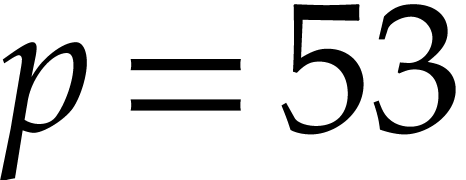 ,
,
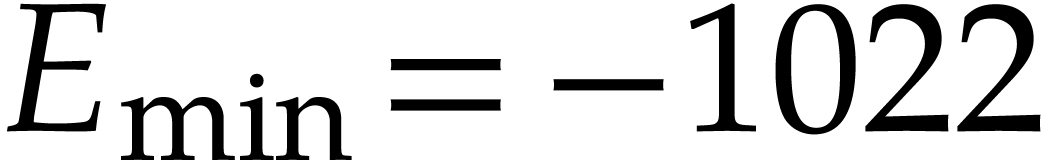 and
and 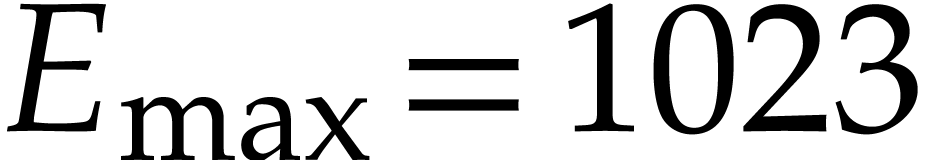 .
We denote the set of hardware floating point numbers by
.
We denote the set of hardware floating point numbers by 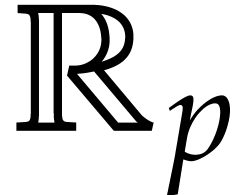 . Given an
. Given an  -algebra
-algebra
 , we will also denote the
corresponding approximate version by
, we will also denote the
corresponding approximate version by 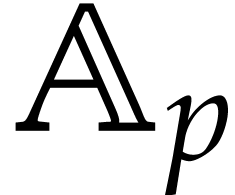 .
For instance, if
.
For instance, if 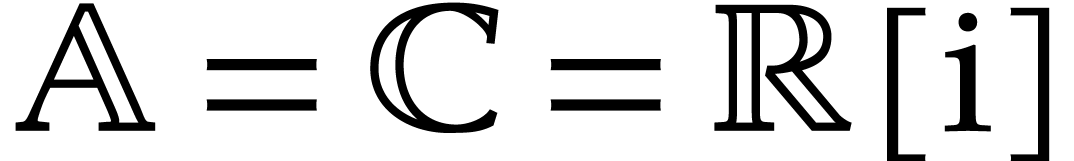 , then we
have
, then we
have 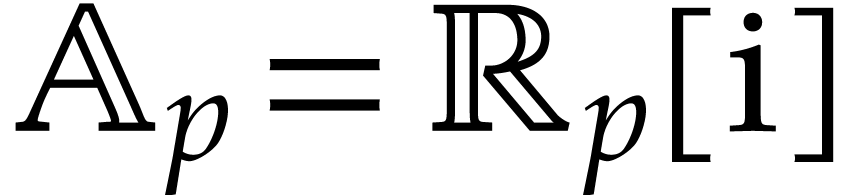 .
.
The IEEE 754 standard imposes correct rounding of all basic arithmetic
operations. In this paper we will systematically use the rounding to
nearest mode. We denote by  the result of
rounding
the result of
rounding  according to this mode. The quantity
according to this mode. The quantity
 stands for the corresponding rounding error,
which may be
stands for the corresponding rounding error,
which may be  . Given a single
operation
. Given a single
operation 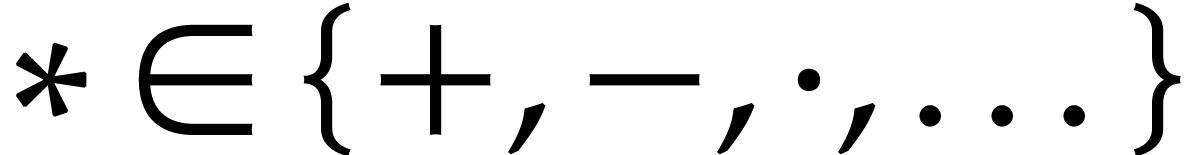 , it will be
convenient to write
, it will be
convenient to write 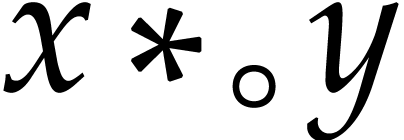 for
for 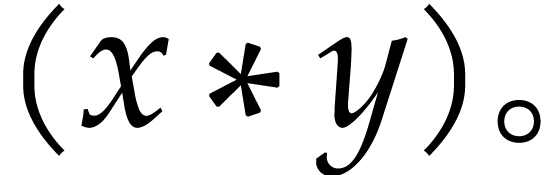 . For compound expressions
. For compound expressions  , we will also write
, we will also write 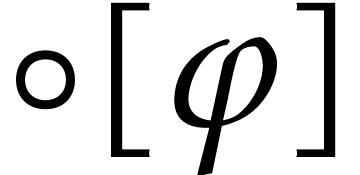 for the
full evaluation of
for the
full evaluation of  using the rounding mode
using the rounding mode  . For instance,
. For instance, 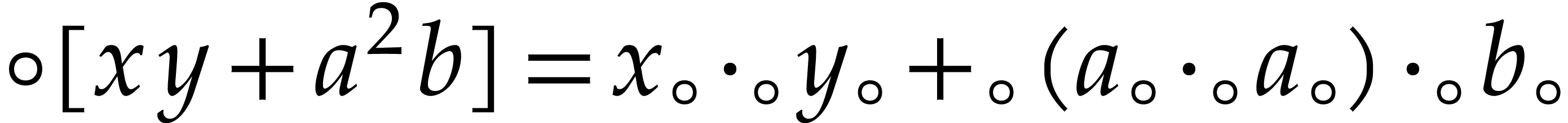 .
.
We denote by 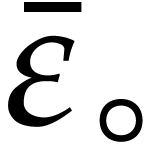 any upper bound function for
any upper bound function for 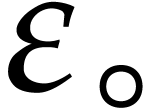 that is easy to compute. In absence of underflow, one
may take
that is easy to compute. In absence of underflow, one
may take  . If we want to
allow for underflows during computations, then we can take
. If we want to
allow for underflows during computations, then we can take 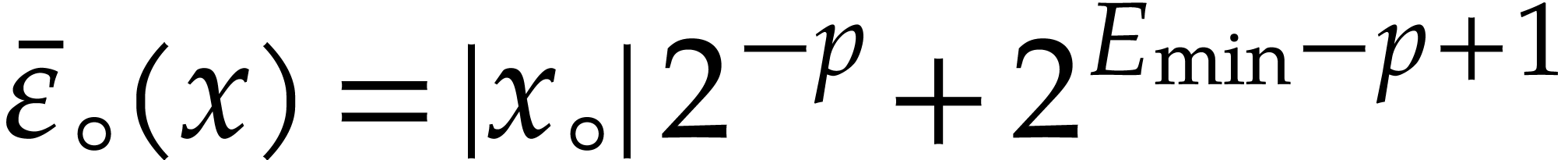 instead, where
instead, where 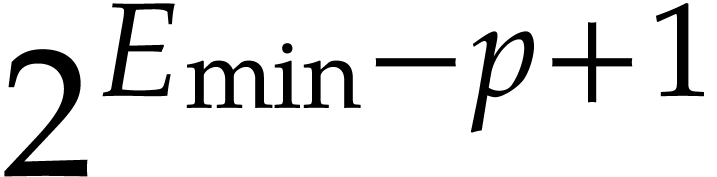 is the smallest
positive subnormal number in
is the smallest
positive subnormal number in 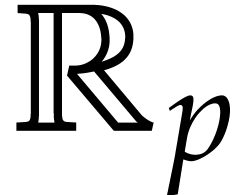 .
If
.
If 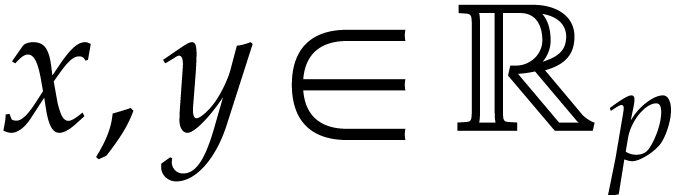 , then we may still take
, then we may still take
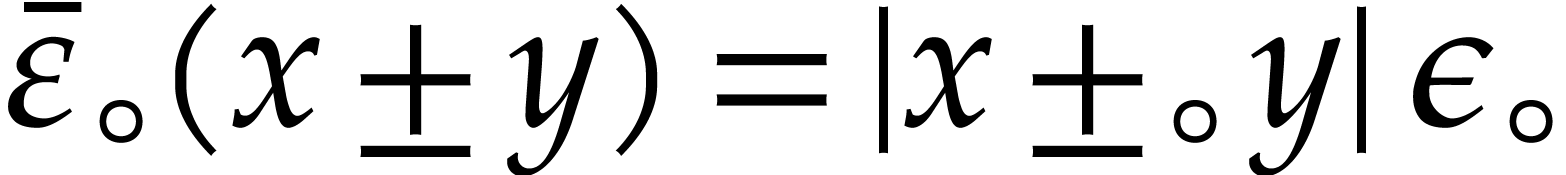 since no underflow occurs in that special case.
See [10, section 2.1] for more details about these facts.
since no underflow occurs in that special case.
See [10, section 2.1] for more details about these facts.
For bounds on rounding errors, the following lemma will be useful.
Proof. Let  for all
for all  . Since
. Since  , we have
, we have
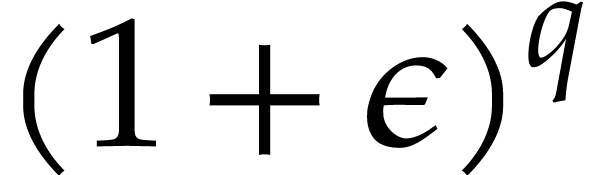 |
 |
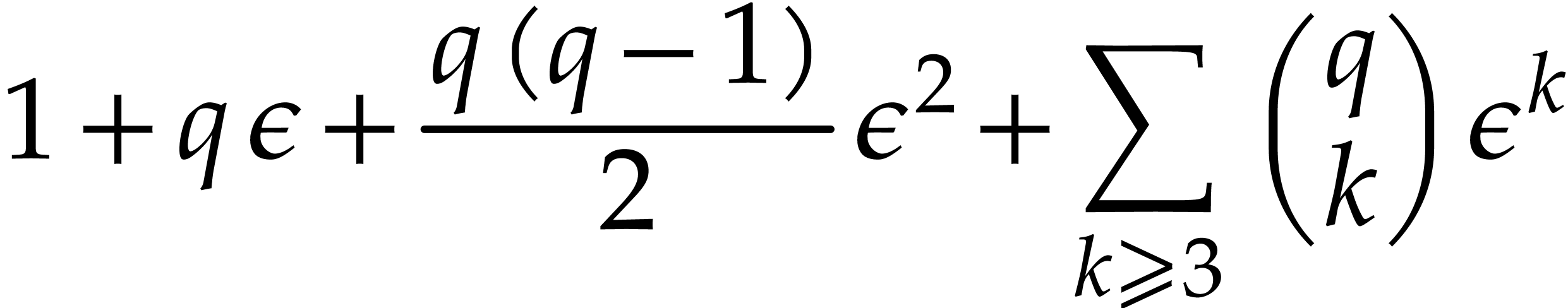 |
|
 |
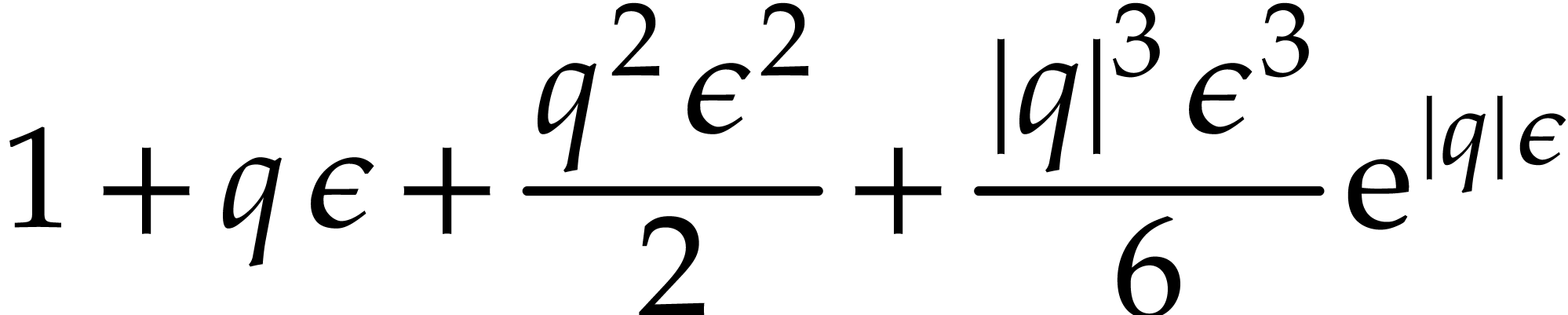 |
||
 |
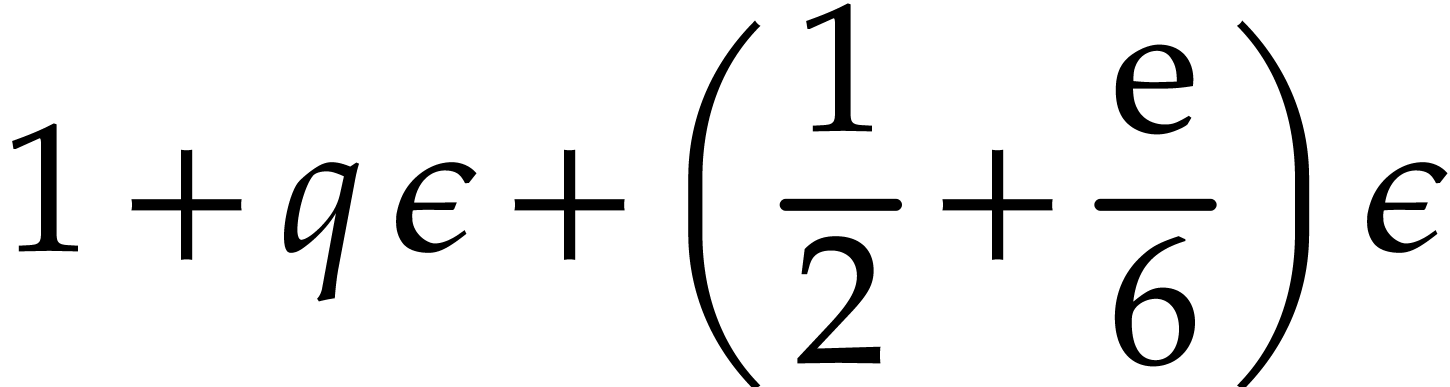 |
||
 |
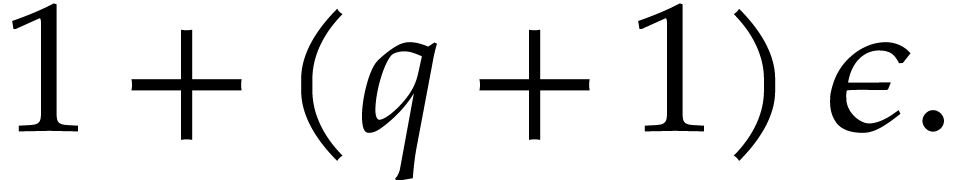 |
 |
Let  be an
be an  -algebra
and let
-algebra
and let  be a norm on
be a norm on  . We will typically take
. We will typically take 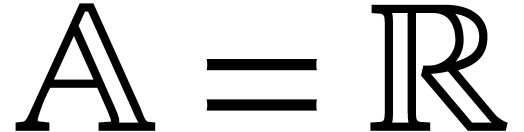 or
or
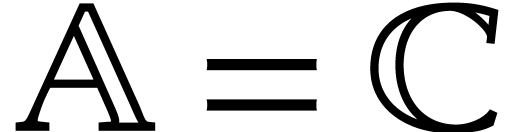 , but more general normed
algebras are also allowed. Given
, but more general normed
algebras are also allowed. Given 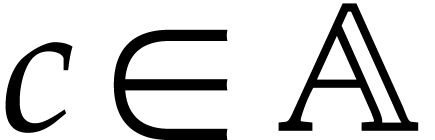 and
and 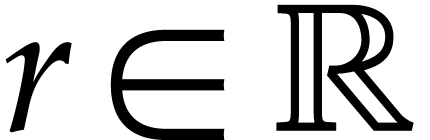 , let
, let  be
the closed ball with center
be
the closed ball with center  and radius
and radius 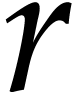 . We denote by
. We denote by  the set of all such balls.
the set of all such balls.
The aim of ball arithmetic is to provide a systematic way to bound the
errors of numerical computations. The idea is to systematically replace
numerical approximations of elements in  by balls
that are guaranteed to contain the true mathematical values. It will be
useful to introduce a separate notation
by balls
that are guaranteed to contain the true mathematical values. It will be
useful to introduce a separate notation  for this
type of semantics: given a ball
for this
type of semantics: given a ball 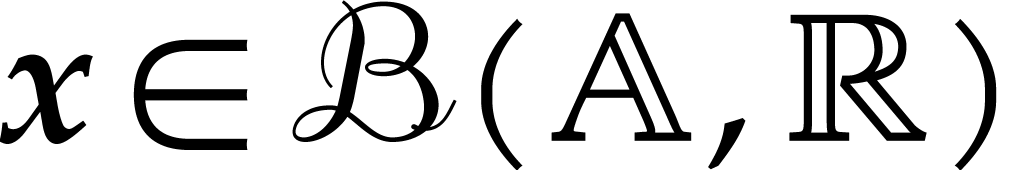 and a number, we
say that
and a number, we
say that  encloses
encloses  if
if  , i.e.
, i.e.

We also introduce poly-balls, which are vectors of balls, for situations
where it is required to reason “coordinate wise”. For all
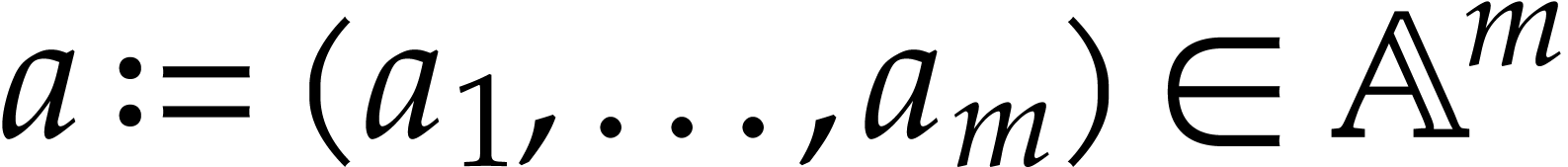 and all
and all 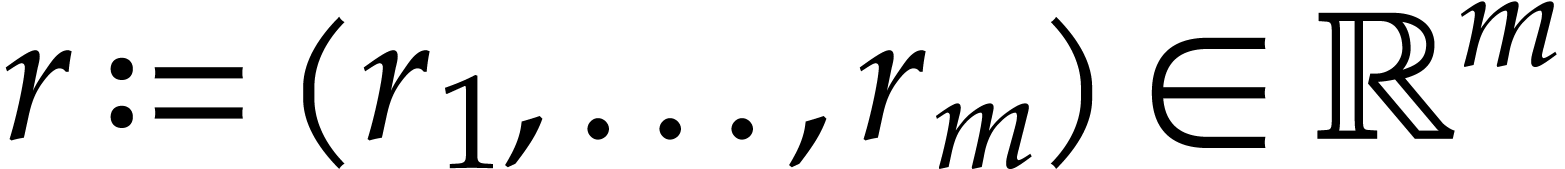 ,
we denote the poly-ball
,
we denote the poly-ball 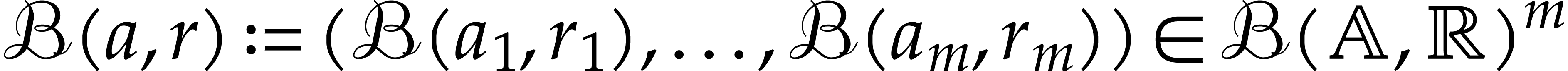 . We
extend this enclosure relation to poly-balls
. We
extend this enclosure relation to poly-balls 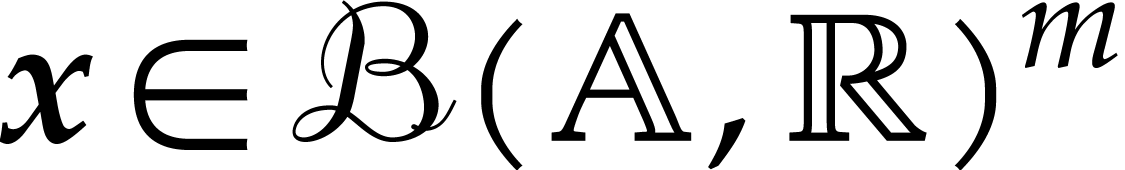 and
and
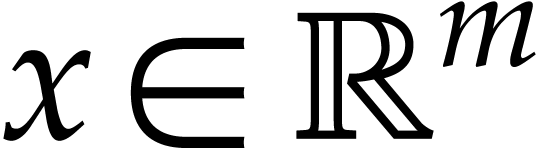 as follows:
as follows:
 |
(2.1) |
In the sequel, we will use a bold font for ball enclosures and a normal
font for values at actual points. Note that the smallest enclosure of
 is the “exact” ball
is the “exact” ball 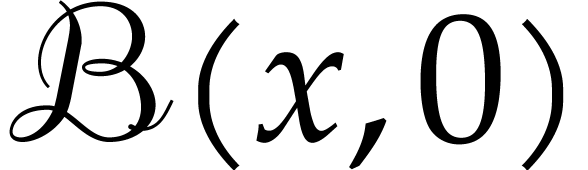 , and we will regard
, and we will regard  as
being embedded into
as
being embedded into  in this way.
in this way.
Let us now recall how to perform arithmetic operations in a way that is
compatible with the “enclosure semantics”. Given a function
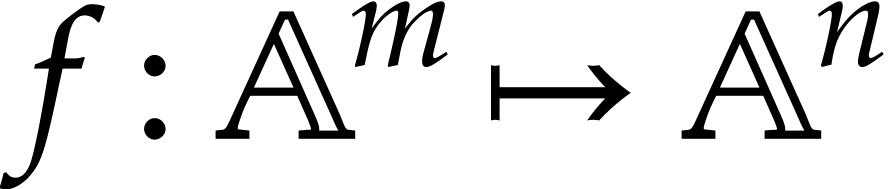 , a ball lift of
, a ball lift of
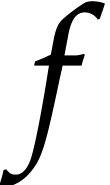 is a function
is a function 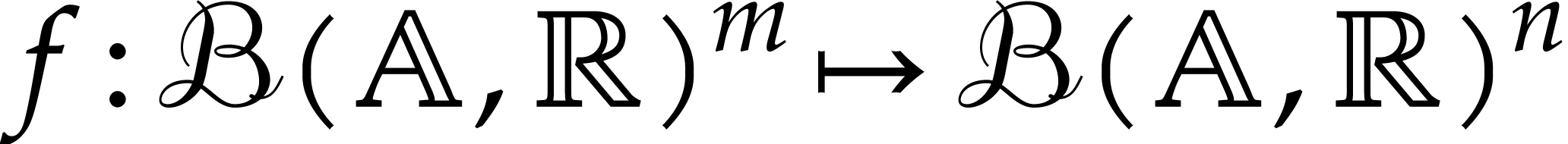 that
satisfies the inclusion property
that
satisfies the inclusion property
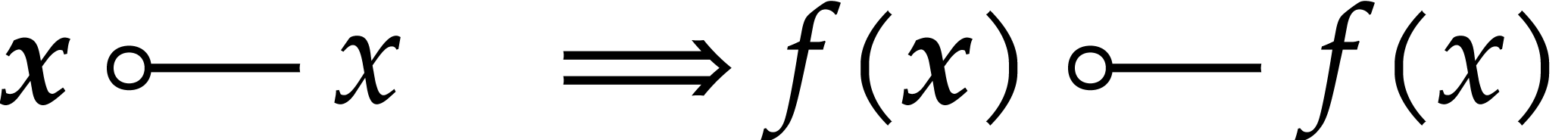
for all 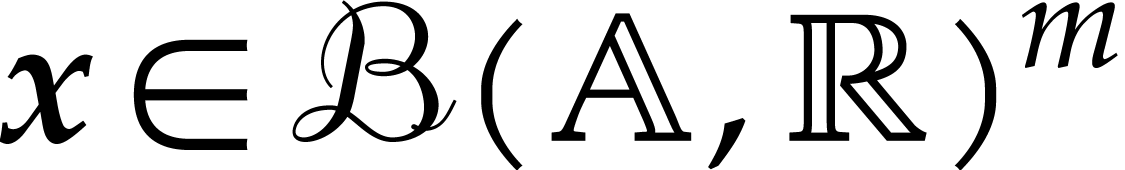 and
and  .
(Note that we voluntarily used the same name
.
(Note that we voluntarily used the same name 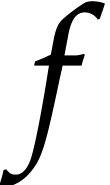 for
the function and its lift.) For instance, the basic arithmetic
operations admit the following ball lifts:
for
the function and its lift.) For instance, the basic arithmetic
operations admit the following ball lifts:
Other operations can be lifted in a similar way (in section 4
below, we will in particular study division). We can also extend the
norm from  to
to  via
via
The extended norm is sub-additive, sub-multiplicative, and positive definite.
For any ball 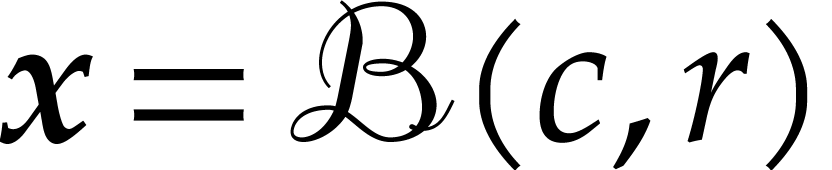 , we have
, we have 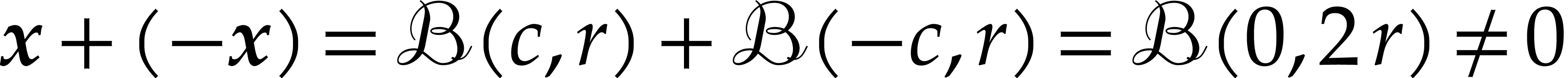 , so
, so  is
clearly not an additive group in the mathematical sense. Nonetheless, we
may consider
is
clearly not an additive group in the mathematical sense. Nonetheless, we
may consider  to be a normed
to be a normed  -algebra from a computer science perspective,
because all the relevant operations
-algebra from a computer science perspective,
because all the relevant operations 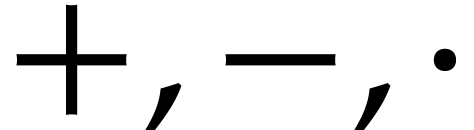 ,
and
,
and  are “implemented”. Allowing
ourselves this shortcut, we may apply the theory from the previous
subsection and formally obtain a ball arithmetic on
are “implemented”. Allowing
ourselves this shortcut, we may apply the theory from the previous
subsection and formally obtain a ball arithmetic on  . It turns out that this construction actually
makes sense from a mathematical perspective, provided that we
appropriately adapt the semantics for the notion of
“enclosure”.
. It turns out that this construction actually
makes sense from a mathematical perspective, provided that we
appropriately adapt the semantics for the notion of
“enclosure”.
Let  . An element
. An element  of
of 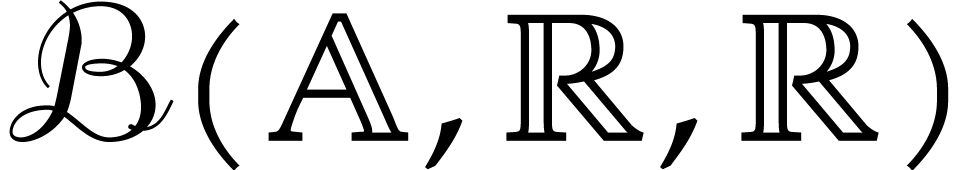 will be called a
matryoshka. Given a matryoshka
will be called a
matryoshka. Given a matryoshka 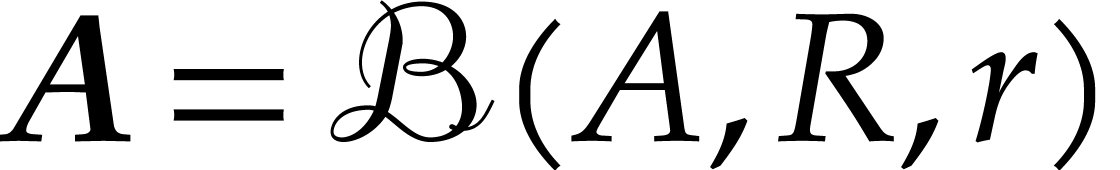 ,
we call
,
we call  its center,
its center,  its large radius, and
its large radius, and  its small
radius. The appropriate enclosure relation for matryoshki is
defined as follows: given a matryoshka
its small
radius. The appropriate enclosure relation for matryoshki is
defined as follows: given a matryoshka 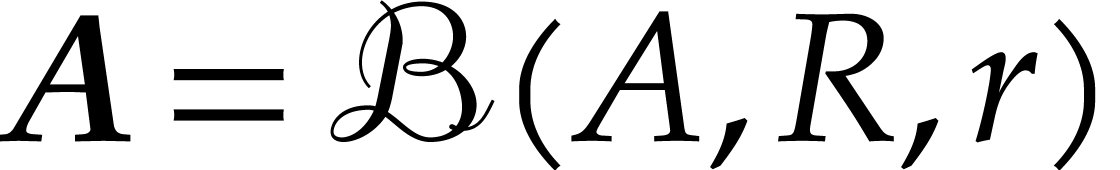 and a
ball
and a
ball 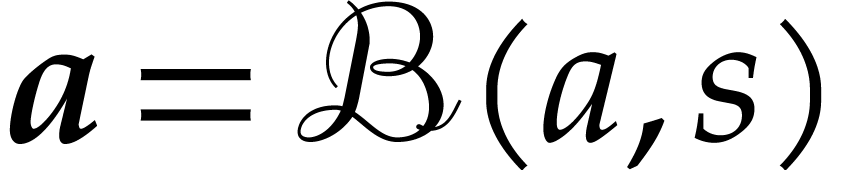 , we define
, we define

Conceptually, the “small embedded ball”
 is contained in the matryoshka, which corresponds to the “big
ball”
is contained in the matryoshka, which corresponds to the “big
ball”
 :
see Figure
2.1
. The enclosure relation naturally extends to vectors as in (
2.1
).
:
see Figure
2.1
. The enclosure relation naturally extends to vectors as in (
2.1
).
We use the abbreviation  for the set of
matryoshki. A function
for the set of
matryoshki. A function 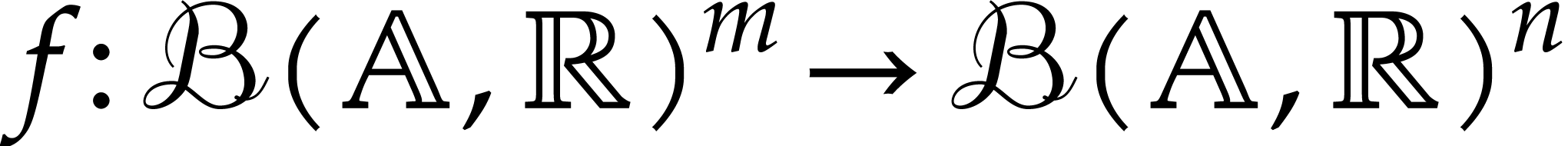 is said to lift
to
is said to lift
to 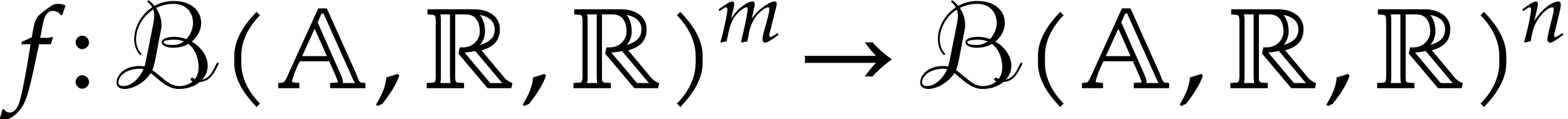 if it satisfies the inclusion principle:
if it satisfies the inclusion principle:

for all  and
and 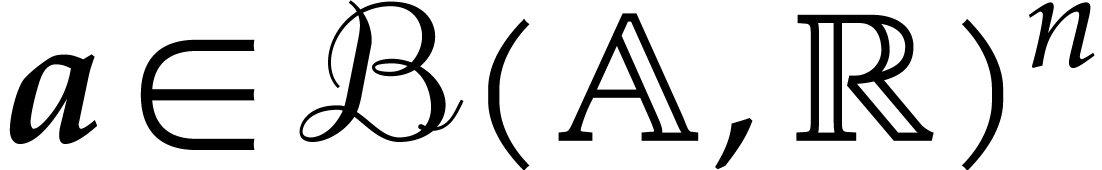 .
Exactly the same formulas (2.2) and (2.3) can
be used in order to lift the basic arithmetic operations:
.
Exactly the same formulas (2.2) and (2.3) can
be used in order to lift the basic arithmetic operations:
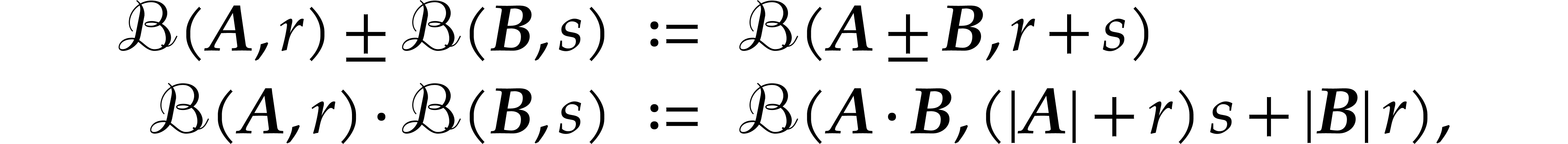
for all 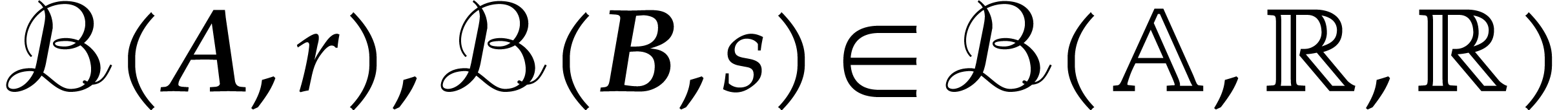 . (Note that it was
this time convenient to use
. (Note that it was
this time convenient to use  ,
,
 as a notation for the centers of our
matryoshki.) We may also extend the norm on
as a notation for the centers of our
matryoshki.) We may also extend the norm on  to
matryoshki via
to
matryoshki via
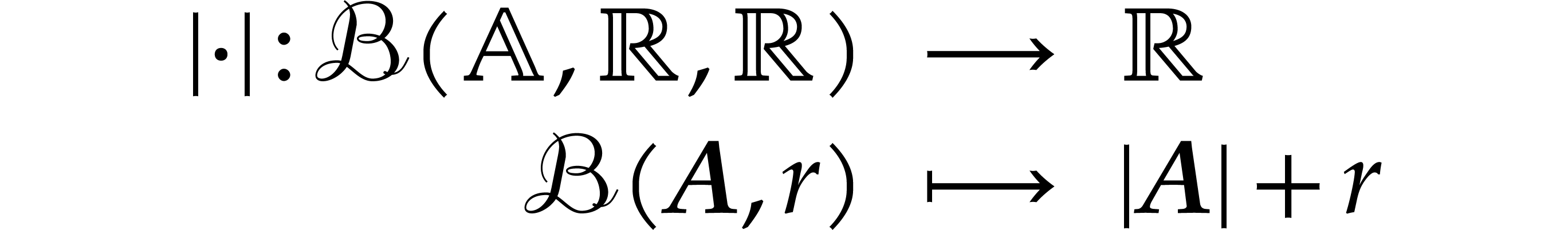
which again remains sub-additive, sub-multiplicative, and positive definite.
Remark
We will write 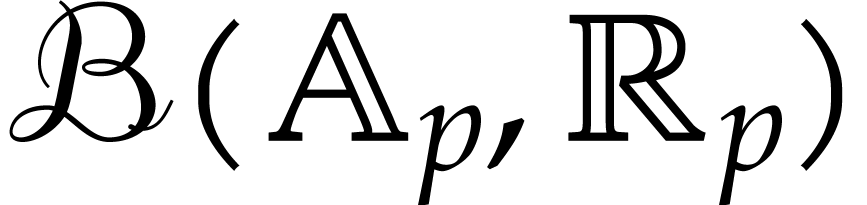 and
and 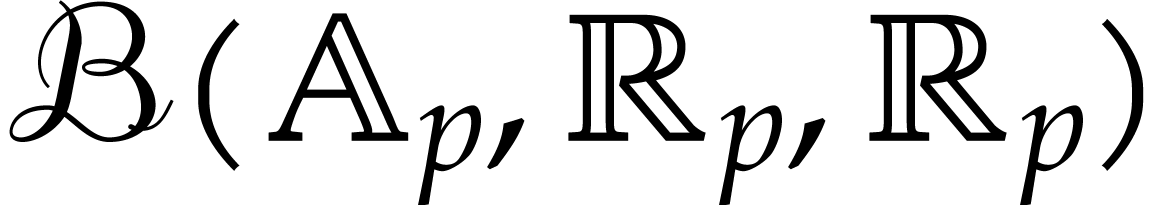 for
the approximate versions of
for
the approximate versions of  and
and 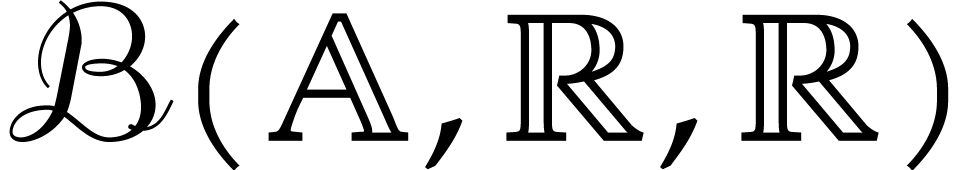 when working with machine floating point numbers in
when working with machine floating point numbers in 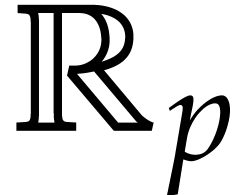 instead of exact real numbers in
instead of exact real numbers in  .
In that case, the formulas from section 2.2 and 2.3
need to be adjusted in order to take into account rounding errors. For
instance, if
.
In that case, the formulas from section 2.2 and 2.3
need to be adjusted in order to take into account rounding errors. For
instance, if 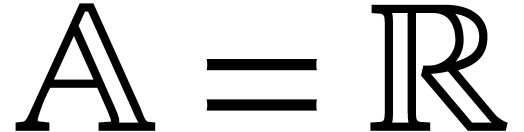 , then one may
replace the formulas (2.2), (2.3), and (2.4) by
, then one may
replace the formulas (2.2), (2.3), and (2.4) by
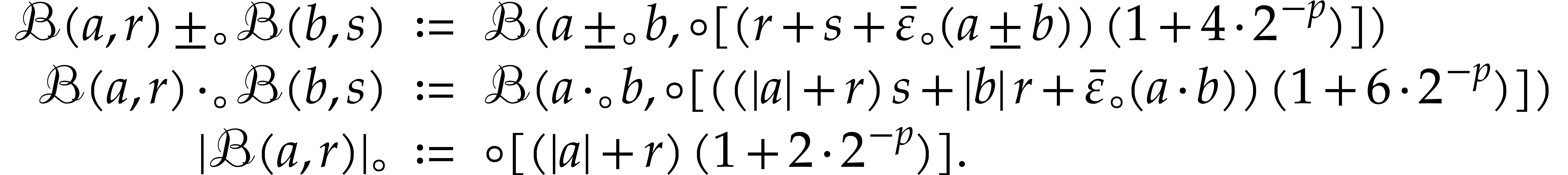 |
(2.5) |
See, e.g., [10]. We will call this rounded ball arithmetic.
Unfortunately, these formulas are far more complicated than (2.2), (2.3), and (2.4), so bounding the rounding errors in this way gives rise to a significant additional computational overhead. An alternative approach is to continue to use the non-adjusted formulas
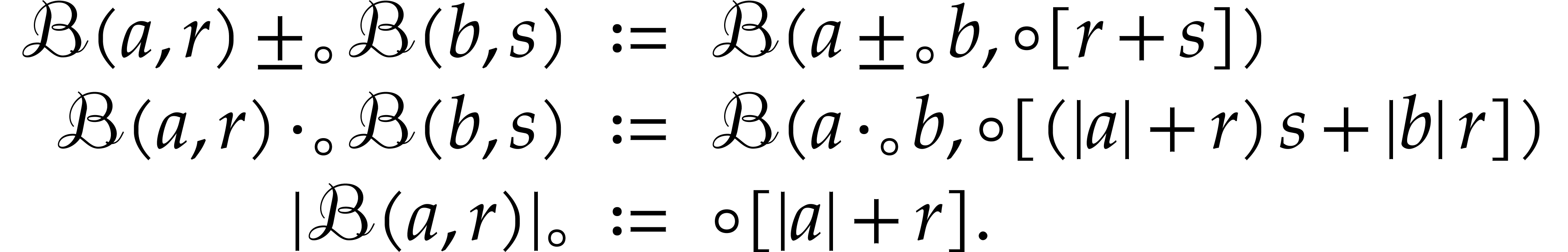 |
(2.6) |
This type of arithmetic was called transient ball arithmetic in [10]. This arithmetic is not a ball lift, but we will see below how to take advantage of it by inflating the radii of the input balls of a given SLP.
Of course, we need to carefully examine the amount of inflation that is
required to ensure the correctness of our final bounds. This will be the
purpose of the next section in the case where we evaluate an entire SLP
using transient ball arithmetic. We denote by 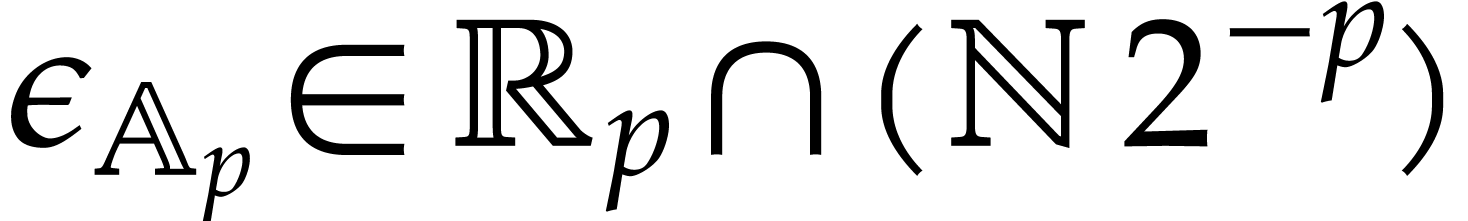 a
quantity that satisfies
a
quantity that satisfies 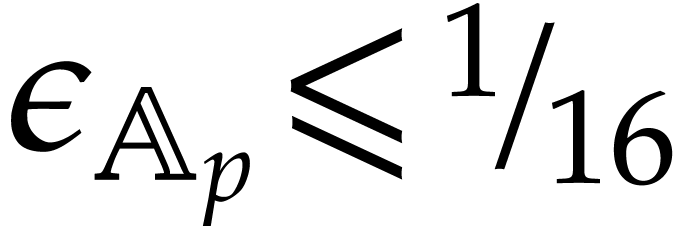 and
and
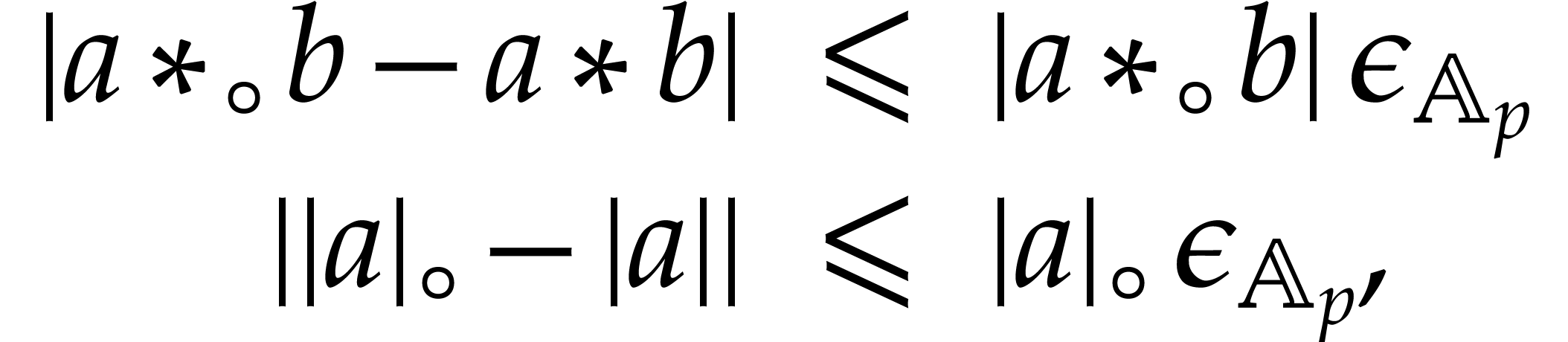 |
(2.7) |
for all  and
and  ,
in absence of underflows and overflows. One may for instance take
,
in absence of underflows and overflows. One may for instance take 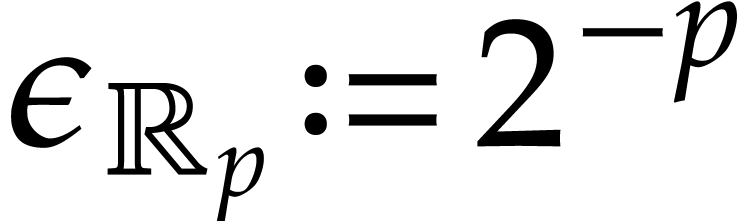 and
and 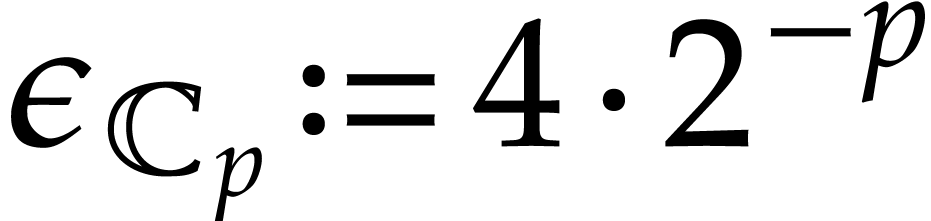 ,
whenever
,
whenever 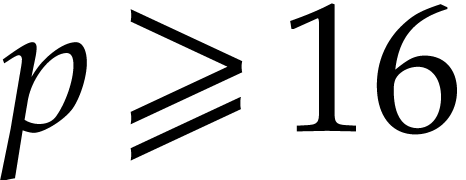 ; see [10,
Appendix A of the preprint version].
; see [10,
Appendix A of the preprint version].
We recall the following lemma, which provides a useful error estimate for the radius of a transient ball product.
 and
and 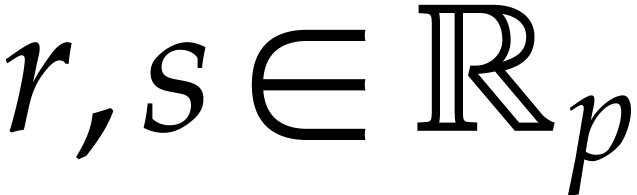 such that the
computation of
such that the
computation of
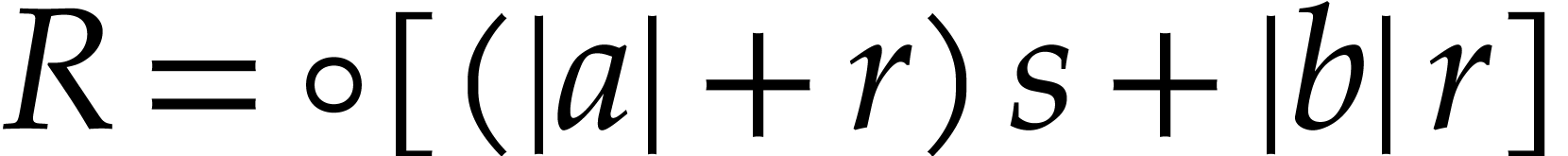
involves no underflows or overflows, we have 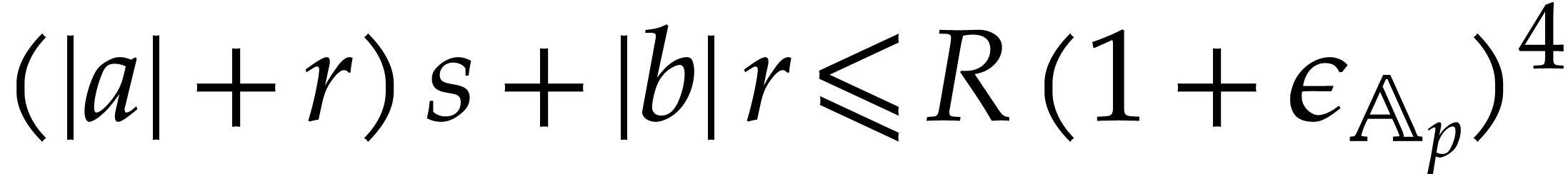 .
.
In the presence of overflows or underflows, additional adjustments are required. Overflows actually cause no problems, because the IEEE 754 standard rounds every number beyond the largest representable floating point number to infinity, so the radii of balls automatically become infinite whenever an overflow occurs. In order to protect ourselves against underflows, the requirements (2.7) need to be changed into
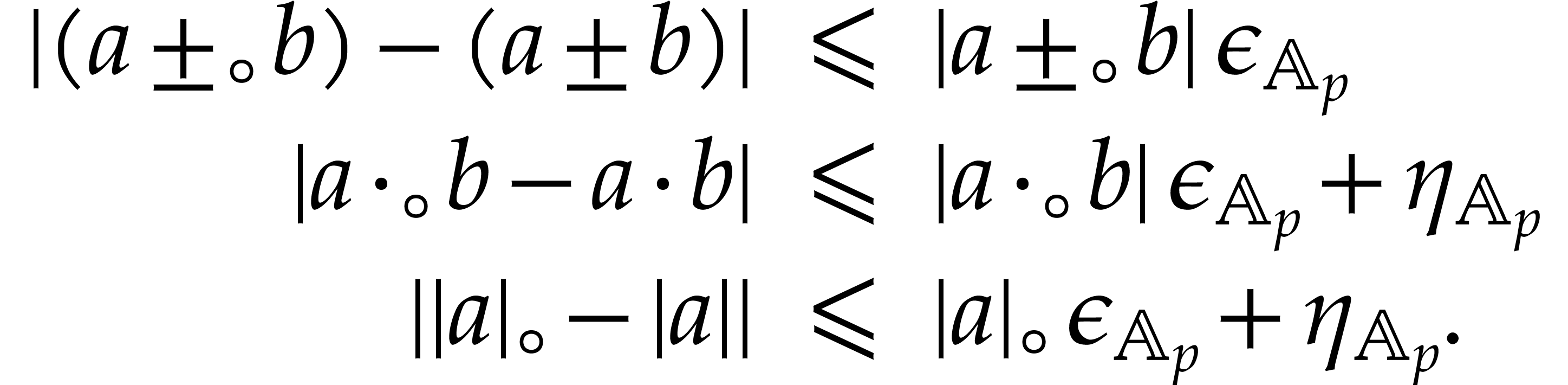 |
(2.8) |
Here we recall that additions and subtractions never lead to underflows.
If 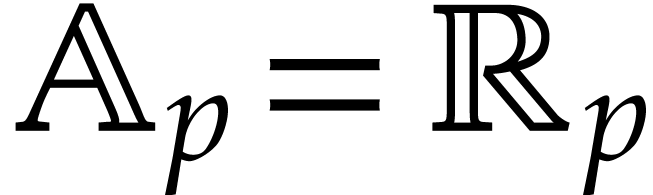 , then we may take
, then we may take 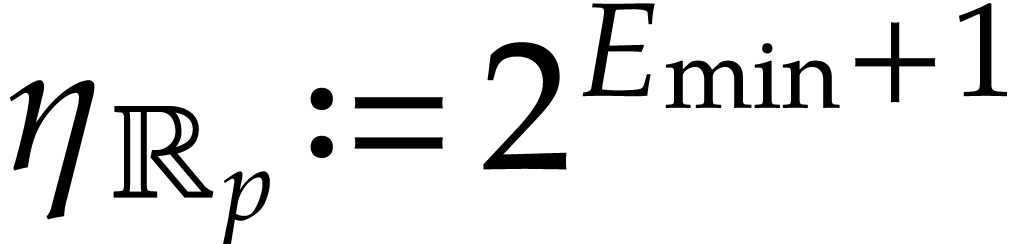 . If
. If 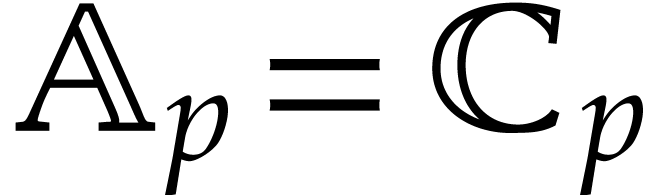 ,
then a safe choice is
,
then a safe choice is 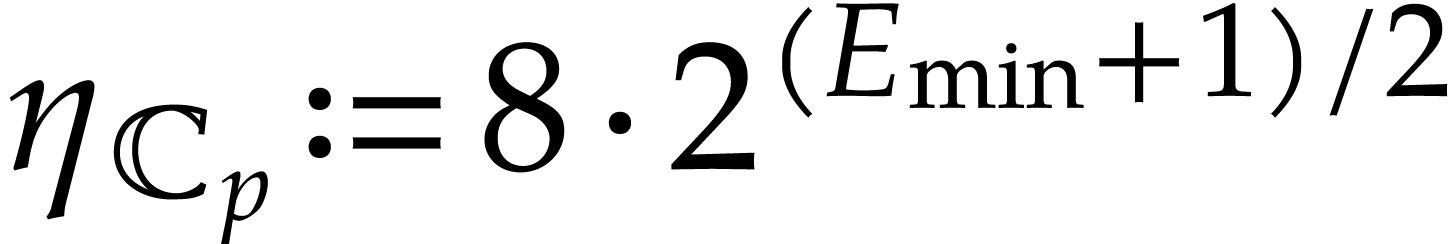 (in fact,
(in fact, 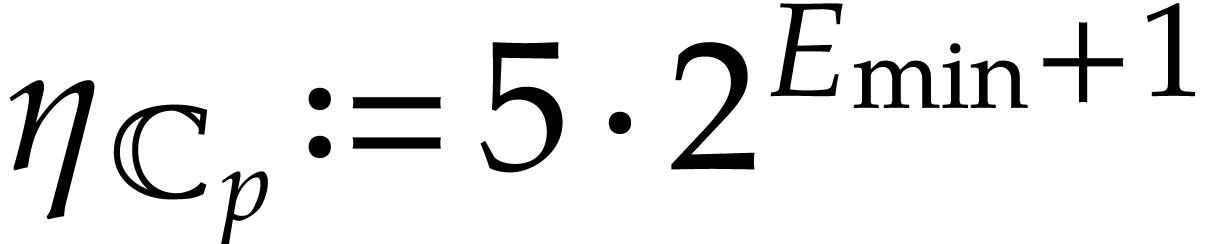 is sufficient for multiplication). We refer to [10, section
3.3] for details.
is sufficient for multiplication). We refer to [10, section
3.3] for details.
Taking  instead of
instead of 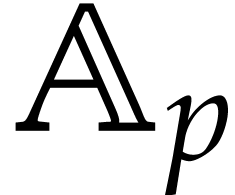 for
our center space, the formulas (2.6) naturally give rise to
transient matryoshka arithmetic:
for
our center space, the formulas (2.6) naturally give rise to
transient matryoshka arithmetic:
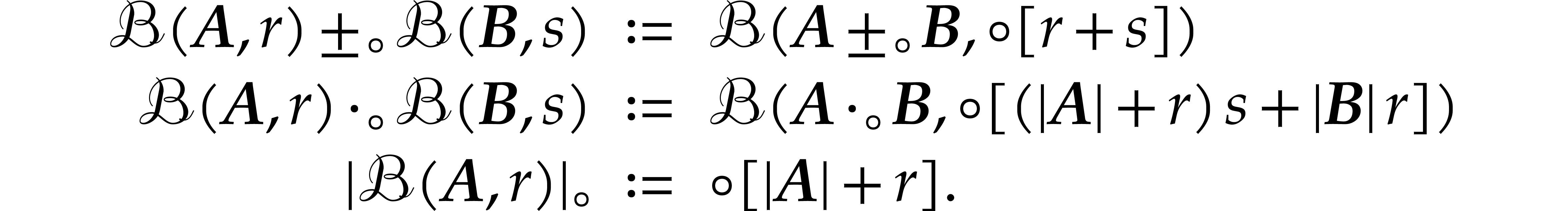
Here we understand the operations 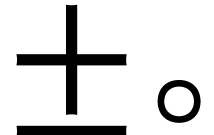 ,
,
 , and
, and  on the centers are done use transient ball arithmetic.
on the centers are done use transient ball arithmetic.
We will need an analogue of Lemma 2.3 for matryoshki. Given
balls 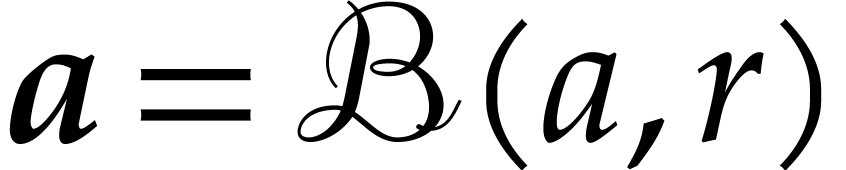 and
and 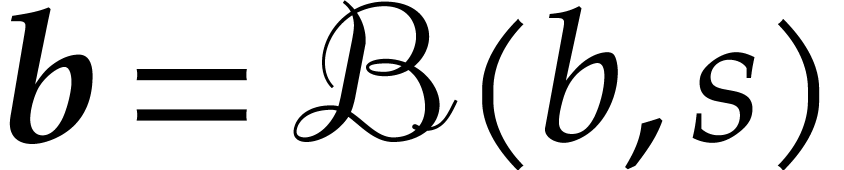 in
in  , we define
, we define 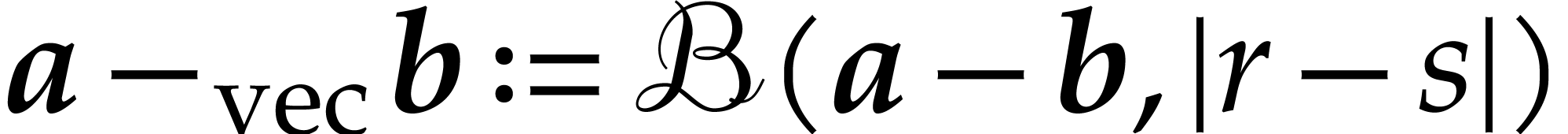 . In what follows, let
. In what follows, let 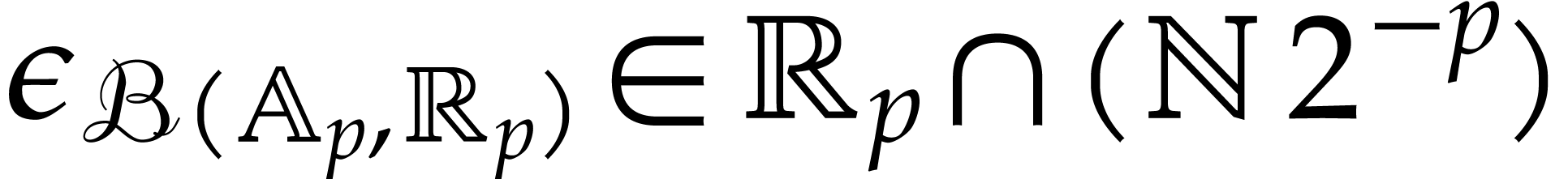 be
such that
be
such that 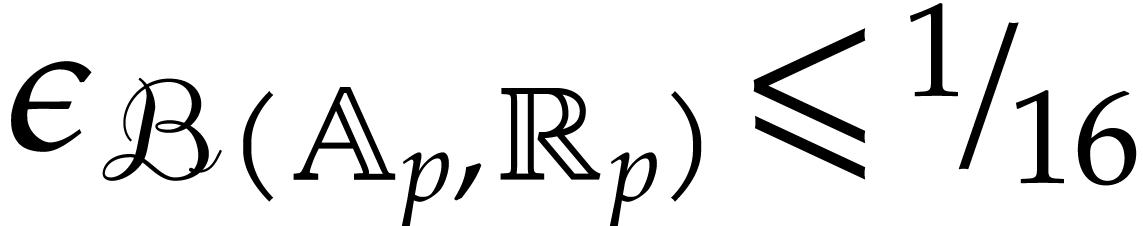 and
and
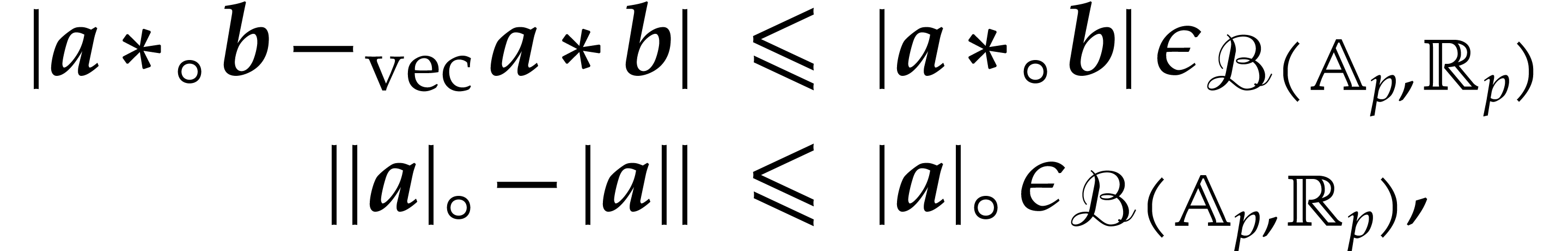 |
(2.9) |
for all 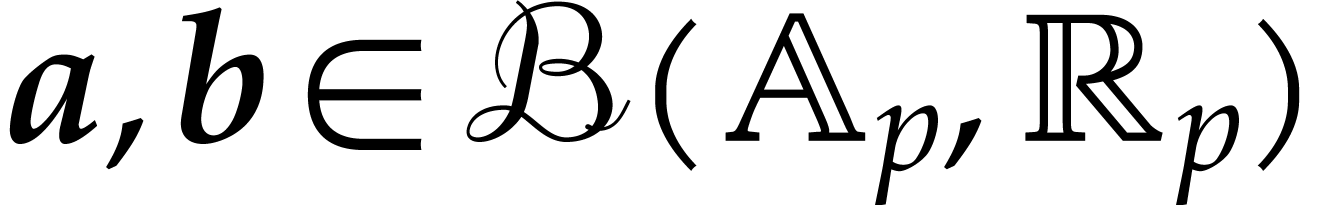 and
and 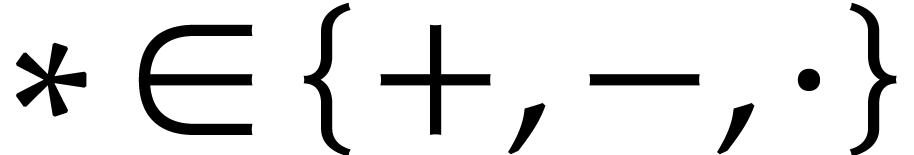 ,
in absence of underflows and overflows.
,
in absence of underflows and overflows.
Let 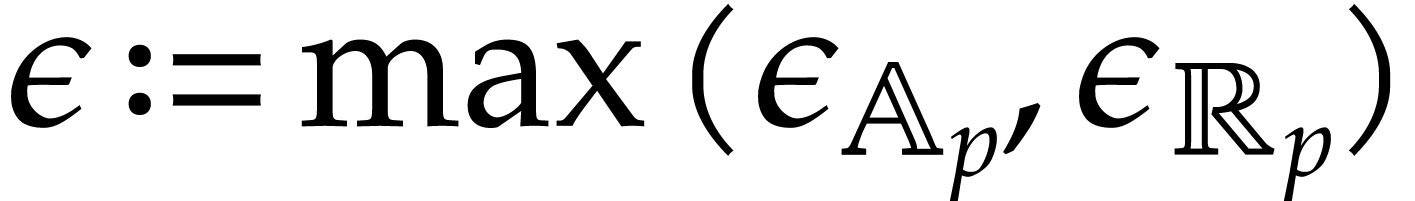 . Given
. Given  and
and  , Lemma 2.3
gives
, Lemma 2.3
gives  ; similarly we have
; similarly we have
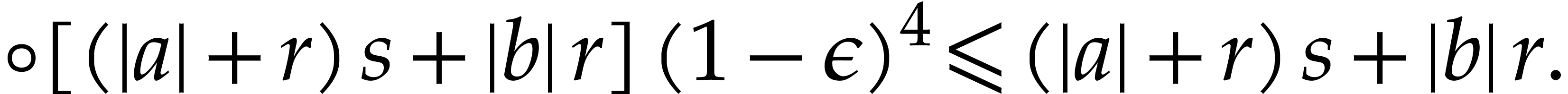
This implies
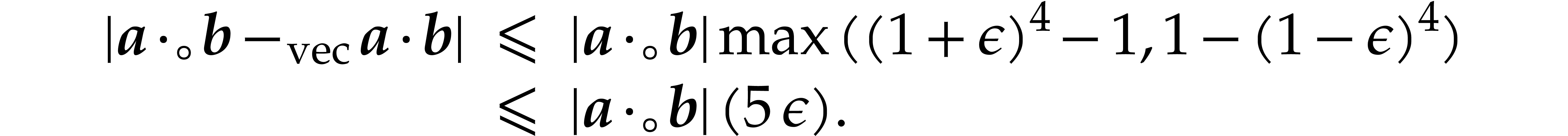
It thus suffices to take 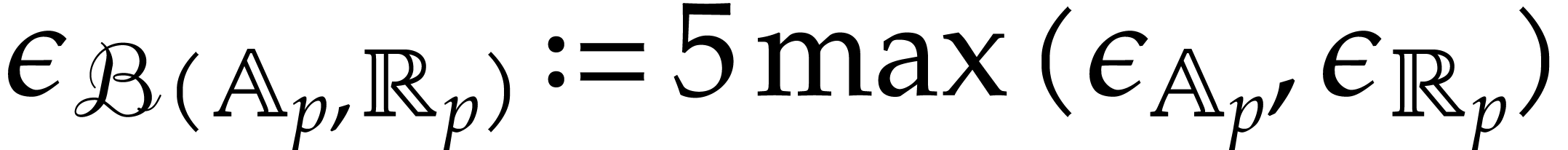 for (2.9)
to hold in the case of multiplication. Simpler similar computations show
that this is also sufficient for the other operations. We can now state
the analogue of Lemma 2.3.
for (2.9)
to hold in the case of multiplication. Simpler similar computations show
that this is also sufficient for the other operations. We can now state
the analogue of Lemma 2.3.
Proof. The same as the proof of [10,
Lemma 1], mutatis mutandis.
A straight-line program  over a ring
over a ring
 is a sequence
is a sequence  of
instructions of the form
of
instructions of the form
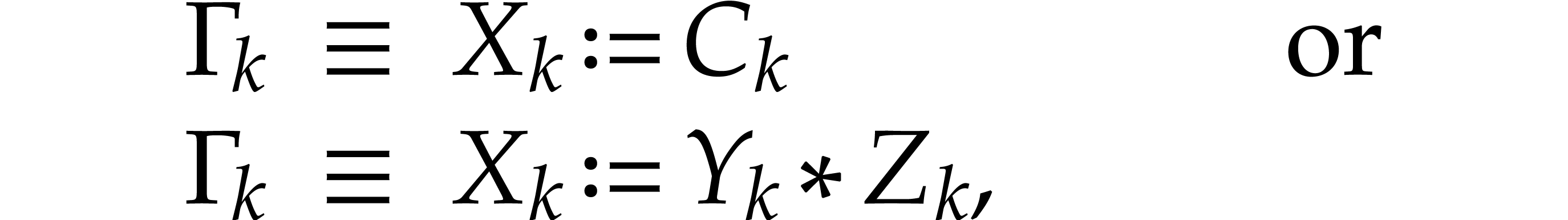
where 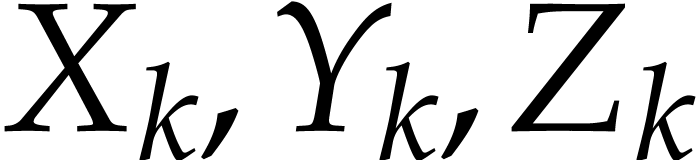 are variables in a finite ordered set
are variables in a finite ordered set
 ,
, 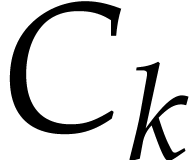 constants in
constants in  , and
, and 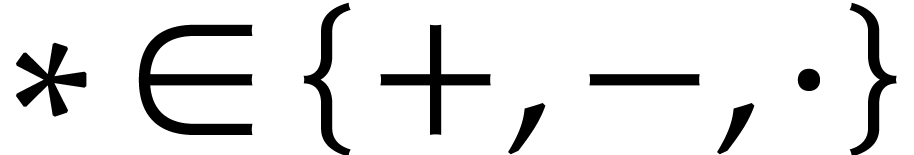 . Variables that appear for the
first time in the sequence in the right-hand side of an instruction are
called input variables. A distinguished subset of the set of
all variables occurring at the left-hand side of instructions is called
the set of output variables. Variables which are not used for
input or output are called temporary variables and determine
the amount of auxiliary memory needed to evaluate the program. The
length
. Variables that appear for the
first time in the sequence in the right-hand side of an instruction are
called input variables. A distinguished subset of the set of
all variables occurring at the left-hand side of instructions is called
the set of output variables. Variables which are not used for
input or output are called temporary variables and determine
the amount of auxiliary memory needed to evaluate the program. The
length  of the sequence is called the
length of
of the sequence is called the
length of  .
.
Let  be the input variables of
be the input variables of  and
and  the output variables, listed in increasing
order. Then we associate an evaluation function
the output variables, listed in increasing
order. Then we associate an evaluation function 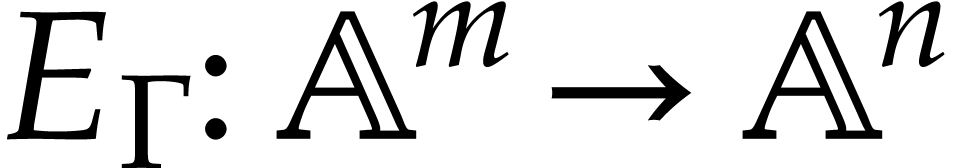 to
to  as follows: given
as follows: given 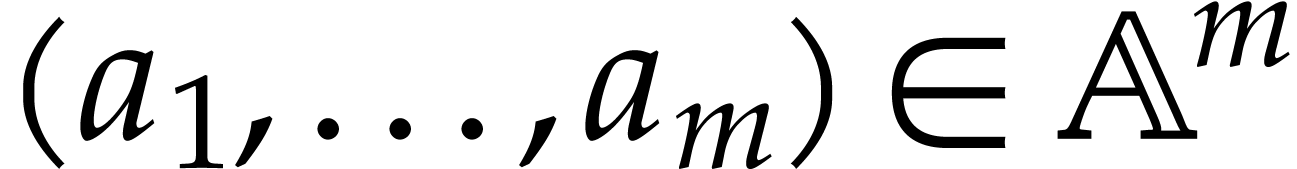 , we assign
, we assign 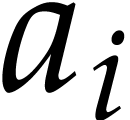 to
to 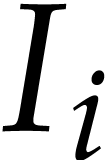 for
for 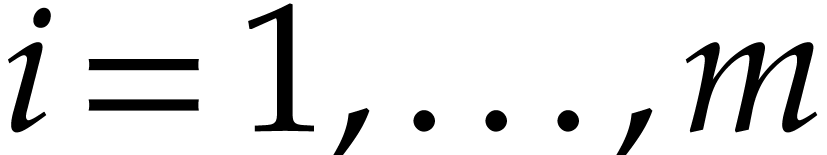 , then
evaluate the instructions of
, then
evaluate the instructions of  in sequence, and
finally read off the values of
in sequence, and
finally read off the values of  ,
which determine
,
which determine  .
.
To each instruction 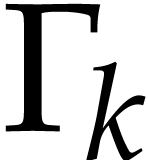 , one may
associate the remaining path lengths
, one may
associate the remaining path lengths 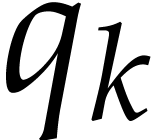 as
follows. Let
as
follows. Let 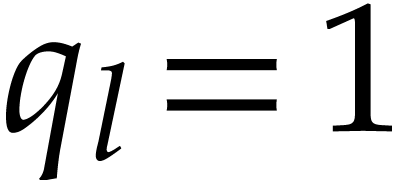 , and assume
that
, and assume
that 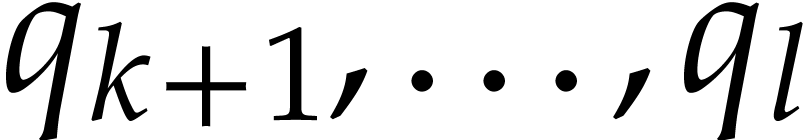 have been defined for some
have been defined for some 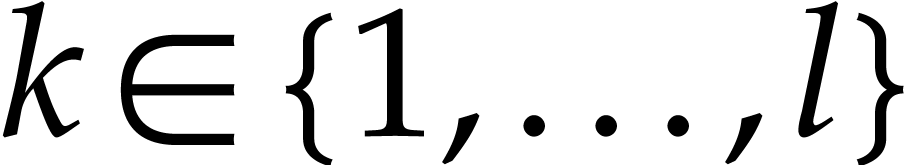 . Then we take
. Then we take 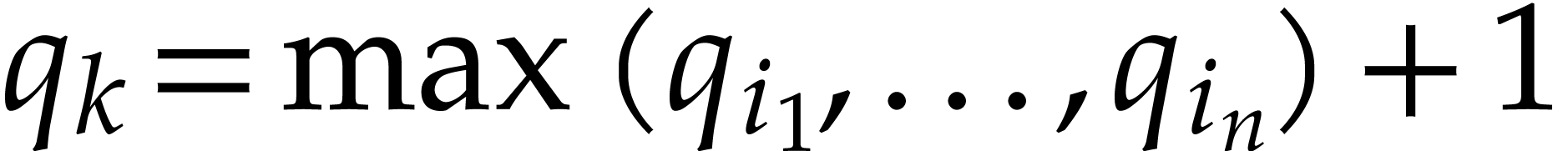 ,
where
,
where  are those indices
are those indices  such that
such that 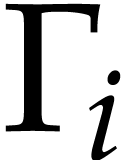 is of the form
is of the form 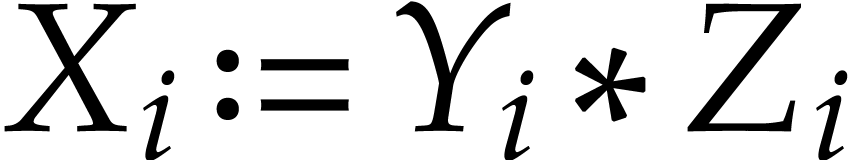 with
with 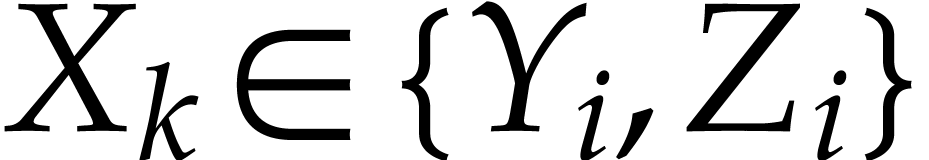 ,
, 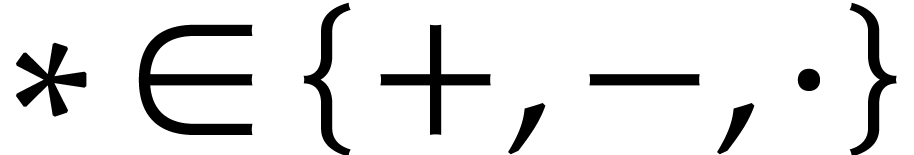 , and
, and 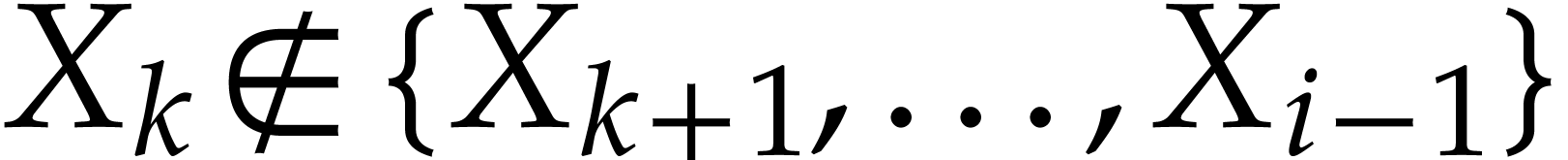 .
If no such indices
.
If no such indices  exist, then we set
exist, then we set 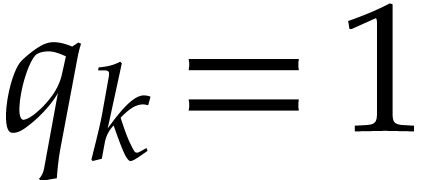 . Similarly, for each input
variable
. Similarly, for each input
variable 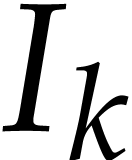 we define
we define 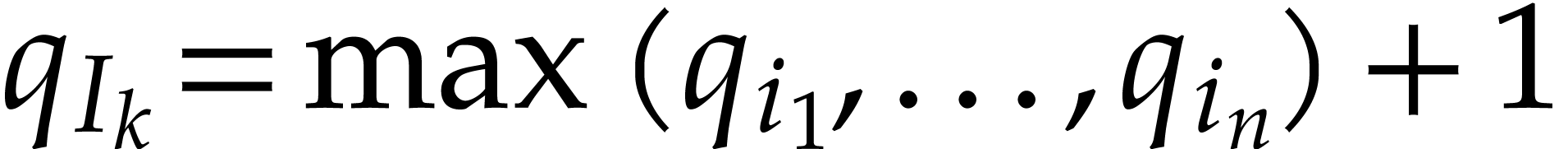 ,
where
,
where  are those indices such that
are those indices such that 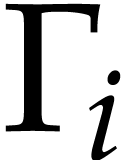 is of the form
is of the form 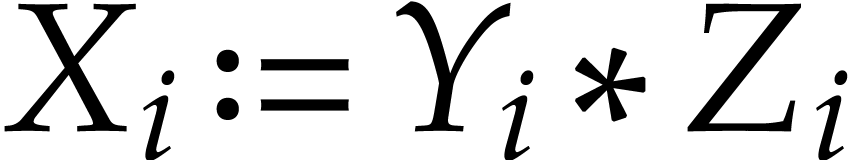 with
with 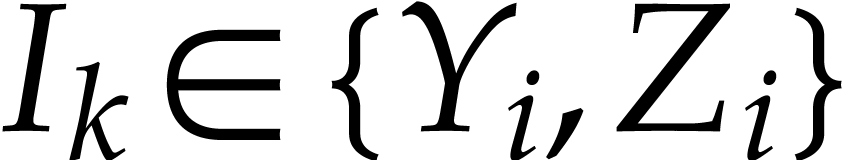 ,
, 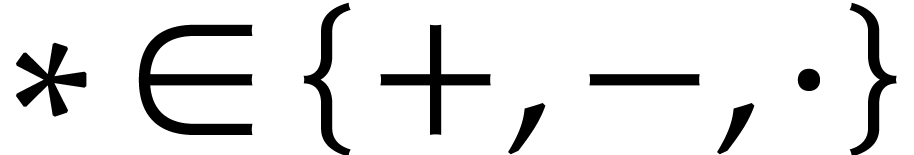 ,
and
,
and 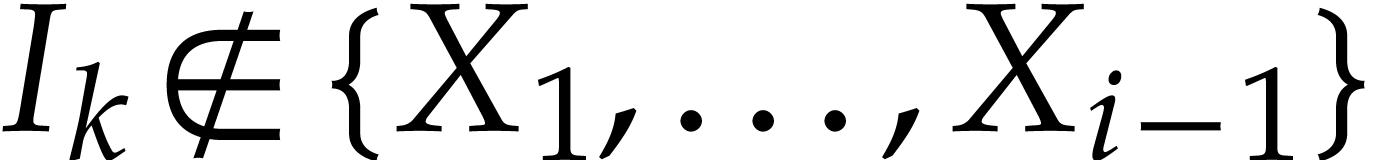 . We also define
. We also define 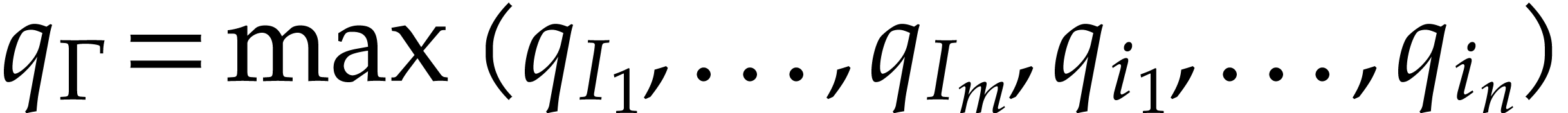 , where
, where  are
the input variables of
are
the input variables of  and
and  all indices
all indices  such that
such that 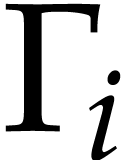 is
of the form
is
of the form 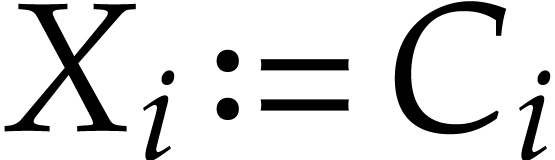 .
.
Example 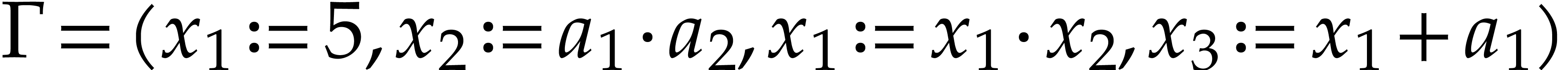 , of length
, of length 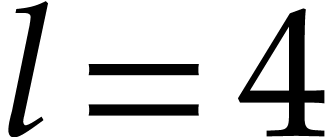 . The input variables are
. The input variables are 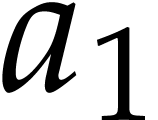 and
and 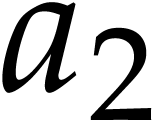 , and we
distinguish
, and we
distinguish 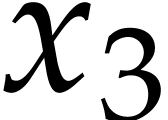 as the sole output variable. This
SLP thus computes the function
as the sole output variable. This
SLP thus computes the function 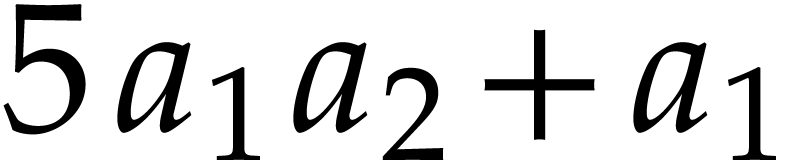 .
The associated computation graph, together with remaining path lengths
are as pictured:
.
The associated computation graph, together with remaining path lengths
are as pictured:
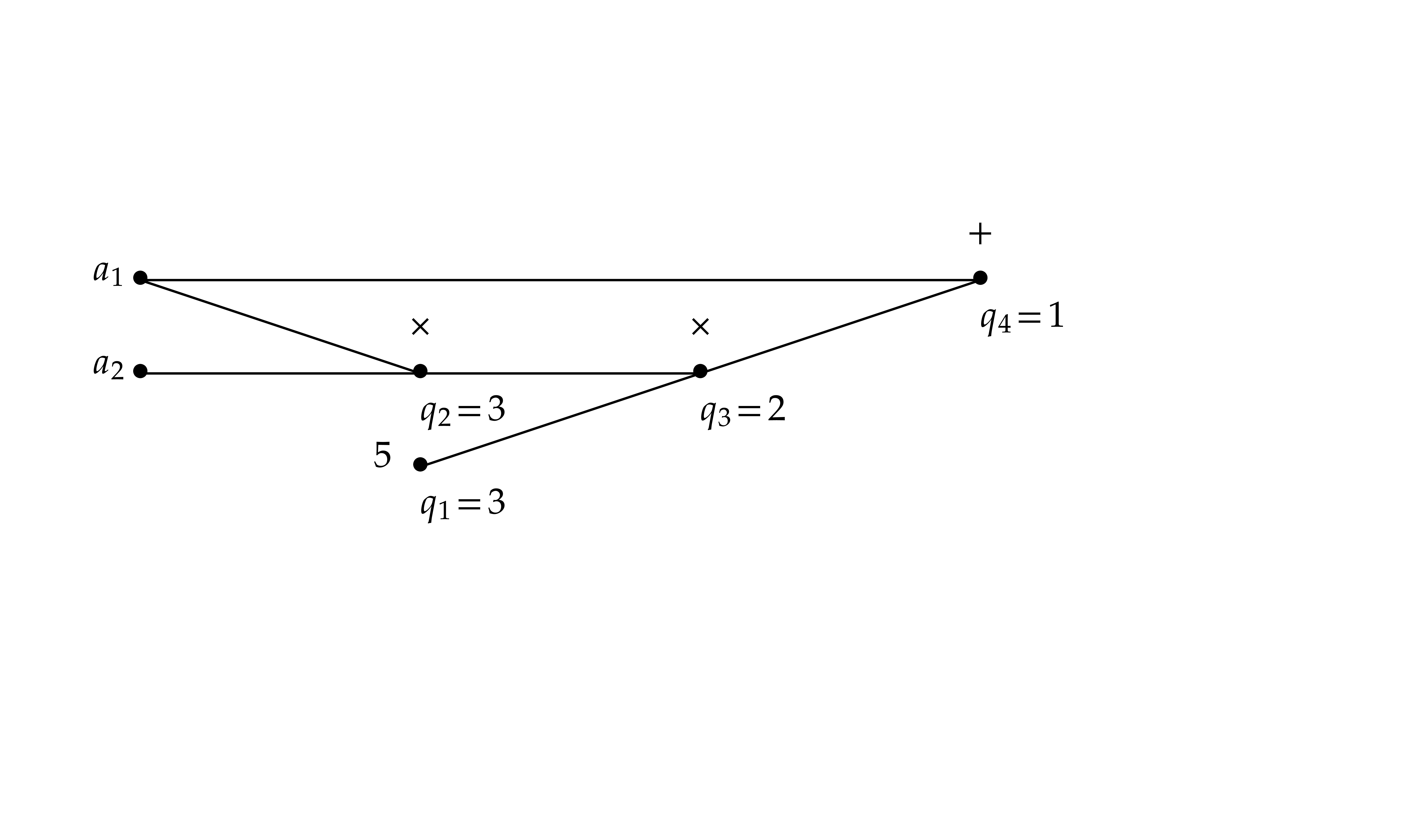
Our goal is to evaluate SLPs using transient ball arithmetic from section 2.4 instead of rounded ball arithmetic. Transient arithmetic is faster, but some adjustments are required in order to guarantee the correctness of the end-results. In order to describe and analyze the correctness of these adjustments, it is useful to introduce one more variant of ball arithmetic.
In semi-exact ball arithmetic, the operations on centers are approximate, but correctly rounded, whereas operations on radii are exact and certified:
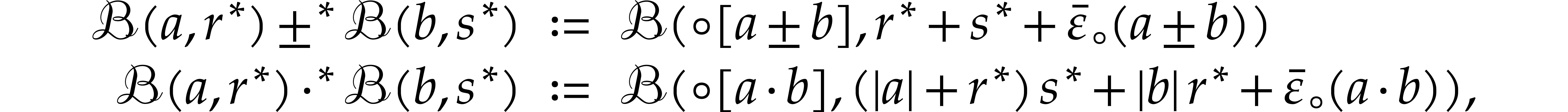
where  and
and  .
The extra terms
.
The extra terms 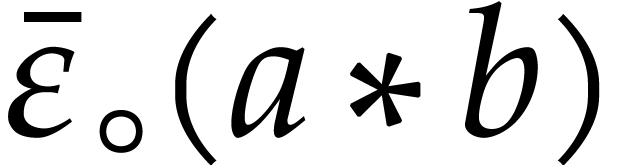 in the radius ensure that these
definitions satisfy the inclusion principle.
in the radius ensure that these
definitions satisfy the inclusion principle.
In order to measure how far transient arithmetic can deviate from this
idealized semi-exact arithmetic, let 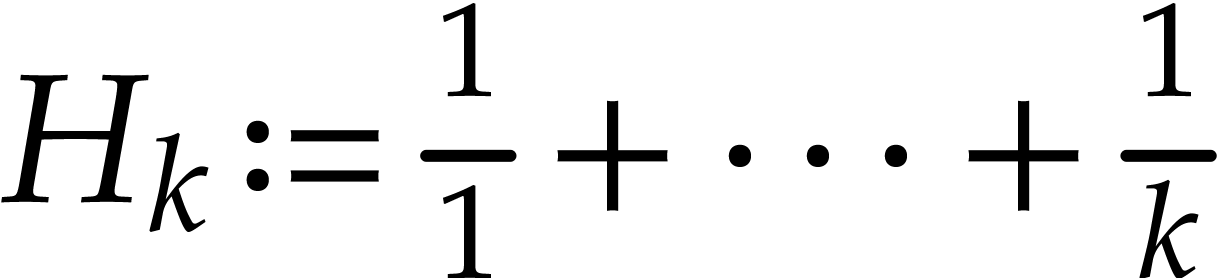 be the
be the
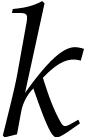 -th harmonic number and let
-th harmonic number and let
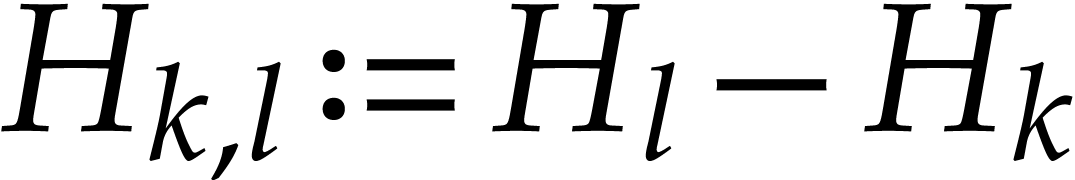 for all
for all 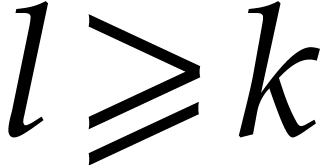 .
The following theorem shows how to certify transient ball evaluations:
.
The following theorem shows how to certify transient ball evaluations:
 be an SLP of length
be an SLP of length 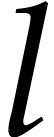 as
above and let
as
above and let 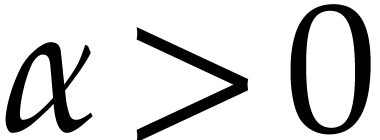 be an arbitrary parameter such
that
be an arbitrary parameter such
that 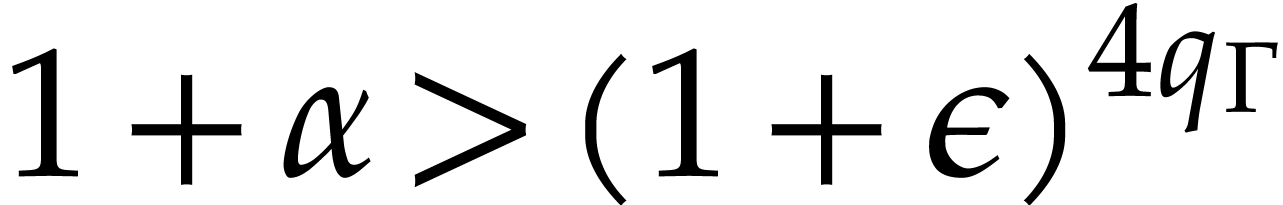 , where
, where 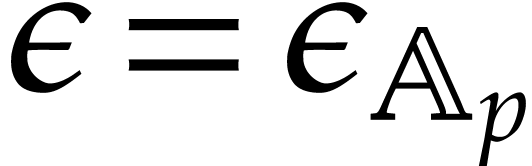 is as in
is as in  for different
types of ball arithmetic. For the first evaluation, we use semi-exact
ball arithmetic with
for different
types of ball arithmetic. For the first evaluation, we use semi-exact
ball arithmetic with 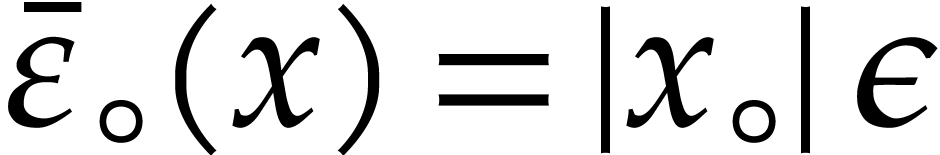 . For
the second evaluation, we use transient ball arithmetic with the
additional property that any input or constant ball
. For
the second evaluation, we use transient ball arithmetic with the
additional property that any input or constant ball 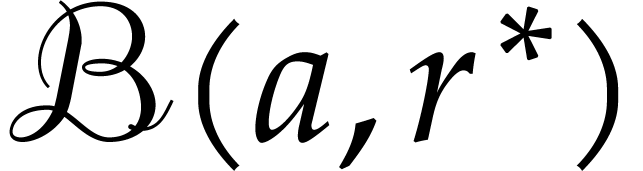 is replaced by a larger ball
is replaced by a larger ball 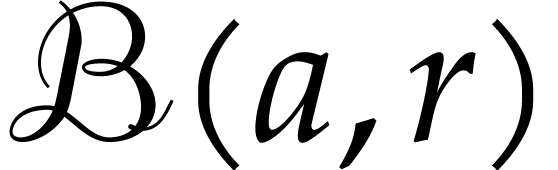 with
with
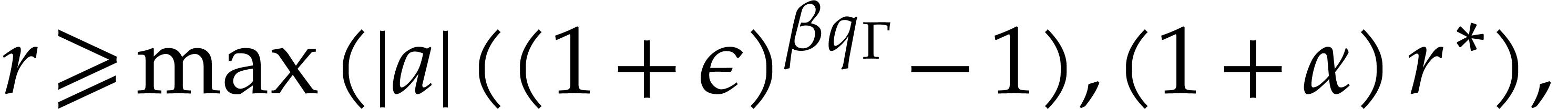
where
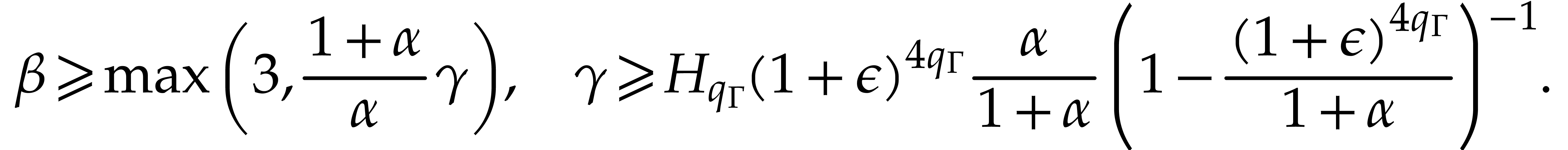
Assume that no underflow or overflow occurs during the second
evaluation. For any corresponding outputs 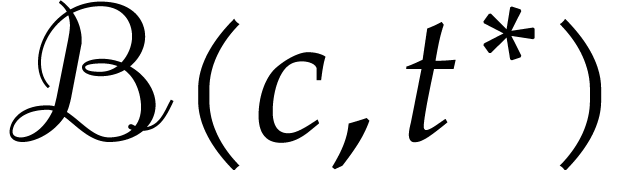 and
and
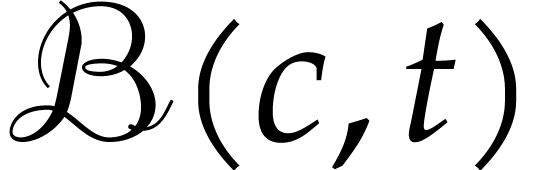 for the first and second evaluations, we then
have
for the first and second evaluations, we then
have 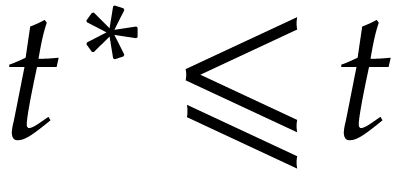 .
.
Given a fixed  and
and  ,
we note that we may take
,
we note that we may take  and
and  such that
such that 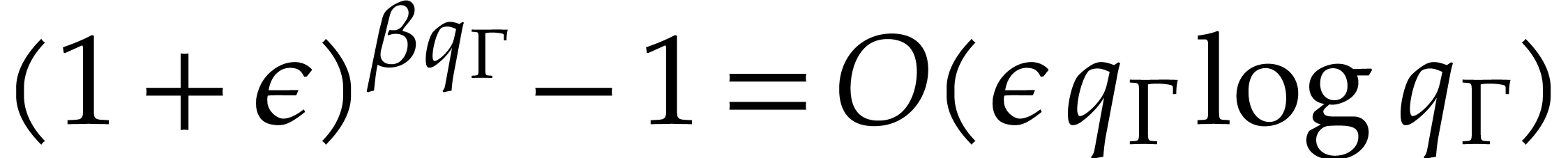 . The value of the
parameter
. The value of the
parameter  may be optimized as a function of the
SLP and the input. Without entering details,
may be optimized as a function of the
SLP and the input. Without entering details,  should be taken large when the input radii are small, and small when
these radii are large. The latter case occurs typically within
subdivision algorithms. For our main application when we want to compute
error bounds, the input radii are typically small or even zero.
should be taken large when the input radii are small, and small when
these radii are large. The latter case occurs typically within
subdivision algorithms. For our main application when we want to compute
error bounds, the input radii are typically small or even zero.
For our implementations in 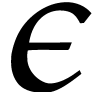 is “sufficiently small”.
is “sufficiently small”.
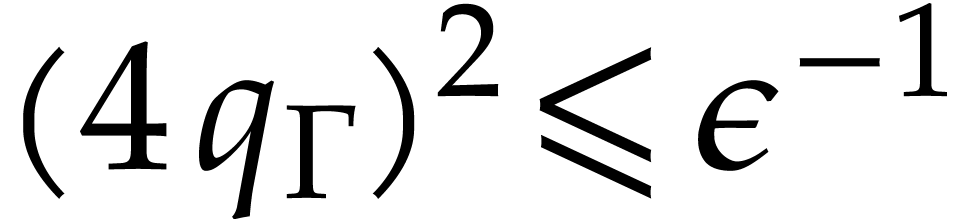 . In order to
apply Theorem 3.2, it is sufficient to take
. In order to
apply Theorem 3.2, it is sufficient to take 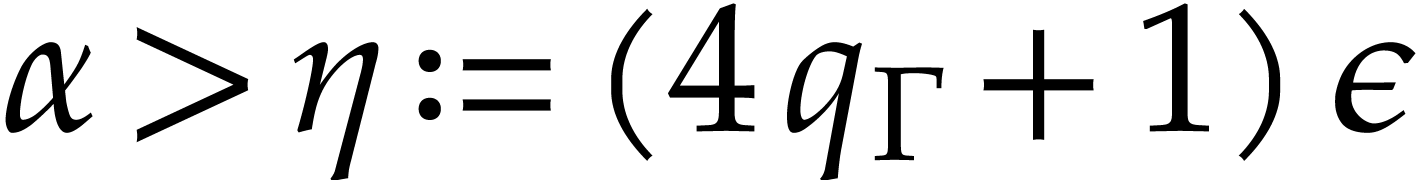 and
and
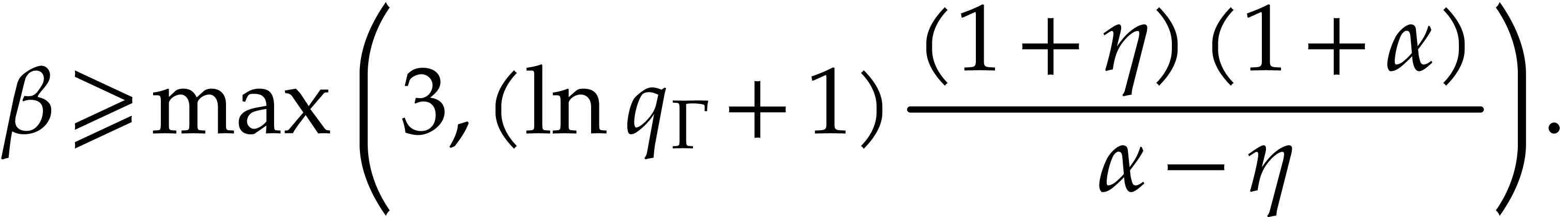
Proof. The harmonic series satisfies the
well-known inequality 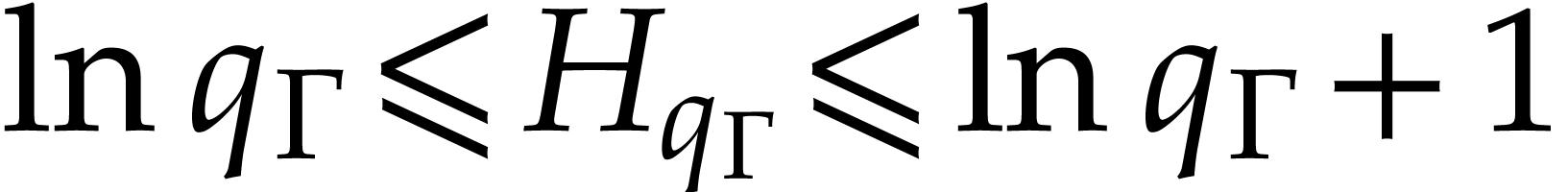 , of
which we only use the right-hand part. Lemma 2.1 also
yields
, of
which we only use the right-hand part. Lemma 2.1 also
yields 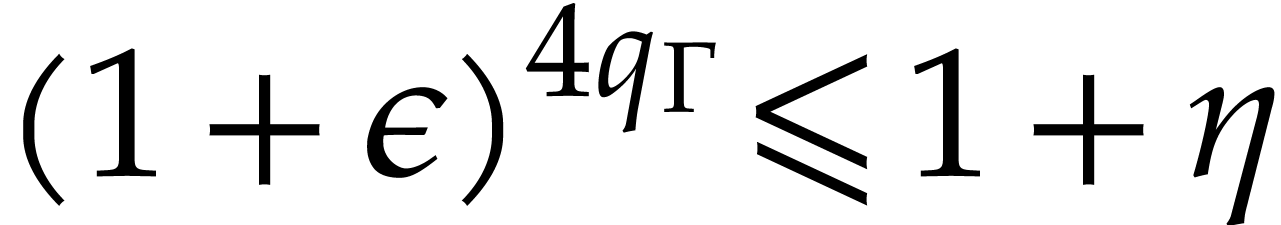 . Given that
. Given that  , it follows that
, it follows that
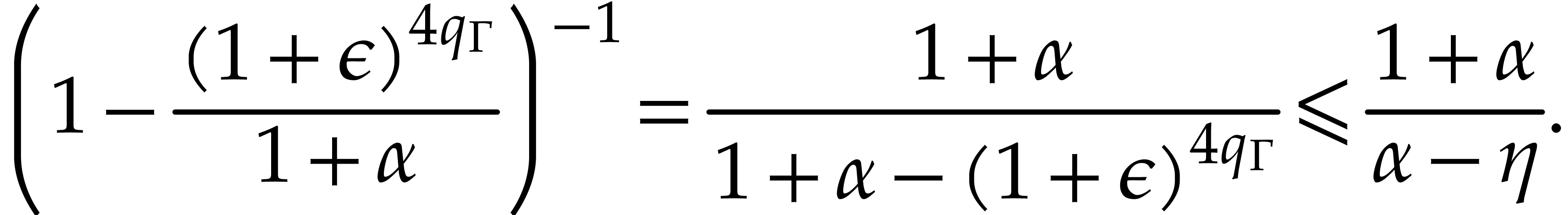
Therefore,
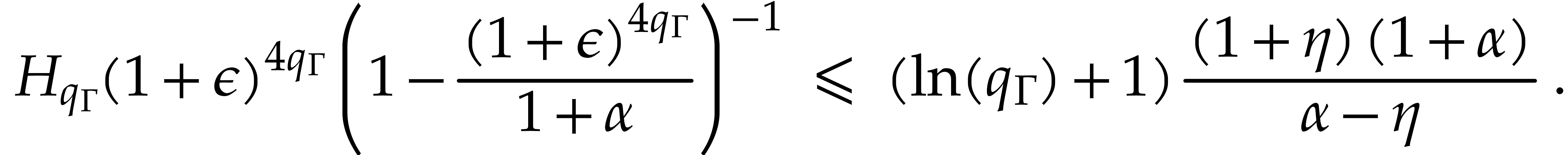

The semi-exact ball arithmetic from the previous subsection naturally
adapts to matryoshki as follows: given 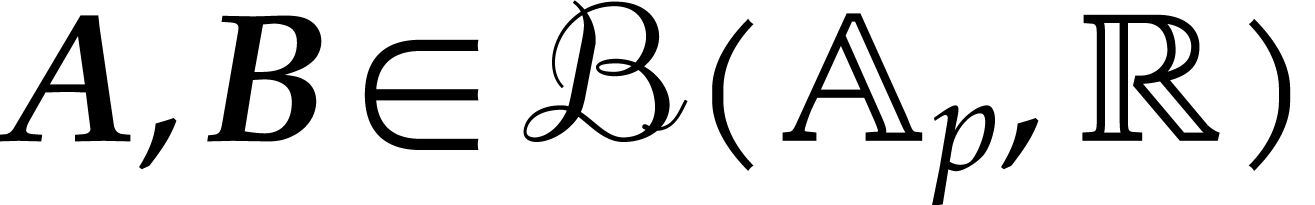 and
and 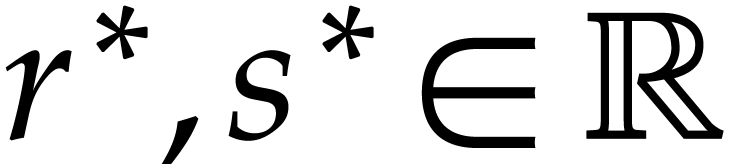 , we define
, we define
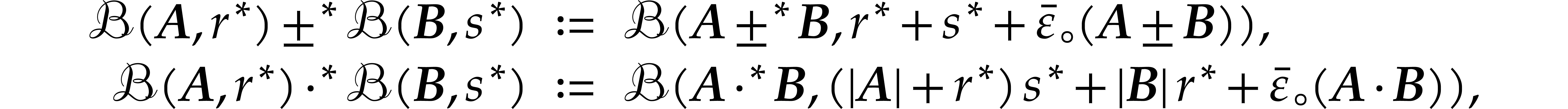
where 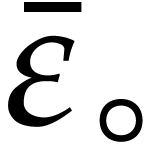 is extended to balls via
is extended to balls via
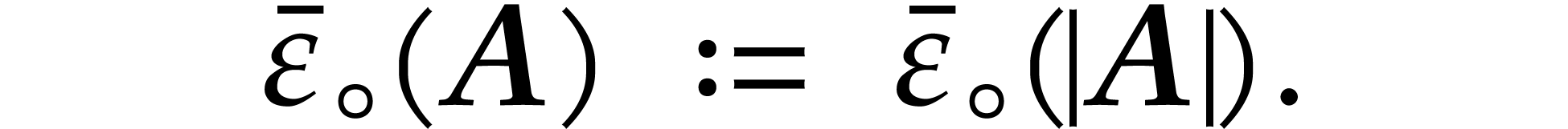
Recall that 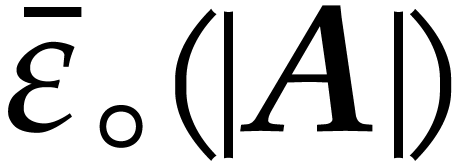 denotes an upper bound on the
rounding errors involved in the computation of the norm of
denotes an upper bound on the
rounding errors involved in the computation of the norm of  . Operations on centers use the semi-exact
arithmetic from the previous subsection. This arithmetic is therefore a
matryoshka lift of the elementary operations. The following theorem
specifies the amount of inflation that is required in order to certify
SLP evaluations using “transient matryoshka arithmetic”.
. Operations on centers use the semi-exact
arithmetic from the previous subsection. This arithmetic is therefore a
matryoshka lift of the elementary operations. The following theorem
specifies the amount of inflation that is required in order to certify
SLP evaluations using “transient matryoshka arithmetic”.
 , and let
, and let 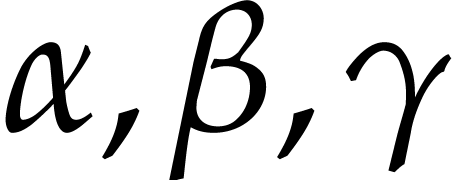 be as in Theorem 3.2. Consider two
evaluations of
be as in Theorem 3.2. Consider two
evaluations of  for two different types of
arithmetic. For the first evaluation, we use semi-exact matryoshka
arithmetic with
for two different types of
arithmetic. For the first evaluation, we use semi-exact matryoshka
arithmetic with 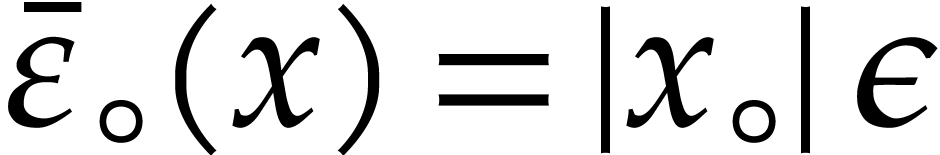 . For the
second evaluation, we use transient matryoshka arithmetic with the
additional property that any input or constant ball
. For the
second evaluation, we use transient matryoshka arithmetic with the
additional property that any input or constant ball 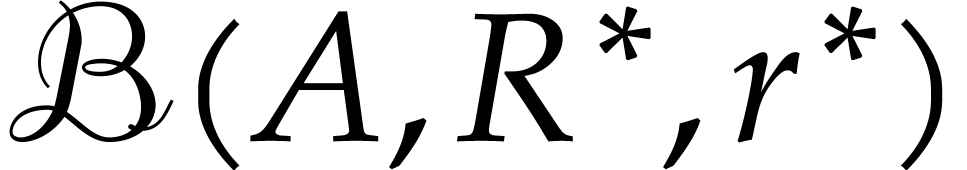 is replaced by a larger ball
is replaced by a larger ball 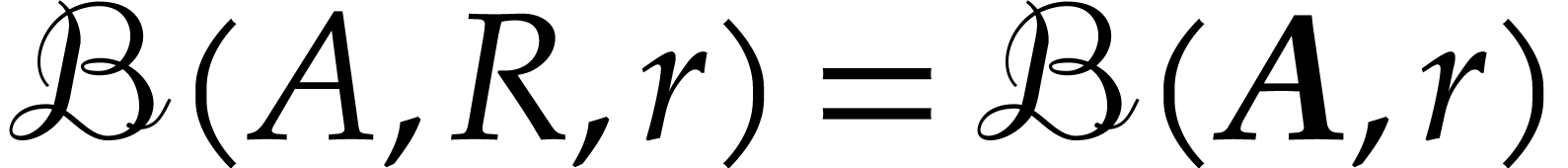 with
with
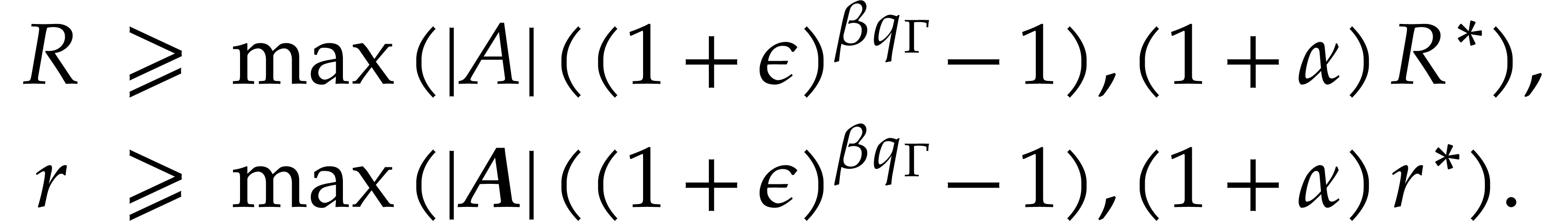
Assume that no underflow or overflow occurs during the second
evaluation. For any corresponding outputs 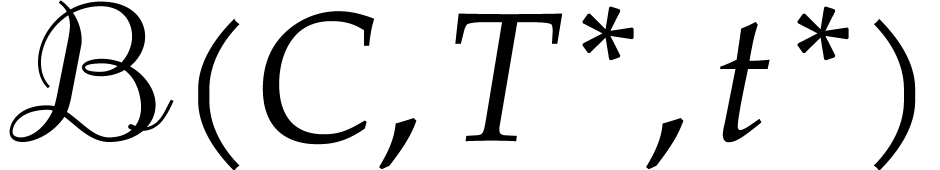 and
and
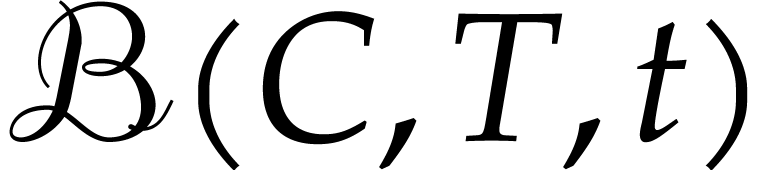 for the first and second evaluations, we then
have
for the first and second evaluations, we then
have 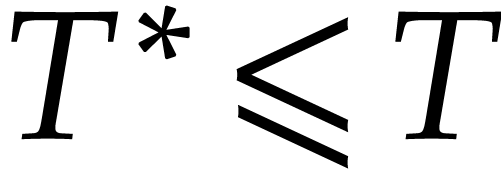 and
and  .
.
Proof. The theorem essentially follows by
applying Theorem 3.2 twice: once for the big and once for
the small radii. This is clear for the big radii  and
and  since the formulas for the big radii of
matryoshki correspond with the formula for the radii of the
corresponding ball arithmetic. For the small radii, we use essentially
the same proof as in [10]. For convenience of the reader,
we reproduce it here with the required minor adaptations.
since the formulas for the big radii of
matryoshki correspond with the formula for the radii of the
corresponding ball arithmetic. For the small radii, we use essentially
the same proof as in [10]. For convenience of the reader,
we reproduce it here with the required minor adaptations.
Let 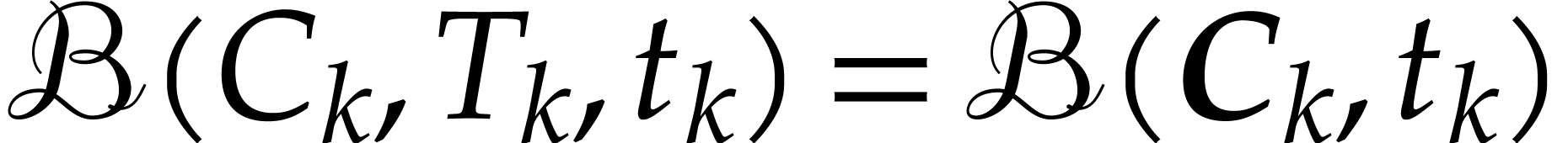 be the value of the variable
be the value of the variable 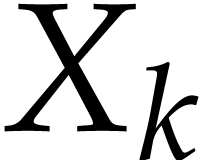 after the evaluation of
after the evaluation of  using
transient matryoshki arithmetic. It will be convenient to systematically
use star superscripts for the corresponding value
using
transient matryoshki arithmetic. It will be convenient to systematically
use star superscripts for the corresponding value 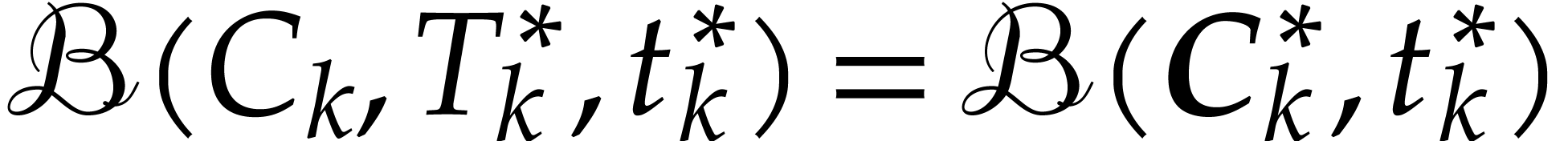 when using semi-exact matryoshka arithmetic. Let us show by induction on
when using semi-exact matryoshka arithmetic. Let us show by induction on
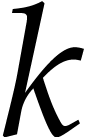 that:
that:
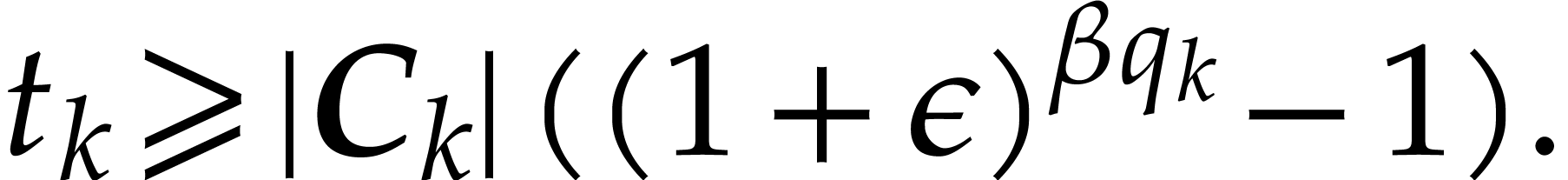 |
(3.1) |
If 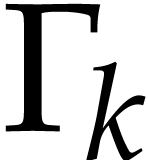 is of the form
is of the form 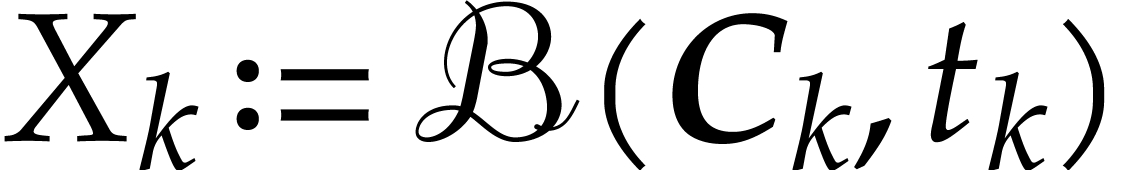 ,
then we are done since
,
then we are done since  .
Otherwise,
.
Otherwise, 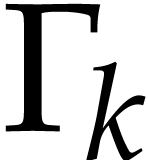 is of the form
is of the form 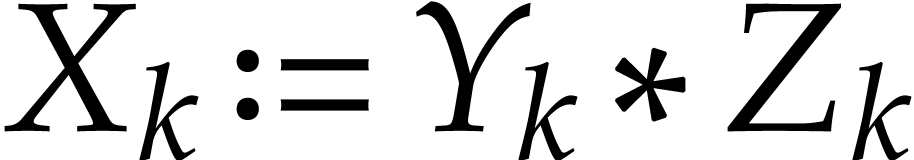 . Writing
. Writing  ,
we claim that
,
we claim that
This holds by assumption if  is an input
variable. Otherwise, let
is an input
variable. Otherwise, let 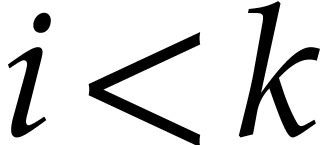 be the largest index
such that
be the largest index
such that 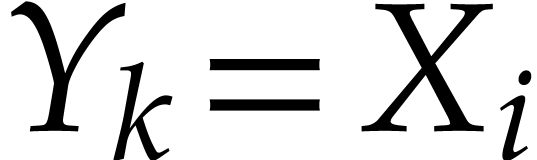 . Then
. Then  by construction of
by construction of  ,
whence our claim follows from the induction hypothesis. Similarly,
writing
,
whence our claim follows from the induction hypothesis. Similarly,
writing  , we have
, we have 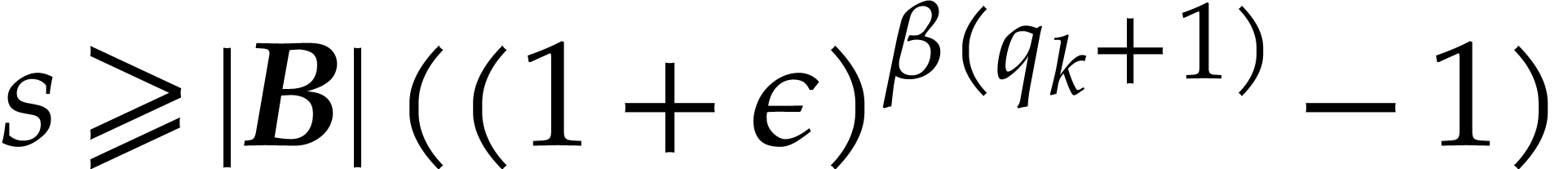 .
.
Having shown our claim, let us first consider the case where 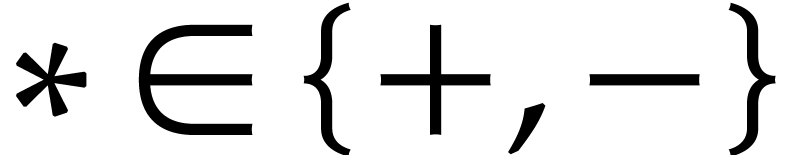 . In this case we obtain
. In this case we obtain
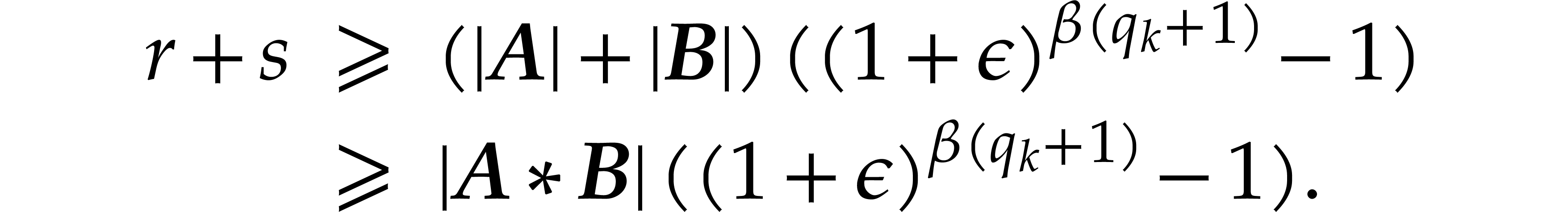
Combined with
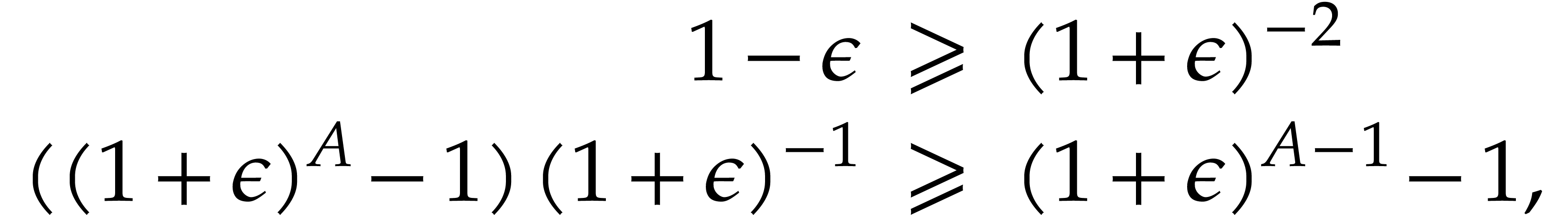 |
(3.2) |
we deduce:
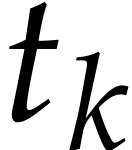 |
 |
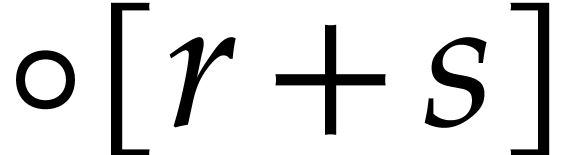 |
|
 |
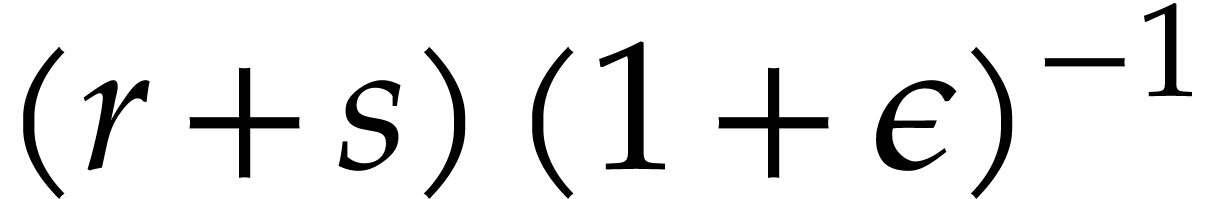 |
||
 |
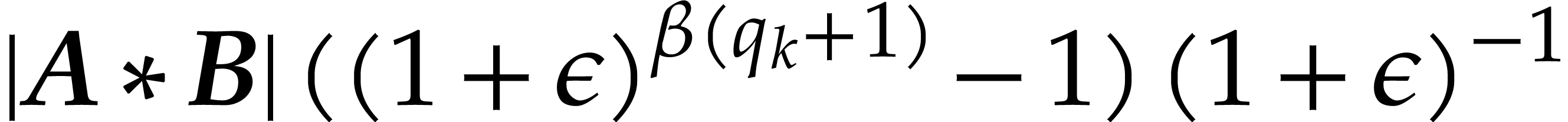 |
||
 |
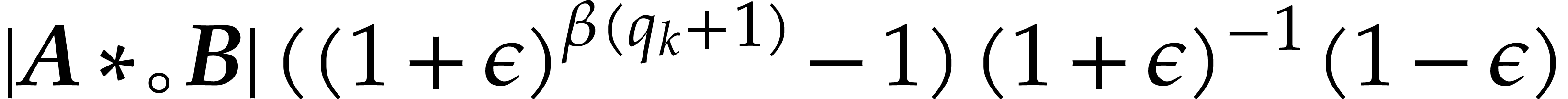 |
||
 |
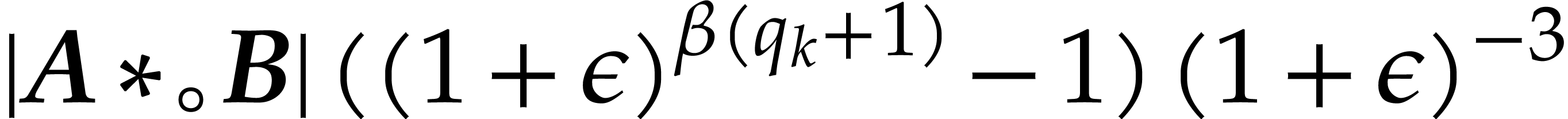 |
||
 |
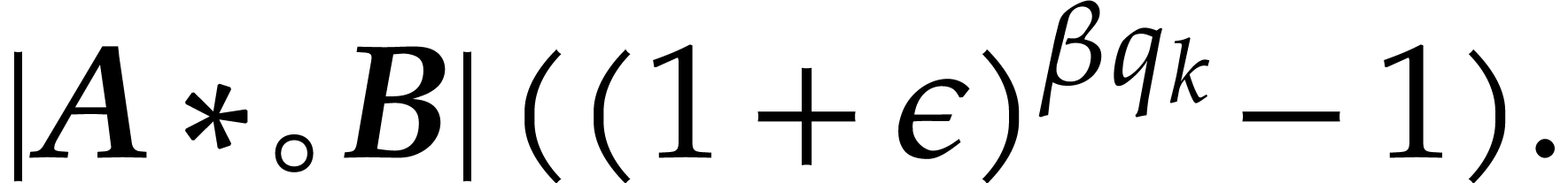 |
In case when  , we obtain
, we obtain
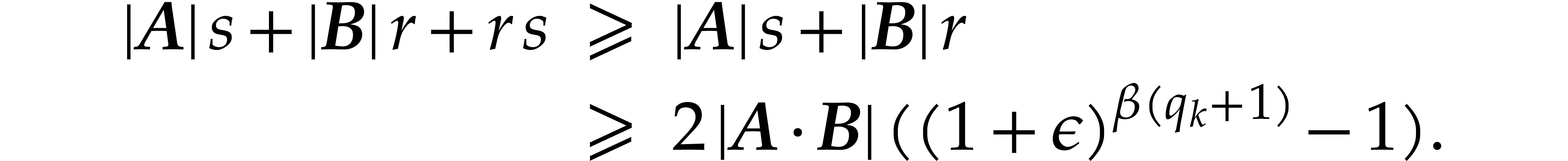
Combined with Lemma 2.4, the inequalities 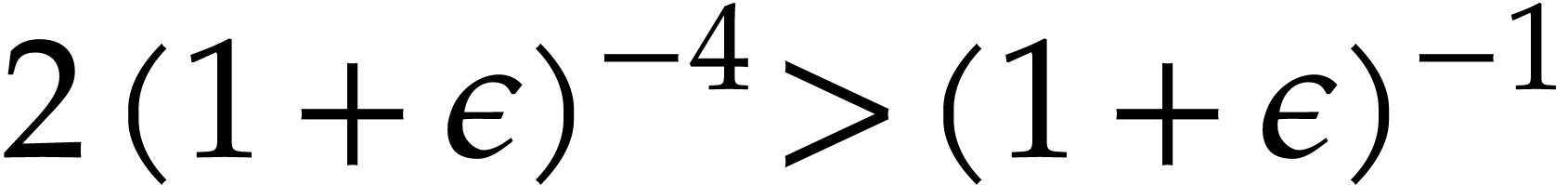 successively imply
successively imply
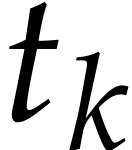 |
 |
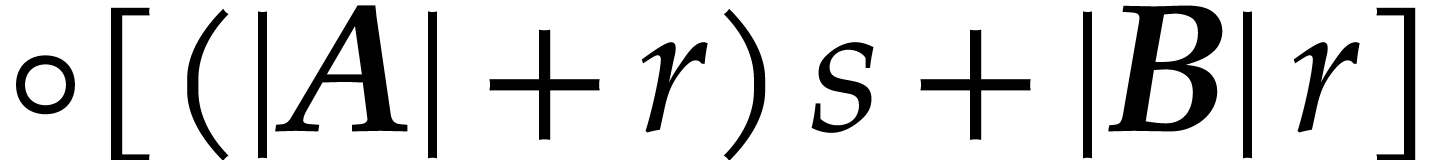 |
|
 |
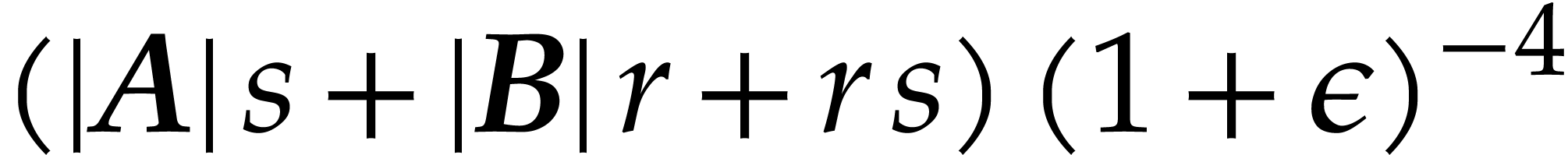 |
||
 |
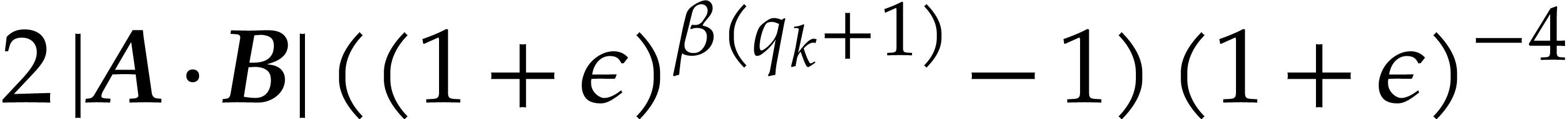 |
||
 |
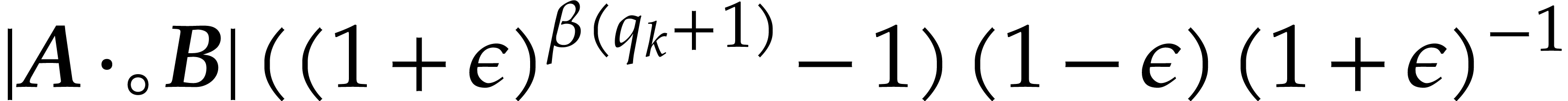 |
||
 |
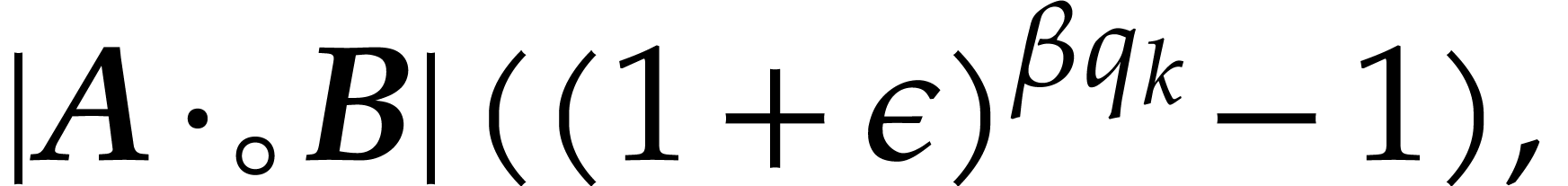 |
which achieves the induction. Then, for all 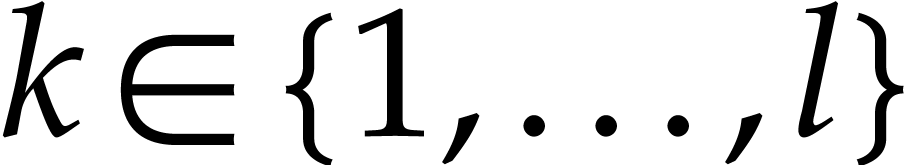 , we define
, we define
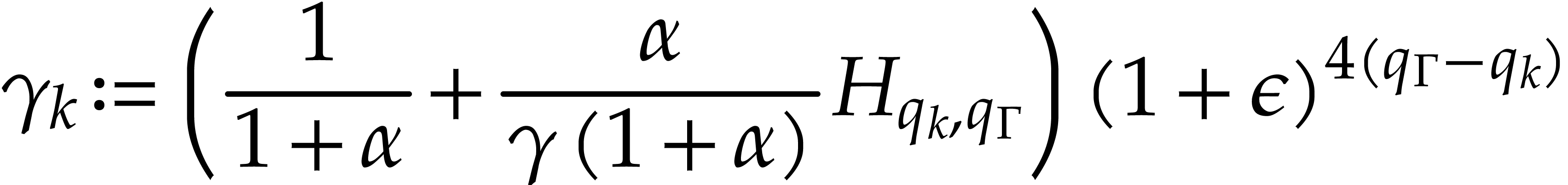
so that 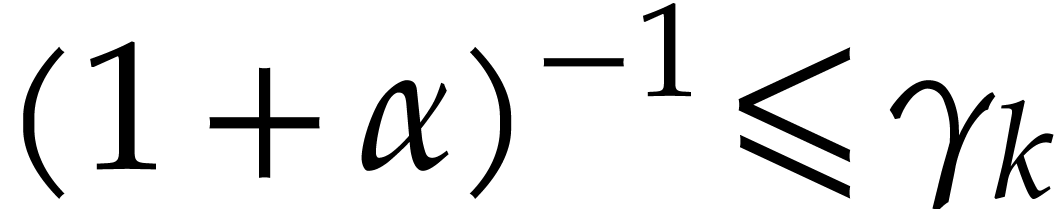 . By the inequality
that we imposed on
. By the inequality
that we imposed on  , we have
, we have
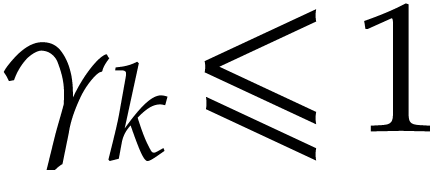 . Using a second induction
over
. Using a second induction
over 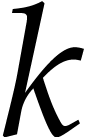 , let us next prove that
, let us next prove that
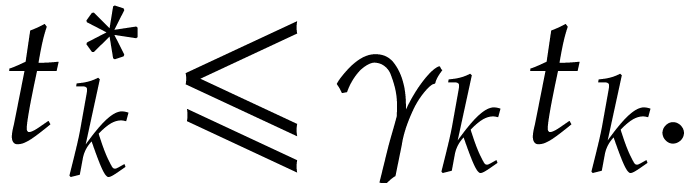 |
(3.3) |
Assume that this inequality holds up until order  . If
. If  is of the form
is of the form  then we are done by the fact that
then we are done by the fact that 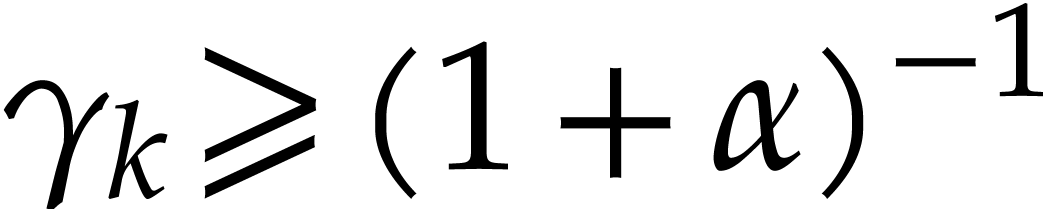 . If
. If 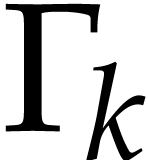 is of the form
is of the form
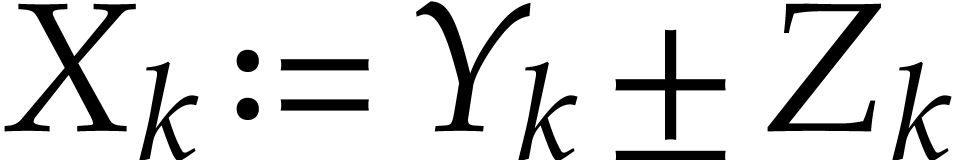 , then let
, then let 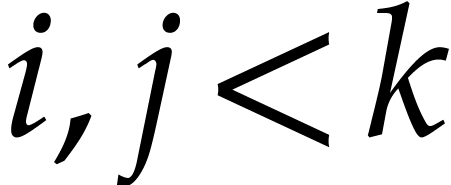 be the largest integers so that
be the largest integers so that 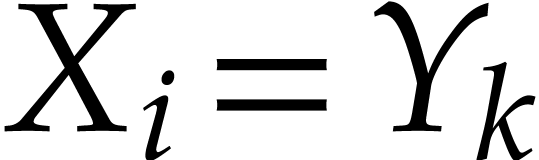 and
and 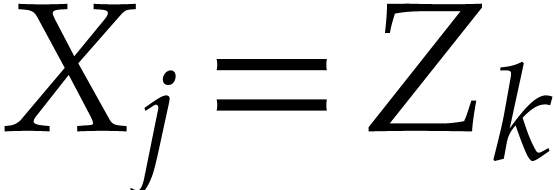 , so we have
, so we have 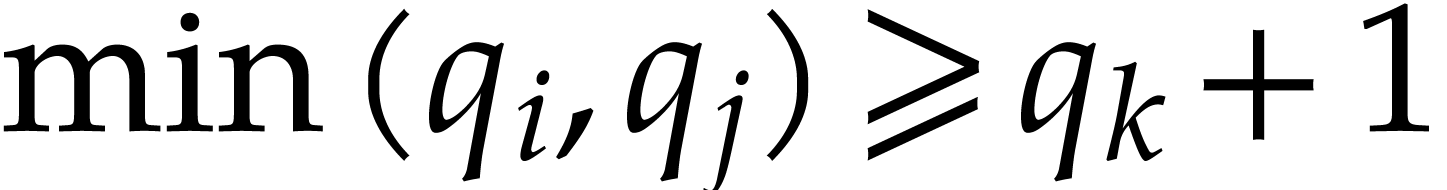 ,
,
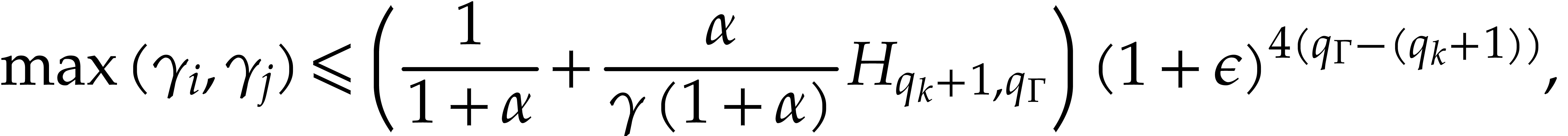
and
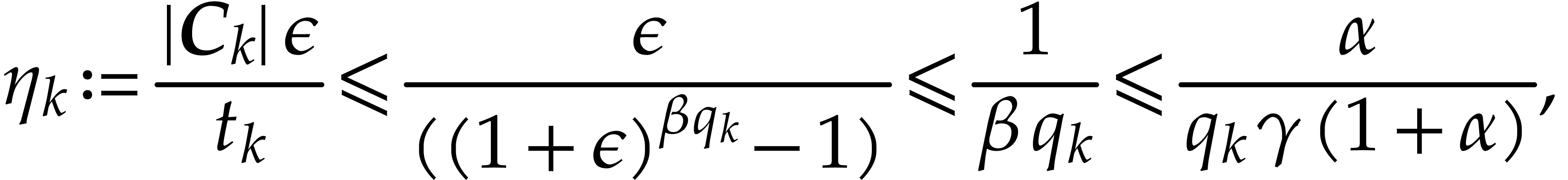
using 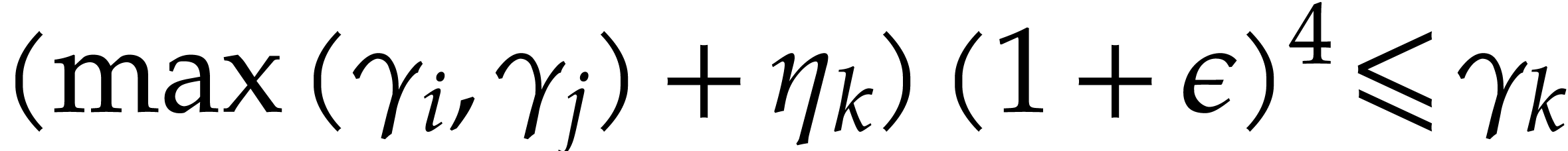 . We denote by
. We denote by  (resp.
(resp.  ) the
matryoshka corresponding to the value of
) the
matryoshka corresponding to the value of  (resp.
(resp.
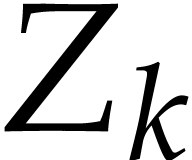 ) in the semi-exact
evaluation. Their corresponding values for the transient evaluation are
denoted without the star superscript. Thanks to Theorem 3.2,
we know that
) in the semi-exact
evaluation. Their corresponding values for the transient evaluation are
denoted without the star superscript. Thanks to Theorem 3.2,
we know that 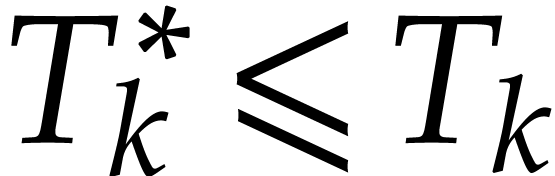 , whence
, whence 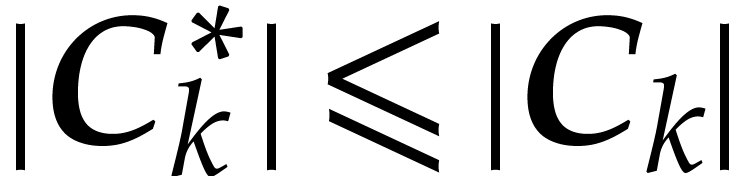 since
since 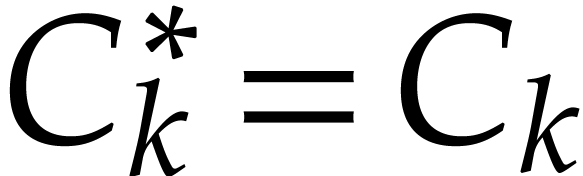 .
With
.
With 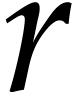 and
and 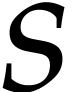 as above, using
as above, using
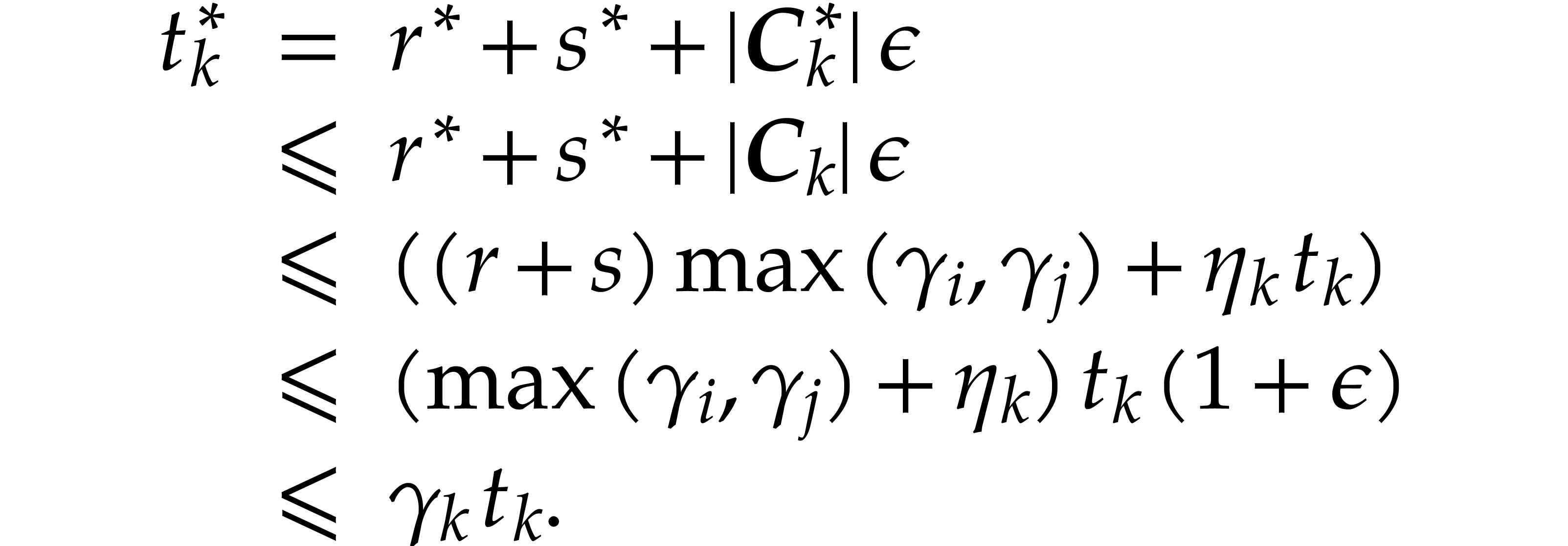
If 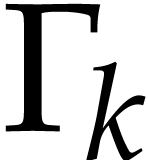 is of the form
is of the form 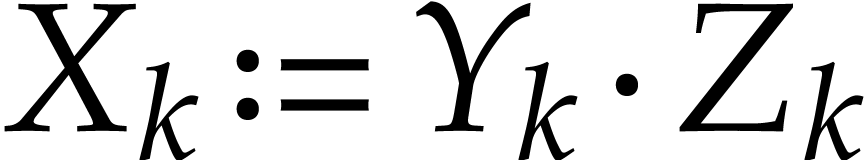 ,
then, thanks to Lemmas 2.3, 2.4, and
inequality
,
then, thanks to Lemmas 2.3, 2.4, and
inequality
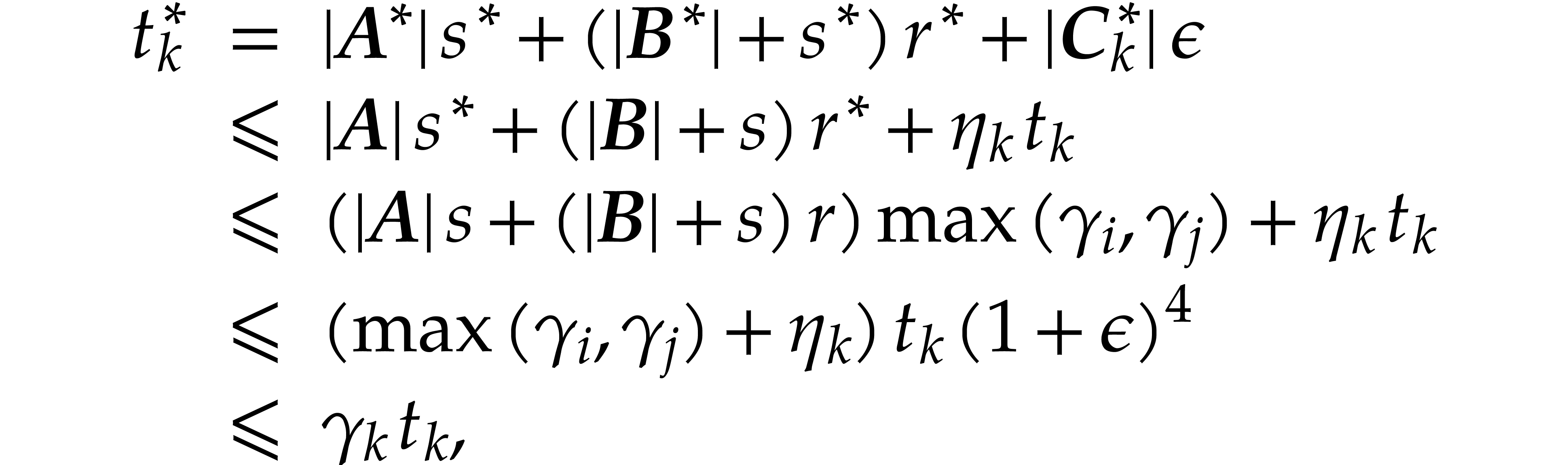
which completes the second induction and the proof of this theorem.
Remark
Let us now give two direct applications of matryoshka arithmetic. Assume
that we are given an SLP  that computes a
function
that computes a
function  and denote by
and denote by 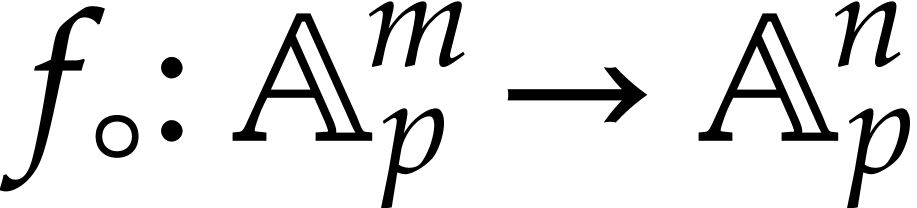 the function obtained by evaluating
the function obtained by evaluating  using
approximate floating point arithmetic over
using
approximate floating point arithmetic over 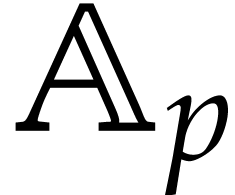 .
Matryoshki yield an efficient way to statically bound the error
.
Matryoshki yield an efficient way to statically bound the error 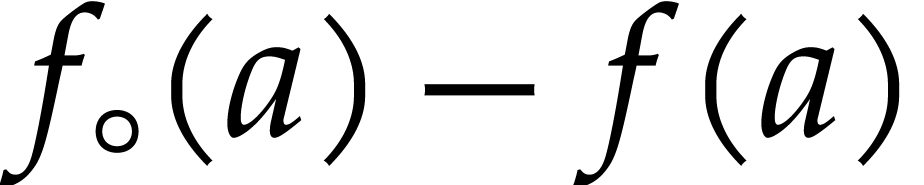 for
for  inside some fixed
poly-ball, as follows:
inside some fixed
poly-ball, as follows:
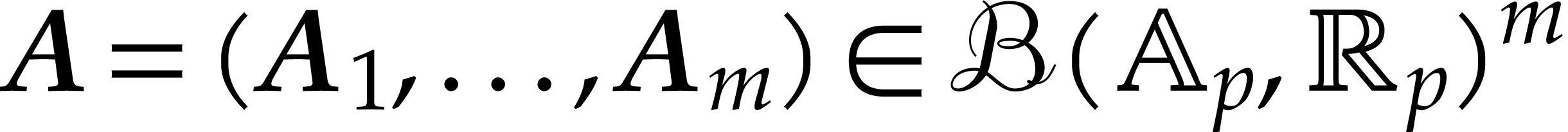 be a fixed poly-ball
and
be a fixed poly-ball
and 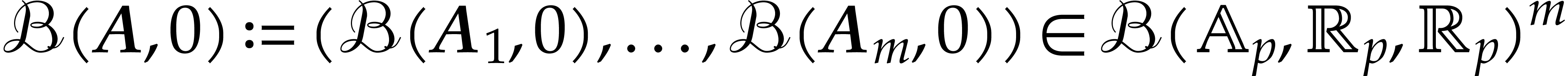 . Let
. Let 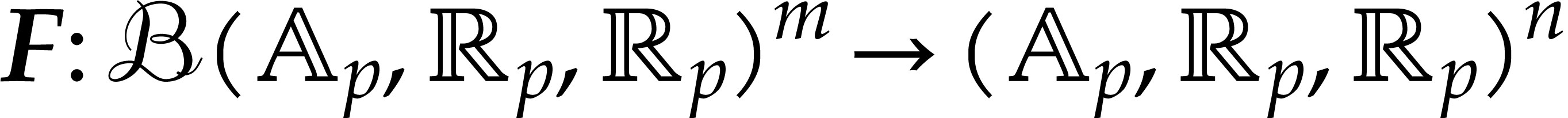 be a poly-matryoshka lift of
be a poly-matryoshka lift of  and
and 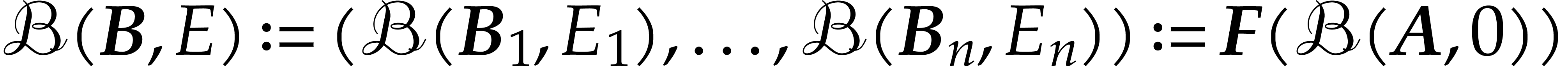 . Then for all
. Then for all  with
with
 and
and  ,
we have
,
we have
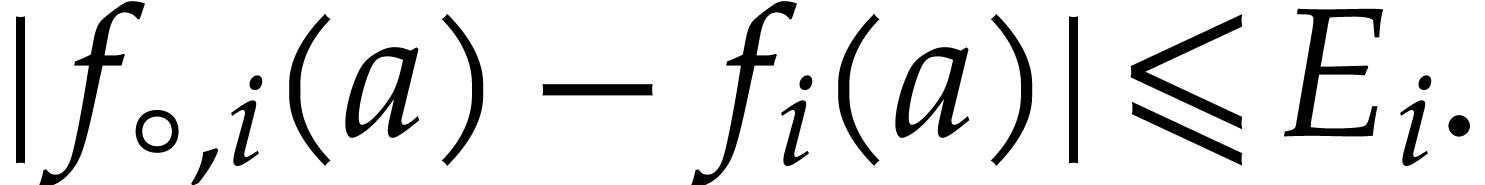
Proof. Let 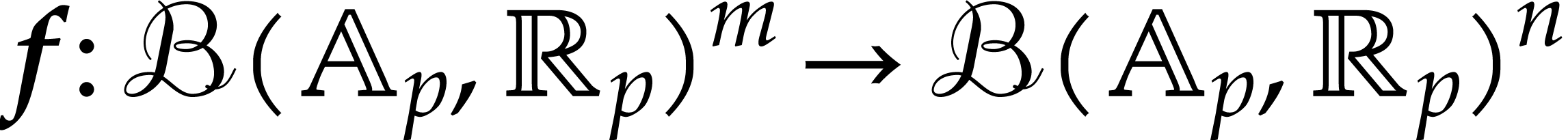 be a ball
lift for which
be a ball
lift for which  satisfies the matryoshka lift
property. Since
satisfies the matryoshka lift
property. Since 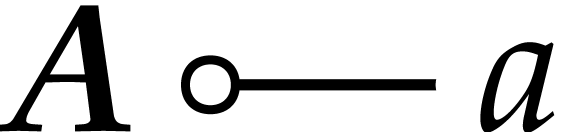 by assumption, we have
by assumption, we have
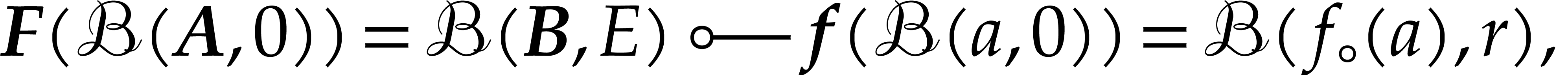
for some 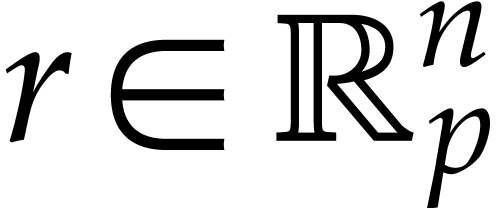 . The ball lift
property also yields
. The ball lift
property also yields
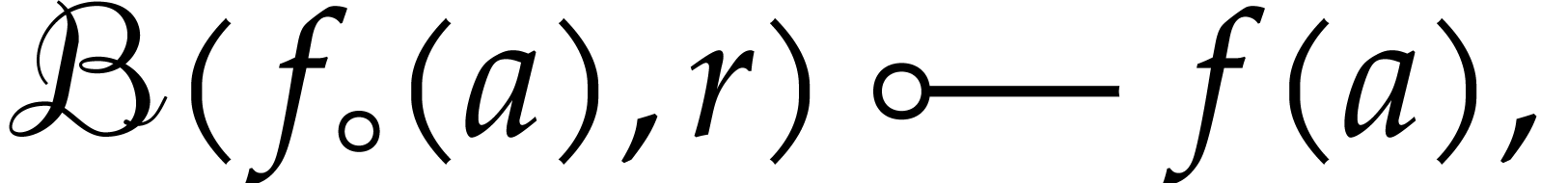
so 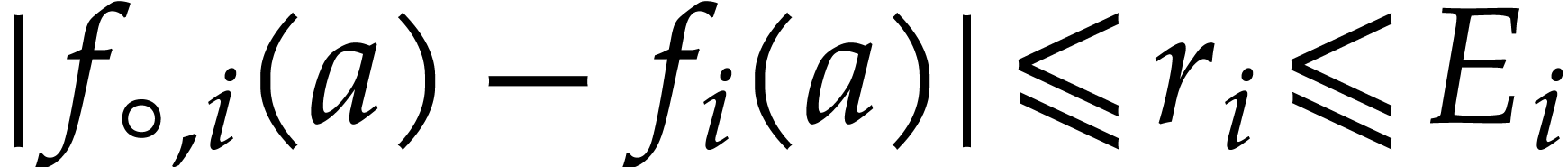 for
for 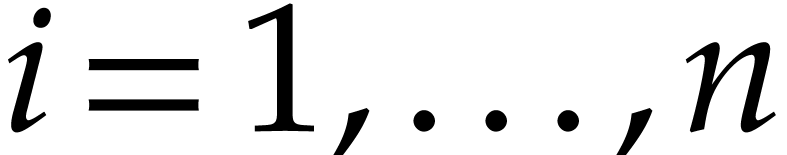 .
.
As our second application, we wish to construct a ball lift of 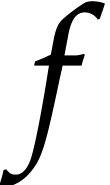 that is almost as efficient to compute as
that is almost as efficient to compute as 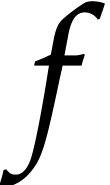 itself, provided that the input balls are included into fixed large
balls
itself, provided that the input balls are included into fixed large
balls 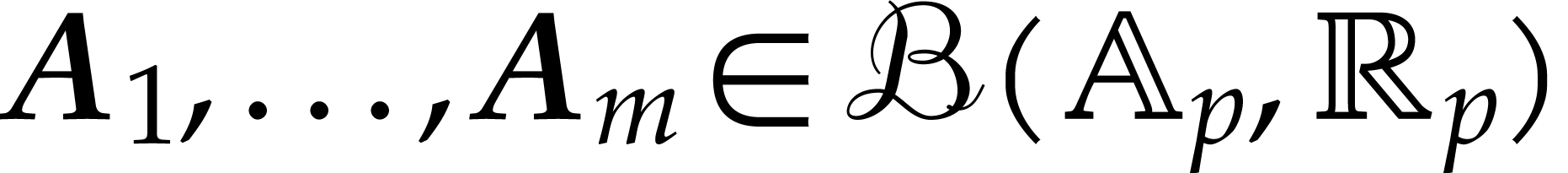 as above. For this, we first compute
bounds
as above. For this, we first compute
bounds 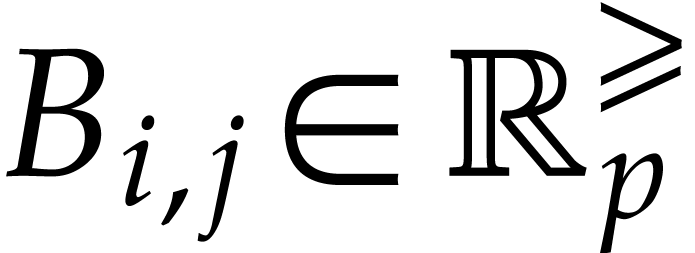 for the Jacobian matrix of
for the Jacobian matrix of 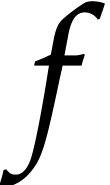 :
:
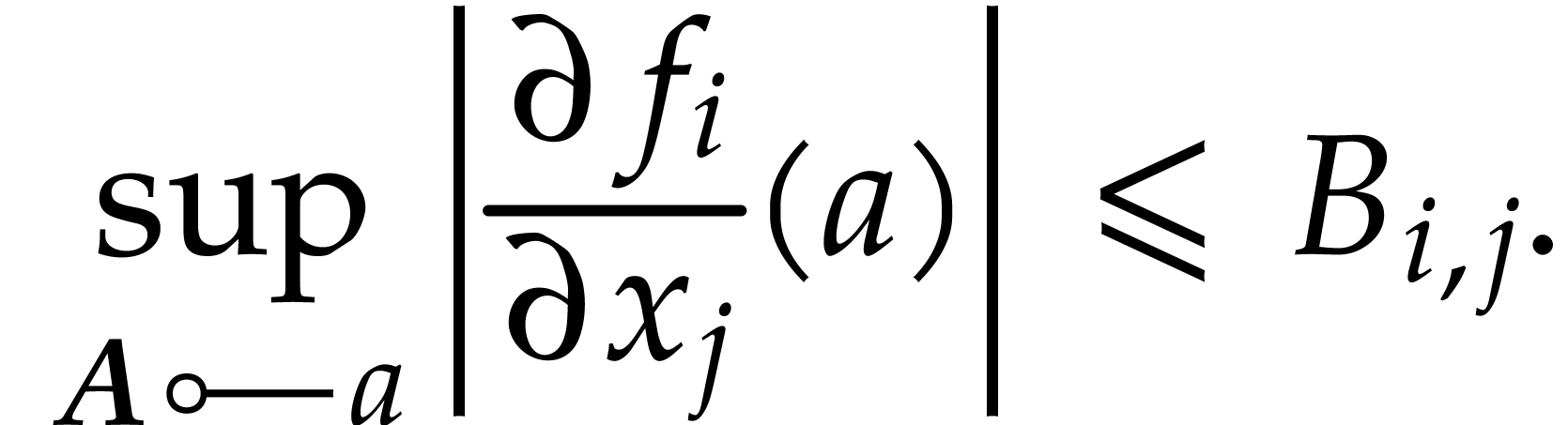 |
(3.4) |
For this, it suffices to evaluate a ball lift of the Jacobian of 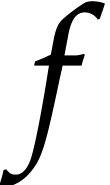 at
at  , which
yields a matrix
, which
yields a matrix 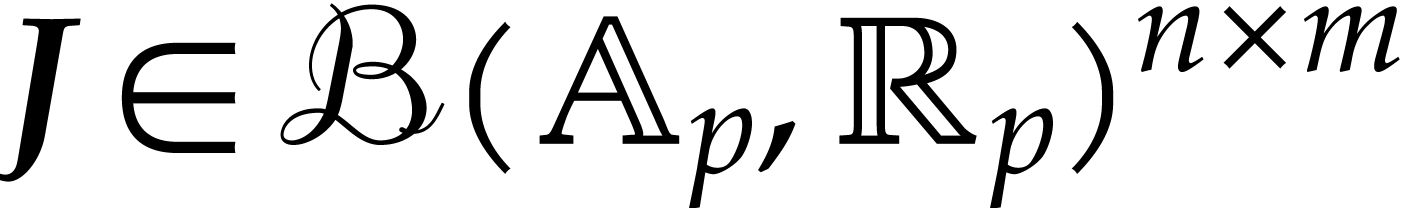 , after which
we take
, after which
we take 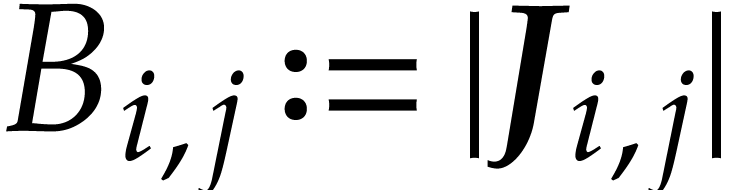 . We recall that an
SLP for the computation of the Jacobian can be constructed using the
algorithm by Baur and Strassen [3].
. We recall that an
SLP for the computation of the Jacobian can be constructed using the
algorithm by Baur and Strassen [3].
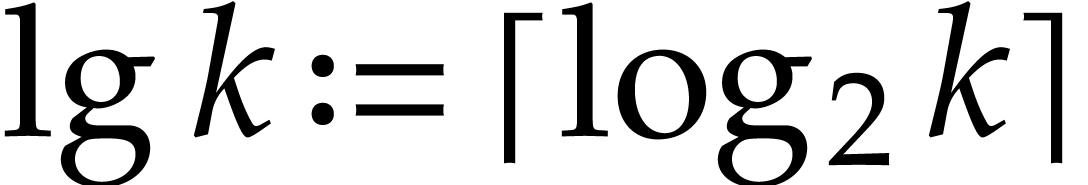 for all integers
for all integers 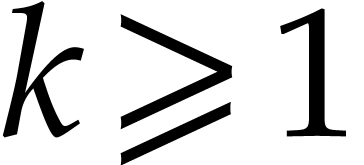 and
and 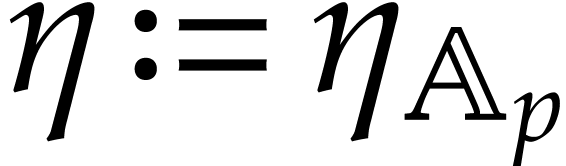 . With
the above notation, assume that
. With
the above notation, assume that 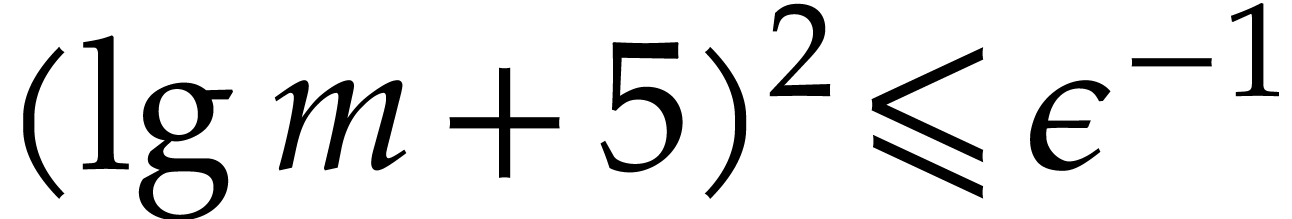 ,
and let
,
and let  be as in Proposition 3.6.
For every
be as in Proposition 3.6.
For every 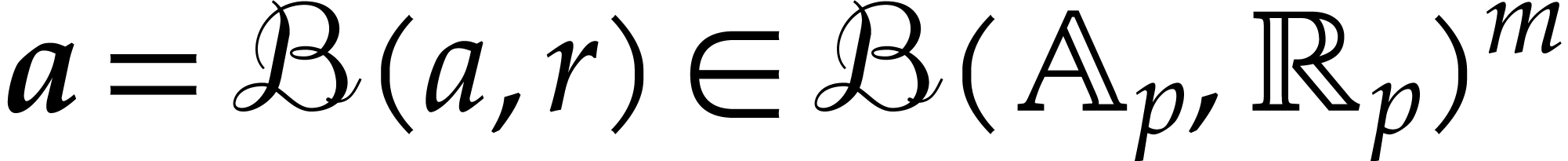 with
with  ,
let
,
let
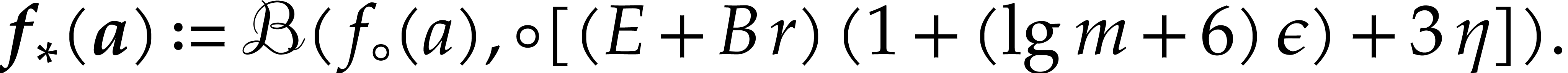
Then  is a ball lift of
is a ball lift of  . (Note that this lift is only defined on the
set of
. (Note that this lift is only defined on the
set of 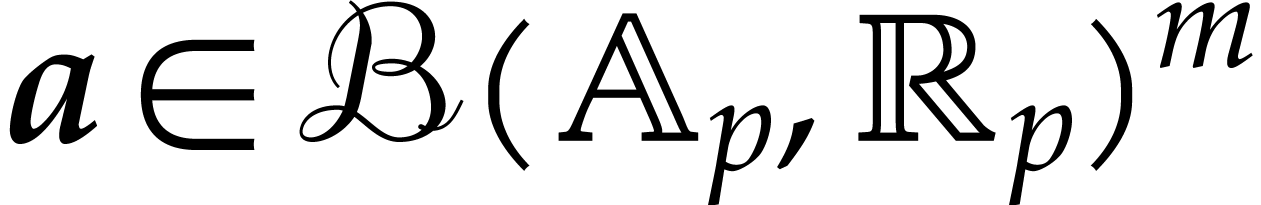 such that
such that  .)
.)
Proof. Let  .
Then, for
.
Then, for 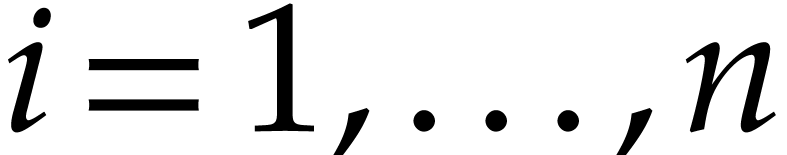 , we have
, we have
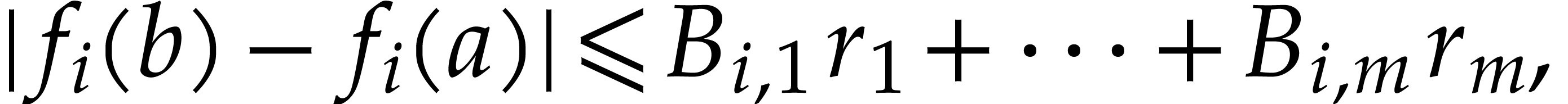
by (3.4) and the mean value theorem. In other words,
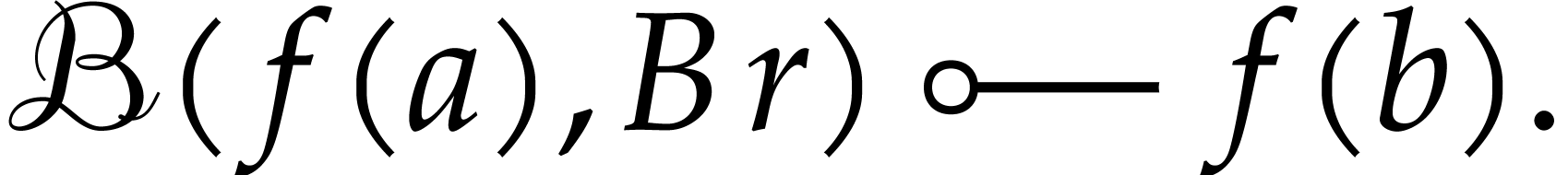
Applying Proposition 3.6, it follows that
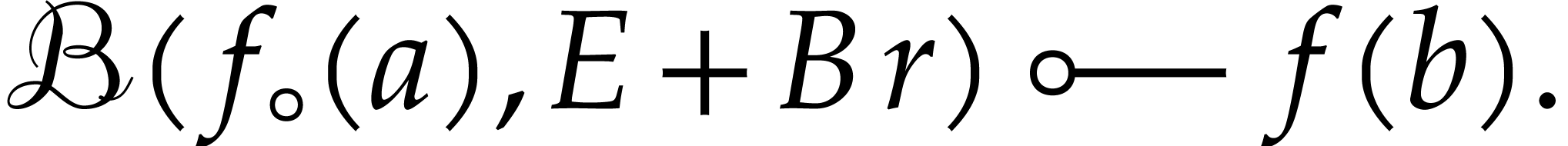
By computing the sum  via a balanced binary tree
and using
via a balanced binary tree
and using
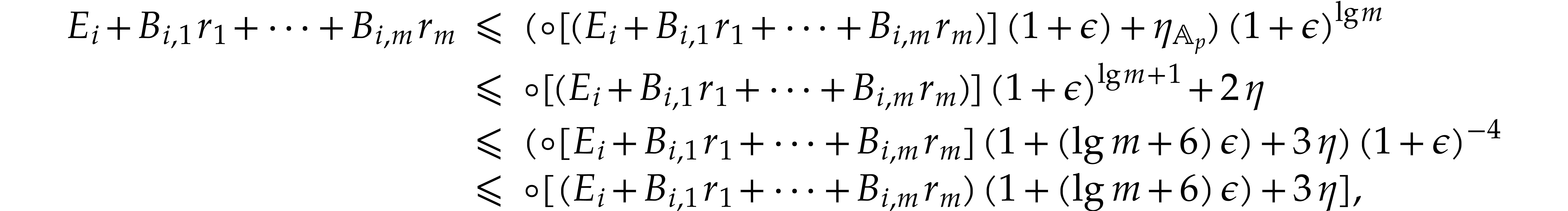
where we also used Lemma 2.1 and the fact that the
computation of 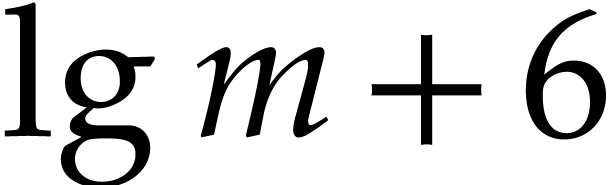 is exact.
is exact.
It is classical to extend ball arithmetic to other operations like
division, exponentiation, logarithm, trigonometric functions, etc. In
this section, we will focus on the particular case of division. It will
actually suffice to study reciprocals 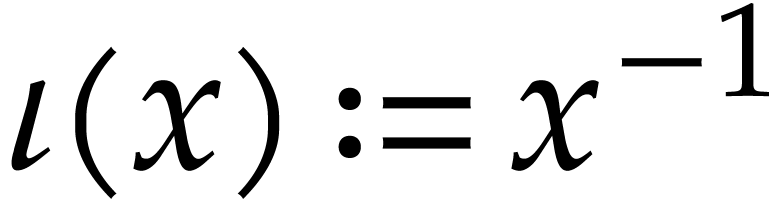 ,
since
,
since 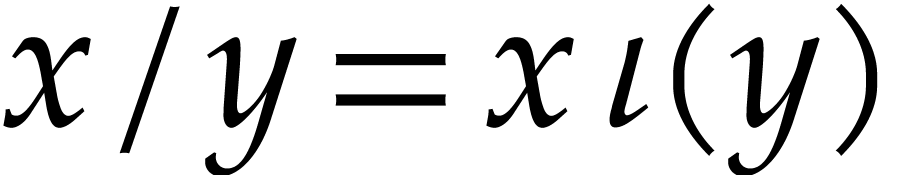 .
.
Divisions and reciprocals raise the new difficulty of divisions by zero.
We recall that the IEEE 754 provides a special not-a-number element NaN
in 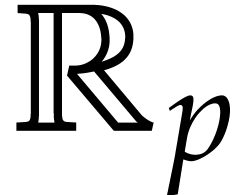 that corresponds to undefined results. All
arithmetic operations on NaN return NaN, so we may check whether some
error occurred during a computation, simply by checking whether one of
the return values is NaN. For exact arithmetic, we will assume that
that corresponds to undefined results. All
arithmetic operations on NaN return NaN, so we may check whether some
error occurred during a computation, simply by checking whether one of
the return values is NaN. For exact arithmetic, we will assume that  is extended in a similar way with an element
is extended in a similar way with an element  such that
such that 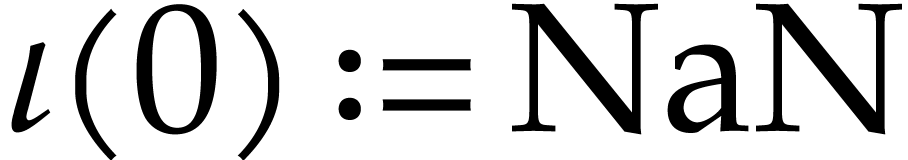 .
.
In the remainder of this section, assume that  or
or
 . In order to extend
reciprocals to balls, it is convenient to introduce the function
. In order to extend
reciprocals to balls, it is convenient to introduce the function
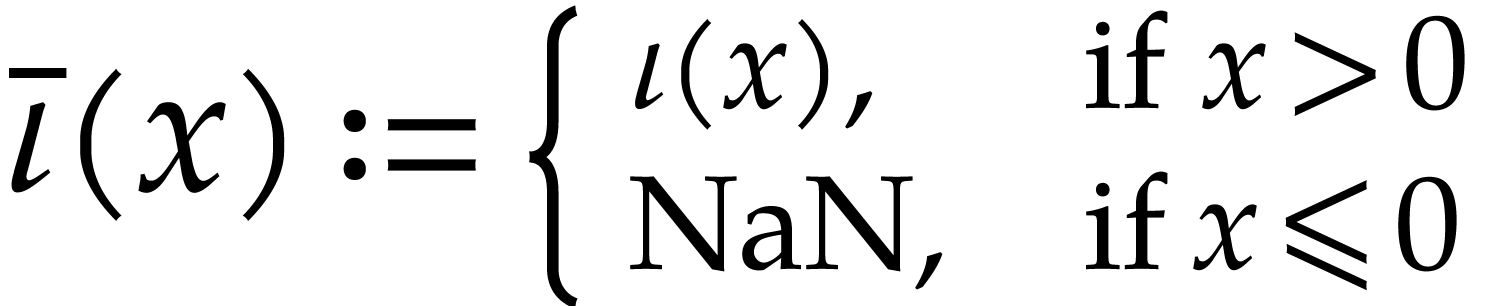
Then the exact reciprocal of a ball 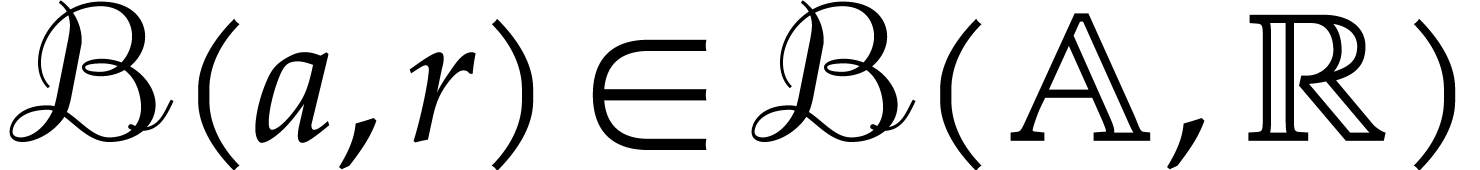 can be
defined as follows:
can be
defined as follows:
where we note that
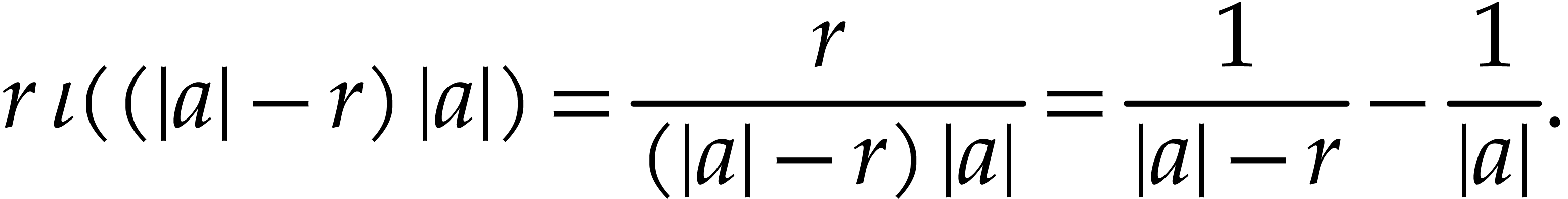
If  then we may also use the following formula
then we may also use the following formula
for transient ball arithmetic and
for semi-exact ball arithmetic.
We assume that the rounded counterpart of the reciprocal verifies the condition
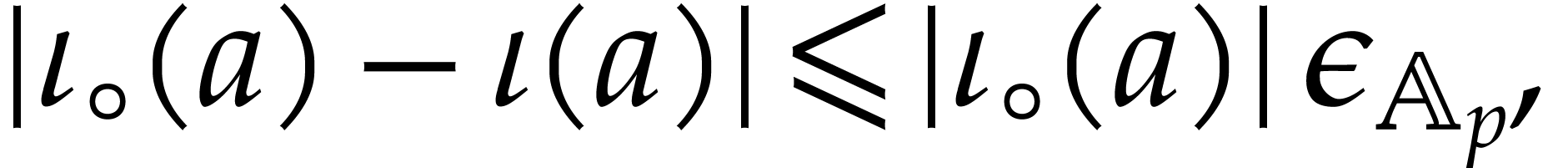 |
(4.4) |
for all invertible  in
in 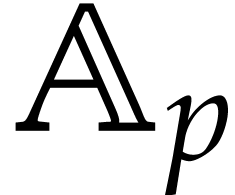 . For IEEE 754 arithmetic, this condition is
naturally satisfied for
. For IEEE 754 arithmetic, this condition is
naturally satisfied for 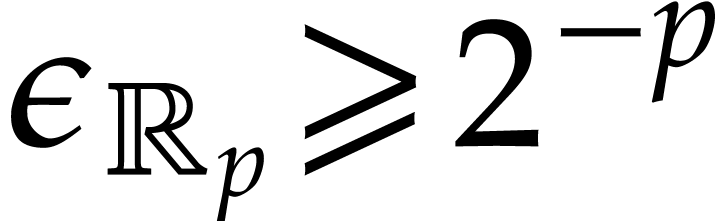 when
when 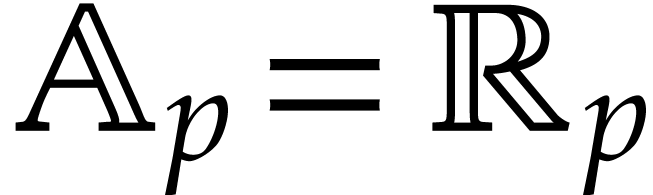 , and in absence of overflows and underflows.
If
, and in absence of overflows and underflows.
If 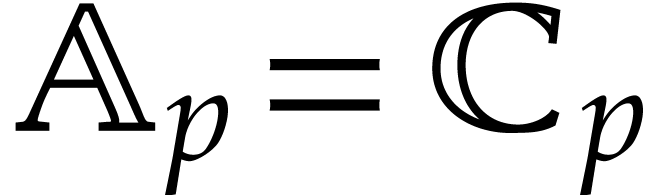 and
and  ,
then we compute reciprocals using the formula
,
then we compute reciprocals using the formula
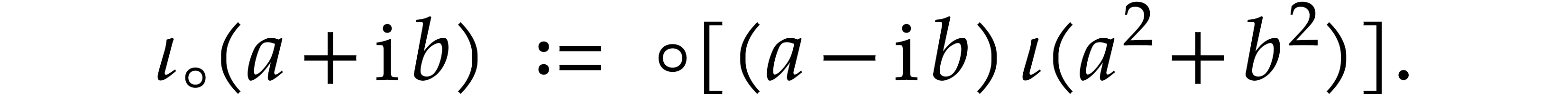
For this definition, we have
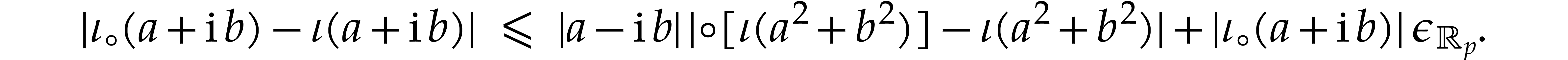
Now
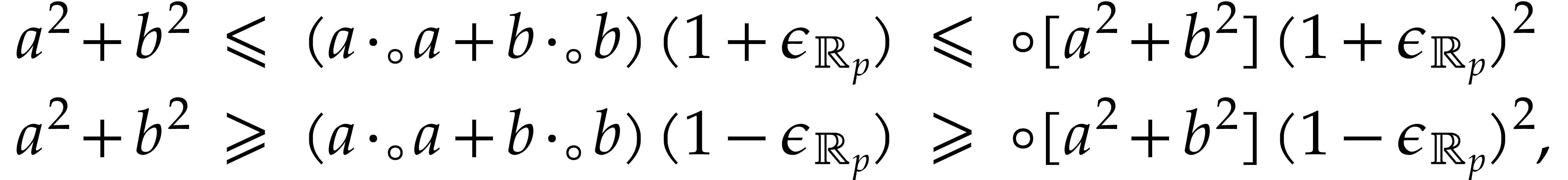
whence
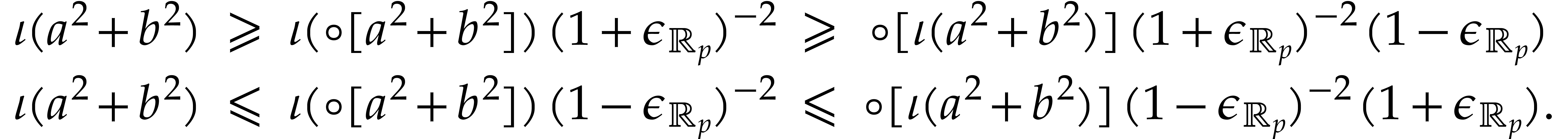
For 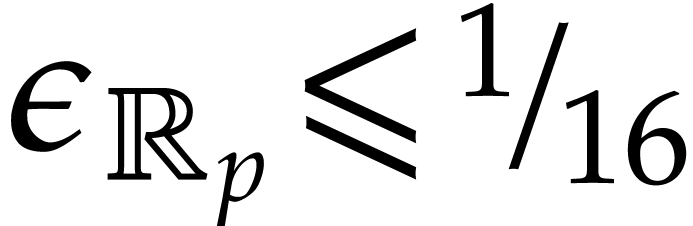 , it follows that
, it follows that
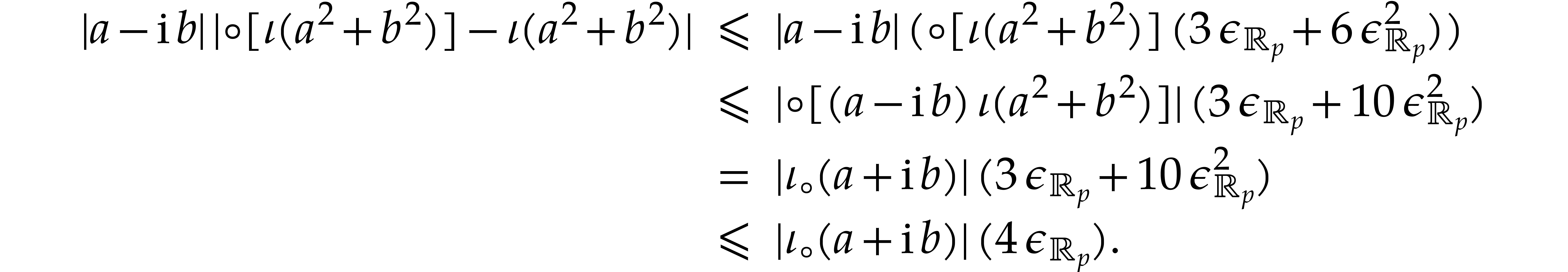
Consequently,
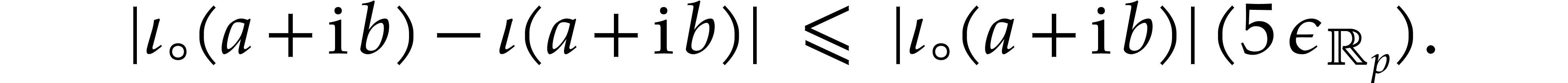
This shows that we may take 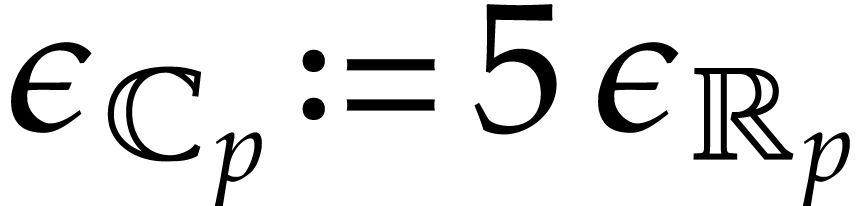 .
.
Let us denote 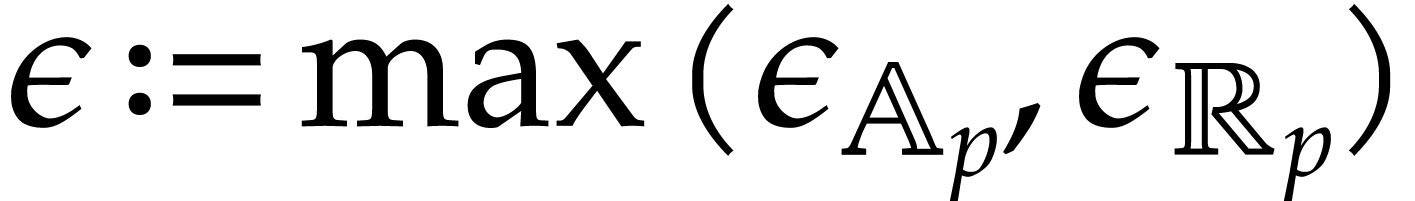 and assume that
and assume that 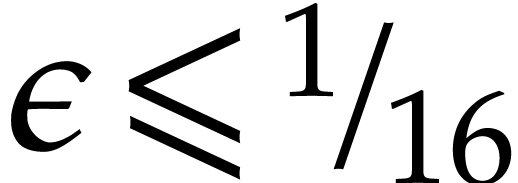 . We are now in a position to prove a
counterpart of Lemma 2.3 for division.
. We are now in a position to prove a
counterpart of Lemma 2.3 for division.
 and
and 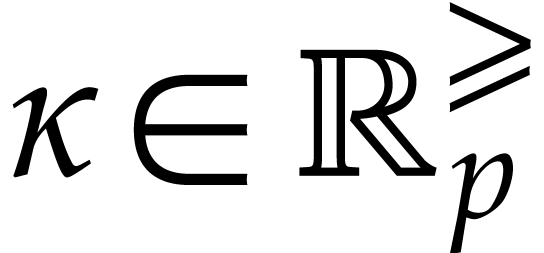 be
such that
be
such that 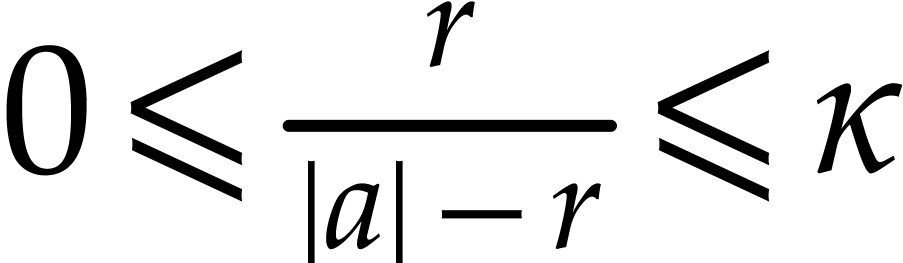 . Assume that the
computation of
. Assume that the
computation of
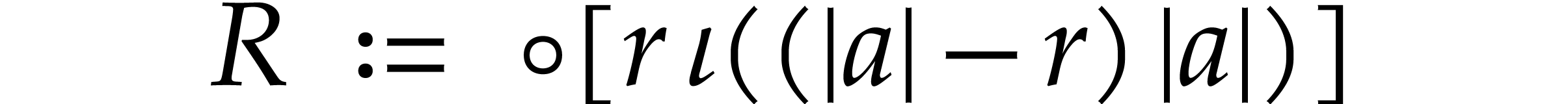
involves no overflows and no underflows. Then 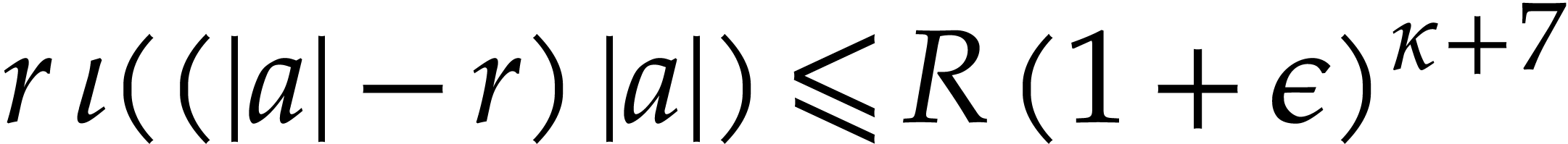 .
.
Proof. We have
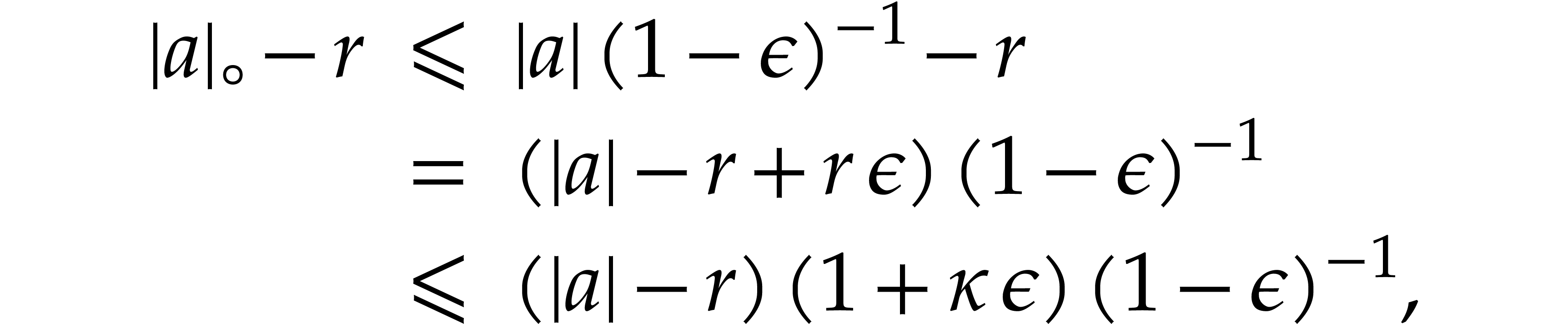
whence
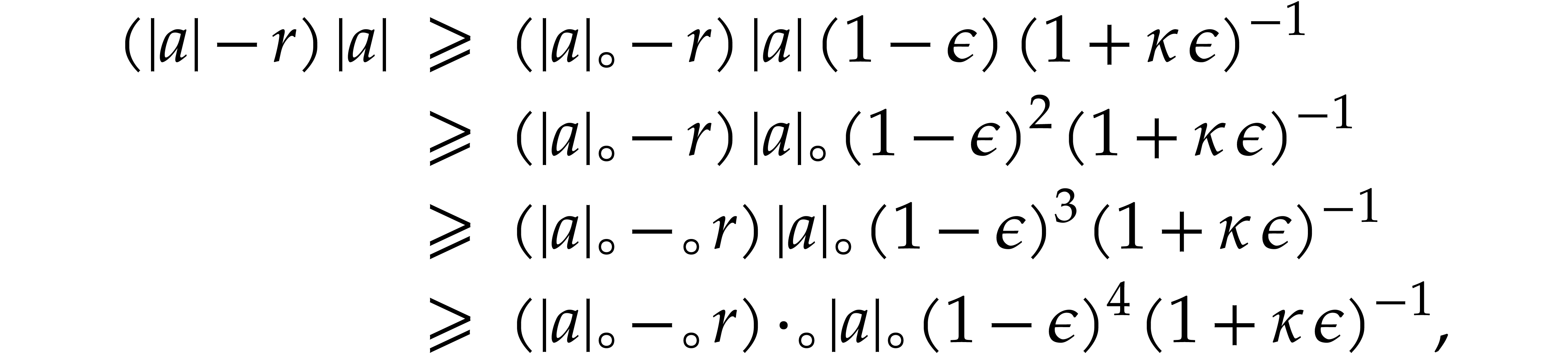
whence
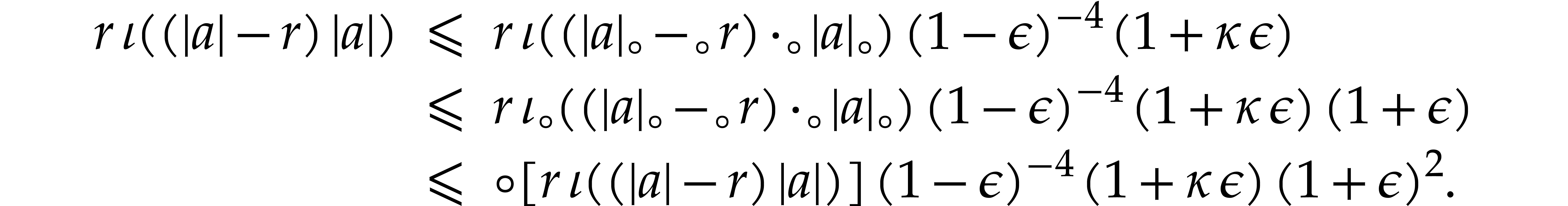
We conclude by observing that 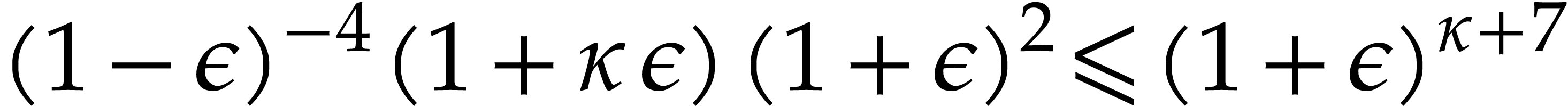 ,
since
,
since 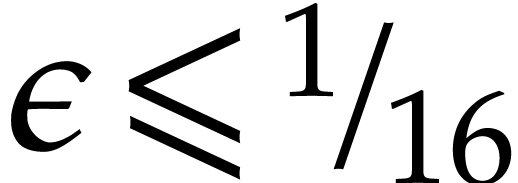 .
.
We adapt the definition of the remaining path length to our extended
notion of SLPs with reciprocals. We now take 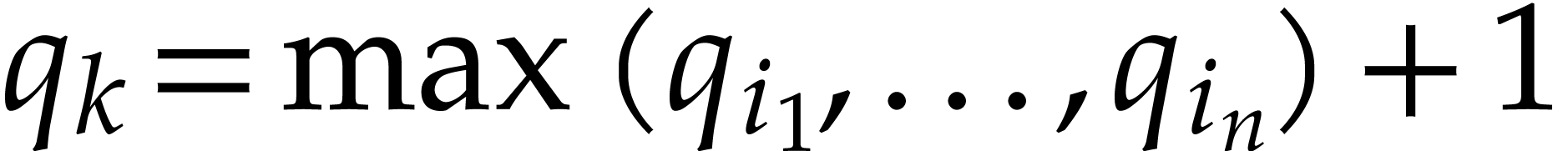 , where
, where  are those indices
are those indices
 such that
such that 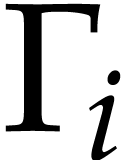 is of the form
is of the form
 with
with  ,
,
 , and
, and 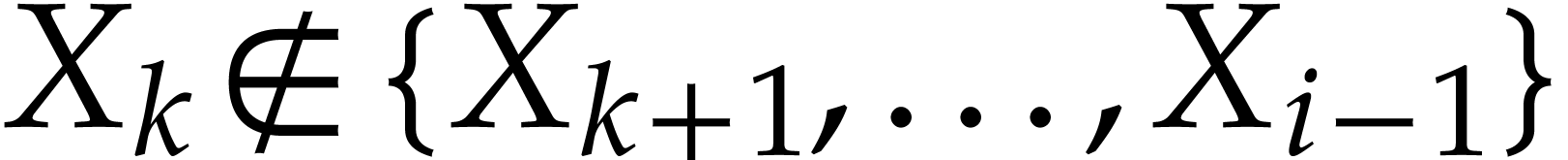 , or
, or  is of the form
is of the form 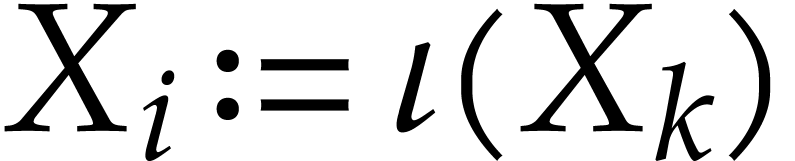 and
and 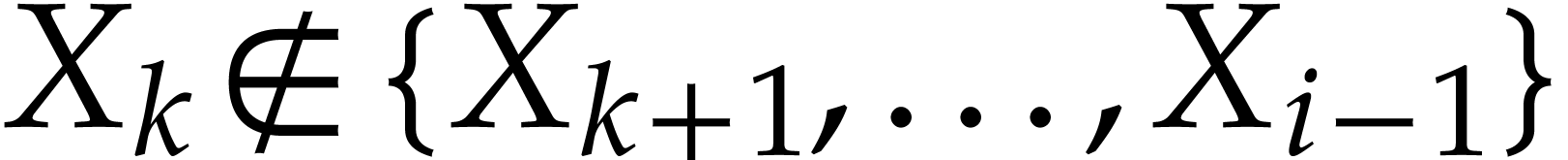 .
Lemma 4.1 allows us to extend Theorem 3.2 as
follows.
.
Lemma 4.1 allows us to extend Theorem 3.2 as
follows.
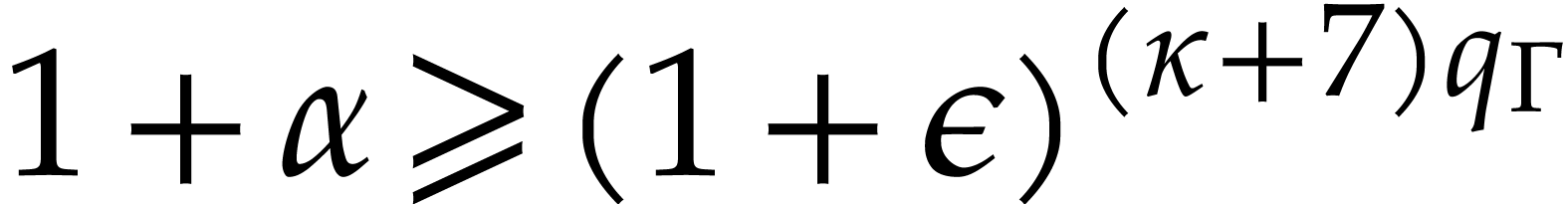 and that
and that  may also contain
reciprocals. During the second evaluation, assume that no underflow or
overflow occurs and that
may also contain
reciprocals. During the second evaluation, assume that no underflow or
overflow occurs and that 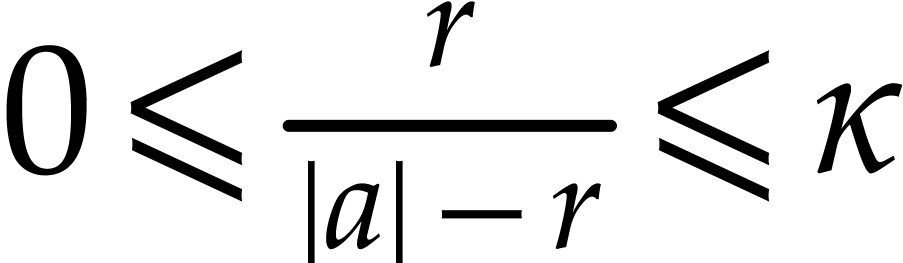 for every computation
of a reciprocal of
for every computation
of a reciprocal of  , where
, where
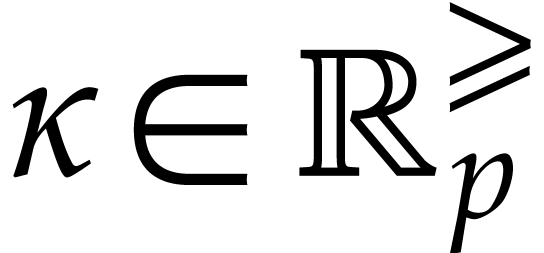 . Assume in addition that
. Assume in addition that
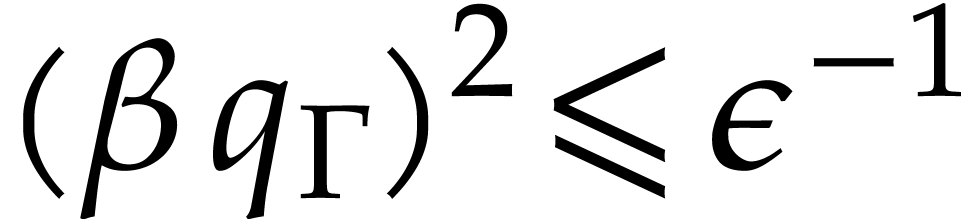 and that the following two inequalities
hold:
and that the following two inequalities
hold:
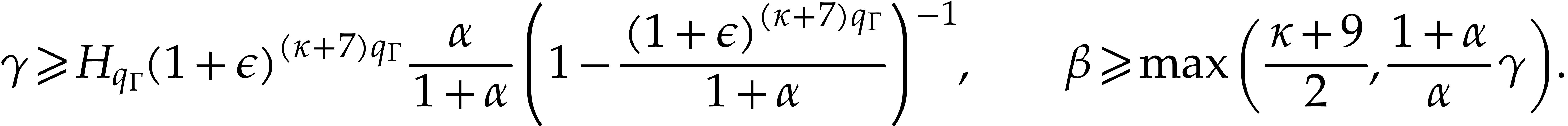
Then  for any corresponding outputs
for any corresponding outputs 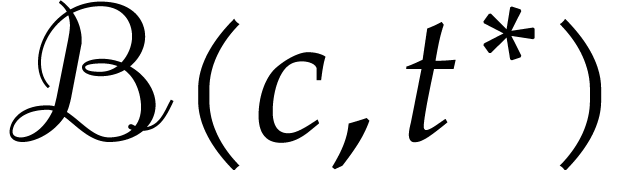 and
and 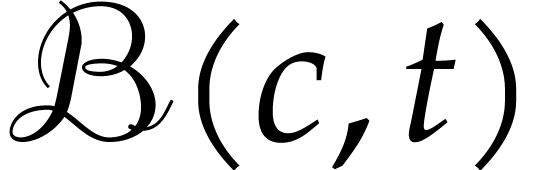 for the two
evaluations.
for the two
evaluations.
Proof. We adapt the proof of [10,
Theorem 5], by showing that the two inductions still go through in the
case of reciprocals. For the first induction, consider an instruction
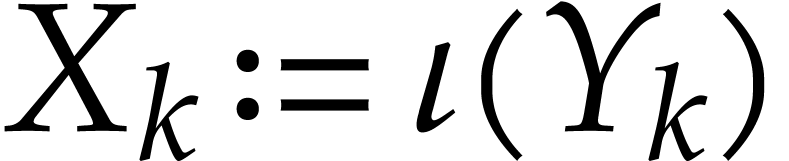 , where
, where  and
and 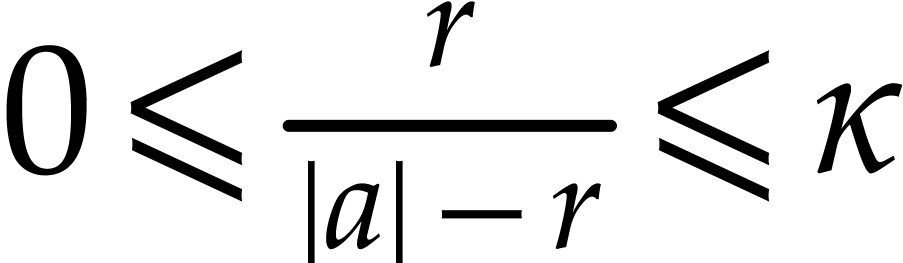 . Recall that
. Recall that
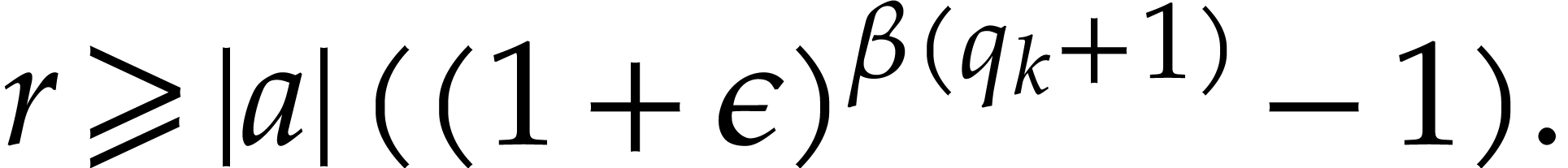
Using  ,
, 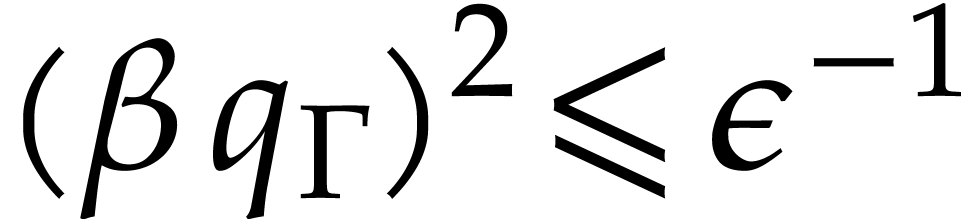 , and Lemma 2.1, we note that
, and Lemma 2.1, we note that
Combined with Lemmas 4.1 and 2.1, we deduce that
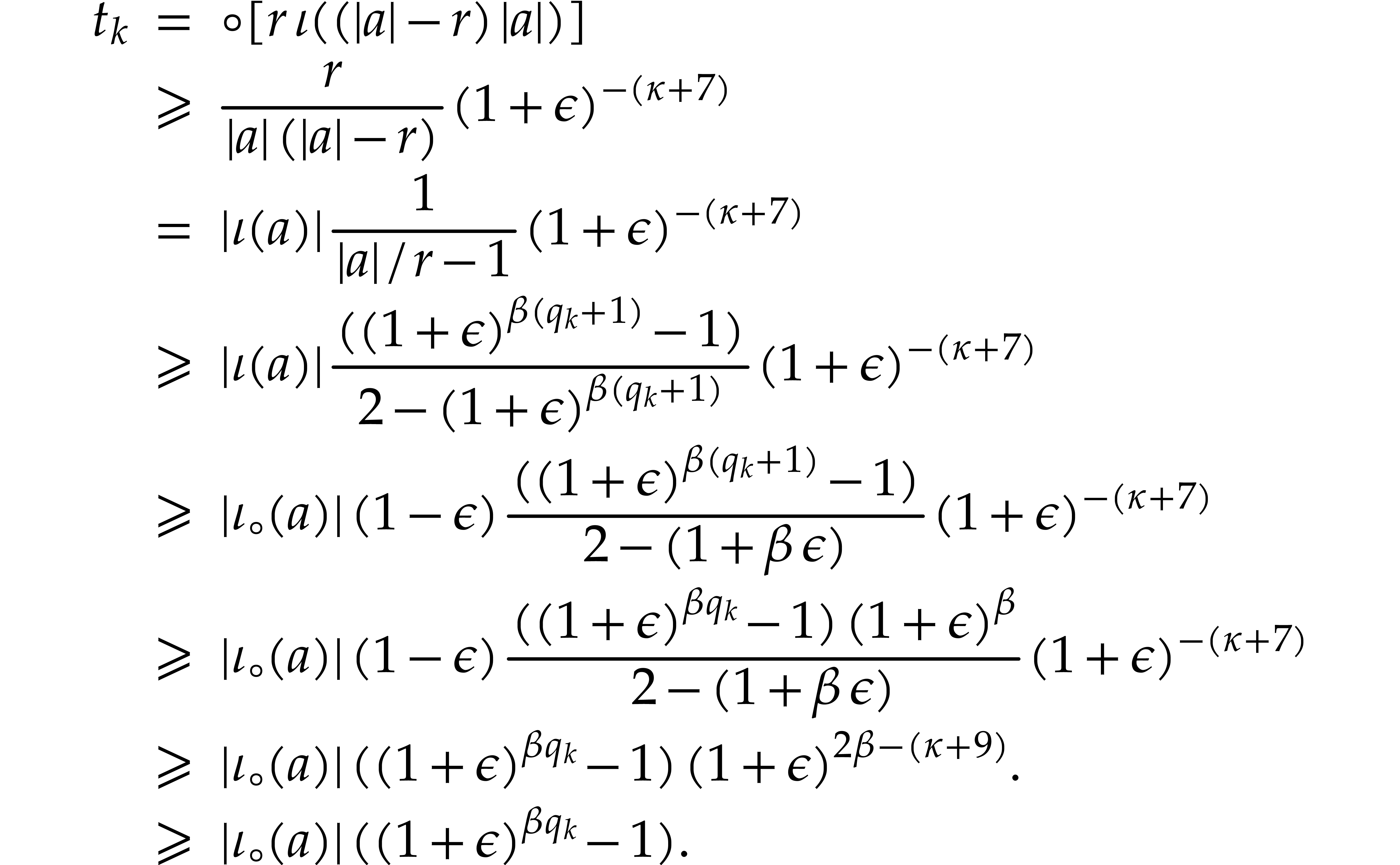
For the second induction, we redefine
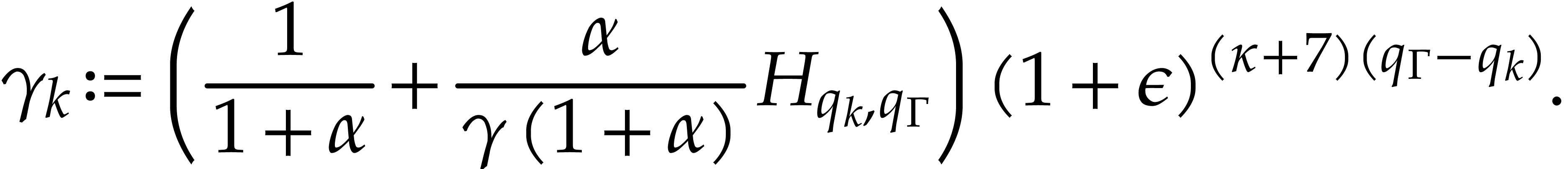
Assume 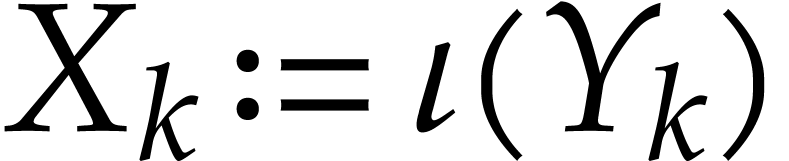 , let
, let 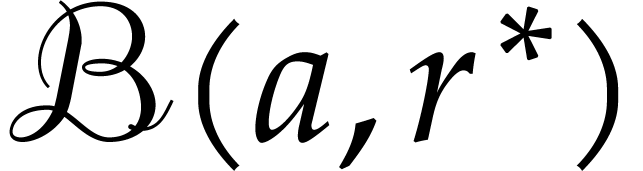 (resp.
(resp. 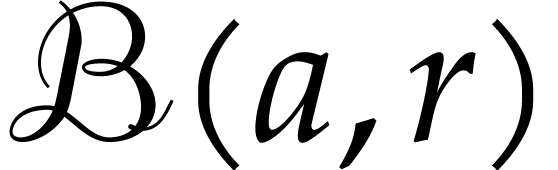 ) be the value of
) be the value of 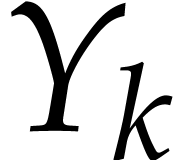 in the semi-exact evaluation (resp. transient
evaluation), and let
in the semi-exact evaluation (resp. transient
evaluation), and let  be the biggest index so
that
be the biggest index so
that 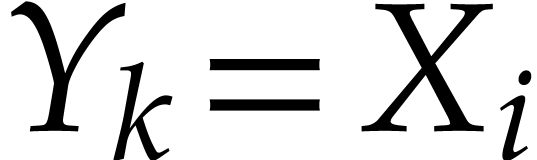 . Then
. Then
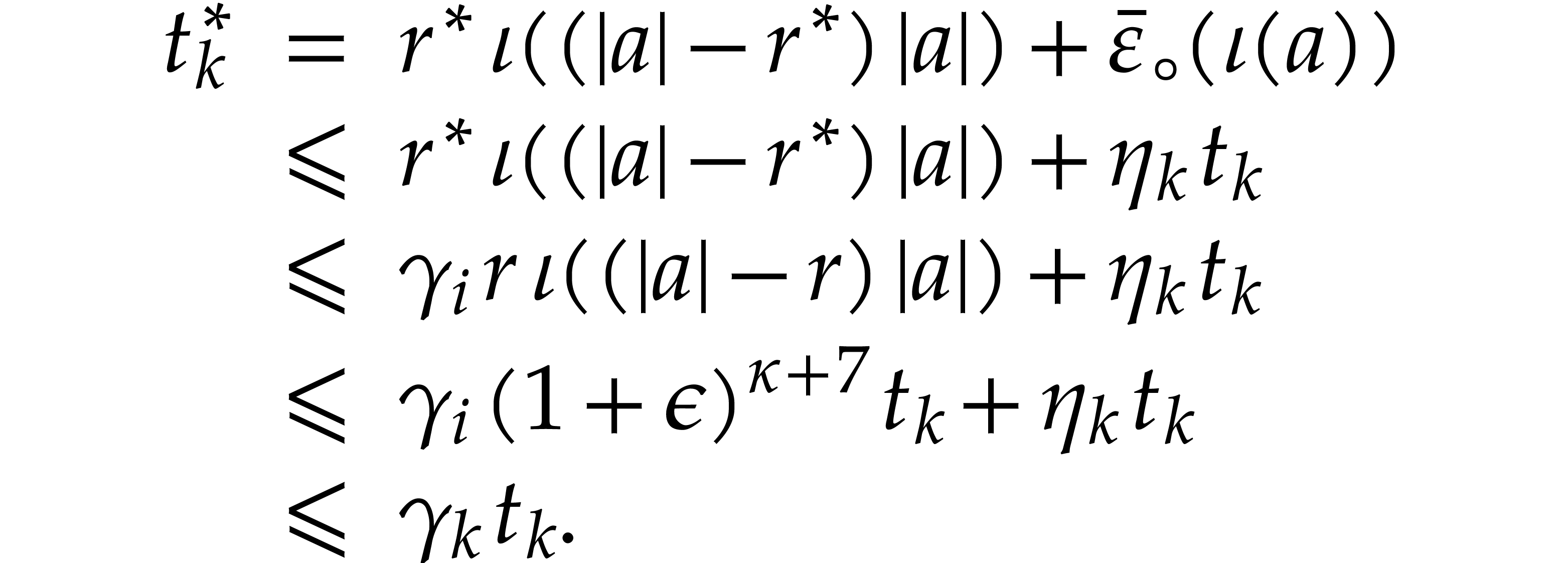
The two inductions still hold for the other operations since we
increased  and
and  .
.
If the conditions of the theorem are all satisfied for a given input
poly-ball 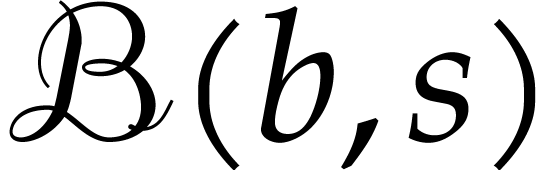 , then we note that
the numeric evaluation of the SLP at any point
, then we note that
the numeric evaluation of the SLP at any point  with
with  never results in a division by zero.
Conversely however, even when all these numerical evaluations are legit,
it may happen that the condition that
never results in a division by zero.
Conversely however, even when all these numerical evaluations are legit,
it may happen that the condition that 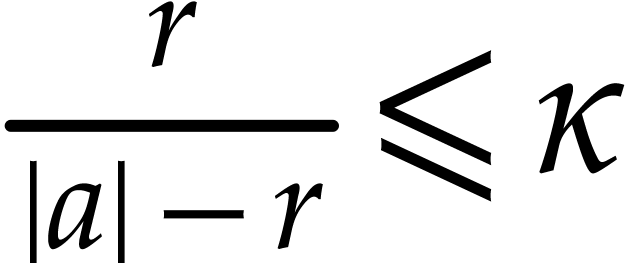 is
violated for the computation of some reciprocal
is
violated for the computation of some reciprocal 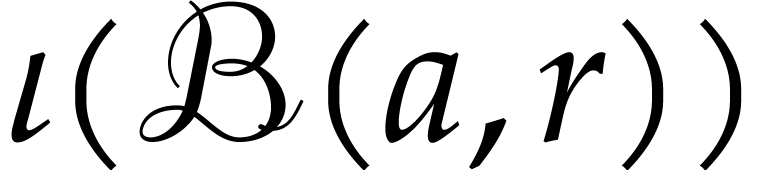 . This can either be due to an overly optimistic
choice of
. This can either be due to an overly optimistic
choice of  or to the classical phenomenon of
overestimation.
or to the classical phenomenon of
overestimation.
Intuitively speaking, a low choice of  means that
balls that need to be inverted should neatly steer away from zero, even
when inflating the radius by a small constant factor. In fact, this is
often a reasonable requirement, in which case one may simply take
means that
balls that need to be inverted should neatly steer away from zero, even
when inflating the radius by a small constant factor. In fact, this is
often a reasonable requirement, in which case one may simply take 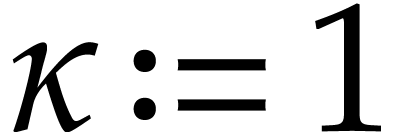 . A somewhat larger choice like
. A somewhat larger choice like
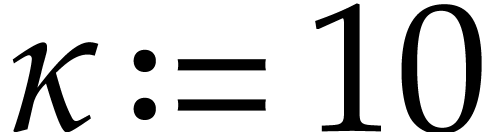 remains appropriate and has the advantage of
increasing the resilience of reciprocal computations (the condition
remains appropriate and has the advantage of
increasing the resilience of reciprocal computations (the condition 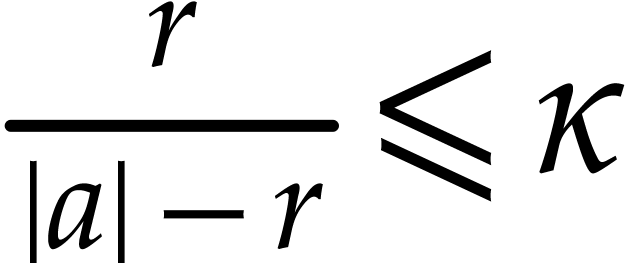 being easier to satisfy). Large values of
being easier to satisfy). Large values of  deteriorate the quality of the obtained bounds for a
dubious further gain in resilience.
deteriorate the quality of the obtained bounds for a
dubious further gain in resilience.
The formulas (4.1), (4.2), and (4.3)
for reciprocals can again be specialized to matryoshki modulo the
precaution that we should interpret  as a lower
bound for the norm. For
as a lower
bound for the norm. For 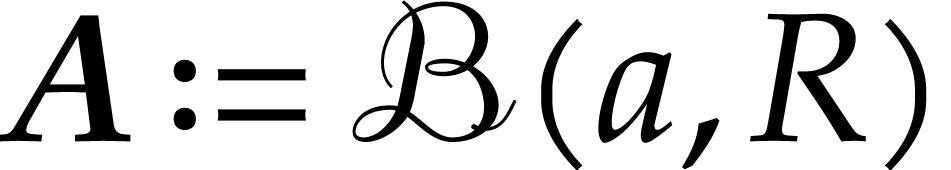 and
and 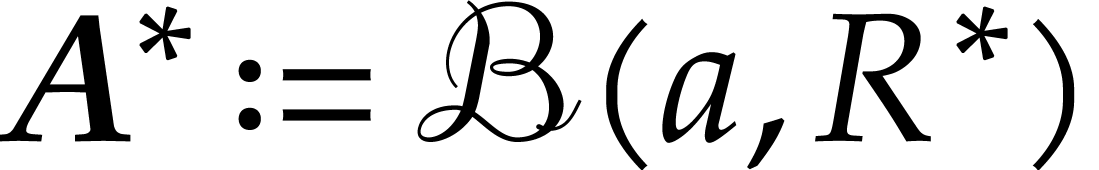 , this leads to the definitions
, this leads to the definitions
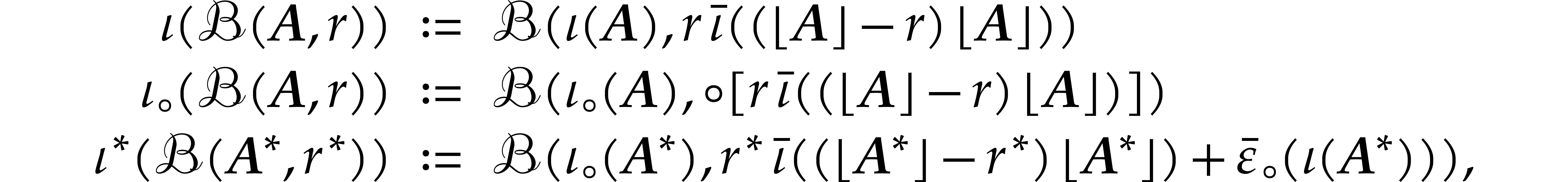
where we use the lower bound notation 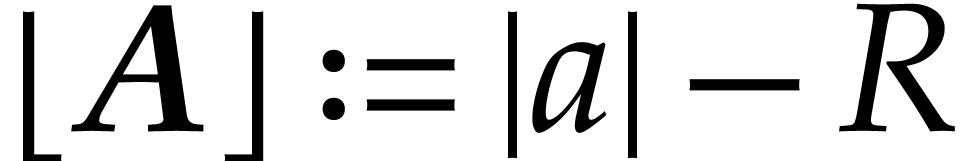 .
In addition to (2.9), we will assume that the rounded
counterpart of the reciprocals also verifies the condition
.
In addition to (2.9), we will assume that the rounded
counterpart of the reciprocals also verifies the condition
for all invertible balls  in
in 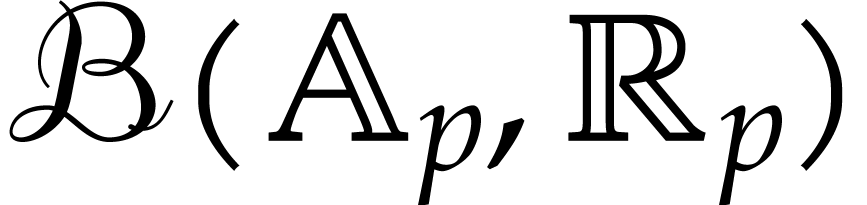 . For what follows, let
. For what follows, let 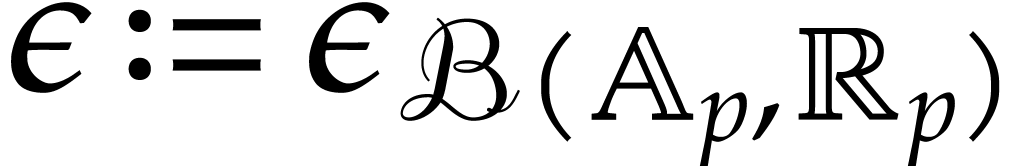 .
.
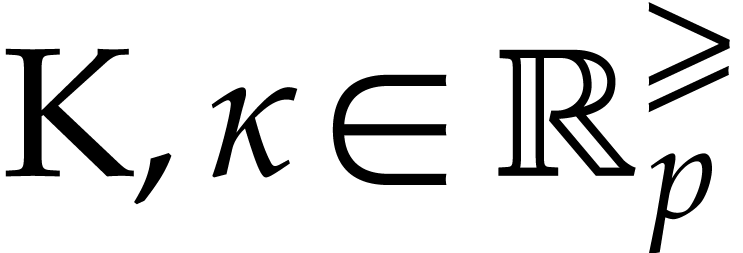 be such that
be such that 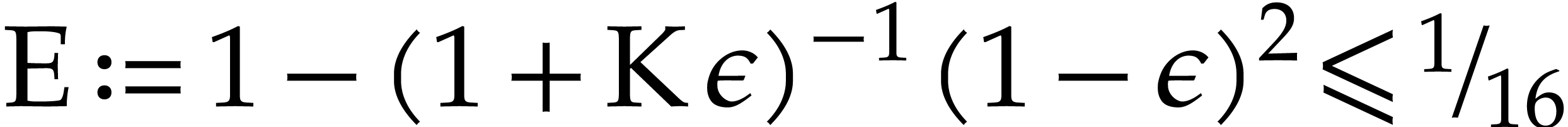 . Let
. Let  be such that
be such that
 and
and  .
If the computation of
.
If the computation of
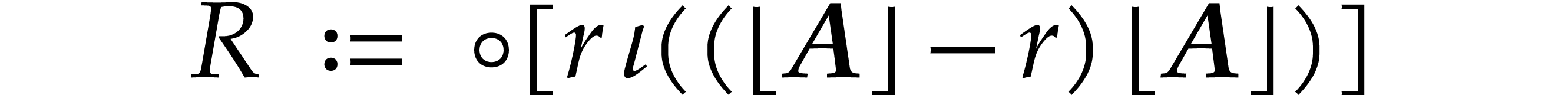
involves no overflows and no underflows, then 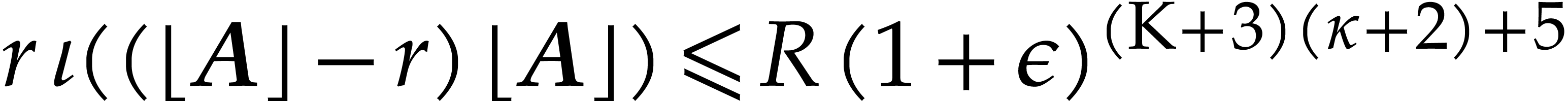 .
.
Proof. From
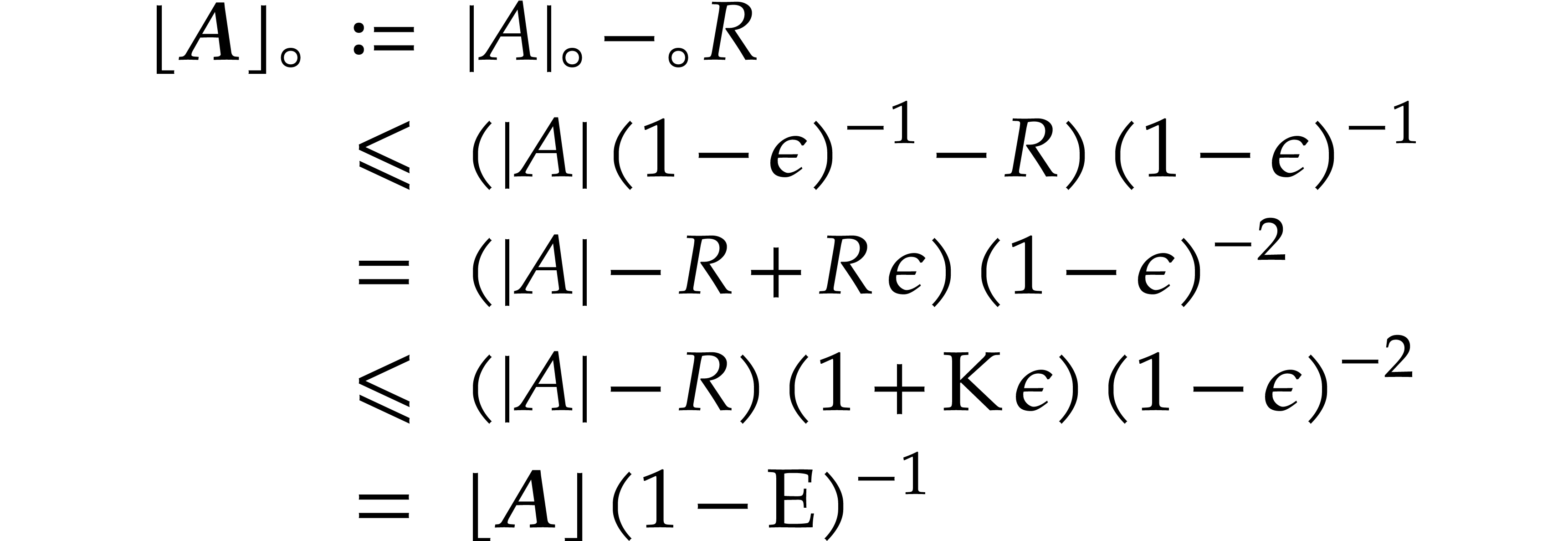
and
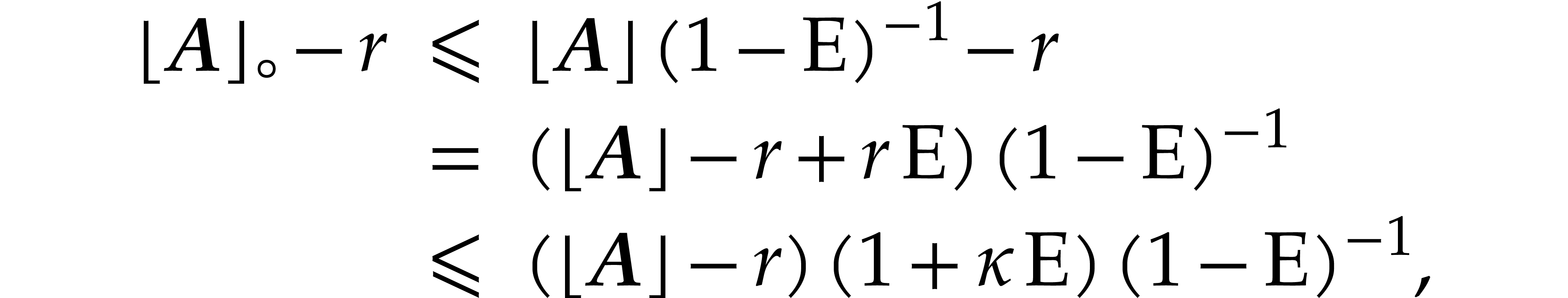
we obtain
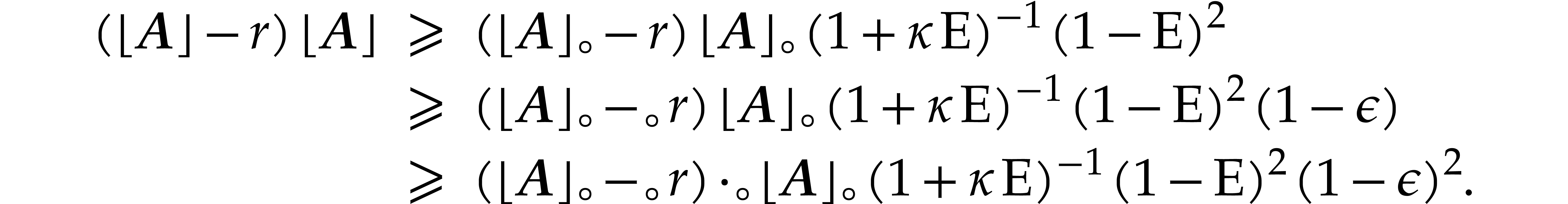
It follows that
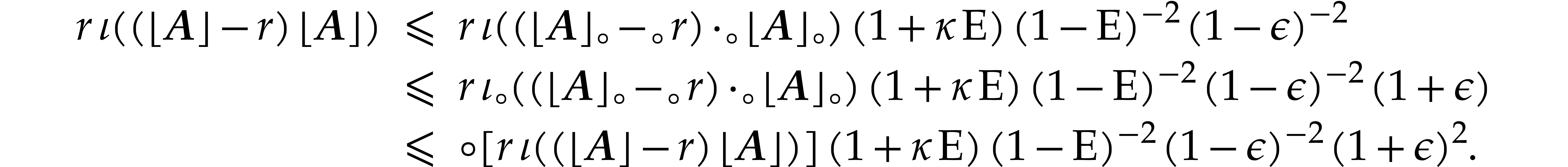
Using 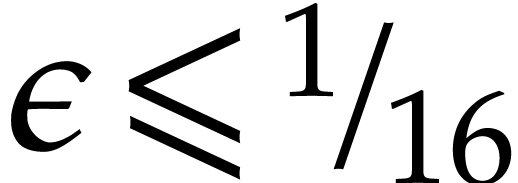 and
and 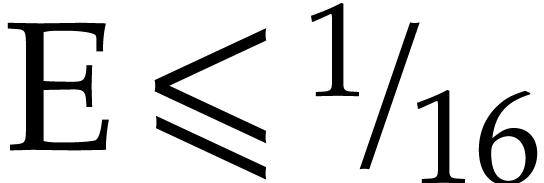 ,
we have
,
we have
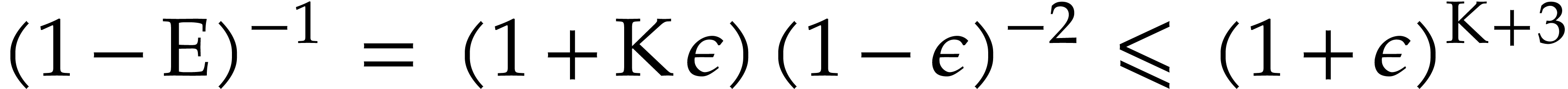
and then
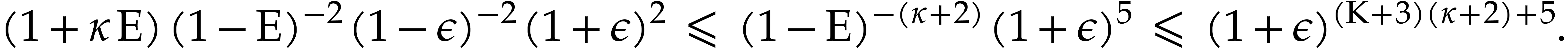

We are now ready to extend Theorem 3.4 to SLPs with reciprocals.
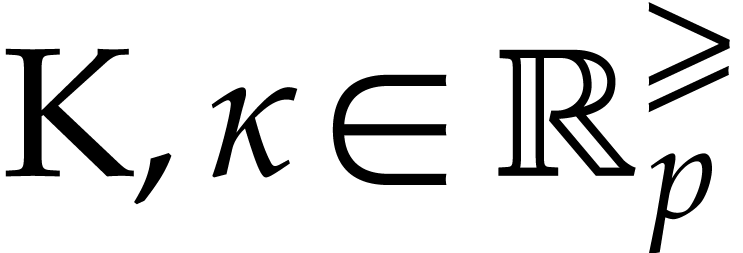 be such that
be such that 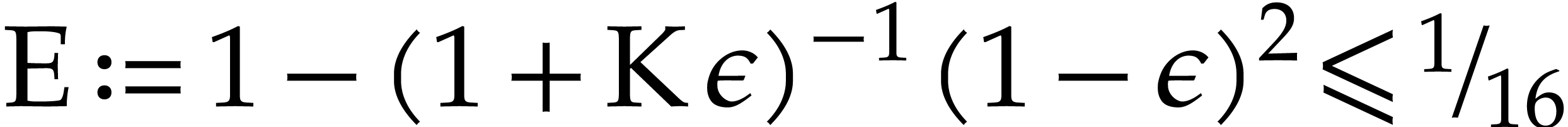 and let
and let
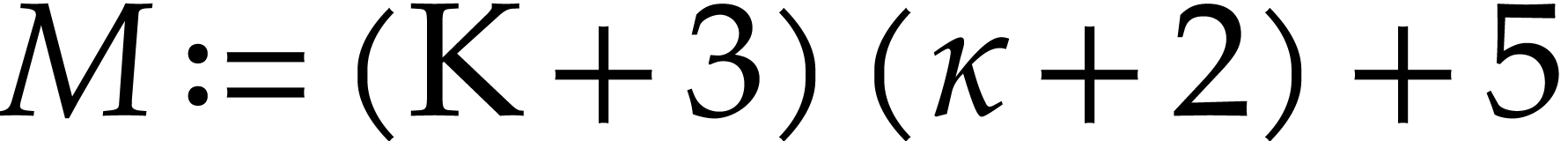 . With the setup from
Theorem 3.4, assume that
. With the setup from
Theorem 3.4, assume that 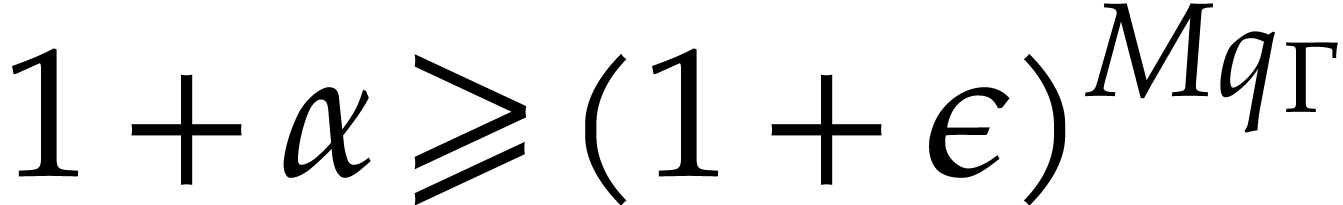 and that
and that
 may also contain reciprocals. During the
second evaluation, assume that no underflow or overflow occurs and
that
may also contain reciprocals. During the
second evaluation, assume that no underflow or overflow occurs and
that 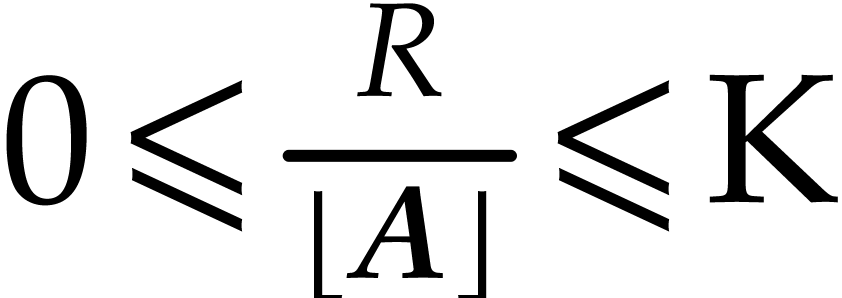 and
and 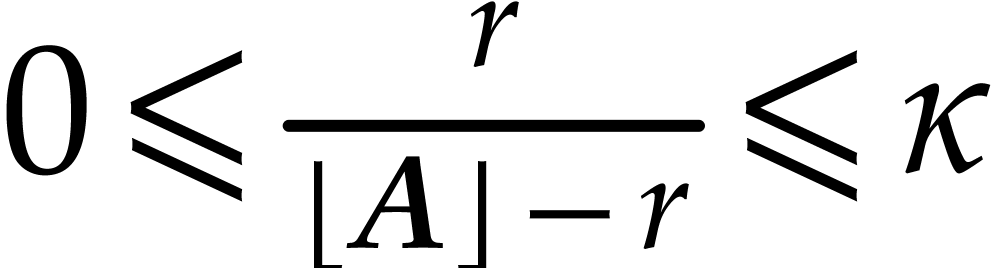 hold for
every computation of a reciprocal of
hold for
every computation of a reciprocal of 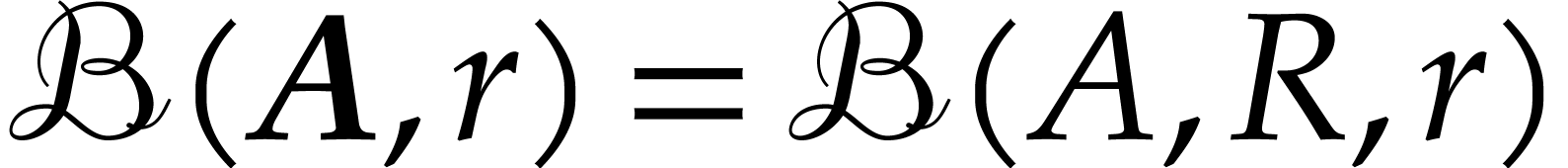 .
Assume in addition that
.
Assume in addition that 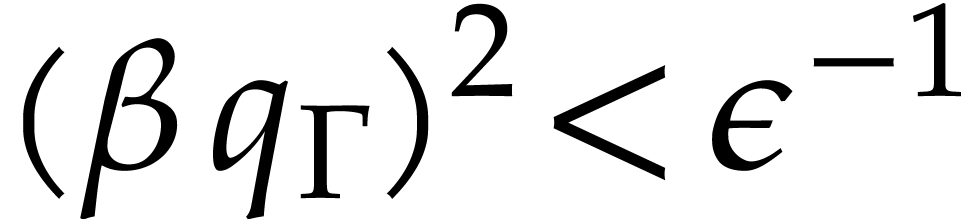 and that the following
two inequalities hold:
and that the following
two inequalities hold:
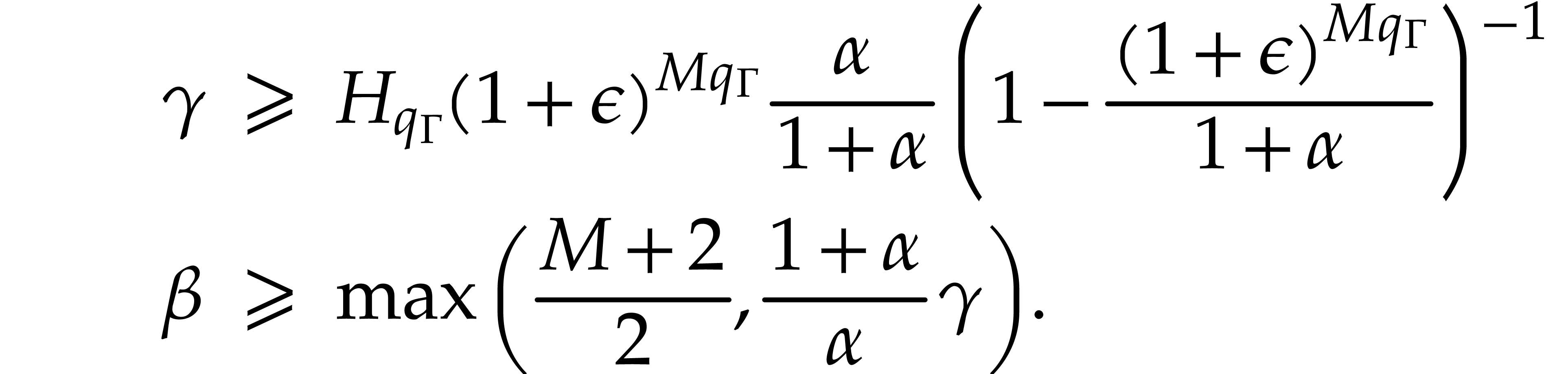
Then  and
and  for any
corresponding outputs
for any
corresponding outputs 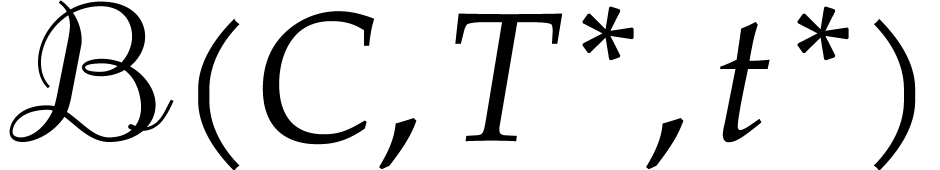 and
and 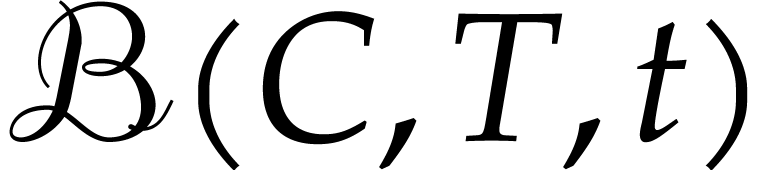 for the first and second evaluations.
for the first and second evaluations.
Proof. We adapt the proof of Theorem 3.4
by showing that the two inductions still go through in the case of
reciprocals. For the first induction, consider an instruction  , where
, where  , with
, with  and
and 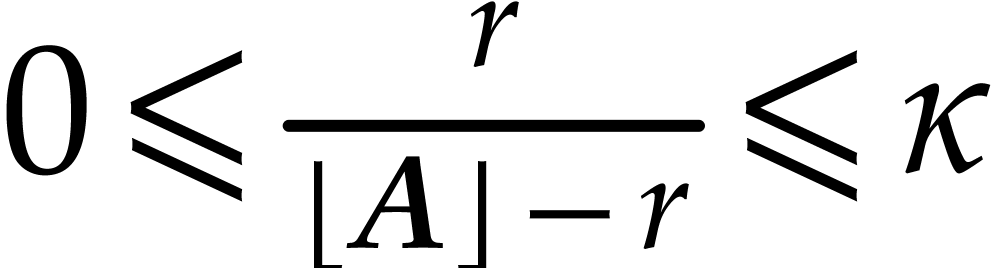 . Recall that
. Recall that
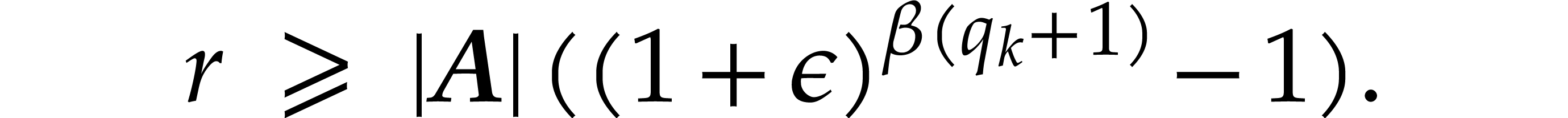
Using Lemma 4.3, the identity  ,
as well as
,
as well as
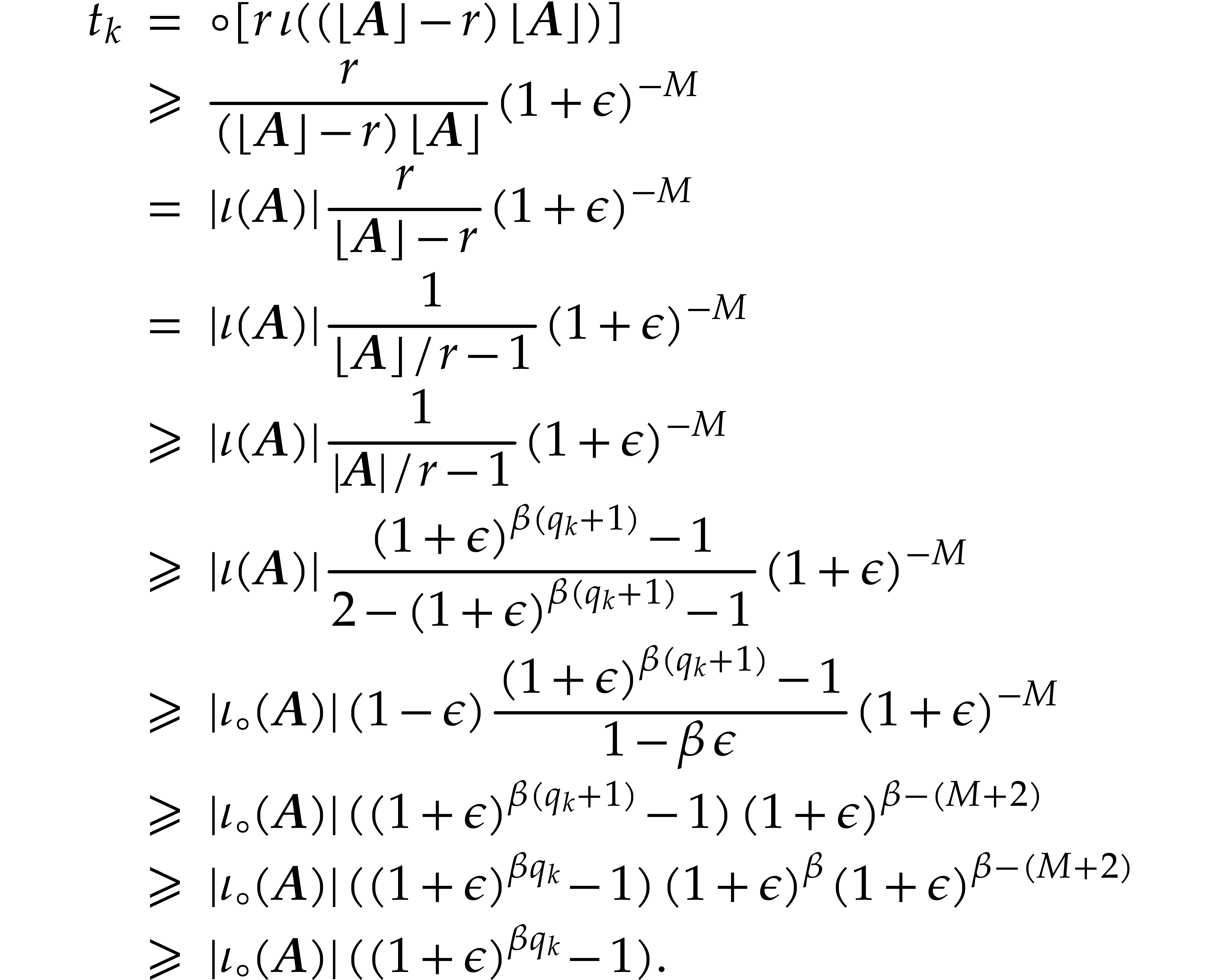
For the second induction, we redefine
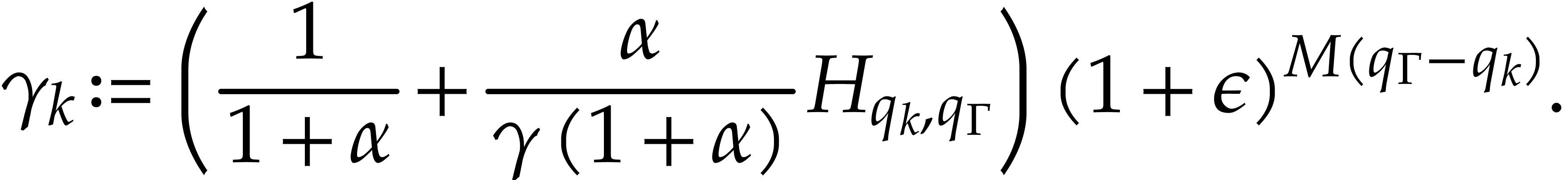
Assume 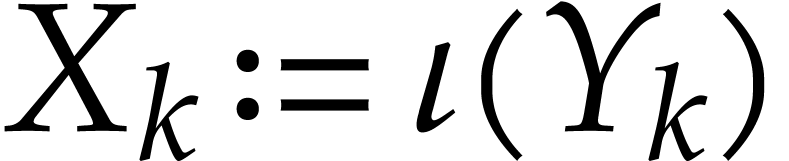 , let
, let  (resp.
(resp.  ) be the value of
) be the value of 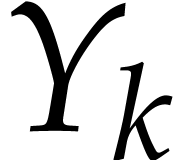 in the semi-exact evaluation (resp. transient
evaluation), and let
in the semi-exact evaluation (resp. transient
evaluation), and let  be the biggest index so
that
be the biggest index so
that 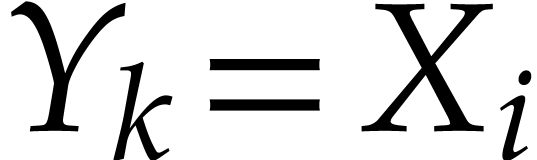 . Then Lemma 4.3
implies
. Then Lemma 4.3
implies
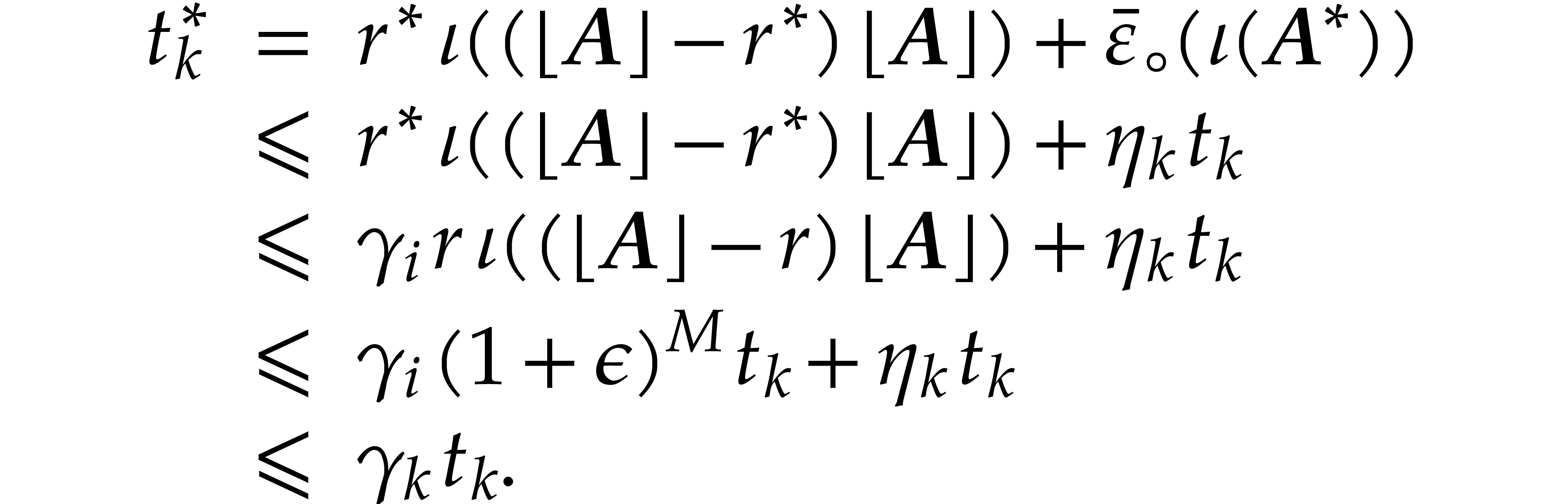
The two inductions still hold for the other operations since we
increased  and
and 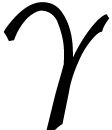 .
.
Similar comments as those made after Theorem 4.2 also apply
to the above theorem. In particular, we recommend taking  .
.
In the previous sections we have focussed on more efficient algorithms
for the reliable evaluation of functions on fixed bounded poly-balls.
This technique applies to very general SLPs that may involve operations
like division, which are only locally defined. Nonetheless, polynomial
SLPs, which only involve the ring operations 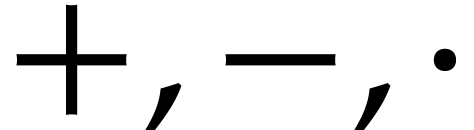 are
important for many applications such as numerical homotopy continuation.
In this special case, we will show how remove the locality restriction
and allow for the global evaluation of such SLPs in a reliable and
efficient way.
are
important for many applications such as numerical homotopy continuation.
In this special case, we will show how remove the locality restriction
and allow for the global evaluation of such SLPs in a reliable and
efficient way.
Consider a polynomial map
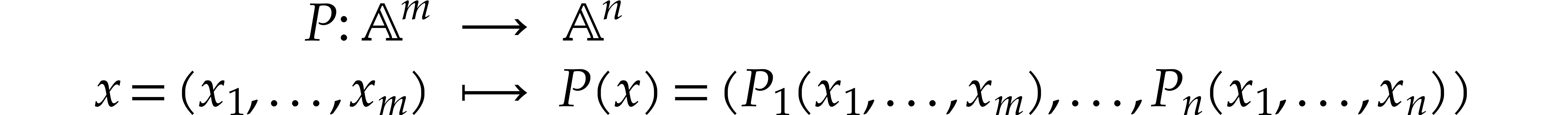
for polynomials  . Given
. Given 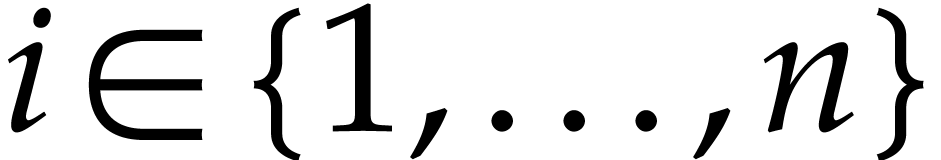 , the polynomial
, the polynomial 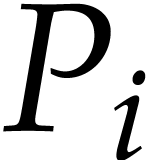 is not homogeneous, in general, but there exists a homogeneous
polynomial
is not homogeneous, in general, but there exists a homogeneous
polynomial 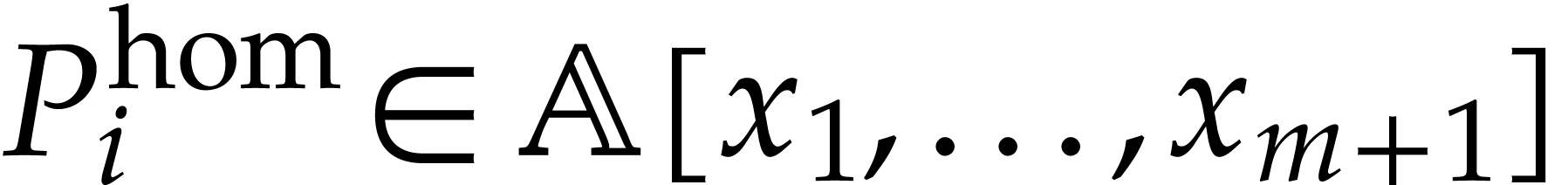 such that
such that 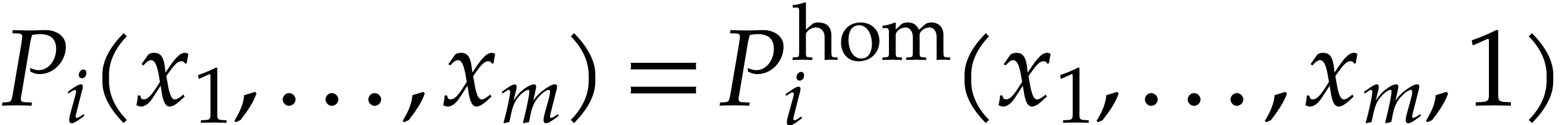 . This polynomial is unique up to multiplication by
powers of
. This polynomial is unique up to multiplication by
powers of 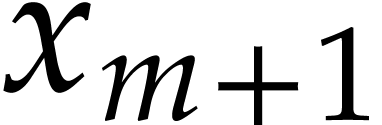 . The polynomials
. The polynomials
 give rise to a polynomial map
give rise to a polynomial map
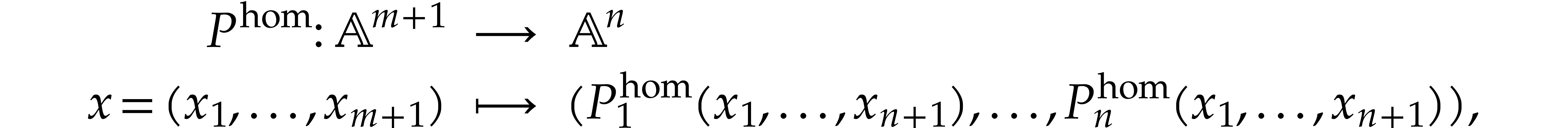
which we call a homogenization of 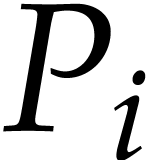 .
.
Assume now that the map 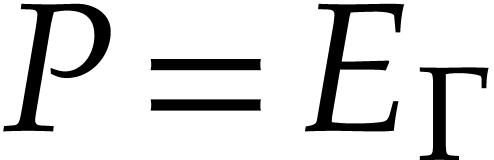 can be computed using an
SLP
can be computed using an
SLP  of length
of length 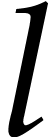 without
divisions. Let us show how to construct an SLP
without
divisions. Let us show how to construct an SLP 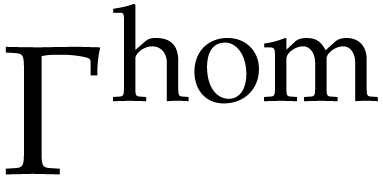 such that
such that 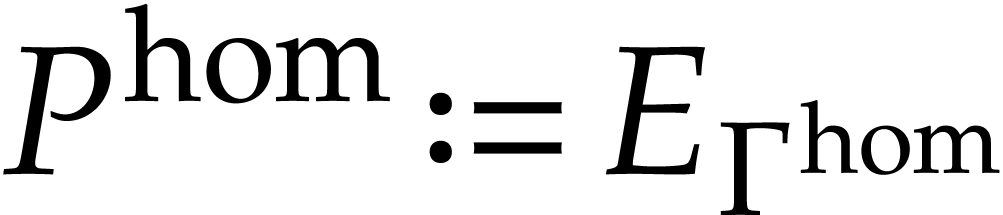 is a homogenization of
is a homogenization of 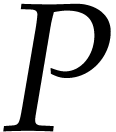 . Consider the formal evaluation of
. Consider the formal evaluation of  over
over  , by
applying
, by
applying  to the input arguments
to the input arguments  . Then the output value
. Then the output value 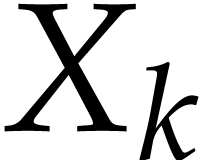 and the input arguments
and the input arguments 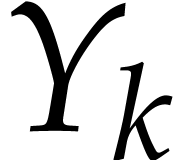 and
and 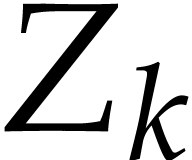 of an instruction
of an instruction 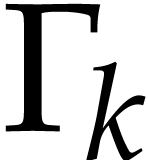 of the form
of the form 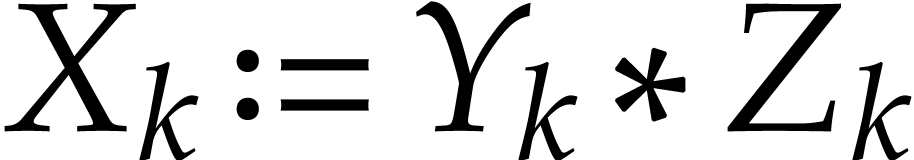 (
(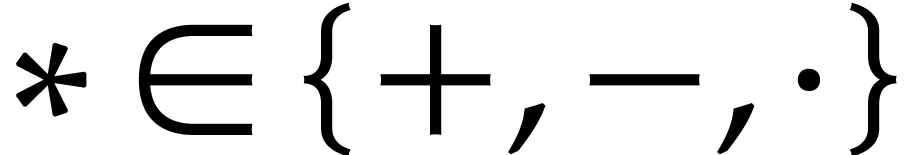 ) are polynomials in
) are polynomials in  that we denote by
that we denote by 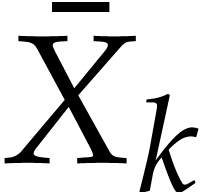
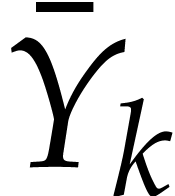 , and
, and 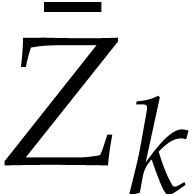 ,
respectively (for instructions
,
respectively (for instructions 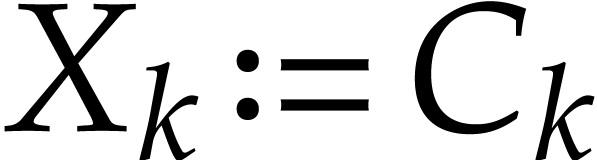 ,
we set
,
we set 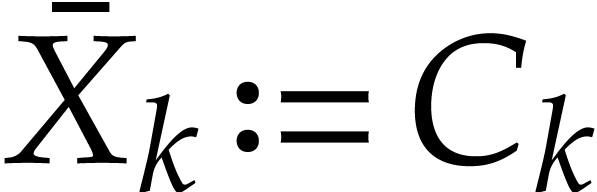 ). We can recursively
compute upper bounds
). We can recursively
compute upper bounds 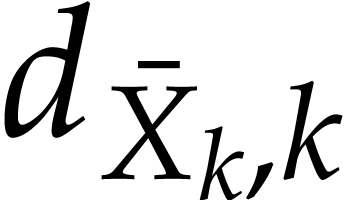 ,
, 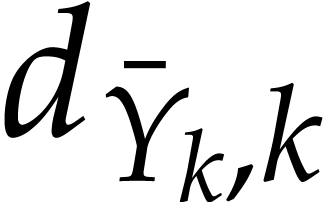 ,
, 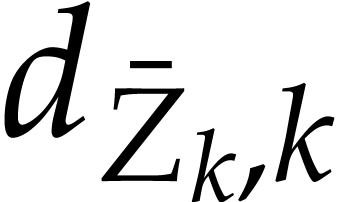 (abbreviated as
(abbreviated as 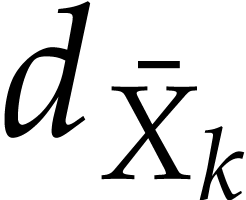 ,
, 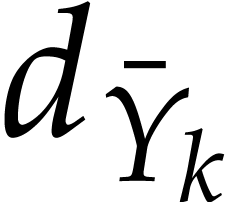 ,
, 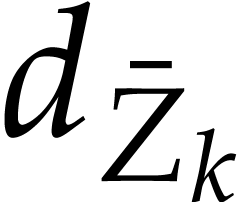 )
for the total degrees of these polynomials:
)
for the total degrees of these polynomials:
If 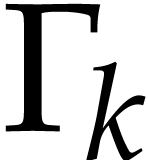 is of the form
is of the form 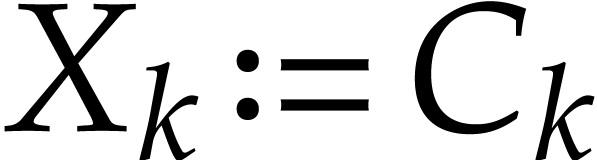 , then we take
, then we take 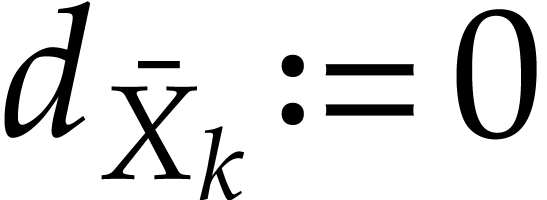 .
.
If  is of the form
is of the form  , then
, then 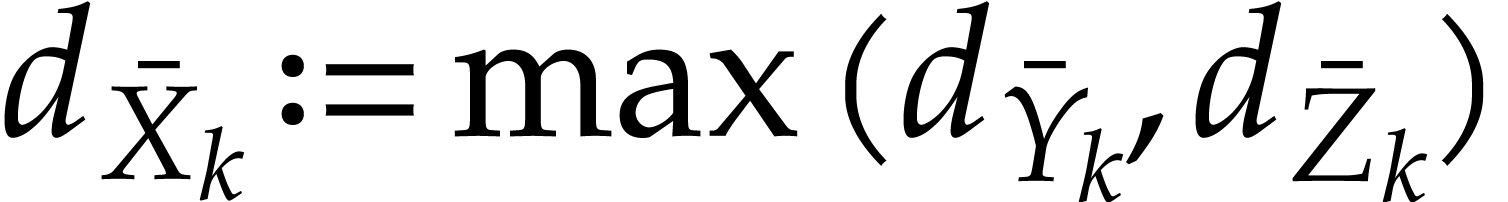 .
.
If 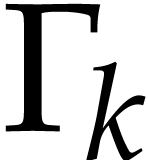 is of the form
is of the form 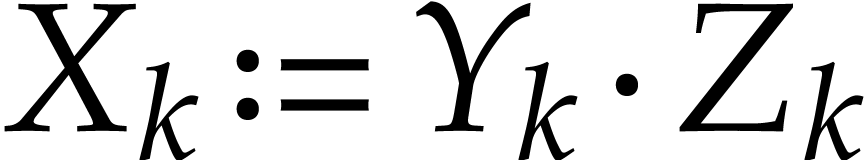 , then
, then 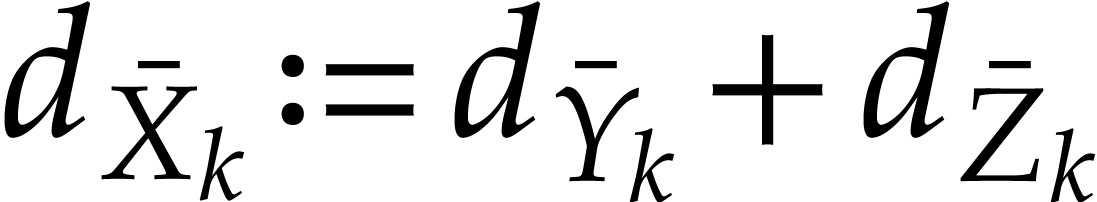 .
.
Here 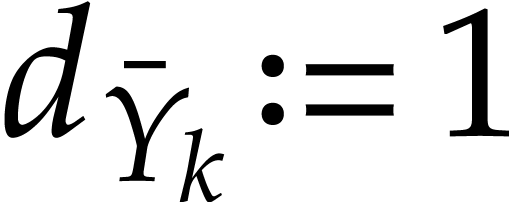 (resp.
(resp. 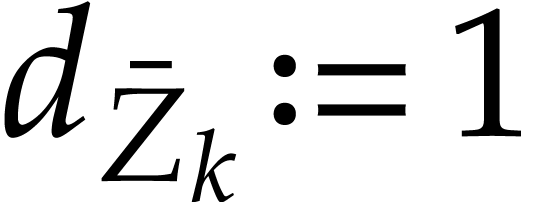 ) whenever
) whenever 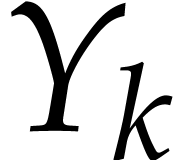 (resp.
(resp. 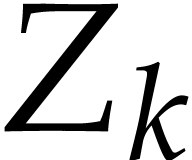 ) is an
input variable.
) is an
input variable.
Now consider the program  obtained by rewriting
each instruction
obtained by rewriting
each instruction 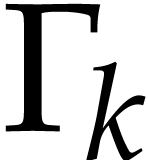 as follows:
as follows:
If 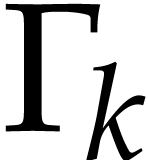 is of the form
is of the form 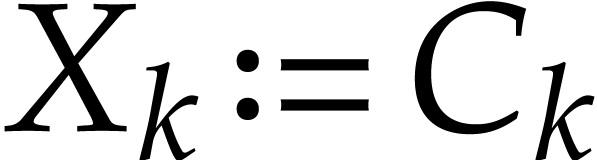 or
or
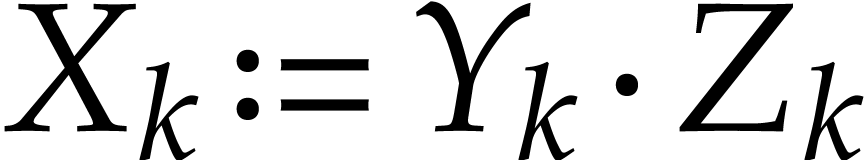 , then
, then 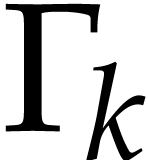 is rewritten into itself.
is rewritten into itself.
If 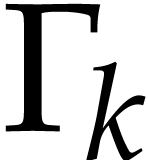 is of the form
is of the form 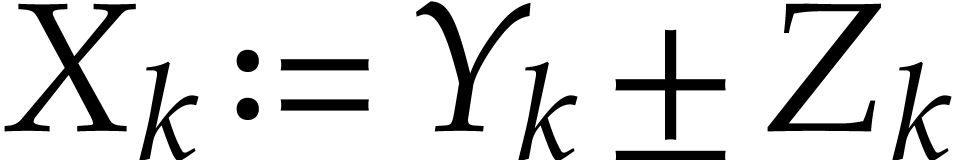 with
with  , then
, then 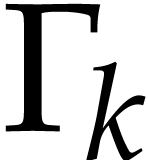 is rewritten into itself.
is rewritten into itself.
If 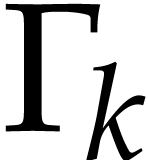 is of the form
is of the form  with
with  , then
, then 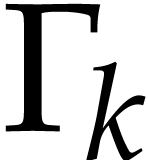 is rewritten into two instructions
is rewritten into two instructions 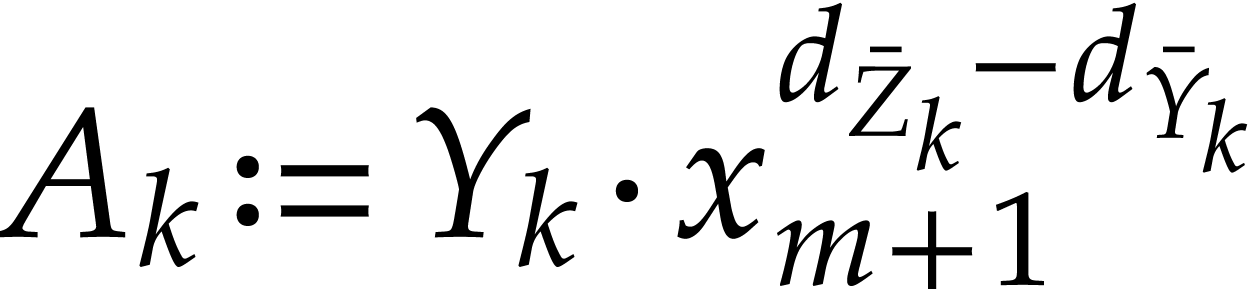 and
and 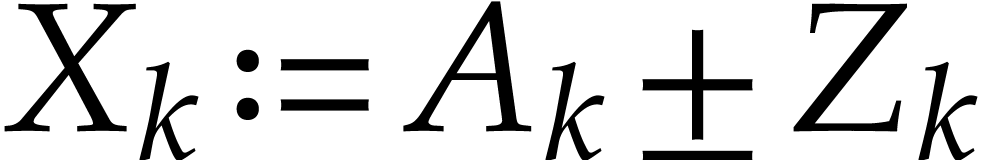 , for some new
auxiliary variable
, for some new
auxiliary variable 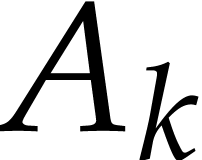 .
.
If  is of the form
is of the form 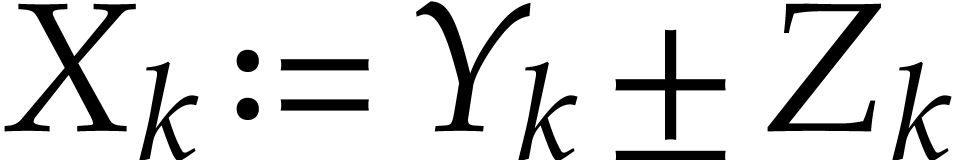 with
with  , then
, then  is rewritten into two instructions
is rewritten into two instructions  and
and 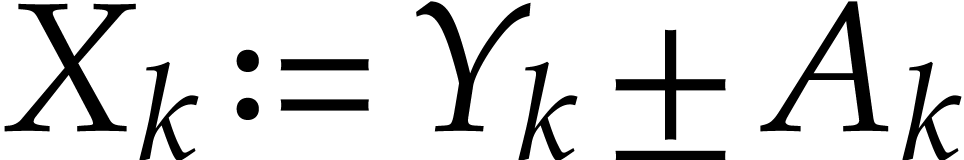 , for some new
auxiliary variable
, for some new
auxiliary variable 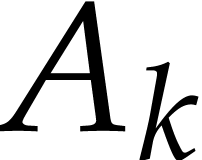 .
.
By induction, one verifies that the image of  under this rewriting computes the unique homogenization
under this rewriting computes the unique homogenization  of
of 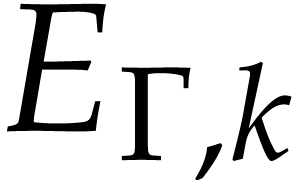 of degree
of degree 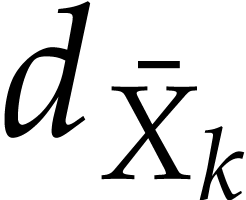 for
for 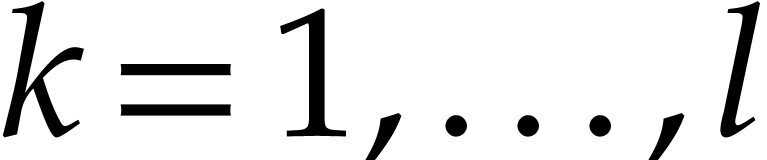 . We obtain
. We obtain 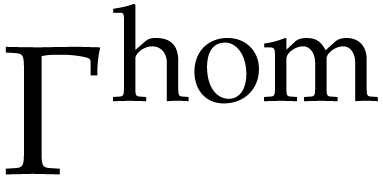 by prepending
by prepending  with instructions that compute all
powers
with instructions that compute all
powers 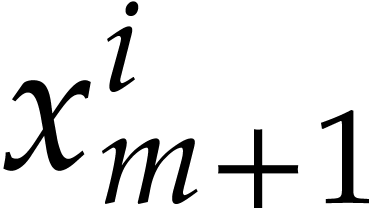 that occur in
that occur in  . This can for instance be done using binary
powering:
. This can for instance be done using binary
powering: 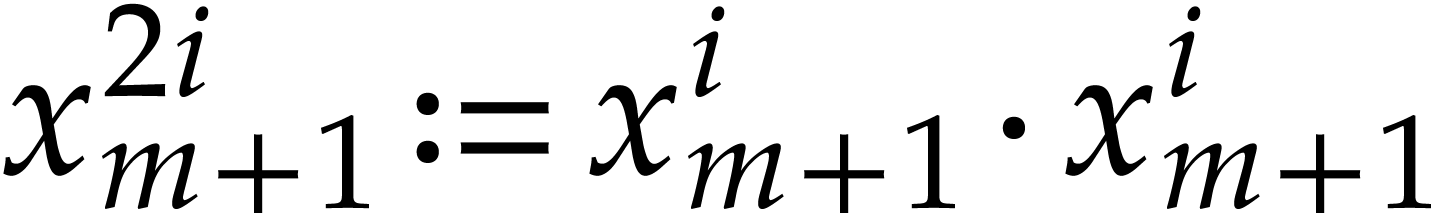 and
and 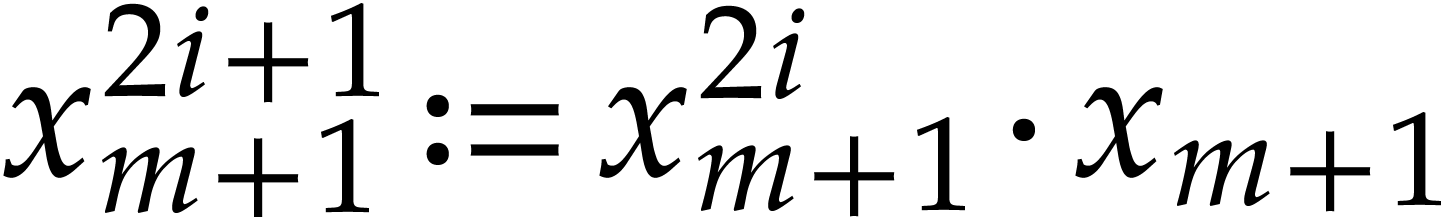 for all
for all
 .
.
Example
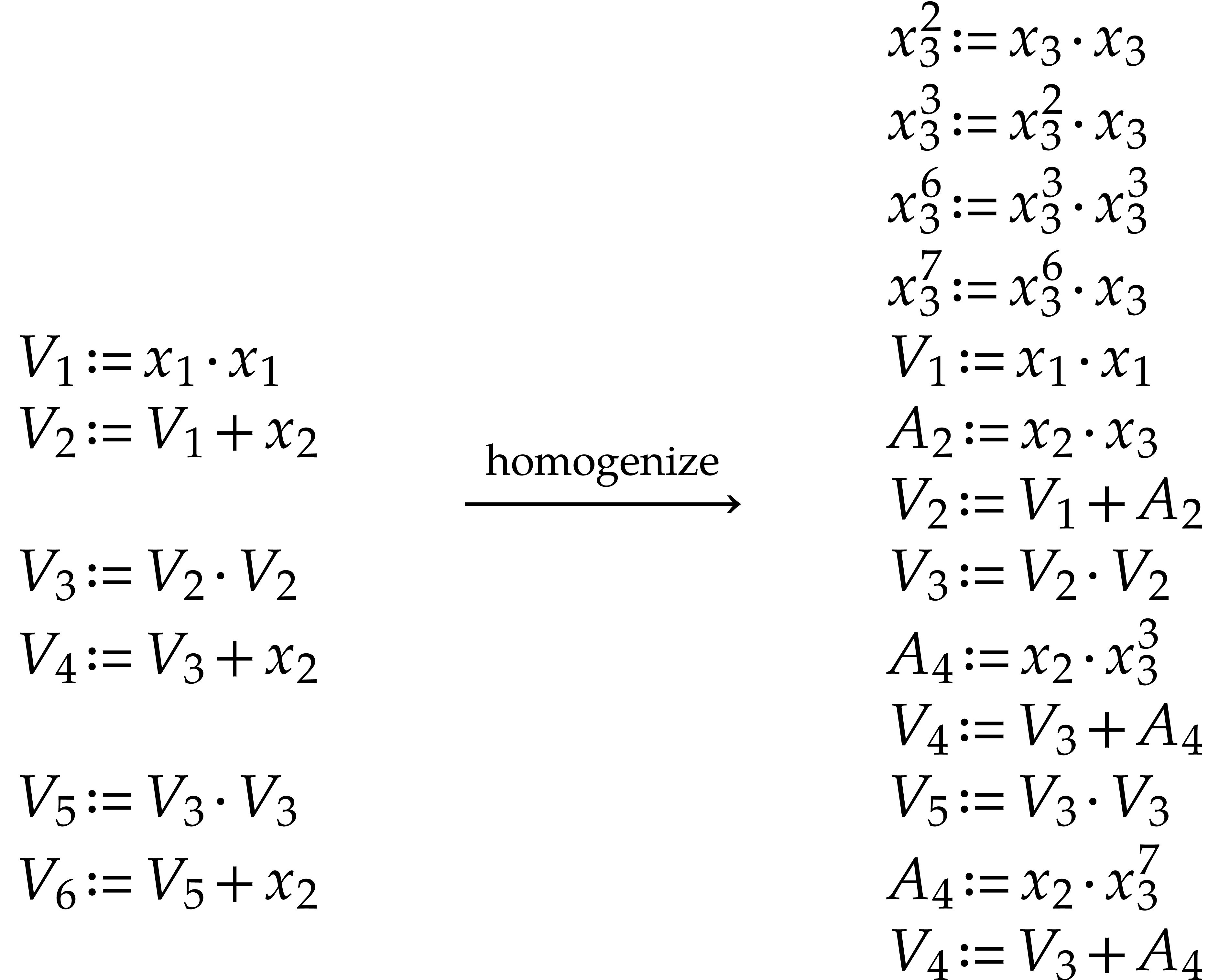
In this example, 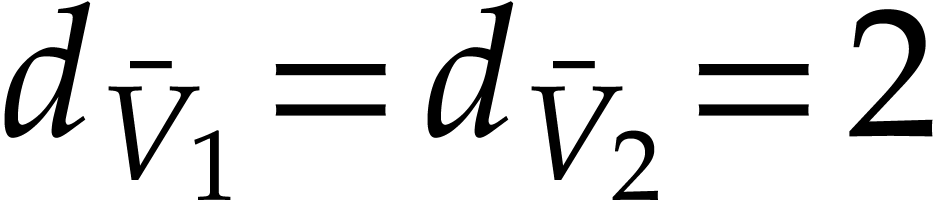 ,
, 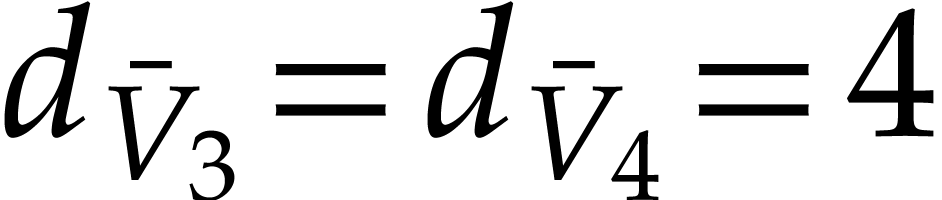 , and
, and 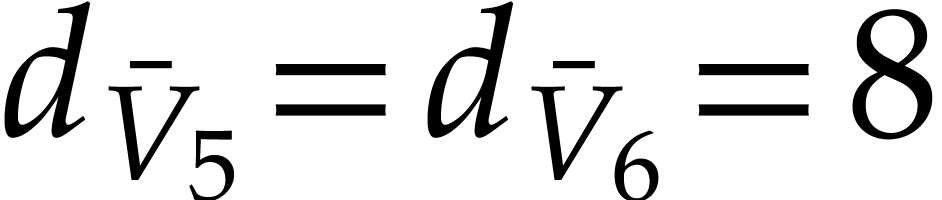 .
In the last instruction, we thus have
.
In the last instruction, we thus have  ,
whence the exponent
,
whence the exponent 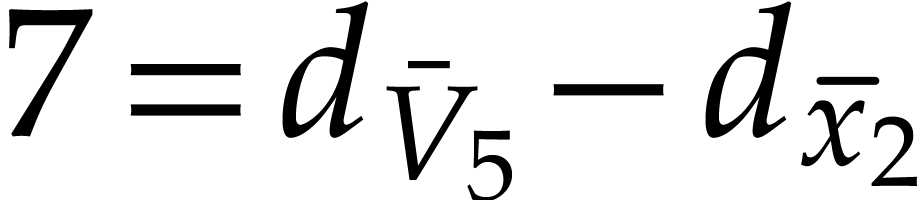 in
in 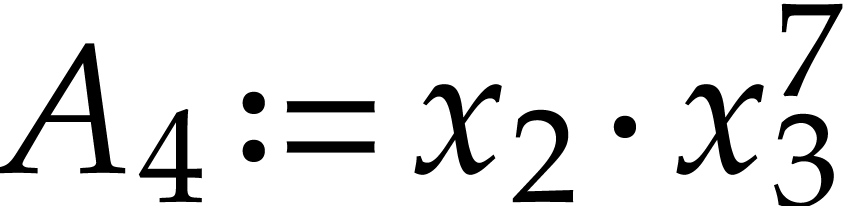 .
.
Remark 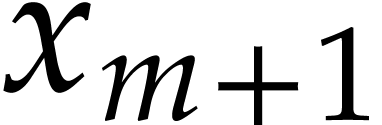 using binary
powering may give rise to a logarithmic overhead. For instance, there is
a straightforward SLP
using binary
powering may give rise to a logarithmic overhead. For instance, there is
a straightforward SLP  of length
of length 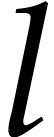 proportional to
proportional to 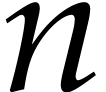 that computes the polynomials
that computes the polynomials
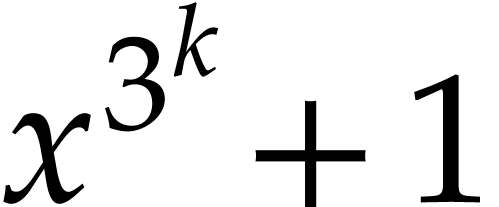 for
for 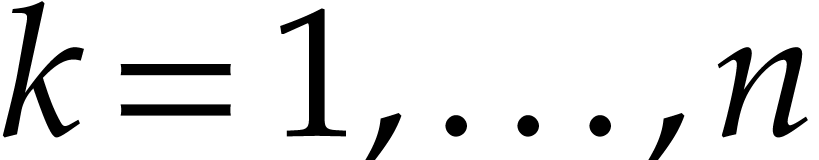 .
But when computing using binary powering in order to compute its
homogenization, the length of
.
But when computing using binary powering in order to compute its
homogenization, the length of 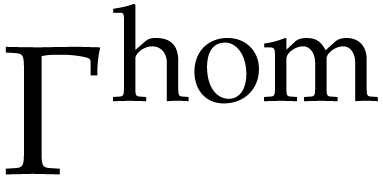 is proportional to
is proportional to
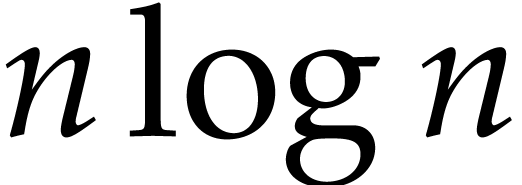 .
.
An alternative way to compute the required powers is to systematically
compute 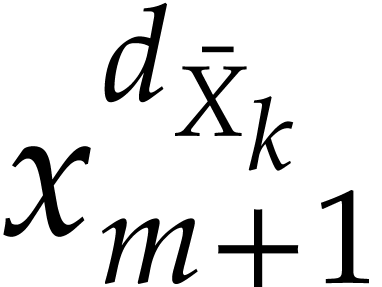 and
and 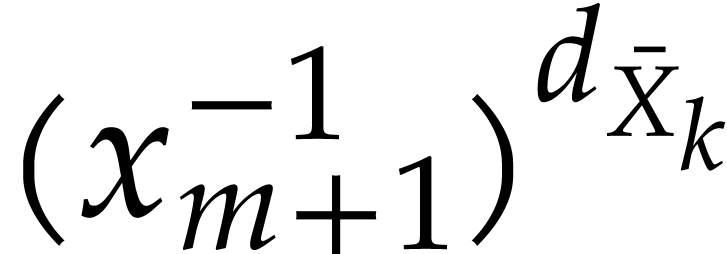 for all
for all
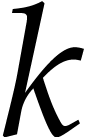 . In that case
. In that case 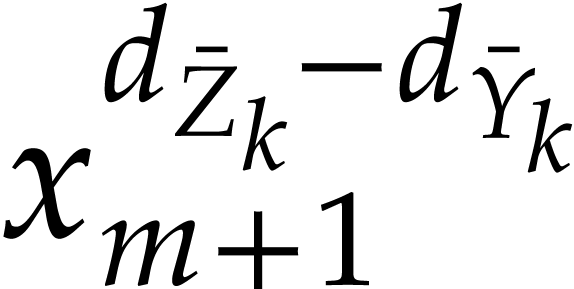 and
and 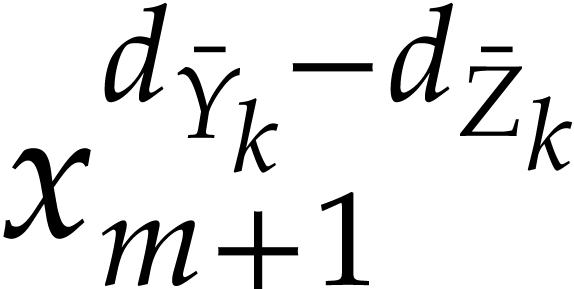 can always be obtained using a
simple multiplication and the length of
can always be obtained using a
simple multiplication and the length of  remains
bounded by
remains
bounded by 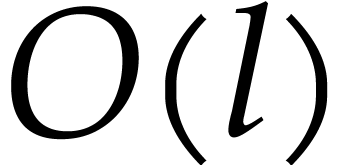 for an SLP
for an SLP  of
length
of
length 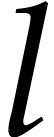 . Of course, this
requires division to be part of the SLP signature, or
. Of course, this
requires division to be part of the SLP signature, or 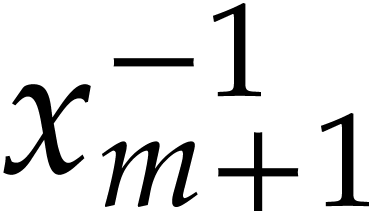 to be passed an argument, in addition to
to be passed an argument, in addition to 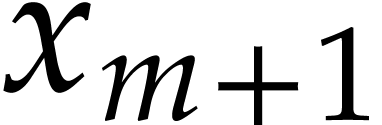 .
.
Consider an output variable 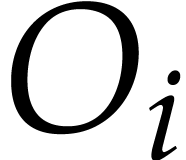 with
with 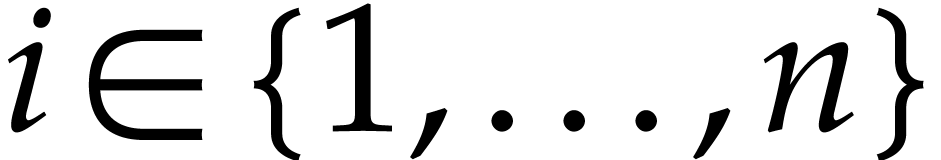 and denote by
and denote by 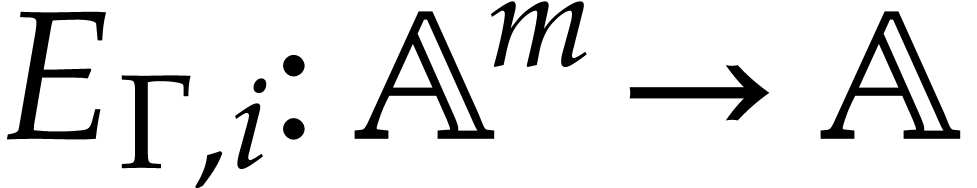 and
and 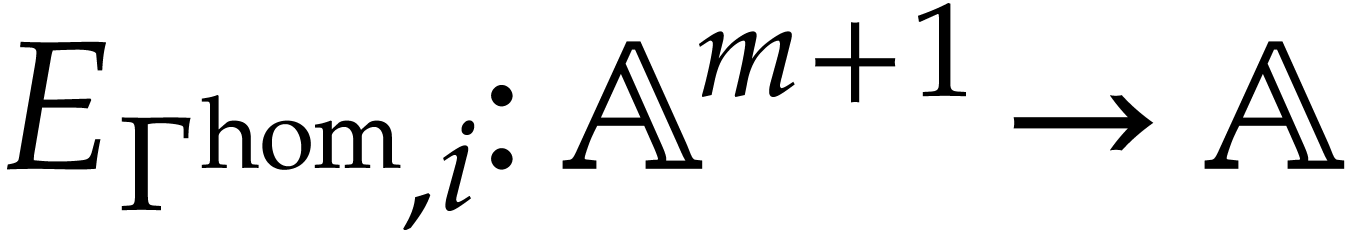 the
the  -th component of
-th component of  and
and  ,
respectively. If
,
respectively. If  is largest with
is largest with  , then we define
, then we define 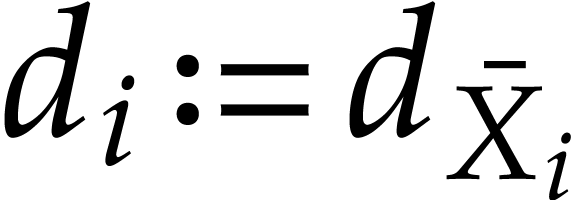 ,
and we note that
,
and we note that  is the unique homogenization of
is the unique homogenization of
 of degree
of degree 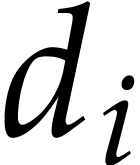 .
Let
.
Let 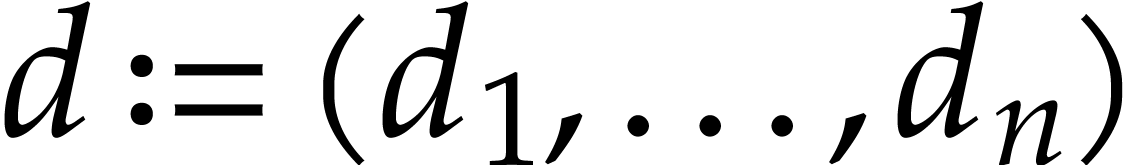 and define
and define 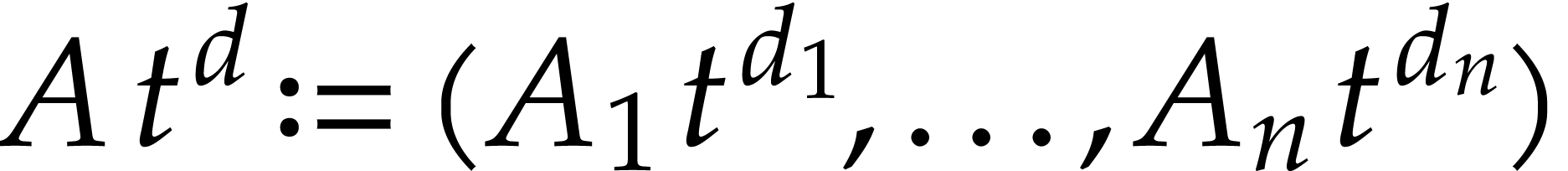 for any
for any
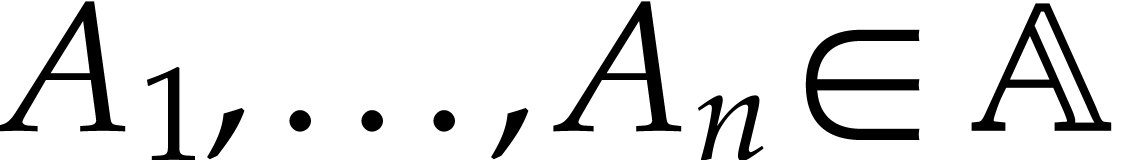 . For any
. For any  and
and  , it then follows that
, it then follows that
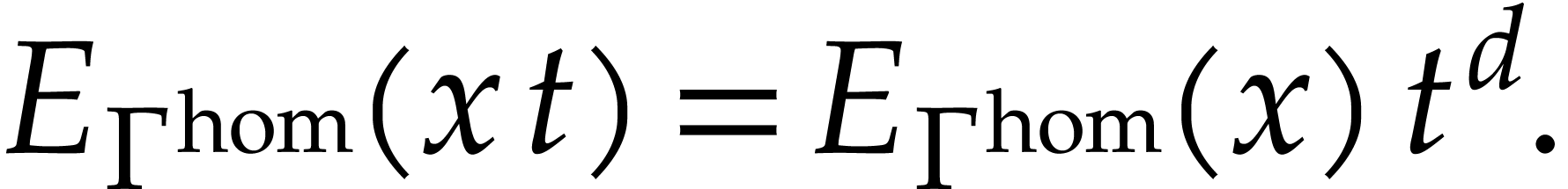 |
(5.1) |
We will denote by 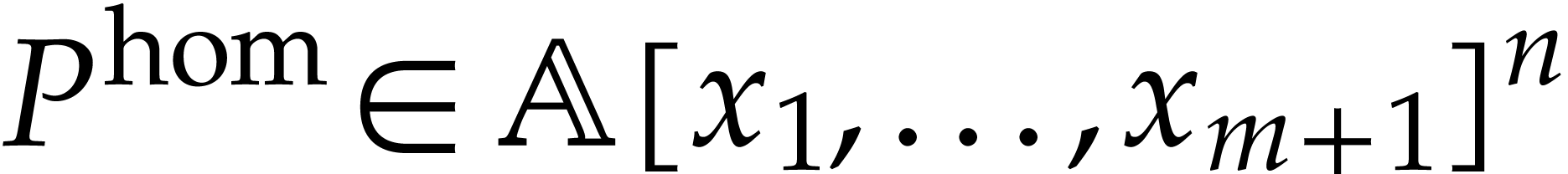 the polynomials with
the polynomials with 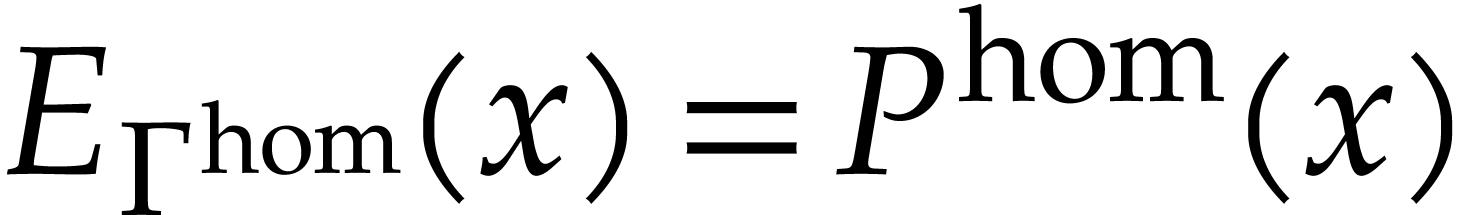 for all
for all  .
.
With the notation from the previous subsection, assume that 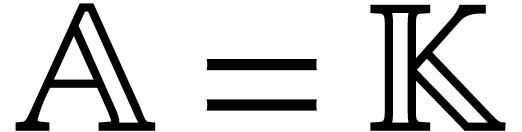 with
with 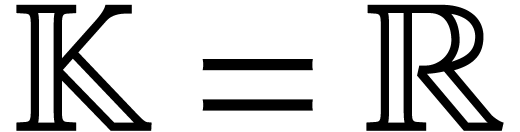 or
or 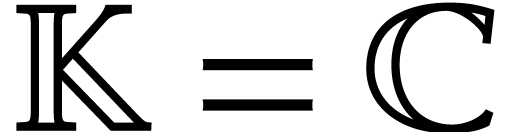 . Suppose that we wish to evaluate
. Suppose that we wish to evaluate  at a point
at a point  and let
and let
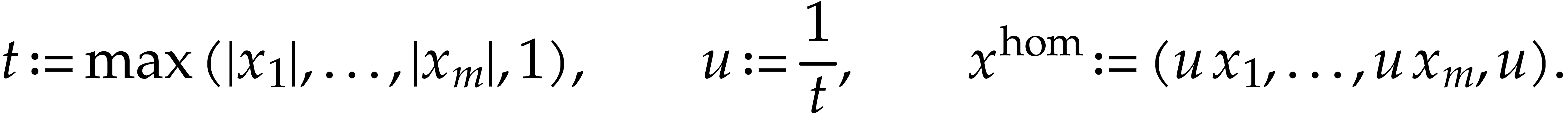 |
(5.2) |
Of course, we may simply evaluate  at
at  , which yields
, which yields 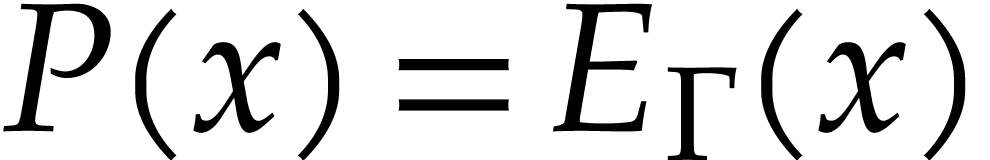 . But thanks to (5.1), we also
have the projective evaluation method
. But thanks to (5.1), we also
have the projective evaluation method

The advantage here is that
 |
(5.3) |
so we only evaluate 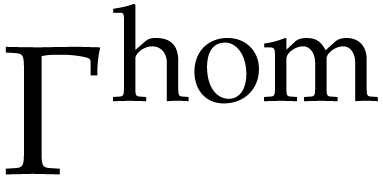 at points in the poly-ball
at points in the poly-ball
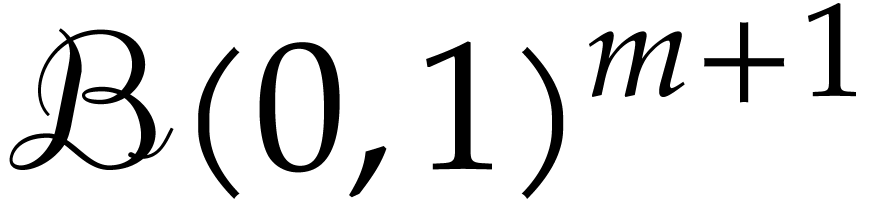 . This allows us to apply the
material from the previous sections concerning the evaluations of SLPs
at points inside a fixed ball. Note that we may easily add the
. This allows us to apply the
material from the previous sections concerning the evaluations of SLPs
at points inside a fixed ball. Note that we may easily add the  function to SLPs since its computation is always exact. If
function to SLPs since its computation is always exact. If
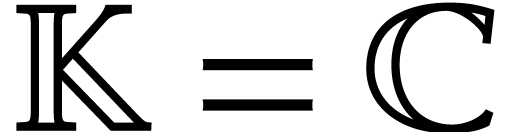 then we apply
then we apply  to the
real and imaginary parts.
to the
real and imaginary parts.
For instance, let 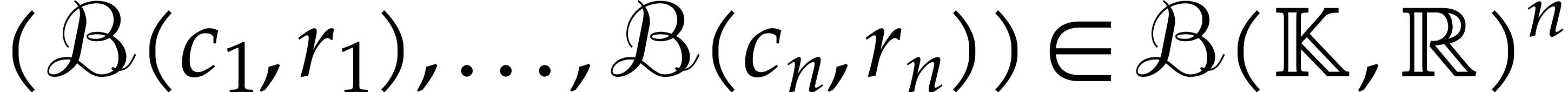 be the evaluation of
be the evaluation of  at
at 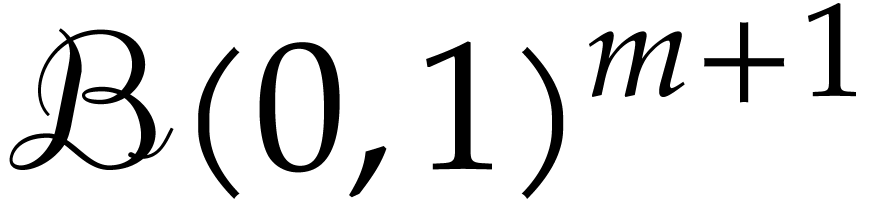 using ball arithmetic and set
using ball arithmetic and set
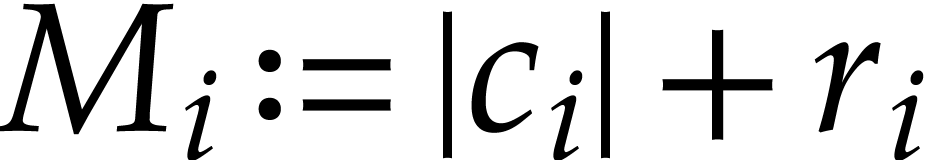 for
for 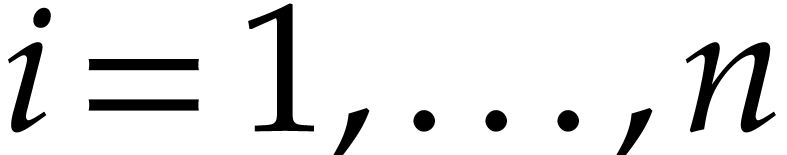 .
Then we have
.
Then we have
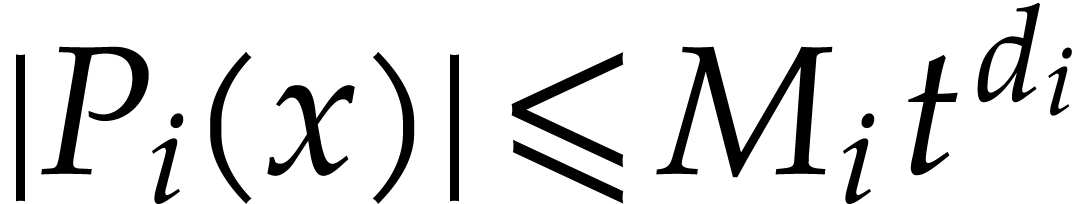 |
(5.4) |
for all  and
and 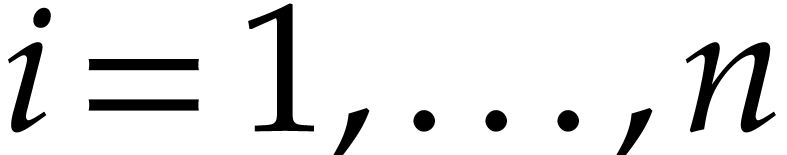 .
Consequently, we may compute upper bounds for
.
Consequently, we may compute upper bounds for  in
time
in
time 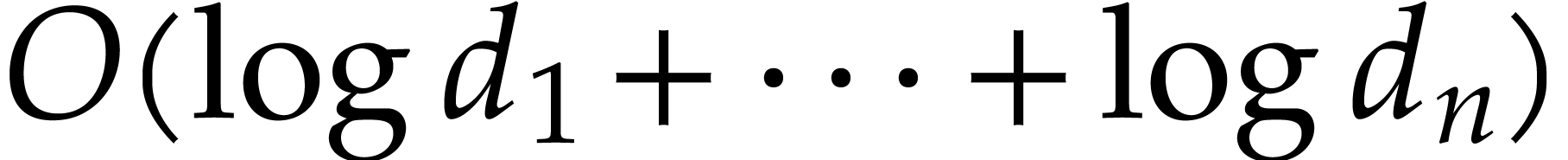 , which is typically
much smaller than the length
, which is typically
much smaller than the length 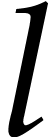 of
of  .
.
We may use such global bounds for the construction of more efficient
ball lifts, although the resulting error bounds may be less sharp. For
this, we first evaluate the Jacobian matrix of  at
at 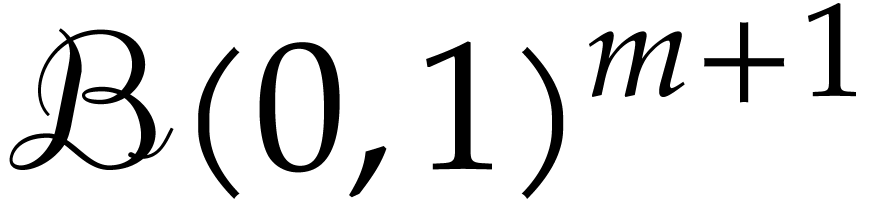 , which yields bounds
, which yields bounds
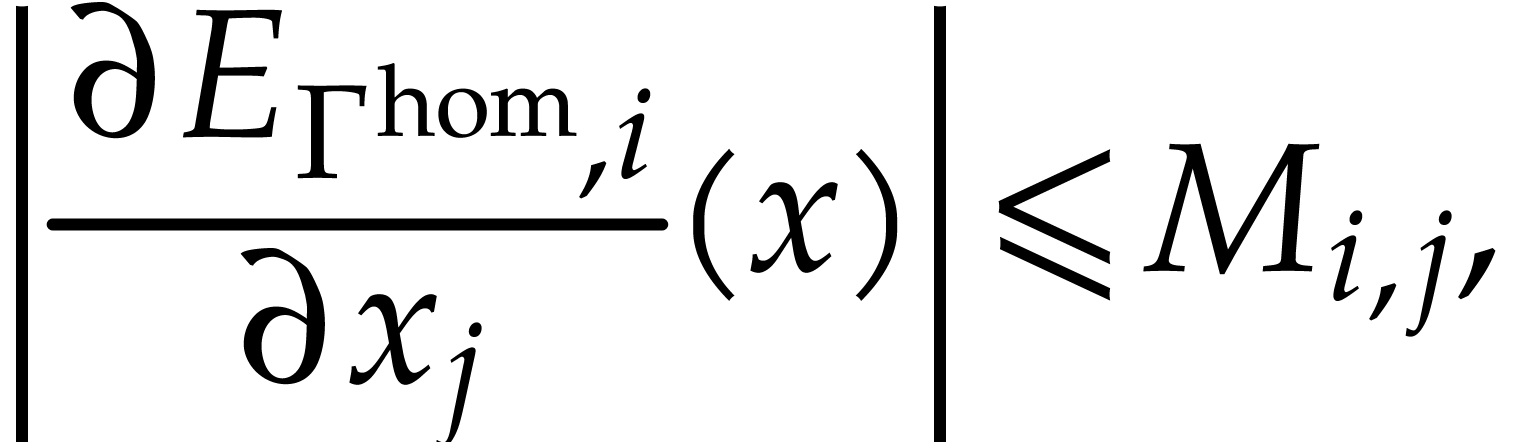 |
(5.5) |
for all 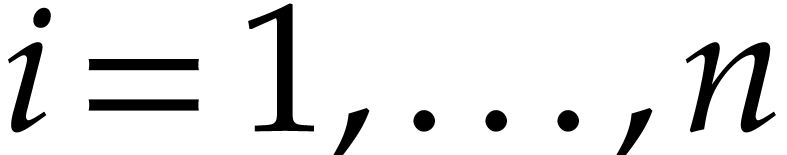 ,
, 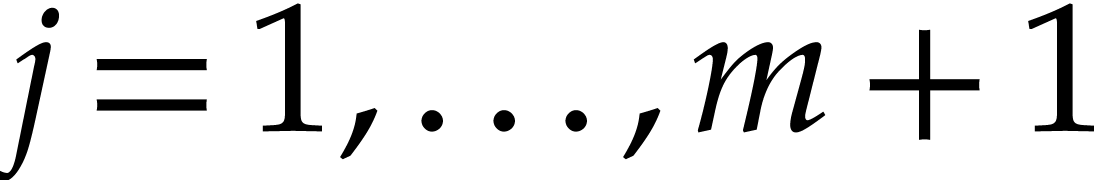 , and
, and 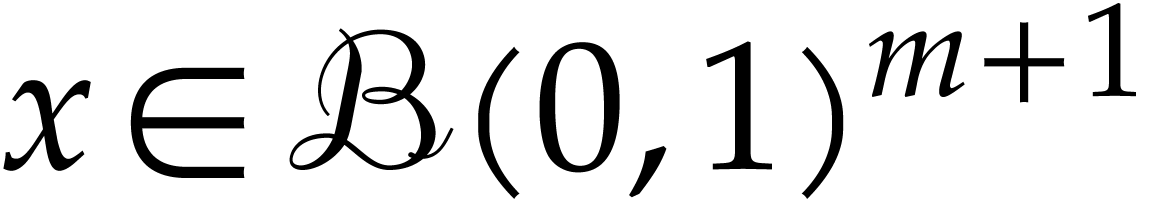 .
For any ball
.
For any ball 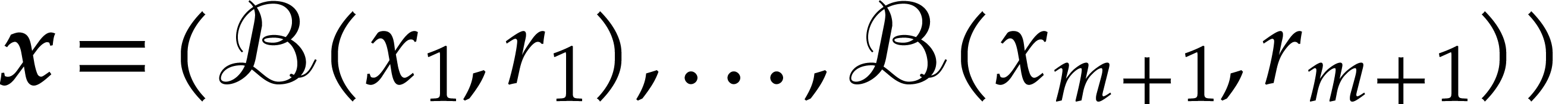 with
with 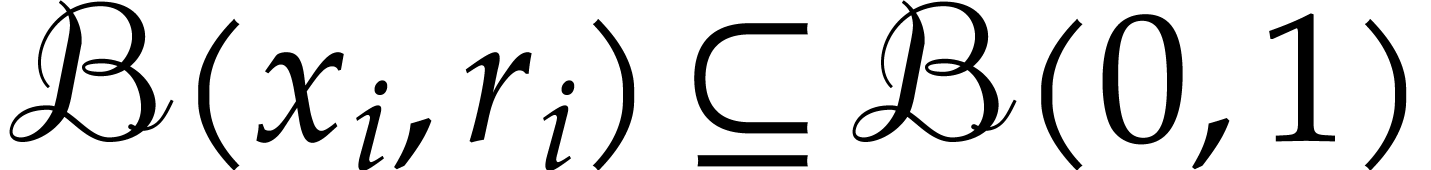 for
for
 , we then have
, we then have
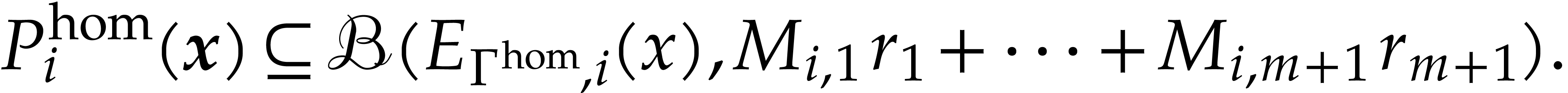 |
(5.6) |
This allows us to compute an enclosure of 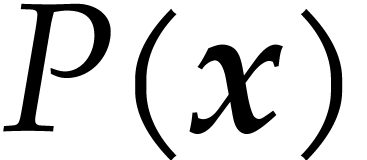 using
a single evaluation of
using
a single evaluation of 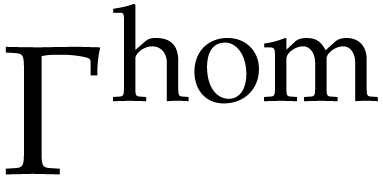 at
at  plus
plus 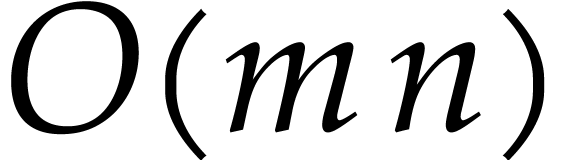 extra operations (the quantity
extra operations (the quantity 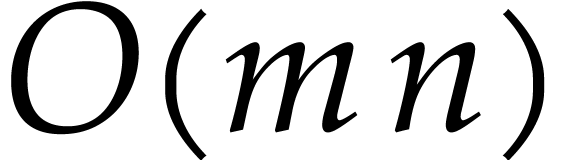 can be further reduced to
can be further reduced to 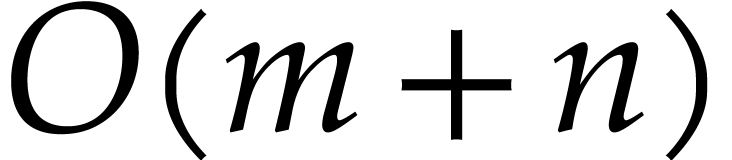 by
replacing the
by
replacing the 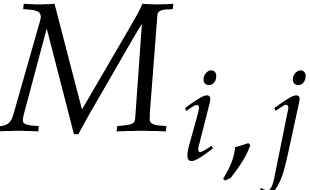 by
by 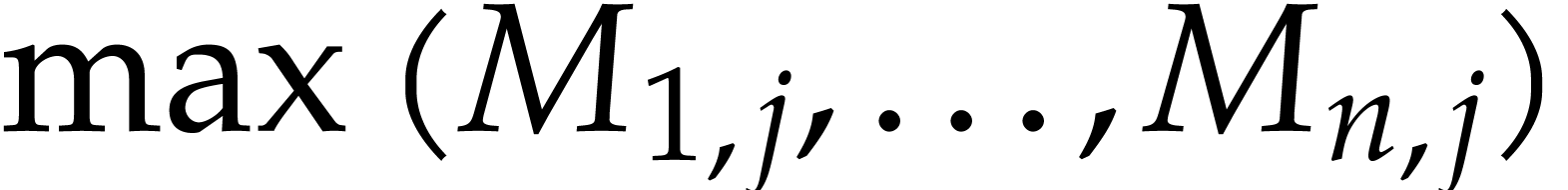 or
or
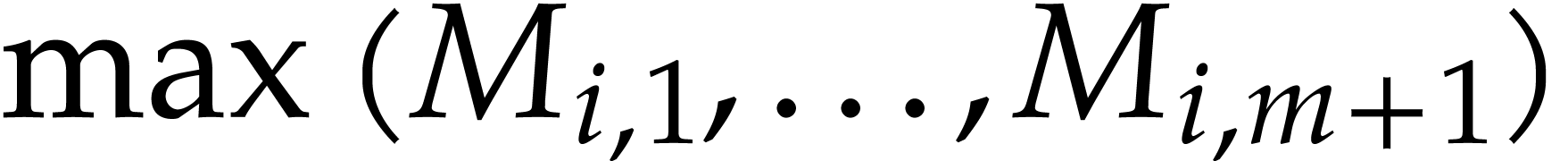 ).
).
Similarly, if 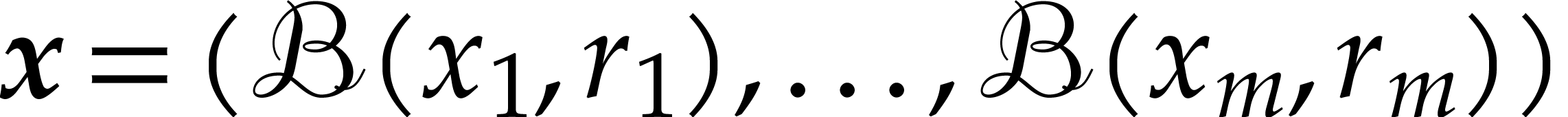 is any ball, then we define
is any ball, then we define
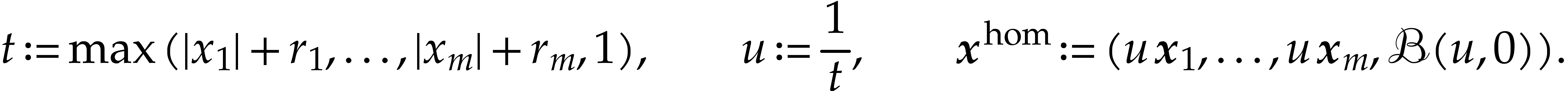 |
(5.7) |
For 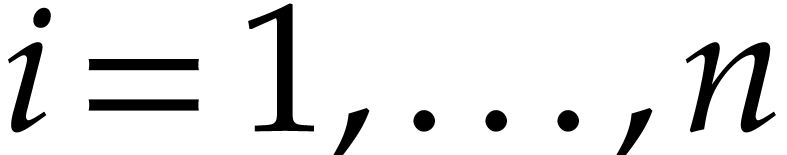 , the relations (5.1)
and (5.6) now yield
, the relations (5.1)
and (5.6) now yield
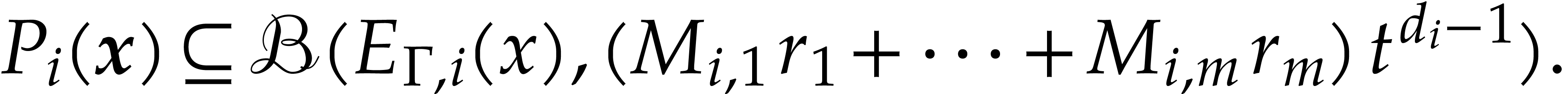 |
(5.8) |
(If 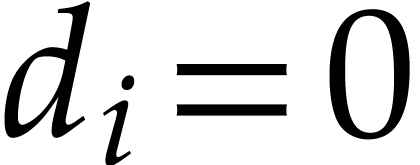 , then
, then 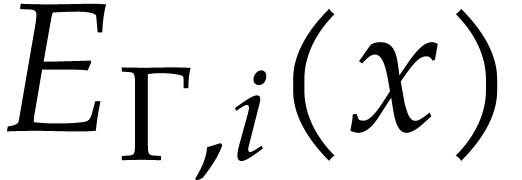 is a constant, and we may use zero as the radius.) This allows us to
compute an enclosure of
is a constant, and we may use zero as the radius.) This allows us to
compute an enclosure of 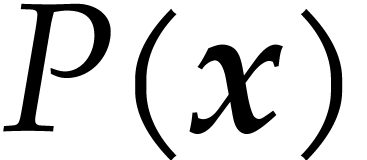 using one evaluation of
using one evaluation of
 at
at  plus
plus 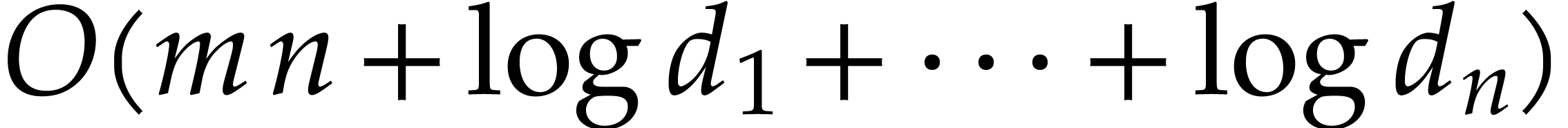 extra operations in
extra operations in  . Note
that the homogenization
. Note
that the homogenization  was only required in
order to compute the constants
was only required in
order to compute the constants  ,
but not for evaluating the right-hand side of (5.8) at a
specific
,
but not for evaluating the right-hand side of (5.8) at a
specific  .
.
In the previous subsection, we assumed infinitely precise arithmetic
over  or
or  .
Let us now show how to adapt this material to the case when
.
Let us now show how to adapt this material to the case when 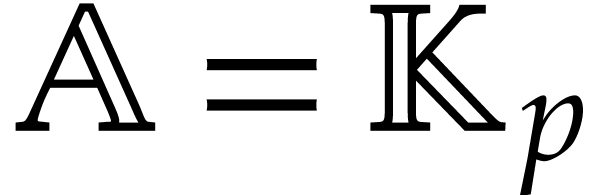 , where
, where 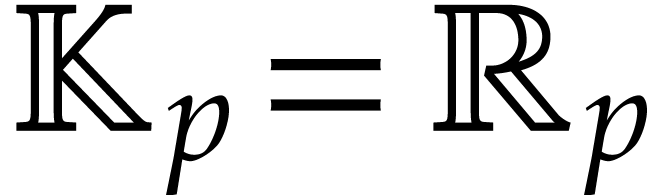 or
or 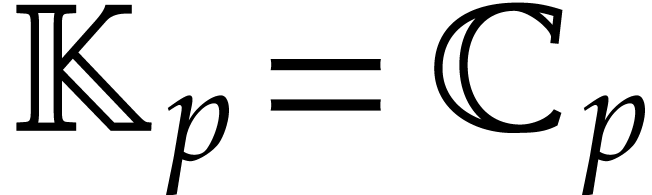 . As usual, assume
. As usual, assume 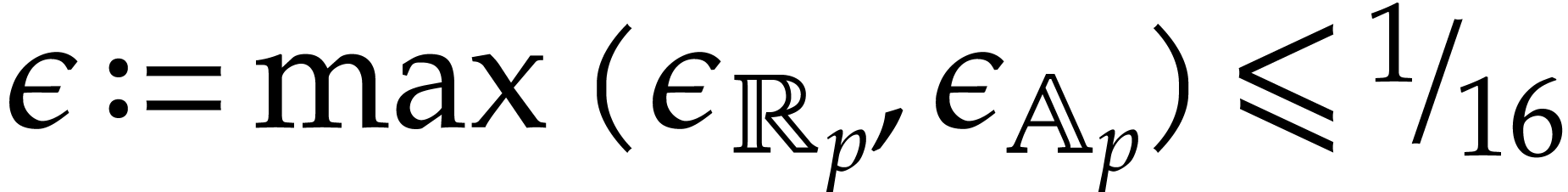 , and let us first show how to deal with rounding
errors in the absence of overflows and underflows. We first replace (5.2) by
, and let us first show how to deal with rounding
errors in the absence of overflows and underflows. We first replace (5.2) by
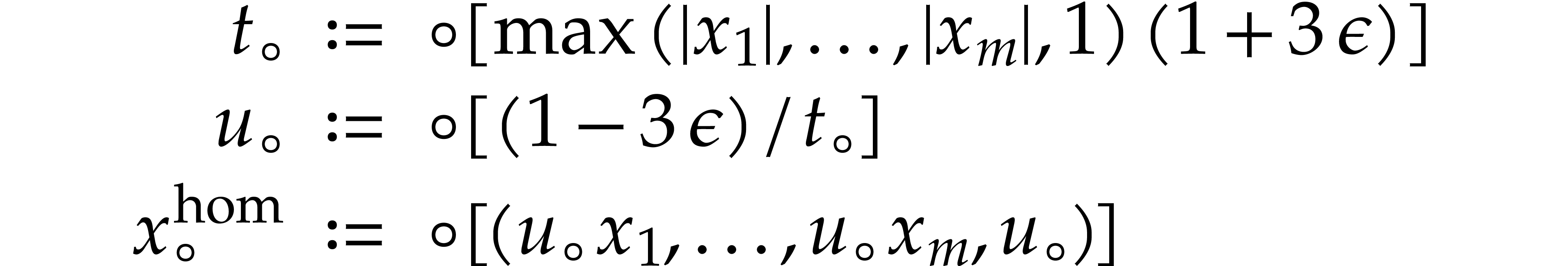
and verify that
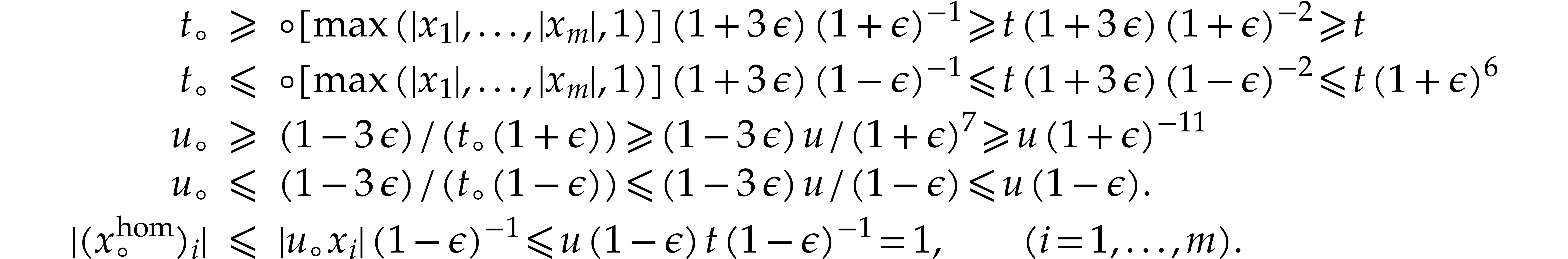
We have
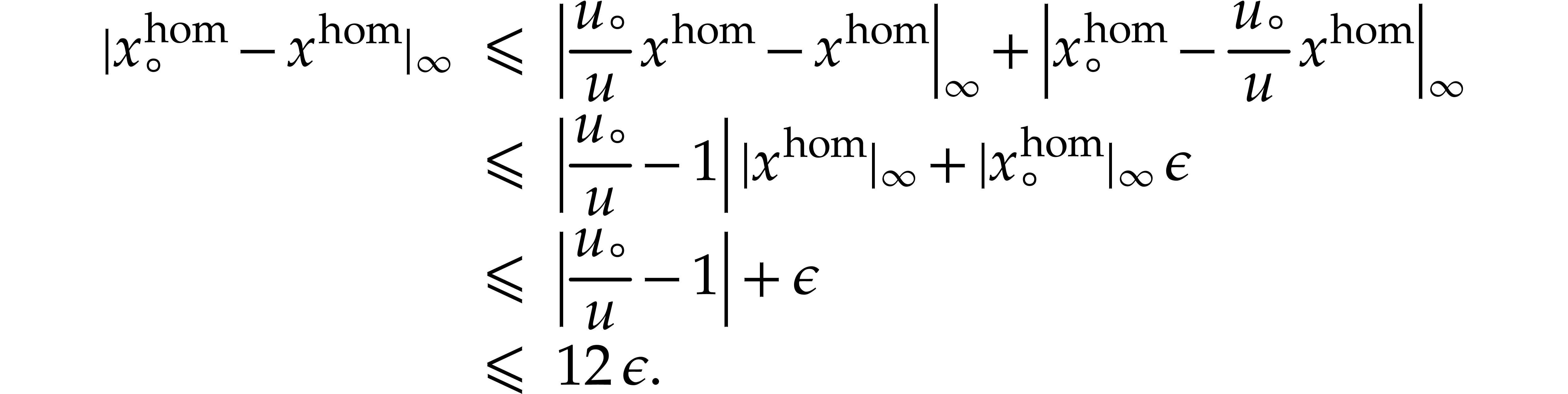
Let  . Evaluating
. Evaluating 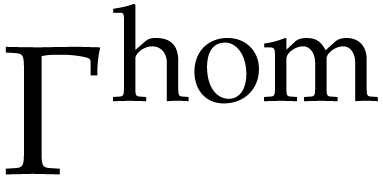 at
at 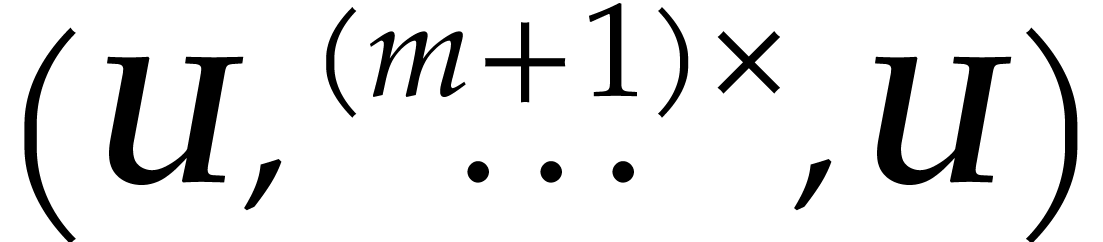 , for the
matryoshka
, for the
matryoshka 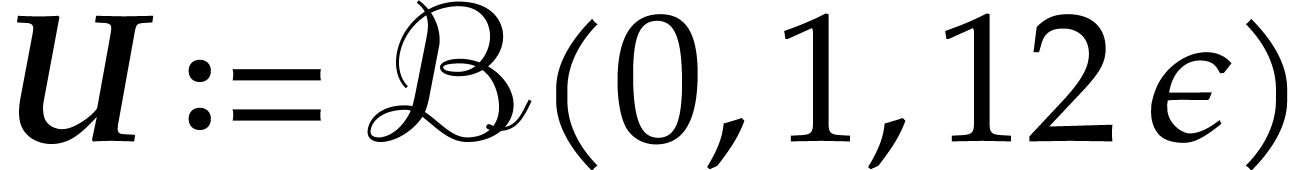 , by Proposition
3.6 for instance, we may compute a
, by Proposition
3.6 for instance, we may compute a  with
with
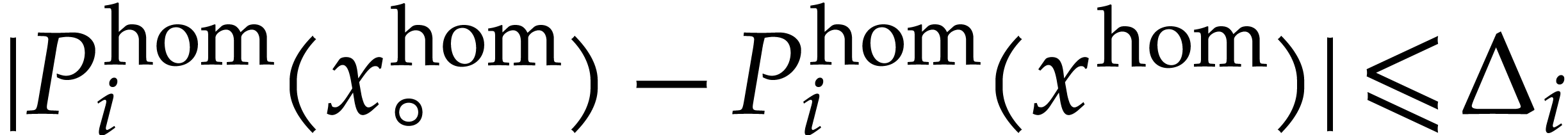
for all 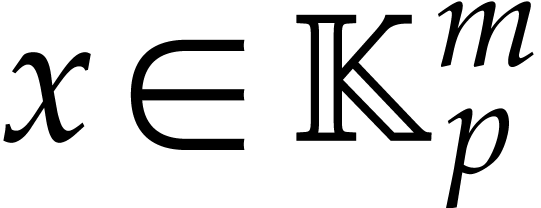 , as well as
, as well as
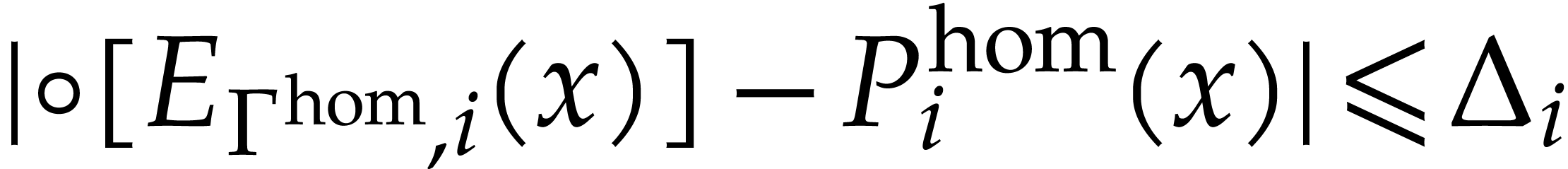
for all 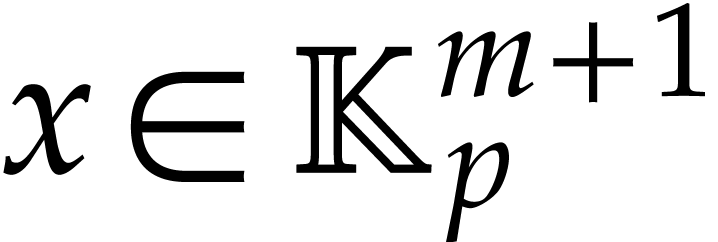 with
with 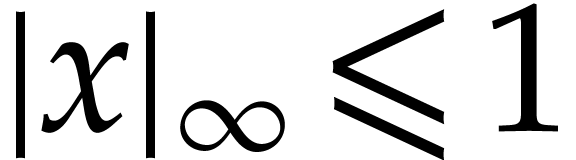 .
It follows that
.
It follows that
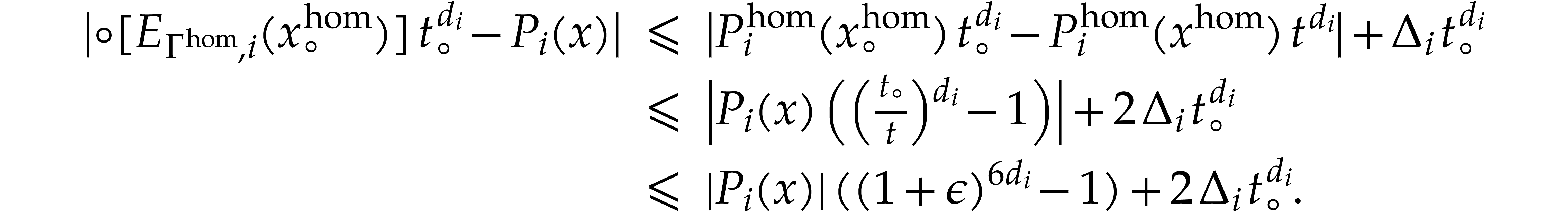
Setting

we then get
Note that for all 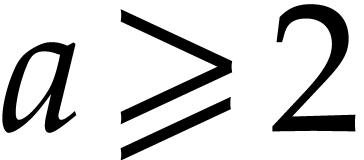 and
and 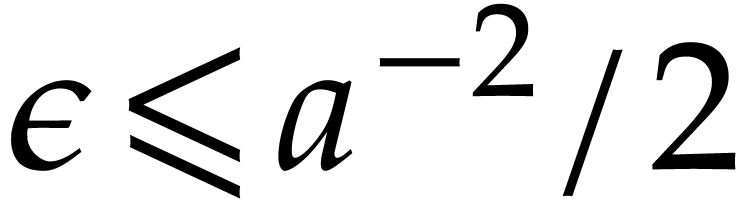 we
have
we
have
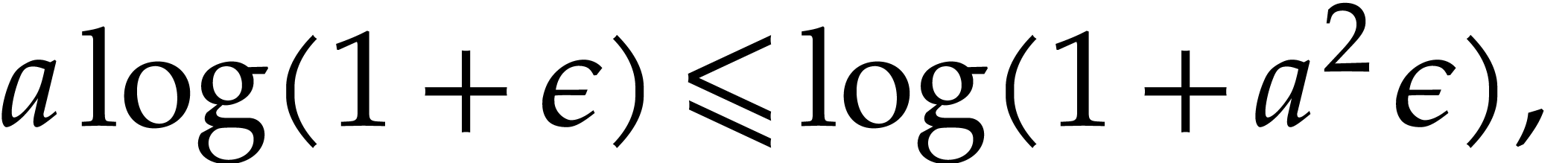
whence 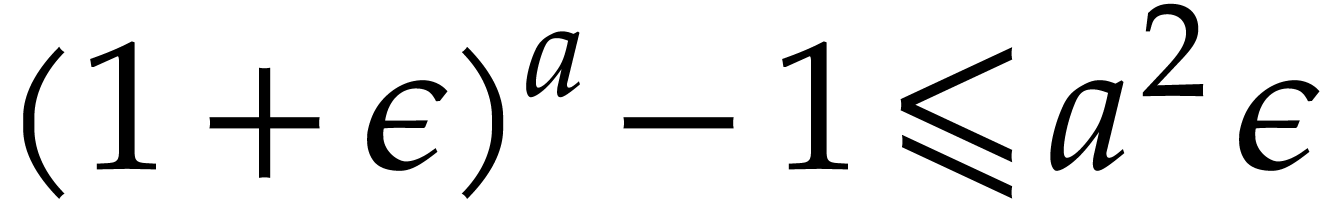 . Consequently,
provided that
. Consequently,
provided that 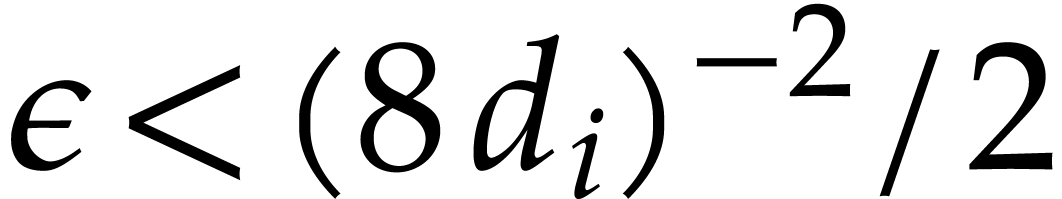 , the bound
, the bound
This yields an easy way to compute error bound
for the approximate numeric evaluation of  at
any point
at
any point 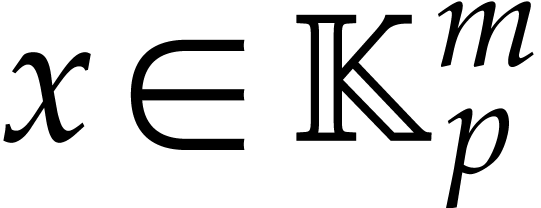 .
.
Let us now turn to the bound (5.4). Using traditional ball
arithmetic (formulas 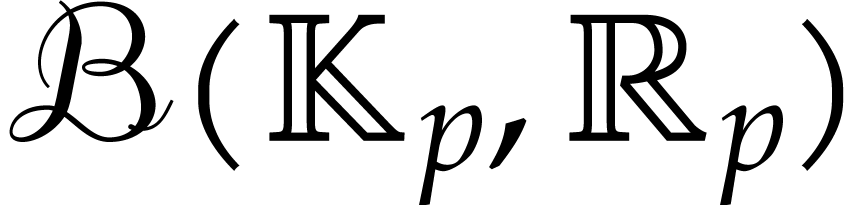 , we may still compute
, we may still compute 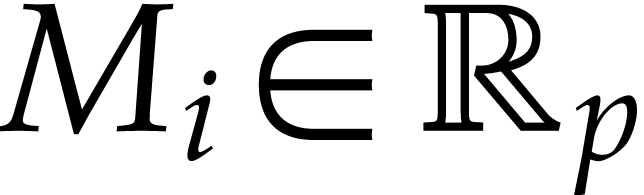 with
with 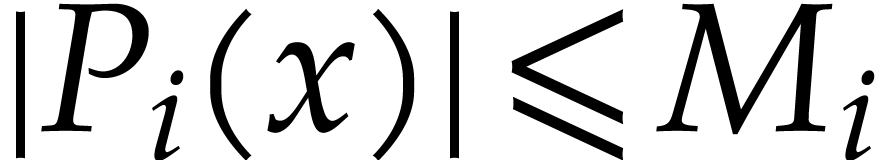 for all
for all 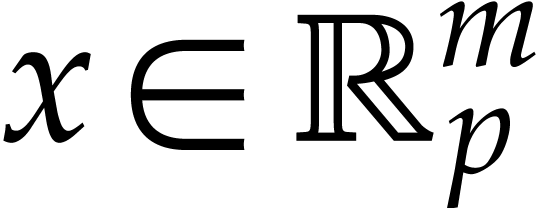 with
with 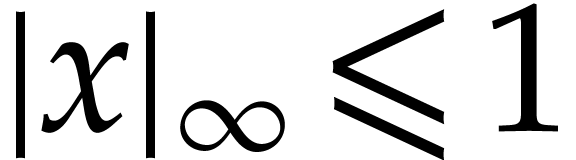 . Then we simply have
. Then we simply have
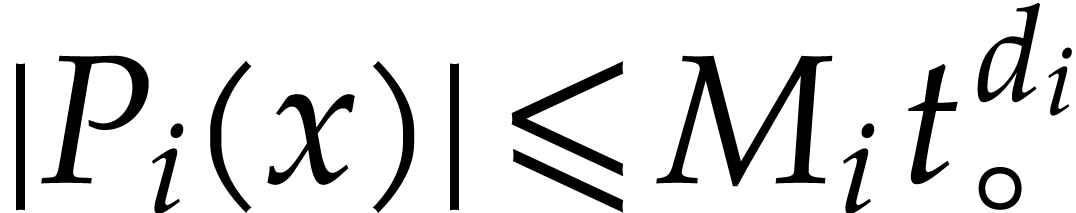
for all 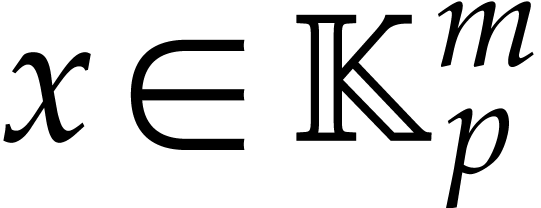 , since
, since 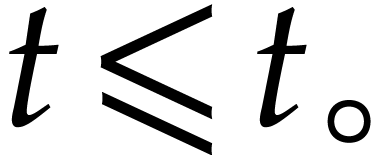 . In a similar way, bounds
. In a similar way, bounds 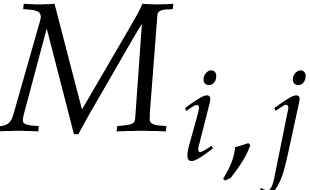 that satisfy (5.5) can be computed using traditional ball
arithmetic. For any ball
that satisfy (5.5) can be computed using traditional ball
arithmetic. For any ball 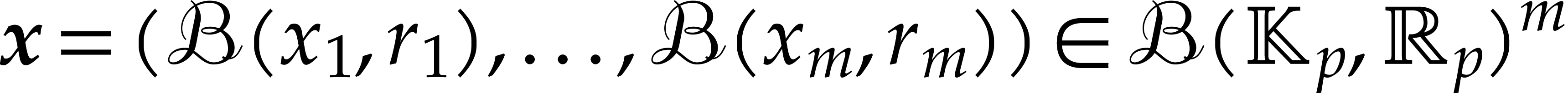 and with we notation
from (5.7), the enclosure (5.8) still holds.
Combining
and with we notation
from (5.7), the enclosure (5.8) still holds.
Combining
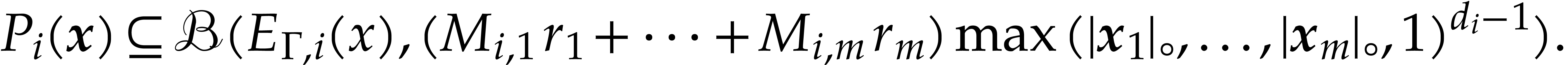
with (5.10), this yields
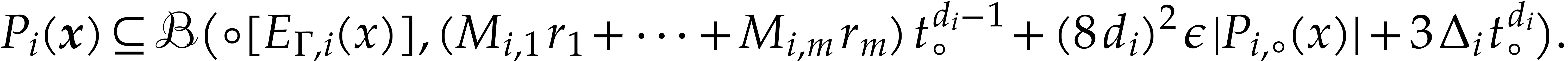
Hence
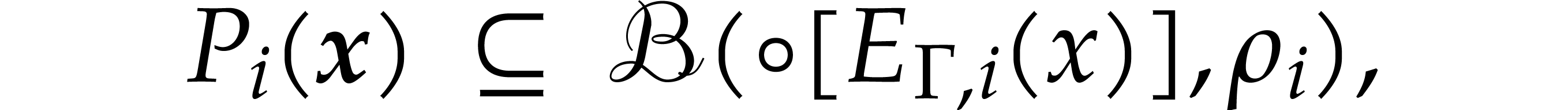
where
This yields a ball lift for 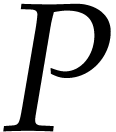 that is almost as
efficient to compute as a mere numeric evaluation of
that is almost as
efficient to compute as a mere numeric evaluation of  .
.
Let us finally analyze how to deal with underflows and overflows. Let
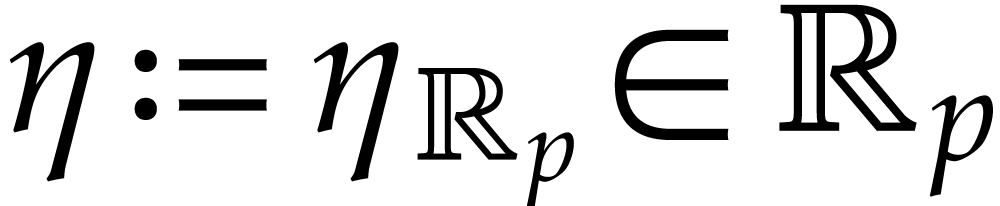 be such that (2.8) holds. As long
as the computation of
be such that (2.8) holds. As long
as the computation of 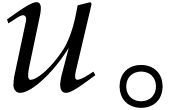 does not underflow, the
inequality
does not underflow, the
inequality  remains valid, even in the case of
overflows (provided that
remains valid, even in the case of
overflows (provided that 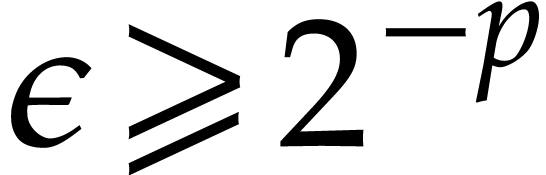 ).
Consequently, the relation (5.10) still holds, so it
suffices to replace (5.11) by
).
Consequently, the relation (5.10) still holds, so it
suffices to replace (5.11) by
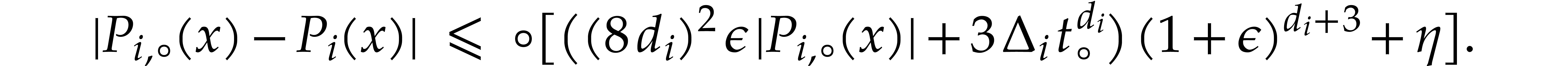
This indeed counters the possible underflow for the multiplication of
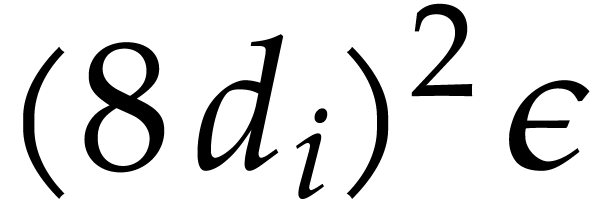 with
with 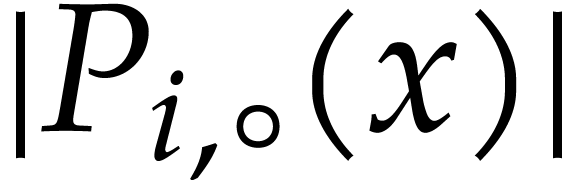 .
Note that the relation trivially holds in the case when the right-hand
side overflows, which happens in particular when the computation of
.
Note that the relation trivially holds in the case when the right-hand
side overflows, which happens in particular when the computation of 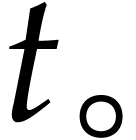 overflows. Similarly, it suffices to replace (5.12) by
overflows. Similarly, it suffices to replace (5.12) by
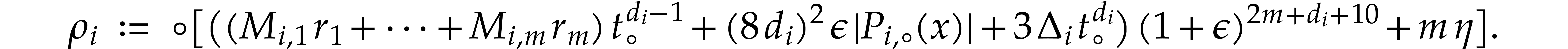
If the computation of  does not overflow, but the
computation of
does not overflow, but the
computation of 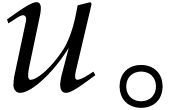 underflows, then the IEEE 754
norm implies that we must have
underflows, then the IEEE 754
norm implies that we must have 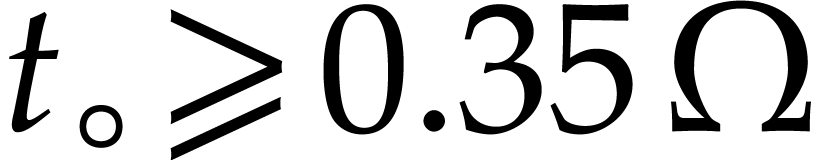 ,
where
,
where  is the largest positive floating point
number in
is the largest positive floating point
number in 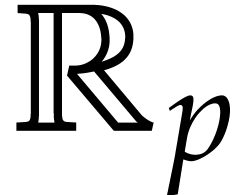 with
with 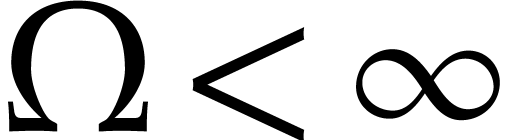 .
Consequently, the computation
.
Consequently, the computation 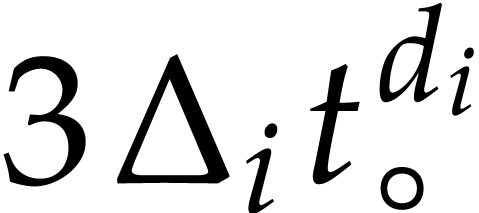 overflows whenever
overflows whenever
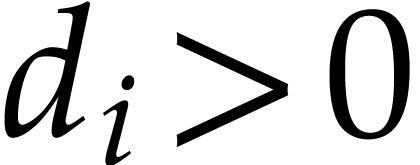 , provided that we compute
this product as
, provided that we compute
this product as 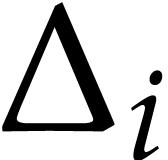 times
times 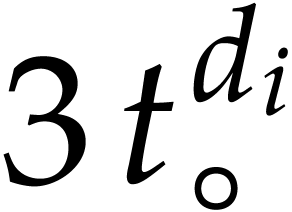 . The adjusted bounds are therefore valid in
general.
. The adjusted bounds are therefore valid in
general.
For several applications, it is useful to not only compute bounds for
the function 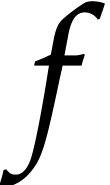 itself, but also for some of its
iterated derivatives.
itself, but also for some of its
iterated derivatives.
Let us first assume that 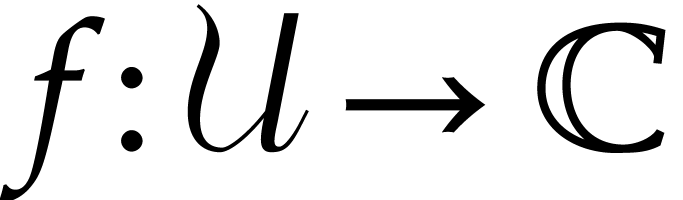 is an analytic function
defined on an open subset
is an analytic function
defined on an open subset 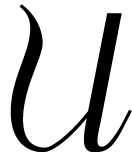 of
of  . Given a derivation order
. Given a derivation order 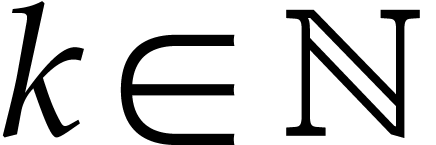 and a ball
and a ball 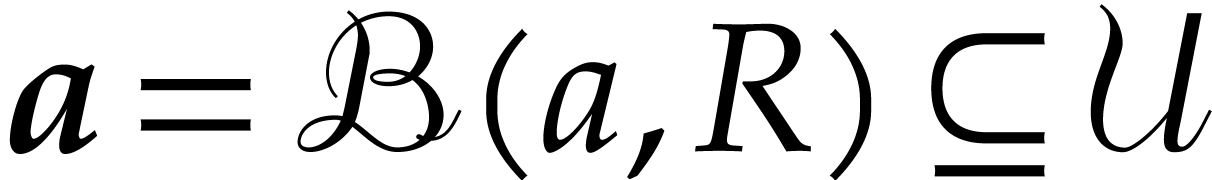 , our goal is to
compute a bound for
, our goal is to
compute a bound for 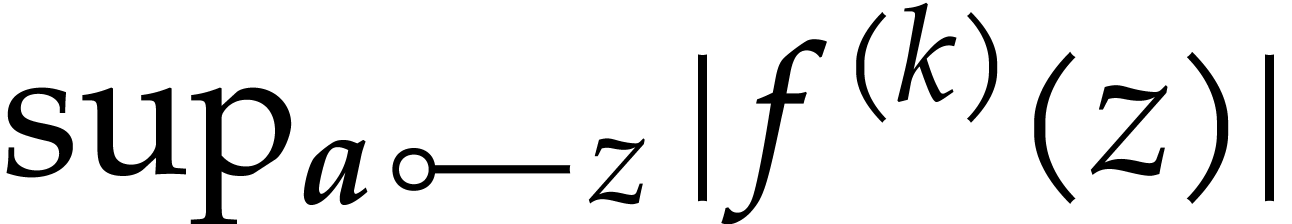 . If
. If 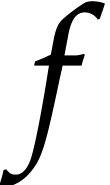 is actually an explicit polynomial
is actually an explicit polynomial
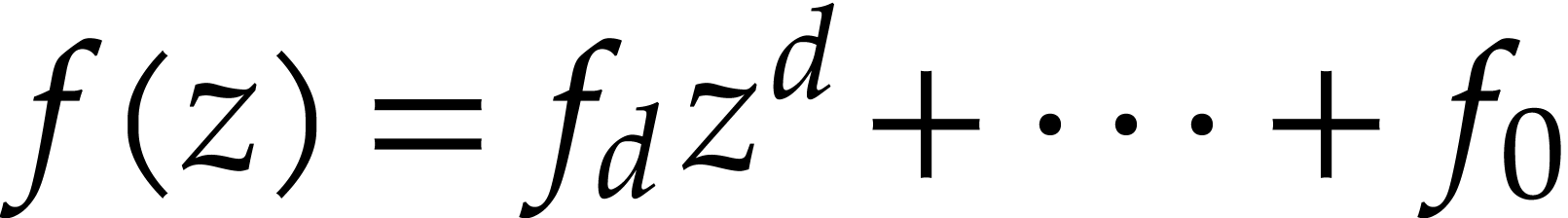
and  , then a first option is
to use the crude bound
, then a first option is
to use the crude bound
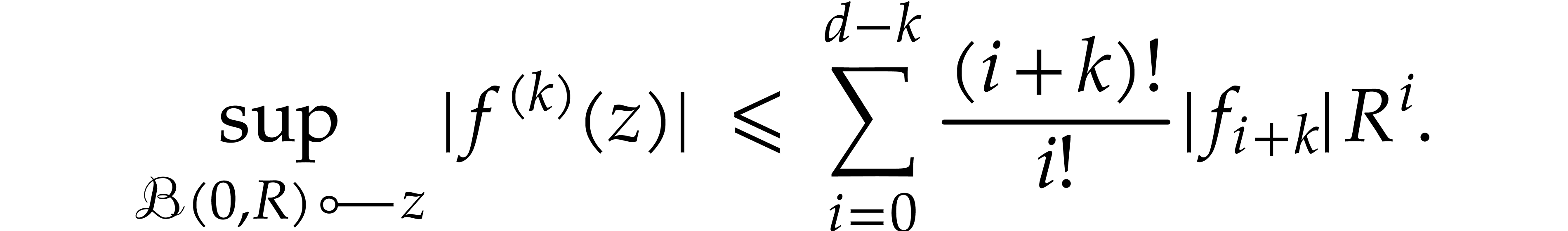
Of course, the case where 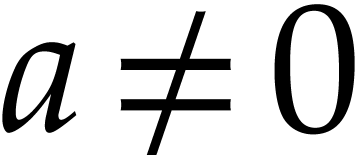 may be reduced to the
case where
may be reduced to the
case where 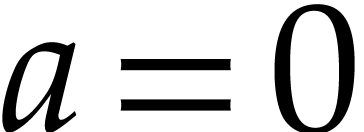 via the change of variables
via the change of variables  .
.
Assume now that 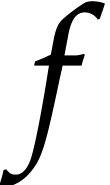 is given through an SLP, which
possibly involves other operations as
is given through an SLP, which
possibly involves other operations as 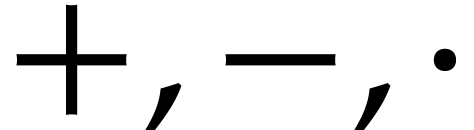 ,
such as division. In that case, the above crude bound typically becomes
suboptimal, and does not even apply if
,
such as division. In that case, the above crude bound typically becomes
suboptimal, and does not even apply if 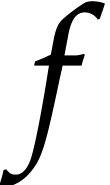 is no
longer a polynomial. A general alternative method to compute iterated
derivatives is to use Cauchy's formula
is no
longer a polynomial. A general alternative method to compute iterated
derivatives is to use Cauchy's formula
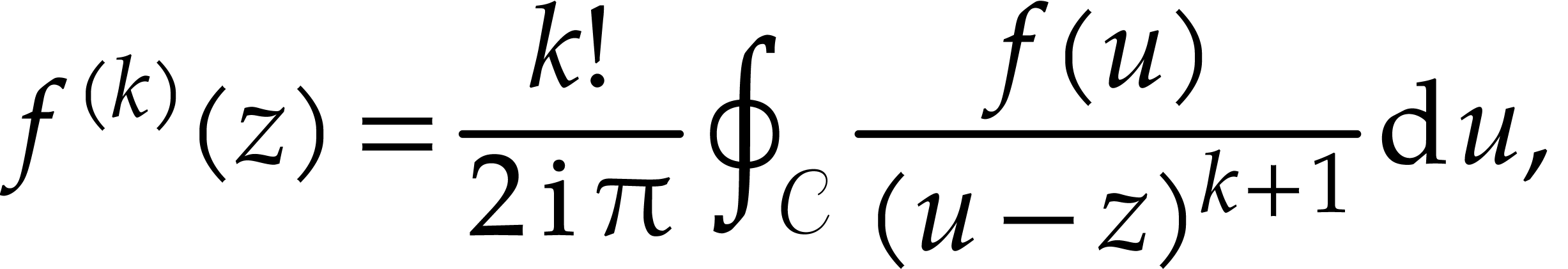 |
(6.1) |
where  is some circle around
is some circle around 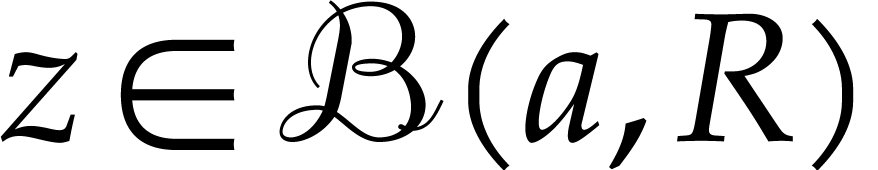 . Taking
. Taking 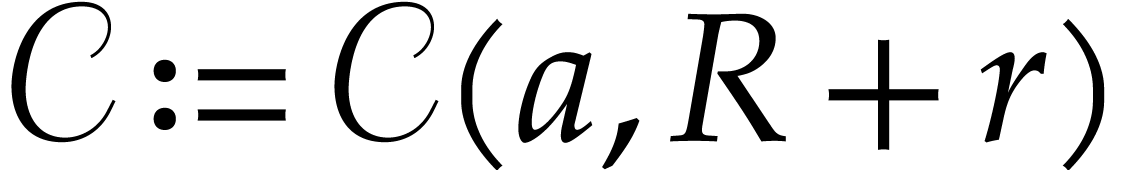 to be the
circle with center
to be the
circle with center  and radius
and radius  for some
for some  , this yields the
bound
, this yields the
bound
where 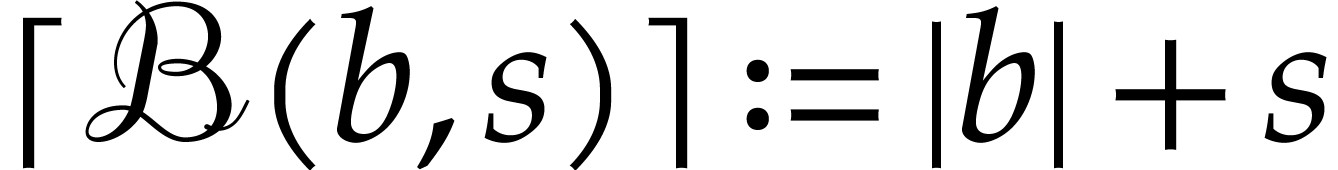 denotes an upper bound for
denotes an upper bound for  where
where 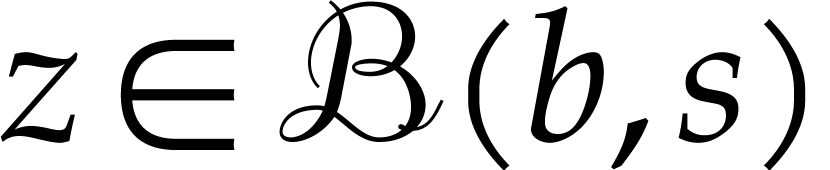 .
.
It is an interesting question how to choose 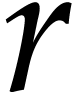 . One practical approach is to start with any
. One practical approach is to start with any  such that
such that  .
Next we may compute both
.
Next we may compute both 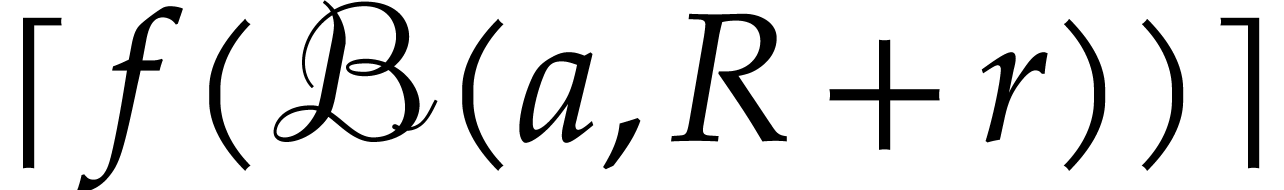 and
and 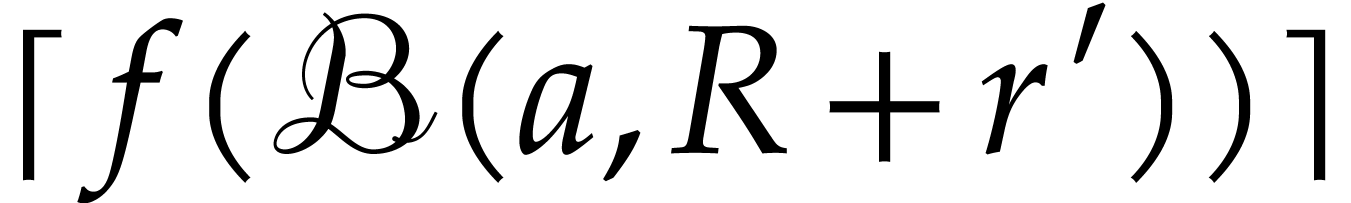 for some other
for some other 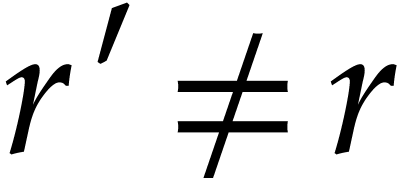 and check which value provided a
better bound. If, say
and check which value provided a
better bound. If, say 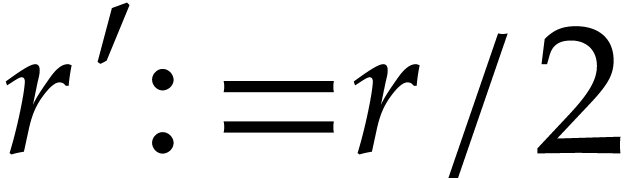 ,
yields a better bound, then we may next try
,
yields a better bound, then we may next try 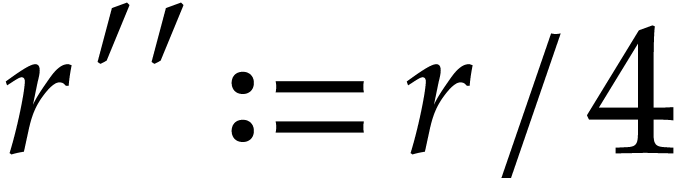 . If the bound for
. If the bound for 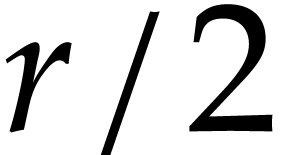 is better
than the one for
is better
than the one for 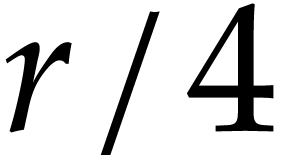 , we may
continue with
, we may
continue with 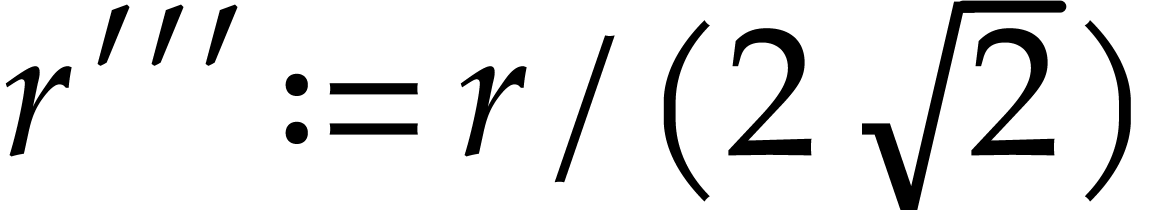 and so on until we find a bound
that suits us.
and so on until we find a bound
that suits us.
For simple explicit functions 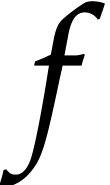 ,
it is also instructive to investigate what is the optimal choice for
,
it is also instructive to investigate what is the optimal choice for
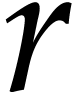 . For instance, if
. For instance, if 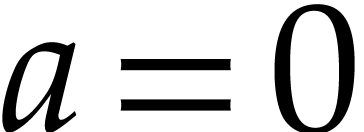 and
and 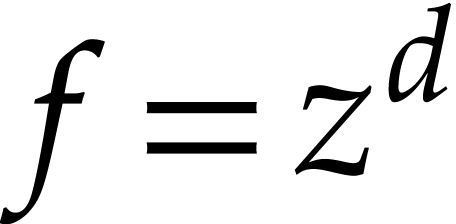 with
with 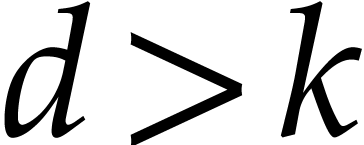 , then we have
, then we have 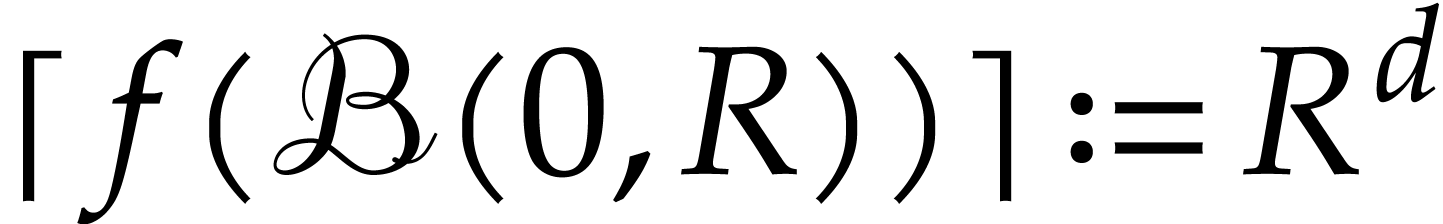 ,
so the bound (6.2) reduces to
,
so the bound (6.2) reduces to
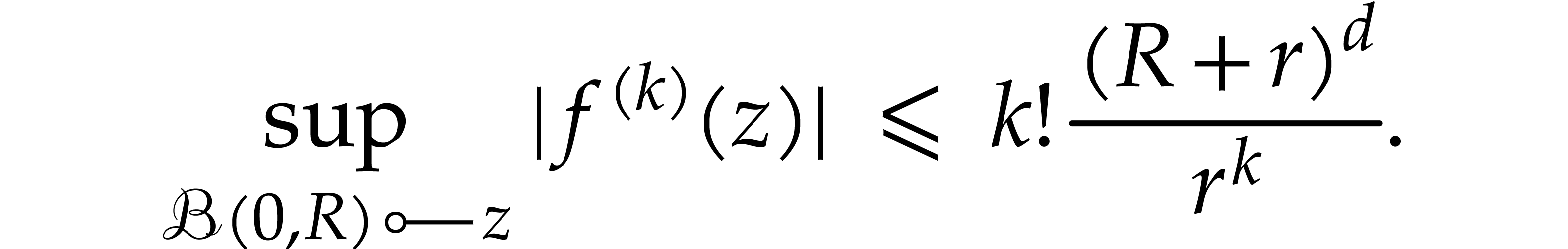
The right-hand side is minimal when
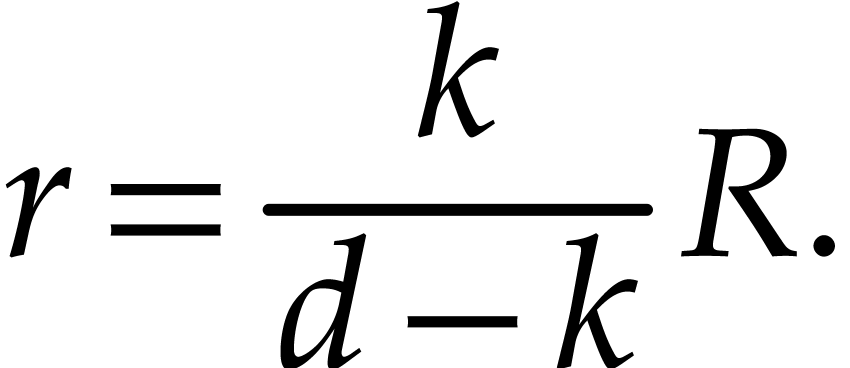 |
(6.3) |
In general, we may consider the power series expansion at 
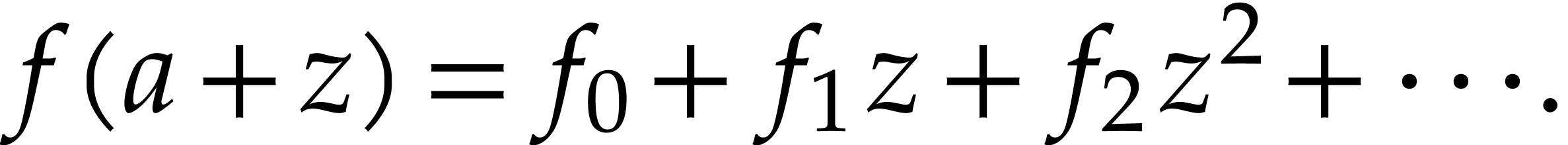
For such a power series expansion and a fixed  with
with  , let
, let  be largest such that
be largest such that 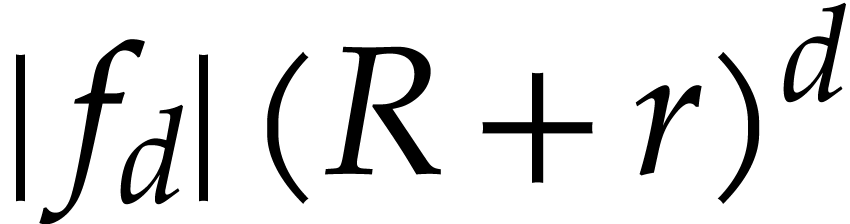 is maximal. We regard
is maximal. We regard 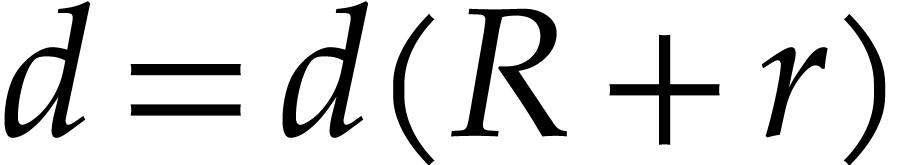 as the “numerical degree” of
as the “numerical degree” of  on the disk
on the disk 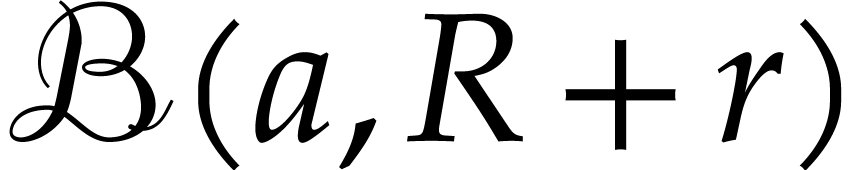 ).
Then the relation (6.3) suggests that we should have
).
Then the relation (6.3) suggests that we should have 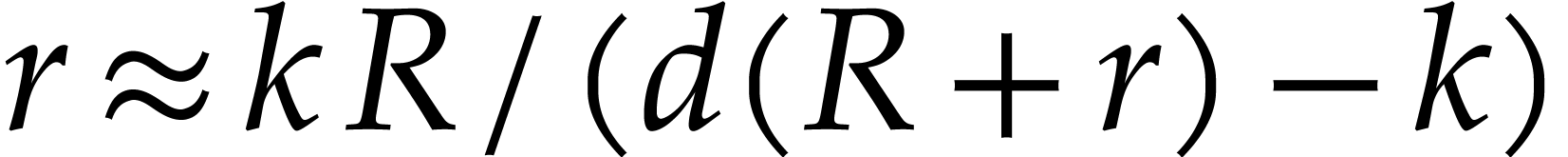 for the optimal value of
for the optimal value of 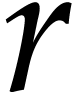 .
.
For higher dimensional generalizations, consider an analytic map 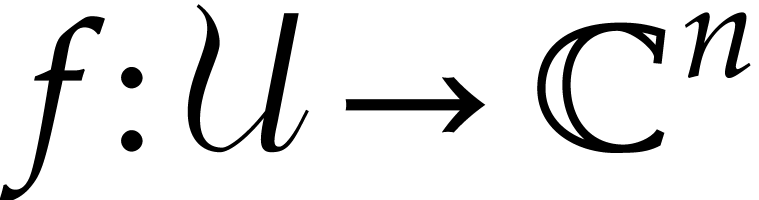 for some open set
for some open set  .
Let
.
Let 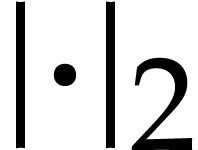 be the standard Euclidean norm on
be the standard Euclidean norm on 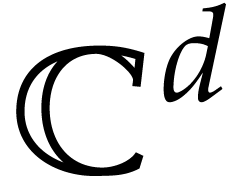 for any
for any  . Given
. Given
 and
and  ,
we denote by
,
we denote by
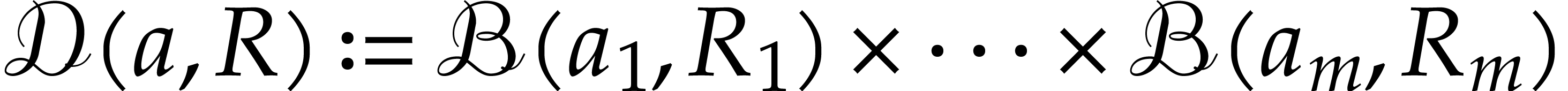
the polydisk associated to the poly-ball 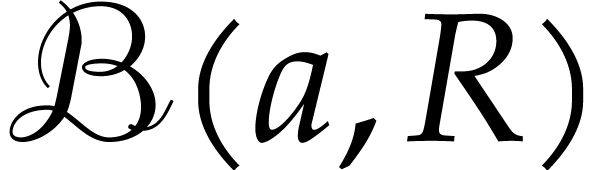 .
For
.
For 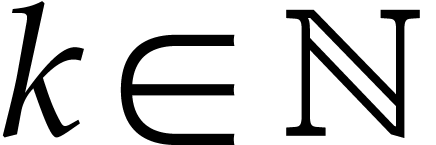 and assuming that
and assuming that 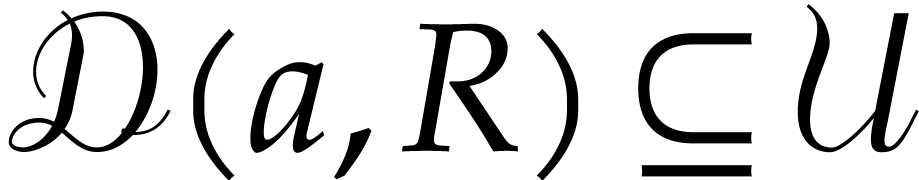 , we denote the operator norm of the
, we denote the operator norm of the 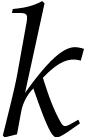 -th derivative
-th derivative 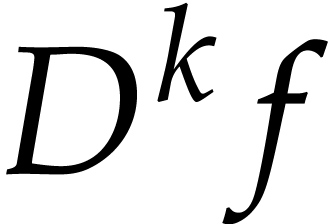 of
of 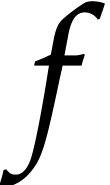 on
on 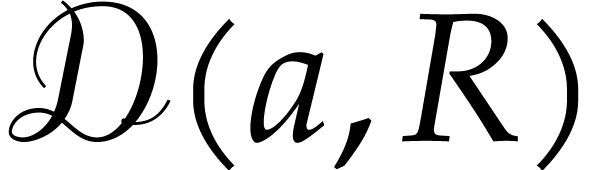 by
by
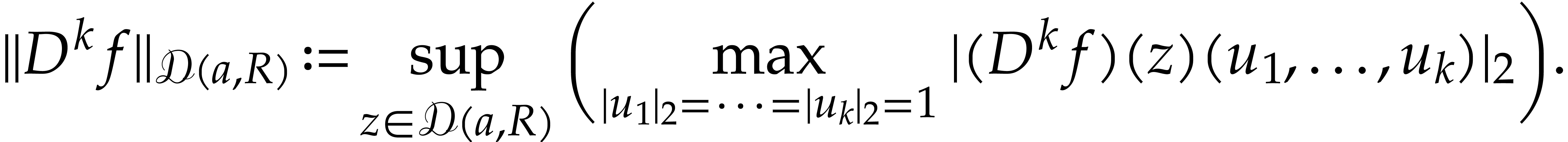
Here we recall that
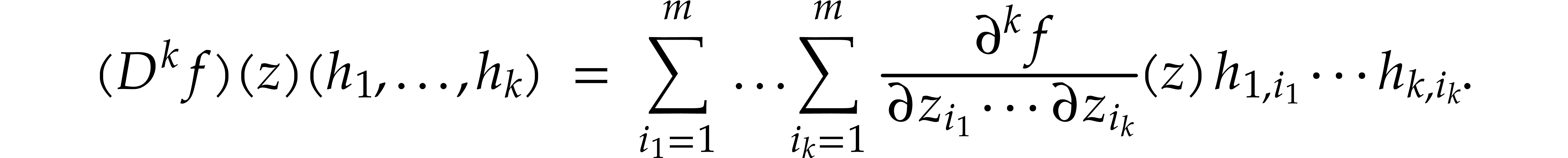
Given 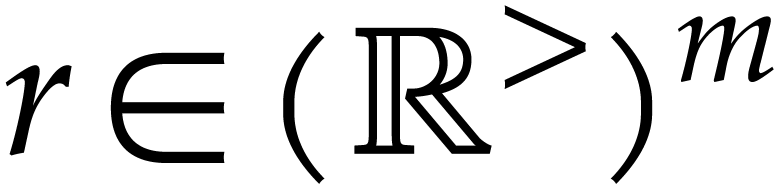 and
and 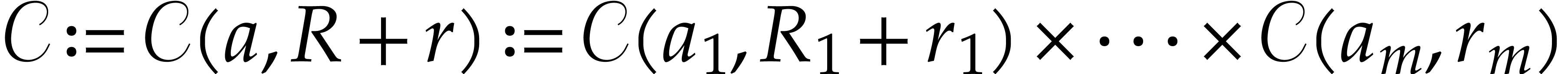 with
with  , we have the following
, we have the following 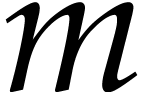 -dimensional generalization of (6.1):
-dimensional generalization of (6.1):
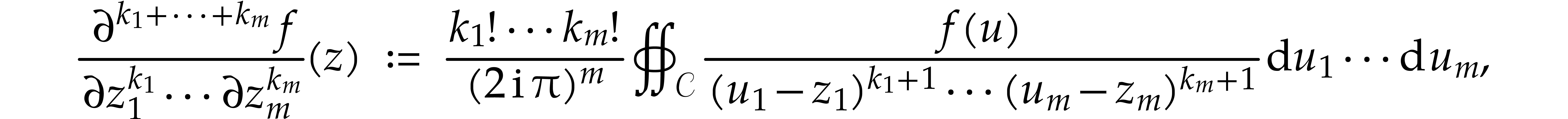
for any 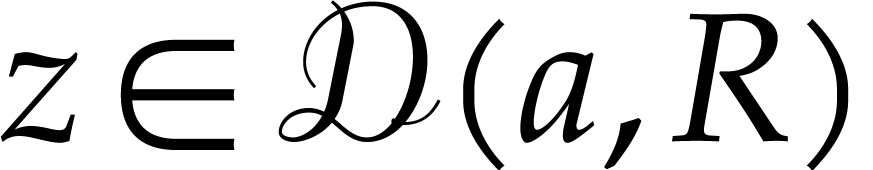 . For any
. For any  , it follows that
, it follows that
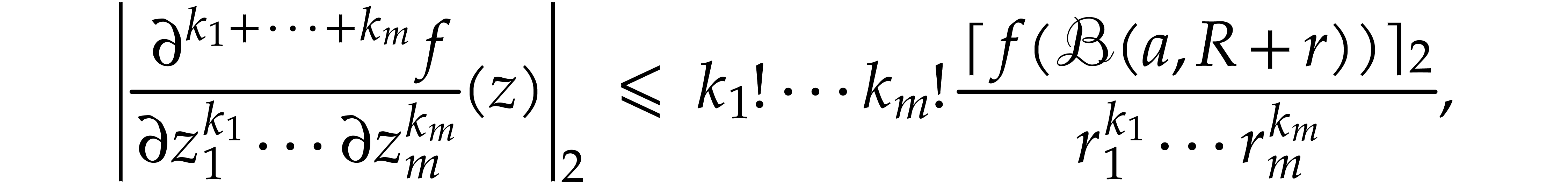
where 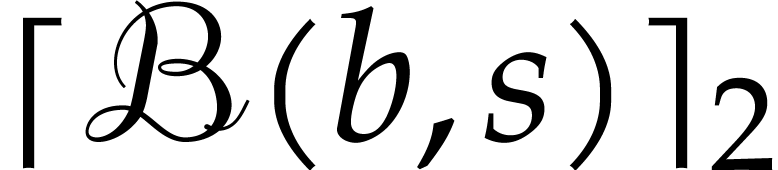 stands for an upper bound for
stands for an upper bound for  with
with 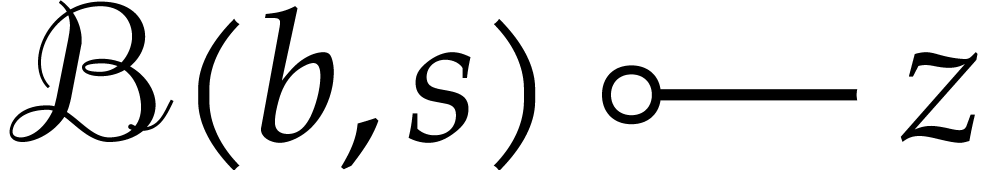 .
Translated into operator norms, this yields
.
Translated into operator norms, this yields
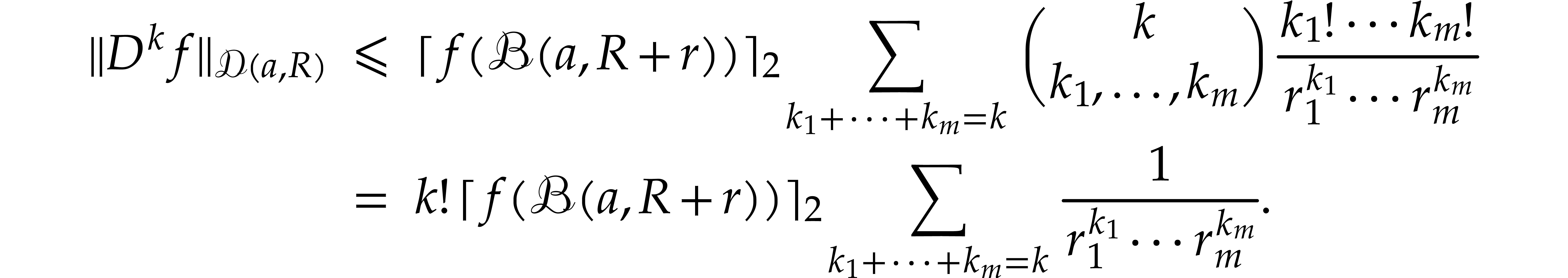
A practical approach to find an 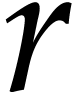 which
approximately minimizes the right-hand side is similar to what we did in
the univariate case: starting from a given
which
approximately minimizes the right-hand side is similar to what we did in
the univariate case: starting from a given 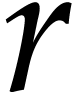 ,
we vary it in a dichotomic way until we reach an acceptably good
approximation. This time, we need to vary the
,
we vary it in a dichotomic way until we reach an acceptably good
approximation. This time, we need to vary the 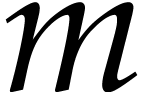 individual components
individual components  of
of 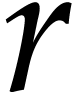 in turn, which makes the approximation process roughly
in turn, which makes the approximation process roughly 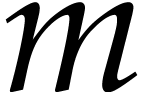 times more expensive. Multivariate analogues of (6.3) are
more complicated and we leave this issue for future work.
times more expensive. Multivariate analogues of (6.3) are
more complicated and we leave this issue for future work.
A. Ahlbäck, J. van der Hoeven, and G. Lecerf. JIL: a high performance library for straight-line programs. https://sourcesup.renater.fr/projects/jil, 2025.
G. Alefeld and J. Herzberger. Introduction to interval computation. Academic Press, New York, 1983.
W. Baur and V. Strassen. The complexity of partial derivatives. Theor. Comput. Sci., 22:317–330, 1983.
C. Beltrán and A. Leykin. Robust certified numerical homotopy tracking. Found. Comput. Math., 13(2):253–295, 2013.
P. Bürgisser, M. Clausen, and M. A. Shokrollahi. Algebraic complexity theory, volume 315 of Grundlehren der Mathematischen Wissenschaften. Springer-Verlag, 1997.
T. Duff and K. Lee. Certified homotopy tracking using the Krawczyk method. In Proceedings of the 2024 International Symposium on Symbolic and Algebraic Computation, ISSAC '24, pages 274–282. New York, NY, USA, 2024. ACM.
A. Guillemot and P. Lairez. Validated numerics for algebraic path tracking. In Proc. ISSAC 2024, pages 36–45. ACM, 2024.
J. van der Hoeven. Ball arithmetic. In A. Beckmann, C. Gaßner, and B. Löwe, editors, Logical approaches to Barriers in Computing and Complexity, number 6 in Preprint-Reihe Mathematik, pages 179–208. Ernst-Moritz-Arndt-Universität Greifswald, February 2010. International Workshop.
J. van der Hoeven. Reliable homotopy continuation. Technical Report, HAL, 2011. https://hal.archives-ouvertes.fr/hal-00589948.
J. van der Hoeven and G. Lecerf. Evaluating straight-line programs over balls. In 23nd IEEE Symposium on Computer Arithmetic (ARITH), pages 142–149. 2016. Extended preprint version with Appendix at https://hal.archives-ouvertes.fr/hal-01225979.
J. van der Hoeven and G. Lecerf. Towards a library for straight-line programs. Technical Report, HAL, 2025. https://hal.science/hal-05075591.
J. van der Hoeven, G. Lecerf, B. Mourrain et al. Mathemagix. 2002. http://www.mathemagix.org.
L. Jaulin, M. Kieffer, O. Didrit, and E. Walter. Applied interval analysis. Springer, London, 2001.
F. Johansson. Arb: a C library for ball arithmetic. ACM Commun. Comput. Algebra, 47(3/4):166–169, 2014.
R. B. Kearfott. An interval step control for continuation methods. SIAM J. Numer. Anal., 31(3):892–914, 1994.
U. W. Kulisch. Computer arithmetic and validity. Theory, implementations and applications. Studies in Mathematics., (33), 2008.
R. E. Moore. Interval analysis. Prentice Hall, Englewood Cliff, 1966.
R. E. Moore, R.B. Kearfott, and M. J. Cloud. Introduction to interval analysis. SIAM Press, 2009.
A. Neumaier. Interval methods for systems of equations. Cambridge University Press, Cambridge, 1990.
S. M. Rump. Fast and parallel interval arithmetic. BIT, 39(3):534–554, 1999.
S. M. Rump. Verification methods: rigorous results using floating-point arithmetic. Acta Numer, 19:287–449, 2010.