Consider an effective differential ring
|
|
Consider an effective differential ring
|
There exist essentially two approaches in computer algebra for the computation with formal solutions of systems of ordinary or partial differential equations.
The first approach is based on the theory of differential algebra [Rit50, Sei56, Ros59, Kap57,
Kol73, Bui92]. We start with an effective
differential field  with derivations
with derivations  and enrich
and enrich  with the formal
solution to a system
with the formal
solution to a system 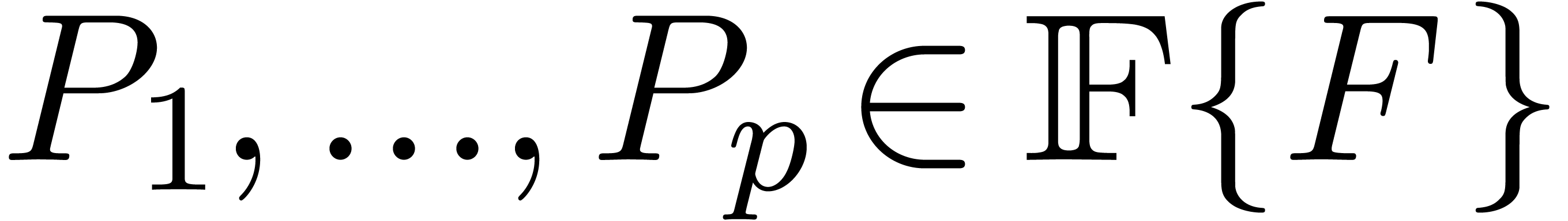 of differential
polynomials. From an algebraic point of view, this formal solution lies
in the differential quotient ring
of differential
polynomials. From an algebraic point of view, this formal solution lies
in the differential quotient ring 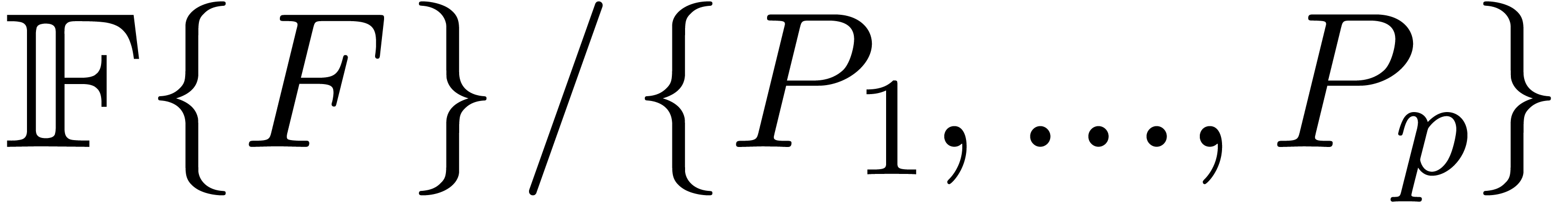 of
of 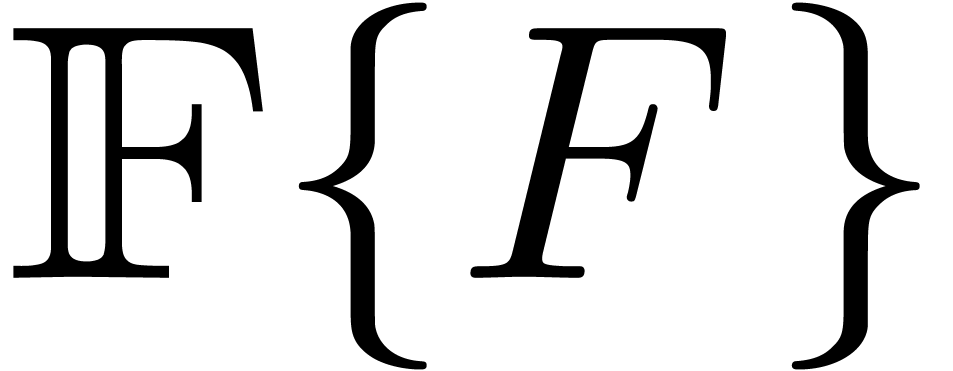 by the perfect ideal
by the perfect ideal  generated by
generated by
 . The theory of differential
algebra is well-established and admits an effective counterpart: see [Bou94] for an overview. In particular, there exists a
zero-test in
. The theory of differential
algebra is well-established and admits an effective counterpart: see [Bou94] for an overview. In particular, there exists a
zero-test in 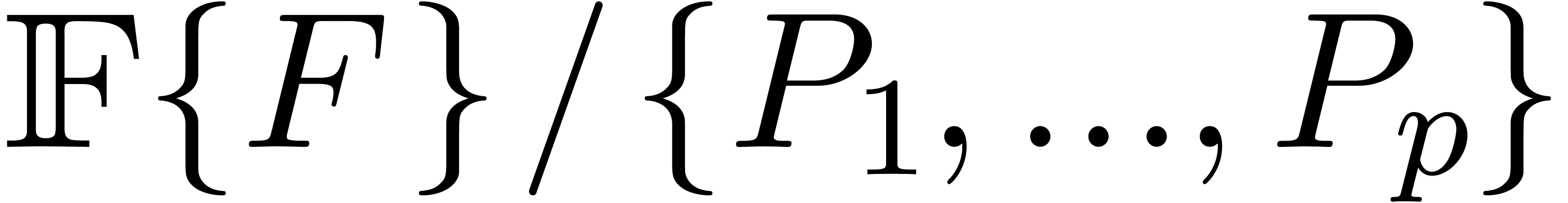 .
.
In practice however, a simple function such as 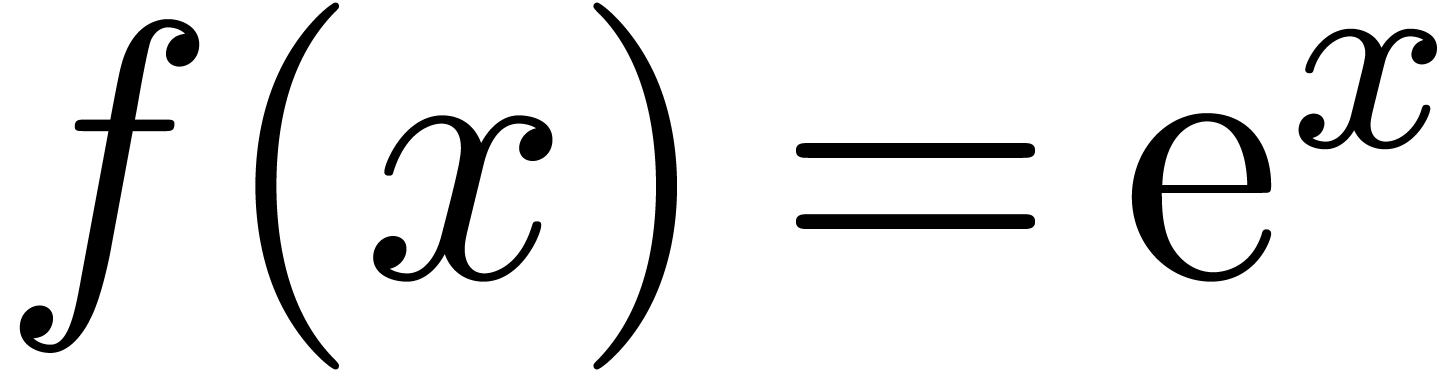 is not just the solution to the differential equation
is not just the solution to the differential equation 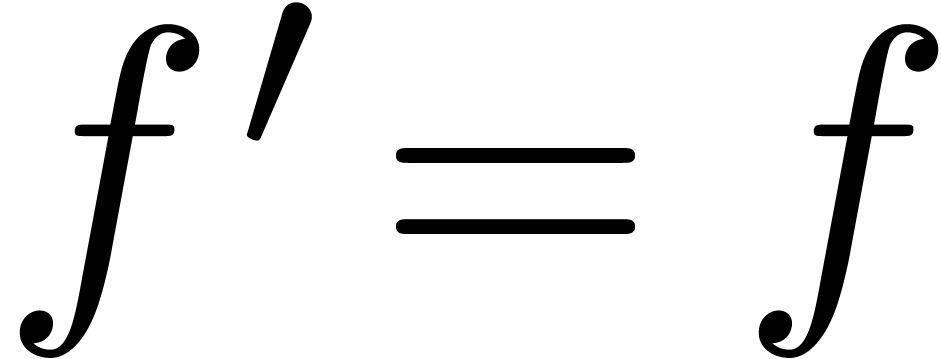 , but it also satisfies the initial condition
, but it also satisfies the initial condition
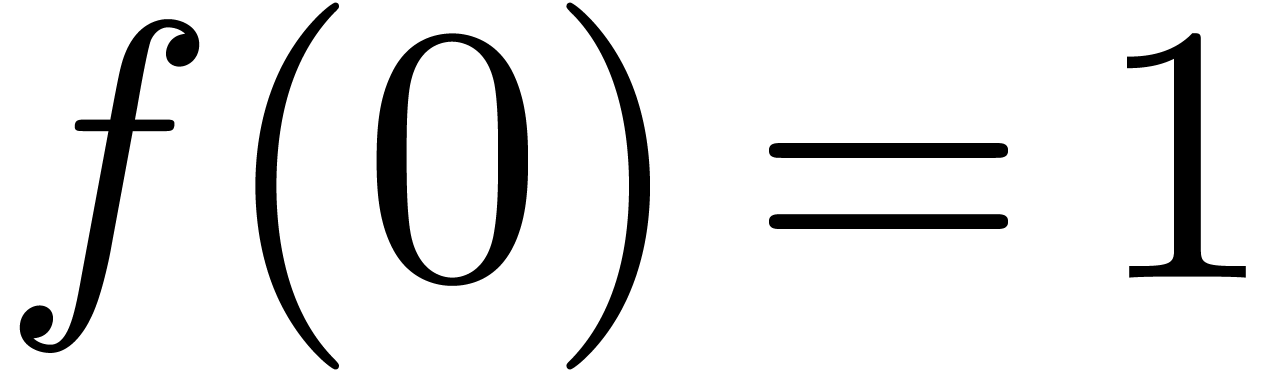 . When taking into account
initial conditions, non-zero elements in
. When taking into account
initial conditions, non-zero elements in 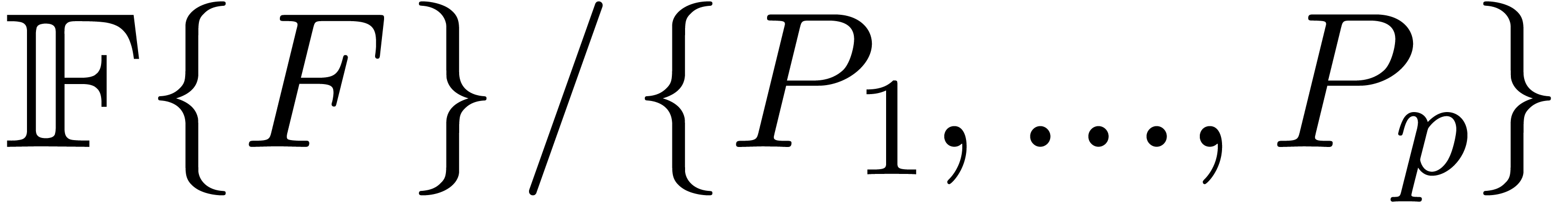 may
vanish when we consider them as functions. For instance, assume that we
redefine
may
vanish when we consider them as functions. For instance, assume that we
redefine 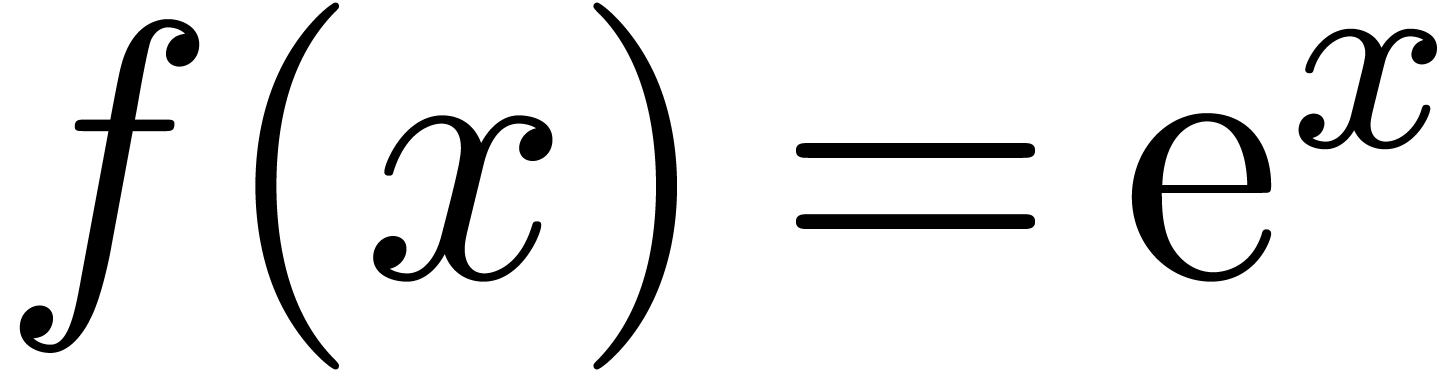 to be the unique solution to
to be the unique solution to 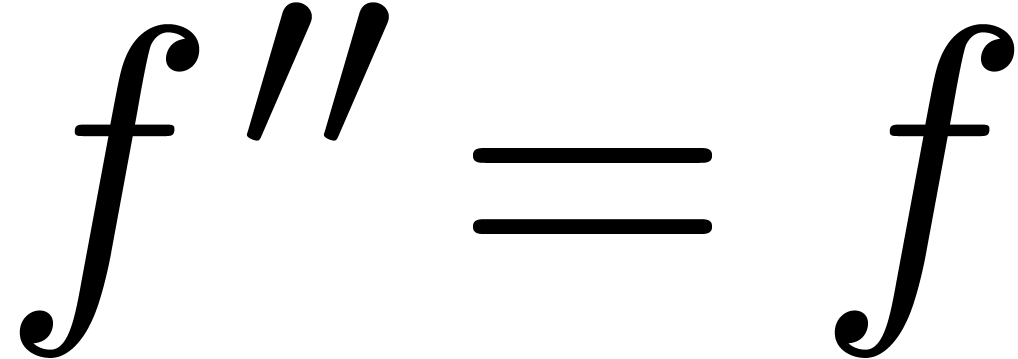 with
with 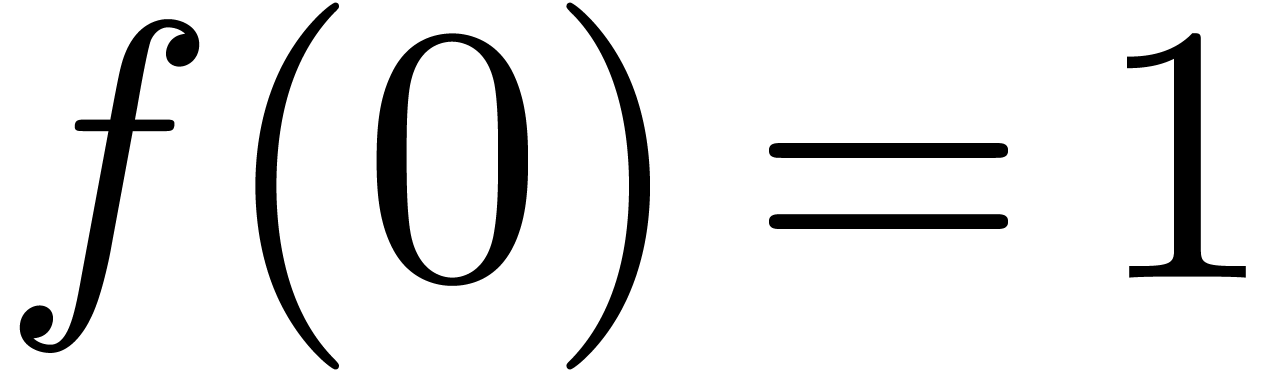 and
and 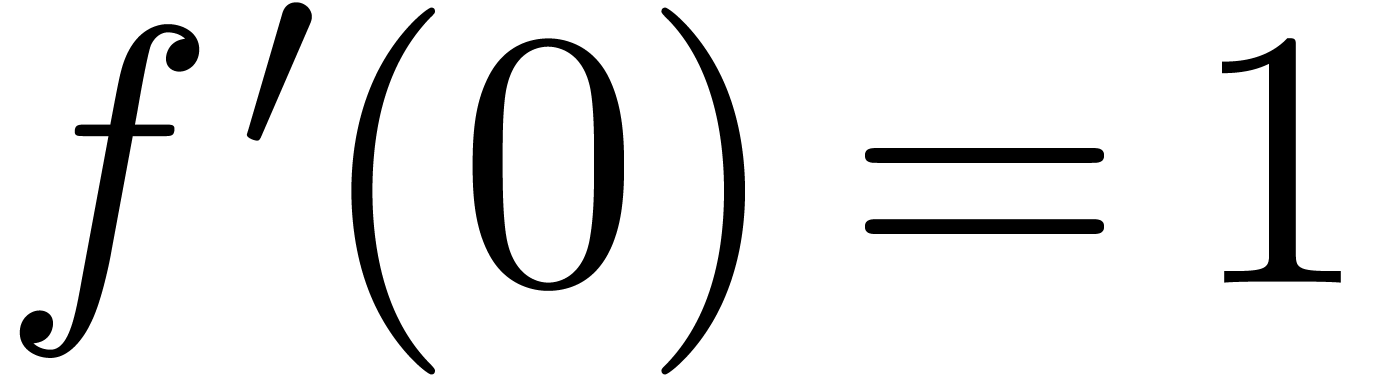 . Then
. Then 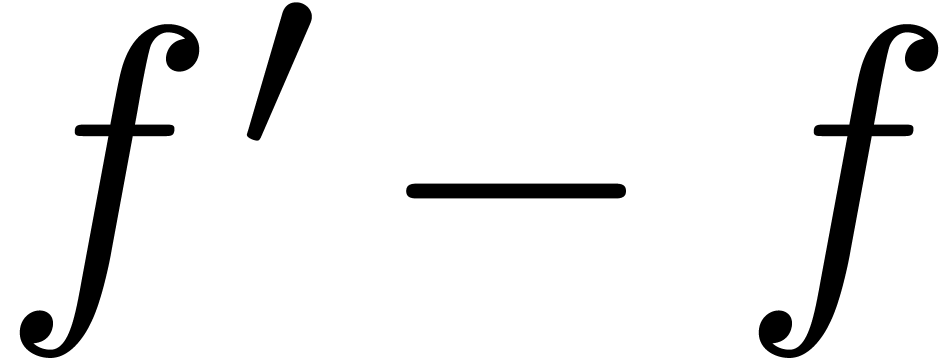 is non-zero as an
element of
is non-zero as an
element of 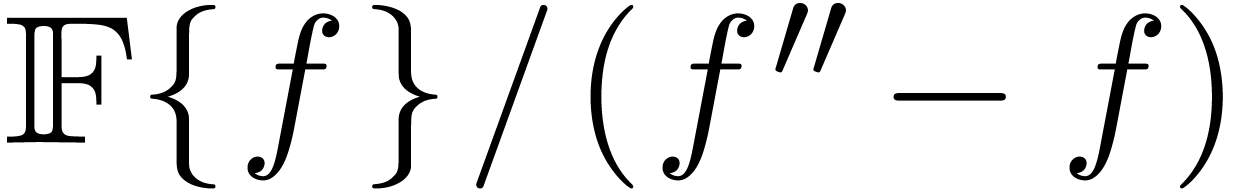 , even though
, even though 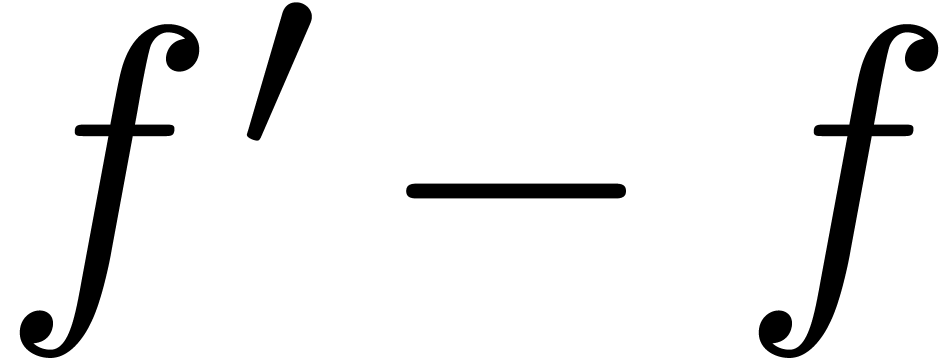 vanishes as a function.
vanishes as a function.
In certain cases, it may therefore be necessary to consider a second approach, in which the new functions are defined to be solutions to systems of differential equations with initial conditions. Since most functions which arise in this way are analytic, it is natural to systematically work with computable power series.
More precisely, given an effective field  ,
a multivariate power series
,
a multivariate power series 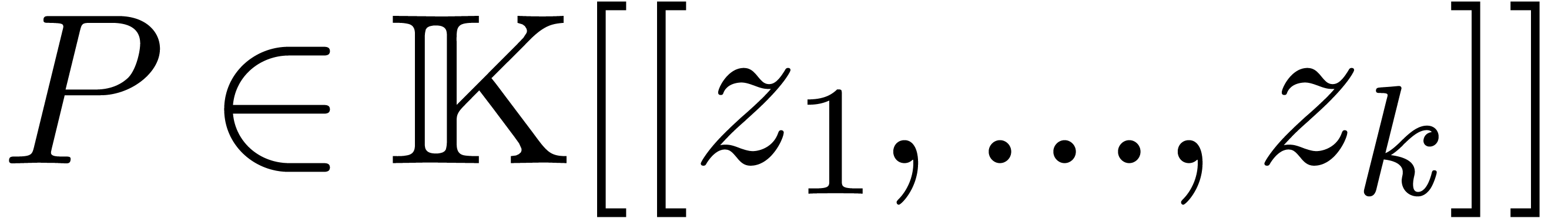 is said to be
computable, if there exists an algorithm which takes
is said to be
computable, if there exists an algorithm which takes 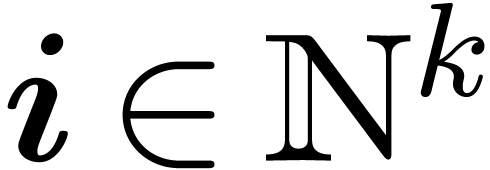 on input and which outputs the corresponding coefficient
on input and which outputs the corresponding coefficient
 of
of  in
in  . The set
. The set  of such
series forms a differential ring, even though
of such
series forms a differential ring, even though  does not come with a zero-test.
does not come with a zero-test.
Now assume that we are given an effective subring  of
of  and let
and let  be the
quotient field of
be the
quotient field of  . We wish
to extend
. We wish
to extend  with power series solutions
with power series solutions 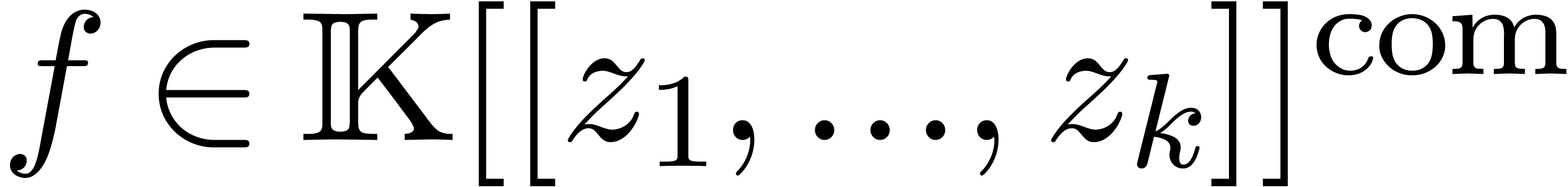 to systems of partial differential equations
to systems of partial differential equations 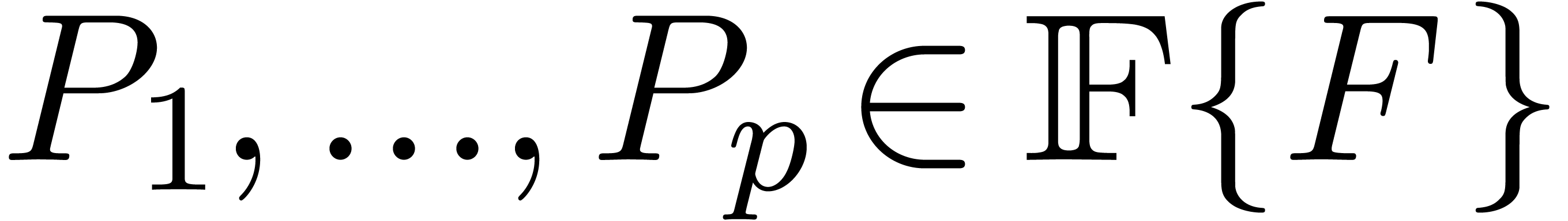 . In the ordinary differential case, the
coefficients of
. In the ordinary differential case, the
coefficients of  can generally be computed as a
function of the equations
can generally be computed as a
function of the equations  and a finite number of
initial conditions in
and a finite number of
initial conditions in  . In
the case of partial differential equations, the initial conditions are
taken in
. In
the case of partial differential equations, the initial conditions are
taken in 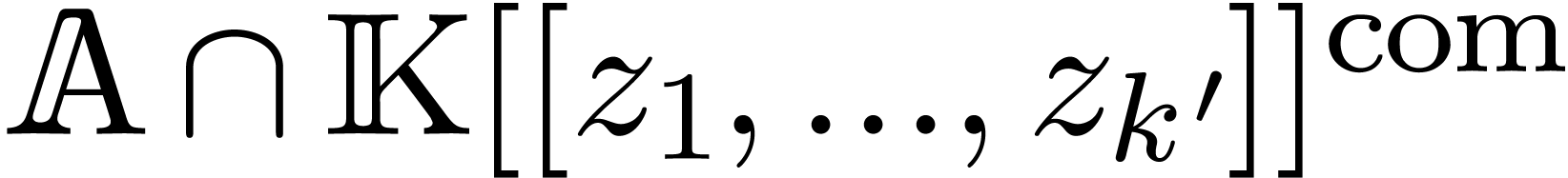 with
with 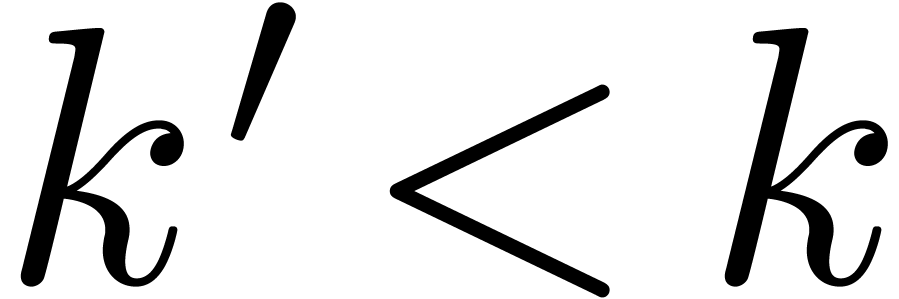 .
.
When extending  with the solution to a system of
differential equations which satisfies explicit initial conditions, an
important problem is to decide whether
with the solution to a system of
differential equations which satisfies explicit initial conditions, an
important problem is to decide whether 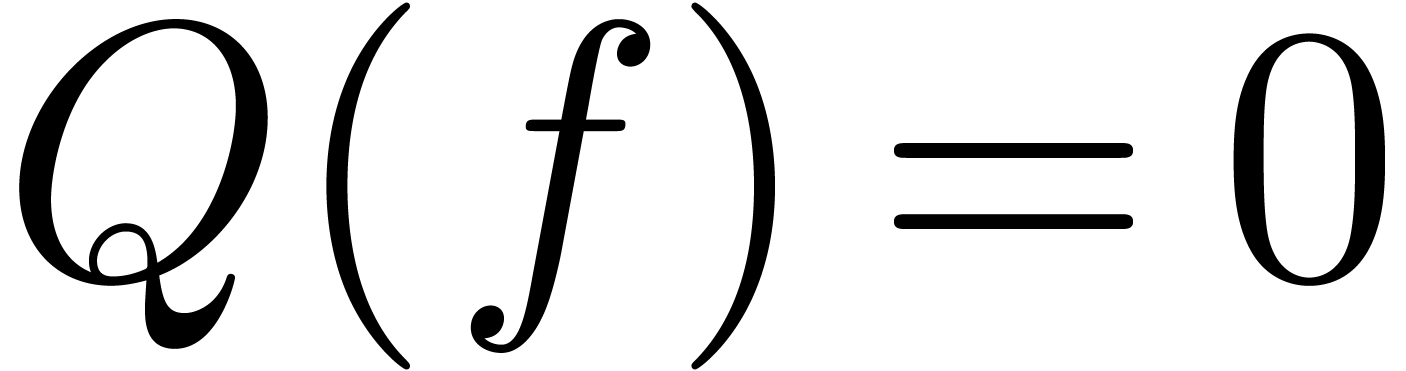 for a
given differential polynomial
for a
given differential polynomial  .
In the case of ordinary differential equations, there exists a variety
of algorithms to solve this problem [DL84, DL89,
Sha89, Sha93, PG95, PG97,
vdH01, vdHS06, vdH02]; see [vdH02] for a discussion. Progress in the case of partial
differential equations has been slower and the best currently known
result [PG02] reduces the zero-test problem to the Ritt
problem concerning the distribution of the singular zeros of a
differential system among its irreducible components. In fact, questions
related to the zero-test problem quickly tend to be undecidable:
.
In the case of ordinary differential equations, there exists a variety
of algorithms to solve this problem [DL84, DL89,
Sha89, Sha93, PG95, PG97,
vdH01, vdHS06, vdH02]; see [vdH02] for a discussion. Progress in the case of partial
differential equations has been slower and the best currently known
result [PG02] reduces the zero-test problem to the Ritt
problem concerning the distribution of the singular zeros of a
differential system among its irreducible components. In fact, questions
related to the zero-test problem quickly tend to be undecidable:
 has a power series solution in
has a power series solution in 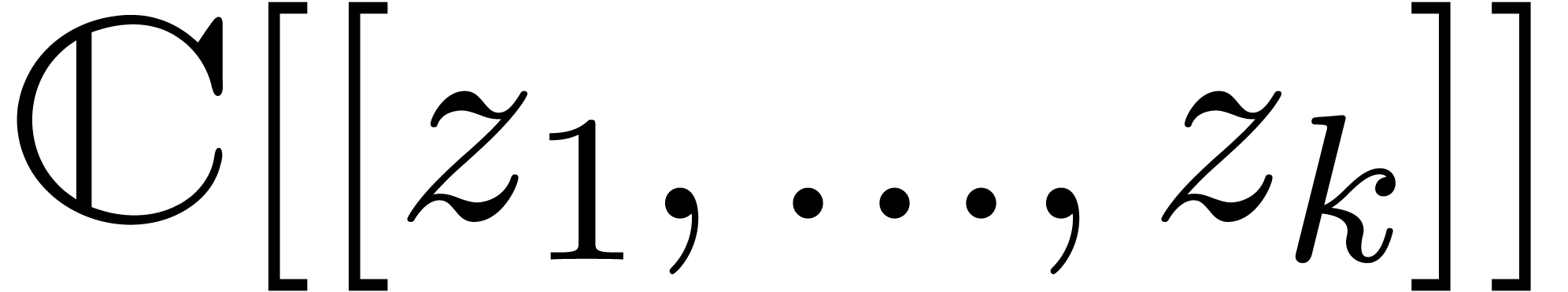 .
.
In this paper, we propose a zero-test in the partial differential case,
which is based on a generalization of the technique from [vdH02,
vdHS06]. In a nutshell, assume that 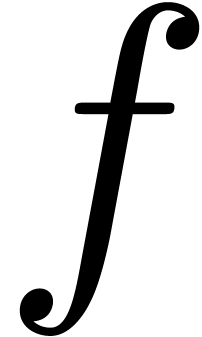 is the unique solution to
is the unique solution to  with
with 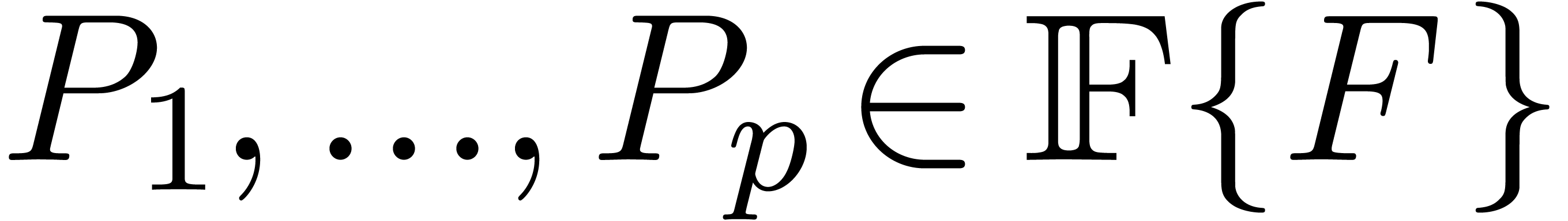 and explicit initial conditions. In order to test whether
and explicit initial conditions. In order to test whether 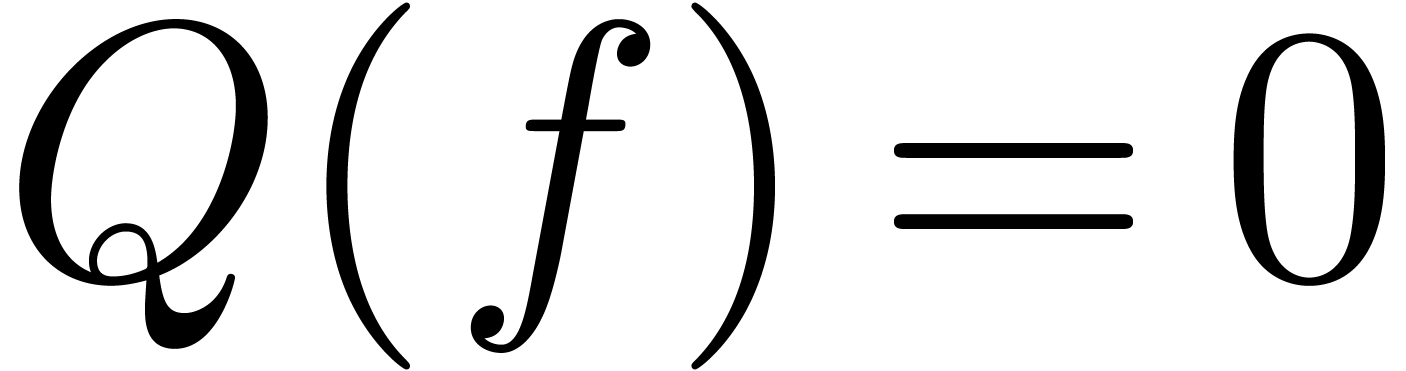 for
for  , we first
simplify the system of equations
, we first
simplify the system of equations 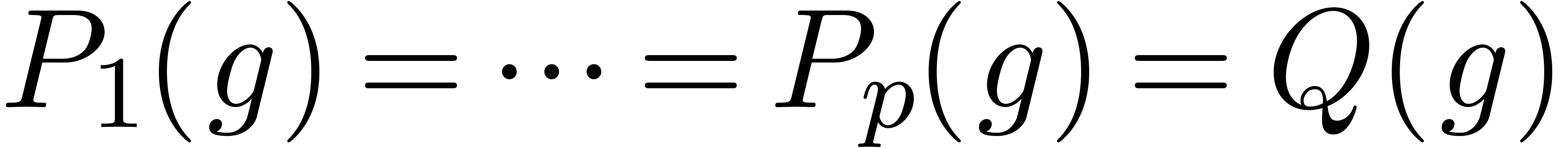 using the
theory of differential algebra. At the end, we obtain a new system of
equations
using the
theory of differential algebra. At the end, we obtain a new system of
equations 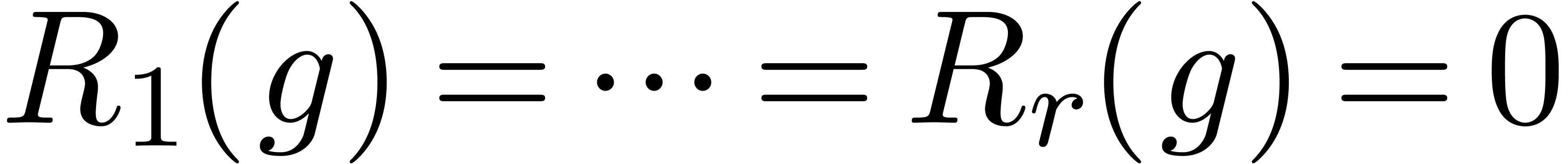 . If we can show
that this system admits a solution
. If we can show
that this system admits a solution  which
satisfies the same initial conditions as
which
satisfies the same initial conditions as 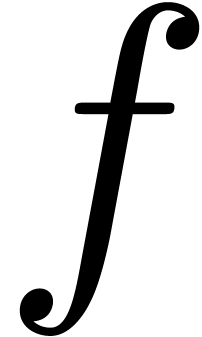 ,
then the fact that
,
then the fact that  implies
implies 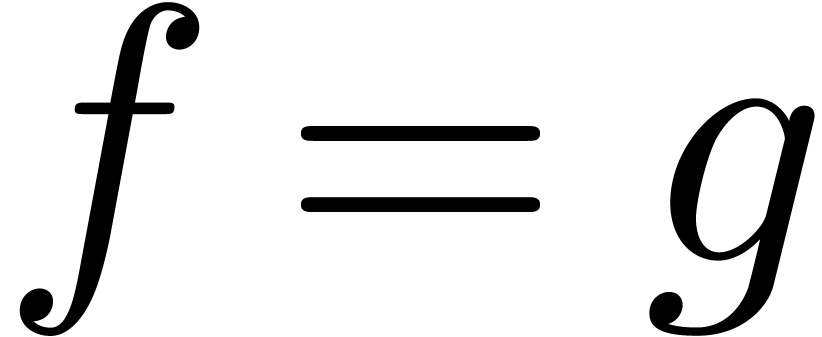 and
and 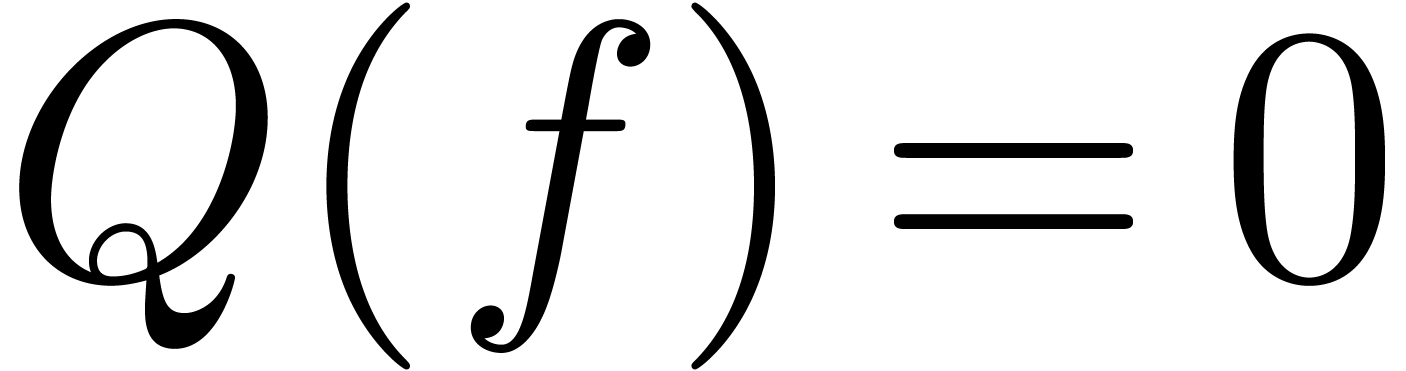 . If
. If 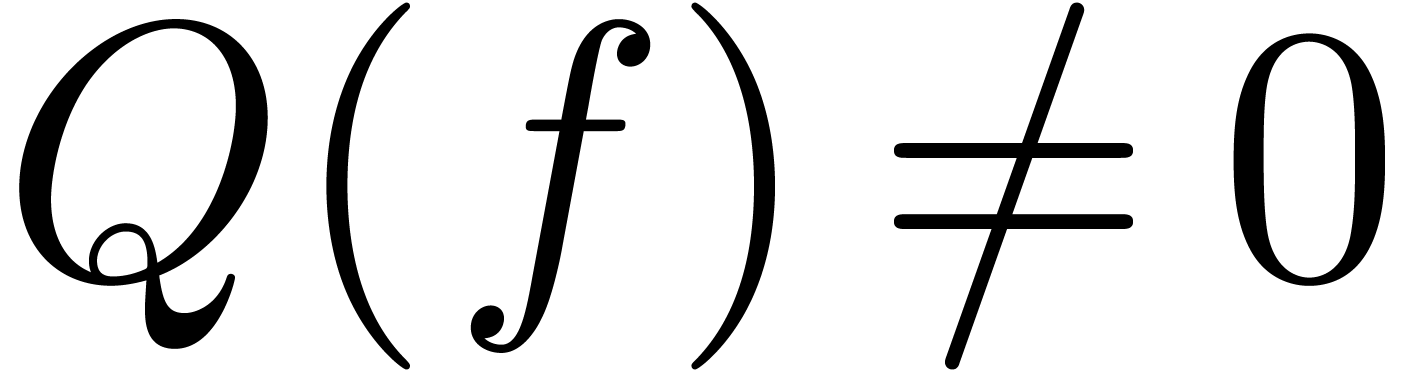 , then it suffices to expand
, then it suffices to expand 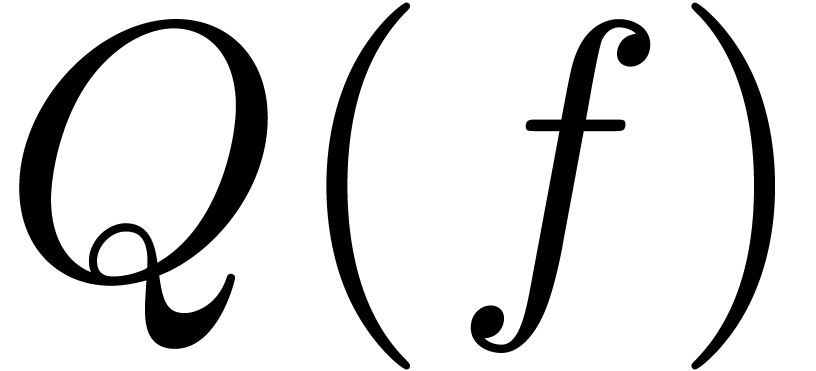 sufficiently far in order to find a non-zero coefficient.
sufficiently far in order to find a non-zero coefficient.
The main difficulty is to ensure the existence of a suitable solution
 to the reduced system
to the reduced system 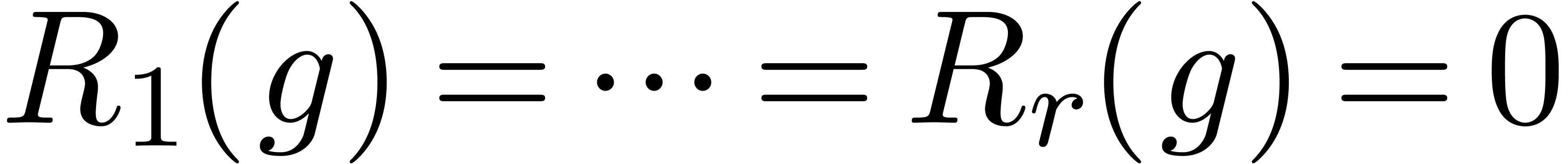 , which may be highly singular. The main part of
this paper is devoted to further reduce the system
, which may be highly singular. The main part of
this paper is devoted to further reduce the system 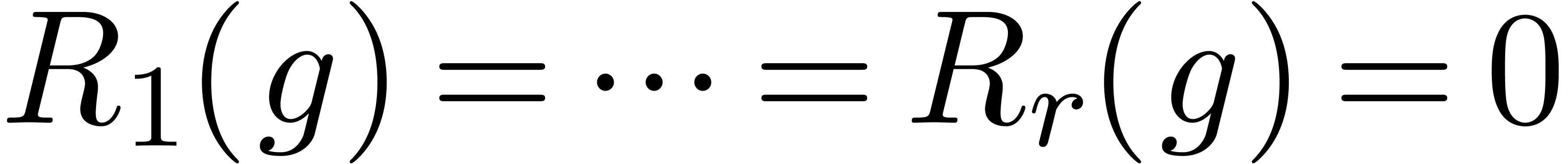 together with the initial conditions into an asymptotic normal form
(called an asymptotic basis). If this asymptotic normal form is
non-contradictory, then we will guarantee the existence of a solution in
a suitable field
together with the initial conditions into an asymptotic normal form
(called an asymptotic basis). If this asymptotic normal form is
non-contradictory, then we will guarantee the existence of a solution in
a suitable field  of power series with
logarithmic coefficients. In order to make our zero-test work, we thus
have to assume that
of power series with
logarithmic coefficients. In order to make our zero-test work, we thus
have to assume that  is also the unique solution
in
is also the unique solution
in  to
to 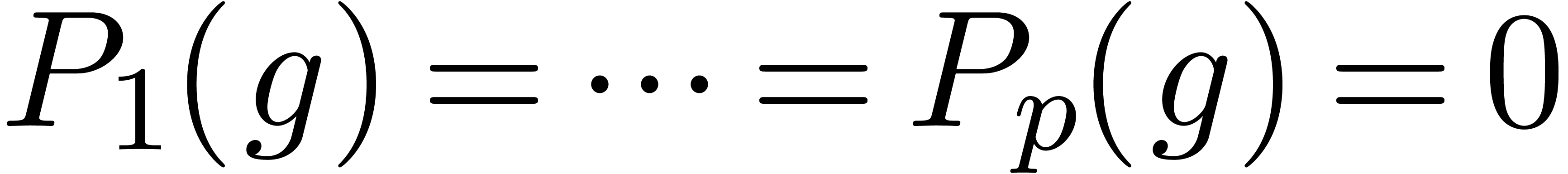 with the
prescribed initial conditions. Fortunately, this is only a mild
additional hypothesis.
with the
prescribed initial conditions. Fortunately, this is only a mild
additional hypothesis.
Let us outline the structure of the paper. In section 2, we start with some quick reminders on so called grid-based power series. For a more detailed treatment, we refer to [vdH06, Chapter 2].
In section 3, we review the elementary theory of
differential algebra. In order to lighten notations, we will only
consider equations in one differential indeterminate. In section 3.6, we also introduce Ritt co-reduction in the “dual
setting” where differential operators in 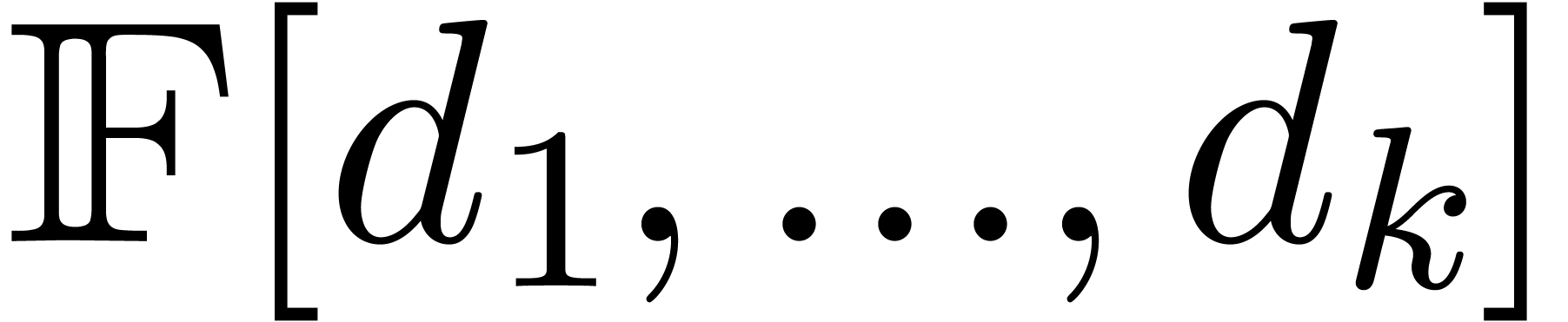 are replaced by operators in
are replaced by operators in 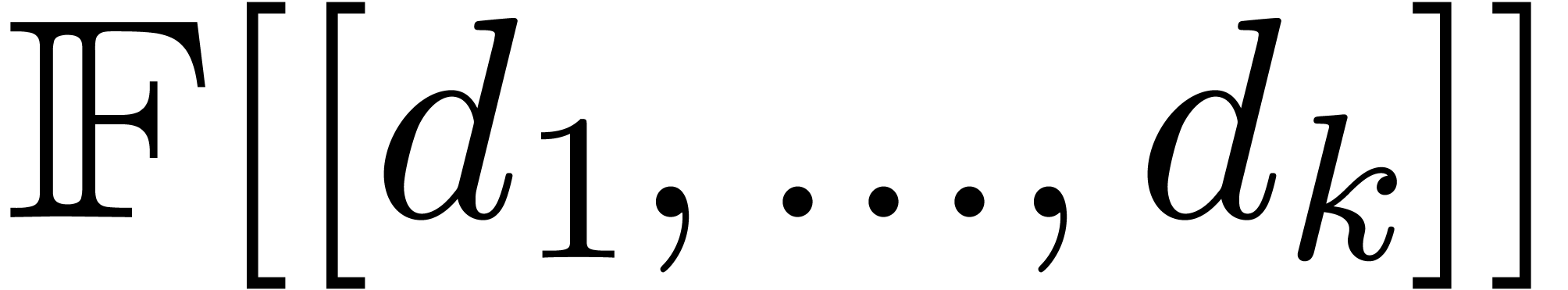 .
This dual setting was considered before in the linear case [vdH07].
.
This dual setting was considered before in the linear case [vdH07].
In section 4, we next switch to the case when we work over
a field  of grid-based power series
of grid-based power series 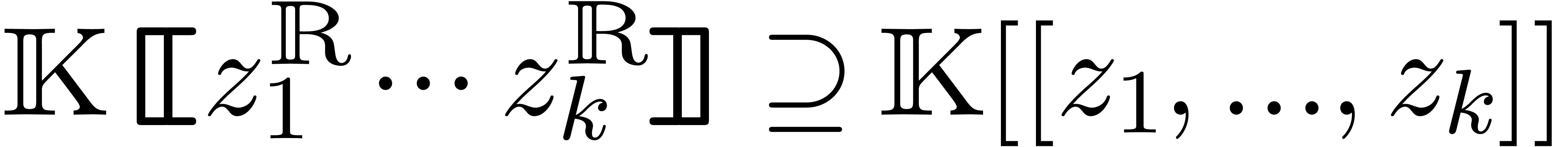 with a suitable monomial ordering on
with a suitable monomial ordering on  . This field comes with natural valuation
preserving derivations
. This field comes with natural valuation
preserving derivations 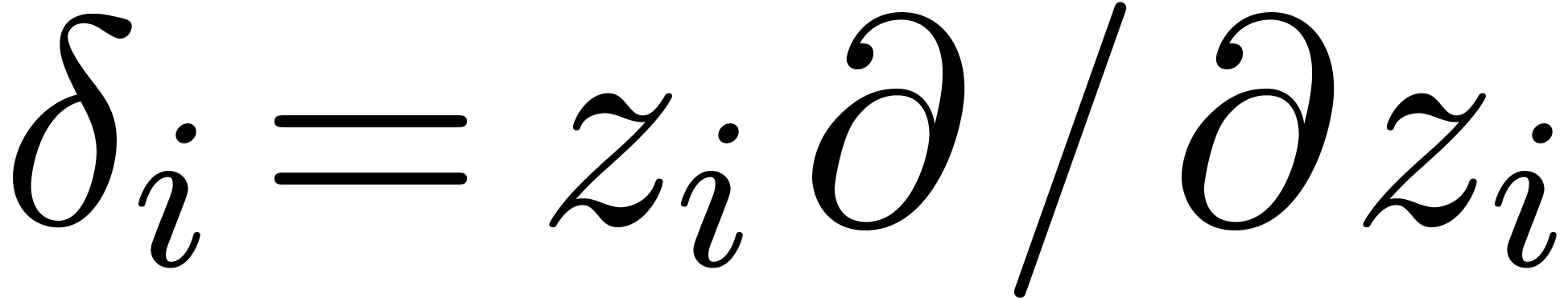 . More
generally, for suitable
. More
generally, for suitable 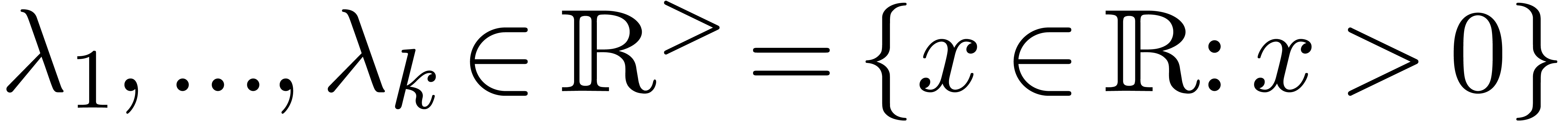 , we
will consider more general derivations
, we
will consider more general derivations 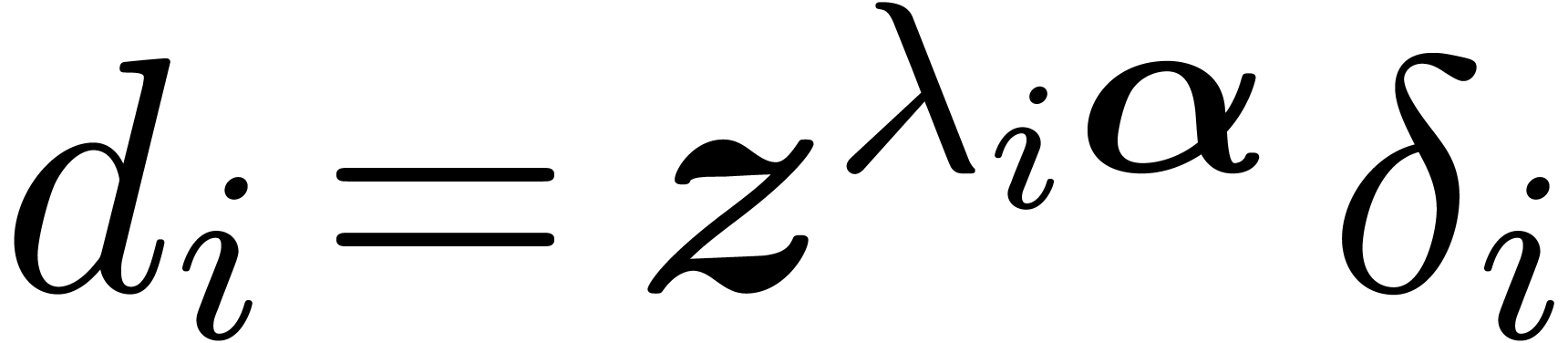 ,
where
,
where 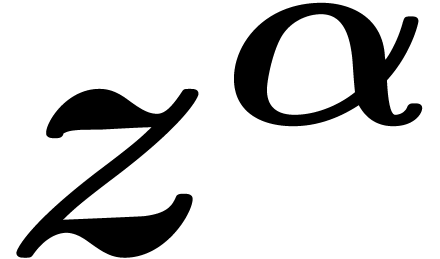 is an infinitesimal monomial. Since
is an infinitesimal monomial. Since  is a field of series, it is naturally to study the
dominant parts of differential equations, which gives rise to a theory
of “asymptotic differential algebra”.
is a field of series, it is naturally to study the
dominant parts of differential equations, which gives rise to a theory
of “asymptotic differential algebra”.
Although a general theory of asymptotic differential algebra is somewhat
difficult to design due to the possible presence of infinite powers of
initials and separants in the asymptotic analogue of Ritt reduction, a
systematic theory can be developed in the case of “quasi-linear
differential ideals”. We will define and outline the basic
properties of such ideals in section 5 and prove the
existence of zeros in 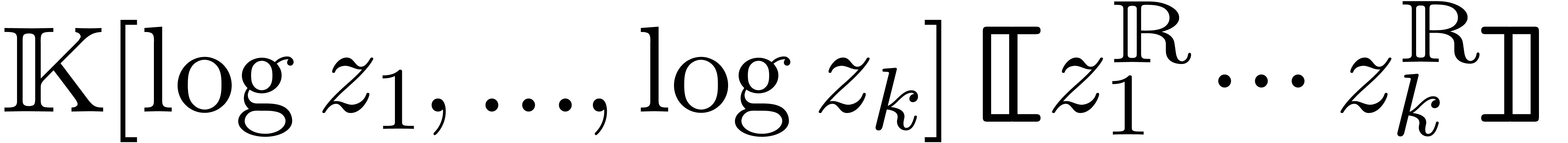 in the case when the
derivations are
in the case when the
derivations are  .
.
Starting with the equations 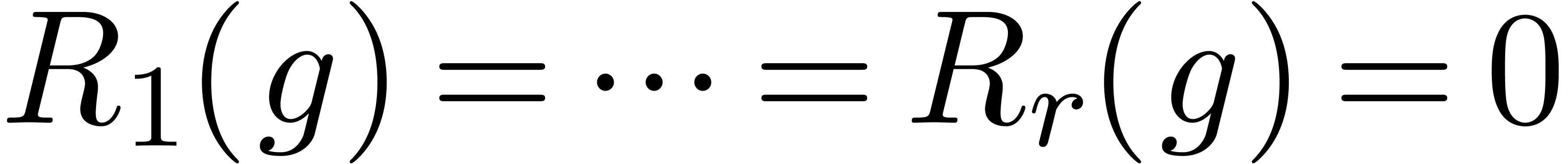 ,
we next have to put the equations in quasi-linear form. This is
automatic for the derivations
,
we next have to put the equations in quasi-linear form. This is
automatic for the derivations 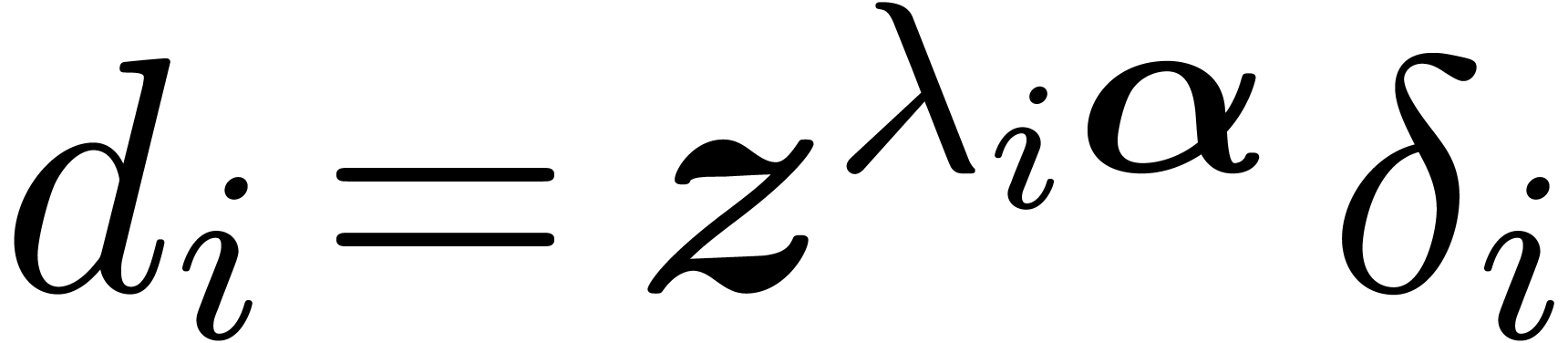 if
if  is sufficiently small. Using a suitable process of
asymptotic dualizations and changes of derivations, we will show in
section 6 how to end up with a system of quasi-linear
equations w.r.t.
is sufficiently small. Using a suitable process of
asymptotic dualizations and changes of derivations, we will show in
section 6 how to end up with a system of quasi-linear
equations w.r.t.  .
In section 7, we will give algorithmic counterparts of this
construction and show how this can be used to elaborate our zero-test.
.
In section 7, we will give algorithmic counterparts of this
construction and show how this can be used to elaborate our zero-test.
When applying the algorithm from this paper in the ordinary differential case, we notice a small difference with [vdH02, vdHS06]. In the present paper, we expand sufficiently far so as to make the equations in the reduced system quasi-linear. This simplifies the existence proof of solutions, but may require expansions up to a higher order than what was necessary before. Indeed, the previous algorithms relied on a theoretical result [vdH02, Theorem 3] for the existence proof (see also [vdH06, Chapter 8]).
For convenience of the reader, we will briefly recall the definition of grid-based power series, as well as some notational conventions. For a more detailed exposition, we refer to [vdH06, Chapter 2].
Let  be an arbitrary ring of coefficients (
be an arbitrary ring of coefficients ( is usually a field) and
is usually a field) and  a
totally ordered multiplicative group (one may also consider partially
ordered monoids). The ordering
a
totally ordered multiplicative group (one may also consider partially
ordered monoids). The ordering  on
on  is called an asymptotic dominance relation and we
call
is called an asymptotic dominance relation and we
call  a monomial group. A subset
a monomial group. A subset  is said to be grid-based if
is said to be grid-based if  for some infinitesimal monomials
for some infinitesimal monomials  and an
arbitrary monomial
and an
arbitrary monomial  . Here
. Here
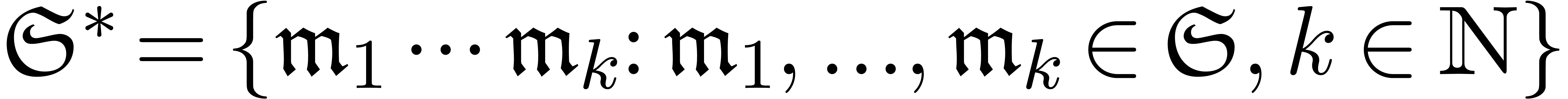 for any
for any  .
.
A grid-based series is a formal sum 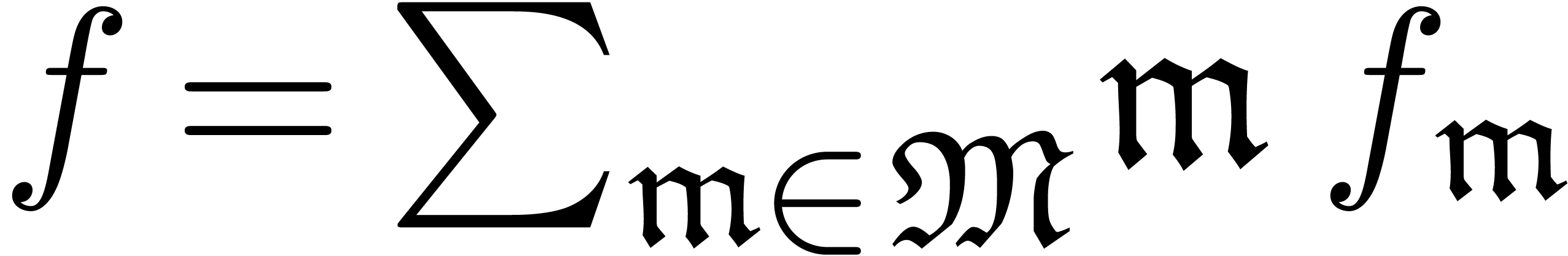 with
with 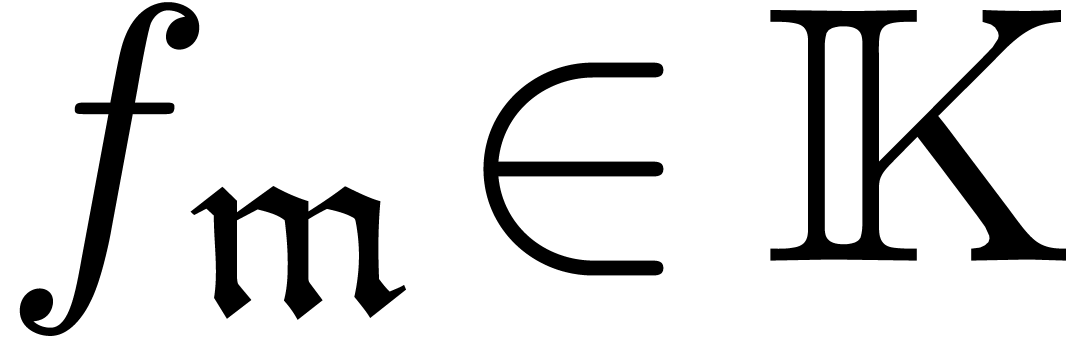 and grid-based support
and grid-based support 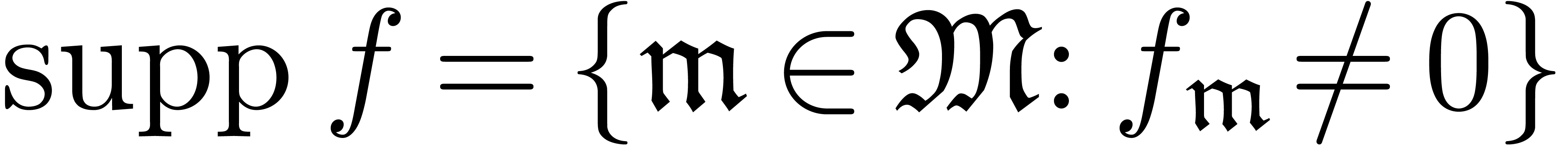 . For reasons which will become clear later in
the paper (when
. For reasons which will become clear later in
the paper (when  will be allowed to be a
non-commutative ring of operators), we multiplied
will be allowed to be a
non-commutative ring of operators), we multiplied  on the right with its corresponding coefficient
on the right with its corresponding coefficient  . The set
. The set  of grid-based
series forms a ring (and a field if
of grid-based
series forms a ring (and a field if  is a field).
is a field).
Any non-zero grid-based series  admits a unique
dominant monomial
admits a unique
dominant monomial 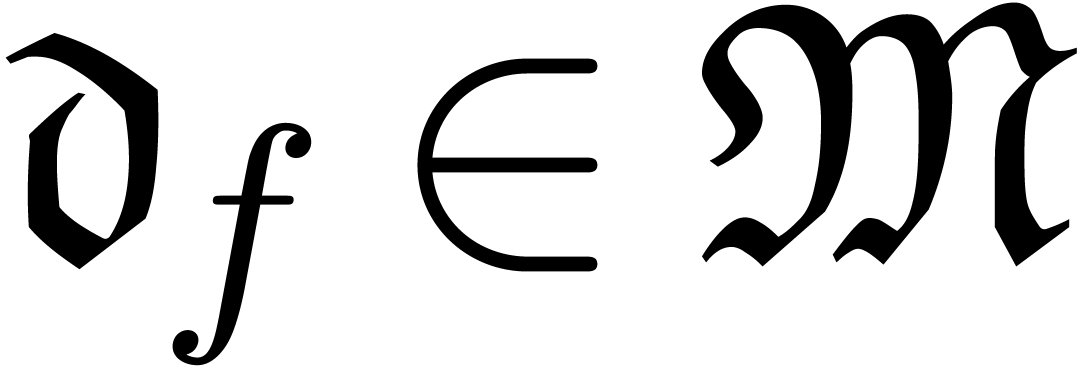 (the maximal element
in its support) and a corresponding dominant coefficient
(the maximal element
in its support) and a corresponding dominant coefficient 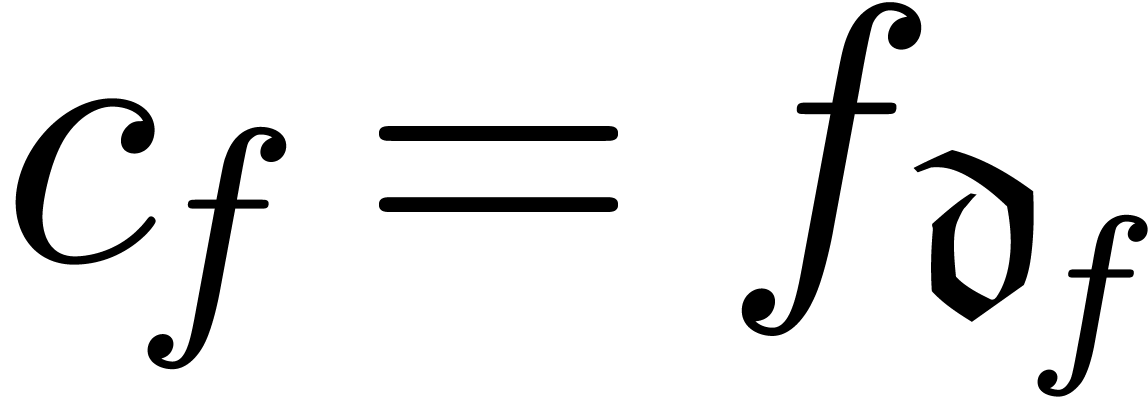 . By convention,
. By convention, 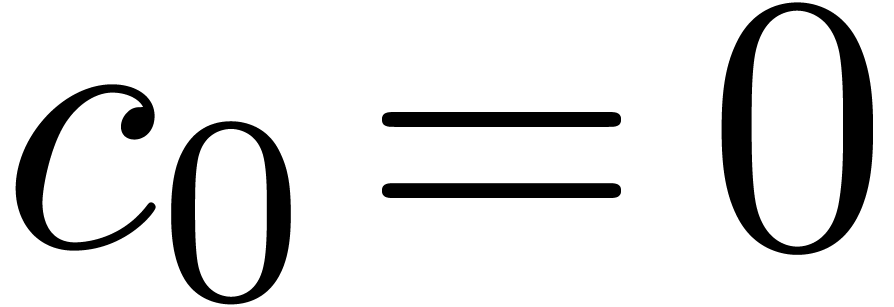 . The dominance relation
. The dominance relation  may be extended to
may be extended to  by setting
by setting  if
if 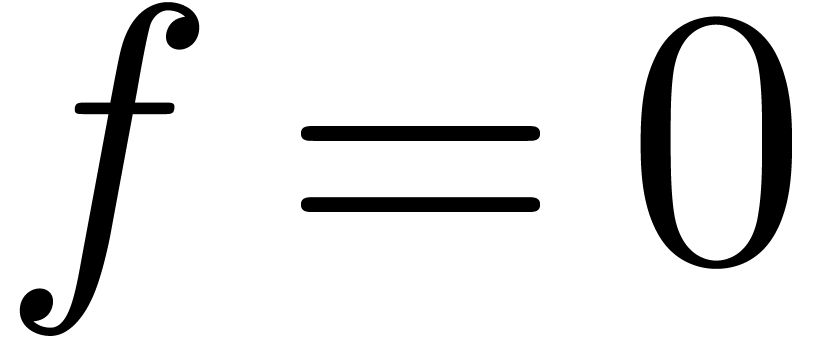 or
or 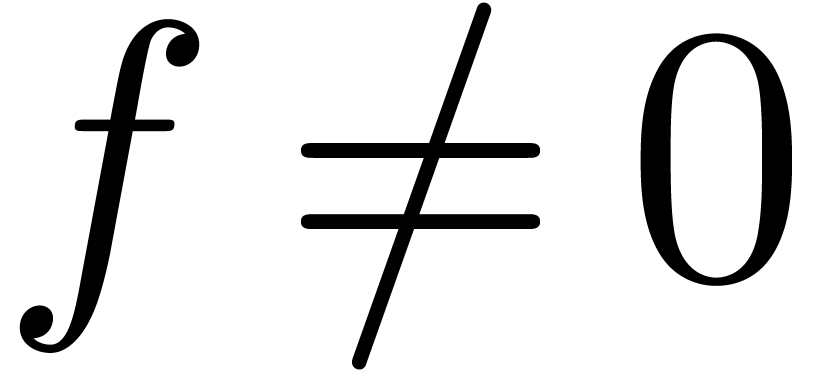 and
and 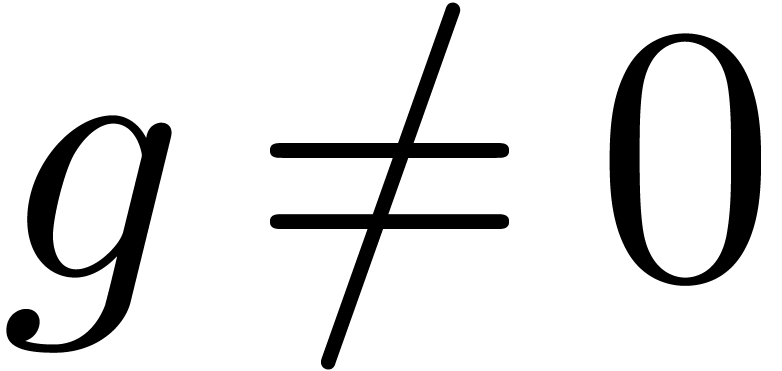 and
and  . This
notation further extends to the case when
. This
notation further extends to the case when 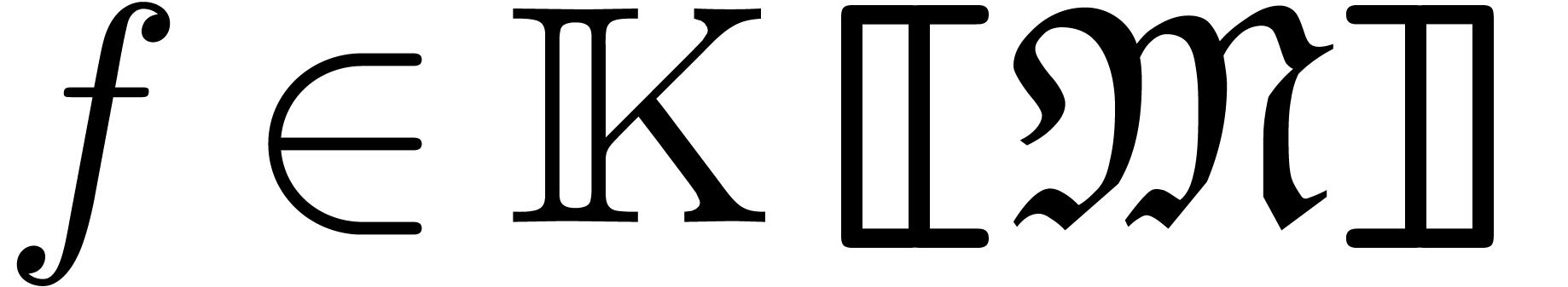 and
and
 for different rings
for different rings  and
and
 . We also write
. We also write  if
if 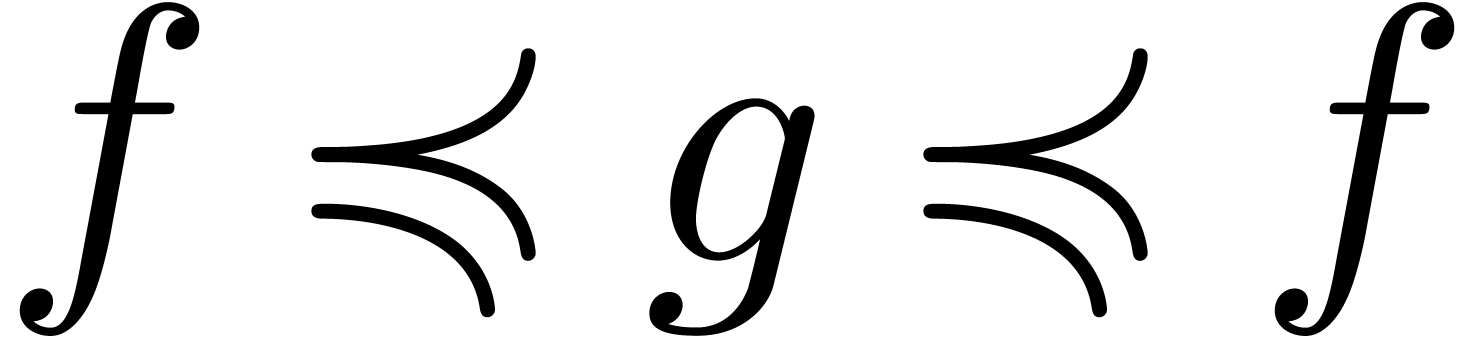 and
and  if
if
 but
but  .
Sometimes, it is convenient to use Landau's notation and write
.
Sometimes, it is convenient to use Landau's notation and write 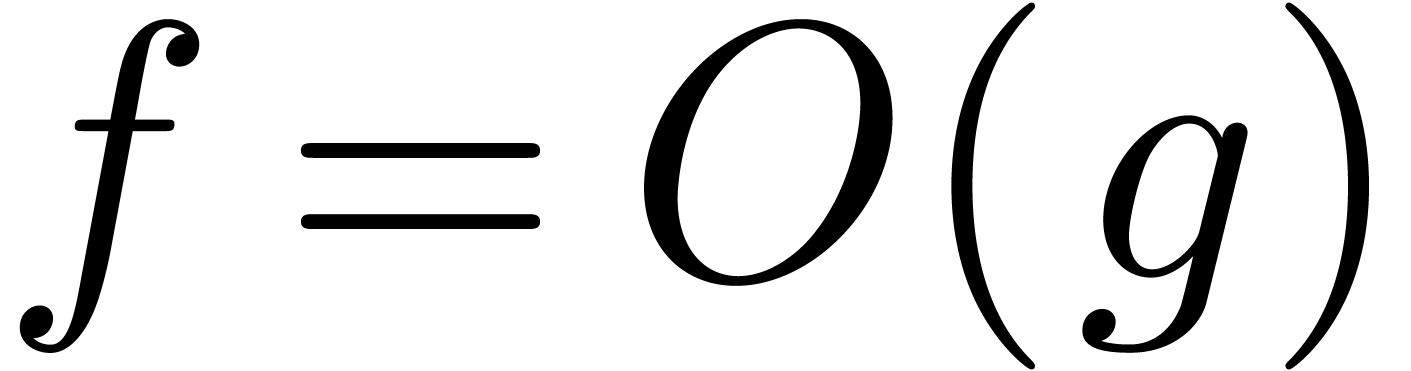 or
or 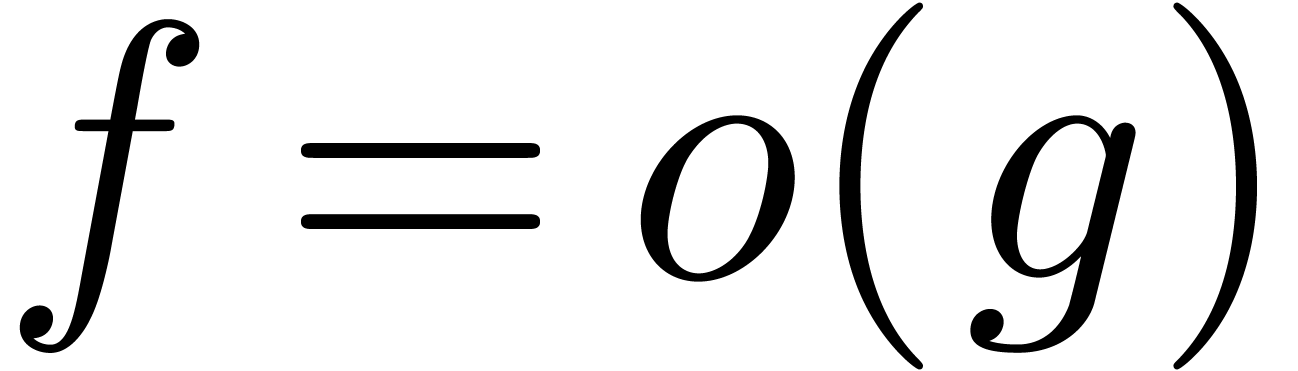 instead of
instead of  resp.
resp.  .
.
A family 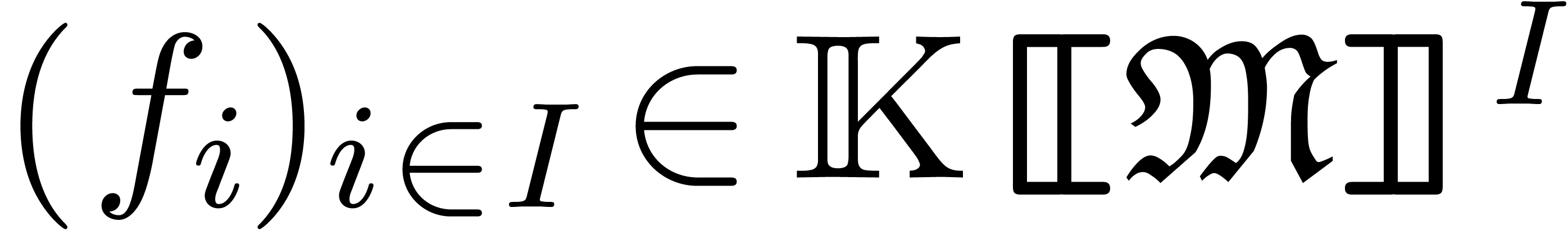 is said to be a grid-based or
summable, if
is said to be a grid-based or
summable, if 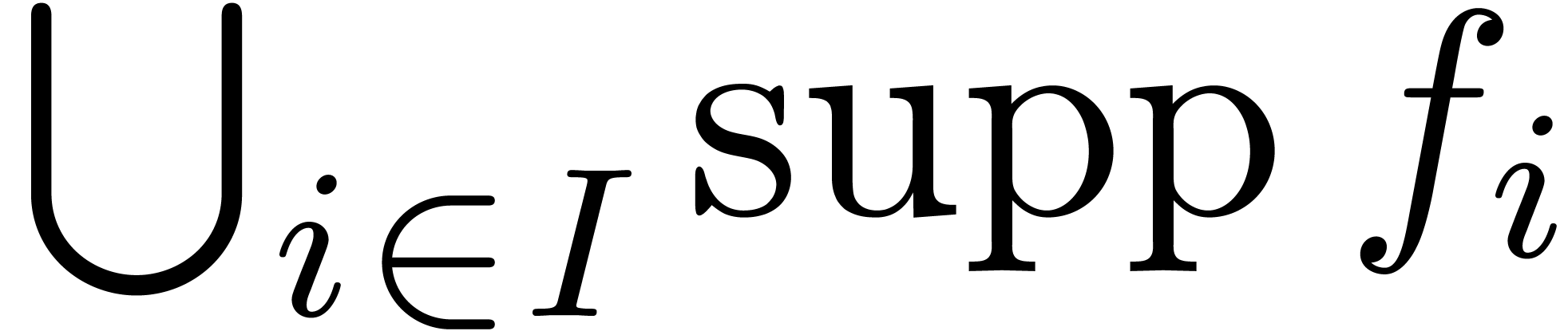 is grid-based and
is grid-based and 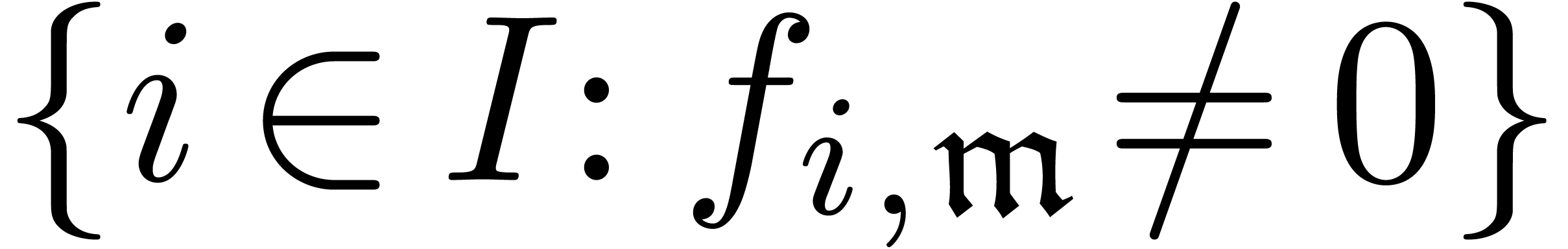 is finite for each
is finite for each  (notice
the double index convention
(notice
the double index convention  ).
In that case, its sum
).
In that case, its sum  with
with 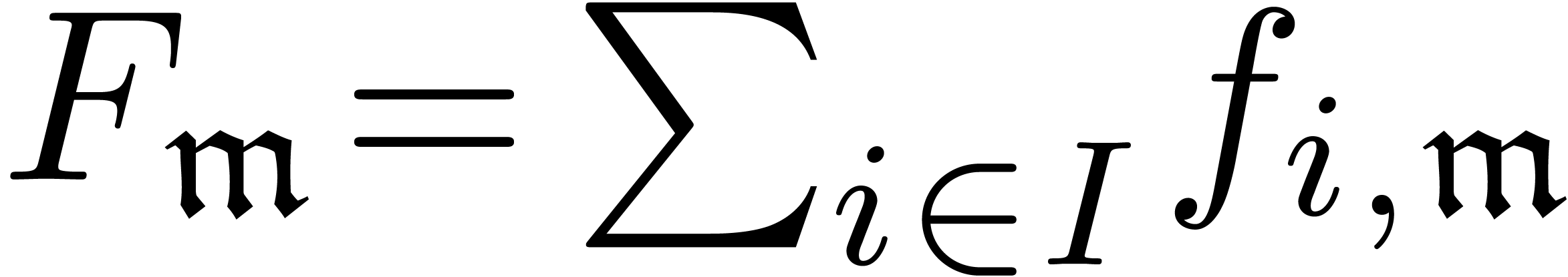 is again in
is again in  .
.
We assume that the reader is familiar with basic results from
differential algebra. Let  be a field with a
finite number of derivations
be a field with a
finite number of derivations  .
We assume that the space
.
We assume that the space  is closed under the Lie
bracket; the
is closed under the Lie
bracket; the  are not required to commute. We
will denote
are not required to commute. We
will denote
Let  be fixed
be fixed  -linearly
independent numbers in
-linearly
independent numbers in  with
with
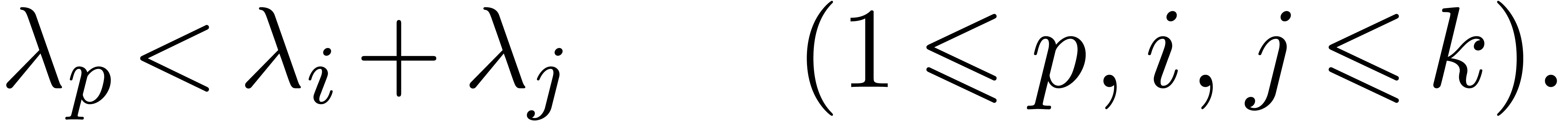 |
(1) |
It is easy to construct such  :
starting with any vector
:
starting with any vector 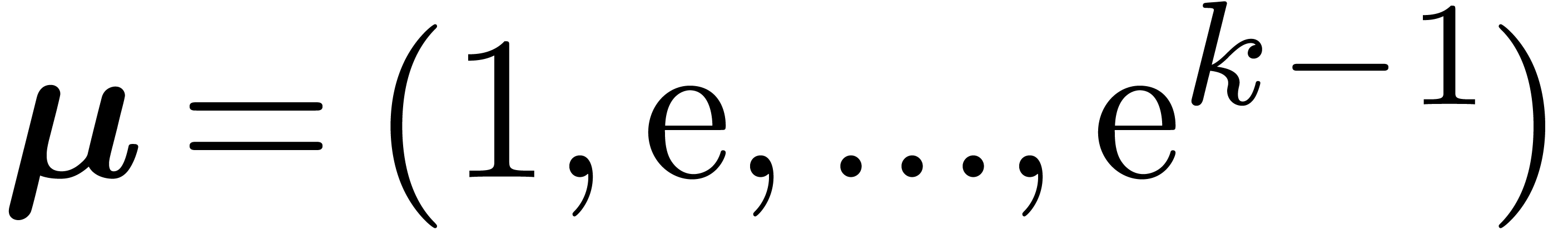 of
of  -linearly independent real numbers, it suffices
to produce a sufficiently precise rational approximation
-linearly independent real numbers, it suffices
to produce a sufficiently precise rational approximation  of
of  and take
and take  . We define a partial ordering
. We define a partial ordering  and a total ordering
and a total ordering 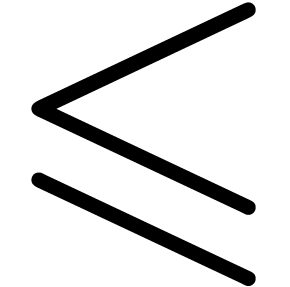 on
on 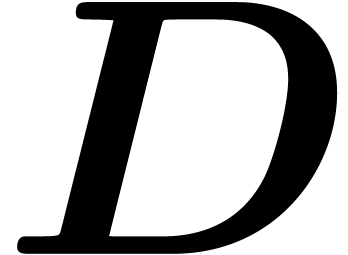 by
by
The total ordering  is admissible in Ritt's
sense.
is admissible in Ritt's
sense.
We will restrict our attention to the ring  of
differential polynomials in one single indeterminate
of
differential polynomials in one single indeterminate  . Given
. Given  ,
we will write
,
we will write 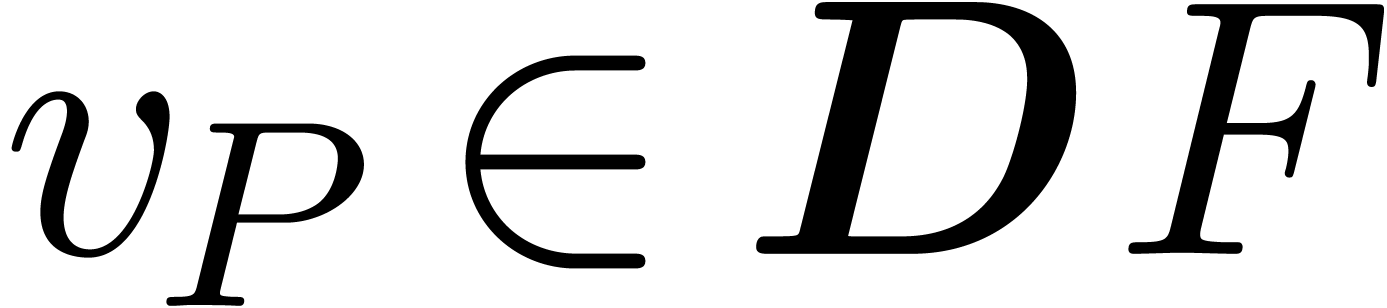 for its leader,
for its leader, 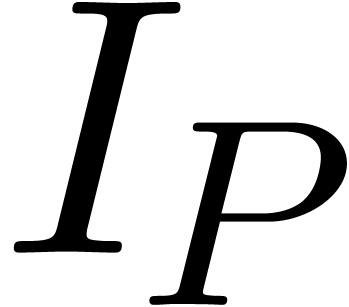 for its initial and
for its initial and 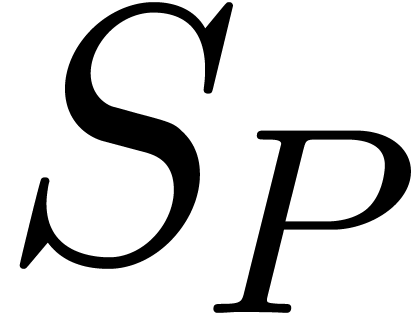 for its separant. The
relation (1) ensures that
for its separant. The
relation (1) ensures that 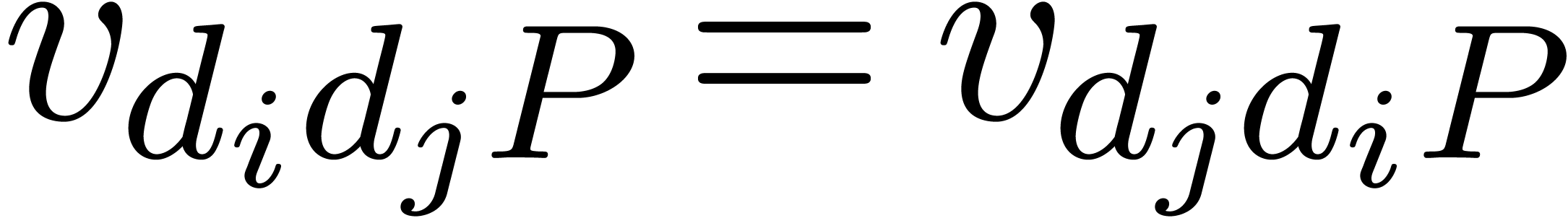 for all
for all
 . Let
. Let  a vector of differential polynomials and denote
a vector of differential polynomials and denote
Given  , Ritt reduction of
, Ritt reduction of
 w.r.t.
w.r.t.  yields a relation
yields a relation
 |
(2) |
where  ,
,  is reduced w.r.t.
is reduced w.r.t.  and
and  is a vector of linear differential operators. We
understand that
is a vector of linear differential operators. We
understand that 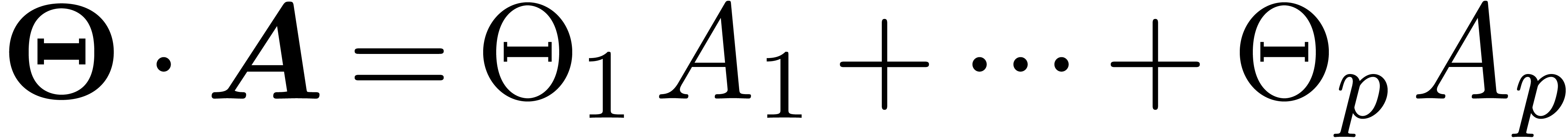 . In
particular, if
. In
particular, if  is a Rosenfeld basis
(i.e. if
is a Rosenfeld basis
(i.e. if  is a coherent auto-reduced
set), then Ritt reduction of the
is a coherent auto-reduced
set), then Ritt reduction of the  -polynomial
of
-polynomial
of 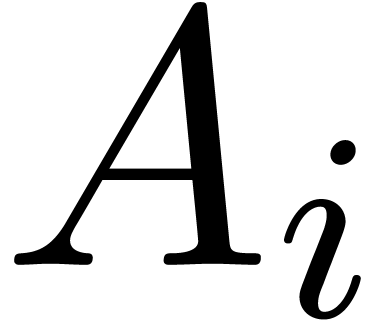 and
and 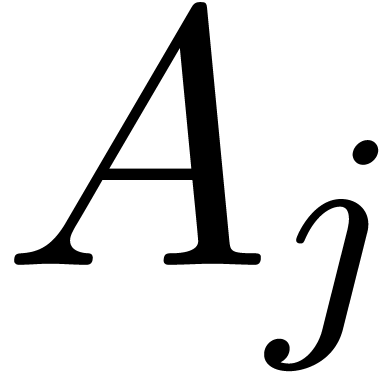 (
( ) gives rise to a relation
) gives rise to a relation
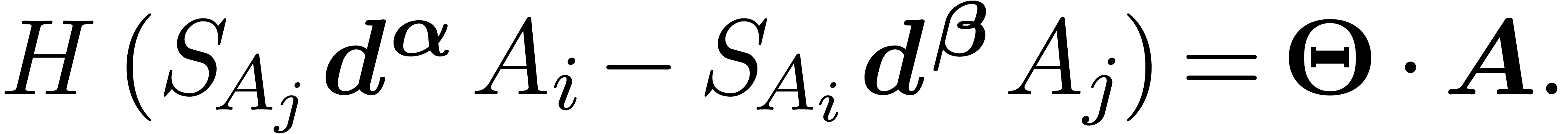 |
(3) |
We will call (3) a critical relation. It can be
rewritten in the form 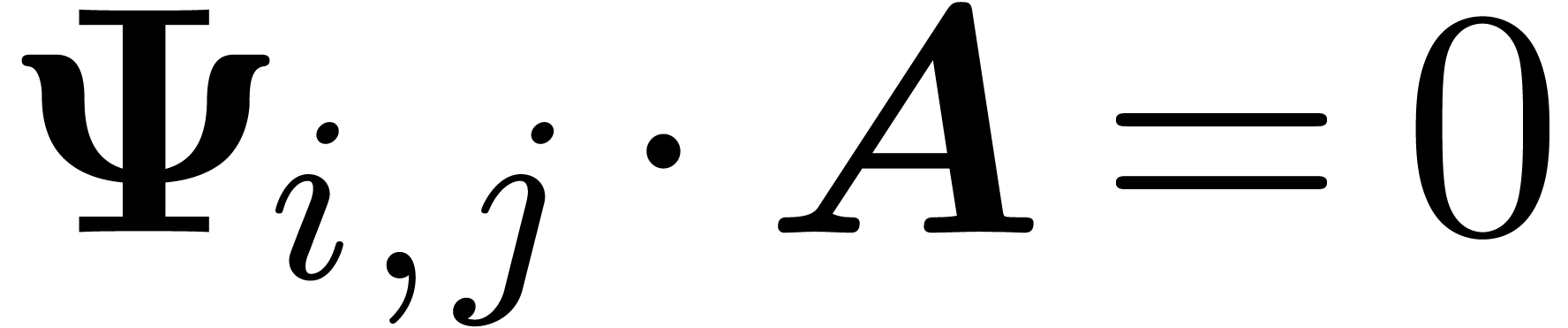 .
.
Given a  and
and  ,
there exist unique differential polynomials
,
there exist unique differential polynomials 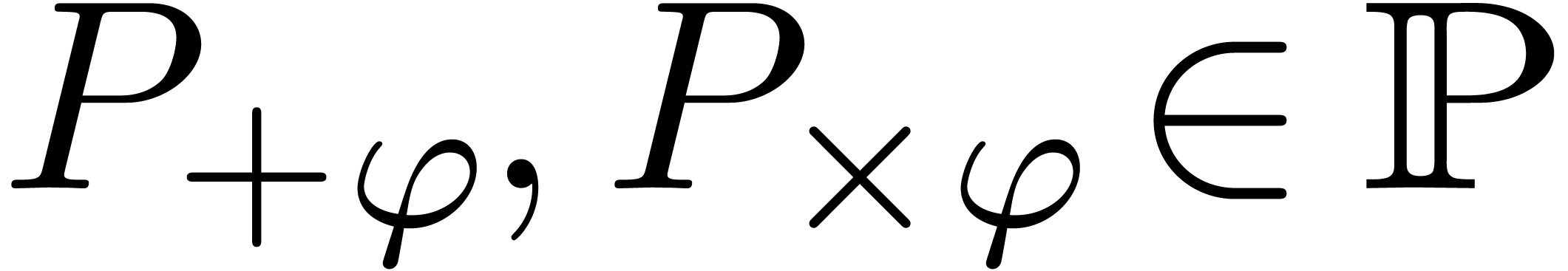 , called additive and multiplicative
conjugates of
, called additive and multiplicative
conjugates of  , with the
properties that
, with the
properties that
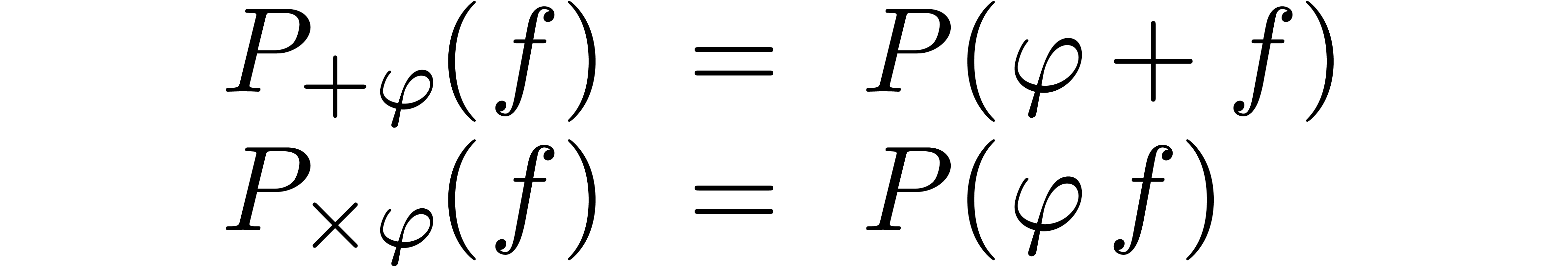
for all 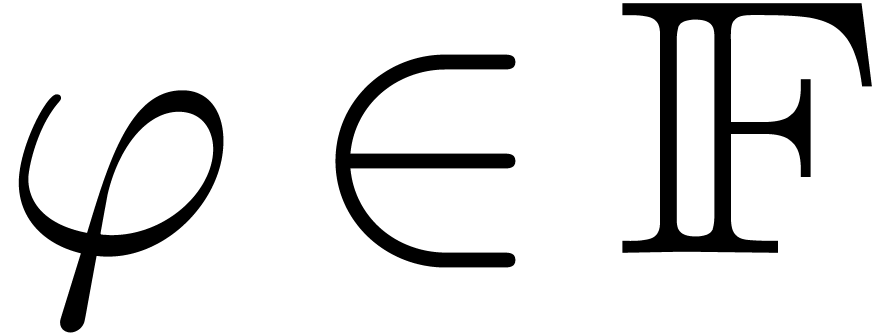 . These notions
naturally extend to vectors and operators
. These notions
naturally extend to vectors and operators 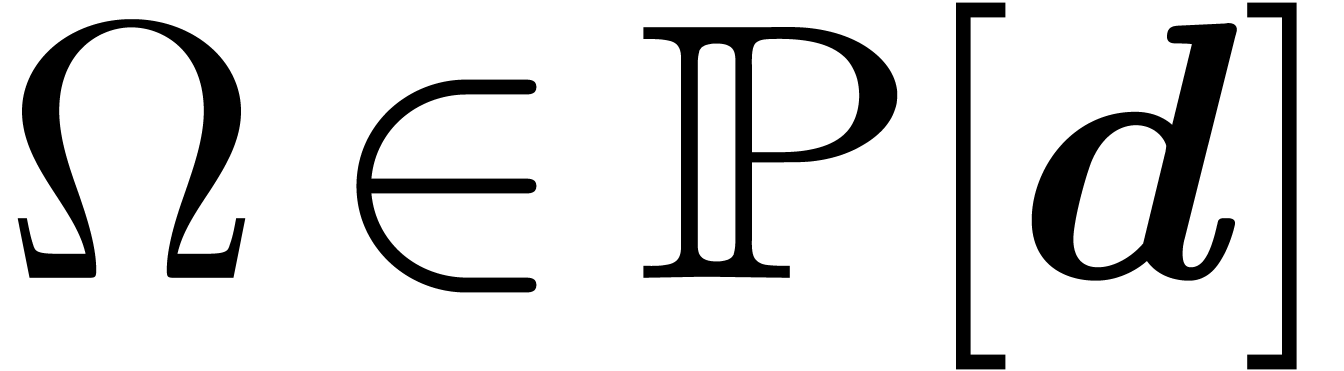 ;
for instance,
;
for instance, 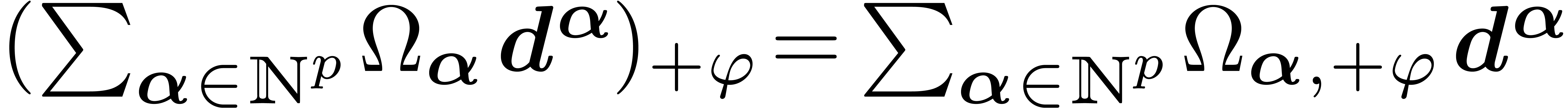 . We have
. We have
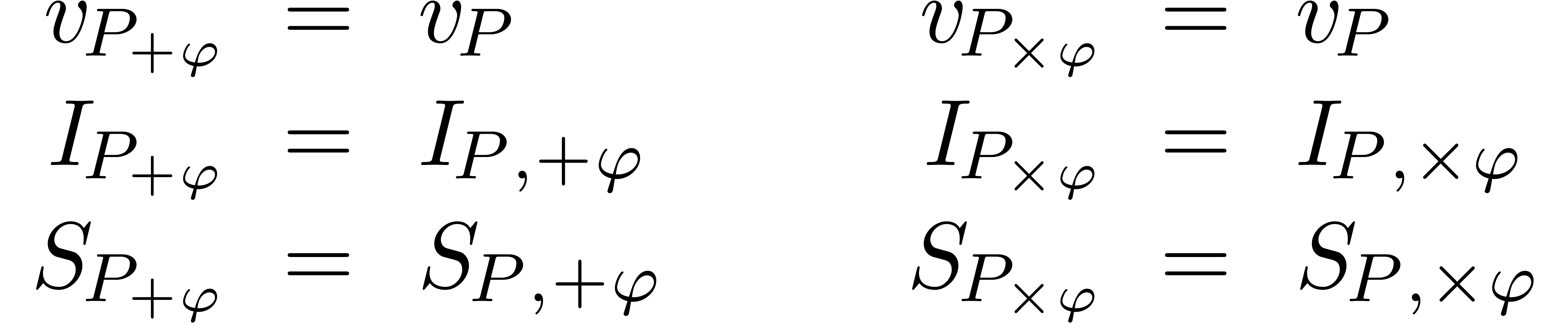
Consequently, if  Ritt reduces to
Ritt reduces to 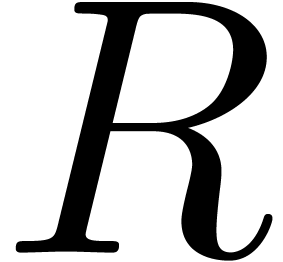 modulo
modulo  , as in
(2), then
, as in
(2), then  and
and  Ritt reduce to
Ritt reduce to  and
and 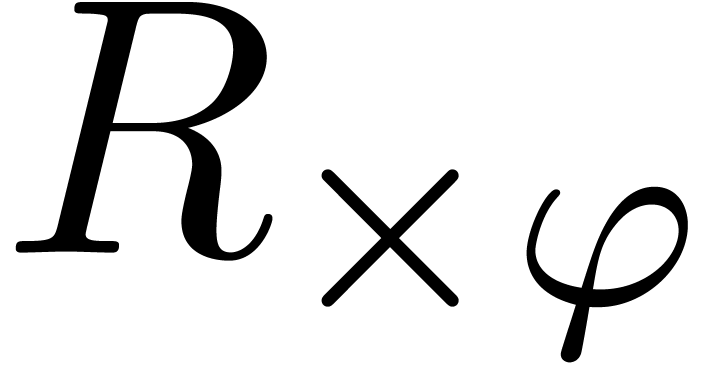 modulo
modulo 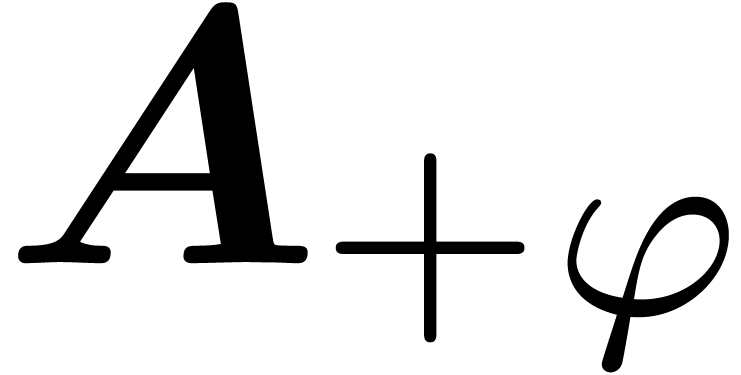 resp.
resp. 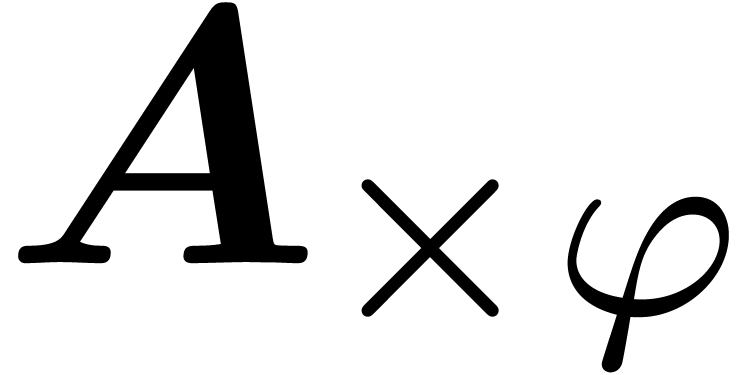 , with
, with
In particular, if  is a Rosenfeld basis with
critical relations
is a Rosenfeld basis with
critical relations 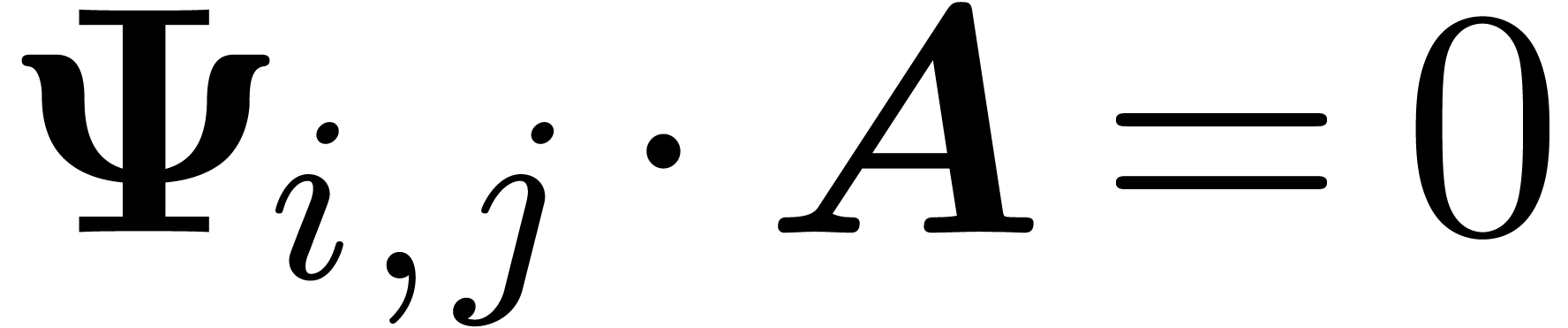 , then so
are
, then so
are  and
and  ,
with critical relations
,
with critical relations  resp.
resp. 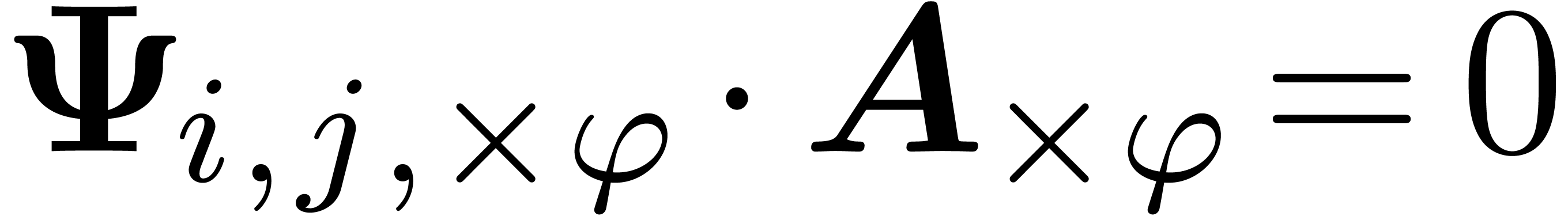 .
.
Another important construction is to change the derivations. Assume that
for certain  . Then any
differential polynomial
. Then any
differential polynomial  can be rewritten into a
differential polynomial
can be rewritten into a
differential polynomial  with respect to the
derivations
with respect to the
derivations  and vice versa. Similarly,
any operator
and vice versa. Similarly,
any operator 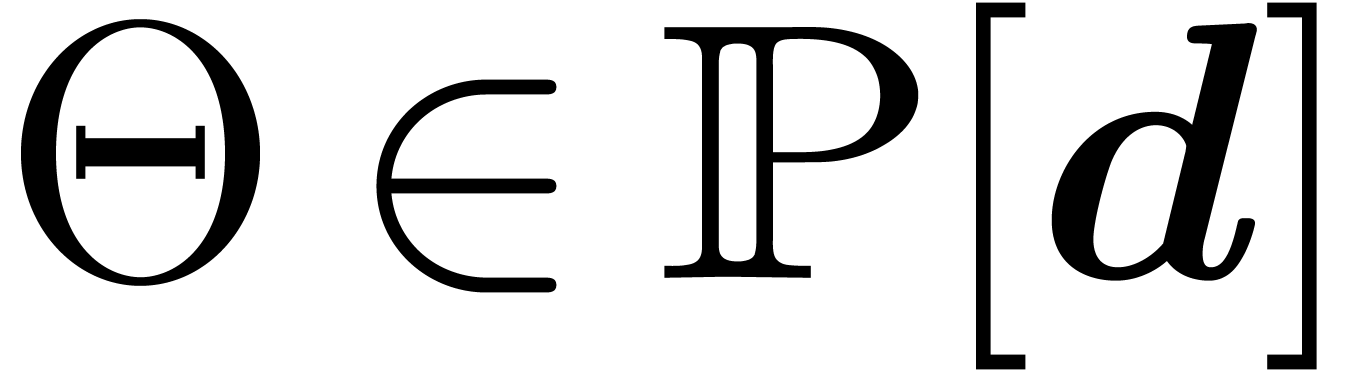 can be rewritten as an operator in
can be rewritten as an operator in
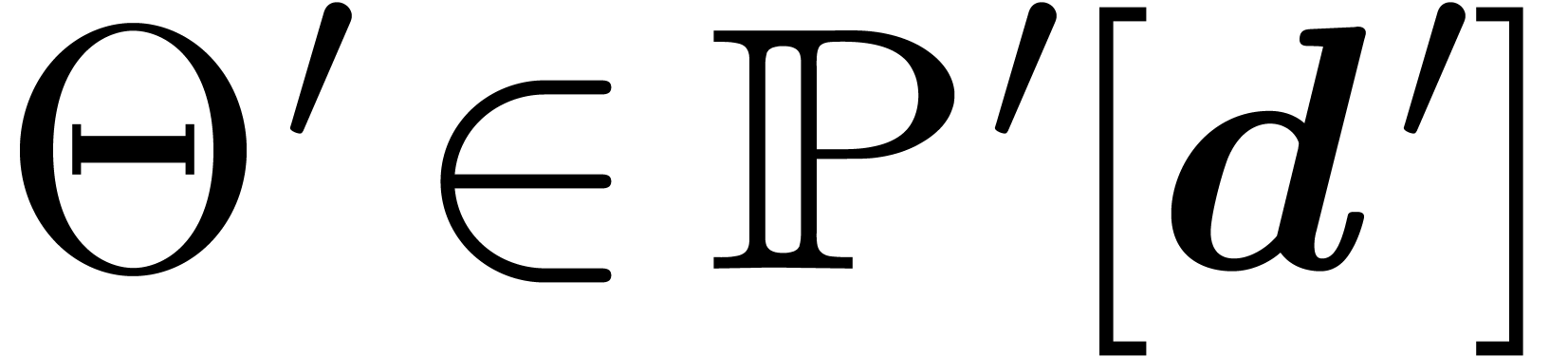 . We again have
. We again have
Consequently, if  Ritt reduces to
Ritt reduces to 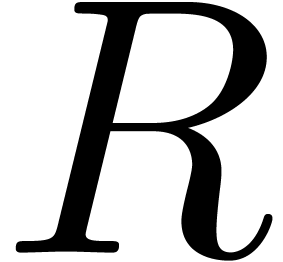 modulo
modulo  , as in
(2), then
, as in
(2), then  Ritt reduces to
Ritt reduces to  modulo
modulo  , with
, with

In particular, if  is a Rosenfeld basis with
critical relations
is a Rosenfeld basis with
critical relations  , then so
are
, then so
are  , with critical relations
, with critical relations
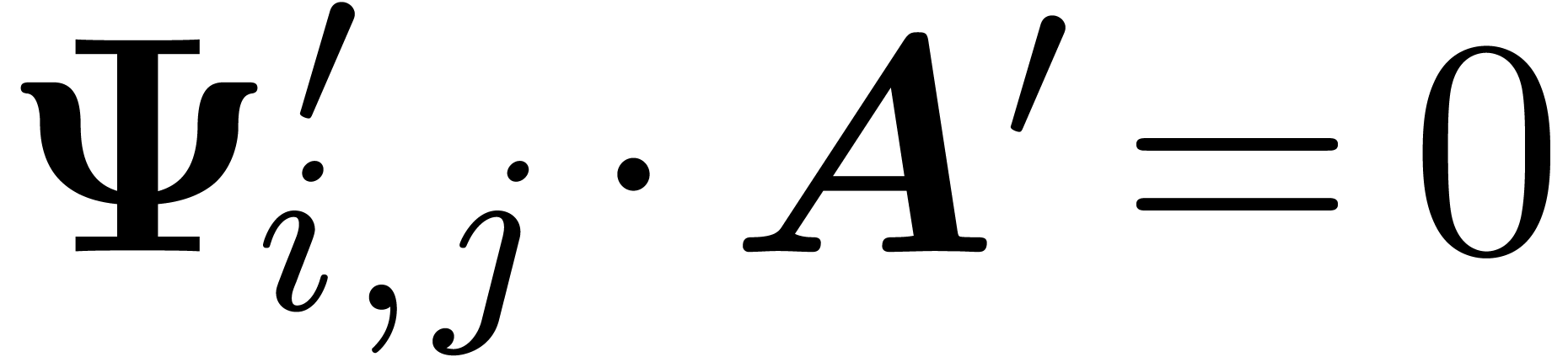 .
.
Let 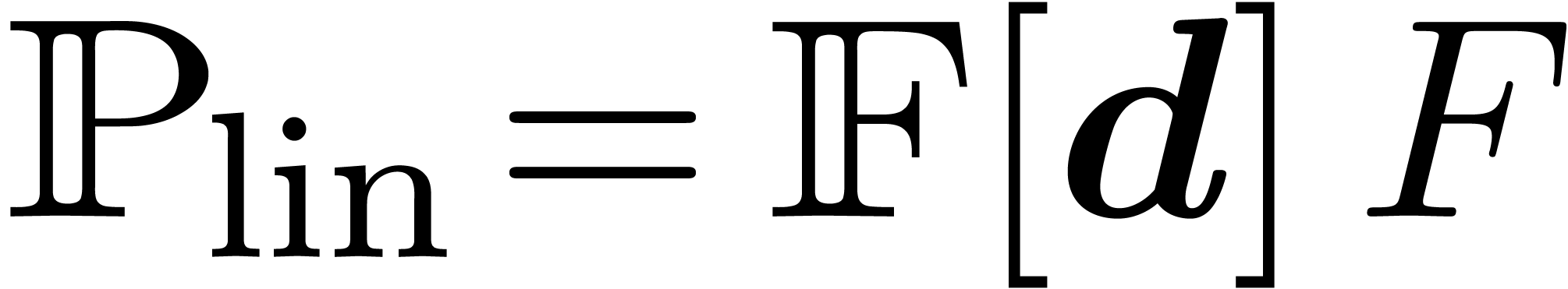 be the set of linear homogeneous
differential polynomials. A differential ideal
be the set of linear homogeneous
differential polynomials. A differential ideal  is said to be linear, if it is generated by
is said to be linear, if it is generated by  . Given
. Given  ,
we will denote by
,
we will denote by  and
and  its linear and constant parts. We also denote
its linear and constant parts. We also denote 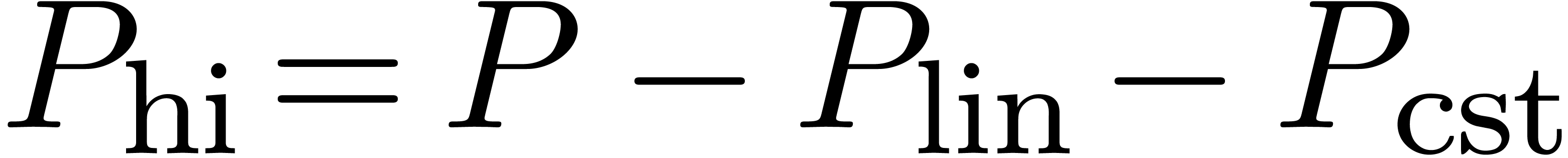 .
.
Given 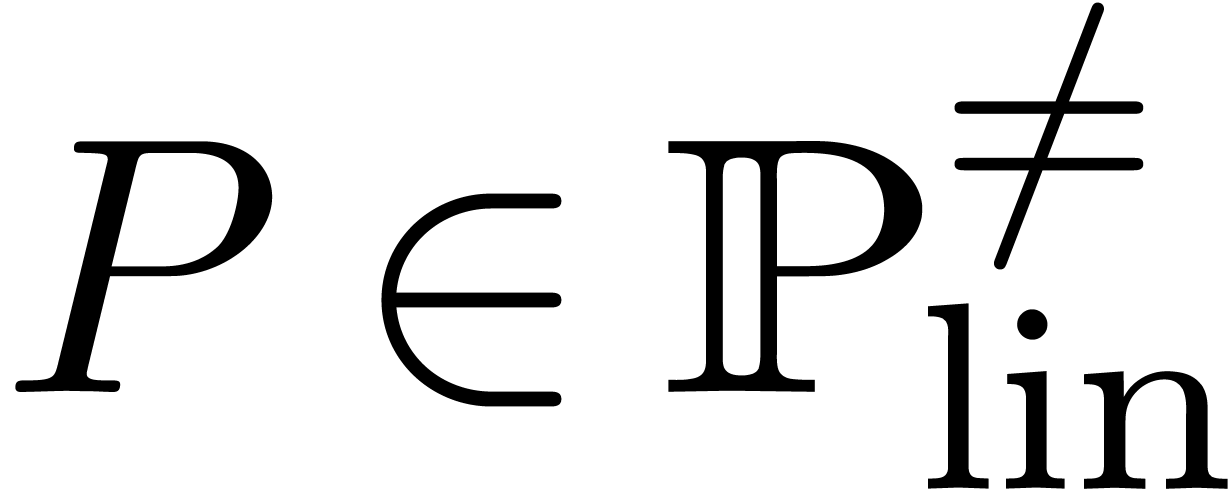 , its initial and
separant
, its initial and
separant  are equal and invertible. Ritt
reduction of
are equal and invertible. Ritt
reduction of 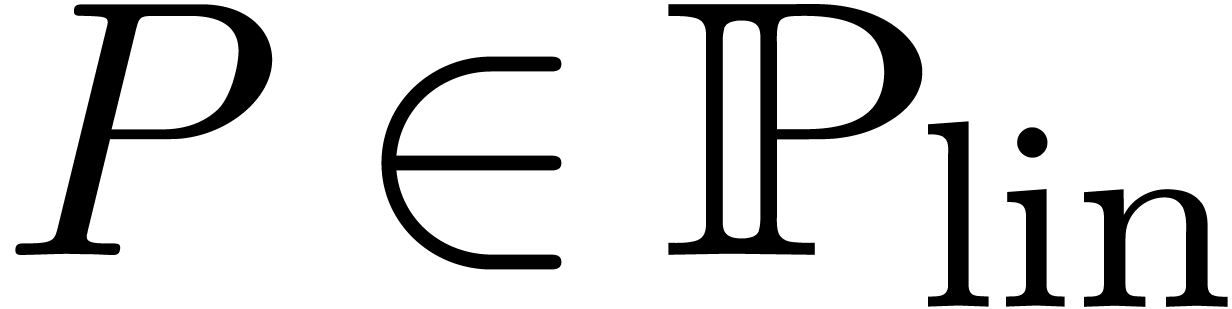 with respect to a system
with respect to a system  yields a relation
yields a relation
 |
(4) |
with 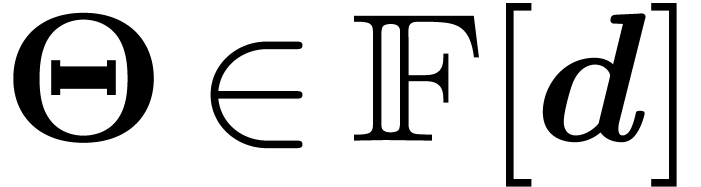 and
and  .
Similarly, the
.
Similarly, the  -polynomial of
two polynomials in
-polynomial of
two polynomials in  is again in
is again in  . In fact,
. In fact,  as a
as a 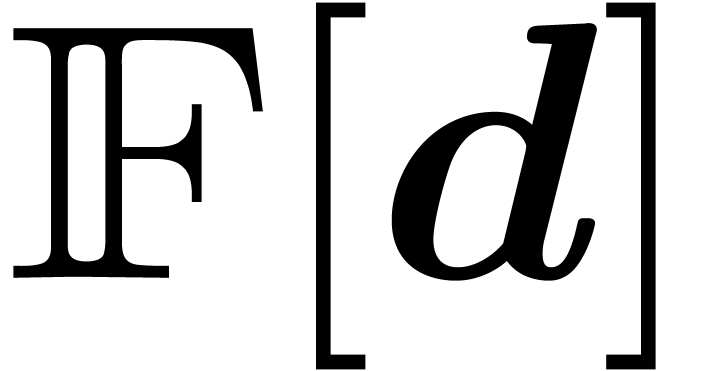 -module is isomorphic to the
skew-ring
-module is isomorphic to the
skew-ring 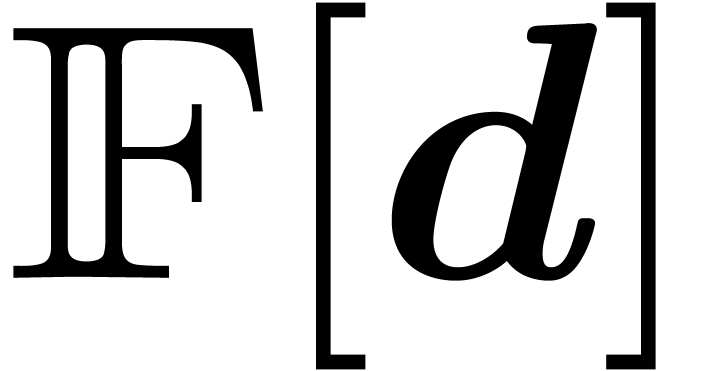 . This leads to the
alternative interpretation of (4) as the reduction of
. This leads to the
alternative interpretation of (4) as the reduction of  w.r.t.
w.r.t.  in the
theory of non-commutative Groebner bases. Similarly,
in the
theory of non-commutative Groebner bases. Similarly,  -polynomials correspond to
-polynomials correspond to  -polynomials and Rosenfeld bases to Groebner
bases.
-polynomials and Rosenfeld bases to Groebner
bases.
Applying Buchberger's algorithm to a linear system  , we thus obtain a Rosenfeld basis
, we thus obtain a Rosenfeld basis  with
with 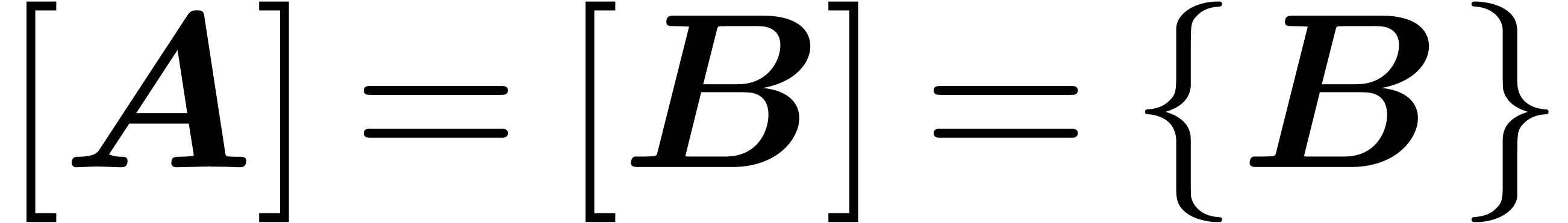 . Any
linear differential ideal
. Any
linear differential ideal 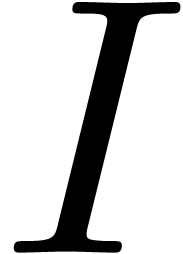 may be represented as
may be represented as
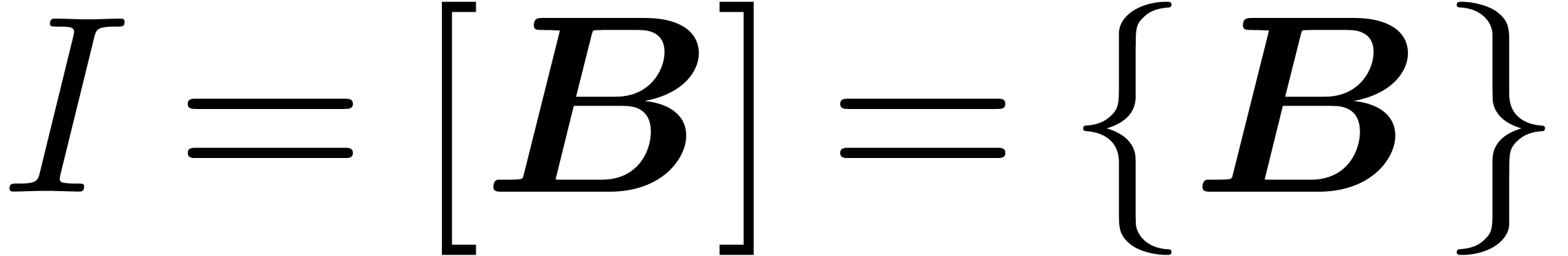 for such a basis
for such a basis  .
.
From now on, we will freely use the concepts of Ritt reduction, critical
relations, etc. for operators in 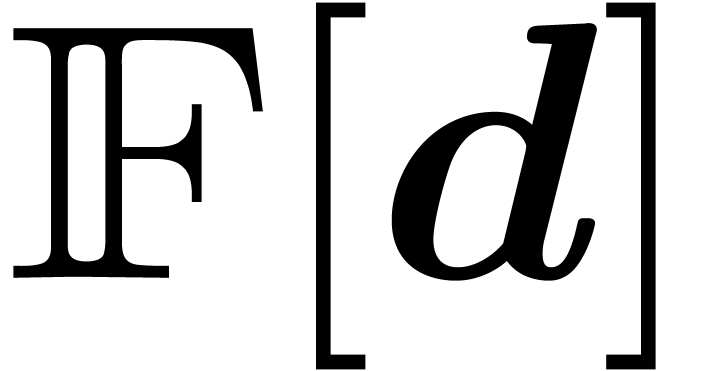 . Given a Rosenfeld basis
. Given a Rosenfeld basis  and
and  , let
, let 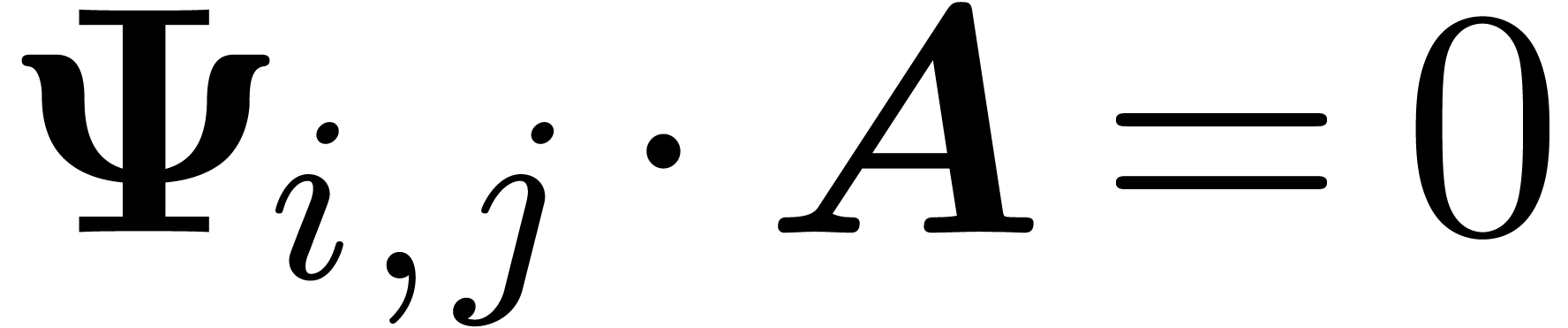 be the critical relation for
be the critical relation for 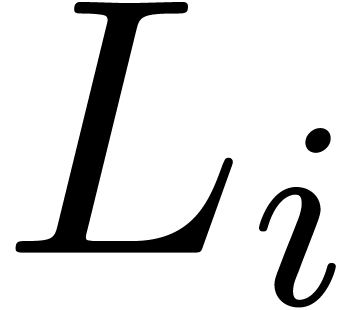 and
and 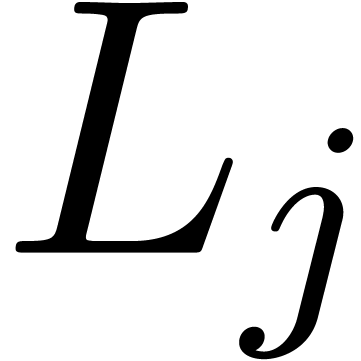 , with
, with 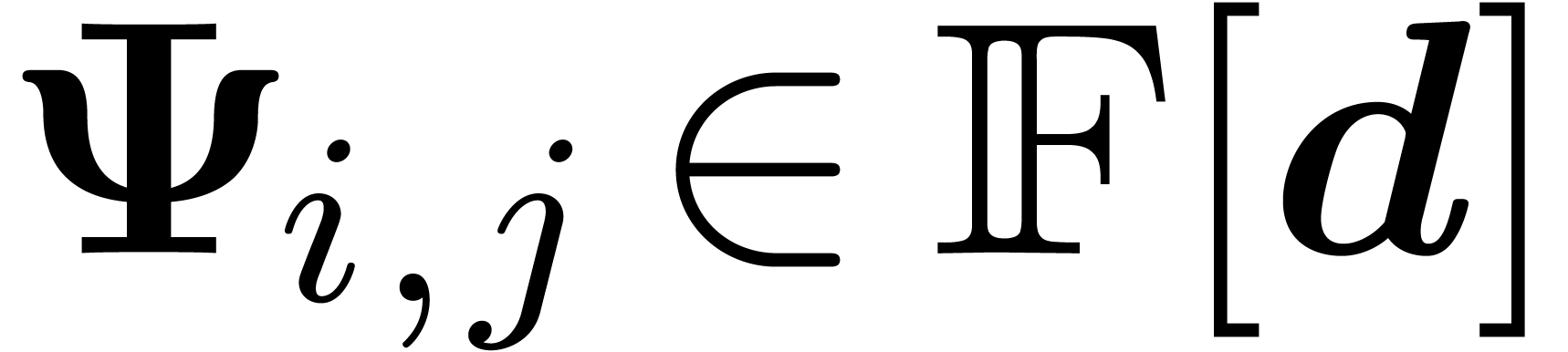 .
Let
.
Let  be the matrix whose rows are the vectors
be the matrix whose rows are the vectors
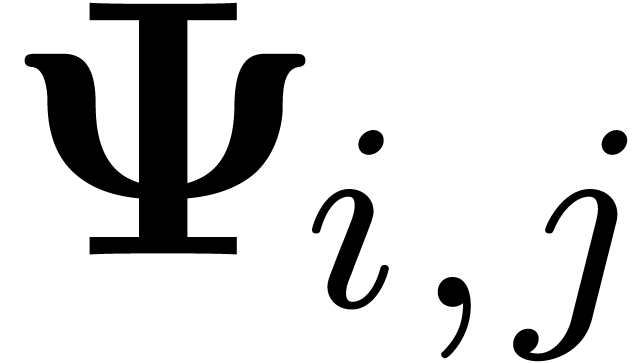 . It is well-known that these
rows generate the module of
. It is well-known that these
rows generate the module of 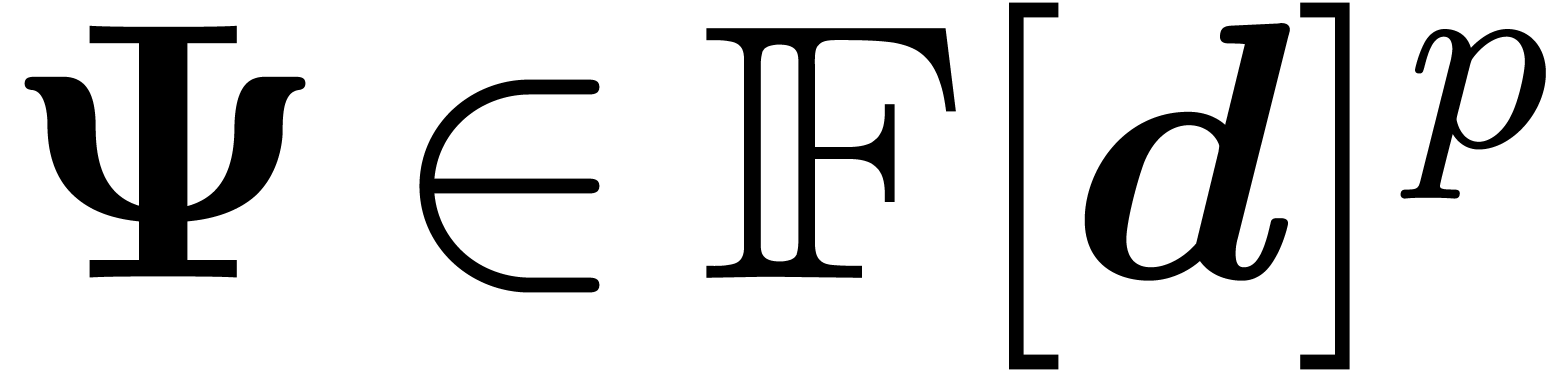 with
with  . In other words, we have a natural exact
sequence
. In other words, we have a natural exact
sequence
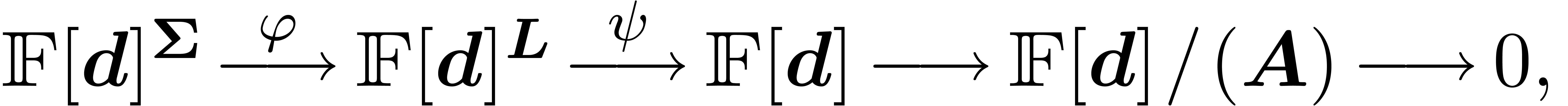 |
(5) |
where
Assuming that  is a field of constants for
is a field of constants for  , we can also consider the natural
power series analogue
, we can also consider the natural
power series analogue 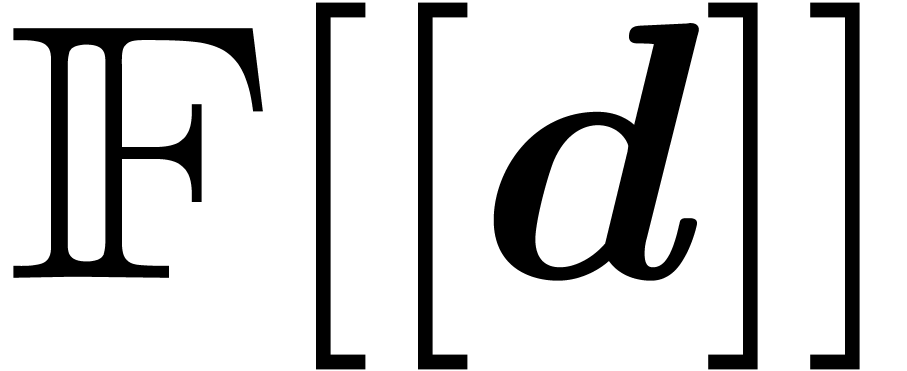 of
of 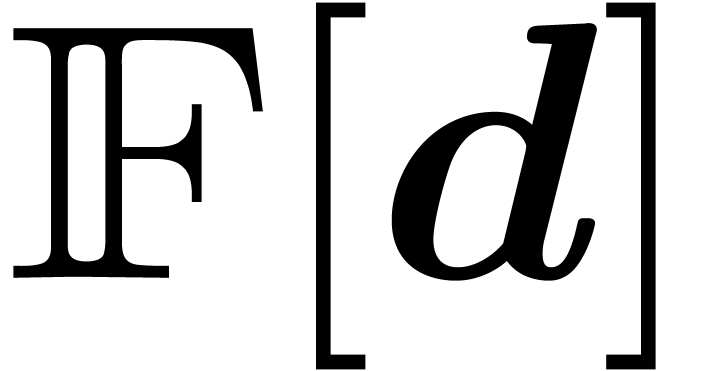 , and apply the theory of standard bases. It will be
convenient to regard this as a dual theory.
, and apply the theory of standard bases. It will be
convenient to regard this as a dual theory.
More precisely, given 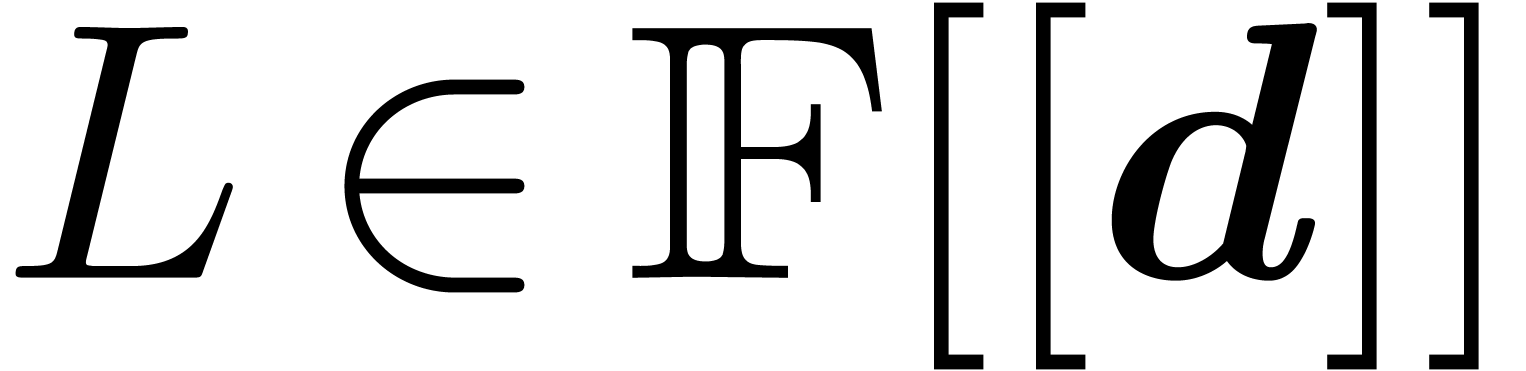 , we
will call the smallest variable
, we
will call the smallest variable 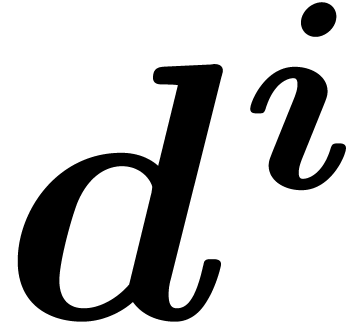 occurring in
occurring in
 its co-leader
its co-leader  . The corresponding coefficient is called the
co-initial
. The corresponding coefficient is called the
co-initial  or co-separant
or co-separant
 . Ritt co-reduction
of
. Ritt co-reduction
of  w.r.t.
w.r.t. 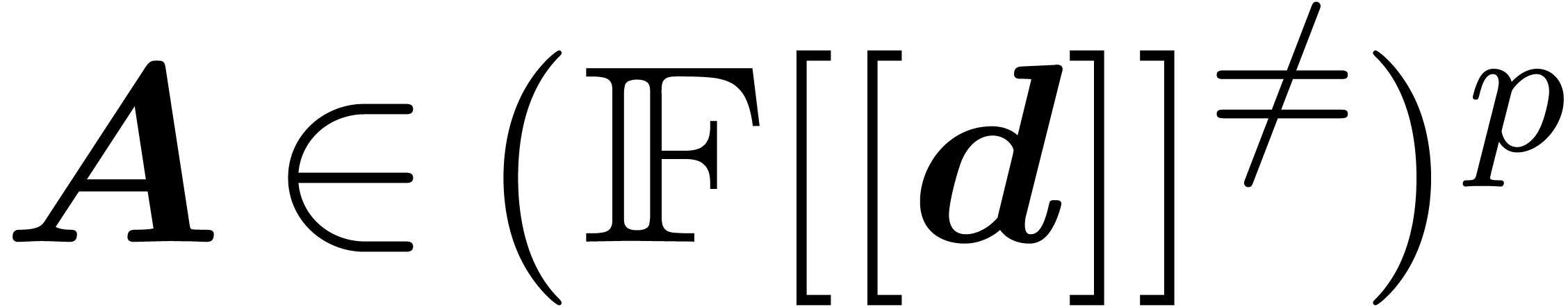 yields a relation
yields a relation
 |
(6) |
with  and
and  such that
such that 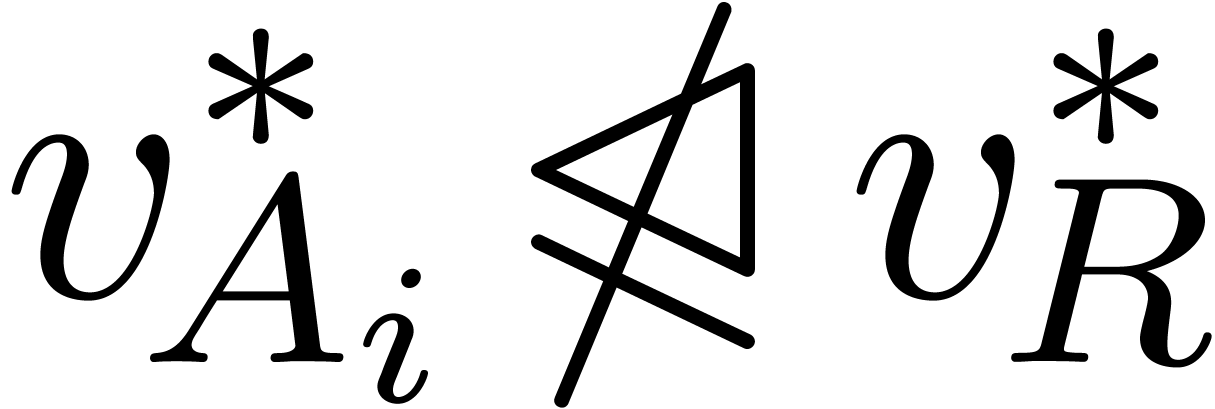 for all
for all  .
If
.
If  is a Rosenfeld co-basis, then Ritt
co-reduction of the co-
is a Rosenfeld co-basis, then Ritt
co-reduction of the co- -polynomial
of
-polynomial
of 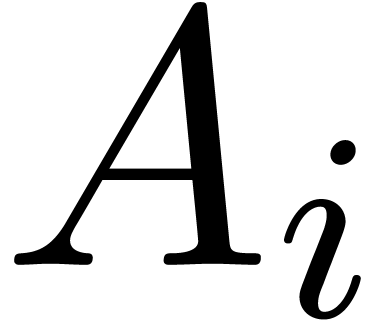 and
and 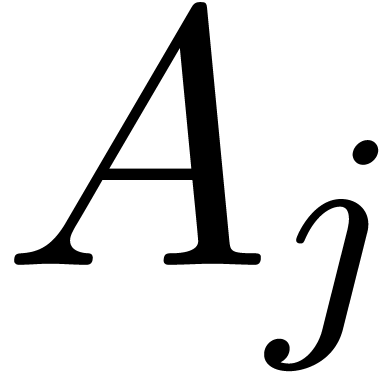 with
with  yields a co-critical relation
yields a co-critical relation
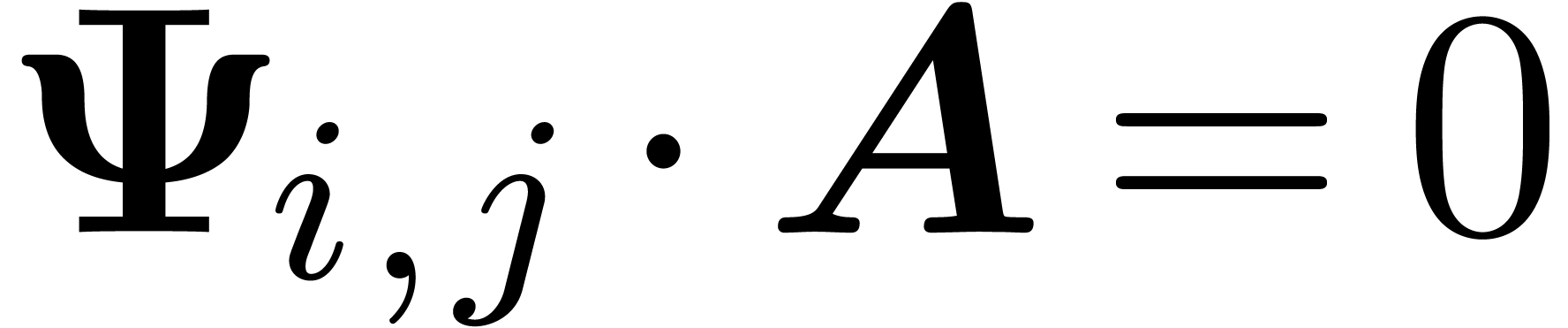
with 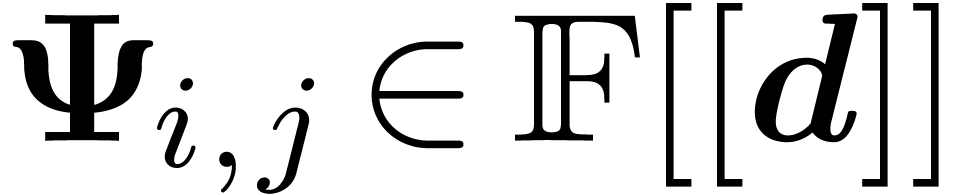 . Denoting by
. Denoting by  the matrix of co-critical relations, we again have a
natural exact sequence
the matrix of co-critical relations, we again have a
natural exact sequence

The process of Ritt co-reduction can be generalized slightly beyond the
linear case. More precisely, let 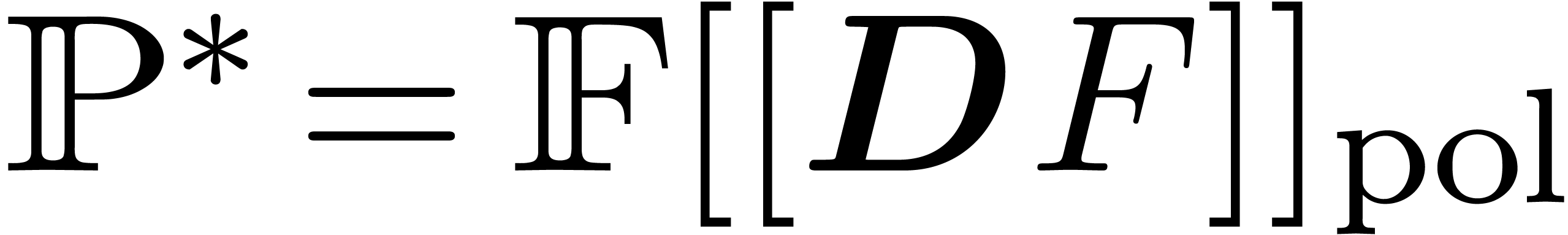 be the set of
series
be the set of
series  in the infinite number of variables
in the infinite number of variables  , such that
, such that  is polynomial in each particular variable in
is polynomial in each particular variable in  . Now let
. Now let 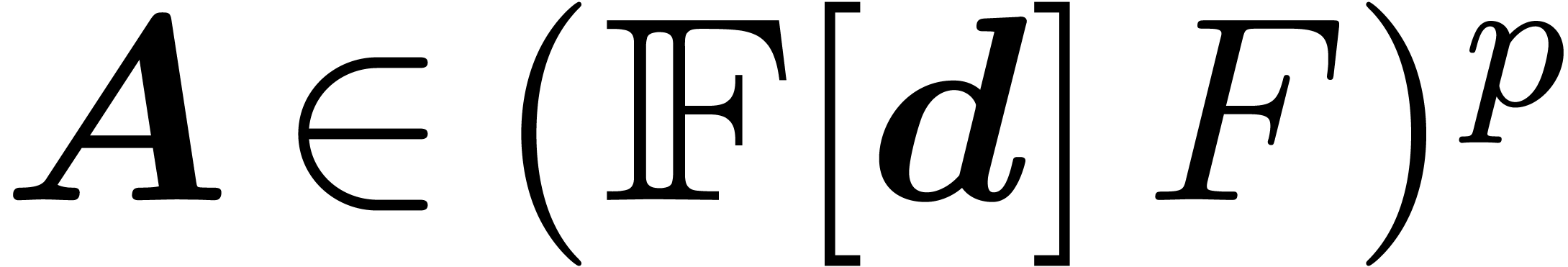 be a linear
system. We say that
be a linear
system. We say that 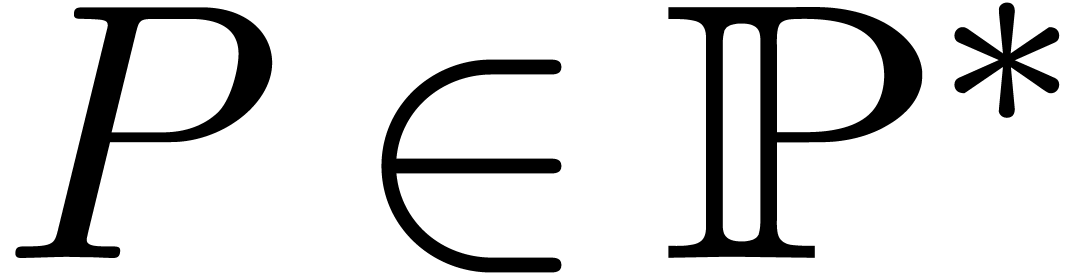 is co-reduced
w.r.t.
is co-reduced
w.r.t.  if its co-leader
if its co-leader 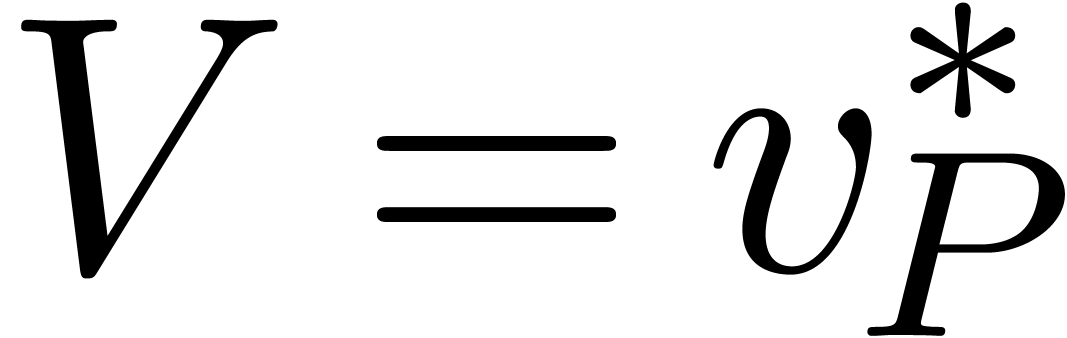 does not satisfy
does not satisfy 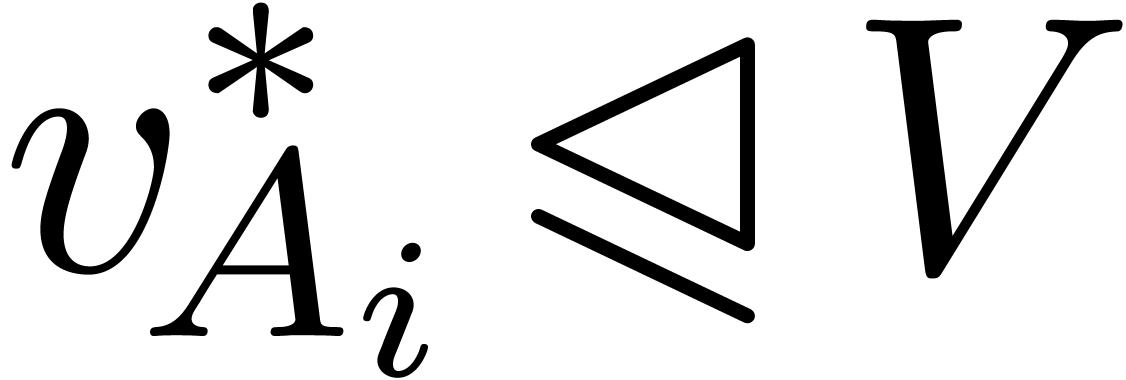 for any
for any 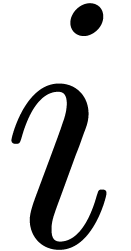 . In the contrary case, we may
consider
. In the contrary case, we may
consider  as a polynomial
as a polynomial 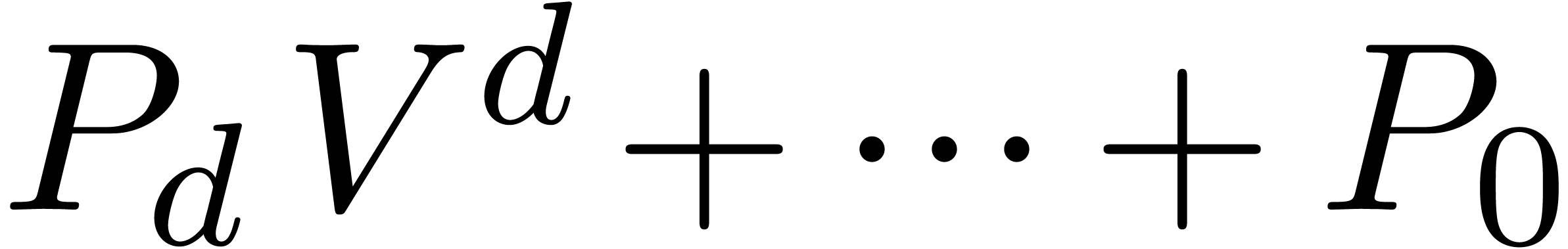 in
in  and write
and write
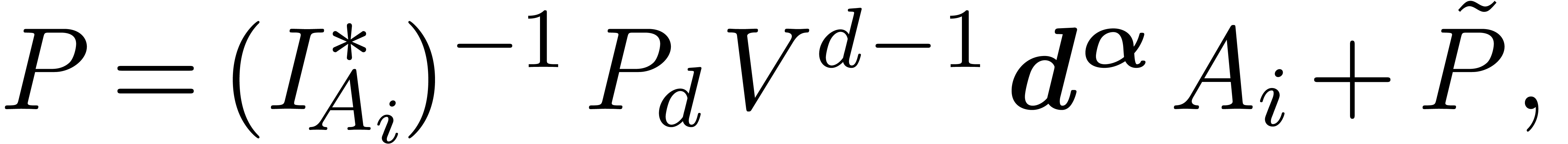 |
(7) |
for the unique  with
with 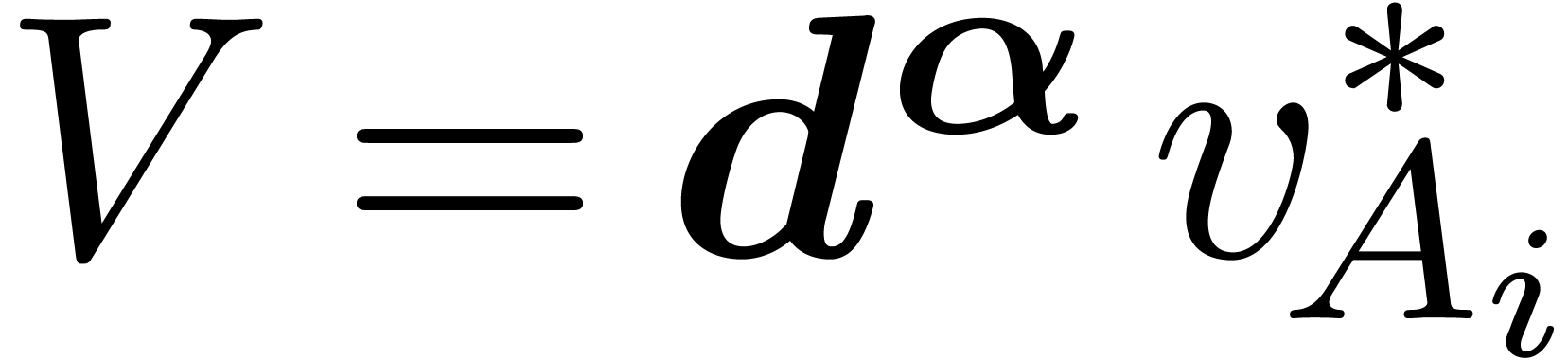 , with
, with  .
After a finite number of such steps, we obtain a relation
.
After a finite number of such steps, we obtain a relation
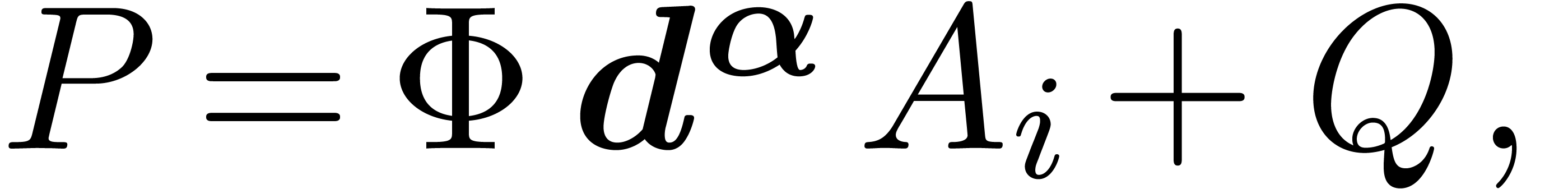 |
(8) |
where  does no longer depend on
does no longer depend on  and
and 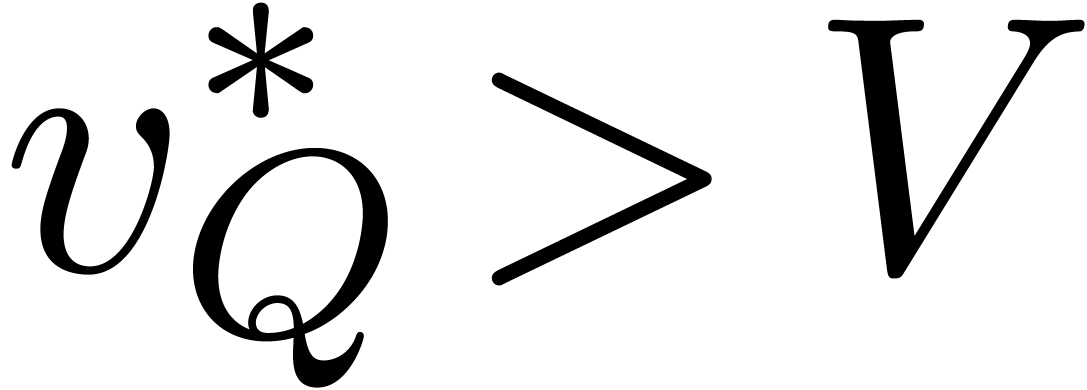 . Continuing the same
process on
. Continuing the same
process on  as long as
as long as  is
not reduced w.r.t.
is
not reduced w.r.t.  results in an
infinite sequence of eliminations which converges to a relation
results in an
infinite sequence of eliminations which converges to a relation
 |
(9) |
where 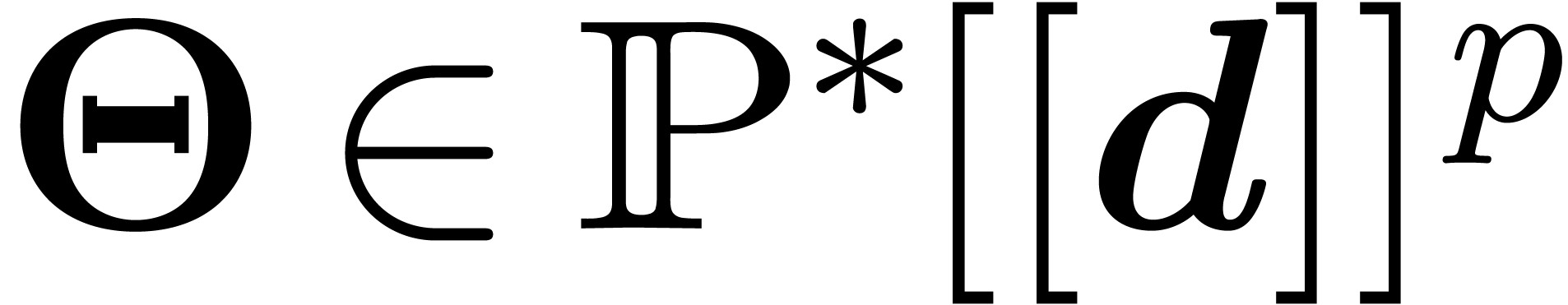 and
and 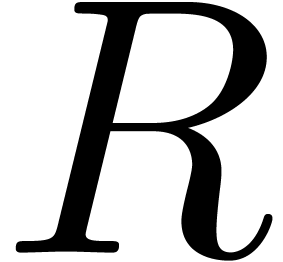 is co-reduced
w.r.t.
is co-reduced
w.r.t.  .
.
Given formal indeterminates  ,
let
,
let  denote the valuation-preserving partial
derivatives
denote the valuation-preserving partial
derivatives
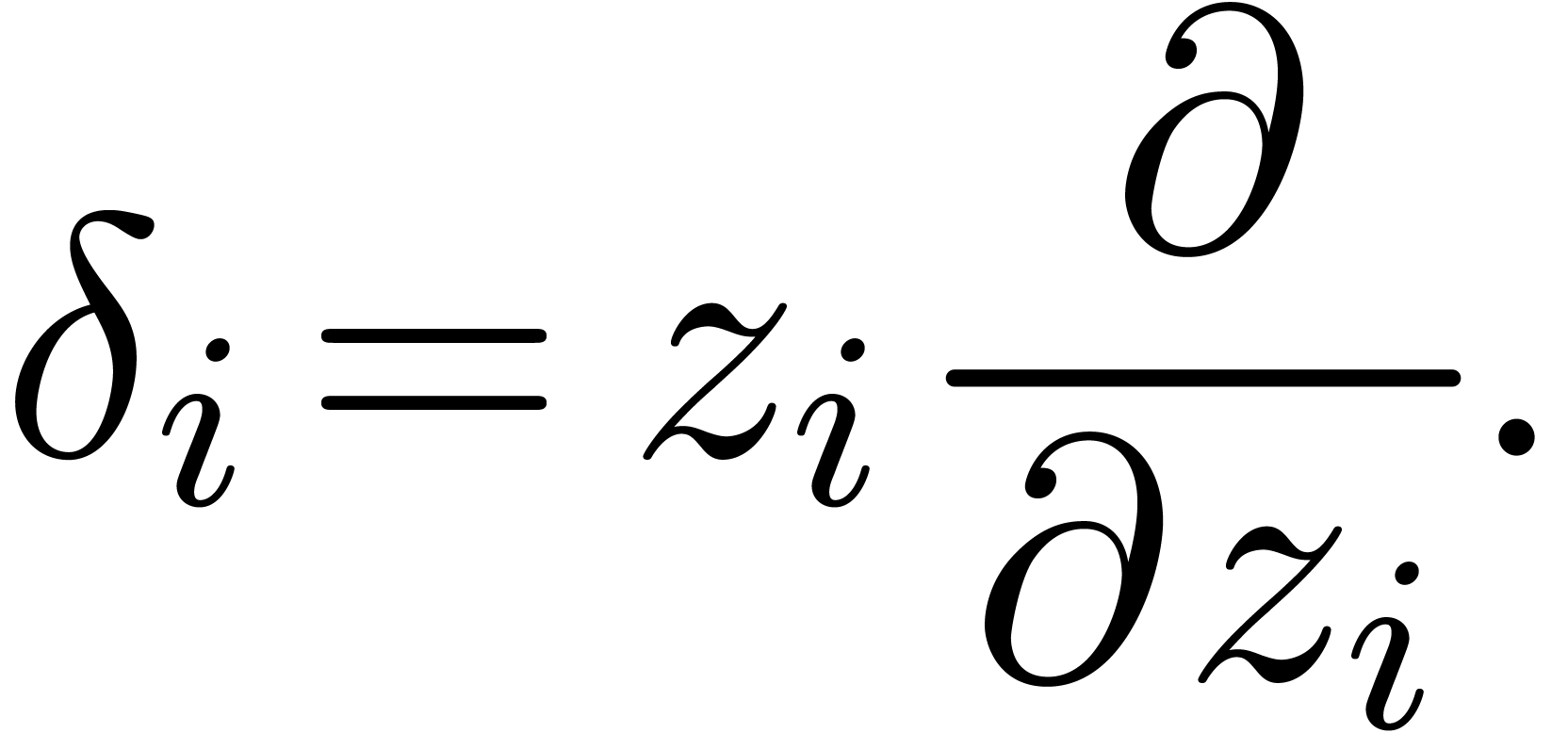
Let 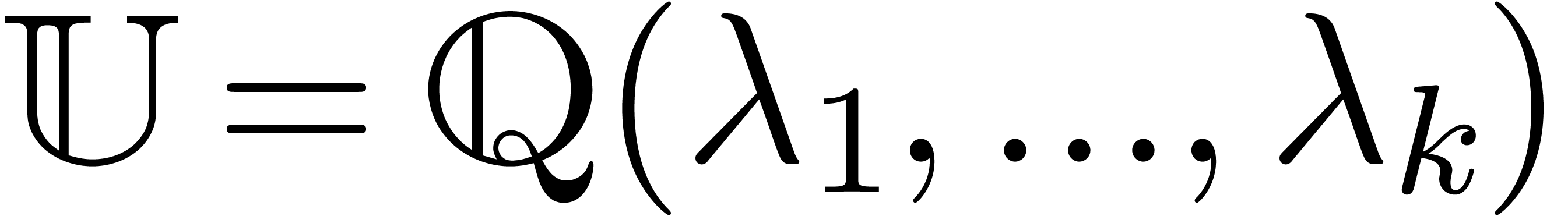 and let
and let  be a vector
of
be a vector
of  -linearly independent
positive real numbers. We give
-linearly independent
positive real numbers. We give 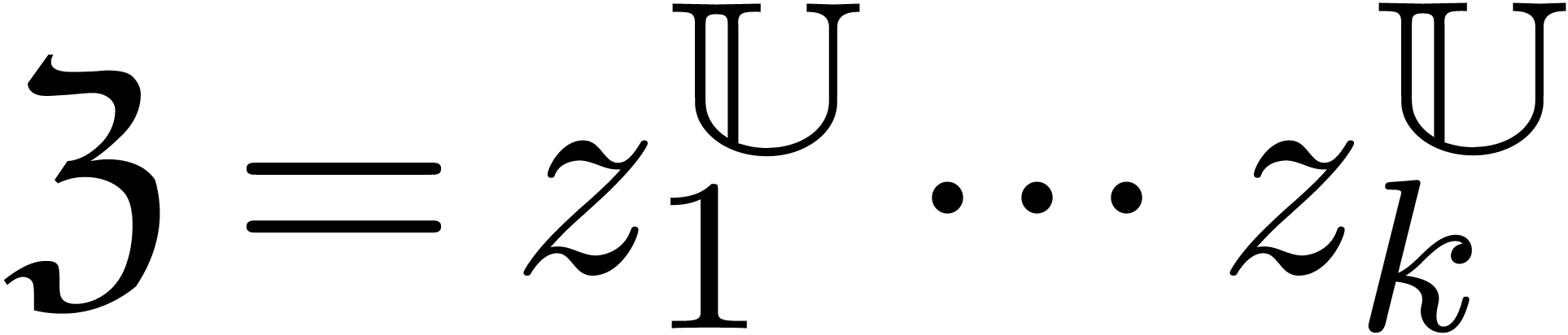 the structure of
a monomial group by
the structure of
a monomial group by

Notice that  is isomorphic to an additive
subgroup of
is isomorphic to an additive
subgroup of  . From now on, we
will assume that
. From now on, we
will assume that  is a field of grid-based series
of the form
is a field of grid-based series
of the form
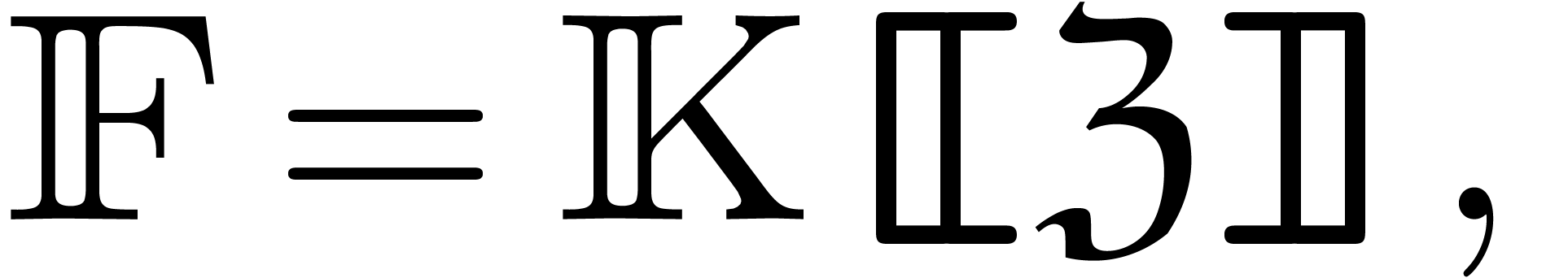
where  is a differential field for the
derivations
is a differential field for the
derivations  .
.
Remark  by any
subgroup of
by any
subgroup of  which contains
which contains  and for any dominance relation
and for any dominance relation  on
on 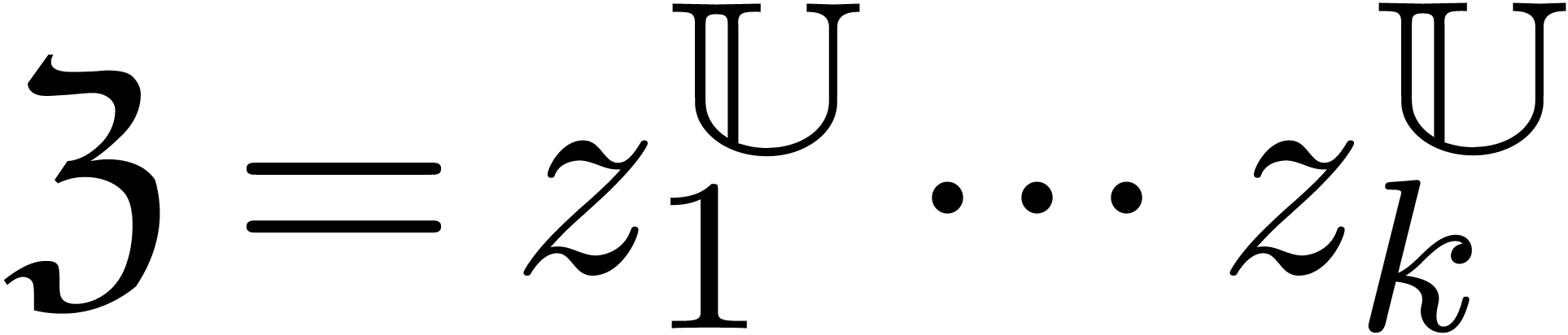 with
with 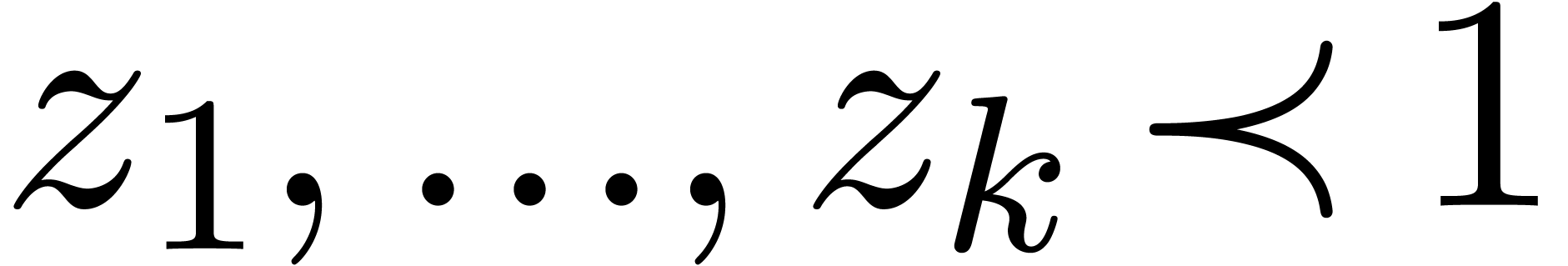 . However,
proofs by induction over grid-based supports in
. However,
proofs by induction over grid-based supports in  generally have to be replaced by transfinite induction proofs.
generally have to be replaced by transfinite induction proofs.
Given  in
in 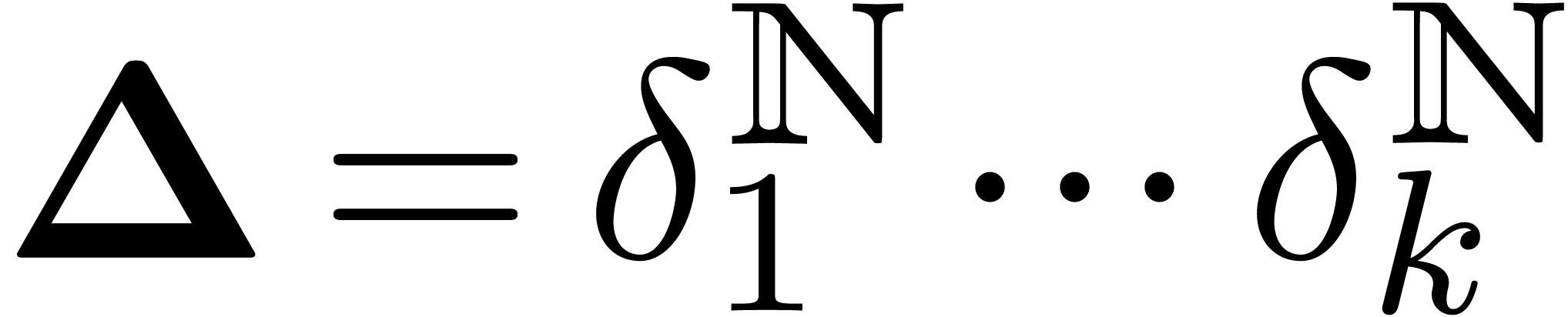 and
and  in
in  , we will
have to consider generalized Newton slopes between terms
, we will
have to consider generalized Newton slopes between terms  and
and  . Both
terms can be “equalized” modulo the change of derivations
. Both
terms can be “equalized” modulo the change of derivations
 , where
, where
If 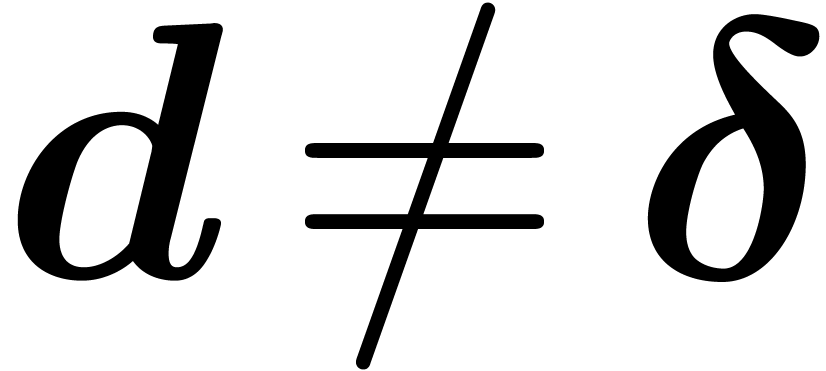 , then the monomials
, then the monomials  are all infinitesimal, and we have
are all infinitesimal, and we have
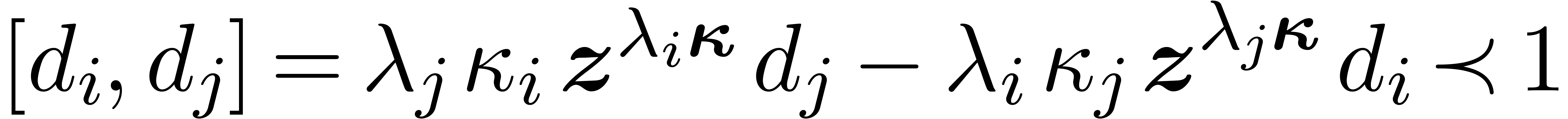 |
(10) |
for all  . In other words,
although the
. In other words,
although the 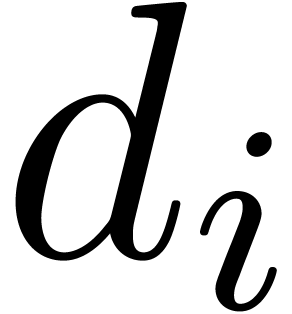 do not commute, they do commute
from the asymptotic point of view. Similarly, if
do not commute, they do commute
from the asymptotic point of view. Similarly, if 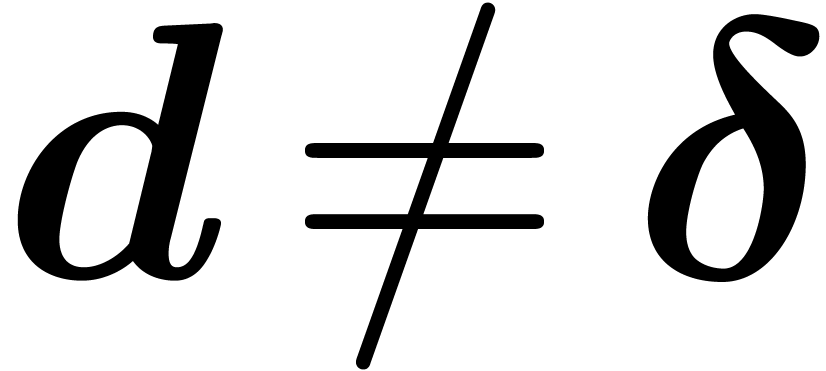 , then each derivation
, then each derivation  asymptotically commutes with elements
asymptotically commutes with elements  in the
operator ring
in the
operator ring  :
:
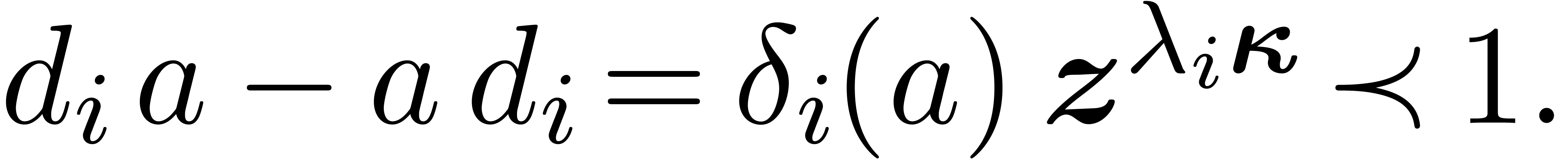 |
(11) |
Let 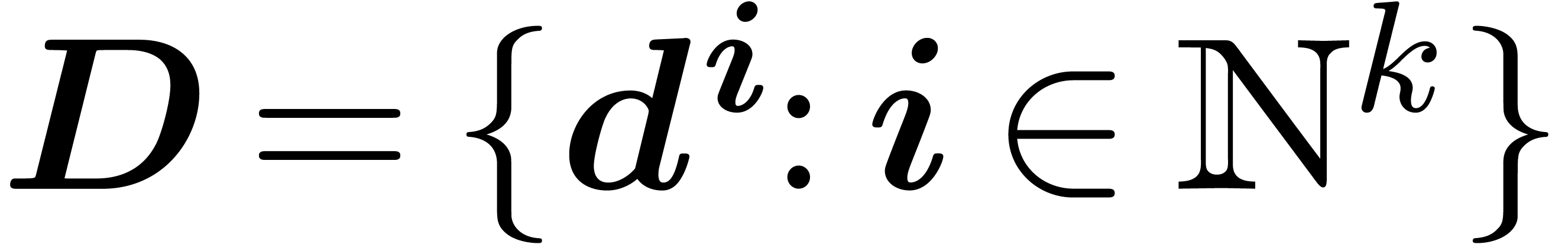 be as before. Any differential polynomial
be as before. Any differential polynomial
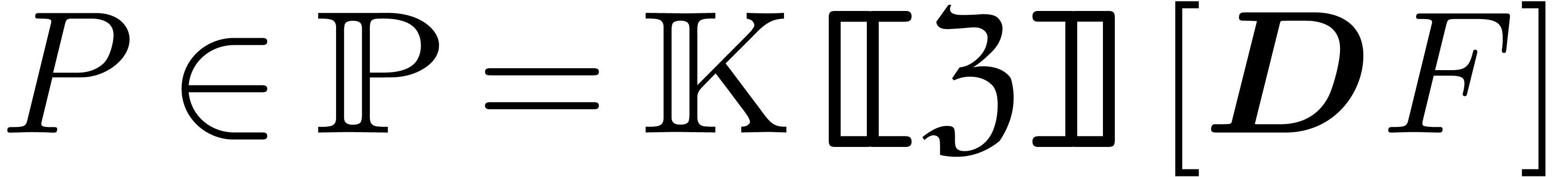 can also be considered as a series
can also be considered as a series 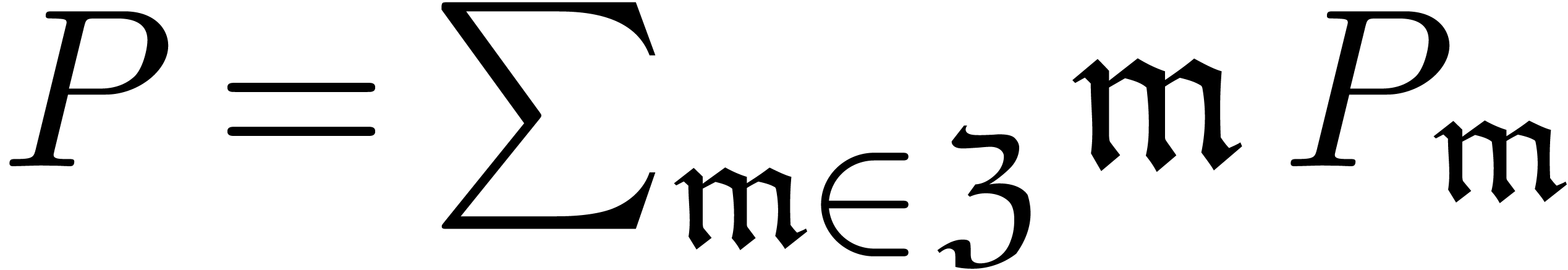 in the ring
in the ring
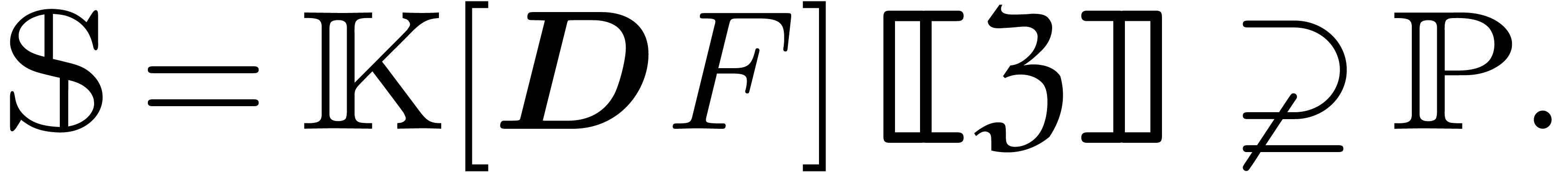
Similarly, an operator 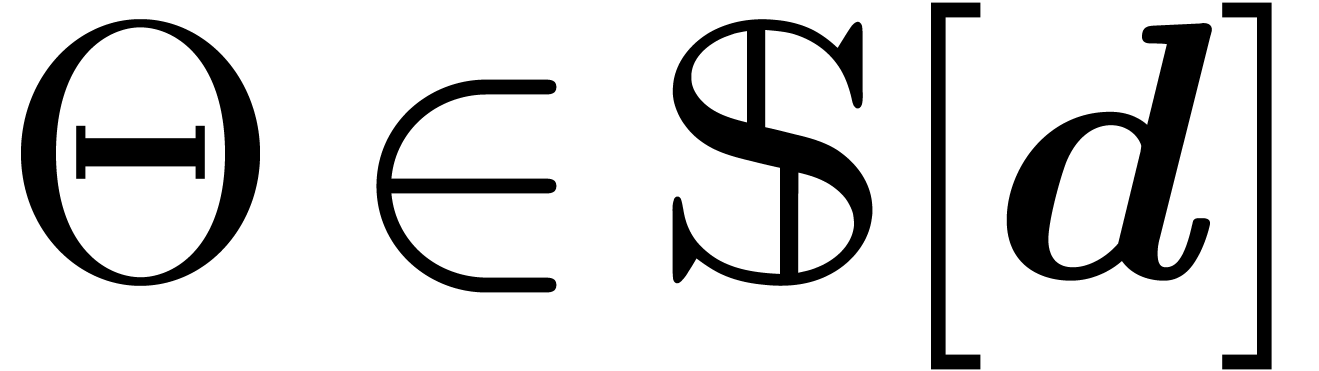 can be considered as a
series
can be considered as a
series 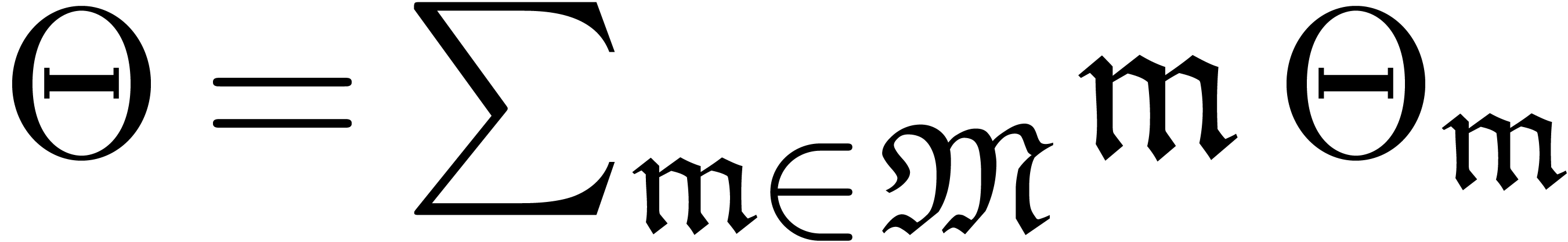 in the ring
in the ring
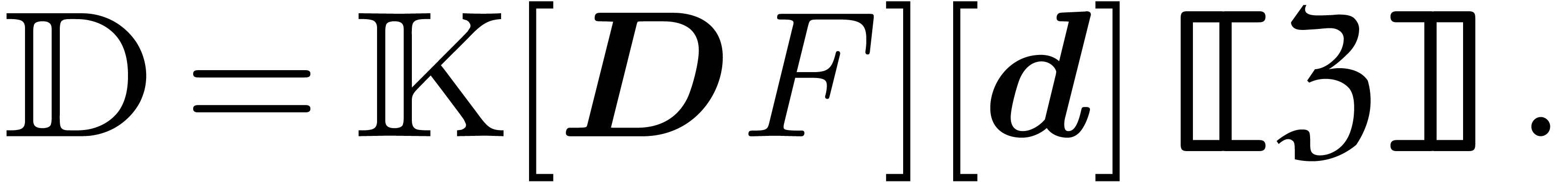
Recall our convention to multiply monomials in the series on the right with the corresponding coefficients.
Because of (10), the set 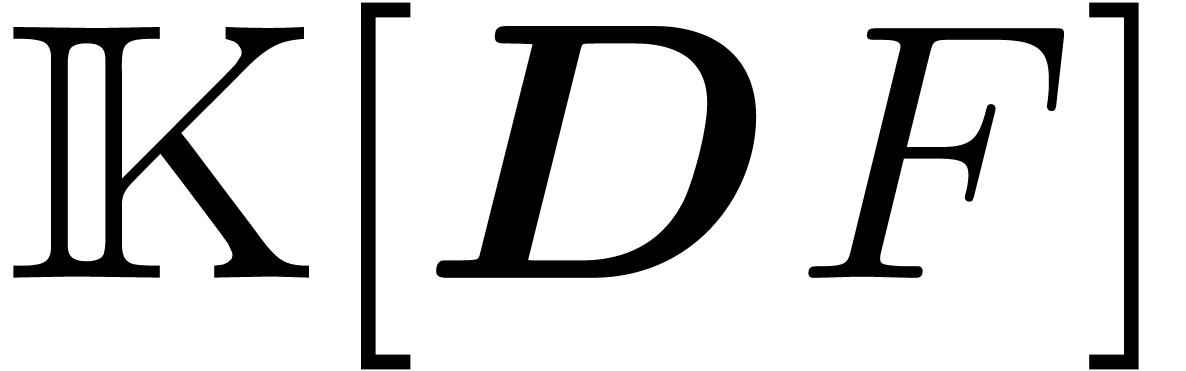 is not
necessarily stable under differentiation. It will be convenient to
introduce the commutative differential ring
is not
necessarily stable under differentiation. It will be convenient to
introduce the commutative differential ring 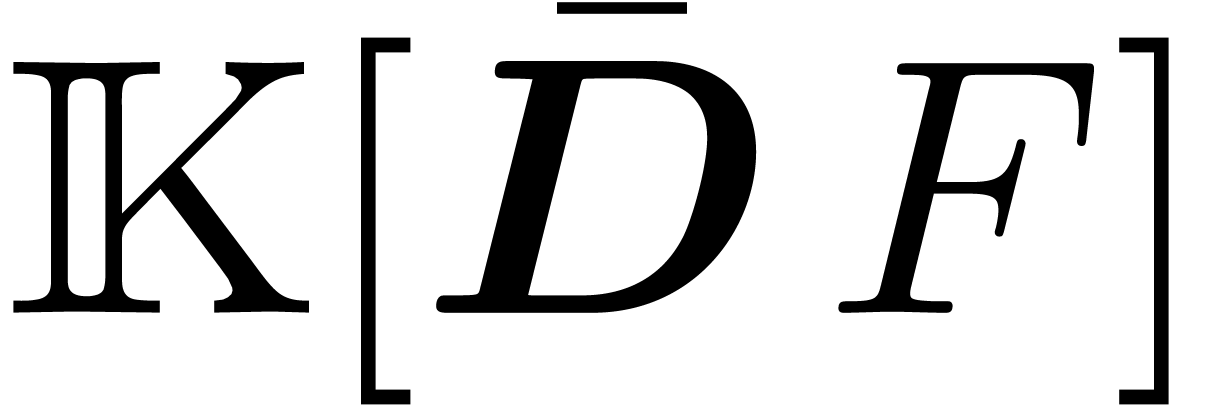 obtained through formal substitution of
obtained through formal substitution of  by
pairwise commuting variants
by
pairwise commuting variants  .
The corresponding bijection
.
The corresponding bijection 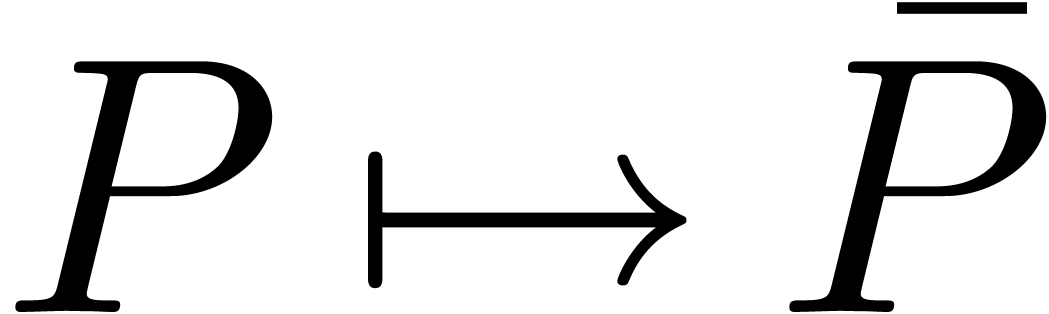 between
between 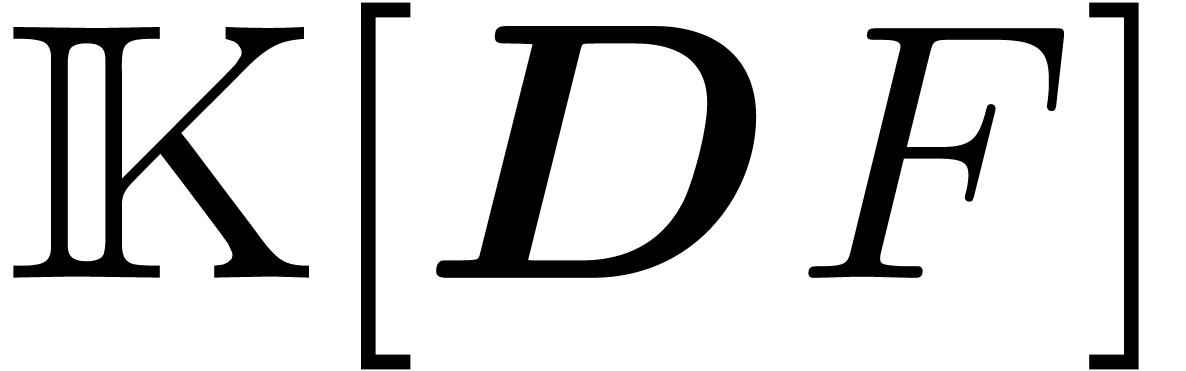 and
and 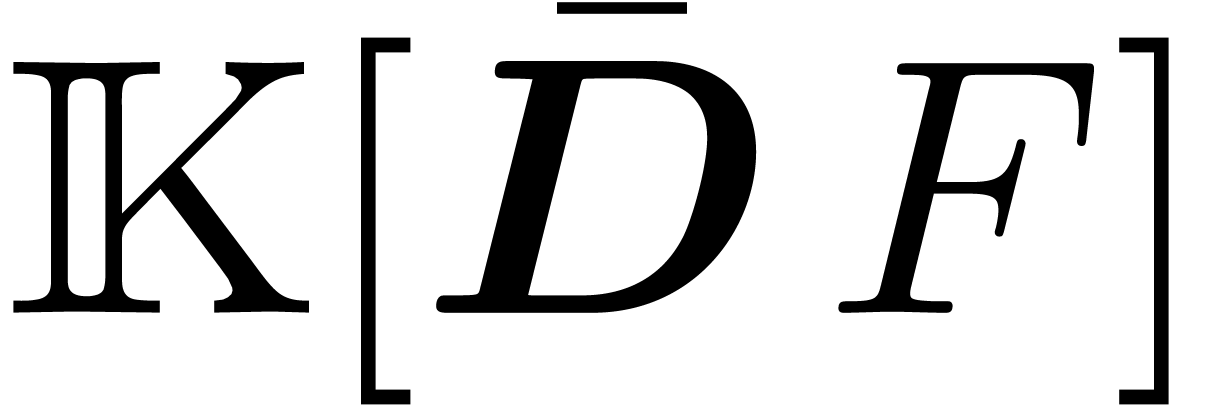 , with
inverse
, with
inverse 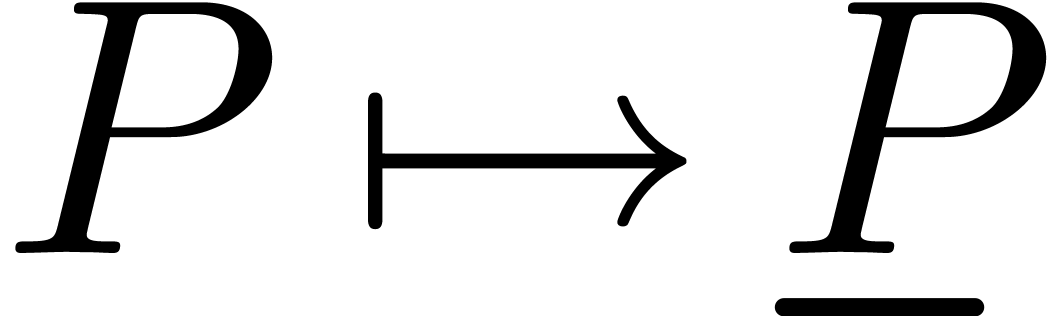 , satisfies
, satisfies
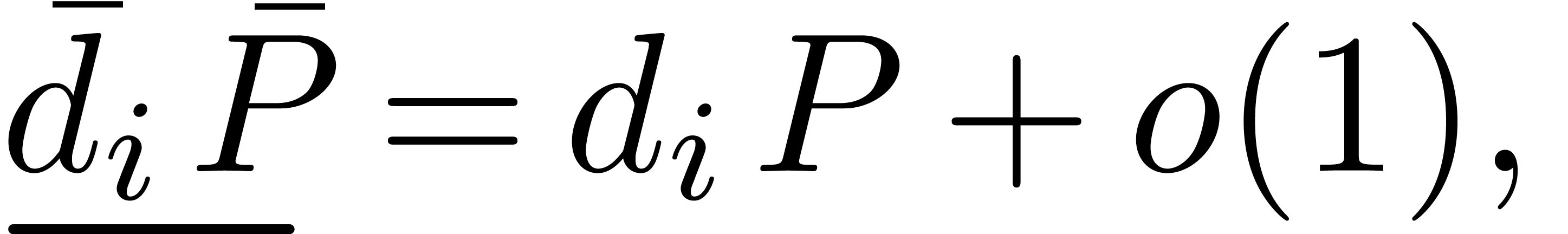
for all  and
and 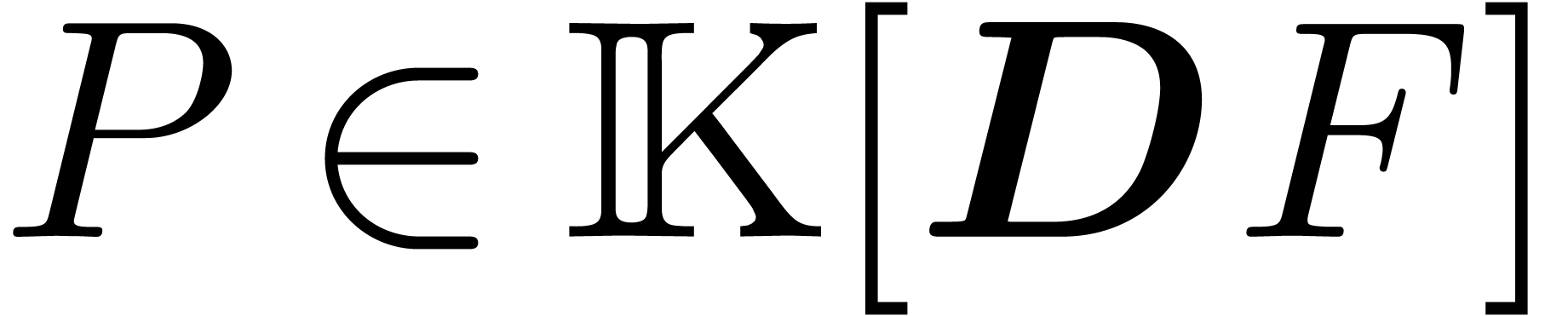 .
If
.
If 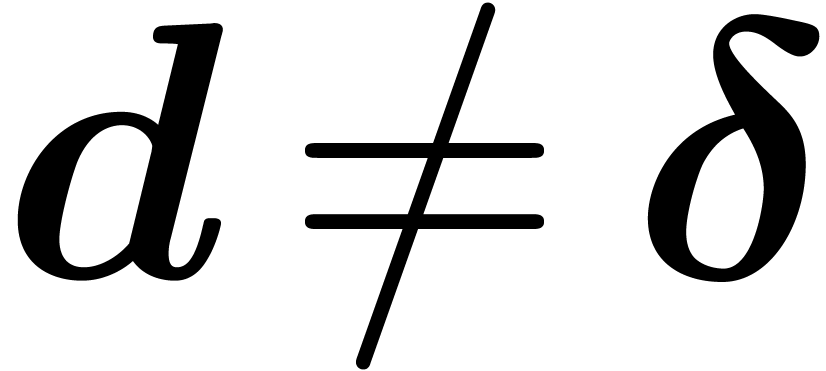 , then (11)
implies that
, then (11)
implies that  is a field of constants for the
derivations
is a field of constants for the
derivations 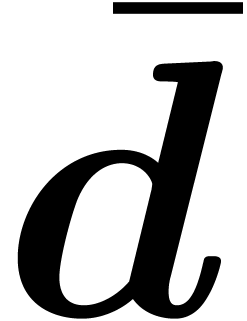 . Given
. Given 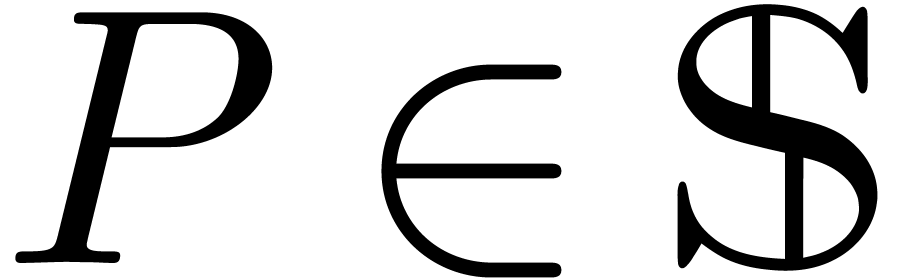 , we will denote
, we will denote 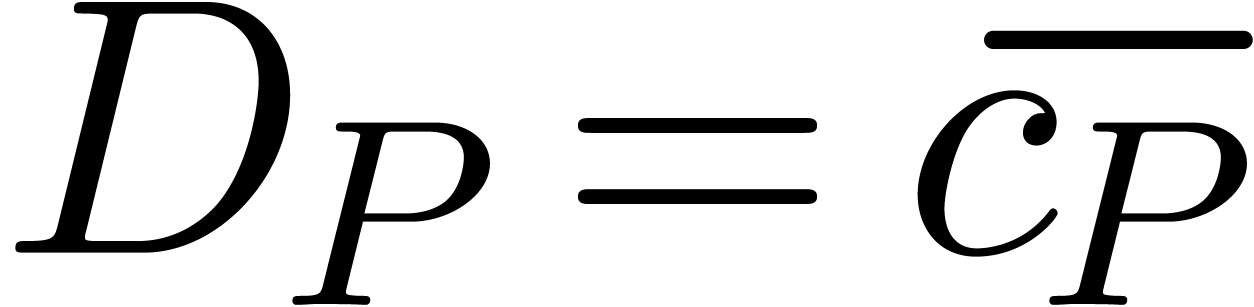 . This notation is extended to differential
ideals
. This notation is extended to differential
ideals  of
of  using
using
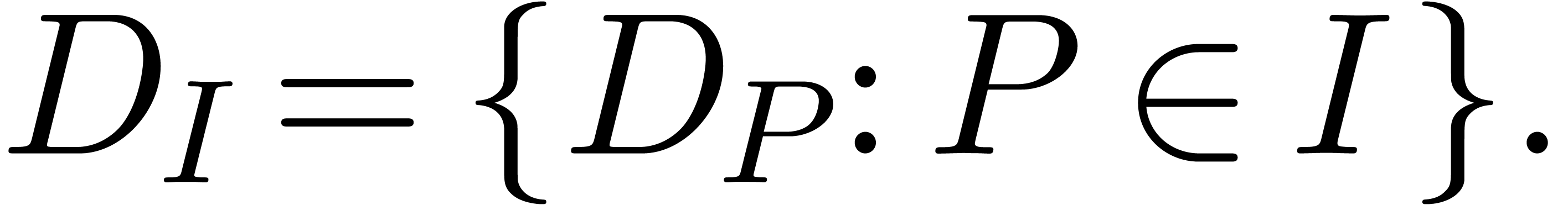
The set 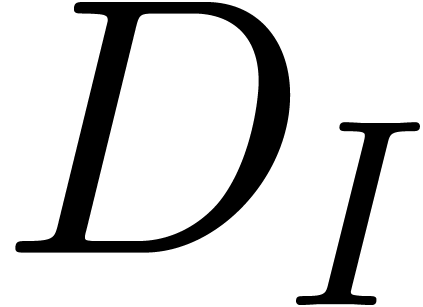 is clearly an ideal of
is clearly an ideal of 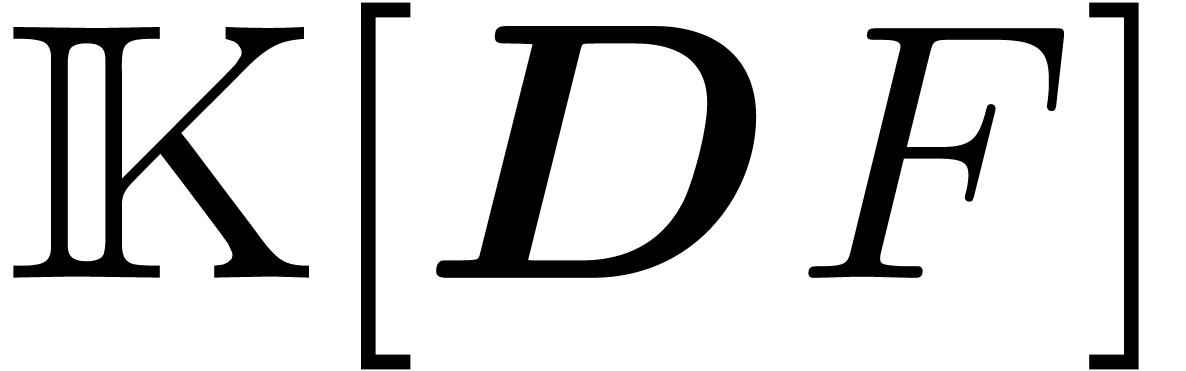 . Assume that
. Assume that 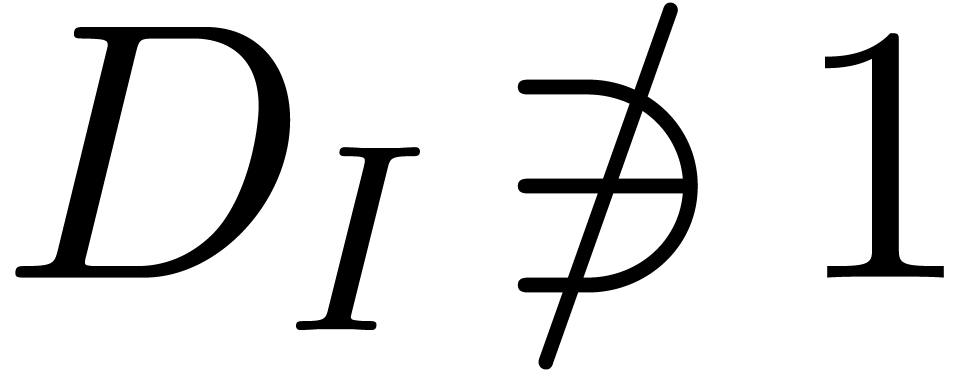 .
Given
.
Given 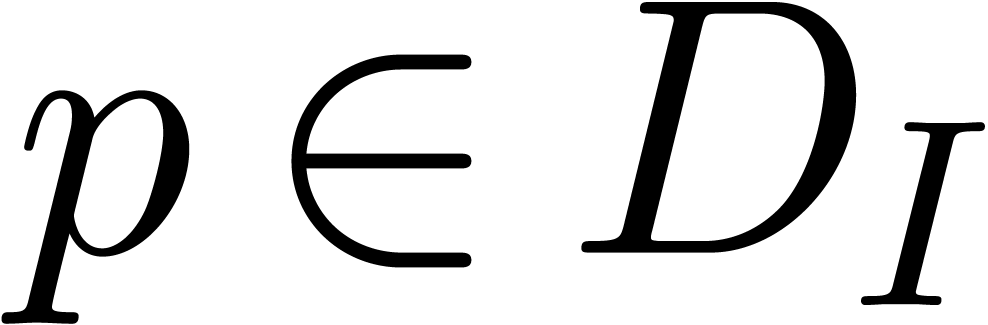 , there exists a
, there exists a  with
with 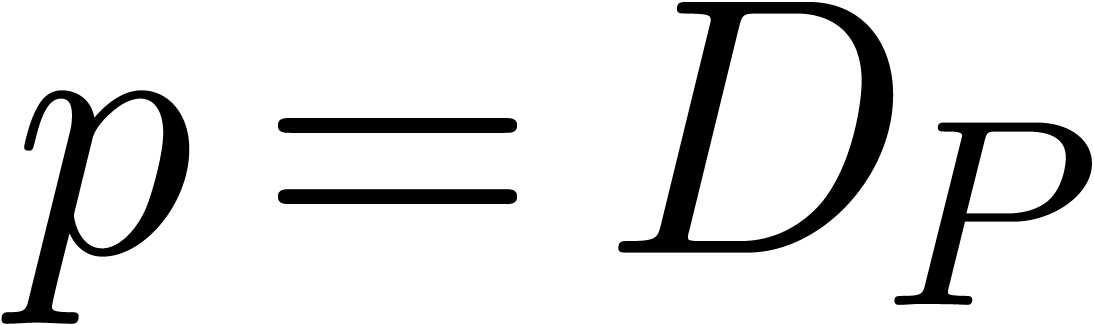 .
Replacing
.
Replacing 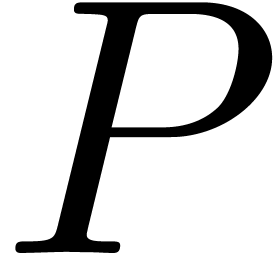 by
by 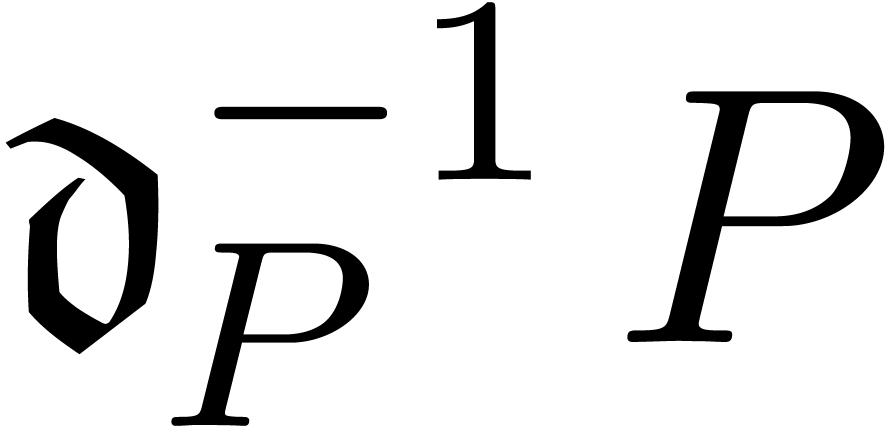 ,
we may assume without loss of generality that
,
we may assume without loss of generality that  , whence
, whence 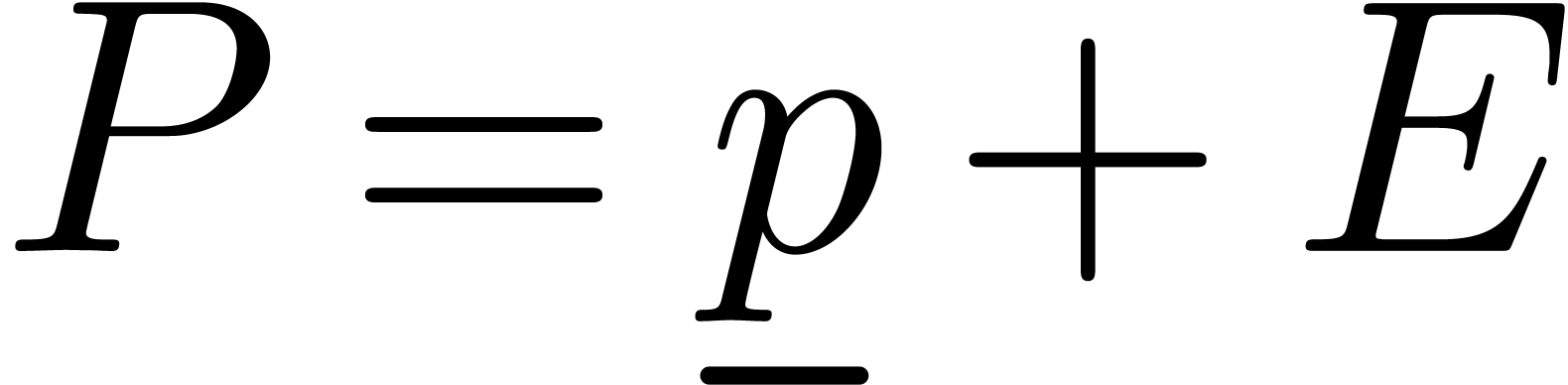 with
with 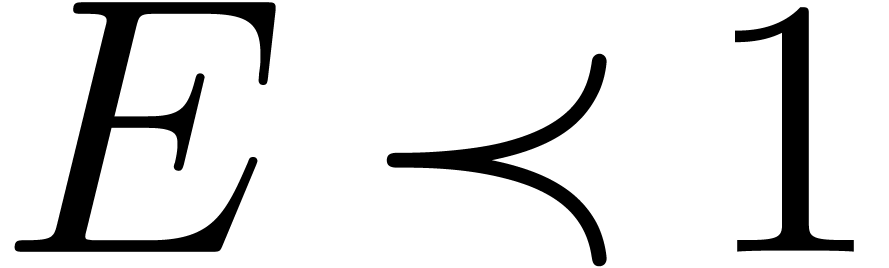 . Now we have
. Now we have 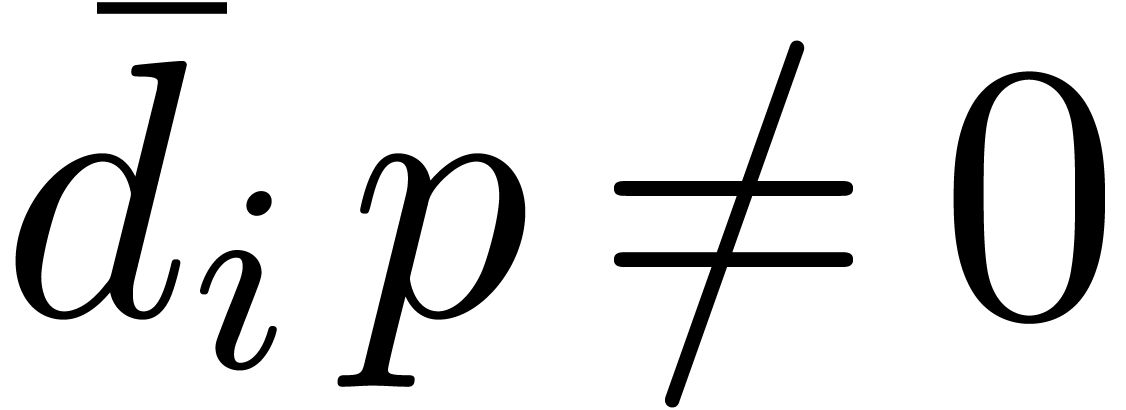 and
and 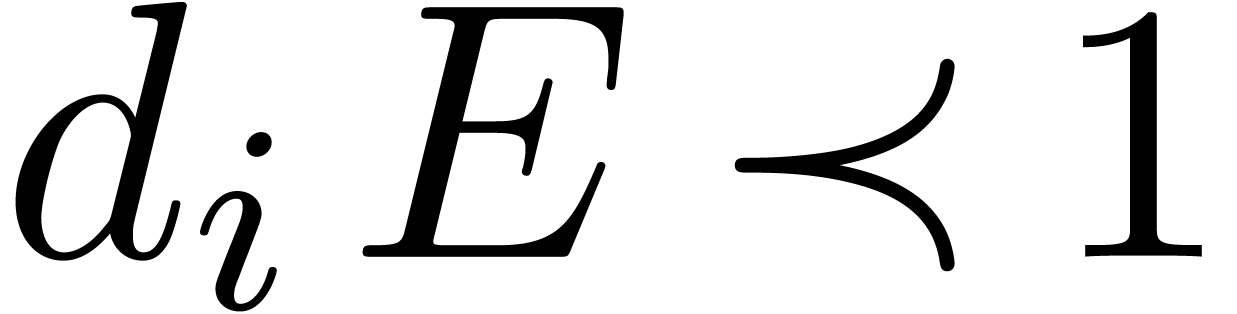 for all
for all 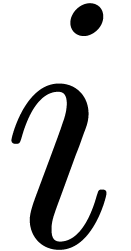 ,
whence
,
whence 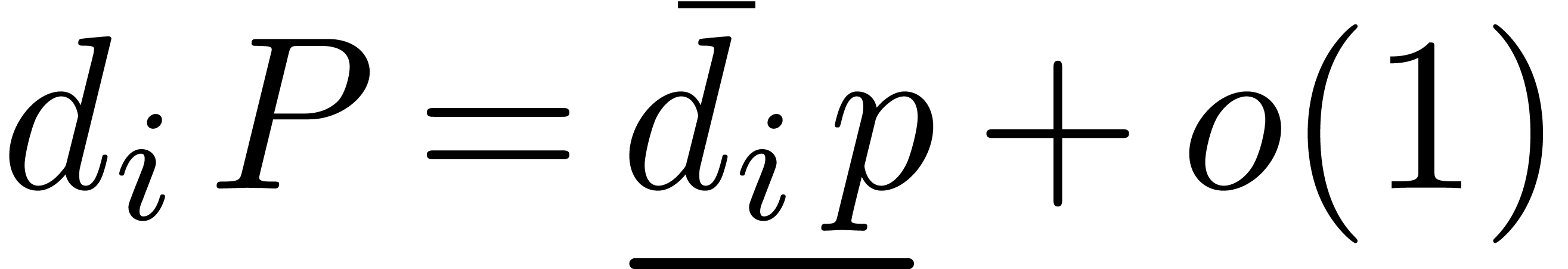 and
and 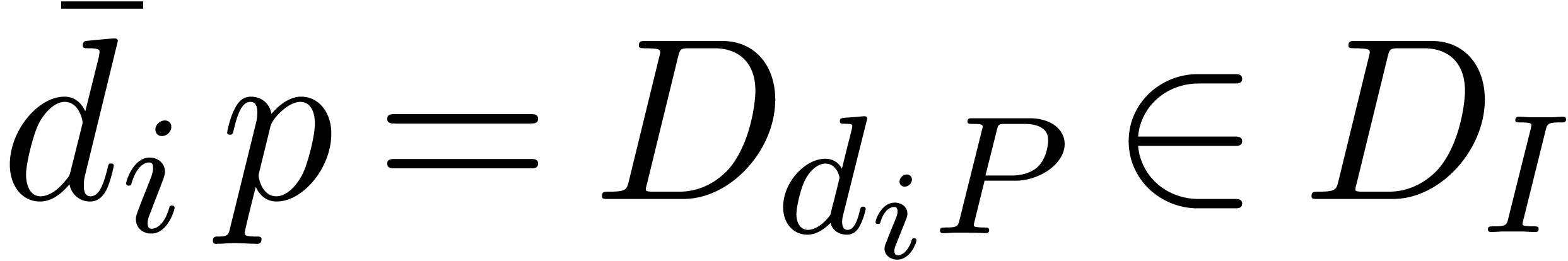 .
This proves that
.
This proves that 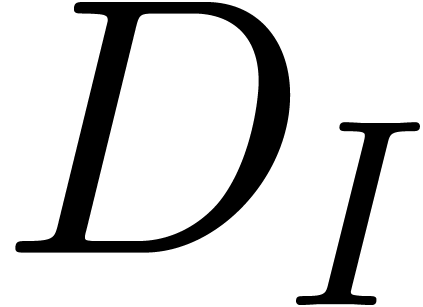 is a differential ideal, called
the dominant differential ideal of
is a differential ideal, called
the dominant differential ideal of 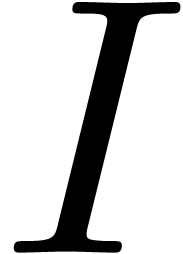 .
.
Remark 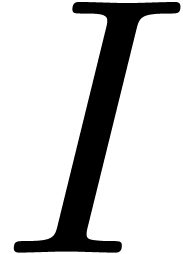 is a radical differential ideal, then
is a radical differential ideal, then 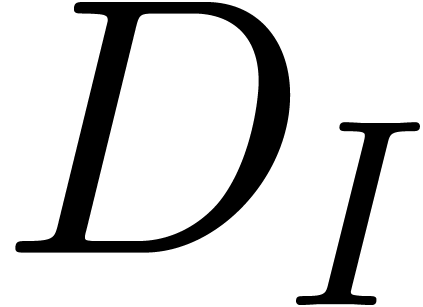 is not necessarily radical. For instance, if we take
is not necessarily radical. For instance, if we take 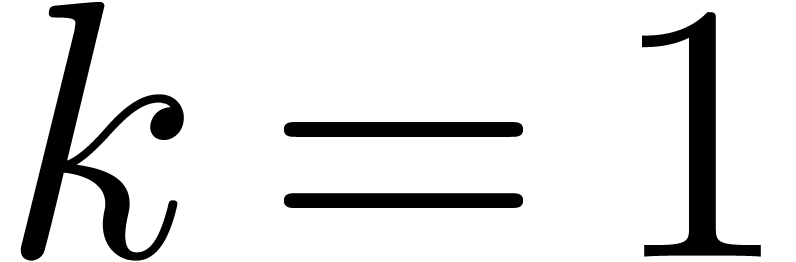 ,
, 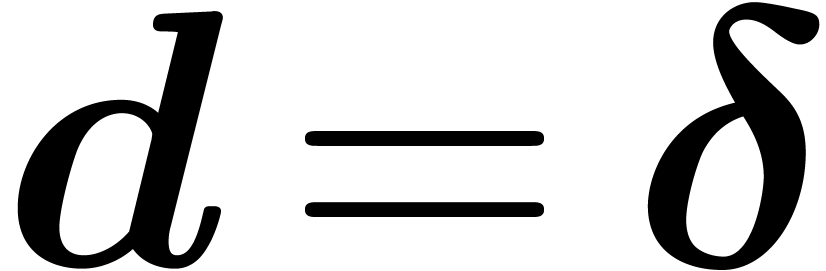 and
and 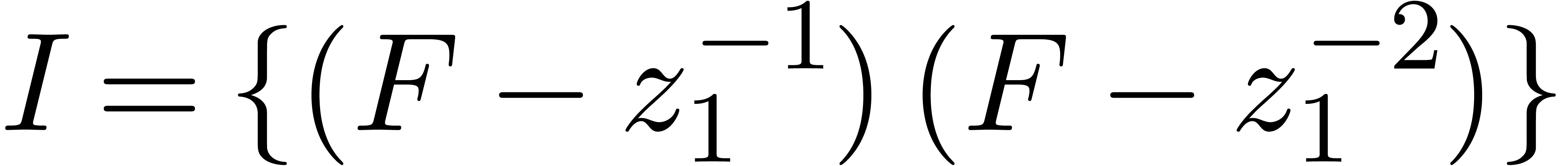 , then
, then 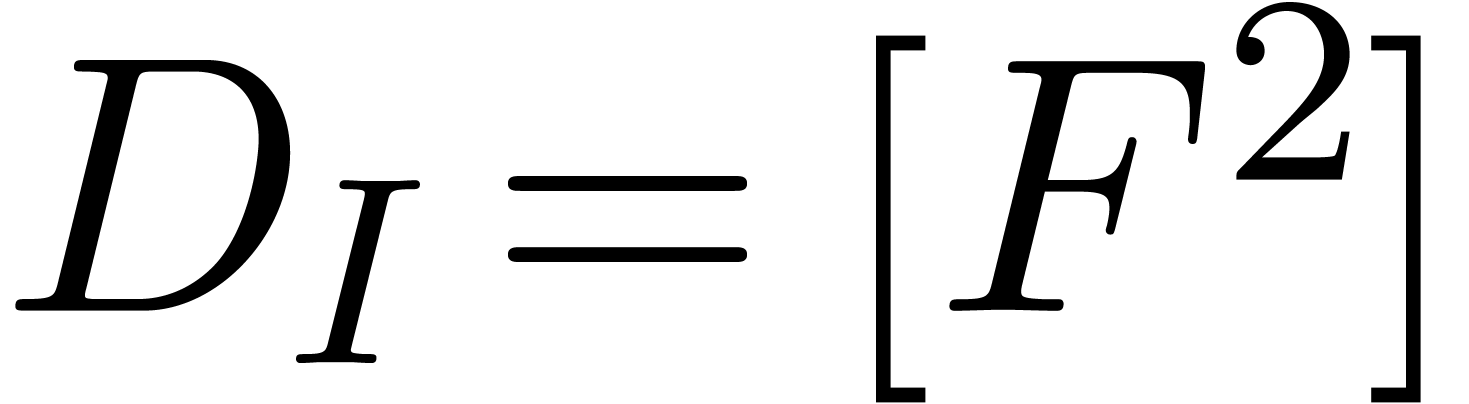 .
.
A differential ideal 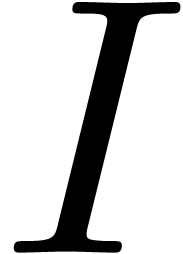 of
of  is said to be strong, if it is closed under grid-based
summation. Since
is said to be strong, if it is closed under grid-based
summation. Since  is archimedian, the strong
differential ideal
is archimedian, the strong
differential ideal 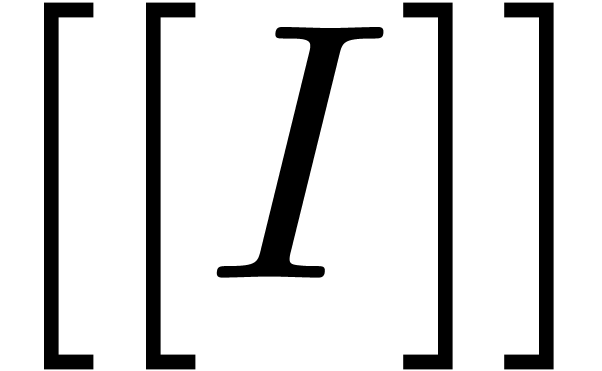 generated by a differential
ideal
generated by a differential
ideal  is just the completion of
is just the completion of 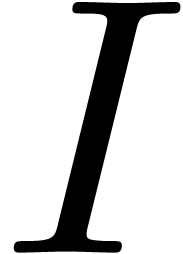 :
:
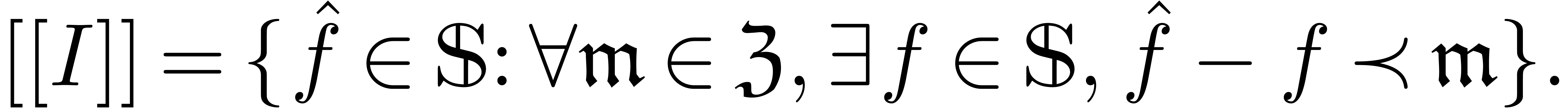 |
(12) |
It follows that 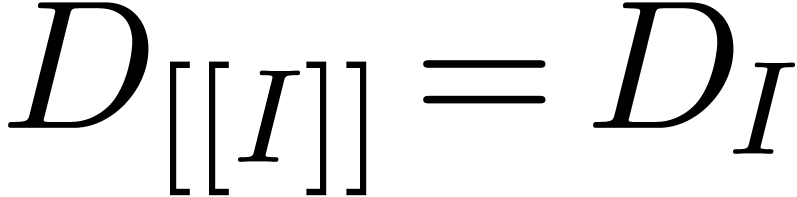 . Any strong
differential ideal
. Any strong
differential ideal 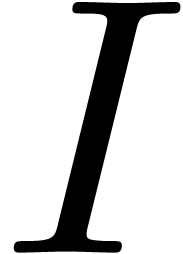 of
of  is
clearly a
is
clearly a 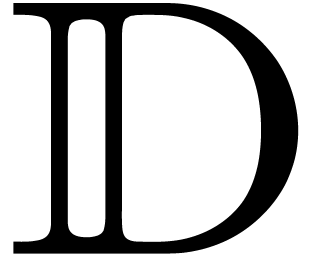 -module. The
contrary is not always true: taking
-module. The
contrary is not always true: taking 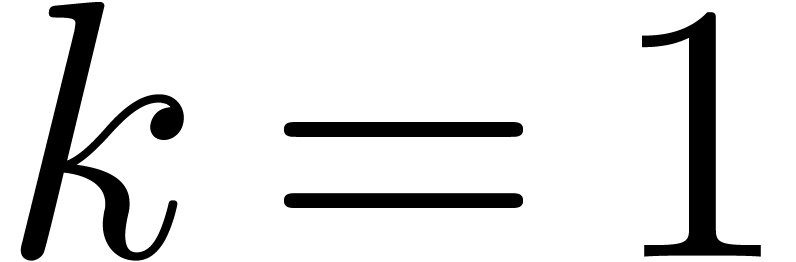 ,
the
,
the  -module generated by
-module generated by
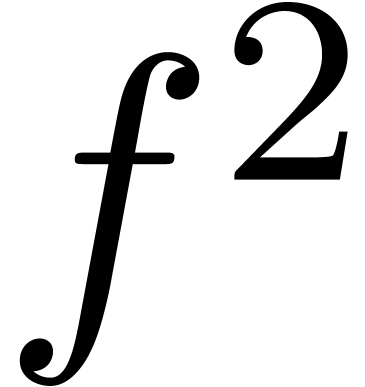 ,
, 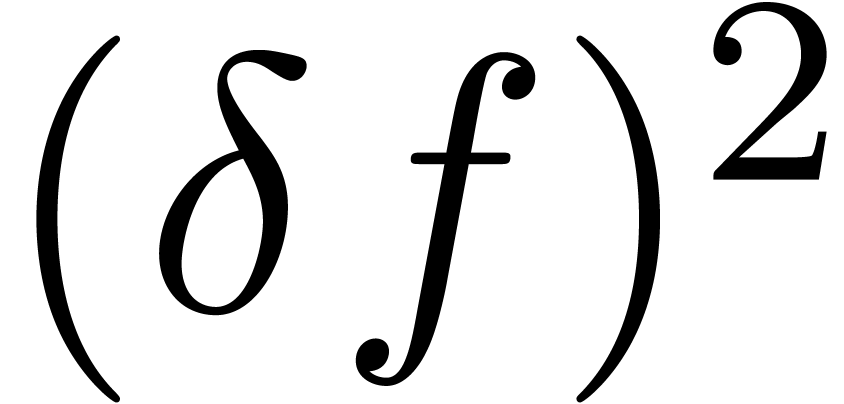 ,
, 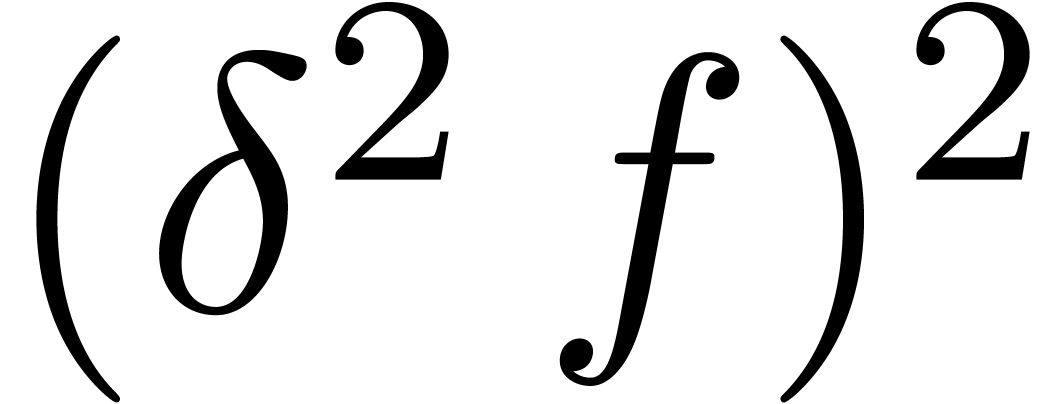 ,
,  does not contain
does not contain 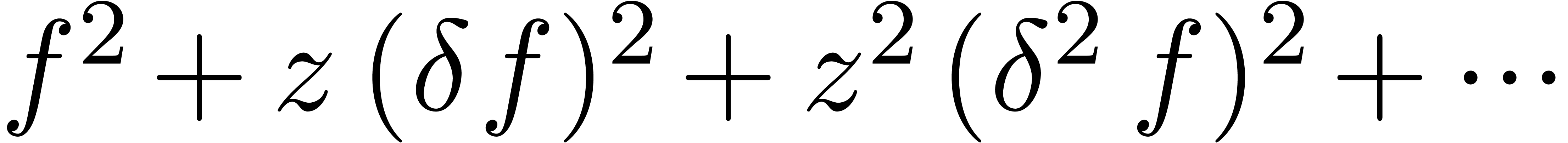 .
.
 be a
be a  -module such that
-module such that 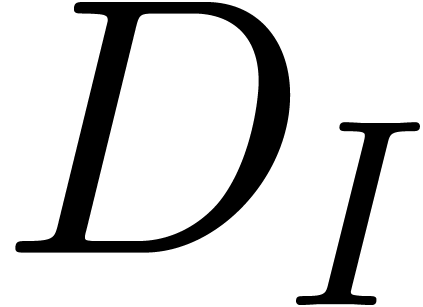 is
finitely generated. Then
is
finitely generated. Then 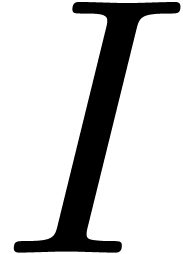 is a strong
differential ideal.
is a strong
differential ideal.
Proof. Let  with
with  be such that
be such that 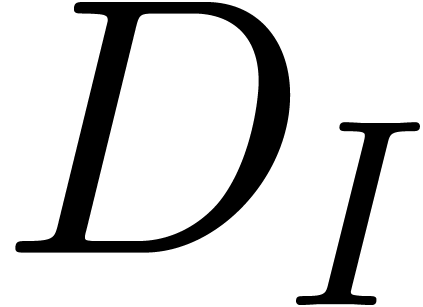 is generated by
is generated by
 . Given
. Given 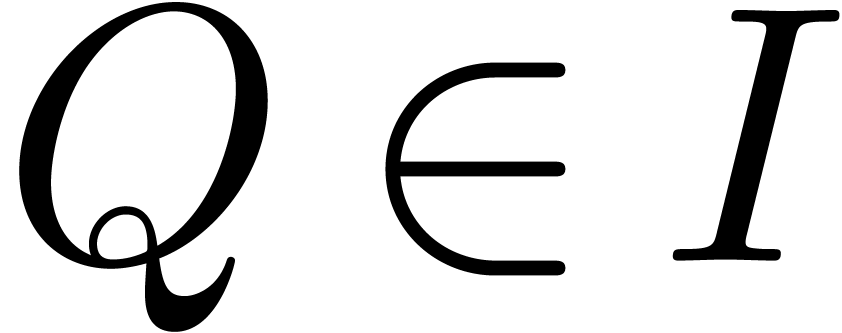 , we claim that there exists an operator
, we claim that there exists an operator 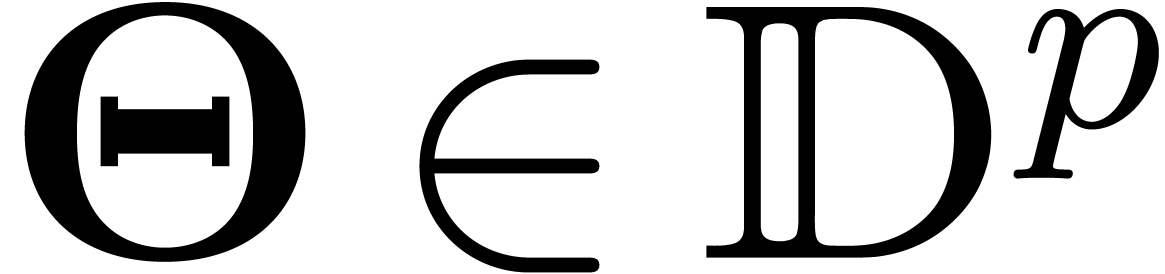 with
with
such that  . We compute the
coefficients
. We compute the
coefficients  of
of  by
induction over
by
induction over 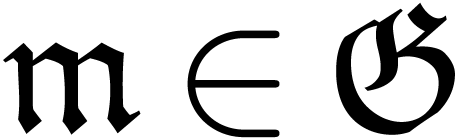 . Assume that
. Assume that
 with
with  has been computed.
Then
has been computed.
Then  and
and  .
Since
.
Since  is generated by
is generated by  , there exists an operator
, there exists an operator 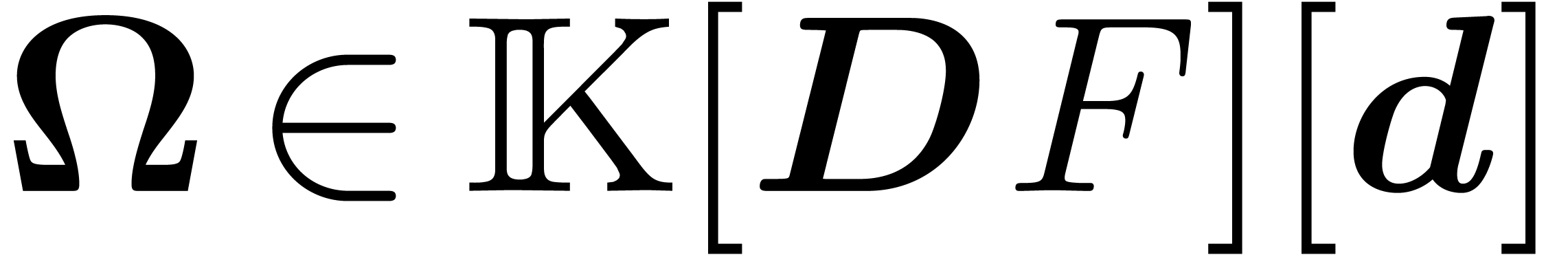 with
with  . Taking
. Taking  , it follows that
, it follows that  ,
so the induction hypothesis is satisfied for the next monomial
,
so the induction hypothesis is satisfied for the next monomial  in
in  . By
induction, we thus compute an operator
. By
induction, we thus compute an operator 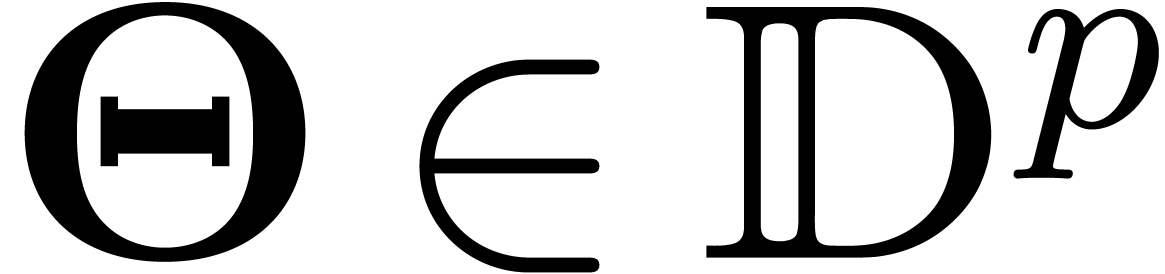 which
satisfies
which
satisfies  for all
for all  .
It follows that
.
It follows that  .
.
Having shown our claim, let  be a grid-based
family. Then there exists a family of operators
be a grid-based
family. Then there exists a family of operators 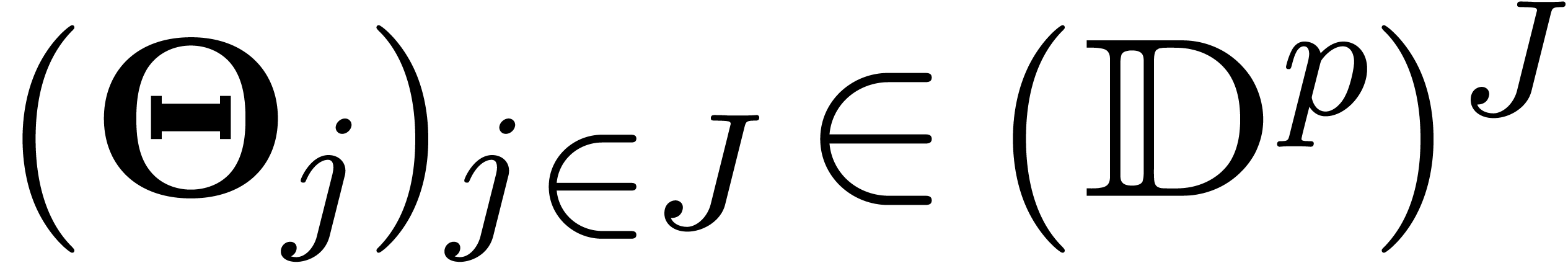 with
with 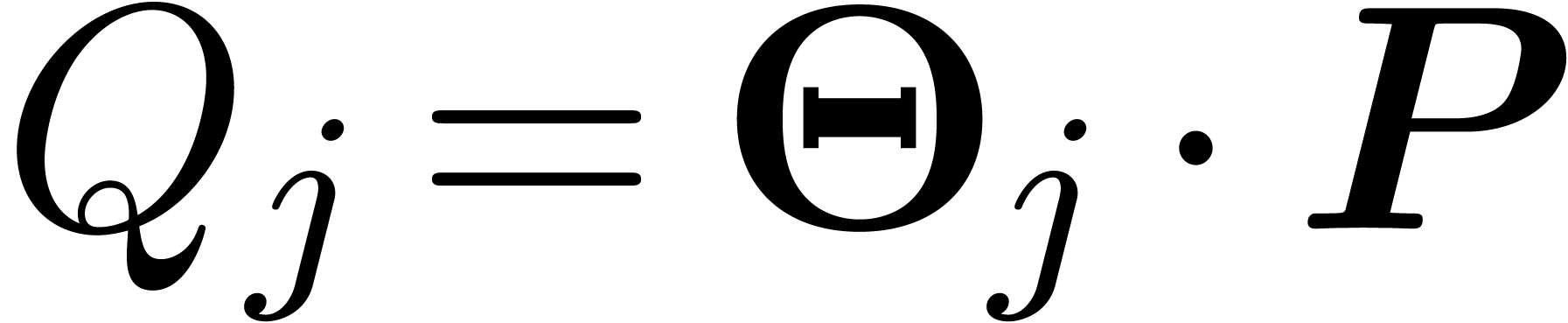 and
and 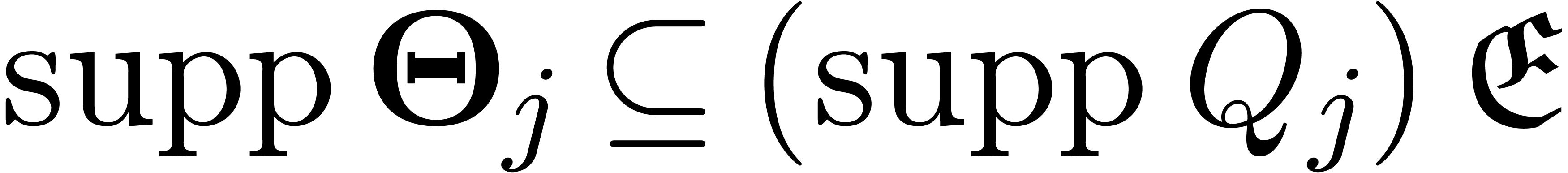 for all
for all  . For each
. For each 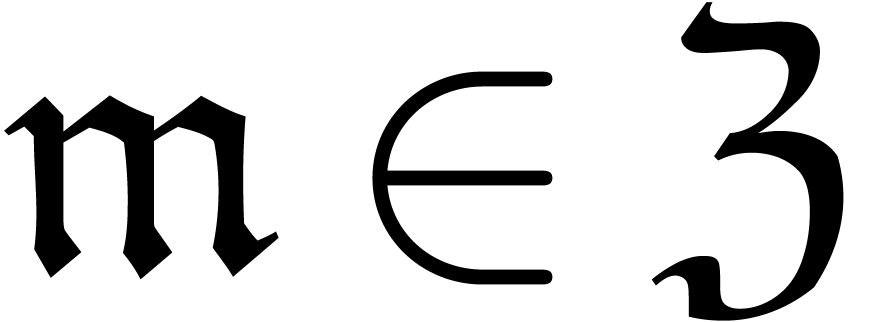 , and using the facts that
, and using the facts that 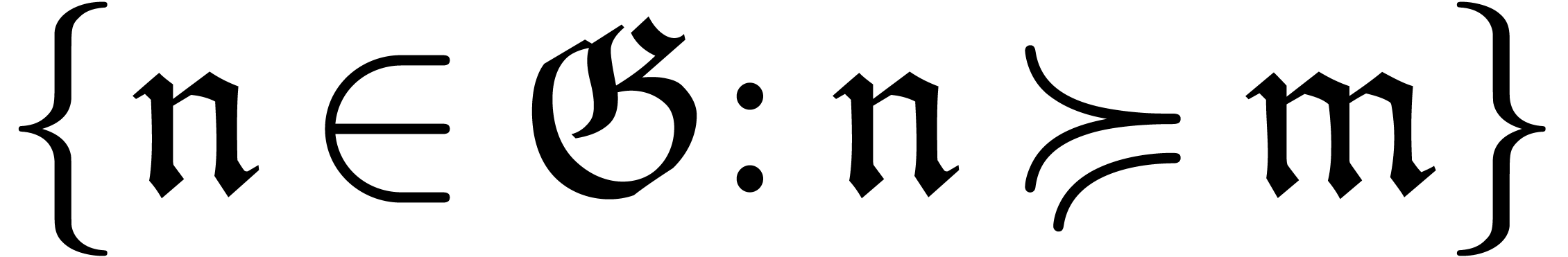 is finite and
is finite and  is grid-based, there are only a
finite number of indices
is grid-based, there are only a
finite number of indices  with
with 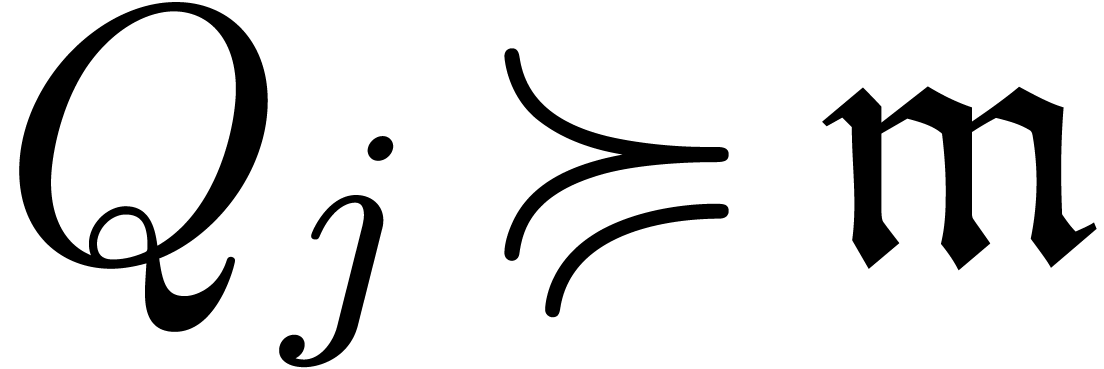 . Consequently,
. Consequently,  is a
grid-based family and
is a
grid-based family and  .
.
Remark  -module is necessarily
finitely generated as well.
-module is necessarily
finitely generated as well.
Let us consider a vector  with
with  for each
for each  . A series
. A series  is said to be asymptotically reduced
w.r.t.
is said to be asymptotically reduced
w.r.t.  if
if  is Ritt reduced w.r.t.
is Ritt reduced w.r.t. 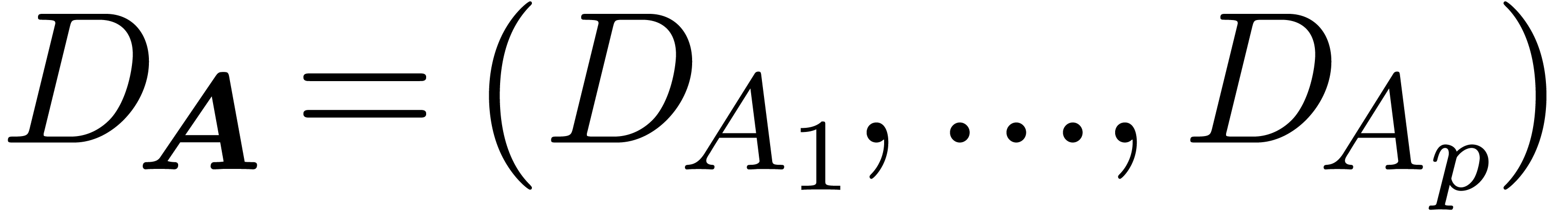 .
.
Due to the presence of  in (2), a
similar division technique as for standard bases will not always work in
the case of asymptotic reduction: infinite sequences of partial
reductions may give rise to infinite powers of initials and separants.
Nevertheless, we will now show that the mechanism does work in the
special but important case when all initials and separants are
in (2), a
similar division technique as for standard bases will not always work in
the case of asymptotic reduction: infinite sequences of partial
reductions may give rise to infinite powers of initials and separants.
Nevertheless, we will now show that the mechanism does work in the
special but important case when all initials and separants are  .
.
We say that  is normal if
is normal if 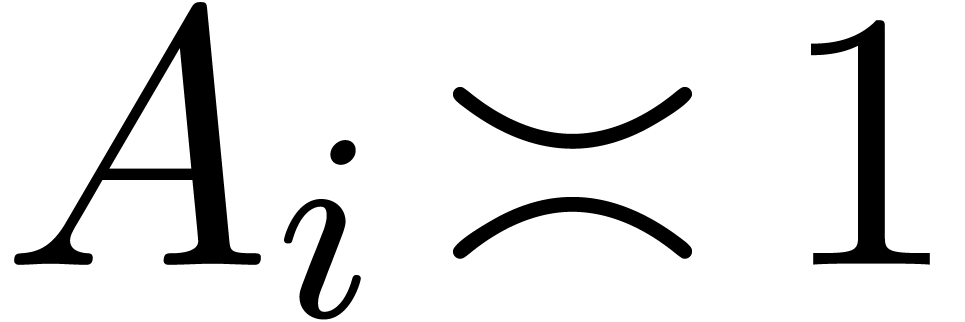 and
and 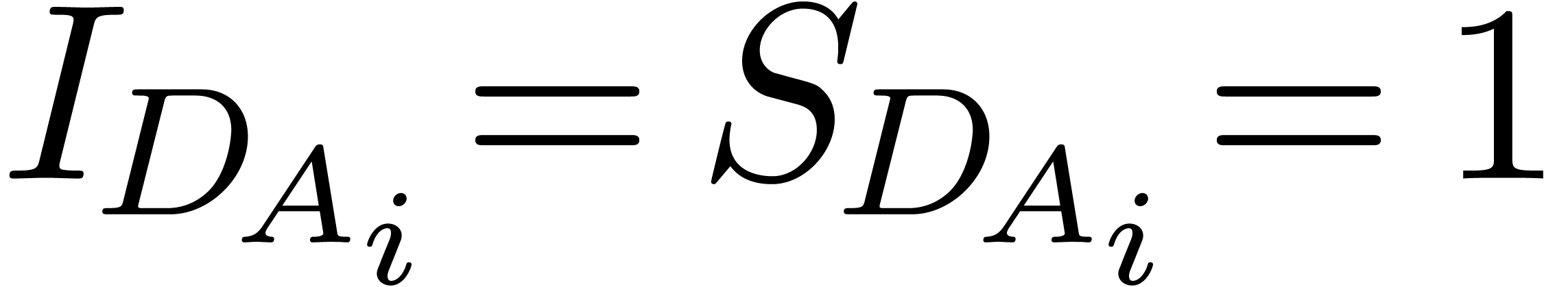 for all
for all  . Given
. Given  ,
we claim that there exists an expression
,
we claim that there exists an expression
 |
(13) |
where  satisfies
satisfies  and
and  is reduced w.r.t.
is reduced w.r.t.  . We will call
. We will call  and
and  the quotient and remainder of the asymptotic
reduction of
the quotient and remainder of the asymptotic
reduction of  w.r.t.
w.r.t.  . The coefficients of
. The coefficients of  and
and  are computed by induction over
the grid-based set
are computed by induction over
the grid-based set
So let 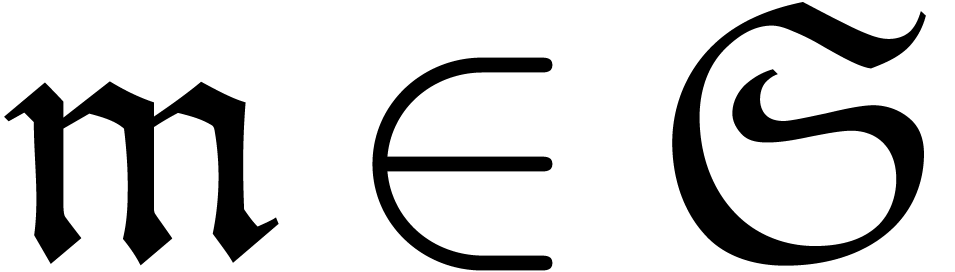 and assume that we computed
and assume that we computed  and
and  for all
for all  , in such a way that
, in such a way that
 |
(14) |
with 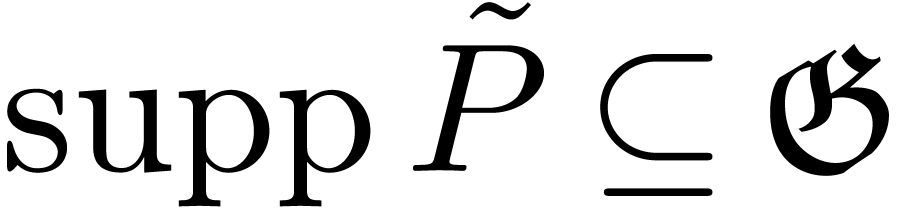 and
and  .
We may assume without loss of generality that
.
We may assume without loss of generality that  (if
(if  , then we may simply take
, then we may simply take
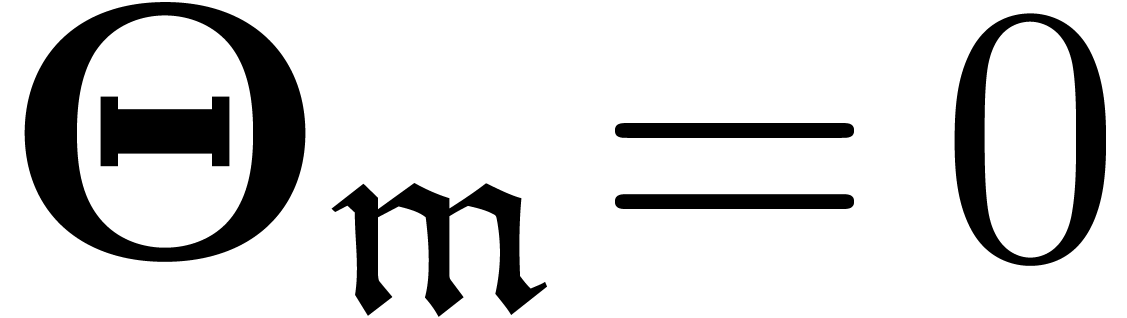 ). Ritt reduction of
). Ritt reduction of 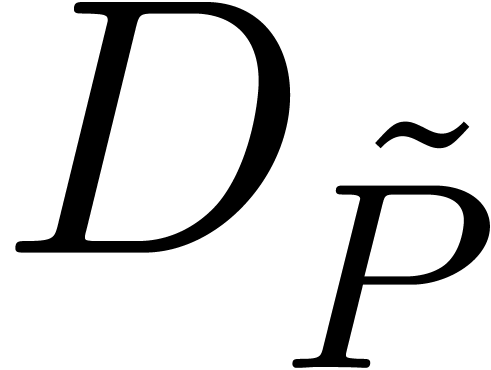 w.r.t.
w.r.t. 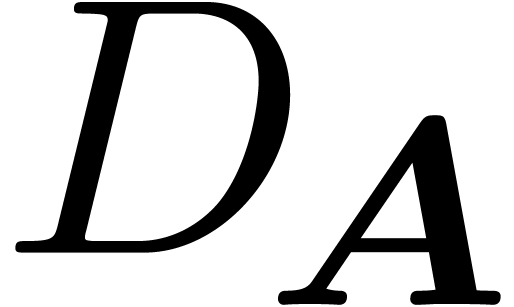 yields a
relation
yields a
relation
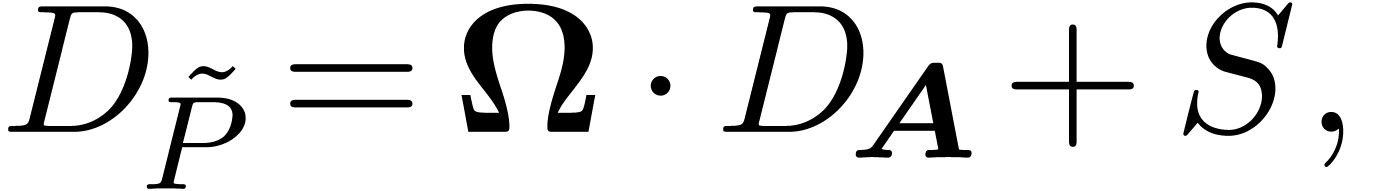
with 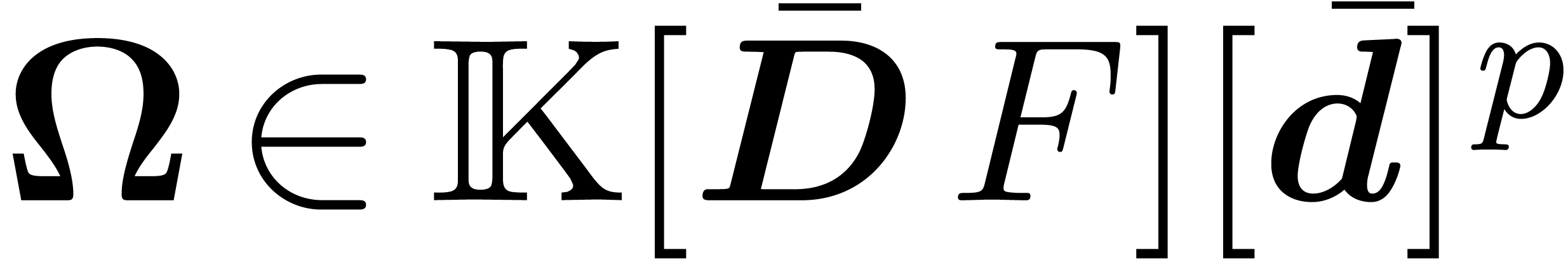 and
and 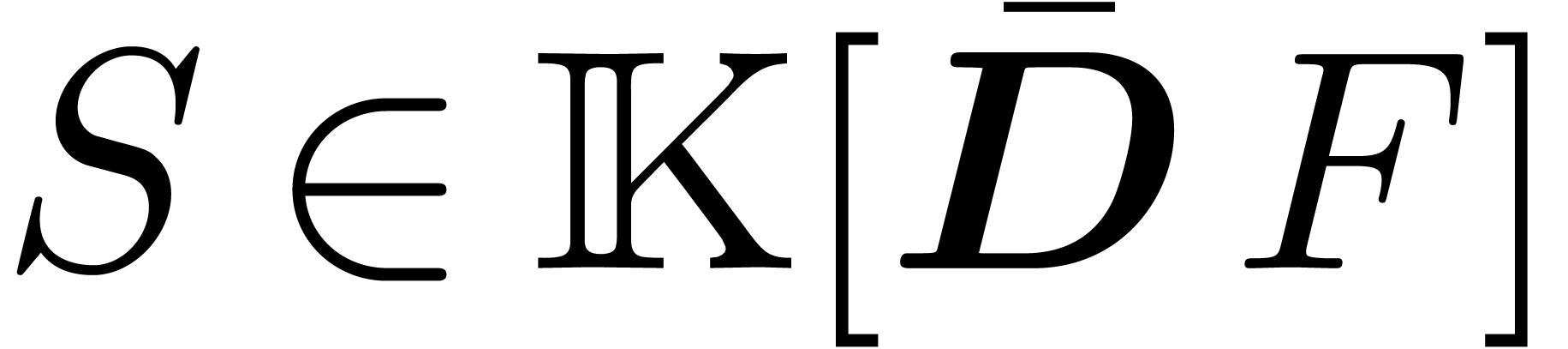 .
In view of (10) and (11), we get
.
In view of (10) and (11), we get
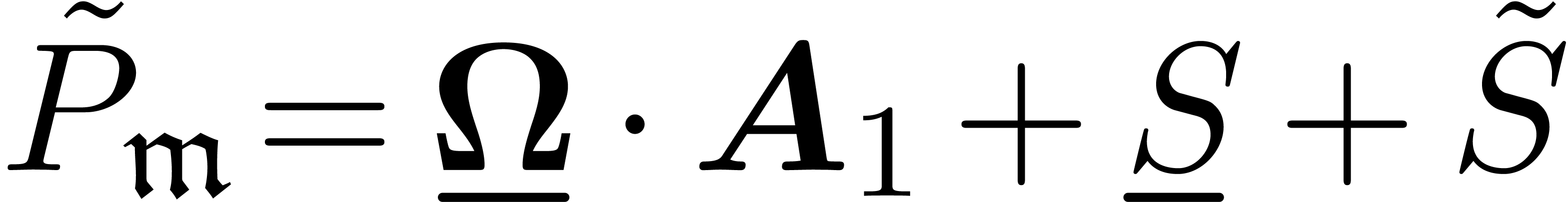 |
(15) |
with 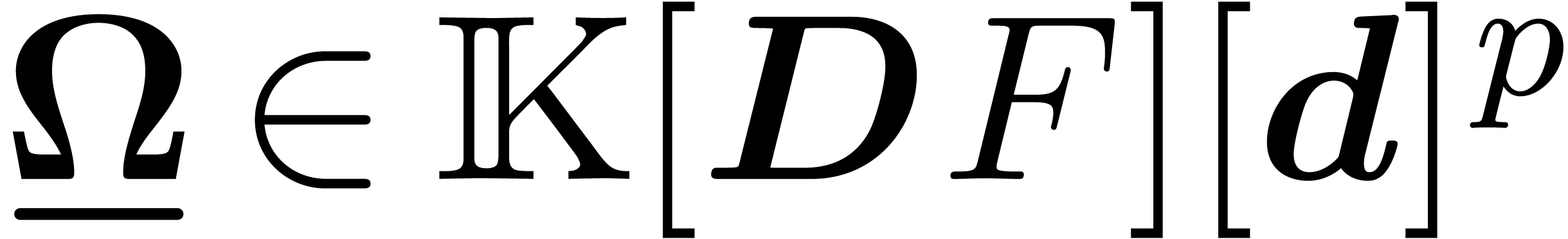 ,
, 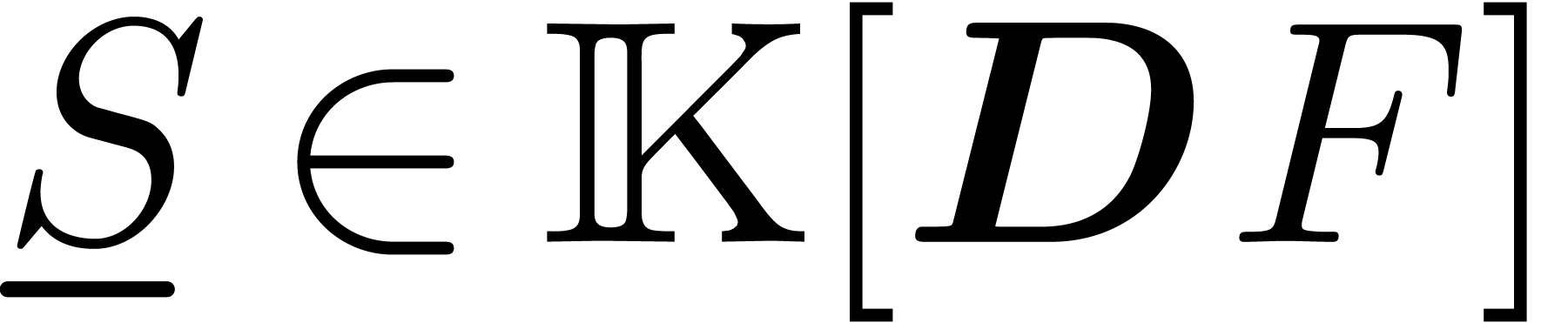 and
and  with
with 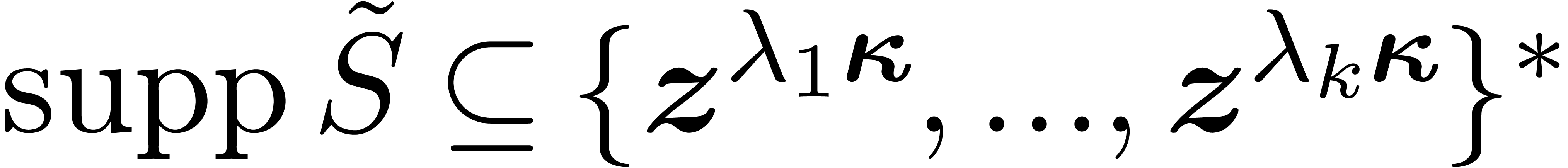 .
Taking
.
Taking 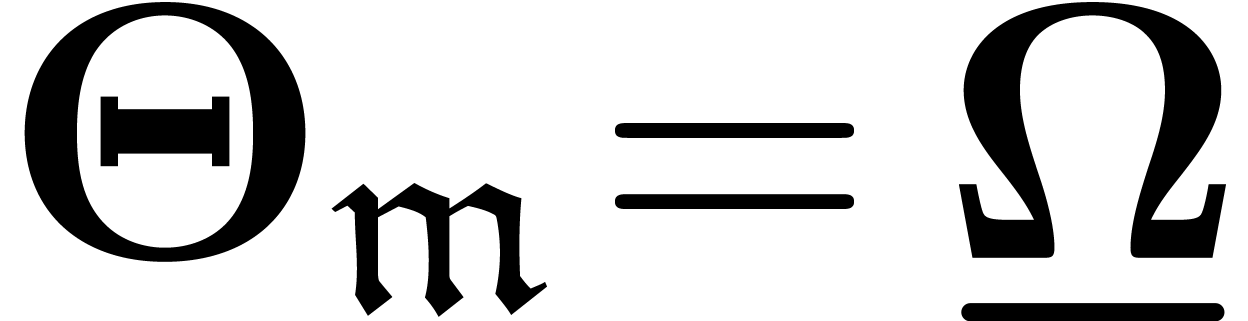 , it follows that
, it follows that
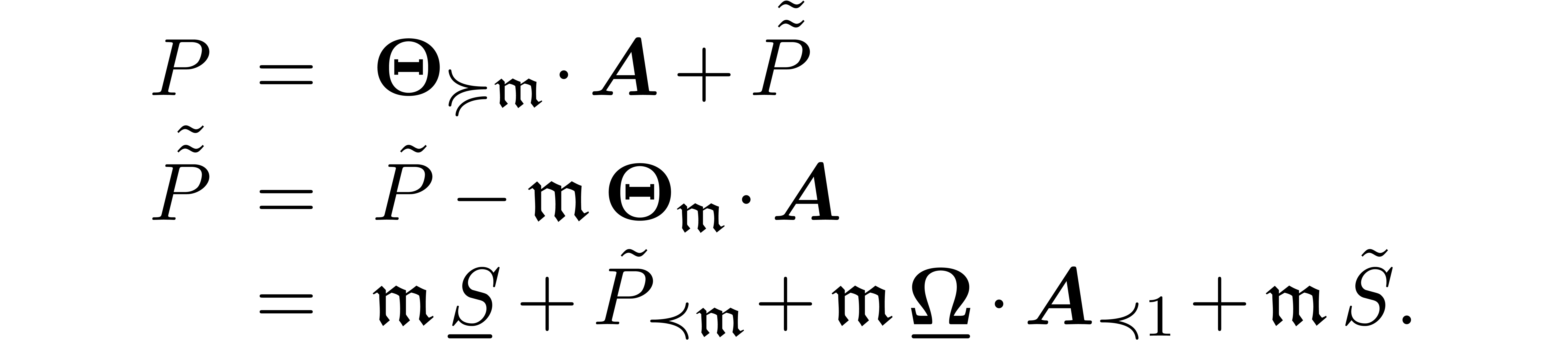
If 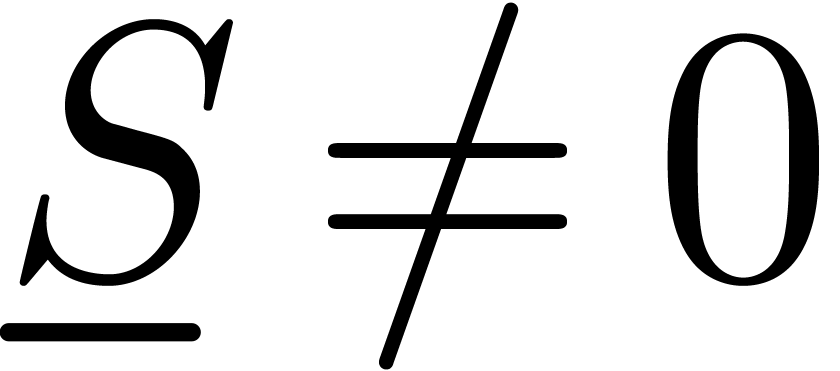 , then
, then 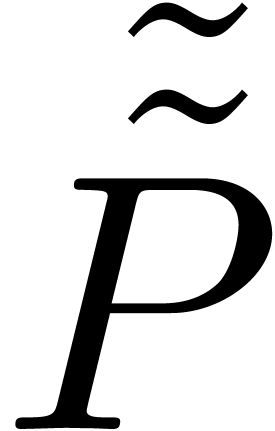 is reduced w.r.t.
is reduced w.r.t.  and the
construction stops. Otherwise, we have
and the
construction stops. Otherwise, we have  and
and  and the induction hypothesis is satisfied for the
next monomial
and the induction hypothesis is satisfied for the
next monomial  .
.
We will say that  is quasi-normal if
is quasi-normal if
 for all
for all 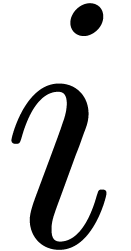 .
In that case, let
.
In that case, let 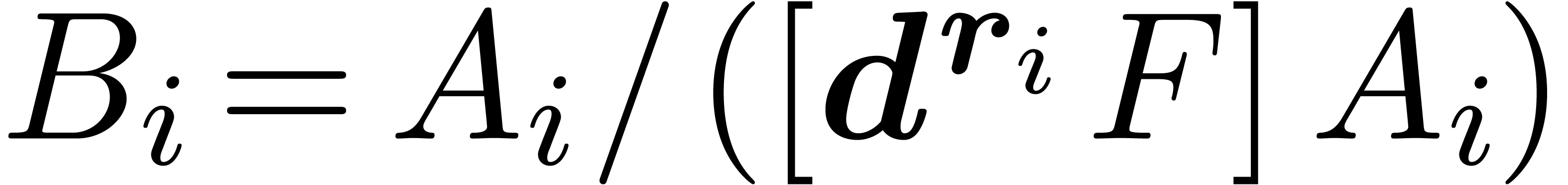 for each
for each  , where
, where 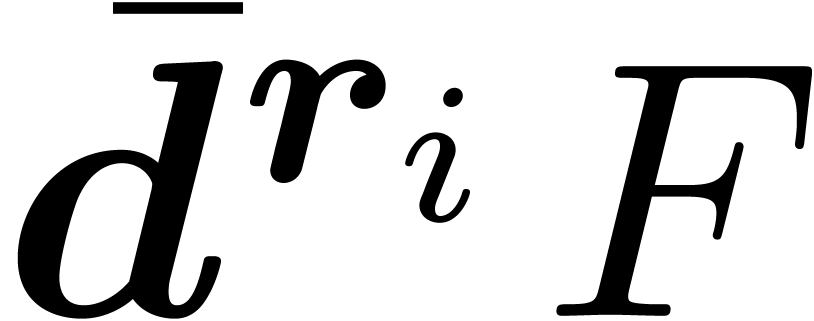 is the leader
of
is the leader
of  and
and  the coefficient
of
the coefficient
of 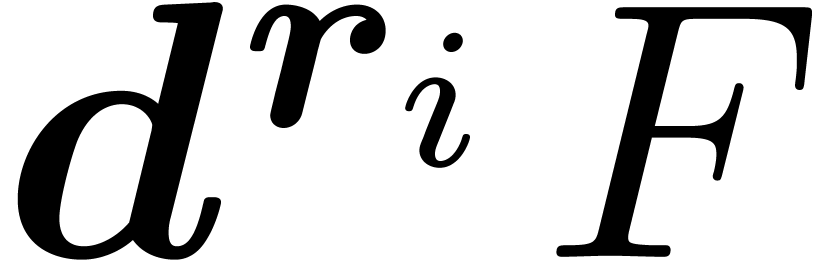 in
in 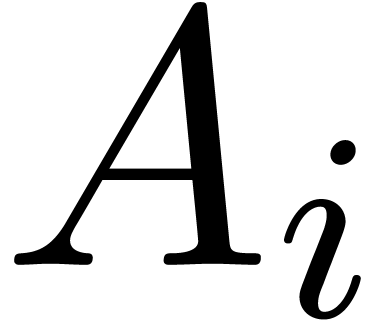 .
Then
.
Then 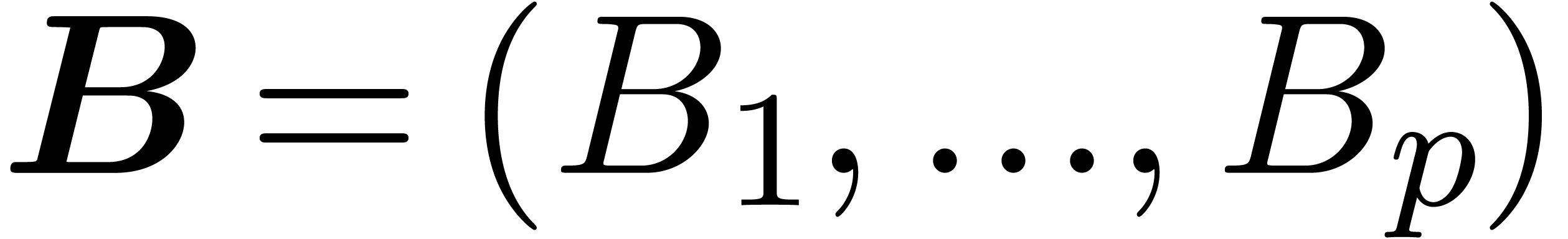 is normal and we call it the
normalization of
is normal and we call it the
normalization of  .
.
Remark  is not quasi-normal, then the same argument still leads to
a relation
is not quasi-normal, then the same argument still leads to
a relation

with  whenever the reduction process stops.
However, we no longer obtain a nice relation in the case when
whenever the reduction process stops.
However, we no longer obtain a nice relation in the case when 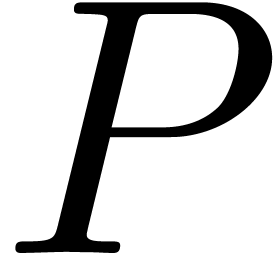 reduces to
reduces to 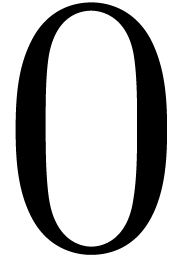 .
.
As we did in section 3.6 for Ritt reduction, it is natural
to introduce asymptotic co-reduction, the dual notion of asymptotic
reduction. Since 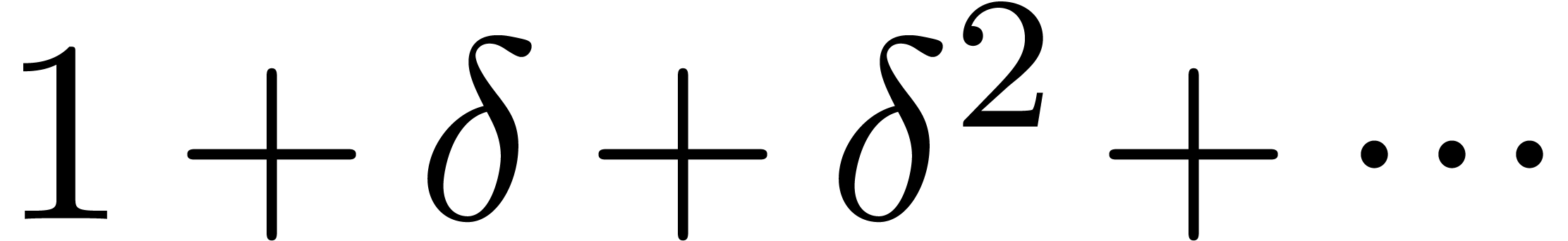 cannot be applied to
cannot be applied to  , we will assume
, we will assume 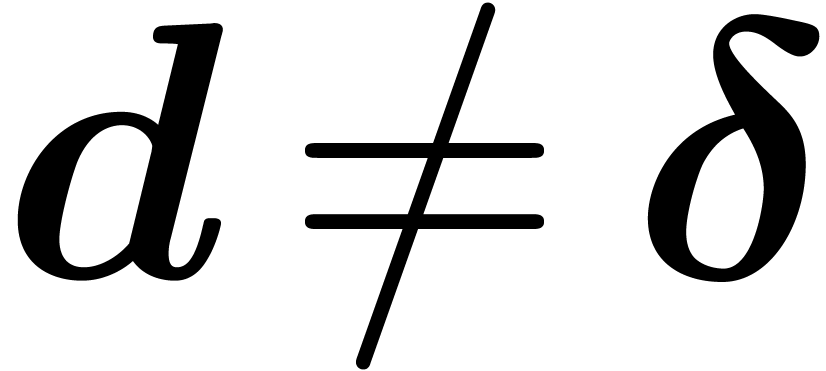 . The set
. The set
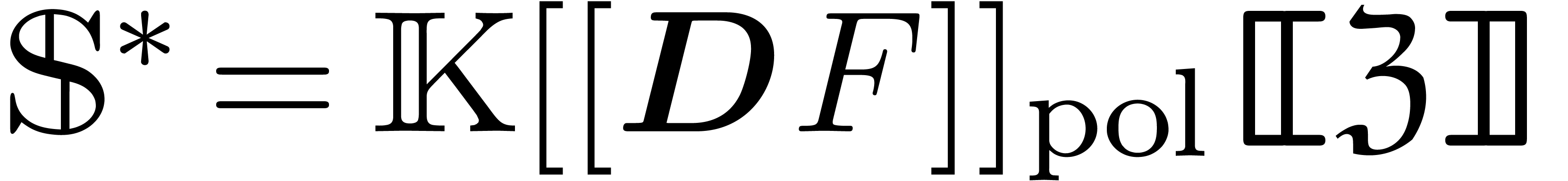
plays the role of  in the dual setting.
Similarly, operator algebra
in the dual setting.
Similarly, operator algebra
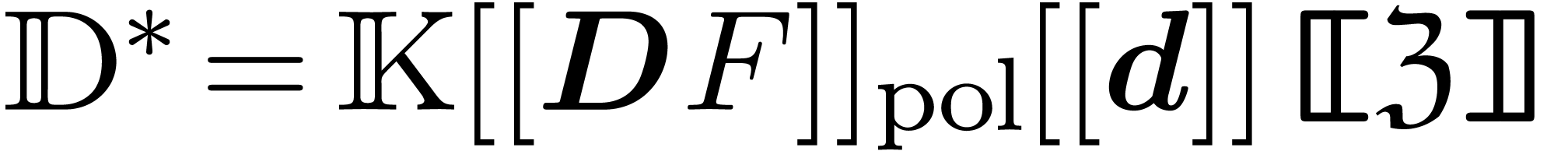
is the natural counterpart of  .
In a similar way as before, one introduces the commutative variant
.
In a similar way as before, one introduces the commutative variant 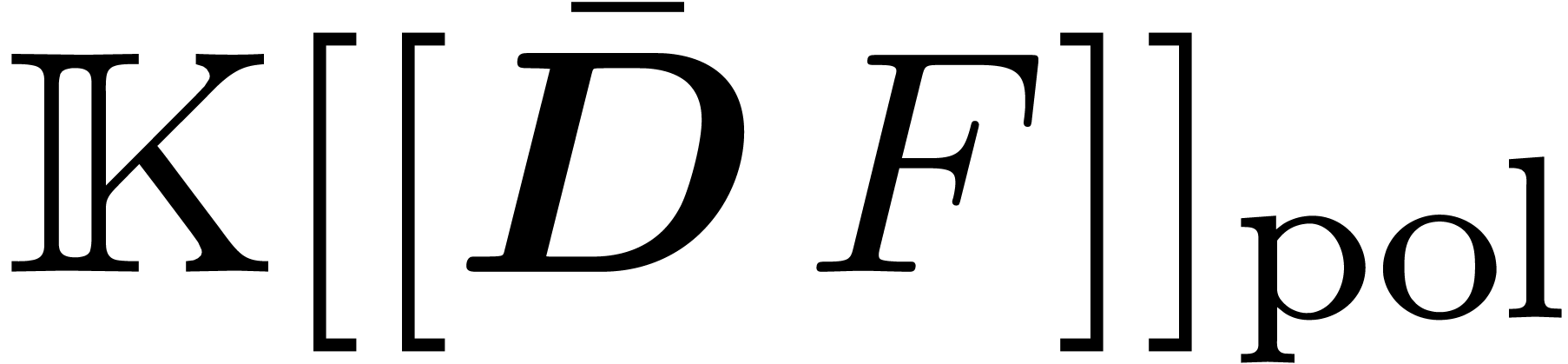 of
of 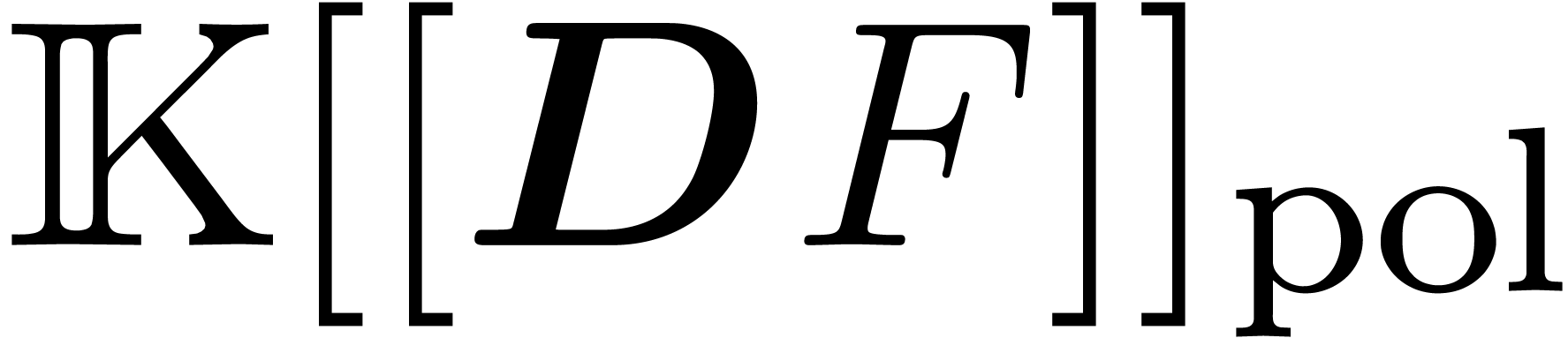 .
Again, the dominant part
.
Again, the dominant part 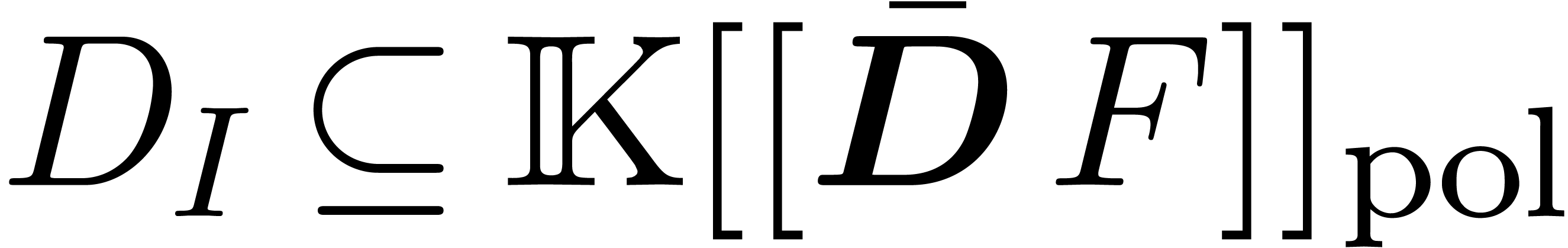 of a differential ideal
of a differential ideal
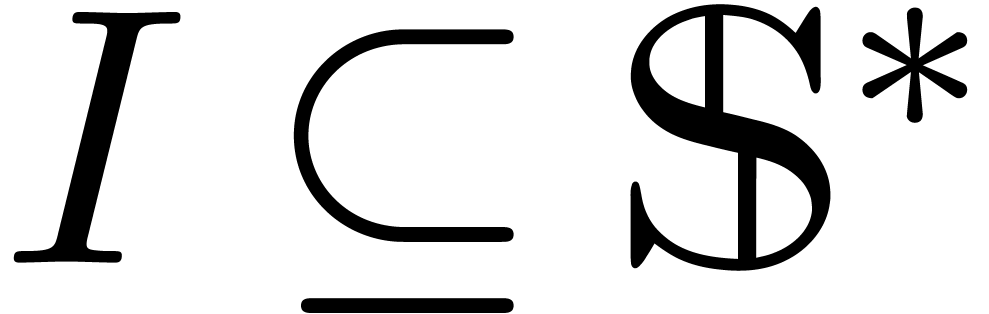 is a differential ideal.
is a differential ideal.
Any series 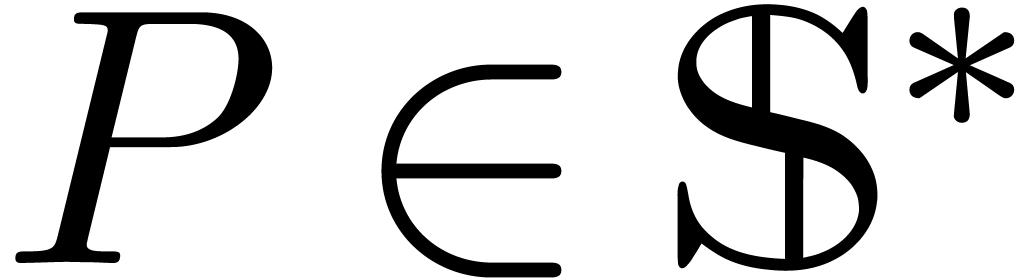 can also be regarded as a series in
the variables
can also be regarded as a series in
the variables  and
and  ,
with a support
,
with a support 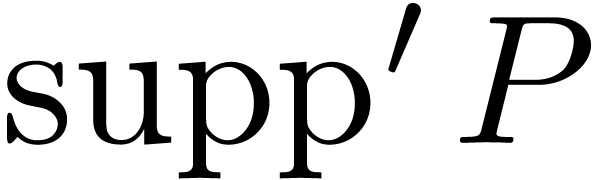 which is a subset of
which is a subset of 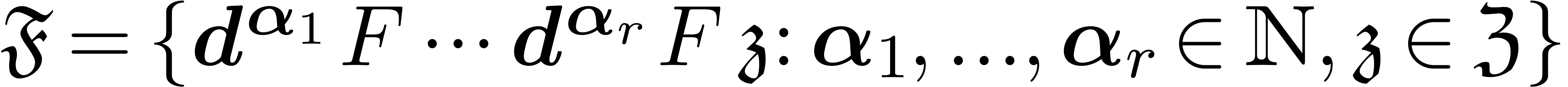 . A subset
. A subset  is said to
be admissible if it occurs as the support of a series in
is said to
be admissible if it occurs as the support of a series in  . A family
. A family 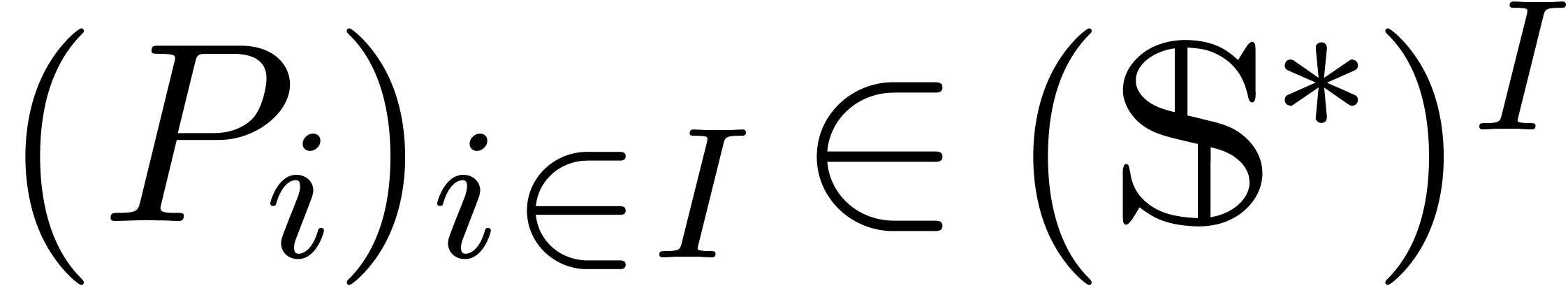 is said to
be summable if
is said to
be summable if  is admissible and
is admissible and  is finite for each
is finite for each  .
In that case,
.
In that case, 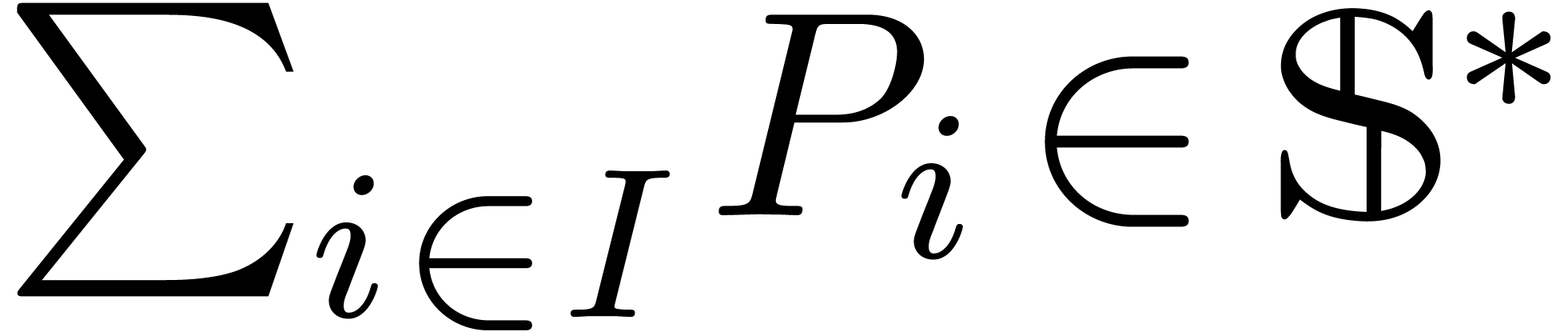 . A
differential ideal
. A
differential ideal 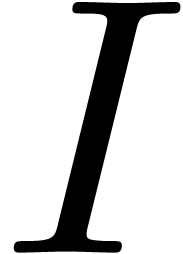 of
of  is
said to be strong if it is closed under infinite summation.
is
said to be strong if it is closed under infinite summation.
Let 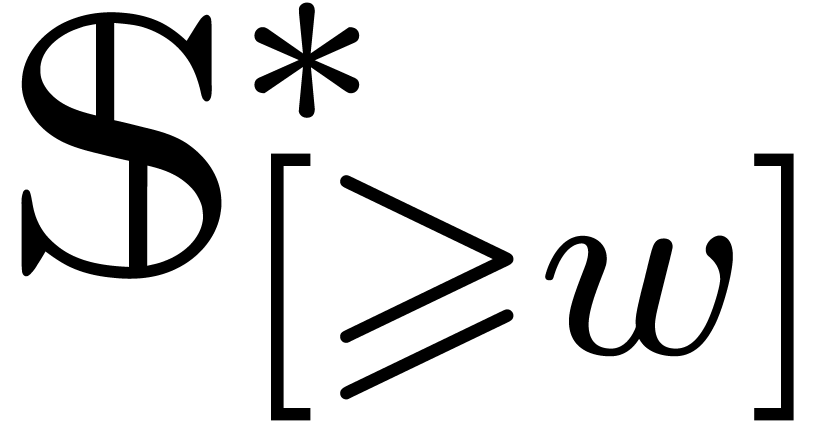 be the set of series in
be the set of series in  which are strong linear combinations of monomials
which are strong linear combinations of monomials 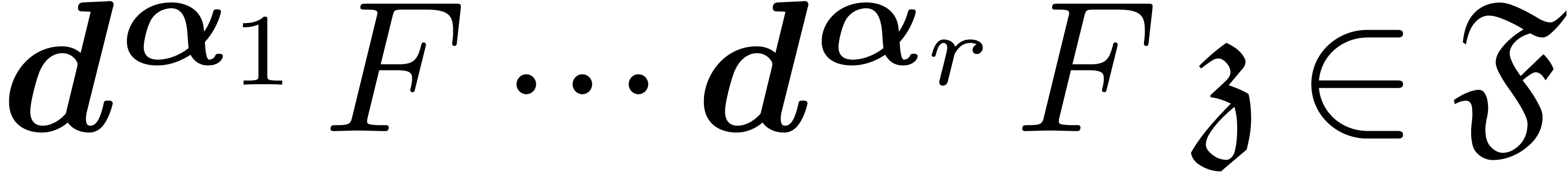 of weight
of weight  at least
at least  .
The strong differential ideal
.
The strong differential ideal 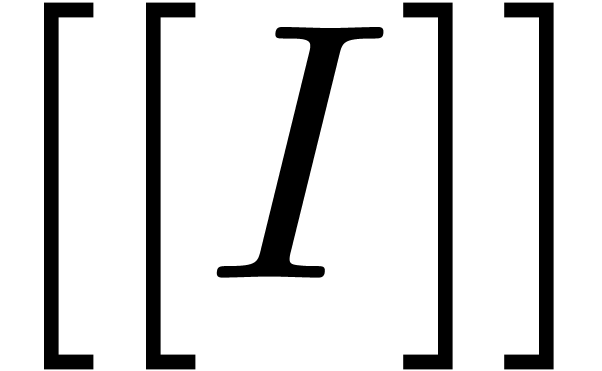 generated by a
differential ideal
generated by a
differential ideal 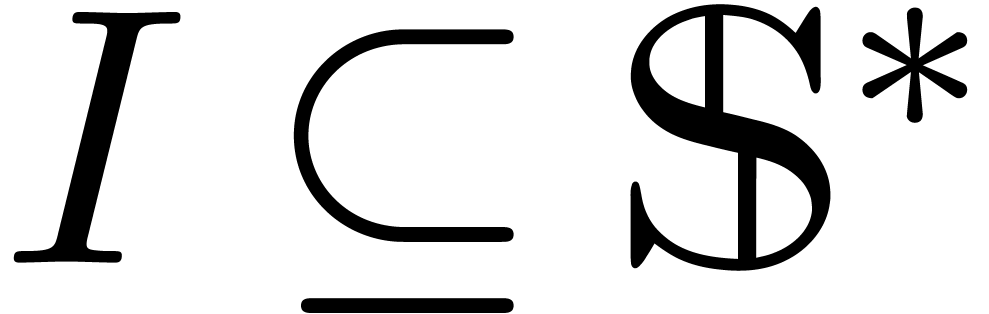 coincides with a suitable
completion of
coincides with a suitable
completion of 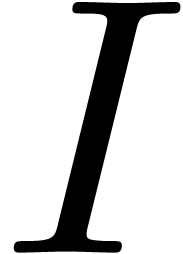 :
:
 |
(16) |
It follows that 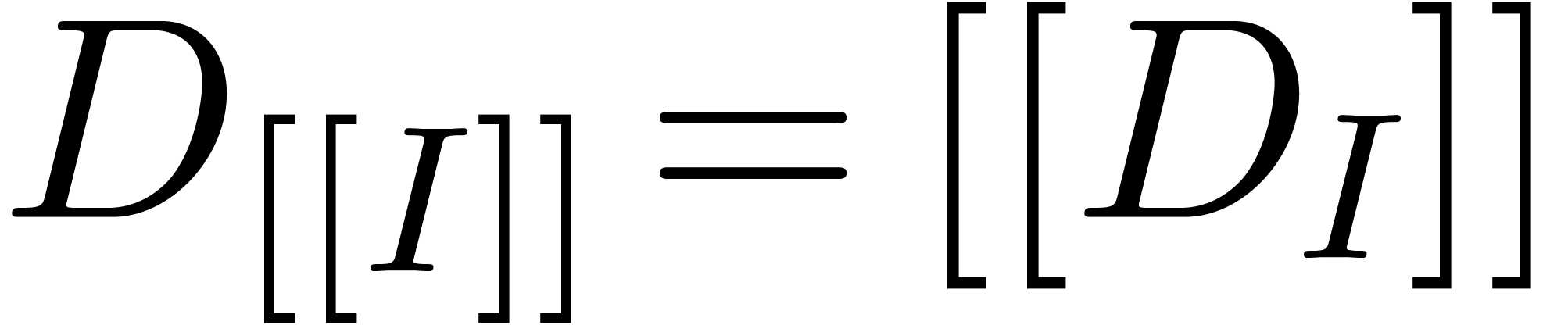 . Any strong
differential ideal of
. Any strong
differential ideal of  is a
is a  -module. Any
-module. Any  -module
-module
 , such that
, such that 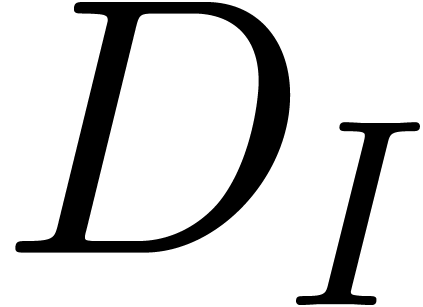 is strong and finitely generated as a strong differential ideal, is a
strong differential ideal.
is strong and finitely generated as a strong differential ideal, is a
strong differential ideal.
Consider a vector 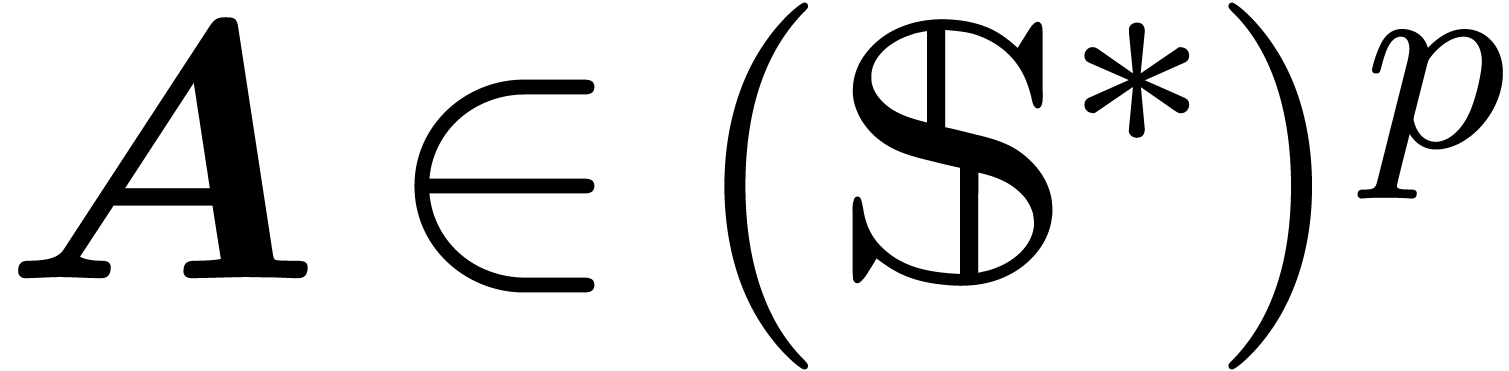 with
with  for all
for all  . We will say that
. We will say that
 is co-normal, if
is co-normal, if  ,
,
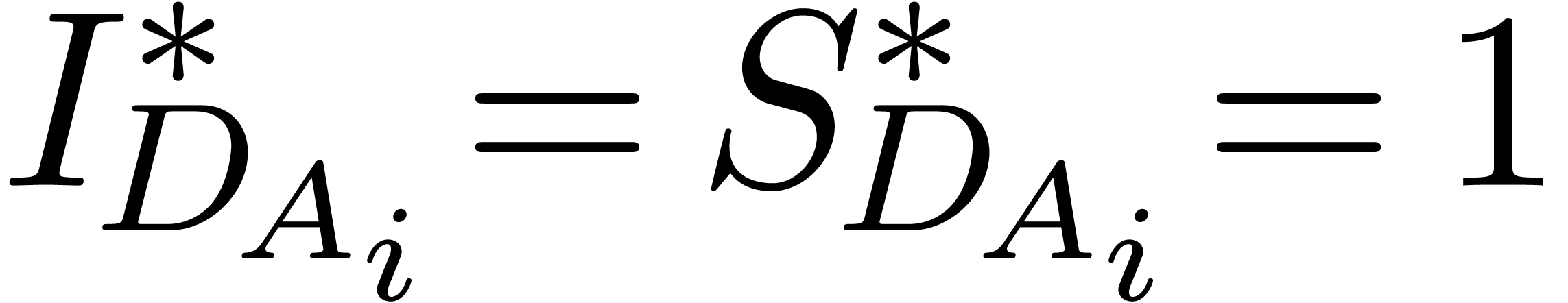 and
and  is linear for all
is linear for all
 . Given
. Given  , we say that
, we say that  is
asymptotically co-reduced w.r.t.
is
asymptotically co-reduced w.r.t.  if
if  or
or 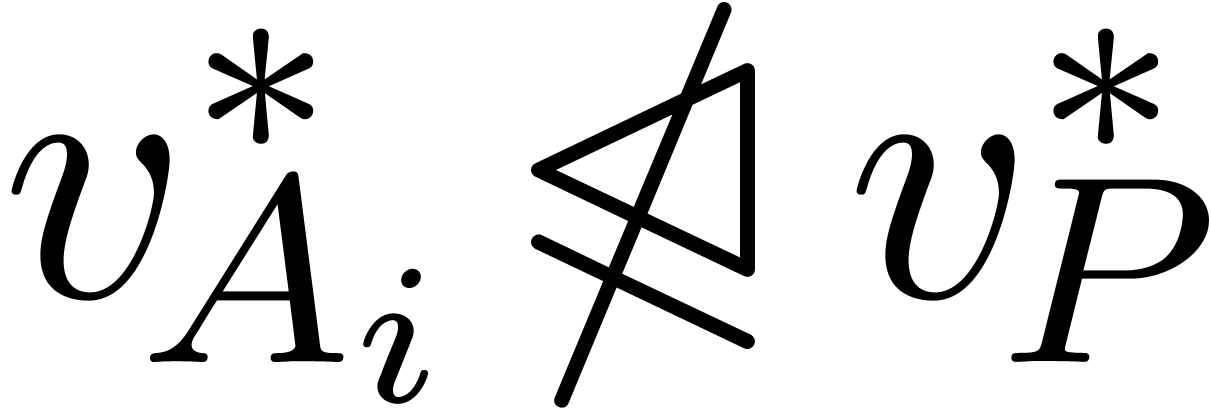 for all
for all  . In a similar way as above,
asymptotic co-reduction of
. In a similar way as above,
asymptotic co-reduction of  w.r.t.
w.r.t.  yields a relation
yields a relation

where  satisfies
satisfies  and
and  is co-reduced w.r.t.
is co-reduced w.r.t.  .
.
Let  be normal in the sense of section 4.3
and assume that
be normal in the sense of section 4.3
and assume that 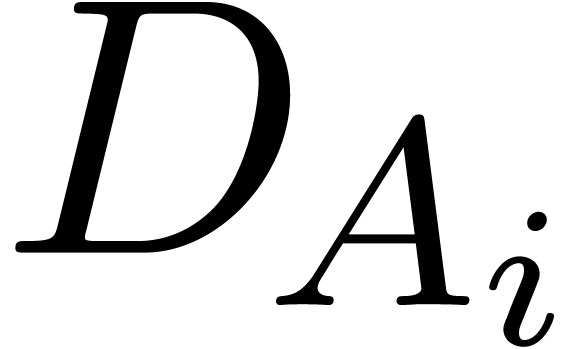 is linear for each
is linear for each 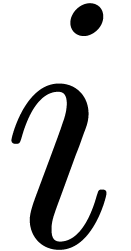 . We say that
. We say that  is an
asymptotic basis, if
is an
asymptotic basis, if 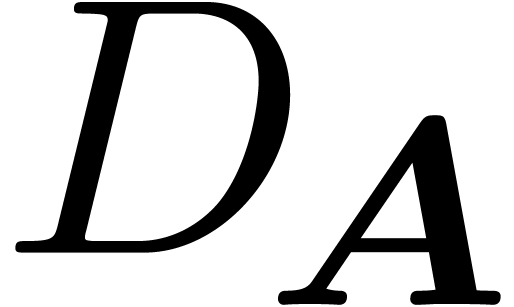 is a Rosenfeld
basis and if each pair
is a Rosenfeld
basis and if each pair 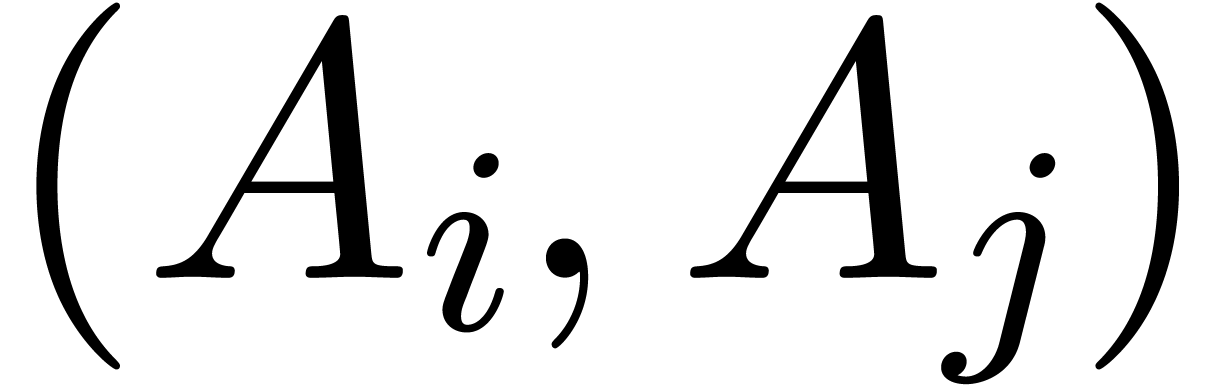 with
with  satisfies an asymptotic critical relation
satisfies an asymptotic critical relation
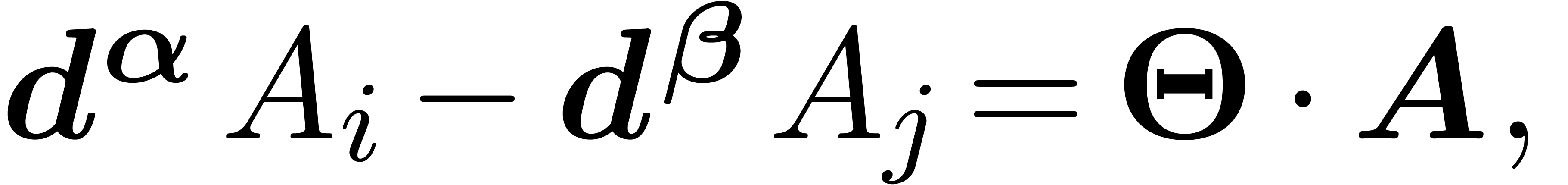 |
(17) |
where 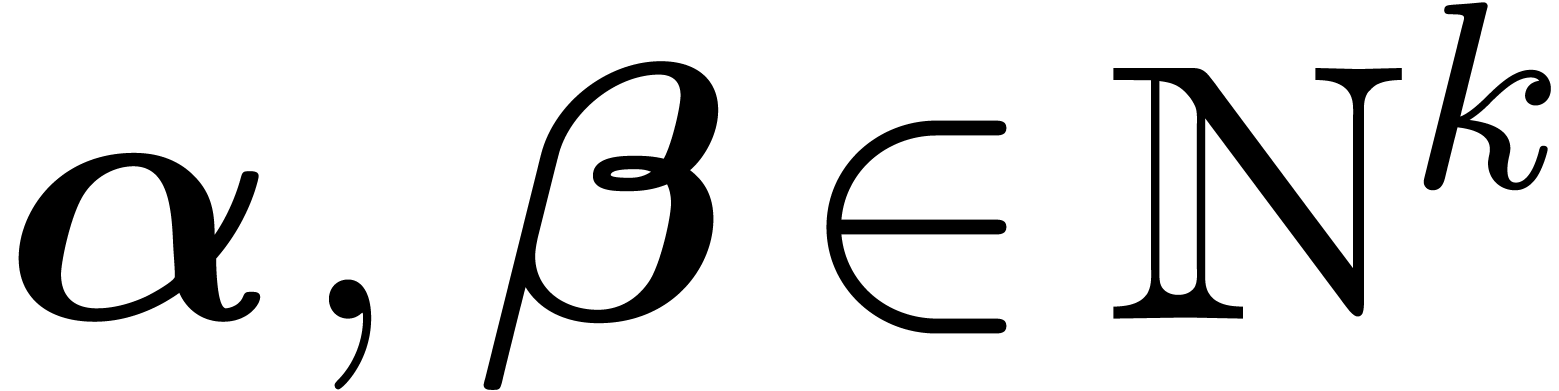 and
and  are such that
are such that
 is a critical relation for
is a critical relation for 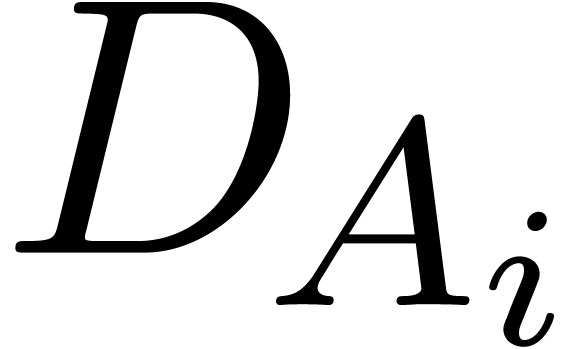 and
and 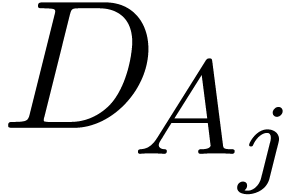 . We call
. We call 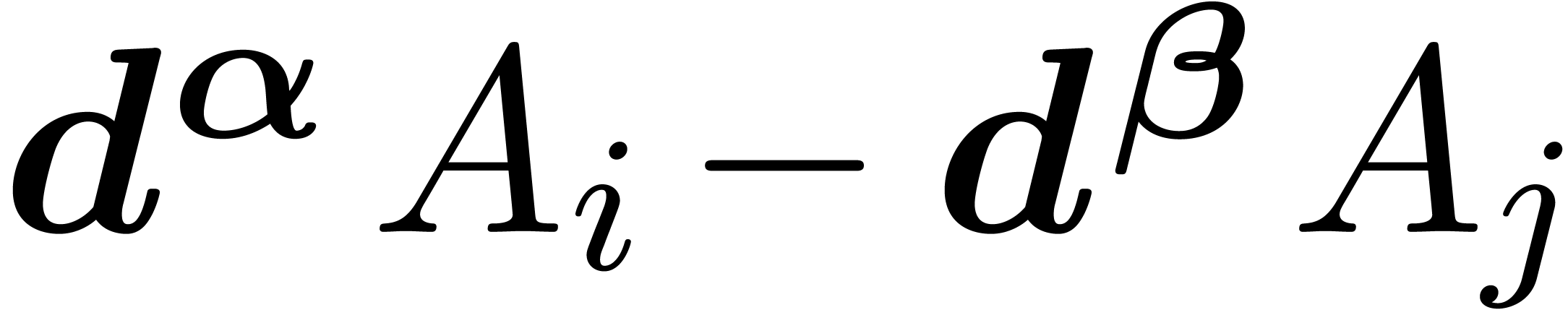 the asymptotic
the asymptotic  -polynomial
of
-polynomial
of 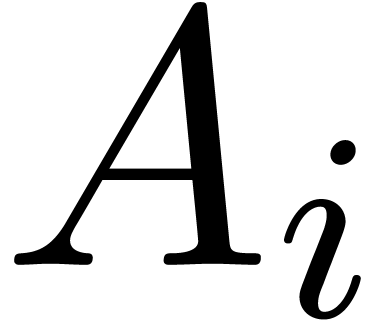 and
and  .
We will denote by
.
We will denote by  the matrix formed by the
the matrix formed by the  row vectors
row vectors 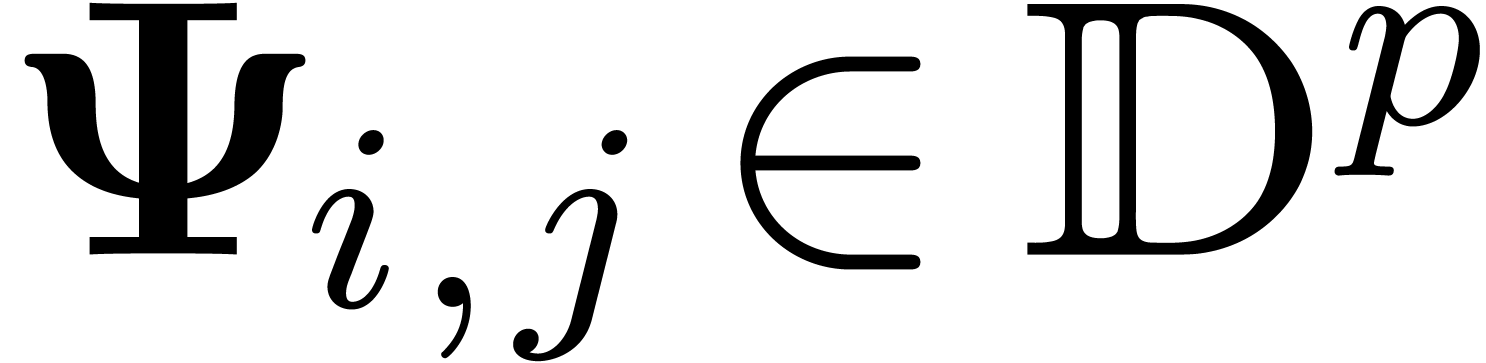 ,
such that
,
such that  is an asymptotic critical relation.
is an asymptotic critical relation.
More generally, we say that 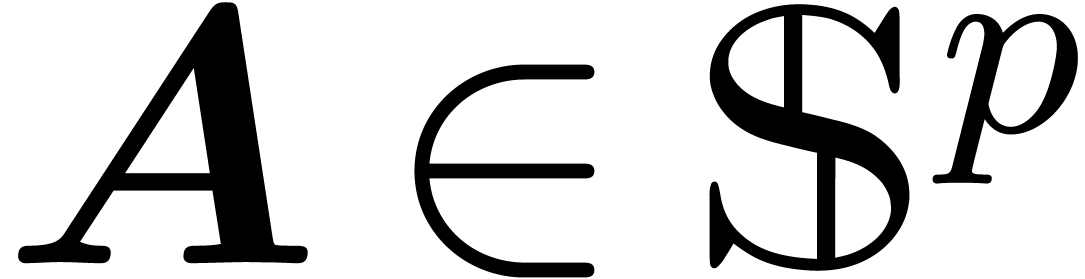 is an asymptotic
basis, if
is an asymptotic
basis, if  is quasi-normal and if its
normalization is an asymptotic basis in the above sense.
is quasi-normal and if its
normalization is an asymptotic basis in the above sense.
Proof. We will construct  by induction over the grid-based set
by induction over the grid-based set
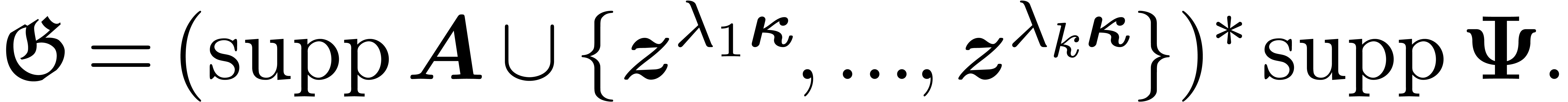
Let 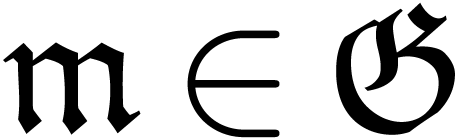 be such that
be such that  has
been computed. As the induction hypothesis, assume that
has
been computed. As the induction hypothesis, assume that  ,
,  and
and

Since  , we have
, we have 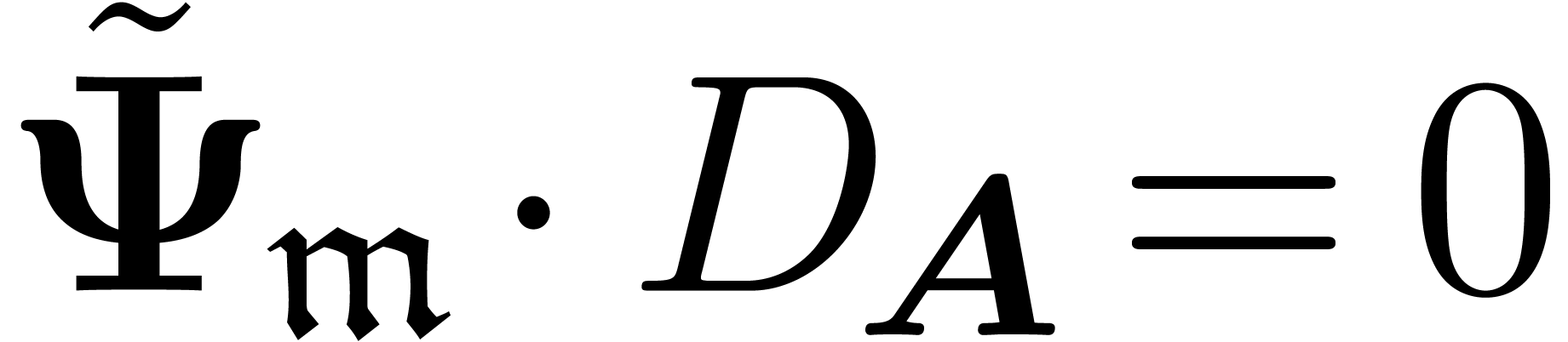 . Hence, the exactness of (5)
implies the existence of a vector
. Hence, the exactness of (5)
implies the existence of a vector  with entries
in
with entries
in 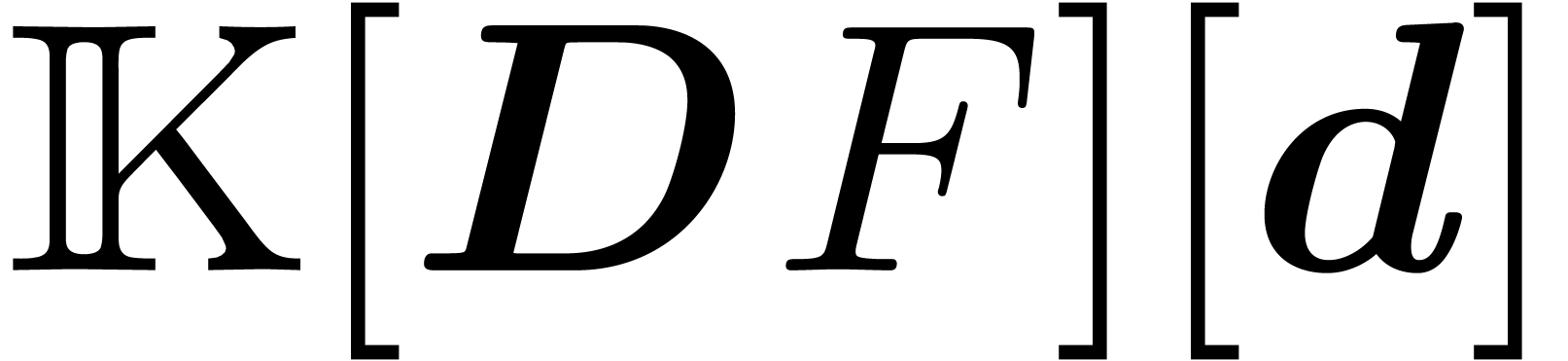 , such that
, such that  . Taking
. Taking  ,
we have
,
we have

and  . By induction over
. By induction over  , we obtain a vector
, we obtain a vector  with
with 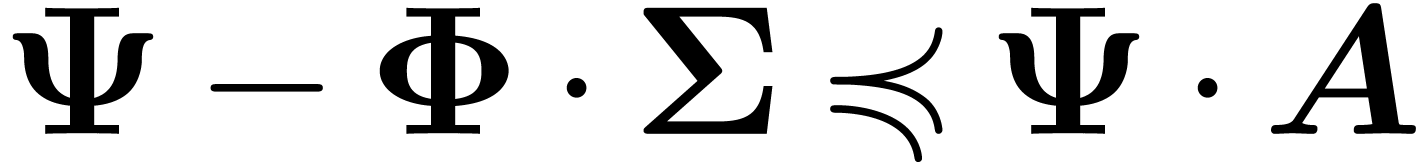 .
.
 -module of
operators
-module of
operators 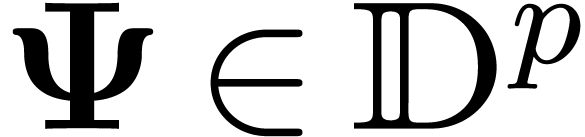 with
with  is
generated by the rows of
is
generated by the rows of  .
.

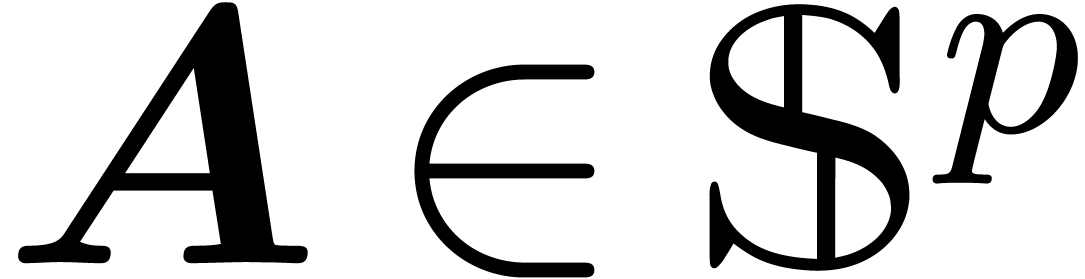 be a normal asymptotic basis. Then
the strong differential ideal generated by
be a normal asymptotic basis. Then
the strong differential ideal generated by  is
given by
is
given by 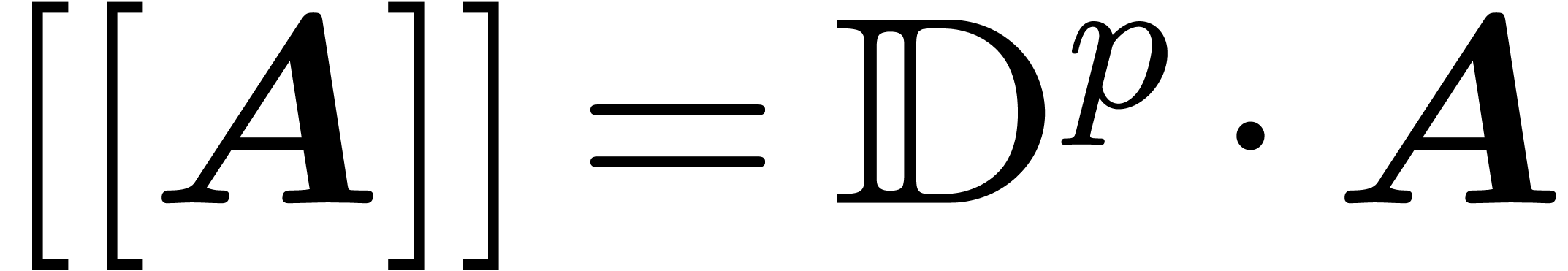 and coincides with the set of
and coincides with the set of 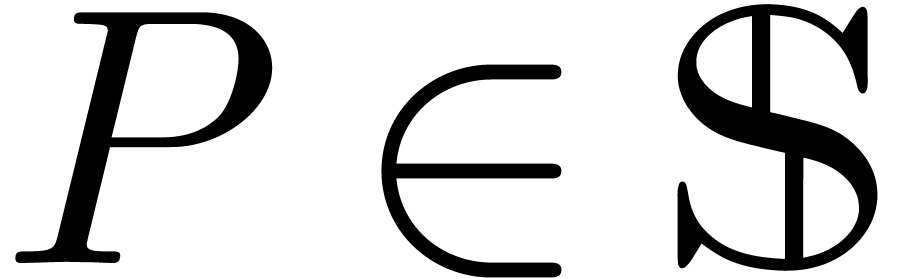 which reduce asymptotically to
which reduce asymptotically to 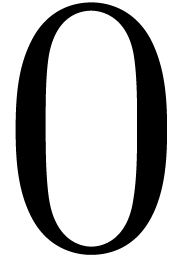 w.r.t.
w.r.t.  .
.
Proof. Given  with
with 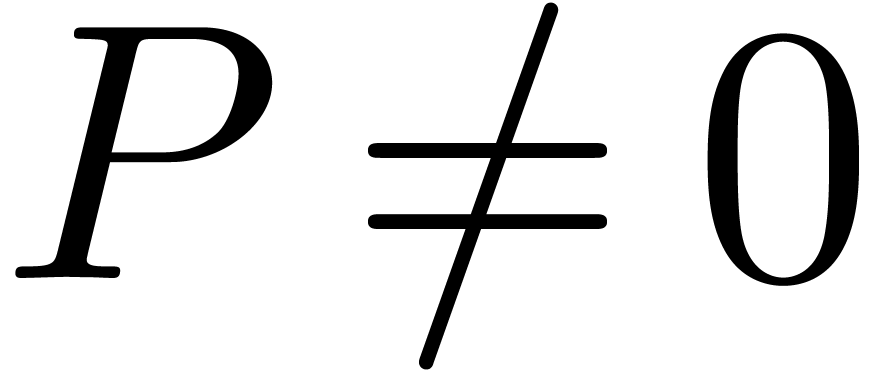 , the lemma implies that there
exists an operator
, the lemma implies that there
exists an operator  with
with  and
and  . In particular,
. In particular,  , so that
, so that  , by proposition 4. Furthermore,
, by proposition 4. Furthermore,  implies that
implies that  is not
asymptotically reduced w.r.t.
is not
asymptotically reduced w.r.t.  .
Now let
.
Now let 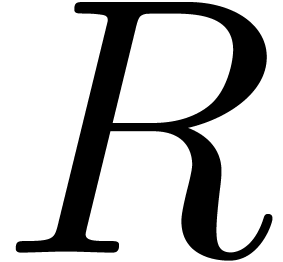 be the remainder of the asymptotic
reduction of
be the remainder of the asymptotic
reduction of 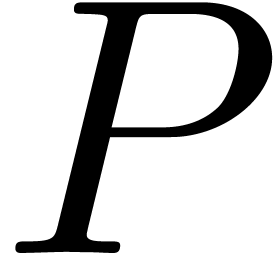 w.r.t.
w.r.t.  . Since
. Since  ,
the above argument shows that
,
the above argument shows that  .
.
A differential ideal 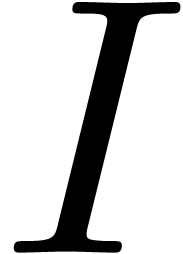 of
of  is said to be quasi-linear if
is said to be quasi-linear if 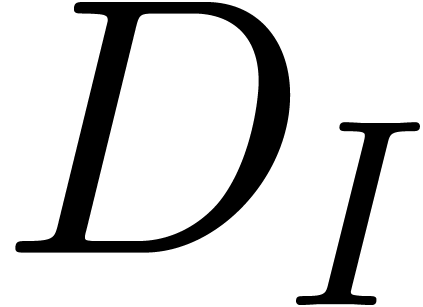 is
linear.
is
linear.
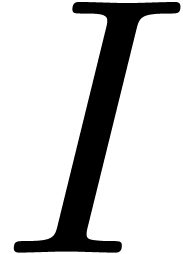 be a strong
differential ideal of
be a strong
differential ideal of  .
Then the following conditions are equivalent:
.
Then the following conditions are equivalent:
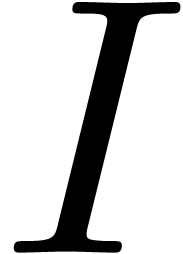 is quasi-linear.
is quasi-linear.
 admits a normal asymptotic basis.
admits a normal asymptotic basis.
Proof. Assume that  is
quasi-linear. By definition, there exists
is
quasi-linear. By definition, there exists 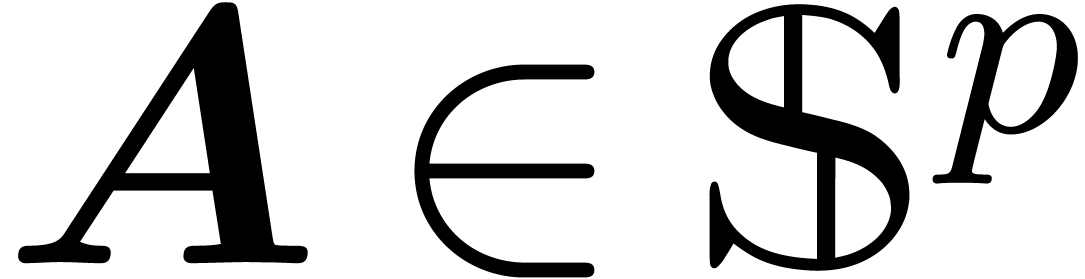 with
with
 ,
,  ,
,  for each
for each  , and such that
, and such that  is a
Rosenfeld basis. Given
is a
Rosenfeld basis. Given  , we
claim that asymptotic Ritt reduction of the asymptotic
, we
claim that asymptotic Ritt reduction of the asymptotic  -polynomial of
-polynomial of 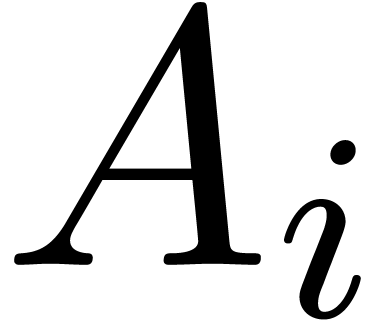 and
and 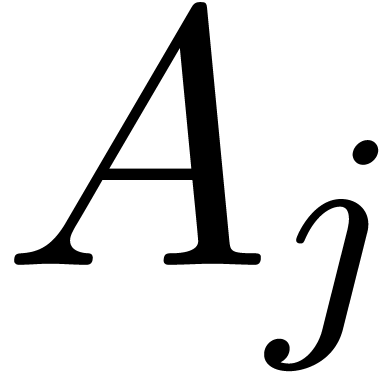 yields an asymptotic critical relation (17).
Indeed, the remainder
yields an asymptotic critical relation (17).
Indeed, the remainder 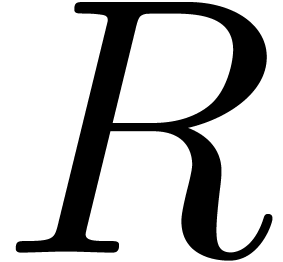 of the asymptotic
reduction must vanish, since
of the asymptotic
reduction must vanish, since 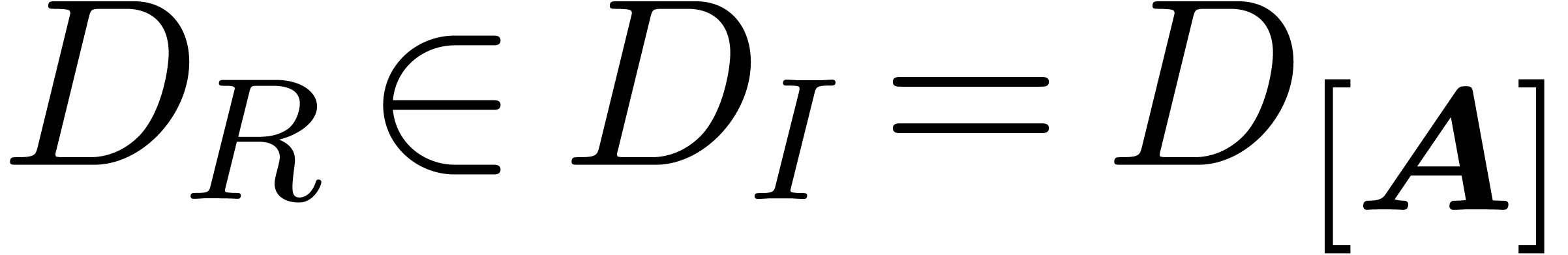 and
and 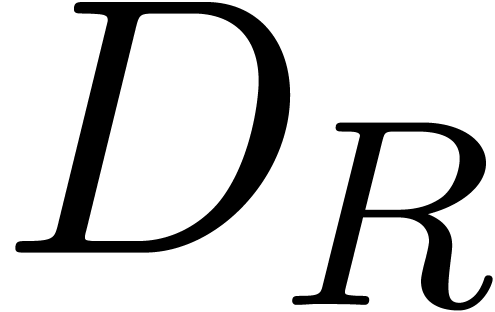 is reduced w.r.t.
is reduced w.r.t.  . We thus get a relation (17).
Furthermore, Ritt reduction of
. We thus get a relation (17).
Furthermore, Ritt reduction of 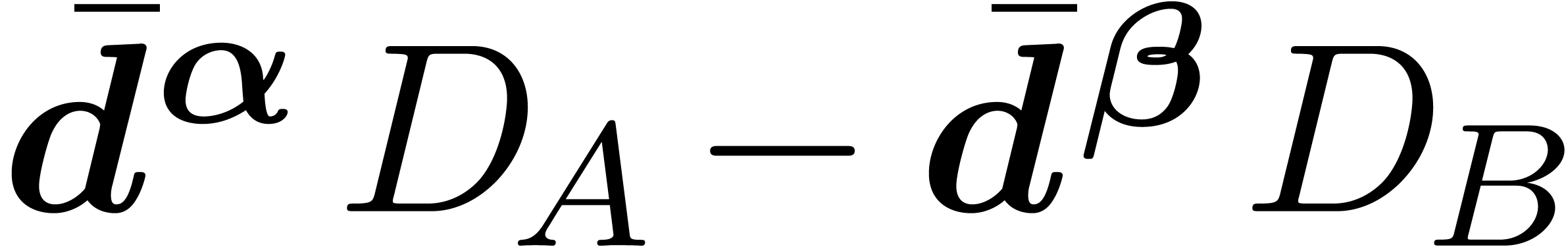 w.r.t.
w.r.t. 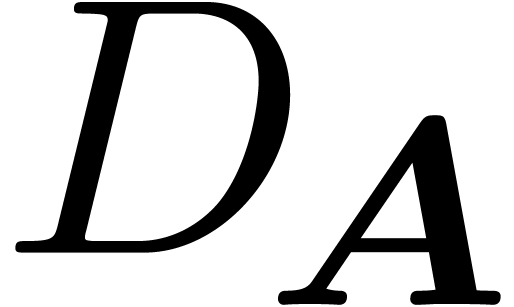 yields
yields 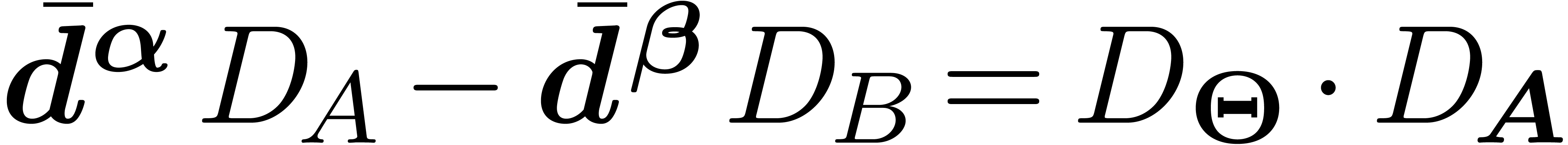 , which is thereby a critical relation for
, which is thereby a critical relation for 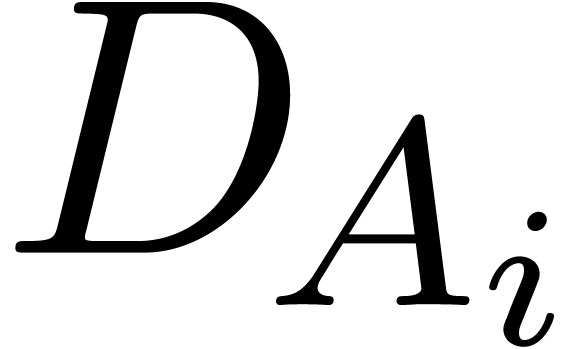 and
and 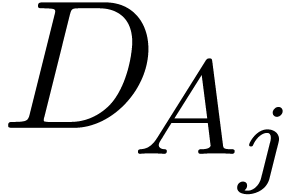 .
.
Inversely, assume that 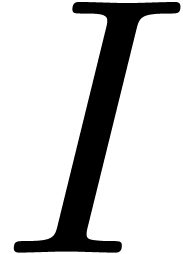 admits a normal
asymptotic basis
admits a normal
asymptotic basis  . Given
. Given
 , corollary 9
implies that
, corollary 9
implies that 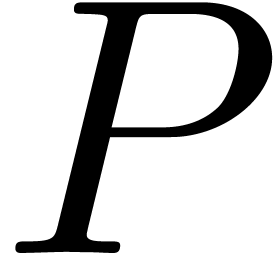 reduces to
reduces to 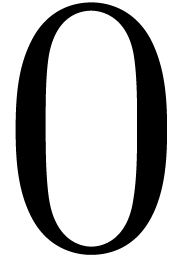 modulo
modulo  . In particular,
. In particular, 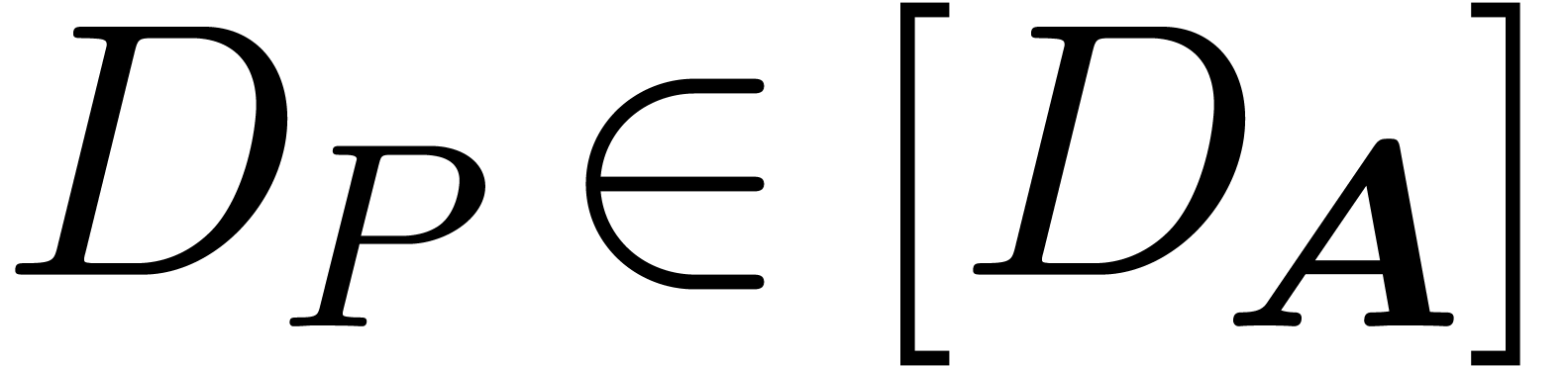 and
and 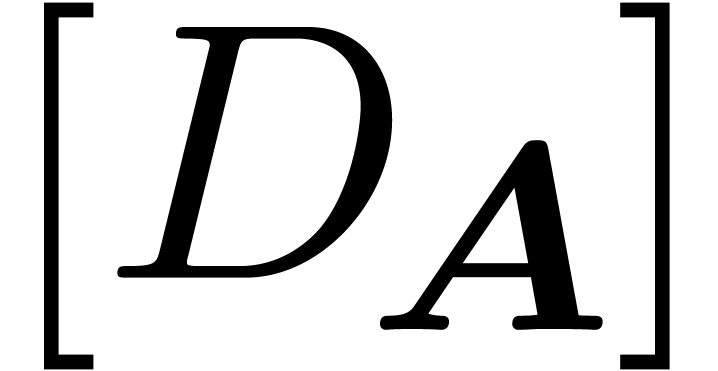 is a linear differential
ideal.
is a linear differential
ideal.
It is rather straightforward to dualize the theory from the previous section. Let us briefly state the dual versions of the main results, while omitting proofs.
Let 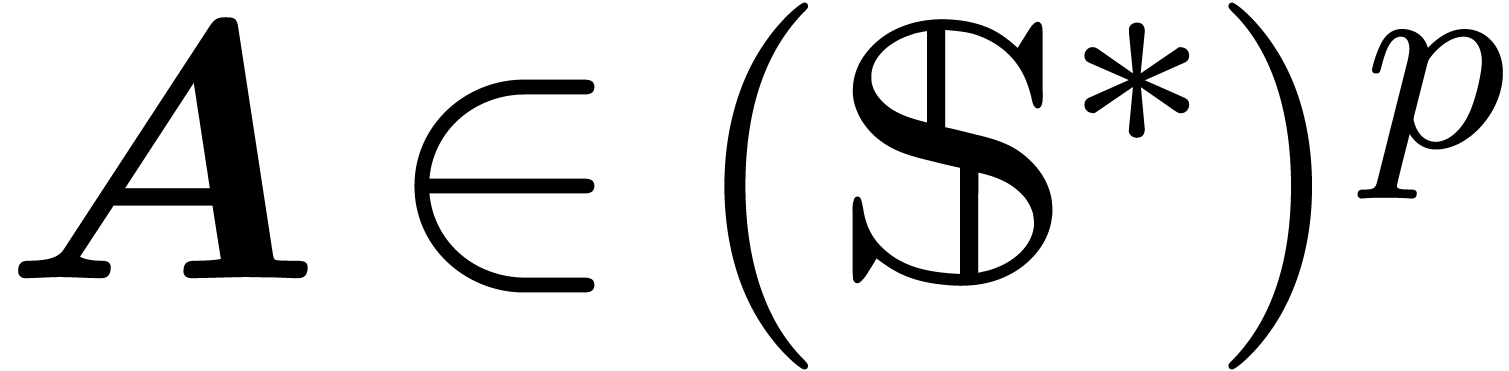 be co-normal in the sense of section 4.4. In particular,
be co-normal in the sense of section 4.4. In particular,  is linear for each
is linear for each
 . We say that
. We say that  is an asymptotic co-basis, if
is an asymptotic co-basis, if  is a Rosenfeld co-basis and if for each pair
is a Rosenfeld co-basis and if for each pair  , we have an asymptotic co-critical
relation
, we have an asymptotic co-critical
relation
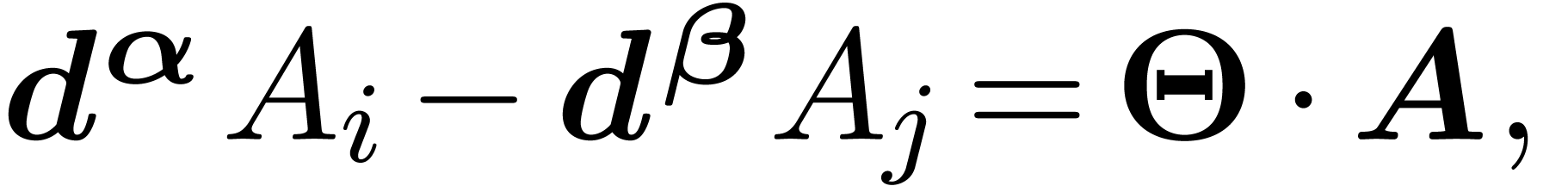 |
(18) |
where 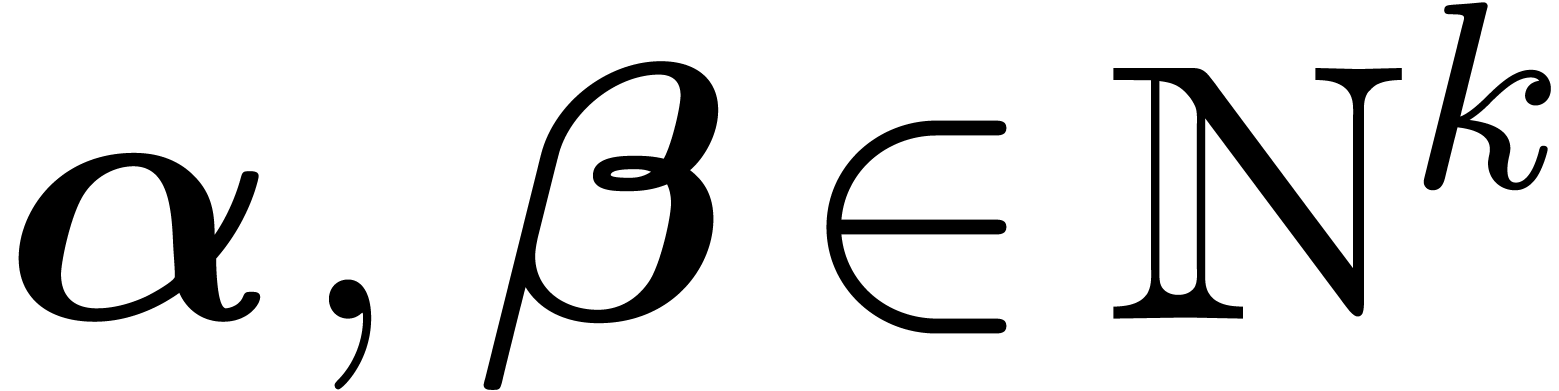 and
and 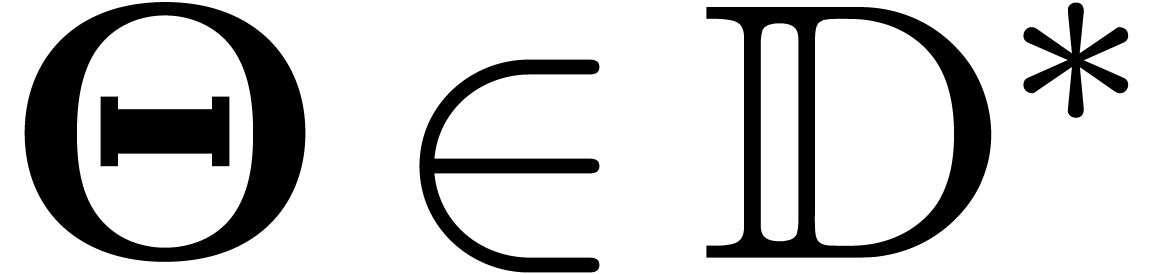 are such that
are such that
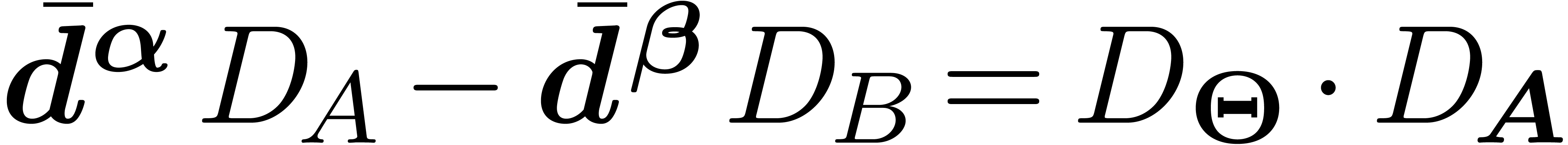 is a co-critical relation for
is a co-critical relation for  and
and 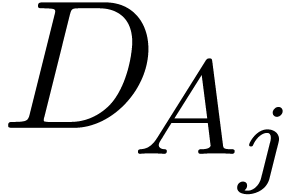 . We will denote by
. We will denote by  the matrix formed by the
the matrix formed by the  row
vectors
row
vectors 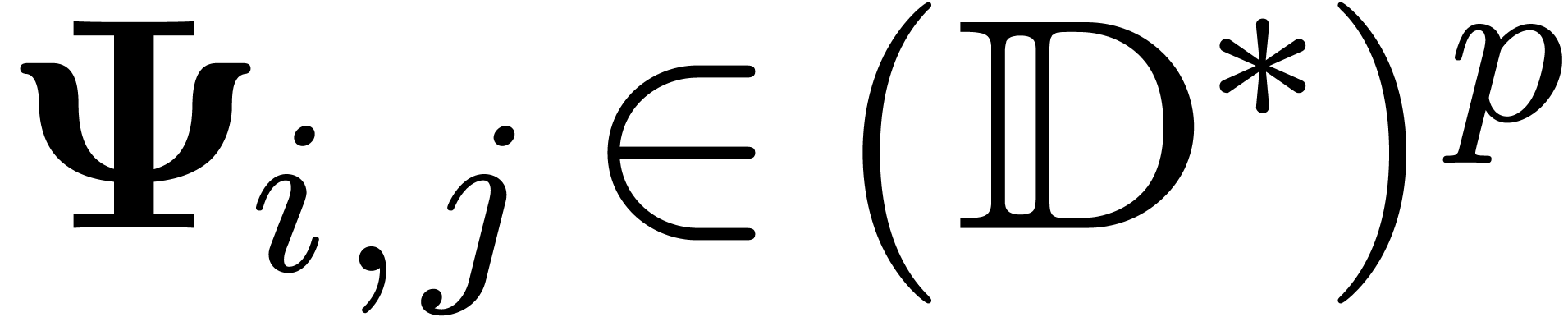 , such that
, such that 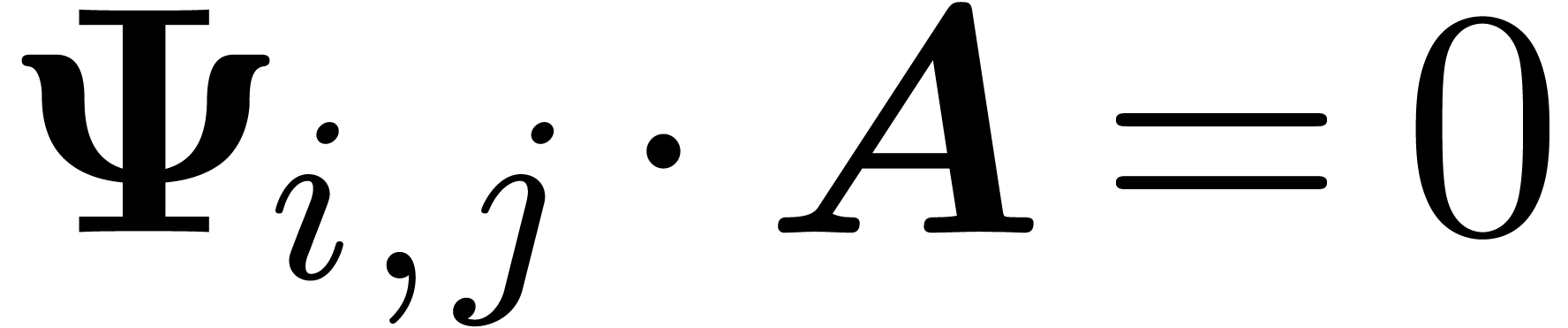 is an asymptotic critical relation. A differential ideal
is an asymptotic critical relation. A differential ideal
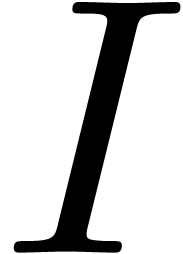 of
of  is said to be
quasi-linear if
is said to be
quasi-linear if  is linear.
is linear.
 be a co-normal asymptotic co-basis. The
strong
be a co-normal asymptotic co-basis. The
strong 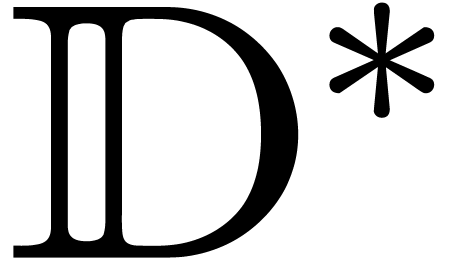 -module of
operators
-module of
operators  with
with  is
generated by the rows of
is
generated by the rows of  .
.

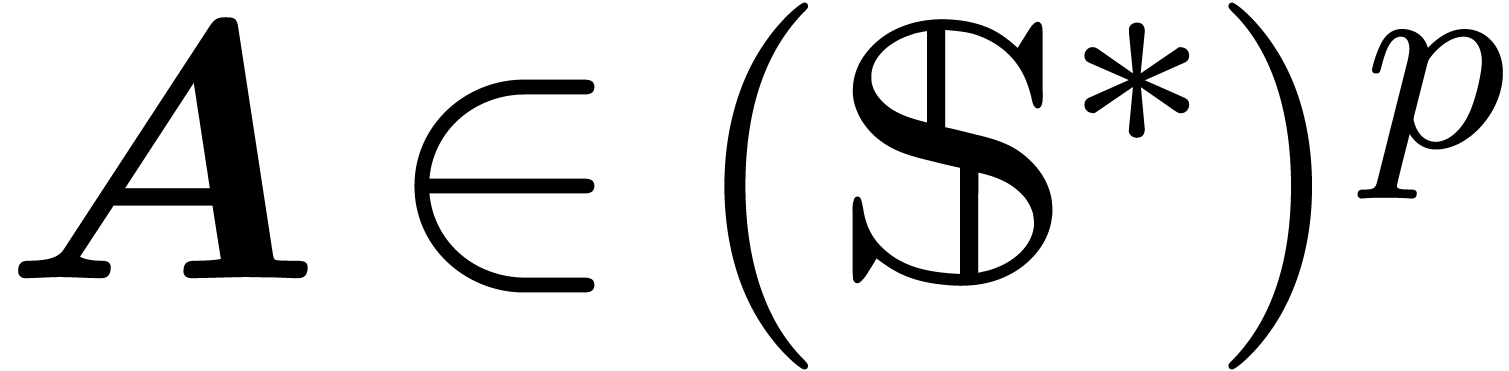 be a co-normal
asymptotic co-basis. Then
be a co-normal
asymptotic co-basis. Then 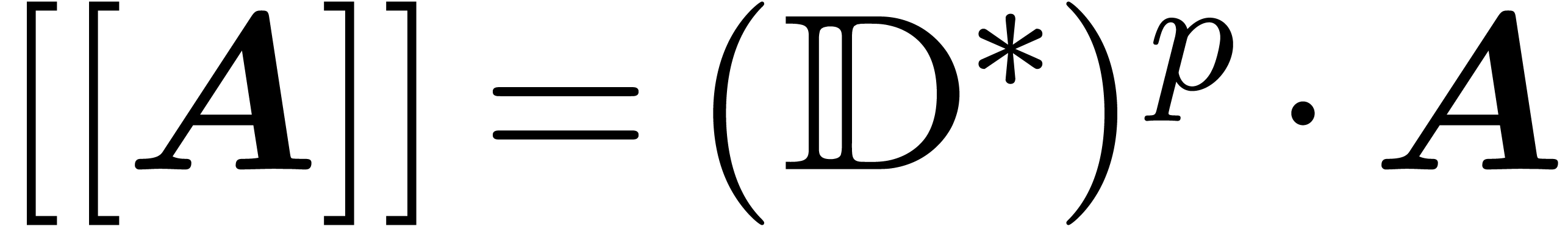 coincides with the
set of
coincides with the
set of  which co-reduce asymptotically to
which co-reduce asymptotically to  w.r.t.
w.r.t.  .
.
 be a strong
differential ideal of
be a strong
differential ideal of  .
Then the following conditions are equivalent:
.
Then the following conditions are equivalent:
 is quasi-linear.
is quasi-linear.
 admits a co-normal asymptotic co-basis.
admits a co-normal asymptotic co-basis.

In this section, we consider an asymptotic basis  in the special case when
in the special case when  and
and  is a field of constants for
is a field of constants for  .
We will show the existence of solutions to the equation
.
We will show the existence of solutions to the equation  in the ring
in the ring 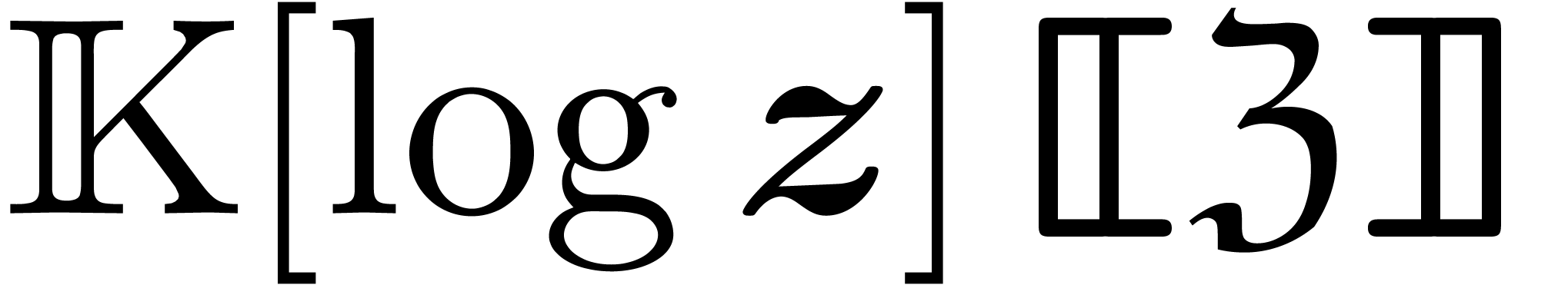 , where
, where 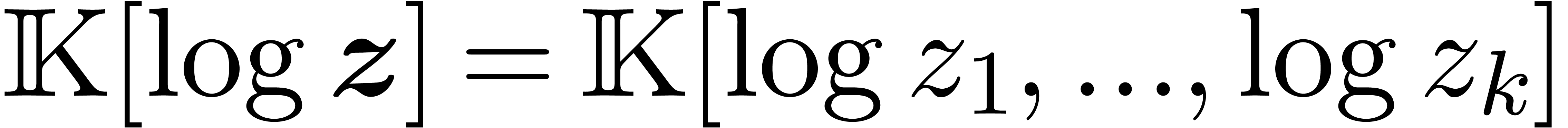 .
.
Proof. Applying the tangent cone algorithm to
 , we obtain a matrix
, we obtain a matrix  with coefficients in
with coefficients in 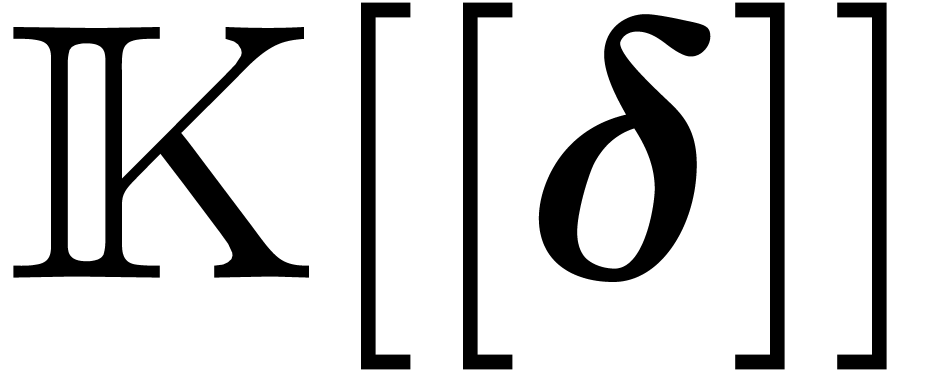 such
that
such
that 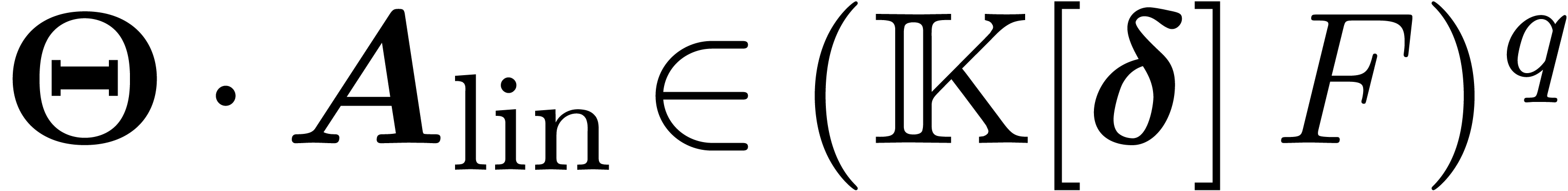 is a Rosenfeld co-basis. We claim that
is a Rosenfeld co-basis. We claim that  is compatible with
is compatible with  in the
sense of [vdH07, Section 3.2], i.e. that
in the
sense of [vdH07, Section 3.2], i.e. that  for any
for any 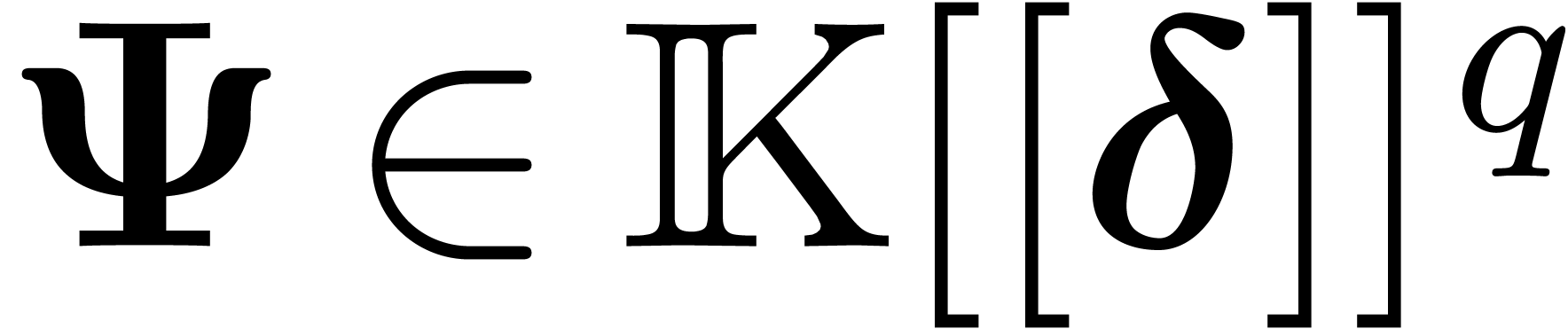 with
with  . Indeed, let
. Indeed, let  be the
matrix of critical relations for the Rosenfeld basis
be the
matrix of critical relations for the Rosenfeld basis  . Since
. Since 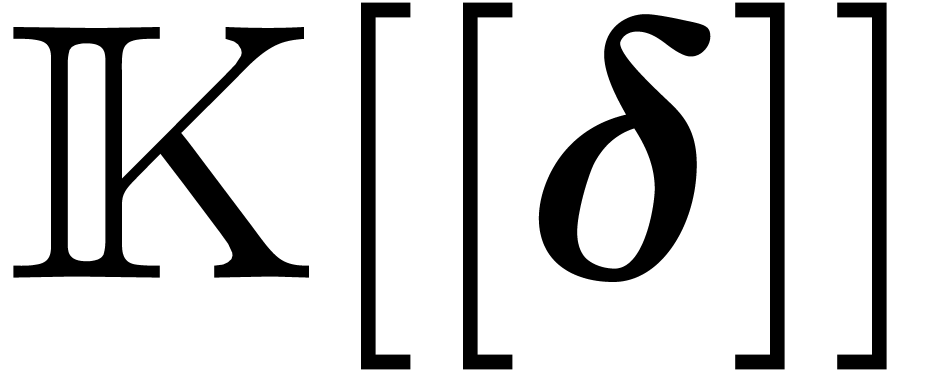 is a flat ring
over
is a flat ring
over 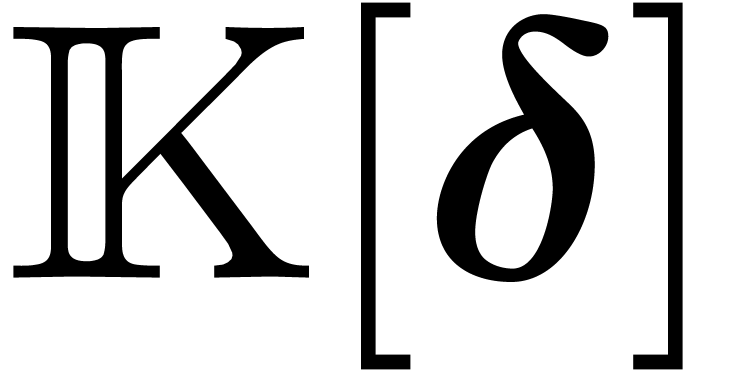 , the exact sequence
, the exact sequence
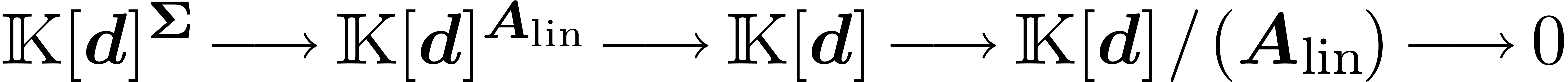
transforms into an exact sequence
In other words, given 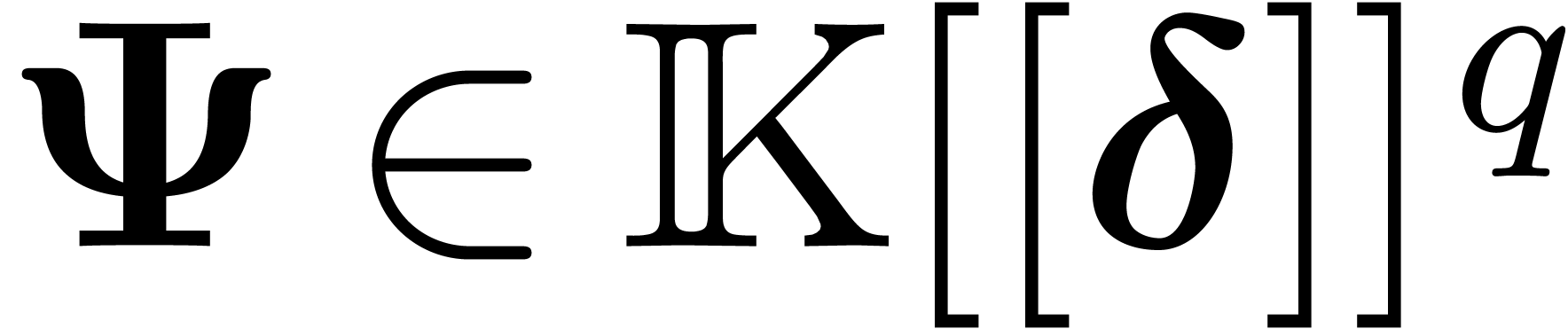 with
with  , there exists a
, there exists a 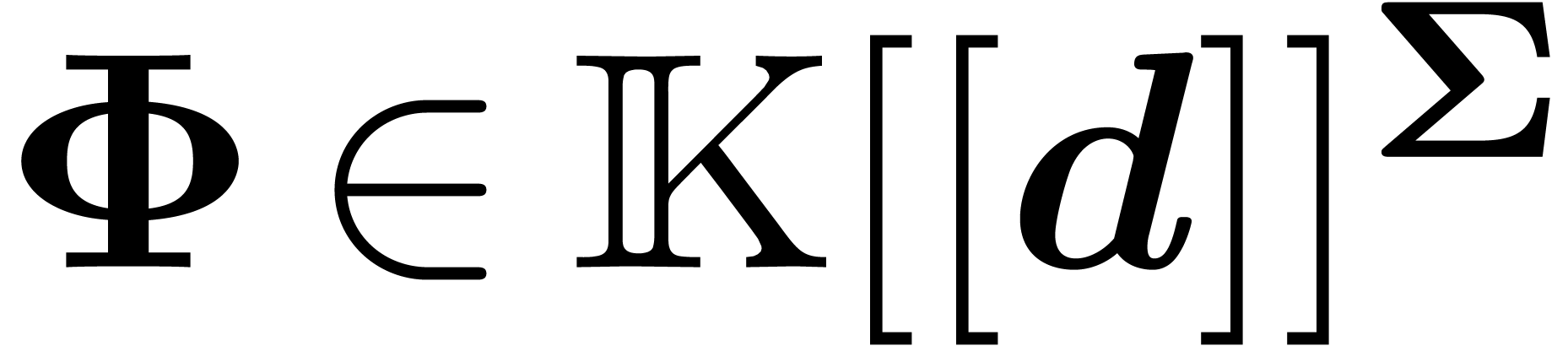 with
with
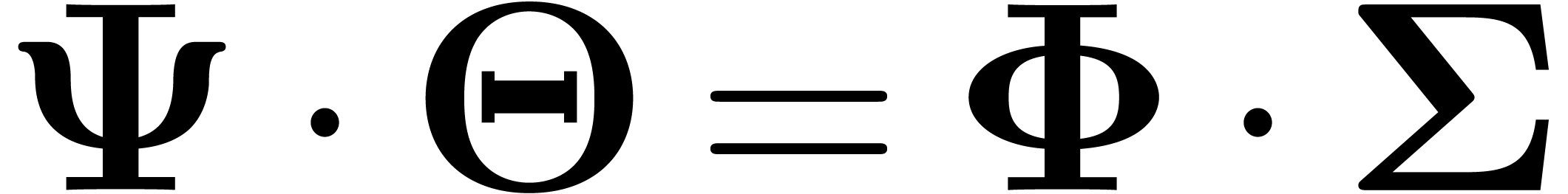 . It follows that
. It follows that
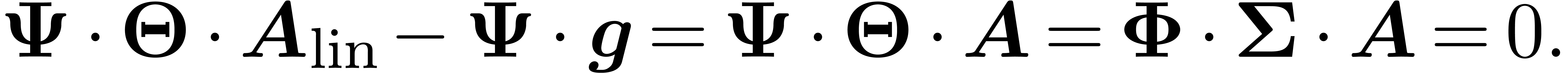
In [vdH07, Section 4.2], we have shown how to compute a
solution in 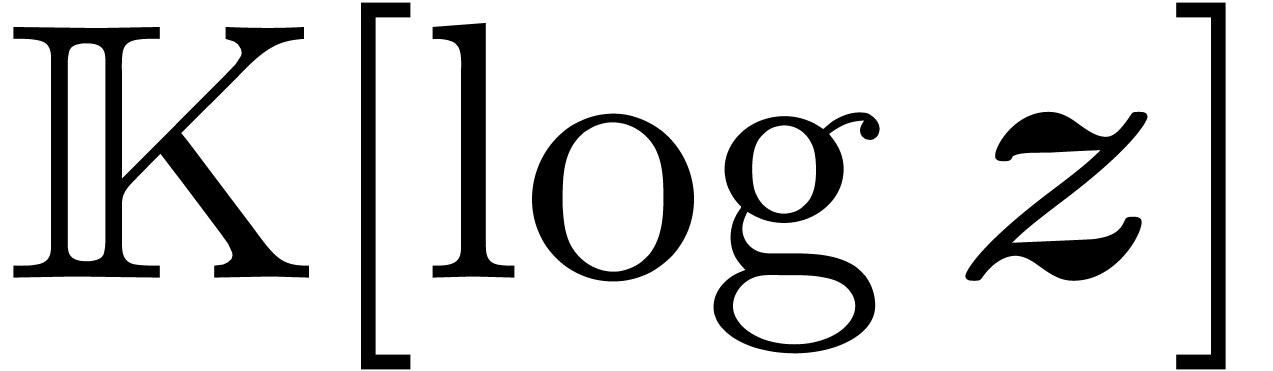 to
to
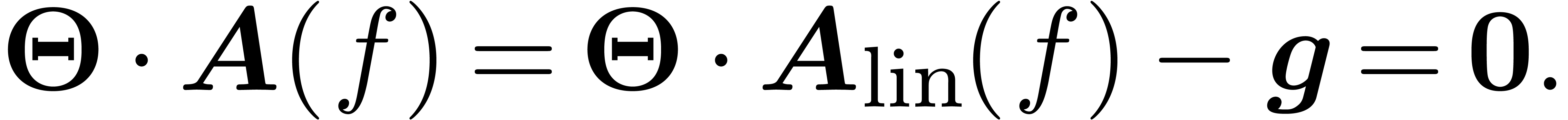
Now  is in the strong ideal generated by
is in the strong ideal generated by 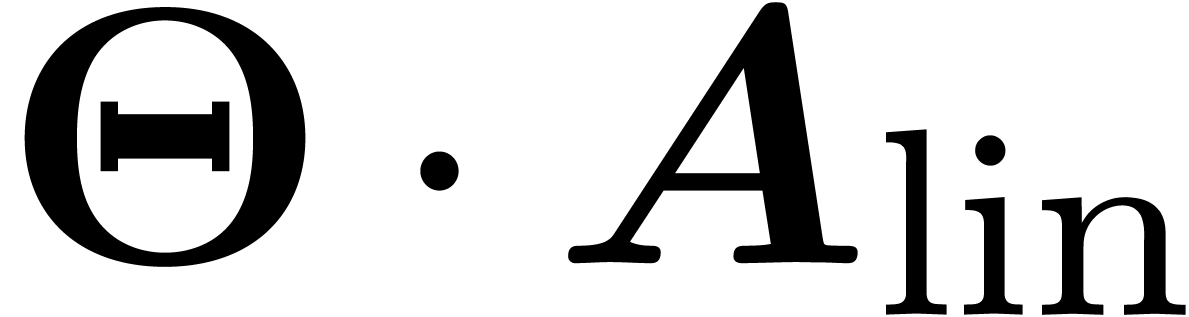 , so there exists a matrix
, so there exists a matrix  with coefficients in
with coefficients in 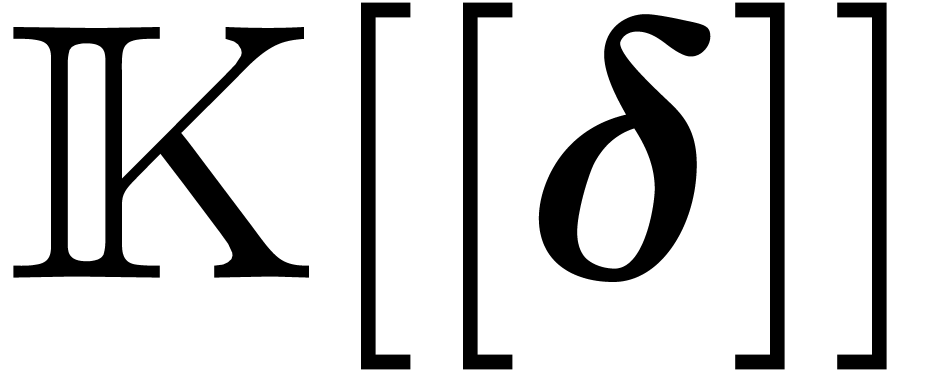 with
with
 . Consequently, there exists
a matrix
. Consequently, there exists
a matrix  with entries in
with entries in 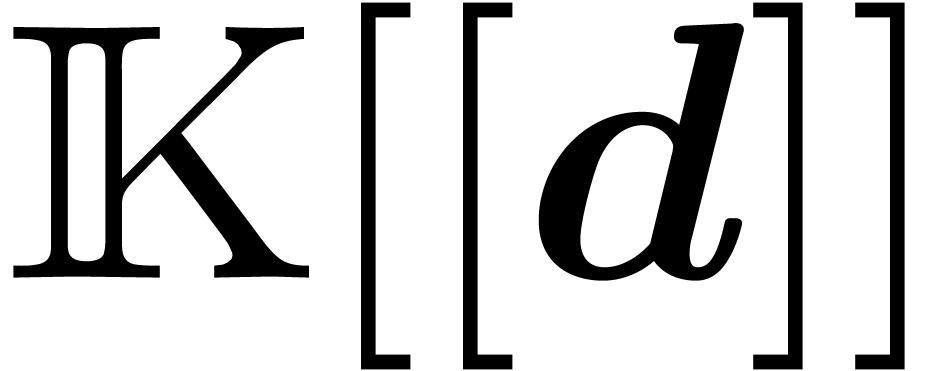 and
and  . We conclude that
. We conclude that 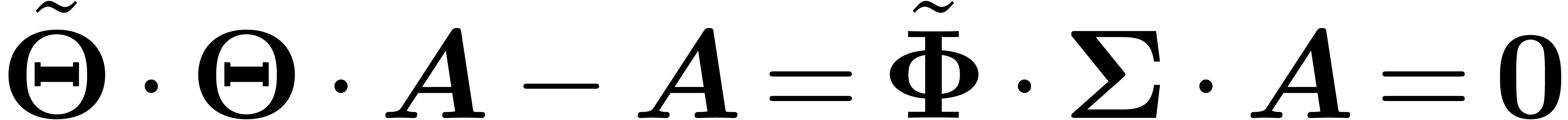 and
and 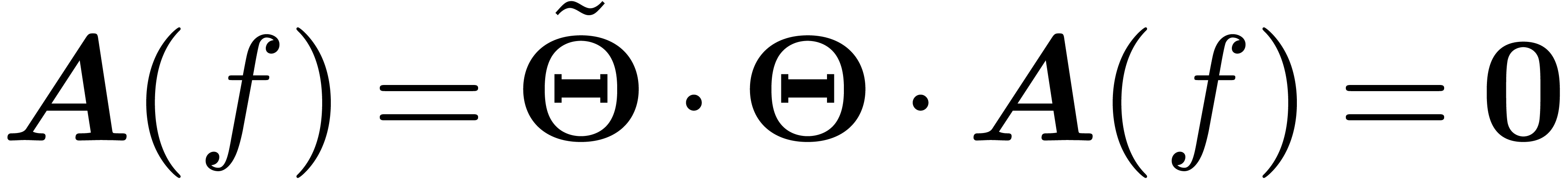 .
.
Proof. We may assume that  is normal. We compute the coefficients
is normal. We compute the coefficients  of a
solution
of a
solution  with
with 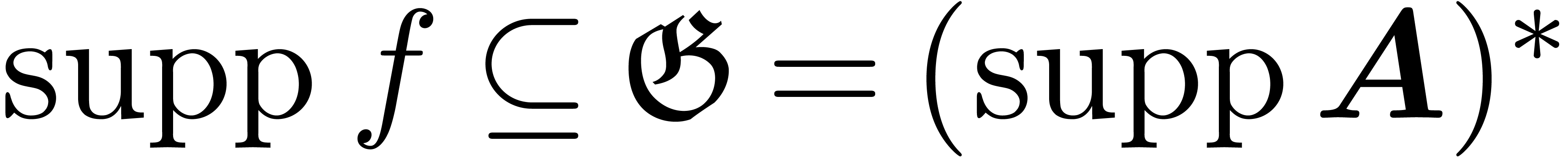 by
induction over
by
induction over 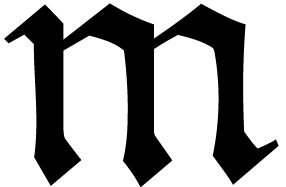 . We have
. We have
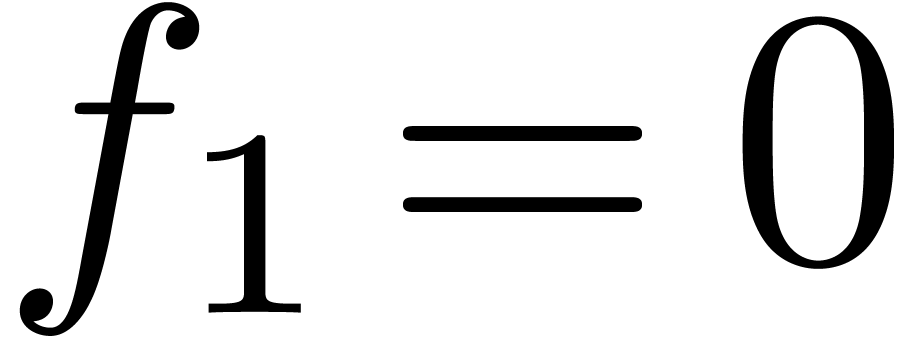 . Given
. Given 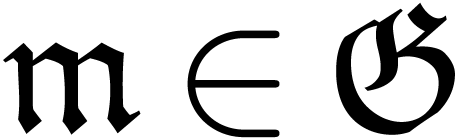 , assume that
, assume that  has been
computed for all
has been
computed for all  , in such a
way that
, in such a
way that  for
for  .
We have
.
We have
and each asymptotic critical relation
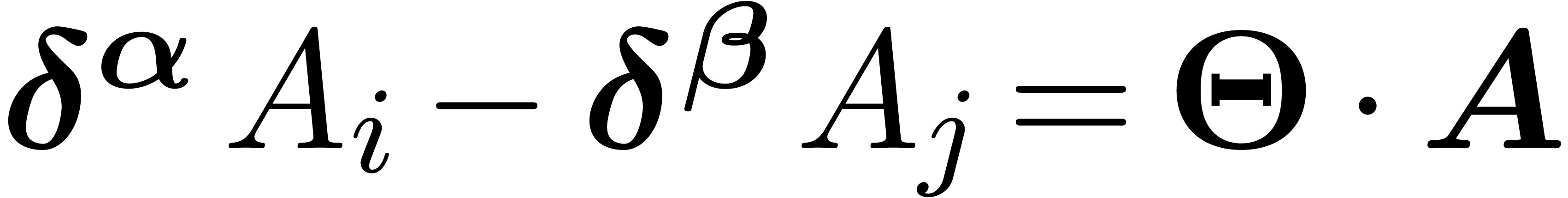
gives rise to a relation
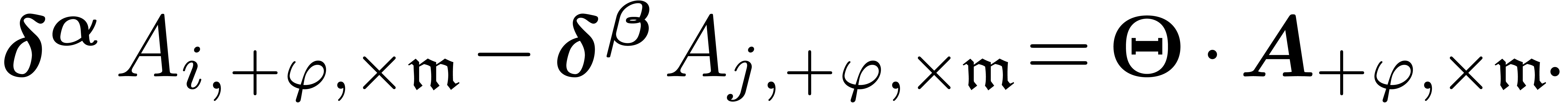
Extracting dominant parts, it follows that 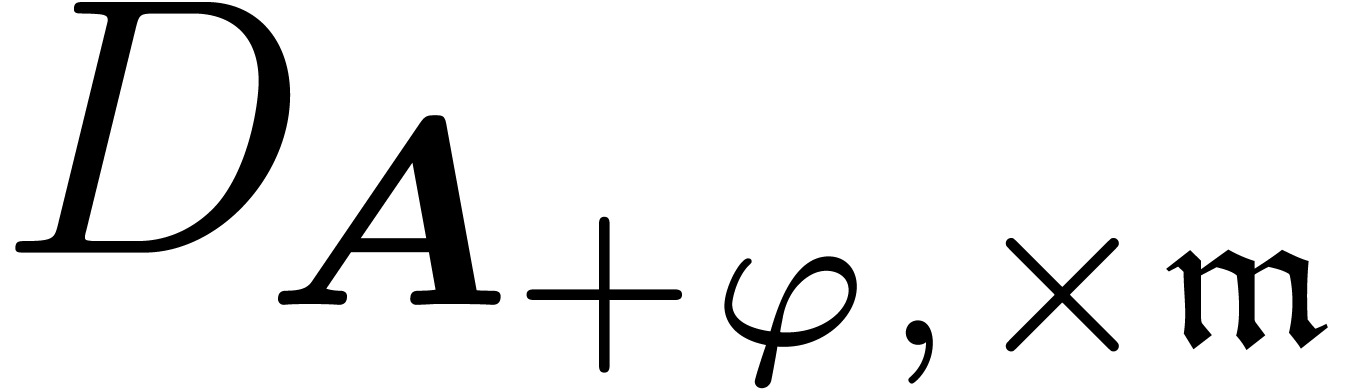 is a
Rosenfeld basis. Moreover,
is a
Rosenfeld basis. Moreover,  ,
whence
,
whence 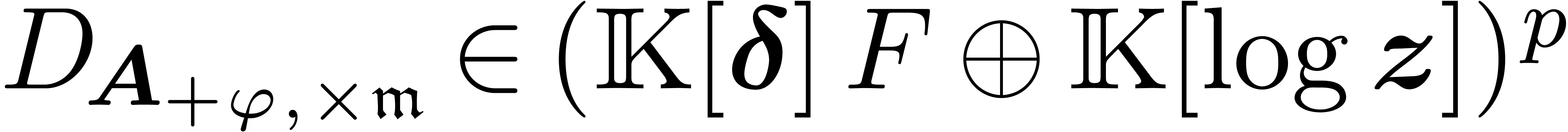 . By lemma 14,
it follows that
. By lemma 14,
it follows that 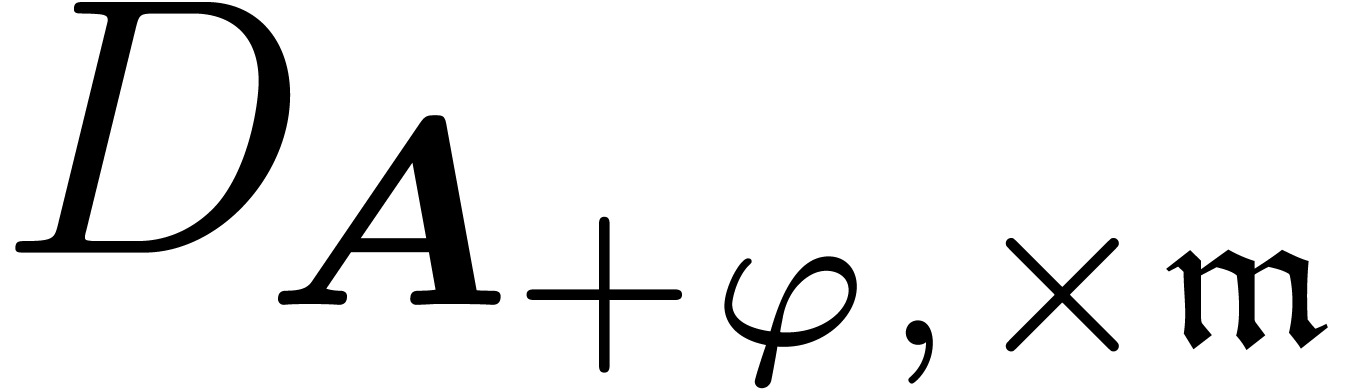 admits a solution
admits a solution 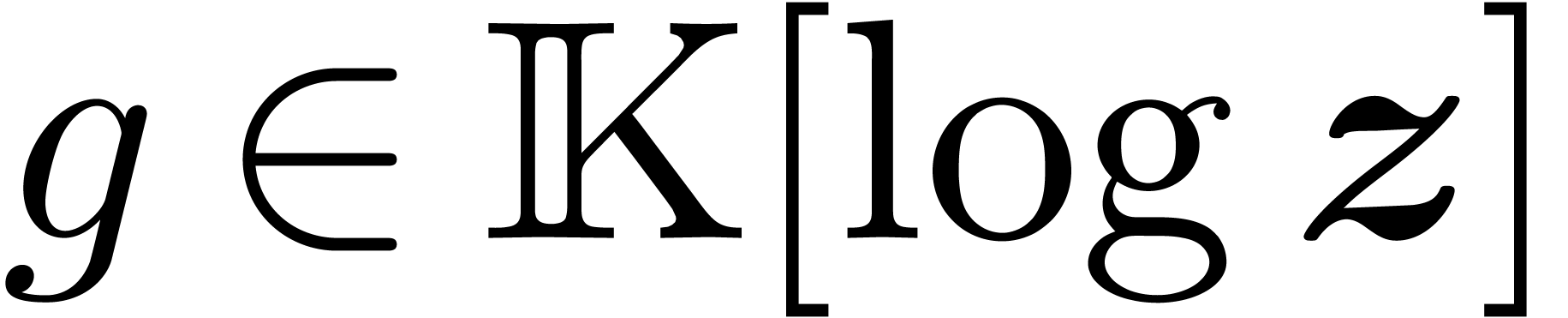 . Taking
. Taking 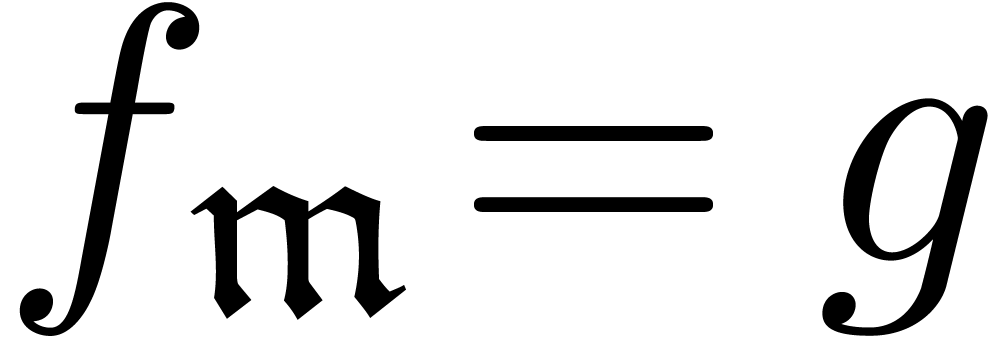 and
and 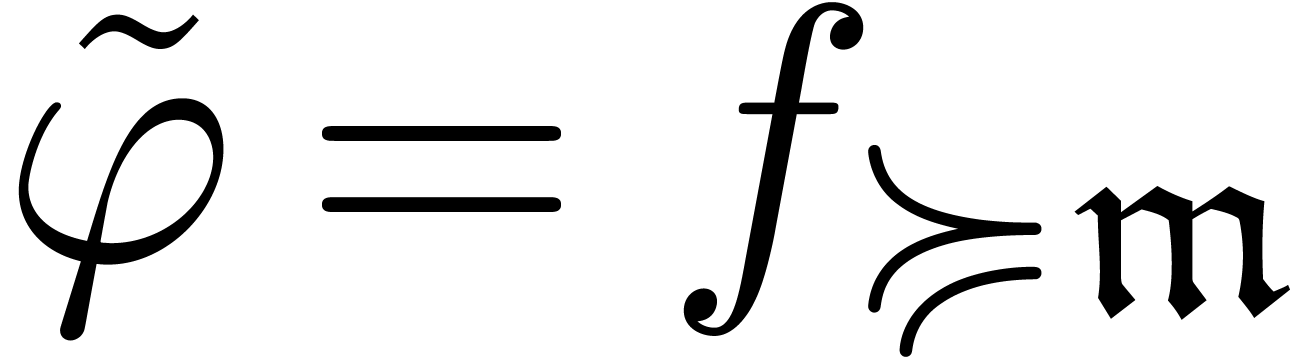 , we have
, we have  and
and 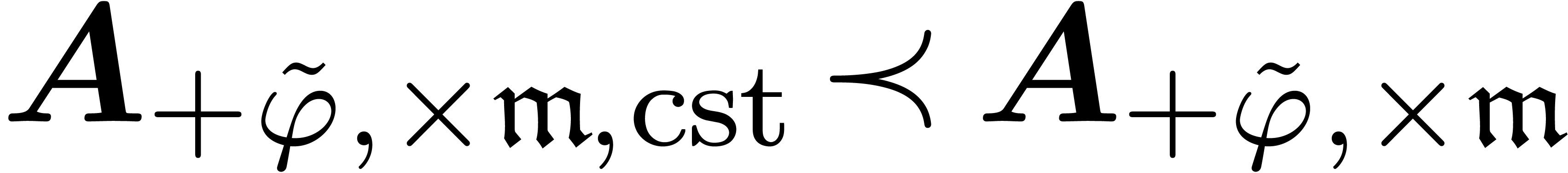 , so the induction
hypothesis is verified for the next monomial in
, so the induction
hypothesis is verified for the next monomial in  .
.
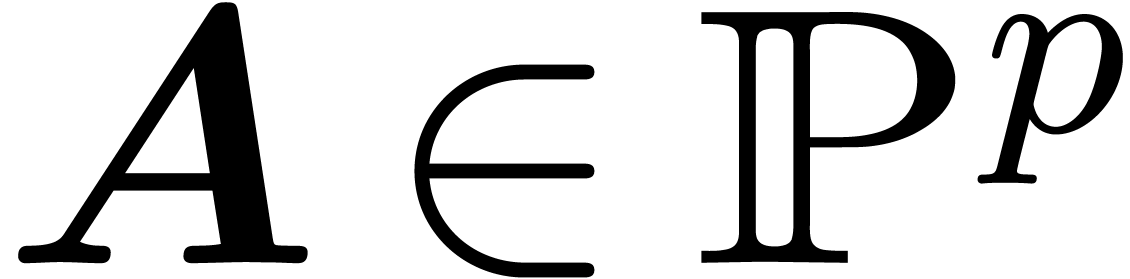 be a Rosenfeld basis w.r.t.
be a Rosenfeld basis w.r.t.  and let
and let  be the leader of
be the leader of
 for each
for each  .
Assume that
.
Assume that  and
and 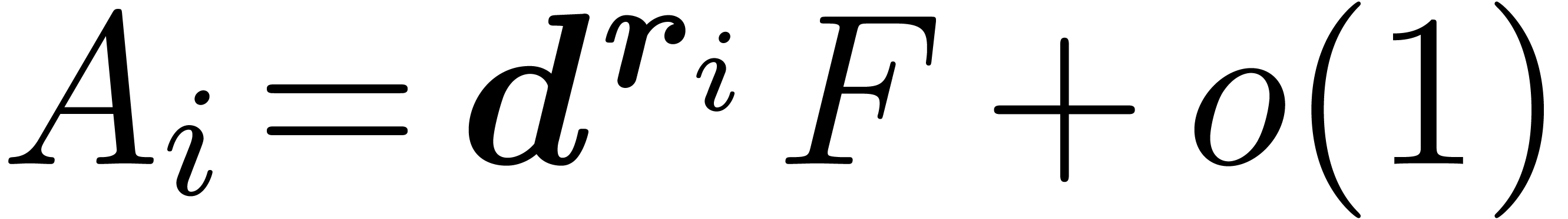 for
all
for
all  . Consider the critical
relation
. Consider the critical
relation
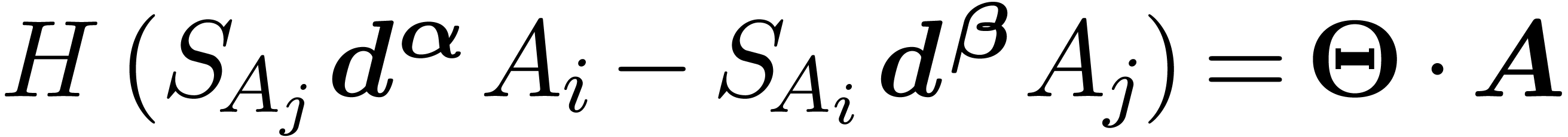 |
(19) |
obtained by Ritt reduction of 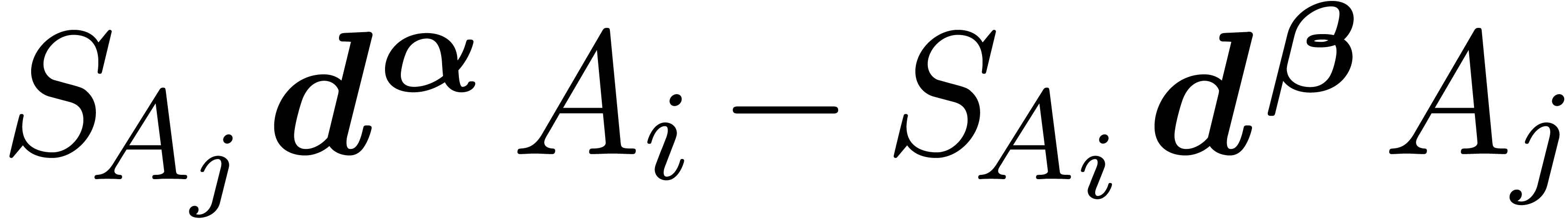 modulo
modulo  . Then
. Then  . Moreover, if
. Moreover, if 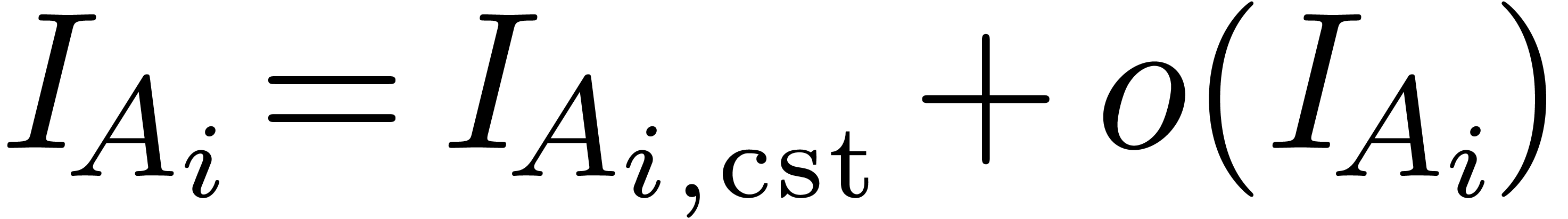 for each
for each
 , then
, then  is an asymptotic basis.
is an asymptotic basis.
Proof. Let 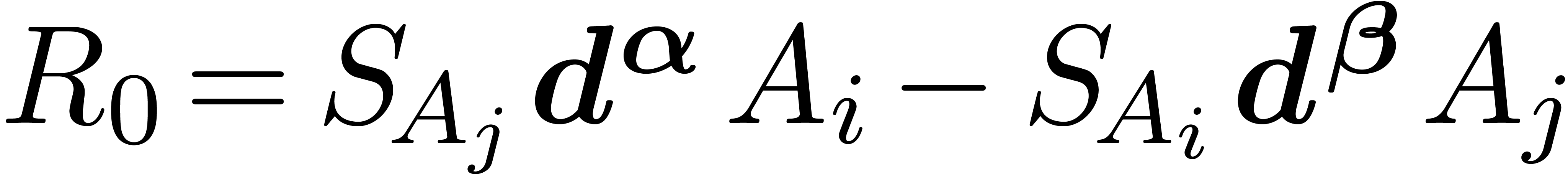 .
The process of Ritt reduction yields a sequence of relations
.
The process of Ritt reduction yields a sequence of relations
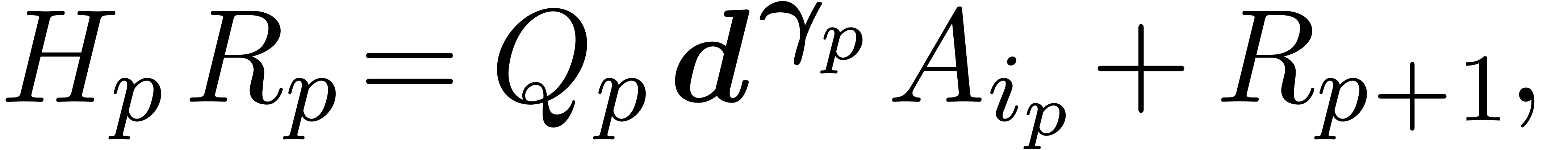 |
(20) |
obtained by pseudo-division of 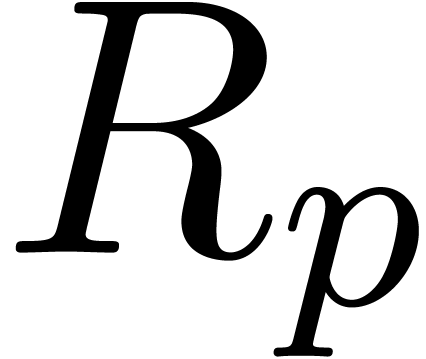 by
by 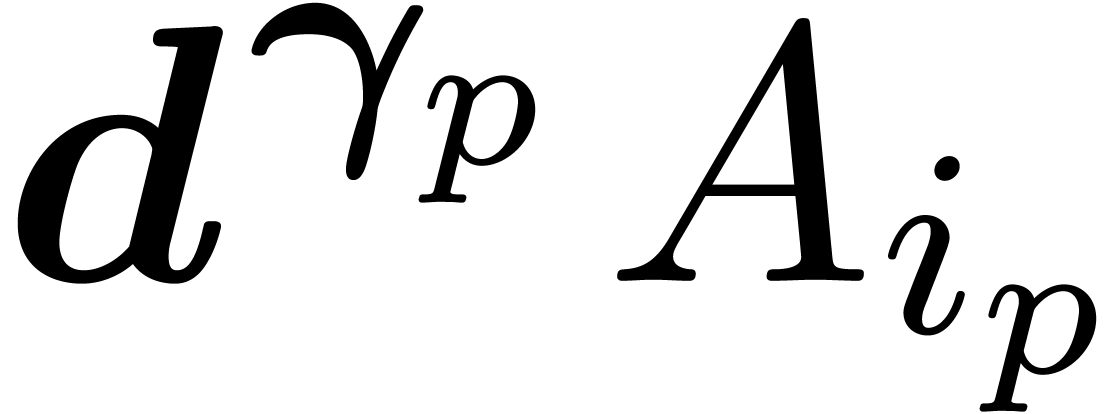 , considered as polynomials in the common
leader
, considered as polynomials in the common
leader 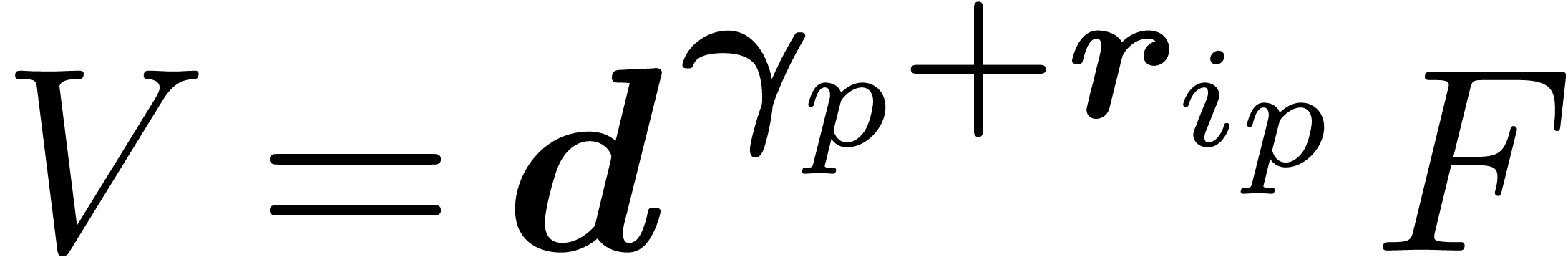 of
of  and
and  . In particular,
. In particular,  is free from
is free from  . At the end of
the reduction process, we have
. At the end of
the reduction process, we have 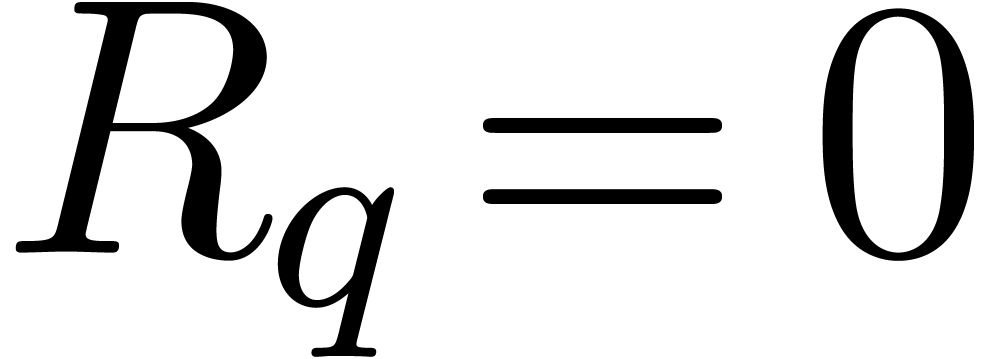 for some
for some  .
.
Let us proof by induction over  that
that  and thus
and thus  . From
. From
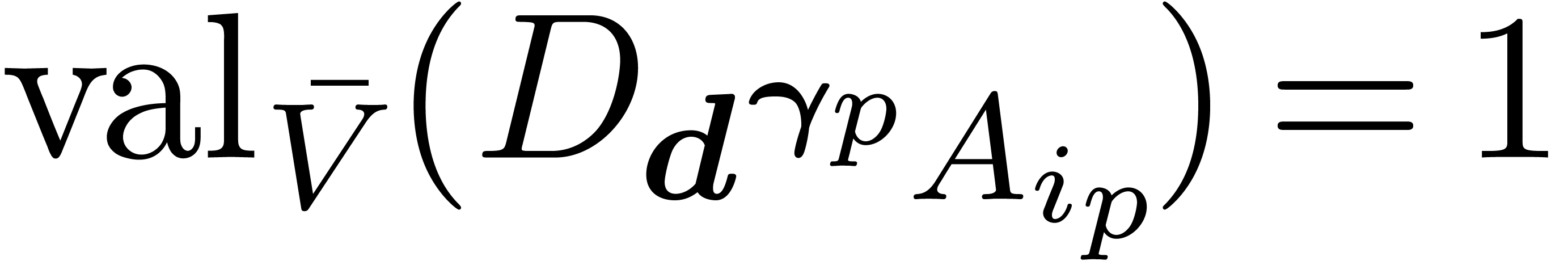 , we deduce
, we deduce 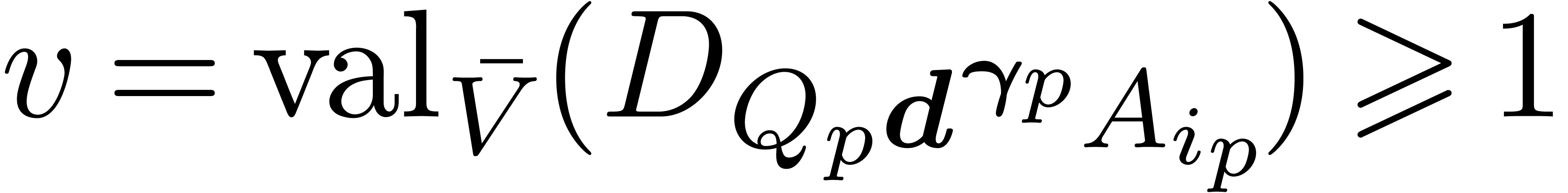 . Let
. Let  be the
coefficient of
be the
coefficient of  in
in  .
Then
.
Then  is also the coefficient of
is also the coefficient of  in
in  , since
, since  is free from
is free from  . In particular,
. In particular,
 . Telescoping the relations
(20) for
. Telescoping the relations
(20) for  , we
get
, we
get  .
.
The hypothesis  implies in particular that
implies in particular that 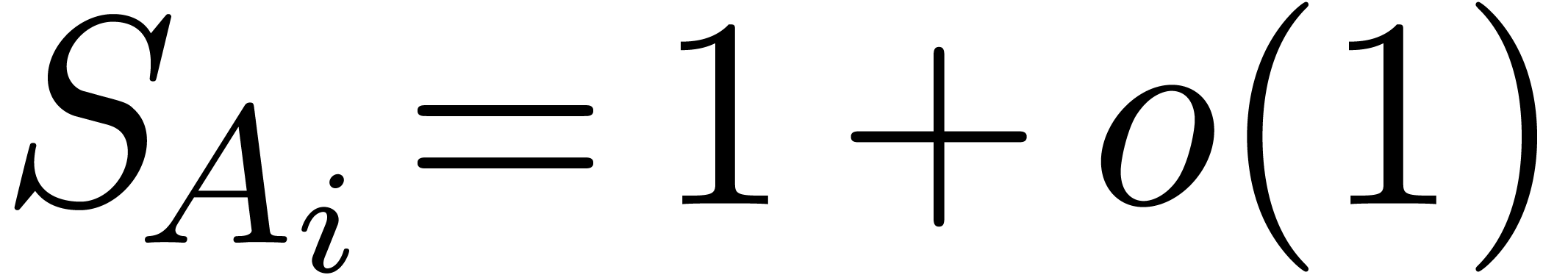 . If we also have
. If we also have 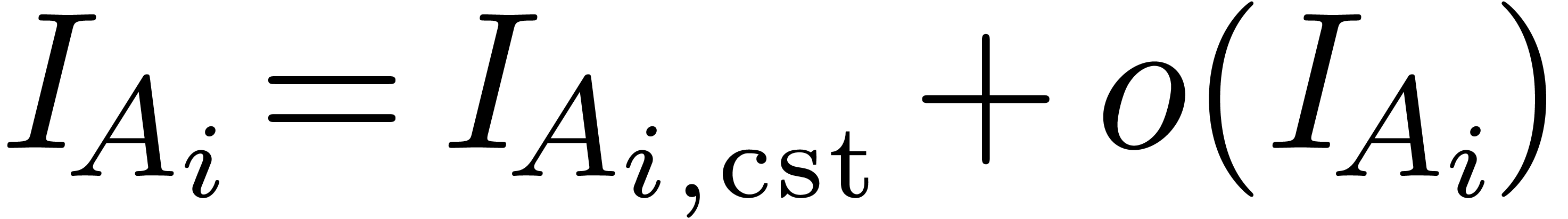 for each
for each 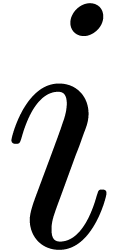 , then
, then  , whence (19) can be divided by
, whence (19) can be divided by
 and rewritten into an asymptotic critical
relation.
and rewritten into an asymptotic critical
relation.
 be a Rosenfeld basis
w.r.t.
be a Rosenfeld basis
w.r.t.  and assume that
and assume that  satisfies
satisfies 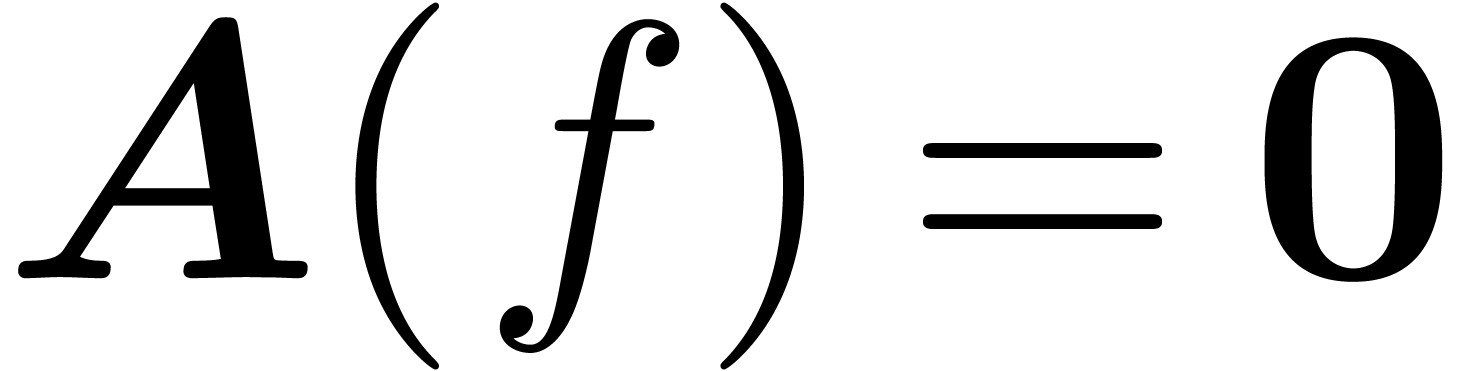 ,
but
,
but 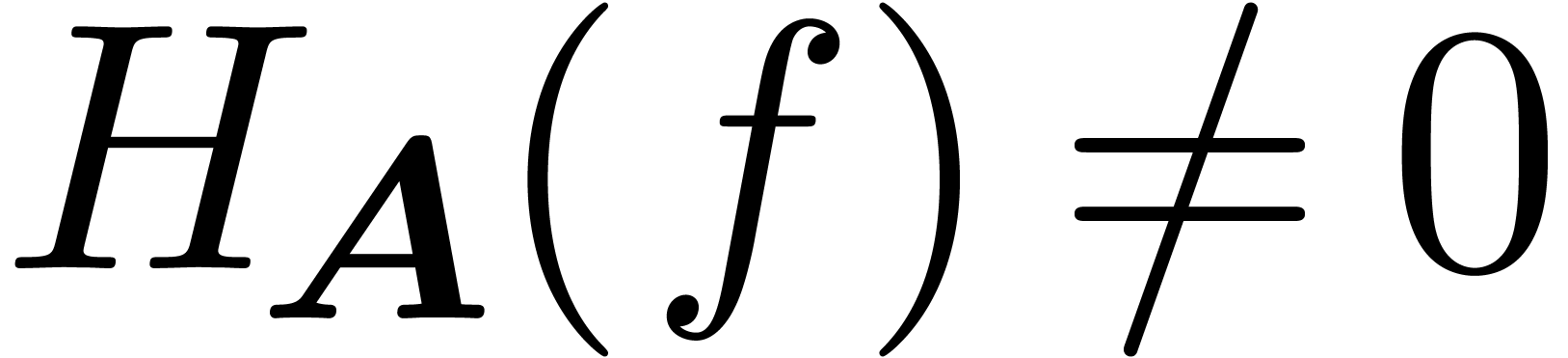 . Then there exist
. Then there exist 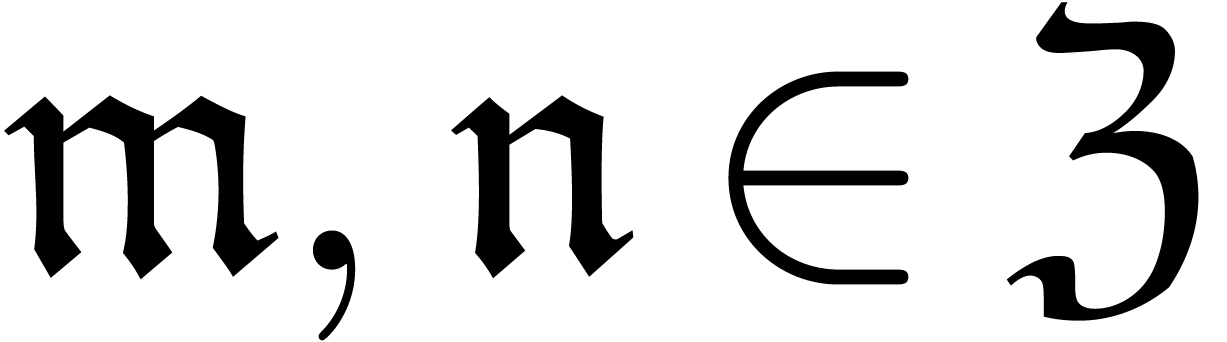 and
and  ,
such that
,
such that 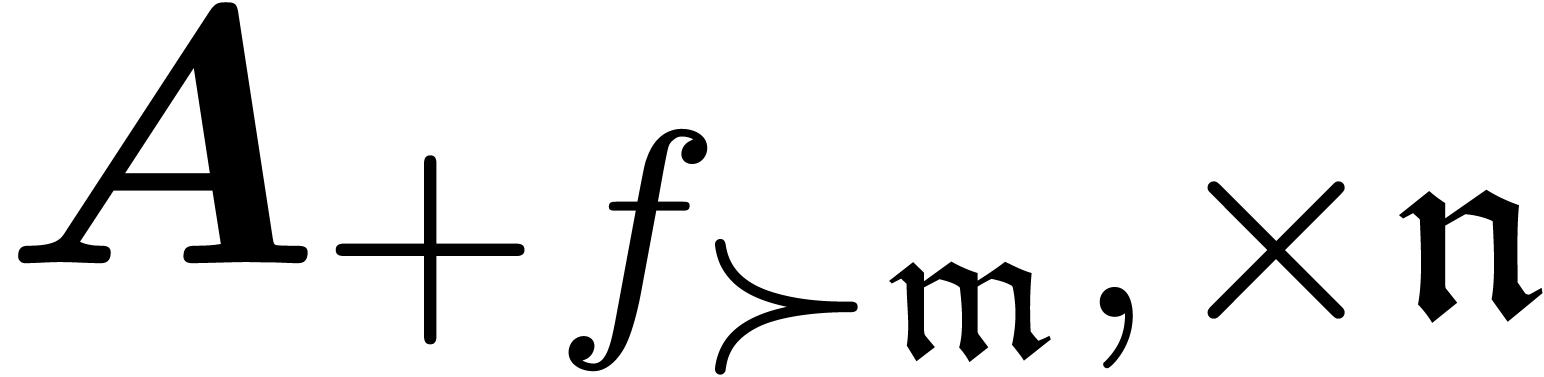 is an asymptotic basis
w.r.t.
is an asymptotic basis
w.r.t.  .
.
Proof. Consider the Rosenfeld basis 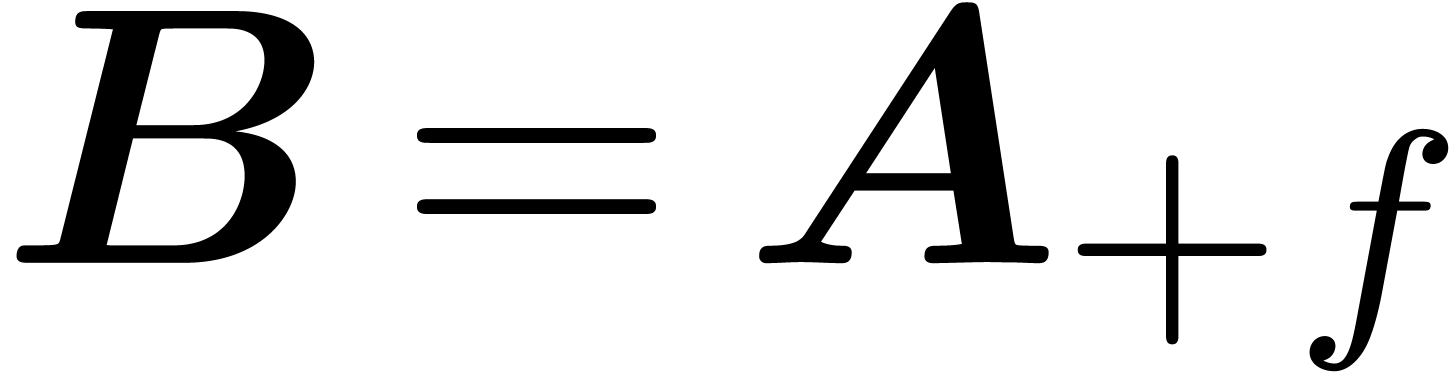 w.r.t.
w.r.t.  ,
which satisfies
,
which satisfies  for all
for all 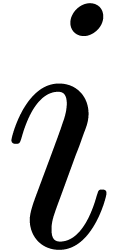 . Let
. Let 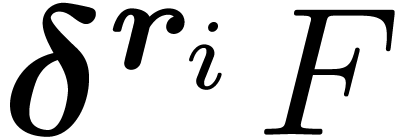 be the leader of
be the leader of 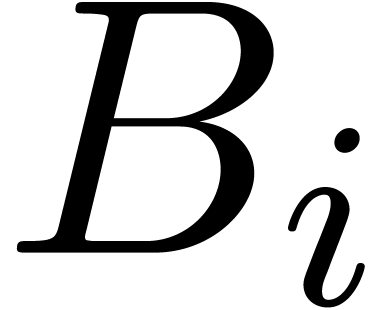 for each
for each  .
Since
.
Since  , the coefficient
, the coefficient 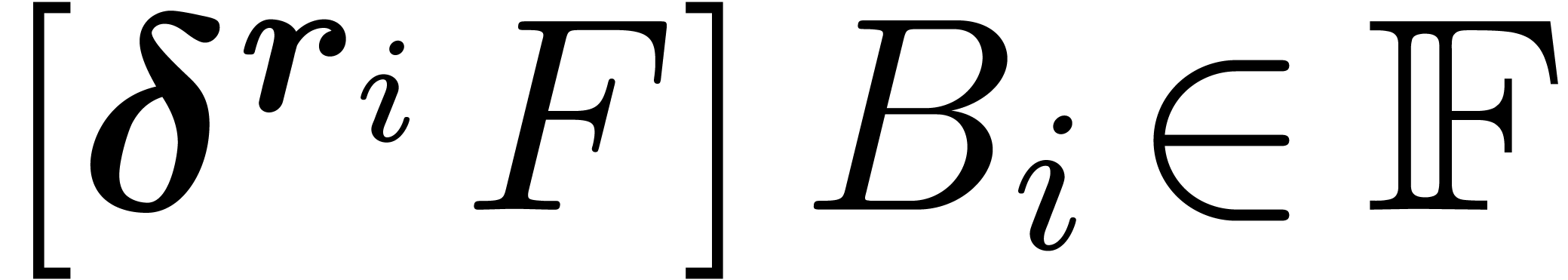 of
of 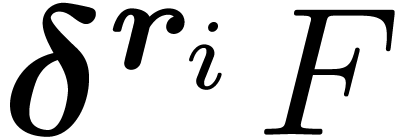 in
in 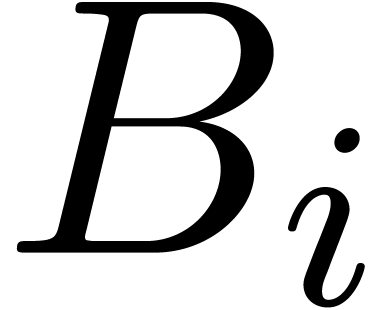 does not vanish. Taking
does not vanish. Taking  sufficiently small, we
have
sufficiently small, we
have 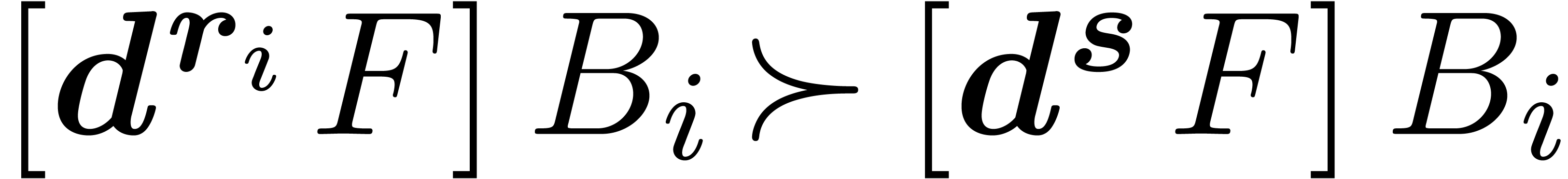 for all
for all 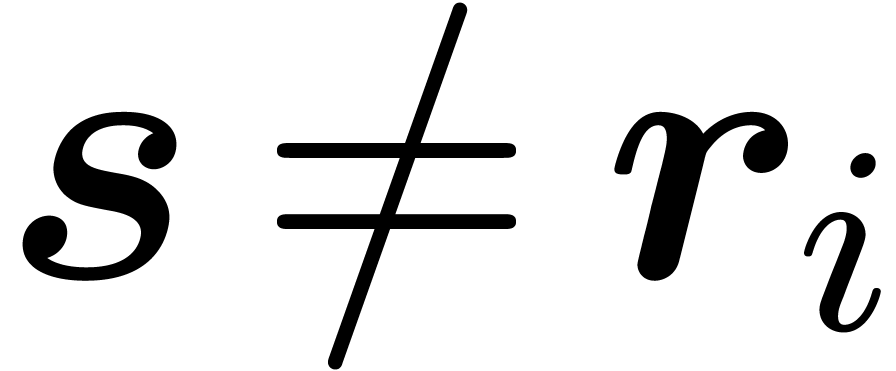 .
From now on, let us consider the entries of
.
From now on, let us consider the entries of  and
and
 as differential polynomials in
as differential polynomials in  . Modulo a multiplicative conjugation by a
sufficiently small
. Modulo a multiplicative conjugation by a
sufficiently small  , we may
assume without loss of generality that
, we may
assume without loss of generality that 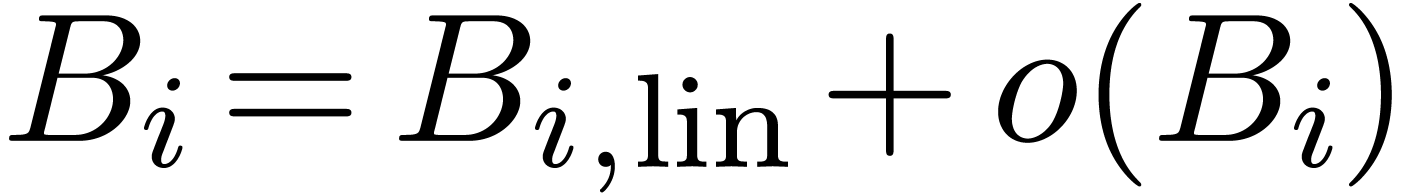 for all
for all
 , while preserving the fact
that
, while preserving the fact
that 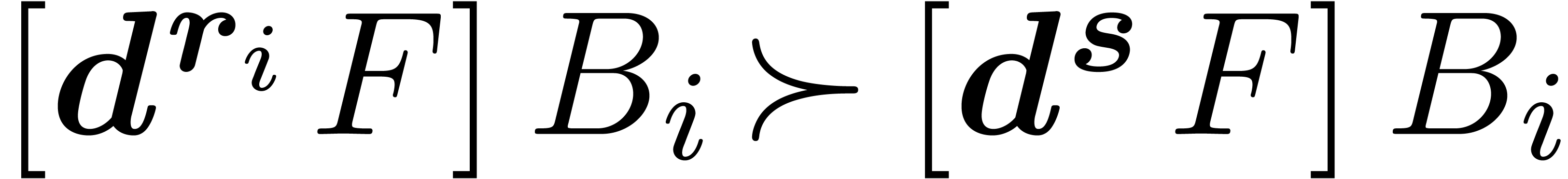 for all
for all 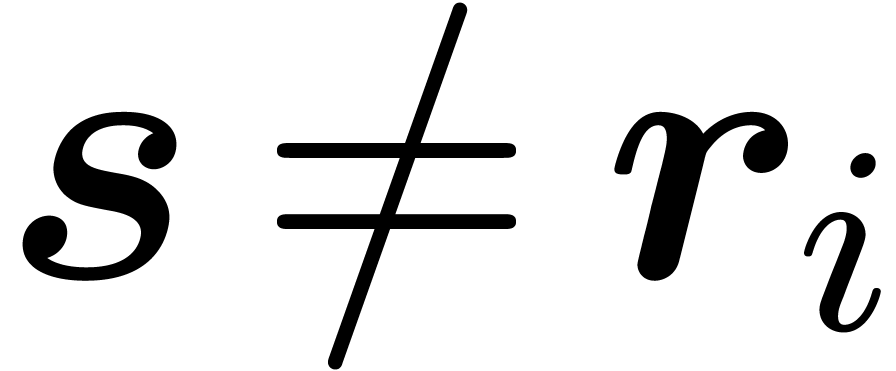 .
Modulo a division of each
.
Modulo a division of each  by
by 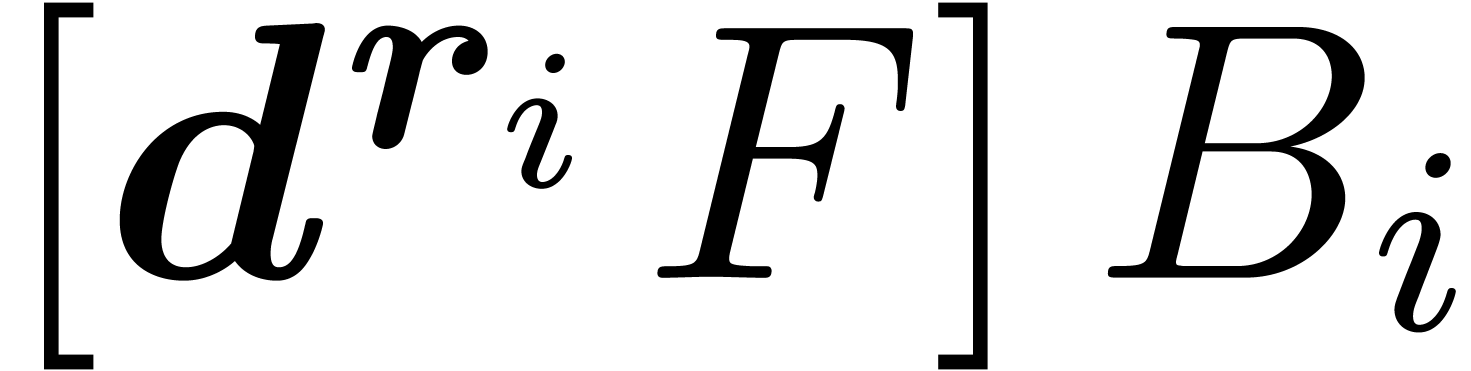 , we are thus in a position where
, we are thus in a position where  satisfies the conditions of lemma 16. We
conclude that
satisfies the conditions of lemma 16. We
conclude that  is an asymptotic basis
w.r.t.
is an asymptotic basis
w.r.t.  , and so
is
, and so
is 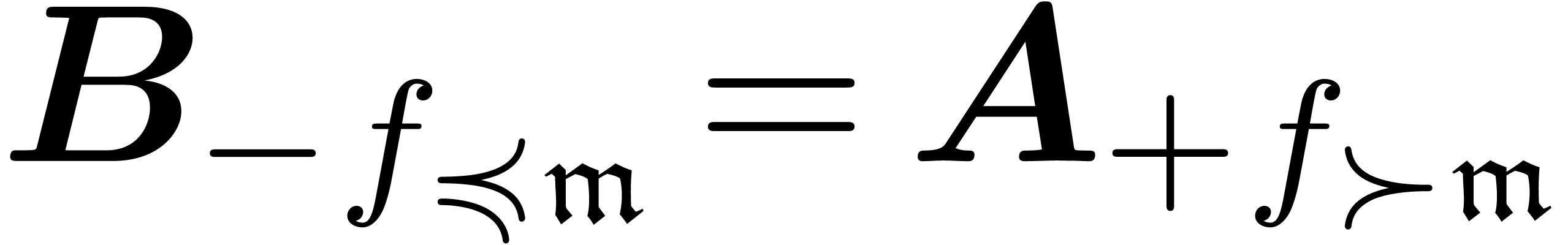 for any
for any  .
.
In this section, we assume that 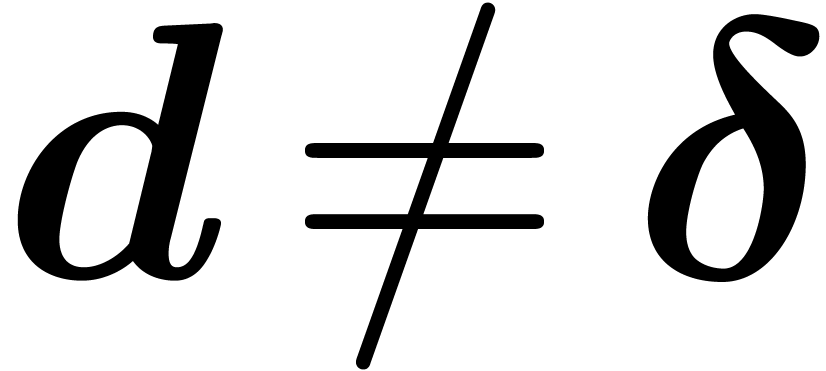 .
Given a strong differential ideal
.
Given a strong differential ideal  ,
the dualization of
,
the dualization of 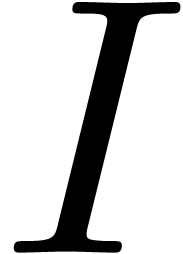 is the smallest
strong differential ideal
is the smallest
strong differential ideal 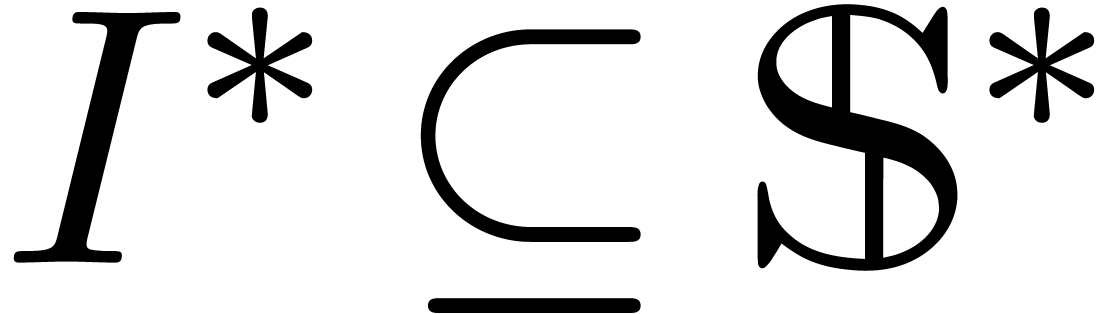 which contains
which contains 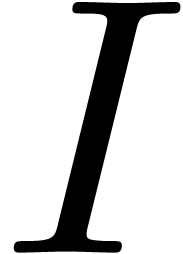 .
.
 ,
its dualization is again quasi-linear and we have
,
its dualization is again quasi-linear and we have 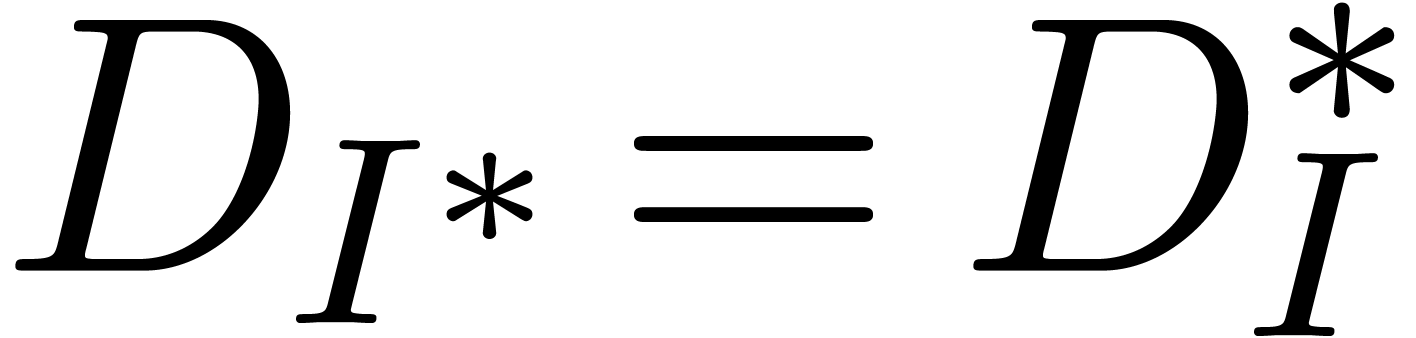 .
.
Proof. Let 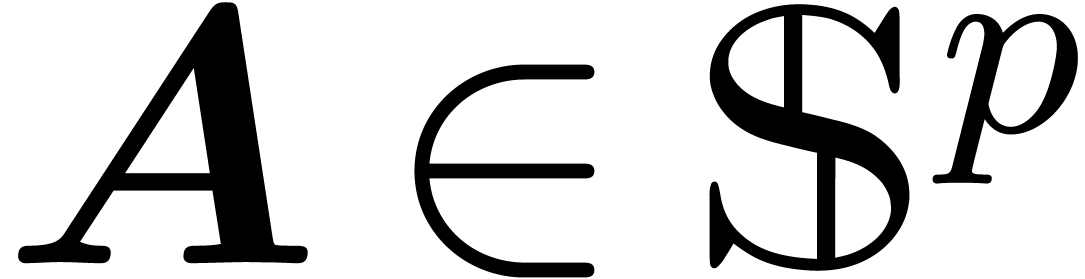 be an
asymptotic basis for
be an
asymptotic basis for 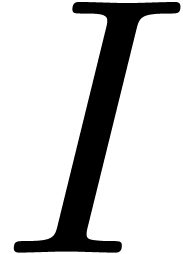 and let
and let  be the vector of critical relations for
be the vector of critical relations for  ,
giving rise to an exact sequence
,
giving rise to an exact sequence
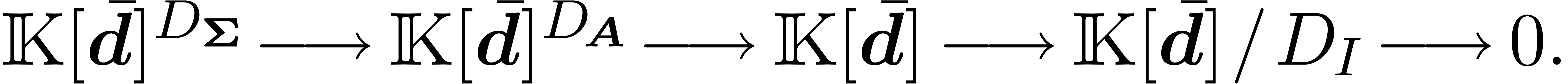 |
(21) |
Since 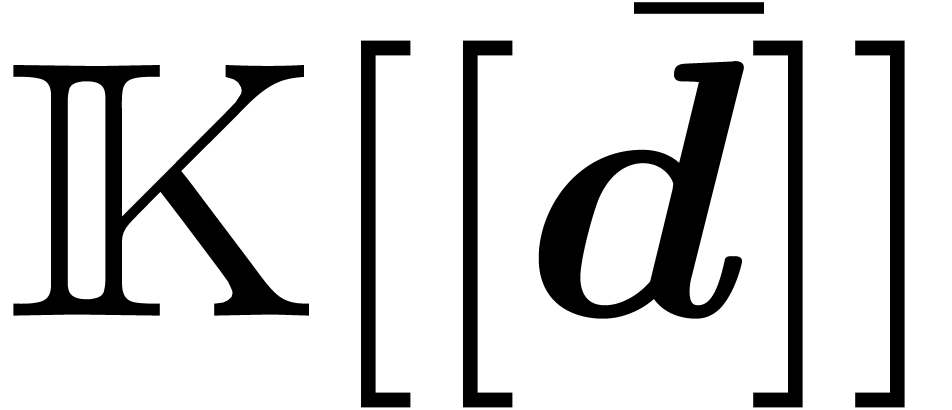 is a flat ring over
is a flat ring over 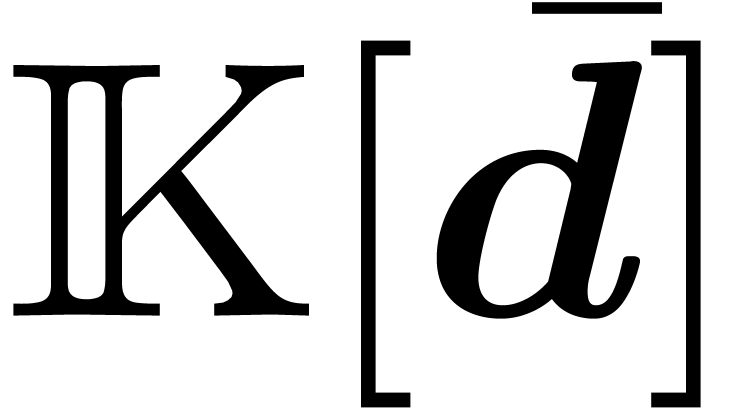 , we also get an exact sequence
, we also get an exact sequence
 |
(22) |
Now consider an element 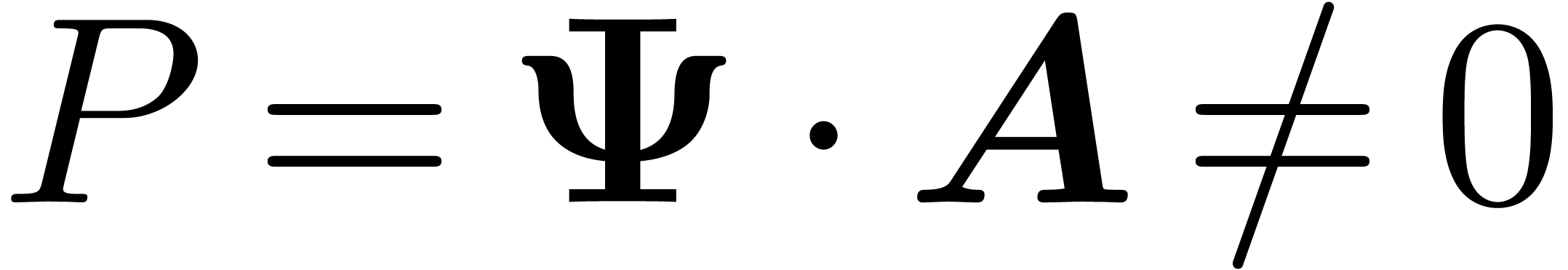 with
with  . We claim that we may rewrite
. We claim that we may rewrite  in such a way that
in such a way that  . Indeed,
using the exactness of (22) instead of the exactness of (5), this is proved in a similar way as lemma 7.
Our claim implies that
. Indeed,
using the exactness of (22) instead of the exactness of (5), this is proved in a similar way as lemma 7.
Our claim implies that  . This
shows that
. This
shows that 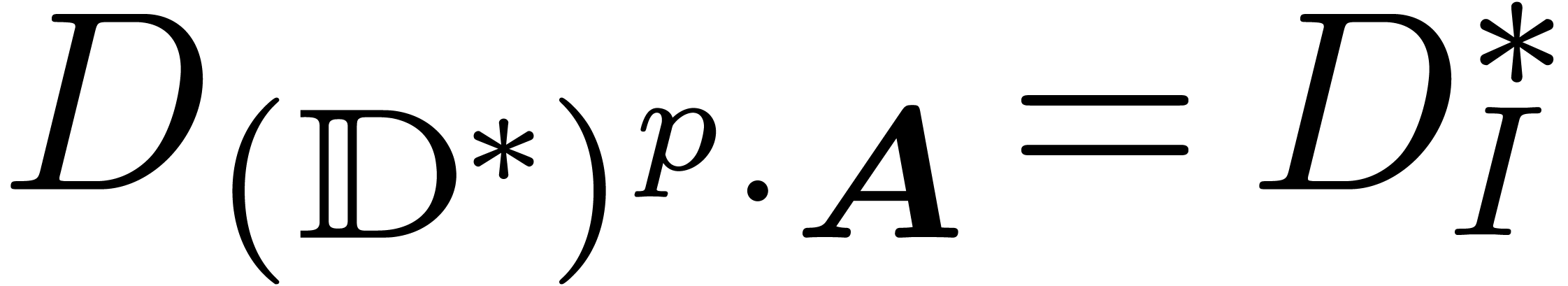 .
.
Now consider a matrix  with entries in
with entries in 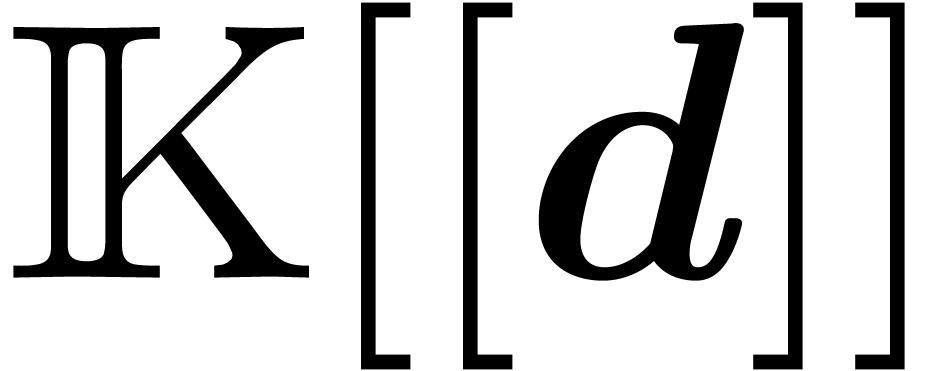 such that
such that  is normal and
is normal and  is a Rosenfeld co-basis. We claim that
is a Rosenfeld co-basis. We claim that  is an asymptotic basis for
is an asymptotic basis for 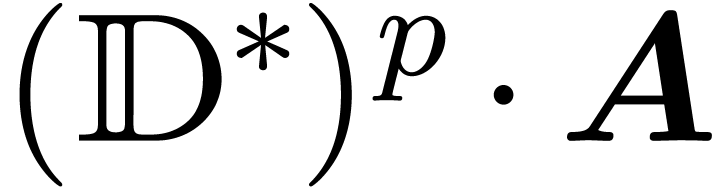 .
Indeed, as in the first part of the proof of proposition 10,
asymptotic co-reduction of the asymptotic co-
.
Indeed, as in the first part of the proof of proposition 10,
asymptotic co-reduction of the asymptotic co- -polynomial of
-polynomial of 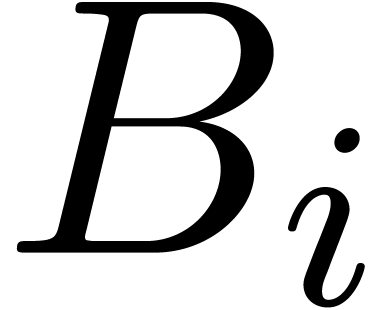 and
and 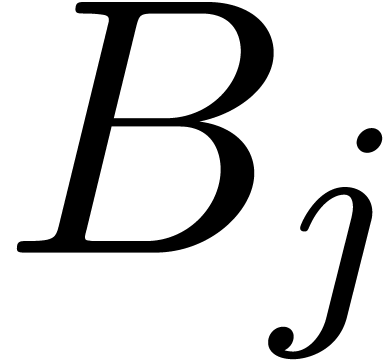 with
with  yields an asymptotic
co-critical relation for
yields an asymptotic
co-critical relation for 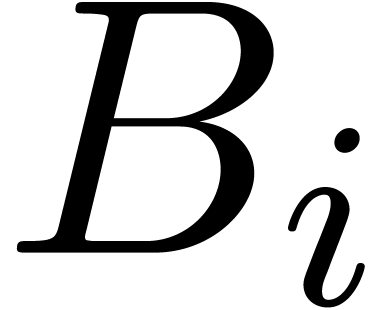 and
and 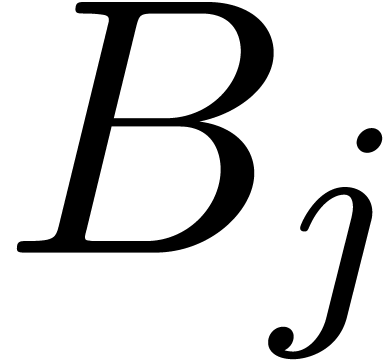 . Our claim and proposition 12
imply that
. Our claim and proposition 12
imply that  is quasi-linear. We conclude that
is quasi-linear. We conclude that
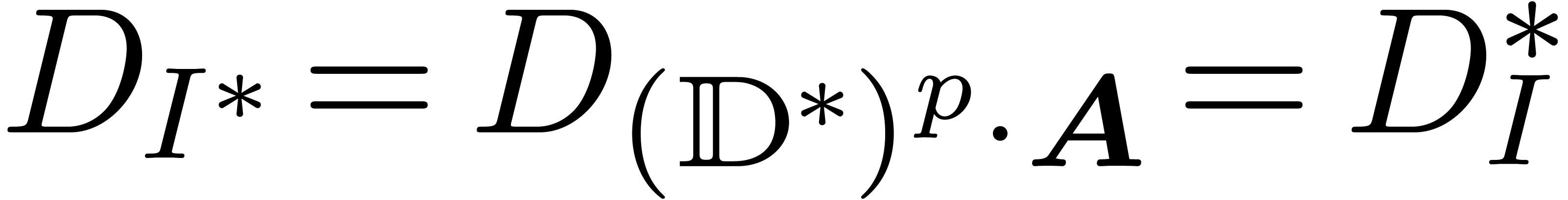 .
.
 is a strong quasi-linear differential ideal,
then so is
is a strong quasi-linear differential ideal,
then so is 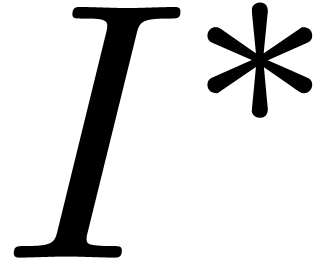 .
.
Proof. Assume that 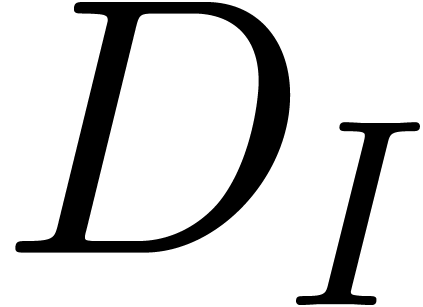 is
generated by
is
generated by  . Then
. Then  is again generated by
is again generated by  .
.
We will now study what happens to quasi-linear differential ideals when changing the derivations. Given two systems of derivations
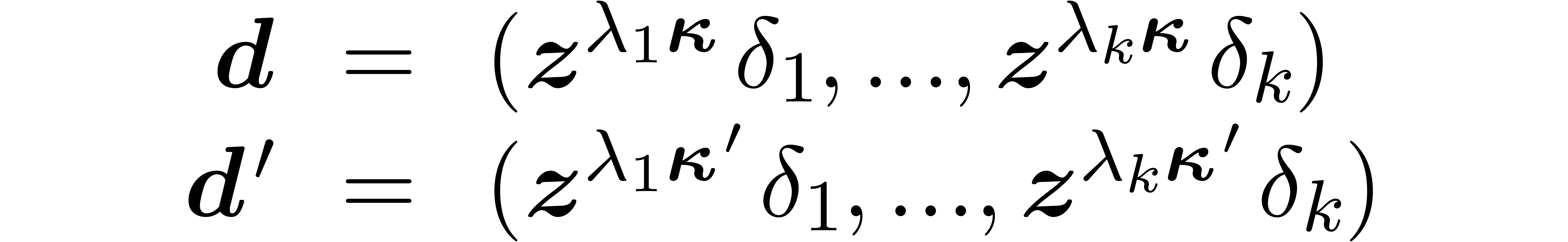
with 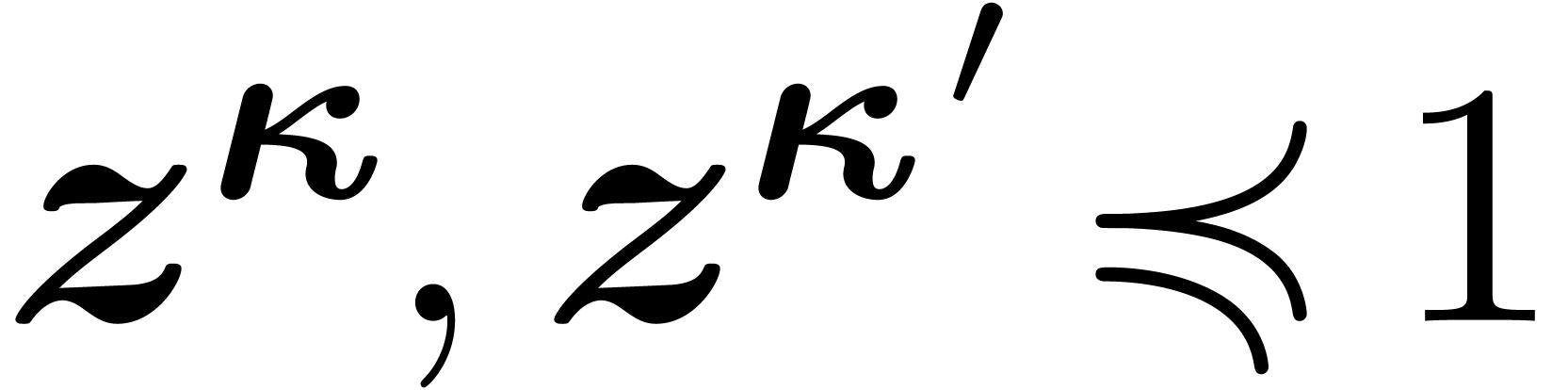 we will write
we will write 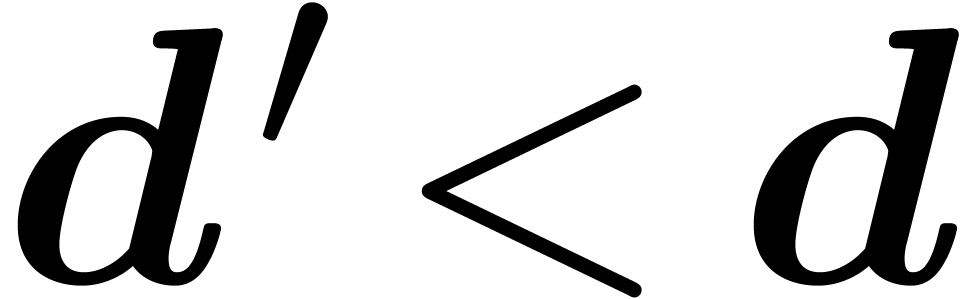 if
if
 . In that case, we have
. In that case, we have
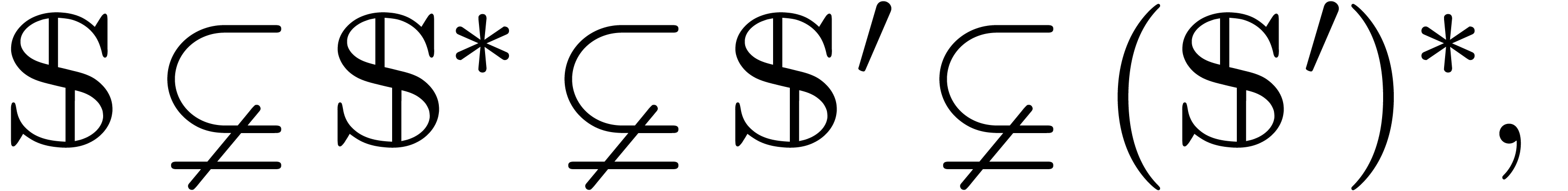
where  and
and  denote the
natural counterparts of
denote the
natural counterparts of  and
and  for
for  . More generally, we will
use primes when working with respect to
. More generally, we will
use primes when working with respect to 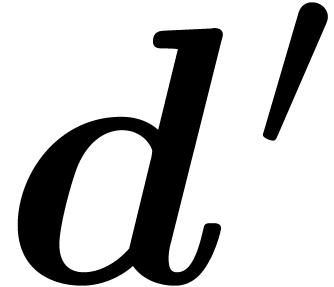 .
.
From now on, let 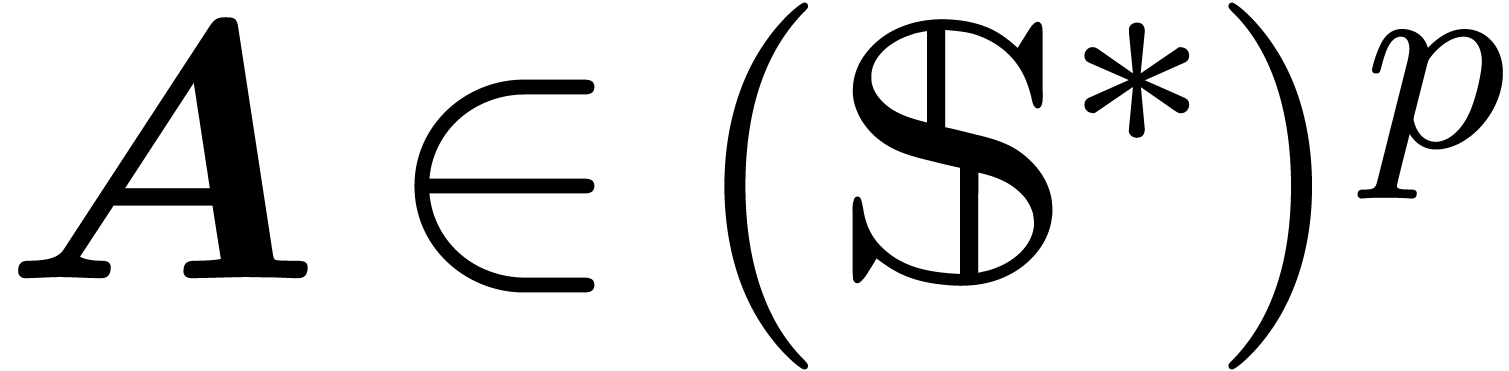 be an asymptotic co-basis. For
each
be an asymptotic co-basis. For
each 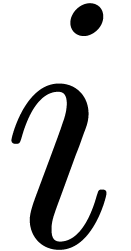 , let
, let 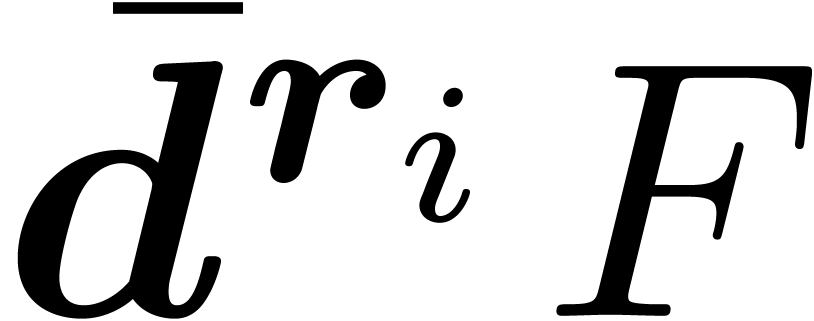 be the co-leader of
be the co-leader of 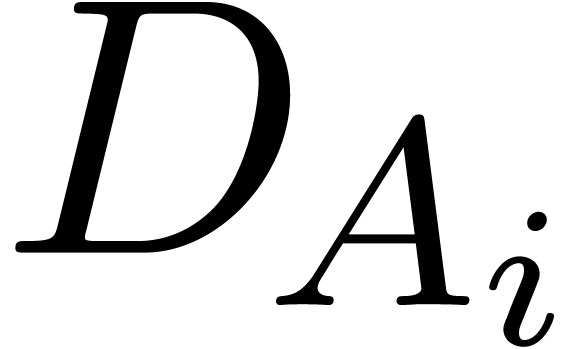 . The
largest
. The
largest  for which
for which 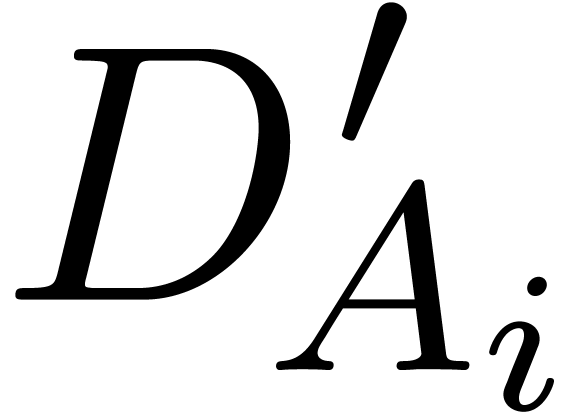 is not
reduced to a single term for some
is not
reduced to a single term for some 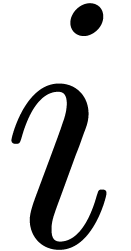 ,
is called the next critical derivation. If
,
is called the next critical derivation. If  is also quasi-normal w.r.t.
is also quasi-normal w.r.t. 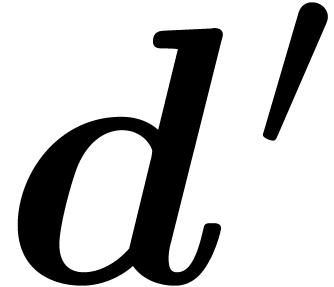 ,
then it follows in particular that
,
then it follows in particular that 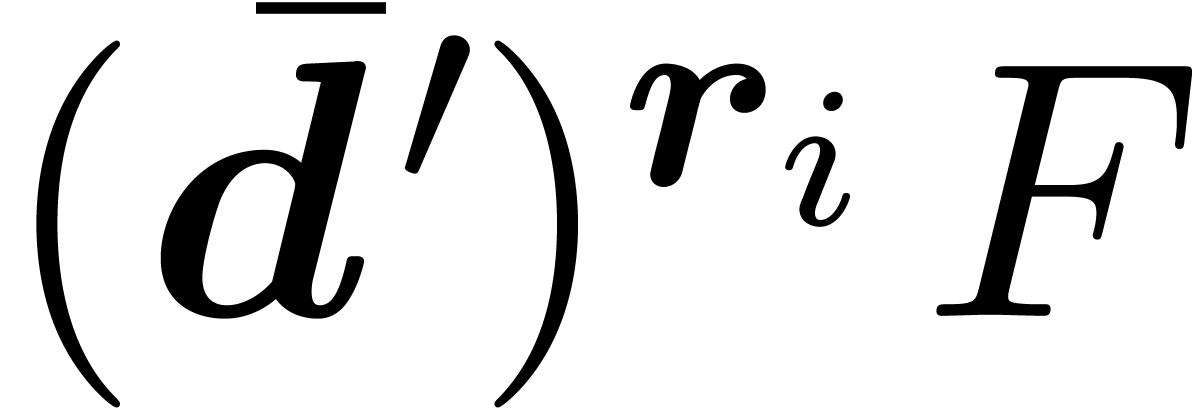 is the leader
of
is the leader
of  for each
for each  .
.
 be an asymptotic co-basis w.r.t.
be an asymptotic co-basis w.r.t.
 and let
and let  be the next
critical derivation. Assume that
be the next
critical derivation. Assume that 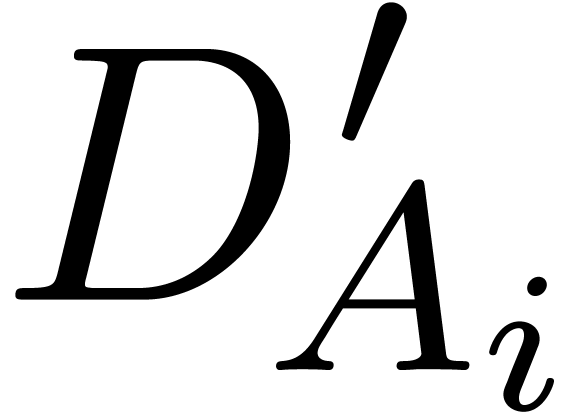 is linear for
each
is linear for
each 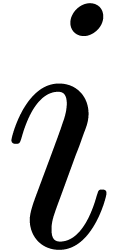 . Then
. Then  is also an asymptotic basis w.r.t.
is also an asymptotic basis w.r.t.  .
.
Proof. Without loss of generality, we may assume
that  is co-normal w.r.t.
is co-normal w.r.t.  . We will denote by
. We will denote by  the normalization of
the normalization of  w.r.t.
w.r.t. 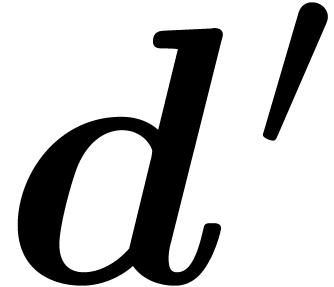 . Let us
prove that any element
. Let us
prove that any element 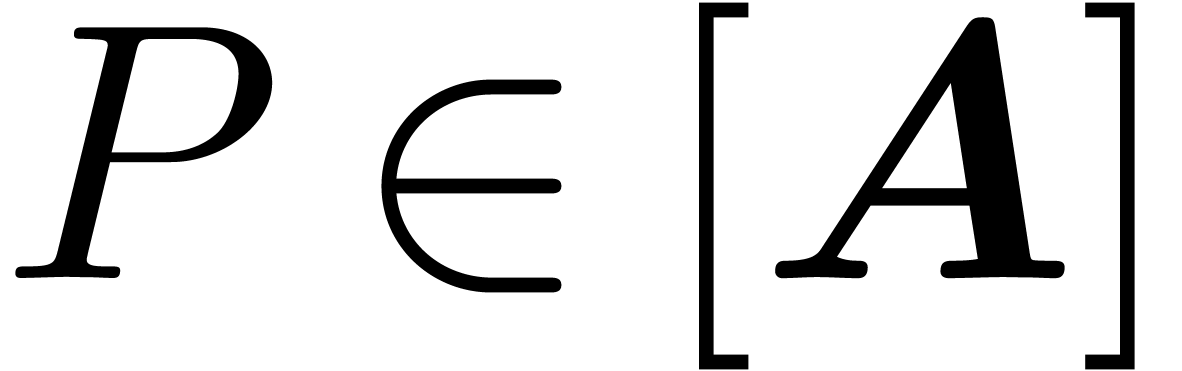 asymptotically reduces to
asymptotically reduces to
 w.r.t.
w.r.t.  . In particular, this will imply that the asymptotic
. In particular, this will imply that the asymptotic
 -polynomials of the form
-polynomials of the form 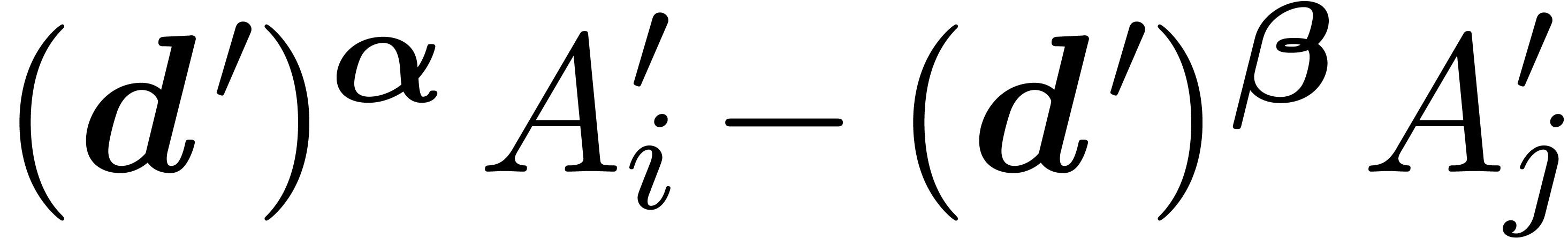 asymptotically reduce to
asymptotically reduce to  w.r.t.
w.r.t.  , and
thereby give rise to the required asymptotic critical relations for
, and
thereby give rise to the required asymptotic critical relations for
 .
.
Assume for contradiction that there exists a  , such that
, such that  is reduced
w.r.t.
is reduced
w.r.t.  . We may
even assume that
. We may
even assume that  is totally reduced
w.r.t.
is totally reduced
w.r.t.  ,
i.e. that each variable
,
i.e. that each variable  with
with  for some
for some 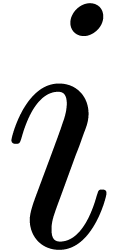 has been eliminated
from
has been eliminated
from 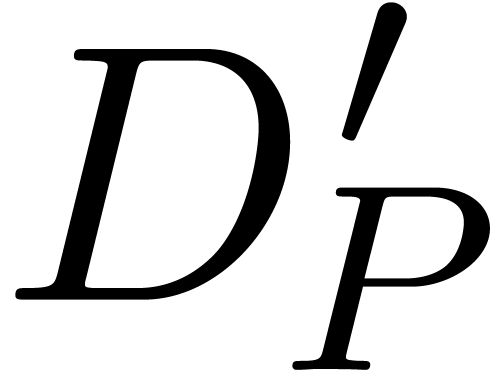 . Since
. Since  is an asymptotic co-basis w.r.t.
is an asymptotic co-basis w.r.t.  , asymptotic co-reduction of
, asymptotic co-reduction of 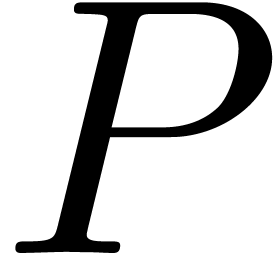 yields a relation
yields a relation  . Let us
prove by induction over
. Let us
prove by induction over  that
that 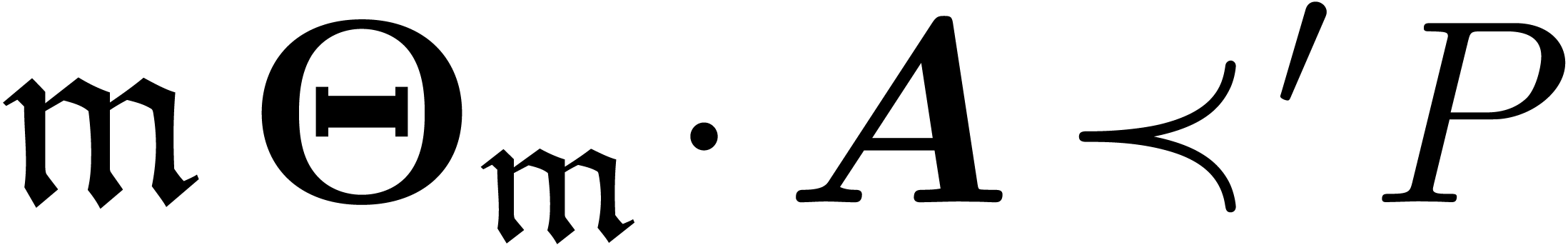 . This yields the desired contradiction, since
this would imply
. This yields the desired contradiction, since
this would imply  , by strong
linearity.
, by strong
linearity.
Let  . Then
. Then  is the quotient of the co-reduction of
is the quotient of the co-reduction of  w.r.t.
w.r.t.  .
Consequently, starting with
.
Consequently, starting with  ,
there exists an infinite sequence of equations
,
there exists an infinite sequence of equations

each of which is induced by a partial co-reduction of the type (7), and such that
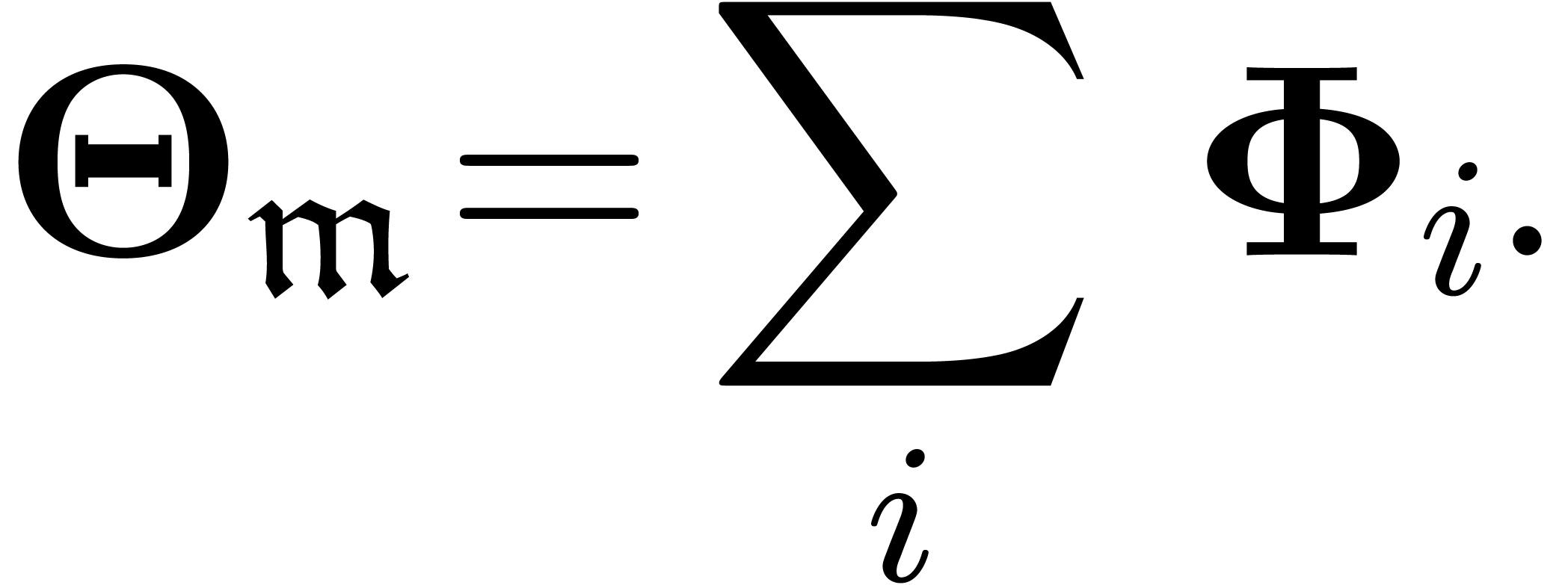
More precisely, let  be the co-leader of
be the co-leader of 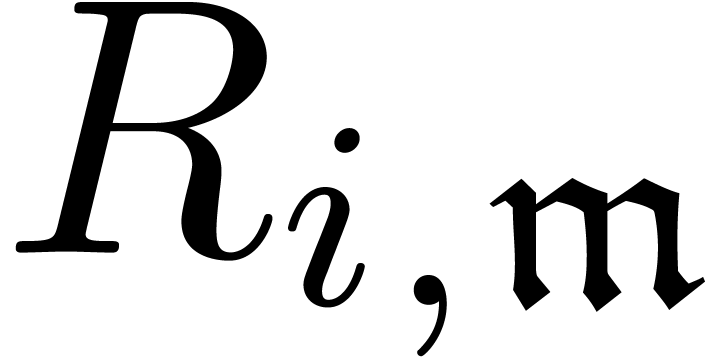 and write
and write 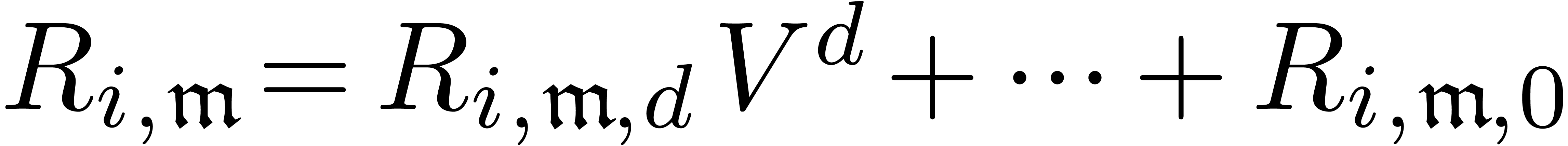 .
Then there exists an index
.
Then there exists an index  with
with 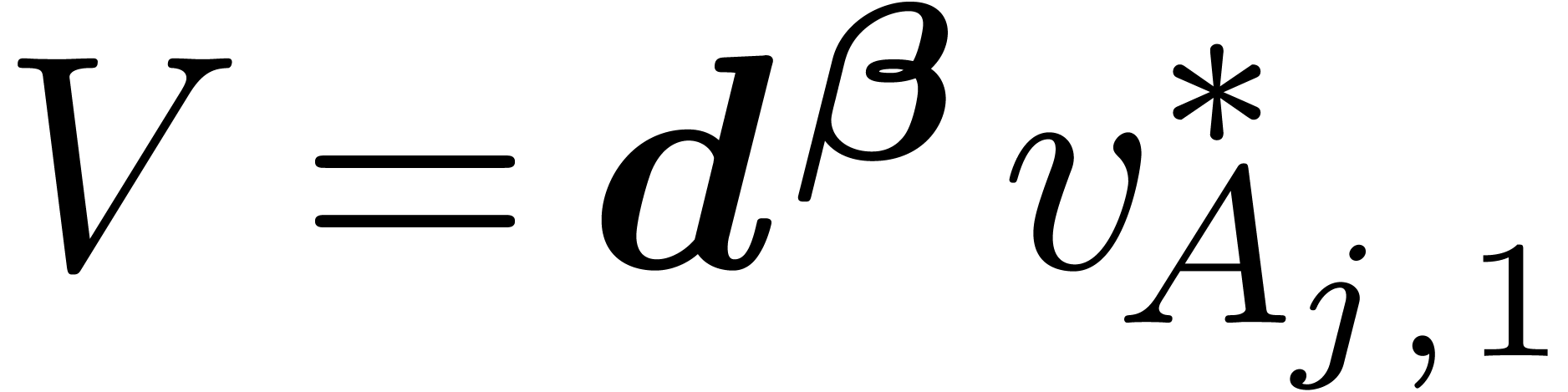 ,
, 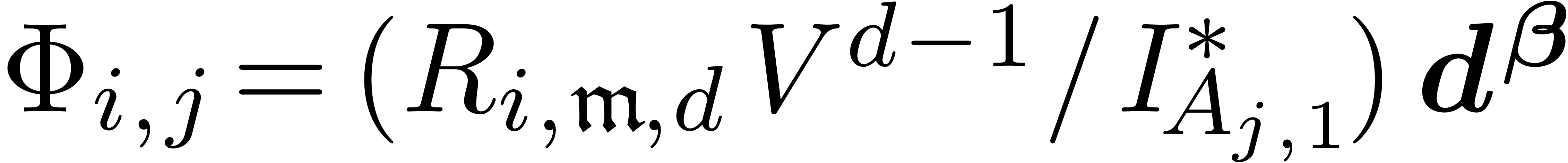 and
and 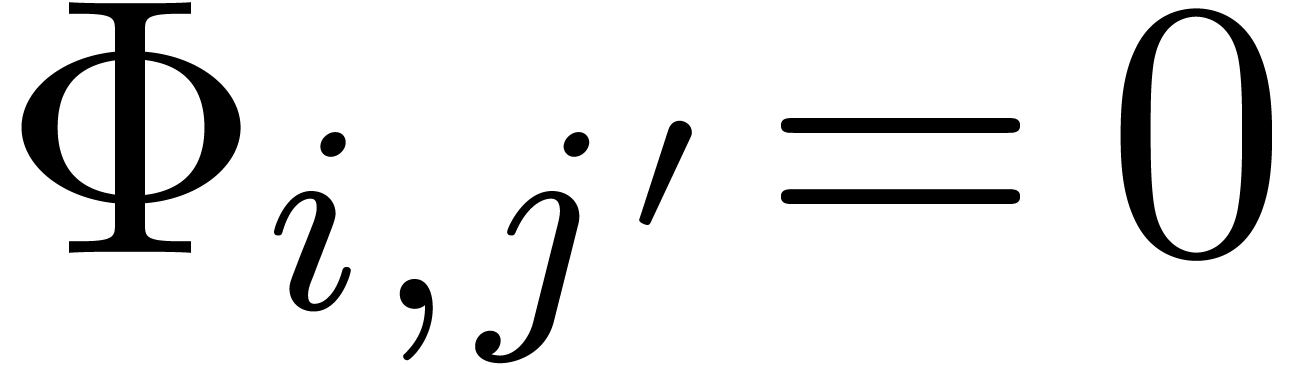 for
for 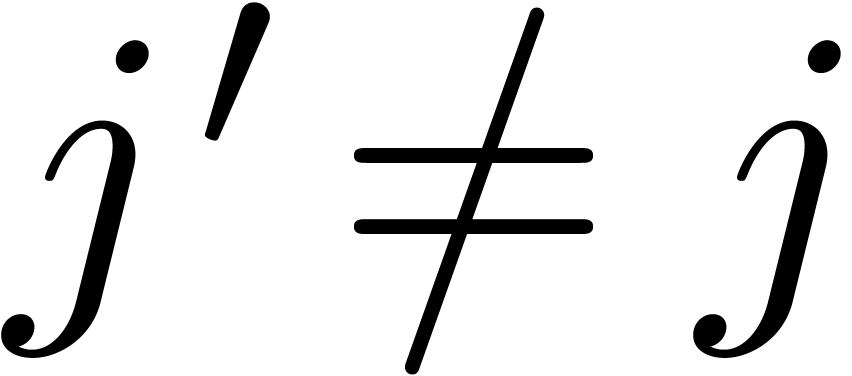 . Assuming that
. Assuming that  , we must have
, we must have 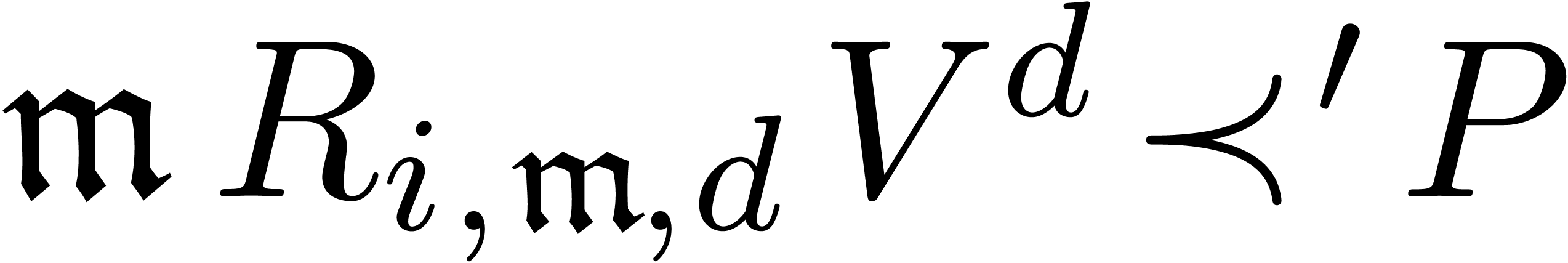 since
since  is totally reduced w.r.t.
is totally reduced w.r.t.
 and
and  involves
involves 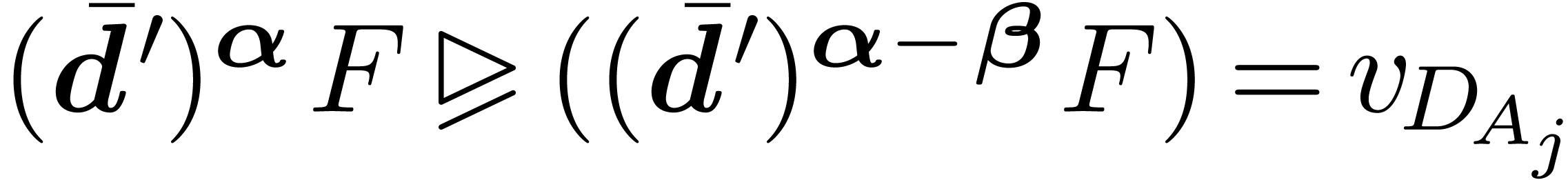 . Combined with the fact that
. Combined with the fact that 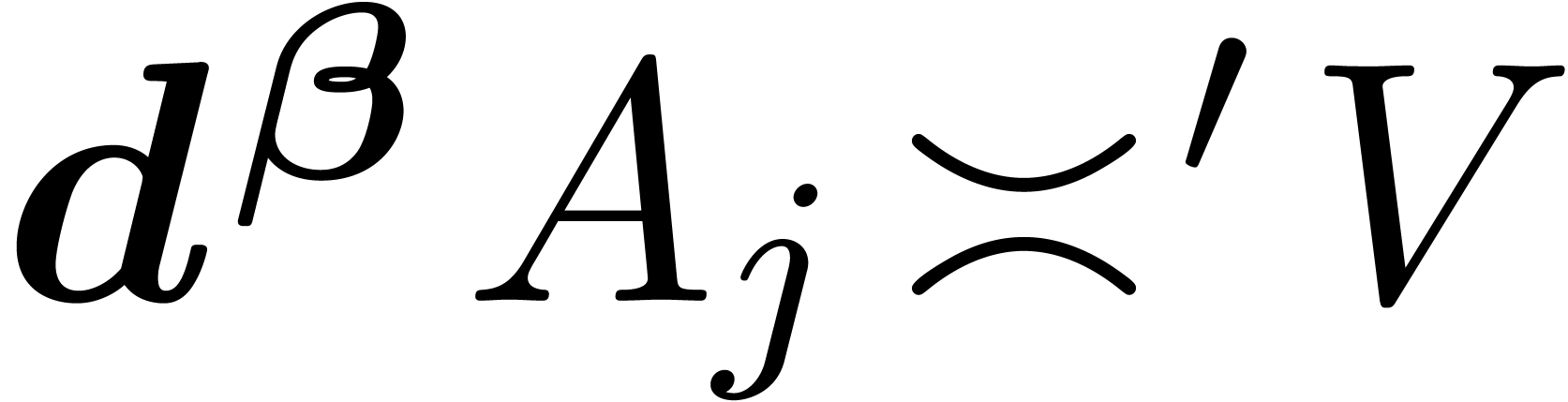 , this yields
, this yields  and
and  . In other words, our
hypothesis
. In other words, our
hypothesis  implies
implies  for
all
for
all  , whence
, whence  .
.
Remark  w.r.t.
w.r.t.
 obtained by asymptotic co-reduction of the
asymptotic co-
obtained by asymptotic co-reduction of the
asymptotic co- -polynomials
continue to provide asymptotic critical relations for
-polynomials
continue to provide asymptotic critical relations for  w.r.t.
w.r.t.  which are sufficiently close
to
which are sufficiently close
to  . Using lemma 10,
it follows that
. Using lemma 10,
it follows that  is an asymptotic basis
w.r.t.
is an asymptotic basis
w.r.t.  . If
. If
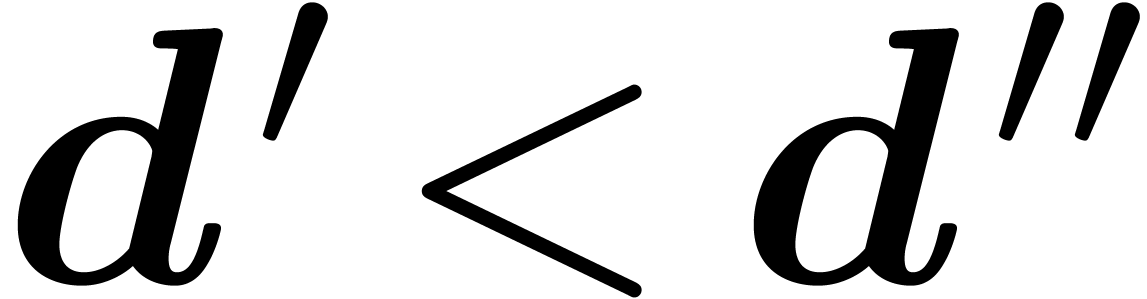 , then asymptotic reduction
of the asymptotic
, then asymptotic reduction
of the asymptotic  -polynomials
w.r.t.
-polynomials
w.r.t. 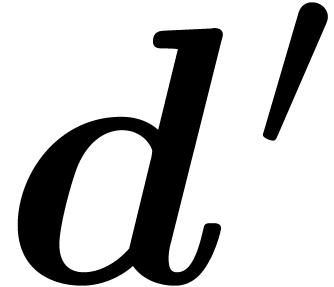 yield new asymptotic
critical and co-critical relations w.r.t.
yield new asymptotic
critical and co-critical relations w.r.t. 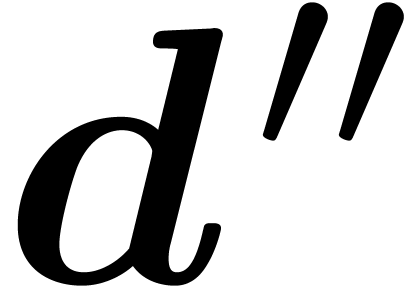 , which allows us to continue the process with
, which allows us to continue the process with
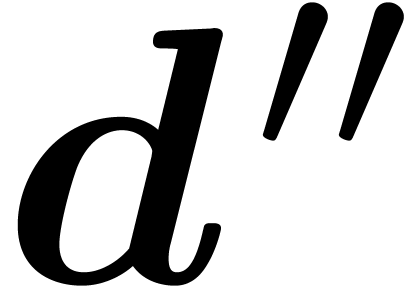 instead of
instead of  .
It can be shown that
.
It can be shown that 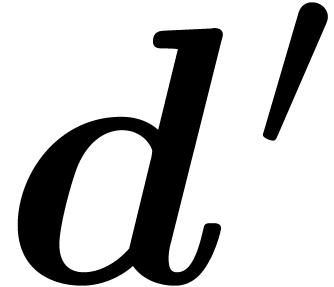 is reached after a finite
number of steps.
is reached after a finite
number of steps.
Given an effective ring  , we
recall that a multivariate power series
, we
recall that a multivariate power series 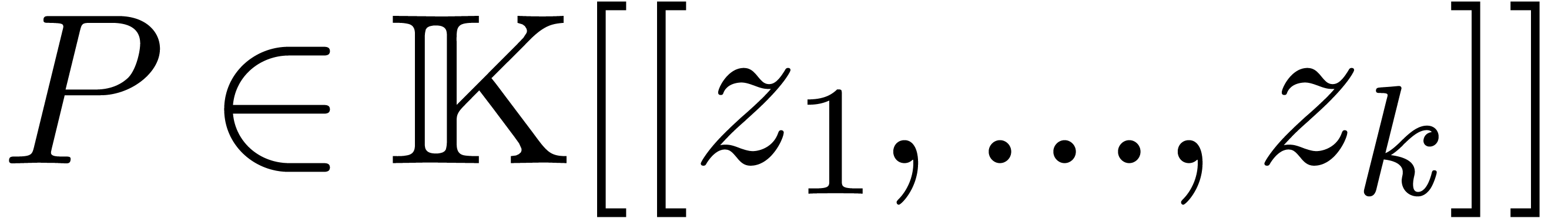 is
computable, if there exists an algorithm which takes
is
computable, if there exists an algorithm which takes 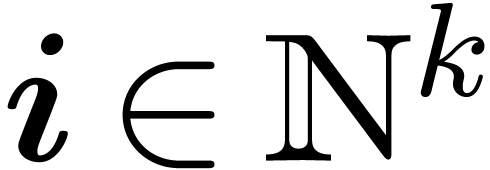 on input and which outputs the corresponding coefficient
on input and which outputs the corresponding coefficient
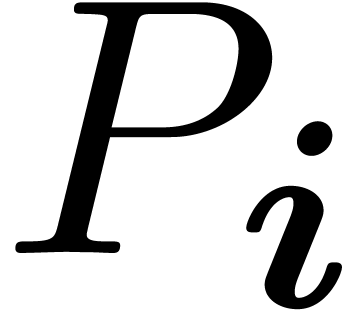 of
of  in
in  . The set
. The set  of such
series forms a differential ring. Although
of such
series forms a differential ring. Although  is
usually a field, it is also allowed to take a non-commutative ring of
operators for
is
usually a field, it is also allowed to take a non-commutative ring of
operators for  .
.
Given an effective monomial group  ,
a grid-based series
,
a grid-based series 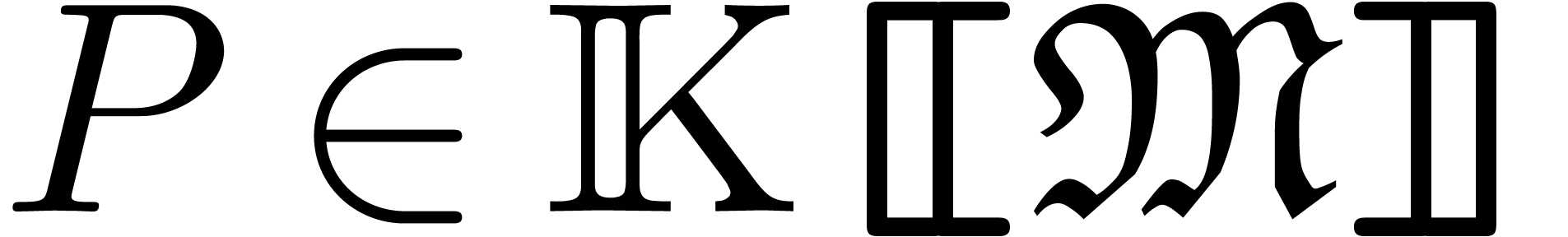 is said to be
computable if there exist infinitesimal
is said to be
computable if there exist infinitesimal  and
and 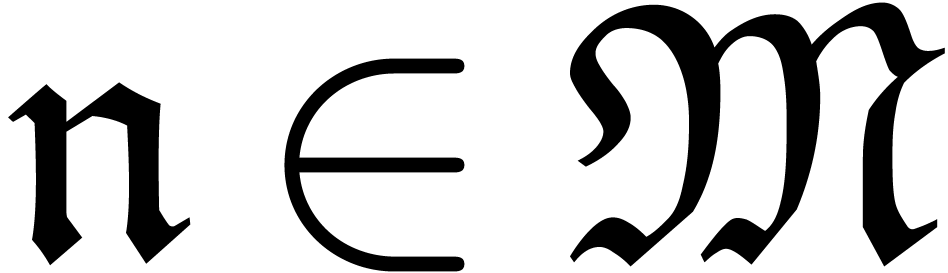 , as well as a computable
series
, as well as a computable
series 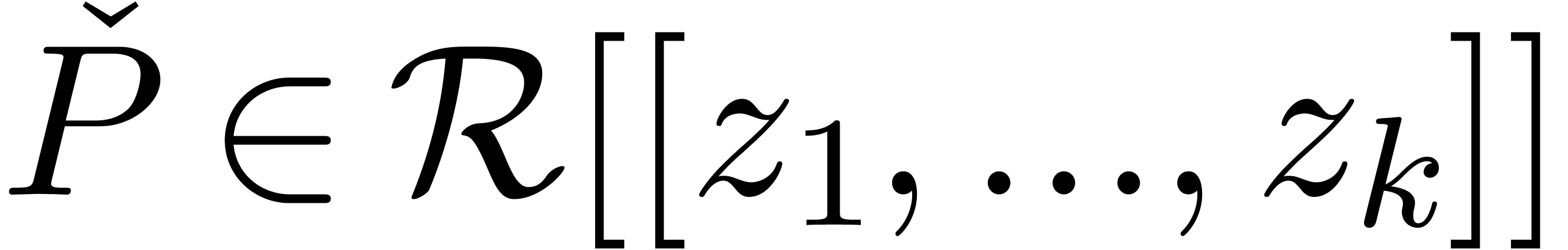 , such that
, such that 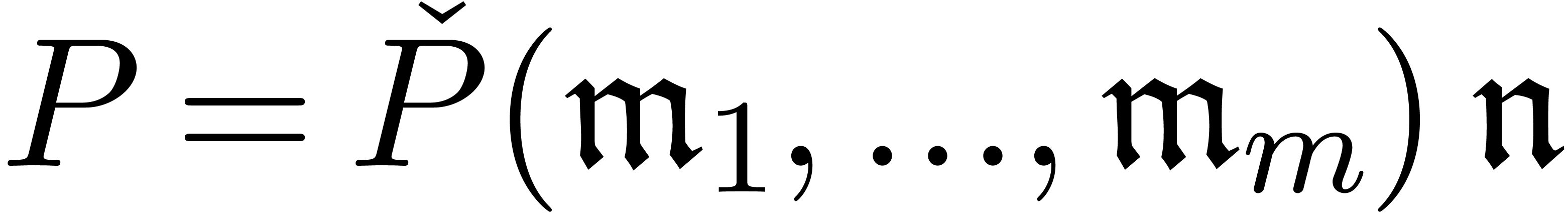 . We denote by
. We denote by  the ring of such series.
the ring of such series.
The definition of computable power series applies in the obvious way to
differential operators 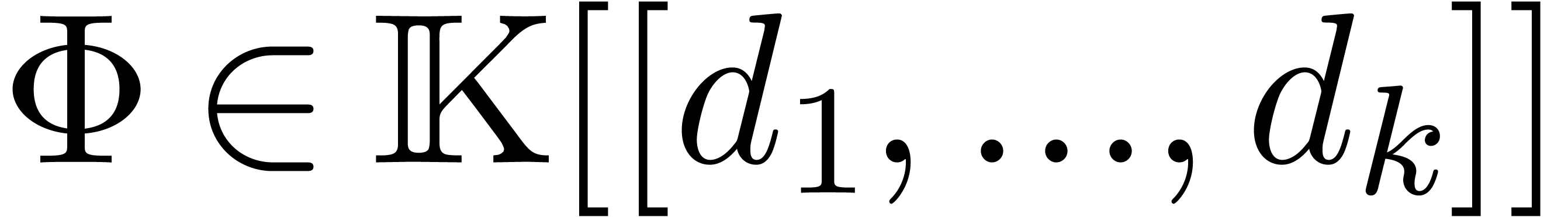 . More
generally, a series
. More
generally, a series 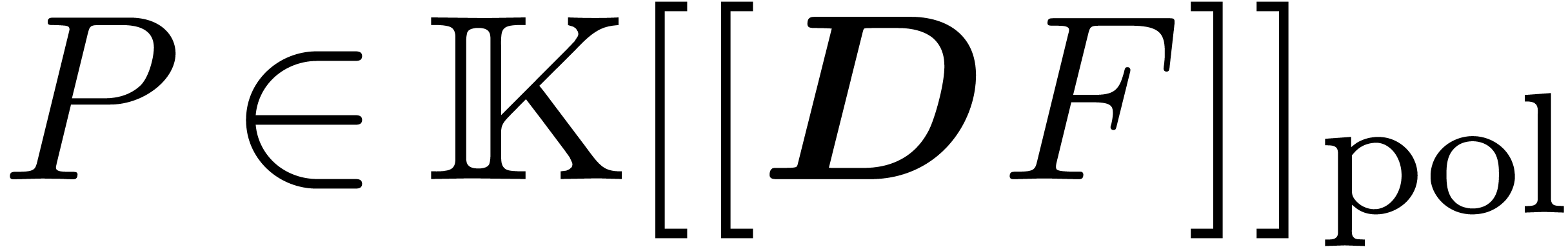 is said to be computable, if
there exists an algorithm which takes a monomial
is said to be computable, if
there exists an algorithm which takes a monomial  on input and which outputs the corresponding coefficient
on input and which outputs the corresponding coefficient  . We denote by
. We denote by 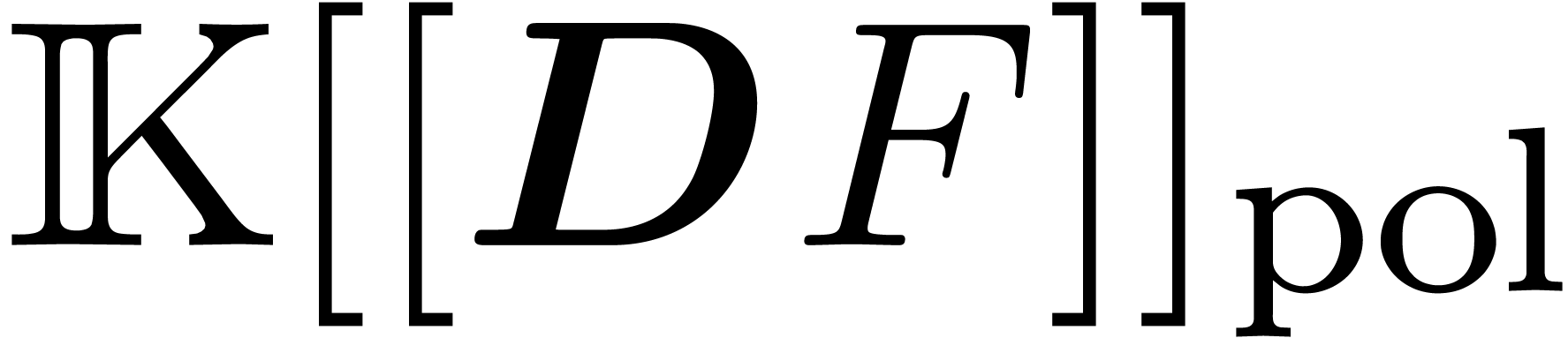 the ring
of such series.
the ring
of such series.
Throughout this section, we will assume that  and
and
 as in sections 3.1 and 4.1
have been fixed and that
as in sections 3.1 and 4.1
have been fixed and that  is an effective field
with an effective zero-test. For instance, we may take
is an effective field
with an effective zero-test. For instance, we may take 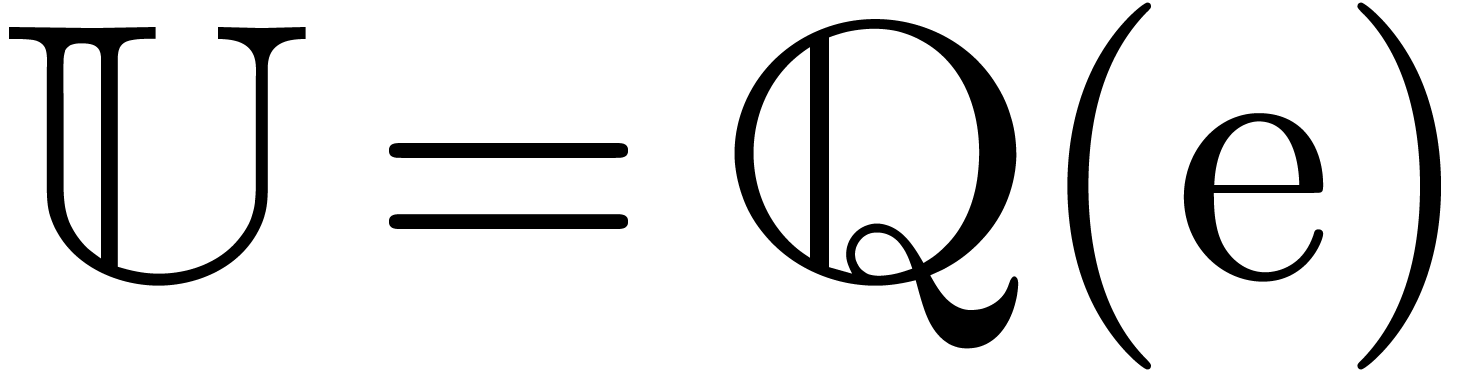 and
and  .
.
Assume that  is an effective field with an
effective zero-test. Let
is an effective field with an
effective zero-test. Let  ,
,
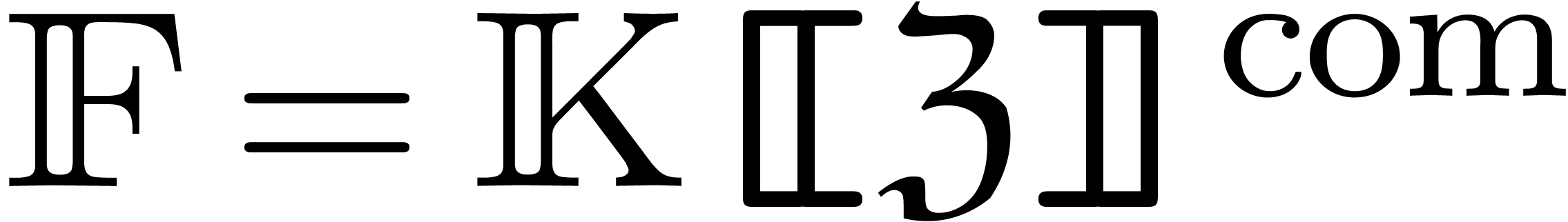 and
and 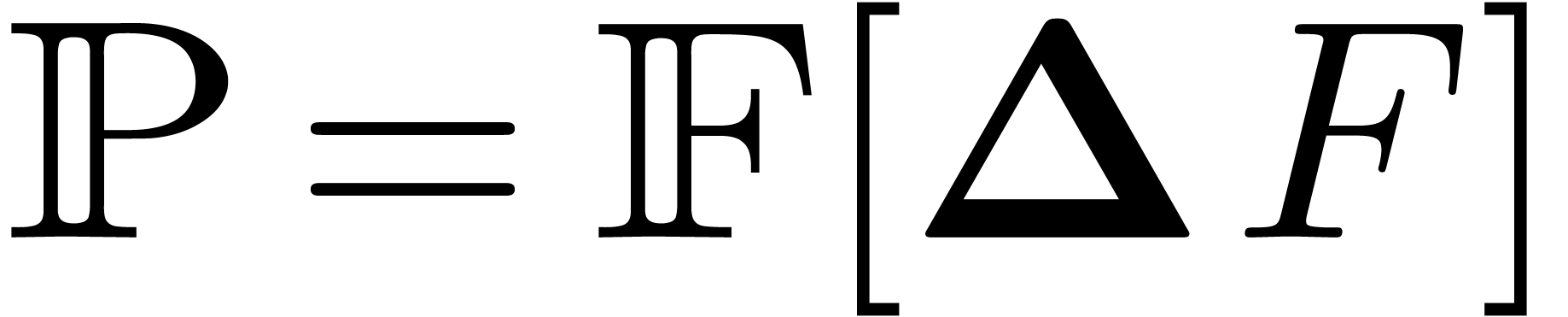 .
Consider a Rosenfeld basis
.
Consider a Rosenfeld basis 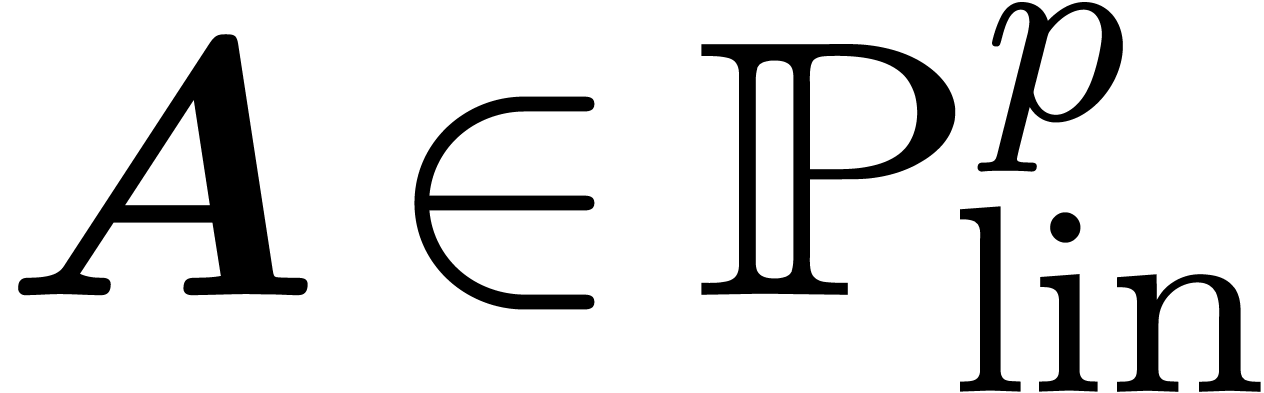 ,
such that the leaders of the
,
such that the leaders of the  are known (remind
that we do not have a zero-test in
are known (remind
that we do not have a zero-test in  ).
Then we may apply the theory from section 6 in order to
find an asymptotic basis for
).
Then we may apply the theory from section 6 in order to
find an asymptotic basis for  w.r.t.
w.r.t.
 .
.
Algorithm asymptotic_basis
Input: a Rosenfeld basis 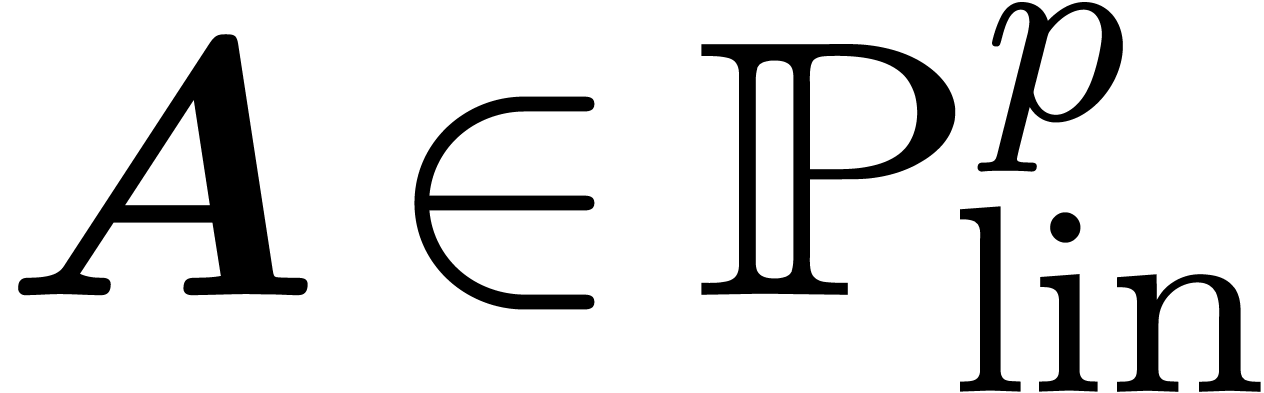 with
known leaders.
with
known leaders.
Output: an asymptotic basis for  .
.
Step 1. [Initial asymptotic basis]
Let 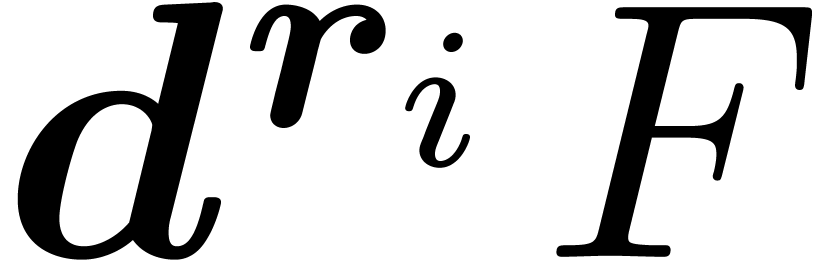 be the leader of
be the leader of 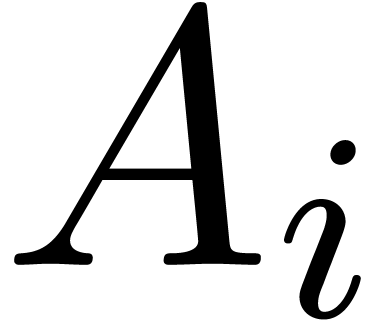 for each
for each 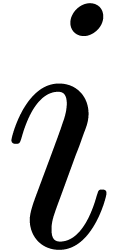 .
.
Take  sufficiently large, such that
sufficiently large, such that 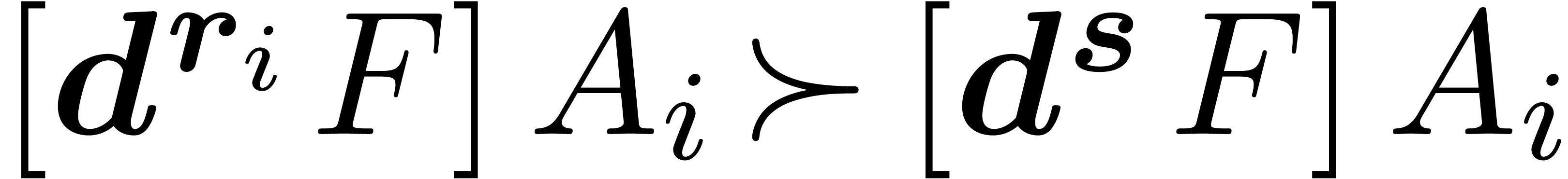 for all
for all 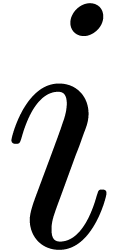 and
and 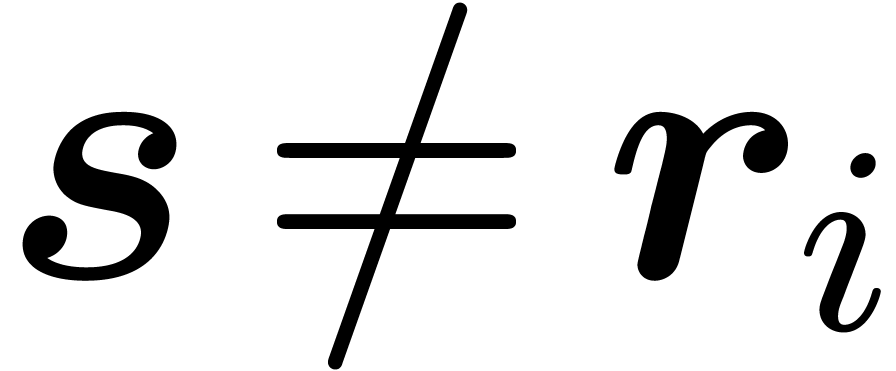 .
.
By lemma 16,  is an asymptotic
basis w.r.t.
is an asymptotic
basis w.r.t.  .
.
Go to step 4.
Step 2. [Dualization]
Normalize  .
.
Compute 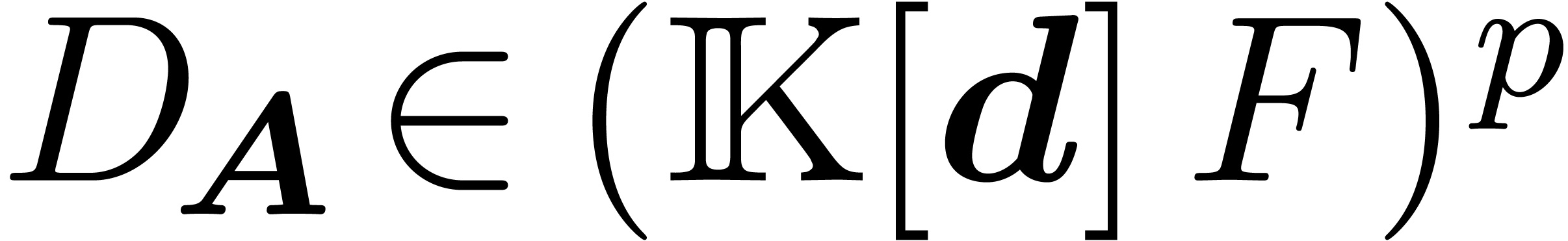 with respect to
with respect to  .
.
Using the tangent cone algorithm, find a Rosenfeld co-basis  for
for 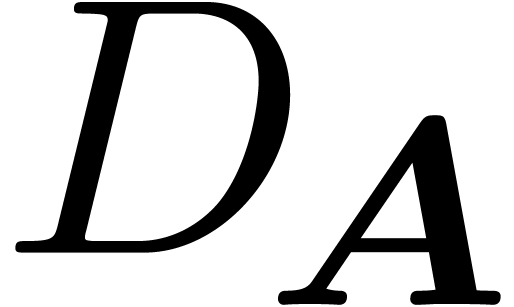 .
.
For each 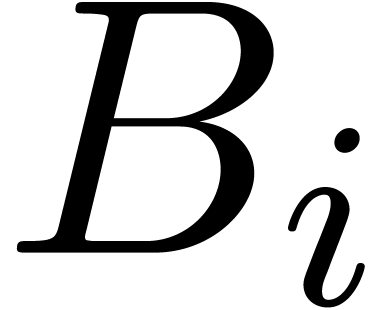 , let
, let 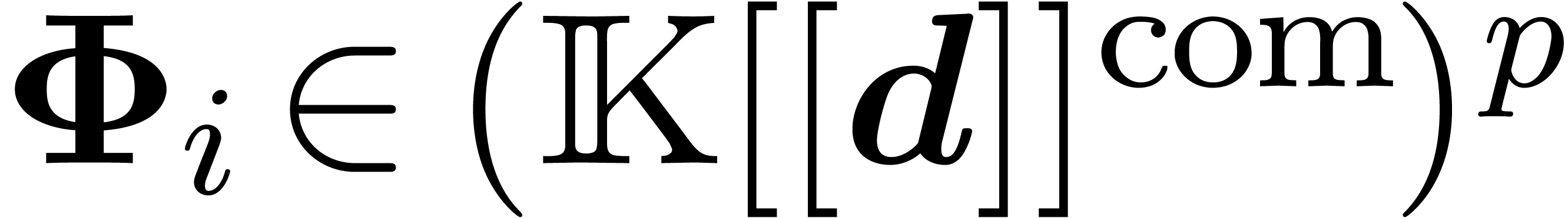 be such that
be such that  .
.
Replace  by
by  .
.
By lemma 18,  is an asymptotic
co-basis w.r.t.
is an asymptotic
co-basis w.r.t.  .
.
Step 3. [Change derivations]
Compute the next critical derivation 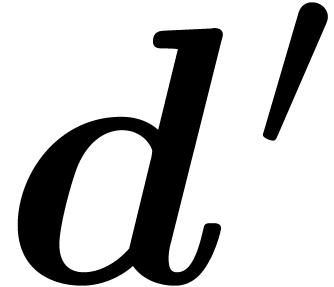 and
replace
and
replace  by
by 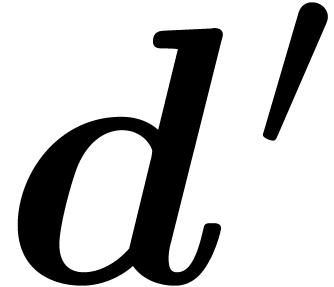 .
.
By lemma 20,  is an asymptotic
basis w.r.t.
is an asymptotic
basis w.r.t.  .
.
Step 4. [Done?]
If 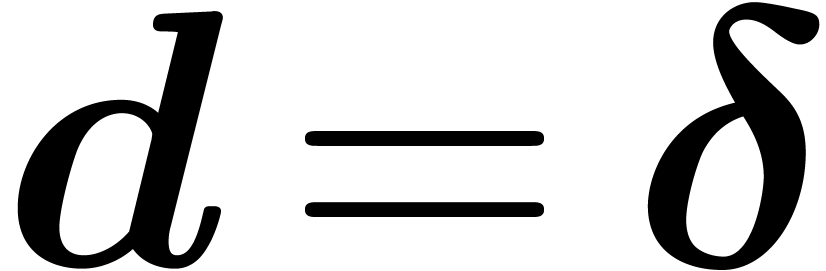 , then return
, then return  .
.
Otherwise, go to step 2.
Remark  . For
instance, in step
. For
instance, in step 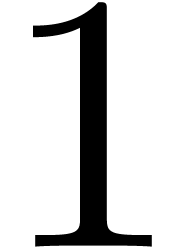 , it
suffices to compute the coefficient
, it
suffices to compute the coefficient  up to the
order of
up to the
order of 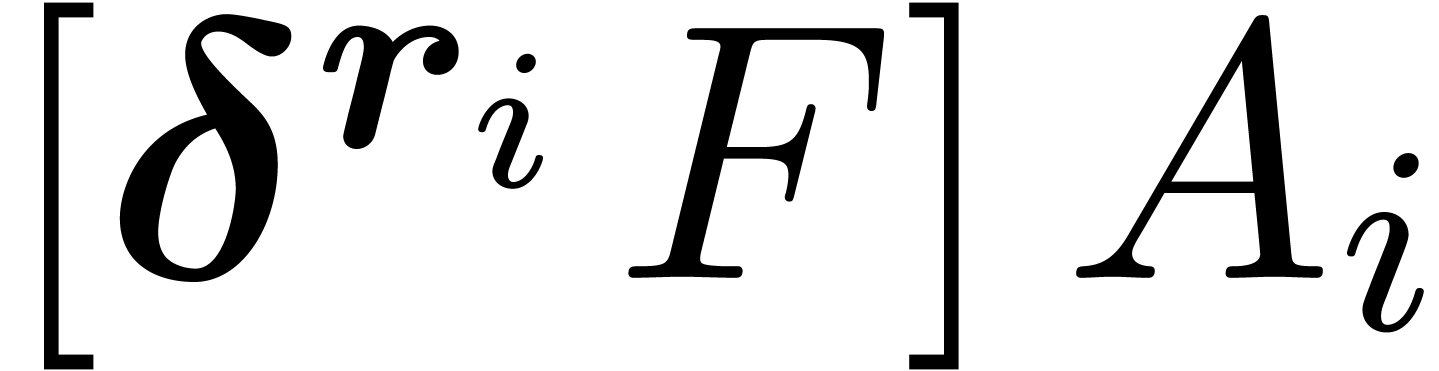 : if
: if  , then
, then 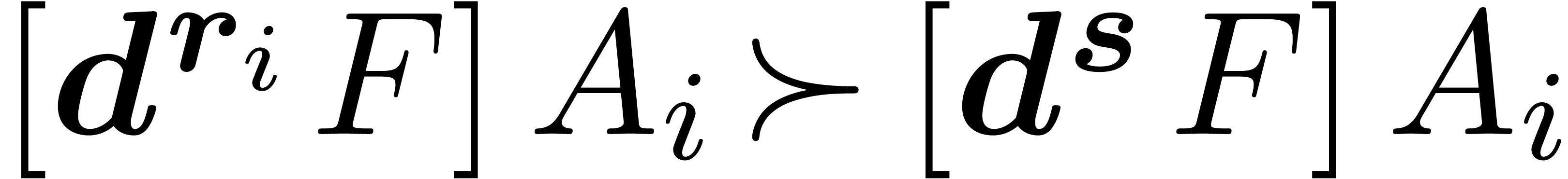 for all
for all  . Similarly, for the computation of
the next critical derivation
. Similarly, for the computation of
the next critical derivation 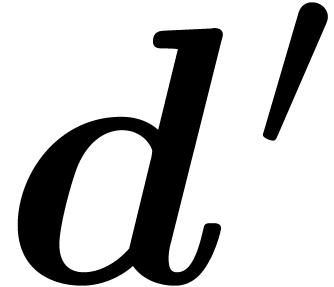 in step 3, it
suffices to evaluate
in step 3, it
suffices to evaluate  up to the order of
up to the order of 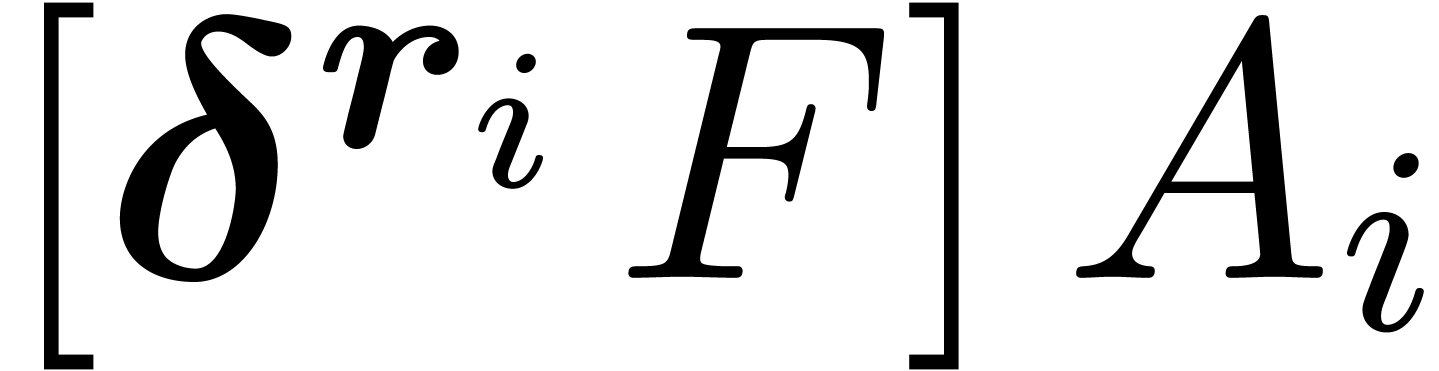 , where
, where 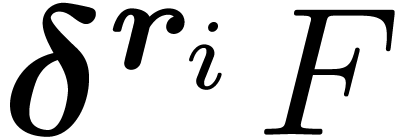 stands for the co-leader of
stands for the co-leader of  .
.
Proof. The correctness being ensured by lemmas
16, 18 and 20, it suffices to
prove the termination. Let  and
and  be the successive values of
be the successive values of  and
and  at the start of step 2. For each
at the start of step 2. For each 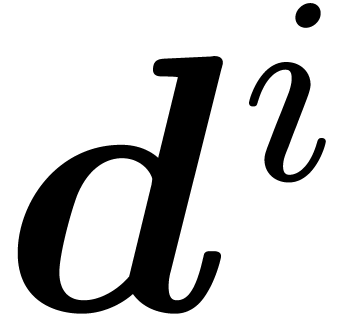 and
and 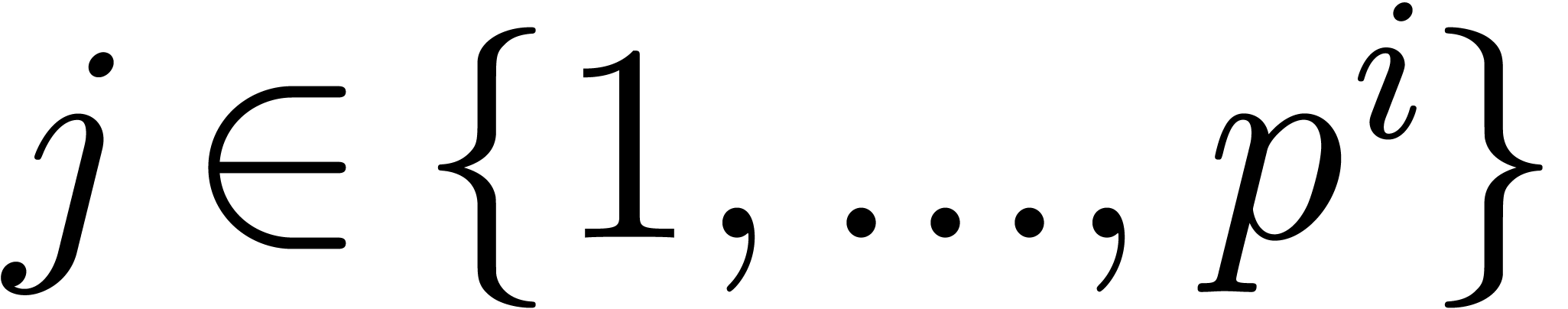 , let
, let 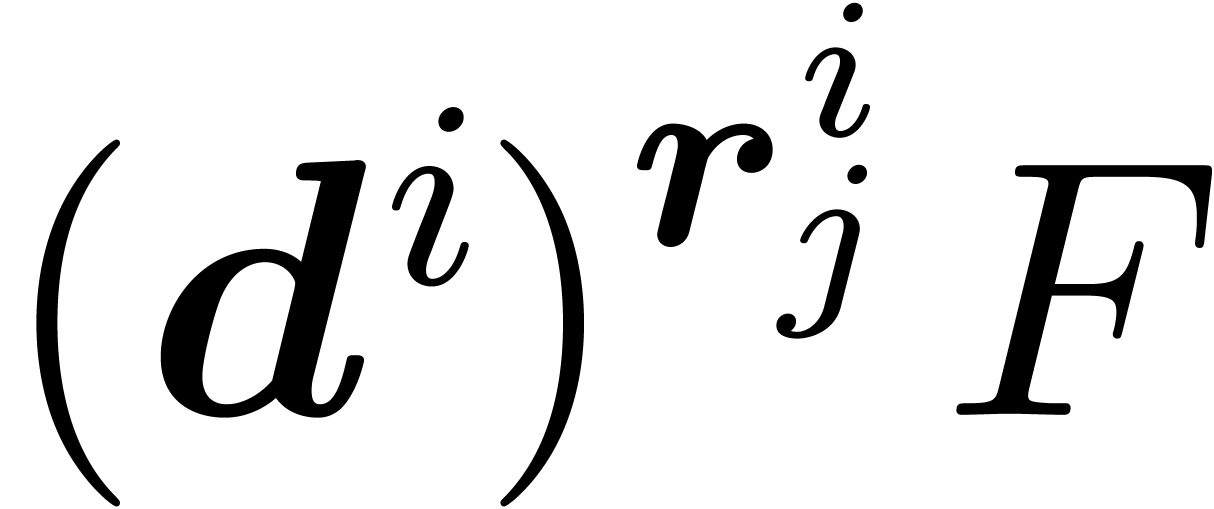 be
the leader of
be
the leader of 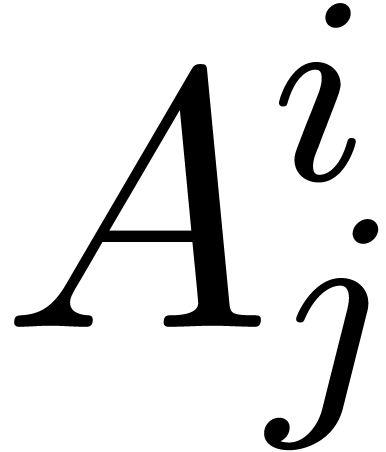 , and consider
the anti-chain
, and consider
the anti-chain 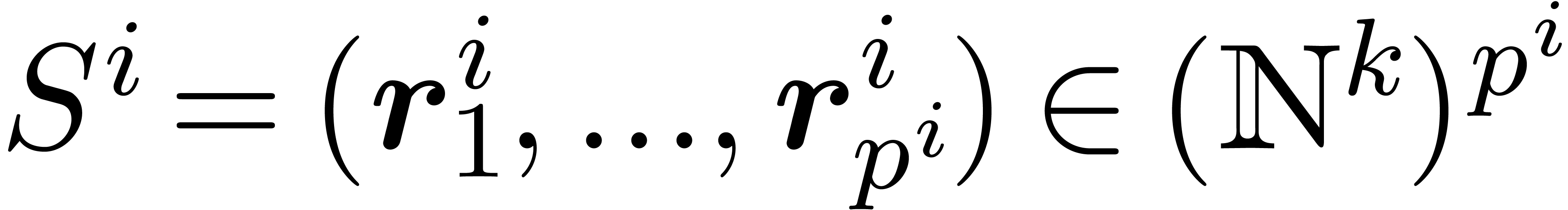 . Then
. Then 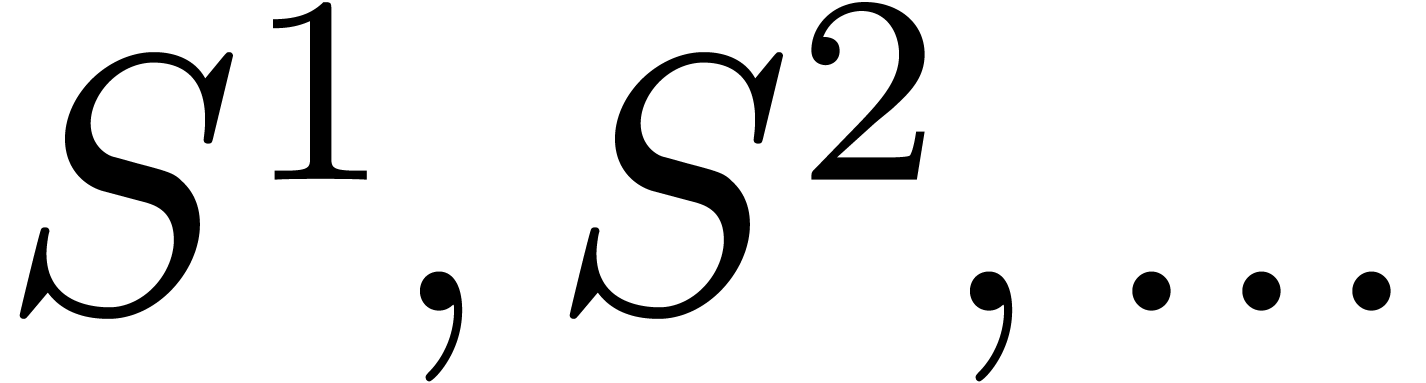 forms a decreasing sequence of anti-chains, which
implies the finiteness of the sequence.
forms a decreasing sequence of anti-chains, which
implies the finiteness of the sequence.
The argument from the proof of proposition 17 can be
generalized so as to provide asymptotic bases w.r.t.  . More precisely, let us consider a
Rosenfeld basis
. More precisely, let us consider a
Rosenfeld basis 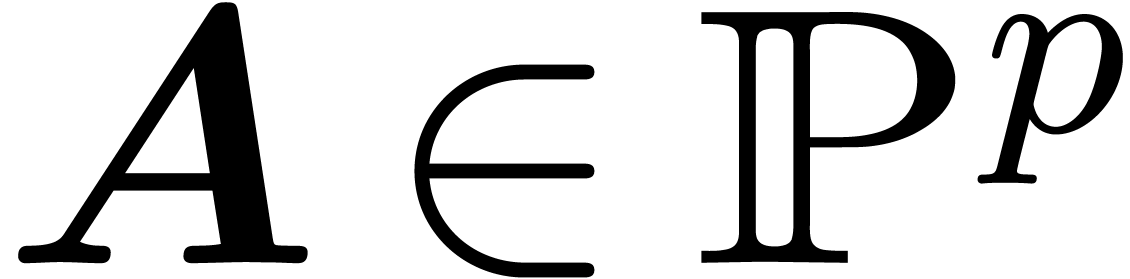 with
with 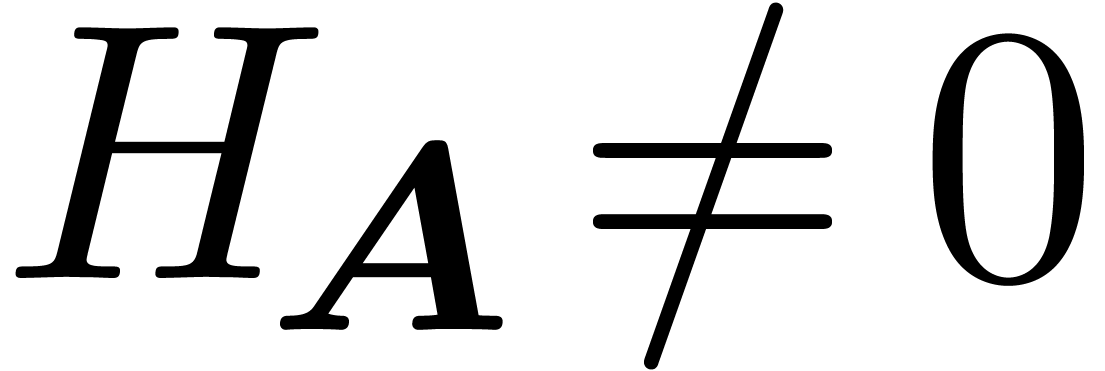 and
whose leaders are known. If
and
whose leaders are known. If 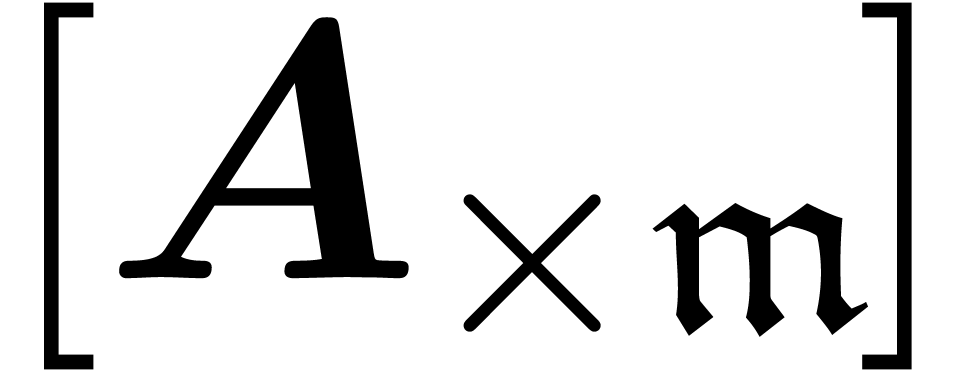 is quasi-linear for
a sufficiently small
is quasi-linear for
a sufficiently small 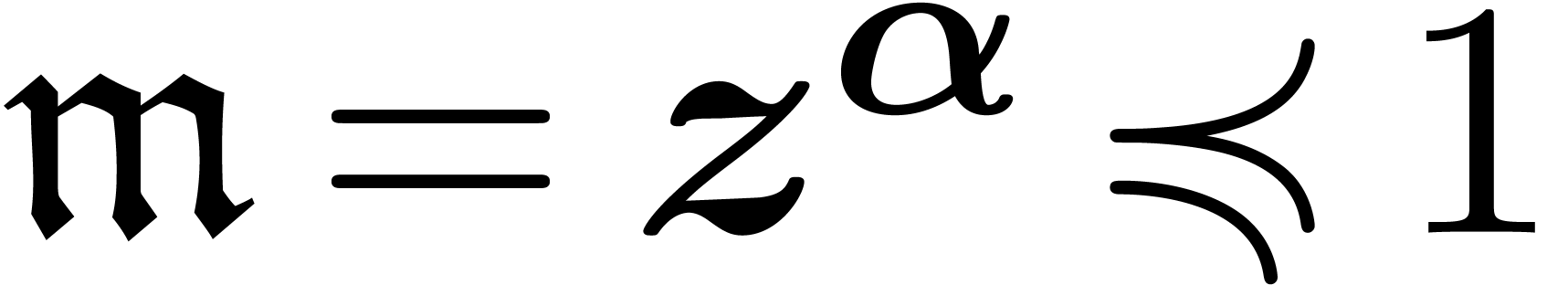 , then
we will show how to compute such an
, then
we will show how to compute such an  and an
asymptotic basis
and an
asymptotic basis  . If the
algorithm fails, then we will provide a proof that
. If the
algorithm fails, then we will provide a proof that  .
.
Algorithm ql_asymptotic_basis
Input: a Rosenfeld basis 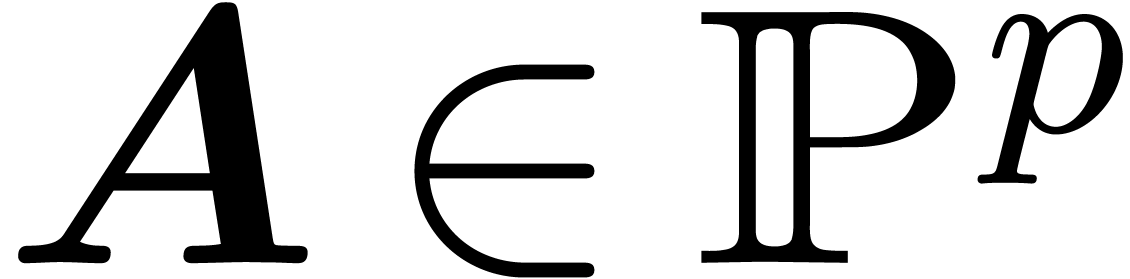 with
with
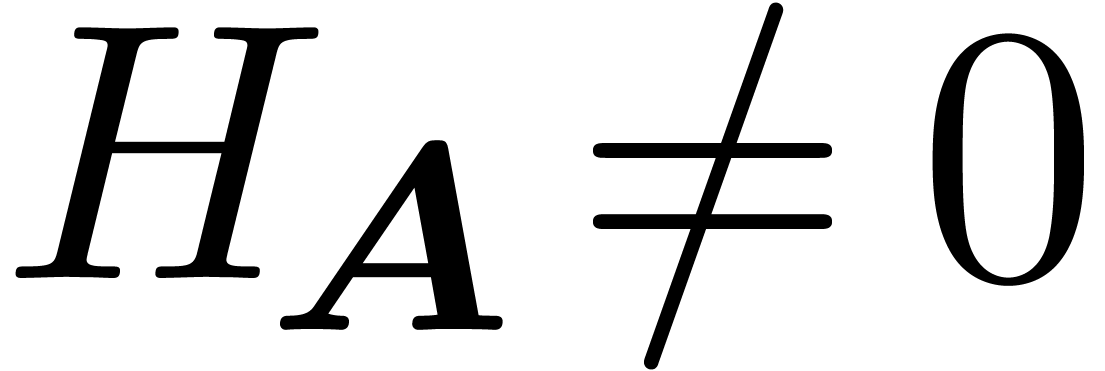 and known leaders.
and known leaders.
| Output: | an asymptotic basis for  for
some for
some  or or |
fail and a certificate that 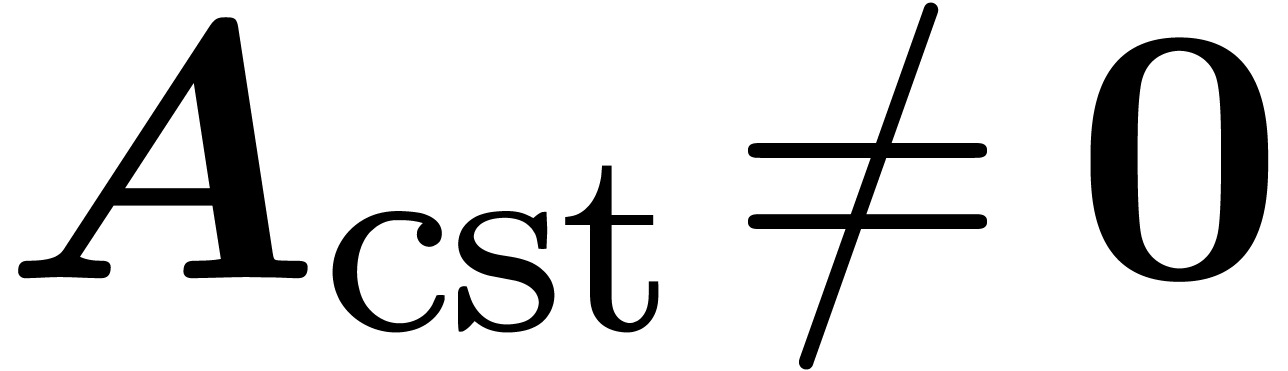 . . |
Step 1. [Initial asymptotic basis]
Let 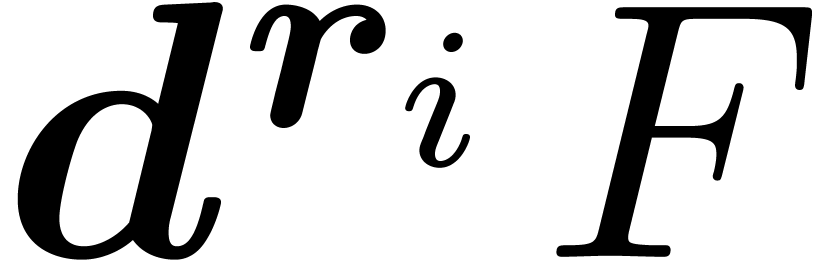 be the leader of
be the leader of  for each
for each  .
.
Take  sufficiently large, such that
sufficiently large, such that 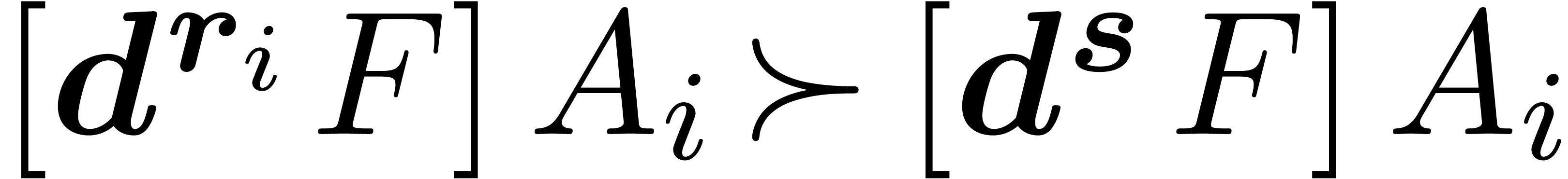 for all
for all  and
and  .
.
Replace  by
by  ,
where
,
where  is sufficiently small such that
is sufficiently small such that 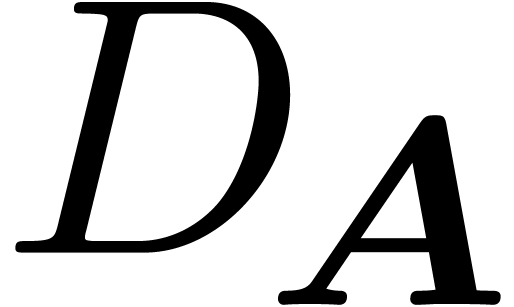 is affine.
is affine.
Go to step 4.
Step 2. [Dualization]
Normalize  .
.
Compute 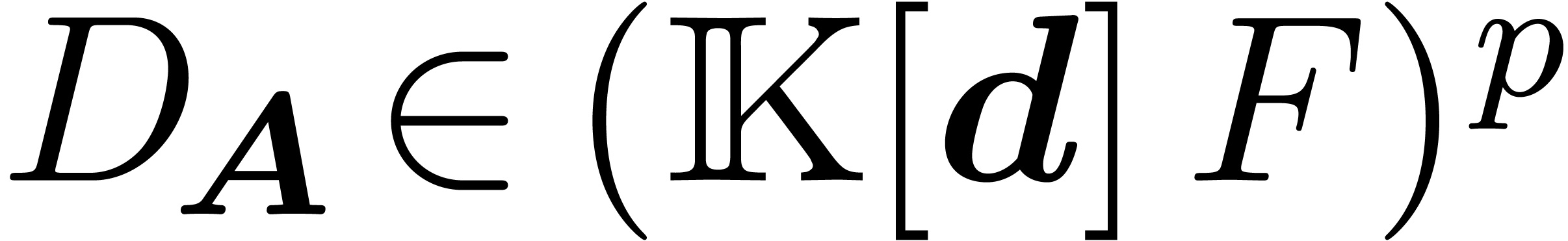 with respect to
with respect to  .
.
Using the tangent cone algorithm, find a Rosenfeld co-basis  for
for 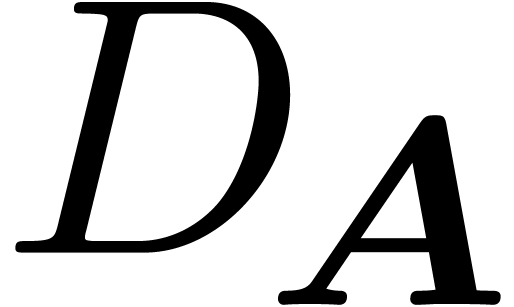 .
.
For each  , let
, let 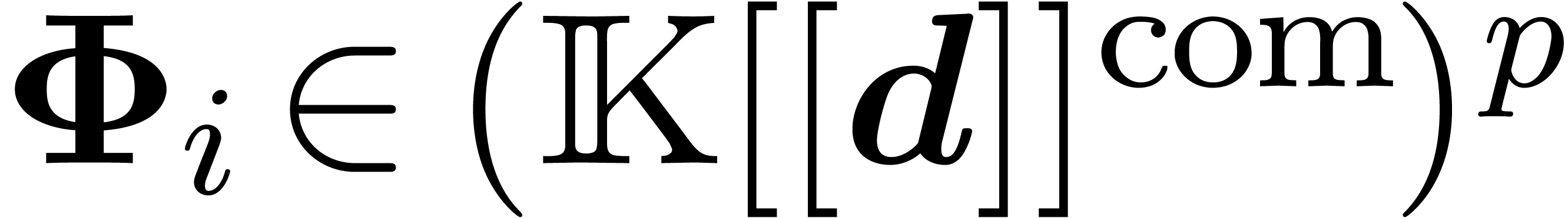 be such that
be such that  .
.
Replace  by
by  .
.
Step 3. [Change derivations]
Compute the next critical derivation 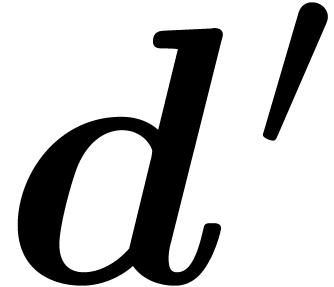 and
replace
and
replace  by
by 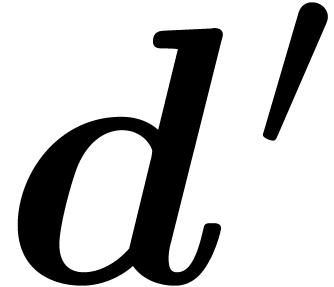 .
.
Replace  by
by  ,
where
,
where  is sufficiently small such that
is sufficiently small such that 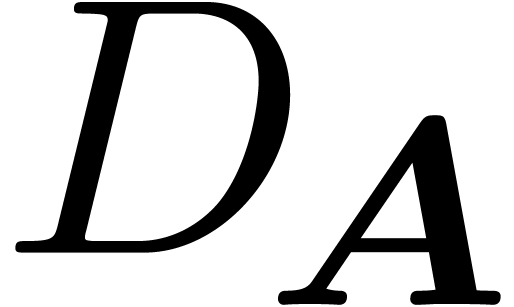 is affine.
is affine.
Step 4. [Done?]
If  , then return
fail.
, then return
fail.
If 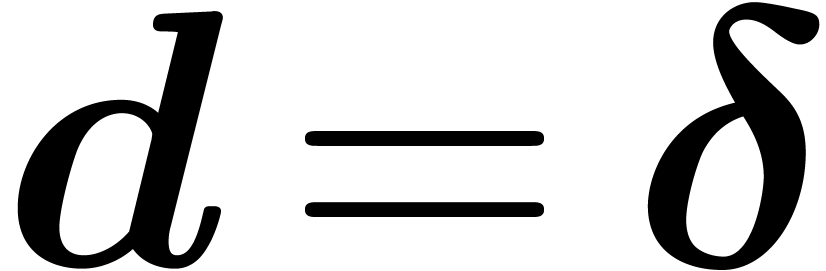 , then return
, then return  .
.
Otherwise, go to step 2.
Proof. The algorithm is a perturbation of the
algorithm  , in which case the previous correction and
termination proof generalizes. Whenever
, in which case the previous correction and
termination proof generalizes. Whenever  in step
4, this implies in particular that
in step
4, this implies in particular that 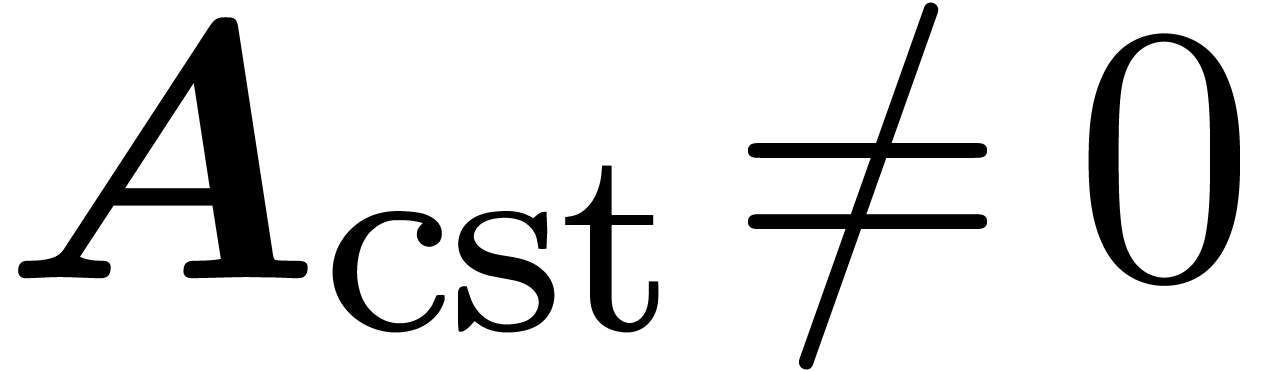 for the input
basis
for the input
basis  .
.
Until now, we have not really used the fact that the derivations are
allowed to act in a non-trivial way on  .
In the next section, we will work over
.
In the next section, we will work over 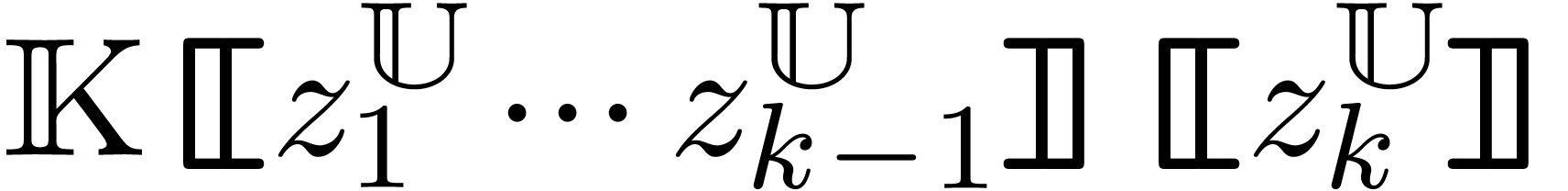 instead
of
instead
of  . This requires some
adaptations of proposition 15.
. This requires some
adaptations of proposition 15.
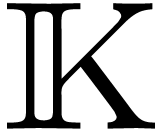 be a field of
constants for
be a field of
constants for  and consider an asymptotic basis
and consider an asymptotic basis
 . Then
. Then 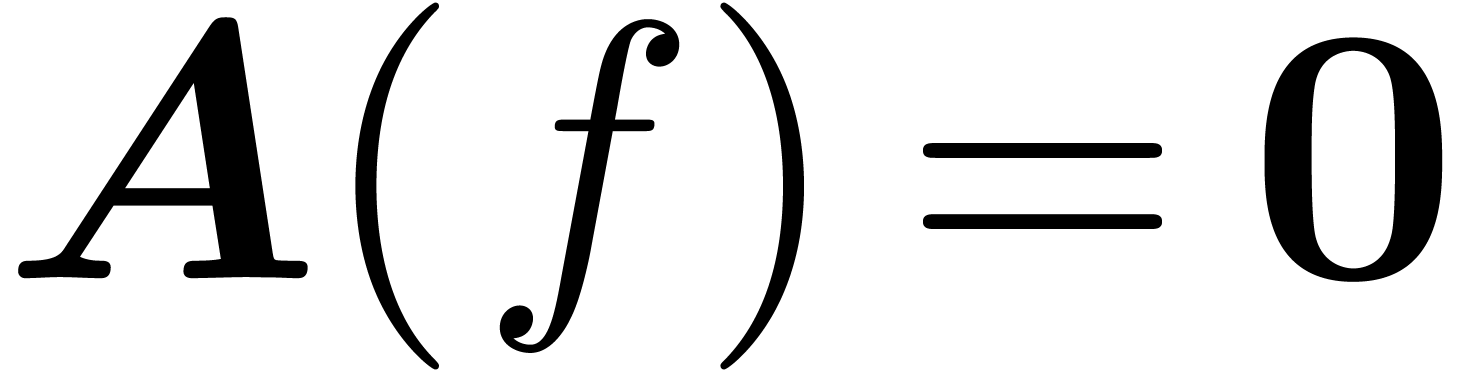 admits a solution in
admits a solution in 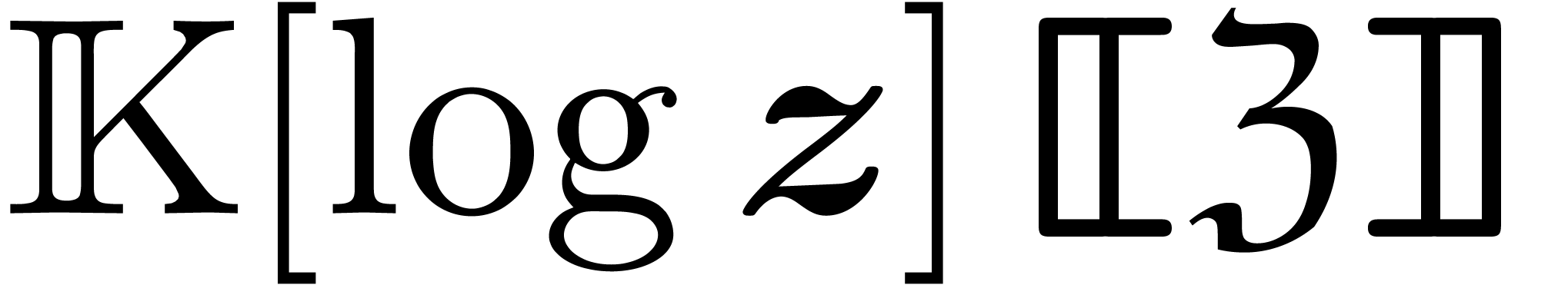 .
.
Proof. This is proved using a straightforward
adaptation of the proof of proposition 15.
 be a field of
constants for
be a field of
constants for  and consider a Rosenfeld basis
and consider a Rosenfeld basis
 . Then
. Then 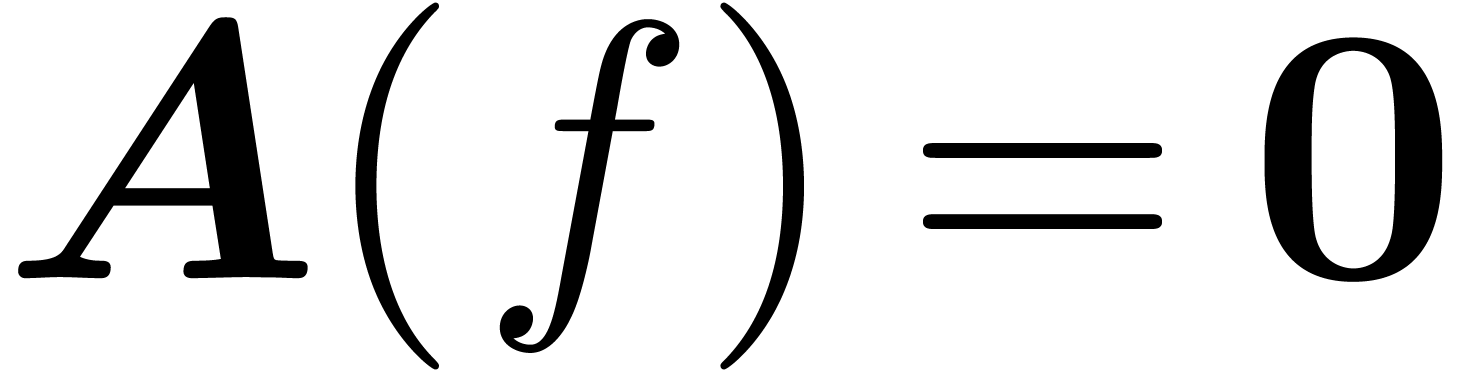 admits a solution in
admits a solution in 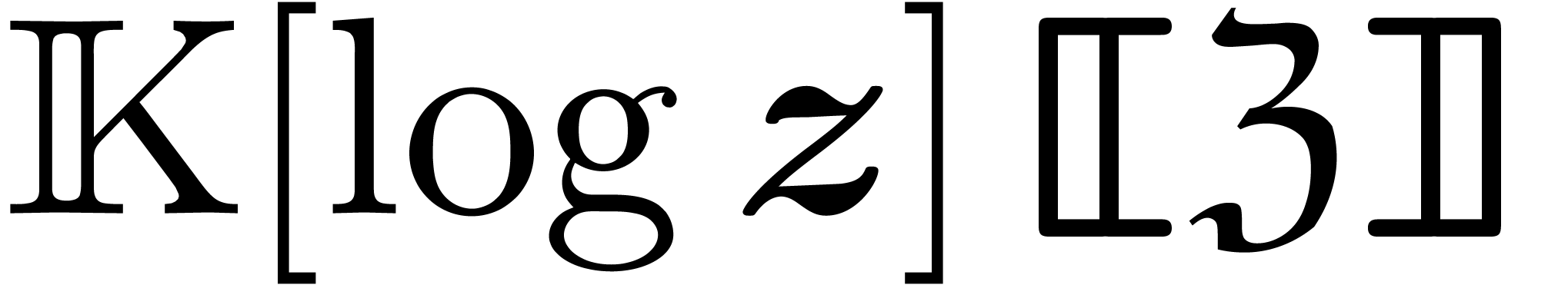 .
.
Proof. Using a procedure similar to ql_asymptotic_basis,
we may compute a monomial  in
in  such that
such that 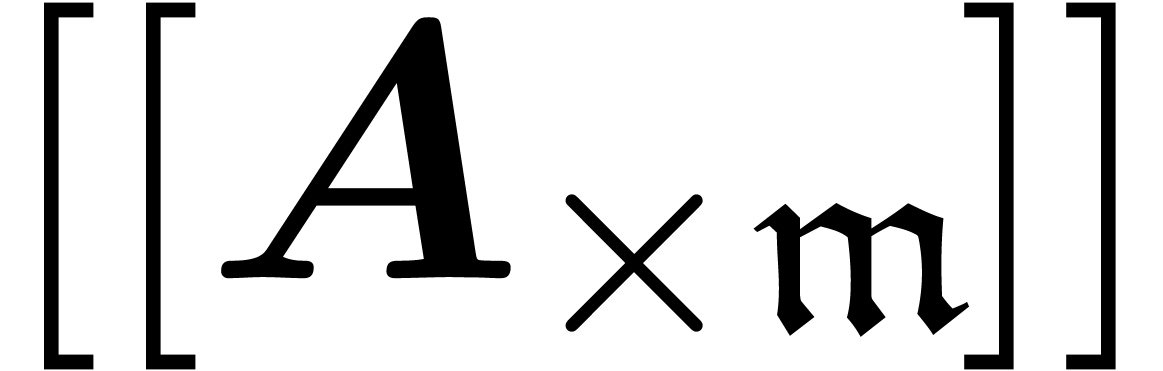 is quasi-linear w.r.t.
is quasi-linear w.r.t.
 . Indeed, since
. Indeed, since  admits no non-linear terms, instead of choosing
admits no non-linear terms, instead of choosing  such that
such that  is affine in steps 1 and
3, we may now choose
is affine in steps 1 and
3, we may now choose  sufficiently large such
that
sufficiently large such
that  is linear. By proposition 25,
is linear. By proposition 25,
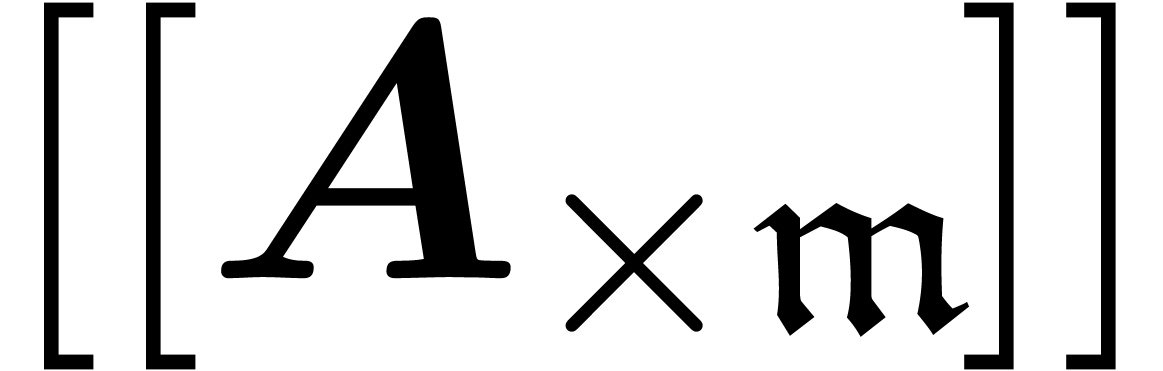 admits a zero
admits a zero  in
in  . It follows that
. It follows that  is a solution to
is a solution to  .
.
Assume now that we wish to work over 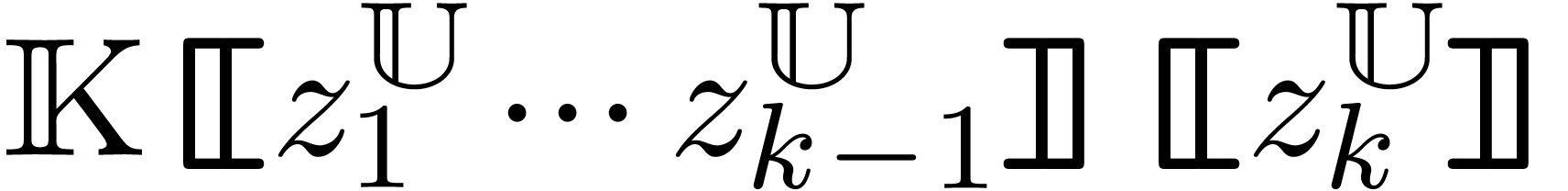 instead of
instead of
 . This fits in our setting by
taking
. This fits in our setting by
taking 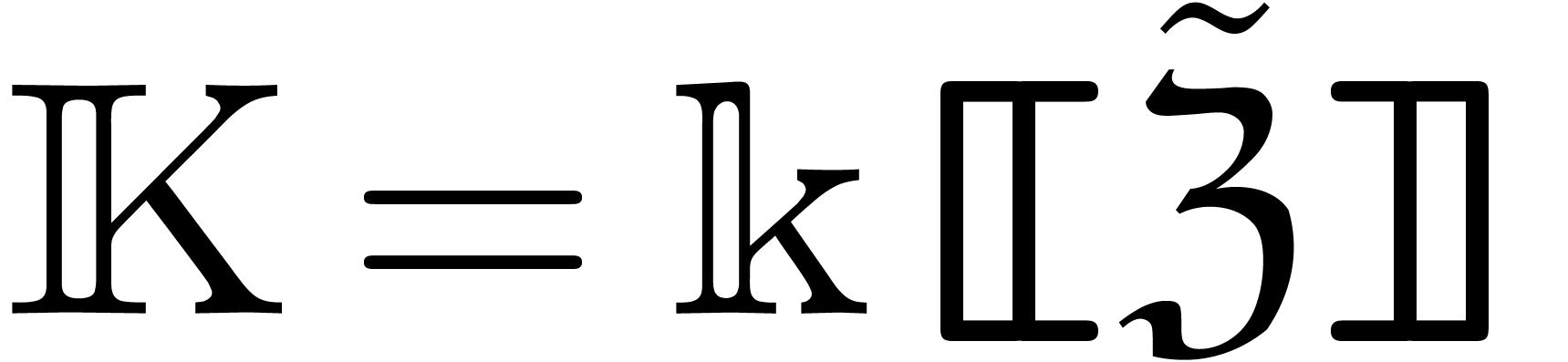 for a constant field
for a constant field  and a copy
and a copy 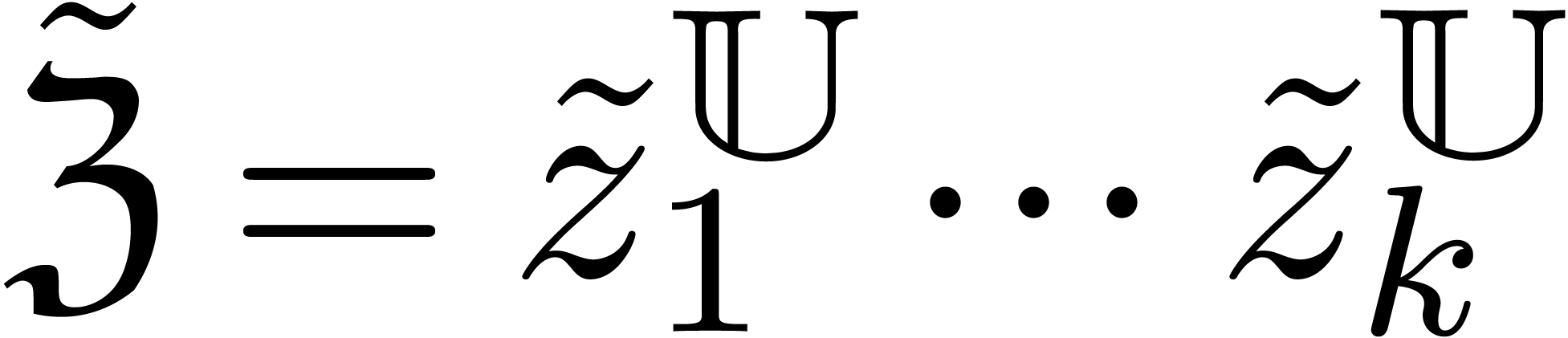 of
of  with
with 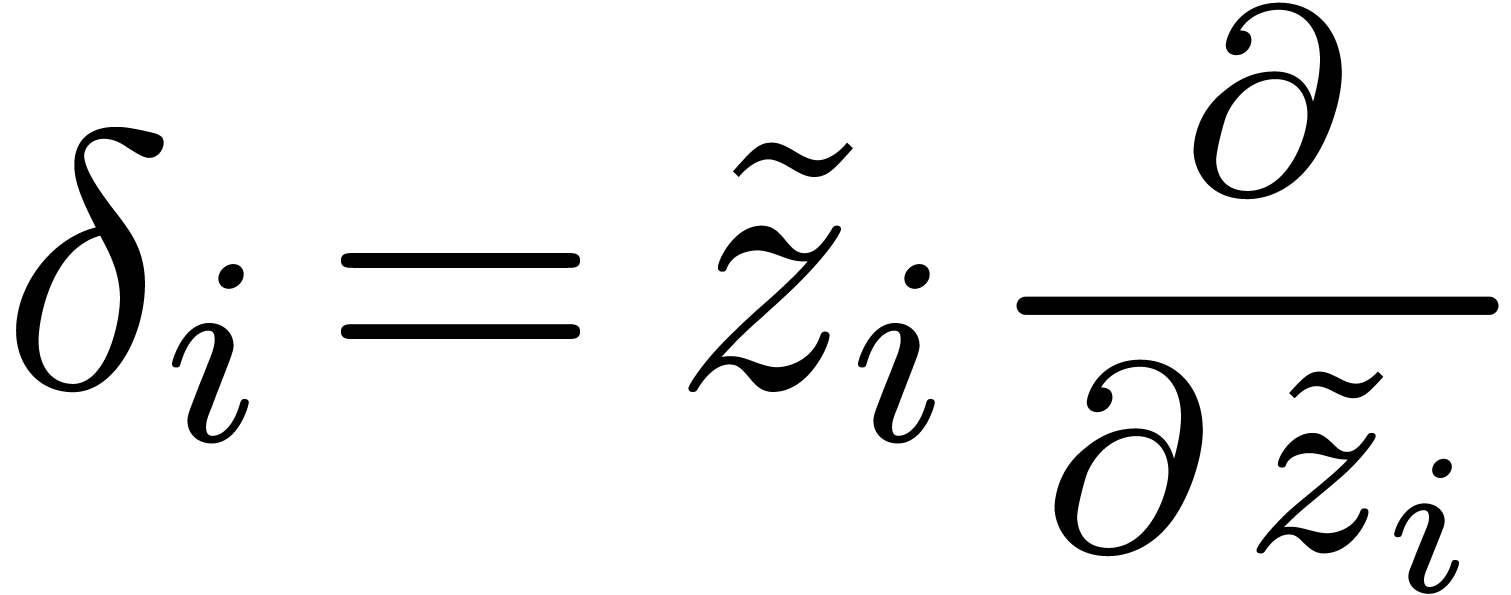 on
on  . The
variables
. The
variables  and
and  will
simply be ignored.
will
simply be ignored.
 be a field of
constants for
be a field of
constants for  . Denote
. Denote 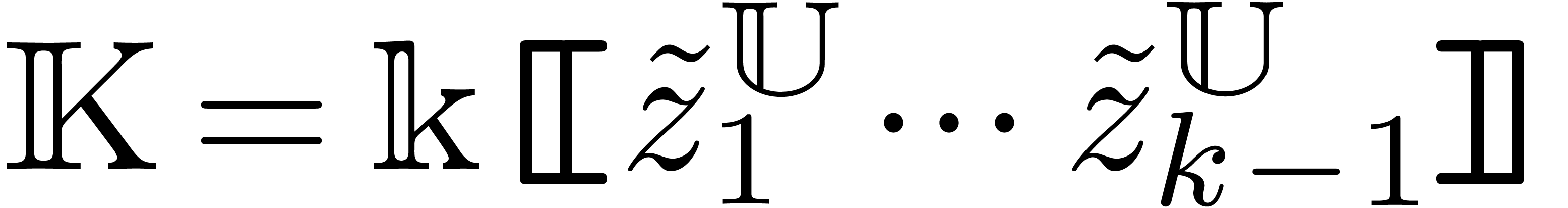 and
and 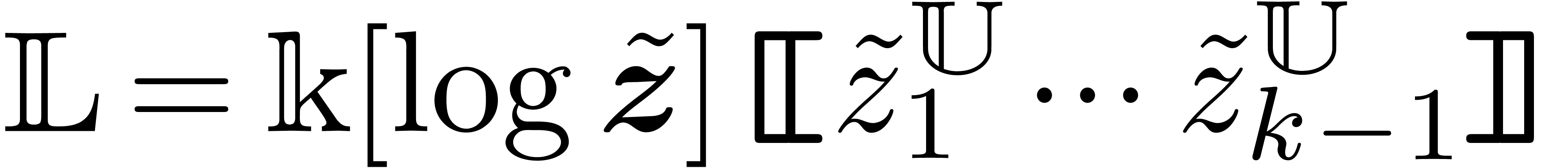 .
Consider an asymptotic basis
.
Consider an asymptotic basis 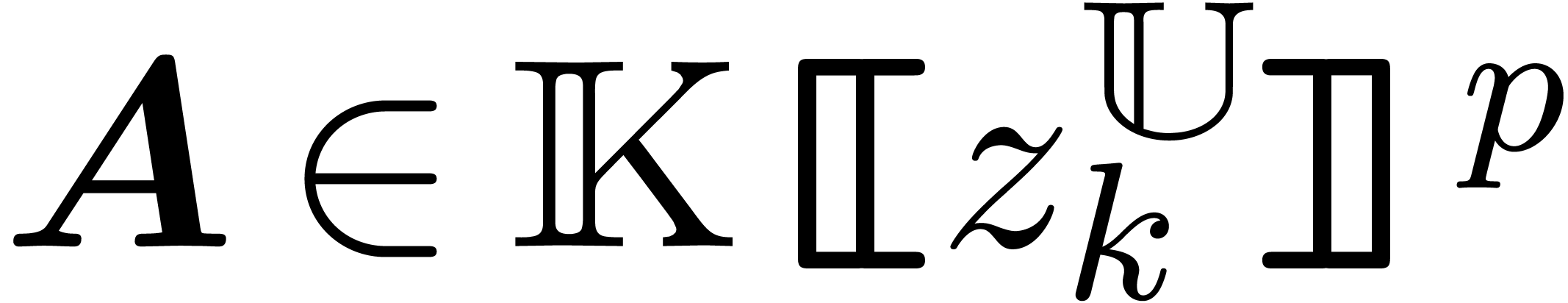 .
Then there exists an
.
Then there exists an 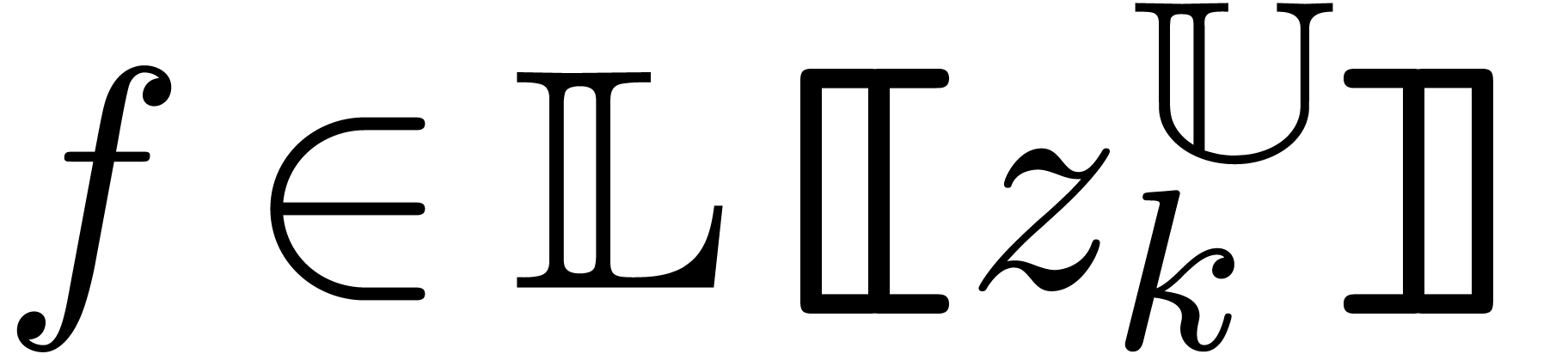 with
with 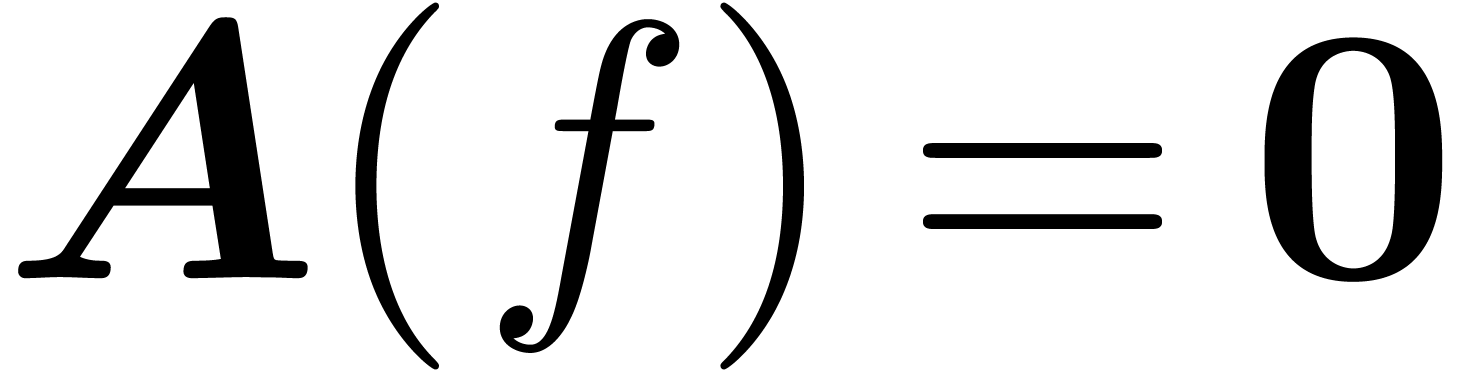 and
and  as a series in
as a series in 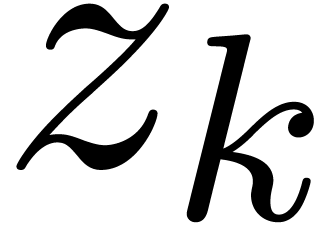 .
.
Proof. The proof is analogous to the proof of
proposition 15. We first notice that the absence of the
variables  from
from  implies
their absence in the asymptotic critical relations and during all
computations in the proof. This time, the Rosenfeld basis
implies
their absence in the asymptotic critical relations and during all
computations in the proof. This time, the Rosenfeld basis  lies in
lies in  instead of
instead of 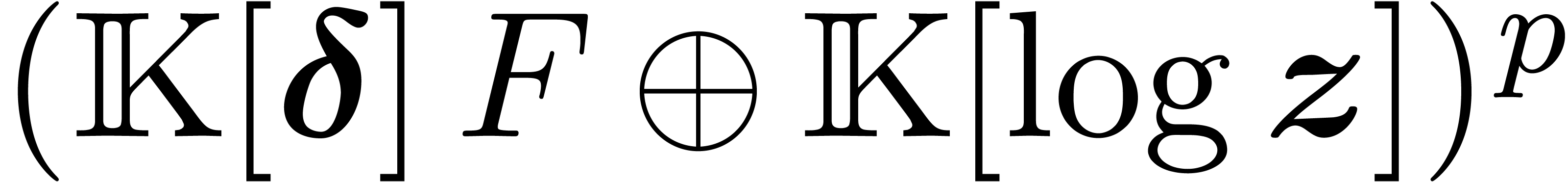 . By proposition 26, the equation
. By proposition 26, the equation
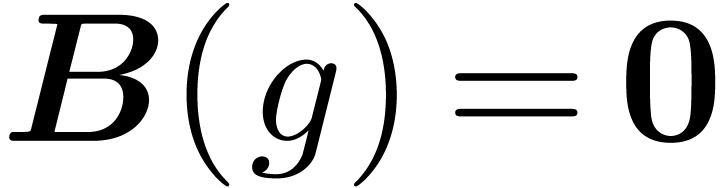 admits a solution in
admits a solution in 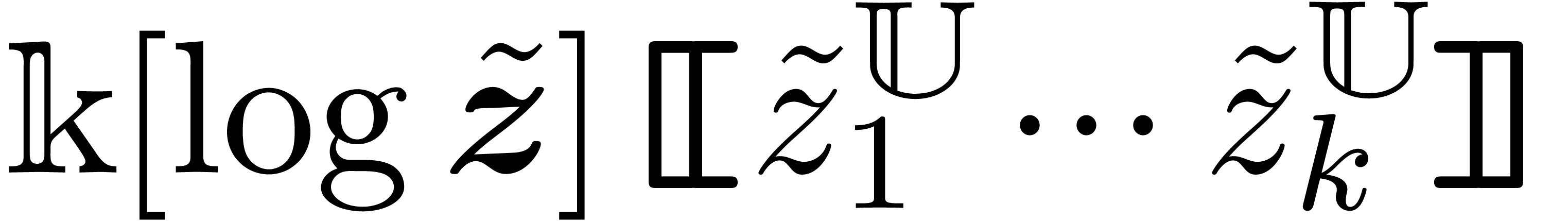 . Since
. Since  does not occur in
does not occur in
 (regarding
(regarding 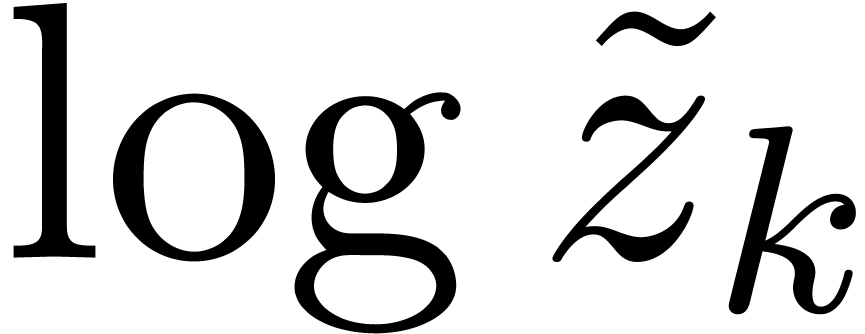 and
and 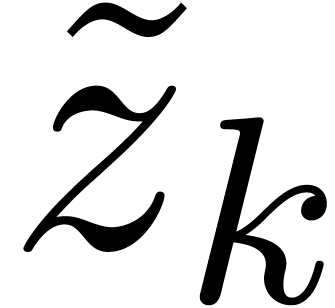 as separate variables), the constant term
as separate variables), the constant term  of
of  w.r.t.
w.r.t. 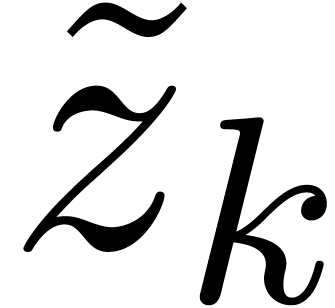 is again a zero of
is again a zero of  . This
ensures that the analogue of the proof of proposition 15
goes through.
. This
ensures that the analogue of the proof of proposition 15
goes through.
Let  be an effective field with an effective
zero-test. Assume that we are given an effective differential subring
be an effective field with an effective
zero-test. Assume that we are given an effective differential subring
 of
of  for
for  with an effective zero-test. Assume also that the coefficients of
with an effective zero-test. Assume also that the coefficients of 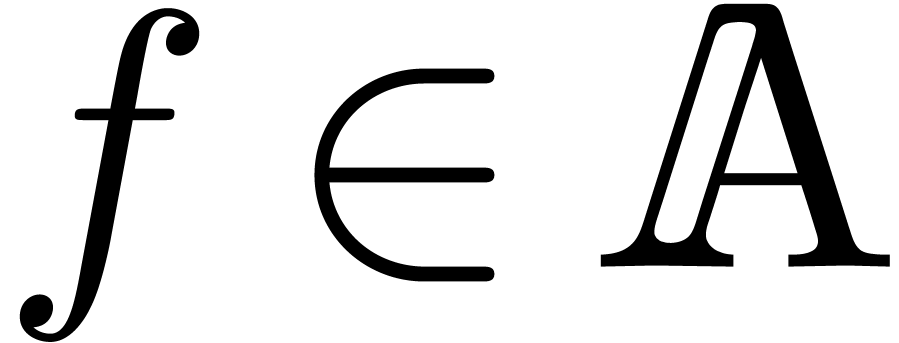 as a series in
as a series in  are still in
are still in
 and that there exists an algorithm to compute
them. These coefficients lie in the effective differential ring
and that there exists an algorithm to compute
them. These coefficients lie in the effective differential ring 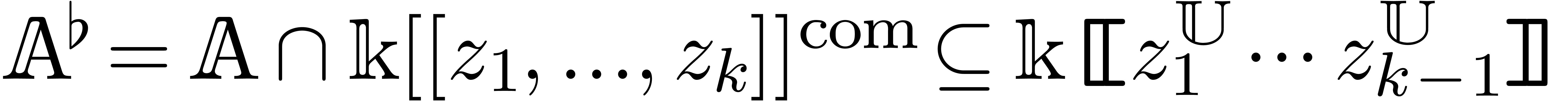 . We will denote by
. We will denote by  the quotient field of
the quotient field of 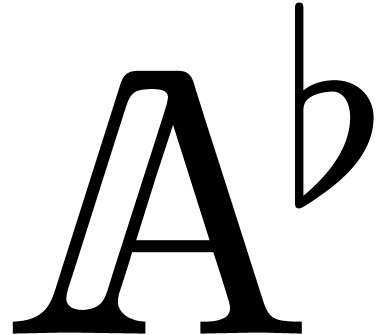 .
In view of the previous section, we may apply the theory from this paper
for series in the field
.
In view of the previous section, we may apply the theory from this paper
for series in the field 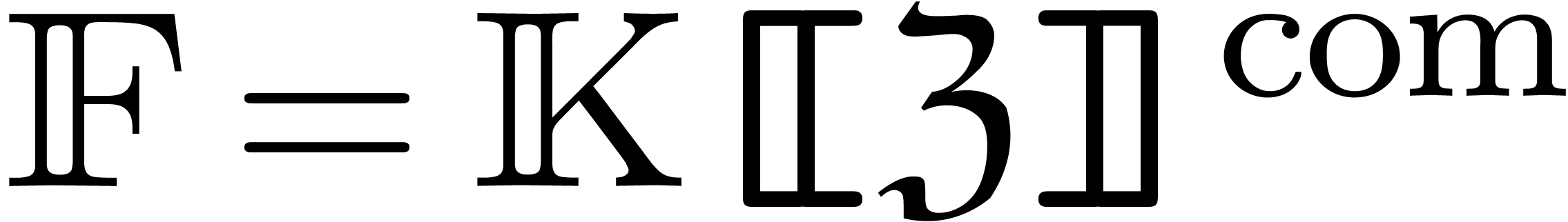 ,
where
,
where 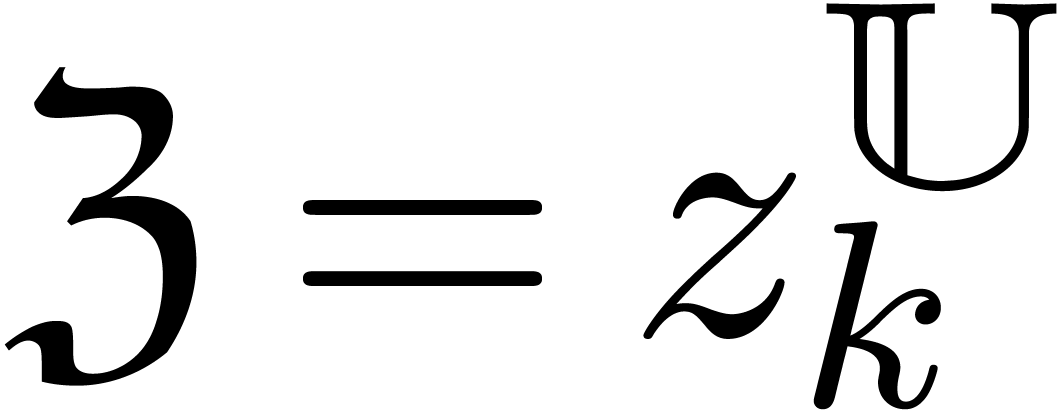 .
.
Let  be a partial differential equation with a
solution
be a partial differential equation with a
solution  and coefficients
and coefficients 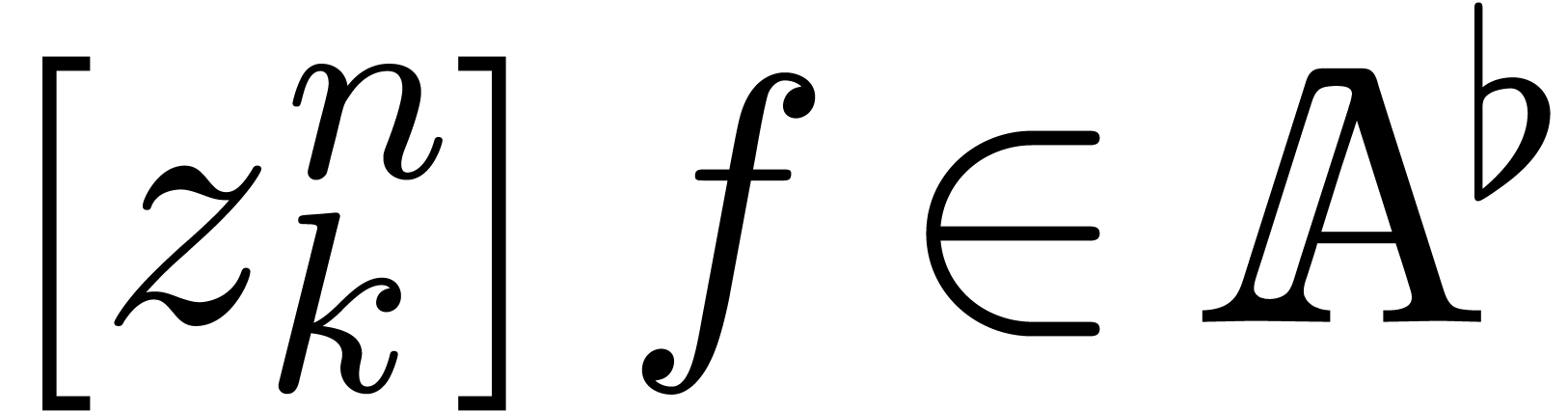 . Assume that there exists an order
. Assume that there exists an order 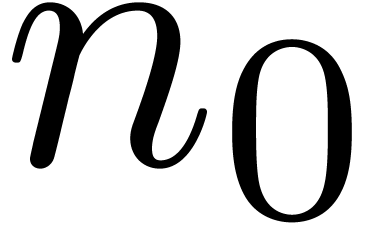 such that the equation
such that the equation
 |
(23) |
admits only  as a solution in
as a solution in  . This is typically the case when
. This is typically the case when  is sufficiently non-singular, so that the coefficients of
is sufficiently non-singular, so that the coefficients of
 in
in 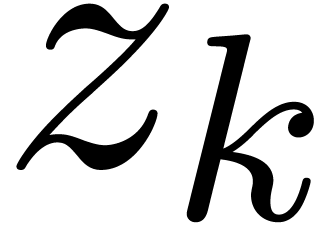 are given by a
recurrence relation. The differential ring
are given by a
recurrence relation. The differential ring  is
clearly a subring of
is
clearly a subring of  . We
will now give an effective zero-test in this ring.
. We
will now give an effective zero-test in this ring.
Algorithm zero_test
Input: a polynomial  .
.
Output: true if 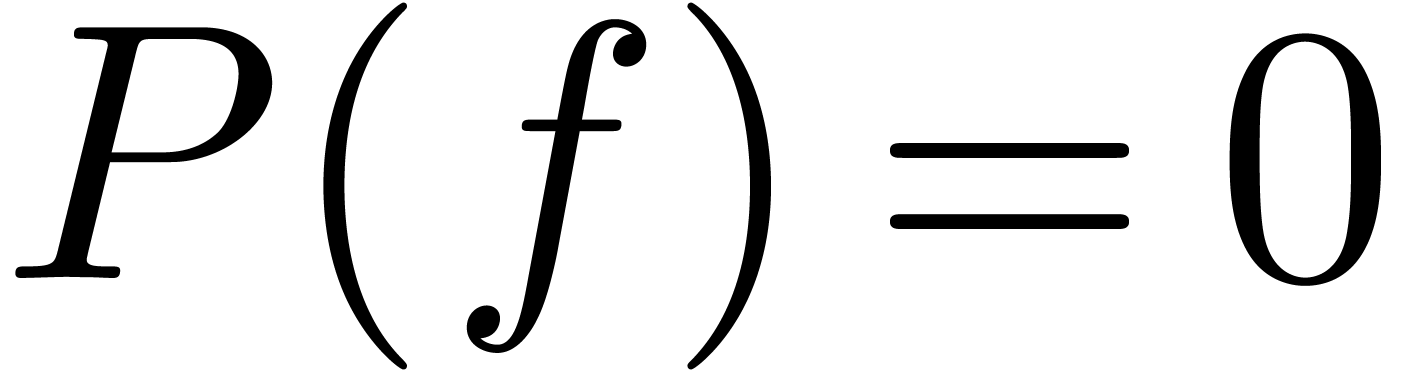 and false otherwise.
and false otherwise.
Step 1. [Initial order]
Set 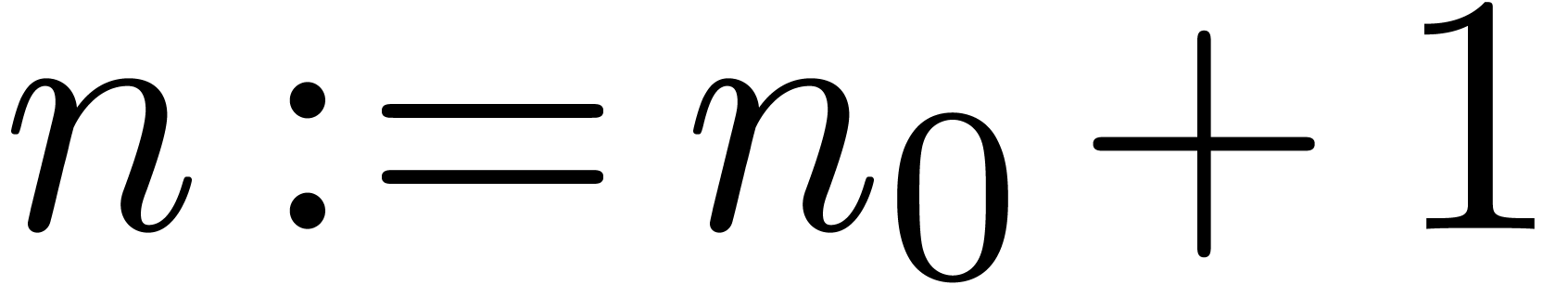 and
and 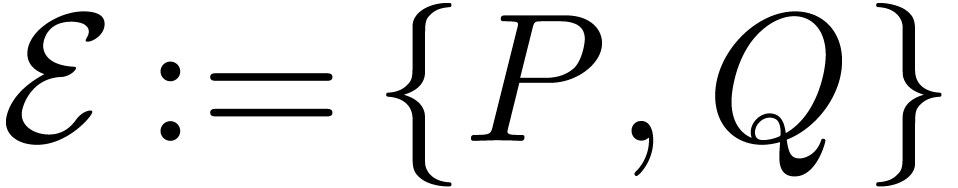 .
.
Step 2. [Rosenfeld basis]
If 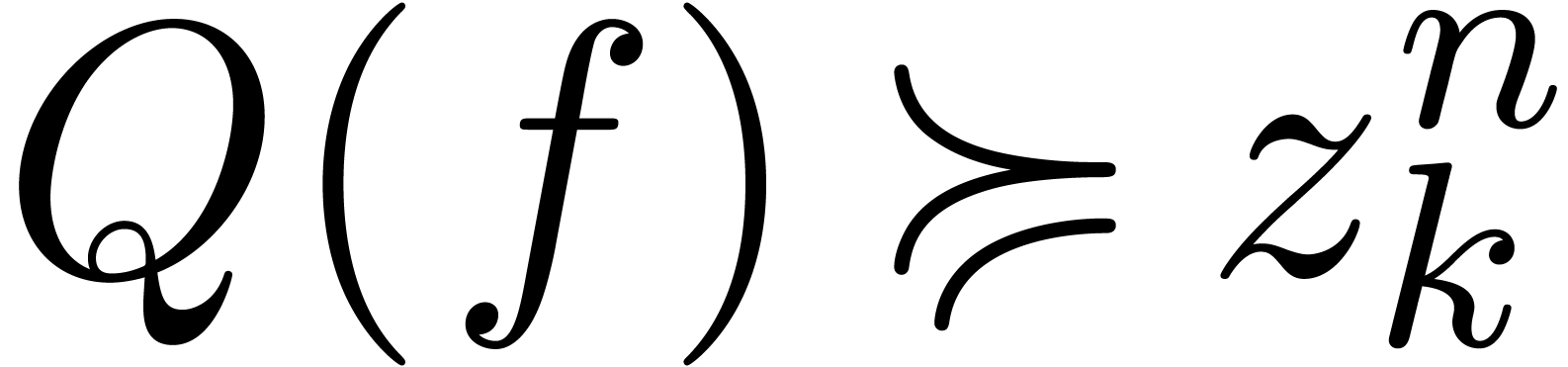 then return false.
then return false.
Compute a Rosenfeld basis  for
for  .
.
Let  be the subset of
be the subset of  with
with 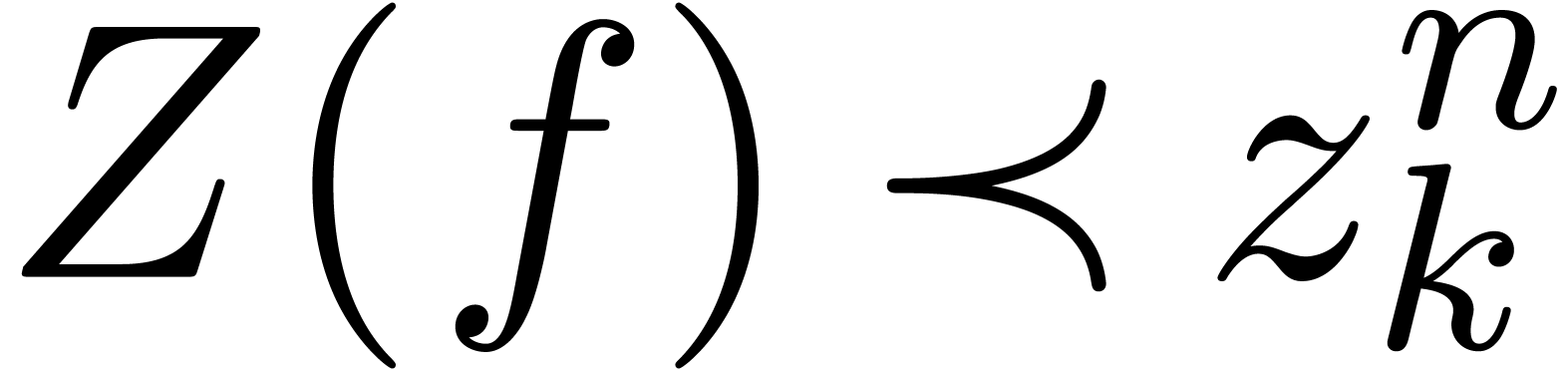 .
.
If  then set
then set  and repeat
step 2.
and repeat
step 2.
Step 3. [Certification]
If ql_asymptotic_basis( )
does not return fail, then return
true.
)
does not return fail, then return
true.
Step 4. [Increase order]
Set  and
and 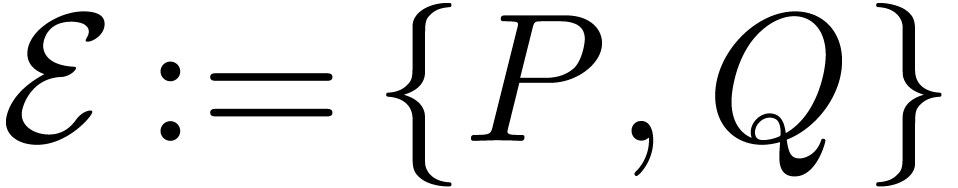 .
.
Return to step 2.
Proof. Let us first prove the correctness. If
the algorithm returns false, then we clearly have 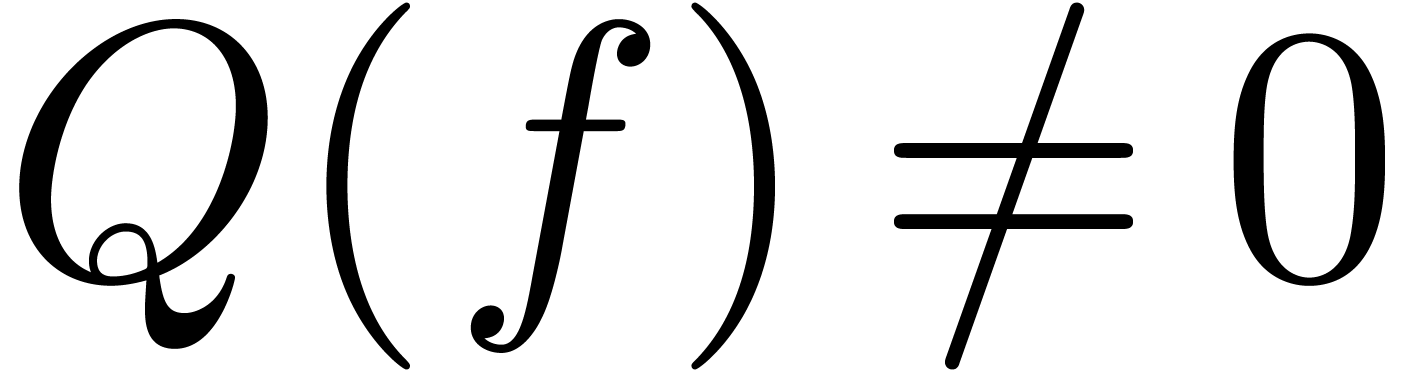 . If the algorithm returns
true, then the ideal
. If the algorithm returns
true, then the ideal  is
quasi-linear in step 3. By proposition 27, this implies the
existence of a zero
is
quasi-linear in step 3. By proposition 27, this implies the
existence of a zero  with
with  . Since
. Since 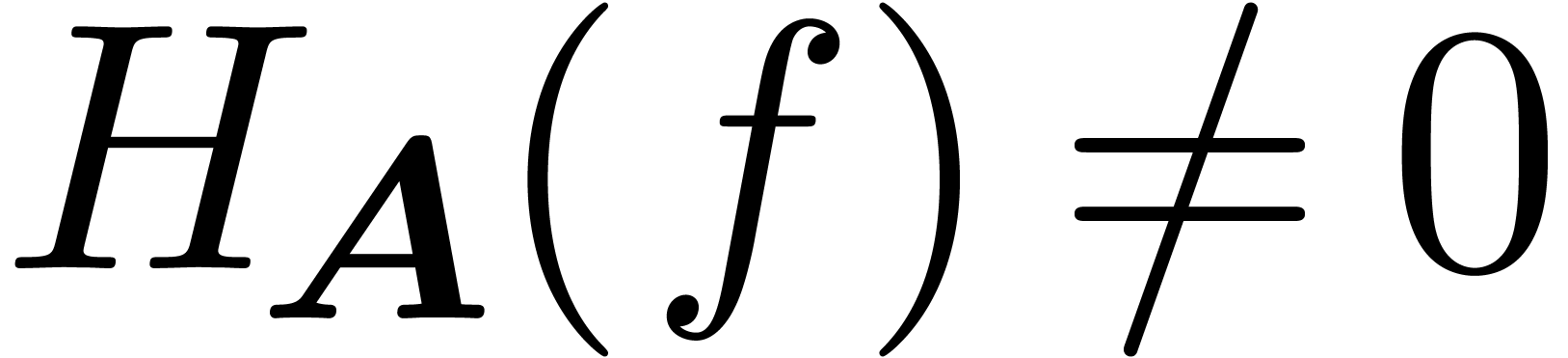 ,
any solution of
,
any solution of  is also a solution of
is also a solution of  and of
and of  . It
follows that
. It
follows that 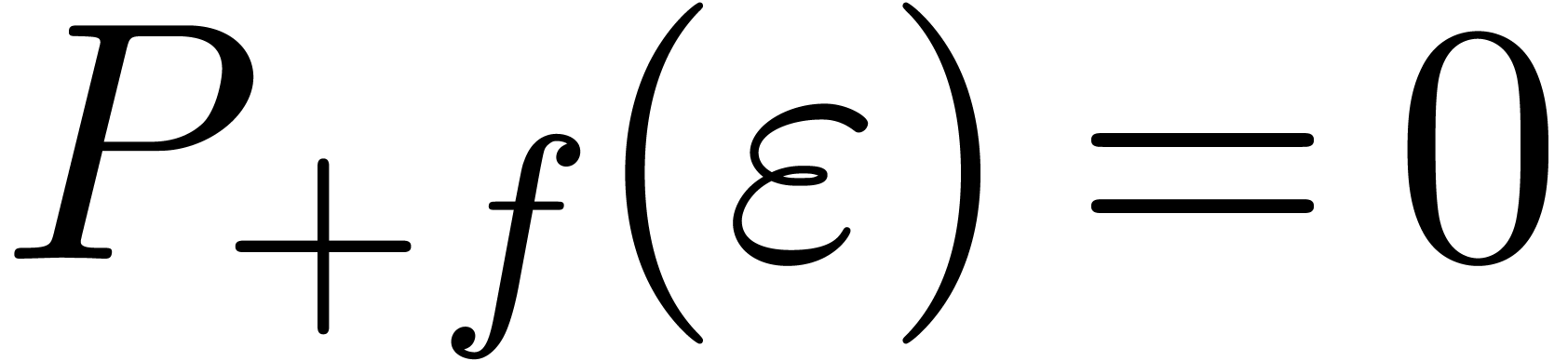 for
for 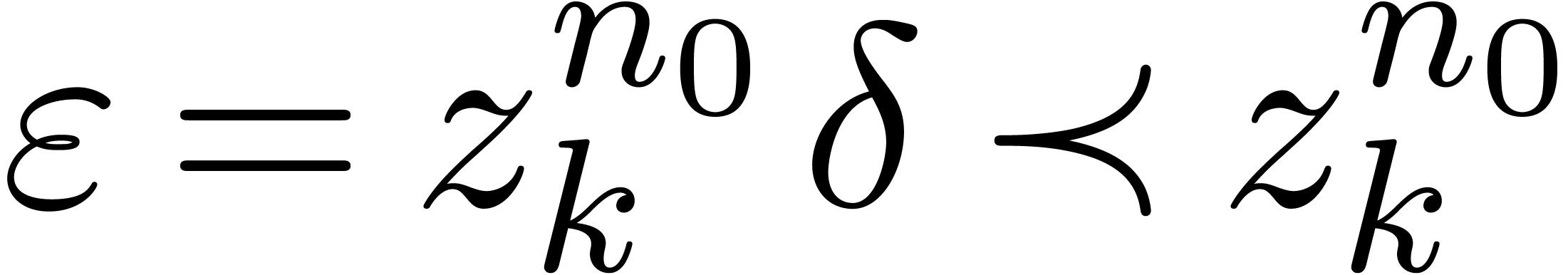 .
But we assumed that
.
But we assumed that 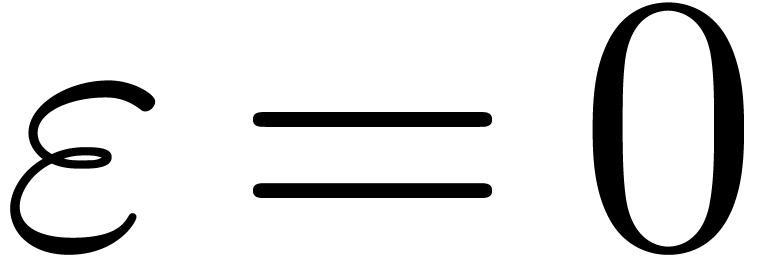 is the only solution to (23). It follows that
is the only solution to (23). It follows that 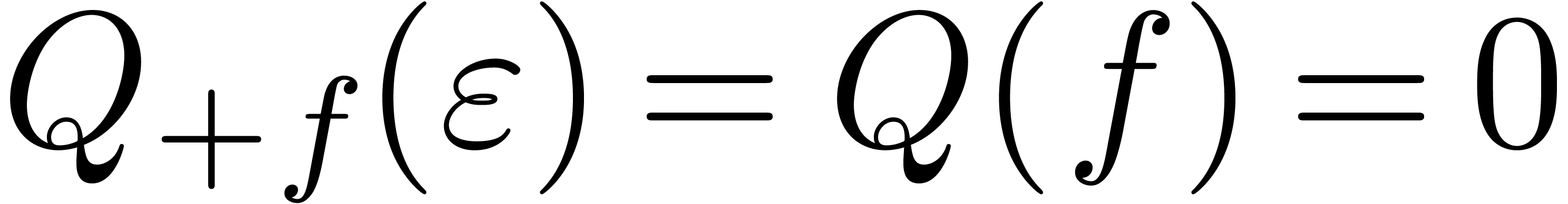 .
.
Let us now prove the termination. For a fixed order 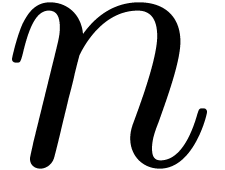 , the loop in step 2 terminates because the
successive rankings of
, the loop in step 2 terminates because the
successive rankings of  are lower and lower. If
are lower and lower. If
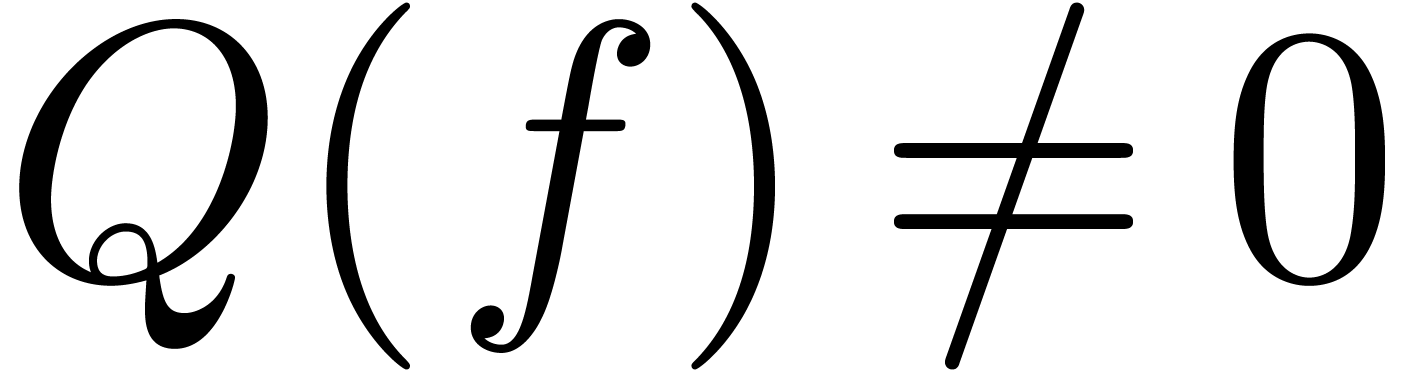 , then we clearly have
, then we clearly have  for a sufficiently large
for a sufficiently large 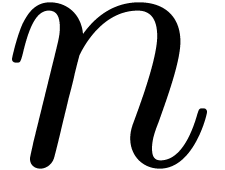 . If
. If 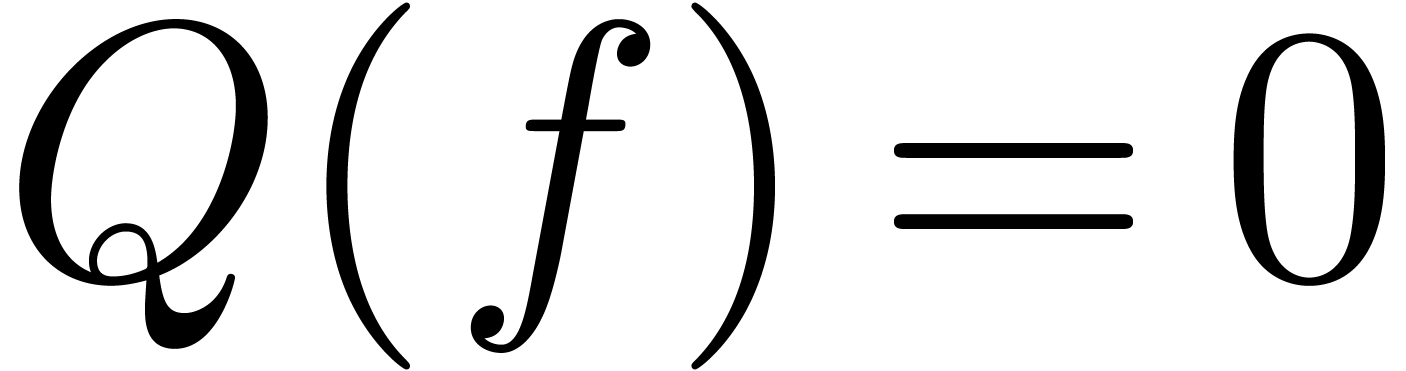 ,
then, for a sufficiently large
,
then, for a sufficiently large  ,
we have
,
we have  for all
for all  considered in step 2. Consequently, the successive values of
considered in step 2. Consequently, the successive values of  in step
in step  all satisfy
all satisfy 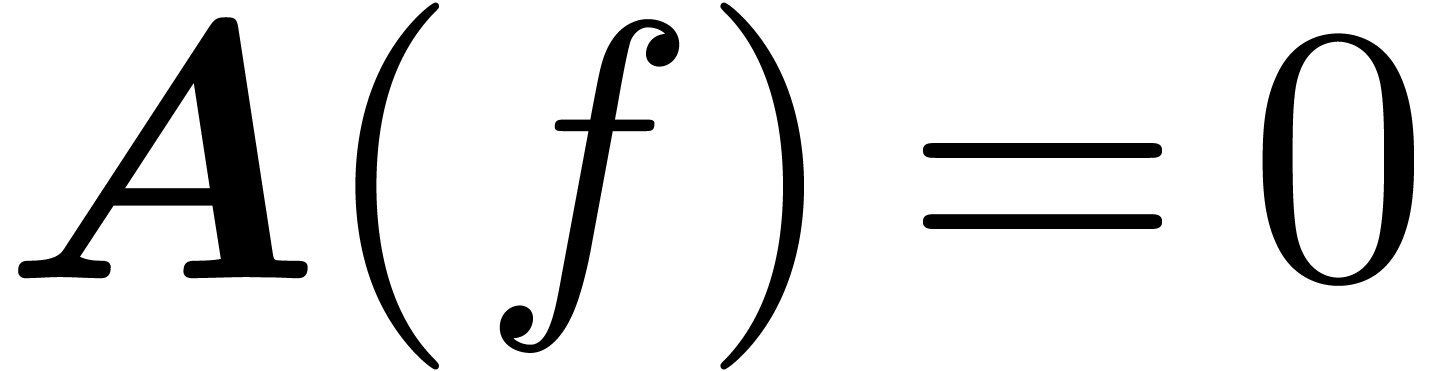 . When entering step 3, we therefore have
. When entering step 3, we therefore have 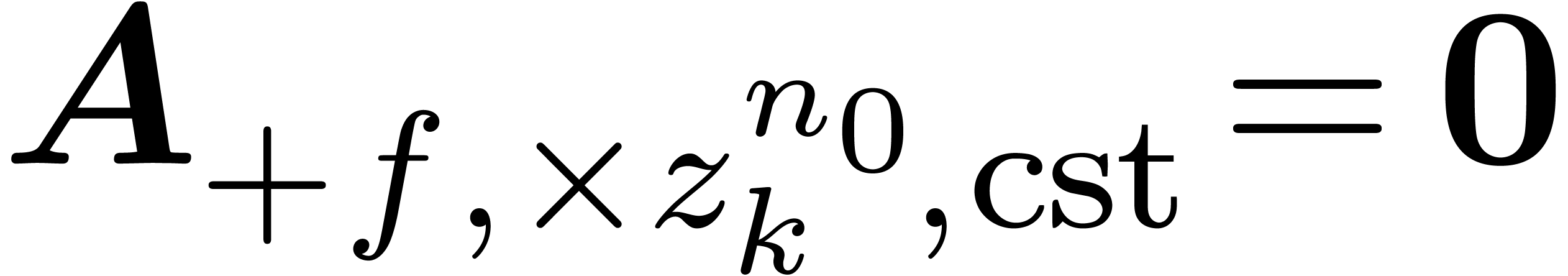 , whence ql_asymptotic_basis
does not return fail.
, whence ql_asymptotic_basis
does not return fail.
Several remarks can be made about the generality of our zero-test. In order to avoid unnecessary complications of the notations, we have presented our algorithm in the case when we adjoin a single solution to a partial differential equation with initial conditions. Of course, the theory of differential algebra also works for differential polynomials in a finite number of indeterminates. It should be straightforward to generalize our zero-test to the case when we adjoin several solutions at the same time.
Similarly, we may replace the single equation 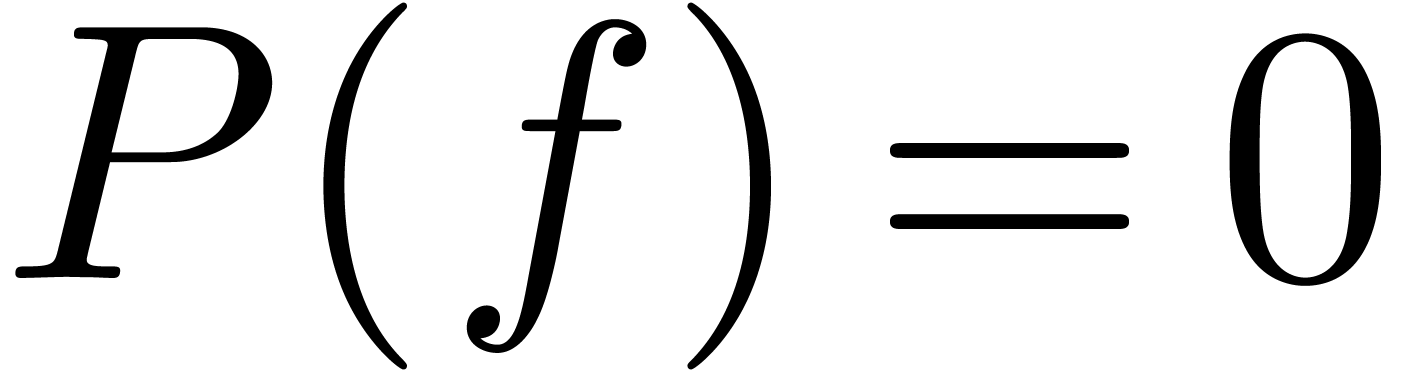 by
a system of equations
by
a system of equations 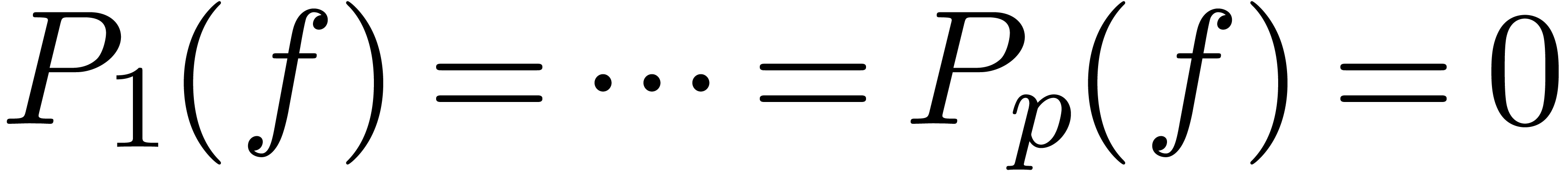 . In
that case, the initial conditions generally lay in the ring
. In
that case, the initial conditions generally lay in the ring 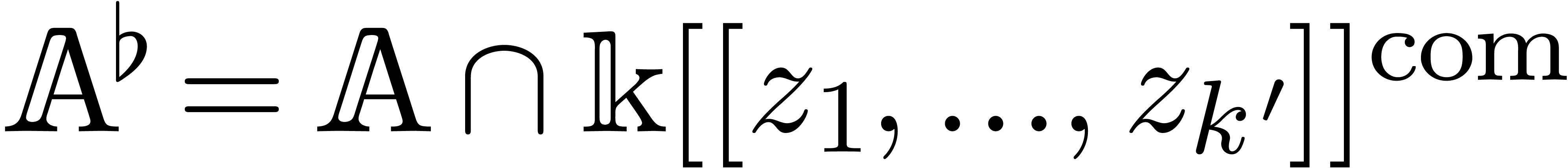 for some
for some  . In
particular, this requires to take
. In
particular, this requires to take 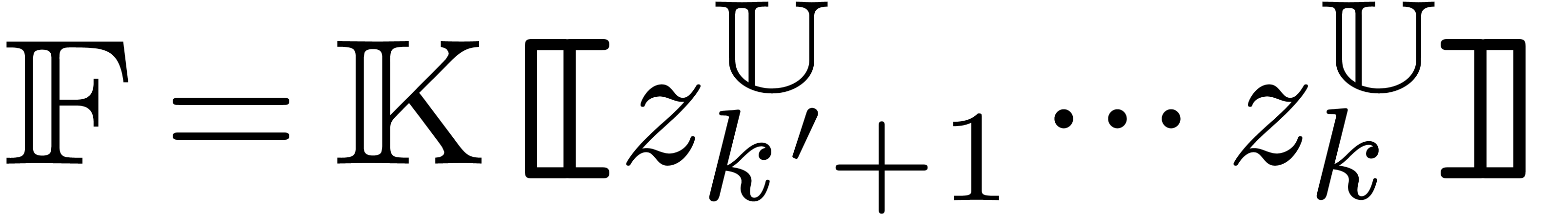 ,
where
,
where  is the quotient field of
is the quotient field of  .
.
We assumed that  is the unique solution in
is the unique solution in  to (23). This condition is usually met
in practice and in particular when Cauchy-Kovalevskaya's theorem
applies. Nevertheless, the condition can probably be weakened to the
existence of a unique solution in
to (23). This condition is usually met
in practice and in particular when Cauchy-Kovalevskaya's theorem
applies. Nevertheless, the condition can probably be weakened to the
existence of a unique solution in 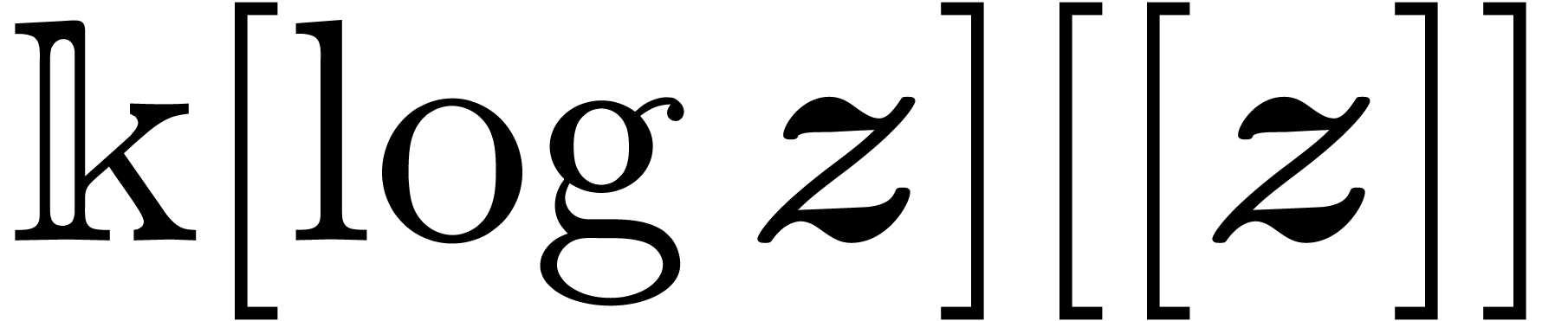 or some ring
in between. In order to prove such a result, one would have to carefully
study the supports of the series which arise during our computations. We
notice that the existence of a unique solution in
or some ring
in between. In order to prove such a result, one would have to carefully
study the supports of the series which arise during our computations. We
notice that the existence of a unique solution in  is a minimal requirement. However, in view of results such as theorem 1, it might be hard to escape from the intrusion of
logarithms. As a matter of fact, the proof of this theorem fails if we
replace
is a minimal requirement. However, in view of results such as theorem 1, it might be hard to escape from the intrusion of
logarithms. As a matter of fact, the proof of this theorem fails if we
replace 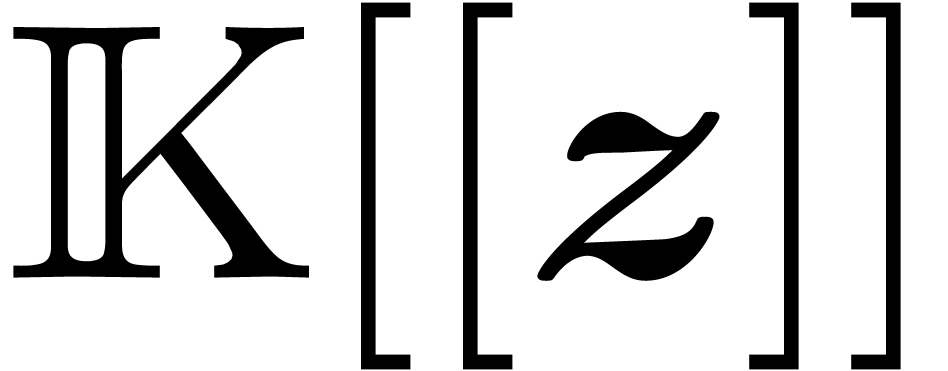 by
by 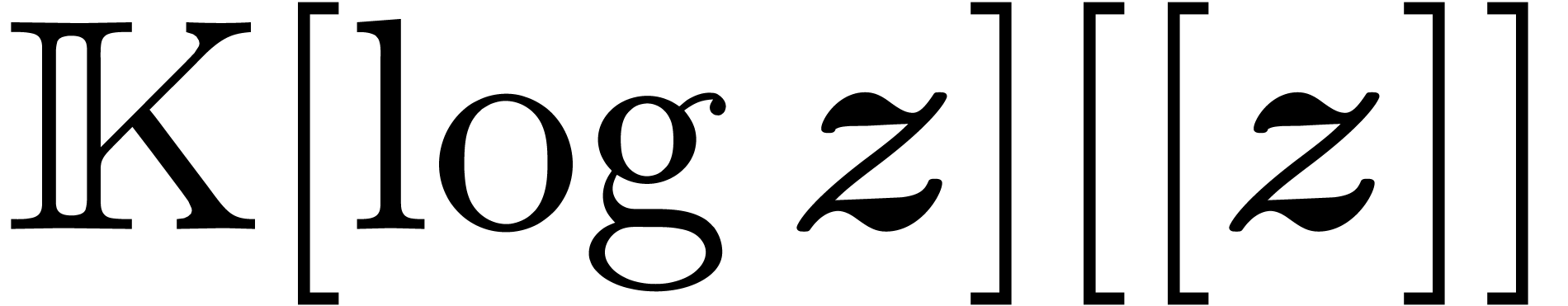 .
.
It is appropriate to notice one important advantage of our setting: we
only required  to be an effective subring of
to be an effective subring of  with an effective zero-test. Such rings can be
constructed via a tower of extensions of
with an effective zero-test. Such rings can be
constructed via a tower of extensions of  of the
type considered in section 7.4. However,
of the
type considered in section 7.4. However,  does not necessarily have to be of this type. For instance, in the case
of ordinary differential equations, we know that the series
does not necessarily have to be of this type. For instance, in the case
of ordinary differential equations, we know that the series  in
in  occurring in Stirling's series
for
occurring in Stirling's series
for  is differentially transcendental over
is differentially transcendental over  . We may thus take
. We may thus take  .
.
Even though the proof of the new zero-test might seem complex, we notice
that the actual algorithm is actually quite simple and can expected to
be reasonably efficient. Indeed, apart from the usual (inevitable?) step
of computing Rosenfeld bases over  ,
we only have to apply the tangent cone algorithm a few times for series
over the simpler field
,
we only have to apply the tangent cone algorithm a few times for series
over the simpler field  .
.
Several points of a more theoretical interest might deserve further
study. First of all, we made a few artificial hypothesis on  and
and  , which one
may try to remove as much as possible. More importantly, it would be
nice to have a genuine theory of asymptotic differential algebra, which
goes beyond the quasi-linear case. In the continuation of [AvdD04],
such a theory might even work for more general “asymptotic
functions fields” than our fields of grid-based series
, which one
may try to remove as much as possible. More importantly, it would be
nice to have a genuine theory of asymptotic differential algebra, which
goes beyond the quasi-linear case. In the continuation of [AvdD04],
such a theory might even work for more general “asymptotic
functions fields” than our fields of grid-based series  .
.
M. Aschenbrenner and L. van den Dries. Asymptotic differential algebra. In Contemporary Mathematics. Amer. Math. Soc., Providence, RI, 2004. To appear.
F. Boulier. Étude et implantation de quelques algorithmes en algèbre différentielle. PhD thesis, University of Lille I, 1994.
A. Buium. Differential algebraic groups of finite dimension, volume 1506 of Lecture Notes in Mathematics. Springer-Verlag, 1992.
J. Denef and L. Lipshitz. Power series solutions of algebraic differential equations. Math. Ann., 267:213–238, 1984.
J. Denef and L. Lipshitz. Decision problems for differential equations. The Journ. of Symb. Logic, 54(3):941–950, 1989.
I. Kaplansky. An introduction to differential algebra. Hermann, 1957.
E.R. Kolchin. Differential algebra and algebraic groups. Academic Press, New York, 1973.
A. Péladan-Germa. Testing identities of series defined by algebraic partial differential equations. In G. Cohen, M. Giusti, and T. Mora, editors, Proc. of AAECC-11, volume 948 of Lect. Notes in Comp. Science, pages 393–407, Paris, 1995. Springer.
A. Péladan-Germa. Tests effectifs de nullité dans des extensions d'anneaux différentiels. PhD thesis, Gage, École Polytechnique, Palaiseau, France, 1997.
A. Péladan-Germa. Testing equality in differential ring extensions defined by pde's and limit conditions. AAECC, 13(4):257–288, 2002.
J.F. Ritt. Differential algebra. Amer. Math. Soc., New York, 1950.
A. Rosenfeld. Specializations in differential algebra. Trans. Amer. Math. Soc., 90:394–407, 1959.
A. Seidenberg. An elimination theorem for differential algebra. Univ. California Publ. Math. (N.S.), pages 31–38, 1956.
J. Shackell. A differential-equations approach to functional equivalence. In Proc. ISSAC '89, pages 7–10, Portland, Oregon, A.C.M., New York, 1989. ACM Press.
J. Shackell. Zero equivalence in function fields defined by differential equations. Proc. of the A.M.S., 336(1):151–172, 1993.
J. van der Hoeven. D-algebraic power series. Technical Report 2001-61, Prépublications d'Orsay, 2001.
J. van der Hoeven. A new zero-test for formal power series. In Teo Mora, editor, Proc. ISSAC '02, pages 117–122, Lille, France, July 2002.
J. van der Hoeven. Transseries and real differential algebra, volume 1888 of Lecture Notes in Mathematics. Springer-Verlag, 2006.
Joris van der Hoeven. Generalized power series solutions to linear partial differential equations. JSC, 42(8):771–791, 2007.
J. van der Hoeven and J.R. Shackell. Complexity bounds for zero-test algorithms. JSC, 41:1004–1020, 2006.