Randomized root finding over finite
fields
using tangent Graeffe transforms |
|
|
Laboratoire d'informatique, de robotique
et de microélectronique de
Montpellier
LIRMM, UMR 5506 CNRS, CC477
Université Montpellier 2
161, rue Ada
34095 Montpellier Cedex 5, France
|
|
|
|
Joris van der Hoeven,
Grégoire Lecerf
|
|
Laboratoire d'informatique de
l'École polytechnique
LIX, UMR 7161 CNRS
Campus de l'École polytechnique
1, rue Honoré d'Estienne d'Orves
Bâtiment Alan Turing, CS35003
91120 Palaiseau, France
|
|
{vdhoeven,lecerf}@lix.polytechnique.fr
|
|
|
|
Abstract
Consider a finite field  whose multiplicative
group has smooth cardinality. We study the problem of computing all
roots of a polynomial that splits over
whose multiplicative
group has smooth cardinality. We study the problem of computing all
roots of a polynomial that splits over  ,
which was one of the bottlenecks for fast sparse interpolation in
practice. We revisit and slightly improve existing algorithms and then
present new randomized ones based on the Graeffe transform. We report on
our implementation in the Mathemagix computer
algebra system, confirming that our ideas gain by an order of magnitude
in practice.
,
which was one of the bottlenecks for fast sparse interpolation in
practice. We revisit and slightly improve existing algorithms and then
present new randomized ones based on the Graeffe transform. We report on
our implementation in the Mathemagix computer
algebra system, confirming that our ideas gain by an order of magnitude
in practice.
Categories and Subject Descriptors
F.2.1 [ANALYSIS OF ALGORITHMS AND PROBLEM COMPLEXITY]: Numerical
Algorithms and Problems–Computations in finite fields; G.4
[MATHEMATICAL SOFTWARE]: Algorithm design and analysis
General Terms
Algorithms, Theory
Keywords
Finite fields, polynomial root finding, algorithm, Mathemagix
1.Introduction
Let  represent the finite field with
represent the finite field with 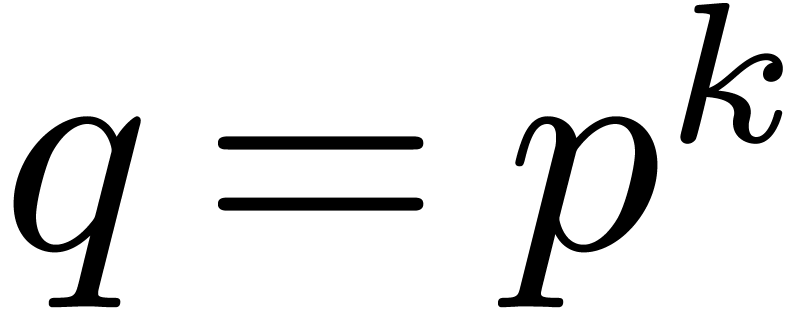 elements, where
elements, where 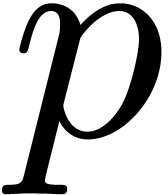 is a prime number,
and
is a prime number,
and 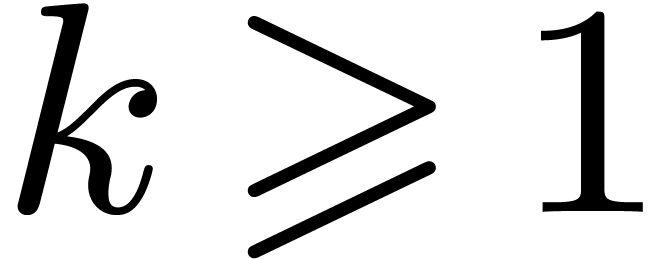 . Throughout this
article, such a field is supposed to be described as a quotient of
. Throughout this
article, such a field is supposed to be described as a quotient of 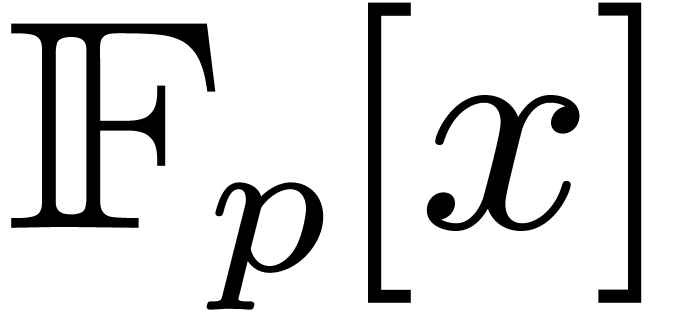 by a monic irreducible polynomial. Let
by a monic irreducible polynomial. Let 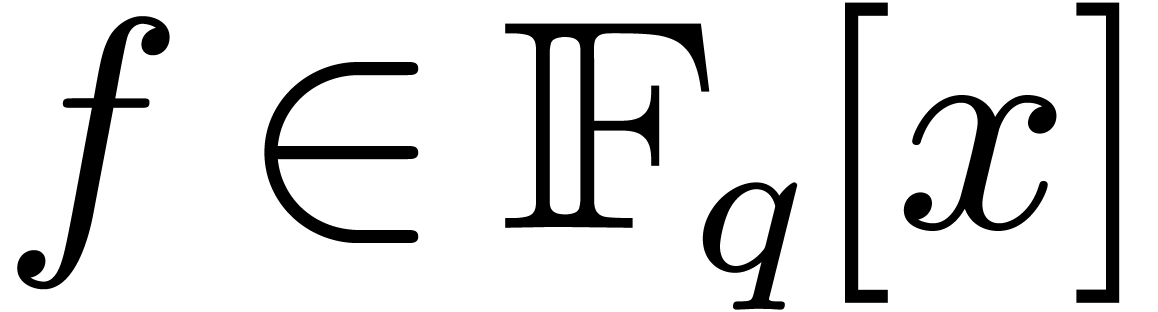 represent a separable monic polynomial of
degree
represent a separable monic polynomial of
degree 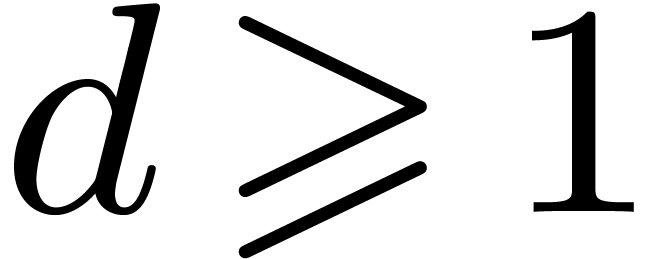 which splits over
which splits over  , which means that all its irreducible factors
have degree one and multiplicity one. In this article we are interested
in computing all the roots of
, which means that all its irreducible factors
have degree one and multiplicity one. In this article we are interested
in computing all the roots of  .
.
1.1Motivation
One of our interests in root finding came from the recent design of
efficient algorithms to interpolate, into the standard monomial basis,
polynomials that are given through evaluation functions. This task is
briefly called sparse interpolation, and root finding often
turns out to be a bottleneck, as reported in [19]. In fact,
in this case, the ground field can be chosen to be 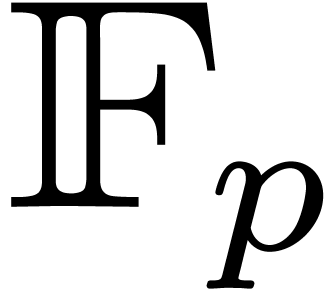 with
with 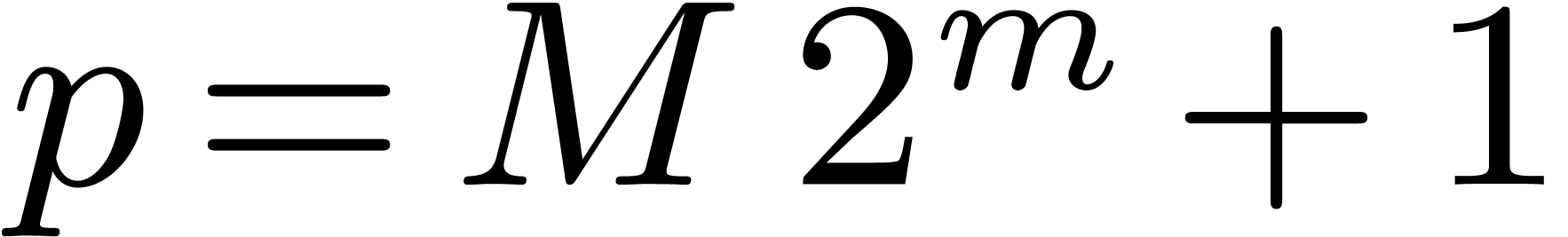 , and where
, and where 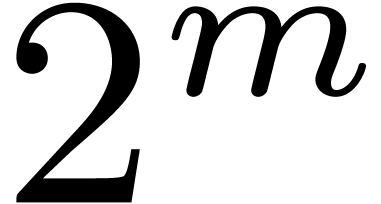 is taken to be much larger than the number of terms to be
discovered. In practice, to minimize the size of
is taken to be much larger than the number of terms to be
discovered. In practice, to minimize the size of 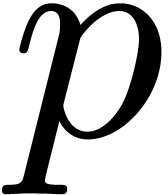 , so that it fits a machine register, we take
, so that it fits a machine register, we take  as small as possible. A typical example is
as small as possible. A typical example is 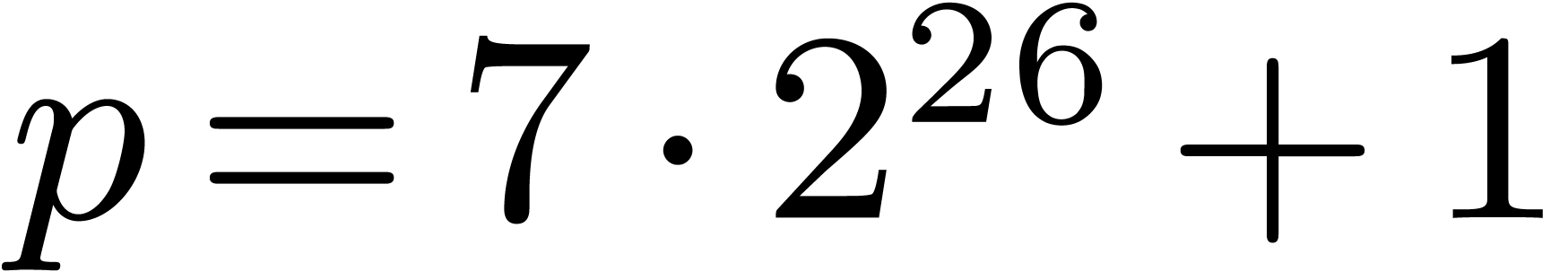 . We informally refer to such
primes as FFT primes.
. We informally refer to such
primes as FFT primes.
Root finding over prime finite fields critically occurs during the
computation of integer and rational roots of polynomials in 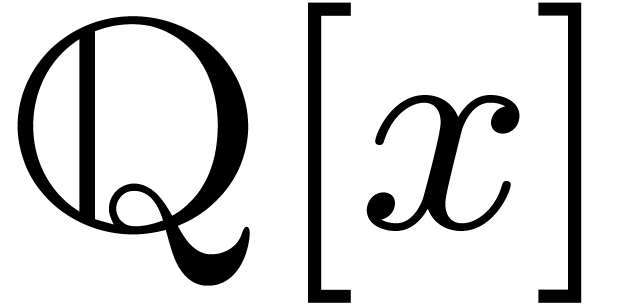 , both for dense and lacunary representations.
Yet other applications concern cryptography and error correcting codes.
Nevertheless, practical root finding has received only moderate
attention so far, existing algorithms with good average complexity
bounds often being sufficient [20, 21].
, both for dense and lacunary representations.
Yet other applications concern cryptography and error correcting codes.
Nevertheless, practical root finding has received only moderate
attention so far, existing algorithms with good average complexity
bounds often being sufficient [20, 21].
In this article, we focus on fast probabilistic root finding algorithms,
targeting primarily FFT prime fields and, more generally, finite fields
whose multiplicative group has smooth cardinality. At a second stage, we
report on practical efficiency of our new algorithms within the Mathemagix computer algebra system [18].
1.2Notations and prerequisites
The multiplicative group 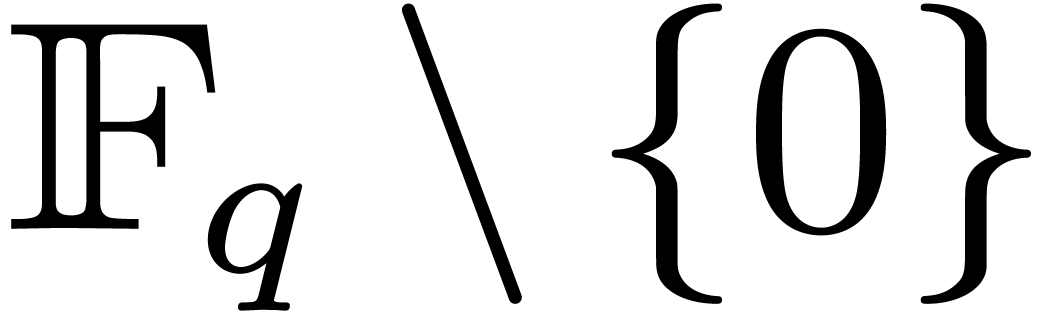 of
of  is written
is written 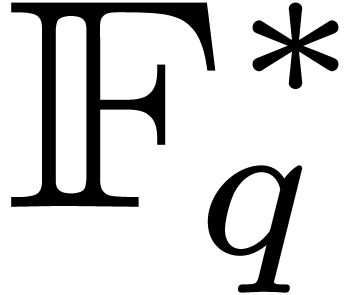 . In
order to simplify the presentation of complexity bounds, we use the
soft-Oh notation:
. In
order to simplify the presentation of complexity bounds, we use the
soft-Oh notation: 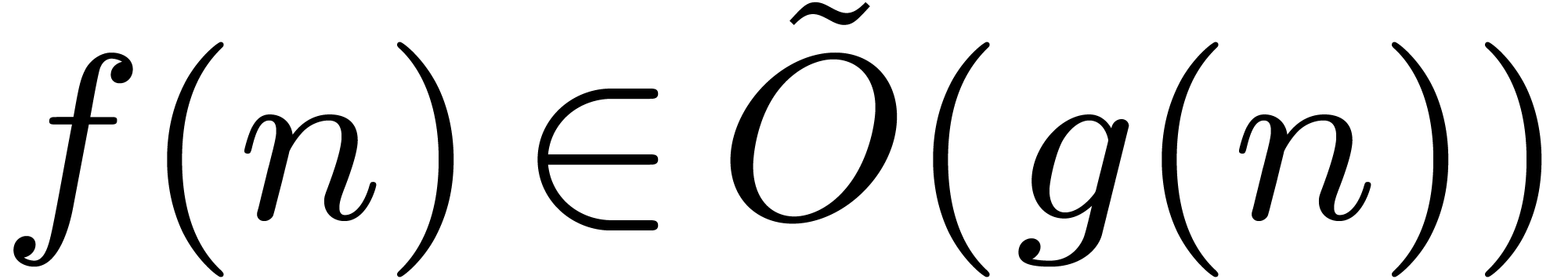 means that
means that 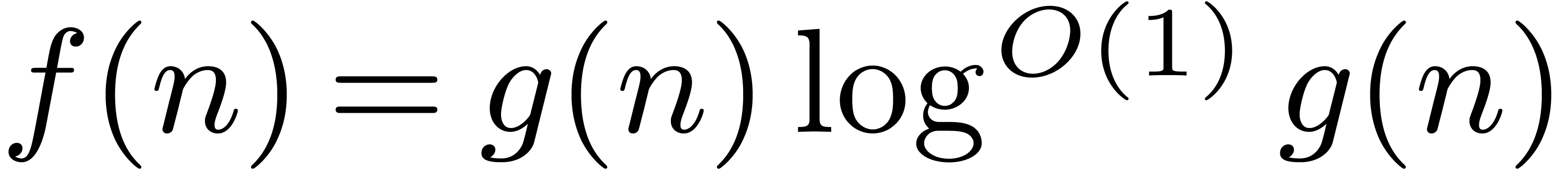 (we refer the reader to [11, Chapter 25,
Section 7] for technical details). The least integer larger or equal to
(we refer the reader to [11, Chapter 25,
Section 7] for technical details). The least integer larger or equal to
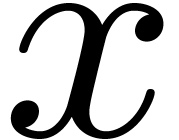 is written
is written 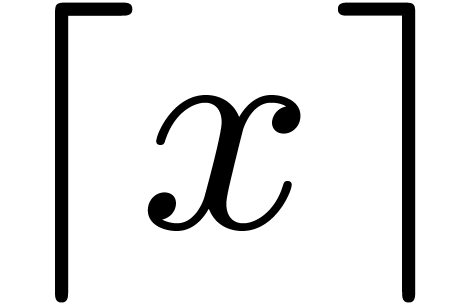 .
The largest integer smaller or equal to
.
The largest integer smaller or equal to 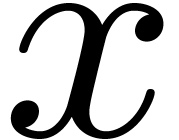 is
written
is
written 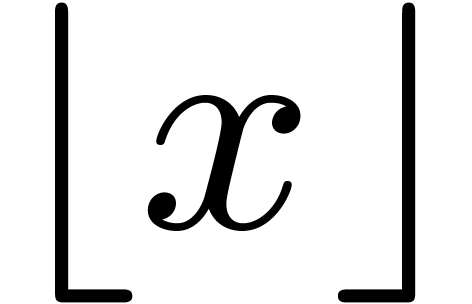 . The
remainder of
. The
remainder of  in the division by
in the division by  is denoted by
is denoted by  .
.
We write  for a function that bounds the total
cost of a polynomial product algorithm in terms of the number of ring
operations performed independently of the coefficient ring, assuming a
unity is available. In other words, two polynomials of degrees at most
for a function that bounds the total
cost of a polynomial product algorithm in terms of the number of ring
operations performed independently of the coefficient ring, assuming a
unity is available. In other words, two polynomials of degrees at most
 over such a ring
over such a ring  can be
multiplied with at most
can be
multiplied with at most 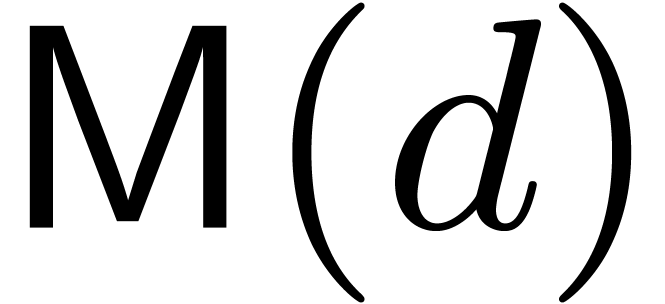 arithmetic operations in
arithmetic operations in
 . The schoolbook algorithm
allows us to take
. The schoolbook algorithm
allows us to take 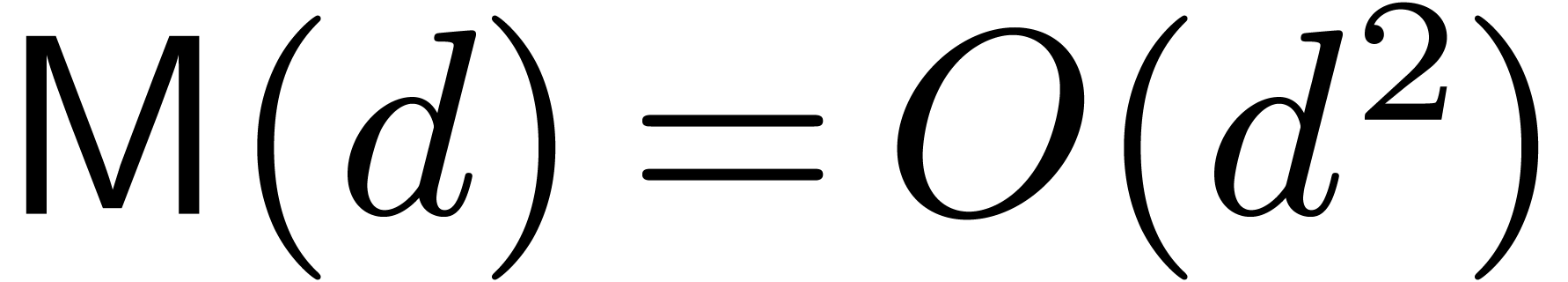 . On the
other hand the fastest known algorithm, due to Cantor and Kaltofen [7], provides us with
. On the
other hand the fastest known algorithm, due to Cantor and Kaltofen [7], provides us with 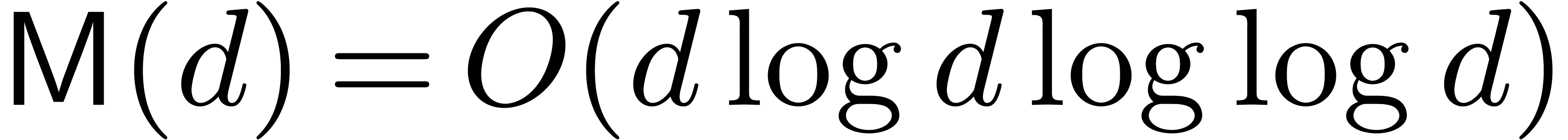 .
In order to simplify the cost analysis of our algorithms we make the
customary assumption that
.
In order to simplify the cost analysis of our algorithms we make the
customary assumption that  for all
for all 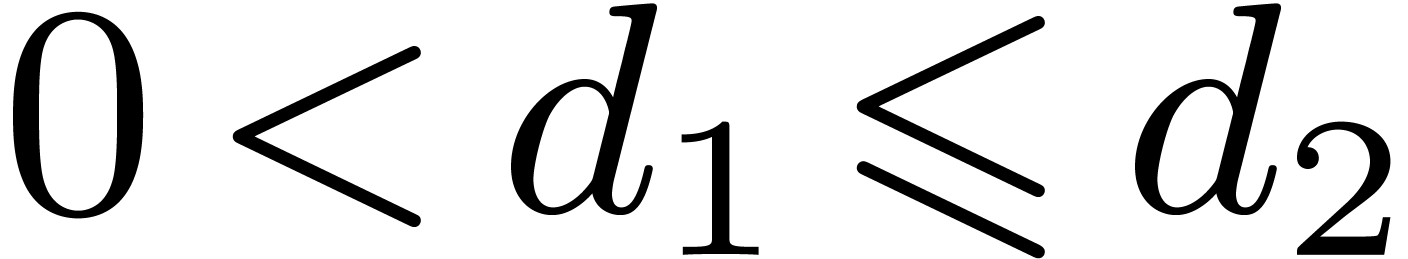 . Notice that this assumption implies the
super-additivity of
. Notice that this assumption implies the
super-additivity of  ,
namely
,
namely 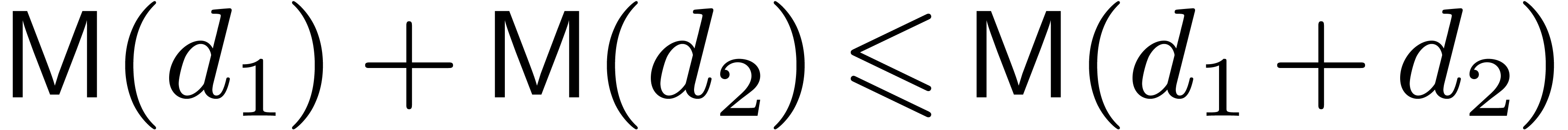 for all
for all 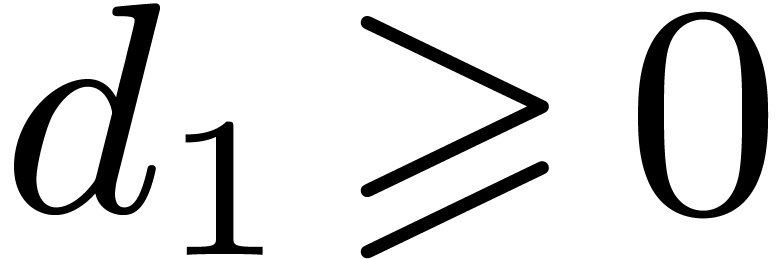 and
and 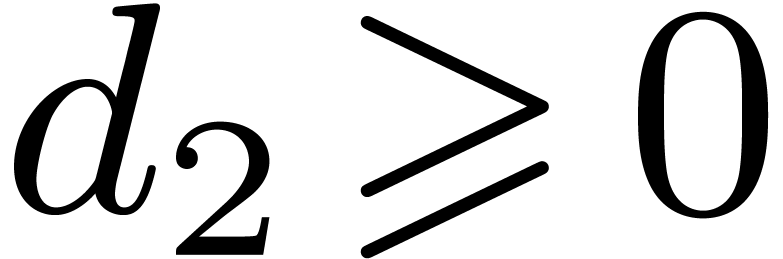 .
.
For operations in  and in finite fields, we are
interested in the Turing machine model, with a sufficiently
large number of tapes. In short, we use the terms bit-cost and
bit-complexity to refer to this model whenever the context is
not clear. For randomized algorithms, we endow Turing machines
with an additional instruction which generates random bits with a
uniform distribution [28].
and in finite fields, we are
interested in the Turing machine model, with a sufficiently
large number of tapes. In short, we use the terms bit-cost and
bit-complexity to refer to this model whenever the context is
not clear. For randomized algorithms, we endow Turing machines
with an additional instruction which generates random bits with a
uniform distribution [28].
We write 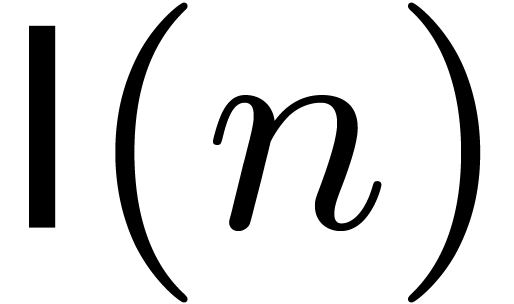 for a function that bounds the bit-cost
of an algorithm which multiplies two integers of bit-sizes at most
for a function that bounds the bit-cost
of an algorithm which multiplies two integers of bit-sizes at most 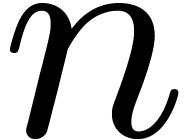 , viewed in classical binary
representation. Recently, the best bound for
, viewed in classical binary
representation. Recently, the best bound for 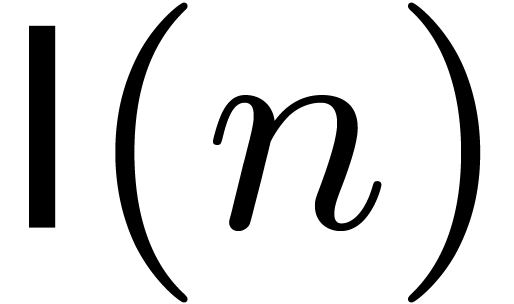 has
been improved to
has
been improved to 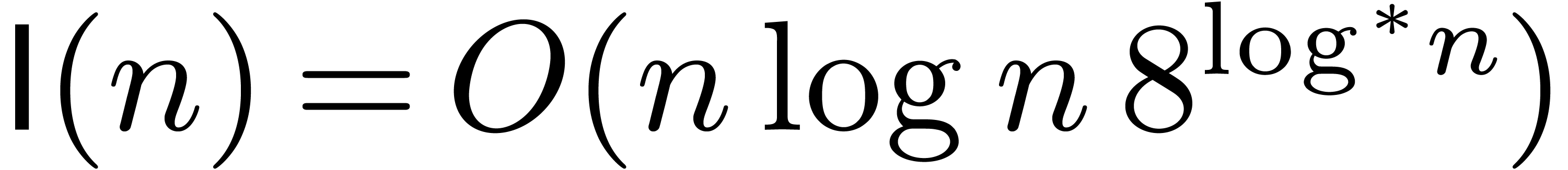 , where
, where 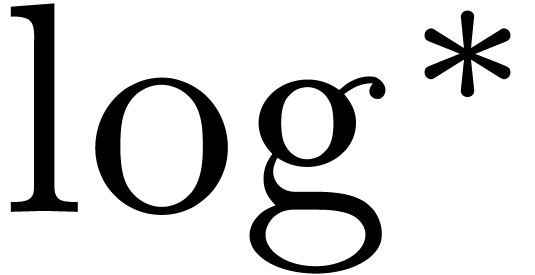 represents the iterated logarithm function
[16]. Again, we make the customary assumption that
represents the iterated logarithm function
[16]. Again, we make the customary assumption that  for all
for all 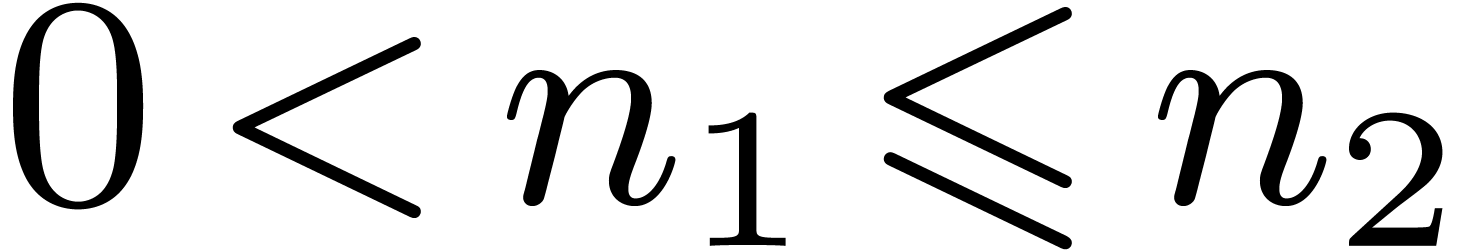 .
We freely use the following classical facts: ring operations in
.
We freely use the following classical facts: ring operations in 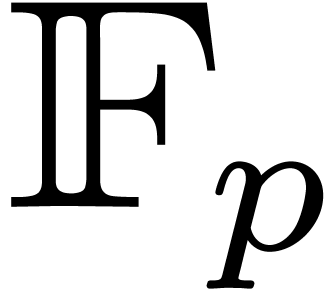 cost
cost 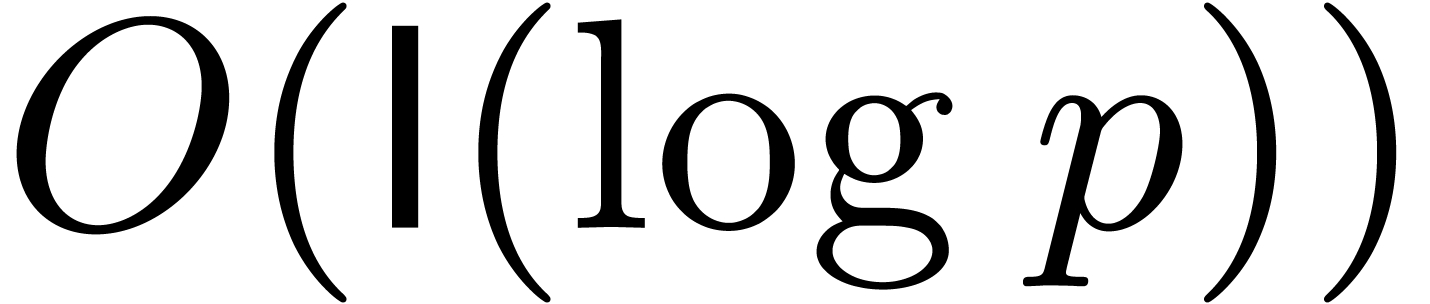 and one division or
inversion in
and one division or
inversion in 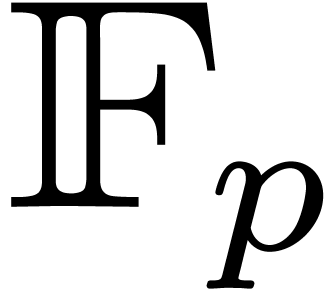 costs
costs 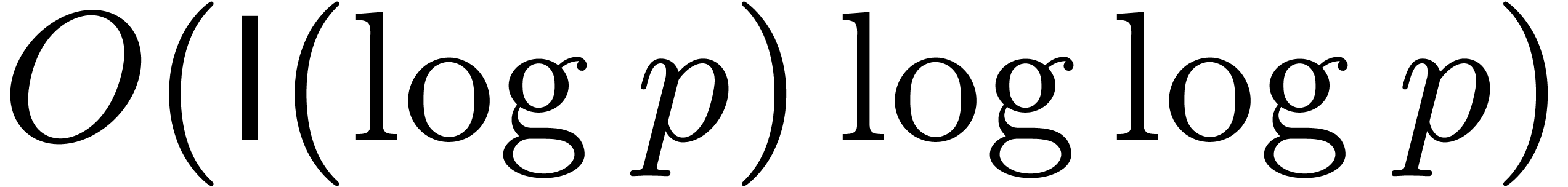 [11, Chapter 11].
[11, Chapter 11].
For polynomial operations over  ,
we let
,
we let 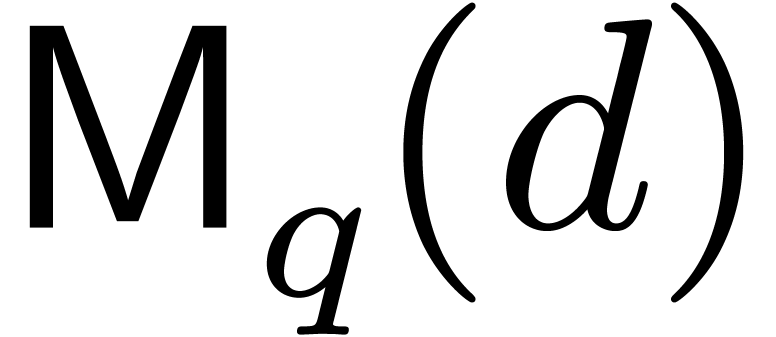 represent a function that bounds the
bit-cost of an algorithm that multiplies two polynomials of degrees at
most
represent a function that bounds the
bit-cost of an algorithm that multiplies two polynomials of degrees at
most 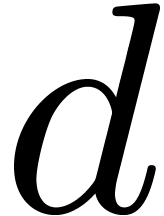 , with the same kind of
assumptions as for
, with the same kind of
assumptions as for  and
and 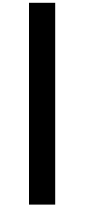 . According to [17], we may take
. According to [17], we may take 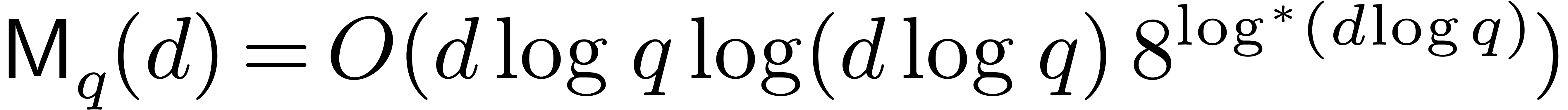 . The ring operations in
. The ring operations in  cost at most
cost at most 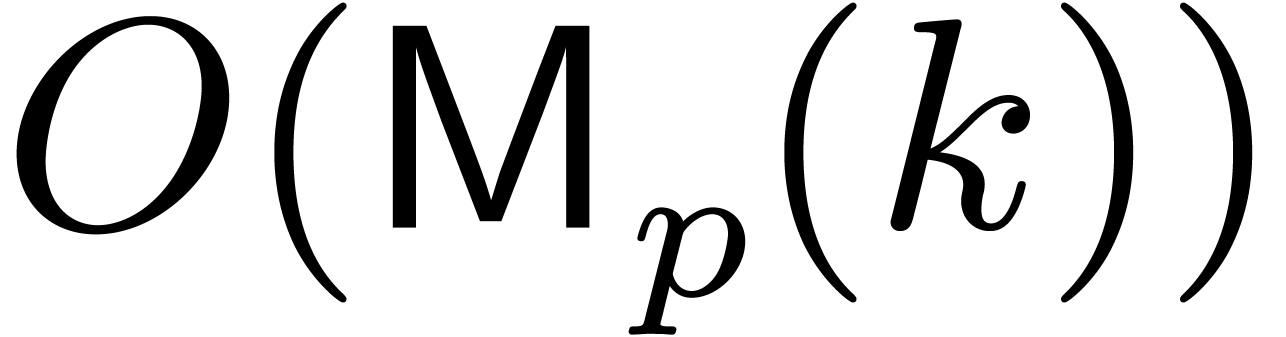 ,
and inversions take at most
,
and inversions take at most 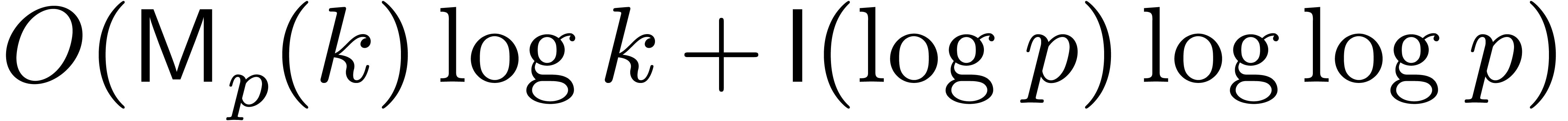 .
For convenience,
.
For convenience, 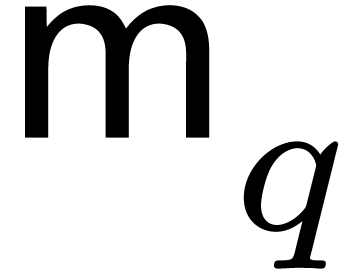 and
and 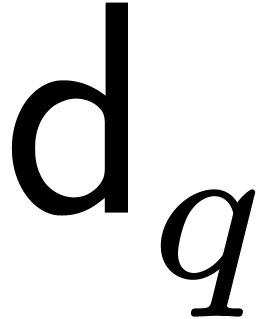 will respectively denote cost functions for the product and the inverse
in
will respectively denote cost functions for the product and the inverse
in  .
.
Let us recall that the gcd of two polynomials of degrees at most 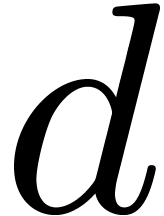 over
over  can be computed in time
can be computed in time
 : One can for instance use
pseudo-remainders in [11, Algorithm 11.4], mutatis
mutandis. Given monic polynomials
: One can for instance use
pseudo-remainders in [11, Algorithm 11.4], mutatis
mutandis. Given monic polynomials  and
and  with
with  and
and 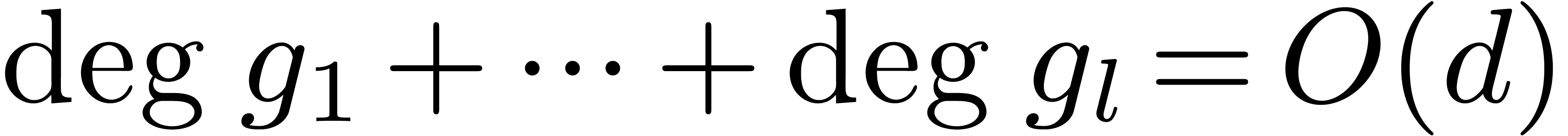 , all the remainders
, all the remainders 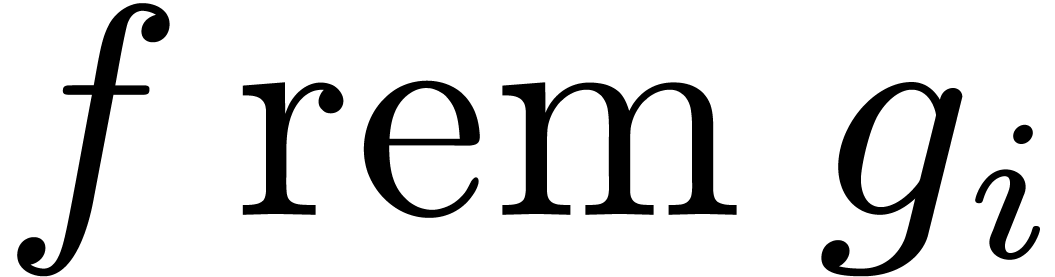 can be computed in time
can be computed in time 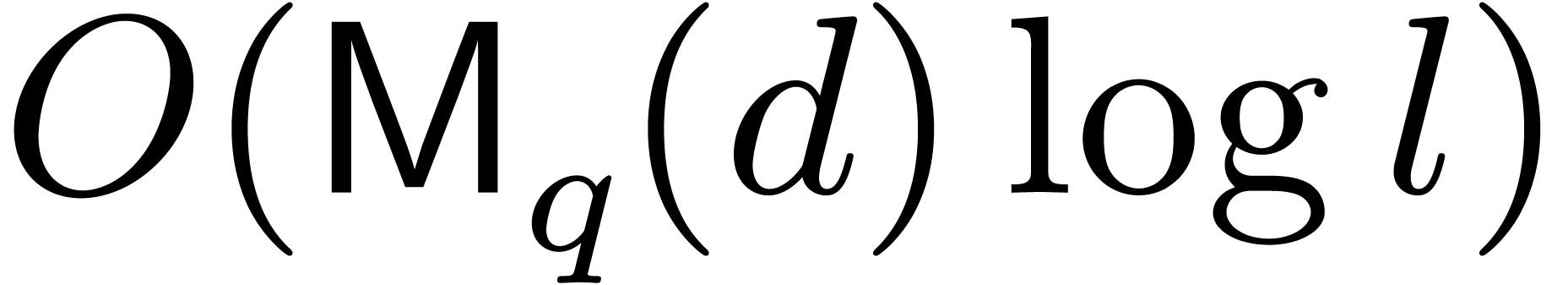 using a subproduct
tree [11, Chapter 10]. The inverse problem, called
Chinese remaindering, can be solved within a similar cost
using a subproduct
tree [11, Chapter 10]. The inverse problem, called
Chinese remaindering, can be solved within a similar cost 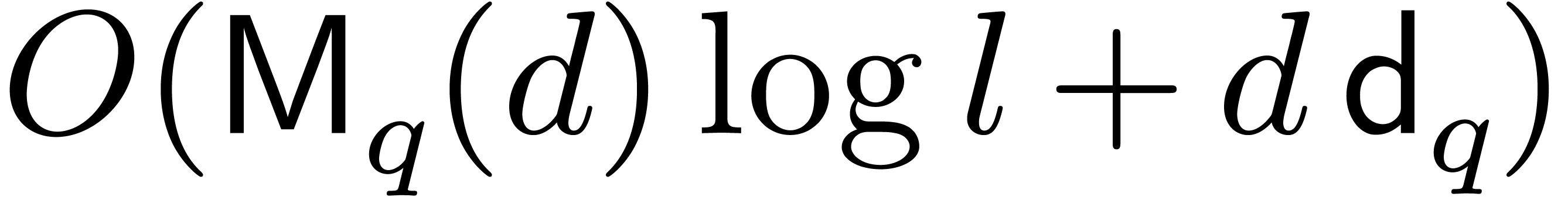 .
.
In this article, when needed, we consider that the factorization of 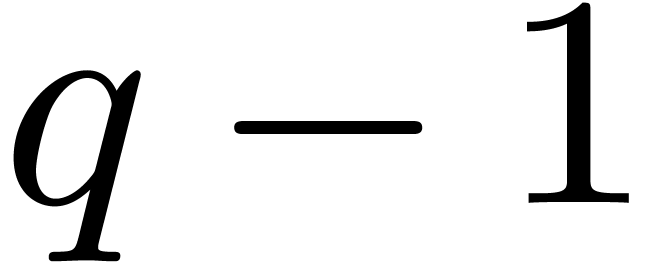 and a primitive element of
and a primitive element of 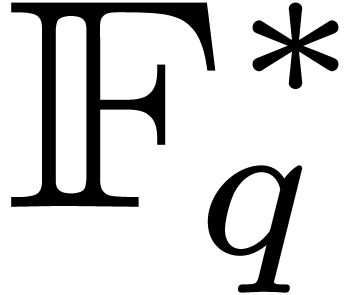 have been precomputed once, and we discard the necessary underlying
costs. In practice, if the factorization of
have been precomputed once, and we discard the necessary underlying
costs. In practice, if the factorization of 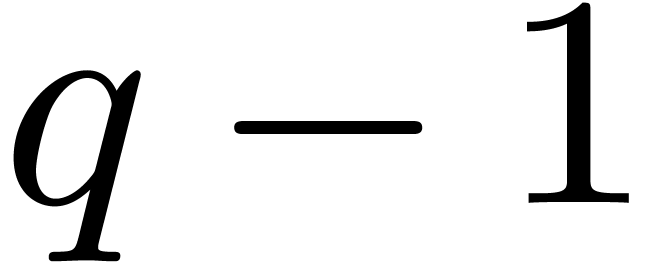 is
given, then it is straightforward to verify whether a given element is
primitive. For known complexity bounds and historical details on these
tasks, we refer the reader to [1, 26, 31].
is
given, then it is straightforward to verify whether a given element is
primitive. For known complexity bounds and historical details on these
tasks, we refer the reader to [1, 26, 31].
1.3Related work and our contributions
Seminal algorithms for polynomial factorization over finite fields are
classically attributed to Berlekamp [2, 3],
and Cantor and Zassenhaus [8], but central earlier ideas
can be found in works of Gauss, Galois, Arwins, Faddeev and Skopin.
Cantor–Zassenhaus' algorithm is randomized and well suited to
compute roots of polynomials of degree 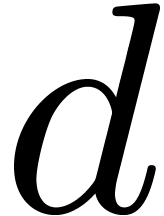 that
split over
that
split over  in average time
in average time 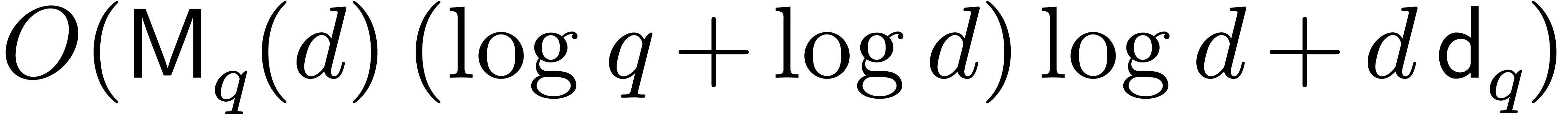 . Of course, if
. Of course, if 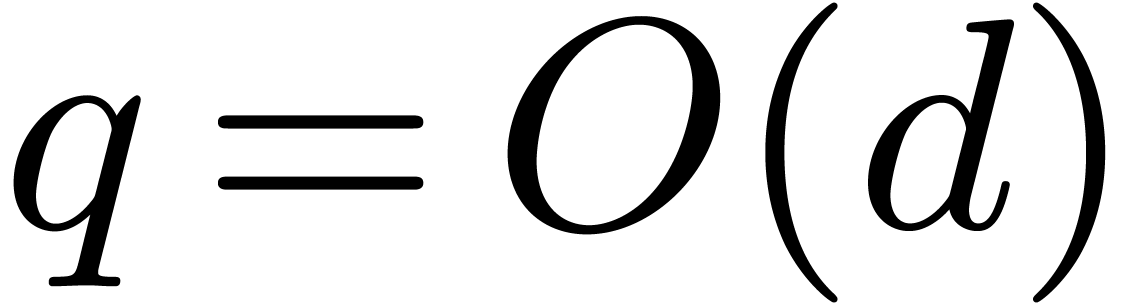 then an
exhaustive search can be naively performed in time
then an
exhaustive search can be naively performed in time 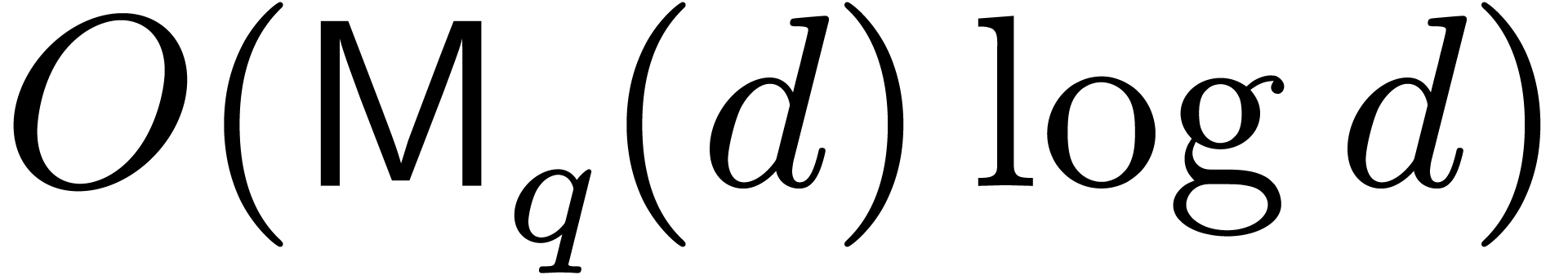 (the factor
(the factor 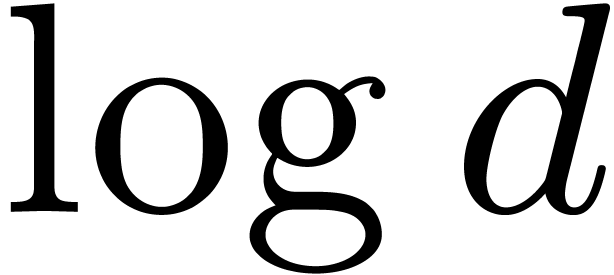 can be discarded if a primitive
element of
can be discarded if a primitive
element of  is given, by means of [6,
Proposition 3]), so that the cost of root finding simplifies to
is given, by means of [6,
Proposition 3]), so that the cost of root finding simplifies to 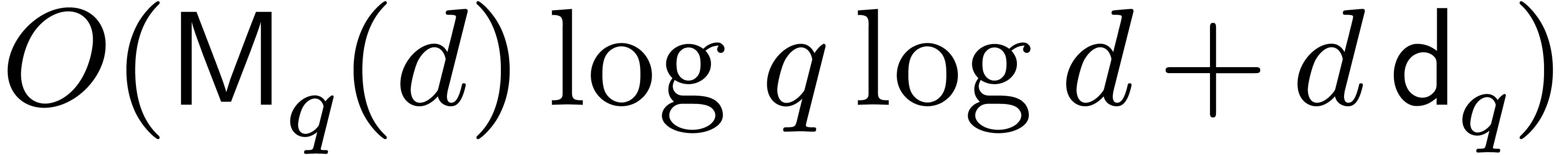 . This classical approach is for
instance implemented in the NTL library written by
Shoup [32]. However neither Berlekamp's nor
Cantor–Zassenhaus' algorithm seems to benefit of particular prime
numbers such as FFT primes. Instead, alternative approaches have been
proposed by Moenck [25], von zur Gathen [10],
Mignotte and Schnorr [24], and then by Rónyai [29].
. This classical approach is for
instance implemented in the NTL library written by
Shoup [32]. However neither Berlekamp's nor
Cantor–Zassenhaus' algorithm seems to benefit of particular prime
numbers such as FFT primes. Instead, alternative approaches have been
proposed by Moenck [25], von zur Gathen [10],
Mignotte and Schnorr [24], and then by Rónyai [29].
In Section 2, for the sake of comparison, we first revisit
Cantor–Zassenhaus' approach and propose a practical trick to
slightly speed it up. We also briefly recall the complexity bound of
Mignotte–Schnorr's algorithm [24].
We then design and analyze fast randomized algorithms based on tangent
Graeffe transforms, leading to an important speed-up for FFT primes. The
practical efficiency of the new algorithms is discussed on the basis of
implementations in the Mathemagix computer algebra
system [18], thus revealing that our fastest variant gains
an order of magnitude over other existing software.
Let us finally mention that our present randomized algorithms admit
deterministic counterparts which are studied in [14].
2.Known algorithms revisted
In this section we revisit efficient root finding algorithms previously
described in the literature, and slightly improve their complexity
analysis. The first stream, followed by Berlekamp [3],
Cantor and Zassenhaus [8], consists in splitting the input
polynomial by computing suitable modular exponentiations and gcds. The
second stream, followed by Moenck [25], and Mignotte and
Schnorr [24], takes advantage of the smoothness of 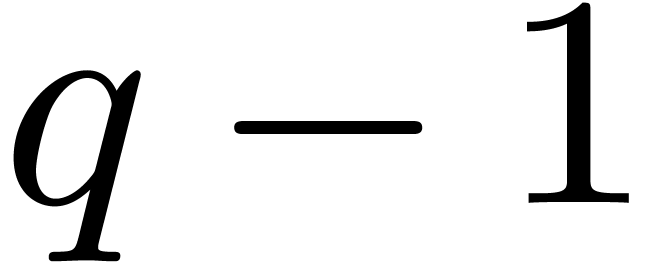 .
.
2.1Cantor–Zassenhaus' algorithm
In this subsection we suppose that  has the form
has the form
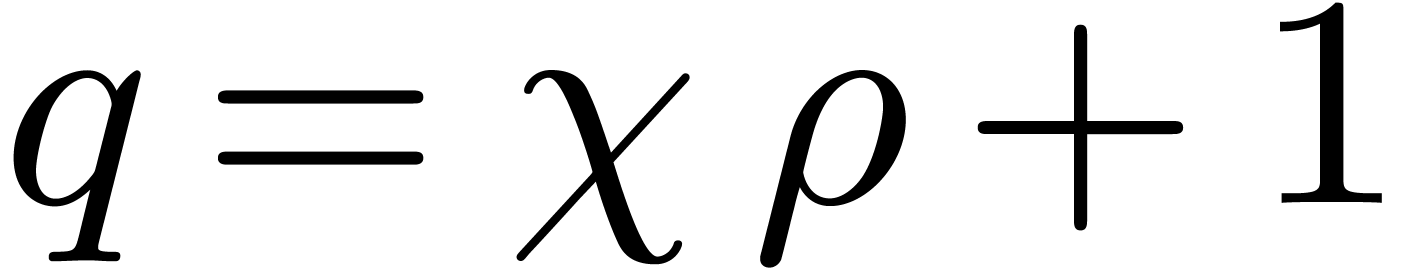 , with
, with 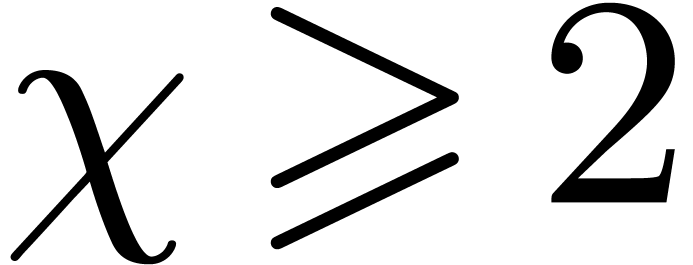 . The following randomized algorithm extends
Cantor–Zassenhaus' one, which corresponds to
. The following randomized algorithm extends
Cantor–Zassenhaus' one, which corresponds to 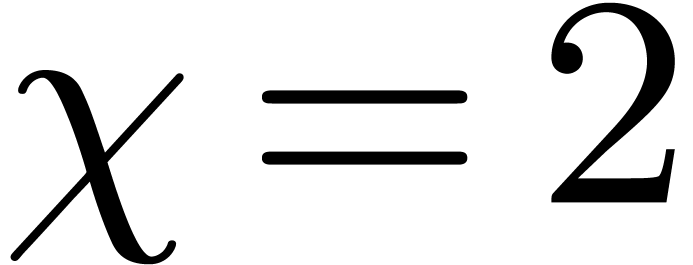 , when
, when  is odd. We need
a primitive root
is odd. We need
a primitive root  of unity of order
of unity of order  .
.
Randomized algorithm 1.
-
Input
 of degree
of degree
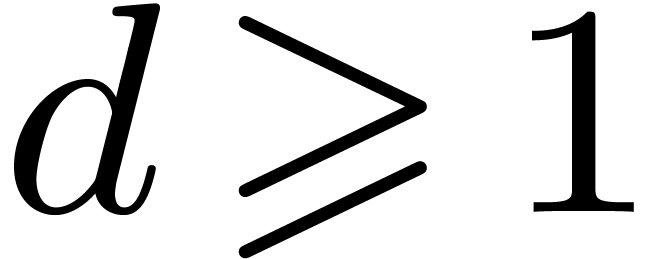 ,
monic, separable, which splits over
,
monic, separable, which splits over
 ,
and such that
,
and such that
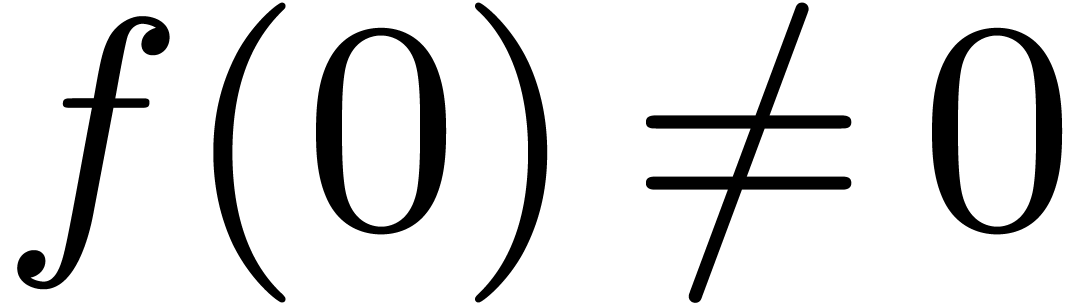 ;
a primitive root
;
a primitive root
 of unity of order
of unity of order
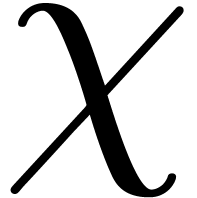 .
.
-
Output
-
The roots of  .
.
-
If  then compute the roots of
then compute the roots of  by calling a fallback root finding algorithm.
by calling a fallback root finding algorithm.
-
Pick up 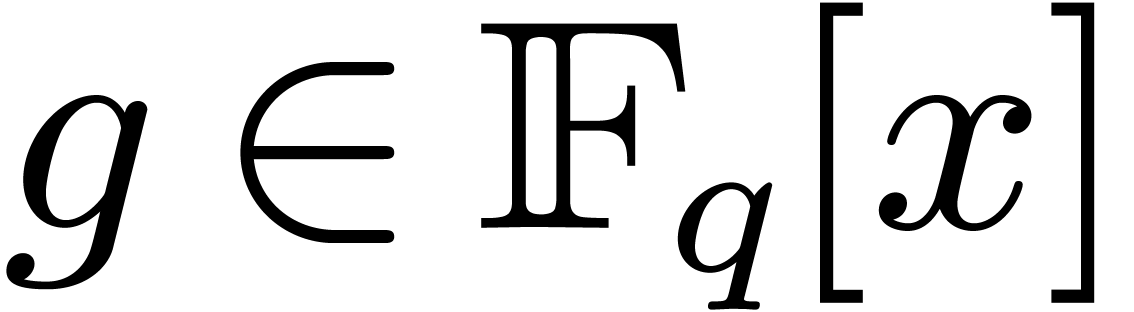 at random of degree at most
at random of degree at most  .
.
-
Compute 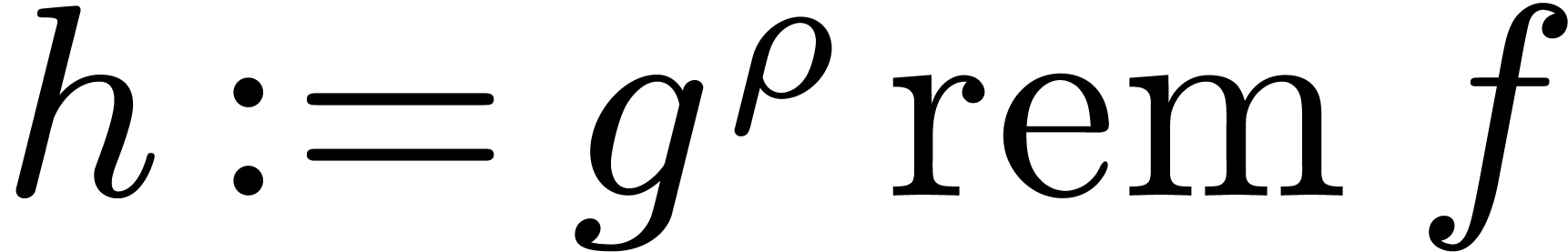 , and set
, and set 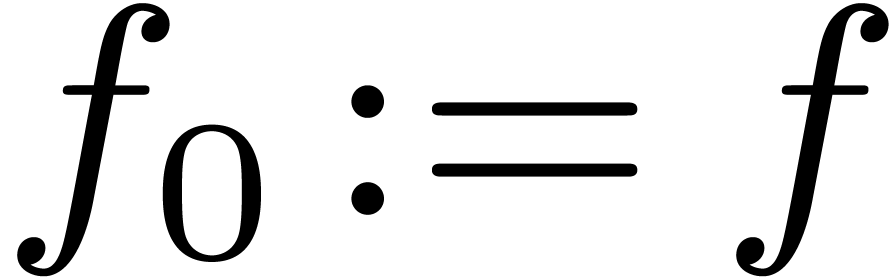 .
.
-
For all 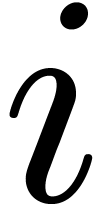 from
from 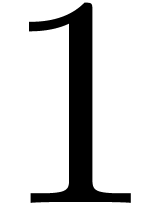 to
to
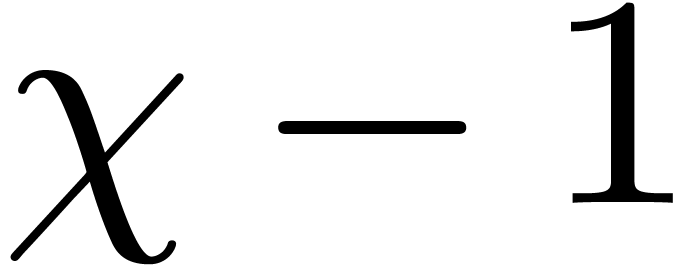 , compute
, compute 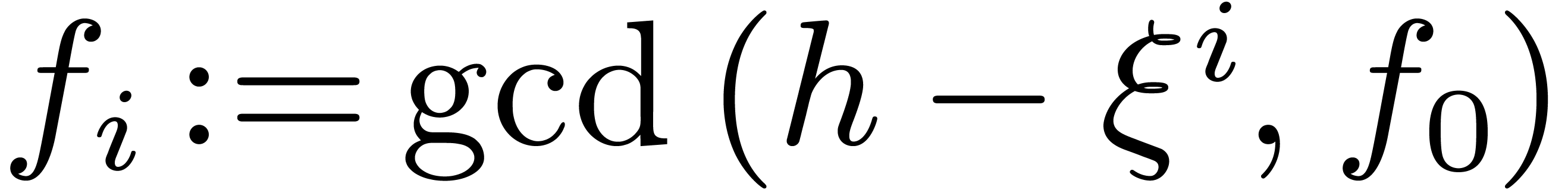 , make it monic, and replace
, make it monic, and replace 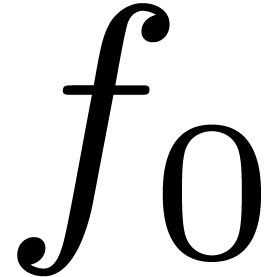 by
by 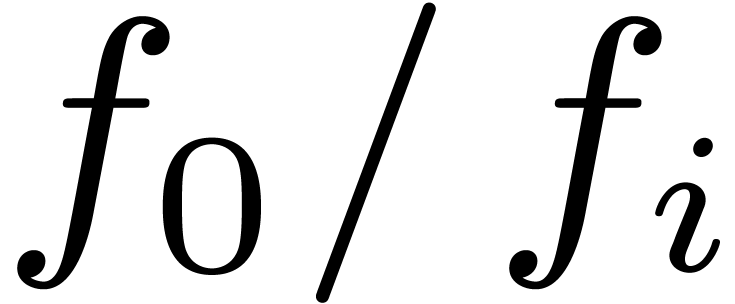 .
.
-
Recursively call the algorithm with those of 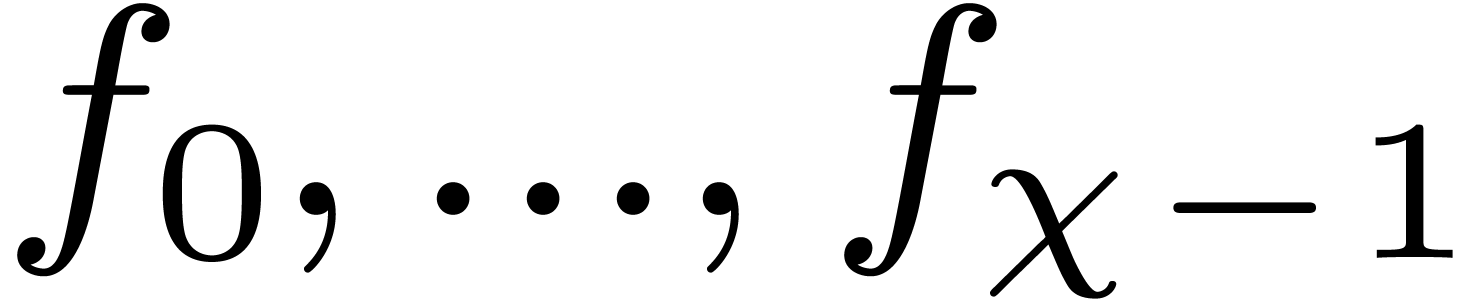 which are not constant, and return the union of the sets of their
roots.
which are not constant, and return the union of the sets of their
roots.
In the classical case when 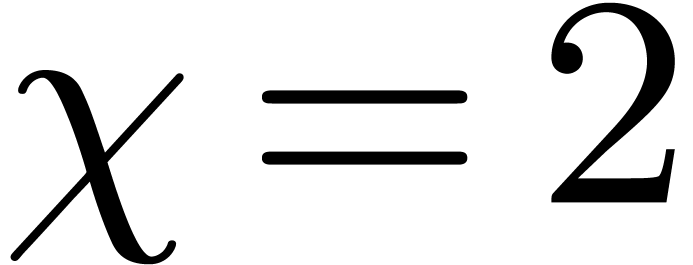 ,
then we recall that step 3 costs
,
then we recall that step 3 costs 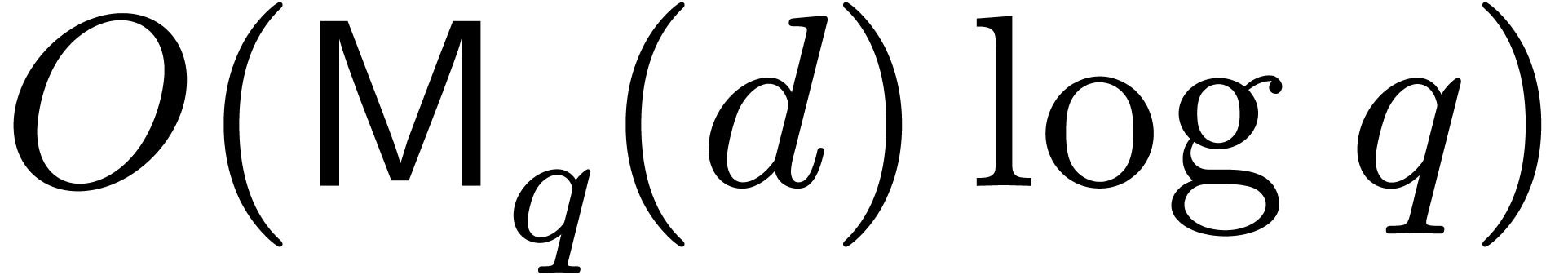 and step 4
takes
and step 4
takes 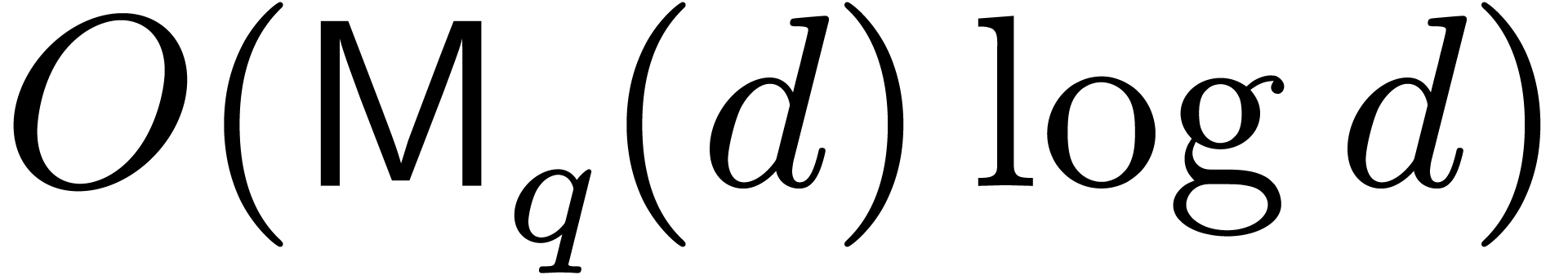 plus one inversion in
plus one inversion in  . Since the average depth of the recursion is
in
. Since the average depth of the recursion is
in 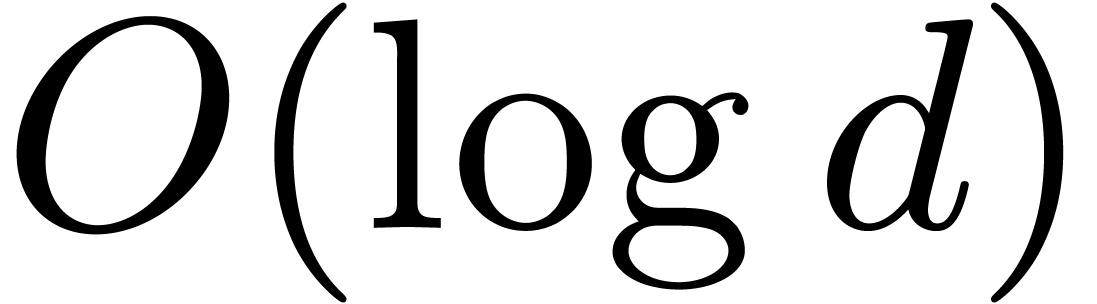 [9], the total average cost
amounts to
[9], the total average cost
amounts to 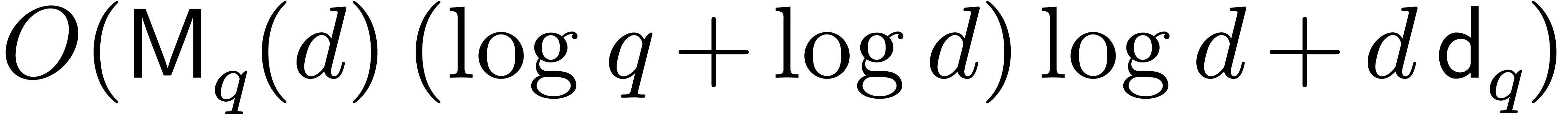 .
.
For the case of arbitrary 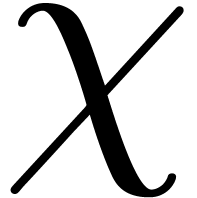 ,
we propose an informal discussion, so as to justify the interest in the
algorithm. If
,
we propose an informal discussion, so as to justify the interest in the
algorithm. If  is a root of
is a root of  , then
, then 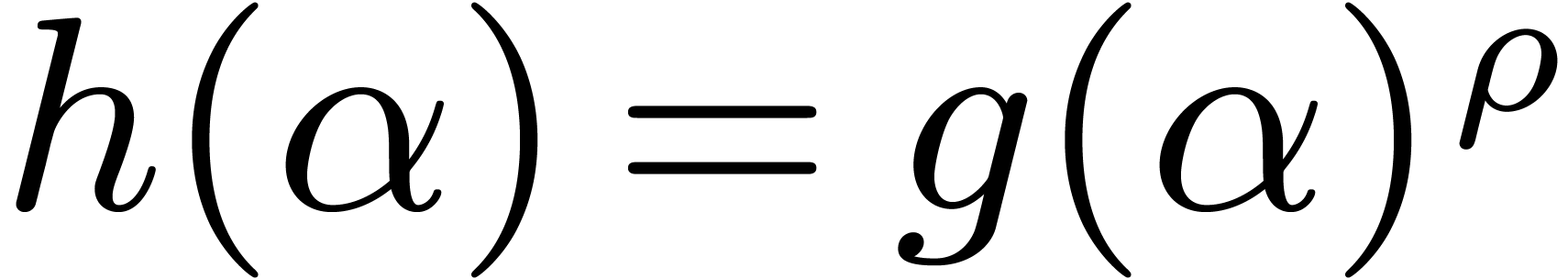 has order
dividing
has order
dividing 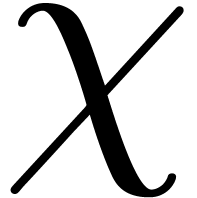 , hence is a power
of
, hence is a power
of  , or zero with a very
small probability. Therefore we have
, or zero with a very
small probability. Therefore we have 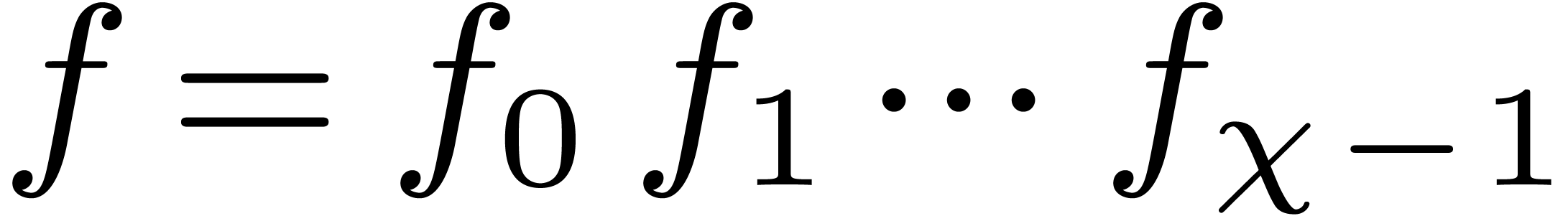 .
Since
.
Since  is taken at random, we might expect that
the values of
is taken at random, we might expect that
the values of 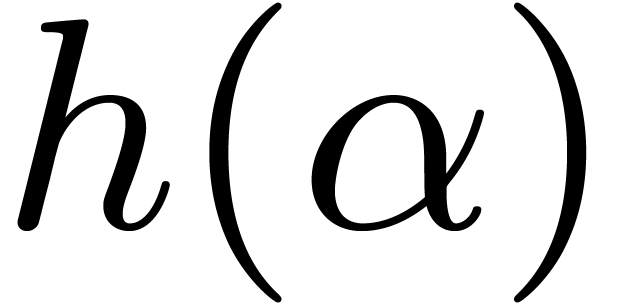 are distributed uniformly among
the powers of
are distributed uniformly among
the powers of  (we discard cases when
(we discard cases when 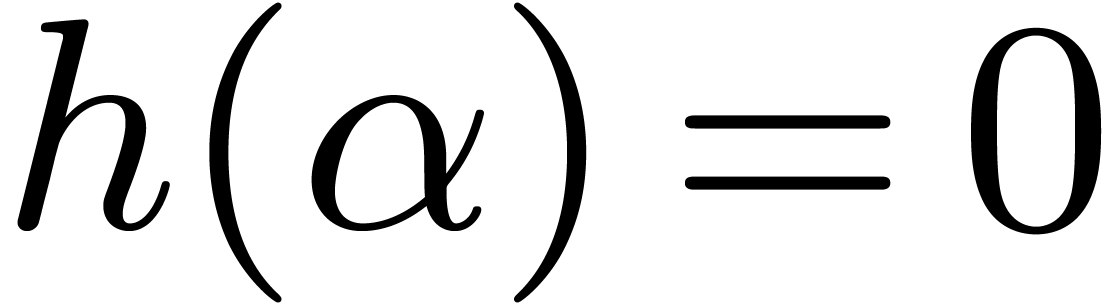 ). In other words, the depth of the
recursive calls is expected to be in
). In other words, the depth of the
recursive calls is expected to be in 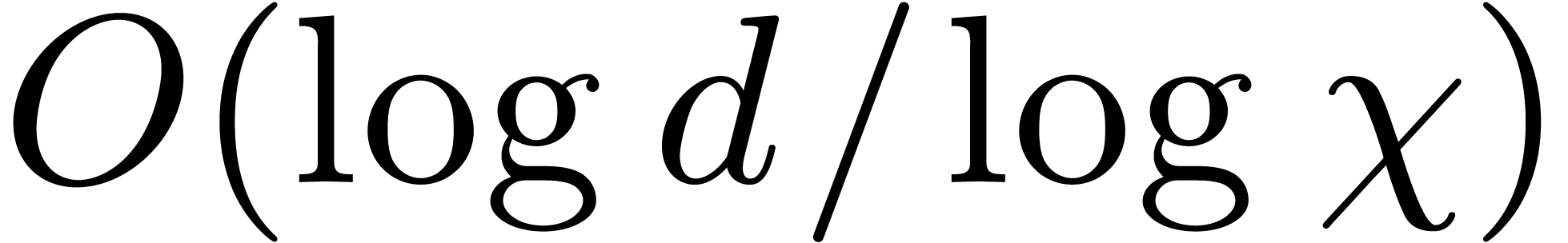 .
.
If we further assume that 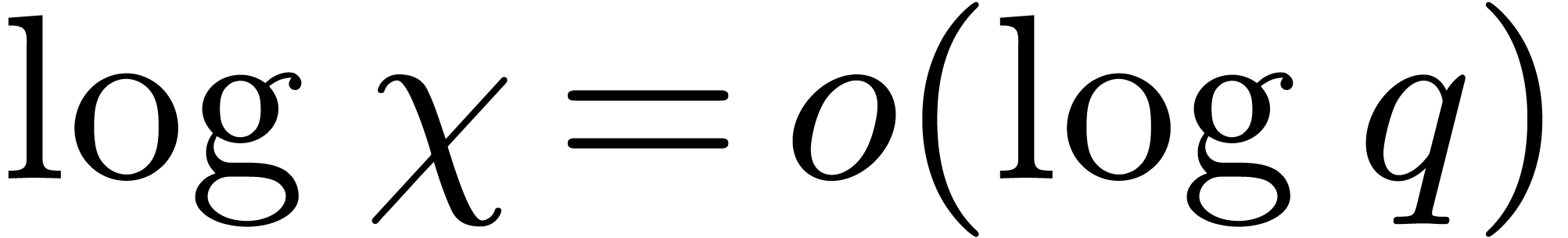 ,
then step 3 takes approximately
,
then step 3 takes approximately 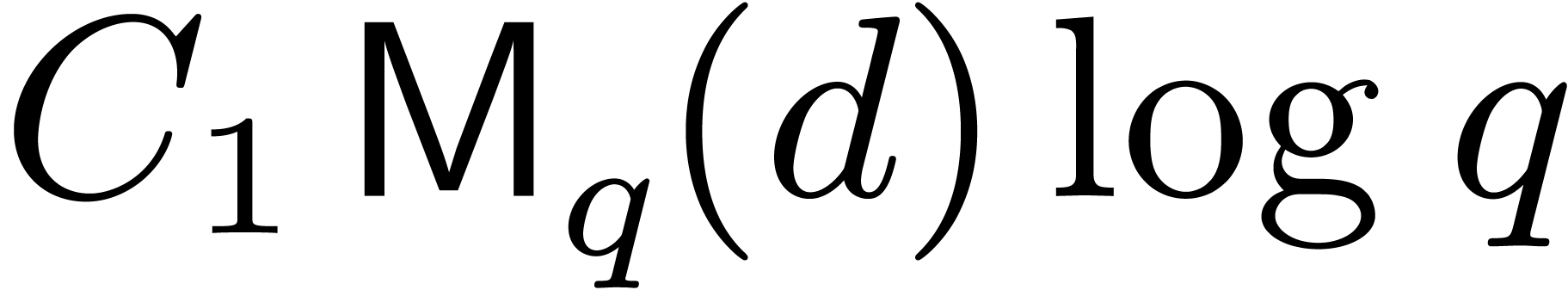 for a certain
constant
for a certain
constant 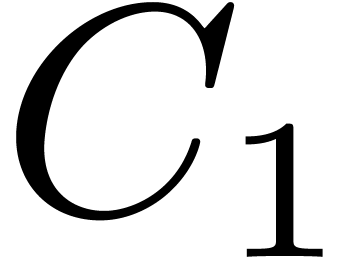 , and step 4 costs
, and step 4 costs
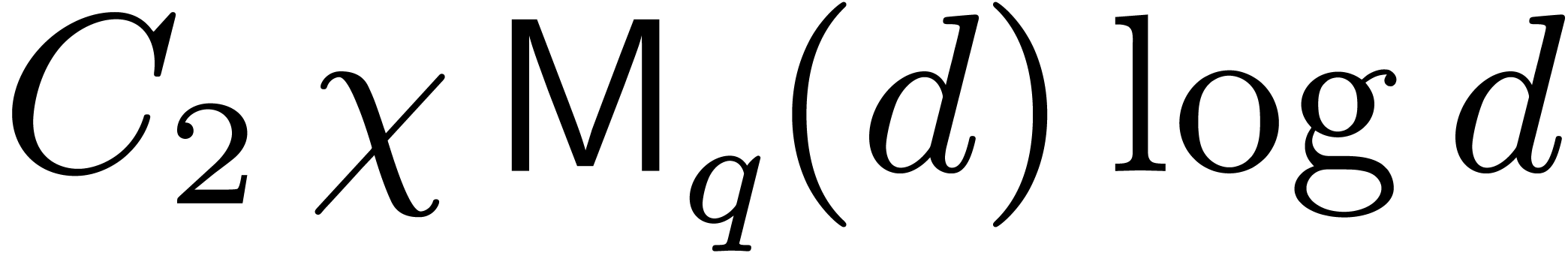 . Discarding the cost of the
inversions, and compared to the case
. Discarding the cost of the
inversions, and compared to the case 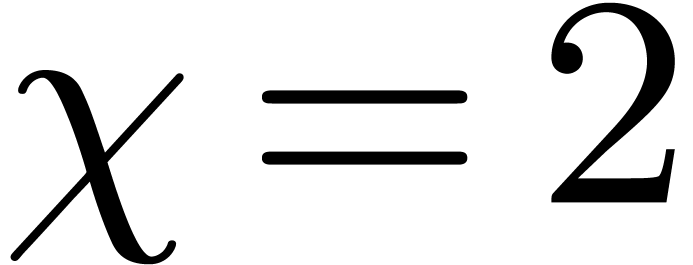 ,
we achieve an approximate speed-up of
,
we achieve an approximate speed-up of
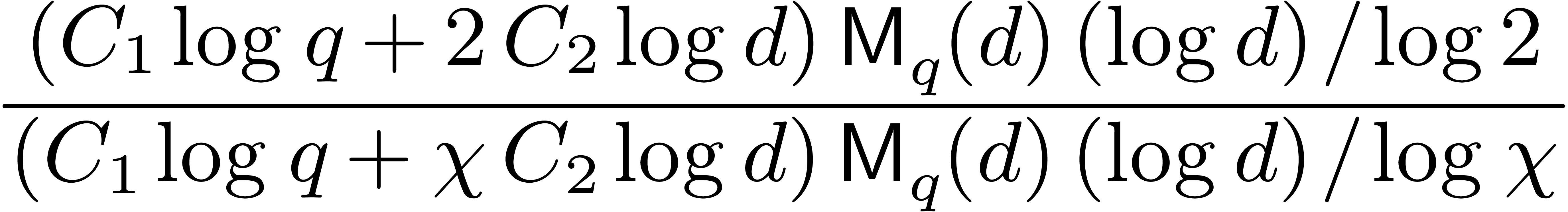
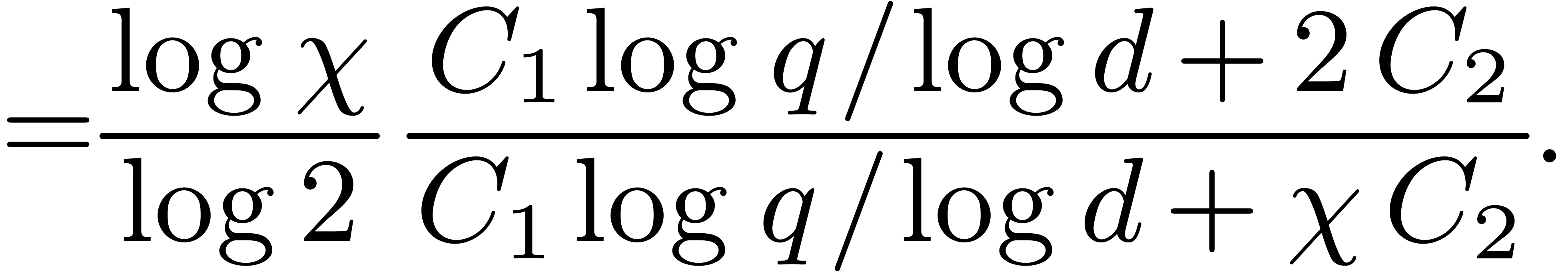
Whenever 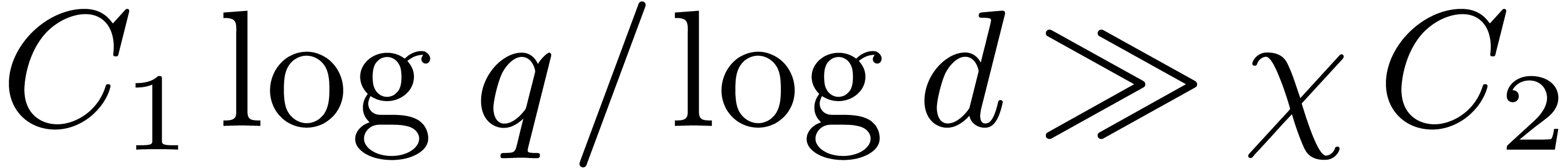 , this speed-up is
of order
, this speed-up is
of order 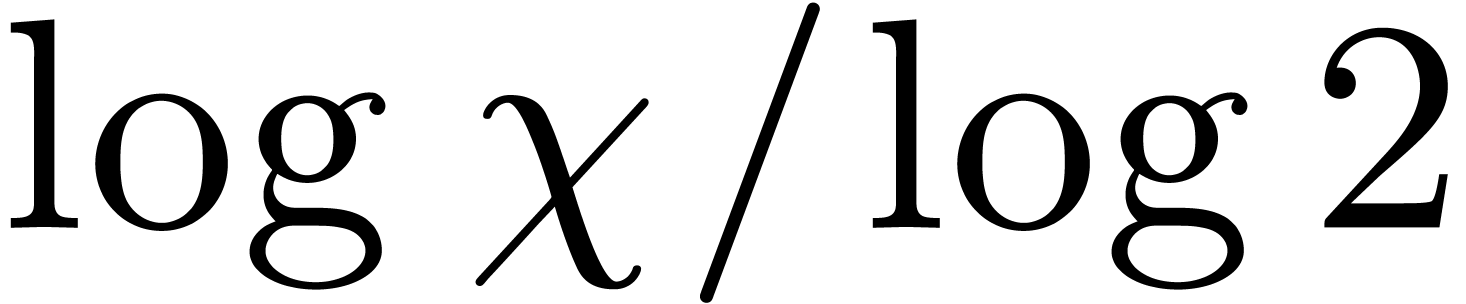 . In general, the
speed-up is maximal if
. In general, the
speed-up is maximal if 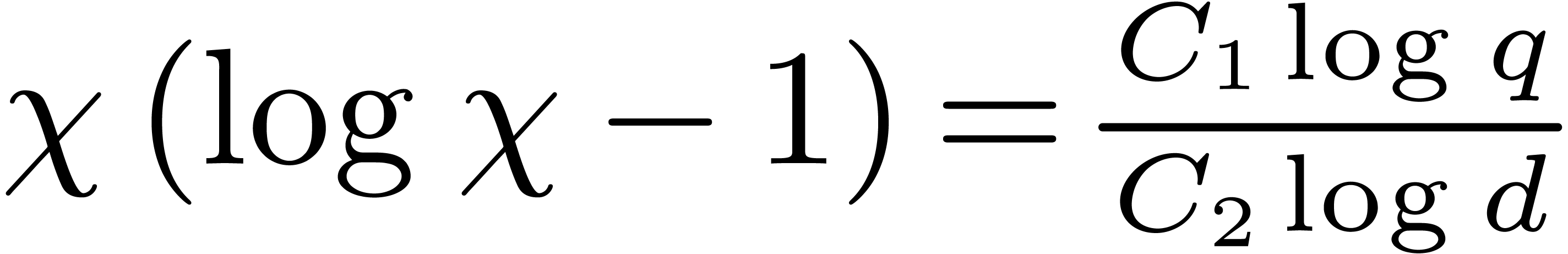 .
.
2.2Mignotte–Schnorr's algorithm
Assuming given a primitive element of 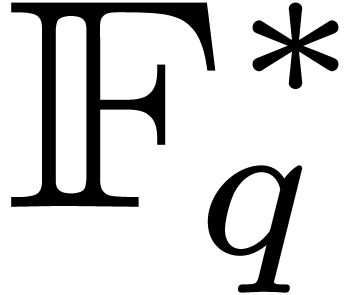 ,
Mignotte and Schnorr proposed a general deterministic root finding
algorithm in [24], that is efficient when
,
Mignotte and Schnorr proposed a general deterministic root finding
algorithm in [24], that is efficient when 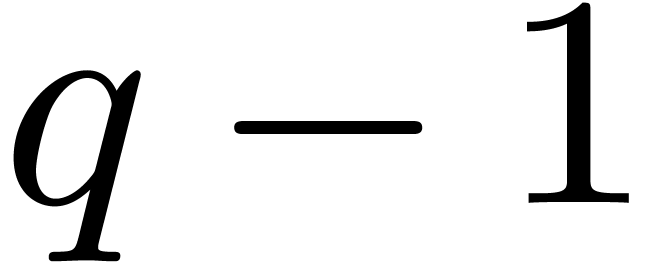 is smooth. For a fair comparison with our new algorithm presented in the
next section (and since their article is written in French) we recall
their method in a different and concise manner.
is smooth. For a fair comparison with our new algorithm presented in the
next section (and since their article is written in French) we recall
their method in a different and concise manner.
Let  be integers
be integers 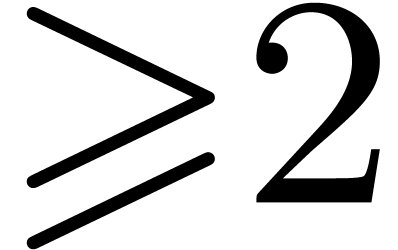 ,
such that
,
such that 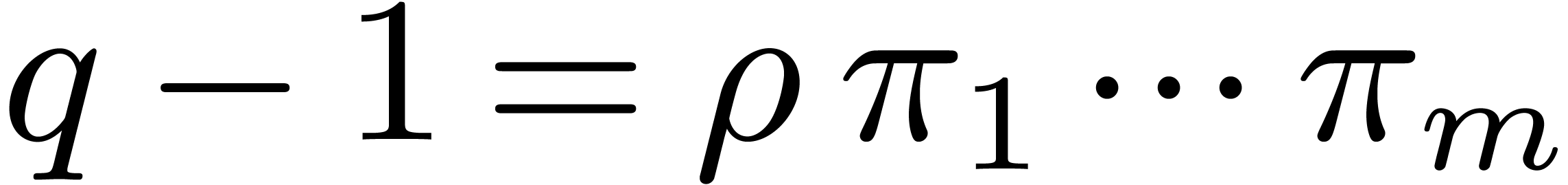 , and let
, and let 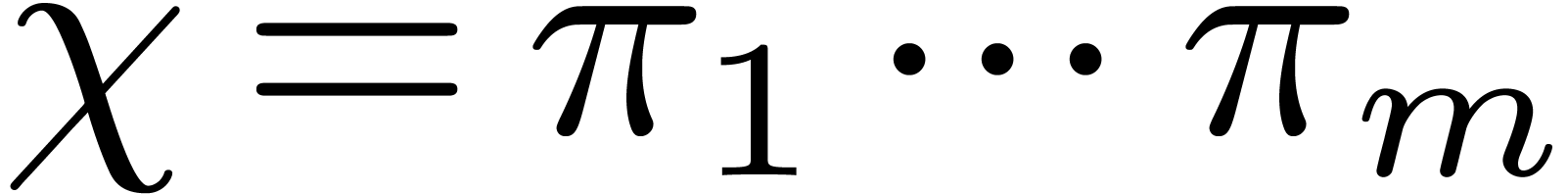 and
and 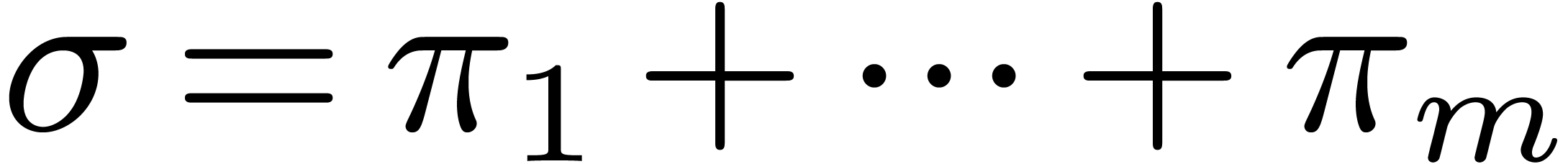 . For
instance, if the irreducible factorization of
. For
instance, if the irreducible factorization of 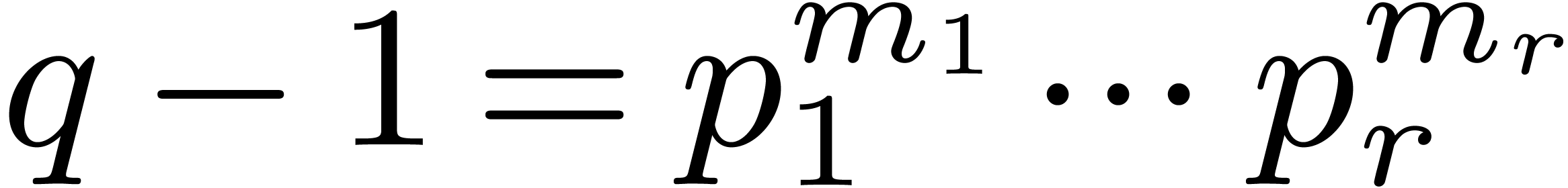 is
known, then we may take
is
known, then we may take  and
and  ,
, 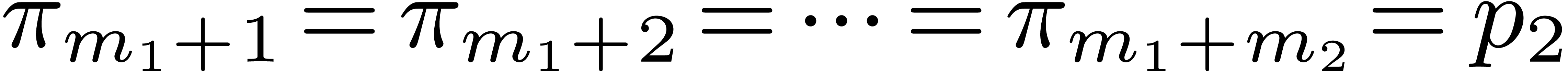 ,
…, and set
,
…, and set  . In order
to split
. In order
to split  into factors of degrees at most
into factors of degrees at most 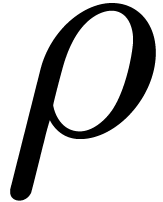 , we may use the following
algorithm.
, we may use the following
algorithm.
Algorithm 2.
-
Input
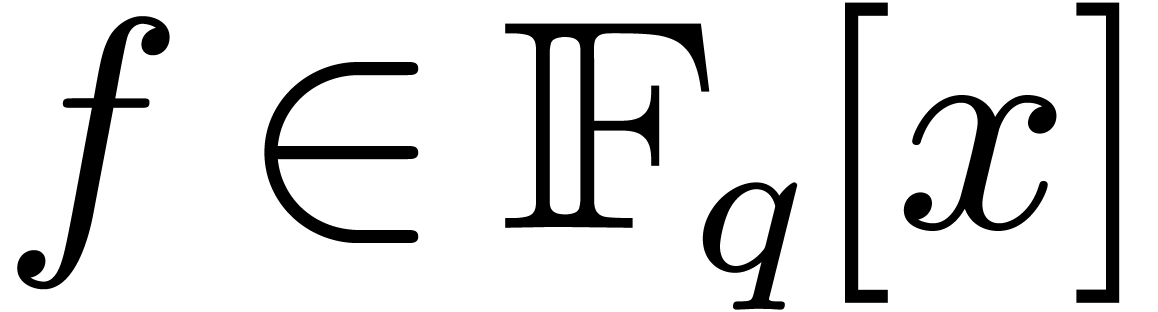 of degree
of degree
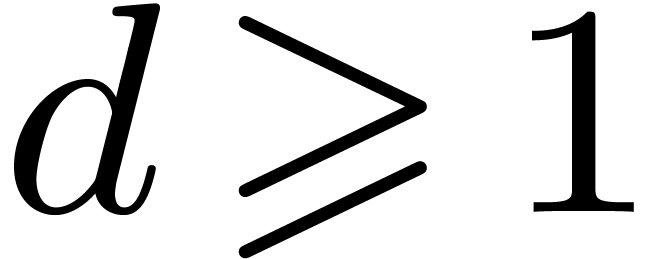 ,
monic, separable, which splits over
,
monic, separable, which splits over
 ,
and such that
,
and such that
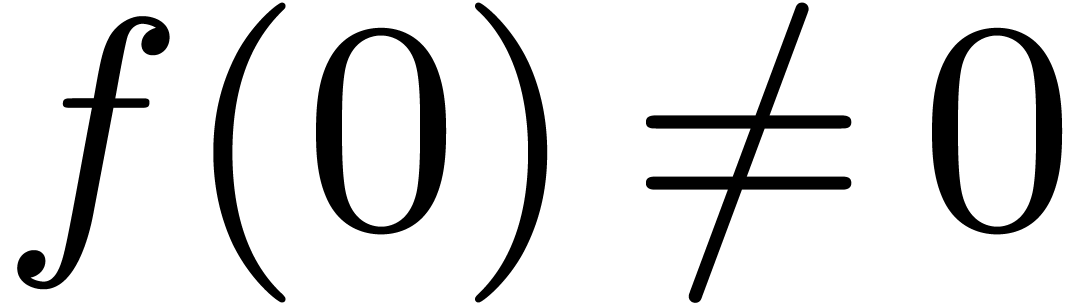 ;
a primitive root
;
a primitive root
 of unity of order
of unity of order
 .
.
-
Output
-
 in
in 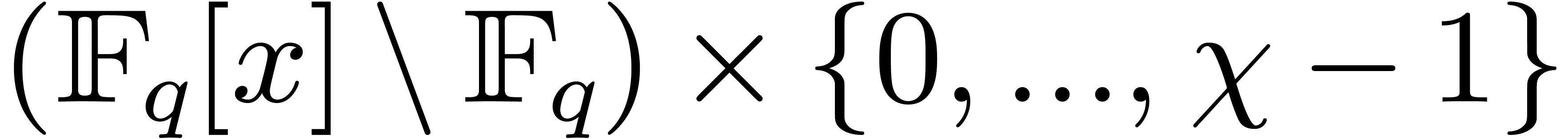 such that
such that 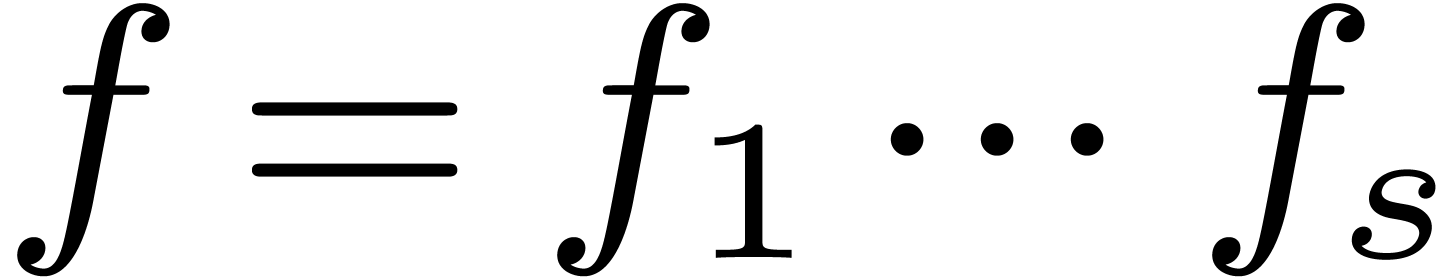 , and the
, and the 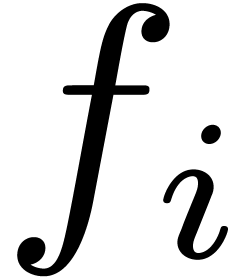 are monic, separable, and divide
are monic, separable, and divide 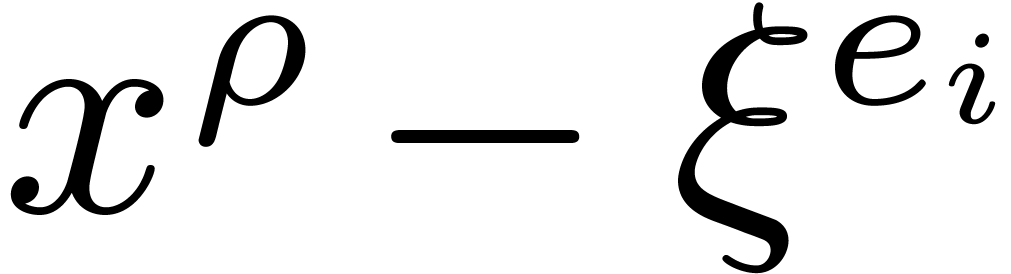 ,
for all
,
for all  .
.
-
Let 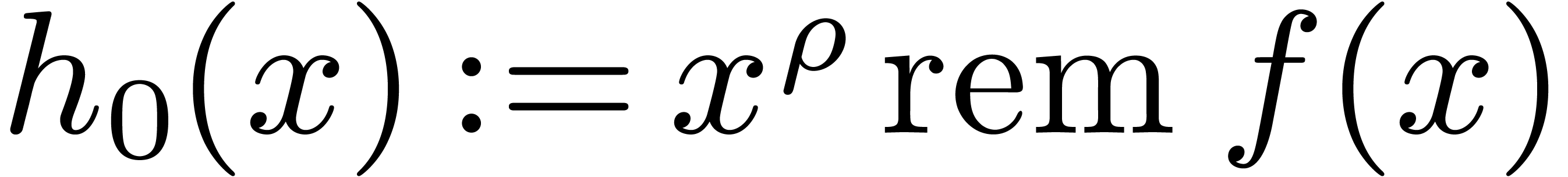 , and
, and
compute 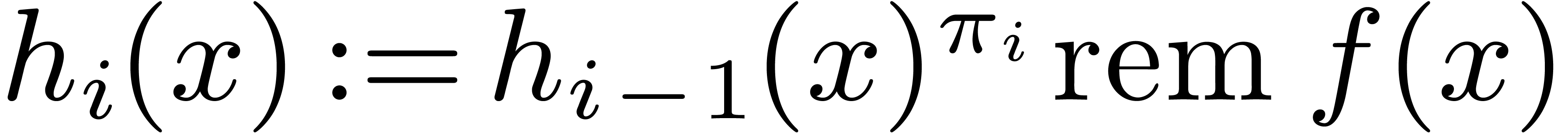 , for all
, for all 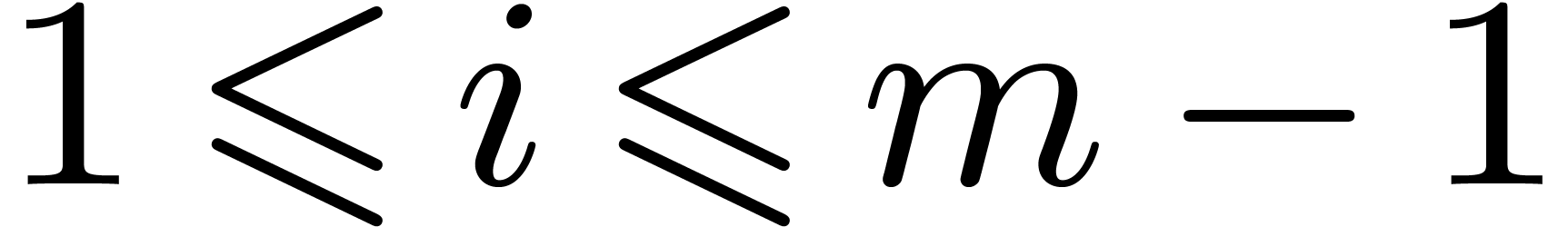 .
.
-
Initialize 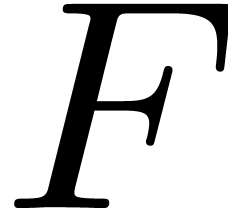 with the list
with the list 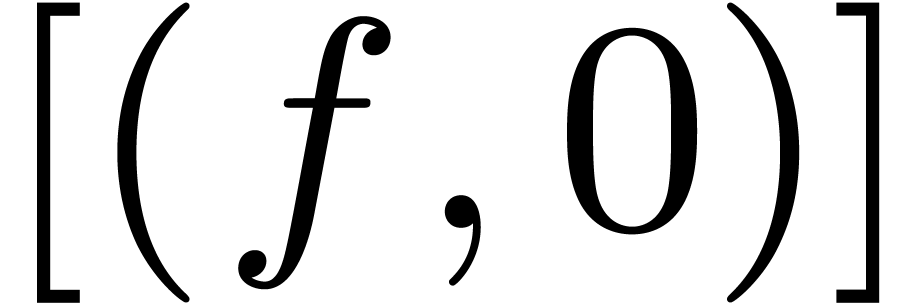 .
.
-
For  from
from  down to
down to
 do
do
-
Compute 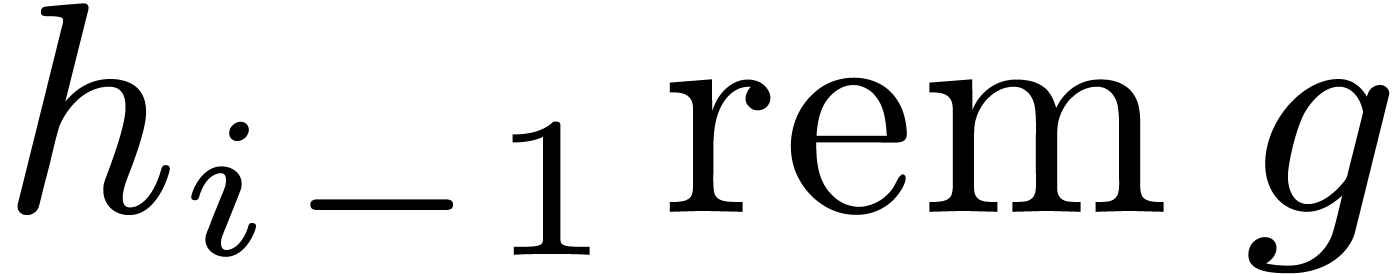 for all pairs
for all pairs 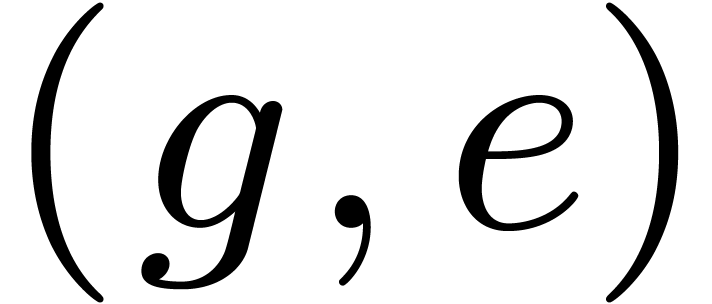 in
in  using a subproduct tree.
using a subproduct tree.
-
Initialize  with the empty list, and for
all
with the empty list, and for
all  from
from  to
to 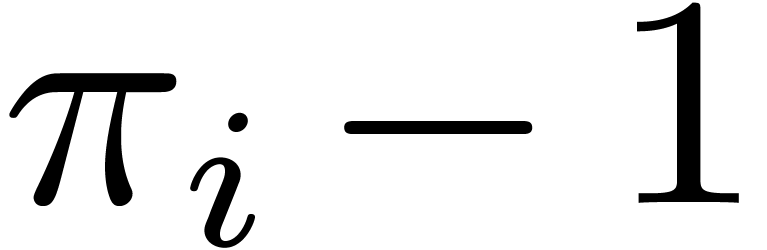 do
do
For each pair  in
in  do
do
Compute 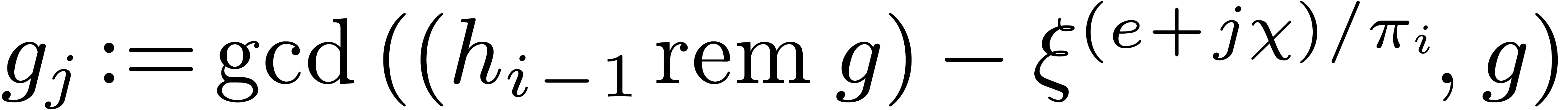 .
.
Let  .
.
Return  .
.
Lemma 3. Algorithm
2 is correct and executes in time  .
.
Proof. We prove the correctness by descending
induction on 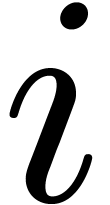 from
from  down
to
down
to 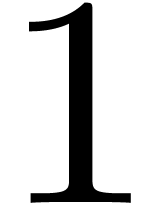 . In fact, at the end of
iteration
. In fact, at the end of
iteration 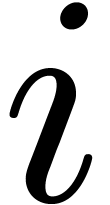 of the loop of step 3, we claim that
of the loop of step 3, we claim that
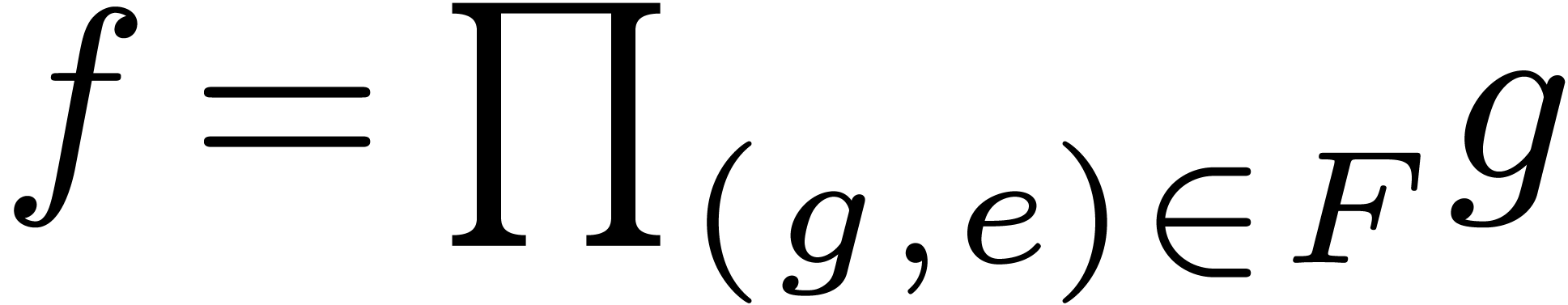 , that
, that  divides
divides  for all
for all 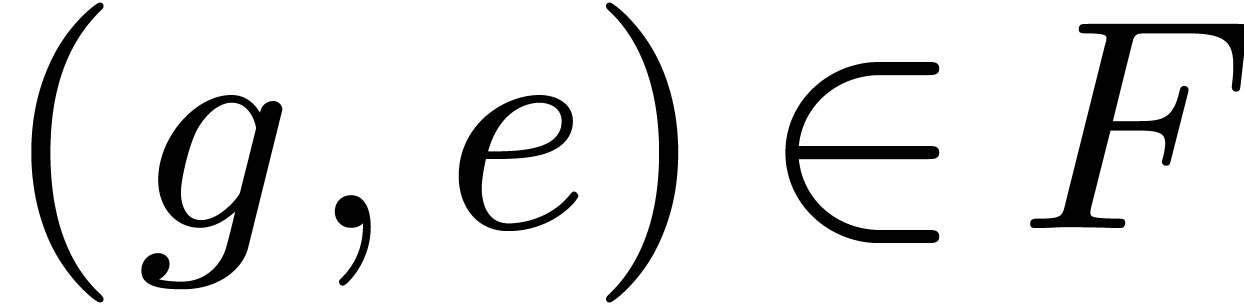 ,
and that the integers
,
and that the integers  in
in 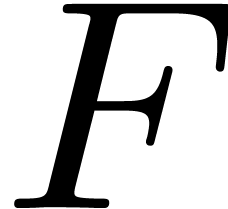 are divisible by
are divisible by 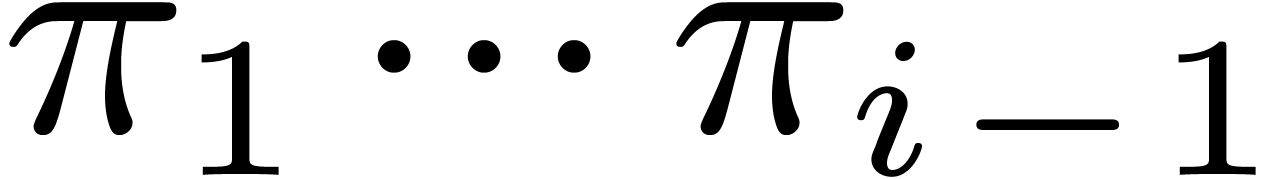 and bounded by
and bounded by 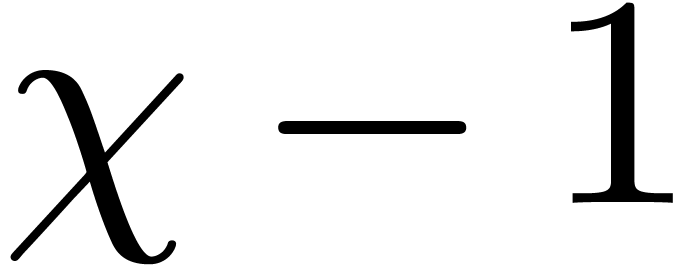 . By construction, these properties are all
true with
. By construction, these properties are all
true with 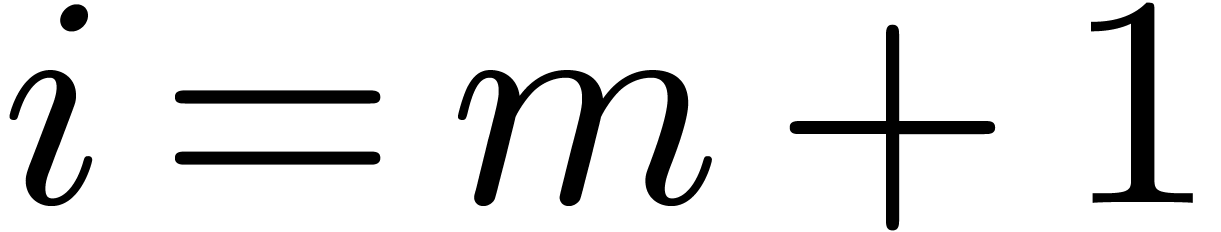 when entering step 3, so that by
induction we can assume that these properties hold for
when entering step 3, so that by
induction we can assume that these properties hold for  when entering the loop at level
when entering the loop at level 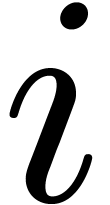 .
Let
.
Let 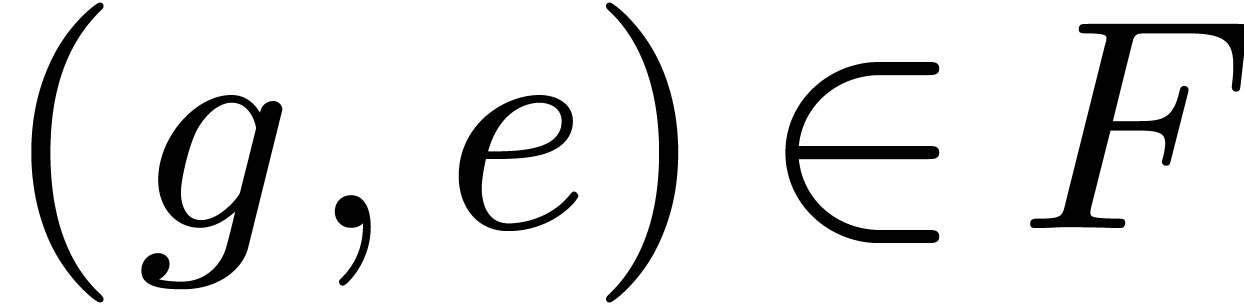 , and let
, and let  be a root of
be a root of  .
From
.
From 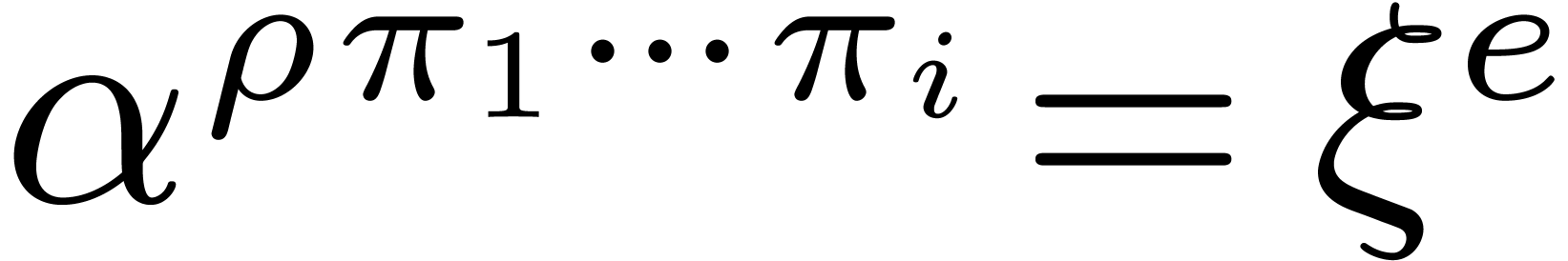 , since
, since  is divisible by
is divisible by  , there
exists
, there
exists  such that
such that  .
We are done with the correctness.
.
We are done with the correctness.
As to the complexity, we can compute the  for
for
 in time
in time 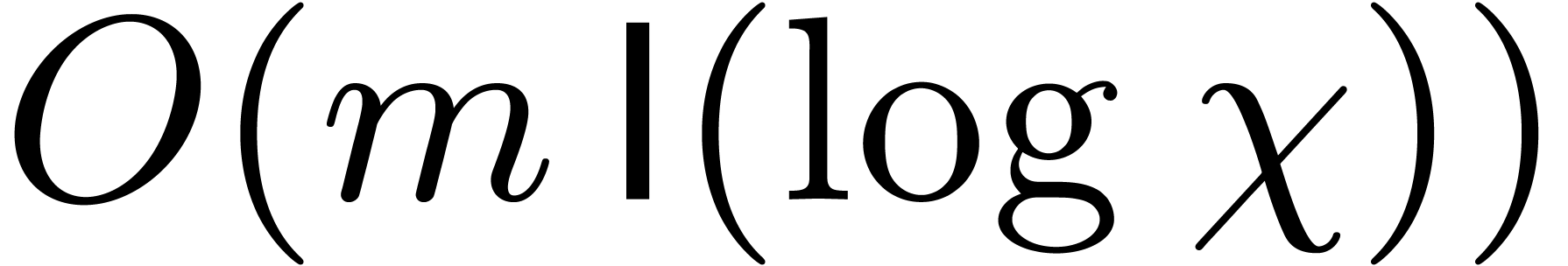 as follows: we
first compute
as follows: we
first compute 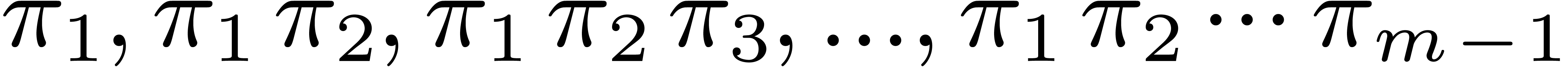 , and
, and 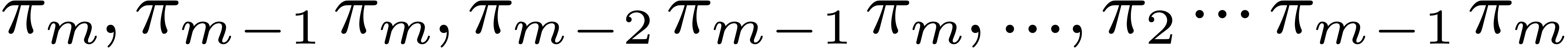 , and then deduce each
, and then deduce each  by multiplying
by multiplying 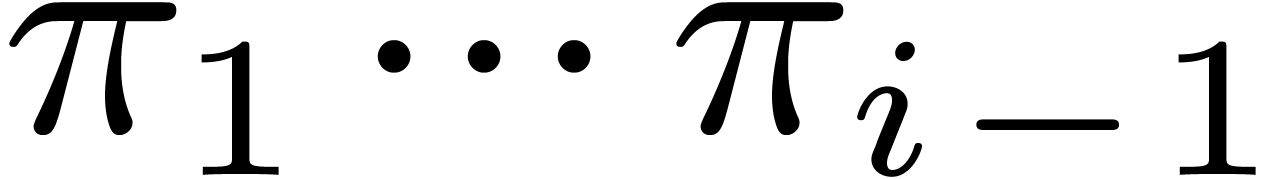 and
and  .
.
Step 1 requires time 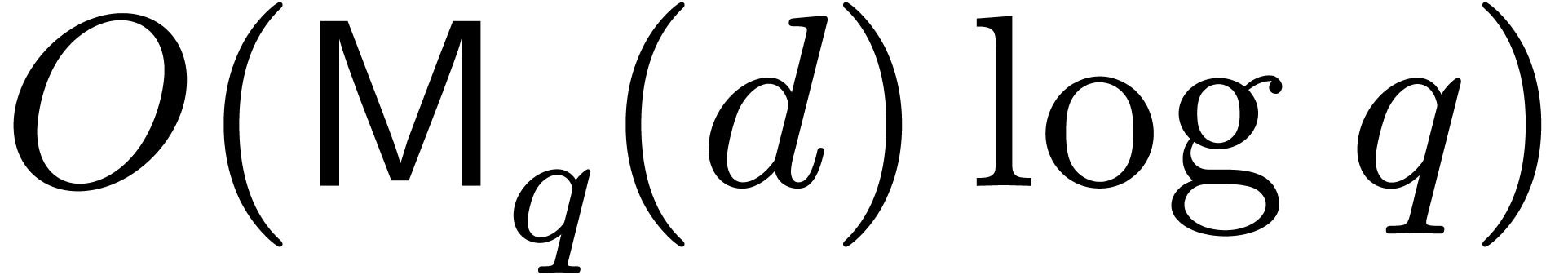 . In
step 3.a, since the sum of the degrees of the polynomials in
. In
step 3.a, since the sum of the degrees of the polynomials in  is at most
is at most 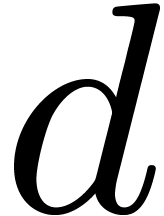 ,
and since these polynomials are monic, this step can be done in time
,
and since these polynomials are monic, this step can be done in time
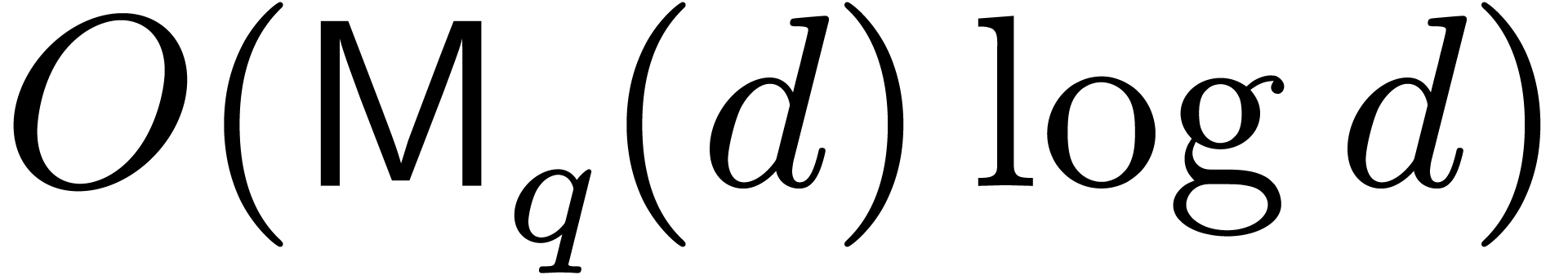 . The cost of the gcds in
step 3.b is
. The cost of the gcds in
step 3.b is 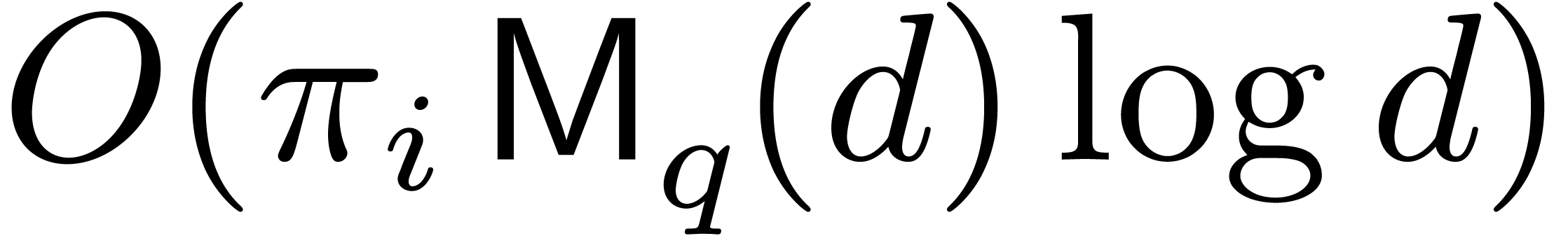 by the super-additivity of
by the super-additivity of 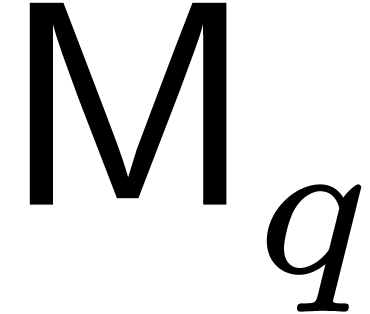 . We compute all the
. We compute all the 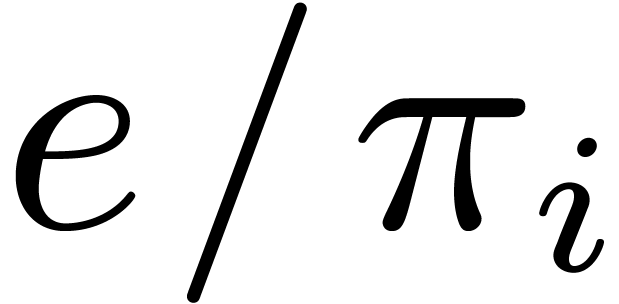 in time
in time 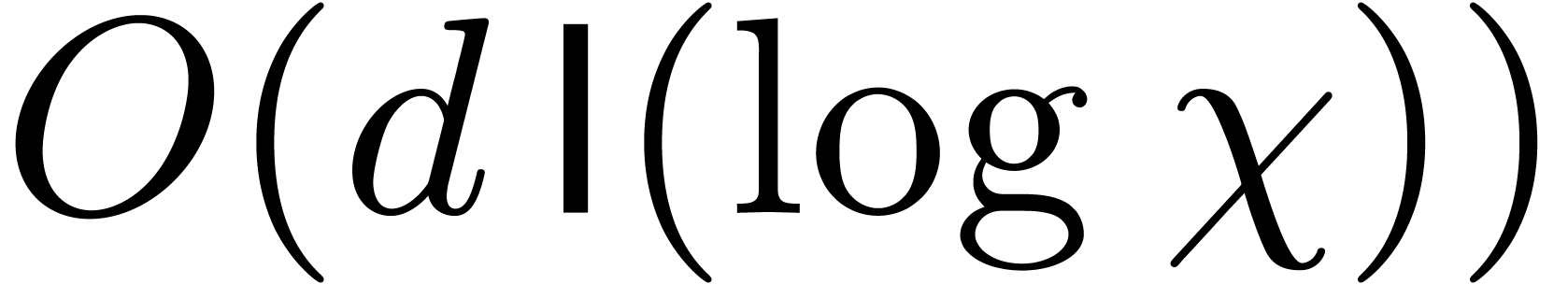 , and
then all the
, and
then all the  and
and  by
means of
by
means of 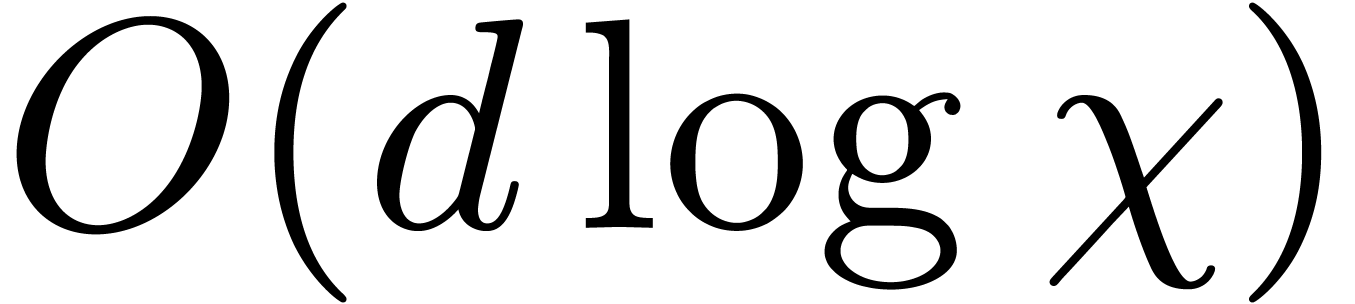 operations in
operations in  . Deducing all the
. Deducing all the 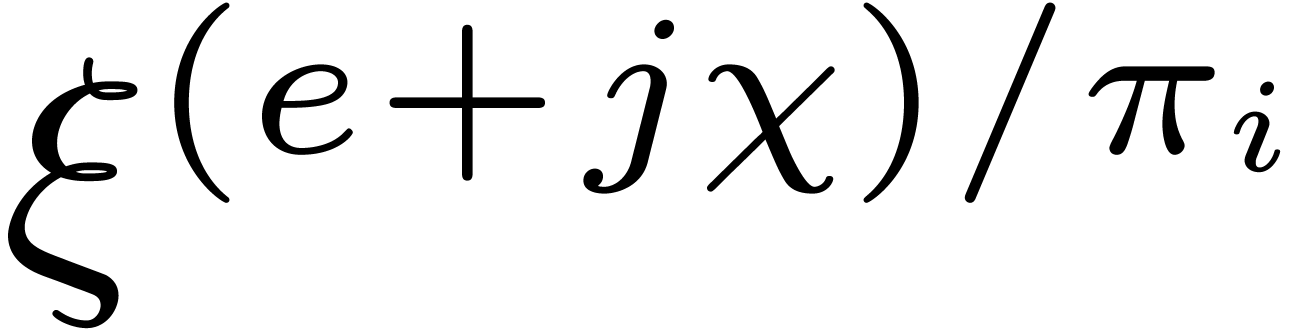 takes
takes
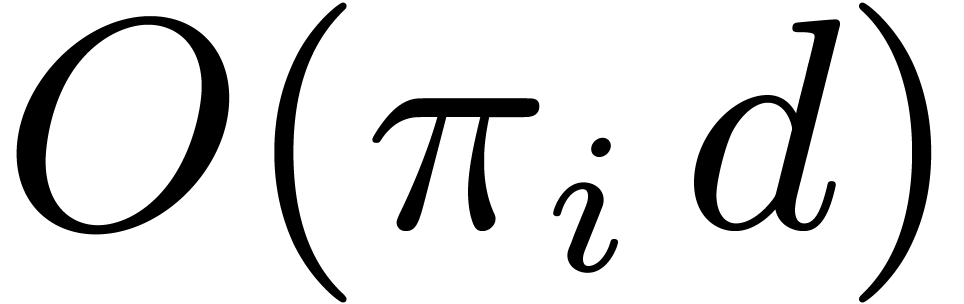 additional products in
additional products in  .
.
Since the cardinality of  cannot exceed
cannot exceed  , the total number of proper
factors
, the total number of proper
factors  in step 3.b is at most
in step 3.b is at most  . Therefore, we need
. Therefore, we need  inversions in order to make all the polynomials in
inversions in order to make all the polynomials in  monic.
monic.
Notice that the dependence on  is good when
is good when 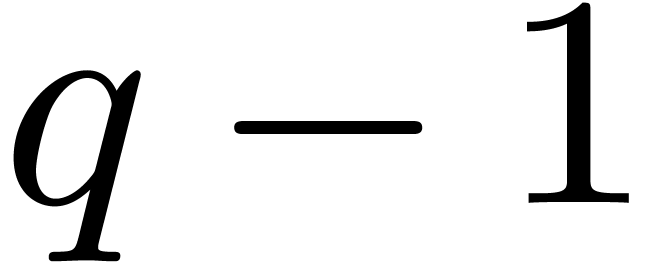 is smooth. For example, if
is smooth. For example, if 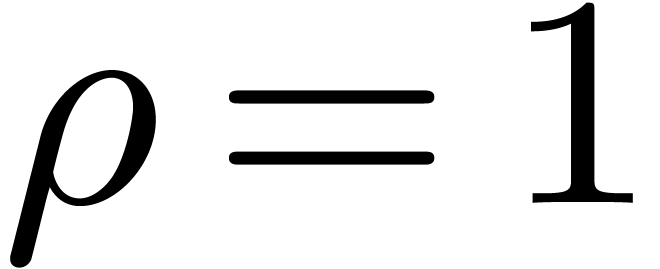 and
and 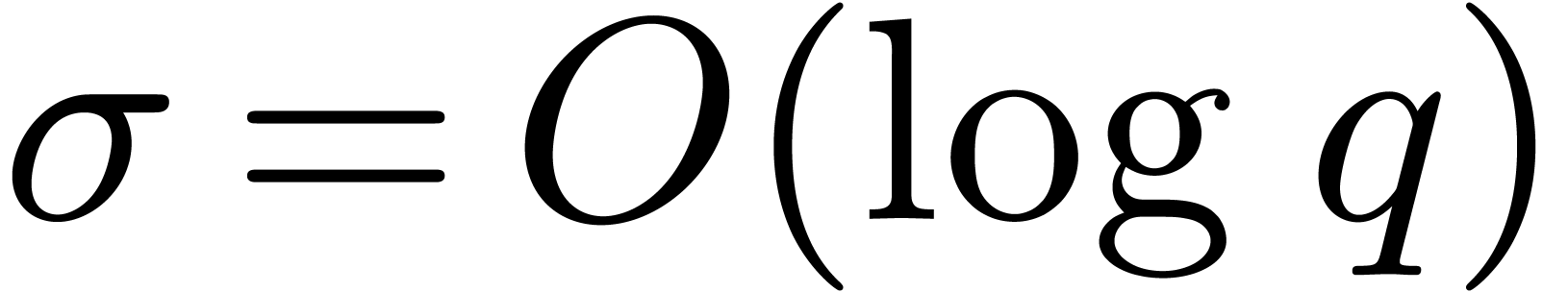 , then the cost of root
finding via the latter proposition drops to
, then the cost of root
finding via the latter proposition drops to 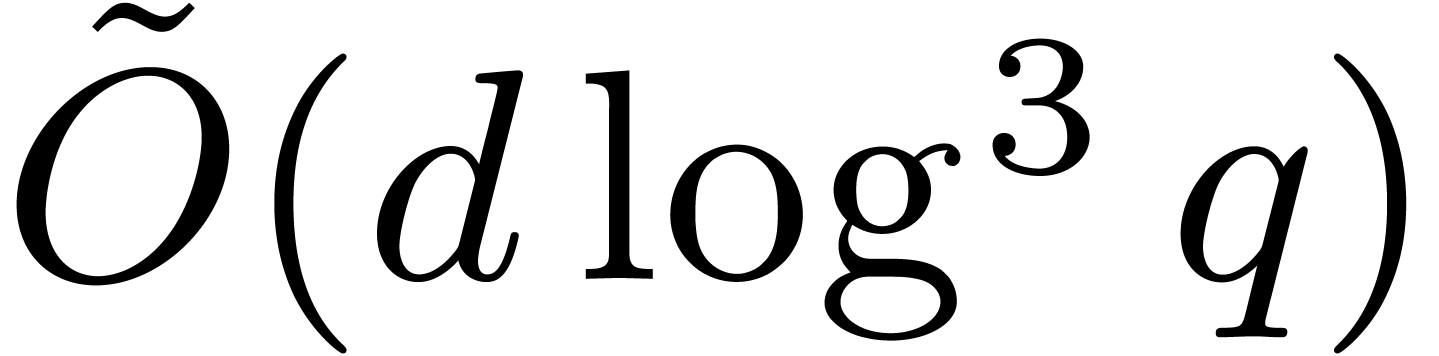 . This is higher than the average
. This is higher than the average 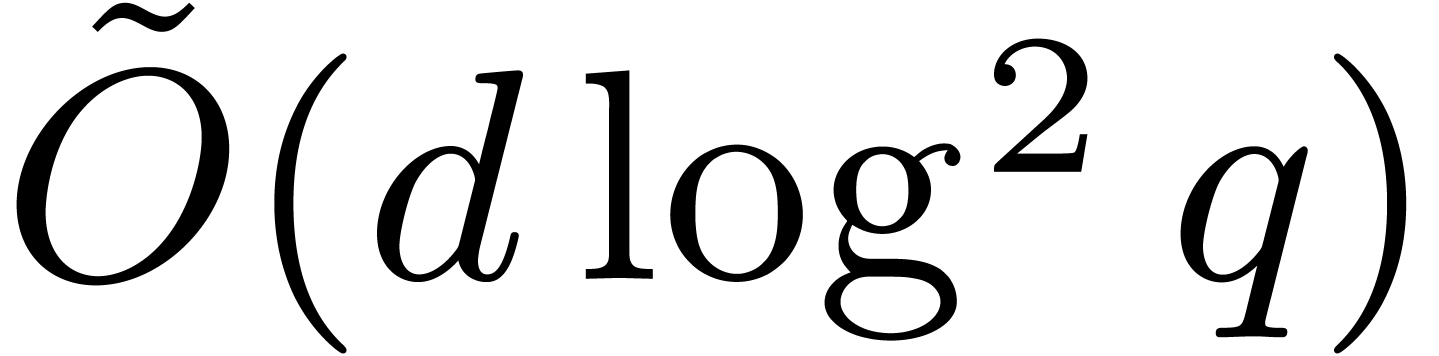 bit-cost of Cantor–Zassenhaus' algorithm.
Nevertheless since the term
bit-cost of Cantor–Zassenhaus' algorithm.
Nevertheless since the term 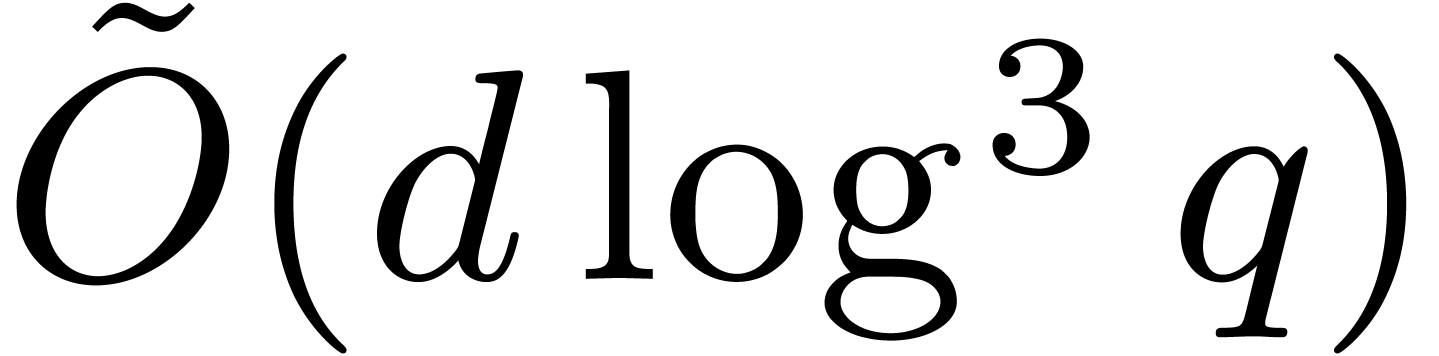 corresponds to
corresponds to 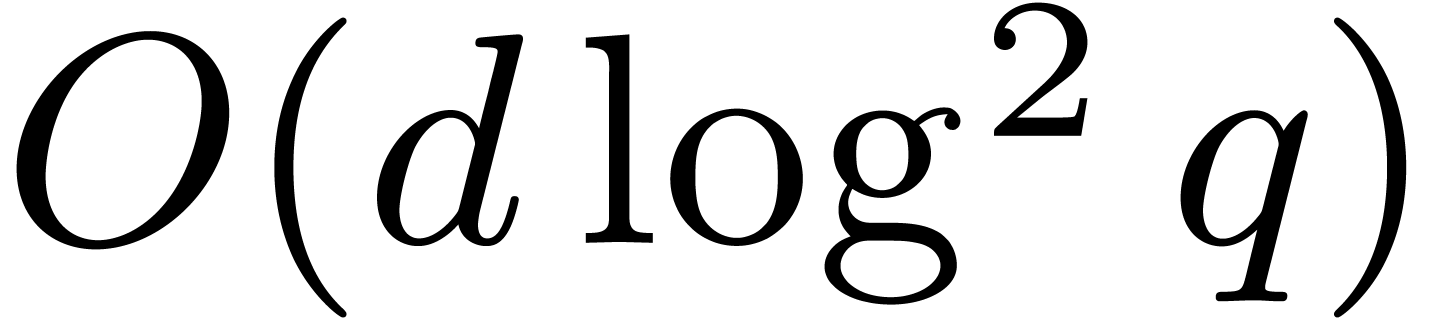 products in
products in  ,
with a small constant hidden in the
,
with a small constant hidden in the  ,
Mignotte–Schnorr's algorithm is competitive for small values of
,
Mignotte–Schnorr's algorithm is competitive for small values of
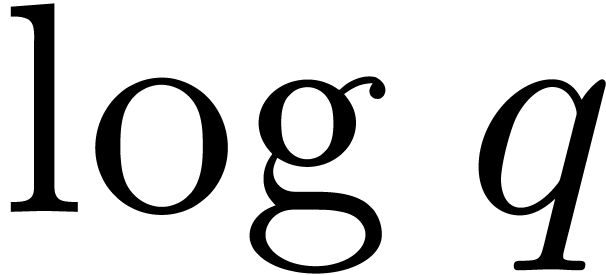 .
.
In the original work of Mignotte and Schnorr [24], the cost
of the algorithm was estimated to 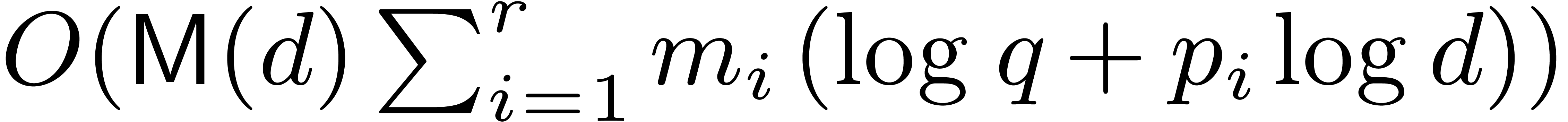 operations in
operations in
 , if
, if 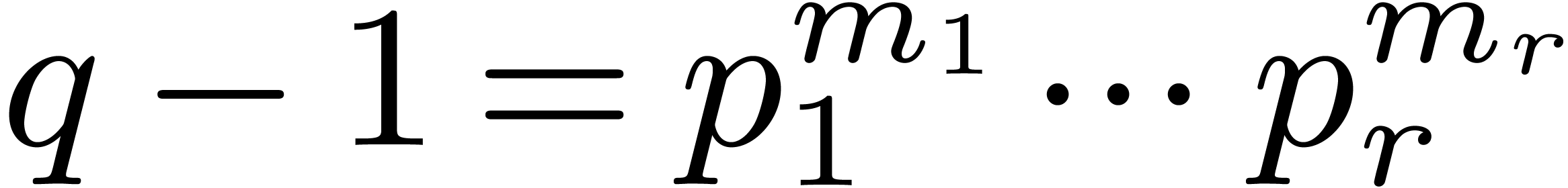 . Our presentation slightly differs by the use of a
subproduct tree in step 3.a.
. Our presentation slightly differs by the use of a
subproduct tree in step 3.a.
Let us briefly mention that a better bound for splitting  was achieved in [10]. Nevertheless, for
finding all the roots, the method of [10] does not seem
competitive in general.
was achieved in [10]. Nevertheless, for
finding all the roots, the method of [10] does not seem
competitive in general.
2.3Moenck's algorithm
Moenck's algorithm [25] deals with the special case when
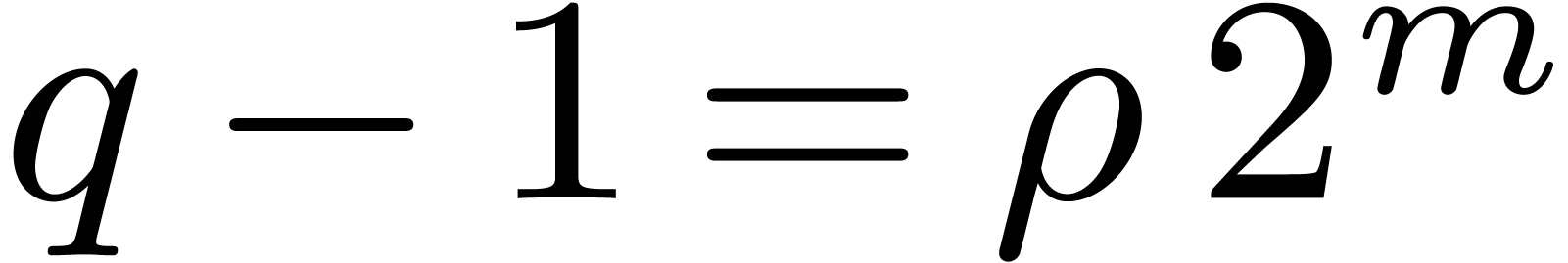 . Let
. Let  be a primitive root of
be a primitive root of 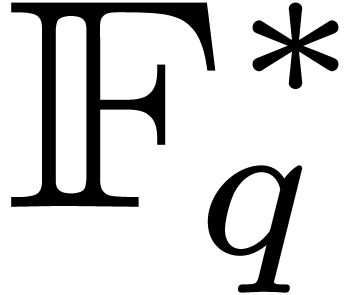 . Let
. Let
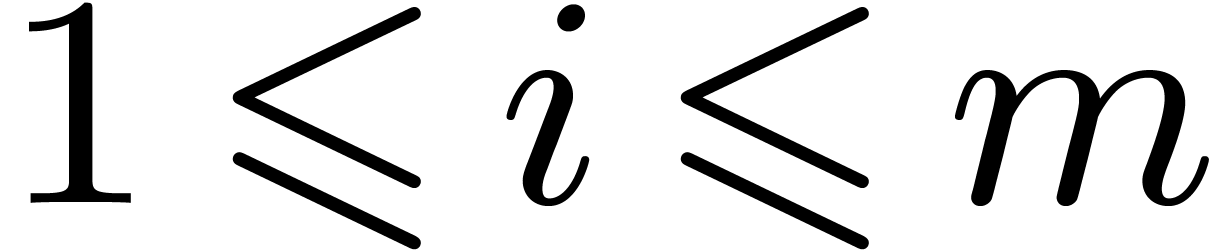 , let
, let  be a polynomial whose roots have orders dividing
be a polynomial whose roots have orders dividing 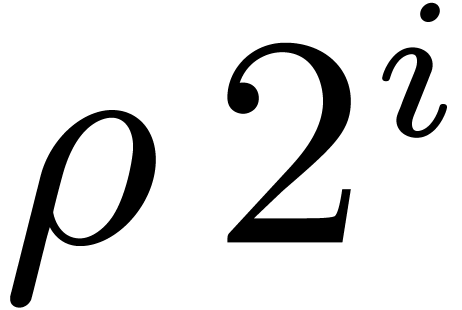 , and let
, and let 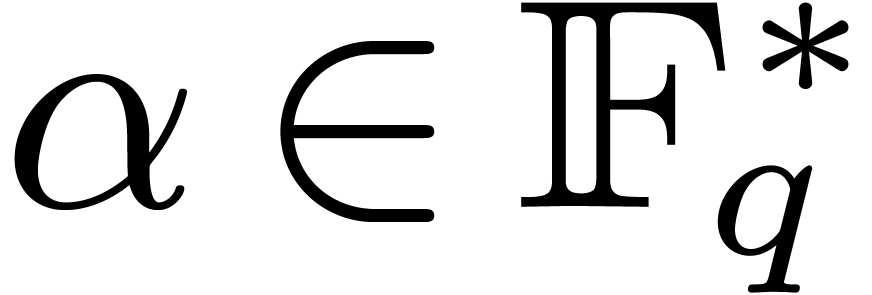 be one of these
roots. Then either this order divides
be one of these
roots. Then either this order divides 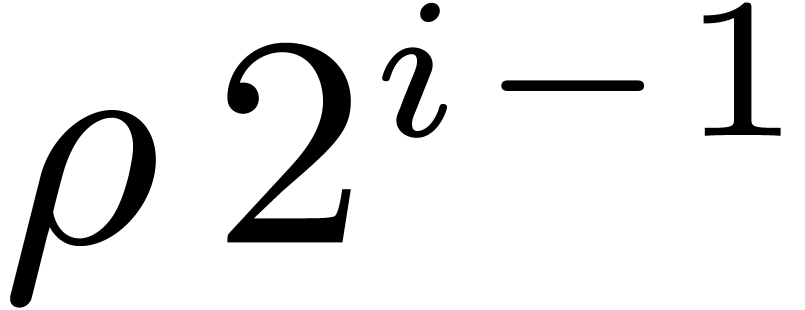 ,
or we have
,
or we have 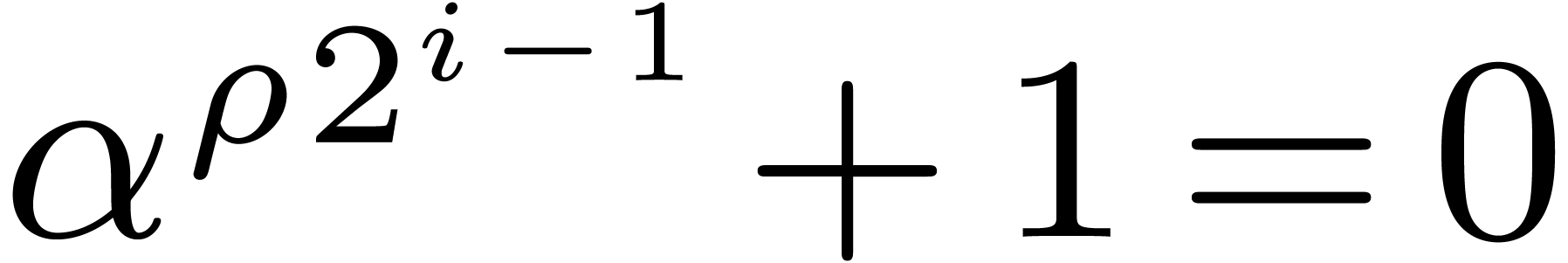 , since
, since 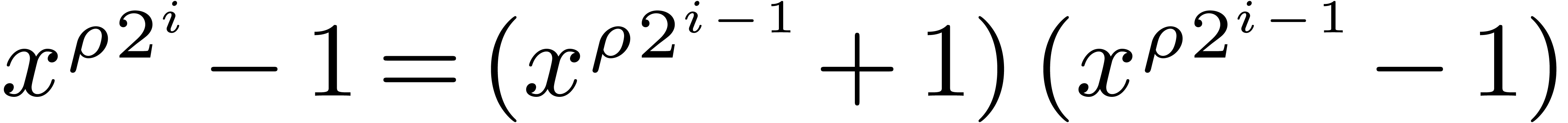 . In the latter case, we obtain
. In the latter case, we obtain
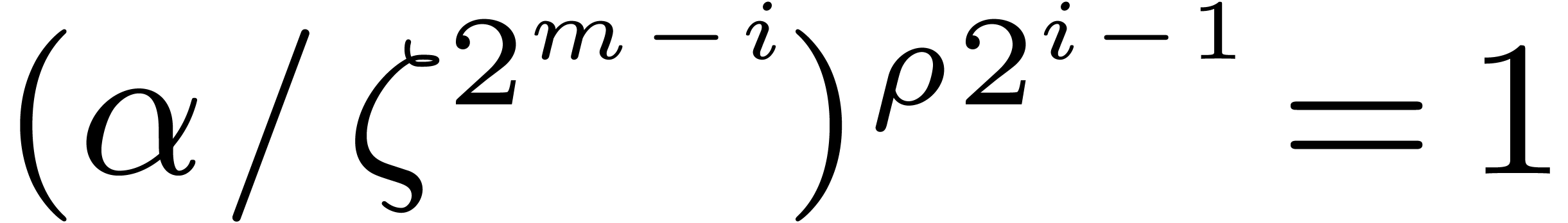 . The polynomials
. The polynomials  and
and 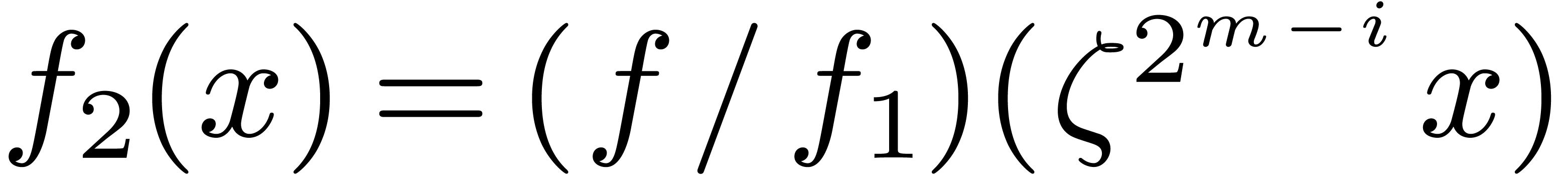 have all their roots of order
dividing
have all their roots of order
dividing 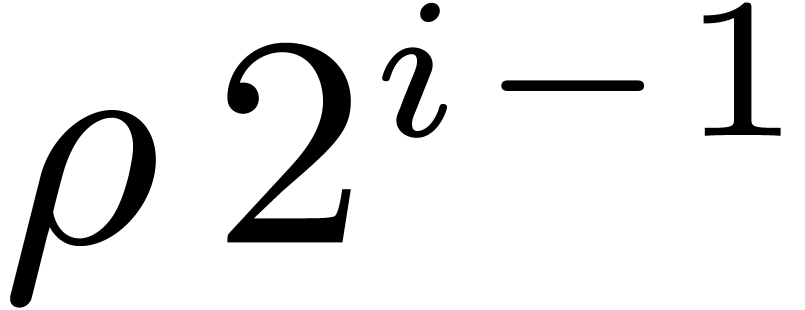 . In this way, the
roots of
. In this way, the
roots of  can be computed inductively starting
from
can be computed inductively starting
from 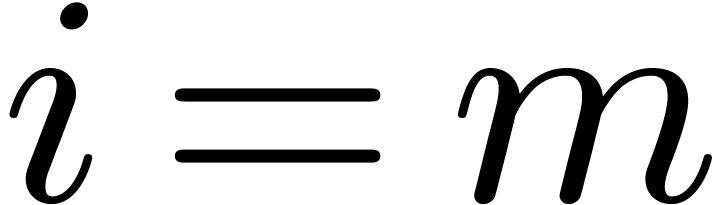 down to
down to 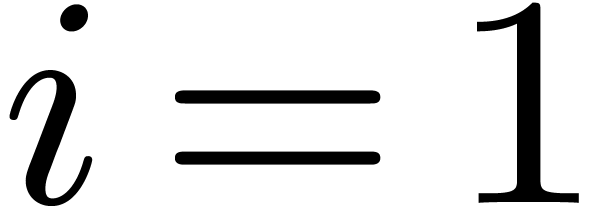 .
At the end, we are reduced to finding roots of several polynomials whose
orders divide
.
At the end, we are reduced to finding roots of several polynomials whose
orders divide  . If
. If  is small, then an exhaustive search easily completes the
computations. Otherwise we may use a fallback algorithm. Moenck's
algorithm summarizes as follows.
is small, then an exhaustive search easily completes the
computations. Otherwise we may use a fallback algorithm. Moenck's
algorithm summarizes as follows.
Algorithm 4.
-
Input
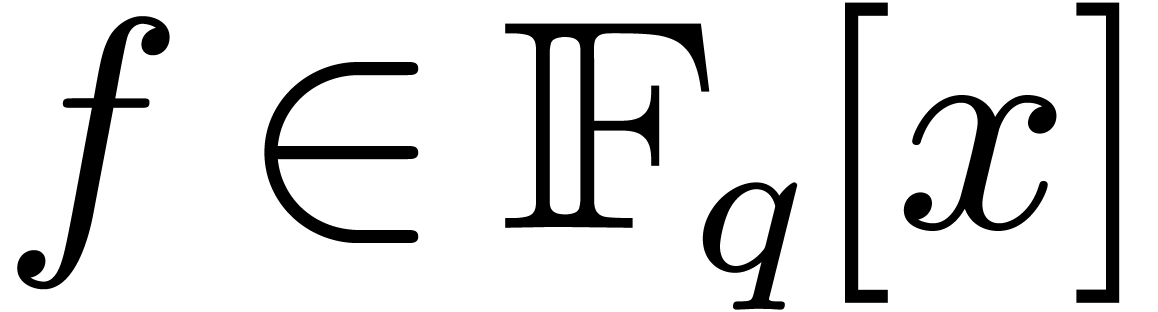 of degree
of degree
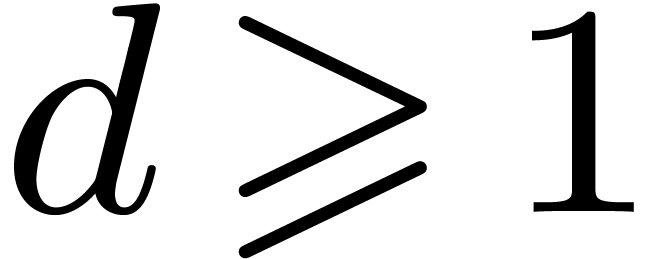 ,
monic, separable, which splits over
,
monic, separable, which splits over
 ,
and such that
,
and such that
 ;
a primitive element
;
a primitive element
 of
of
 .
.
-
Output
-
 in
in  such that
such that , the
, the 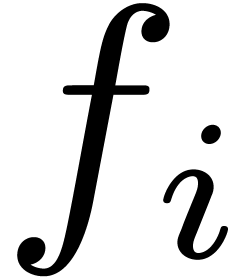 are monic, separable, and the roots of
are monic, separable, and the roots of 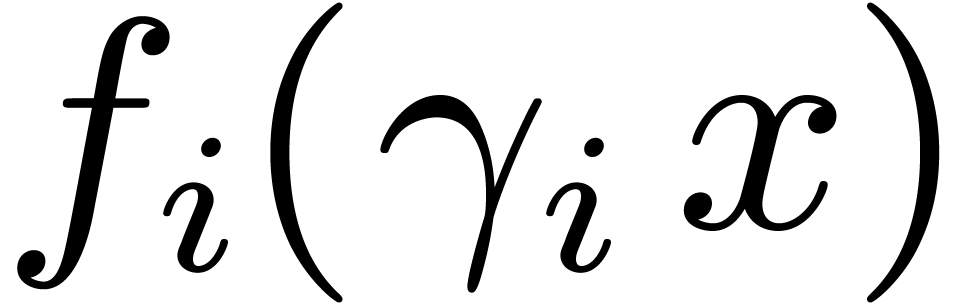 have orders dividing
have orders dividing  .
.
-
Compute 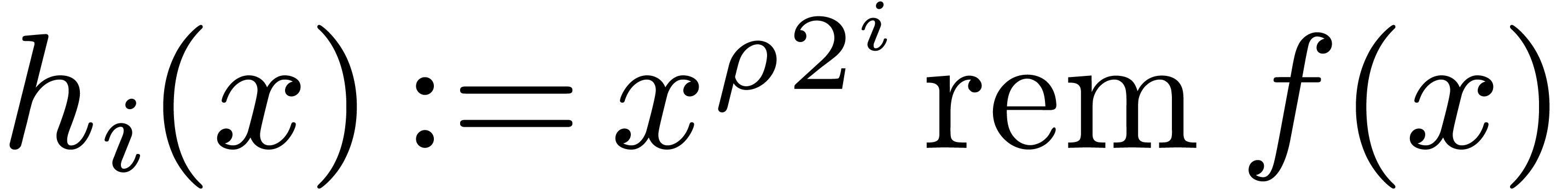 for all
for all  .
.
-
Initialize  with the list
with the list  .
.
-
For  from
from  down to
down to
 do
do
-
Compute the remainders of 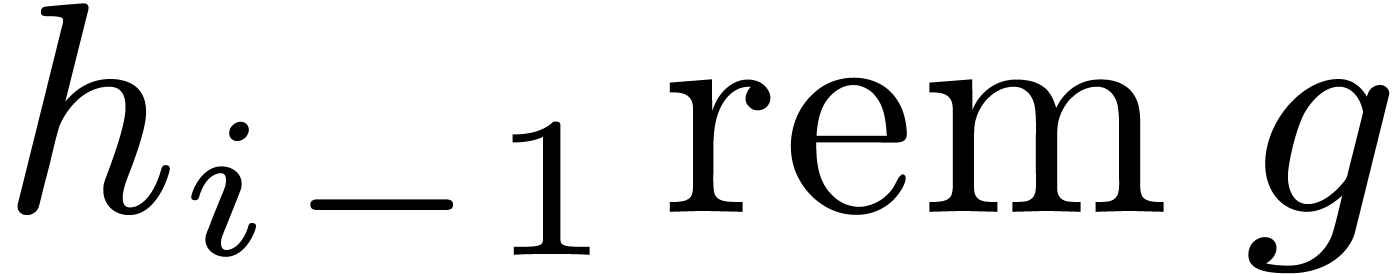 for all
triples
for all
triples  in
in  using
a subproduct tree.
using
a subproduct tree.
-
Initialize  as an empty list.
as an empty list.
-
For all  in
in  do
do
-
Compute  . If
. If  is not constant then make it monic and
append
is not constant then make it monic and
append  to
to  .
.
-
Compute 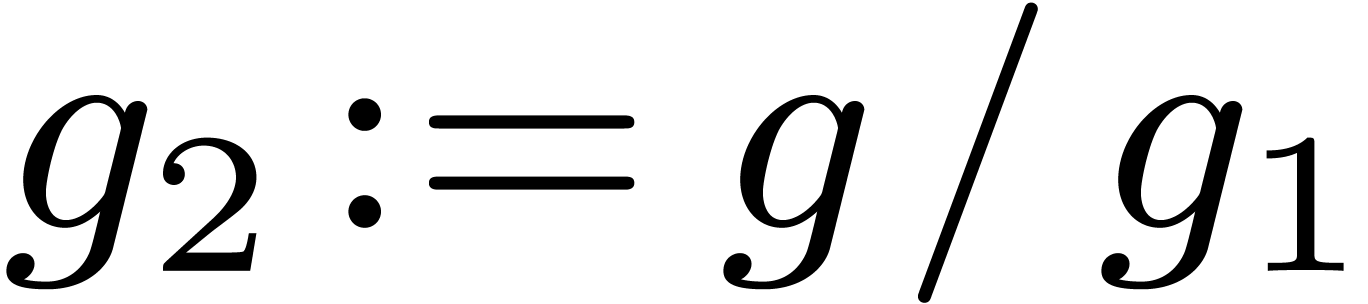 . If
. If 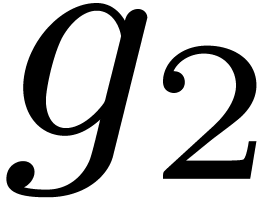 is not constant then make it monic, and
append
is not constant then make it monic, and
append  to
to  .
.
-
Replace  by
by  .
.
-
Return  .
.
Our presentation differs from [25]. We also introduced step
3.a, which yields a sensible theoretical speed-up, similarly to
Mignotte–Schnorr's algorithm. In fact Moenck's and
Mignotte–Schnorr's algorithms are quite similar from the point of
view of the successive splittings of  ,
and the intermediate operations. We thus leave out the details on
correctness and cost analysis. As an advantage, the logarithms of the
successive roots are not needed. Nevertheless computing all the powers
of
,
and the intermediate operations. We thus leave out the details on
correctness and cost analysis. As an advantage, the logarithms of the
successive roots are not needed. Nevertheless computing all the powers
of  in steps 3.c amounts to a bit-cost
in steps 3.c amounts to a bit-cost 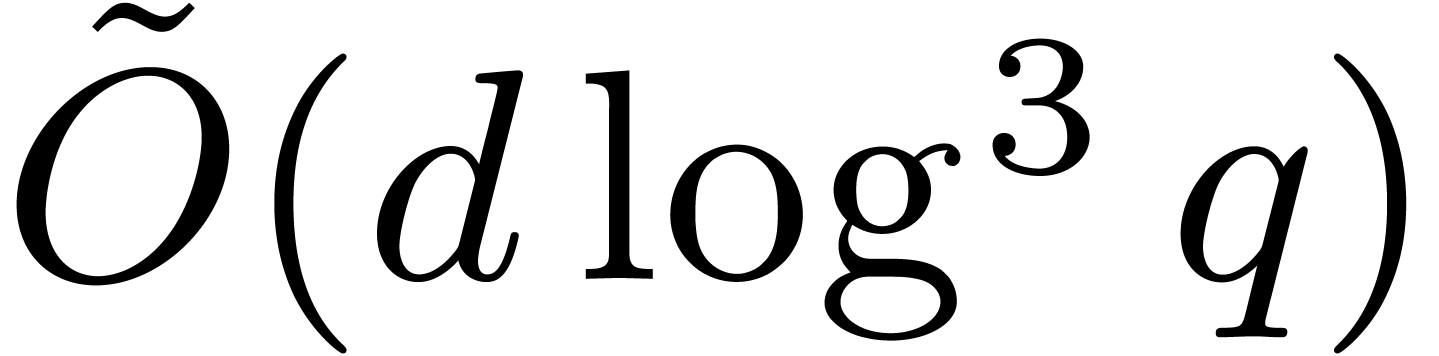 .
.
3.Using Graeffe transforms
One advantage of Cantor–Zassenhaus' algorithm is its average depth
in the recursive calls in 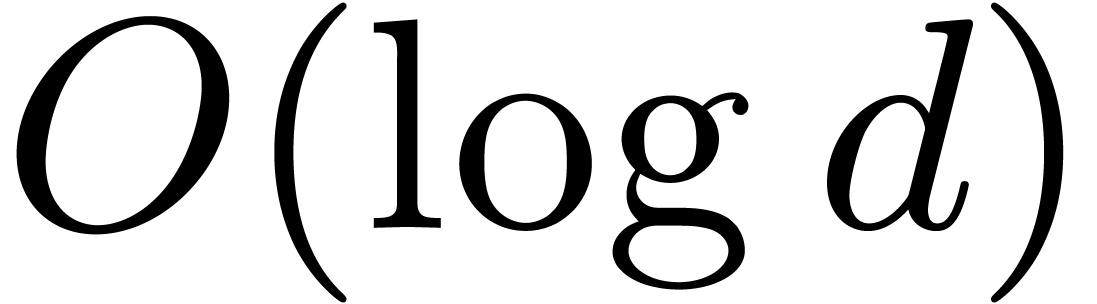 .
This is to be compared to the
.
This is to be compared to the 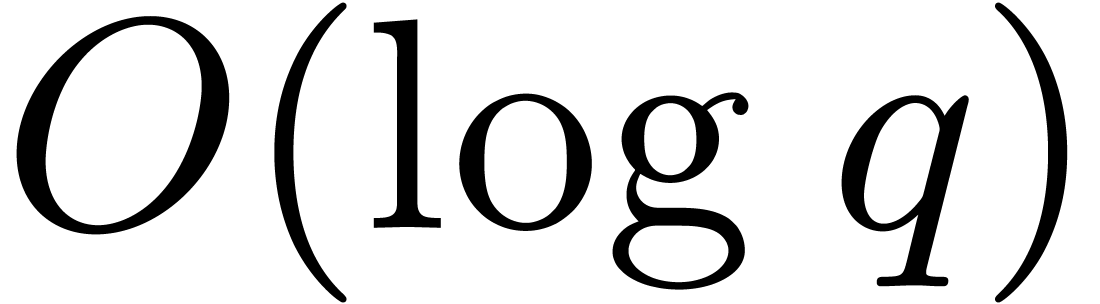 iterations of
Algorithms 2 and 4. In this section we propose
a new kind of root finder based on the tangent Graeffe transform, which
takes advantage of a FFT prime field, with an average cost not exceeding
the one of Cantor–Zassenhaus.
iterations of
Algorithms 2 and 4. In this section we propose
a new kind of root finder based on the tangent Graeffe transform, which
takes advantage of a FFT prime field, with an average cost not exceeding
the one of Cantor–Zassenhaus.
3.1Generalized Graeffe
transforms
Classically, the Graeffe transform of a polynomial 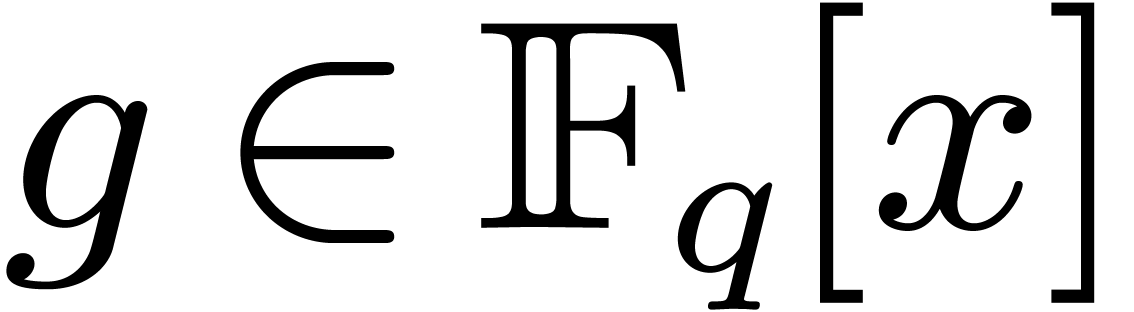 of degree
of degree 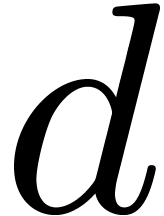 is the unique polynomial
is the unique polynomial
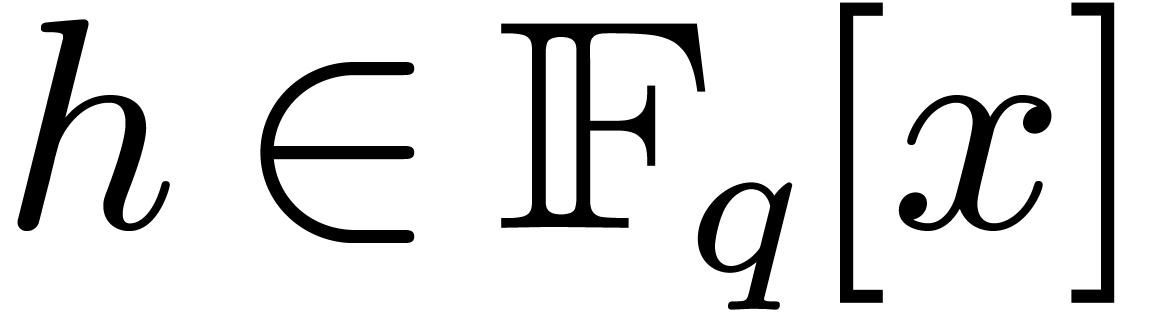 satisfying
satisfying 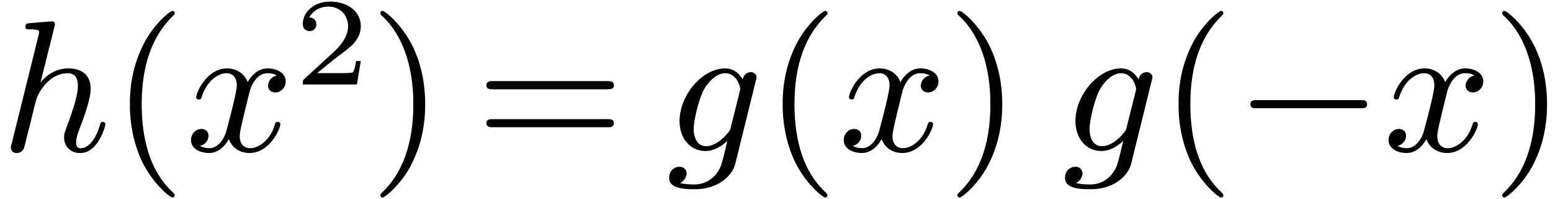 .
If
.
If  , then
, then  . This construction can be extended to higher
orders as follows: the generalized Graeffe transform of
. This construction can be extended to higher
orders as follows: the generalized Graeffe transform of  of order
of order  ,
written
,
written 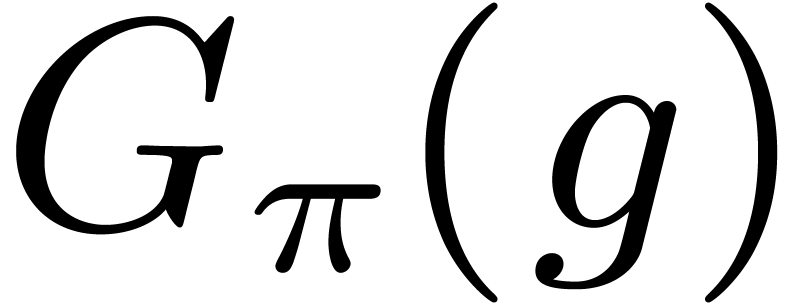 , is defined as the
resultant
, is defined as the
resultant
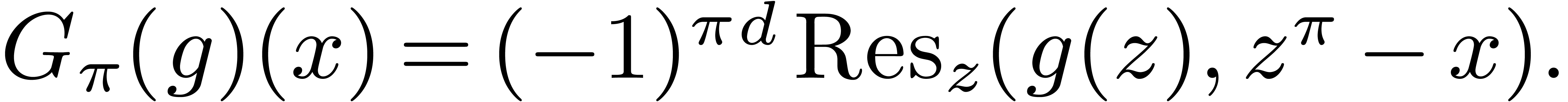
If 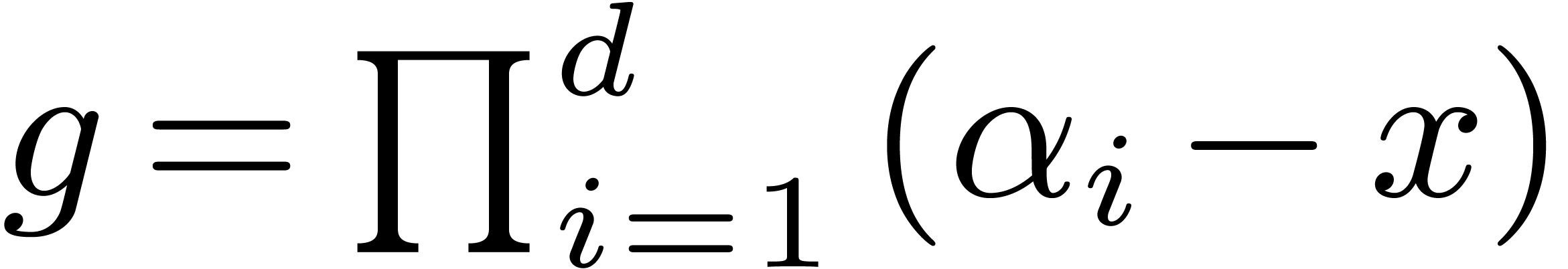 , then
, then 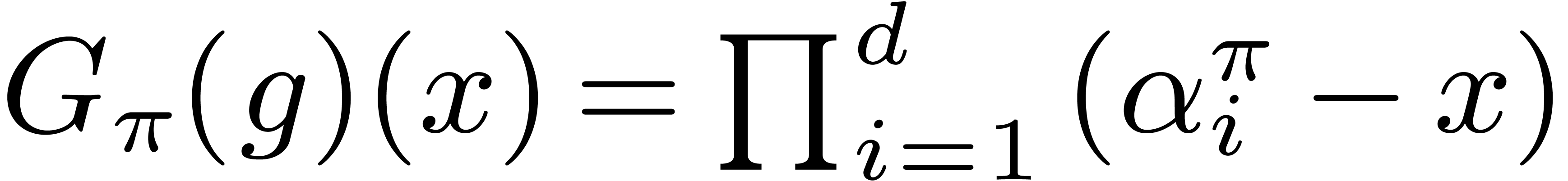 . Equivalently,
. Equivalently, 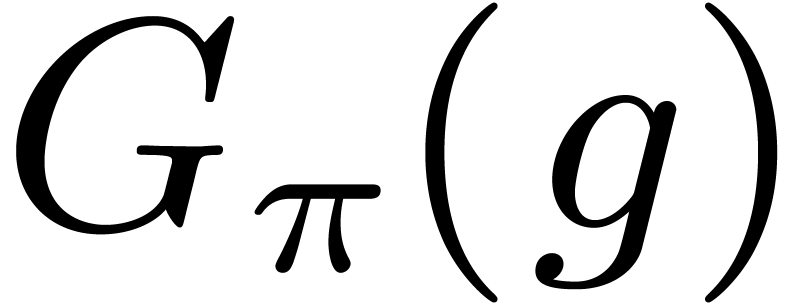 is the
characteristic polynomial of multiplication by
is the
characteristic polynomial of multiplication by 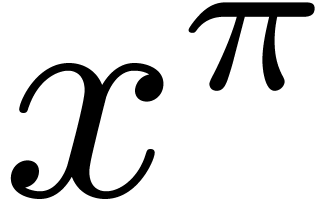 in
in 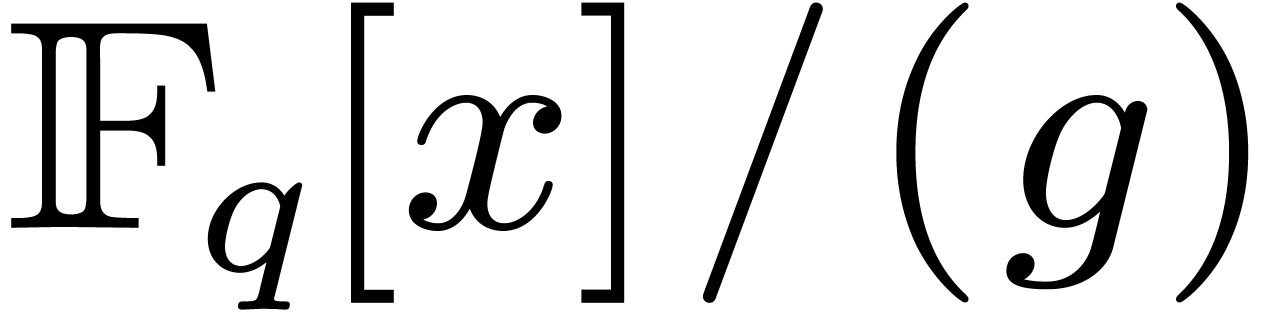 (up to the sign). For our root finding
algorithms, the most important case is when
(up to the sign). For our root finding
algorithms, the most important case is when 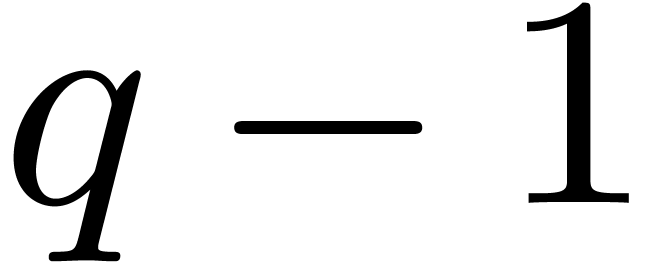 is
smooth and the order
is
smooth and the order  of the generalized Graeffe
transform divides
of the generalized Graeffe
transform divides 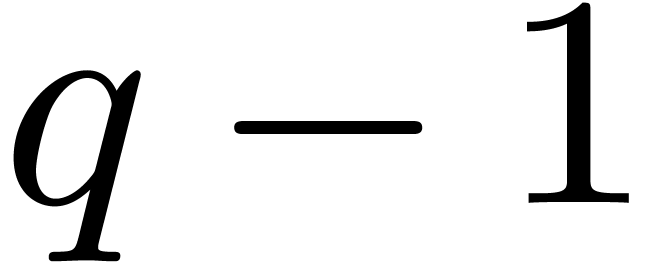 .
.
Proposition 5. Let
 be integers
be integers 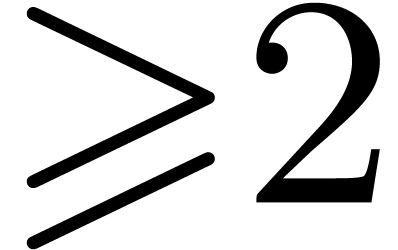 ,
such that
,
such that 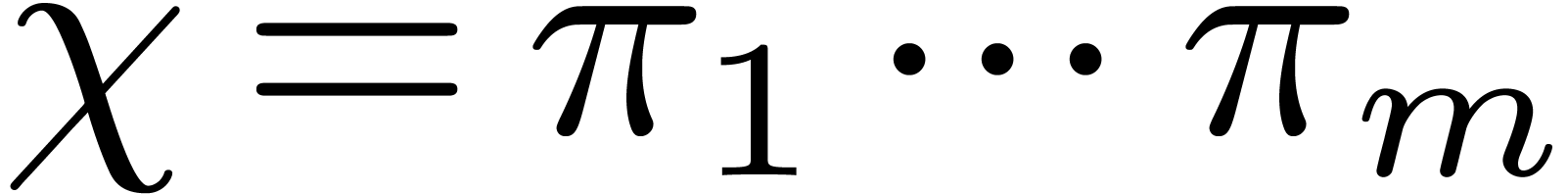 divides
divides 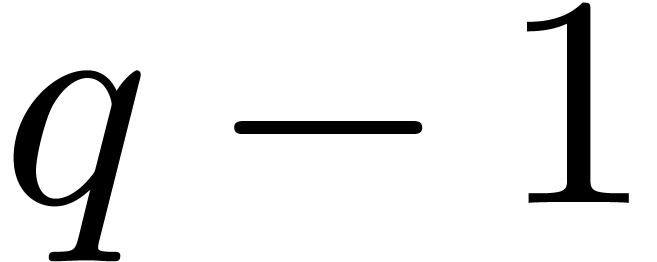 ,
and let
,
and let  be given primitive roots of unity of
orders
be given primitive roots of unity of
orders  , for all
, for all 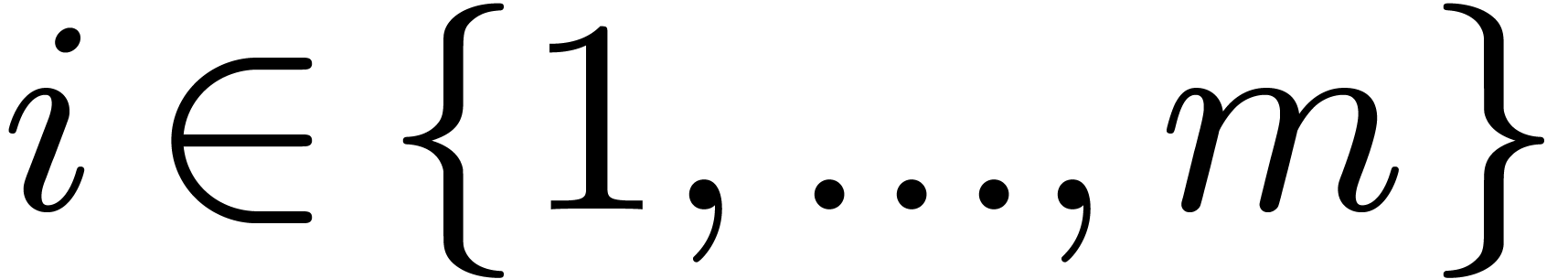 . If
. If  is a monic
polynomial in
is a monic
polynomial in 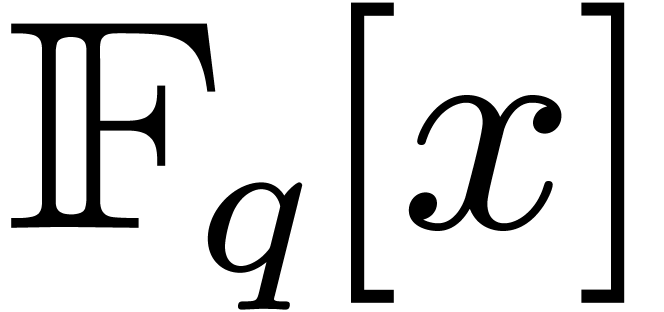 of degree
of degree  , then the generalized Graeffe transforms of orders
, then the generalized Graeffe transforms of orders
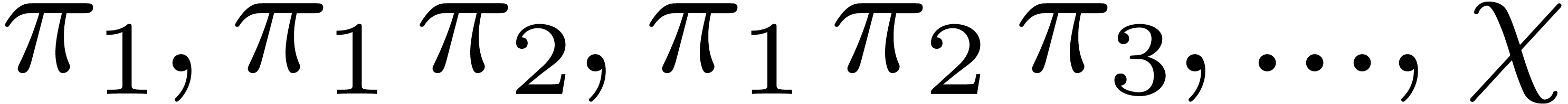 of
of  can be computed in
time
can be computed in
time 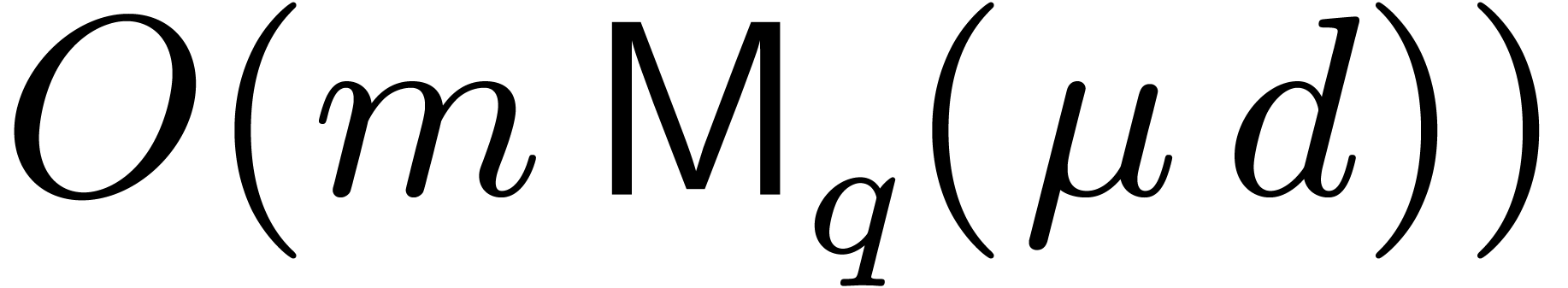 or
or 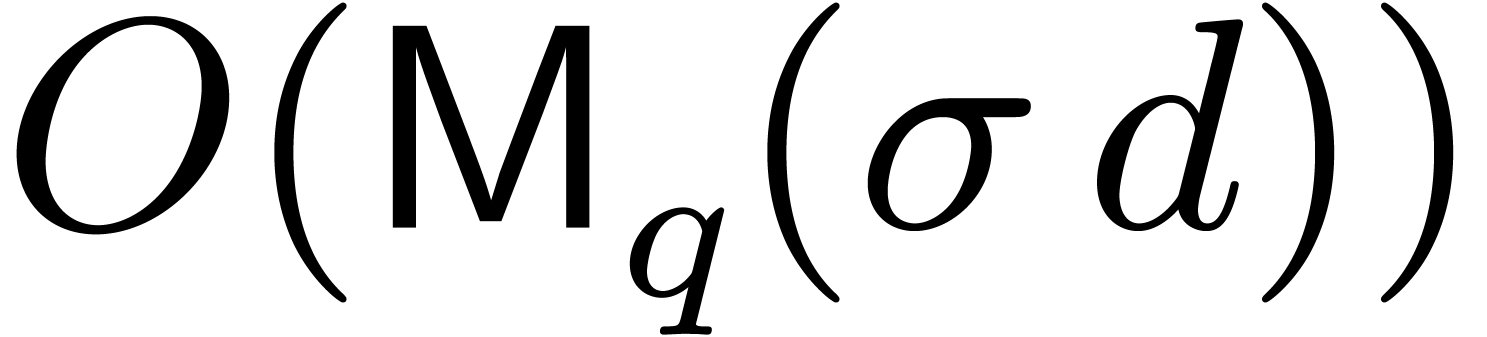 ,
where
,
where  and
and 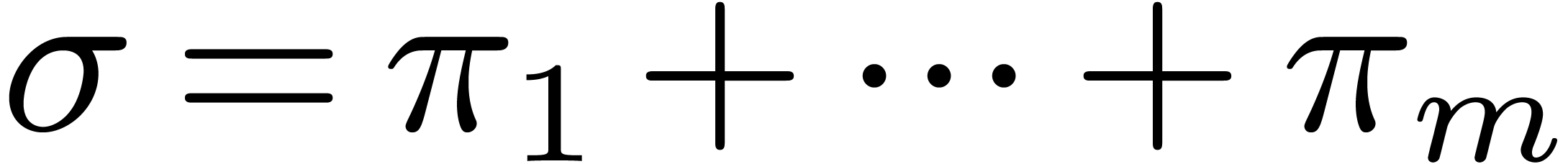 .
.
Proof. Writing 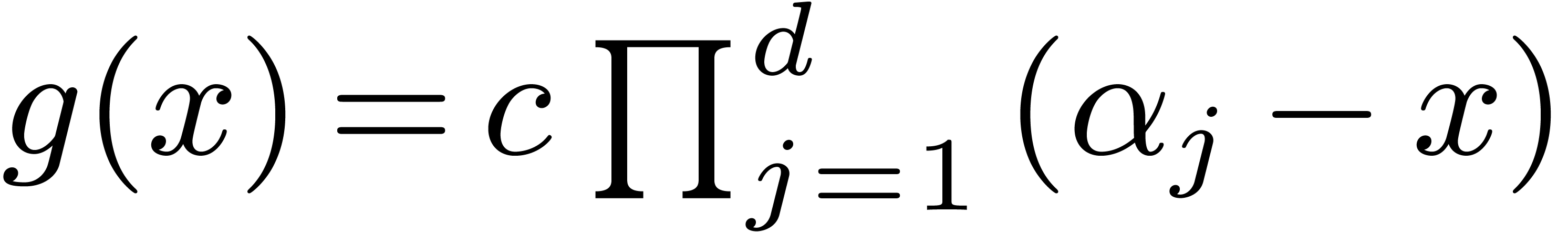 in an
algebraic closure of
in an
algebraic closure of  , the
Graeffe transform of
, the
Graeffe transform of  of order
of order  is
is  . Consequently this leads
to
. Consequently this leads
to  . Using the latter
formula, by Lemma 6 below, the transform can be obtained in
time
. Using the latter
formula, by Lemma 6 below, the transform can be obtained in
time 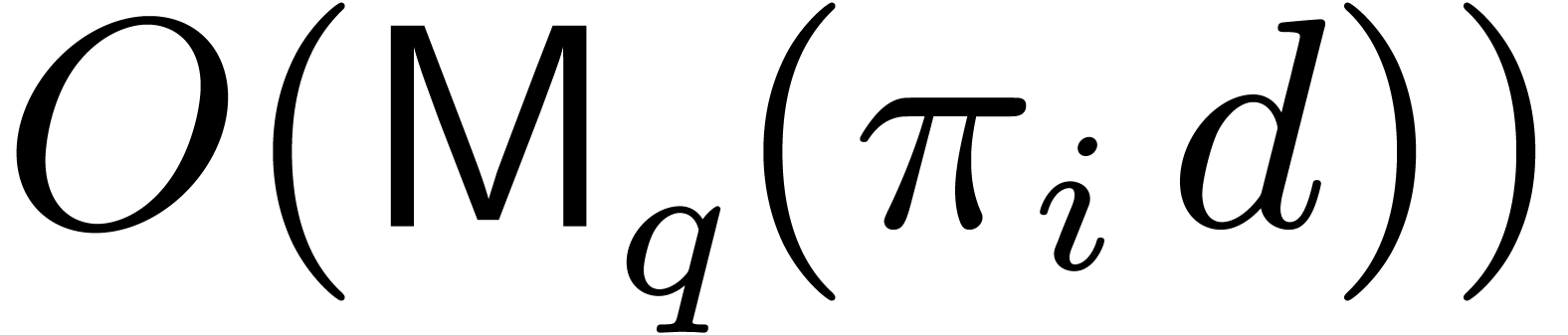 . Taking the sum over
. Taking the sum over
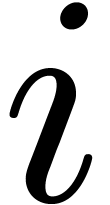 concludes the proof.
concludes the proof.
Lemma 6. Let
 be a polynomial of degree
be a polynomial of degree 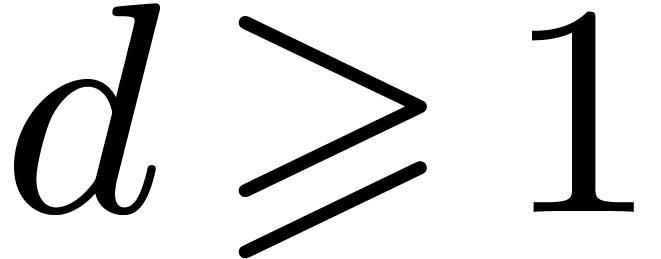 in
in 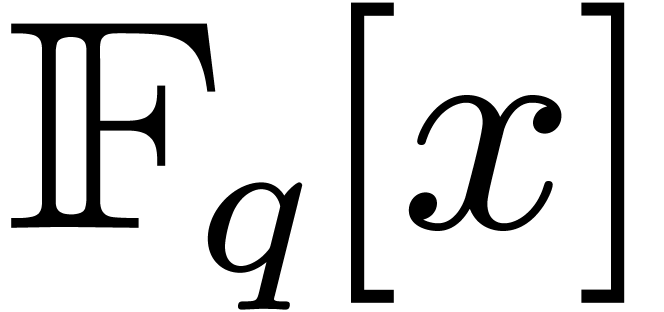 , let
, let 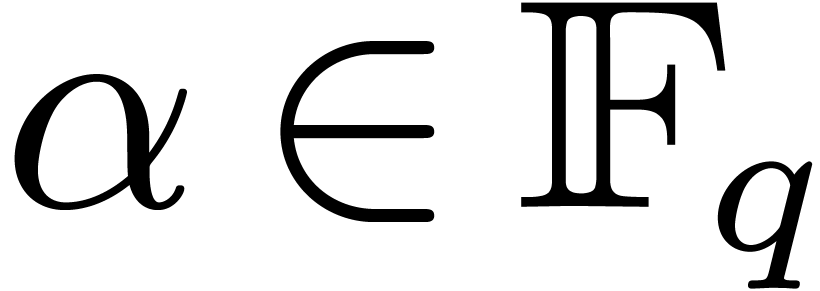 , and let
, and let 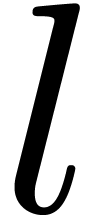 be an
integer. Then the product
be an
integer. Then the product  can be computed in
time
can be computed in
time 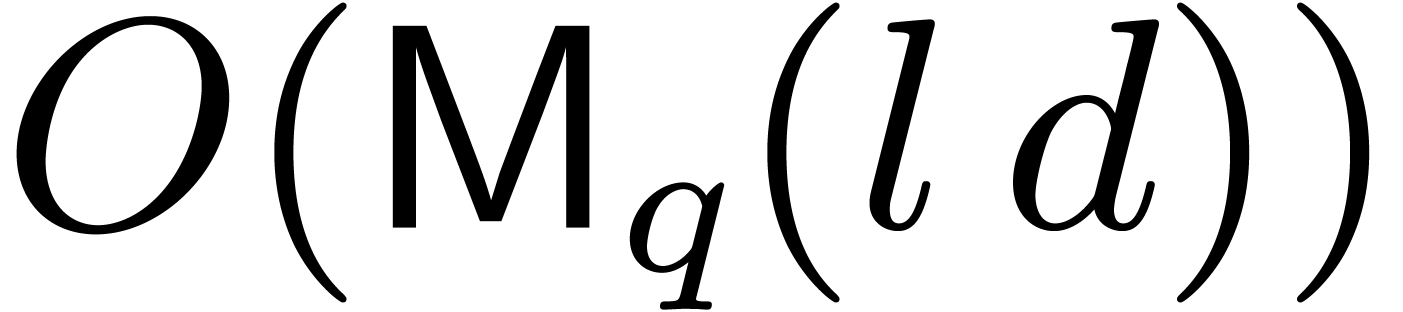 .
.
Proof. Let 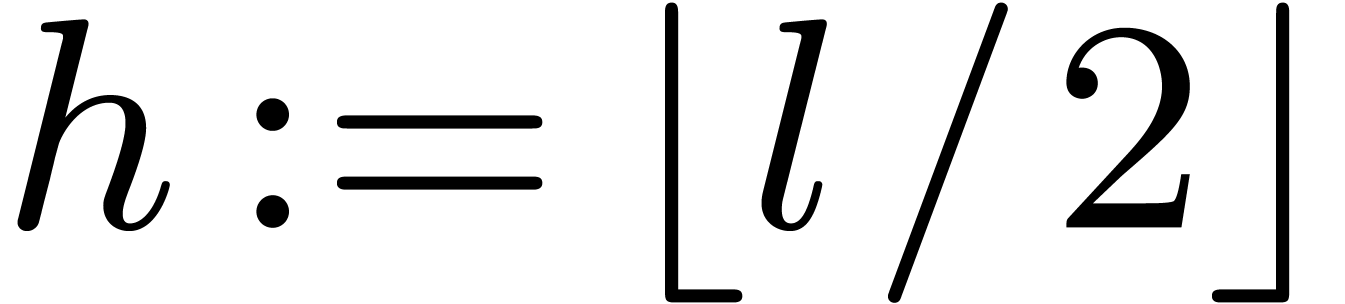 .
If
.
If  is even, then we have
is even, then we have 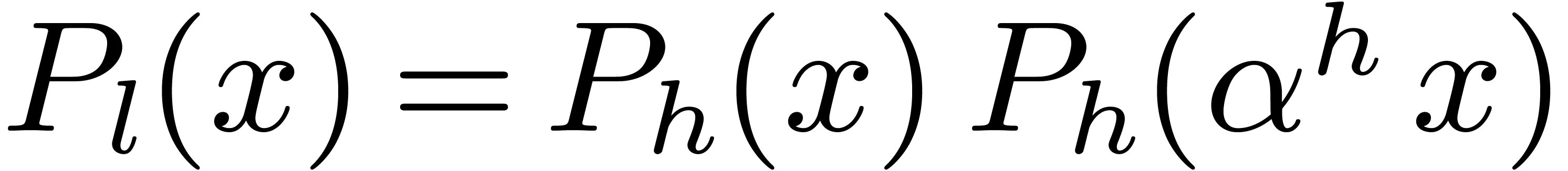 , otherwise we have
, otherwise we have 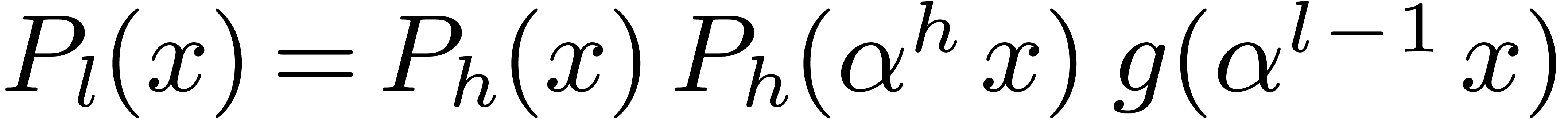 .
These formulas lead to an algorithm with the claimed cost.
.
These formulas lead to an algorithm with the claimed cost.
Let us mention that good complexity bounds for Graeffe transforms for
general finite fields can be found in [14].
3.2Tangent Graeffe transforms
Introducing a formal parameter  with
with 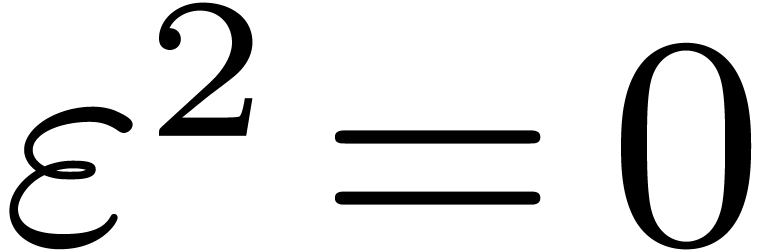 , we define the generalized tangent Graeffe
transform of
, we define the generalized tangent Graeffe
transform of  of order
of order  as being
as being  . For any ring
. For any ring  , computations with “tangent
numbers” in
, computations with “tangent
numbers” in  can be done with constant
overhead with respect to computations in
can be done with constant
overhead with respect to computations in  (in the
FFT model, the overhead is asymptotically limited to a factor of two).
Whenever a Graeffe transform preserves the number of distinct simple
roots, the tangent Graeffe transform can be used to directly recover the
original simple roots from the transformed polynomial, as follows:
(in the
FFT model, the overhead is asymptotically limited to a factor of two).
Whenever a Graeffe transform preserves the number of distinct simple
roots, the tangent Graeffe transform can be used to directly recover the
original simple roots from the transformed polynomial, as follows:
Lemma 7. Let
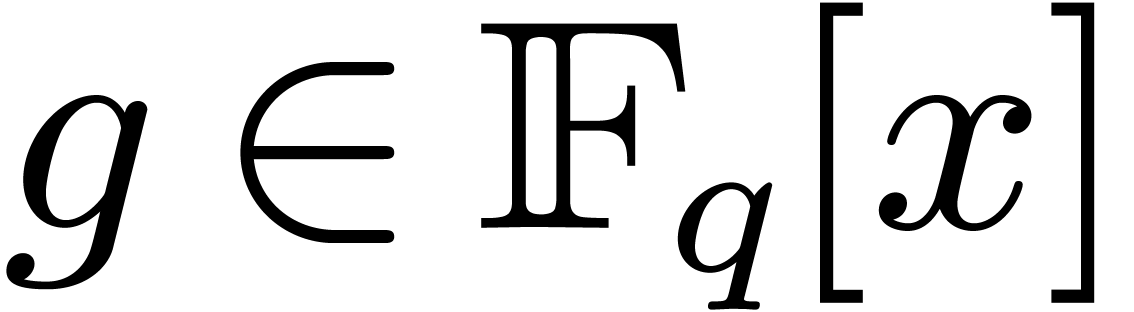 be separable of degree
be separable of degree 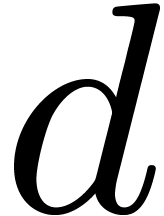 , let
, let  be coprime to
be coprime to 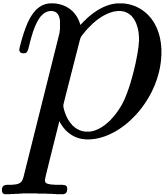 , and let
, and let 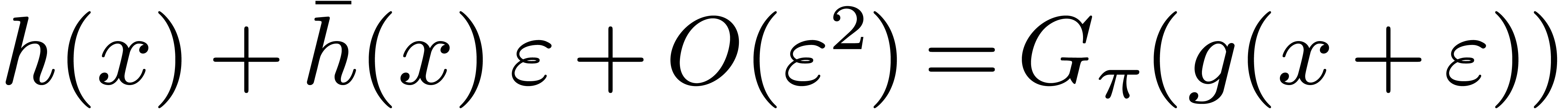 . A nonzero root
. A nonzero root 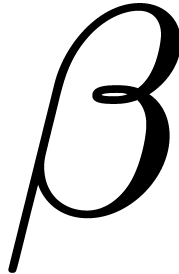 of h is
simple if, and only if,
of h is
simple if, and only if, 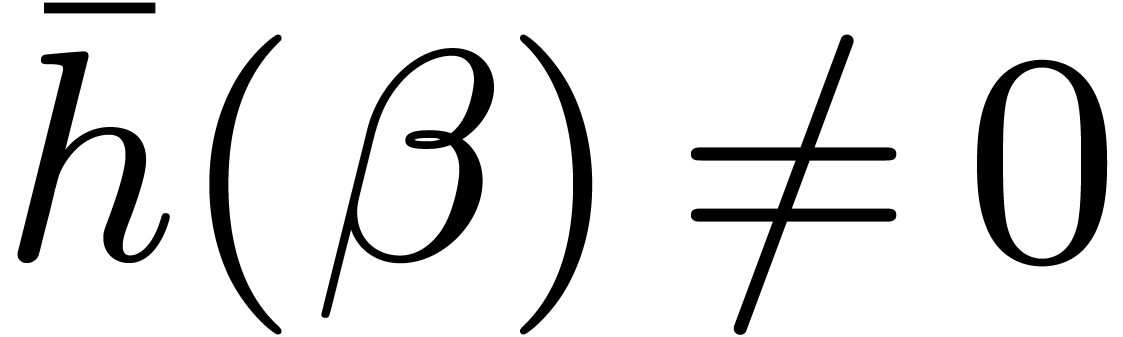 . For
such a root,
. For
such a root, 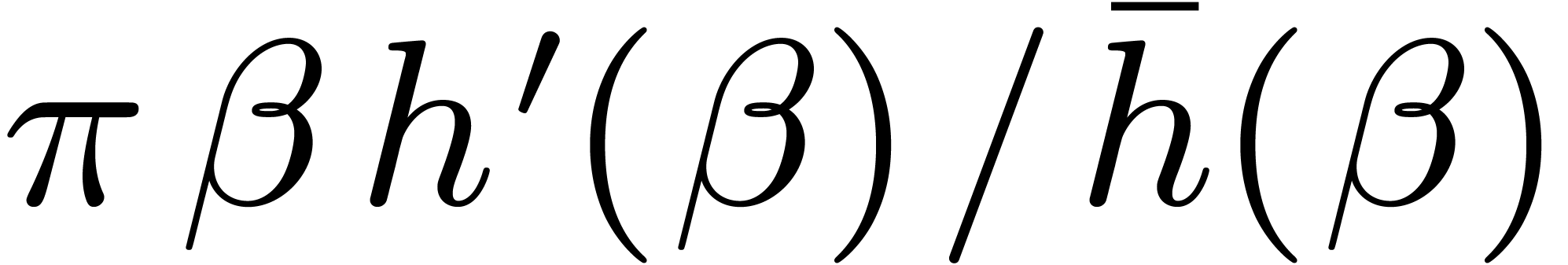 is the unique root
is the unique root  of
of  such that
such that 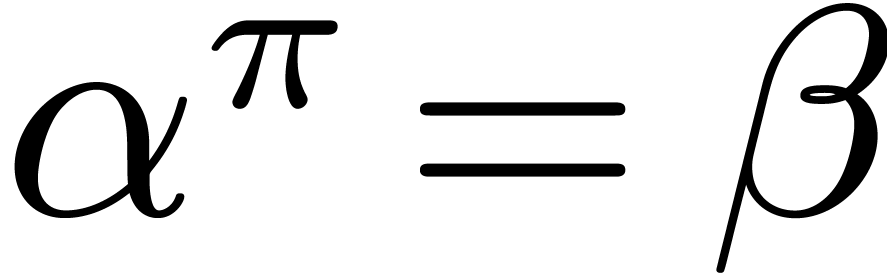 .
.
Proof. Let  be a root of
be a root of
 in an algebraic closure of
in an algebraic closure of  . The lemma follows from the formula
. The lemma follows from the formula 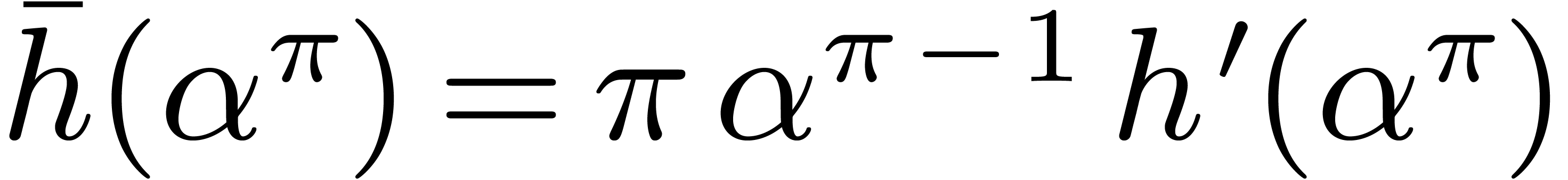 , obtained by direct
calculation.
, obtained by direct
calculation.
In the context of the Graeffe method, the tangent transform is classical
(for instance, see [23, 27] for history,
references, and use in numerical algorithms). The generalized tangent
Graeffe transform can also be seen as the tangent characteristic
polynomial of 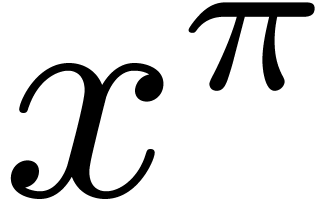 modulo
modulo 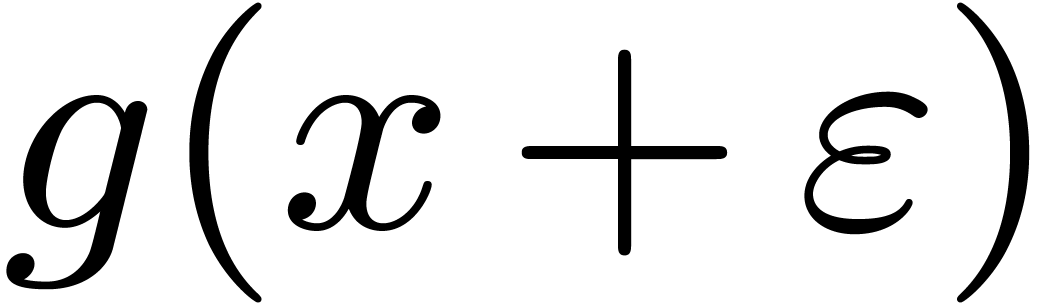 , and this construction is often attributed to
Kronecker in algebraic geometry [22].
, and this construction is often attributed to
Kronecker in algebraic geometry [22].
3.3Overview of our methods
Let us write 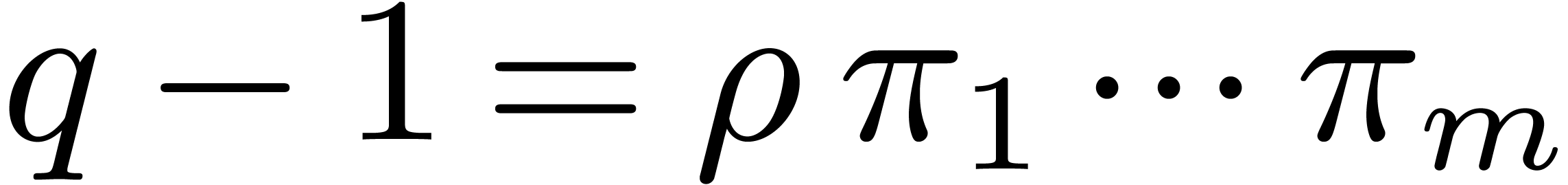 . Let
. Let 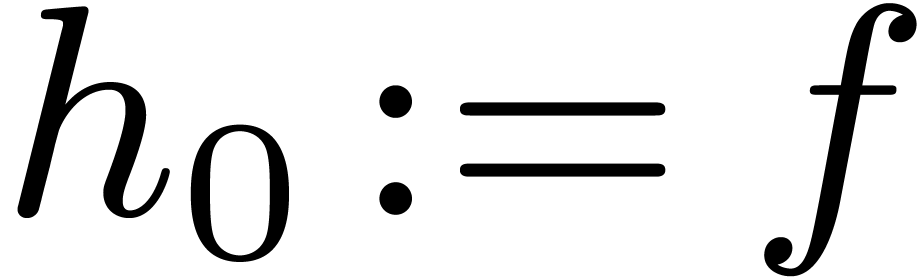 , and let
, and let 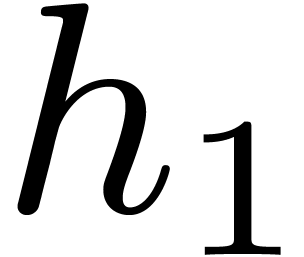 , …,
, …, 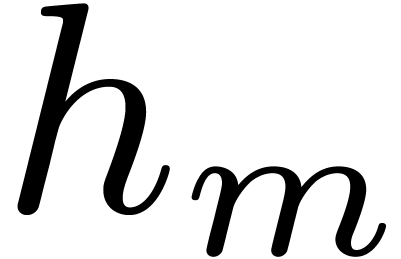 be the Graeffe
transforms of orders
be the Graeffe
transforms of orders  ,
,  , …,
, …,  of
of  . The roots of
. The roots of  are to be found among the elements of order
are to be found among the elements of order  . One may then find the roots of
. One may then find the roots of 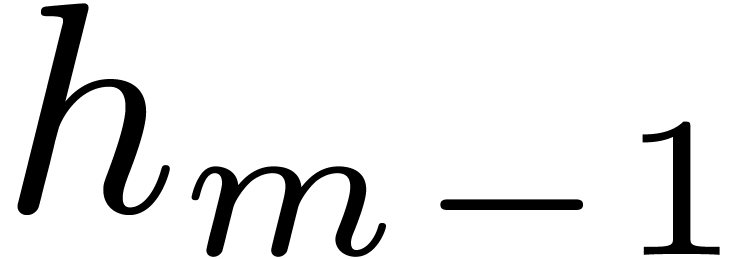 among the
among the 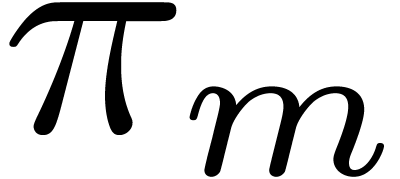 -th
roots of the roots of
-th
roots of the roots of 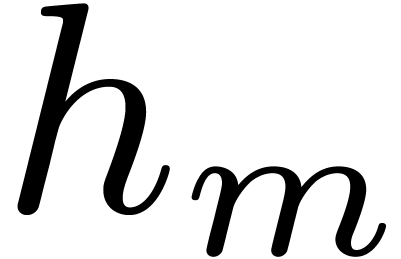 , and,
by induction, the roots of
, and,
by induction, the roots of 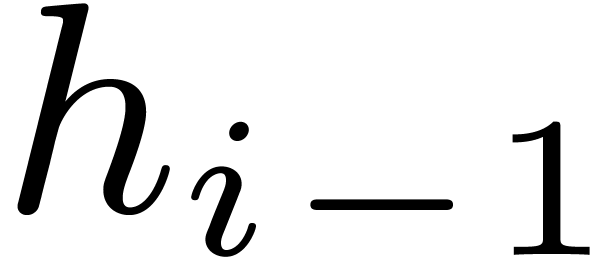 are to be found among
the
are to be found among
the 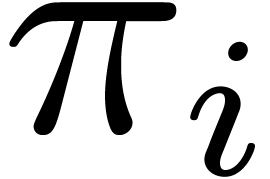 -th roots of the roots of
-th roots of the roots of
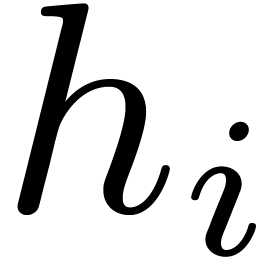 . This is the starting point
of the efficient deterministic algorithm designed in [14].
But in order to make it much more efficient than
Cantor–Zassenhaus's algorithm we introduce and analyze two types
of randomizations in the next sections. First we avoid computing
. This is the starting point
of the efficient deterministic algorithm designed in [14].
But in order to make it much more efficient than
Cantor–Zassenhaus's algorithm we introduce and analyze two types
of randomizations in the next sections. First we avoid computing 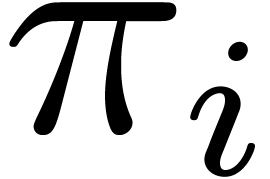 -th roots by combining random
variable shifts and tangent transforms. Second we analyze the behaviour
for random polynomials, which leads us to a very efficient heuristic
algorithm.
-th roots by combining random
variable shifts and tangent transforms. Second we analyze the behaviour
for random polynomials, which leads us to a very efficient heuristic
algorithm.
3.4A randomized algorithm
Our randomized algorithms can be competitive to Cantor–Zassenhaus'
algorithm only for very smooth values of 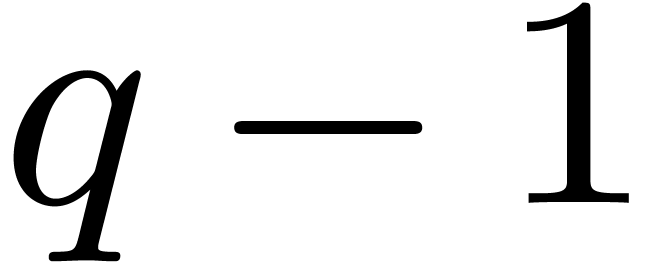 .
For simplicity we focus on the important case of an FFT field where
.
For simplicity we focus on the important case of an FFT field where
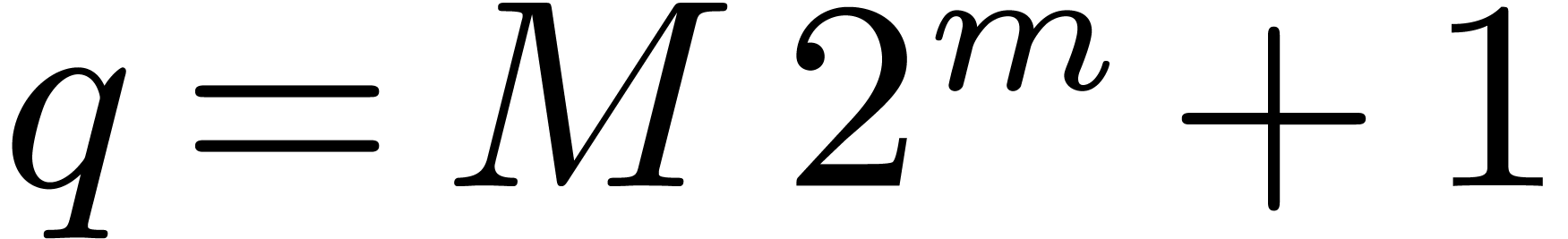 , with
, with 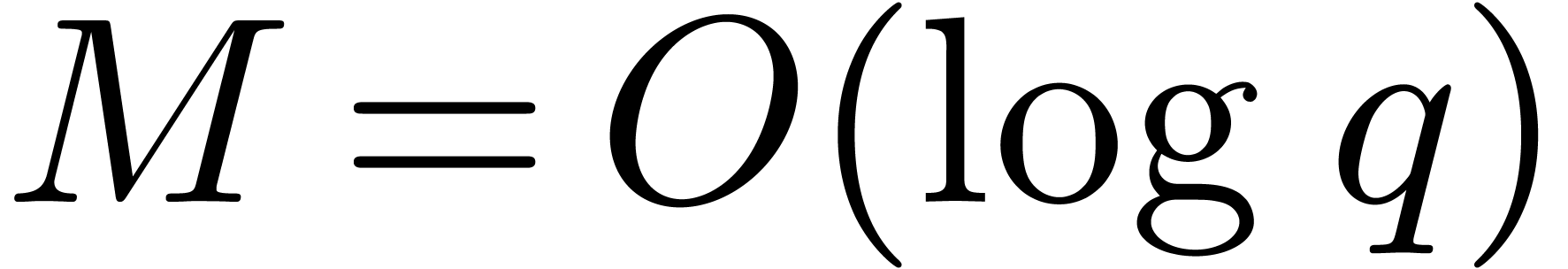 .
.
We introduce the parameter  .
Let
.
Let 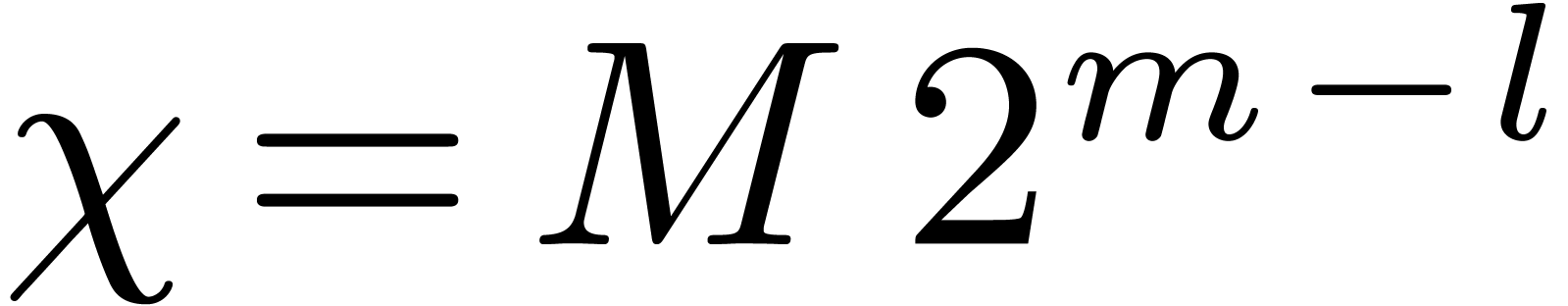 be a divisor of
be a divisor of 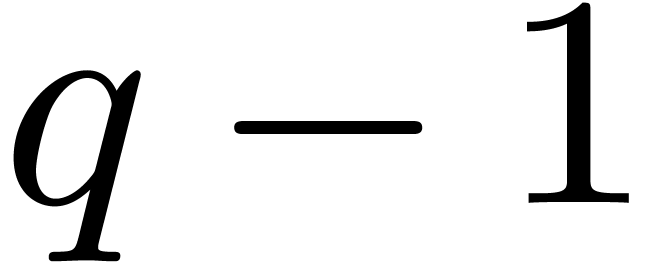 , and let
, and let 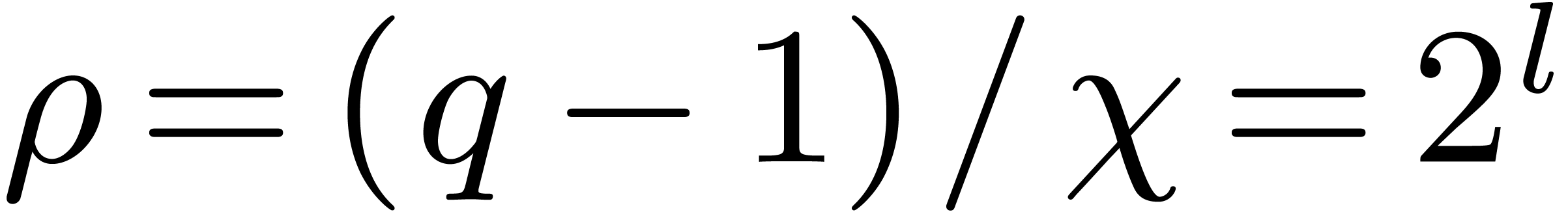 .
Let
.
Let  denote the roots of
denote the roots of  . The Graeffe transform
. The Graeffe transform 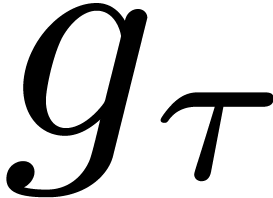 of
of
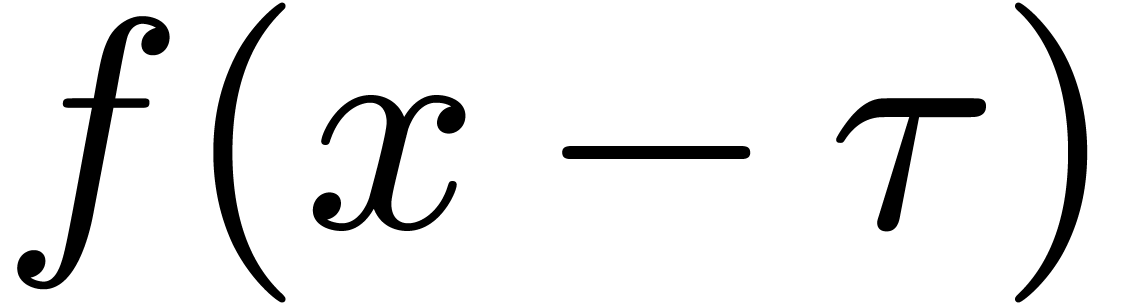 of order
of order  equals
equals 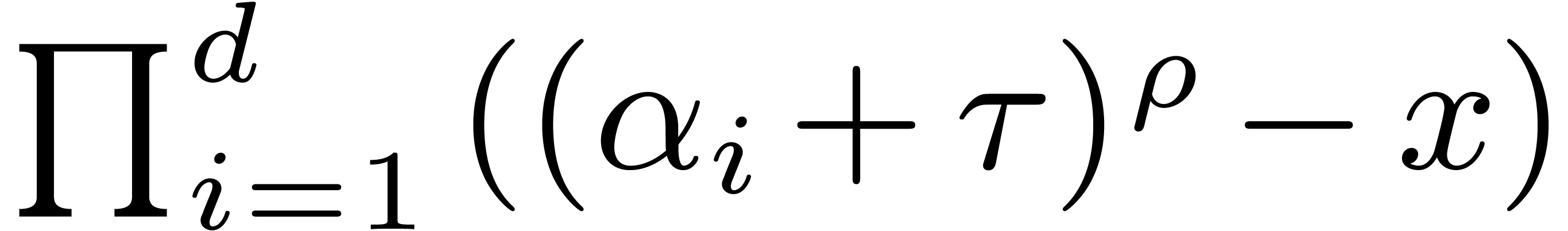 .
.
Given a pair of distinct roots 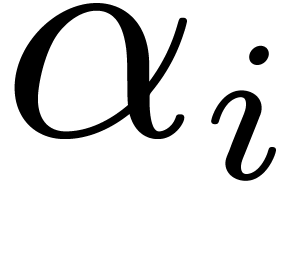 and
and 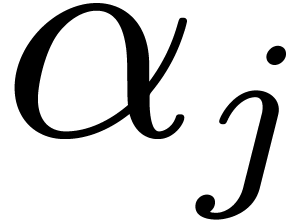 of
of  , we have
, we have
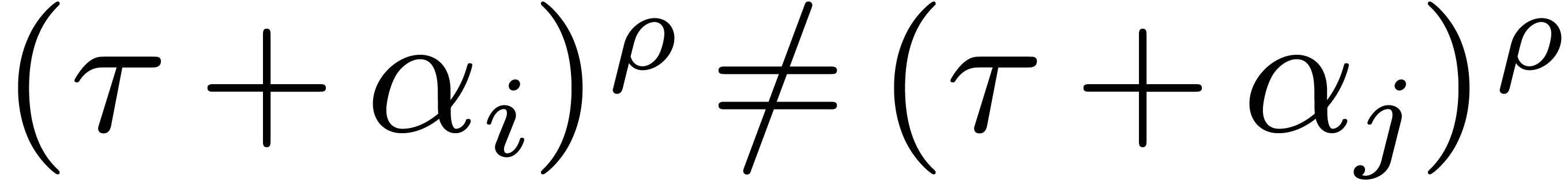 for all but at most
for all but at most 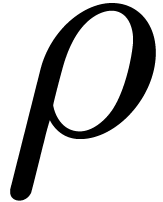 values of
values of  . Therefore for all
but at most
. Therefore for all
but at most 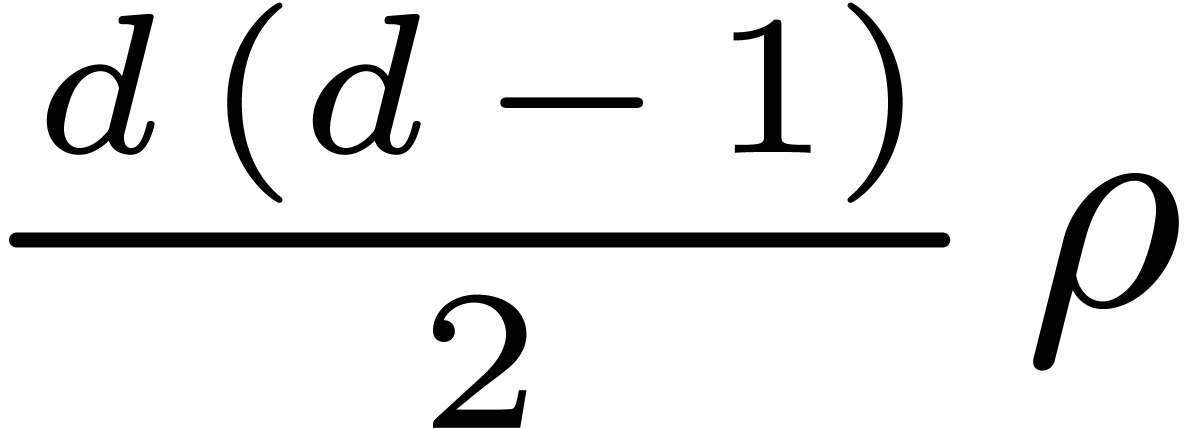 values of
values of  , the polynomial
, the polynomial 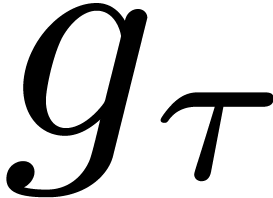 has no
multiple root. Considering that
has no
multiple root. Considering that  is taken
uniformly at random in
is taken
uniformly at random in  , the
probability that
, the
probability that 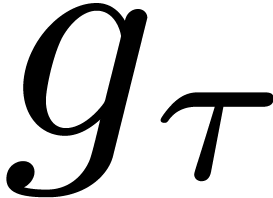 has multiple roots is at most
has multiple roots is at most
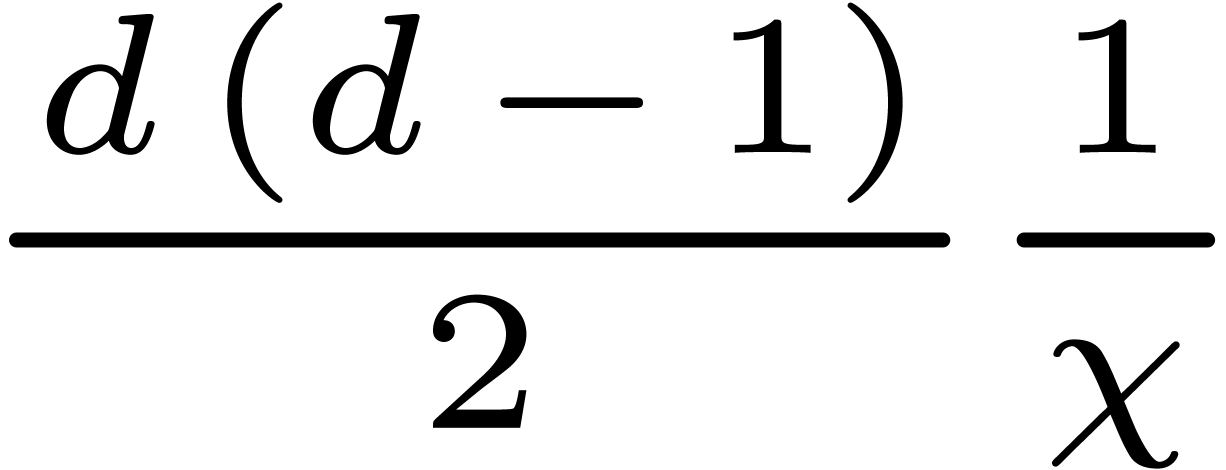 . This yields the following
randomized algorithm.
. This yields the following
randomized algorithm.
Randomized algorithm 8.
-
Input
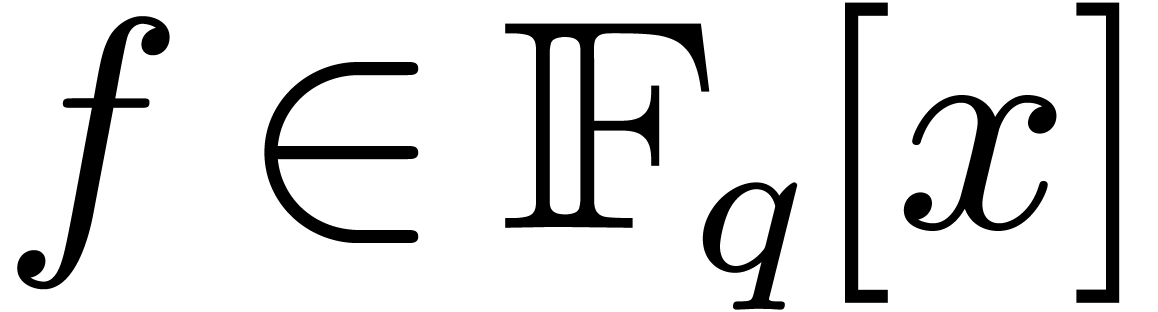 of degree
of degree
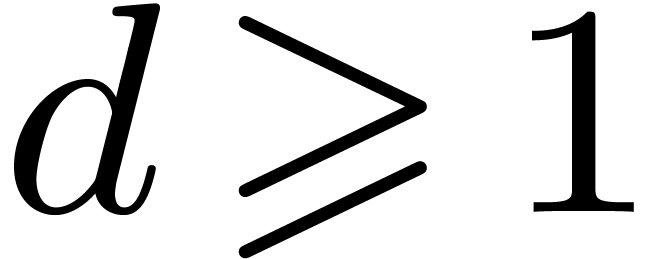 ,
monic, separable, which splits over
,
monic, separable, which splits over
 ,
and such that
,
and such that
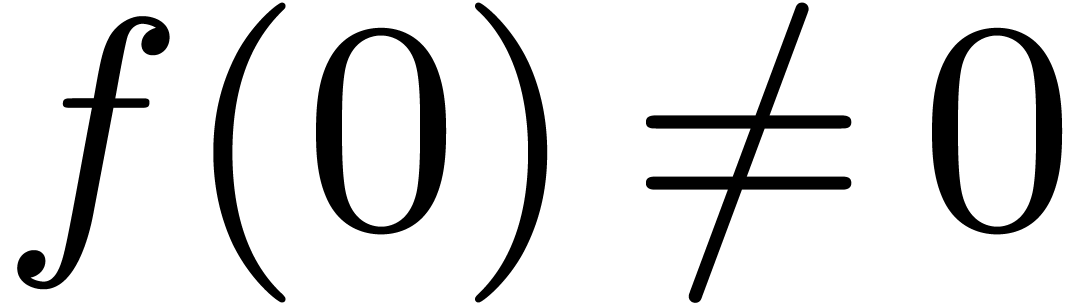 ;
a primitive root
;
a primitive root
 of
of
 .
.
-
Output
-
The roots of  .
.
-
If  then set
then set 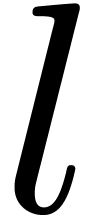 to
to 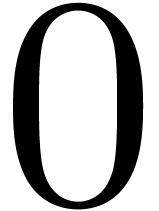 . Otherwise set
. Otherwise set  to the largest integer in
to the largest integer in 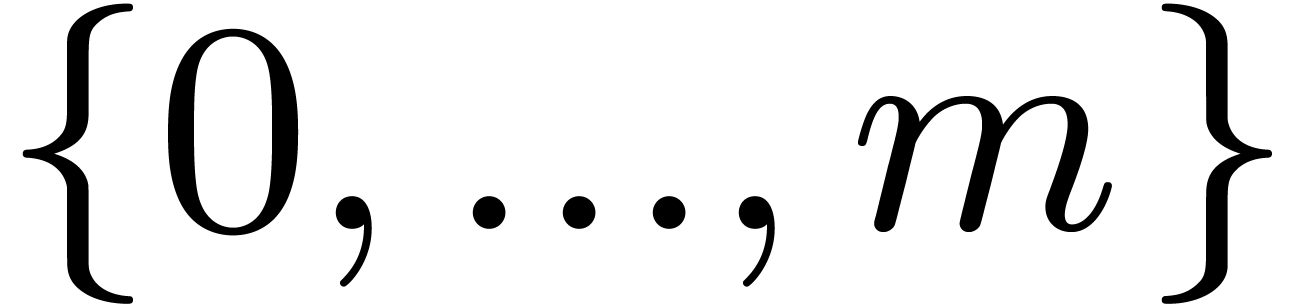 such
that
such
that  . Compute
. Compute 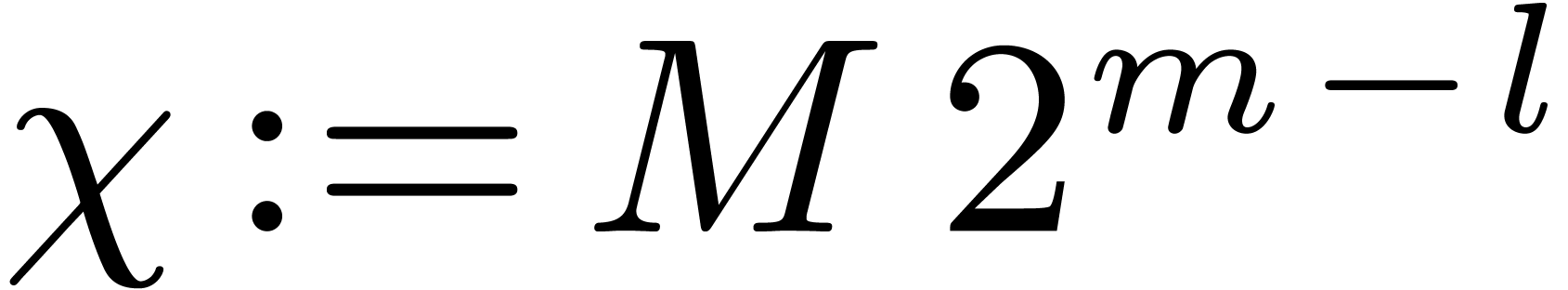 and
and 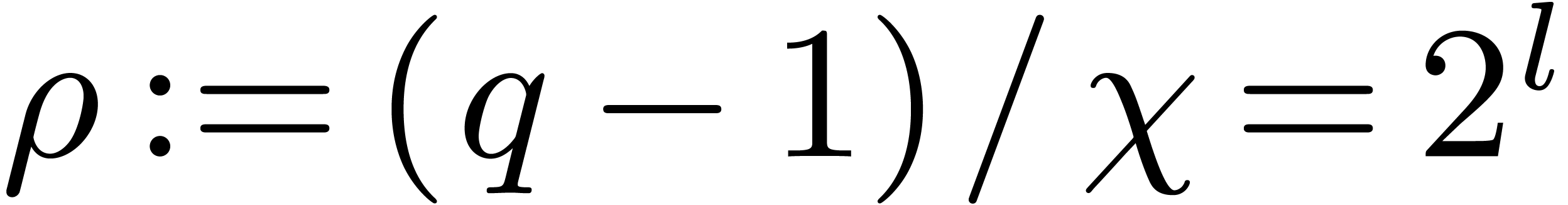 .
.
-
Pick 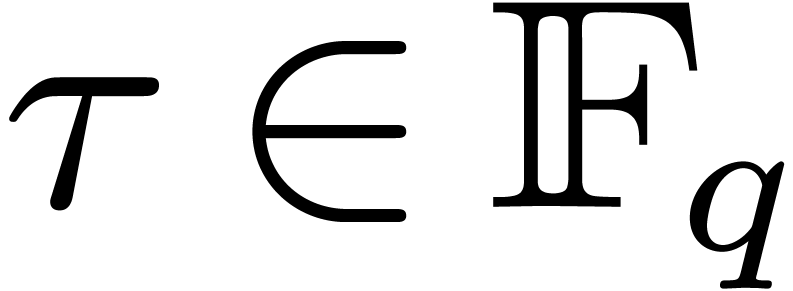 uniformly at random, and compute
uniformly at random, and compute 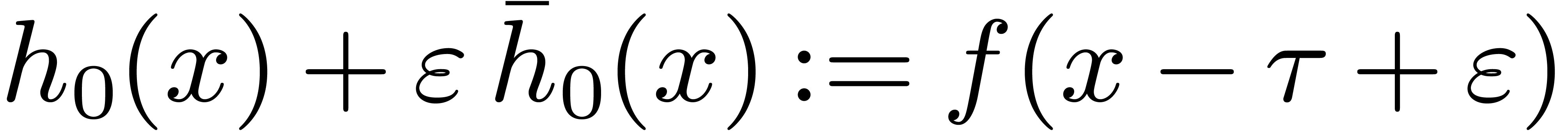 , where
, where  .
.
-
Recursively compute the Graeffe transform 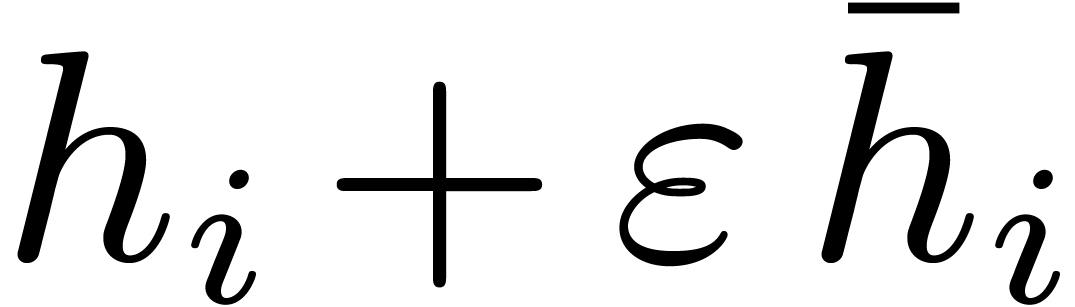 of
order
of
order  of
of 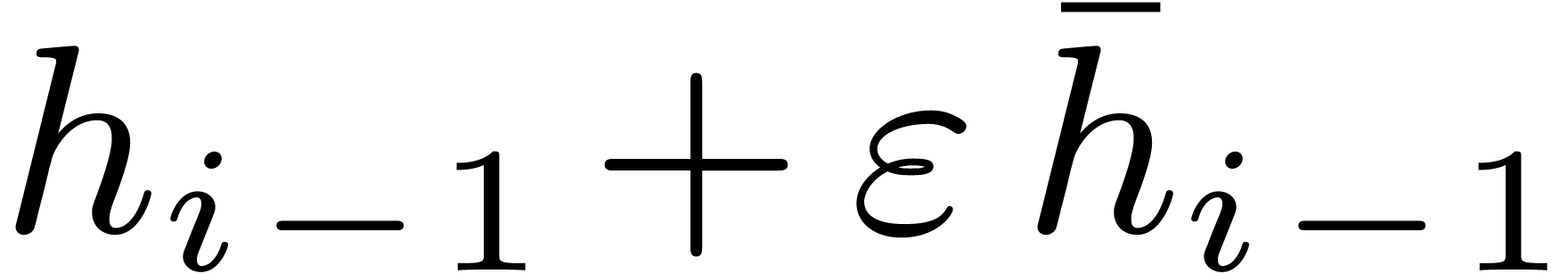 ,
for all
,
for all 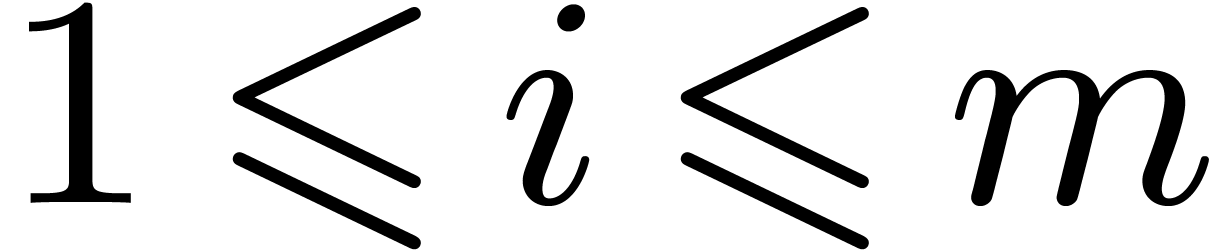 .
.
-
Compute the list 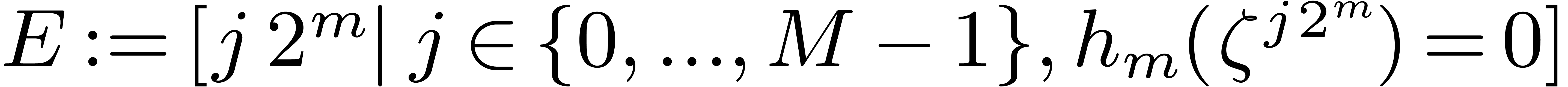 of
of  -logarithms of the roots of
-logarithms of the roots of 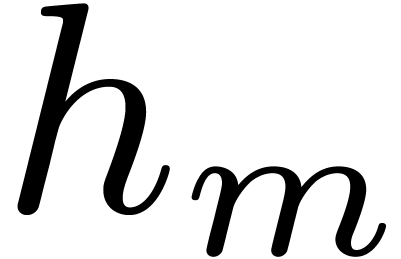 .
.
-
For  from
from  down to
down to
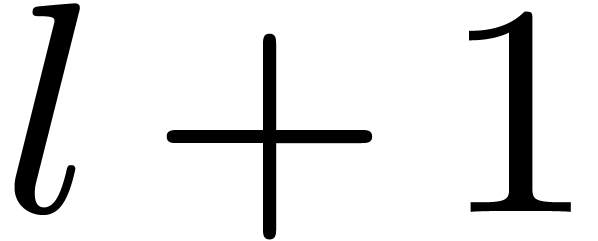 do
do
-
Replace  by the concatenation of
by the concatenation of  for
for 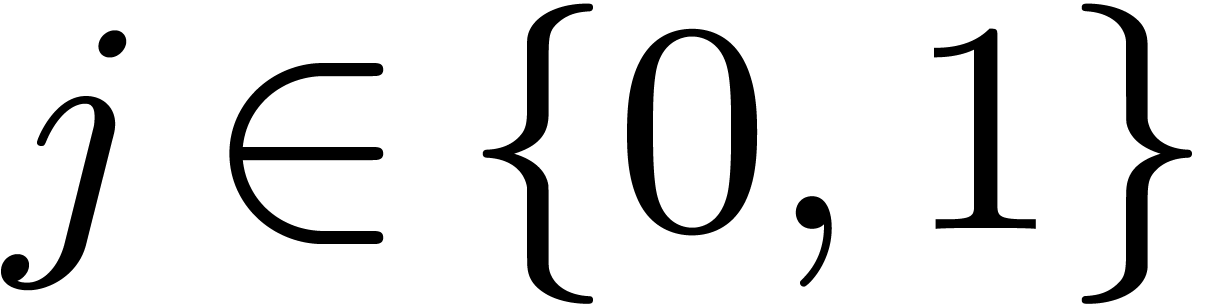 .
.
-
If  has cardinality more than
has cardinality more than 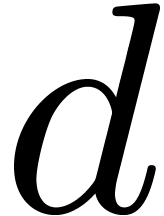 then remove the elements
then remove the elements  from
from  such that
such that 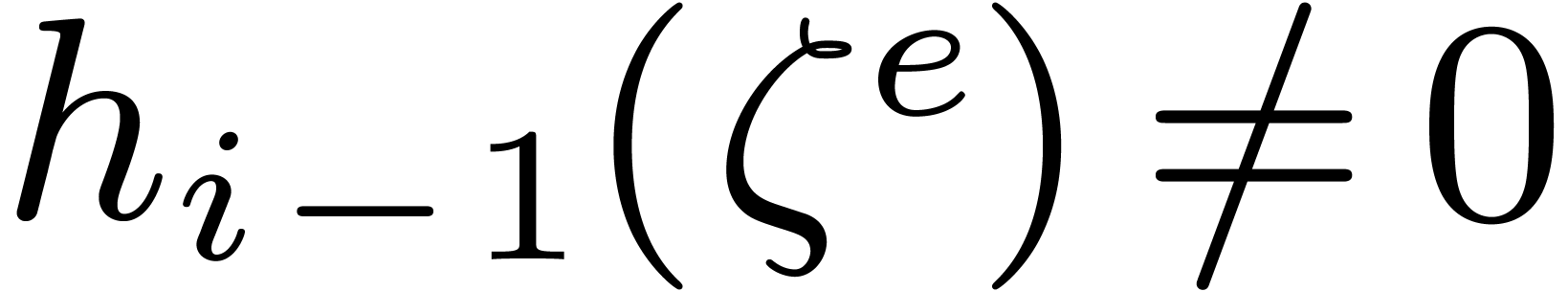 .
.
-
If 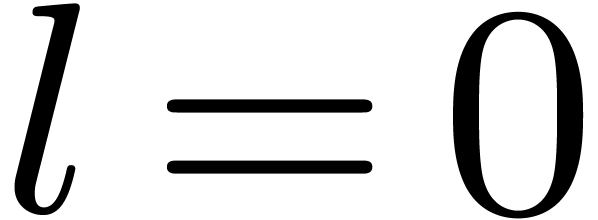 then return
then return 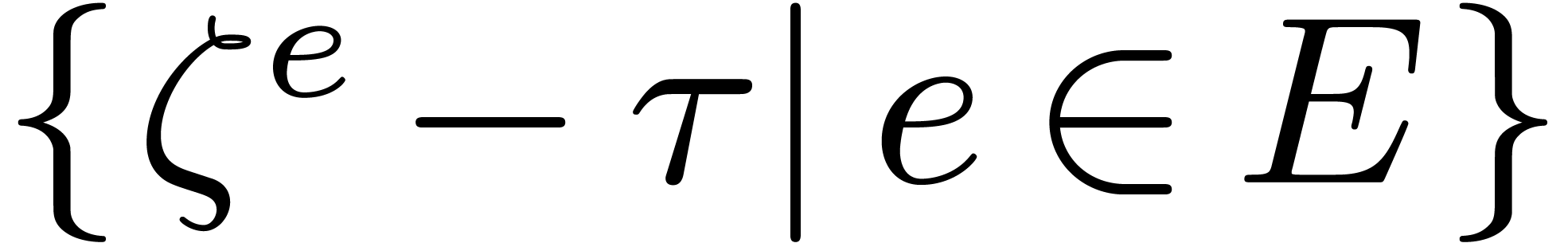 .
.
-
Compute 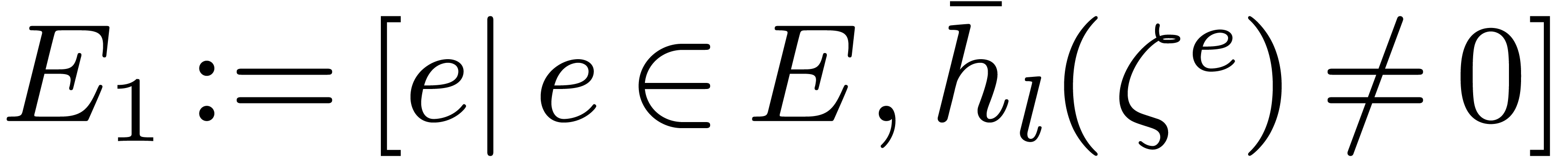 .
.
-
Compute 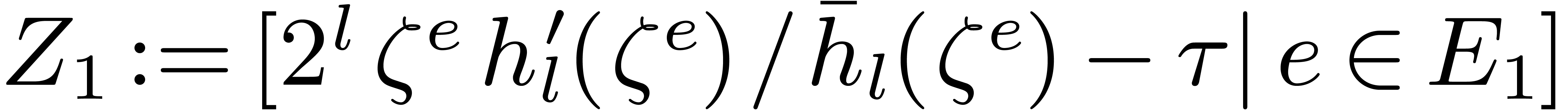 .
.
Add  to
to 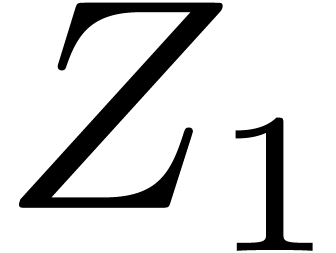 if
if 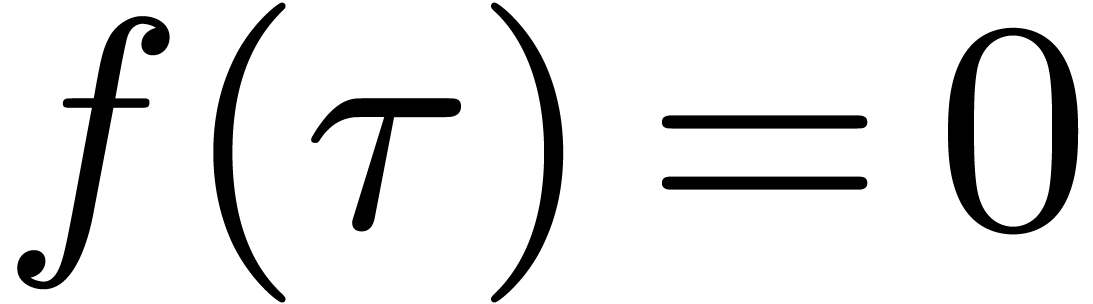 .
.
-
Compute 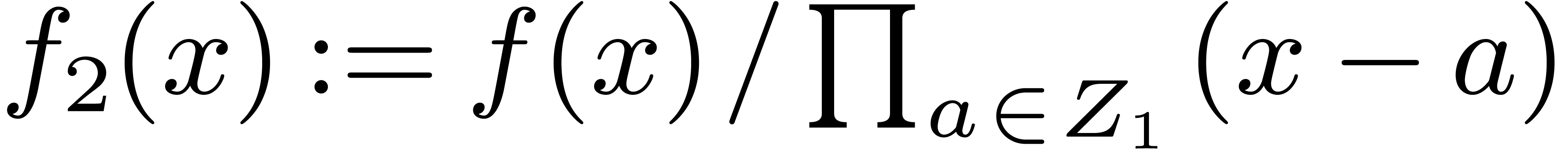 .
.
-
Compute recursively the roots 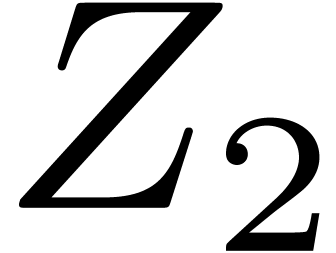 of
of 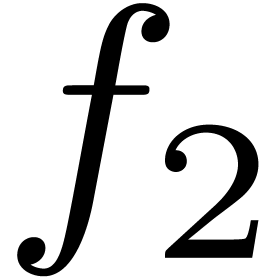 .
.
-
Return  .
.
Proposition 9. Algorithm
8 is correct, and takes an average time 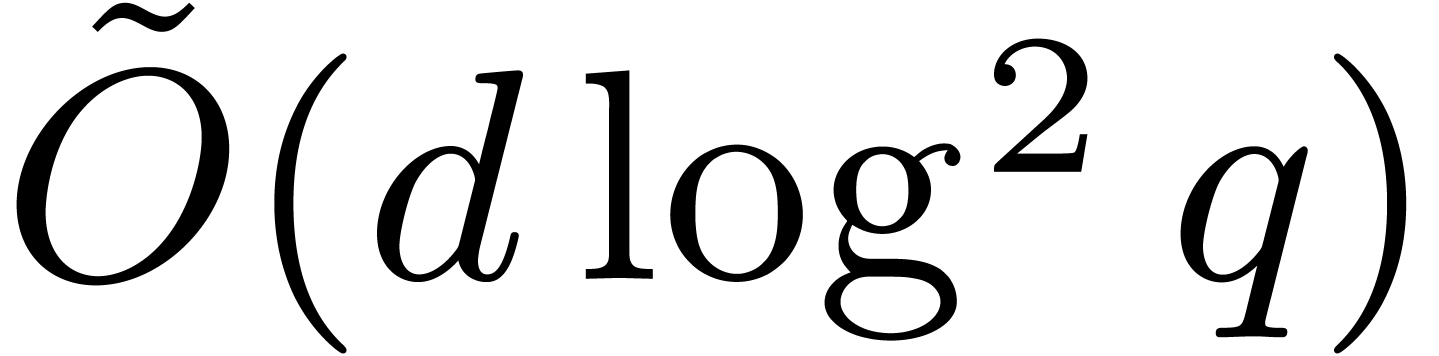 , if
, if 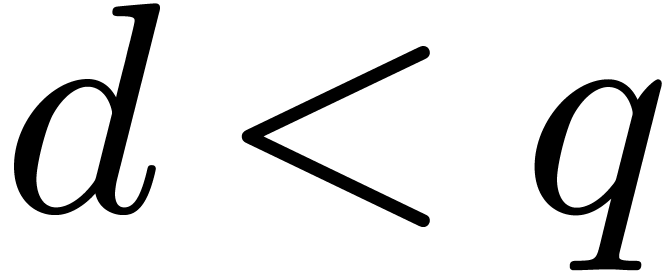 and
and 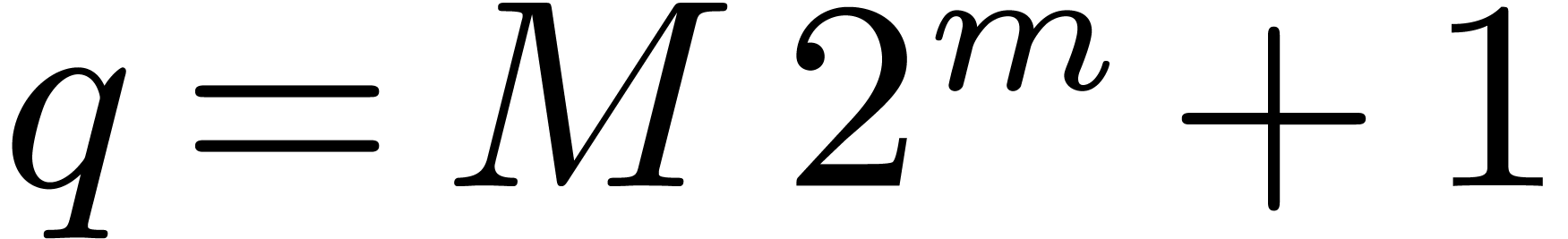 with
with 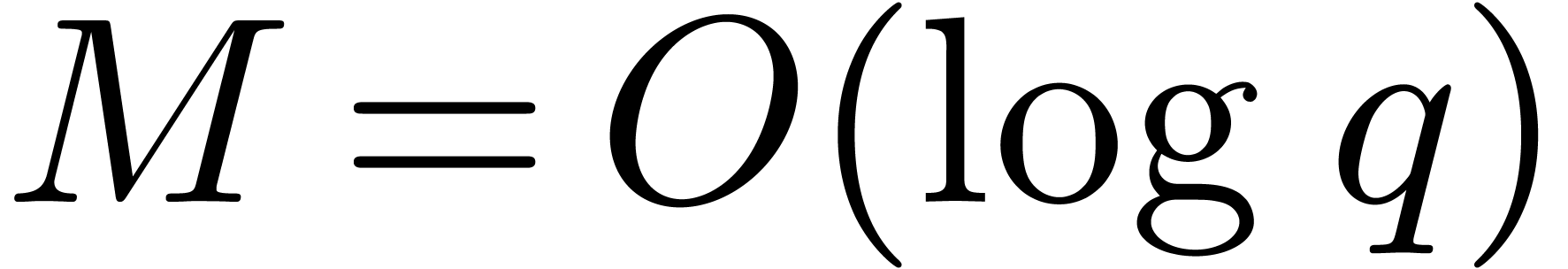 .
.
Proof. The correctness follows from Lemma 7,
which asserts that  is a subset of the roots of
is a subset of the roots of
 .
.
Step 3 takes 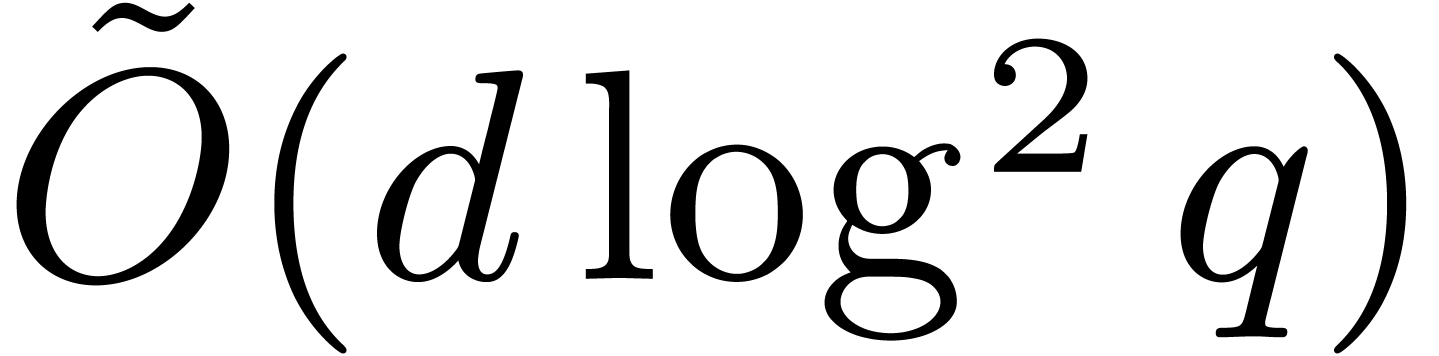 by Proposition 5.
Steps 2, 5.a, 5.b, 6, 7, 8, 9 execute in time
by Proposition 5.
Steps 2, 5.a, 5.b, 6, 7, 8, 9 execute in time 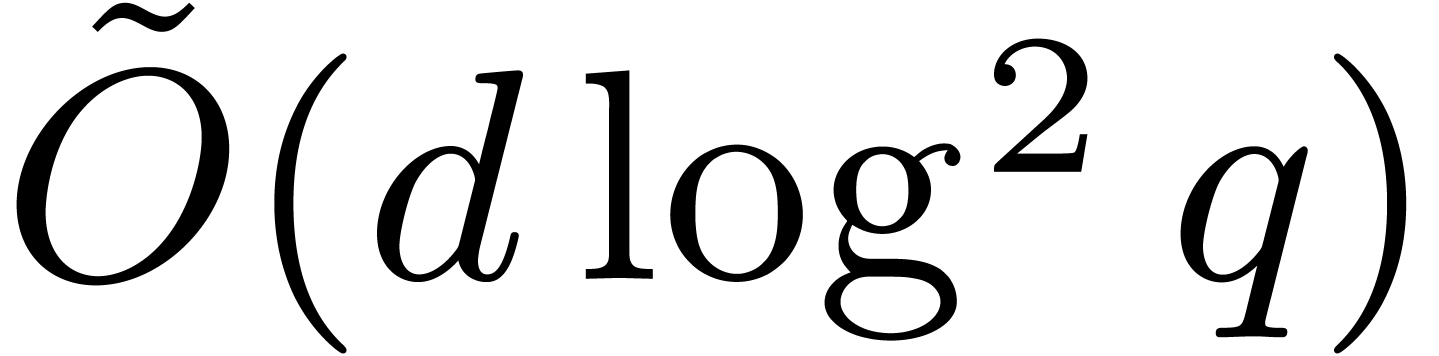 . Step 4 costs
. Step 4 costs 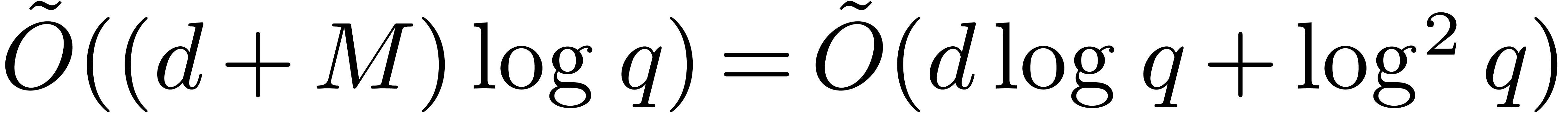 .
If
.
If  then the number of iterations in step 5 is
then the number of iterations in step 5 is
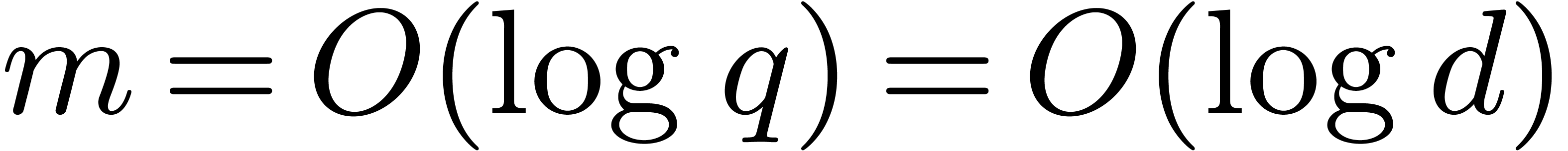 . Otherwise the number of
iterations is
. Otherwise the number of
iterations is 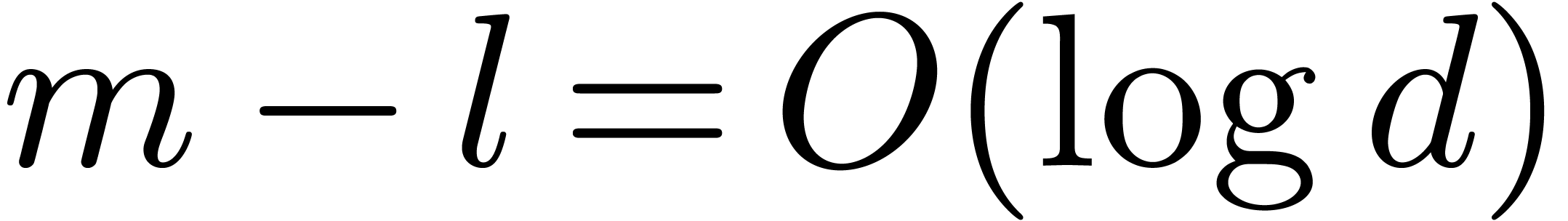 . Consequently,
the total cost of all steps but step 10 is
. Consequently,
the total cost of all steps but step 10 is 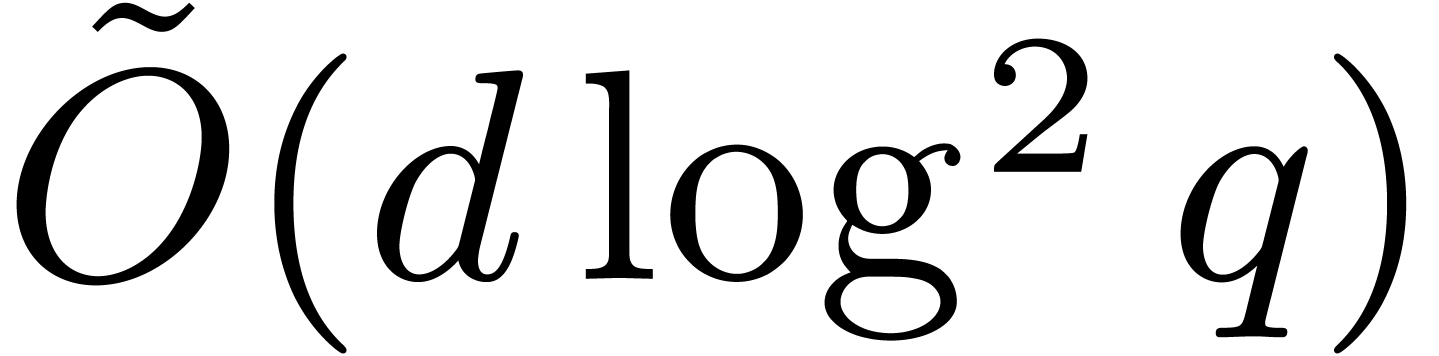 .
From the choice of
.
From the choice of 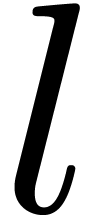 , we have
already seen that the degree of
, we have
already seen that the degree of 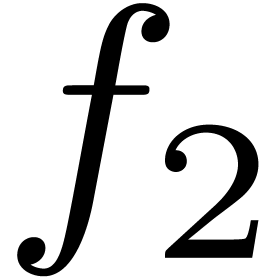 equals
equals 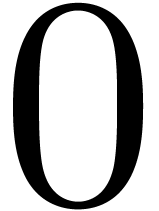 with probability at least
with probability at least 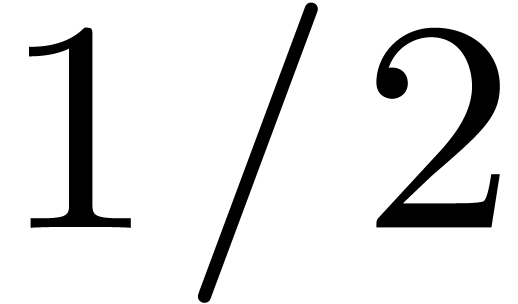 .
Writing
.
Writing 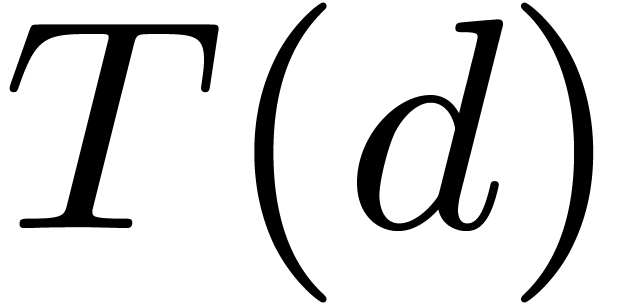 for the average execution time, we thus
have
for the average execution time, we thus
have 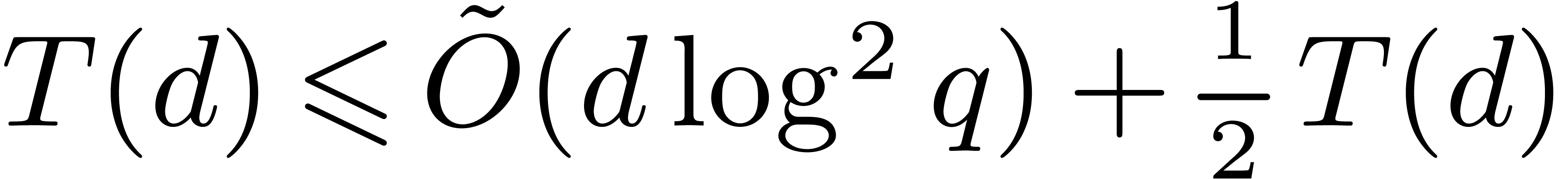 , which implies
, which implies 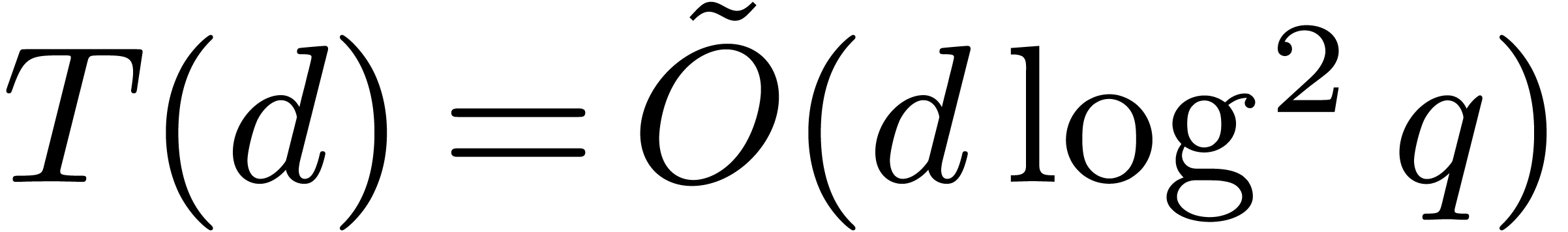 .
.
Since the base field supports FFTs it is important to perform all
intermediate computations by taking advantage of sharing transforms.
This technique was popularized within the NTL library for many
algorithms. In addition we notice that the first few iterates of the
loop of step 5 can be reduced to direct FFT computations instead of
generic multi-point evaluations.
3.5Random polynomials which split over 
Taking a monic random polynomial of degree 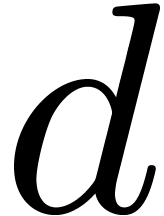 which
splits over
which
splits over  , for a uniform
distribution, is equivalent to taking its
, for a uniform
distribution, is equivalent to taking its 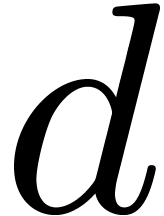 roots
at random in
roots
at random in  . Let
. Let  represent the roots of
represent the roots of  .
We examine the behavior of tangent Graeffe transforms of such random
polynomials.
.
We examine the behavior of tangent Graeffe transforms of such random
polynomials.
Let 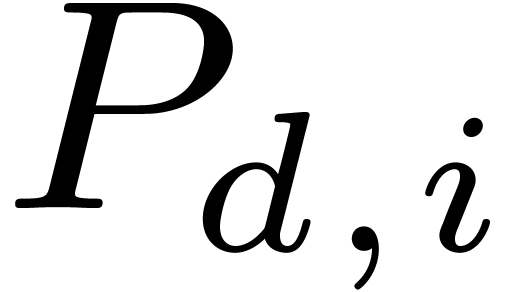 be the number of monic polynomials of degree
be the number of monic polynomials of degree
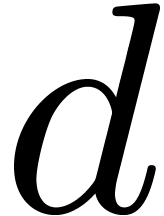 which split over
which split over  and
have
and
have 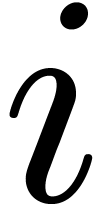 distinct nonzero roots of order dividing
distinct nonzero roots of order dividing
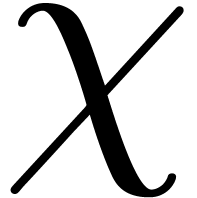 . Such a polynomial uniquely
corresponds to the choice of
. Such a polynomial uniquely
corresponds to the choice of  distinct values
among
distinct values
among 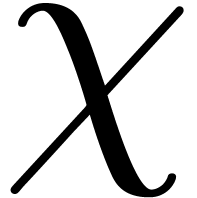 , namely the roots, and
then of the multiplicities of these roots with sum
, namely the roots, and
then of the multiplicities of these roots with sum 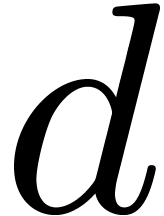 . Therefore we have
. Therefore we have 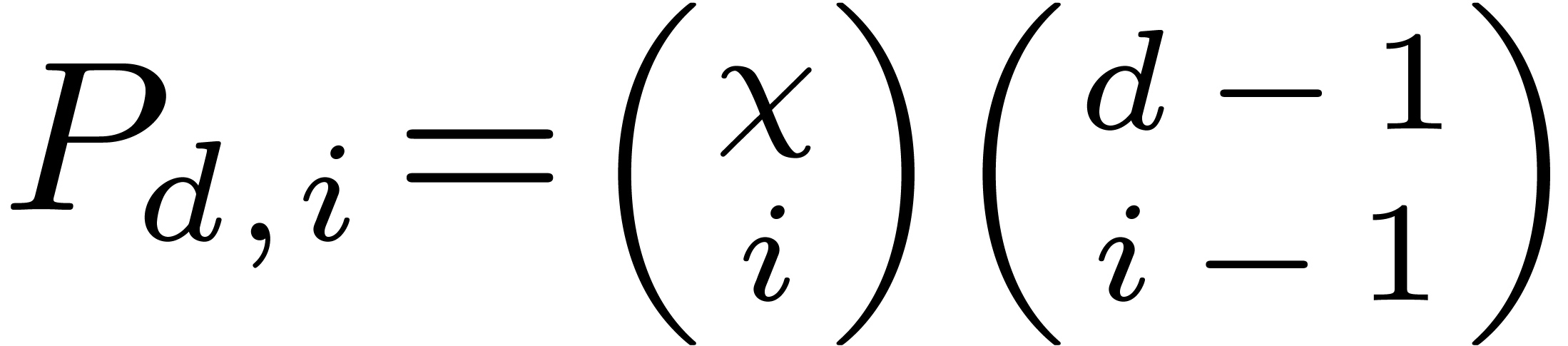 . One can check that
. One can check that 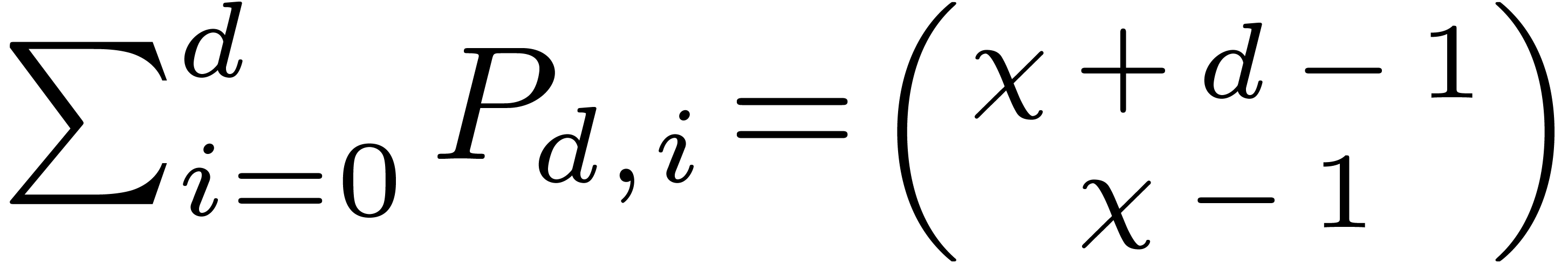 ,
which corresponds to choosing a multiplicity in
,
which corresponds to choosing a multiplicity in  for each element of order dividing
for each element of order dividing 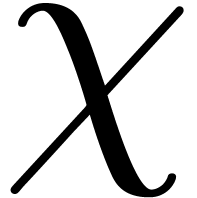 ,
under the constraint that the sum of the multiplicities is exactly
,
under the constraint that the sum of the multiplicities is exactly 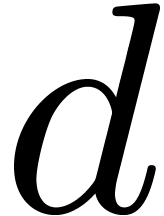 . The average number of roots of
such polynomials is
. The average number of roots of
such polynomials is
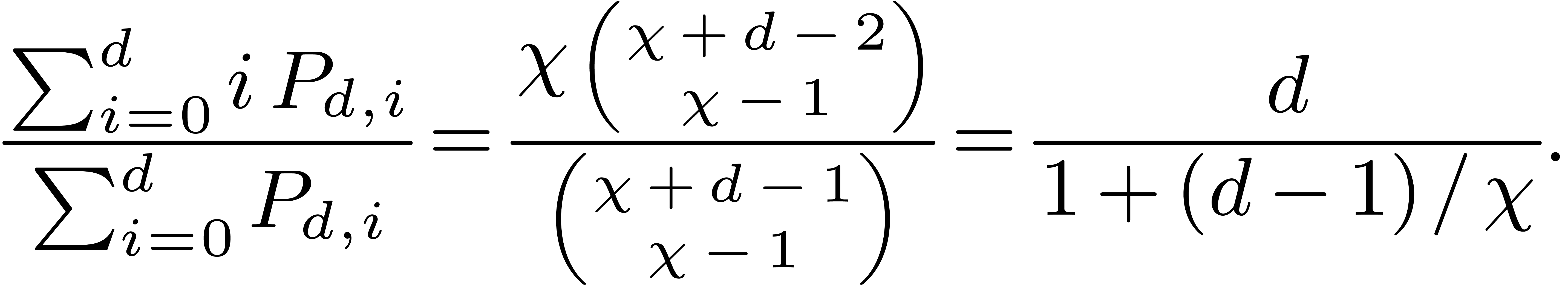
The latter formulas are direct consequences of the classical
Chu–Vandermonde identity. Assuming that 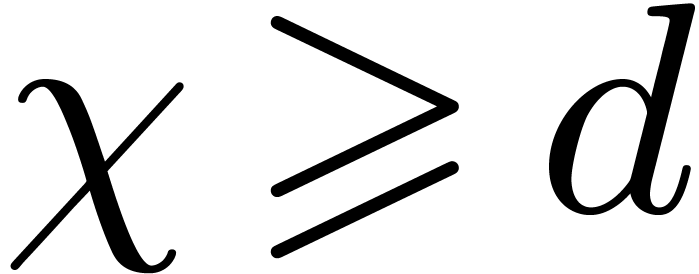 , the average number of distinct roots is at least
, the average number of distinct roots is at least
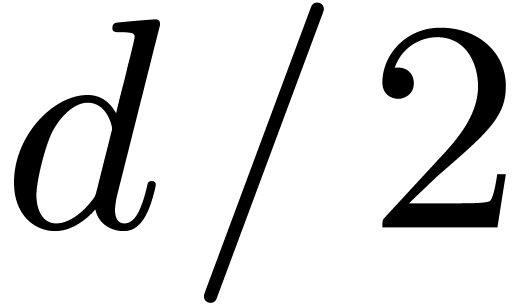 . When
. When  is much greater than
is much greater than  then this lower bound is
getting close to
then this lower bound is
getting close to  .
.
Proposition 10. Let
 be a fixed divisor of
be a fixed divisor of 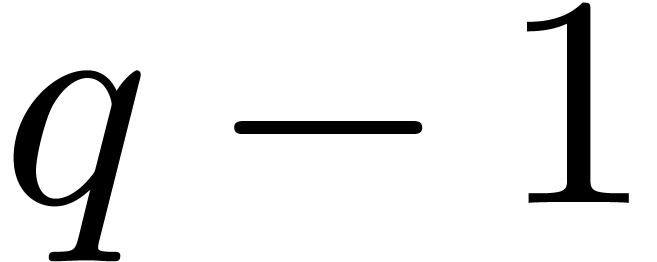 , and let
, and let 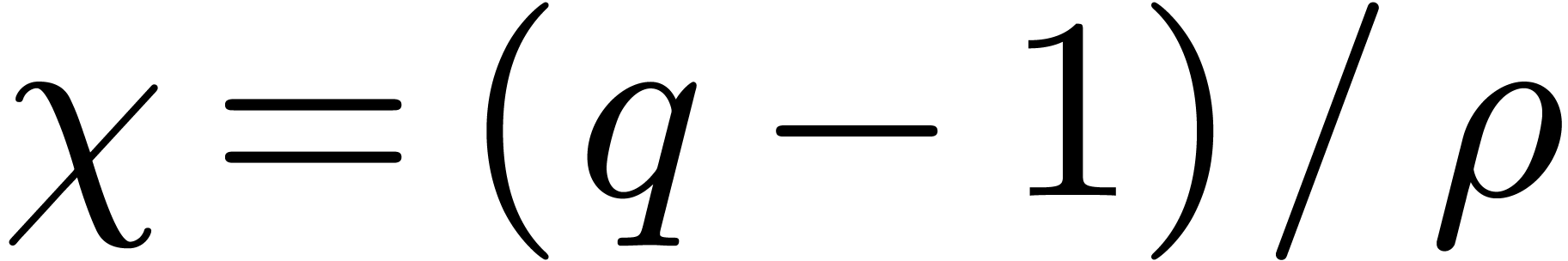 .
Let
.
Let 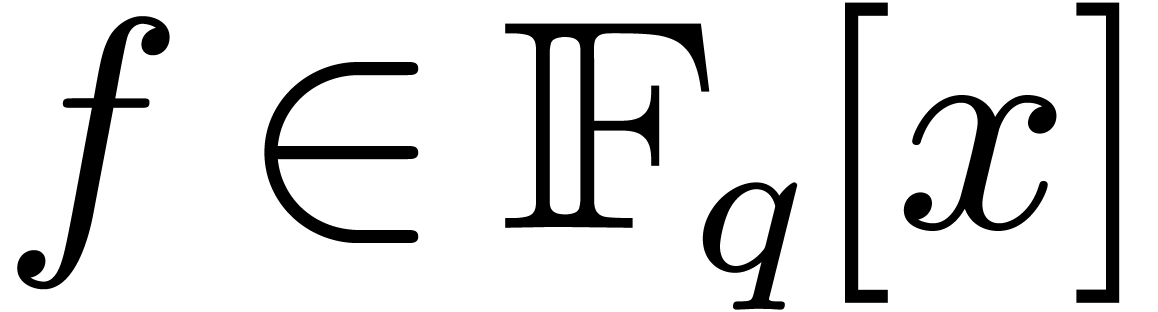 be a monic separable polynomial of degree
be a monic separable polynomial of degree
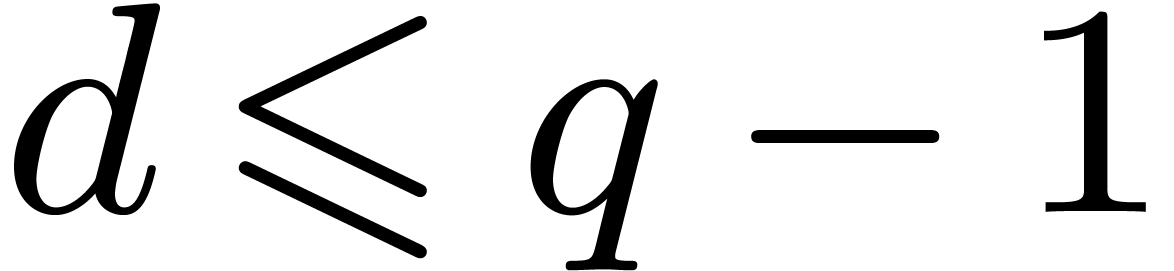 , which splits over
, which splits over  , and such that
, and such that 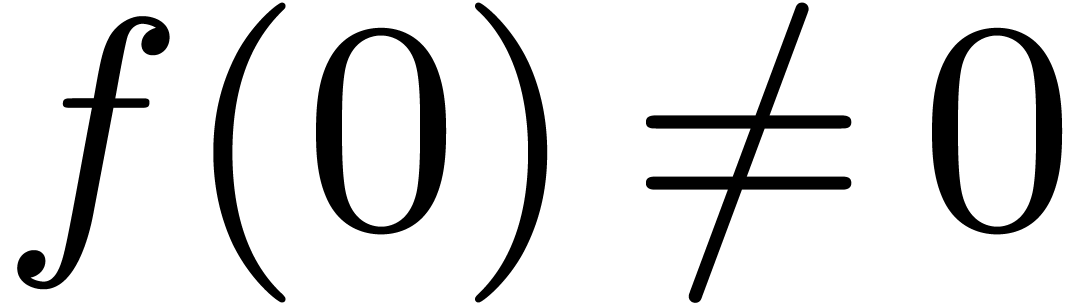 . Let
. Let  be the Graeffe
transform of
be the Graeffe
transform of 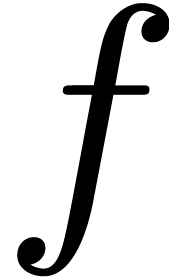 of order
of order 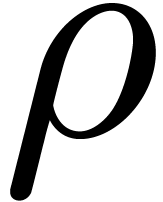 . The average number of simple roots of
. The average number of simple roots of  over all such polynomials
over all such polynomials 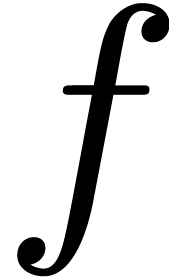 endowed
with a uniform distribution is at least
endowed
with a uniform distribution is at least 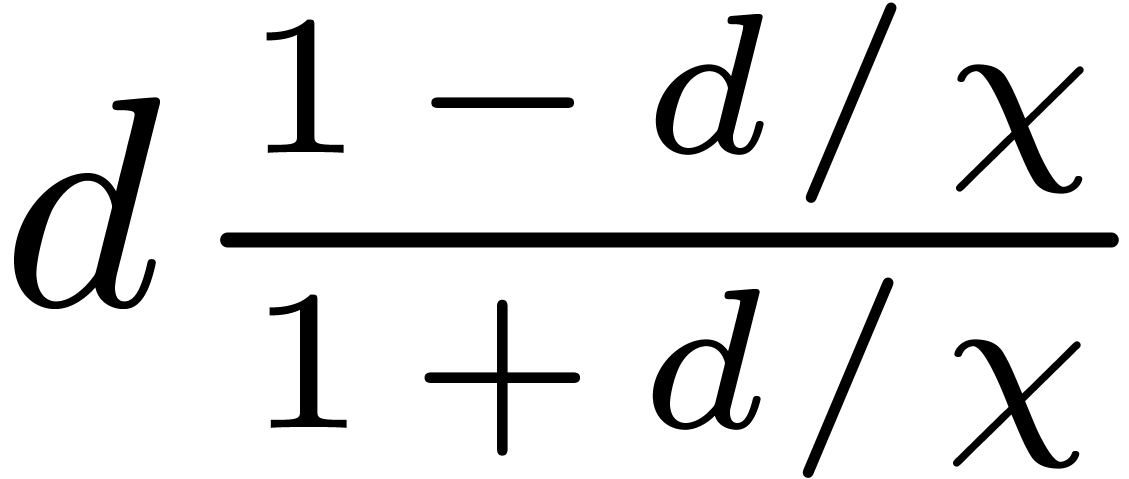 .
.
Moreover, assuming that 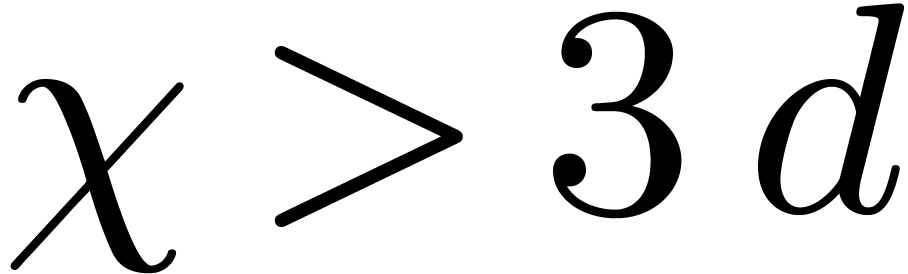 the probability that
the probability that
 has at least
has at least 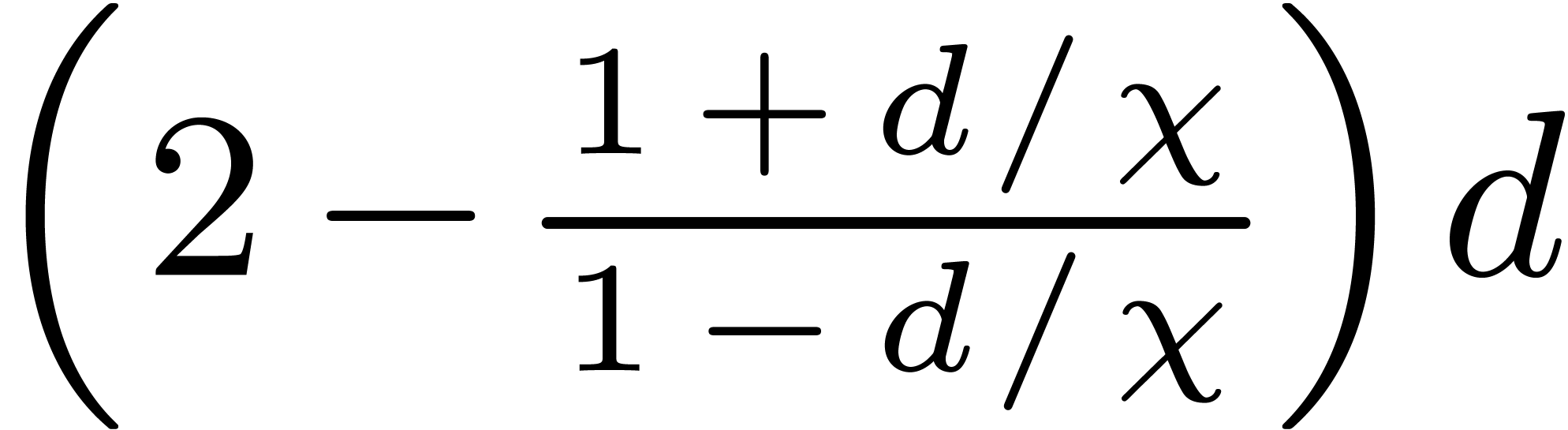 simple
roots is at least
simple
roots is at least 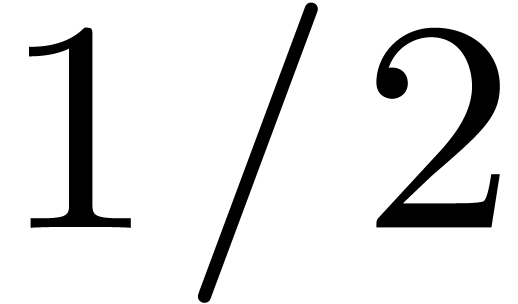 .
.
Proof. The polynomial  is
uniformly distributed in the set of monic polynomials with roots of
order
is
uniformly distributed in the set of monic polynomials with roots of
order 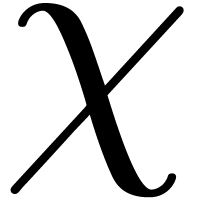 . Let
. Let  and
and  be the respective numbers of simple and
multiple roots of
be the respective numbers of simple and
multiple roots of  , so that
, so that
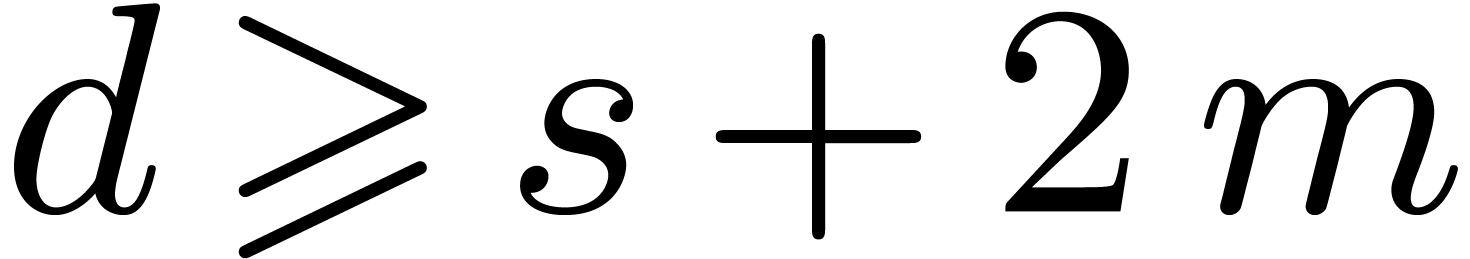 . We have just seen that the
average number
. We have just seen that the
average number  of distinct roots of
of distinct roots of  is at least
is at least 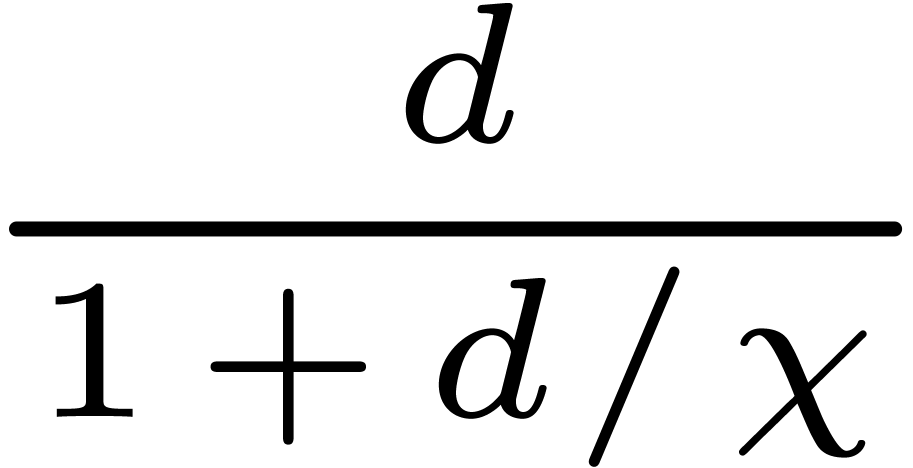 .
Hence,
.
Hence, 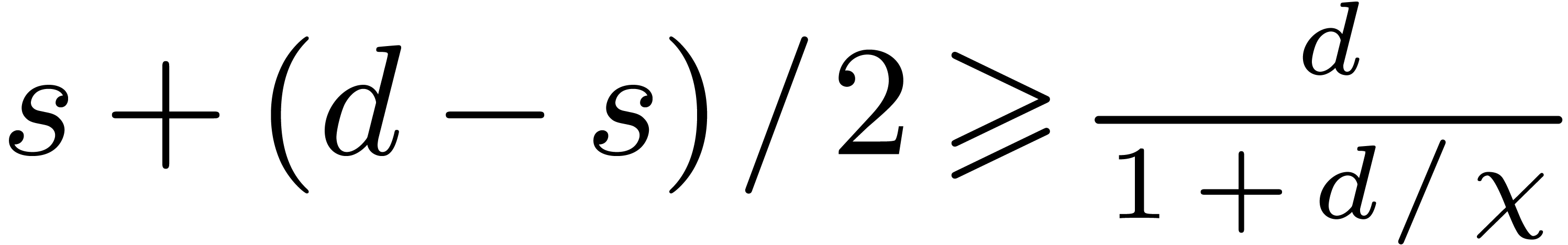 and
and 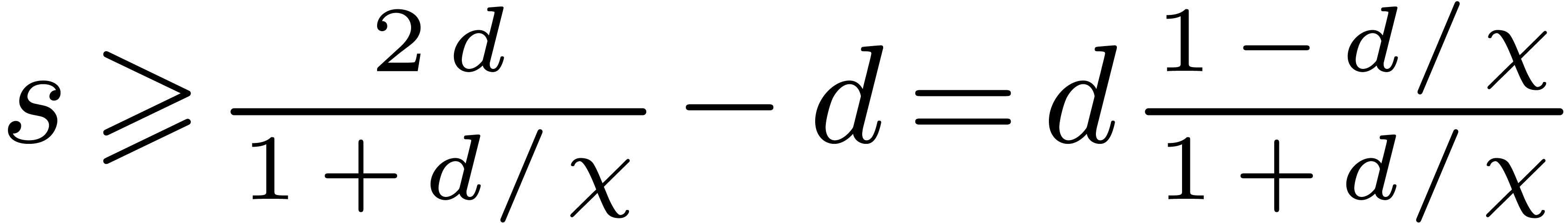 .
.
Setting 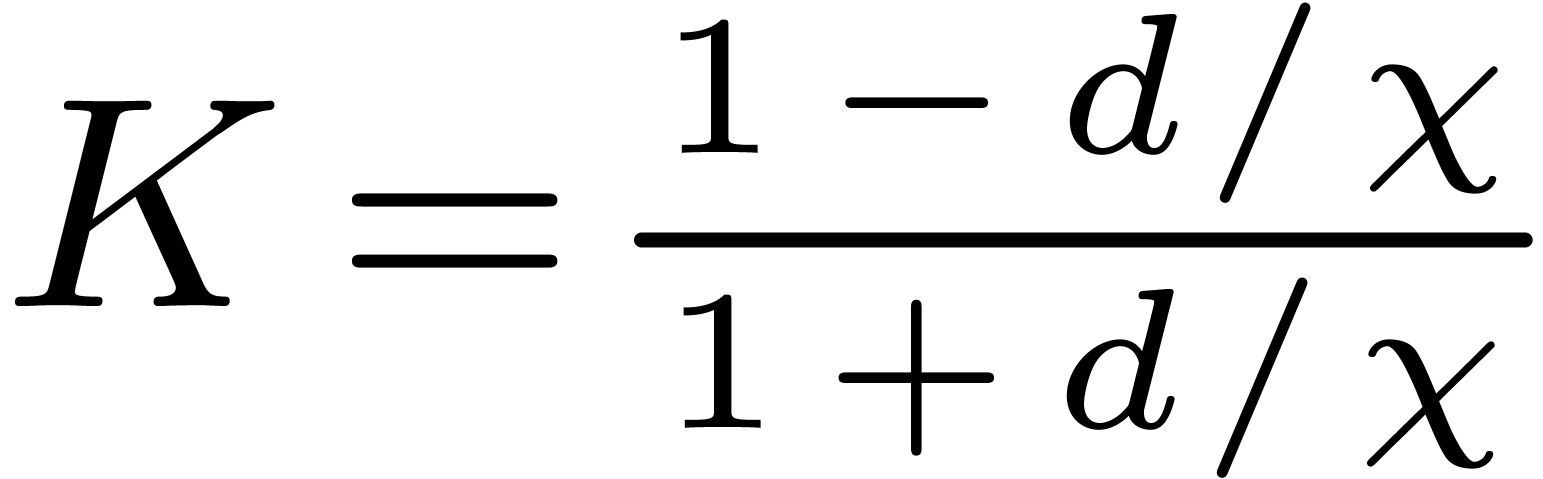 and assuming that
and assuming that  , so that
, so that 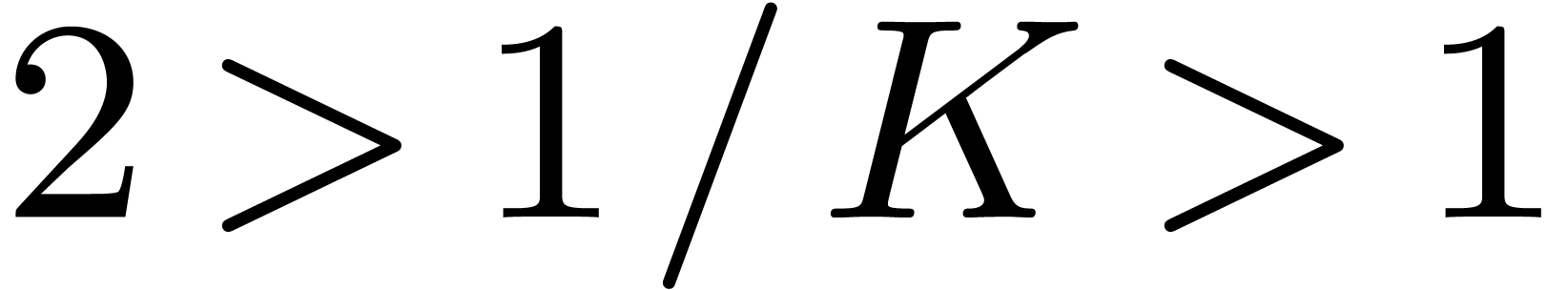 ,
let
,
let 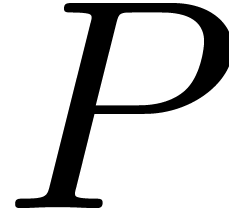 be the probability that
be the probability that  has less than
has less than 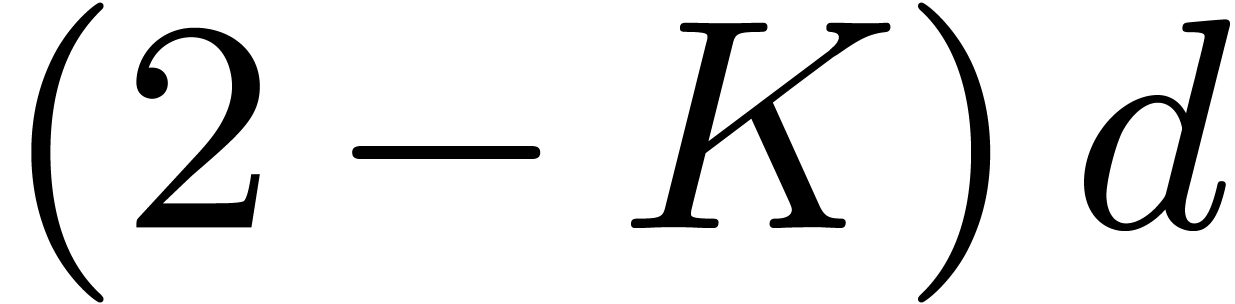 simple roots. Then the average
number of roots
simple roots. Then the average
number of roots  is at most
is at most  , whence
, whence  .
We conclude that
.
We conclude that 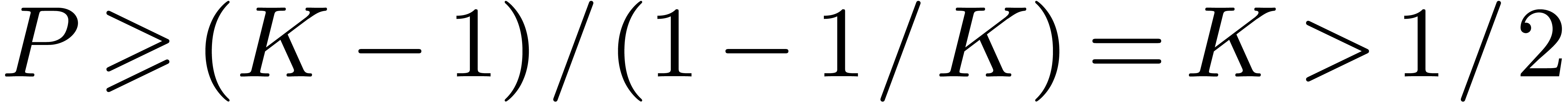 .
.
3.6A heuristic randomized algorithm
Let 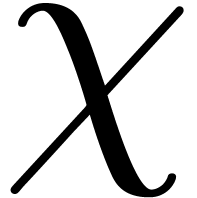 be a divisor of
be a divisor of  ,
,  and consider a polynomial
and consider a polynomial
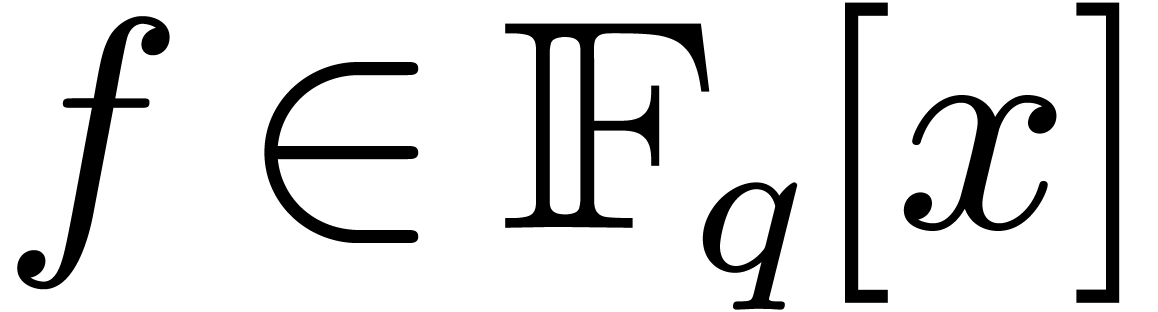 of degree
of degree 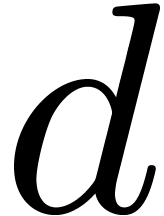 .
In Section 3.4, we have shown that for all but at most
.
In Section 3.4, we have shown that for all but at most 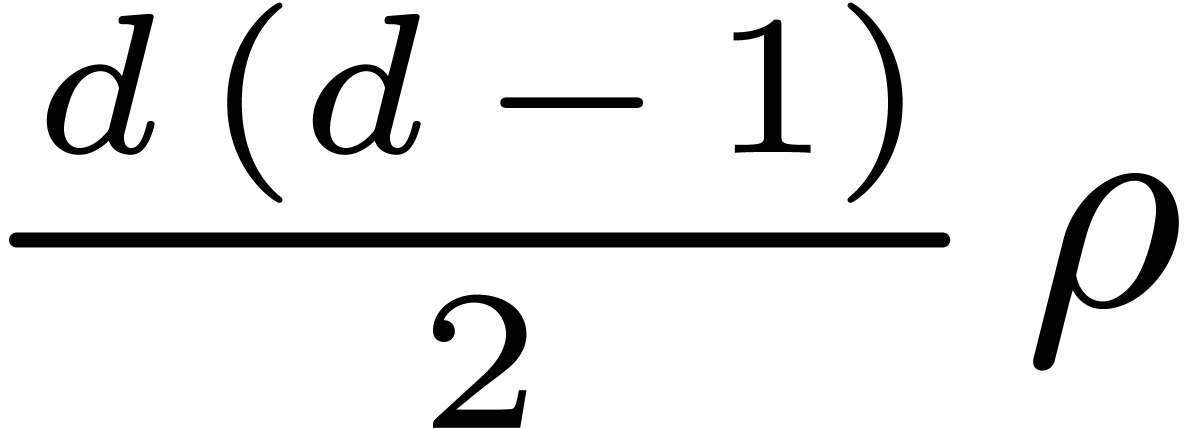 values of
values of  ,
the Graeffe transform
,
the Graeffe transform 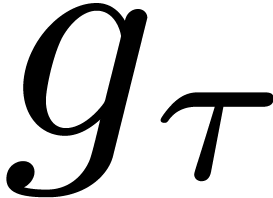 of order
of order 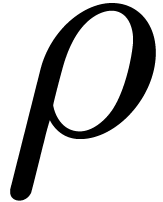 of
of 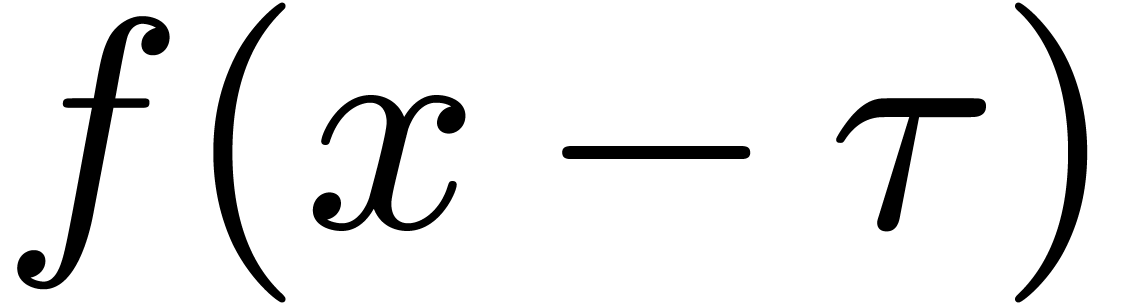 has no multiple root. Taking
has no multiple root. Taking 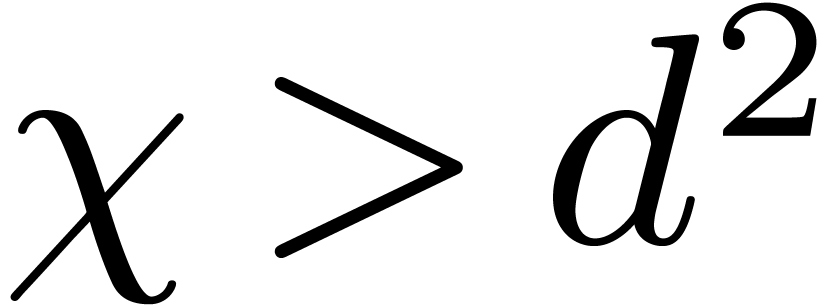 , this implies that
, this implies that 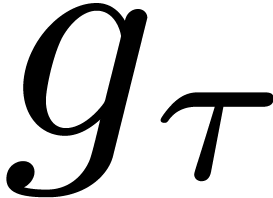 has
no multiple roots with probability at least
has
no multiple roots with probability at least  , when picking
, when picking  at random.
Now Proposition 10 implies that at least one third of the
roots remain simple with probability at least
at random.
Now Proposition 10 implies that at least one third of the
roots remain simple with probability at least  under the weaker condition that
under the weaker condition that 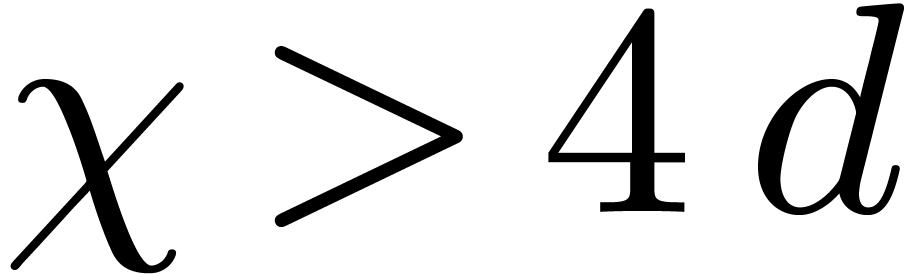 and for random
and for random
 . It is an interesting
question whether this fact actually holds for any
. It is an interesting
question whether this fact actually holds for any  if
if  is randomly chosen:
is randomly chosen:
Heuristic. Let 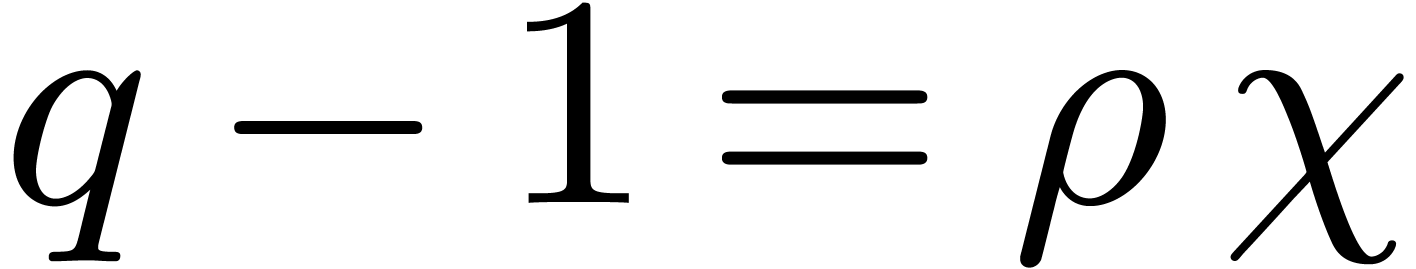 with
with
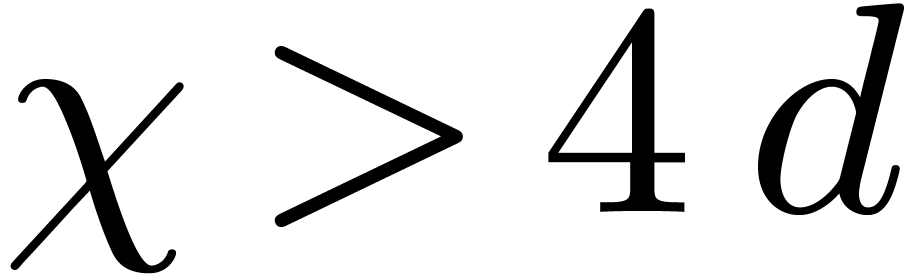 and let
and let 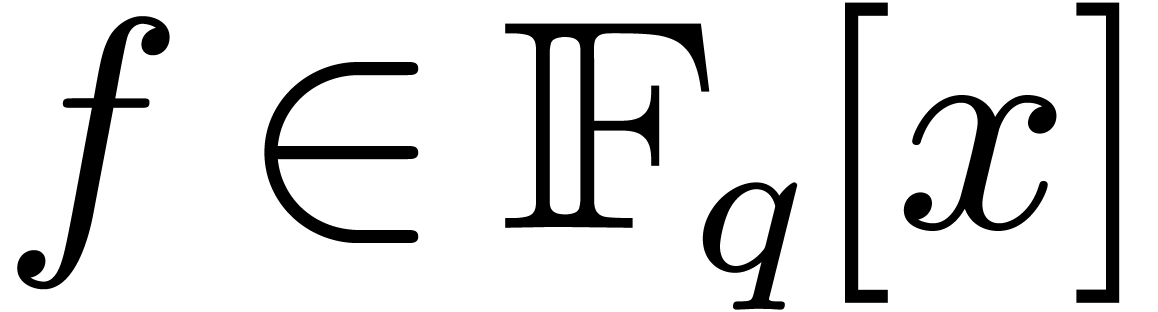 be a monic,
separable polynomial of degree
be a monic,
separable polynomial of degree 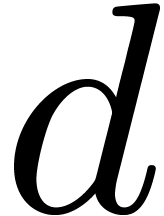 which splits over
which splits over
 . Then there exist at least
. Then there exist at least
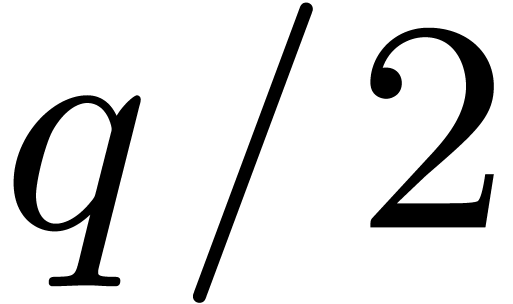 elements
elements 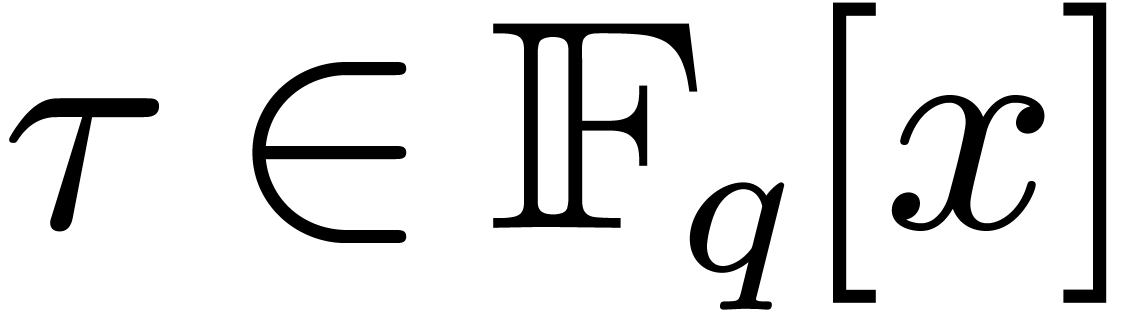 such that the
Graeffe transform of order
such that the
Graeffe transform of order 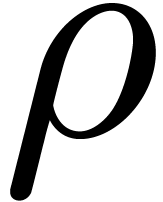 of
of 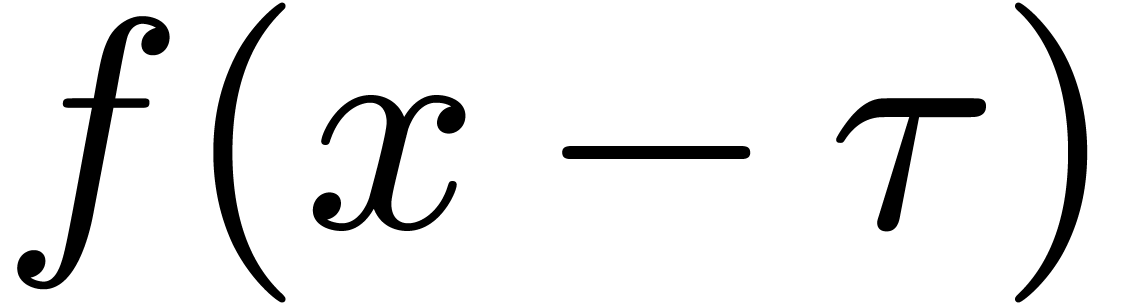 has at least
has at least 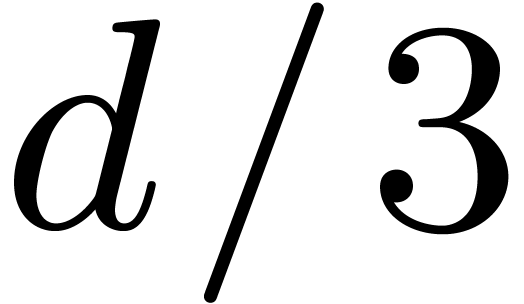 simple roots.
simple roots.
From now on, assume that  is picked at random or
that the above heuristic holds and
is picked at random or
that the above heuristic holds and  is chosen at
random. Taking
is chosen at
random. Taking  , we may then
find the roots of
, we may then
find the roots of 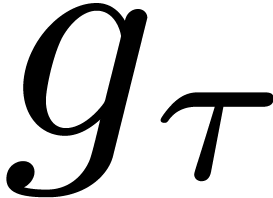 by computing a few discrete
Fourier transforms of length
by computing a few discrete
Fourier transforms of length  ,
instead of more expensive multi-point evaluations. Using tangent Graeffe
transforms, the simple roots can be lifted back for almost no cost.
These considerations lead to the following efficient randomized
algorithm.
,
instead of more expensive multi-point evaluations. Using tangent Graeffe
transforms, the simple roots can be lifted back for almost no cost.
These considerations lead to the following efficient randomized
algorithm.
Randomized algorithm 11.
-
Input
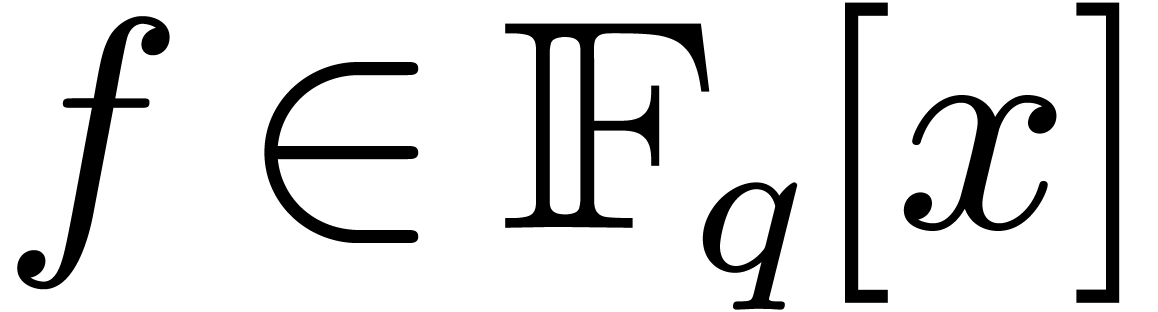 of degree
of degree
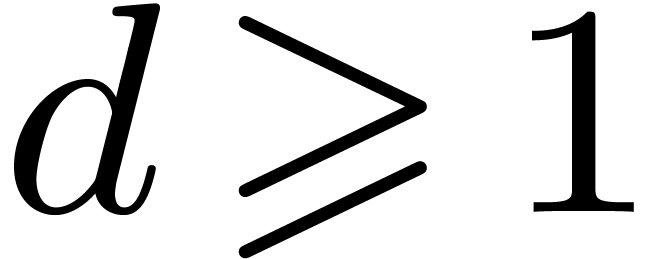 ,
monic, separable, which splits over
,
monic, separable, which splits over
 ,
and such that
,
and such that
 ;
a primitive element
;
a primitive element
 of
of
 .
.
-
Output
-
The roots of  .
.
-
If  then evaluate
then evaluate  on
all the elements of
on
all the elements of  , and
return the roots.
, and
return the roots.
-
Otherwise set  to be the largest integer in
to be the largest integer in
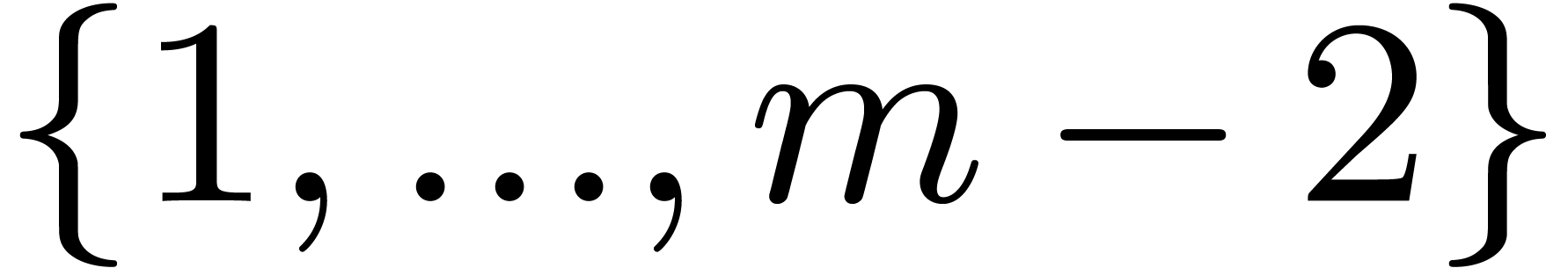 such that
such that 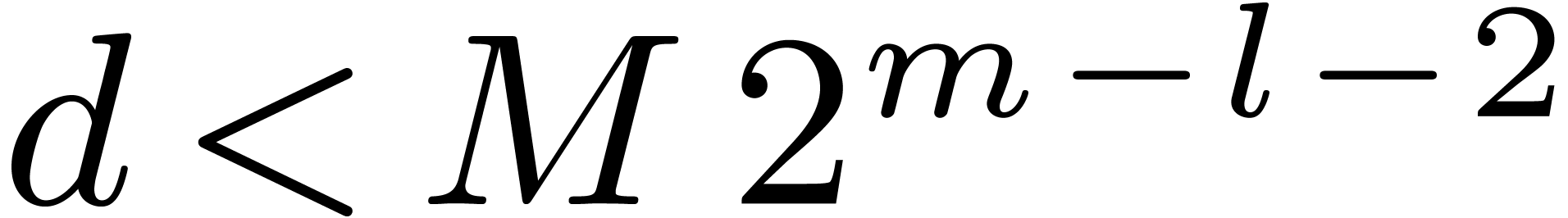 .
Compute
.
Compute 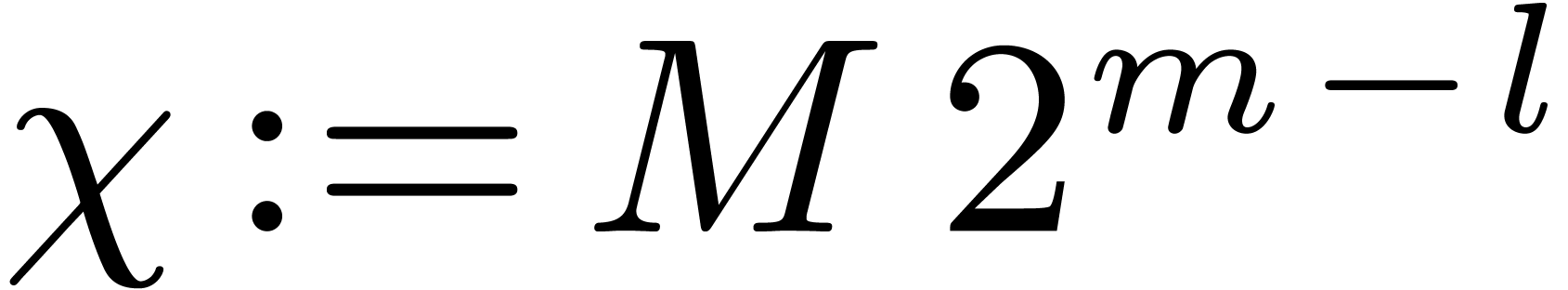 and
and 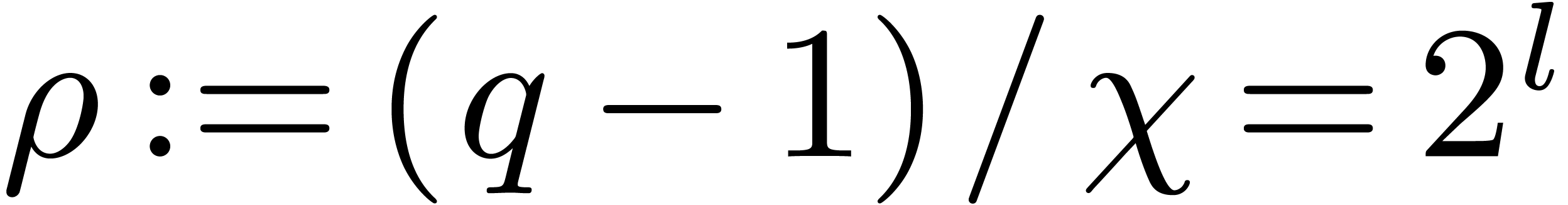 .
.
-
Pick a random  in
in  , and compute the Graeffe transform
, and compute the Graeffe transform 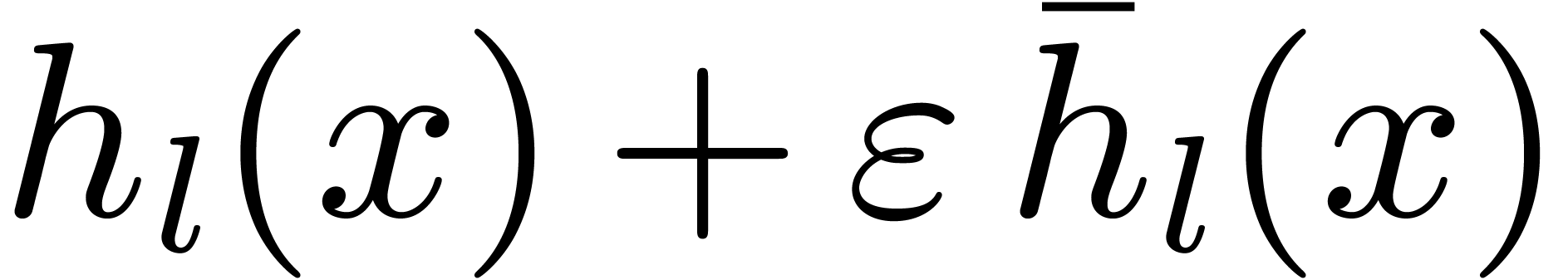 of order
of order 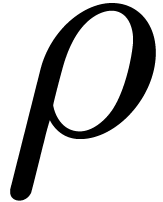 of
of 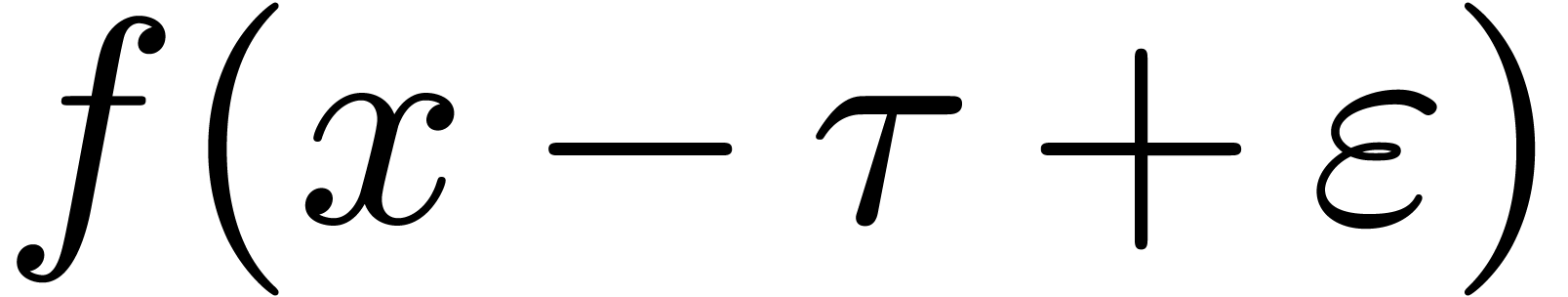 with
with 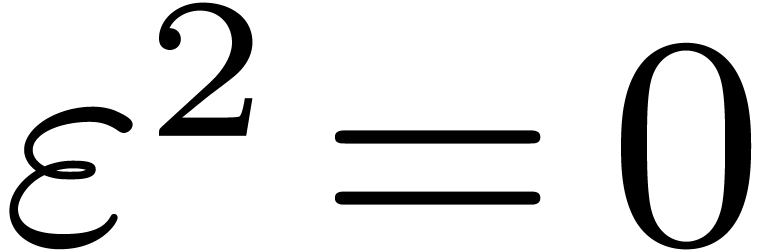 .
.
-
Compute 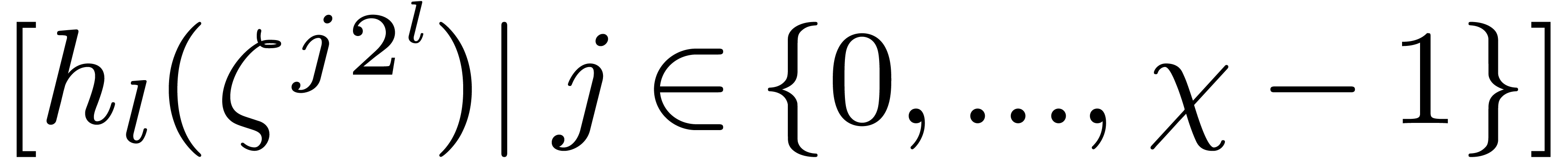 ,
, 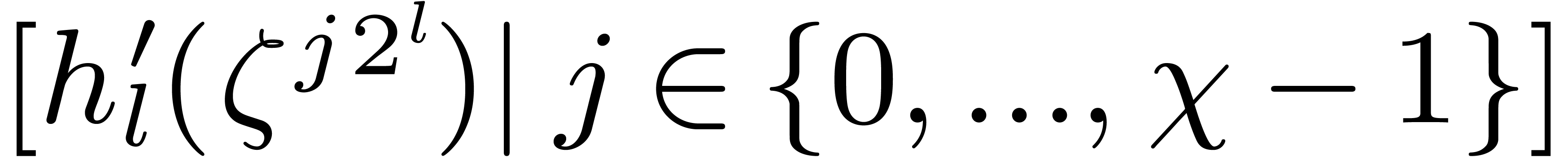 ,
, 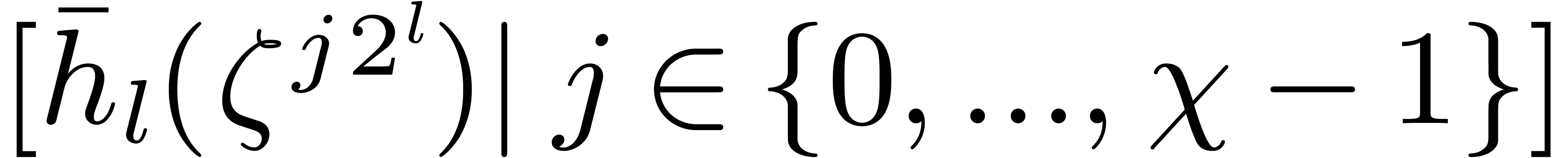 .
.
-
Compute  . Add
. Add  to
to 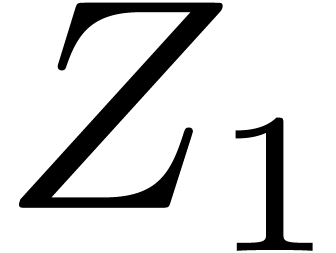 if
if 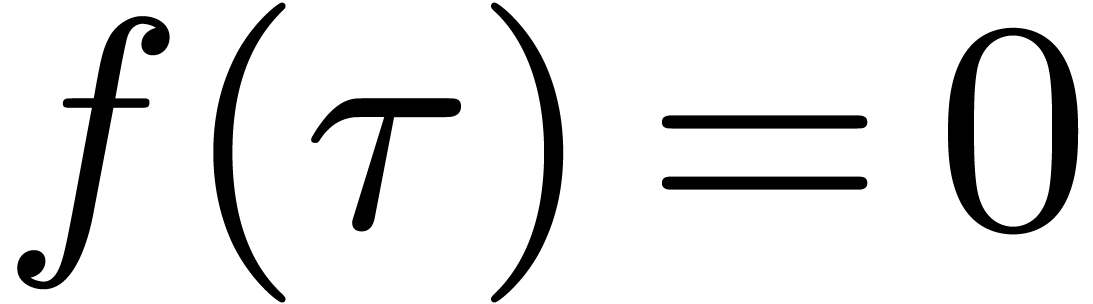 .
.
-
Compute  .
.
-
Compute recursively the roots  of
of  .
.
-
Return  .
.
Proposition 12. Assume
the heuristic or that  is chosen at random among
the monic, separable polynomials with
is chosen at random among
the monic, separable polynomials with  and which
split over
and which
split over  . Then Algorithm
11 takes an average time
. Then Algorithm
11 takes an average time 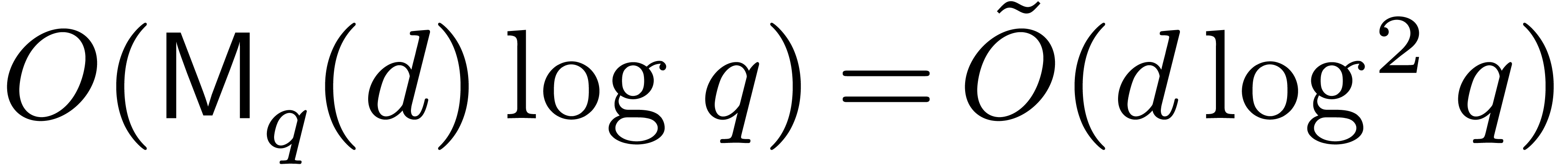 ,
whenever
,
whenever  and
and 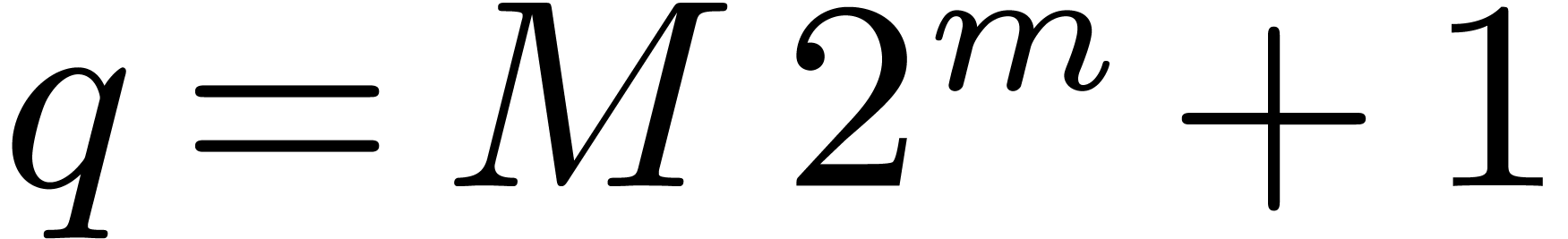 with
with 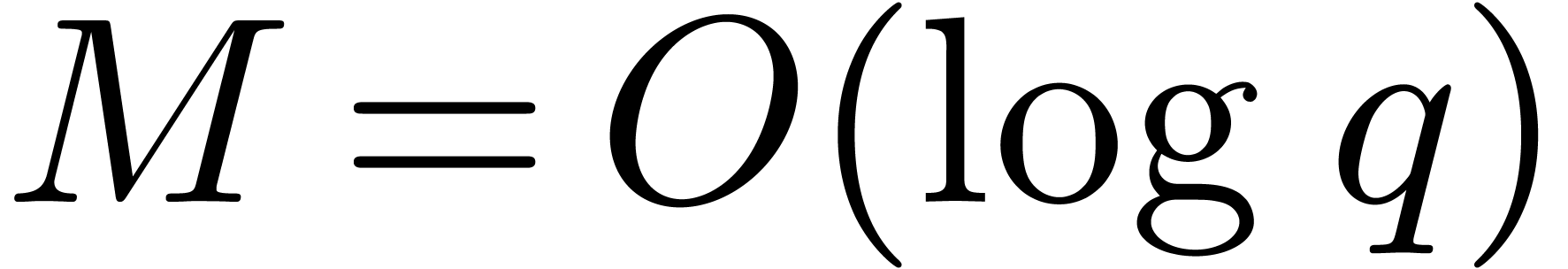 .
.
Proof. Of course if 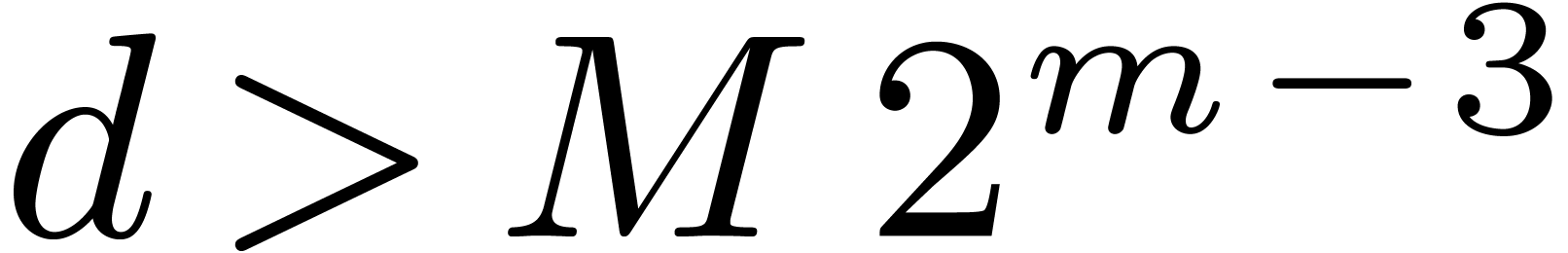 then
the cost is
then
the cost is 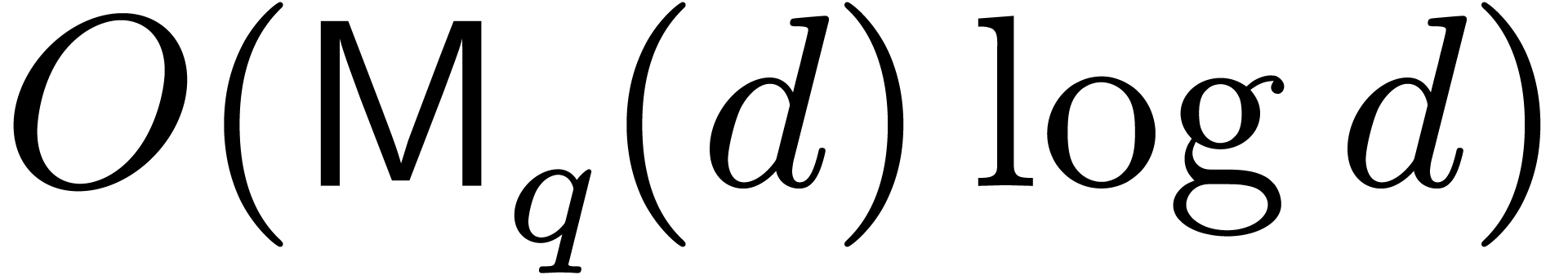 . Now suppose we
arrive in step 2. The roots of
. Now suppose we
arrive in step 2. The roots of 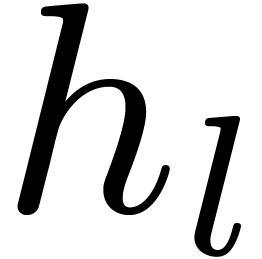 have order
dividing
have order
dividing 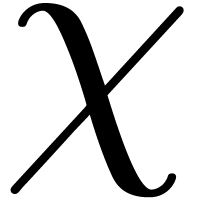 , and we have
, and we have 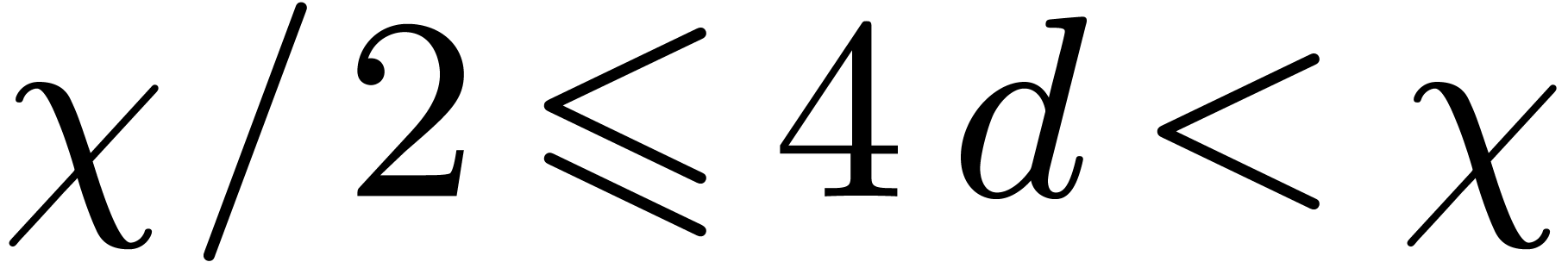 . If the algorithm terminates then
it is correct by the same arguments as for Algorithm 8.
. If the algorithm terminates then
it is correct by the same arguments as for Algorithm 8.
The cost of step 3 is bounded by 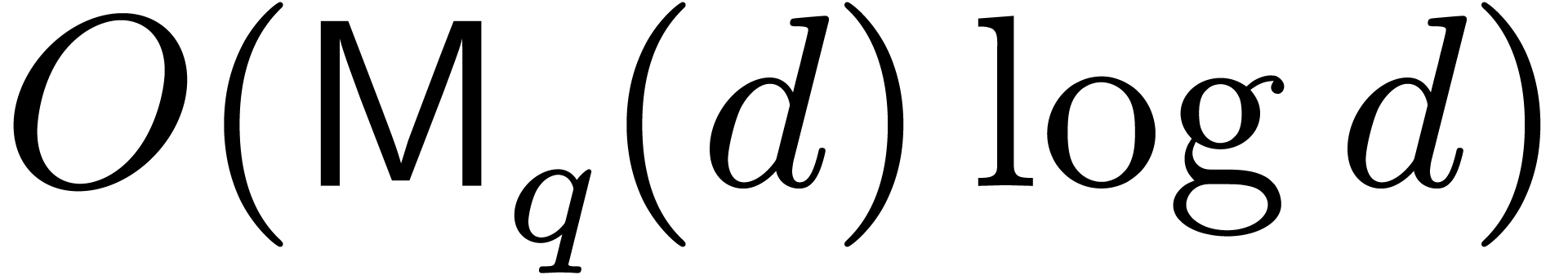 (and even by
(and even by
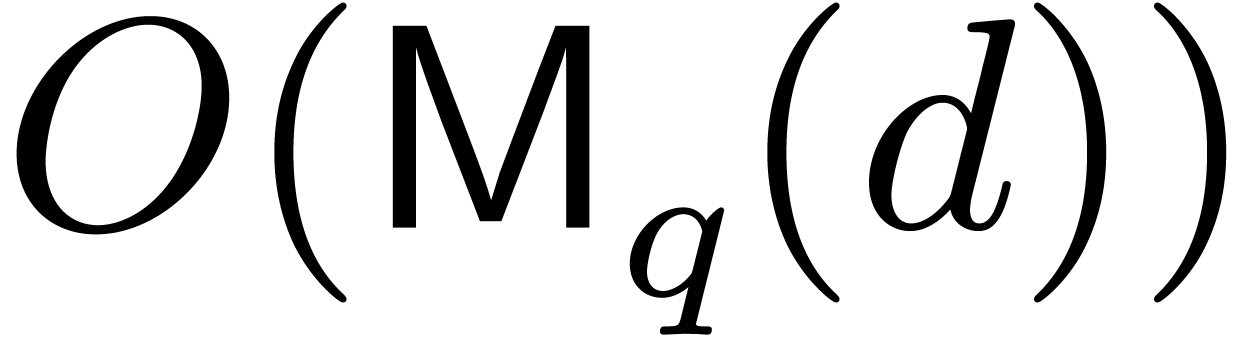 if
if  according to [4, Chapter 1, Section 2]). When computing
according to [4, Chapter 1, Section 2]). When computing 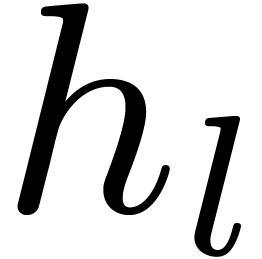 using
using 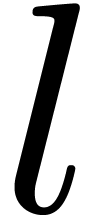 tangent Graeffe transforms of order
tangent Graeffe transforms of order  , the cost of step 3 is bounded by
, the cost of step 3 is bounded by
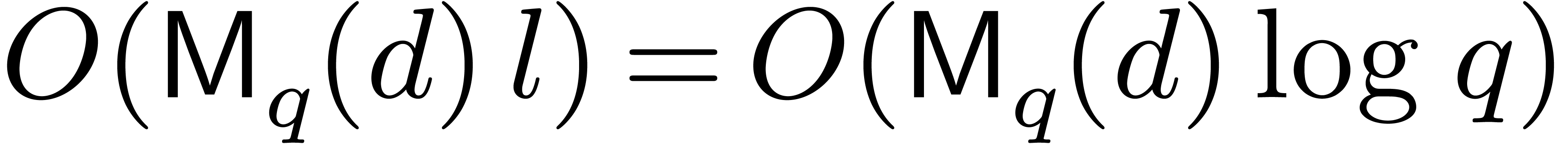 . Steps 4 and 5 can be done
in time
. Steps 4 and 5 can be done
in time 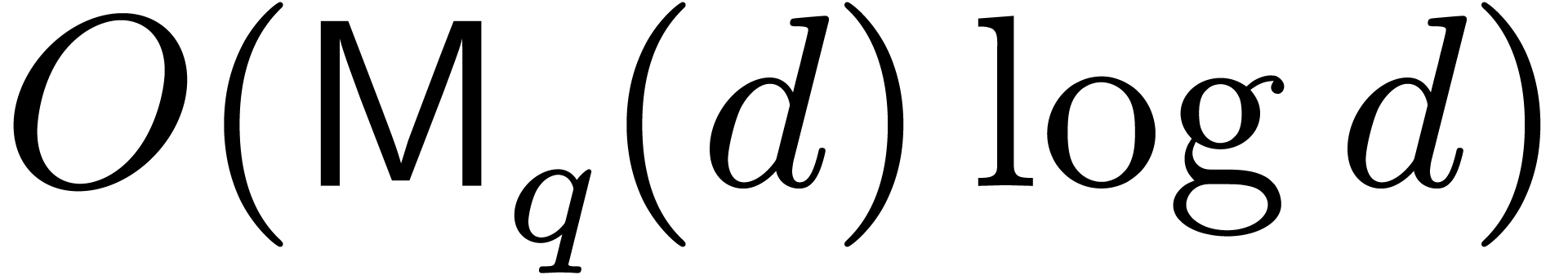 . The average
execution time
. The average
execution time 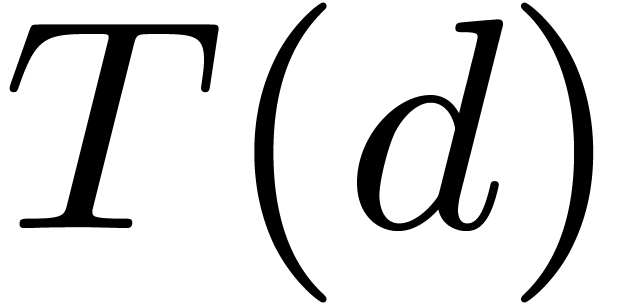 thus satisfies
thus satisfies
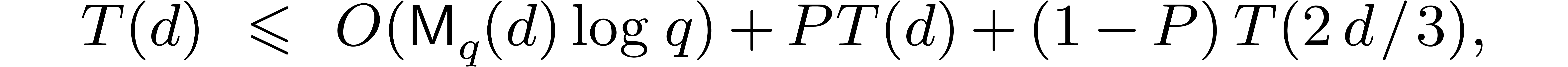
where 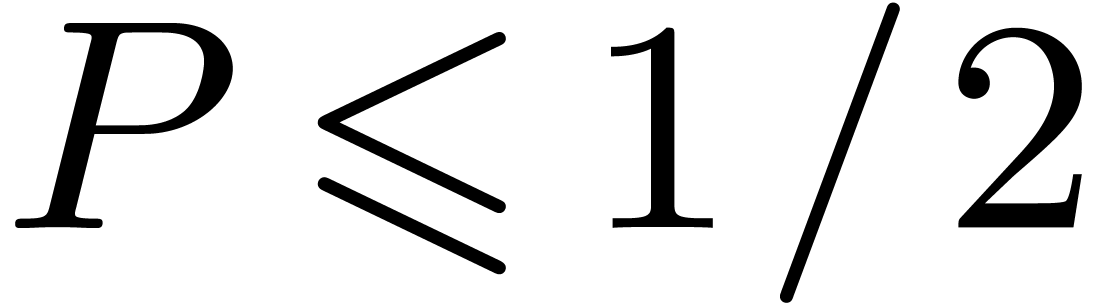 is the probability that
is the probability that  contains more than
contains more than 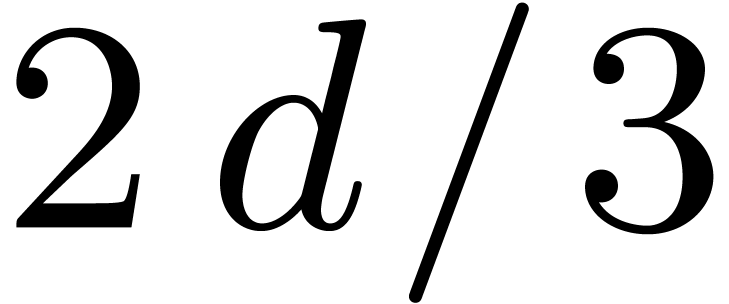 elements in step 7. It
follows that
elements in step 7. It
follows that  , whence
, whence 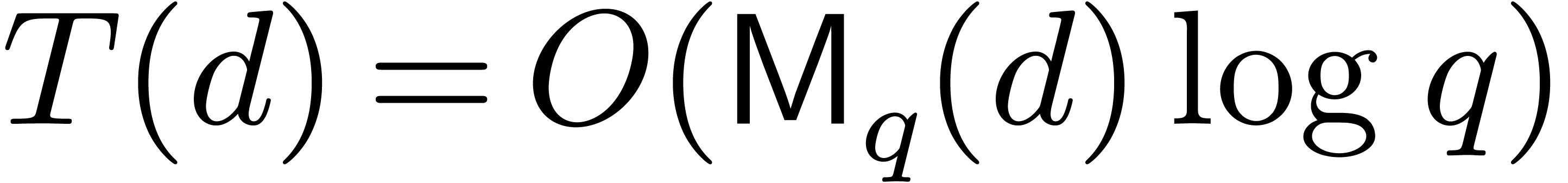 .
.
The main bottleneck for Algorithm 11 is step 3. It would be
possible to improve our complexity bound if a better algorithm were
known to compute Graeffe transforms of order 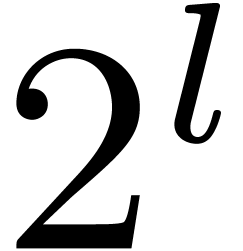 . In the FFT model, the tangent Graeffe transform of
a polynomial of degree
. In the FFT model, the tangent Graeffe transform of
a polynomial of degree 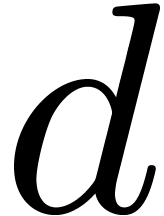 can be computed in time
can be computed in time
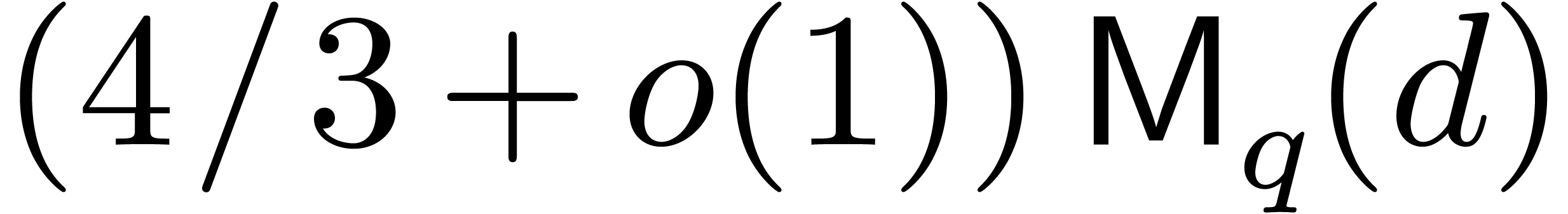 . In practice, this means
that the asymptotic complexity of Algorithm 11 is
equivalent to
. In practice, this means
that the asymptotic complexity of Algorithm 11 is
equivalent to 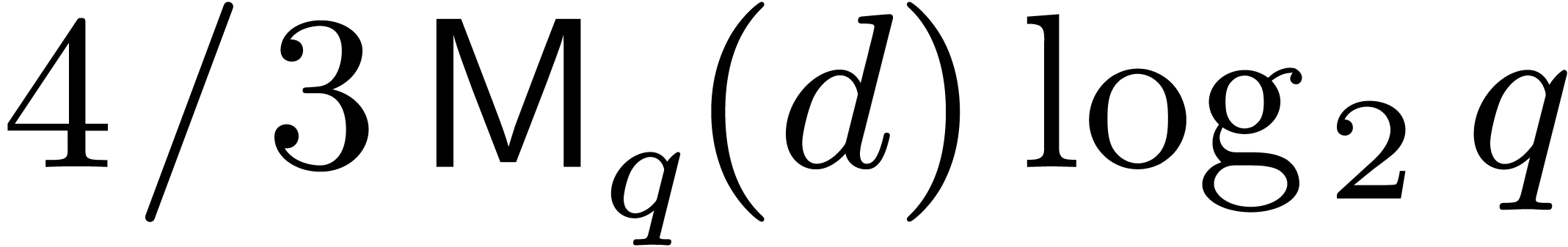 .
.
In order to reduce the cost of the Graeffe transforms, it is relevant to
choose 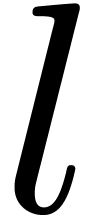 such that
such that 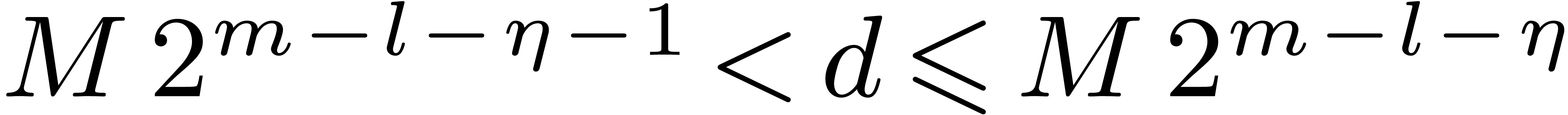 for
some small
for
some small  , which is to be
determined in practice as a function of
, which is to be
determined in practice as a function of 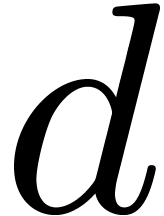 and
and
 . In this way more time is
spent in multi-point evaluations. For the multi-point evaluations in
step 4, one may use
. In this way more time is
spent in multi-point evaluations. For the multi-point evaluations in
step 4, one may use  FFTs of size
FFTs of size 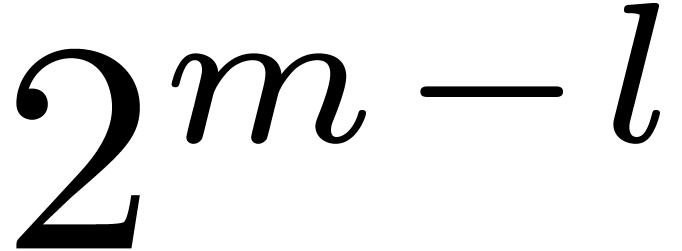 for small values of
for small values of  ,
or appeal to Bluestein's chirp transform [5].
,
or appeal to Bluestein's chirp transform [5].
4.Timings
In this section we report on timings for the algorithms presented above.
We use a platform equipped with an Intel CoreTM
i7-4770 CPU at 3.40 GHz, and 8 GB of 1600 MHz DDR3. It
runs the Jessie GNU Debian
CoreTM
i7-4770 CPU at 3.40 GHz, and 8 GB of 1600 MHz DDR3. It
runs the Jessie GNU Debian operating system with a Linux
operating system with a Linux kernel version 3.14 in 64 bit mode. We compile with GCC
[12] version 4.9.1.
kernel version 3.14 in 64 bit mode. We compile with GCC
[12] version 4.9.1.
We use revision 9738 of Mathemagix. For the sake
of comparison to other software, we installed the NTL library version
8.0.0 [32] (configured to benefit from GMP [13]
version 6.0.0), and Flint version 2.4.4 [15].
For our benchmark family we simply build polynomials  of degree
of degree  from random pairwise distinct roots.
from random pairwise distinct roots.
Table 1 shows timings for the FFT prime field 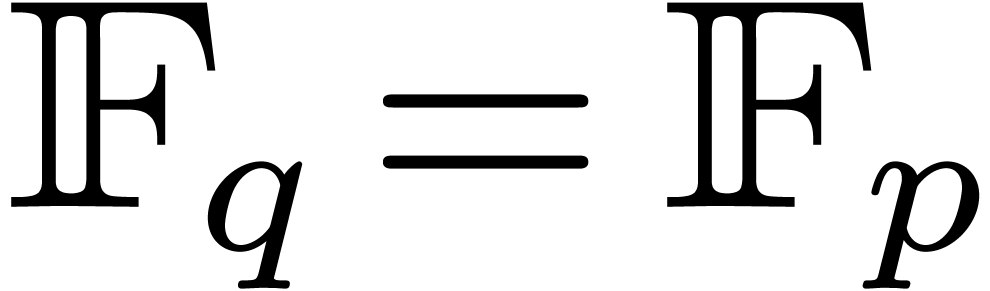 with
with 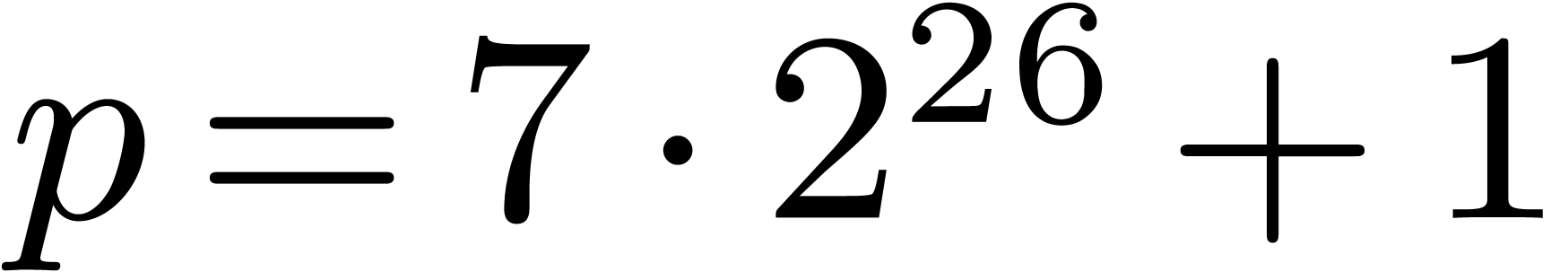 . The row
NTL corresponds to the function FindRoots, which
contains an optimization with respect to Algorithm 1 with
. The row
NTL corresponds to the function FindRoots, which
contains an optimization with respect to Algorithm 1 with
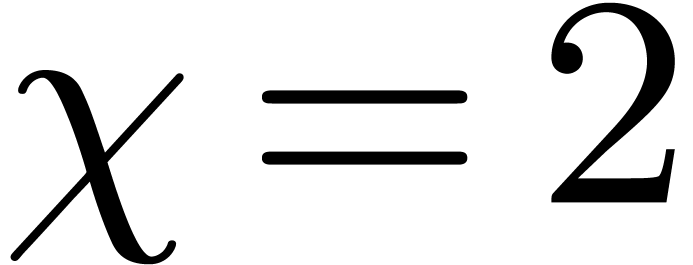 : in fact, the polynomials
: in fact, the polynomials
 in step
in step  are taken of
degree
are taken of
degree 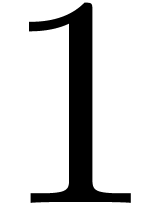 (see [30] for details). We
implemented the same optimization in our versions of
Cantor–Zassenhaus in Mathemagix. The row
Flint corresponds to the function nmod_poly_factor_equal_deg,
that does not take advantage of this optimization, which mainly explains
a loss of efficiency. The rows “Alg. 1” to
“Alg. 11” correspond to our own implementations
in Mathemagix of the above algorithms (see files
algebramix/polynomial_modular_int.hpp and algebramix/bench/polynomial_modular_int_bench.cpp).
Our modified version of Cantor–Zassenhaus' algorithm, with
(see [30] for details). We
implemented the same optimization in our versions of
Cantor–Zassenhaus in Mathemagix. The row
Flint corresponds to the function nmod_poly_factor_equal_deg,
that does not take advantage of this optimization, which mainly explains
a loss of efficiency. The rows “Alg. 1” to
“Alg. 11” correspond to our own implementations
in Mathemagix of the above algorithms (see files
algebramix/polynomial_modular_int.hpp and algebramix/bench/polynomial_modular_int_bench.cpp).
Our modified version of Cantor–Zassenhaus' algorithm, with  , does not reveal to be of
practical interest for this prime size.
, does not reveal to be of
practical interest for this prime size.
Concerning the deterministic algorithms, let us precise that we take
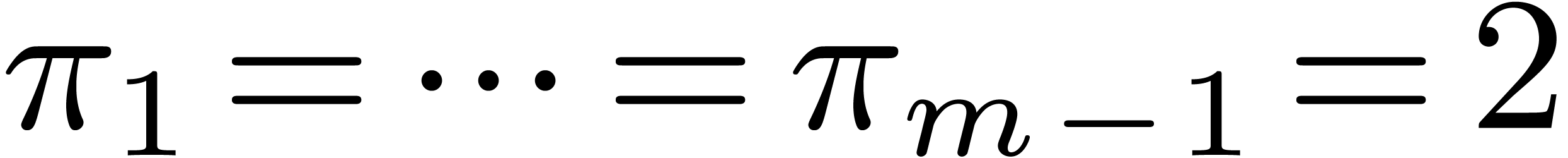 and
and 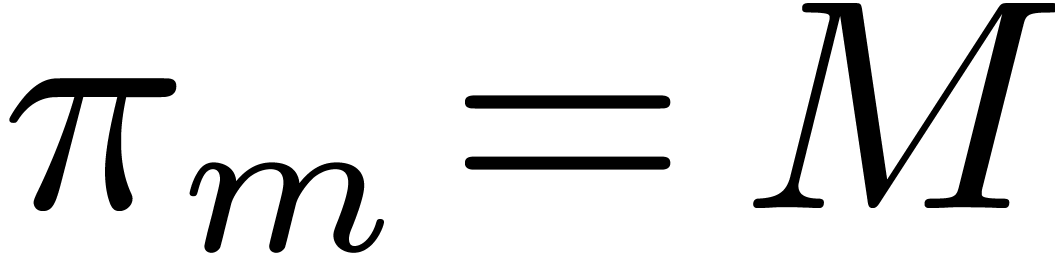 in Algorithm 2. In addition, in our implementation of Algorithm 4,
when
in Algorithm 2. In addition, in our implementation of Algorithm 4,
when  and
and  are small, for
efficiency reasons, we compute
are small, for
efficiency reasons, we compute 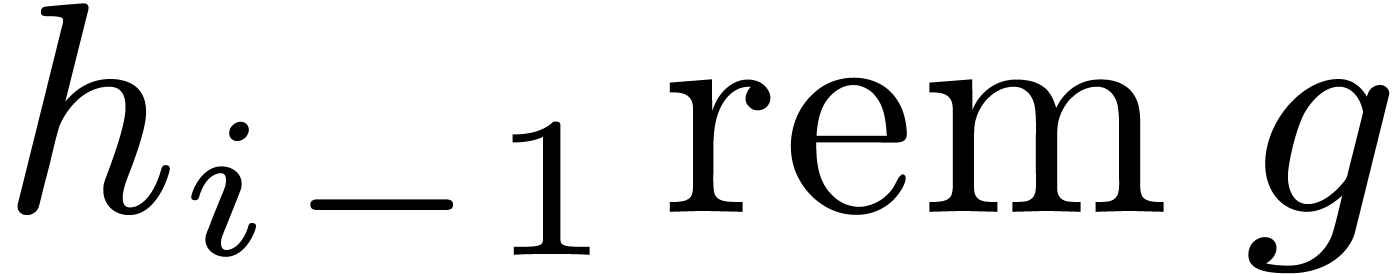 using binary
powering instead of simultaneous remainders. These deterministic methods
turn out to be quite competitive.
using binary
powering instead of simultaneous remainders. These deterministic methods
turn out to be quite competitive.
Our Table 2 is similar to Table 1 for the FFT
prime field 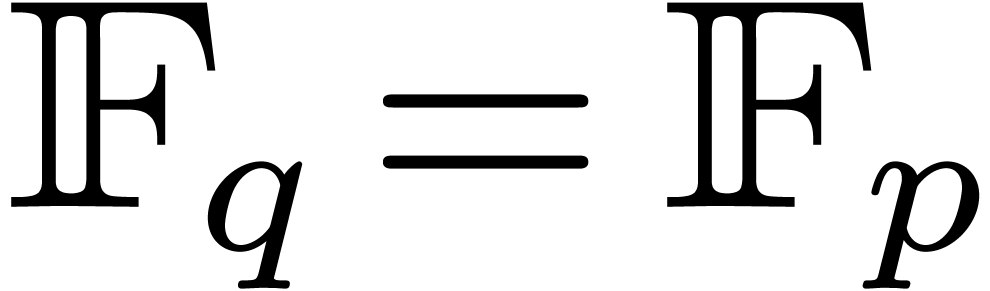 with
with 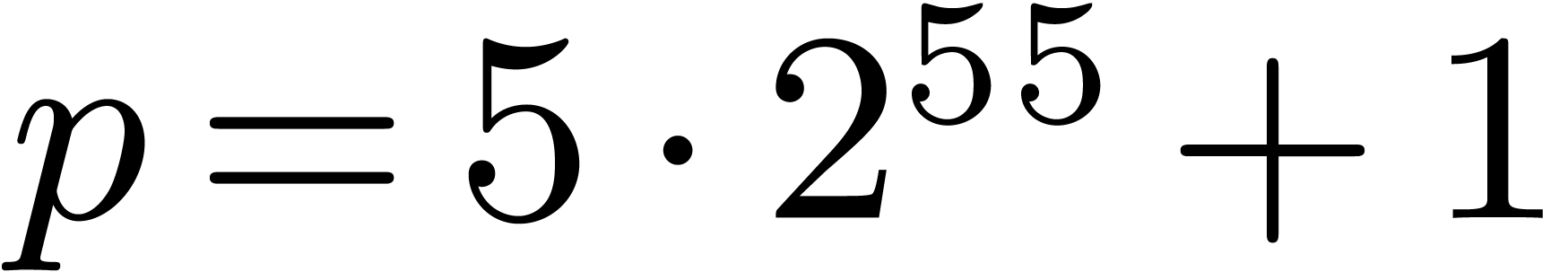 .
Nevertheless NTL does not support this larger prime within its type zz_p. This larger prime starts to reveal the interest in our
modified version of Cantor–Zassenhaus with
.
Nevertheless NTL does not support this larger prime within its type zz_p. This larger prime starts to reveal the interest in our
modified version of Cantor–Zassenhaus with  . The speed-up measured with the modified version
even more increases with larger primes: With
. The speed-up measured with the modified version
even more increases with larger primes: With 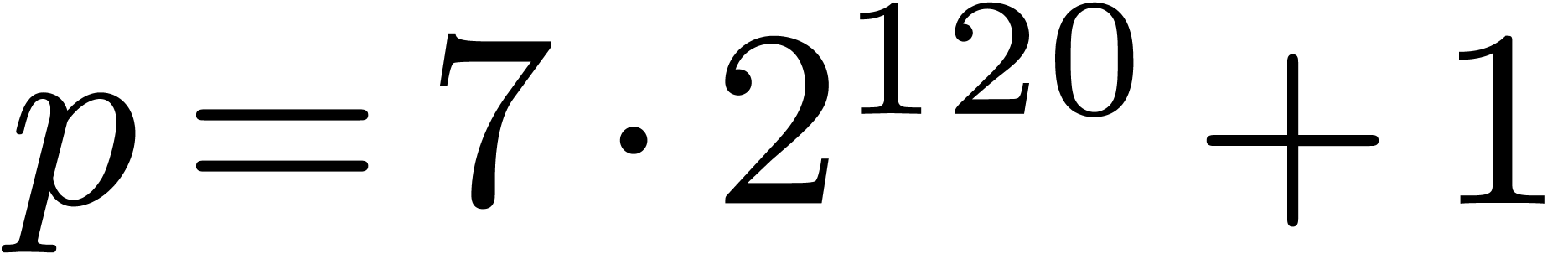 , it reaches a factor 1.6 in size
, it reaches a factor 1.6 in size 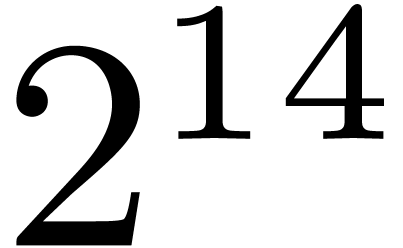 .
.
Using Graeffe transforms as in Algorithm 8 is not very
competitive. However, in final, it is satisfactory to observe that our
Algorithm 11, exploiting the tangent transform, gains by an
order of magnitude over other existing methods in both tables.
 |
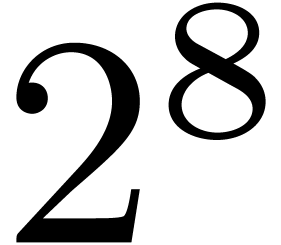 |
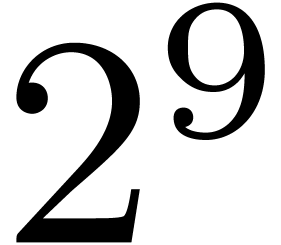 |
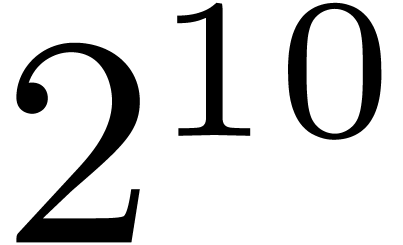 |
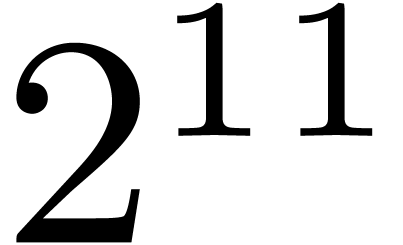 |
 |
 |
 |
 |
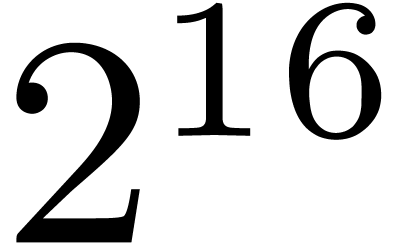 |
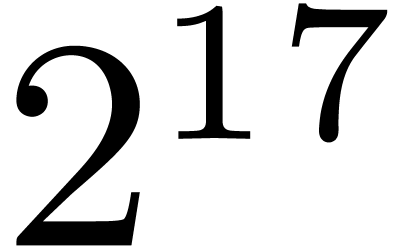 |
 |
| NTL |
0.0065 |
0.015 |
0.037 |
0.090 |
0.20 |
0.48 |
1.1 |
2.5 |
5.4 |
12 |
26 |
| Flint |
0.0093 |
0.025 |
0.065 |
0.17 |
0.45 |
1.2 |
3.0 |
8.0 |
22 |
63 |
250 |
Alg. 1, Cantor–Zassenhaus, 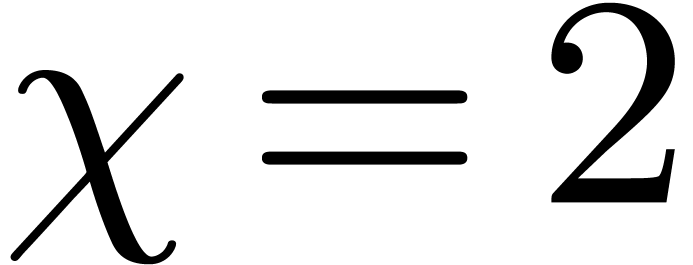 |
0.010 |
0.020 |
0.043 |
0.092 |
0.20 |
0.42 |
0.90 |
1.9 |
4.0 |
8.6 |
18 |
| Alg. 1, Cantor–Zassenhaus,
modified |
0.009 |
0.018 |
0.036 |
0.091 |
0.20 |
0.41 |
0.96 |
2.1 |
4.4 |
10 |
22 |
| Alg. 2, Mignotte–Schnorr |
0.063 |
0.12 |
0.25 |
0.51 |
1.0 |
2.0 |
3.9 |
7.8 |
15 |
31 |
62 |
| Alg. 4, Moenck |
0.025 |
0.051 |
0.10 |
0.21 |
0.44 |
0.91 |
1.9 |
3.9 |
8.2 |
17 |
35 |
| Alg. 8, Graeffe, randomized |
0.003 |
0.006 |
0.021 |
0.074 |
0.25 |
0.70 |
1.7 |
3.6 |
7.5 |
15 |
29 |
| Alg. 11, Graeffe, heuristic |
0.001 |
0.002 |
0.003 |
0.007 |
0.015 |
0.031 |
0.065 |
0.13 |
0.24 |
0.59 |
1.4 |
|
|
|
 |
 |
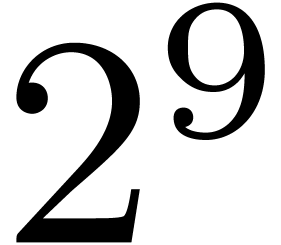 |
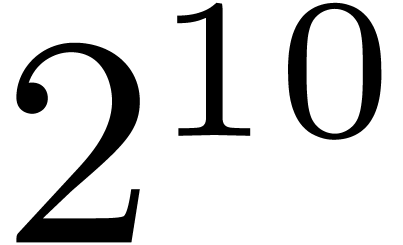 |
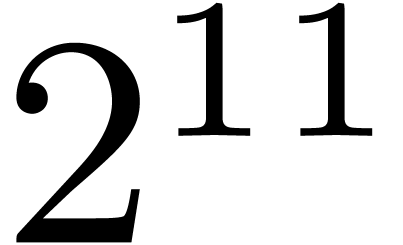 |
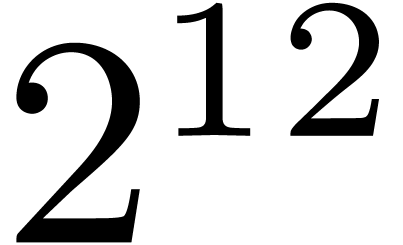 |
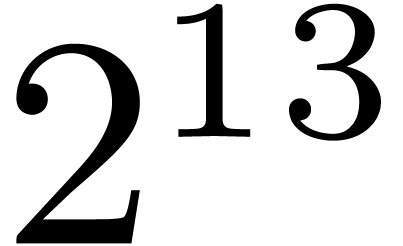 |
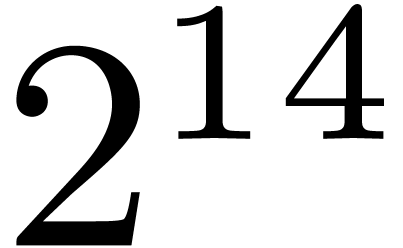 |
 |
 |
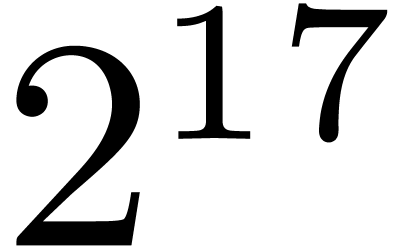 |
 |
| Flint |
0.032 |
0.084 |
0.22 |
0.58 |
1.5 |
3.8 |
9.5 |
23 |
58 |
150 |
470 |
Alg. 1, Cantor–Zassenhaus, 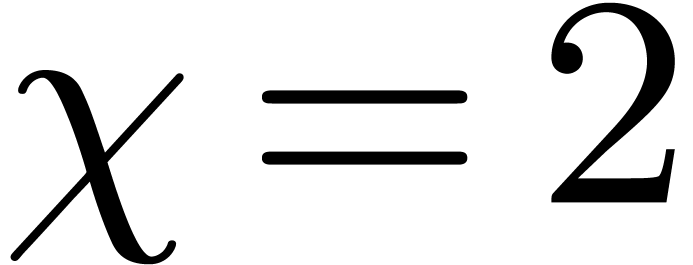 |
0.035 |
0.075 |
0.16 |
0.37 |
0.78 |
1.7 |
3.8 |
8.6 |
19 |
41 |
90 |
| Alg. 1, Cantor–Zassenhaus,
modified |
0.025 |
0.055 |
0.11 |
0.28 |
0.63 |
1.3 |
3.1 |
7.0 |
14 |
33 |
76 |
| Alg. 2, Mignotte–Schnorr |
0.22 |
0.46 |
0.96 |
2.0 |
4.2 |
8.7 |
18 |
39 |
83 |
180 |
370 |
| Alg. 4, Moenck |
0.89 |
0.18 |
0.37 |
0.76 |
1.6 |
3.4 |
7.2 |
16 |
33 |
72 |
150 |
| Alg. 8, Graeffe, randomized |
0.011 |
0.038 |
0.14 |
0.56 |
1.1 |
2.6 |
6.8 |
16 |
40 |
92 |
210 |
| Alg. 11, Graeffe, heuristic |
0.005 |
0.007 |
0.016 |
0.032 |
0.067 |
0.14 |
0.29 |
0.61 |
1.3 |
2.7 |
5.6 |
|
|
|
Coming back to our initial motivation for sparse polynomial
interpolation, let us mention that plugging Algorithm 11
into our implementations reported in [19] leads to quite
good speed-ups. The total time for Example 1 of [19],
concerning the product of random sparse polynomials, decreases from 12 s
to 7.6 s with the “coefficient ratios” technique. In fact,
the time spent in root finding decreases from 50 % to 8 % during the
sole determination of the support.
Example 2 of [19] concerns the sparse interpolation of the
determinant of the generic  matrix. For
matrix. For 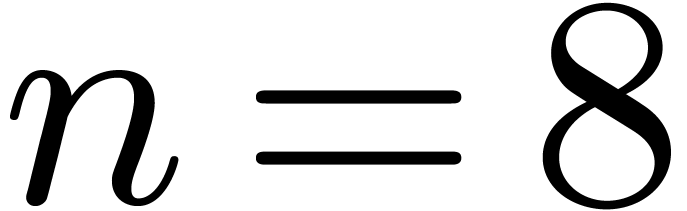 , the time for the “Kronecker
substitution” technique with a prime of 68 bits decreases from 95
s to 43 s. The time elapsed in root finding during the sole
determination of the support drops from 70 % to 20 %. Thanks to
additional optimizations, the “coefficient ratios” technique
now runs this example in
, the time for the “Kronecker
substitution” technique with a prime of 68 bits decreases from 95
s to 43 s. The time elapsed in root finding during the sole
determination of the support drops from 70 % to 20 %. Thanks to
additional optimizations, the “coefficient ratios” technique
now runs this example in 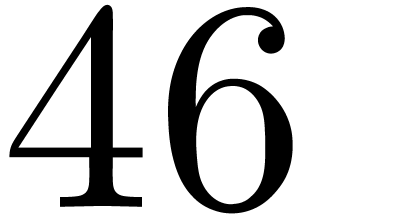 s.
s.
Acknowledgements
Bruno Grenet was partially supported by a LIX–Qualcomm –Carnot postdoctoral fellowship.
–Carnot postdoctoral fellowship.
5.References
-
[1]
-
E. Bach. Comments on search procedures for
primitive roots. Math. Comp., 66:1719–1727, 1997.
-
[2]
-
E. R. Berlekamp. Factoring polynomials over finite
fields. Bell System Tech. J., 46:1853–1859, 1967.
-
[3]
-
E. R. Berlekamp. Factoring polynomials over large
finite fields. Math. Comp., 24:713–735, 1970.
-
[4]
-
D. Bini and V. Y. Pan. Polynomial and matrix
computations. Vol. 1. Fundamental algorithms. Progress in
Theoretical Computer Science. Birkhäuser, 1994.
-
[5]
-
L. I. Bluestein. A linear filtering approach to the
computation of discrete Fourier transform. IEEE
Transactions on Audio and Electroacoustics,
18(4):451–455, 1970.
-
[6]
-
A. Bostan and É. Schost. Polynomial
evaluation and interpolation on special sets of points. J.
Complexity, 21(4):420–446, 2005.
-
[7]
-
D. G. Cantor and E. Kaltofen. On fast
multiplication of polynomials over arbitrary algebras. Acta
Infor., 28(7):693–701, 1991.
-
[8]
-
D. G. Cantor and H. Zassenhaus. A new algorithm for
factoring polynomials over finite fields. Math. Comp.,
36(154):587–592, 1981.
-
[9]
-
Ph. Flajolet and J.-M. Steyaert. A branching
process arising in dynamic hashing, trie searching and
polynomial factorization. In M. Nielsen and E. M. Schmidt,
editors, Automata, Languages and Programming. Proceedings
of the 9th ICALP Symposium, volume 140 of Lecture Notes
in Comput. Sci., pages 239–251. Springer Berlin
Heidelberg, 1982.
-
[10]
-
J. von zur Gathen. Factoring polynomials and
primitive elements for special primes. Theoret. Comput.
Sci., 52(1-2):77–89, 1987.
-
[11]
-
J. von zur Gathen and J. Gerhard. Modern
computer algebra. Cambridge University Press, 2nd edition,
2003.
-
[12]
-
GCC, the GNU Compiler Collection. Software
available at http://gcc.gnu.org, from
1987.
-
[13]
-
T. Granlund et al. GMP, the GNU multiple precision
arithmetic library, from 1991. Software available at http://gmplib.org.
-
[14]
-
B. Grenet, J. van der Hoeven, and G. Lecerf.
Deterministic root finding over finite fields using Graeffe
transforms. Technical report, École polytechnique,
2015.
-
[15]
-
W. Hart, F. Johansson, and S. Pancratz. FLINT: Fast
Library for Number Theory, 2014. Version 2.4.4, http://flintlib.org.
-
[16]
-
D. Harvey, J. van der Hoeven, and G. Lecerf. Even
faster integer multiplication. http://arxiv.org/abs/1407.3360,
2014.
-
[17]
-
D. Harvey, J. van der Hoeven, and G. Lecerf. Faster
polynomial multiplication over finite fields. http://arxiv.org/abs/1407.3361,
2014.
-
[18]
-
J. van der Hoeven et al. Mathemagix, from 2002. http://www.mathemagix.org.
-
[19]
-
J. van der Hoeven and G. Lecerf. Sparse polynomial
interpolation in practice. ACM Commun. Comput. Algebra,
48(4), 2014. In section "ISSAC 2014 Software
Presentations".
-
[20]
-
E. Kaltofen and V. Shoup. Subquadratic-time
factoring of polynomials over finite fields. Math.
Comp., 67(223):1179–1197, 1998.
-
[21]
-
K. S. Kedlaya and C. Umans. Fast modular
composition in any characteristic. In A. Z. Broder et al.,
editors, 49th Annual IEEE Symposium on Foundations of
Computer Science 2008 (FOCS '08), pages 146–155.
IEEE, 2008.
-
[22]
-
L. Kronecker. Grundzüge einer arithmetischen
Theorie der algebraischen Grössen. J. reine angew.
Math., 92:1–122, 1882.
-
[23]
-
G. Malajovich and J. P. Zubelli. Tangent Graeffe
iteration. Numer. Math., 89(4):749–782, 2001.
-
[24]
-
M. Mignotte and C. Schnorr. Calcul
déterministe des racines d'un polynôme dans un
corps fini. C. R. Acad. Sci. Paris Sér. I Math.,
306(12):467–472, 1988.
-
[25]
-
R. T. Moenck. On the efficiency of algorithms for
polynomial factoring. Math. Comp., 31:235–250,
1977.
-
[26]
-
G. L. Mullen and D. Panario. Handbook of Finite
Fields. Discrete Mathematics and Its Applications. Chapman
and Hall/CRC, 2013.
-
[27]
-
V. Pan. Solving a polynomial equation: Some history
and recent progress. SIAM Rev., 39(2):187–220,
1997.
-
[28]
-
C. H. Papadimitriou. Computational
Complexity. Addison-Wesley, 1994.
-
[29]
-
L. Rónyai. Factoring polynomials modulo
special primes. Combinatorica, 9(2):199–206,
1989.
-
[30]
-
V. Shoup. A fast deterministic algorithm for
factoring polynomials over finite fields of small
characteristic. In S. M. Watt, editor, ISSAC '91:
Proceedings of the 1991 International Symposium on Symbolic
and Algebraic Computation, pages 14–21. ACM Press,
1991.
-
[31]
-
V. Shoup. Searching for primitive roots in finite
fields. Math. Comp., 58:369–380, 1992.
-
[32]
-
V. Shoup. NTL: A Library for doing Number
Theory, 2014. Software, version 8.0.0. http://www.shoup.net/ntl.
 whose multiplicative
group has smooth cardinality. We study the problem of computing all
roots of a polynomial that splits over
whose multiplicative
group has smooth cardinality. We study the problem of computing all
roots of a polynomial that splits over  ,
which was one of the bottlenecks for fast sparse interpolation in
practice. We revisit and slightly improve existing algorithms and then
present new randomized ones based on the Graeffe transform. We report on
our implementation in the
,
which was one of the bottlenecks for fast sparse interpolation in
practice. We revisit and slightly improve existing algorithms and then
present new randomized ones based on the Graeffe transform. We report on
our implementation in the 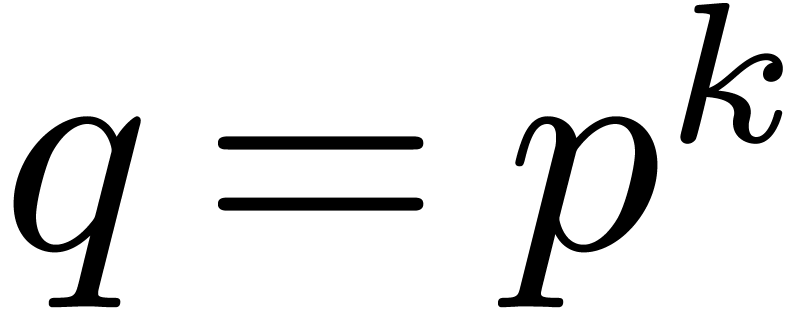 elements, where
elements, where 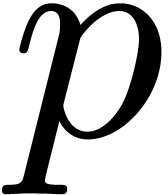 is a prime number,
and
is a prime number,
and 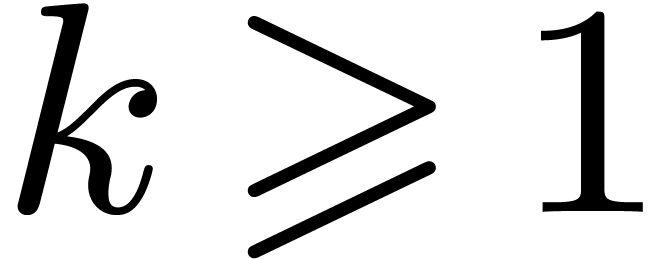 .
.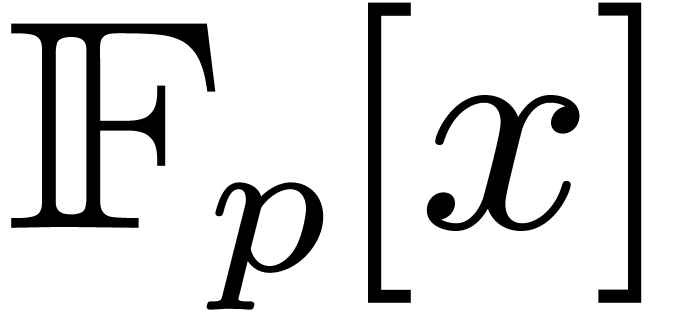 by a monic irreducible polynomial. Let
by a monic irreducible polynomial. Let 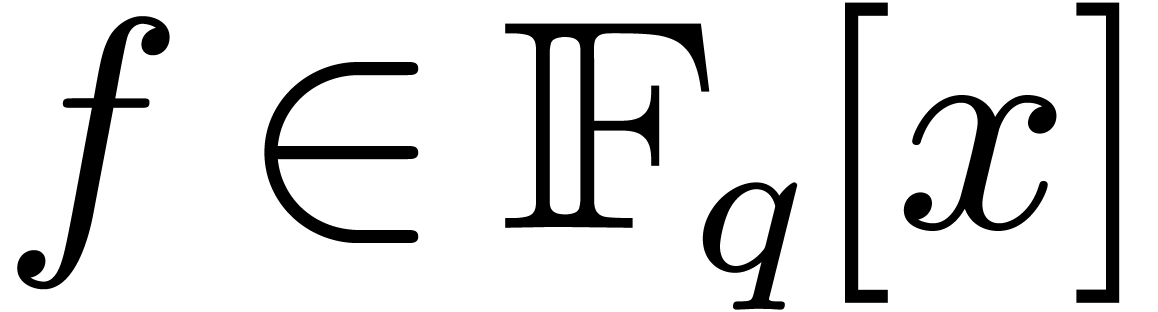 represent a separable monic polynomial of
degree
represent a separable monic polynomial of
degree 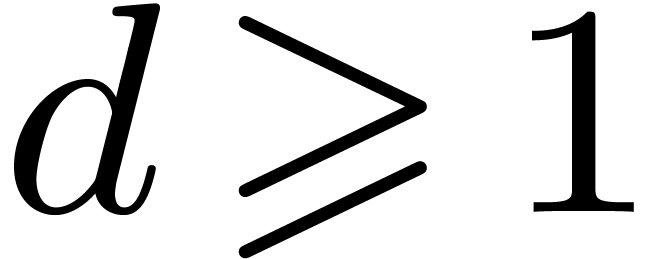 which splits over
which splits over  .
.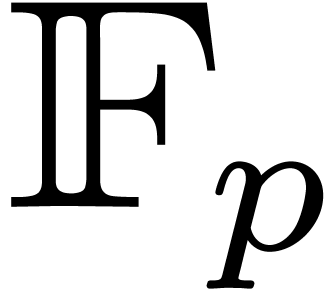 with
with 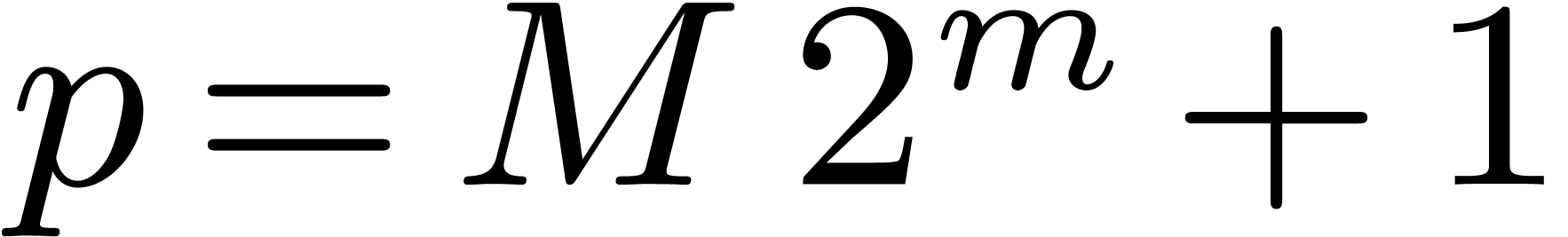 ,
,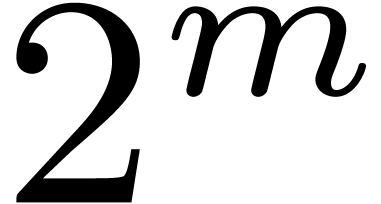 is taken to be much larger than the number of terms to be
discovered. In practice, to minimize the size of
is taken to be much larger than the number of terms to be
discovered. In practice, to minimize the size of  as small as possible. A typical example is
as small as possible. A typical example is  .
. ,
, of
of 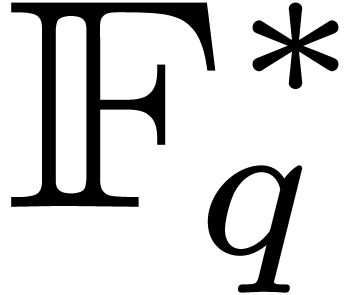 .
.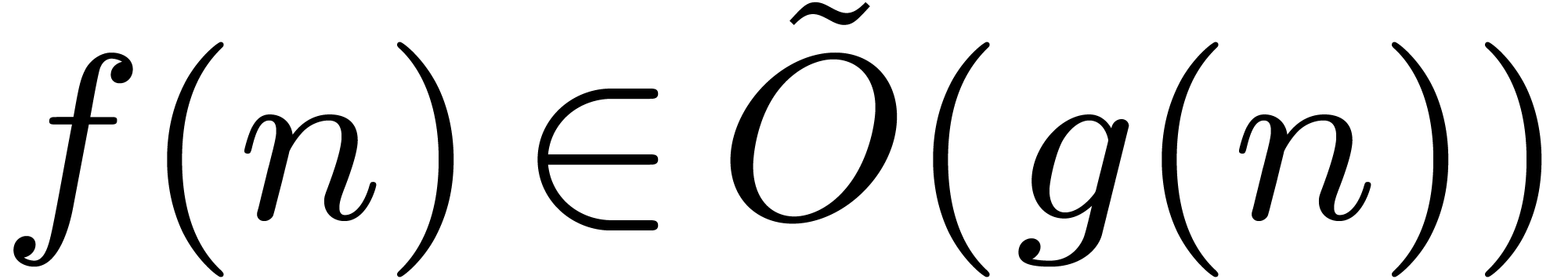 means that
means that  (we refer the reader to [
(we refer the reader to [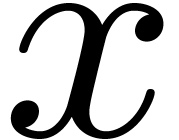 is written
is written 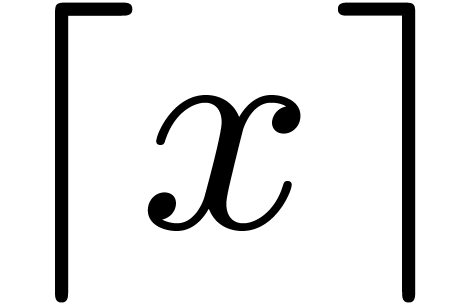 .
.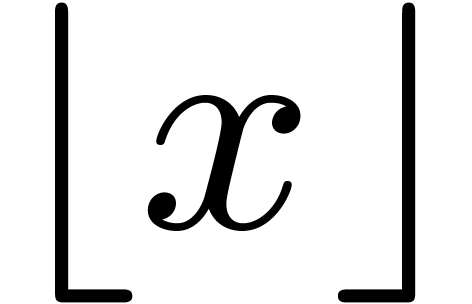 .
. in the division by
in the division by  .
.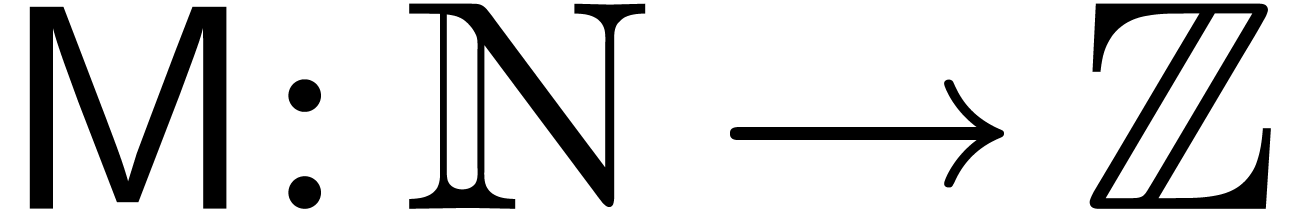 for a function that bounds the total
cost of a polynomial product algorithm in terms of the number of ring
operations performed independently of the coefficient ring, assuming a
unity is available. In other words, two polynomials of degrees at most
for a function that bounds the total
cost of a polynomial product algorithm in terms of the number of ring
operations performed independently of the coefficient ring, assuming a
unity is available. In other words, two polynomials of degrees at most
 over such a ring
over such a ring  can be
multiplied with at most
can be
multiplied with at most 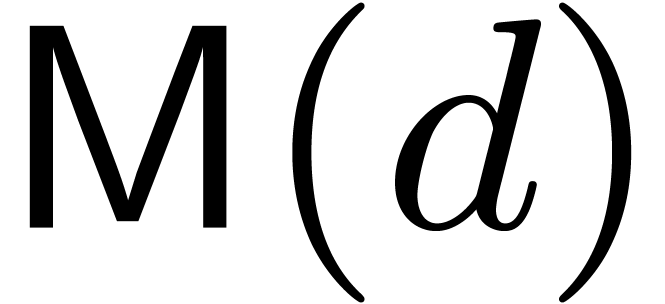 arithmetic operations in
arithmetic operations in
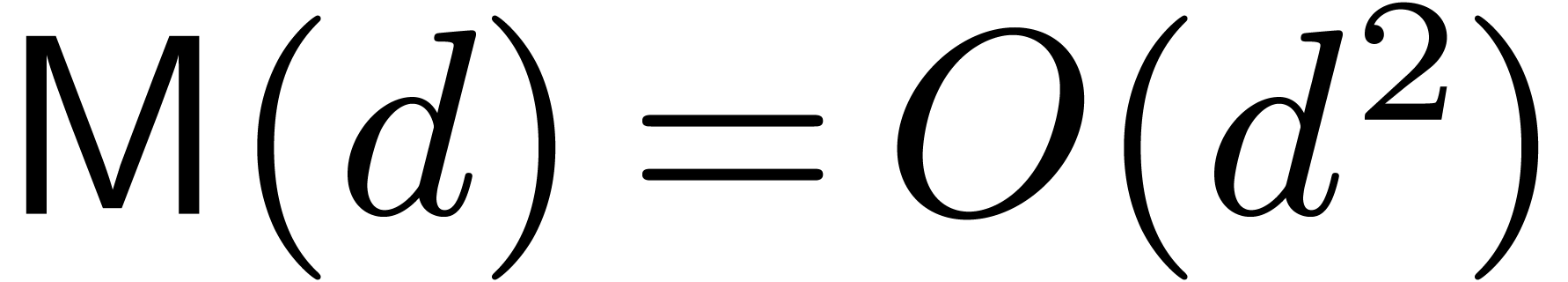 .
.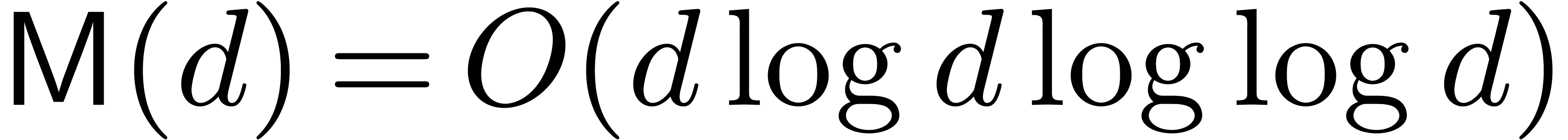 .
. for all
for all 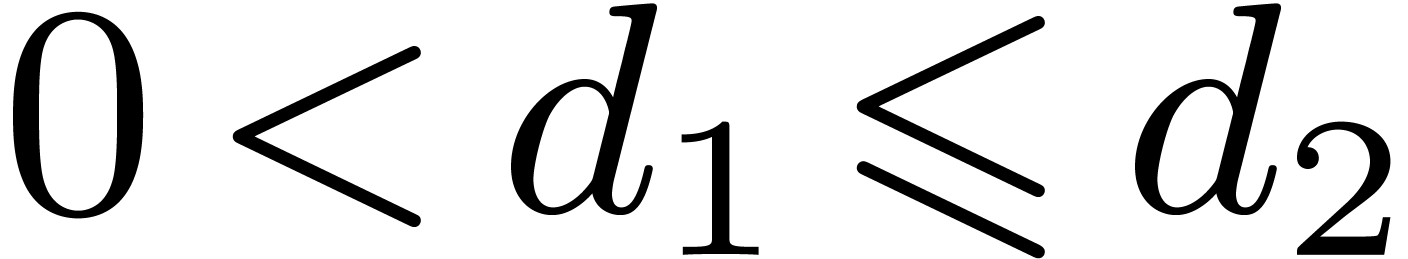 .
. ,
,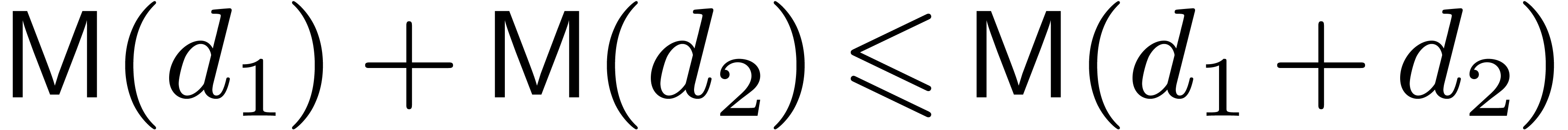 for all
for all 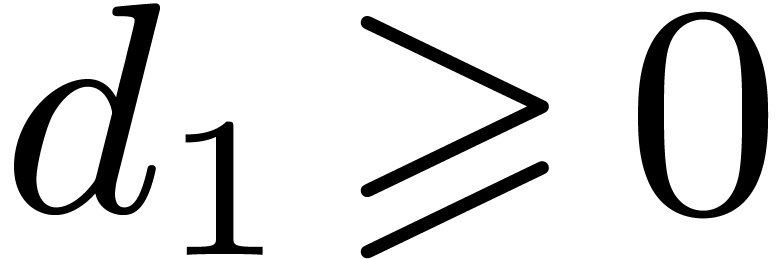 and
and  .
. and in finite fields, we are
interested in the Turing machine model, with a sufficiently
large number of tapes. In short, we use the terms bit-cost and
bit-complexity to refer to this model whenever the context is
not clear. For randomized algorithms, we endow Turing machines
with an additional instruction which generates random bits with a
uniform distribution [
and in finite fields, we are
interested in the Turing machine model, with a sufficiently
large number of tapes. In short, we use the terms bit-cost and
bit-complexity to refer to this model whenever the context is
not clear. For randomized algorithms, we endow Turing machines
with an additional instruction which generates random bits with a
uniform distribution [ for a function that bounds the bit-cost
of an algorithm which multiplies two integers of bit-sizes at most
for a function that bounds the bit-cost
of an algorithm which multiplies two integers of bit-sizes at most  ,
,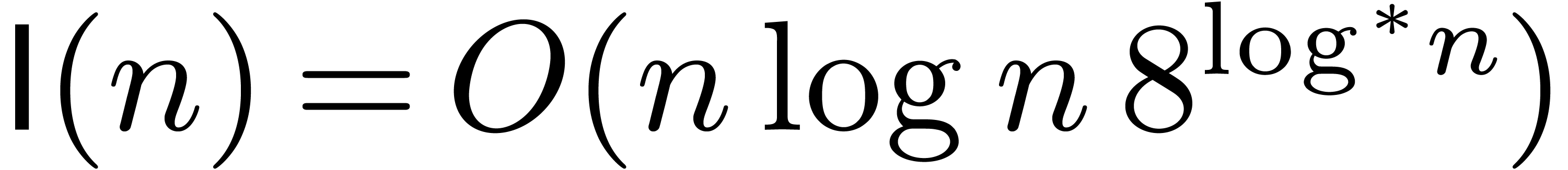 ,
, represents the iterated logarithm function
[
represents the iterated logarithm function
[ for all
for all  .
. and one division or
inversion in
and one division or
inversion in  [
[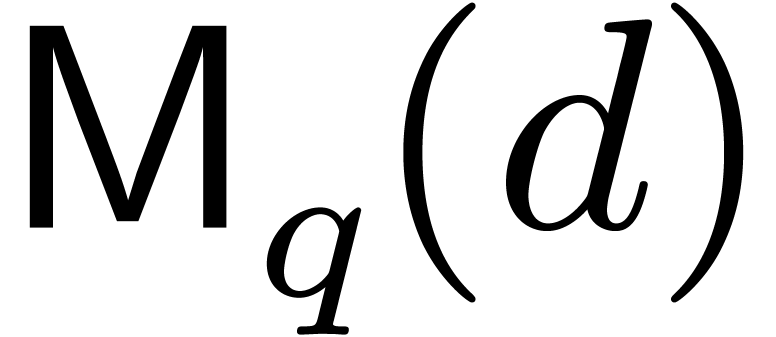 represent a function that bounds the
bit-cost of an algorithm that multiplies two polynomials of degrees at
most
represent a function that bounds the
bit-cost of an algorithm that multiplies two polynomials of degrees at
most  .
.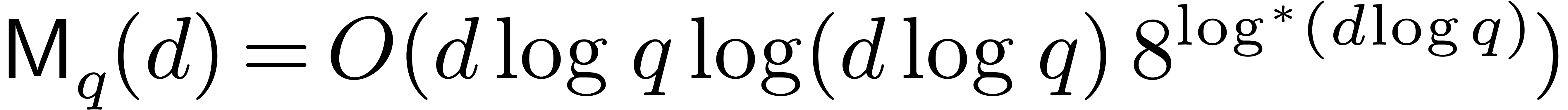 .
.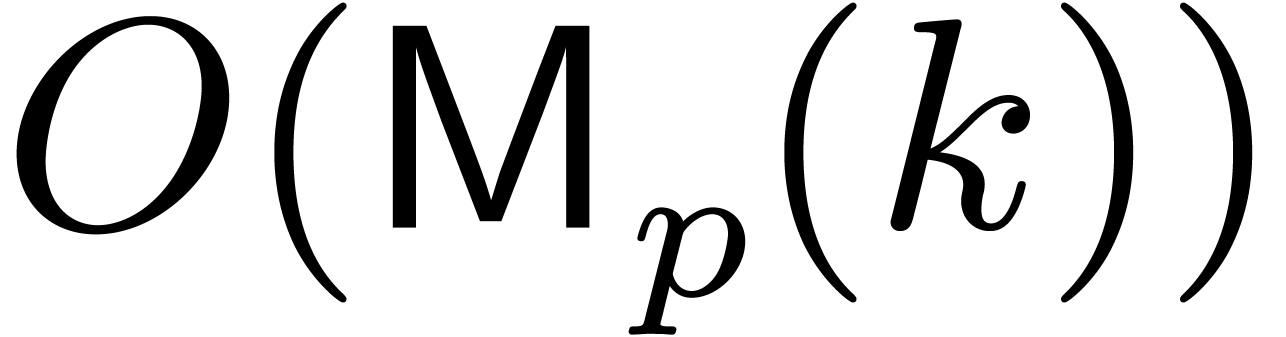 ,
,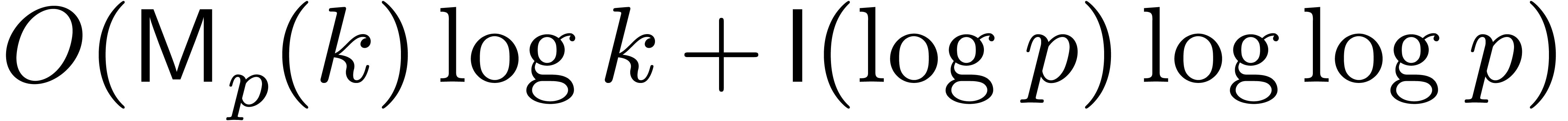 .
.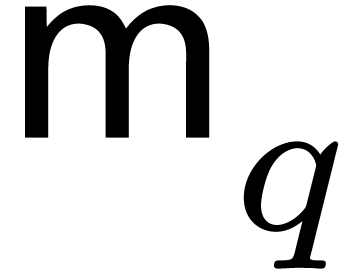 and
and 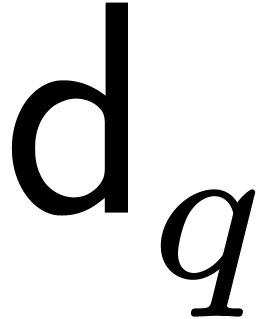 will respectively denote cost functions for the product and the inverse
in
will respectively denote cost functions for the product and the inverse
in 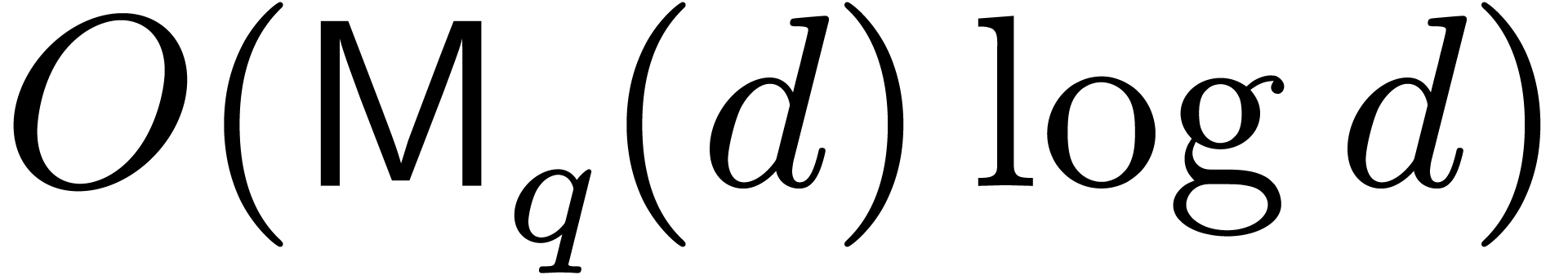 :
: with
with 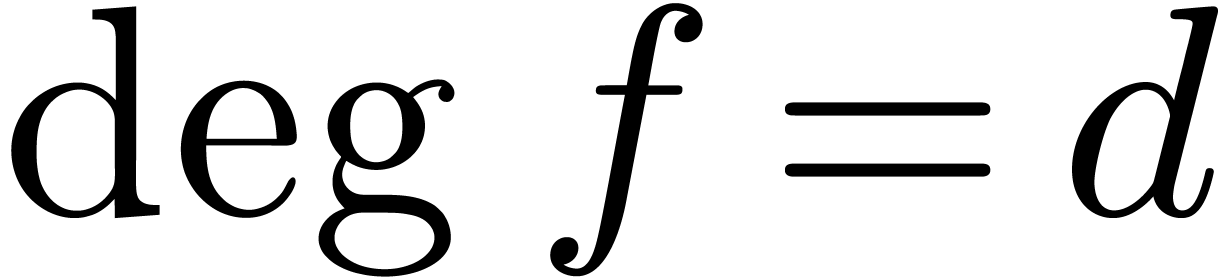 and
and 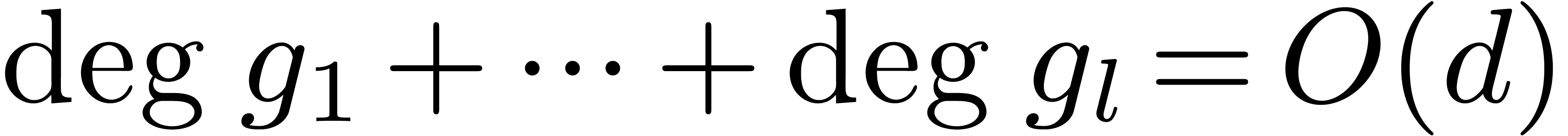 ,
,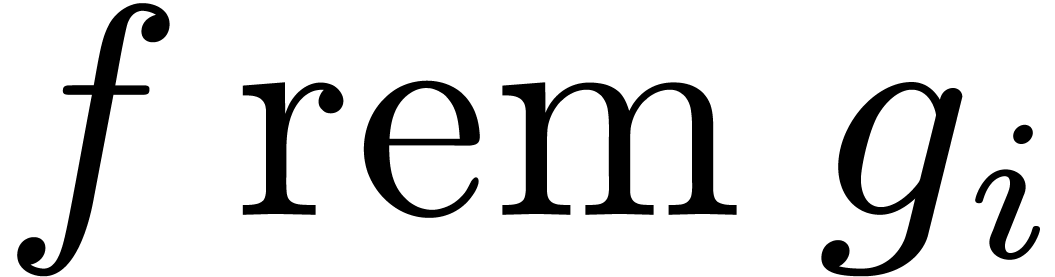 can be computed in time
can be computed in time 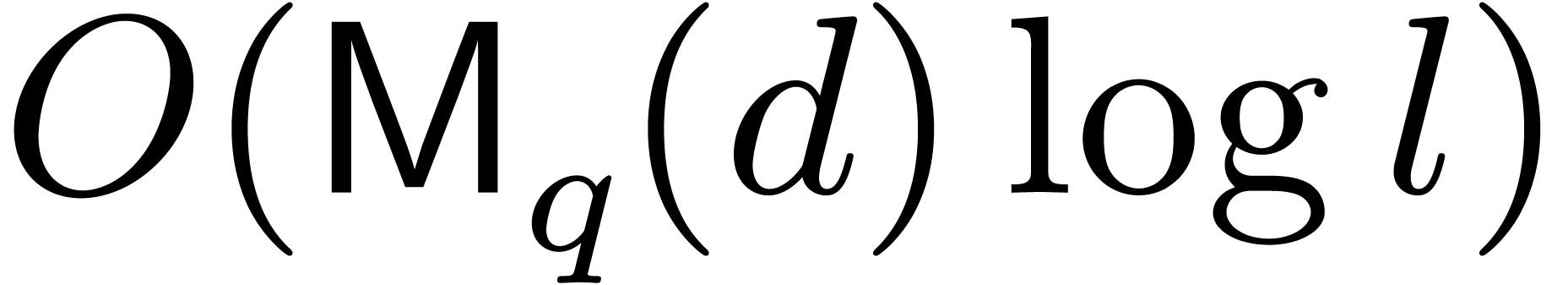 using a subproduct
tree [
using a subproduct
tree [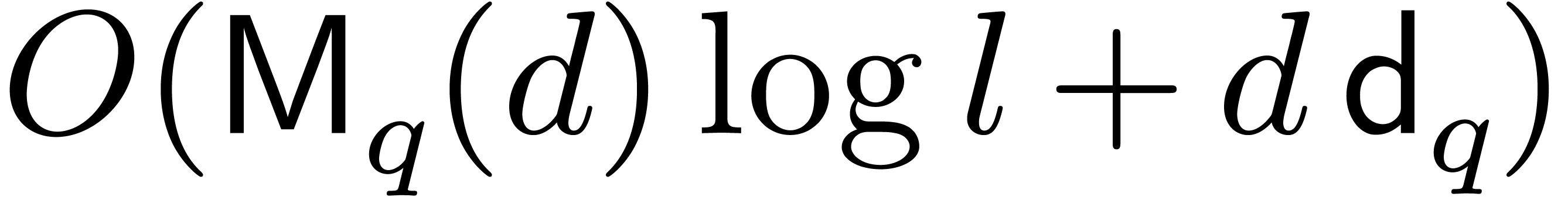 .
.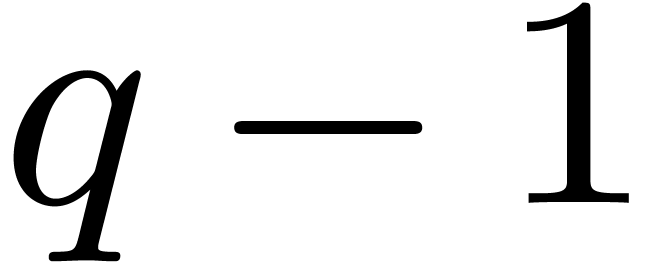 and a primitive element of
and a primitive element of 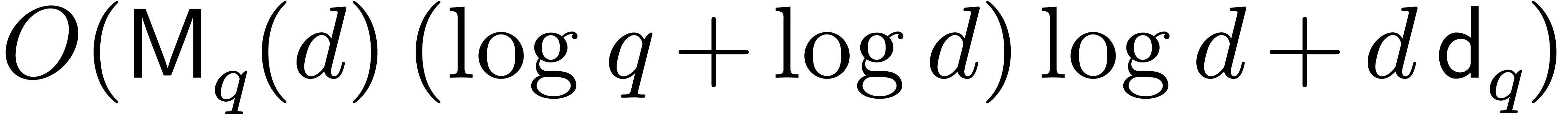 .
.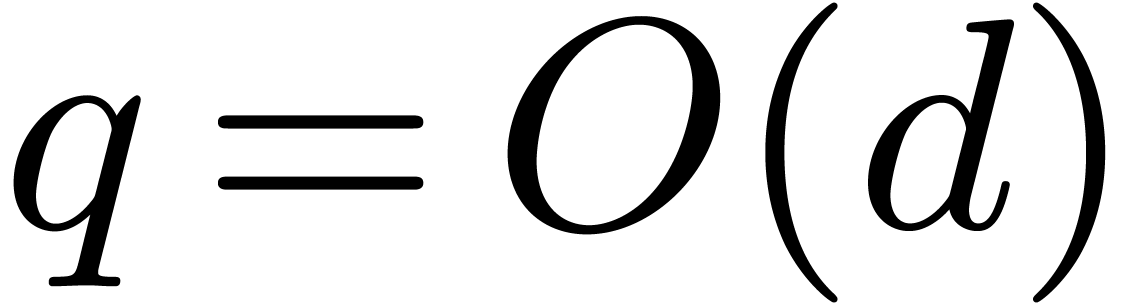 then an
exhaustive search can be naively performed in time
then an
exhaustive search can be naively performed in time  can be discarded if a primitive
element of
can be discarded if a primitive
element of  .
. has the form
has the form
 ,
, .
. ,
, of unity of order
of unity of order 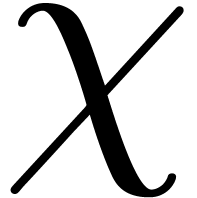 .
.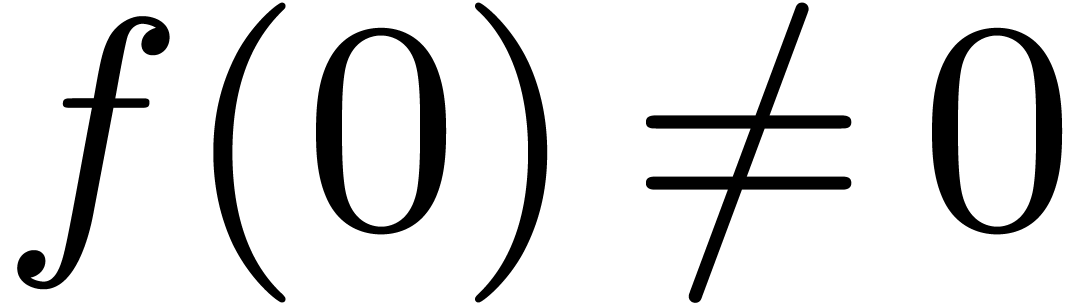 ;
; then compute the roots of
then compute the roots of  at random of degree at most
at random of degree at most  .
. ,
,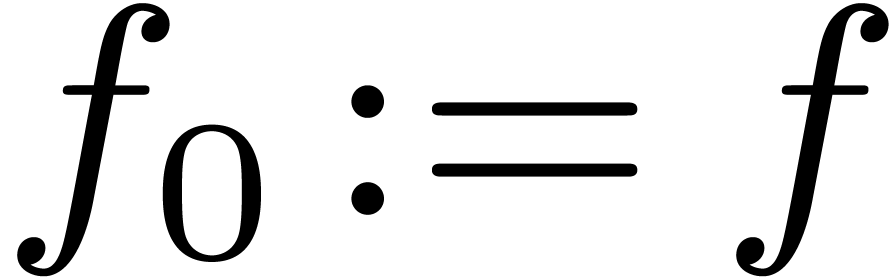 .
. from
from  to
to
 ,
,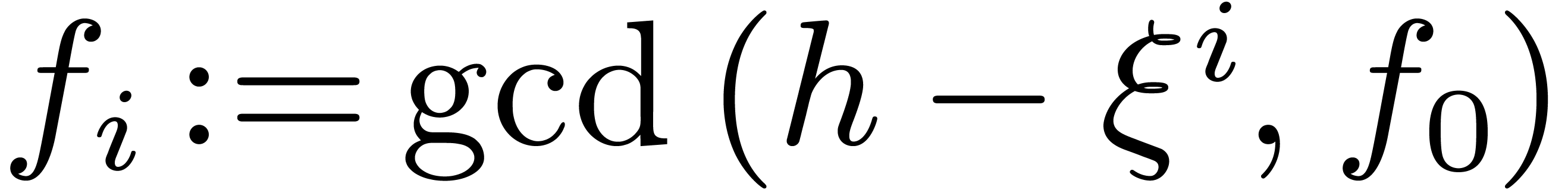 ,
,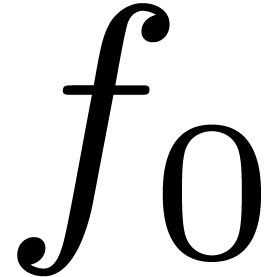 by
by 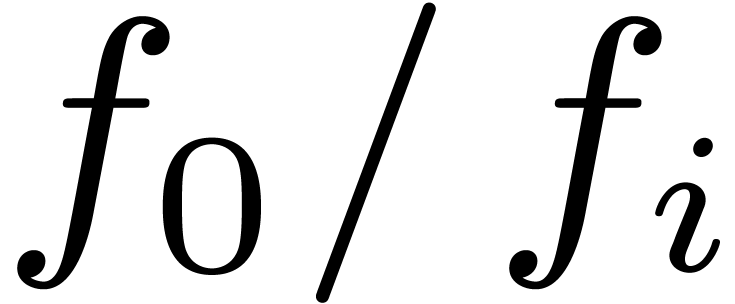 .
.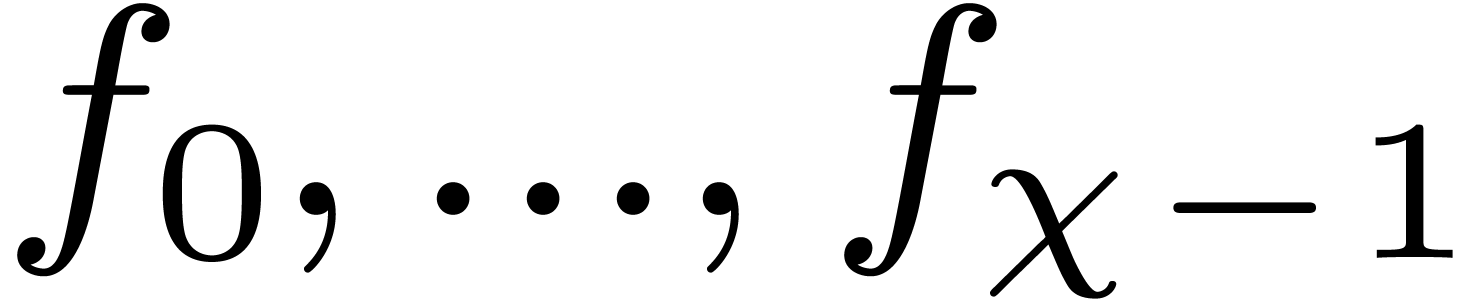 which are not constant, and return the union of the sets of their
roots.
which are not constant, and return the union of the sets of their
roots.
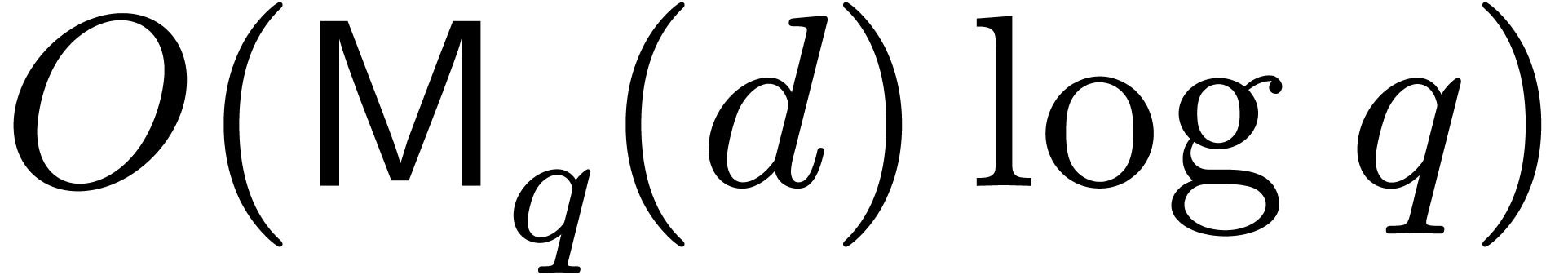 and step 4
takes
and step 4
takes 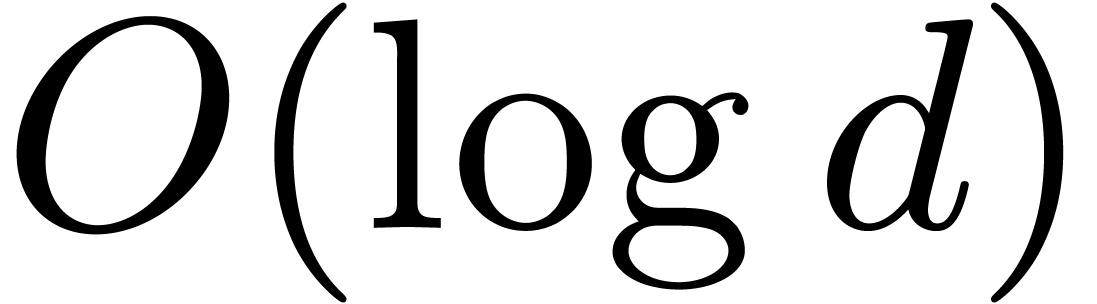 [
[ is a root of
is a root of  has order
dividing
has order
dividing  .
.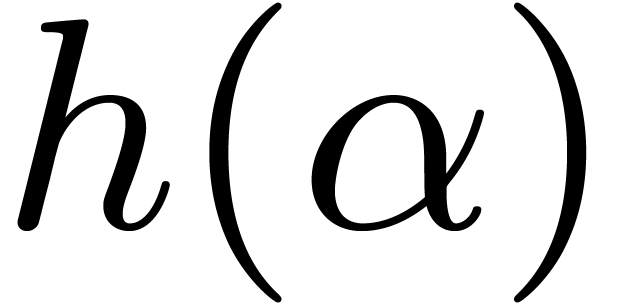 are distributed uniformly among
the powers of
are distributed uniformly among
the powers of 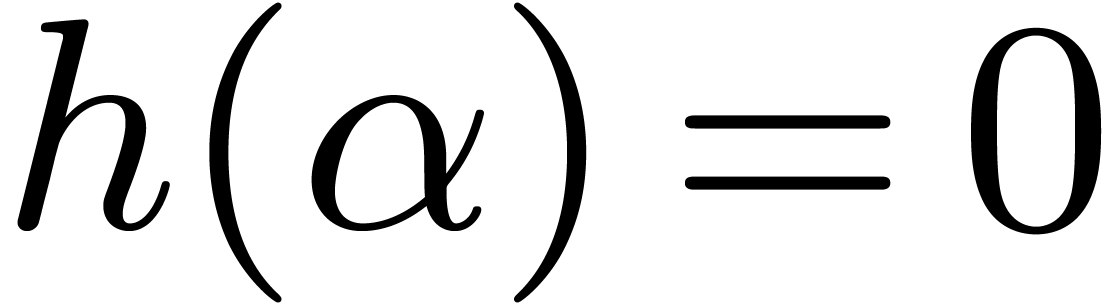 ).
).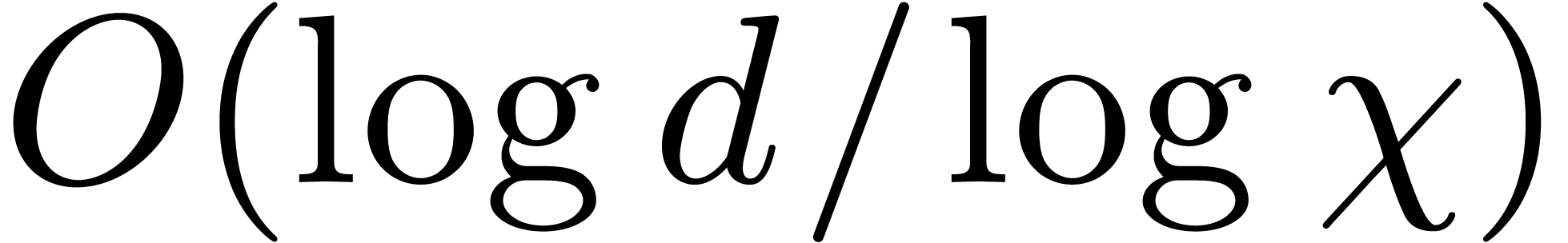 .
.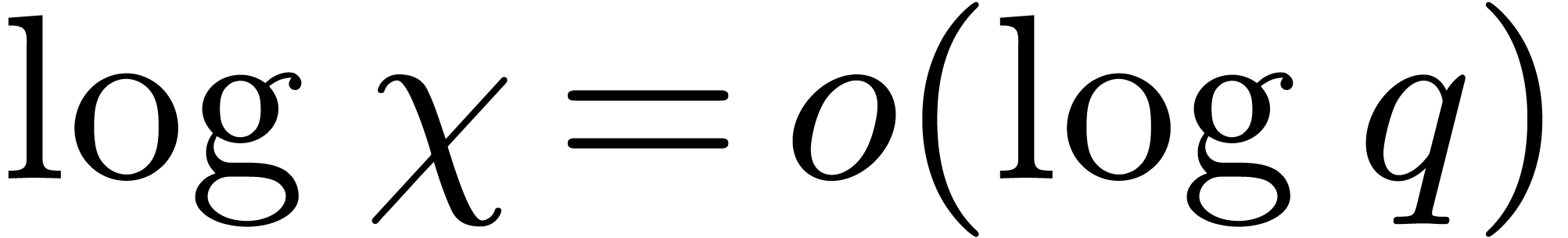 ,
,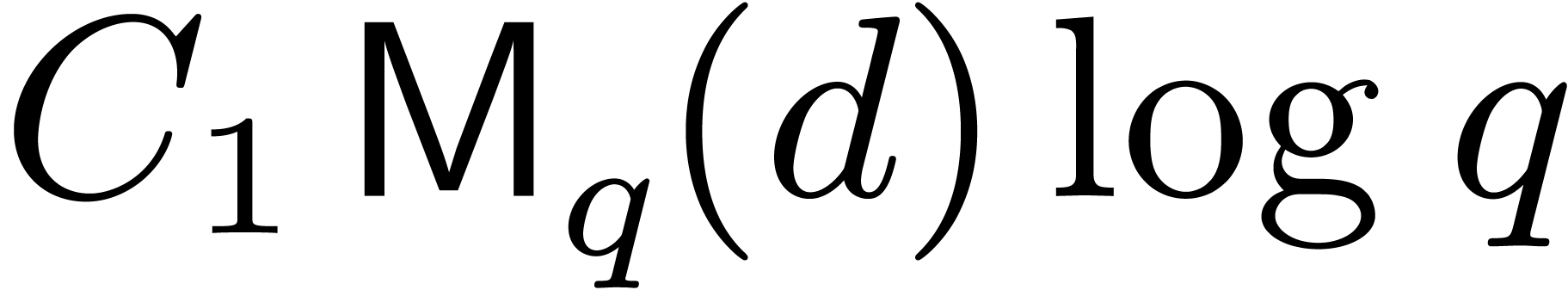 for a certain
constant
for a certain
constant 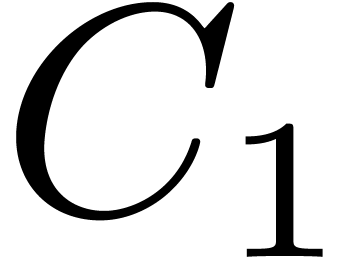 ,
,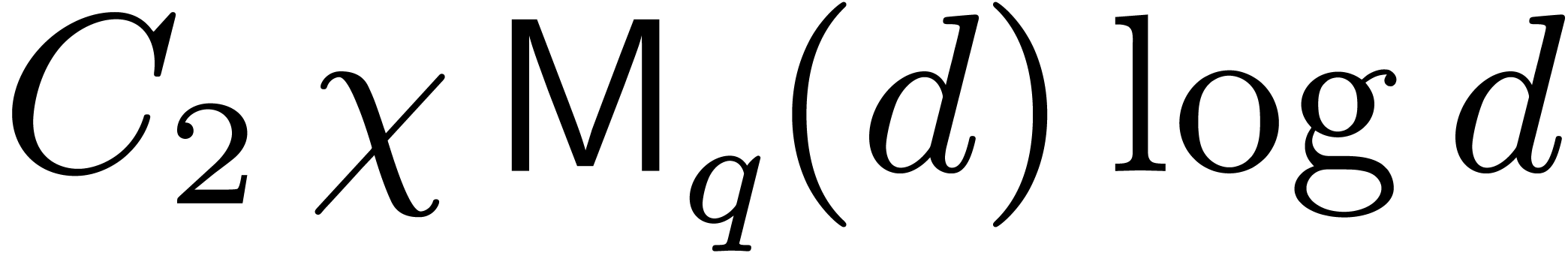 .
.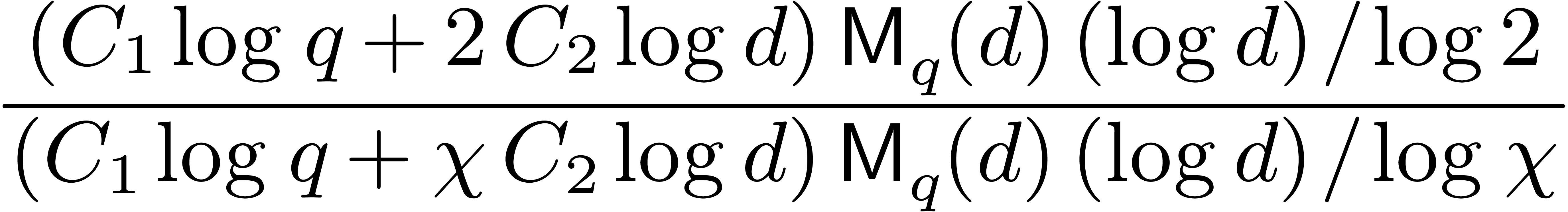
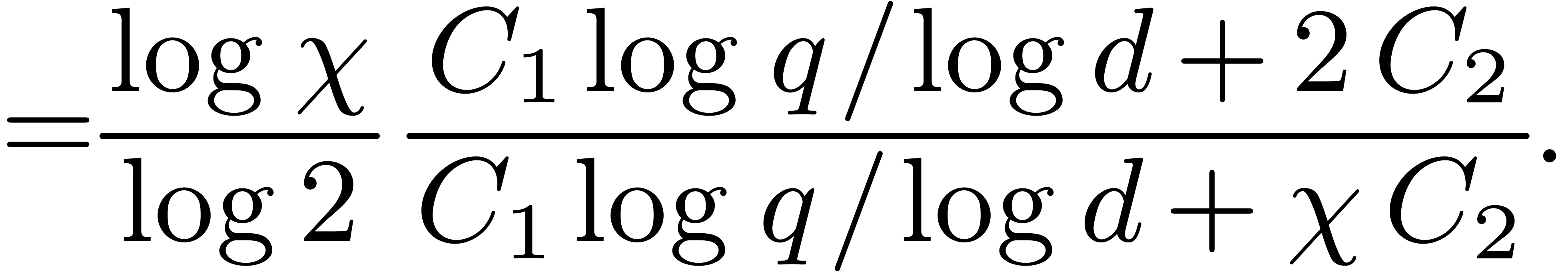
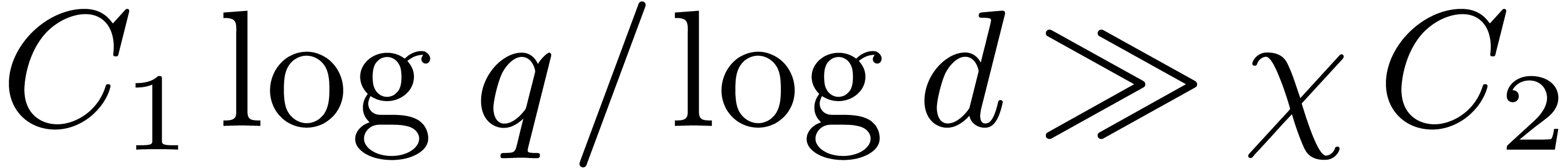 ,
, .
.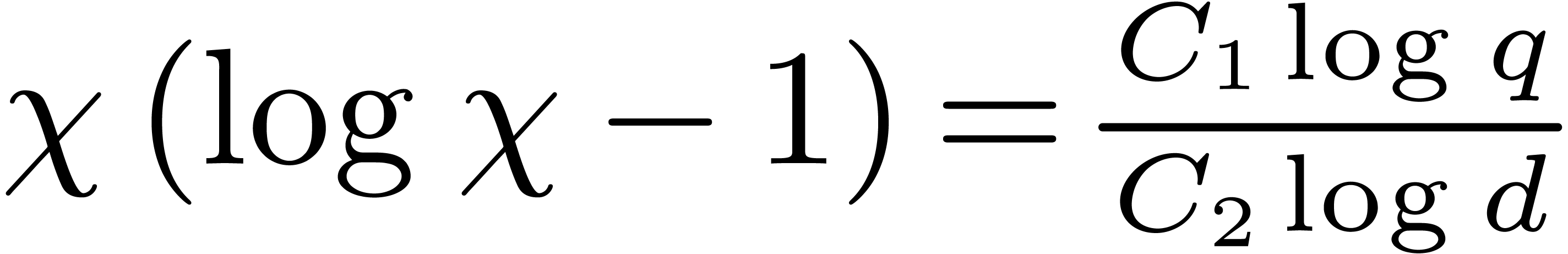 .
. be integers
be integers  ,
,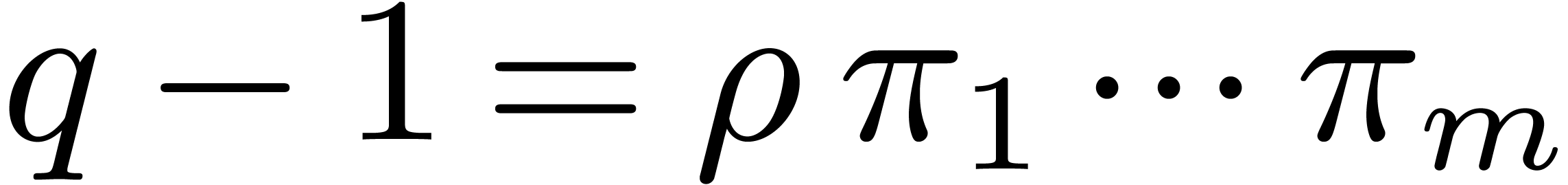 ,
,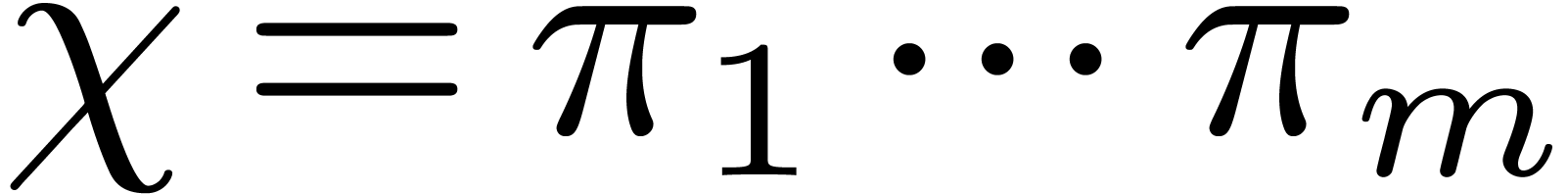 and
and 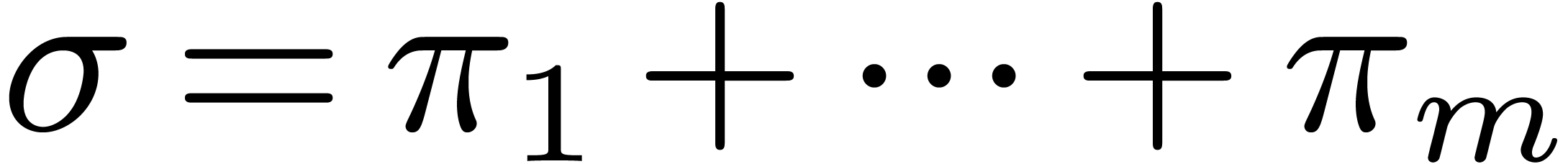 .
.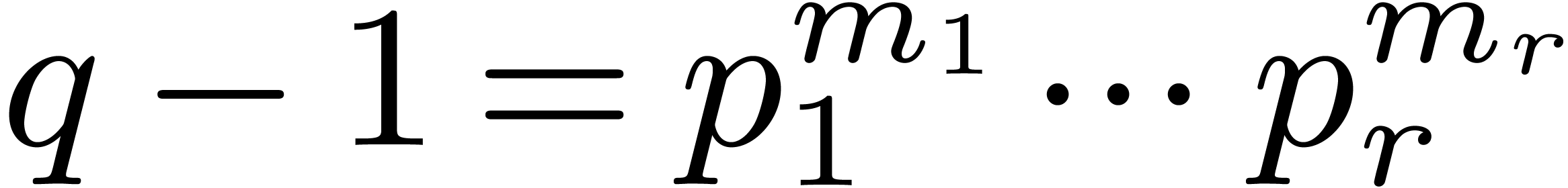 is
known, then we may take
is
known, then we may take  and
and  ,
,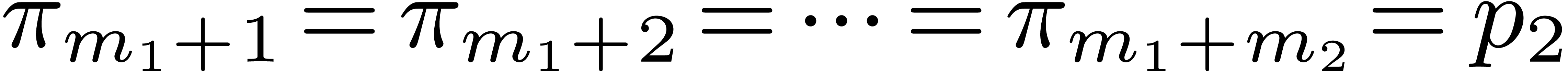 ,
, .
. ,
, in
in 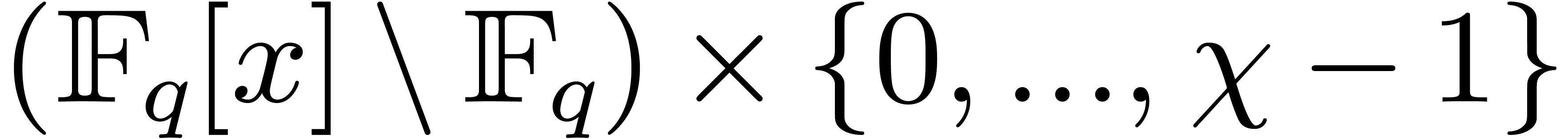 such that
such that 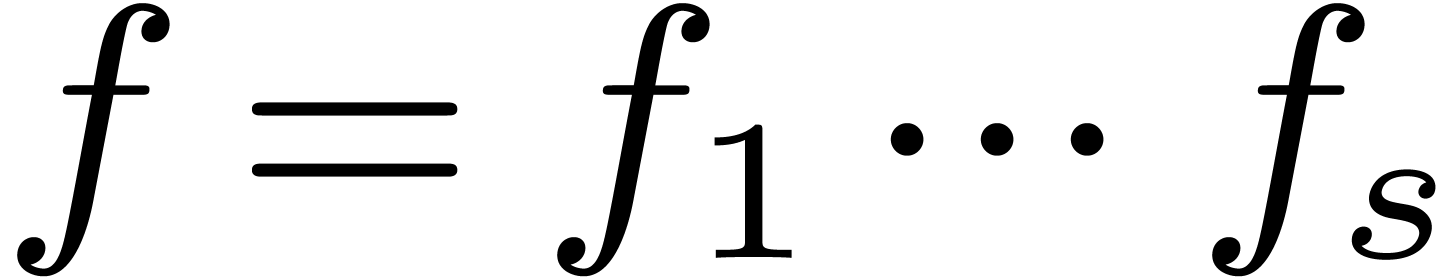 ,
, are monic, separable, and divide
are monic, separable, and divide  ,
,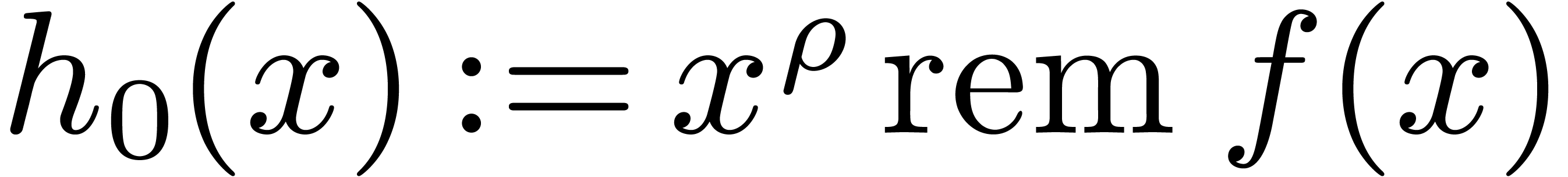 ,
,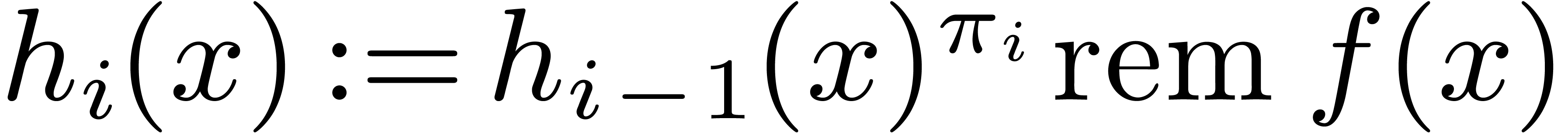 ,
,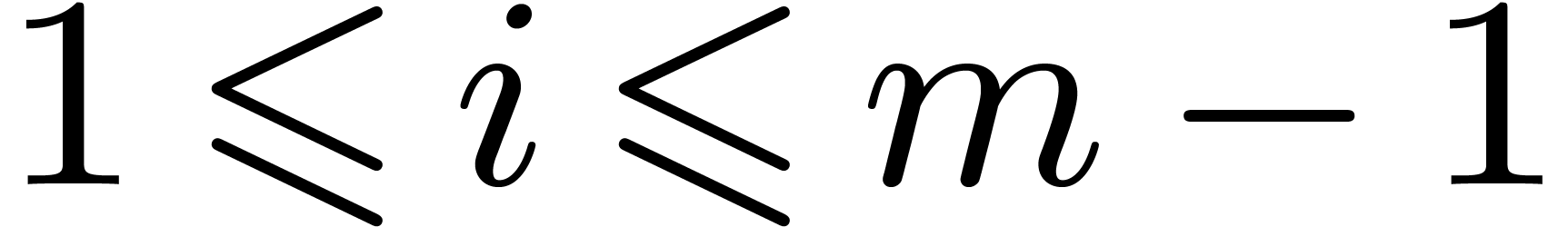 .
. with the list
with the list 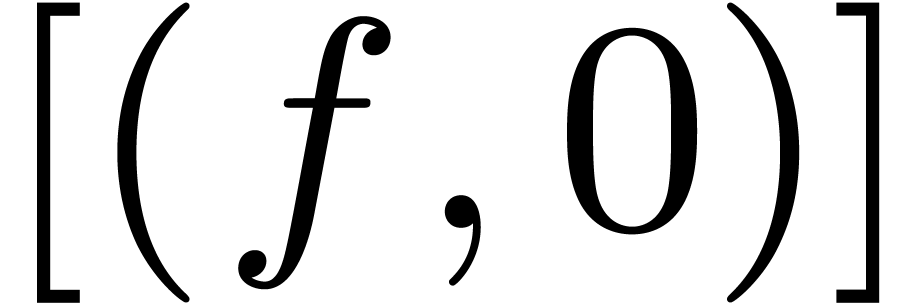 .
. down to
down to
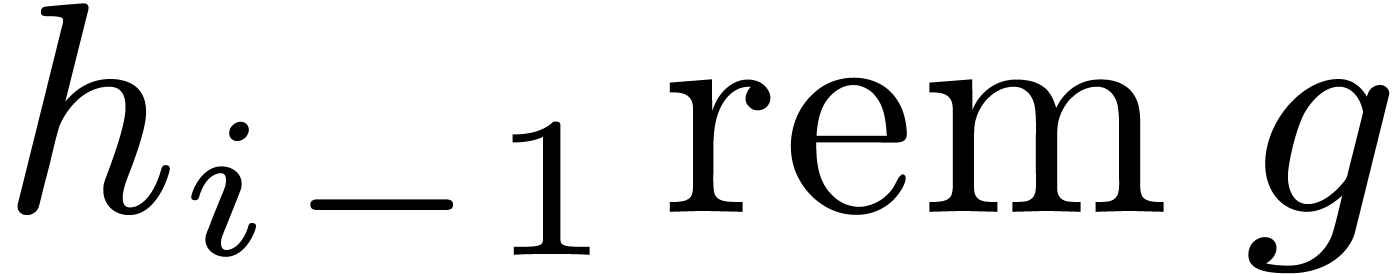 for all pairs
for all pairs 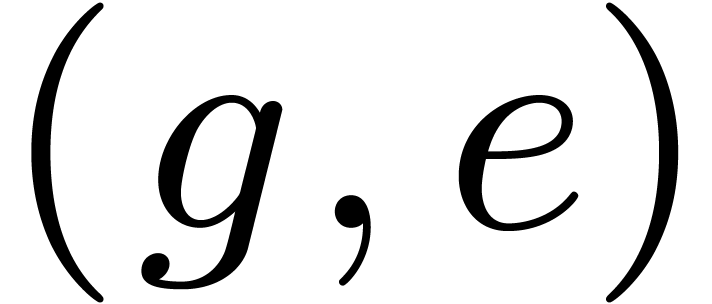 in
in  with the empty list, and for
all
with the empty list, and for
all  from
from  to
to  do
do
 in
in  do
do
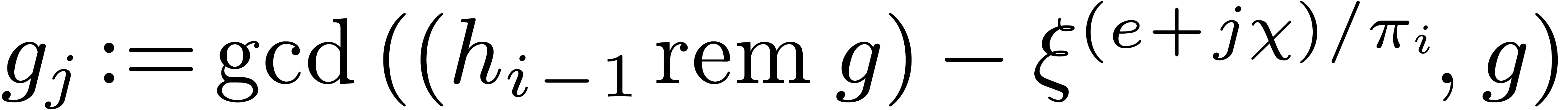 .
. is not constant, then make it monic
and append
is not constant, then make it monic
and append  to
to  .
. .
. .
. from
from  down
to
down
to  .
.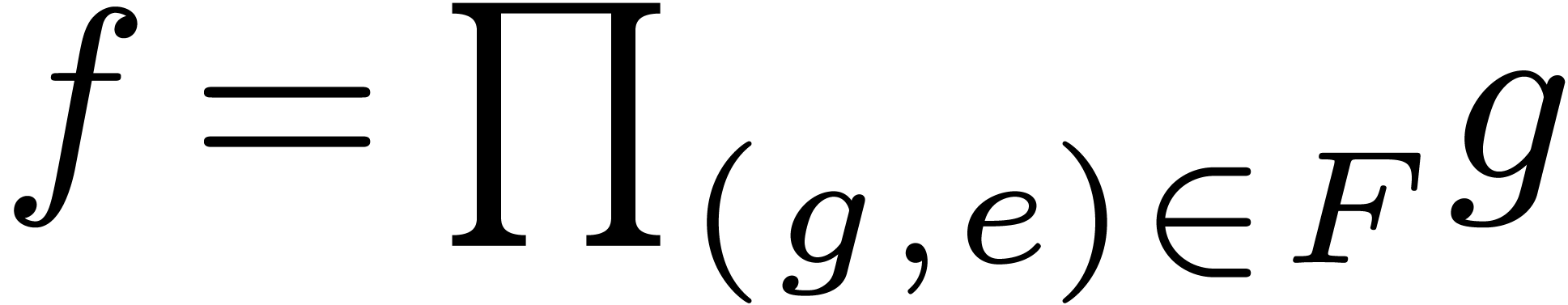 ,
, divides
divides 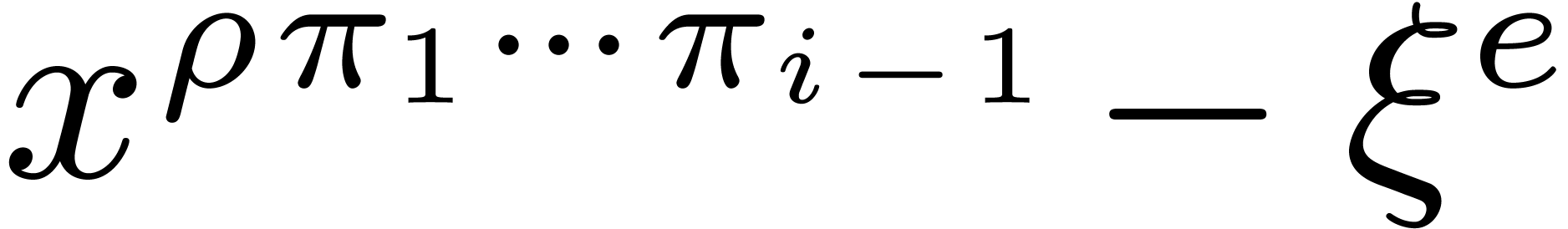 for all
for all 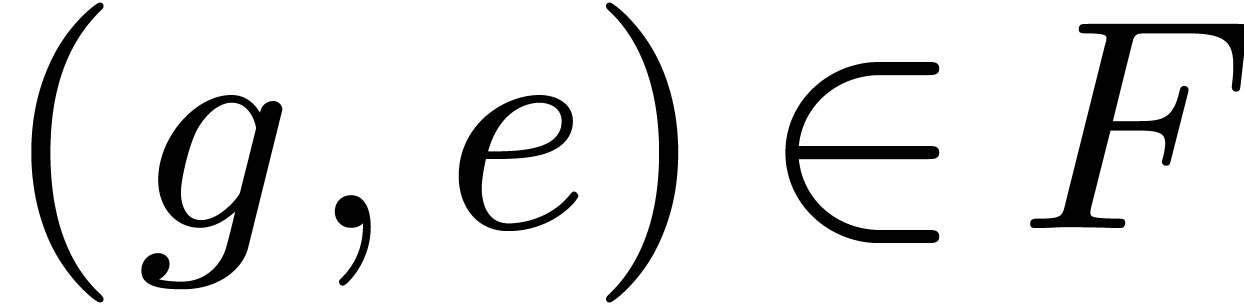 ,
, in
in 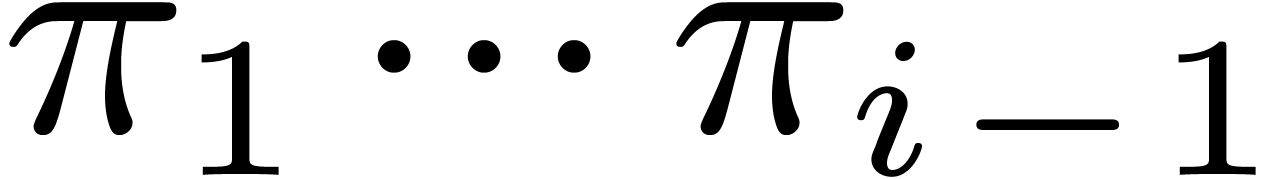 and bounded by
and bounded by 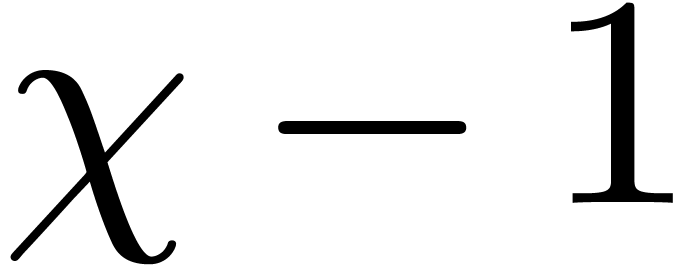 .
.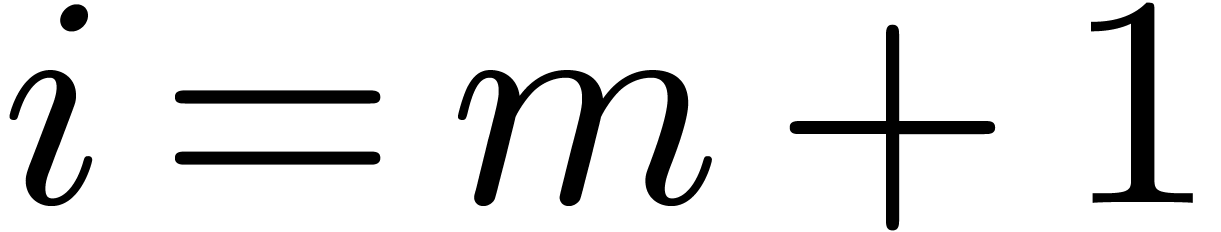 when entering step 3, so that by
induction we can assume that these properties hold for
when entering step 3, so that by
induction we can assume that these properties hold for  when entering the loop at level
when entering the loop at level  be a root of
be a root of 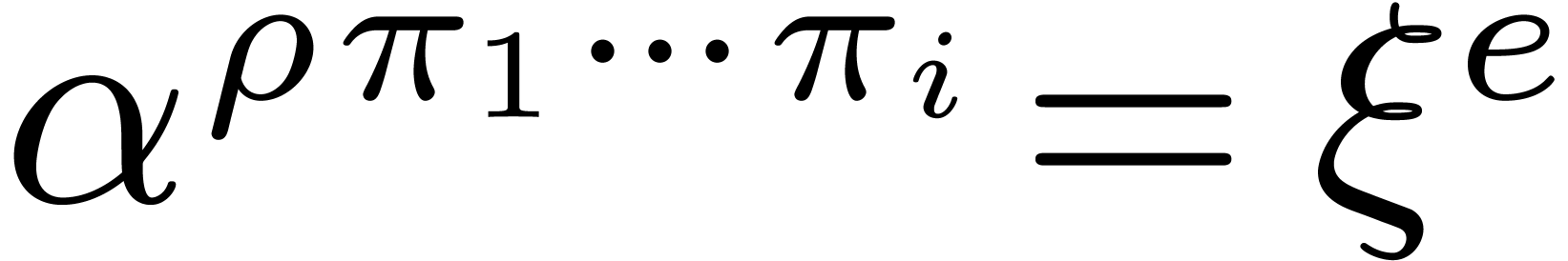 ,
, ,
, such that
such that  .
. for
for
 in time
in time 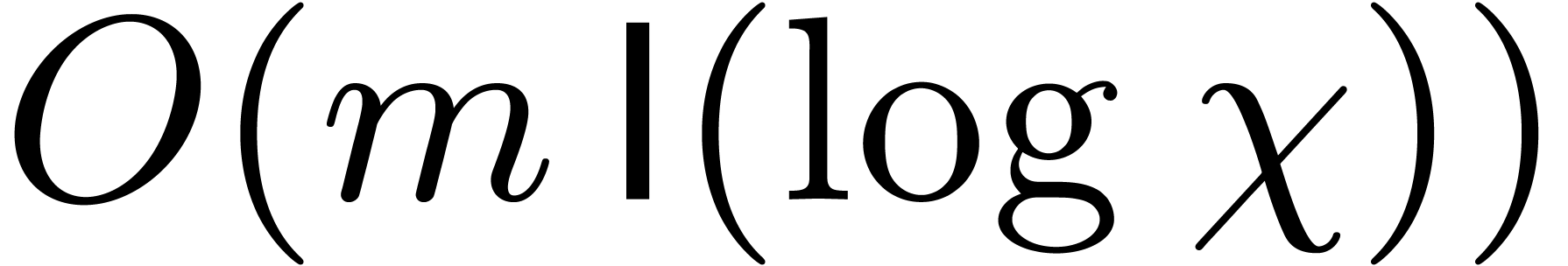 as follows: we
first compute
as follows: we
first compute  ,
, ,
, .
. ,
,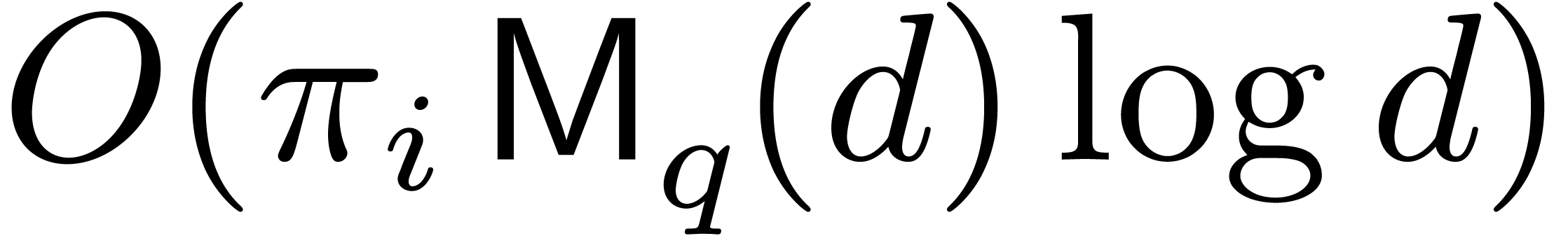 by the super-additivity of
by the super-additivity of 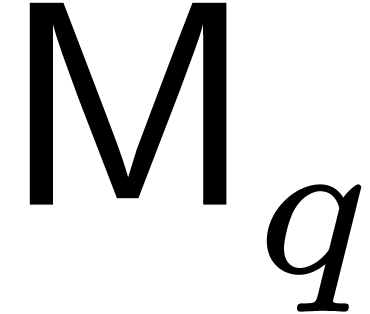 .
. in time
in time 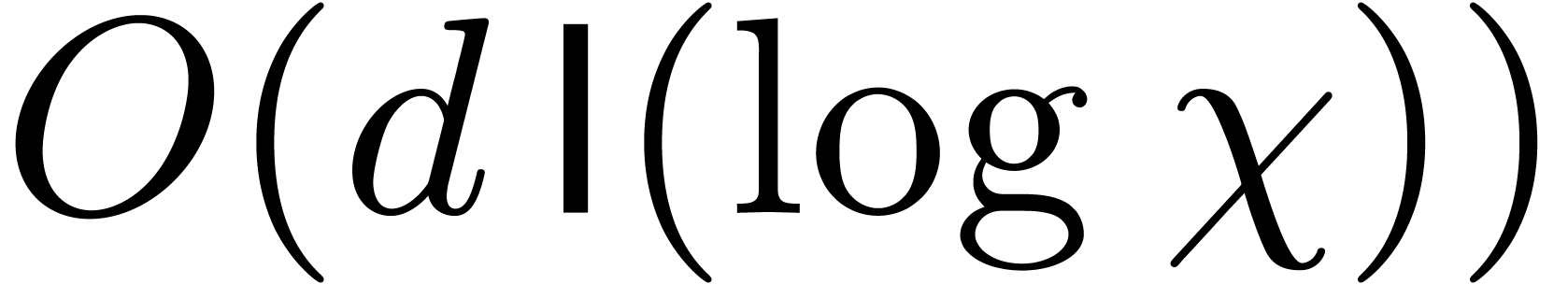 ,
,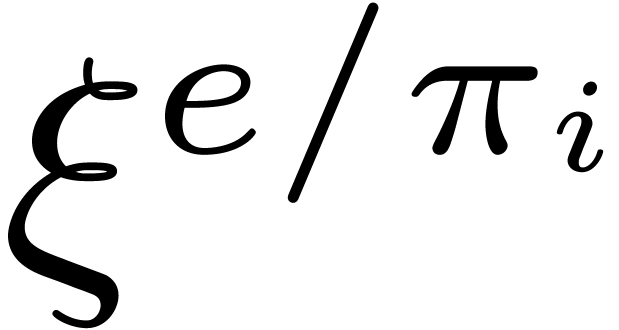 and
and 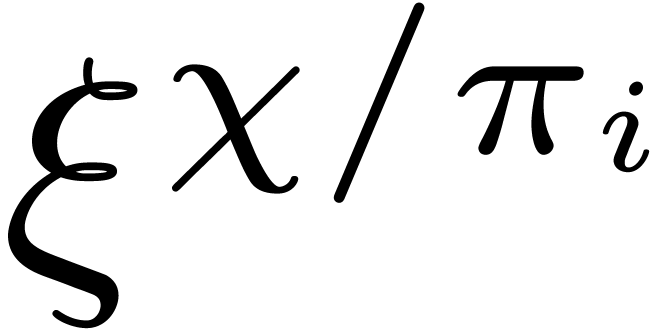 by
means of
by
means of 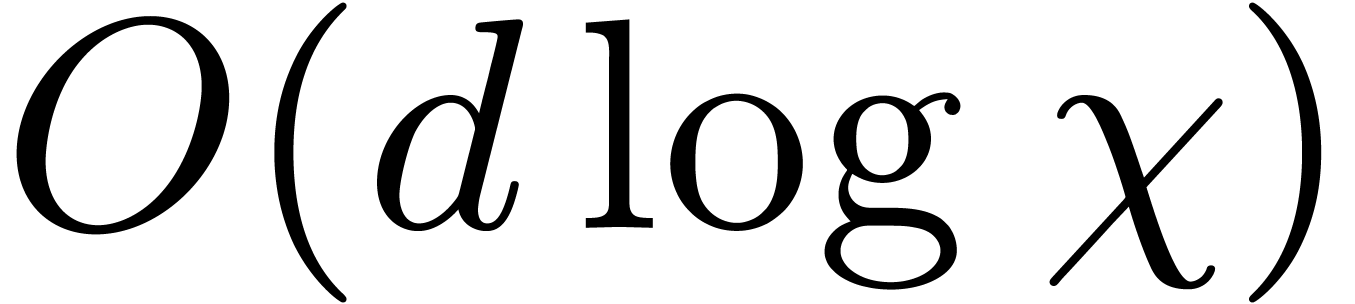 operations in
operations in 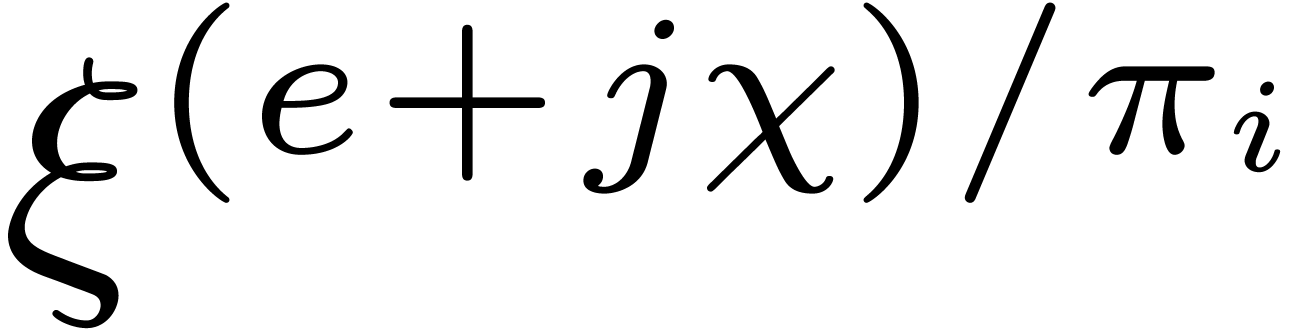 takes
takes
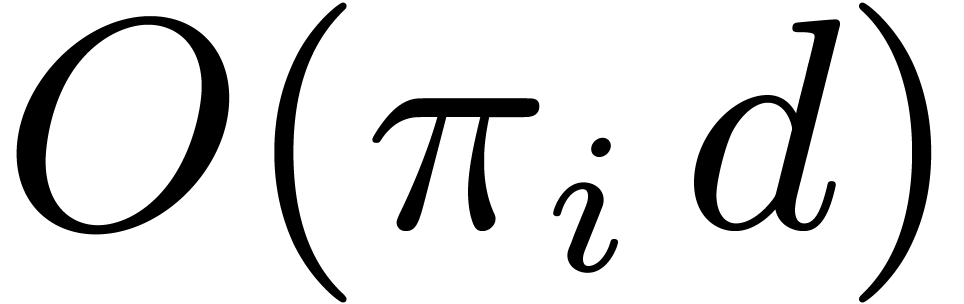 additional products in
additional products in 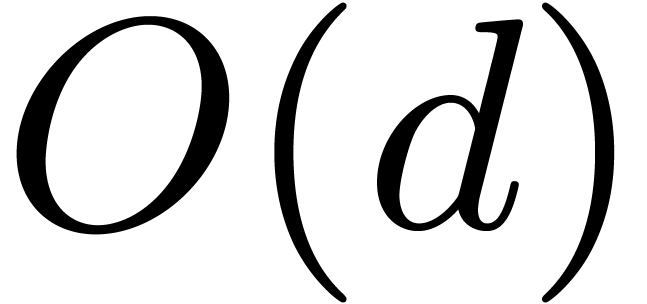 inversions in order to make all the polynomials in
inversions in order to make all the polynomials in 
 is good when
is good when  ,
,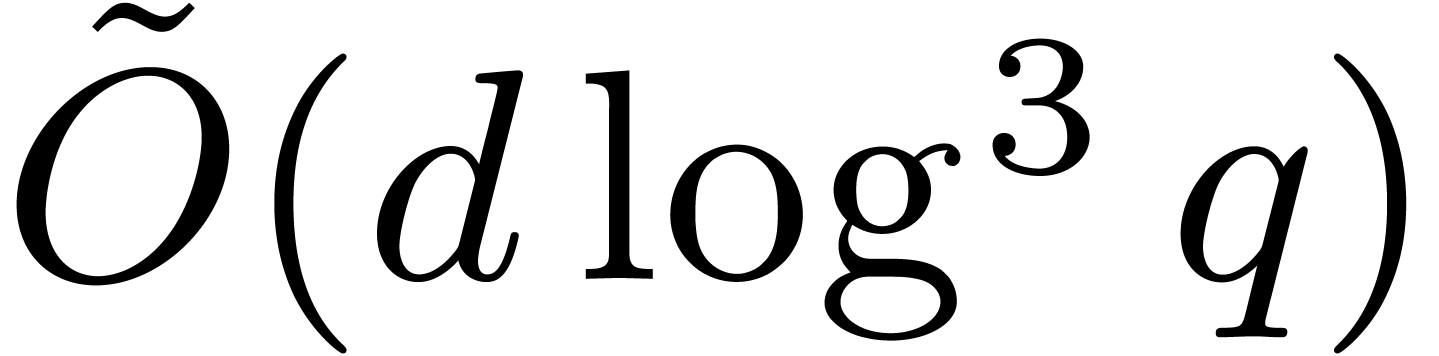 .
.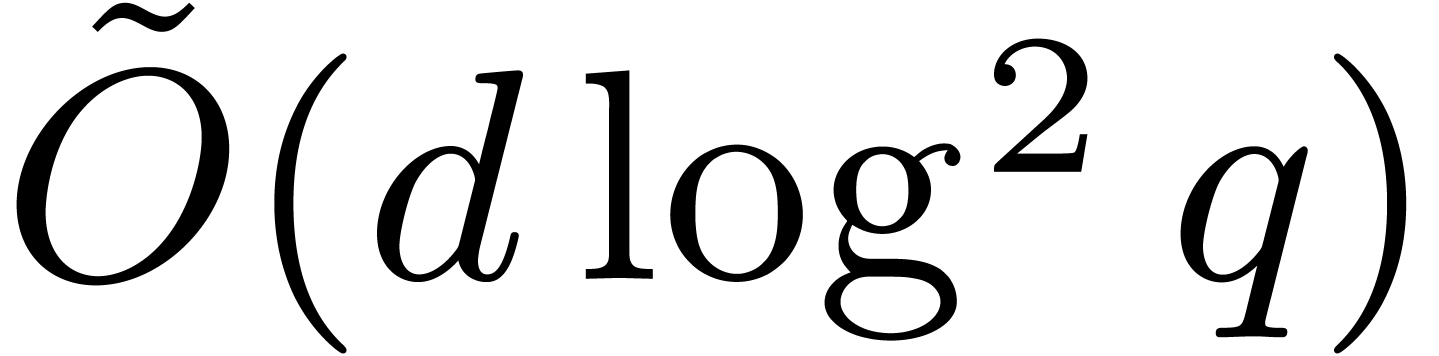 bit-cost of Cantor–Zassenhaus' algorithm.
Nevertheless since the term
bit-cost of Cantor–Zassenhaus' algorithm.
Nevertheless since the term 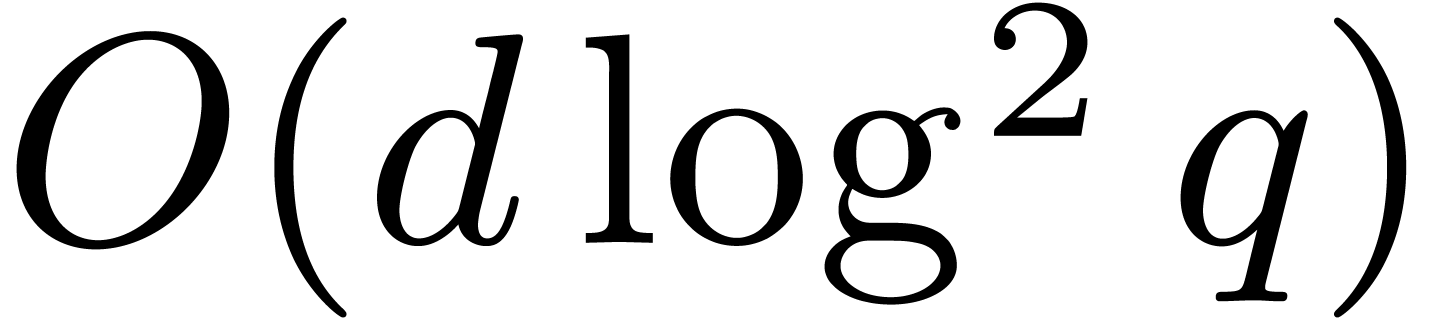 products in
products in  ,
, .
.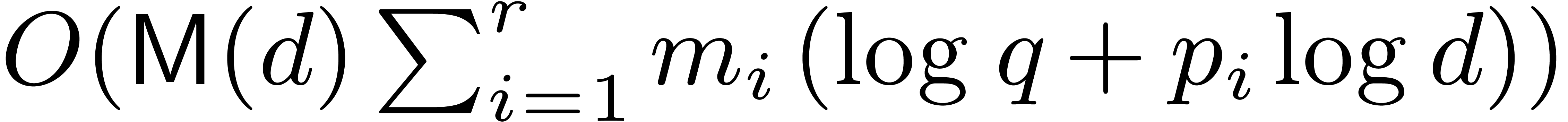 operations in
operations in
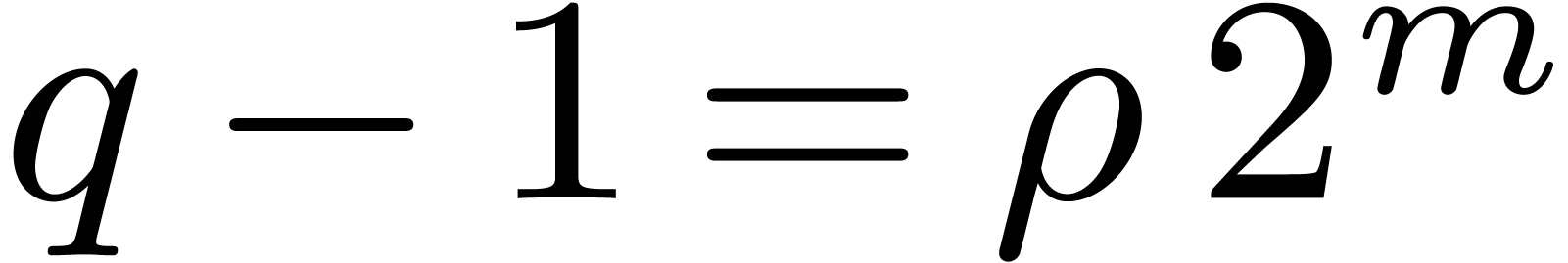 .
. be a primitive root of
be a primitive root of 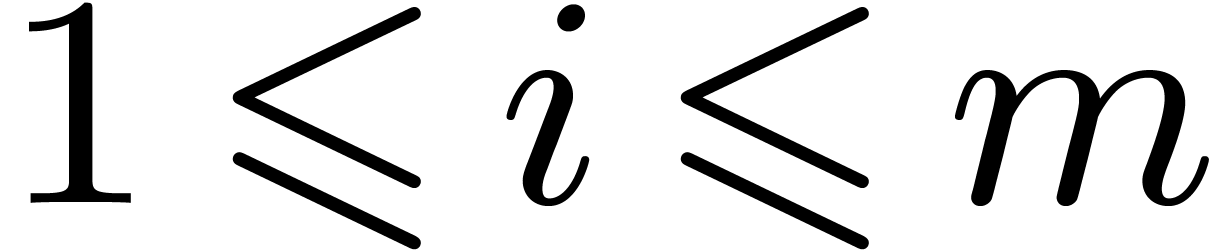 ,
,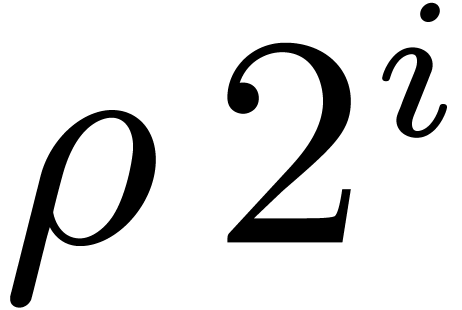 ,
,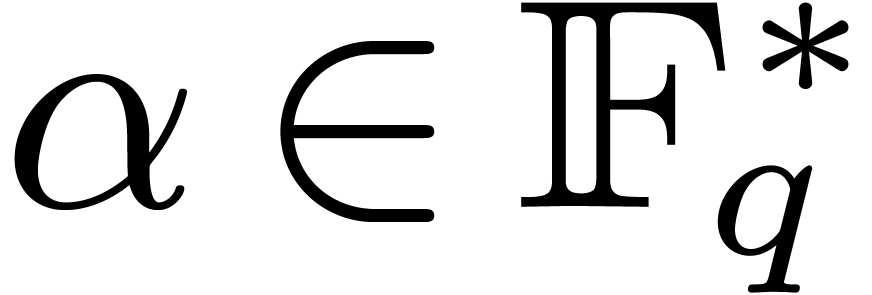 be one of these
roots. Then either this order divides
be one of these
roots. Then either this order divides 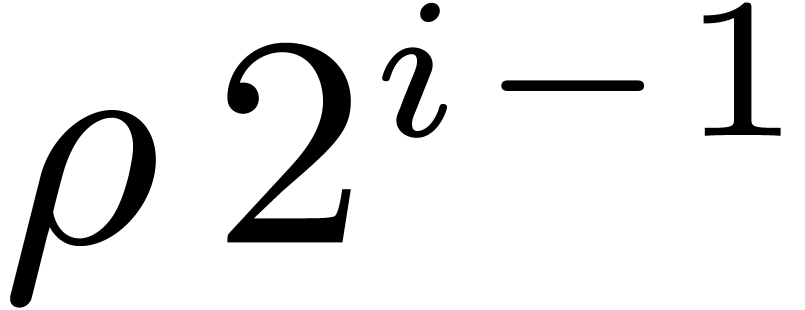 ,
,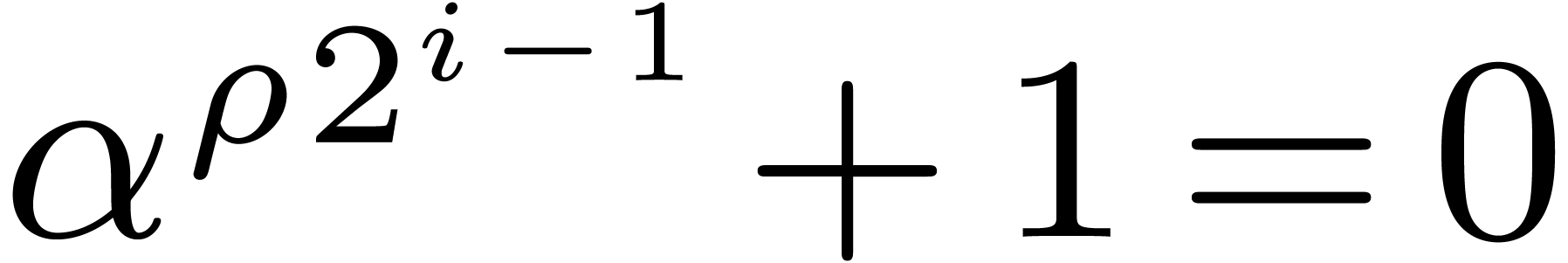 ,
,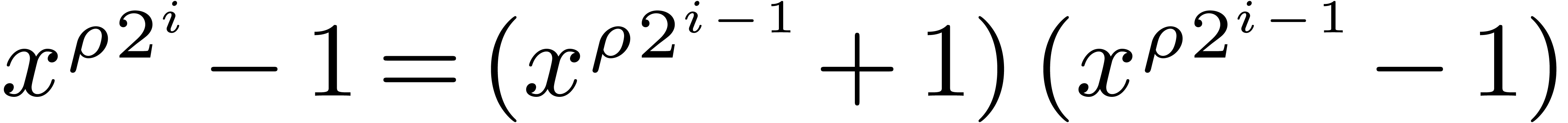 .
.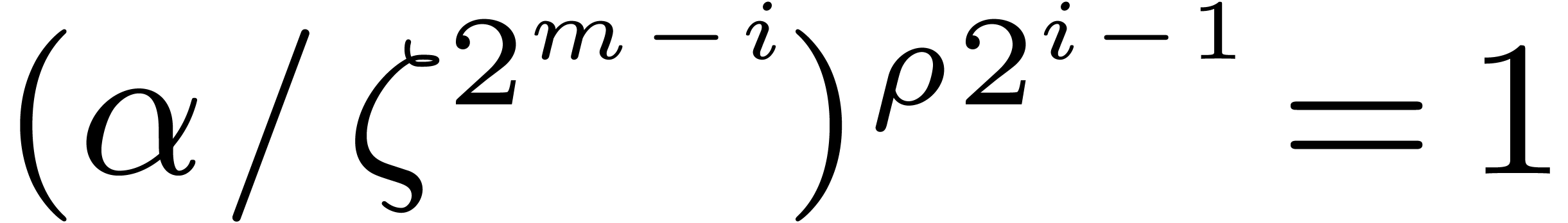 .
.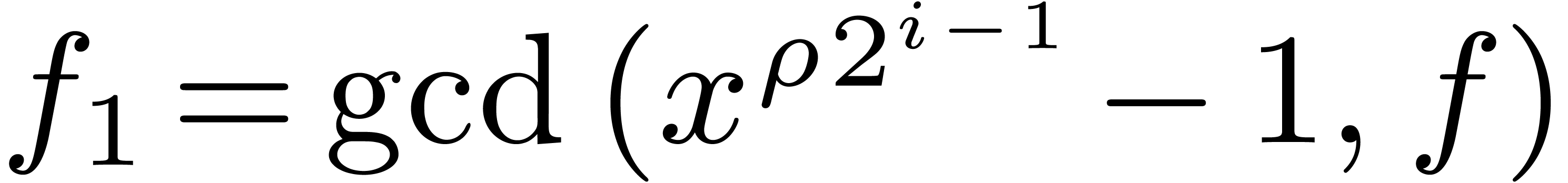 and
and 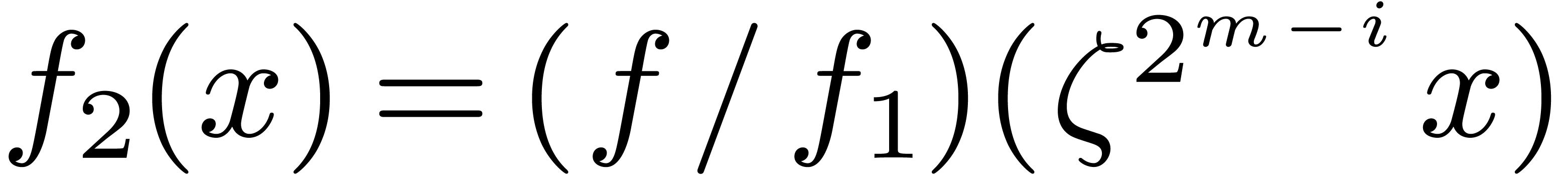 have all their roots of order
dividing
have all their roots of order
dividing 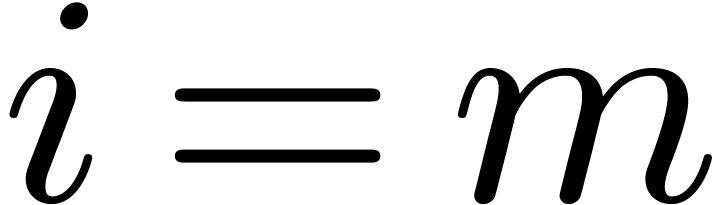 down to
down to 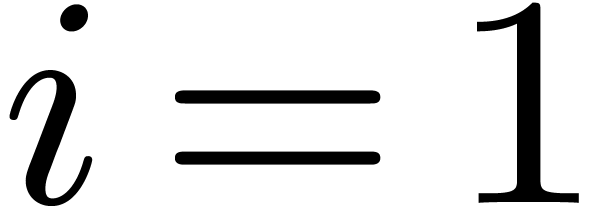 .
. in
in 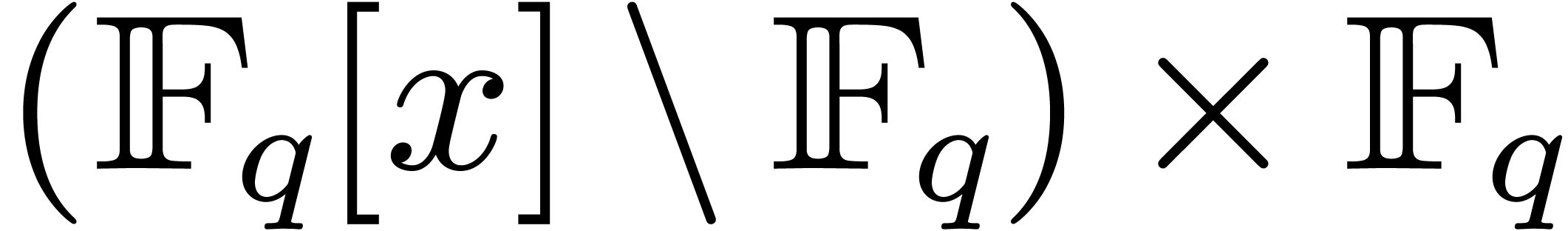 such that
such that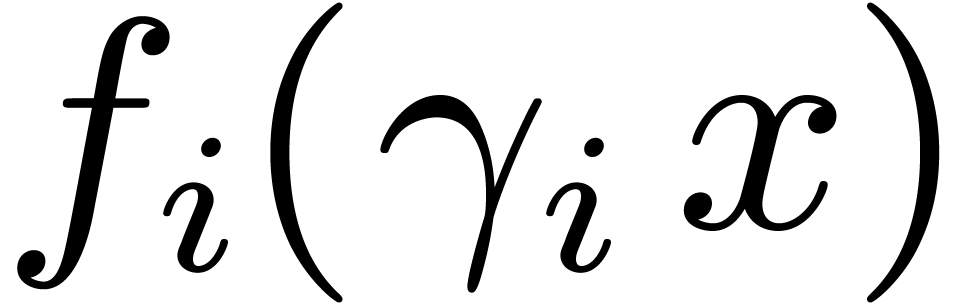 have orders dividing
have orders dividing 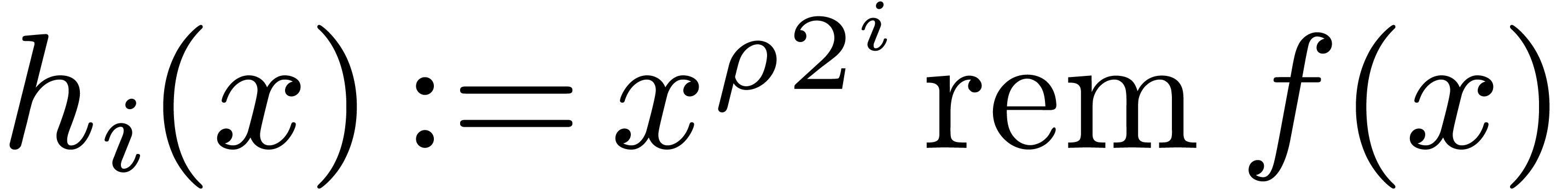 for all
for all  .
.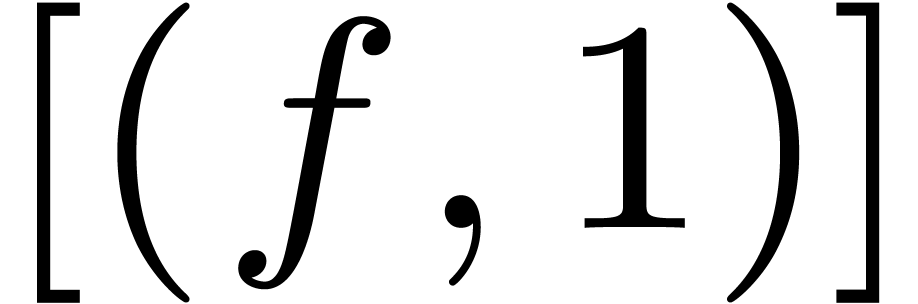 .
. in
in  .
. is not constant then make it monic and
append
is not constant then make it monic and
append  to
to  .
.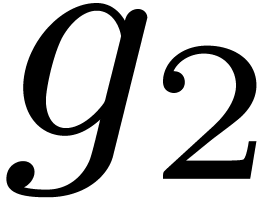 is not constant then make it monic, and
append
is not constant then make it monic, and
append 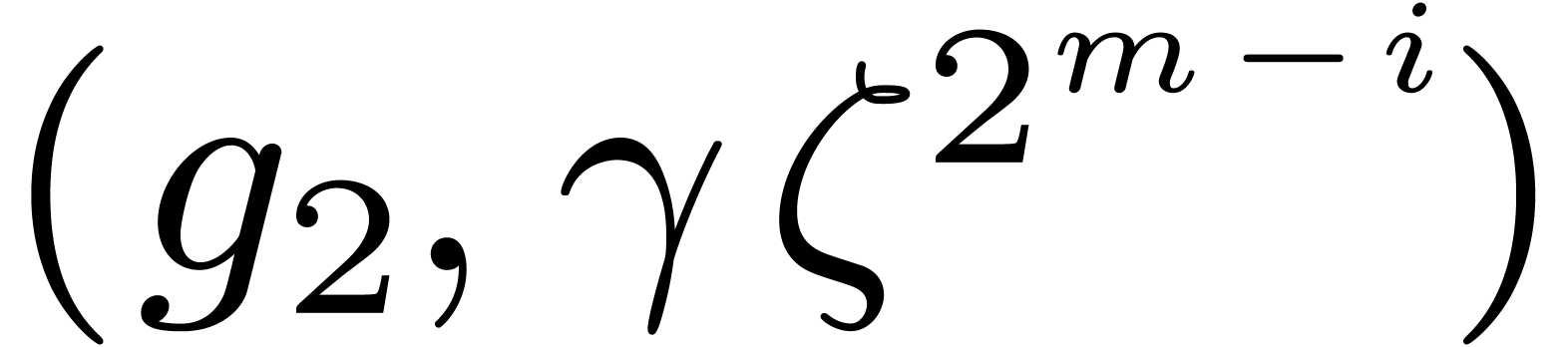 to
to  .
. in steps 3.c amounts to a bit-cost
in steps 3.c amounts to a bit-cost 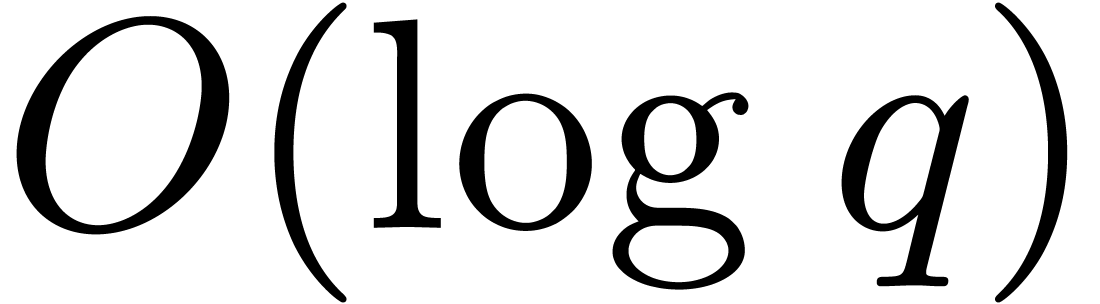 iterations of
Algorithms
iterations of
Algorithms 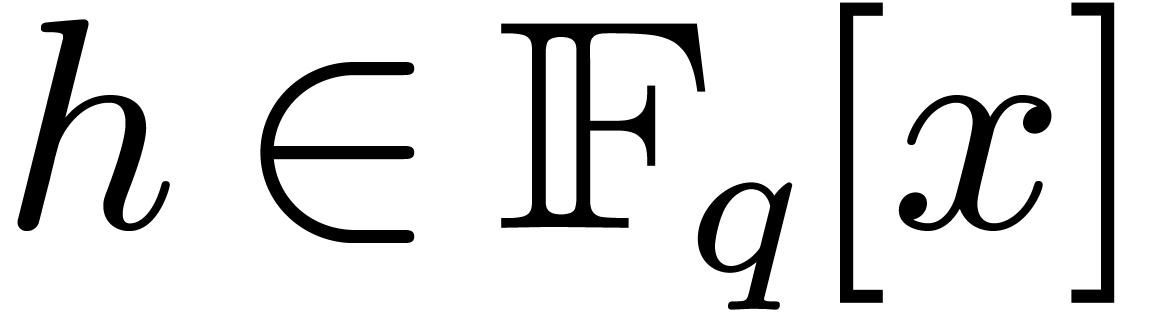 satisfying
satisfying 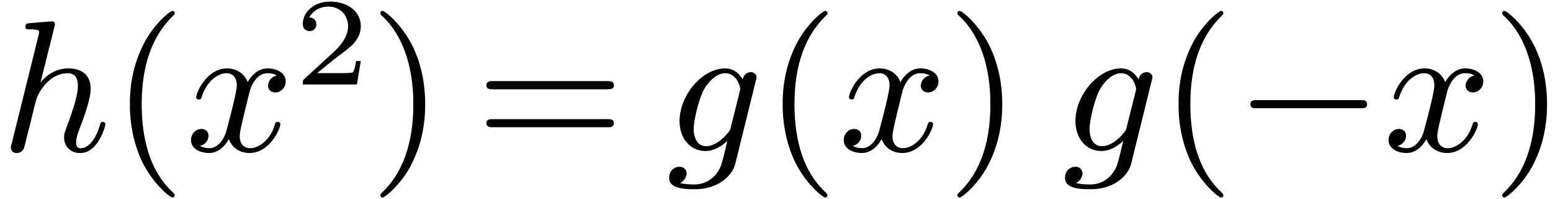 .
.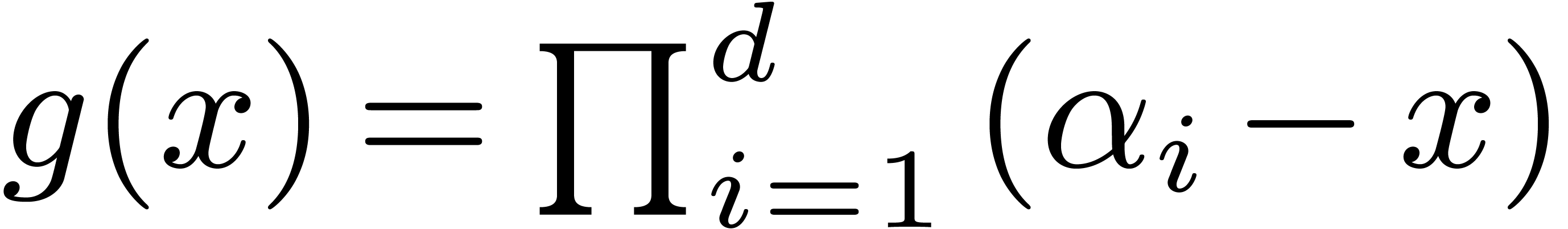 ,
,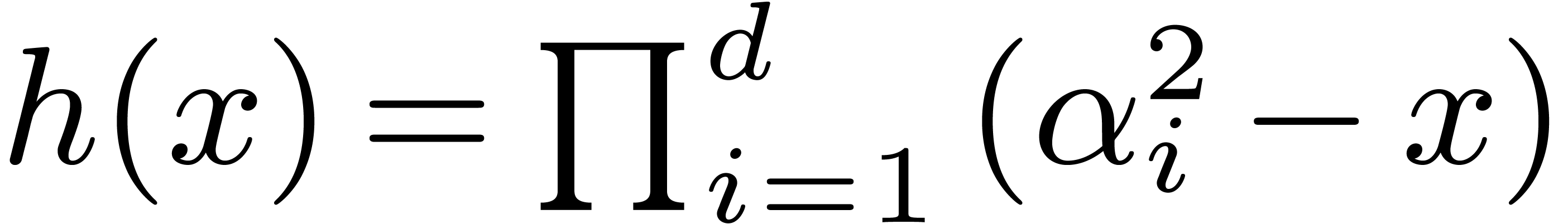 .
. ,
,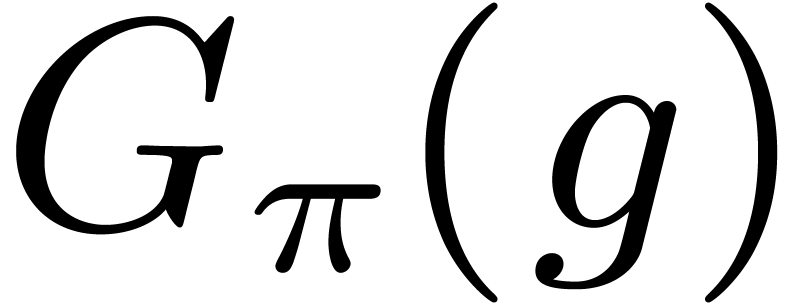 ,
,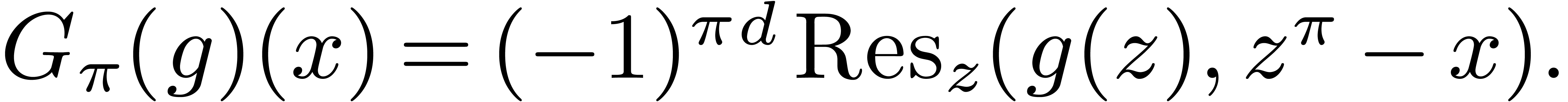
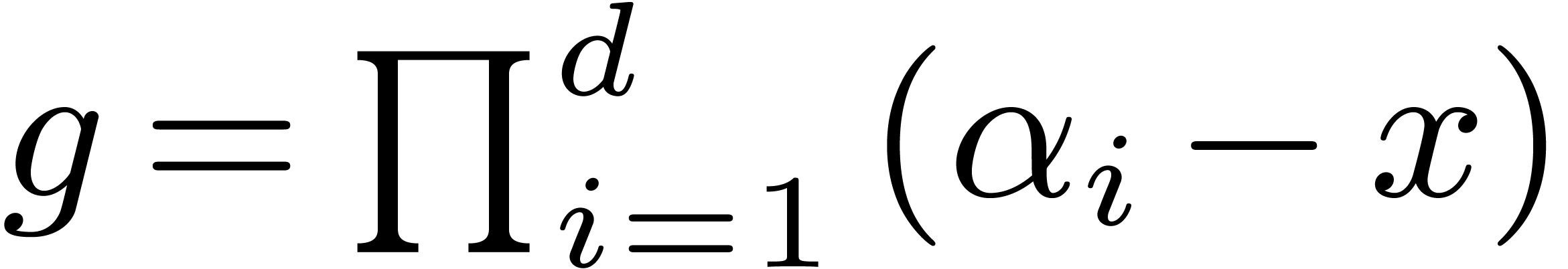 ,
,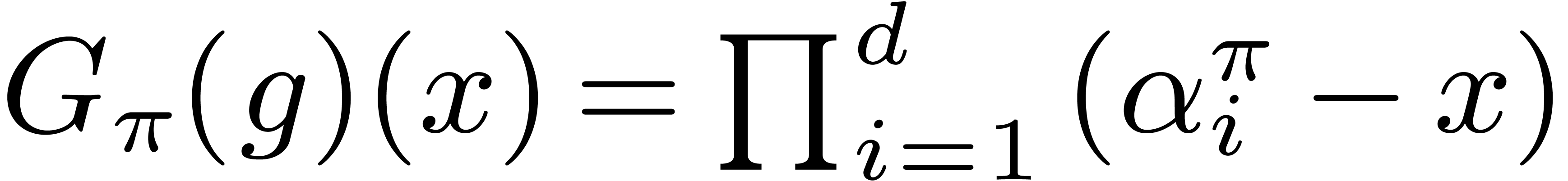 .
.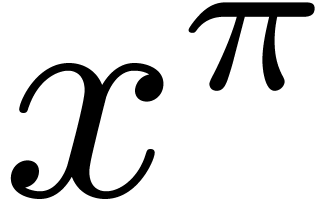 in
in 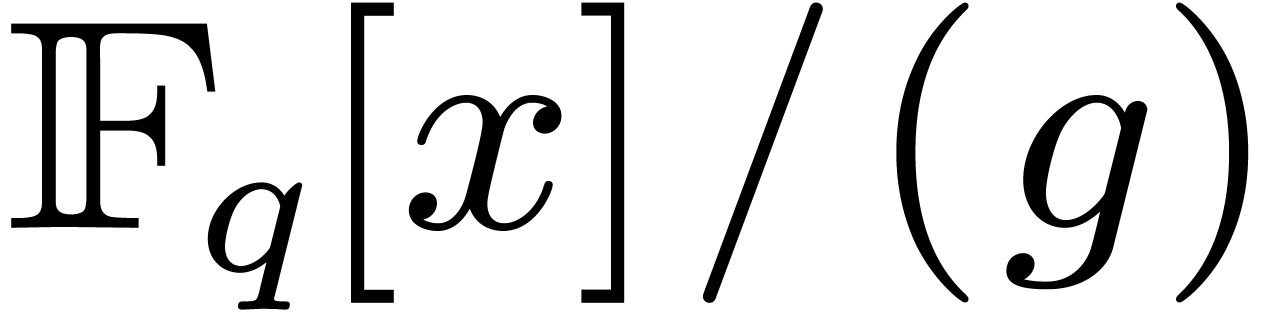 (up to the sign). For our root finding
algorithms, the most important case is when
(up to the sign). For our root finding
algorithms, the most important case is when 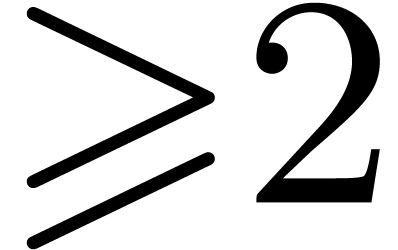 ,
, ,
, be given primitive roots of unity of
orders
be given primitive roots of unity of
orders 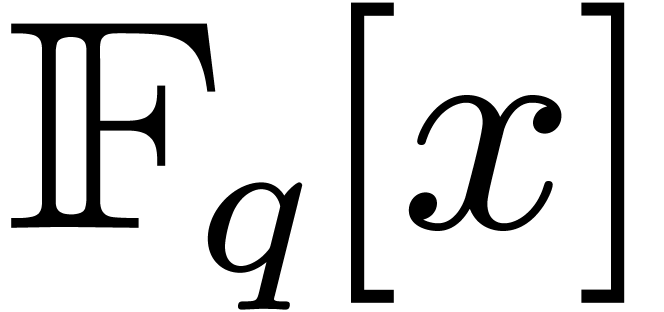 of degree
of degree 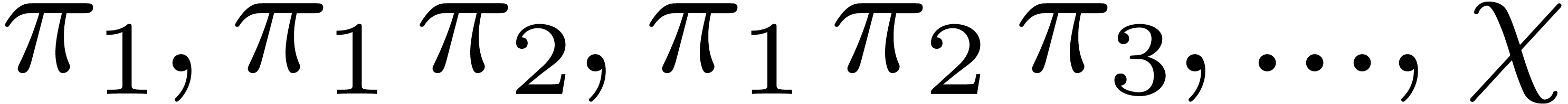 of
of 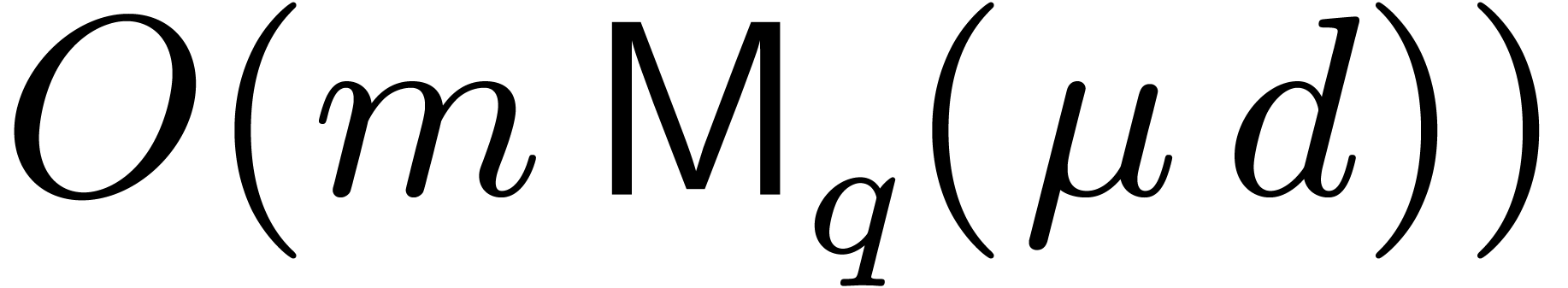 or
or 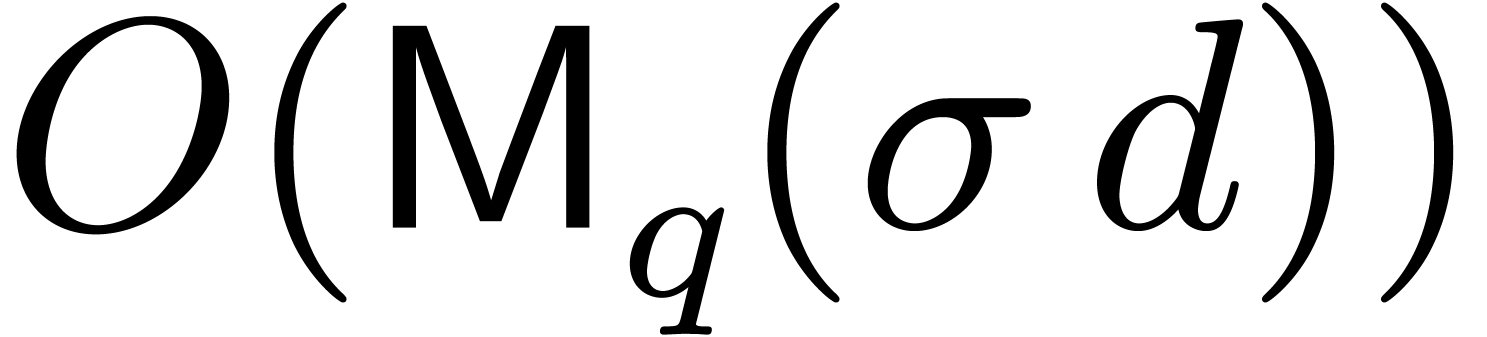 ,
, and
and 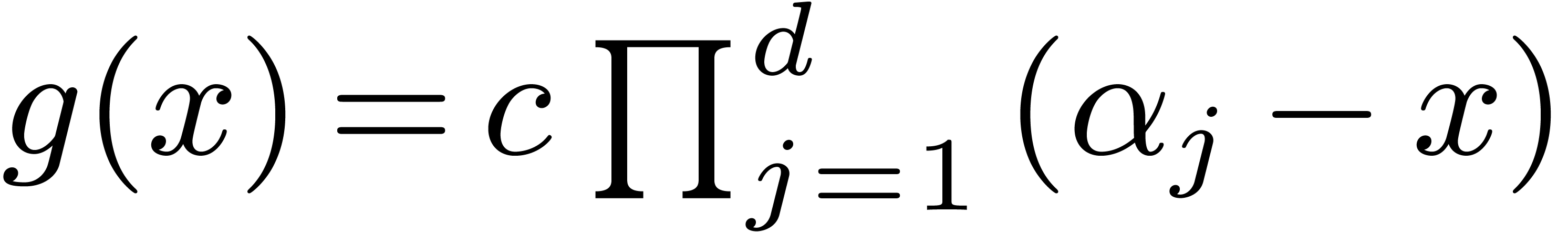 in an
algebraic closure of
in an
algebraic closure of 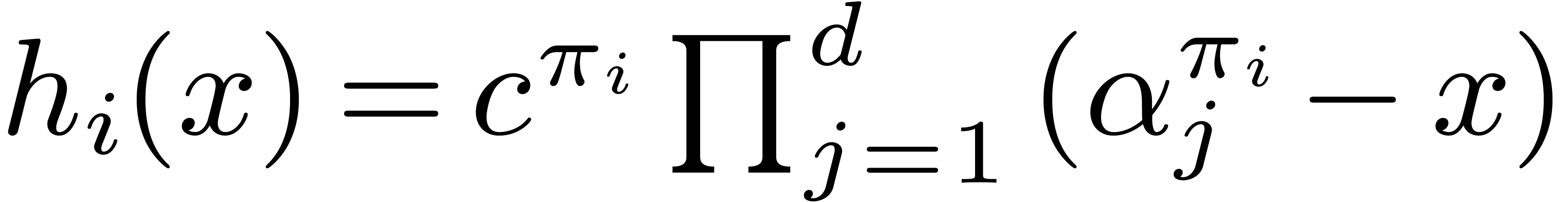 .
.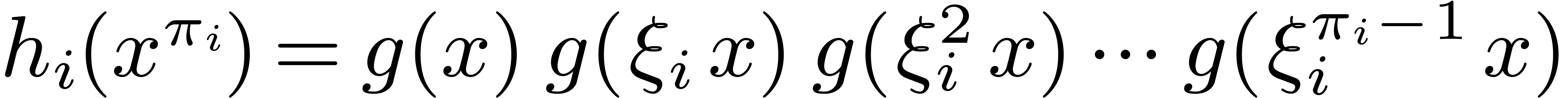 .
.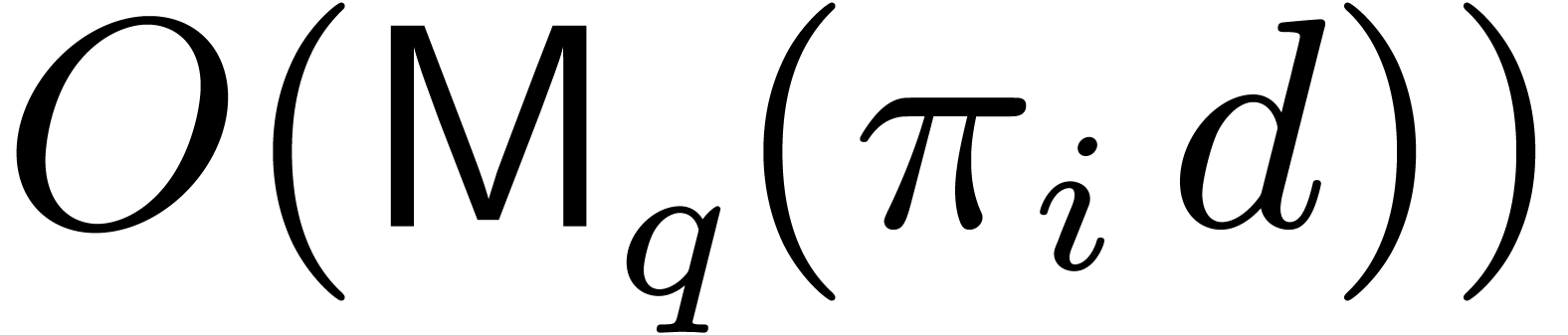 .
.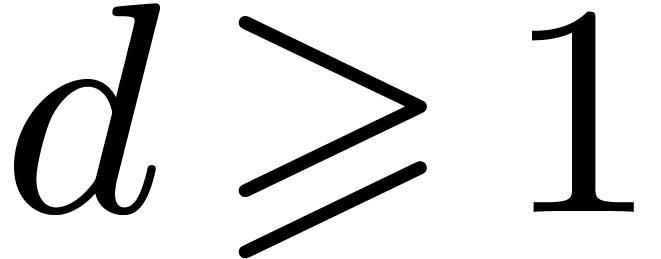 in
in  ,
, be an
integer. Then the product
be an
integer. Then the product 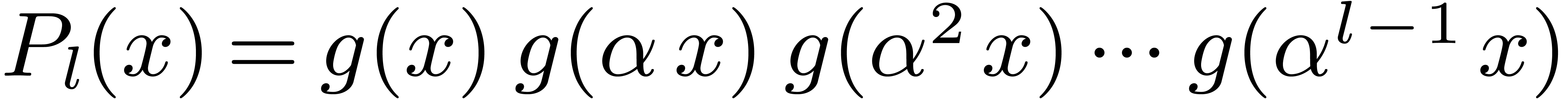 can be computed in
time
can be computed in
time 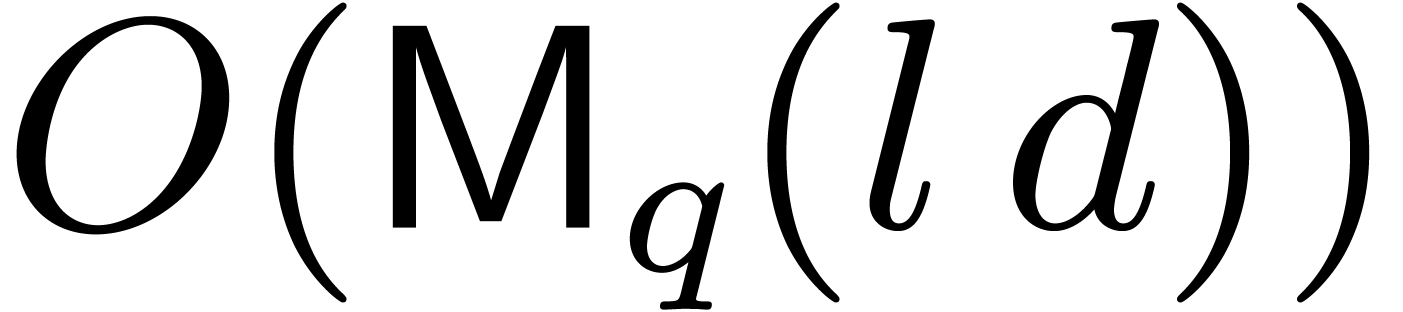 .
.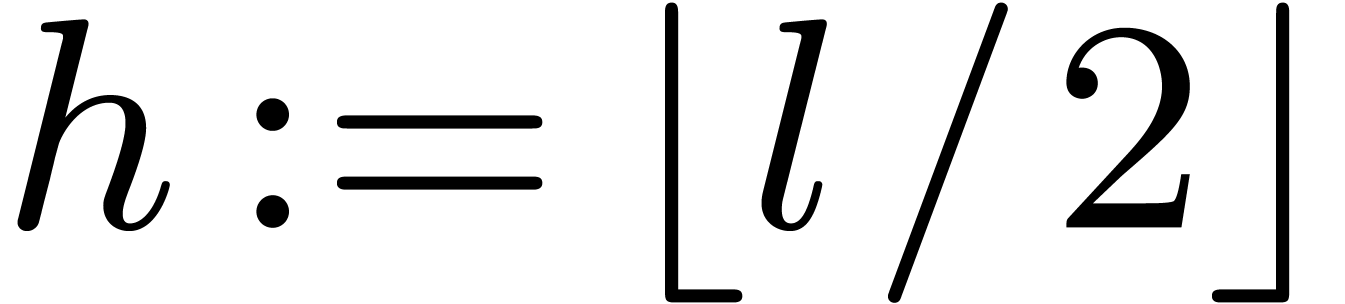 .
.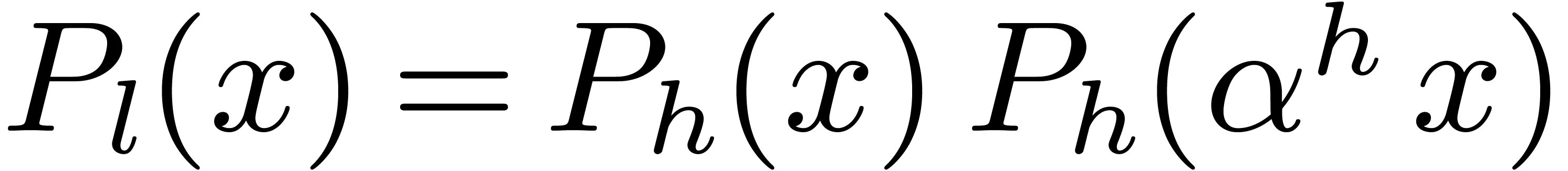 ,
,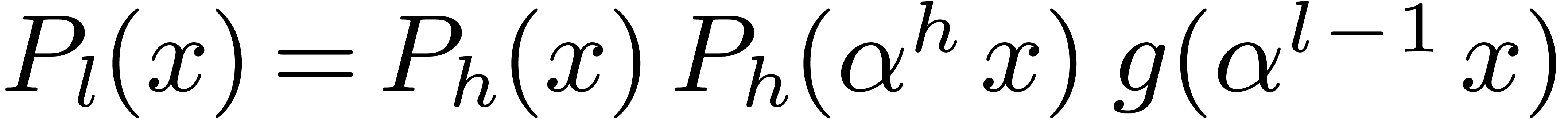 .
. with
with 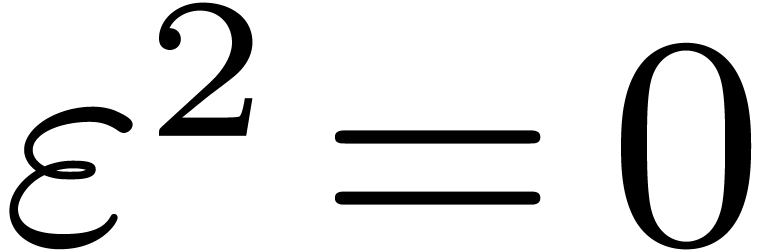 ,
, .
. ,
,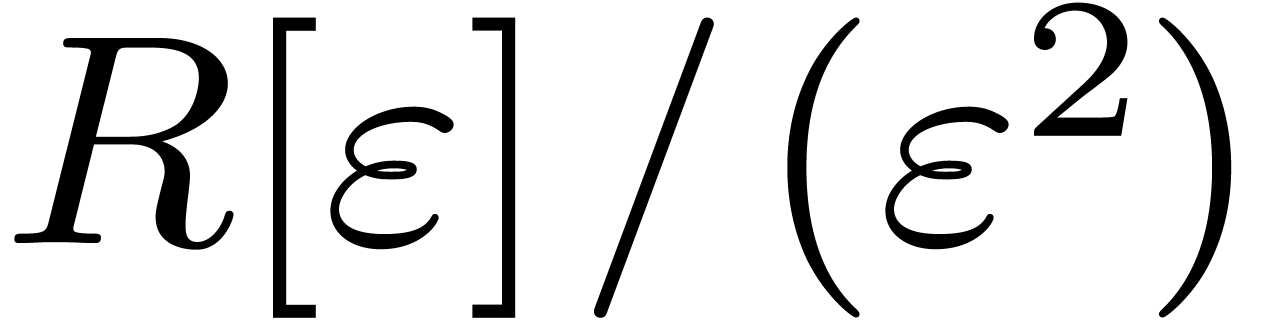 can be done with constant
overhead with respect to computations in
can be done with constant
overhead with respect to computations in  be coprime to
be coprime to  ,
,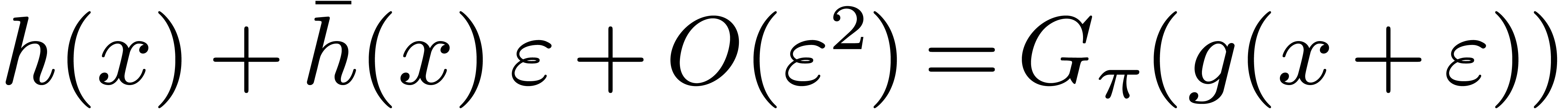 .
. of h is
simple if, and only if,
of h is
simple if, and only if, 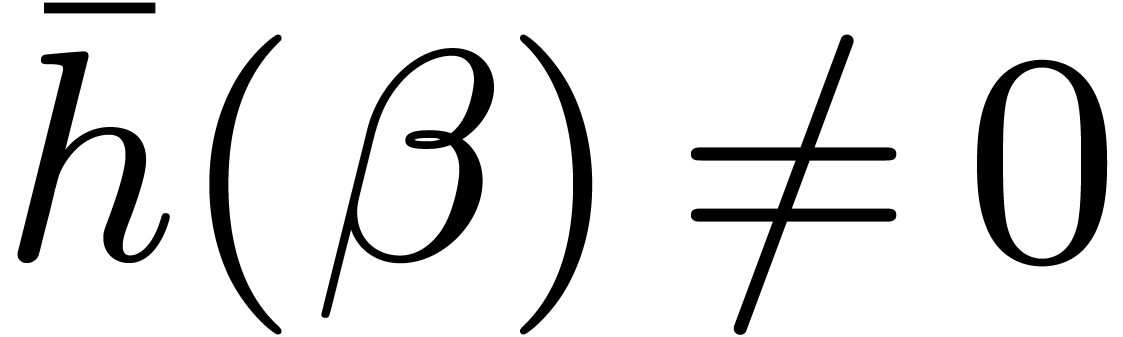 .
.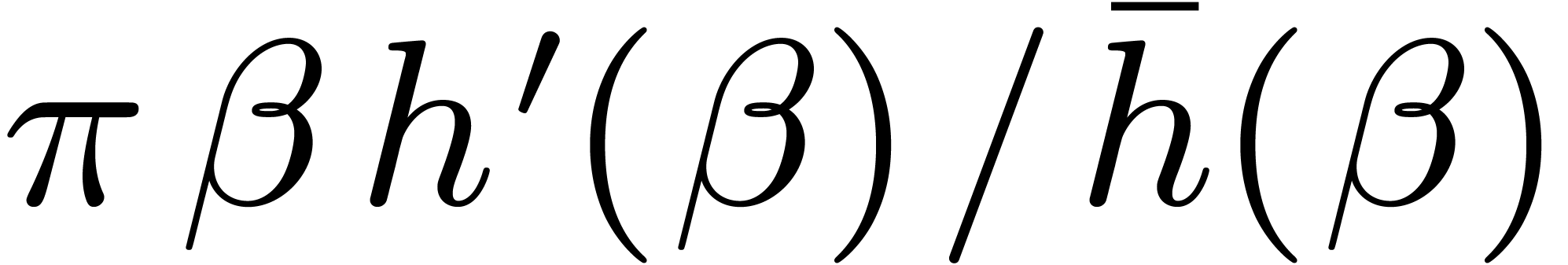 is the unique root
is the unique root  .
. ,
,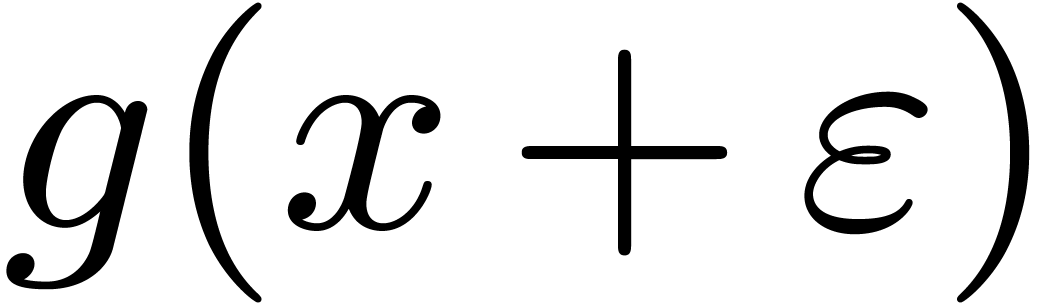 ,
, ,
, ,
, be the Graeffe
transforms of orders
be the Graeffe
transforms of orders  ,
, ,
, of
of  among the
among the  -th
-th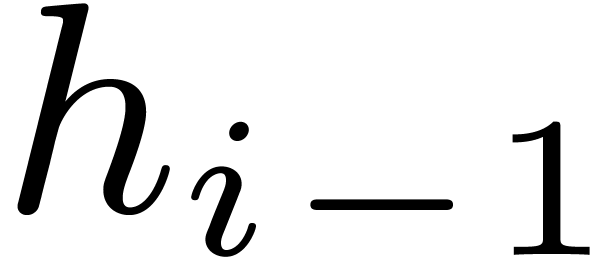 are to be found among
the
are to be found among
the  .
.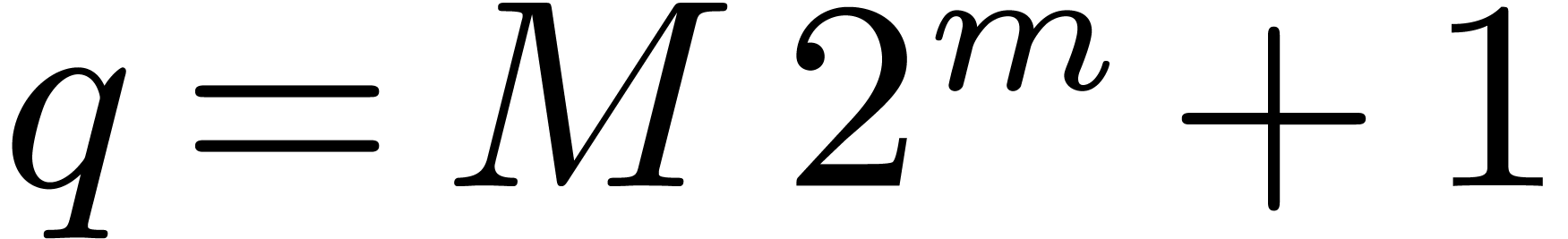 ,
,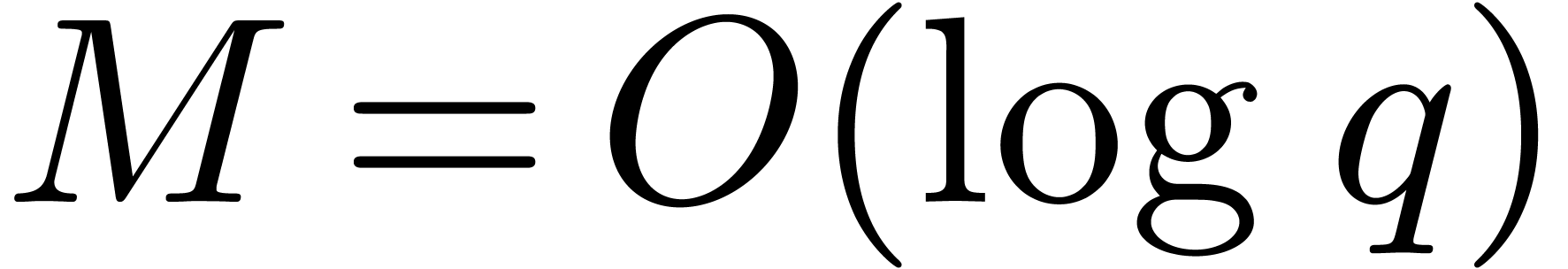 .
.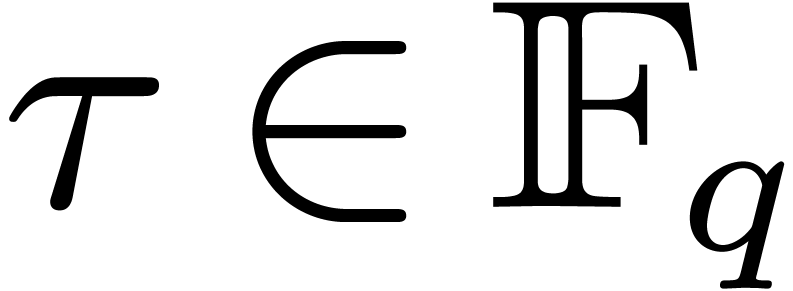 .
.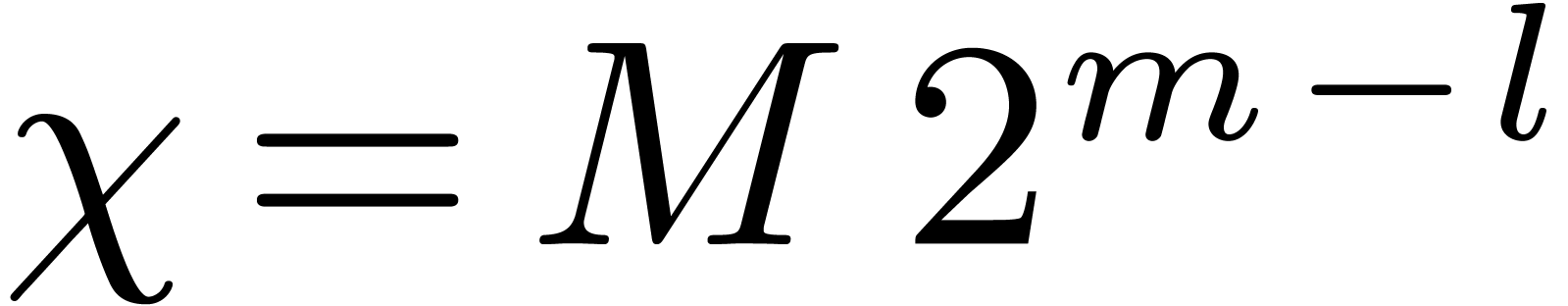 be a divisor of
be a divisor of 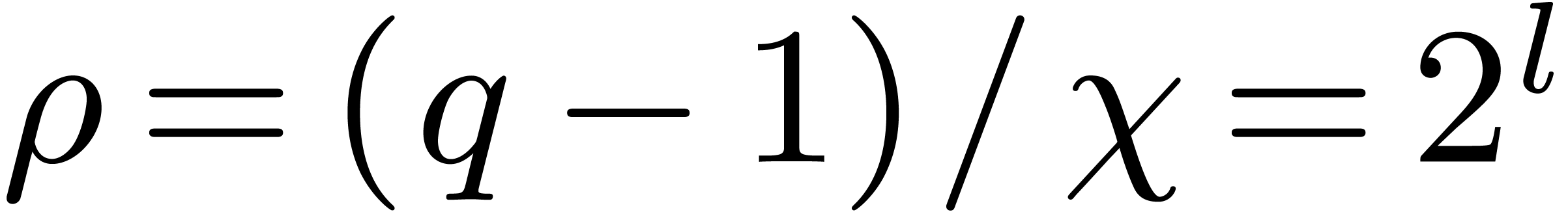 .
. denote the roots of
denote the roots of 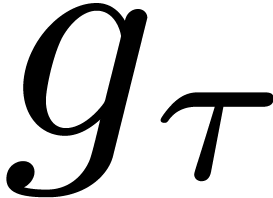 of
of
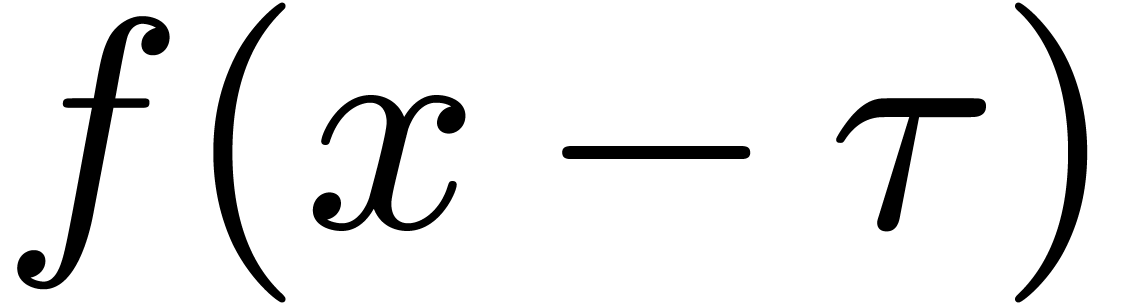 of order
of order 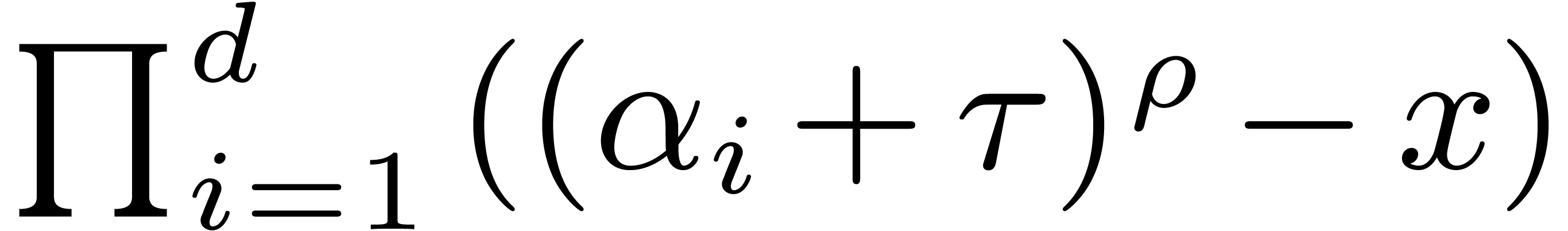 .
. and
and  of
of 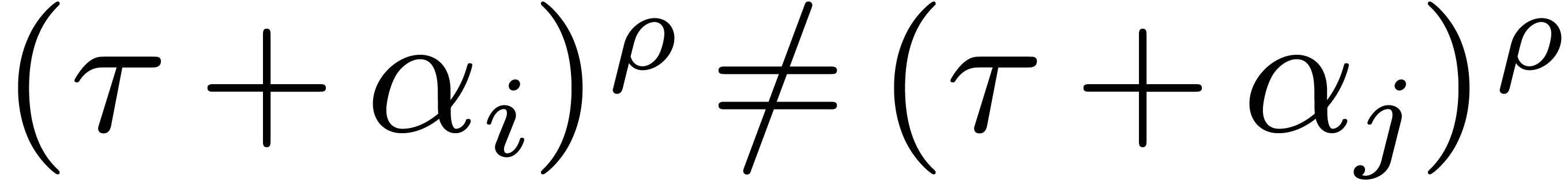 for all but at most
for all but at most  .
.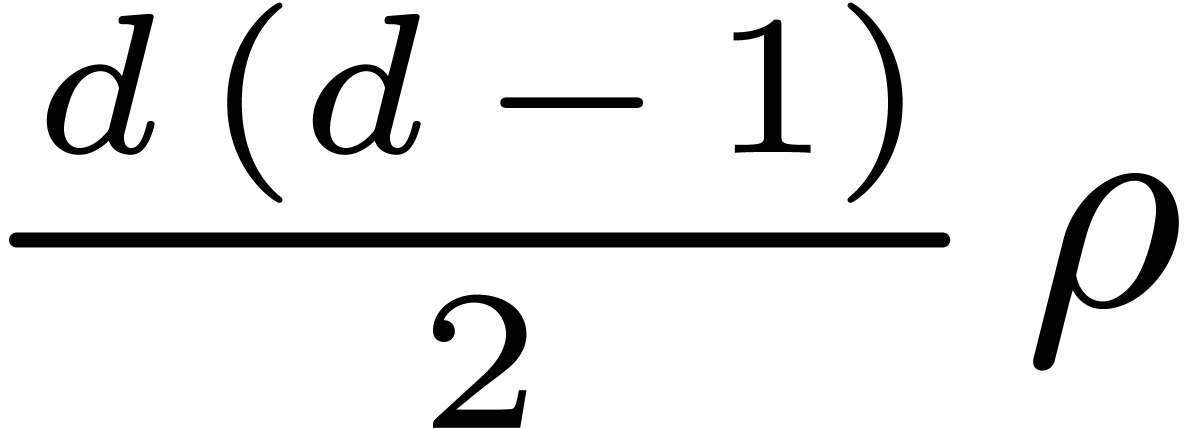 values of
values of 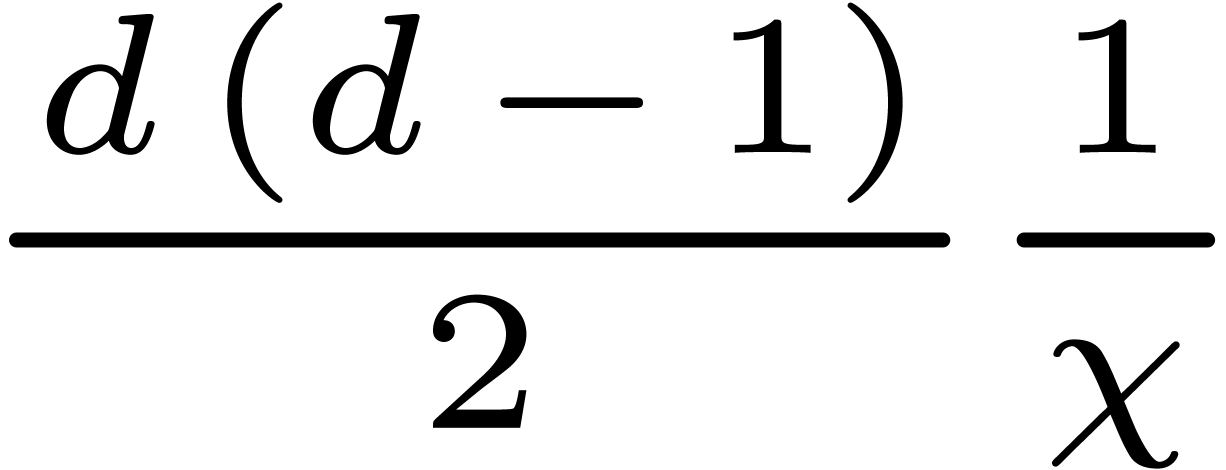 .
. then set
then set  to
to 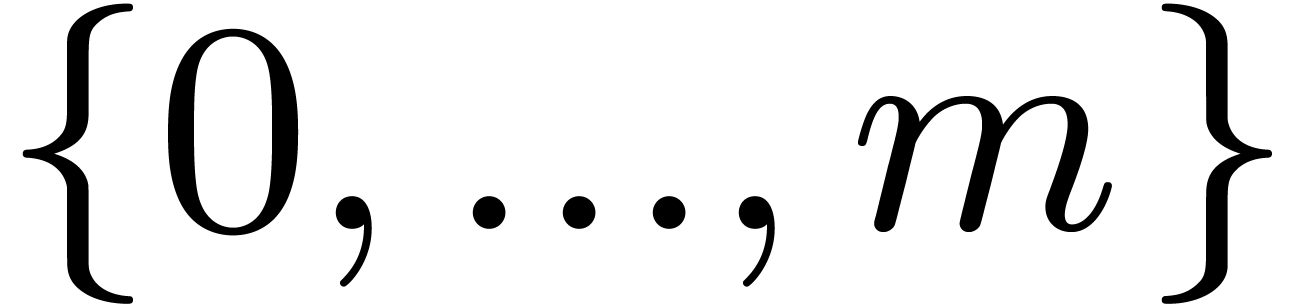 such
that
such
that  .
.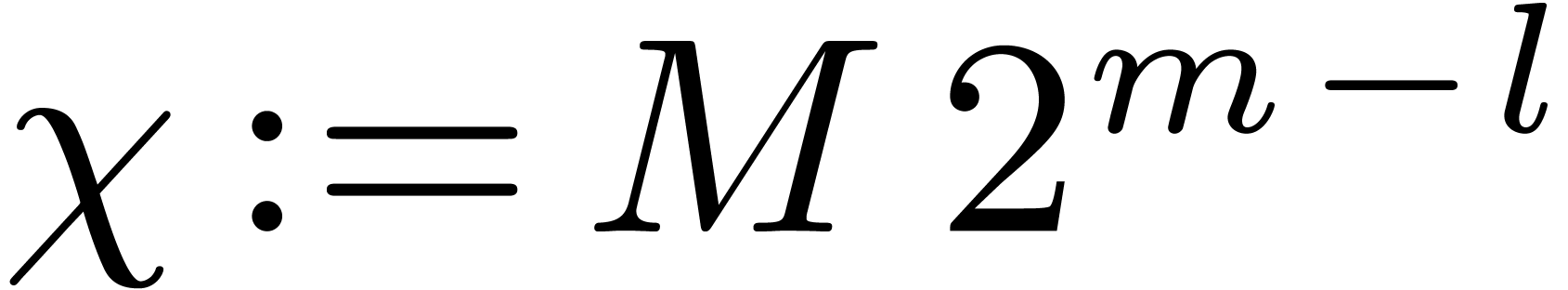 and
and 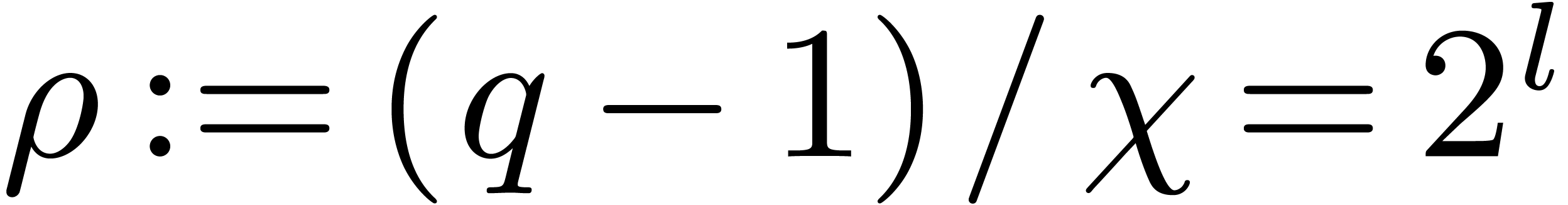 .
.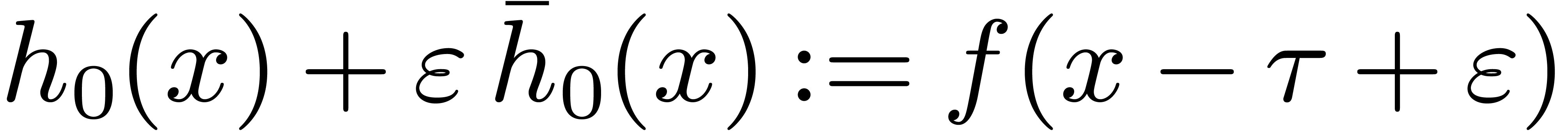 ,
,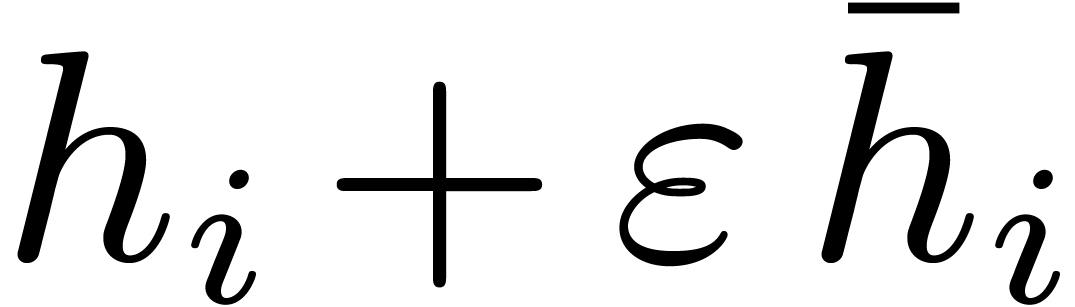 of
order
of
order  of
of 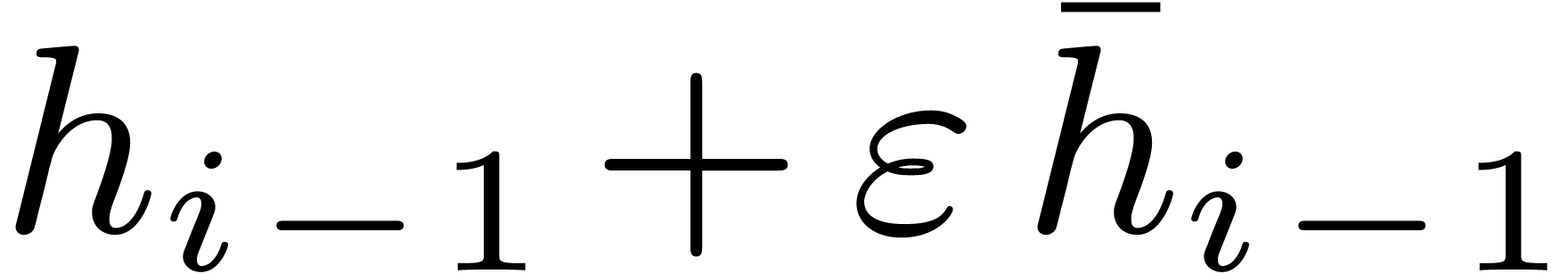 ,
,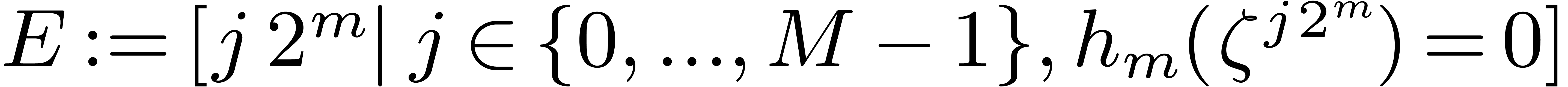 of
of  do
do
 by the concatenation of
by the concatenation of 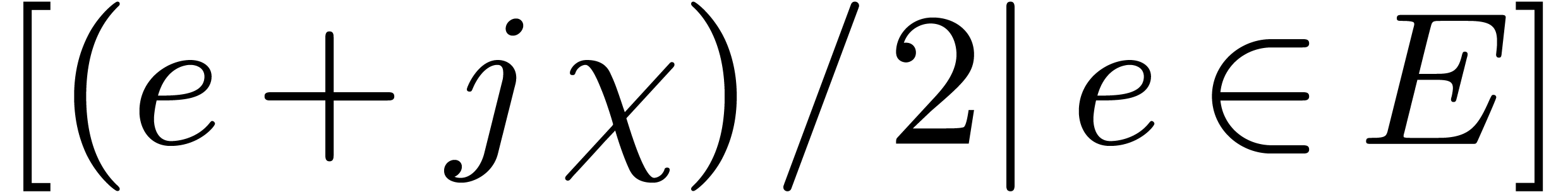 for
for 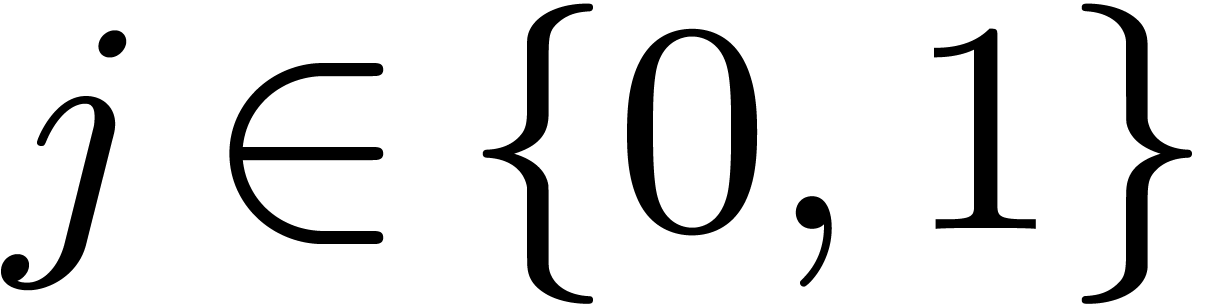 .
. from
from 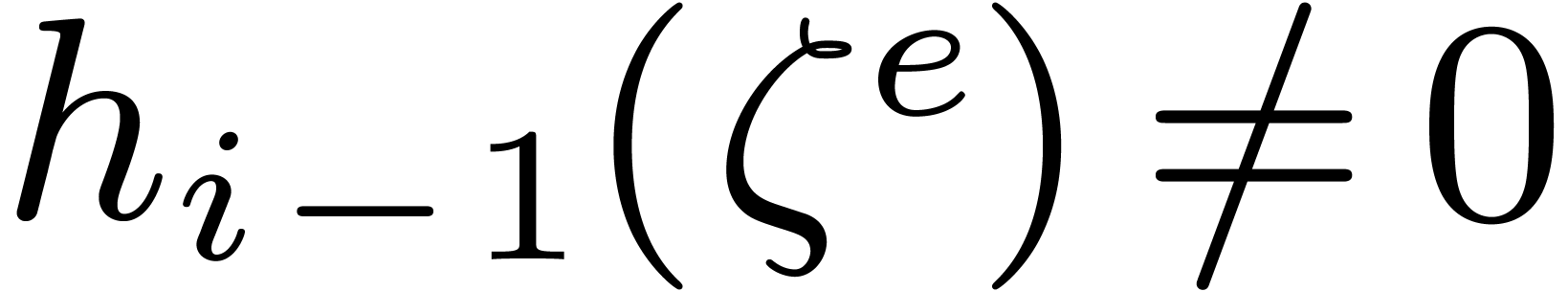 .
. then return
then return 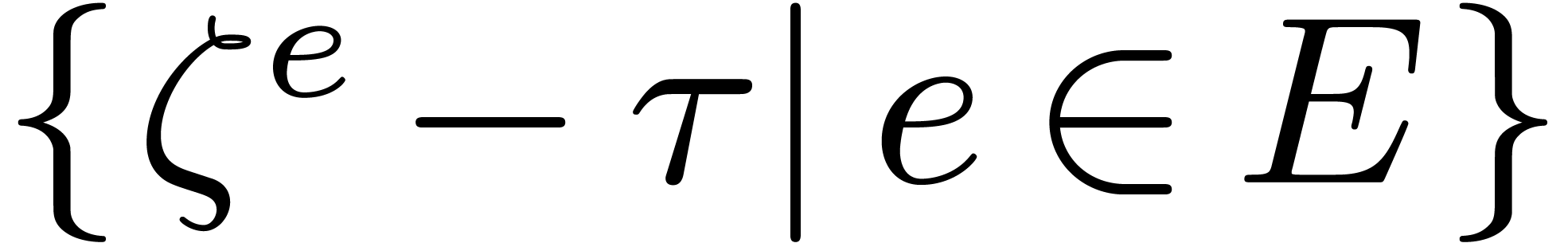 .
.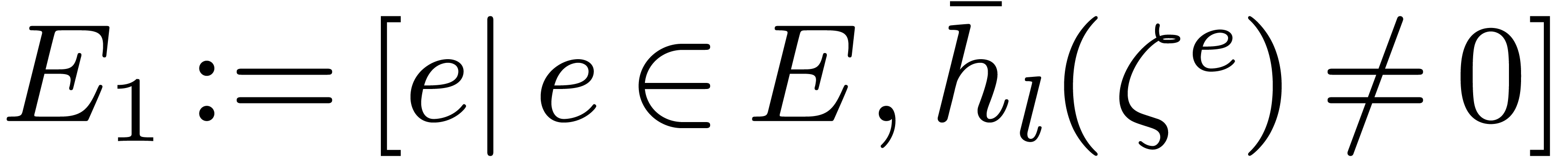 .
.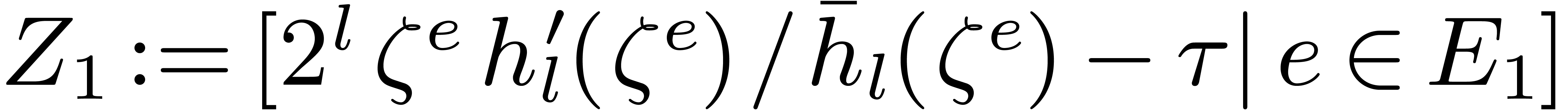 .
. if
if 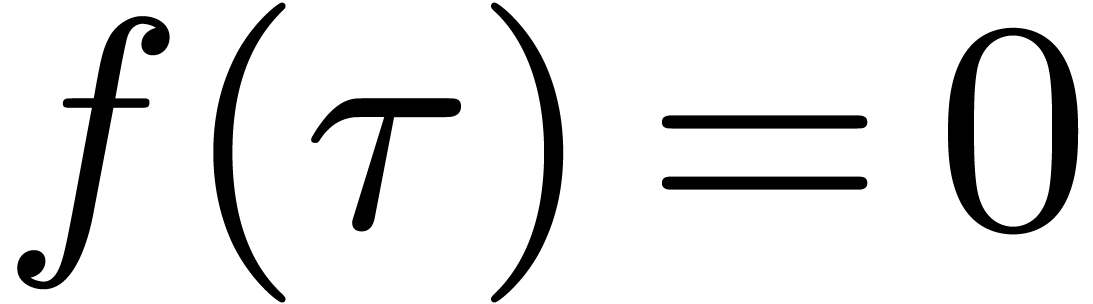 .
.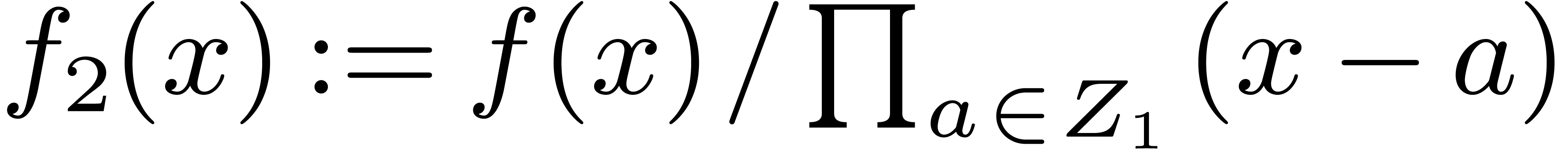 .
. of
of  .
. .
. and
and  .
.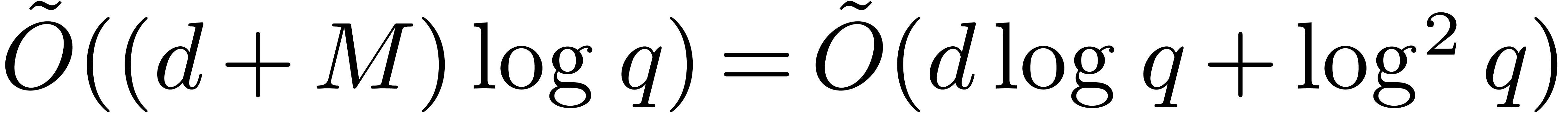 .
.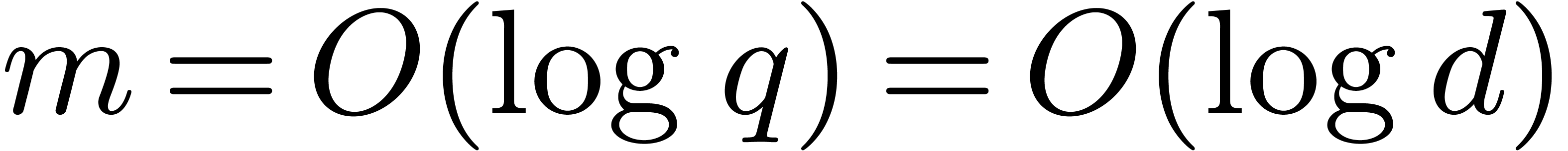 .
.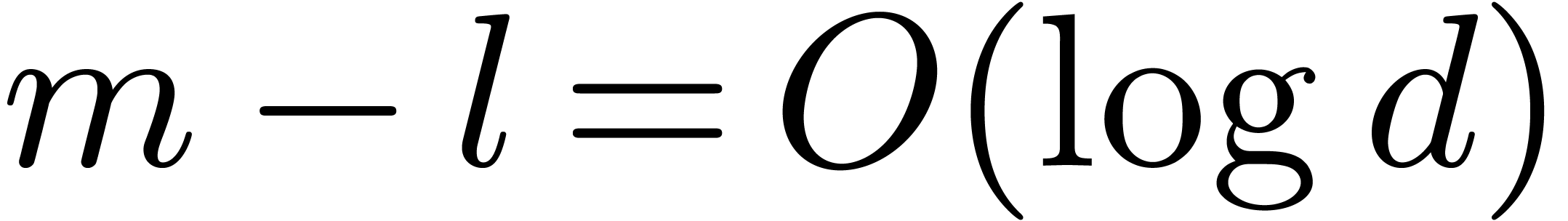 .
. with probability at least
with probability at least  .
.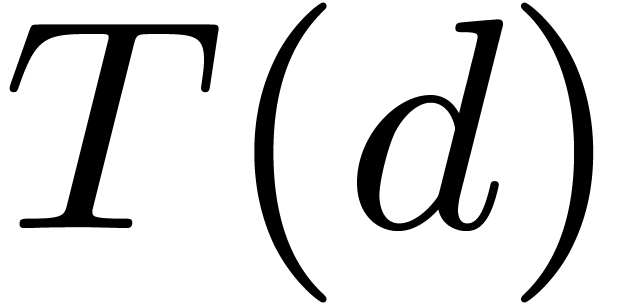 for the average execution time, we thus
have
for the average execution time, we thus
have 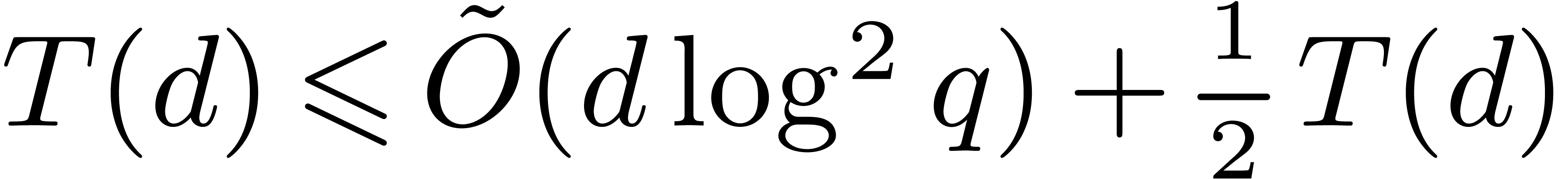 ,
,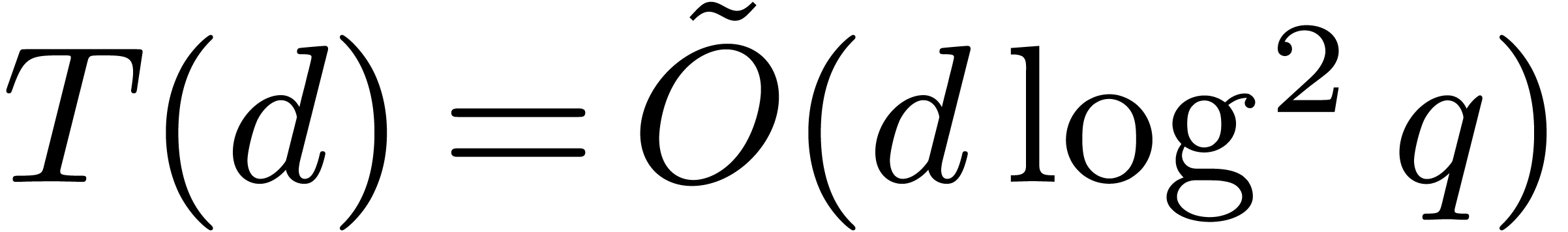 .
. be the number of monic polynomials of degree
be the number of monic polynomials of degree
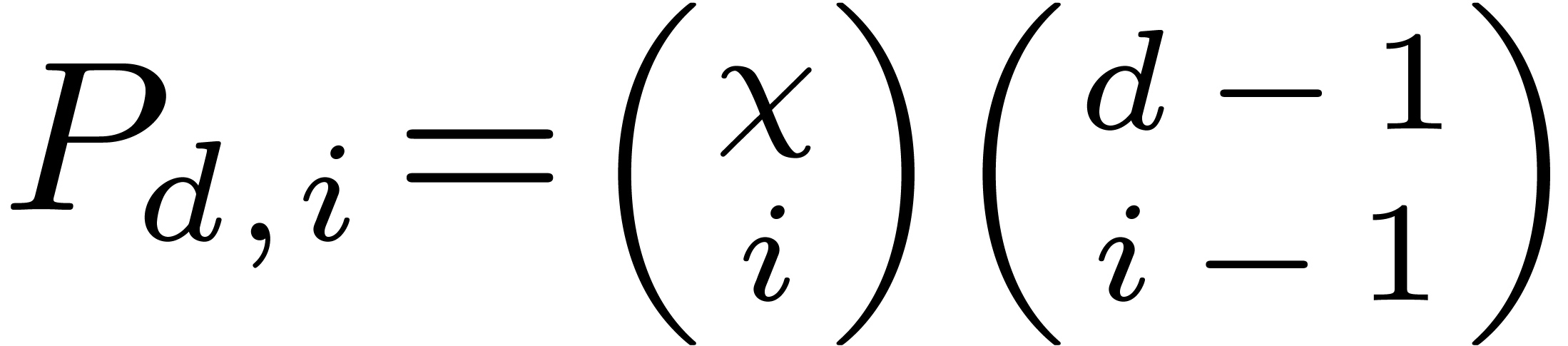 .
.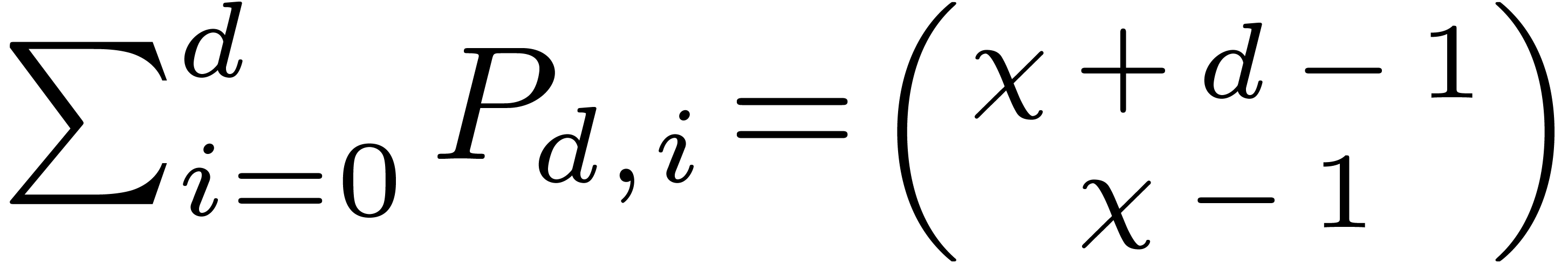 ,
, for each element of order dividing
for each element of order dividing 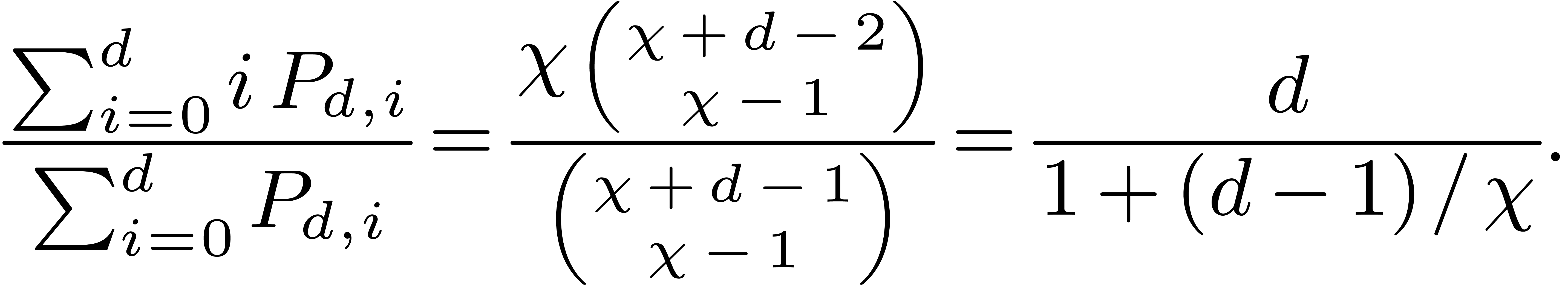
 ,
,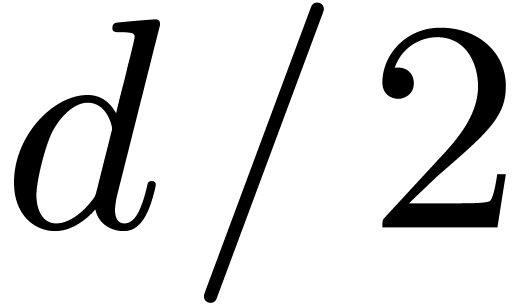 .
.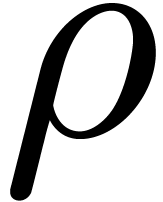 be a fixed divisor of
be a fixed divisor of 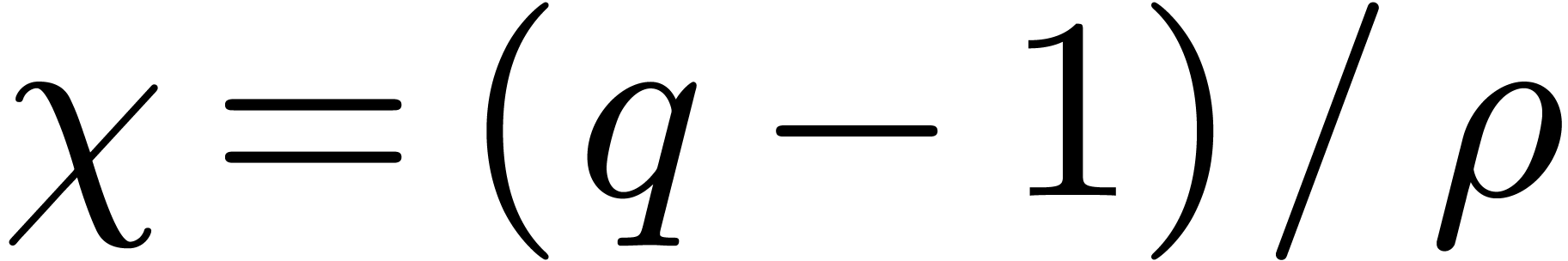 .
.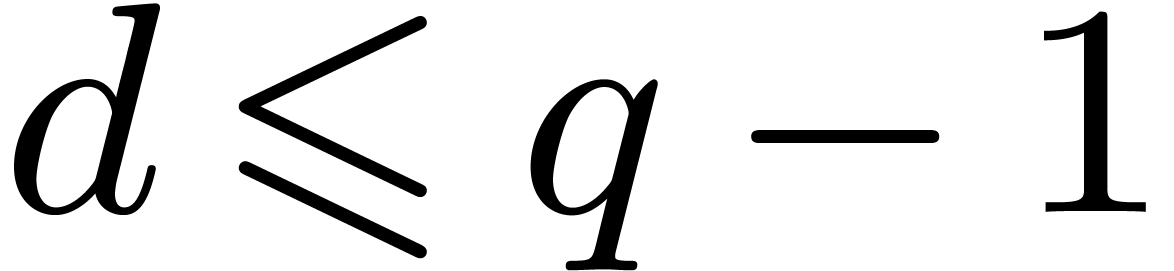 ,
,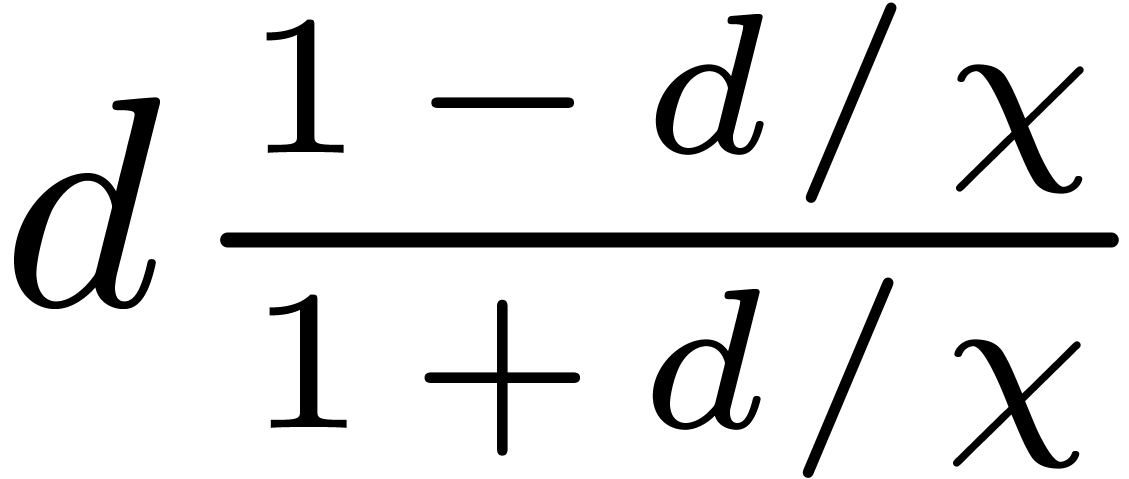 .
. the probability that
the probability that
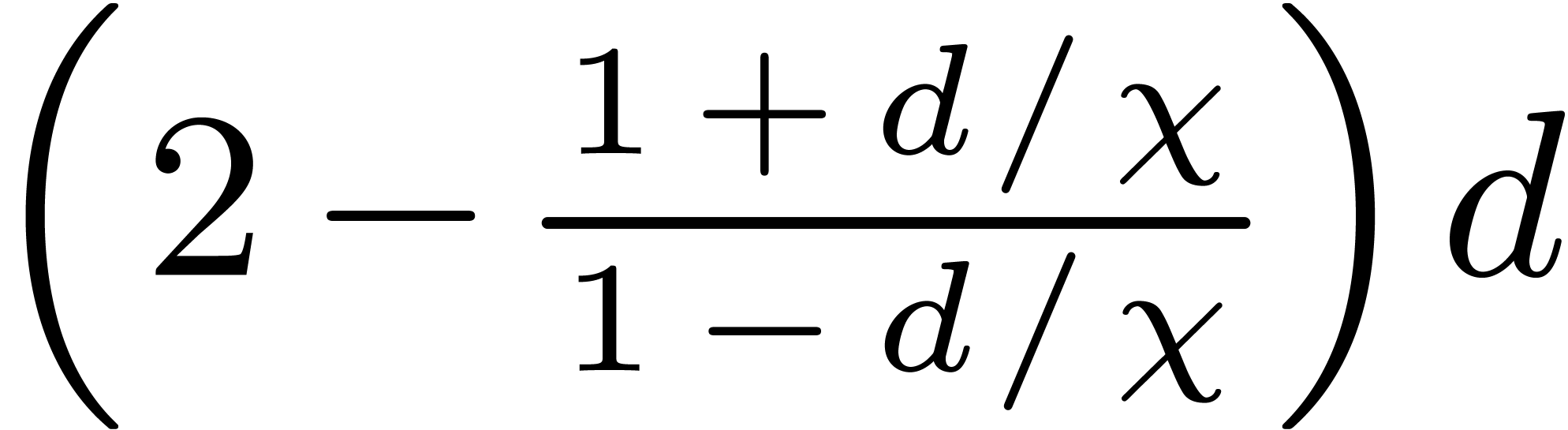 simple
roots is at least
simple
roots is at least  .
. and
and 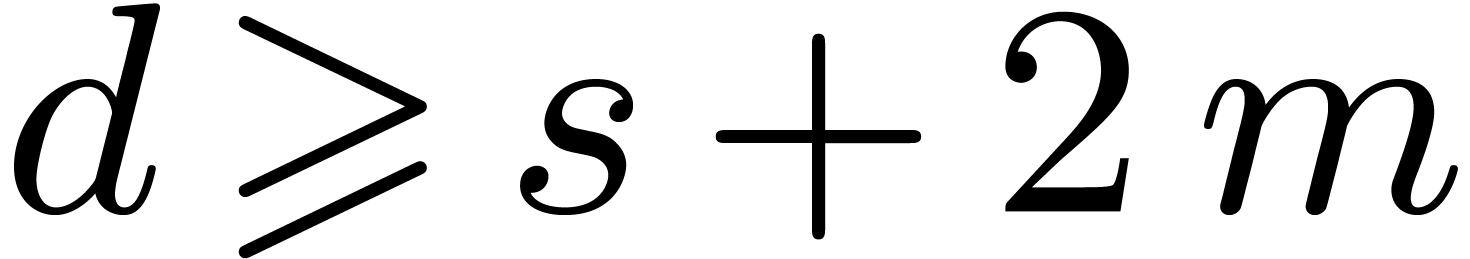 .
. of distinct roots of
of distinct roots of  .
. and
and  .
.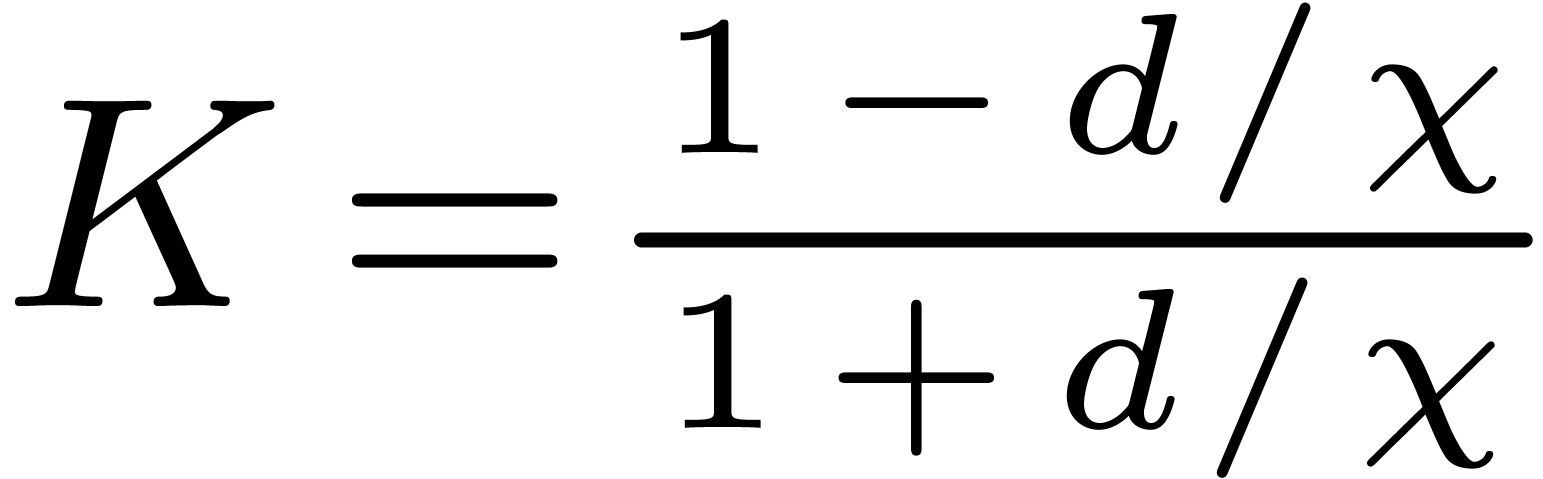 and assuming that
and assuming that 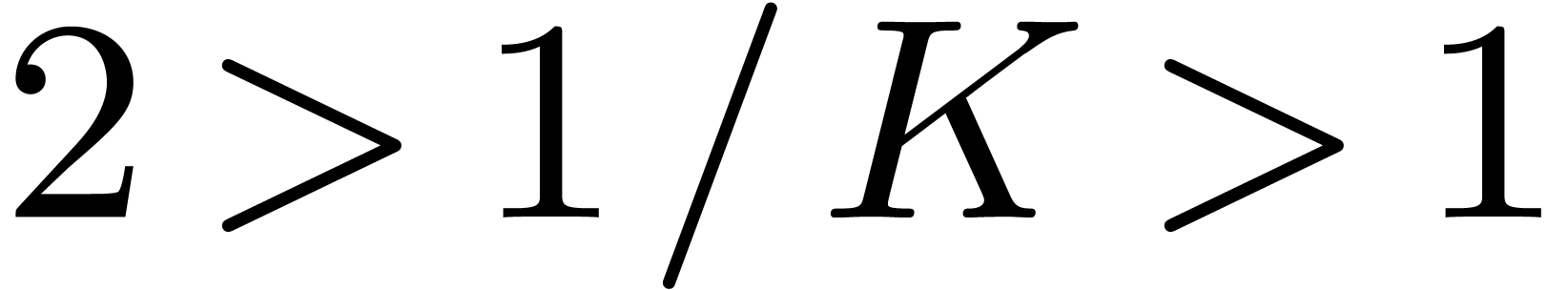 ,
, be the probability that
be the probability that 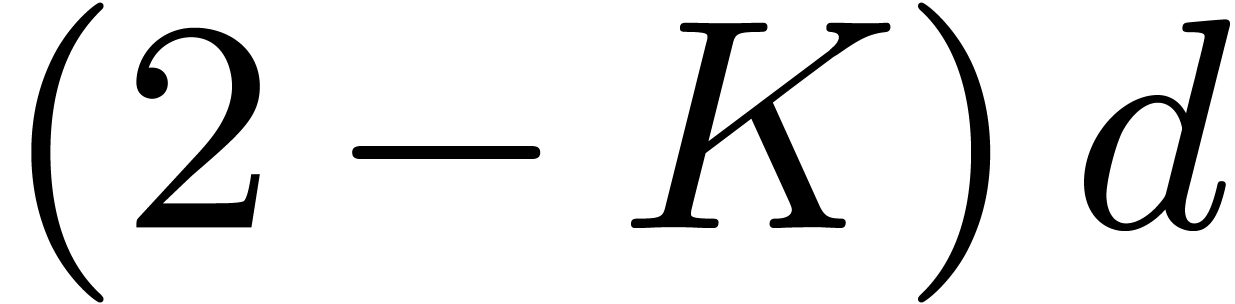 simple roots. Then the average
number of roots
simple roots. Then the average
number of roots  is at most
is at most 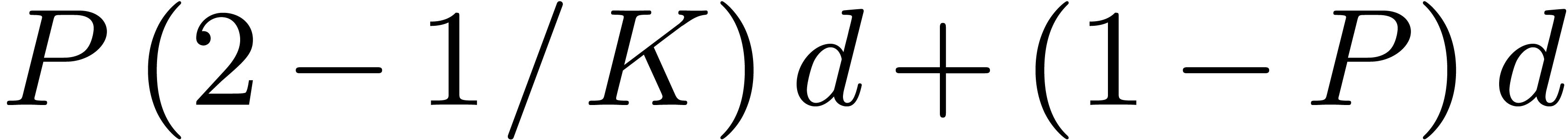 ,
,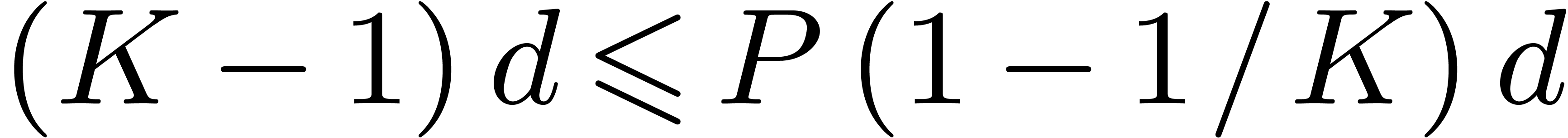 .
.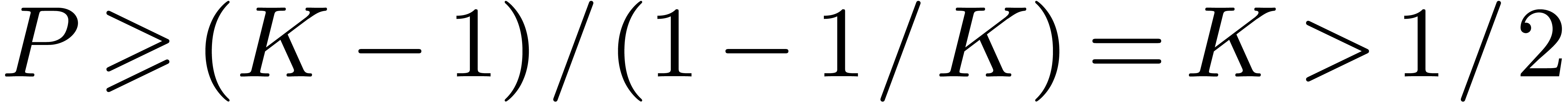 .
.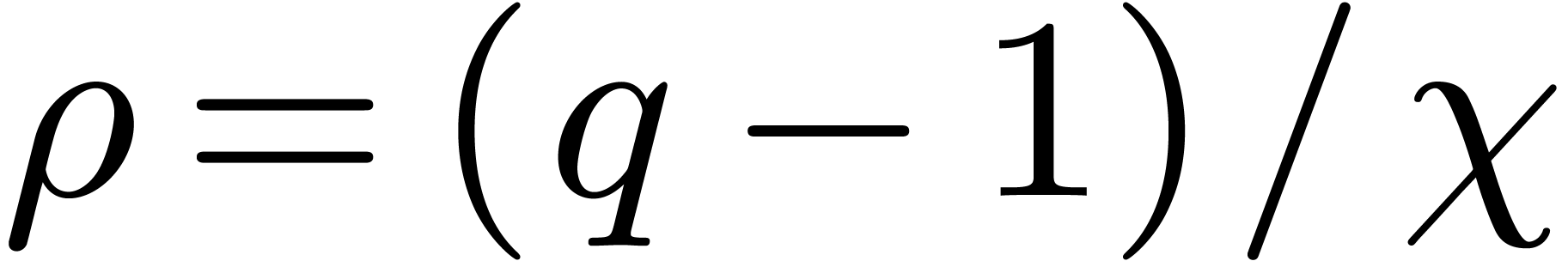 and consider a polynomial
and consider a polynomial
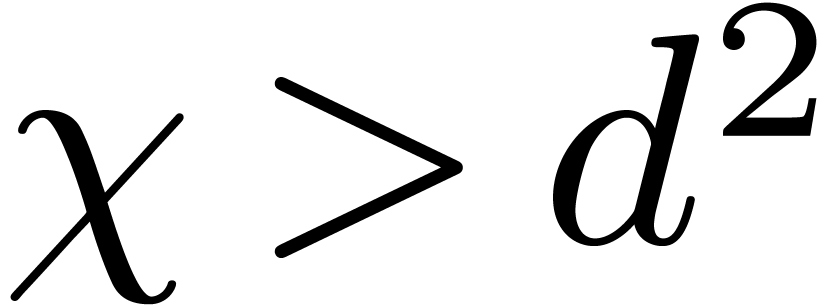 ,
, ,
, and for random
and for random
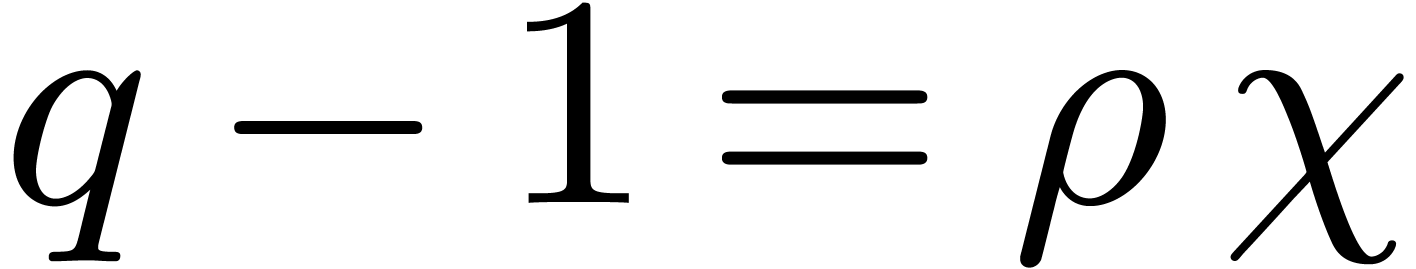 with
with
 and let
and let 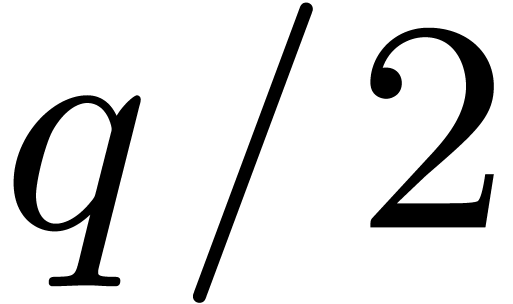 elements
elements 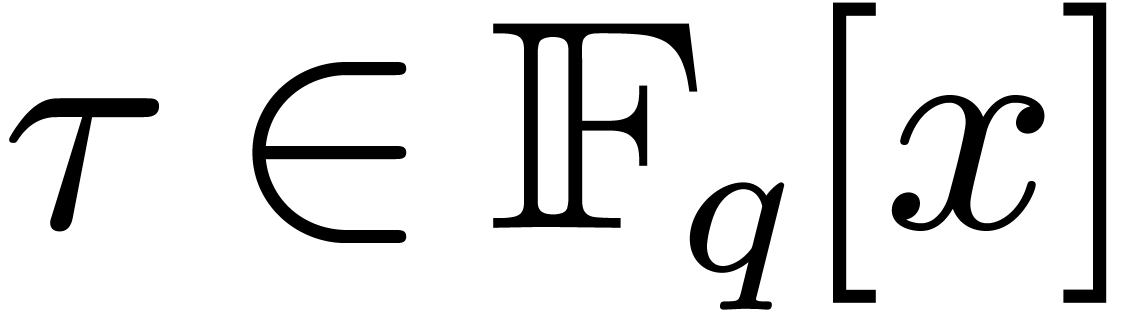 such that the
Graeffe transform of order
such that the
Graeffe transform of order 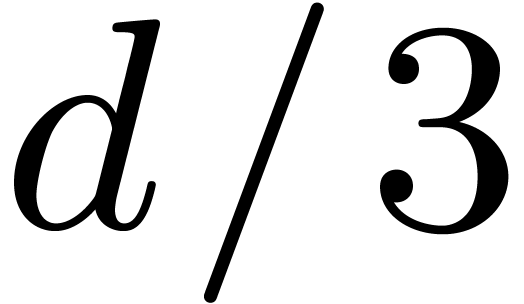 simple roots.
simple roots.
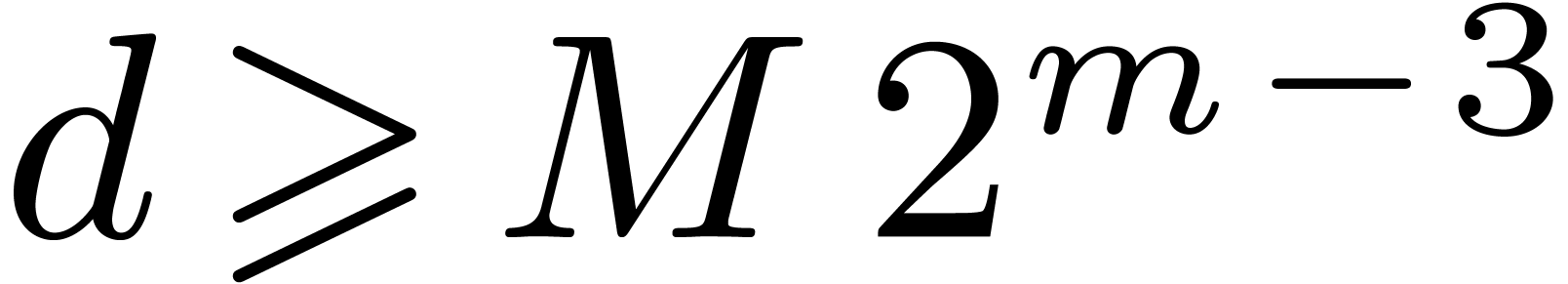 then evaluate
then evaluate 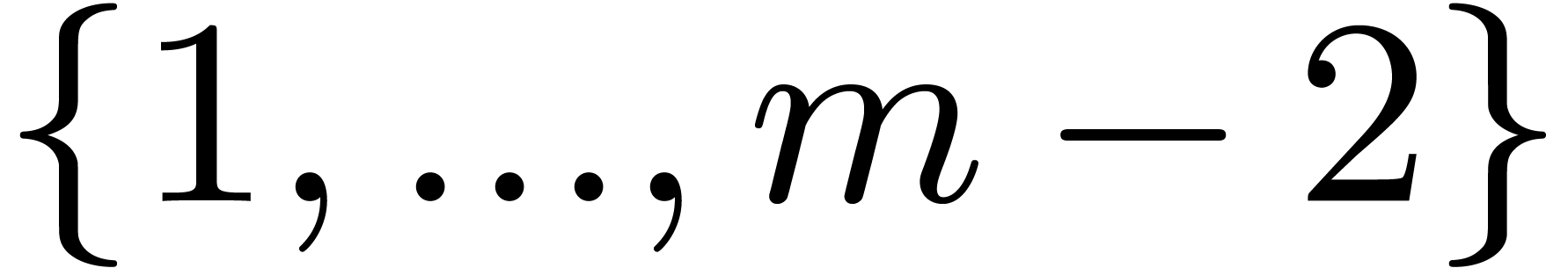 such that
such that 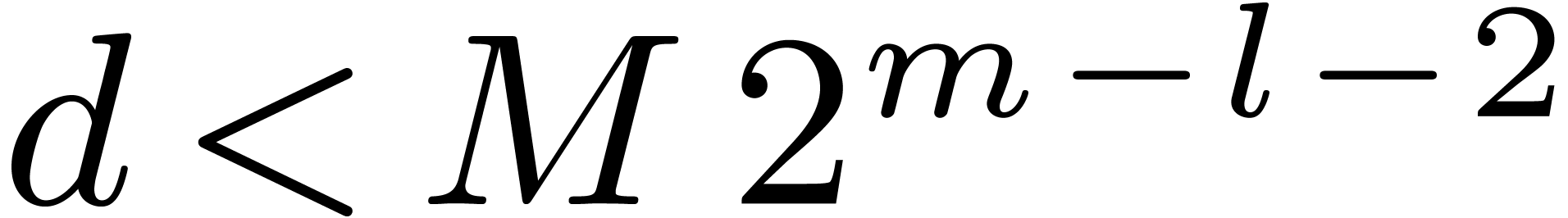 .
.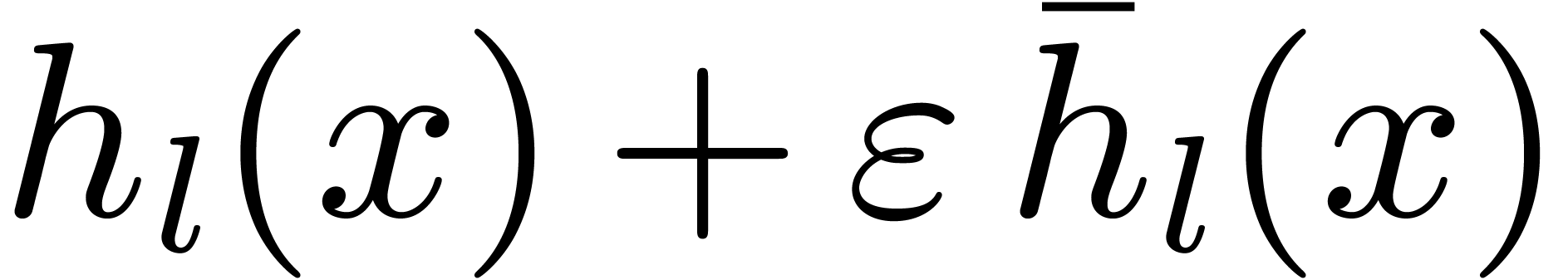 of order
of order 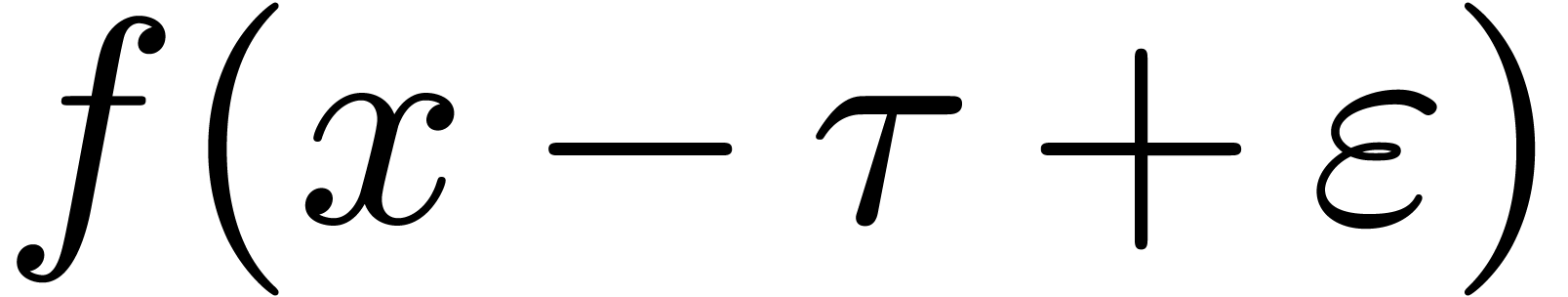 with
with 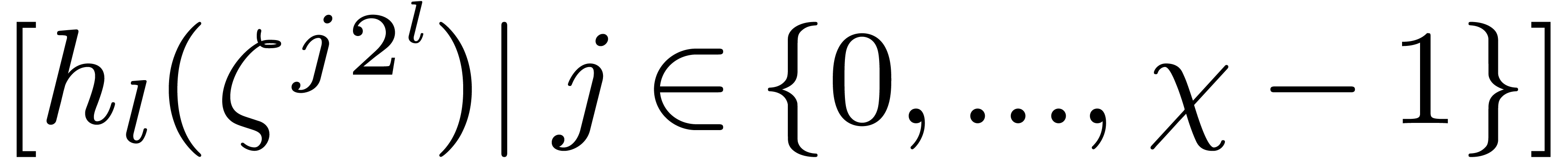 ,
,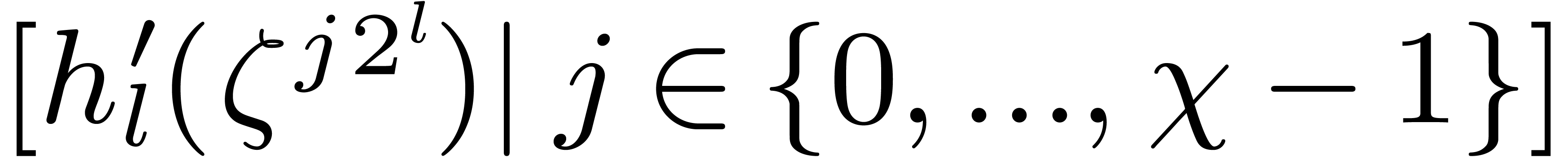 ,
,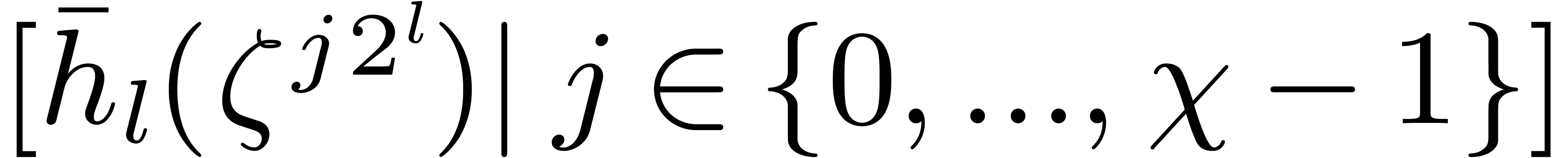 .
. .
.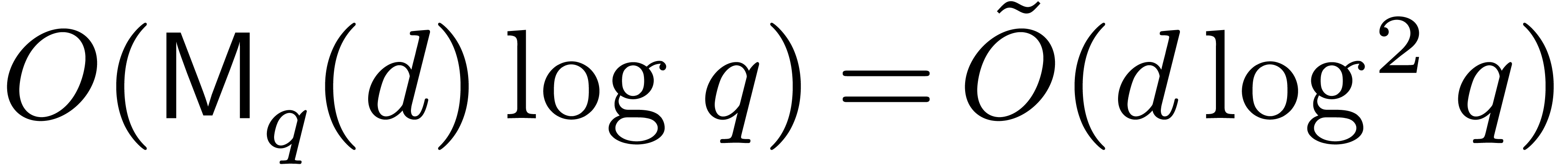 ,
,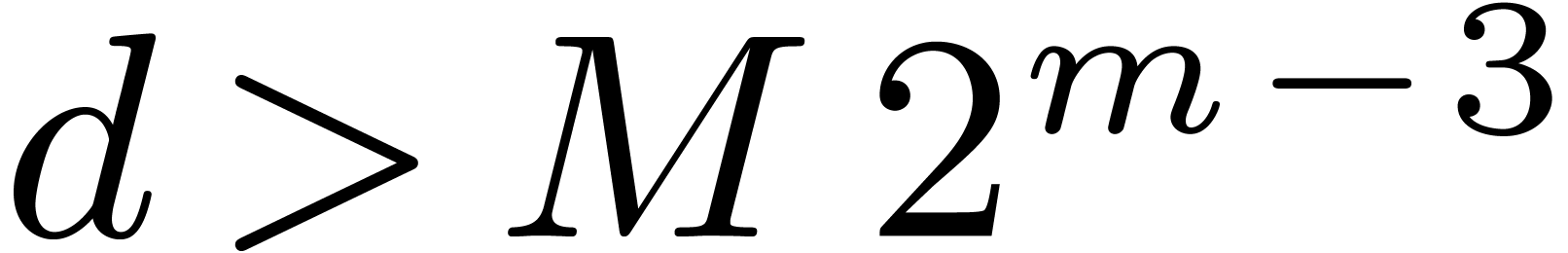 then
the cost is
then
the cost is  have order
dividing
have order
dividing 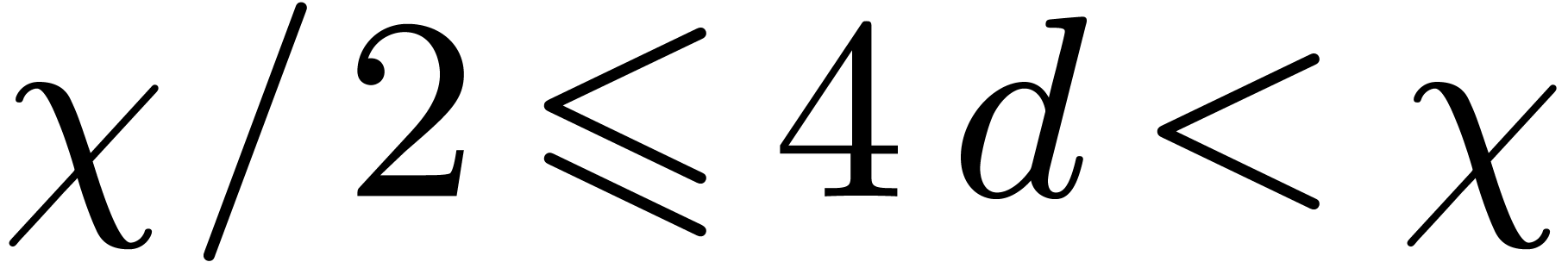 .
.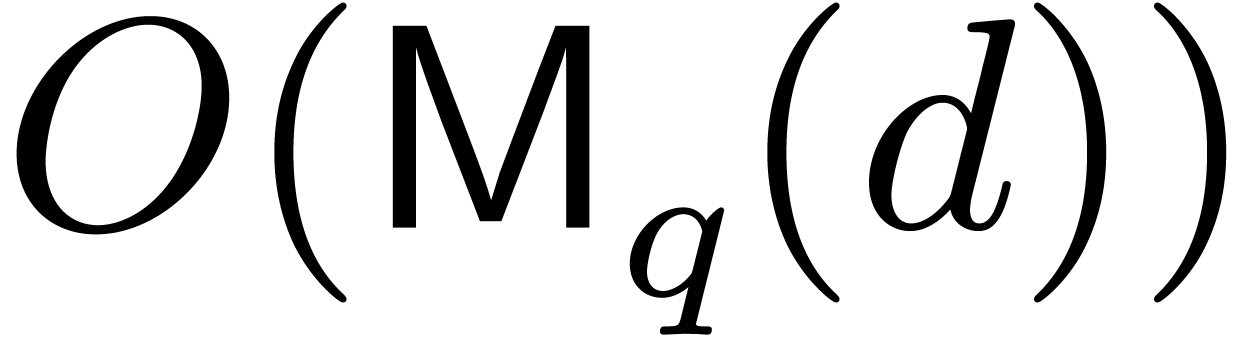 if
if  according to [
according to [ ,
,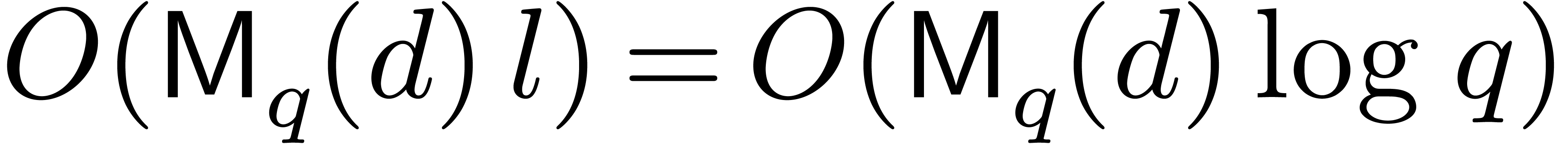 .
.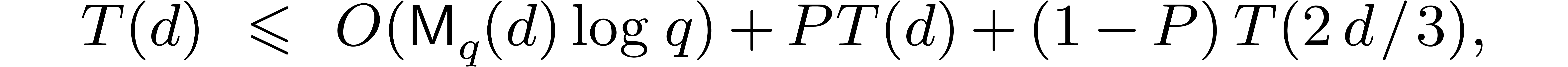
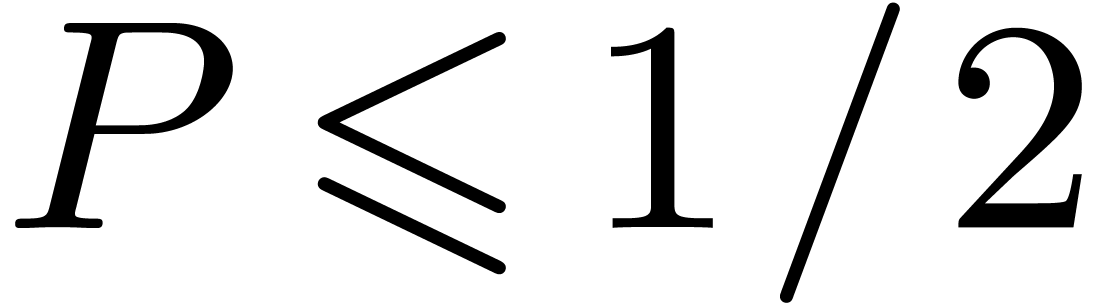 is the probability that
is the probability that 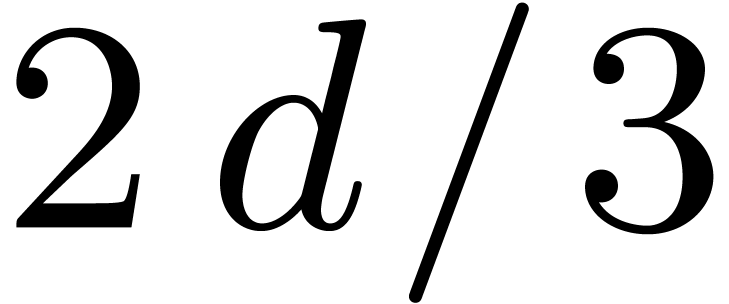 elements in step 7. It
follows that
elements in step 7. It
follows that 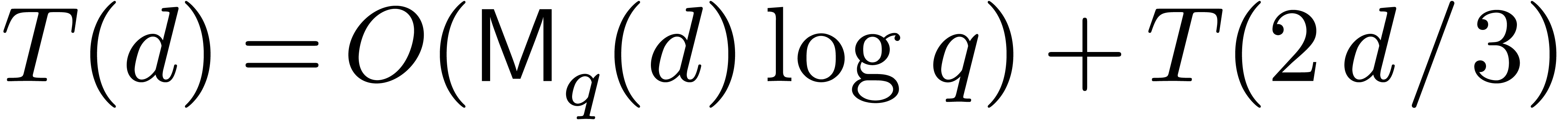 ,
,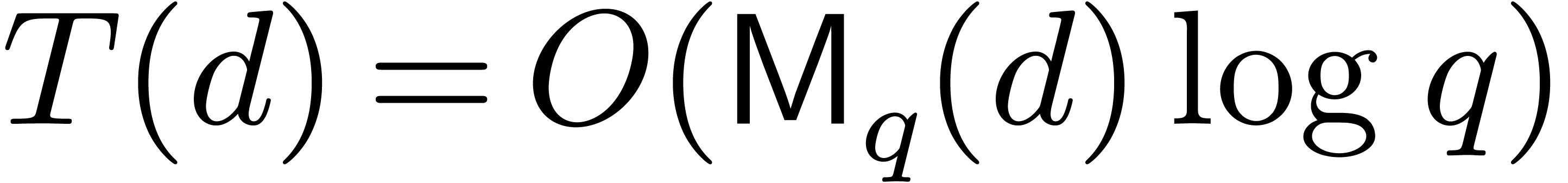 .
.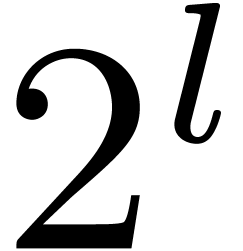 .
.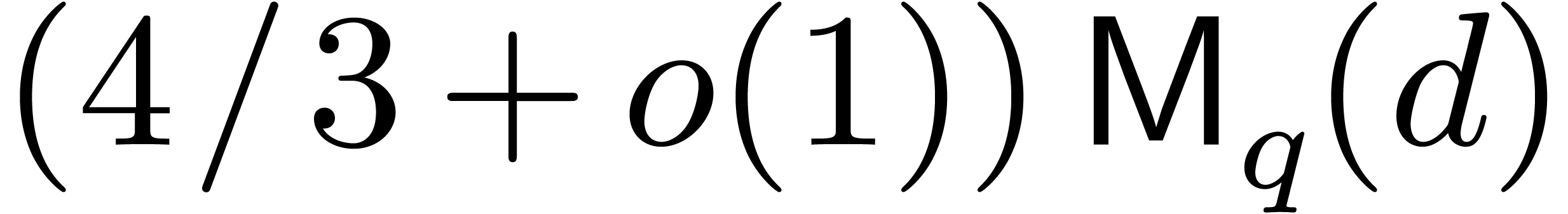 .
.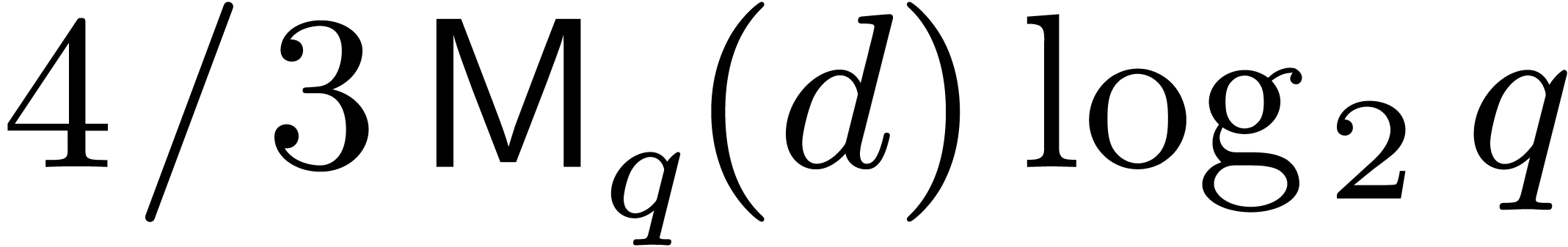 .
.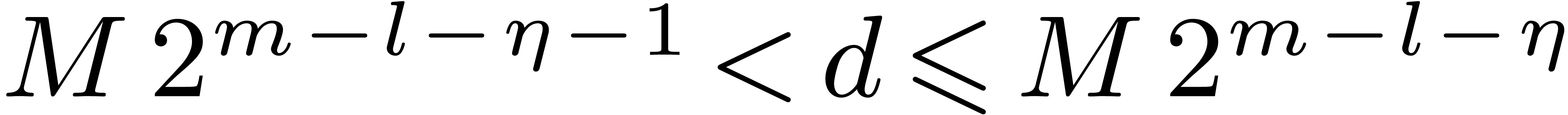 for
some small
for
some small  ,
, FFTs of size
FFTs of size 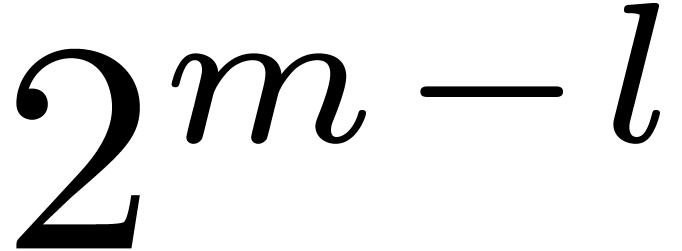 for small values of
for small values of 
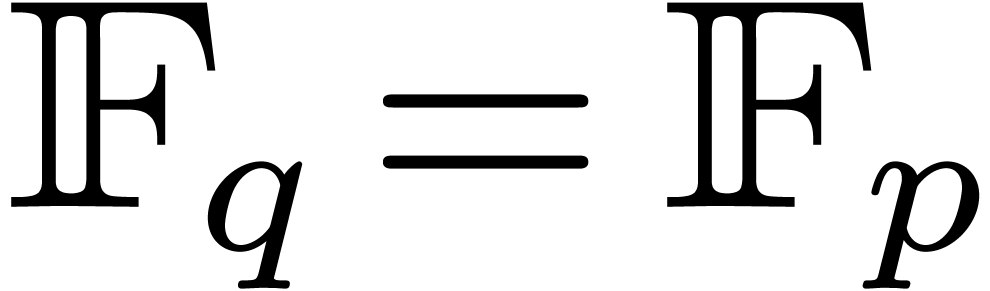 with
with 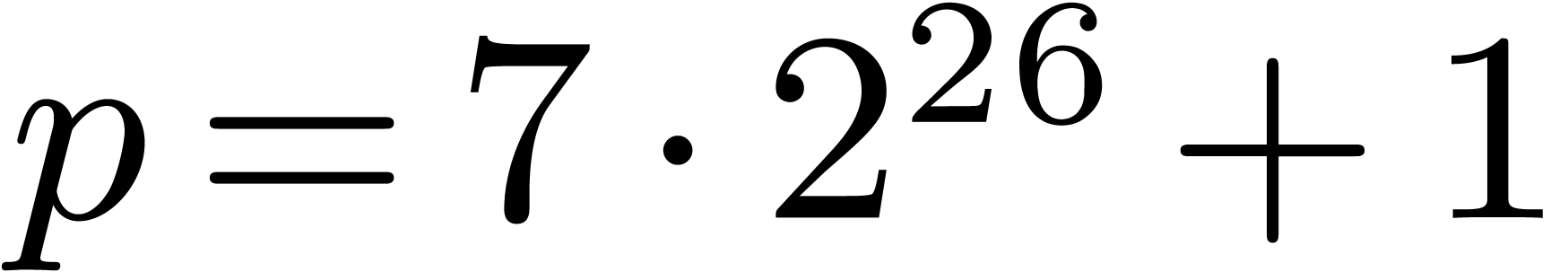 .
. ,
,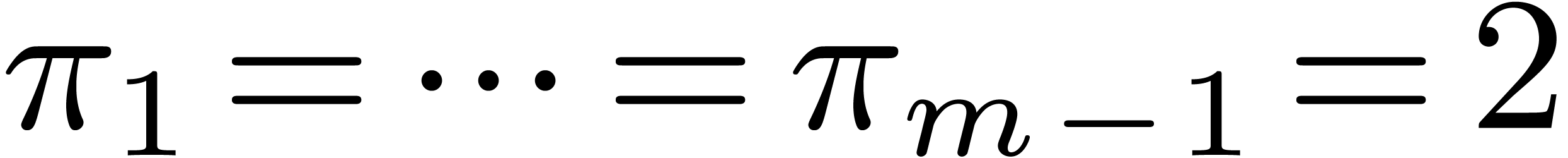 and
and 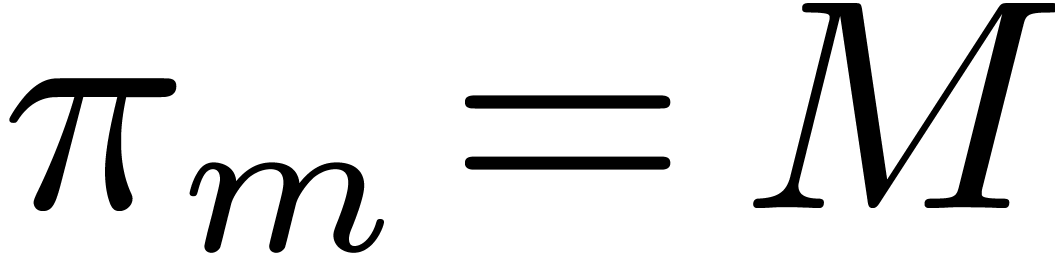 in Algorithm
in Algorithm 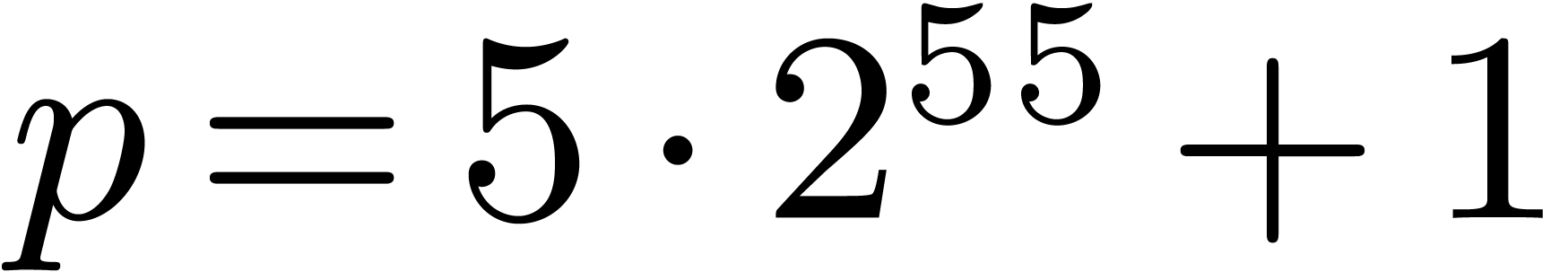 .
.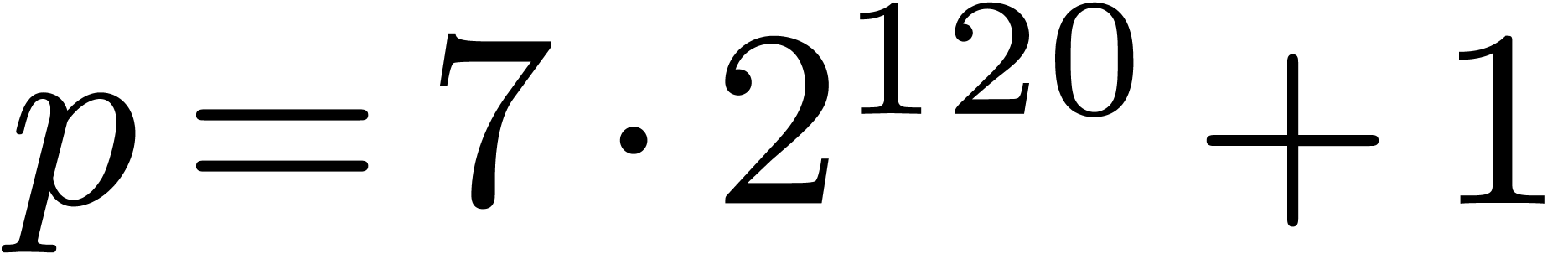 ,
, .
.
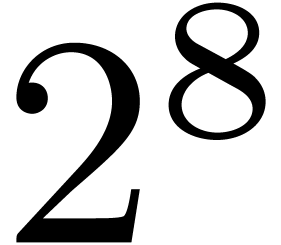
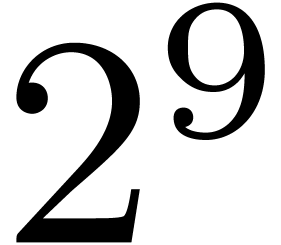
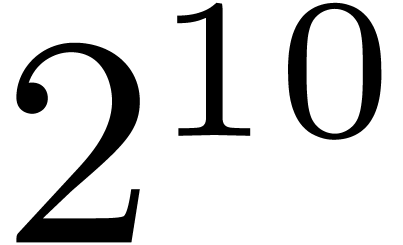
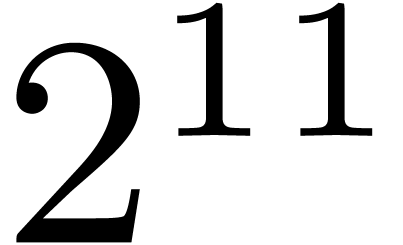
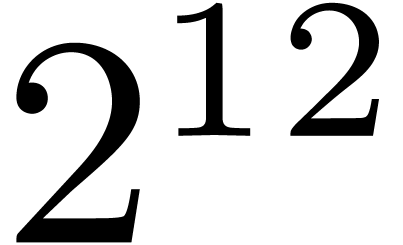
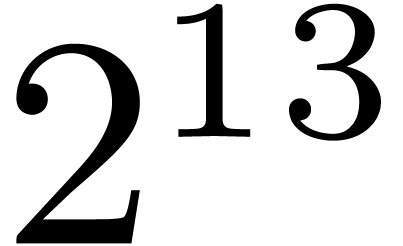
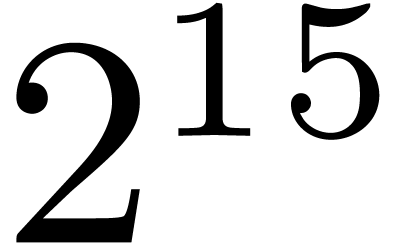
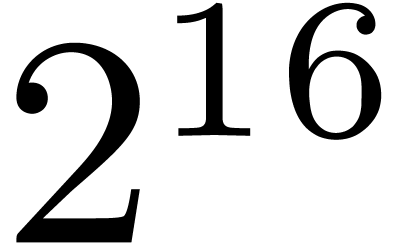

 matrix. For
matrix. For  ,
, s.
s.