Yet another differential shape
lemma |
|
| September 18, 2025 |
|
 . The first author
has been supported by an ERC-2023-ADG grant for the ODELIX
project (number 101142171). The second author has been
supported by the ANR-22-CE48-0008 (OCCAM) and ANR-22-CE48-0016
(NODE) grants.
. The first author
has been supported by an ERC-2023-ADG grant for the ODELIX
project (number 101142171). The second author has been
supported by the ANR-22-CE48-0008 (OCCAM) and ANR-22-CE48-0016
(NODE) grants.
Funded by the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. |
 |
Throughout this note, let  be a field of
characteristic zero. Consider a zero-dimensional ideal
be a field of
characteristic zero. Consider a zero-dimensional ideal 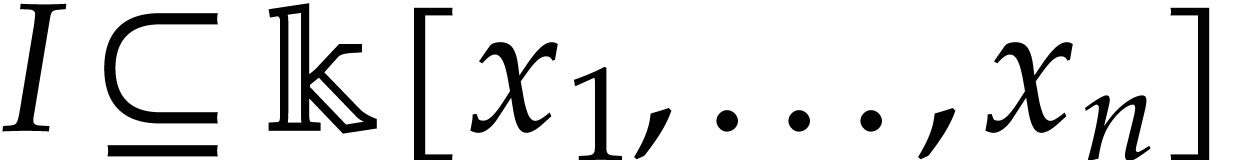 . Modulo a linear change of coordinates, one
may put
. Modulo a linear change of coordinates, one
may put 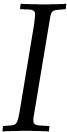 in general position, in the sense that
distinct roots of
in general position, in the sense that
distinct roots of 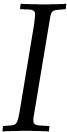 have distinct
have distinct 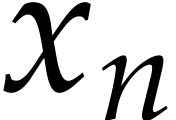 -coordinates. The original shape lemma was
proposed by Gianni and Mora [2] in order to describe the
shape of a lexicographical Gröbner basis of
-coordinates. The original shape lemma was
proposed by Gianni and Mora [2] in order to describe the
shape of a lexicographical Gröbner basis of  . In the simplest case when the ideal is radical and
in general position, they show that it has a lexicographical
Gröbner basis of the form
. In the simplest case when the ideal is radical and
in general position, they show that it has a lexicographical
Gröbner basis of the form
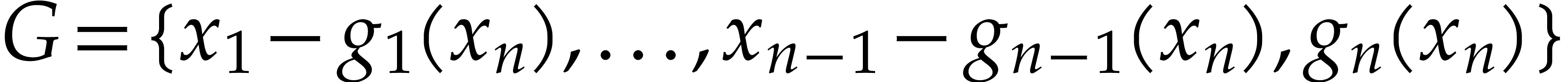
where  is monic and
is monic and 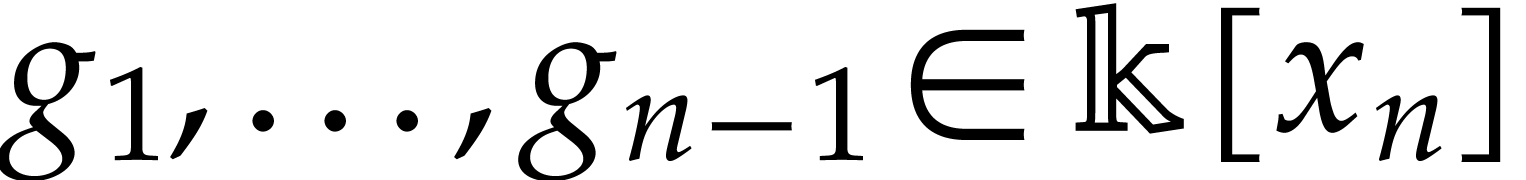 are
of degree
are
of degree 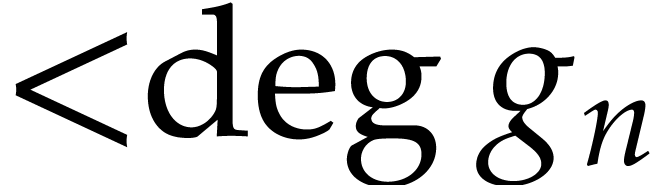 .
.
More recently, a non-commutative version of the shape lemma was proposed
in [4] for zero-dimensional left ideals 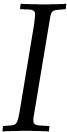 of the algebra
of the algebra 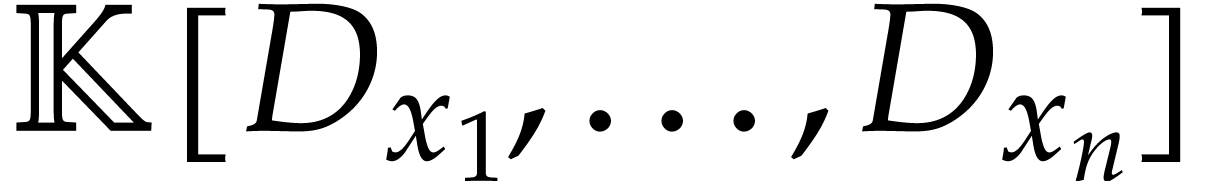 , where
, where 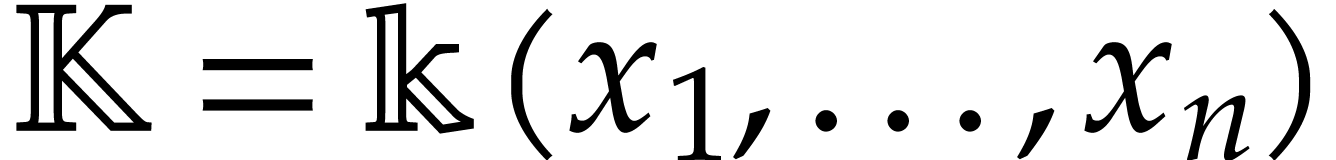 and
and  are the partial
derivations with respect to
are the partial
derivations with respect to  .
If
.
If 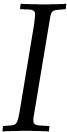 is generated by operators with constant
coefficients, then the “non-commutative” shape lemma
directly follows from the classical shape lemma, since
is generated by operators with constant
coefficients, then the “non-commutative” shape lemma
directly follows from the classical shape lemma, since 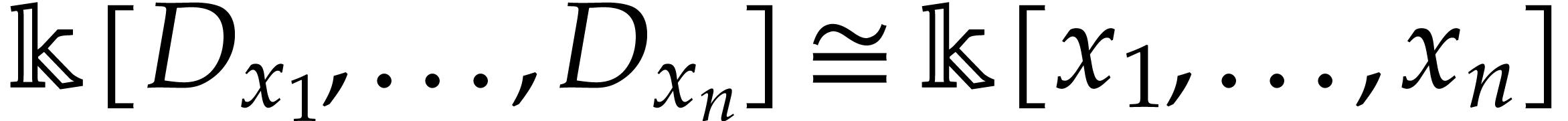 as
as  -algebras. For the general
case, the authors introduce the notion of D-radical ideals as a
non-commutative counterpart of radical ideals. They then generalize the
classical shape lemma to D-radical ideals. It turns out that only
constant linear changes of coordinates are required in order to put
D-radical ideals into general position.
-algebras. For the general
case, the authors introduce the notion of D-radical ideals as a
non-commutative counterpart of radical ideals. They then generalize the
classical shape lemma to D-radical ideals. It turns out that only
constant linear changes of coordinates are required in order to put
D-radical ideals into general position.
In this paper, we take the perspective of differential algebra. In that
case, any differential ideal generated by linear differential
polynomials is automatically radical. There is also a counterpart for
the classical correspondence between radical ideals and solutions sets:
in suitable polynomial exponential function spaces, left ideals of 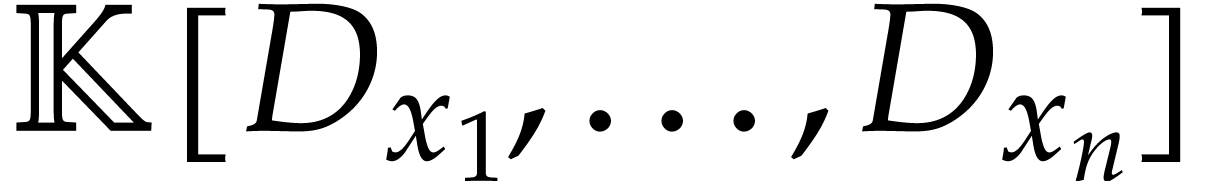 are in one-to-one correspondence with solutions sets;
see, e.g., [3, section 4.3].
are in one-to-one correspondence with solutions sets;
see, e.g., [3, section 4.3].
For any zero-dimensional left ideal 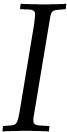 of
of 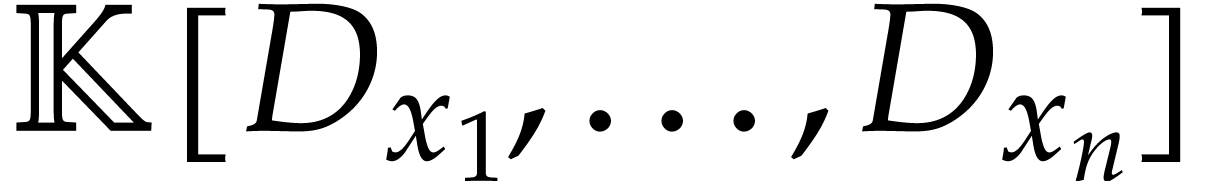 , we shall prove that we may put it
in shape position modulo a linear change of derivations
, we shall prove that we may put it
in shape position modulo a linear change of derivations
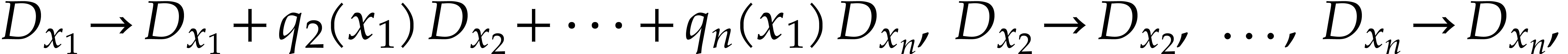
where 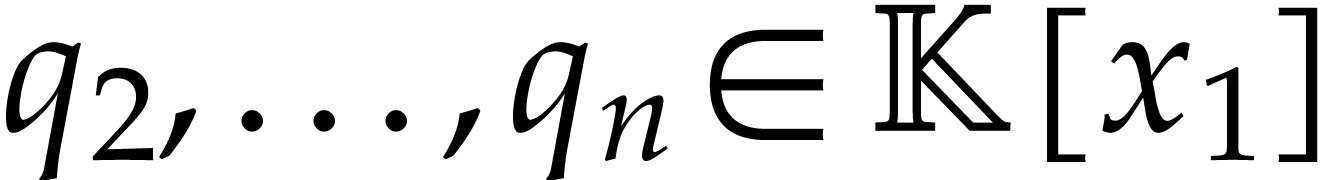 are polynomials. This corresponds to the
change of coordinates
are polynomials. This corresponds to the
change of coordinates
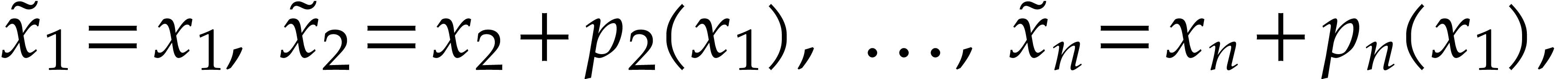
where 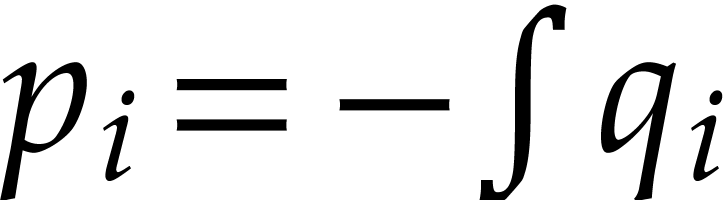 for
for 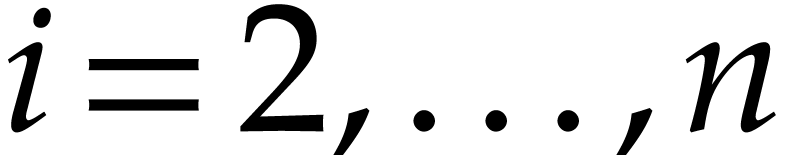 .
Contrary to the shape lemma from [4], our change of
derivations may have non-constant coefficients. On the other hand, no
further assumptions (like the D-radicality assumption) are required for
our result.
.
Contrary to the shape lemma from [4], our change of
derivations may have non-constant coefficients. On the other hand, no
further assumptions (like the D-radicality assumption) are required for
our result.
We start with the presentation of our main result in the bivariate case.
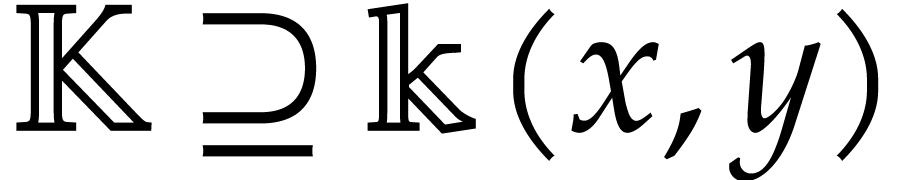 be a field equipped with commuting
derivations
be a field equipped with commuting
derivations 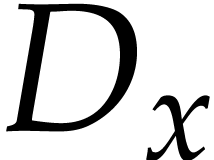 and
and 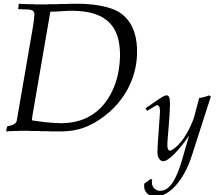 such
that
such
that 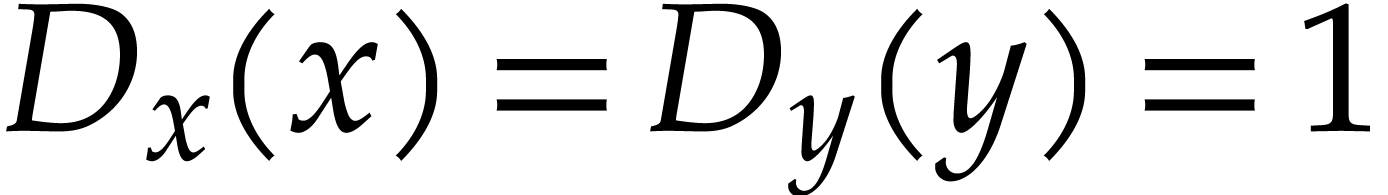 and
and 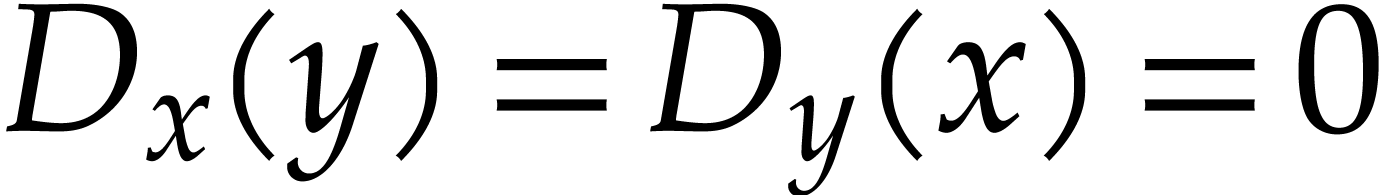 .
Let
.
Let 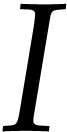 be a left ideal in
be a left ideal in 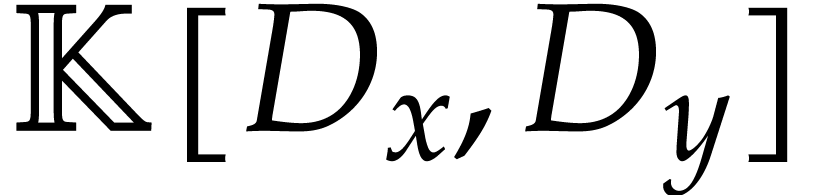 such that the quotient
such that the quotient 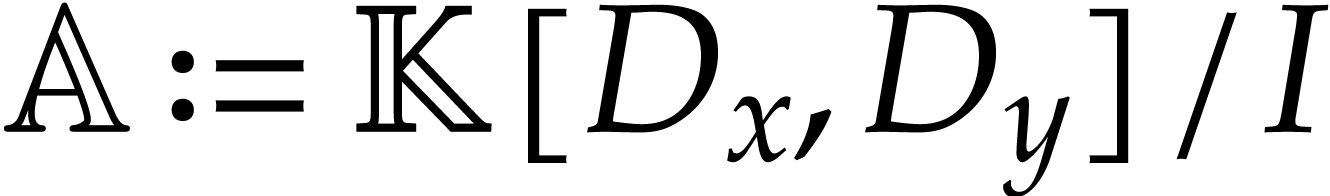 is finite-dimensional
over
is finite-dimensional
over  . Then there exists a
polynomial
. Then there exists a
polynomial 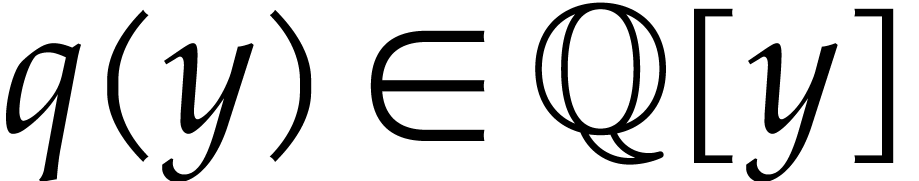 such that the powers of the
projection of
such that the powers of the
projection of 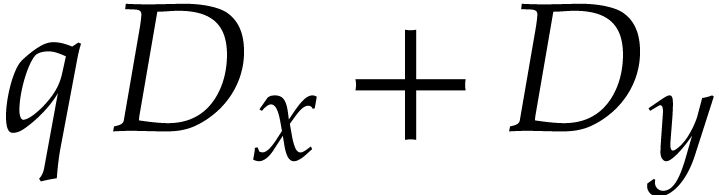 in
in  span
span
 as a
as a  -vector
space.
-vector
space.
Proof. For an element 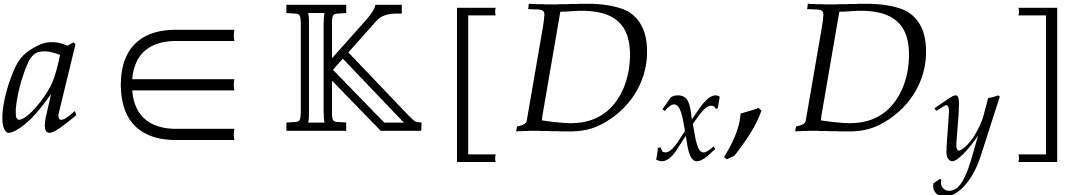 , let
, let  denote its projection
in
denote its projection
in  . Let
. Let  . We pick
. We pick 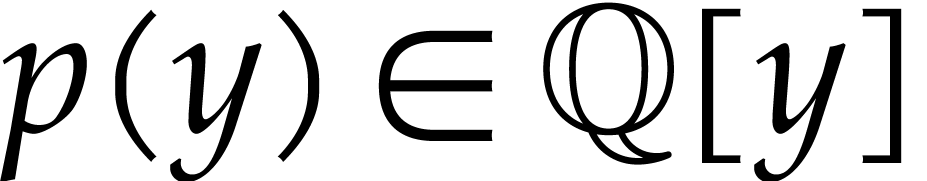 such that the
dimension of the subspace spanned by
such that the
dimension of the subspace spanned by 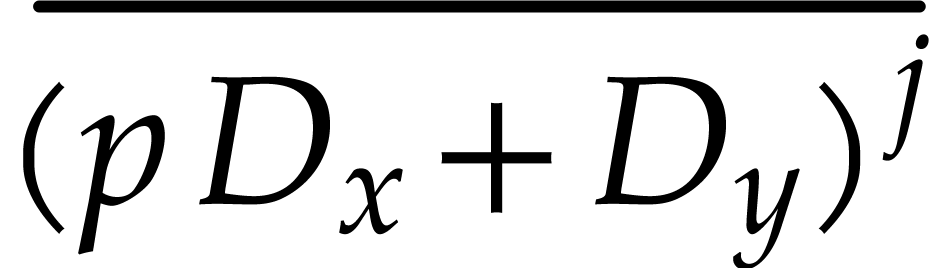 for
for  is largest possible. We denote this subspace by
is largest possible. We denote this subspace by  and its dimension by
and its dimension by  ,
and will prove that
,
and will prove that  . We also
introduce
. We also
introduce 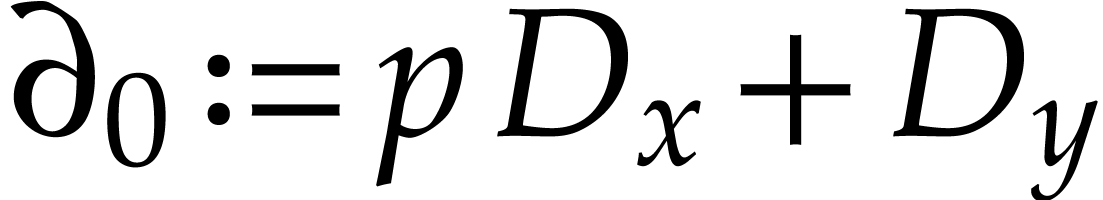 .
.
We adjoin a countable set of variables 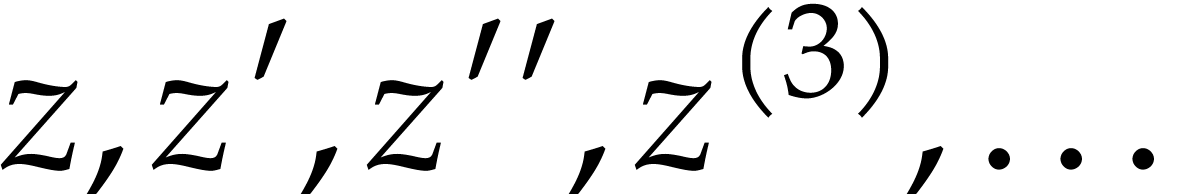 to
to  and let our derivatives act via
and let our derivatives act via 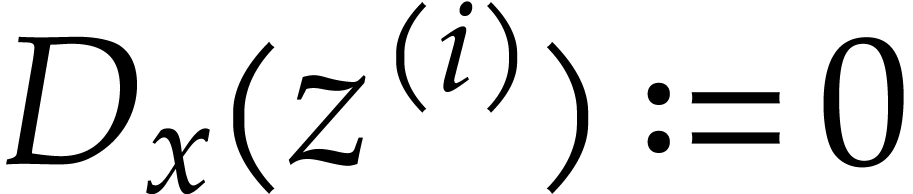 and
and 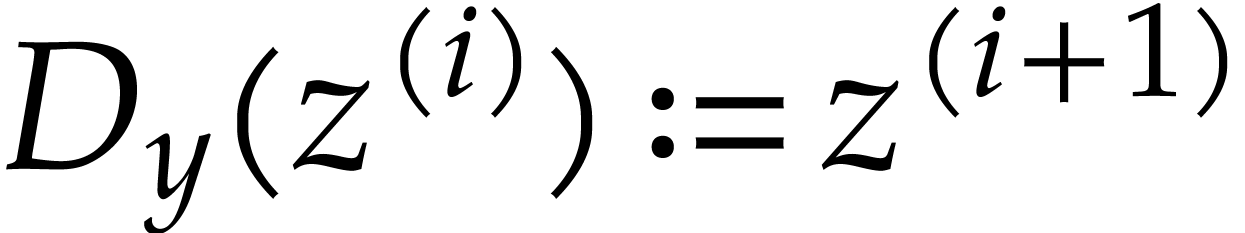 . We also define the
differential operator
. We also define the
differential operator 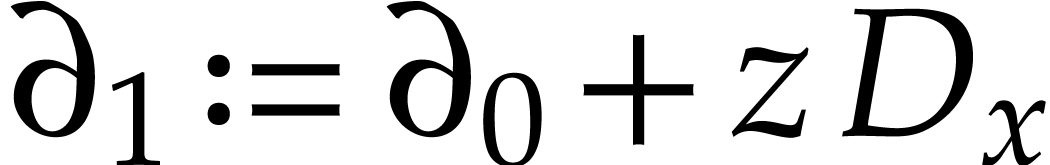 on
on 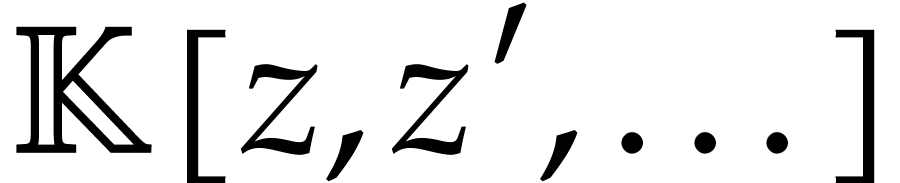 . Now consider the following element in the
. Now consider the following element in the 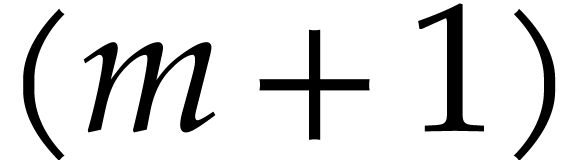 -st exterior power of
-st exterior power of 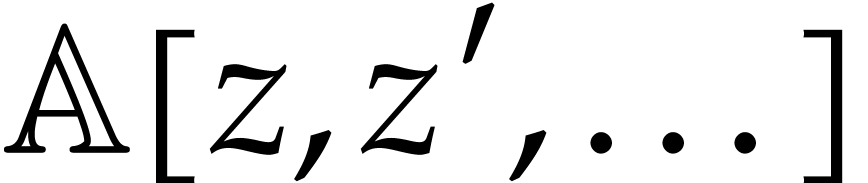 as a
as a 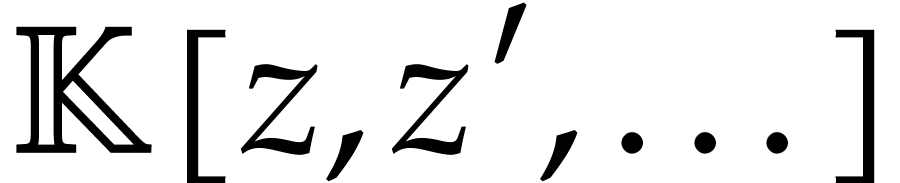 -module:
-module:
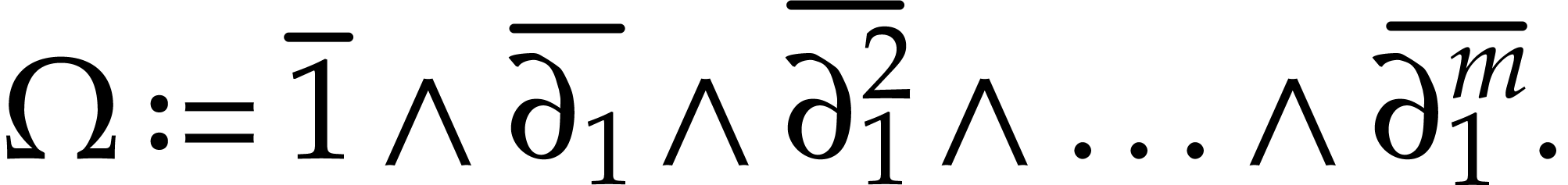 |
(1) |
By using the commutation rules between 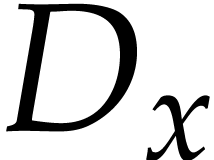 and
and 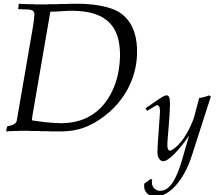 and elements of
and elements of 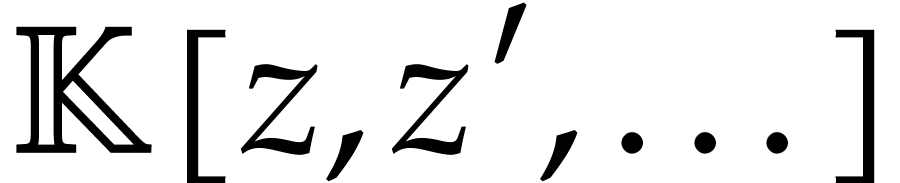 ,
we can write every
,
we can write every 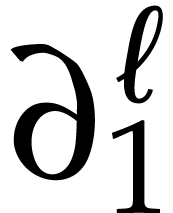 in the standard differential
operator form
in the standard differential
operator form 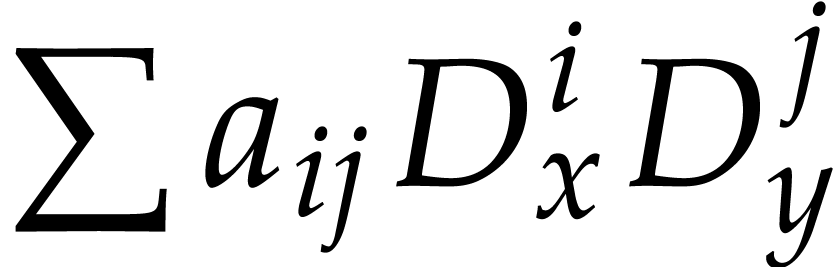 with
with 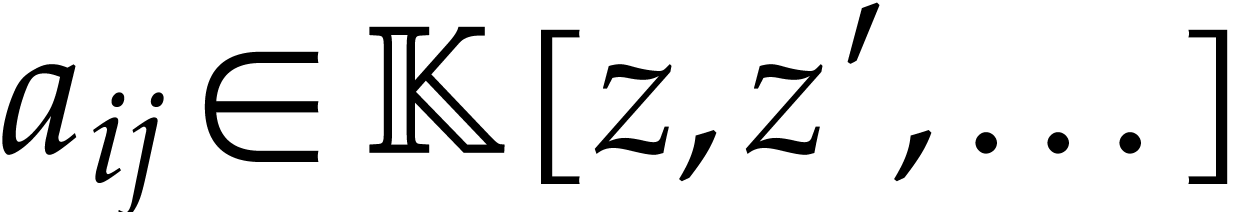 .
Substituting this representation into (1) and expanding by
linearity, we can regard
.
Substituting this representation into (1) and expanding by
linearity, we can regard  as a polynomial in
as a polynomial in 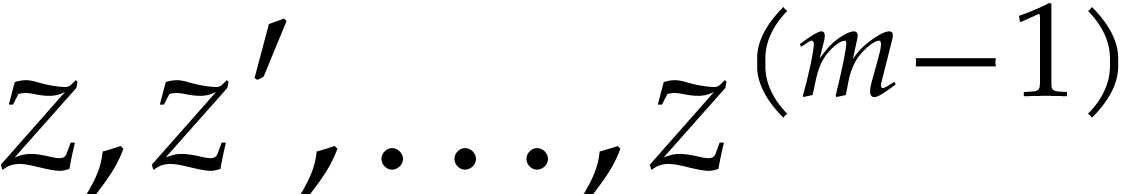 with coefficients in
with coefficients in 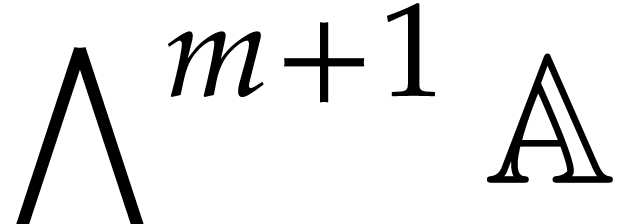 ,
of the following precise form:
,
of the following precise form:
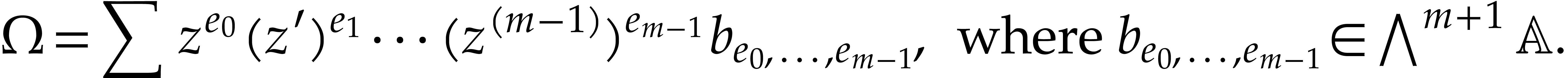
By the assumption on the maximality of the dimension of  , this polynomial vanishes under any
substitution of the form
, this polynomial vanishes under any
substitution of the form 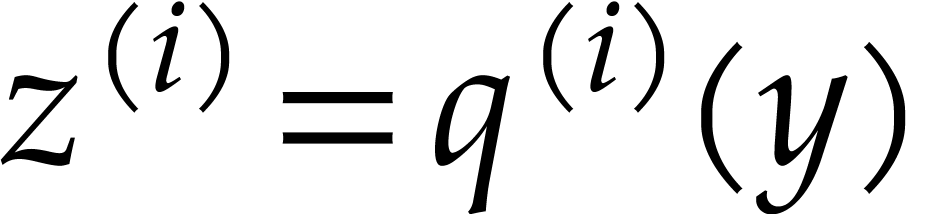 ,
where
,
where  is a polynomial. But this implies that
is a polynomial. But this implies that
 must vanish itself [5, p.35], so
all its coefficients
must vanish itself [5, p.35], so
all its coefficients 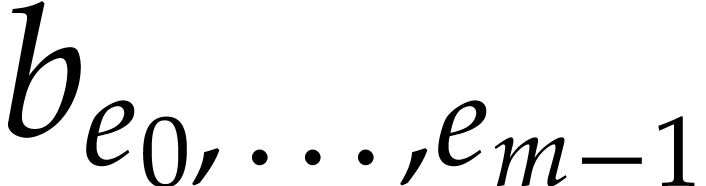 are zero in
are zero in 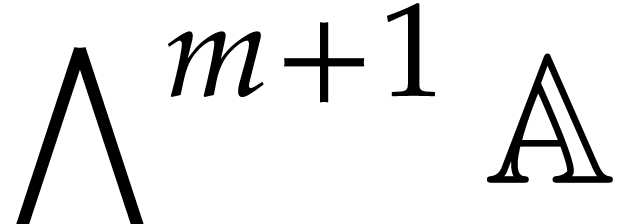 . Consider the coefficient of the monomial
. Consider the coefficient of the monomial
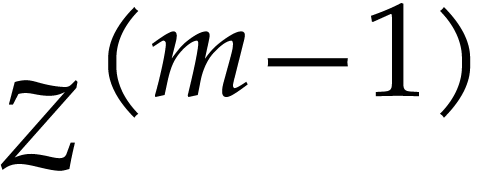 . Since the variable
. Since the variable 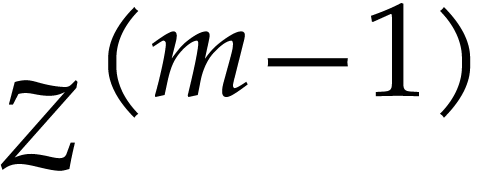 appears only in the last power of
appears only in the last power of 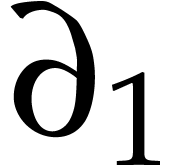 , we have
, we have
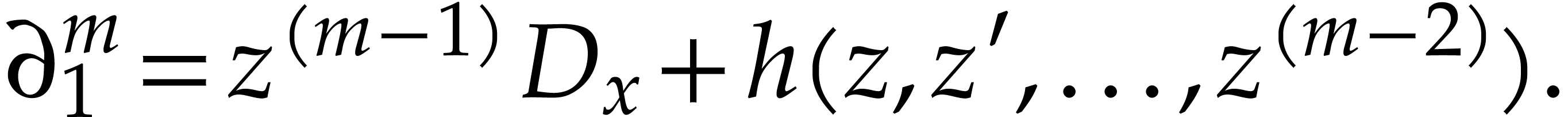
Hence the coefficient of 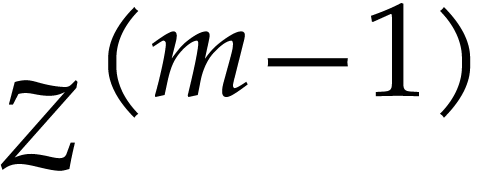 in (1) is
the wedge product of the
in (1) is
the wedge product of the  -free
parts
-free
parts  of the terms
of the terms  and
the coefficient
and
the coefficient 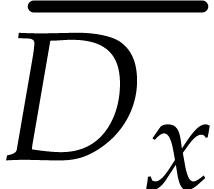 of
of 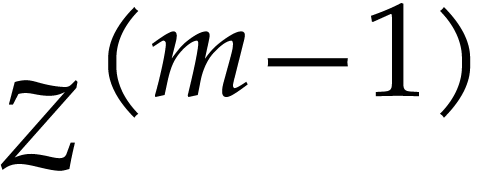 in
in
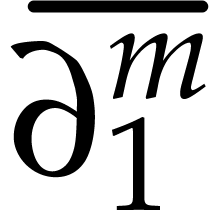 . Therefore,
. Therefore,
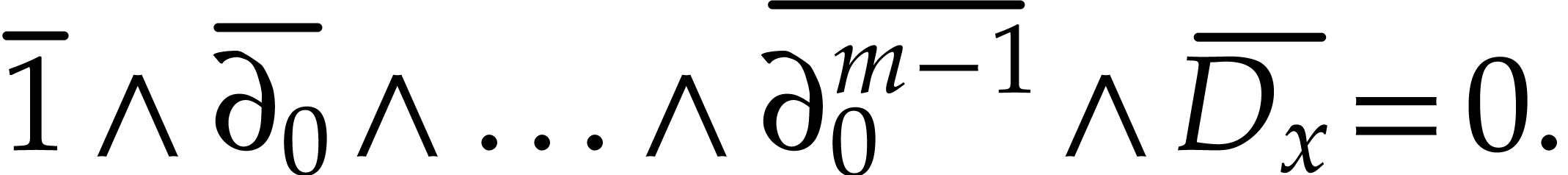
This implies that 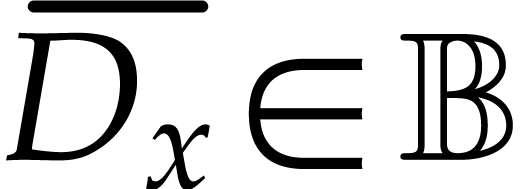 . Since
. Since
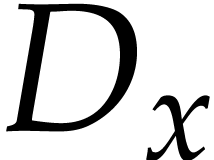 and
and 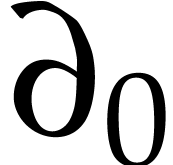 commute and generate
the whole
commute and generate
the whole 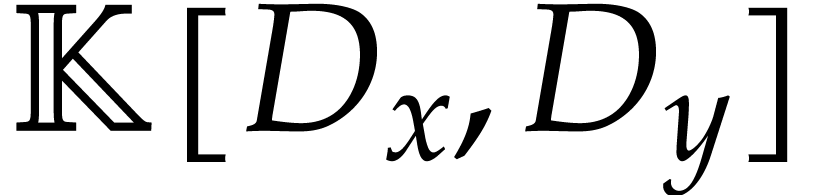 over
over  ,
we conclude that
,
we conclude that 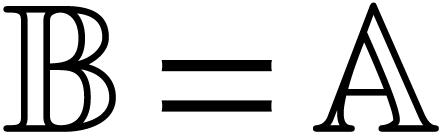 .
.
Remark
The following corollary gives an alternative formulation of Theorem 1 in terms of a change of variables.
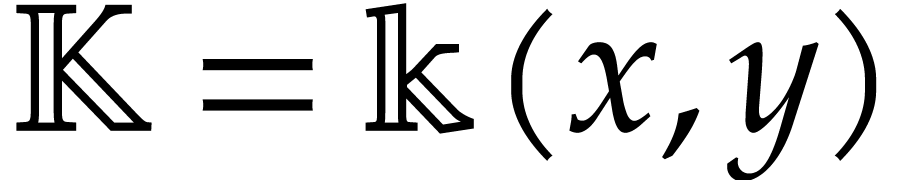 , where
, where 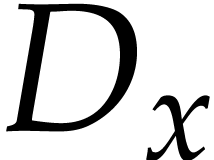 and
and 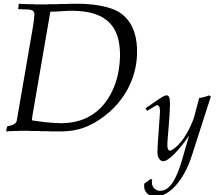 are the partial derivatives with respect to
are the partial derivatives with respect to  and
and 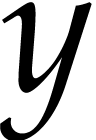 . Then
there exists a polynomial
. Then
there exists a polynomial  with the following
property. Consider an invertible polynomial change of variables
with the following
property. Consider an invertible polynomial change of variables 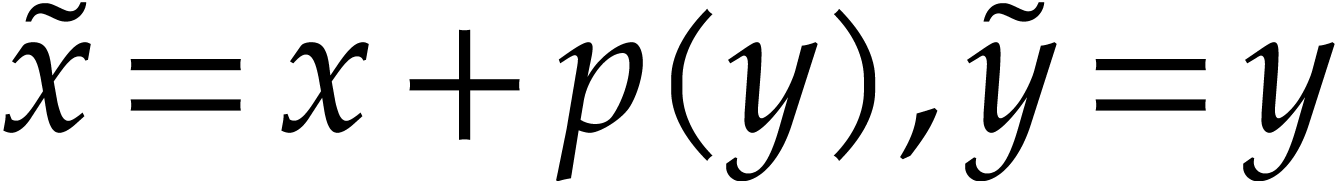 and denote the partial derivatives with respect to
and denote the partial derivatives with respect to
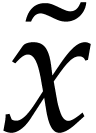 and
and 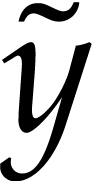 by
by  and
and 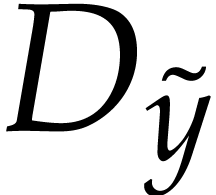 ,
respectively. Then the projections of powers of
,
respectively. Then the projections of powers of 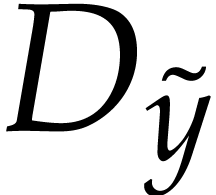 generate
generate  .
.
Proof. Applying Theorem 1, let 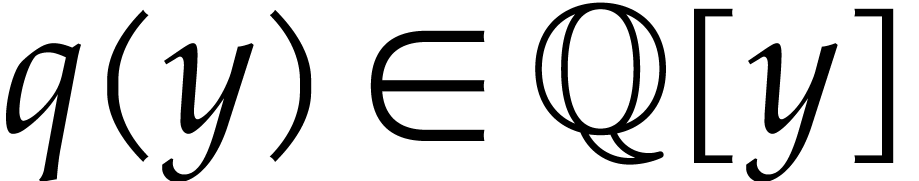 be the resulting polynomial and take
be the resulting polynomial and take 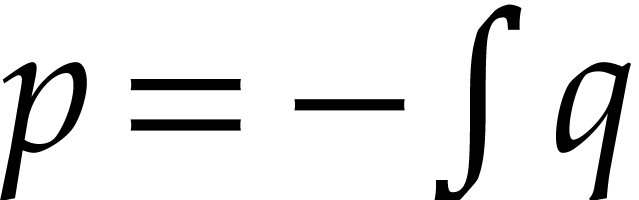 . Direct computation shows that
. Direct computation shows that 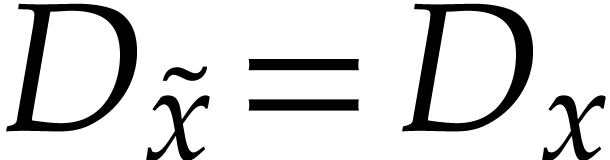 and
and 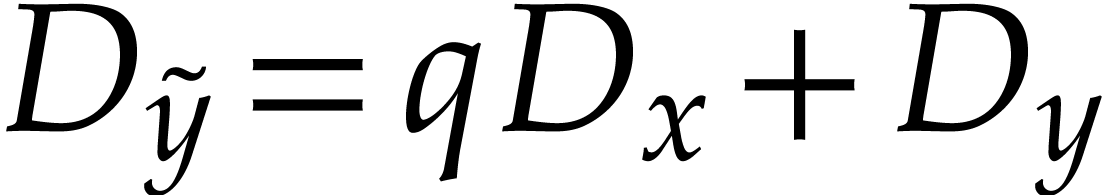 , so
, so 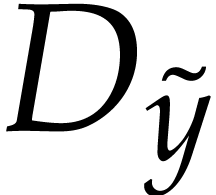 has the desired property.
has the desired property.
Example 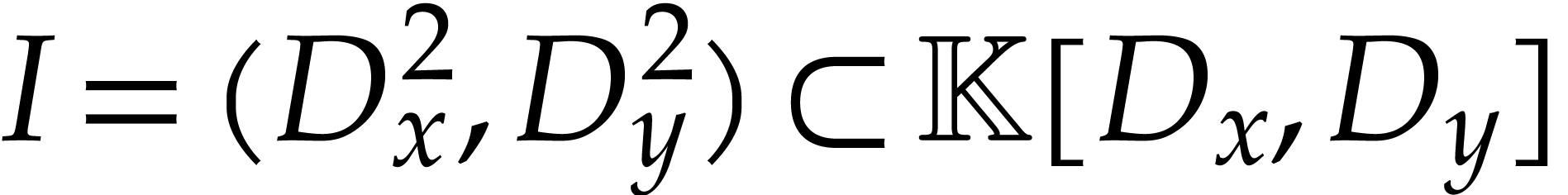 . Note that the results of [4] are not
applicable to this ideal since it is not D-radical. We consider
. Note that the results of [4] are not
applicable to this ideal since it is not D-radical. We consider 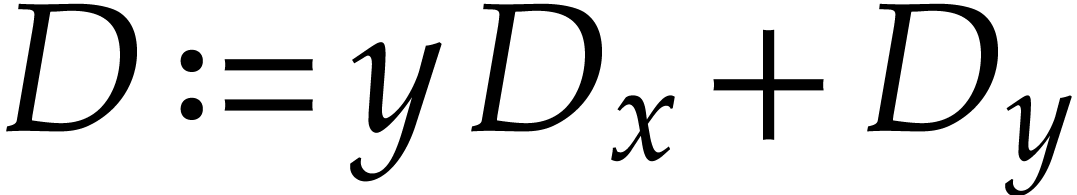 and compute its powers modulo
and compute its powers modulo 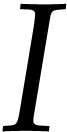 :
:
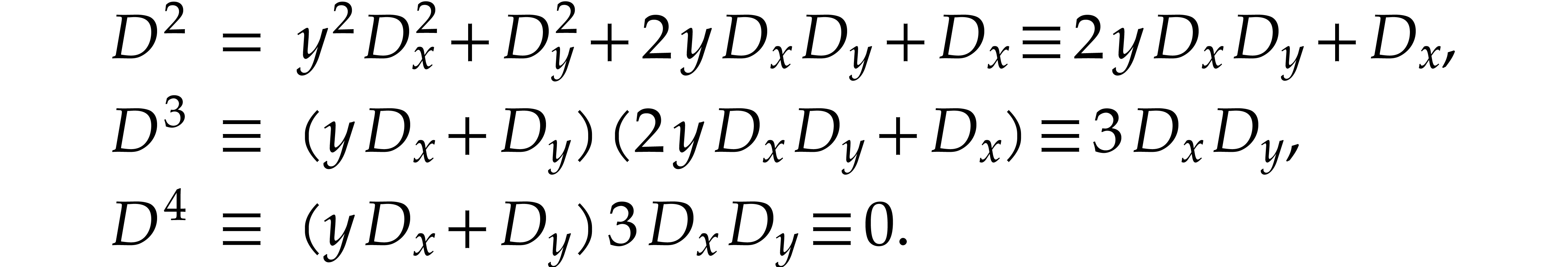
Thus, modulo 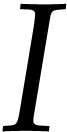 , we have
, we have 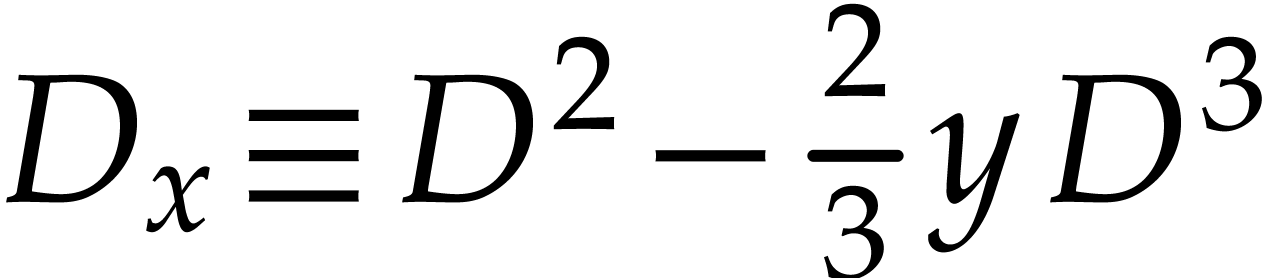 and
and 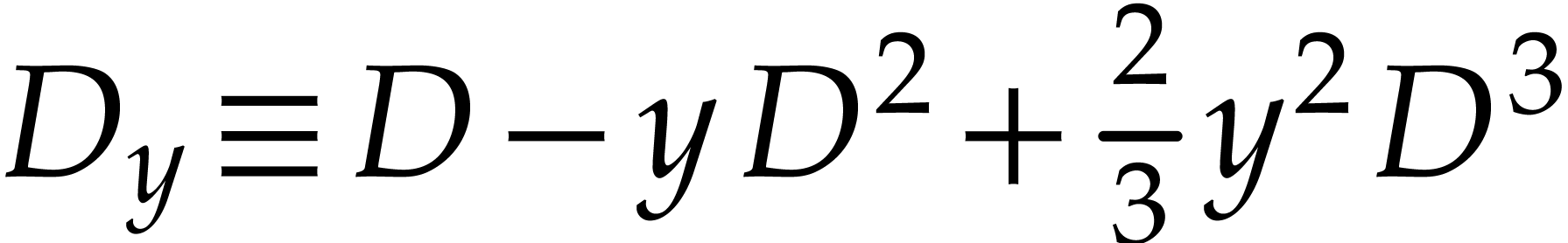 . The
corresponding change of variables is
. The
corresponding change of variables is 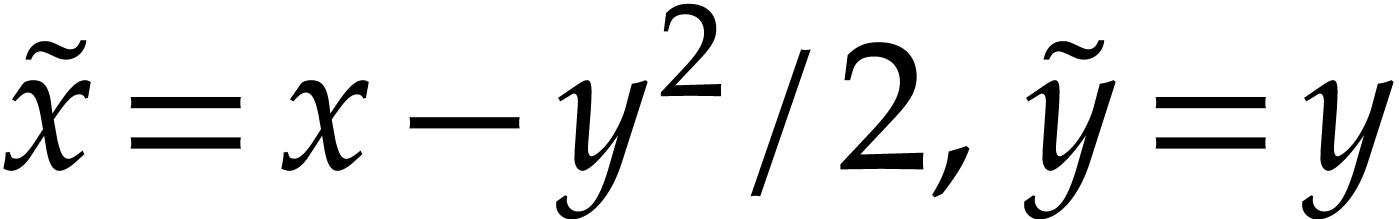 ,
and it transforms the ideal into
,
and it transforms the ideal into
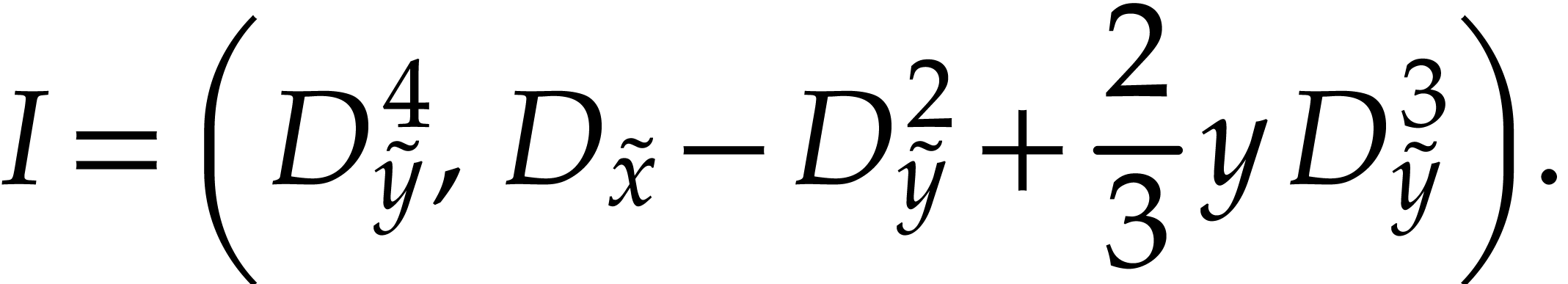
We now pursue with the multivariate case, by showing how to reduce it to the bivariate case from the previous section.
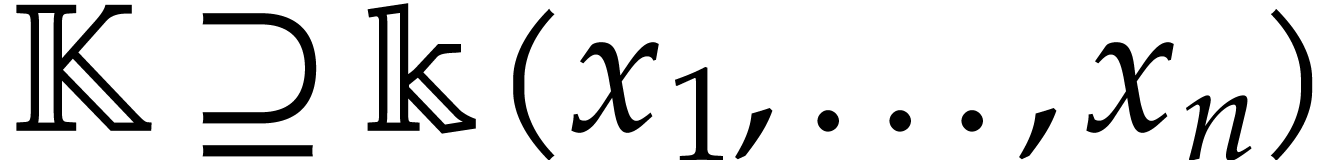 be a field equipped with pairwise
commuting derivations
be a field equipped with pairwise
commuting derivations  such that
such that 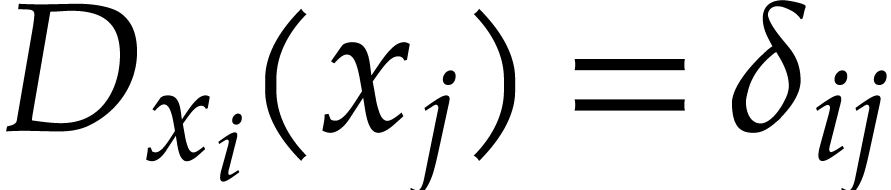 for all
for all 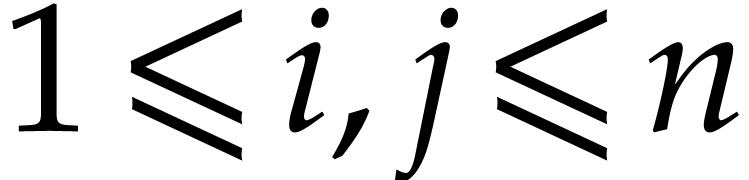 . Let
. Let
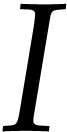 be a left ideal in
be a left ideal in 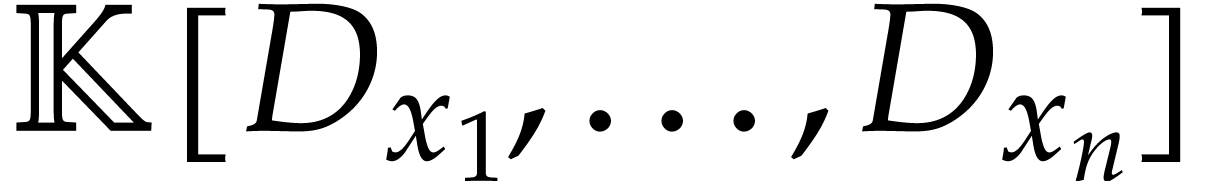 such that the quotient
such that the quotient 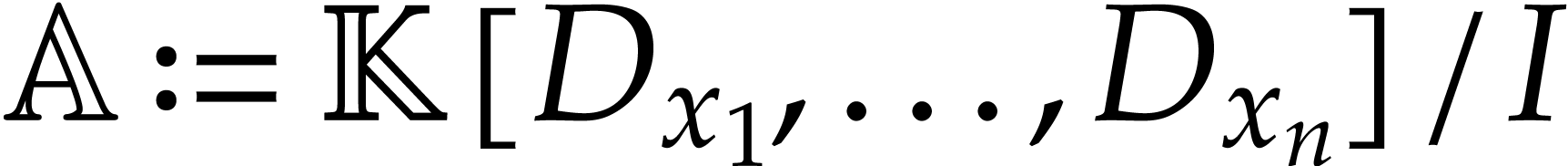 is finite-dimensional
over
is finite-dimensional
over  . Then there exist
univariate polynomials
. Then there exist
univariate polynomials 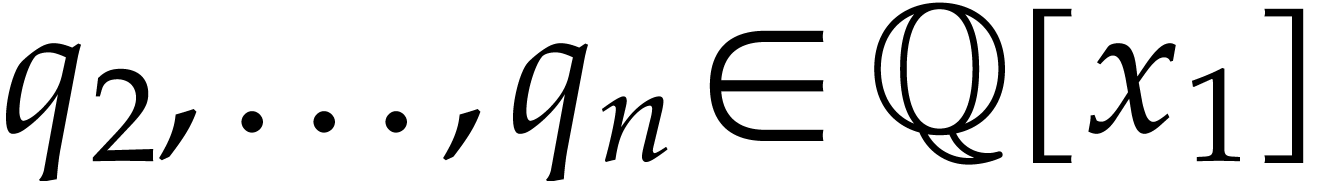 such that the
projections of powers of
such that the
projections of powers of
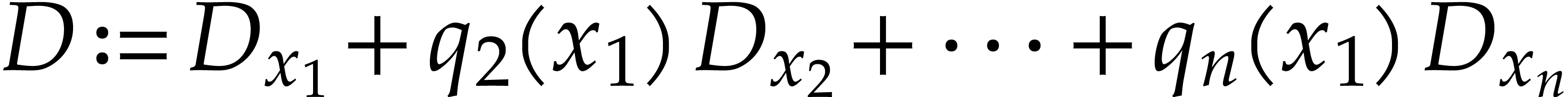
generate  as a
as a  -vector
space.
-vector
space.
Proof. We proceed by induction on 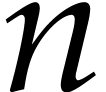 . The base case
. The base case 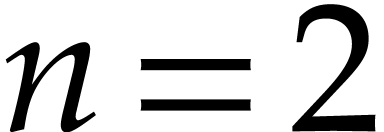 follows
from Theorem 1. Assume that
follows
from Theorem 1. Assume that 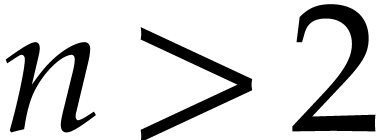 .
We apply the induction hypothesis to the ideal
.
We apply the induction hypothesis to the ideal 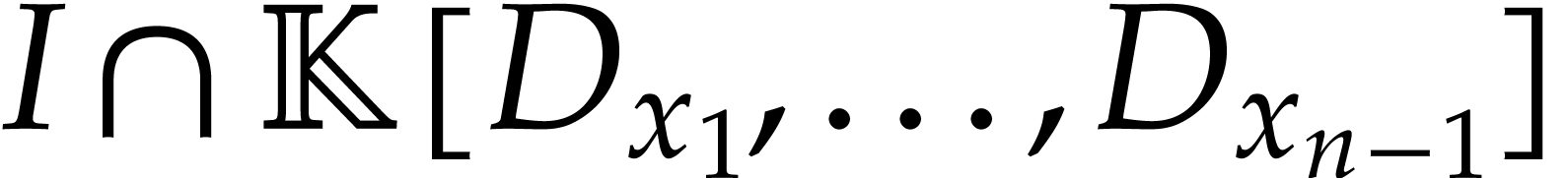 and
and  and obtain polynomials
and obtain polynomials 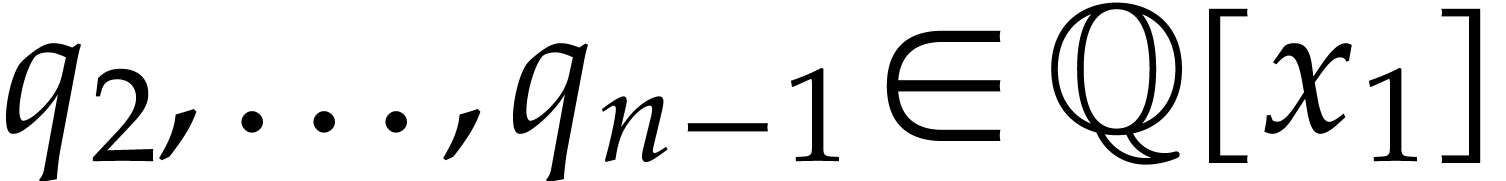 such that the projections of powers of
such that the projections of powers of
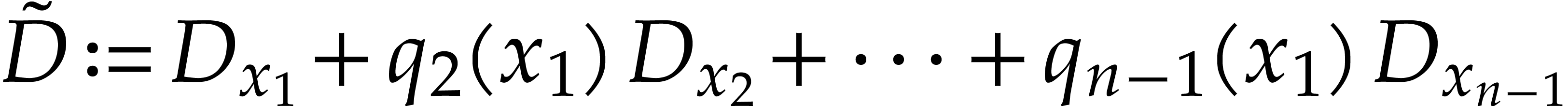
generate
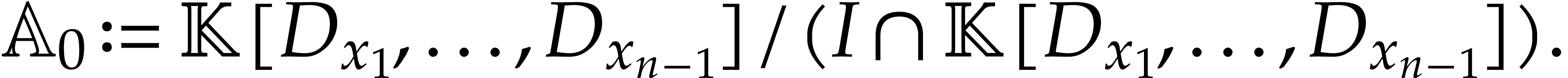
The embedding 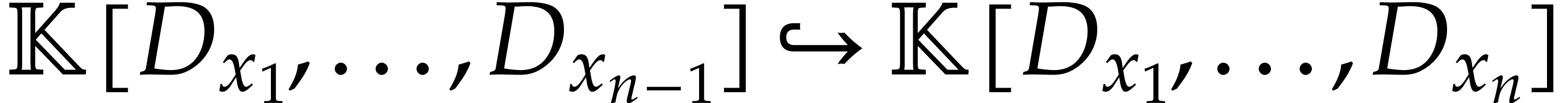 yields an embedding
yields an embedding  . Then
. Then  is generated by
the projection of
is generated by
the projection of 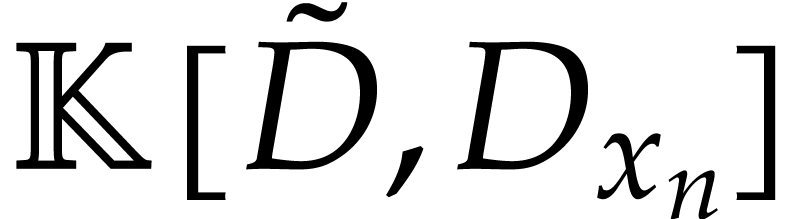 . We apply
Theorem 1, this time to the ideal
. We apply
Theorem 1, this time to the ideal 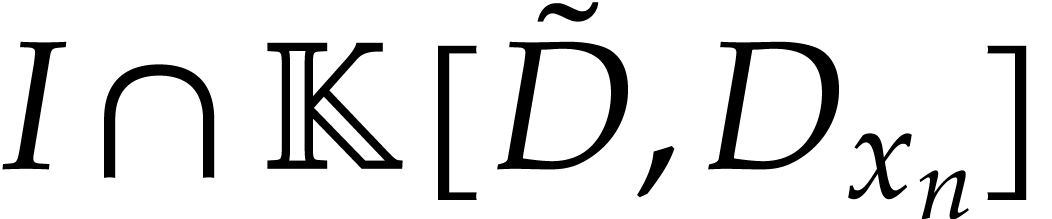 with
with 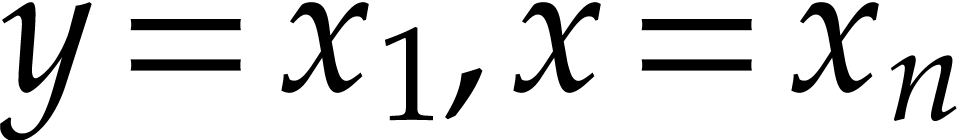 , and
, and 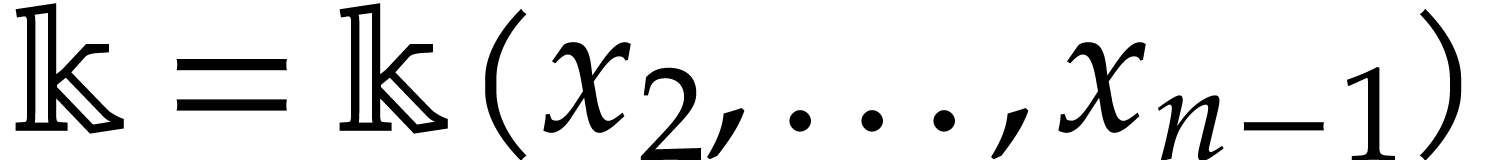 . This gives us a polynomial
. This gives us a polynomial  such that the projections of powers of
such that the projections of powers of
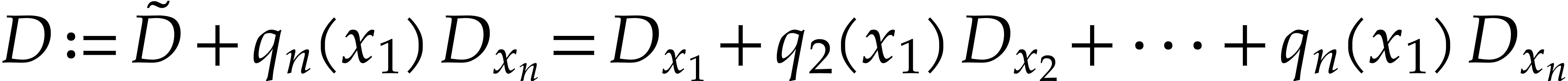
generate  . This finishes the
proof.
. This finishes the
proof.
Again, we may reformulate this result in terms of changes of variables.
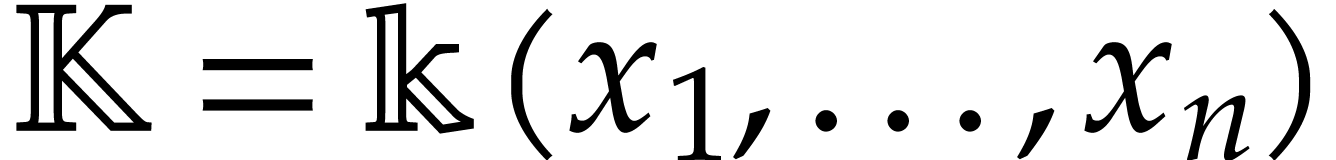 , so
, so  are
the respective partial derivatives. Then there exist polynomials
are
the respective partial derivatives. Then there exist polynomials 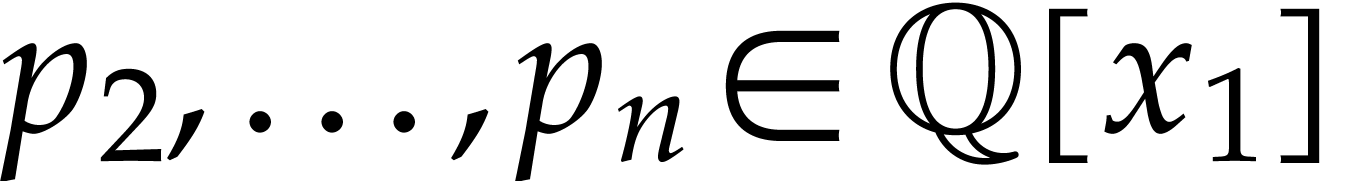 with the following property. Consider an invertible
polynomial change of variables
with the following property. Consider an invertible
polynomial change of variables
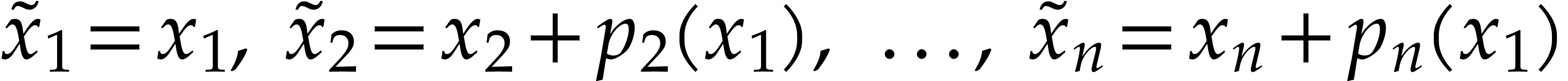
and denote the partial derivatives with respect to  by
by  , respectively. Then the
projections of powers of
, respectively. Then the
projections of powers of 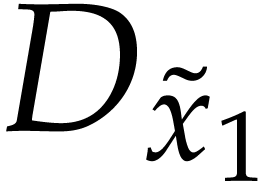 generate
generate  .
.
Proof. Applying Theorem 5, let 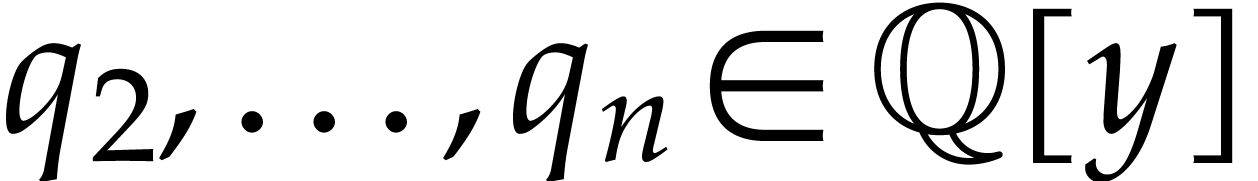 be the obtained polynomials. We take
be the obtained polynomials. We take 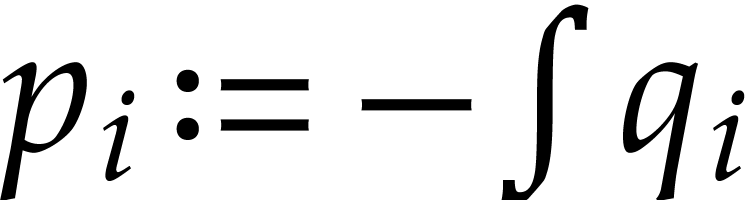 for
for 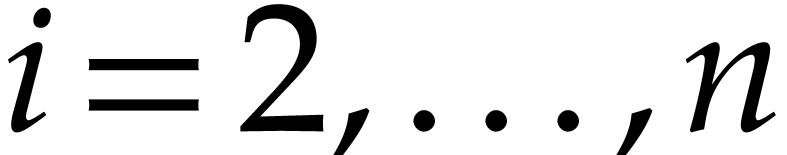 . Direct computation
shows that
. Direct computation
shows that
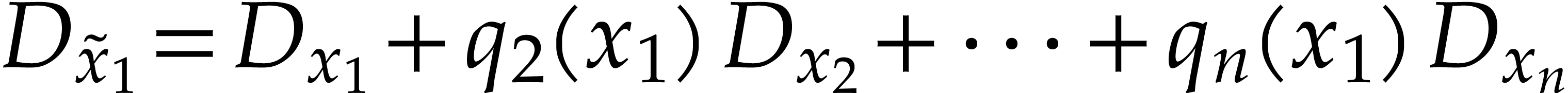
and 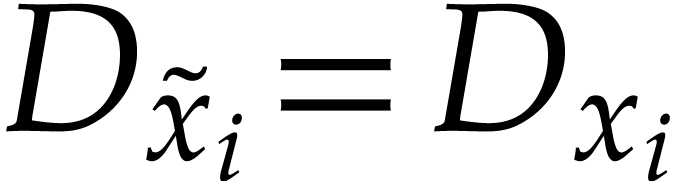 for
for 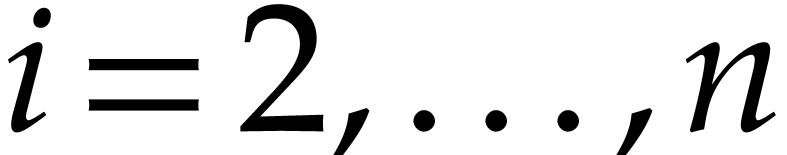 ,
so
,
so 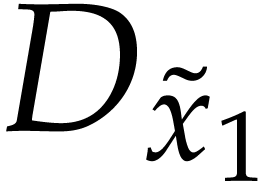 has the desired property.
has the desired property.
It is instructive to further examine the structure of modules that are generated by powers of a single derivation. For this, we recall [4, Theorem 8]:
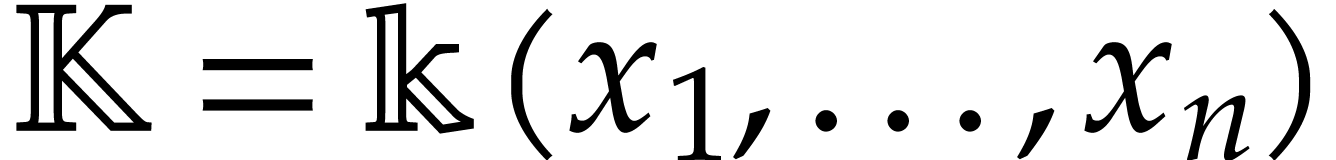 and let
and let  be the partial derivatives with respect to
be the partial derivatives with respect to  , respectively. Let
, respectively. Let 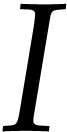 be a left ideal in
be a left ideal in 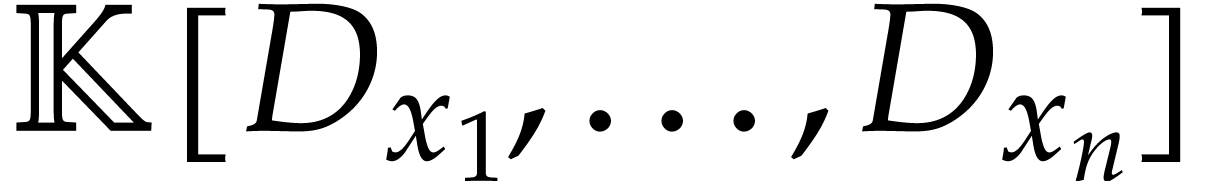 such that the quotient
such that the quotient 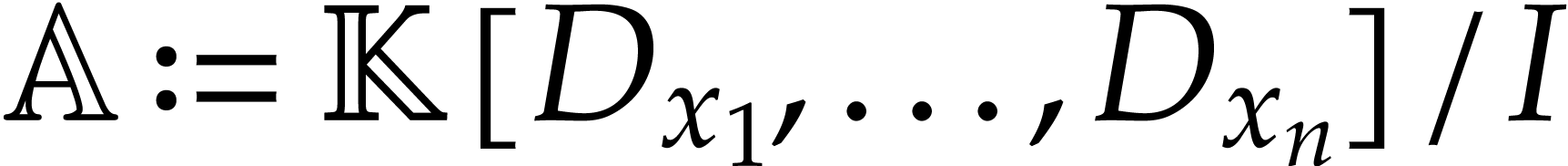 is finite-dimensional over
is finite-dimensional over  . Then, for a differential operator
. Then, for a differential operator 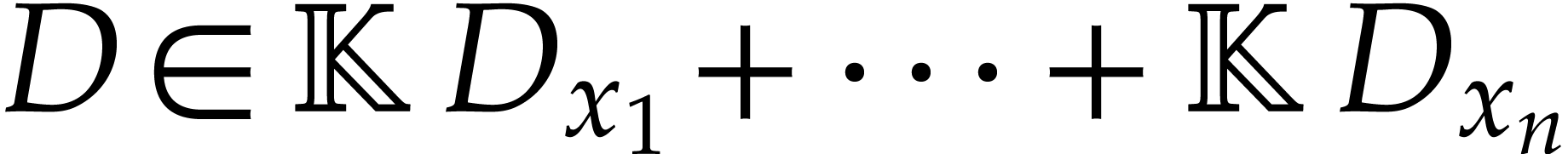 , the following conditions are
equivalent:
, the following conditions are
equivalent:
Proof. i  ii. As any element in A, the projection of
ii. As any element in A, the projection of 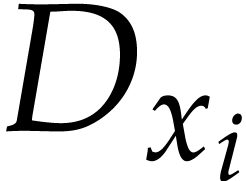 in
in  can be written as a
can be written as a  -linear combination of the
projections of powers of
-linear combination of the
projections of powers of 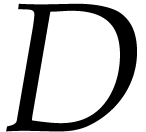 . We
can take this combination of powers as our polynomial
. We
can take this combination of powers as our polynomial 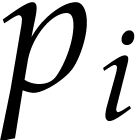 .
.
ii  i.
Since
i.
Since  is spanned by power products of
is spanned by power products of 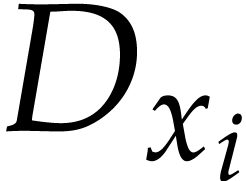 's and each of the
's and each of the 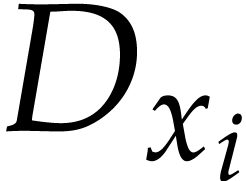 's is congruent modulo
's is congruent modulo 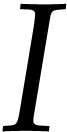 to a polynomial in
to a polynomial in 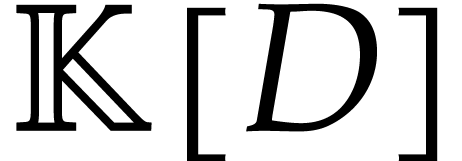 , the
projection of this polynomial ring is the whole
, the
projection of this polynomial ring is the whole  .
.
This section is dedicated to a more abstract version of Theorem 5. We start with a lemma that is essentially contained in the proof of [6, Lemma 2.2], but that we will reprove here for convenience of the reader.
 be a field of characteristic zero equipped
with pairwise commuting derivations
be a field of characteristic zero equipped
with pairwise commuting derivations  ,
which are linearly independent over
,
which are linearly independent over  .
Let
.
Let  be the column vector with entries
be the column vector with entries  . Then there exist elements
. Then there exist elements 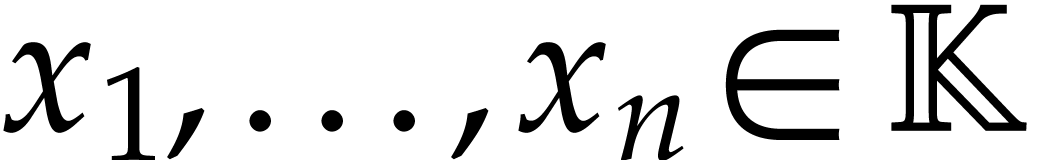 and a nonsingular matrix
and a nonsingular matrix  such that the derivations
such that the derivations  with
with 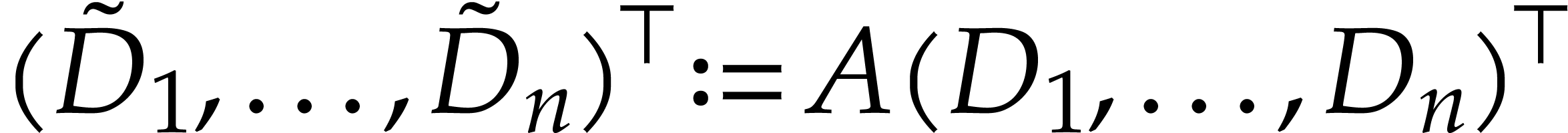 pairwise commute and
pairwise commute and 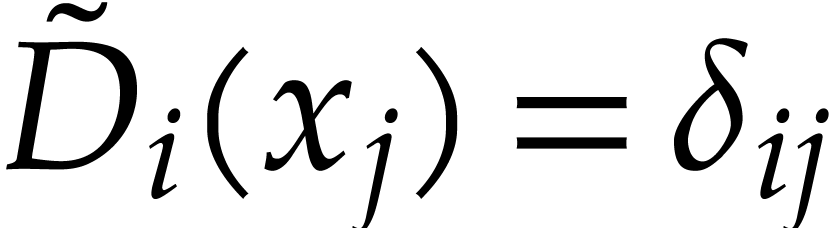 for every
for every
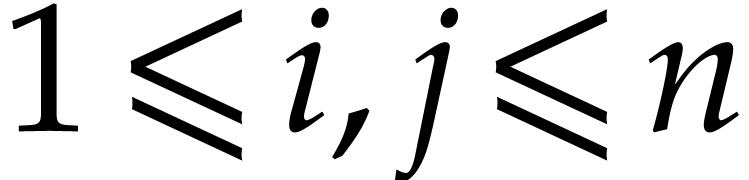 .
.
Proof. Linear independence of  implies that there exist elements
implies that there exist elements  such that the
vectors
such that the
vectors  for
for 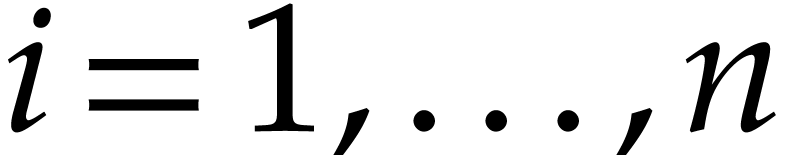 are linearly
independent. Consider a matrix
are linearly
independent. Consider a matrix  whose rows are
these vectors. We set
whose rows are
these vectors. We set 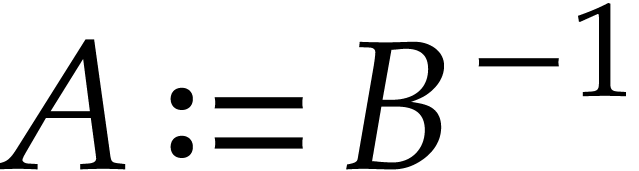 and
and 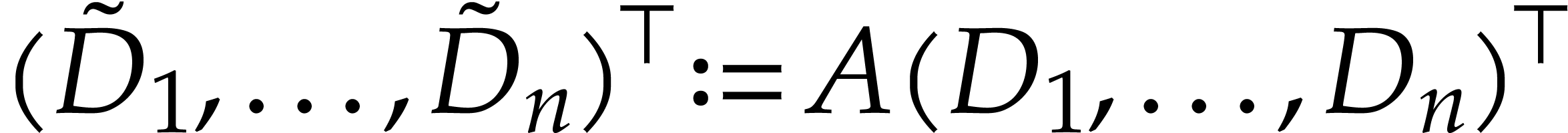 . For every
. For every 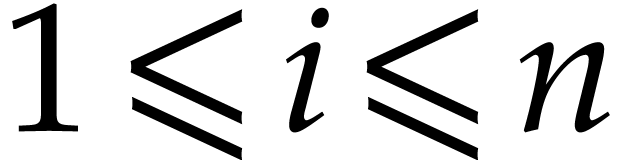 ,
since
,
since 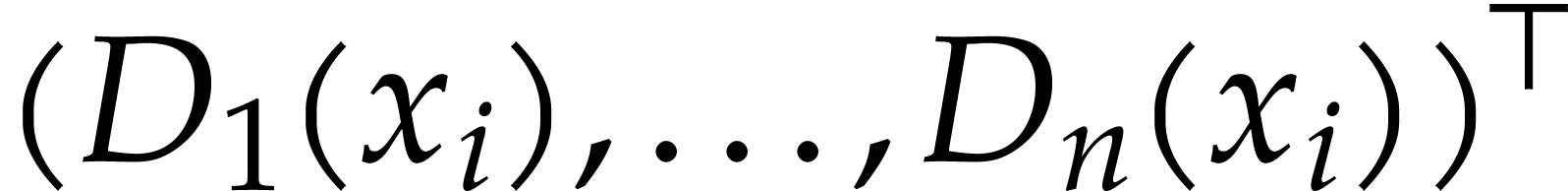 is the
is the  -th
column of
-th
column of  , we have
, we have 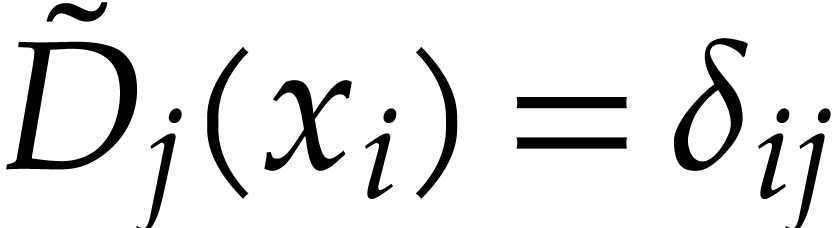 .
.
In order to show that  pairwise commute, consider
pairwise commute, consider
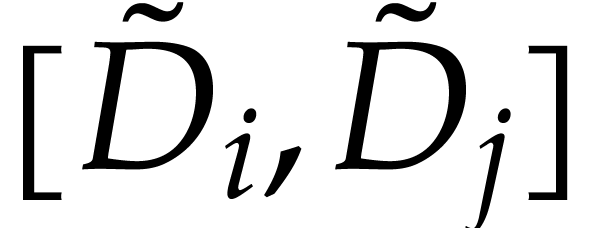 for
for 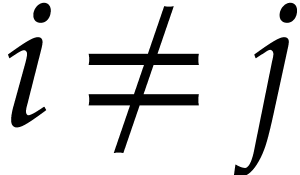 .
This Lie bracket can be written as a linear combination
.
This Lie bracket can be written as a linear combination  with
with 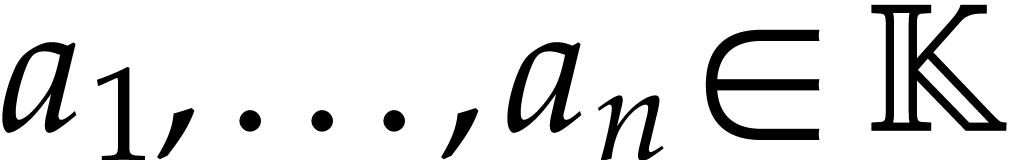 . On the other hand,
. On the other hand,
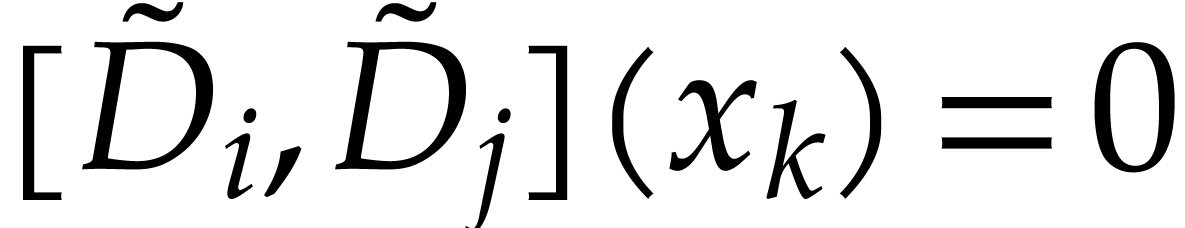 for every
for every 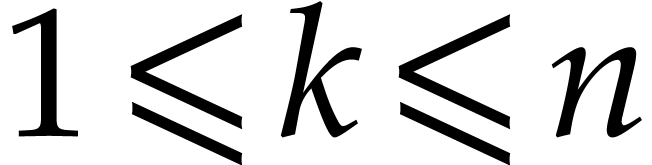 ,
so
,
so 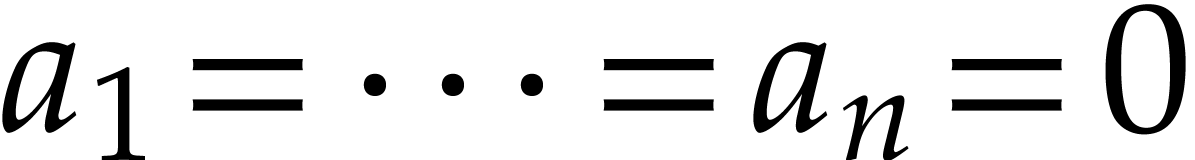 . This concludes the
commutativity proof.
. This concludes the
commutativity proof.
 be a field of characteristic
zero equipped with pairwise commuting derivations
be a field of characteristic
zero equipped with pairwise commuting derivations  , which are linearly independent over
, which are linearly independent over  . Let
. Let 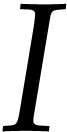 be
a left ideal in
be
a left ideal in  such that the quotient
such that the quotient 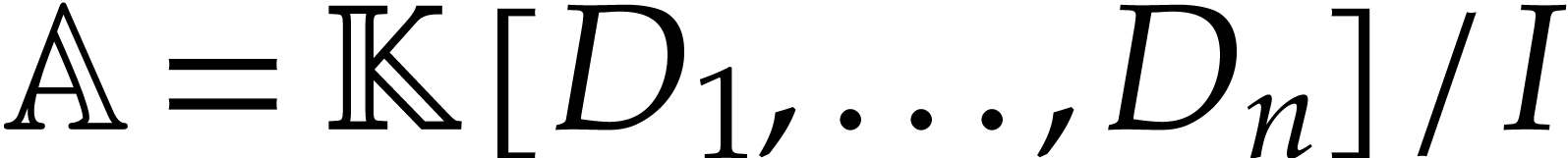 has finite dimension over
has finite dimension over  . Then there exist pairwise commuting
. Then there exist pairwise commuting  -linear combinations
-linear combinations  of
of  , which are linearly
independent over
, which are linearly
independent over  , and such
that the projections of powers of
, and such
that the projections of powers of 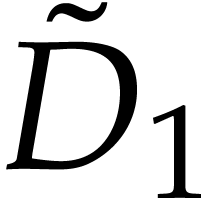 generate
generate
 as a
as a  -vector
space.
-vector
space.
Proof. By Lemma 8, there exist  and a matrix
and a matrix  such that
such that 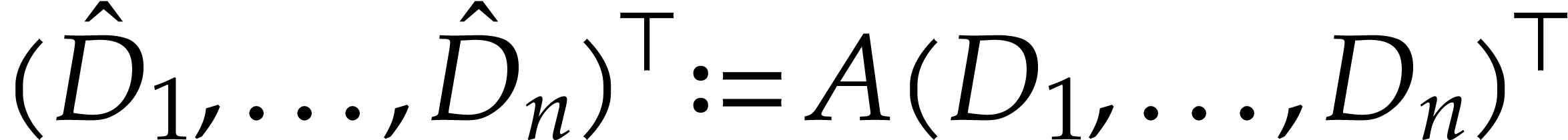 commute pairwise and
commute pairwise and 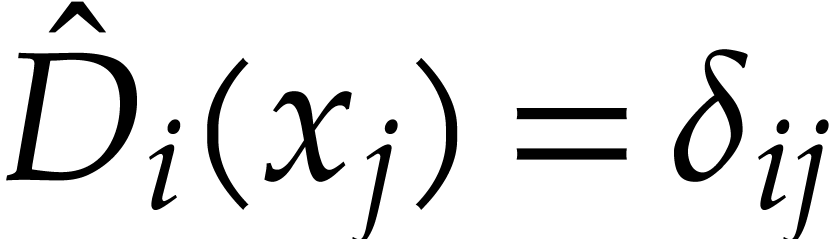 .
We apply Theorem 5 with
.
We apply Theorem 5 with 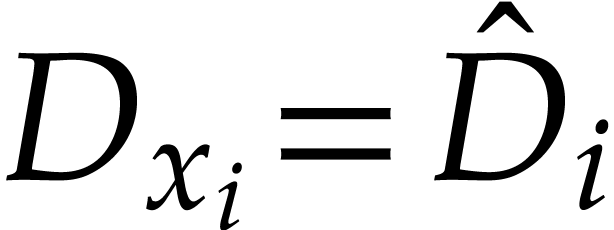 for
for 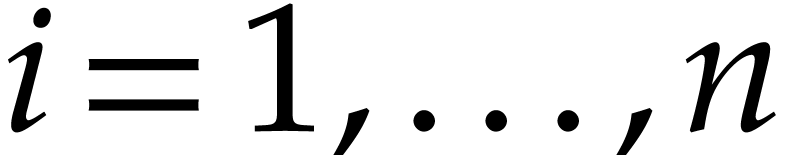 and obtain a
and obtain a  -linear
transformation of
-linear
transformation of  to
to  , where
, where 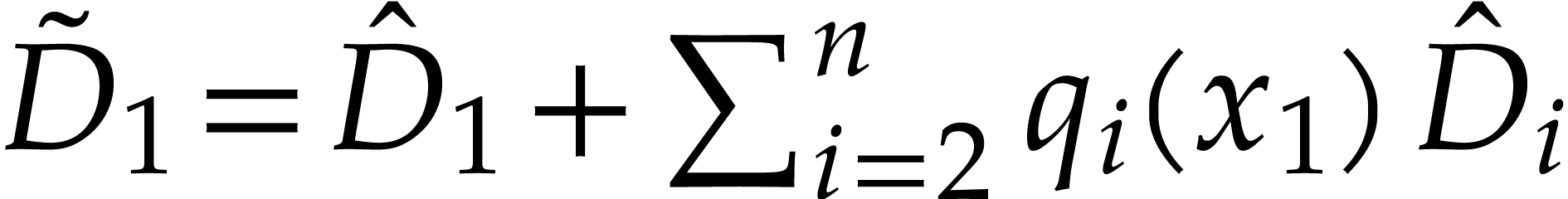 and
and 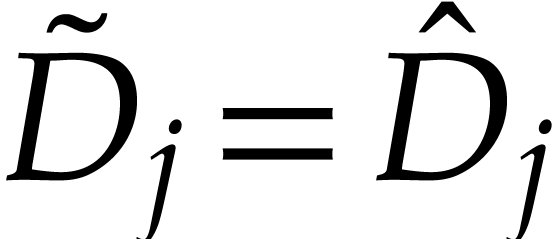 for
for 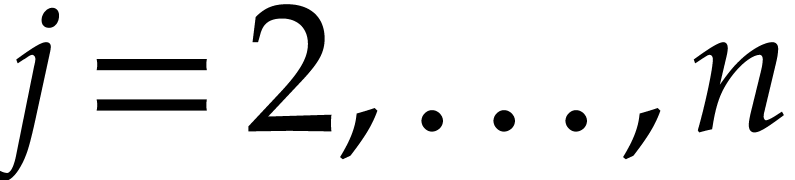 , such that the
projections of powers of
, such that the
projections of powers of 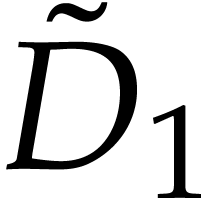 span
span  as a
as a  -vector space. Composing
the invertible transformations
-vector space. Composing
the invertible transformations  and
and  , we obtain the desired change of
derivations.
, we obtain the desired change of
derivations.
B. Dwork, G. Gerotto, and F. J. Sullivan. An
instroduction to  -functions.
Princeton University Press, 1994.
-functions.
Princeton University Press, 1994.
P. Gianni and T. Mora. Algebraic solutions of systems of polynomial equations using Gröbner bases. In Proc. of the 5th International Conference on Applied Algebra, Algebraic Algorithms and Error-Correcting Codes, volume 356 of Lect. Notes in Comp. Sc., pages 247–257. 1989.
J. van der Hoeven. Generalized power series solutions to linear partial differential equations. JSC, 42(8):771–791, 2007.
M. Kauers, C. Koutschan, and T. Verron. A shape lemma for ideals of differential operators. Journal of Algebra, 677(1):448–459, 2025.
J. F. Ritt. Differential algebra, volume 33 of Colloquium Publications. Amer. Math. Soc., 1948.
M. F. Singer. Model theory of partial differential fields: From commuting to noncommuting derivations. Proc. of A.M.S., 135:1929–1934, 2007.