Guessing singular dependencies |
|
| November 4, 2013 |
|
 . This work was
partially supported by the ANR Gecko and ANR-09-JCJC-0098-01
. This work was
partially supported by the ANR Gecko and ANR-09-JCJC-0098-01
Given
|
Consider an infinite sequence 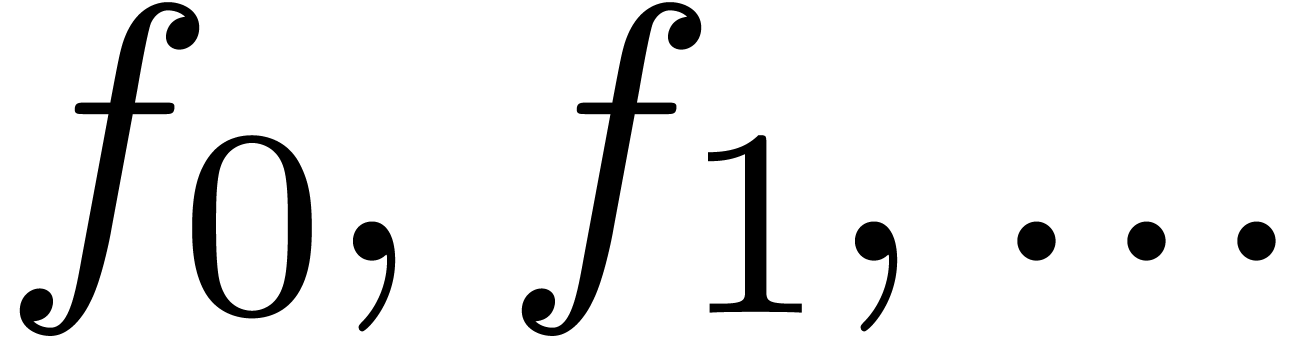 of complex
numbers. If
of complex
numbers. If 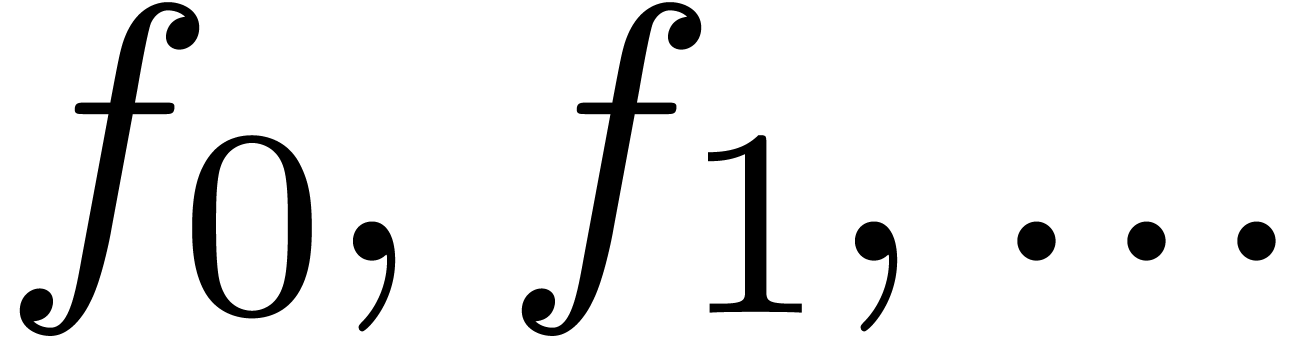 are the coefficients of a formal
power series
are the coefficients of a formal
power series  , then it is
well-known [Pól37, Wil94, FS96]
that the asymptotic behaviour of the sequence
, then it is
well-known [Pól37, Wil94, FS96]
that the asymptotic behaviour of the sequence 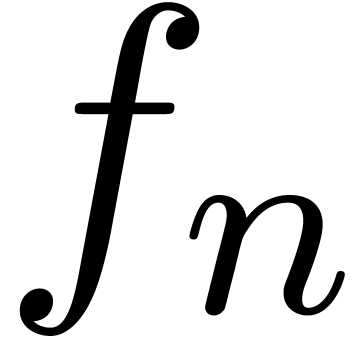 is
closely related to the behaviour of the generating function
is
closely related to the behaviour of the generating function 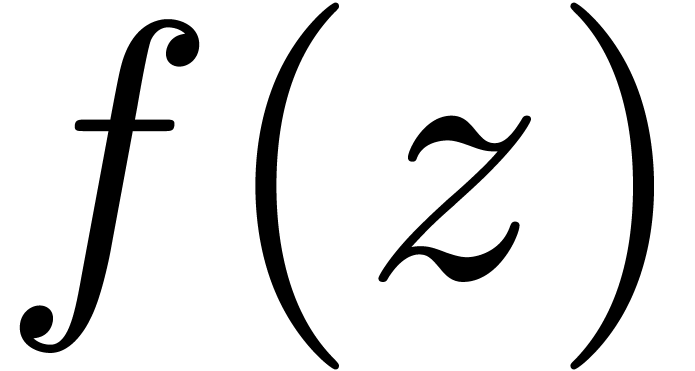 near its dominant singularity. Now, if
near its dominant singularity. Now, if  is the solution to some complicated equation, then it can be hard to
compute the asymptotic behaviour using formal methods. On the other
hand, the coefficients
is the solution to some complicated equation, then it can be hard to
compute the asymptotic behaviour using formal methods. On the other
hand, the coefficients 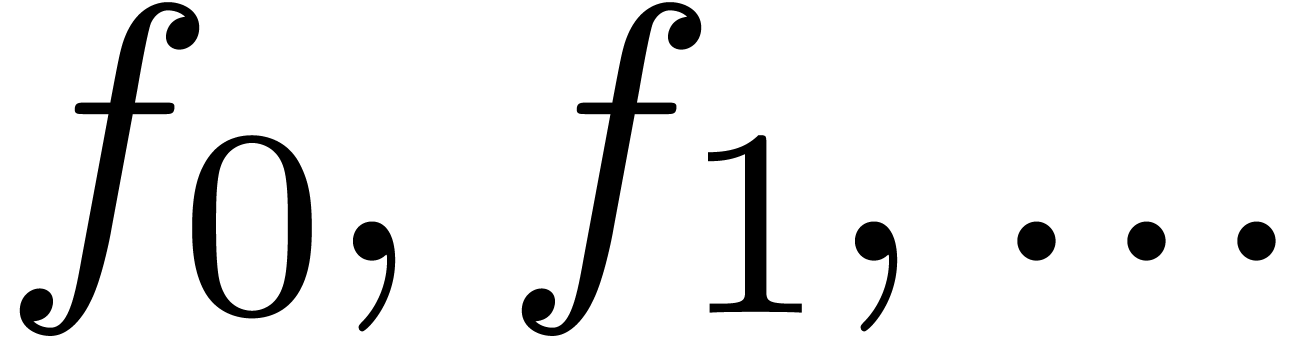 of such a solution
of such a solution  can often be computed numerically up to a high order.
With this numerical evidence at hand, it is natural to raise the
following questions:
can often be computed numerically up to a high order.
With this numerical evidence at hand, it is natural to raise the
following questions:
Can we guess the asymptotic behaviour of 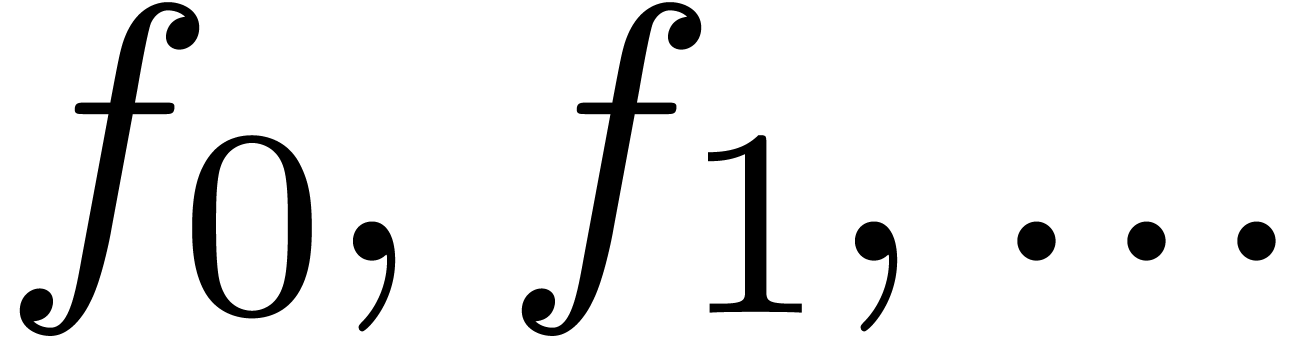 ?
?
Can we guess the behaviour of 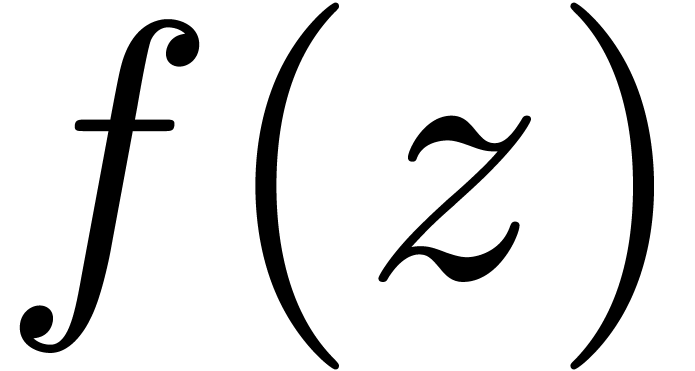 near its
dominant singularity?
near its
dominant singularity?
These questions can be regarded as part of the construction of a more general toolbox for the “experimental mathematician” [BBKW06, BD09]. More specifically, we advocate the systematic integration of “guessing tools” into symbolic computation packages. Indeed, current systems can be quite good at all kinds of formal manipulations. However, in the daily practice of scientific discovery, it would be helpful if these systems could also detect hidden properties, which may not be directly apparent or expected. Furthermore, the guessing tool is allowed to be heuristic, so that it only suggests hidden properties; at a second stage, one may then search for full proofs using other techniques.
One well-known tool in this direction is the LLL-algorithm [LLL82].
Given 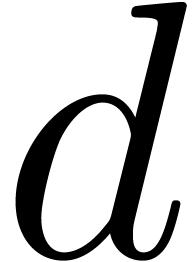 numbers
numbers 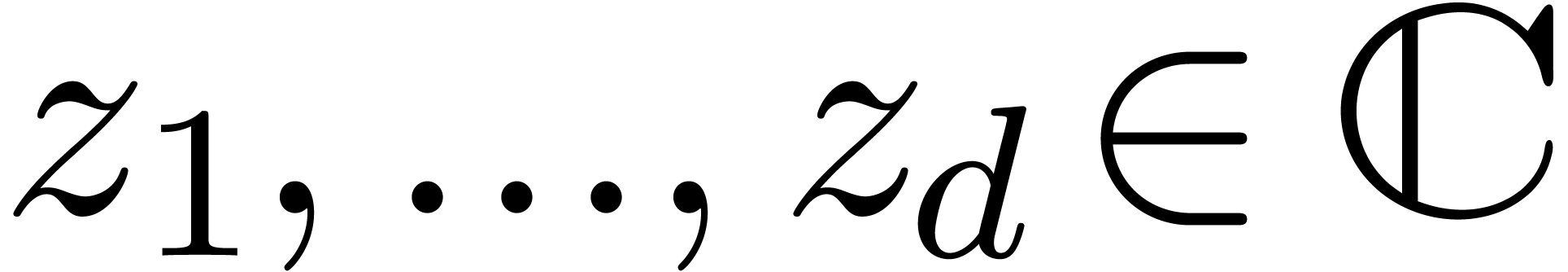 ,
it can be used in order to guess relations of the form
,
it can be used in order to guess relations of the form
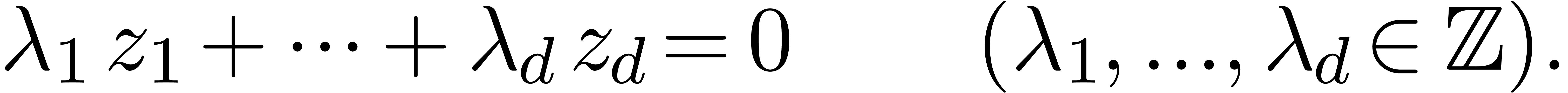 |
(1) |
Given  formal power series
formal power series 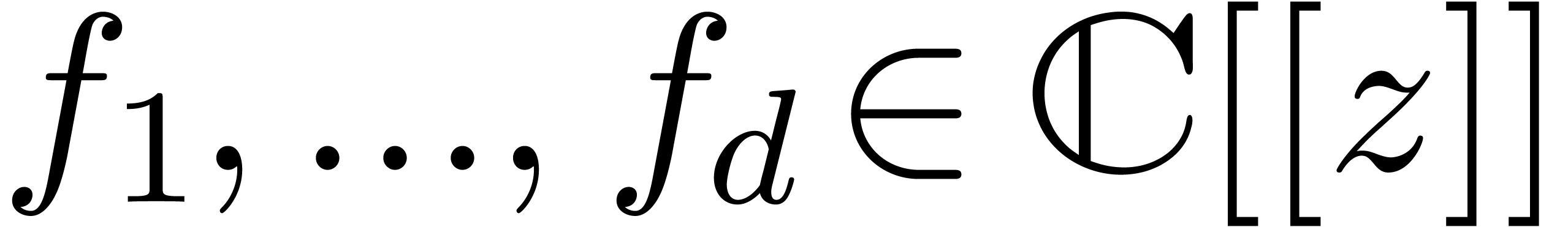 , algorithms for the computation of
Padé-Hermite forms [BL94, Der94] can be
used in order to guess linear relations
, algorithms for the computation of
Padé-Hermite forms [BL94, Der94] can be
used in order to guess linear relations
 |
(2) |
A well-known implementation is provided by the  , the
, the
 or a linear differential equation
with coefficients in
or a linear differential equation
with coefficients in 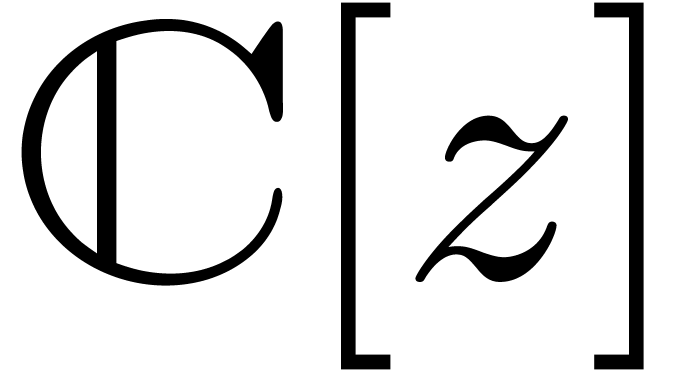 satisfied by
satisfied by  . Indeed, it suffices to take
. Indeed, it suffices to take 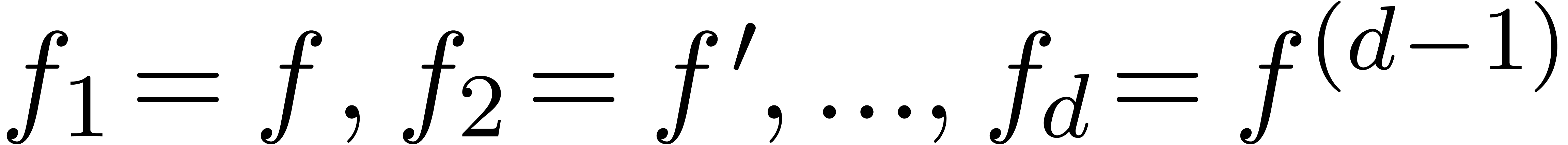 in (2) in order search for small linear differential
equations satisfied by
in (2) in order search for small linear differential
equations satisfied by  .
.
Unfortunately, many interesting formal power series  do not admit closed form formulas and do not satisfy linear differential
equations with polynomial coefficients. In that case, we can still use
asymptotic extrapolation [Hoe09] in order to guess the
asymptotic behaviour of the coefficients. However, this only provides us
some rough idea about the behaviour of
do not admit closed form formulas and do not satisfy linear differential
equations with polynomial coefficients. In that case, we can still use
asymptotic extrapolation [Hoe09] in order to guess the
asymptotic behaviour of the coefficients. However, this only provides us
some rough idea about the behaviour of  at its
dominant singularity. In practice, it often happens that
at its
dominant singularity. In practice, it often happens that  locally satisfies an algebraic or differential equation
with analytic coefficients, even though these coefficients fail to be
polynomials. For instance, combinatorics [Pól37, FS96] is full with examples of generating functions which are
not algebraic, but whose dominant singularities are algebraic.
locally satisfies an algebraic or differential equation
with analytic coefficients, even though these coefficients fail to be
polynomials. For instance, combinatorics [Pól37, FS96] is full with examples of generating functions which are
not algebraic, but whose dominant singularities are algebraic.
In this paper, we will describe two approaches to detect analytic
dependencies on a compact disk: the first one assumes that we have an
algorithm for the analytic continuation of  and
relies on the monodromy of
and
relies on the monodromy of  at its singularities.
The second approach is purely numerical and makes no special assumptions
on
at its singularities.
The second approach is purely numerical and makes no special assumptions
on  . On our way, we will
encounter various interesting related problems, such as the
determination of the radius of convergence or the singularities of
. On our way, we will
encounter various interesting related problems, such as the
determination of the radius of convergence or the singularities of  . We will also propose heuristic
solutions to these problems, thereby extending the basic toolbox for
experimenting with analytic functions.
. We will also propose heuristic
solutions to these problems, thereby extending the basic toolbox for
experimenting with analytic functions.
Since all algorithms in this paper are directly or indirectly based on heuristics, it is important to investigate how much confidence we can attach to the computed results. In section 2, we will present a survey of different kinds of heuristic algorithms which are used in symbolic computation. Some of these heuristics are relatively benign when compared to others, so it will be useful to have some general insights on the reliability of different types of heuristic algorithms.
The remainder of the paper is divided into two main parts. In the first
part (sections 3, 4 and 5), we
will develop some basic tools for later use. In the second part, we turn
to the main topic of this paper: the disclosure of local analytic
relations between analytic functions. Two main types of analytic input
functions  will be considered:
will be considered:
Functions for which we can merely compute a large number of the
Taylor coefficients  at the origin.
at the origin.
Functions for which we have a reasonably efficient algorithm for
their analytic continuation, so that we can also compute the
Taylor coefficients of  at other points
besides the origin.
at other points
besides the origin.
The second situation typically arises when  is
the solution of a differential or more general functional equation; see
section 4.1 for a further discussion on analytic
continuation.
is
the solution of a differential or more general functional equation; see
section 4.1 for a further discussion on analytic
continuation.
One of the most basic problems concerning an analytic function  which is only known by its Taylor coefficients, is to
determine its radius of convergence. In section 3, we will
present two methods. The first one is related Cauchy-Hadamard's formula
and provides rough approximations under mild assumptions on
which is only known by its Taylor coefficients, is to
determine its radius of convergence. In section 3, we will
present two methods. The first one is related Cauchy-Hadamard's formula
and provides rough approximations under mild assumptions on  . The second method provides much better
approximations, but only works if
. The second method provides much better
approximations, but only works if  admits a
single dominant singularity of a simple type.
admits a
single dominant singularity of a simple type.
Building on the algorithm for approximating the radius of convergence of
 , we next turn our attention
to the problem of locating its singularities. In section 4.2,
we first restrict ourselves to the dominant singularities of
, we next turn our attention
to the problem of locating its singularities. In section 4.2,
we first restrict ourselves to the dominant singularities of  (i.e. the singularities of minimal norm).
Assuming AN2, we next present algorithms for the
exploration of the Riemann surface of
(i.e. the singularities of minimal norm).
Assuming AN2, we next present algorithms for the
exploration of the Riemann surface of  beyond its
dominant singularities.
beyond its
dominant singularities.
In the special case when  is meromorphic on a
compact disk
is meromorphic on a
compact disk 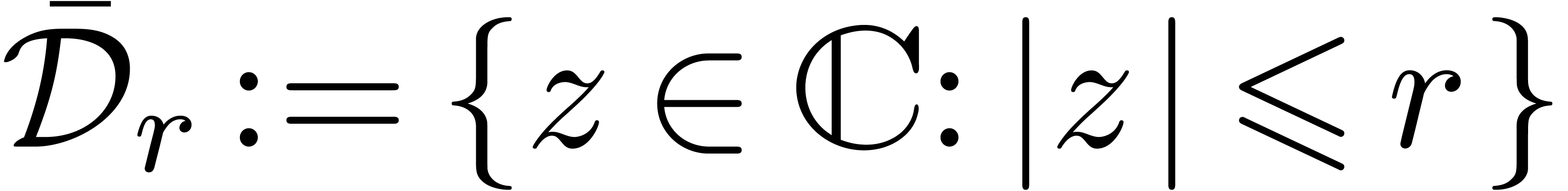 , section 5 contains a special purpose algorithm for the determination
of a polynomial
, section 5 contains a special purpose algorithm for the determination
of a polynomial 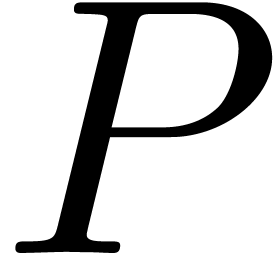 such that
such that 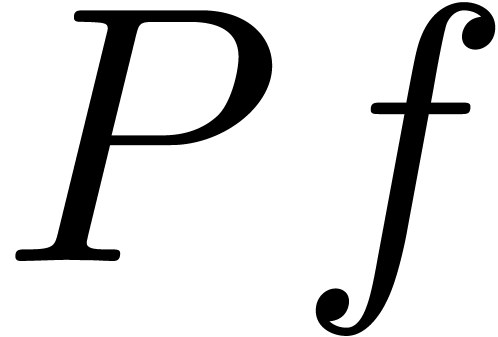 is analytic on
is analytic on  . This
algorithm works under the hypothesis AN1 and induces
better algorithms for the problems in sections 3 and 4 in this special case.
. This
algorithm works under the hypothesis AN1 and induces
better algorithms for the problems in sections 3 and 4 in this special case.
In the second part of this paper, we turn to the detection of
dependencies between analytic functions on a compact disk  . More precisely, assume that
. More precisely, assume that 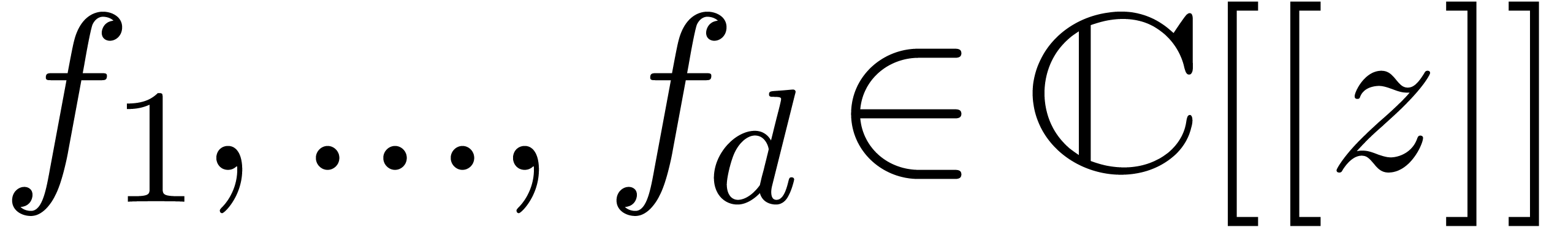 are fixed convergent power series. We are interested in the
determination of linear dependencies of the form
are fixed convergent power series. We are interested in the
determination of linear dependencies of the form
 |
(3) |
where 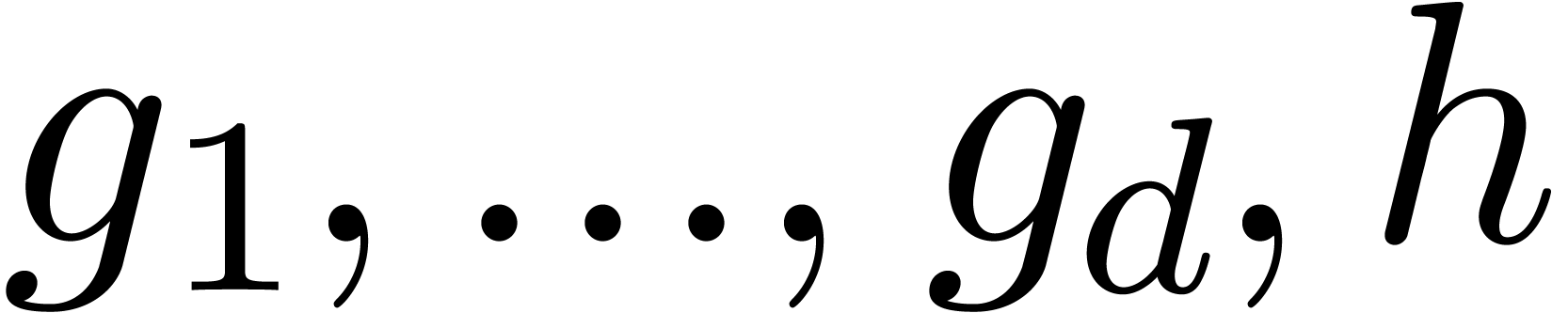 are analytic on
are analytic on  . Modulo a scaling
. Modulo a scaling  ,
we may assume without loss of generality that
,
we may assume without loss of generality that  .
.
In section 6, we assume AN2 and first
consider the two special cases of algebraic and Fuchsian dependencies.
In the case of algebraic dependencies, we take 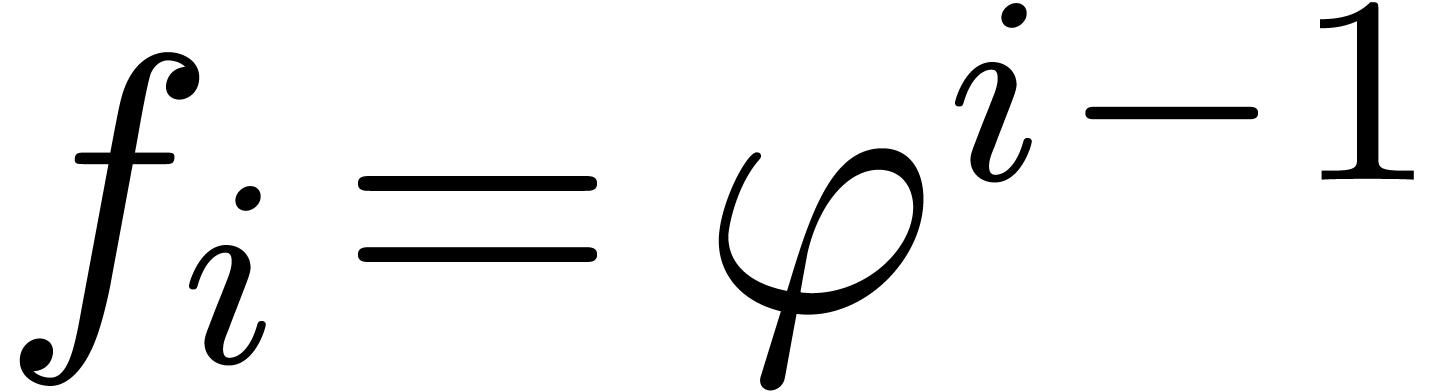 for a fixed function
for a fixed function  , and
also require that
, and
also require that 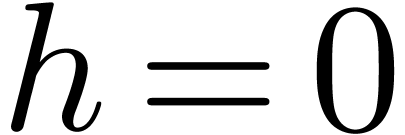 . In the
case of Fuchsian dependencies, we take
. In the
case of Fuchsian dependencies, we take 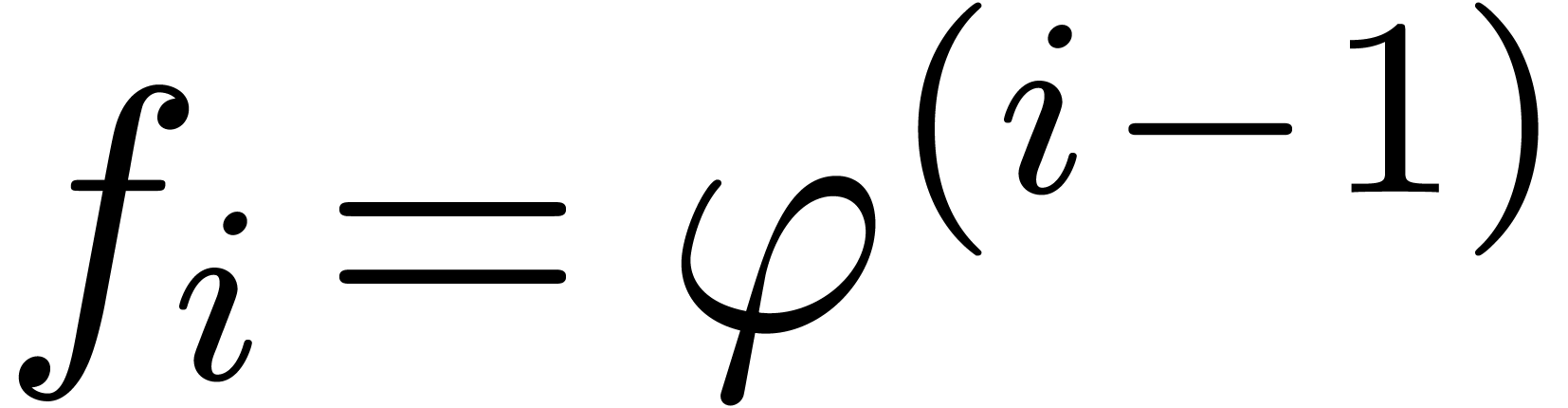 for a
fixed function
for a
fixed function  , and again
require that
, and again
require that 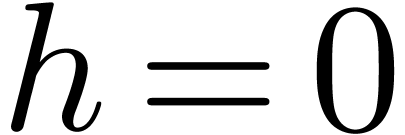 . The second
algorithm only succeeds in the case when all singularities of
. The second
algorithm only succeeds in the case when all singularities of  on the disk are of Fuchsian type (see sections 3.2
and 6.2 for detailed definitions). The main idea behind the
method is to compute the set of of functions generated by
on the disk are of Fuchsian type (see sections 3.2
and 6.2 for detailed definitions). The main idea behind the
method is to compute the set of of functions generated by  and its analytic continuation around its singularities in
and its analytic continuation around its singularities in
 . If there exists an
algebraic dependency, then this set is finite and we may use it to find
the dependency. If there exists a Fuchsian dependency, then the set is
contained in finite dimensional vector space, and we may construct the
dependency from a basis of this vector space.
. If there exists an
algebraic dependency, then this set is finite and we may use it to find
the dependency. If there exists a Fuchsian dependency, then the set is
contained in finite dimensional vector space, and we may construct the
dependency from a basis of this vector space.
In section 7, we only assume AN1 and consider the general problem of determining dependencies of the form (3). We will describe a purely numerical algorithm based on Gram-Schmidt orthogonalization for finding such relations. The idea is to simply truncate the power series expansions and then apply the numerical method. We will prove that an asymptotic convergence theorem which shows that this approach is at least correct “at the limit”.
In the last section 8, we will present some numerical
experiments with the algorithm from section 7. In section
8.1, we first consider some examples of relations which
were recognized by the algorithm. In section 8.2, we will
also examine the behaviour of the algorithm in the case when  are analytically independent. In fact, the algorithm from
section 7 still requires some human cooperation for
deciding whether we really found a relation. Based on the numerical
experiments, we conclude with some perspectives for the design of a
fully automatic algorithm.
are analytically independent. In fact, the algorithm from
section 7 still requires some human cooperation for
deciding whether we really found a relation. Based on the numerical
experiments, we conclude with some perspectives for the design of a
fully automatic algorithm.
Acknowledgments. We would like to thank the three referees for their detailed and valuable comments on a first version of this paper.
As soon as we enter the area of heuristic and non mathematically proven algorithms, it is natural to ask how much confidence can be attached to the output. In fact, there is a large spectrum of situations which can occur, depending on the precise nature of the heuristics. There may also be a trade-off between computational complexity and correctness: is it better to rely on a slow deterministic algorithm for polynomial factorisation over a finite field, or on a fast probabilistic algorithm?
Without striving for exhaustion, section 2.1 a catalogue of different kinds of heuristic algorithms which occur in the area of symbolic computation. Each of the heuristic algorithms considered in this paper will fit into one of these categories. We will also describe some standard strategies in order to increase the level of confidence and examine typical examples for which heuristic algorithms may fail.
For example, consider the class of exp-log constants, built up
from the rationals  using the operations
using the operations  , exp and log. The following
conjecture [Lan71] is a major open problem in number
theory:
, exp and log. The following
conjecture [Lan71] is a major open problem in number
theory:
 be complex numbers which are linearly
independent over the rational numbers
be complex numbers which are linearly
independent over the rational numbers  .
Then the transcendence degree of
.
Then the transcendence degree of
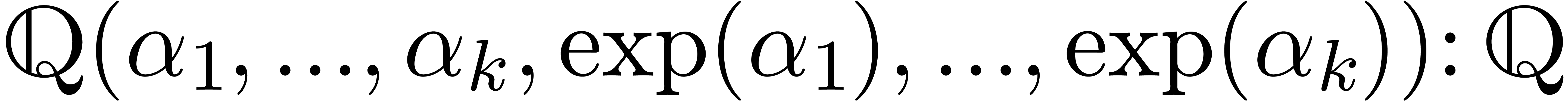
is at least 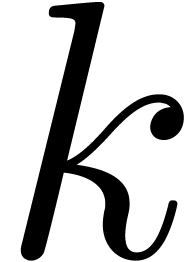 .
.
From the computer algebra point of view, the conjecture implies [CP78] that all numerical relations between exp-log constants
can be deduced from the usual rules 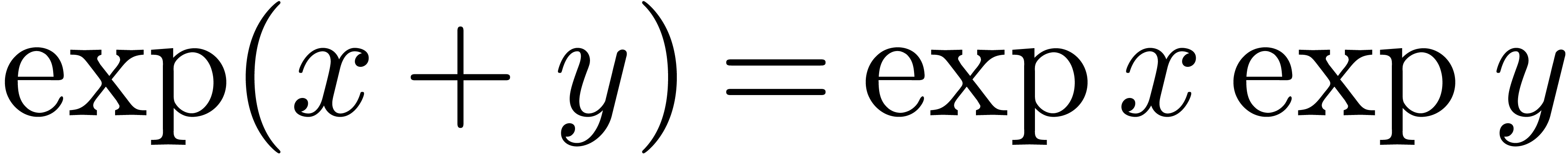 and
and 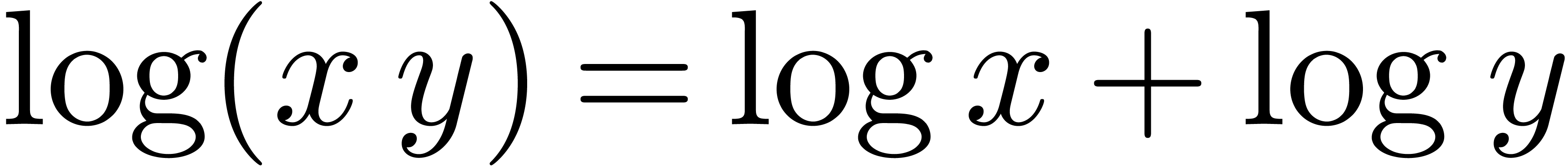 . Based on this fact, Richardson
has given a zero test for exp-log constants [Ric97, Ric07] with the following properties: (1) if the algorithm
terminates on a given input, then the result is correct; (2) if the
conjecture holds, then the algorithm always terminates; (3) if the
algorithm does not terminate on a given input, then a counterexample to
the conjecture can be constructed from this input.
. Based on this fact, Richardson
has given a zero test for exp-log constants [Ric97, Ric07] with the following properties: (1) if the algorithm
terminates on a given input, then the result is correct; (2) if the
conjecture holds, then the algorithm always terminates; (3) if the
algorithm does not terminate on a given input, then a counterexample to
the conjecture can be constructed from this input.
Similar situations occur in algorithmic number theory, depending on the correctness of Riemann's hypothesis [Bel11]. In this paper, the algorithms in sections 4.3 and 6 rely on zero tests for analytic functions. If we know that our analytic functions lie in special classes (such as the class of exp-log functions, or the class of differentially algebraic functions), then these zero tests might be reduced to suitable conjectures [Hoe01].
For instance, in section 3, we will give heuristic algorithms for the computation of the radius of convergence of an analytic function. This will be a basic building block for many of the other algorithms in this paper. Nevertheless, the correctness of several of these other algorithms reduces to the correctness of this basic building block.
If, for input functions in a more restricted class, we may determine their convergence radii with larger accuracy, then this will immediately make all the other algorithms more reliable. For instance, if we consider a class (e.g. rational or algebraic functions) for which convergence radii can be computed exactly, then the algorithms in section 4.2 are no longer heuristic.
 is zero, it
suffices to pick a random number
is zero, it
suffices to pick a random number  and test
whether
and test
whether 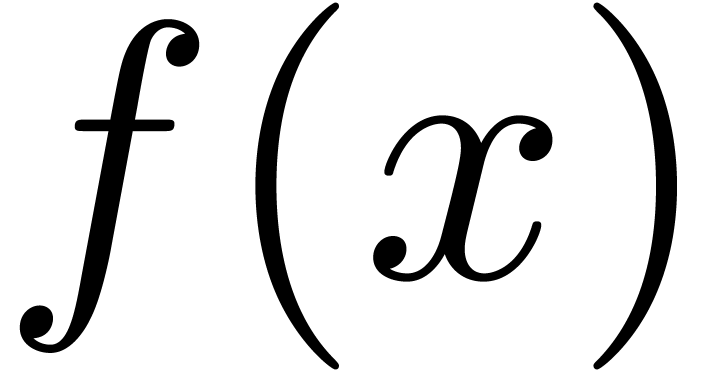 vanishes.
vanishes.
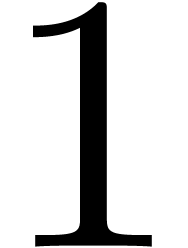 ” are really correct
with probability
” are really correct
with probability 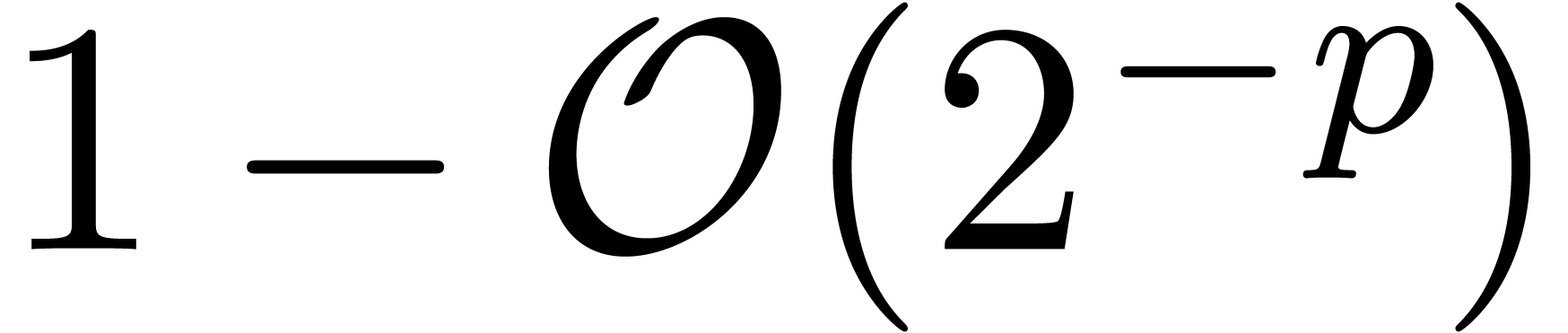 , where
, where
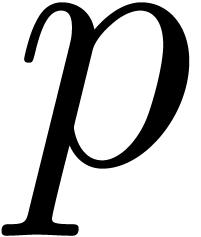 is the working precision. There are many other
examples of heuristic algorithms which are correct with high
probability. For instance, in order to show that two polynomials
is the working precision. There are many other
examples of heuristic algorithms which are correct with high
probability. For instance, in order to show that two polynomials  in
in 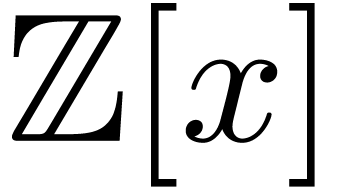 have no common divisors,
it suffices to pick a “sufficiently random” prime
have no common divisors,
it suffices to pick a “sufficiently random” prime 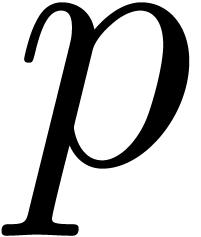 and show that the reductions of
and show that the reductions of  and
and  in
in 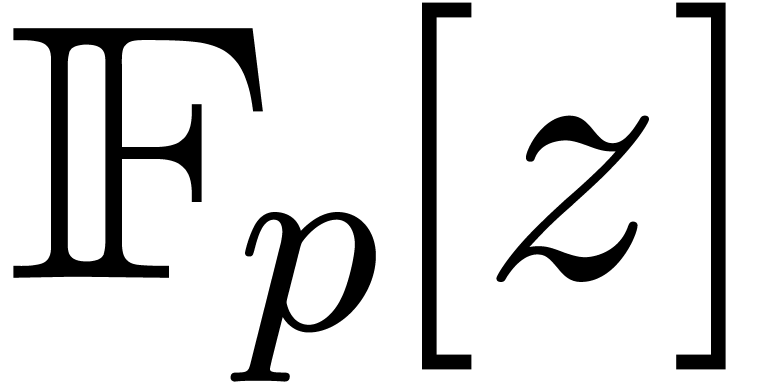 have no common
divisors.
have no common
divisors.
We also recall that there are two classical types of probabilistic
algorithms. The examples mentioned above are only correct with high
probability and fall into the class of so-called Monte Carlo algorithms.
The second kind of Las Vegas algorithms are always correct, but only
fast with high probability. For instance, all known fast algorithms for
factoring polynomials over a finite field  are
probabilistic Las Vegas type algorithms [GG02].
are
probabilistic Las Vegas type algorithms [GG02].
This does not withstand that experts in this area have a great sense of how accurate and trustworthy various methods are. Ideally speaking, any numerical algorithm comes with a detailed error analysis. Most textbooks on numerical analysis start with a section on the various sources of error and how to take into account the machine accuracy [PTVF07, section 1.1]. For more statistical algorithms, there is also a tradition of trying to quantify the level of trust that can be attached to the computed results. Finally, for many algorithms, it is possible to automate the error analysis by using interval arithmetic [Moo66].
 . From a theoretical point of
view [Wei00, Hoe11], it can be investigated
whether a given numerical algorithm is at least “ultimately
correct” in the sense that the computed output tends to the
mathematically correct result if
. From a theoretical point of
view [Wei00, Hoe11], it can be investigated
whether a given numerical algorithm is at least “ultimately
correct” in the sense that the computed output tends to the
mathematically correct result if  tends to
infinity. If the numerical algorithm comes with a rigourous error
analysis, then we have a means for controlling the distance
tends to
infinity. If the numerical algorithm comes with a rigourous error
analysis, then we have a means for controlling the distance  between our approximations at a given precision
between our approximations at a given precision  and the ultimate limit. In particular, for any
and the ultimate limit. In particular, for any
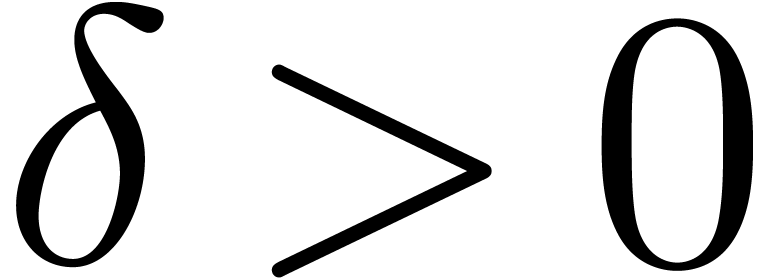 , we may then select a
precision
, we may then select a
precision  with
with 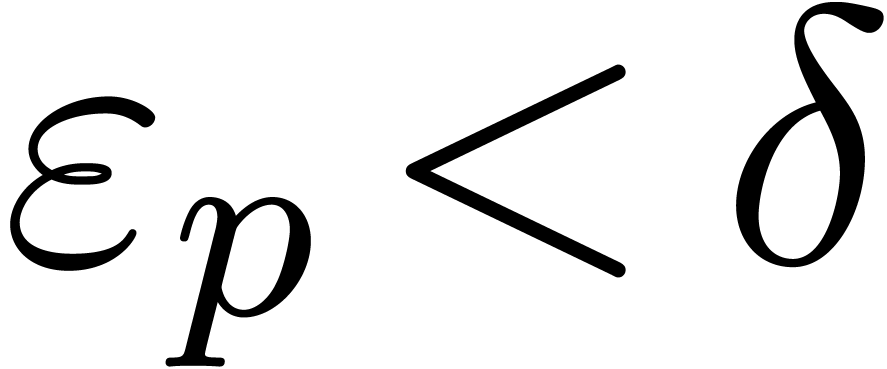 .
.
However, there are many situation in which we have no means for
controlling the distance 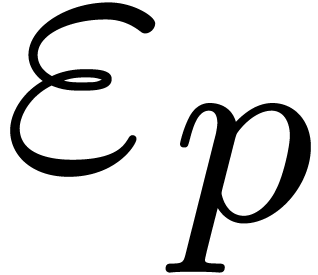 ,
even though our algorithm is ultimately correct. For instance, the
computation of the radius of convergence
,
even though our algorithm is ultimately correct. For instance, the
computation of the radius of convergence  of a
differentially algebraic function is undecidable [DL89],
even though there exists an algorithm [Hoe05, Hoe07]
for the computation of a sequence
of a
differentially algebraic function is undecidable [DL89],
even though there exists an algorithm [Hoe05, Hoe07]
for the computation of a sequence  with
with  . Similarly, for a large class of
functions, the formula (4) below gives an approximation for
the radius of convergence of a series (when computing with a precision
of
. Similarly, for a large class of
functions, the formula (4) below gives an approximation for
the radius of convergence of a series (when computing with a precision
of 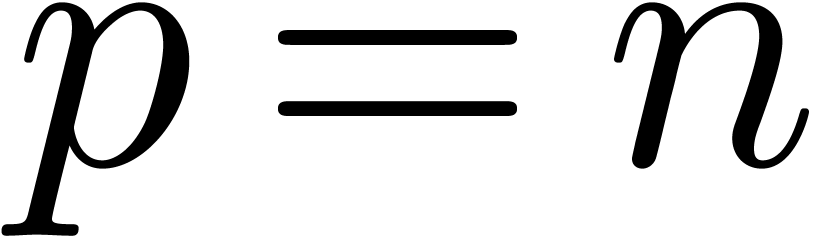 bits), but the formula is only ultimately
correct (5).
bits), but the formula is only ultimately
correct (5).
For instance, in numerical analysis, a frequent trick is to rerun the same algorithm for different working precisions and compare the results. Similarly, probabilistic algorithms of Monte Carlo type can be rerun several times in order to increase our confidence that we obtained the correct result.
We also mentioned the fact that equality testing of exp-log constants is quite asymmetric in the sense that proving equalities is usually much harder than proving inequalities. This suggests the use of a mixed strategy for this problem, which combines a heuristic equality test with a deterministic, interval arithmetic based, inequality prover. In case of equality, we may optionally run Richardson's more expensive algorithm and try to prove the equality.
In applications, we notice that heuristic algorithms are often used in a similar way: to speed up the main algorithm, which can be perfectly deterministic. A nice example is the computation of a Gröbner basis over the rationals using modular arithmetic. In Faugère's software, modular arithmetic is used in order to get a precise idea about those S-polynomials that reduce to zero, thereby avoiding many unnecessary reductions when performing the actual computations over the rationals [Fau94].
In the particular case of a heuristic algorithm whose purpose is to guess dependencies, we finally notice that we may always build in the trivial safeguard to check all proposed relations a posteriori; see also remark 10 in section 6.1.
One particular angle of attack concerns the computational complexity or the numerical stability. This means that we search for examples for which the heuristic algorithm is very slow or numerically unstable. This line of thought underlies much of the numerical experiments which are presented in section 8.
Instead of attacking the heuristic algorithms, it is also possible to look for interesting classes of examples on which the heuristic provably works (or works better). In this paper, some interesting special classes of analytic functions are meromorphic, algebraic and so-called Fuchsian functions on a compact disk (see section 6.2). Typical classes which have to be considered for counterexamples are lacunary series, functions with a natural boundary, or holonomic functions that are not Fuchsian.
Let  be an analytic function which is given by
its power series
be an analytic function which is given by
its power series 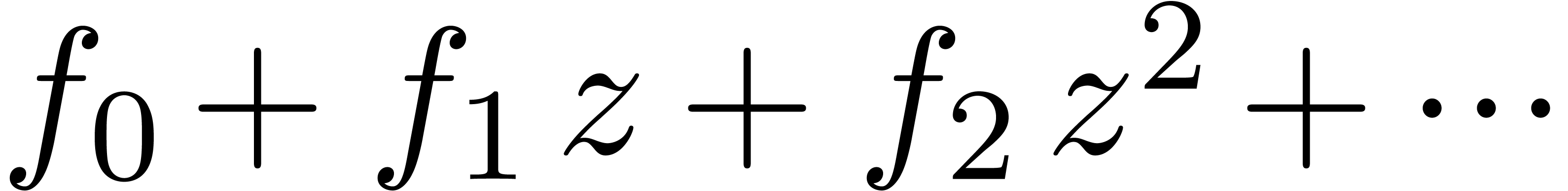 at the origin. A natural
problem is to compute the radius of convergence
at the origin. A natural
problem is to compute the radius of convergence  of
of  . For sufficiently large
classes of analytic functions, such as solutions to algebraic
differential equations over the rationals, this problem is generally
undecidable [DL89, Hoe07], although efficient
and high quality algorithms for the computation of lower bounds for
. For sufficiently large
classes of analytic functions, such as solutions to algebraic
differential equations over the rationals, this problem is generally
undecidable [DL89, Hoe07], although efficient
and high quality algorithms for the computation of lower bounds for 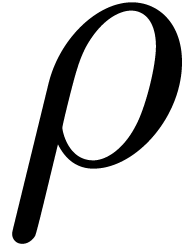 do exist in this case [Hoe07]. In this
section, we will consider heuristic algorithms, and only assume that a
large number of coefficients
do exist in this case [Hoe07]. In this
section, we will consider heuristic algorithms, and only assume that a
large number of coefficients  of
of  are known numerically.
are known numerically.
The first idea which comes into our mind is to apply Cauchy-Hadamard's
formula for the radius of convergence 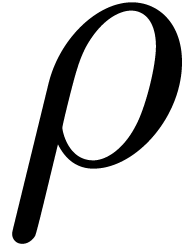 :
:
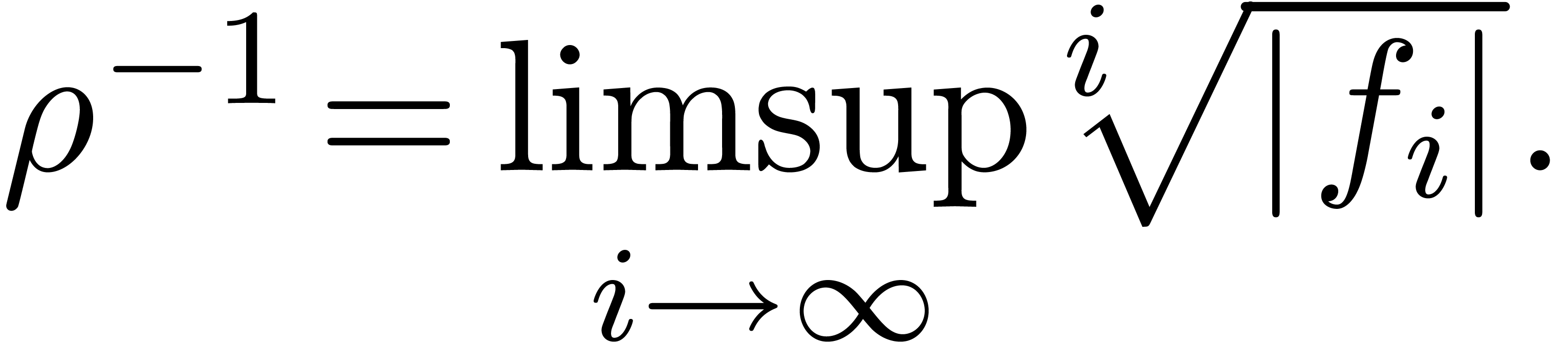
Given  coefficients
coefficients  of
of
 , we may for instance use the
approximation
, we may for instance use the
approximation
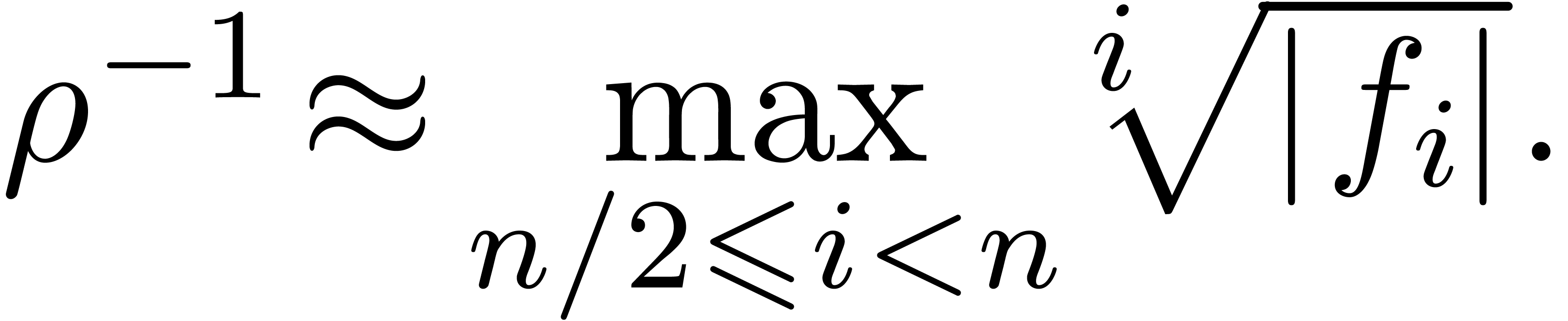 |
(4) |
For most convergent power series  ,
this formula is ultimately exact in the sense that
,
this formula is ultimately exact in the sense that
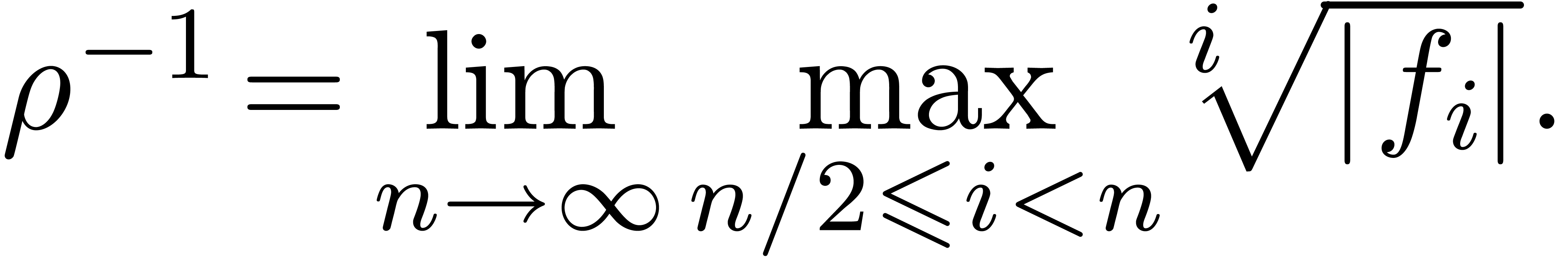 |
(5) |
This is in particular the case when  is
ultimately convex or ultimately concave (this follows from the fact that
the sequence
is
ultimately convex or ultimately concave (this follows from the fact that
the sequence  converges in an ultimately monotone
way to
converges in an ultimately monotone
way to 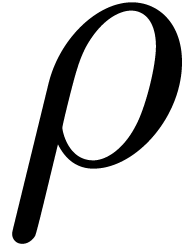 , in this case). The
set of
, in this case). The
set of  for which (5) holds is also
stable under the transformation
for which (5) holds is also
stable under the transformation 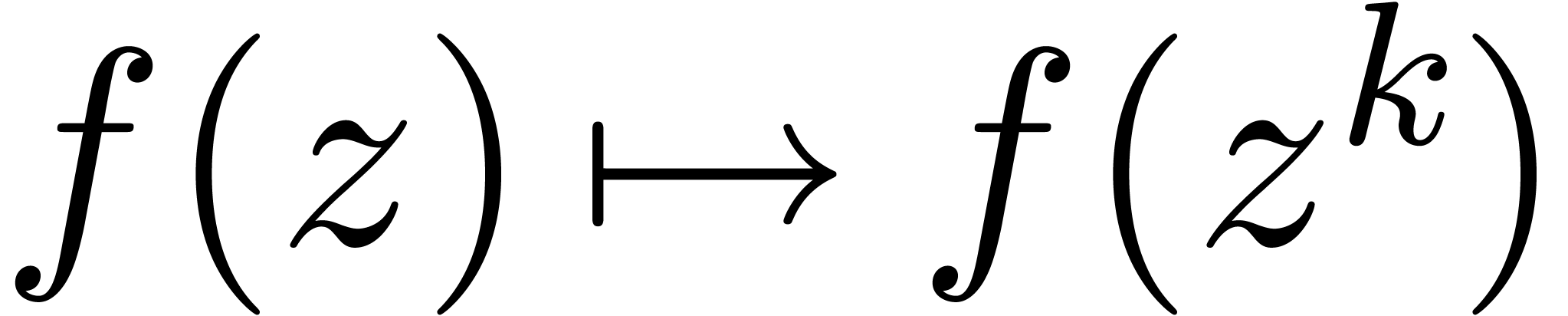 for any
for any 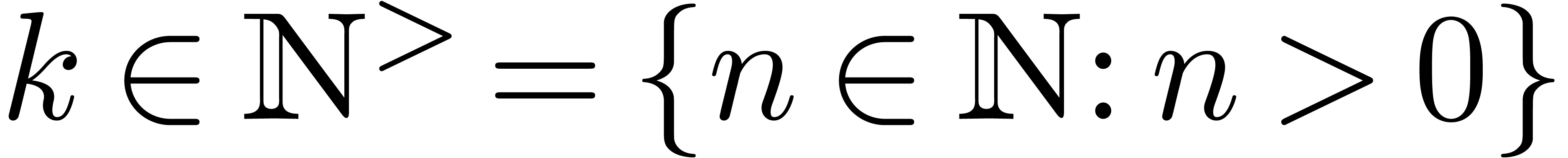 . Of course, we may replace
. Of course, we may replace 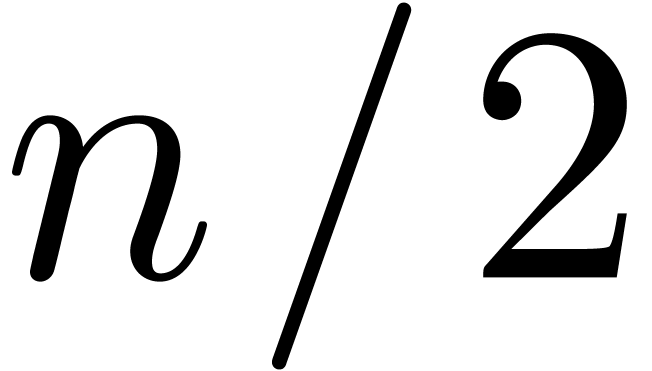 by
by 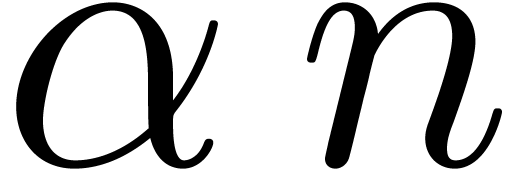 in (5) for
any
in (5) for
any 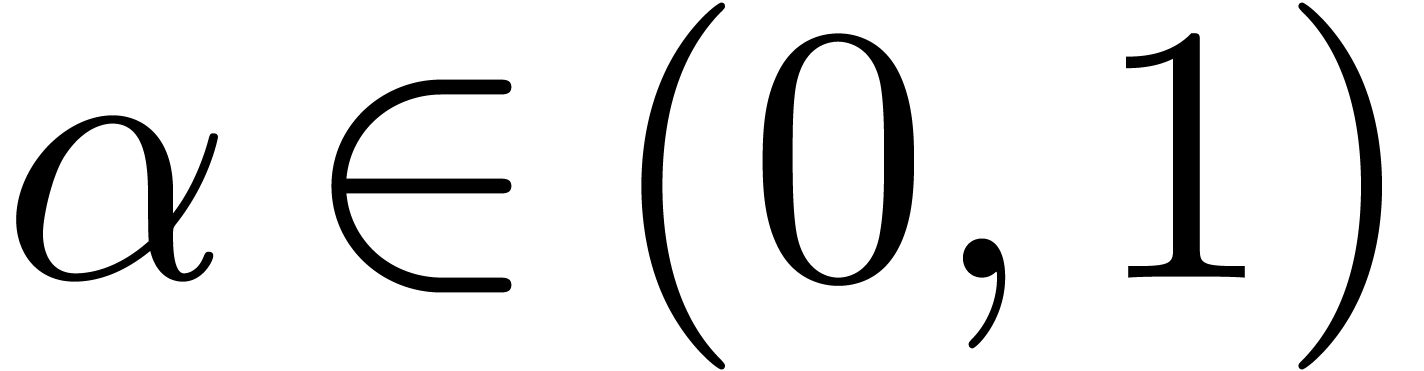 . Notice however that the
lacunary power series
. Notice however that the
lacunary power series 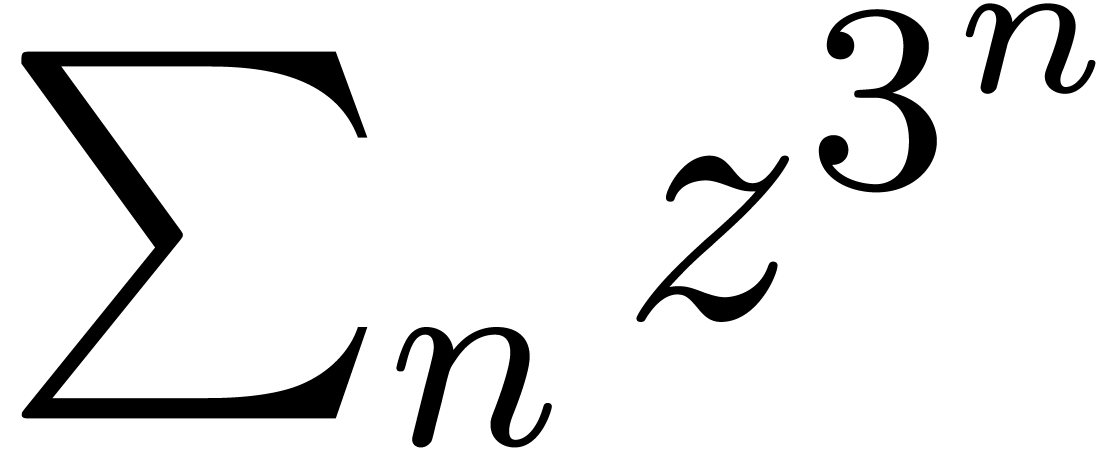 does not satisfy (5).
does not satisfy (5).
The formula (4) has the disadvantage that it has not been
scaled appropriately: when replacing  by
by  , where
, where 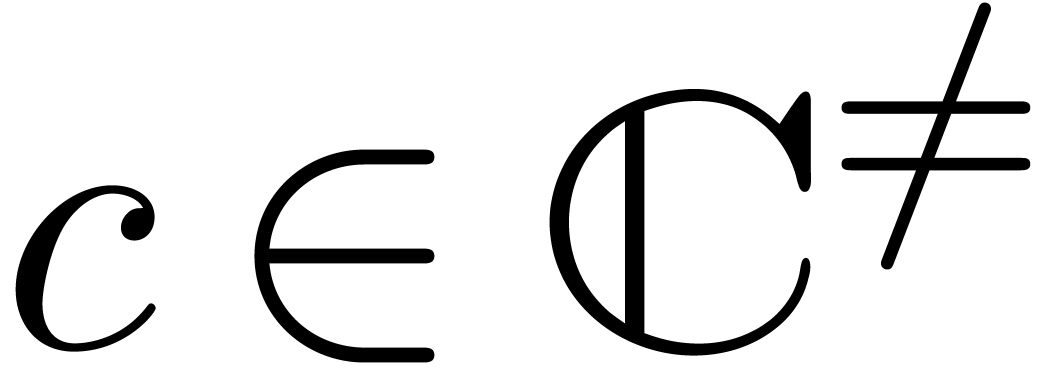 is
such that
is
such that  , we obtain
different approximations for
, we obtain
different approximations for  and
and  . This drawback can be removed by replacing
. This drawback can be removed by replacing
 by
by 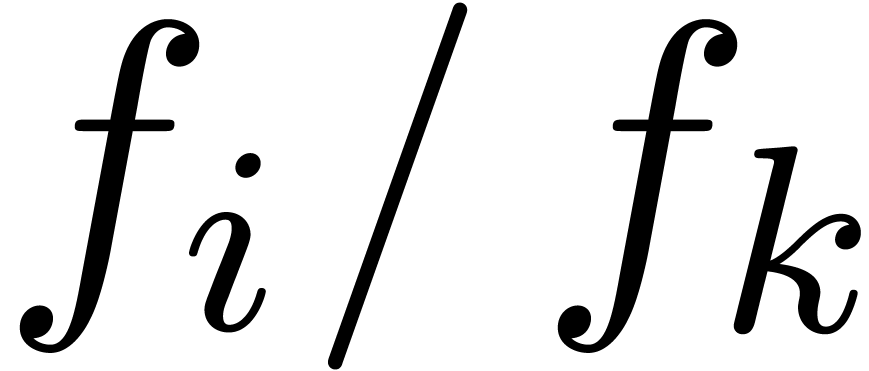 for some appropriate
coefficient index
for some appropriate
coefficient index 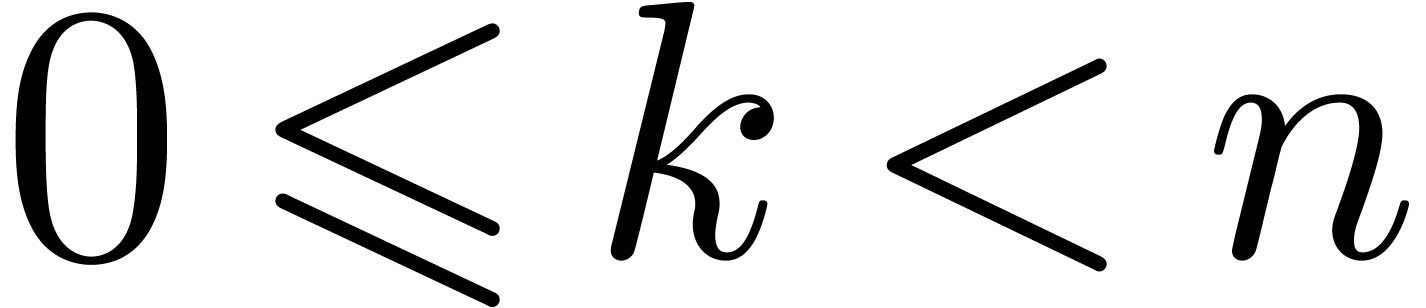 with
with 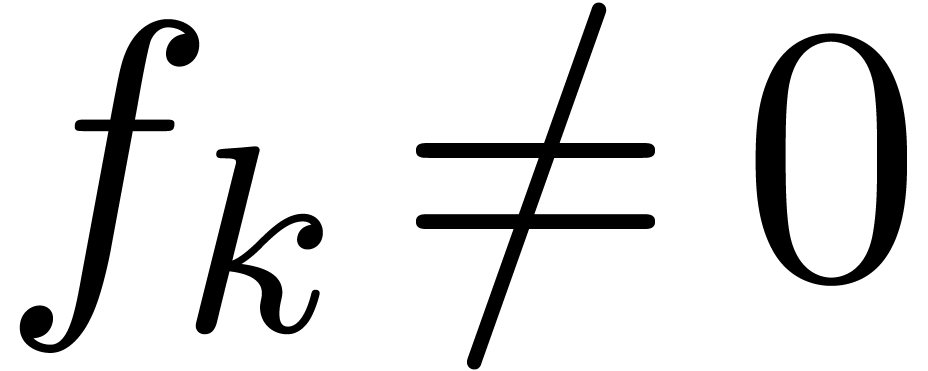 . In fact, one can even do better, and compute
. In fact, one can even do better, and compute  using the formula
using the formula 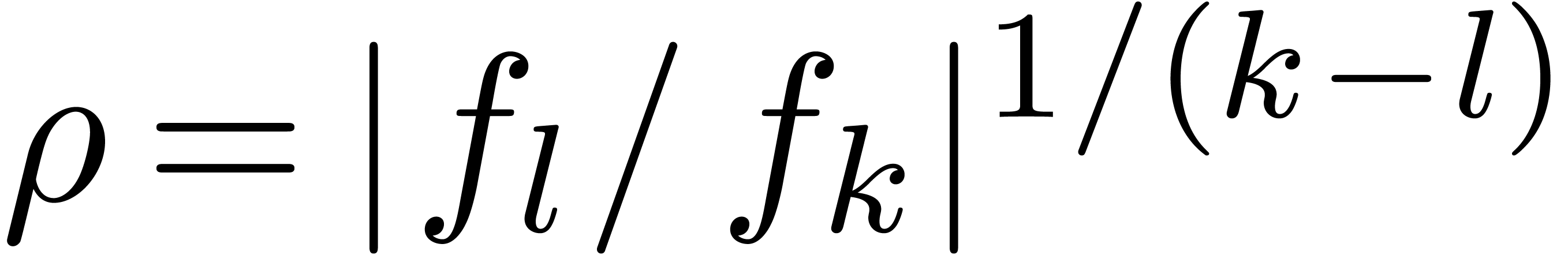 for
appropriate indices
for
appropriate indices  with
with 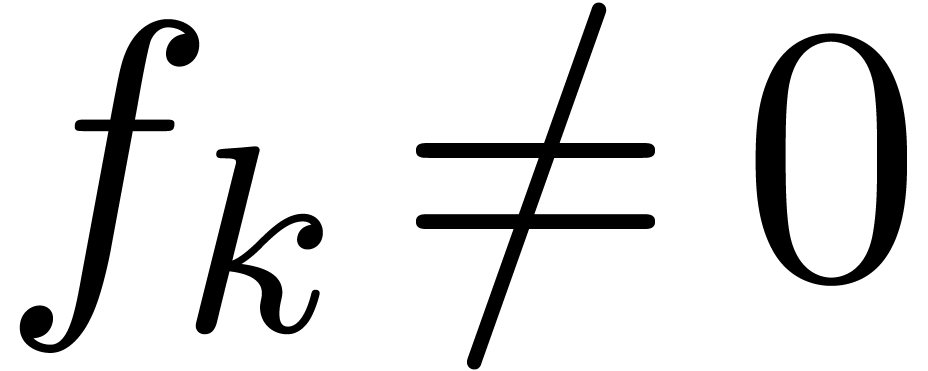 and
and 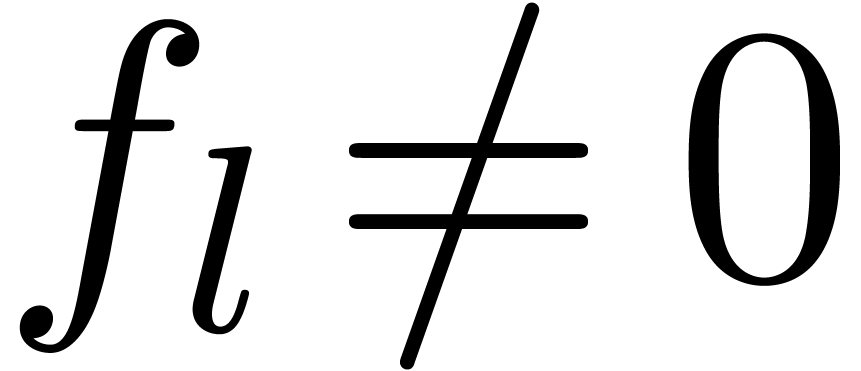 . Let us now show how to
read off such indices from the numerical Newton diagram of
. Let us now show how to
read off such indices from the numerical Newton diagram of  .
.
Let 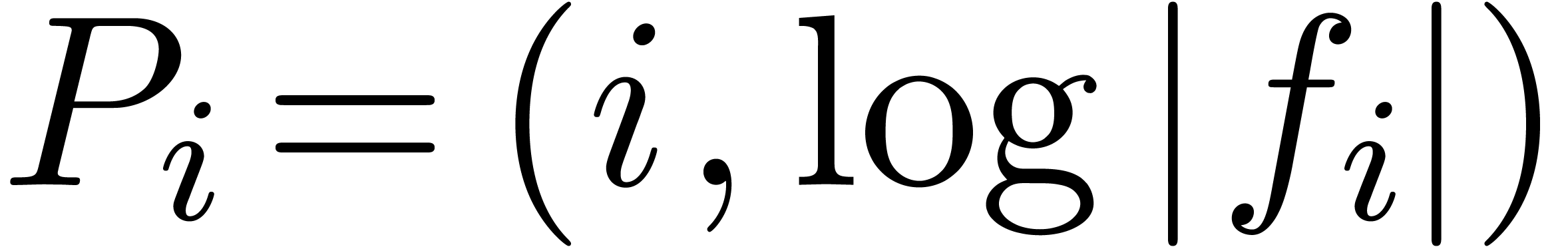 , where we understand
that
, where we understand
that 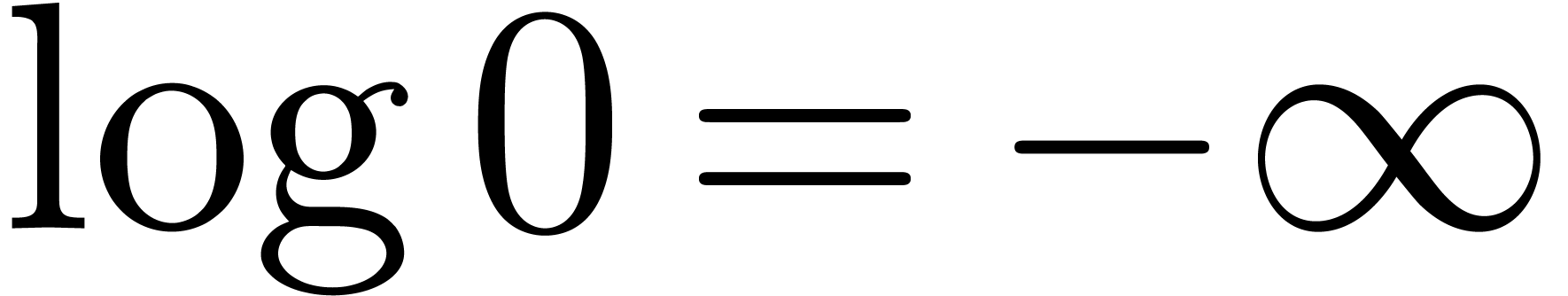 . Then the Newton
diagram of
. Then the Newton
diagram of  is the convex hull of the half
lines
is the convex hull of the half
lines
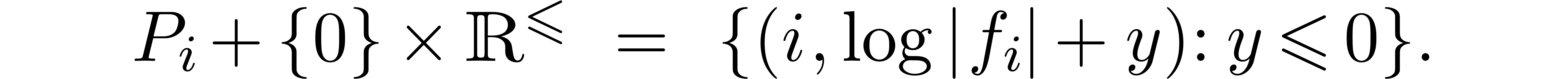
For a fixed  , say
, say 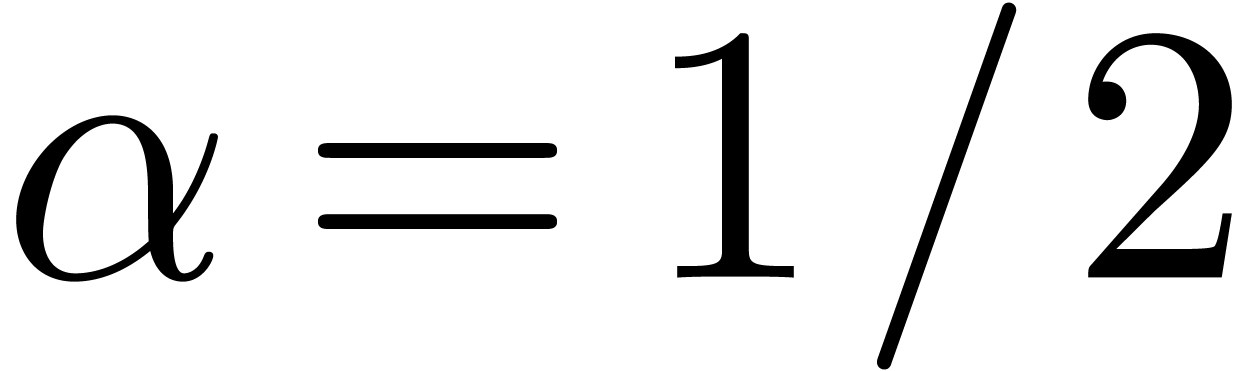 , let
, let 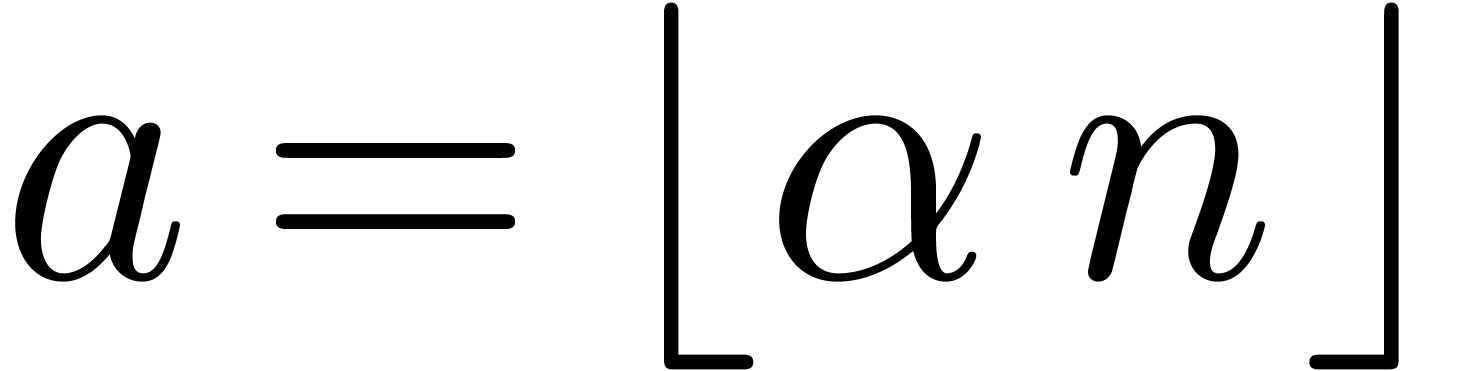 ,
and consider the Newton diagram of
,
and consider the Newton diagram of  .
There exists a minimal subset
.
There exists a minimal subset 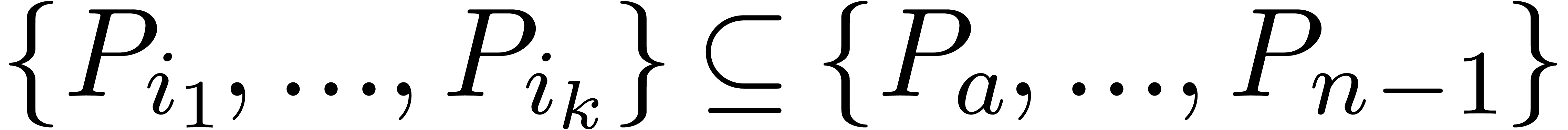 with
with  , such that the Newton diagram is also the
convex hull of the half lines
, such that the Newton diagram is also the
convex hull of the half lines 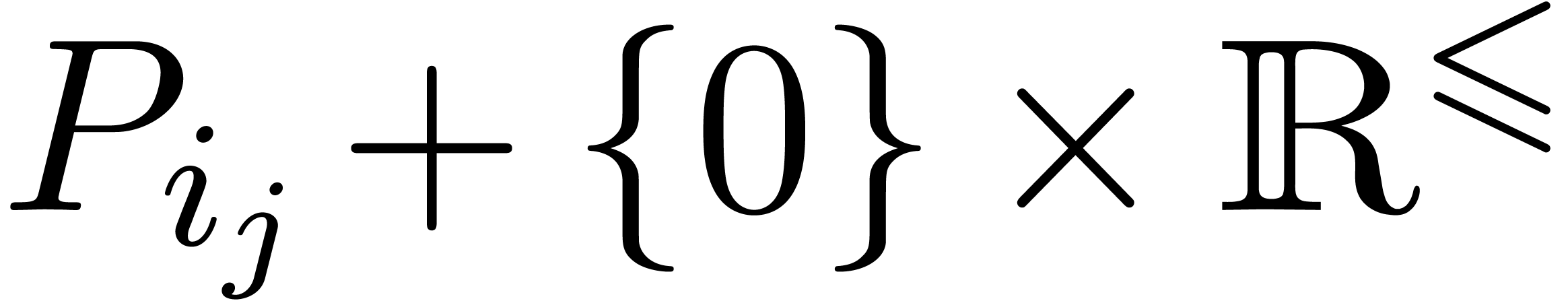 for
for  . Graphically speaking, the
. Graphically speaking, the  are the vertices of the Newton diagram (see figure 1).
are the vertices of the Newton diagram (see figure 1).
For a fixed 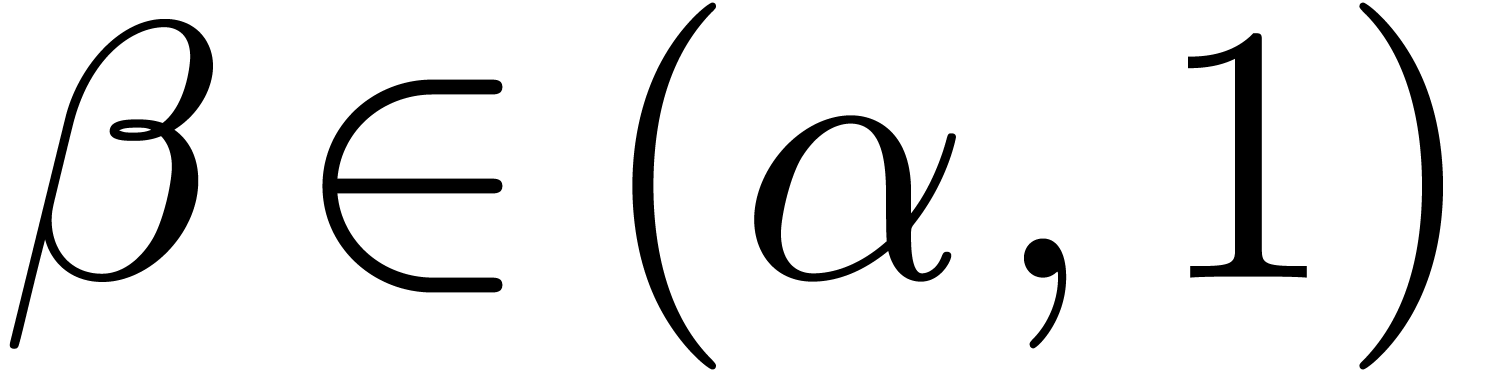 , say
, say  , we may now determine the unique
edge
, we may now determine the unique
edge  of the Newton diagram such that
of the Newton diagram such that  , and replace the formula (4)
by
, and replace the formula (4)
by
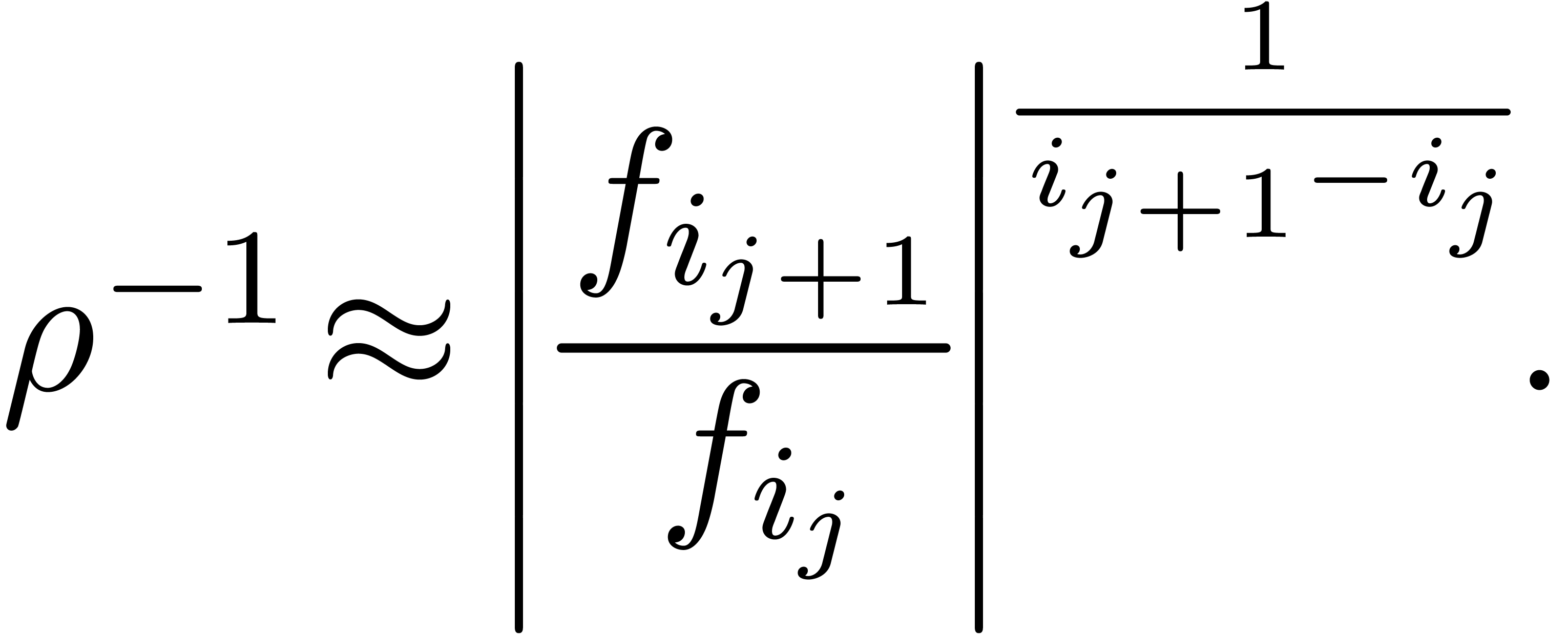 |
(6) |
For a large class of convergent power series  , the formula (6) is again ultimately
exact. The indices
, the formula (6) is again ultimately
exact. The indices  can be computed from the
coefficients
can be computed from the
coefficients 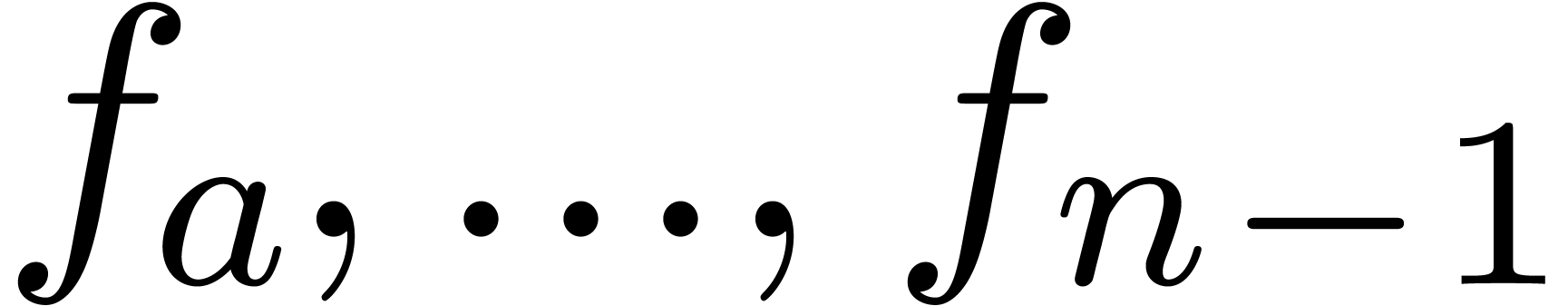 using a linear traversal in time
using a linear traversal in time
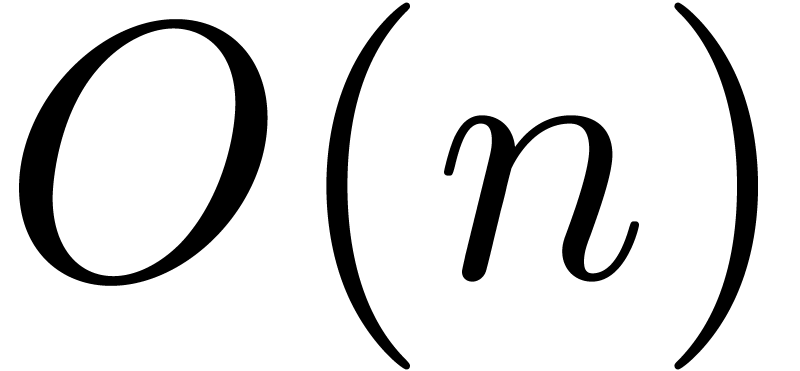 . This yields an efficient
algorithm for the approximation of
. This yields an efficient
algorithm for the approximation of  which turns
out to be more accurate than (4) in practice. The formula
(6) has been implemented in the
which turns
out to be more accurate than (4) in practice. The formula
(6) has been implemented in the  ,
the computed radius is usually correct up to one decimal digit in the
relative error.
,
the computed radius is usually correct up to one decimal digit in the
relative error.
 |
The formula (6) usually yields a reasonable estimate for
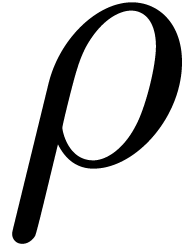 , even in very degenerate
cases when there are several singularities at distance
, even in very degenerate
cases when there are several singularities at distance 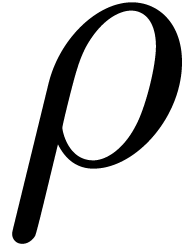 or close to
or close to 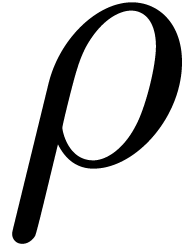 . However, if
. However, if
 admits a single isolated singularity
admits a single isolated singularity  at distance
at distance 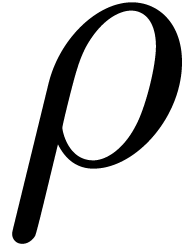 of the origin, with no
other singularities at distance close to
of the origin, with no
other singularities at distance close to 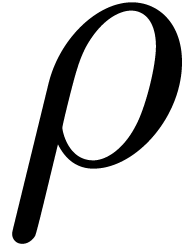 ,
then it is often possible to read off much more information about this
singularity from the coefficients
,
then it is often possible to read off much more information about this
singularity from the coefficients  .
.
For instance, it frequently (always?) occurs that the quotients 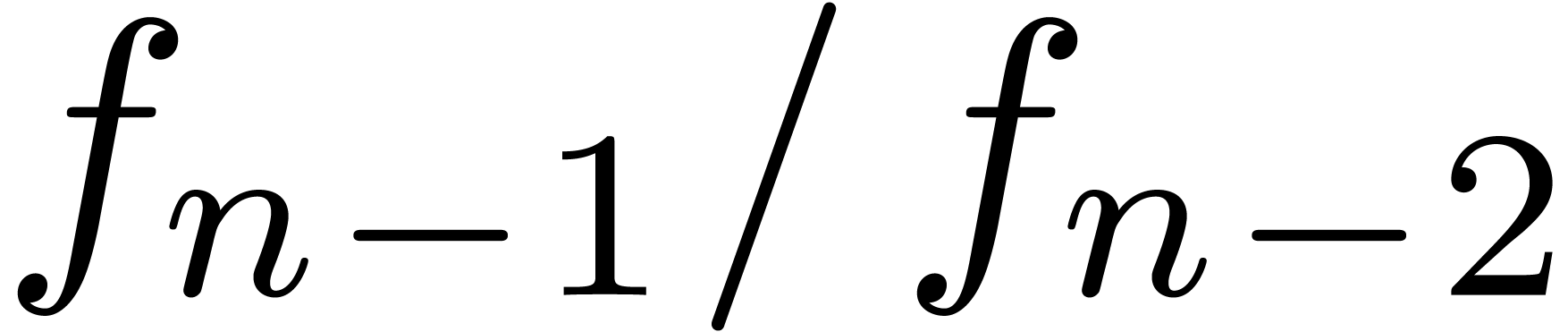 simply tend to
simply tend to  for
for  . Moreover, as we will show below,
if the singularity at
. Moreover, as we will show below,
if the singularity at  has a known type, then the
approximation
has a known type, then the
approximation 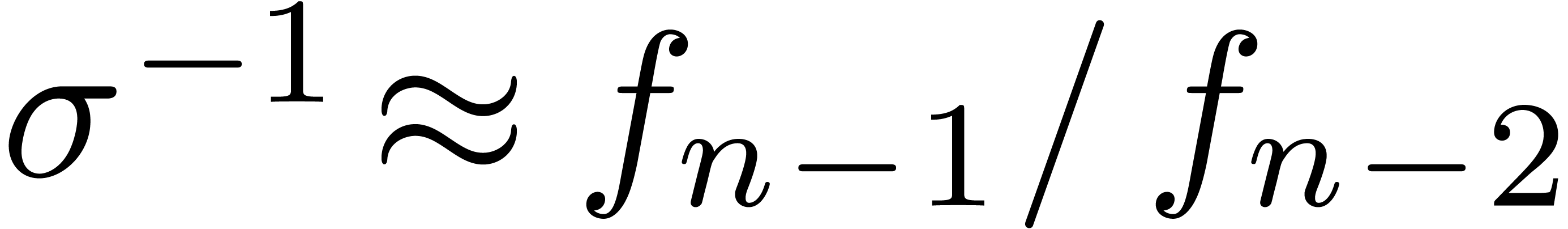 can be further improved. If
nothing is known about the singularity at
can be further improved. If
nothing is known about the singularity at  ,
then we may still try and see what happens if we apply such specialized
algorithms for various frequent types of singularities: with a bit of
luck, we will both obtain useful information about the type of
singularity and the numerical value of
,
then we may still try and see what happens if we apply such specialized
algorithms for various frequent types of singularities: with a bit of
luck, we will both obtain useful information about the type of
singularity and the numerical value of  .
.
We say that  is algebraic at
is algebraic at  , if
, if  satisfies a polynomial equation
satisfies a polynomial equation
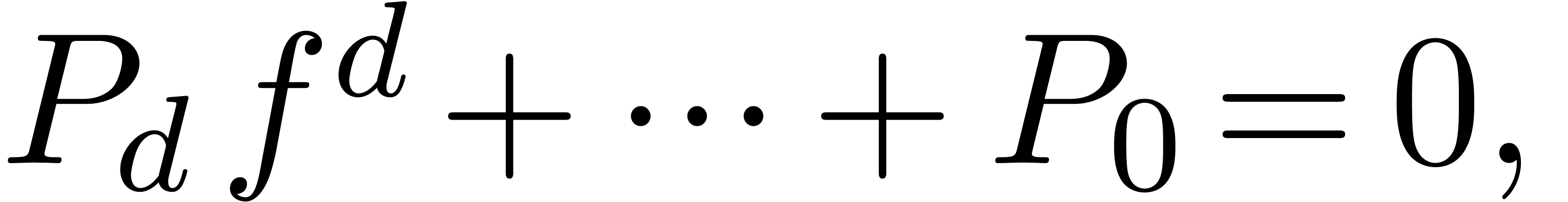
where  are analytic functions at
are analytic functions at  with
with 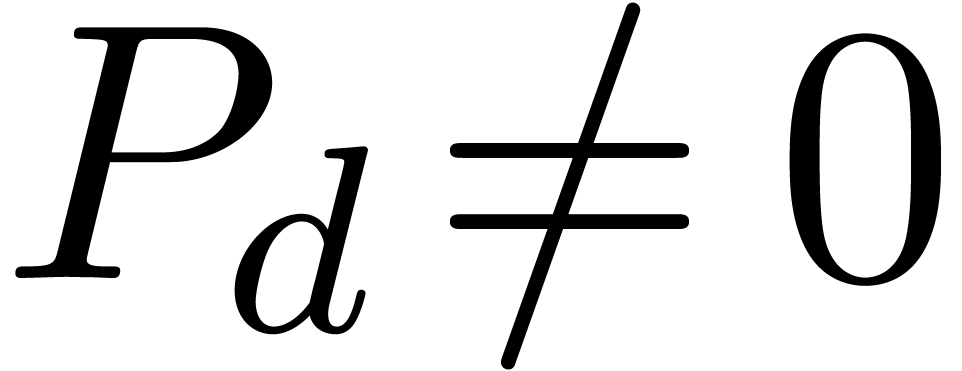 . In that case, we have
. In that case, we have
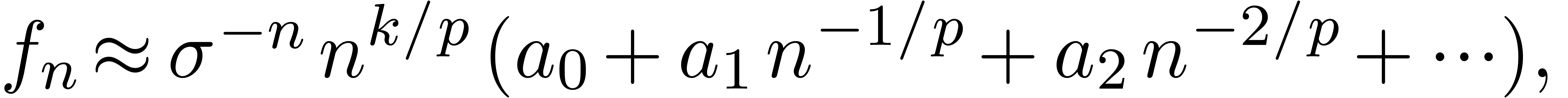
with  and ramification index
and ramification index 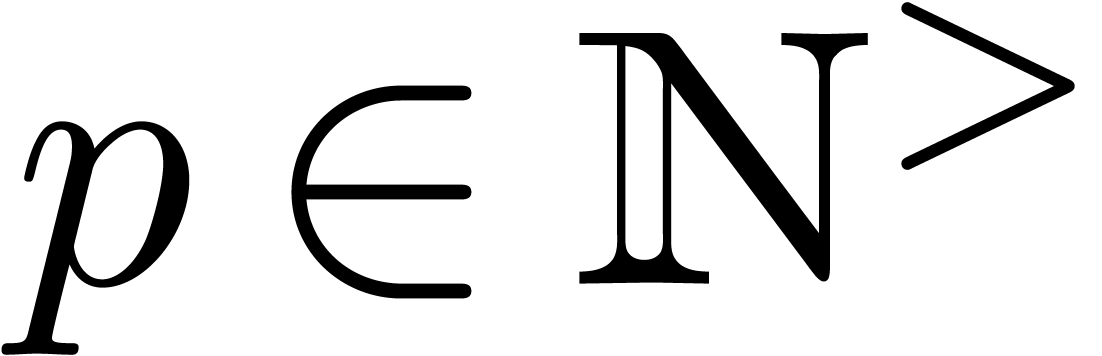 , whence
, whence
 |
(7) |
Using the E-algorithm [Wen01, BZ91], we may
now compute simultaneous approximations for the first
coefficients  ,
, 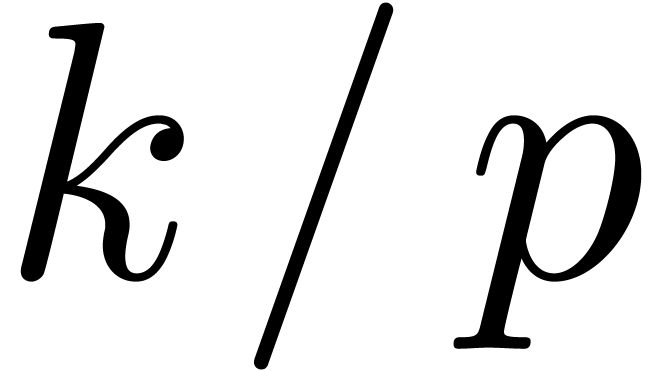 ,
, 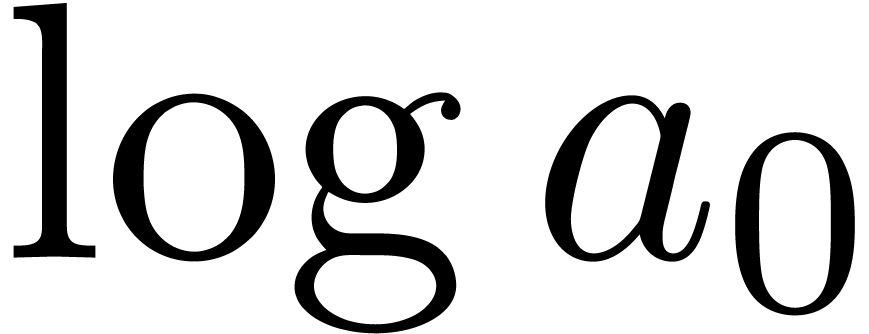 ,
,
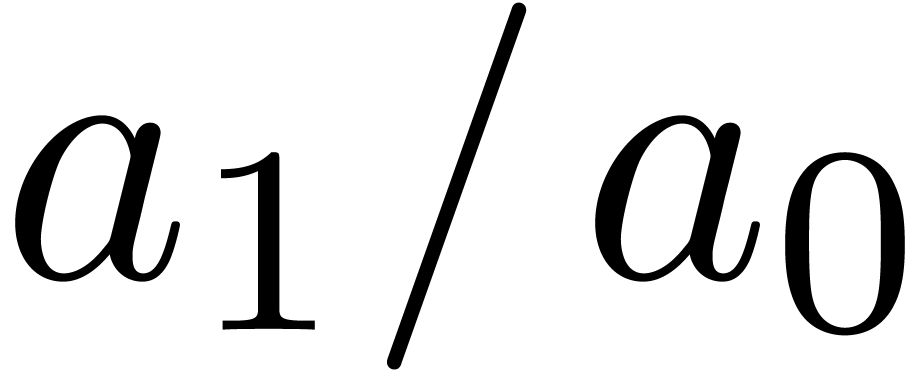 , etc. of the
expansion (7). It turns out that this strategy greatly
improves the accuracy of the approximation of
, etc. of the
expansion (7). It turns out that this strategy greatly
improves the accuracy of the approximation of  (see also [Hoe09]).
(see also [Hoe09]).
Similarly, we say that  is Fuchsian at
is Fuchsian at
 , if
, if  satisfies a linear differential equation
satisfies a linear differential equation
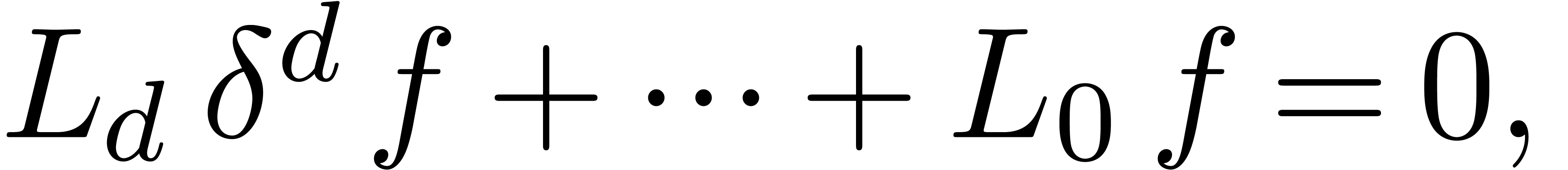
where  and
and  are analytic
functions at
are analytic
functions at  with
with 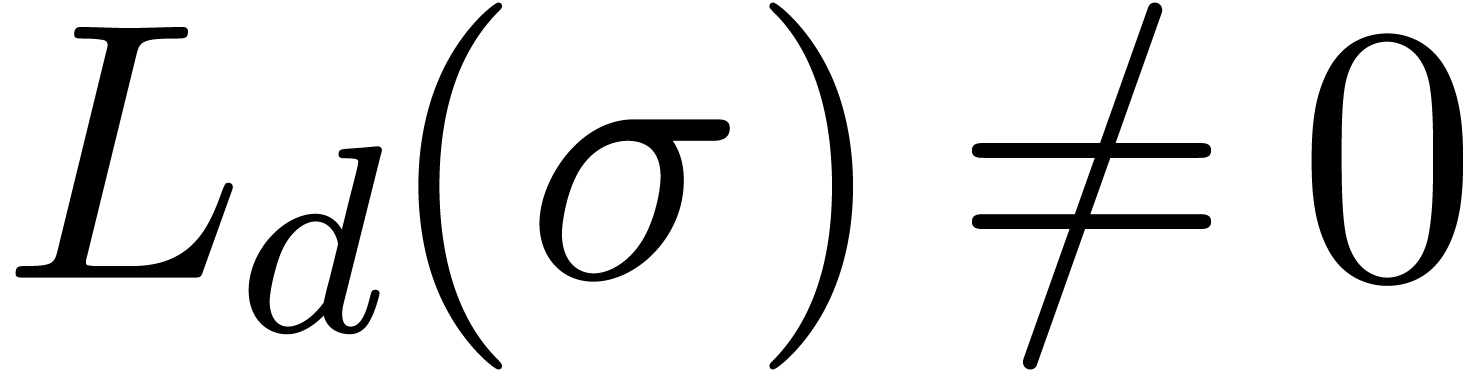 .
In that case, the Taylor coefficients
.
In that case, the Taylor coefficients  satisfy
the asymptotic expansion
satisfy
the asymptotic expansion
where  ,
, 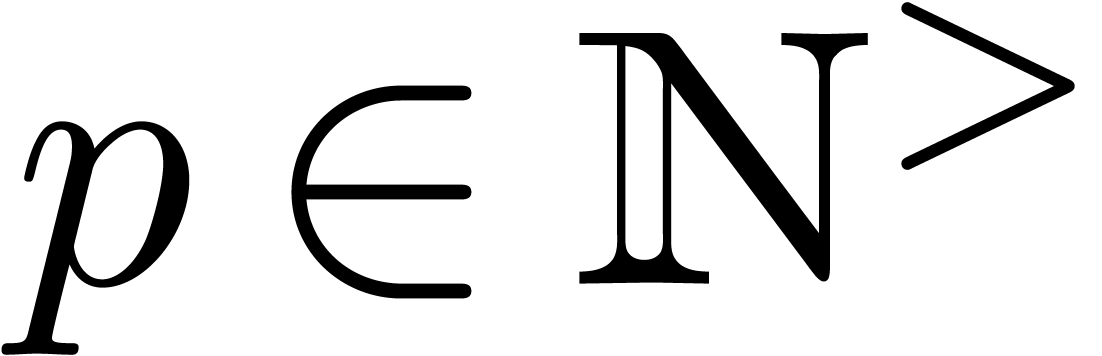 and the
and the 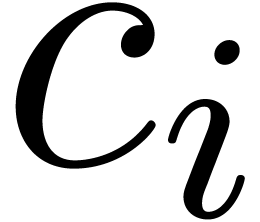 are polynomials in
are polynomials in  of degrees
of degrees  [Fab85, Poi86,
Bir13, Was67]. Again, the E-algorithm or more
general algorithms for asymptotic extrapolation [Hoe09] can
be used to compute
[Fab85, Poi86,
Bir13, Was67]. Again, the E-algorithm or more
general algorithms for asymptotic extrapolation [Hoe09] can
be used to compute  with a high accuracy. Notice
that these algorithms also provide estimates for the accuracies of the
computed approximations.
with a high accuracy. Notice
that these algorithms also provide estimates for the accuracies of the
computed approximations.
In cases where nothing particular is known about the behaviour of  at its dominant singularity, the strategy of
asymptotic extrapolation [Hoe09] still may work and both
provide useful information about the nature of the singularity and the
numerical value of
at its dominant singularity, the strategy of
asymptotic extrapolation [Hoe09] still may work and both
provide useful information about the nature of the singularity and the
numerical value of  .
.
In order to explore the analytic function 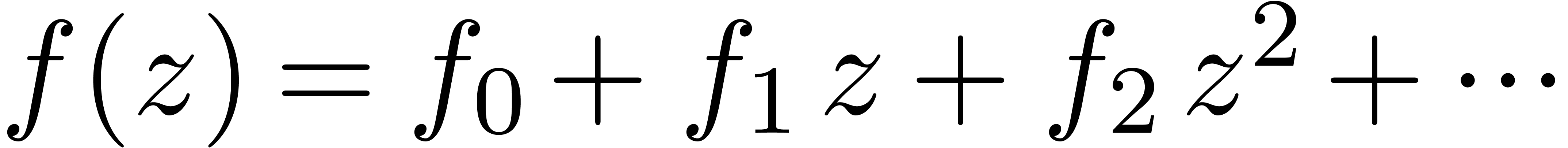 determined by the coefficients
determined by the coefficients 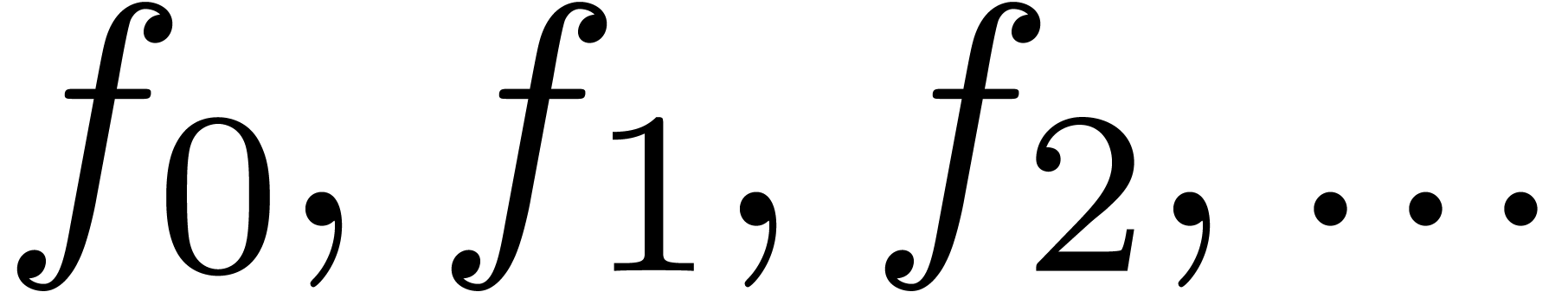 more closely, and
in particular determine its singularities in a given region, it is
useful to have a means for performing the analytic continuation of
more closely, and
in particular determine its singularities in a given region, it is
useful to have a means for performing the analytic continuation of  .
.
The way  is given sometimes provides us with such
a means. For instance, if
is given sometimes provides us with such
a means. For instance, if  is the solution to an
initial value problem
is the solution to an
initial value problem
then the continuation  of
of  at any sufficiently small
at any sufficiently small  is again the solution
of an initial value problem
is again the solution
of an initial value problem
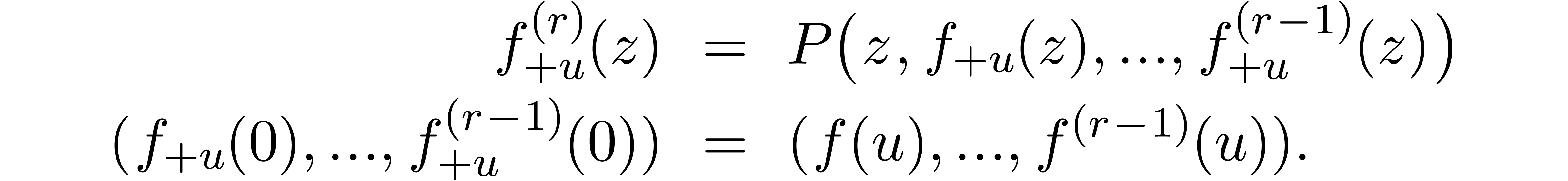
In [Hoe05, Hoe07] it is shown in detail how to
turn this into an algorithm for the analytic continuation of  . Notice also that the power series
solutions to an initial value problem can be computed efficiently using
the algorithms from [BK78, Hoe02].
. Notice also that the power series
solutions to an initial value problem can be computed efficiently using
the algorithms from [BK78, Hoe02].
In general, it is always possible to compute the continuation 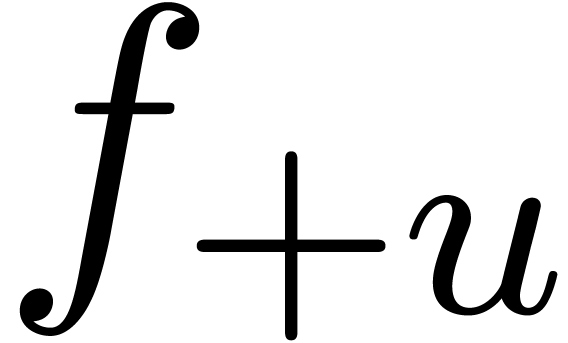 numerically. However, this kind of “poor
man's” analytic continuation induces a big loss of accuracy. Let
us illustrate this on the fundamental example
numerically. However, this kind of “poor
man's” analytic continuation induces a big loss of accuracy. Let
us illustrate this on the fundamental example
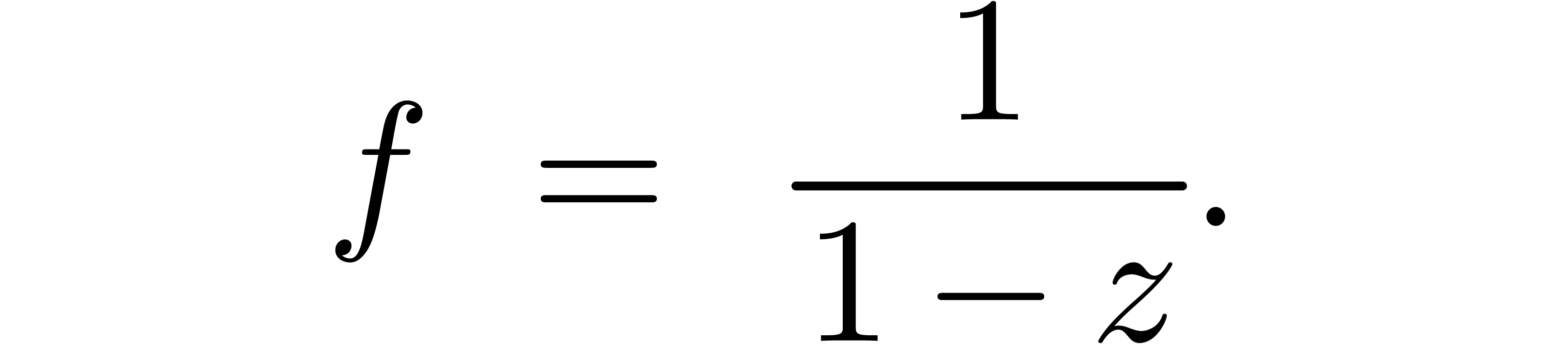
In order to compute 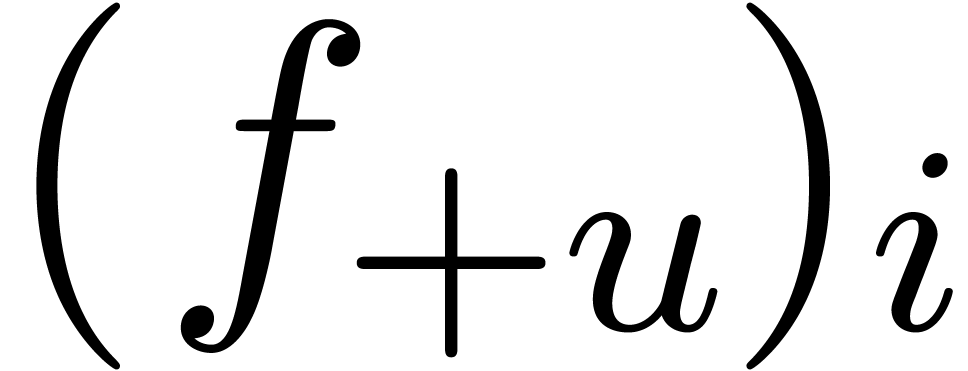 with a precision of
with a precision of  bits using the formula
bits using the formula
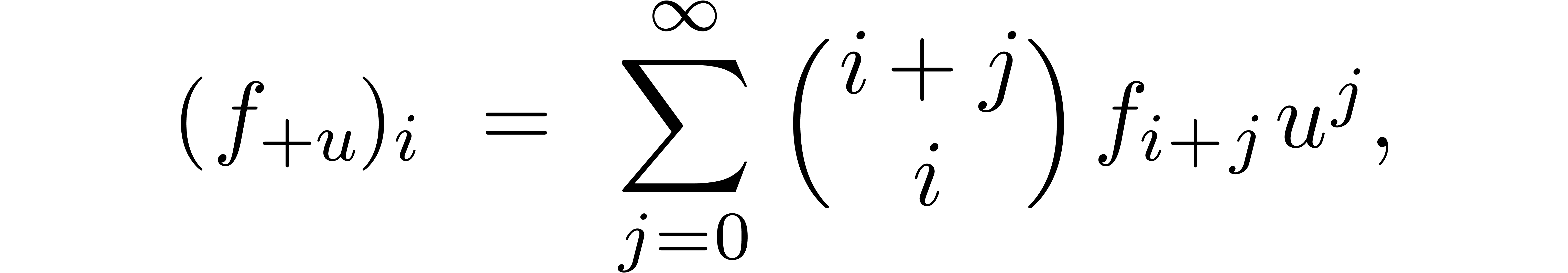
we need to truncate this expansion at an order  for which
for which
Putting 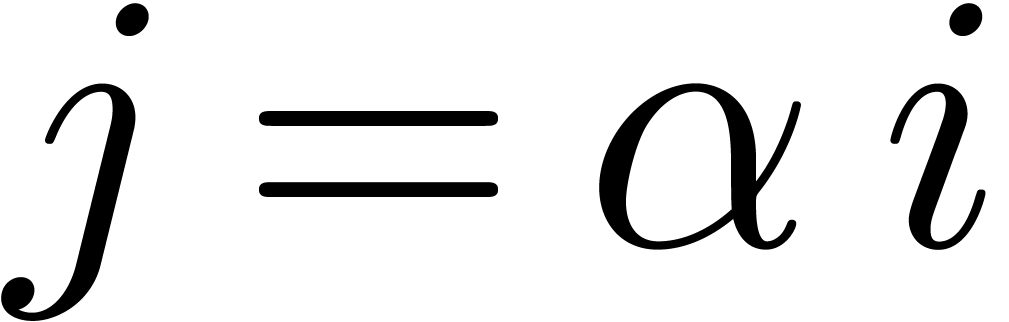 and using Stirling's formula, this
yields
and using Stirling's formula, this
yields
For instance, in order to expand 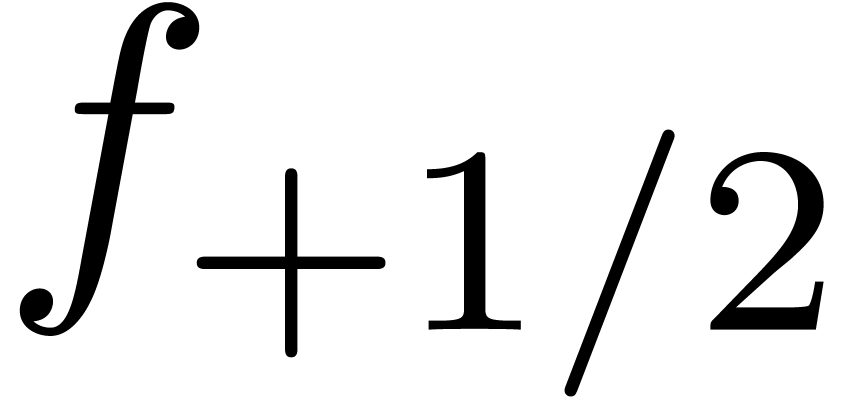 at order
at order  with precision
with precision  ,
we get
,
we get
and we need an expansion of  at the origin at
order
at the origin at
order 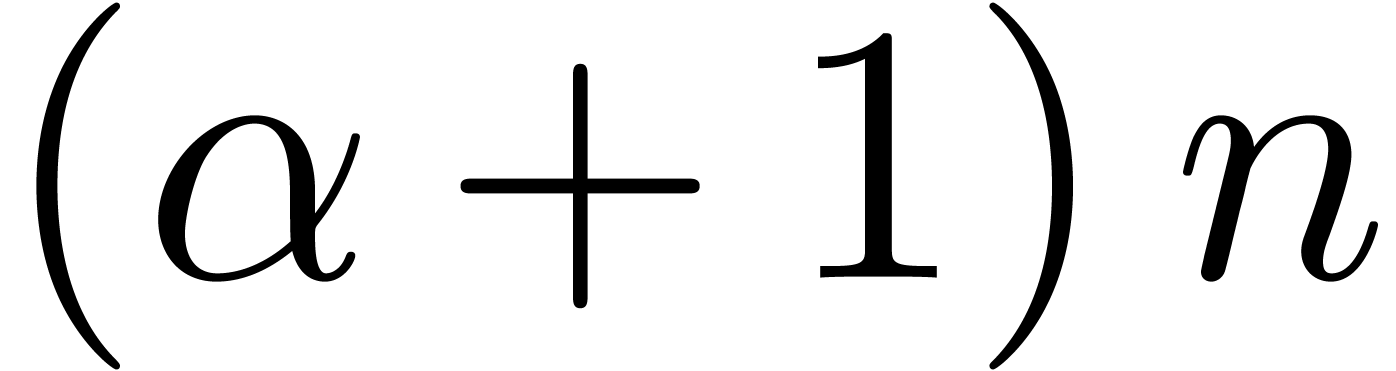 . In general, for every
analytic continuation step, we need to multiply the expansion order by a
constant factor which depends on the desired precision and the ratio
between the step size and the radius of convergence.
. In general, for every
analytic continuation step, we need to multiply the expansion order by a
constant factor which depends on the desired precision and the ratio
between the step size and the radius of convergence.
An experimentally better strategy for poor man's analytic continuation
is to postcompose  with a suitable analytic
function
with a suitable analytic
function 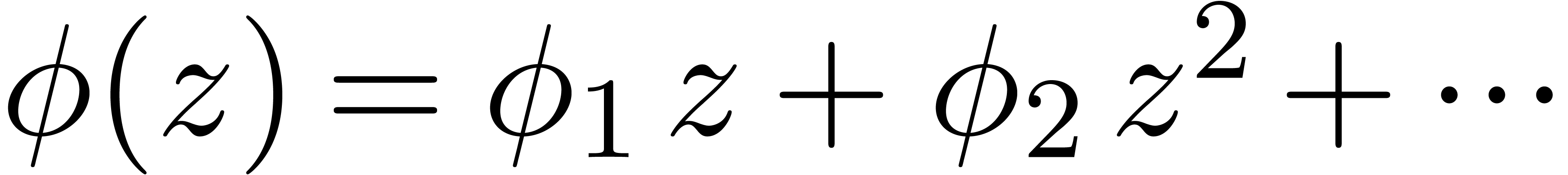 instead of
instead of 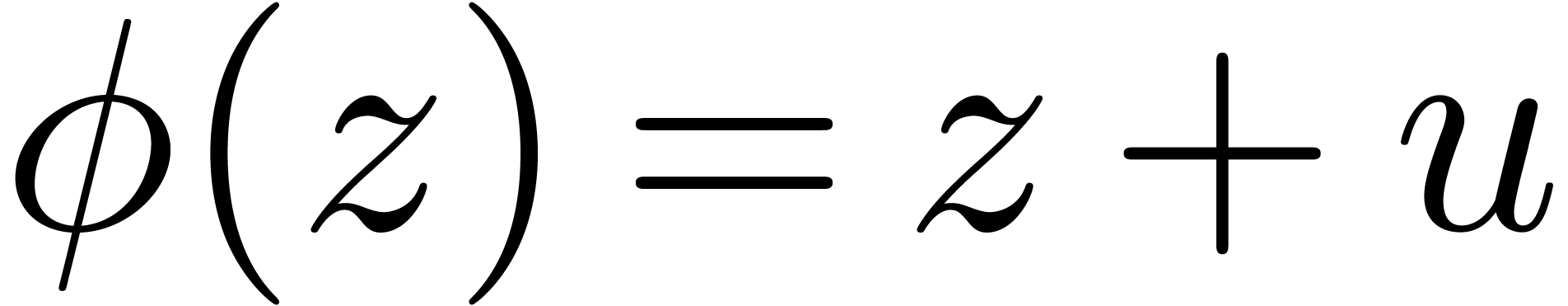 . If
. If  admits a dominant
singularity at
admits a dominant
singularity at  , then
, then 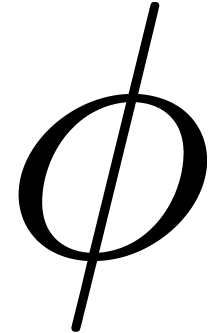 should be chosen in such a way that
should be chosen in such a way that  has
has 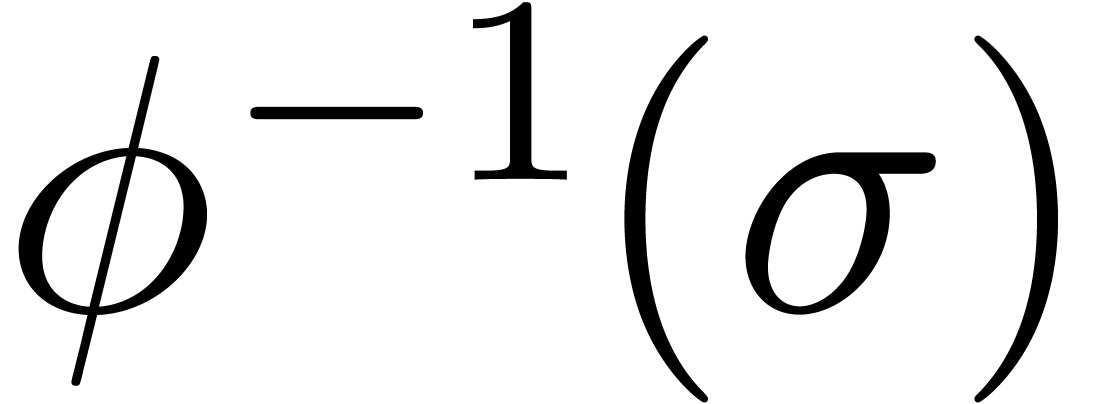 as its only singularity in the unit disk,
and such that
as its only singularity in the unit disk,
and such that 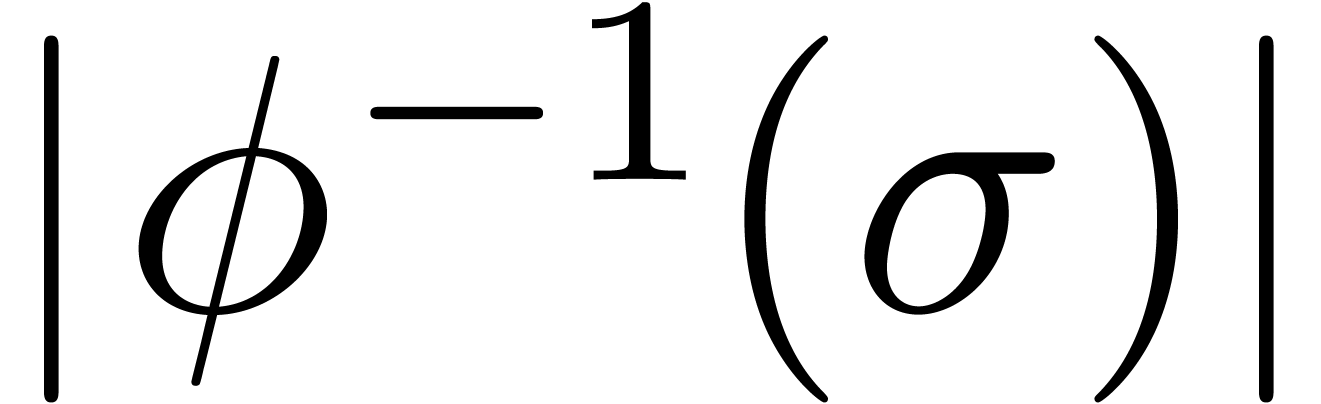 is as small as possible. One may
typically take
is as small as possible. One may
typically take  to be a composition of rational
functions of the form
to be a composition of rational
functions of the form 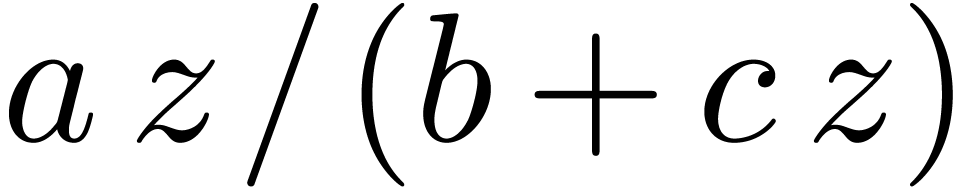 . Yet
another strategy would be to consider a Padé-Hermite
approximation
. Yet
another strategy would be to consider a Padé-Hermite
approximation 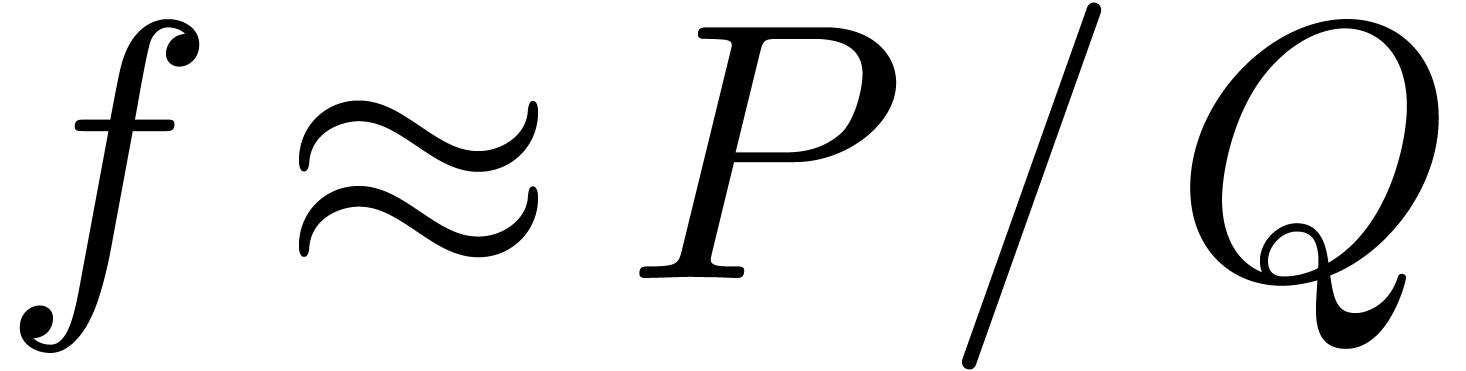 of
of  and
then to expand
and
then to expand 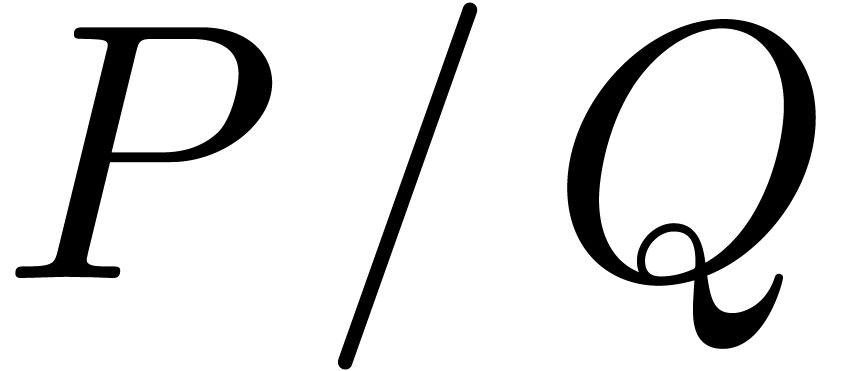 (instead of
(instead of  ) at
) at  .
.
Assuming that we have a means for analytic continuation (whether this
means is efficient and accurate or only a “poor man's”
solution), a natural question is to gather information about the
singularities of  . First of
all, we may want to locate the dominant singularity (or singularities)
of
. First of
all, we may want to locate the dominant singularity (or singularities)
of  with a good precision.
with a good precision.
Let us first assume that  admits a unique
dominant singularity at
admits a unique
dominant singularity at  and no other
singularities of norm
and no other
singularities of norm 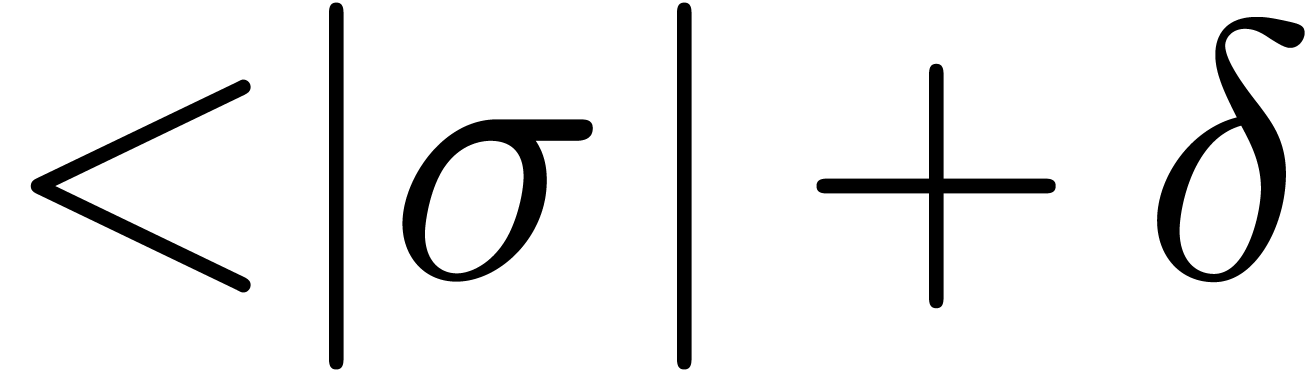 .
Section 3 provides us with heuristic algorithms for the
computation of
.
Section 3 provides us with heuristic algorithms for the
computation of 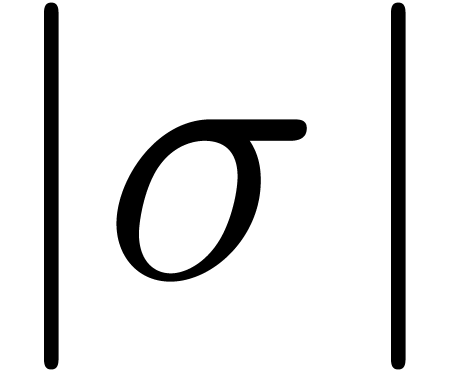 . More
generally, for any
. More
generally, for any 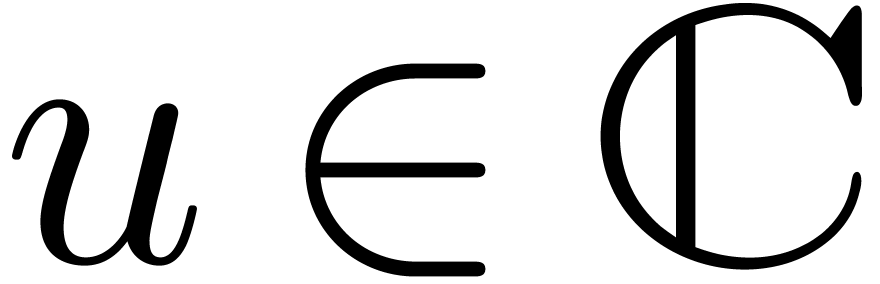 with
with 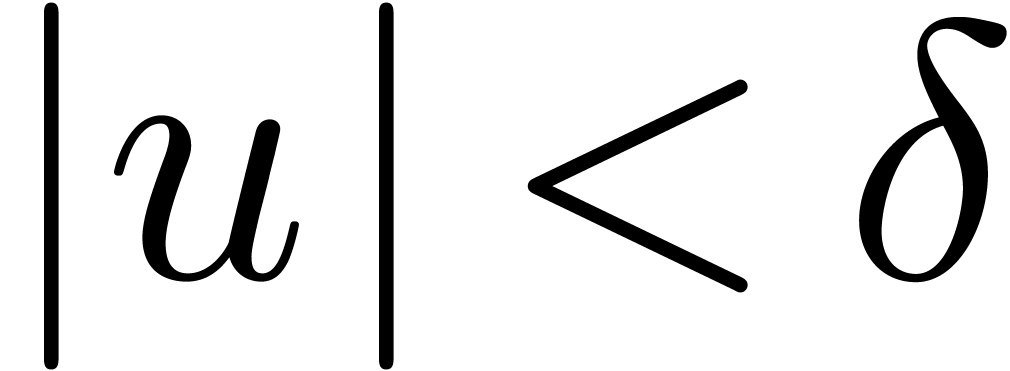 , the point
, the point 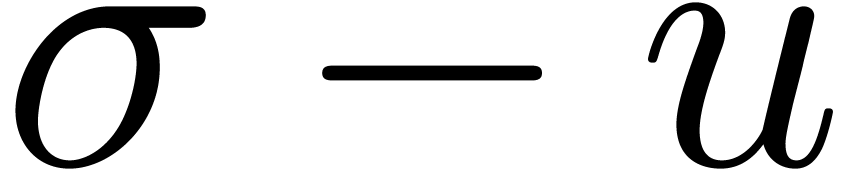 is also the
dominant singularity of
is also the
dominant singularity of  , so
we may compute
, so
we may compute 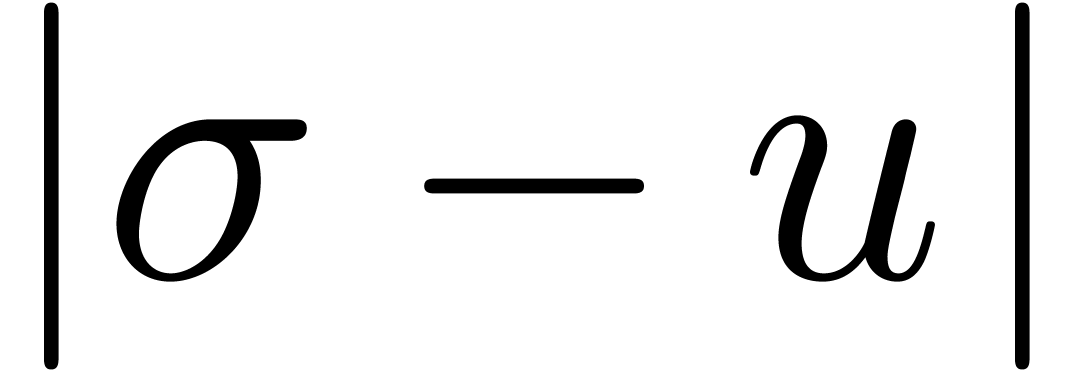 using the same heuristic
algorithms. Computing
using the same heuristic
algorithms. Computing 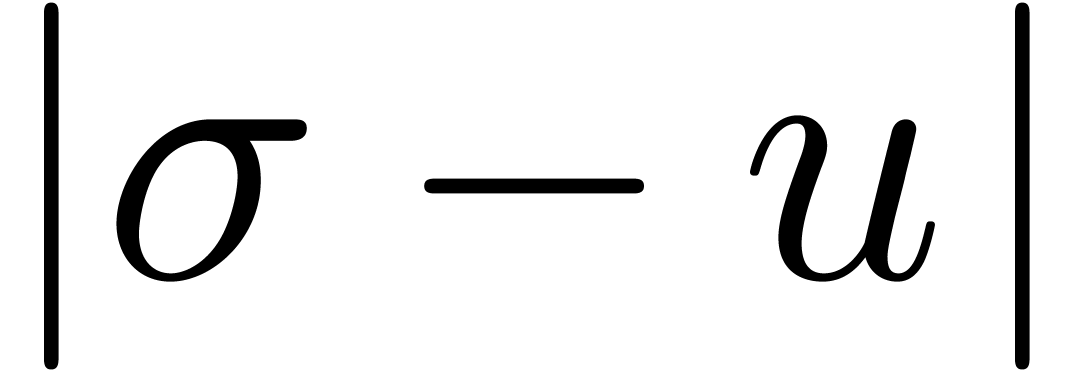 and
and 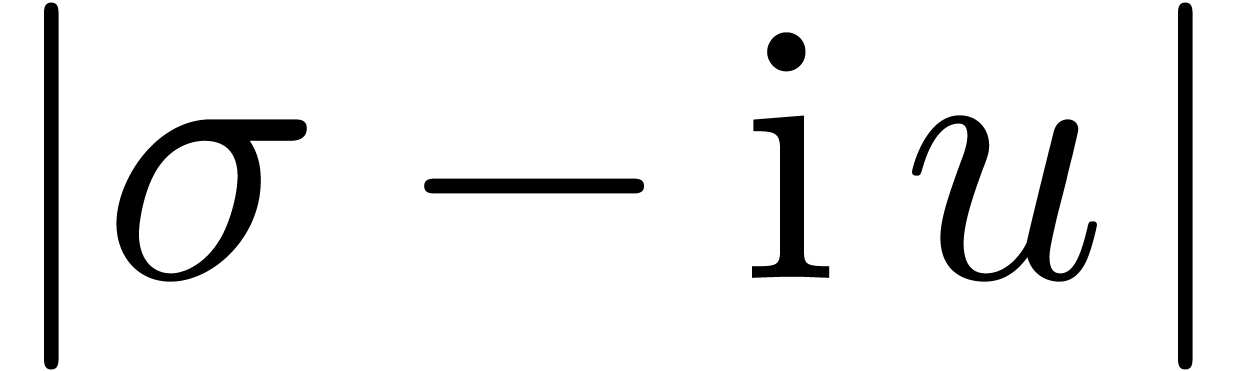 for two such points, the singularity
for two such points, the singularity  is now
uniquely determined by its distances
is now
uniquely determined by its distances  ,
,
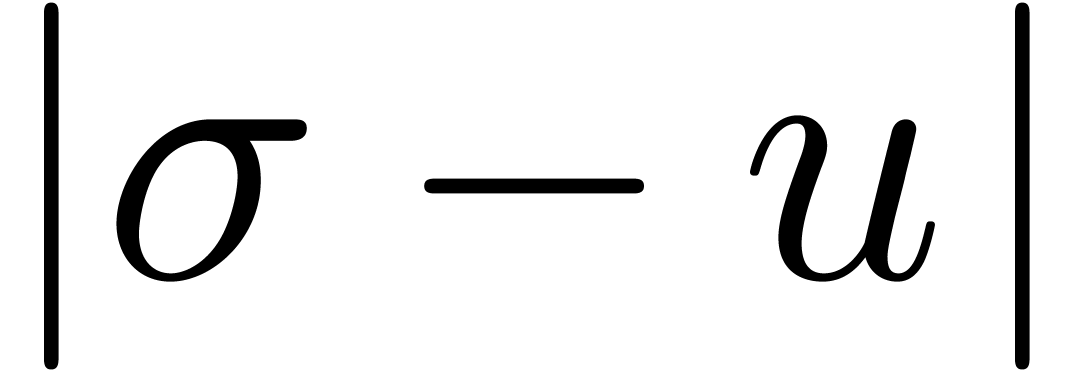 and
and 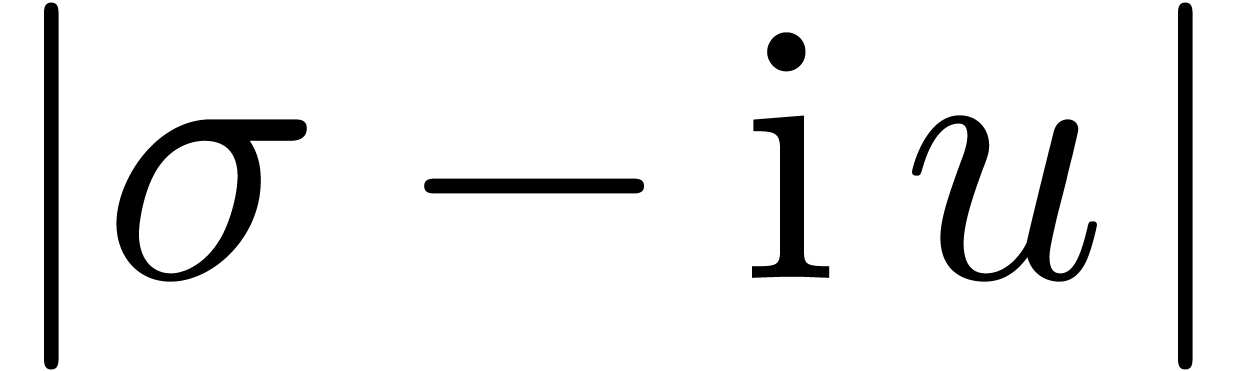 to
to  ,
,  and
and  (see figure 2).
(see figure 2).
Even if we do not know  beforehand, then we apply
the above method for
beforehand, then we apply
the above method for  with
with  , for some
, for some 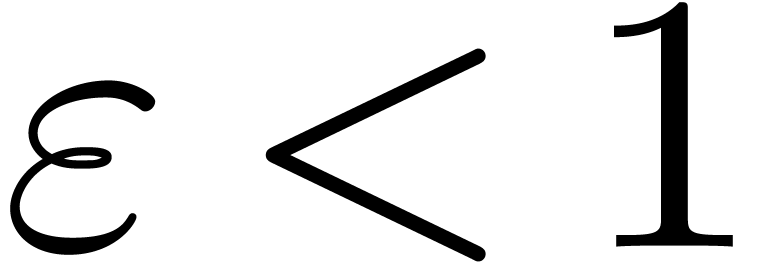 .
In order to check the correctness of the computed value of
.
In order to check the correctness of the computed value of  a posteriori, we also compute the radius of
convergence
a posteriori, we also compute the radius of
convergence 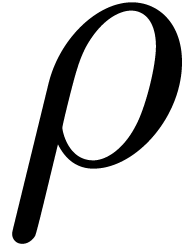 of
of 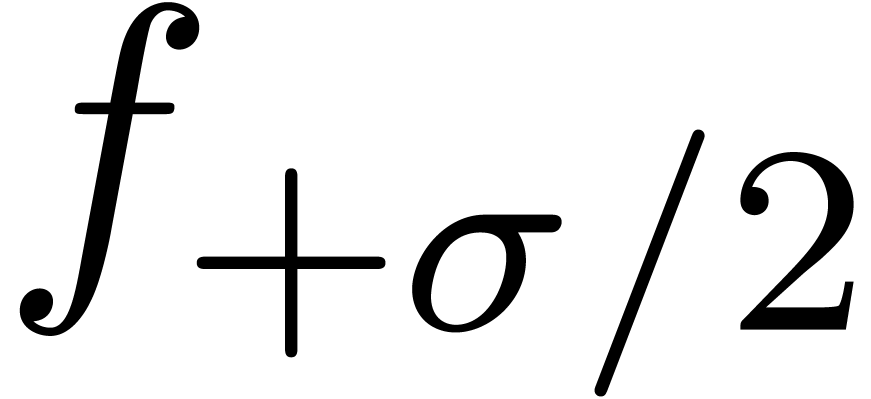 .
Then
.
Then  is a dominant singularity of
is a dominant singularity of  if and only if
if and only if 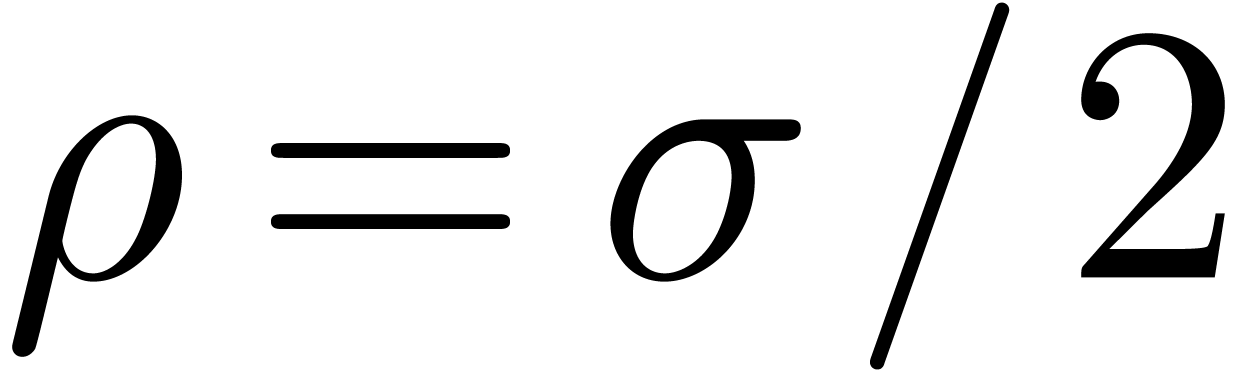 .
If this check fails, then we simply divide
.
If this check fails, then we simply divide  by
two and repeat the same procedure until the right value of
by
two and repeat the same procedure until the right value of  is found.
is found.
In practice, the convergence radii can only be approximated, so all
equality tests have to be replaced by approximate equality tests, for
which the tolerance in relative precision is slightly larger than the
estimated relative precision with which the convergence radii are
computed. In particular, the above method computes  with approximately the same accuracy as the radius of convergence
with approximately the same accuracy as the radius of convergence  .
.
Furthermore, if our procedure for analytic continuation is accurate
enough, then we may “zoom in” on a singularity, and
determine its location with higher precision. More precisely, assume
that we have a rough approximation  of the
dominant singularity
of the
dominant singularity  . For
some small
. For
some small  , we then compute
an approximation
, we then compute
an approximation  of the dominant singularity of
of the dominant singularity of
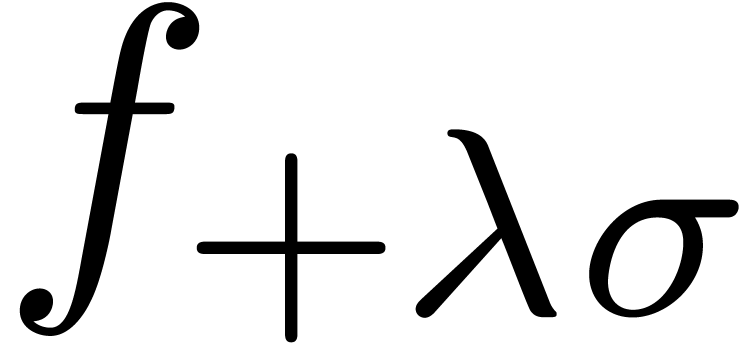 with
with  .
This yields the improved approximation
.
This yields the improved approximation 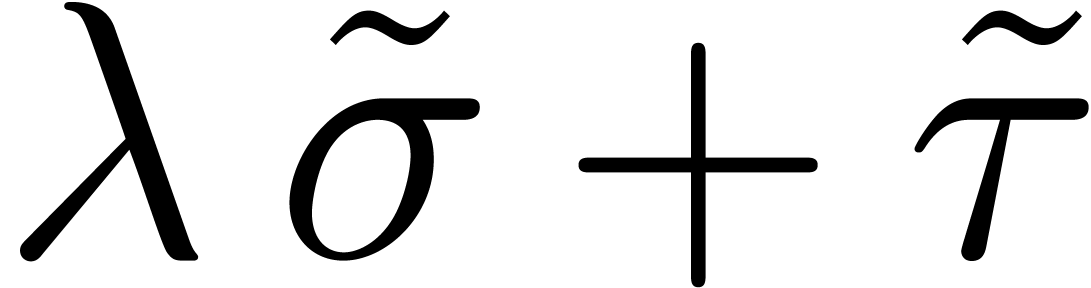 of
of  .
.
Assume now that  admits more than one dominant
singularity (or other singularities of norms close to
admits more than one dominant
singularity (or other singularities of norms close to  ), but still a finite number of them. On the
one hand, by computing the radii of convergence of
), but still a finite number of them. On the
one hand, by computing the radii of convergence of 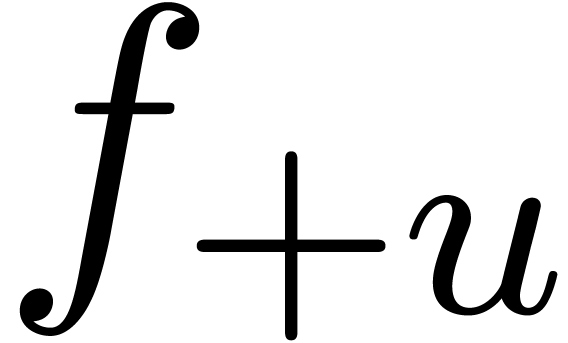 for a sufficiently large number of points
for a sufficiently large number of points  with
with
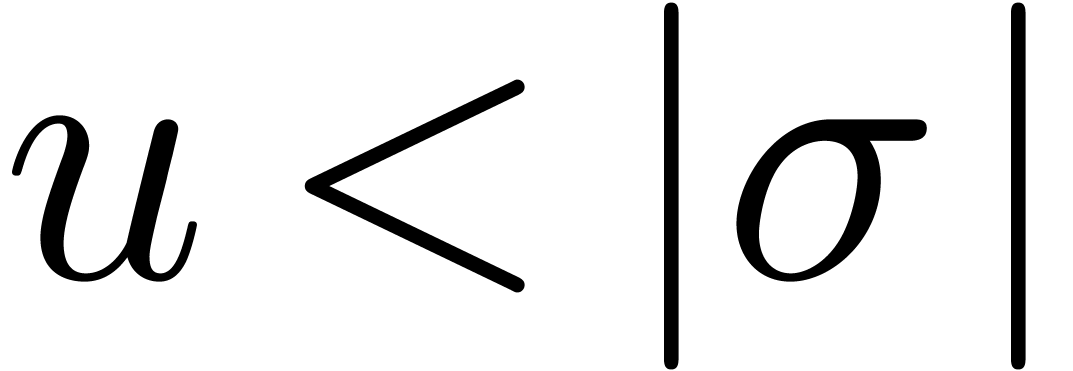 , we may determine all
dominant singularities. On the other hand, for any two adjacent dominant
singularities
, we may determine all
dominant singularities. On the other hand, for any two adjacent dominant
singularities  and
and 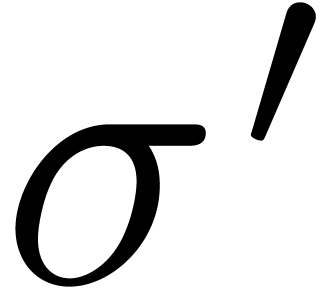 with
with
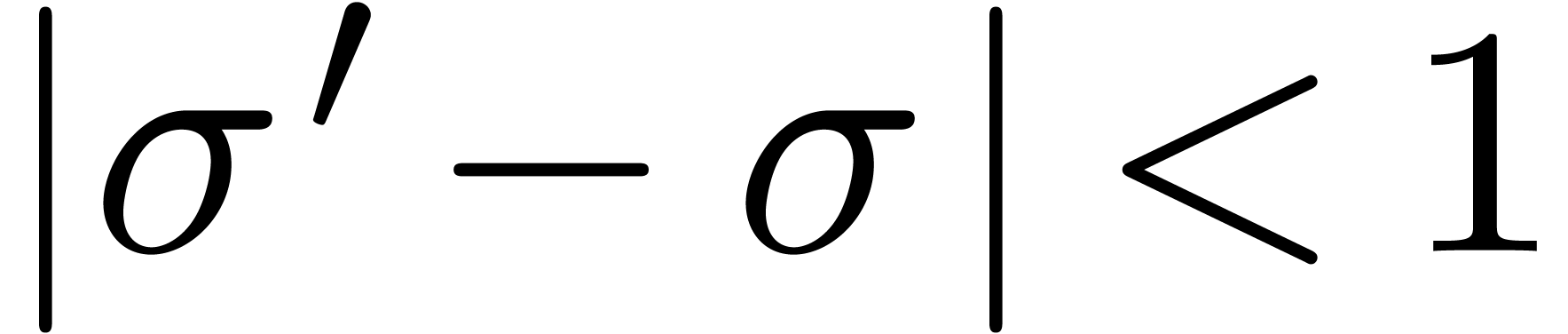 , we may check the absence of
other singularities in between by looking at the radii of convergence of
, we may check the absence of
other singularities in between by looking at the radii of convergence of
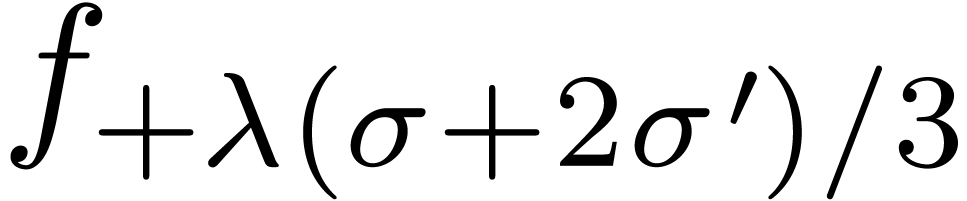 and
and 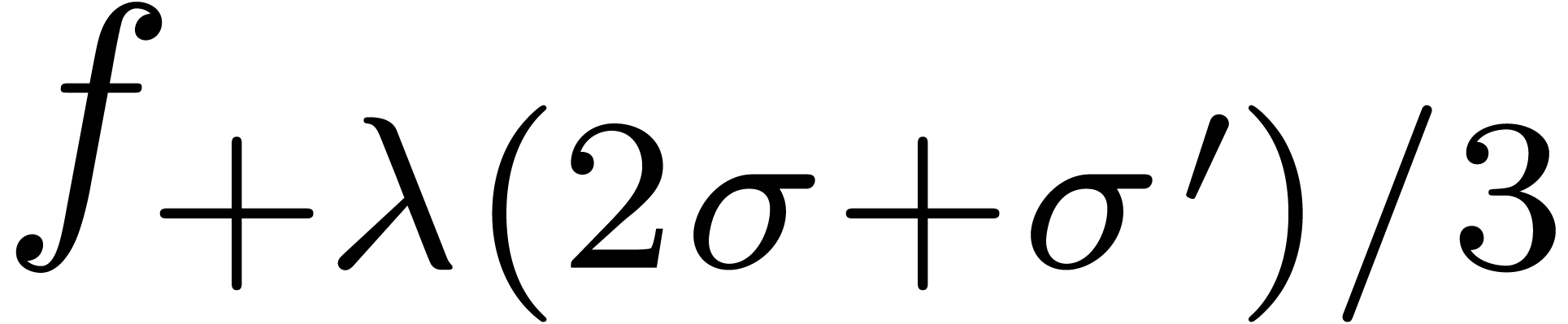 for some
for some  . This yields a criterion for
deciding whether we took a “sufficiently large number of points
. This yields a criterion for
deciding whether we took a “sufficiently large number of points
 ”.
”.
From the numerical point of view, rough initial rough approximations can be further improved by zooming in. In figure 3 we have shown an example where we zoomed in on one among eight singularities. After zooming in, we see that all other singularities are far away, so they do not pollute the computation of the radius of convergence.
The generalized algorithm is particularly useful in the special case when there are two dominant singularities which are complex conjugates. This annoying situation prevents us from using the technique of asymptotic extrapolation in a direct way. Nevertheless, we may use it after zooming in on one of the two singularities.
In the case when our method for analytic continuation allows us to turn
around singularities, it is natural to ask whether we can explore the
Riemann surface of  beyond the dominant
singularities. In general, it is always possible to approximate the
Riemann surface of
beyond the dominant
singularities. In general, it is always possible to approximate the
Riemann surface of  by an organically growing
sequence of more and more precise Riemann surfaces of a special form; we
refer to [Hoe07] for details. In this section, we will
restrict ourselves to a more particular situation: given the closed disk
by an organically growing
sequence of more and more precise Riemann surfaces of a special form; we
refer to [Hoe07] for details. In this section, we will
restrict ourselves to a more particular situation: given the closed disk
 of center
of center 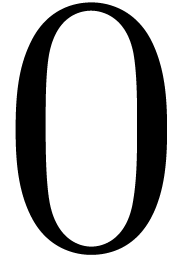 and radius
and radius
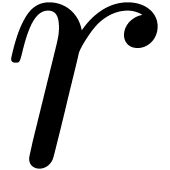 , we will assume that there
exist a finite number of points
, we will assume that there
exist a finite number of points 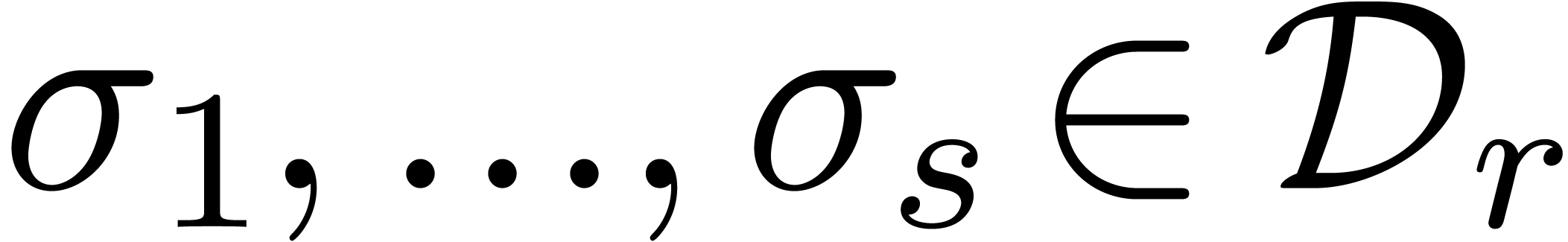 in its interior
such that
in its interior
such that  is defined above
is defined above 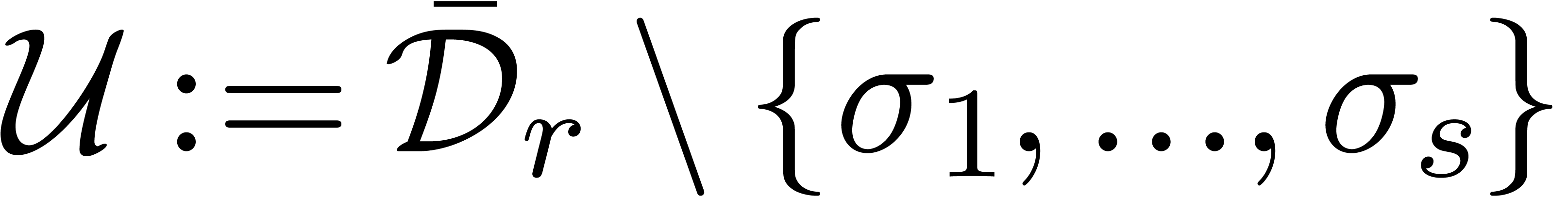 . Our task is to find the points
. Our task is to find the points  .
.
One complication is that some of the singularities 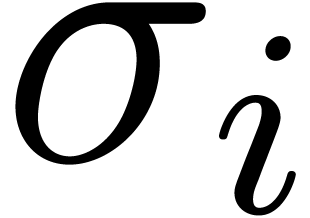 may not directly be visible from the origin by following a straight
line, but only after turning around one or more other singularities. In
principle, more and more singularities might therefore be disclosed by
making successive turns around the singularities which were already
found. In order to ensure our algorithm to terminate, we will make the
additional assumption
may not directly be visible from the origin by following a straight
line, but only after turning around one or more other singularities. In
principle, more and more singularities might therefore be disclosed by
making successive turns around the singularities which were already
found. In order to ensure our algorithm to terminate, we will make the
additional assumption
There exists a finite dimensional vector space of analytic
functions above  , which
contains
, which
contains  and all its analytic
continuations.
and all its analytic
continuations.
This is in particular the case if
The Riemann surface of  admits a finite
number of sheets above
admits a finite
number of sheets above  .
.
In sections 6.1 and 6.2, we will encounter two natural situations in which the assumptions A resp. H are satisfied.
Consider a finite number of points 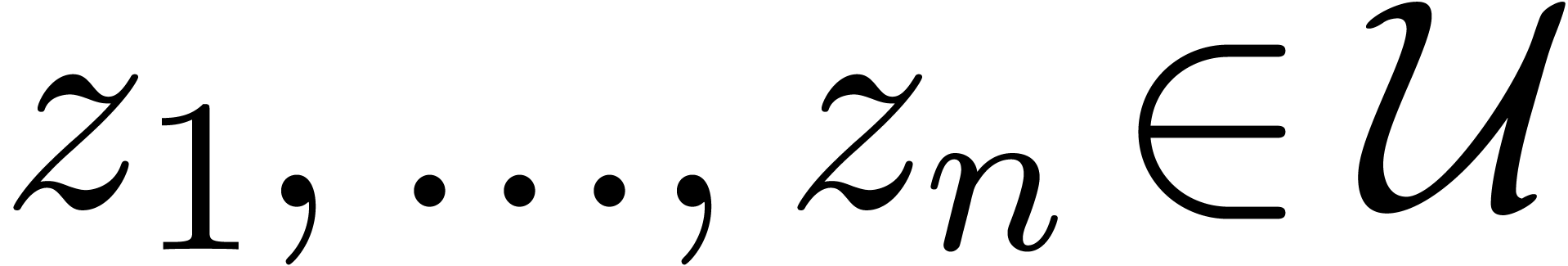 together with
a graph
together with
a graph  which admits
which admits 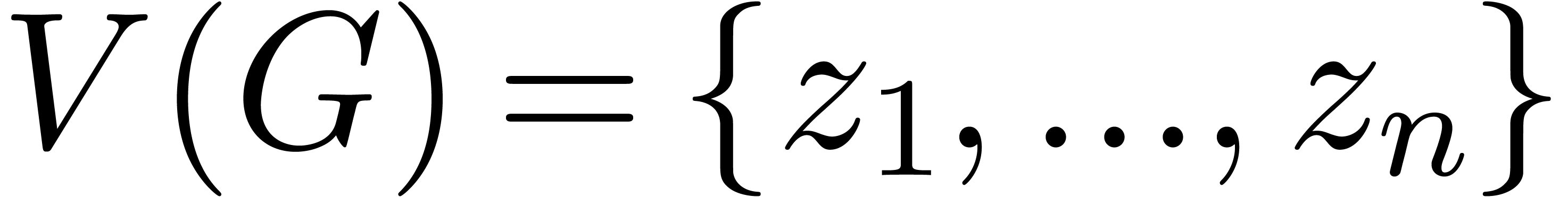 as
its vertices. We will say that
as
its vertices. We will say that  is
admissible if
is
admissible if  is connected and for
every edge
is connected and for
every edge 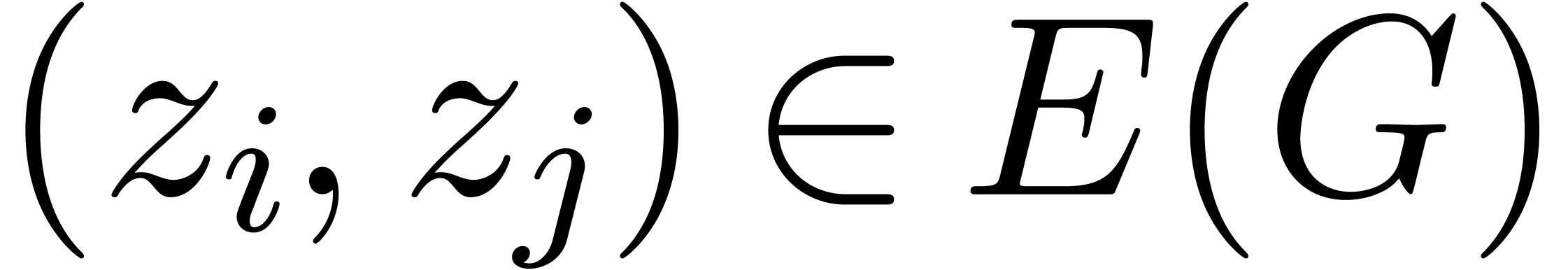 , the straightline
segment between
, the straightline
segment between 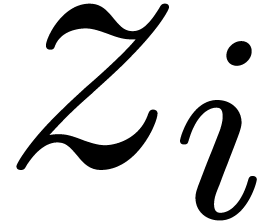 and
and 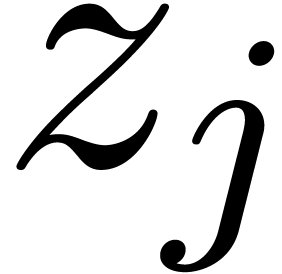 lies
in
lies
in  . Assume that
. Assume that  is known at one of the points
is known at one of the points 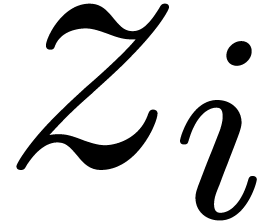 . For each
. For each 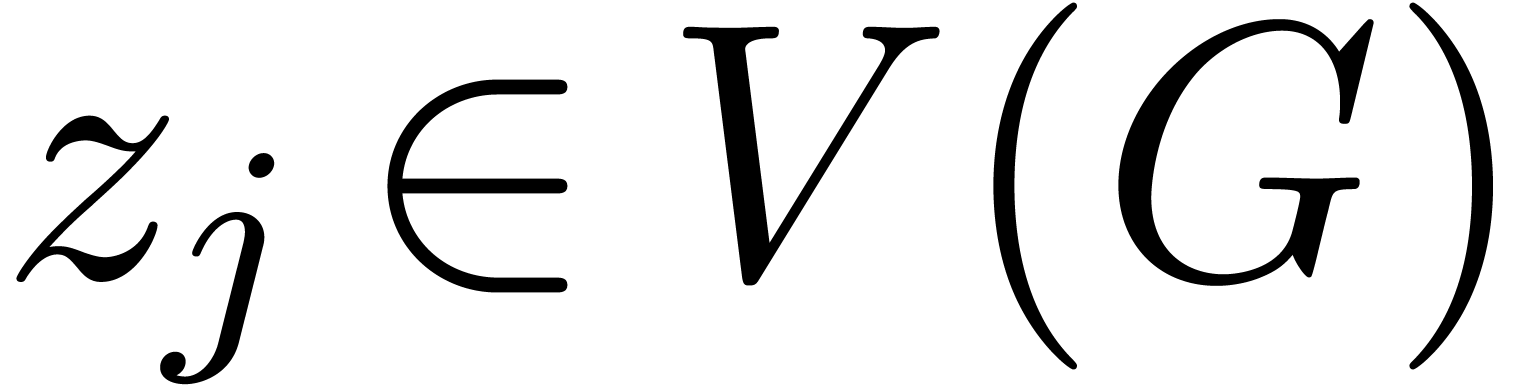 ,
we may then define
,
we may then define  to be the vector space
spanned by all analytic continuations of
to be the vector space
spanned by all analytic continuations of  by
following edges of
by
following edges of  . We may
compute the collection
. We may
compute the collection  of these vector spaces
using the following algorithm:
of these vector spaces
using the following algorithm:
Algorithm continue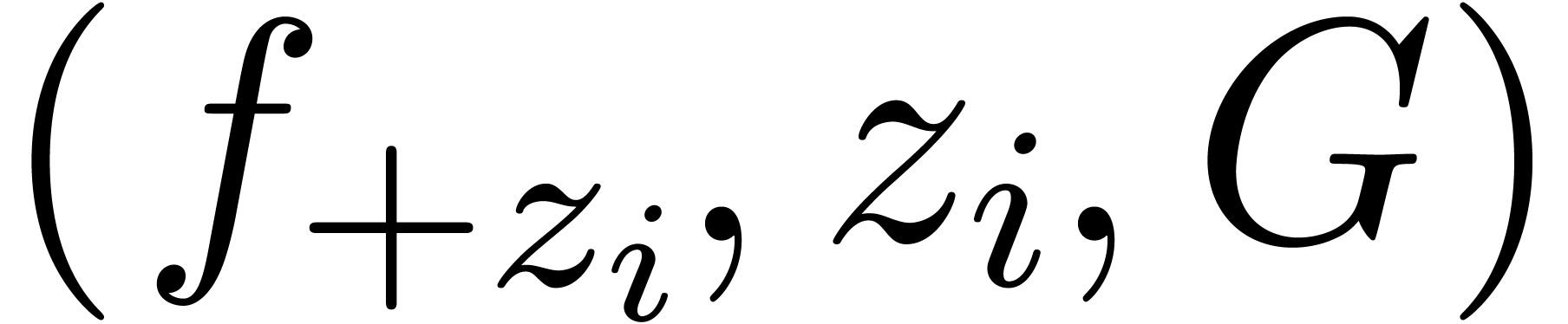
 at
at  and an admissible graph
and an admissible graph  with
with 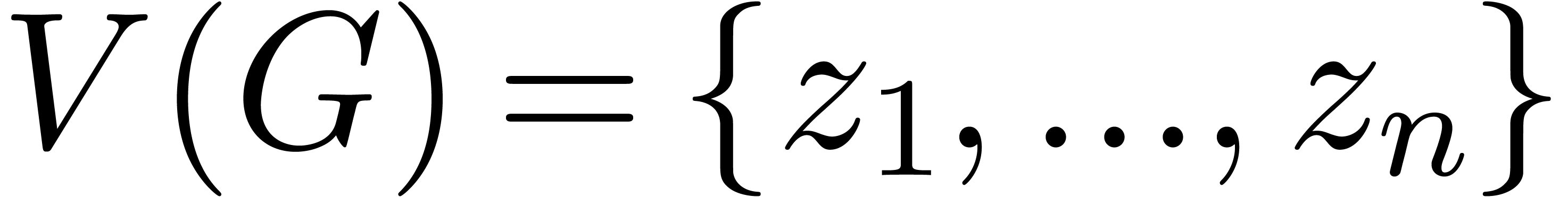
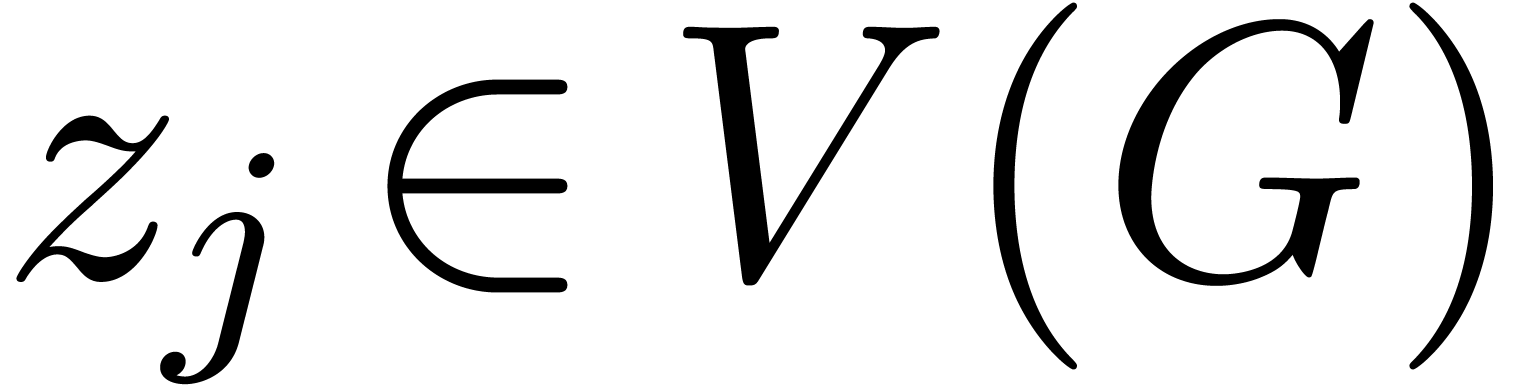 ,
a basis
,
a basis 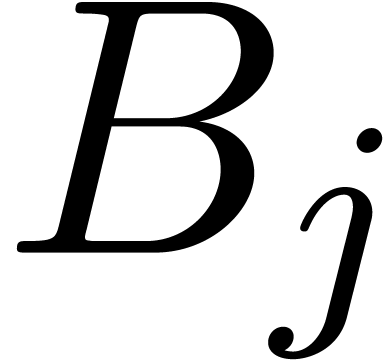 of
of 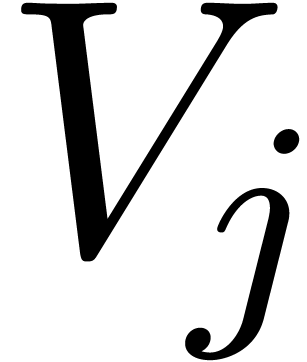
Step 1. [Initialize]
Set 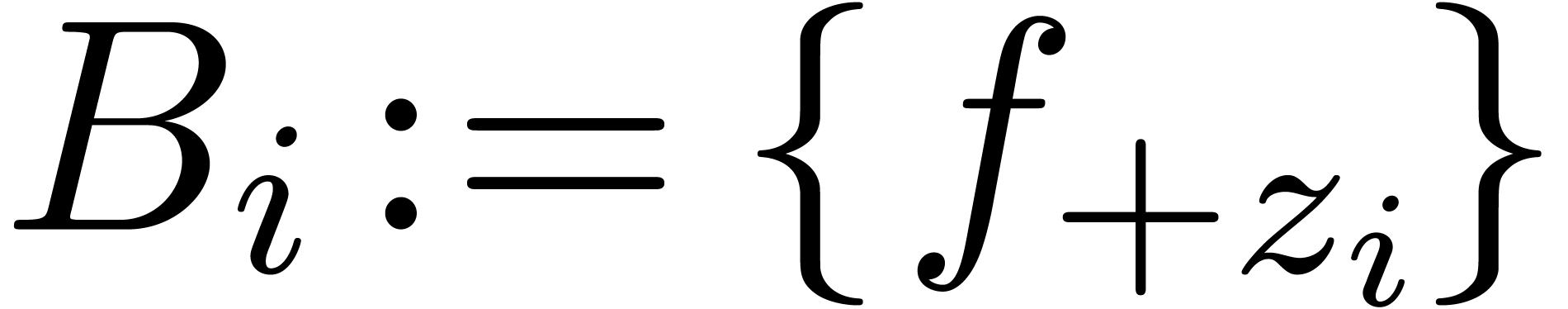 and
and 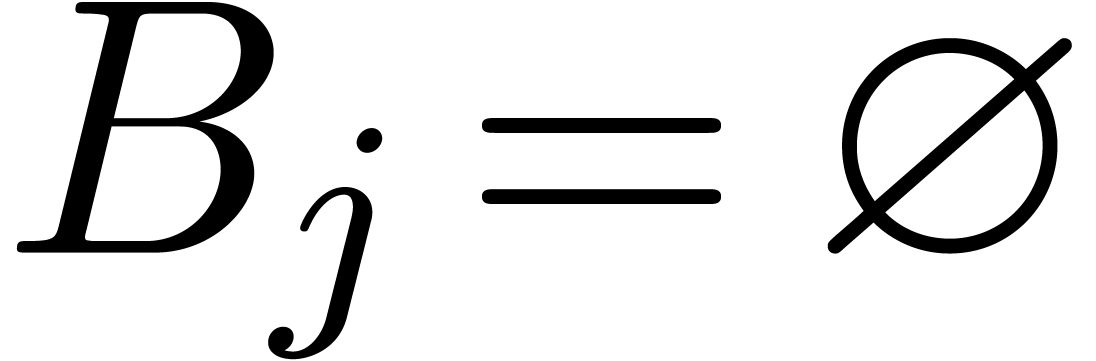 for all
for all 
Step 2. [Saturate]
For any 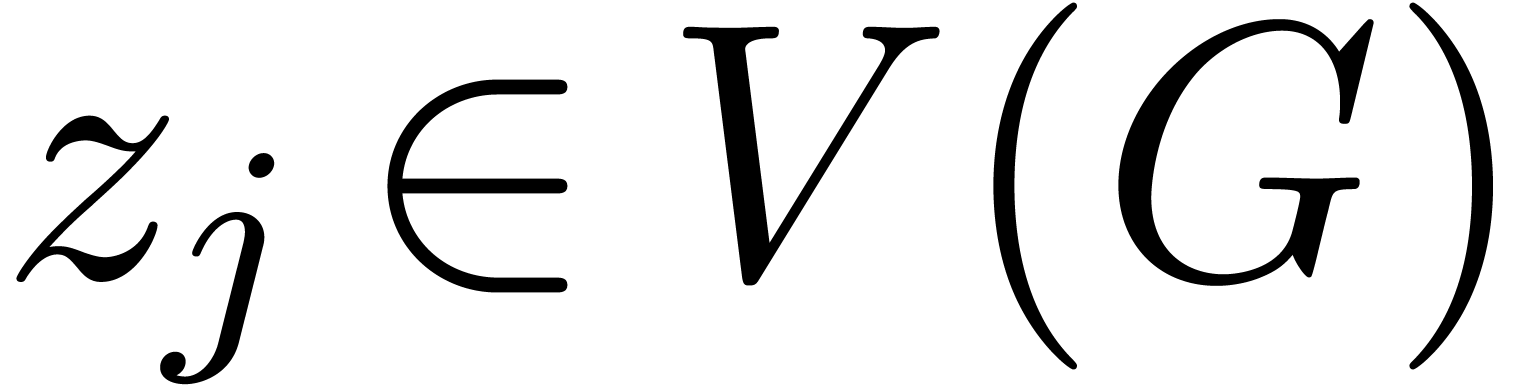 ,
, 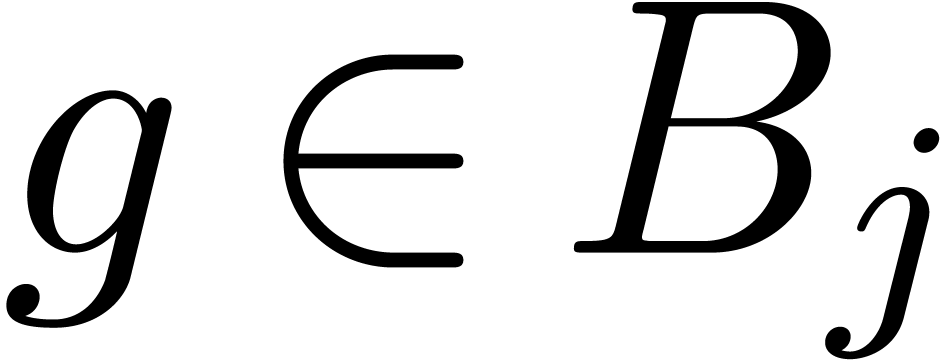 and
and 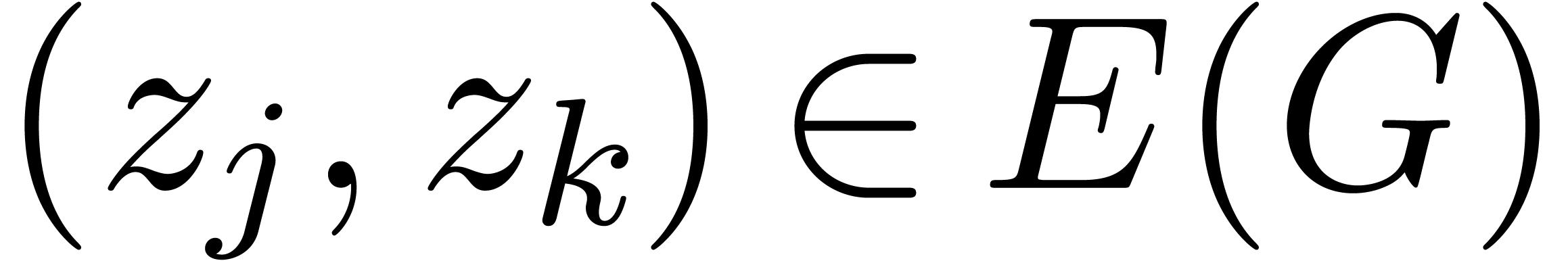 do
do
If 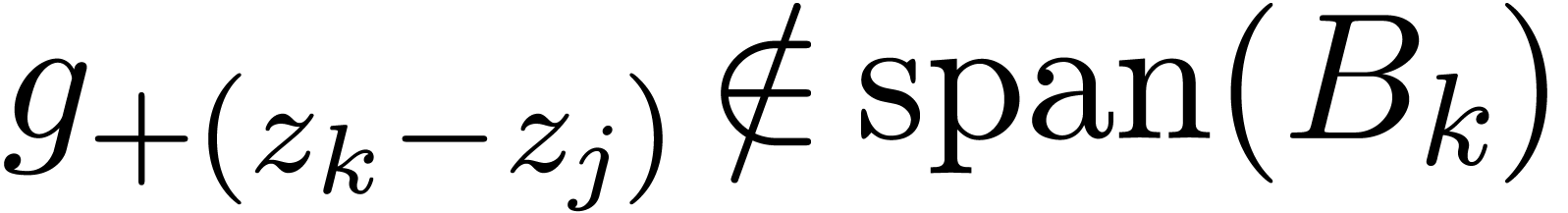 , then
, then
Set 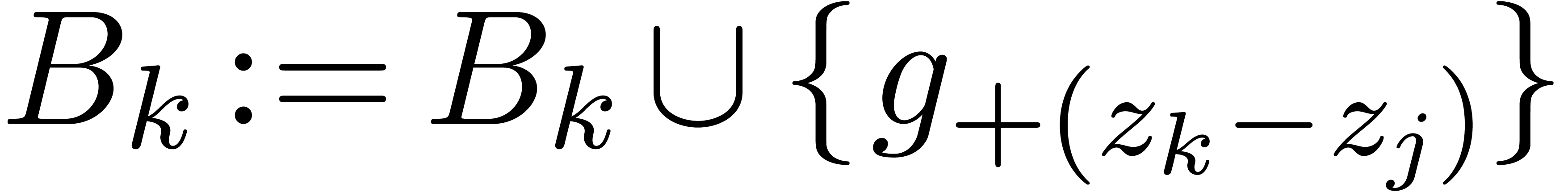 and repeat step 2
and repeat step 2
Step 3. [Terminate]
Return 
Remark 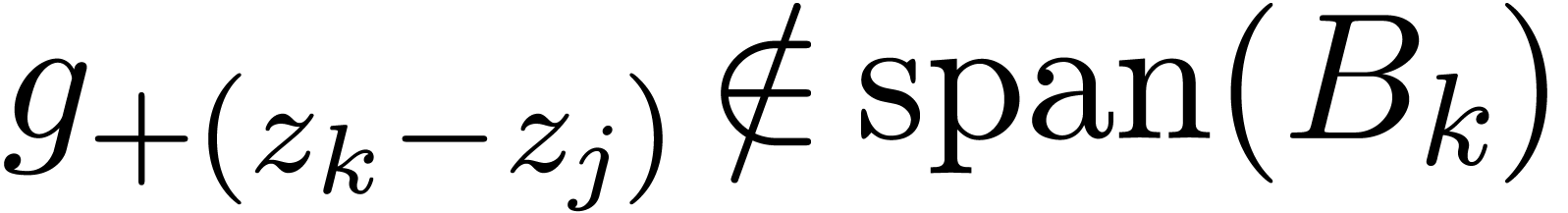 requires an equality test for analytic
functions. From the heuristic point of view, we may simply fix two
numbers
requires an equality test for analytic
functions. From the heuristic point of view, we may simply fix two
numbers 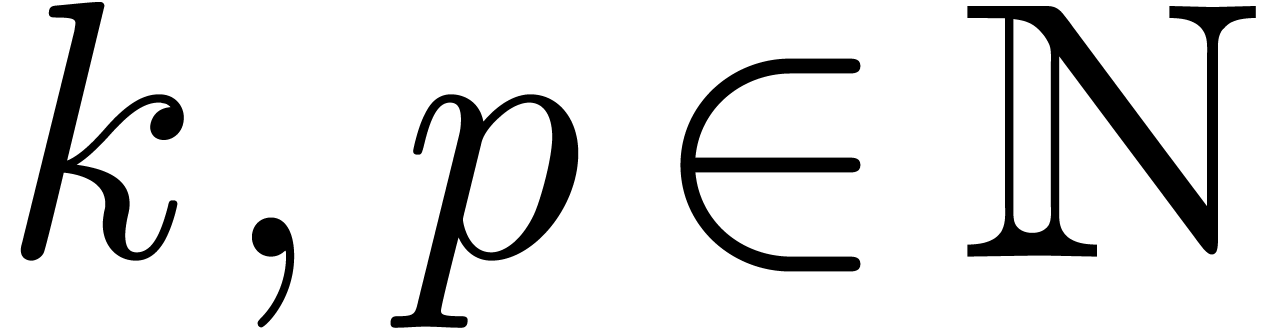 and test whether the first
and test whether the first  Taylor coefficients coincide up to a relative error
Taylor coefficients coincide up to a relative error  .
.
Assume now that 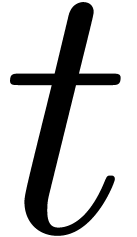 singularities in
singularities in  are known, say
are known, say  .
We need a test in order to check whether
.
We need a test in order to check whether 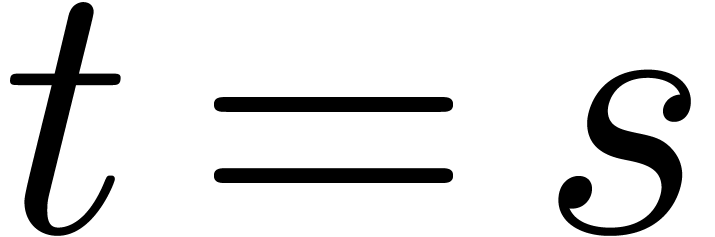 ,
as well as a way to find at least one of the remaining singularities in
,
as well as a way to find at least one of the remaining singularities in
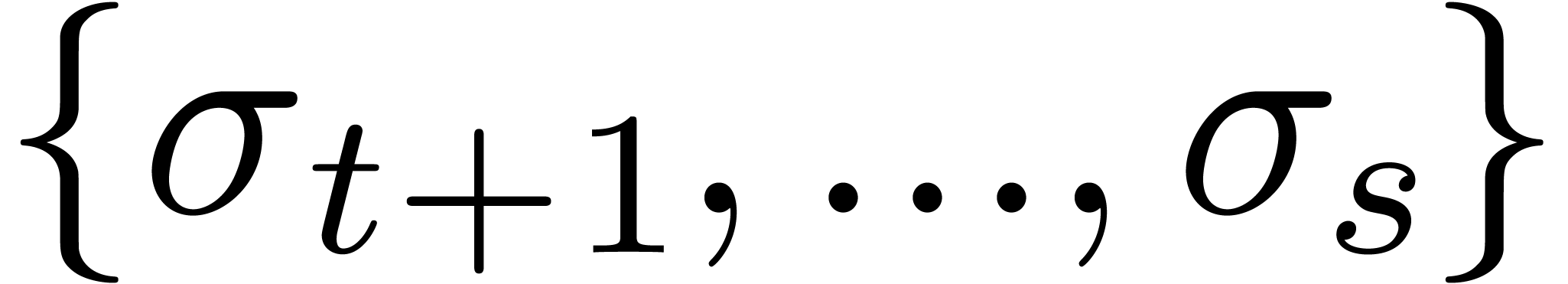 if
if 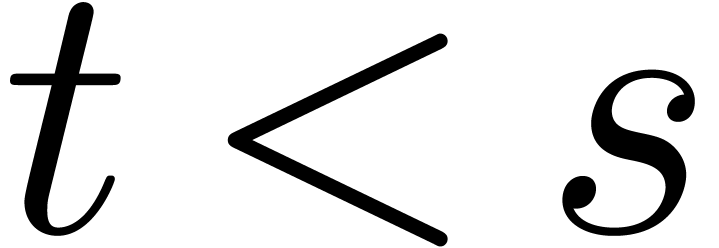 .
.
Let  be such that
be such that 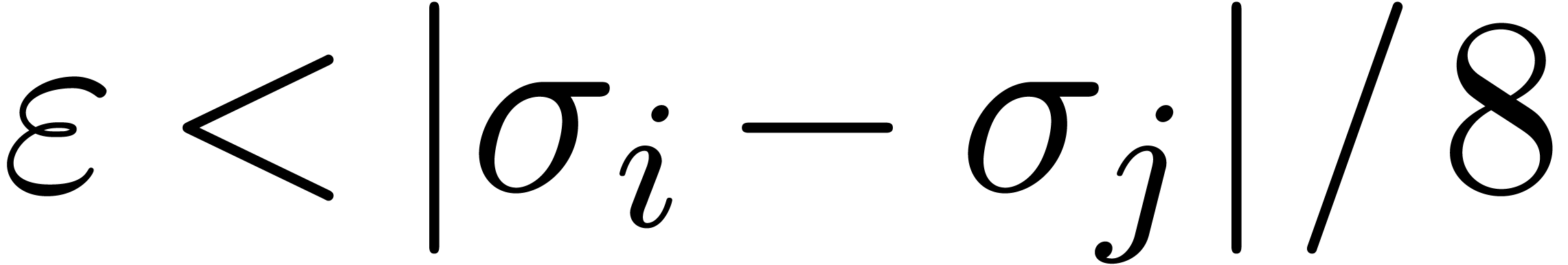 for all
for all
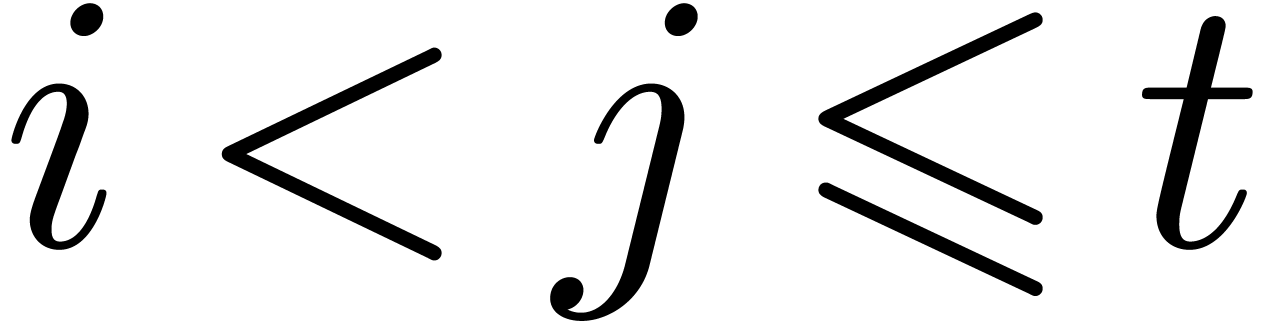 and
and 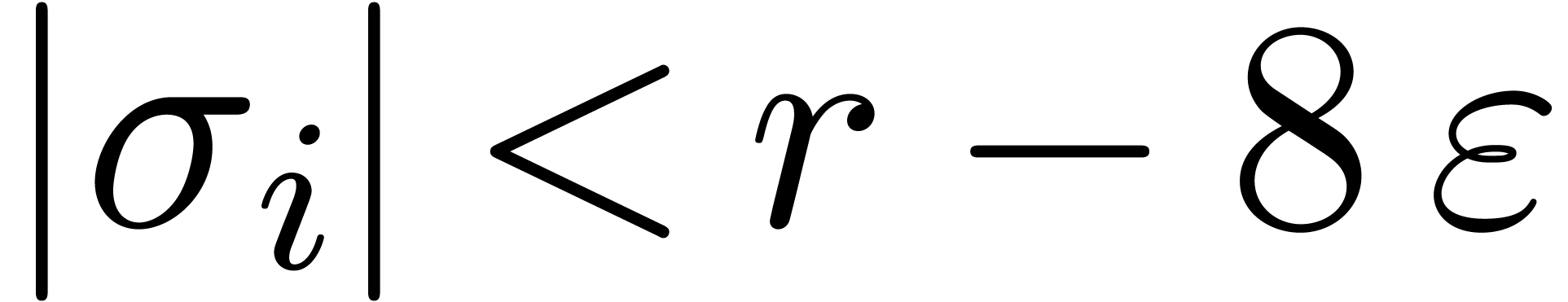 .
We now consider a graph
.
We now consider a graph  in the form of a
hexagonal honeycomb, which fills up the disk
in the form of a
hexagonal honeycomb, which fills up the disk  and
such that each edge
and
such that each edge 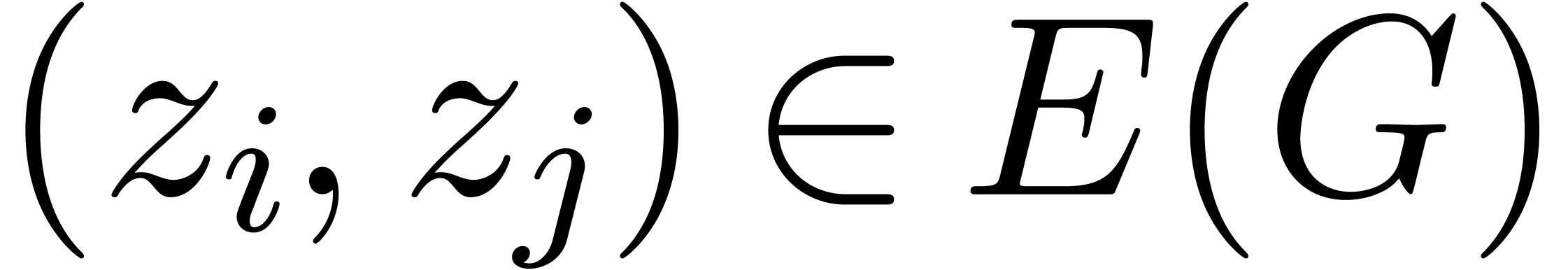 has length
has length 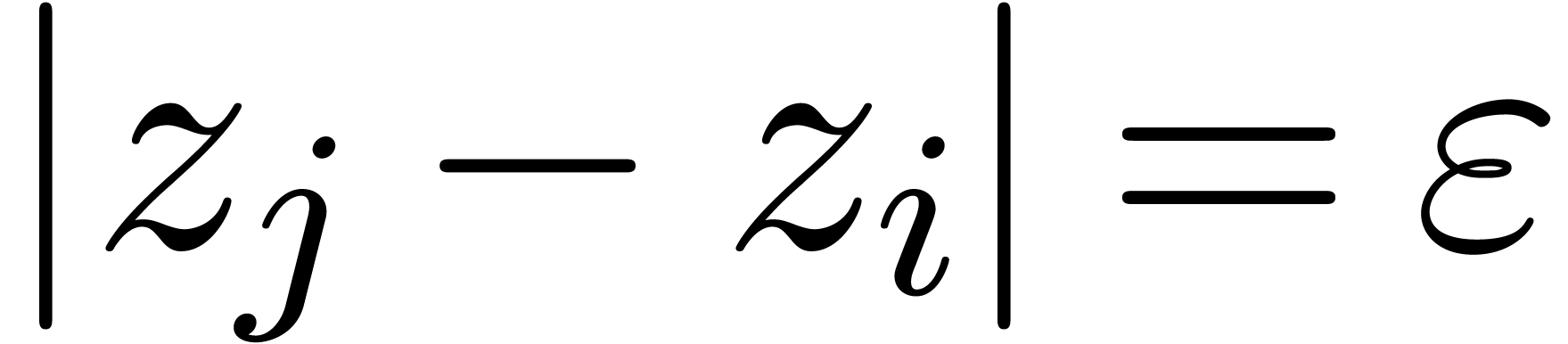 (see also figure 4 below). Picking
(see also figure 4 below). Picking  sufficiently at random, the graph
sufficiently at random, the graph  is also
admissible, so we may apply the algorithm continue. For
each vertex
is also
admissible, so we may apply the algorithm continue. For
each vertex  , we also compute
the minimum
, we also compute
the minimum 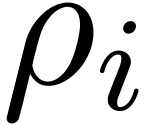 of the convergence radii of the
elements in
of the convergence radii of the
elements in 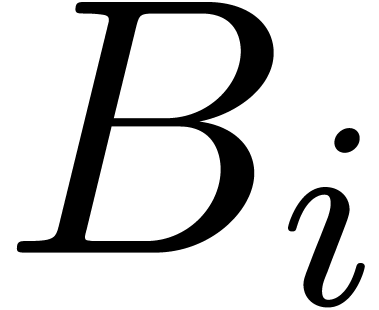 . We claim that
. We claim that
 if and only if
if and only if
for all  . Indeed, if
. Indeed, if 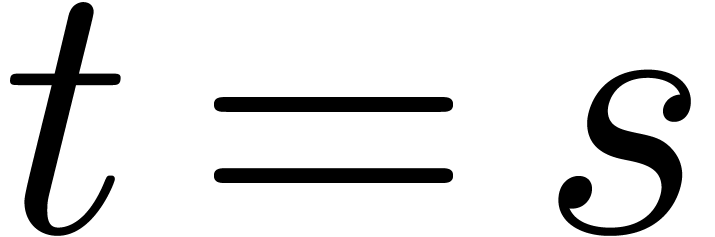 , then the equality clearly holds.
Assume for contradiction that the equality holds for all
, then the equality clearly holds.
Assume for contradiction that the equality holds for all  , even though
, even though  .
For each of the outermost vertices
.
For each of the outermost vertices  of the
honeycomb with
of the
honeycomb with 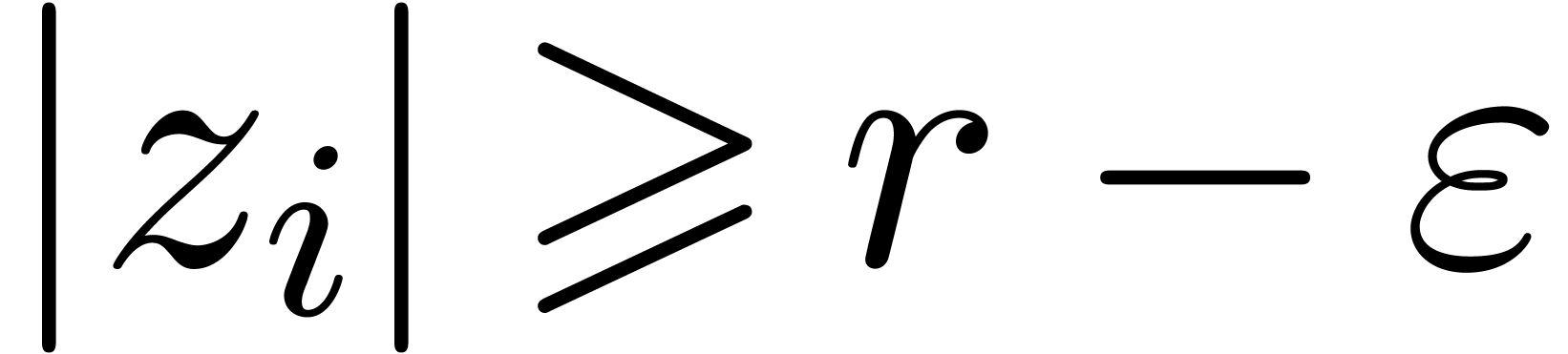 , we have
, we have
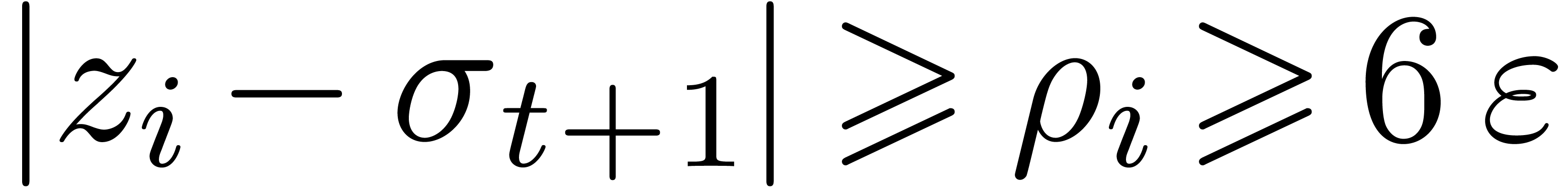 . This implies that
. This implies that 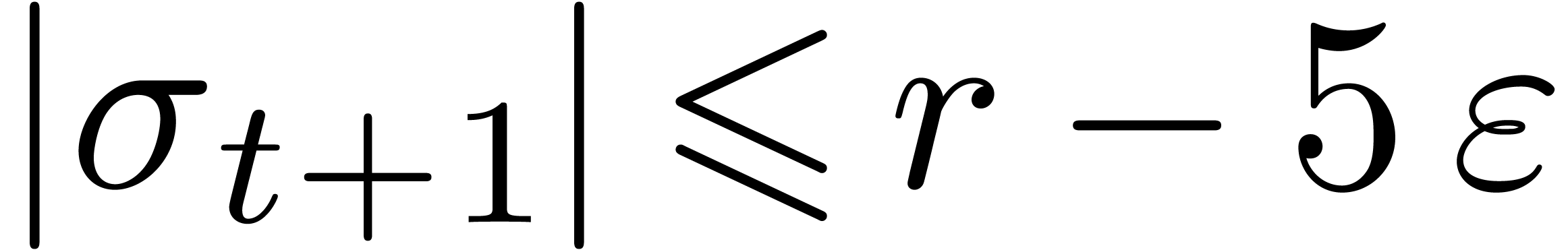 , whence
, whence 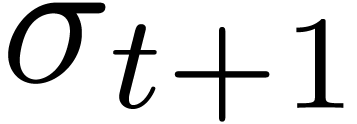 lies in the interior of one of the cells of the honeycomb. Let
lies in the interior of one of the cells of the honeycomb. Let 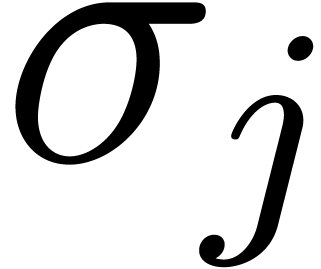 with
with 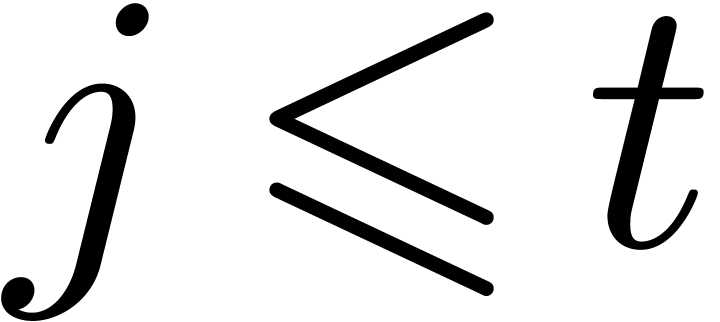 be such that
be such that 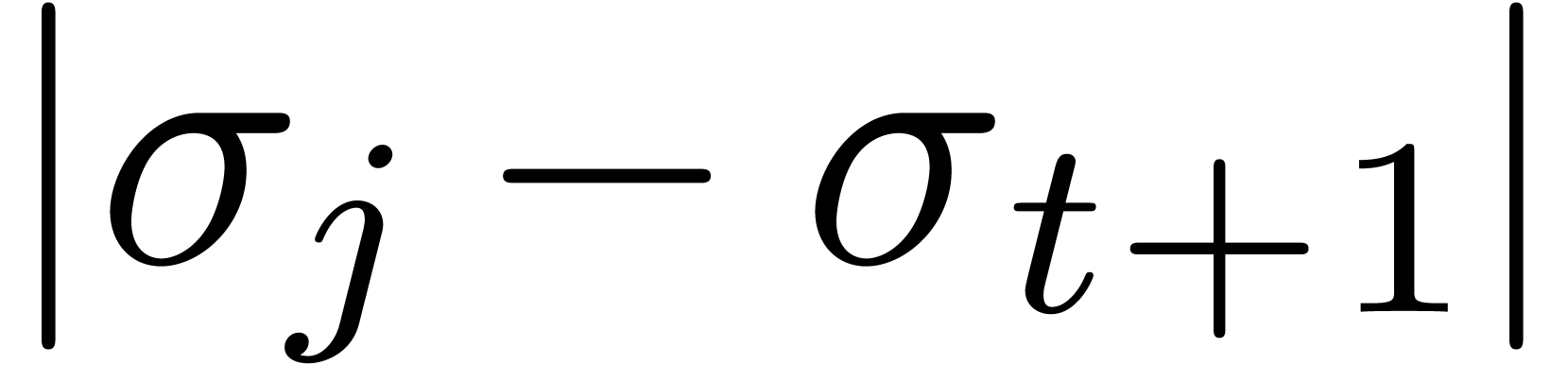 is minimal. Now consider a vertex
is minimal. Now consider a vertex  of the cell of
the honeycomb which contains
of the cell of
the honeycomb which contains 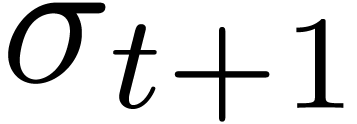 such that
such that 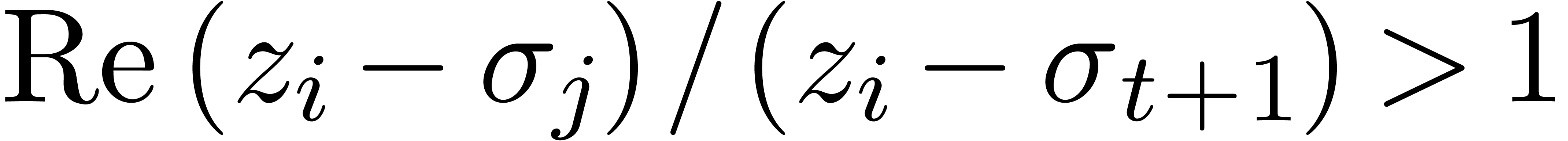 (see figure 4). Then
(see figure 4). Then 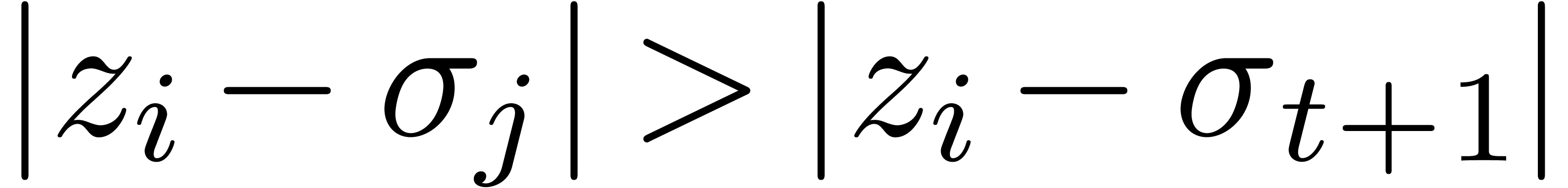 . Now
. Now 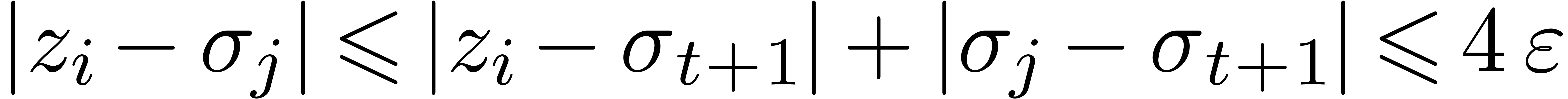 also implies that
also implies that
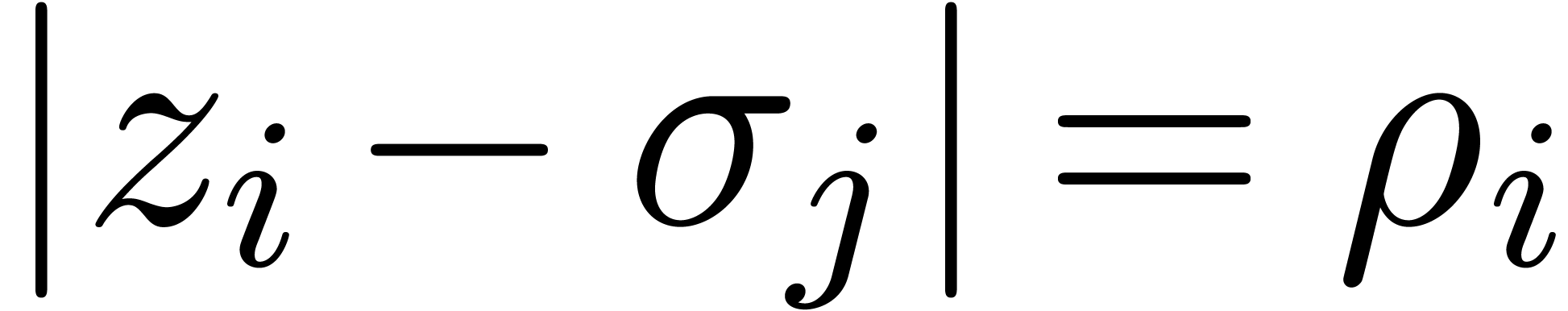 . Consequently,
. Consequently, 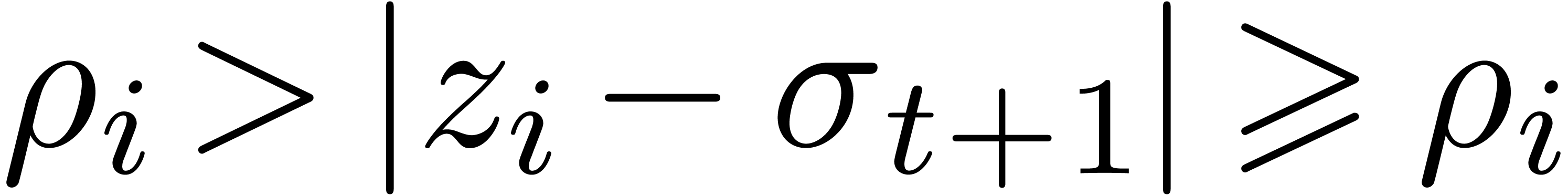 . This contradiction completes the proof of our
claim.
. This contradiction completes the proof of our
claim.
Whenever (9) does not hold for some 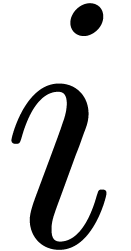 , then this indicates the presence of a
singularity in
, then this indicates the presence of a
singularity in  near
near 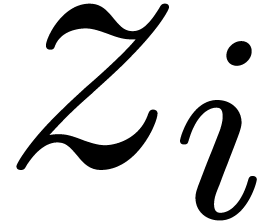 . It thus suffices to determine the dominant
singularities of the elements in
. It thus suffices to determine the dominant
singularities of the elements in  in order to
find at least one of these missing singularities.
in order to
find at least one of these missing singularities.
Remark 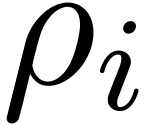 . Therefore, and as in the previous subsection,
the test (9) should really be replaced by an approximate
equality test.
. Therefore, and as in the previous subsection,
the test (9) should really be replaced by an approximate
equality test.
Remark  edges and not
edges and not 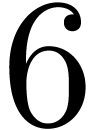 (at least in the case when
(at least in the case when 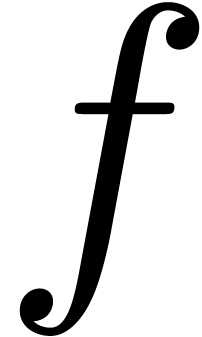 is
the solution to a differentially algebraic equation).
is
the solution to a differentially algebraic equation).
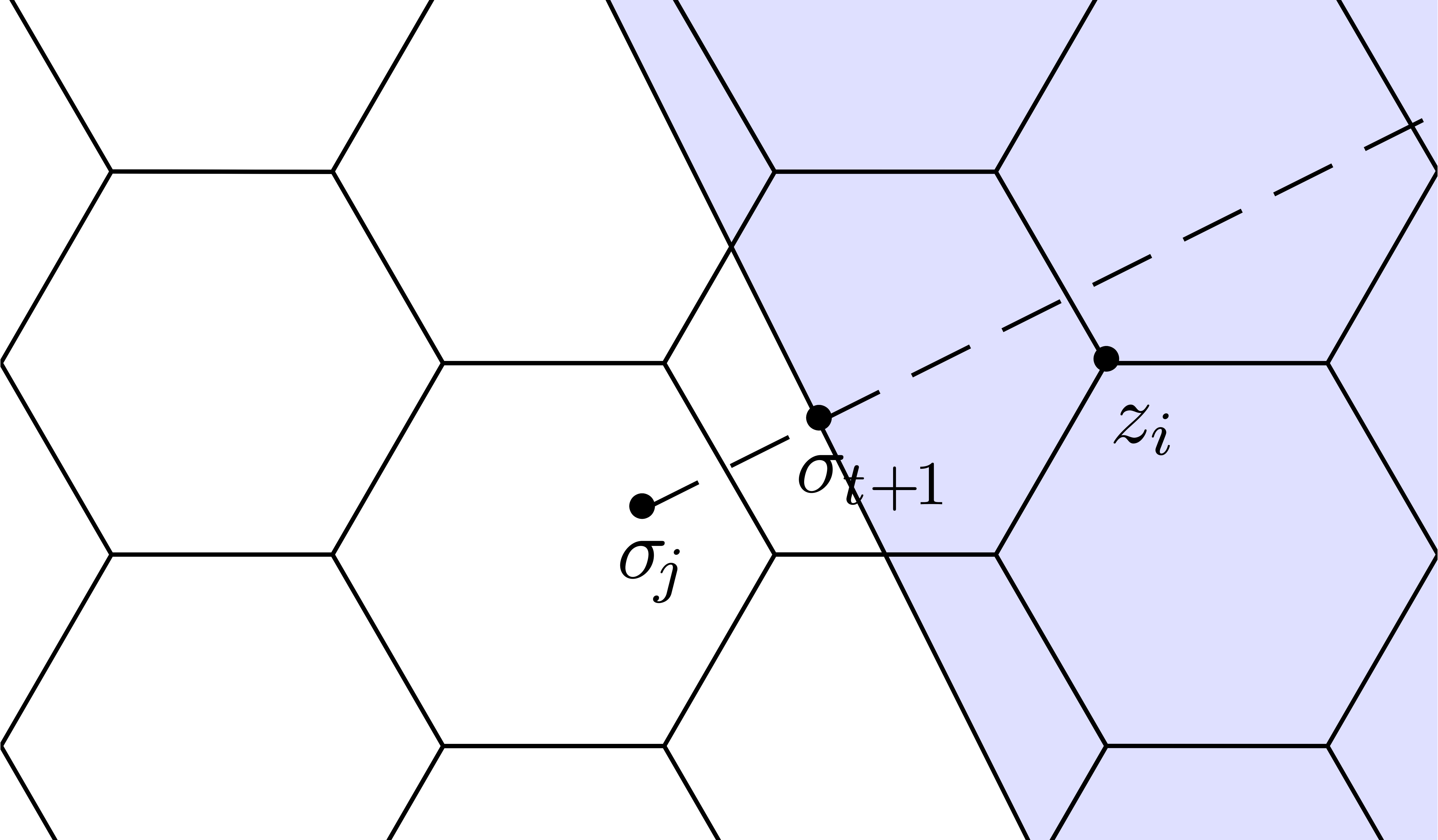 |
Figure 4. Illustration of the proof
of our claim that |
In the case when  is meromorphic on the compact
disk
is meromorphic on the compact
disk  of radius
of radius 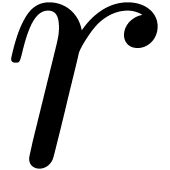 ,
then there exists an alternative for the algorithms from section 4: we may directly search for a polynomial
,
then there exists an alternative for the algorithms from section 4: we may directly search for a polynomial 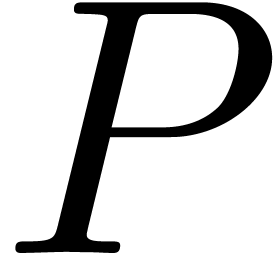 such that the radius of convergence of
such that the radius of convergence of  is
strictly larger than
is
strictly larger than 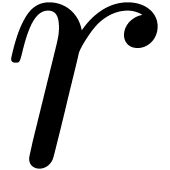 . If
such a polynomial
. If
such a polynomial 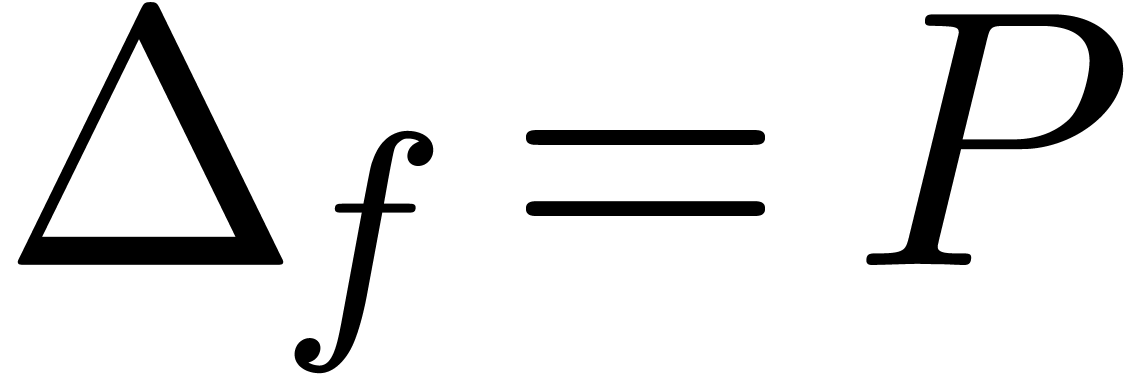 exists, then we may select
exists, then we may select
 to be monic and of minimal degree; this
particular polynomial
to be monic and of minimal degree; this
particular polynomial  will be called the
denominator of
will be called the
denominator of  on
on  . If
. If  is not meromorphic
on
is not meromorphic
on  , then we define
, then we define 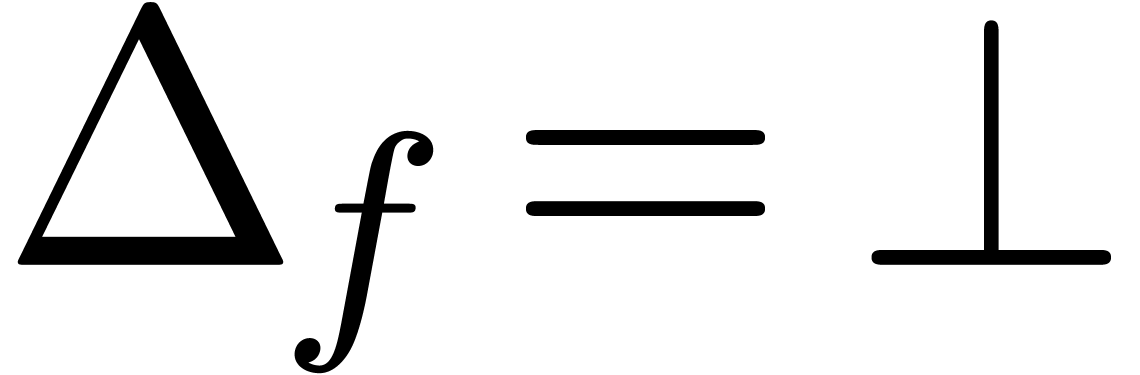 . Given
. Given  , we also define the guarded denominator
, we also define the guarded denominator
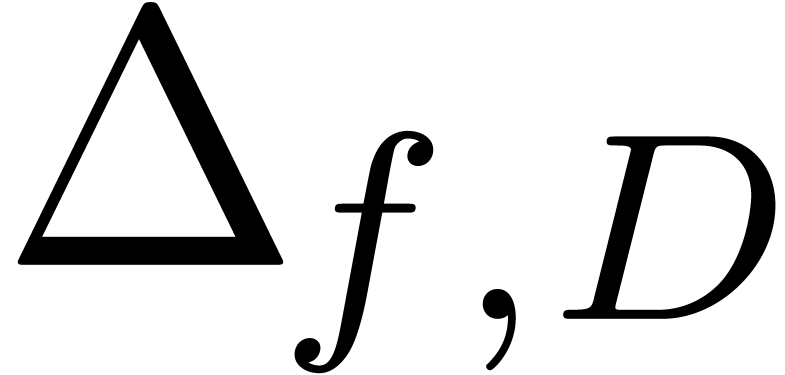 by
by 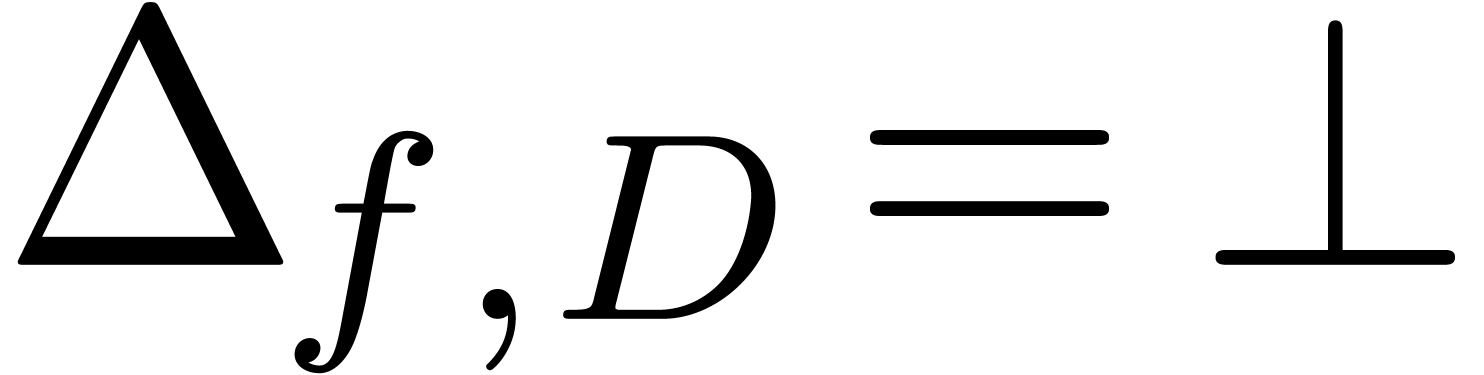 if
if 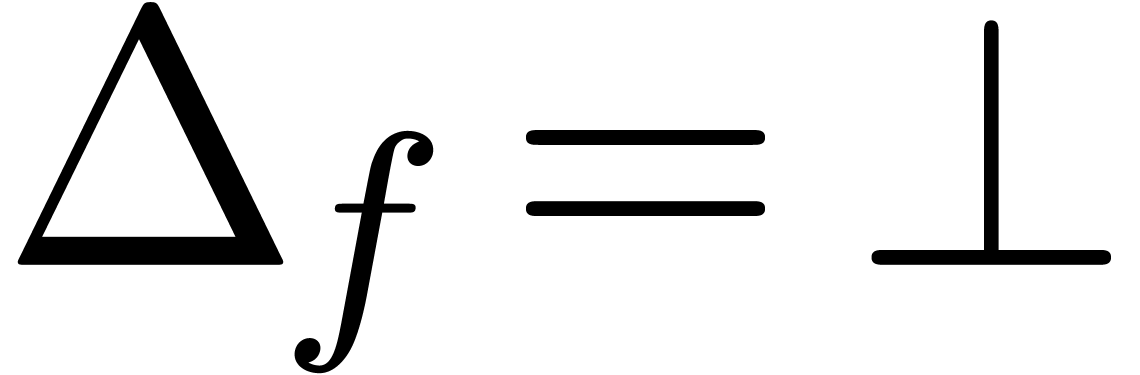 or
or 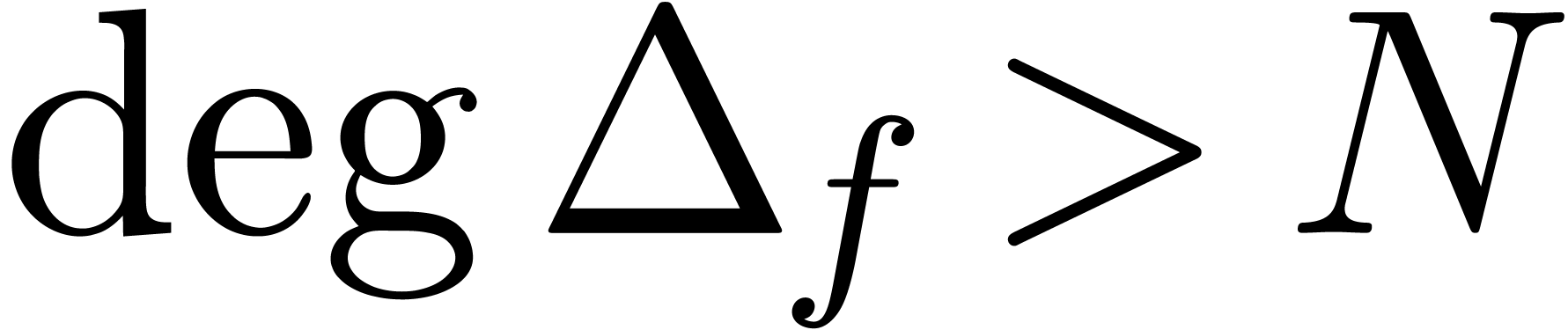 and
and 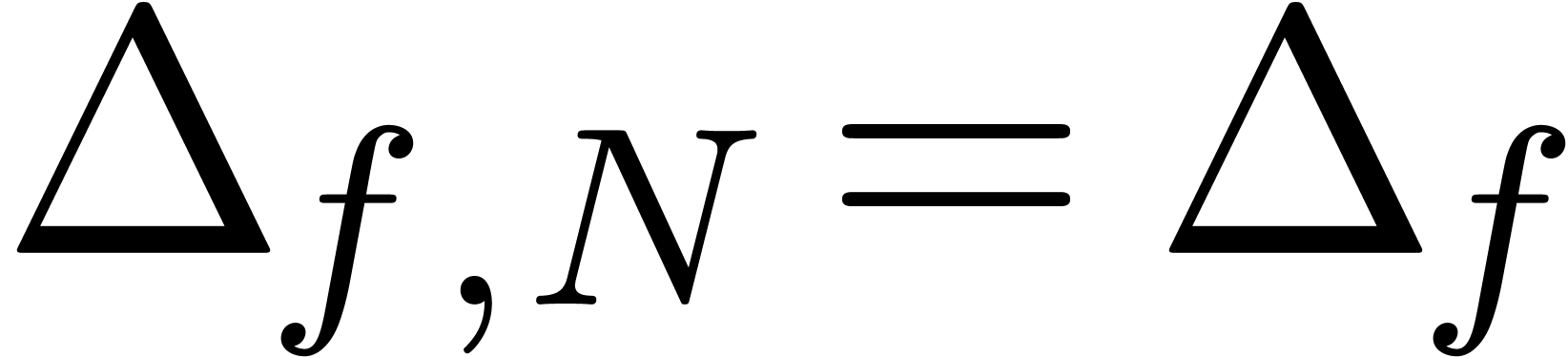 otherwise.
Guarded denominators may be computed using simple linear algebra, as
follows:
otherwise.
Guarded denominators may be computed using simple linear algebra, as
follows:
Algorithm denom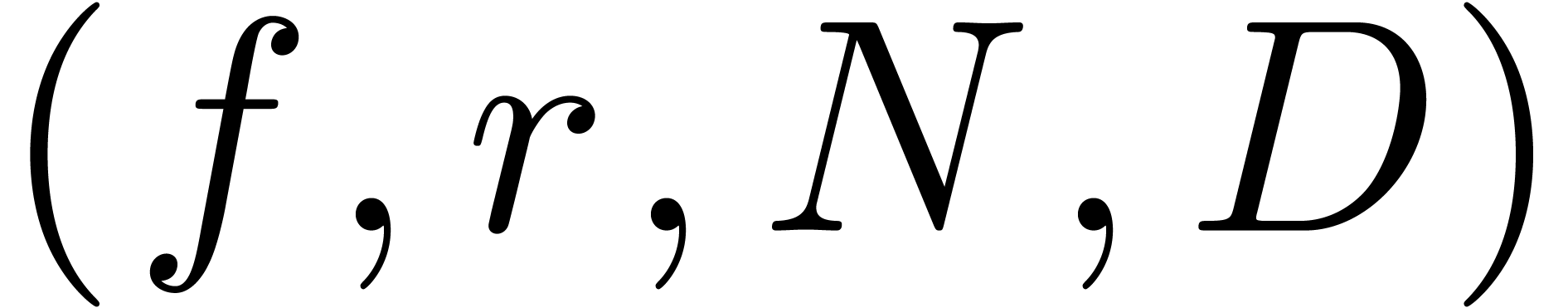
 coefficients of
coefficients of 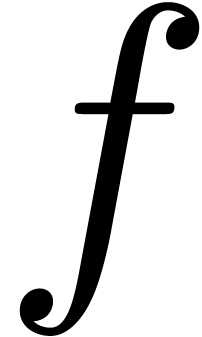 , a radius
, a radius
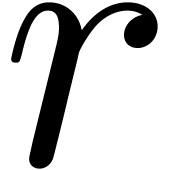 and a degree bound
and a degree bound 
 with
with 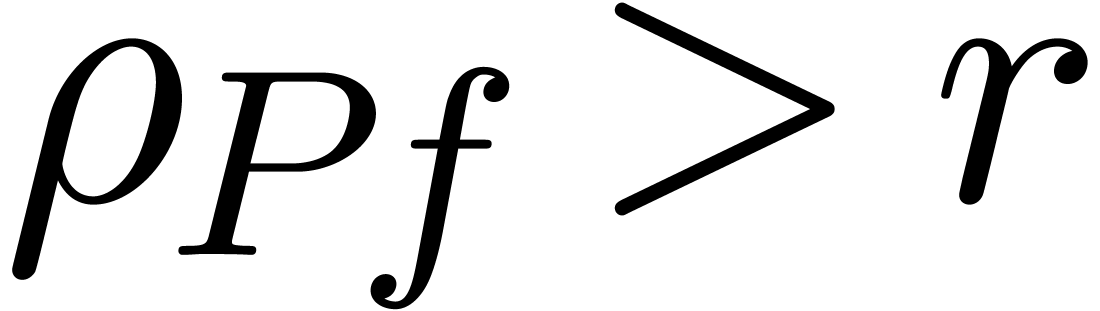 ,
,
chosen of minimal degree 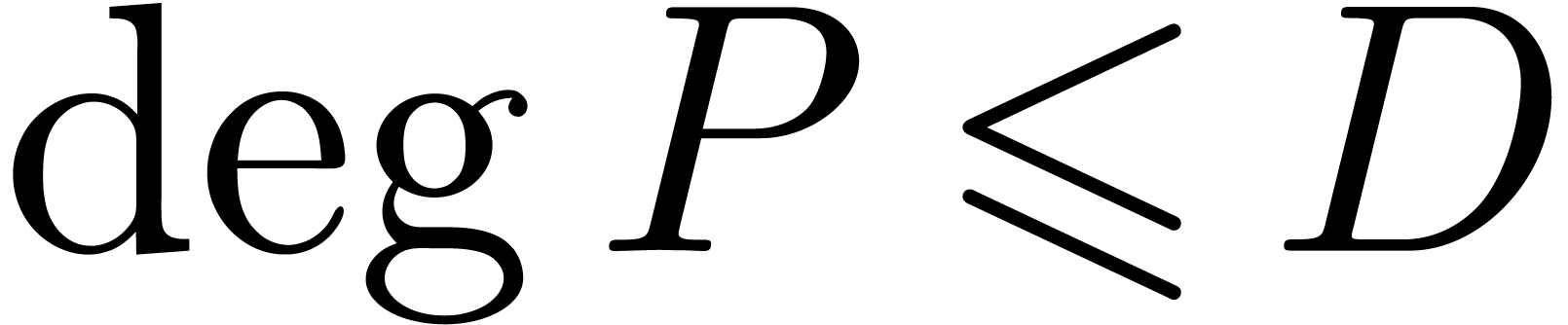 ,
or
,
or  (failed)
(failed)
Step 1. [Initialize]
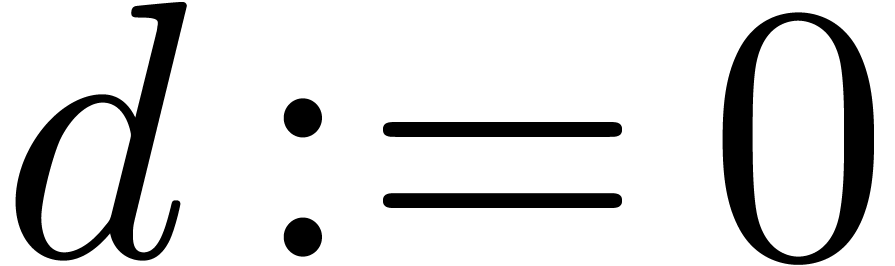
Step 2. [Determine  ]
]
Solve the linear system
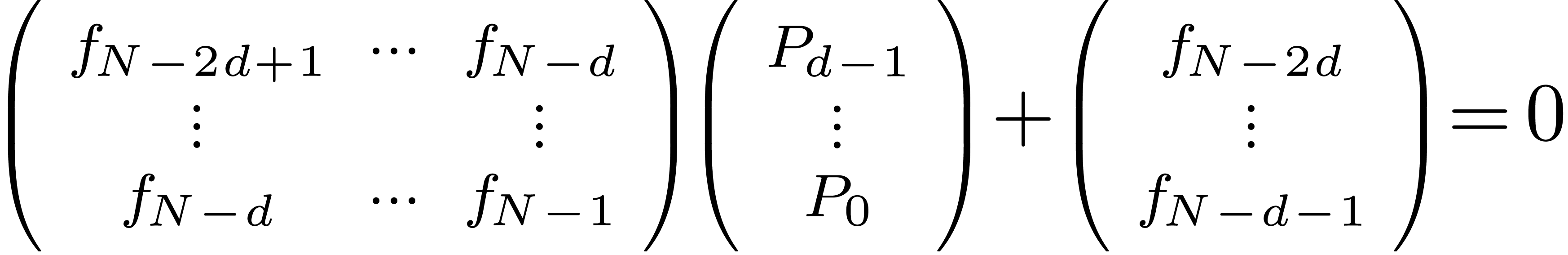 |
(10) |
Set 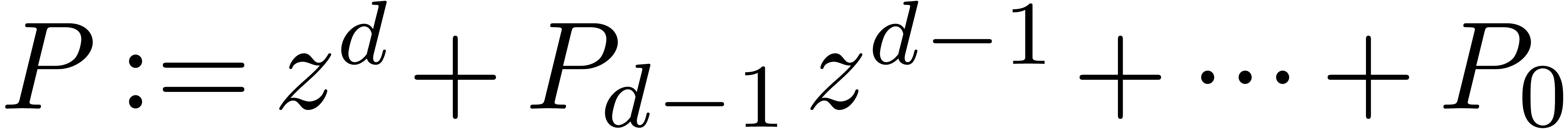
Step 3. [Terminate or loop]
Heuristically determine 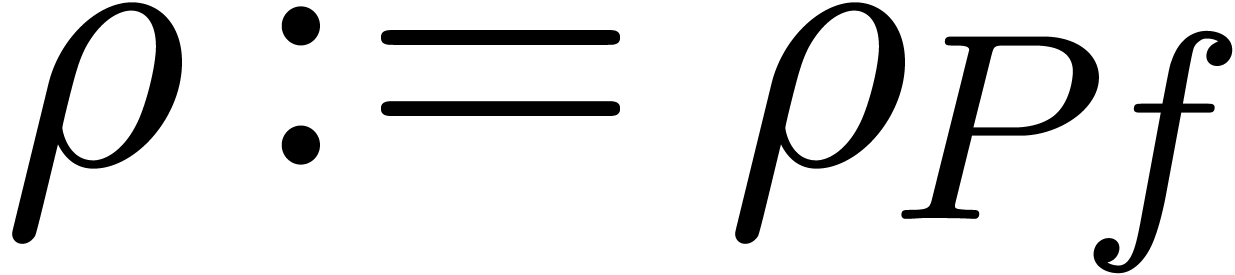 ,
based on the first
,
based on the first  coefficients of
coefficients of 
If  then return
then return 
If 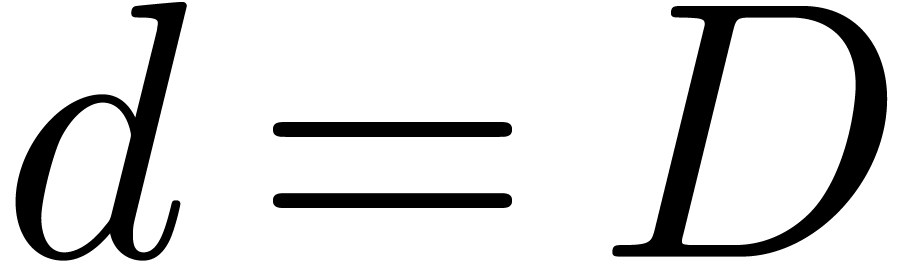 then return
then return 
Set 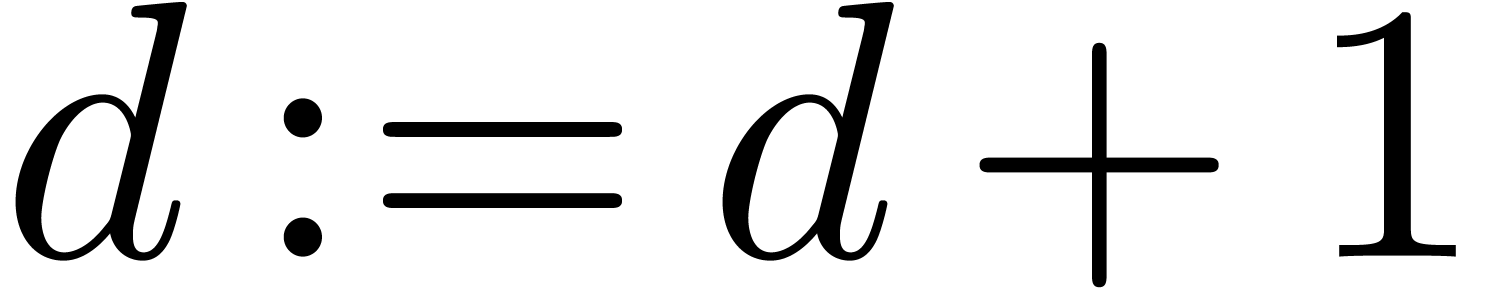 and go to step 2
and go to step 2
In order to study the reliability of this algorithm, let us first
introduce some more notations. First of all, given integers  and
and  , we will
denote
, we will
denote
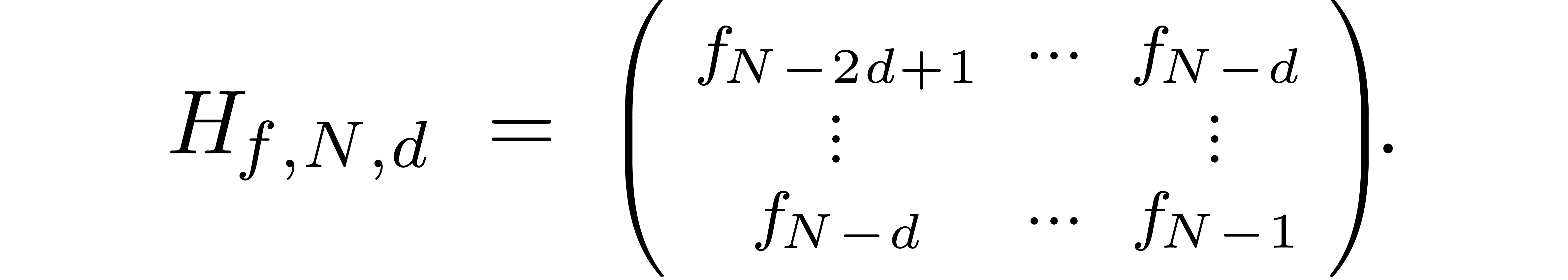
The approximate correctness of the algorithm relies on the following technical lemma which will be proved in the next section.
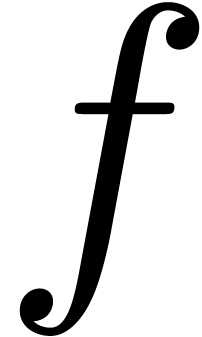 admits exactly
admits exactly 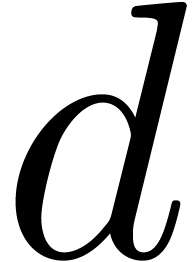 roots
in the closed unit disk, when counted with multiplicities, then the
matrix norm of
roots
in the closed unit disk, when counted with multiplicities, then the
matrix norm of 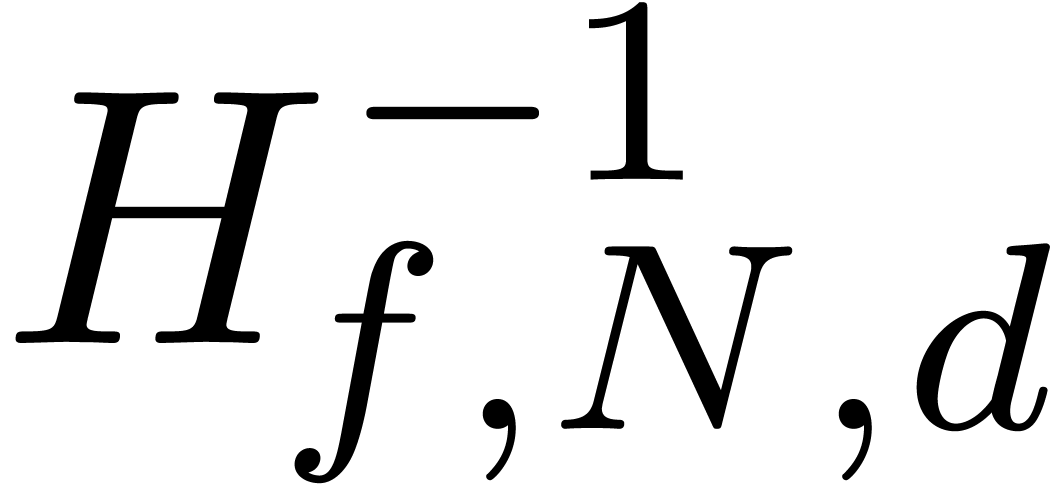 satisfies
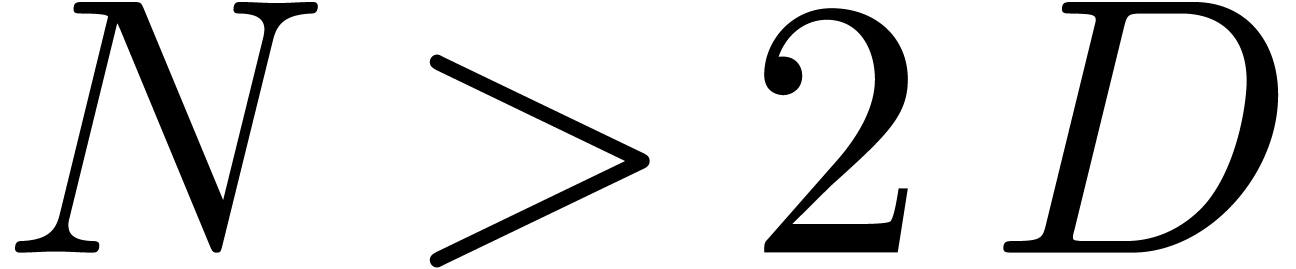
satisfies 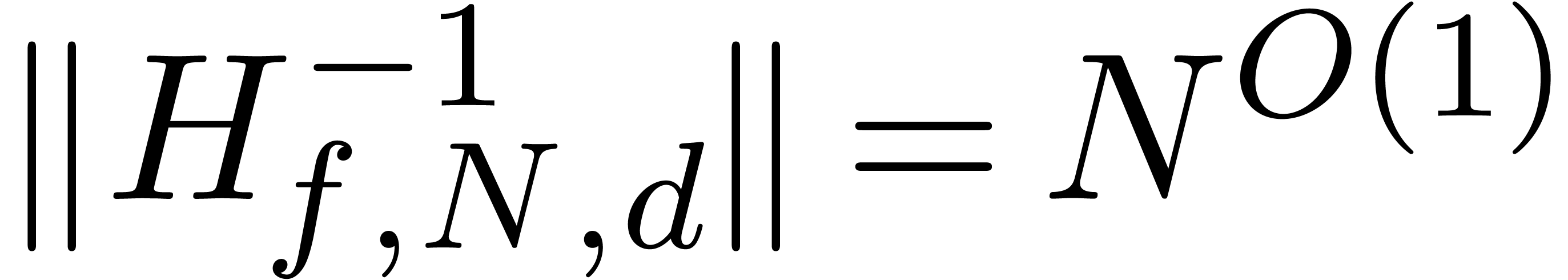 for
for 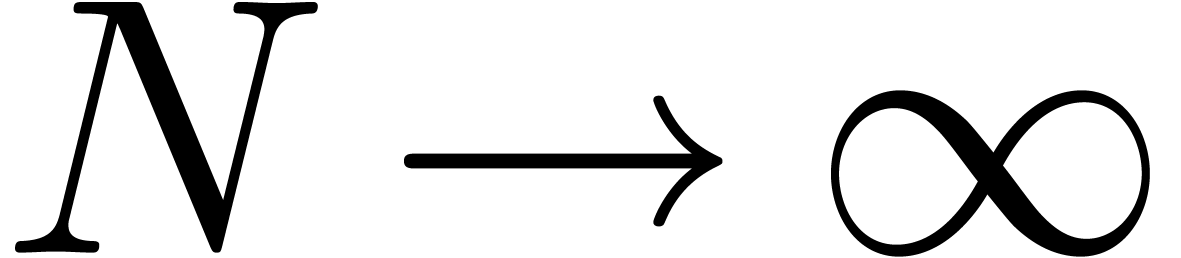 .
.
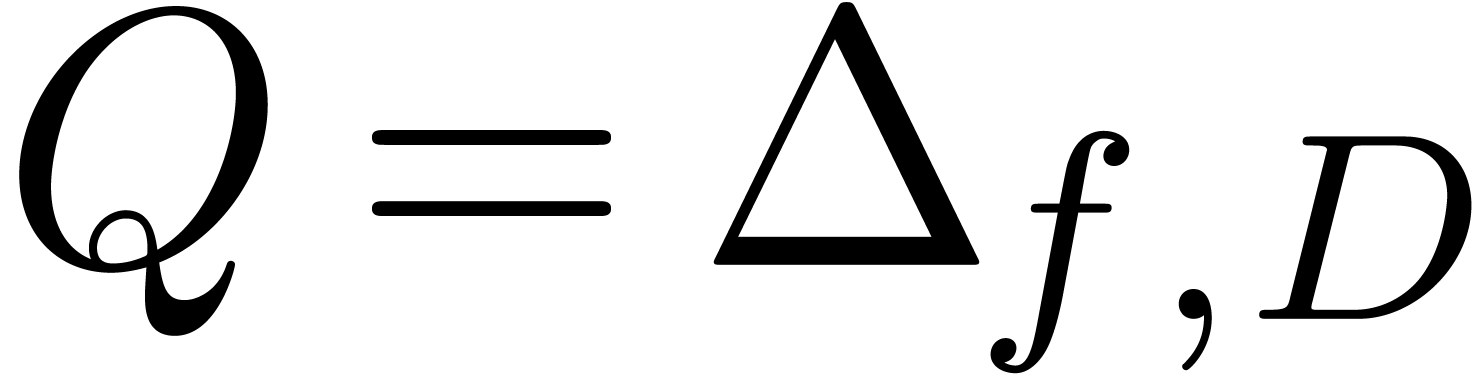 and assume that the test
and assume that the test 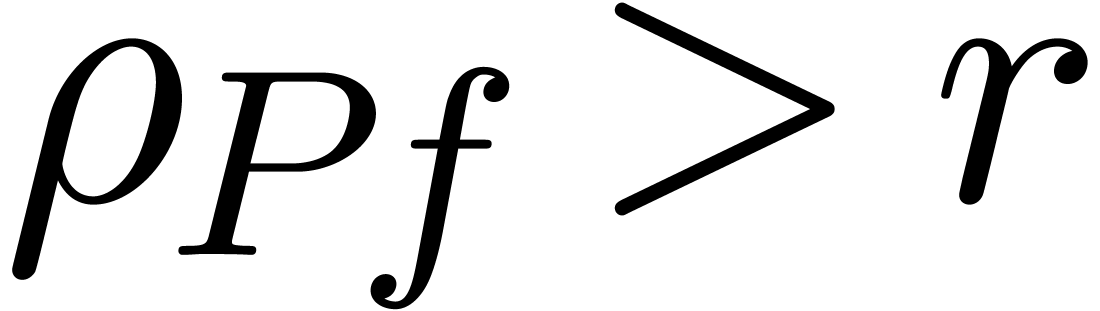 in the algorithm always returns true if and only if
in the algorithm always returns true if and only if 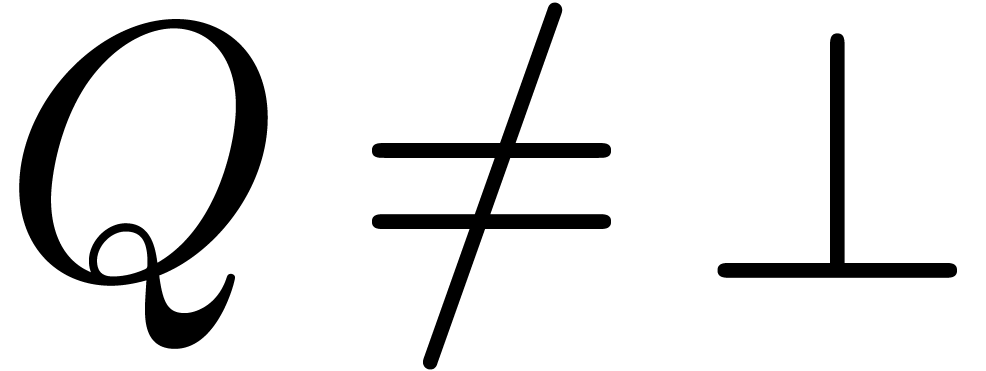 and
and  . Then
. Then  if and only if
if and only if 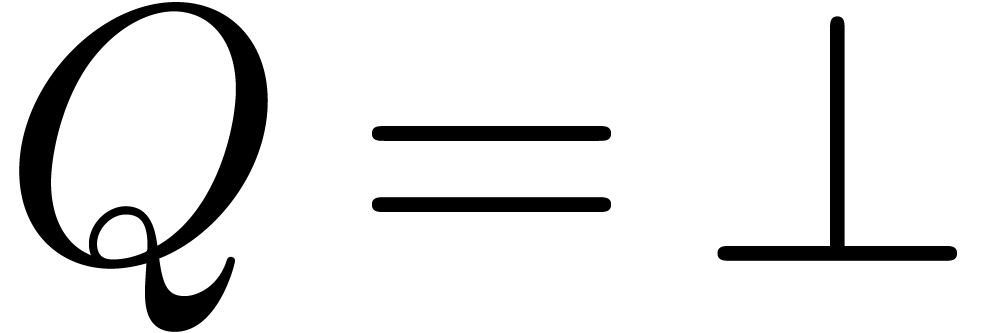 . Moreover,
if
. Moreover,
if 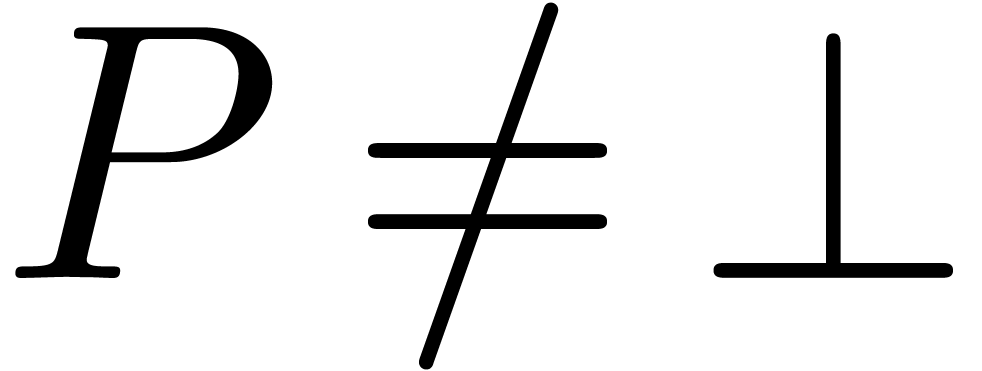 , then
, then
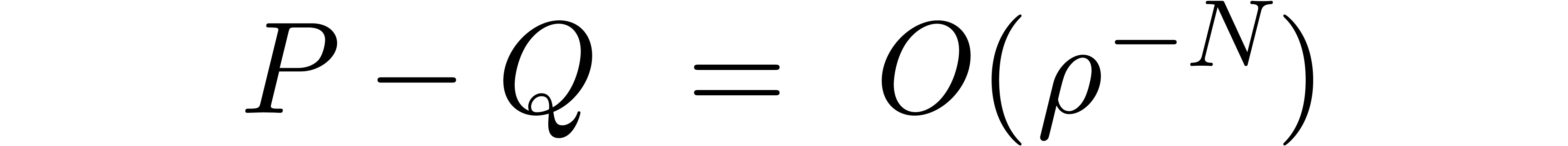
for  and any
and any 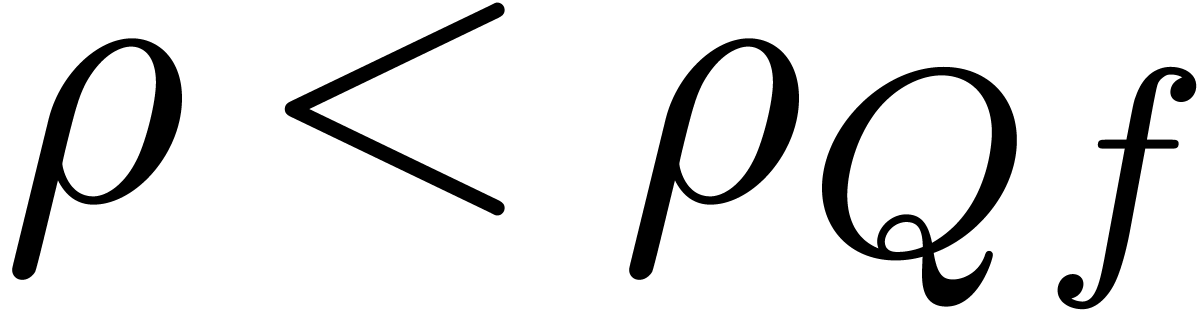 .
.
Proof. Modulo a scaling 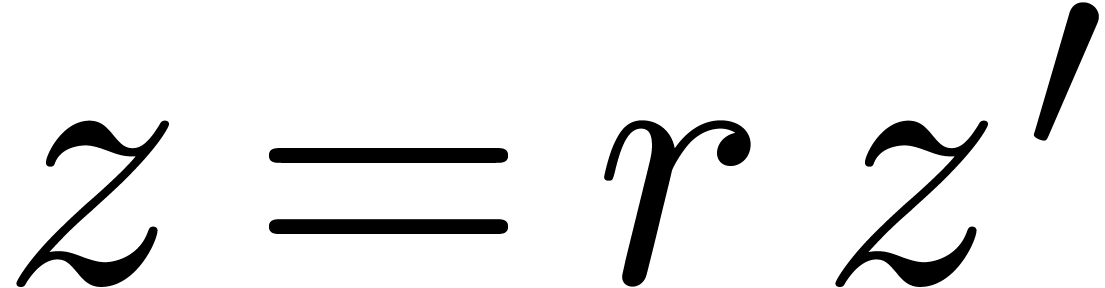 , we may assume without loss of generality that
, we may assume without loss of generality that
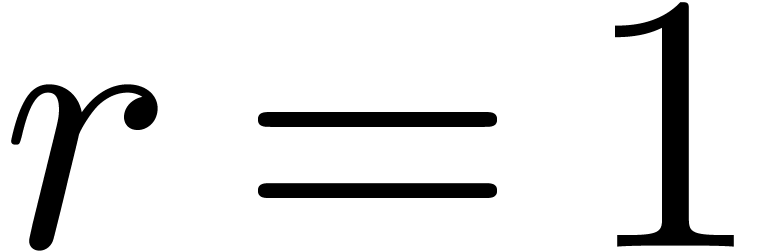 . Furthermore, the proof is
clear if
. Furthermore, the proof is
clear if 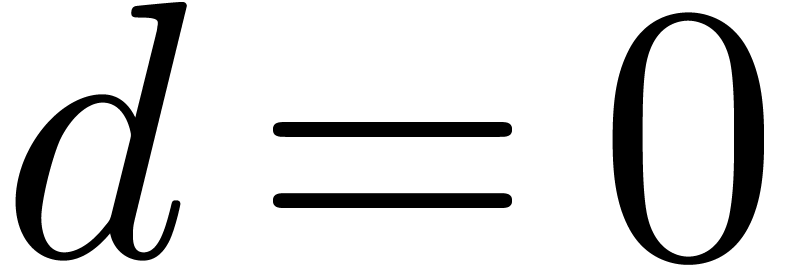 , so we will assume
that
, so we will assume
that 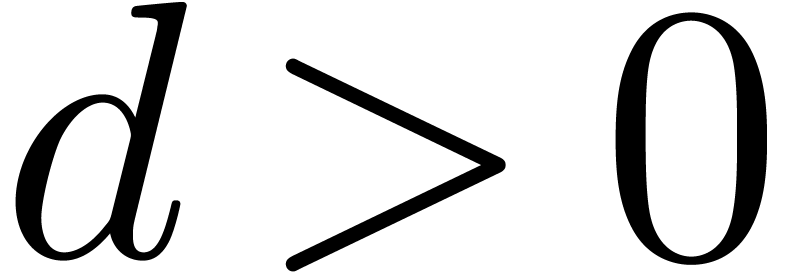 and
and 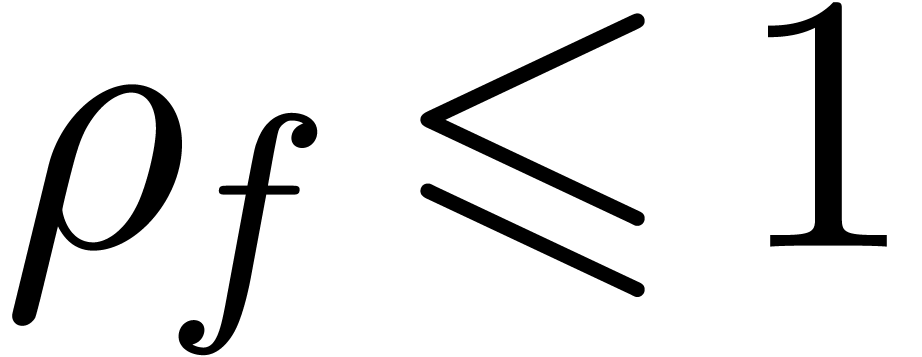 .
The test
.
The test 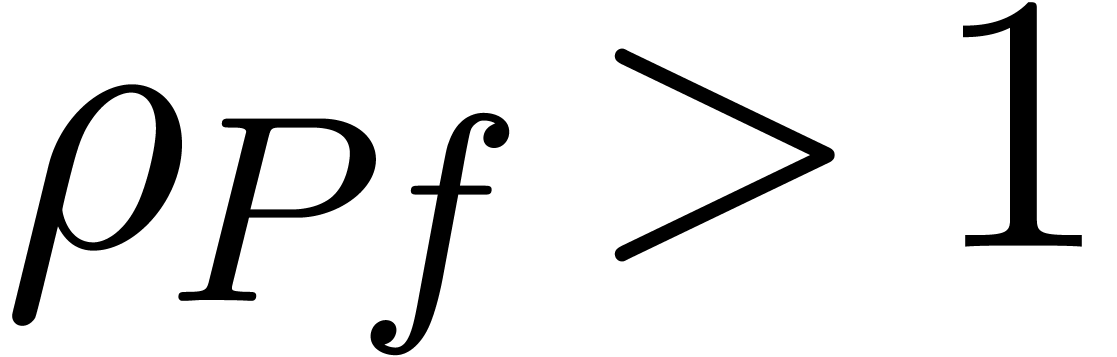 returns false as long as
returns false as long as  (or if
(or if  ).
Assume now that
).
Assume now that 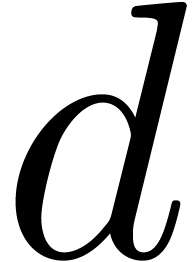 reaches
reaches 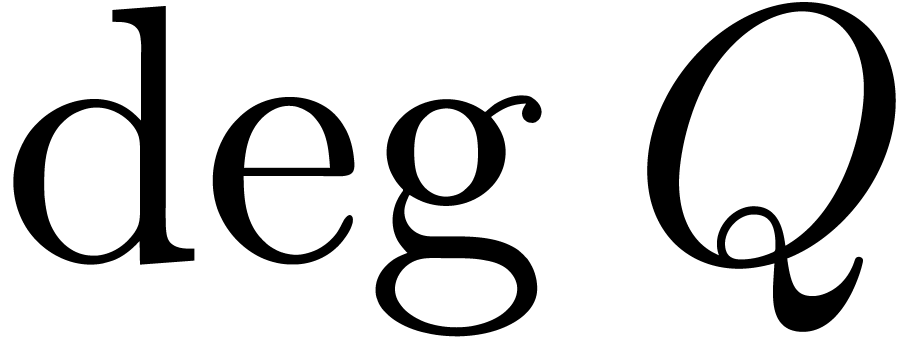 in the algorithm. Then the computed
in the algorithm. Then the computed 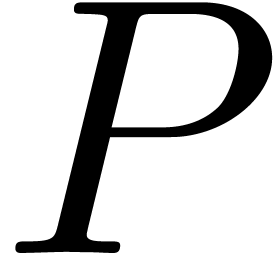 satisfies
satisfies
since
Now let 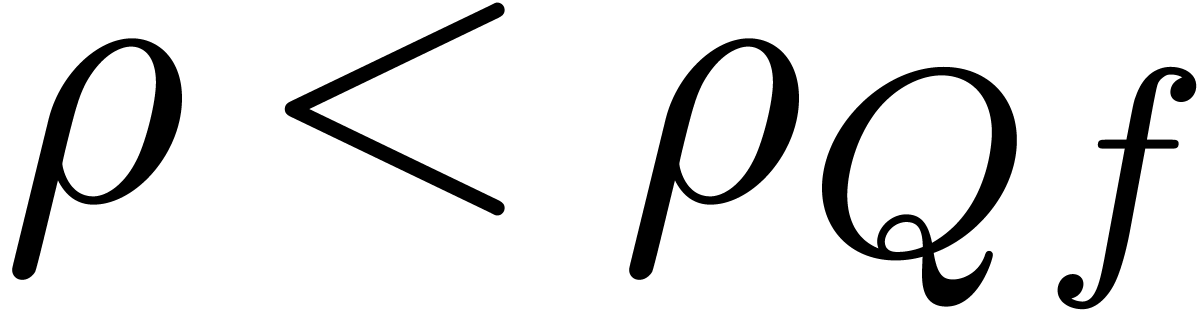 . Given
. Given 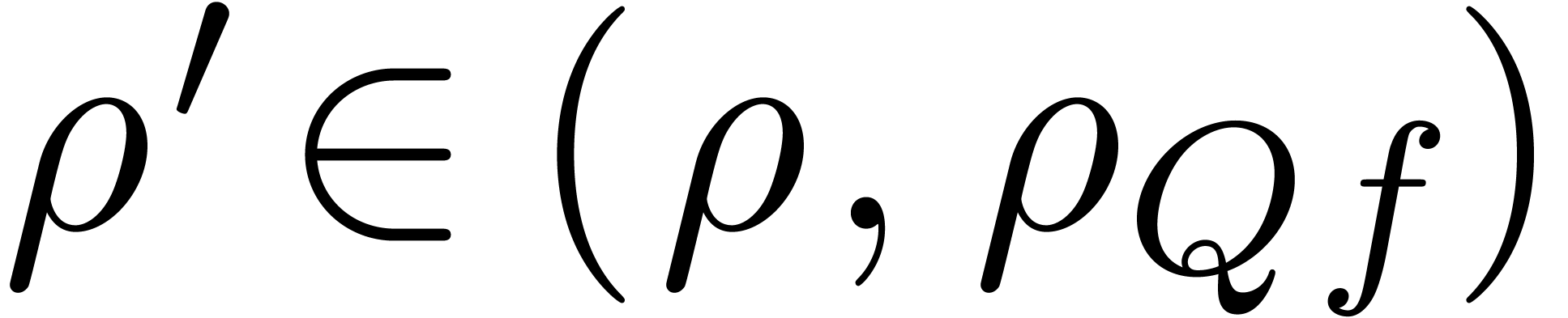 , we have
, we have 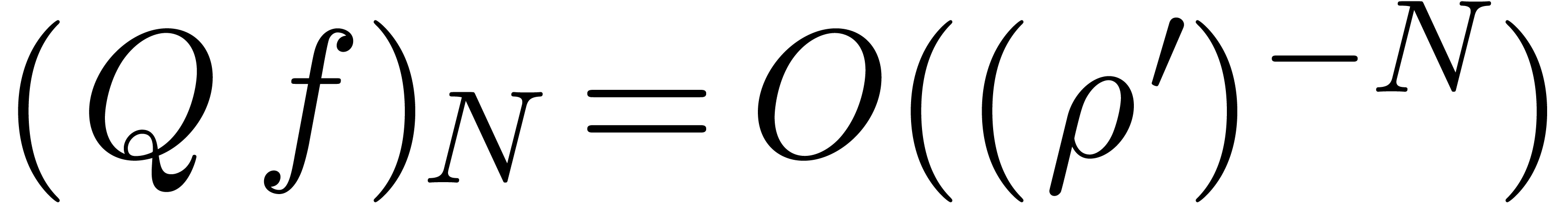 .
Using lemma 5, it follows that
.
Using lemma 5, it follows that 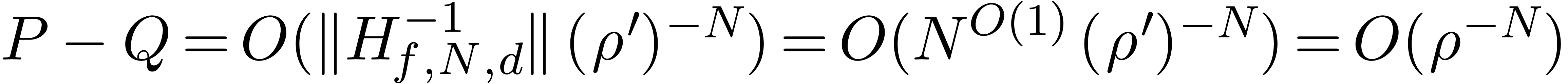 .
.
Remark 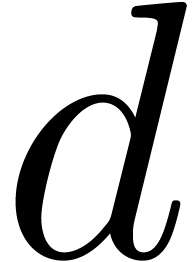 -step
search for finding a polynomial of minimal degree
-step
search for finding a polynomial of minimal degree 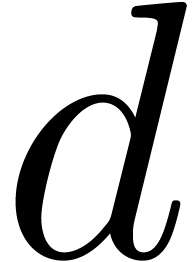 with
with 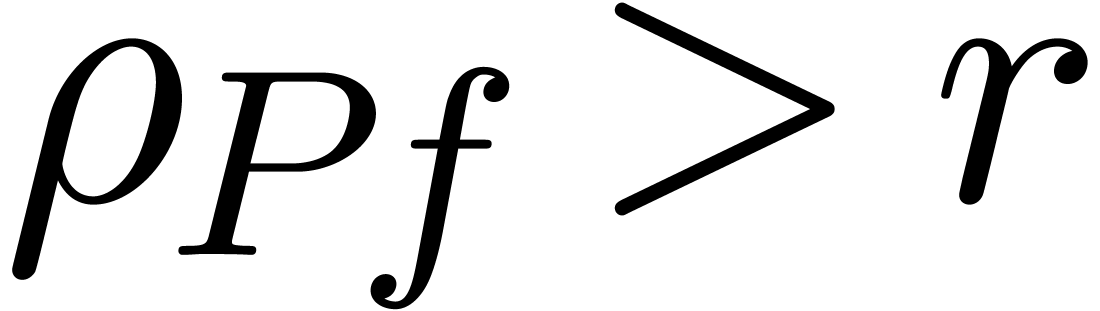 . Using a binary search
(doubling
. Using a binary search
(doubling 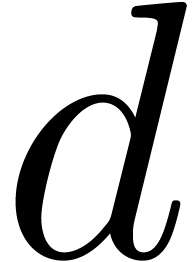 at each step at a first stage, and
using a dichotomic search at a second stage), the number of steps can be
reduced to
at each step at a first stage, and
using a dichotomic search at a second stage), the number of steps can be
reduced to 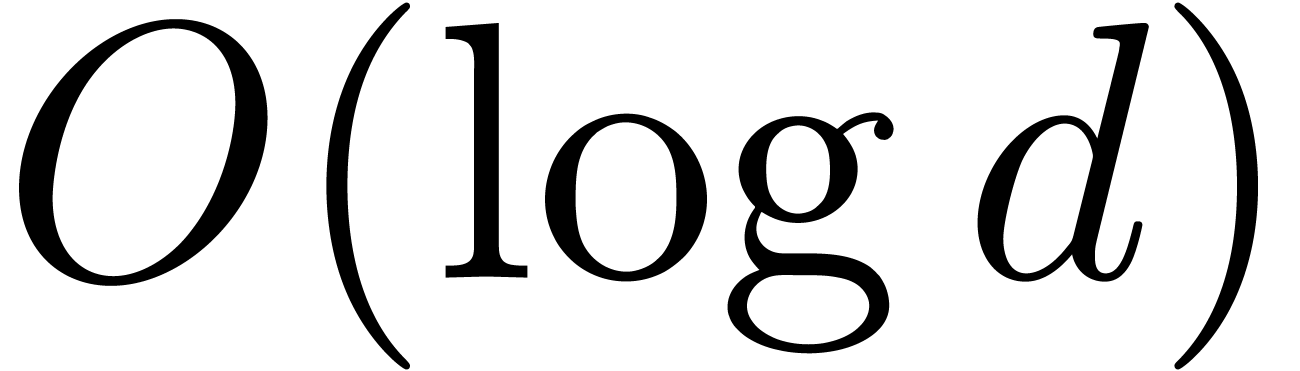 .
.
Proof. Let us first consider the case when 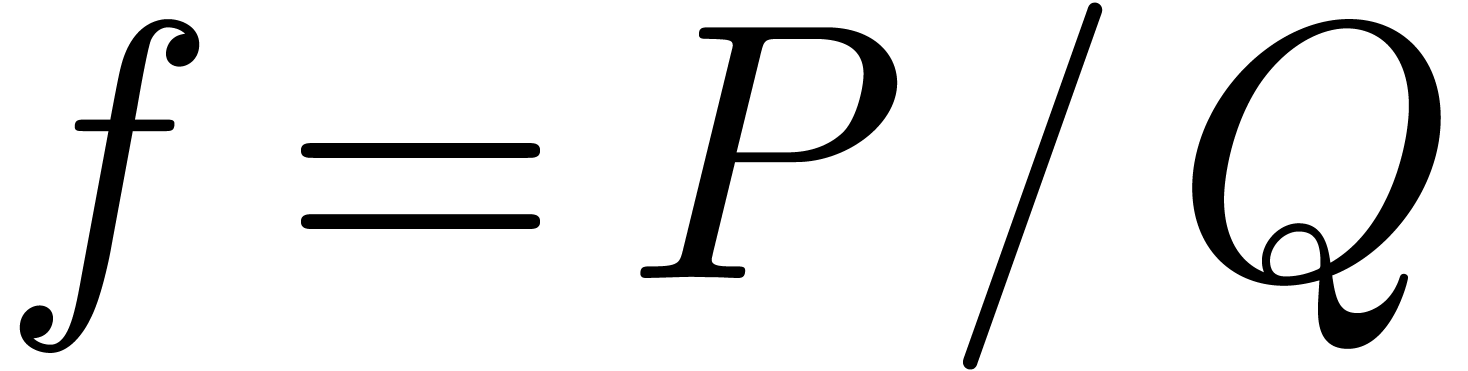 is a rational function with
is a rational function with 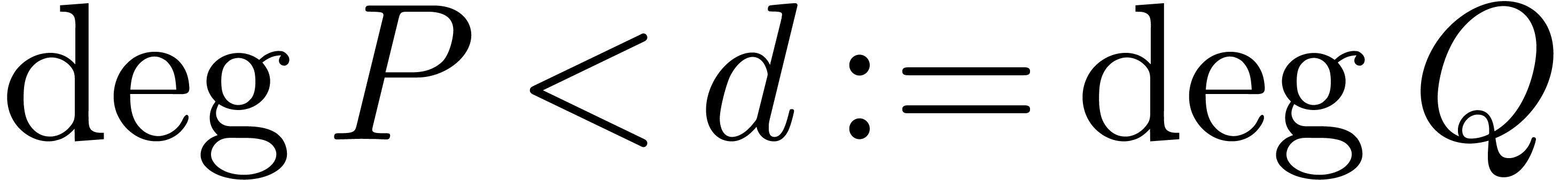 ,
, 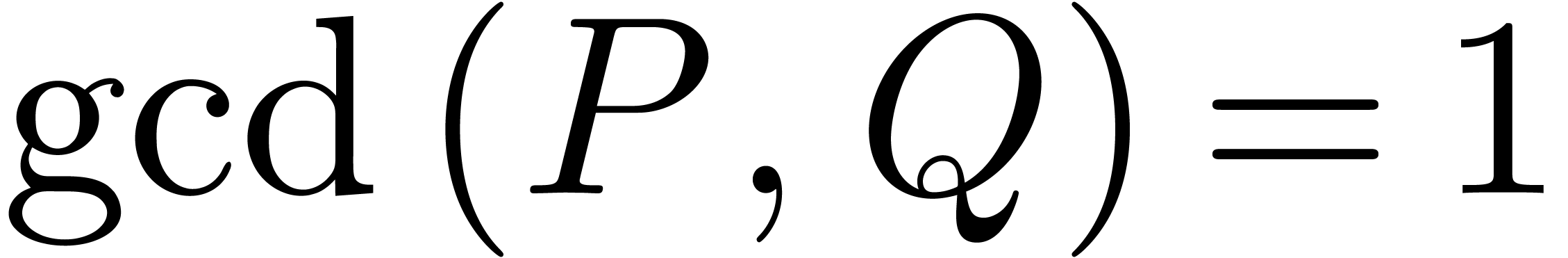 , and
such that
, and
such that  only admits roots in the closed unit
disk. We denote
only admits roots in the closed unit
disk. We denote  and
and  for
each
for
each 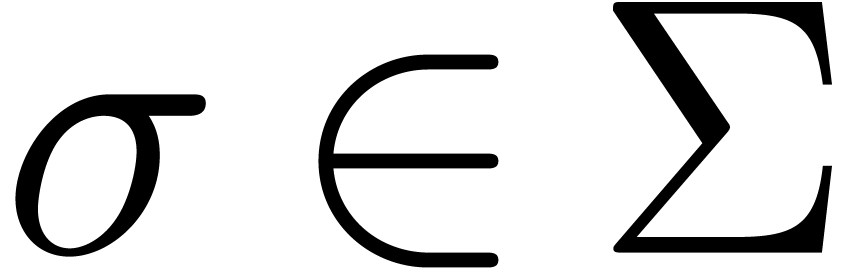 . Using partial fraction
decomposition, there exist numbers
. Using partial fraction
decomposition, there exist numbers  with
with  such that
such that
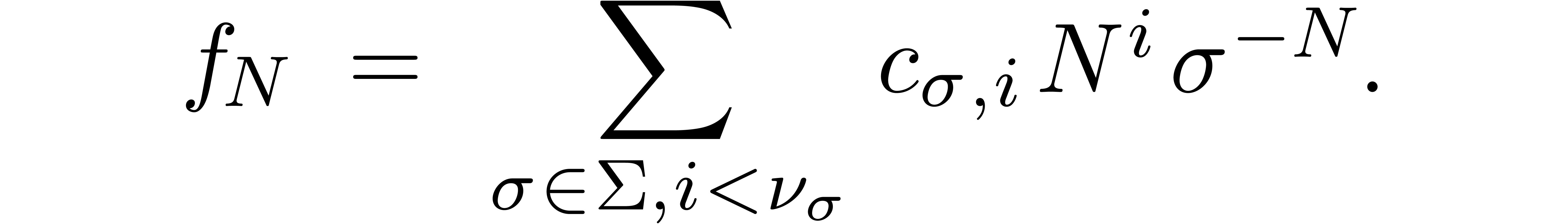
In particular, we may factor
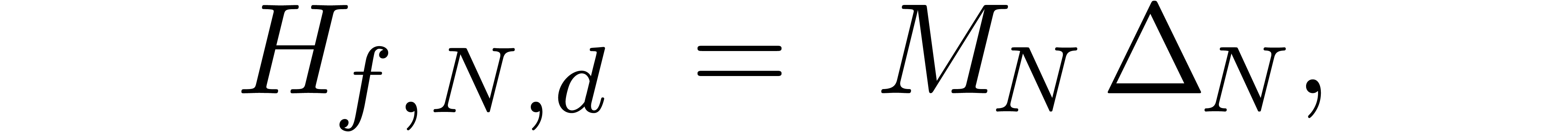
where  is a matrix with entries in
is a matrix with entries in  and
and  is a diagonal matrix with
entries
is a diagonal matrix with
entries  (and such that each
(and such that each  occurs
occurs  times). The functions
times). The functions 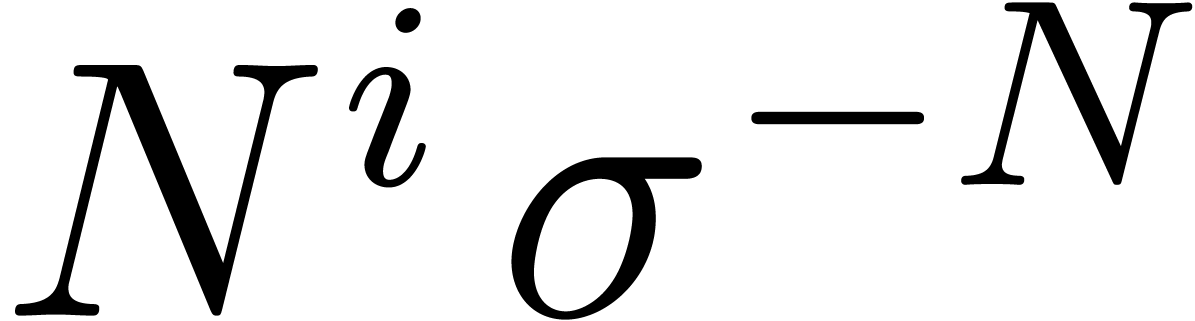 with
with  being linearly independent, the matrix
being linearly independent, the matrix  is invertible in
is invertible in 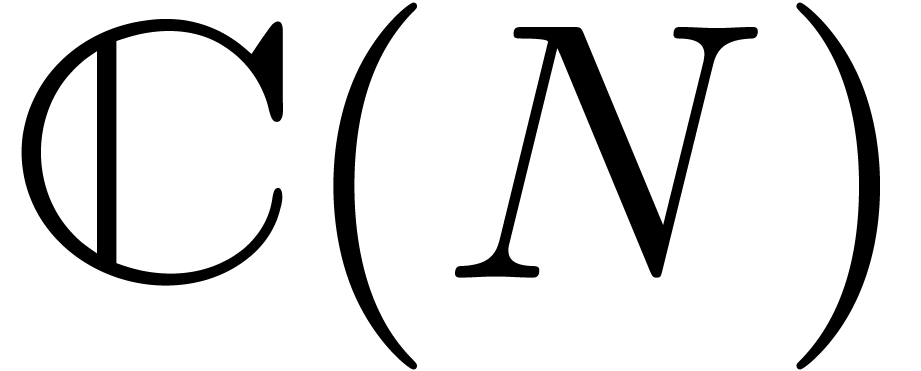 ,
whence
,
whence
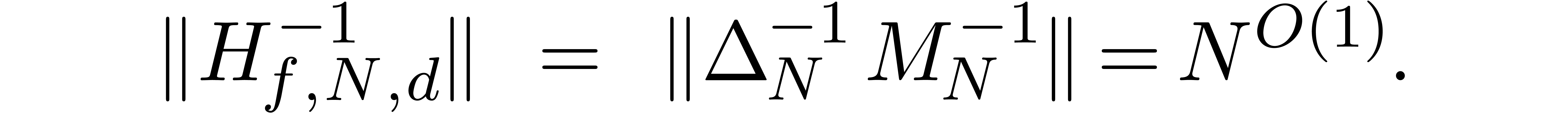
This completes the proof of the lemma in the special case.
In general, we may write 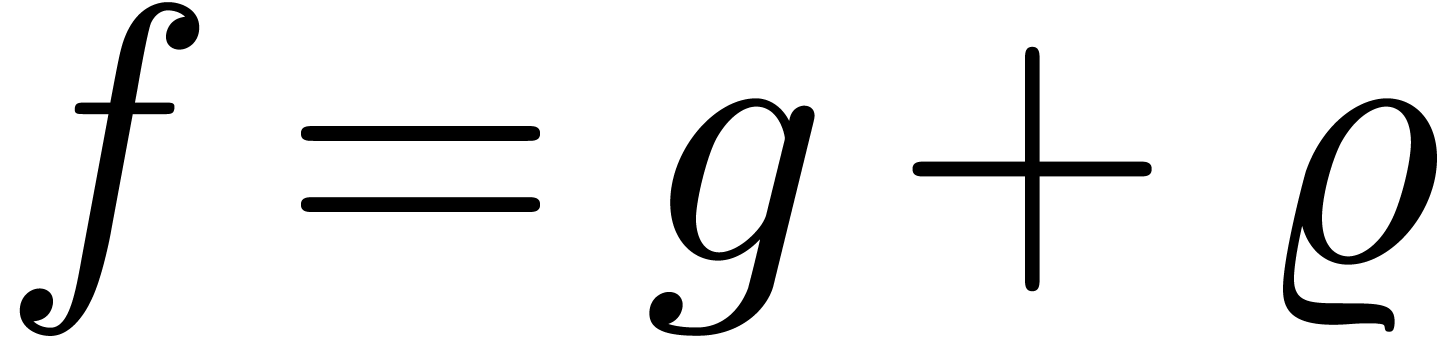 ,
with
,
with 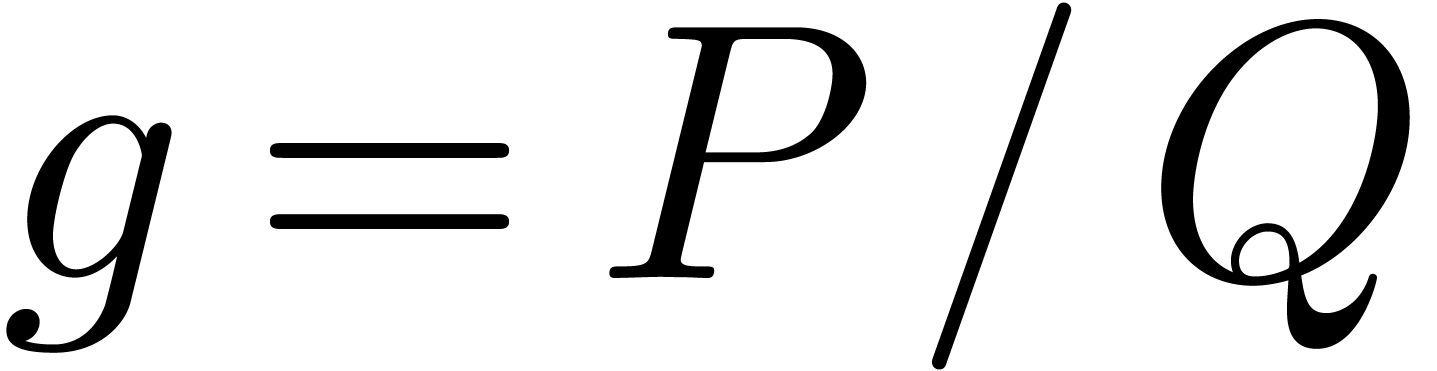 as above and where
as above and where 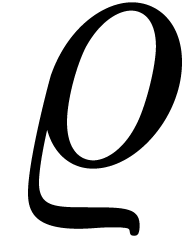 is an analytic function on the closed unit disk. Then
is an analytic function on the closed unit disk. Then
since
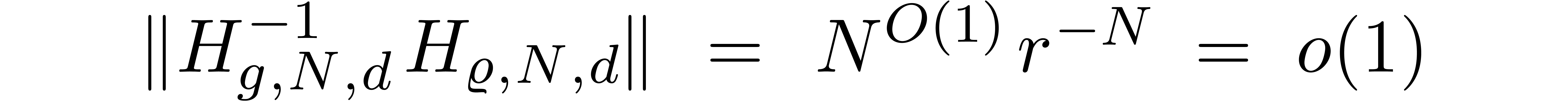
for some  . This completes the
proof in the general case.
. This completes the
proof in the general case.
Keeping the same spirit as in section 5, we will now turn
our attention to two larger classes of algebraic and Fuchsian analytic
functions on the compact disk  of radius
of radius 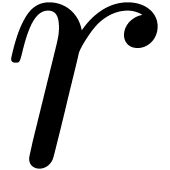 . Given a function
. Given a function  in one of these classes, we will show how to find the defining equation
for
in one of these classes, we will show how to find the defining equation
for  , under the assumption
that we have a high accuracy algorithm for its analytic continuation. As
in remark 2, we will also assume the existence of a
heuristic equality test for analytic functions.
, under the assumption
that we have a high accuracy algorithm for its analytic continuation. As
in remark 2, we will also assume the existence of a
heuristic equality test for analytic functions.
Let  be an analytic function which is given by
its power series
be an analytic function which is given by
its power series 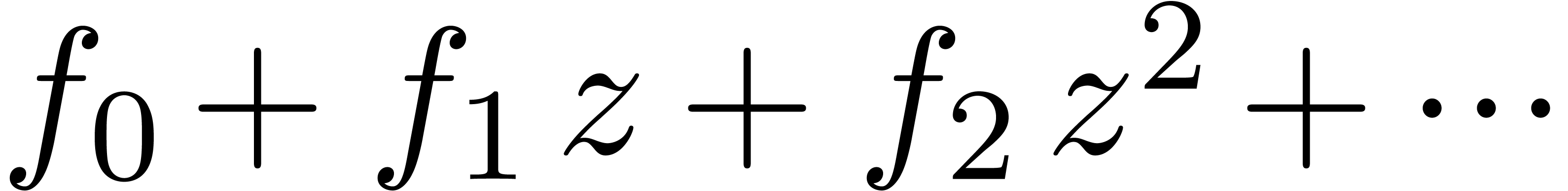 at the origin. Assume that
at the origin. Assume that  can be continued analytically on a Riemann surface
can be continued analytically on a Riemann surface
 above the closed disk
above the closed disk  of
radius
of
radius  minus a finite set of points
minus a finite set of points  . Let
. Let  be the set of
analytic functions on
be the set of
analytic functions on  . We
say that
. We
say that  is algebraic on
is algebraic on  if there exists a polynomial relation
if there exists a polynomial relation
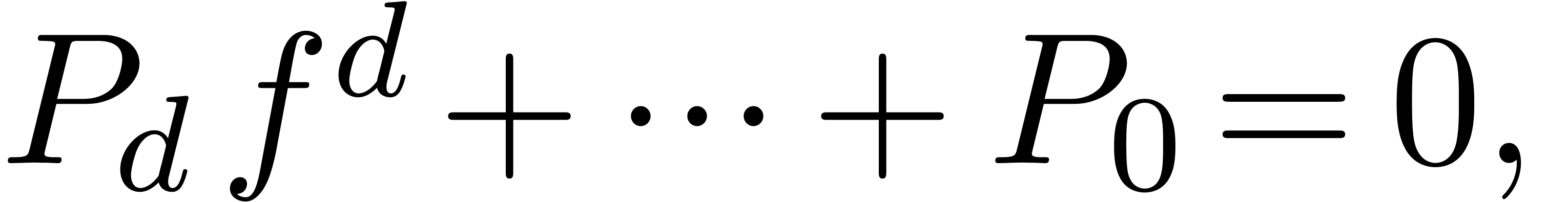 |
(11) |
with  . In that case, we may
normalize the relation such that
. In that case, we may
normalize the relation such that  has minimal
degree and such that
has minimal
degree and such that 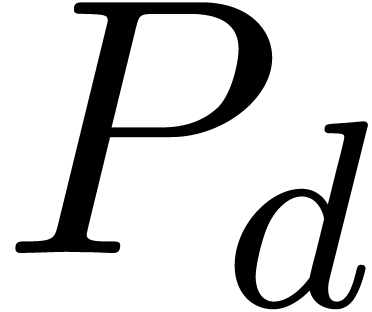 is a monic polynomial of
minimal degree. In particular, all roots of
is a monic polynomial of
minimal degree. In particular, all roots of 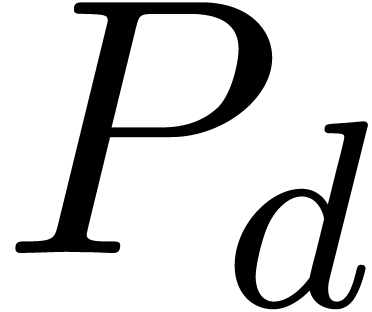 are
inside the disk
are
inside the disk  .
.
Given a function  which is algebraic on
which is algebraic on  , this function clearly satisfies
the assumption A in section 4.3, whence we
may compute the singularities
, this function clearly satisfies
the assumption A in section 4.3, whence we
may compute the singularities  using the
algorithm described there. Conversely, the example
using the
algorithm described there. Conversely, the example
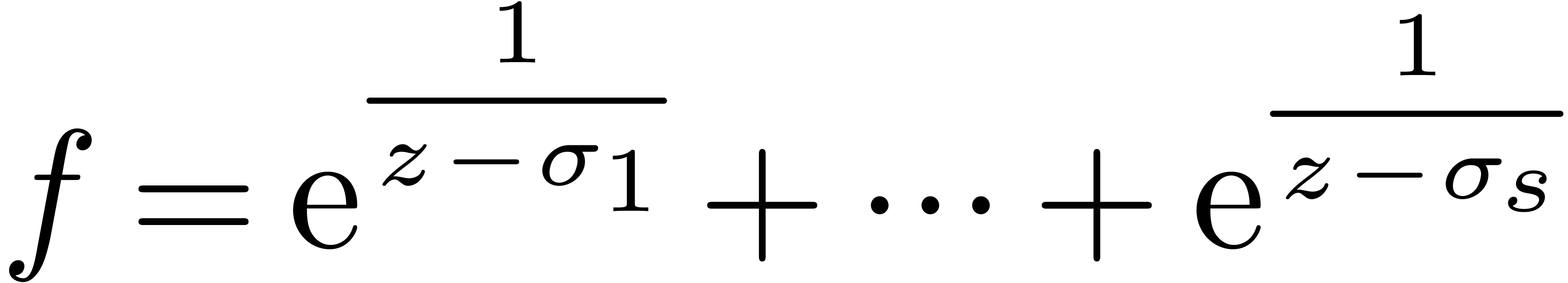
shows that there are functions which satisfy the assumption
A, but which are not algebraic on the disk  .
.
Assume that  is algebraic on
is algebraic on  . For each singularity
. For each singularity 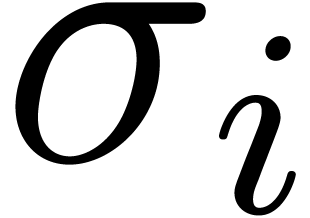 , consider a path
, consider a path 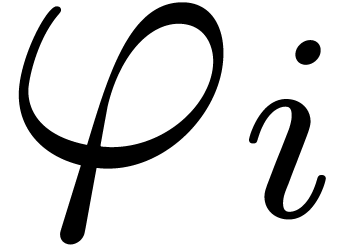 from the
origin to a point near
from the
origin to a point near 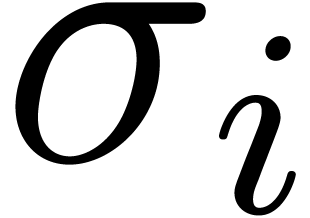 which avoids the other
singularities, and let
which avoids the other
singularities, and let 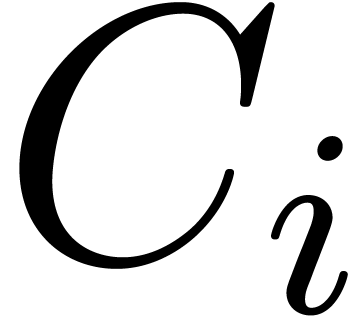 be the operator which
performs an analytic continuation along
be the operator which
performs an analytic continuation along 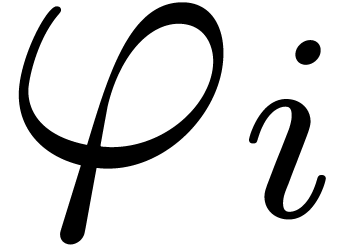 ,
one turn around
,
one turn around 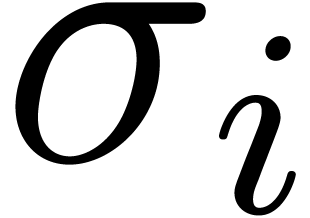 , followed by
an analytic continuation along
, followed by
an analytic continuation along 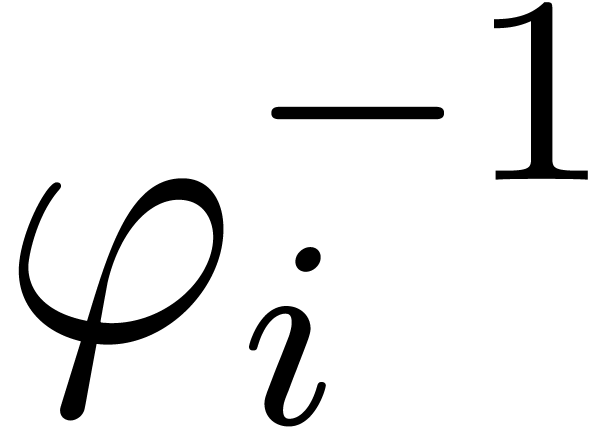 .
With these operators, we may use the following algorithm for the
detection of algebraic dependencies:
.
With these operators, we may use the following algorithm for the
detection of algebraic dependencies:
Algorithm alg_dep
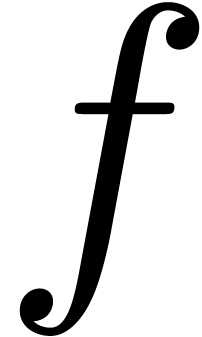 above
above 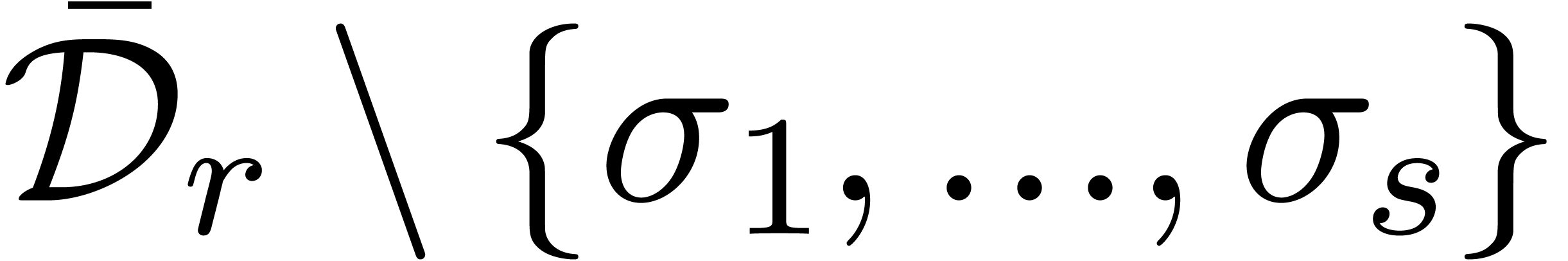 and bounds
and bounds  ,
,
 and
and 
 and
and 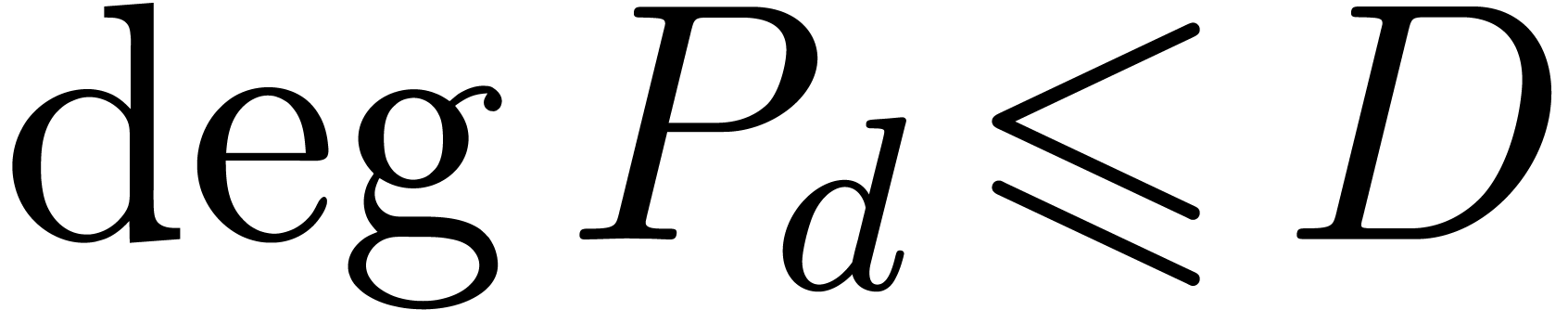 , or
, or  (failed)
(failed)
Step 1. [Initialize]
Set 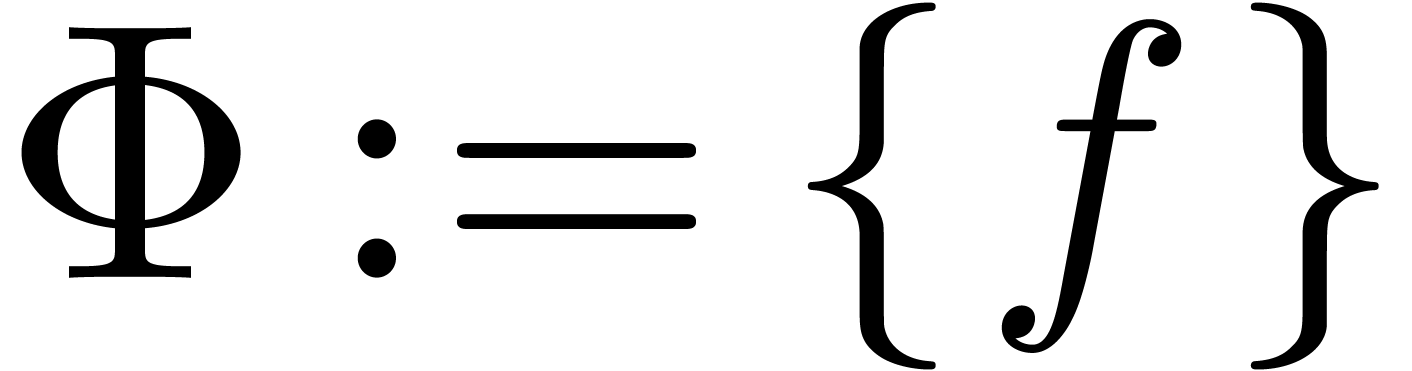
Step 2. [Saturate]
If  then return
then return 
If 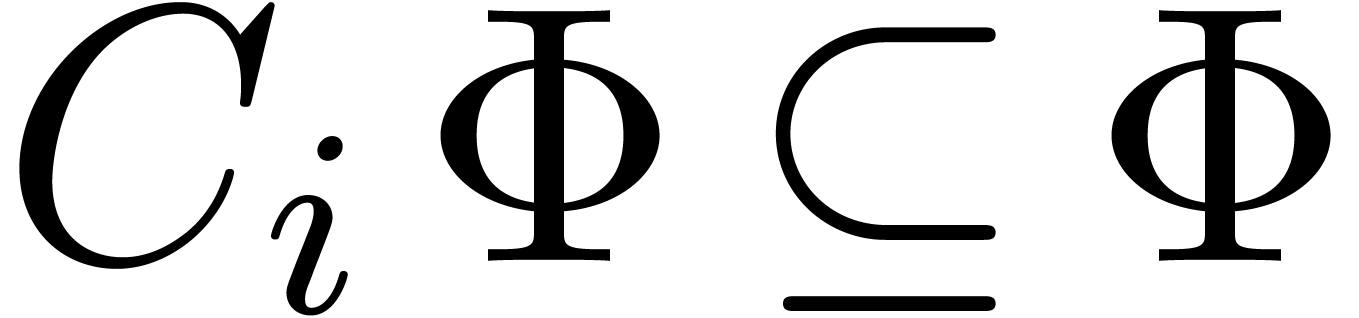 for all
for all  ,
then go to step 3
,
then go to step 3

Repeat step 2
Step 3. [Terminate]
Denote 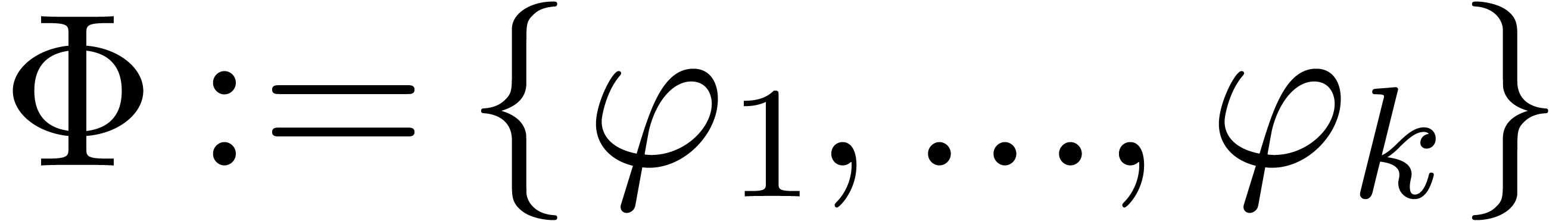
Compute 
For each 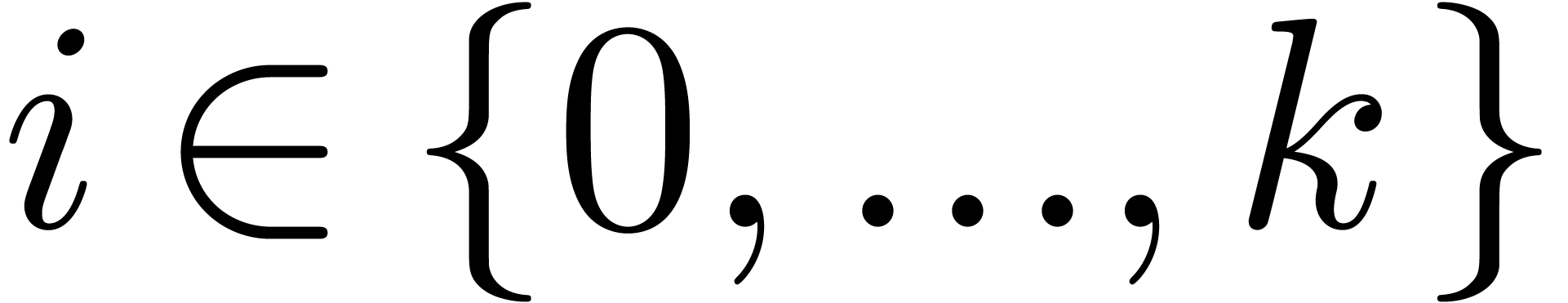 , compute
, compute 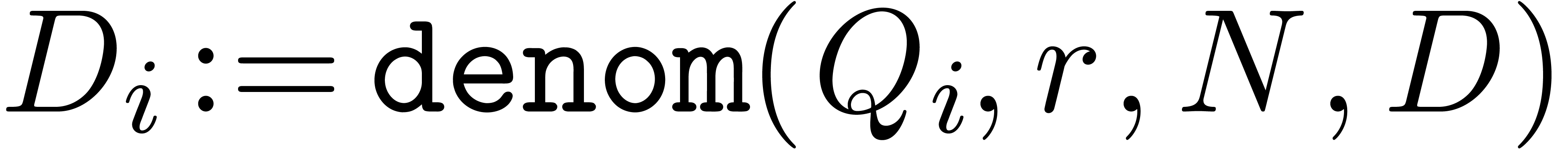
If 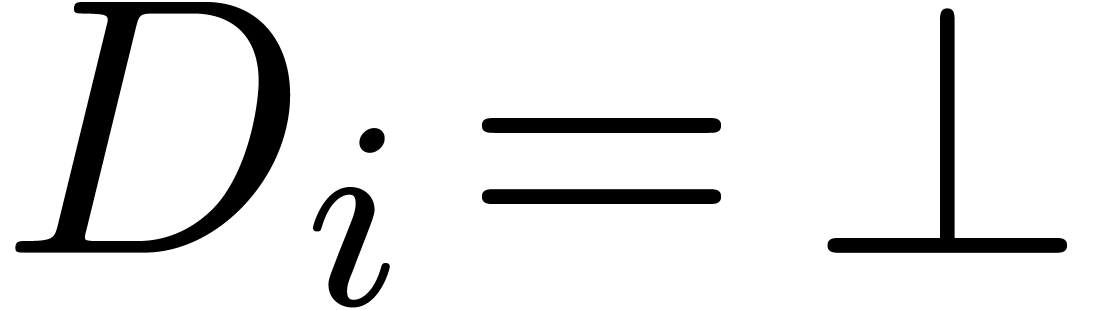 for some
for some 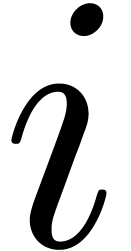 ,
then return
,
then return 
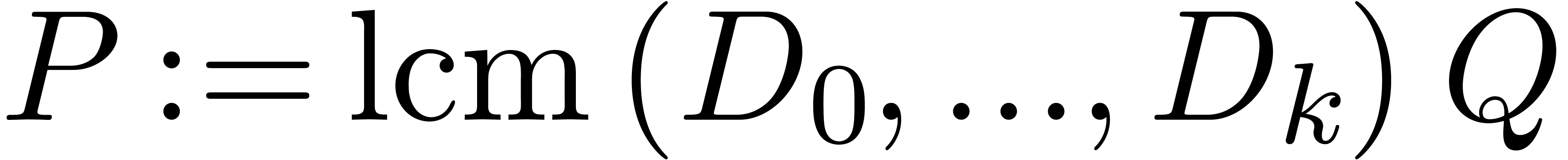
If  then return
then return 
Return 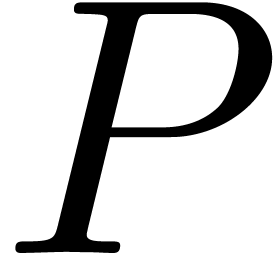
Proof. Assume that  satisfies a normalized relation (11), with
satisfies a normalized relation (11), with  and
and  . Since
. Since  only contains distinct roots of
only contains distinct roots of 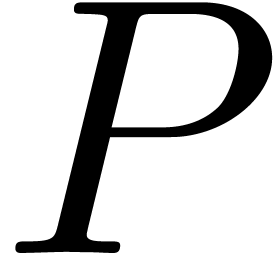 ,
we have
,
we have 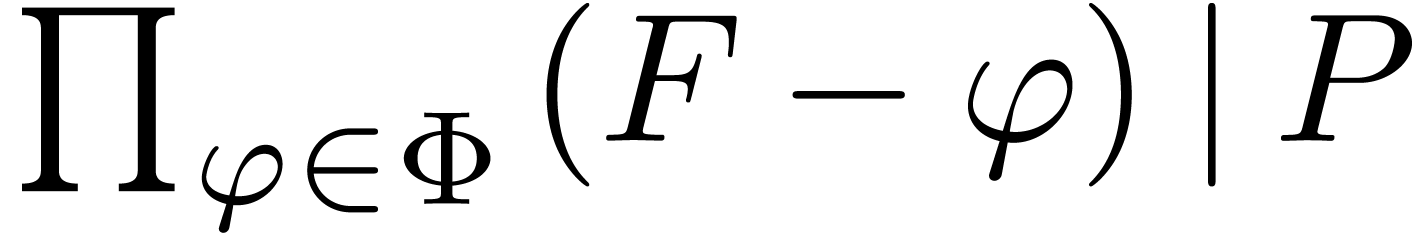 in
in 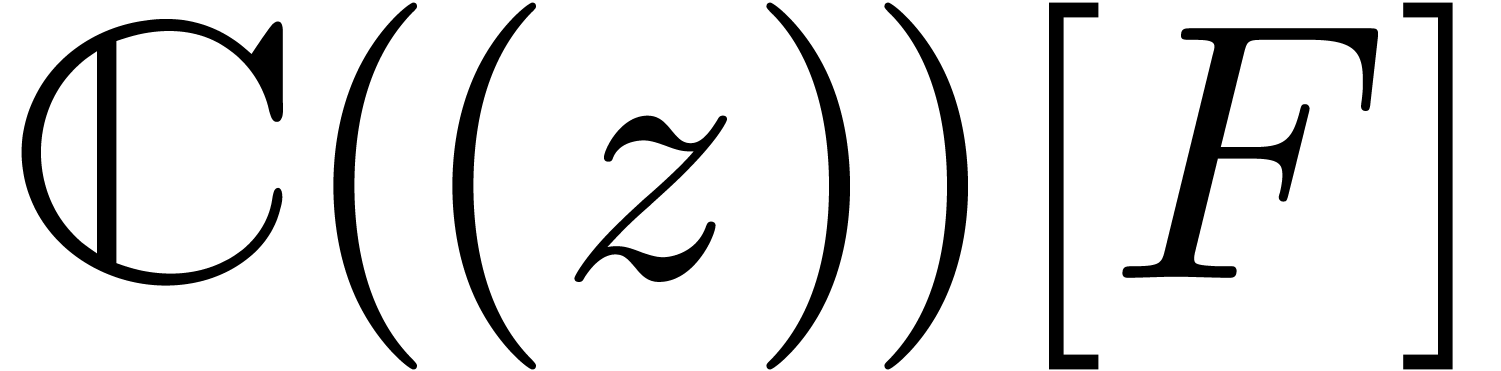 throughout
the algorithm. In particular
throughout
the algorithm. In particular  ,
and we ultimately obtain stabilization
,
and we ultimately obtain stabilization  .
.
At this point, analytic continuation around any of the points  leaves the polynomial
leaves the polynomial  invariant,
so the coefficients of
invariant,
so the coefficients of  are analytic and
single-valued on
are analytic and
single-valued on 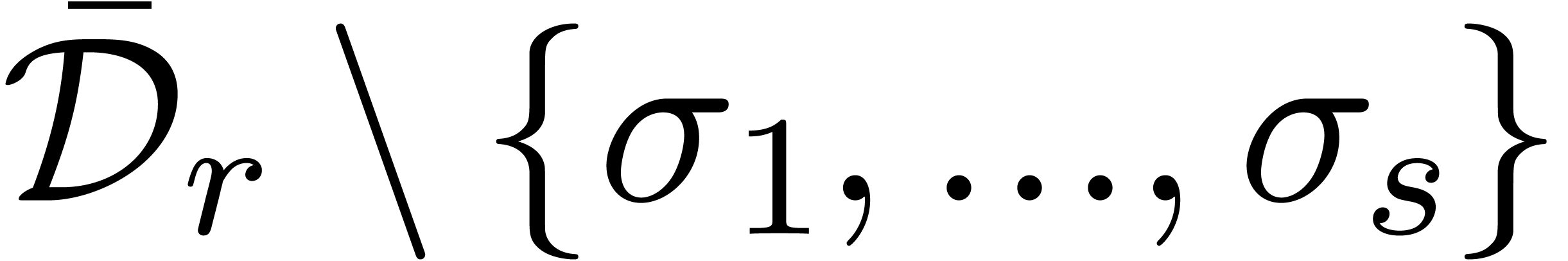 . On the
other hand, given a singularity
. On the
other hand, given a singularity 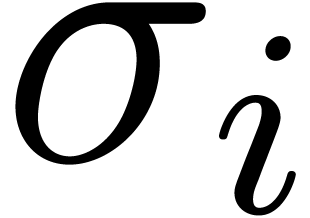 ,
each solution
,
each solution  is also given by a convergent
Puiseux series near
is also given by a convergent
Puiseux series near 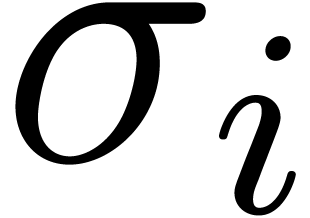 , whence
so are the coefficients of
, whence
so are the coefficients of  .
Since the only Puiseux series without monodromy around
.
Since the only Puiseux series without monodromy around 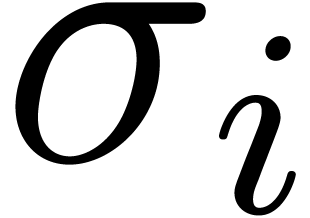 are Laurent series, it follows that the coefficients of
are Laurent series, it follows that the coefficients of  are meromorphic on
are meromorphic on  .
.
By the minimality assumption on 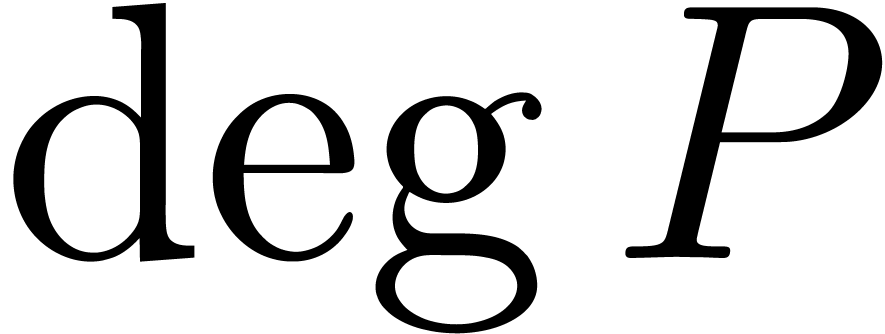 ,
it follows that
,
it follows that 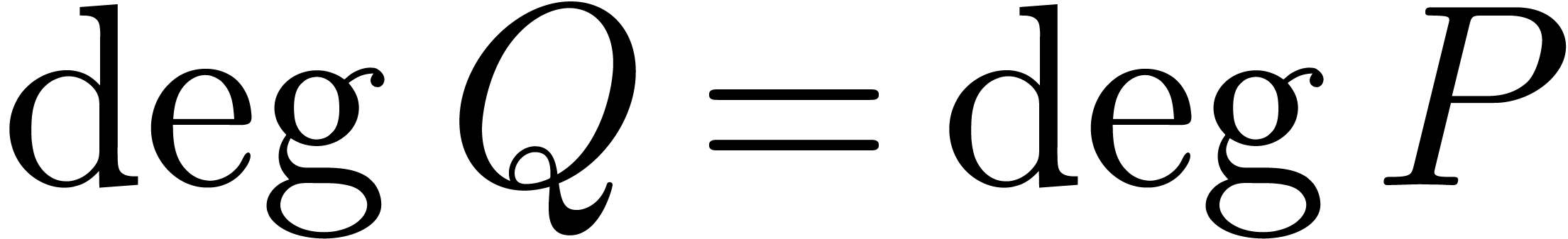 and
and 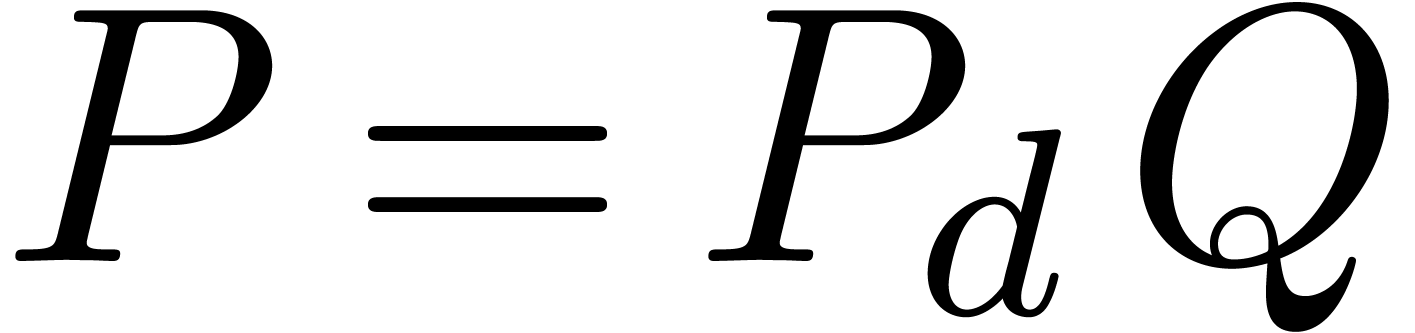 . Since each coefficient
. Since each coefficient 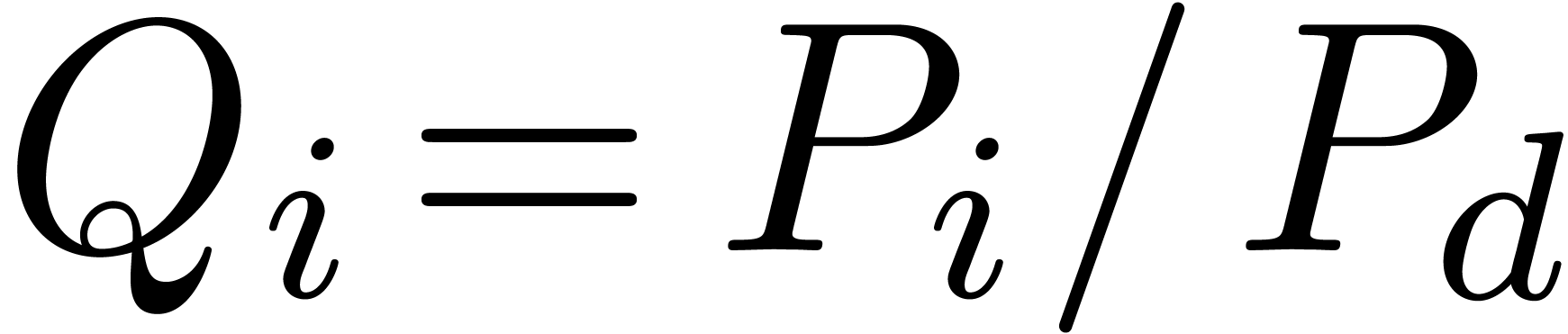 is
meromorphic on
is
meromorphic on  , we may use
the algorithm denom from the previous section in order
to compute a polynomial
, we may use
the algorithm denom from the previous section in order
to compute a polynomial 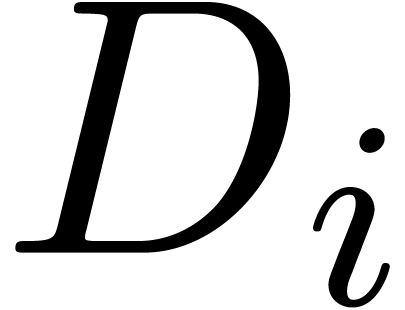 of minimal degree
of minimal degree 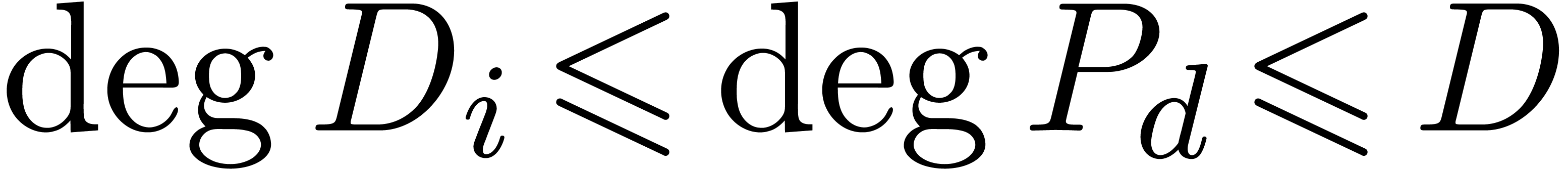 such that
such that 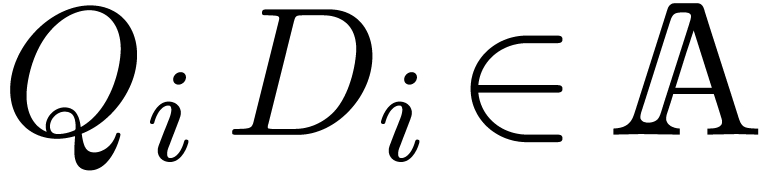 .
The monic least common multiple
.
The monic least common multiple 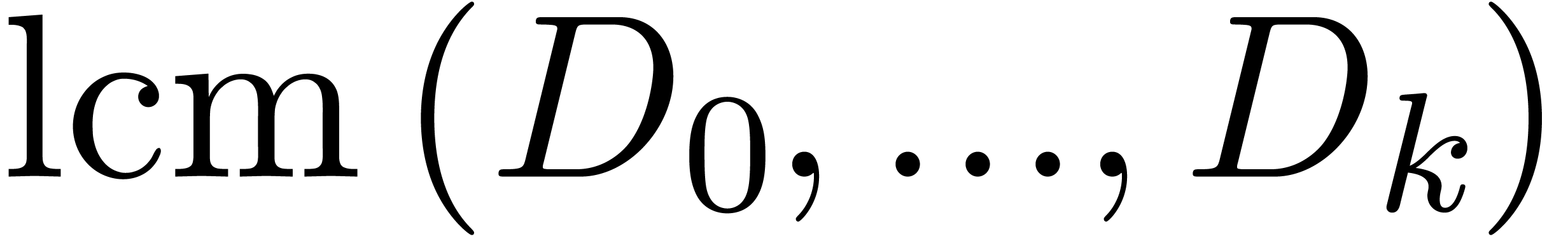 is nothing but
the monic polynomial
is nothing but
the monic polynomial 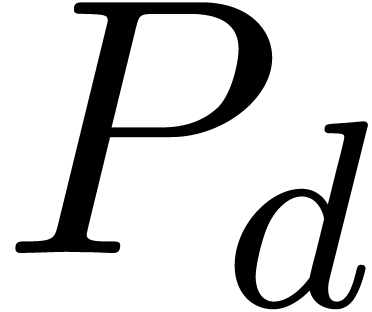 of minimal degree such that
of minimal degree such that
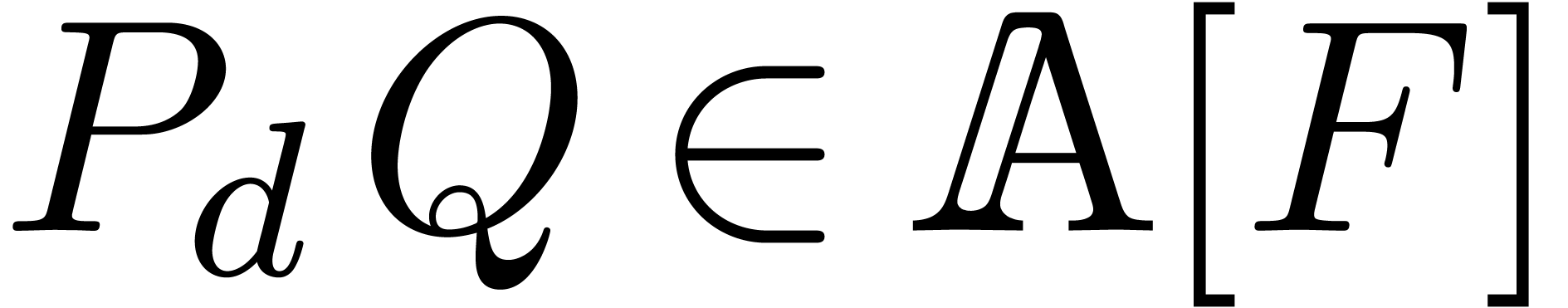 .
.
Remark  and
and 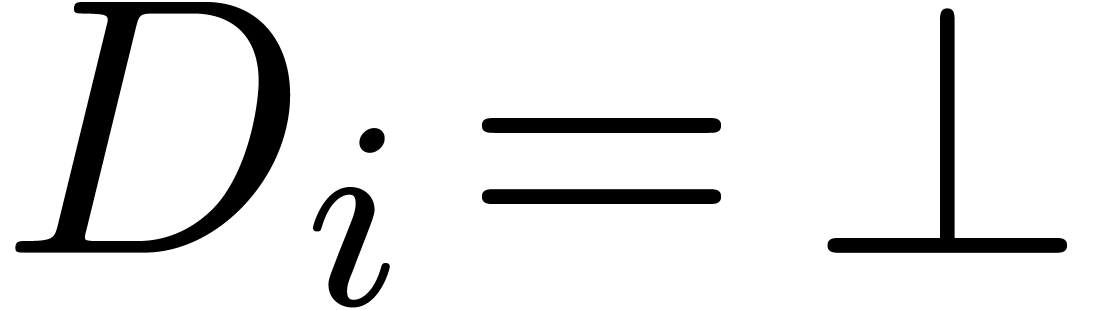 always
return the right answer, then we will reach the line
always
return the right answer, then we will reach the line 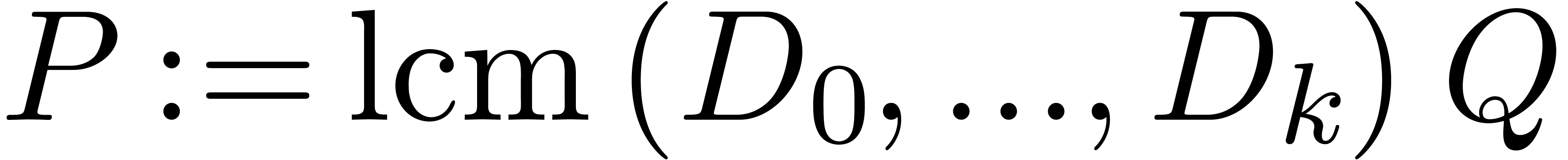 whenever the desired relation exists. For the final normalization step,
we need a numerical algorithm for the computation of least common
multiples which allows for small errors in the input coefficients. This
is similar to the computation of approximate g.c.d.s for
which there exists an extensive literature; see for example [CGTW95,
KL96], or [Zen04] and references therein.
whenever the desired relation exists. For the final normalization step,
we need a numerical algorithm for the computation of least common
multiples which allows for small errors in the input coefficients. This
is similar to the computation of approximate g.c.d.s for
which there exists an extensive literature; see for example [CGTW95,
KL96], or [Zen04] and references therein.
Remark  and check whether they are indeed
superior to
and check whether they are indeed
superior to 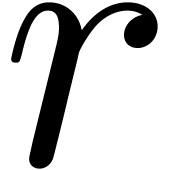 .
.
We say that  is Fuchsian on
is Fuchsian on  , if
, if  satisfies a linear
differential equation
satisfies a linear
differential equation
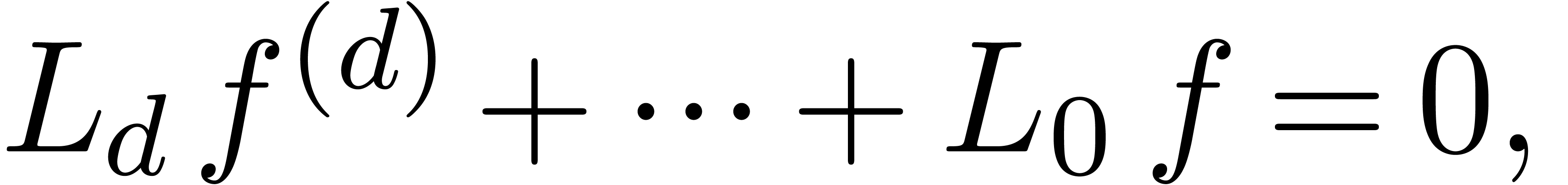 |
(12) |
where  , and
, and 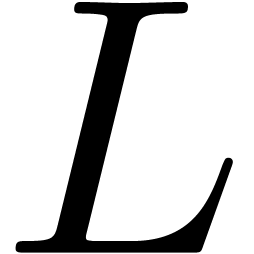 is Fuchsian at each point in
is Fuchsian at each point in  .
Again, we may normalize (12) such that
.
Again, we may normalize (12) such that 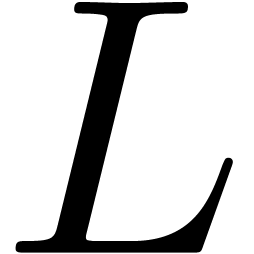 has minimal order
has minimal order  and such that
and such that  is a monic polynomial of minimal degree.
is a monic polynomial of minimal degree.
Given a function  which is Fuchsian on
which is Fuchsian on  , the function now satisfies the
assumption H in section 4.3, so we may
again compute the singularities
, the function now satisfies the
assumption H in section 4.3, so we may
again compute the singularities  using the
algorithm described there. With
using the
algorithm described there. With  as in the
previous section, we may detect Fuchsian dependencies as follows:
as in the
previous section, we may detect Fuchsian dependencies as follows:
Algorithm fuch_dep
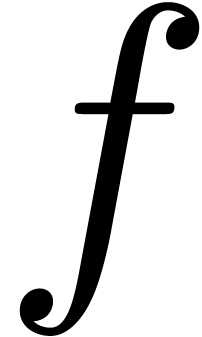 above
above 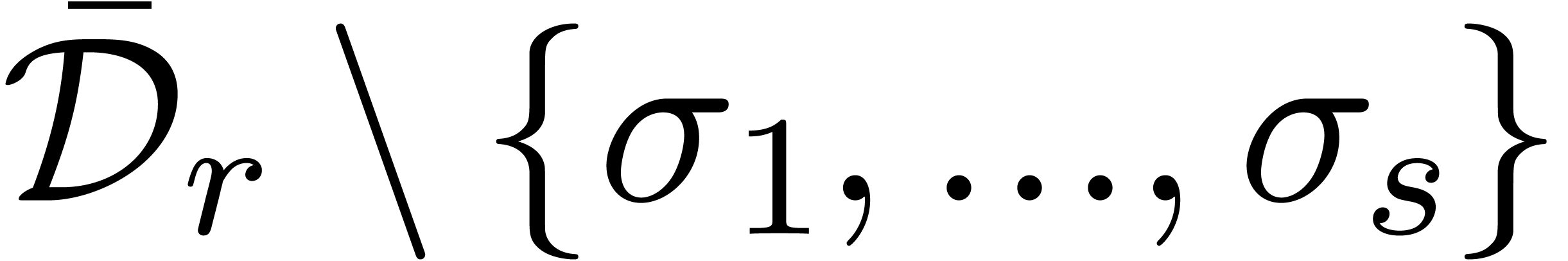 and bounds
and bounds 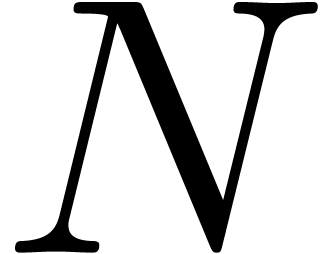 ,
,
 and
and 
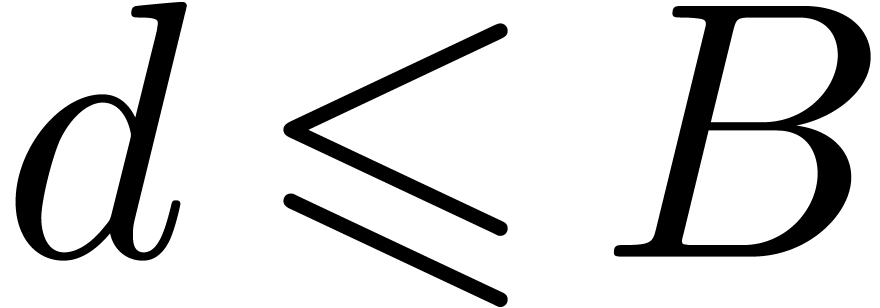 and
and 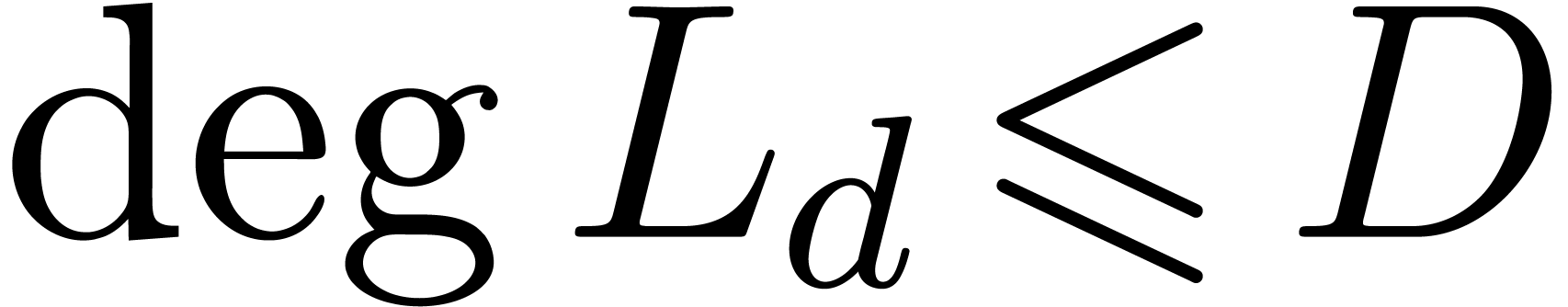 , or
, or  (failed)
(failed)
Step 1. [Initialize]
Set 
Step 2. [Saturate]
If  then return
then return 
Let  denote the vector space generated by a
finite set of vectors
denote the vector space generated by a
finite set of vectors 
If 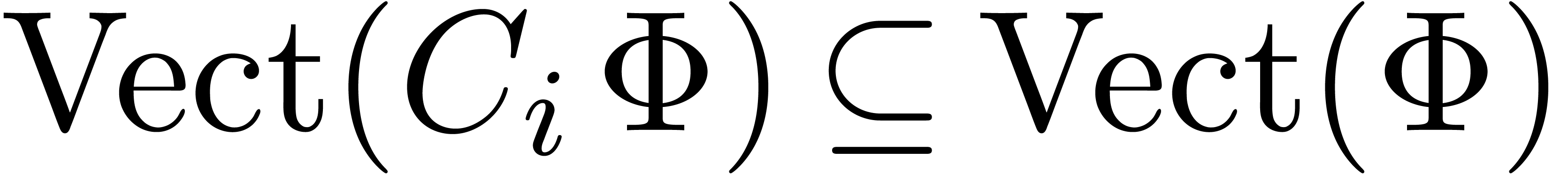 for all
for all  ,
then go to step 3
,
then go to step 3
 for
for  and
and  with
with 
Repeat step 2
Step 3. [Terminate]
Denote 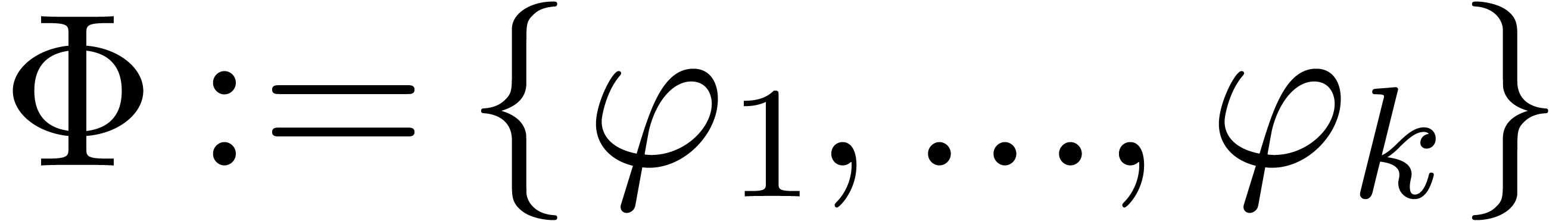
Compute 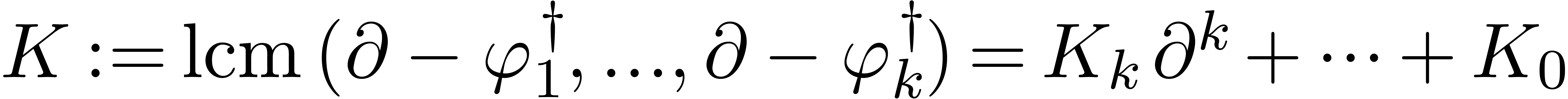
in the skew polynomial ring 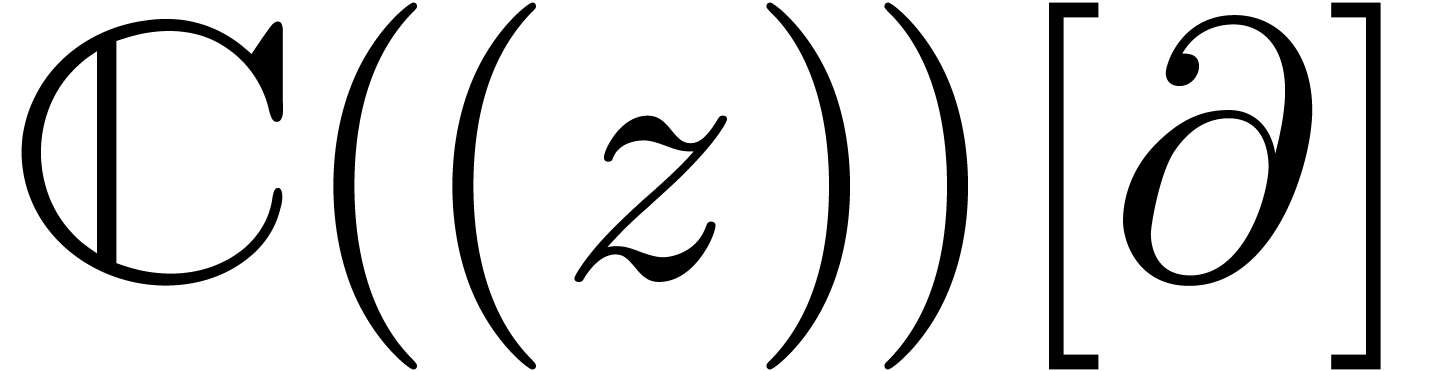 ,
where
,
where  denotes
denotes 
For each 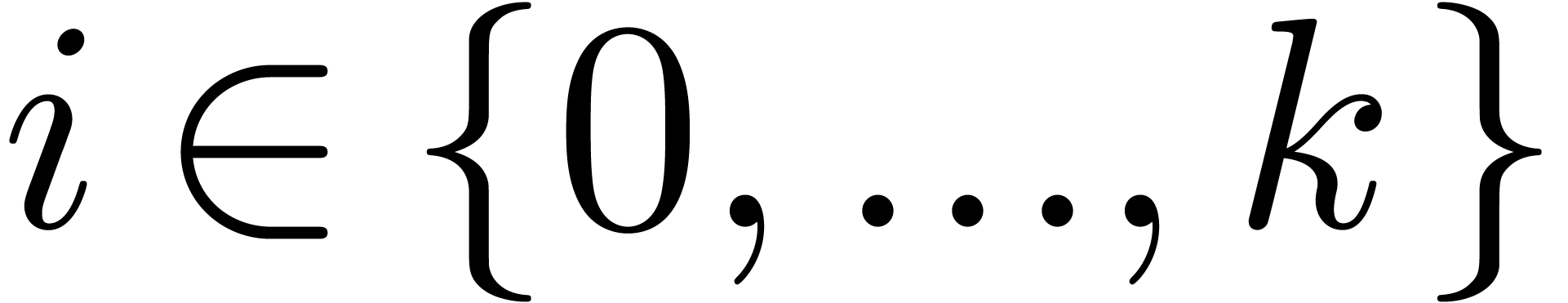 , compute
, compute 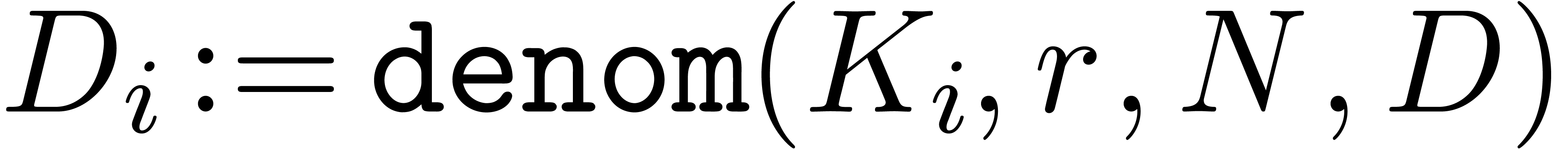
If 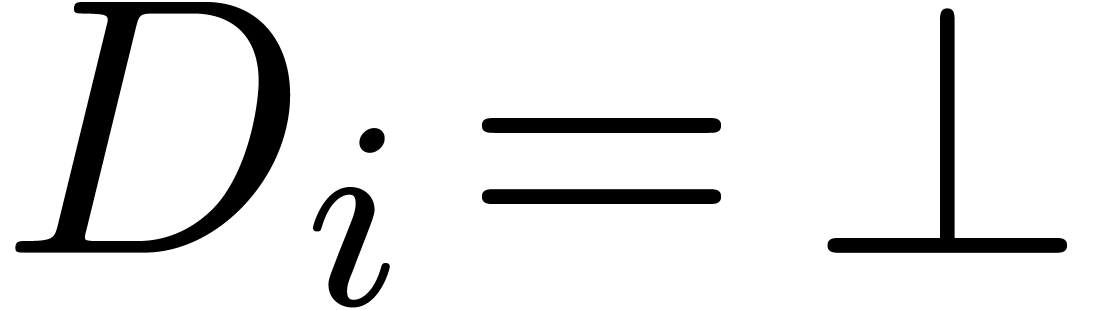 for some
for some 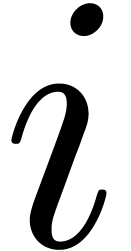 ,
then return
,
then return 
If  then return
then return 
Return 
Proof. Assume that  satisfies a normalized Fuchsian relation (12), with
satisfies a normalized Fuchsian relation (12), with 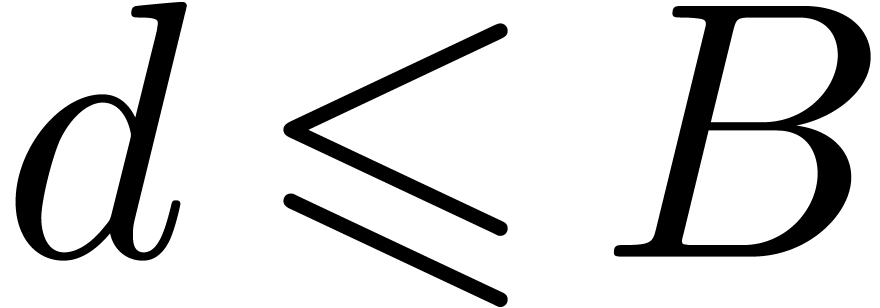 and
and 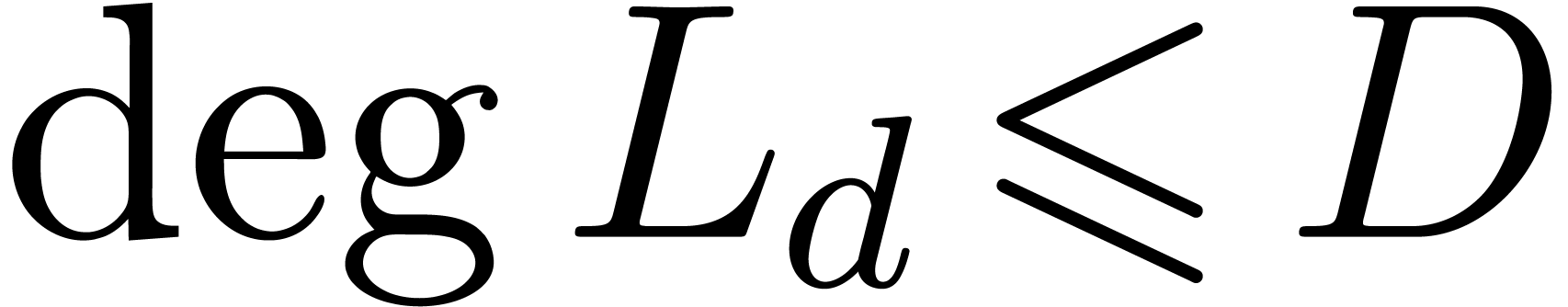 .
Throughout the algorithm, the set
.
Throughout the algorithm, the set  only contains
linearly independent solutions to
only contains
linearly independent solutions to 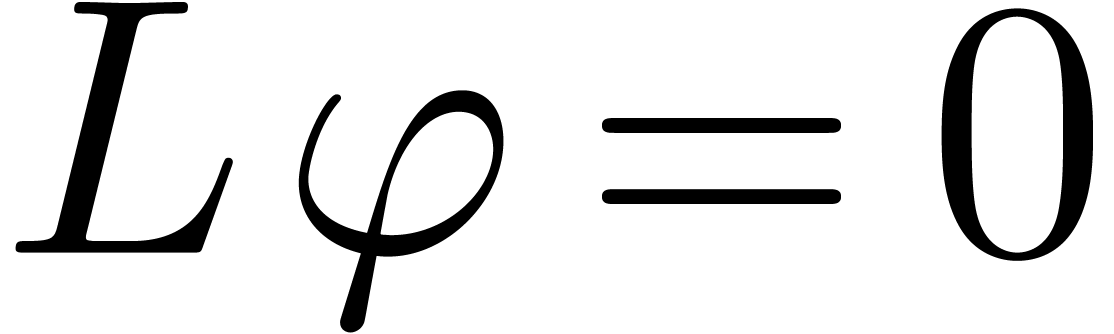 .
Therefore, the smallest operator
.
Therefore, the smallest operator 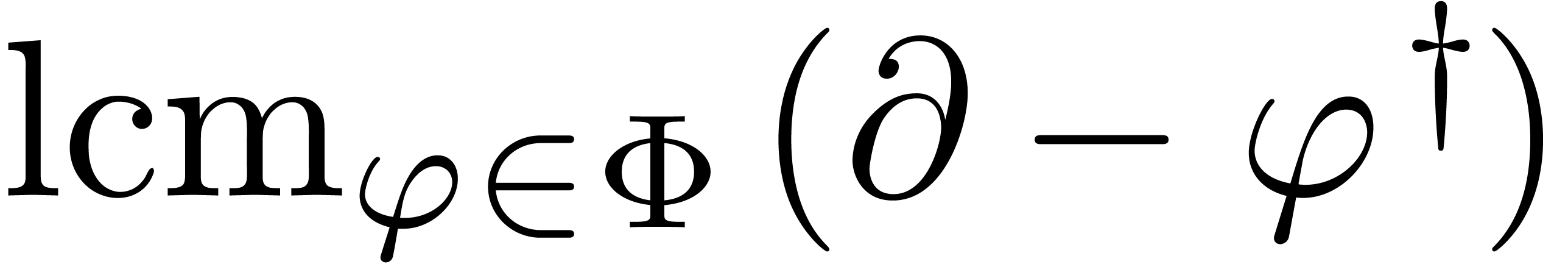 which vanishes
on
which vanishes
on  divides
divides  in
in 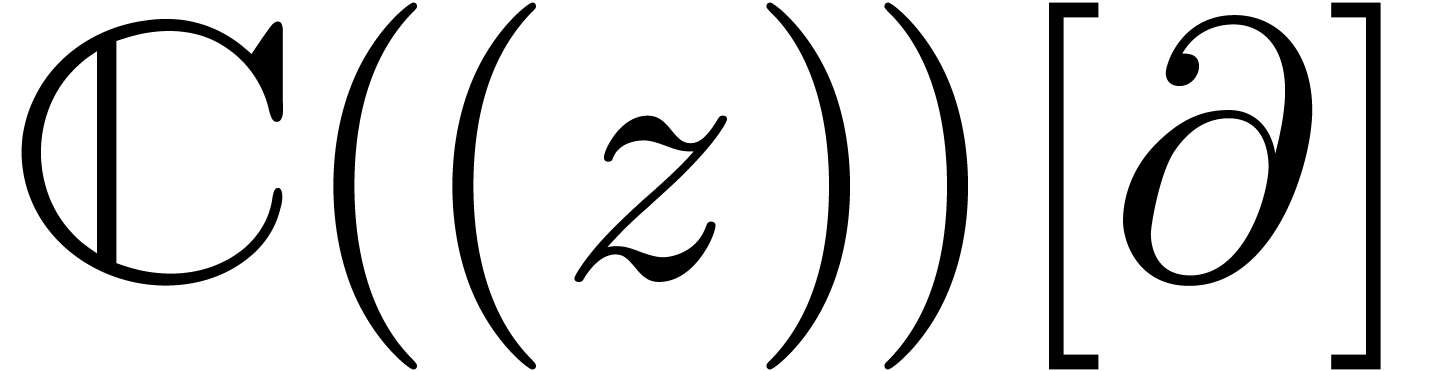 on the right. In particular
on the right. In particular  ,
and we ultimately obtain stabilization
,
and we ultimately obtain stabilization  .
.
Consider one of the singularities 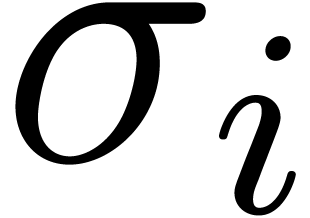 .
Since
.
Since 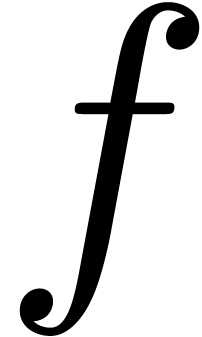 is Fuchsian at
is Fuchsian at 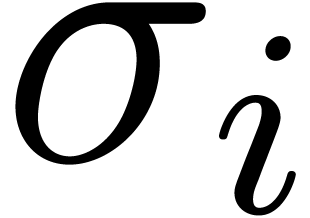 , the equation
, the equation 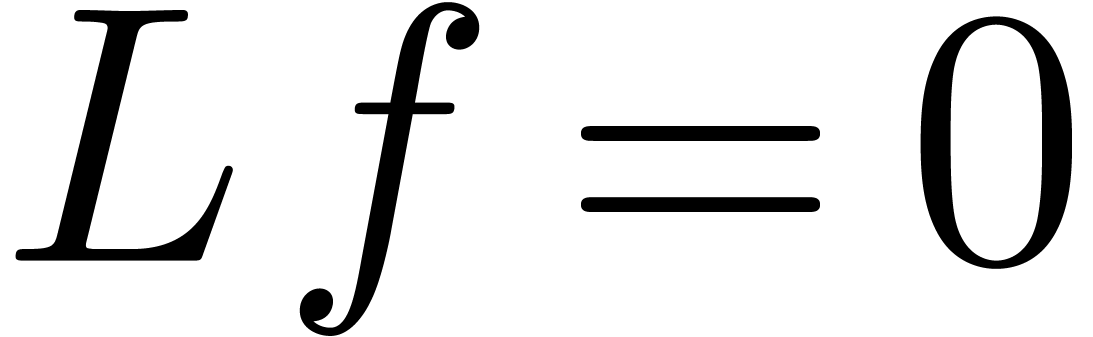 admits a
fundamental system of solutions of the form
admits a
fundamental system of solutions of the form
where 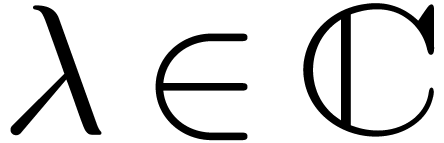 and
and  are convergent
power series. The coefficients of
are convergent
power series. The coefficients of  lie in the
field
lie in the
field  generated by all generalized power series
of this form. Again, the only elements of
generated by all generalized power series
of this form. Again, the only elements of  with a
trivial monodromy around
with a
trivial monodromy around  are convergent Laurent
series at
are convergent Laurent
series at 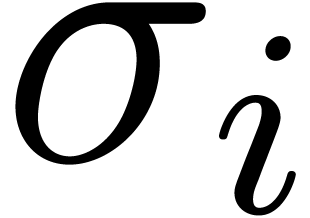 . Since analytic
continuation around
. Since analytic
continuation around 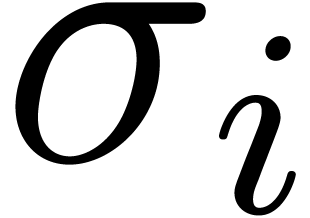 leaves the operator
leaves the operator  unchanged, it follows that the coefficients of
unchanged, it follows that the coefficients of  are meromorphic on
are meromorphic on  .
We conclude in a similar way as in the proof of theorem 8.
.
We conclude in a similar way as in the proof of theorem 8.
Remark 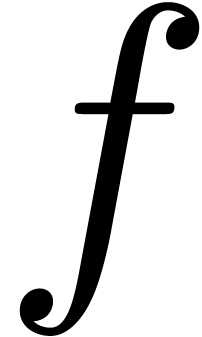 admits at worse a Fuchsian singularity at
admits at worse a Fuchsian singularity at
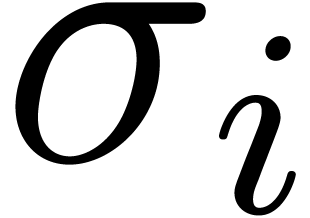 is essential for the algorithm to work. For
instance, in the case of the function
is essential for the algorithm to work. For
instance, in the case of the function
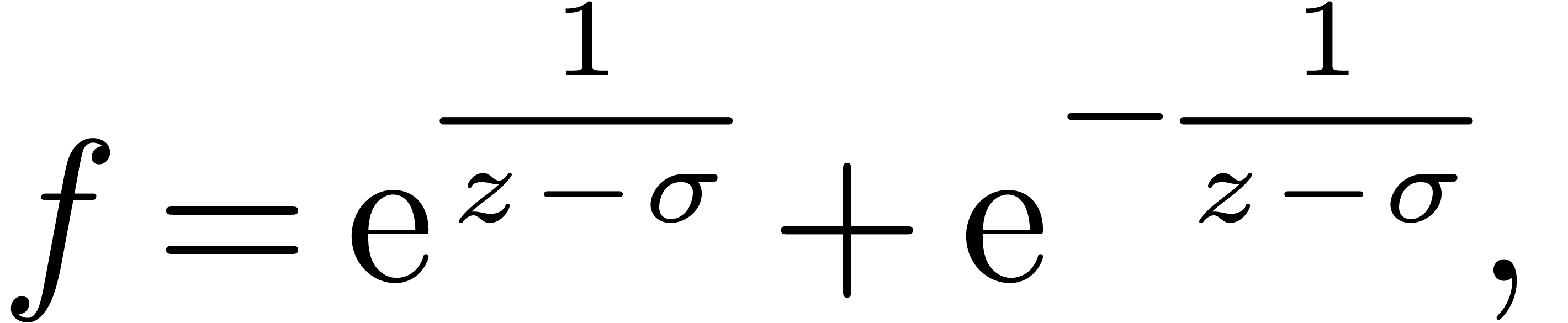
the monodromy around  is trivial, whence applying
the algorithm for
is trivial, whence applying
the algorithm for  would simply result in having
would simply result in having
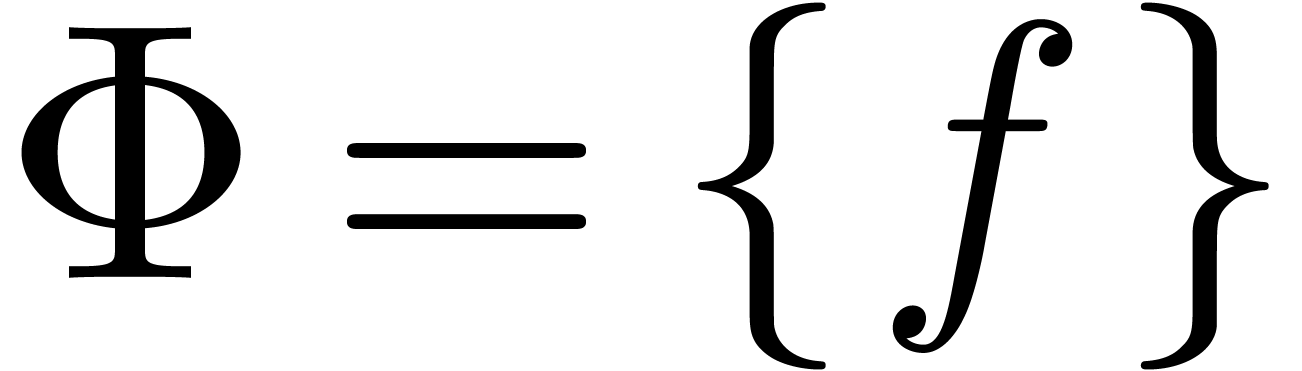 at step 3. Even though
at step 3. Even though 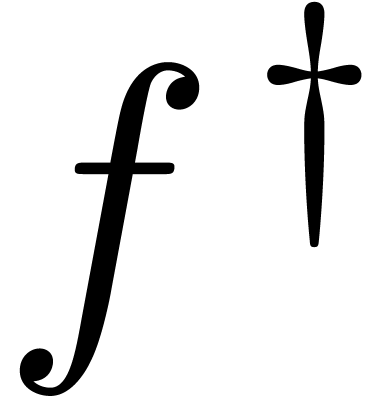 has no monodromy around
has no monodromy around  ,
this function is no longer a Laurent series. In fact, the desired
vanishing operator has second order in this case, but it cannot be read
off directly from
,
this function is no longer a Laurent series. In fact, the desired
vanishing operator has second order in this case, but it cannot be read
off directly from  .
.
In the case when we have no algorithm or no efficient algorithm for the
analytic continuation of  ,
the algorithms of section 6 can no longer be used. In this
section, we will describe a purely numerical approach for the detection
of analytic relations on a closed disk of radius
,
the algorithms of section 6 can no longer be used. In this
section, we will describe a purely numerical approach for the detection
of analytic relations on a closed disk of radius 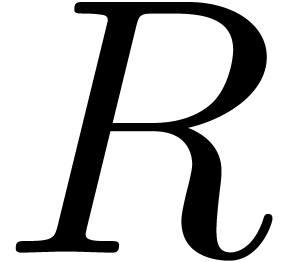 . Modulo the change of variables
. Modulo the change of variables 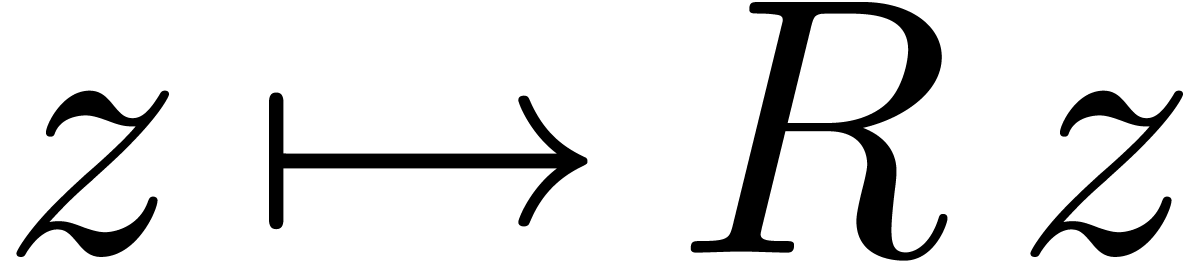 , it suffices to consider the case when
, it suffices to consider the case when 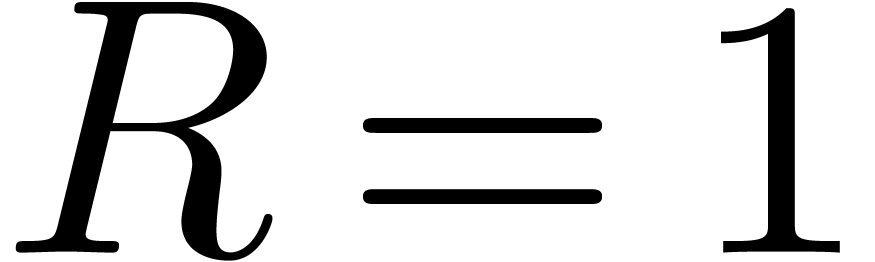 .
.
Given an order 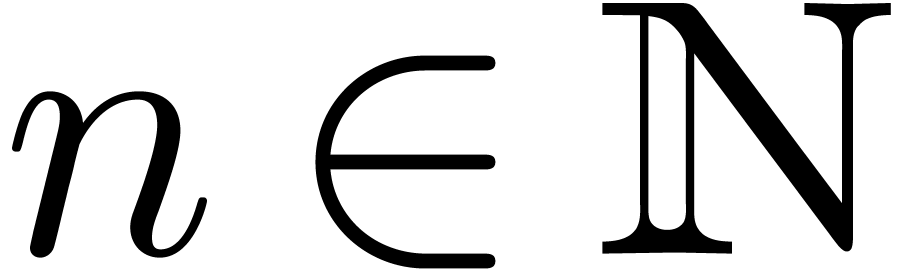 , we will
denote by
, we will
denote by 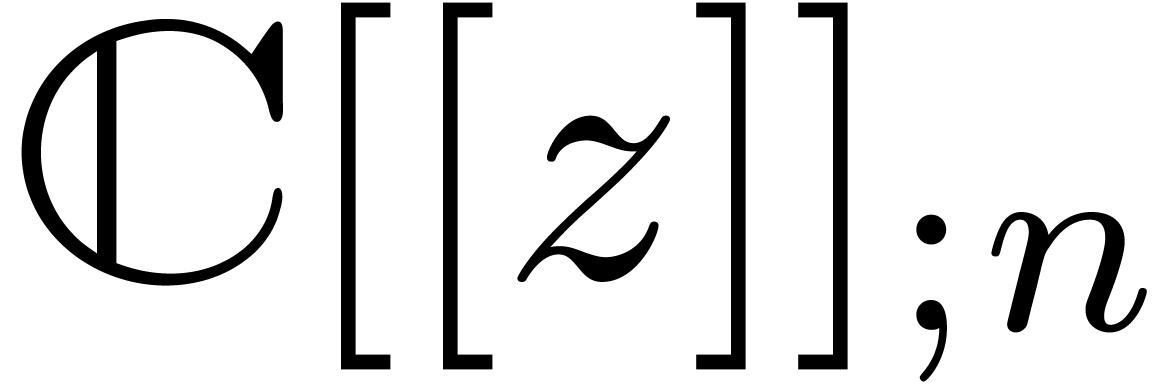 the set of power series
the set of power series  with
with 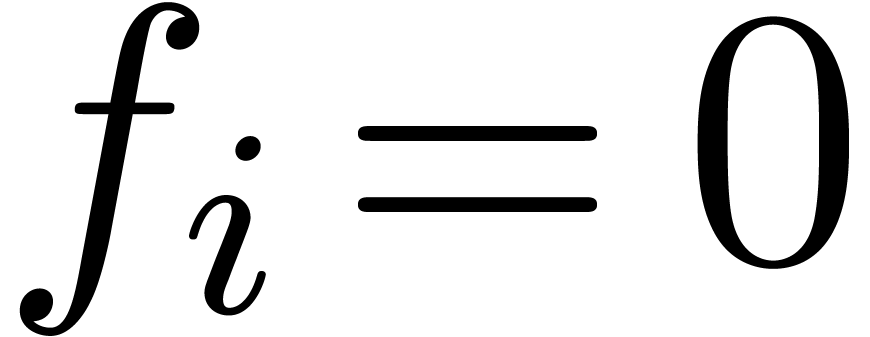 for all
for all 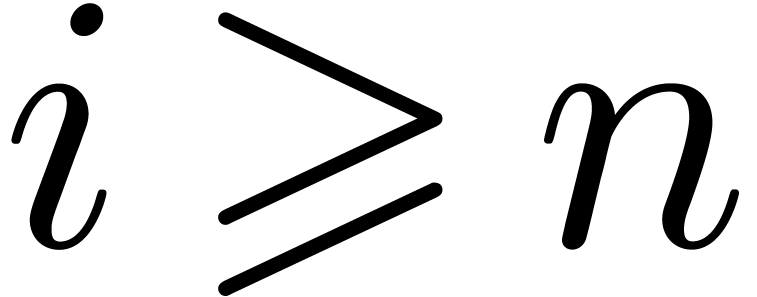 . When truncating the usual multiplication on
. When truncating the usual multiplication on
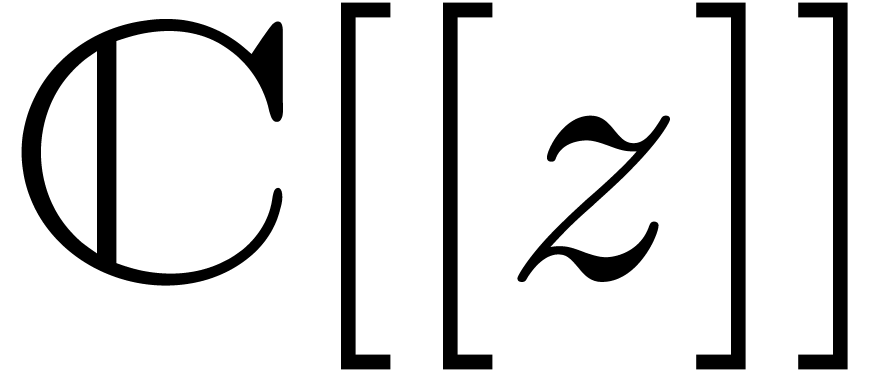 at order
at order  ,
we give
,
we give  a ring structure, which is isomorphic to
a ring structure, which is isomorphic to
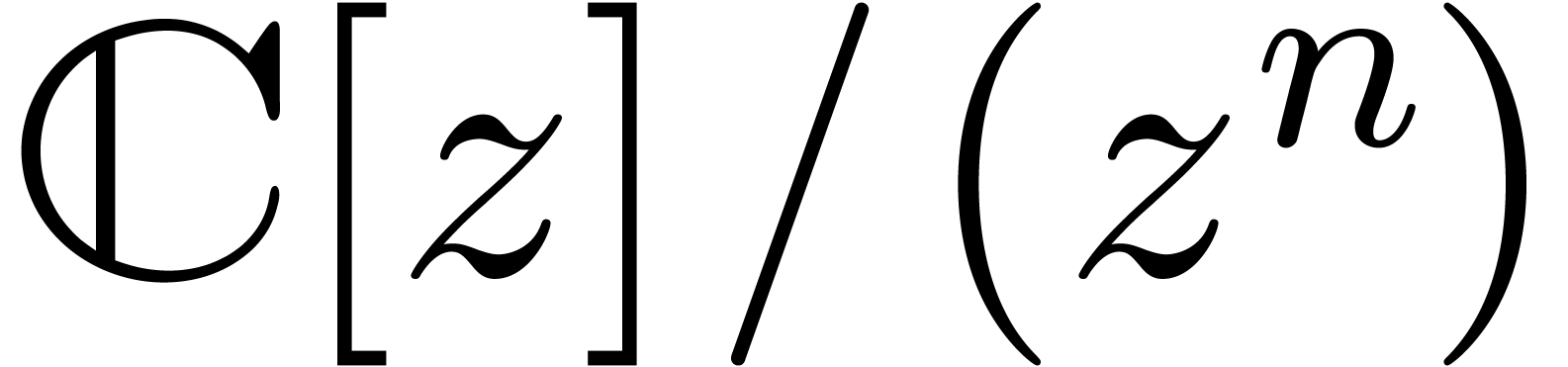 . We will denote by
. We will denote by 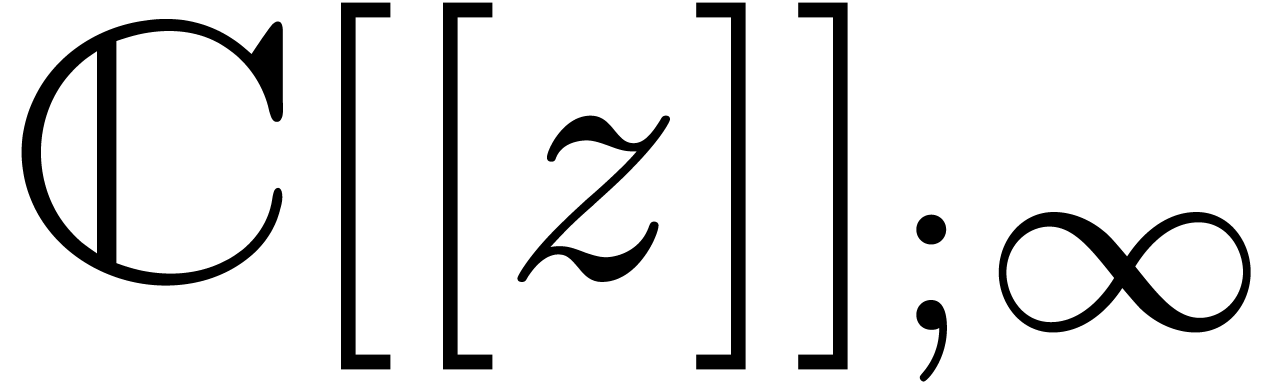 the Hilbert space of all power series
the Hilbert space of all power series  with finite
with finite 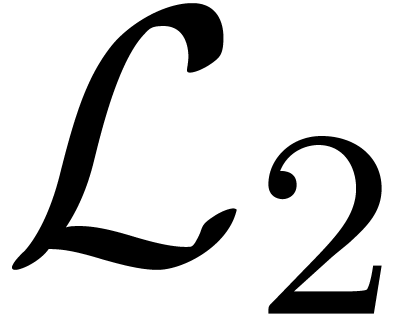 norm
norm
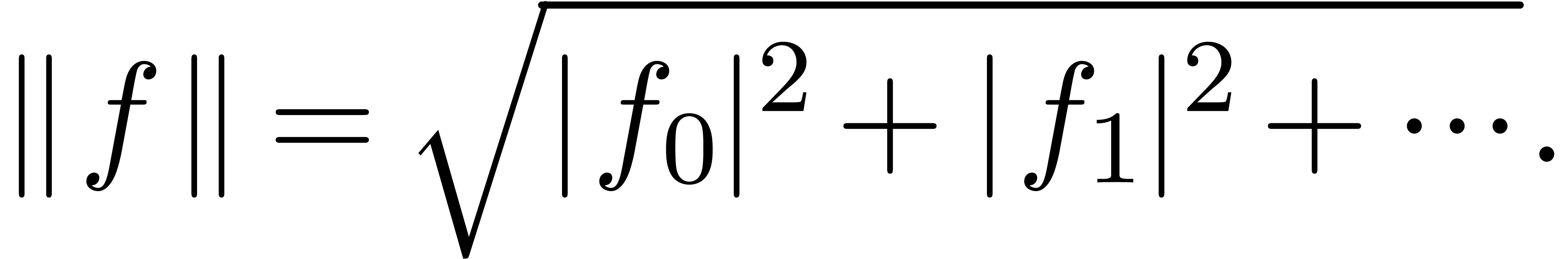
Notice that any power series that converges on the closed unit disk has
finite norm, but a power series with finite norm is only guaranteed to
converge on the open unit disk. More generally, the norm of a vector
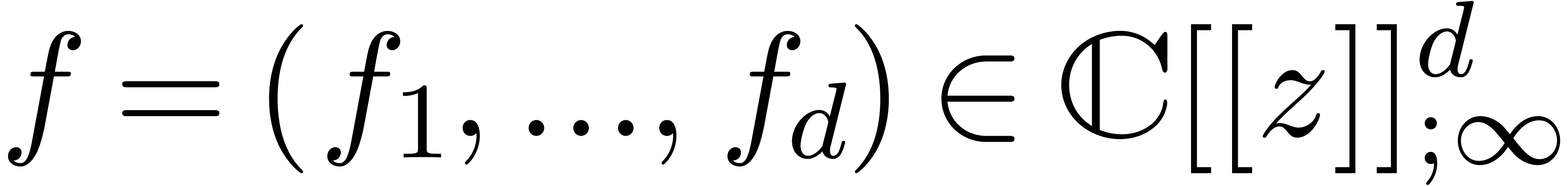 is given by
is given by
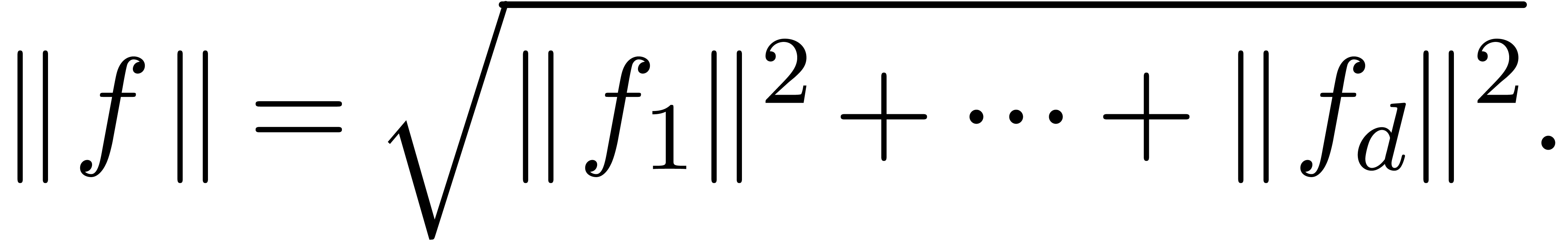
The spaces  can be considered as an increasing
sequence of Hilbert spaces, for the restrictions of the norm on
can be considered as an increasing
sequence of Hilbert spaces, for the restrictions of the norm on 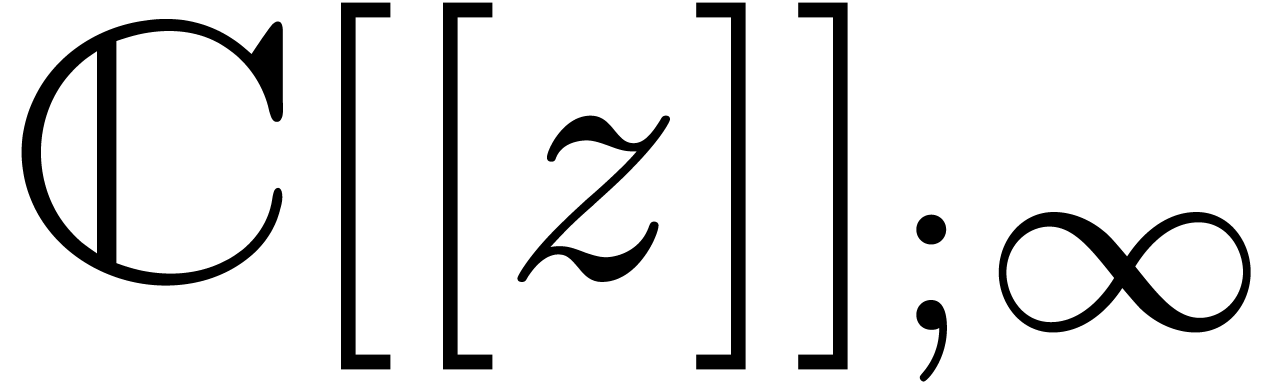 to the
to the  .
.
Let  and assume that
and assume that 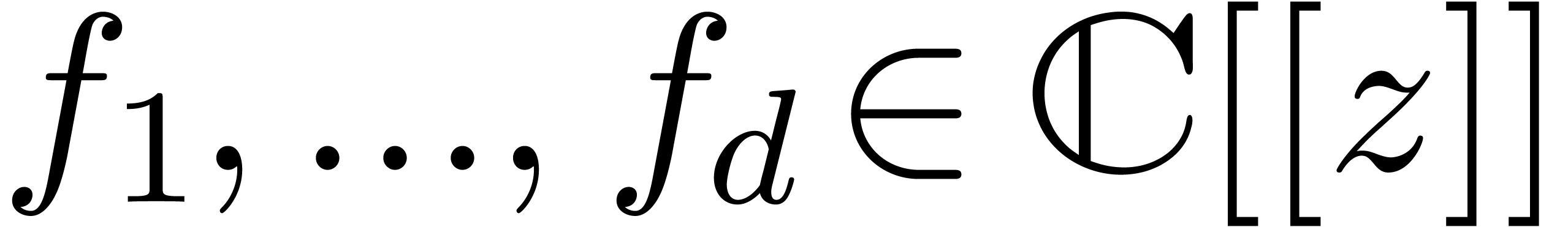 are
power series with radii of convergence at least
are
power series with radii of convergence at least  (notice that we do not assume the
(notice that we do not assume the  to be
of finite norm). We want to solve the equation
to be
of finite norm). We want to solve the equation
 |
(13) |
We will denote the vector space of all such relations 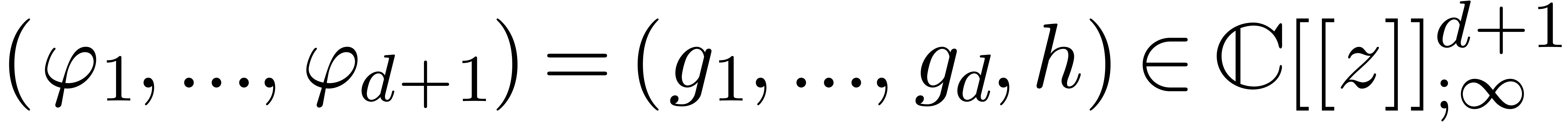 by
by  . Since the equation (13) involves an infinite number of coefficients, we need to
consider its truncated version at a finite order
. Since the equation (13) involves an infinite number of coefficients, we need to
consider its truncated version at a finite order 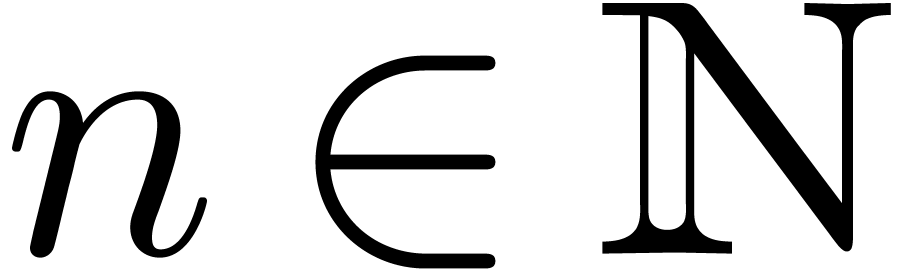 . Replacing
. Replacing  by their
truncations in
by their
truncations in  , we will
search for non-trivial solutions of the equation
, we will
search for non-trivial solutions of the equation
 |
(14) |
In a way which will be made more precise below, we will require the
norms of 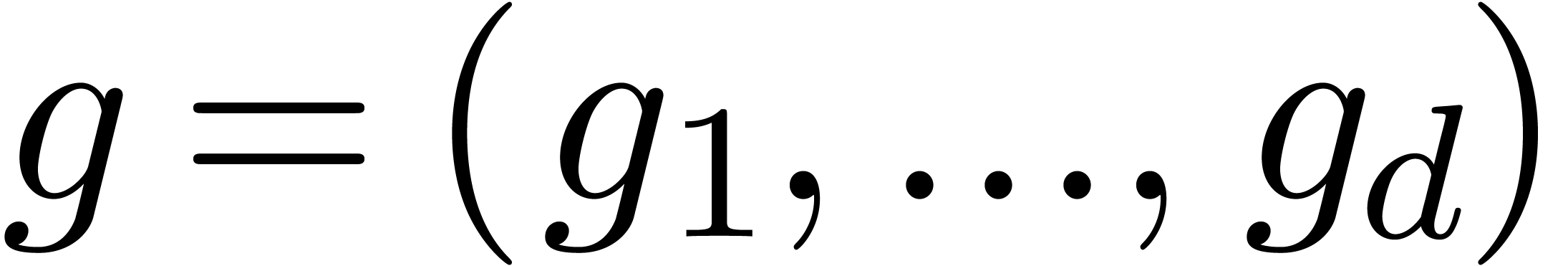 and
and 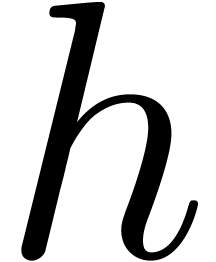 to remain
of the same orders of magnitude as the vector
to remain
of the same orders of magnitude as the vector  . We will denote by
. We will denote by 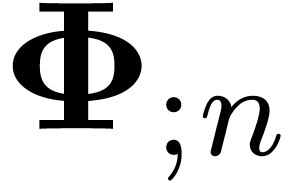 the
vector space of all
the
vector space of all 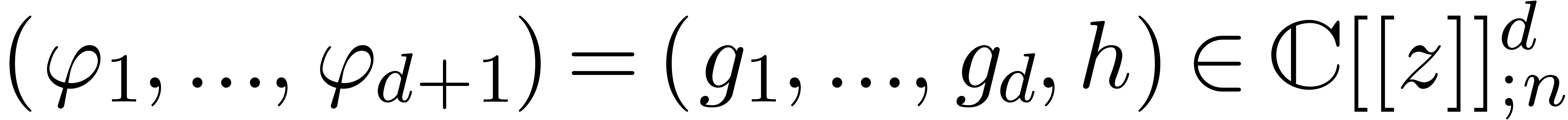 which satisfy (14).
If the norms of the solutions to the truncated problems tend to a limit
for
which satisfy (14).
If the norms of the solutions to the truncated problems tend to a limit
for  , then we will prove that
these solutions tend to a solution of the original problem (13).
, then we will prove that
these solutions tend to a solution of the original problem (13).
Let us reformulate the truncated problem in terms of linear algebra. The
series  give rise to an
give rise to an 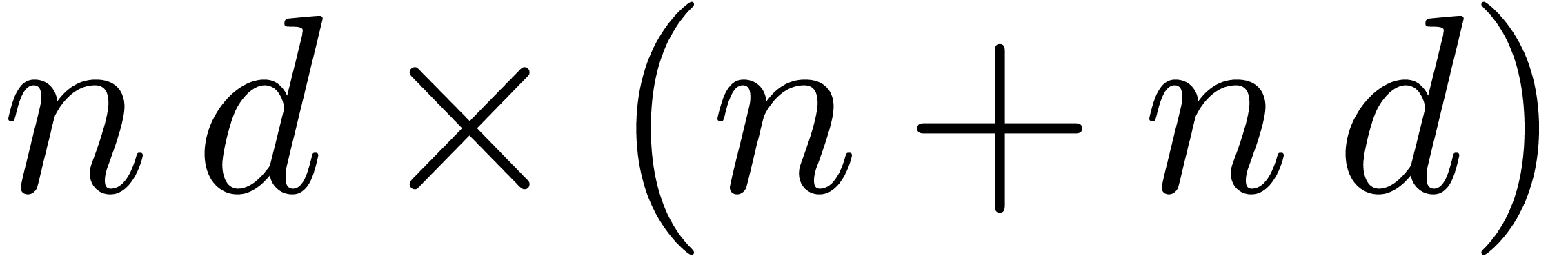 matrix
matrix
The unknown series  give rise to a row vector
give rise to a row vector
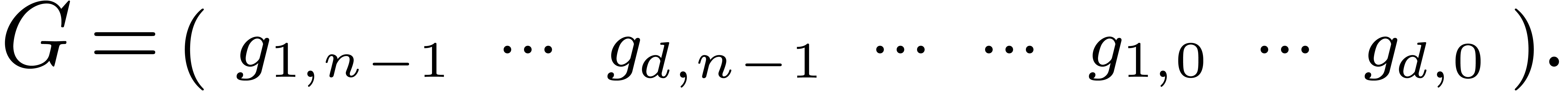
Setting  , we then have
, we then have
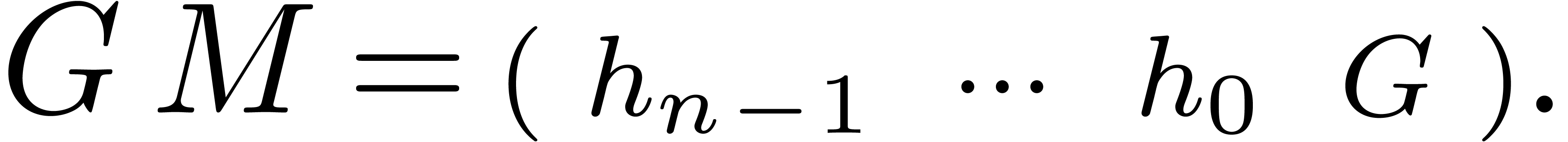
Putting the first  entries on the right hand side
and grouping by packets of
entries on the right hand side
and grouping by packets of  entries, it follows
that
entries, it follows
that 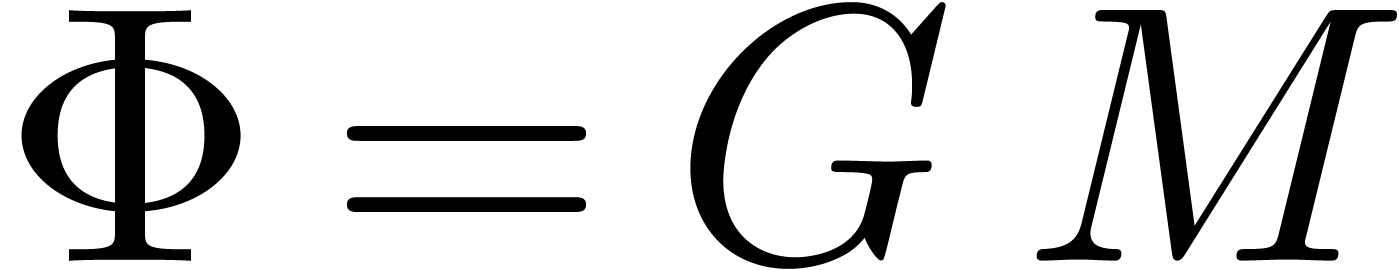 encodes the relation
encodes the relation 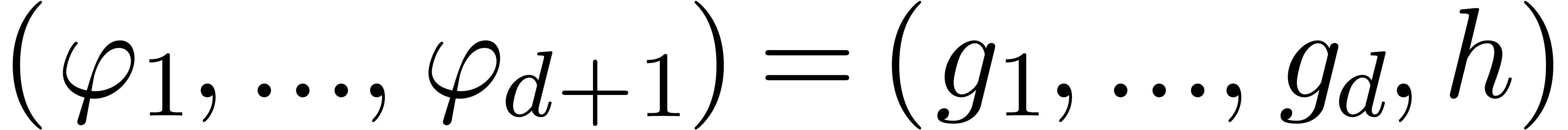 . This reduces the problem to finding those vectors
. This reduces the problem to finding those vectors
 for which
for which 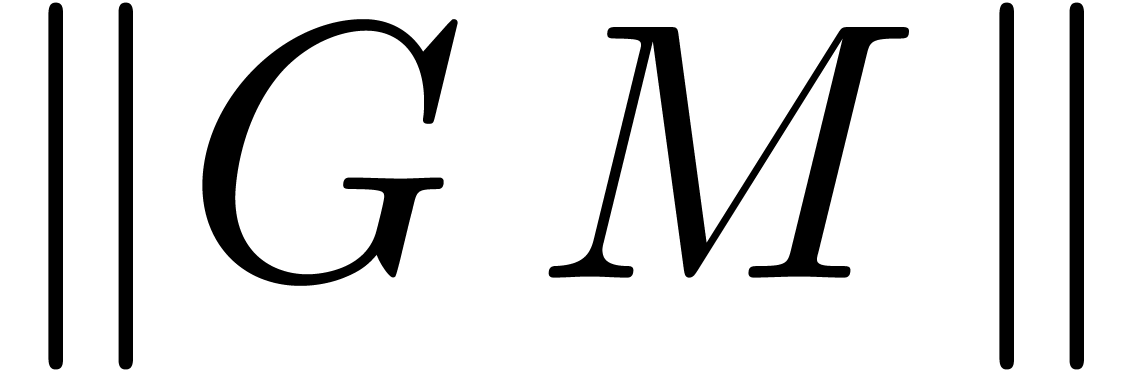 is of the same
order of magnitude as the vector
is of the same
order of magnitude as the vector  .
.
We start with the computation of a thin LQ decomposition of 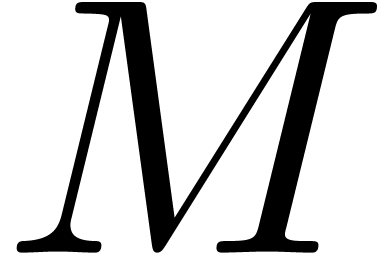 . This can for instance be done using the
Gram-Schmidt process: starting with the first row, we orthogonally
project each row on the vector space spanned by the previous rows. This
results in a decomposition
. This can for instance be done using the
Gram-Schmidt process: starting with the first row, we orthogonally
project each row on the vector space spanned by the previous rows. This
results in a decomposition
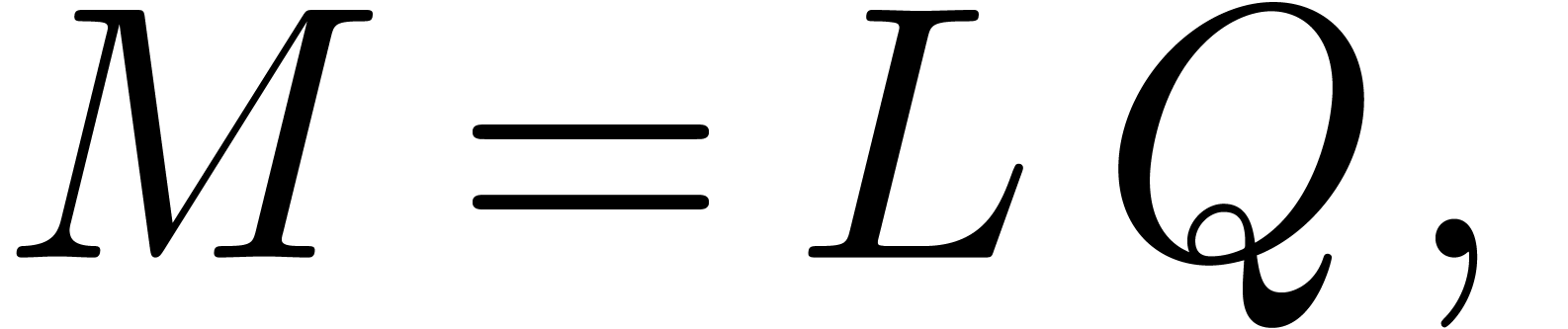
where  is a lower triangular
is a lower triangular  matrix with ones on the diagonal and
matrix with ones on the diagonal and  is an
is an 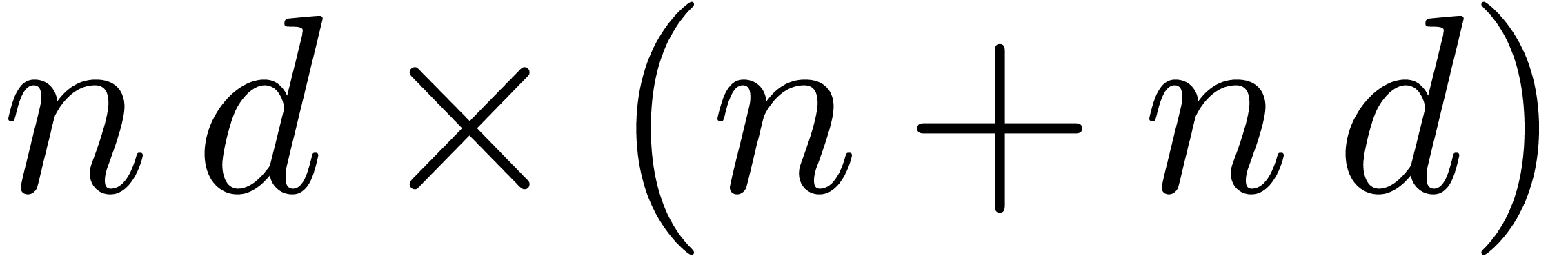 matrix, whose rows are mutually orthogonal
(i.e.
matrix, whose rows are mutually orthogonal
(i.e. 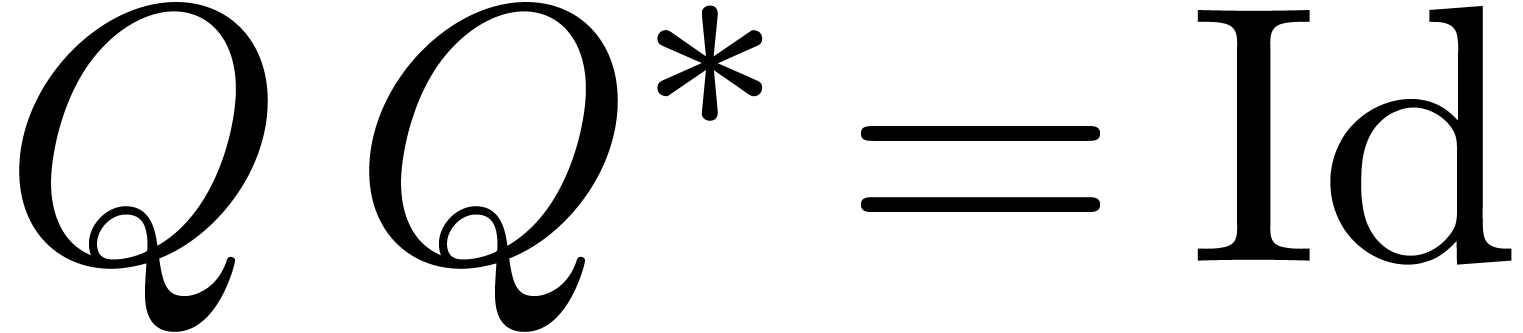 ). Now
consider the matrix
). Now
consider the matrix  formed by the
formed by the 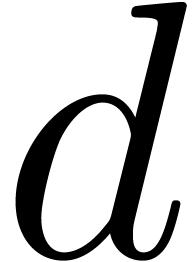 last rows of
last rows of 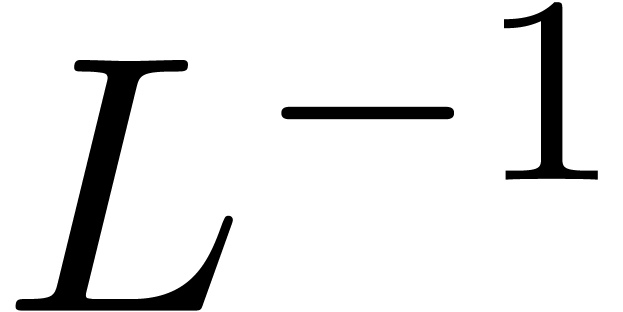 .
Then each row
.
Then each row 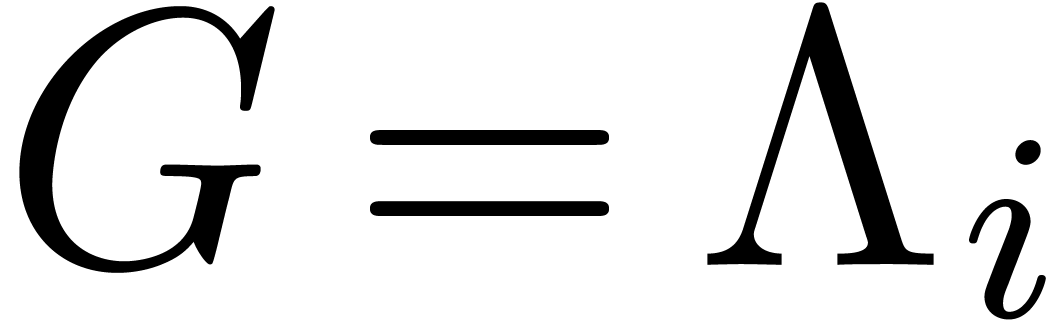 gives rise to a relation (14),
encoded by
gives rise to a relation (14),
encoded by 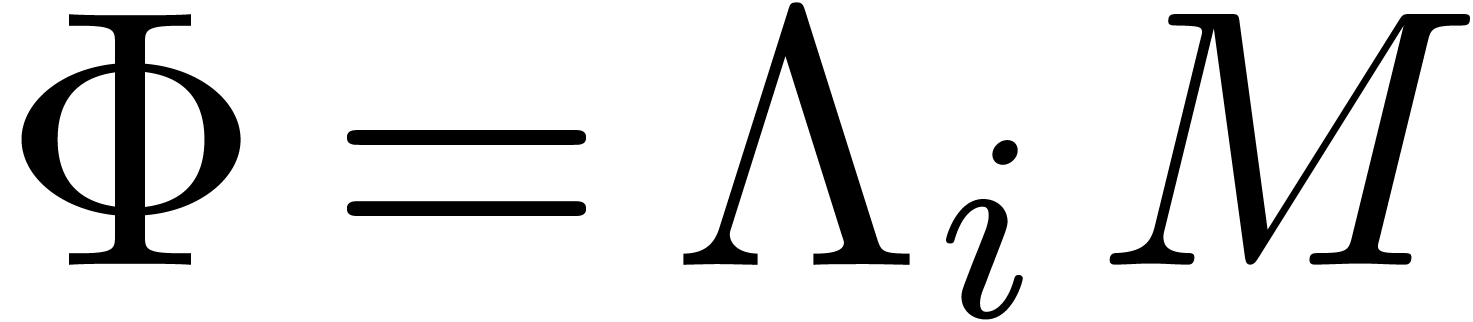 . Moreover, this
relation is normal or
. Moreover, this
relation is normal or 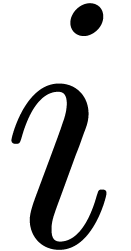 -normal,
in the sense that
-normal,
in the sense that 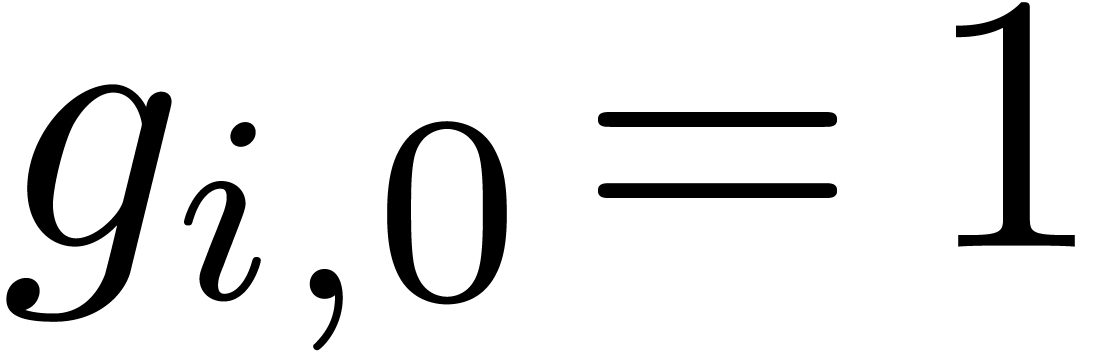 and
and 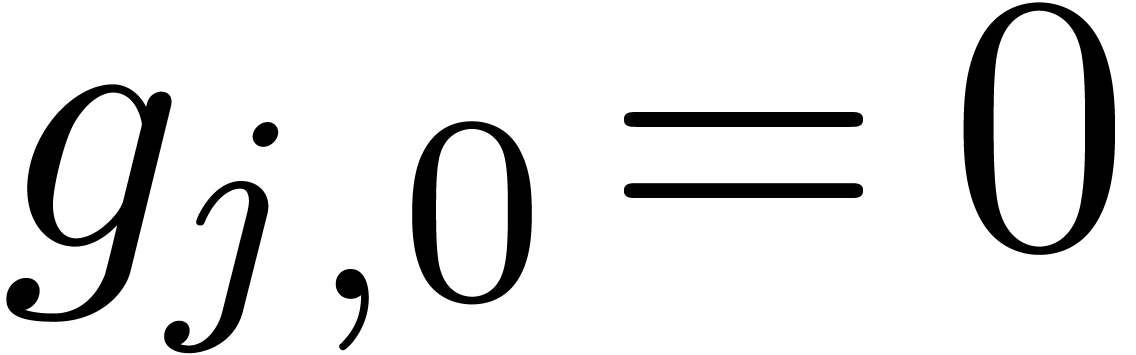 for all
for all  . Since
. Since  is the shortest vector in
is the shortest vector in 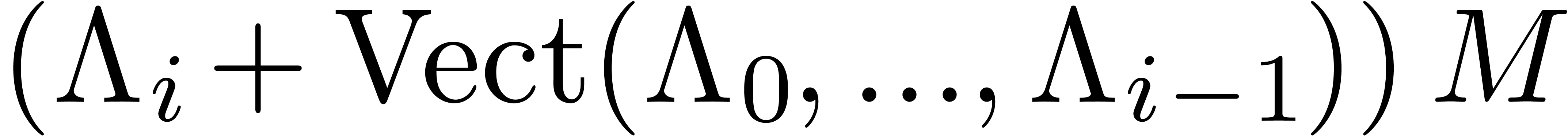 ,
the relation is also minimal in norm, among all
,
the relation is also minimal in norm, among all  -normal relations. Choosing the row
-normal relations. Choosing the row  for which
for which 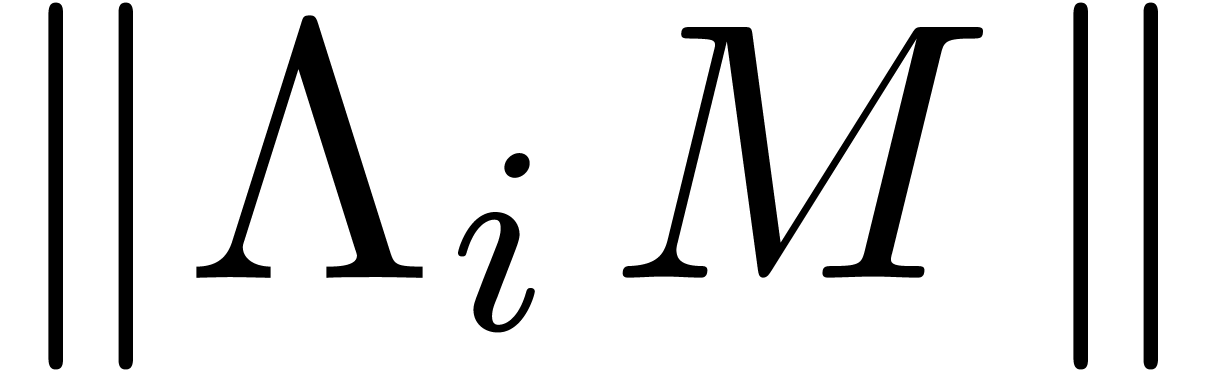 is minimal, our algorithm simply
returns the corresponding relation. Then our algorithm has the following
fundamental property:
is minimal, our algorithm simply
returns the corresponding relation. Then our algorithm has the following
fundamental property:
 for which
for which 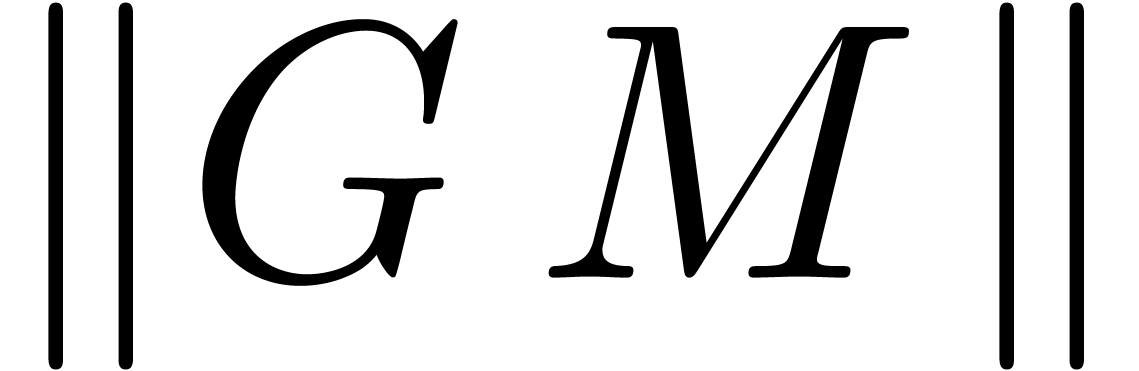 is minimal.
is minimal.
Let us now return to the case when 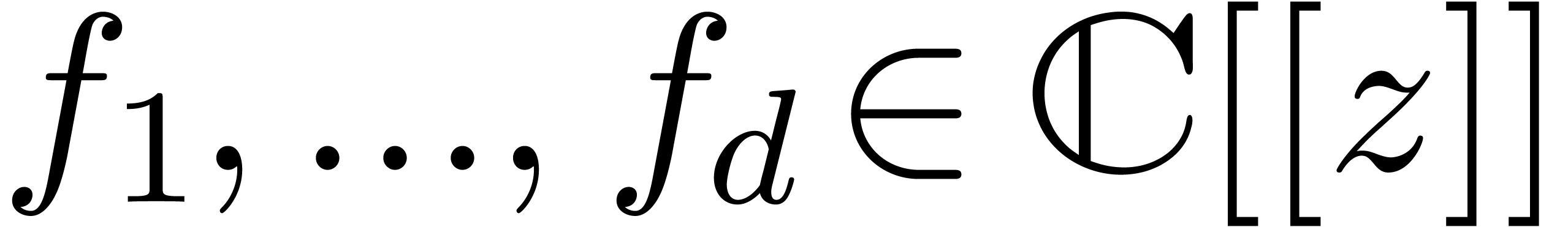 are no longer
truncated, but all have a radius of convergence
are no longer
truncated, but all have a radius of convergence 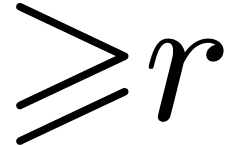 . A relation (13) is again said to be
normal or
. A relation (13) is again said to be
normal or  -normal
if
-normal
if 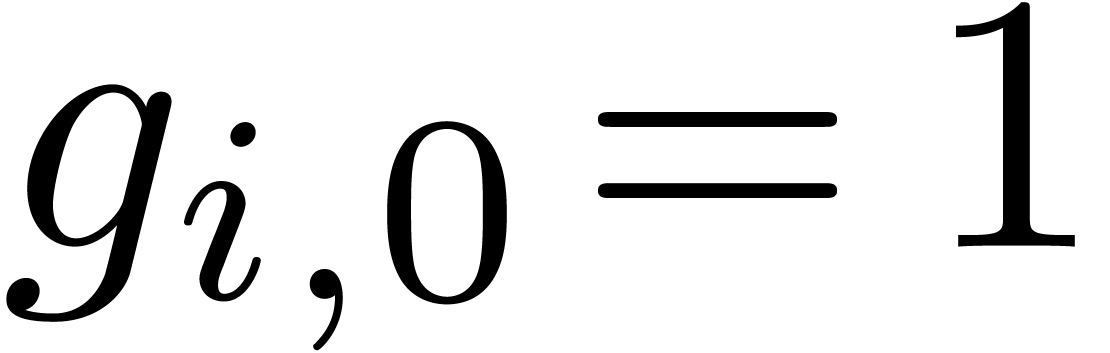 and
and 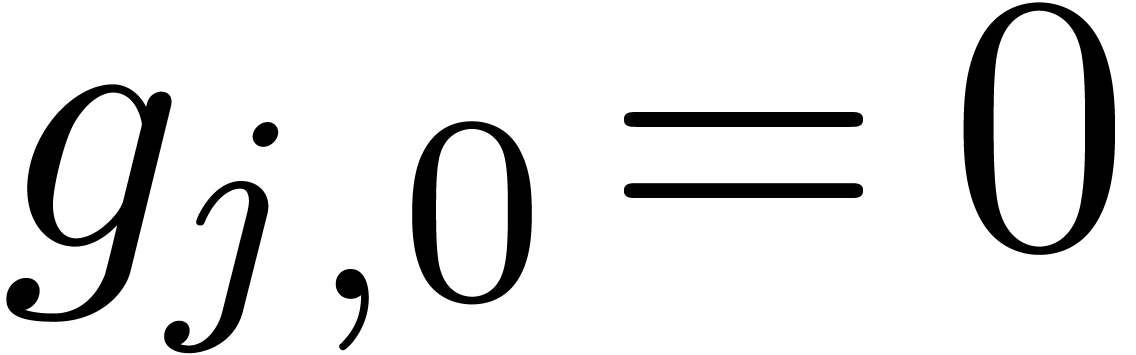 for all
for all  . Under the limit
. Under the limit  , we claim that our algorithm finds a minimal
normal relation, if there exists a relation of the form (13):
, we claim that our algorithm finds a minimal
normal relation, if there exists a relation of the form (13):
Assume that 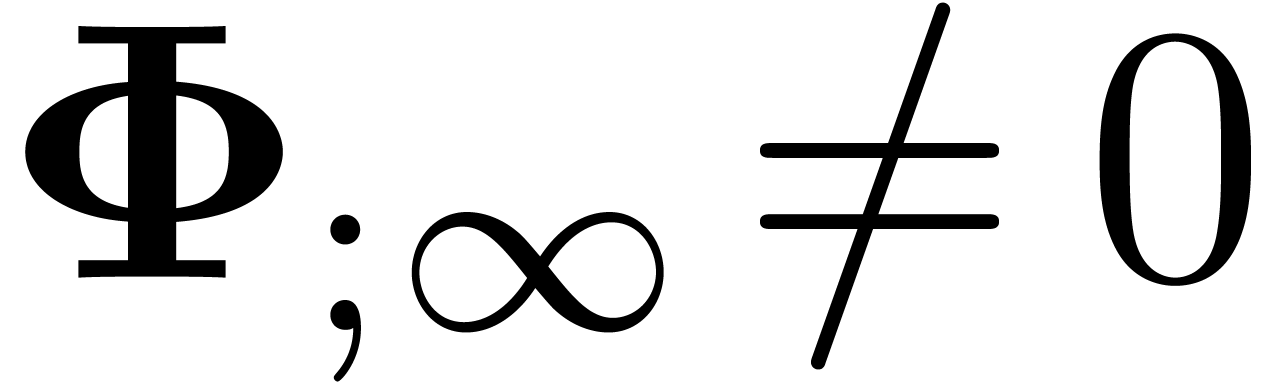 . Then
. Then
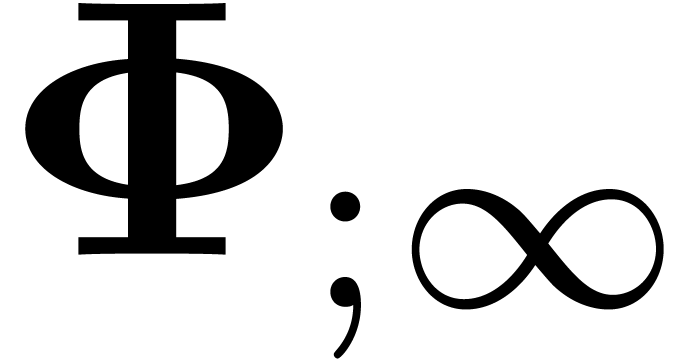 contains a minimal normal relation. For
each
contains a minimal normal relation. For
each  ,
,  contains at most one minimal
contains at most one minimal  -normal relation.
-normal relation.
Assume that  is a minimal
is a minimal 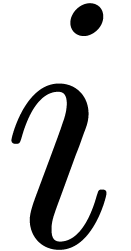 -normal relation. For each
-normal relation. For each 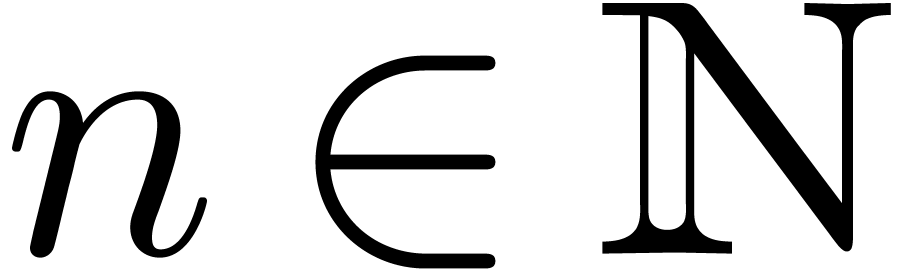 , let
, let 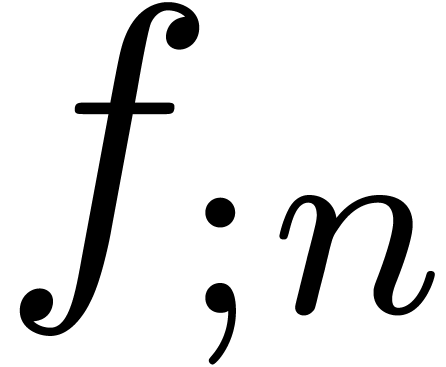 be the
truncation of
be the
truncation of  at order
at order 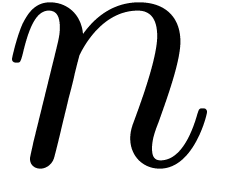 and consider the corresponding minimal
and consider the corresponding minimal  -normal relation
-normal relation 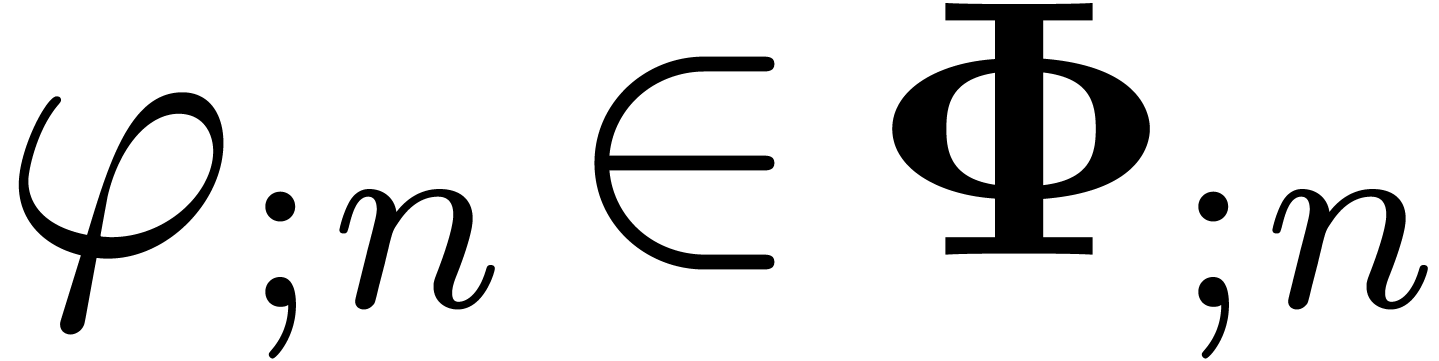 . Then the relations
. Then the relations  converge to
converge to  in
in  .
.
If 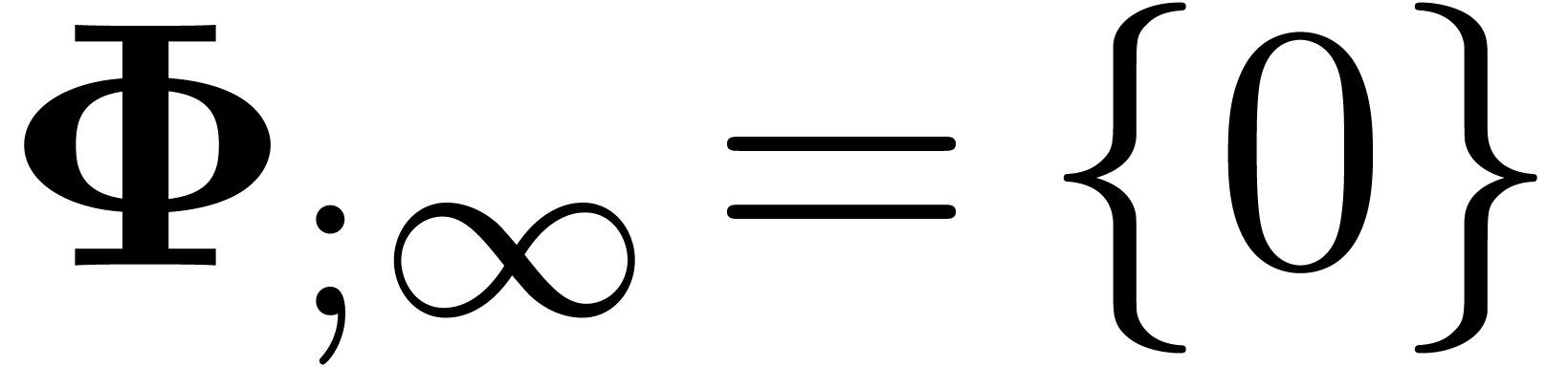 , then the norms
, then the norms
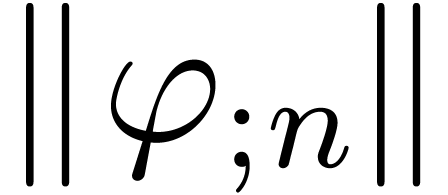 , with
, with 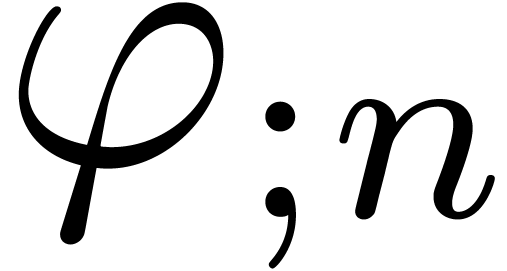 as in
as in  .
.
Proof. A non trivial relation 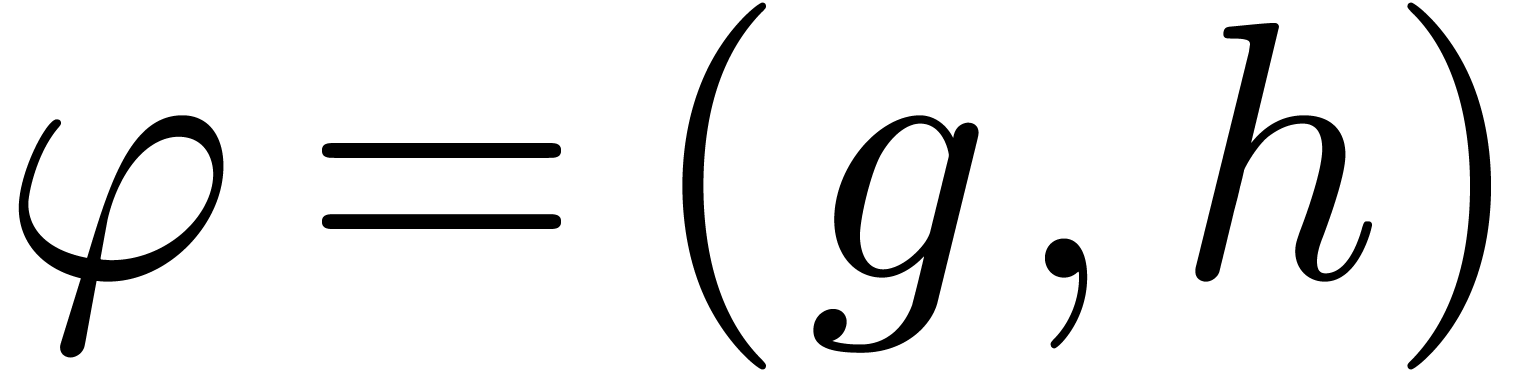 is easily normalized: we first divide
is easily normalized: we first divide  by
by  , where
, where 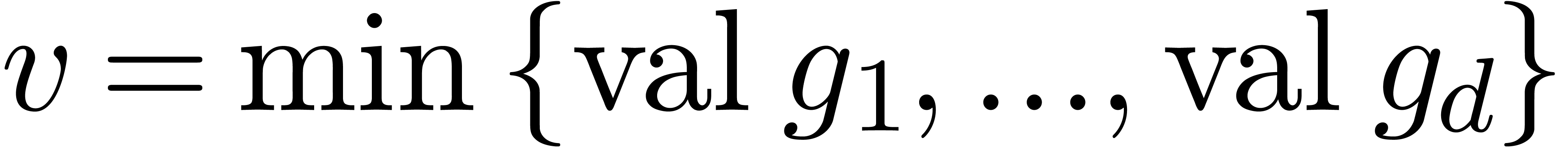 . We next divide by
. We next divide by 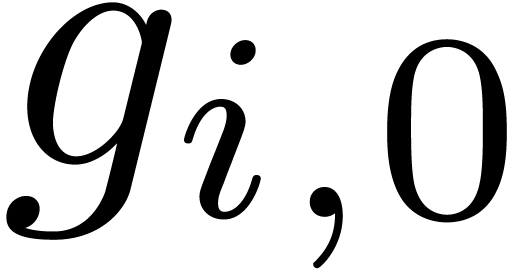 ,
where
,
where  is largest with
is largest with 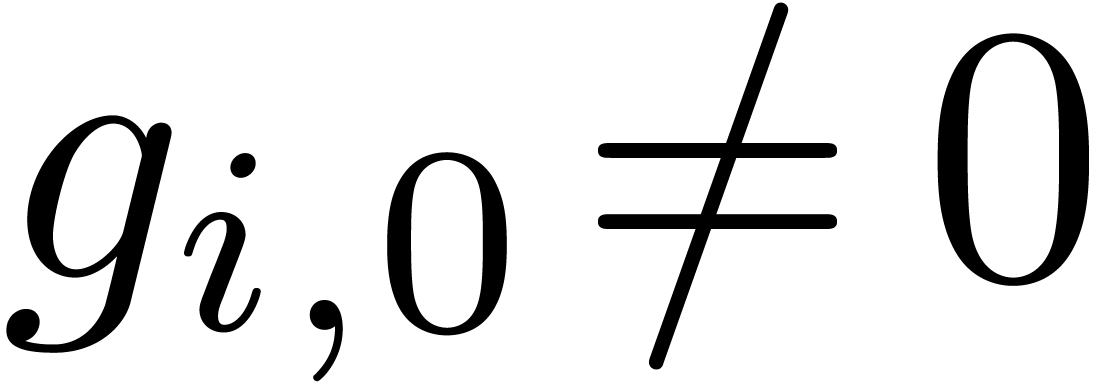 . Now the set of all
. Now the set of all  -normal
relations is a closed affine subspace of
-normal
relations is a closed affine subspace of  .
The orthogonal projection of
.
The orthogonal projection of  on this subspace
yields a unique
on this subspace
yields a unique  -normal
relation of minimal norm. This proves (a).
-normal
relation of minimal norm. This proves (a).
Assume that there exists an  -normal
relation
-normal
relation 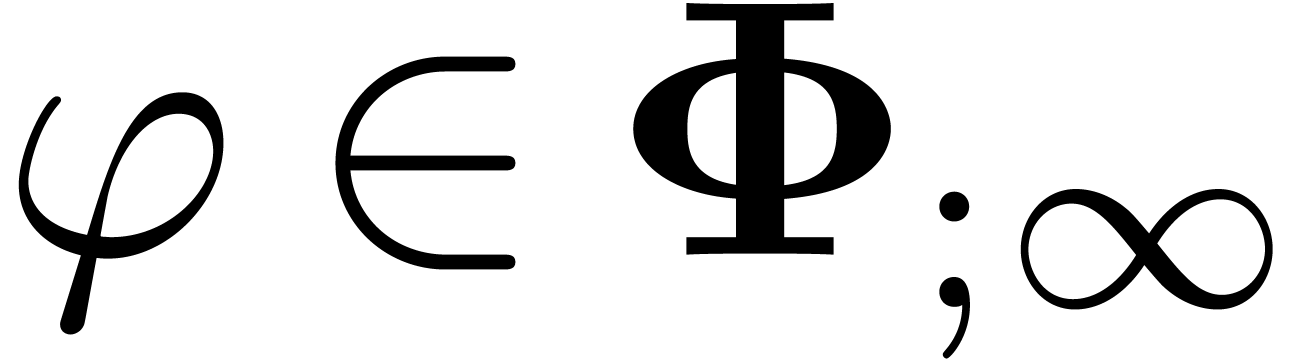 be the minimal such relation. Given an order
be the minimal such relation. Given an order 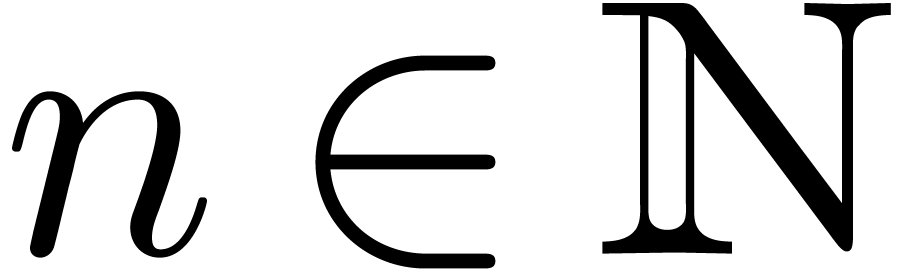 , consider the minimal
, consider the minimal  -normal relation
-normal relation 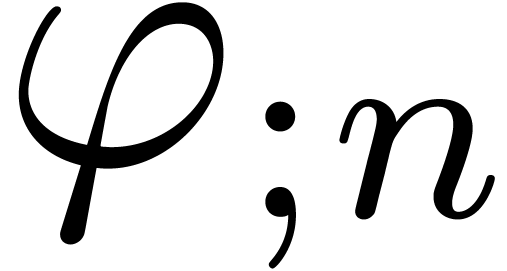 at this
order. Truncation of this relation at a smaller order
at this
order. Truncation of this relation at a smaller order 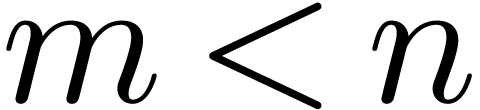 yields an
yields an  -normal relation
-normal relation
 at order
at order  with
with 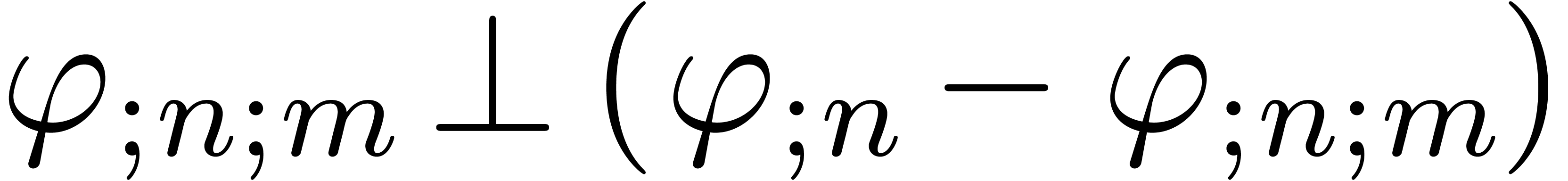 , whence
, whence
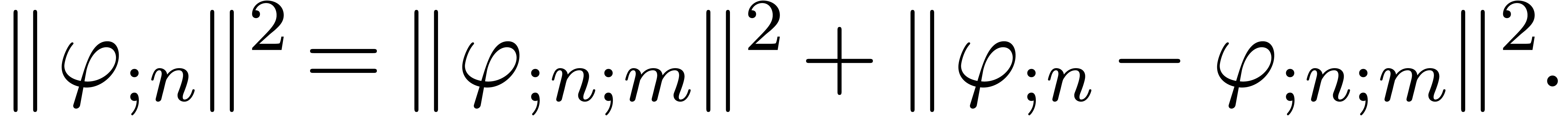 |
(15) |
Moreover, since 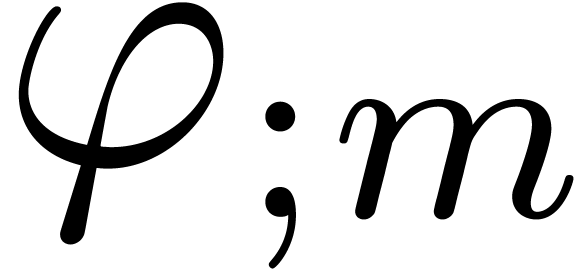 is the projection of
is the projection of  on the affine space of
on the affine space of  -normal
relations at order
-normal
relations at order 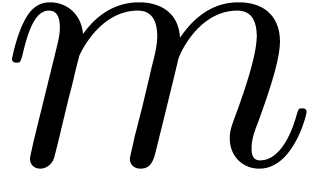 , we have
, we have
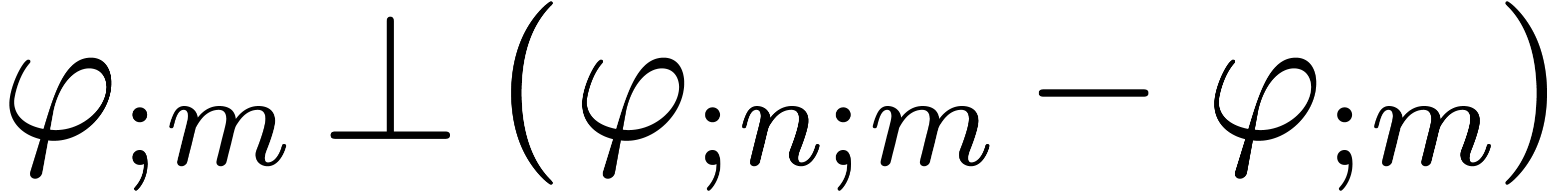 and
and
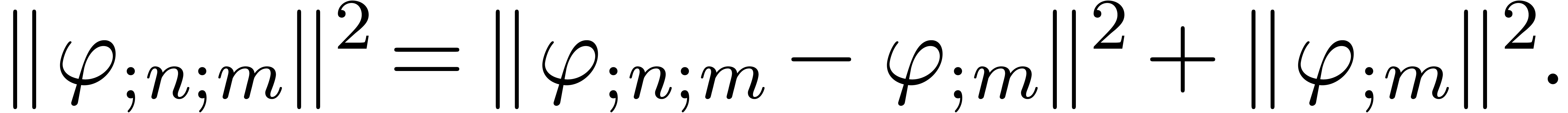 |
(16) |
Similarly, truncation of the relation  at finite
order
at finite
order 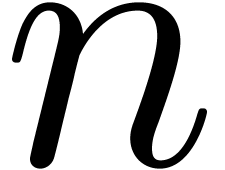 yields an
yields an 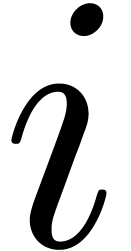 -normal
relation
-normal
relation  which satisfies
which satisfies
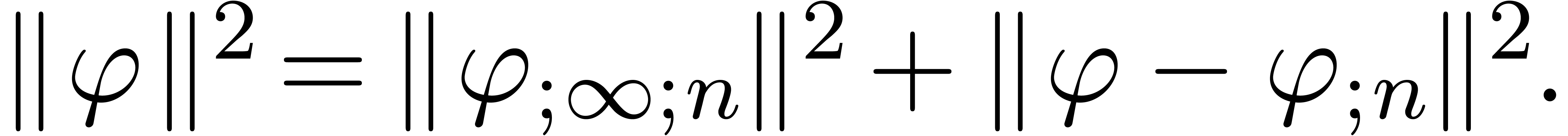
In particular, 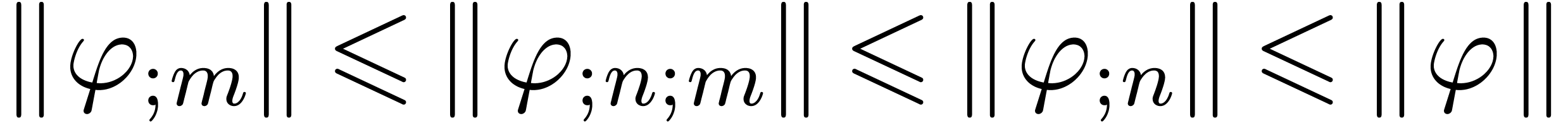 , so that
, so that
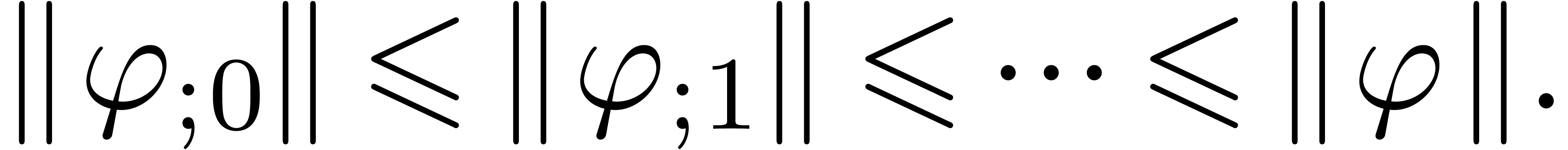
For 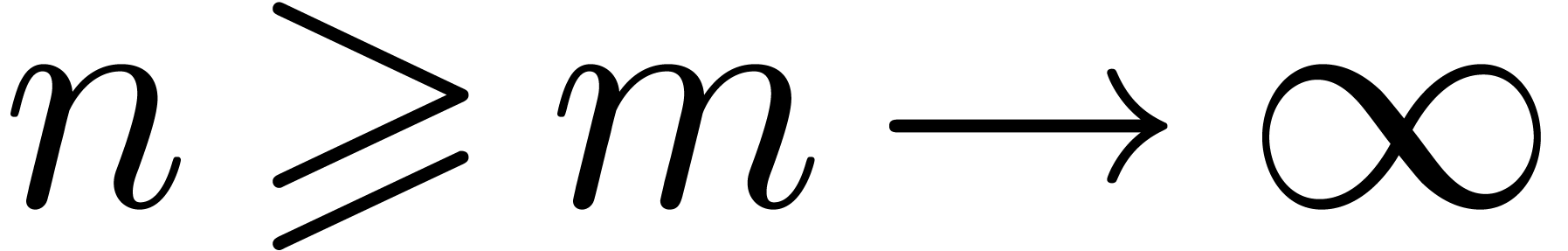 , it follows that
, it follows that 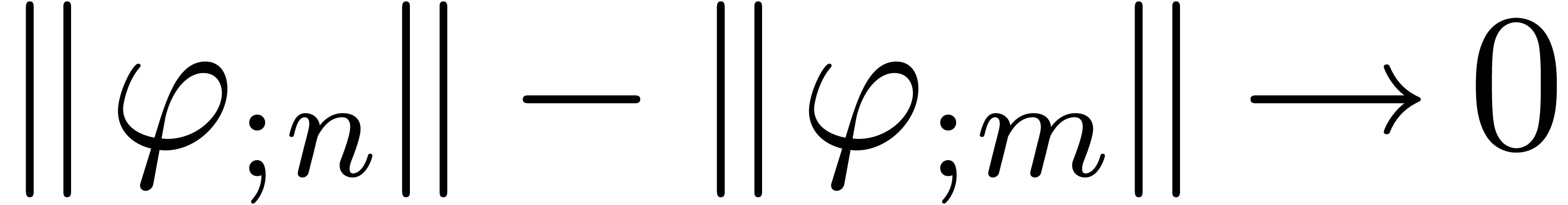 , whence
, whence
and
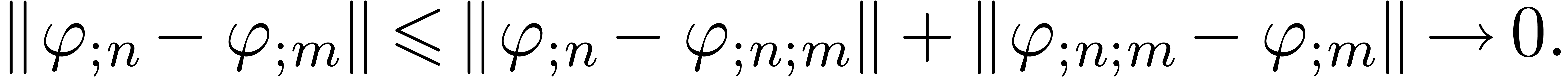
In other words, 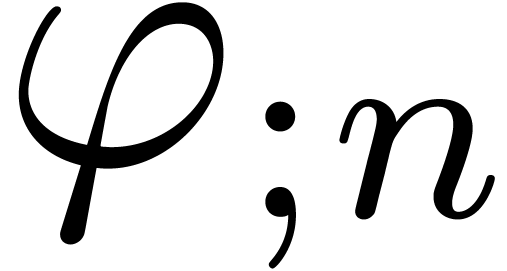 is a Cauchy sequence, which
converges to a limit
is a Cauchy sequence, which
converges to a limit 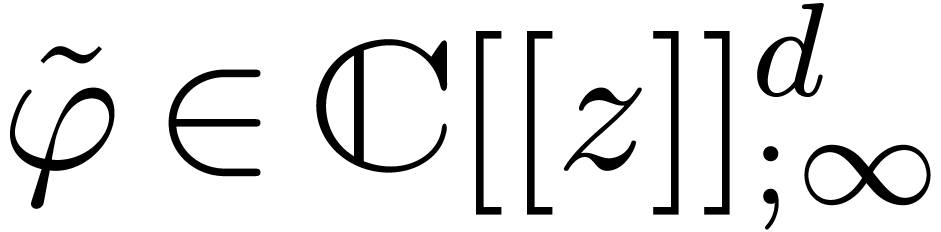 with
with  . Now for each
. Now for each 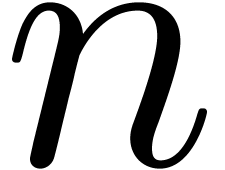 ,
we may write
,
we may write  and denote by
and denote by  the truncation of the vector
the truncation of the vector  at order
at order  . By assumption, the inner products
. By assumption, the inner products
 and
and  vanish. Since
vanish. Since 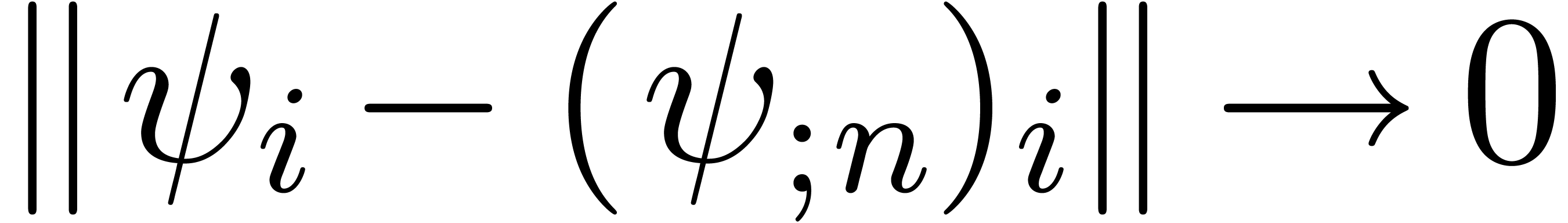 for all
for all  and
and  , we also have
, we also have  for
for
 , whence
, whence 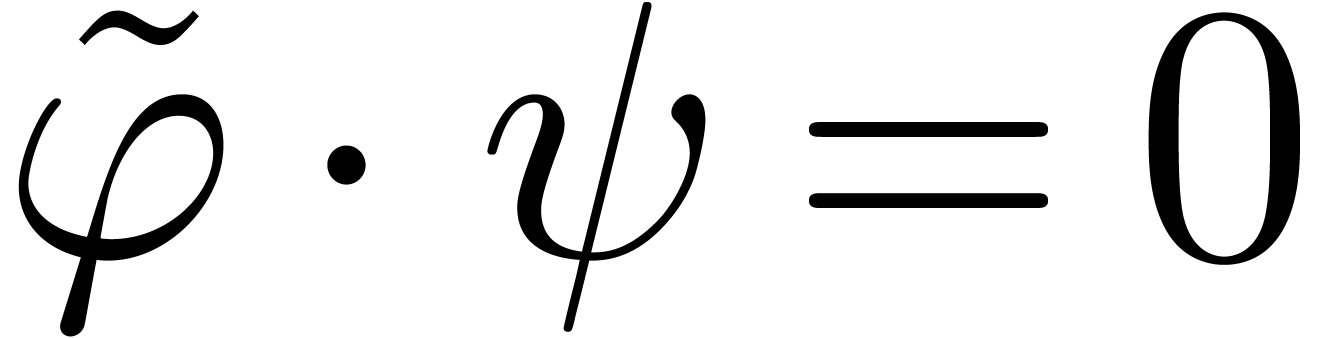 . Consequently,
. Consequently,  is an
is an
 -normal relation in
-normal relation in  . By the minimality hypothesis on
. By the minimality hypothesis on
 , we conclude that
, we conclude that  , which proves (b).
, which proves (b).
In general, the existence of a bound  with
with
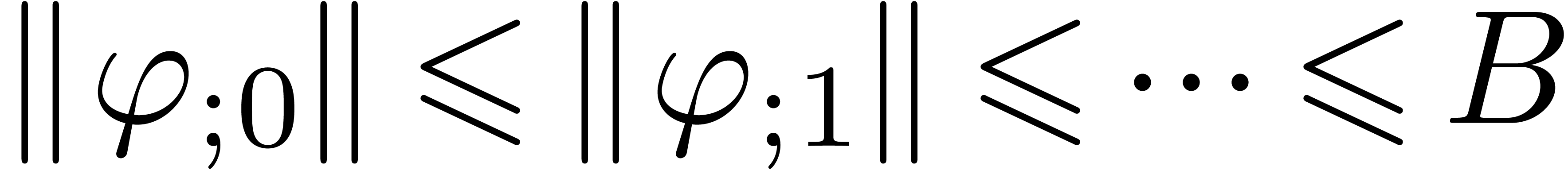
still ensures  to be a Cauchy sequence, and its
limit yields an
to be a Cauchy sequence, and its
limit yields an  -normal
relation (13). This proves the last assertion
(c).
-normal
relation (13). This proves the last assertion
(c).
Remark  with an isolated smallest singularity
at
with an isolated smallest singularity
at  of the form
of the form
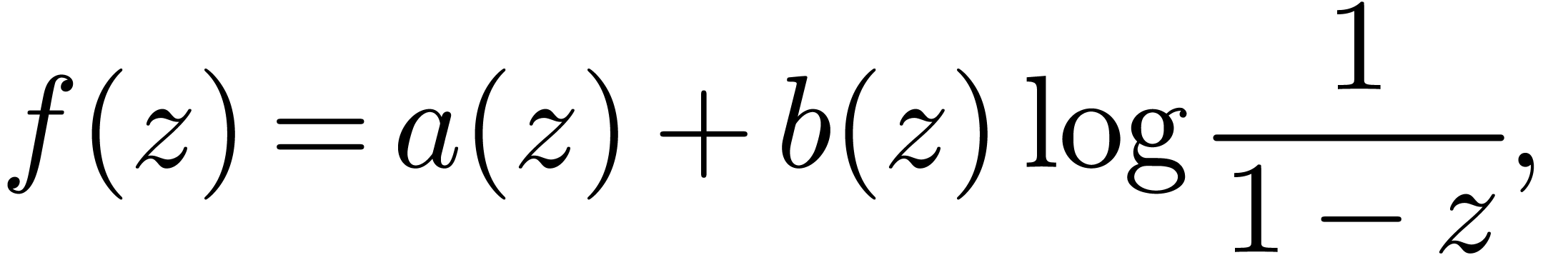
where  and
and  are analytic
at
are analytic
at  . Then the asymptotic
extrapolation of
. Then the asymptotic
extrapolation of 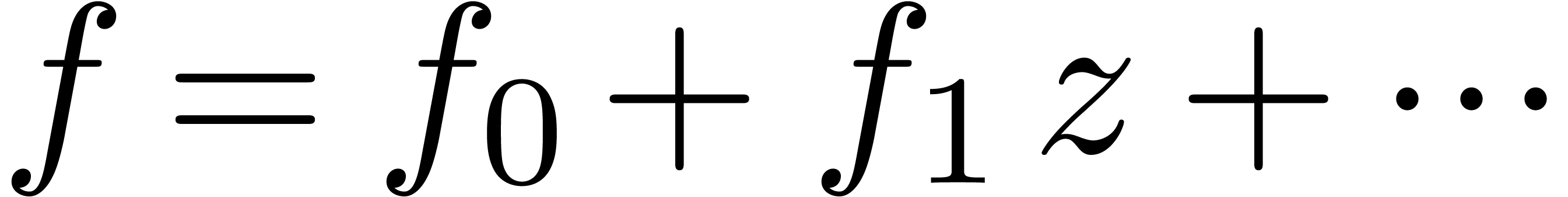 yields an asymptotic expansion
of the form
yields an asymptotic expansion
of the form
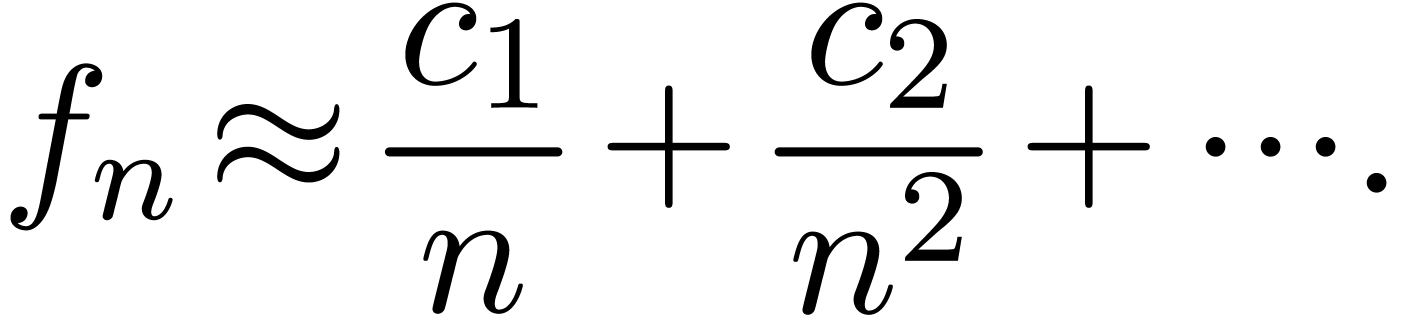
Using singularity analysis [FS96], we may then recover the
function  from the coefficients
from the coefficients 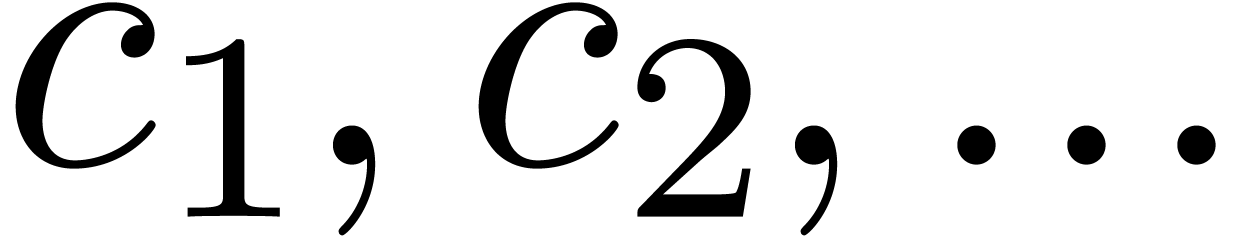 . However, this technique only works in special
cases, since the first
. However, this technique only works in special
cases, since the first  terms of the asymptotic
expansion may hide other terms, which need to be taken into account when
searching for exact dependencies.
terms of the asymptotic
expansion may hide other terms, which need to be taken into account when
searching for exact dependencies.
A first implementation of the guessing algorithm from section 7
has been made in the 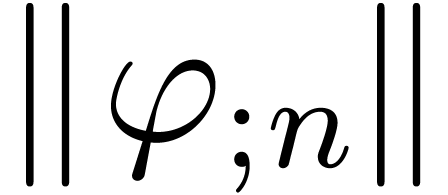 .
.
We have tested the orthogonalization algorithm on three examples of increasing difficulty, for which linear dependencies are known to exist. In order to avoid problems due to numerical instability, we have used a large working precision, of 1024 or 2048 bits.
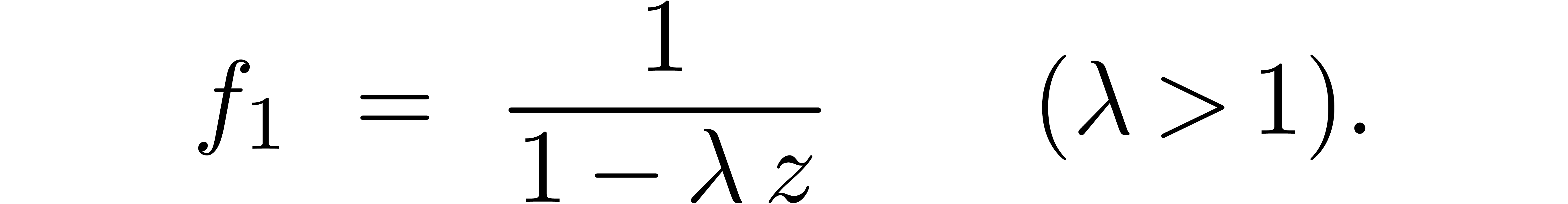
Here follow the values for 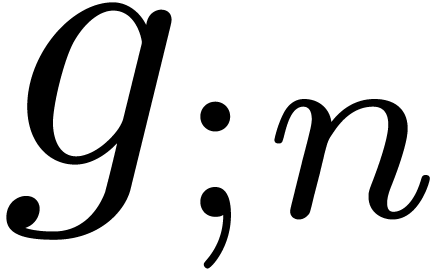 at different orders
and
at different orders
and 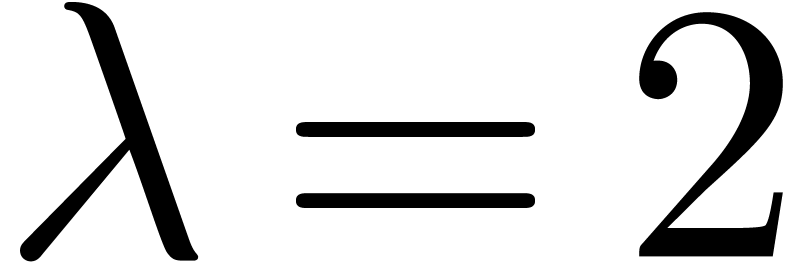 :
:
The 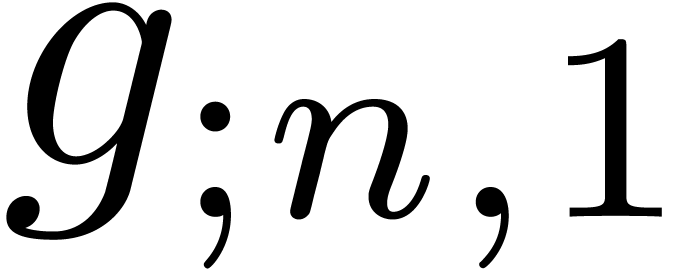 clearly converge to a limit
clearly converge to a limit 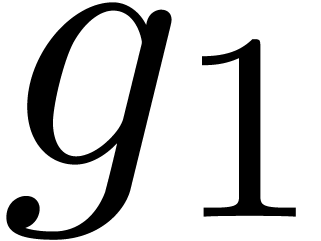 with radius of convergence
with radius of convergence  .
It should be noticed that we do not have
.
It should be noticed that we do not have 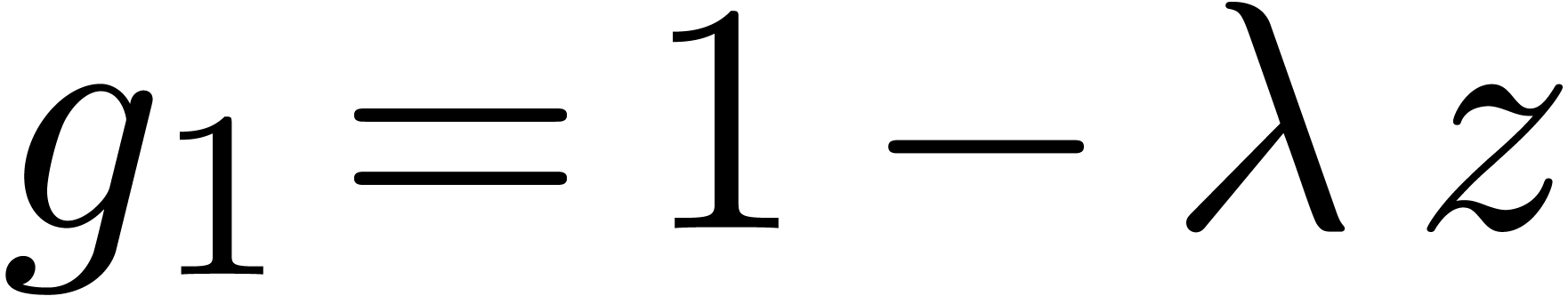 .
In other words, the “best” numeric relation (from the point
of view of
.
In other words, the “best” numeric relation (from the point
of view of  -norms) does not
coincide with the “best” algebraic relation (as found by
using Padé-Hermite approximation). A closer examination of the
result shows that
-norms) does not
coincide with the “best” algebraic relation (as found by
using Padé-Hermite approximation). A closer examination of the
result shows that
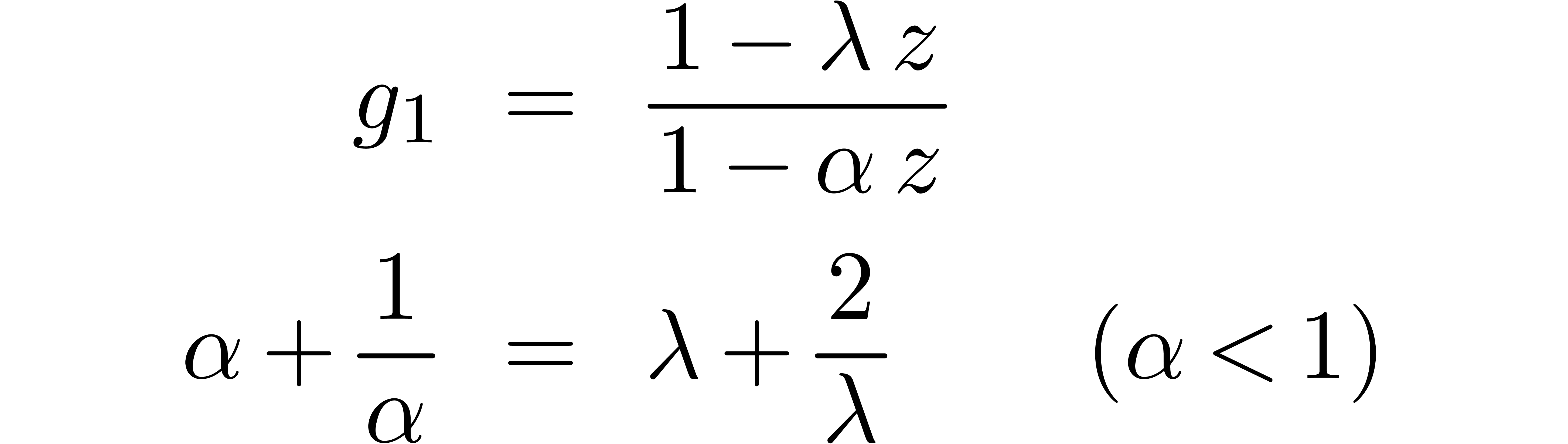
In particular,  decreases if
decreases if  increases.
increases.
We obtain:

The convergence only becomes apparent at higher orders. Contrary to the
previous example, it seems that the series in the computed relation all
have a radius of convergence  .
The norms of the computed results are given by
.
The norms of the computed results are given by 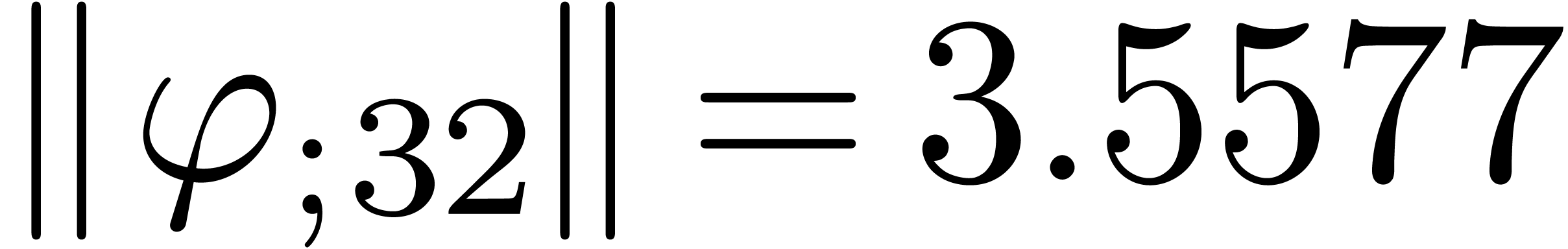 ,
, 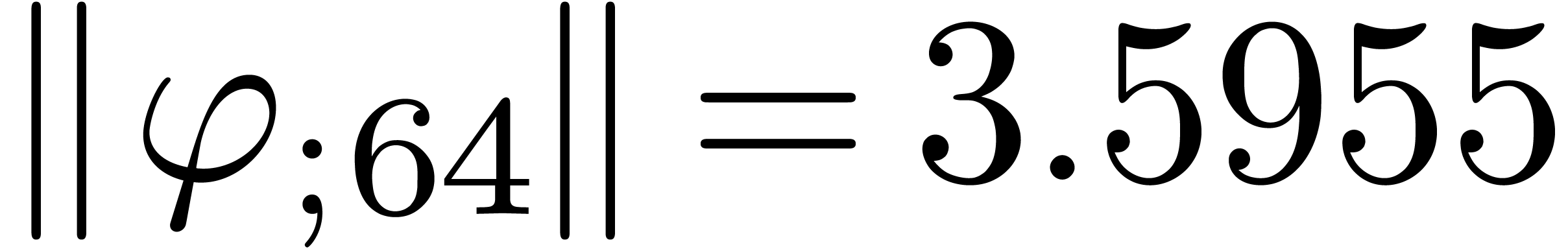 ,
, 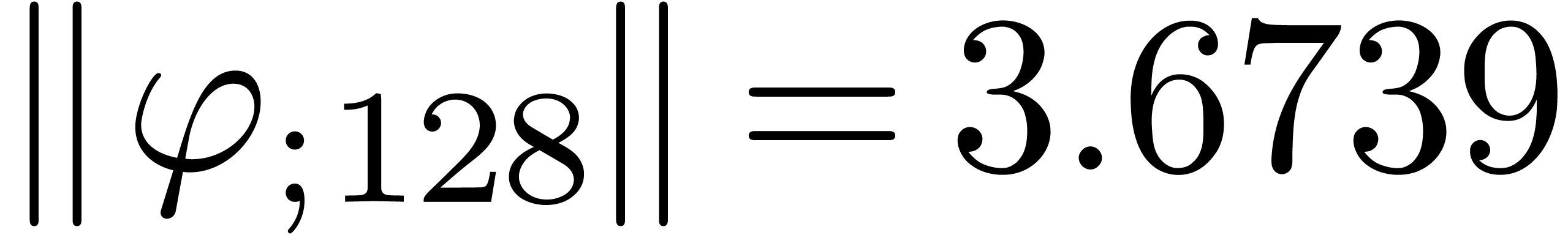 and
and 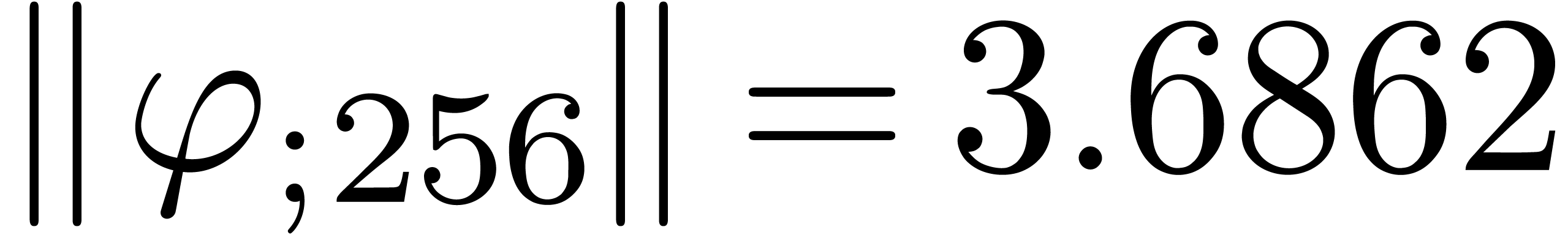 .
.
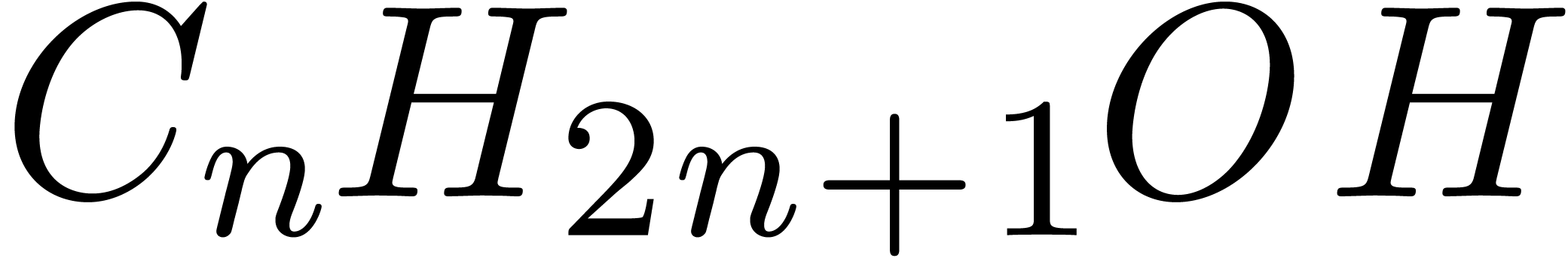 [Pól37].
Its generating series satisfies the functional equation
[Pól37].
Its generating series satisfies the functional equation
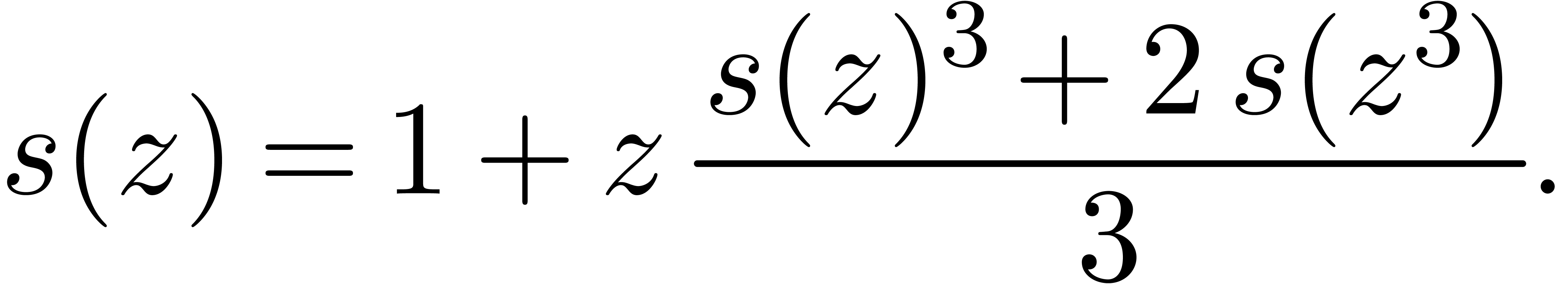
The asymptotic behaviour of the coefficients 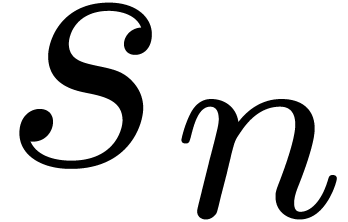 is
determined by the asymptotic behaviour of
is
determined by the asymptotic behaviour of 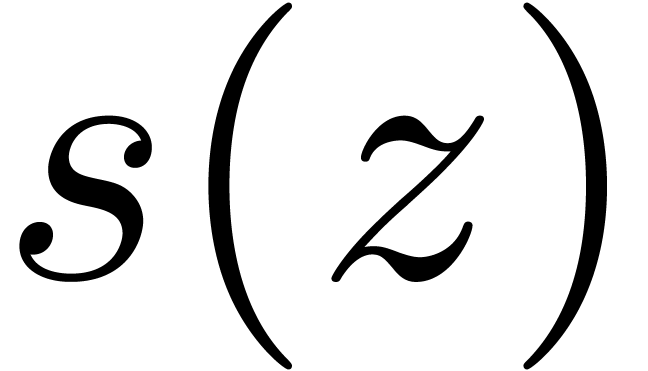 at its
singularity of smallest norm. Since
at its
singularity of smallest norm. Since 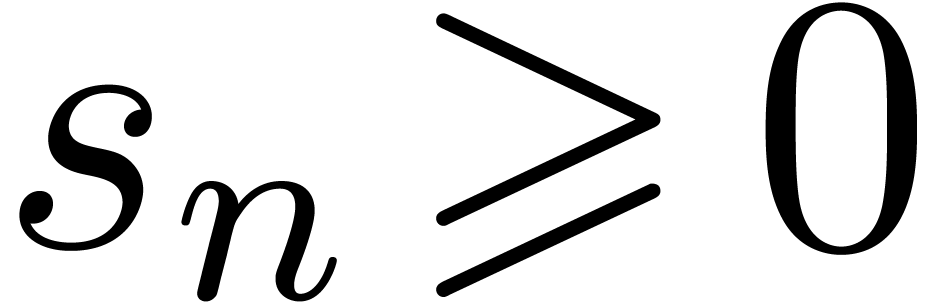 for all
for all
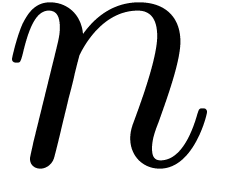 , this so-called dominant
singularity necessarily lies on the positive real axis, and coincides
with the radius of convergence
, this so-called dominant
singularity necessarily lies on the positive real axis, and coincides
with the radius of convergence 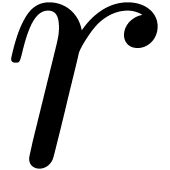 of
of  . Using asymptotic extrapolation [Hoe09],
we find that
. Using asymptotic extrapolation [Hoe09],
we find that 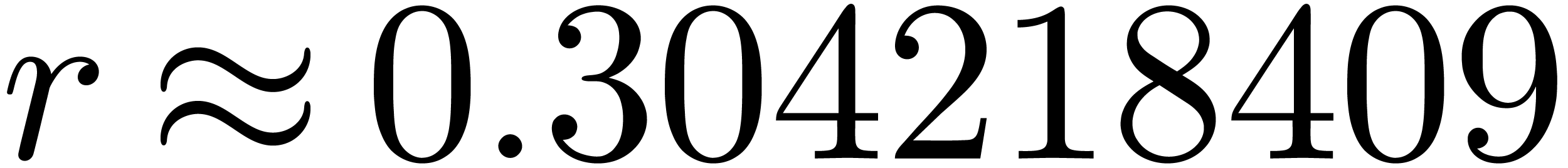 . In order to
investigate
. In order to
investigate 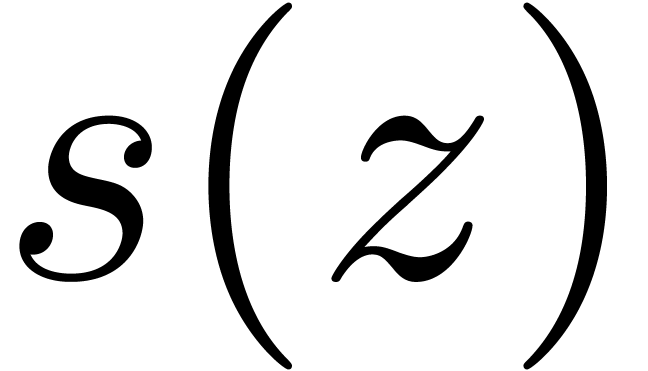 for
for  close to
close to
 , we apply our algorithm to
, we apply our algorithm to
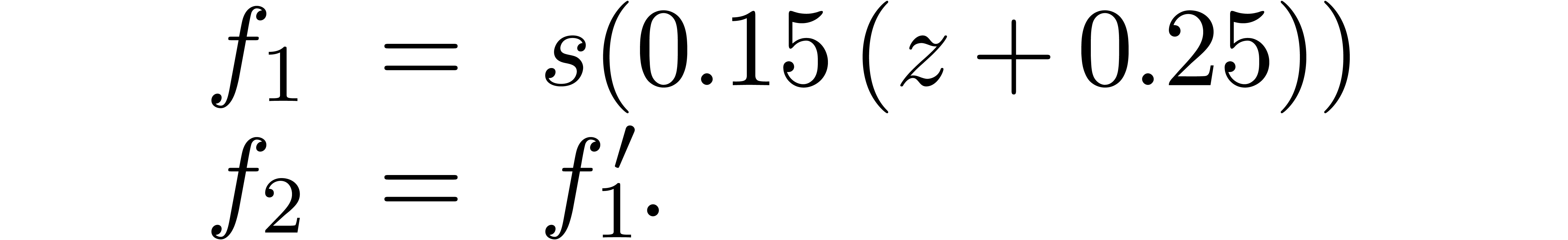
The translation  is done using power series
evaluation until stabilization at the working precision. Although this
was most straightforward to implement for this particular example, there
exist better strategies for zooming in, as mentioned at the end of
section 4.1. At different orders, we obtain:
is done using power series
evaluation until stabilization at the working precision. Although this
was most straightforward to implement for this particular example, there
exist better strategies for zooming in, as mentioned at the end of
section 4.1. At different orders, we obtain:

The corresponding norms are given by 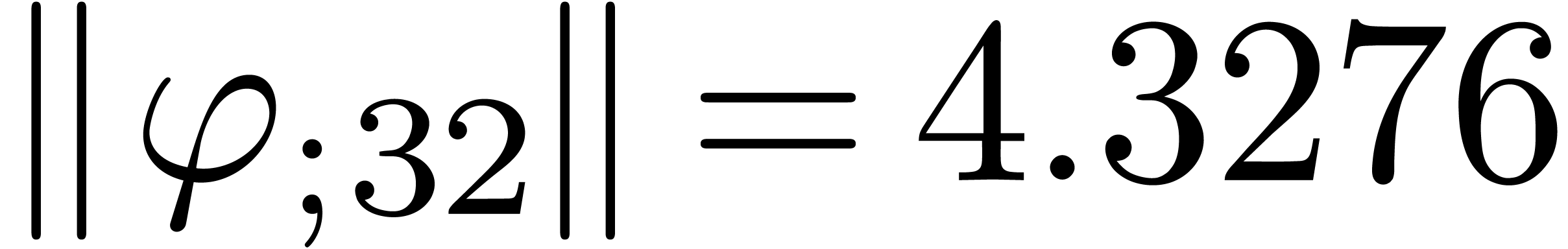 ,
,
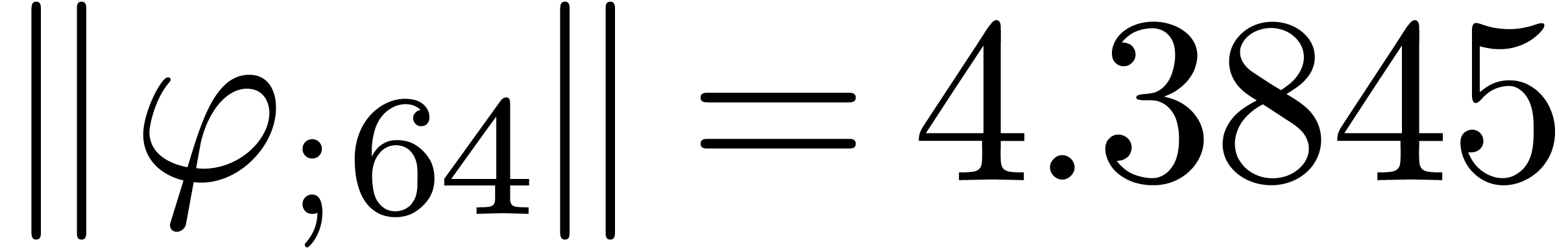 ,
, 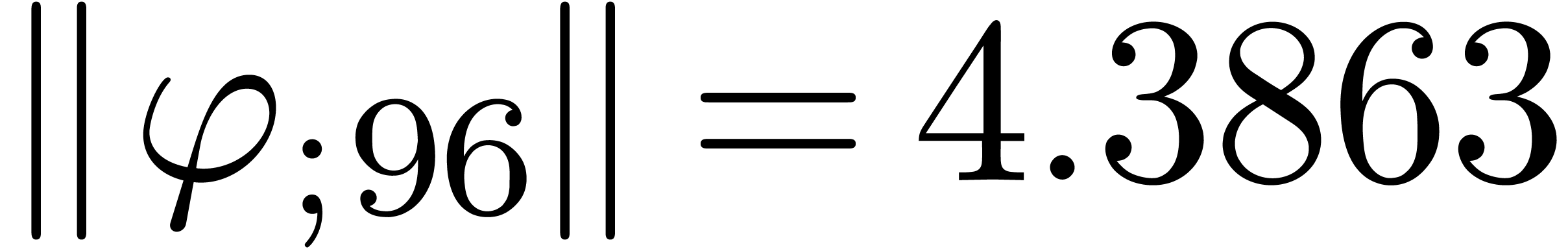 and
and
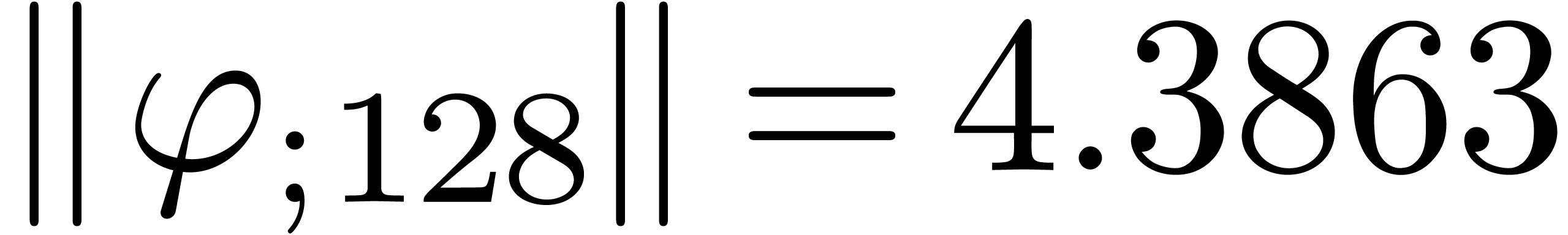 . Again, the convergence is
rather slow, and the computed series all seem to have radius of
convergence
. Again, the convergence is
rather slow, and the computed series all seem to have radius of
convergence  . Since
. Since 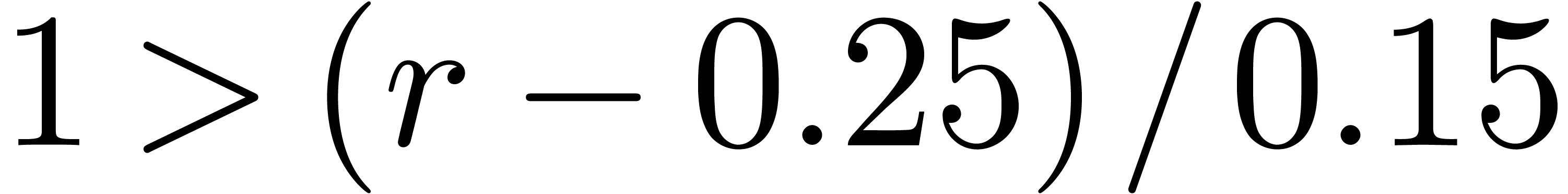 , this means that we indeed guessed
an analytic relation between
, this means that we indeed guessed
an analytic relation between  and
and  on the unit disk.
on the unit disk.
Remark 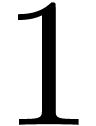 ,
if such a relation indeed exists. Larger radii of convergence
,
if such a relation indeed exists. Larger radii of convergence 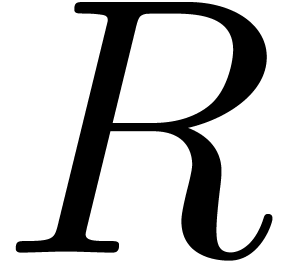 can be obtained simply by running the algorithm on
can be obtained simply by running the algorithm on 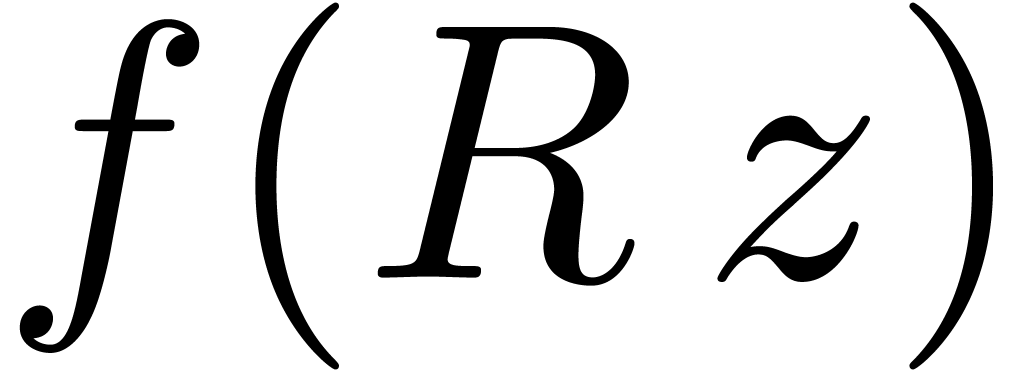 and scaling back the result.
and scaling back the result.
It is also instructive to run the algorithm on examples where the 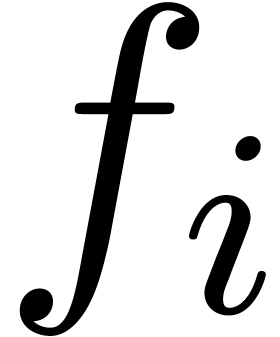 are known to be analytically independent. In that
case, it is important to examine the behaviour of the norms
are known to be analytically independent. In that
case, it is important to examine the behaviour of the norms 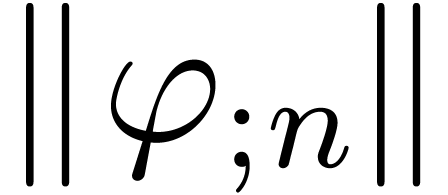 for
for  and find more precise criteria
which will enable us to discard the existence of a nice dependency with
a reasonable degree of certainty.
and find more precise criteria
which will enable us to discard the existence of a nice dependency with
a reasonable degree of certainty.
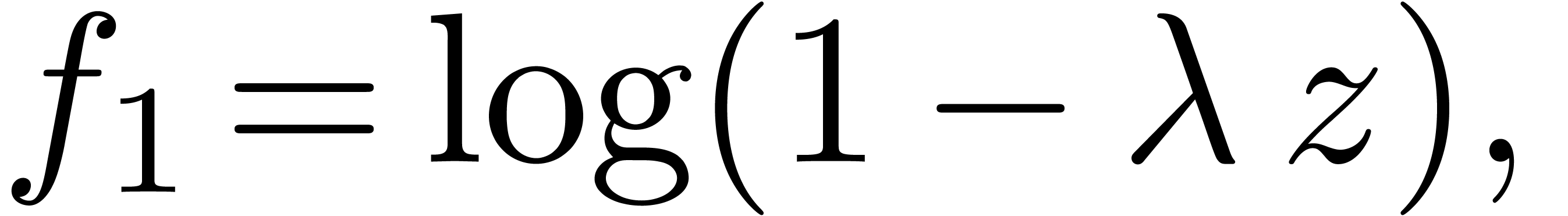
where  . Running our algorithm
directly on this function yields the following results for
. Running our algorithm
directly on this function yields the following results for 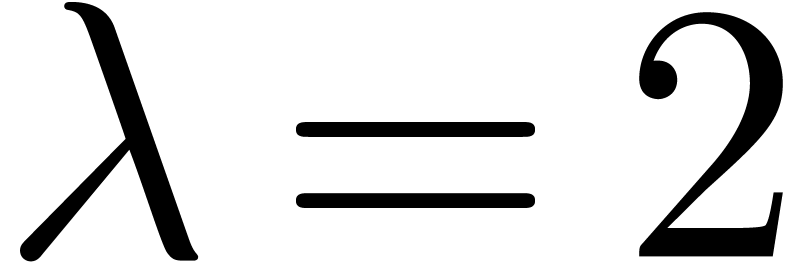 :
:
The results indeed do not converge and the corresponding sequence of
norms 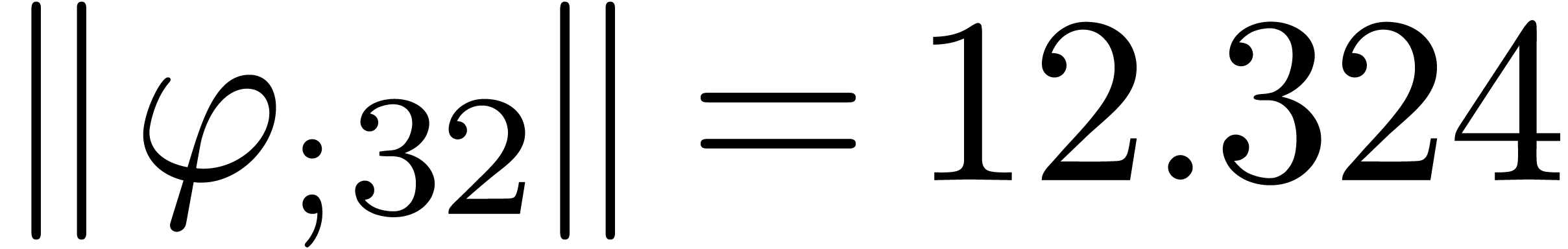 ,
, 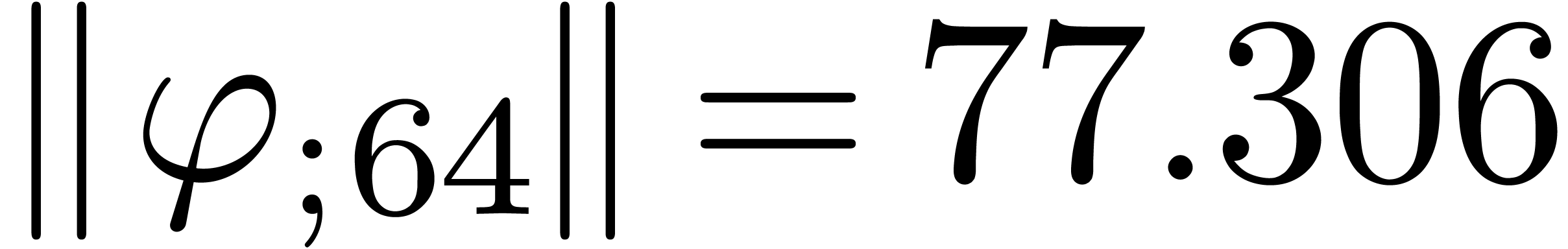 ,
, 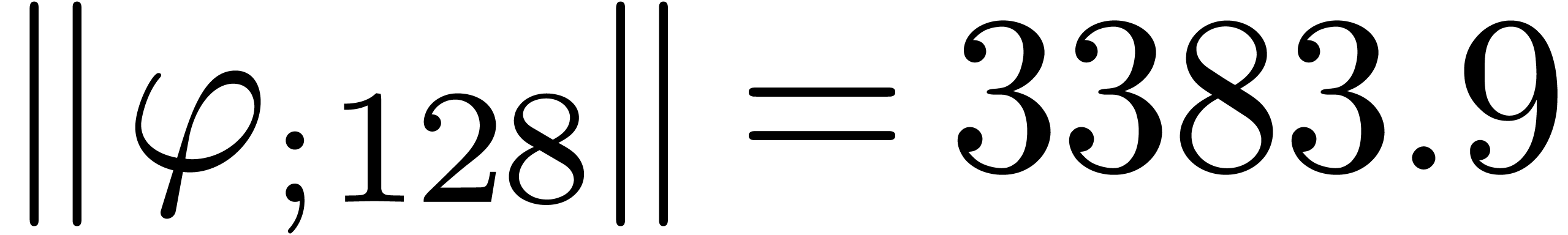 and
and 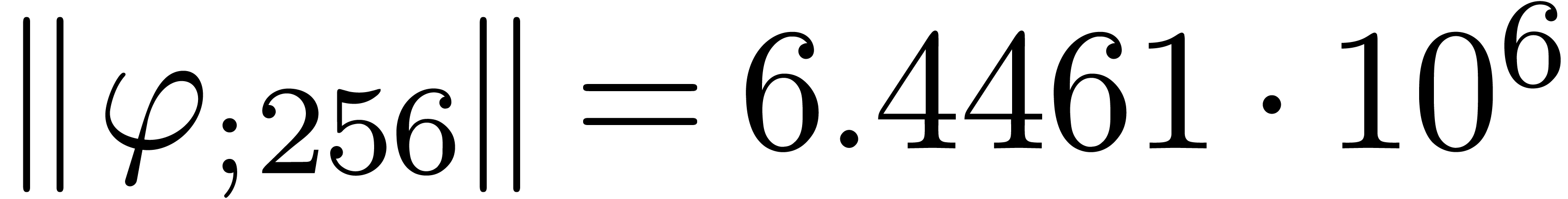 diverges at moderate exponential speed.
diverges at moderate exponential speed.
 . More generally, we can consider various
types of singularities, such as
. More generally, we can consider various
types of singularities, such as
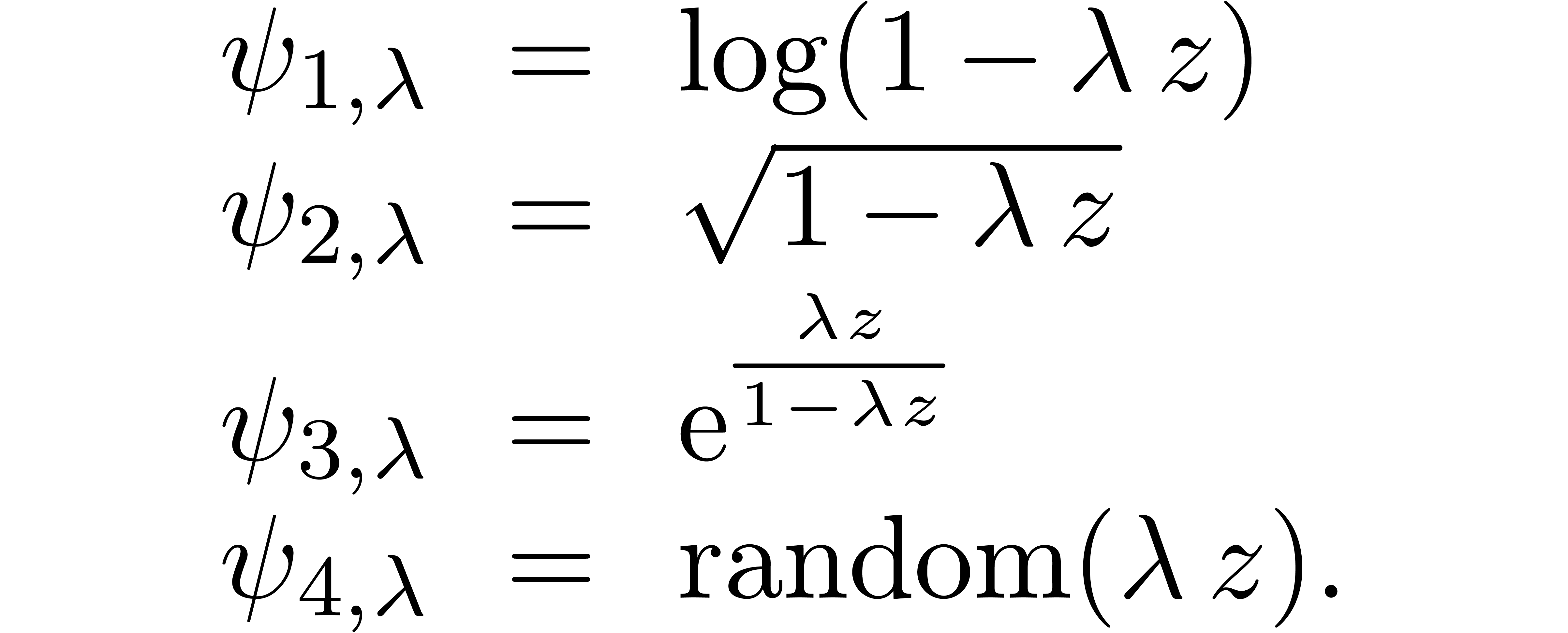
The series  is a series whose coefficients are
chosen according to a random uniform distribution on
is a series whose coefficients are
chosen according to a random uniform distribution on  . The results are shown in table 1
below. For
. The results are shown in table 1
below. For  ,
, 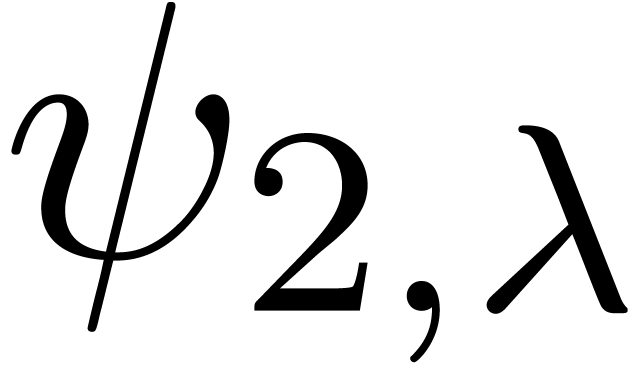 and
and 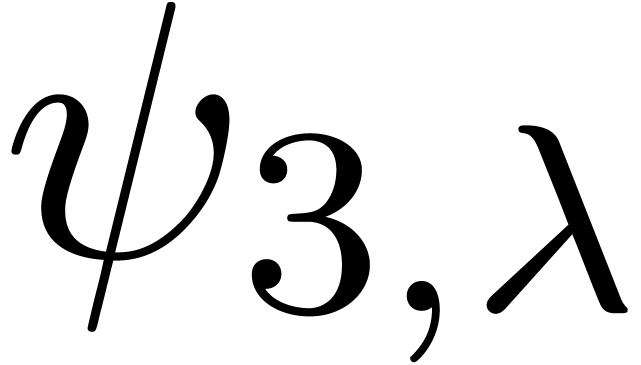 , it seems that the norm
does not much depend on the precise type of singularity, but only on
, it seems that the norm
does not much depend on the precise type of singularity, but only on
 and the truncation order
and the truncation order  . For the last series
. For the last series 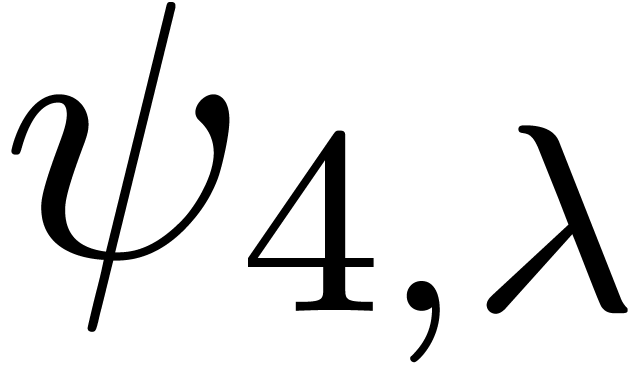 ,
the dependencies on
,
the dependencies on  and
and  approximately seem to follow the law
approximately seem to follow the law
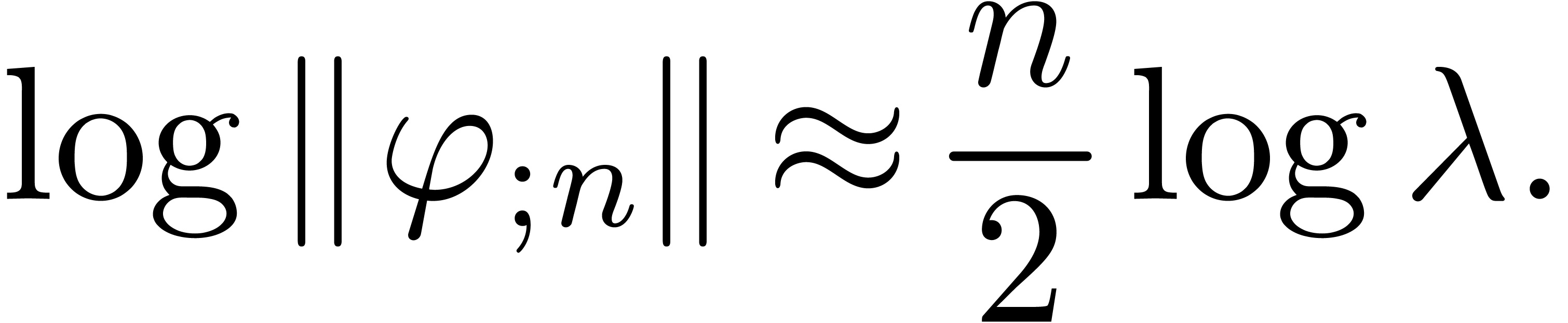 |
(17) |
This idealized law needs to be adjusted for functions 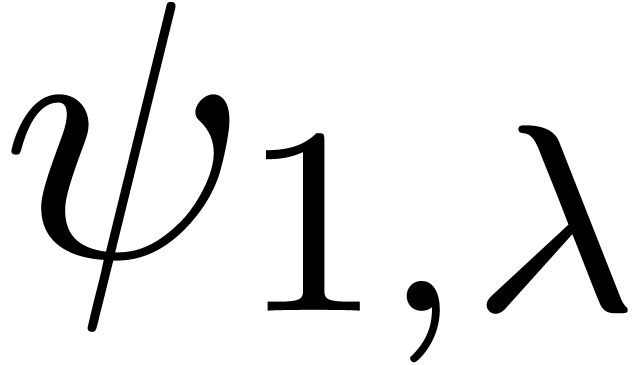 ,
, 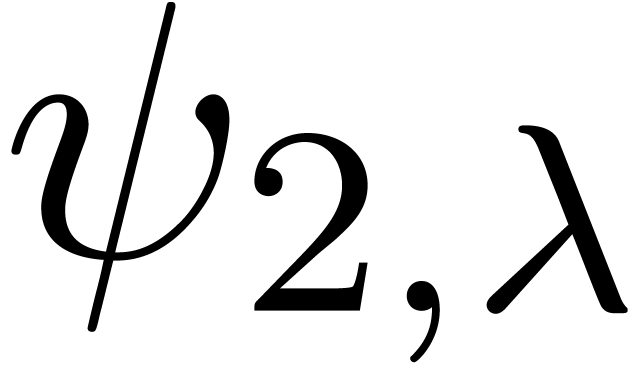 ,
,
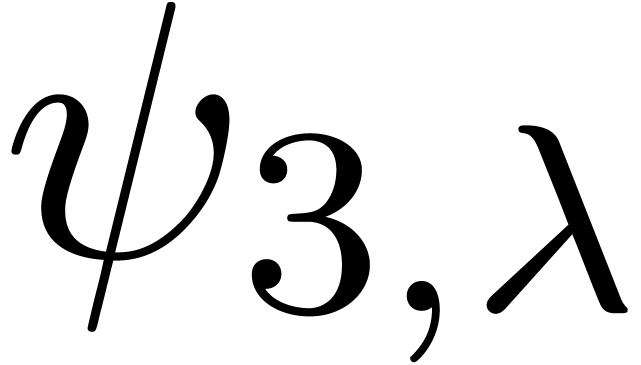 with more common types of singularities.
Although (17) remains asymptotically valid for large values
of
with more common types of singularities.
Although (17) remains asymptotically valid for large values
of 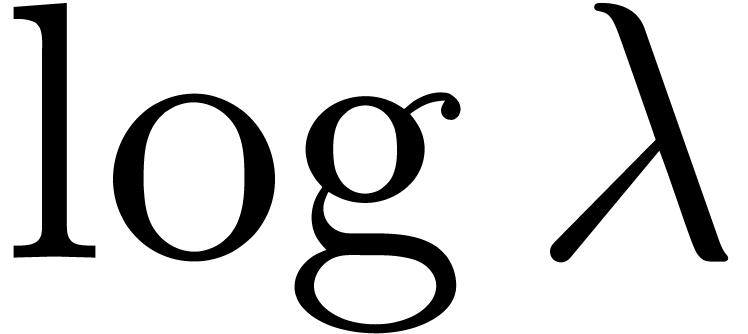 , the factor
, the factor 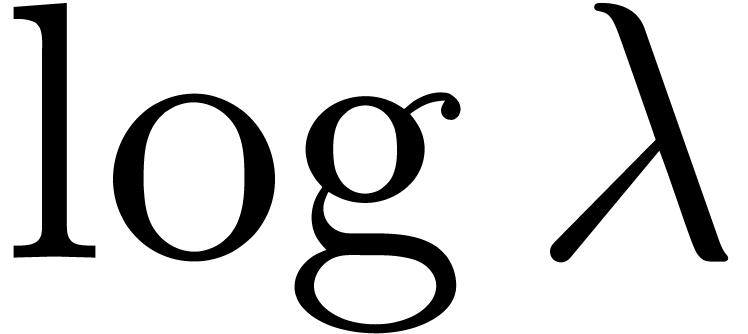 needs to be replaced by a smaller number for moderate
values. For
needs to be replaced by a smaller number for moderate
values. For 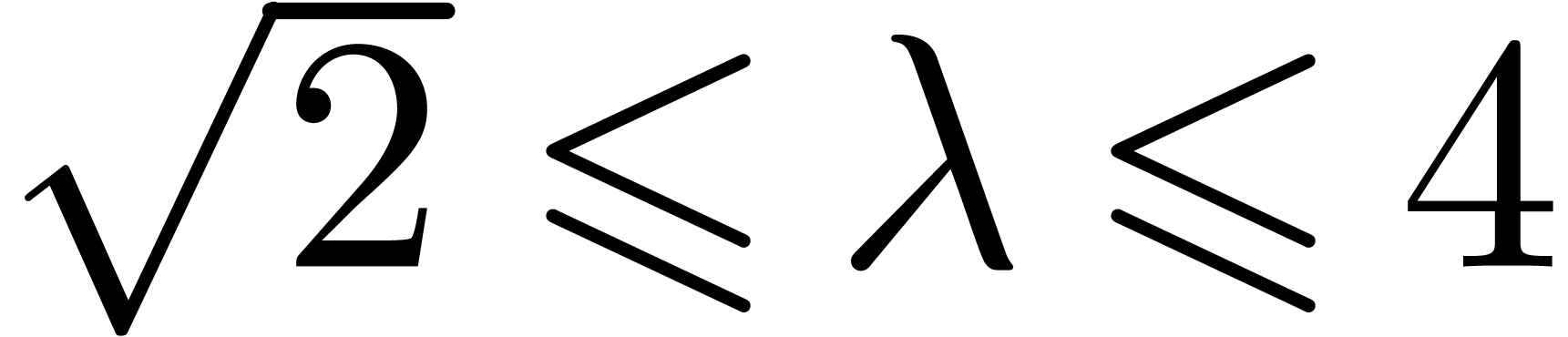 , this factor
rather seems to be of the form
, this factor
rather seems to be of the form  ,
where the constant
,
where the constant  depends on the nature of the
singularity. Also, the linear dependency of
depends on the nature of the
singularity. Also, the linear dependency of 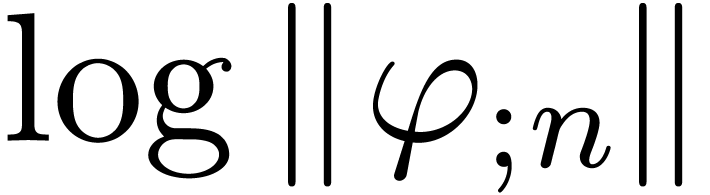 on
on
 is only reached for large values of
is only reached for large values of  .
.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
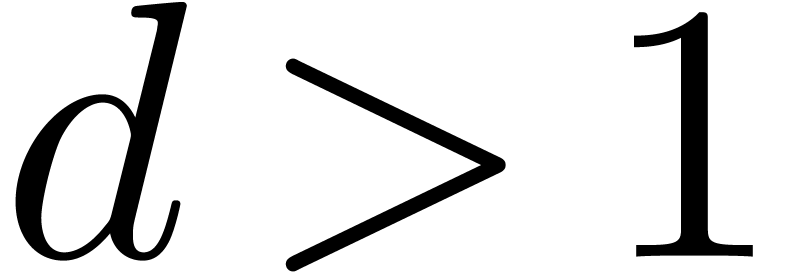
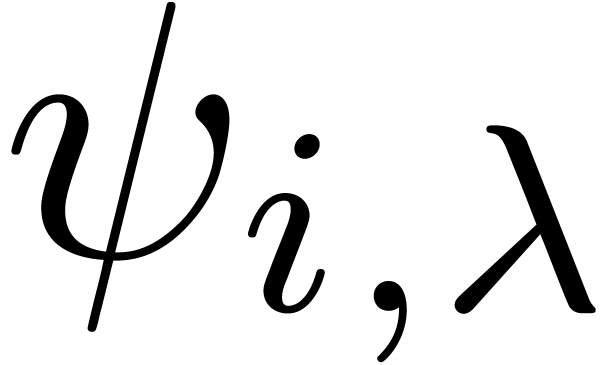 as above and studied the dependency of
as above and studied the dependency of 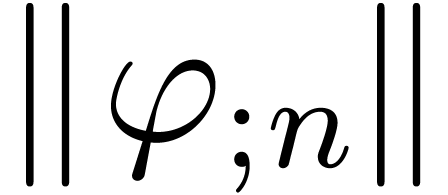 on
on
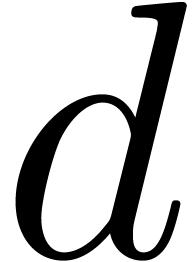 . The results are shown in
table 2 below. In the bottom rows,
. The results are shown in
table 2 below. In the bottom rows, 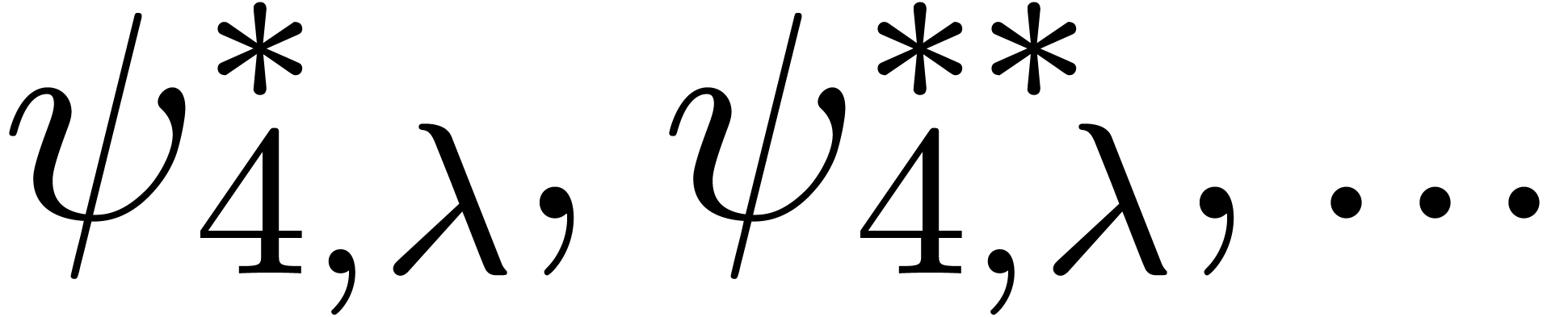 stand for distinct uncorrelated random series
stand for distinct uncorrelated random series 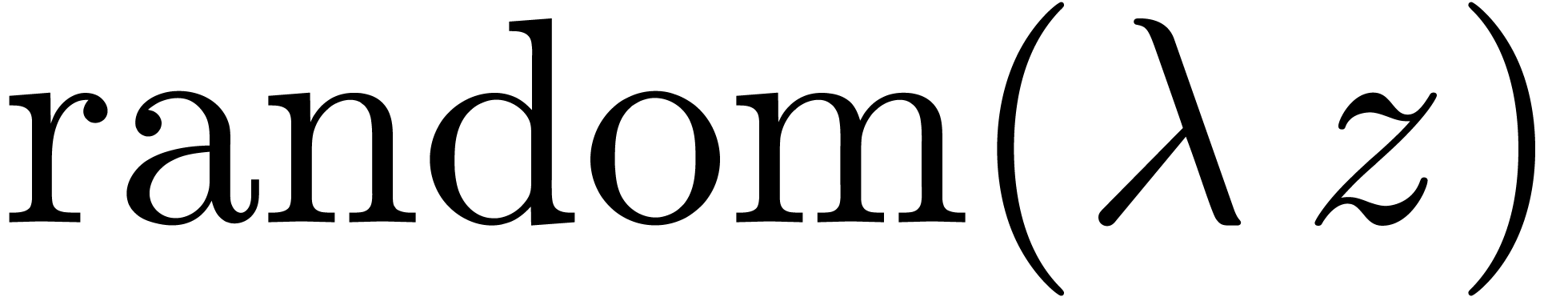 . In that case, the relation (17)
generalizes to
. In that case, the relation (17)
generalizes to
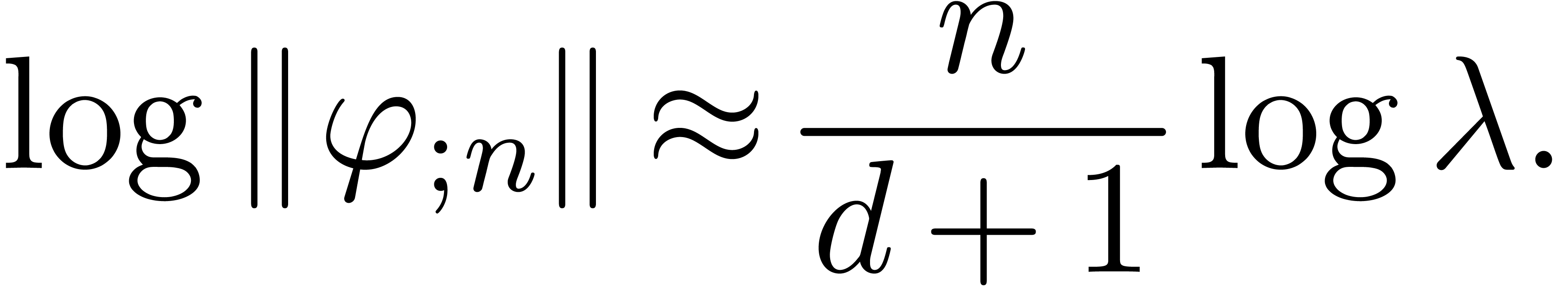 |
(18) |
It also seems that the law can be adapted to functions with more common
types of singularities, along similar lines as before. It would be
interesting to have a theoretical explanation for the empirical laws (17) and (18). The division by  in (18) is probably due to the fact that there are
in (18) is probably due to the fact that there are  unknowns in the equation (13).
unknowns in the equation (13).
Of course, in the case that we are considering functions  with several singularities
with several singularities  on our
disk of interest, only the singularities
on our
disk of interest, only the singularities 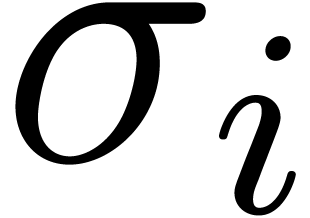 for
which
for
which 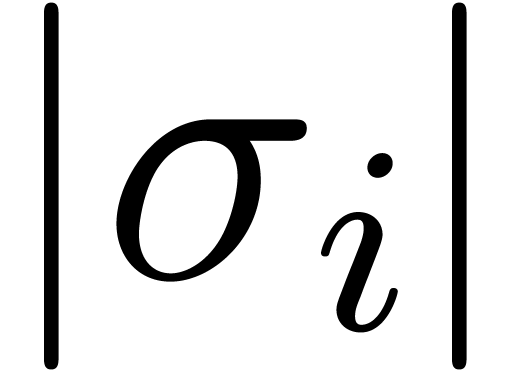 is smallest are “numerically
visible” (except when there exist relations which not involve
these dominant singularities
is smallest are “numerically
visible” (except when there exist relations which not involve
these dominant singularities 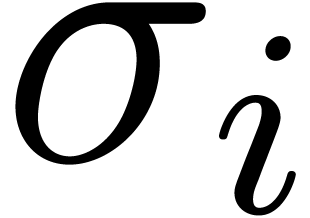 ).
).
In order to design a blackbox algorithm for the detection of dependencies (13), we need to make a final decision on whether we declare the input functions to be dependent or not. In view of the empirical law (18), and whatever decision criterion we implement, the outcome can only be trusted if the following two conditions are satisfied:
The number  should not be too large.
should not be too large.
There exists a large constant  for which all
singularities of
for which all
singularities of  are concentrated inside the
disk of radius
are concentrated inside the
disk of radius 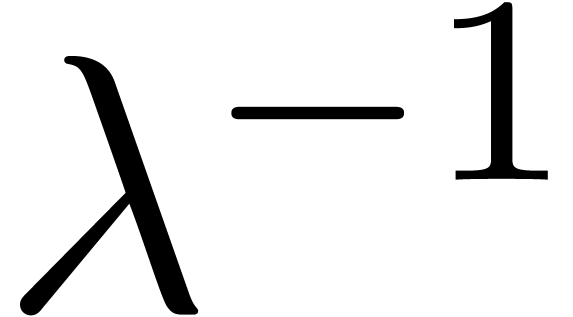 or outside the disk of radius
or outside the disk of radius
 .
.
As usual, if we are interested in dependencies near an isolated singularity, then the second condition can often be achieved by zooming in on the singularity.
Our empirical observations in the previous section suggest that we
should base the final decision on the empirical law (18).
First of all, in the case of independence, we should observe a more or
less geometric increase of the norm  when running
the algorithm for different orders
when running
the algorithm for different orders 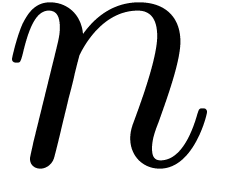 .
If
.
If  only admits an isolated singularity in
only admits an isolated singularity in  , then we may also compute its norm
, then we may also compute its norm
 and compare the computed values of
and compare the computed values of  with the expected values, as given by the law (18),
or a suitable adaptation of this law when
with the expected values, as given by the law (18),
or a suitable adaptation of this law when  becomes small. This method is most effective when
becomes small. This method is most effective when  is large, so it is usually recommended to zoom in on the singularity
before doing this comparison. In fact, if the law (18) is
satisfied for different zooming factors, then this may further
increase our confidence that the input functions are independent.
is large, so it is usually recommended to zoom in on the singularity
before doing this comparison. In fact, if the law (18) is
satisfied for different zooming factors, then this may further
increase our confidence that the input functions are independent.
For any numerical checks based on the law (18) or a
refinement of it, we also recommend to precondition the input series
 . In particular, we recommend
to multiply each
. In particular, we recommend
to multiply each  by a suitable constant,
ensuring that
by a suitable constant,
ensuring that
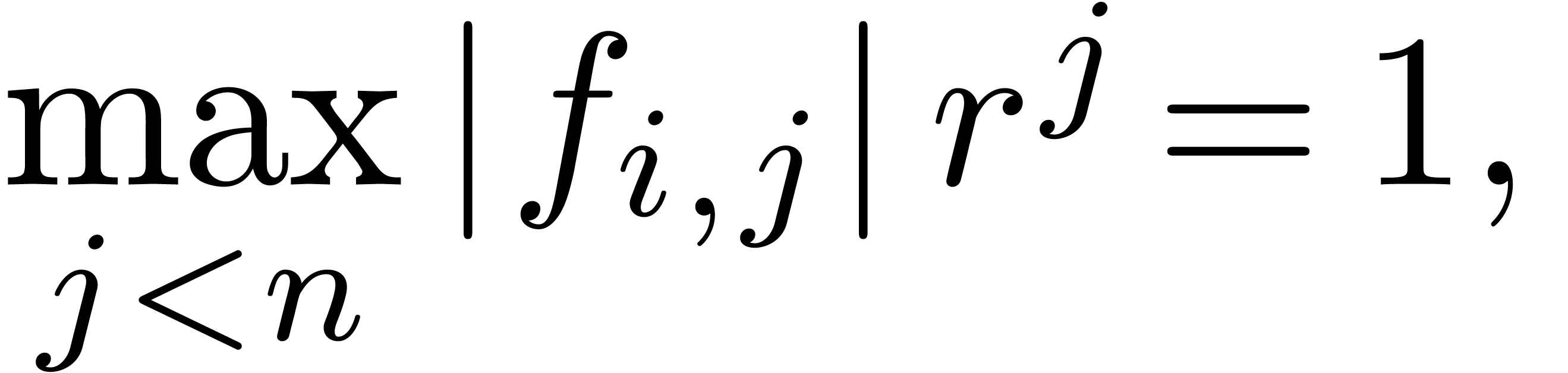
whenever we apply our algorithm at order 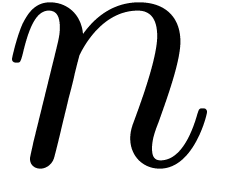 .
Here
.
Here 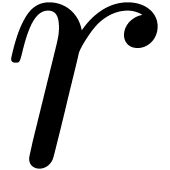 is computed using one of the algorithms
from section 3.
is computed using one of the algorithms
from section 3.
In fact, there is a trade-off between zooming in on the dominant
singularity (thereby ensuring a large value of  ) and using the original input coefficients (which
are given with a higher accuracy and order). In order to get more
insight in how far we should zoom in, we need to analyze the cost of the
algorithm from section 7.
) and using the original input coefficients (which
are given with a higher accuracy and order). In order to get more
insight in how far we should zoom in, we need to analyze the cost of the
algorithm from section 7.
The current working precision 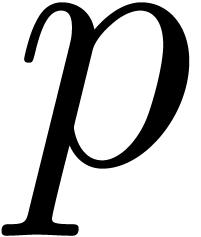 should in general
be taken larger than
should in general
be taken larger than 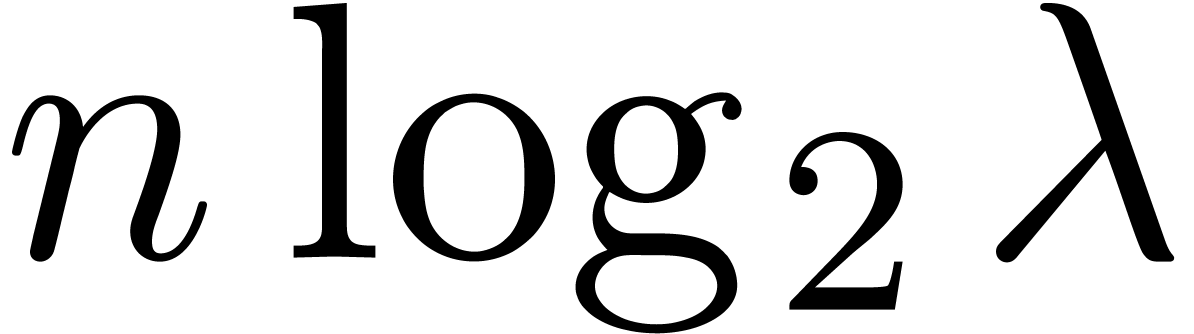 in order to keep the method
numerically stable. Denoting by
in order to keep the method
numerically stable. Denoting by 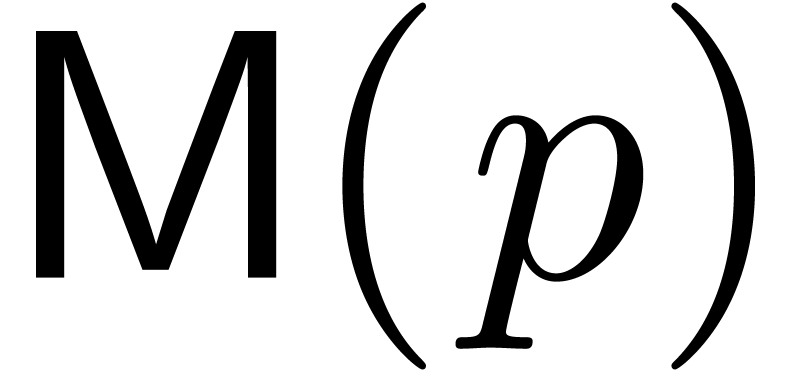 the cost for
multiplying two
the cost for
multiplying two  -bit numbers,
a naive implementation of the Gram-Schmidt orthogonalization procedure
yields a total cost of
-bit numbers,
a naive implementation of the Gram-Schmidt orthogonalization procedure
yields a total cost of 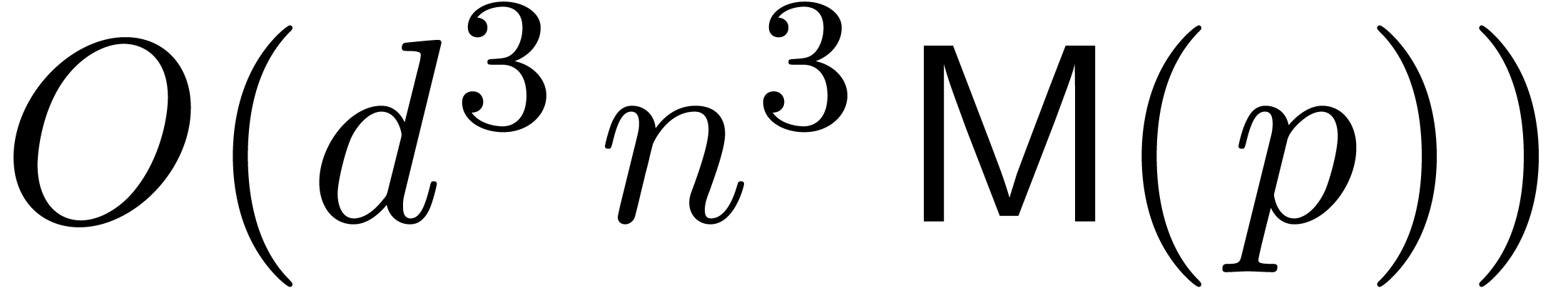 .
Denoting by
.
Denoting by 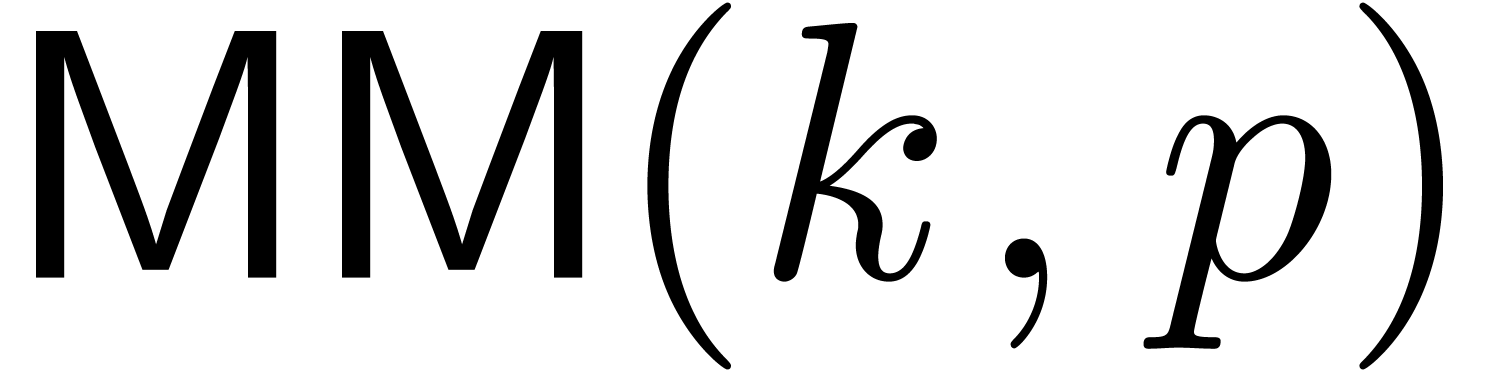 the cost of multiplying two
the cost of multiplying two  matrices with
matrices with 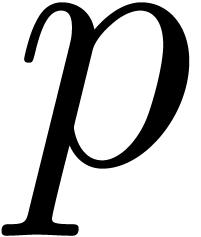 bit entries,
and using a blockwise Gram-Schmidt procedure (similar to the procedure
for matrix inversion in [Str69]), we obtain the better
bound
bit entries,
and using a blockwise Gram-Schmidt procedure (similar to the procedure
for matrix inversion in [Str69]), we obtain the better
bound 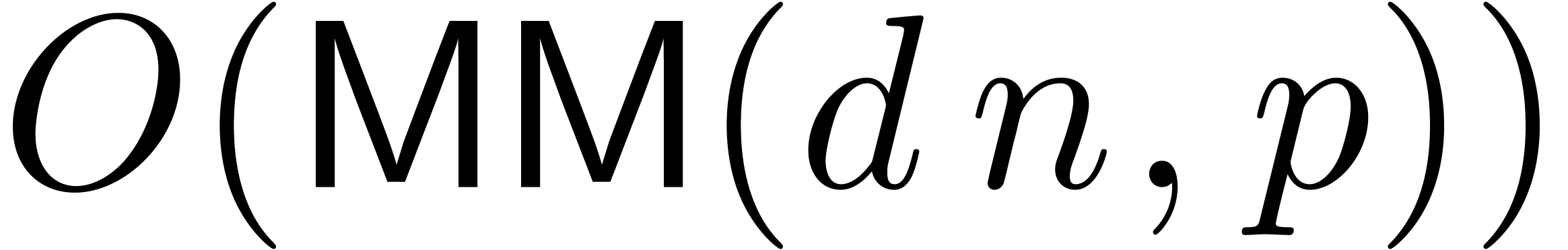 . However, the matrix
. However, the matrix
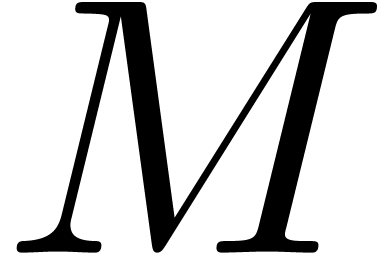 from section 7 has a very special
form. With more work, it might therefore be possible to save an
additional factor
from section 7 has a very special
form. With more work, it might therefore be possible to save an
additional factor 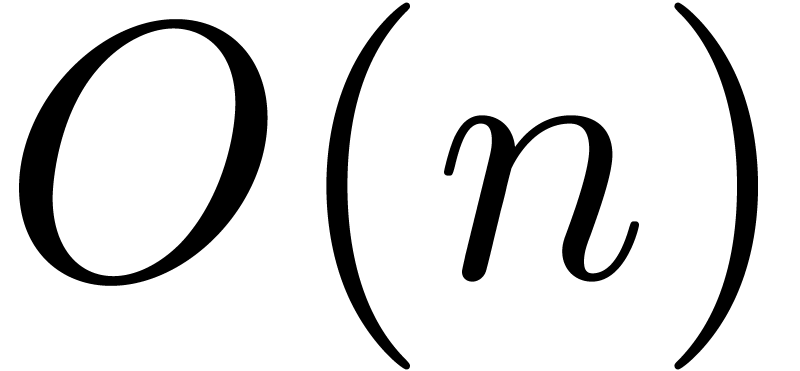 , but we
have not actively tried to do so yet.
, but we
have not actively tried to do so yet.
Taking into account the effect of a possible zoom, we may next evaluate
the computational cost in terms of the desired “output
quality”. As a definition of the output quality, we may take the
expected value 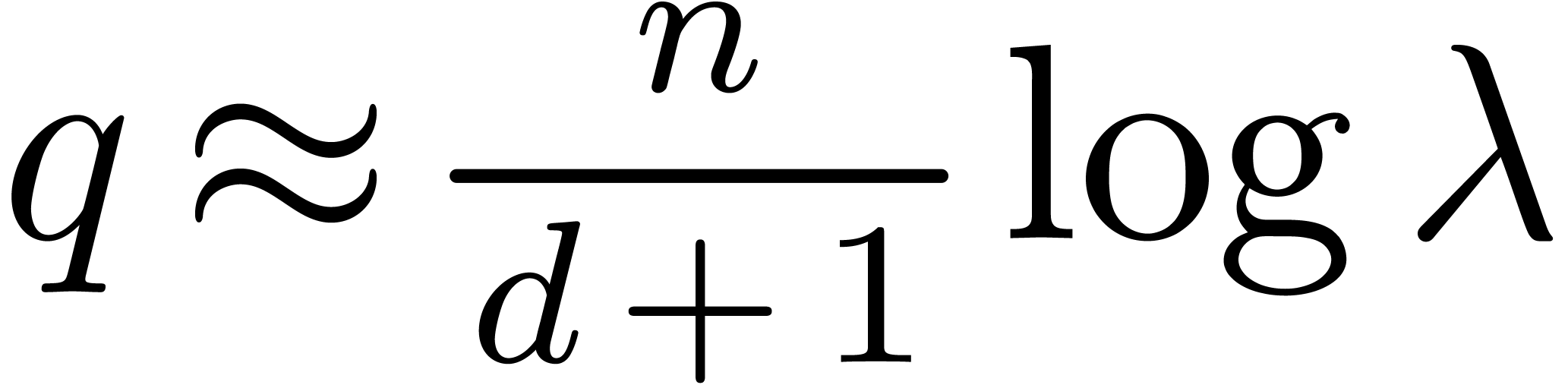 of
of 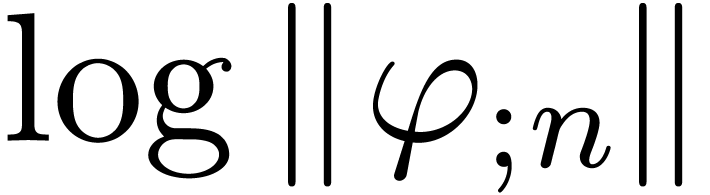 in the
case when
in the
case when  are independent. In order to obtain
accurate results, we need to compute with a bit precision larger than
are independent. In order to obtain
accurate results, we need to compute with a bit precision larger than
 . In terms of
. In terms of  , the time complexity thus becomes
, the time complexity thus becomes
where 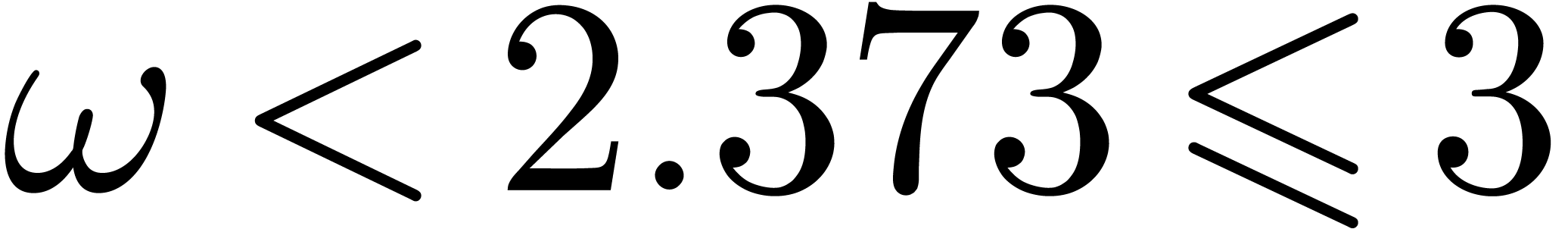 is the exponent of matrix multiplication
[Str69, Pan84, CW87, Vas12].
The complexity bound makes it clear that we should put a lot of effort
into keeping
is the exponent of matrix multiplication
[Str69, Pan84, CW87, Vas12].
The complexity bound makes it clear that we should put a lot of effort
into keeping 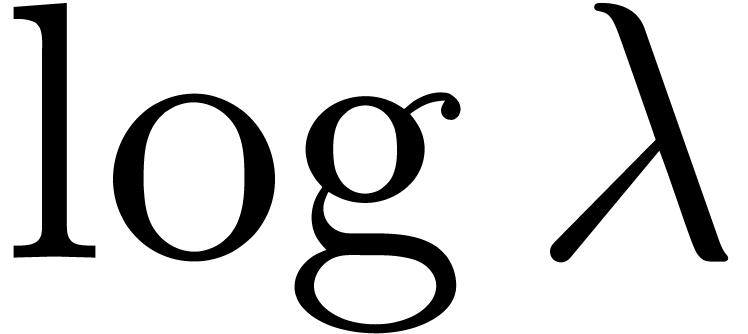 large. If
large. If  satisfies a differential equation, then zooming in can be done with low
computational cost (see section 4.1). Otherwise, the
required expansion order grows quickly with the inverse of the distance
to the singularity. Indeed, for
satisfies a differential equation, then zooming in can be done with low
computational cost (see section 4.1). Otherwise, the
required expansion order grows quickly with the inverse of the distance
to the singularity. Indeed, for  ,
the formula (8) becomes
,
the formula (8) becomes
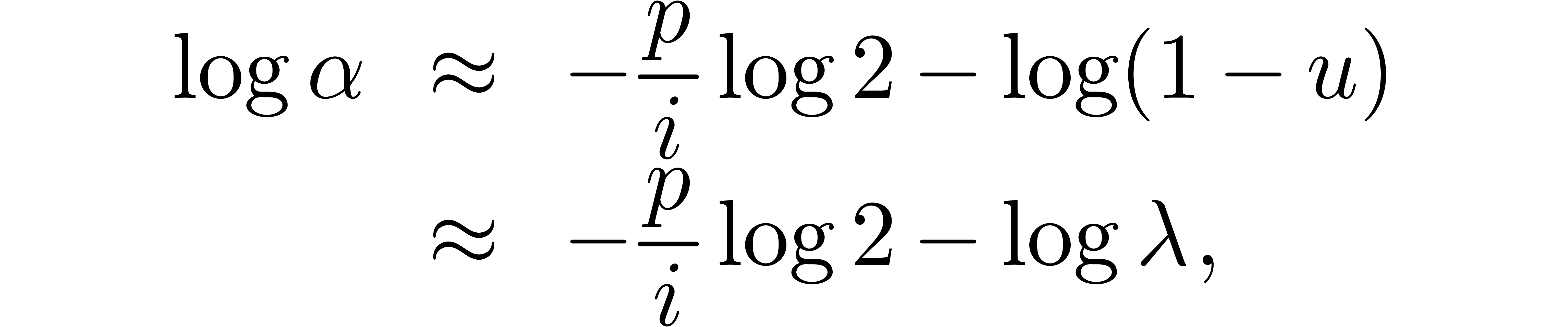
where we recall that, in order to apply the orthogonalization process
after zooming in, we need to expand  at an order
which is
at an order
which is  times larger than before.
times larger than before.
D. Bailey, J.M. Borwein, V. Kapoor, and E.W. Weisstein. Ten problems in experimental mathematics. The American Mathematical Monthly, 113(6):481–509, 2006.
J.M. Borwein and K.J. Devlin. The Computer As Crucible: An Introduction to Experimental Mathematics. A.K. Peters Series. A.K. Peters, 2009.
K. Belabas. Journées Nationales de Calcul Formel (2011), volume 2 of Les cours du CIRM, chapter Théorie algébrique des nombres et calcul formel. CEDRAM, 2011. Exp. No. 1, 40 pages, http://ccirm.cedram.org/ccirm-bin/item?id=CCIRM_2011__2_1_A1_0.
G.D. Birkhoff. Equivalent singular points of ordinary differential equations. Math. Ann., 74:134–139, 1913.
R.P. Brent and H.T. Kung. Fast algorithms for manipulating formal power series. Journal of the ACM, 25:581–595, 1978.
B. Beckermann and G. Labahn. A uniform approach for the fast computation of matrix-type Padé approximants. SIAM J. Matrix Analysis and Applications, 15:804–823, 1994.
C. Brezinski and R. Zaglia. Extrapolation Methods. Theory and Practice. North-Holland, Amsterdam, 1991.
D.V. Chudnovsky and G.V. Chudnovsky. Computer algebra in the service of mathematical physics and number theory (computers in mathematics, stanford, ca, 1986). In Lect. Notes in Pure and Applied Math., volume 125, pages 109–232, New-York, 1990. Dekker.
R. M. Corless, P. M. Gianni, B. M. Trager, and S. M. Watt. The singular value decomposition for polynomial systems. In Proc. ISSAC '95, pages 195–207. ACM Press, 1995.
B. F. Caviness and M. J. Prelle. A note on algebraic independence of logarithmic and exponential constants. SIGSAM Bull., 12/2:18–20, 1978.
D. Coppersmith and S. Winograd. Matrix multiplication
via arithmetic progressions. In Proc. of the  Annual Symposium on Theory of Computing, pages 1–6,
New York City, may 25–27 1987.
Annual Symposium on Theory of Computing, pages 1–6,
New York City, may 25–27 1987.
H. Derksen. An algorithm to compute generalized Padé-Hermite forms. Technical Report Rep. 9403, Catholic University Nijmegen, January 1994.
J. Denef and L. Lipshitz. Decision problems for differential equations. The Journ. of Symb. Logic, 54(3):941–950, 1989.
E. Fabry. Sur les intégrales des équations différentielles linéaires à coefficients rationnels. PhD thesis, Paris, 1885.
J.-C. Faugère. Parallelization of Gröbner basis. In Hoon Hong, editor, Parallel and Symbolic Computation, volume 5 of Lect. Notes Series in Computing. Pasco'94, World Scientific, 1994.
Ph. Flajolet and R. Sedgewick. An introduction to the analysis of algorithms. Addison Wesley, Reading, Massachusetts, 1996.
J. von zur Gathen and J. Gerhard. Modern Computer Algebra. Cambridge University Press, 2-nd edition, 2002.
J. van der Hoeven, G. Lecerf, B. Mourrain, et al. Mathemagix, 2002. http://www.mathemagix.org.
J. van der Hoeven. Fast evaluation of holonomic functions. TCS, 210:199–215, 1999.
J. van der Hoeven. Zero-testing, witness conjectures and differential diophantine approximation. Technical Report 2001-62, Prépublications d'Orsay, 2001.
J. van der Hoeven. Relax, but don't be too lazy. JSC, 34:479–542, 2002.
J. van der Hoeven. Effective complex analysis. JSC, 39:433–449, 2005.
J. van der Hoeven. On effective analytic continuation. MCS, 1(1):111–175, 2007.
J. van der Hoeven. On asymptotic extrapolation. JSC, 44(8):1000–1016, 2009.
J. van der Hoeven. Journées Nationales de Calcul Formel (2011), volume 2 of Les cours du CIRM, chapter Calcul analytique. CEDRAM, 2011. Exp. No. 4, 85 pages, http://ccirm.cedram.org/ccirm-bin/fitem?id=CCIRM_2011__2_1_A4_0.
N. K. Karmarkar and Y. N. Lakshman. Approximate polynomial greatest common divisors and nearest singular polynomials. In Y.N. Lakhsman, editor, Proc. ISSAC '96, pages 35–42, Zürich, Switzerland, July 1996. ACM Press.
S. Lang. Transcendental numbers and diophantine approximation. Bull. Amer. Math. Soc., 77/5:635–677, 1971.
A.K. Lenstra, H.W. Lenstra, and L. Lovász. Factoring polynomials with rational coefficients. Math. Ann., 261:515–534, 1982.
R.E. Moore. Interval Analysis. Prentice Hall, Englewood Cliffs, N.J., 1966.
V. Pan. How to multiply matrices faster, volume 179 of Lect. Notes in Math. Springer, 1984.
H. Poincaré. Sur les intégrales irrégulières des équations linéaires. Acta Math., 8:295–344, 1886.
G. Pólya. Kombinatorische Anzahlbestimmungen für Gruppen, Graphen und chemische Verbindungen. Acta Mathematica, 68:145–254, 1937.
W.H. Press, S.A. Teukolsky, W.T. Vetterling, and B.P. Flannery. Numerical recipes, the art of scientific computing. Cambridge University Press, 3rd edition, 2007.
D. Richardson. How to recognise zero. JSC, 24:627–645, 1997.
D. Richardson. Zero tests for constants in simple scientific computation. MCS, 1(1):21–37, 2007.
V. Strassen. Gaussian elimination is not optimal. Numer. Math., 13:352–356, 1969.
A.J. Sommese and C.W. Wampler. The Numerical Solution of Systems of Polynomials Arising in Engineering and Science. World Scientific, 2005.
B. Salvy and P. Zimmermann. Gfun: a Maple package for the manipulation of generating and holonomic functions in one variable. ACM Trans. on Math. Software, 20(2):163–177, 1994.
V. Vassilevska Williams. Multiplying matrices faster
than Coppersmith-Winograd. In  ACM
Symp. on Theory of Computing (STOC'12), 2012. To appear.
Preliminary version available at http://cs.berkeley.edu/~virgi/matrixmult.pdf.
ACM
Symp. on Theory of Computing (STOC'12), 2012. To appear.
Preliminary version available at http://cs.berkeley.edu/~virgi/matrixmult.pdf.
J. Verschelde. Homotopy continuation methods for solving polynomial systems. PhD thesis, Katholieke Universiteit Leuven, 1996.
W. Wasow. Asymptotic expansions for ordinary differential equations. Dover, New York, 1967.
K. Weihrauch. Computable analysis. Springer-Verlag, Berlin/Heidelberg, 2000.
E. J. Weniger. Nonlinear sequence transformations: Computational tools for the acceleration of convergence and the summation of divergent series. Technical Report math.CA/0107080, Arxiv, 2001.
H.S. Wilf. Generating functionology. Academic Press, 2nd edition, 1994. http://www.math.upenn.edu/~wilf/DownldGF.html.
Z. Zeng. The approximate gcd of inexact polynomials Part I: a univariate algorithm. http://www.neiu.edu/~zzeng/uvgcd.pdf, 2004.