On the complexity of skew
arithmetic |
|
| September 1, 2015 |
|
 . This work has
been supported by the ANR-09-JCJC-0098-01
. This work has
been supported by the ANR-09-JCJC-0098-01
In this paper, we study the complexity of several basic operations on linear differential operators with polynomial coefficients. As in the case of ordinary polynomials, we show that these complexities can be expressed almost linearly in terms of the cost of multiplication.
|
Let  be an effective field of constants of
characteristic zero, so that all field operations can be carried out by
algorithms. Given an indeterminate
be an effective field of constants of
characteristic zero, so that all field operations can be carried out by
algorithms. Given an indeterminate  and the
derivation
and the
derivation 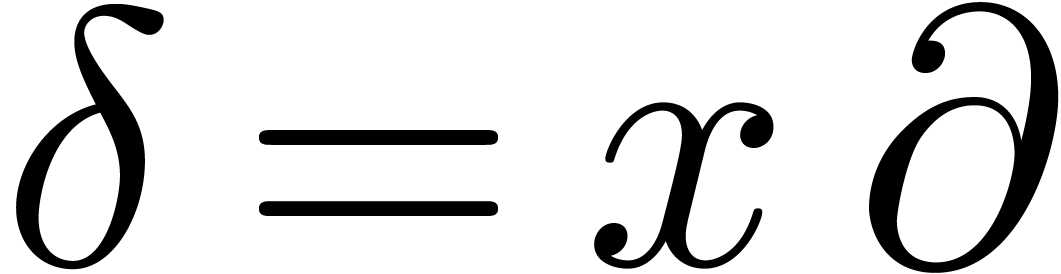 , where
, where 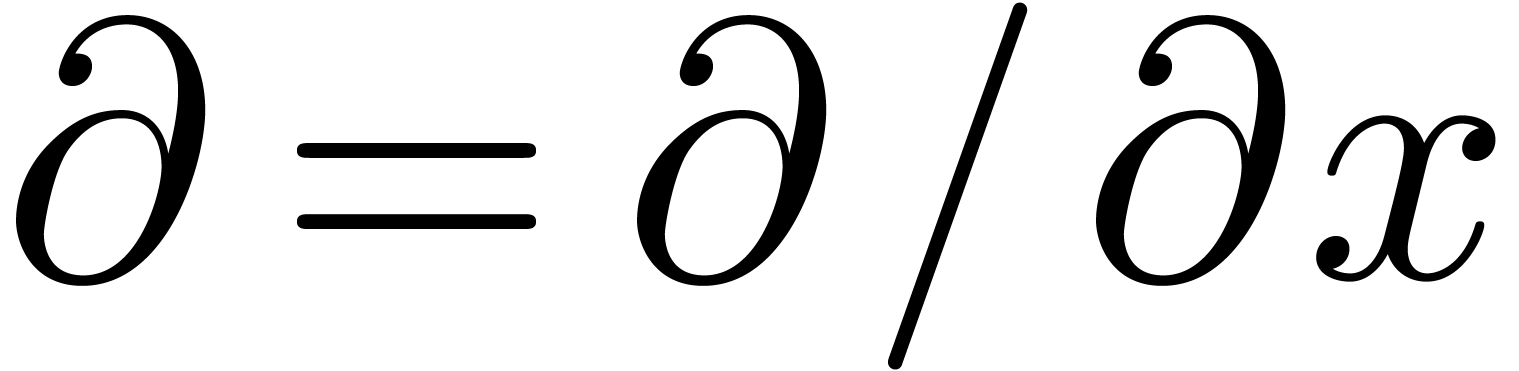 , it is well known [26,
8, 12, 28, 29] that
the skew polynomial ring
, it is well known [26,
8, 12, 28, 29] that
the skew polynomial ring 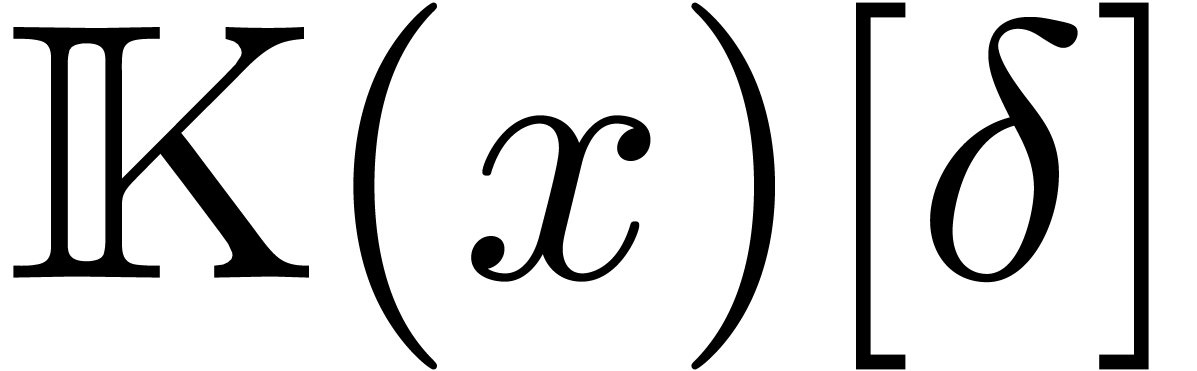 behaves very much like
an ordinary polynomial ring: there are skew analogues for each of the
classical operations of division with remainder, greatest common
divisors, least common multiples, etc. In this paper, we will study the
complexity of these operations. For this purpose, it will be more
appropriate to work in the ring
behaves very much like
an ordinary polynomial ring: there are skew analogues for each of the
classical operations of division with remainder, greatest common
divisors, least common multiples, etc. In this paper, we will study the
complexity of these operations. For this purpose, it will be more
appropriate to work in the ring 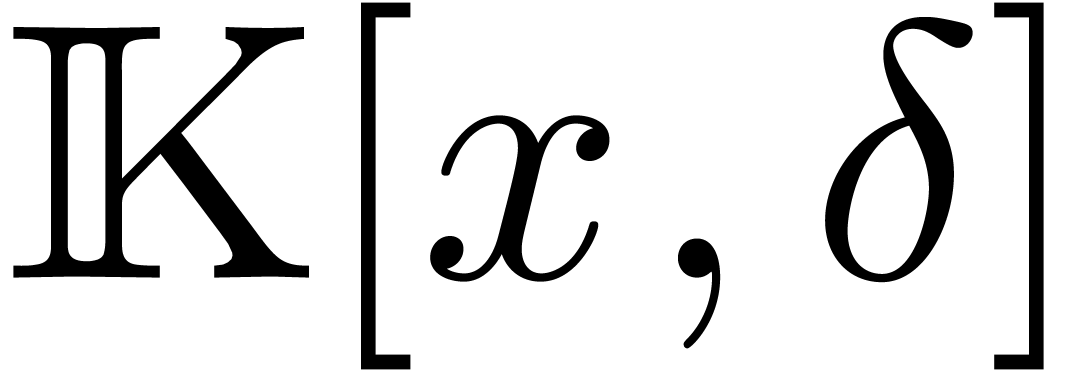 instead of
instead of 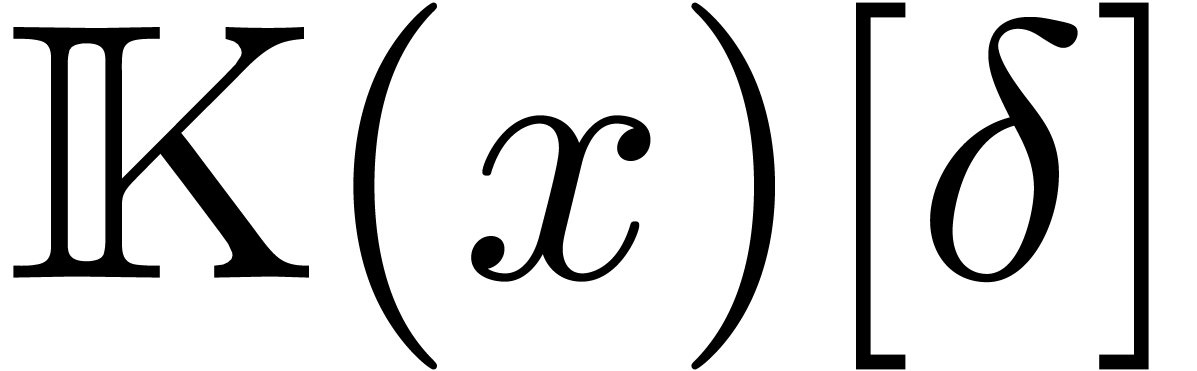 . In analogy with the commutative
case, we will give bounds for the computational complexities of the
various operations in terms of the complexity of operator
multiplication.
. In analogy with the commutative
case, we will give bounds for the computational complexities of the
various operations in terms of the complexity of operator
multiplication.
For our complexity measures, we make the customary assumption that all
field operations in 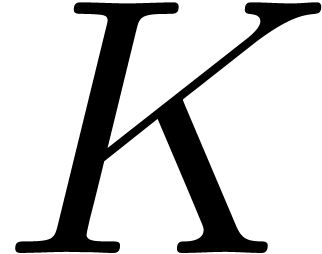 can be carried out in
constant time
can be carried out in
constant time 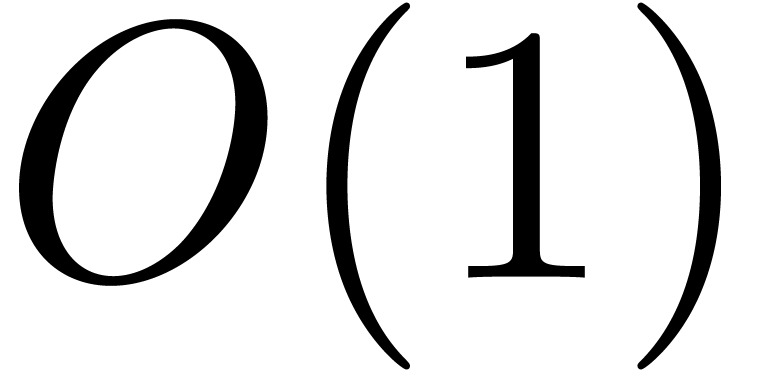 . We will try
to express the complexities of our algorithms in terms of the following
standard complexities:
. We will try
to express the complexities of our algorithms in terms of the following
standard complexities:
The time 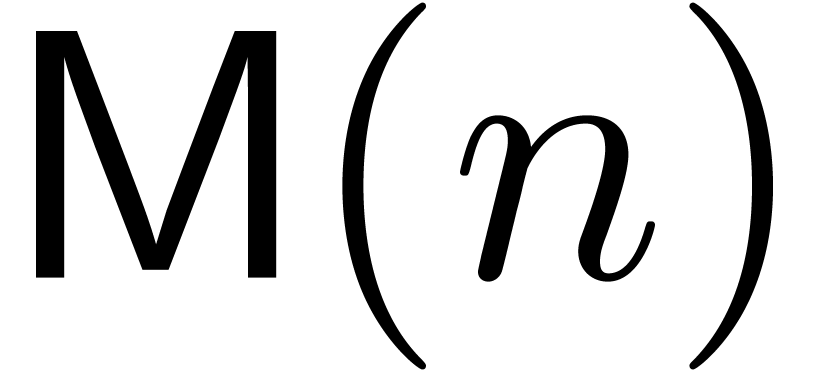 required for the multiplication of
two polynomials of degrees
required for the multiplication of
two polynomials of degrees 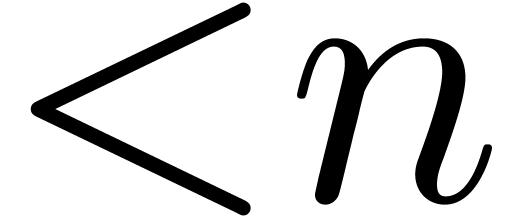 and coefficients
in
and coefficients
in  . It is classical [32, 31, 9] that
. It is classical [32, 31, 9] that 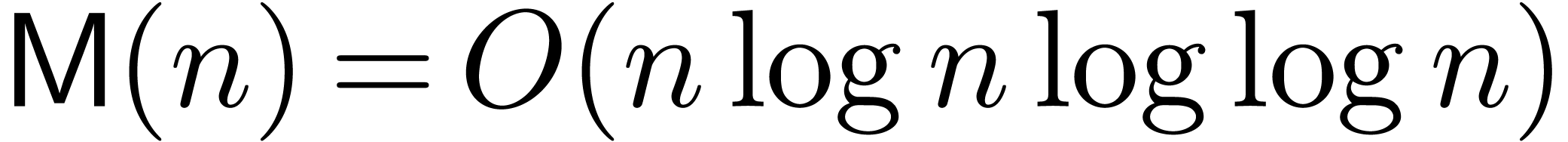 and
and 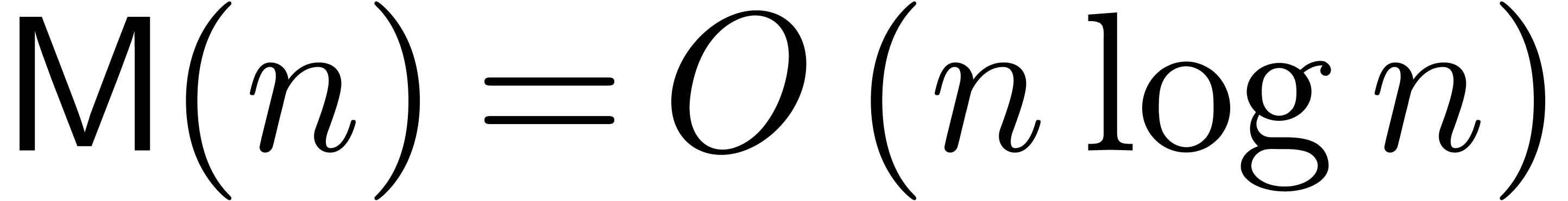 if
if  admits
sufficiently many
admits
sufficiently many 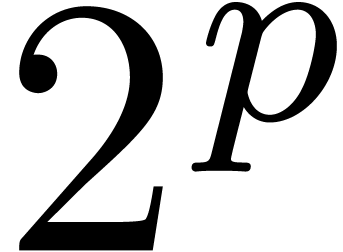 -th
roots of unity [10].
-th
roots of unity [10].
The complexity 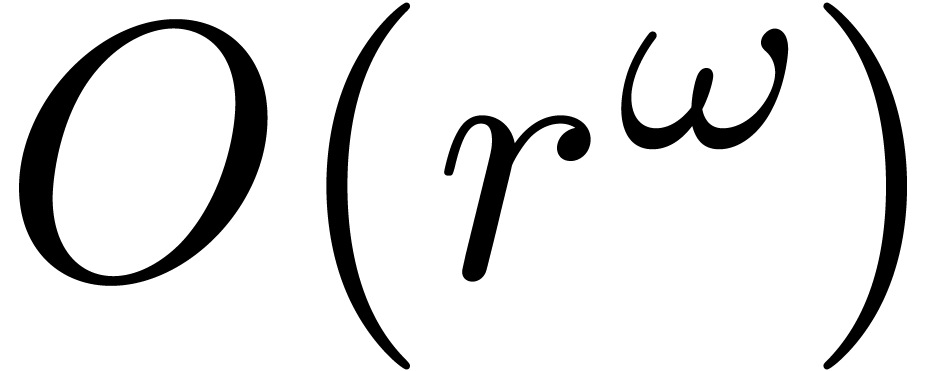 of multiplying two
of multiplying two  matrices with entries in
matrices with entries in  .
It is classical [34, 30, 11,
13] that
.
It is classical [34, 30, 11,
13] that 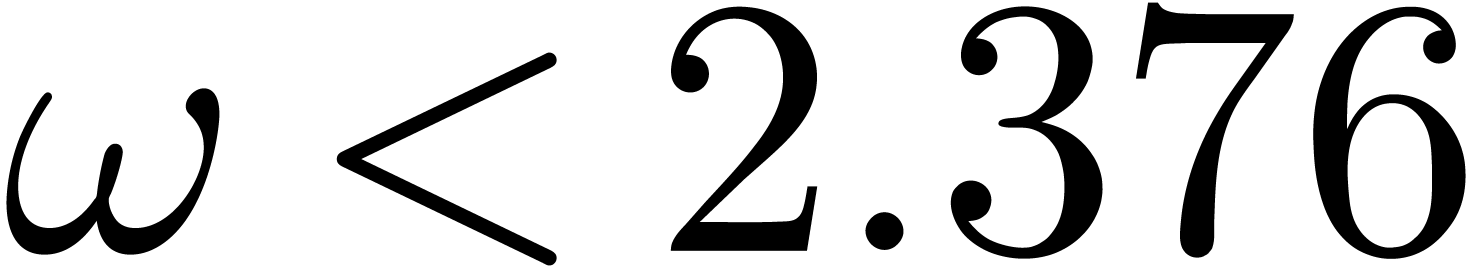 ,
although
,
although  in practice.
in practice.
We will denote by 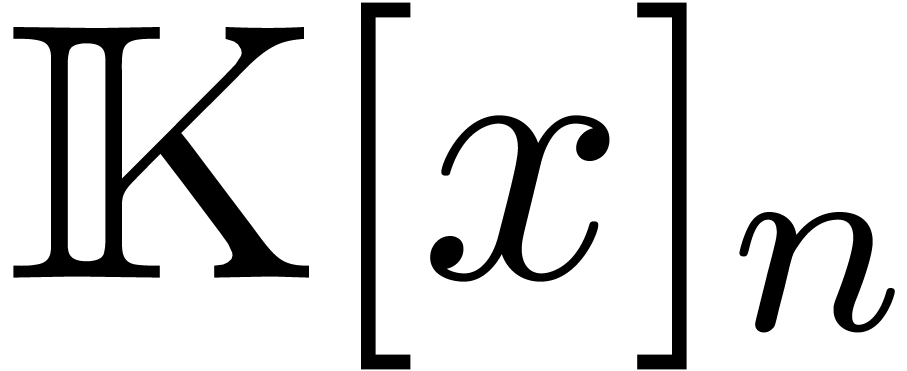 the subset of
the subset of 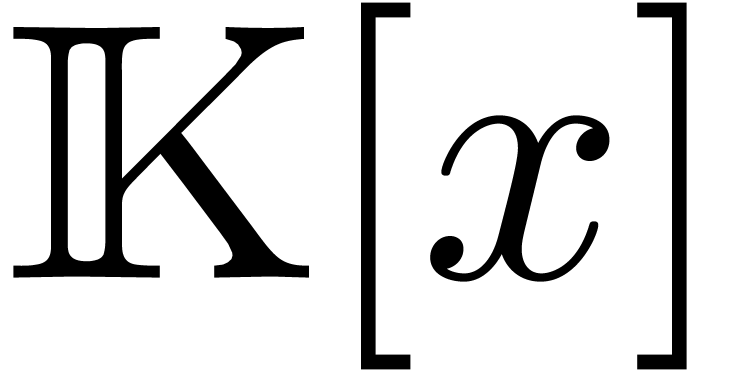 of polynomials of degree
of polynomials of degree 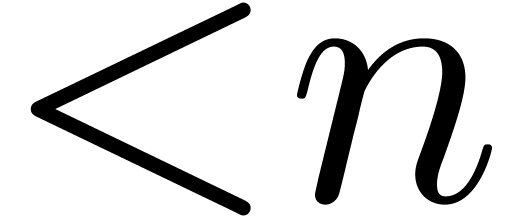 .
Likewise, we denote by
.
Likewise, we denote by 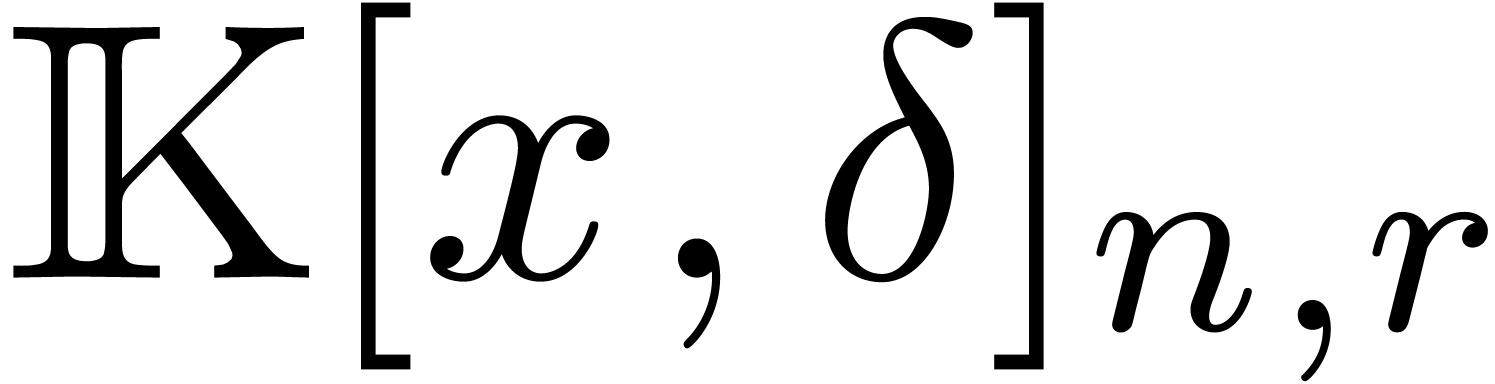 the set of operators
the set of operators 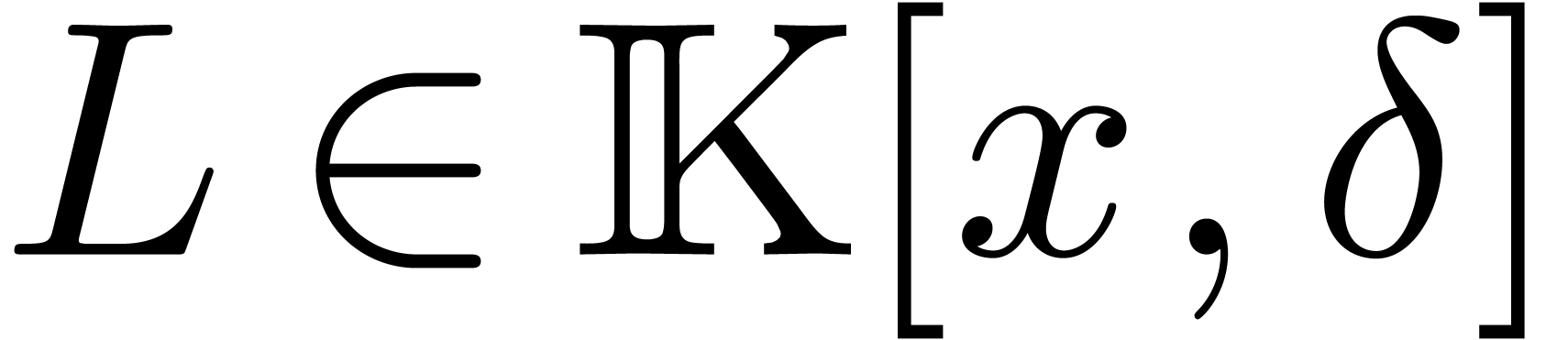 of degree
of degree 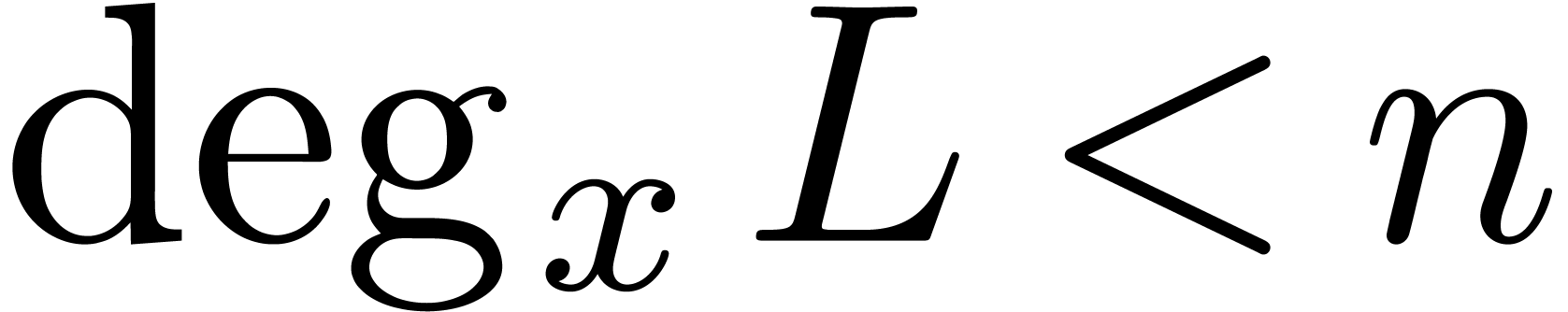 in
in  and degree
and degree 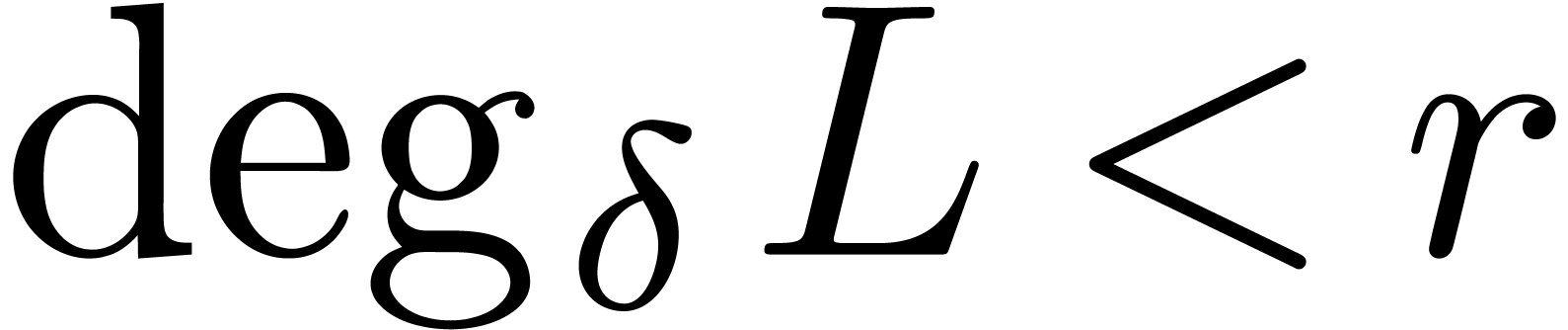 in
in 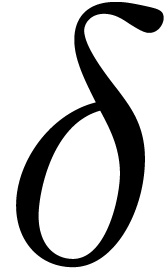 .
.
Now consider two linear differential operators 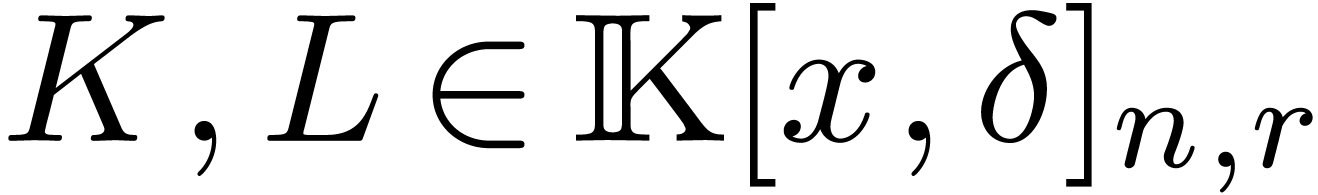 . We start with studying the following complexities:
. We start with studying the following complexities:
The complexity 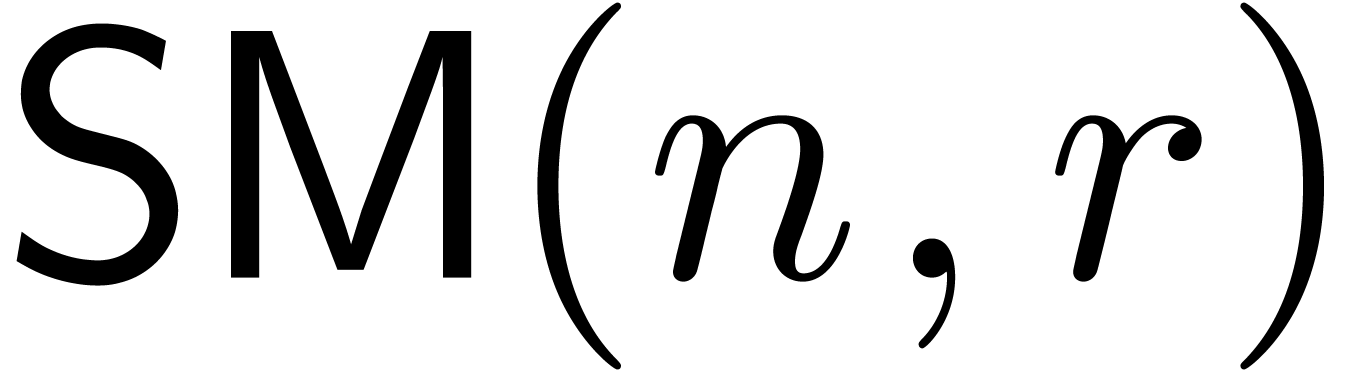 of multiplying
of multiplying  and
and  .
.
The complexity  of applying
of applying  to a vector of
to a vector of 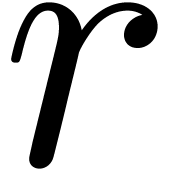 polynomials in
polynomials in 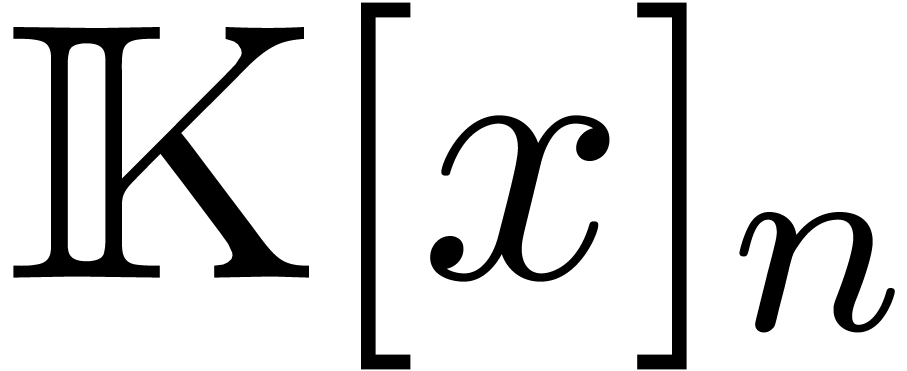 .
.
The cost 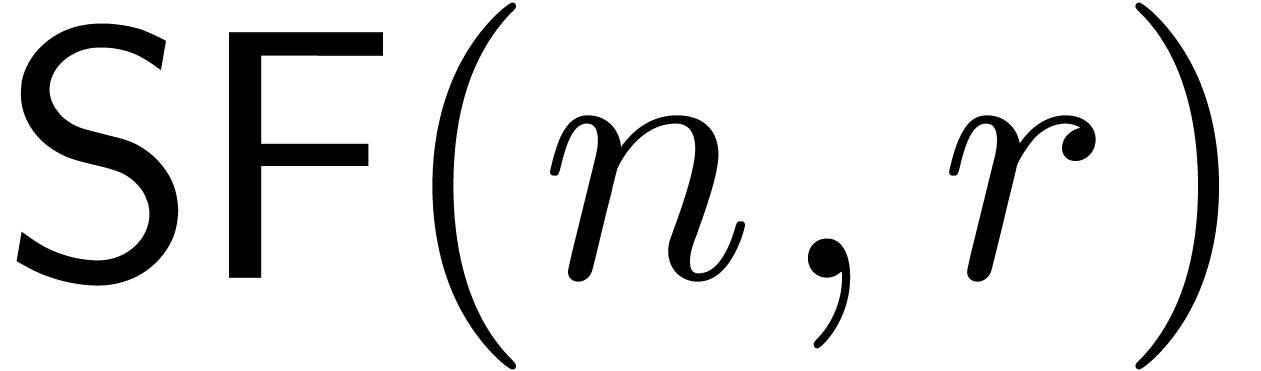 to compute a fundamental system of
to compute a fundamental system of
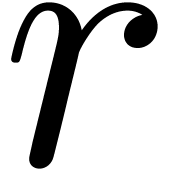 solutions to the monic equation
solutions to the monic equation 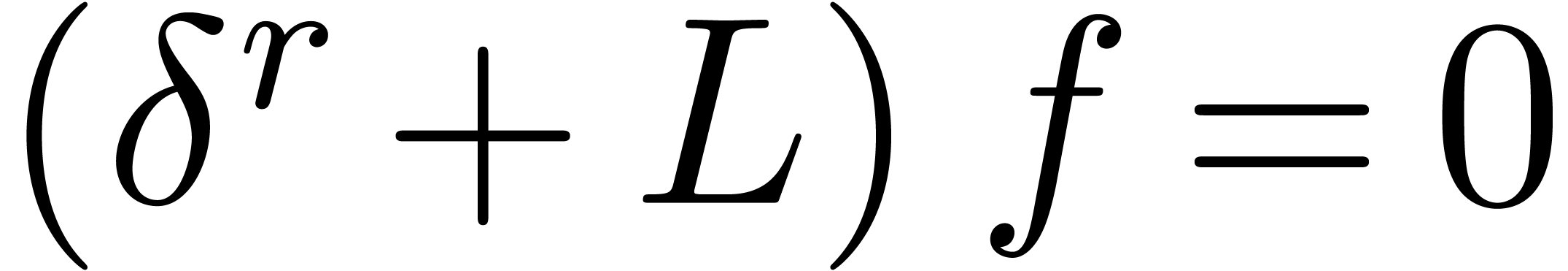 in
in 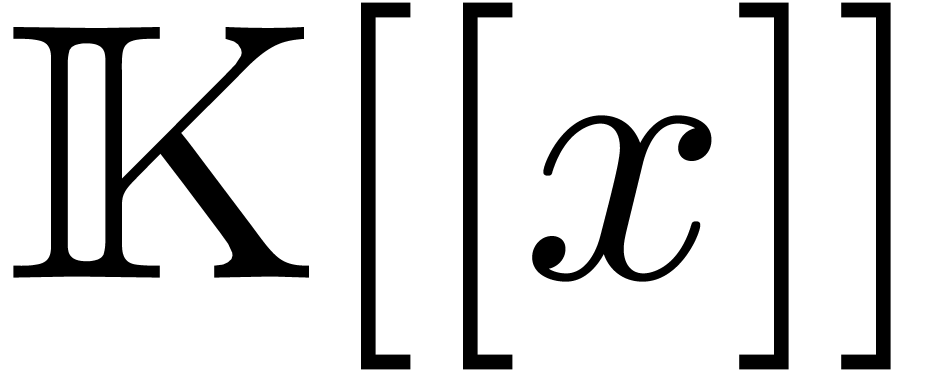 , up to
order
, up to
order 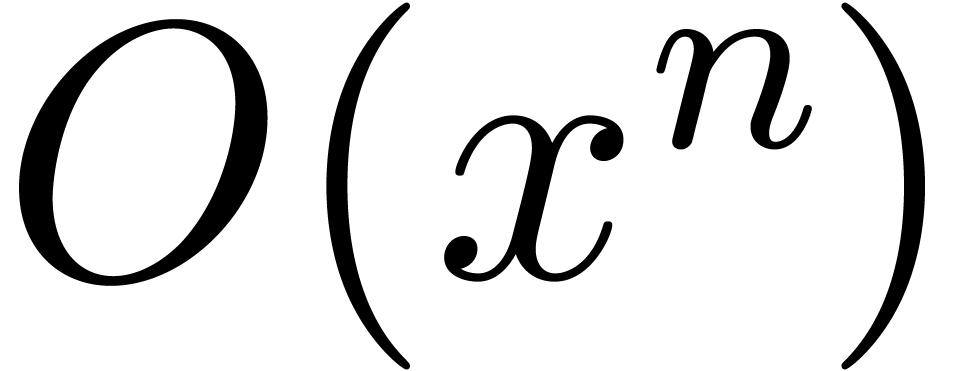 , while assuming
the existence of such a fundamental system.
, while assuming
the existence of such a fundamental system.
Given a vector  of
of 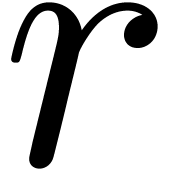 truncated power series in
truncated power series in 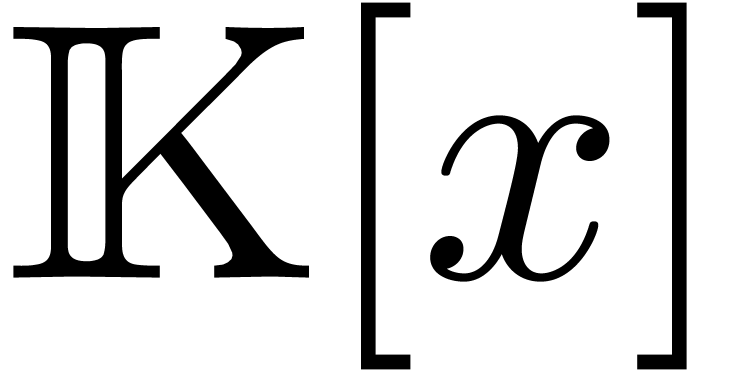 ,
the cost
,
the cost  of computing a monic operator in
of computing a monic operator in
 with
with  .
.
The special case 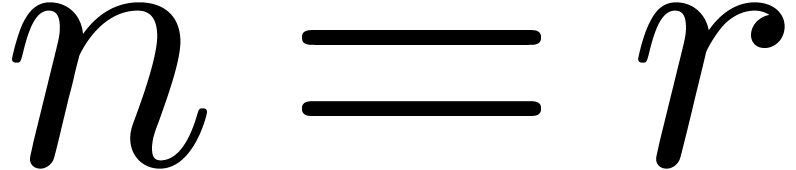 was first studied in [20],
where it was shown that
was first studied in [20],
where it was shown that 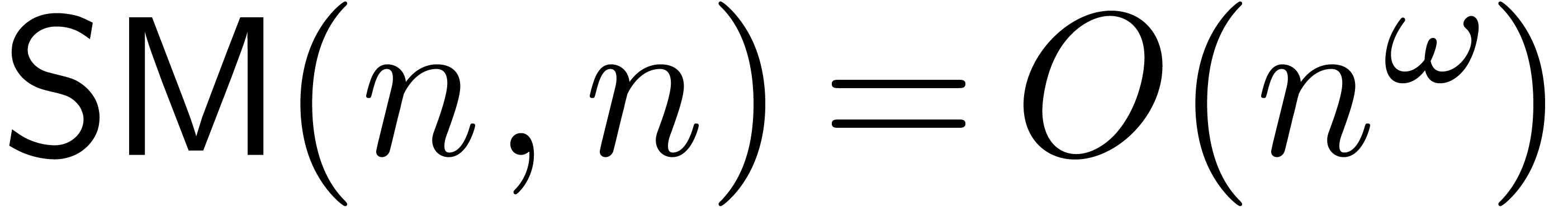 ,
using evaluation-interpolation techniques. The inverse bound
,
using evaluation-interpolation techniques. The inverse bound  has been proved in [5]; this paper also
contains detailed information on the constant factors involved in these
bounds. Recently (and after the writing of a first version of this
paper), the quasi-optimal bound
has been proved in [5]; this paper also
contains detailed information on the constant factors involved in these
bounds. Recently (and after the writing of a first version of this
paper), the quasi-optimal bound 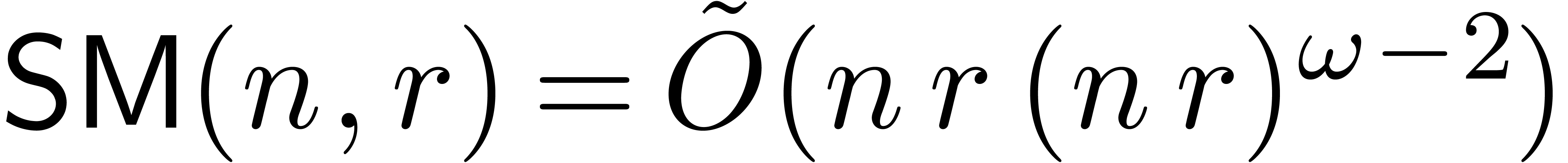 was proved in
[2].
was proved in
[2].
For fixed constants 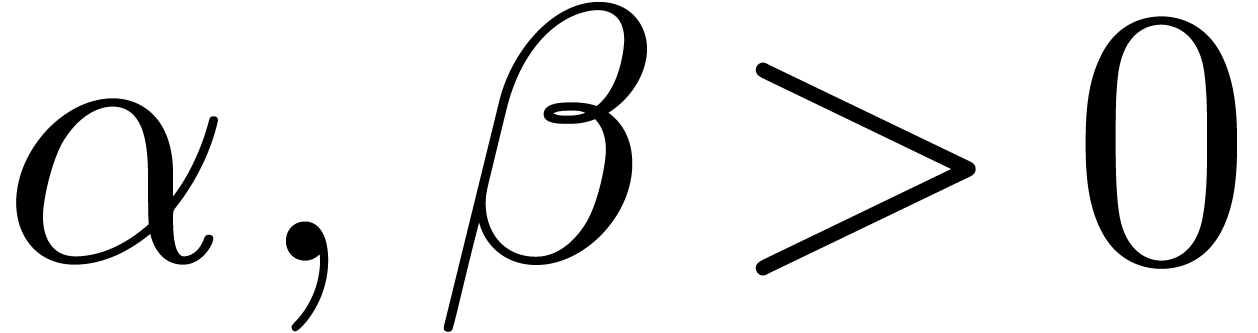 , one has
, one has
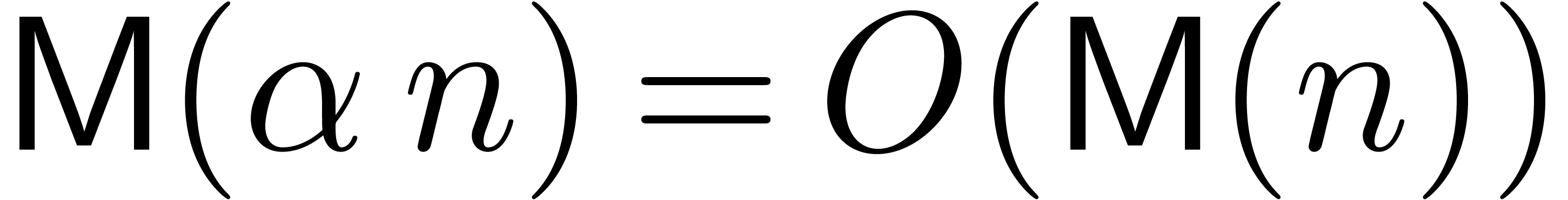 ,
, 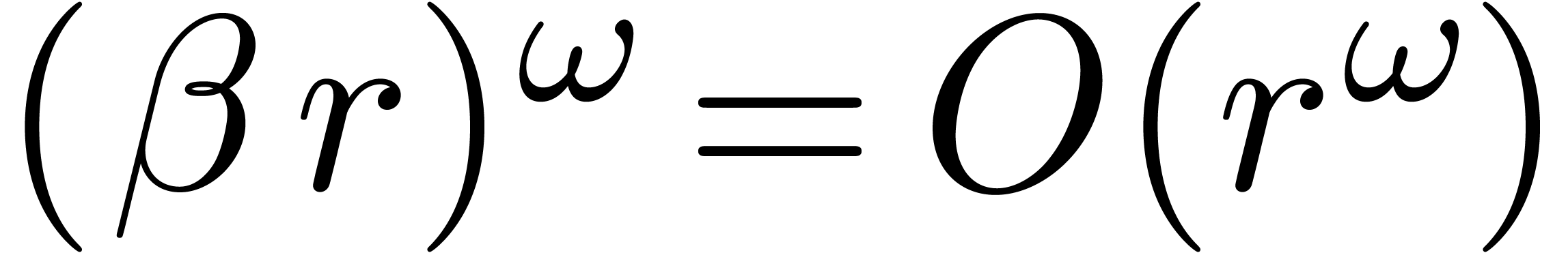 ,
, 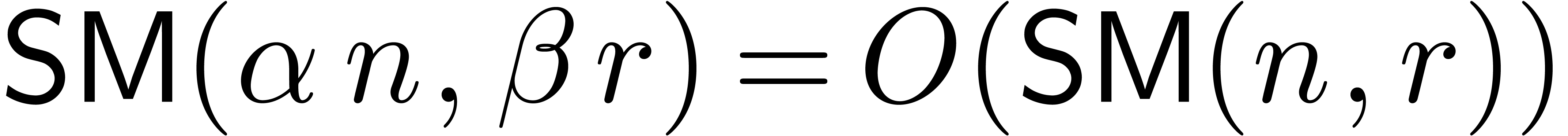 , etc.,
by splitting the multiplicands in a finite number of pieces. In this
paper, we will freely use this remark without further mention. In order
to simplify our complexity estimates, it will be convenient to make a
few additional assumptions. First of all, we will assume that
, etc.,
by splitting the multiplicands in a finite number of pieces. In this
paper, we will freely use this remark without further mention. In order
to simplify our complexity estimates, it will be convenient to make a
few additional assumptions. First of all, we will assume that 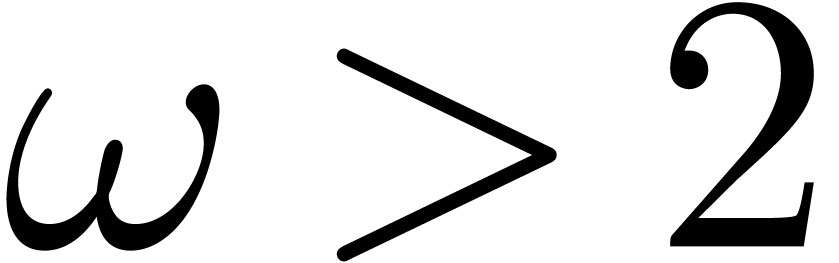 , whence in particular
, whence in particular 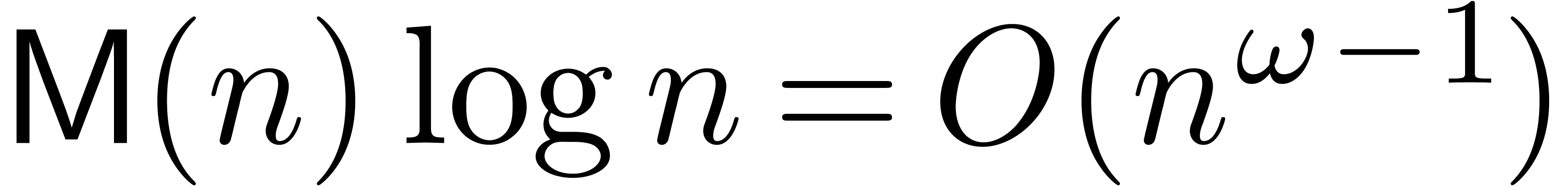 . We will also assume that the function
. We will also assume that the function 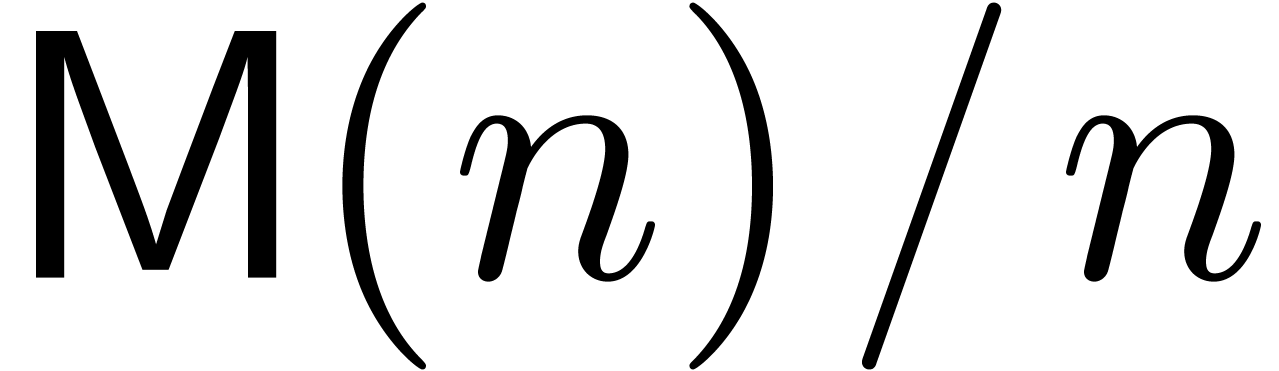 is increasing and that
is increasing and that 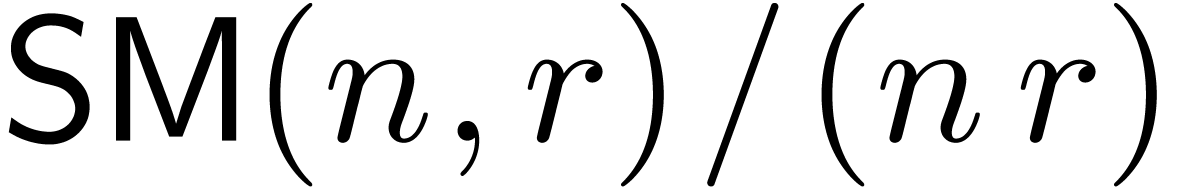 is
increasing in both
is
increasing in both 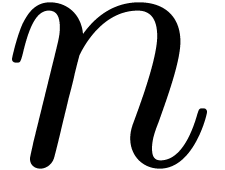 and
and 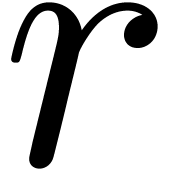 . This will indeed be the case for the complexity
bounds for
. This will indeed be the case for the complexity
bounds for  that will be given in Section 3.
that will be given in Section 3.
In Section 2, we will first prove (see Theorems 2
and 3) that the problems of multiplication and
operator-vector application are essentially equivalent when 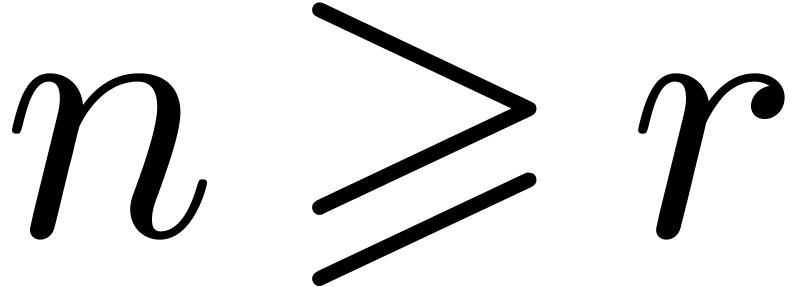 . We also recall the best existing bounds for
operator multiplication.
. We also recall the best existing bounds for
operator multiplication.
In Section 3, we show that the problems of computing
fundamental systems of solutions and its inverse can be reduced to
operator multiplication modulo a logarithmic overhead (see Theorems 7 and 8). This provides a dual way to perform
operations on differential operators by working on their fundamental
systems of solutions. In Section 3 and all subsequent
sections, we always assume that  .
This is indeed required for the truncations of the fundamental systems
of solutions at order
.
This is indeed required for the truncations of the fundamental systems
of solutions at order 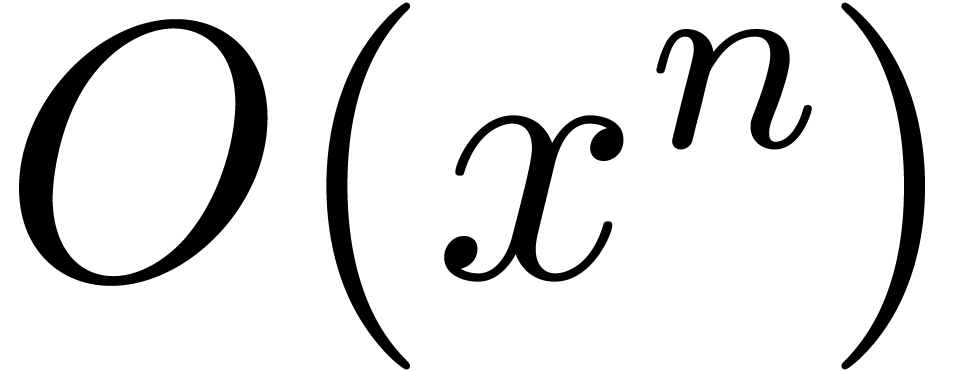 to be linearly
independent.
to be linearly
independent.
In Section 4, we start with the operations of exact right
division and right division with remainder. In Section 5,
we consider greatest common right divisors (gcrds) and least common left
multiples (lclms). Again, we will show how to express the complexities
of these operations essentially in terms of the complexity 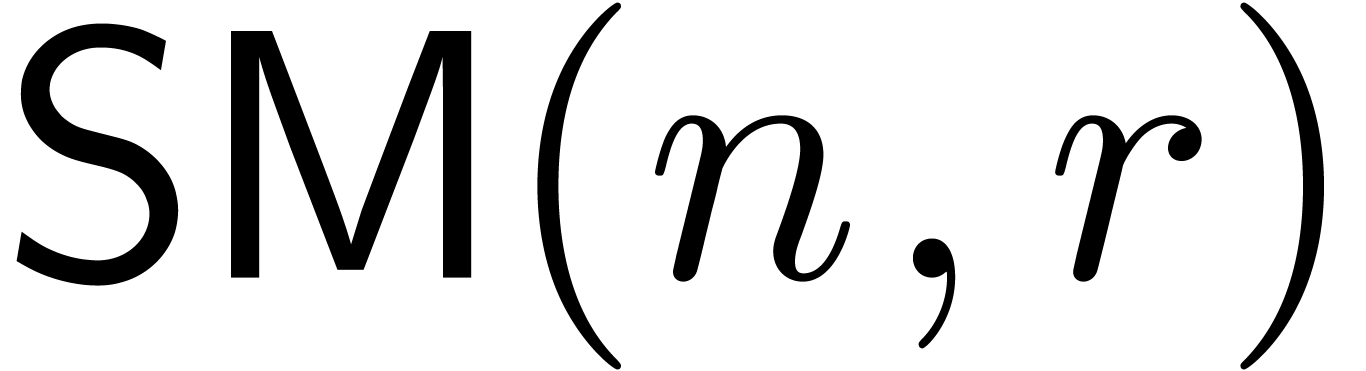 of multiplication (see Theorems 13, 15,
18 and 21).
of multiplication (see Theorems 13, 15,
18 and 21).
For several of our algorithms, we need to work at a point where certain operators are non singular. If we only need the input operators to be non singular, then it is easy to find a point where this is the case. If we also need the output operators or certain auxiliary operators to be non singular (as in Section 5), then we resort to picking random points, which are non singular with probability 1. In Section 5.2 we present additional techniques for turning algorithms which rely on random point picking into randomized algorithms of Las Vegas type and into fully deterministic algorithms.
For technical reasons, we found it convenient to work with respect to
the Euler derivation 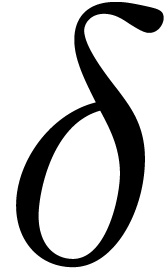 instead of
instead of  . Nevertheless, operators
. Nevertheless, operators  in
in 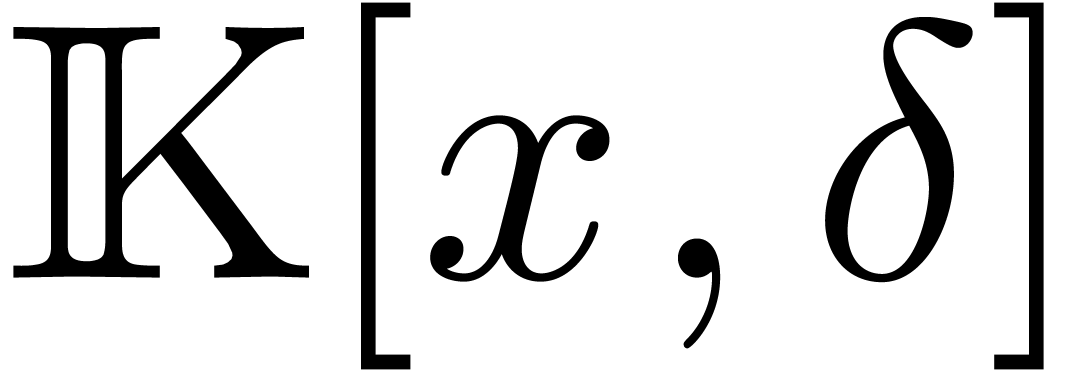 can be converted efficiently into operators
in
can be converted efficiently into operators
in 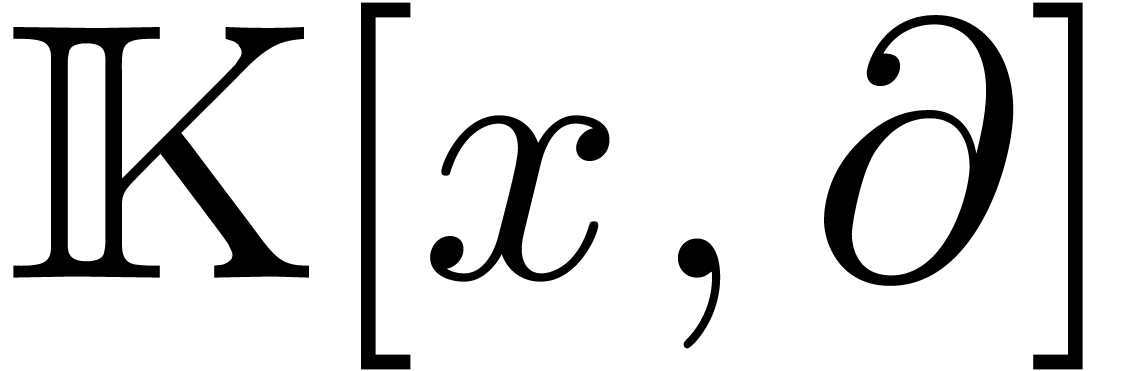 and vice versa, modulo an increase
of the degree
and vice versa, modulo an increase
of the degree 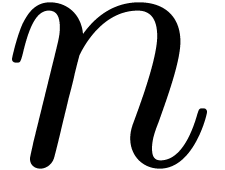 in
in  with
the degree
with
the degree 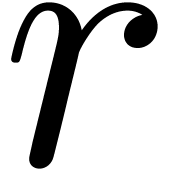 in
in 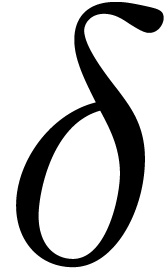 or
or  (see Lemma 6). Using our assumption that
(see Lemma 6). Using our assumption that
 , such increases of the
degree
, such increases of the
degree 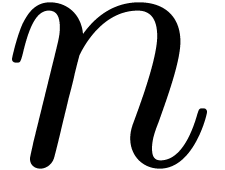 by
by 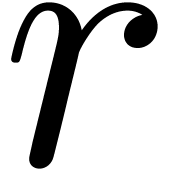 only gives
rise to constant overheads in the complexity bounds. Hence, the
complexity bounds for our main algorithms from Sections 3,
4 and 5 still hold when replacing
only gives
rise to constant overheads in the complexity bounds. Hence, the
complexity bounds for our main algorithms from Sections 3,
4 and 5 still hold when replacing 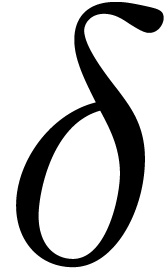 by
by  . In
addition, some of the algorithms can be adapted to directly use
. In
addition, some of the algorithms can be adapted to directly use  instead of
instead of 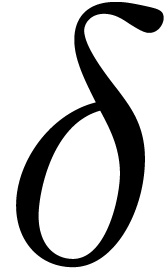 ,
without the need for any conversions (see Remark 11).
,
without the need for any conversions (see Remark 11).
To the best of our knowledge, the idea to perform operations on linear differential operators via power series solutions was first proposed (but only partially worked out) in [4, Chapter 10]. In this paper, we use a slightly different technique: instead of a single power series solution, we prefer to consider a fundamental system of solutions. This has the advantage of forcing a clean bijection between operators and solution spaces, thereby avoiding part of the randomness in the proposals from [4, Chapter 10].
It is also possible to mimic classical divide and conquer algorithms for
right division, greatest common right divisors and least common left
multiples, while using adjoints in order to perform the recursive
operations on the appropriate side. Such algorithms were partially
implemented inside
Various complexity results for computations with linear differential operators and other skew polynomials were previously obtained [17, 14, 15, 25, 16, 4]. Especially the computation of greatest common right divisors and least common left multiples of two or more operators has received particular attention. After the publication of a first version of this paper [23], the complexities of several classical algorithms [19, 33, 25] for the computation of least common right multiples were studied in great detail in [6], and new improvements were proposed there.
The complexities of most of the algorithms in this paper are stated in terms of the input and output sizes. The uncertified randomized algorithms for gcrds and lclms are optimal up to logarithmic factors from this perspective, which yields an improvement with respect to the previously known complexity bounds. In the context of certified randomized algorithms (i.e. of Las Vegas type), the complexity bounds remain quasi-optimal in terms of the size of a suitable certificate. From the deterministic point of view, the new algorithms for gcrds and lclms are suboptimal.
Acknowledgment. We are grateful to the second referee whose questions and remarks have lead to several improvements with respect to the first version of this paper.
The key argument behind the proof from [20] that 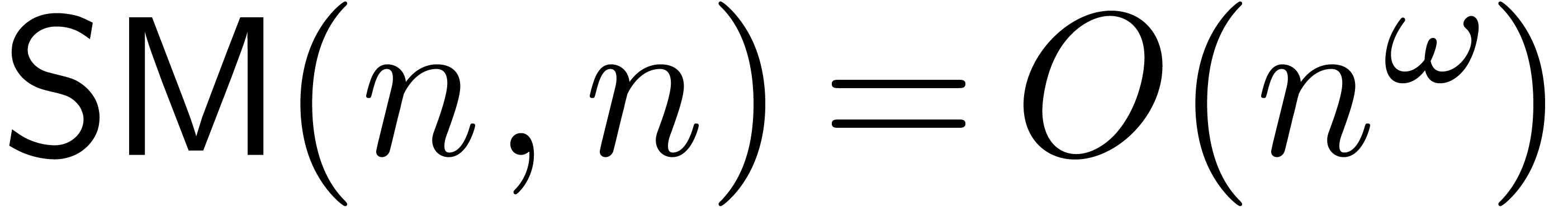 is the observation that an operator
is the observation that an operator 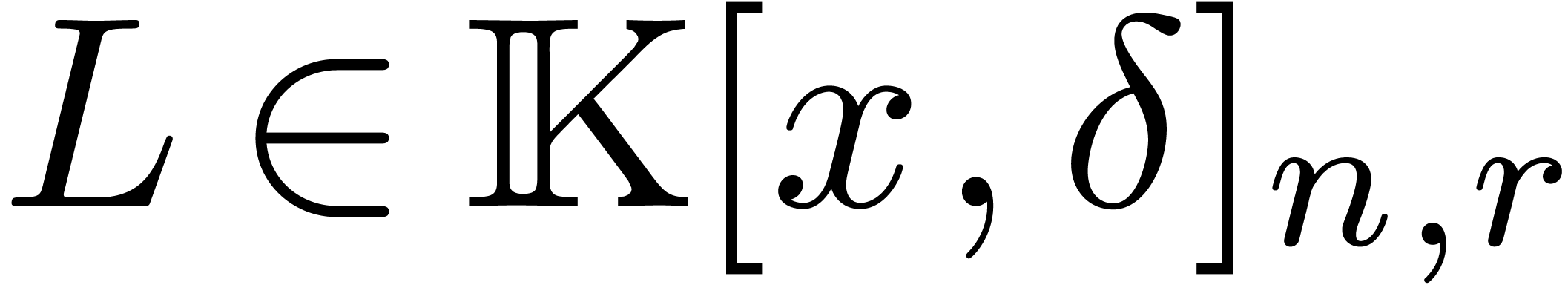 is uniquely determined by its images on the vector
is uniquely determined by its images on the vector  . This makes it possible to use a similar
evaluation-interpolation strategy for the multiplication of differential
operators as in the case of FFT-multiplication of commutative
polynomials. More precisely, given
. This makes it possible to use a similar
evaluation-interpolation strategy for the multiplication of differential
operators as in the case of FFT-multiplication of commutative
polynomials. More precisely, given 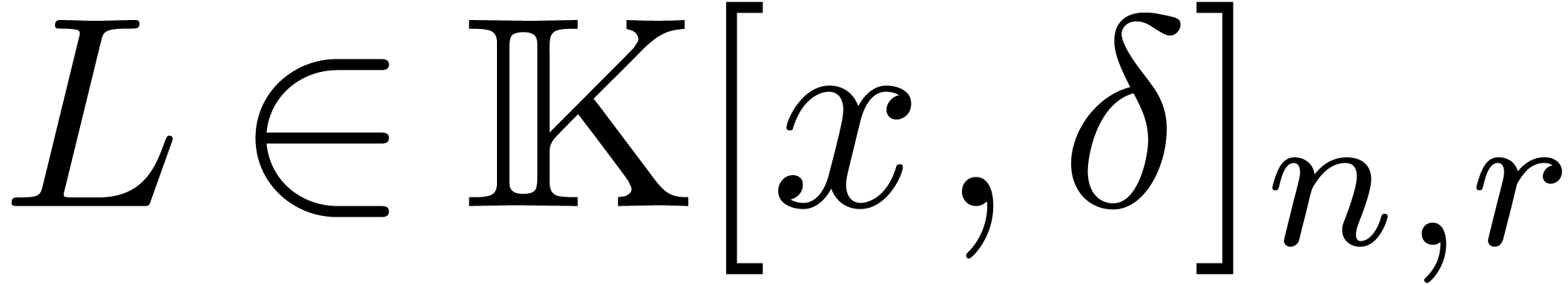 ,
let
,
let 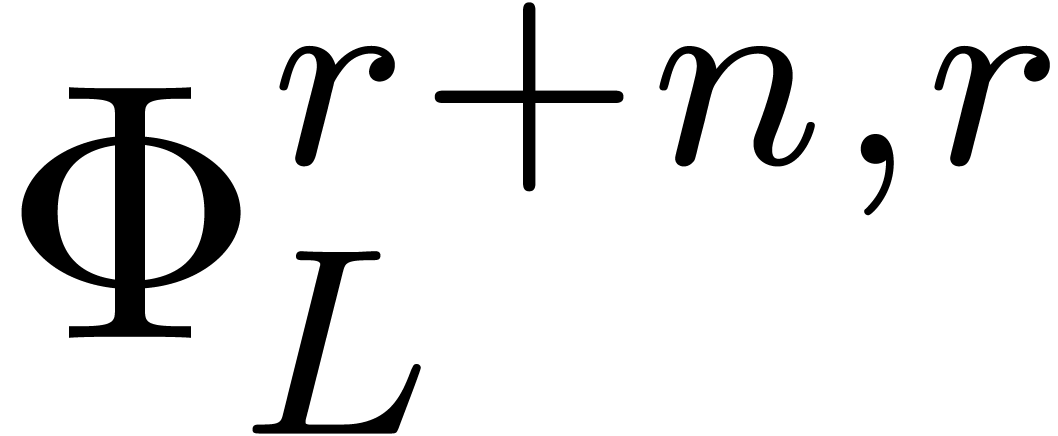 be the matrix of the mapping
be the matrix of the mapping 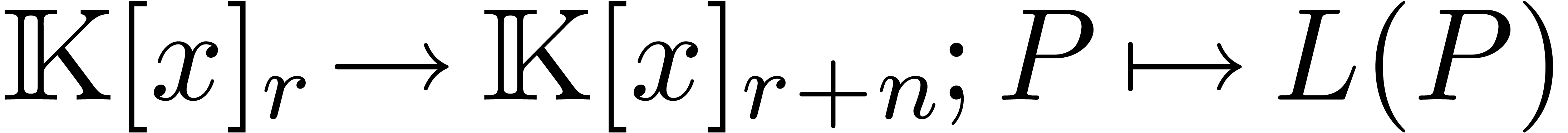 with respect to the bases
with respect to the bases 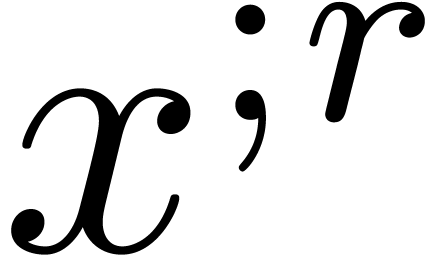 and
and
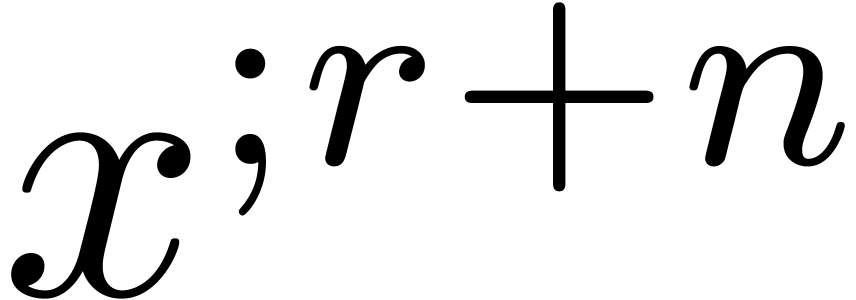 :
:
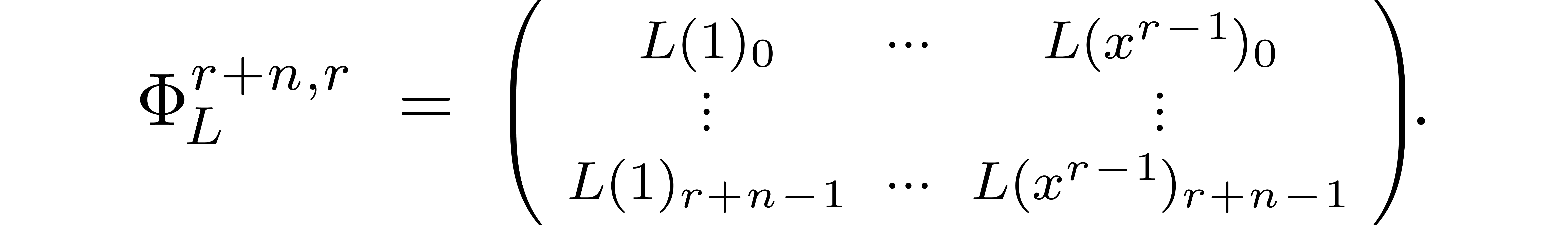
The evaluation and interpolation steps can be done efficiently using the following lemma, which is essentially contained in [5]:
Proof. Consider the expansion of  with respect to
with respect to 
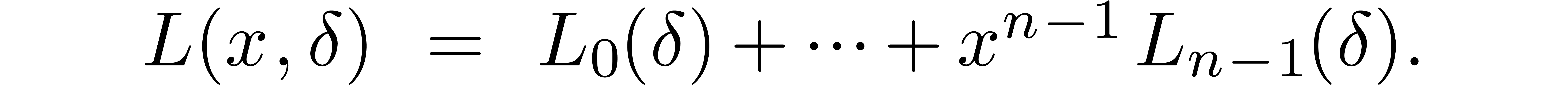
For all  , we have
, we have
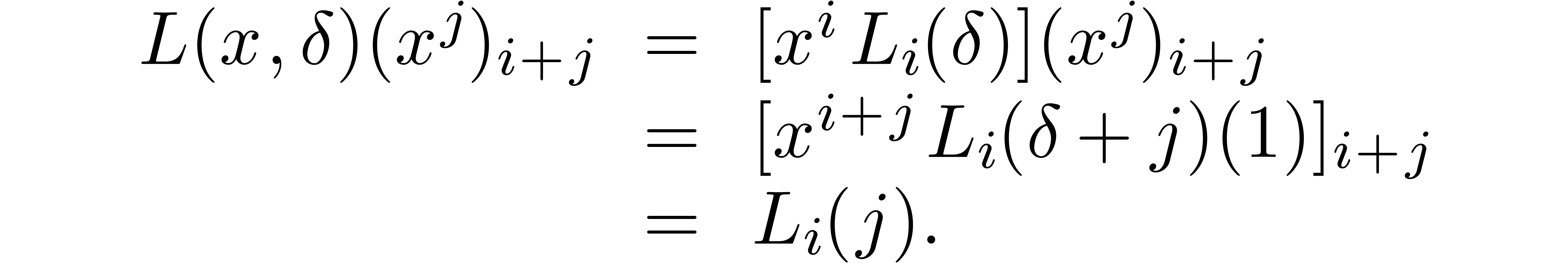
In other words, 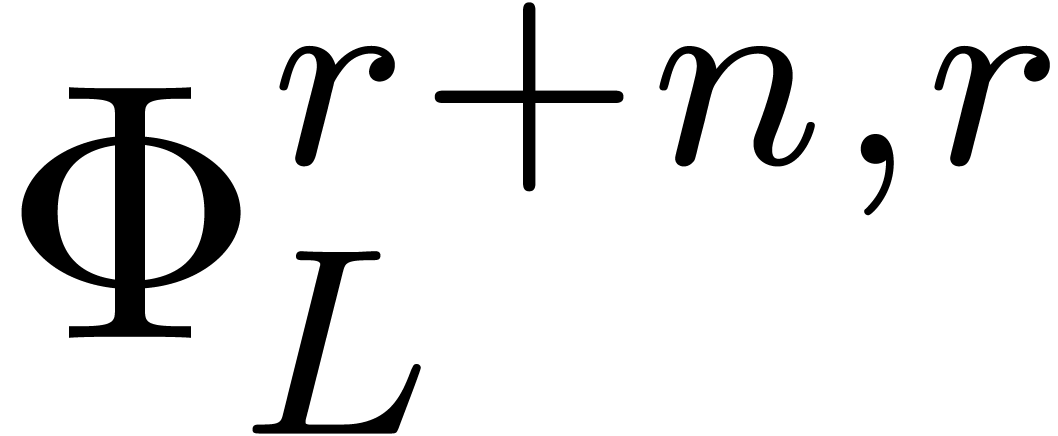 is a lower triangular band
matrix
is a lower triangular band
matrix
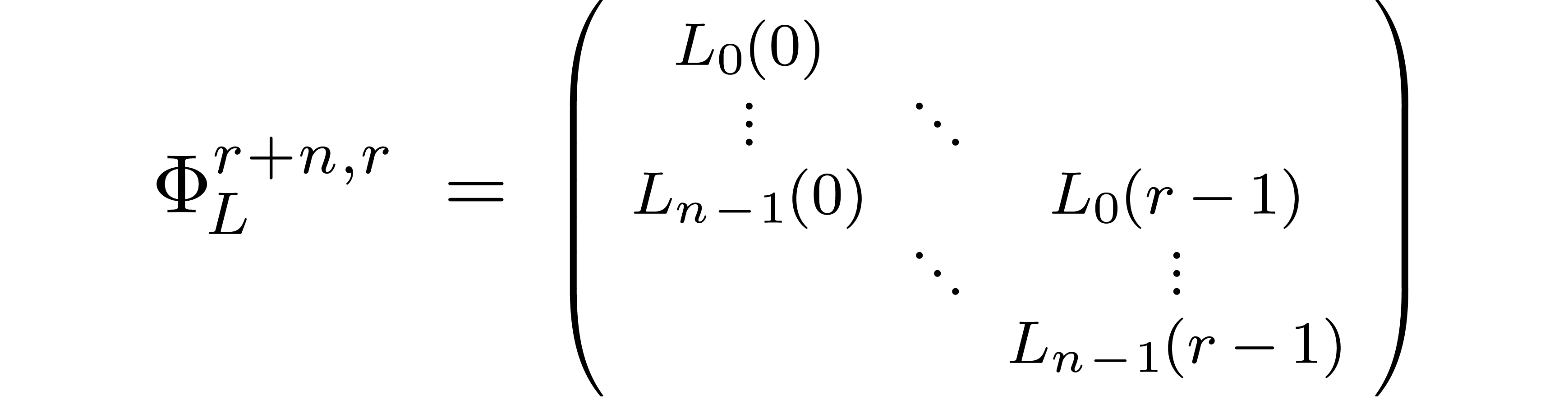
of bandwidth 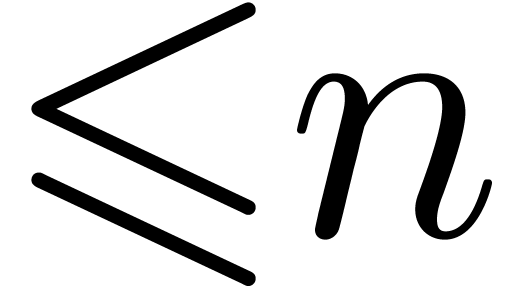 . The
coefficients on the
. The
coefficients on the 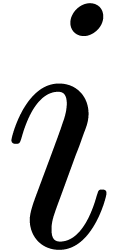 -th
subdiagonal of
-th
subdiagonal of 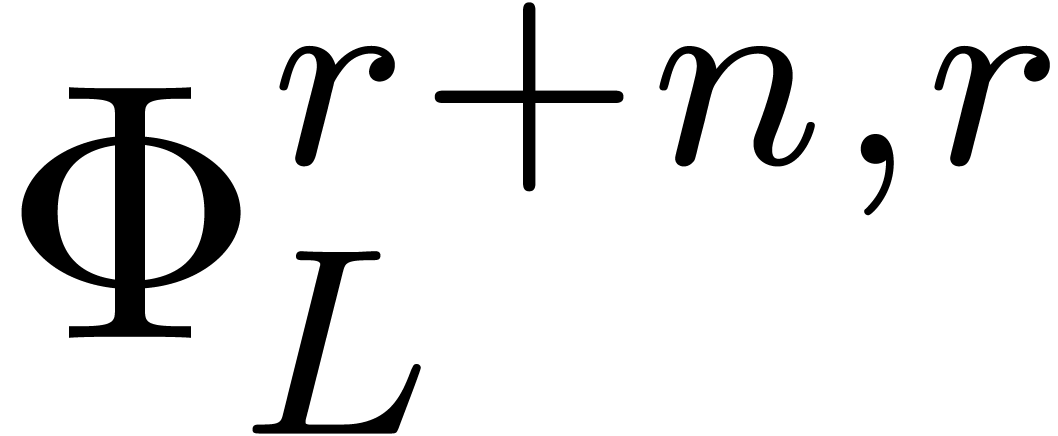 are exactly the result of a
multipoint evaluation of
are exactly the result of a
multipoint evaluation of 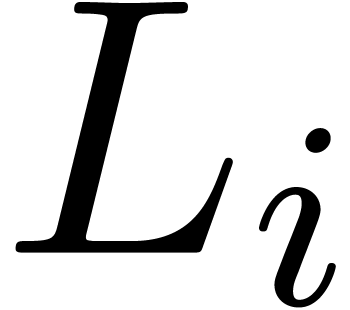 at
at 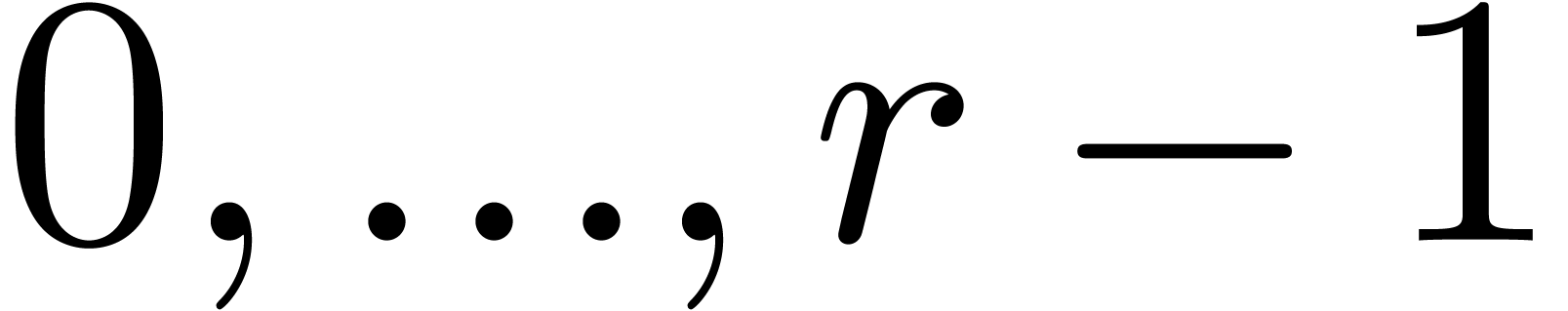 . It is classical [27, 35,
3] that both multipoint evaluation and the inverse
operation of interpolation can be performed in time
. It is classical [27, 35,
3] that both multipoint evaluation and the inverse
operation of interpolation can be performed in time 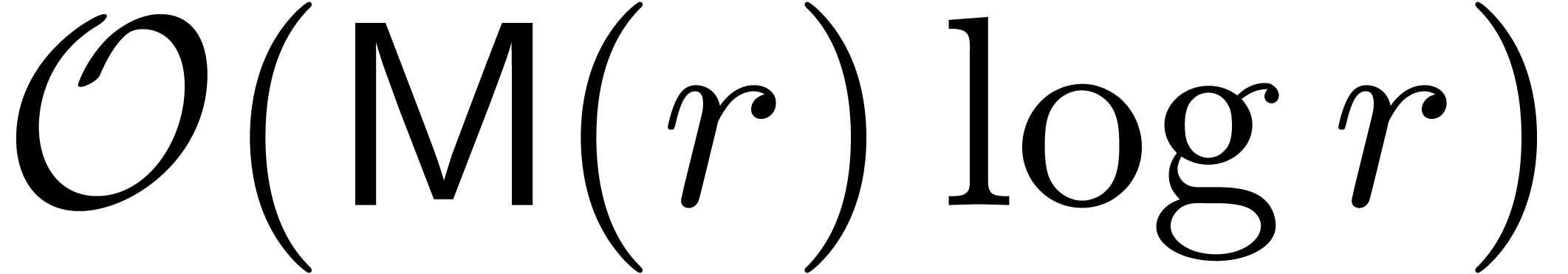 . Doing this for each of the polynomials
. Doing this for each of the polynomials 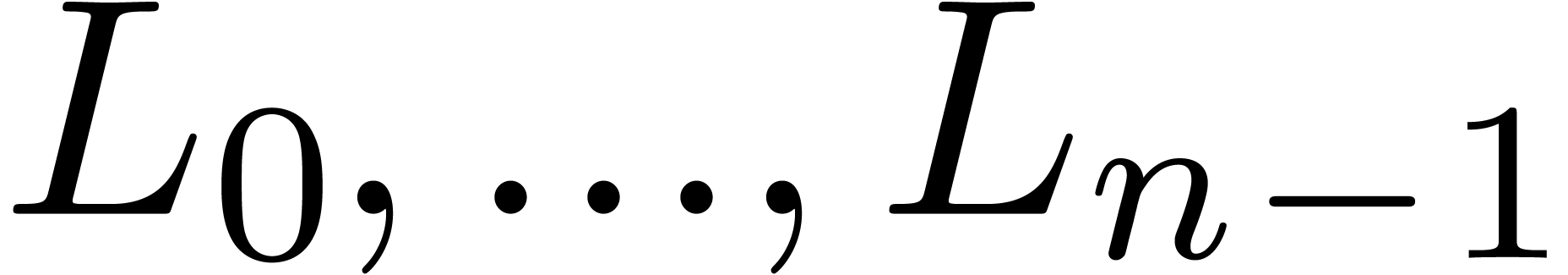 yields the result.
yields the result.
Proof. Let 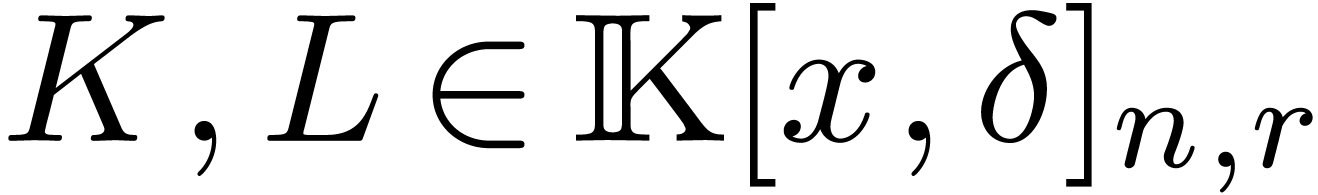 and assume
that we want to compute
and assume
that we want to compute  . We
may evaluate
. We
may evaluate 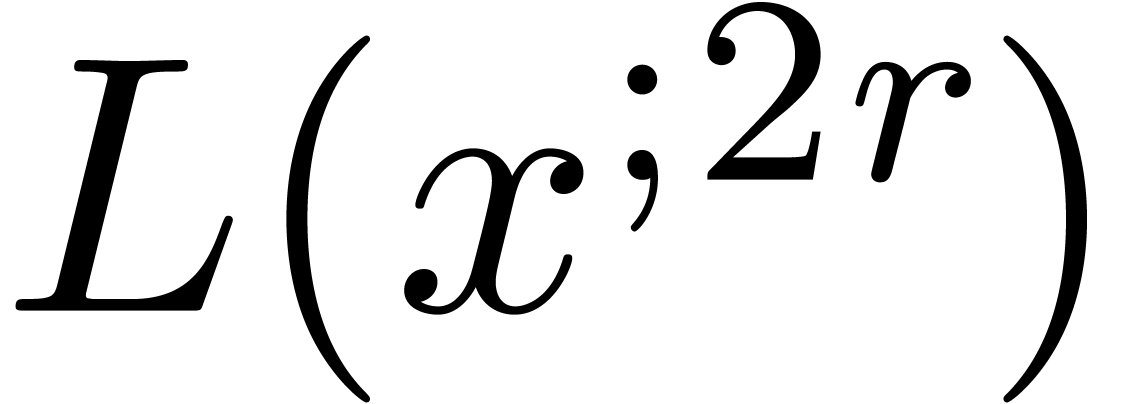 in time
in time 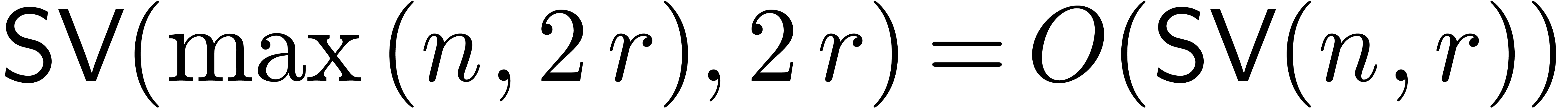 . We may also evaluate
. We may also evaluate 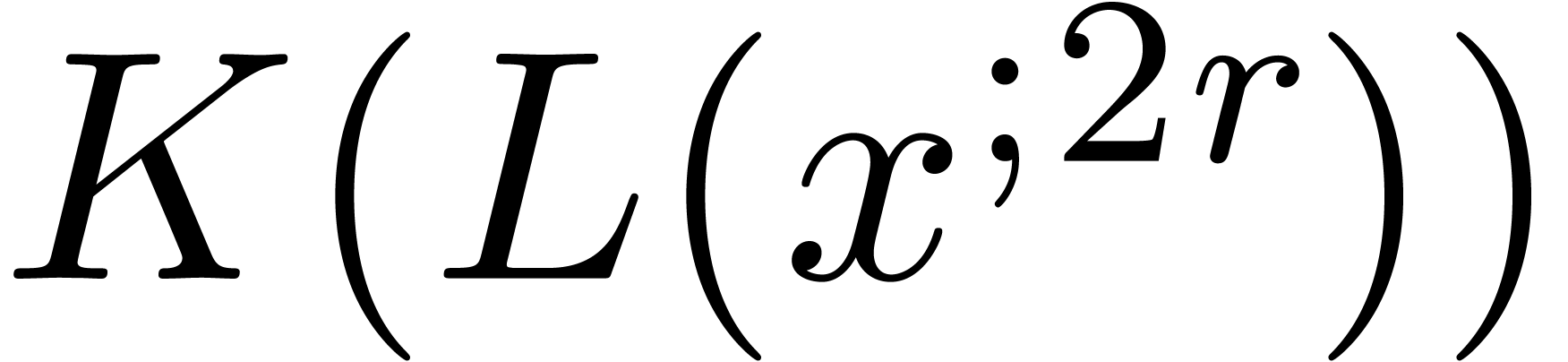 in
time
in
time 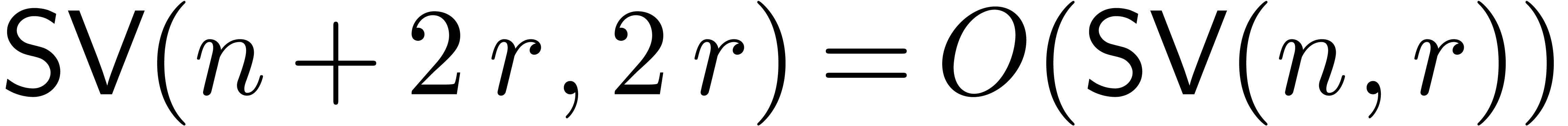 . Using Lemma 1,
we may recover
. Using Lemma 1,
we may recover  from
from 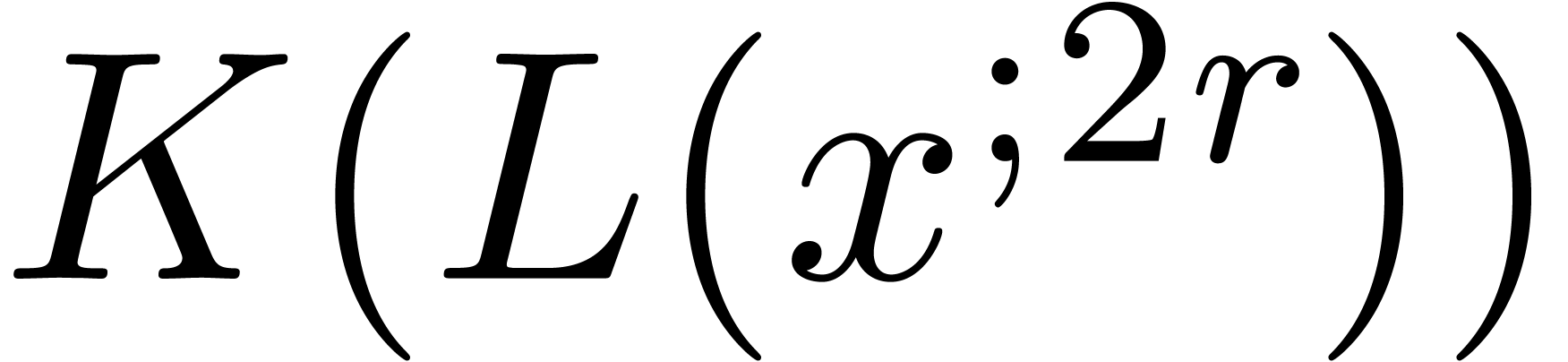 in
time
in
time 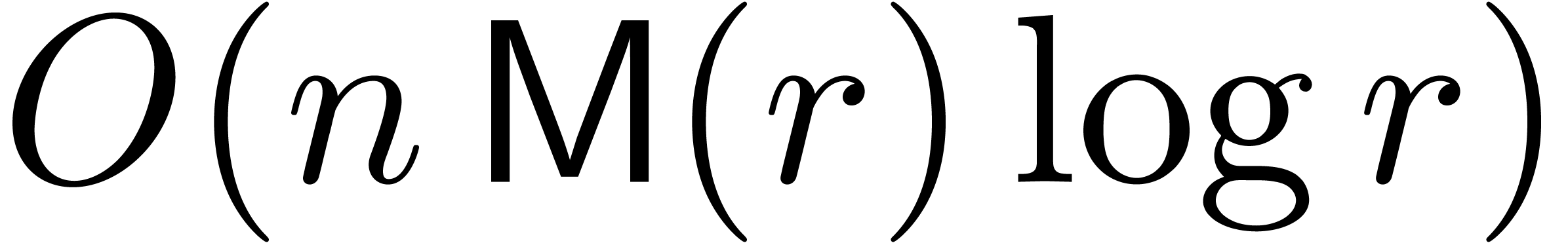 . This completes the
proof.
. This completes the
proof.
Proof. Assume now that we are given 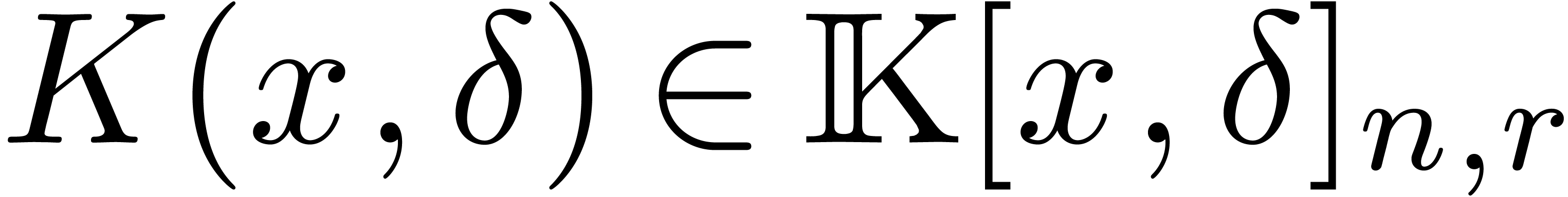 , as well as a vector
, as well as a vector 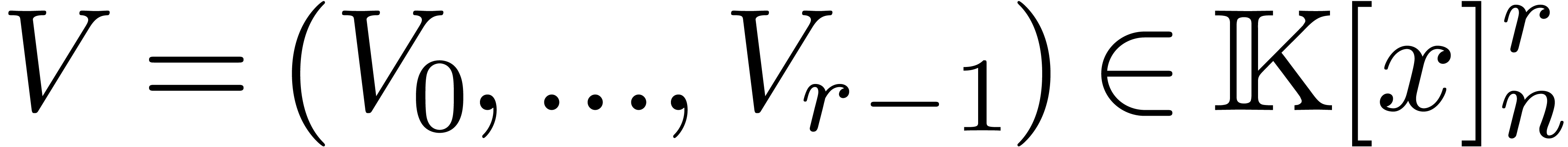 and that we want to evaluate
and that we want to evaluate 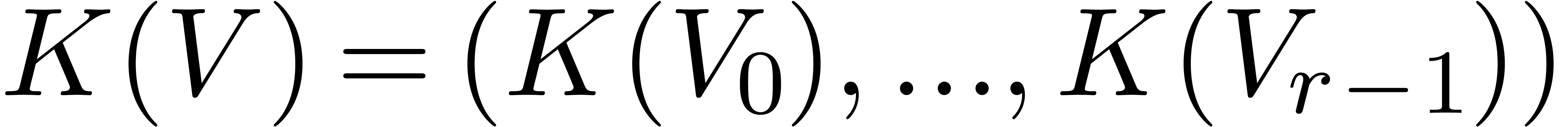 .
This is equivalent to evaluating the operator
.
This is equivalent to evaluating the operator 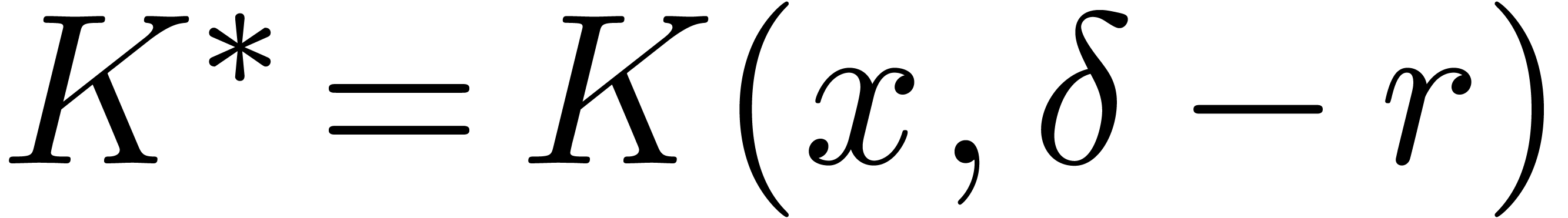 at
the vector
at
the vector 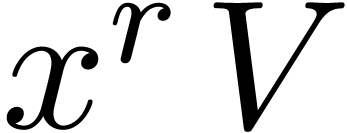 . It is classical
[1] that
. It is classical
[1] that 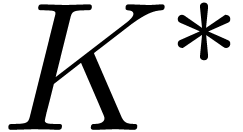 can be computed in time
can be computed in time
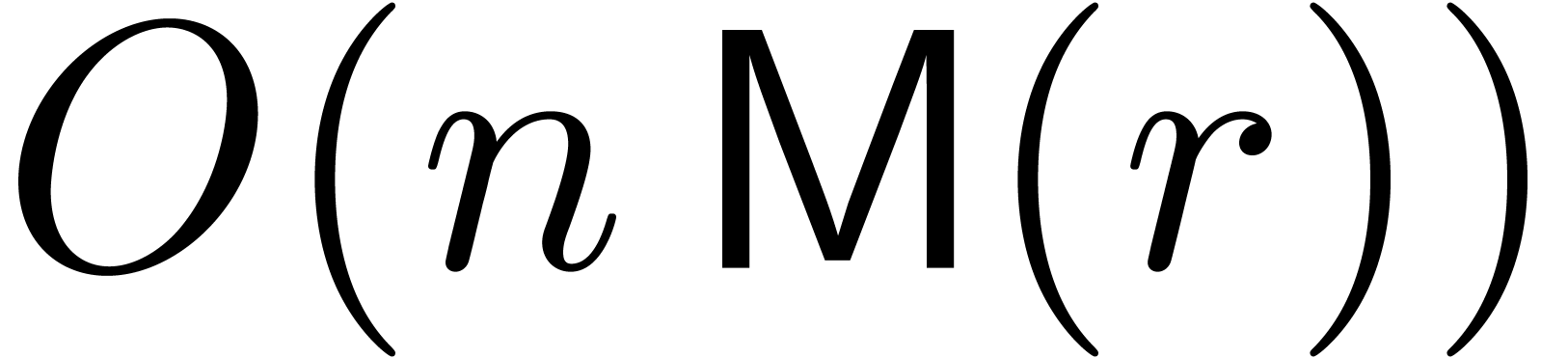 . Using Lemma 1,
we may compute the unique operator
. Using Lemma 1,
we may compute the unique operator 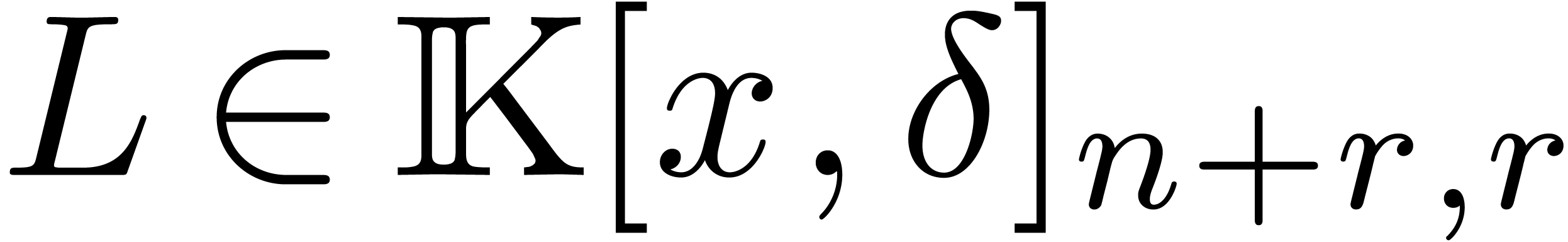 with
with 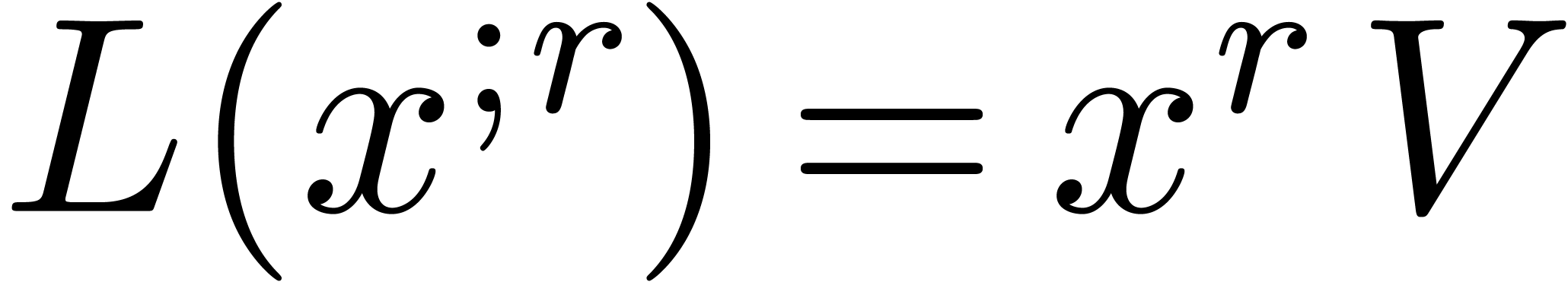 in time
in time 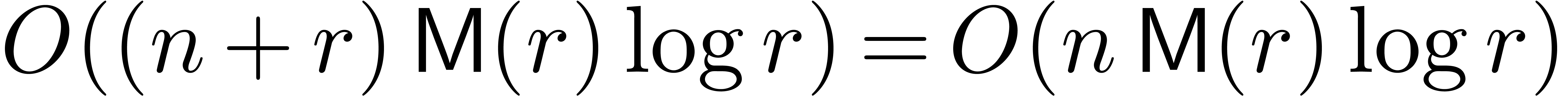 .
We may next compute the product
.
We may next compute the product  in time
in time 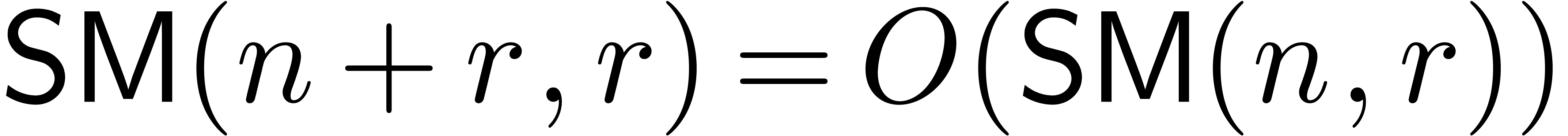 . Lemma 1 finally
allows us to evaluate
. Lemma 1 finally
allows us to evaluate  at
at 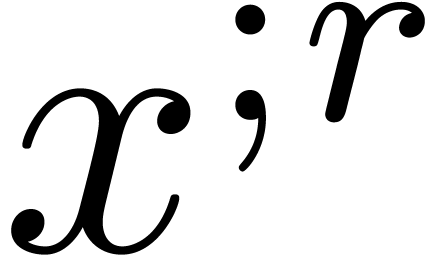 in time
in time 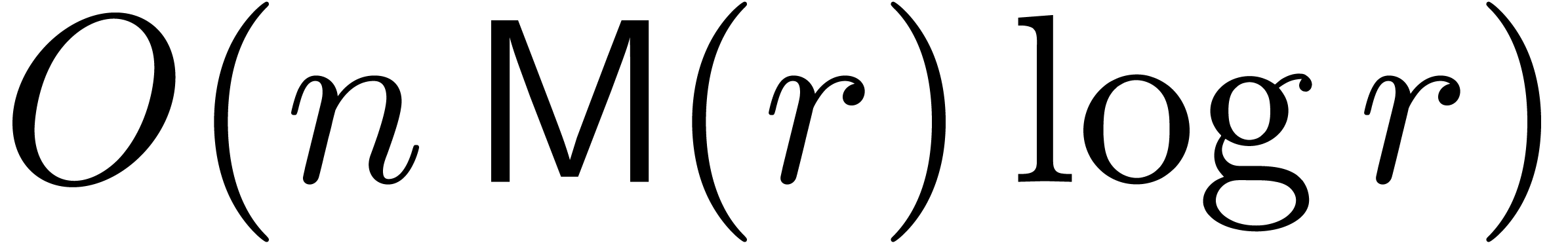 , thereby yielding
, thereby yielding
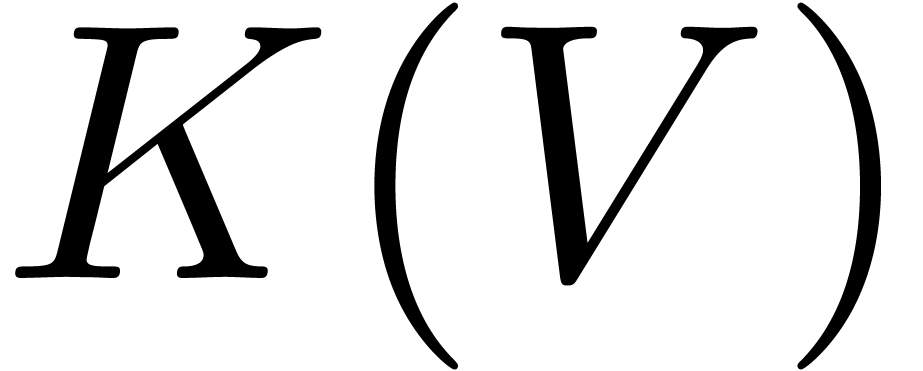 .
.
The above results immediately imply the bound 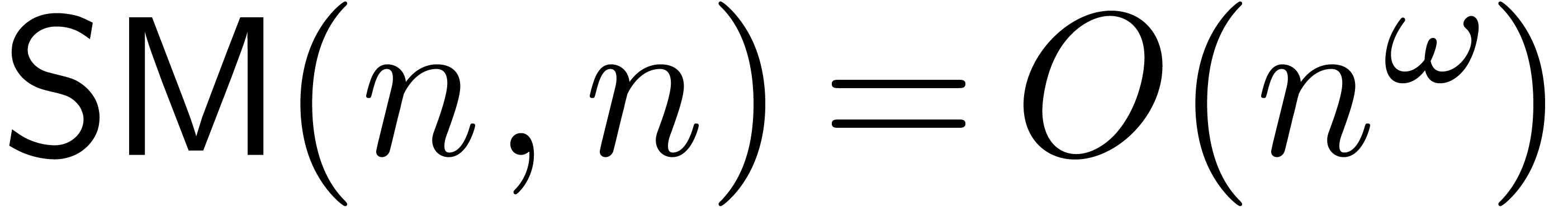 from [20] by the computation of a product
from [20] by the computation of a product 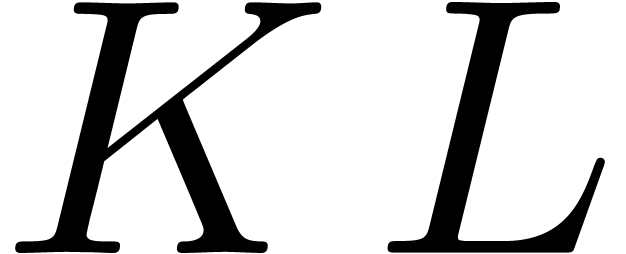 to the computation of a matrix product
to the computation of a matrix product
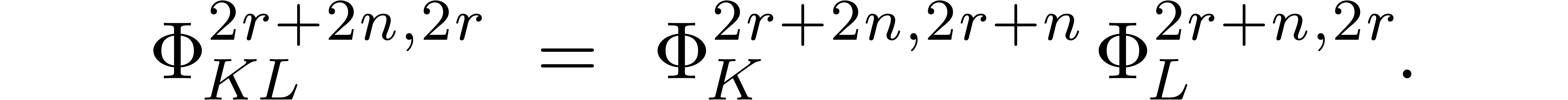
After the publication of a first version of this paper, the following
quasi-optimal bound for 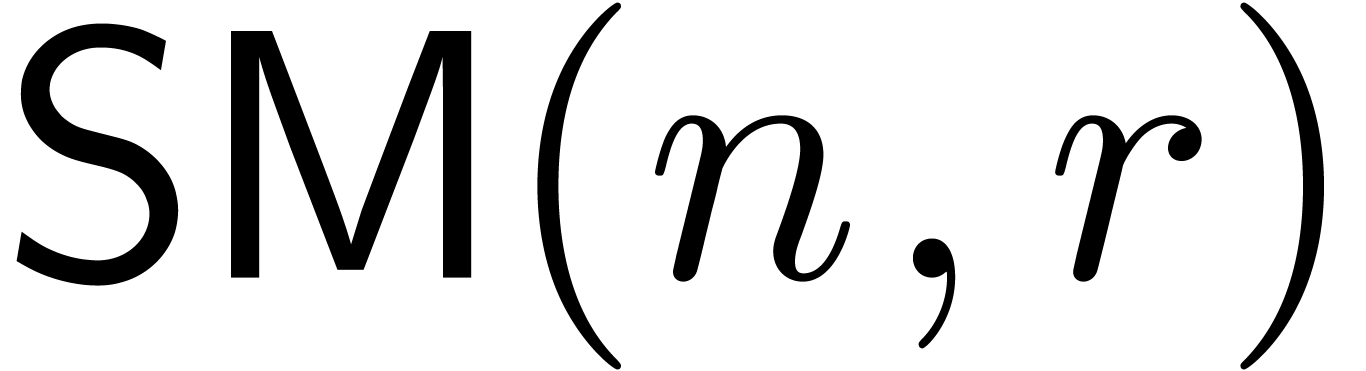 was established in [2, Theorems 3 and 5].
was established in [2, Theorems 3 and 5].
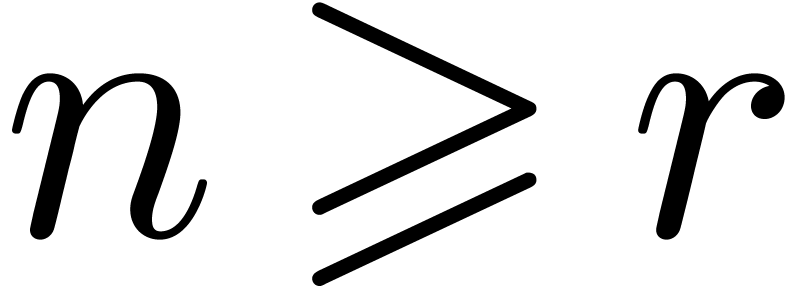
The inverse bound  from [5] can also
be generalized:
from [5] can also
be generalized:
 , then the
product of an
, then the
product of an  matrix and an
matrix and an  matrix with coefficients in
matrix with coefficients in  can be computed in
time
can be computed in
time 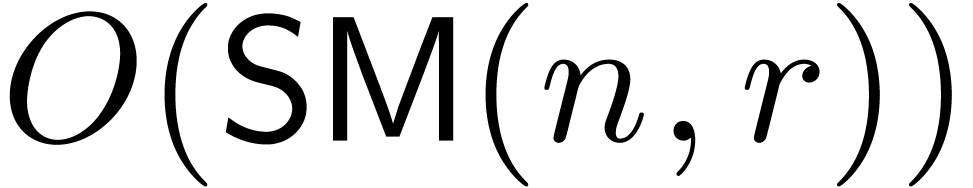 .
.
Proof. By the result from [5], the
problem is equivalent to the computation of 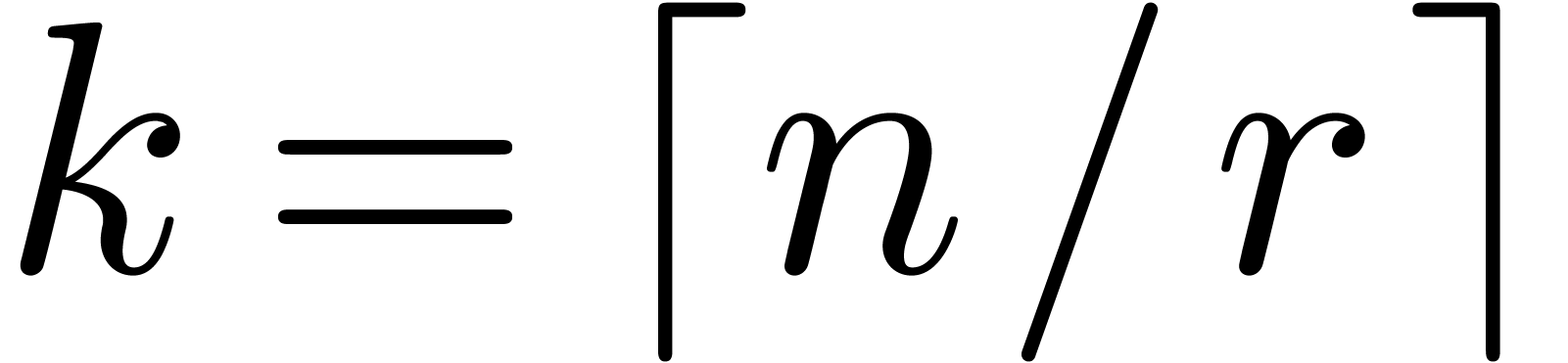 operators
operators 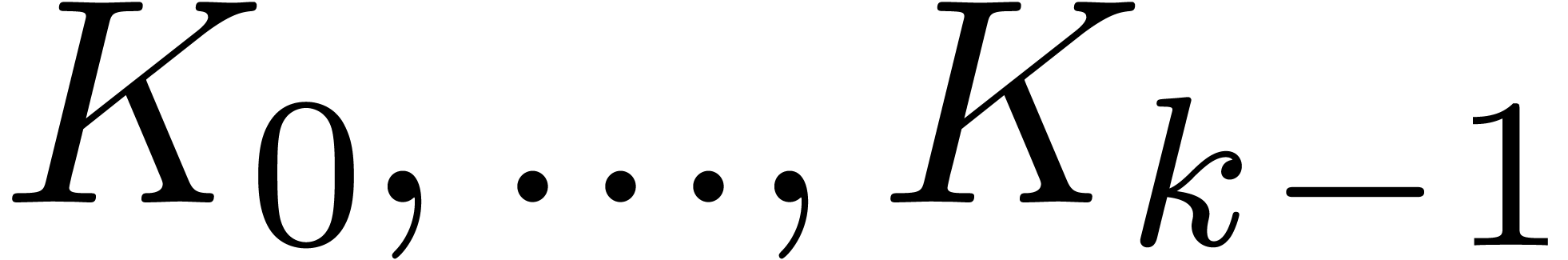 in
in 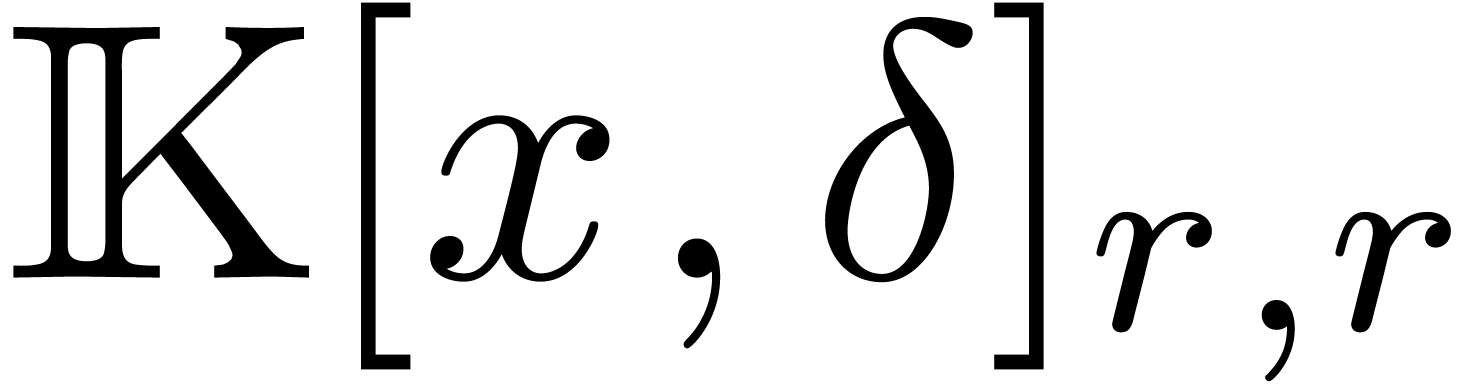 with a
fixed operator
with a
fixed operator 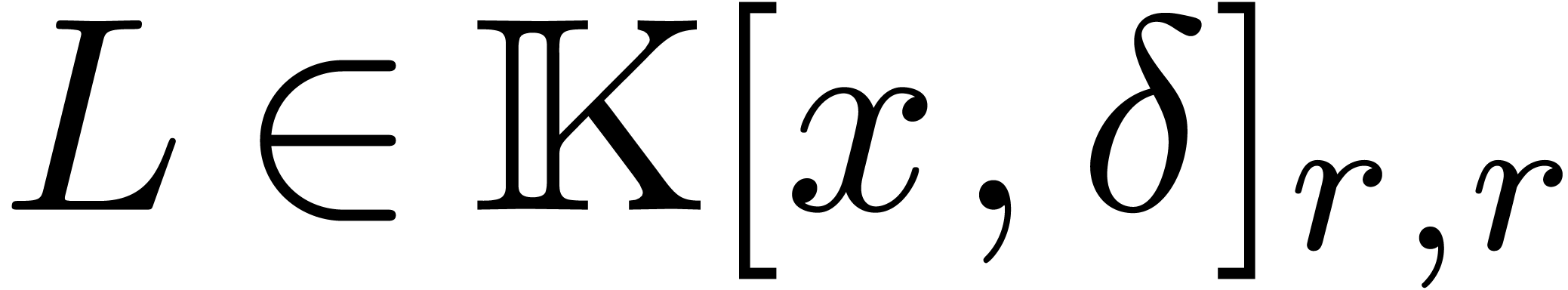 . Setting
. Setting
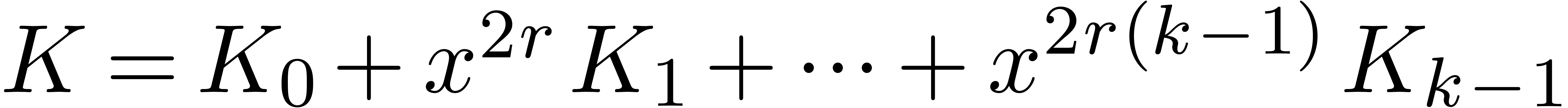 , we may compute
, we may compute  in time
in time 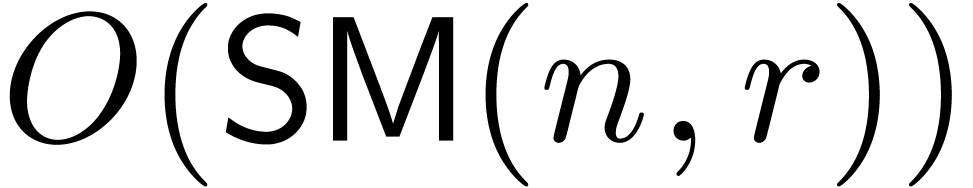 . We
may directly read off the products
. We
may directly read off the products 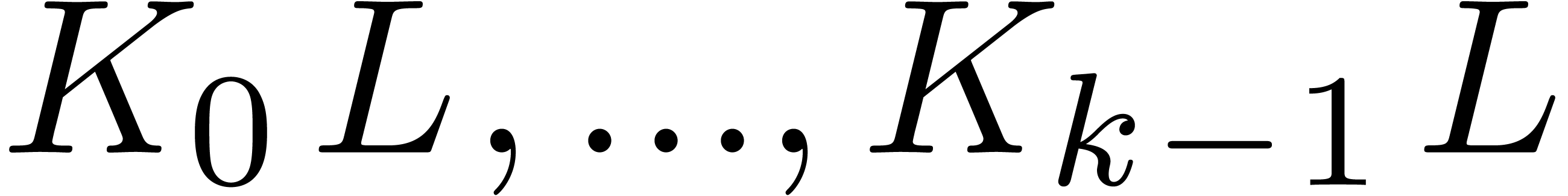 from the
result.
from the
result.
In this paper, we have chosen to work with respect to the derivation
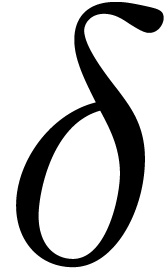 instead of
instead of  .
The following result from [5, Section 3.3] can be used to
efficiently convert between operators in
.
The following result from [5, Section 3.3] can be used to
efficiently convert between operators in 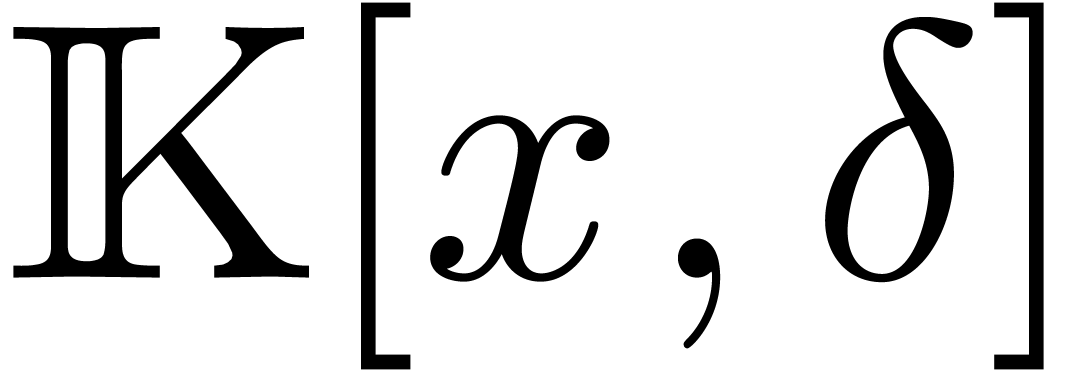 and
and
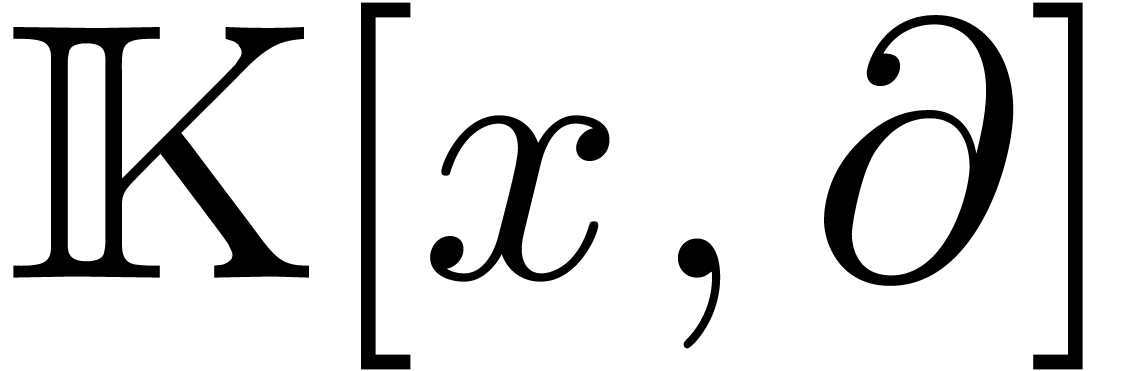 (in [20], we proved a somewhat
weaker result which would also suffice for the purposes of this paper).
We have written
(in [20], we proved a somewhat
weaker result which would also suffice for the purposes of this paper).
We have written 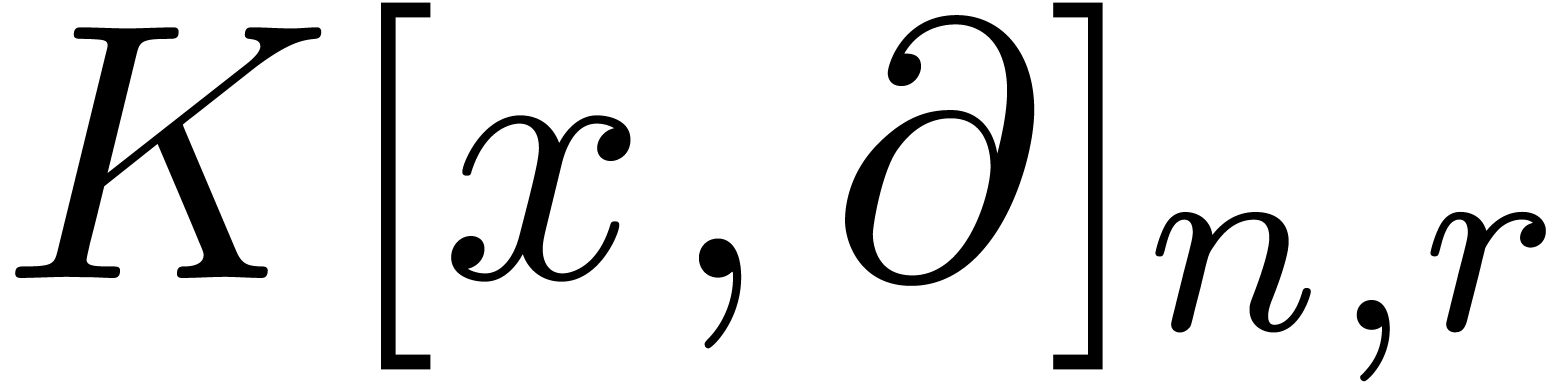 for the set of operators of
degree
for the set of operators of
degree 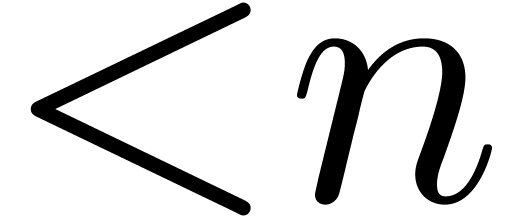 in
in  and degree
and degree
 in
in  .
.
Any operator in 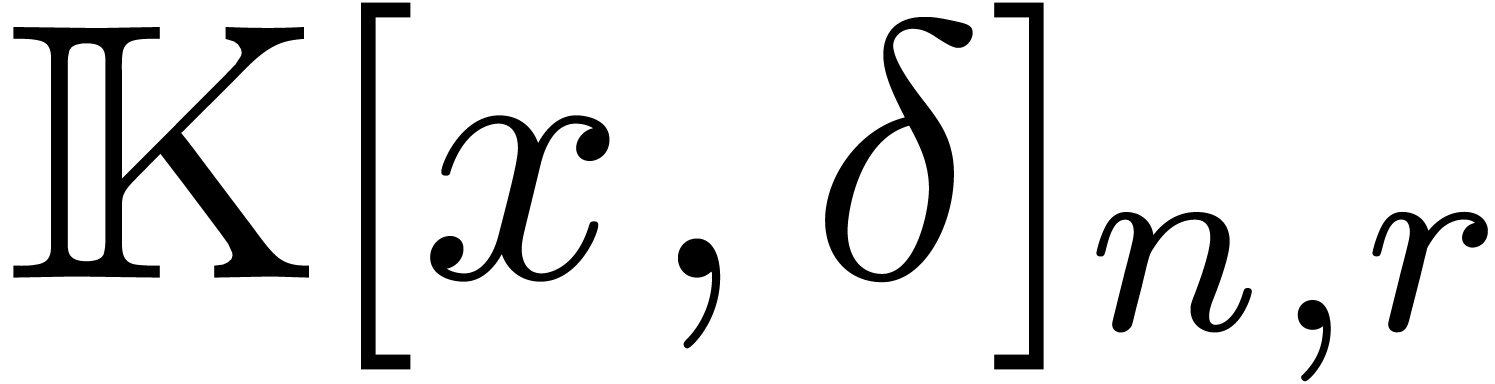 can be converted into an
operator in
can be converted into an
operator in 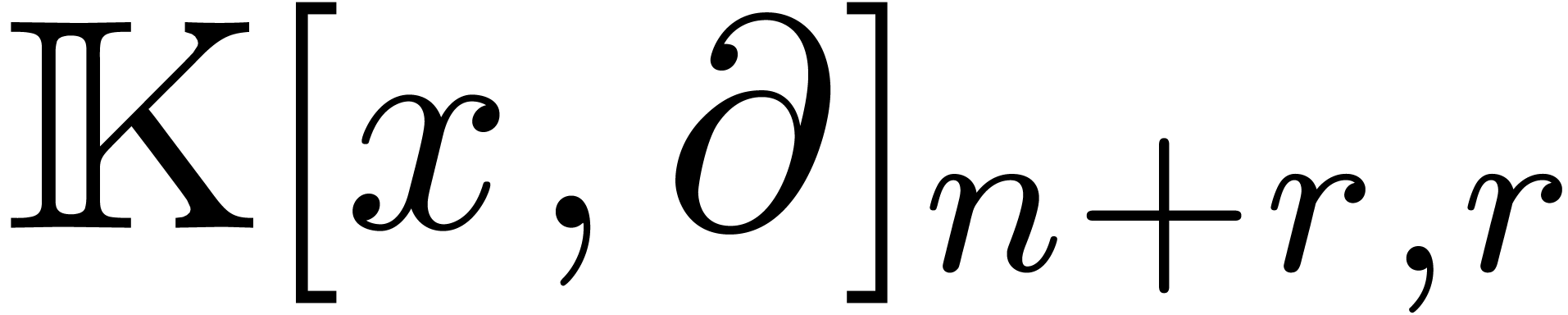 in time
in time 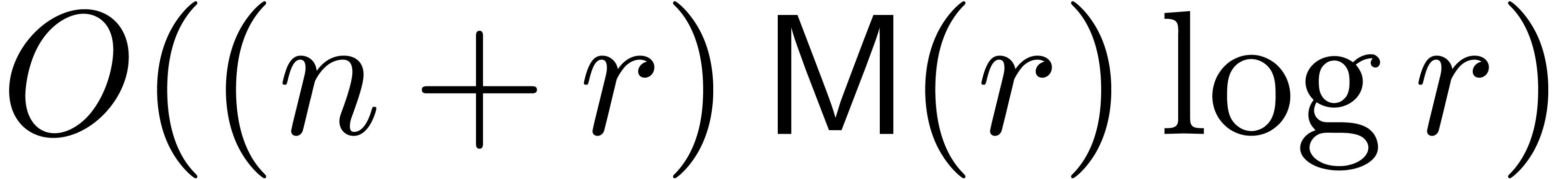 .
.
Any operator in 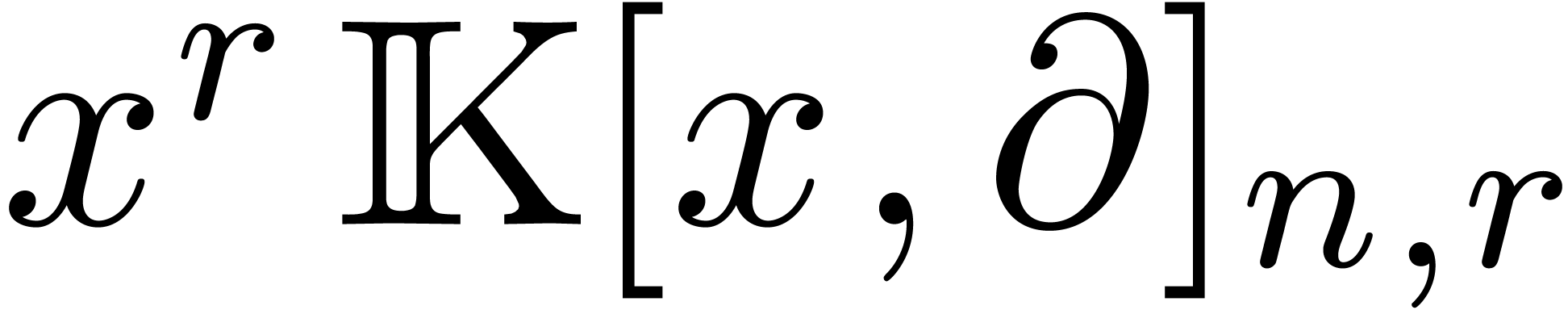 can be converted into an
operator in
can be converted into an
operator in 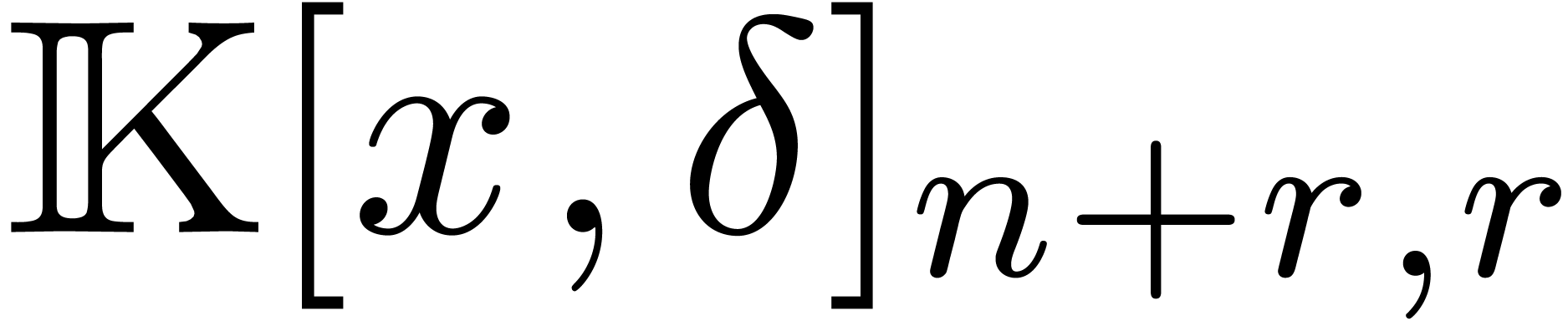 in time
in time 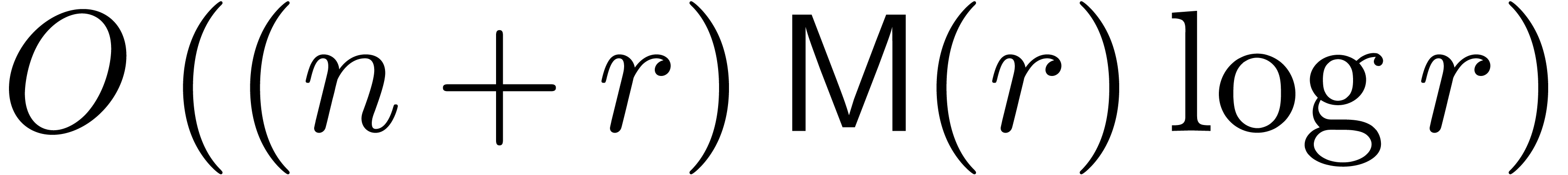 .
.
From now on, we will assume that  .
We recall that an operator
.
We recall that an operator 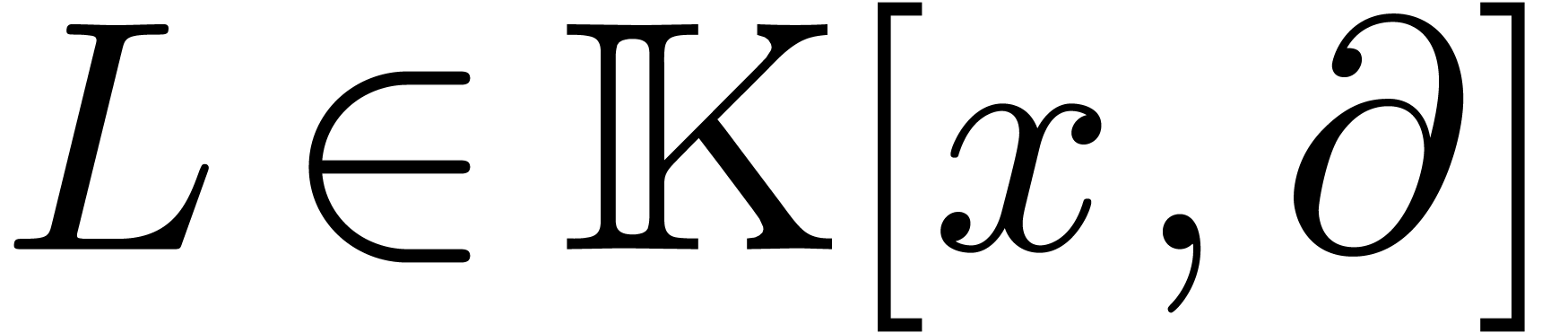 of order
of order 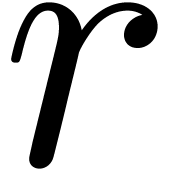 is said to be non singular at
is said to be non singular at 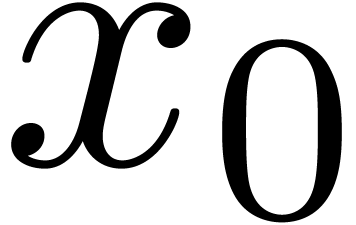 , if its leading coefficient
, if its leading coefficient  does not vanish at
does not vanish at 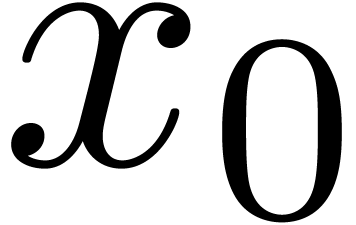 . We will
say that an operator
. We will
say that an operator 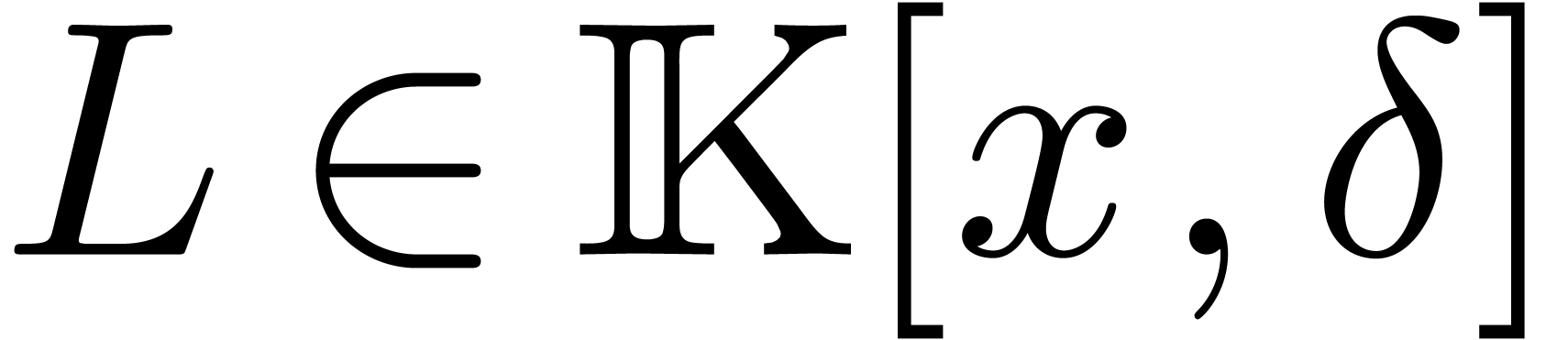 of order
of order  is non singular (at the origin) if
is non singular (at the origin) if 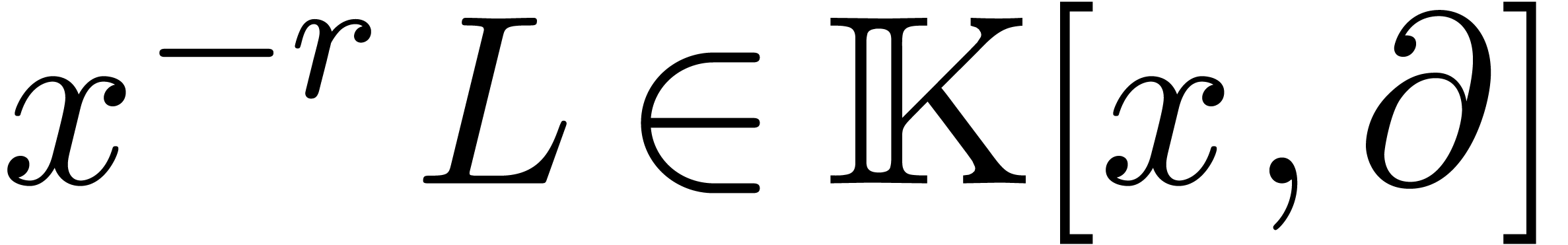 and
and 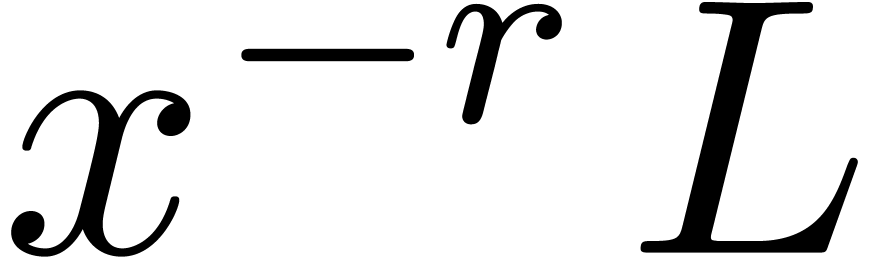 is non singular as an operator in
is non singular as an operator in  .
.
Given a non singular differential operator 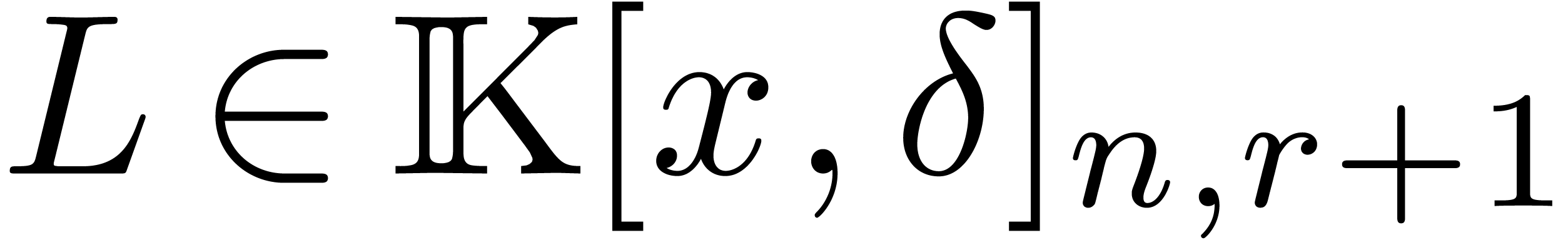 of
order
of
order  , the equation
, the equation 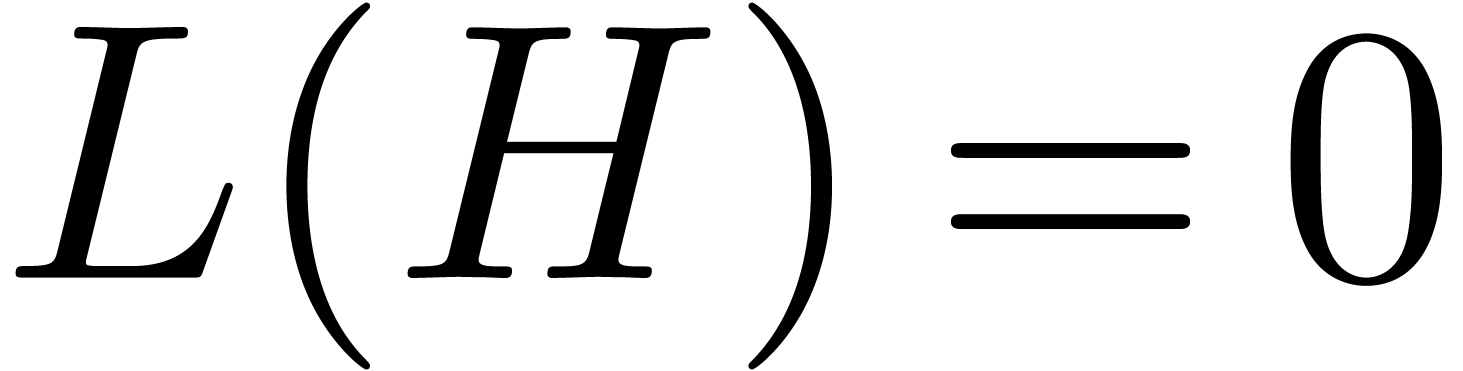 admits a canonical fundamental system
admits a canonical fundamental system 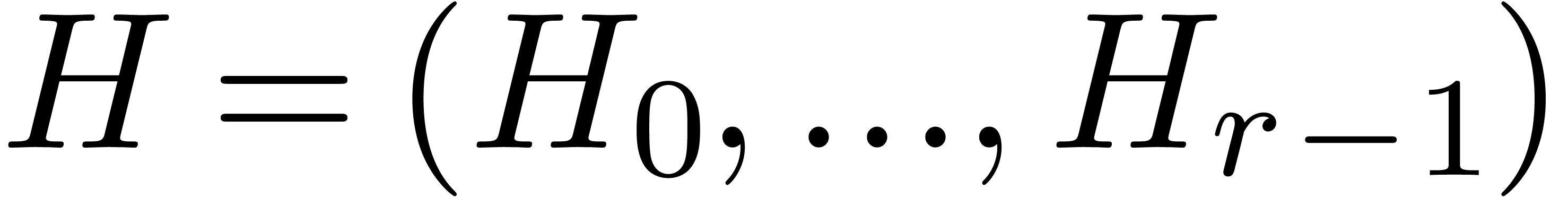 of solutions in
of solutions in 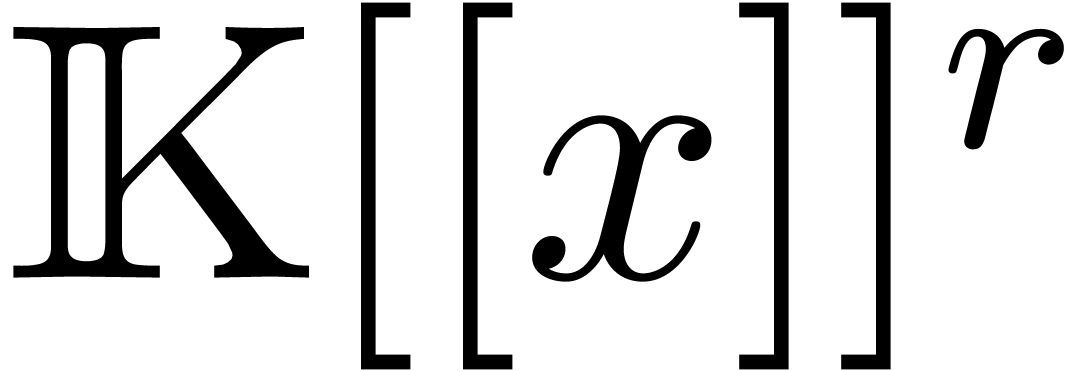 ,
with the property that
,
with the property that 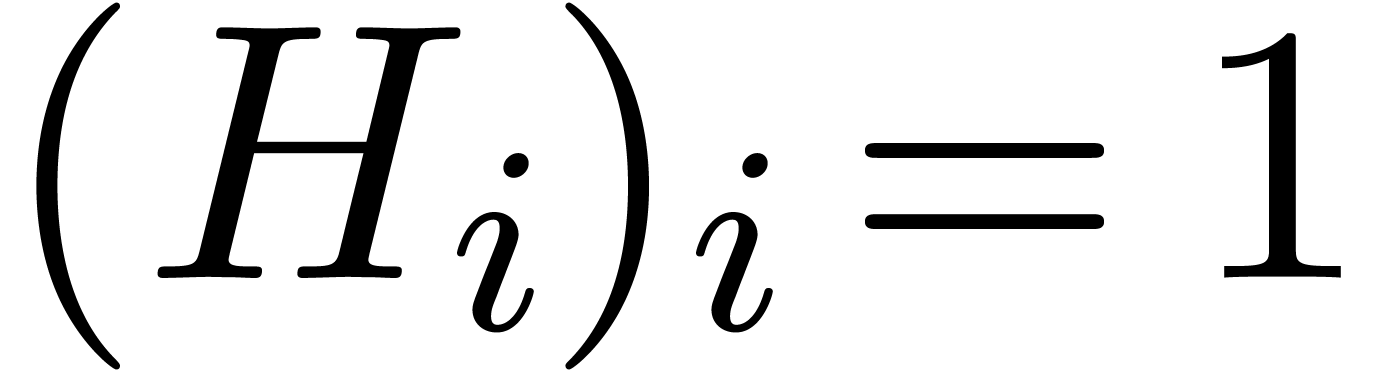 and
and 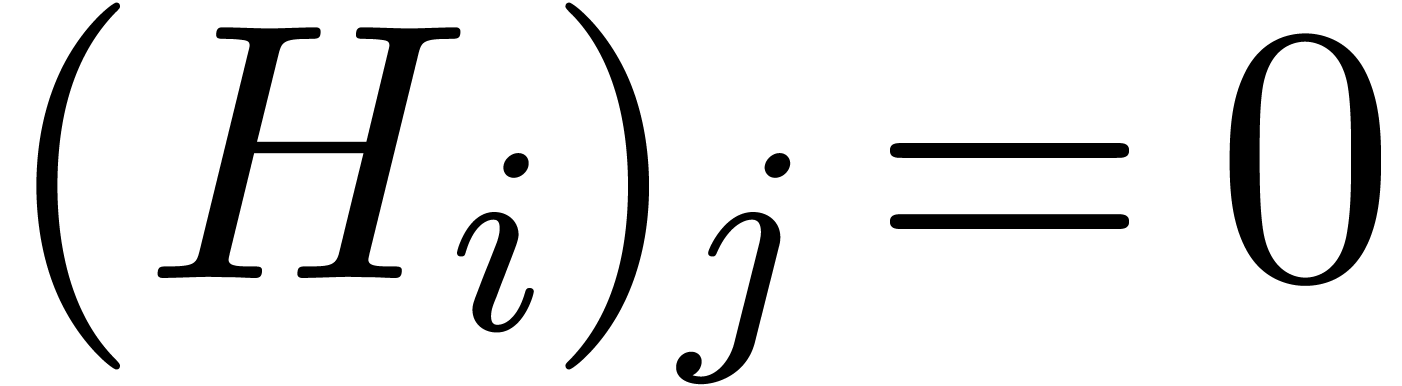 for all
for all 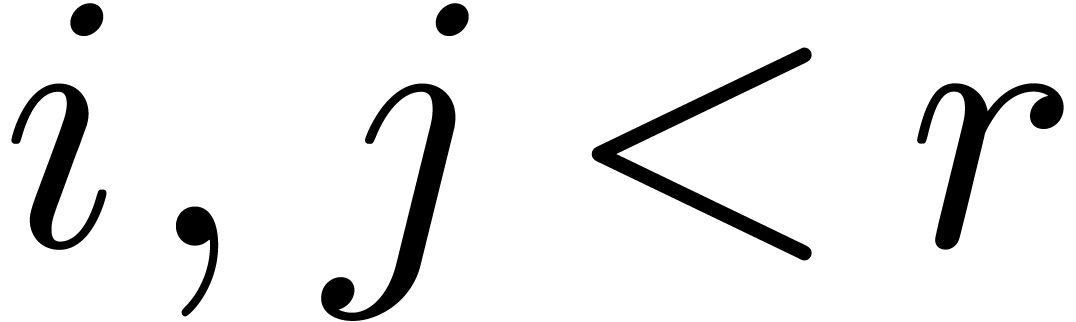 with
with 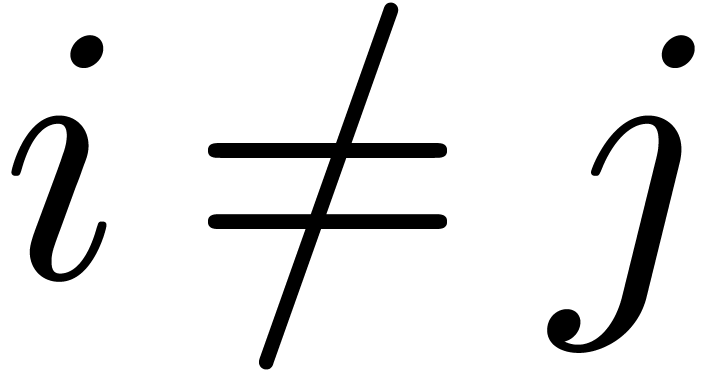 .
Conversely, given a
.
Conversely, given a  -linearly
independent vector of power series
-linearly
independent vector of power series  ,
there exists a unique monic operator
,
there exists a unique monic operator  of order
of order
 with
with 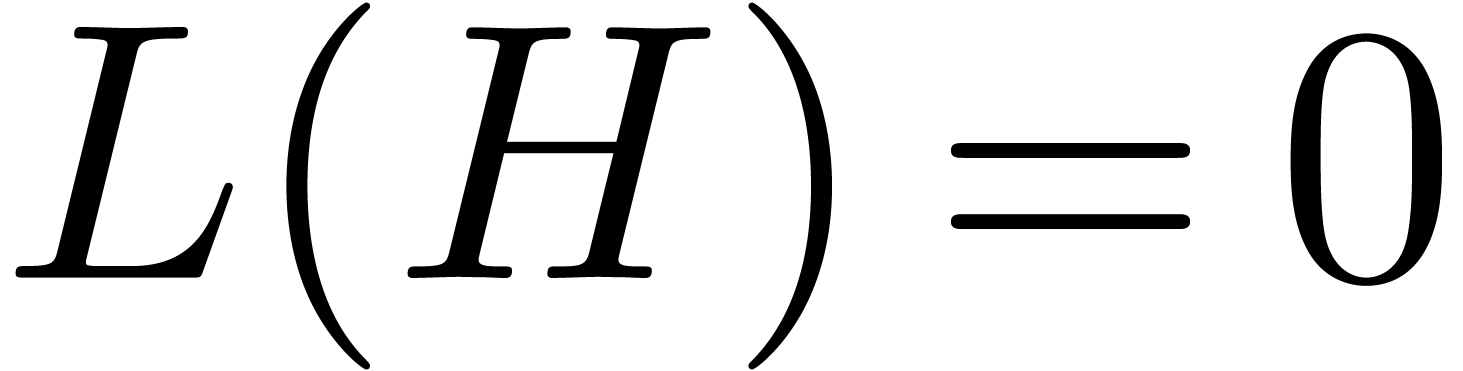 .
Let us show how to convert efficiently between these two
representations.
.
Let us show how to convert efficiently between these two
representations.
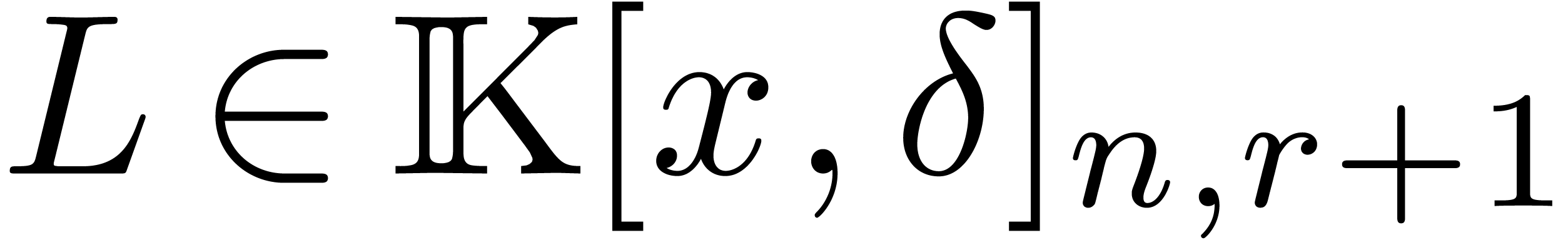 be a differential operator of
order
be a differential operator of
order 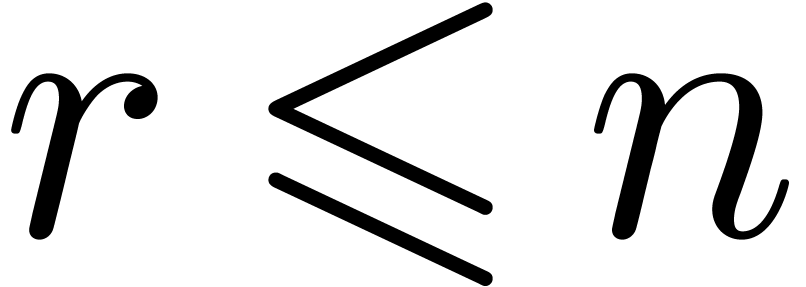 , which is non
singular at the origin, and let
, which is non
singular at the origin, and let  be its
canonical fundamental system of solutions. Then we may compute
be its
canonical fundamental system of solutions. Then we may compute  up to order
up to order 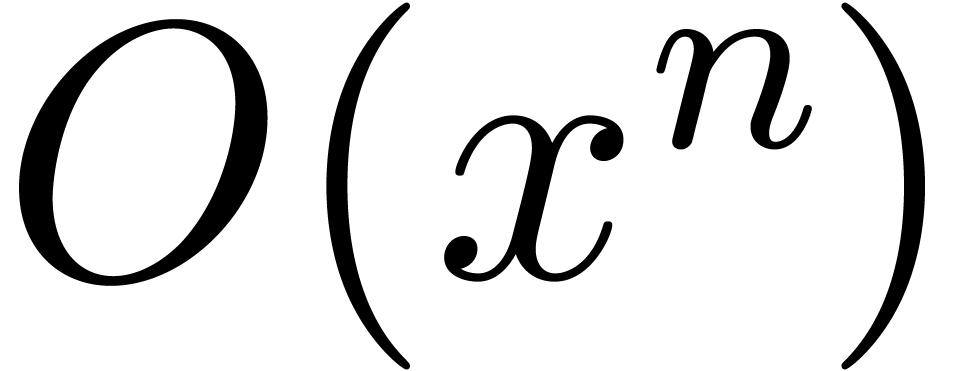 in time
in time 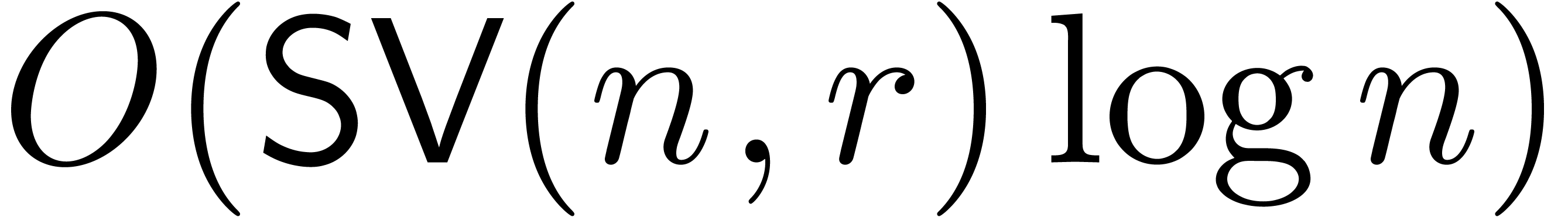 . In other words,
. In other words,
Proof. Modulo multiplying  on the left by
on the left by 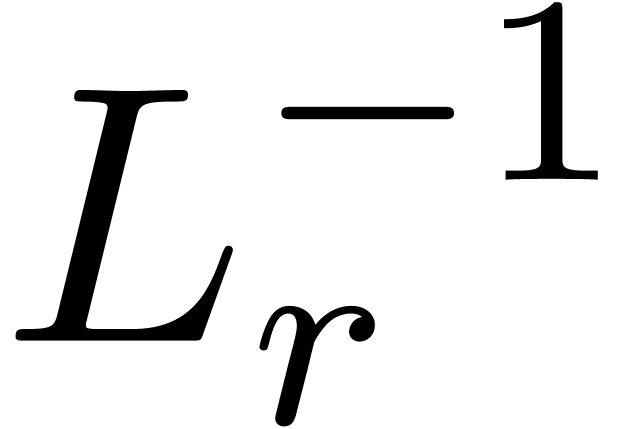 , we may
assume without loss of generality that
, we may
assume without loss of generality that  is monic.
Since
is monic.
Since  is non singular at the origin, we have
is non singular at the origin, we have
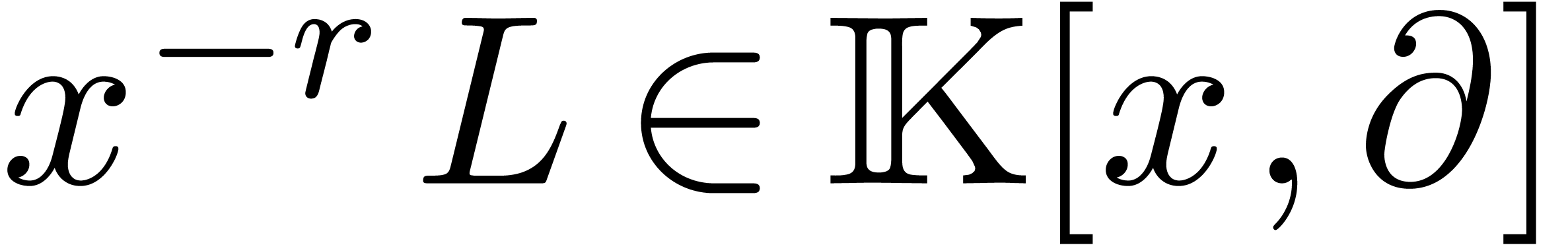 . Rewritten in terms of
. Rewritten in terms of 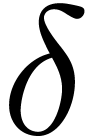 , this means that
, this means that  is of the form
is of the form
for certain 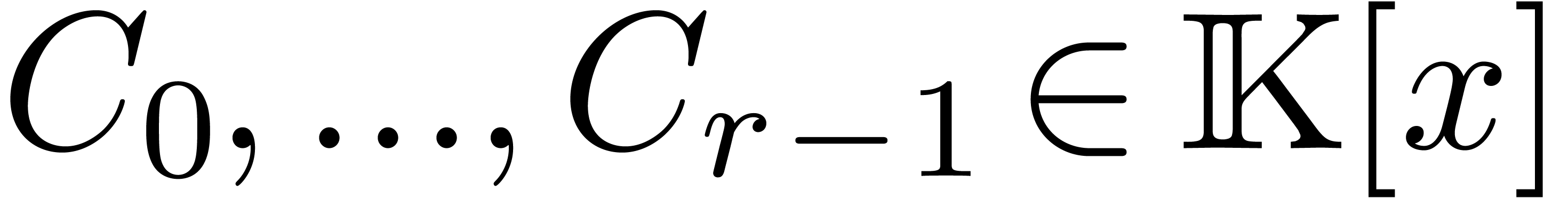 . Setting
. Setting 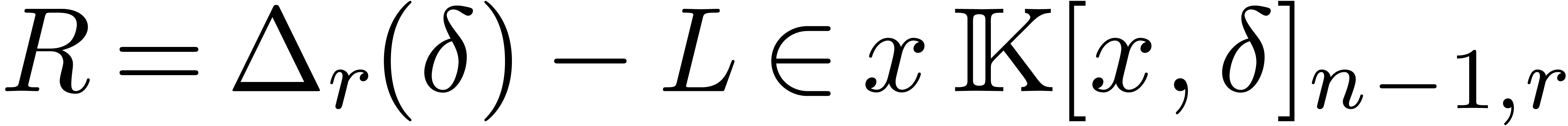 , we observe that
, we observe that 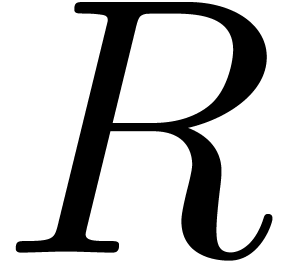 maps
maps 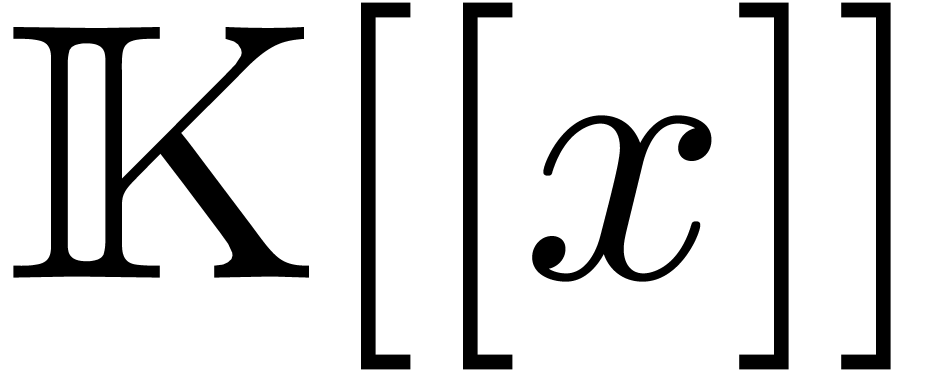 into
into 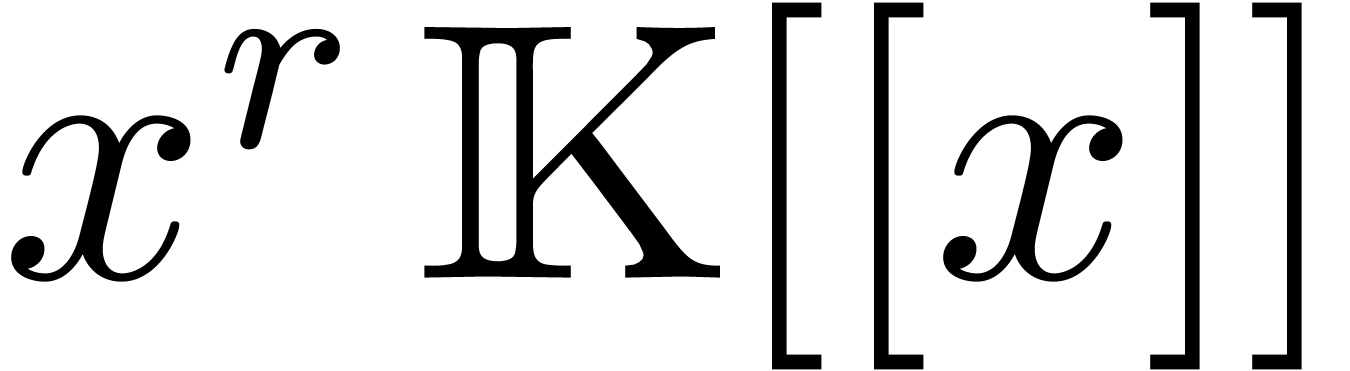 .
We now compute
.
We now compute  using the “recursive”
formula
using the “recursive”
formula
where
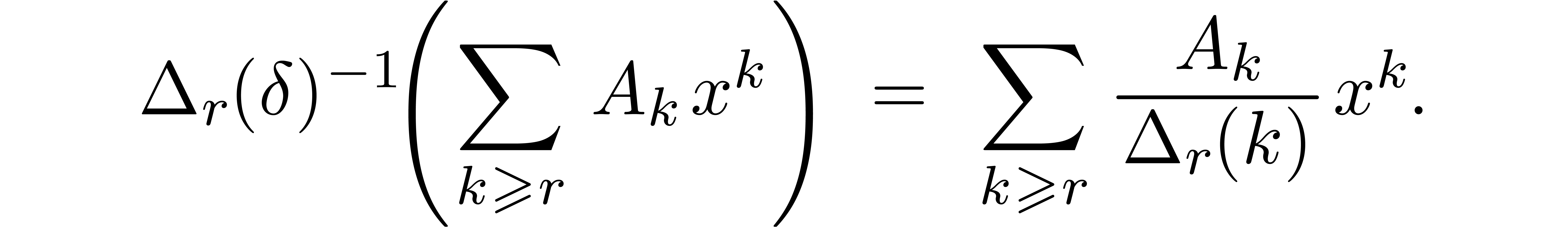
The equation (4) is a schoolbook example for applying the
strategy of relaxed resolution of power series equations [21,
22]. Since 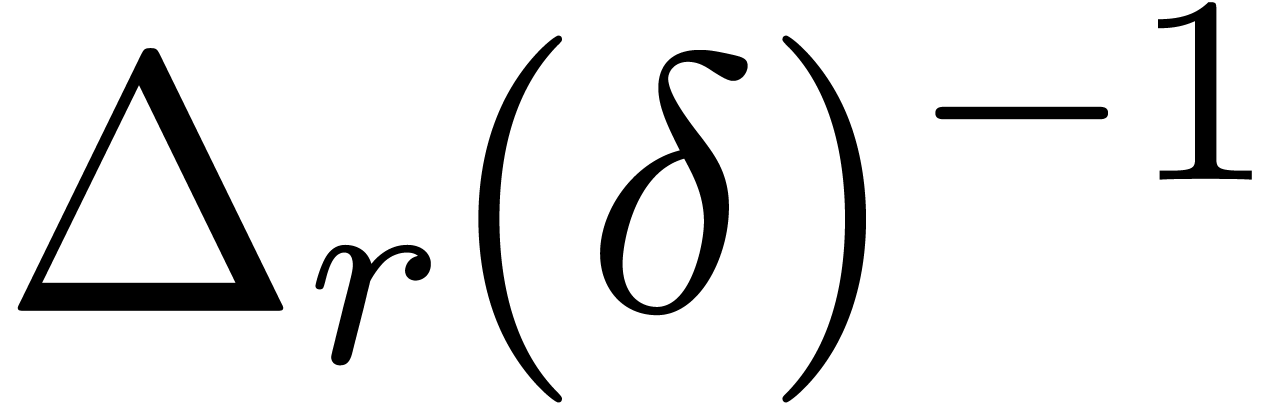 operates
coefficientwise, it can be computed in linear time. The main cost of the
computation therefore reduces to the relaxed evaluation of
operates
coefficientwise, it can be computed in linear time. The main cost of the
computation therefore reduces to the relaxed evaluation of 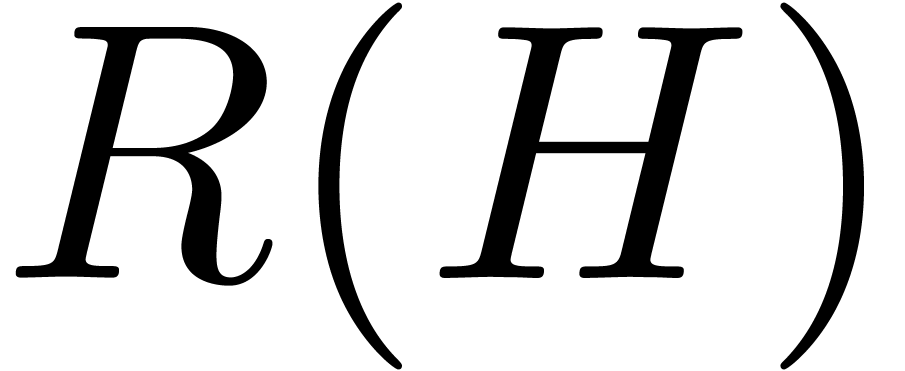 . Using fast relaxed multiplication, this
amounts to a cost
. Using fast relaxed multiplication, this
amounts to a cost

Using the monotonicity assumption and Theorem 3, the result
follows.
In what follows, given a non zero series 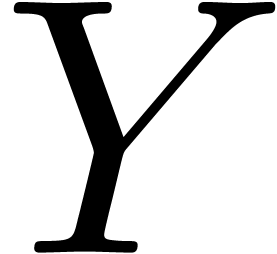 in
in
 , we denote by
, we denote by 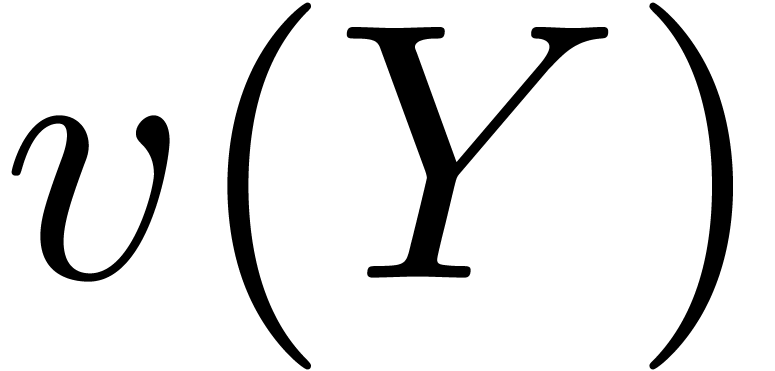 its valuation. Given a vector
its valuation. Given a vector  of
elements in a
of
elements in a  -vector space,
we will also denote by
-vector space,
we will also denote by 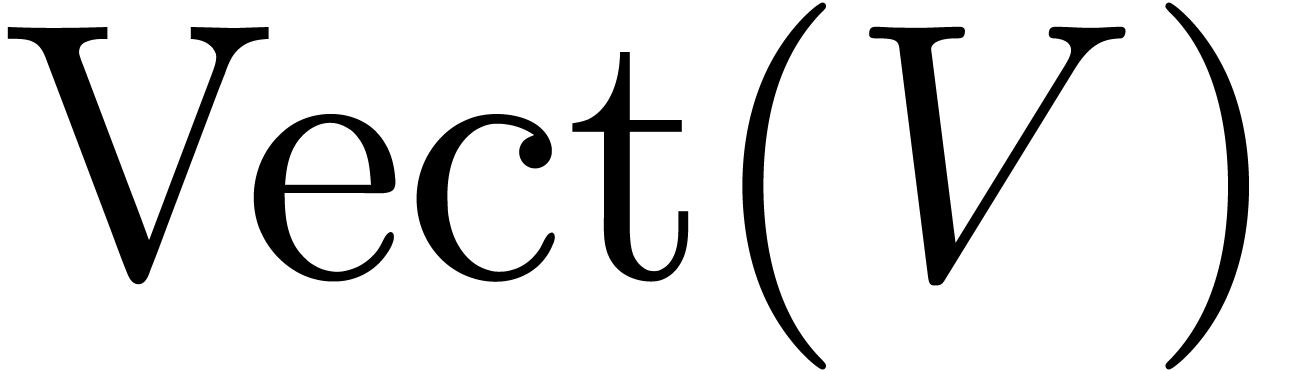 the subvector space
generated by the entries of
the subvector space
generated by the entries of  ,
and
,
and
Notice that  .
.
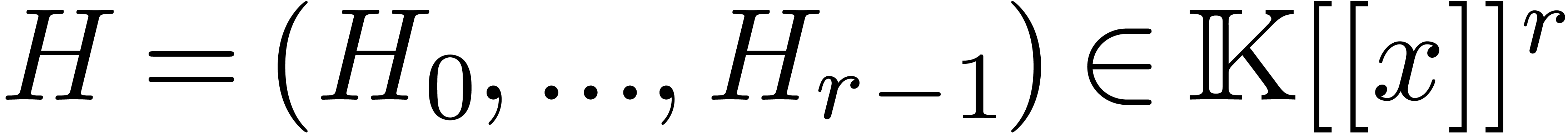 be
be  -linearly
independent. Then there exists a unique monic operator
-linearly
independent. Then there exists a unique monic operator 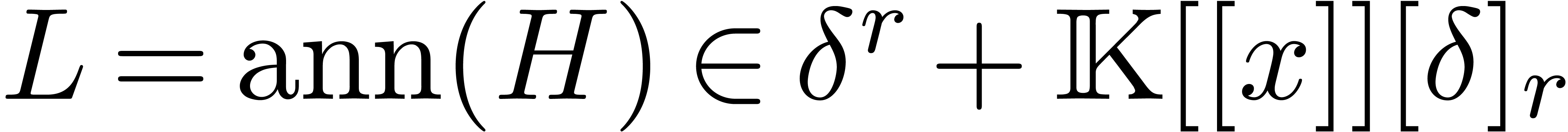 with
with 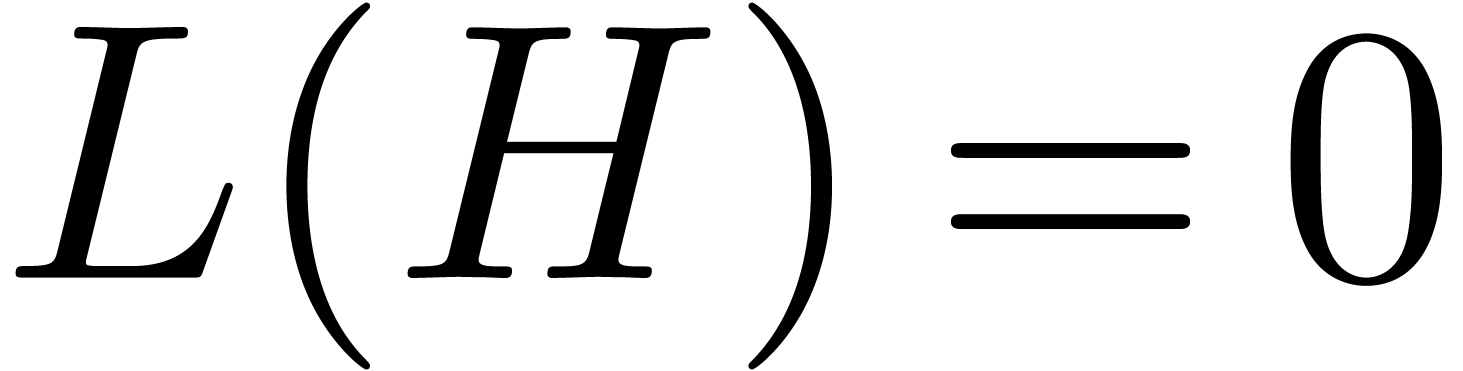 .
Moreover, given the truncation of
.
Moreover, given the truncation of  at order
at order
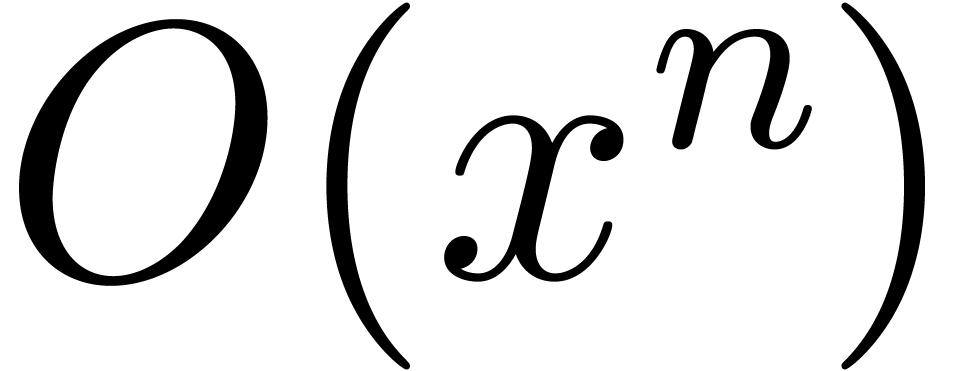 , we may compute
, we may compute  at order
at order 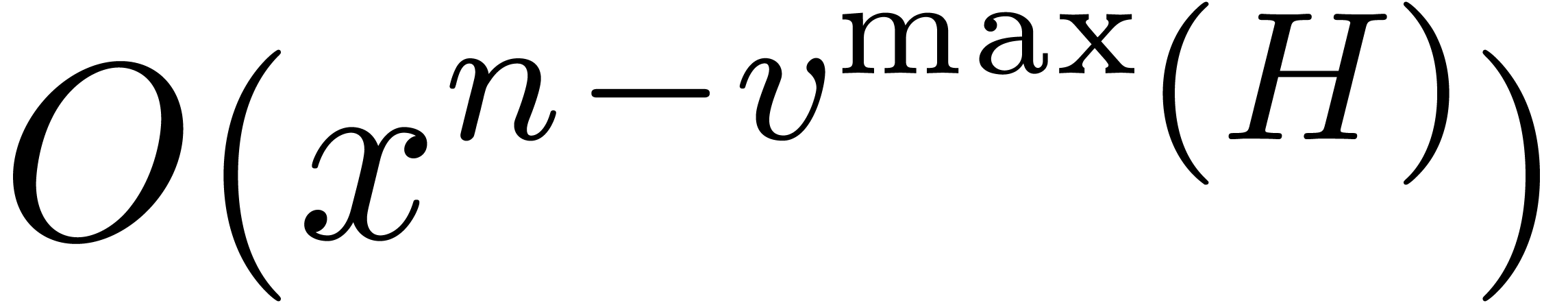 in time
in time 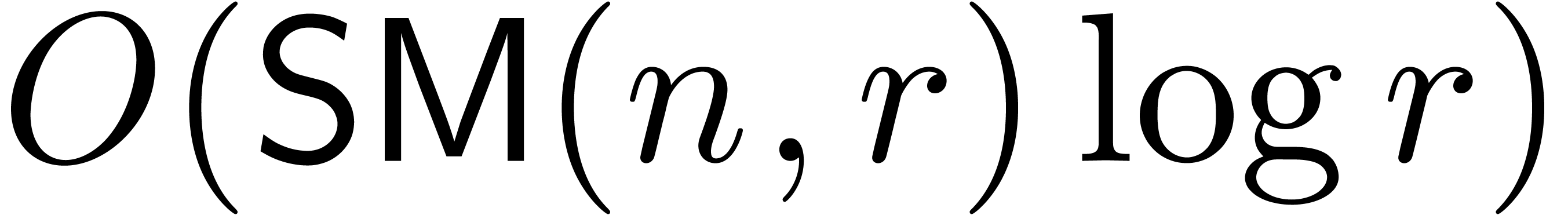 . In other words,
. In other words,
Proof. Modulo a triangularization of  , we may assume without loss of
generality that
, we may assume without loss of
generality that 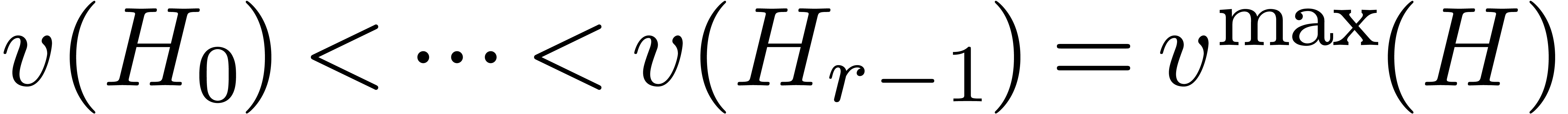 . We define
operators
. We define
operators  by
by
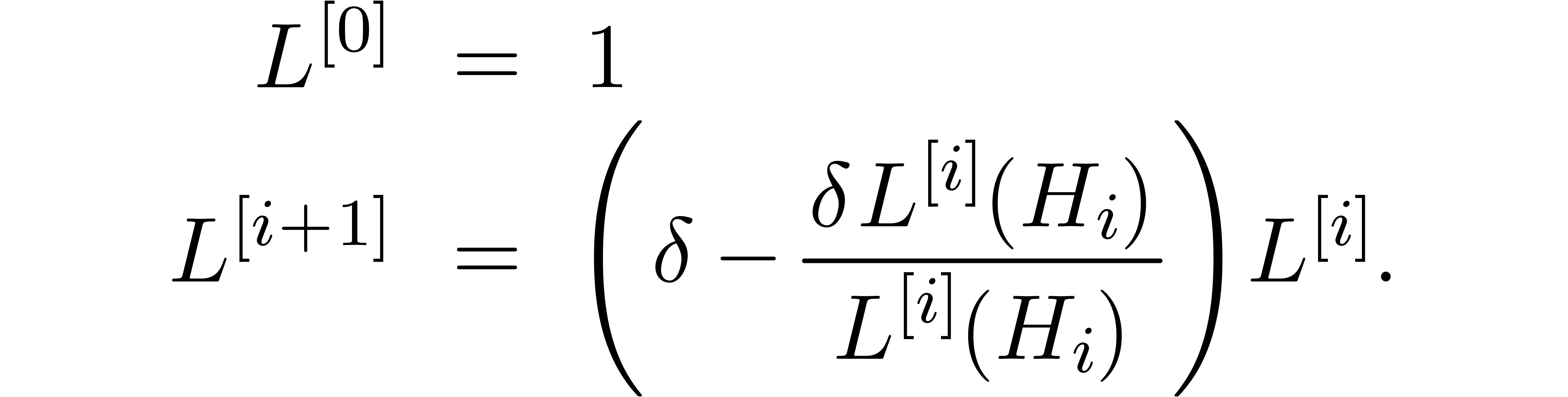
Then 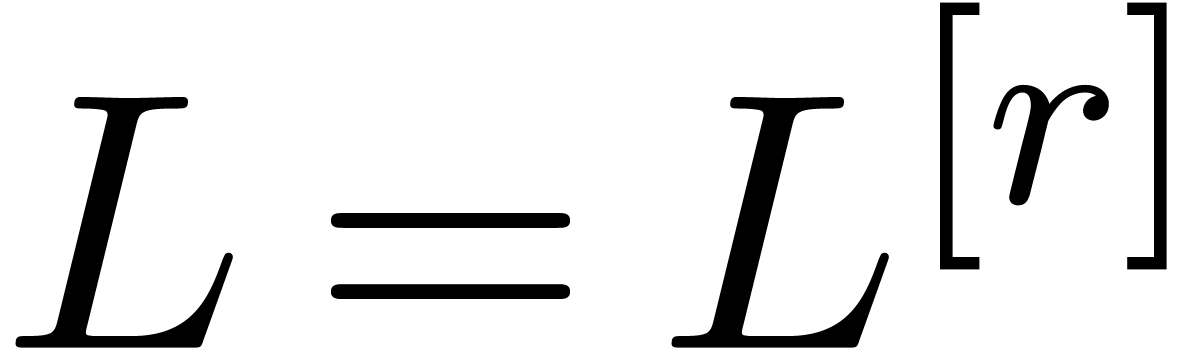 annihilates
annihilates  and for
any other operator
and for
any other operator 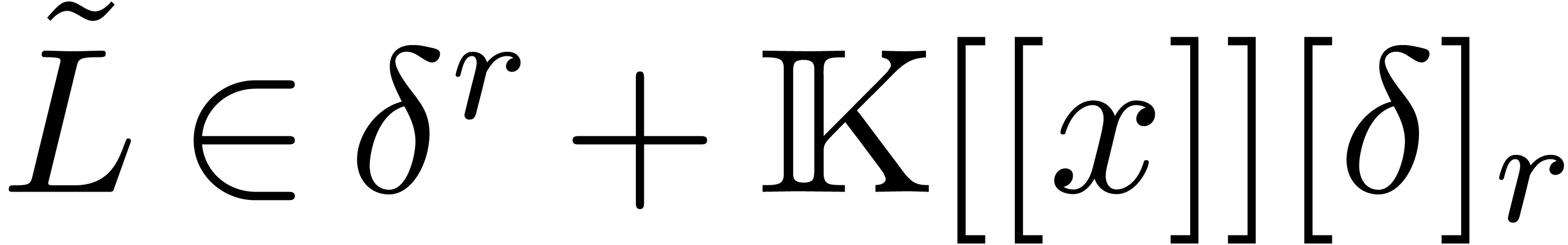 with
with 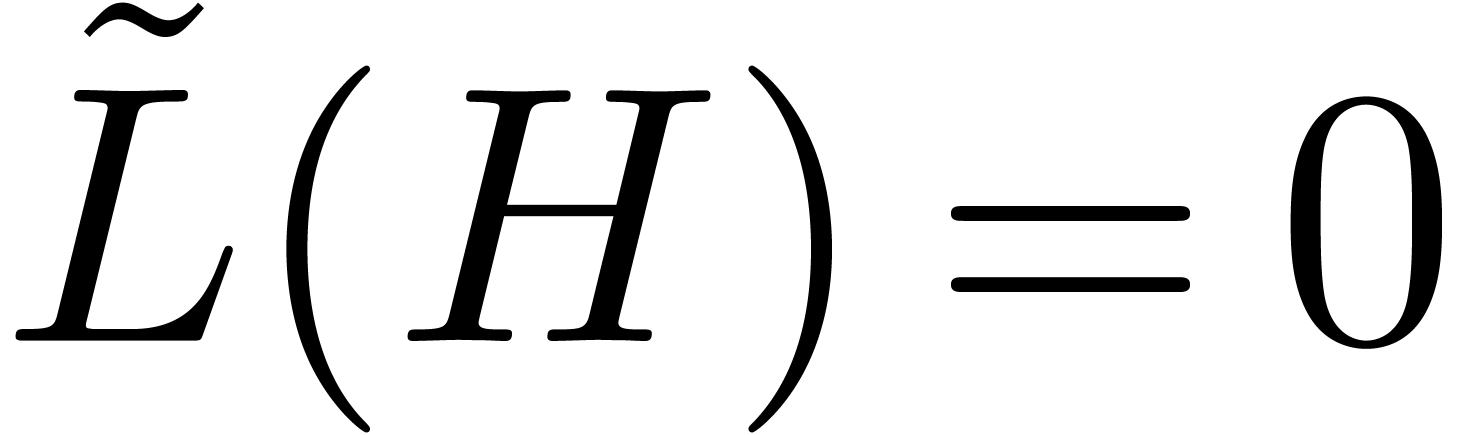 , we would have
, we would have 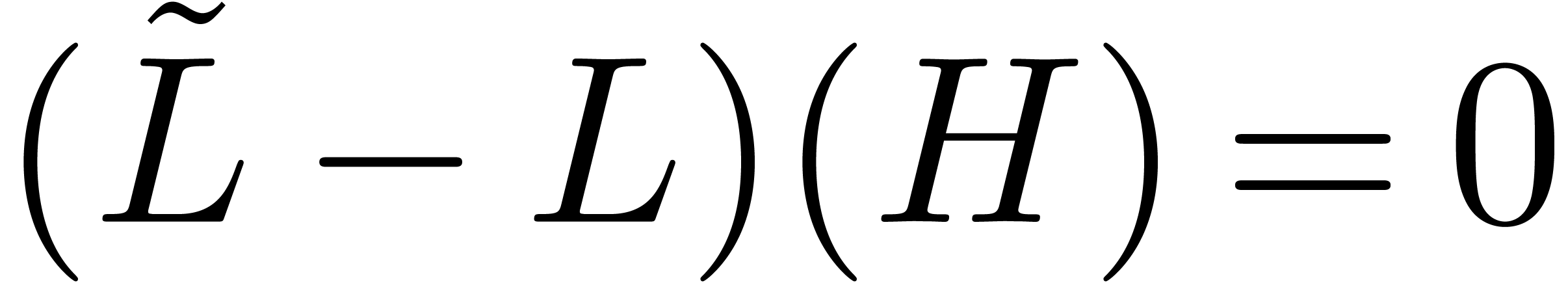 ,
which is in contradiction with the fact that
,
which is in contradiction with the fact that 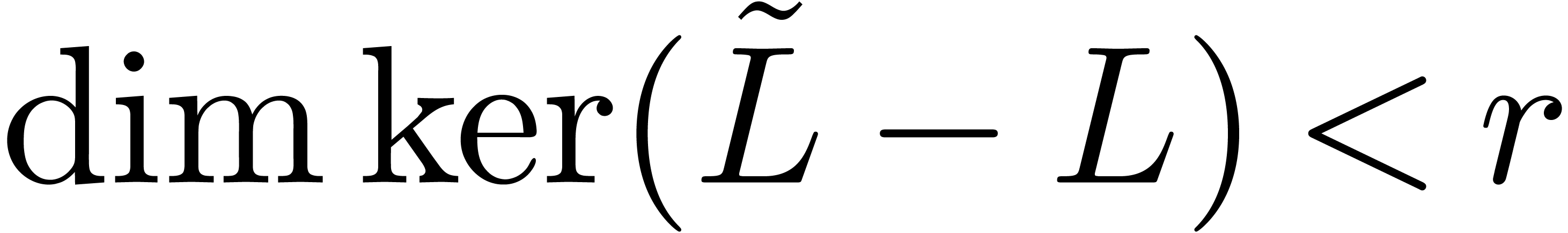 . Moreover, by induction over
. Moreover, by induction over 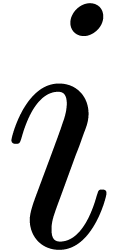 , we observe that the coefficient of
, we observe that the coefficient of 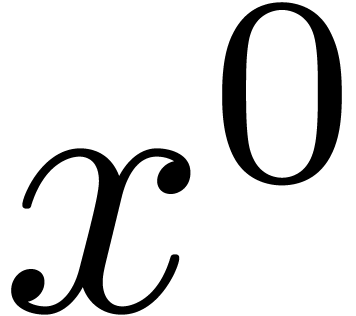 in
in 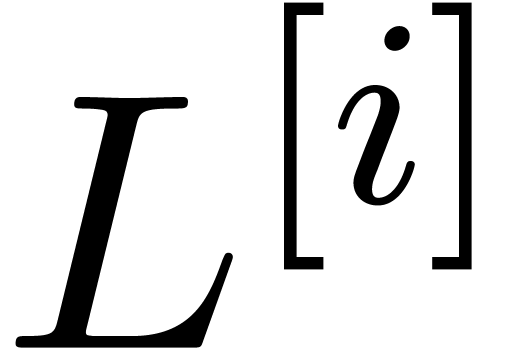 is given by
is given by  and the coefficients of
and the coefficients of 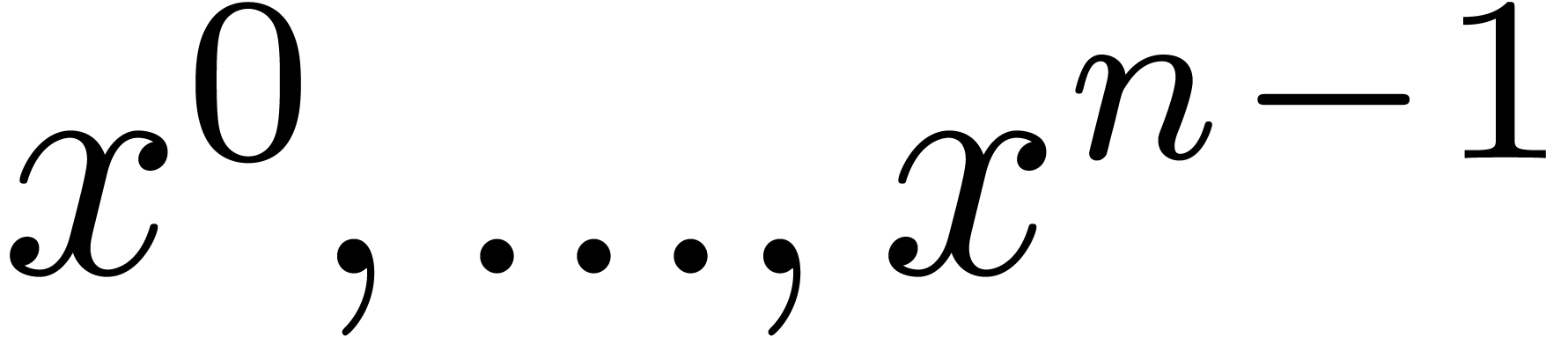 in
in 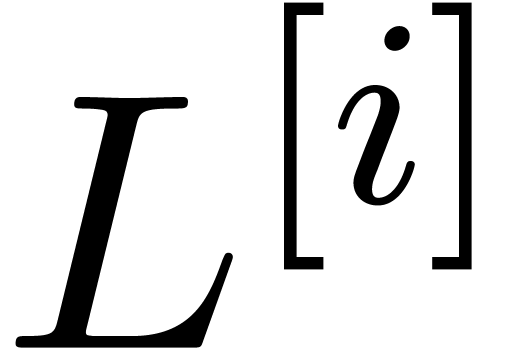 can be expressed in terms of the coefficients of
can be expressed in terms of the coefficients of 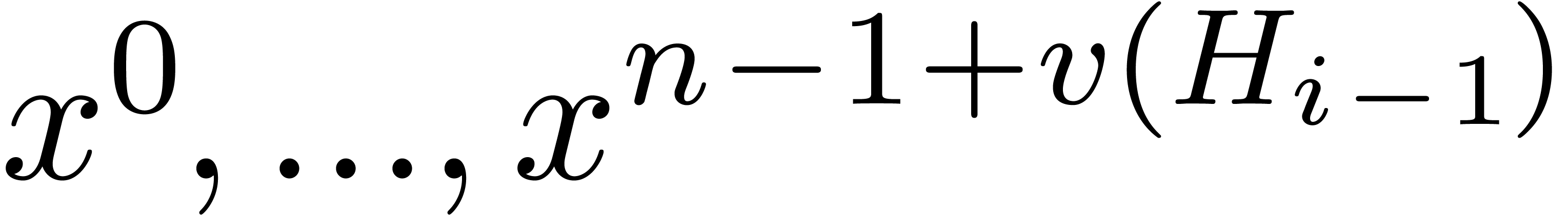 in
in 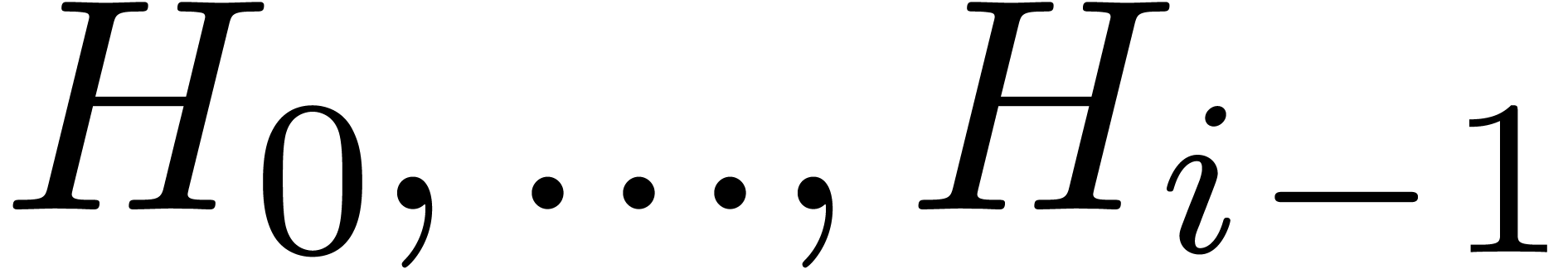 . In particular, the
truncation of
. In particular, the
truncation of  at order
at order 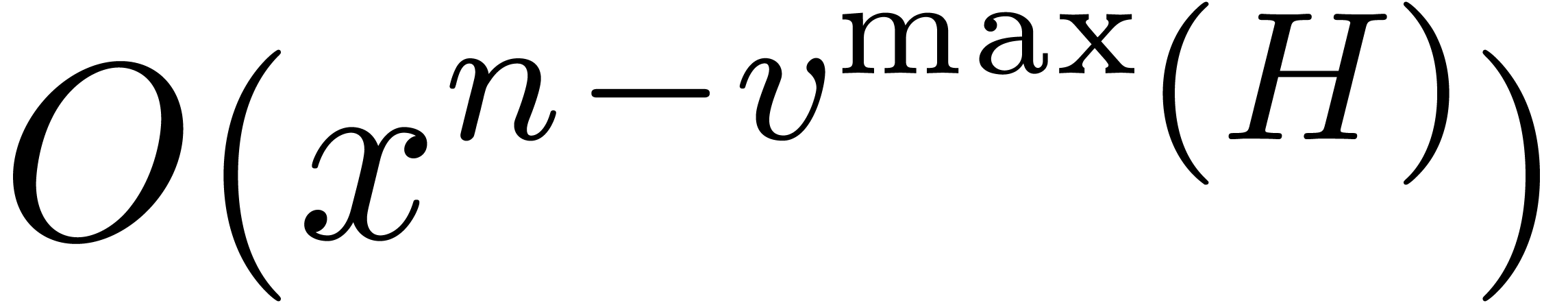 is uniquely determined by the truncation of
is uniquely determined by the truncation of  at
order
at
order 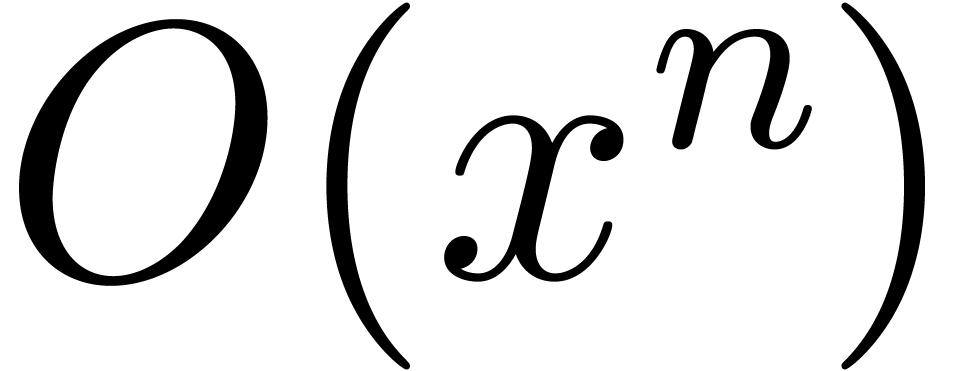 .
.
In order to explicitly compute  up to a given
order, it is more efficient to use a divide and conquer approach. More
precisely, given
up to a given
order, it is more efficient to use a divide and conquer approach. More
precisely, given 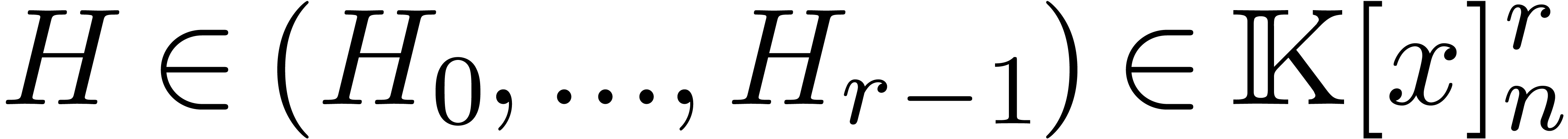 we compute
we compute 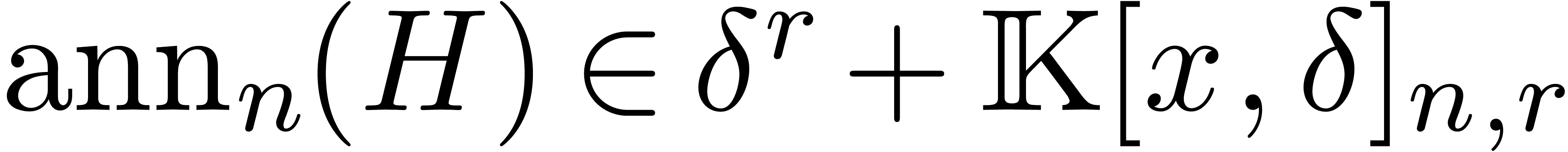 using the following method:
using the following method:
If 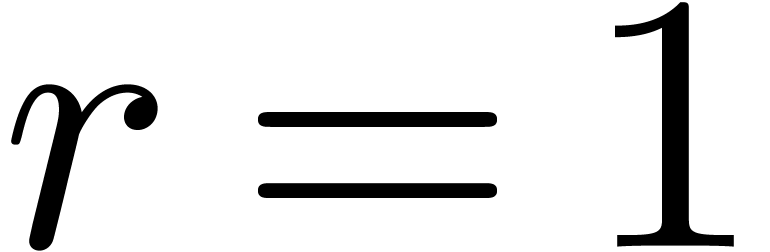 , then we take
, then we take 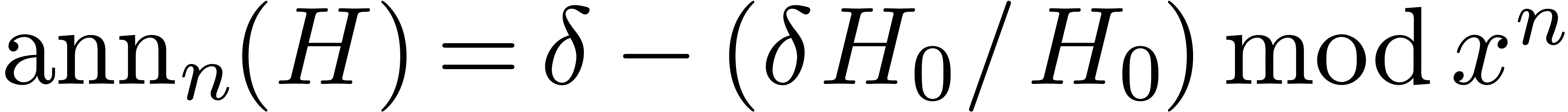 .
.
Otherwise, let  with
with 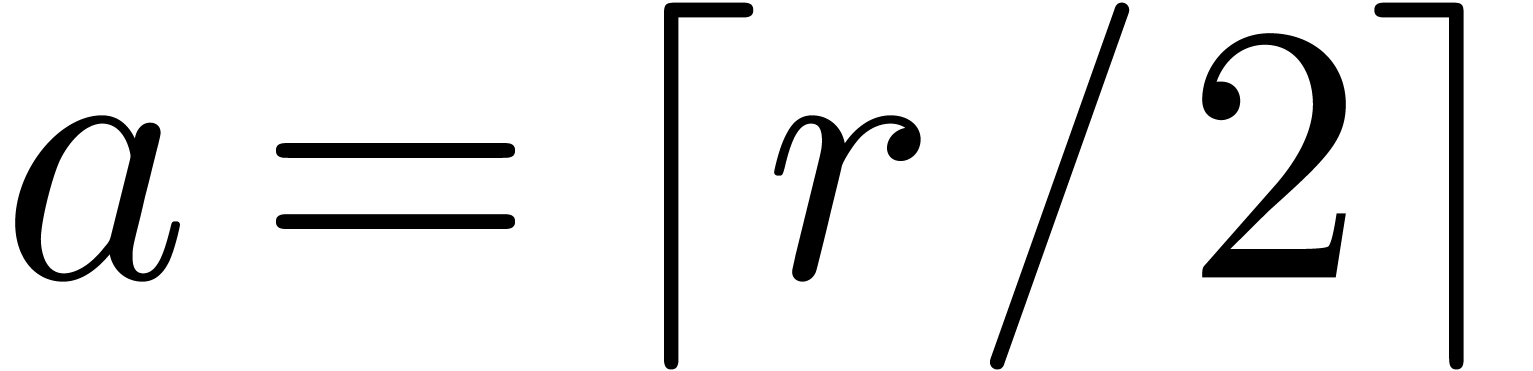 .
.
Compute 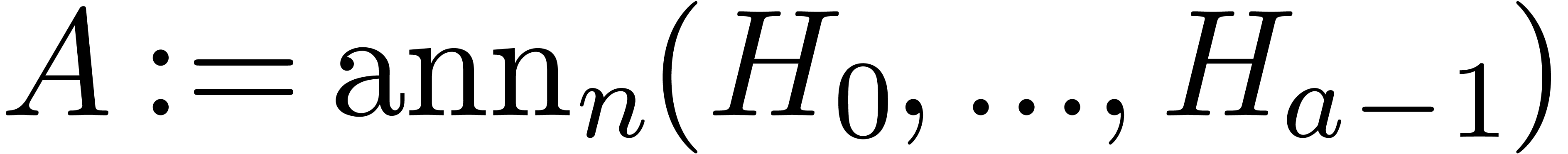 .
.
Evaluate  .
.
Compute 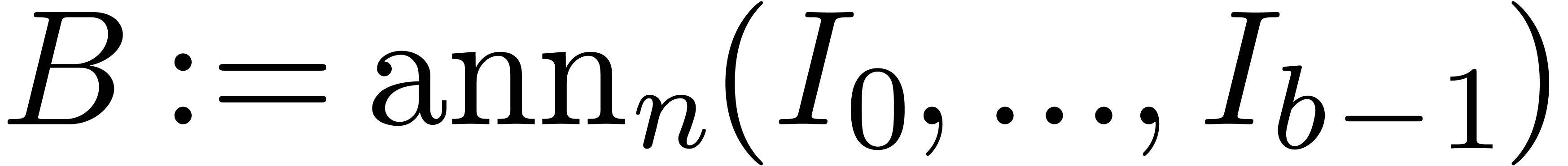 .
.
Return  .
.
If 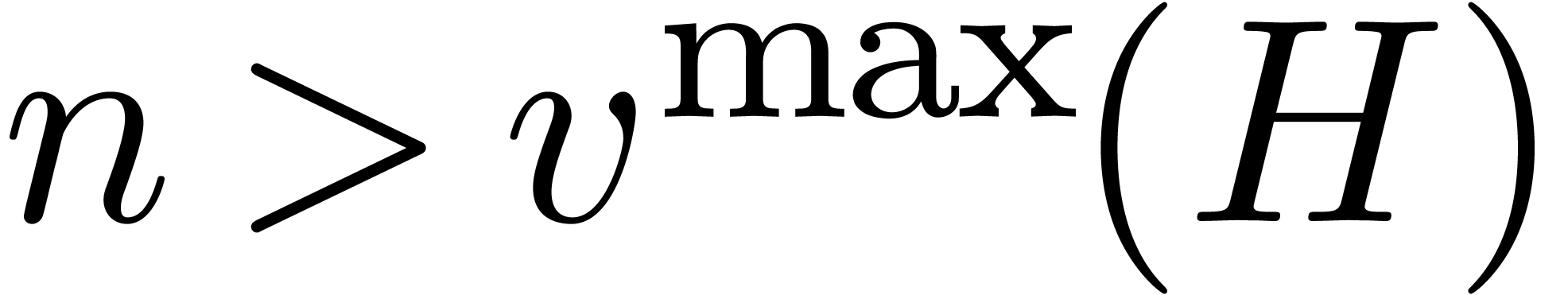 , then it is easy to check
that
, then it is easy to check
that 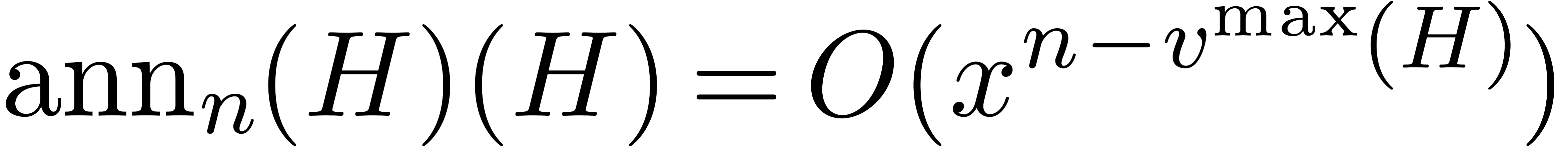 . For a fixed constant
. For a fixed constant
 , we thus have
, we thus have
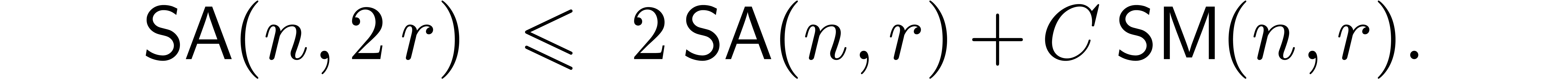
The result now follows from the monotonicity assumption.
Remark 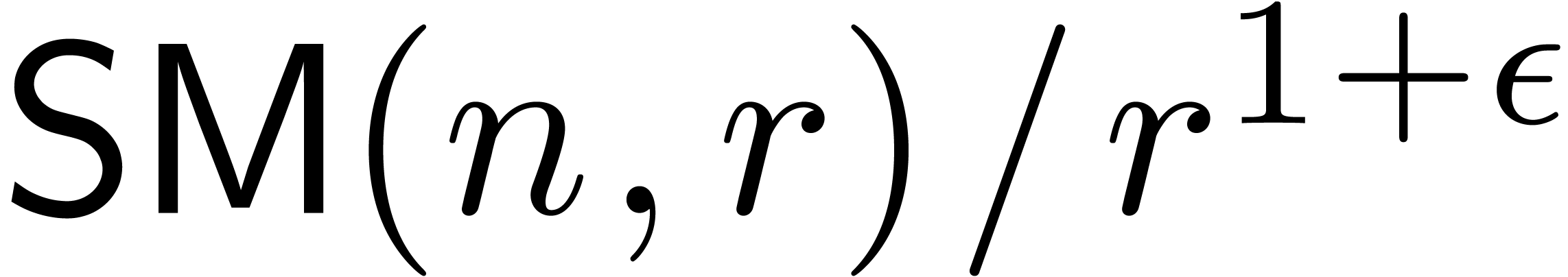 is increasing in
is increasing in 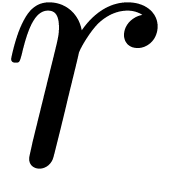 for some
for some 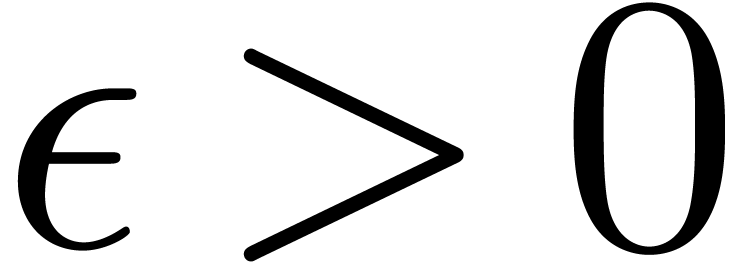 , then the bound further simplifies
to
, then the bound further simplifies
to  .
.
Remark  in Theorem 8 is
singular if and only if
in Theorem 8 is
singular if and only if 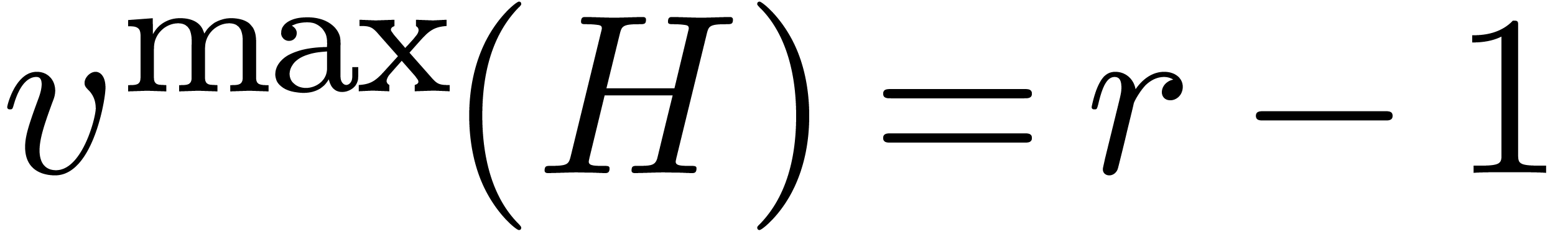 , and
if and only if
, and
if and only if 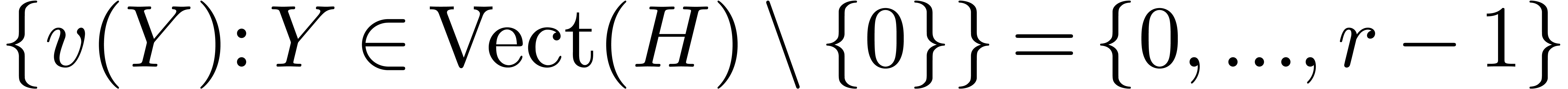 .
.
Remark  instead of
instead of 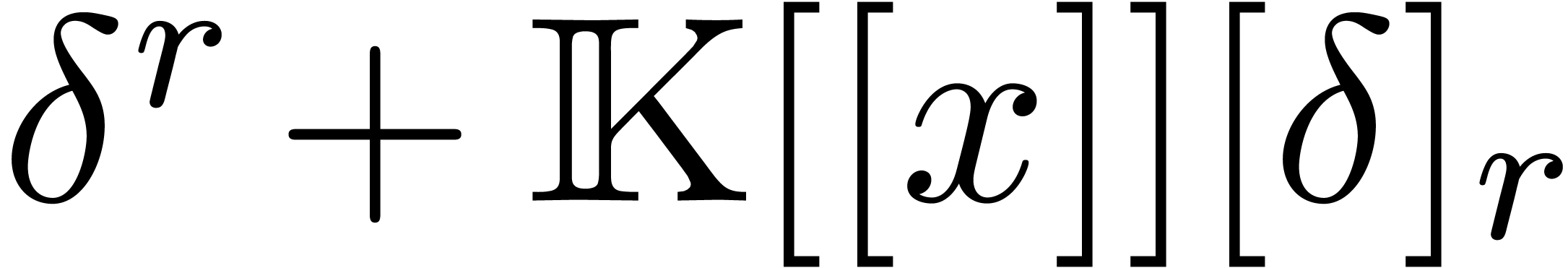 . Indeed, for this, it suffices to take
. Indeed, for this, it suffices to take
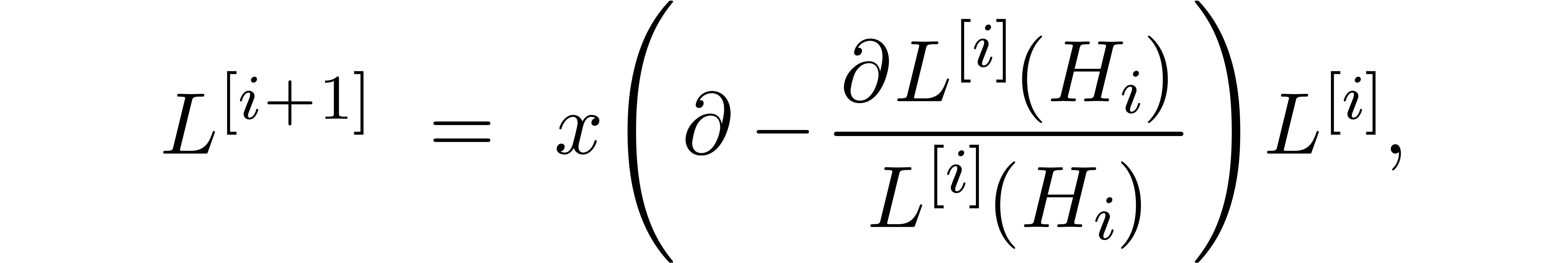
and carefully adapt the truncation orders.
Although a general operator 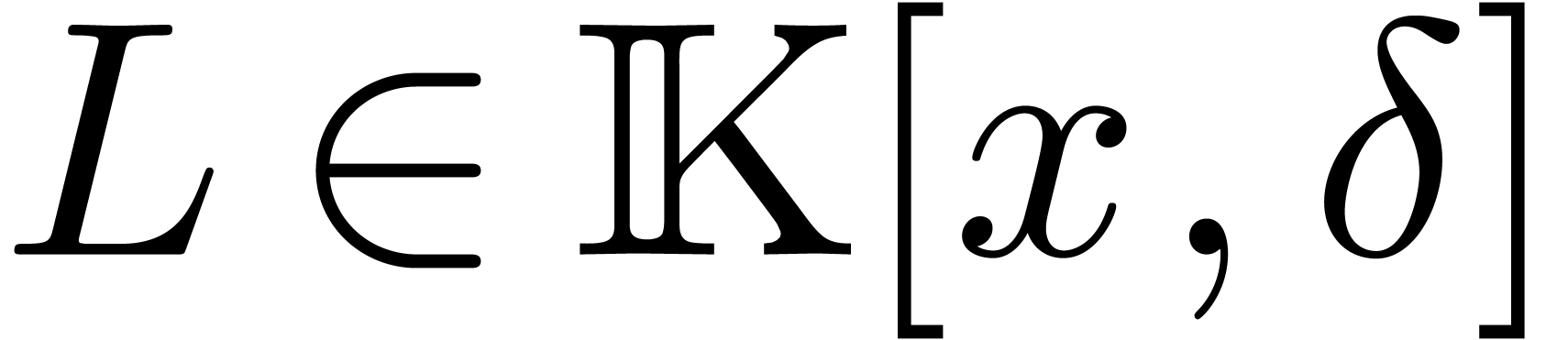 can be singular at
the origin, many operations on operators (such as right division and
greatest common right divisors) commute with translations
can be singular at
the origin, many operations on operators (such as right division and
greatest common right divisors) commute with translations 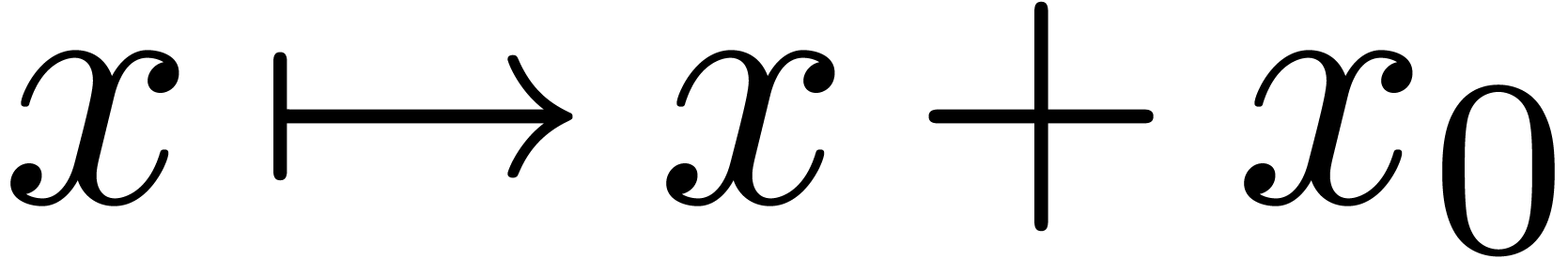 , and Lemma 6 may be used in
conjunction with the following lemma in order to reduce to the case when
, and Lemma 6 may be used in
conjunction with the following lemma in order to reduce to the case when
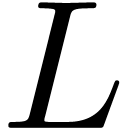 is non singular at the origin.
is non singular at the origin.
Proof. Let 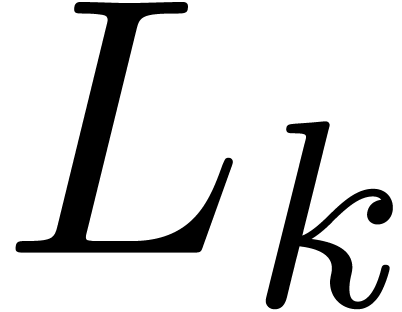 be the
leading coefficient of
be the
leading coefficient of  .
Since
.
Since 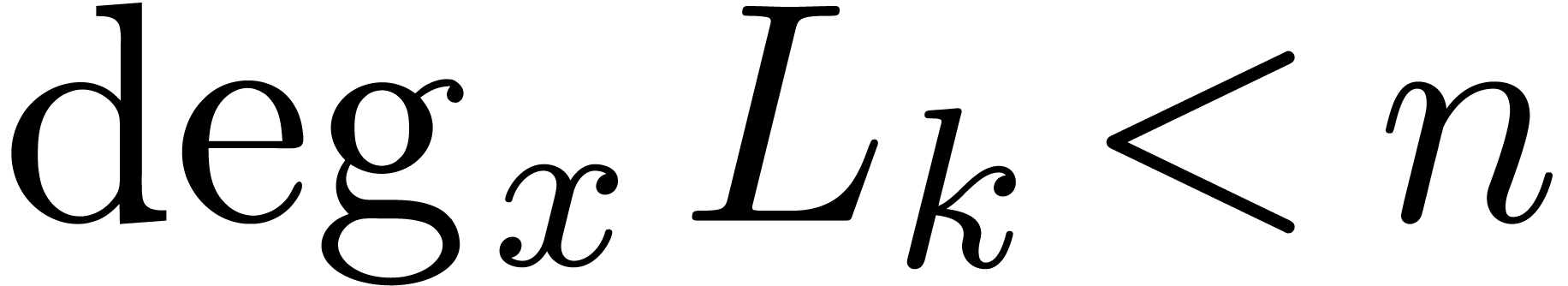 , we have
, we have 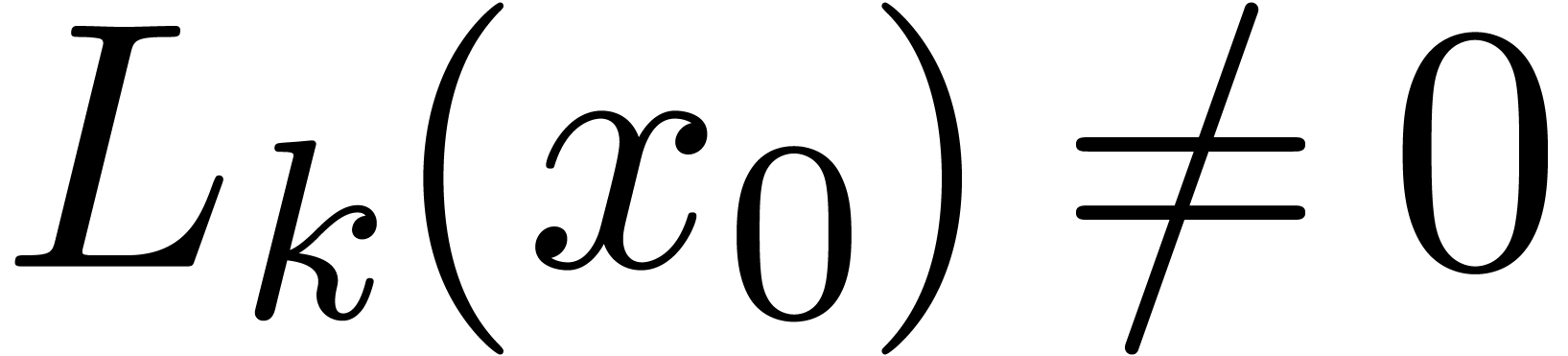 for some
for some 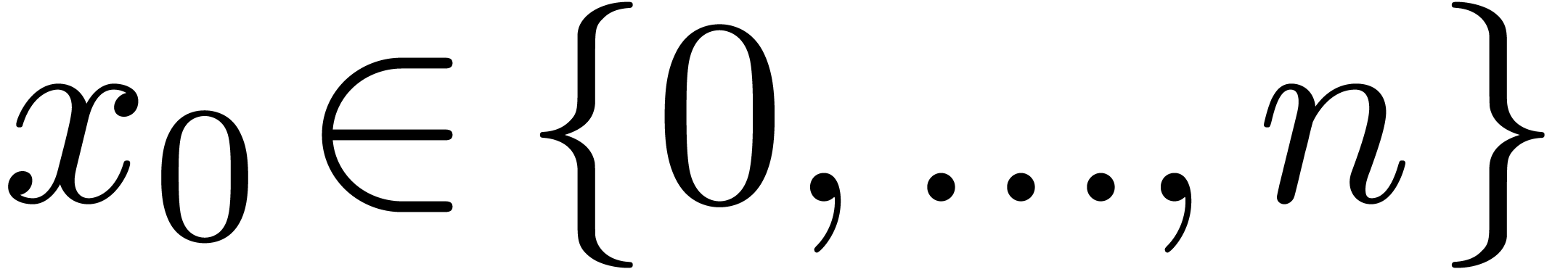 .
Using fast multipoint evaluation [7], we may find such a
point
.
Using fast multipoint evaluation [7], we may find such a
point 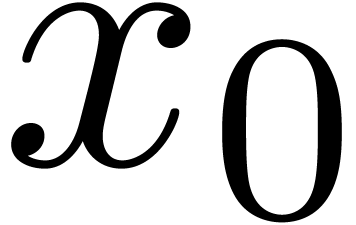 in time
in time 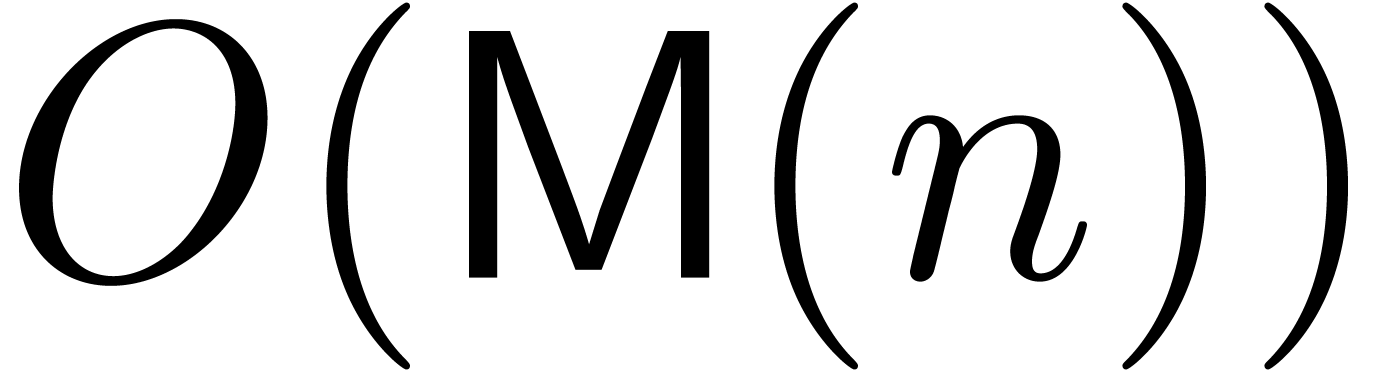 .
.
From the formula (?) it is clear that both the degrees in
 and
and 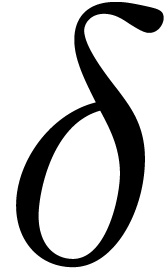 are additive for the
multiplication of operators
are additive for the
multiplication of operators 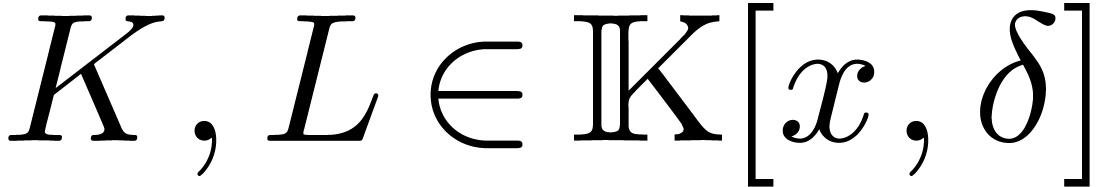 .
In particular, if
.
In particular, if 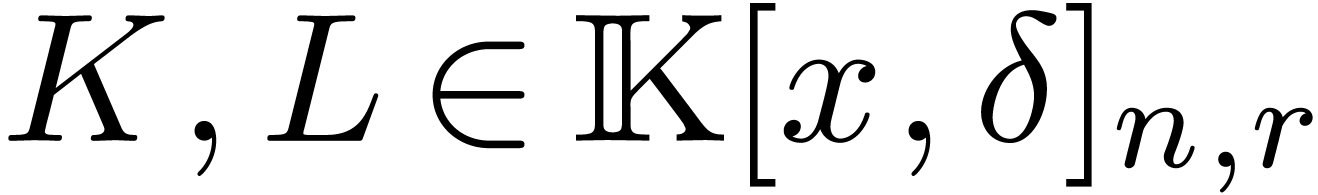 and
and  is
left or right divisible by
is
left or right divisible by  ,
then the quotient is again in
,
then the quotient is again in 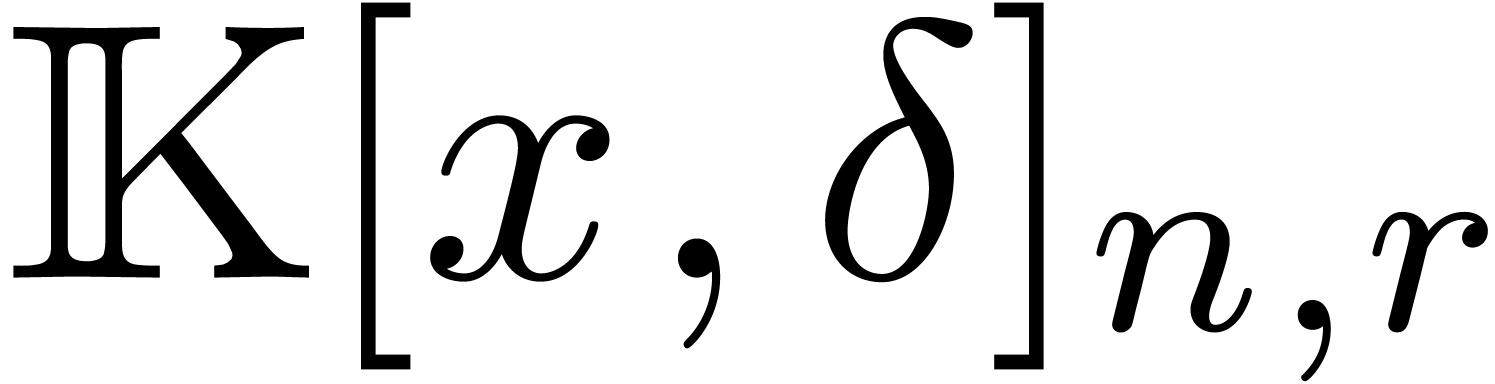 .
.
Proof. By Lemmas ? and 12,
and modulo a shift 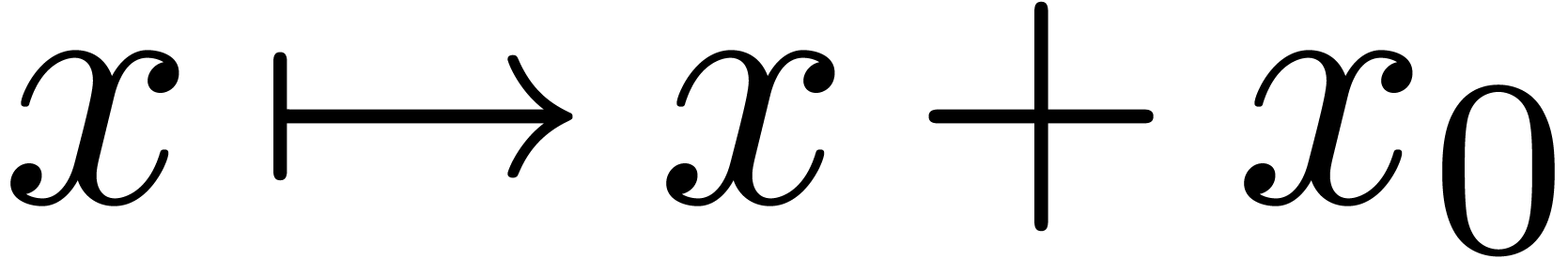 , we may
assume without loss of generality that
, we may
assume without loss of generality that  and
and  are non singular at the origin. We now use the
following algorithm:
are non singular at the origin. We now use the
following algorithm:
We first compute the canonical fundamental system of solutions  to
to 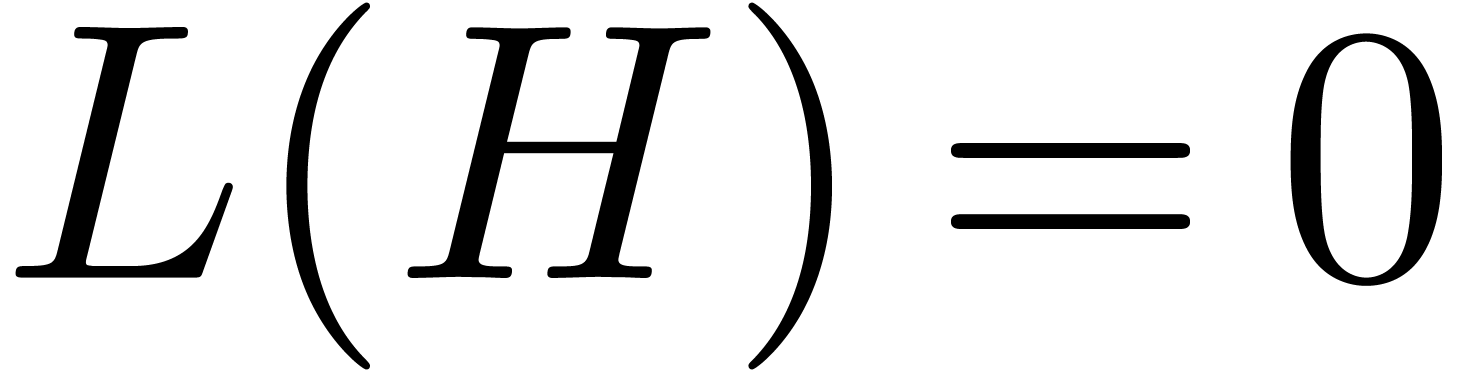 up to order
up to order 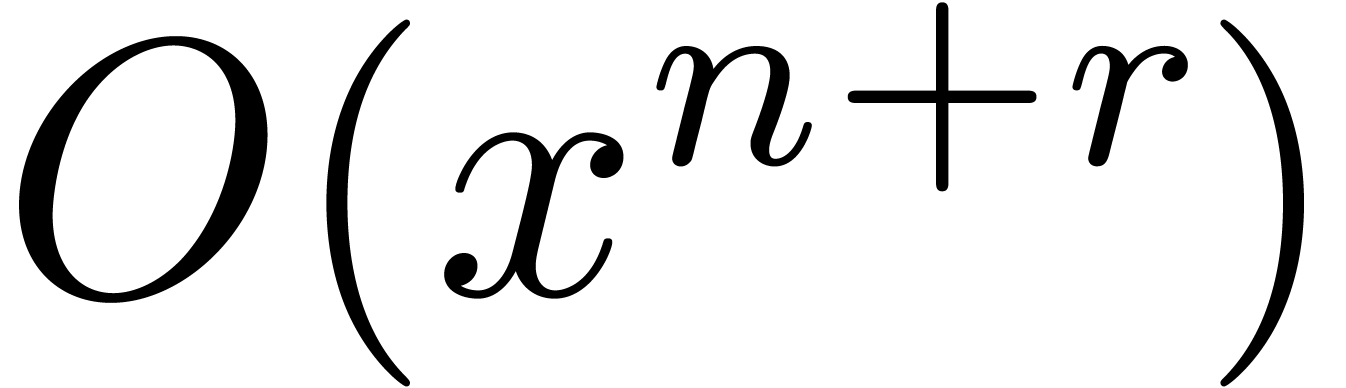 . By Theorem 7,
this can be done in time
. By Theorem 7,
this can be done in time 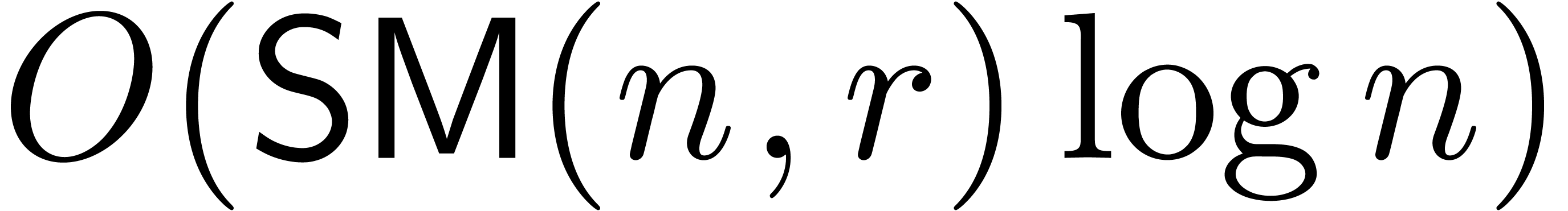 .
.
We next evaluate 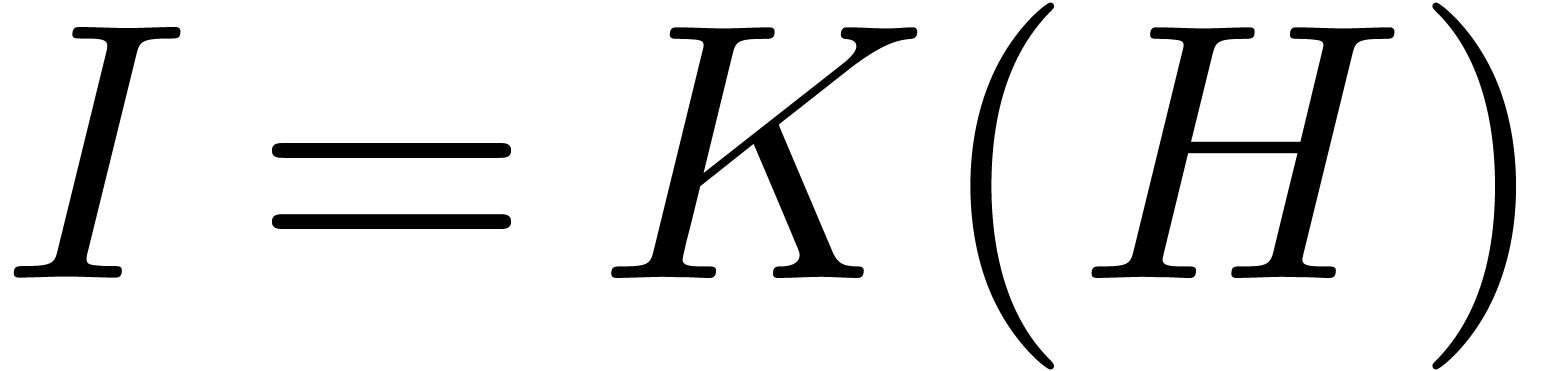 and compute a
and compute a  -basis
-basis  for
for 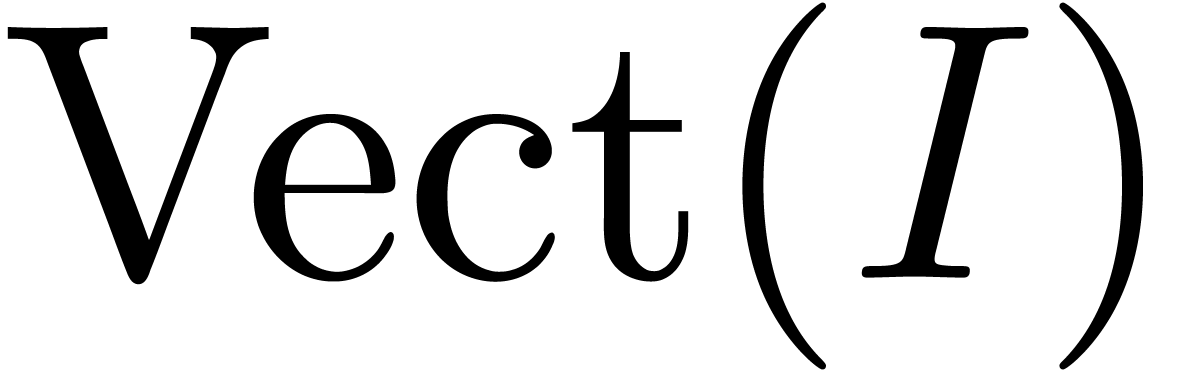 at order
at order 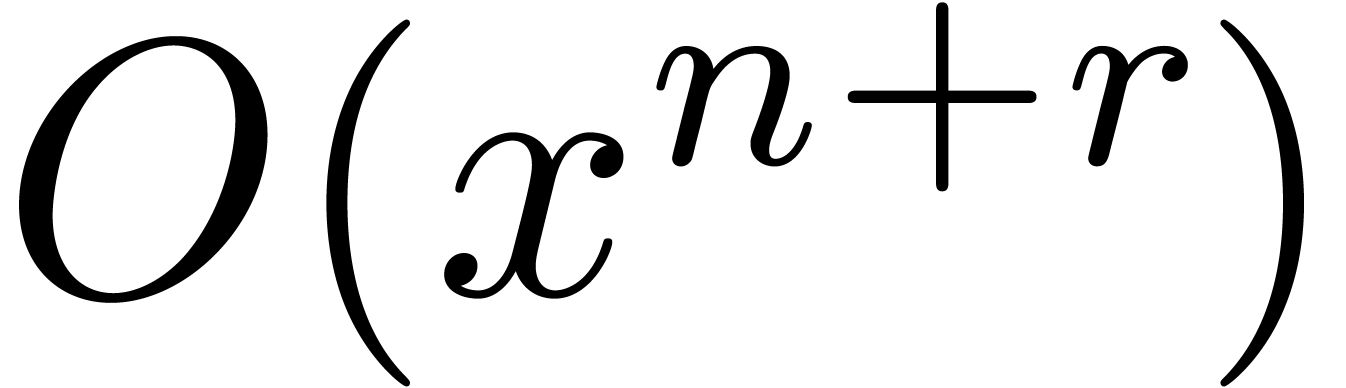 .
This can be done in time
.
This can be done in time 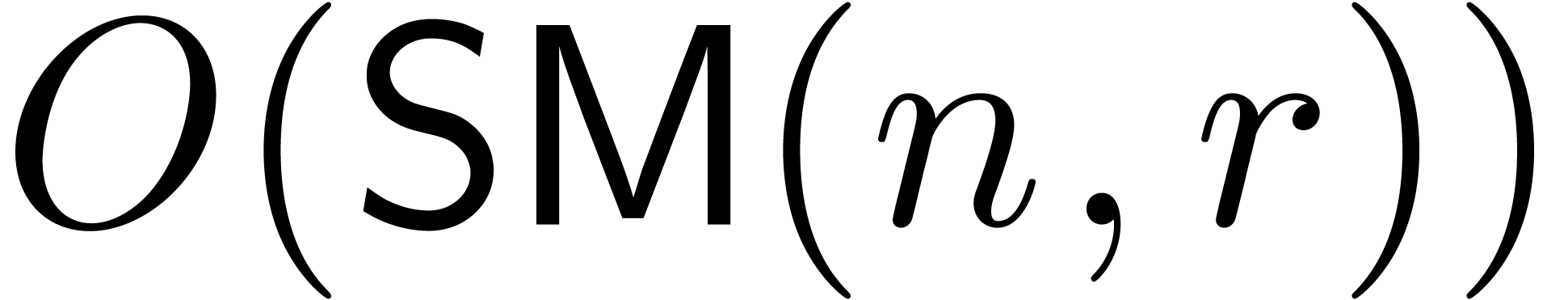 ,
by Theorems 3 and 5, and using linear
algebra. Since
,
by Theorems 3 and 5, and using linear
algebra. Since  is non singular, we have
is non singular, we have 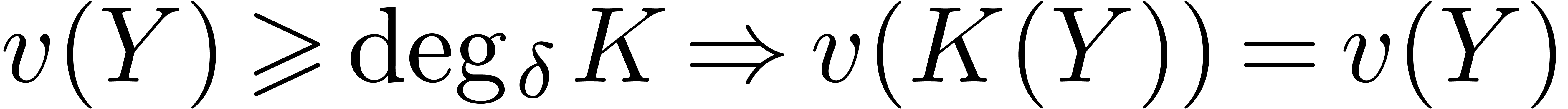 for all
for all  .
In particular, the
.
In particular, the 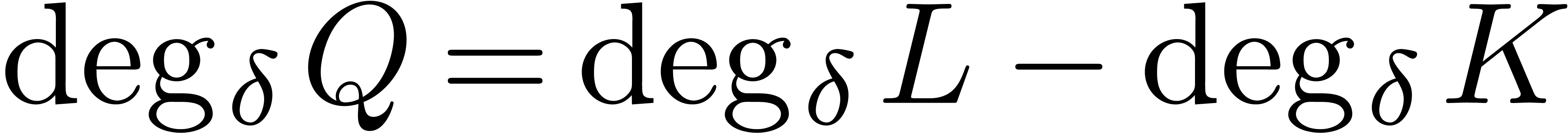 elements of
elements of  of valuations
of valuations 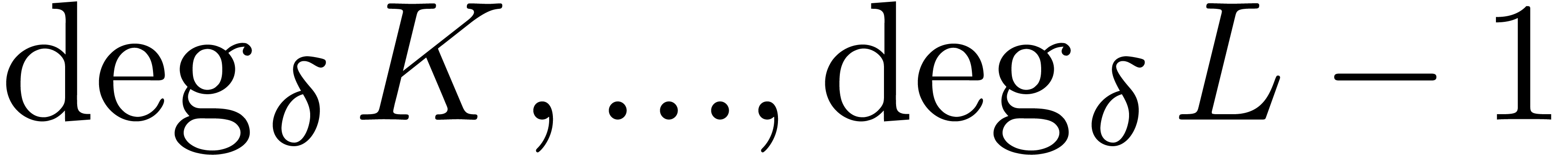 are mapped to
set which spans a vector space of dimension
are mapped to
set which spans a vector space of dimension 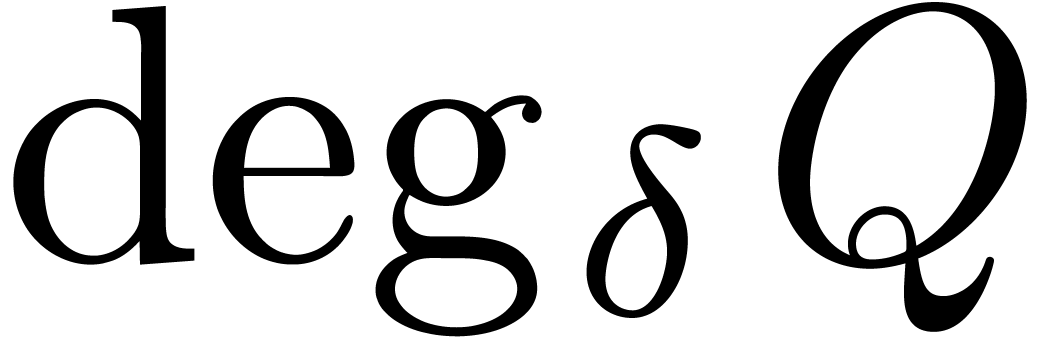 . This shows that
. This shows that 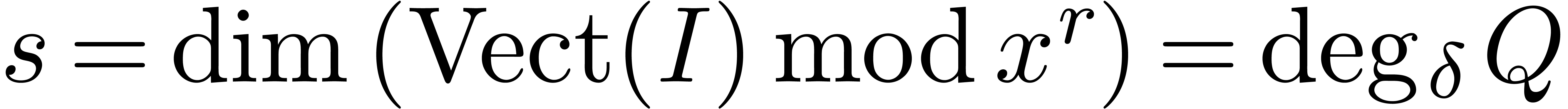 .
.
We now compute the monic annihilator 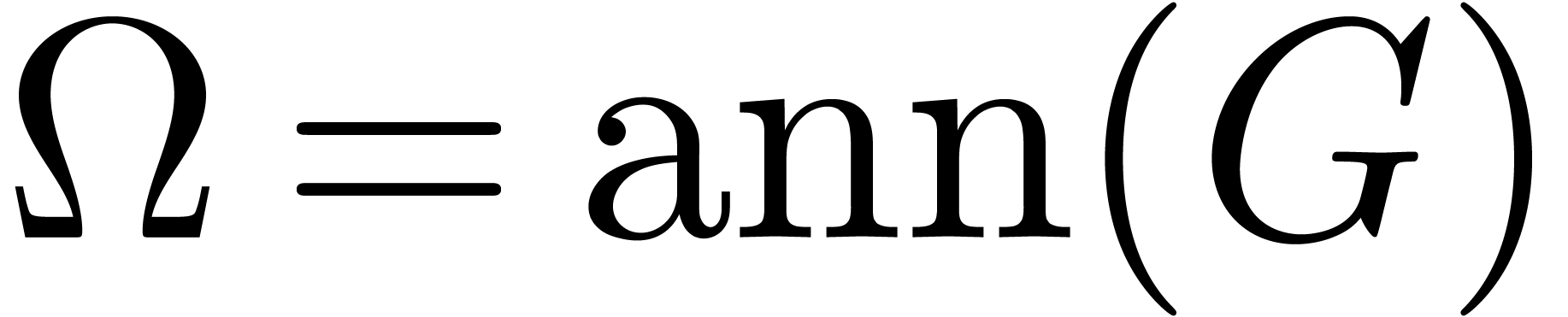 of
of  at order
at order 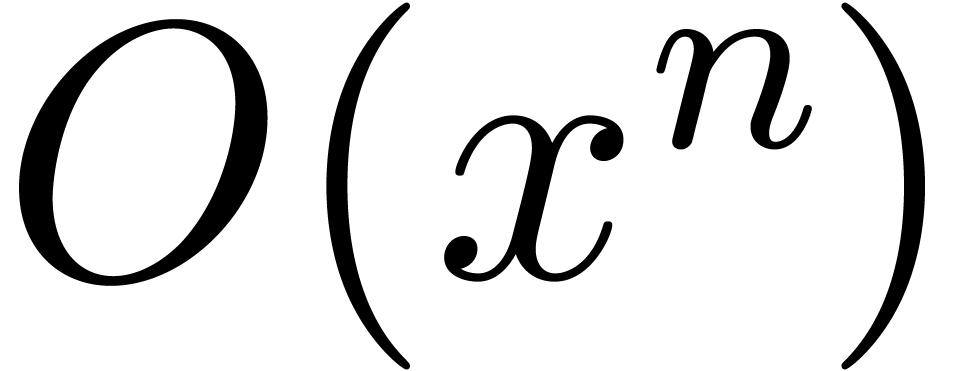 .
This can be done in time
.
This can be done in time 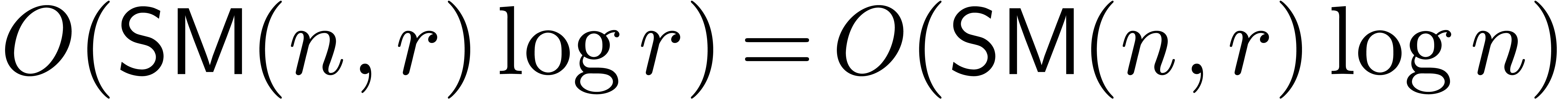 ,
by Theorem 8.
,
by Theorem 8.
We return the truncation of  at order
at order  , where
, where  .
.
Since each of the steps can be carried out in time 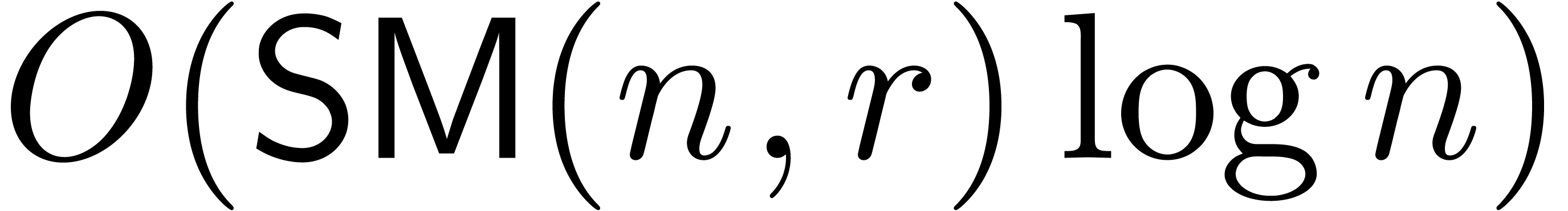 , the result follows.
, the result follows.
It is classical that euclidean division generalizes to the skew
polynomial ring 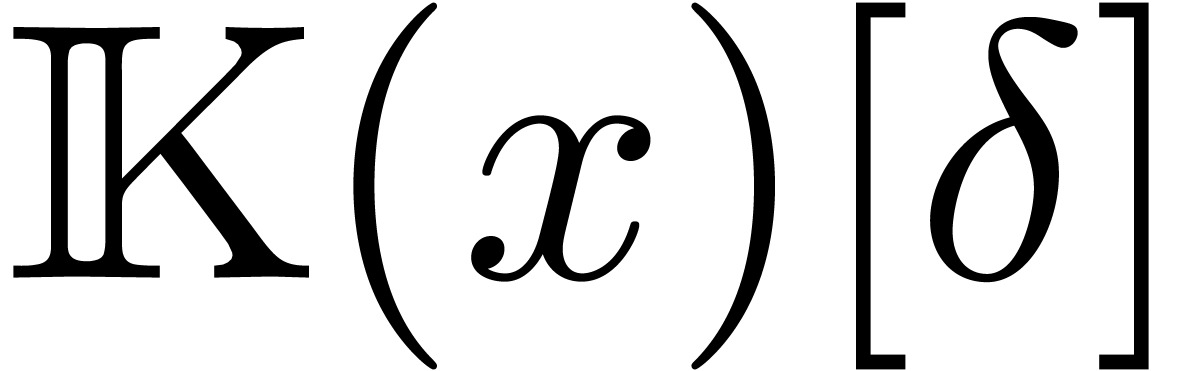 . In other
words, given operators
. In other
words, given operators 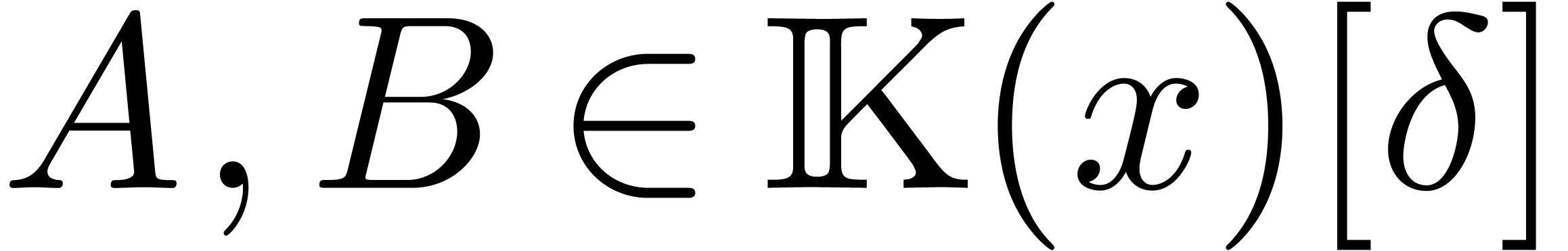 where
where 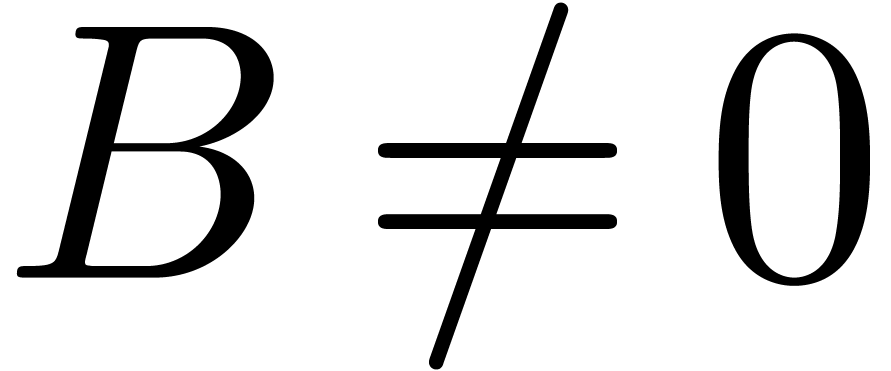 , there exist unique operators
, there exist unique operators 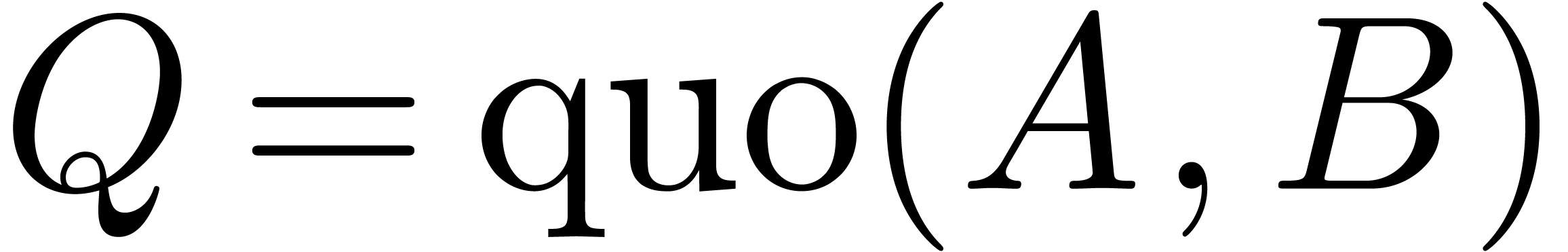 and
and 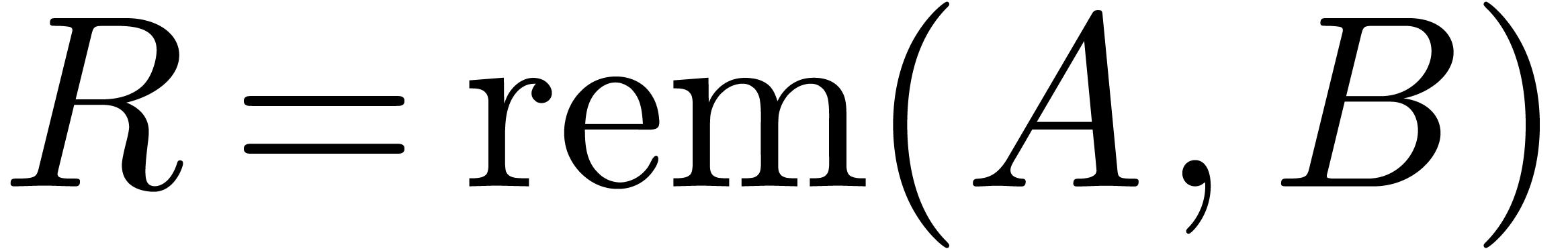 in
in 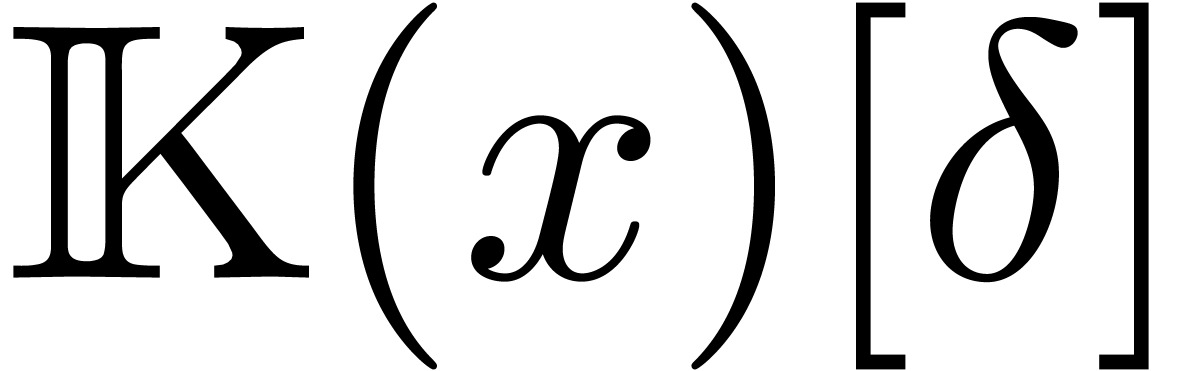 with
with

and  . If
. If 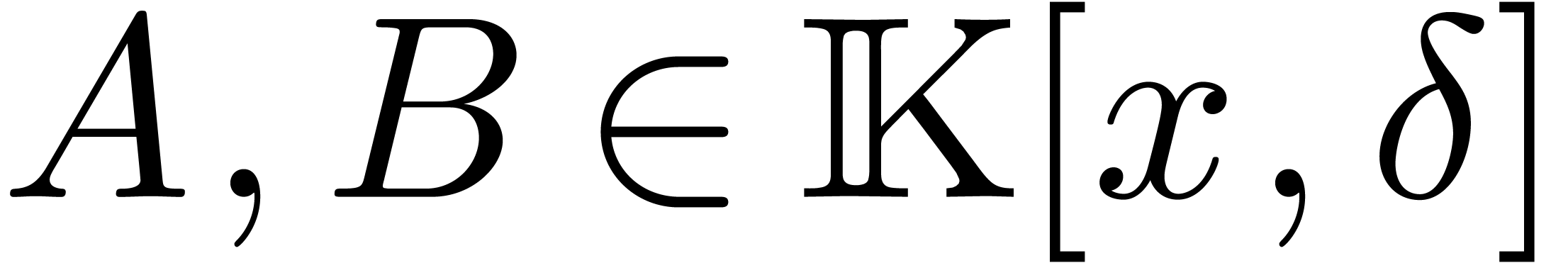 and
and 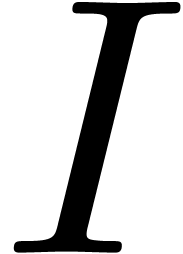 is the leading term of
is the leading term of  with respect to
with respect to 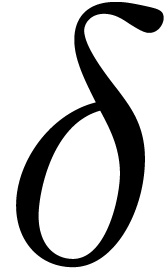 , then left
multiplication of
, then left
multiplication of  by
by 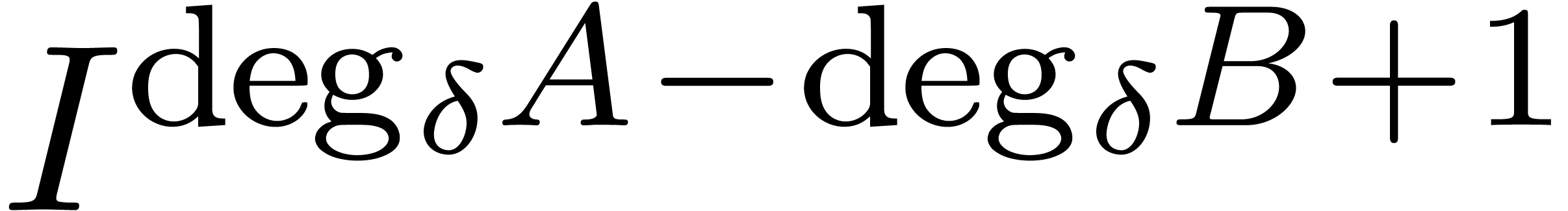 allows us to remain in the domain
allows us to remain in the domain 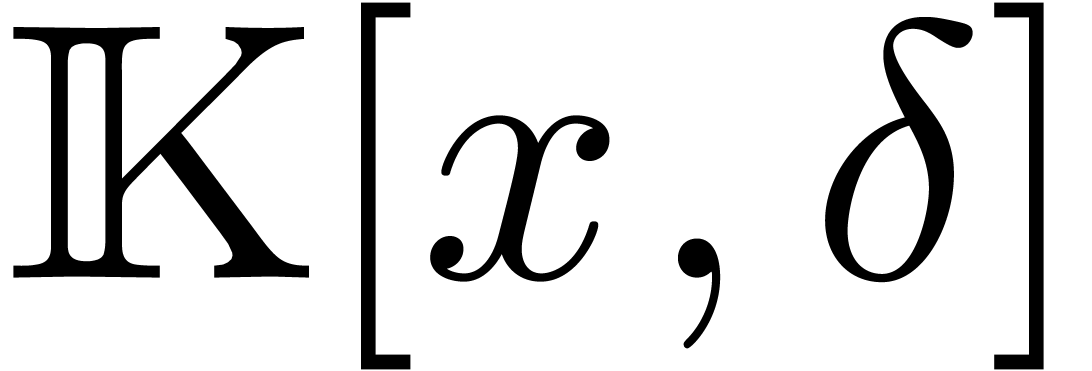 :
there exist unique
:
there exist unique 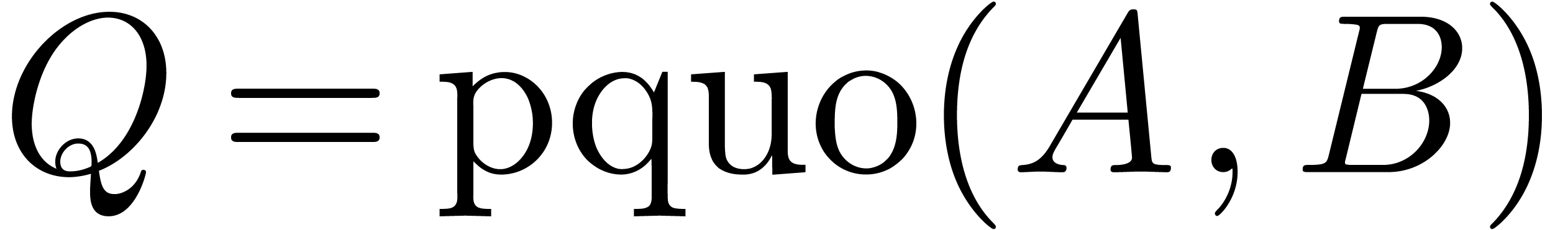 and
and 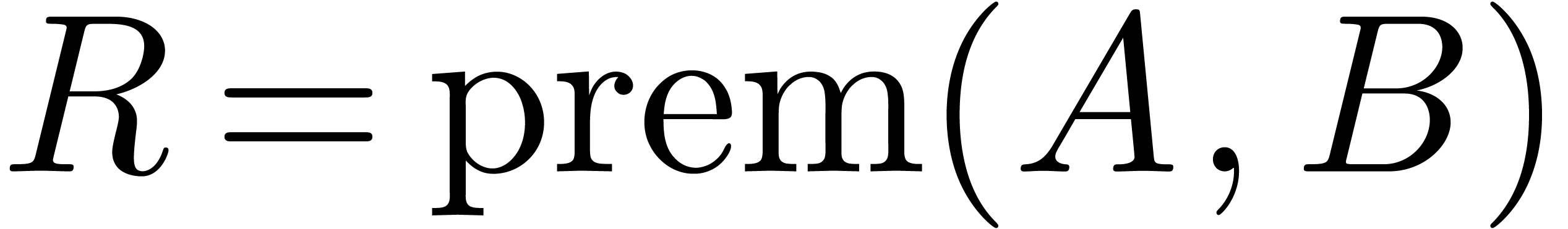 in
in 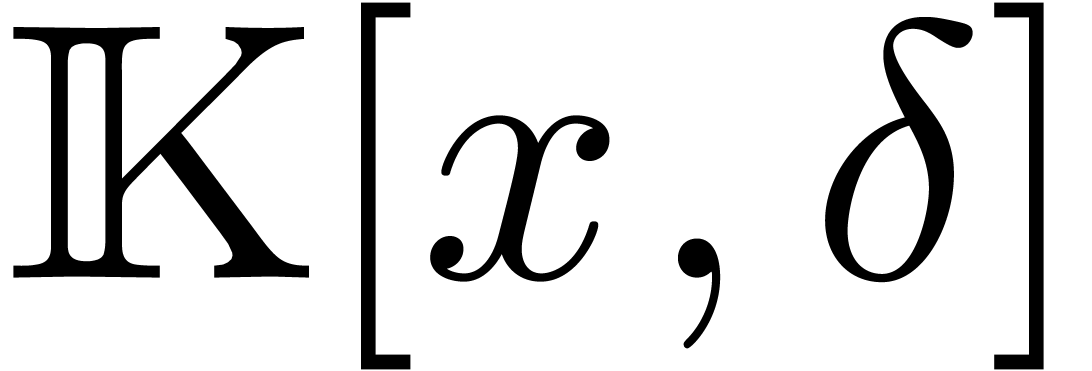 with
with
and  . The operators
. The operators  and
and  are usually called
pseudo-quotients and pseudo-remainders. In some cases, a non trivial
polynomial can be factored out in the relation (6). Let
are usually called
pseudo-quotients and pseudo-remainders. In some cases, a non trivial
polynomial can be factored out in the relation (6). Let
 be monic, of maximal degree, such that
be monic, of maximal degree, such that 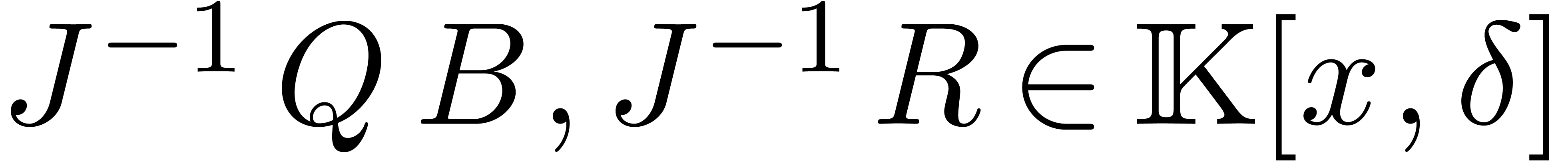 . Then we call
. Then we call 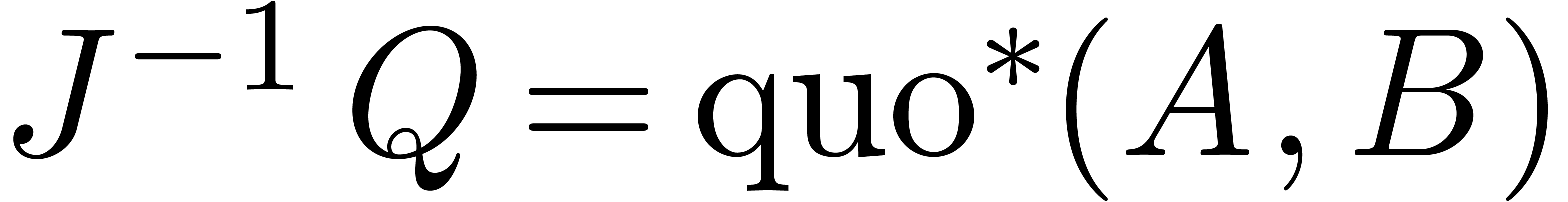 and
and  the “simplified” pseudo-quotient
and pseudo-remainder of
the “simplified” pseudo-quotient
and pseudo-remainder of  and
and  .
.
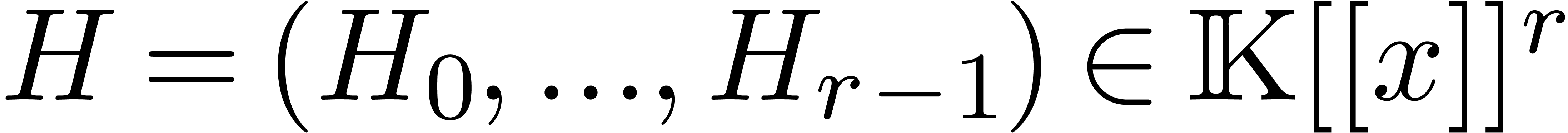 be
be  -linearly
independent and define
-linearly
independent and define 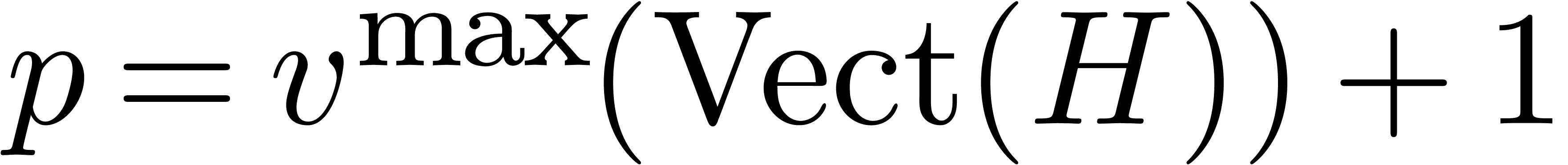 .
Given
.
Given  , there exists a
unique operator
, there exists a
unique operator 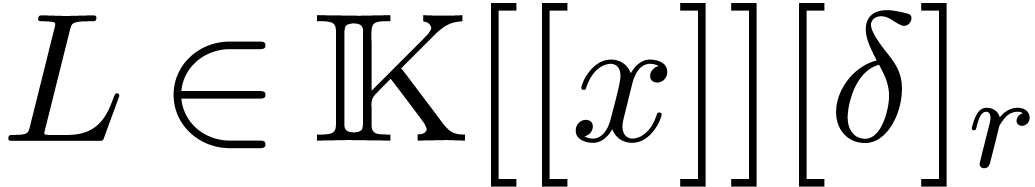 of order
of order 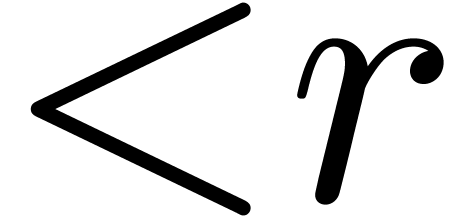 with
with  and we may compute its first
and we may compute its first  terms with respect to
terms with respect to  in time
in time
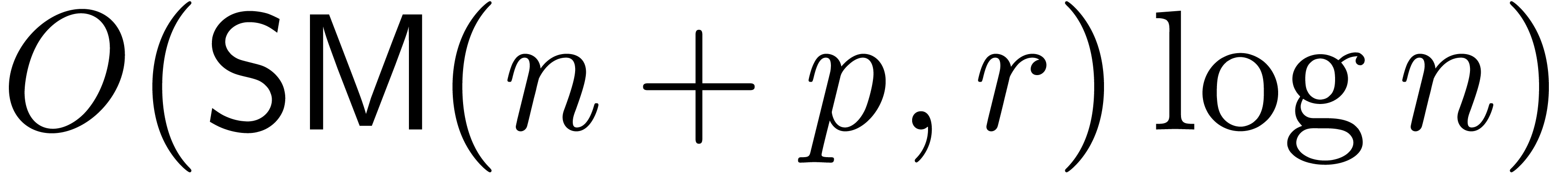 .
.
Proof. Let 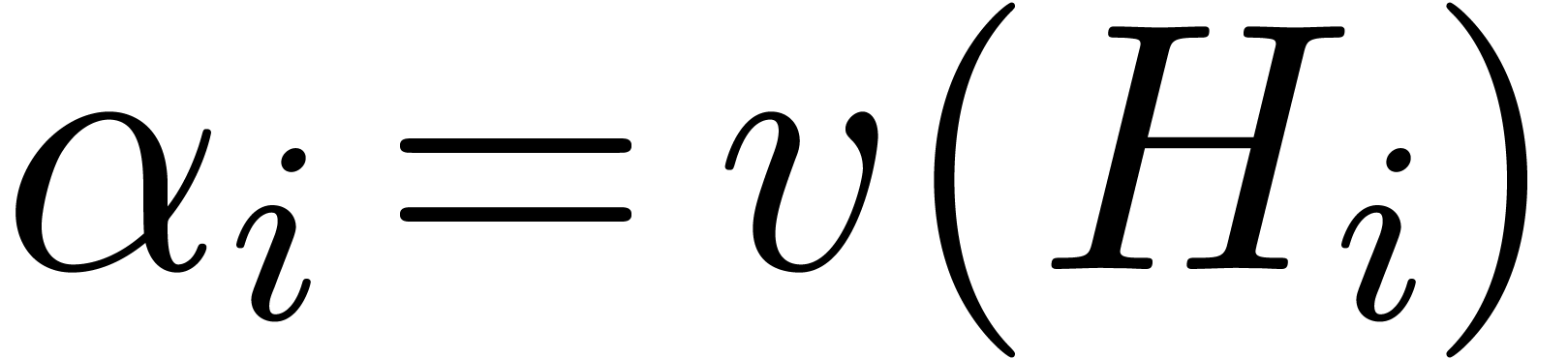 for each
for each
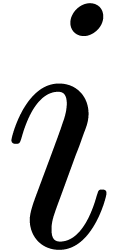 . Modulo a base change, we
may assume without loss of generality that
. Modulo a base change, we
may assume without loss of generality that  .
Let
.
Let 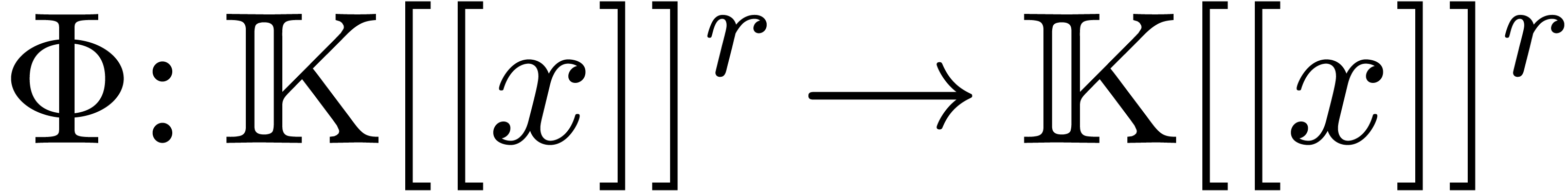 be the operator with
be the operator with
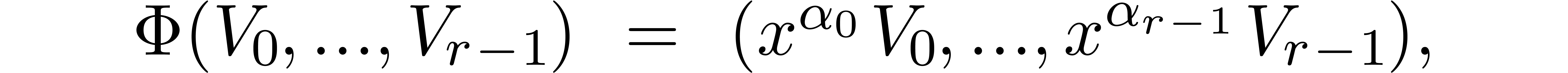
and let 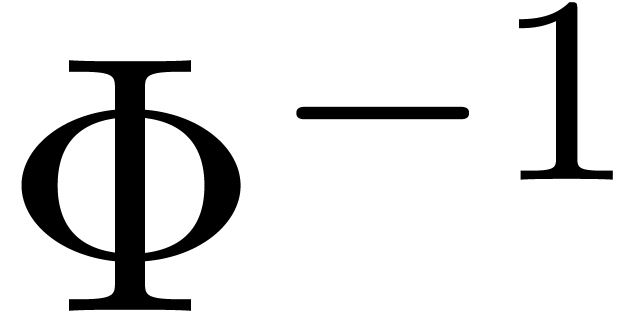 denote the inverse operator. Let
denote the inverse operator. Let  be the operator with
be the operator with
Writing 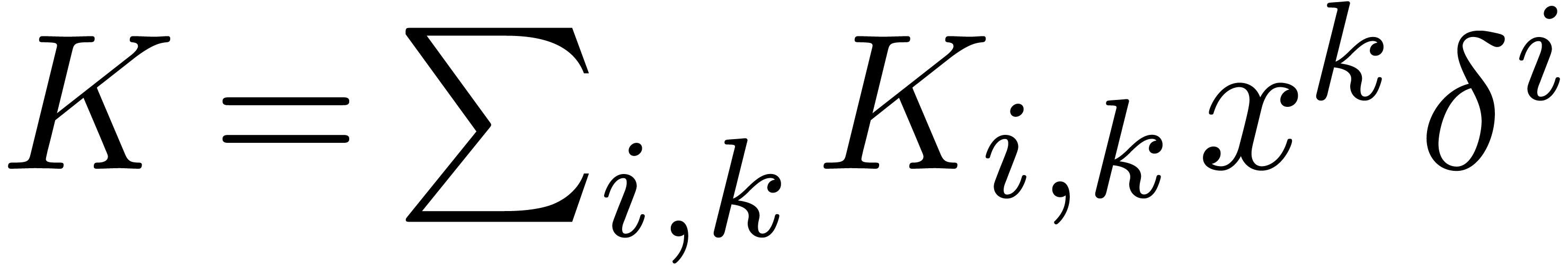 and
and 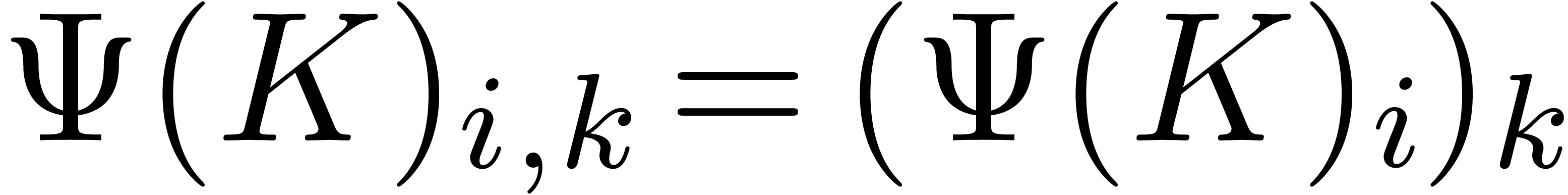 ,
we have
,
we have
In other words,  and its inverse
and its inverse 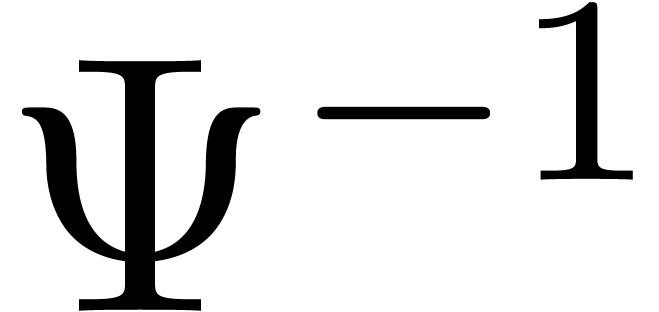 operate coefficientwise and
operate coefficientwise and 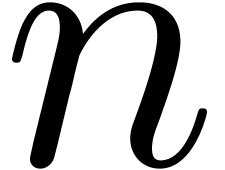 coefficients can be
computed in time
coefficients can be
computed in time 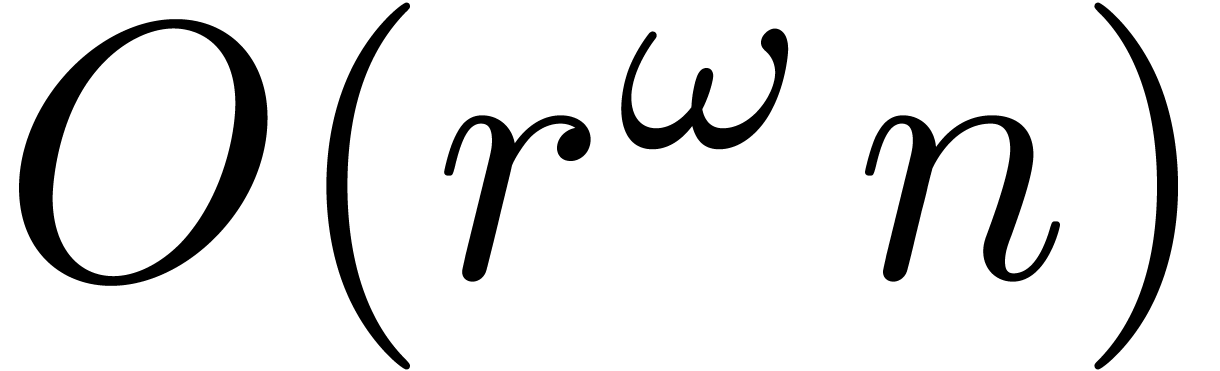 .
.
Putting  with
with  for each
for each
 , we may rewrite the equation
, we may rewrite the equation
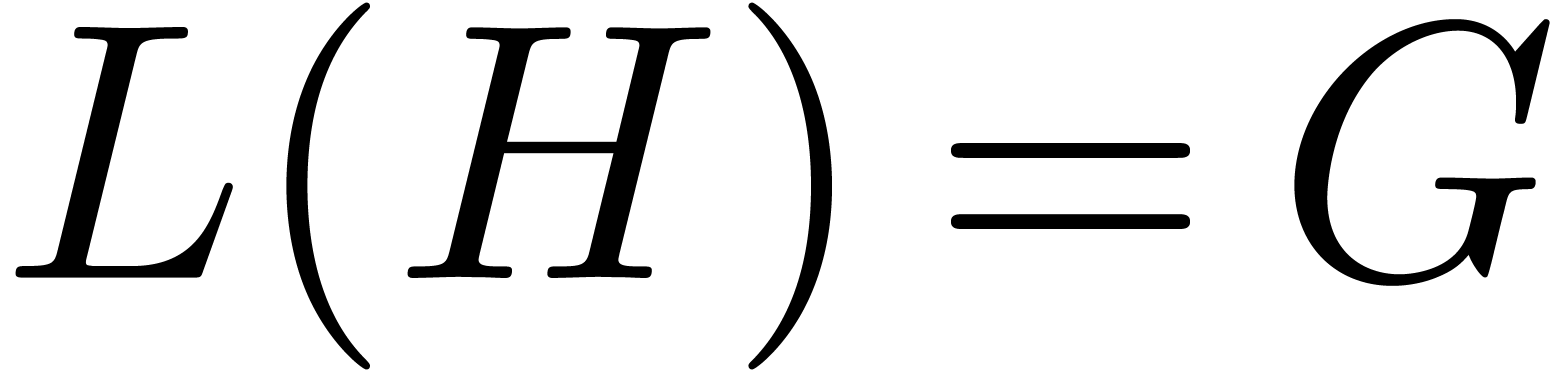 as
as
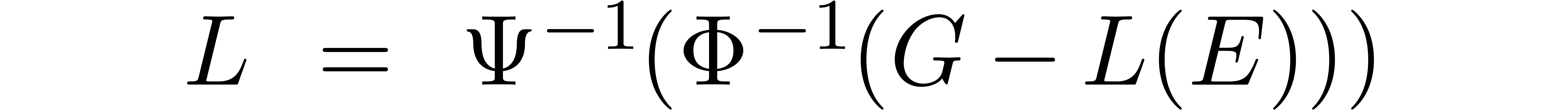
and we observe that the coefficient of 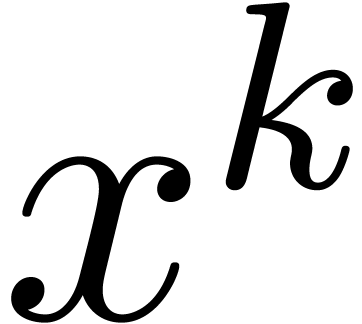 in the
righthand side of (?) only depends on earlier coefficients
of
in the
righthand side of (?) only depends on earlier coefficients
of 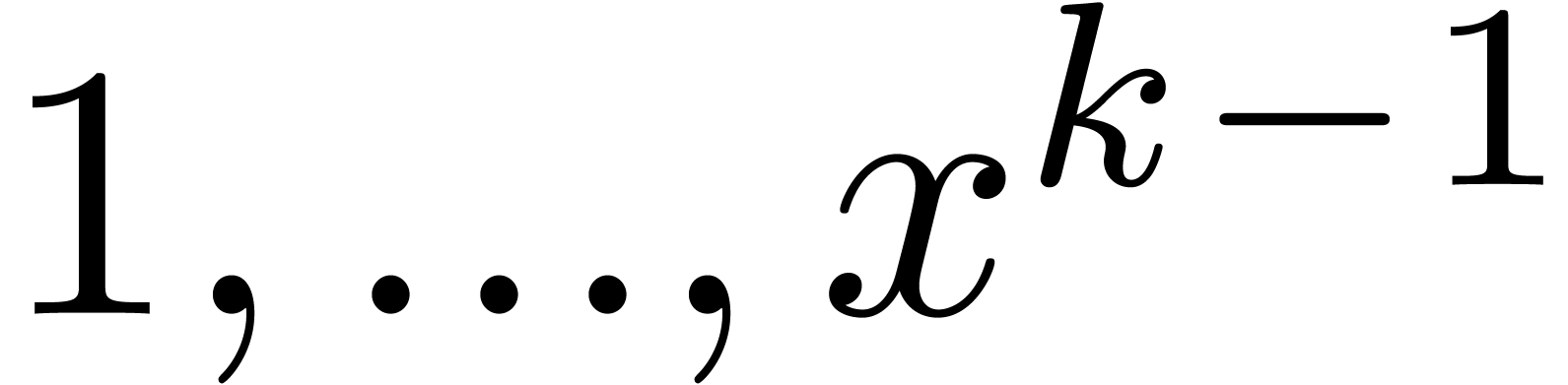 in
in  .
In particular, we may solve the equation using a relaxed algorithm. Then
the main cost is concentrated in the relaxed evaluation of
.
In particular, we may solve the equation using a relaxed algorithm. Then
the main cost is concentrated in the relaxed evaluation of 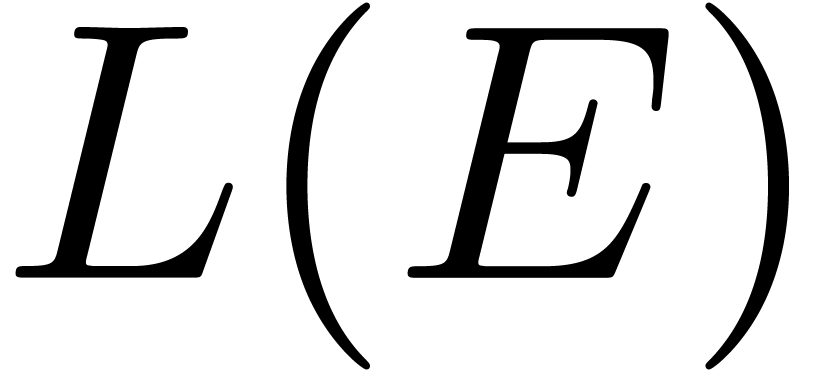 . As in the proof of Theorem 7,
this evaluation can be done in time
. As in the proof of Theorem 7,
this evaluation can be done in time 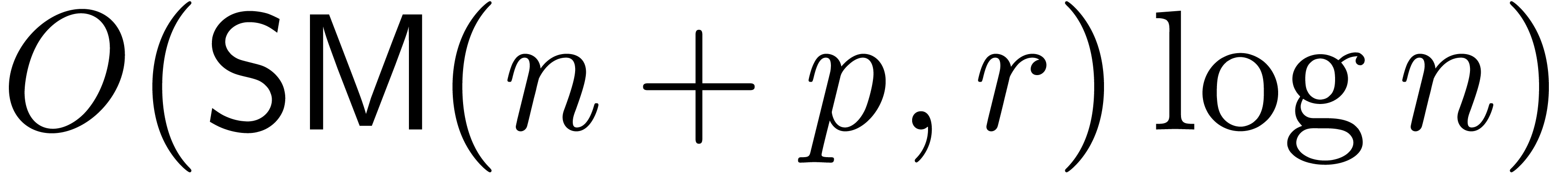 .
.
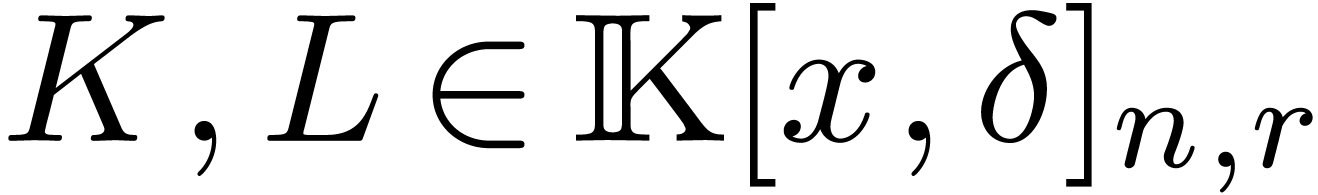 with
with  and
and
 . Right pseudo-division of
. Right pseudo-division of
 by
by  and simplification
yields a relation
and simplification
yields a relation

where  . If
. If  is such that
is such that 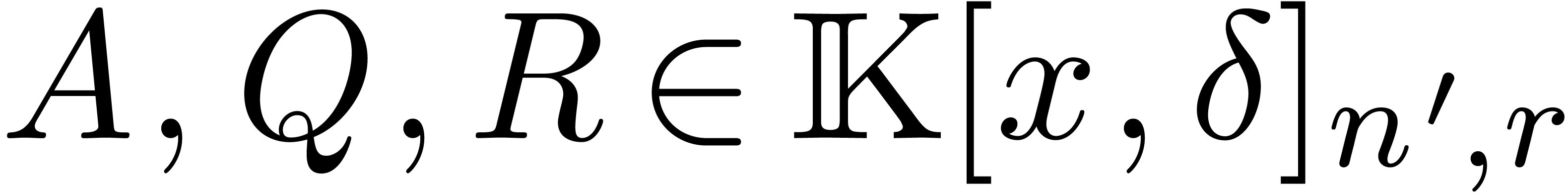 ,
then
,
then  and
and  can be
computed in time
can be
computed in time 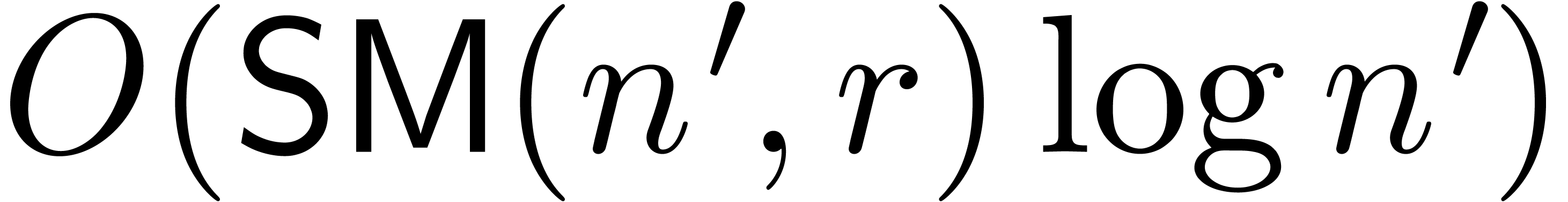 .
.
Proof. Modulo a shift 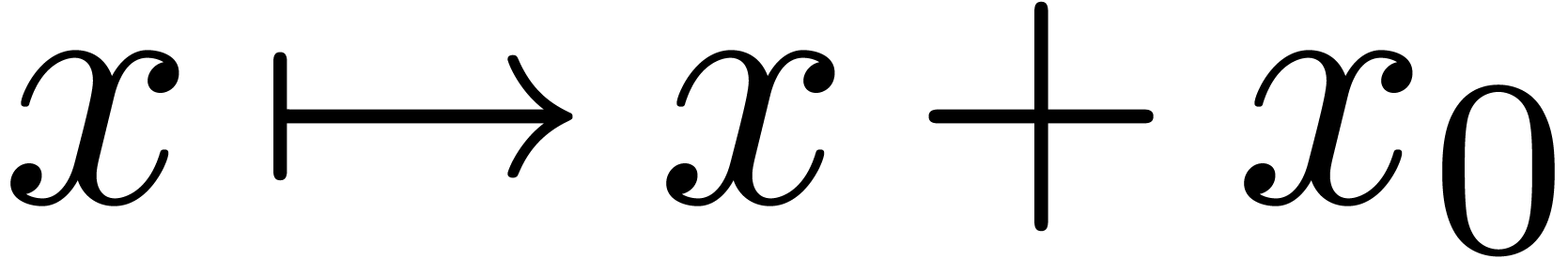 , we may assume without loss of generality that
, we may assume without loss of generality that 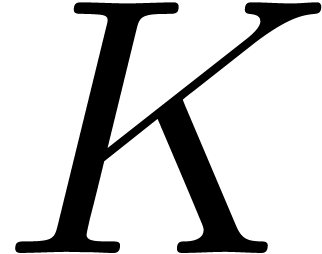 and
and  are non singular at the
origin. We now use the following algorithm:
are non singular at the
origin. We now use the following algorithm:
We compute the canonical fundamental system  of solutions to
of solutions to  up to order
up to order 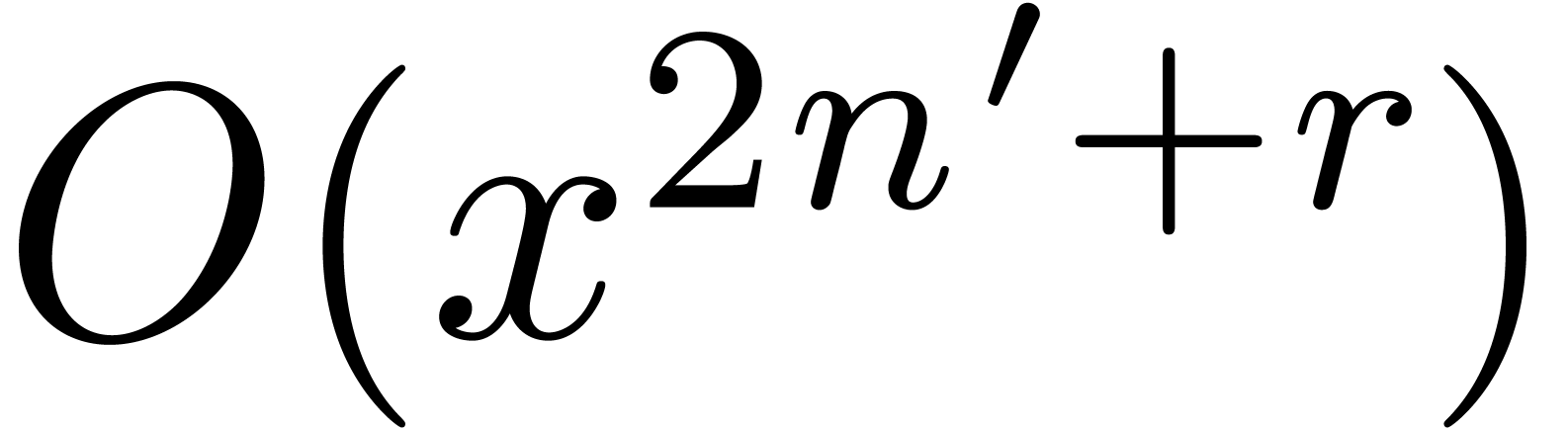 . This requires a time
. This requires a time 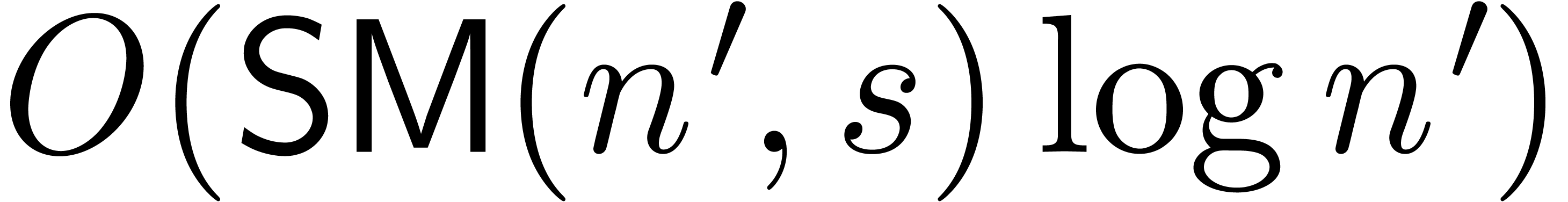 .
.
We compute 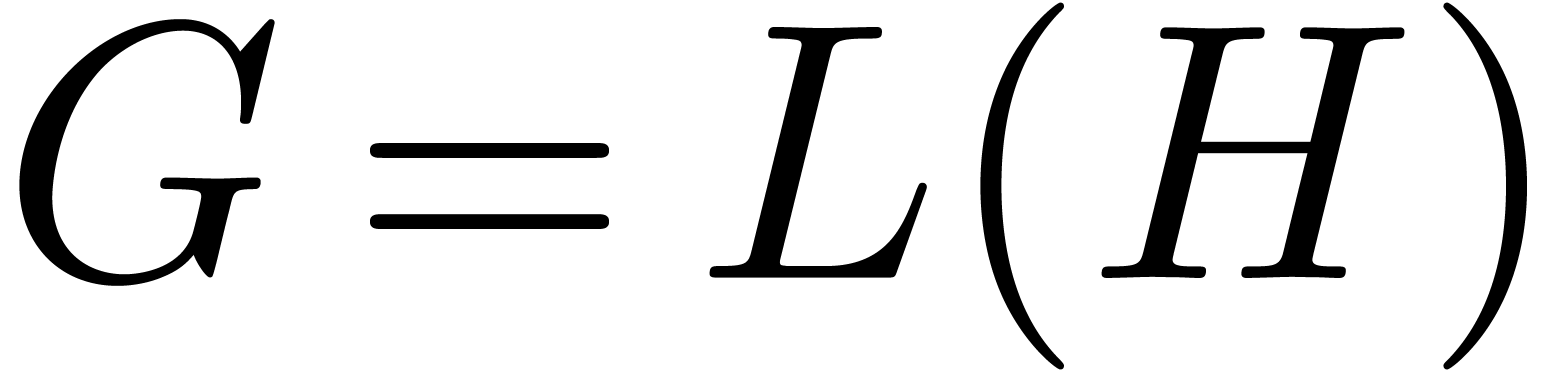 with
with 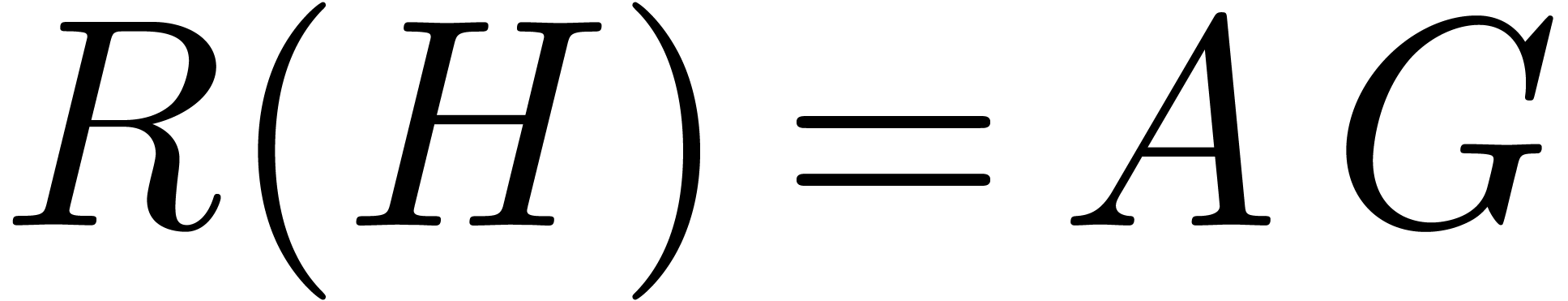 up
to order
up
to order 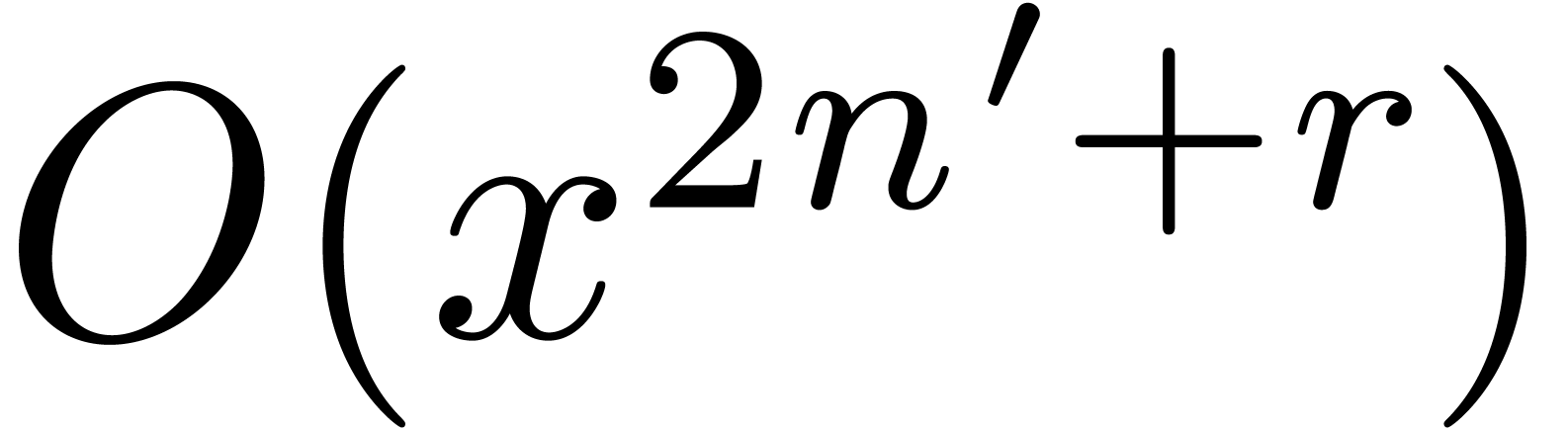 . This requires
a time
. This requires
a time 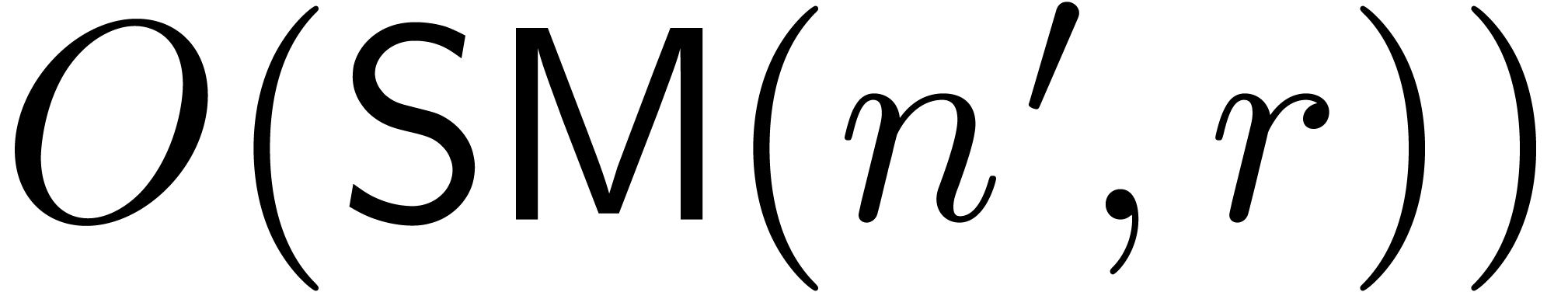 .
.
We determine the operator 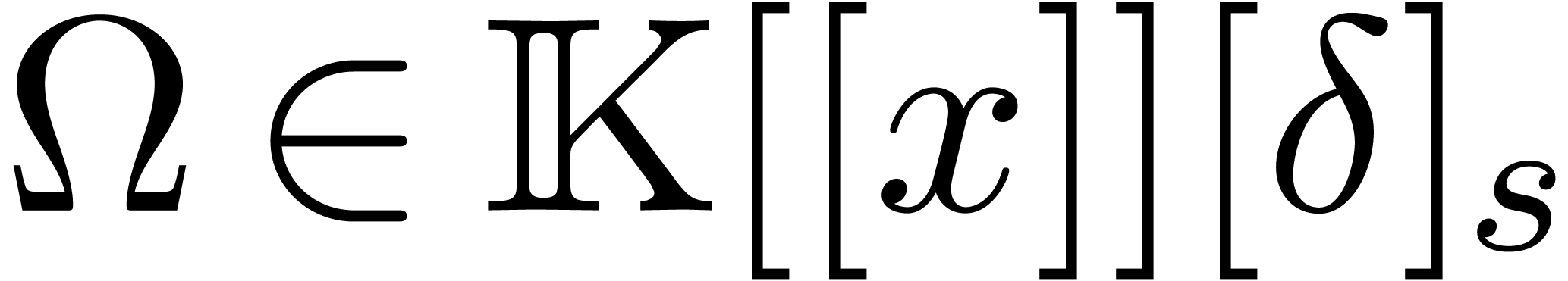 with
with 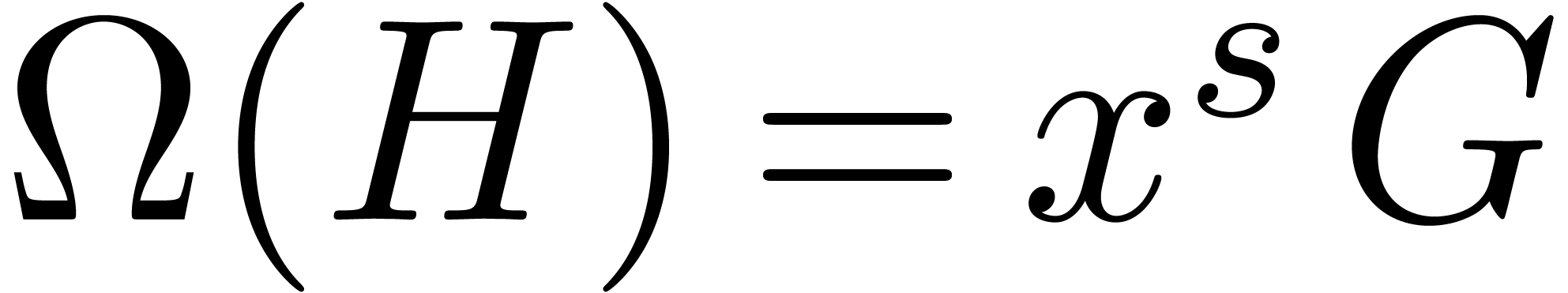 up to order
up to order 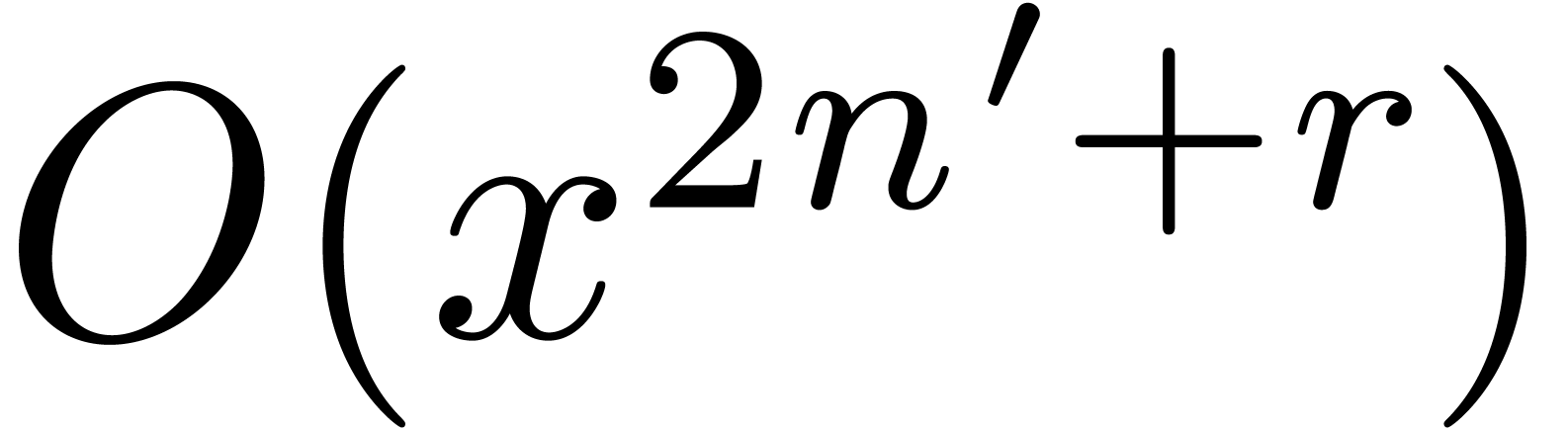 .
Lemma 14 shows that this can be done in time
.
Lemma 14 shows that this can be done in time 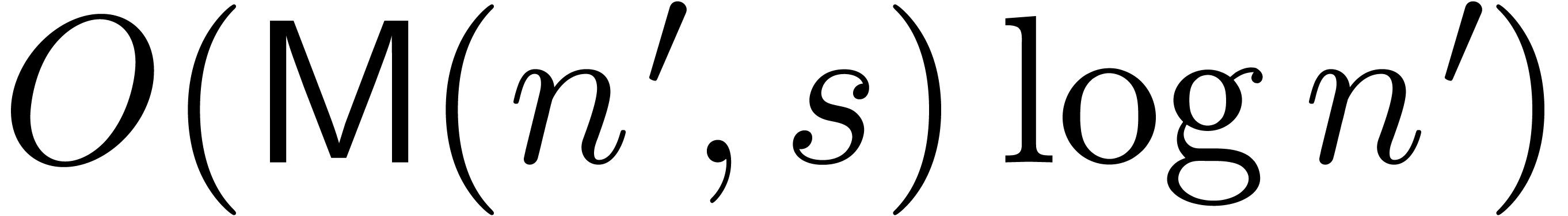 .
.
By Theorem 8, we have 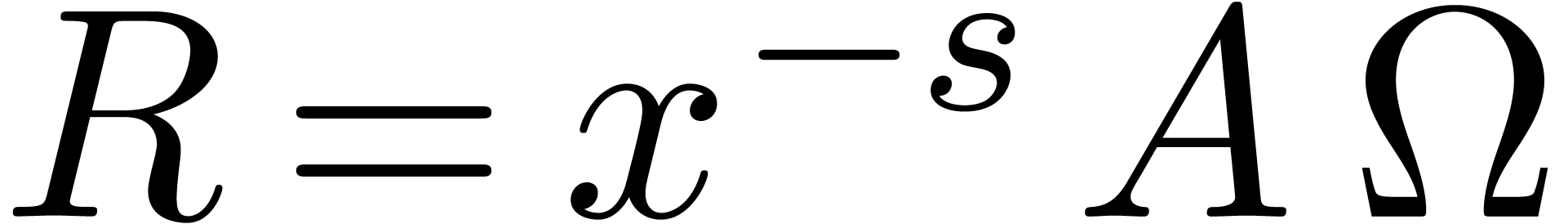 and
and 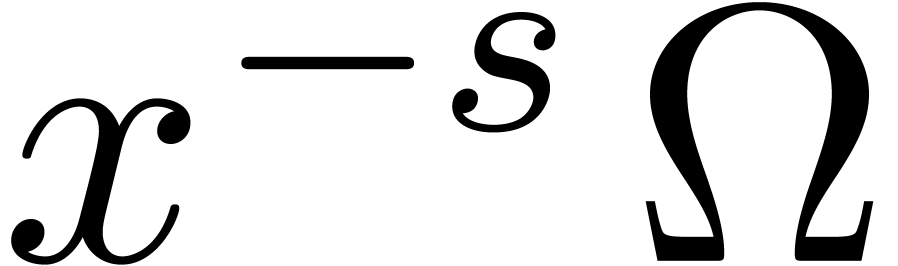 is known up to order
is known up to order 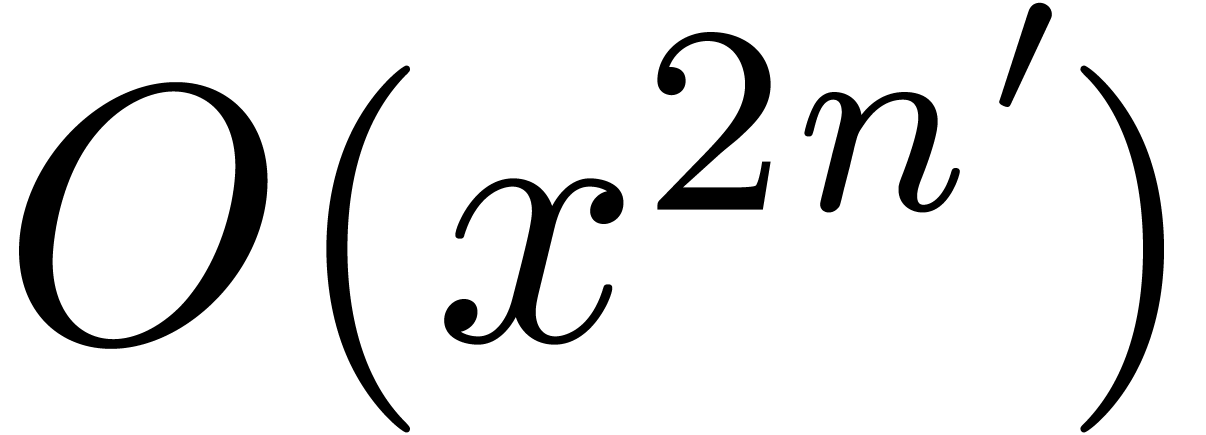 . Now
. Now 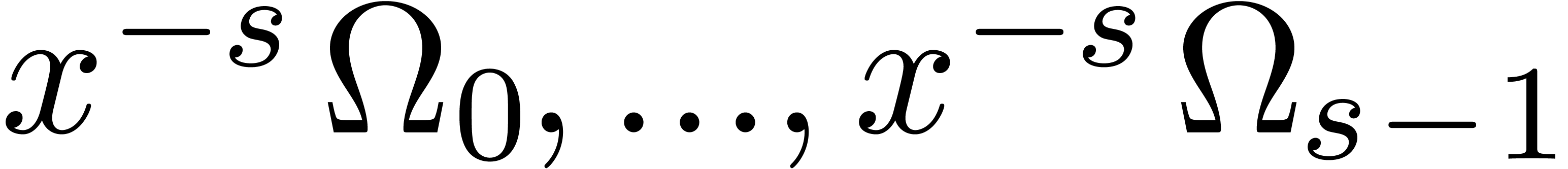 are truncated
rational functions, for which the degrees of the numerators and
denominators are bounded by
are truncated
rational functions, for which the degrees of the numerators and
denominators are bounded by 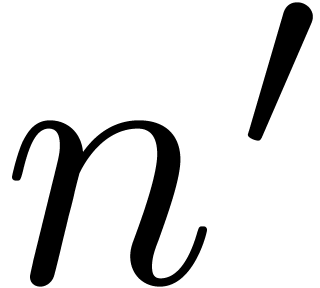 .
Using rational function reconstruction [18], we may
thus compute
.
Using rational function reconstruction [18], we may
thus compute 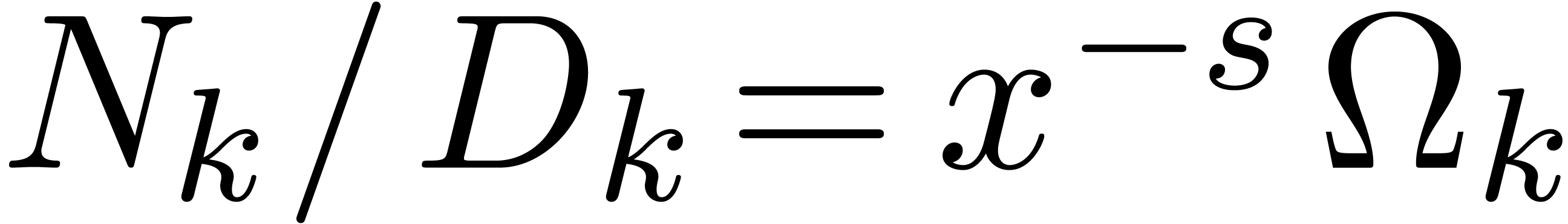 with
with 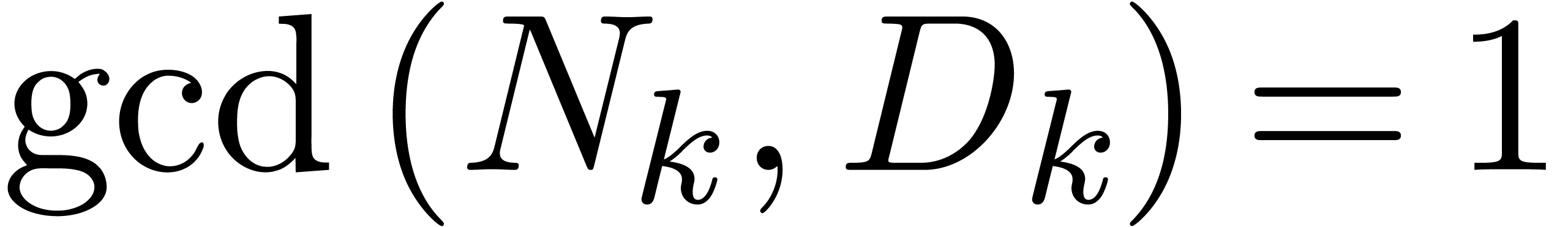 in
time
in
time  . Taking
. Taking 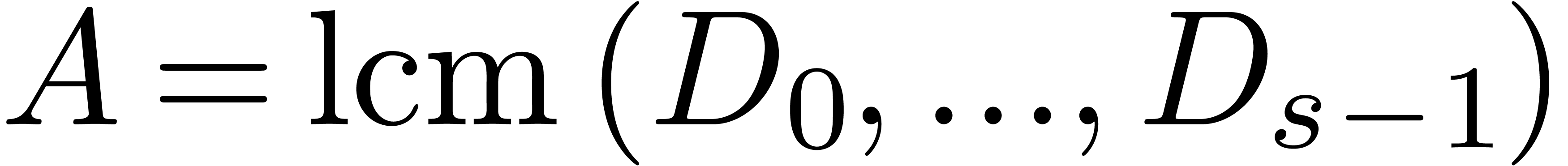 , we find
, we find 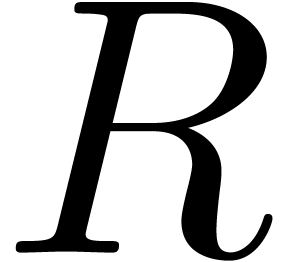 .
.
Once  and
and 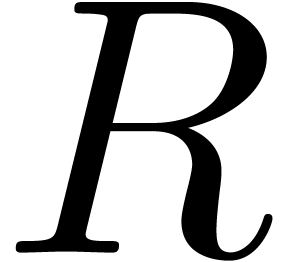 are known,
we compute
are known,
we compute  using the algorithm from Theorem
13.
using the algorithm from Theorem
13.
The total complexity of this algorithm is bounded by 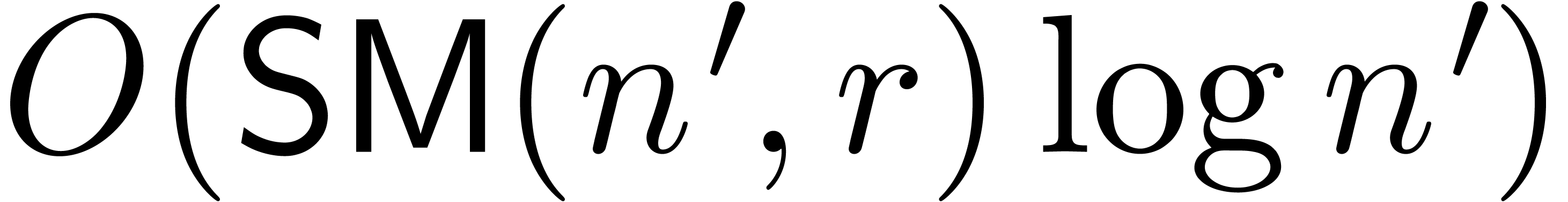 .
.
Remark 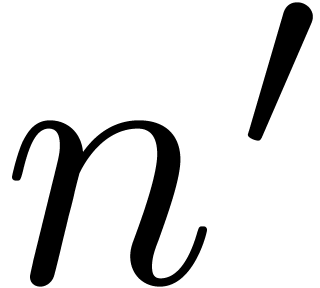 is known
beforehand. In general, we may still apply the above algorithm for a
trial value
is known
beforehand. In general, we may still apply the above algorithm for a
trial value 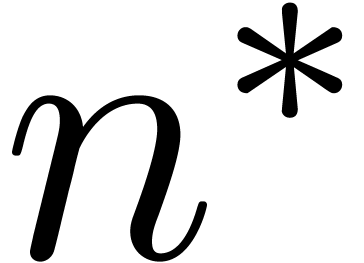 . Then the
algorithm may either fail (for instance, if
. Then the
algorithm may either fail (for instance, if  ), or return the triple
), or return the triple  under the assumption that
under the assumption that 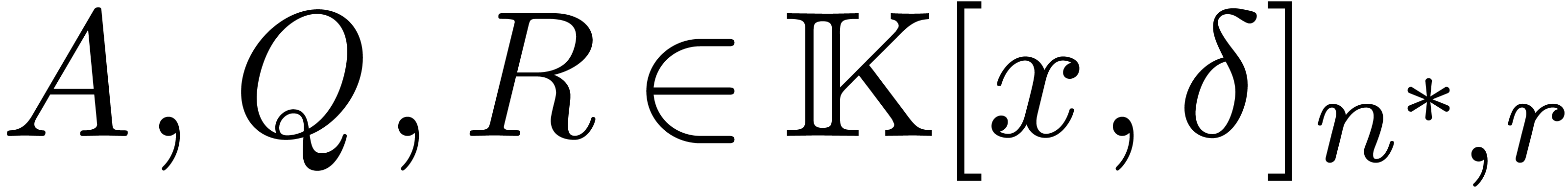 .
We may then check whether the triple is correct in time
.
We may then check whether the triple is correct in time 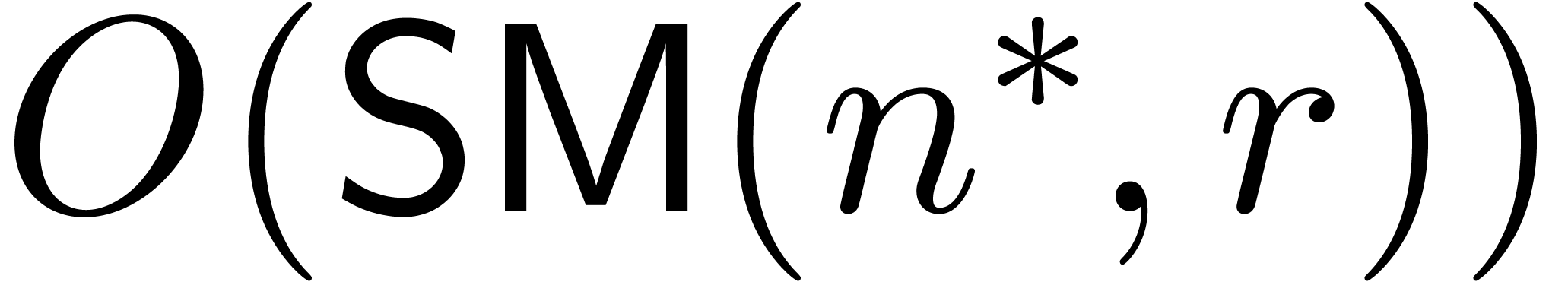 . Applying this procedure for successive
guesses
. Applying this procedure for successive
guesses 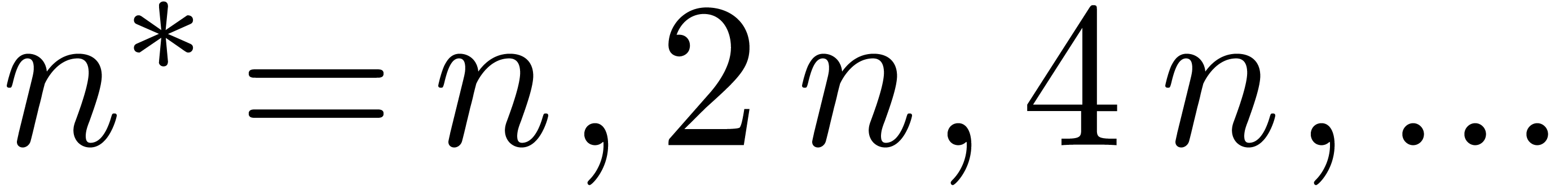 , the algorithm
ultimately succeeds for an
, the algorithm
ultimately succeeds for an 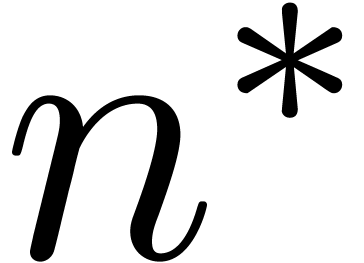 with
with 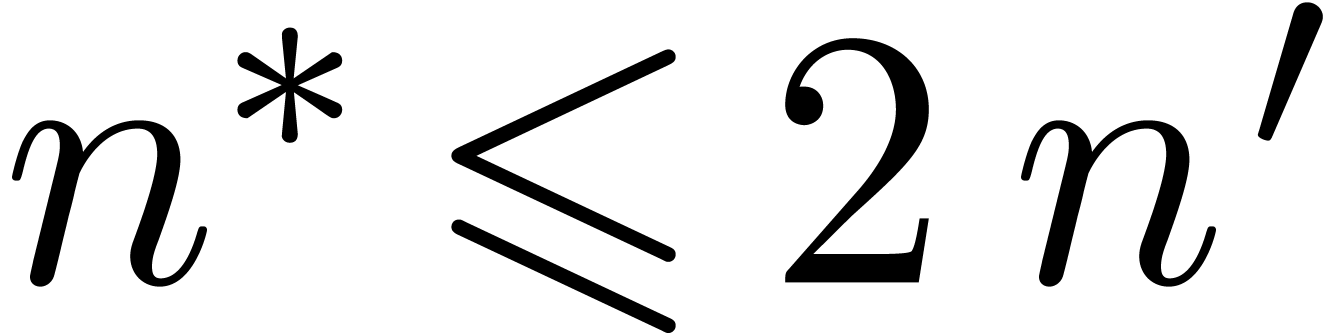 . Using the monotonicity hypothesis, the total
running time thus remains bounded by
. Using the monotonicity hypothesis, the total
running time thus remains bounded by 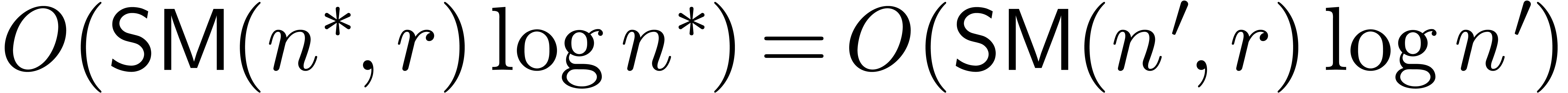 .
.
It is classical that greatest common right divisors and least common
left multiples exist in the skew euclidean domain 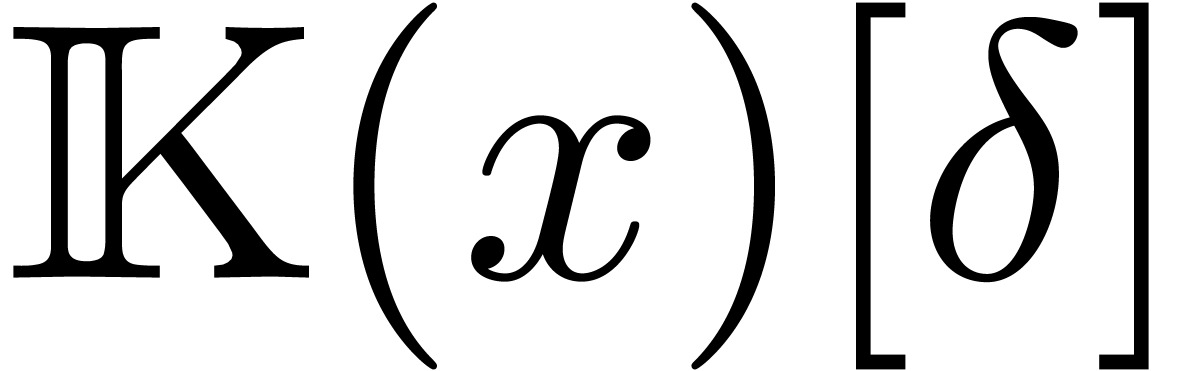 : given two operators
: given two operators 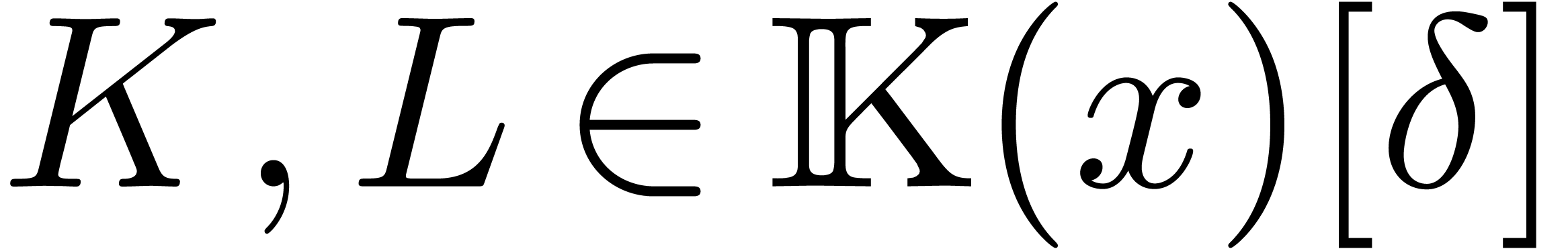 ,
the greatest common right divisor
,
the greatest common right divisor 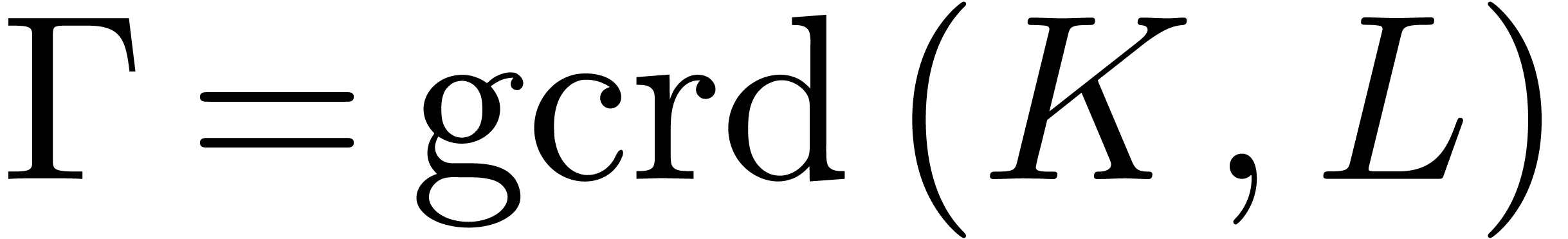 and the least
common left multiple
and the least
common left multiple  are the unique monic
operators with
are the unique monic
operators with
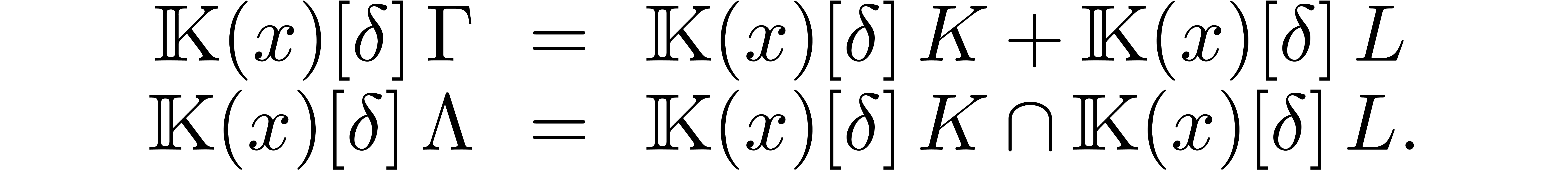
Assume now that 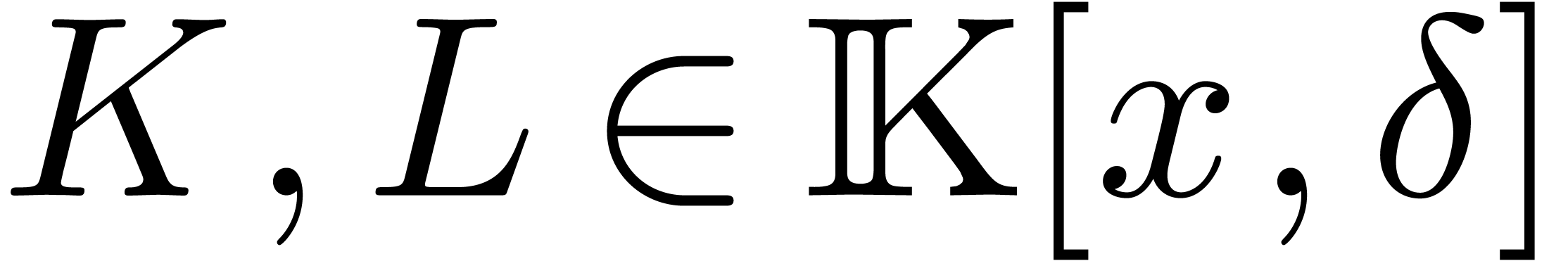 and let
and let  and
and  be monic polynomials of minimal degrees,
such that
be monic polynomials of minimal degrees,
such that  and
and  are in
are in
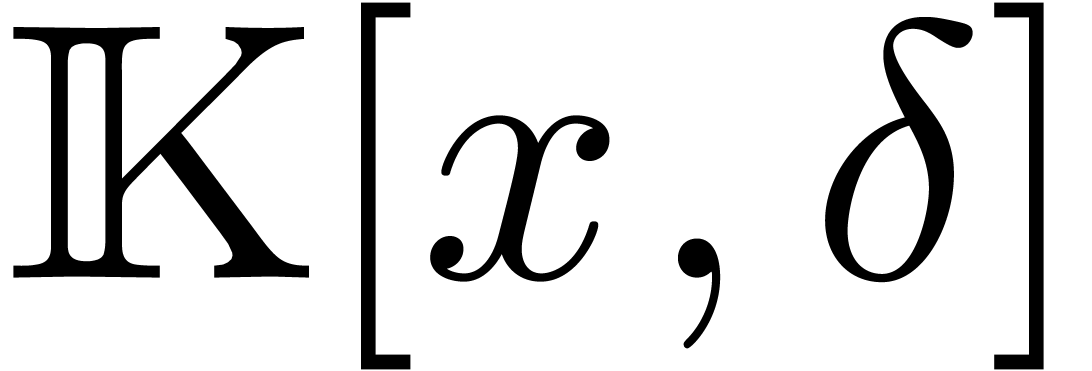 . Then we call
. Then we call  and
and 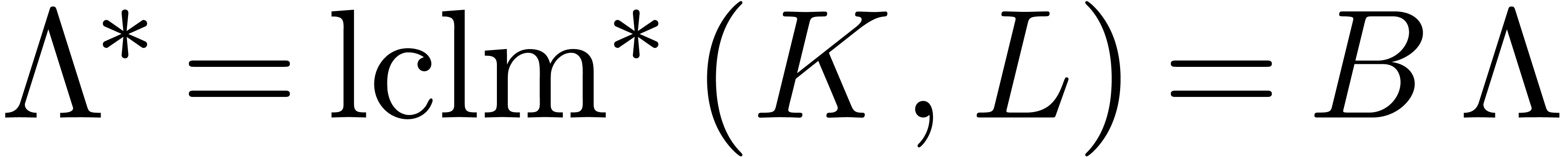 the (simplified) pseudo-gcrd
and pseudo-lclm of
the (simplified) pseudo-gcrd
and pseudo-lclm of 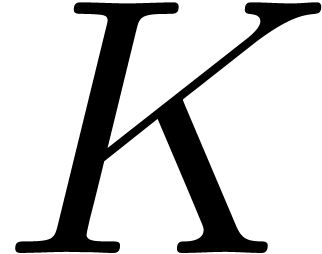 and
and 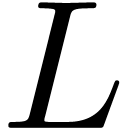 .
.
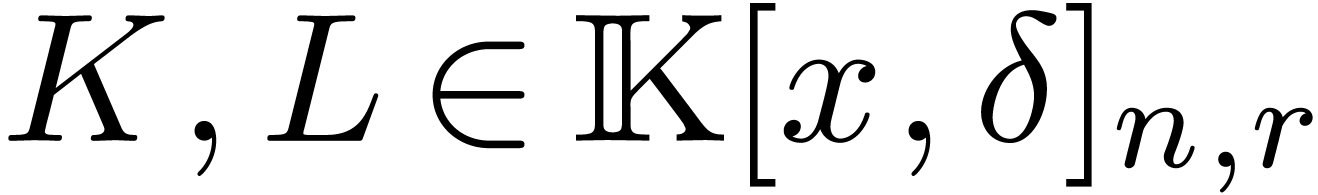 be such that
be such that  and
and  are non singular at the origin, as well as
are non singular at the origin, as well as 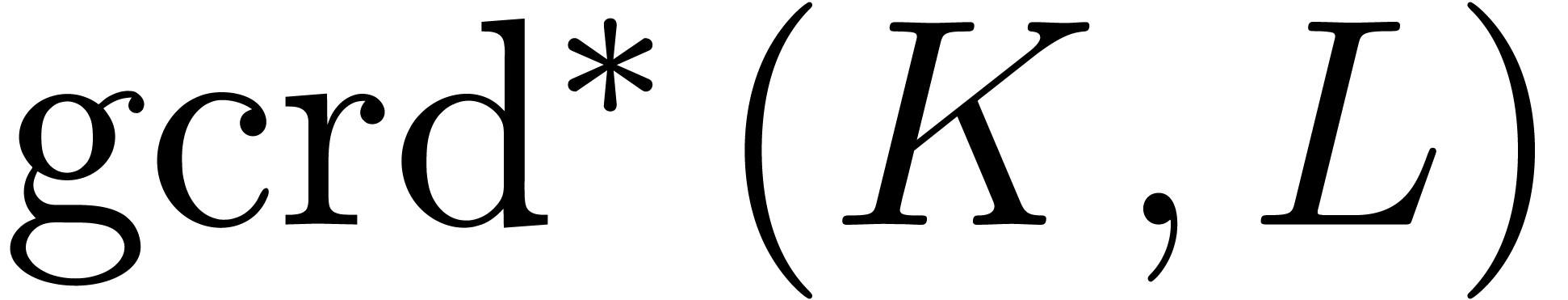 or
or 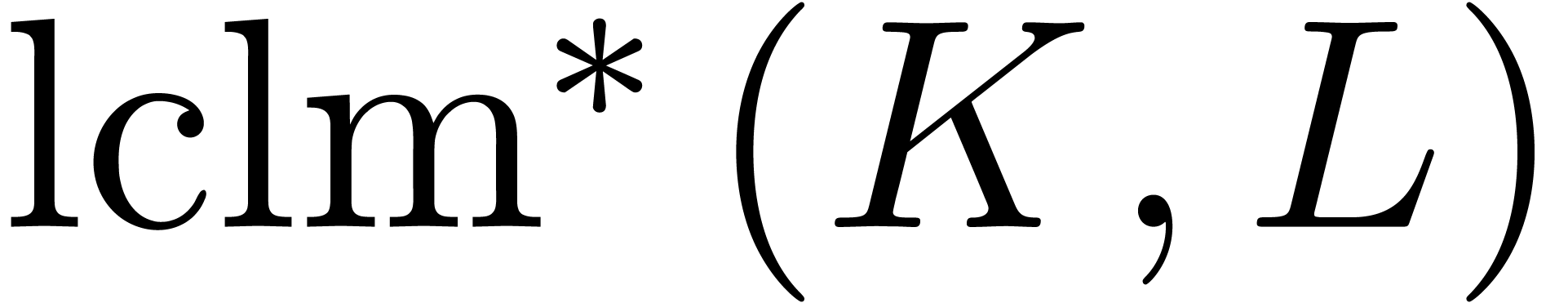 . Let
. Let
 and
and  be the canonical
fundamental systems of solutions to
be the canonical
fundamental systems of solutions to 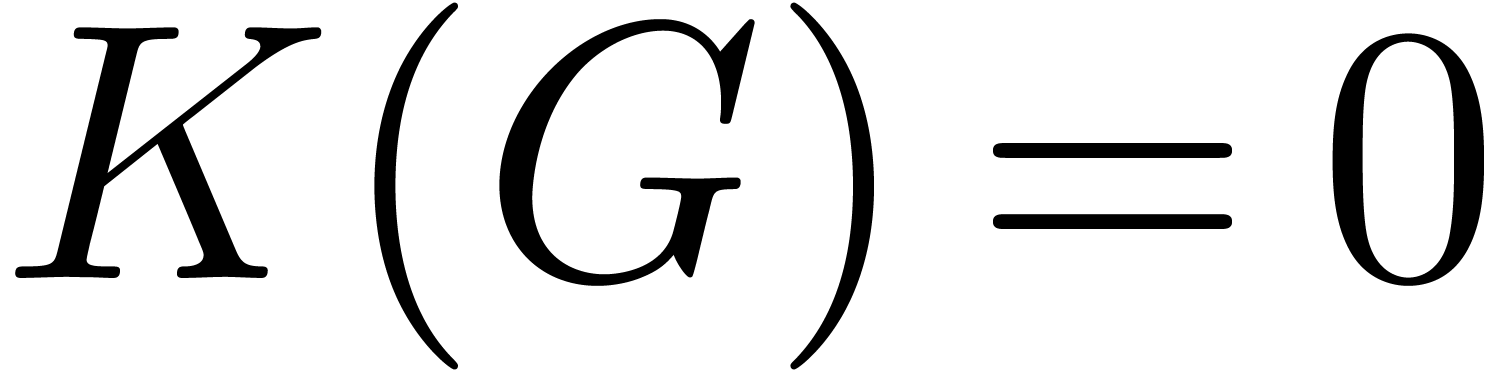 and
and 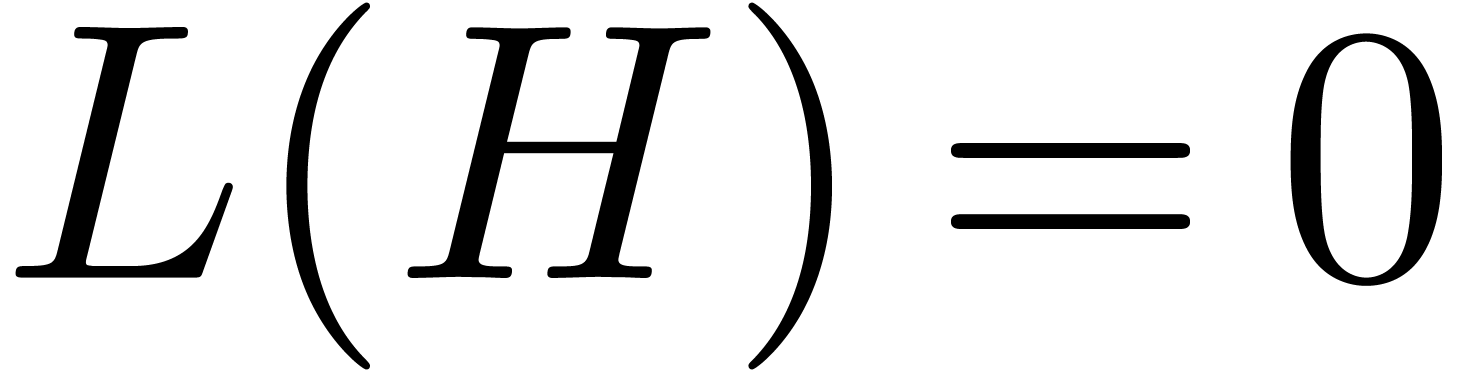 . Then
. Then
Proof. Let 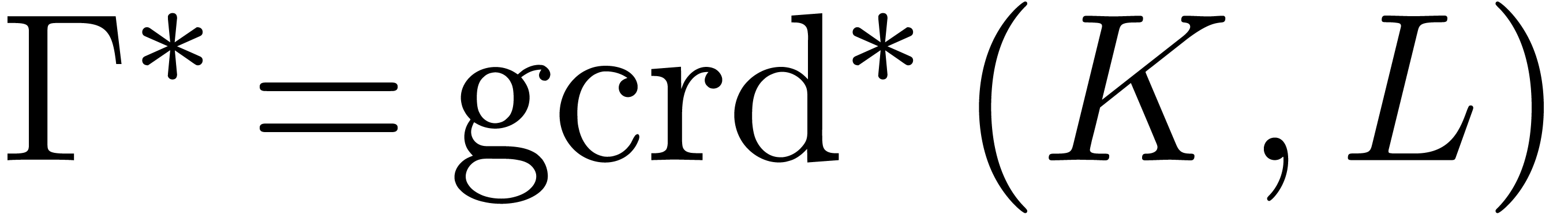 ,
,
 ,
,  and
and
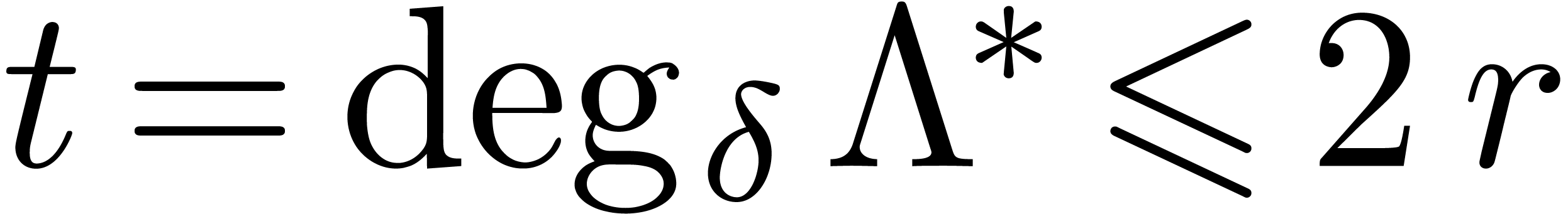 . If
. If  is non singular, then it admits a canonical fundamental system of
solutions
is non singular, then it admits a canonical fundamental system of
solutions 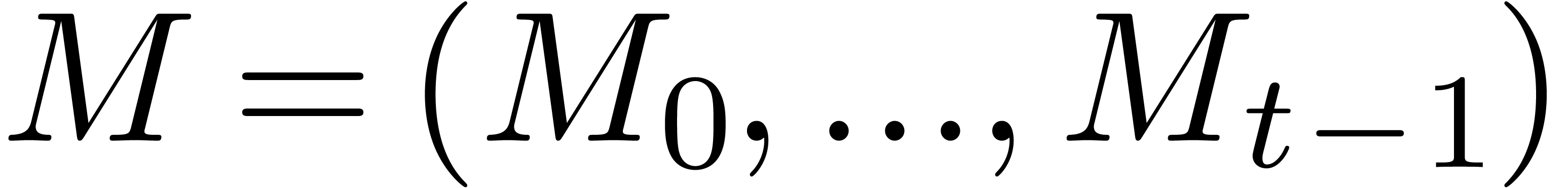 with
with 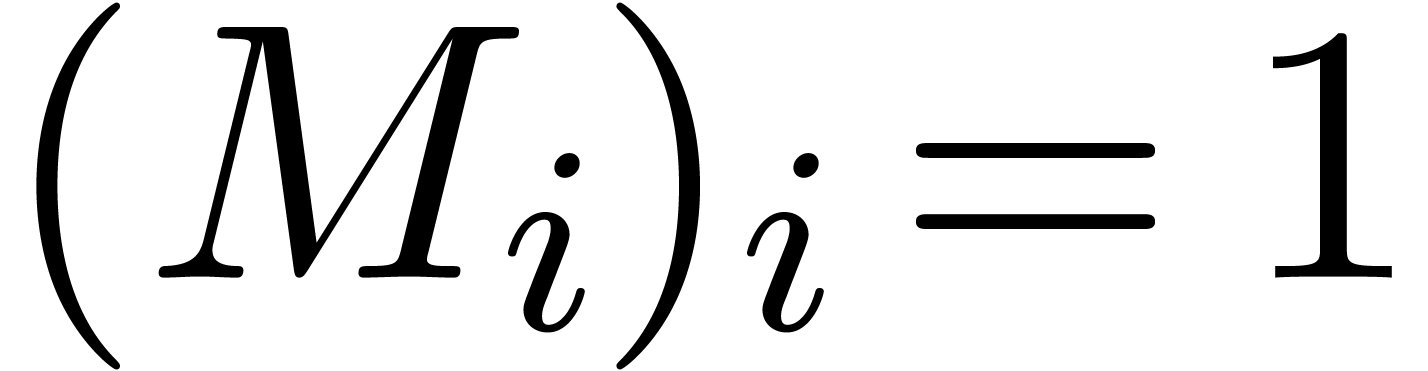 and
and 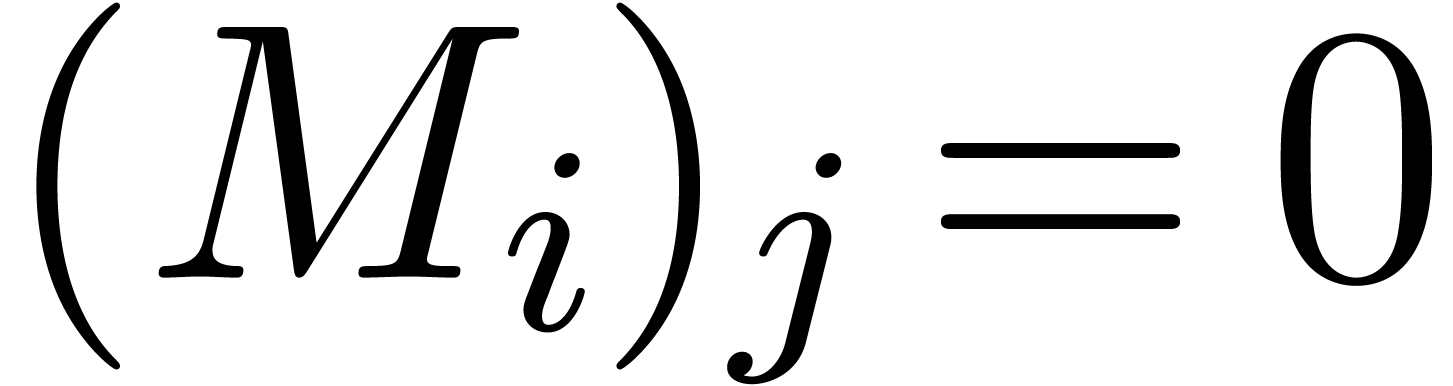 for all
for all 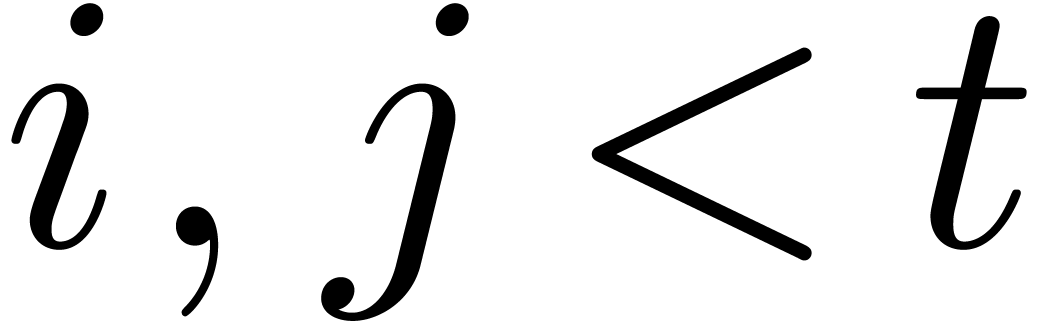 with
with 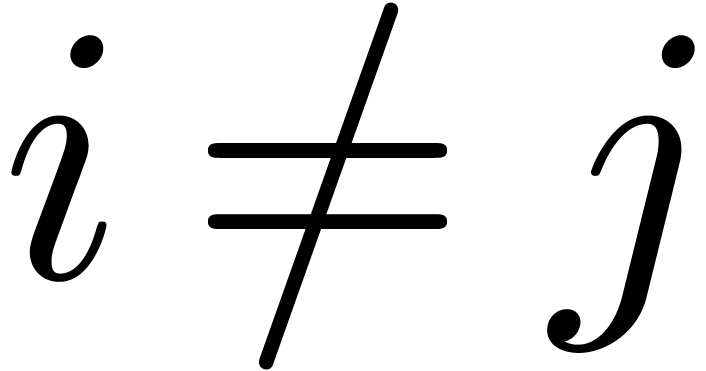 . In particular,
. In particular,  .
Since
.
Since  is the least common left multiple of
is the least common left multiple of  and
and  , we
also have
, we
also have 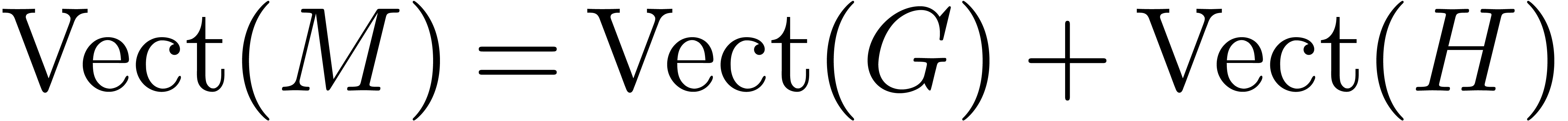 , which completes
the proof of the first equality. If
, which completes
the proof of the first equality. If  is non
singular, then we obtain the second equality in a similar way.
is non
singular, then we obtain the second equality in a similar way.
If  is non singular, then we also have
is non singular, then we also have  and
and  , since
, since
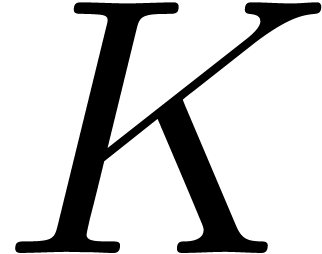 and
and  are non singular.
Now
are non singular.
Now  , whence
, whence  . If
. If  is non singular,
then we obtain the first equality in a similar way.
is non singular,
then we obtain the first equality in a similar way.
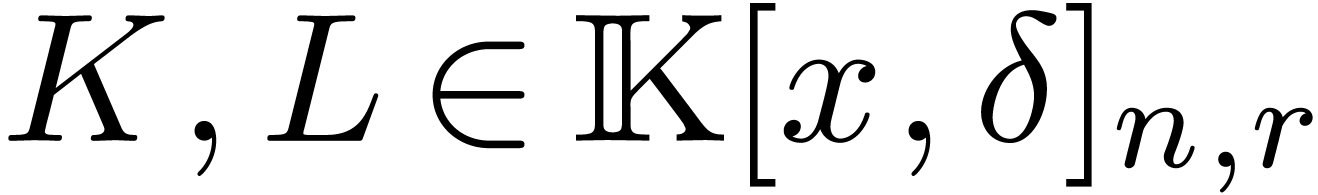 and
and 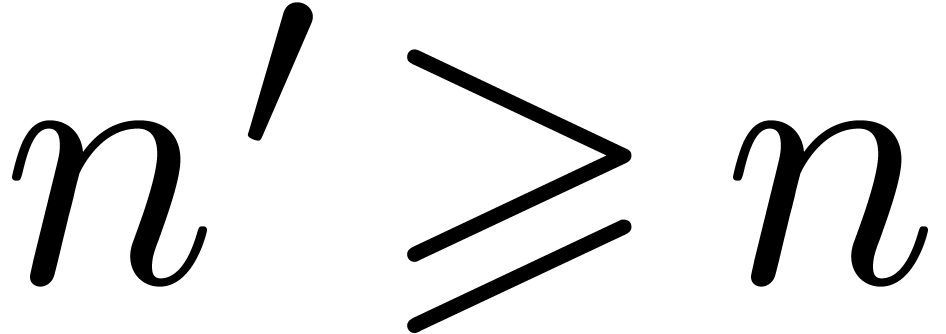 be
such that
be
such that 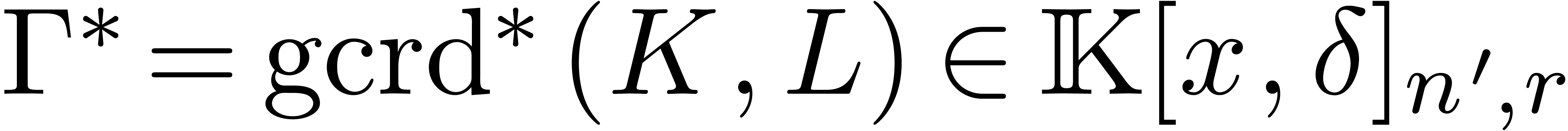 and
and  .
Assume that
.
Assume that  ,
,  and
and 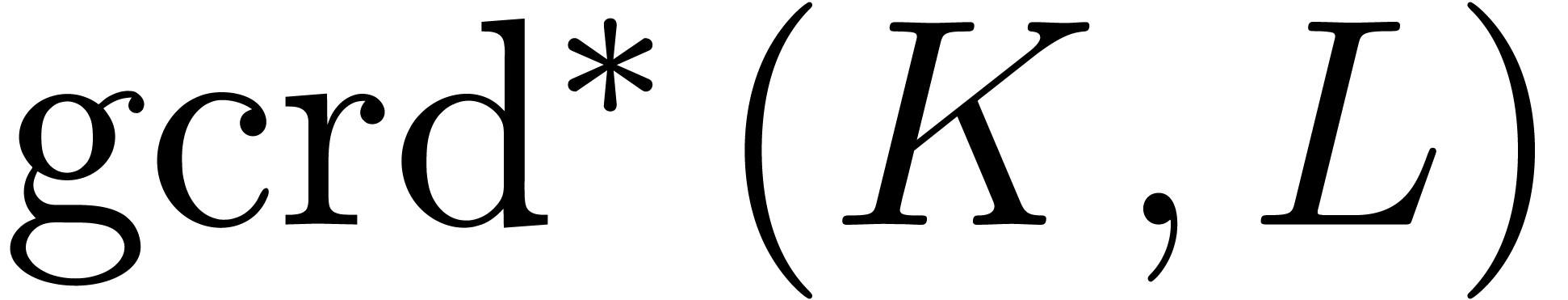 (or
(or 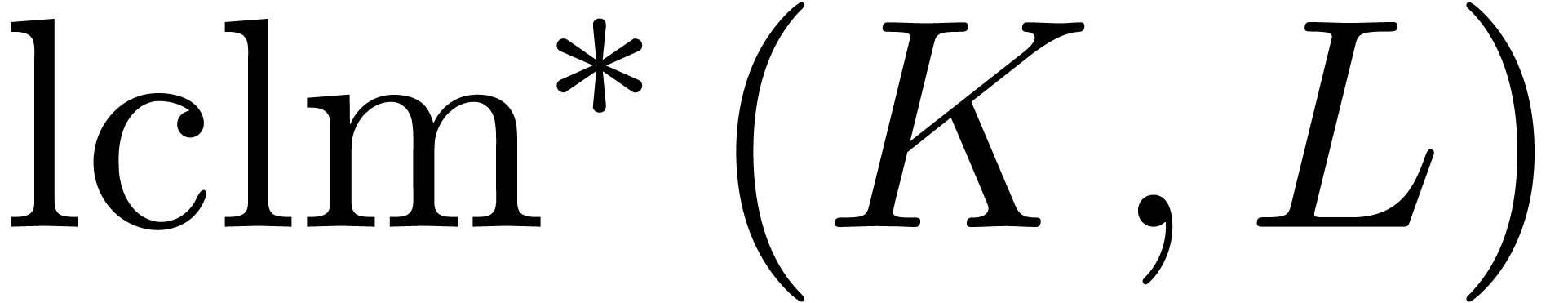 ) are non singular at the origin. Then we may
compute
) are non singular at the origin. Then we may
compute  in time
in time 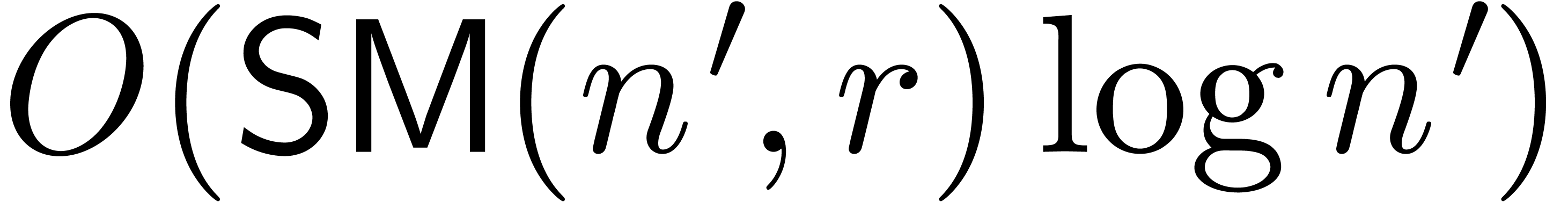 .
.
Proof. We compute  using
the following algorithm:
using
the following algorithm:
We compute the canonical fundamental systems of solutions  and
and  to
to 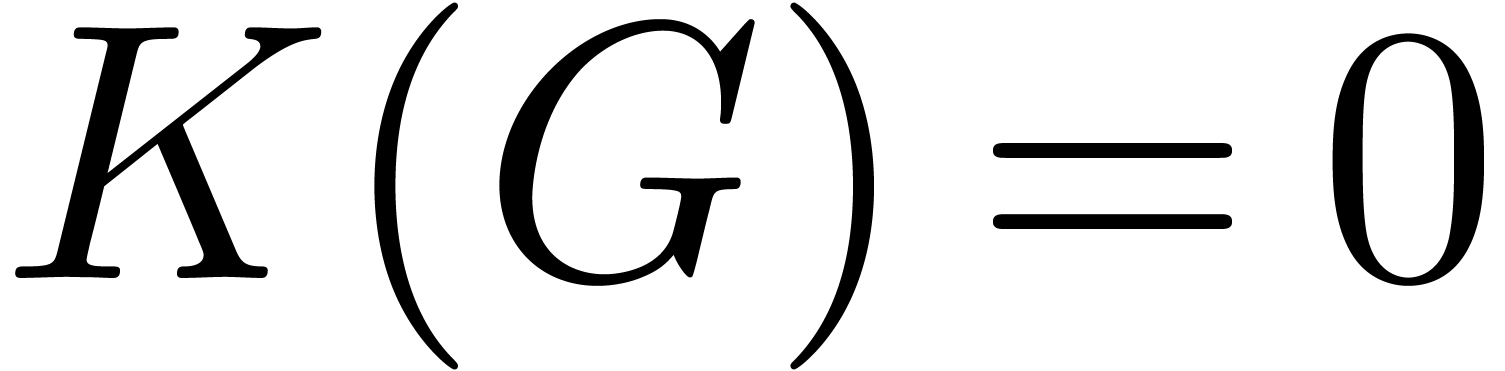 and
and 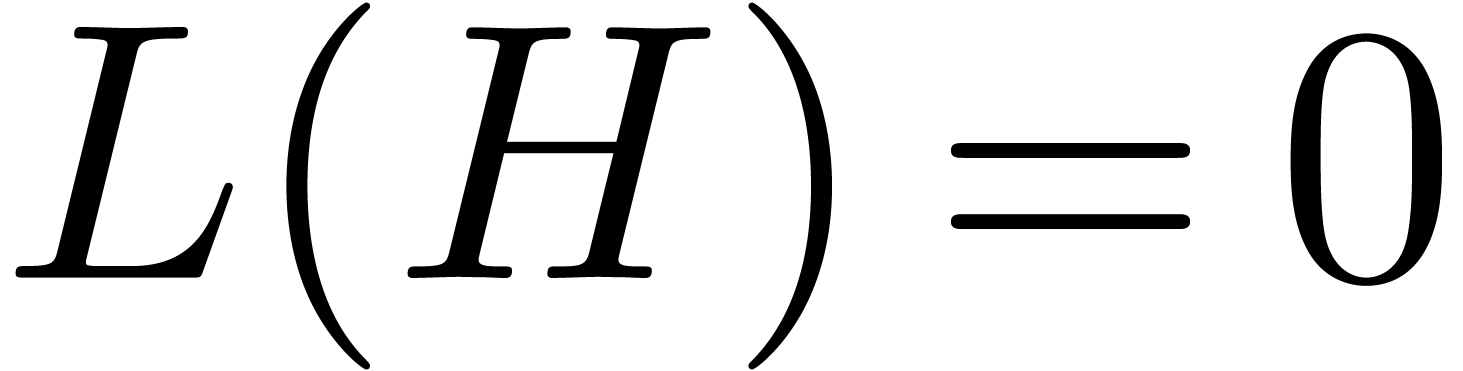 at order
at order 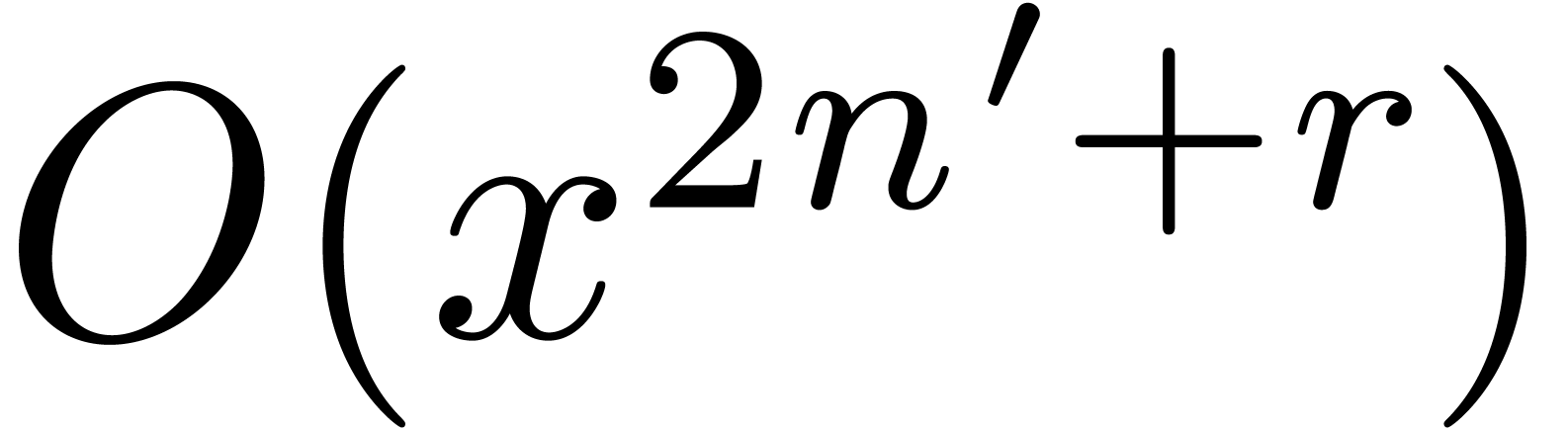 .
This can be done in time
.
This can be done in time 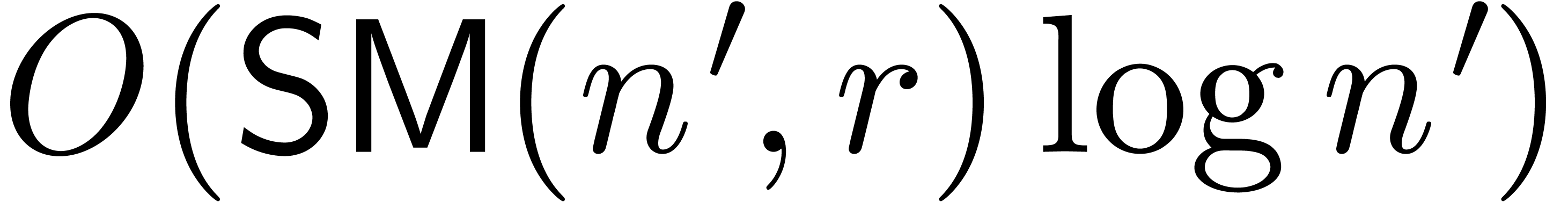 .
.
Using linear algebra, we compute a basis  for
for
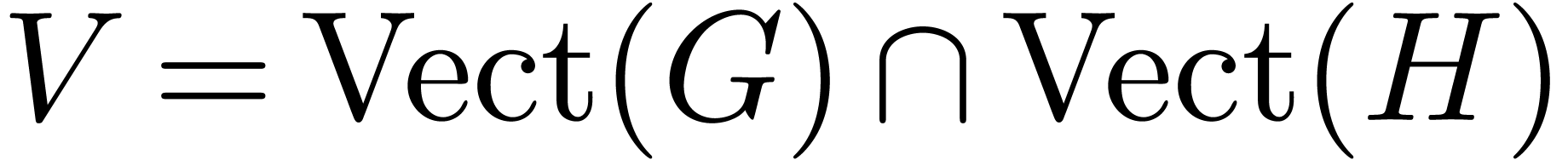 at order
at order 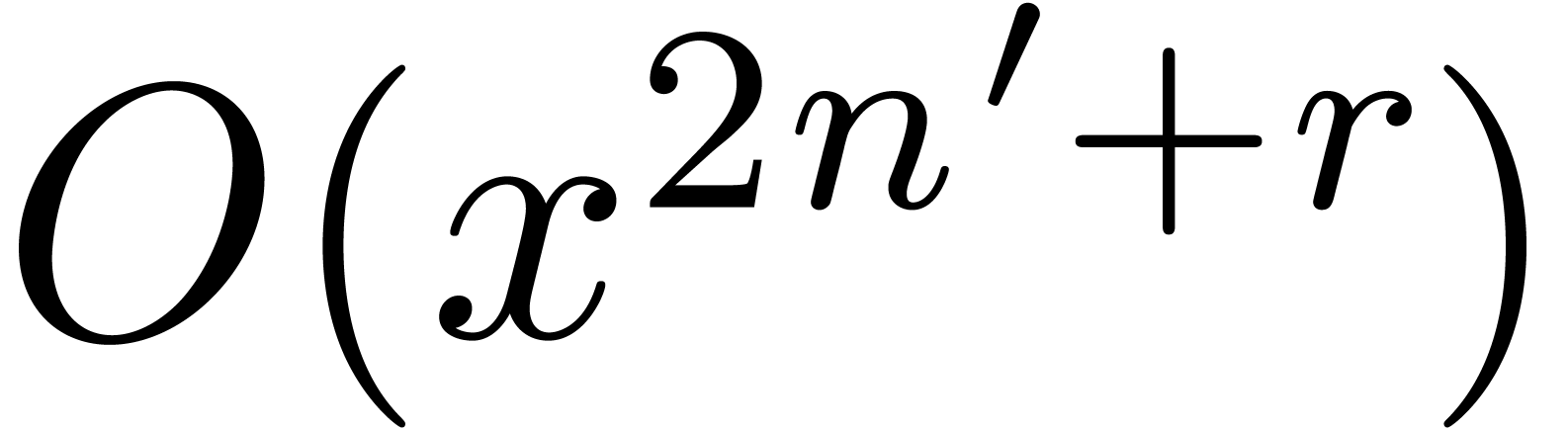 .
This can be done in time
.
This can be done in time 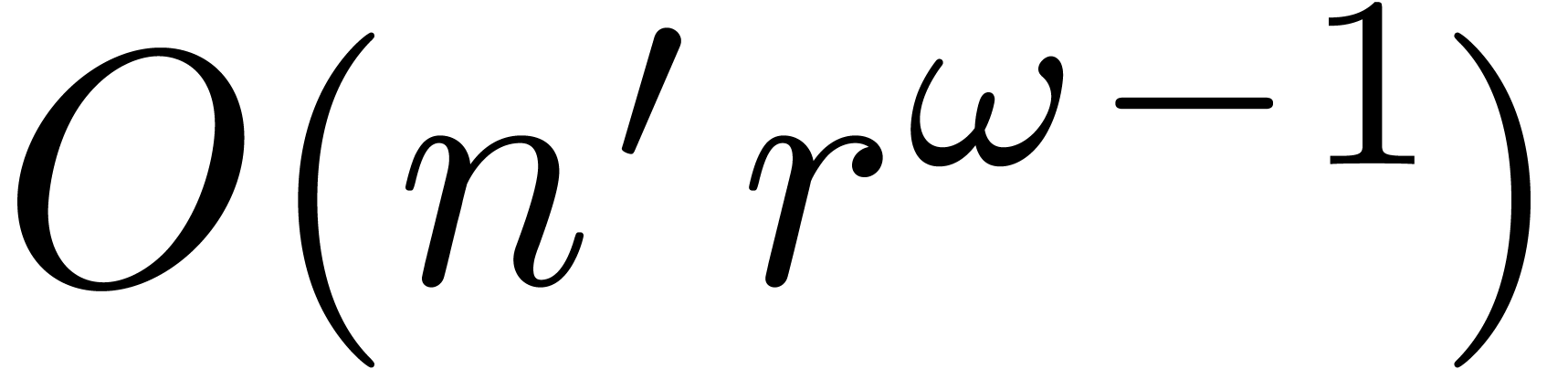 .
By Lemma 17, we have
.
By Lemma 17, we have 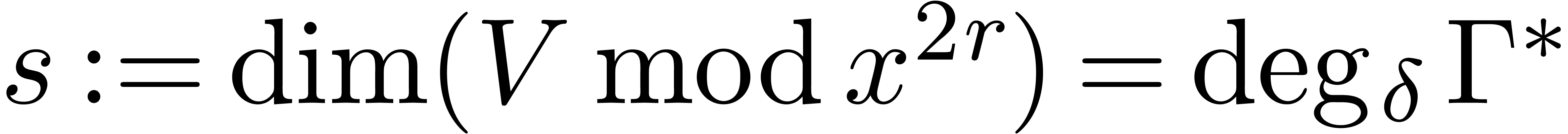 .
We also notice that
.
We also notice that 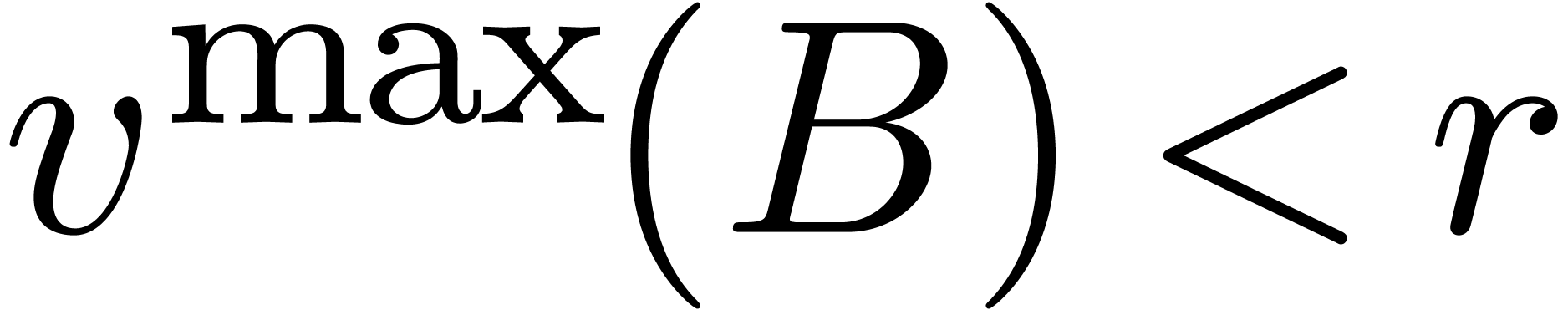 .
.
We compute 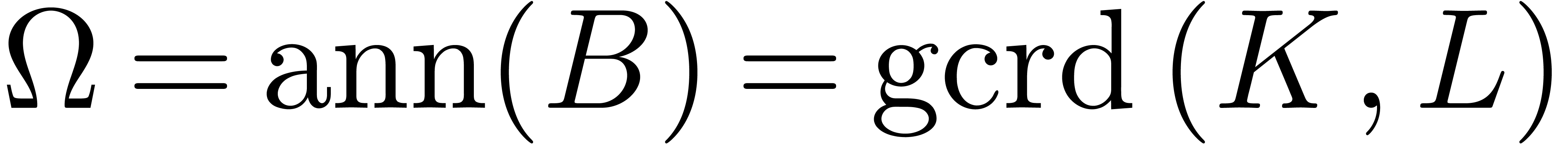 at order
at order 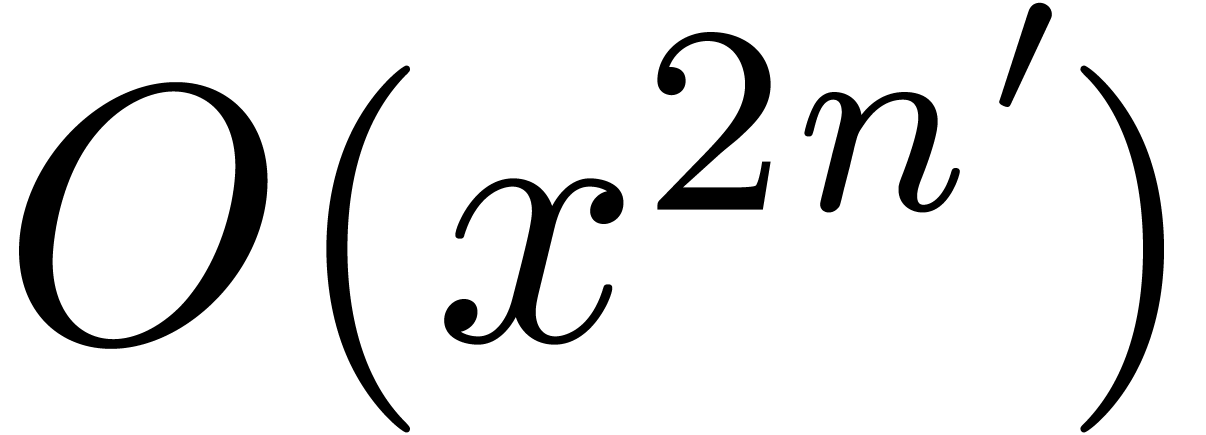 . By Theorem 8, this can be done in
time
. By Theorem 8, this can be done in
time 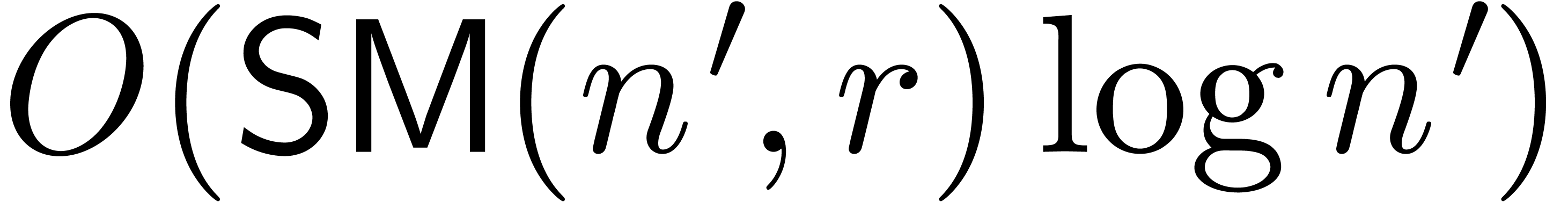 .
.
We compute  from
from  using rational function reconstruction.
using rational function reconstruction.
This algorithm requires a total running time 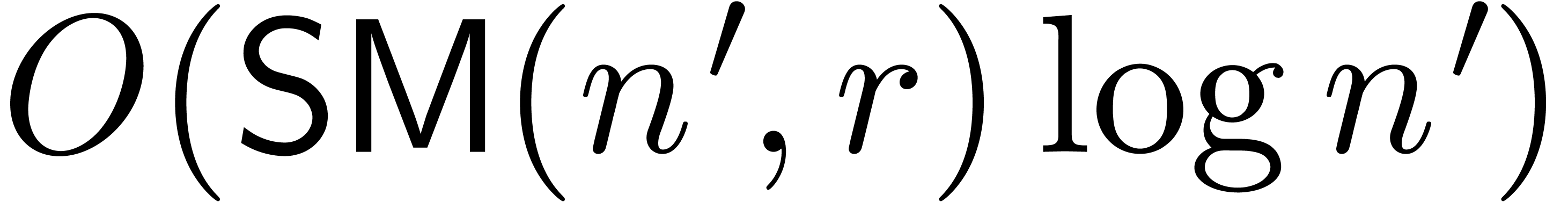 .
.
Remark 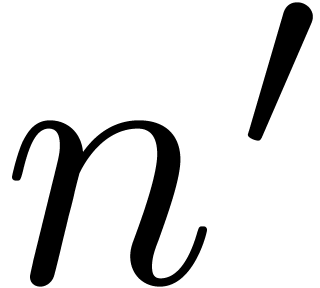 is known
beforehand. Below, we will discuss ways to check the correctness of the
computed result for a trial value
is known
beforehand. Below, we will discuss ways to check the correctness of the
computed result for a trial value 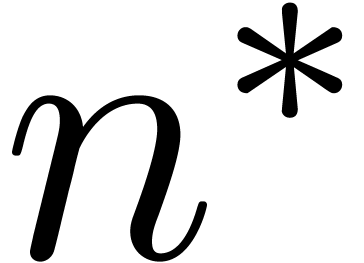 ,
after which a similar strategy as in remark 16 can be
applied. During the relaxed computation of
,
after which a similar strategy as in remark 16 can be
applied. During the relaxed computation of  and
and
 , we may also check whether
, we may also check whether
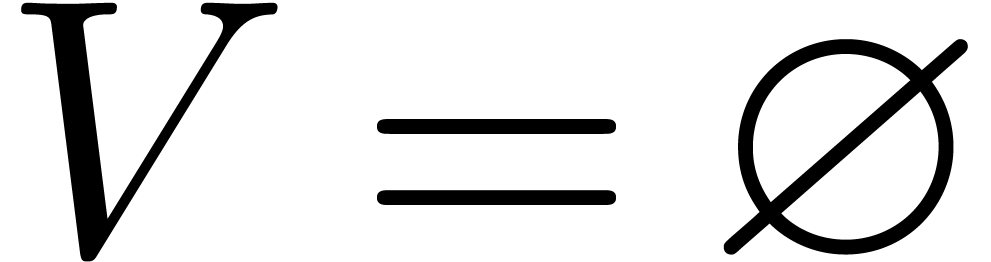 at each next coefficient. In the particular case
when
at each next coefficient. In the particular case
when 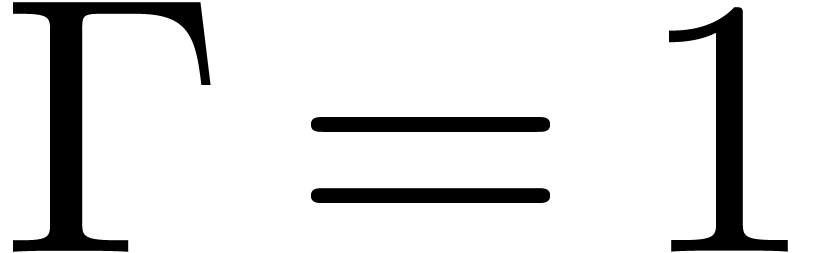 , the running time of
the algorithm will then be bounded by
, the running time of
the algorithm will then be bounded by 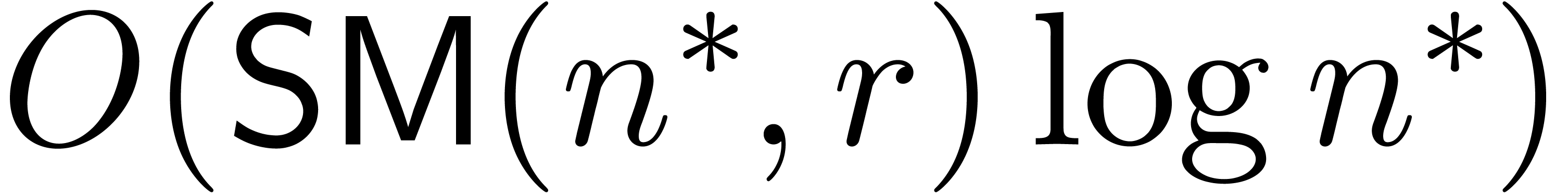 ,
where
,
where 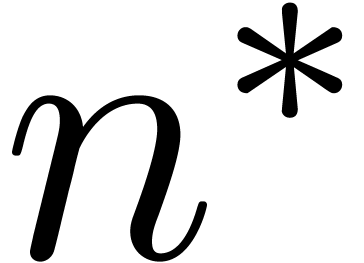 is the smallest order at which common
solutions no longer exist. This kind of early termination only works for
this very special case.
is the smallest order at which common
solutions no longer exist. This kind of early termination only works for
this very special case.
Remark  might be singular at the origin, even if
might be singular at the origin, even if 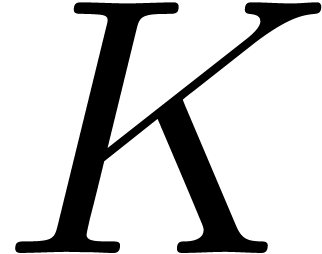 ,
,  and
and 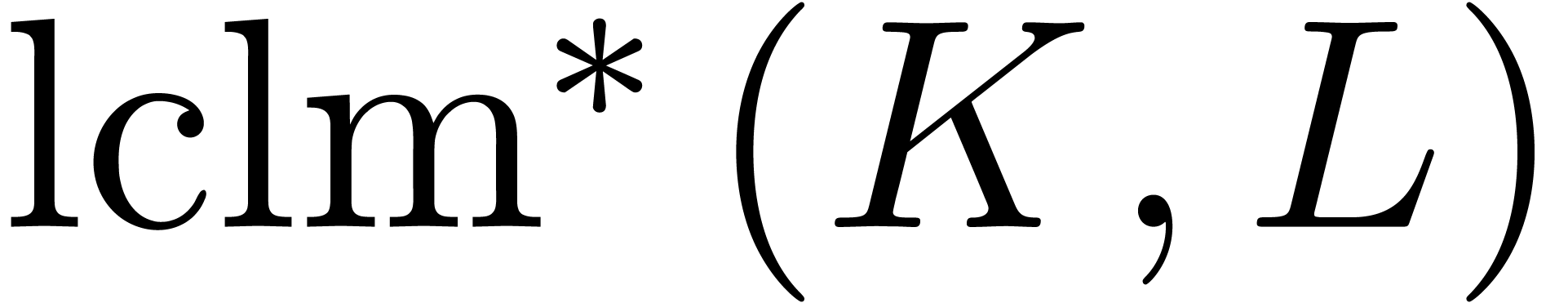 are not. This happens for instance when
are not. This happens for instance when 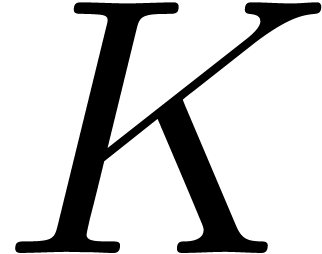 is the minimal annihilator of the vector
is the minimal annihilator of the vector 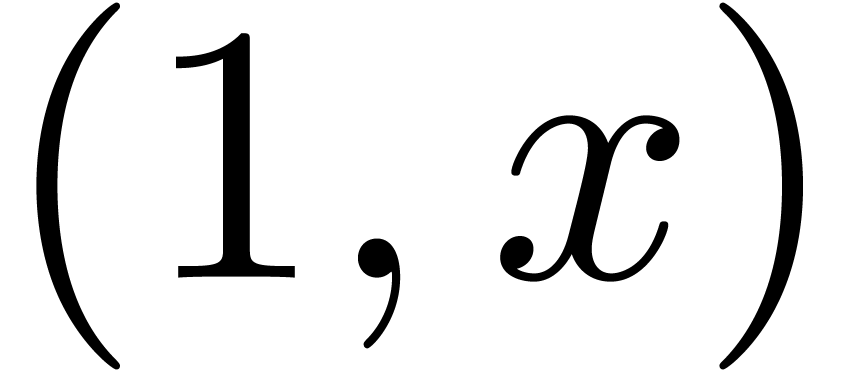 and
and  the minimal annihilator of the vector
the minimal annihilator of the vector 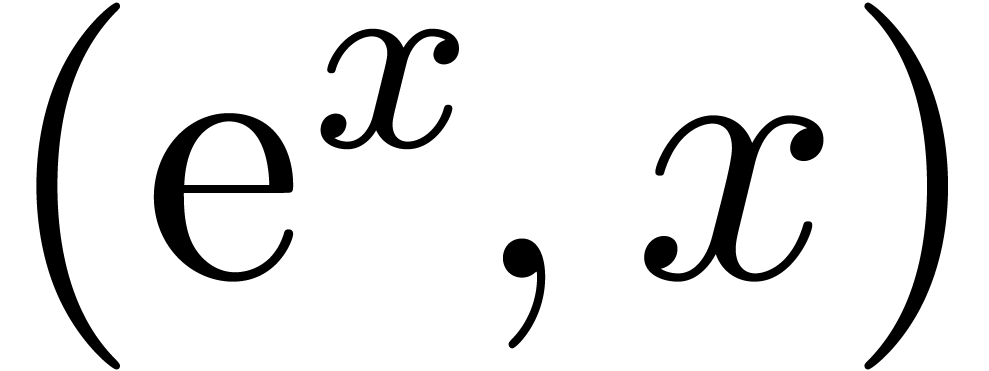 , so that
, so that  .
.
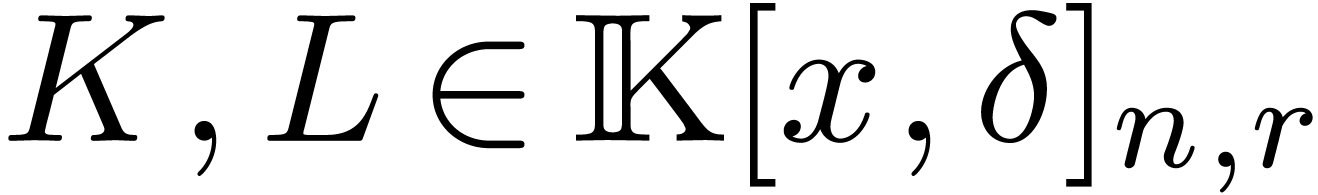 and
and 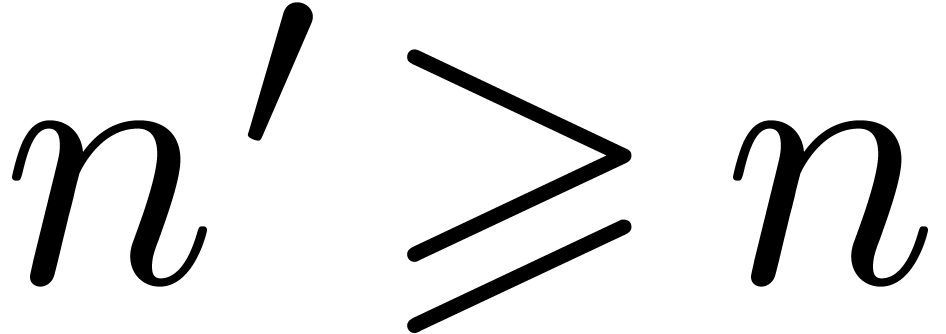 be
such that
be
such that 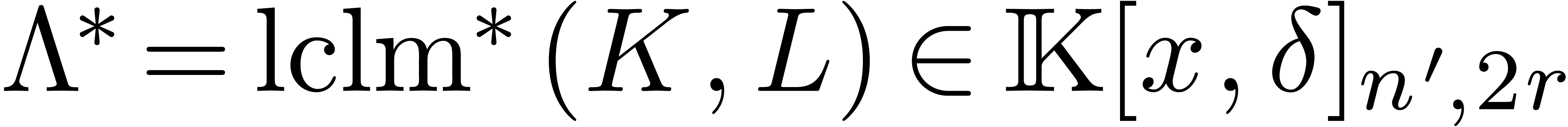 and
and  .
If
.
If 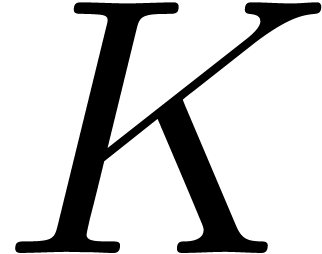 ,
,  and
and 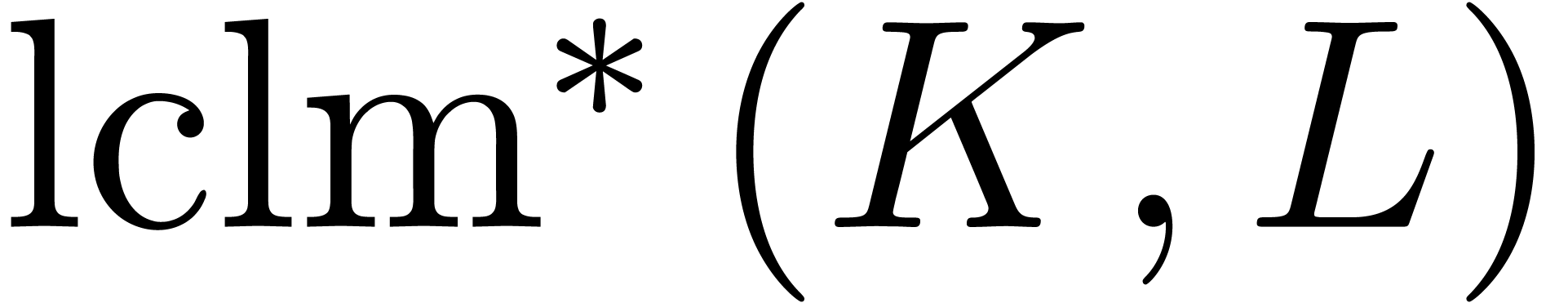 (or
(or 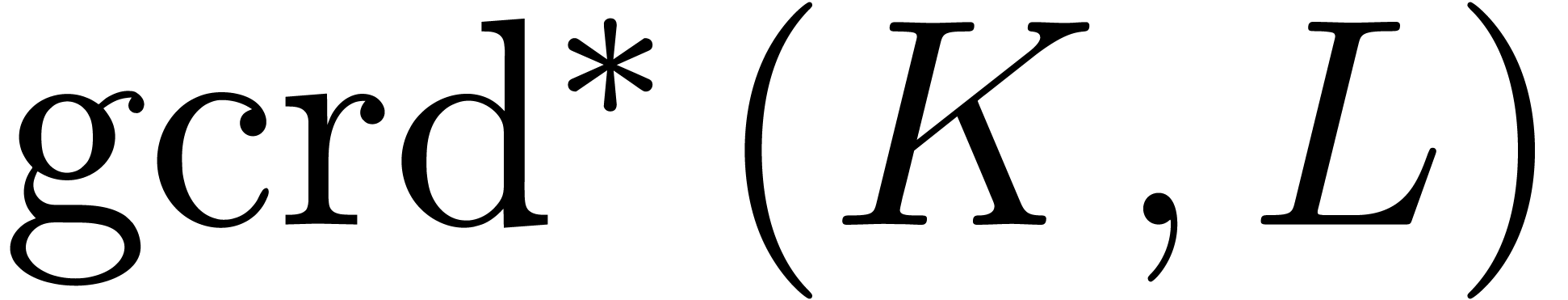 )
are non singular at the origin, then we may compute
)
are non singular at the origin, then we may compute  in time
in time 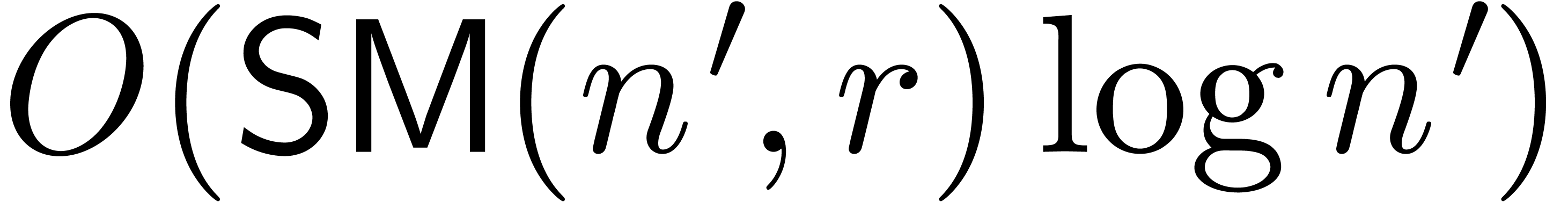 .
.
Proof. Similar to the proof of Theorem 18,
by taking 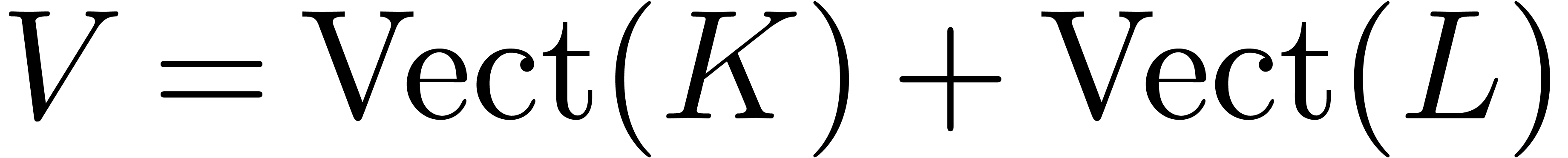 instead of
instead of 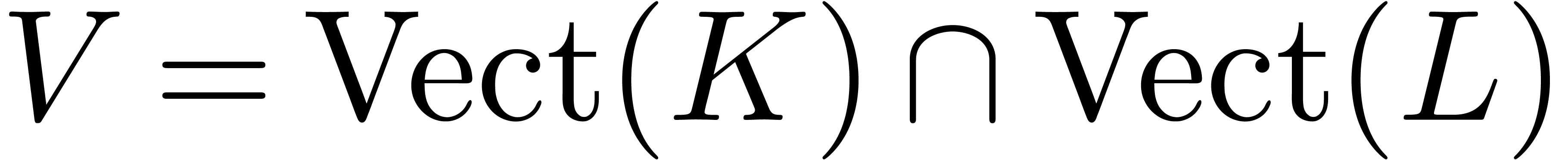 .
.
The assumption that 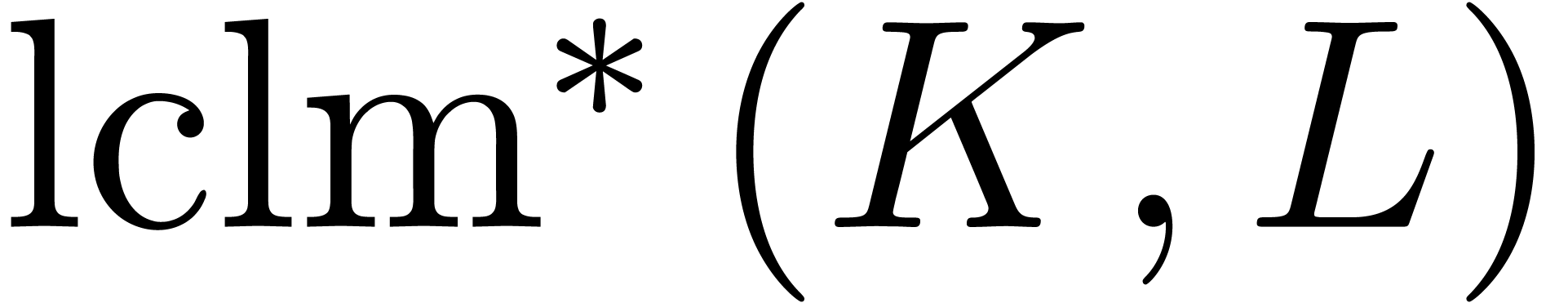 should be non singular is
still a bit unsatisfactory in Theorems 18 and 21,
even though the probability that a randomly chosen point is singular is
infinitesimal. If we drop this assumption, then we still have
should be non singular is
still a bit unsatisfactory in Theorems 18 and 21,
even though the probability that a randomly chosen point is singular is
infinitesimal. If we drop this assumption, then we still have  in the proof of Theorem 18. Consequently,
“candidate” pseudo-gcrds
in the proof of Theorem 18. Consequently,
“candidate” pseudo-gcrds  found by
the algorithm are genuine pseudo-gcrds whenever
found by
the algorithm are genuine pseudo-gcrds whenever  pseudo-divides both
pseudo-divides both 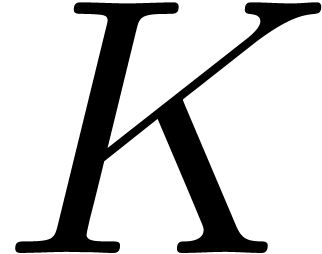 and
and 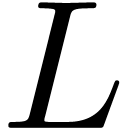 . Using the right division algorithms from the
previous section, this can be checked in time
. Using the right division algorithms from the
previous section, this can be checked in time 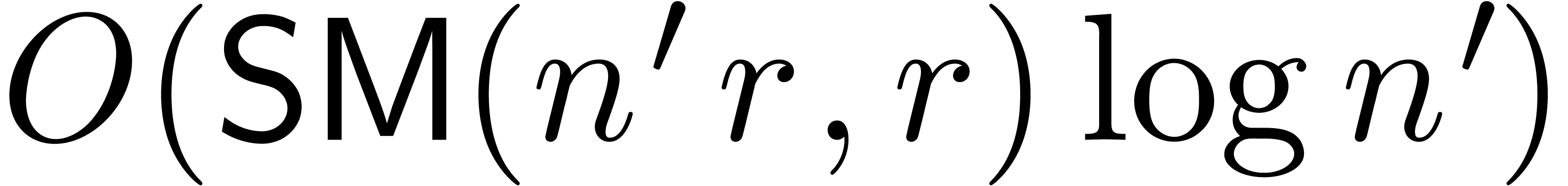 in
the case of gcrds and
in
the case of gcrds and 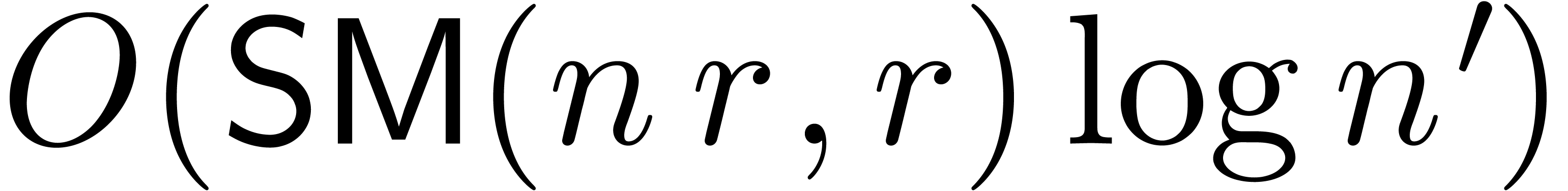 in the case of lclms.
in the case of lclms.
Remark 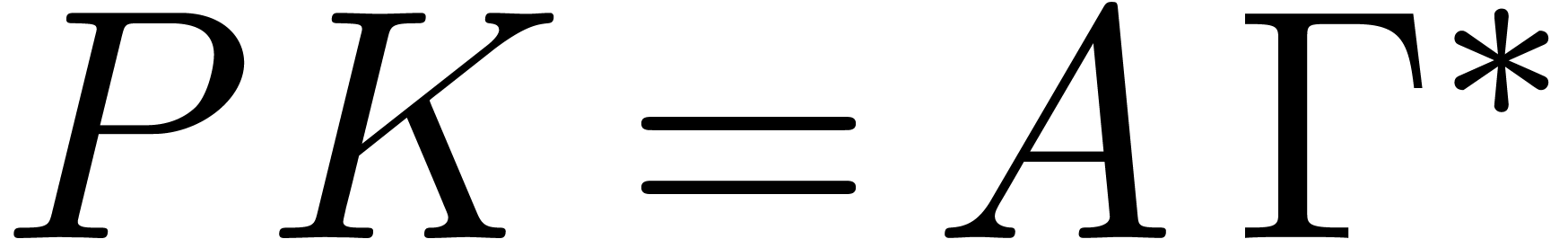 for some
for some
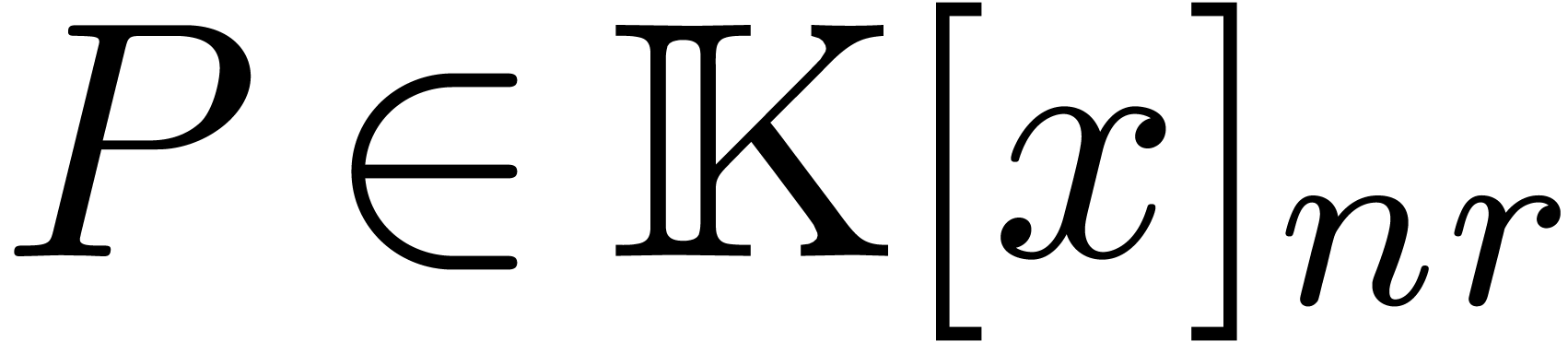 and
and 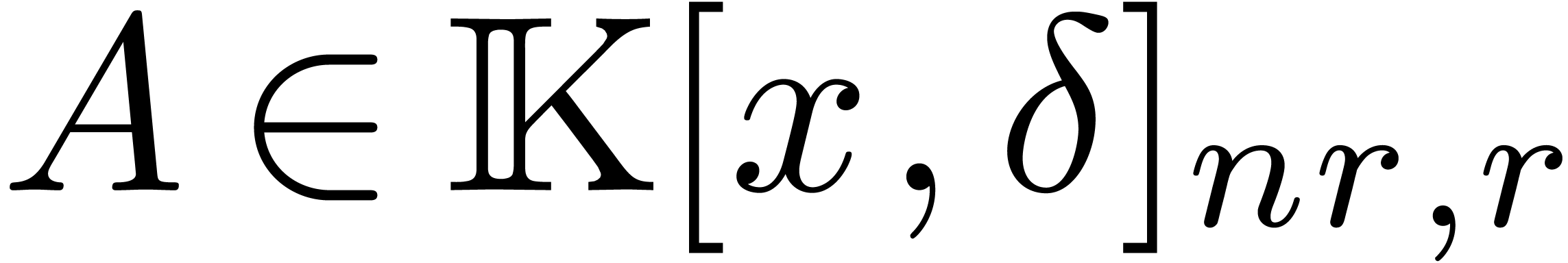 .
If this is indeed the case, then the trial divisions of
.
If this is indeed the case, then the trial divisions of  and
and  by
by  can actually be
carried out in time
can actually be
carried out in time 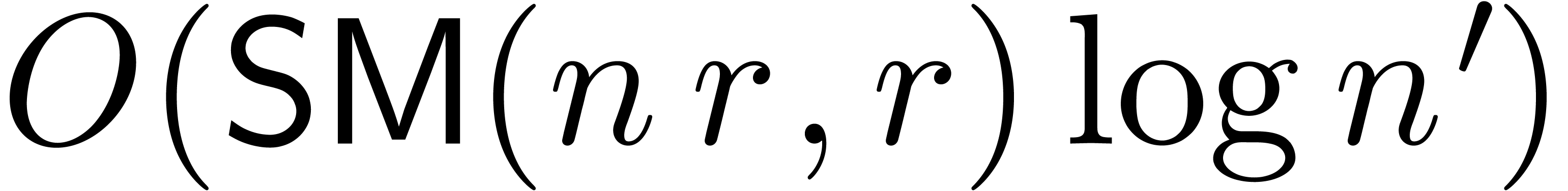 .
.
An alternative way to check whether candidate gcrds and lclms are
correct is to compute Bezout and Ore relations. More precisely, given
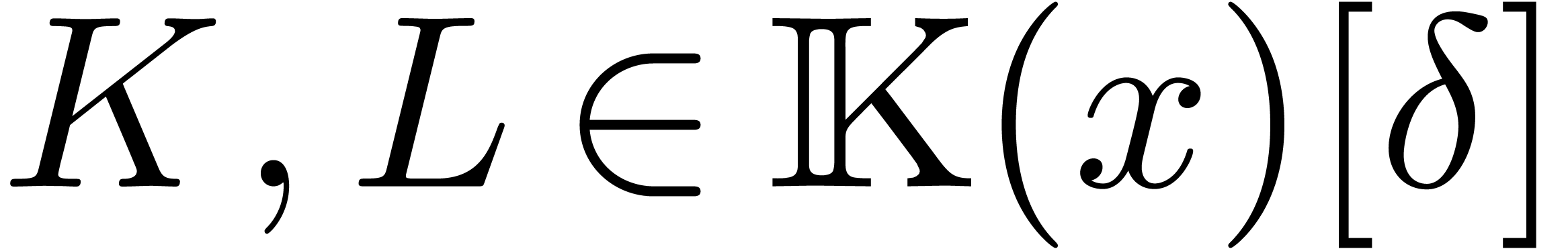 with
with 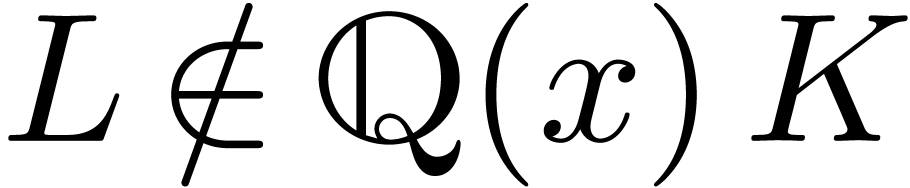 ,
there exist operators
,
there exist operators 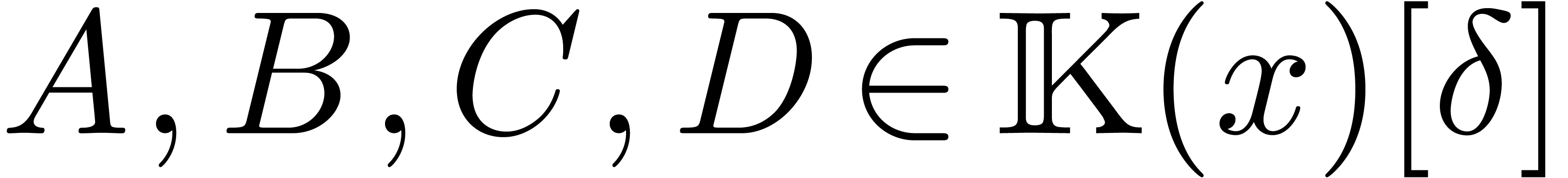 with
with
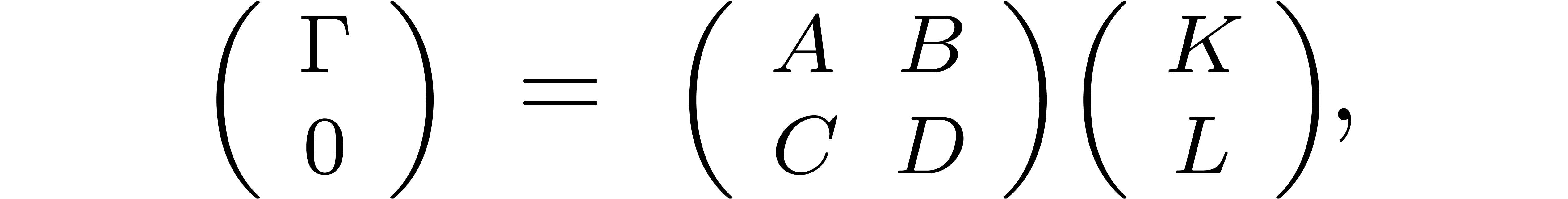
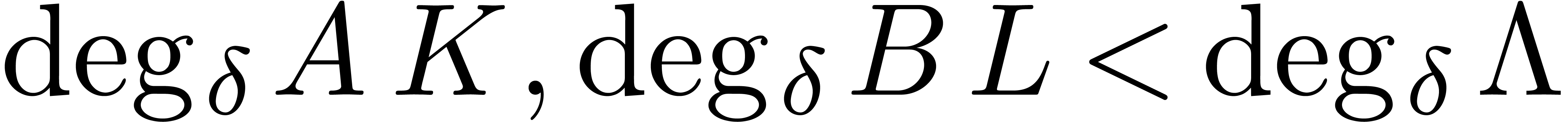 and
and 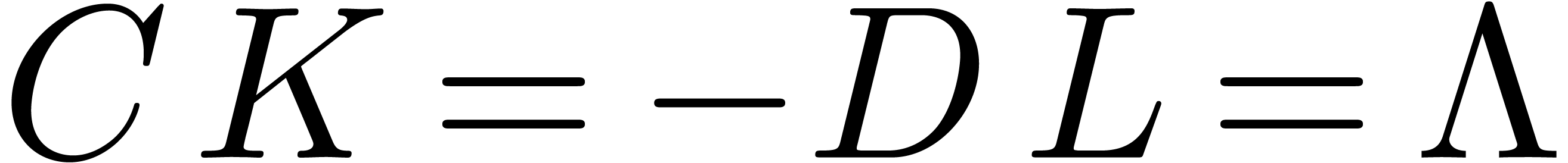 .
The
.
The  matrix at the righthand side will be called
the Euclidean matrix
matrix at the righthand side will be called
the Euclidean matrix 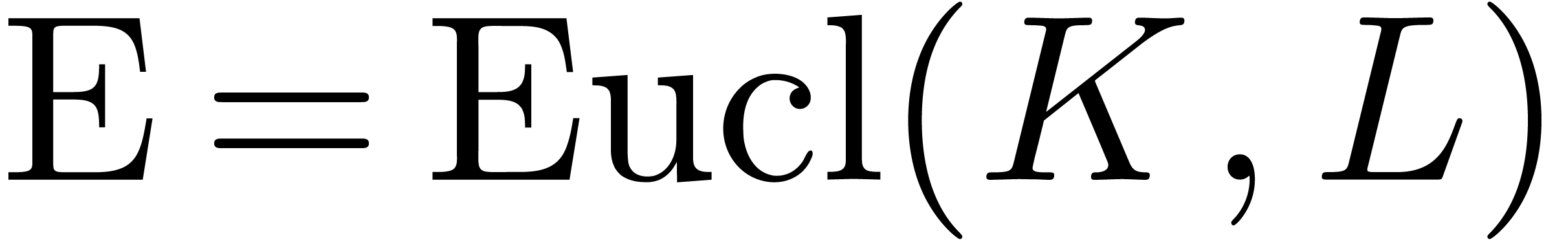 of
of 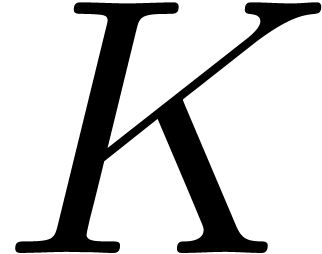 and
and 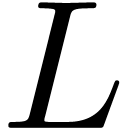 . In a similar way as
above, we may define a (simplified) pseudo-Euclidean matrix
. In a similar way as
above, we may define a (simplified) pseudo-Euclidean matrix 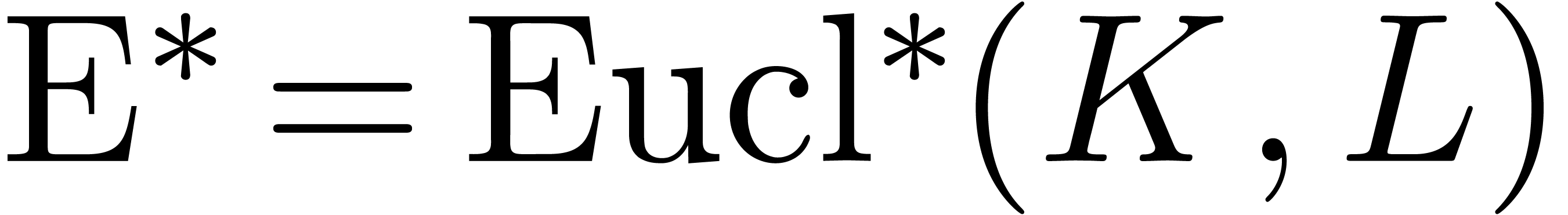 with entries
with entries 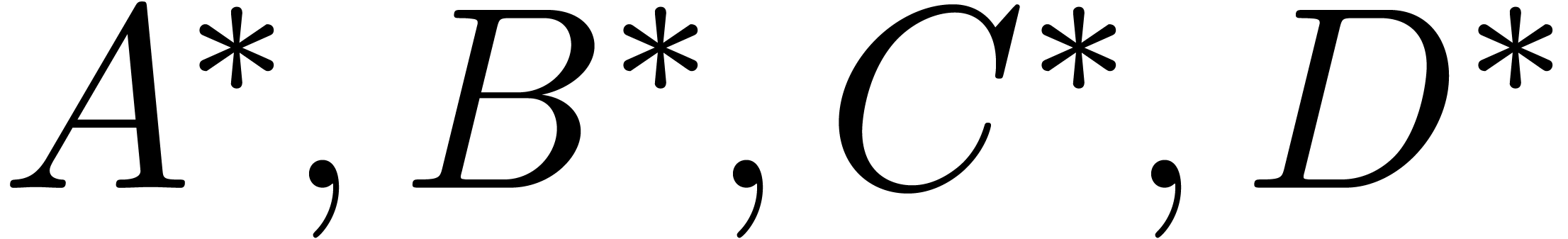 in
in 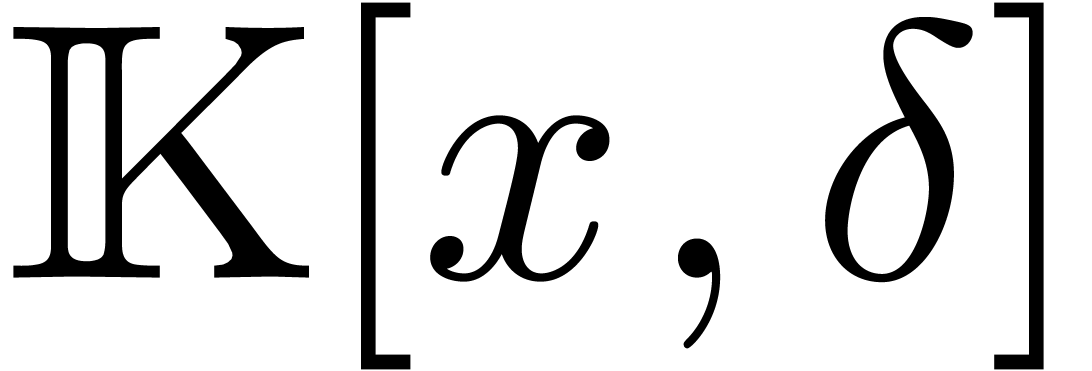 , whenever
, whenever 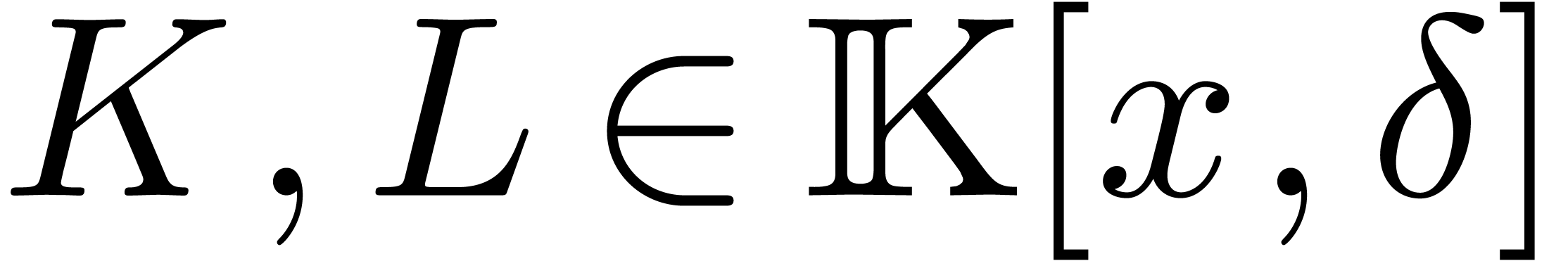 .
We will say that
.
We will say that 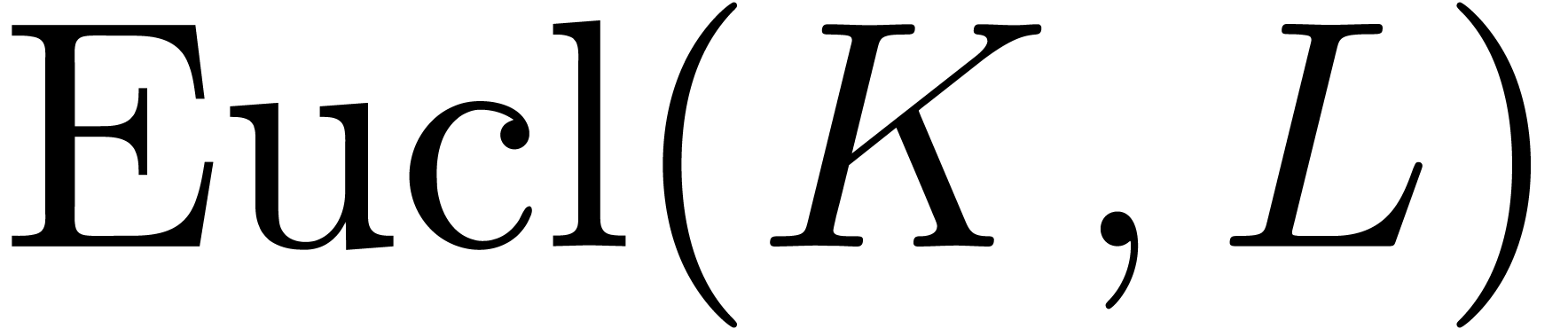 is non singular at
is non singular at 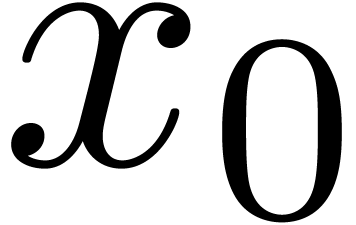 , if the denominators of
, if the denominators of  and
and 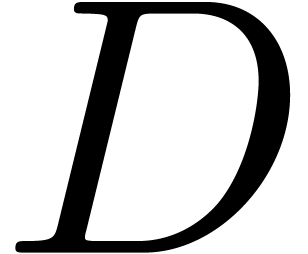 do not vanish at
do not vanish at 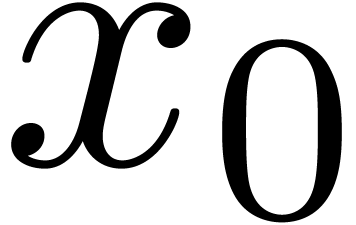 .
.
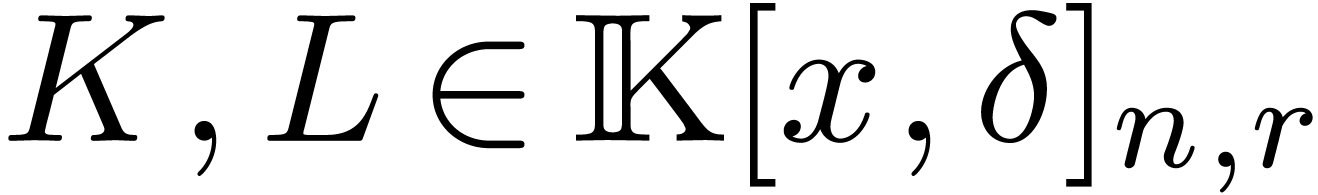 and
and 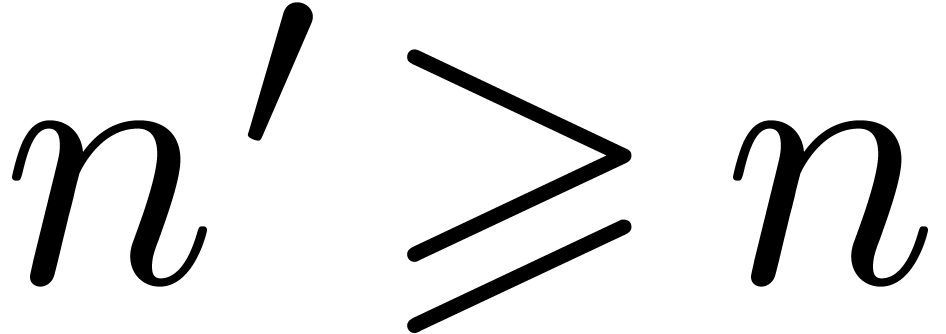 be
such that
be
such that 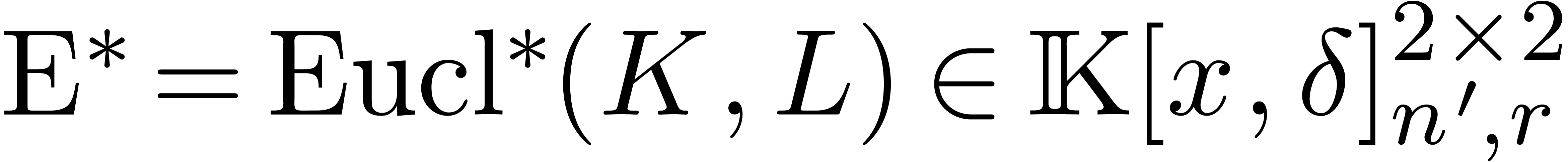 and
and  .
If
.
If 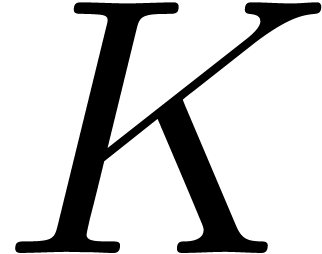 ,
,  ,
, 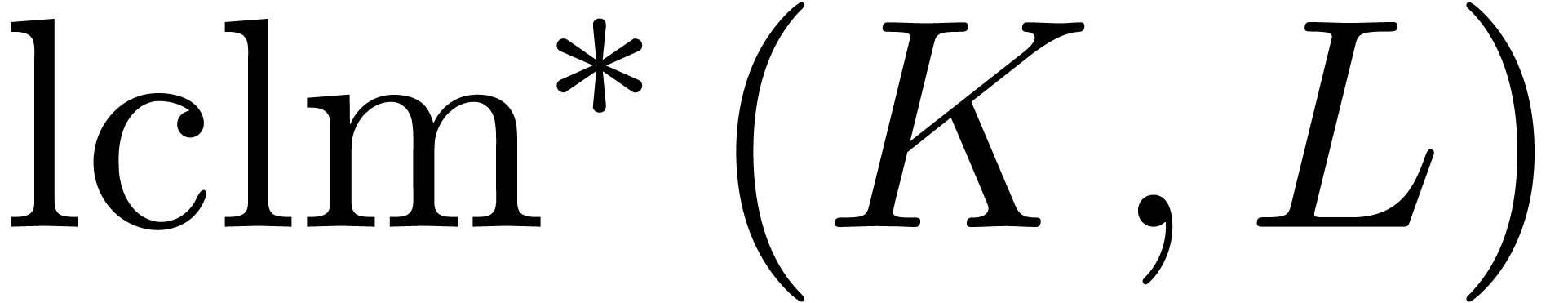 and
and 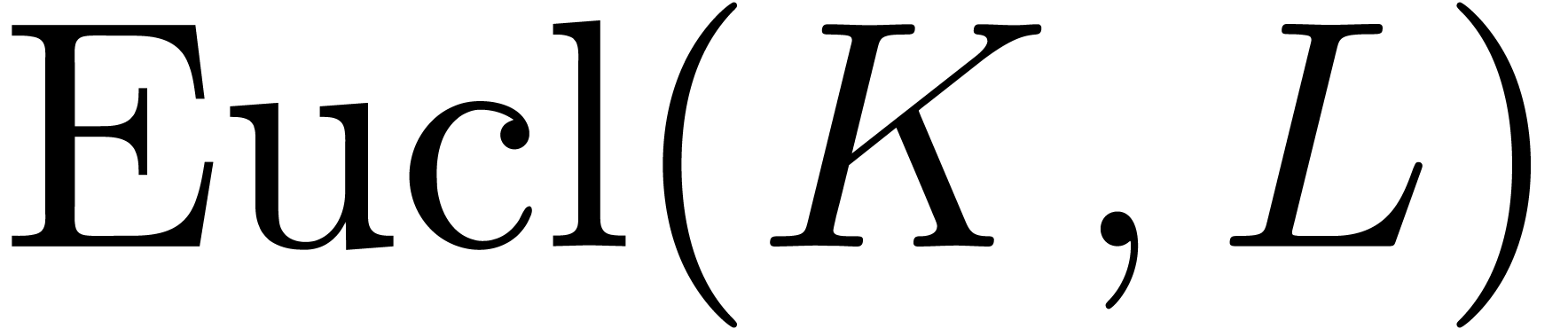 are non singular at the origin, then we may compute
are non singular at the origin, then we may compute  in time
in time 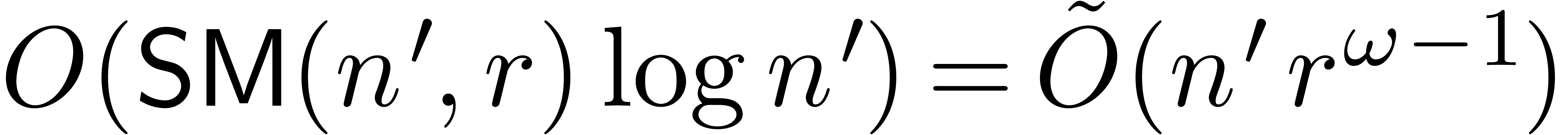 .
.
Proof. Assuming 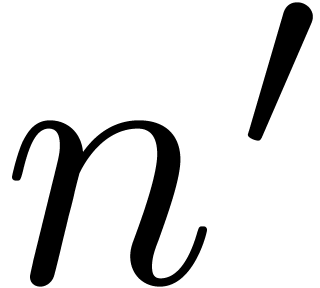 known,
we compute
known,
we compute 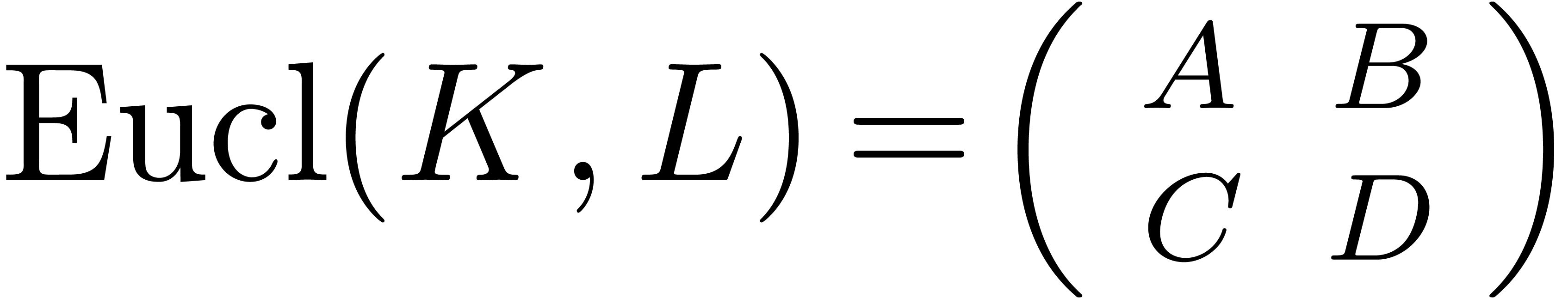 at order
at order 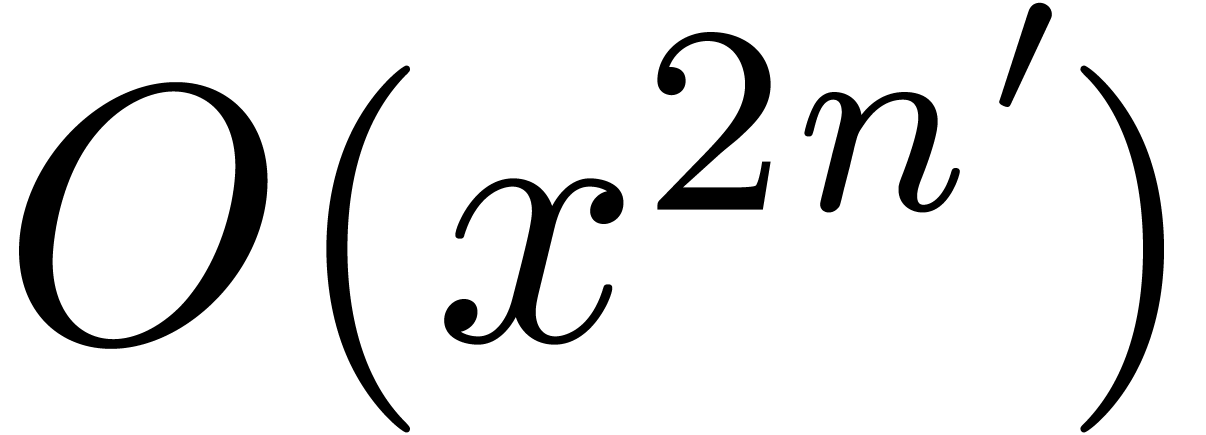 as
follows:
as
follows:
We compute the canonical fundamental systems of solutions  and
and  to
to  and
and  at order
at order 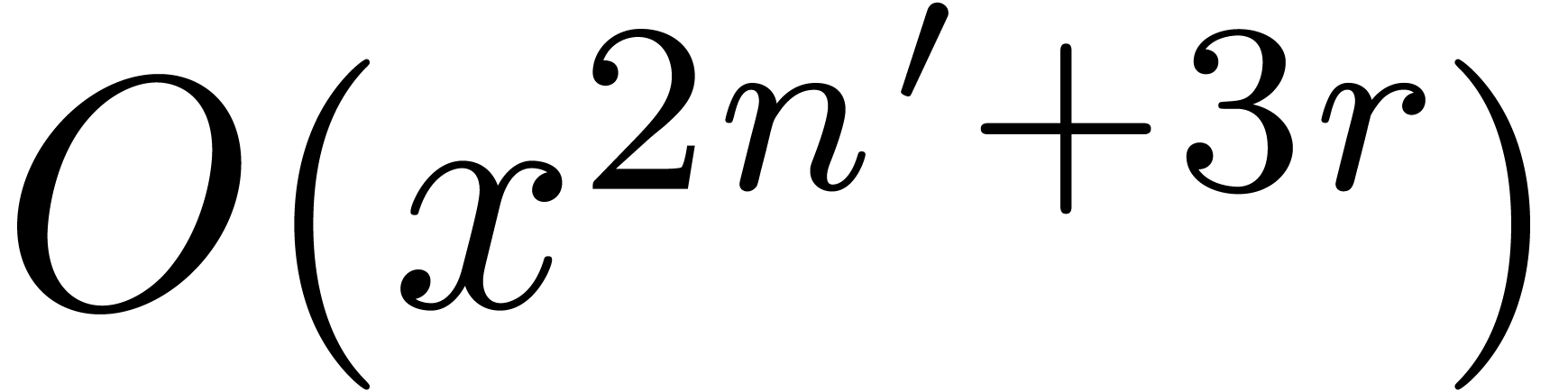 .
.
We compute a basis  for
for  at order
at order  , together with
bases
, together with
bases  and
and  for the
supplements of
for the
supplements of 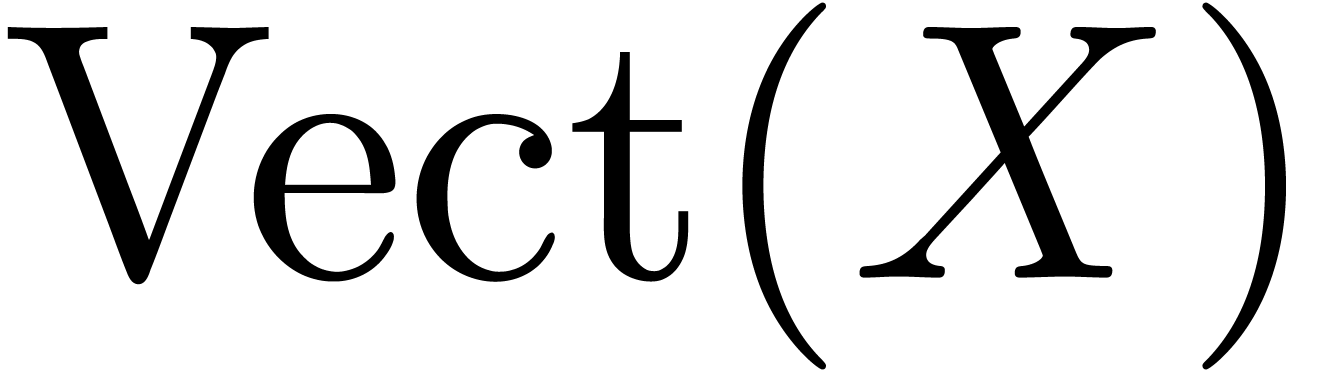 in
in 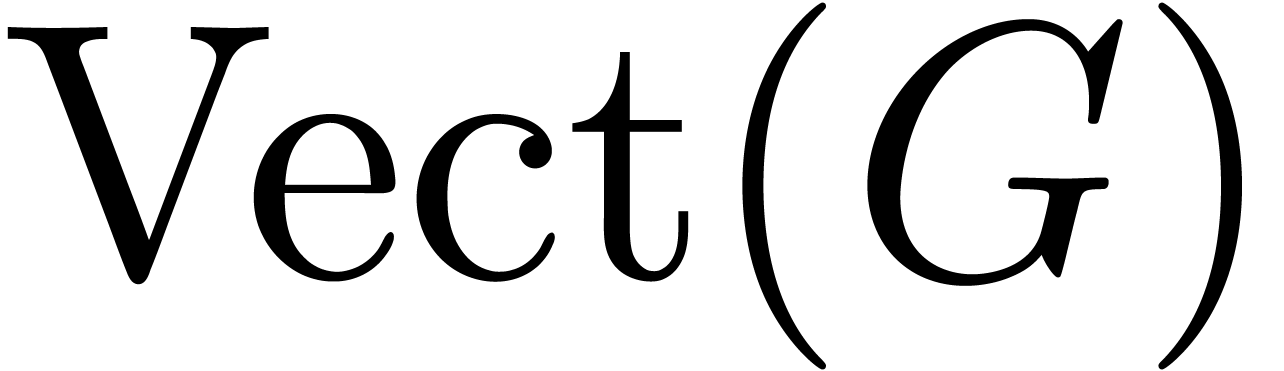 resp.
resp. 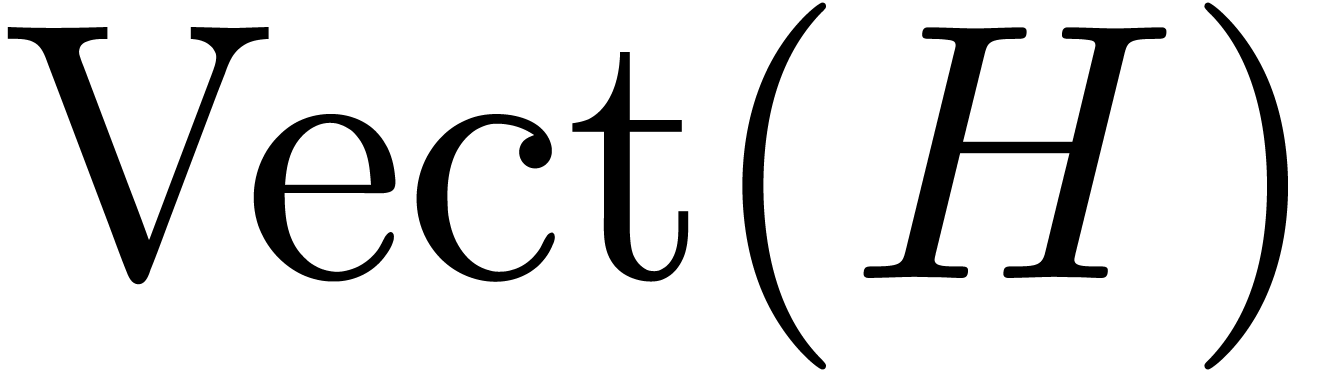 . We
also compute
. We
also compute 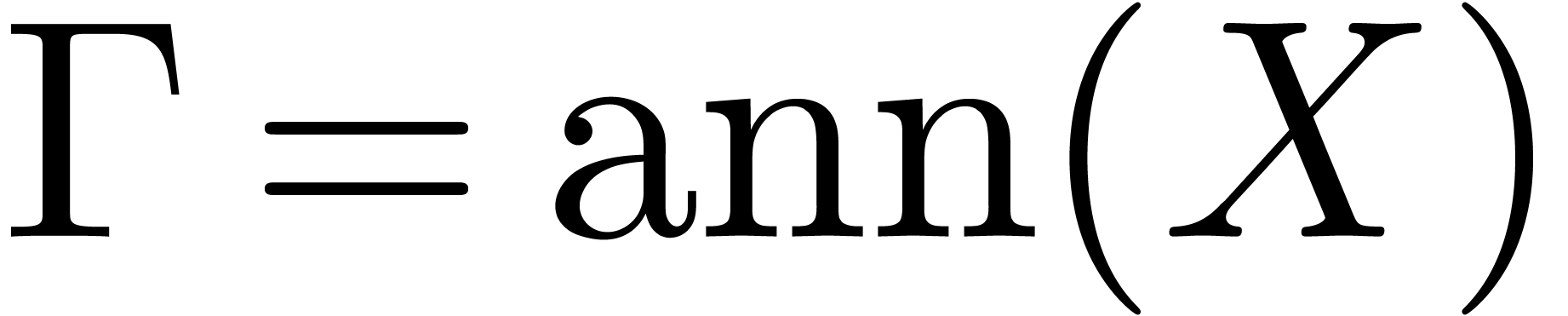 at order
at order 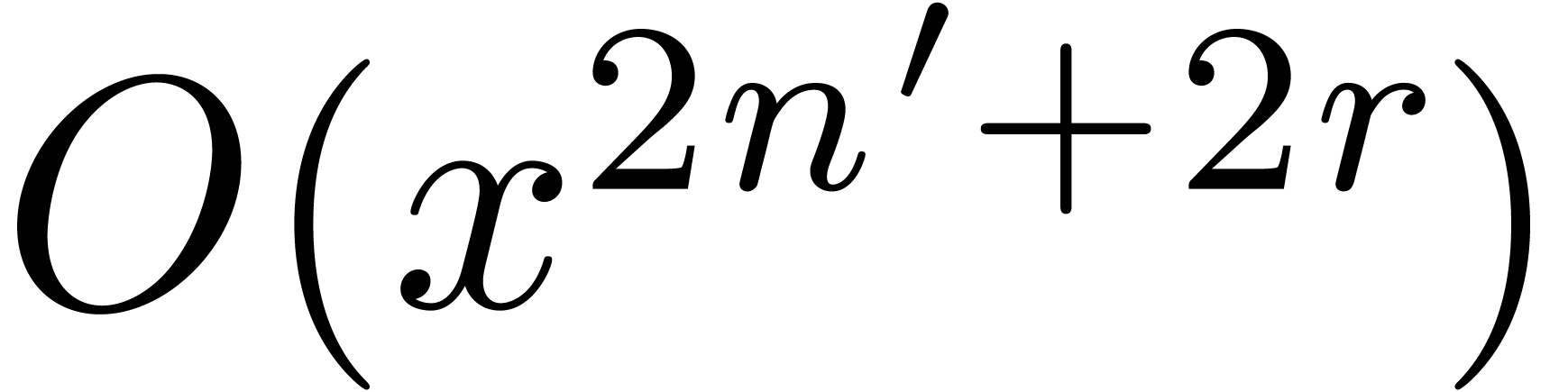 .
.
We solve the systems  and
and  in
in  resp.
resp.  at order
at order 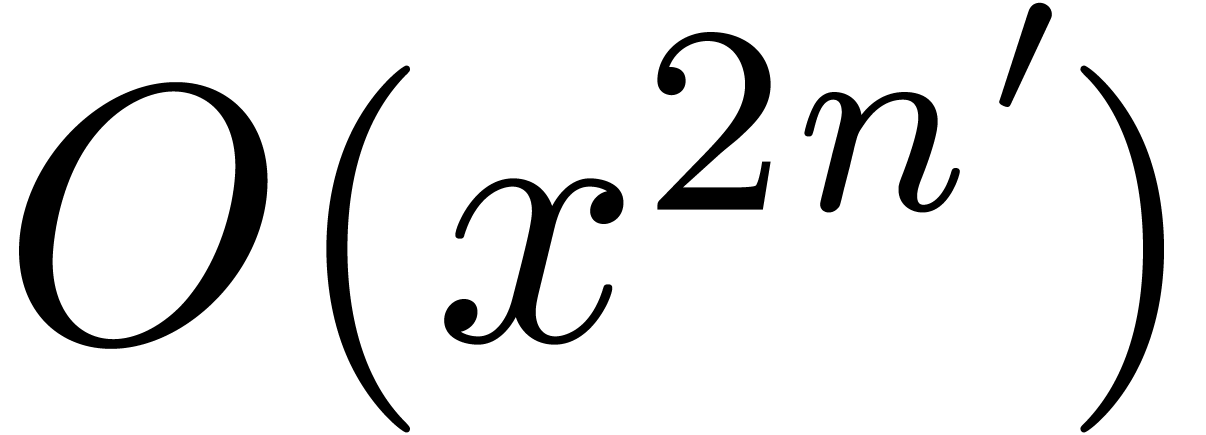 , using Lemma 14.
, using Lemma 14.
We compute a basis  for
for  at order
at order  , as well as
bases
, as well as
bases  and
and  for the
vector spaces
for the
vector spaces  resp.
resp. 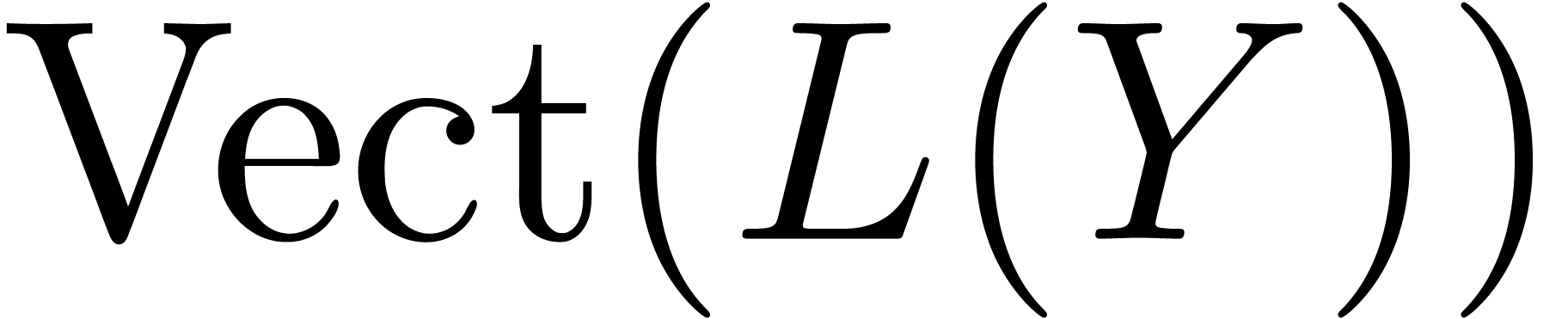 at order
at order 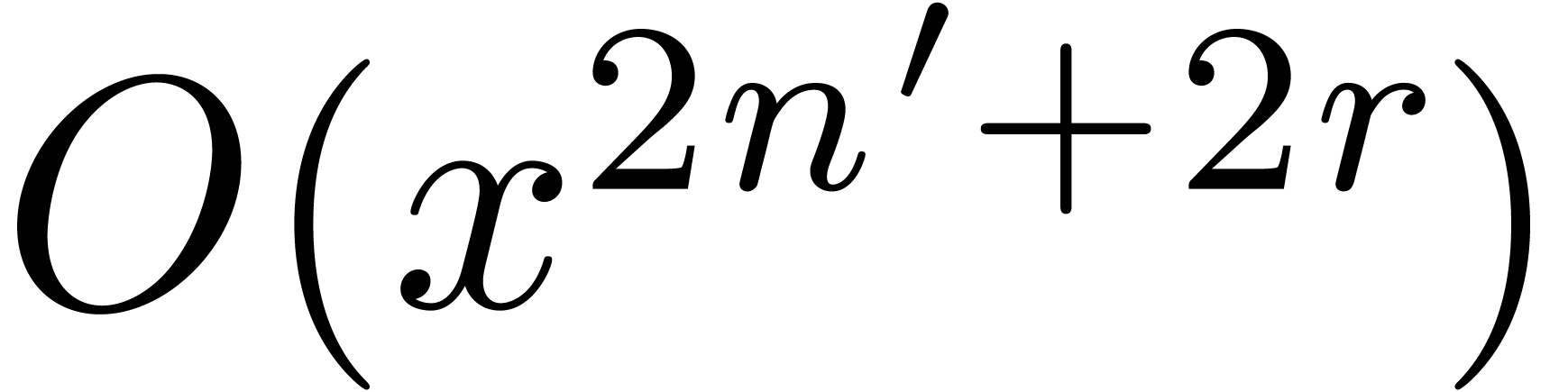 .
.
We compute 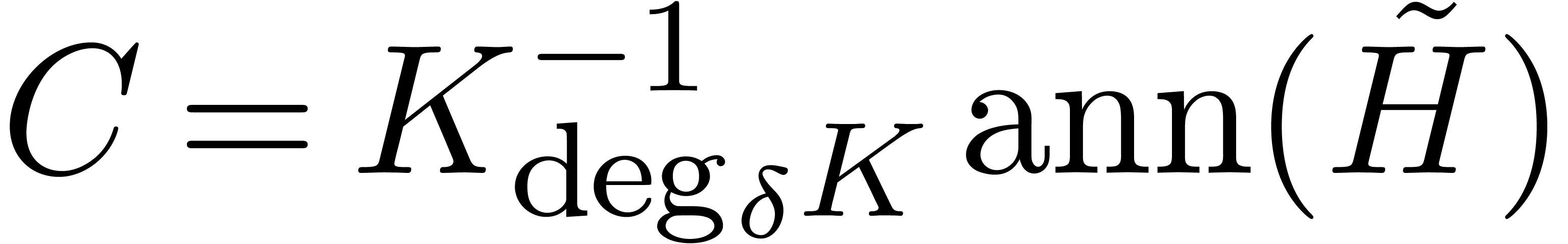 and
and 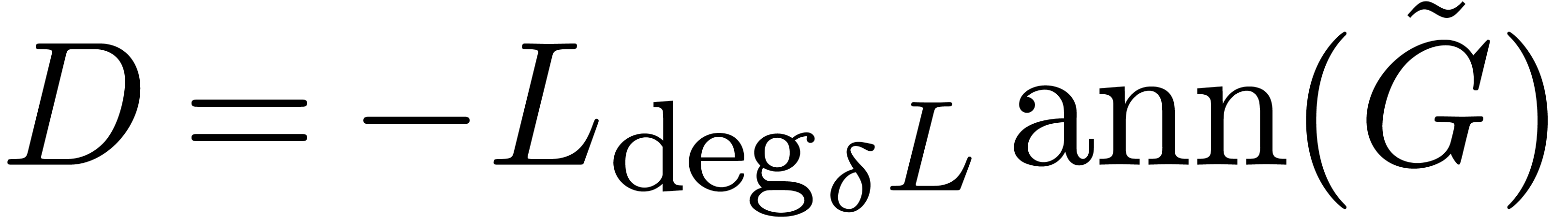 at
order
at
order 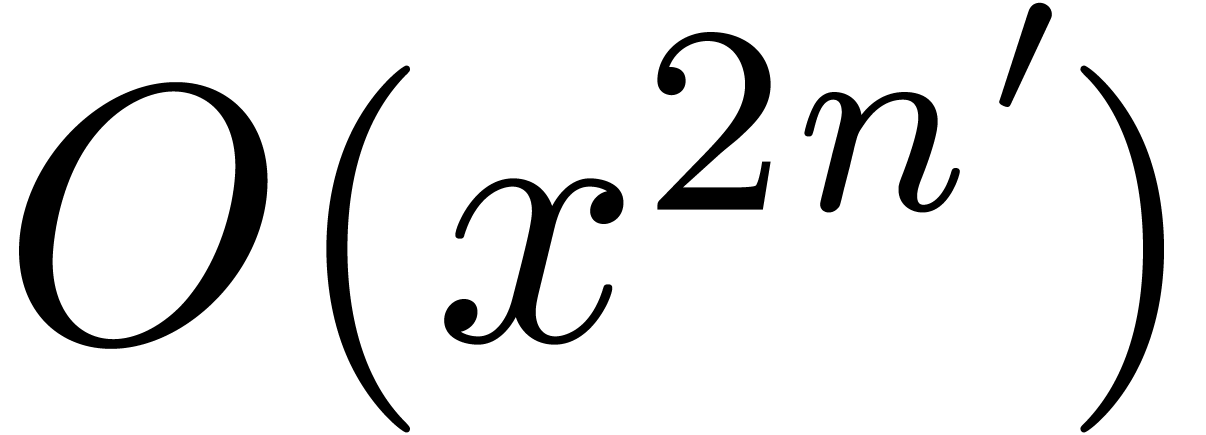 .
.
We finally compute  from
from  and
and 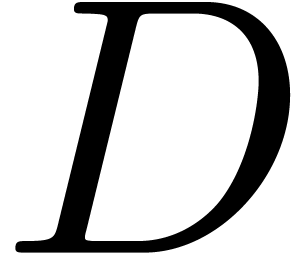 using rational function reconstruction. The
complexity analysis and the remainder of the proof is done in a similar
way as in the proofs of Theorems 15 and 18.
using rational function reconstruction. The
complexity analysis and the remainder of the proof is done in a similar
way as in the proofs of Theorems 15 and 18.
With the above techniques, we may at least verify whether computed
pseudo-gcrds or pseudo-lclms are correct. For a fully deterministic
algorithm, we still need a way to find a point where 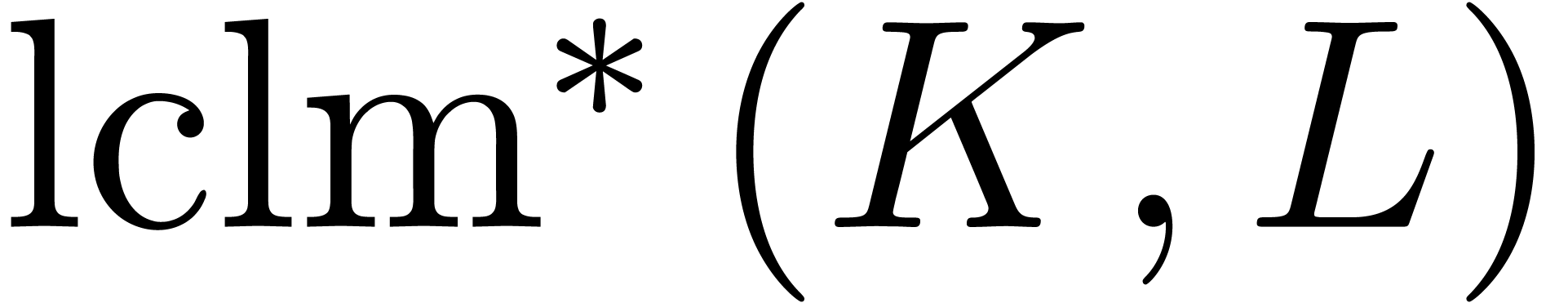 is non singular. This can be done by brute force. Let us state the
result in the most general setting of pseudo-Euclidean matrices.
is non singular. This can be done by brute force. Let us state the
result in the most general setting of pseudo-Euclidean matrices.
Proof. Let 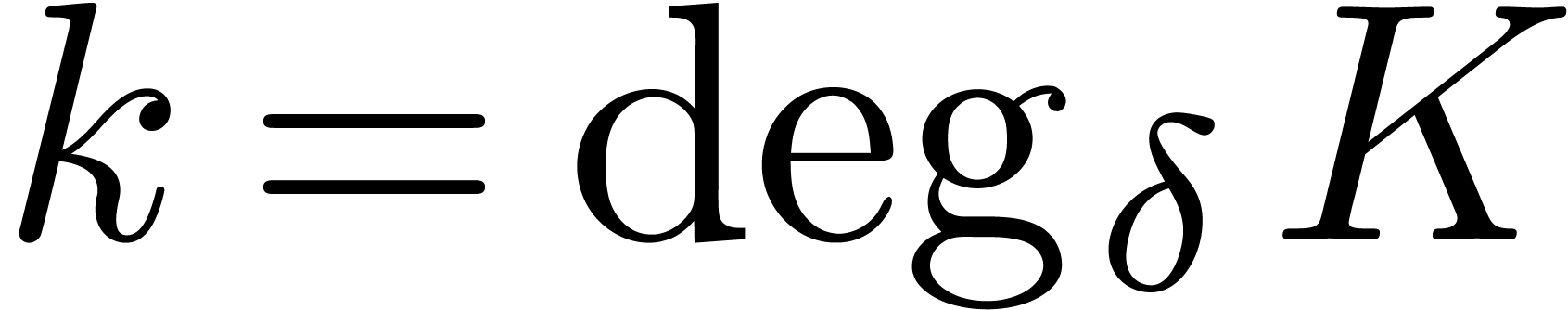 ,
,
 , and assume first that we
know
, and assume first that we
know  . Let
. Let 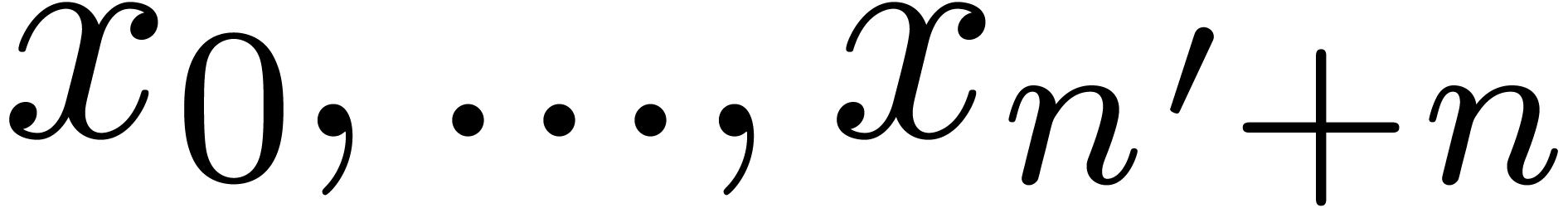 be
be  be pairwise distinct, randomly chosen points
in
be pairwise distinct, randomly chosen points
in  at which
at which  and
and  are non singular. At each
are non singular. At each 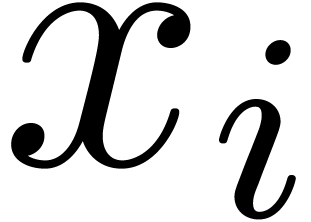 , we compute canonical fundamental systems of
solutions
, we compute canonical fundamental systems of
solutions  and
and  for
for 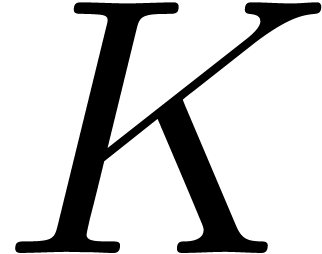 and
and  at order
at order 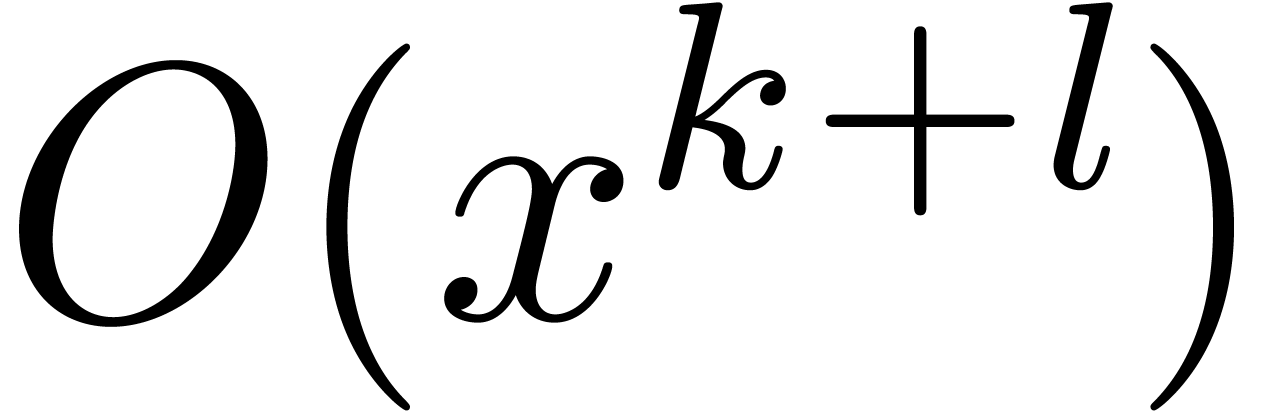 . We claim that this can be done in time
. We claim that this can be done in time 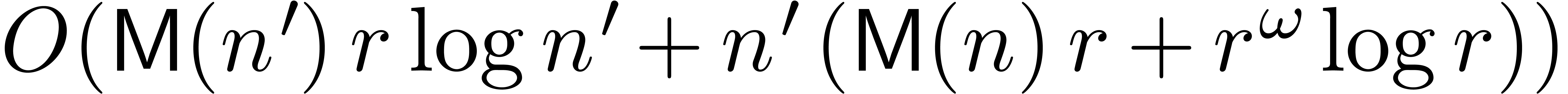 .
.
Indeed, it requires a time 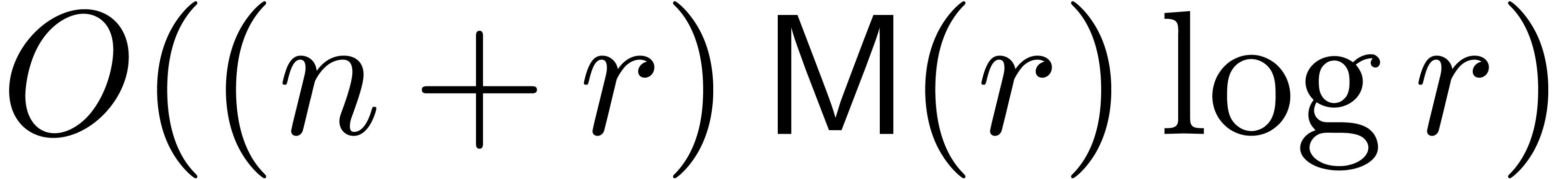 to rewrite each
operator with respect to
to rewrite each
operator with respect to  . We
next perform a multipoint evaluation of the coefficients of these
operators to obtain the shifted operators at
. We
next perform a multipoint evaluation of the coefficients of these
operators to obtain the shifted operators at 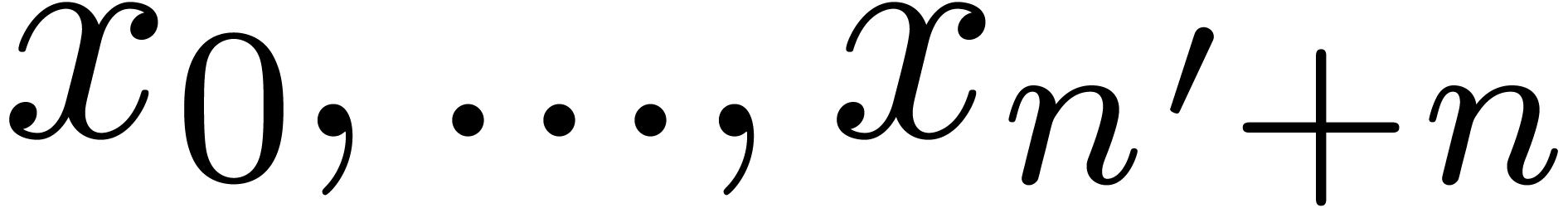 (this requires a time
(this requires a time 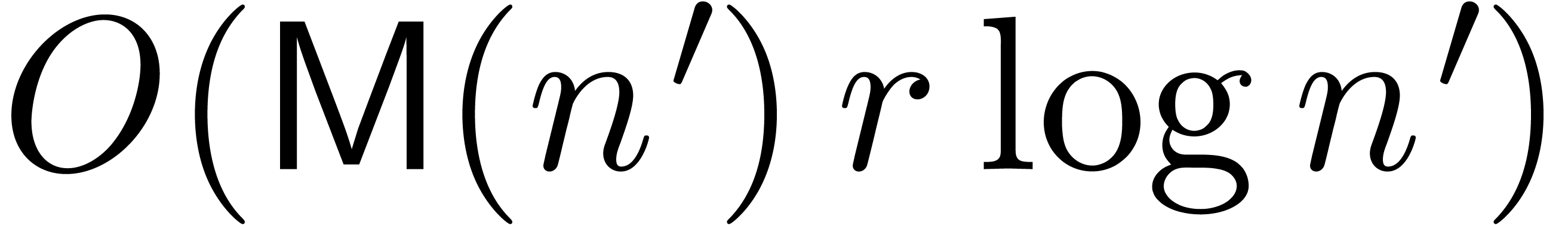 ). The
truncations of these operators at order
). The
truncations of these operators at order 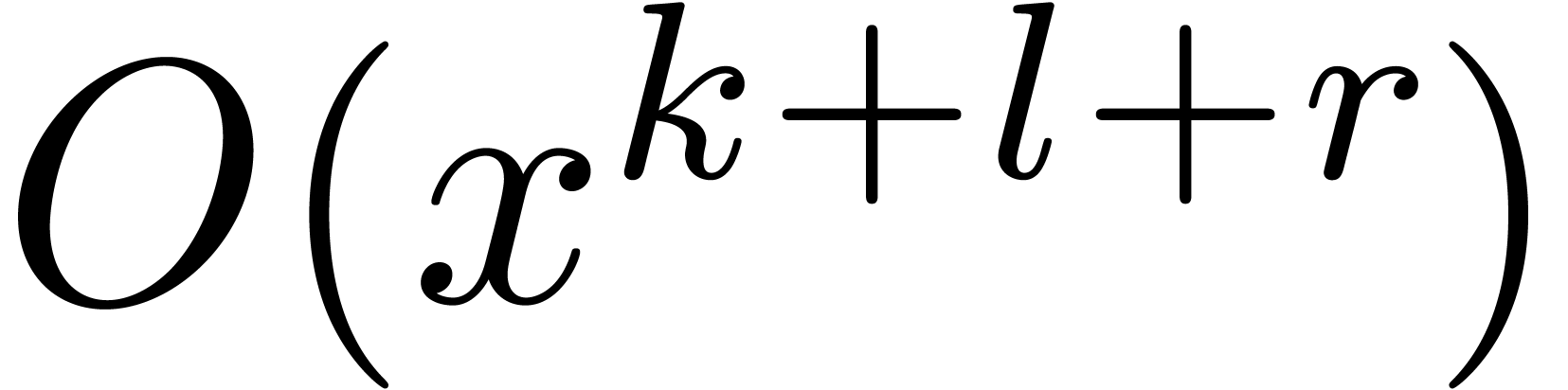 are then
converted back to the respresentation with respect to
are then
converted back to the respresentation with respect to 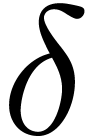 . This can be done in time
. This can be done in time 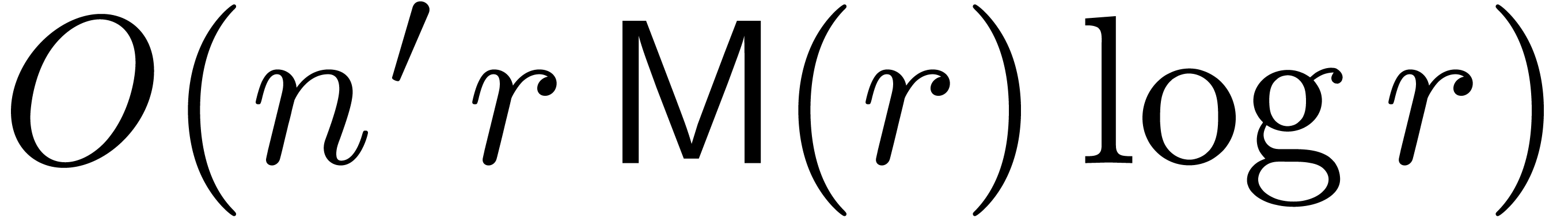 . Using Theorem 7, we finally
compute the required fundamental systems of solutions in time
. Using Theorem 7, we finally
compute the required fundamental systems of solutions in time 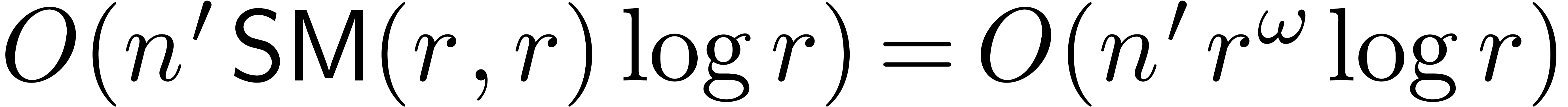 .
.
From 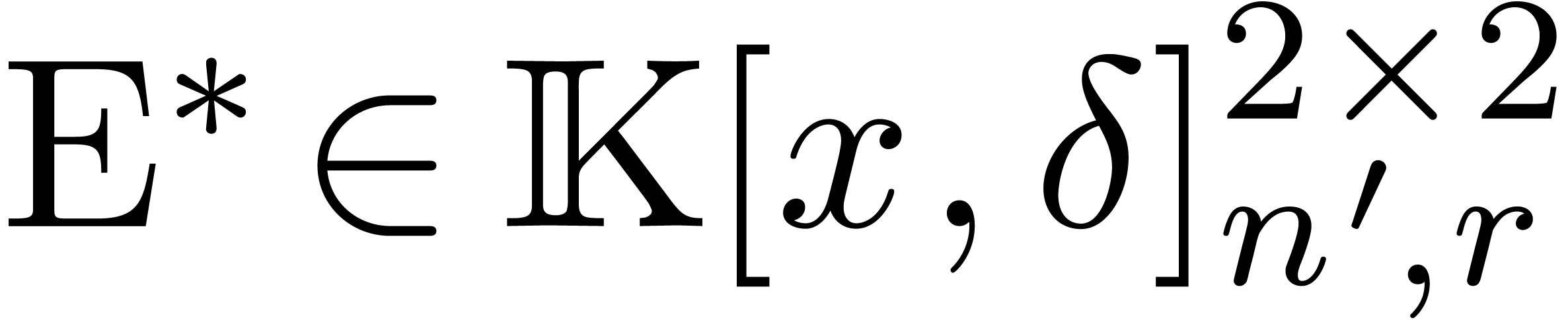 , we get
, we get 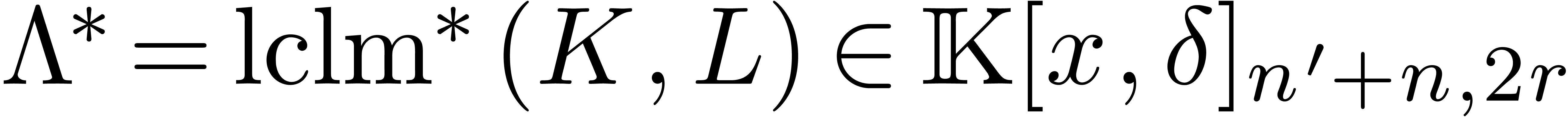 . Since we assumed
. Since we assumed 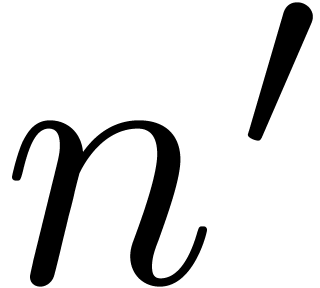 to
be sufficiently large, it follows that
to
be sufficiently large, it follows that  is non
singular at one of the points
is non
singular at one of the points 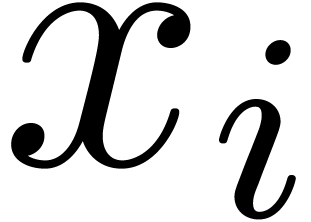 .
At such a point
.
At such a point 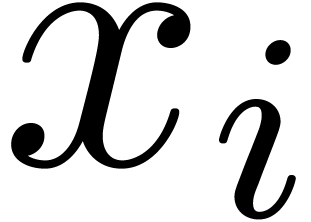 , the
canonical fundamental systems of solutions
, the
canonical fundamental systems of solutions  and
and
 generate a vector space
generate a vector space 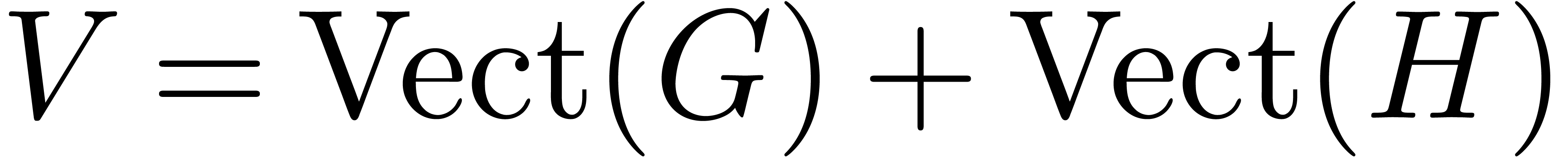 of maximal dimension
of maximal dimension  , and
with a basis
, and
with a basis  such that
such that 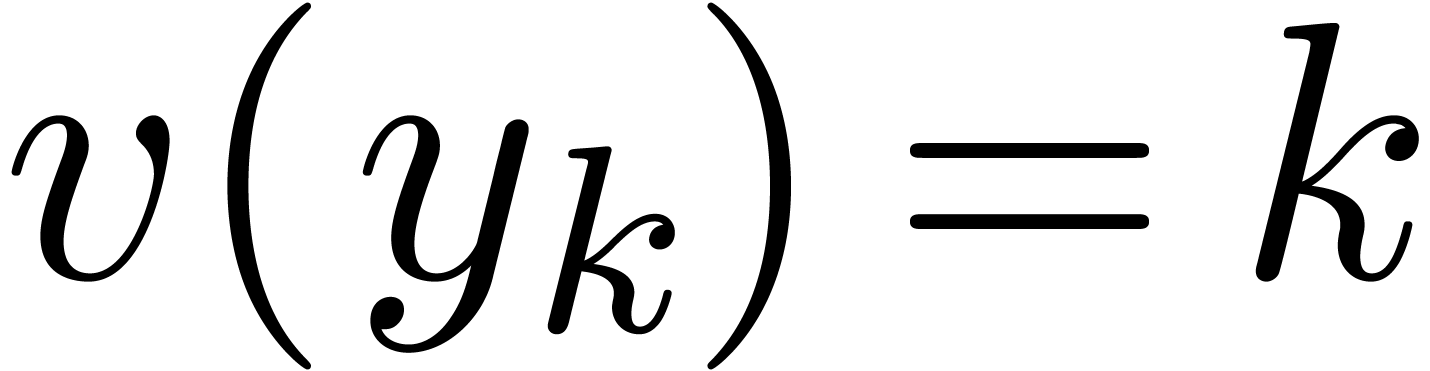 for all
for all 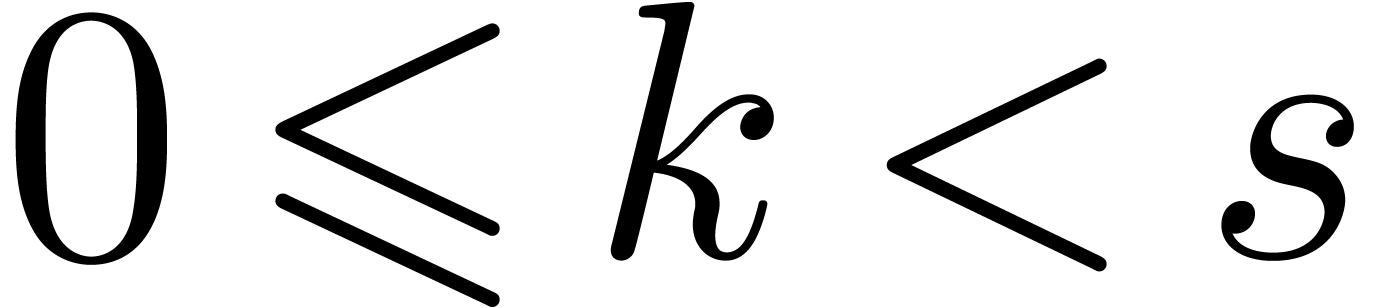 . We finally apply
Theorem 23 in order to obtain
. We finally apply
Theorem 23 in order to obtain  .
If
.
If 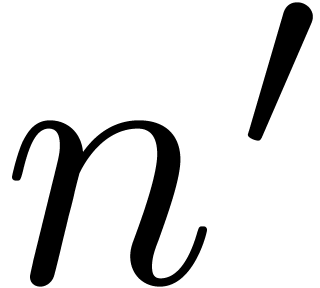 is unknown, then we use a sequence of guesses
is unknown, then we use a sequence of guesses
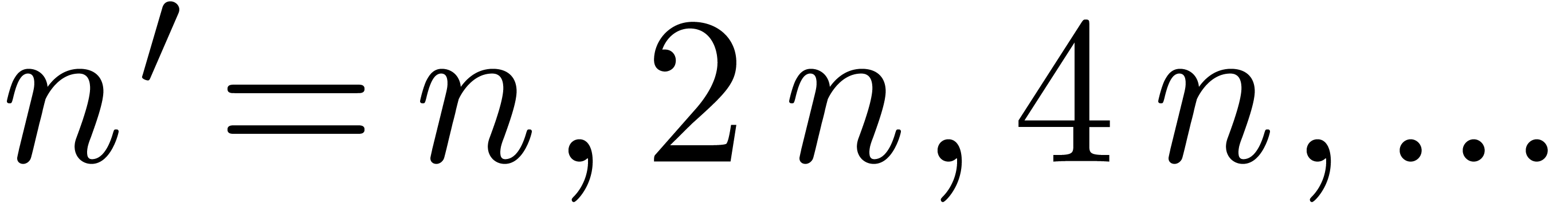 , as in the previous
proofs.
, as in the previous
proofs.
Remark  using Theorem 21 and certify the result using trial
division by
using Theorem 21 and certify the result using trial
division by 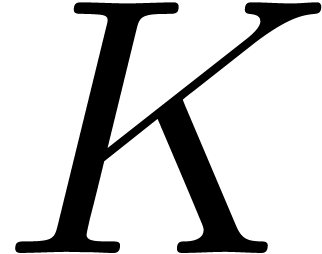 and
and  .
This allows us to use the weaker assumption
.
This allows us to use the weaker assumption 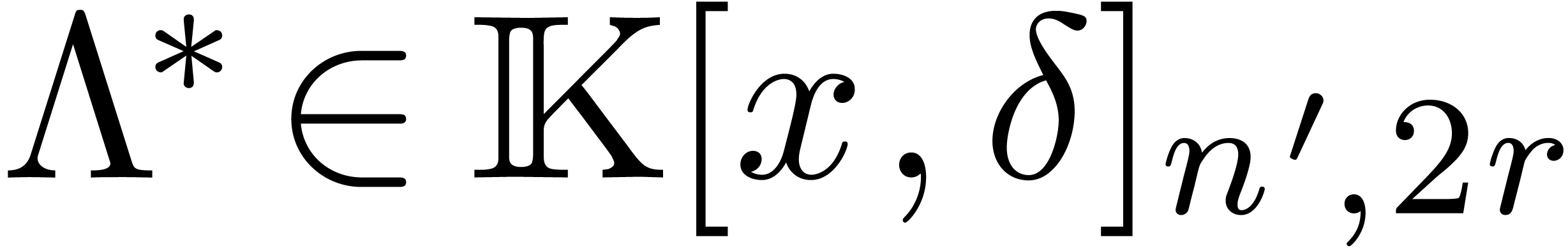 instead of
instead of 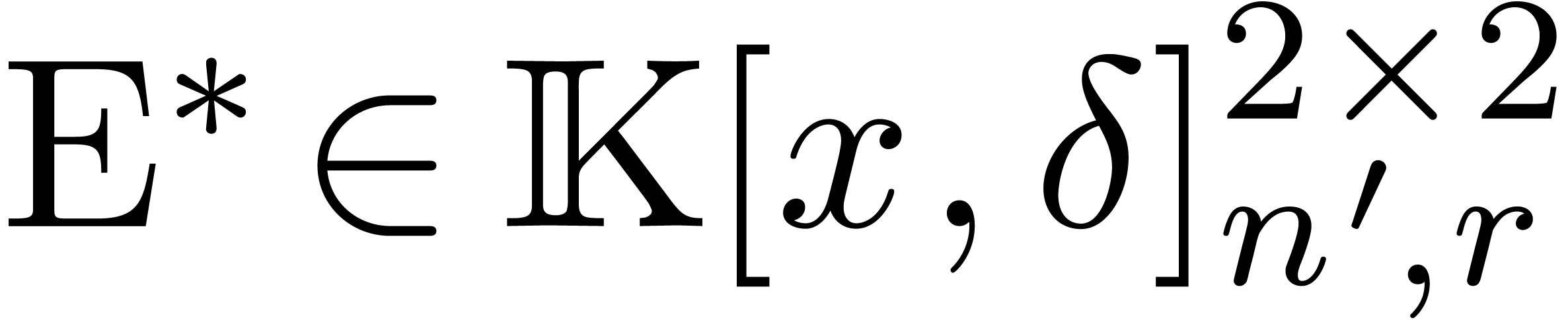 , whereas the
complexity bound becomes
, whereas the
complexity bound becomes  .
.
We have summarized our complexity bounds for Euclidean operations on two
operators 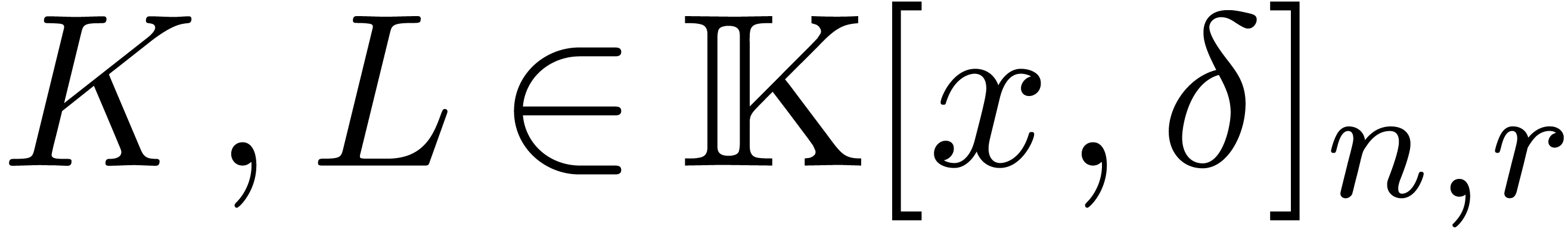 in Table 1. We
systematically write
in Table 1. We
systematically write 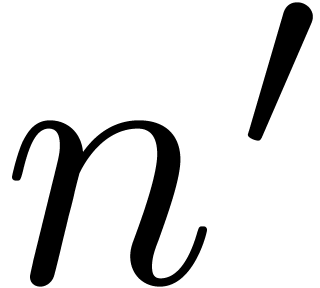 for the degree in
for the degree in  of the result. We also write
of the result. We also write 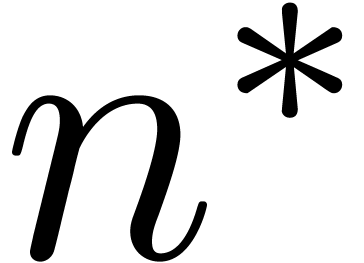 for
the degree of the Euclidean matrix in
for
the degree of the Euclidean matrix in  .
.
The algorithms in the first line correspond to applying Theorems 18, 21 and 23 at a randomly chosen
point, without checking the result. The second line corresponds to the
Las Vegas randomized algorithm for which the answers are certified
through trial division (the bound for gcrds might further drop to 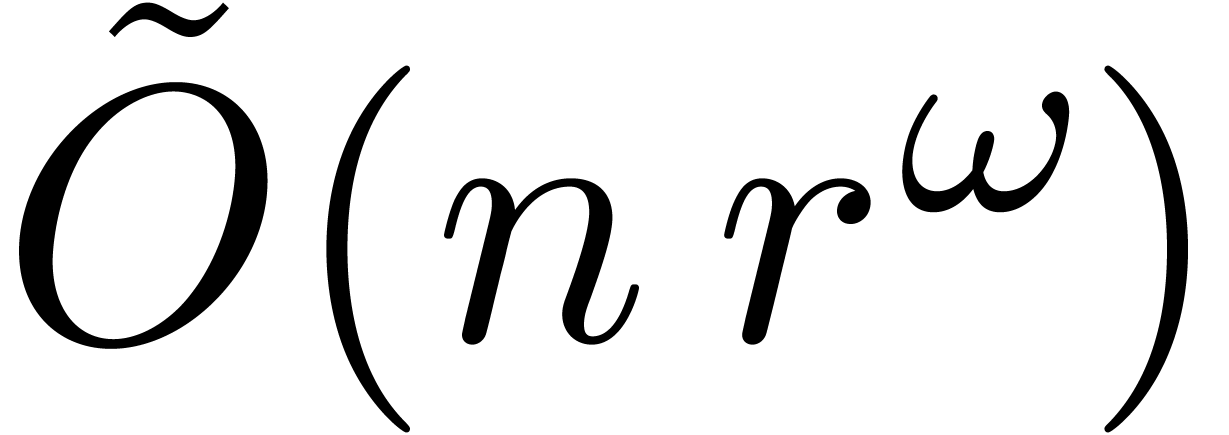 in view of Remark 22; more generally,
the bounds can be restated in terms of sizes of certificates). In the
third line, we rather use Euclidean matrices for the certification. The
fourth line shows complexity bounds for the deterministic versions of
our algorithms.
in view of Remark 22; more generally,
the bounds can be restated in terms of sizes of certificates). In the
third line, we rather use Euclidean matrices for the certification. The
fourth line shows complexity bounds for the deterministic versions of
our algorithms.
In comparison, several randomized Las Vegas algorithms were given in [6] that achieve the complexity bound 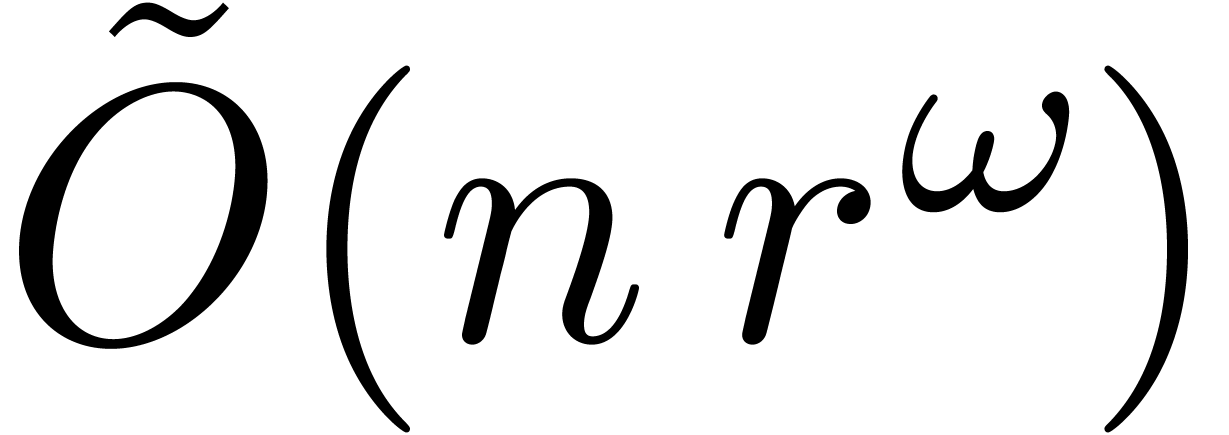 for lclms. This is in particular the case for Heffter's algorithm [19], when using Theorem 4. The non determinism is
due to the use of a fast Las Vegas randomized algorithm for the
computation of kernels of matrices with polynomial entries [6,
Theorem 2]. Grigoriev established complexity bounds for gcrds which rely
on a similar reduction to polynomial linear algebra. Along the same
lines as in [6], this should lead to a Las Vegas randomized
algorithm of complexity
for lclms. This is in particular the case for Heffter's algorithm [19], when using Theorem 4. The non determinism is
due to the use of a fast Las Vegas randomized algorithm for the
computation of kernels of matrices with polynomial entries [6,
Theorem 2]. Grigoriev established complexity bounds for gcrds which rely
on a similar reduction to polynomial linear algebra. Along the same
lines as in [6], this should lead to a Las Vegas randomized
algorithm of complexity 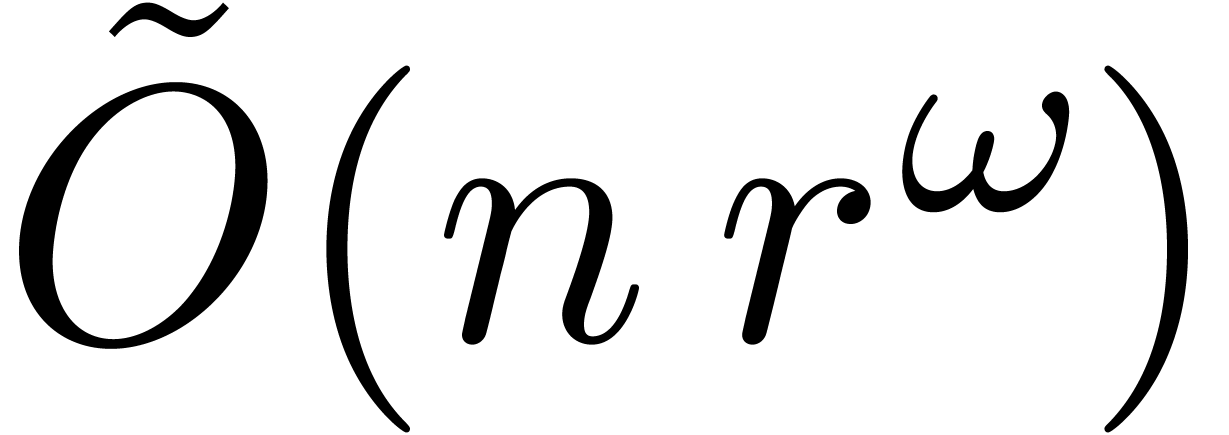 ,
although we did not check this in detail.
,
although we did not check this in detail.
In summary, the new algorithms do not achieve any improvements in the
worst case. Nevertheless, the uncertified versions of our algorithms
admit optimal running times up to logarithmic factors in terms of the
combined input and output size. The certified randomized
versions satisfy similar complexity bounds in terms of the size of a
suitable certificate; such bounds can sometimes be better than the
previously known worst case bounds. When performing our expansions at a
randomly chosen point in  , we
also recall that the probability of failure is exponentially small as a
function of the bitsize of this point.
, we
also recall that the probability of failure is exponentially small as a
function of the bitsize of this point.
|
||||||||||||||||||||
The algorithms from Section 5.1 extend in a straightforward way to the computation of greatest common right divisors and least common left multiples of more than two operators. For instance, using obvious notations, we obtain the following generalizations of Theorems 21 and 18.
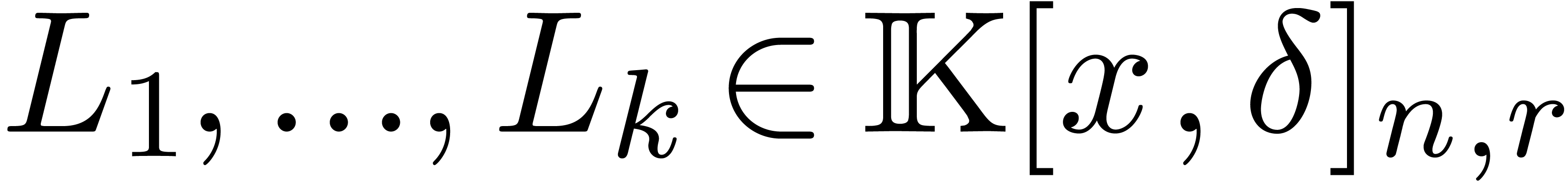 with
with  and
and
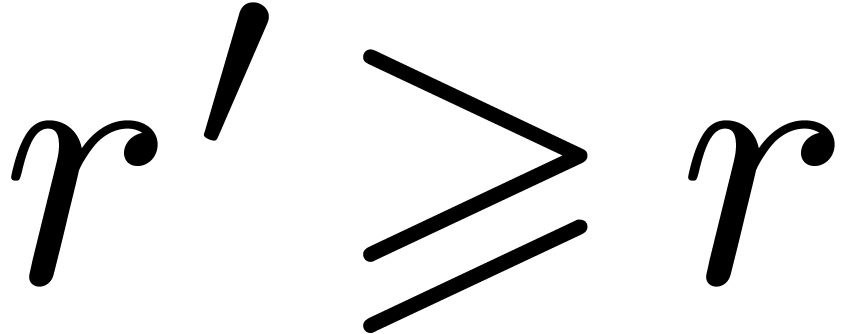 ,
, 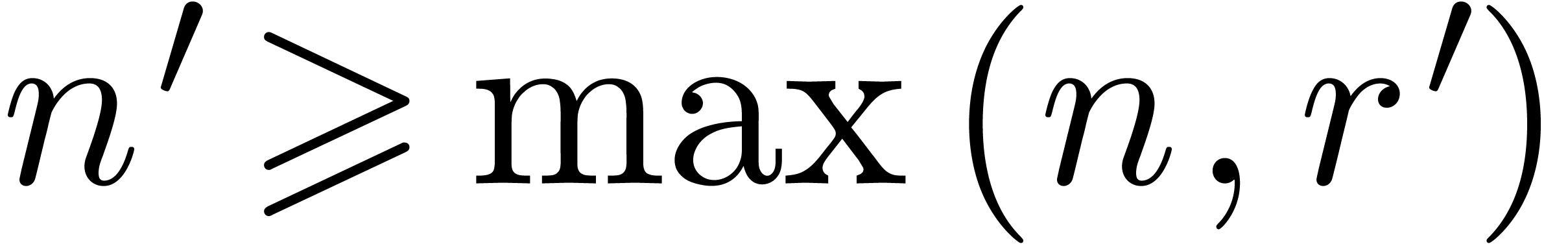 be such that
be such that 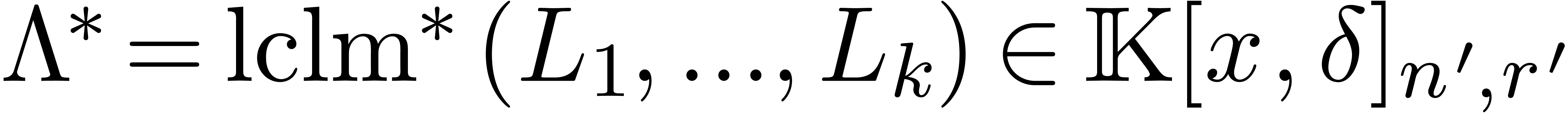 . Assume that
. Assume that
 and
and  are all non
singular at the origin. Then we may compute
are all non
singular at the origin. Then we may compute  in
time
in
time  .
.
Proof. We compute  using
the following algorithm:
using
the following algorithm:
We first compute the canonical fundamental systems of solutions 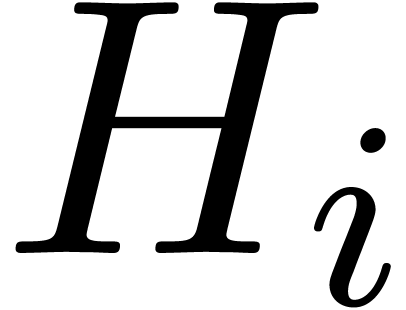 to
to  at order
at order  . This can be done in time
. This can be done in time  .
.
Let 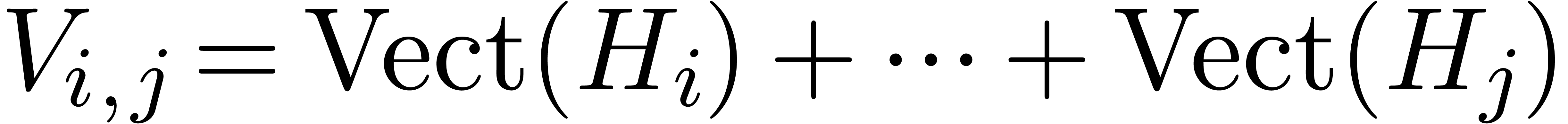 for all
for all  .
Using linear algebra, we may recursively compute a basis
.
Using linear algebra, we may recursively compute a basis 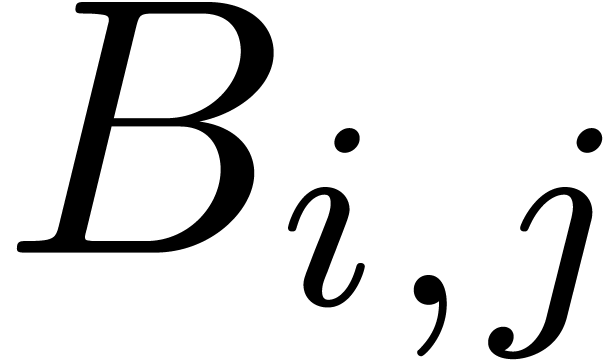 for
for 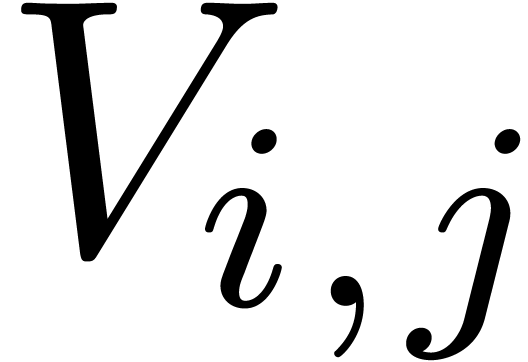 from bases
from bases 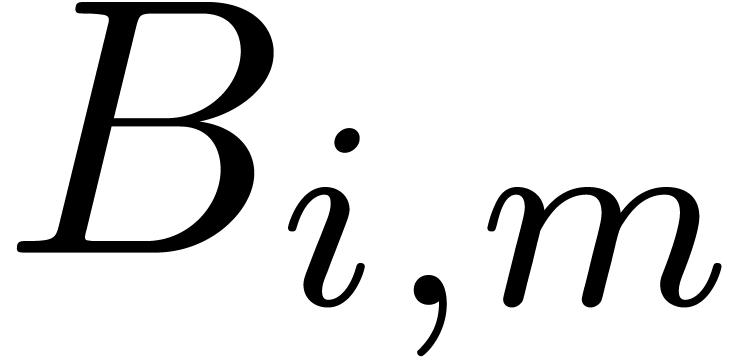 and
and 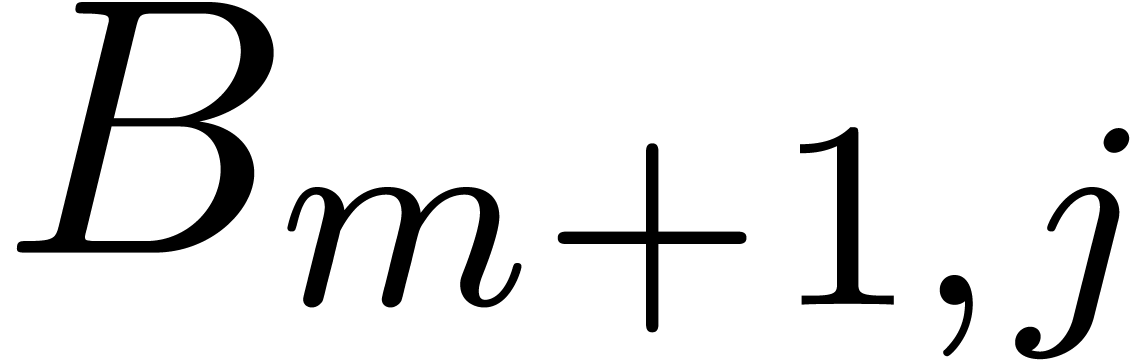 for
for 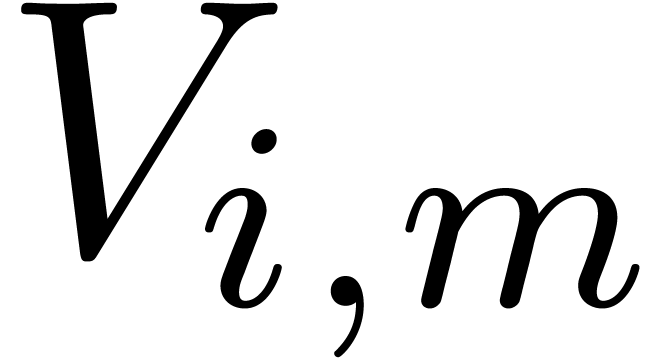 and
and 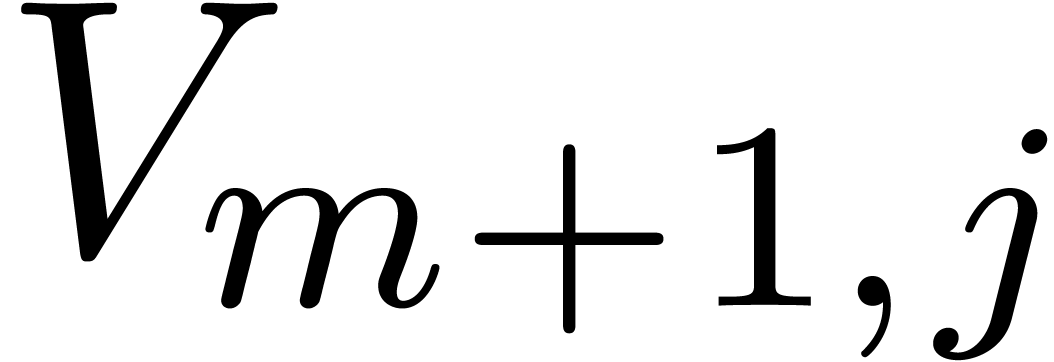 , where
, where 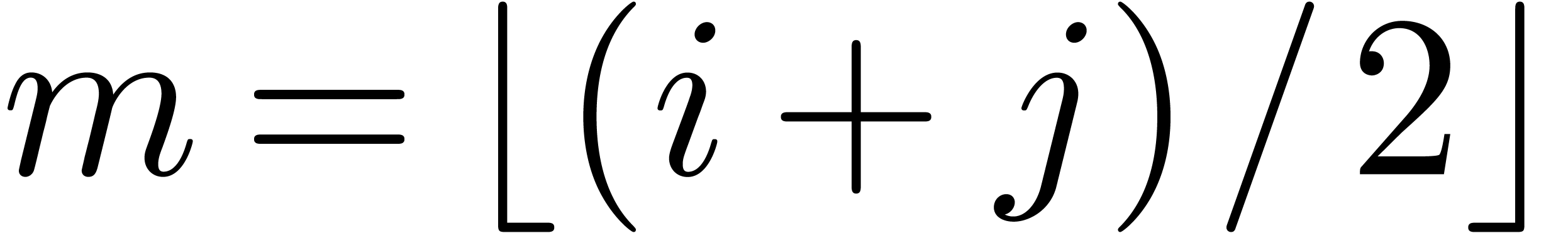 . This algorithm yields a basis
. This algorithm yields a basis  for
for 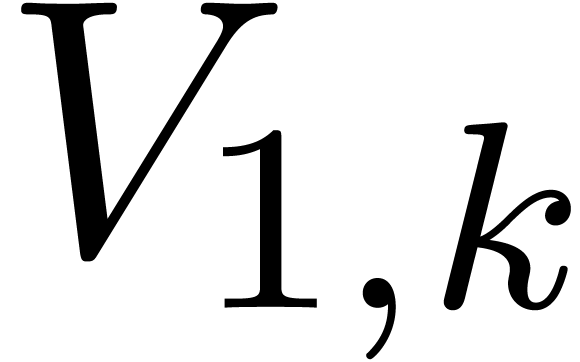 in time
in time 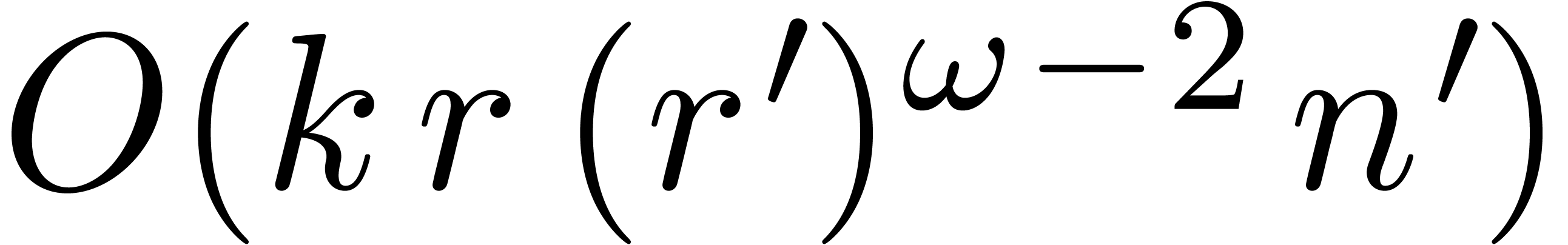 . Using a suitable generalization of Lemma
17, we also notice that
. Using a suitable generalization of Lemma
17, we also notice that 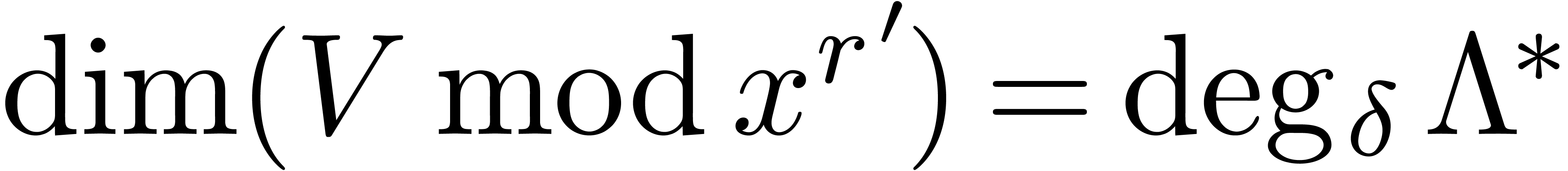 .
.
We compute 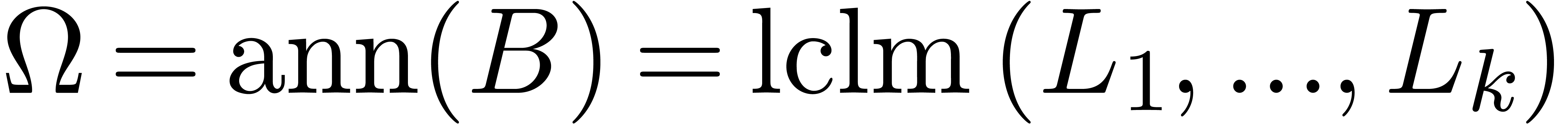 at order
at order 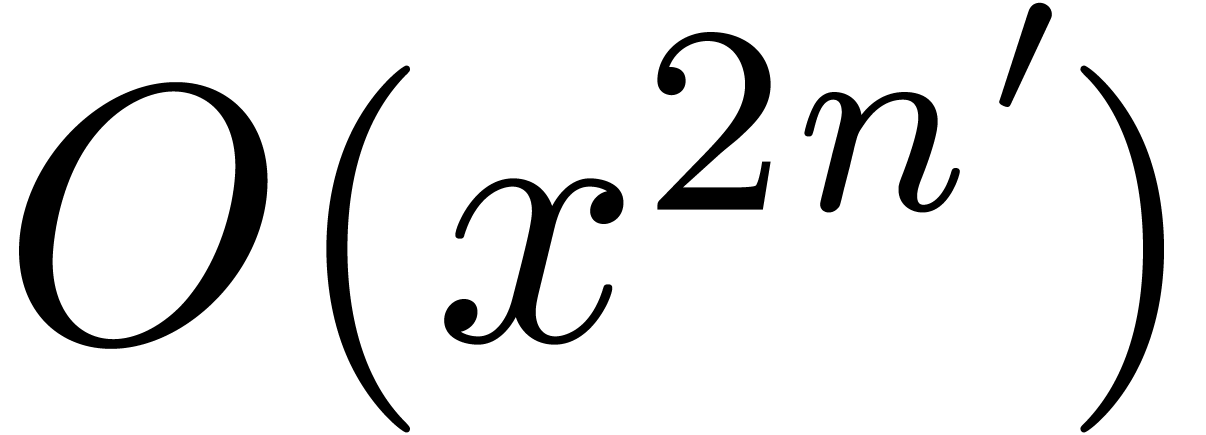 . By Theorem 8, this can be done in
time
. By Theorem 8, this can be done in
time 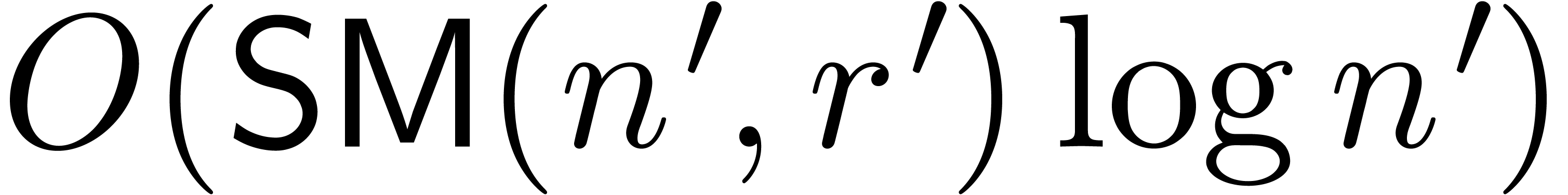 .
.
We compute  from
from  using rational function reconstruction.
using rational function reconstruction.
We obtain the result by adding up all complexity bounds.
Remark 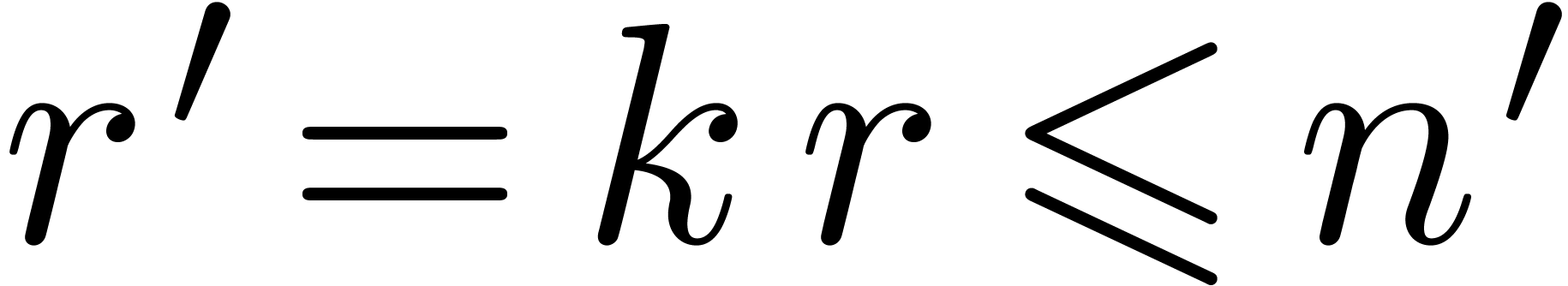 and using [2], the complexity bound
simplifies to
and using [2], the complexity bound
simplifies to  . By [6,
Theorem 6], we may always take
. By [6,
Theorem 6], we may always take 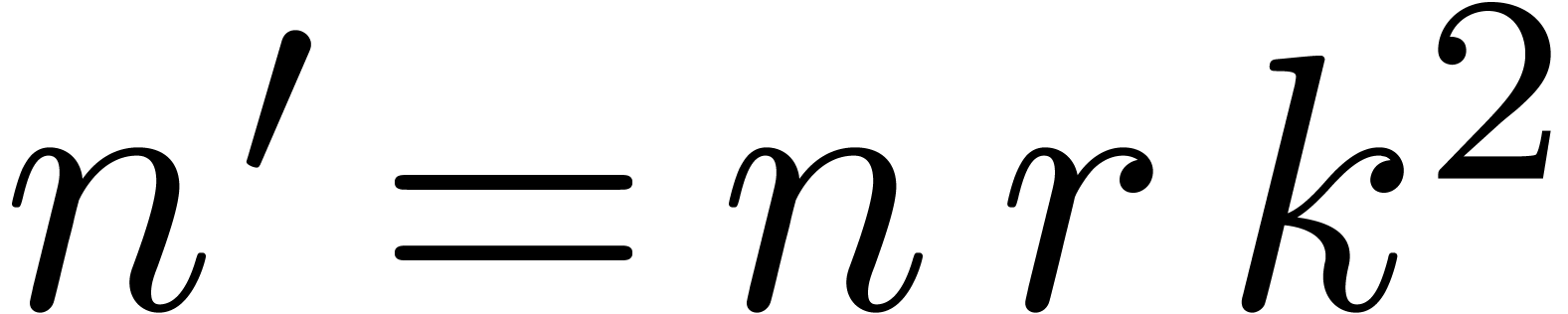 ,
after which the bound further reduces to
,
after which the bound further reduces to 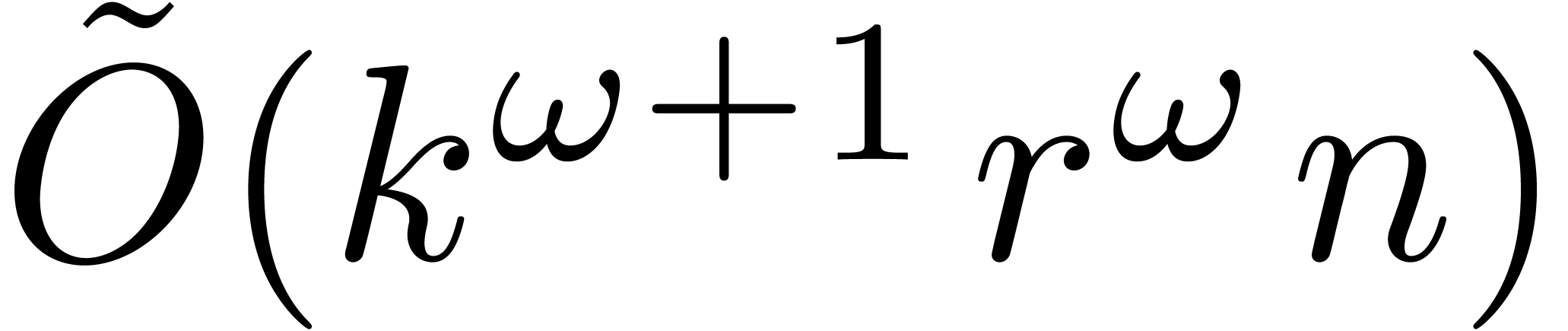 .
In our randomized setting, this improves upon the bounds from [6,
Figure 1].
.
In our randomized setting, this improves upon the bounds from [6,
Figure 1].
Remark 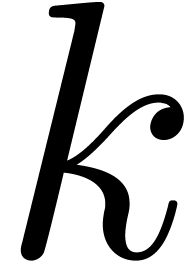 exact
divisions of operators in
exact
divisions of operators in 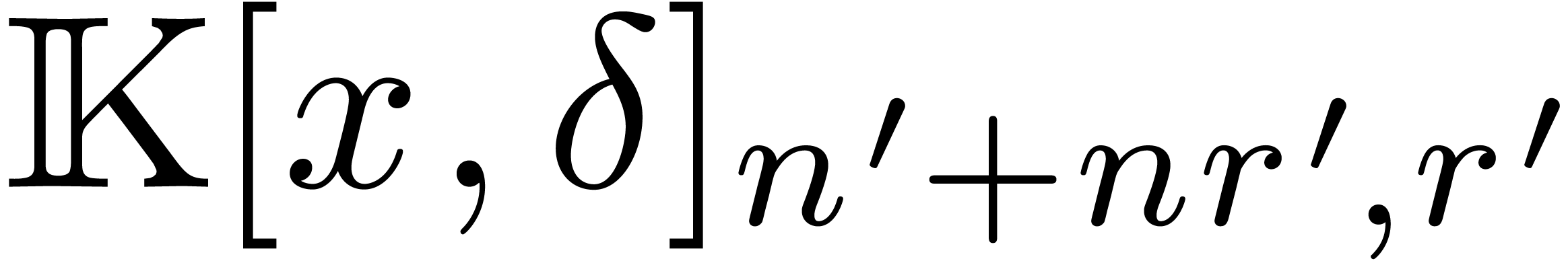 by
by  . Using the division algorithm from Section 4, and taking
. Using the division algorithm from Section 4, and taking 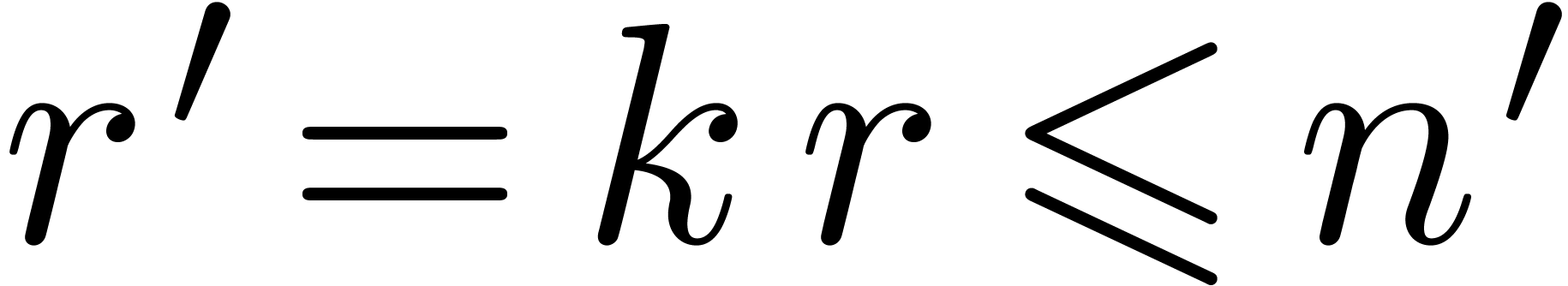 and
and 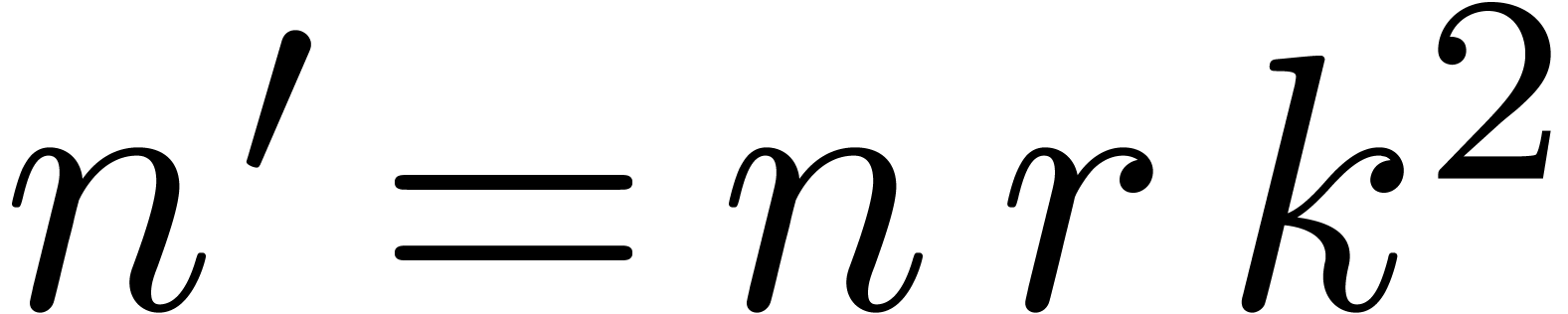 as above, this can be done in time
as above, this can be done in time
This is slightly better than the new bound from [6].
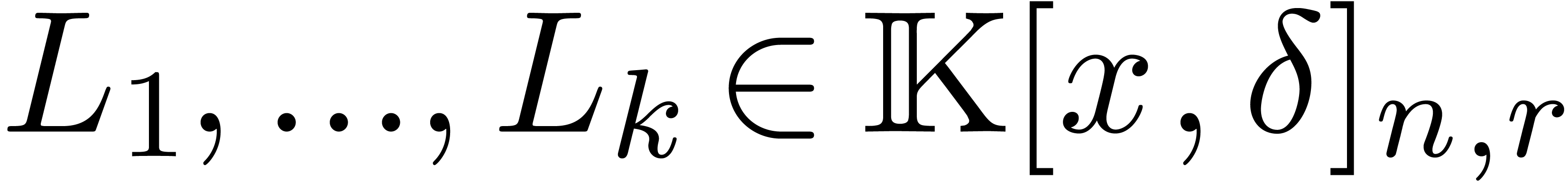 and
and 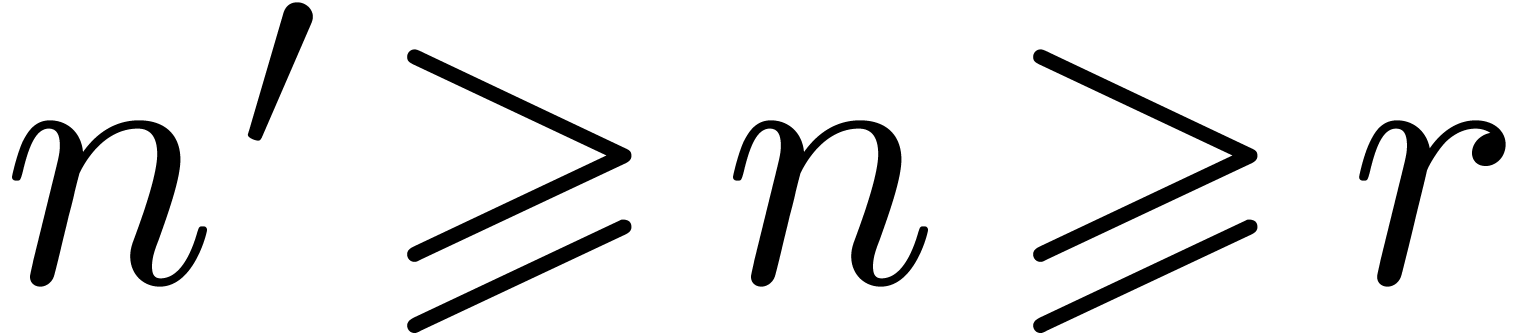 be
such that
be
such that  . Assume that
. Assume that
 and
and  are all non
singular at the origin. Then we may compute
are all non
singular at the origin. Then we may compute  in
time
in
time 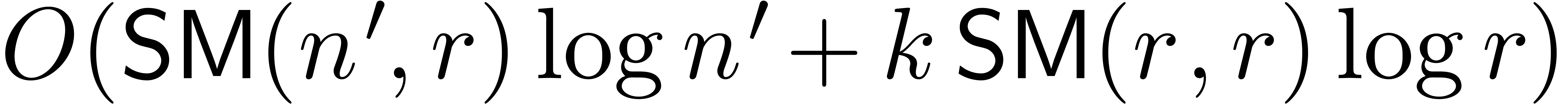 .
.
Proof. The proof is similar to the one of
Theorem 26, except for the way how we compute a basis for
 . Indeed, we first compute a
basis
. Indeed, we first compute a
basis  for
for  .
This requires a time
.
This requires a time 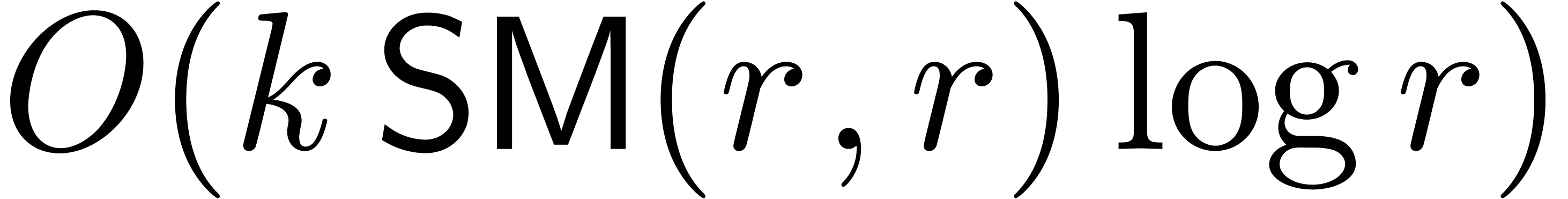 for the computation of
for the computation of  modulo
modulo 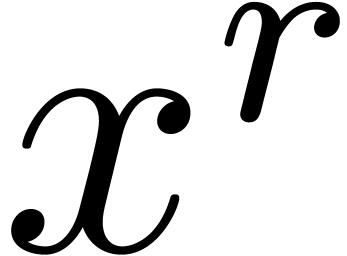 and a time
and a time 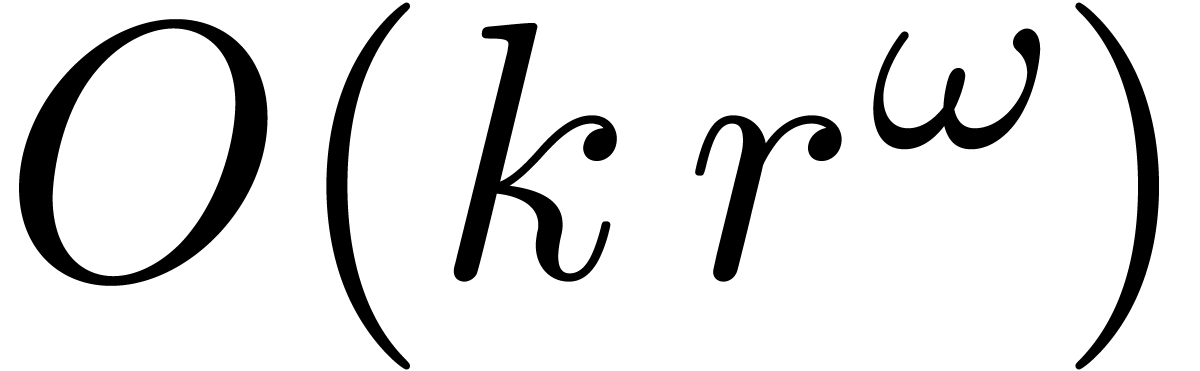 for the remaining linear algebra. We next compute the
unique constant matrix
for the remaining linear algebra. We next compute the
unique constant matrix  such that
such that 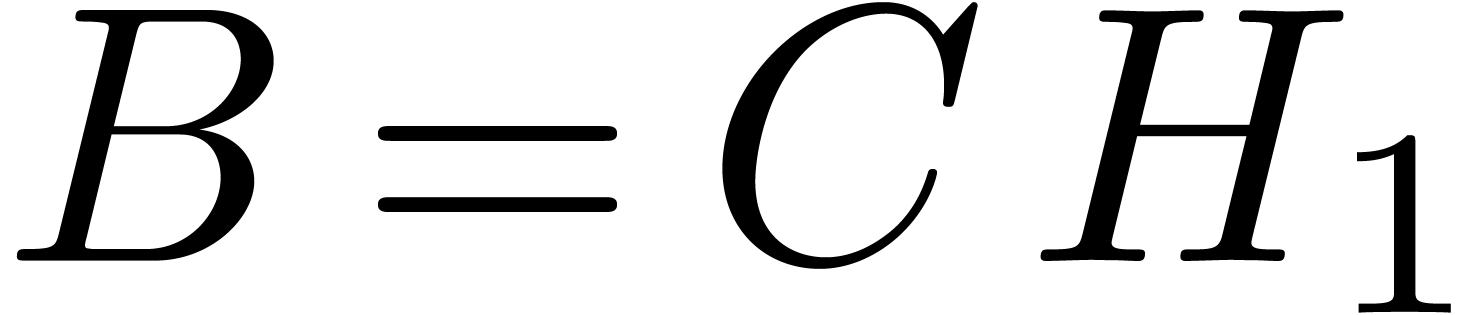 modulo
modulo 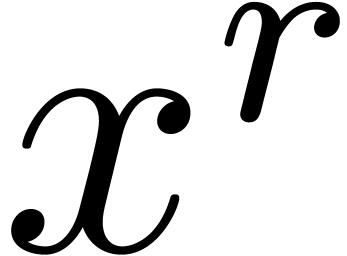 . Since
. Since
 is non singular, we have
is non singular, we have 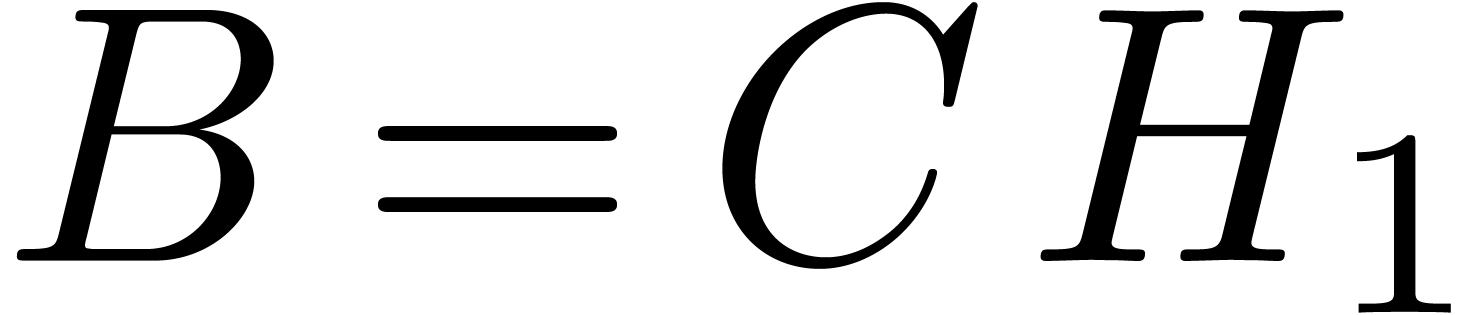 at any order, so it suffices to compute
at any order, so it suffices to compute  up to
order
up to
order 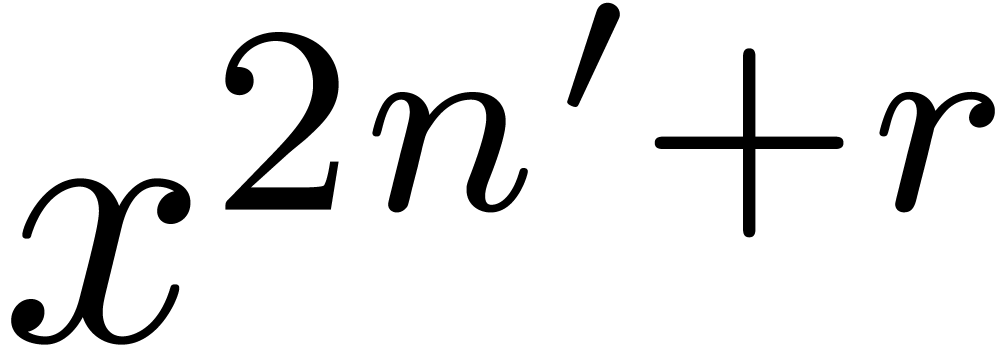 in order to obtain
in order to obtain  up to order
up to order 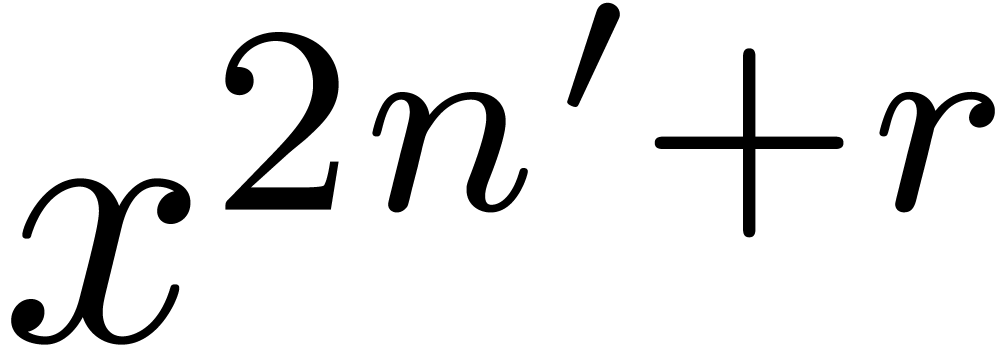 .
.
Remark  and
and  of
of 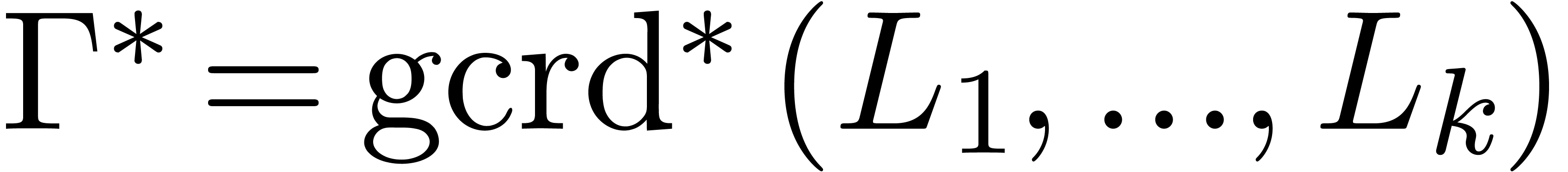 and
and 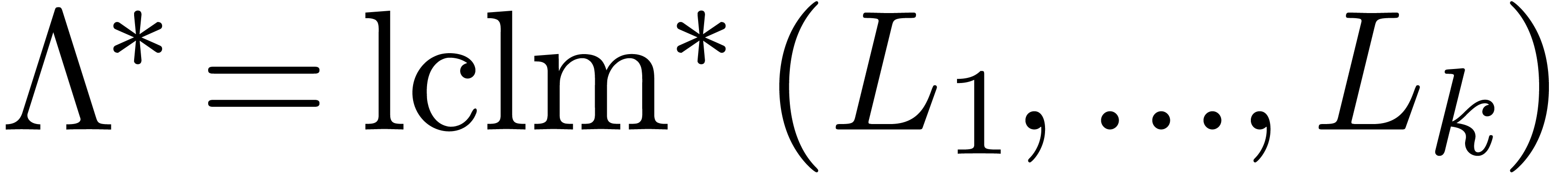 , without
computing
, without
computing  and
and  themselves. For this, it suffices to compute the dimensions of
themselves. For this, it suffices to compute the dimensions of  and
and  . Assuming
that we are at a “non singular point”, the answer is
therefore yes: using the techniques from the proofs of Theorems 29
and 26, we may compute
. Assuming
that we are at a “non singular point”, the answer is
therefore yes: using the techniques from the proofs of Theorems 29
and 26, we may compute  in time
in time 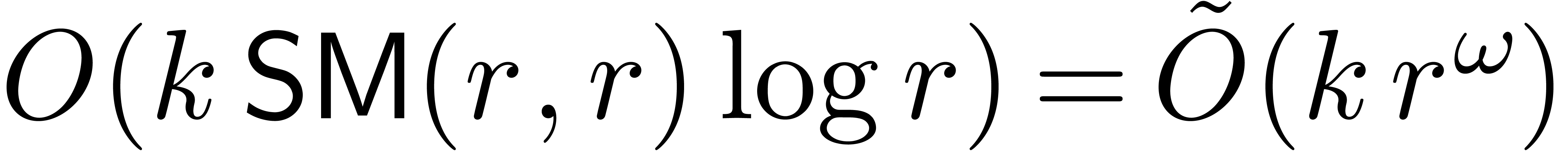 and
and 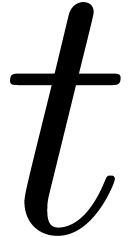 in time
in time 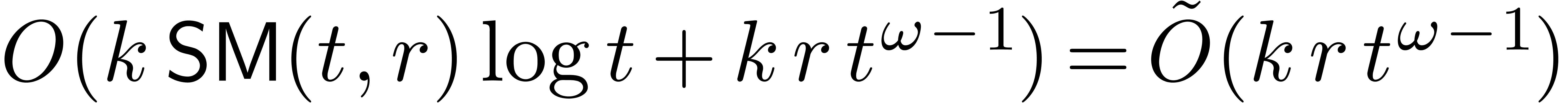 .
.
A. V. Aho, K. Steiglitz, and J. D. Ullman. Evaluating polynomials on a fixed set of points. SIAM Journ. of Comp., 4:533–539, 1975.
A. Benoit, A. Bostan, and J. van der Hoeven. Quasi-optimal multiplication of linear differential operators. In Proc. FOCS '12, pages 524–530. New Brunswick, October 2012. IEEE.
A. Borodin and R.T. Moenck. Fast modular transforms. Journal of Computer and System Sciences, 8:366–386, 1974.
A. Bostan. Algorithmique efficace pour des opérations de base en calcul formel. PhD thesis, École polytechnique, 2003.
A. Bostan, F. Chyzak, and N. Le Roux. Products of ordinary differential operators by evaluation and interpolation. In J. Rafael Sendra and Laureano González-Vega, editors, ISSAC, pages 23–30. Linz/Hagenberg, Austria, July 2008. ACM Press.
A. Bostan, F. Chyzak, B. Salvy, and Z. Li. Fast computation of common left multiples of linear ordinary differential operators. In J. van der Hoeven and M. van Hoeij, editors, Proc. ISSAC '12, pages 99–106. Grenoble, France, July 2012.
A. Bostan and É. Schost. Polynomial evaluation and interpolation on special sets of points. Journal of Complexity, 21(4):420–446, August 2005. Festschrift for the 70th Birthday of Arnold Schönhage.
E. Brassine. Analogie des équations différentielles linéaires à coefficients variables, avec les équations algébriques, pages 331–347. Note III du Tome 2 du Cours d'analyse de Ch. Sturm. École polytechnique, 1864.
D.G. Cantor and E. Kaltofen. On fast multiplication of polynomials over arbitrary algebras. Acta Informatica, 28:693–701, 1991.
J.W. Cooley and J.W. Tukey. An algorithm for the machine calculation of complex Fourier series. Math. Computat., 19:297–301, 1965.
D. Coppersmith and S. Winograd. Matrix multiplication
via arithmetic progressions. In Proc. of the  Annual Symposium on Theory of Computing, pages 1–6.
New York City, may 25–27 1987.
Annual Symposium on Theory of Computing, pages 1–6.
New York City, may 25–27 1987.
S.S. Demidov. On the history of the theory of linear differential equations. Arch. Hist. Exact. Sci., 28(4):369–387, 1983.
F. Le Gall. Powers of tensors and fast matrix multiplication. In Proc. ISSAC 2014, pages 296–303. Kobe, Japan, July 23–25 2014.
M. Giesbrecht. Factoring in skew polynomial rings over finite fields. In Proc. LATIN '92, volume 583 of LNCS, pages 191–203. 1992.
M. Giesbrecht. Factoring in skew polynomial rings over finite finite fields. JSC, 26:463–486, 1998.
M. Giesbrecht and Y. Zhang. Factoring and decomposing
ore polynomials over  .
In Manuel Bronstein, editor, Proc. ISSAC '03, pages
127–134. Philadelphia, USA, August 2003.
.
In Manuel Bronstein, editor, Proc. ISSAC '03, pages
127–134. Philadelphia, USA, August 2003.
D. Yu. Grigoriev. Complexity of factoring and calculating the gcd of linear ordinary differential operators. J. Symb. Comput., 10(1):7–37, 1990.
J. von zur Gathen and J. Gerhard. Modern Computer Algebra. Cambridge University Press, 2-nd edition, 2002.
L. Heffter. Über gemeinsame Vielfache linearer Differentialausdrücke und lineare Differentialgleichungen derselben Klasse. J. Reine Angew. Math., 116:157–166, 1896.
J. van der Hoeven. FFT-like multiplication of linear differential operators. JSC, 33(1):123–127, 2002.
J. van der Hoeven. Relax, but don't be too lazy. JSC, 34:479–542, 2002.
J. van der Hoeven. Relaxed multiplication using the middle product. In Manuel Bronstein, editor, Proc. ISSAC '03, pages 143–147. Philadelphia, USA, August 2003.
J. van der Hoeven. On the complexity of skew arithmetic. Technical Report, HAL, 2011. http://hal.archives-ouvertes.fr/hal-00557750.
J. van der Hoeven, G. Lecerf, B. Mourrain et al. Mathemagix. 2002. http://www.mathemagix.org.
Z. Li. A subresultant theory for ore polynomials with applications. In O. Gloor, editor, Proc. ISSAC '98, pages 132–139. Rostock, Germany, August 1998.
G. Libri. Mémoire sur la résolution des équations algébriques dont les racines ont entre elles un rapport donné, et sur l'intégration des équations différentielles linéaires dont les intégrales particulières peuvent s'exprimer les unes par les autres. J. Reine und Angew. Math., 10:167–194, 1833.
R.T. Moenck and A. Borodin. Fast modular transforms via division. In Thirteenth annual IEEE symposium on switching and automata theory, pages 90–96. Univ. Maryland, College Park, Md., 1972.
O. Ore. Theorie der linearen Differentialgleichungen. J. Reine und Angew. Math., 167:221–234, 1932.
O. Ore. Theory of non-commutative polynomials. Ann. of Math., 34(3):480–508, 1933.
V. Pan. How to multiply matrices faster, volume 179 of Lect. Notes in Math. Springer, 1984.
A. Schönhage. Schnelle Multiplikation von Polynomen über Körpern der Charakteristik 2. Acta Informatica, 7:395–398, 1977.
A. Schönhage and V. Strassen. Schnelle Multiplikation großer Zahlen. Computing, 7:281–292, 1971.
R.P. Stanley. Differentially finite power series. European J. Combin., 1:175–188, 1980. MR #81m:05012.
V. Strassen. Gaussian elimination is not optimal. Numer. Math., 13:352–356, 1969.
V. Strassen. Die Berechnungskomplexität von elementarsymmetrischen Funktionen und von Interpolationskoeffizienten. Numer. Math., 20:238–251, 1973.