Towards a library for straight-line
programs  |
|
| Preliminary version of May 20, 2025 |
| This work is dedicated to the memory of Joos Heintz. |
|
 . This work has
been supported by an ERC-2023-ADG grant for the ODELIX project
(number 101142171).
. This work has
been supported by an ERC-2023-ADG grant for the ODELIX project
(number 101142171).
Funded by the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. |
 |
 . This article has
been written using GNU TeXmacs [65].
. This article has
been written using GNU TeXmacs [65].
Straight-line programs have proved to be an extremely useful framework both for theoretical work on algebraic complexity and for practical implementations. In this paper, we expose ideas for the development of high performance libraries dedicated to straight-line programs, with the hope that they will allow to fully leverage the theoretical advantages of this framework for practical applications. |
A straight-line program (or SLP) is a program that takes a finite number
of input arguments, then executes a sequence of simple arithmetic
instructions, and finally returns a finite number of output values. For
instance, the function 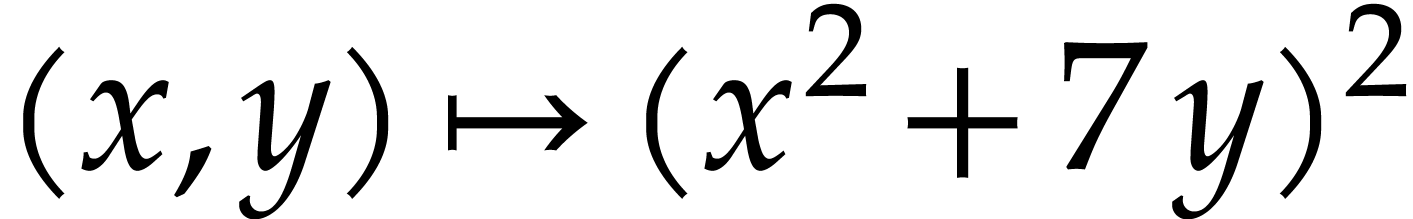 can be computed using the
following SLP:
can be computed using the
following SLP:
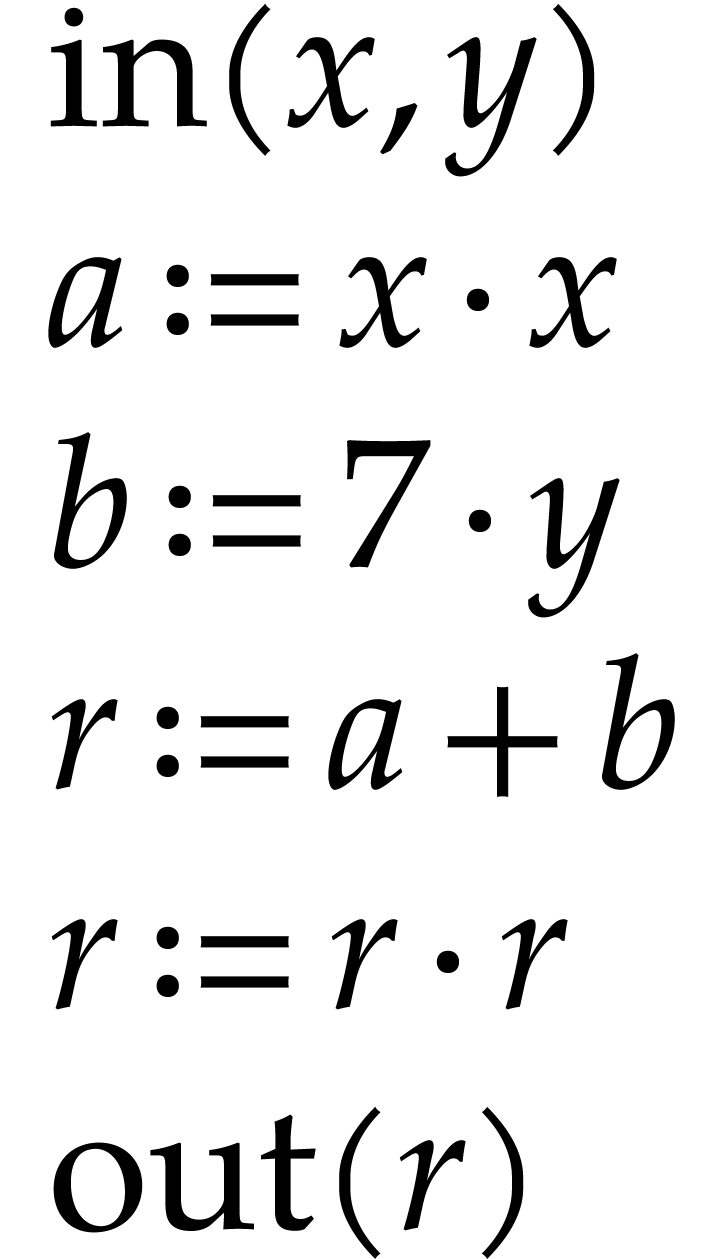 |
(1.1) |
The instructions operate on a finite list of variables (here 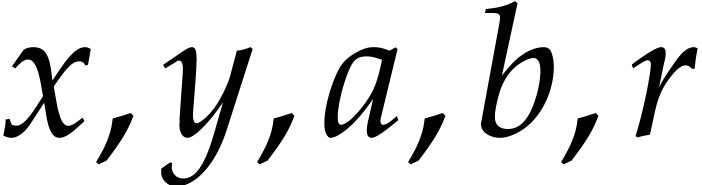 ) and constants (here
) and constants (here  ). There are no restrictions on how variables
are allowed to be reused: they can be reassigned several times (like
). There are no restrictions on how variables
are allowed to be reused: they can be reassigned several times (like
 ) and they may occur multiple
times in the input and output of an operation (like in the operations
) and they may occur multiple
times in the input and output of an operation (like in the operations
 and
and 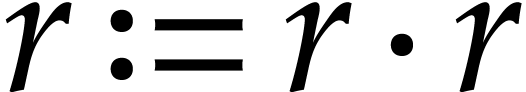 ).
).
SLPs have a profoundly dual nature as programs and data. As programs, SLPs are eligible for a range of operations and techniques from the theory of compilation [3]: constant folding, common subexpression elimination, register allocation, etc. Although the expressive power of SLPs is very limited, their simplicity can be turned into an advantage: many program optimizations that are hard to implement for general purpose programs become simpler and more efficient when restricted to SLPs. In particular, most classical program transformations can be done in linear time. Traditional general purpose compilation techniques also rarely exploit mathematical properties (beyond basic algebraic rules that are useful during simplifications). In the SLP world, algebraic transformations such as automatic differentiation [14] and transposition [17] are easy to implement; more examples will be discussed in this paper.
Let us now turn to the data side. The example SLP (1.1) can
be regarded as a polynomial 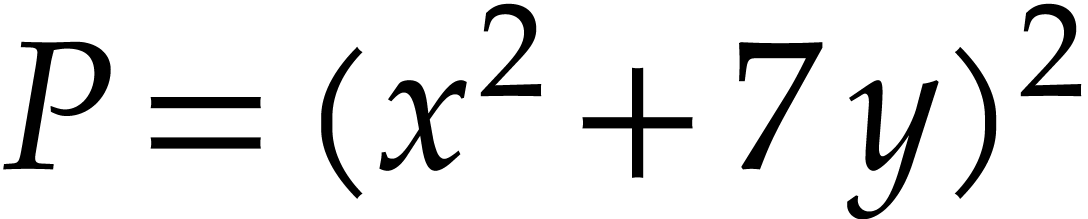 .
In this sense, SLPs constitute a data structure for the representation
of multivariate polynomials. Note that this representation is more
compact than the (expanded) sparse representation
.
In this sense, SLPs constitute a data structure for the representation
of multivariate polynomials. Note that this representation is more
compact than the (expanded) sparse representation 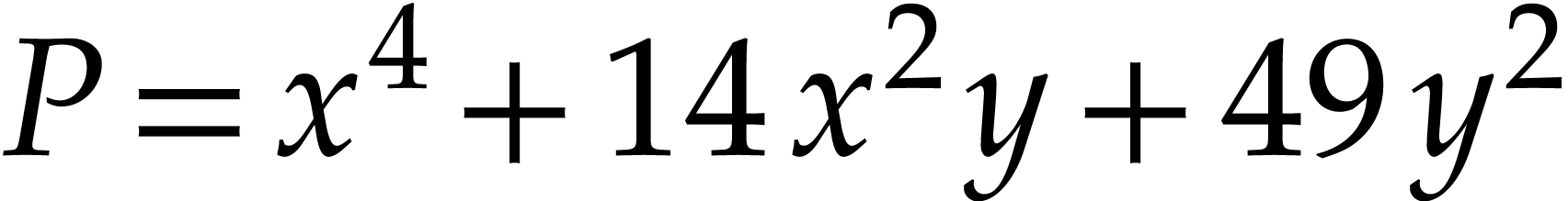 and way more compact than the dense “total degree”
representation
and way more compact than the dense “total degree”
representation 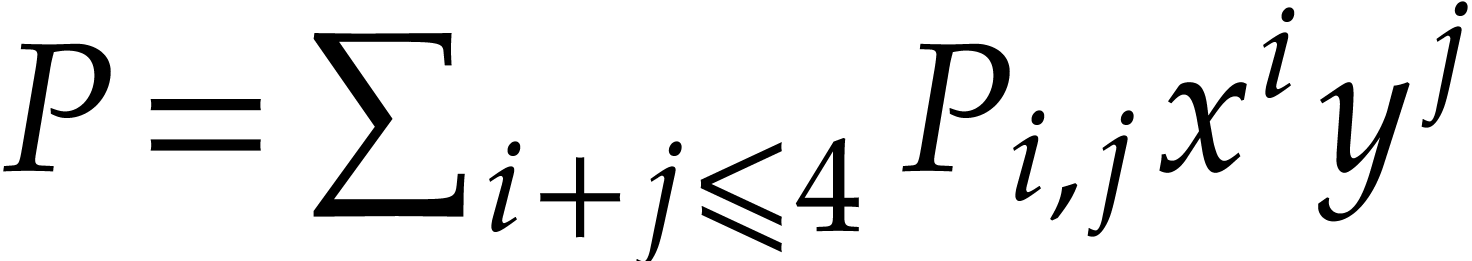 . If our main
goal is to evaluate a given polynomial many times, then the SLP
representation tends to be particularly efficient. However, for explicit
computations on polynomials, other representations may be
preferred: for instance, the dense representation allows for FFT
multiplication [40, section 8.2] and the sparse
representation also allows for special evaluation-interpolation
techniques [101].
. If our main
goal is to evaluate a given polynomial many times, then the SLP
representation tends to be particularly efficient. However, for explicit
computations on polynomials, other representations may be
preferred: for instance, the dense representation allows for FFT
multiplication [40, section 8.2] and the sparse
representation also allows for special evaluation-interpolation
techniques [101].
The above efficiency considerations explain why SLPs have become a central framework in the area of algebraic complexity [21]. Joos Heintz has been an early proponent of polynomial SLPs in computer algebra. Together with Schnorr, he designed a polynomial time algorithm to test if an SLP represents the zero function or not, up to precomputations that only depend on the size of the SLP [55]. Later, Giusti and Heintz proposed an efficient algorithm to compute the dimension of the solution set of a system of homogeneous polynomials given by SLPs [43]. Then, Heintz and his collaborators showed that the polynomials involved in the Nullstellensatz had good evaluation properties, and could therefore be better represented by SLPs [47, 33] than by dense polynomials. These results led to a new method, called geometric resolution, which allows polynomial systems to be solved in a time that is polynomial in intrinsic geometric quantities [41, 44, 46, 51, 87].
In order to implement the geometric resolution algorithm, it was
necessary to begin with programming efficient evaluation data
structures. The first steps were presented at the TERA'1996 conference
held in Santander (Spain) by Aldaz, and by Castaño, Llovet, and
Martìnez [22]. Later on, a
There are a few other concepts that are very similar to SLPs. Trees and directed acyclic graphs (DAGs) are other popular structures for the representation of mathematical expressions. Conversions to and from SLPs are rather straightforward, but SLPs have the advantage that they expose more low-level execution details. Since performance is one of our primary concerns, we therefore prefer the framework of SLPs in this paper.
Another related concept is the blackbox representation. Blackbox
programs can be evaluated, but their “source code” is not
available. This representation is popular in numerical analysis and the
complexity of various numerical methods [98, Chapters 4, 9,
10, and 17] can be expressed in terms of the required number of function
evaluations (the length of an SLP corresponds to the cost of one
function evaluation in this context). The blackbox representation is
also popular in computer algebra, especially in the area of sparse
interpolation [81, 26, 101].
However, for programs that we write ourselves, it is unnatural to
disallow opening the blackboxes. This restriction makes it artificially
hard to perform many algebraic transformations such as modular
reduction, automatic differentiation, etc. On the other hand, computing
the determinant of an  matrix can easily be done
in time
matrix can easily be done
in time 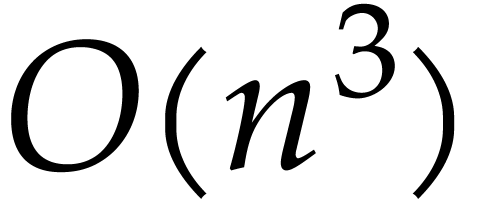 by a blackbox using Gaussian
elimination. This task is less trivial for SLPs, since branching to find
appropriate pivots is forbidden.
by a blackbox using Gaussian
elimination. This task is less trivial for SLPs, since branching to find
appropriate pivots is forbidden.
Despite the importance of SLPs for theoretical and practical purposes,
they have not yet been the central target of a dedicated high
performance library, up to our knowledge. (We refer to [36,
22, 20] for early packages for polynomial
SLPs.) In contrast, such libraries exist for integer and rational
numbers (
In 2015, we started the development of such a dedicated library for
SLPs, called
Performance is a primary motivation behind our work. Both operations on SLPs and their execution should be as efficient as possible. At the same time, we wish to be able to fully exploit the generality of the SLP framework. This requires a suitable representation of SLPs that is both versatile and efficient to manipulate. As will be detailed in section 2, we will represent SLPs using a suitable low-level encoding of pseudo-code as in (1.1), while allowing its full semantic richness to be expressed. For instance, the ordering of the instructions in (1.1) is significant, as well as the ability to assign values multiple times to the same variables. One may also specify a precise memory layout.
One typical workflow for SLP libraries is the following:
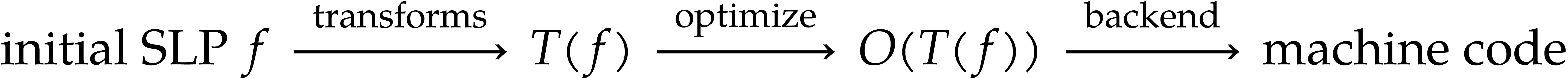 |
(1.2) |
For instance, we might start with an SLP  that
computes the determinant of a
that
computes the determinant of a  matrix
multiplication, then compute its gradient using automatic
differentiation, then optimize this code, and finally generate
executable machine code.
matrix
multiplication, then compute its gradient using automatic
differentiation, then optimize this code, and finally generate
executable machine code.
The initial SLP can be specified directly using low-level pseudo-code.
But this is usually not most convenient, except maybe for very simple
SLPs. In section 3, we describe a higher level recording
mechanism. Given an existing, say, C++ template implementation for the
computation of determinants of matrices, we may specialize this routine
for a special “recorder” type and run it on a  matrix with generic entries. The recording mechanism will
then be able to recover a trace of this computation and produce an SLP
for determinants of
matrix with generic entries. The recording mechanism will
then be able to recover a trace of this computation and produce an SLP
for determinants of  matrices.
matrices.
In section 4, we turn to common program transformations like simplification, register allocation, etc. Although this is part of the classical theory of compilation, the SLP framework gives rise to several twists. Since our libraries are required to be very efficient, they allow us to efficiently generate SLPs on the fly. Such SLPs become disposable as soon as they are no longer needed. Consequently, our SLPs can be very large, which makes it crucial that transformations on SLPs run in linear time. The philosophy is to sacrifice expensive optimizations that require more time, but to make up for this by generating our SLPs in such a way that cheaper optimizations already produce almost optimal code. That being said, there remains a trade-off between speed of compilation and speed of execution: when a short SLP needs to be executed really often, it could still make sense to implement more expensive optimizations. But the primary focus of our libraries is on transformations that run in linear time.
When considering SLPs over specific algebraic domains such as integers, modular integers, floating point numbers, polynomials, matrices, balls, etc., it may be possible to exploit special mathematical properties of these domains in order to generate more efficient SLPs. This type of transformations, which can be problematic to implement in general purpose compilers, are the subject of section 5.
Popular examples from computer algebra are automatic differentiation [14] and transposition [17]. Another example was described in [70]: ball arithmetic allows us to lift any numerical algorithm into a reliable one that also produces guaranteed error bounds for all results. However, rounding errors need to be taken into account when implementing a generic ball arithmetic, which leads to a non-trivial overhead. When the algorithm is actually an SLP, this overhead can be eliminated through a static analysis. Similarly, assume given an SLP over arbitrary precision integers, together with a bound for the inputs. Then one may statically compute bounds for all intermediate results and generate a dedicated SLP that eliminates the need to examine the precisions during runtime. This may avoid many branches and subroutine calls.
Several applications that motivated our work are discussed in section 6. From the perspective of a high level application, the SLP library is a mixture of a compiler and a traditional computer algebra library. Instead of directly calling a high level function like a matrix product or a discrete Fourier transform (DFT), the idea is rather to compute a function that is able to efficiently compute matrix products or DFTs of a specified kind (i.e. over a particular coefficient ring and for particular dimensions). In this scenario, the library is used as a tool to accelerate critical operations.
High level master routines for matrix products and DFTs may automatically compile and cache efficient machine code for matrices and DFTs of small or moderate sizes. Products and DFTs of large sizes can be reduced to these base cases. It is an interesting question whether these master routines should also be generated by the SLP library. In any case, the SLP framework allows for additional flexibility: instead of statically instantiating C++ templates for a given type, we may generate these instantiations dynamically. Moreover, using the techniques from section 5, this can be done in a way that exploits mathematical properties of the type, which are invisible for the C++ compiler.
More specifically, we will discuss applications to numerical homotopy continuation, discrete Fourier transforms, power series computations, differential equations, integer arithmetic, and geometric resolution of polynomial systems. There are many other applications, starting with linear algebra, but our selection will allow us to highlight various particular advantages and challenges for the SLP framework.
The last section 7 is dedicated to benchmarks. Some timings
for the
Notation. Throughout this paper, we denote  . For every
. For every  ,
we also define
,
we also define  .
.
Acknowledgments. We wish to thank Albin
We start this section with an abstract formalization of SLPs. Our presentation is slightly different from [21] or [70], in order to be somewhat closer to the actual machine representation that we will describe next.
Let  be a set of operation symbols together with
a function
be a set of operation symbols together with
a function 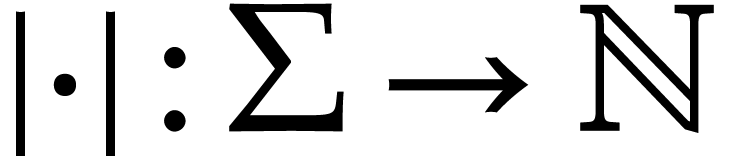 . We call
. We call  a signature and
a signature and  the
arity of
the
arity of  , for any
operation
, for any
operation 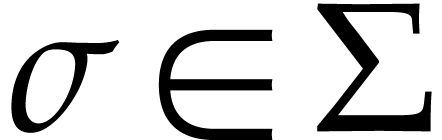 . A domain
with signature
. A domain
with signature  is a set
is a set  together with a function
together with a function 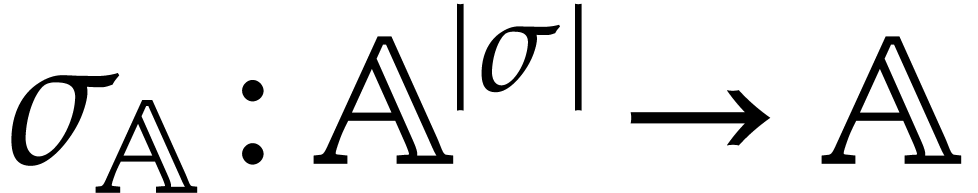 for every
for every 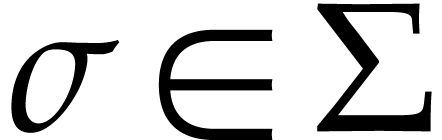 . We often write
. We often write  instead of
instead of  if no confusion can arise. The domain
if no confusion can arise. The domain
 is said to be effective if we have data
structures for representing the elements of
is said to be effective if we have data
structures for representing the elements of  and
and
 on a computer and if we have programs for
on a computer and if we have programs for  and
and  , for
all
, for
all 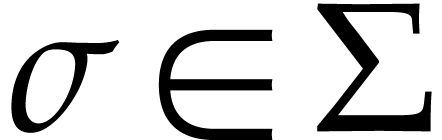 .
.
Example 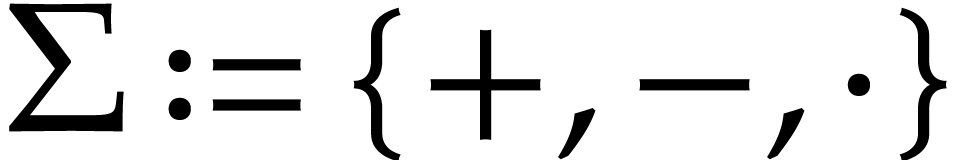 to be the signature of rings with
to be the signature of rings with  and
and  to be the ring
to be the ring  or
or
 .
.
Remark 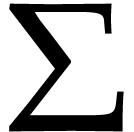 is also
called a language (without relation symbols) and
is also
called a language (without relation symbols) and  a structure for this language; see, e.g., [7, Appendix B]. For simplicity, we restricted ourselves to
one-sorted languages, but extensions to the multi-sorted case are
straightforward.
a structure for this language; see, e.g., [7, Appendix B]. For simplicity, we restricted ourselves to
one-sorted languages, but extensions to the multi-sorted case are
straightforward.
Let  be an effective domain with signature
be an effective domain with signature  . An instruction is a
tuple
. An instruction is a
tuple
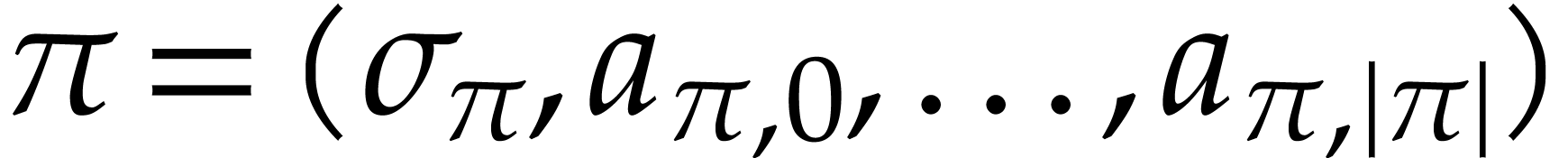
with  and arguments
and arguments 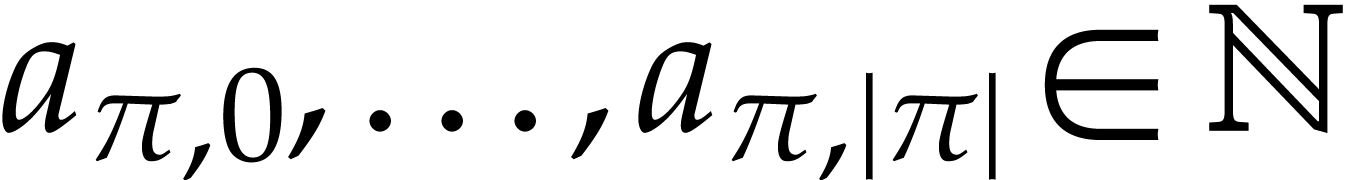 , where
, where  .
We call
.
We call 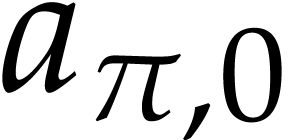 the destination argument or
operand and
the destination argument or
operand and  the source
arguments or operands. We denote by
the source
arguments or operands. We denote by 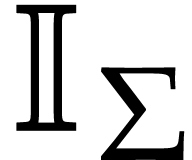 the set of such instructions. Given
the set of such instructions. Given  ,
we also let
,
we also let 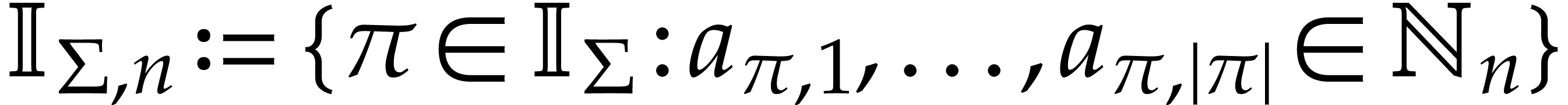 . A
straight-line program (SLP) over
. A
straight-line program (SLP) over  is a quadruple
is a quadruple 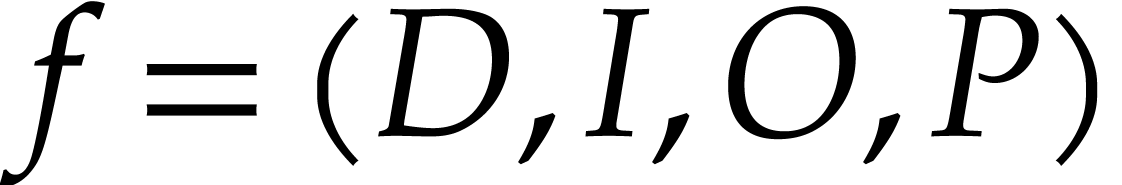 , where
, where
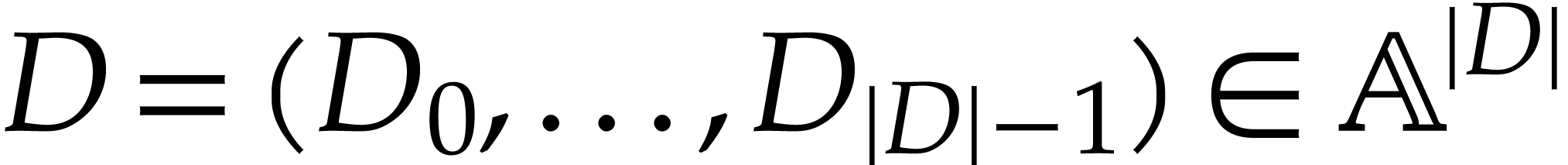 is a tuple of data fields,
is a tuple of data fields,
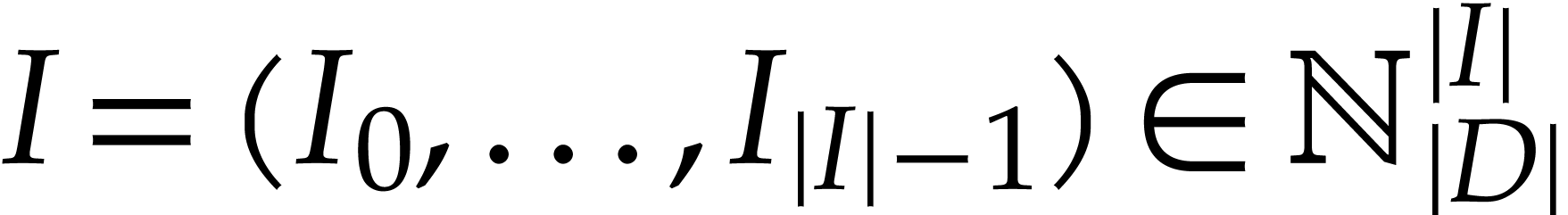 is a tuple of pairwise distinct input
locations,
is a tuple of pairwise distinct input
locations,
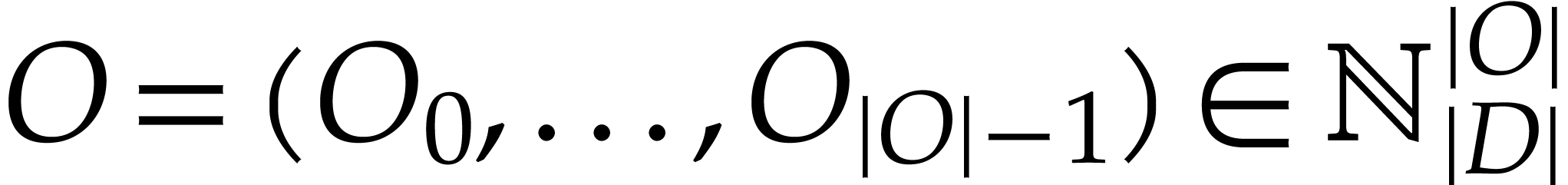 is a tuple of output locations,
is a tuple of output locations,
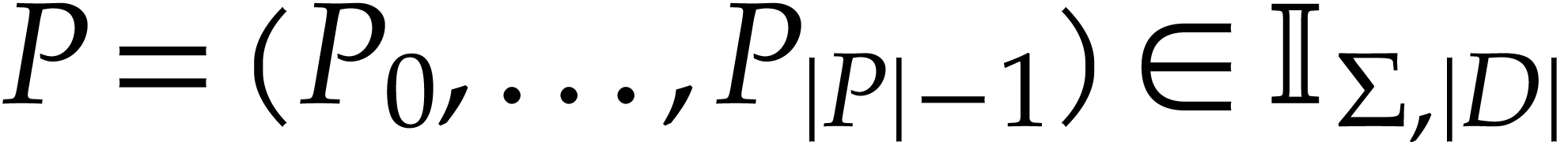 is a tuple of instructions.
is a tuple of instructions.
We regard 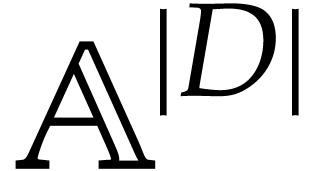 as the working space for our SLP. Each
location in this working space can be represented using an integer in
as the working space for our SLP. Each
location in this working space can be represented using an integer in
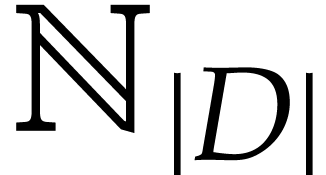 and instructions directly operate on the working
space as we will describe now.
and instructions directly operate on the working
space as we will describe now.
Given a state  of our working space, the
execution of an instruction
of our working space, the
execution of an instruction 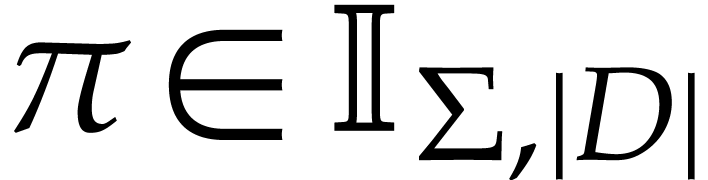 gives rise
to a new state
gives rise
to a new state 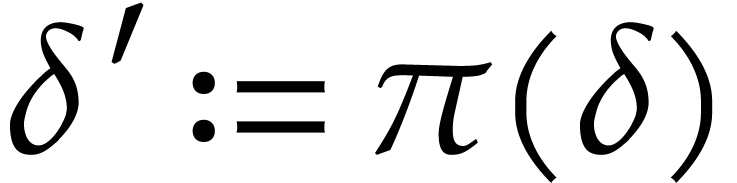 where
where 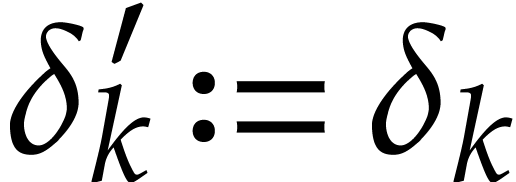 if
if
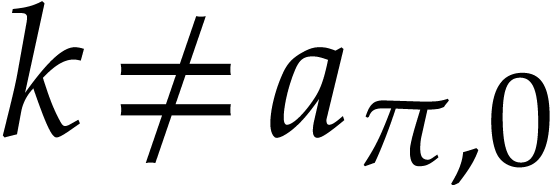 and
and 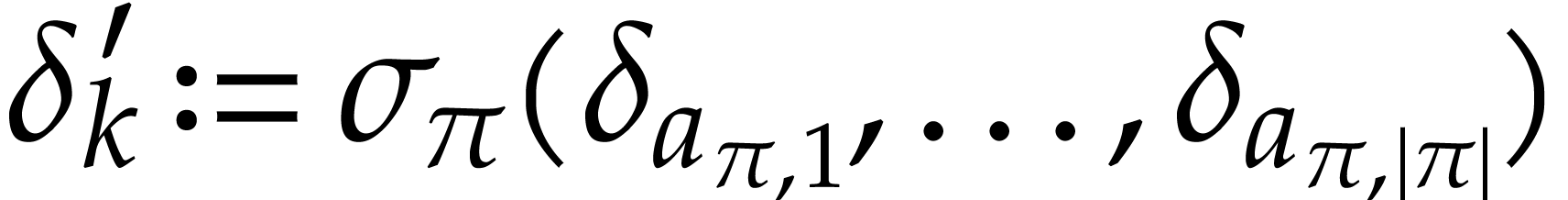 if
if 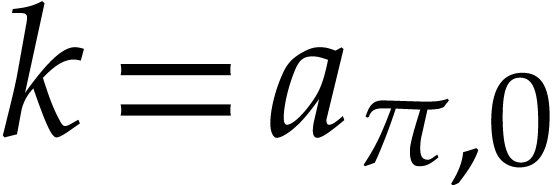 . Given input values
. Given input values 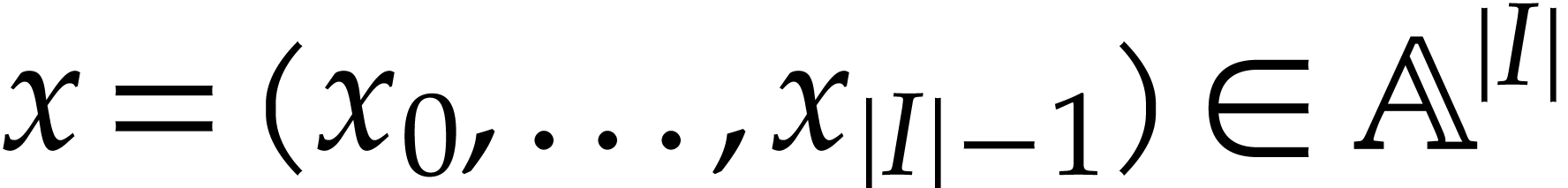 , the corresponding begin state
, the corresponding begin state 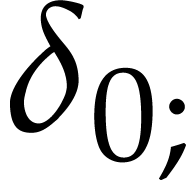 of our SLP is given by
of our SLP is given by 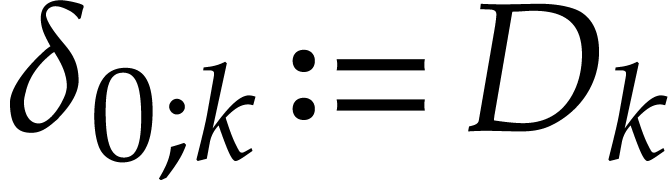 if
if  and
and 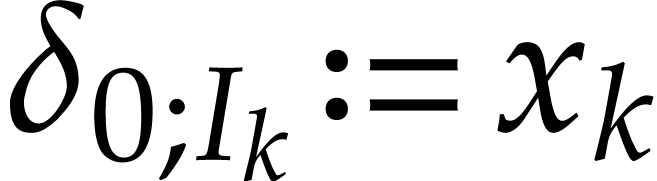 for
for 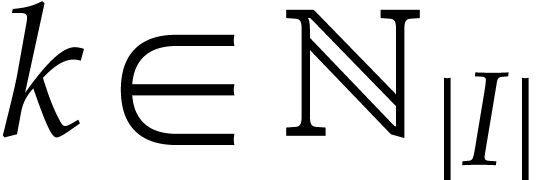 . Execution of the SLP next gives rise to a
sequence of states
. Execution of the SLP next gives rise to a
sequence of states 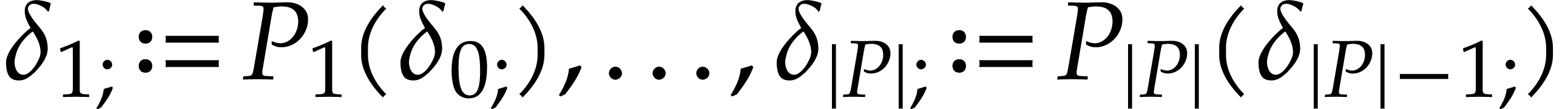 . The
output values
. The
output values 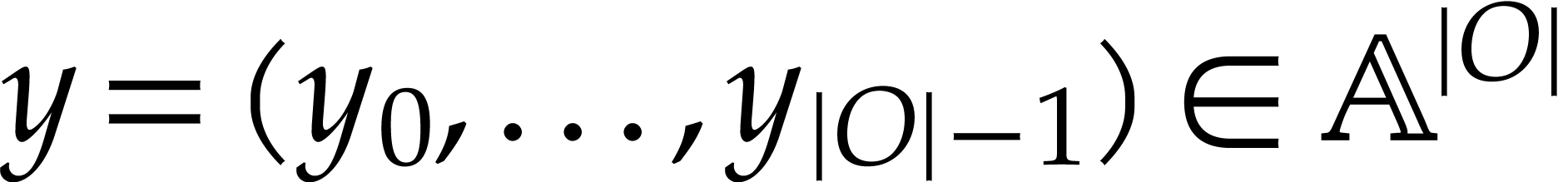 of our SLP are now given
by
of our SLP are now given
by 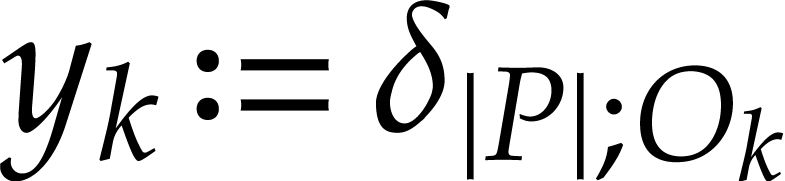 for
for 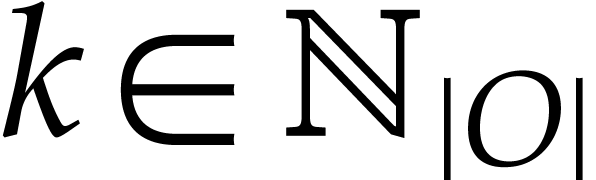 .
In this way our SLP
.
In this way our SLP  gives rise to a function
gives rise to a function
 that we will also denote by
that we will also denote by  . Two SLPs will be said to be
equivalent if they compute the same function.
. Two SLPs will be said to be
equivalent if they compute the same function.
Example  and
and  as in Example 2.1,
our introductory example (1.1) can be represented as
follows:
as in Example 2.1,
our introductory example (1.1) can be represented as
follows: 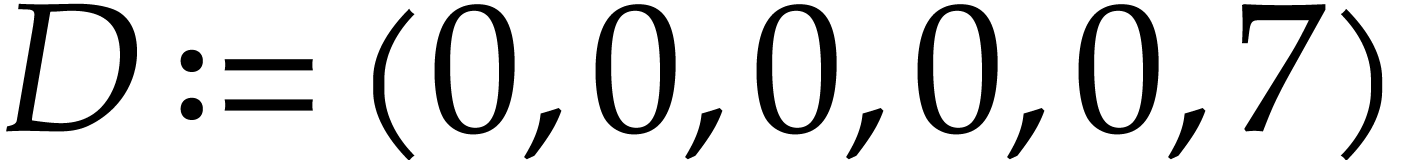 ,
, 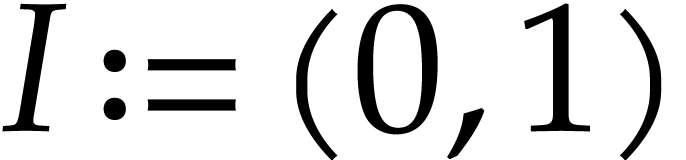 ,
, 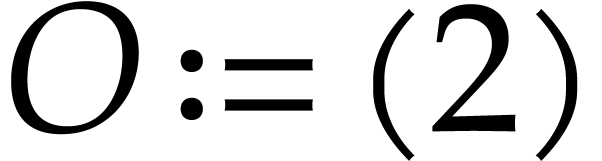 ,
and
,
and 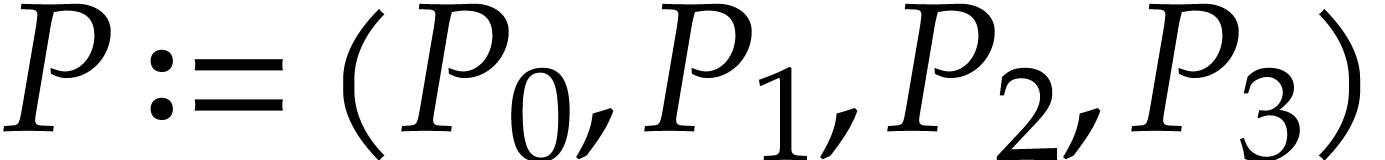 with
with
One may check that this SLP indeed computes the intended function when
using the above semantics. Note that we may chose arbitrary values for
the input fields 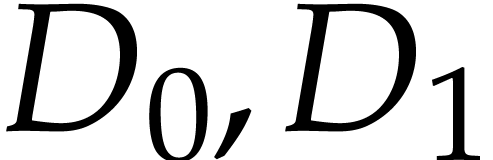 , the output
field
, the output
field 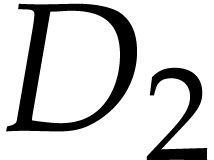 , and the auxiliary
data fields
, and the auxiliary
data fields 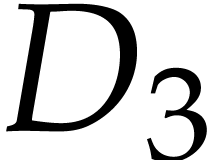 ,
, 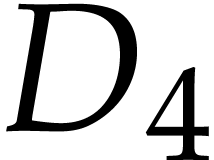 . So we may just as well take them to be zero,
as we did.
. So we may just as well take them to be zero,
as we did.
For the sake of readability, we will continue to use the notation (1.1) instead (2.1), the necessary rewritings
being clear. If we wish to make the numbering of registers precise in
(1.1), then we will replace 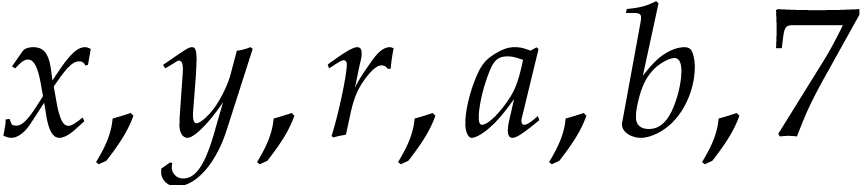 by
by
 :
:
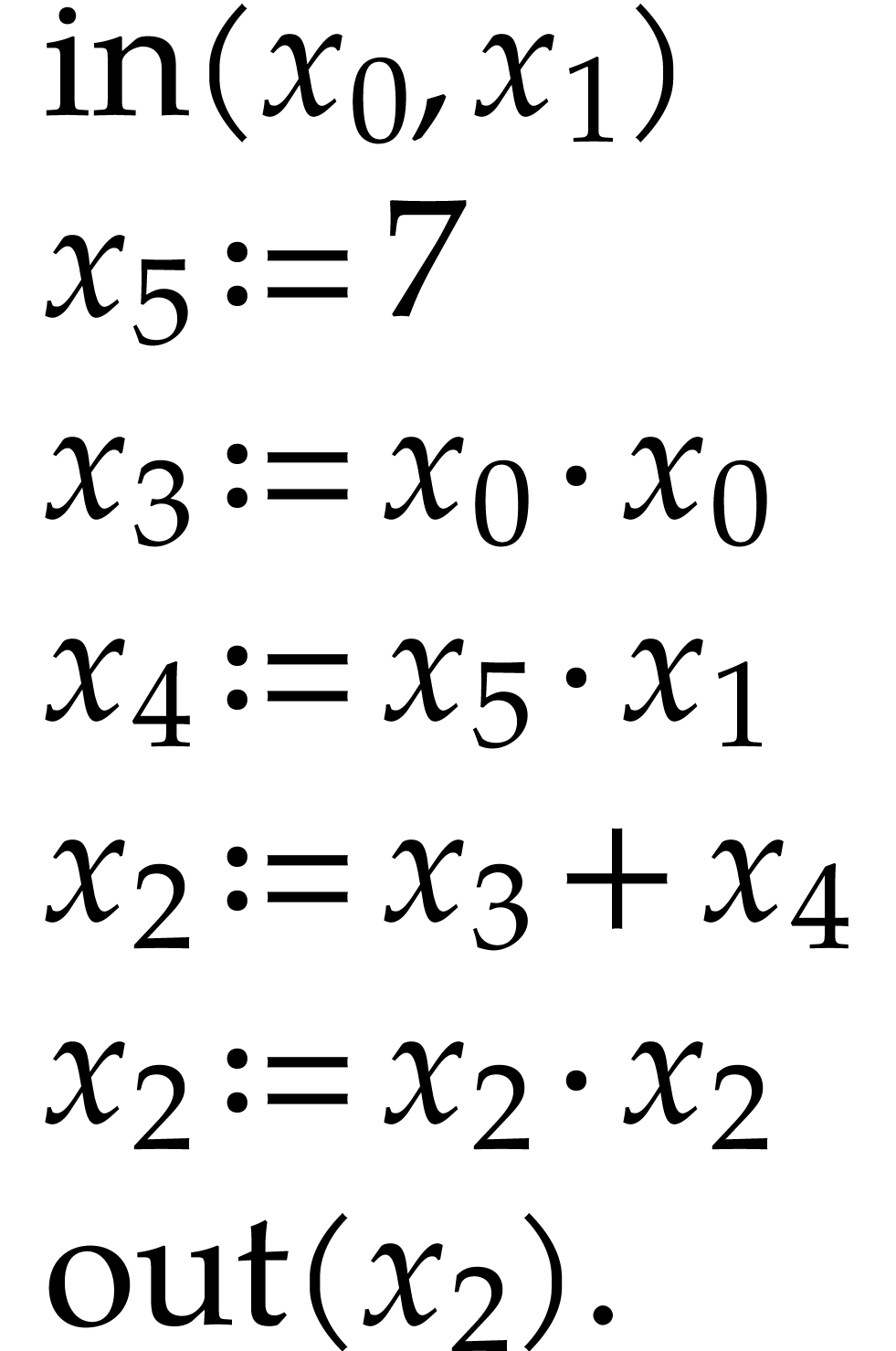 |
(2.2) |
Note that 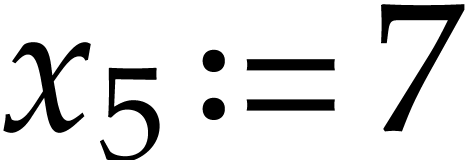 is not really an instruction, but
rather a way to indicate that the data field
is not really an instruction, but
rather a way to indicate that the data field 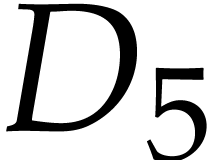 contains the constant
contains the constant  .
.
It will be useful to call elements of 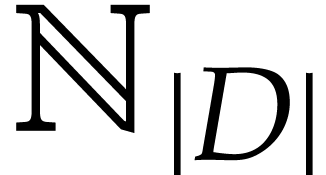 variables and denote them by more intelligible symbols like
variables and denote them by more intelligible symbols like
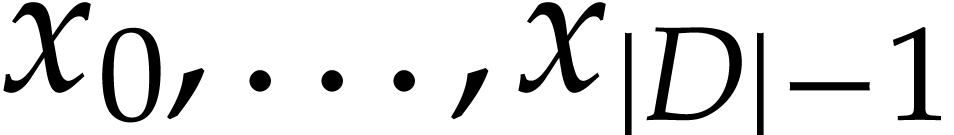 whenever convenient. The entries of
whenever convenient. The entries of  and
and  are called input and
output variables, respectively. Non-input variables that also
do not occur as destination operands of instructions in
are called input and
output variables, respectively. Non-input variables that also
do not occur as destination operands of instructions in  are called constants. An auxiliary variable is a
variable that is neither an input variable, nor an output variable, nor
a constant. Given a variable
are called constants. An auxiliary variable is a
variable that is neither an input variable, nor an output variable, nor
a constant. Given a variable 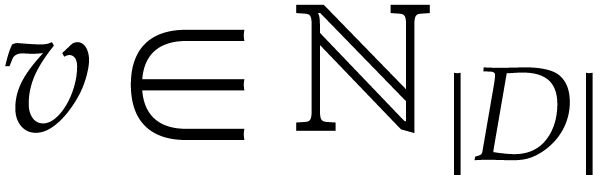 the corresponding
data field is
the corresponding
data field is 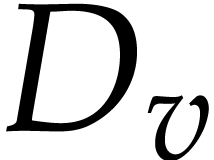 .
Input variables, output variables, and constants naturally correspond to
input fields, output fields, and constant
fields.
.
Input variables, output variables, and constants naturally correspond to
input fields, output fields, and constant
fields.
Remark 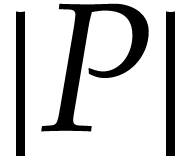 of the SLP as small
as possible.
of the SLP as small
as possible.
Remark
One crucial design decision concerns the choice of the signature  and the way how operations are represented.
and the way how operations are represented.
On the one hand, we do not want to commit ourselves to one specific
signature, so it is important to plan future extensions and even allow
users to specify their own dynamic signatures. This kind of flexibility
requires no extra implementation effort for many
“signature-agnostic” operations on SLPs, such as common
subexpression elimination, register allocation, etc. On the other hand,
the precise signature does matter for operations like simplification,
automatic differentiation, etc. We need our code to be as efficient as
possible for the most common operations in  ,
while providing the possibility to smoothly extend our implementations
to more exotic operations whenever needed.
,
while providing the possibility to smoothly extend our implementations
to more exotic operations whenever needed.
In the  by abstract expressions.
Exploiting pattern matching facilities inside
by abstract expressions.
Exploiting pattern matching facilities inside
What about the choice of a subsignature 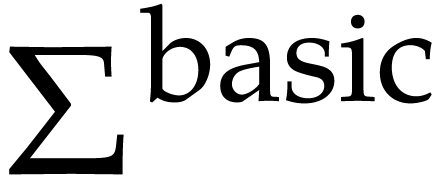 of
operations that we deem to be “most common” and that should
benefit from particularly efficient support in the library? At the end
of the day, we wish to turn our SLPs into efficient machine code. It is
therefore useful to draw inspiration from the instruction sets of modern
CPUs and GPUs. For example, this motivated our decision to include the
fused multiply add (FMA) operation
of
operations that we deem to be “most common” and that should
benefit from particularly efficient support in the library? At the end
of the day, we wish to turn our SLPs into efficient machine code. It is
therefore useful to draw inspiration from the instruction sets of modern
CPUs and GPUs. For example, this motivated our decision to include the
fused multiply add (FMA) operation 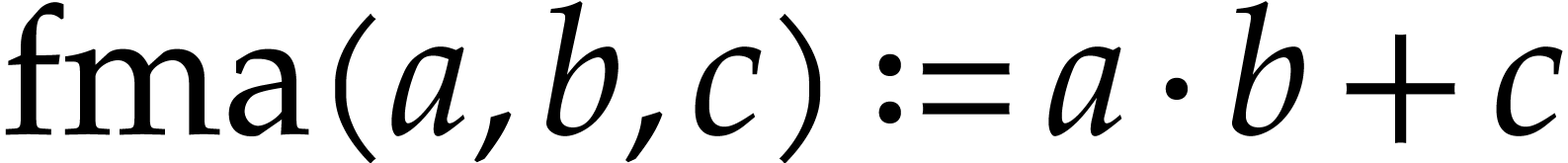 in
in
 , together with its signed
variants
, together with its signed
variants 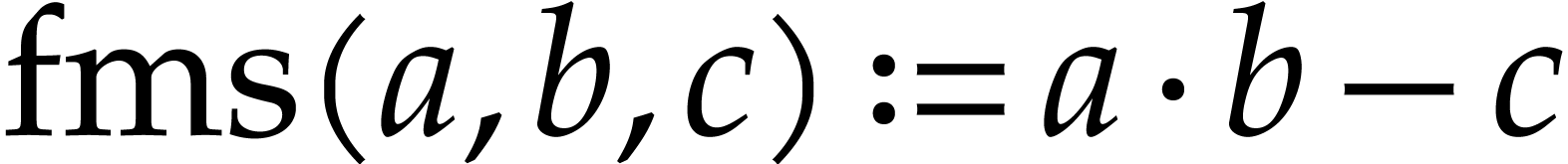 ,
, 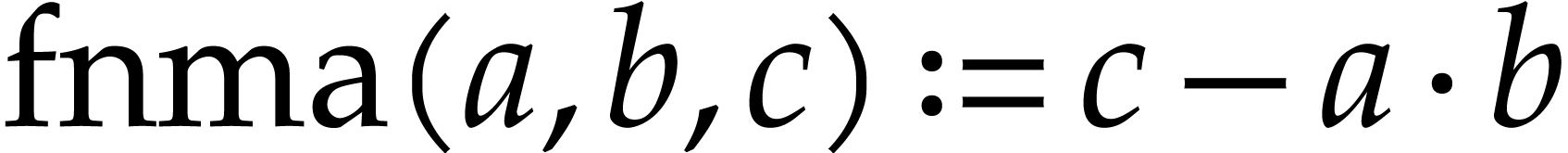 , and
, and 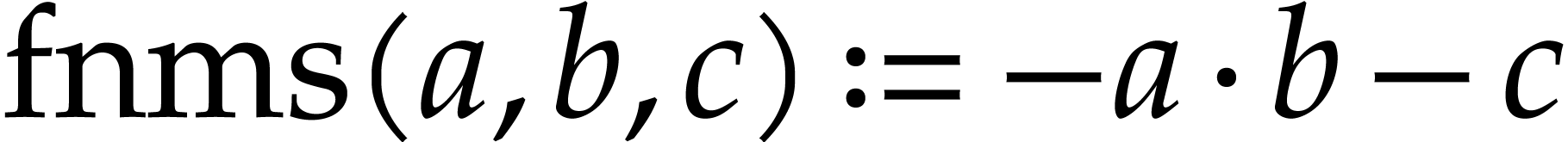 .
Although this adds to the complexity of
.
Although this adds to the complexity of  (why not
emulate FMA using multiplication and addition?), this decision tends to
result in better machine code (more about this below; see also section
5.7).
(why not
emulate FMA using multiplication and addition?), this decision tends to
result in better machine code (more about this below; see also section
5.7).
However, the instructions sets of modern processors are very large. In order to keep our SLP library as simple as possible, it would be unreasonable to directly support all these instructions. Much of the complexity of modern instruction sets is due to multiple instances of the same instruction for different data types, SIMD vector widths, immediate arguments, addressing modes, guard conditions, etc. In the SLP setting it is more meaningful to implement general mechanisms for managing such variants. Modern processors also tend to provide a large number of exotic instructions, which are only needed at rare occasions, and which can typically be emulated using simpler instructions.
One useful criterion for deciding when and where to support particular operations is to ask the question how easily the operation can be emulated, while resulting in final machine code of the same quality. Let us illustrate this idea on a few examples.
Imagine that our hardware supports FMA, but that we did not include this
operation in  . In order to
exploit this hardware feature, we will need to implement a special
post-processing transformation on SLPs for locating and replacing pairs
of instructions like
. In order to
exploit this hardware feature, we will need to implement a special
post-processing transformation on SLPs for locating and replacing pairs
of instructions like 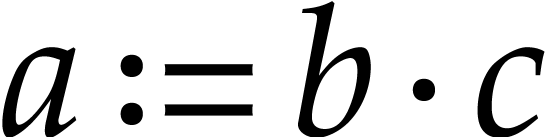 and
and  by FMAs, even when they are separated by several independent
instructions. This is doable, but not so easy. Why bother, if it
suffices to add FMA to our signature and generate high quality code with
FMAs from the outset? Maybe it will require more implementation efforts
to systematically support FMAs inside our routines on SLPs, but we won't
need a separate and potentially expensive post-processing step.
by FMAs, even when they are separated by several independent
instructions. This is doable, but not so easy. Why bother, if it
suffices to add FMA to our signature and generate high quality code with
FMAs from the outset? Maybe it will require more implementation efforts
to systematically support FMAs inside our routines on SLPs, but we won't
need a separate and potentially expensive post-processing step.
In fact, for floating point numbers that follow the IEEE 754 standard
[5], the FMA instruction cannot be emulated using one
multiplication and one addition. This is due to the particular semantics
of correct rounding: if 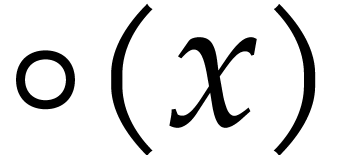 denotes the double
precision number that is nearest to a real number
denotes the double
precision number that is nearest to a real number  , then we do not always have
, then we do not always have  . The IEEE 754 rounding semantics can be exploited
for the implementation of extended precision arithmetic [25,
99, 69, 77] and modular
arithmetic [13, 73]. This provides additional
motivation for including FMA in our basic signature
. The IEEE 754 rounding semantics can be exploited
for the implementation of extended precision arithmetic [25,
99, 69, 77] and modular
arithmetic [13, 73]. This provides additional
motivation for including FMA in our basic signature 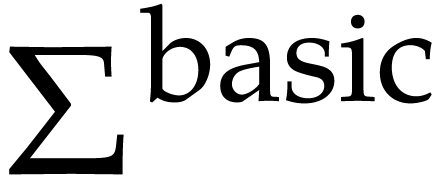 .
.
We do not only have flexibility regarding the signature  , but also when it comes to the domains
, but also when it comes to the domains  that we wish to support. For the selection of
operations in
that we wish to support. For the selection of
operations in  , it is also
important to consider their implementations for higher level domains,
such as modular integers, matrices, truncated power series, etc. Now the
implementation of
, it is also
important to consider their implementations for higher level domains,
such as modular integers, matrices, truncated power series, etc. Now the
implementation of 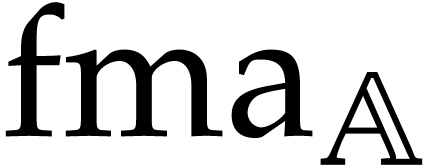 is often simpler than the
combined implementation of
is often simpler than the
combined implementation of  and
and 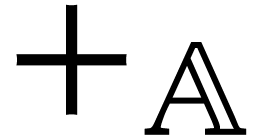 . For instance, if
. For instance, if 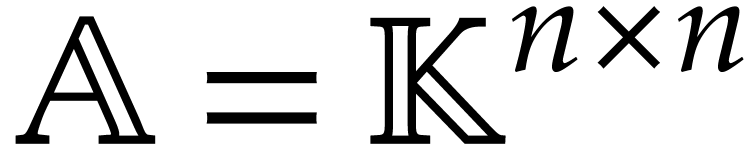 is
the domain of
is
the domain of  matrices over a field, then
matrices over a field, then 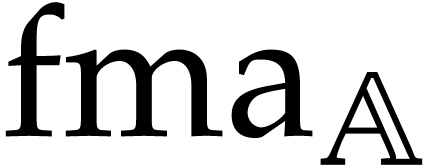 can be implemented using
can be implemented using 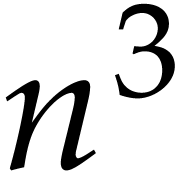 FMAs
over
FMAs
over  , whereas its emulation
via
, whereas its emulation
via  and
and 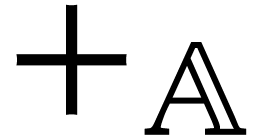 would require
would require
 instructions. One may argue that the better code
should be recoverable using a suitable post-processing step as described
above. This is true for matrix multiplication, but turns out to become
more problematic for other domains, such as modular integers that are
implemented using floating point FMAs. Once more, the inclusion of FMA
into our signature
instructions. One may argue that the better code
should be recoverable using a suitable post-processing step as described
above. This is true for matrix multiplication, but turns out to become
more problematic for other domains, such as modular integers that are
implemented using floating point FMAs. Once more, the inclusion of FMA
into our signature 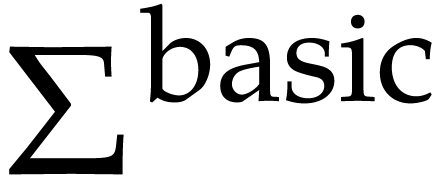 tends to facilitate the
generation of high quality machine code.
tends to facilitate the
generation of high quality machine code.
Let us finish with an example of some operations that we do not
wish to include in 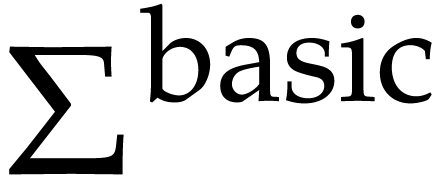 .
Instruction sets of CPUs allow us to work with integers and floating
point numbers of various precisions. How can we do computations with
mixed types in our framework? Instead of mimicking the CPUs instruction
set within
.
Instruction sets of CPUs allow us to work with integers and floating
point numbers of various precisions. How can we do computations with
mixed types in our framework? Instead of mimicking the CPUs instruction
set within 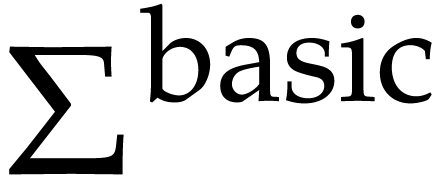 , the idea is
rather to provide a general mechanism to dynamically enrich
, the idea is
rather to provide a general mechanism to dynamically enrich  . Here we may exploit the fact that our
framework made very few assumptions on
. Here we may exploit the fact that our
framework made very few assumptions on  and
and  . Given domains
. Given domains  of signatures
of signatures 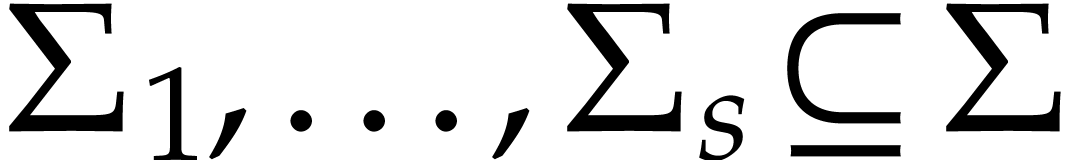 , the idea is
to dynamically create a signature
, the idea is
to dynamically create a signature 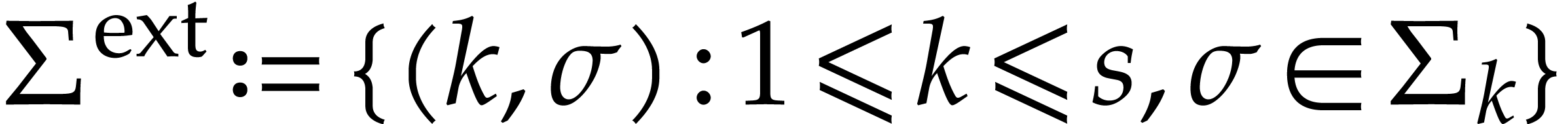 and a domain
and a domain
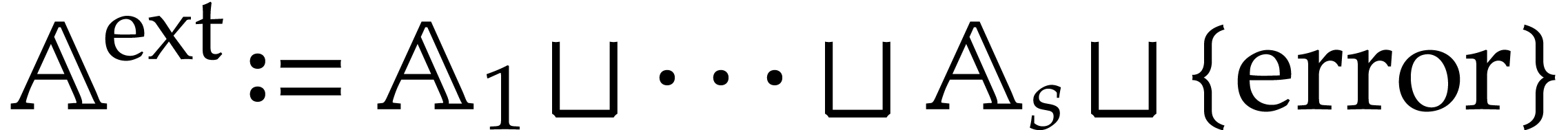 such that
such that 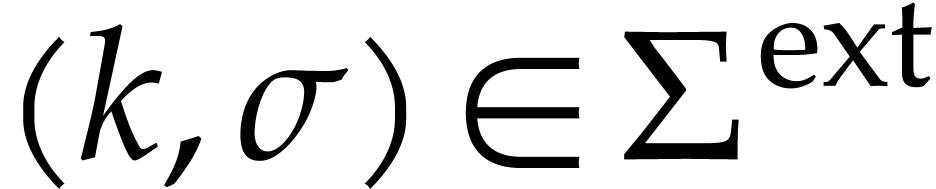 operates on
operates on
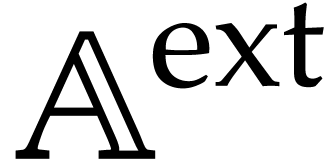 via
via 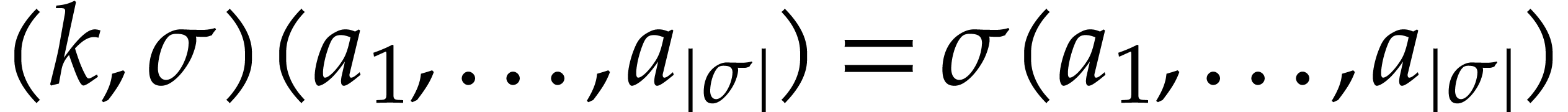 if
if 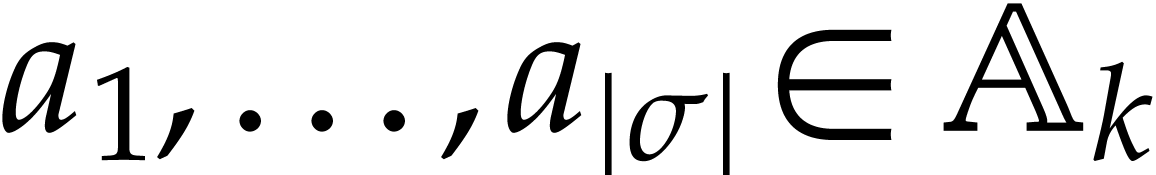 and
and  otherwise. We regard
otherwise. We regard  and
and  as being disjoint, which allows us to
dynamically add
as being disjoint, which allows us to
dynamically add  to
to  .
.
In this way, it is easy to emulate computations with mixed types and signatures in our abstract SLP framework (and thereby support multi-sorted structures as in Remark 2.2). This kind of emulation comes with some overhead though. But we consider this to be a small price to pay for the simplicity that we gain by avoiding the management of multiple types and signatures in the framework itself.
The SLP framework is more general than it may seem at first sight due to
the fact that we are completely free to chose the signature  and the underlying domain
and the underlying domain  .
In principle, this allows for all data types found in computer algebra
systems. Nonetheless, for our library it is wise to include privileged
support for a more restricted set of domains, similarly to what we did
with
.
In principle, this allows for all data types found in computer algebra
systems. Nonetheless, for our library it is wise to include privileged
support for a more restricted set of domains, similarly to what we did
with  in the case of signatures.
in the case of signatures.
First of all, we clearly wish to be able to have domains for all the
machines types that can be found in hardware. In traditional CPUs, these
types were limited to floating point numbers and (signed and unsigned)
integers of various bit-sizes. In modern CPUs and GPUs, one should add
SIMD vector versions of these types for various widths and possibly a
few more special types like matrices and polynomials over  of several sizes and degrees.
of several sizes and degrees.
On top of the machine types, we next require support for basic
arithmetical domains such as vectors, matrices, polynomials, jets,
modular integers and polynomials, extended precision numbers, intervals,
balls, etc. Such functionality is commonplace in computer algebra
systems or specialized HPC libraries such as 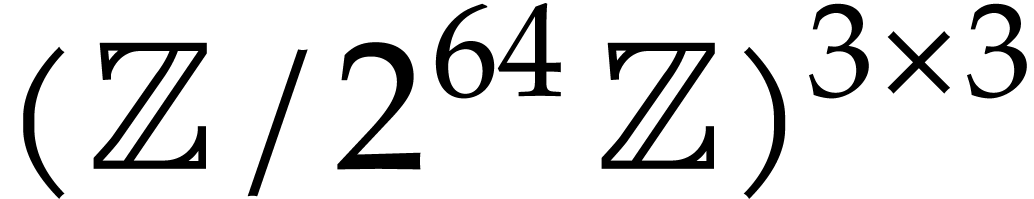 of
of  matrices with 64 bit integer coefficients in a typical
example of an SLP algebra. One advantage is that instances can always be
represented as dense vectors of a fixed size.
matrices with 64 bit integer coefficients in a typical
example of an SLP algebra. One advantage is that instances can always be
represented as dense vectors of a fixed size.
In the  of our domain must be specified. In our implementation, we use
of our domain must be specified. In our implementation, we use 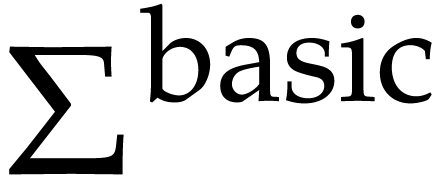 as the signature, while agreeing that operations in
as the signature, while agreeing that operations in 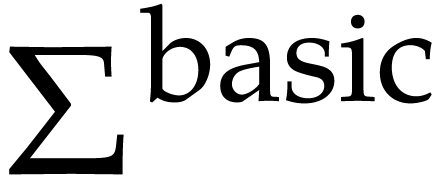 that are not implemented for a given domain simply
raise an error. We also provide default implementations for operations
like FMA that can be emulated using other operations. In order to
achieve full extensibility, it suffices to add a generic operation to
our signature for all operations in
that are not implemented for a given domain simply
raise an error. We also provide default implementations for operations
like FMA that can be emulated using other operations. In order to
achieve full extensibility, it suffices to add a generic operation to
our signature for all operations in 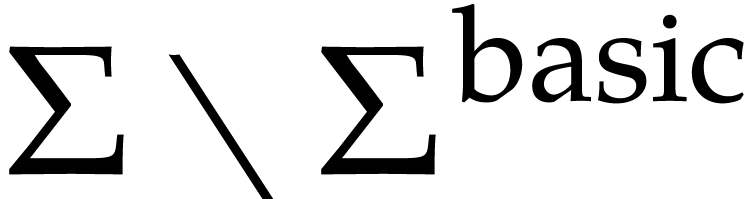 ;
the arguments of this generic operation are the concrete operation in
;
the arguments of this generic operation are the concrete operation in
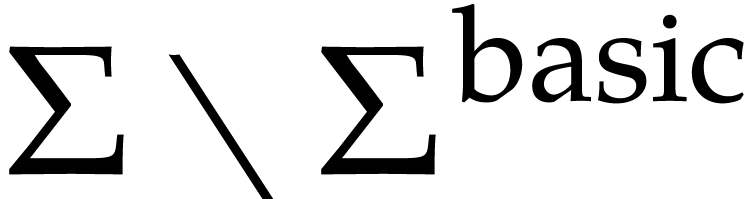 and the (variable number of) arguments of this
operation.
and the (variable number of) arguments of this
operation.
In our lower level C++ implementation in 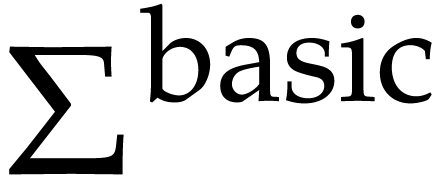 gives rise to a
virtual method for this type which can carry out the operation for the
concrete domain at hand. An element of a domain is represented as one
consecutive block of data inside memory. The size of this block is fixed
and can be retrieved using another virtual method of the domain
type. This mechanism is essentially the same as the one from the
gives rise to a
virtual method for this type which can carry out the operation for the
concrete domain at hand. An element of a domain is represented as one
consecutive block of data inside memory. The size of this block is fixed
and can be retrieved using another virtual method of the domain
type. This mechanism is essentially the same as the one from the
Given an abstract SLP 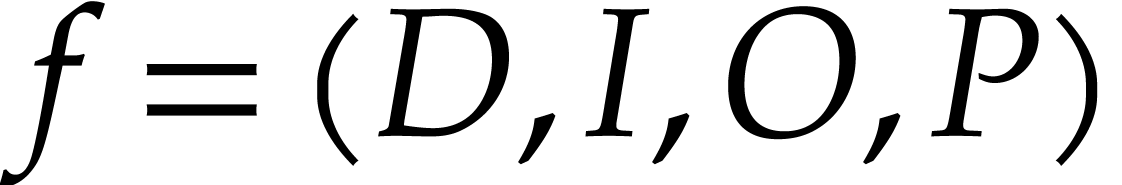 , it is
natural to represent
, it is
natural to represent 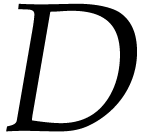 ,
, 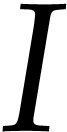 , and
, and  as
actual vectors in contiguous memory. In the cases of
as
actual vectors in contiguous memory. In the cases of 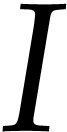 and
and  , these vectors have
machine integer coefficients. If elements of
, these vectors have
machine integer coefficients. If elements of  can
themselves be represented by vectors of a fixed size, then one may use
the additional optimization to concatenate all entries of
can
themselves be represented by vectors of a fixed size, then one may use
the additional optimization to concatenate all entries of 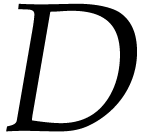 into a single vector, which we do in the
into a single vector, which we do in the
For the representation of programs  ,
we have several options. In the
,
we have several options. In the 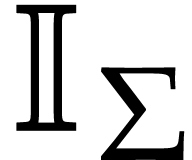 , so that
, so that  is simply
represented as a vector of instructions. In
is simply
represented as a vector of instructions. In  and the arguments of
instructions are represented by machine integers. Consequently,
instructions in
and the arguments of
instructions are represented by machine integers. Consequently,
instructions in 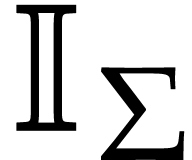 can be represented by machine
integer vectors. This again makes it possible to concatenate all
instructions into a single machine integer vector, which can be thought
of as “byte code”.
can be represented by machine
integer vectors. This again makes it possible to concatenate all
instructions into a single machine integer vector, which can be thought
of as “byte code”.
The systematic concatenation of vector entries of vectors in  is required in order to build a table
with the offsets of the individual instructions. Alternatively, we could
have imposed a maximal arity for the operations in
is required in order to build a table
with the offsets of the individual instructions. Alternatively, we could
have imposed a maximal arity for the operations in  , which would have allowed us to represent all
instructions by vectors of the same length. This alternative
representation is less compact but has the advantage that individual
instructions can be addressed more easily. It is also not so clear what
would be a good maximal arity.
, which would have allowed us to represent all
instructions by vectors of the same length. This alternative
representation is less compact but has the advantage that individual
instructions can be addressed more easily. It is also not so clear what
would be a good maximal arity.
The  and
and 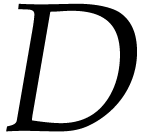 should really be considered as output
streams rather than vectors. Moreover, it is almost always possible to
give a simple and often tight a priori bound for the lengths of
should really be considered as output
streams rather than vectors. Moreover, it is almost always possible to
give a simple and often tight a priori bound for the lengths of
 and
and 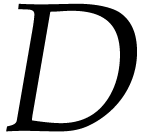 at the end of this
streaming process. This makes it possible to allocate these vectors once
and for all and directly stream the entries without being preoccupied by
range checks or reallocations of larger memory blocks.
at the end of this
streaming process. This makes it possible to allocate these vectors once
and for all and directly stream the entries without being preoccupied by
range checks or reallocations of larger memory blocks.
We have considered but discarded a few alternative design options. All
operations in  have a single output value in our
implementation. Since SLPs are allowed to have multiple output values,
it might be interesting to allow the same thing for operations in
have a single output value in our
implementation. Since SLPs are allowed to have multiple output values,
it might be interesting to allow the same thing for operations in  . Some instructions in CPUs are
indeed of this kind, like long multiplication (x86) or loading several
registers from memory (ARM). However, this elegant feature requires an
additional implementation effort for almost all operations on SLPs. This
also incurs a performance penalty, even for the vast majority of SLPs
that do not need this feature.
. Some instructions in CPUs are
indeed of this kind, like long multiplication (x86) or loading several
registers from memory (ARM). However, this elegant feature requires an
additional implementation effort for almost all operations on SLPs. This
also incurs a performance penalty, even for the vast majority of SLPs
that do not need this feature.
Note finally that it is still possible to emulate instructions with multiple outputs by considering single vector outputs and then introducing extra instructions for extracting entries of these vectors. Unfortunately however, this is really inelegant, because it forces us to use more convoluted non-fixed-sized vector domains. It is also non-trivial to recombine these multiple instructions into single machines instruction when building the final machine code.
Similar considerations apply for in-place semantics like in the C
instruction 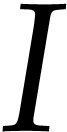 and
and  are not
required to be disjoint. But it is also easy to emulate an instruction
like
are not
required to be disjoint. But it is also easy to emulate an instruction
like
Yet another interesting type of alternative design philosophy would be to systematically rule out redundant computations by carrying out common subexpression elimination during the very construction of SLPs. However, for cache efficiency, it is sometimes more efficient to recompute a value rather than retrieving it from memory. Our representation provides greater control over what is stored where and when. The systematic use of common subexpression elimination through hash tables also has a price in performance.
Recall that two SLPs are equivalent if they compute the same mathematical function. Among two equivalent SLPs, the shorter one is typically most efficient. But the length of an SLP is not the only factor for its practical performance. It is also important to keep an eye on dependency chains, data locality, and cache performance. Besides performance, “readability” of an SLP may also be an issue: we often change the numbering of data fields in a way that makes the SLP more readable.
We catch all these considerations under the concept of quality. This concept is deliberately vague, because the practical benefits of SLPs of “higher quality” depend greatly on our specific hardware. Operations on SLPs should be designed carefully in order to avoid needless quality deteriorations. This can often be achieved by touching the input SLPs “as least as possible” and only in “straightforward ways”.
Let us briefly review how dependency chains and data layout may affect the performance. Consider the following two SLPs for complex multiplication:
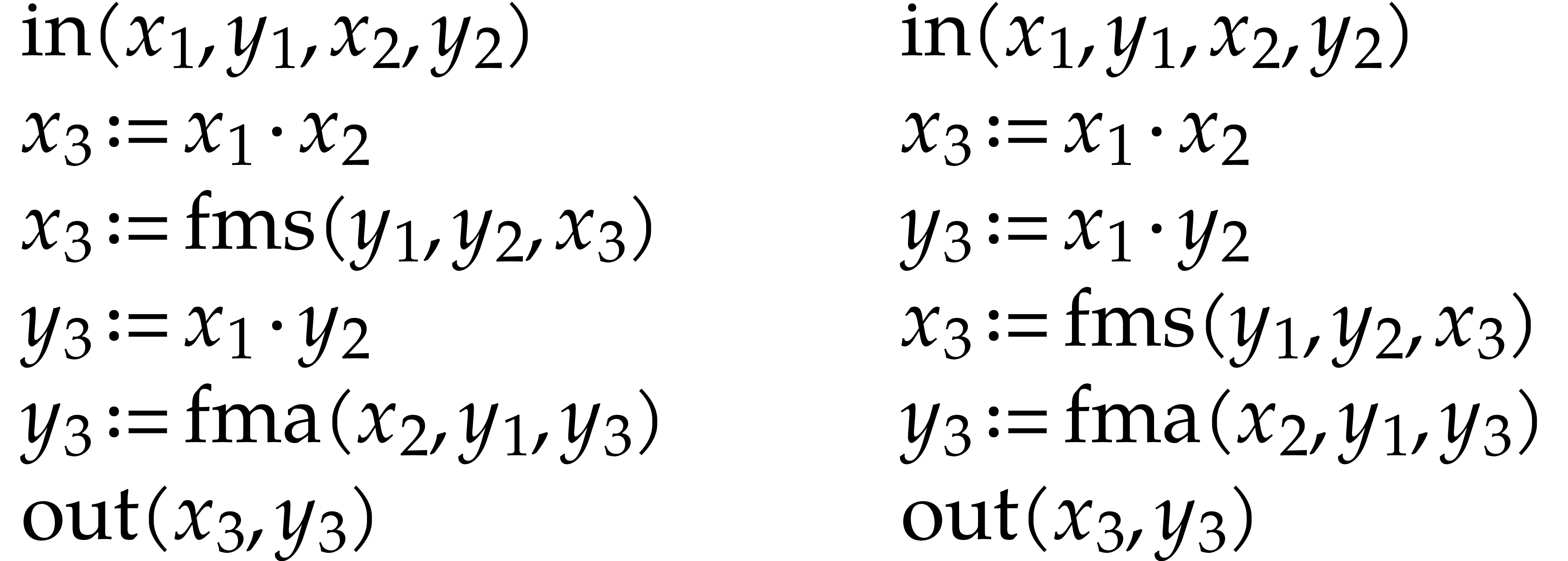 |
(2.3) |
Here 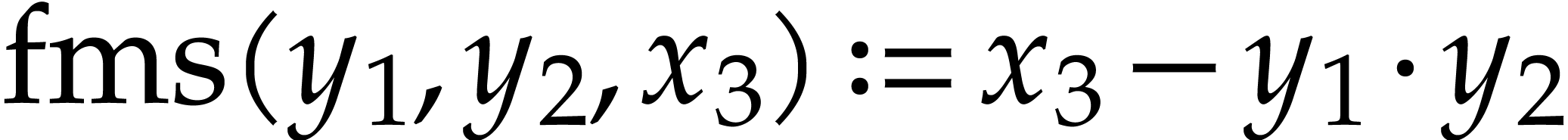 stands for “fused multiply
subtract” and
stands for “fused multiply
subtract” and 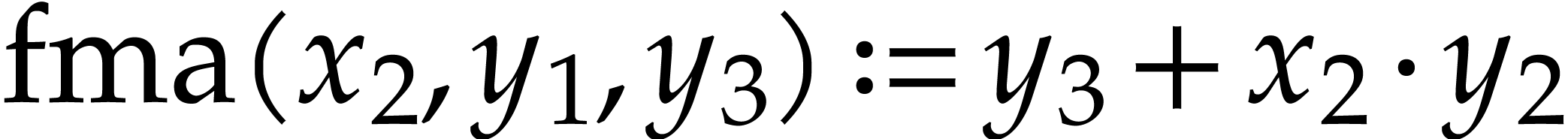 for “fused multiply
add”. Modern hardware tends to contain multiple execution
units for additions, multiplications, fused multiplications, etc.,
which allow for out of order execution [75, 6, 34]. In the right SLP, this means that the
instruction
for “fused multiply
add”. Modern hardware tends to contain multiple execution
units for additions, multiplications, fused multiplications, etc.,
which allow for out of order execution [75, 6, 34]. In the right SLP, this means that the
instruction 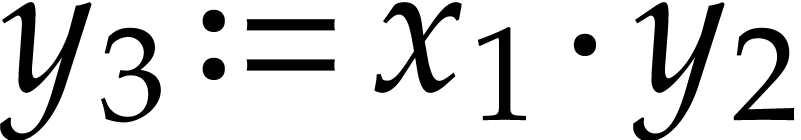 can be dispatched to a
second multiplication unit while
can be dispatched to a
second multiplication unit while 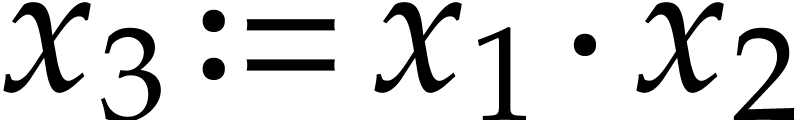 is still being
executed by a first unit. However, in the left SLP, the instruction
is still being
executed by a first unit. However, in the left SLP, the instruction 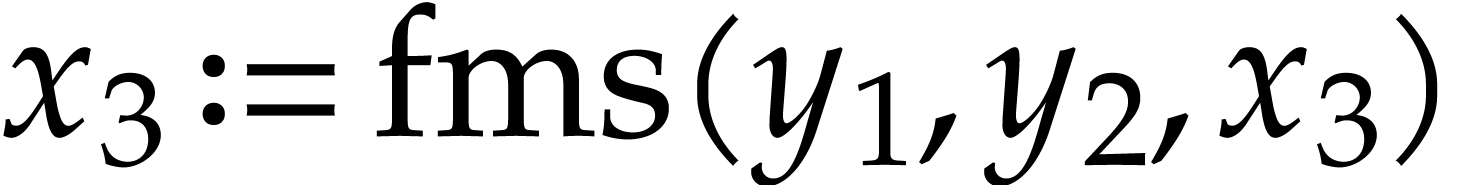 has to wait the for the outcome of
has to wait the for the outcome of 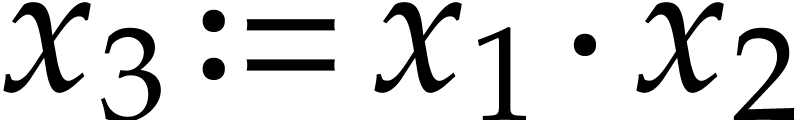 . Whereas the fused multiplications in both
SLPs depend on the result of one earlier multiplication, these
dependencies are better spread out in time in the right SLP, which
typically leads to better performance.
. Whereas the fused multiplications in both
SLPs depend on the result of one earlier multiplication, these
dependencies are better spread out in time in the right SLP, which
typically leads to better performance.
Let us now turn to the numbering of our data fields in  . When generating the final machine code for
our SLP, we typically cut
. When generating the final machine code for
our SLP, we typically cut 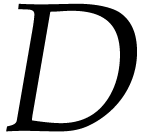 into a small number of
contiguous blocks, which are then mapped into contiguous chunks in
memory. For instance, we might put the input, output, auxiliary, and
constant fields in successive blocks of
into a small number of
contiguous blocks, which are then mapped into contiguous chunks in
memory. For instance, we might put the input, output, auxiliary, and
constant fields in successive blocks of 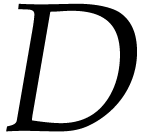 and map
them to separate chunks in memory.
and map
them to separate chunks in memory.
Now memory accesses are most efficient when done per cache line. For
instance, if cache lines are 1024 bits long and if we are working over
64 bit double precision numbers, then fetching 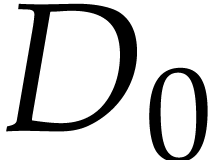 from memory will also fetch
from memory will also fetch  .
The cache performance of an SLP will therefore be best when large
contiguous portions of the program
.
The cache performance of an SLP will therefore be best when large
contiguous portions of the program  access only a
proportionally small number of data fields
access only a
proportionally small number of data fields 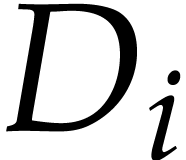 ,
preferably by chunks of 16 contiguous fields. The theoretical notion of
cache oblivious algorithms [39] partially captures
these ideas. Divide and conquer algorithms tend to be cache oblivious
and thereby more efficient. Computing the product of two
,
preferably by chunks of 16 contiguous fields. The theoretical notion of
cache oblivious algorithms [39] partially captures
these ideas. Divide and conquer algorithms tend to be cache oblivious
and thereby more efficient. Computing the product of two  matrices using a naive triple loop is not cache oblivious
(for large
matrices using a naive triple loop is not cache oblivious
(for large 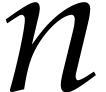 ) and can
therefore be very slow. In the terminology of this subsection, high
quality SLP should in particular be cache oblivious.
) and can
therefore be very slow. In the terminology of this subsection, high
quality SLP should in particular be cache oblivious.
Where does the “initial SLP”  come
from in the workflow (1.2)? It is not very convenient to
oblige users to specify
come
from in the workflow (1.2)? It is not very convenient to
oblige users to specify  using pseudo-code like
(1.1), (2.1), or (2.2). Now we
often already have some existing implementation of
using pseudo-code like
(1.1), (2.1), or (2.2). Now we
often already have some existing implementation of  , albeit not in our SLP framework. In this
section we explain how to derive an SLP for
, albeit not in our SLP framework. In this
section we explain how to derive an SLP for  from
an existing implementation, using a mechanism that records the trace of
a generic execution of
from
an existing implementation, using a mechanism that records the trace of
a generic execution of  .
.
Modulo the creation of appropriate wrappers for recording, this
mechanism applies for any existing code in any language, as long as the
code is either generic or templated by a domain  that implements at most the signature
that implements at most the signature  .
By “at most”, we mean that the only allowed operations on
elements from
.
By “at most”, we mean that the only allowed operations on
elements from  are the ones from
are the ones from  .
.
Recording can be thought of as a more powerful version of inlining,
albeit restricted to the SLP setting: instead of using complex
compilation techniques for transforming the existing code, it suffices
to implement a cheap wrapper that records the trace of an execution.
Hence the names
Let us describe how to implement the recording mechanism for existing C
or C++ code over a domain  .
For this we introduce a type recorder, which could
either be a template with
.
For this we introduce a type recorder, which could
either be a template with  as a parameter, or a
generic but slower recorder type that works over all domains. In order
to record a function, say
as a parameter, or a
generic but slower recorder type that works over all domains. In order
to record a function, say 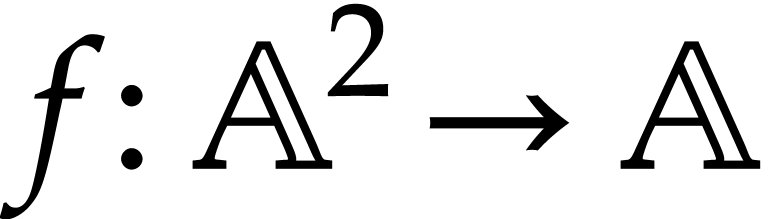 ,
we proceed as follows:
,
we proceed as follows:
|
In this code we use global variables for the state of the recorder. This
state mainly consists of the current quadruple 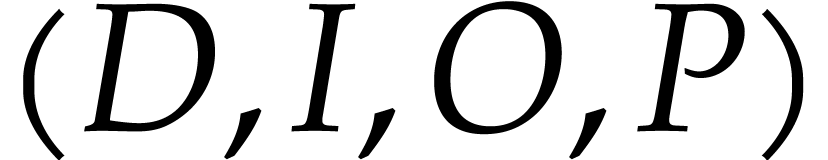 , where
, where 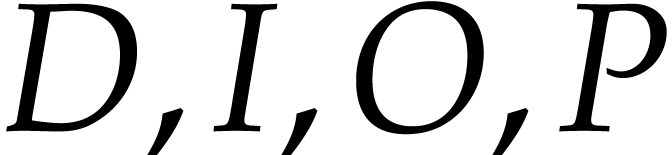 are thought of as
output streams (rather than vectors).
are thought of as
output streams (rather than vectors).
When starting the recorder, we reset  to being
empty. Instances of the recorder type represent indices
of data fields in
to being
empty. Instances of the recorder type represent indices
of data fields in  .
.
The instruction  , adds
the corresponding index (
, adds
the corresponding index ( in this case) to
in this case) to 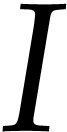 , and next stores it in
, and next stores it in 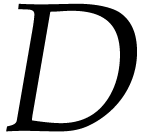 ,
adds the corresponding index
,
adds the corresponding index  to
to 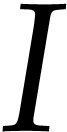 , and then stores it in
, and then stores it in
We next execute the actual function  on our input
data. For this, the data type recorder should implement
a default constructor, a constructor from
on our input
data. For this, the data type recorder should implement
a default constructor, a constructor from  ,
and the operations from
,
and the operations from  (as well as copy and
assignment operators to comply with C++). The default constructor adds a
new auxiliary data field to
(as well as copy and
assignment operators to comply with C++). The default constructor adds a
new auxiliary data field to 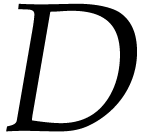 ,
whereas the constructor from
,
whereas the constructor from  adds a new constant
field. An operation like multiplication of
adds a new constant
field. An operation like multiplication of  and
and
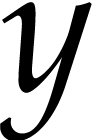 creates a new auxiliary destination field
creates a new auxiliary destination field 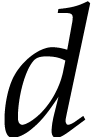 in
in 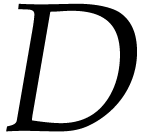 and streams the
instruction
and streams the
instruction 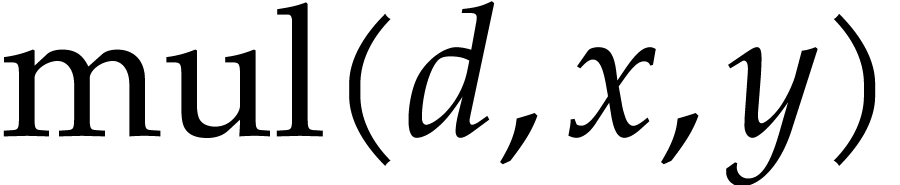 into
into  .
.
At the end, the instruction  and
and 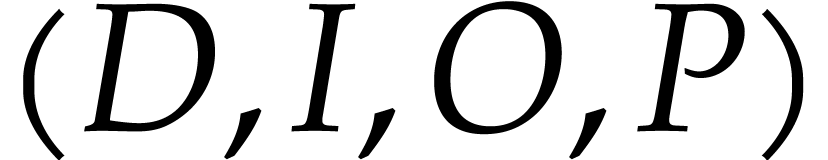 .
.
Remark
Remark  , the above recording
algorithm will put them in separate data fields. Another useful
optimization is to maintain a table of constants (as part of the global
state) and directly reuse constants that where allocated before.
, the above recording
algorithm will put them in separate data fields. Another useful
optimization is to maintain a table of constants (as part of the global
state) and directly reuse constants that where allocated before.
 matrix
multiplication
matrix
multiplication
Let us investigate in detail what kind of SLPs are obtained through
recording on the example of  matrix
multiplication. Assume that matrices are implemented using a C++
template type matrix<C> with the expected
constructors and accessors. Assume that matrix multiplication is
implemented in the following way:
matrix
multiplication. Assume that matrices are implemented using a C++
template type matrix<C> with the expected
constructors and accessors. Assume that matrix multiplication is
implemented in the following way:
|
When applying this code for two generic  input
matrices in a similar way as in the previous subsection, without the
optimizations from Remarks 3.1 and 3.2, we
obtain the following SLP:
input
matrices in a similar way as in the previous subsection, without the
optimizations from Remarks 3.1 and 3.2, we
obtain the following SLP:
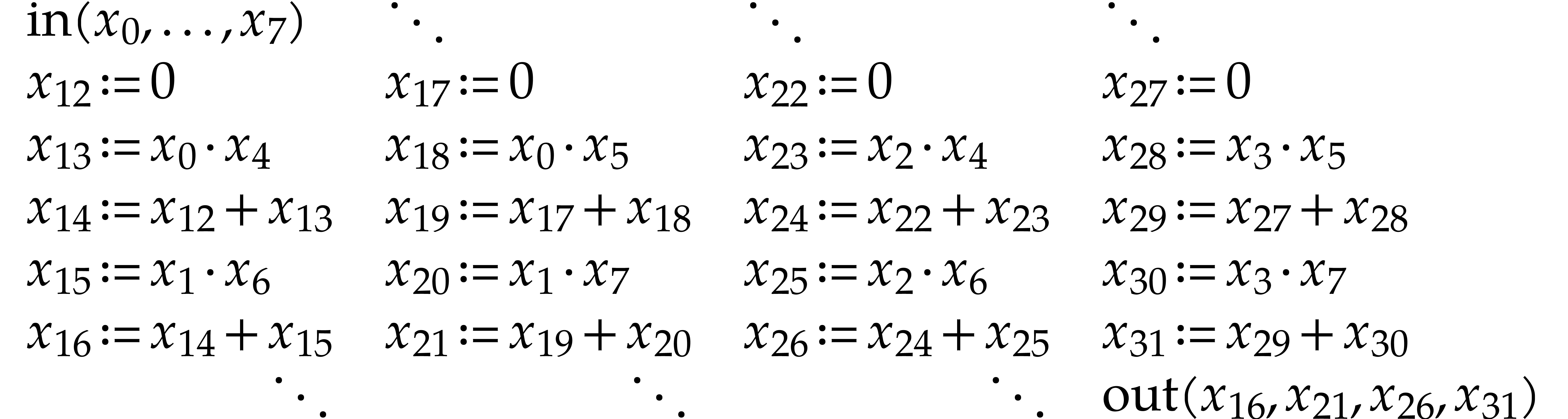 |
(3.1) |
(The order of this code is column by column from left to right.) In
order to understand the curious numbering here, one should remind how
constructors work: the declaration of 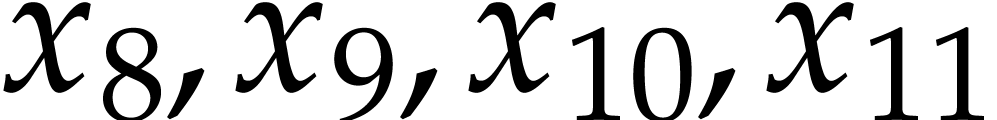 but never used. The constructor
of sum next creates the constant
but never used. The constructor
of sum next creates the constant 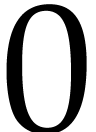 , which is put in
, which is put in 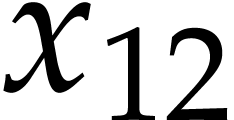 .
We then record the successive instructions, the results of which are all
put in separate data fields. Note that
.
We then record the successive instructions, the results of which are all
put in separate data fields. Note that  are not
really instructions, but rather a convenient way to indicate the
constant fields
are not
really instructions, but rather a convenient way to indicate the
constant fields  all contain zero.
all contain zero.
When applying the optimizations from Remarks 3.1 and 3.2, the generated code becomes as follows:
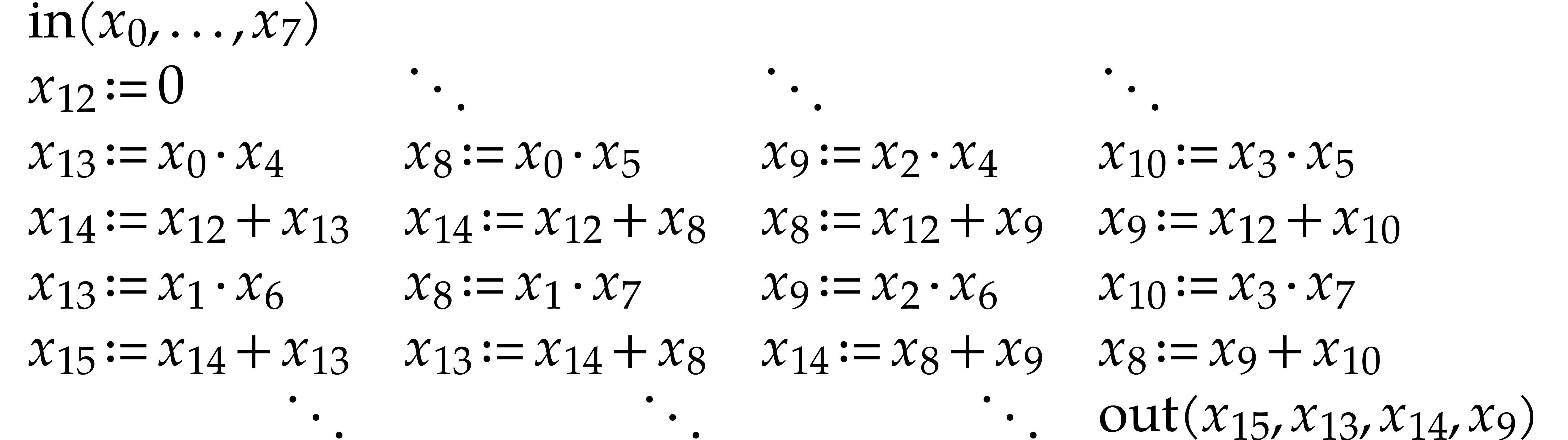 |
(3.2) |
The numbering may look even odder (although we managed to decrease the
length of  ). This is due to
the particular order in which auxiliary data fields are freed and
reclaimed via the stack.
). This is due to
the particular order in which auxiliary data fields are freed and
reclaimed via the stack.
The example from the previous subsection shows that the recording mechanism does not generate particularly clean SLPs. This is not per se a problem, because right after recording a function we typically simplify the resulting SLP, as will be detailed in section 4.4 below. However, the simplifier may not be able to correct all problems that we introduced when doing the recording in a naive manner. Simplification also tends to be faster for shorter and cleaner SLPs. Simplification might not even be needed at all.
The advantage of the mechanism from the previous section is that it can be applied to an external template C++ library over which we have no control. One reason for the somewhat messy results (3.1) and (3.2) is that C++ incites us to create classes with nice high level mathematical interfaces. Behind the scene, this gives rise to unnecessary temporary variables and copying of data. We may avoid these problems by using a lower level in-place interface for C and matrix<C>. For instance:
|
When recording our SLP using this kind of code, we obtain a much cleaner result:
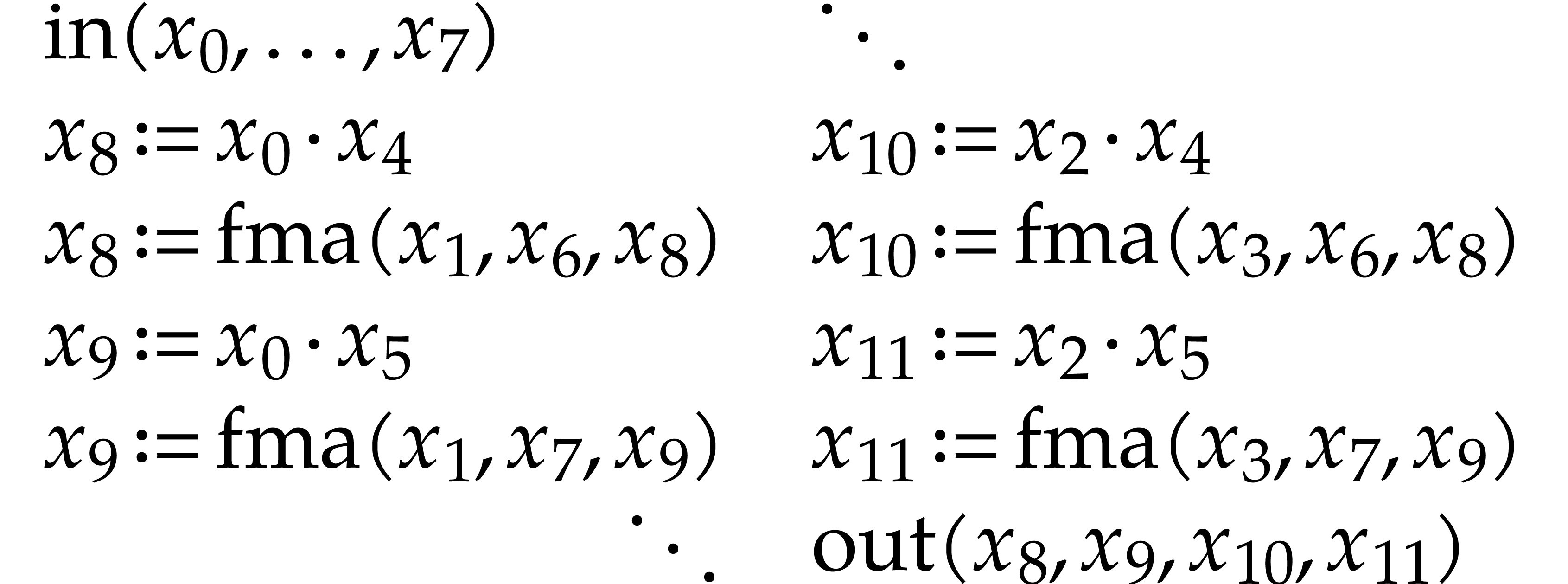 |
(3.3) |
For this reason, the
Remark
It is a pain because the above multiplication algorithm becomes incorrect in this situation. Fortunately there is the easy remedy to copy colliding arguments into auxiliary variables. Testing for collisions induces additional overhead when recording the code, but the generated SLP is not impacted if no collisions occur.
What is more, if collisions do occur, then we actually have the opportunity to generate an even better SLP. This is for instance interesting for discrete Fourier transforms (DFTs), which can either be done in-place or out-of-place. In our framework, we may implement a single routine which tests in which case we are and then uses the best code in each case.
The shifted perspective from efficiency of execution to quality of recorded code cannot be highlighted enough.
One consequence is that the overhead of control structures only concerns
the cost of recording the SLP, but not the cost of executing the SLP
itself. For example, in Remark 3.3, this holds for the cost
of checking whether there are collisions between input and output
arguments. But the same holds for the overhead of recursive function
calls. For instance, one may implement matrix multiplication
recursively, by reducing an 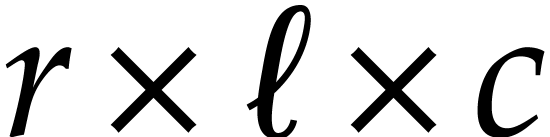 product into an
product into an 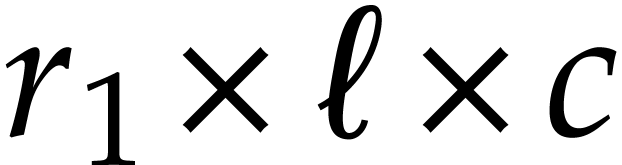 and an
and an 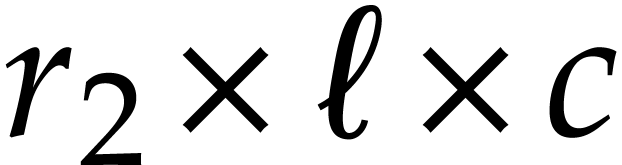 product with
product with  and
and  (or using a similar
decomposition for
(or using a similar
decomposition for  or
or  if
these are larger). The advantage of such a recursive strategy is that it
tends to have a better cache efficiency. Now traditional implementations
typically recurse down only until a certain threshold, like
if
these are larger). The advantage of such a recursive strategy is that it
tends to have a better cache efficiency. Now traditional implementations
typically recurse down only until a certain threshold, like 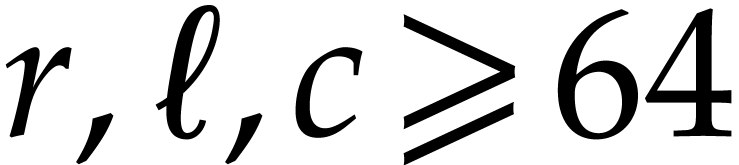 , because of the overhead of the recursive
calls. But this overhead disappears when the multiplication is recorded
as an SLP, so we may just as well recurse down to
, because of the overhead of the recursive
calls. But this overhead disappears when the multiplication is recorded
as an SLP, so we may just as well recurse down to 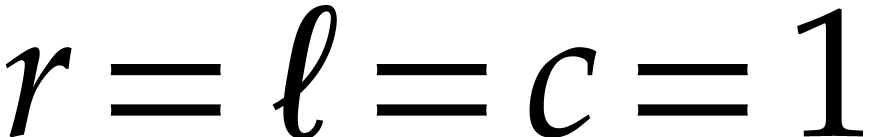 .
.
An even more extreme example is relaxed power series arithmetic.
Consider basic arithmetic operations on truncated power series such as
inversion, exponentiation, etc. If the series are truncated at a fixed
order 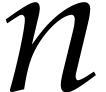 that is not too large (say
that is not too large (say 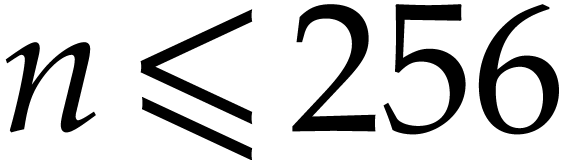 ), then lazy or relaxed algorithms are
particularly efficient (see [57] and section 6.3
below). However, they require highly non-conventional control
structures, which explains that they are not as widely used in computer
algebra systems as they might be. This disadvantage completely vanishes
when these operations are recorded as SLPs: there is still a little
overhead while recording an SLP, but not when executing it.
), then lazy or relaxed algorithms are
particularly efficient (see [57] and section 6.3
below). However, they require highly non-conventional control
structures, which explains that they are not as widely used in computer
algebra systems as they might be. This disadvantage completely vanishes
when these operations are recorded as SLPs: there is still a little
overhead while recording an SLP, but not when executing it.
The shifted perspective means that we should focus our attention on the
SLP that we wish to generate, not on the way that we generate it. For
instance, the SLP (3.3) is still not satisfactory, because
it contains several annoying dependency chains: the execution of the
instruction 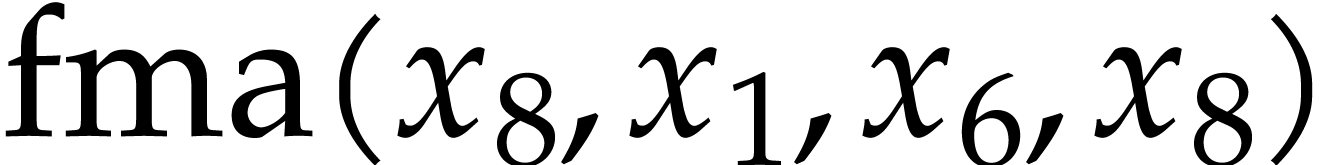 cannot start before completing the
previous instruction
cannot start before completing the
previous instruction 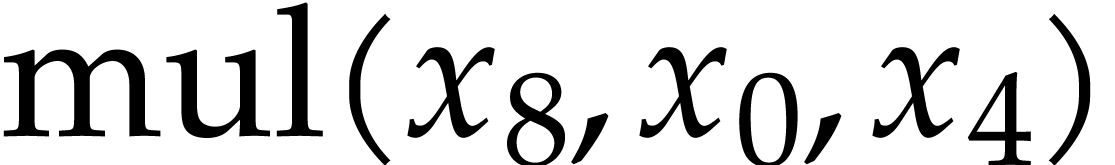 and similarly for the other
FMAs. For CPUs with at least 12 registers, the following SLP would
behave better:
and similarly for the other
FMAs. For CPUs with at least 12 registers, the following SLP would
behave better:
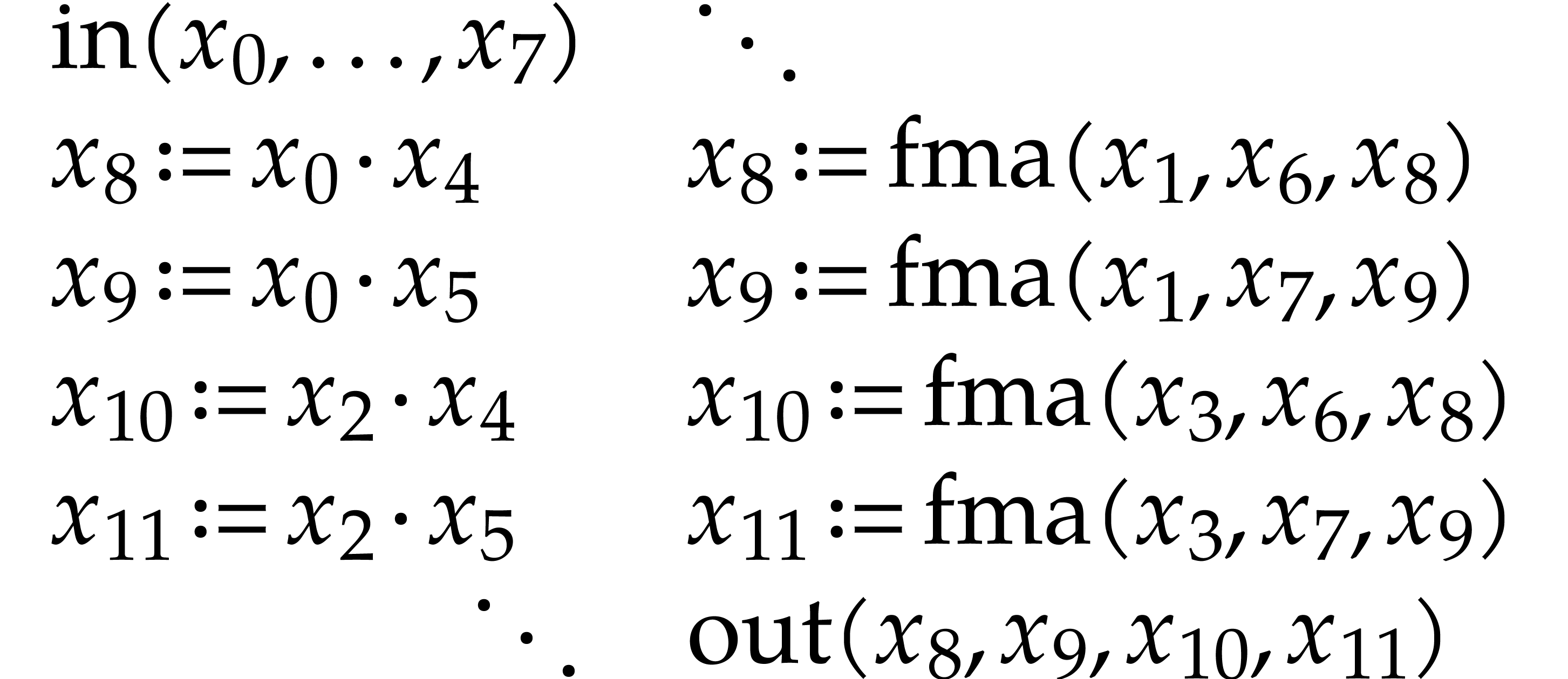 |
(3.4) |
Again, the SLP (3.3) could have been rewritten into this
form automatically, using an appropriate optimization that detects
dependency chains and reschedules instructions. Another observation is
that the dependency chains were not present in (3.1), so
they were introduced by the optimizations from Remark 3.1;
this problem can be mitigated by replacing the first-in-first-out
“stack allocator” by one that disallows the last  freed registers to be immediately reused. But then again,
it is even better to design the routines that we wish to record in such
a way that none of these remedies are needed. For instance, when doing
freed registers to be immediately reused. But then again,
it is even better to design the routines that we wish to record in such
a way that none of these remedies are needed. For instance, when doing
 matrix products in the above recursive fashion,
it suffices to recurse on
matrix products in the above recursive fashion,
it suffices to recurse on 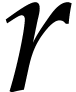 or
or  when
when  and
and 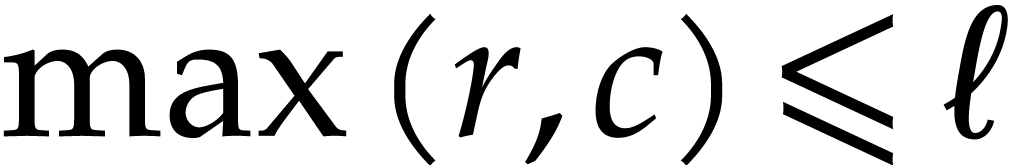 .
.
The
This section is dedicated to classical program transformations like common subexpression elimination, simplification, register allocation, etc. As explained in the introduction, this is part of the traditional theory of compilation, but the SLP framework gives rise to several twists. SLPs can become very large and should therefore be disposable as soon as they are no longer needed. Our resulting constraint is that all algorithms should run in linear time (or in expected linear time if hash tables are required).
We recall that another important general design goal is to preserve the “quality” of an SLP as much as possible during transformations. The example SLPs (3.1), (3.2), (3.3), and (3.4) from the previous subsection are all equivalent, but their quality greatly differs in terms of code length, data locality, cache efficiency, dependency chains, and general elegance. It is the responsibility of the user to provide initial SLPs of high quality in (1.2). But it is on the SLP library to not deteriorate this quality during transformations, or, at least, to not needlessly do so. An extreme case of this principle is when the input SLP already accomplishes the task that a transformation is meant to achieve. Ideally speaking, the transformation should then simply return the input SLP. One typical example is the simplification of an already simplified SLP.
For the sake of completeness, we first describe with some very basic and straightforward operations on SLPs that are essentially related to their representation. These operations are often used as building blocks inside more complex transformations.
We start with the extraction of useful information about a given SLP.
Concerning the variables in 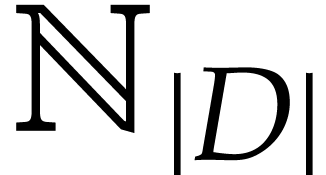 ,
we may build boolean lookup tables of length
,
we may build boolean lookup tables of length  for
the following predicates:
for
the following predicates:
Is  an input variable?
an input variable?
Is  an output variables?
an output variables?
Is  a constant?
a constant?
Is  an auxiliary variable?
an auxiliary variable?
Is  modified (i.e. does it occur
as the destination of an instruction)?
modified (i.e. does it occur
as the destination of an instruction)?
Is  used (i.e. does it occur as
the argument of an instruction)?
used (i.e. does it occur as
the argument of an instruction)?
Does  occur in the SLP at all
(i.e. as an input/output or left/right hand side)?
occur in the SLP at all
(i.e. as an input/output or left/right hand side)?
We may also build lookup tables to collect information about the program
 itself. Let us focus on
itself. Let us focus on 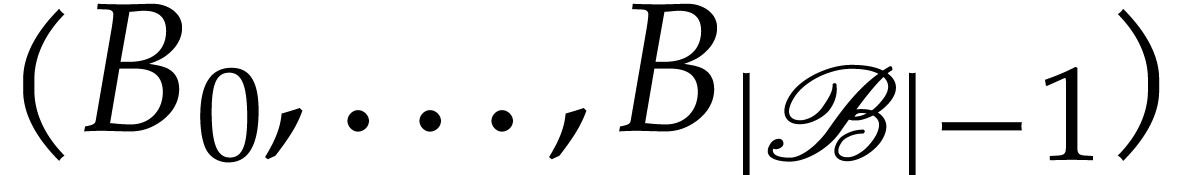 for the internal low level representation of
for the internal low level representation of  . Every instruction
. Every instruction 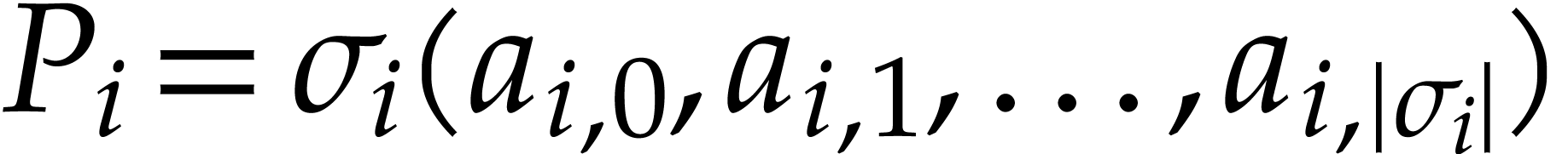 thus
corresponds to a part of the byte code: for some offset
thus
corresponds to a part of the byte code: for some offset 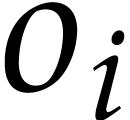 (with
(with  and
and  otherwise), we
have
otherwise), we
have  ,
, 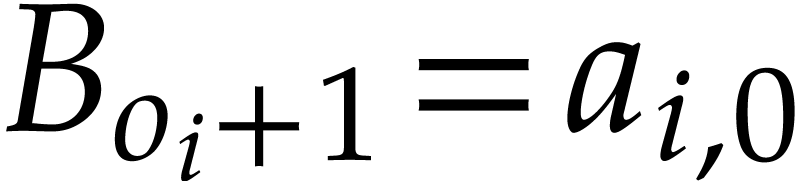 ,
, 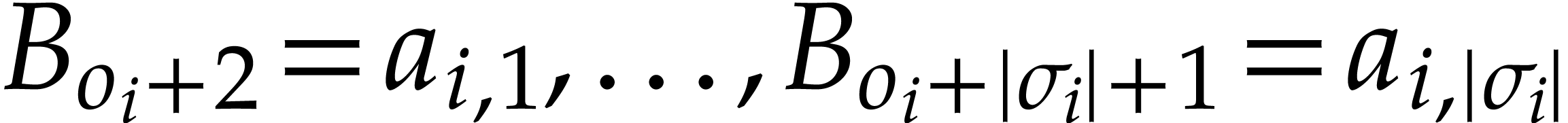 . For
this representation, the following information is typically useful:
. For
this representation, the following information is typically useful:
An index table for the offsets 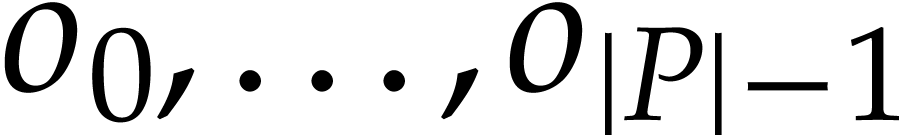 .
.
For every destination or source argument 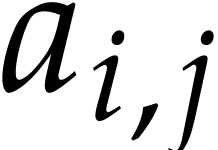 , the next location in the byte code where it is
being used. Here we use the special values
, the next location in the byte code where it is
being used. Here we use the special values 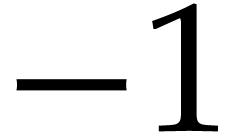 and
and  to indicate when it is not reused at all
or when it is only used for the output. We also understand that an
argument is never “reused” as soon as it gets modified.
to indicate when it is not reused at all
or when it is only used for the output. We also understand that an
argument is never “reused” as soon as it gets modified.
For every destination or source argument 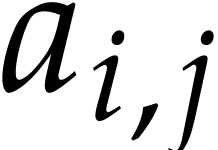 , the next location in the byte code where it is
being assigned a new value or
, the next location in the byte code where it is
being assigned a new value or 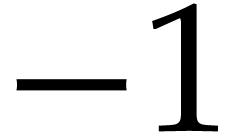 if this never
happens.
if this never
happens.
For every instruction, the maximal length of a dependency chain ending with this instruction.
Clearly, all these types of information can easily be obtained using one
linear pass through the program  .
.
We discussed several design options for the representations of SLPs in section 2. The options that we selected impose few restrictions, except for the one that all instructions have a single destination operand. This freedom allows us to express low level details that matter for cache efficiency and instruction scheduling. However, it is sometimes useful to impose additional constraints on the representation. We will now describe several basic operations on SLPs for this purpose.
The function computed by an SLP clearly does not depend on the precise
numbering of the data fields in 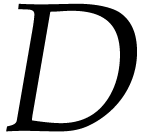 .
If the input and output variables are pairwise distinct, then we may
always impose them to be numbered as
.
If the input and output variables are pairwise distinct, then we may
always impose them to be numbered as 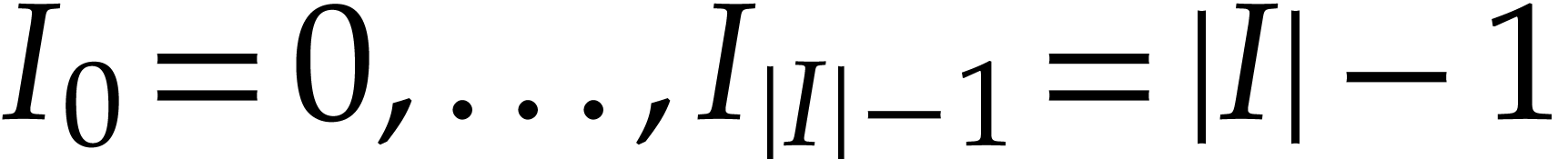 and
and 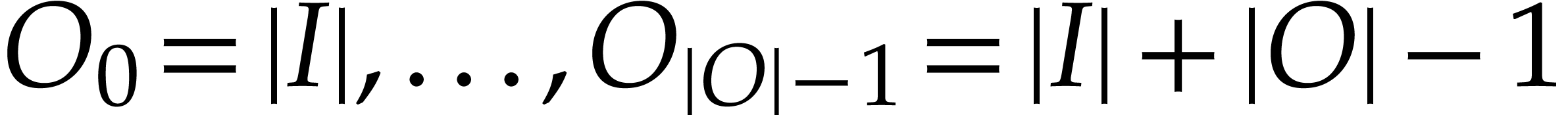 : for this it suffices to permute
the data fields.
: for this it suffices to permute
the data fields.
Similarly, we may require that all variables actually occur in the
input, the output, or in the program  itself: if
itself: if
 are the variables that occur in the SLP, then it
suffices to renumber
are the variables that occur in the SLP, then it
suffices to renumber 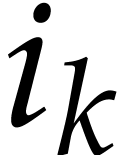 into
into 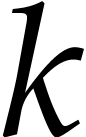 , for
, for  .
When applied to the SLP from (3.1), we have
.
When applied to the SLP from (3.1), we have 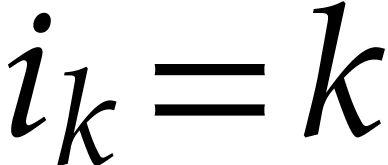 for
for 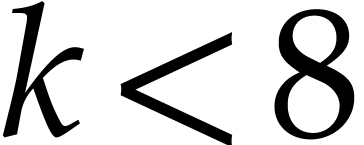 and
and 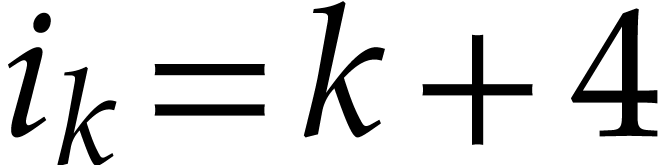 for
for 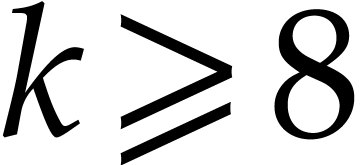 , so we suppress
, so we suppress  useless data fields.
useless data fields.
A stronger natural condition that we may impose on an SLP is that every
instruction participates in the computation of the output. This can be
achieved using classical dead code optimization, which does one linear
pass through  in reverse direction. When combined
with the above “dead data” optimization, we thus make sure
that our SLPs contain no obviously superfluous instructions or data
fields.
in reverse direction. When combined
with the above “dead data” optimization, we thus make sure
that our SLPs contain no obviously superfluous instructions or data
fields.
Our representation of SLPs allows the same variables to be reassigned
several times. This is useful in order to reduce memory consumption and
improve cache efficiency, but it may give rise to unwanted dependency
chains. For instance, the SLP (3.2) contains more
dependency chains than (3.1): the instruction 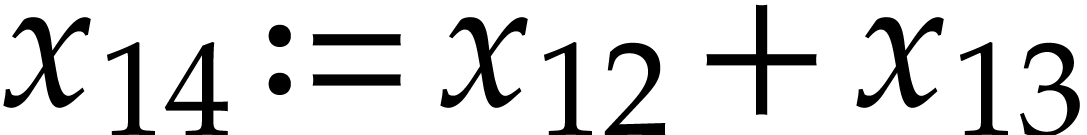 must be executed before
must be executed before 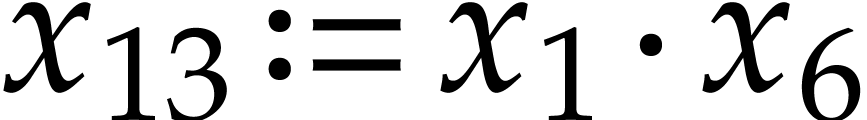 ,
but the instructions
,
but the instructions 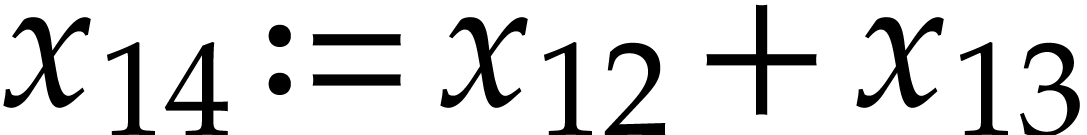 and
and  can be swapped. In order to remove all dependency chains due to
reassignments, we may impose the strong condition that all destination
operands in our SLP are pairwise distinct. This can again easily be
achieved through renumbering. Note that the non-optimized recording
strategy from section 3.1 has this property.
can be swapped. In order to remove all dependency chains due to
reassignments, we may impose the strong condition that all destination
operands in our SLP are pairwise distinct. This can again easily be
achieved through renumbering. Note that the non-optimized recording
strategy from section 3.1 has this property.
In Remark 3.3, we discussed the in-place calling
convention that is allowed by our formalism and we saw that aliasing may
negatively impact the correctness of certain algorithms. For some
applications, one may therefore wish to forbid aliasing, which can
easily be achieved through numbering. This can be strengthened further
by imposing all input and output variables 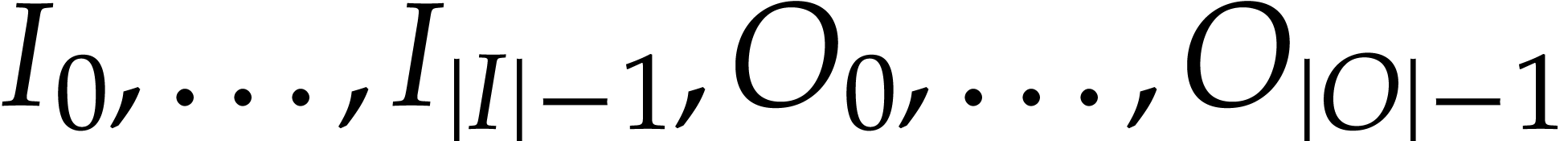 to be
pairwise distinct.
to be
pairwise distinct.
A powerful optimization in order to avoid superfluous computations is
common subexpression elimination (CSE). The result of each instruction
in  can be regarded as a mathematical expression
in the input variables of our SLP. We may simply discard instructions
that recompute the same expression as an earlier instruction. In order
to do this, it suffices to build a hash table with all expressions that
we encountered so far, using one linear pass through
can be regarded as a mathematical expression
in the input variables of our SLP. We may simply discard instructions
that recompute the same expression as an earlier instruction. In order
to do this, it suffices to build a hash table with all expressions that
we encountered so far, using one linear pass through  .
.
In our more algebraic setting, this mechanism can actually be improved,
provided that our domain  admits an algebraic
hash function. Assume for instance that
admits an algebraic
hash function. Assume for instance that 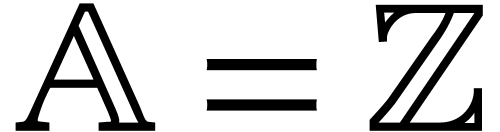 and let
and let
 be a large prime number. Let
be a large prime number. Let  be the arguments of the function computed by our SLP and let
be the arguments of the function computed by our SLP and let  be uniformly random elements of
be uniformly random elements of 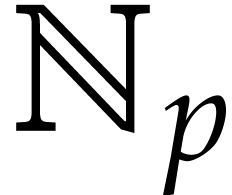 , regarded as a subset of the finite field
, regarded as a subset of the finite field  . Given any polynomial expression
. Given any polynomial expression
 , we may use
, we may use 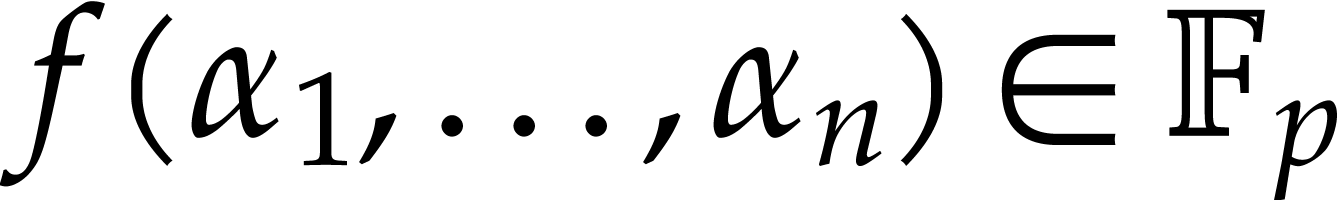 as an algebraic hash value for
as an algebraic hash value for  .
The probability that two distinct expressions have the same hash value
is proportional to
.
The probability that two distinct expressions have the same hash value
is proportional to 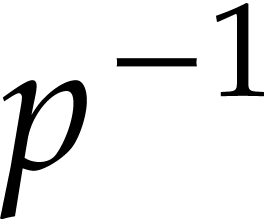 , and can
therefore be made exponentially small in the bit-size of
, and can
therefore be made exponentially small in the bit-size of  and the cost of hashing.
and the cost of hashing.
When using this algebraic hash function for common subexpression
elimination (both for hashing and equality testing), mathematically
equivalent expressions (like  and
and  or
or 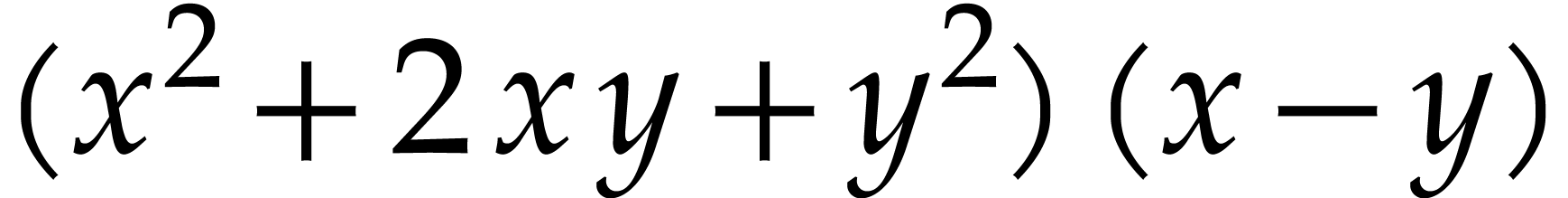 and
and 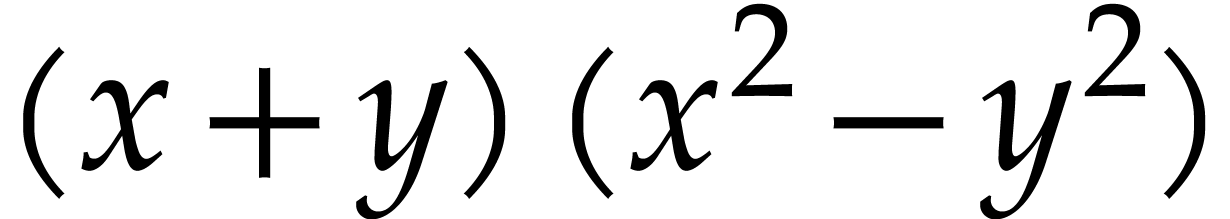 ) will be considered as equal, which may result in
the elimination of more redundant computations. However, this algorithm
is only “Monte Carlo probabilistic” in the sense that it may
fail, albeit with a probability that can be made arbitrarily (and
exponentially) small. Due to its probabilistic nature, we do not use
this method by default in our libraries. The approach also applies when
) will be considered as equal, which may result in
the elimination of more redundant computations. However, this algorithm
is only “Monte Carlo probabilistic” in the sense that it may
fail, albeit with a probability that can be made arbitrarily (and
exponentially) small. Due to its probabilistic nature, we do not use
this method by default in our libraries. The approach also applies when
 , in which case divisions by
zero (in
, in which case divisions by
zero (in  but not in
but not in  ) only arise with exponentially small probability.
) only arise with exponentially small probability.
When implementing CSE in a blunt way, it is natural to use a separate data field for every distinct expression that we encounter. However, this heavily deteriorates the cache efficiency and reuse of data in registers. In order to preserve the quality of SLPs, our implementation first generates a blunt SLP with separate fields for every expression (but without removing dead code). This SLP has exactly the same shape as the original one (same inputs, outputs, and instructions, modulo renumbering). During a second pass, we renumber the new SLP using numbers of the original one, and remove all superfluous instructions.
Simplification is an optimization that is even more powerful than common subexpression elimination. Mathematically speaking, an SLP always computes a function, but different SLPs may compute the same function. In particular, the output of CSE computes the same function as the input. But there might be even shorter and efficient SLPs with this property.
In full generality, finding the most efficient SLP for a given task is a difficult problem [21, 103, 93]. This is mainly due to the fact that an expression may first need to be expanded before an actual simplification occurs:
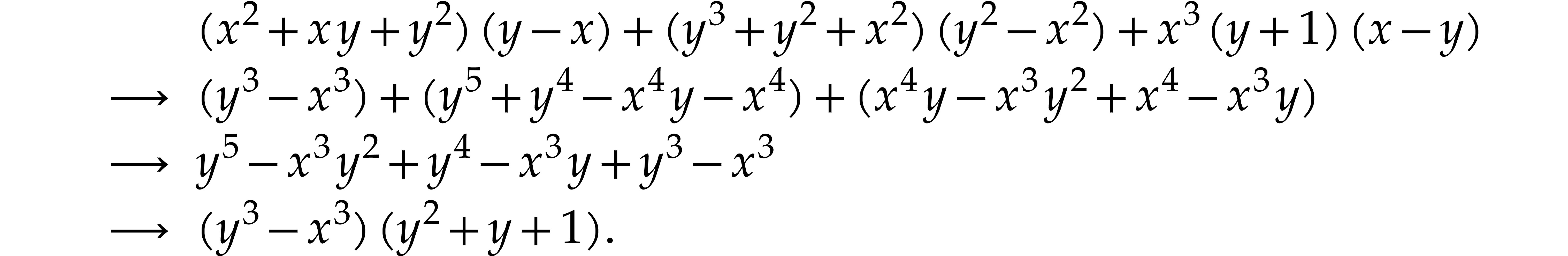
In our implementation, we therefore limited ourselves to simple algebraic rules that never increase the size of expressions and that can easily be applied in linear time using a single pass through the input SLP:
Constant folding: whenever an expression has only constant arguments, then we replace it by its evaluation.
Basic algebraic simplifications like 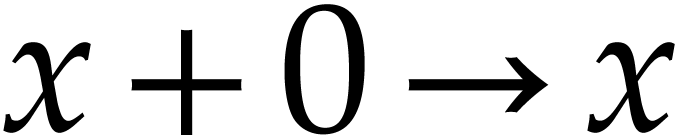 ,
,
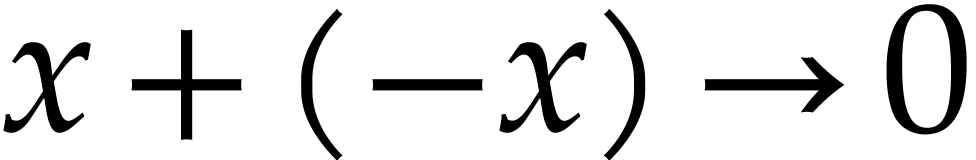 ,
, 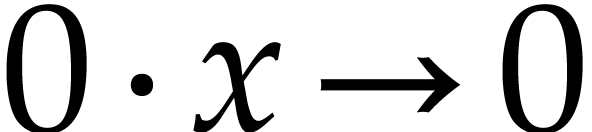 ,
, 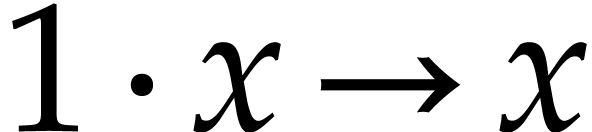 ,
,
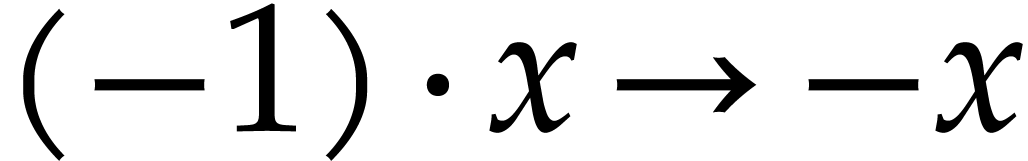 ,
, 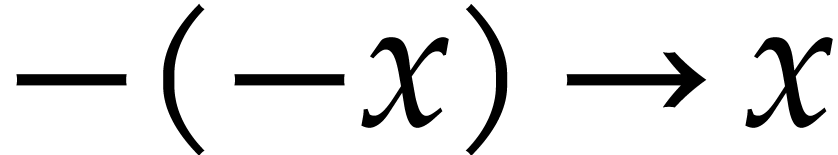 ,
, 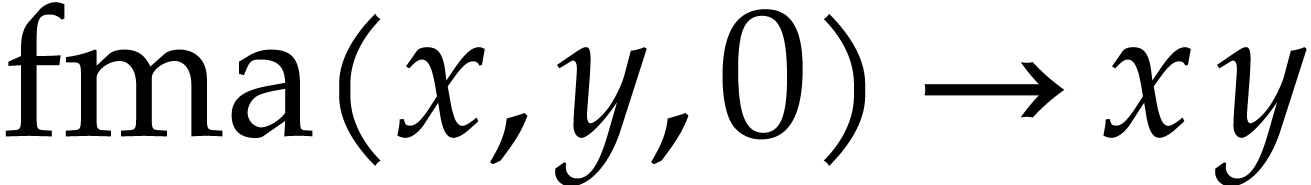 ,
,
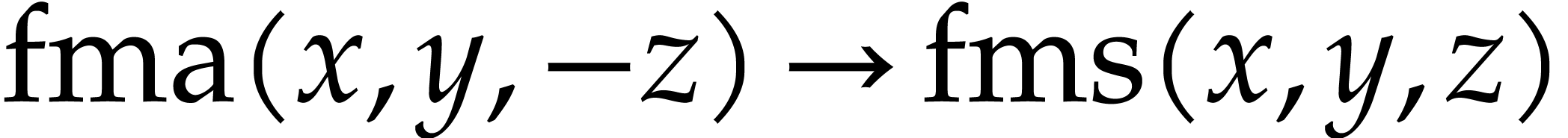 , etc.
, etc.
Imposing an ordering on the arguments of commutative operations:
 ,
,  , etc. In addition to this rewriting rule, we
also use a hash function for CSE that returns the same value for
expressions like
, etc. In addition to this rewriting rule, we
also use a hash function for CSE that returns the same value for
expressions like  and
and  .
.
Simplification is a particularly central operation of the
In the 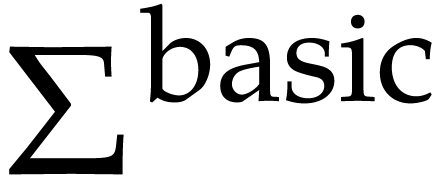 of basic
operations with the set of simplification rules by introducing all
possible versions of signed multiplication: besides the four versions
of basic
operations with the set of simplification rules by introducing all
possible versions of signed multiplication: besides the four versions
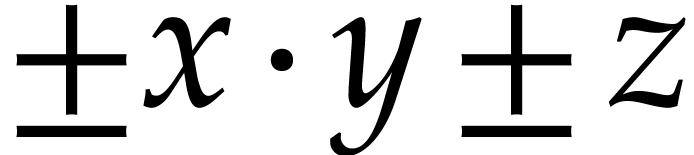 of signed FMAs, our signature
of signed FMAs, our signature 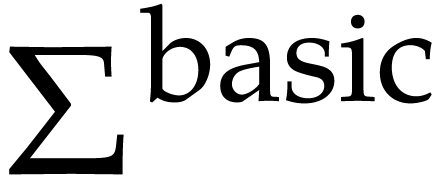 also contains the operation
also contains the operation  .
The resulting uniform treatment of signs is particularly beneficial for
complex arithmetic, linear algebra (when computing determinants),
polynomial and series division, automatic differentiation, and various
other operations that make intensive use of signs.
.
The resulting uniform treatment of signs is particularly beneficial for
complex arithmetic, linear algebra (when computing determinants),
polynomial and series division, automatic differentiation, and various
other operations that make intensive use of signs.
Just before generating machine code for our SLP in the workflow (1.2), it is useful to further “massage” our SLP while taking into account specific properties of the target hardware. Register allocation is a particularly crucial preparatory operation.
Consider a target CPU or GPU with 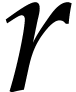 registers. In
our SLP formalism, the goal of register allocation is to transform an
input SLP into an equivalent SLP with the following properties:
registers. In
our SLP formalism, the goal of register allocation is to transform an
input SLP into an equivalent SLP with the following properties:
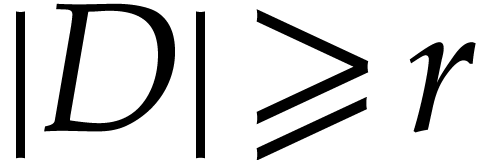 and the first
and the first 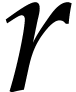 data
fields of
data
fields of 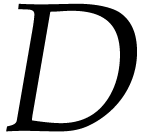 are reserved for
“registers”.
are reserved for
“registers”.
For all operations in  except
“move”, all arguments are registers.
except
“move”, all arguments are registers.
Moving registers to other data fields “in memory” or vice versa are thought of as expensive operations that should be minimized in number.
In our implementations, we also assume that  for
all input/output variables and constants, but this constraint can easily
be relaxed if needed.
for
all input/output variables and constants, but this constraint can easily
be relaxed if needed.
There is a rich literature on register allocation. The problem of finding an optimal solution is NP-complete [24], but practically efficient solutions exist, based on graph coloring [24, 23, 19] and linear scanning [96]. The second approach is more suitable for us, because it is guaranteed to run in linear time, so we implemented a variant of it.
More precisely, using one linear pass in backward direction, for each
operand of an instruction, we first determine the next location where it
is used (if anywhere). We next use a greedy algorithm that does one more
forward pass through  . During
this linear pass, we maintain lookup tables with the correspondence
between data fields and the registers they got allocated to. Whenever we
need to access a data field that is not in one of the registers, we
search for a register that is not mapped to a data field or whose
contents are no longer needed. If such a register exists, then we take
it. Otherwise, we determine the register whose contents are needed
farthest in the future. We then save its contents in the corresponding
data field, after which the register becomes available to hold new data.
. During
this linear pass, we maintain lookup tables with the correspondence
between data fields and the registers they got allocated to. Whenever we
need to access a data field that is not in one of the registers, we
search for a register that is not mapped to a data field or whose
contents are no longer needed. If such a register exists, then we take
it. Otherwise, we determine the register whose contents are needed
farthest in the future. We then save its contents in the corresponding
data field, after which the register becomes available to hold new data.
This simple strategy efficiently produces reasonably good (and sometimes very good) code on modern hardware. In the future, we might still implement some of the alternative strategies based on graph coloring, for cases when it is reasonable to spend more time on optimization.
The complexity of our current implementation is bounded by 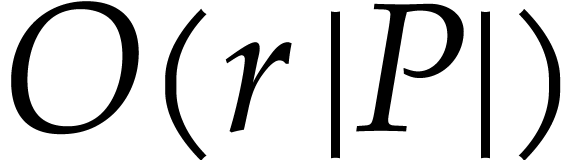 , because we loop over all registers whenever
we need to allocate a new one. The dependence on
, because we loop over all registers whenever
we need to allocate a new one. The dependence on 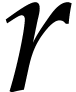 could be lowered to
could be lowered to 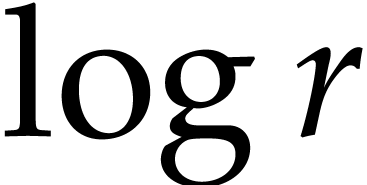 by using heaps in order to
find the registers that are needed farthest in the future. This
optimization would in fact be worth implementing: for very large SLPs,
one may regard different L1 and L2 cache levels as generalized register
files. It thus makes sense to successively apply register allocation
for, say,
by using heaps in order to
find the registers that are needed farthest in the future. This
optimization would in fact be worth implementing: for very large SLPs,
one may regard different L1 and L2 cache levels as generalized register
files. It thus makes sense to successively apply register allocation
for, say, 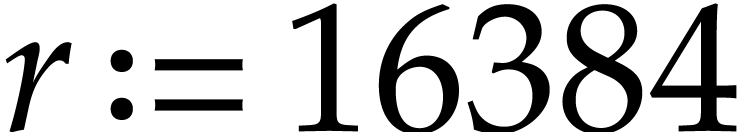 ,
,  , and
, and 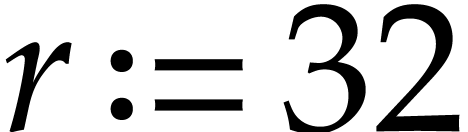 .
The efficiency of this optimization might be disappointing though if our
SLP does not entirely fit into the instruction cache: in that case the
mere execution of the SLP will become a major source of cache misses.
.
The efficiency of this optimization might be disappointing though if our
SLP does not entirely fit into the instruction cache: in that case the
mere execution of the SLP will become a major source of cache misses.
Unfortunately, the above simple allocation strategy is not always
satisfactory from the dependency chain point of view. For instance,
consider the evaluation of a constant dense polynomial of high degree
 using Horner's rule. The greedy algorithm might
systematically reallocate the last
using Horner's rule. The greedy algorithm might
systematically reallocate the last  constant
coefficients to same register. This unnecessarily puts a “high
pressure” on this register, which results in unnecessary
dependencies. The remedy is to pick a small number
constant
coefficients to same register. This unnecessarily puts a “high
pressure” on this register, which results in unnecessary
dependencies. The remedy is to pick a small number  , say
, say 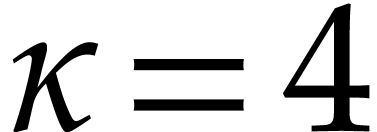 ,
and blacklist the last
,
and blacklist the last  allocated registers from
being reallocated. As a result, the pressure will be spread out over
allocated registers from
being reallocated. As a result, the pressure will be spread out over
 registers instead of a single one.
registers instead of a single one.
Remark
Consider the following two SLPs:
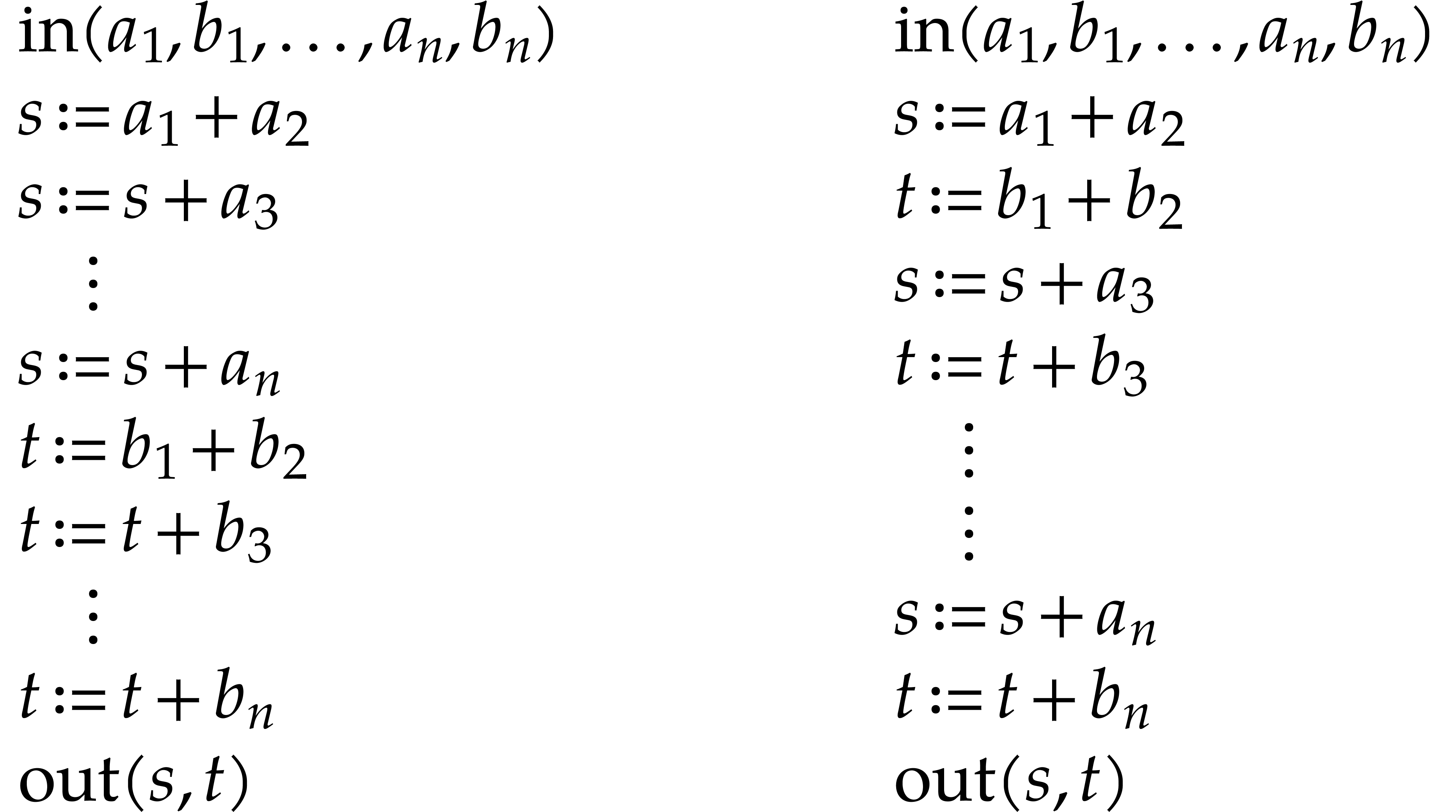 |
(4.1) |
Both SLPs are equivalent and compute the sums 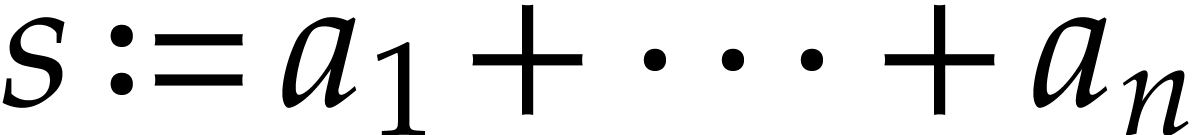 and
and 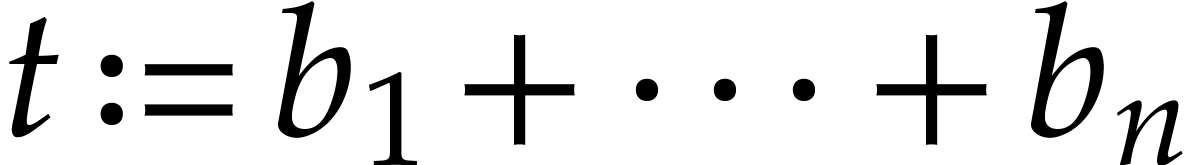 . However, the first SLP
contains two long dependency chains of length
. However, the first SLP
contains two long dependency chains of length 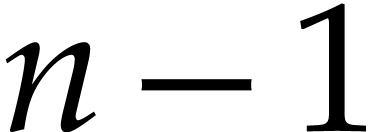 , whereas these dependency chains got interleaved in
the second SLP.
, whereas these dependency chains got interleaved in
the second SLP.
Modern CPUs contain multiple execution units for addition. This allows
the processor to execute the instructions  and
and
 in parallel for
in parallel for  ,
as well as the first instructions
,
as well as the first instructions 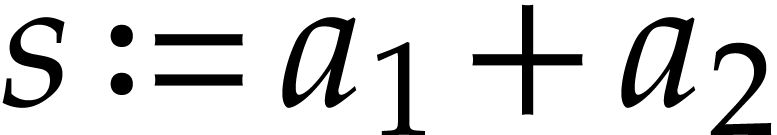 and
and 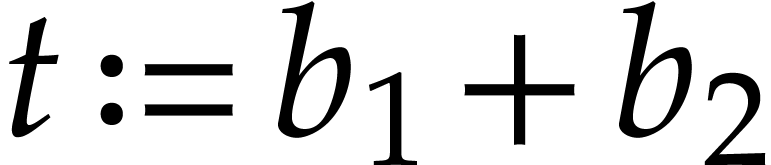 . Modern hardware has also become
particularly good at scheduling (i.e. dispatching
instruction to the various execution units): if
. Modern hardware has also become
particularly good at scheduling (i.e. dispatching
instruction to the various execution units): if  is not so large, then the execution of
is not so large, then the execution of 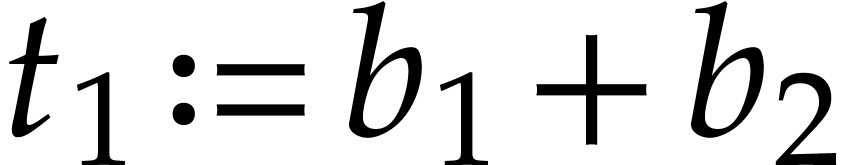 in the
first SLP may start while the execution of
in the
first SLP may start while the execution of 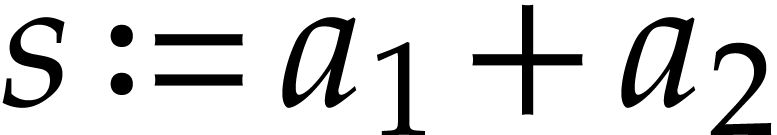 or
or
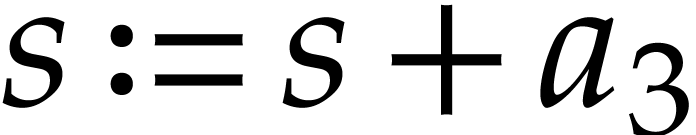 is still in progress. However, processors have a
limited “look-ahead capacity”, so this fails to work when
is still in progress. However, processors have a
limited “look-ahead capacity”, so this fails to work when
 exceeds a certain threshold. In that case, the
second SLP may be executed almost twice as fast, and it may be desirable
to find a way to automatically rewrite the first SLP into the second
one.
exceeds a certain threshold. In that case, the
second SLP may be executed almost twice as fast, and it may be desirable
to find a way to automatically rewrite the first SLP into the second
one.
A nice way to accomplish this task is to emulate what a good hardware
scheduler does, but without being limited by look-ahead thresholds. For
this, we first need to model our hardware approximately in our SLP
framework: we assume that we are given  execution
units
execution
units  , where each
, where each 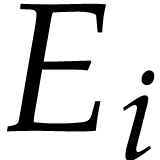 is able to execute a subset
is able to execute a subset  of
operations with prescribed latencies and reciprocal throughputs.
of
operations with prescribed latencies and reciprocal throughputs.
We next emulate the execution of  using these
execution units. At every point in time, we have executed a subset of
the instructions in
using these
execution units. At every point in time, we have executed a subset of
the instructions in  and we maintain a list of
instructions that are ready to be executed next (an instruction being
ready if the values of all its arguments have already been computed).
Whenever this list contains an instruction for which there exists an
available execution unit, we take the first such instruction and
dispatch it to the available unit.
and we maintain a list of
instructions that are ready to be executed next (an instruction being
ready if the values of all its arguments have already been computed).
Whenever this list contains an instruction for which there exists an
available execution unit, we take the first such instruction and
dispatch it to the available unit.
We implemented this approach in the
Note finally that it is often possible to interleave instructions from
the outset (as in the right-hand SLP of (4.1)) when
generating initial SLPs in the workflow (1.2). For
instance, if we just need to execute the same SLP twice on different
data, then we may work over the domain  instead
of
instead
of  (see sections 5.1 and 5.5
below). More generally, good SLP libraries should provide a range of
tools that help with the design of well-scheduled initial SLPs.
(see sections 5.1 and 5.5
below). More generally, good SLP libraries should provide a range of
tools that help with the design of well-scheduled initial SLPs.
Several operations in our signature  may not be
supported by our target hardware. Before transforming our SLP into
executable machine code, we have to emulate such operations using other
operations that are supported. Within a chain of transformations of the
initial SLP, there are actually several moments when we may do this.
may not be
supported by our target hardware. Before transforming our SLP into
executable machine code, we have to emulate such operations using other
operations that are supported. Within a chain of transformations of the
initial SLP, there are actually several moments when we may do this.
One option is to directly let the backend for our target hardware take
care of emulating missing instructions. In that case, we typically have
to reserve one or more scratch registers for emulation purposes. For
instance, if we have an  operation but no
operation but no  operation, then the instruction
operation, then the instruction 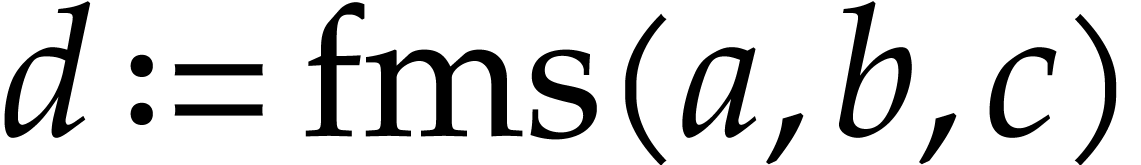 can be emulated using two instructions
can be emulated using two instructions 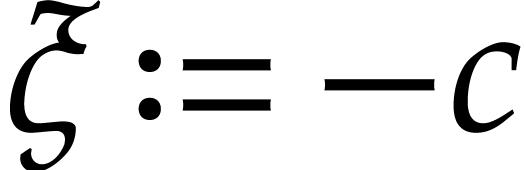 and
and 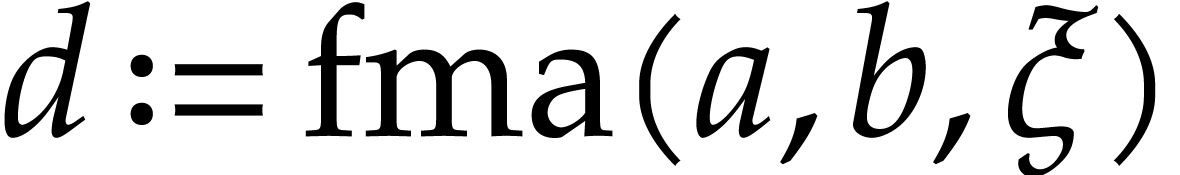 , where
, where  stands for the scratch register. However, this strategy has two
disadvantages: we diminish the number of available registers, even in
the case of an SLP that does not require the emulation of any
instructions. For SLPs that contain many
stands for the scratch register. However, this strategy has two
disadvantages: we diminish the number of available registers, even in
the case of an SLP that does not require the emulation of any
instructions. For SLPs that contain many  instructions in a row, we also create long dependency chains, by putting
a lot of pressure on the scratch register.
instructions in a row, we also create long dependency chains, by putting
a lot of pressure on the scratch register.
Another option is to perform the emulation using a separate
transformation on SLPs. This has the disadvantage of adding an
additional step before the backend (even for SLPs that contain no
instructions that need to be emulated), but it generally results in
better code. For instance, for a long sequence of  instructions as above, we may emulate them using
instructions as above, we may emulate them using  scratch variables
scratch variables  that are used in turn (very
similar to what we did at the end of section 4.5). When
doing the emulation before register allocation, the scratch variables
need not be mapped to fixed registers, which allows for an even better
use of the available hardware registers.
that are used in turn (very
similar to what we did at the end of section 4.5). When
doing the emulation before register allocation, the scratch variables
need not be mapped to fixed registers, which allows for an even better
use of the available hardware registers.
It is finally an interesting challenge how to support certain types of instructions inside our SLP framework, such as carry handling, SIMD instructions, guarded instructions, etc. We plan to investigate the systematic incorporation and emulation of such features in future work.
There exist several general purpose libraries for building machine code
on the fly inside memory [8, 95, 11].
This avoids the overhead of writing any code to disk, which is a useful
feature for JIT compilers. In our SLP framework, where we can further
restrict our attention to a specific signature  and a specific domain
and a specific domain  , it is
possible to reduce the overhead of this building process even further.
, it is
possible to reduce the overhead of this building process even further.
Especially in our new
Our SLP library ultimately aims at providing a uniform interface for a
wide variety of target architectures, including GPUs. Our current
implementation in
Building efficient machine code for our SLPs is only interesting if we
wish to evaluate our SLPs many times. When all input data for these
evaluations are available beforehand, then this evaluation task becomes
embarrassingly parallel. The SLP library should easily allow us to
exploit the available parallelism on the target architecture. If our
hardware supports SIMD parallelism of width  for
our domain
for
our domain  , then we
systematically support builders for the SIMD type
, then we
systematically support builders for the SIMD type  and provide a wrapper for doing multiple evaluations of our SLP
approximately
and provide a wrapper for doing multiple evaluations of our SLP
approximately  times faster. In the case of GPUs,
times faster. In the case of GPUs,
 may become as large as the number of available
threads. For modern CPUs with multiple cores, we also provide a
multi-threaded interface for evaluating SLPs many times.
may become as large as the number of available
threads. For modern CPUs with multiple cores, we also provide a
multi-threaded interface for evaluating SLPs many times.
The implementation of an efficient and versatile SLP library requires a lot of efforts. Some of this work might be useful beyond the strict framework of SLPs. In this section, we briefly mention some low hanging fruit within hand's reach.
The SLP framework can be overkill for some applications. The typical workflow (1.2) is indeed relatively long: we first construct an SLP, then transform and optimize it, then prepare it for the backend (register allocation, emulation, etc.), and finally generate the machine code. The full building cost is often about thousand times higher than the cost of a single execution of the final machine code. For particularly simple programs, it is tempting to bypass the entire SLP layer and directly build the machine code. This might for instance be useful for the repeated evaluation of dense or sparse polynomials. We also plan to implement special shortcuts for bilinear and trilinear SLPs. Such SLPs can often be evaluated more efficiently for transformed representations of the inputs and outputs (e.g. modulo several primes or in a suitable FFT model). One may even considering rewriting general SLPs to benefit from such accelerations [61, sections 4.4.2 and 4.4.3].
In other circumstances, we may miss basic control structures. One common application is the repeated evaluation of an SLP on different inputs, as discussed at the end of the previous subsection. Instead of generating a function for our SLP and calling this function inside a loop, one may eliminate the overhead of function calls by putting this loop directly around the code of our SLP. This is also useful for the generation of efficient codelets for discrete Fourier transforms (see section 6.2 below). Another common design pattern is the repeated evaluation of an SLP until some condition is met. This is for instance useful for numerical homotopy continuation (see section 6.1).
The recording strategy from section 3 also reaches its limits when the resulting SLP is so large that the corresponding machine code does not fit into the instruction cache. In that case, we may wish to automatically factor out large identical sub-SLPs (up to renumbering) and automatically replace them by function calls. This could be achieved by tagging function calls during recording or by using a dedicated post-processing step.
We plan to extend our builders to generate light-weight control sugar for the above purposes and gracefully intertwine it with the machine code for the SLPs themselves. It is not yet clear to us yet how far these extensions should go. For particularly useful design patterns, it will be faster to develop dedicated implementations and optimizations. But if we need too many types of control sugar, we may end up with a general purpose compiler.
As a general rule, there is clearly a trade-off between the speed of generating machine code and the quality of the generated code (and its speed of execution). The best choice essentially depends on the number of times that we wish to execute our code. An ideal library should be able to efficiently support the largest possible range of “numbers of executions”.
The full strength of the SLP framework becomes apparent for algebraic transformations. Traditional compilers may exploit some algebraic properties during the optimization and code generation phases, but this typically remains limited to the kind of constant folding and basic rewriting rules that we have discussed in section 4.4. One reason is that general purpose languages possess no deeper knowledge about mathematical types that a user might introduce. Since there is typically no way to easily compute with programs themselves, it is also not straightforward to extend the compiler with such knowledge. Another reason is that more sophisticated algebraic optimizations are typically easier to design for SLPs than for full blown programs in a high level language.
In this section we discuss operations on SLPs that exploit mathematical
properties of the domain  .
The algorithms still use rewriting and static analysis techniques from
the traditional theory of compilation, but also heavily rely on
mathematical manipulations that can commonly be found in computer
algebra systems. We will first recall a few classical techniques like
vectorization and automatic differentiation. We next introduce the
concept of SLP algebras which provides a general framework for the
design of algebraic transformations. We finish with several less
classical transformations and examples how to use SLP algebras.
.
The algorithms still use rewriting and static analysis techniques from
the traditional theory of compilation, but also heavily rely on
mathematical manipulations that can commonly be found in computer
algebra systems. We will first recall a few classical techniques like
vectorization and automatic differentiation. We next introduce the
concept of SLP algebras which provides a general framework for the
design of algebraic transformations. We finish with several less
classical transformations and examples how to use SLP algebras.
A simple but useful transformation is SIMD-style vectorization. In a
traditional language that supports templates, like C++,  for vectors of length
for vectors of length  with
entries in
with
entries in  . Given a function
. Given a function
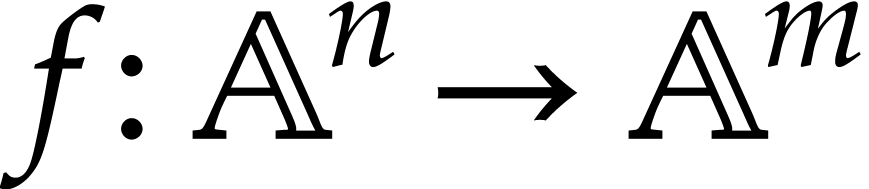 that is templated by
that is templated by  , the instantiation of this function for
, the instantiation of this function for  then allows for the
then allows for the  -fold
evaluation of
-fold
evaluation of  , provided that
this instantiation is legit.
, provided that
this instantiation is legit.
In the SLP setting, vectorization is also straightforward to implement:
it essentially suffices to duplicate all inputs, outputs, data fields,
and instructions  times. For instance, consider
the SLP
times. For instance, consider
the SLP
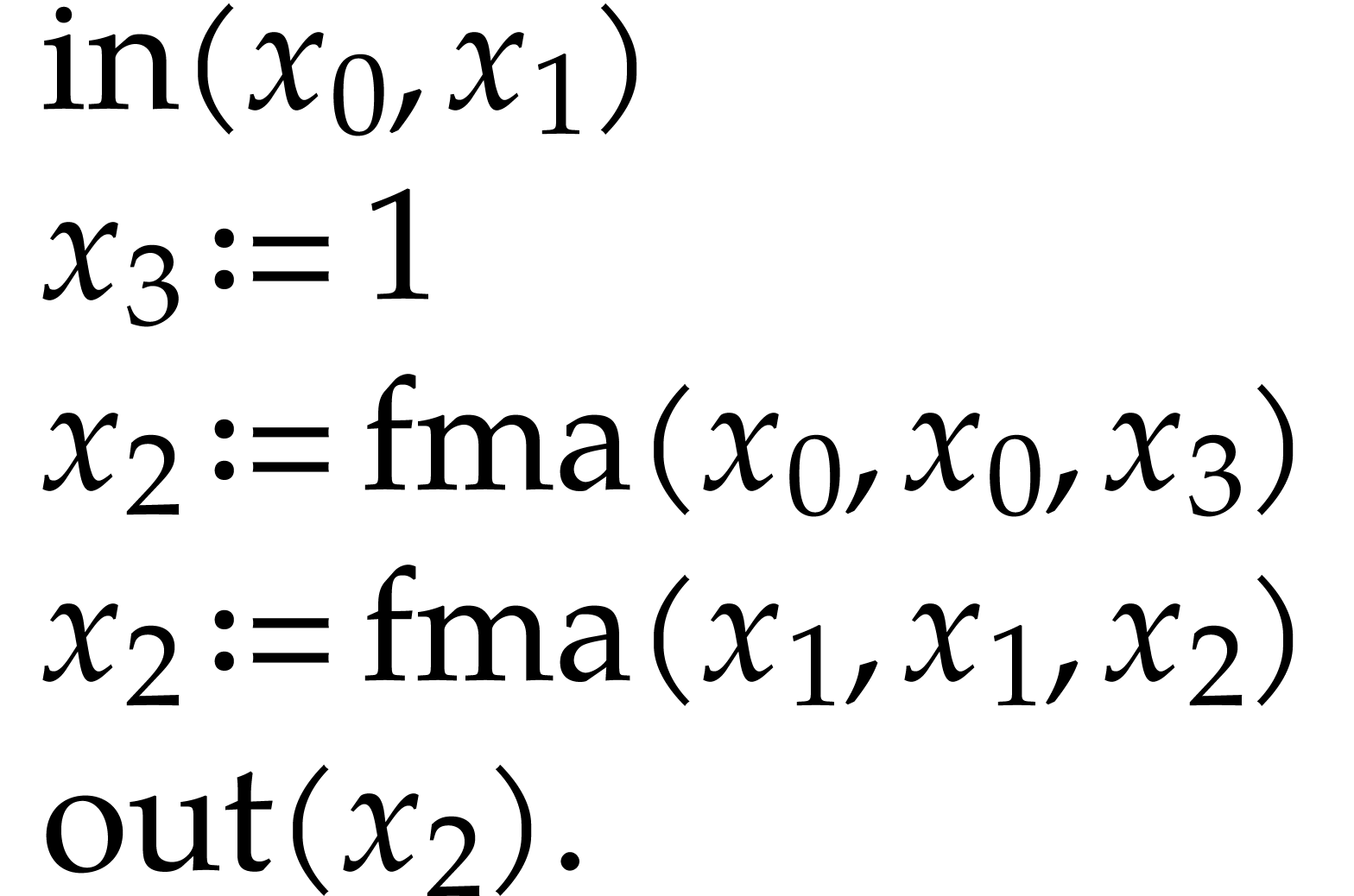 |
(5.1) |
Vectorizing this SLP for 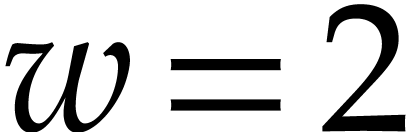 yields the following
SLP:
yields the following
SLP:
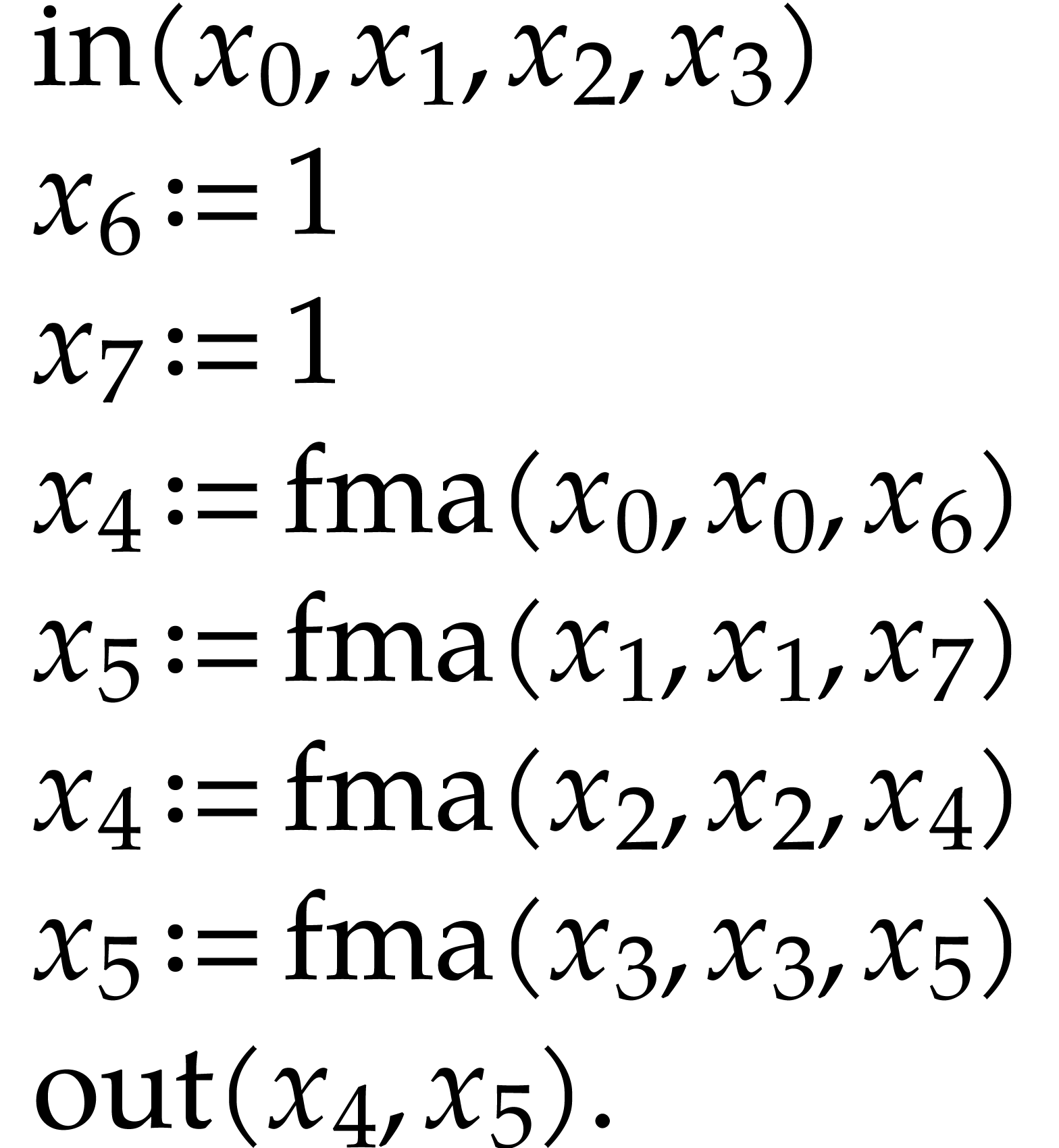
Note that this vectorized SLP has a high quality in the sense of section
2.5, because dependency chains are well interleaved.
Whenever an SLP needs to be executed several times, it may therefore be
beneficial to vectorize it this way (for a small 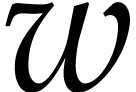 like
like 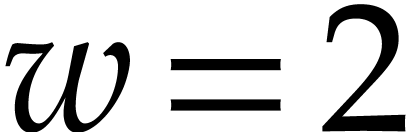 ) and then perform the
execution by groups of
) and then perform the
execution by groups of  .
.
Although most compilers do not directly integrate support for automatic differentiation, dedicated tools for this task are available for many languages; see e.g. [9, 10, 79]. Automatic differentiation can be done in two modes: the forward mode (differentiating with respect a variable) and the backward mode (computing gradients).
The forward mode is the easiest to implement. Mathematically speaking,
in order to differentiate 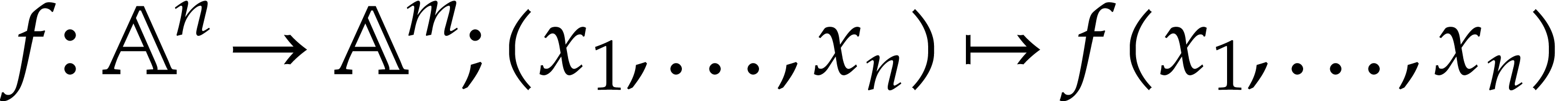 with respect to, say,
with respect to, say,
 with
with 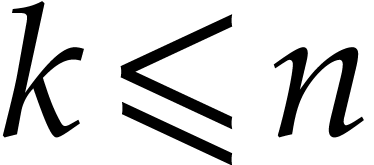 ,
it suffices to evaluate
,
it suffices to evaluate  in the algebra
in the algebra  :
:
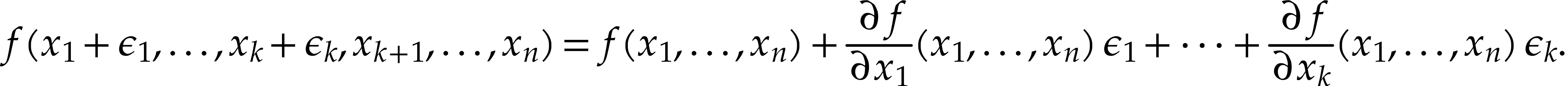
The forward mode can therefore be implemented directly in the language
itself, provided that the language allows us to implement  as a template and instantiate it for
as a template and instantiate it for  .
.
Forward differentiation can be implemented for SLPs in a similar way as
vectorization: with the notation from the section 5.1, we
now take  and replace every instruction by one or
more instructions according to the action of
and replace every instruction by one or
more instructions according to the action of  in
in
 . For instance, for
. For instance, for  , the forward derivative of the SLP
(5.1) is as follows:
, the forward derivative of the SLP
(5.1) is as follows:
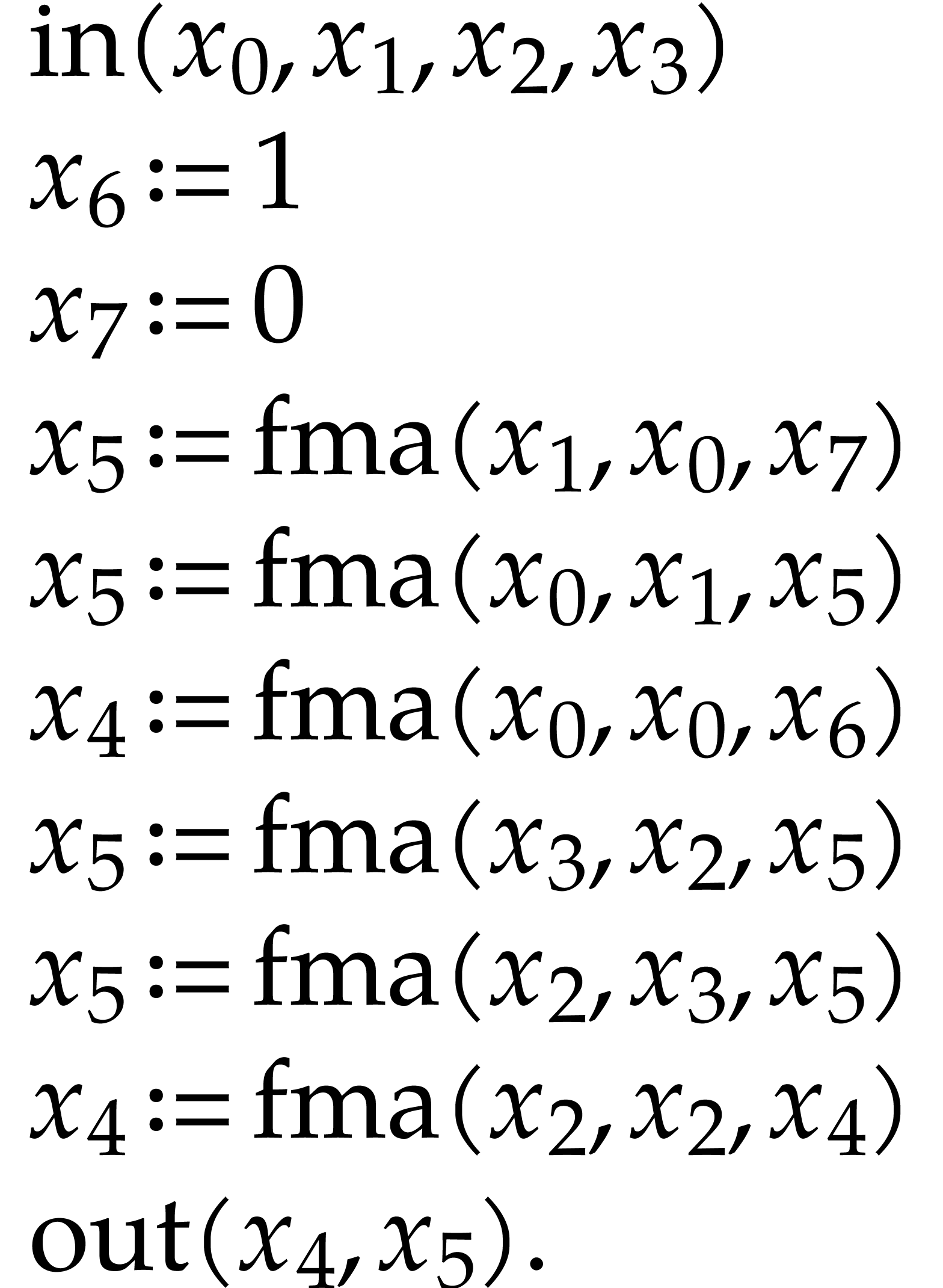
The value of 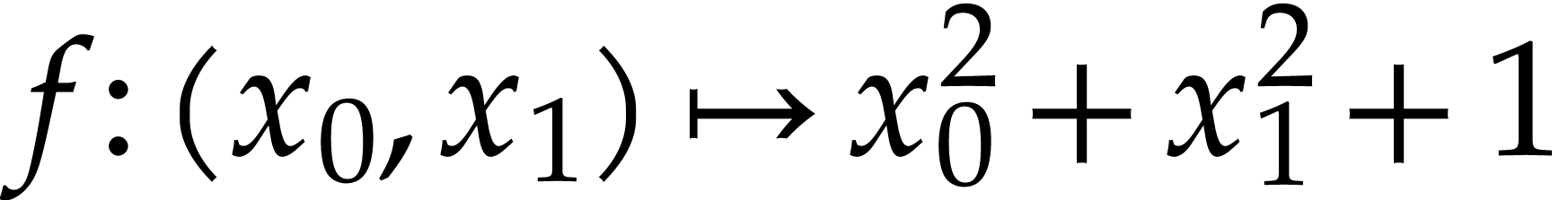 and its derivative with respect to
and its derivative with respect to
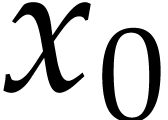 can be computed simultaneously by evaluating
this SLP at
can be computed simultaneously by evaluating
this SLP at 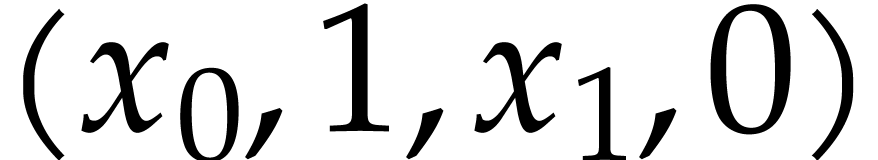 .
.
Baur and Strassen also proposed an efficient algorithm for automatic
differentiation in the backward mode [14]. Their method
relies on applying the chain rule in backward direction. As a
consequence, it can not be implemented by evaluating  in the usual forward direction over some suitable
in the usual forward direction over some suitable  -algebra. Instead, specific compiler support or a
dedicated program is required in order to use this method. In the SLP
setting, where programs are treated as data, the forward and backward
modes can be implemented in a similar way; we only need to reverse the
direction in which we process
-algebra. Instead, specific compiler support or a
dedicated program is required in order to use this method. In the SLP
setting, where programs are treated as data, the forward and backward
modes can be implemented in a similar way; we only need to reverse the
direction in which we process  and apply the
chain rule.
and apply the
chain rule.
Automatic differentiation in both directions typically generates a lot
of trivial instructions of the kind  or
or 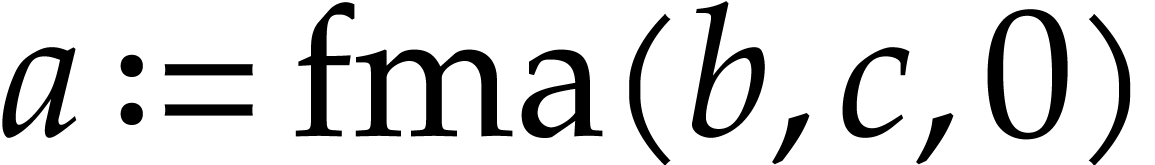 . It is therefore recommended to
always simplify the resulting SLP as explained in section 4.4.
In fact, automatic differentiation is an excellent test case for
simplification routines. Note also that it is less straightforward to
benefit from simplification when implementing forward differentiation
using templates in a general purpose language, as described above.
. It is therefore recommended to
always simplify the resulting SLP as explained in section 4.4.
In fact, automatic differentiation is an excellent test case for
simplification routines. Note also that it is less straightforward to
benefit from simplification when implementing forward differentiation
using templates in a general purpose language, as described above.
Assume that  is a ring and consider a linear map
is a ring and consider a linear map
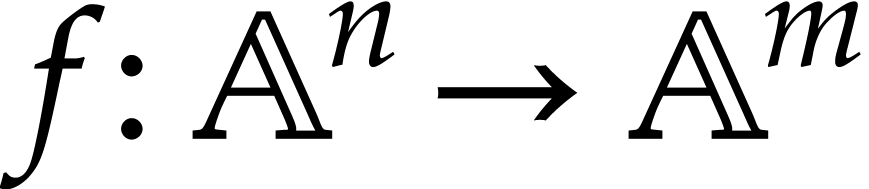 that can be computed by an SLP of length
that can be computed by an SLP of length  . Then the transposition
principle states that the transposed map
. Then the transposition
principle states that the transposed map  can be computed by another SLP of length
can be computed by another SLP of length 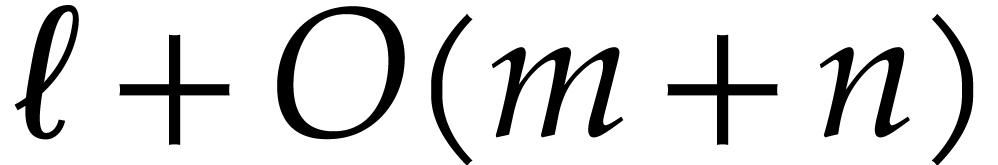 .
The principle can be traced back to [16], in a different
terminology of electrical networks. An early statement in terms of
computational complexity can be found in [32, Theorems 4
and 5]. See [17] for some applications in computer algebra.
.
The principle can be traced back to [16], in a different
terminology of electrical networks. An early statement in terms of
computational complexity can be found in [32, Theorems 4
and 5]. See [17] for some applications in computer algebra.
Like in the case of backward differentiation, the transposition
principle can be implemented using one backward linear pass. Sometimes,
the input SLP is only linear in a subset of the input variables, in
which case we may apply the transposition principle with respect to
these variables only, while considering the other input variables as
parameters. Backward differentiation can then be regarded as a special
case of the transposition principle, the SLP  together with its Jacobian being linear with respect to the variables
that correspond to infinitesimal perturbations.
together with its Jacobian being linear with respect to the variables
that correspond to infinitesimal perturbations.
Example
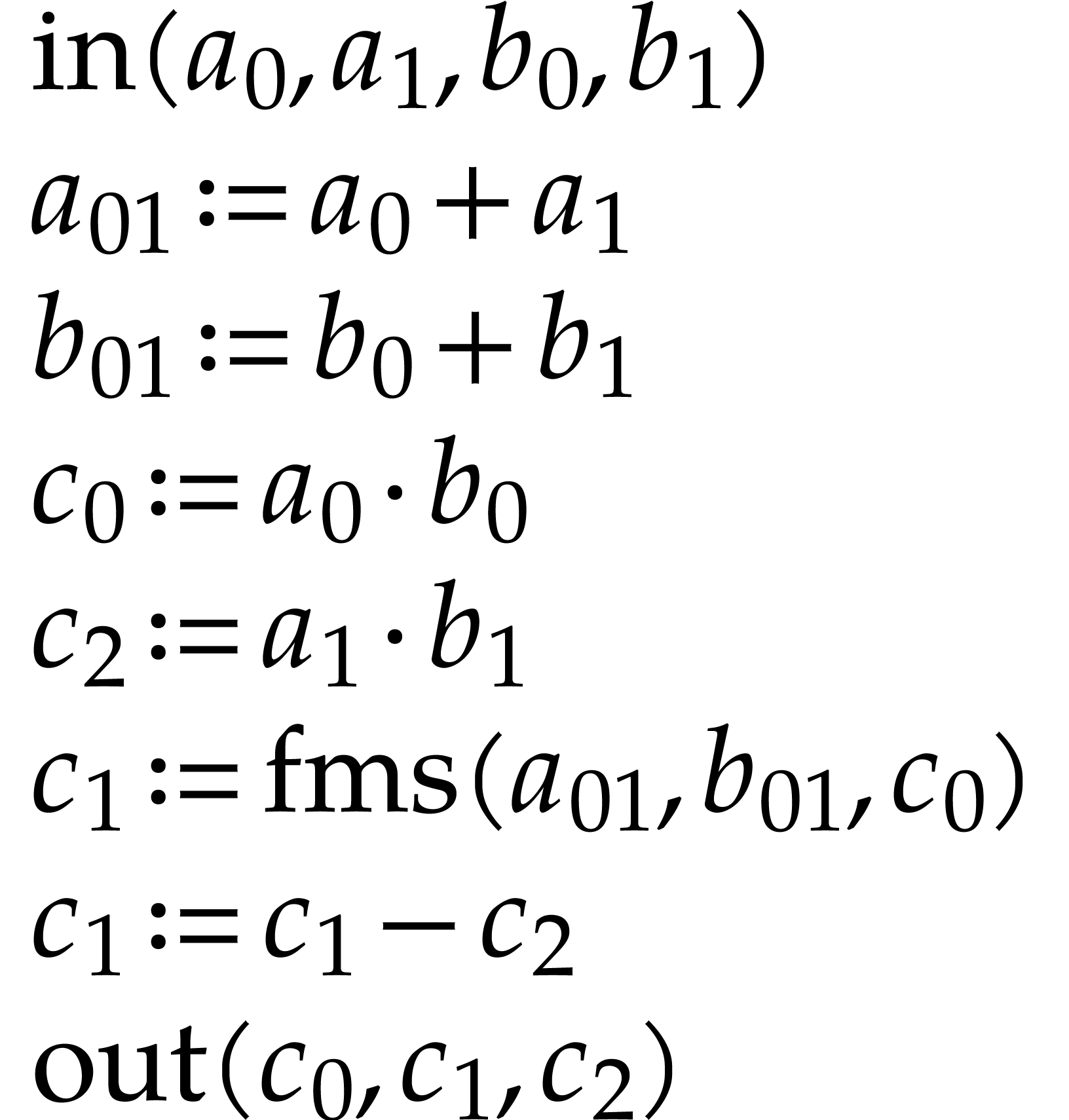 |
(5.2) |
This SLP 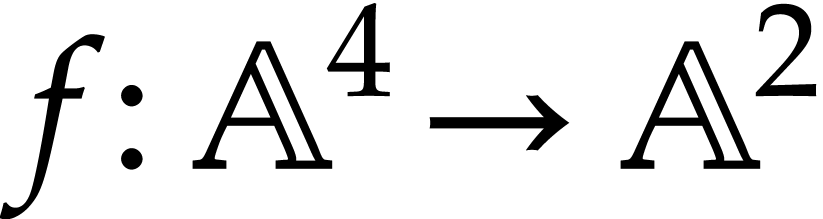 computes the product
computes the product 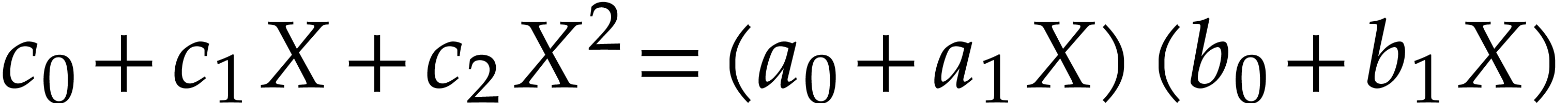 using Karatsuba's algorithm [40, Section 8.1]. For fixed
using Karatsuba's algorithm [40, Section 8.1]. For fixed
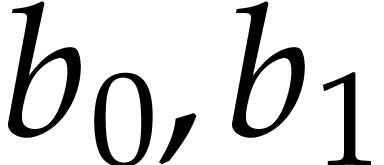 , the map
, the map 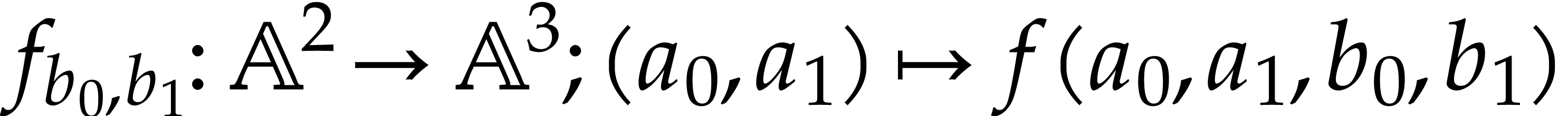 is linear in
is linear in 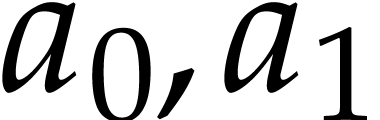 . The transposed
map
. The transposed
map 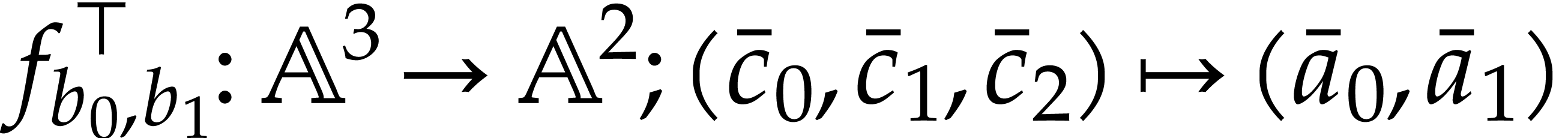 computes the so-called middle
product [52] of
computes the so-called middle
product [52] of 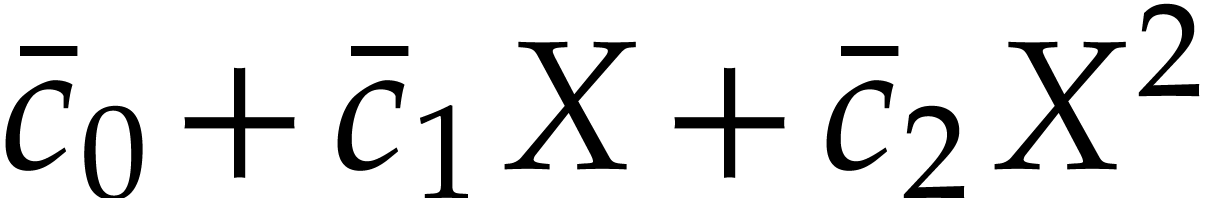 and
and 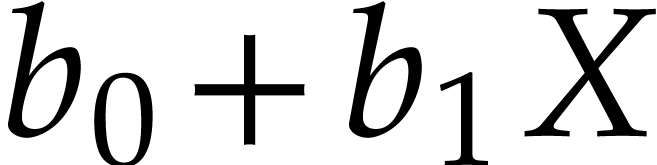 . We may obtain an SLP for the map
. We may obtain an SLP for the map
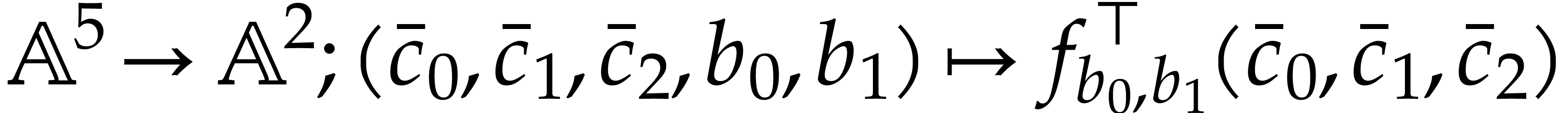 in three steps:
in three steps:

The left-hand SLP is a renumbered version of (5.2) to which
we appended three instructions to copy the output (without this, the
transposed SLP would override the input arguments). The middle SLP shows
its raw unsimplified transposition. The background colors indicate the
images of the individual instructions. For instance, the instruction
 is equivalent to
is equivalent to
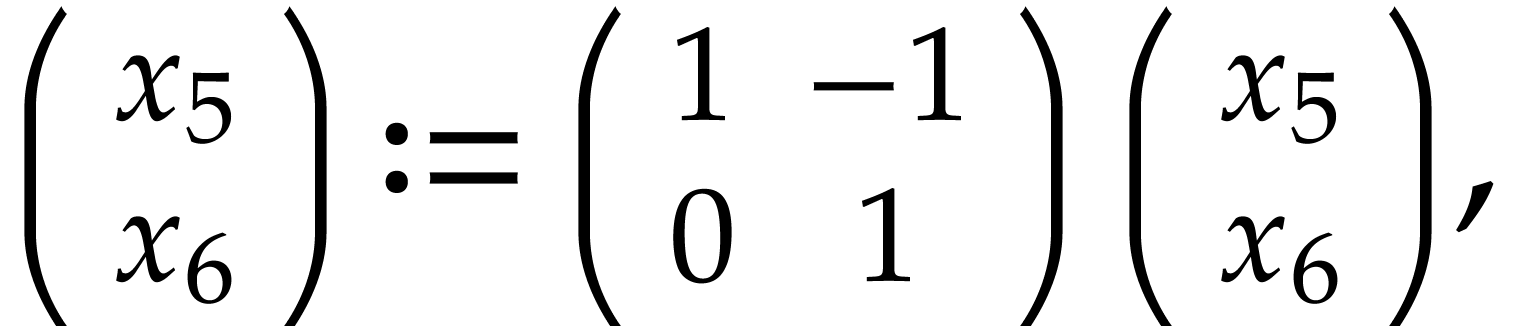
which leads to the transposed code 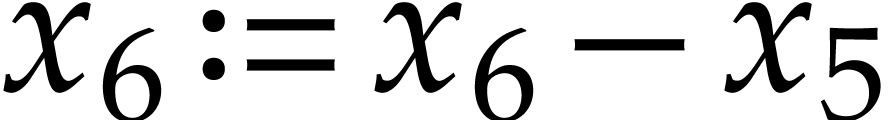 .
The instruction
.
The instruction  is treated apart, because it
only depends on the parameters
is treated apart, because it
only depends on the parameters  and not on the
main input variables
and not on the
main input variables 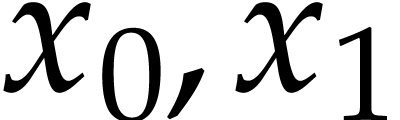 : all
instructions of this kind are extracted from the input SLP and prepended
as is to the transposed SLP. For the transposition itself, the
parameters
: all
instructions of this kind are extracted from the input SLP and prepended
as is to the transposed SLP. For the transposition itself, the
parameters 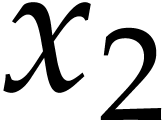 ,
, 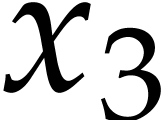 and variables like
and variables like 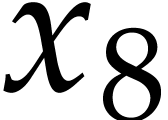 are considered as constants.
The right-hand SLP shows the simplification of the raw transposed SLP.
We both applied usual simplification as in section 4.4 and
an optimization that combines multiplications and additions into FMA
instructions.
are considered as constants.
The right-hand SLP shows the simplification of the raw transposed SLP.
We both applied usual simplification as in section 4.4 and
an optimization that combines multiplications and additions into FMA
instructions.
Consider a rational map 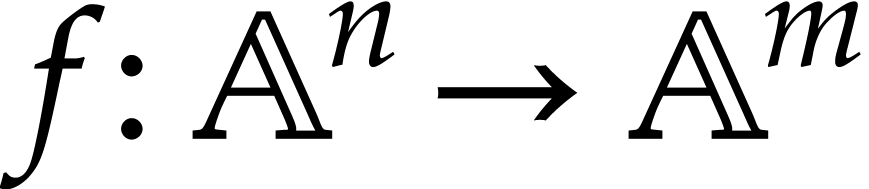 . Its
homogenization is the rational map
. Its
homogenization is the rational map 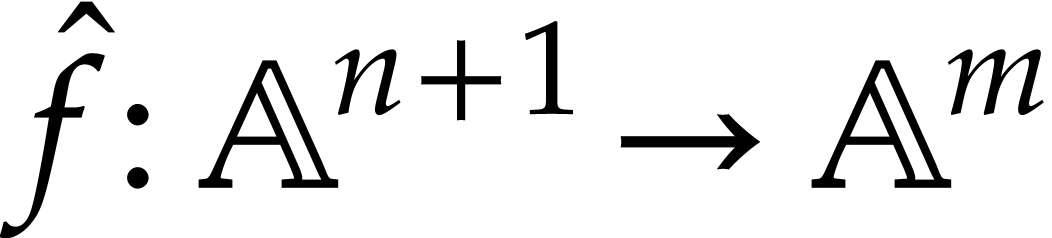 such
that
such
that  is homogeneous with
is homogeneous with  for
for  . The homogenization of
an SLP can be constructed using a single linear pass, during which we
keep track of the degrees of all intermediate results that were
“computed” so far. The algorithm is best illustrated on an
example:
. The homogenization of
an SLP can be constructed using a single linear pass, during which we
keep track of the degrees of all intermediate results that were
“computed” so far. The algorithm is best illustrated on an
example:
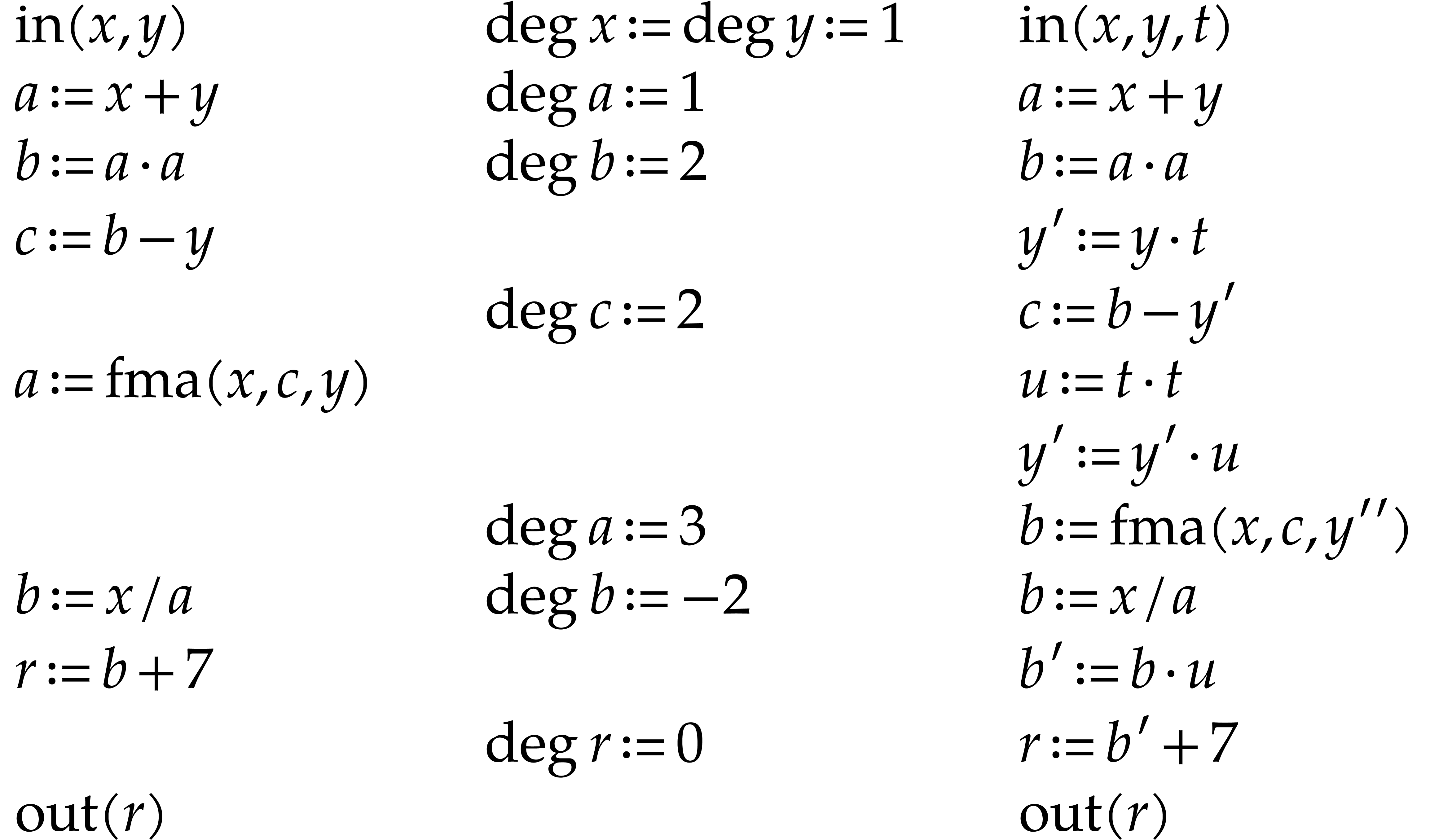
The left-hand side shows the input SLP and the right-hand side its
homogenization. We also indicate the degrees of all intermediate
results. During additions, subtractions, and FMAs, we multiply with
appropriate powers of  to keep things
homogeneous. We also maintain a table of powers of
to keep things
homogeneous. We also maintain a table of powers of  that were computed so far, in order to avoid needless recomputations.
that were computed so far, in order to avoid needless recomputations.
This procedure actually extends to other operations, as long as the
notion of degree extends in a reasonable way. For instance, for the
operations  ,
,  , and
, and  ,
we may take
,
we may take 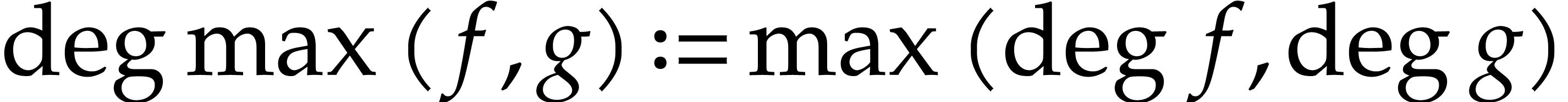 ,
, 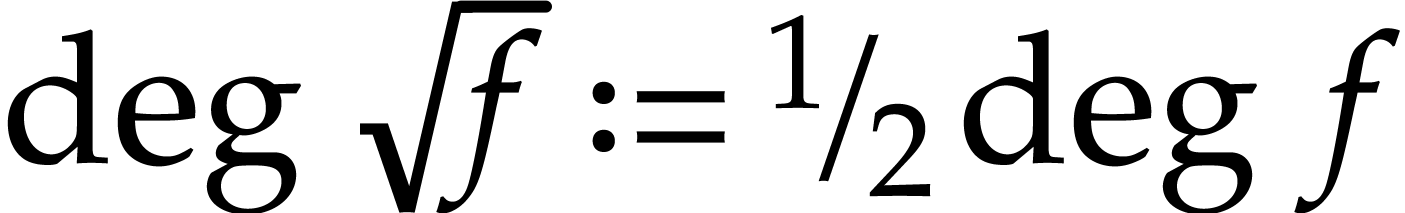 , and
, and 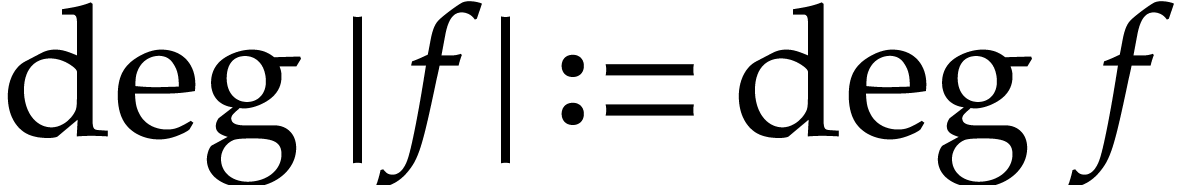 .
.
Let  be a fixed signature and let
be a fixed signature and let  ,
,  be domains. We say
that
be domains. We say
that  is a domain over
is a domain over  if we have a function
if we have a function  in order to reinterpret
elements in
in order to reinterpret
elements in  as elements in
as elements in  .
.  , like the domain
, like the domain  from section 5.1 or the domain
from section 5.1 or the domain  from section 5.2. As we saw in section 2.3, the
from section 5.2. As we saw in section 2.3, the  over
over  .
.
Now consider the case when elements of  are
represented as vectors in
are
represented as vectors in 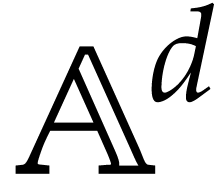 and that
and that  is implemented as an SLP
is implemented as an SLP 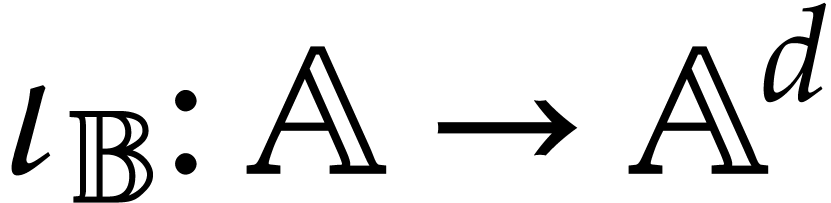 .
Assume also that every operation
.
Assume also that every operation  is implemented
on
is implemented
on  as an SLP
as an SLP 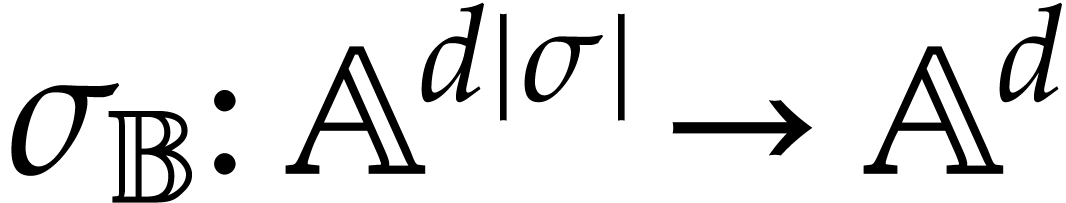 ,
where inputs
,
where inputs  are represented as
are represented as 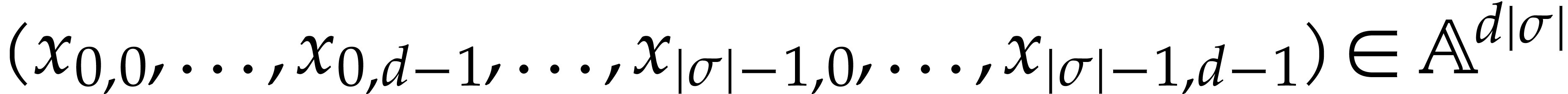 . Then we call
. Then we call  an
SLP algebra and call
an
SLP algebra and call 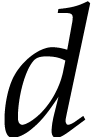 its
dimension over
its
dimension over  . The
recording technique from section 3 yields a convenient way
to turn any domain
. The
recording technique from section 3 yields a convenient way
to turn any domain  over
over  into an SLP algebra: we obtain
into an SLP algebra: we obtain  and every
and every  by recording
by recording  and
and 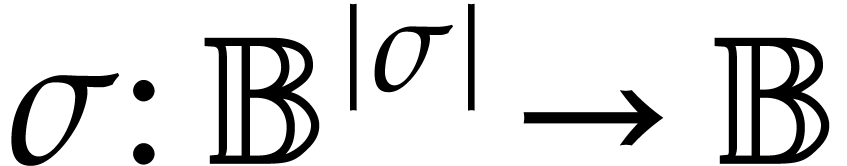 over
over  .
Conversely,
.
Conversely, 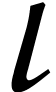 and
and  can be
obtained from
can be
obtained from 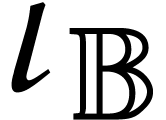 and
and  through evaluation.
through evaluation.
Remark  and
and  from
sections 5.1 and 5.2 are indeed
from
sections 5.1 and 5.2 are indeed  -algebras in the mathematical sense. In
general, the signature
-algebras in the mathematical sense. In
general, the signature 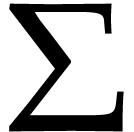 typically contains the
algebra operations, but we do not insist on
typically contains the
algebra operations, but we do not insist on  to
verify all mathematical axioms of an
to
verify all mathematical axioms of an  -algebra.
-algebra.
Let  be a domain over
be a domain over  , whose elements are represented as vectors in
, whose elements are represented as vectors in 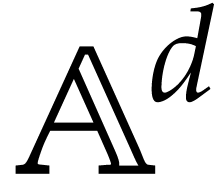 . Given an SLP
. Given an SLP  over
over  , we may naturally
execute
, we may naturally
execute  over
over  .
Using the recording technique from section 3, we may then
obtain a new SLP, which we call the reinterpretation of
.
Using the recording technique from section 3, we may then
obtain a new SLP, which we call the reinterpretation of  as an SLP over
as an SLP over  .
Similarly, since every operation in
.
Similarly, since every operation in 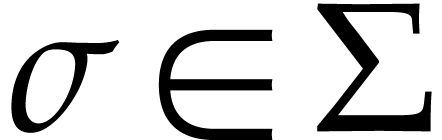 can be
applied over both
can be
applied over both  and
and  , and constants in
, and constants in  can be
lifted to a constant in
can be
lifted to a constant in  , any
SLP
, any
SLP  over
over  can be
evaluated over
can be
evaluated over  . Recording
the trace of such an evaluation, we obtain a new SLP that we call the
lift of
. Recording
the trace of such an evaluation, we obtain a new SLP that we call the
lift of  to
to  . Note that this is still an SLP over
. Note that this is still an SLP over  .
.
If  is actually an SLP algebra over
is actually an SLP algebra over  , then SLPs can be reinterpreted or lifted more
efficiently using
, then SLPs can be reinterpreted or lifted more
efficiently using  and the
and the  , while bypassing the recording technique. In
sections 5.1 and 5.2, this is what we did in
an ad hoc way for vectorization and forward differentiation.
But something similar can be done to lift SLPs to general SLP algebras
, while bypassing the recording technique. In
sections 5.1 and 5.2, this is what we did in
an ad hoc way for vectorization and forward differentiation.
But something similar can be done to lift SLPs to general SLP algebras
 . Given an input SLP
. Given an input SLP 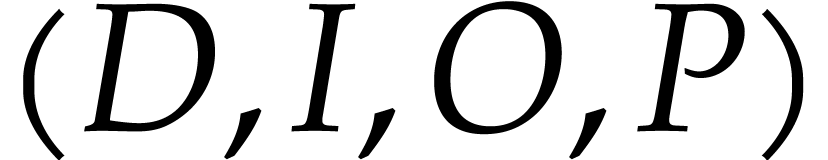 , we first renumber all data fields
in
, we first renumber all data fields
in  and the
and the  such that
they carry numbers
such that
they carry numbers  and such that each operations
acts on separate data fields (some optimizations are actually possible
here, but this is not crucial for the general idea). Essentially, it
then suffices to replace every instruction
and such that each operations
acts on separate data fields (some optimizations are actually possible
here, but this is not crucial for the general idea). Essentially, it
then suffices to replace every instruction  in
the input SLP by
in
the input SLP by  , while
substituting
, while
substituting 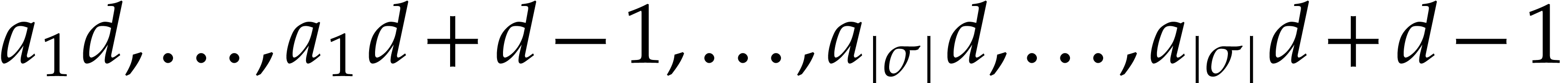 for the input arguments and
for the input arguments and 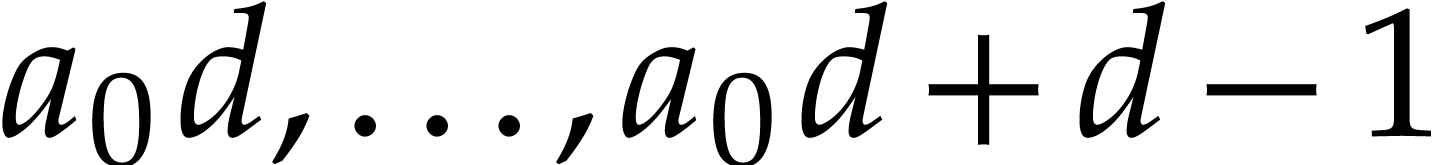 for the output arguments. The constant fields are
lifted using
for the output arguments. The constant fields are
lifted using  .
.
However, additional adjustments need to be made for instructions that
involve aliasing. For instance, assume that  is
the algebra of complex numbers over
is
the algebra of complex numbers over  ,
where
,
where  is implemented using the right-hand SLP
from (2.3). Assume that
is implemented using the right-hand SLP
from (2.3). Assume that 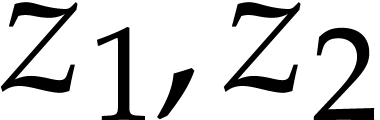 are
variables that get lifted into
are
variables that get lifted into  .
Then the instruction
.
Then the instruction  would a priori be
lifted into
would a priori be
lifted into
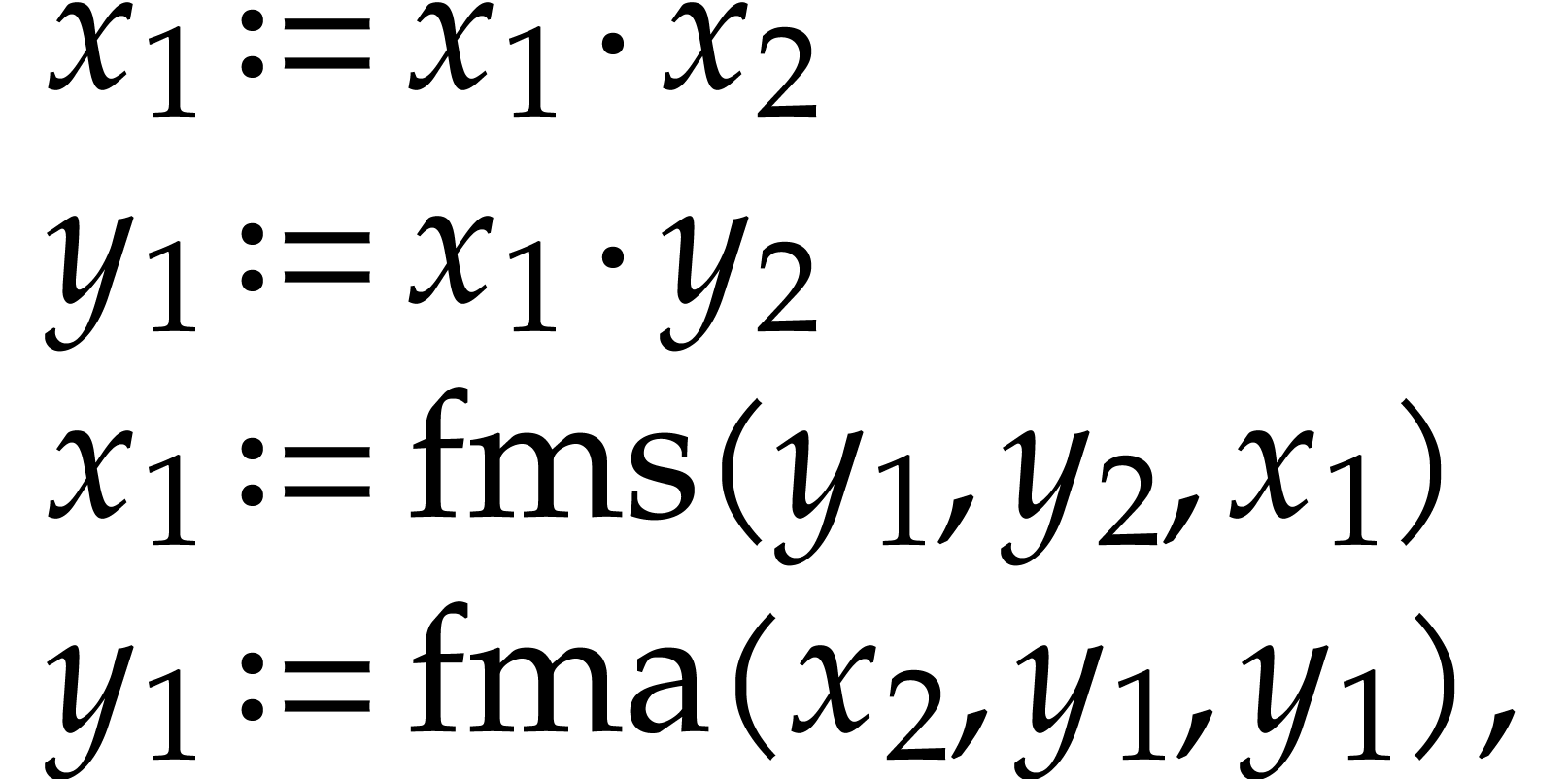 |
(5.3) |
which is incorrect due to the aliasing. We thus have to do some additional renaming and/or copying in order to restore the correctness. In our example, it suffices to replace (5.3) by
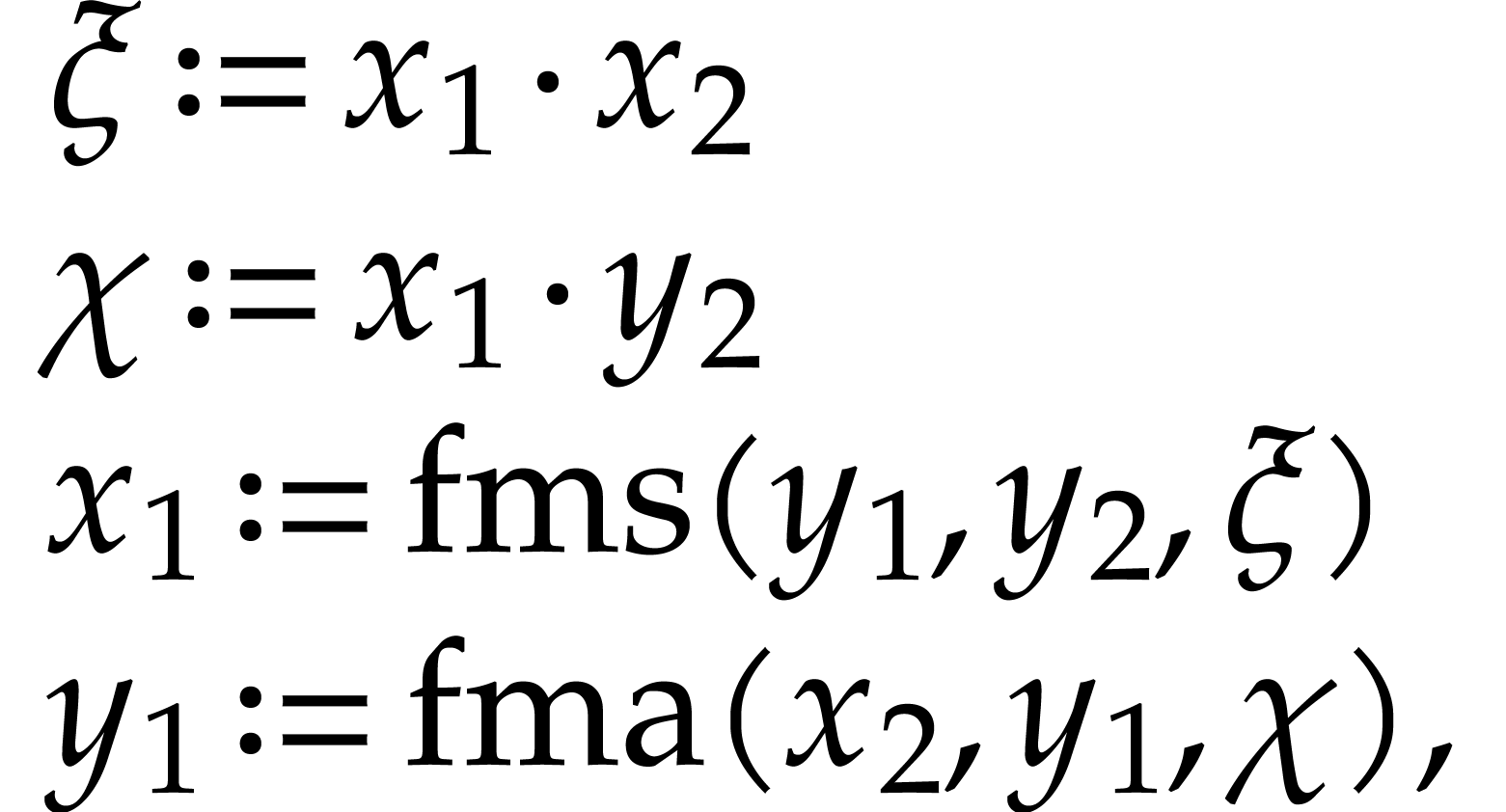
where  are separate scratch variables. This
corresponds to replacing our SLP (2.3) for complex
multiplication by the following one in presence of aliasing:
are separate scratch variables. This
corresponds to replacing our SLP (2.3) for complex
multiplication by the following one in presence of aliasing:
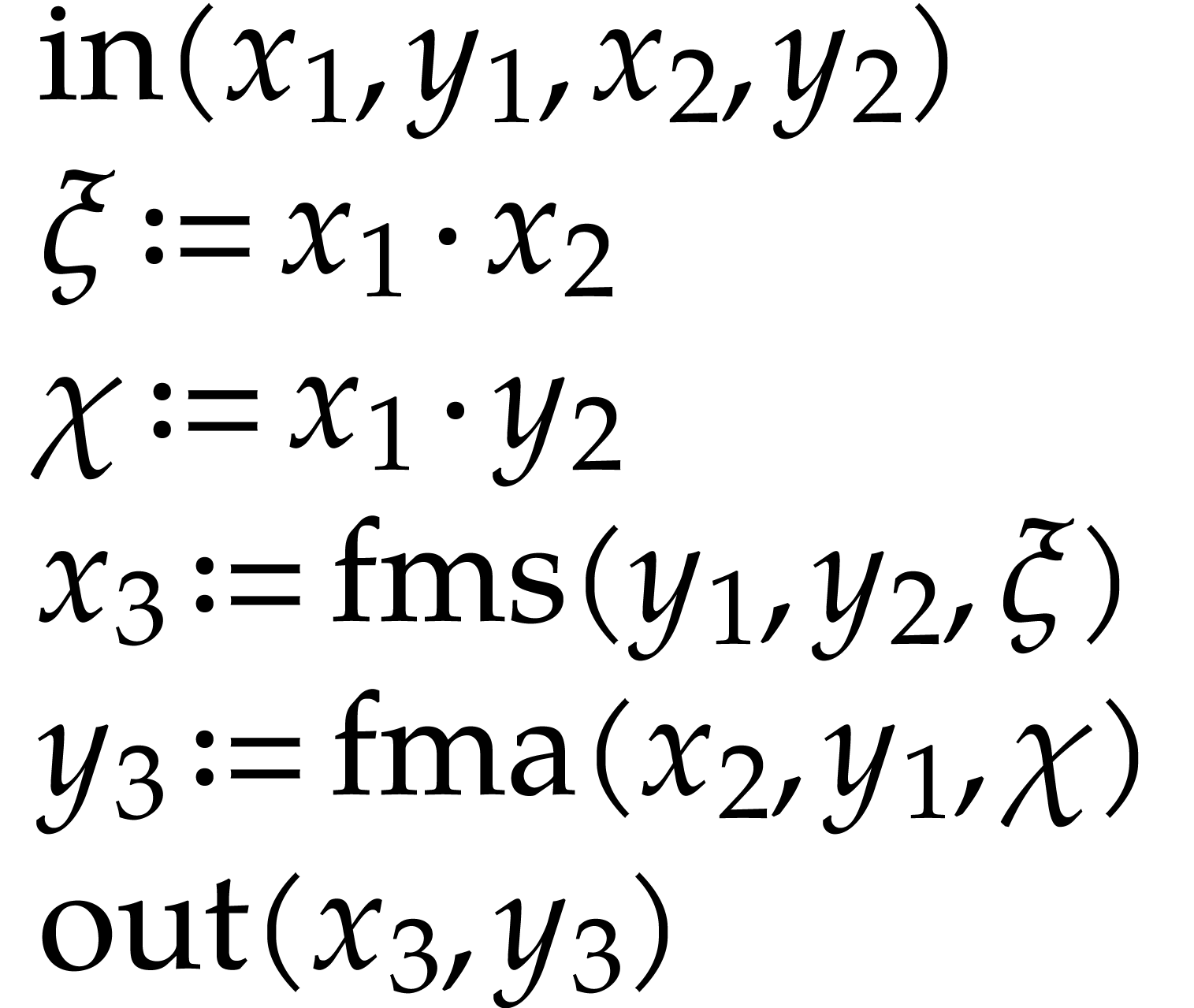 |
(5.4) |
In a similar way as at the end of sections 4.5 and 4.7,
we should also avoid putting too much register pressure on the scratch
variables  . This can be done
by circulating the scratch variables among
. This can be done
by circulating the scratch variables among  possibilities, as usual.
possibilities, as usual.
Note that it can be detected automatically whether an SLP like the right-hand of (2.3) needs to be corrected when some of the arguments are aliased. Moreover, the appropriate correction may depend on the precise arguments that are aliased. For instance, consider the following implementation of complex FMAs:
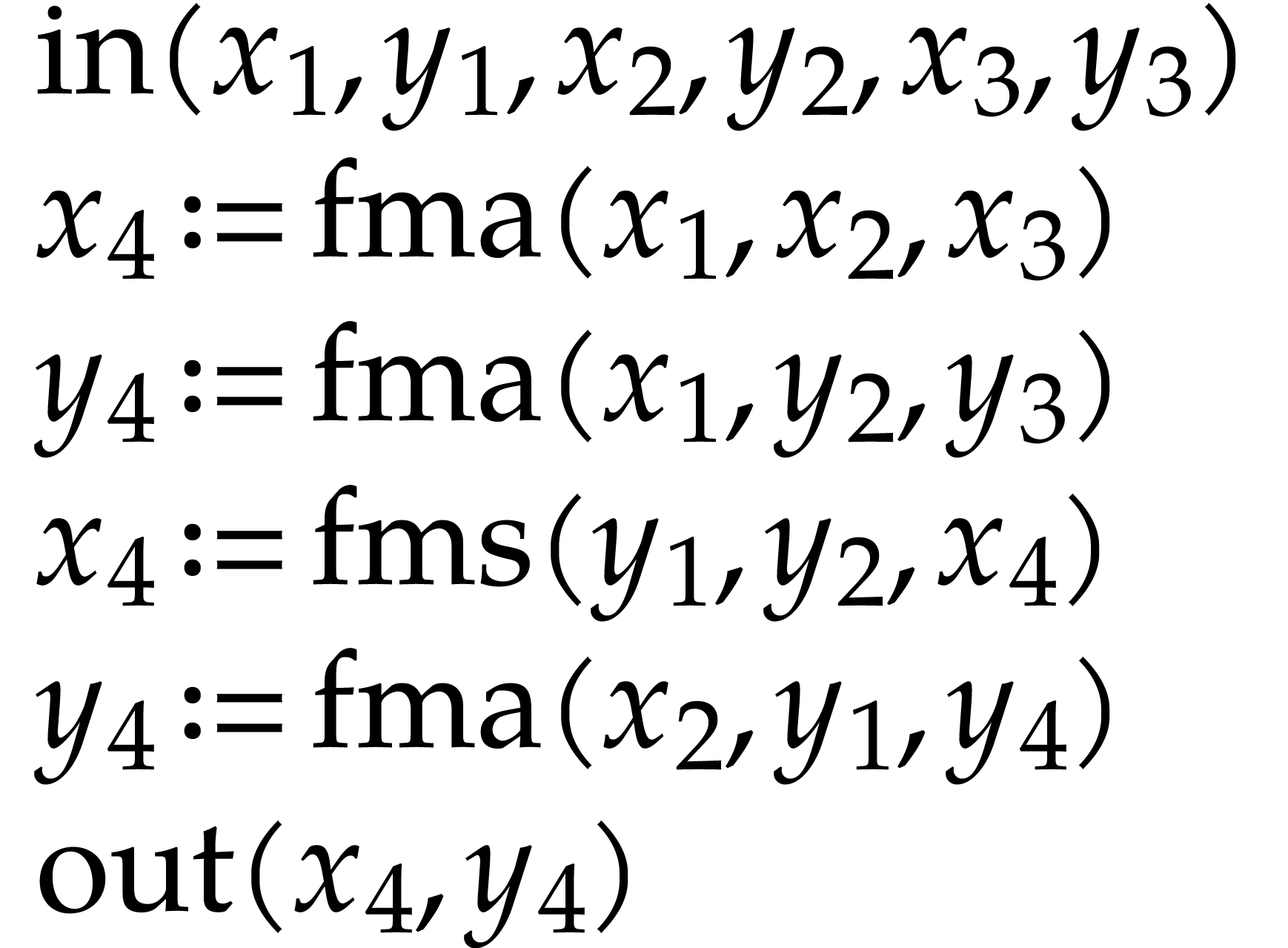
A similar correction as in (5.4) is needed when lifting
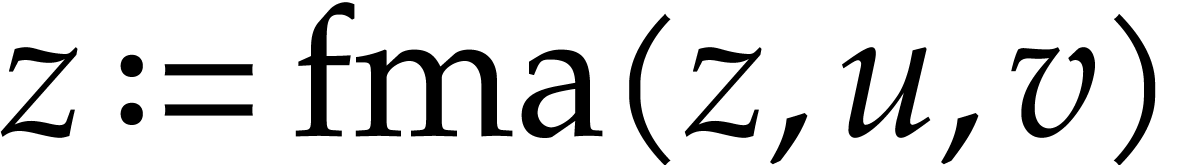 , but no correction is needed
when lifting
, but no correction is needed
when lifting 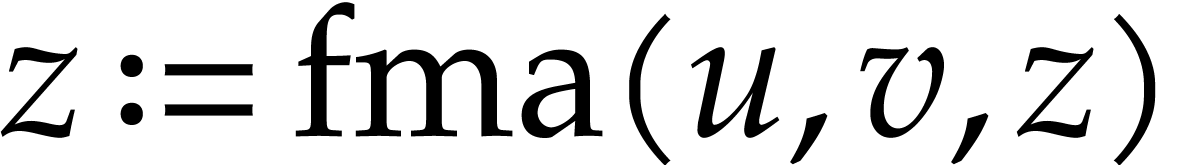 . In the
. In the
An interesting direction for future research would be to automatically combine certain instructions and lift them jointly. This would allow for heavier optimizations of the “joint lift” of the combined instructions. For instance, assume that we wish to lift an SLP that repeatedly contains the following pattern:
where 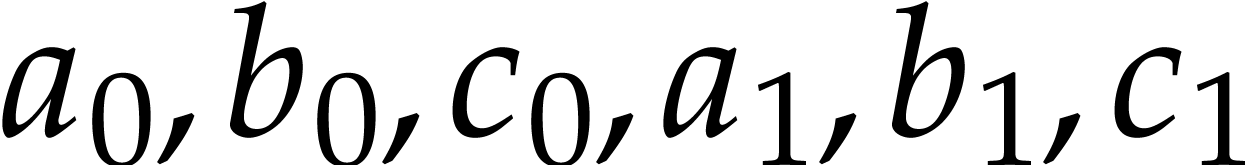 are pairwise distinct. We may view this
pair of instructions as a joint instruction
are pairwise distinct. We may view this
pair of instructions as a joint instruction
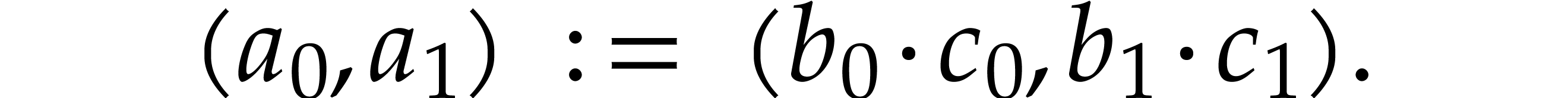
This instruction might be lifted as a single instruction over the SIMD
type  . As highlighted in
section 5.1, this typically yields a “joint
lift” of better quality than sequentially lifting the instructions
. As highlighted in
section 5.1, this typically yields a “joint
lift” of better quality than sequentially lifting the instructions
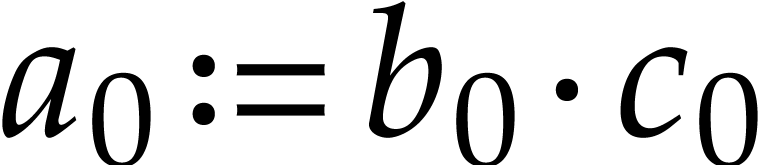 and
and 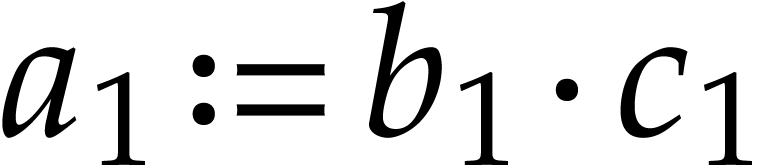 .
More generally, we expect rescheduling as in section 4.6 to
be an interesting optimization on this kind of joined lifts.
.
More generally, we expect rescheduling as in section 4.6 to
be an interesting optimization on this kind of joined lifts.
Ball arithmetic [60, 76] is a variant of interval arithmetic [91, 92, 102]. Given a numerical algorithm and an input, the aim is to automatically compute a rigorous bound for the error of the output. In our case, the algorithm will be given by an SLP.
The idea behind ball arithmetic is to systematically replace approximate
numbers by balls that enclose the true mathematical values. According to
this semantics, a ball lift of an operation  (which we will still denote by
(which we will still denote by  )
takes balls
)
takes balls  as inputs and produces a ball
as inputs and produces a ball  that satisfies the inclusion property:
that satisfies the inclusion property:
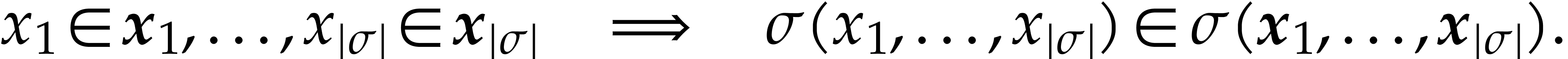
In order to construct such ball lifts, we also have to take into account rounding errors, when working with finite precision.
For instance, let  be the set of standard
IEEE-754 double precision floating point numbers. Given an operation
be the set of standard
IEEE-754 double precision floating point numbers. Given an operation
 on real numbers, let
on real numbers, let 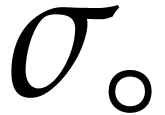 denote its correctly rounded variant on
denote its correctly rounded variant on  .
Given
.
Given 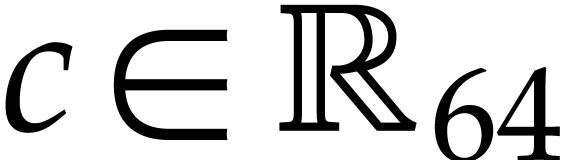 and
and 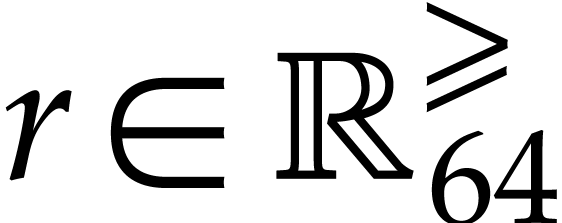 ,
let
,
let 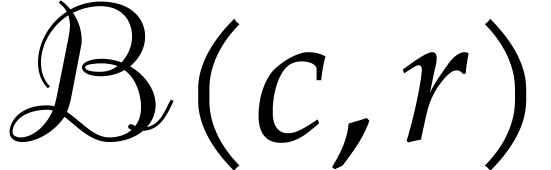 be the ball with center
be the ball with center  and radius
and radius  . Then the
standard arithmetic operations can be lifted as follows:
. Then the
standard arithmetic operations can be lifted as follows:
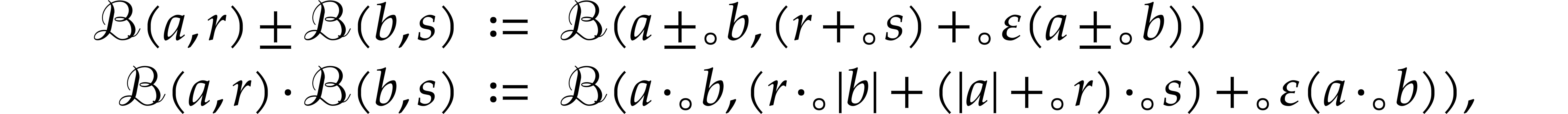
where 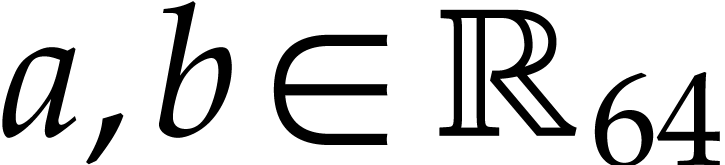 ,
, 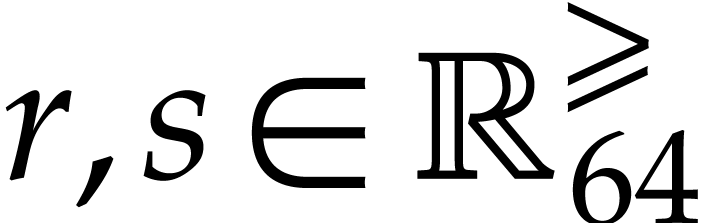 , and for all
, and for all 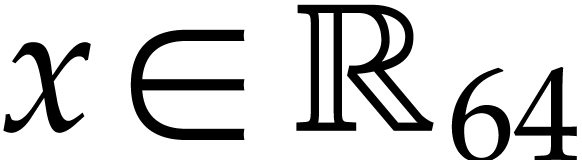 ,
,
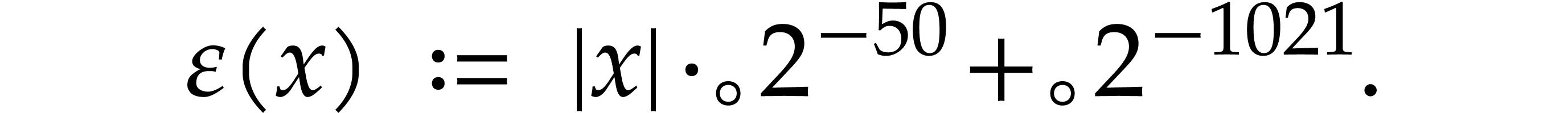
Other operations can be lifted similarly. Taking 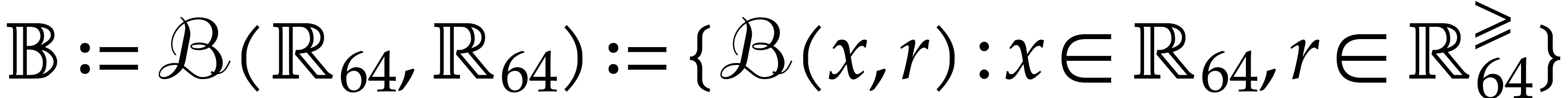 , this allows us to implement
, this allows us to implement  as an SLP algebra (note that
as an SLP algebra (note that  is not an algebra
in the mathematical sense though: remind Remark 5.2).
Lifting an SLP
is not an algebra
in the mathematical sense though: remind Remark 5.2).
Lifting an SLP  over
over  to
to
 , we obtain a new SLP
, we obtain a new SLP 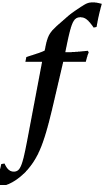 that computes the usual numerical evaluation of
that computes the usual numerical evaluation of  , together with a rigorous error
bound for the obtained approximate value.
, together with a rigorous error
bound for the obtained approximate value.
The SLP 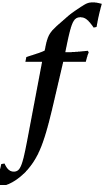 obtained through direct lifting has the
disadvantage that a lot of time is spent on evaluations of
obtained through direct lifting has the
disadvantage that a lot of time is spent on evaluations of  , i.e. on bounding rounding
errors. It turns out that this can entirely be avoided by slightly
increasing the radii of input balls. The precise amount of inflation can
be computed as a function of the input SLP
, i.e. on bounding rounding
errors. It turns out that this can entirely be avoided by slightly
increasing the radii of input balls. The precise amount of inflation can
be computed as a function of the input SLP  :
see [70, Theorem 5] for a formula. The fact our program
:
see [70, Theorem 5] for a formula. The fact our program
 is an SLP allows us to do this computation
statically, i.e. while building the output program
is an SLP allows us to do this computation
statically, i.e. while building the output program
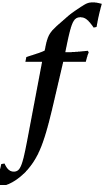 and not merely while executing it. This is not
possible for general purpose programs
and not merely while executing it. This is not
possible for general purpose programs  that may
involve loops of unpredictable lengths or recursions of unpredictable
depths.
that may
involve loops of unpredictable lengths or recursions of unpredictable
depths.
Ball arithmetic can be generalized [59, 70] to
balls with centers in more general algebras such as the complexification
 of
of  .
However, the formula
.
However, the formula  for the absolute value of a
complex number
for the absolute value of a
complex number 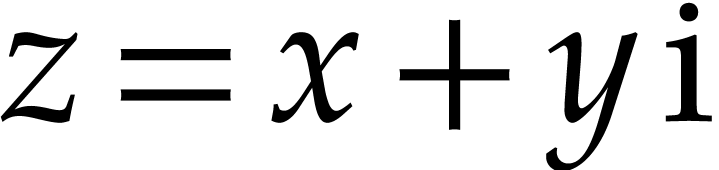 involves a square root, which is
fairly expensive to compute. In [70], we proposed to
compute these absolute values using the formula
involves a square root, which is
fairly expensive to compute. In [70], we proposed to
compute these absolute values using the formula  whenever we need to lift a product
whenever we need to lift a product  .
In
.
In  ,
where
,
where 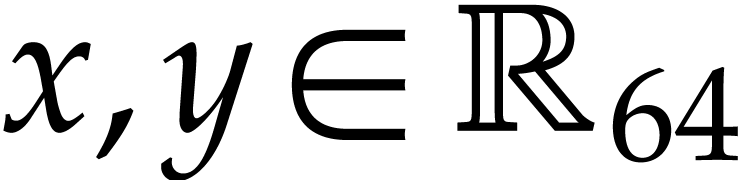 ,
, 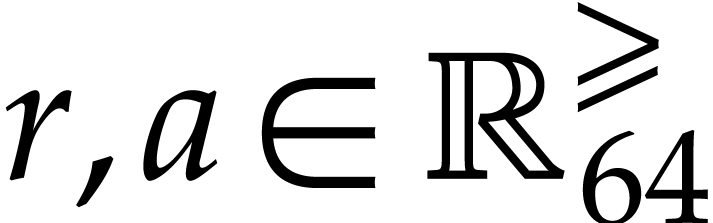 , and
, and 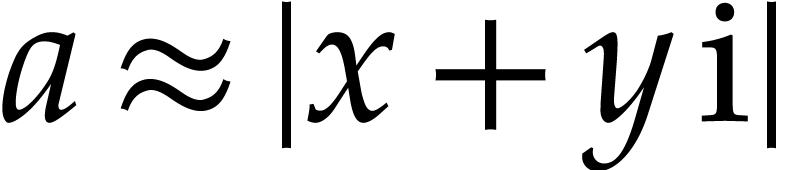 .
Ignoring rounding errors, we may implement the standard arithmetic
operations as follows:
.
Ignoring rounding errors, we may implement the standard arithmetic
operations as follows:
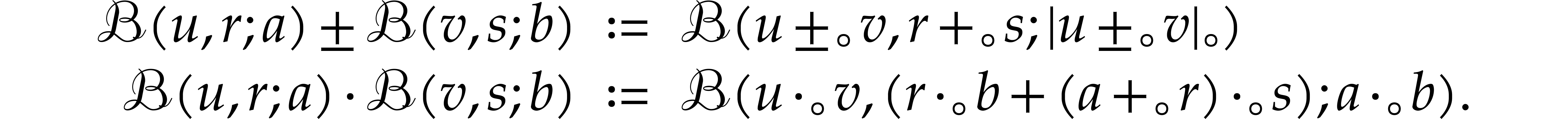
After lifting an SLP over  to
to 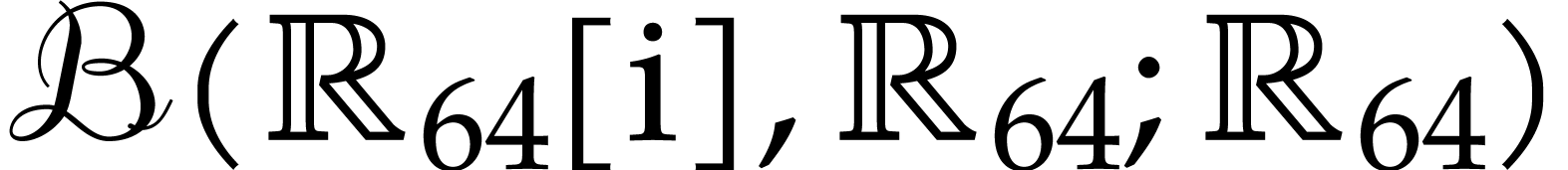 , we may again “forget” about the
absolute values and project the output down to
, we may again “forget” about the
absolute values and project the output down to 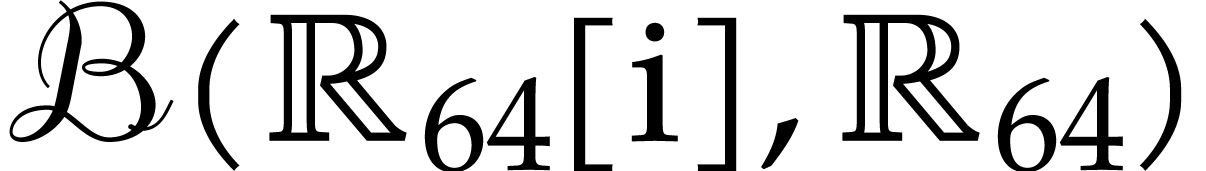 . Removing all dead code from the resulting SLP (see
section 4.2), we essentially obtain the same SLP as using
the ad hoc implementation from
. Removing all dead code from the resulting SLP (see
section 4.2), we essentially obtain the same SLP as using
the ad hoc implementation from
There are several ways to implement modular arithmetic in  when
when  . We refer
to [73] for a survey of efficient methods that can benefit
from SIMD acceleration. In this section, we will use a variant of
modular arithmetic that is based on machine double precision arithmetic,
but the material can easily be adapted to other variants.
. We refer
to [73] for a survey of efficient methods that can benefit
from SIMD acceleration. In this section, we will use a variant of
modular arithmetic that is based on machine double precision arithmetic,
but the material can easily be adapted to other variants.
As in the previous subsection, we assume that our hardware implements
the IEEE-754 standard for floating point arithmetic and we use rounding
to the nearest. Recall that integers in  can be
represented exactly in
can be
represented exactly in  . We
assume that our modulus is odd with
. We
assume that our modulus is odd with 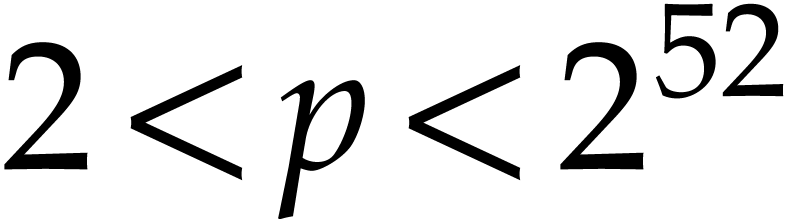 and also
assume that
and also
assume that 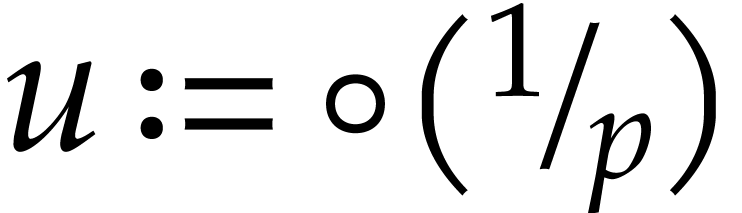 has been precomputed.
has been precomputed.
We represent a normalized residue modulo  as an integer in
as an integer in  between
between  and
and  . The normal form
. The normal form 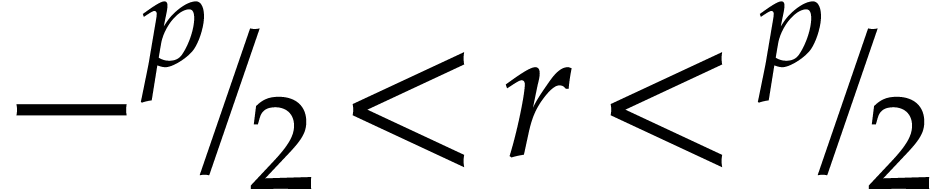 of an integer
of an integer  can be computed
efficiently using the
can be computed
efficiently using the  operation as follows:
operation as follows:
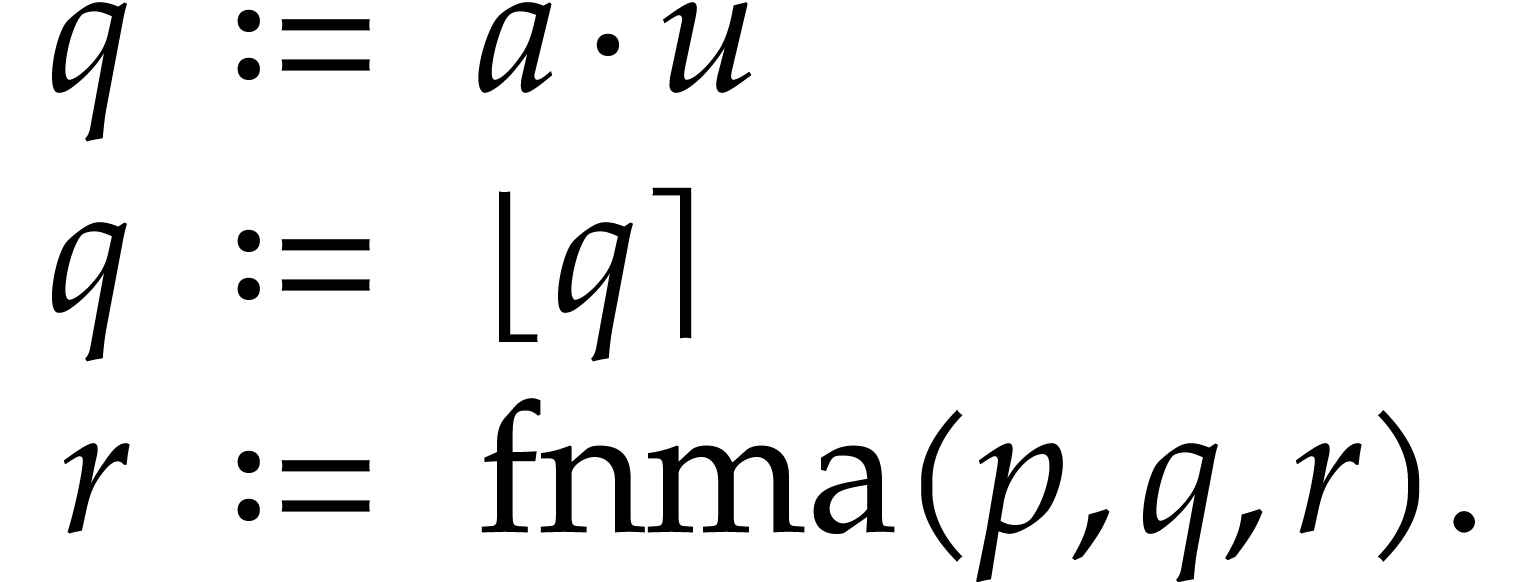 |
(5.5) |
Here 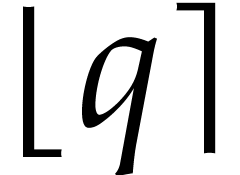 stands for the closest integer near
stands for the closest integer near 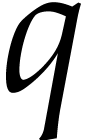 . Abbreviating this code by
. Abbreviating this code by  , this naturally leads to the
following algorithms to compute the modular sum, difference, and product
, this naturally leads to the
following algorithms to compute the modular sum, difference, and product
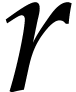 of
of  and
and 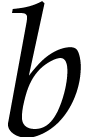 :
:
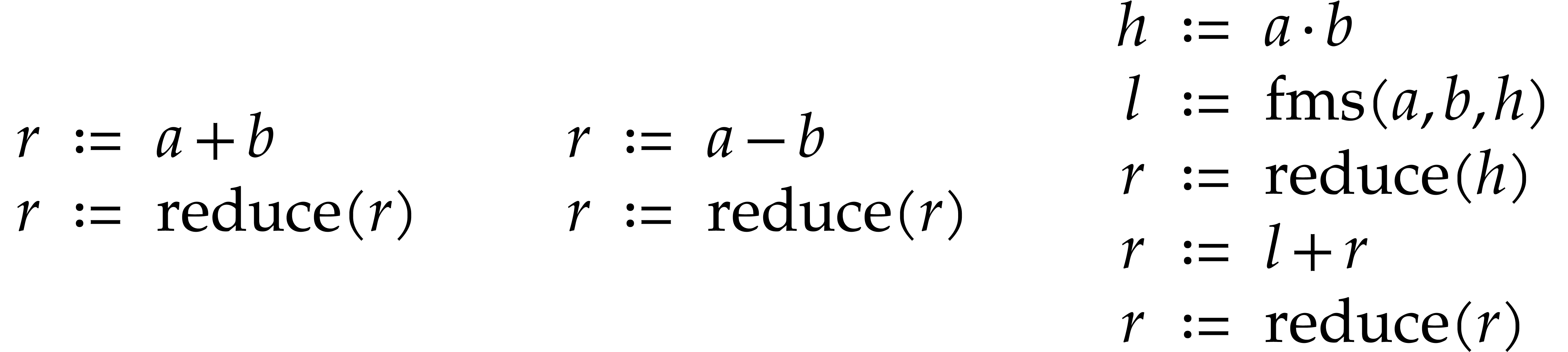 |
(5.6) |
Let  be the SLP algebra over
be the SLP algebra over  , where the arithmetic operations are
implemented in this way.
, where the arithmetic operations are
implemented in this way.
In the algorithms (5.6), we note that the bulk of the
computation time is spent on modular reductions. A common technique to
avoid reductions is to delay them as much as possible [28,
29, 54, 18, 105].
This can be achieved by switching to a non-normalized or
redundant representation of residues modulo  by integers in the range
by integers in the range  . In
the above algorithms (5.6), we may then suppress the final
reduction
. In
the above algorithms (5.6), we may then suppress the final
reduction 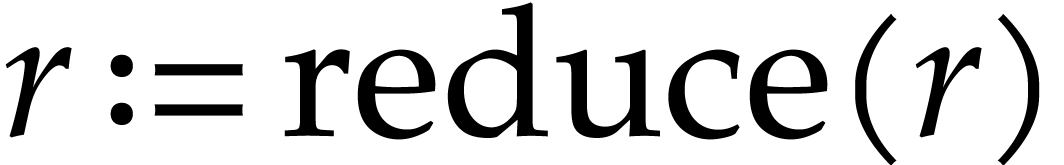 , whenever we are
able to guarantee that
, whenever we are
able to guarantee that 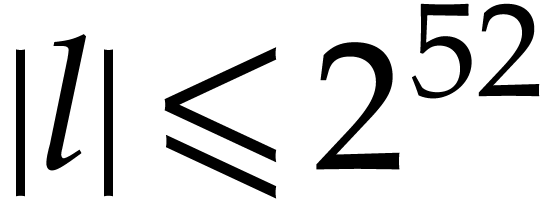 . In
the contrary case, we will say that the operation overflows for
the corresponding inputs
. In
the contrary case, we will say that the operation overflows for
the corresponding inputs  and
and 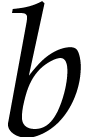 .
.
Let  be the SLP algebra that corresponds to the
above kind of non-normalized modular arithmetic:
be the SLP algebra that corresponds to the
above kind of non-normalized modular arithmetic:
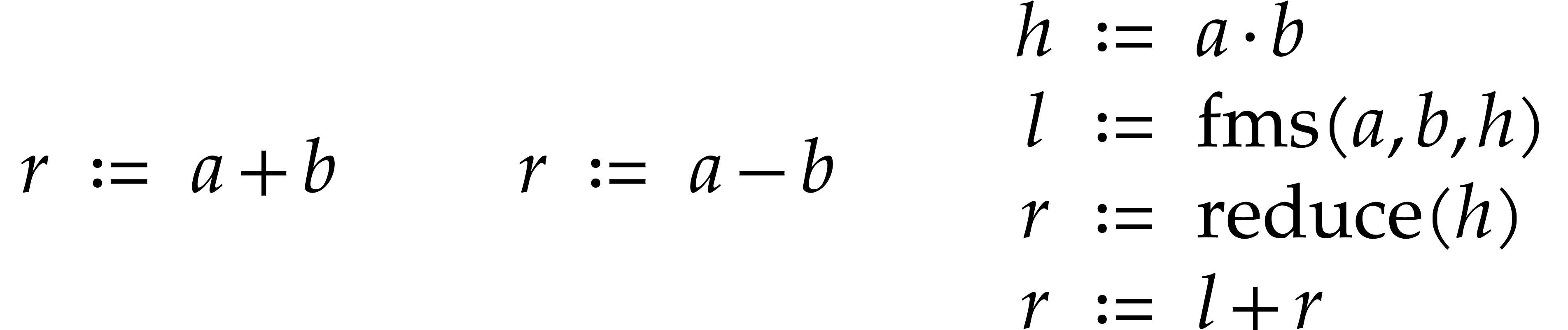 |
(5.7) |
We also extend 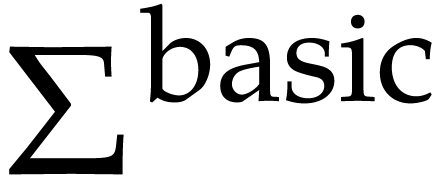 with an operation “
with an operation “ ” that is implemented as the
identity operation by default and as modular reduction (5.5)
on
” that is implemented as the
identity operation by default and as modular reduction (5.5)
on 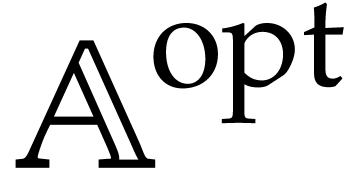 . Now consider an SLP
. Now consider an SLP  over
over  with inputs
with inputs 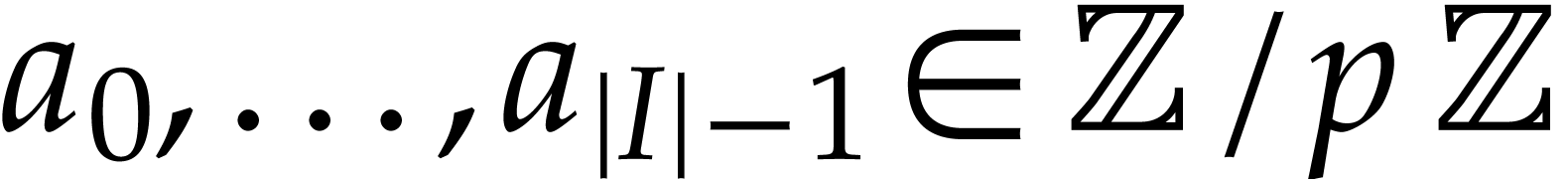 . In absence of overflows, its execution over
. In absence of overflows, its execution over
 produces the same output modulo
produces the same output modulo  as its execution over
as its execution over  . The
correctness of the optimized execution over
. The
correctness of the optimized execution over  can
be restored in presence of overflows by inserting a reduction after
every instruction that may cause an overflow.
can
be restored in presence of overflows by inserting a reduction after
every instruction that may cause an overflow.
How to determine and correct the instructions that may cause overflows?
In [72, section 4.1], we described a simple greedy
algorithm for doing this. Roughly speaking, we start with the bounds
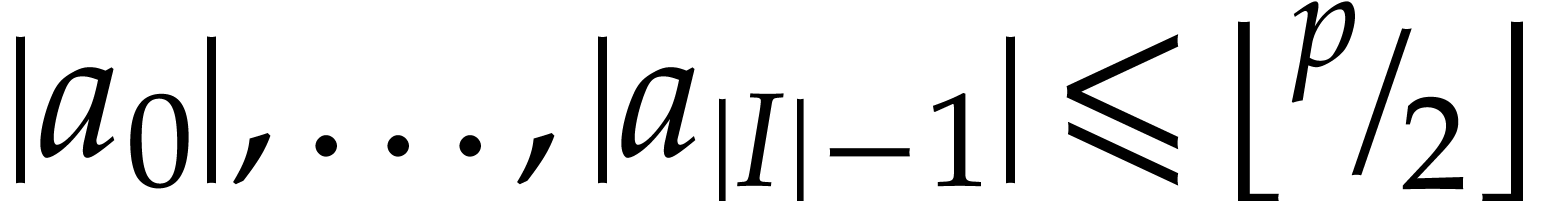 for the absolute values of our inputs. Using a
linear pass through our SLP, we next compute bounds for the results of
every instruction: for additions and subtractions
for the absolute values of our inputs. Using a
linear pass through our SLP, we next compute bounds for the results of
every instruction: for additions and subtractions 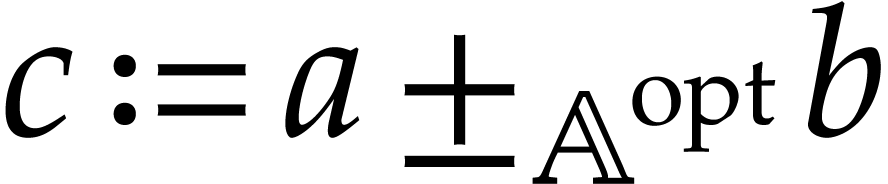 , we have
, we have 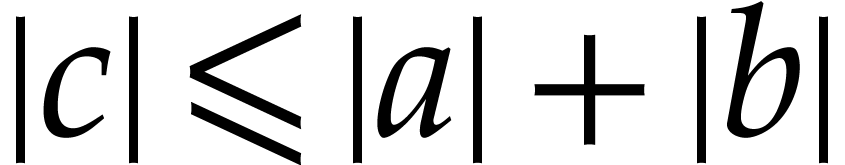 ;
for multiplications
;
for multiplications 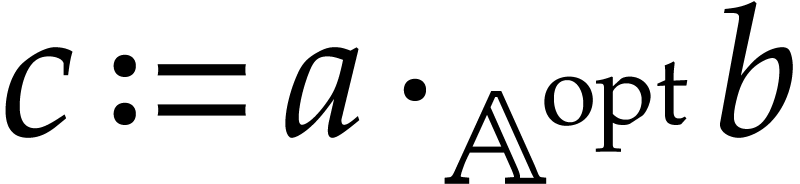 , we have
, we have
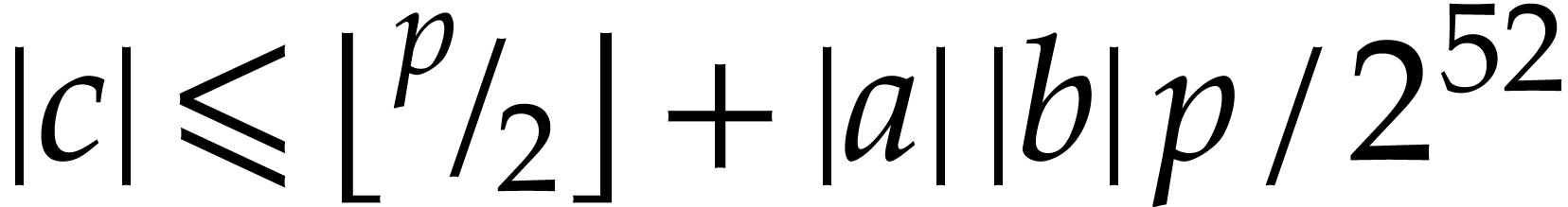 . Whenever the bound for
. Whenever the bound for 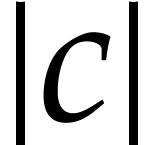 exceeds
exceeds 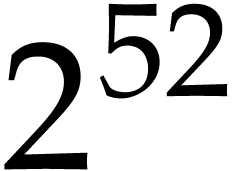 ,
we insert the instruction
,
we insert the instruction 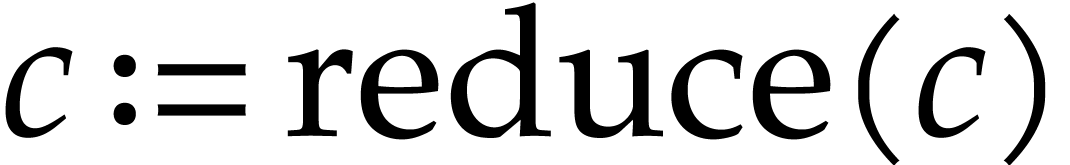 ,
and replace the bound by
,
and replace the bound by 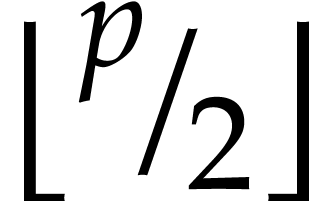 .
Optionally, we also insert instructions to reduce all output values at
the end of the SLP.
.
Optionally, we also insert instructions to reduce all output values at
the end of the SLP.
The redundant representation for the residues modulo  allows for some additional optimizations. For instance, we may use the
following algorithm for the fused operation
allows for some additional optimizations. For instance, we may use the
following algorithm for the fused operation 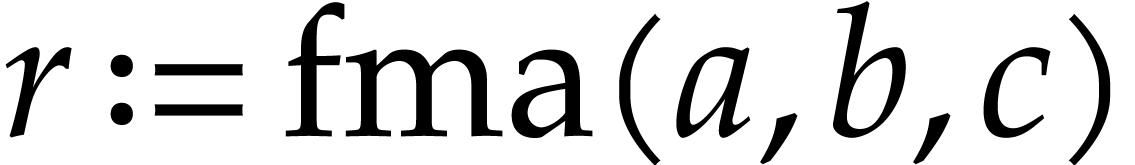 modulo
modulo  :
:
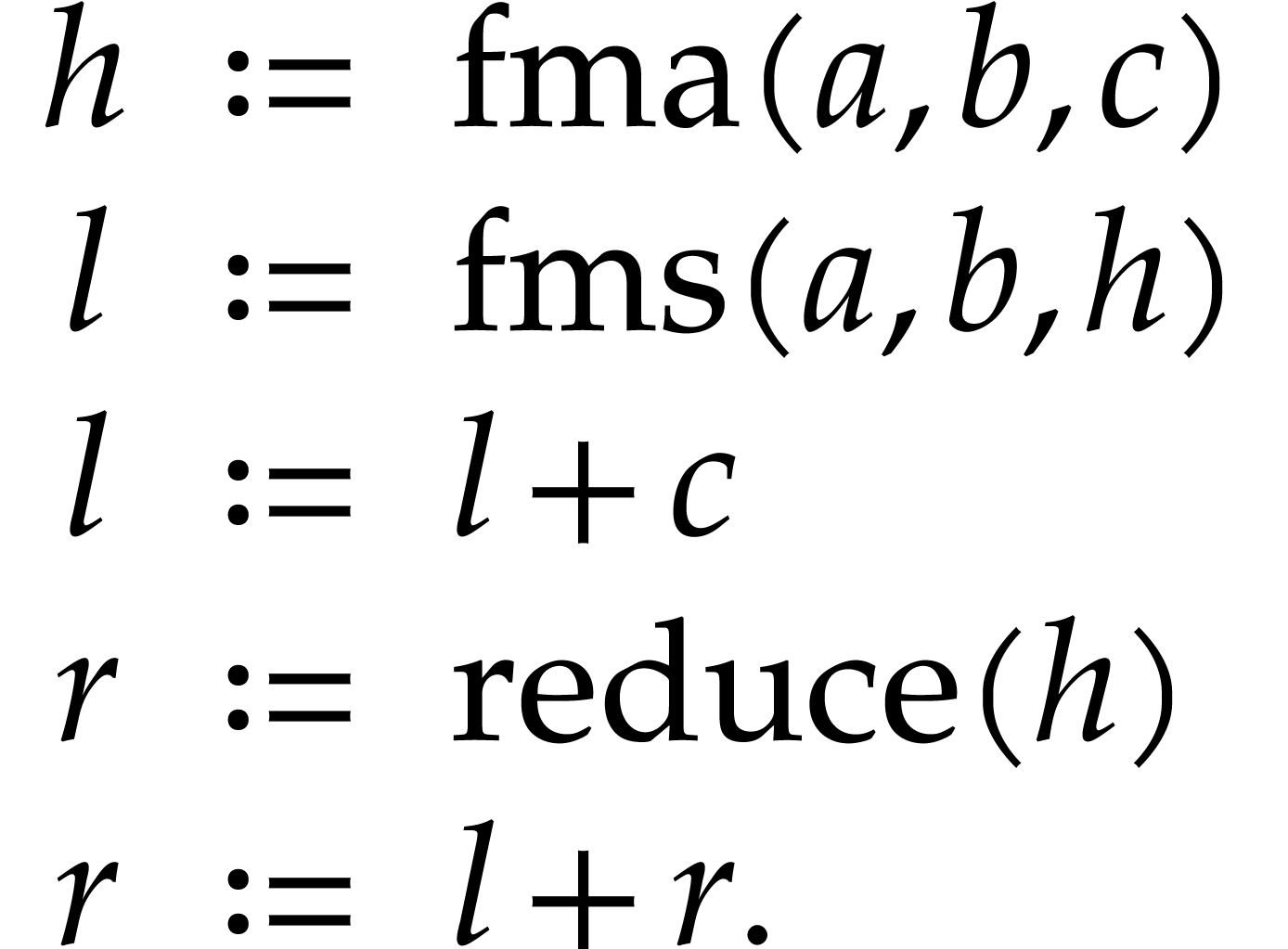
Although this implementation is not faster than the default
implementation (a modular multiplication followed by a modular
addition), it yields a better bound for the result: we obtain  instead of
instead of  .
This optimization may therefore help to lower the number of reductions
that need to be inserted in order to counter potential overflows. Note
that this subtle improvement is hard to find automatically and also
requires us to include the “fma” operation into
.
This optimization may therefore help to lower the number of reductions
that need to be inserted in order to counter potential overflows. Note
that this subtle improvement is hard to find automatically and also
requires us to include the “fma” operation into  (remember the discussion in section 2.2).
(remember the discussion in section 2.2).
Let us finally investigate the role of the modulus  . In a typical C++ implementation, this is
either a template parameter (in which case a recompilation is necessary
in order to use a new
. In a typical C++ implementation, this is
either a template parameter (in which case a recompilation is necessary
in order to use a new  ) or we
pass it as an additional function argument (in which case, we cannot
exploit special properties of
) or we
pass it as an additional function argument (in which case, we cannot
exploit special properties of  at compile time).
In our SLP setting, we dynamically generate specific code for any
required modulus
at compile time).
In our SLP setting, we dynamically generate specific code for any
required modulus  , while
relying on the ability to “efficiently generate disposable machine
code”. The specific value of
, while
relying on the ability to “efficiently generate disposable machine
code”. The specific value of  was for
instance used during the above bound computations. Certain
simplifications may also exploit it, e.g. if a constant
happens to be a multiple of
was for
instance used during the above bound computations. Certain
simplifications may also exploit it, e.g. if a constant
happens to be a multiple of  plus zero, one, or
minus one.
plus zero, one, or
minus one.
We may sometimes prefer to create SLPs for generic moduli  . This remains possible, e.g. by
treating
. This remains possible, e.g. by
treating  as an input variable when recording. Of
course, special restrictions will apply in this case, since it is no
longer possible to do static optimizations that take into account the
specific value of
as an input variable when recording. Of
course, special restrictions will apply in this case, since it is no
longer possible to do static optimizations that take into account the
specific value of  . For
instance, it is necessary to tweak the above procedure to counter
overflows: the bound
. For
instance, it is necessary to tweak the above procedure to counter
overflows: the bound 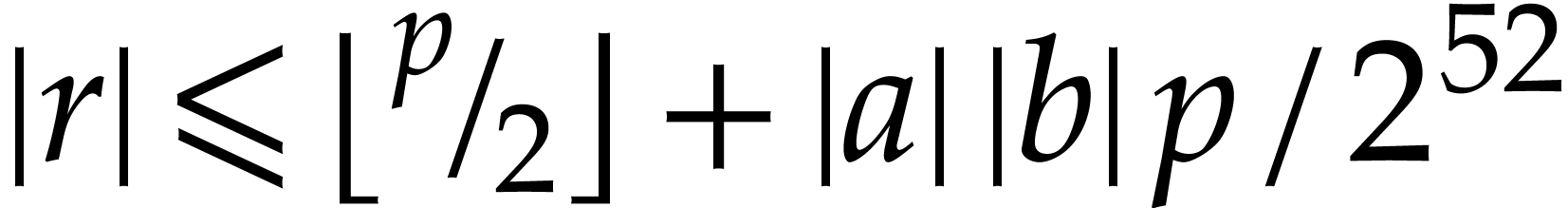 for multiplication must be
replaced by
for multiplication must be
replaced by 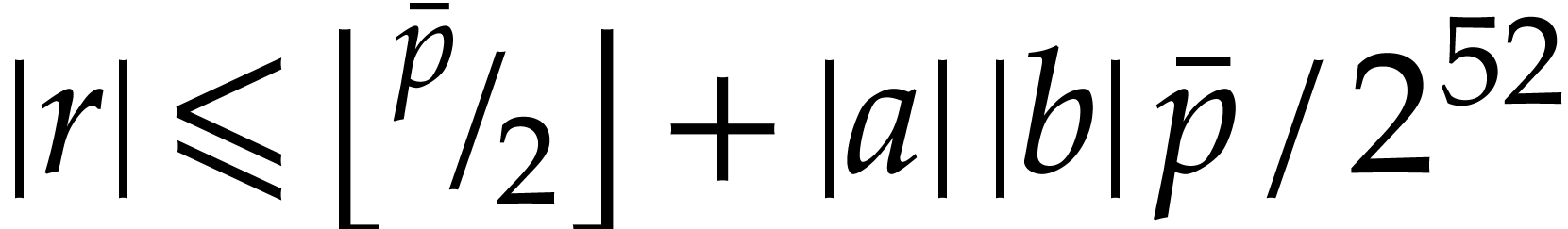 , where
, where 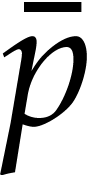 is a fixed upper bound for the target moduli
is a fixed upper bound for the target moduli  .
.
There are various ways to conduct numerical computations with a
precision that exceeds the hardware precision. Popular libraries like
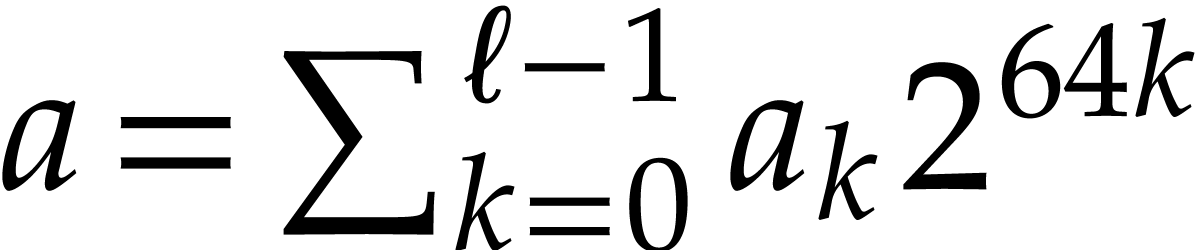 , where
, where 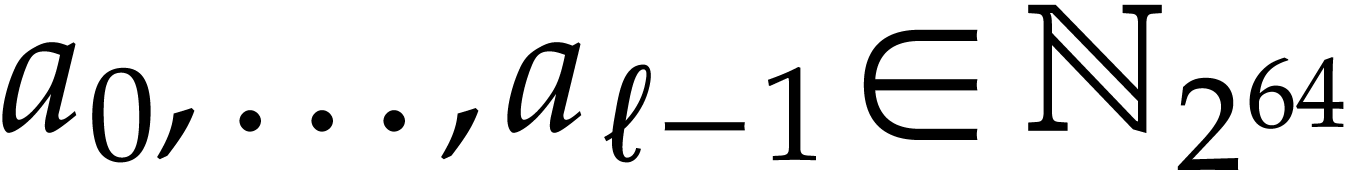 are
machine integers that are often called limbs. The efficient
implementation of basic arithmetic then relies on hardware support for
carry handling. For instance, the addition of two numbers of
are
machine integers that are often called limbs. The efficient
implementation of basic arithmetic then relies on hardware support for
carry handling. For instance, the addition of two numbers of  limbs is implemented as follows on traditional hardware:
limbs is implemented as follows on traditional hardware:
 |
(5.8) |
Unfortunately, this code is not an SLP according to our definition, because the semantics of the carry handling is implicit: if this were an SLP, then the three additions would be independent, so permuting them in any order would yield an equivalent SLP. Various approaches to reconcile carry handling with our SLP framework will be presented in a forthcoming paper. Of course, one may also directly generate assembly code for programs like (5.8), as a function of the desired extended precision [2].
Another disadvantage of the reliance on carries is that SIMD units do
not always support them. For instance, neither 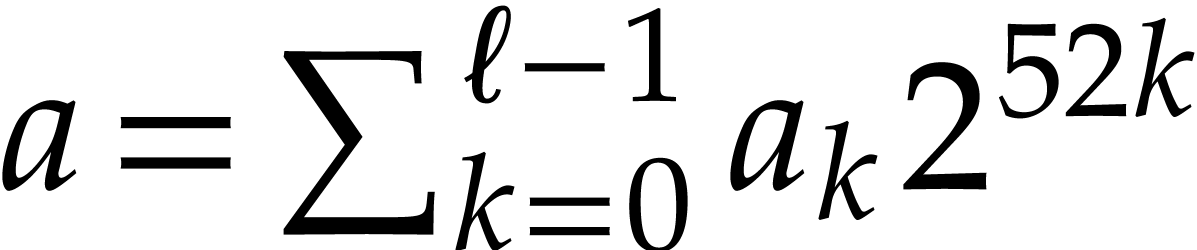 with
with 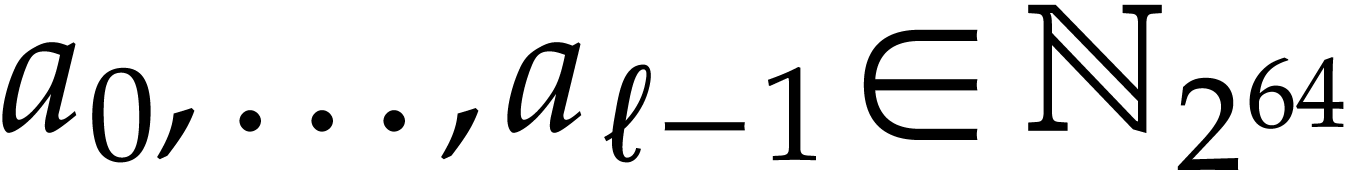 , and reserve the
, and reserve the  highest bits of
highest bits of 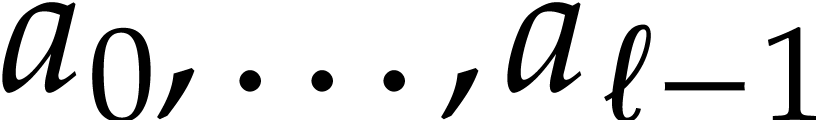 for carry handling. This
representation is particularly interesting on recent
for carry handling. This
representation is particularly interesting on recent 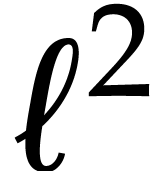 cycles [50,
31].
cycles [50,
31].
On CPUs and GPUs without efficient carry handling or IFMA instructions,
one may rely on floating point arithmetic for efficient SIMD
implementations of extended precision arithmetic. This is particularly
interesting if the hardware favors floating point over integer
arithmetic. In [69], we showed how to efficiently implement
medium precision fixed point arithmetic in this way. Fixed point numbers
can be represented redundantly as 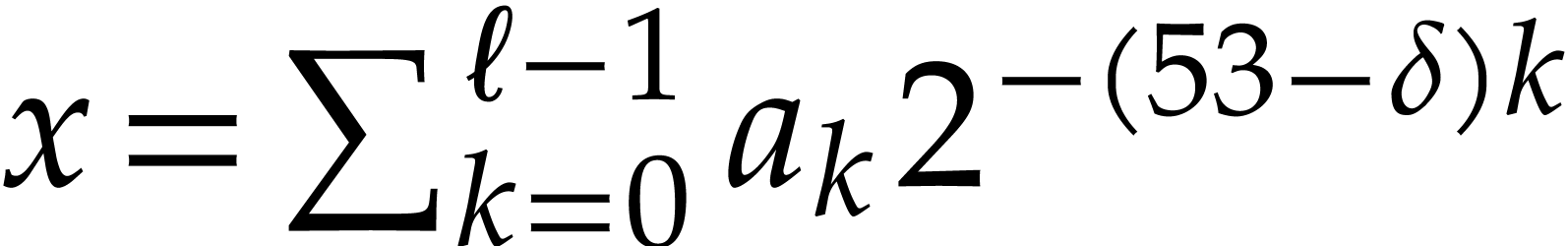 ,
with
,
with 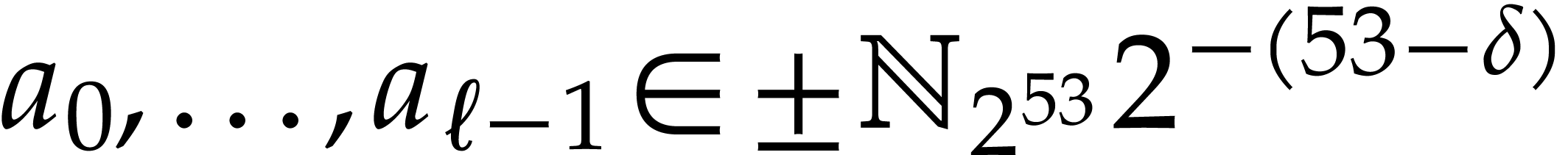 , where
, where  is a small number that corresponds to the number of “carry
bits” (one typically has
is a small number that corresponds to the number of “carry
bits” (one typically has  ).
The unnormalized SIMD multiplication of two such numbers takes
approximately
).
The unnormalized SIMD multiplication of two such numbers takes
approximately 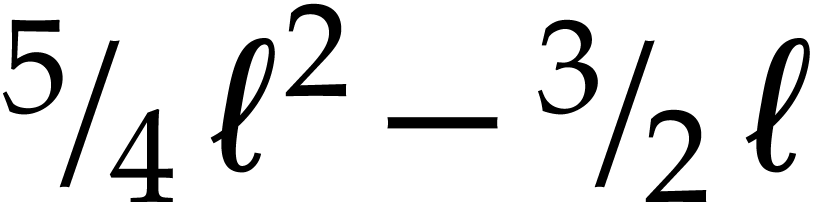 cycles. The techniques from [69] can be adapted to multiple precision integer arithmetic.
cycles. The techniques from [69] can be adapted to multiple precision integer arithmetic.
The above fixed point numbers form an SLP algebra, when  and
and  are fixed. As in the case of modular
arithmetic, there is an operation “
are fixed. As in the case of modular
arithmetic, there is an operation “ ”
to put numbers in an almost normal form with
”
to put numbers in an almost normal form with 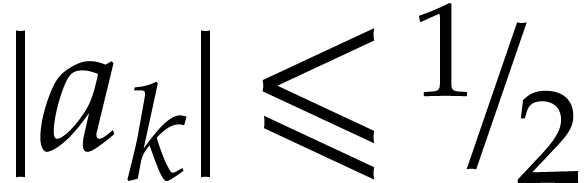 for
for
 . Using a similar greedy
algorithm as in the previous subsection, we may detect potential
overflows and deal with them by inserting appropriate reductions. In the
case of fixed point arithmetic, this gives rise to a trade-off: if we
increase
. Using a similar greedy
algorithm as in the previous subsection, we may detect potential
overflows and deal with them by inserting appropriate reductions. In the
case of fixed point arithmetic, this gives rise to a trade-off: if we
increase  by one, then we may lower the number of
reductions, but also lose
by one, then we may lower the number of
reductions, but also lose  bits of precision.
bits of precision.
We may next develop floating point arithmetic on top of integer or fixed
point arithmetic by managing all exponents ourselves. This approach is
for instance used in
Another way to extend the precision of floating point arithmetic is to
use compensated algorithms such as 2Sum [89]. In that case,
a floating point number with 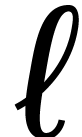 -fold
precision is represented as
-fold
precision is represented as  ,
where
,
where 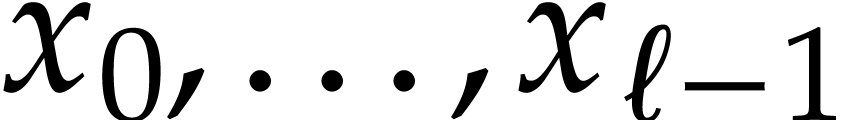 are hardware floating point numbers that
do not overlap (for double precision, this typically means that
are hardware floating point numbers that
do not overlap (for double precision, this typically means that 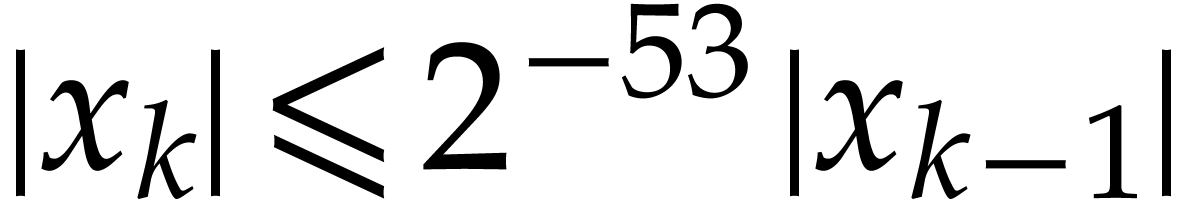 for
for  ).
Algorithms for basic arithmetic operations in doubled precision (
).
Algorithms for basic arithmetic operations in doubled precision (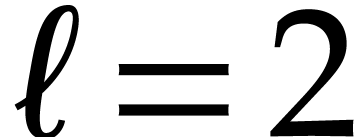 ) go back to [25]. We
refer to [99, 12, 78] for
generalizations to higher precisions. For a fixed value of
) go back to [25]. We
refer to [99, 12, 78] for
generalizations to higher precisions. For a fixed value of 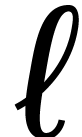 , this type of arithmetic again gives rise to
an SLP algebra. Since the representation is normalized, no special
reductions are needed to counter carry overflows. (However, additional
efforts are required in order to fully treat floating point errors,
overflows, and underflows.) Unfortunately, the overhead of the
compensated algorithms approach tends to increase rapidly as a function
of
, this type of arithmetic again gives rise to
an SLP algebra. Since the representation is normalized, no special
reductions are needed to counter carry overflows. (However, additional
efforts are required in order to fully treat floating point errors,
overflows, and underflows.) Unfortunately, the overhead of the
compensated algorithms approach tends to increase rapidly as a function
of 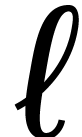 , which limits its
practical usefulness to the case when
, which limits its
practical usefulness to the case when 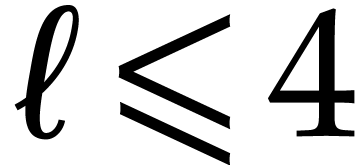 .
.
In this section, we discuss several applications for which we started using or plan to use our SLP libraries. We will highlight the added value of the SLP framework, and also investigate limitations and ideas to work around them. The list of selected applications is by no means exhaustive, but it will allow us to cover a variety of issues that are relevant for the development of SLP libraries.
Numerical homotopy continuation [4, 104] is the archetype application of SLPs. Assume that we wish to solve a polynomial system
 |
(6.1) |
where  . Assume also that we
can construct a “similar” system
. Assume also that we
can construct a “similar” system
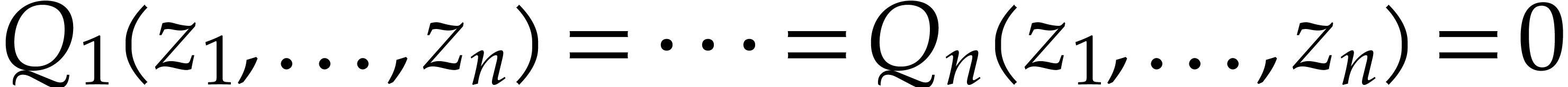 |
(6.2) |
that is easy to solve. This typically means that both systems have the
same number of solutions and the same total degrees:  . Now consider the following system that
depends a “time” parameter
. Now consider the following system that
depends a “time” parameter 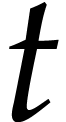 :
:
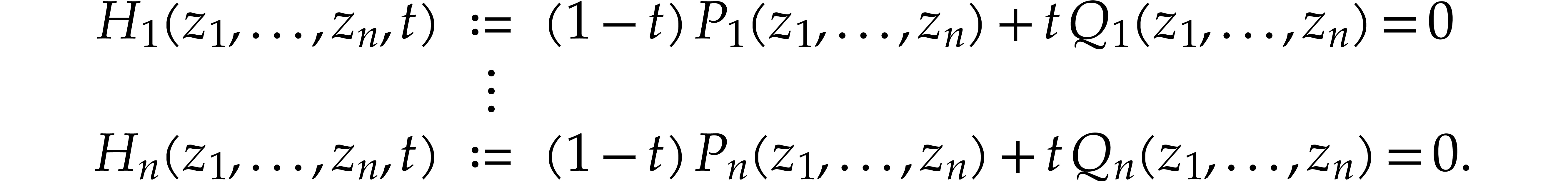
For 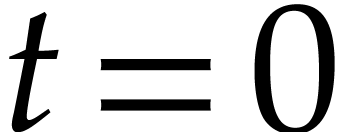 and
and 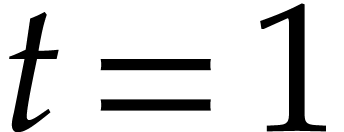 this system
reduces to (6.1) and (6.2), respectively. The
idea is then to follow the solutions of (6.2) from
this system
reduces to (6.1) and (6.2), respectively. The
idea is then to follow the solutions of (6.2) from 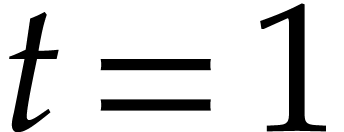 to
to 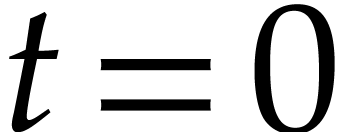 . This
can be achieved using various “path tracking” algorithms.
The most straightforward method uses Euler–Newton iterations:
given an approximate solution
. This
can be achieved using various “path tracking” algorithms.
The most straightforward method uses Euler–Newton iterations:
given an approximate solution 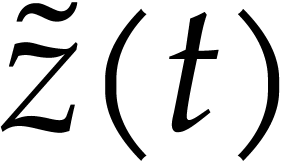 at time
at time 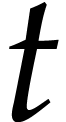 , we get an approximate solution
, we get an approximate solution
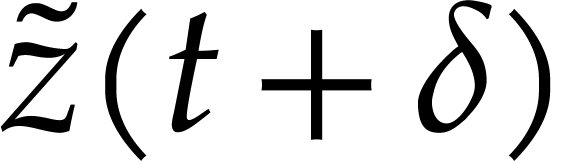 at time
at time  using
using
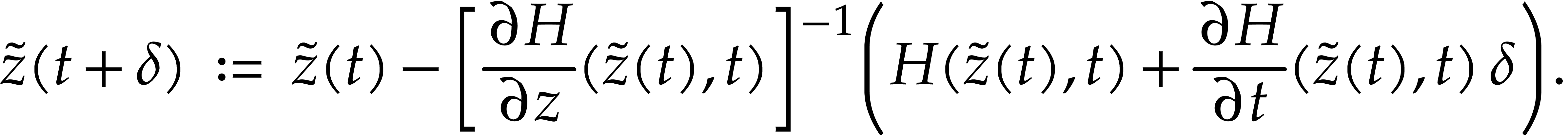 |
(6.3) |
This formula can be used both as a predictor (with 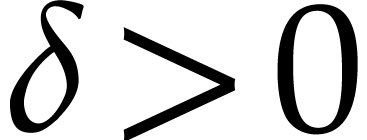 ) and as a corrector (with
) and as a corrector (with 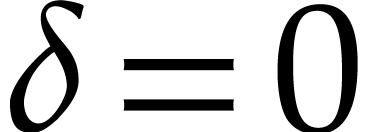 ). One typically alternates prediction and
correction steps. In order to control the step-size
). One typically alternates prediction and
correction steps. In order to control the step-size  , one uses a predicate for deciding whether a
step needs to be accepted: in case of acceptance, we increase the
step-size (say
, one uses a predicate for deciding whether a
step needs to be accepted: in case of acceptance, we increase the
step-size (say 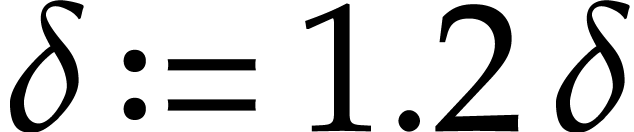 ); otherwise,
we decrease it (say
); otherwise,
we decrease it (say 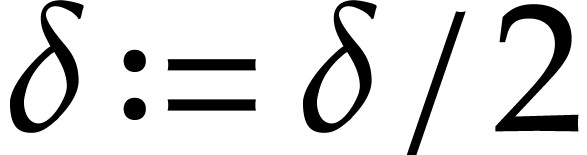 ). A
simple predicate that one may use is
). A
simple predicate that one may use is
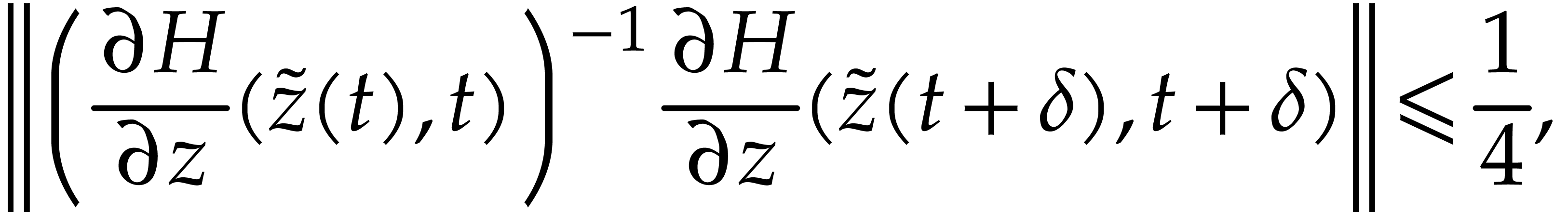 |
(6.4) |
but other predicates may be suitable for certain systems. The quality of
the first order approximation (6.3) can also be improved:
if we have approximations 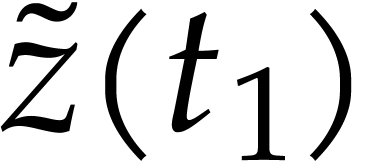 and
and 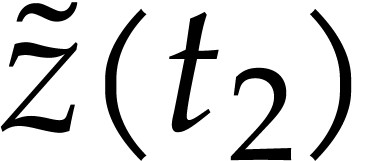 of the solution
of the solution 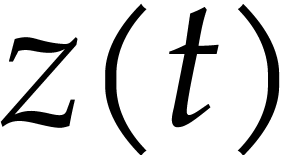 at two successive times
at two successive times 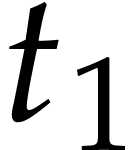 ,
, 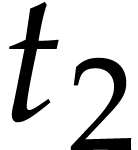 ,
together with approximations
,
together with approximations 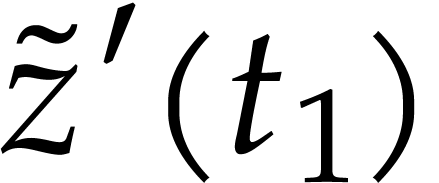 and
and 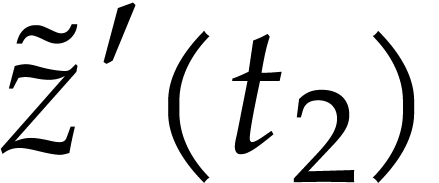 of the gradient
of the gradient 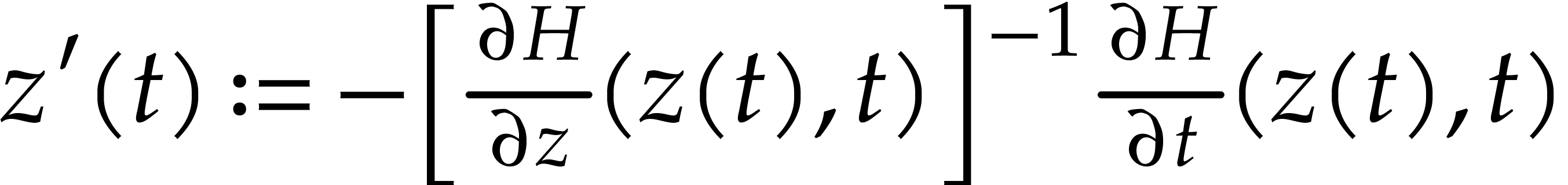 ,
then we may fit
,
then we may fit 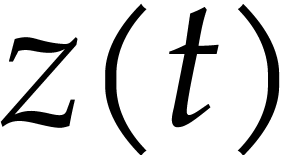 using a polynomial of degree
using a polynomial of degree
 or
or  ,
and use that to obtain a higher order approximation at a new time
,
and use that to obtain a higher order approximation at a new time 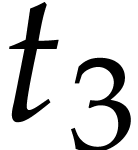 .
.
In the context of this paper, it is convenient to regard our systems as
zeros of polynomial mappings 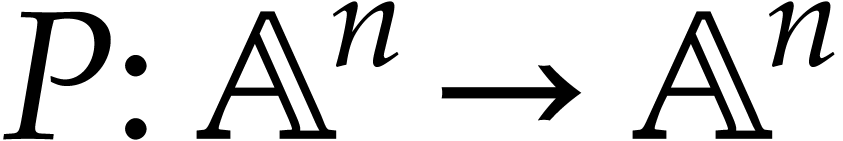 ,
,
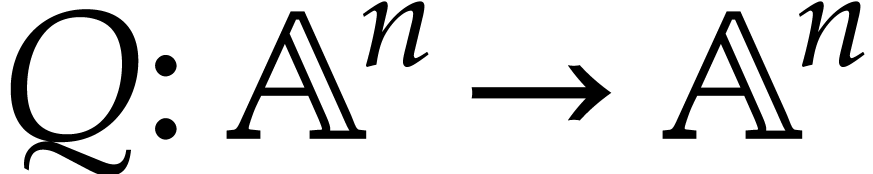 , and
, and 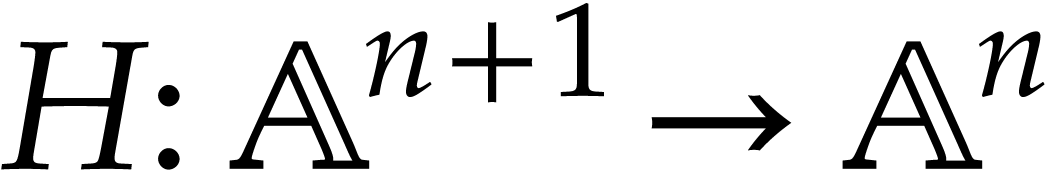 that are given through SLPs. Using automatic differentiation, we may
then construct SLPs for
that are given through SLPs. Using automatic differentiation, we may
then construct SLPs for 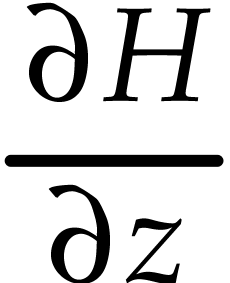 and
and 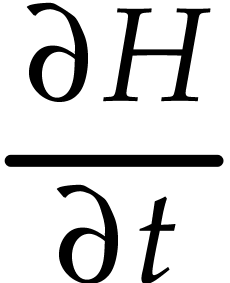 . We may also record linear algebra routines
for matrix multiplication, inversion, and norm computation. This enables
us to construct SLPs for steppers (6.3) and verifiers (6.4).
. We may also record linear algebra routines
for matrix multiplication, inversion, and norm computation. This enables
us to construct SLPs for steppers (6.3) and verifiers (6.4).
The SLP framework has several advantages here. If our polynomials are
sparse, then evaluation in the SLP representation may be significantly
faster. Moreover, the sparsity is conserved by automatic
differentiation. Even in the dense representation, the monomials are
shared subexpressions between  ,
so the evaluation of
,
so the evaluation of  is typically faster than
the separate evaluation of
is typically faster than
the separate evaluation of  .
Furthermore, we generate machine code for the evaluation, which is
faster then using a loop over the terms of an expanded representation of
.
Furthermore, we generate machine code for the evaluation, which is
faster then using a loop over the terms of an expanded representation of
 .
.
Full fledged SLP libraries also provide a lot of flexibility concerning
the domain  . Usually, we take
. Usually, we take
 to be the domain of machine complex floating
point numbers at double precision. But we may easily lift our SLPs to
extended precision, as we saw in section 5.8. The
techniques from section 5.6 also allow us to efficiently
evaluate SLPs over balls and then use this to construct certified path
trackers [83, 62]. Generating machine code for
evaluating a given SLP over
to be the domain of machine complex floating
point numbers at double precision. But we may easily lift our SLPs to
extended precision, as we saw in section 5.8. The
techniques from section 5.6 also allow us to efficiently
evaluate SLPs over balls and then use this to construct certified path
trackers [83, 62]. Generating machine code for
evaluating a given SLP over  is fast, provided
that we have efficient implementations for the methods from sections 3, 4 and 5.5. In the SLP framework
such codelets can thus be constructed on-the-fly whenever needed for the
resolution of our specific input system. Similarly, if a system has
multiple solutions, then automatic differentiation can be used to
“deflate” it on-the-fly into a system which turns these
solutions into isolated ones.
is fast, provided
that we have efficient implementations for the methods from sections 3, 4 and 5.5. In the SLP framework
such codelets can thus be constructed on-the-fly whenever needed for the
resolution of our specific input system. Similarly, if a system has
multiple solutions, then automatic differentiation can be used to
“deflate” it on-the-fly into a system which turns these
solutions into isolated ones.
Numerical homotopy methods lend themselves very well to parallelization,
since every separate path can be tracked using a different thread. SIMD
acceleration of width 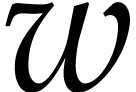 may also be used to
simultaneously track
may also be used to
simultaneously track 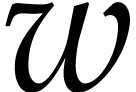 paths using a single
thread. However, the required number of steps may differ from one path
to another, so an ad hoc mechanism is needed to detect complete
paths and to feed the corresponding threads (or SIMD lanes) with new
paths. The strict SLP framework is slightly insufficient for
implementing such a mechanism. A minima, when generating
machine code for our SLP, we wish to be able to surround it by a loop
that allows for multiple executions until some condition is met. As
briefly discussed in section 4.9, this kind of control
sugar is a welcome extension of the framework from this paper.
paths using a single
thread. However, the required number of steps may differ from one path
to another, so an ad hoc mechanism is needed to detect complete
paths and to feed the corresponding threads (or SIMD lanes) with new
paths. The strict SLP framework is slightly insufficient for
implementing such a mechanism. A minima, when generating
machine code for our SLP, we wish to be able to surround it by a loop
that allows for multiple executions until some condition is met. As
briefly discussed in section 4.9, this kind of control
sugar is a welcome extension of the framework from this paper.
Another major application of SLP libraries is the automatic generation of codelets for discrete Fourier transforms (DFTs) and variants.
The codelet approach was pioneered in FFTW3 [37, 38] and later applied in other implementations [100, 72]. Given any desired order, the idea is to automatically generate a dedicated and highly optimized codelet to perform DFTs of this order. For small orders, the appropriate codelet is typically unrolled as an SLP and pre-compiled into the library. For larger orders, the idea is to decompose the transform into DFTs of smaller orders using classical techniques due to Good, Cooley–Tukey, Rader, etc. There are often many competing algorithms to compute a DFT, in which case we automatically compare running times and select the best strategy for the target length. This tuning phase may be expensive, but the best strategies can be cached.
In order to achieve really high performance, it is actually profitable
to unroll DFTs up till “not so small” orders like  . When pre-compiling all these
“not so small” DFTs into the library, this may considerably
blow up its size. This is all the more true if one also wishes to
include variants of DFTs such as the truncated Fourier transform [56, 58, 84]. In the SLP framework,
one may efficiently build and compile these codelets on-the-fly, while
preserving or even improving the efficiency at execution time.
. When pre-compiling all these
“not so small” DFTs into the library, this may considerably
blow up its size. This is all the more true if one also wishes to
include variants of DFTs such as the truncated Fourier transform [56, 58, 84]. In the SLP framework,
one may efficiently build and compile these codelets on-the-fly, while
preserving or even improving the efficiency at execution time.
The SLP approach is also more versatile, because it allows us to
dynamically choose our ground ring  .
Traditional DFTs over
.
Traditional DFTs over  may therefore be generated
on-the-fly for various working precisions. But one may also generate
number theoretic transforms over
may therefore be generated
on-the-fly for various working precisions. But one may also generate
number theoretic transforms over 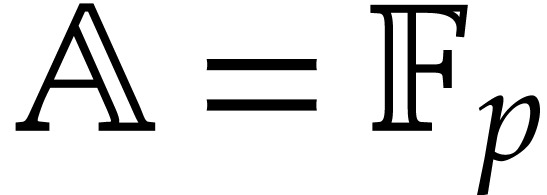 for various
prime numbers
for various
prime numbers  [97], and Nussbaumer
polynomial transforms [94] over
[97], and Nussbaumer
polynomial transforms [94] over 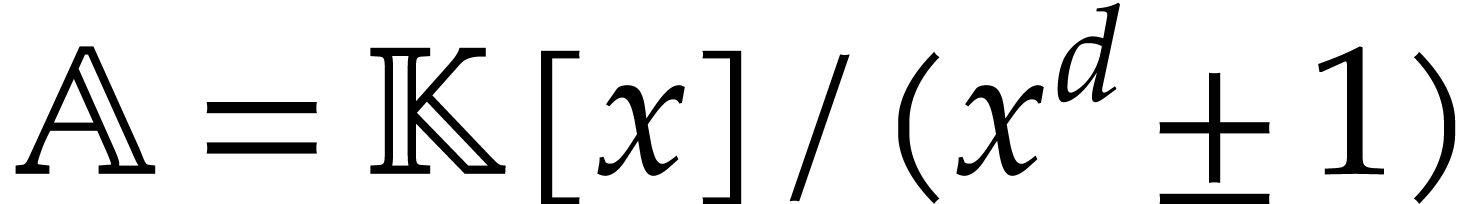 for
various degrees
for
various degrees 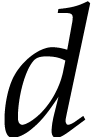 . In
addition, we may apply algebraic optimization techniques from section 5, while exploiting particular mathematical properties of the
ground ring
. In
addition, we may apply algebraic optimization techniques from section 5, while exploiting particular mathematical properties of the
ground ring  . This idea has
been applied successfully in [69, 66, 72]
for DFTs in medium precision and number theoretic transforms over
. This idea has
been applied successfully in [69, 66, 72]
for DFTs in medium precision and number theoretic transforms over  ,
, 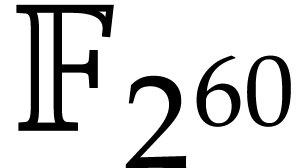 ,
and
,
and 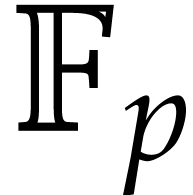 for so-called smooth FFT primes
for so-called smooth FFT primes  .
.
A few technical issues need to be addressed though in order to use an
SLP library for this application. First of all, the design of DFTs of
large orders heavily relies on tensor products [100]: given
an SLP 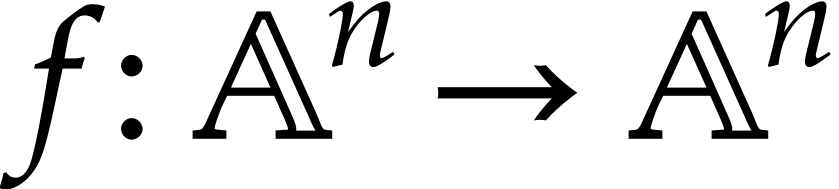 that computes a DFT (or another linear
map) of order
that computes a DFT (or another linear
map) of order  , we often need
highly optimized code for
, we often need
highly optimized code for  and
and  . If
. If 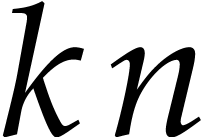 is small, then we
simply generate SLPs for these tensor products. However, if
is small, then we
simply generate SLPs for these tensor products. However, if 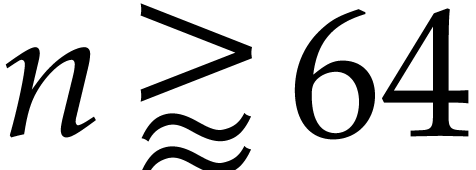 and
and  are both “not so
small”, then it is best to automatically put the code of
are both “not so
small”, then it is best to automatically put the code of  inside a loop of length
inside a loop of length  .
This is another instance where control sugar is useful (see also
sections 4.9 and 6.1). Moreover, we may wish
to pass
.
This is another instance where control sugar is useful (see also
sections 4.9 and 6.1). Moreover, we may wish
to pass 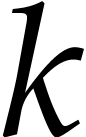 as a parameter to the functions
as a parameter to the functions 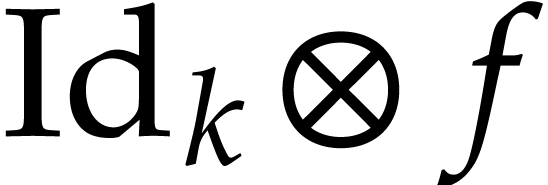 and
and 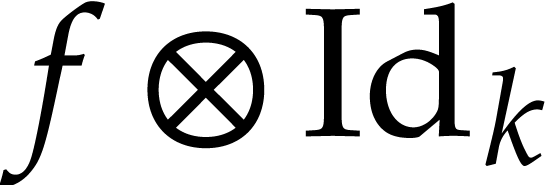 .
.
Another issue is to find the best strategy for computing a particular
DFT. Our SLP library must therefore contain support for benchmarking
competing strategies on-the-fly and selecting the best ones. Such a
mechanism can be expensive, so this should be complemented by a caching
system that remembers the best strategies. This is a non-trivial problem
that we have not yet addressed in our present implementations. For
instance, for DFTs of a fixed length over 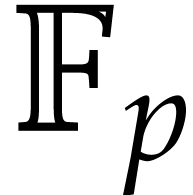 ,
should we use the same strategy for different values of
,
should we use the same strategy for different values of  ? We might also attempt to cleverly bench a
reduced number of DFTs and try to build a model that can predict the
running time of other DFTs.
? We might also attempt to cleverly bench a
reduced number of DFTs and try to build a model that can predict the
running time of other DFTs.
Consider the multiplication 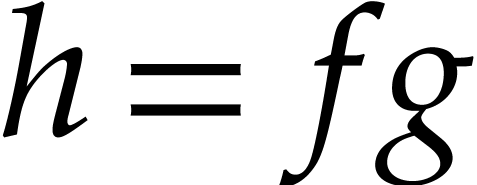 of two formal power
series
of two formal power
series  . From an algorithmic
perspective, we may deal with the infinite nature of power series in
several ways. One idea is to work at a finite truncation order: given
. From an algorithmic
perspective, we may deal with the infinite nature of power series in
several ways. One idea is to work at a finite truncation order: given
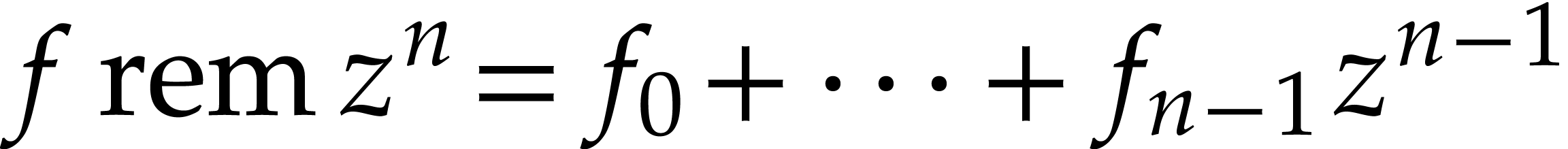 and
and 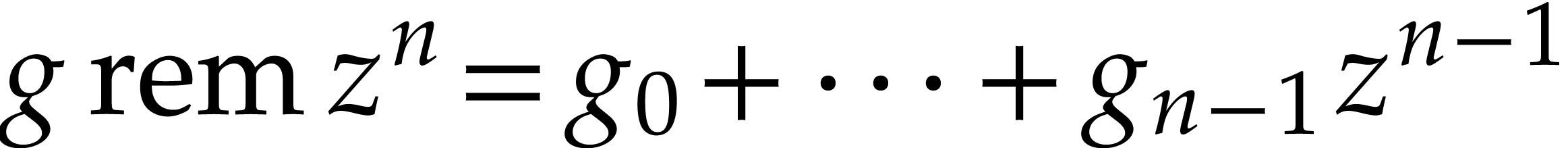 ,
we then wish to compute
,
we then wish to compute 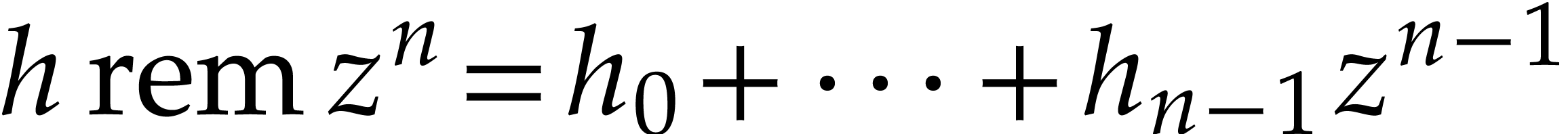 .
Another approach [57], the relaxed (or
online) one, is to regard
.
Another approach [57], the relaxed (or
online) one, is to regard  and
and  as streams of coefficients and to insist that
as streams of coefficients and to insist that
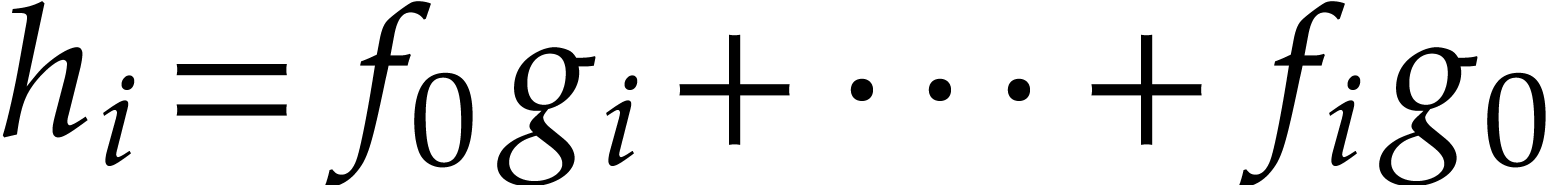 |
(6.5) |
needs to be output as soon as  and
and  are known. The naive way to compute the product
are known. The naive way to compute the product  in a relaxed manner is to directly use (6.5).
At order three, this yields
in a relaxed manner is to directly use (6.5).
At order three, this yields
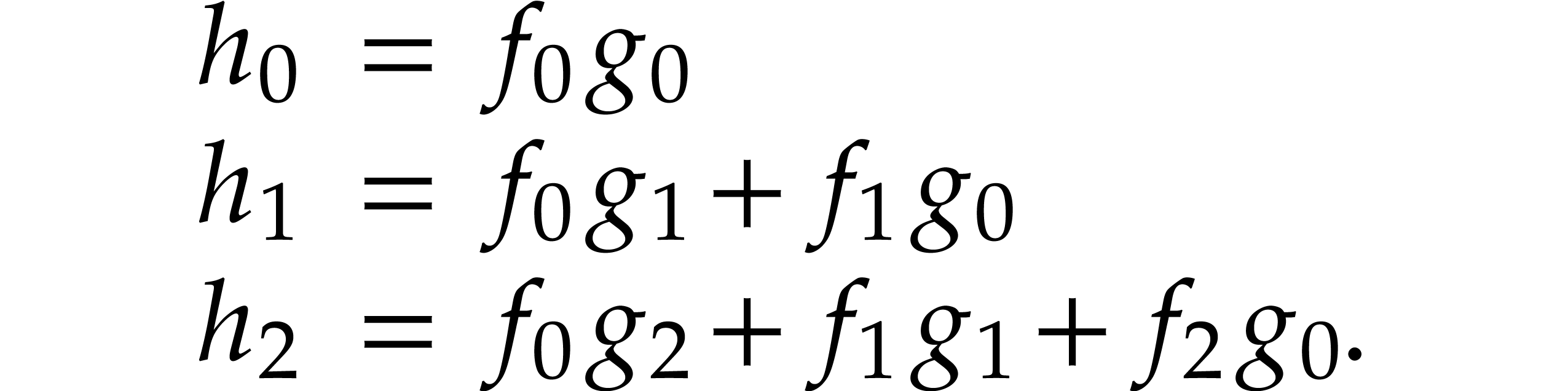
But we may save one multiplication using Karatsuba's trick:
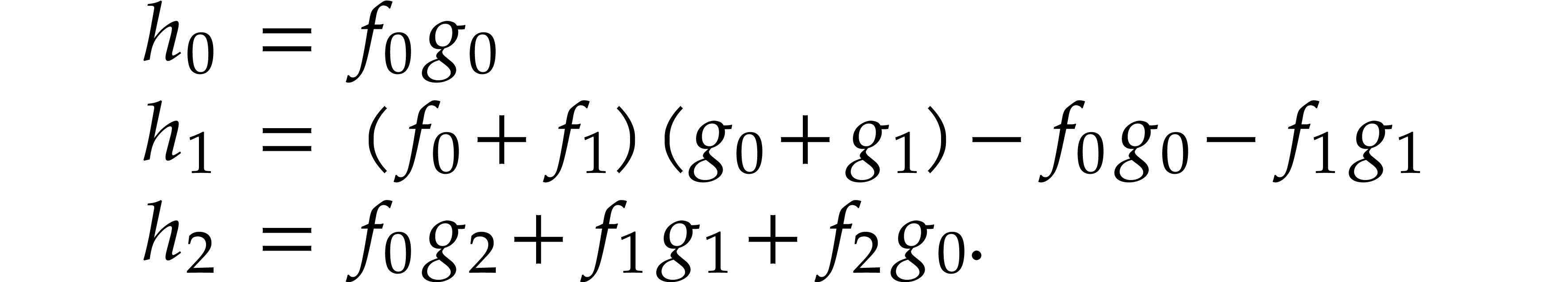
In fact, Karatsuba's algorithm is essentially relaxed [57], modulo reordering the instructions in an appropriate way. However, this reordering is non-trivial to program and the appropriate control structures induce a significant overhead. Our SLP framework has a big advantage here, since, no matter how complex these control structures are, the overhead vanishes when recording the multiplication.
Example 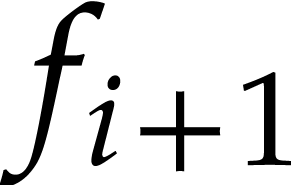 and
and 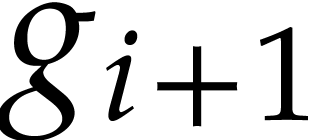 of the inputs are allowed to depend on
earlier coefficients
of the inputs are allowed to depend on
earlier coefficients  of the output. This yields
a convenient way to solve power series equations. For instance, the
inverse
of the output. This yields
a convenient way to solve power series equations. For instance, the
inverse 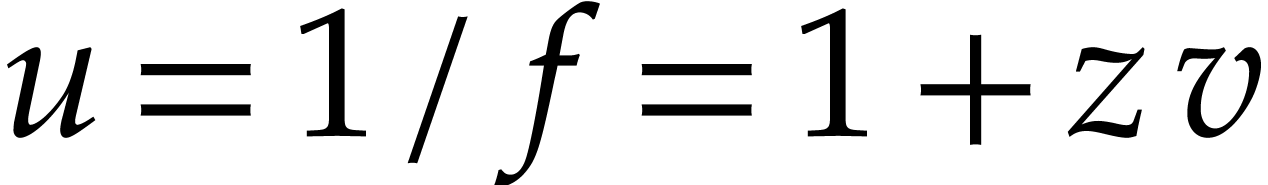 of a power series of the form
of a power series of the form 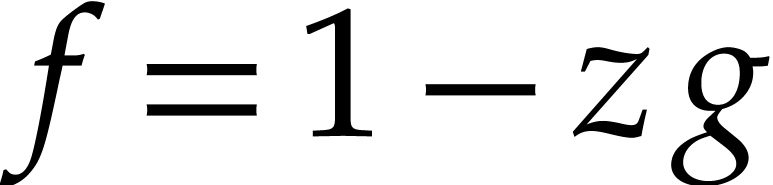 satisfies the equation
satisfies the equation
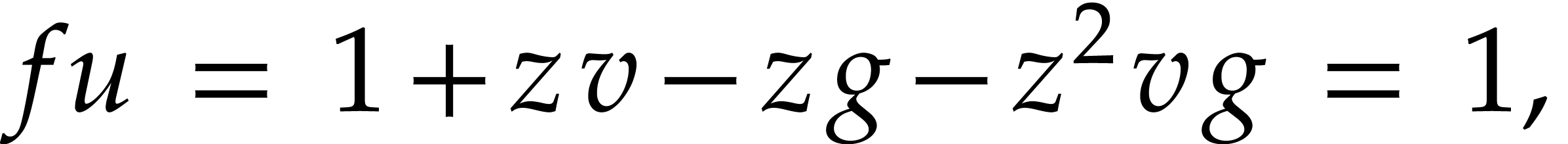
whence
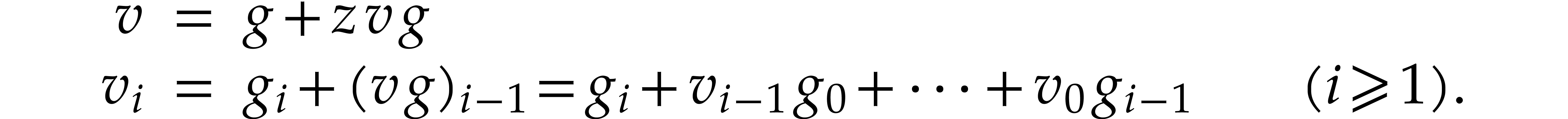
Now assume that we compute  using the formula
using the formula
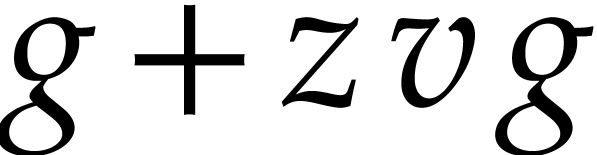 and Karatsuba's algorithm. When recording the
trace of an expansion at order
and Karatsuba's algorithm. When recording the
trace of an expansion at order  ,
we obtain the following SLP, after simplification:
,
we obtain the following SLP, after simplification:
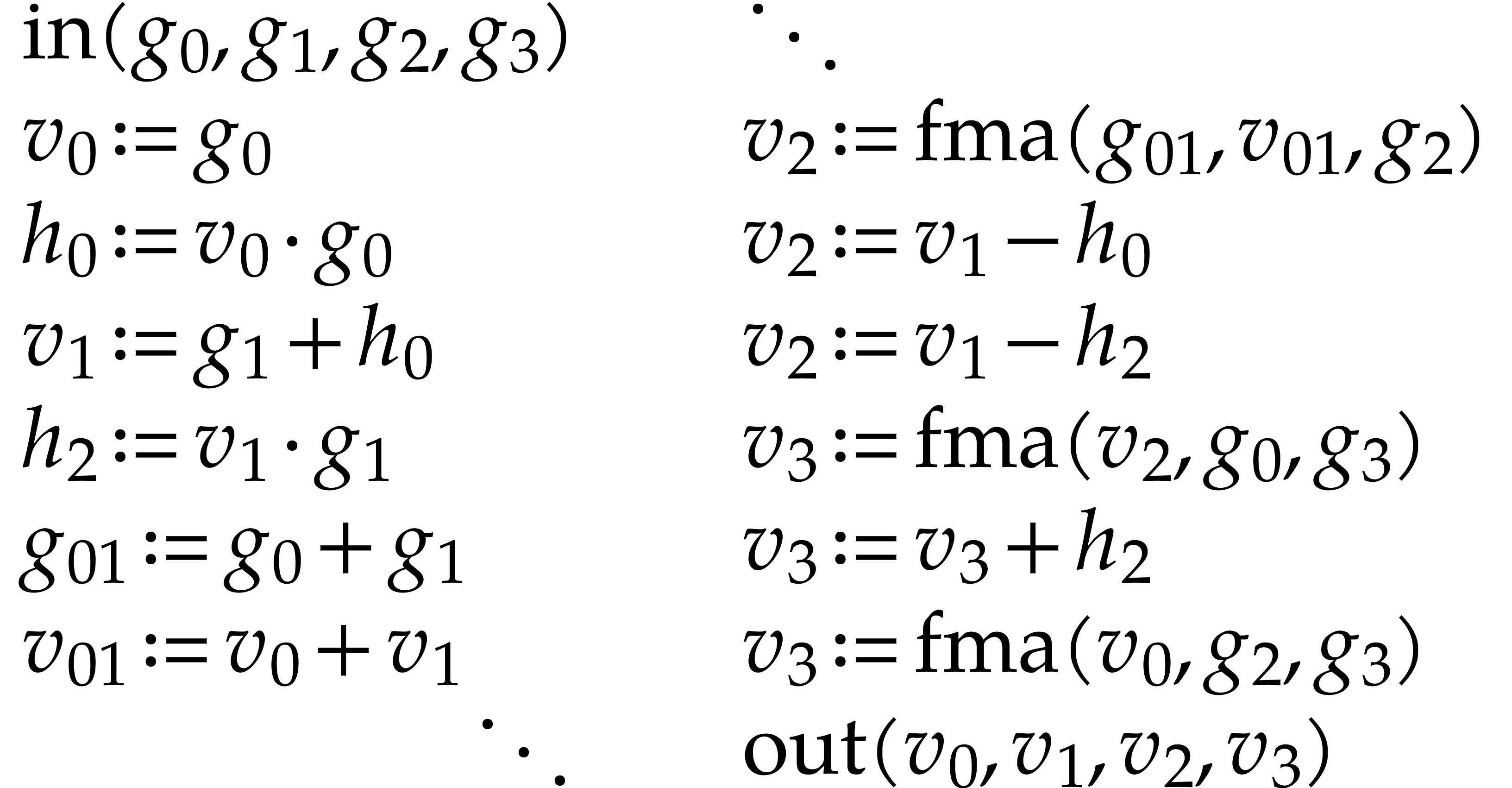
Trading one multiplication against several additions and subtractions
may not seem worth the effort, except maybe for larger orders. However,
when lifting the SLP to a domain like  from
section 5.7, multiplications may be far more expensive than
additions and subtractions. Even for small orders, the relaxed approach
may then lead to significant savings.
from
section 5.7, multiplications may be far more expensive than
additions and subtractions. Even for small orders, the relaxed approach
may then lead to significant savings.
If  , then the relaxed
approach can in particular be used in order to solve a system of
ordinary differential equations (ODEs) of the form
, then the relaxed
approach can in particular be used in order to solve a system of
ordinary differential equations (ODEs) of the form
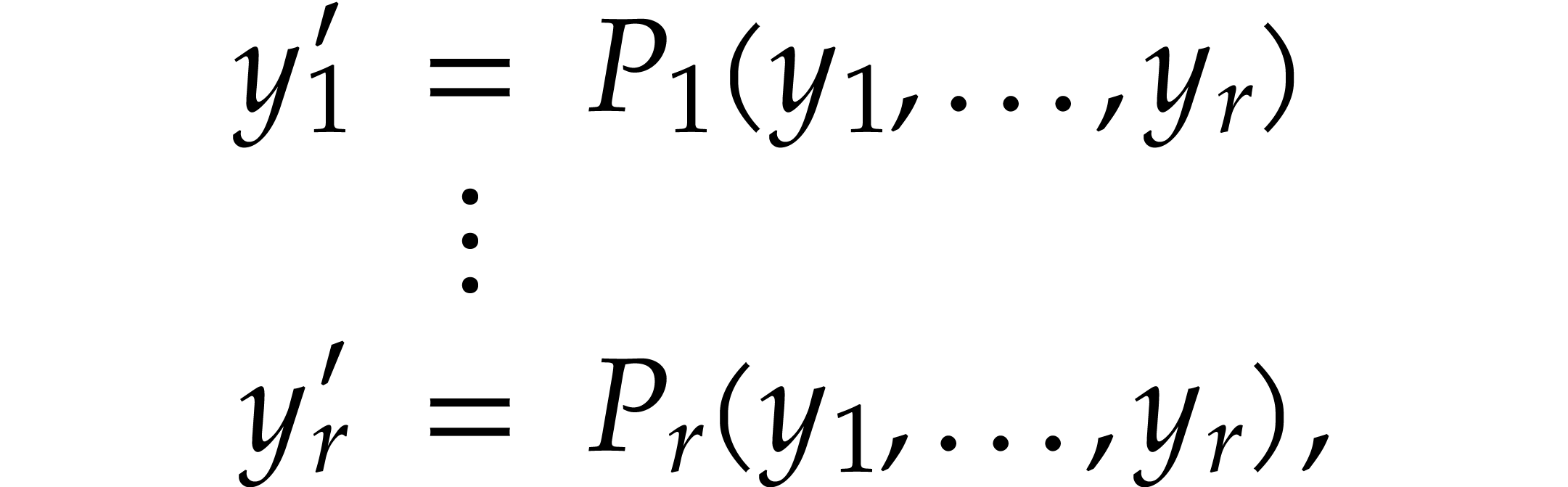
where  . Indeed, it suffices
to rewrite the system as
. Indeed, it suffices
to rewrite the system as
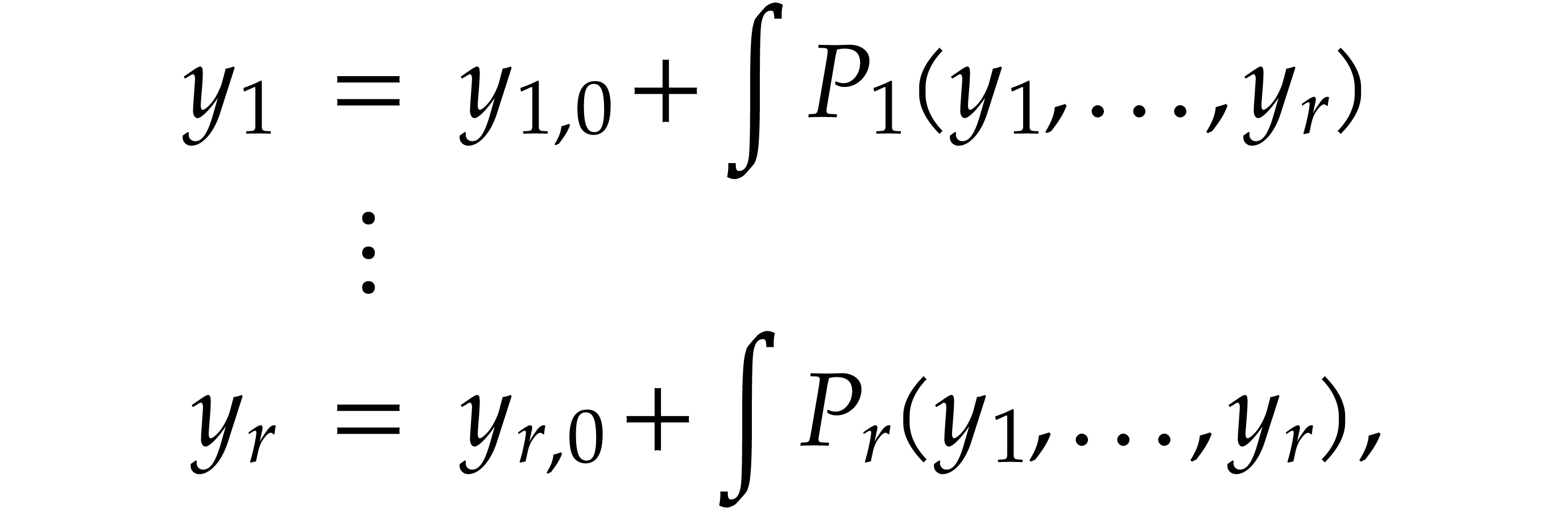
after which one may check that the coefficients  only depend on earlier coefficients when evaluating the right-hand
sides.
only depend on earlier coefficients when evaluating the right-hand
sides.
For any given truncation order 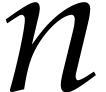 ,
we may record the resolution process as an SLP. The power series
solution naturally gives rise to a “stepper” for the
numerical integration of the system. However, the size of the SLP
increases with
,
we may record the resolution process as an SLP. The power series
solution naturally gives rise to a “stepper” for the
numerical integration of the system. However, the size of the SLP
increases with 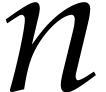 : the factor
is
: the factor
is  for the naive method,
for the naive method,  for Karatsuba's method, and
for Karatsuba's method, and 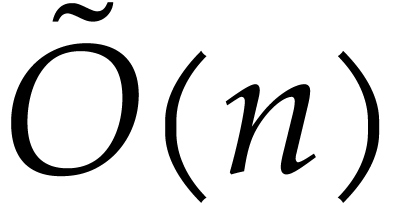 for large
for large 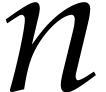 (see [57, 63] for asymptotically
fast methods). It is an interesting problem to rewrite this SLP as
multiple applications of a few SLPs of significantly smaller sizes
(about
(see [57, 63] for asymptotically
fast methods). It is an interesting problem to rewrite this SLP as
multiple applications of a few SLPs of significantly smaller sizes
(about 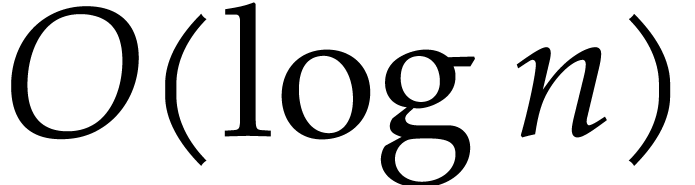 SLPs of the size of the original SLP
might do, by associating one type of SLP to each size of squares in [57, Figure 3] and doing the required transforms separately).
This also raises the practical challenge of generating SLPs that call
other SLPs: another example of control sugar.
SLPs of the size of the original SLP
might do, by associating one type of SLP to each size of squares in [57, Figure 3] and doing the required transforms separately).
This also raises the practical challenge of generating SLPs that call
other SLPs: another example of control sugar.
Traditional Runge-Kutta methods for the numerical integration of ODEs
are also very suitable for the SLP framework. They have the advantage
that they just require an SLP for the evaluation of the polynomials
 . However, efficient
Runge–Kutta schemes are only known up till order
. However, efficient
Runge–Kutta schemes are only known up till order  : for larger orders, we need many evaluations,
so Taylor series methods are currently more efficient.
: for larger orders, we need many evaluations,
so Taylor series methods are currently more efficient.
In section 5.8 we already discussed the generation of SLPs
for arithmetic operations with extended precision. The typical
application that we had in mind there was to allow for SLPs over
numerical domains with a fixed higher precision. In order to support
integers and rational numbers as domains  ,
we also need to consider mixed precisions. The same holds when solving
some equation over high precision floating point numbers using Newton's
method: in this case, it is best to double the working precision at
every iteration.
,
we also need to consider mixed precisions. The same holds when solving
some equation over high precision floating point numbers using Newton's
method: in this case, it is best to double the working precision at
every iteration.
The most straightforward way to compute with mixed precisions is to use
a similar interface as 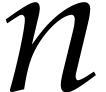 limbs. For small values of
limbs. For small values of 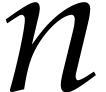 , we may automatically generate a dedicated
routine, similarly as in section 5.8. We may still do this
for “not so small values” of
, we may automatically generate a dedicated
routine, similarly as in section 5.8. We may still do this
for “not so small values” of 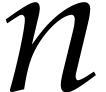 ,
in which case we may unroll Karatsuba's and Toom's more sophisticated
multiplication algorithms [82, 106]. For
larger
,
in which case we may unroll Karatsuba's and Toom's more sophisticated
multiplication algorithms [82, 106]. For
larger 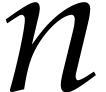 , we may recurse down
to these base cases for which we generated dedicated implementations.
For very high precisions, we may resort to FFT-multiplication [97],
where the appropriate number theoretic transforms are automatically
generated using the techniques from section 6.2. A similar
strategy can be applied for the multiplication of two integers of
different sizes in limbs.
, we may recurse down
to these base cases for which we generated dedicated implementations.
For very high precisions, we may resort to FFT-multiplication [97],
where the appropriate number theoretic transforms are automatically
generated using the techniques from section 6.2. A similar
strategy can be applied for the multiplication of two integers of
different sizes in limbs.
It is a good question whether the general master routine for integer
multiplication should also be generated automatically by the SLP
library. It is not unreasonable to require that the implementation of
such routines should be done in a separate higher level library. But it
might also be interesting if the SLP library could automatically
generate a full library like
Another mixed precision scenario is the evaluation of an SLP over the
integers  , where we have
bounds for the input arguments. In that case, we can statically
determine bounds for the results of all instructions and their sizes in
limbs. We may next replace each instruction by a dedicated SLP for the
corresponding number of limbs. Consider for instance the computation of
the product
, where we have
bounds for the input arguments. In that case, we can statically
determine bounds for the results of all instructions and their sizes in
limbs. We may next replace each instruction by a dedicated SLP for the
corresponding number of limbs. Consider for instance the computation of
the product 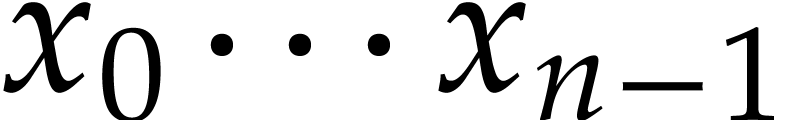 of integers
of integers 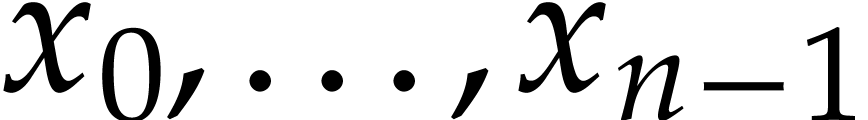 that all fit into one limb. This can efficiently be done using the
technique of product trees: for
that all fit into one limb. This can efficiently be done using the
technique of product trees: for  ,
we compute
,
we compute 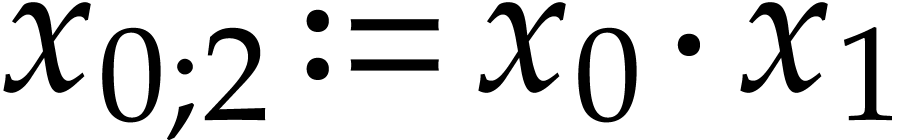 ,
, 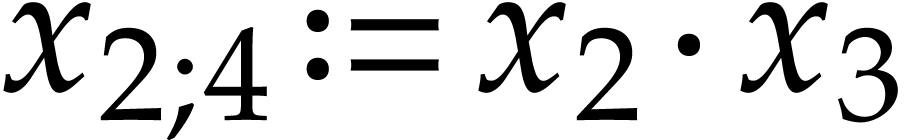 ,
, 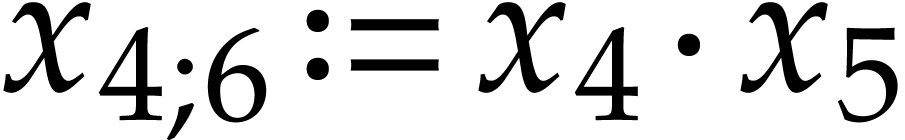 ,
,
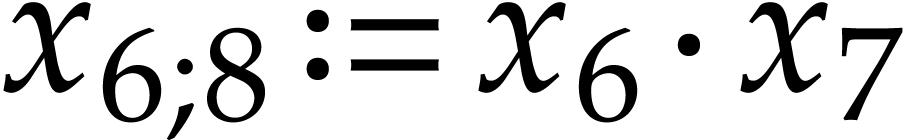 using an SLP for
using an SLP for  limb
multiplication,
limb
multiplication, 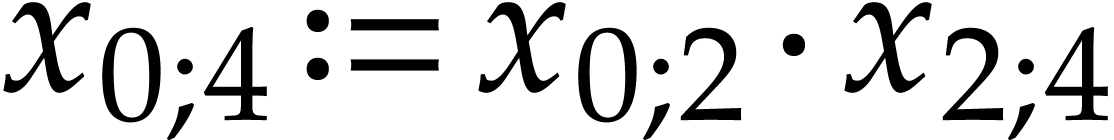 and
and 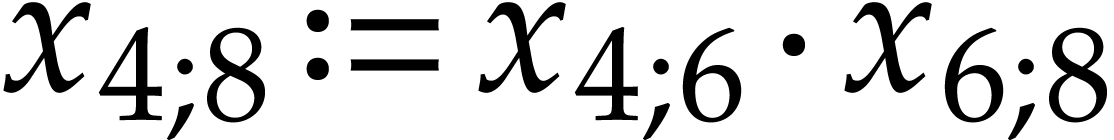 using an SLP for
using an SLP for  limb multiplication, and
limb multiplication, and 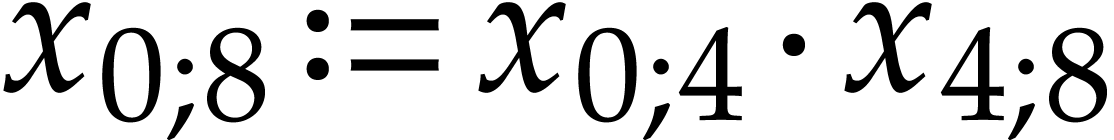 using an SLP for
using an SLP for  limb
multiplication.
limb
multiplication.
A major shortcoming of existing multiple precision libraries like 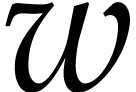 integers at a
time:
integers at a
time:  . This is not entirely
convenient, because an SIMD routine for doing this requires all
. This is not entirely
convenient, because an SIMD routine for doing this requires all 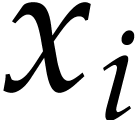 to be of the same limb size and similarly for the
to be of the same limb size and similarly for the
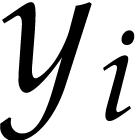 . But there exist many
applications for which the sizes of integers are indeed predictable and
uniform. The SLP framework naturally allows us to speed up such
applications by generating SIMD versions of operations on integers.
. But there exist many
applications for which the sizes of integers are indeed predictable and
uniform. The SLP framework naturally allows us to speed up such
applications by generating SIMD versions of operations on integers.
Last but not least, we hope that our new SLP libraries will be useful in
order to speed up polynomial system solving using the method of
geometric resolution. This method can be thought of as a purely
algebraic counterpart of homotopy continuation from section 6.1,
although the technical details are very different. It was first
developed by Joos
The aim is again to solve a system of polynomial equations (6.1),
but we now work over an effective field  instead
of
instead
of  . The solutions typically
lie in an extension field
. The solutions typically
lie in an extension field  of
of  . A primitive representation
. A primitive representation 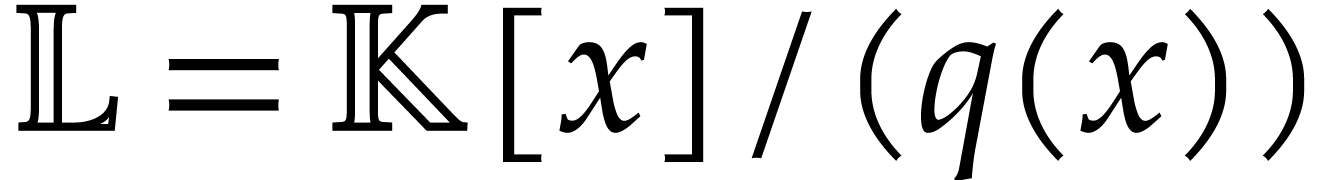 of
of 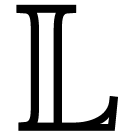 is therefore computed along with the
solutions itself, where
is therefore computed along with the
solutions itself, where  us a monic irreducible
polynomial. For sufficiently generic systems, the degree of
us a monic irreducible
polynomial. For sufficiently generic systems, the degree of  coincides with the number of solutions and all solutions
can be represented simultaneously via a single point in
coincides with the number of solutions and all solutions
can be represented simultaneously via a single point in 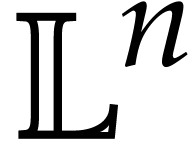 (each root of
(each root of 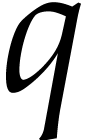 giving rise to
an actual solution).
giving rise to
an actual solution).
Unlike numerical homotopy continuation, the geometric resolution method
proceeds by an induction over the dimension. Assume that we have a
solution of the 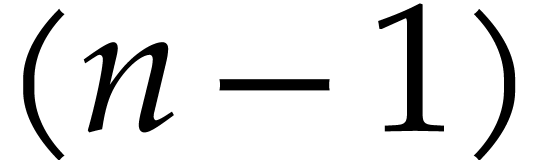 -dimensional
system
-dimensional
system
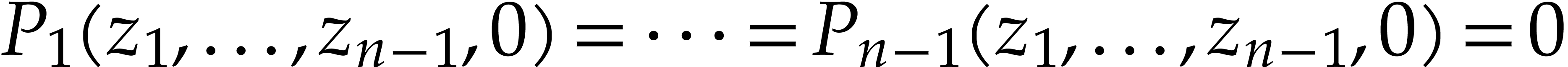 |
(6.6) |
over 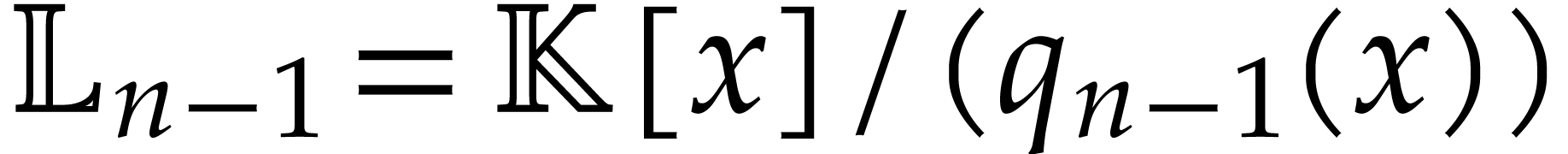 . Then the idea is to
first lift it into a solution of
. Then the idea is to
first lift it into a solution of
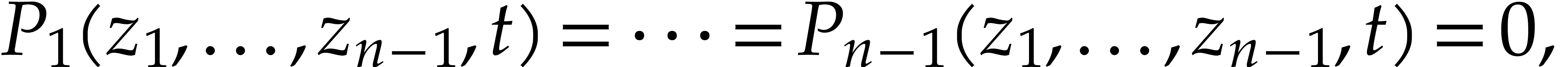 |
(6.7) |
over 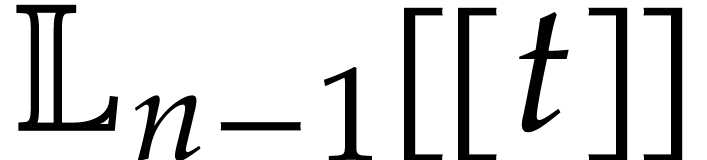 , where
, where  is a time parameter as in section 6.1. Expansions of order
is a time parameter as in section 6.1. Expansions of order
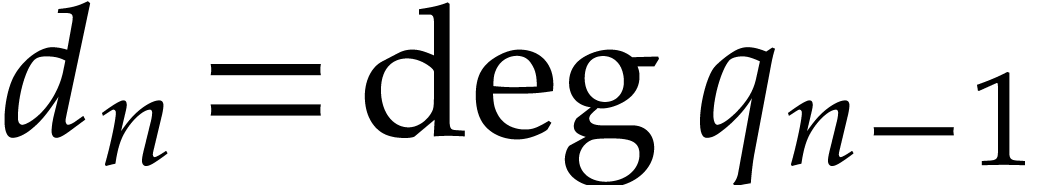 in
in 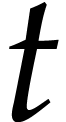 will generically
suffice. We next intersect the “solution curve”
will generically
suffice. We next intersect the “solution curve”  of the system (6.7) with the hypersurface of
zeros of
of the system (6.7) with the hypersurface of
zeros of 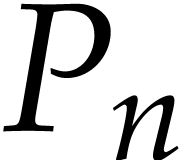 . It turns out that
the resulting equation
. It turns out that
the resulting equation
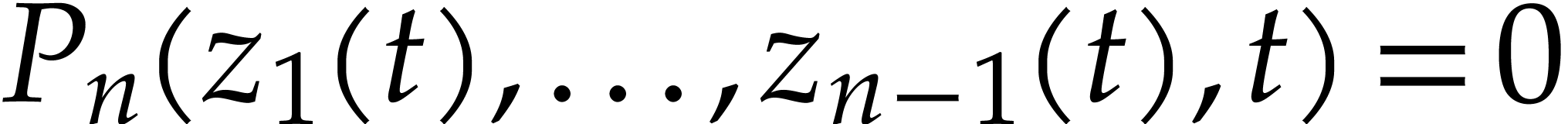
can be solved using one big resultant computation. If  , then it is also profitable to first reduce
the system modulo a small and suitable “machine” prime
, then it is also profitable to first reduce
the system modulo a small and suitable “machine” prime  , solve the resulting system over
, solve the resulting system over
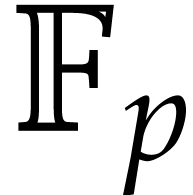 , Hensel lift the solution to
, Hensel lift the solution to
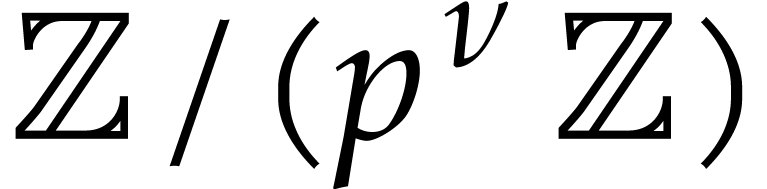 , and finally obtain the
desired solution using rational number reconstruction [40,
section 5.10].
, and finally obtain the
desired solution using rational number reconstruction [40,
section 5.10].
In order to implement this strategy efficiently, the following basic
building blocks are particularly crucial: fast univariate polynomial
arithmetic over 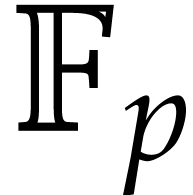 , fast
arithmetic modulo
, fast
arithmetic modulo 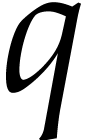 , efficient
evaluations of SLPs over
, efficient
evaluations of SLPs over 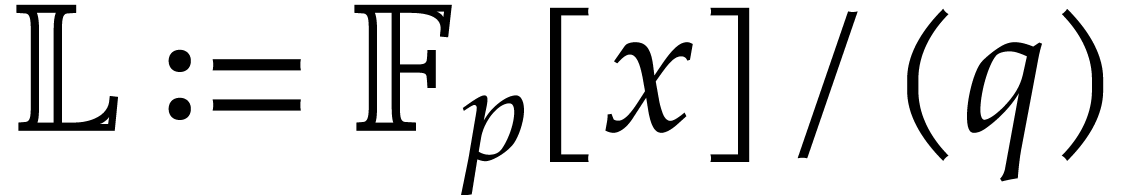 and
and 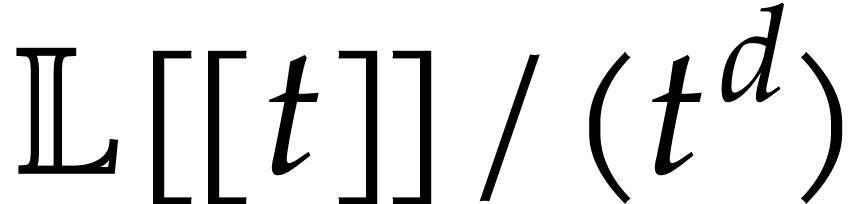 , efficient algorithms for resultants and
subresultants, and variants of these building blocks when working over
, efficient algorithms for resultants and
subresultants, and variants of these building blocks when working over
 instead of
instead of 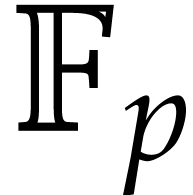 .
Now univariate polynomial arithmetic over
.
Now univariate polynomial arithmetic over 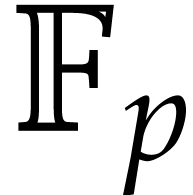 or
or
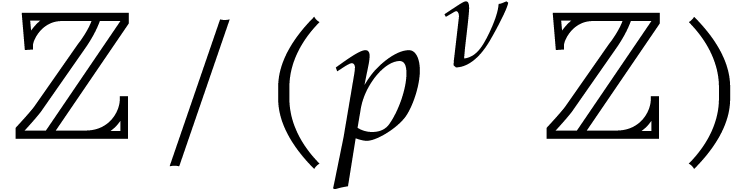 is very similar to integer arithmetic. Using a
similar approach as in the previous subsection, we may benefit from the
SLP framework to automatically generate the required routines.
is very similar to integer arithmetic. Using a
similar approach as in the previous subsection, we may benefit from the
SLP framework to automatically generate the required routines.
If the degree of  gets large, then
multiplications in
gets large, then
multiplications in 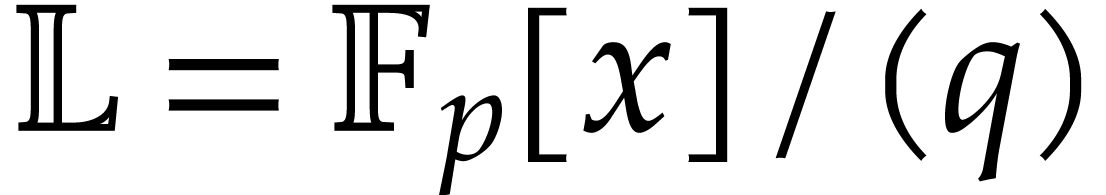 are done using fast Fourier
methods. When evaluating an SLP over
are done using fast Fourier
methods. When evaluating an SLP over 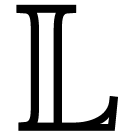 ,
a lot of the required DFTs can often be shared, which significantly
reduces the cost. Similarly, reductions modulo
,
a lot of the required DFTs can often be shared, which significantly
reduces the cost. Similarly, reductions modulo 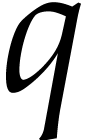 can often be postponed to the end. For instance, the
can often be postponed to the end. For instance, the  matrix product (3.4) can be lifted from
matrix product (3.4) can be lifted from 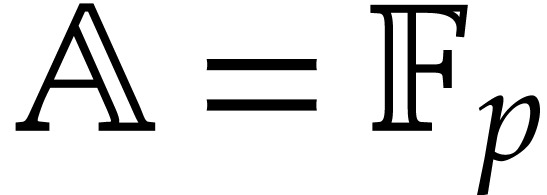 to
to 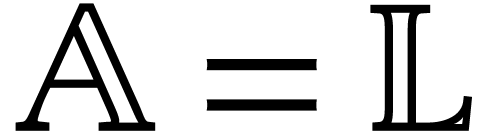 as follows: we first convert the input
arguments
as follows: we first convert the input
arguments  into the FFT representation using
DFTs, then perform the
into the FFT representation using
DFTs, then perform the  matrix multiplication
while using the FFT representation, next convert the result back into
the usual polynomial representation, and finally reduce modulo
matrix multiplication
while using the FFT representation, next convert the result back into
the usual polynomial representation, and finally reduce modulo 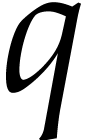 .
.
In order to implement such optimizations within our SLP framework, it is
convenient to extend the signature  with
converters between the polynomial and FFT representations and with
operations on the FFT representations. This will allow us to lift (3.4) as follows from
with
converters between the polynomial and FFT representations and with
operations on the FFT representations. This will allow us to lift (3.4) as follows from  to
to  :
:
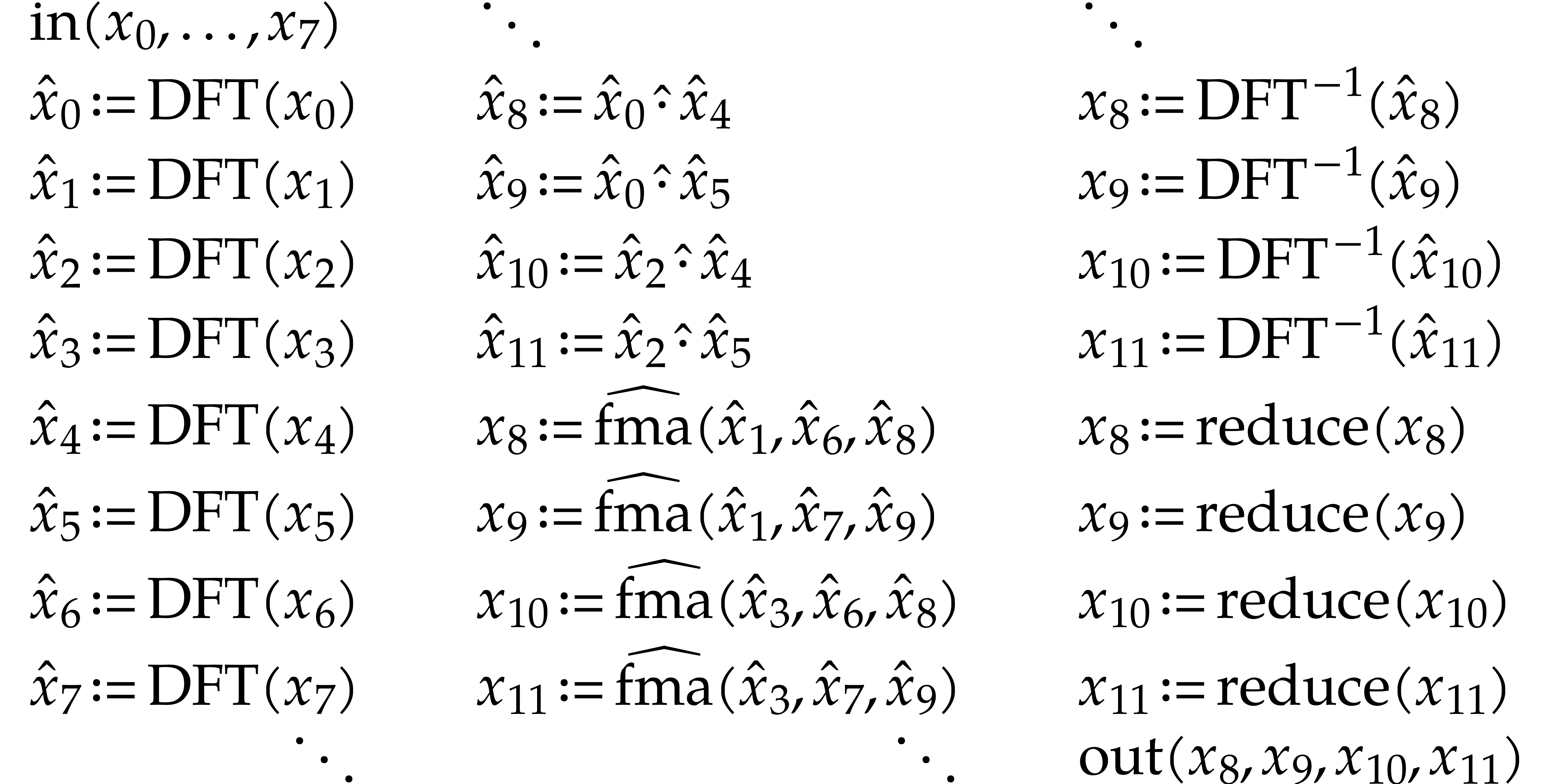
Here elements of  are represented redundantly by
polynomials of degree
are represented redundantly by
polynomials of degree 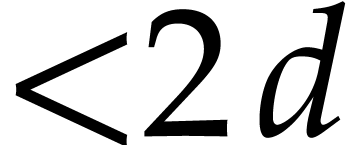 , where
, where
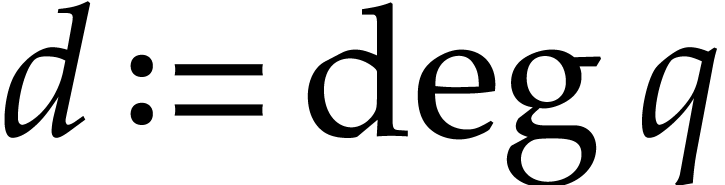 . The operation
“reduce” computes the remainder of the division by
. The operation
“reduce” computes the remainder of the division by  . The input arguments are assumed
to be reduced. The map
. The input arguments are assumed
to be reduced. The map 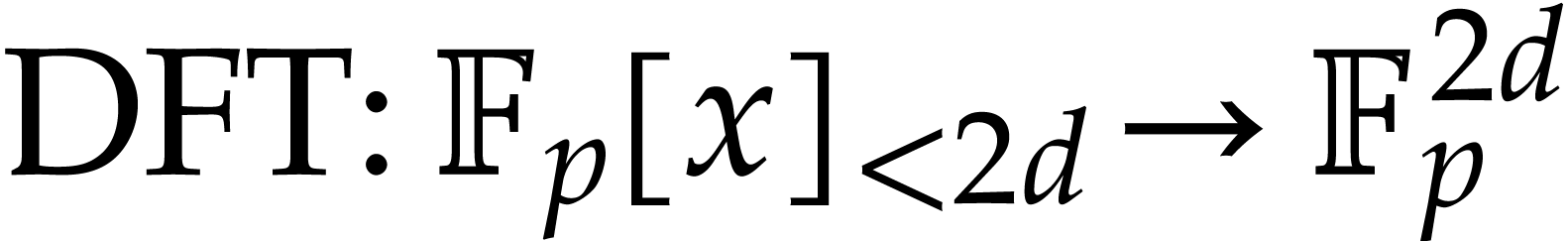 computes a discrete
Fourier transform of length
computes a discrete
Fourier transform of length 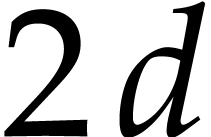 (assuming that
(assuming that 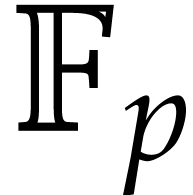 has a
has a 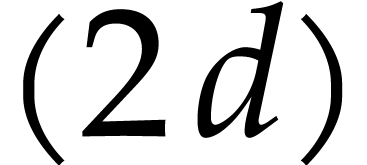 -th
primitive root of unity), where
-th
primitive root of unity), where 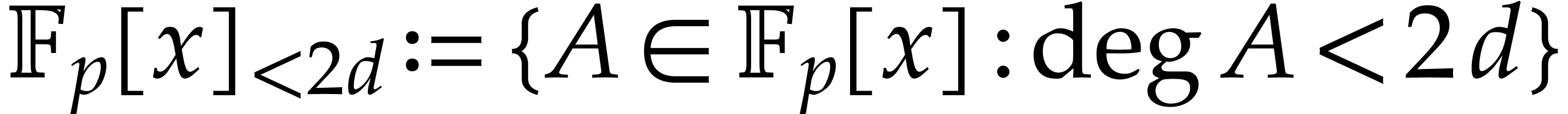 .
This map is
.
This map is  -linear and we
have
-linear and we
have  for polynomials
for polynomials 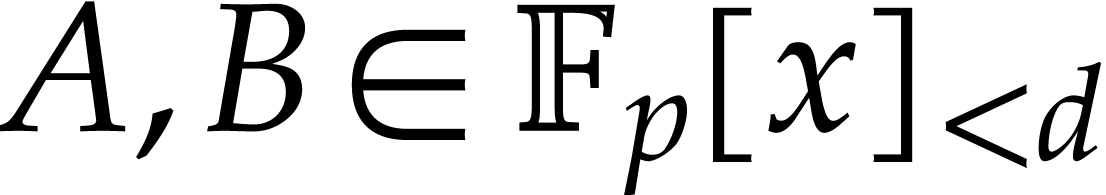 . We noted
. We noted  and
and  for the vector lifts of
for the vector lifts of  and
and  to
to  .
.
In fact, the cost of the reductions (which also require FFT
multiplications) can be further reduced by switching to a polynomial
analogue [88] of the Montgomery representation [90]
for elements of  . One may
also consider Fourier representations of larger sizes
. One may
also consider Fourier representations of larger sizes 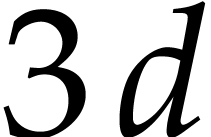 ,
, 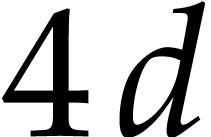 ,
...: this increases the cost of individual transforms, but
may dramatically reduce the number of transforms that need to be done.
We plan to further work out the details of these ideas in a forthcoming
paper.
,
...: this increases the cost of individual transforms, but
may dramatically reduce the number of transforms that need to be done.
We plan to further work out the details of these ideas in a forthcoming
paper.
As stated in the introduction, our previous papers [70, 66] internally rely on the  -version
that has just been released [1].
-version
that has just been released [1].
We tested our libraries on the following platforms:
An
The machine ships with an AMD
A
This machine also incorporates an
An
Our first benchmark concerns the computation of determinants of  matrices. We consider two types of input SLPs for
computing this determinant:
matrices. We consider two types of input SLPs for
computing this determinant:
The naive SLP, which adds up all 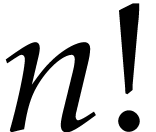 terms when
expanding the determinant. Note that this method requires no
divisions, contrary to the asymptotically faster method based on
Gaussian elimination.
terms when
expanding the determinant. Note that this method requires no
divisions, contrary to the asymptotically faster method based on
Gaussian elimination.
The simplification of the naive SLP. The size of this SLP is still
exponential as a function of 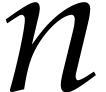 ,
but much smaller than the naive SLP.
,
but much smaller than the naive SLP.
The Tables 7.1, 7.2, and 7.3 have been subdivided into two main left-hand and right-hand parts which correspond to the naive and simplified SLPs, respectively. The first “len” column shows the number of instructions of the input SLP. Each other column reports the timing of a specific operation on the input SLP in cycles per instruction:
Simplification of the SLP.

Computing the gradient of the SLP.
Lifting the SLP to the complexification  of
the domain
of
the domain  .
.
Register allocation, using  registers.
registers.
Complete machine code generation, including the register allocation.
Executing the generated machine code over (scalar) double precision numbers.
Tables
7.1
,
7.2
, and
7.3
report timings for our three test platforms
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table 7.1. Timings in cycles
per instruction on the |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table 7.2. Timings in cycles
per instruction on the AMD |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table 7.3. Timings in cycles
per instruction on the |
One major observation concerning these tables is that all operations on
SLPs require between 100 and 1000 cycles per instruction, approximately.
The older Intel
For small values of 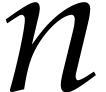 , the
timings involve a large overhead. This overhead tends to disappear for
SLPs with more than 100 instructions. The timings remain relatively
stable in the midrange, for SLPs of lengths between 100 and 100000. Very
large SLPs cause cache problems and we observe a significant overhead
for such SLPs.
, the
timings involve a large overhead. This overhead tends to disappear for
SLPs with more than 100 instructions. The timings remain relatively
stable in the midrange, for SLPs of lengths between 100 and 100000. Very
large SLPs cause cache problems and we observe a significant overhead
for such SLPs.
For input SLPs of midrange lengths, we note that instructions tend to execute in less than one cycle. This is due to out of order execution by multiple execution units, which is particularly well done on M3 processors. We also note that all cycle times are reported with respect to the base clock speed.
We recall that domain for all timings in Tables 7.1, 7.2, and 7.3 is the scalar domain 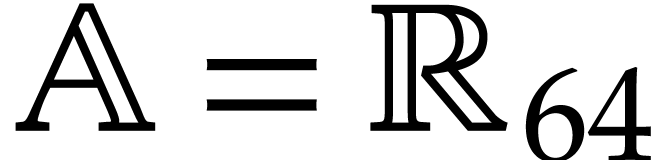 of double precision floating point numbers. For many
applications, it is possible to work over the SIMD domain
of double precision floating point numbers. For many
applications, it is possible to work over the SIMD domain 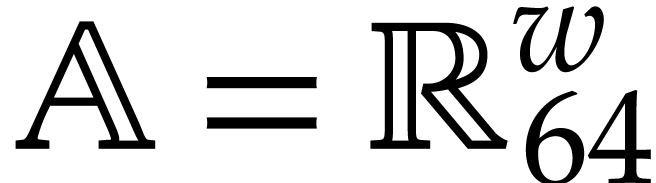 for some
for some 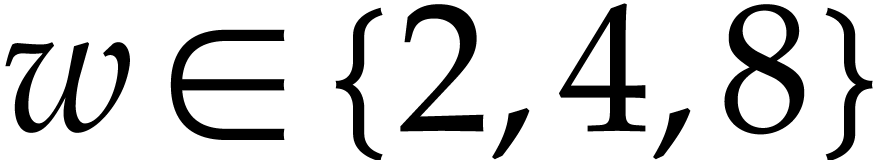 , in
which case multiple executions are accelerated by an approximately
factor of
, in
which case multiple executions are accelerated by an approximately
factor of  with respect to
with respect to 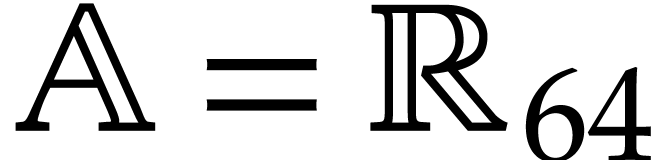 . This allows the
. This allows the 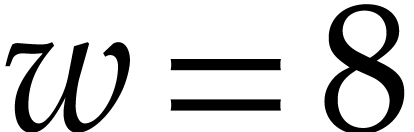 ) to make up for the smaller number
of execution units with respect to the M3 platform (on
which
) to make up for the smaller number
of execution units with respect to the M3 platform (on
which 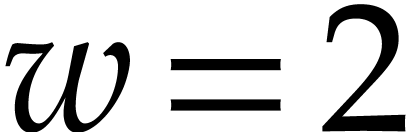 ). See [72,
section 5.1] for more details on this point and further benchmarks.
). See [72,
section 5.1] for more details on this point and further benchmarks.
Let us finally examine the kind of code that is generated by our SLP
simplifier. In Figure
7.1
, we show the simplified SLP for computing a
 determinant, as well as the corresponding machine code on X86
platforms. We observe that the code makes efficient use of fused
multiply add instructions. The generated machine code also tends to
exploit the indirect addressing mode for arithmetic instructions whose
arguments are only required once. For small values of
determinant, as well as the corresponding machine code on X86
platforms. We observe that the code makes efficient use of fused
multiply add instructions. The generated machine code also tends to
exploit the indirect addressing mode for arithmetic instructions whose
arguments are only required once. For small values of
 ,
the simplified SLPs are quite competitive with Gaussian elimination.
They have the advantage that they require no divisions and no
conditional code to find appropriate pivots.
,
the simplified SLPs are quite competitive with Gaussian elimination.
They have the advantage that they require no divisions and no
conditional code to find appropriate pivots.
|
||
One major motivation for our work on SLP libraries is the development of a fast tool for numerical homotopy continuation at double precision.
We did a first prototype implementation in
We recently started a C++ reimplementation inside the
In Table
7.4
, we reported timings for the classical Katsura
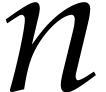 benchmark. We also consider a few dense random systems Posso
benchmark. We also consider a few dense random systems Posso
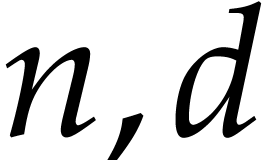 of dimension
of dimension
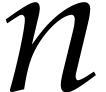 and total degree
and total degree
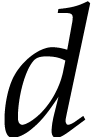 .
The first “sols” column shows the total number of
solutions. The columns labeled by “jit” indicate the time
spent on building the machine code. The columns labeled by “exe
.
The first “sols” column shows the total number of
solutions. The columns labeled by “jit” indicate the time
spent on building the machine code. The columns labeled by “exe
 ” show the actual time that was needed to solve the system using
” show the actual time that was needed to solve the system using
 threads.
threads.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The main benefit of switching to our lower level implementation in
More extensive benchmarking reveals that the performance scales well
with the number of threads and the SIMD width on our test platforms. The
last two columns of Table 7.4 show that this even holds
when passing from 6 to 12 threads on the M3 processor: for
the particular application of path tracking, efficiency cores perform
almost as well as performance cores. Curiously, on the 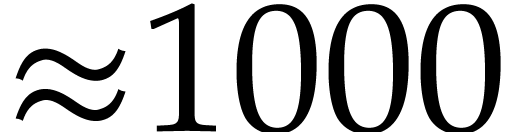 solutions; we are still investigating the reason
for this.
solutions; we are still investigating the reason
for this.
One major objective of the
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
A. Ahlbäck, J. van der Hoeven, and G. Lecerf. https://sourcesup.renater.fr/projects/jil, 2025.
A. Ahlbäck and F. Johansson. Fast basecases for arbitrary-size multiplication. In 2025 IEEE 32nd Symposium on Computer Arithmetic (ARITH), pages 53–60. 2025.
A. V. Aho, M. S. Lam, R. Sethi, and J. D. Ullman. Compilers principles, techniques & tools. Pearson Education, 2nd edition, 2007.
Georg, K. Allgower, E. L. Numerical Continuation Methods. Springer-Verlag, 1990.
ANSI/IEEE. IEEE standard for binary floating-point arithmetic. Technical Report, ANSI/IEEE, New York, 2008. ANSI-IEEE Standard 754-2008. Revision of IEEE 754-1985, approved on June 12, 2008 by IEEE Standards Board.
ARM corporation. Fast models user guide. https://developer.arm.com/documentation/100965/latest. Version 11.29.
M. Aschenbrenner, L. van den Dries, and J. van der Hoeven. Asymptotic Differential Algebra and Model Theory of Transseries. Number 195 in Annals of Mathematics studies. Princeton University Press, 2017.
AsmJit: low-latency machine code generation. https://github.com/asmjit/asmjit.
Autodiff: automatic differentiation in C++ couldn't be simpler. https://autodiff.github.io.
Torch.autograd: automatic differentiation package in pytorch. https://docs.pytorch.org/docs/stable/autograd.html.
Awesome-JIT. https://github.com/wdv4758h/awesome-jit. Ressources for JIT compilation.
D. H. Bailey, Y. Hida, and X. S. Li. Algorithms for quad-double precision floating point arithmetic. In 15th IEEE Symposium on Computer Arithmetic, pages 155–162. IEEE, 2001.
H. G. Baker. Computing A*B (mod N) efficiently in ANSI C. SIGPLAN Not., 27(1):95–98, 1992.
W. Baur and V. Strassen. The complexity of partial derivatives. Theor. Comput. Sci., 22:317–330, 1983.
Blas (basic linear algebra subprograms). https://netlib.org/blas/.
J. L. Bordewijk. Inter-reciprocity applied to electrical networks. Applied Scientific Research B: Electrophysics, Acoustics, Optics, Mathematical Methods, 6:1–74, 1956.
A. Bostan, G. Lecerf, and É. Schost. Tellegen's principle into practice. In Proceedings of the 2003 International Symposium on Symbolic and Algebraic Computation, ISSAC '03, pages 37–44. New York, NY, USA, 2003. ACM Press.
J. Bradbury, N. Drucker, and M. Hillenbrand. NTT software optimization using an extended Harvey butterfly. Cryptology ePrint Archive, Paper 2021/1396, 2021. https://eprint.iacr.org/2021/1396.
P. Briggs, K. D. Cooper, and L. Torczon. Rematerialization. In Proceedings of the ACM SIGPLAN 1992 Conference on Programming Language Design and Implementation, PLDI '92, pages 311–321. New York, NY, USA, 1992. ACM.
N. Bruno, J. Heintz, G. Matera, and R. Wachenchauzer. Functional programming concepts and straight-line programs in computer algebra. Math. Comput. Simulation, 60(6):423–473, 2002.
P. Bürgisser, M. Clausen, and M. A. Shokrollahi. Algebraic complexity theory. Springer-Verlag, Berlin, 1997.
B. Castaño, J. Heintz, J. Llovet, and R. Martìnez. On the data structure straight-line program and its implementation in symbolic computation. Math. Comput. Simulation, 51(5):497–528, 2000.
G. J. Chaitin. Register allocation & spilling via graph coloring. ACM Sigplan Notices, 17(6):98–101, 1982.
G. J. Chaitin, M. A. Auslander, A. K. Chandra, J. Cocke, M. E. Hopkins, and P. W. Markstein. Register allocation via coloring. J. Comput. Lang., 6(1):47–57, 1981.
T. J. Dekker. A floating-point technique for extending the available precision. Numer. Math., 18(3):224–242, 1971.
A. Díaz and E. Kaltofen. FoxBox: a system for manipulating symbolic objects in black box representation. In Proceedings of the 1998 International Symposium on Symbolic and Algebraic Computation, ISSAC '98, pages 30–37. New York, NY, USA, 1998. ACM.
J.-G. Dumas, T. Gautier, M. Giesbrecht, P. Giorgi, B. Hovinen, E. Kaltofen, B. D. Saunders, W. J. Turner, and G. Villard. LinBox: a generic library for exact linear algebra. In A. M. Cohen, X. S. Gao, and N. Takayama, editors, Proceedings of the 2002 International Congress of Mathematical Software, Beijing, China, pages 40–50. World Scientific, 2002. https://linalg.org.
J.-G. Dumas, P. Giorgi, and C. Pernet. FFPACK: finite field linear algebra package. In J. Schicho, editor, Proceedings of the 2004 International Symposium on Symbolic and Algebraic Computation, ISSAC '04, pages 119–126. New York, NY, USA, 2004. ACM.
J.-G. Dumas, P. Giorgi, and C. Pernet. Dense linear algebra over word-size prime fields: the FFLAS and FFPACK packages. ACM Trans. Math. Softw., 35(3):19–1, 2008.
C. Durvye and G. Lecerf. A concise proof of the Kronecker polynomial system solver from scratch. Expo. Math., 26(2):101–139, 2008.
T. Edamatsu and D. Takahashi. Accelerating large integer multiplication using intel AVX-512IFMA. In Algorithms and Architectures for Parallel Processing: 19th International Conference, ICA3PP 2019, Melbourne, Australia, pages 60–74. Springer-Verlag, 2019.
Ch. M. Fiduccia. On the algebraic complexity of matrix multiplication. PhD thesis, Brown University, 1973.
N. Fitchas, M. Giusti, and F. Smietanski. Sur la complexité du théorème des zéros. In M. Florenzano and J. Guddat, editors, Approximation and optimization in the Caribbean, II (Havana, 1993), volume 8 of Approx. Optim., pages 274–329. Frankfurt am Main, 1995. Lang.
A. Fog. Software optimization resources. https://www.agner.org/optimize.
L. Fousse, G. Hanrot, V. Lefèvre, P. Pélissier, and P. Zimmermann. MPFR: a multiple-precision binary floating-point library with correct rounding. ACM Trans. Math. Software, 33(2), 2007. Software available at https://www.mpfr.org.
T. S. Freeman, G. M. Imirzian, E. Kaltofen, and Y. Lakshman. DAGWOOD: a system for manipulating polynomials given by straight-line programs. ACM Trans. Math. Software, 14:218–240, 1988.
M. Frigo. A fast Fourier transform compiler. In Proc. 1999 ACM SIGPLAN Conf. on Programming Language Design and Implementation, volume 34, pages 169–180. ACM, May 1999.
M. Frigo and S. G. Johnson. The design and implementation of FFTW3. Proc. IEEE, 93(2):216–231, 2005.
M. Frigo, C. E. Leiserson, H. Prokop, and S. Ramachandran. Cache-oblivious algorithms. In 40th Annual Symposium on Foundations of Computer Science, pages 285–297. IEEE, 1999.
J. von zur Gathen and J. Gerhard. Modern Computer Algebra. Cambridge University Press, 3rd edition, 2013.
M. Giusti, K. Hägele, J. Heintz, J. L. Montaña, J. E. Morais, and L. M. Pardo. Lower bounds for diophantine approximations. J. Pure Appl. Algebra, 117/118:277–317, 1997.
M. Giusti, K. Hägele, G. Lecerf, J. Marchand, and B. Salvy. The projective Noether Maple package: computing the dimension of a projective variety. J. Symbolic Comput., 30(3):291–307, 2000.
M. Giusti and J. Heintz. La détermination des points isolés et de la dimension d'une variété algébrique peut se faire en temps polynomial. In D. Eisenbud and L. Robbiano, editors, Computational algebraic geometry and commutative algebra (Cortona, 1991), Sympos. Math., XXXIV, pages 216–256. Cambridge Univ. Press, 1993.
M. Giusti, J. Heintz, J. E. Morais, J. Morgenstern, and L. M. Pardo. Straight-line programs in geometric elimination theory. J. Pure Appl. Algebra, 124(1-3):101–146, 1998.
M. Giusti, J. Heintz, J. E. Morais, and L. M. Pardo. When polynomial equation systems can be “solved” fast? In G. Cohen, M. Giusti, and T. Mora, editors, Applied Algebra, Algebraic Algorithms and Error-Correcting Codes. AAECC 1995, volume 948 of Lect. Notes Comput. Sci., pages 205–231. Springer-Verlag, 1995.
M. Giusti, J. Heintz, J. E. Morais, and L. M. Pardo. Le rôle des structures de données dans les problèmes d'élimination. C. R. Acad. Sci. Paris Sér. I Math., 325(11):1223–1228, 1997.
M. Giusti, J. Heintz, and J. Sabia. On the efficiency of effective Nullstellensätze. Comput. Complexity, 3(1):56–95, 1993.
M. Giusti, G. Lecerf, and B. Salvy. A Gröbner free alternative for polynomial system solving. J. Complexity, 17(1):154–211, 2001.
T. Granlund et al. GMP, the GNU multiple precision arithmetic library. 1991. https://gmplib.org.
S. Gueron and V. Krasnov. Accelerating big integer arithmetic using intel IFMA extensions. In 2016 IEEE 23nd Symposium on Computer Arithmetic (ARITH), pages 32–38. 2016.
K. Hägele, J. E. Morais, L. M. Pardo, and M. Sombra. On the intrinsic complexity of the arithmetic Nullstellensatz. J. Pure Appl. Algebra, 146(2):103–183, 2000.
G. Hanrot, M. Quercia, and P. Zimmermann. The middle product algorithm I. Speeding up the division and square root of power series. Appl. Algebra Eng. Commun. Comput., 14:415–438, 2004.
W. Hart, F. Johansson, and S. Pancratz. FLINT: Fast Library for Number Theory. 2013. Version 2.4.0, https://flintlib.org.
D. Harvey. Faster arithmetic for number-theoretic transforms. J. Symbolic Comput., 60:113–119, 2014.
J. Heintz and C.-P. Schnorr. Testing polynomials which are easy to compute. In Logic and algorithmic (Zurich, 1980), volume 30 of Monograph. Enseign. Math., pages 237–254. Geneva, 1982. Univ. Genève.
J van der Hoeven. The truncated Fourier transform and applications. In J. Schicho, editor, Proceedings of the 2004 International Symposium on Symbolic and Algebraic Computation, ISSAC '04, pages 290–296. New York, NY, USA, 2004. ACM.
J. van der Hoeven. Relax, but don't be too lazy. J. Symbolic Comput., 34:479–542, 2002.
J. van der Hoeven. Notes on the Truncated Fourier Transform. Technical Report 2005-5, Université Paris-Sud, Orsay, France, 2005.
J. van der Hoeven. Ball arithmetic. Technical Report, HAL, 2009. https://hal.archives-ouvertes.fr/hal-00432152.
J. van der Hoeven. Ball arithmetic. In A. Beckmann, Ch. Gaßner, and B. Löwe, editors, Logical approaches to Barriers in Computing and Complexity, number 6 in Preprint-Reihe Mathematik, pages 179–208. Ernst-Moritz-Arndt-Universität Greifswald, 2010.
J. van der Hoeven. Calcul analytique. In Journées Nationales de Calcul Formel. 14 – 18 Novembre 2011, volume 1 of Les cours du CIRM, pages 1–85. CIRM, 2011. https://www.numdam.org/articles/10.5802/ccirm.16/.
J. van der Hoeven. Reliable homotopy continuation. Technical Report, HAL, 2011. http://hal.archives-ouvertes.fr/hal-00589948.
J. van der Hoeven. Faster relaxed multiplication. In Proceedings of the 39th International Symposium on Symbolic and Algebraic Computation, ISSAC '14, pages 405–412. New York, NY, USA, 2014. ACM.
J. van der Hoeven. Multiple precision floating-point arithmetic on SIMD processors. In 24th IEEE Symposium on Computer Arithmetic (ARITH), pages 2–9. July 2017.
J. van der Hoeven. The Jolly Writer. Your Guide to GNU TeXmacs. Scypress, 2020.
J. van der Hoeven, R. Larrieu, and G. Lecerf. Implementing fast carryless multiplication. In Mathematical Aspects of Computer and Information Sciences. MACIS 2017, volume 10693 of Lect. Notes in Comput. Sci., pages 121–136. Springer International Publishing, 2017.
J. van der Hoeven and G. Lecerf. Interfacing Mathemagix with C++. In Proceedings of the 38th International Symposium on Symbolic and Algebraic Computation, ISSAC '13, pages 363–370. New York, NY, USA, 2013. ACM.
J. van der Hoeven and G. Lecerf. Mathemagix User Guide. HAL, 2013. https://hal.archives-ouvertes.fr/hal-00785549.
J. van der Hoeven and G. Lecerf. Faster FFTs in medium precision. In 22nd IEEE Symposium on Computer Arithmetic (ARITH), pages 75–82. June 2015.
J. van der Hoeven and G. Lecerf. Evaluating straight-line programs over balls. In P. Montuschi, M. Schulte, J. Hormigo, S. Oberman, and N. Revol, editors, 2016 IEEE 23nd Symposium on Computer Arithmetic, pages 142–149. IEEE, 2016.
J. van der Hoeven and G. Lecerf. On the complexity exponent of polynomial system solving. Found. Comput. Math., 21:1–57, 2021.
J. van der Hoeven and G. Lecerf. Implementing number theoretic transforms. Technical Report, HAL, 2024. https://hal.science/hal-04841449.
J. van der Hoeven, G. Lecerf, and G. Quintin. Modular SIMD arithmetic in Mathemagix. ACM Trans. Math. Softw., 43(1):5–1, 2016.
J. van der Hoeven et al. Mathemagix. 2002. https://www.mathemagix.org.
Intel corporation. Intel® 64 and IA-32 architectures software developer's manual. https://www.intel.com/content/www/us/en/developer/articles/technical/intel-sdm.html.
F. Johansson. Arb: a C library for ball arithmetic. ACM Commun. Comput. Algebra, 47(3/4):166–169, 2014.
M. Joldeş, O. Marty, J.-M. Muller, and V. Popescu. Arithmetic algorithms for extended precision using floating-point expansions. IEEE Trans. Comput., 65(4):1197–1210, 2015.
M. Joldes, J.-M. Muller, V. Popescu, and W. Tucker. CAMPARY: cuda multiple precision arithmetic library and applications. In Mathematical Software – ICMS 2016, pages 232–240. Cham, 2016. Springer.
Juliadiff: differentiation tools in Julia. https://juliadiff.org.
V. Kabanets and R. Impagliazzo. Derandomizing polynomial identity tests means proving circuit lower bounds. Computational Complexity, 13:1–46, 2004.
E. Kaltofen and B. M. Trager. Computing with polynomials given by black boxes for their evaluations: greatest common divisors, factorization, separation of numerators and denominators. J. Symb. Comput., 9(3):301–320, 1990.
A. Karatsuba and J. Ofman. Multiplication of multidigit numbers on automata. Soviet Physics Doklady, 7:595–596, 1963.
R. B. Kearfott. An interval step control for continuation methods. SIAM J. Numer. Anal., 31(3):892–914, 1994.
R. Larrieu. The truncated Fourier transform for mixed radices. In M. Burr, editor, Proceedings of the 2017 ACM International Symposium on Symbolic and Algebraic Computation, ISSAC '17, pages 261–268. New York, NY, USA, 2017. ACM.
G. Lecerf. Computing an equidimensional decomposition of an algebraic variety by means of geometric resolutions. In Proceedings of the 2000 International Symposium on Symbolic and Algebraic Computation, ISSAC '00, pages 209–216. New York, NY, USA, 2000. ACM.
G. Lecerf. Une alternative aux méthodes de
réécriture pour la résolution des syst es algébriques.
PhD thesis, École polytechnique, 2001.
es algébriques.
PhD thesis, École polytechnique, 2001.
G. Matera. Probabilistic algorithms for geometric elimination. Appl. Algebra Engrg. Comm. Comput., 9(6):463–520, 1999.
P. Mihăilescu. Fast convolutions meet montgomery. Math. Comp., 77(262):1199–1221, 2008.
O. Møller. Quasi double-precision in floating point addition. BIT Numer. Math., 5:37–50, 1965.
P. L. Montgomery. An FFT extension of the elliptic curve method of factorization. PhD thesis, U. of California at Los Angeles, 1992.
R. E. Moore. Interval Analysis. Prentice Hall, Englewood Cliffs, N.J., 1966.
R. E. Moore, R. B. Kearfott, and M. J. Cloud. Introduction to interval analysis. Society for Industrial and Applied Mathematics, 2009.
C. D. Murray and R. R. Williams. On the (non) NP-Hardness of computing circuit complexity. Theory of Computing, 13(4):1–22, 2017.
H. J. Nussbaumer and P. Quandalle. Computation of convolutions and discrete Fourier transforms by polynomial transforms. IBM J. Res. Develop., 22(2):134–144, 1978.
LLVM ORC design and implementation. https://www.llvm.org/docs/ORCv2.html.
M. Poletto and V. Sarkar. Linear scan register allocation. ACM Trans. Program. Lang. Syst., 21(5):895–913, 1999.
J. M. Pollard. The fast Fourier transform in a finite field. Math. Comp., 25(114):365–374, 1971.
W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. Numerical recipes, the art of scientific computing. Cambridge University Press, 3rd edition, 2007.
D. M. Priest. On Properties of Floating Point Arithmetics: Numerical Stability and the Cost of Accurate Computations. PhD thesis, University of California at Berkeley, 1992.
M. Püschel, J. M. F. Moura, J. Johnson, D. Padua, M. Veloso, B. Singer, J. Xiong, F. Franchetti, A. Gacic, Y. Voronenko, K. Chen, R. W. Johnson, and N. Rizzolo. SPIRAL: code generation for DSP transforms. Proceedings of the IEEE, special issue on “Program Generation, Optimization, and Adaptation”, 93(2):232–275, 2005.
D. S. Roche. What can (and can't) we do with sparse polynomials? In C. Arreche, editor, Proceedings of the 2018 ACM International Symposium on Symbolic and Algebraic Computation, ISSAC '18, pages 25–30. New York, NY, USA, 2018. ACM Press.
S. M. Rump. Verification methods: rigorous results using floating-point arithmetic. Acta Numer., 19:287–449, 2010.
A. Shpilka and A. Yehudayoff. Arithmetic circuits: a survey of recent results and open questions. Foundations and Trends in Theoretical Computer Science, 5(3–4):207–388, 2010.
A. J. Sommese, J. Verschelde, and C. W. Wampler. Introduction to numerical algebraic geometry, pages 301–337. Springer, 2005.
D. Takahashi. An implementation of parallel number-theoretic transform using Intel AVX-512 instructions. In F. Boulier, M. England, T. M. Sadykov, and E. V. Vorozhtsov, editors, Computer Algebra in Scientific Computing. CASC 2022., volume 13366 of Lect. Notes Comput. Sci., pages 318–332. Springer, Cham, 2022.
A. L. Toom. The complexity of a scheme of functional elements realizing the multiplication of integers. Soviet Mathematics, 4(2):714–716, 1963.