| On sparse interpolation of rational functions and gcds   |
|
| Preliminary version of November 11, 2020 |
|
 . This paper is
part of a project that has received funding from the French
“Agence de l'innovation de défense”.
. This paper is
part of a project that has received funding from the French
“Agence de l'innovation de défense”.
 . This article has
been written using GNU TeXmacs [8].
. This article has
been written using GNU TeXmacs [8].
In this note, we present a variant of a probabilistic algorithm by Cuyt and Lee for the sparse interpolation of multivariate rational functions. We also present an analogous method for the computation of sparse gcds. |
Let 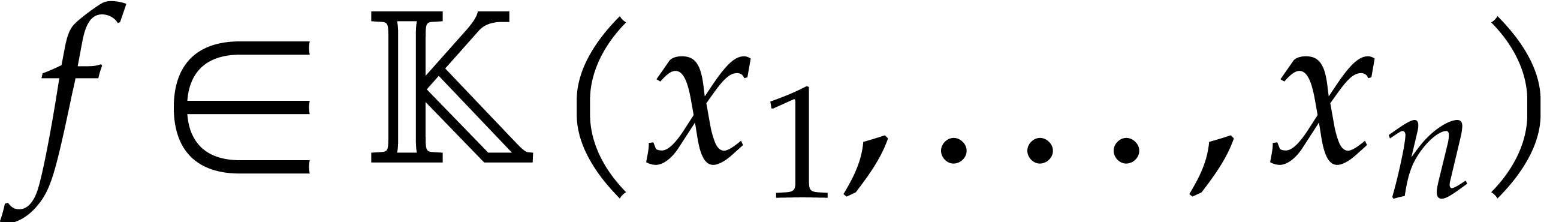 be a rational function over an effective
field
be a rational function over an effective
field  , presented as a
blackbox that can be evaluated at points in
, presented as a
blackbox that can be evaluated at points in 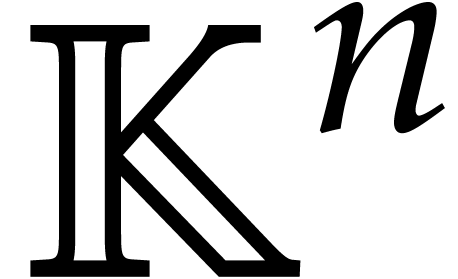 . The problem of sparse interpolation is to
recover
. The problem of sparse interpolation is to
recover  in its usual representation, as a
quotient of the form
in its usual representation, as a
quotient of the form
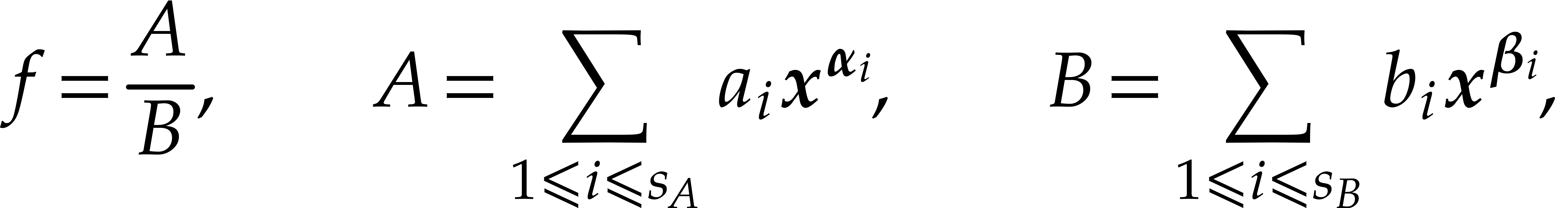
where 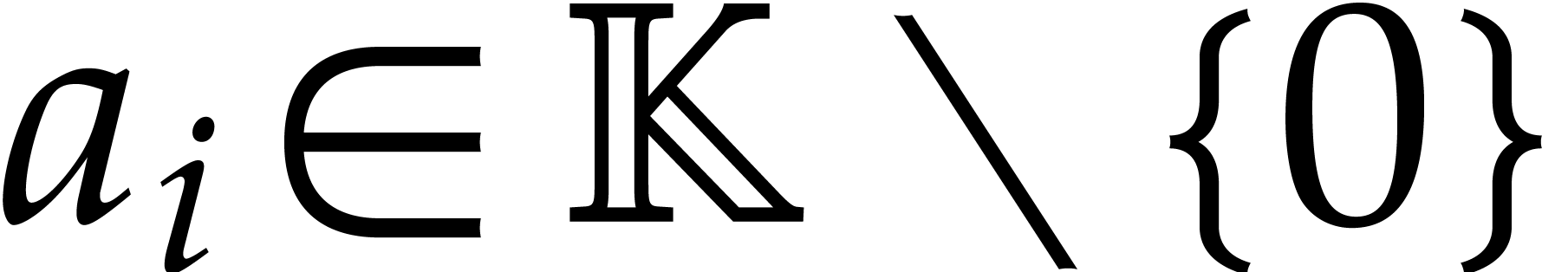 and
and 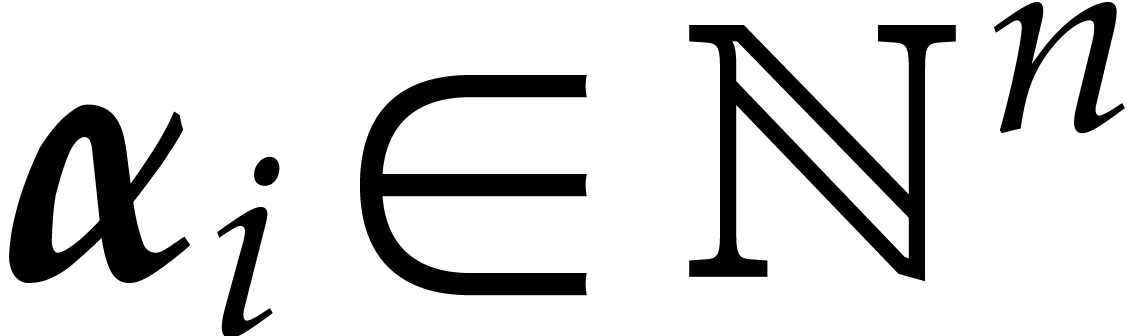 for
for 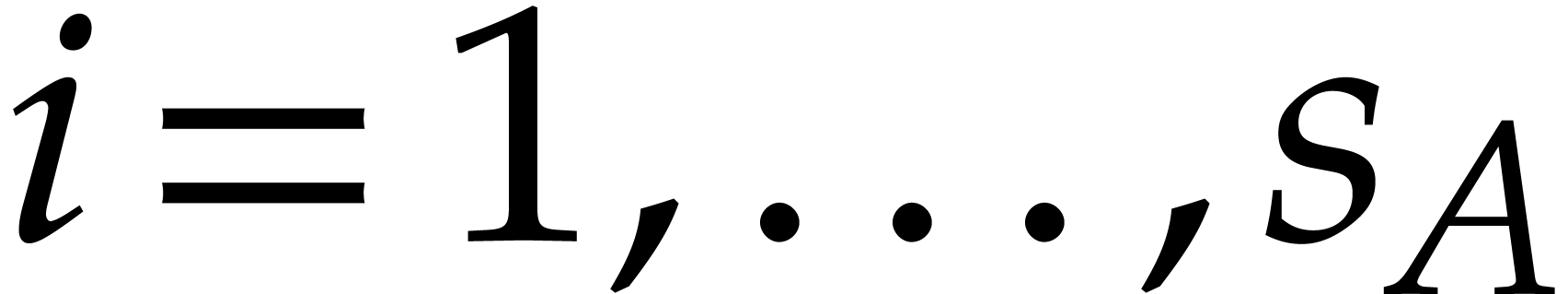 , where
, where 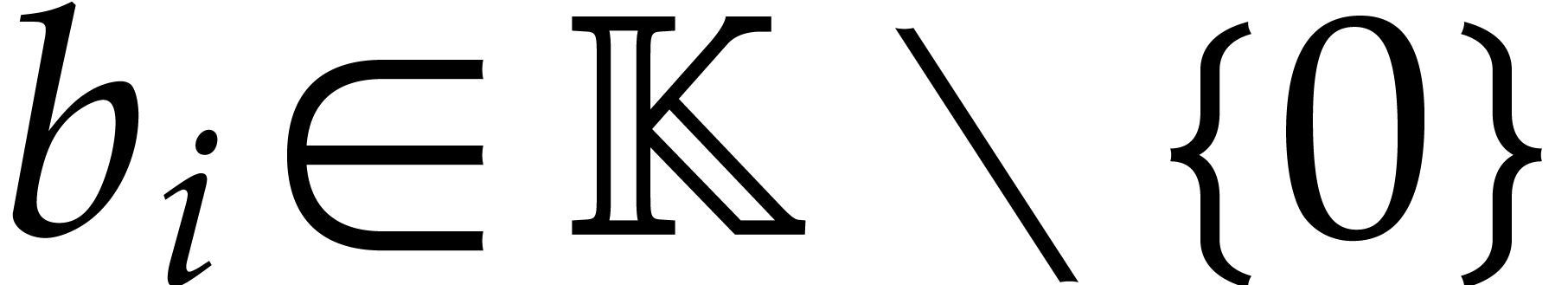 and
and
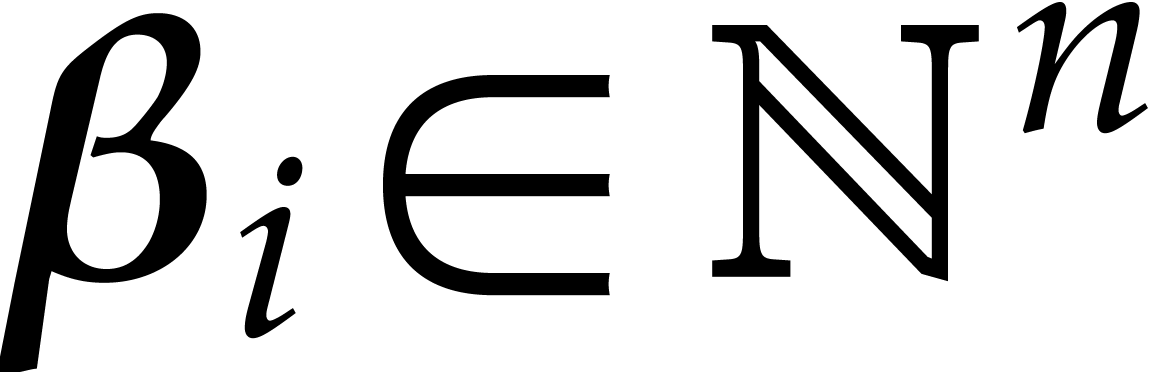 for
for 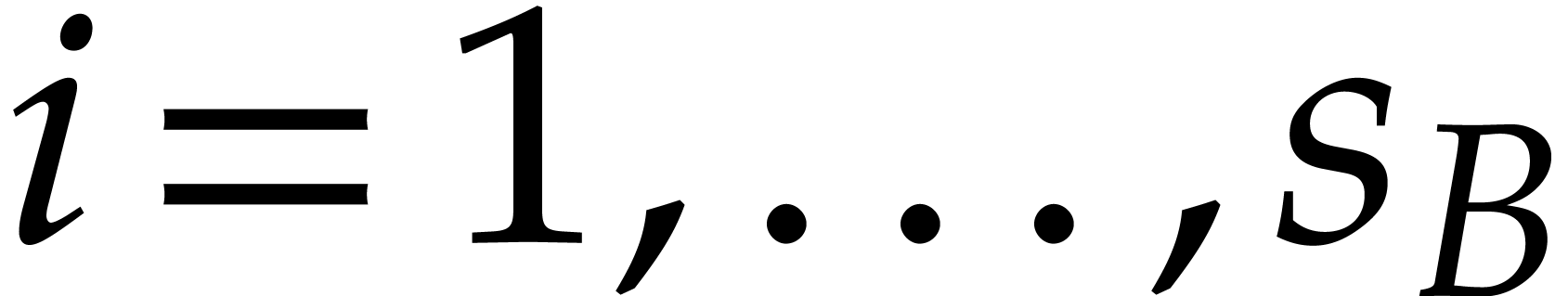 ,
where
,
where 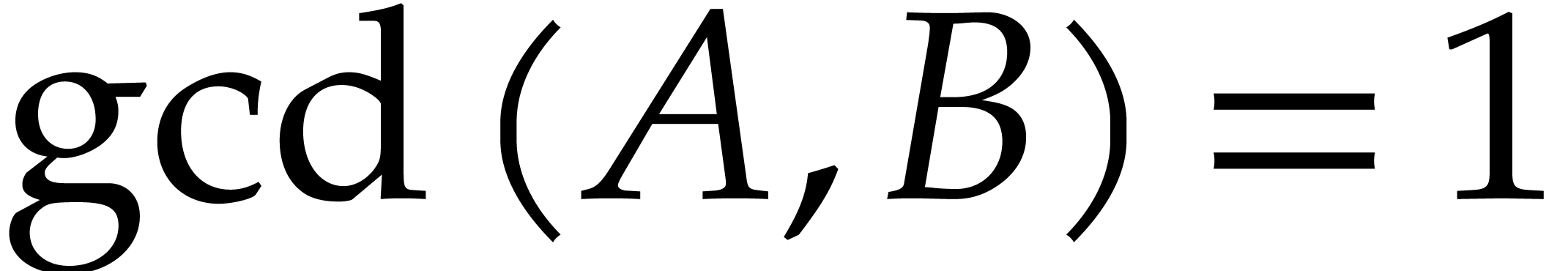 , and where
, and where 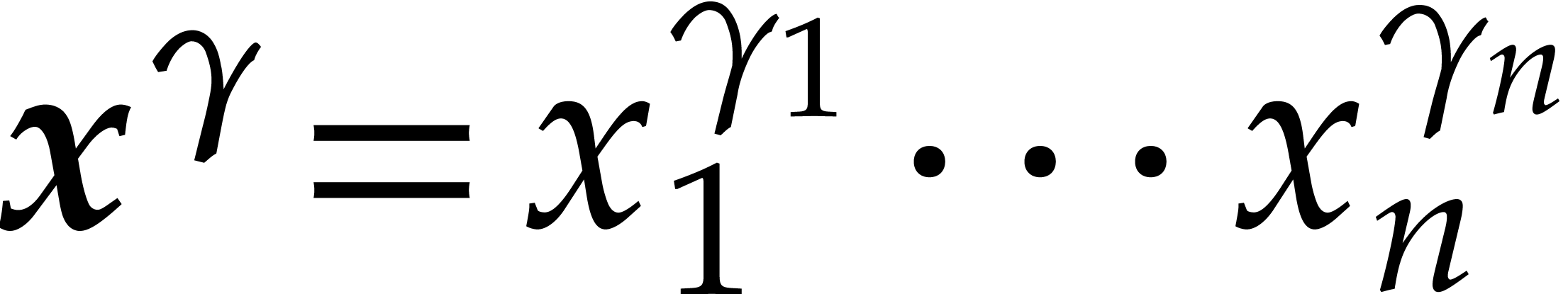 for any
for any  .
.
Here, “sparse” means that we use a sparse representation for
multivariate polynomials: only the set of the non-zero terms is stored
and each term is represented by a pair made of a coefficient and an
exponent vector. When using a sparse representation, the natural
complexity measures are the number of non-zero terms and the maximum bit
size of the exponents. On the contrary, a dense representation of a
polynomial 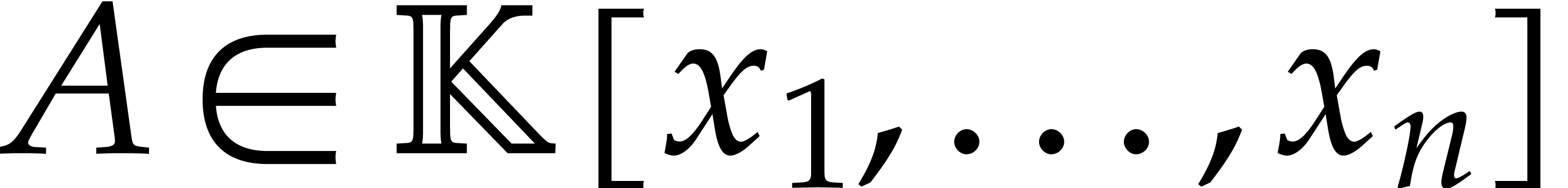 , say of total
degree
, say of total
degree  , is the vector of all
its coefficients up to degree
, is the vector of all
its coefficients up to degree  for a prescribed
monomial ordering.
for a prescribed
monomial ordering.
The sparse interpolation of a blackbox polynomial 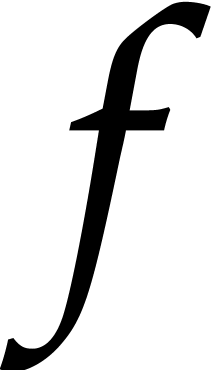 has been widely studied in computer algebra, and very efficient
algorithms are known. In this paper, we will use this polynomial case as
a basic building block, with an abstract specification. We refer to [1, 4, 8, 9, 13,
17] for state of the art algorithms for polynomial sparse
interpolation and further historical references.
has been widely studied in computer algebra, and very efficient
algorithms are known. In this paper, we will use this polynomial case as
a basic building block, with an abstract specification. We refer to [1, 4, 8, 9, 13,
17] for state of the art algorithms for polynomial sparse
interpolation and further historical references.
Our main problem here is to find an efficient reduction of the general
sparse interpolation problem for rational functions to the special case
of polynomials. We focus on the case when the total degrees 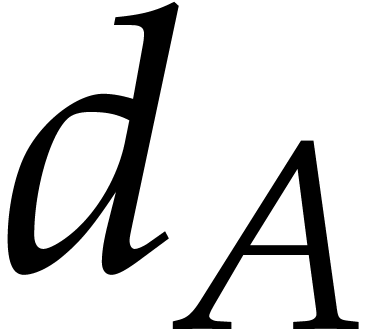 and
and 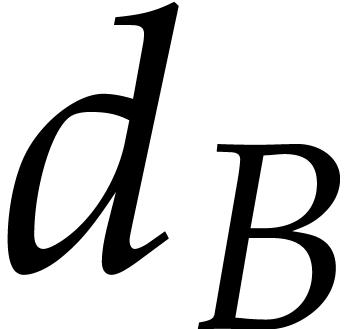 are “modest” with
respect to the total number of terms
are “modest” with
respect to the total number of terms  .
This is typically the case for applications in computer algebra. We also
recall that algorithms in this area are usually probabilistic, of Monte
Carlo type; our new algorithms are no exception. In a similar vein, we
assume that the cardinality of
.
This is typically the case for applications in computer algebra. We also
recall that algorithms in this area are usually probabilistic, of Monte
Carlo type; our new algorithms are no exception. In a similar vein, we
assume that the cardinality of  is
“sufficiently large”, so that random points in
is
“sufficiently large”, so that random points in  are “generic” with high probability.
are “generic” with high probability.
One efficient reduction from sparse rational function interpolation to sparse polynomial interpolation was proposed by Cuyt and Lee [2]. Our new method is a variant of their algorithm; through the use of projective coordinates, we are able to prove a better complexity bound: see section 3.
Computations with rational functions are intimately related to gcd
computations. In section 4, we show that our approach also
applies to gcd computations: given a blackbox function for the
computation of two sparse polynomials 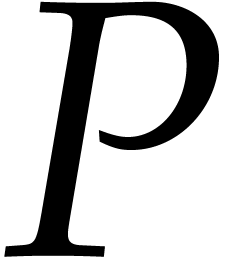 and
and 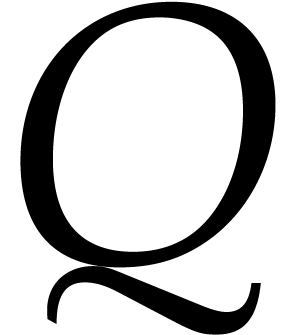 , we present a new complexity bound
for the sparse interpolation of
, we present a new complexity bound
for the sparse interpolation of 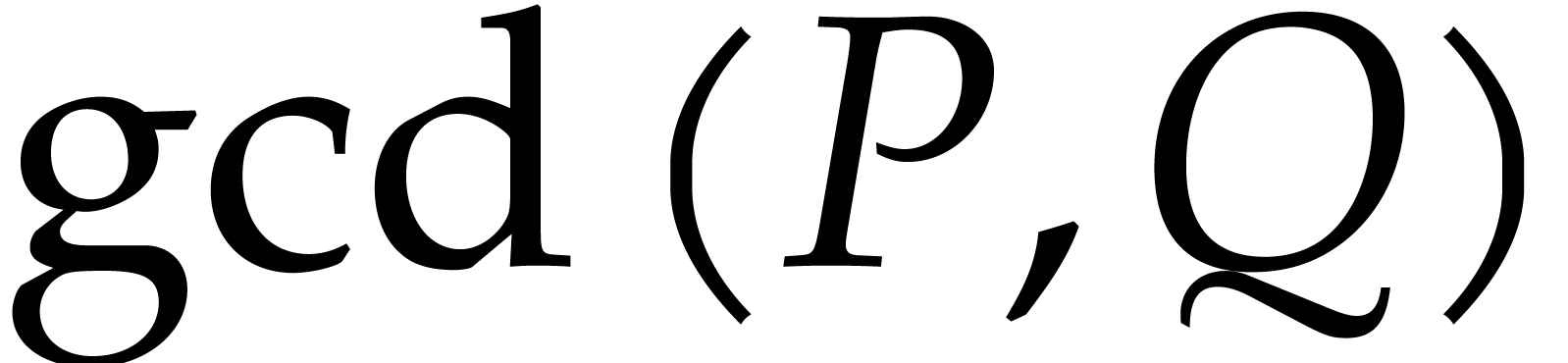 .
We also present an alternative heuristic algorithm for the case when
.
We also present an alternative heuristic algorithm for the case when
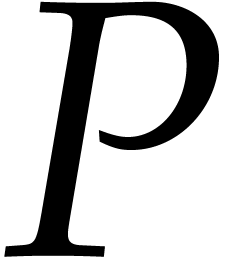 and
and  are given
explicitly, in sparse representation.
are given
explicitly, in sparse representation.
For simplicity, all time complexities are measured in terms of the
required number of operations in  .
Since our algorithms are probabilistic, we assume that a random element
in
.
Since our algorithms are probabilistic, we assume that a random element
in  can be produced in unit time. Our complexity
bounds are valid in several complexity models. For definiteness, one may
assume a probabilistic RAM model that supports operations in
can be produced in unit time. Our complexity
bounds are valid in several complexity models. For definiteness, one may
assume a probabilistic RAM model that supports operations in  .
.
The algorithms in this paper all rely on a given base algorithm for the
interpolation of sparse polynomials. For a polynomial in 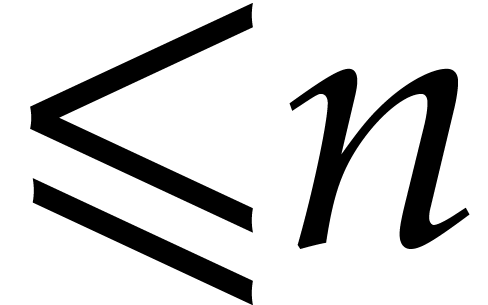 variables of total degree
variables of total degree 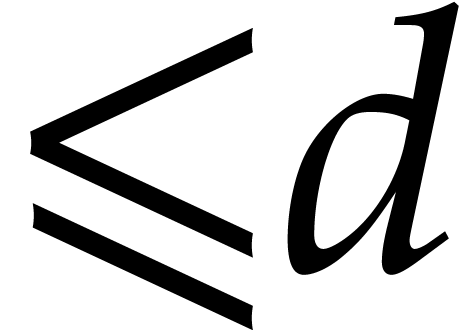 with
with
 terms, given by a blackbox function
terms, given by a blackbox function  , we assume that this algorithm requires
, we assume that this algorithm requires 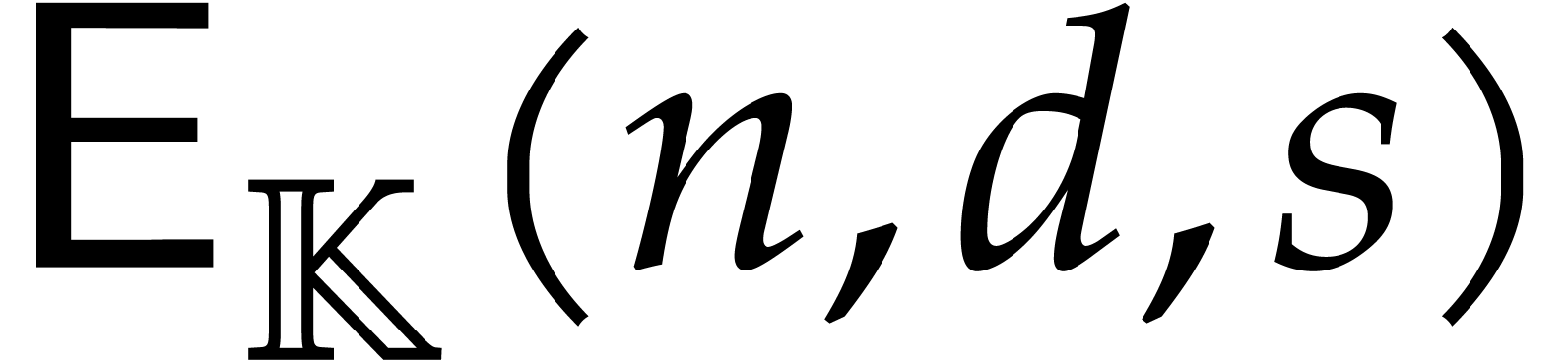 evaluations of
evaluations of  ,
as well as
,
as well as 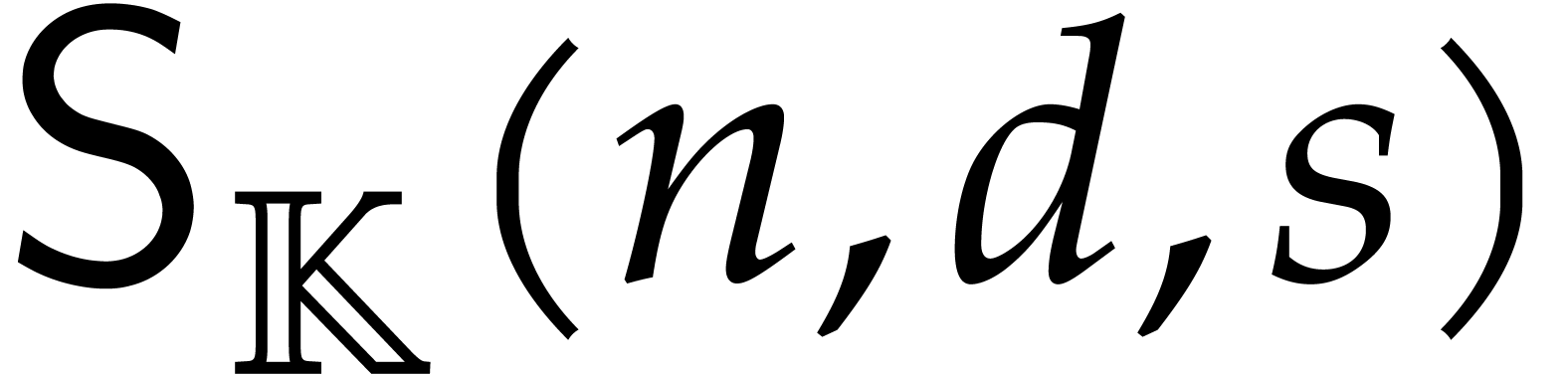 additional operations for the actual
interpolation from the latter values of
additional operations for the actual
interpolation from the latter values of  .
We recall that this algorithm is allowed to be probabilistic, of Monte
Carlo type.
.
We recall that this algorithm is allowed to be probabilistic, of Monte
Carlo type.
As a particular example of interest, consider the case when 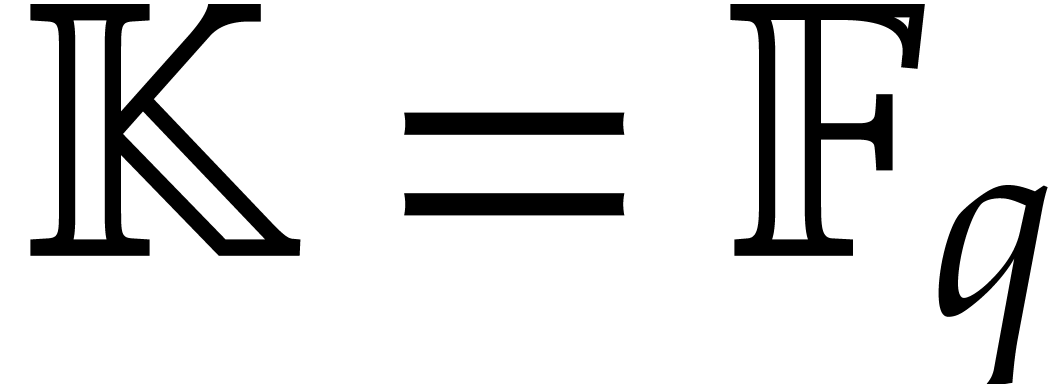 , and let
, and let 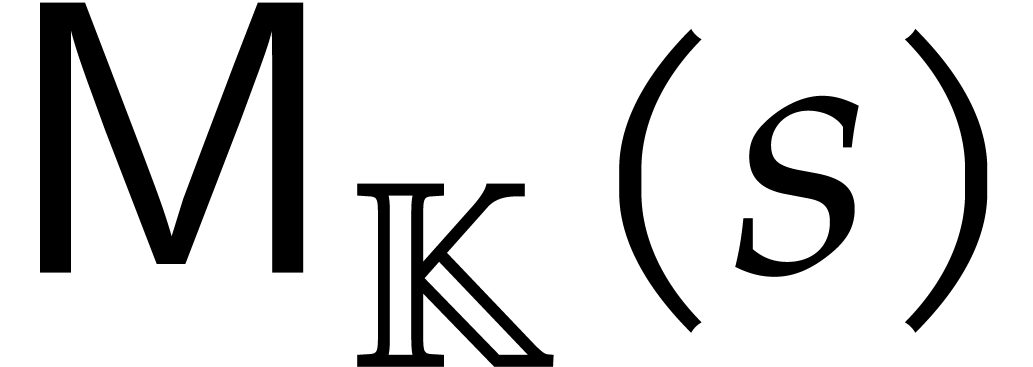 be the cost to multiply two polynomials of degree
be the cost to multiply two polynomials of degree  in
in 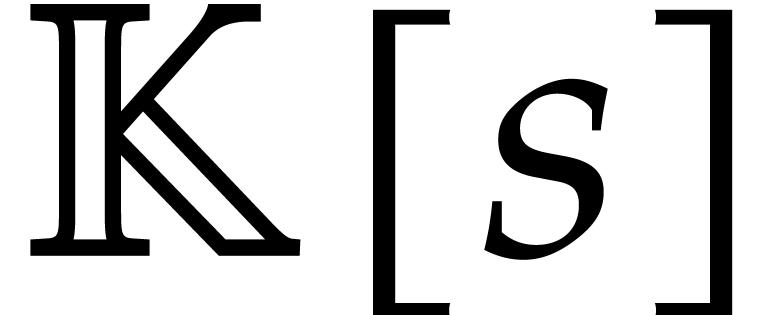 . In a suitable asymptotic
region where
. In a suitable asymptotic
region where  and
and 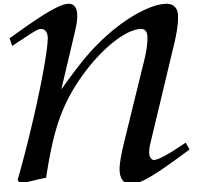 do not
grow too fast, Prony's traditional probabilistic geometric progression
technique yields
do not
grow too fast, Prony's traditional probabilistic geometric progression
technique yields
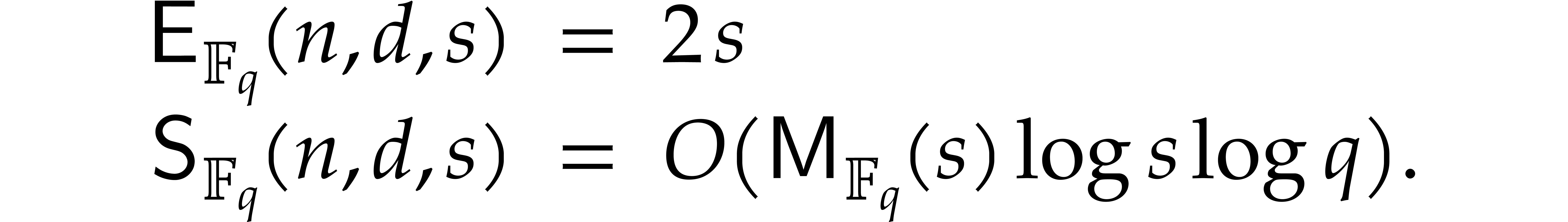
For FFT-primes 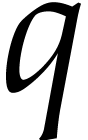 , one may also
apply the tangent Graeffe method, which yields
, one may also
apply the tangent Graeffe method, which yields
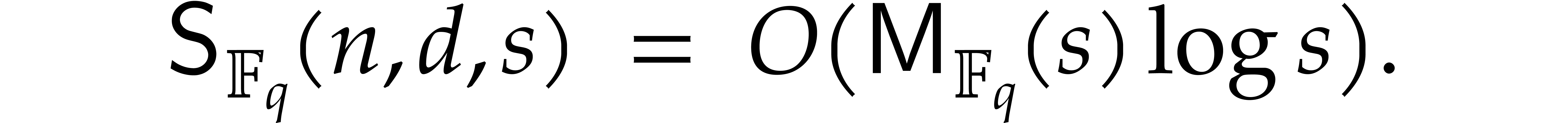
We refer to [9] for a survey of recent complexity bounds
for sparse polynomial interpolation. In what follows, we always assume
that 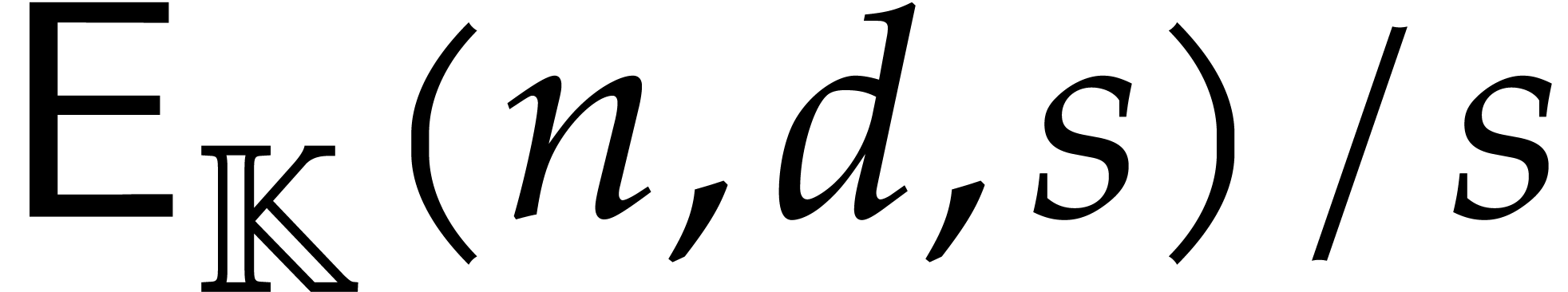 and
and 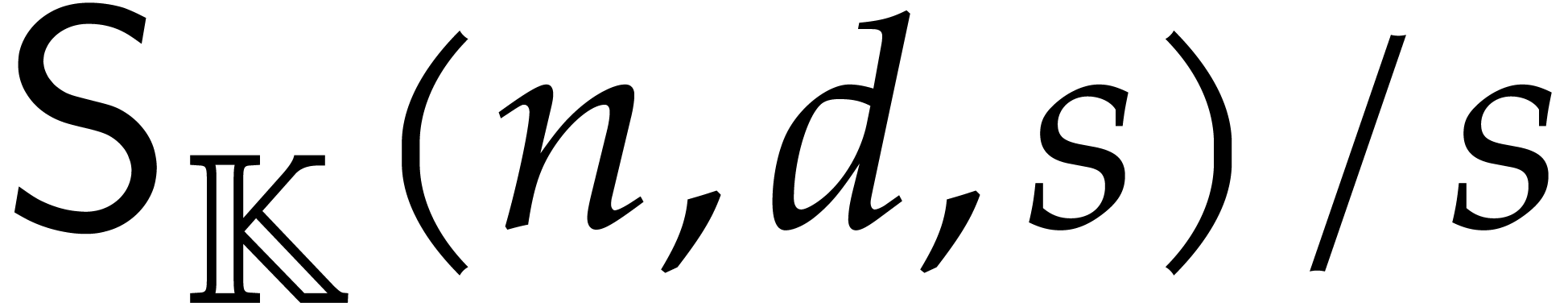 are
non-decreasing in
are
non-decreasing in  .
.
Consider a polynomial or rational blackbox function 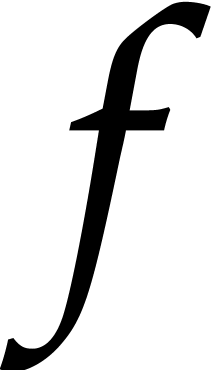 . We assume that a blackbox function over
. We assume that a blackbox function over  only involves field operations in
only involves field operations in  (which includes equality testing and branching, if needed), and that the
number of these operations is uniformly bounded.
(which includes equality testing and branching, if needed), and that the
number of these operations is uniformly bounded.
Efficient algorithms for the sparse interpolation of 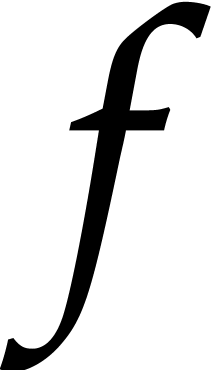 typically evaluate
typically evaluate 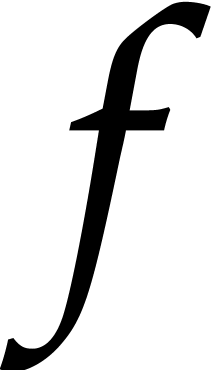 at a specific sequence of
points, such as a geometric progression. For the algorithms in this
paper, it is convenient to systematically make the assumption that we
only evaluate
at a specific sequence of
points, such as a geometric progression. For the algorithms in this
paper, it is convenient to systematically make the assumption that we
only evaluate 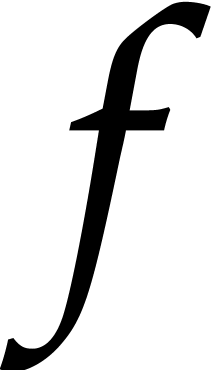 at points
at points 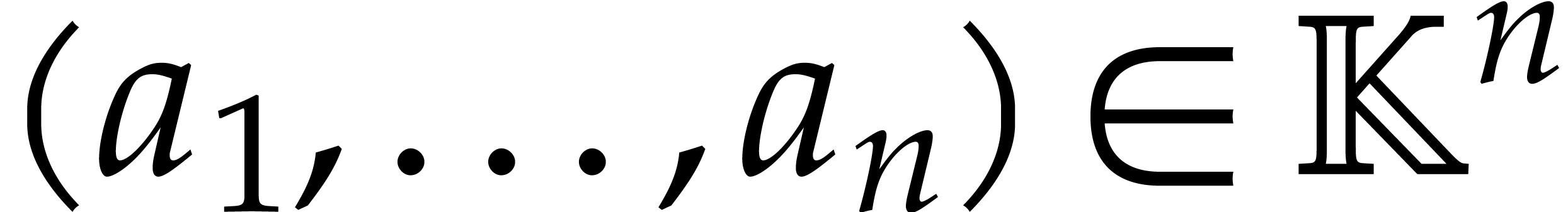 with
with 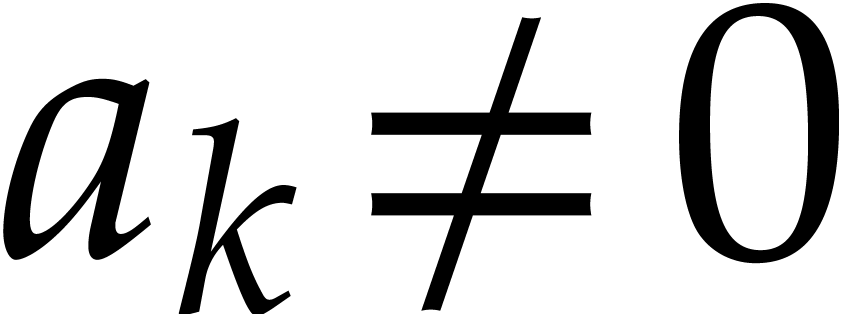 for
for 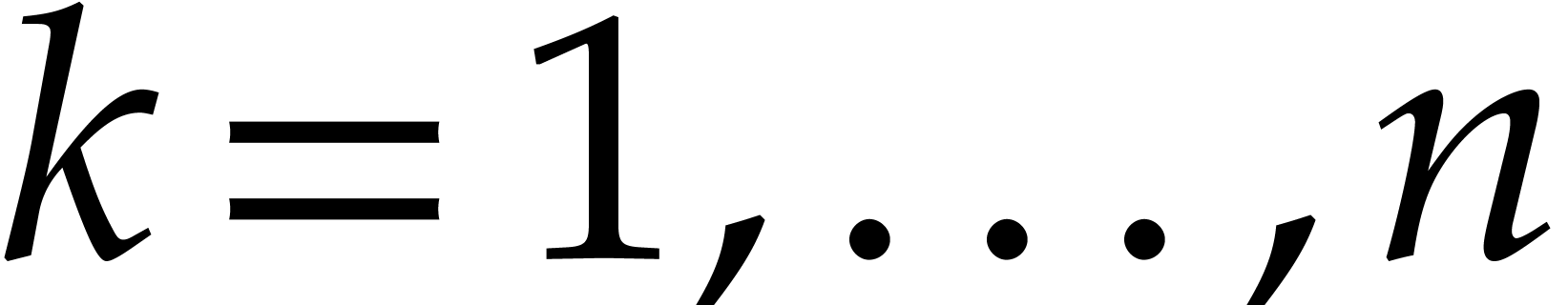 .
This assumption holds in particular for points in geometric
progressions.
.
This assumption holds in particular for points in geometric
progressions.
One problem with the evaluation of a blackbox function that involves divisions is that the evaluation may fail whenever a division by zero occurs. An evaluation point for which this happens is colloquially called a bad point. Such bad points must be discarded and the same holds for sequences of evaluation points that contain at least one bad point. Of course, it would in principle suffice to choose another sequence of evaluation points. However, in general, sufficiently generic sequences are not readily at our disposal with high probability. This problem may be overcome using randomization, as follows.
Since our blackbox function 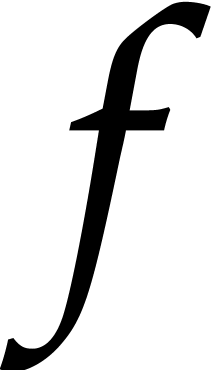 only involves a
bounded number of field operations in
only involves a
bounded number of field operations in  ,
the set of bad evaluation points is a constructible subset of
,
the set of bad evaluation points is a constructible subset of 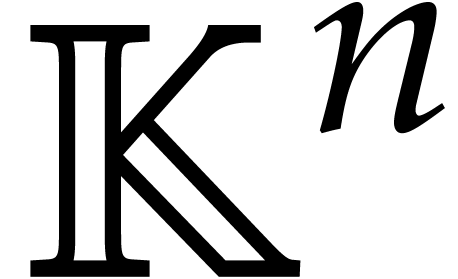 . We assume that this subset is not
Zariski dense. Consequently, there exists a polynomial
. We assume that this subset is not
Zariski dense. Consequently, there exists a polynomial 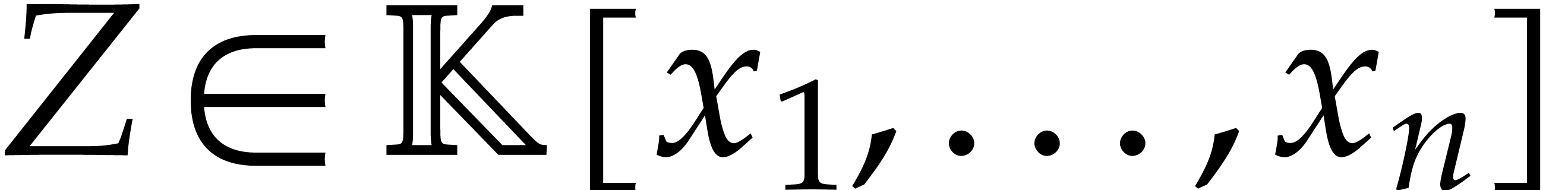 such that
such that  whenever
whenever  is a
bad point. Given
is a
bad point. Given  , the
probability that a point
, the
probability that a point  satisfies
satisfies

is at least
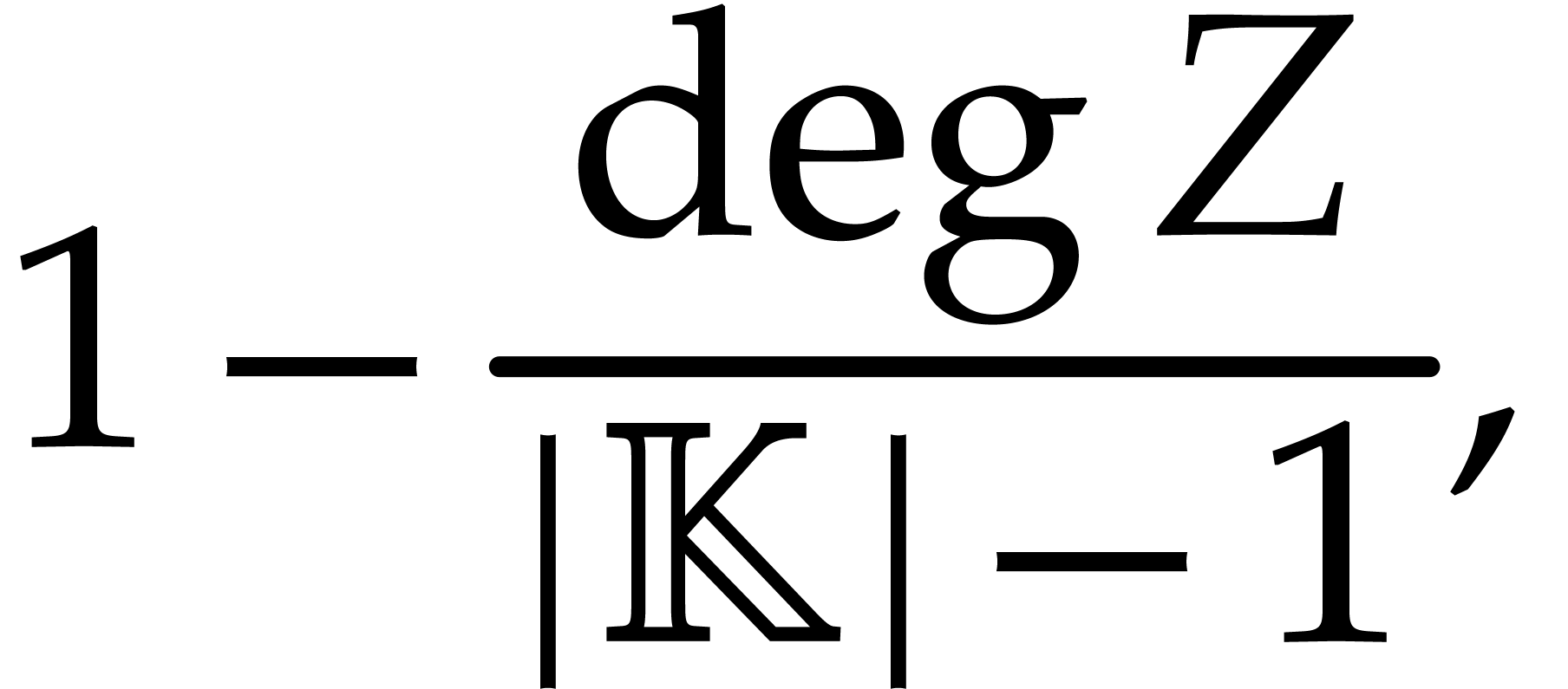
by the Schwartz–Zippel lemma [5, Lemma 6.44], where
 denotes the cardinality of
denotes the cardinality of  .
.
Now assume that we are given a method for the sparse interpolation of
any blackbox function with the same support as  . The evaluation points for such a method form a
fixed finite subset
. The evaluation points for such a method form a
fixed finite subset  of
of 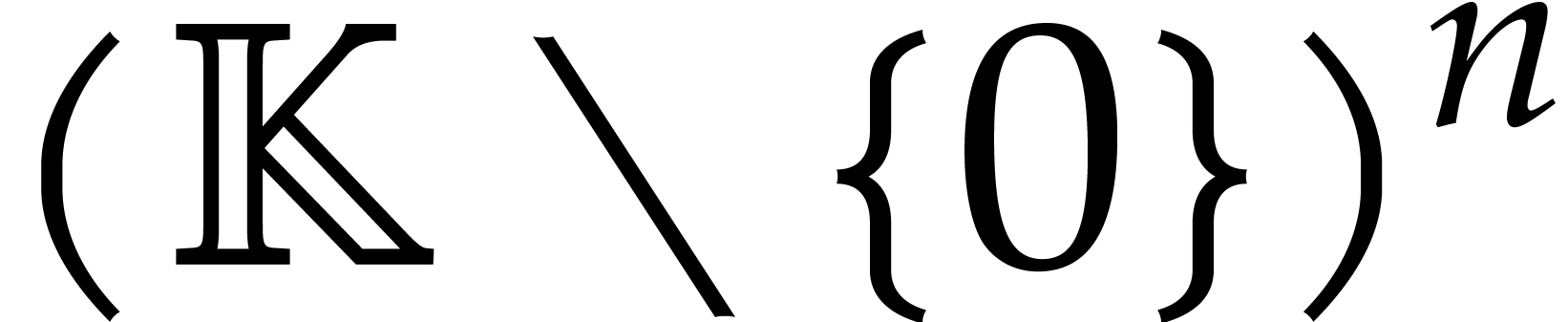 . If
. If  is sufficiently large,
then it follows with high probability that
is sufficiently large,
then it follows with high probability that  for
all
for
all  , when taking
, when taking  at random. We may thus interpolate
at random. We may thus interpolate
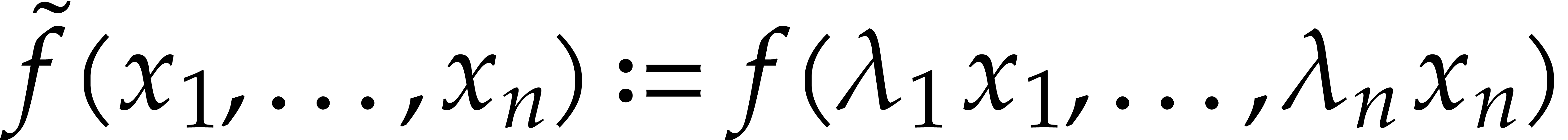
instead of  , with high
probability. Since
, with high
probability. Since  are non-zero, we may next
recover the sparse interpolation of
are non-zero, we may next
recover the sparse interpolation of 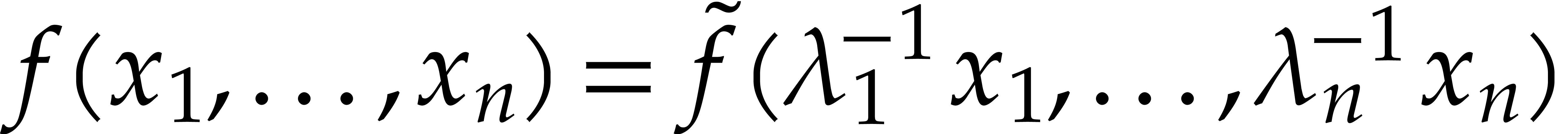 itself.
itself.
This section concerns the sparse interpolation of a rational function
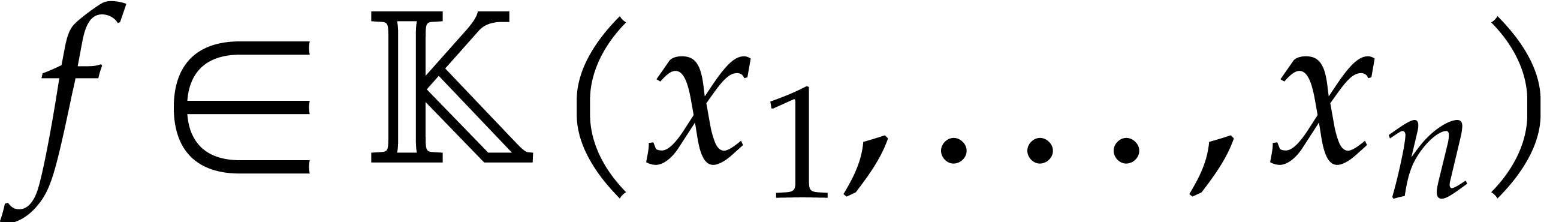 given as a blackbox.
given as a blackbox.
The natural idea to interpolate a univariate rational function  given as a blackbox is to evaluate it at many points and
then use Cauchy interpolation [5, Corollary 5.18] in
combination with the fast Euclidean algorithm [5, chapter
11]; this idea appears in early works on the topic [14]. If
the numerator and denominator of
given as a blackbox is to evaluate it at many points and
then use Cauchy interpolation [5, Corollary 5.18] in
combination with the fast Euclidean algorithm [5, chapter
11]; this idea appears in early works on the topic [14]. If
the numerator and denominator of 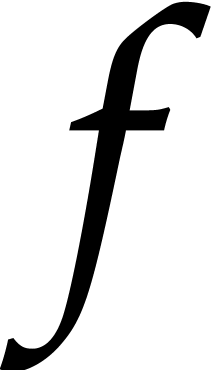 have respective
degrees
have respective
degrees 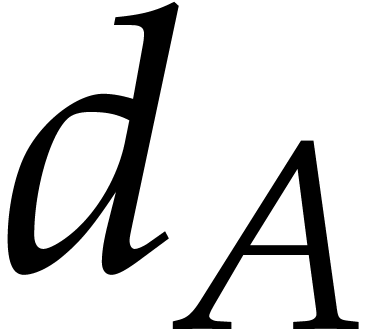 and
and 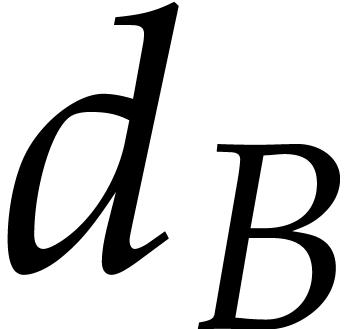 ,
then the total cost decomposes into
,
then the total cost decomposes into 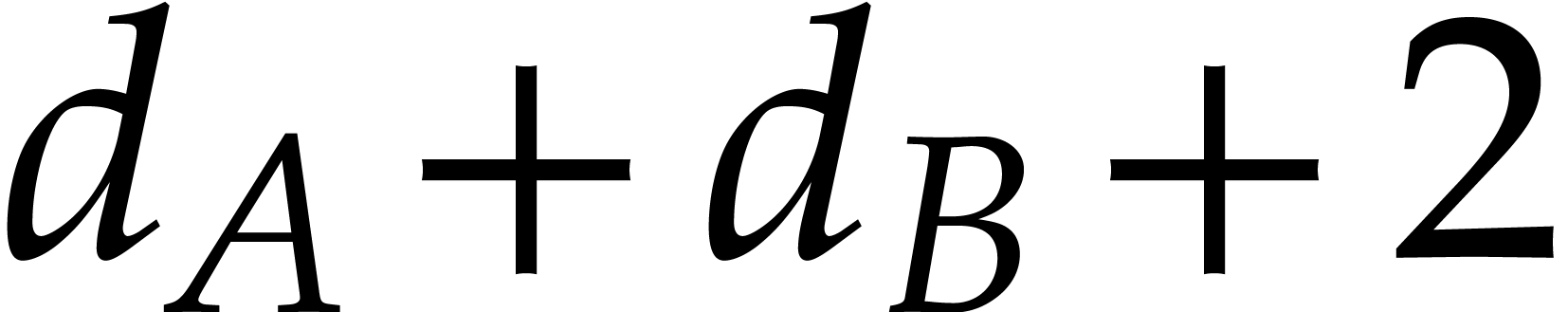 evaluations
of
evaluations
of  and
and
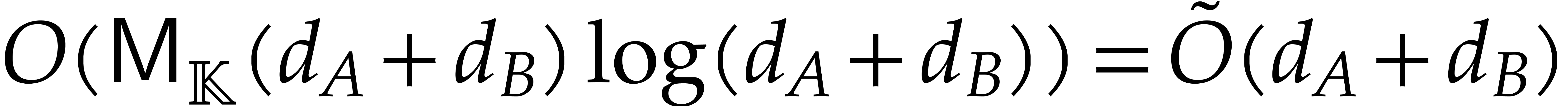
operations in  for the Cauchy interpolation. Here
for the Cauchy interpolation. Here
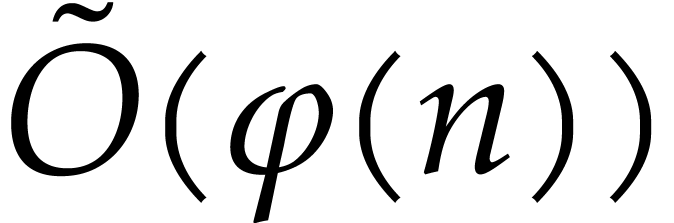 is the usual shorthand for
is the usual shorthand for 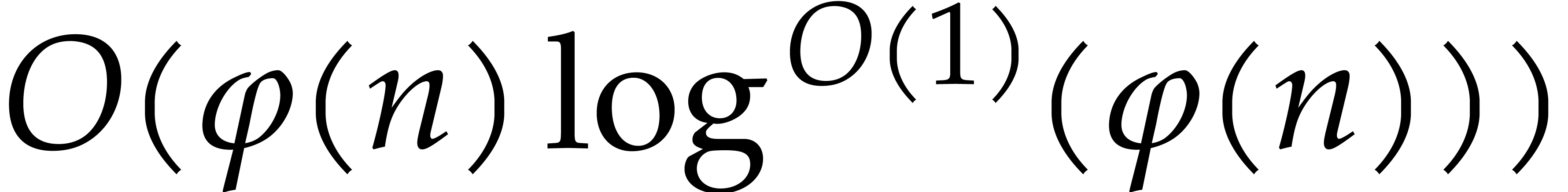 , as in [5].
, as in [5].
Interpolating rational functions seems more difficult than polynomials.
In high degree, it is still a challenging problem to design efficient
algorithms in terms of the sparse size  of the
function. An algorithm with exponential time complexity is known from
[6].
of the
function. An algorithm with exponential time complexity is known from
[6].
In the multivariate case, the interpolation problem can be handled as a
dense one with respect to one of the variables and as a sparse one with
respect to the other variables. Although no general polynomial
complexity bound is known in terms of the sparse size, this approach is
extremely useful in practice, as soon as one of the variables has small
degree. Roughly speaking, one proceeds as follows: for a fixed point
 we reconstruct the univariate function
we reconstruct the univariate function 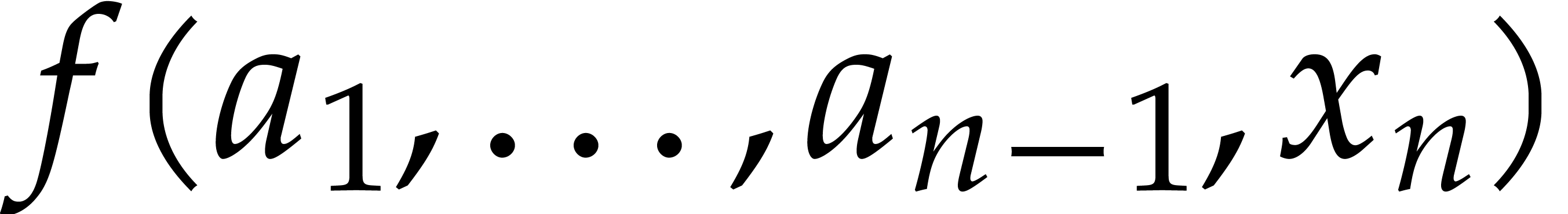 with the dense representation in
with the dense representation in 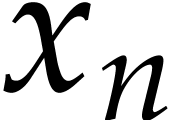 . Then we regard the numerator
. Then we regard the numerator  and the denominator
and the denominator  as polynomials in
as polynomials in 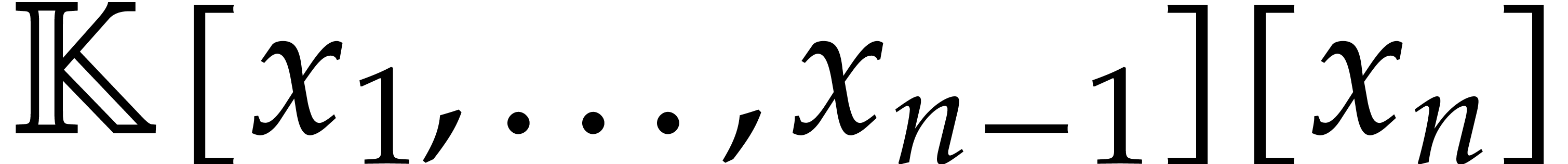 , and it remains to interpolate
their sparse coefficients using sufficiently many evaluation points
, and it remains to interpolate
their sparse coefficients using sufficiently many evaluation points
 .
.
The difficulty with the latter interpolation is that the values of 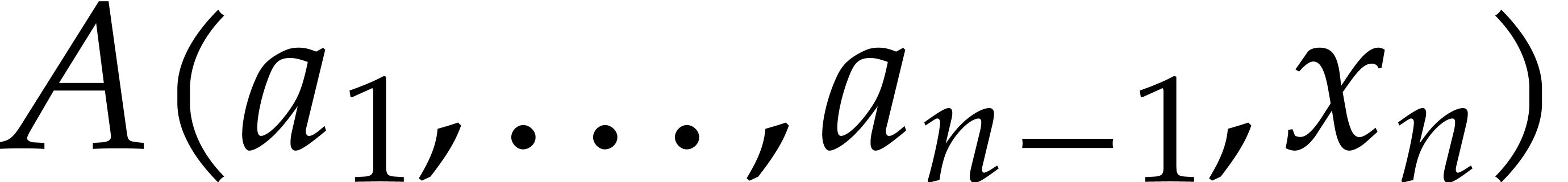 and
and 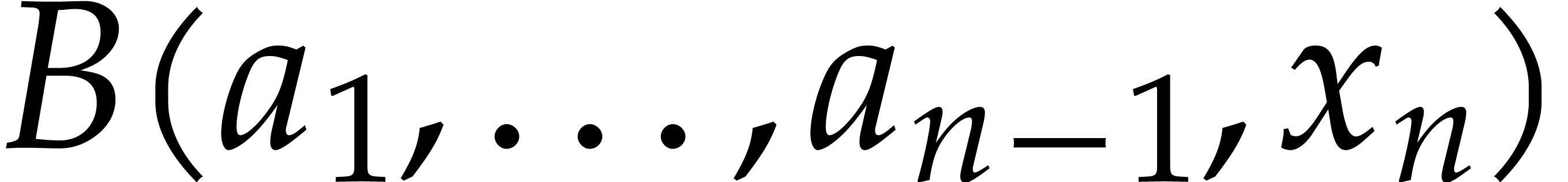 are only determined up to
a scalar in
are only determined up to
a scalar in  . In order to
compute this scalar, a normalization assumption is necessary. For
instance we may require
. In order to
compute this scalar, a normalization assumption is necessary. For
instance we may require  to be monic in
to be monic in 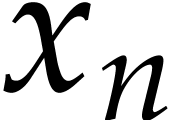 , which can be achieved through a
random linear change of coordinates [14]. Another kind of
normalization has been proposed by Cuyt and Lee [2]: they
introduce a new auxiliary variable to decompose
, which can be achieved through a
random linear change of coordinates [14]. Another kind of
normalization has been proposed by Cuyt and Lee [2]: they
introduce a new auxiliary variable to decompose  and
and  into their homogeneous components. Their
approach is sketched below. Let us finally mention [12],
which addresses the special case
into their homogeneous components. Their
approach is sketched below. Let us finally mention [12],
which addresses the special case 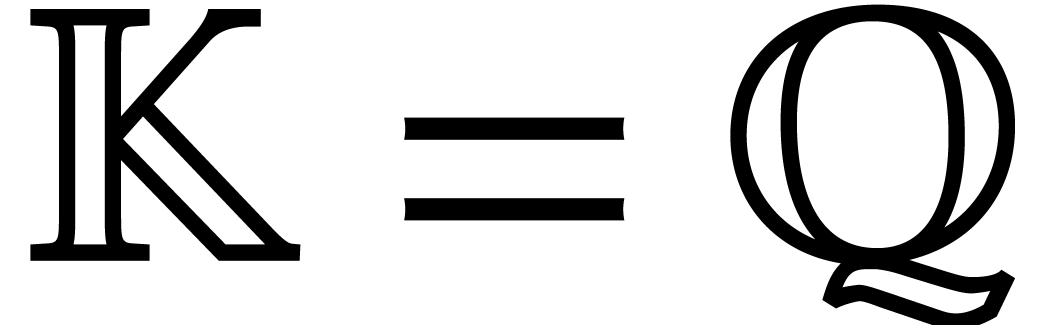 using a
specific strategy.
using a
specific strategy.
An efficient reduction of sparse interpolation from rational functions
to polynomials was proposed by Cuyt and Lee in [2]. Their
approach starts by introducing a homogenizing variable 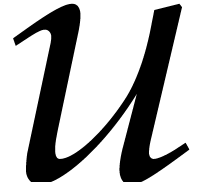 and
and
With high probability, they next reduce to the case when 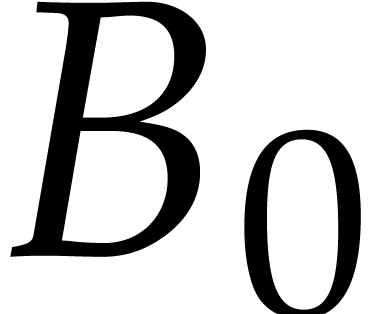 is non-zero, by choosing a random point
is non-zero, by choosing a random point 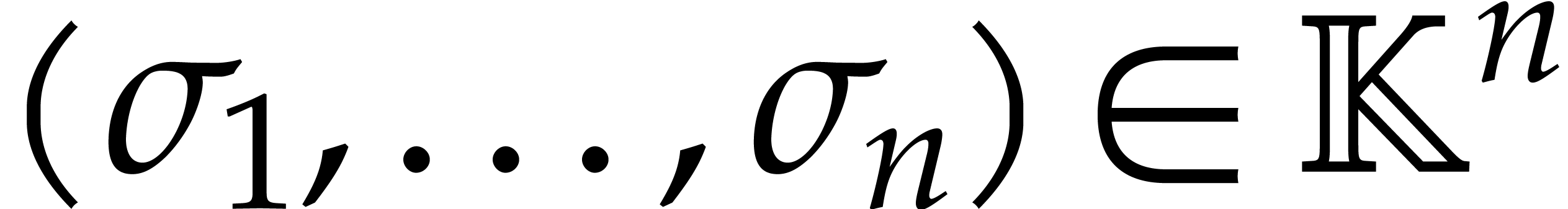 and performing a shift:
and performing a shift:
For a fixed point 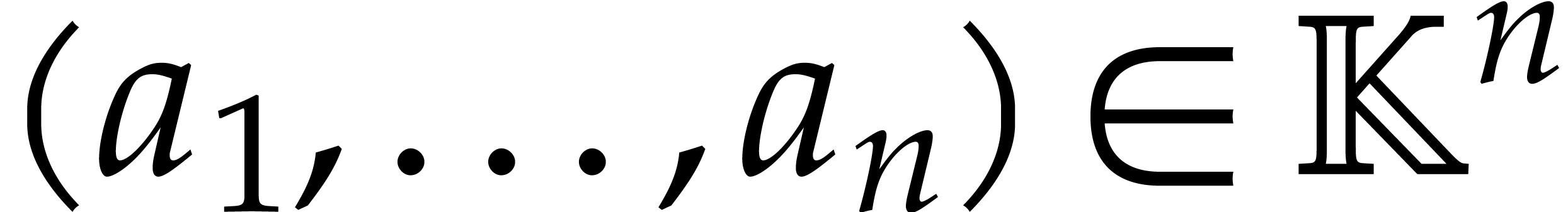 , we may
consider
, we may
consider 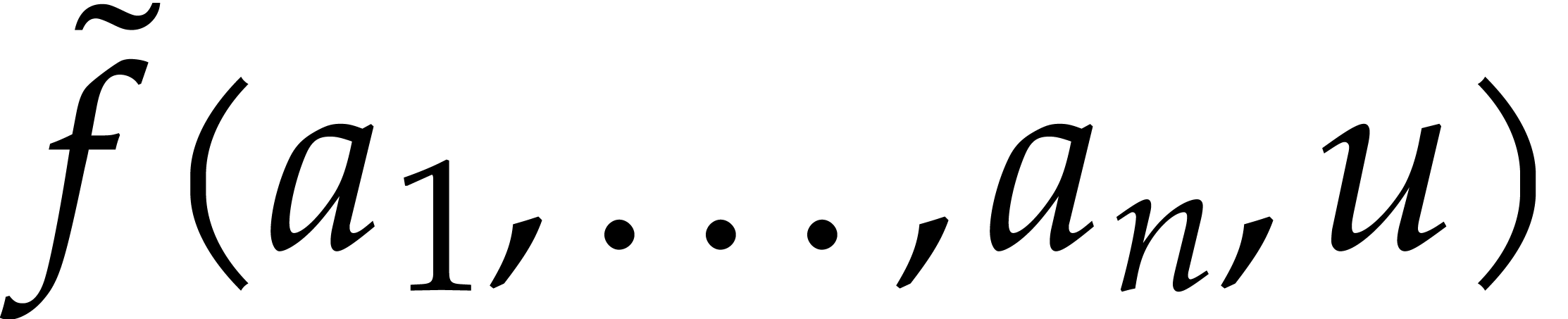 as a univariate rational function in
as a univariate rational function in
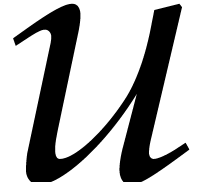 , which can generically be
interpolated from
, which can generically be
interpolated from 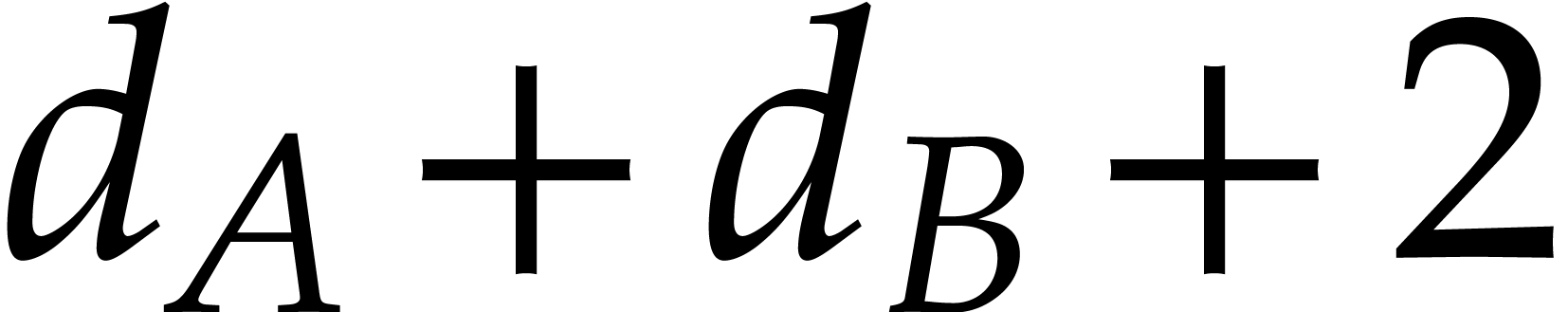 evaluations for different
values of
evaluations for different
values of 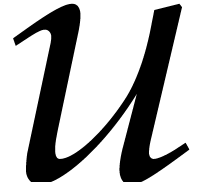 .
.
The first main idea from [2] is to normalize the resulting rational function in such a way that the constant coefficient of the denominator is equal to one:
This yields blackbox functions that take  as
input and produce
as
input and produce
as output. We may now use sparse polynomial interpolation for each of
these blackbox functions and determine the sparse expressions for the
above polynomials. We finally obtain 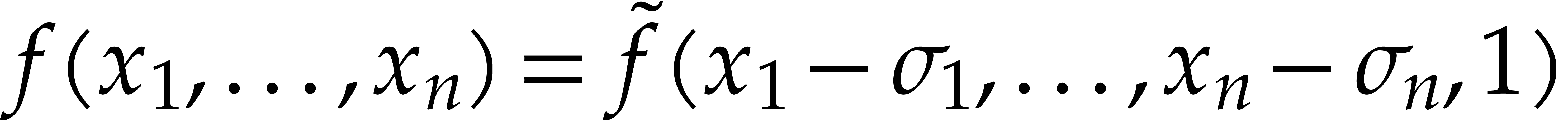 using a
simple shift.
using a
simple shift.
One complication here is that shifts

destroy the sparsity. The second main observation by Cuyt and Lee is
that this drawback only occurs for the non-leading terms: the
coefficient 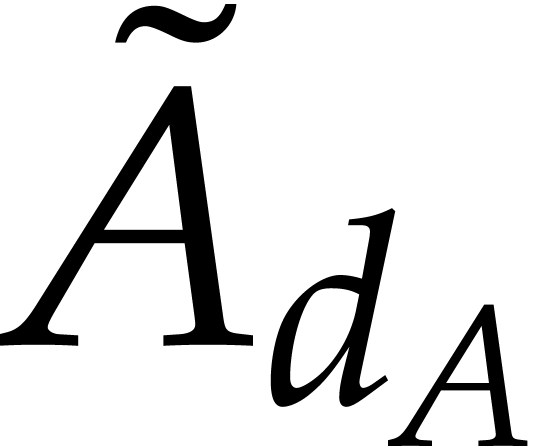 (resp.
(resp. 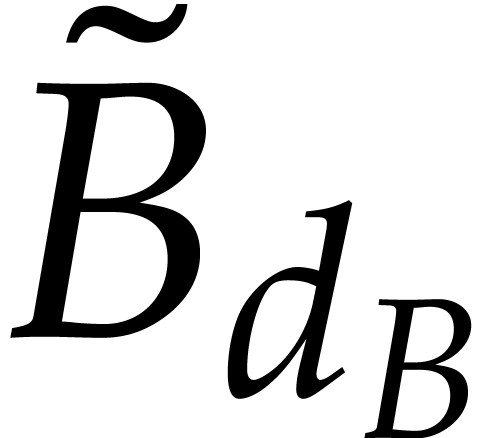 )
coincides with
)
coincides with 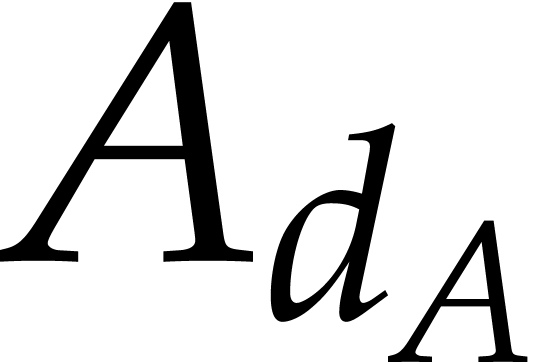 (resp.
(resp. 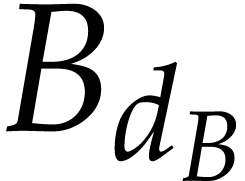 ). Using this observation recursively in a clever
way, it is possible to obtain the non-leading coefficients as well,
using at most
). Using this observation recursively in a clever
way, it is possible to obtain the non-leading coefficients as well,
using at most
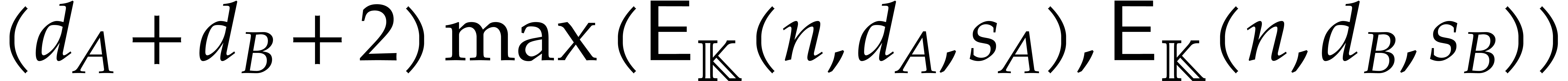
blackbox evaluations [2, section 2.2]. However, even though sparse interpolations of shifted polynomials can be avoided, the resulting algorithm still requires evaluations of shifted polynomials in their interpolated form: see the remarks at the end of [2, section 2.2]. In fact, the focus of [2] is on minimizing the number of blackbox evaluations; the overall complexity of the algorithm is not analyzed in detail.
Instead of using the recursive method from [2, section 2.2]
for determining the non-leading coefficients, we propose to avoid the
mere existence of such terms altogether. At the start of our algorithm,
we assume that the total degrees 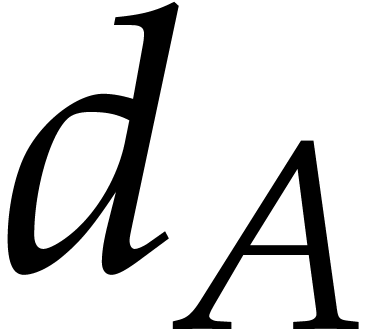 and
and 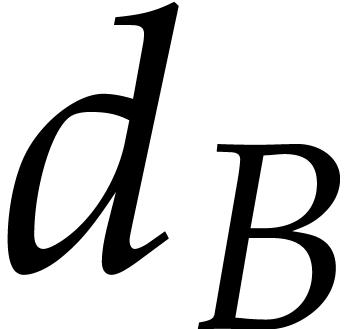 of the numerator
of the numerator  and the
denominator
and the
denominator 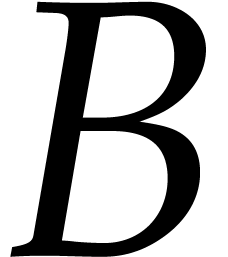 of
of 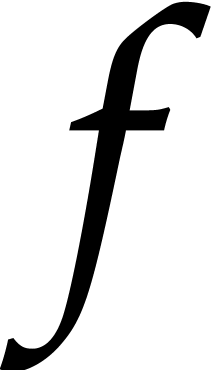 are
known. If we are only given a rough upper bound
are
known. If we are only given a rough upper bound 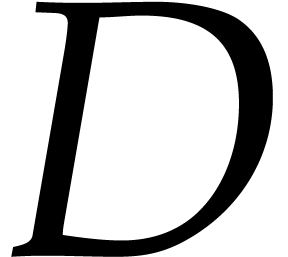 on these degrees, then we may reduce to this case as follows: take a
point
on these degrees, then we may reduce to this case as follows: take a
point 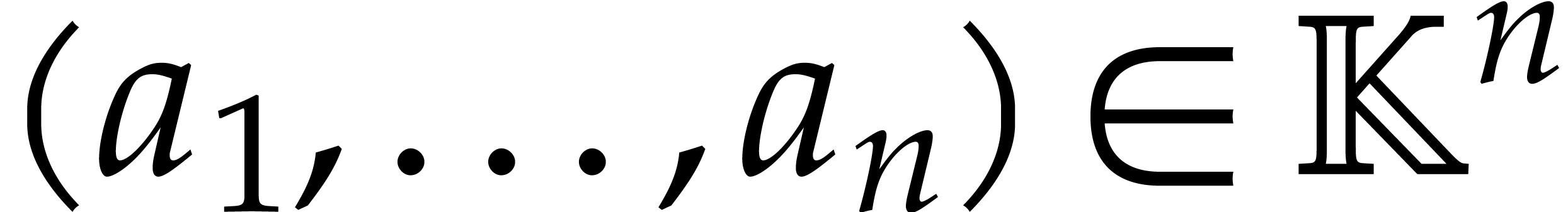 at random, and interpolate
at random, and interpolate 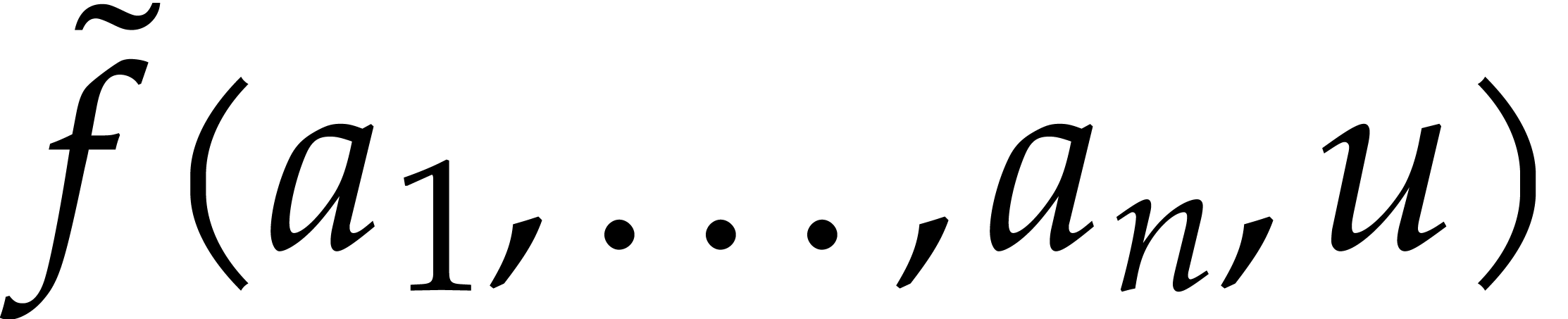 as a univariate rational function in
as a univariate rational function in 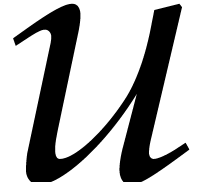 , from
, from 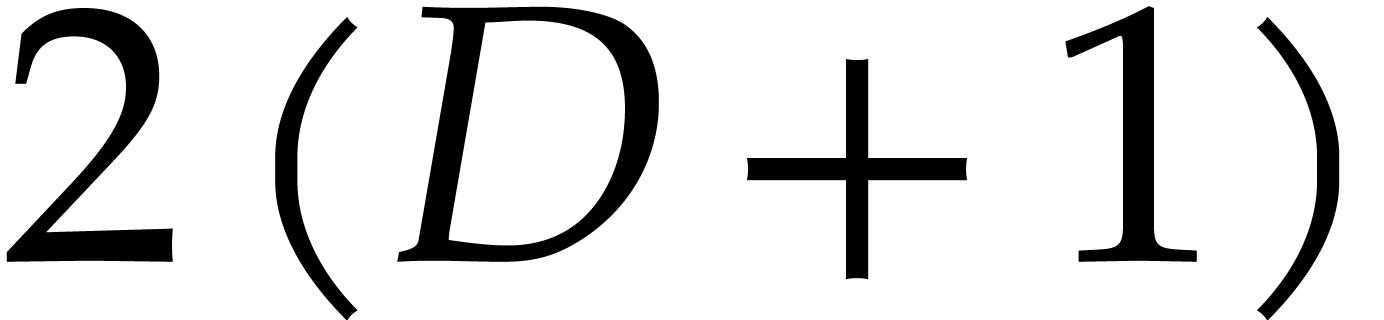 evaluations at
different values of
evaluations at
different values of 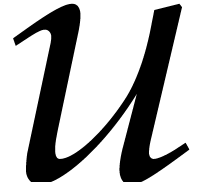 . With
high probability,
. With
high probability, 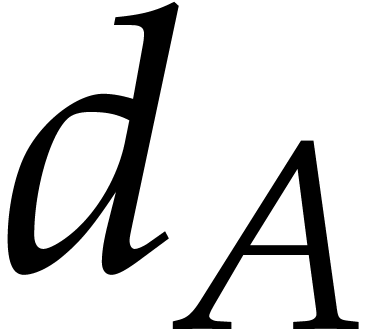 and
and 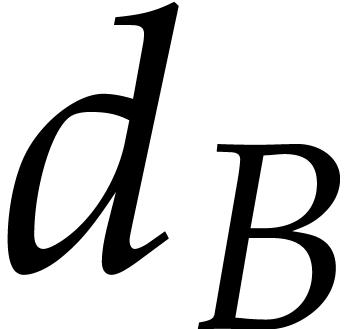 coincide with the degrees of the numerator and denominator of
coincide with the degrees of the numerator and denominator of 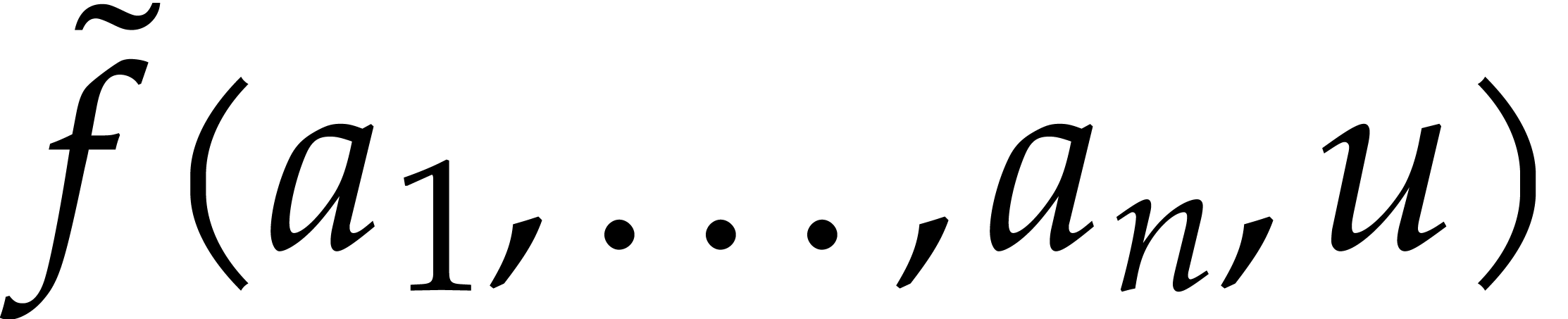 .
.
Our key observation is the following: if  and
and
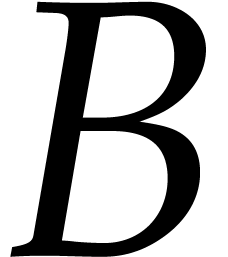 are homogeneous polynomials then
are homogeneous polynomials then 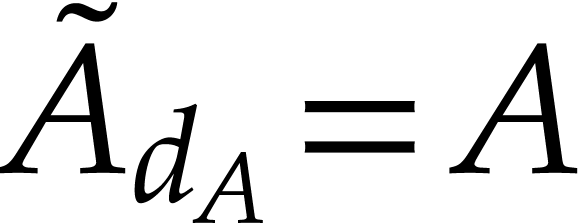 and
and 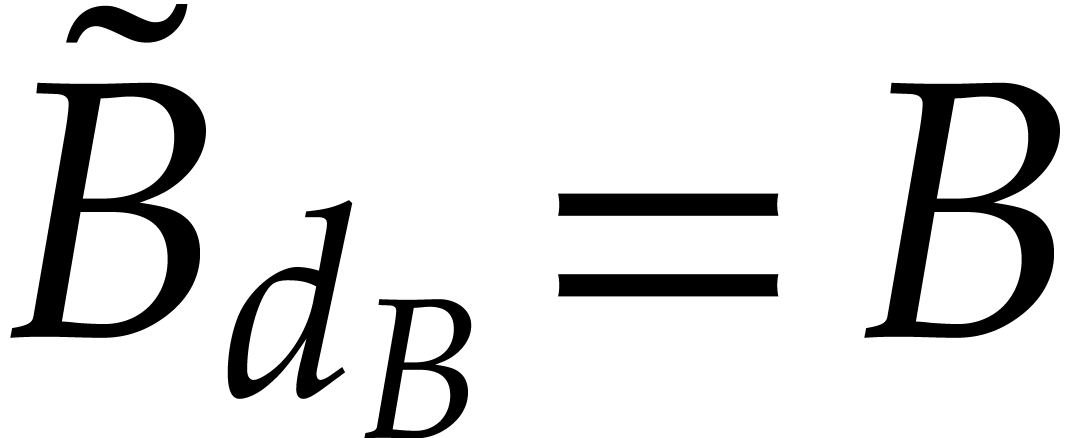 , so Cuyt
and Lee's method mostly reduces to two sparse polynomial interpolations.
Our method is therefore to force the polynomials
, so Cuyt
and Lee's method mostly reduces to two sparse polynomial interpolations.
Our method is therefore to force the polynomials  and
and 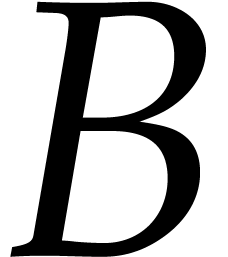 to become homogeneous by introducing a new
projective coordinate
to become homogeneous by introducing a new
projective coordinate 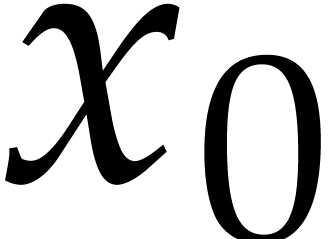 .
.
More precisely, we introduce the rational function
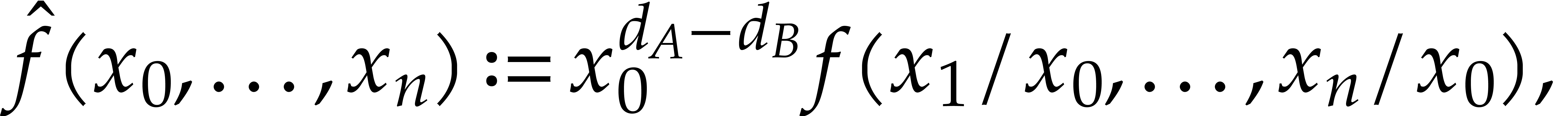
and we write
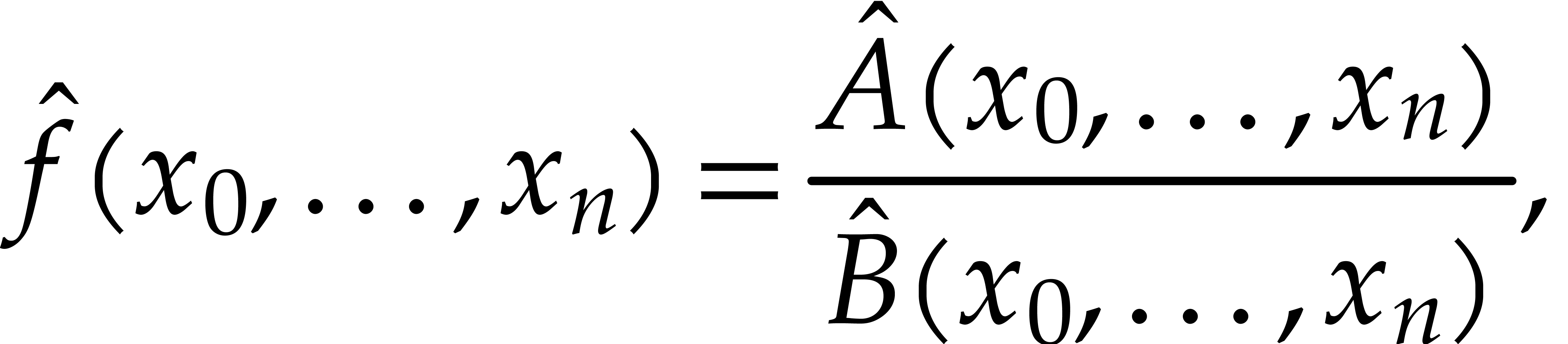
where
The numerator 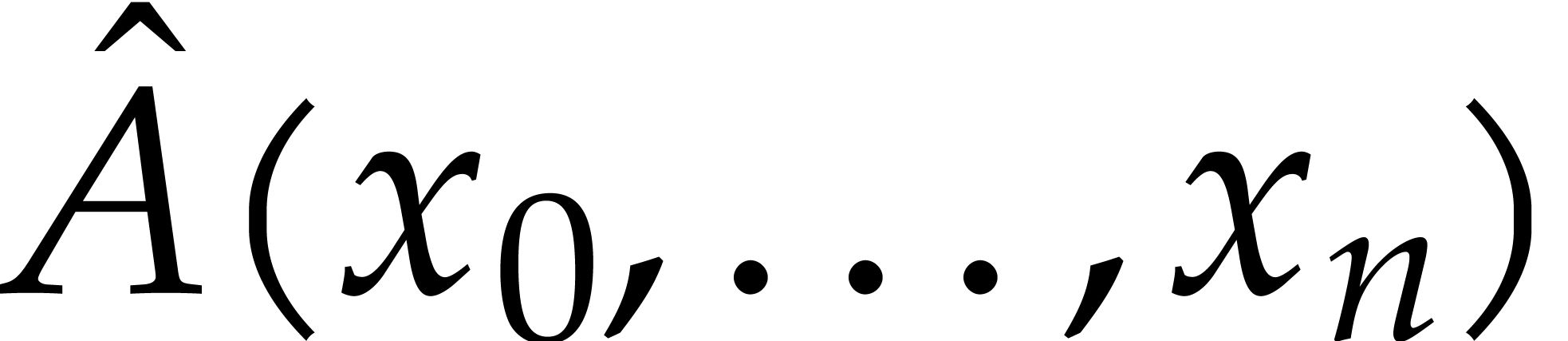 and denominator
and denominator  of
of 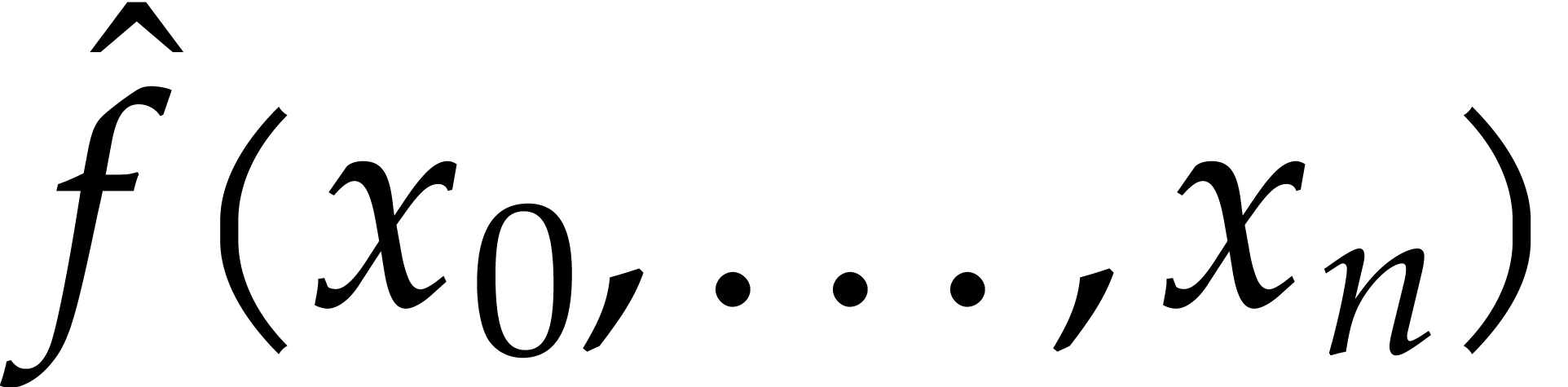 are both homogeneous and coprime. One
evaluation of
are both homogeneous and coprime. One
evaluation of  requires one evaluation of
requires one evaluation of  plus
plus 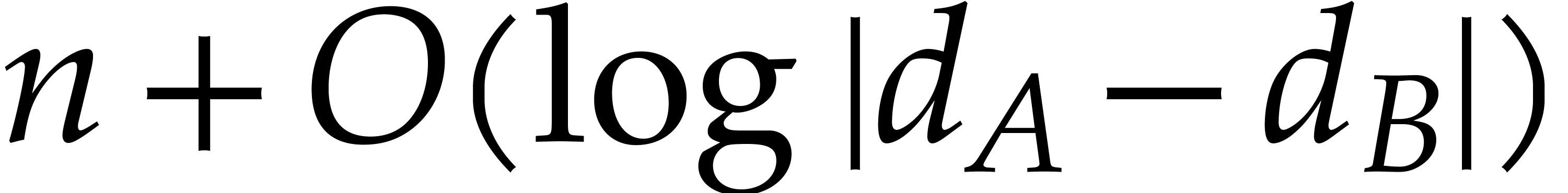 operations in
operations in  .
.
For some random shift 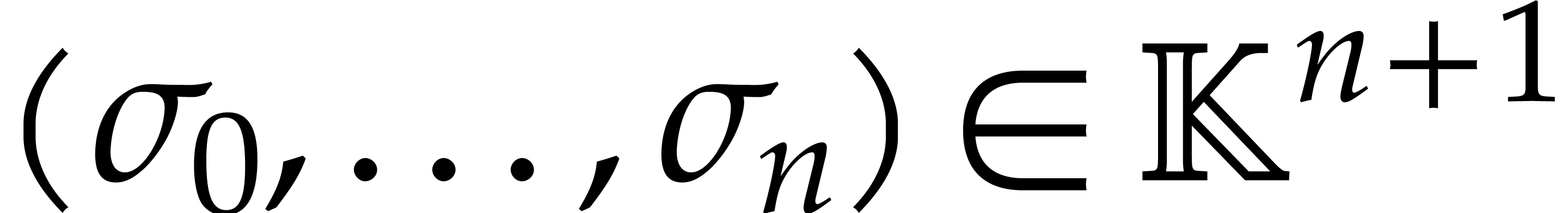 , we
next consider
, we
next consider
One evaluation of 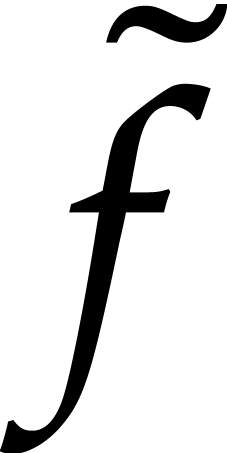 requires one evaluation of
requires one evaluation of
 plus
plus 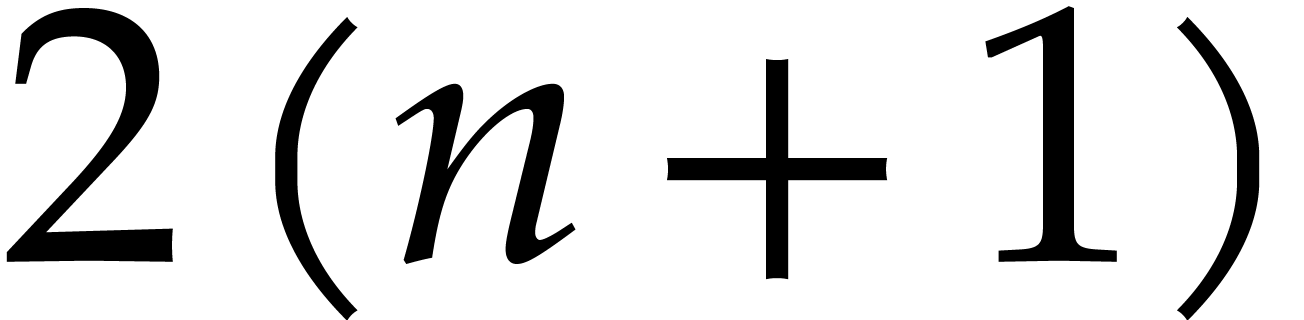 operations in
operations in  . Before addressing the
interpolation algorithm for
. Before addressing the
interpolation algorithm for  ,
let us show that
,
let us show that  is the canonical representative
of
is the canonical representative
of 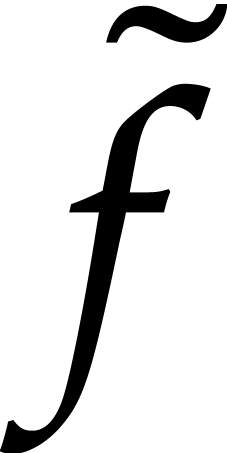 .
.
Proof. We consider the following weighted degree:
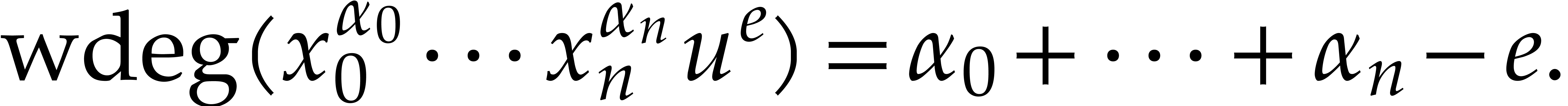
For this weight,  and
and  are
quasi-homogeneous, whence so are their respective irreducible factors
and therefore their gcd, written
are
quasi-homogeneous, whence so are their respective irreducible factors
and therefore their gcd, written 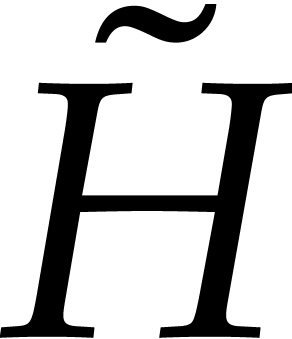 .
Consequently, there exists a non-negative integer
.
Consequently, there exists a non-negative integer 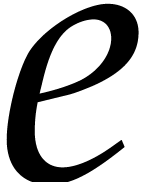 such that
such that
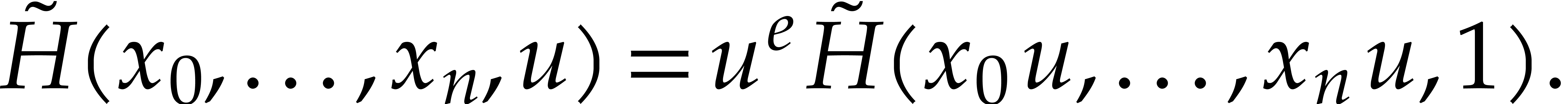
By construction,  and
and  are
coprime, whence
are
coprime, whence 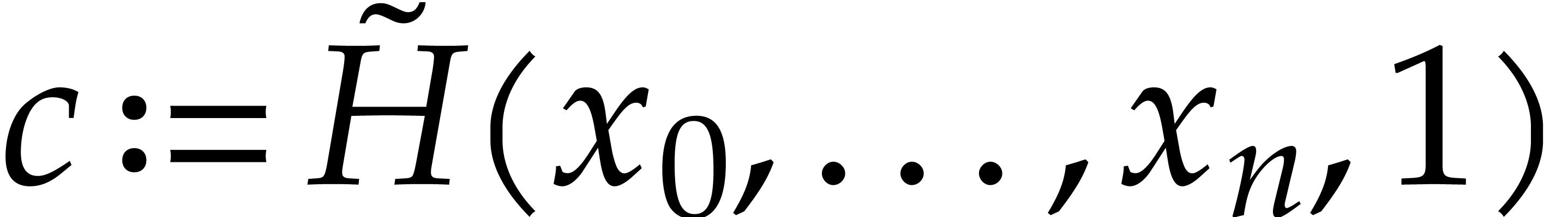 is a non-zero constant and
is a non-zero constant and 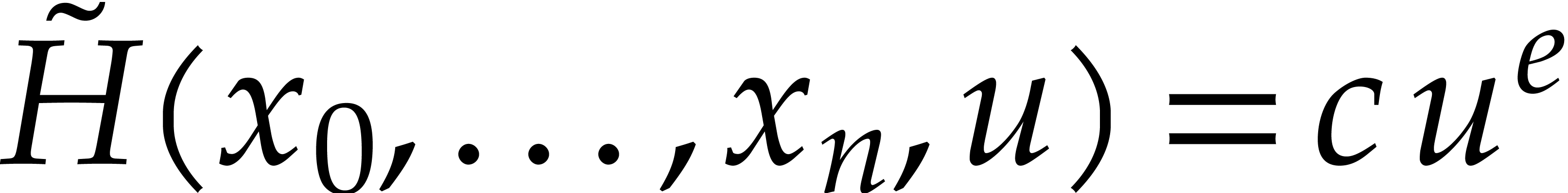 . Since
. Since 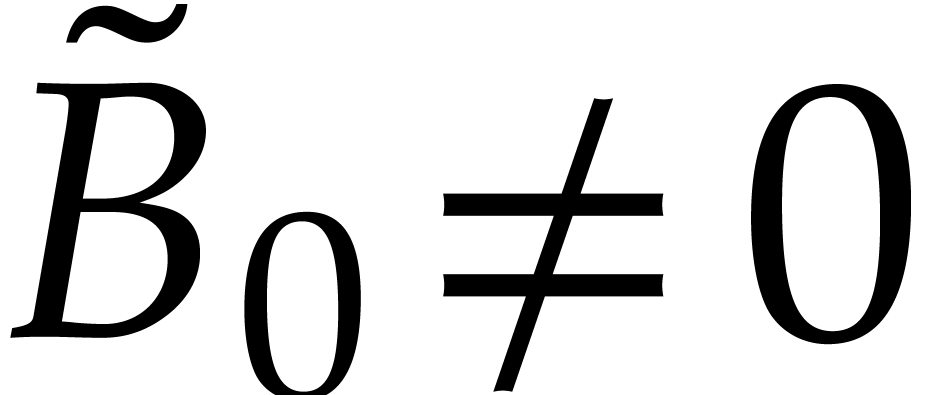 , we conclude that
, we conclude that  .
.
 be a rational blackbox function whose
evaluation requires
be a rational blackbox function whose
evaluation requires 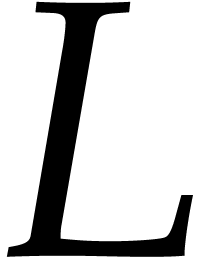 operations in
operations in  . Let
. Let  ,
where
,
where  and
and 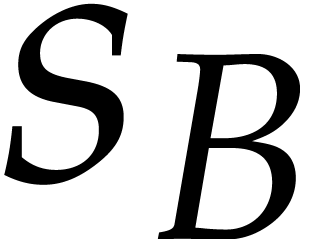 are bounds
for the number of terms of
are bounds
for the number of terms of  and
and 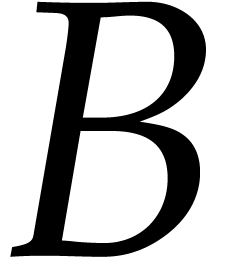 . Let
. Let  ,
where
,
where 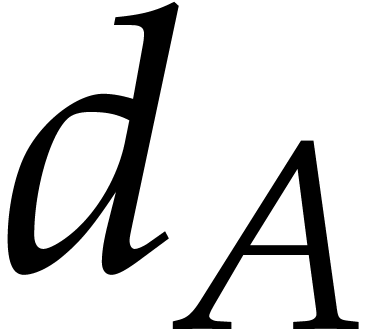 and
and 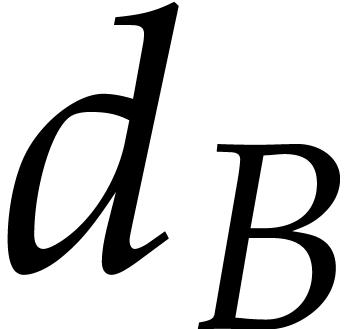 are the
total degrees of
are the
total degrees of  and
and 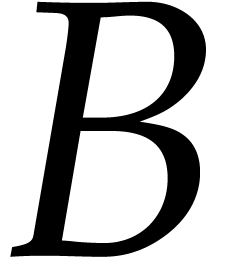 . Using a probabilistic algorithm of Monte Carlo
type, the sparse interpolation of
. Using a probabilistic algorithm of Monte Carlo
type, the sparse interpolation of 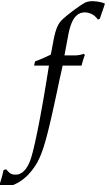 takes at
most
takes at
most
operations in  , provided
that the cardinality of
, provided
that the cardinality of  is sufficiently
large.
is sufficiently
large.
Proof. First of all, a point  is taken at random, so
is taken at random, so 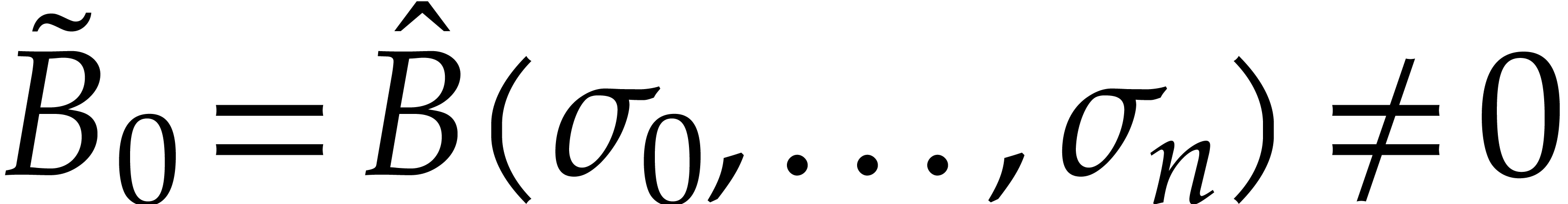 holds with high
probability. Let us describe a blackbox for evaluating
holds with high
probability. Let us describe a blackbox for evaluating 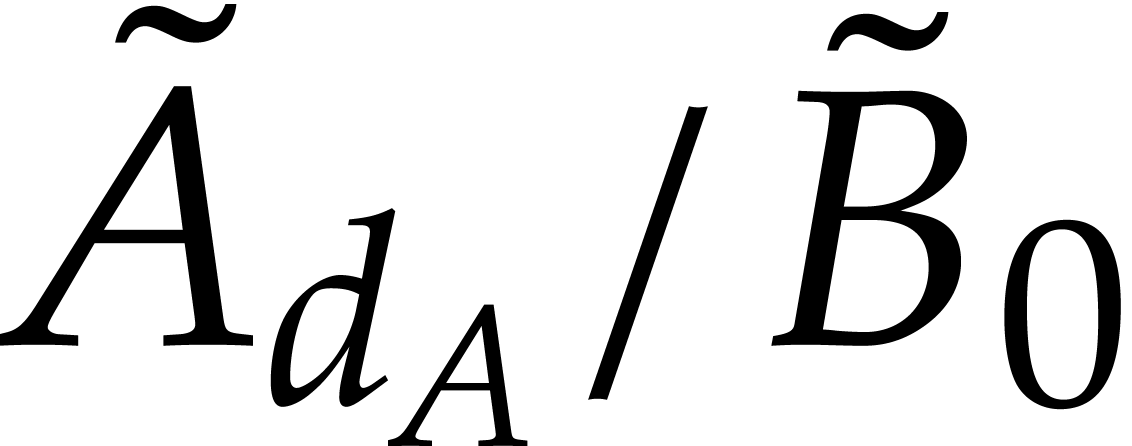 and
and 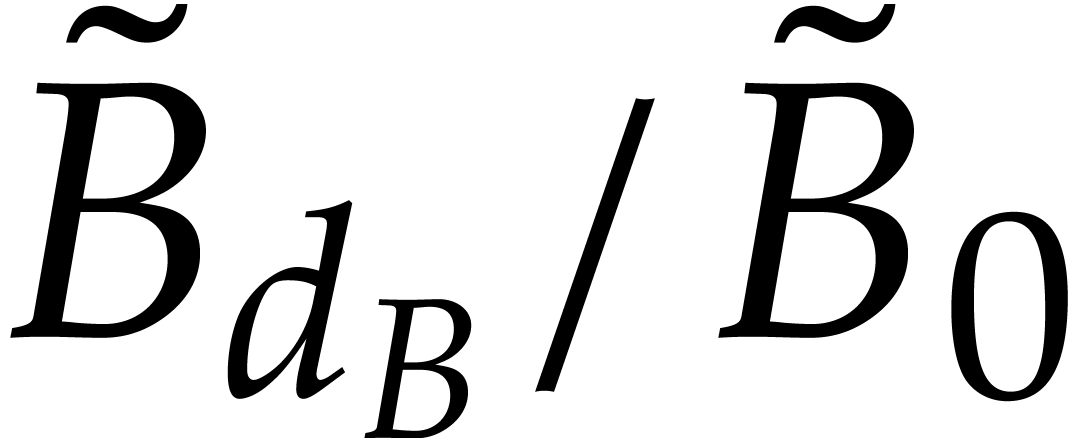 at a point
at a point  :
:
We perform 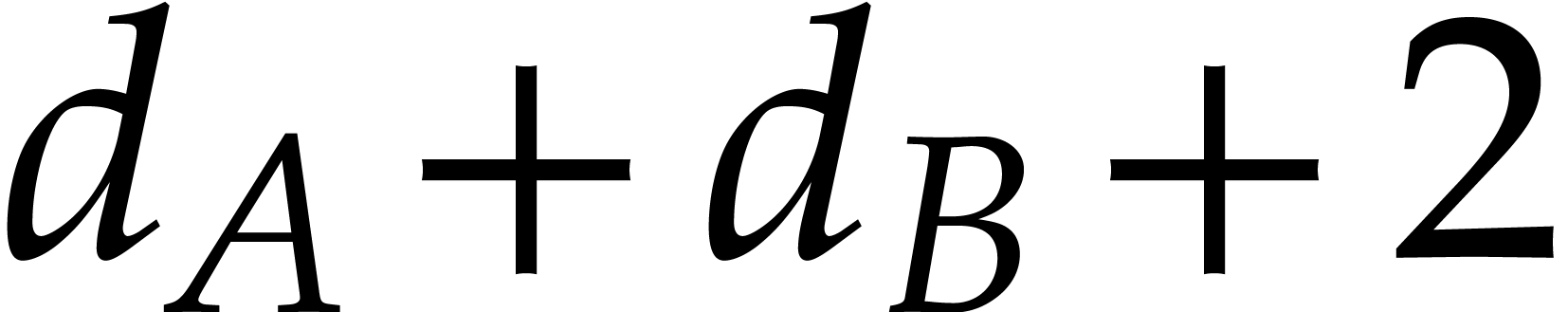 evaluations of
evaluations of 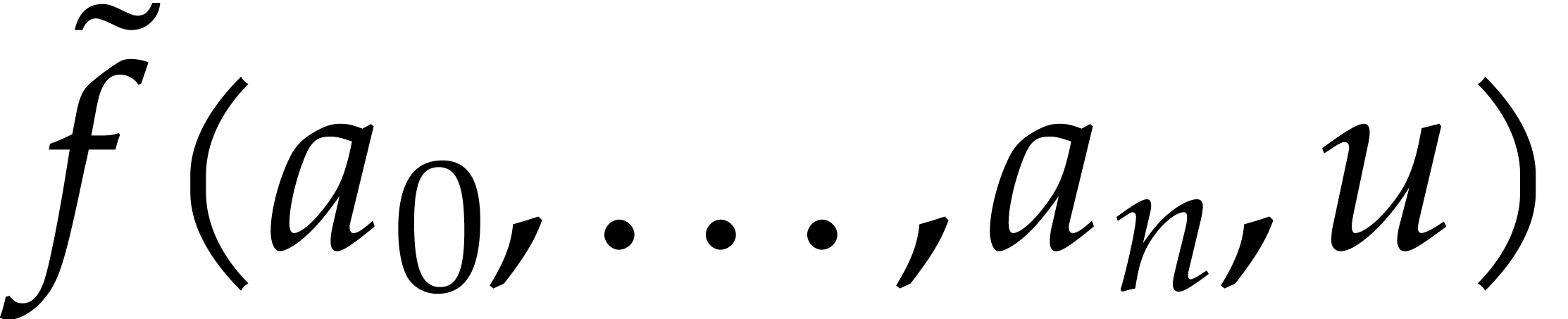 for different values of
for different values of 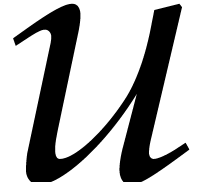 ,
which give rise to at most
,
which give rise to at most
operations in  .
.
If the latter evaluations do not fail, then we perform the
univariate Cauchy interpolation of 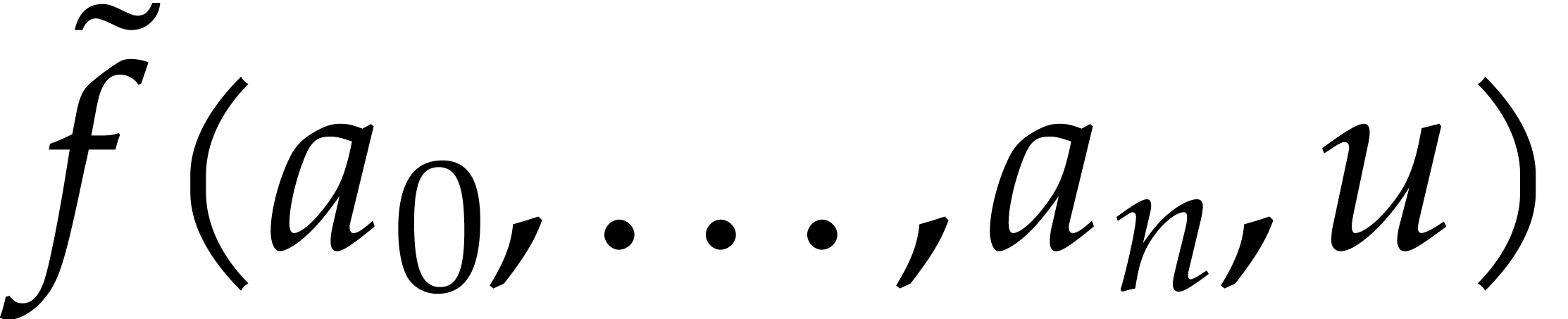 ,
which takes
,
which takes 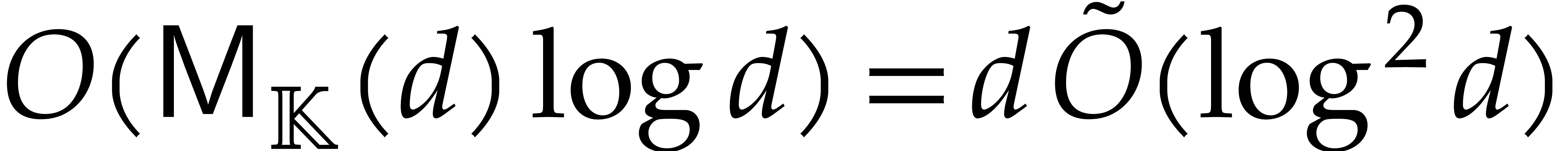 operations in
operations in  . If this Cauchy interpolation fails, then
the evaluation of
. If this Cauchy interpolation fails, then
the evaluation of 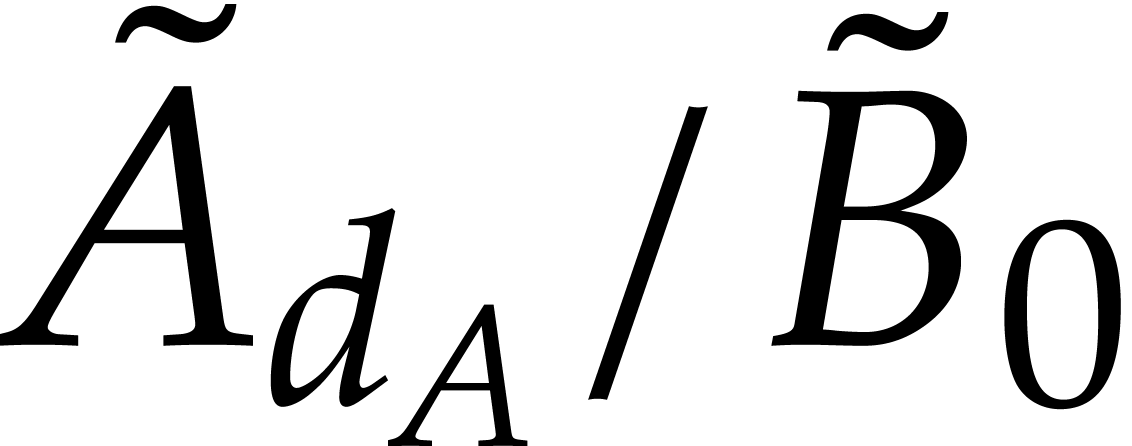 and
and 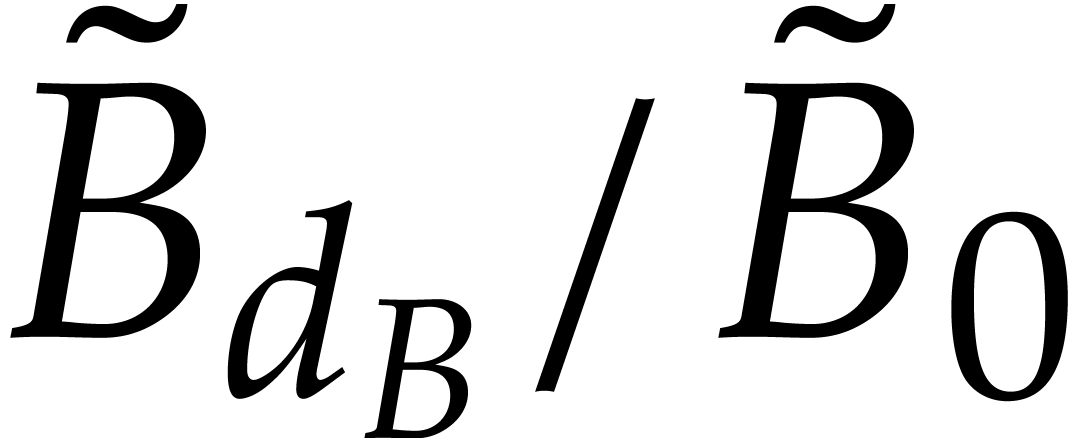 aborts.
aborts.
The failure of the Cauchy interpolation of  depends on the actual procedure being used, but we may design it to
succeed on a Zariski dense subset of points
depends on the actual procedure being used, but we may design it to
succeed on a Zariski dense subset of points  in
in
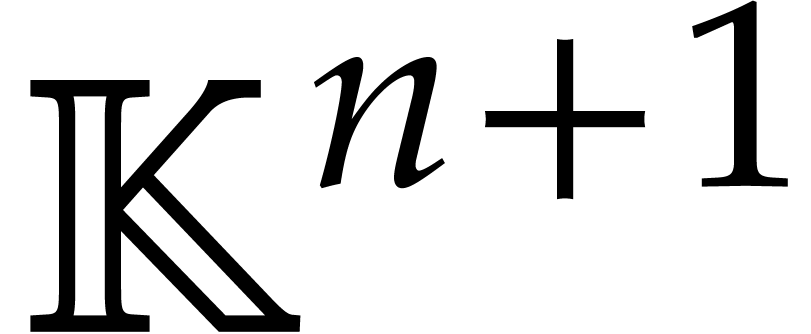 . For instance, with the
aforementioned method of [5, Corollary 5.18], the
reconstruction succeeds whenever the degrees of the reconstructed
numerator and denominator are
. For instance, with the
aforementioned method of [5, Corollary 5.18], the
reconstruction succeeds whenever the degrees of the reconstructed
numerator and denominator are 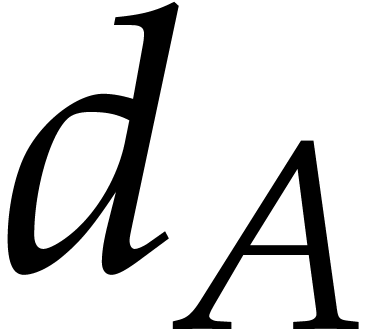 and
and 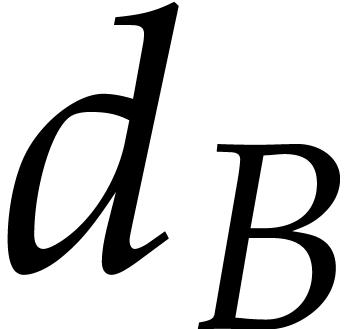 , respectively. This holds when
, respectively. This holds when  , where
, where
Since  is primitive as an element of
is primitive as an element of  , the gcd of
, the gcd of  and
and  in
in  can be obtained as the
primitive representative in
can be obtained as the
primitive representative in  of the gcd of
of the gcd of  and
and  in
in  ; see [15, chapter IV, Theorem 2.3],
for instance. Using Lemma 1, we deduce that
; see [15, chapter IV, Theorem 2.3],
for instance. Using Lemma 1, we deduce that  is not identically zero. Consequently, the evaluation of
is not identically zero. Consequently, the evaluation of
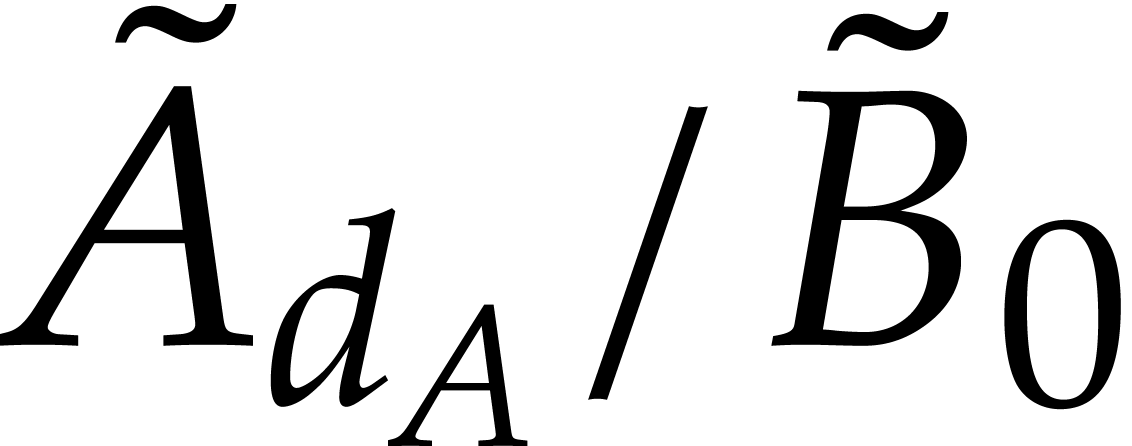 and
and 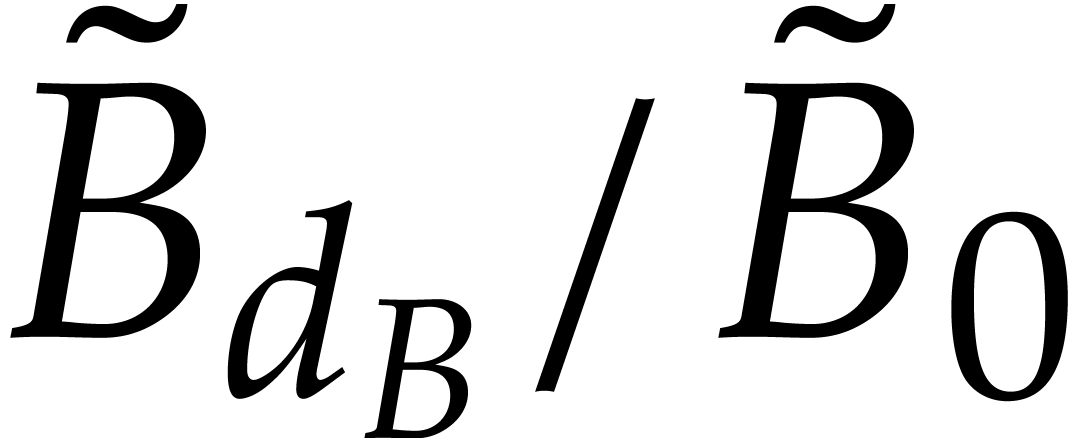 at a point
at a point  does not fail on a Zariski dense subset of
does not fail on a Zariski dense subset of 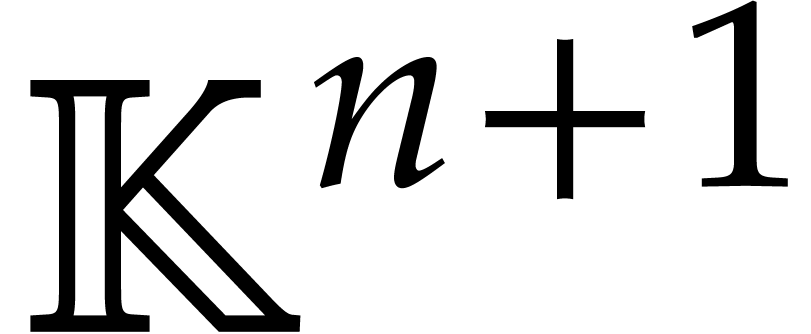 .
.
In order to ensure the sparse polynomial interpolation to succeed with
high probability, we appeal to the discussion from section 2.2
for the evaluations of 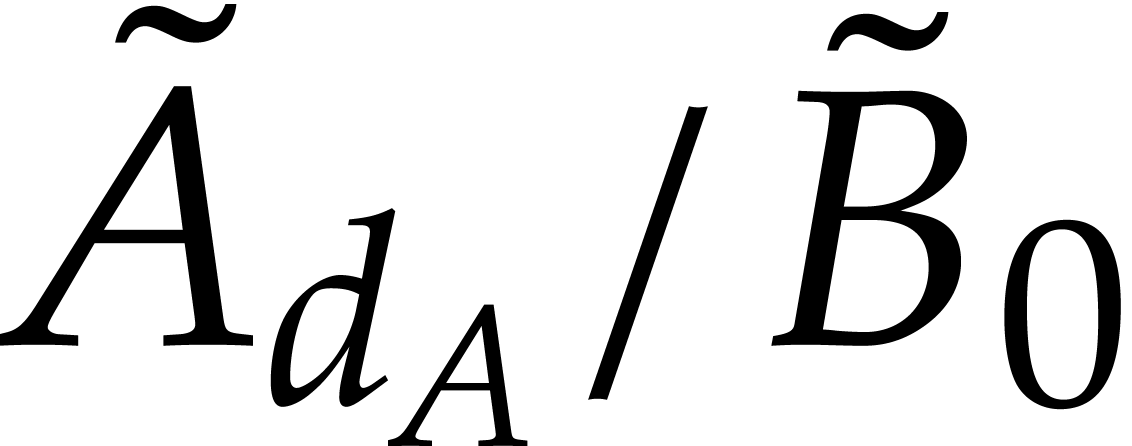 and
and 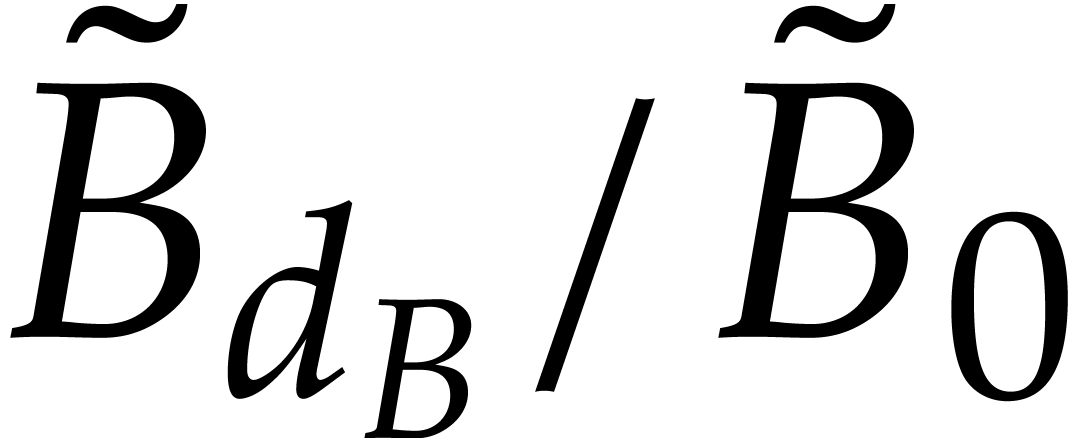 . More precisely, by taking
. More precisely, by taking 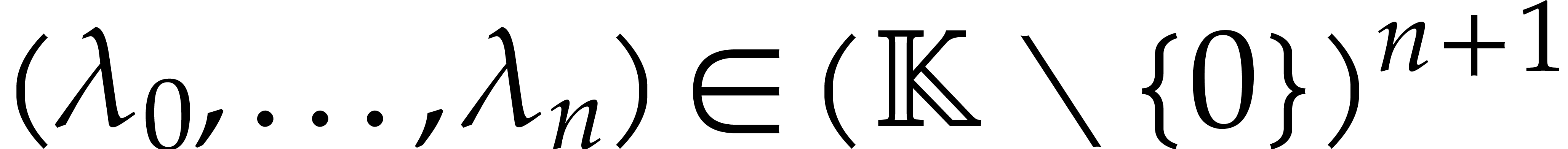 at random, we can interpolate
at random, we can interpolate 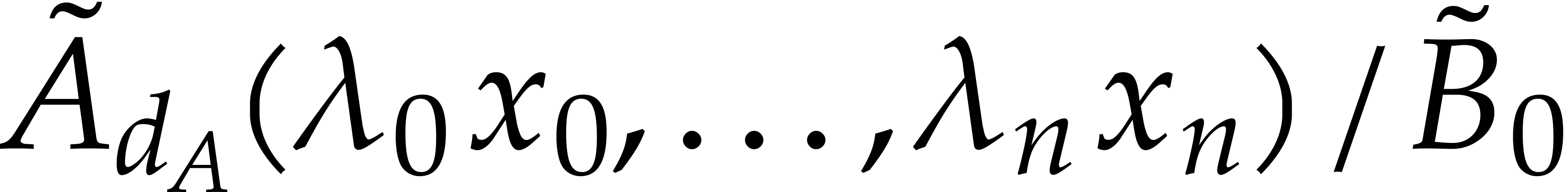 and
and 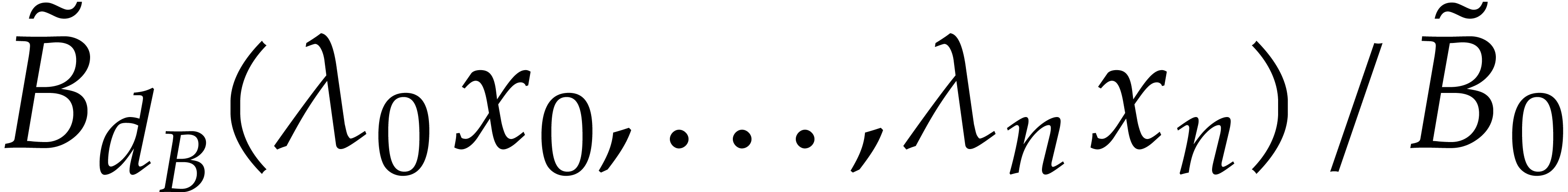 with high probability. This random dilatation further
increases the cost of each blackbox evaluation by
with high probability. This random dilatation further
increases the cost of each blackbox evaluation by  operations in
operations in  .
.
The required number of evaluation points  is
is
Once all evaluations are done, we need
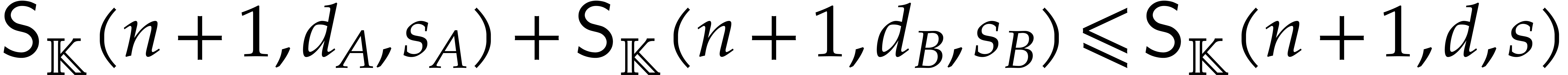
further operations to reconstruct the sparse representations of 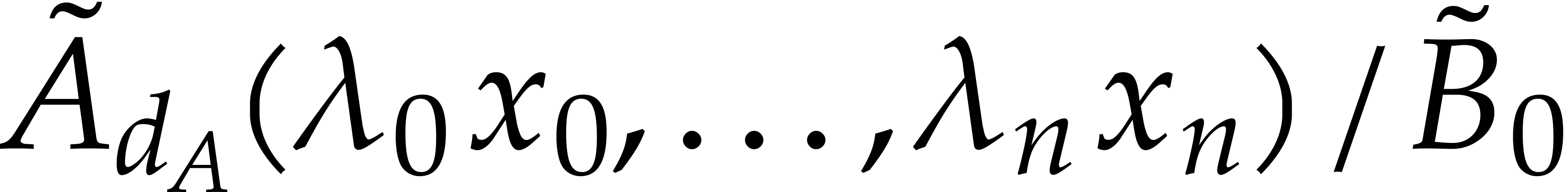 and
and 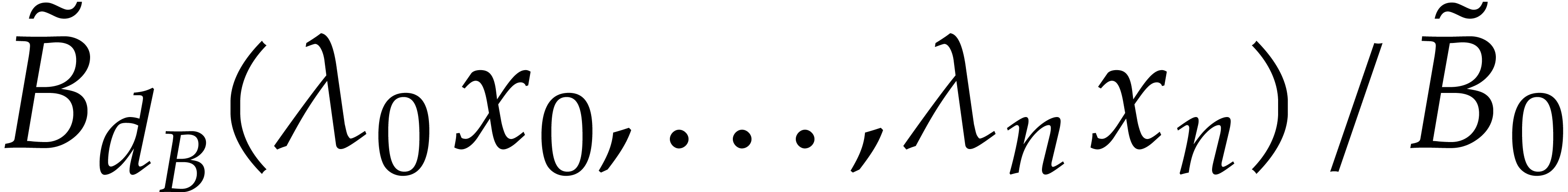 . The
backward dilatation to recover
. The
backward dilatation to recover  and
and 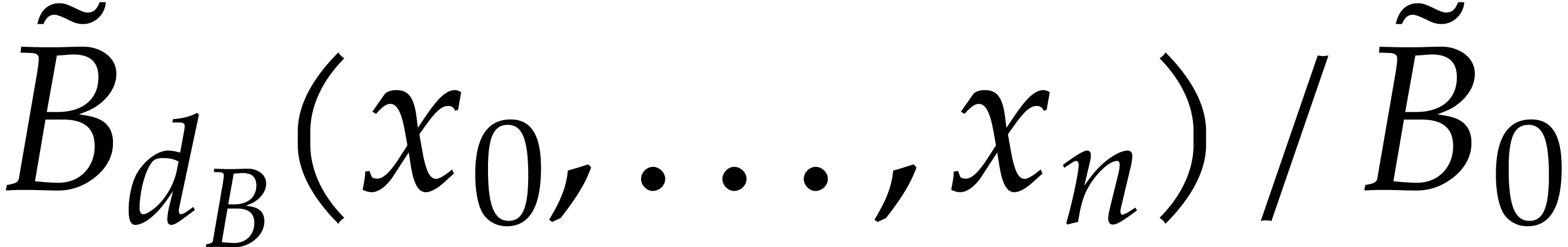 takes
takes
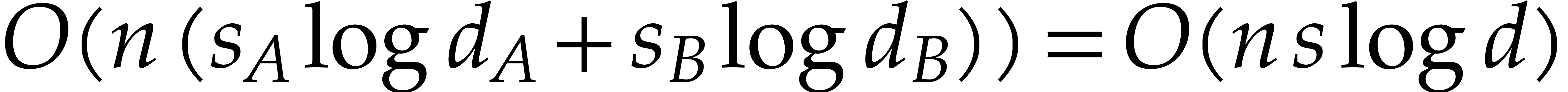
further operations in  .
.
To conclude the proof, we observe that 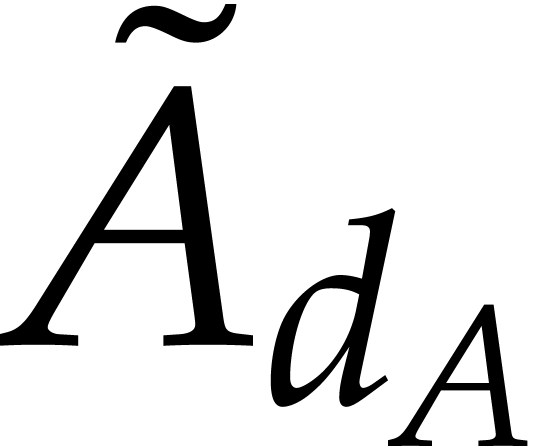 and
and 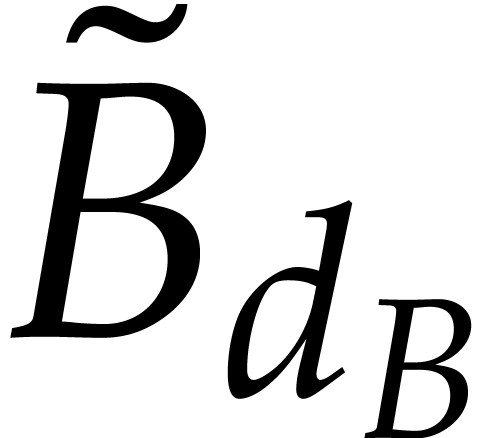 coincide with
coincide with 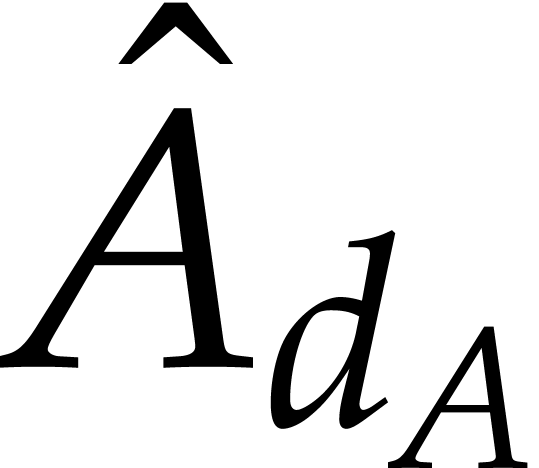 and
and 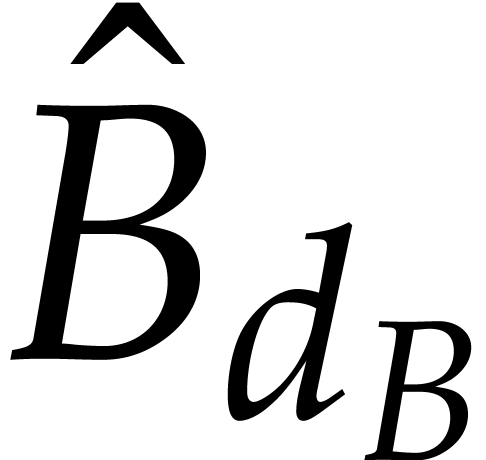 . But since
. But since  are
are  are homogeneous, this means that
are homogeneous, this means that 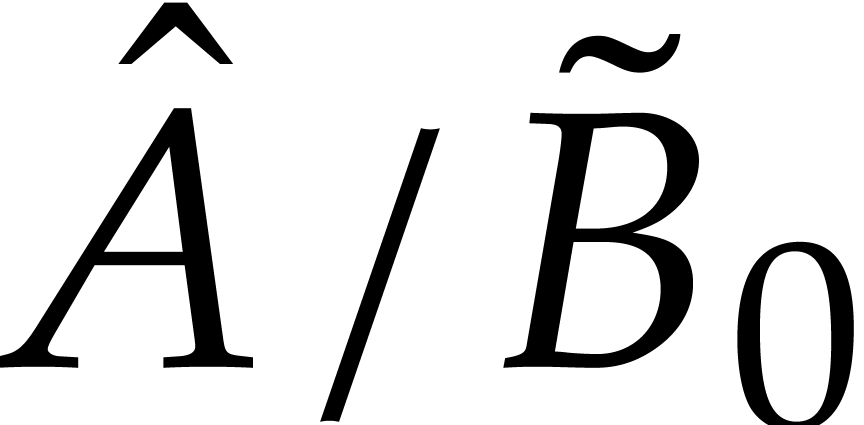 and
and 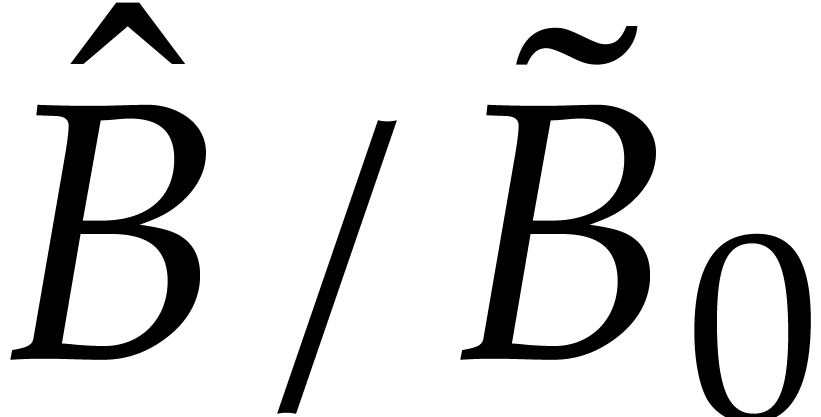 actually coincide with
actually coincide with 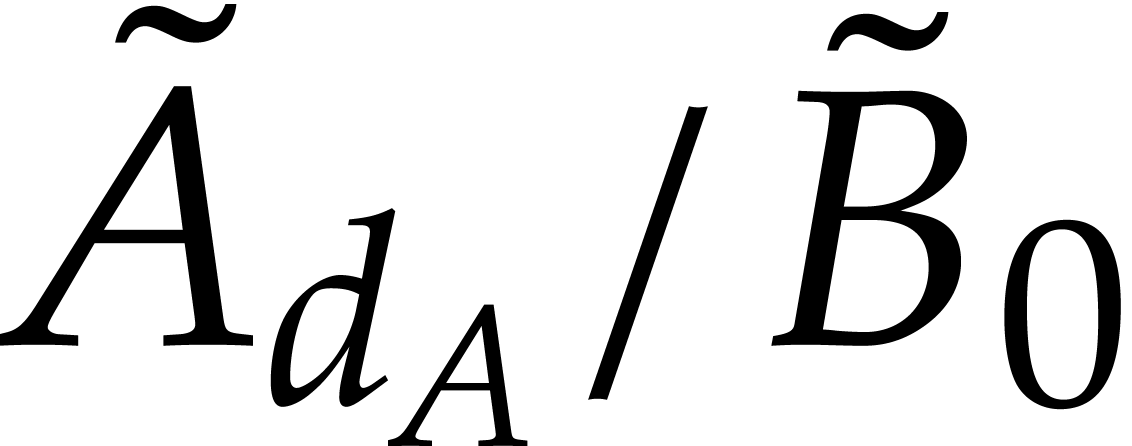 and
and 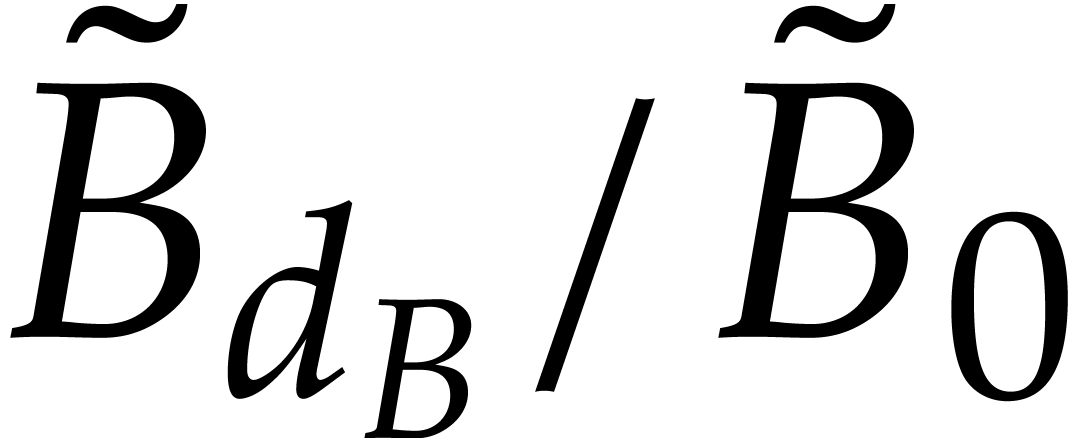 .
.
Remark
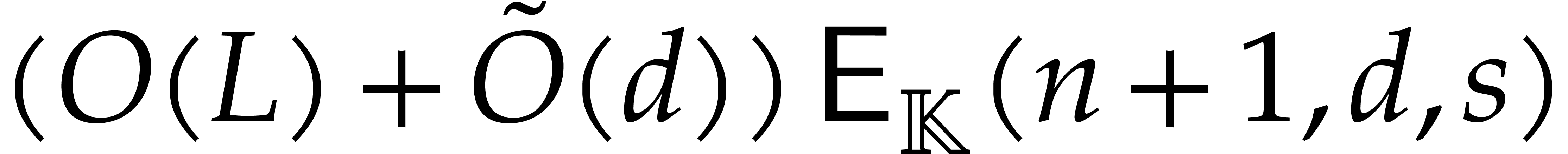
if the terms of  and
and  are
more or less equally distributed over their homogeneous components. With
our method, we always pay the maximal possible overhead
are
more or less equally distributed over their homogeneous components. With
our method, we always pay the maximal possible overhead 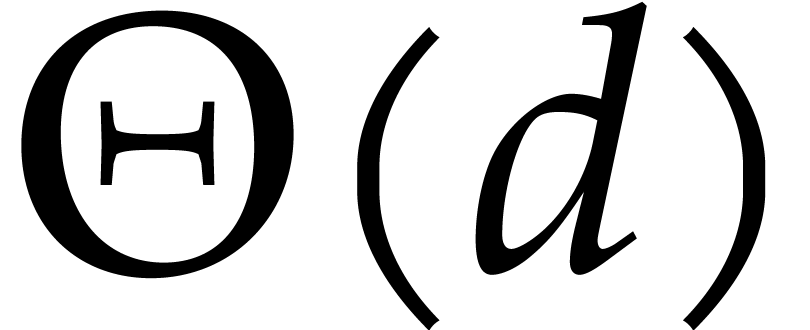 with respect to sparse interpolation of polynomials.
with respect to sparse interpolation of polynomials.
Let 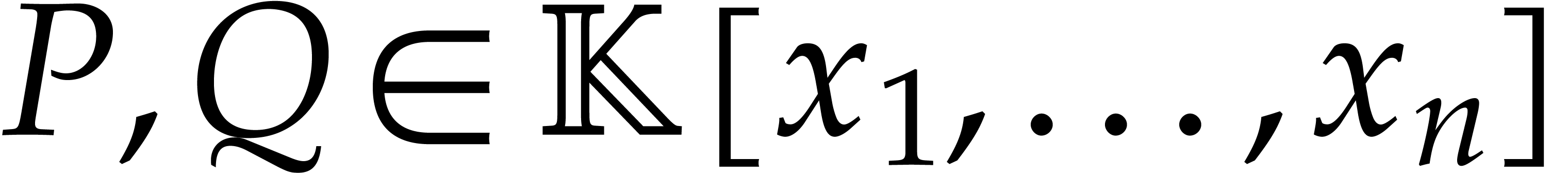 be polynomials that are given through a
common blackbox. In this section we show how to adapt the technique from
the previous section to the computation of
be polynomials that are given through a
common blackbox. In this section we show how to adapt the technique from
the previous section to the computation of 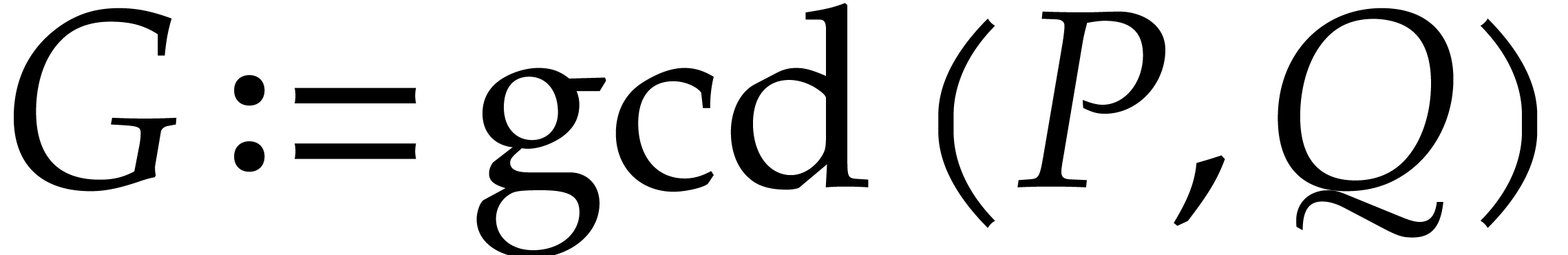 .
.
A classical approach for multivariate gcds relies on
evaluation/interpolation for all but one of the variables, say 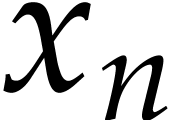 , and thus on the computation of
many univariate gcds; see for instance [5, chapter 6]. This
turns out to be similar to rational function interpolation: the
univariate case is handled using dense representations and a suitable
normalization is necessary to recombine the specialized gcds.
, and thus on the computation of
many univariate gcds; see for instance [5, chapter 6]. This
turns out to be similar to rational function interpolation: the
univariate case is handled using dense representations and a suitable
normalization is necessary to recombine the specialized gcds.
In general and without generic coordinates, the gcd  does not admit a natural normalization. This issue has been studied in
[3]. Basically one piece of their solution is to consider
does not admit a natural normalization. This issue has been studied in
[3]. Basically one piece of their solution is to consider
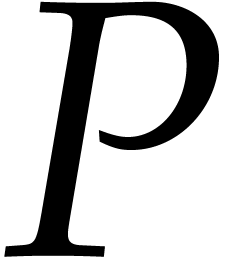 and
and 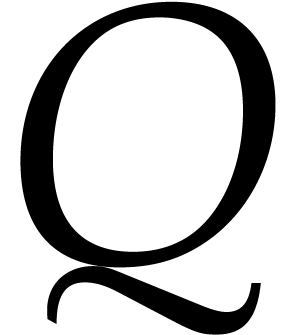 as polynomials in
as polynomials in
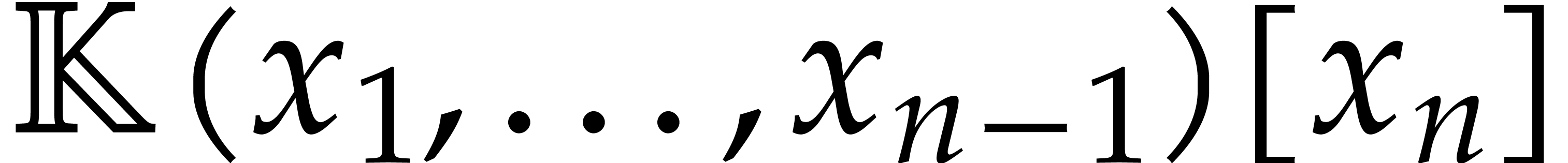 and to force
and to force  to be monic
in
to be monic
in 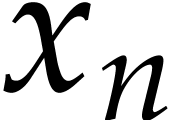 . This leads to
interpolate rational functions instead of polynomials, and the technique
of the previous section may be used. But it is even more efficient to
adapt our main idea for rational functions to gcds.
. This leads to
interpolate rational functions instead of polynomials, and the technique
of the previous section may be used. But it is even more efficient to
adapt our main idea for rational functions to gcds.
The sparse gcd problem was first investigated by Zippel, who proposed a variable by variable approach [18]. Then, subresultant polynomials turned out to be useful to avoid rational function interpolations. For historical references we refer the reader to [3, 14]. Software implementations and a recent state of the art can be found in [11].
Let us mention that probabilistic sparse gcd algorithms may be turned into Las Vegas type algorithms by interpolating the full Bézout relation, at the price of an increased computational cost; see for instance [5, chapter 6]. In this paper we content ourselves with Monte Carlo algorithms and we focus on gcd computations only.
Let 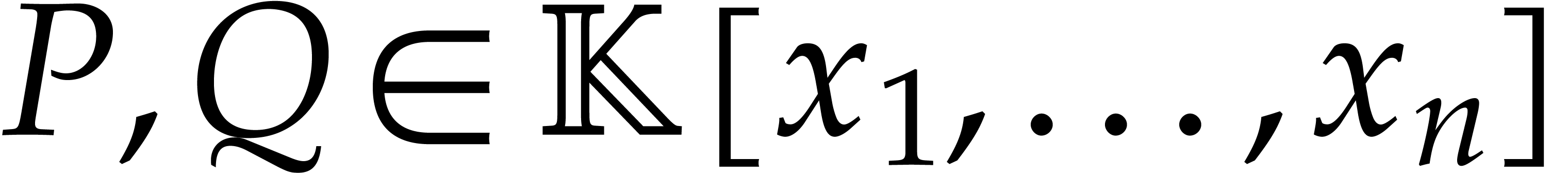 be polynomials that are given through a
common blackbox, and assume that
be polynomials that are given through a
common blackbox, and assume that 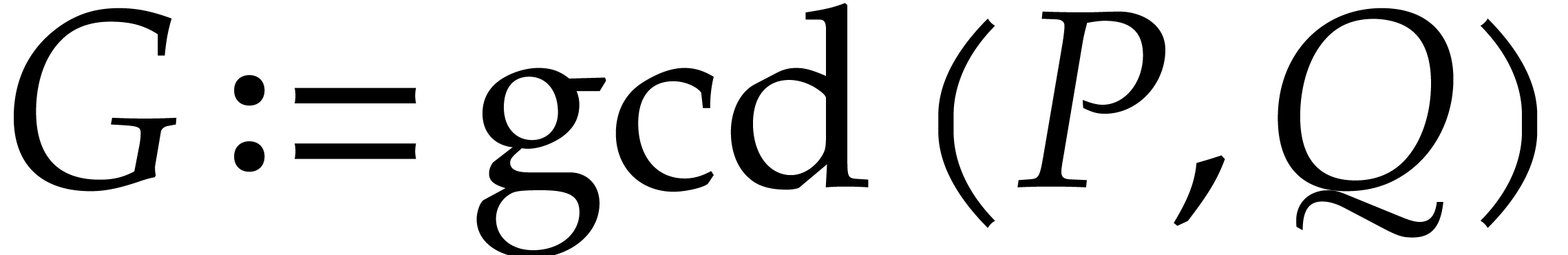 contains
contains  terms. We let
terms. We let 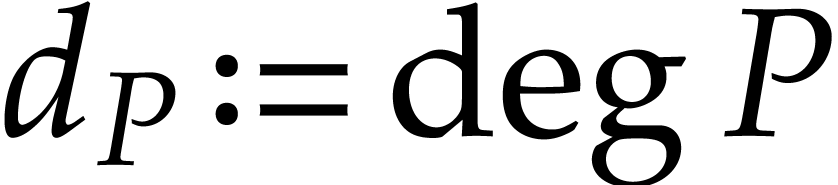 ,
,
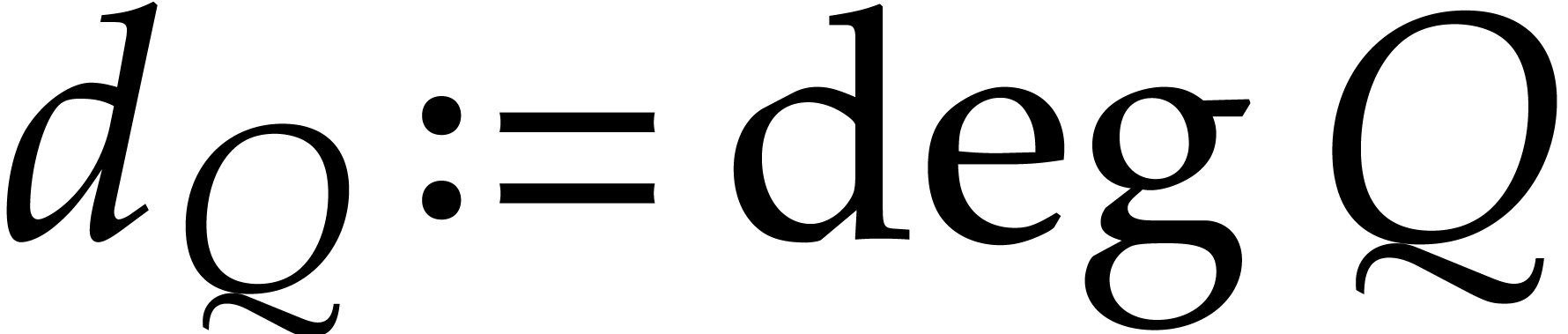 ,
,  . Using the technique from the previous section we
first reduce to the case when
. Using the technique from the previous section we
first reduce to the case when 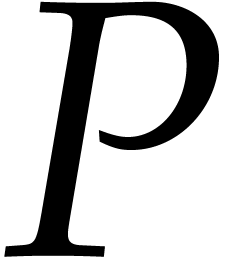 and
and 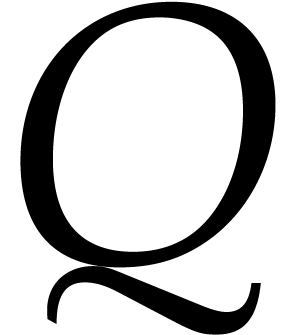 are homogeneous (without increasing their total degrees),
so we let:
are homogeneous (without increasing their total degrees),
so we let:
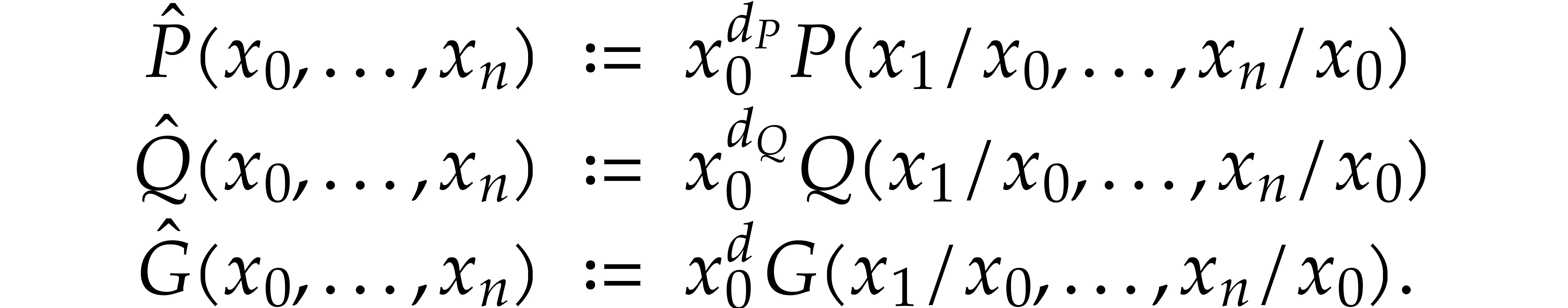
For 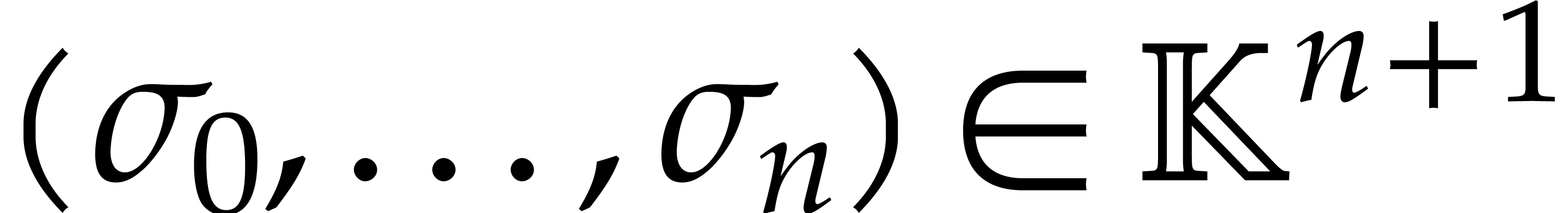 , we let
, we let
Example 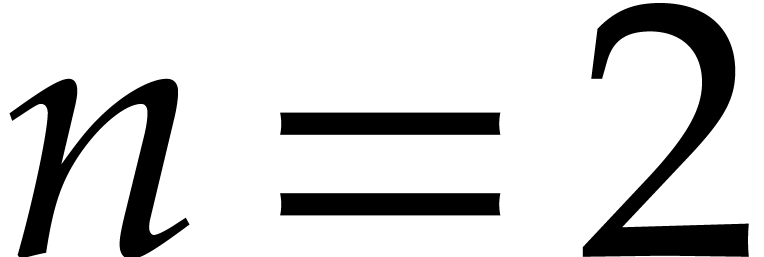 ,
, 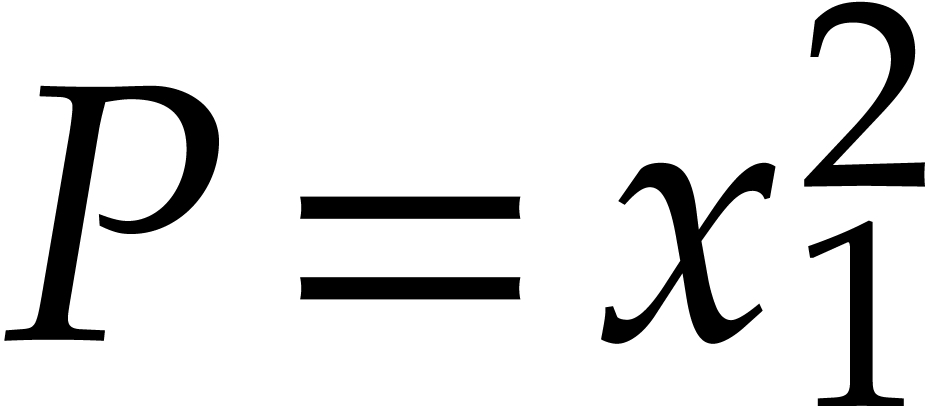 ,
,
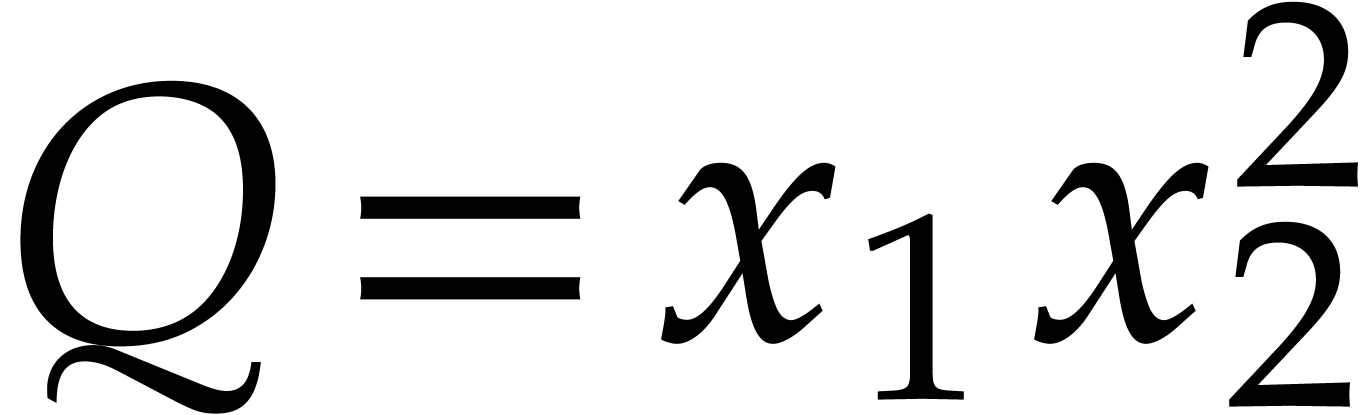 ,
, 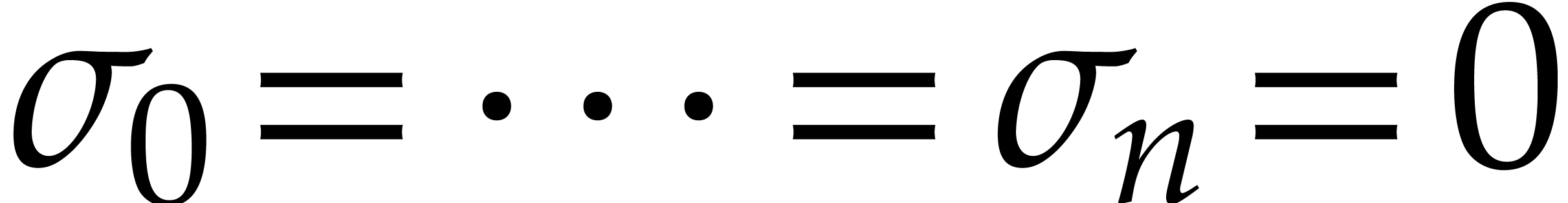 , we have
, we have 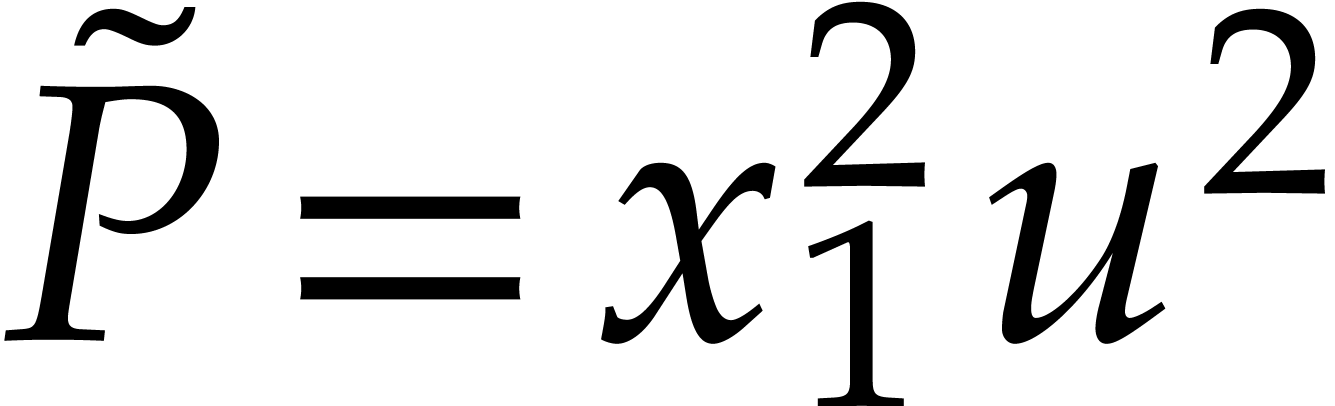 and
and 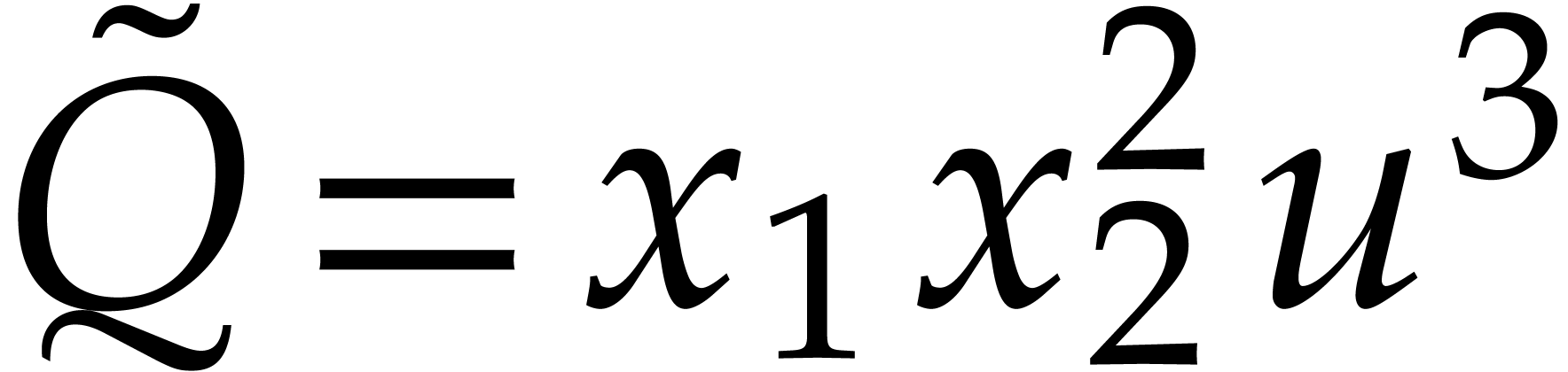 . We note that
. We note that 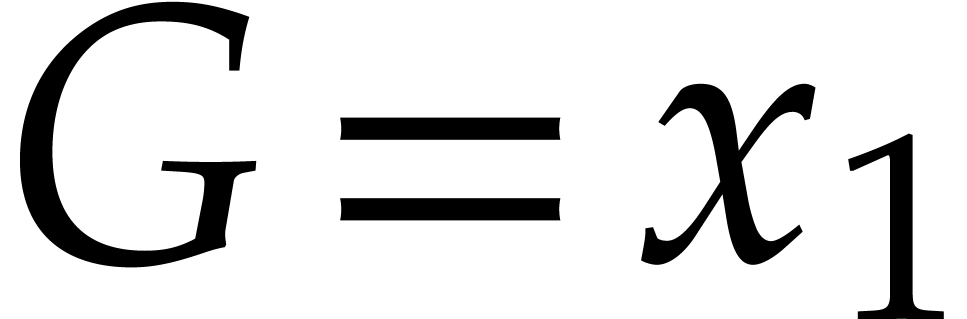 ,
and then that
,
and then that 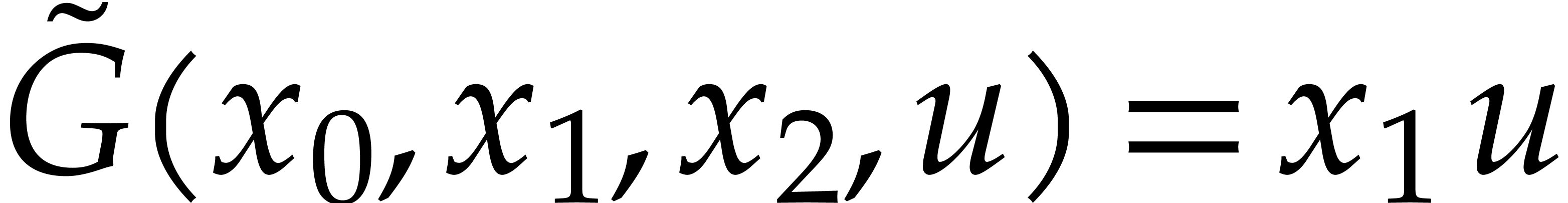 . However
. However 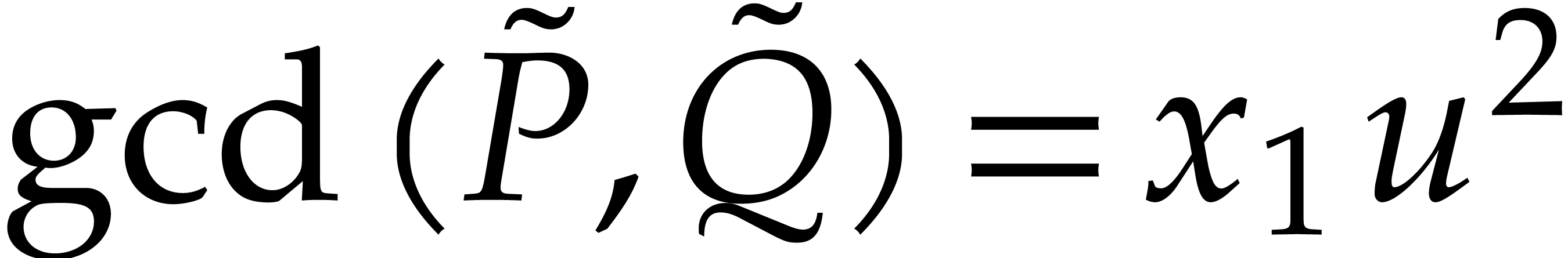 .
.
The latter example shows that we need to take care of the relationship
between  and
and 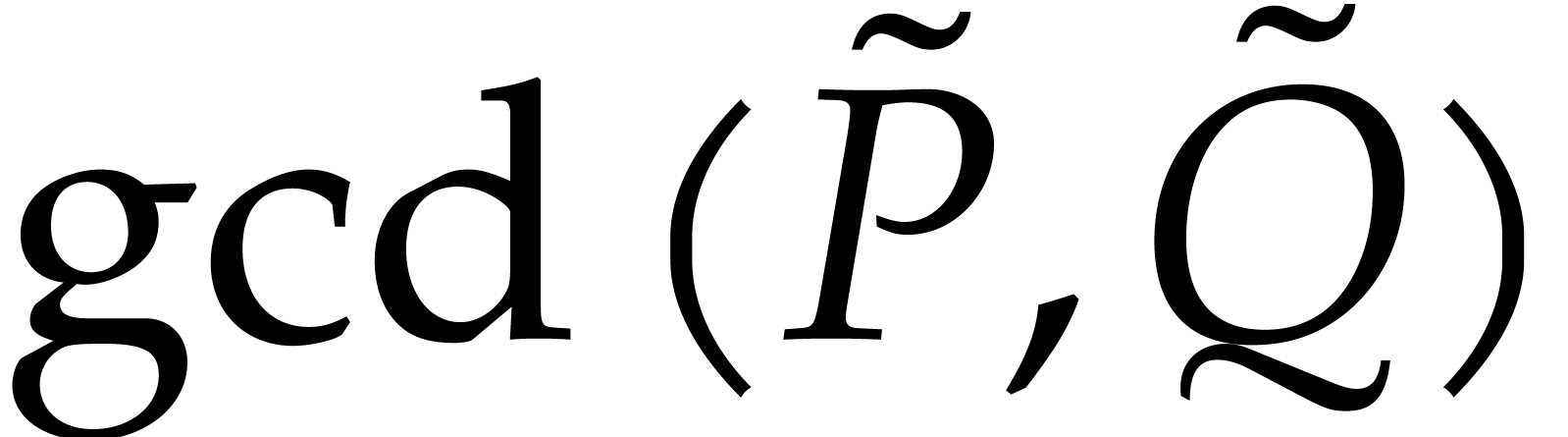 .
This is the purpose of the following lemma, which extends Lemma 1.
.
This is the purpose of the following lemma, which extends Lemma 1.
Proof. Let 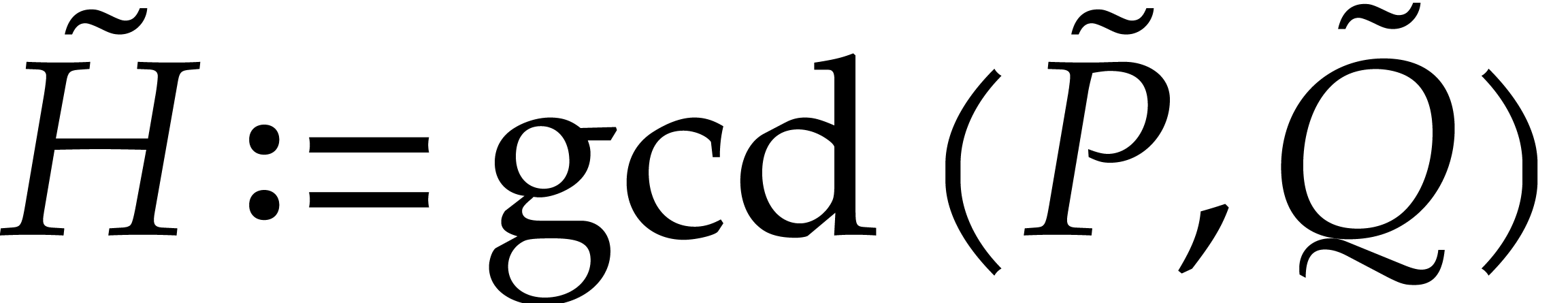 .
In the proof of Lemma 1 we have shown that
.
In the proof of Lemma 1 we have shown that
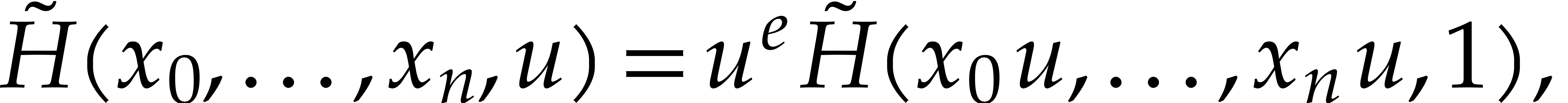
for some 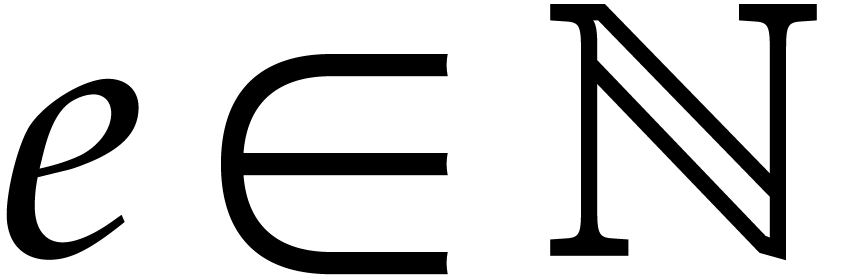 . By construction,
we have
. By construction,
we have 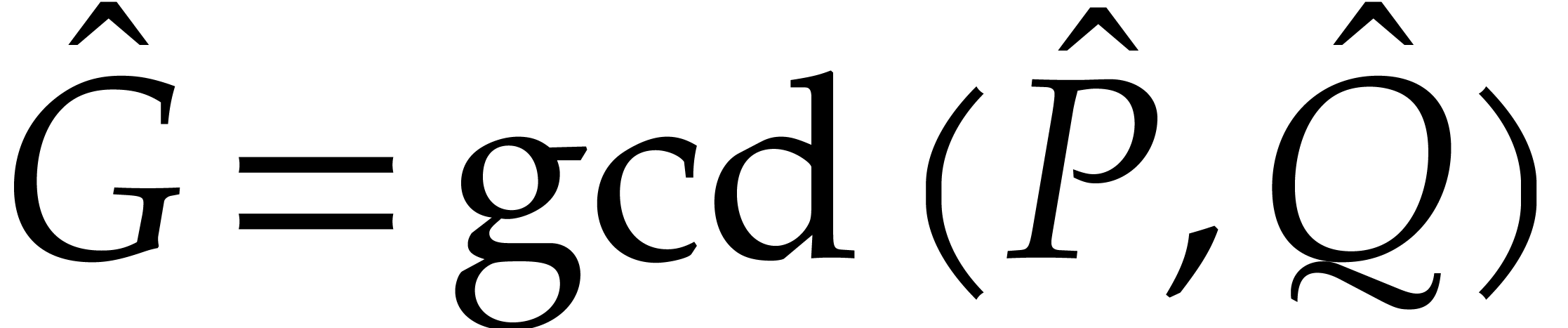 , so
, so 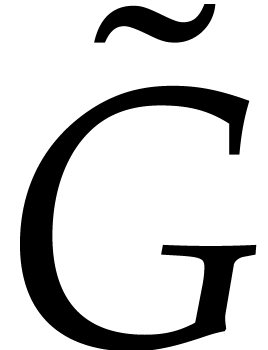 divides
divides 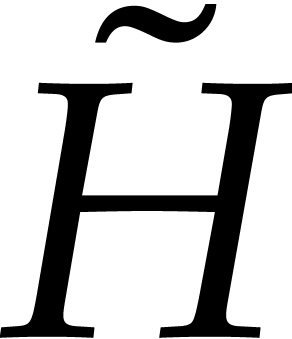 . Conversely,
. Conversely,  divides
divides  ,
so there exists a non-zero constant
,
so there exists a non-zero constant 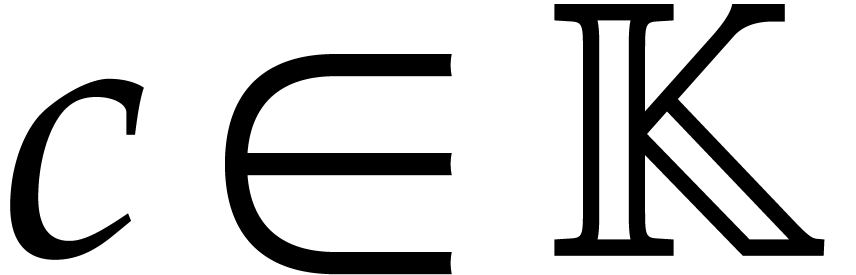 with
with
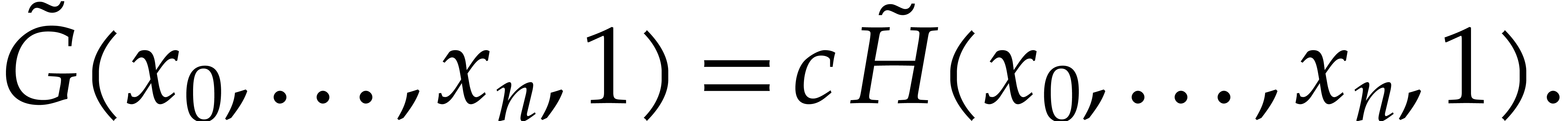
It follows that
Since  or
or  ,
we finally have
,
we finally have 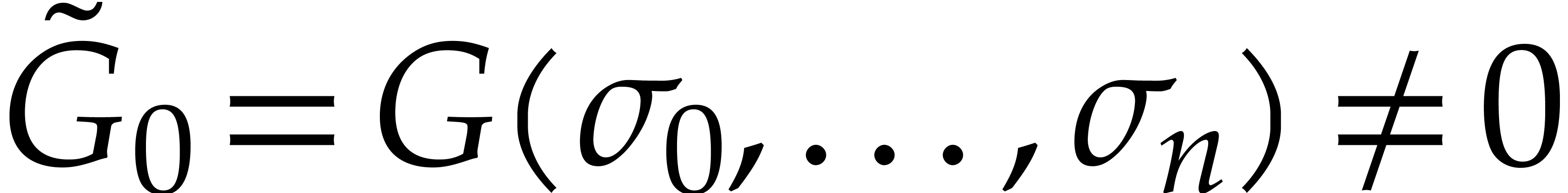 , so that
, so that
 .
.
From now on we assume that  or
or  , so that
, so that 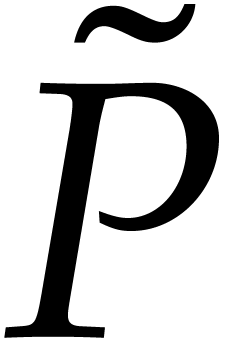 or
or  is primitive as an element in
is primitive as an element in  . By Lemma 5 and [15,
chapter IV, Theorem 2.3], their gcd
. By Lemma 5 and [15,
chapter IV, Theorem 2.3], their gcd 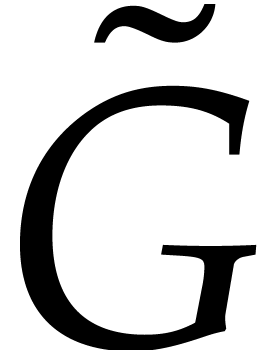 in
in  can be obtained as the primitive representative
can be obtained as the primitive representative 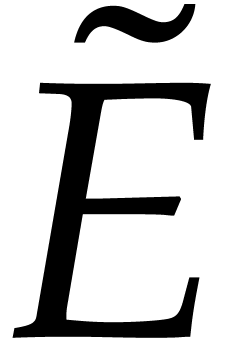 in
in  of the gcd of
of the gcd of 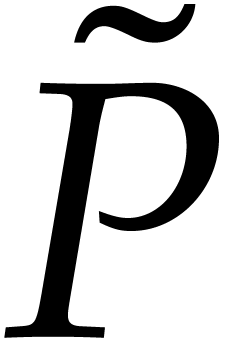 and
and  in
in  .
We further observe that
.
We further observe that 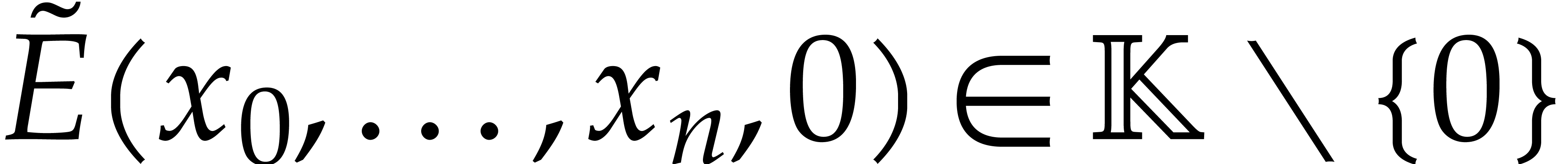 ,
whence
,
whence
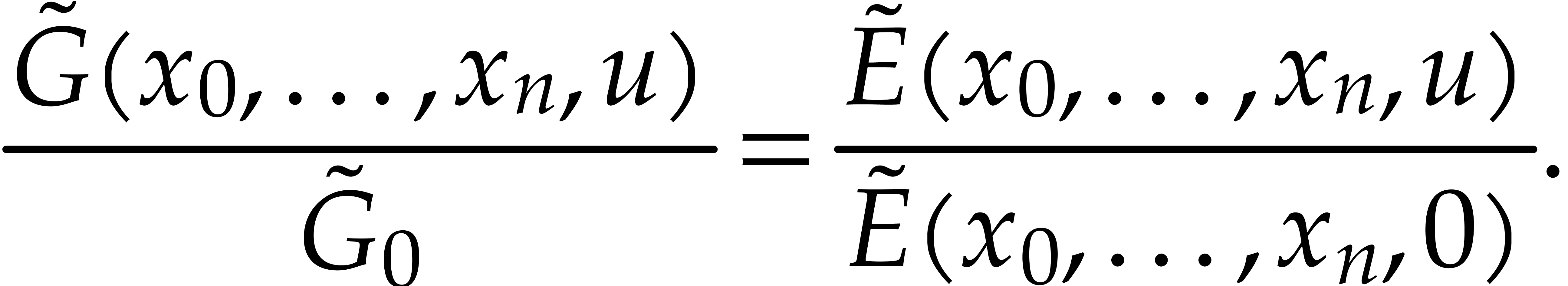 |
(1) |
This allows us to obtain
as the gcd of 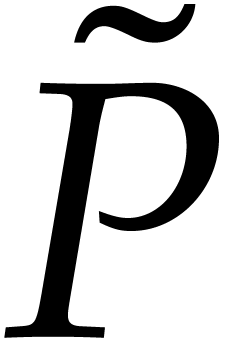 and
and  in
in
 , and to recover
, and to recover  via
via
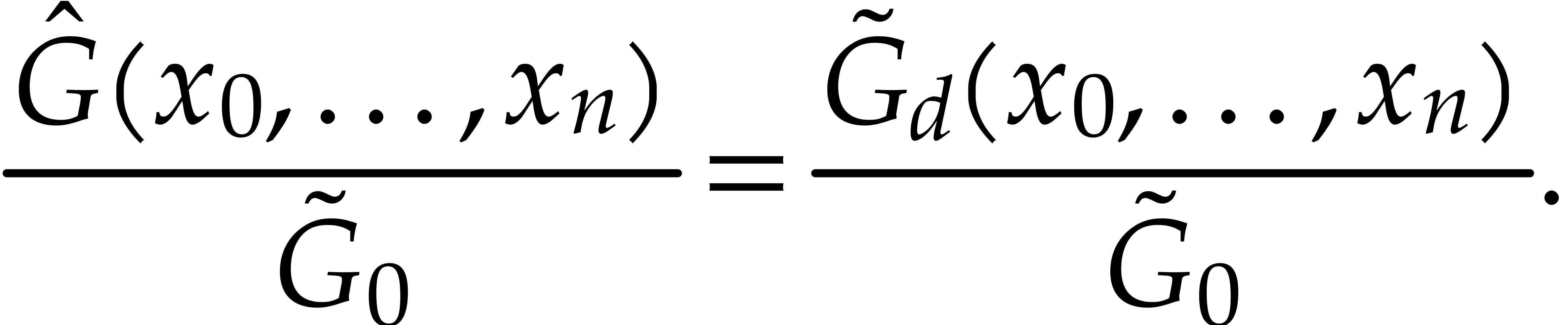
This approach yields the following complexity bound for the sparse
interpolation of 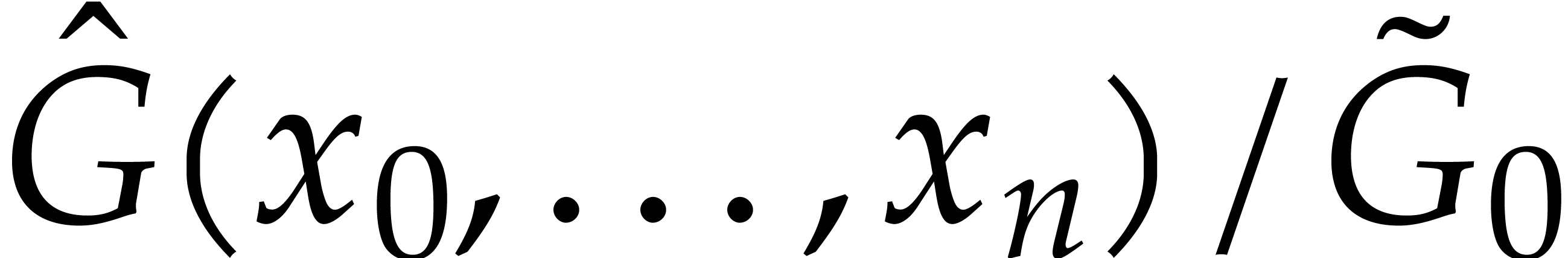 .
.
 and
and  in
in  using
using  operations in
operations in  . Let
. Let 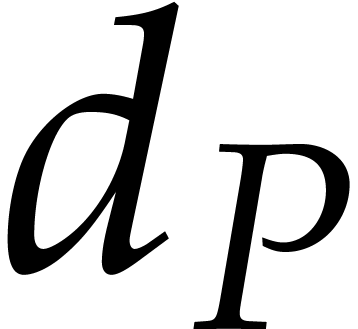 ,
,
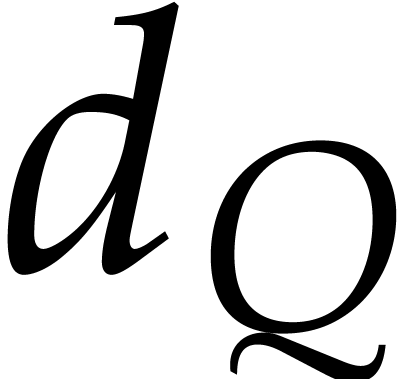 , and
, and 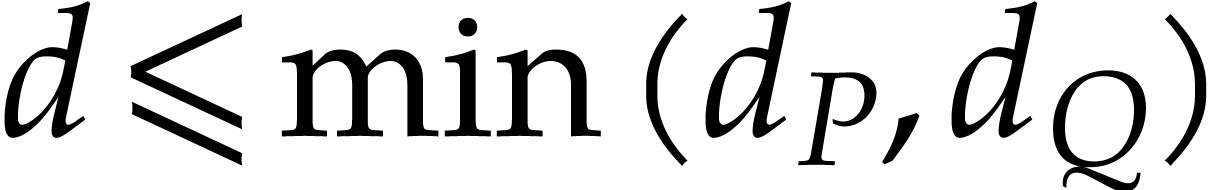 be the respective total degrees of
be the respective total degrees of 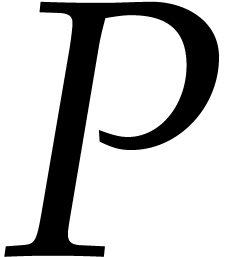 ,
,
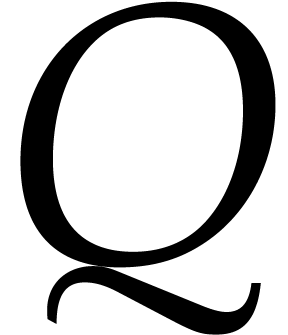 , and
, and  . Let
. Let 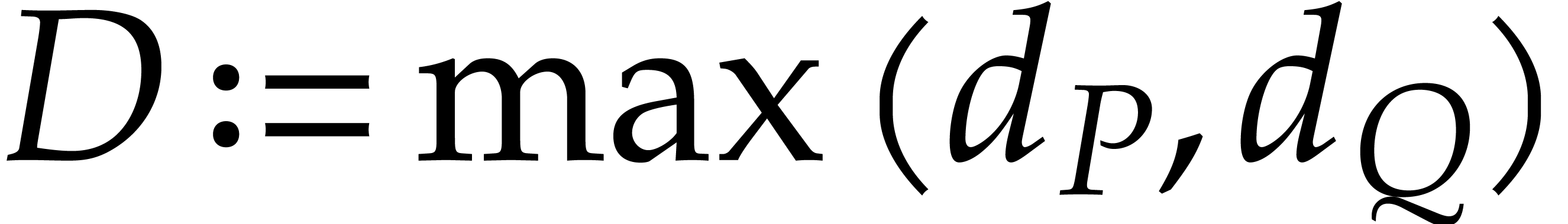 .
Using a probabilistic algorithm of Monte Carlo type, we may
interpolate
.
Using a probabilistic algorithm of Monte Carlo type, we may
interpolate  using
using
operations in  , provided
that the cardinality of
, provided
that the cardinality of  is sufficiently
large.
is sufficiently
large.
Proof. We first take  at
random, so
at
random, so  or
or  with high
probability. In order to evaluate
with high
probability. In order to evaluate  at a point
at a point
 we proceed as follows:
we proceed as follows:
We evaluate  and
and  for
for
 different values of
different values of  . The evaluation of
. The evaluation of 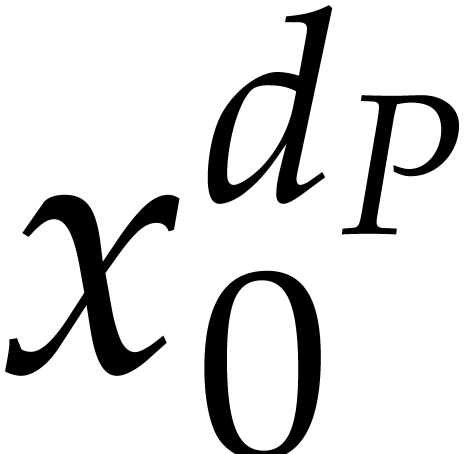 ,
, 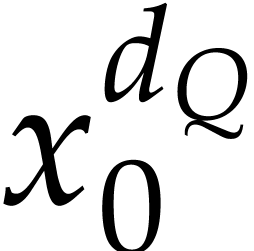 ,
,
 takes
takes
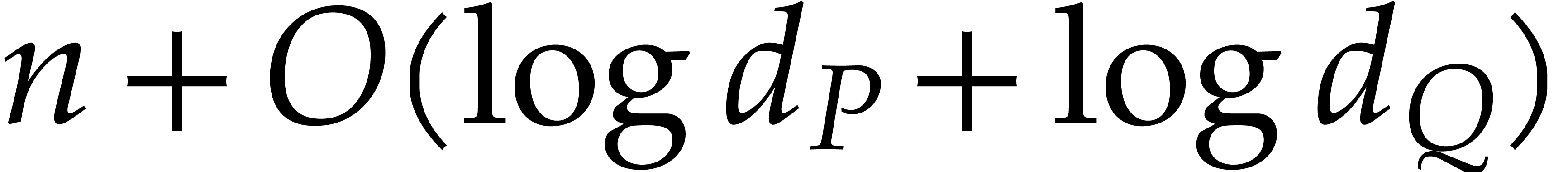
operations in  . The
evaluation of
. The
evaluation of  involves
involves 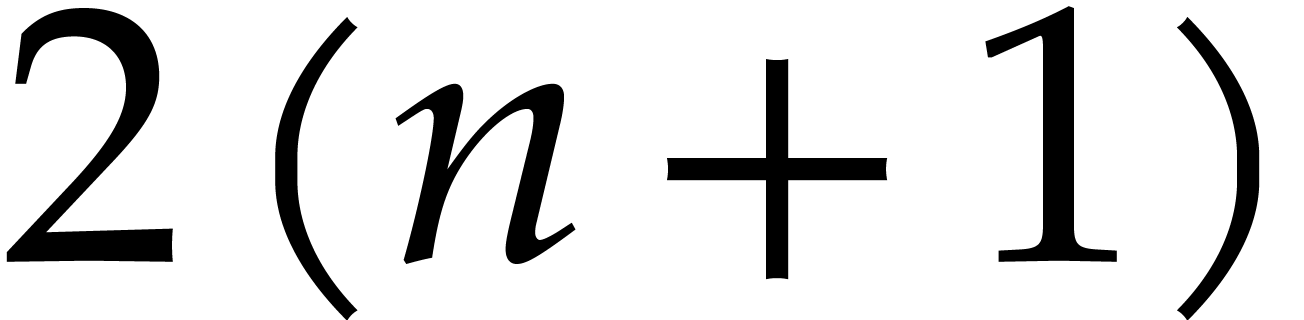 more operations. Therefore, one evaluation of
more operations. Therefore, one evaluation of 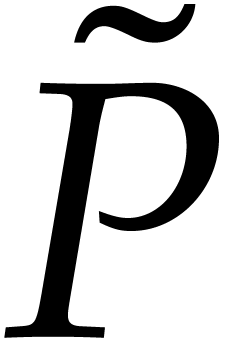 and
and  amounts to
amounts to
operations in  .
.
We interpolate  and
and  , and then compute
, and then compute
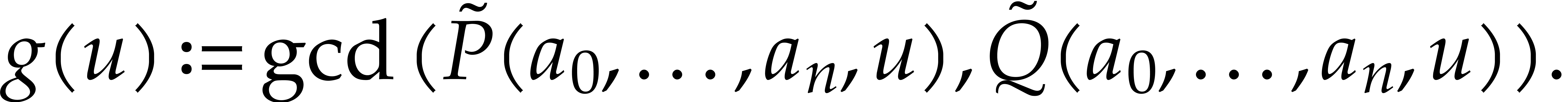
This requires 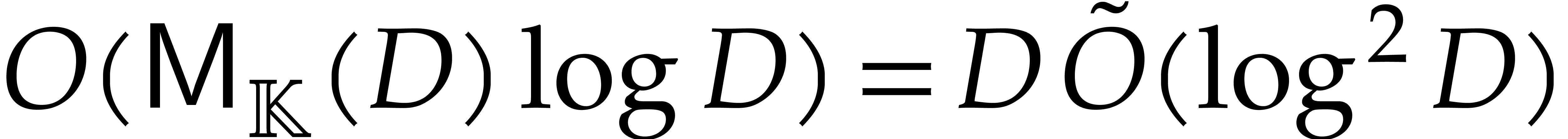 operations in
operations in  . By (1), the normalization
. By (1), the normalization
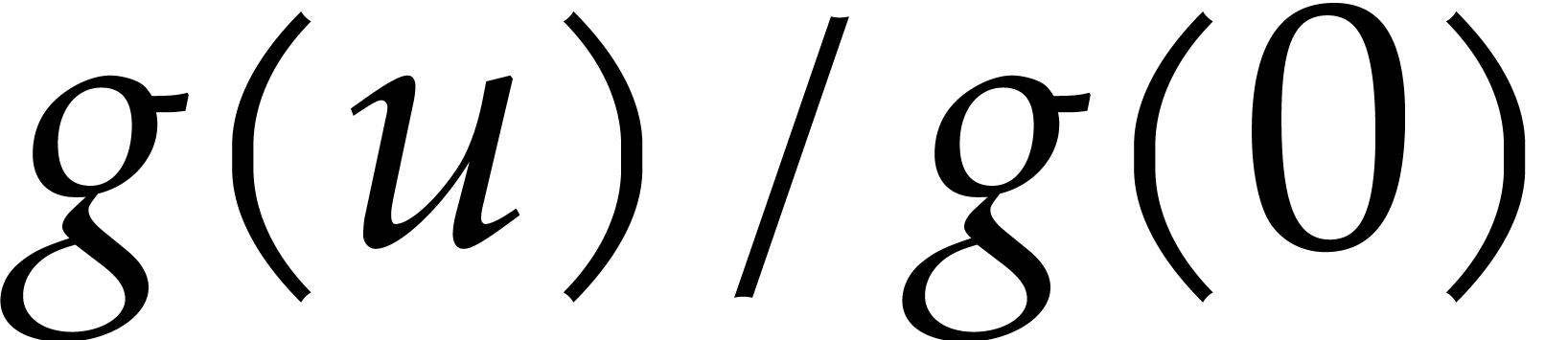 coincides with
coincides with 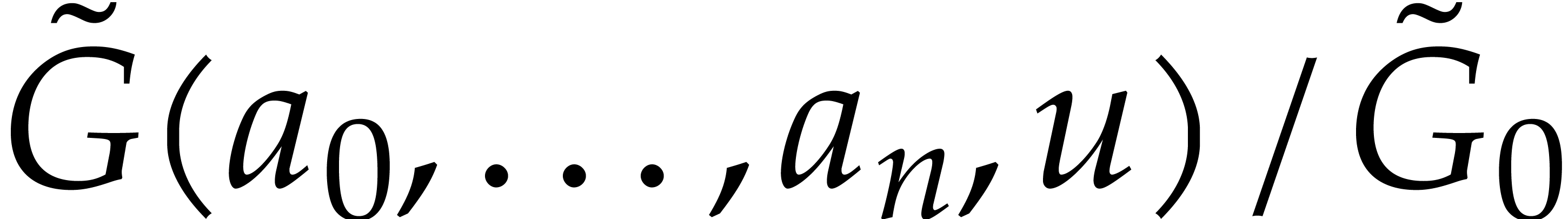 whenever
whenever 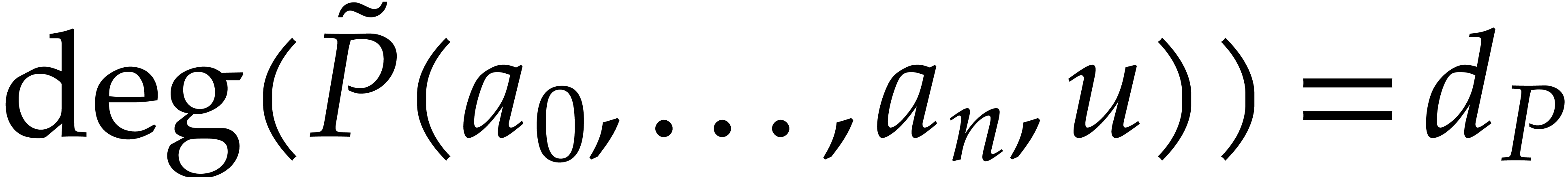 ,
,  , and the subresultant coefficient of
degree
, and the subresultant coefficient of
degree  of
of  and
and  is non-zero: see [5, chapter 6] or
[16], for instance.
is non-zero: see [5, chapter 6] or
[16], for instance.
In this way, we have built a blackbox that evaluates 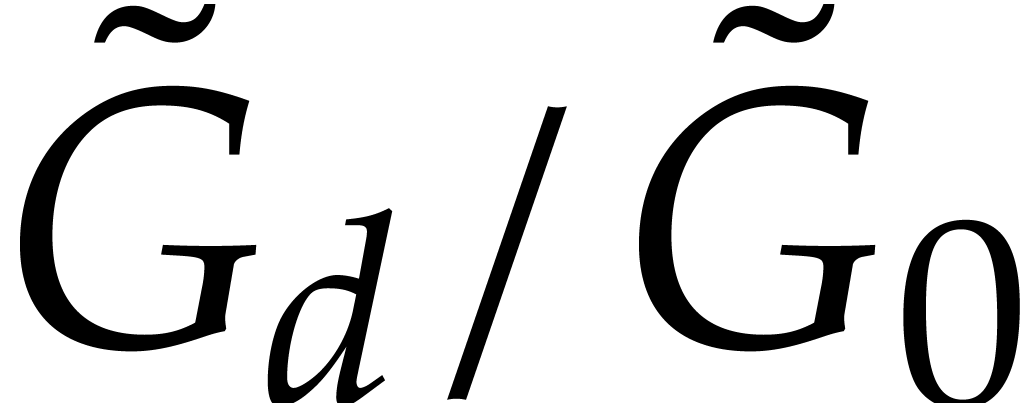 on a Zariski dense subset of
on a Zariski dense subset of 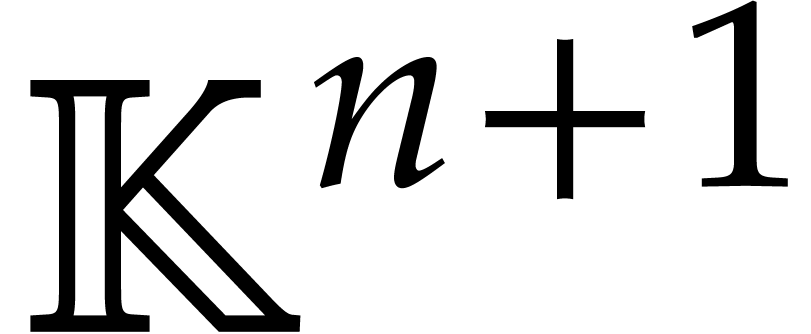 .
In order to ensure that the sparse interpolation of
.
In order to ensure that the sparse interpolation of 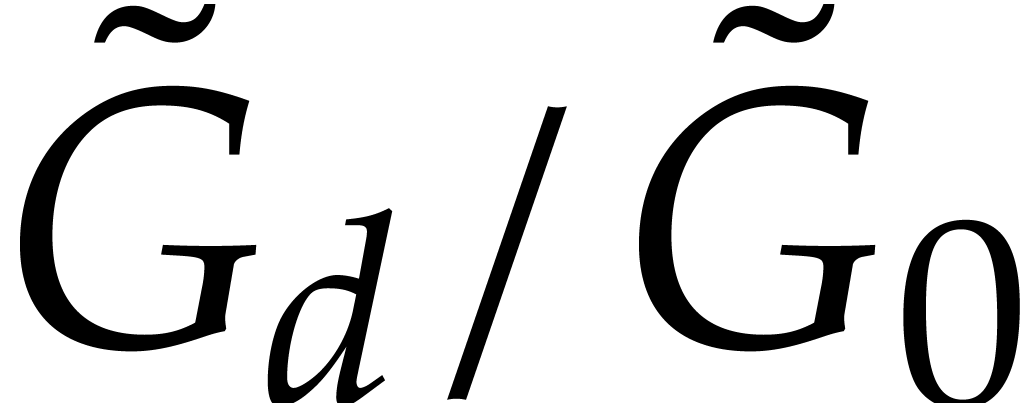 succeeds with high probability, we appeal to the discussion from section
2.2. Precisely, we take
succeeds with high probability, we appeal to the discussion from section
2.2. Precisely, we take 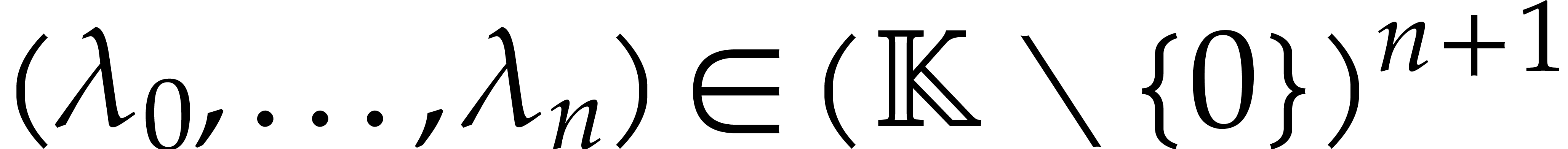 at random
and we interpolate
at random
and we interpolate  . This
random dilatation further increases the cost of each blackbox evaluation
by
. This
random dilatation further increases the cost of each blackbox evaluation
by  operations in
operations in  .
.
We need 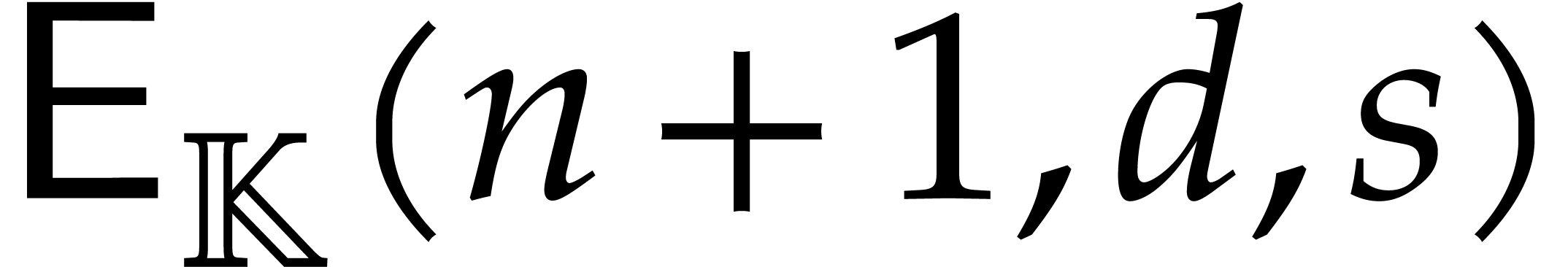 evaluation points, together with
evaluation points, together with 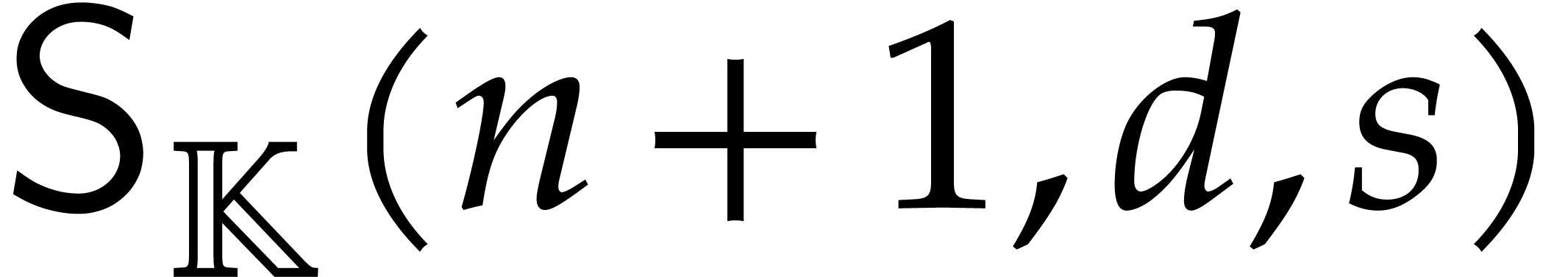 further operations in
further operations in  ,
for the sparse interpolation of
,
for the sparse interpolation of 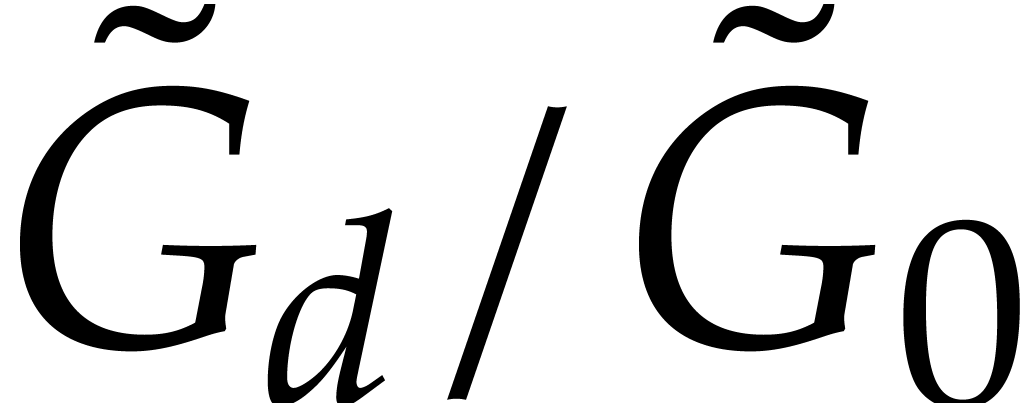 .
Finally, we recover the requested gcd of
.
Finally, we recover the requested gcd of 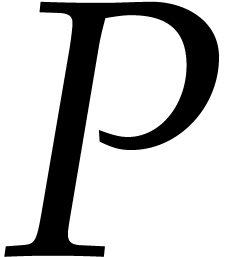 and
and
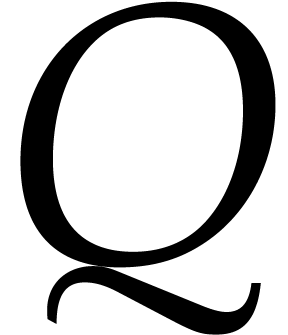 from
from 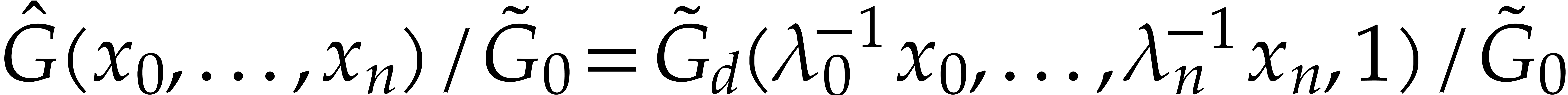 ,
using
,
using 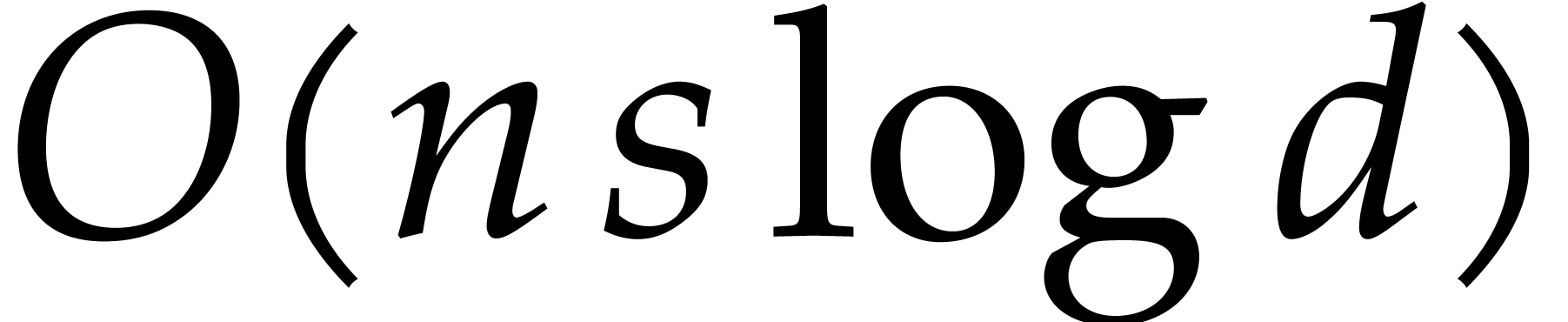 extra operations in
extra operations in  .
.
Let us now focus on the case when 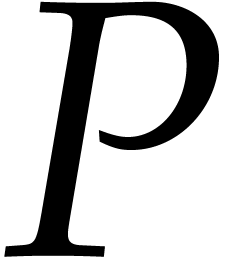 and
and 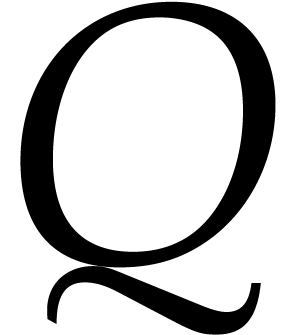 are presented as sparse polynomials instead of blackbox
functions (more generally, one may consider the model from [7,
section 5.3]). The number of terms of
are presented as sparse polynomials instead of blackbox
functions (more generally, one may consider the model from [7,
section 5.3]). The number of terms of 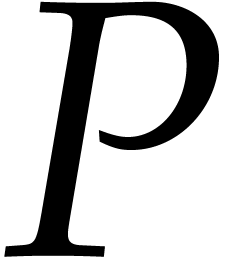 (resp. of
(resp. of
 ) is written
) is written 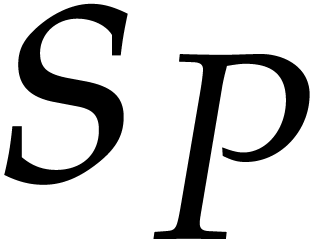 (resp.
(resp.  ). The above method
has the disadvantage that we need to evaluate
). The above method
has the disadvantage that we need to evaluate 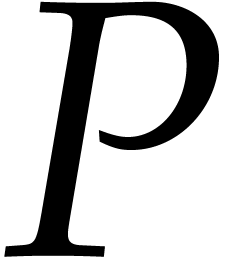 and
and  at many shifted points that are generally
not (e.g.) in a geometric progression. Such evaluations are
typically more expensive, when using a general algorithm for multi-point
evaluation, so it is better to avoid shifting altogether in this case.
at many shifted points that are generally
not (e.g.) in a geometric progression. Such evaluations are
typically more expensive, when using a general algorithm for multi-point
evaluation, so it is better to avoid shifting altogether in this case.
Now consider the particular case when
and  contains a single term
contains a single term 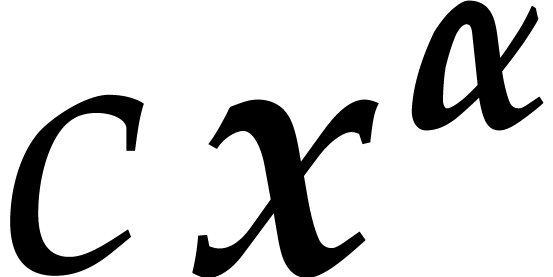 . Then we may use an alternative normalization
where we divide by
. Then we may use an alternative normalization
where we divide by 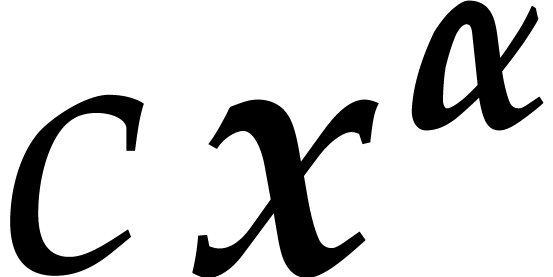 instead of
instead of  , and multiply by
, and multiply by  to
keep things polynomial. For a random point
to
keep things polynomial. For a random point  ,
we may check whether we are in this case (with high probability) by
testing whether
,
we may check whether we are in this case (with high probability) by
testing whether

Once 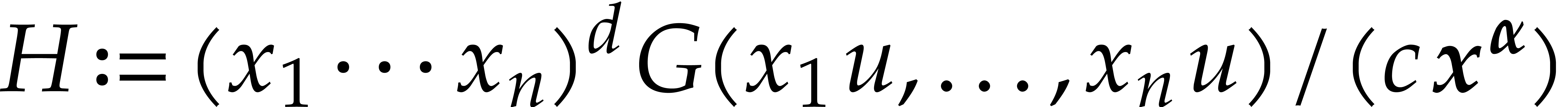 has been interpolated, we recover
has been interpolated, we recover  as
as
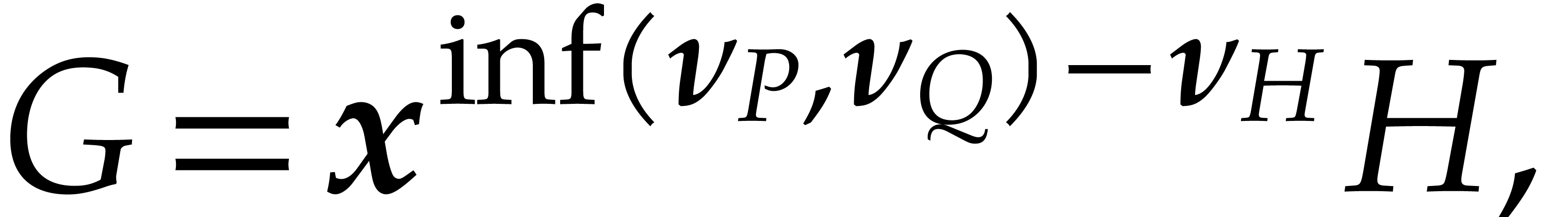
where 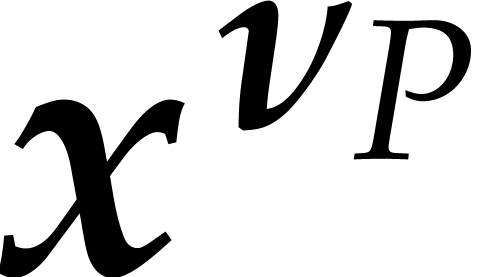 stands for the gcd of all monomials
occurring in
stands for the gcd of all monomials
occurring in 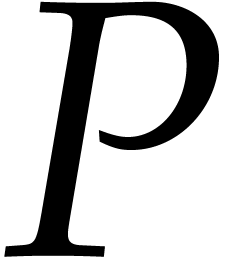 and similarly for
and similarly for 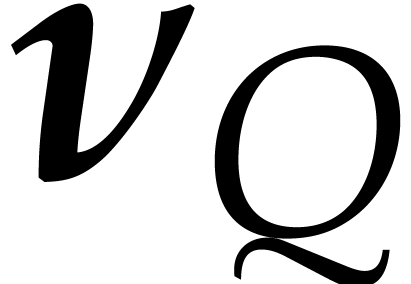 and
and 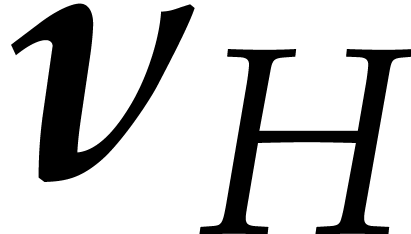 . With these
modifications, the complexity bound of Theorem 6 becomes
. With these
modifications, the complexity bound of Theorem 6 becomes
The same approach can be used if 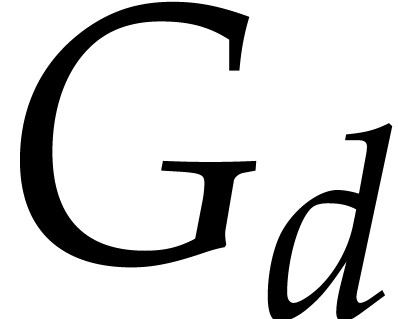 contains a
single term
contains a
single term 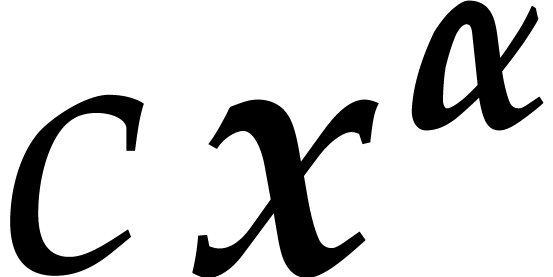 .
.
In the case when  contains several terms, we
consider
contains several terms, we
consider
for a suitable vector 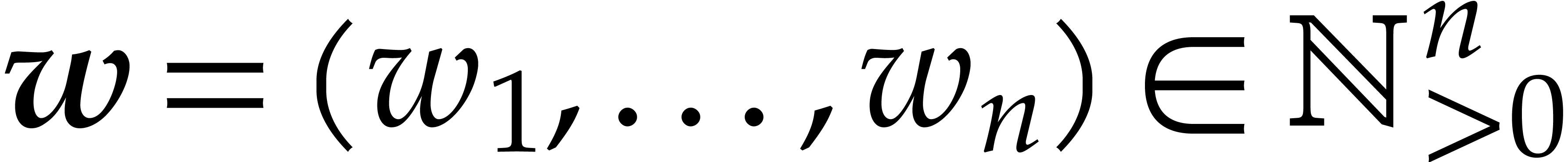 of weights. Whenever
of weights. Whenever 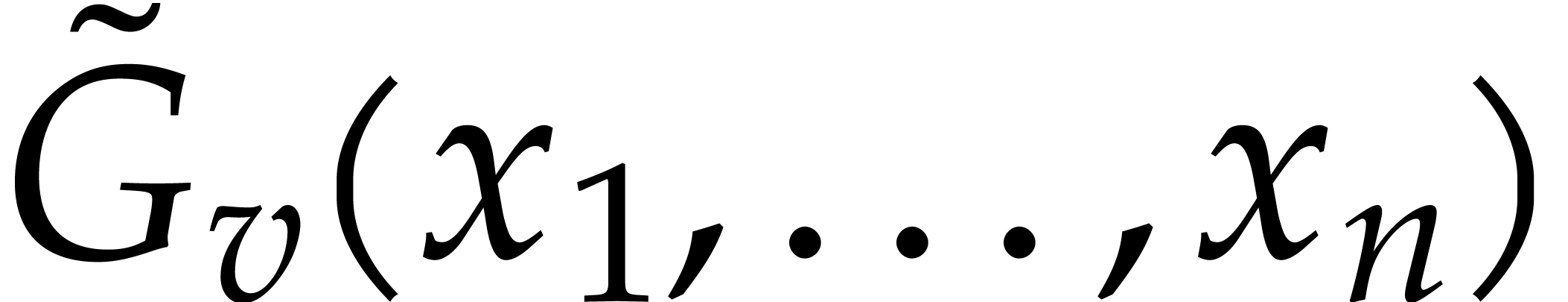 contains a single term, we may use the above method
to compute
contains a single term, we may use the above method
to compute  and then
and then  . However, the degree
. However, the degree  of
of
 is potentially
is potentially  times
larger than the degree
times
larger than the degree  of
of  , where
, where 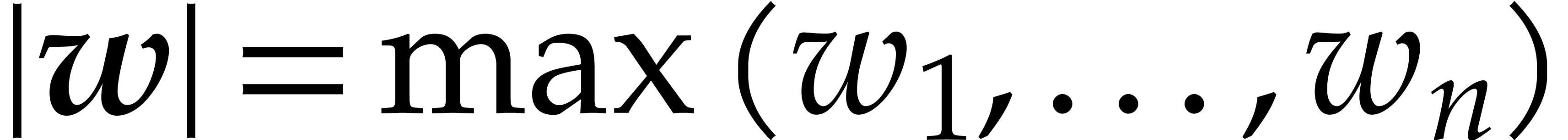 .
This leads to the question how small we can take
.
This leads to the question how small we can take  while ensuring that
while ensuring that  contains a single term with
probability at least
contains a single term with
probability at least 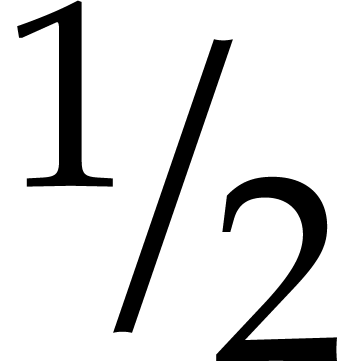 . We
conjecture that this is the case when taking
. We
conjecture that this is the case when taking  at
random with
at
random with 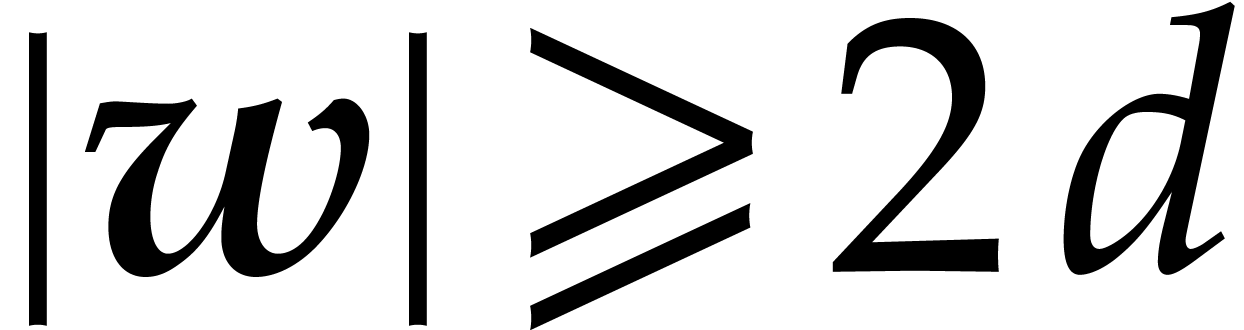 . In practice,
the idea is to try a sequence of random weights
. In practice,
the idea is to try a sequence of random weights  for which
for which  follows a slow geometric progression.
follows a slow geometric progression.
Let us provide some partial evidence for our conjecture. In dimension
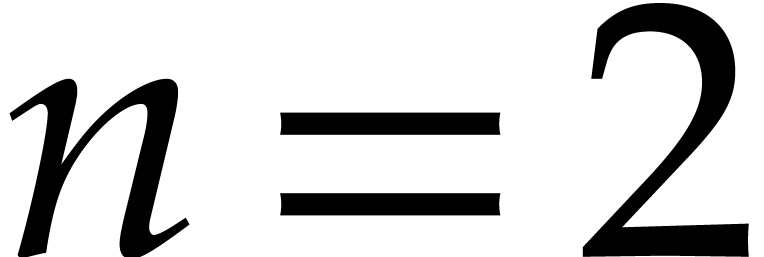 , consider the Newton polygon
at
, consider the Newton polygon
at  of a polynomial of degree
of a polynomial of degree  made of the maximal number of slopes
made of the maximal number of slopes 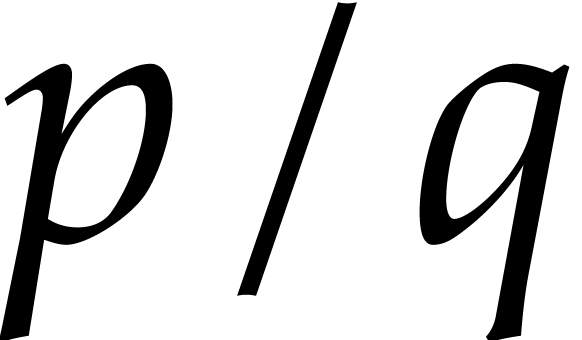 with
with 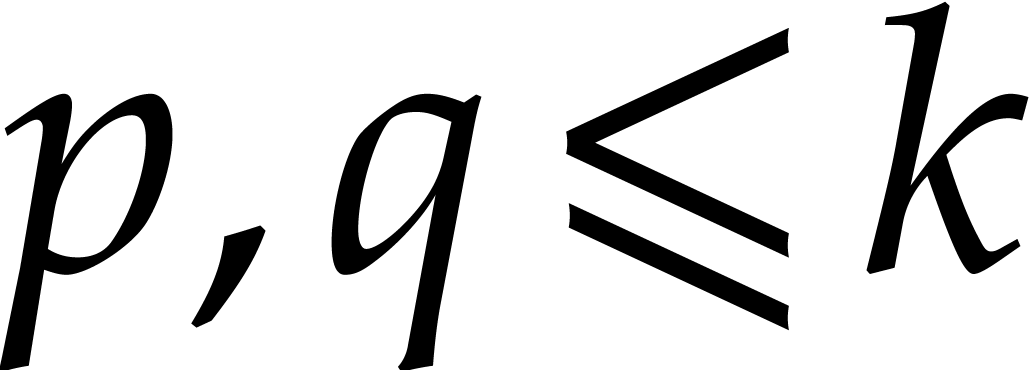 . For each integer
. For each integer 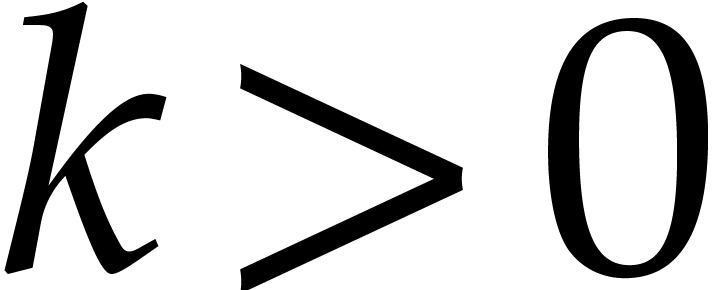 , let
, let 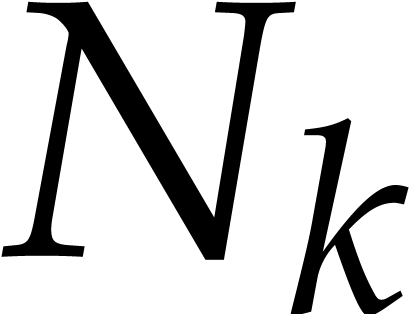 be the number of
slopes
be the number of
slopes  with
with 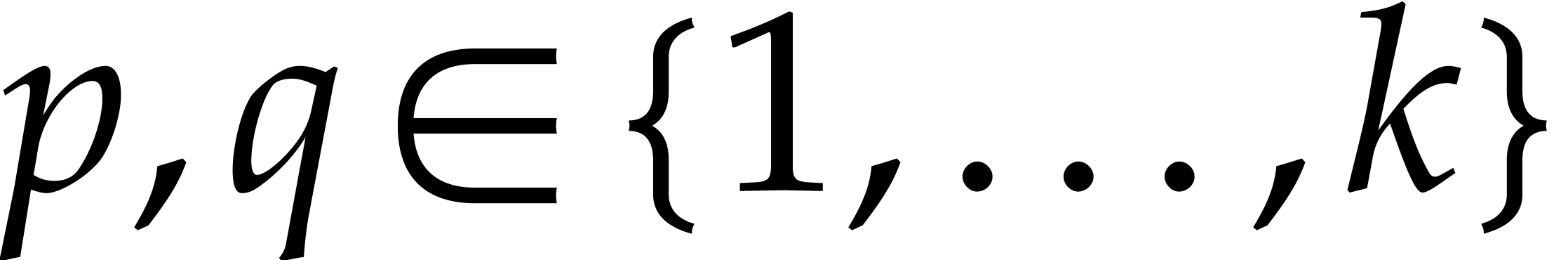 ,
,
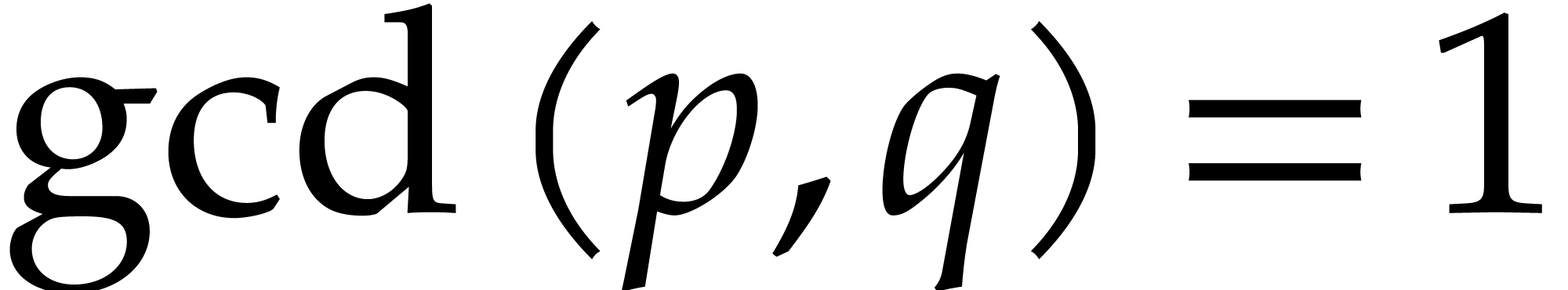 , and
, and 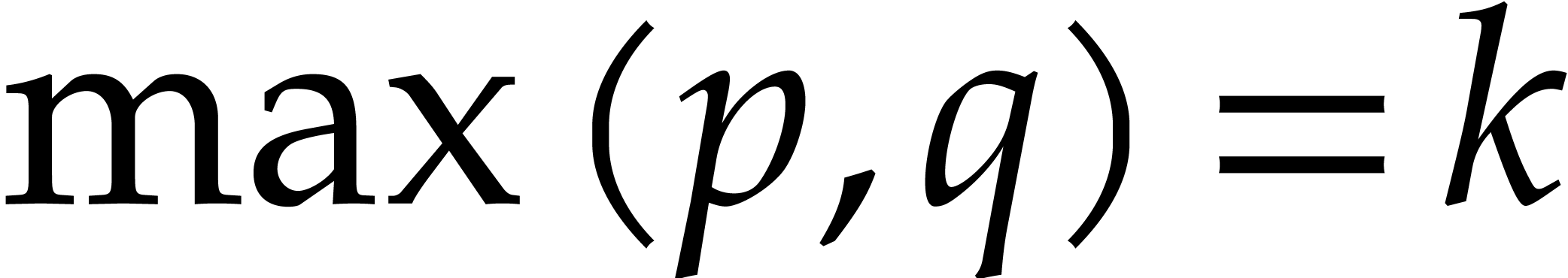 . We have
. We have

Under this constraint, the sum  is maximized by
considering Newton polygons that first exhaust all slopes
is maximized by
considering Newton polygons that first exhaust all slopes  for which
for which 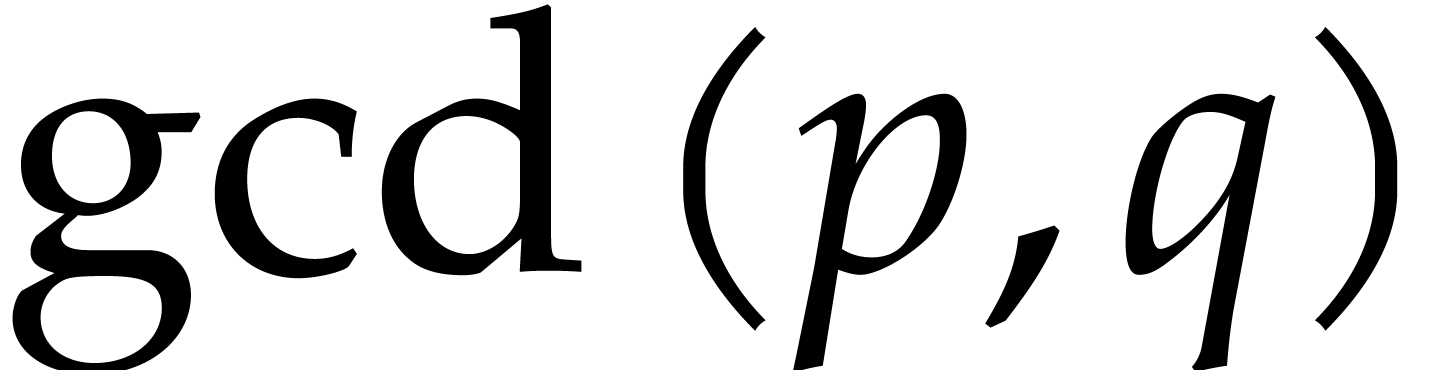 is minimal. Now
is minimal. Now 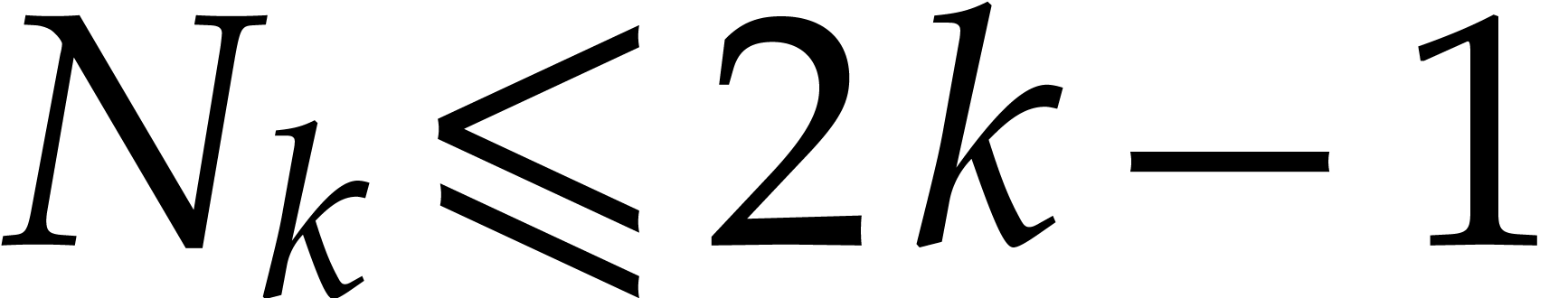 for all
for all  .
Taking
.
Taking 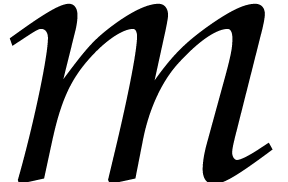 minimal with
minimal with 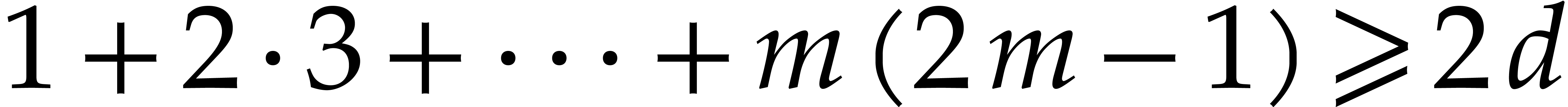 , it follows that
, it follows that
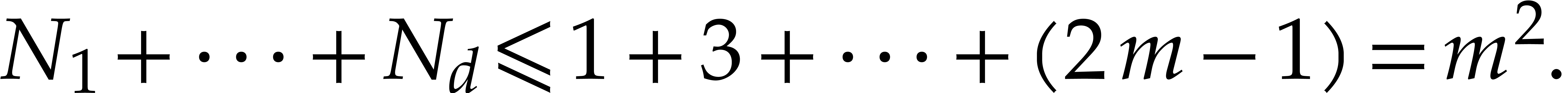
Now 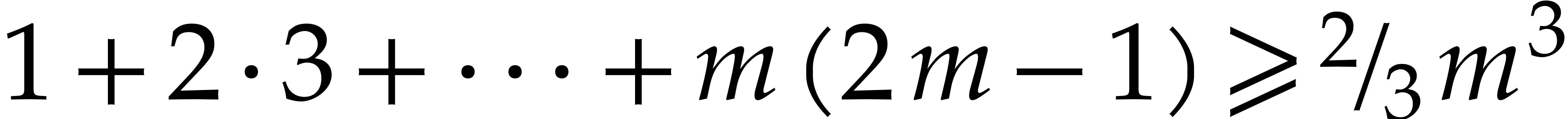 , so
, so 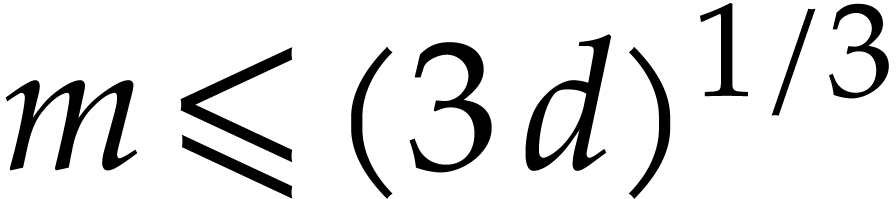 and
and
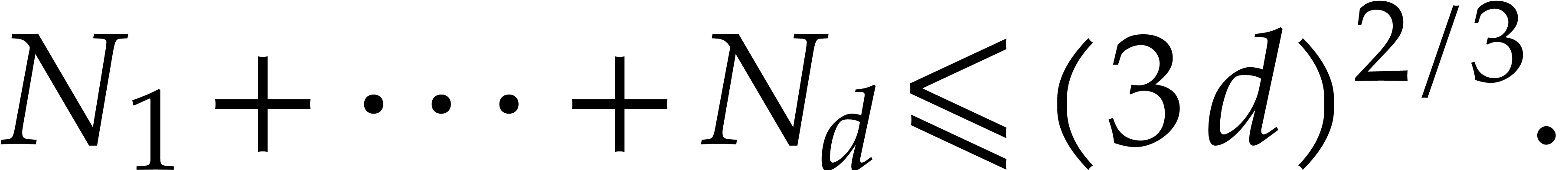
On the other hand, for any 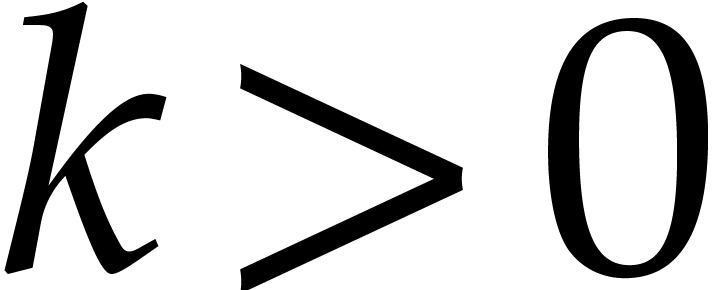 ,
the number of rational numbers
,
the number of rational numbers 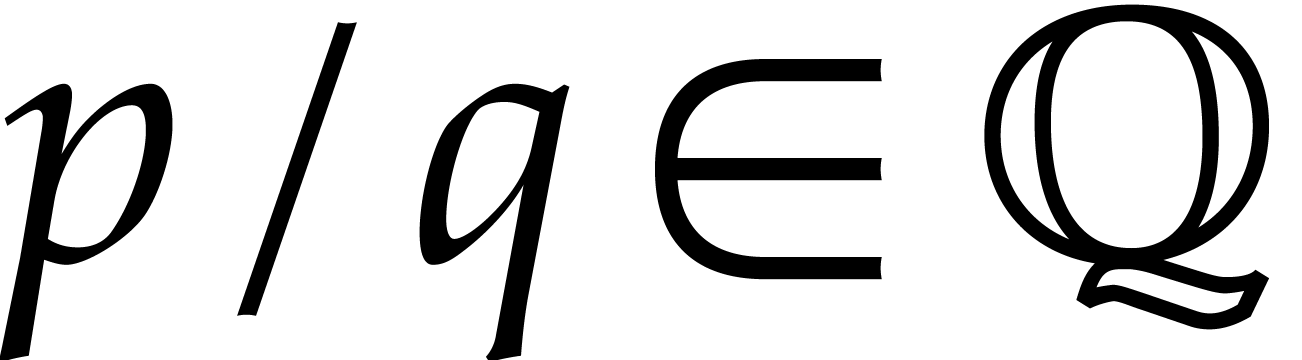 with
with 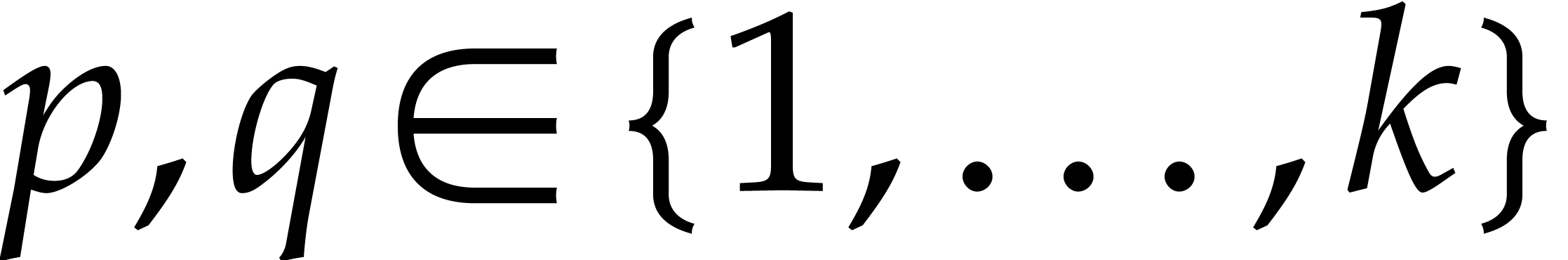 is at least
is at least
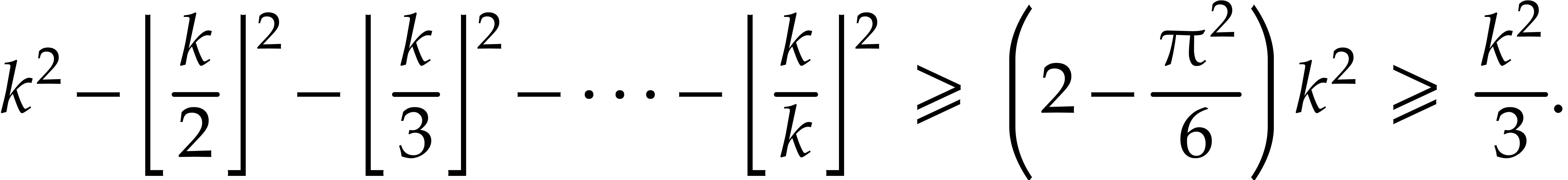
Now let 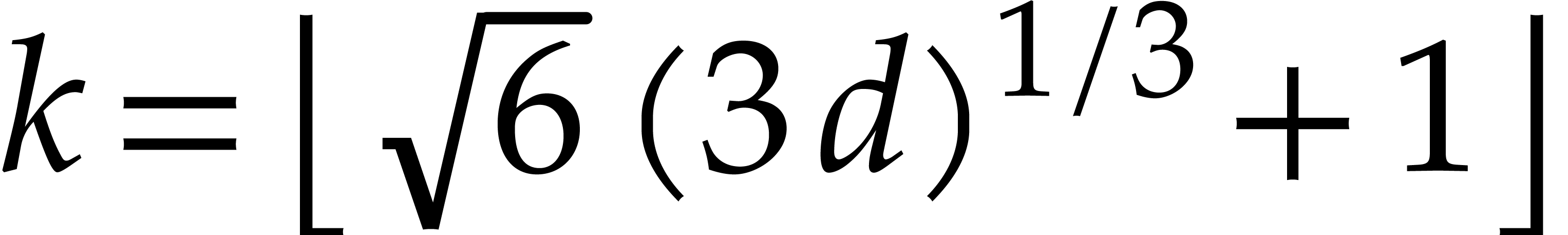 be the smallest integer with
be the smallest integer with 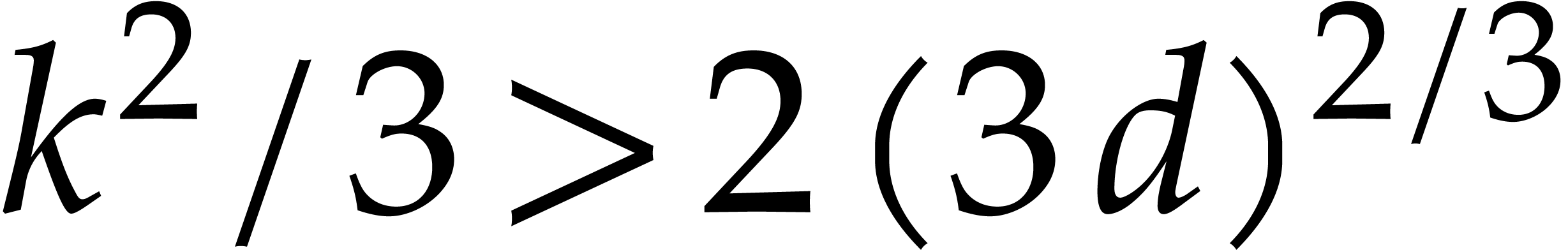 . For a random weight
. For a random weight 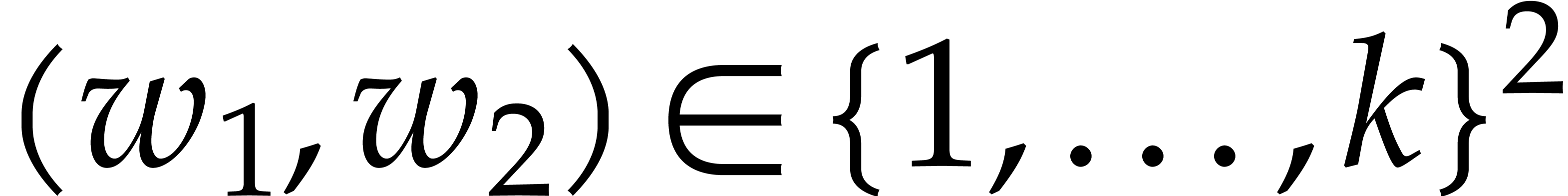 with
with 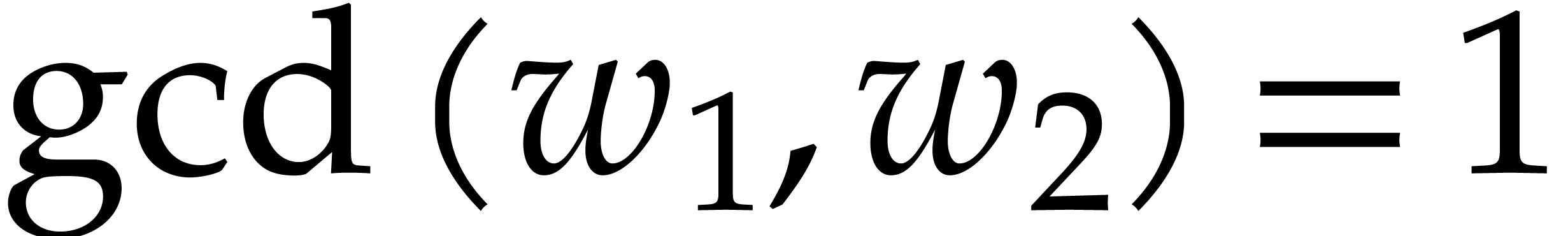 , we then
conclude that
, we then
conclude that 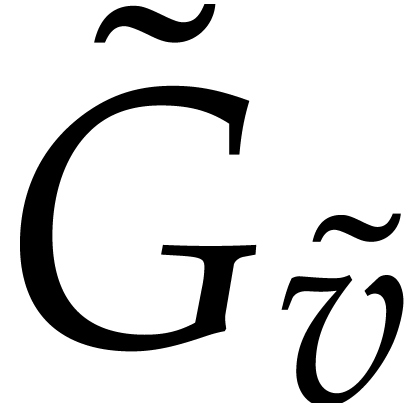 has a unique term with probability
at least
has a unique term with probability
at least 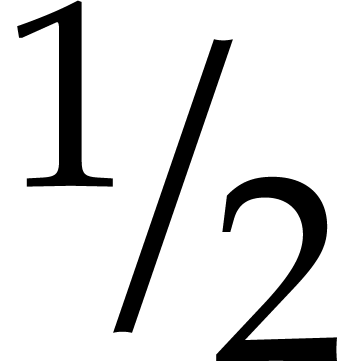 .
.
As a second piece of evidence, let us show that there always
exists a weight vector 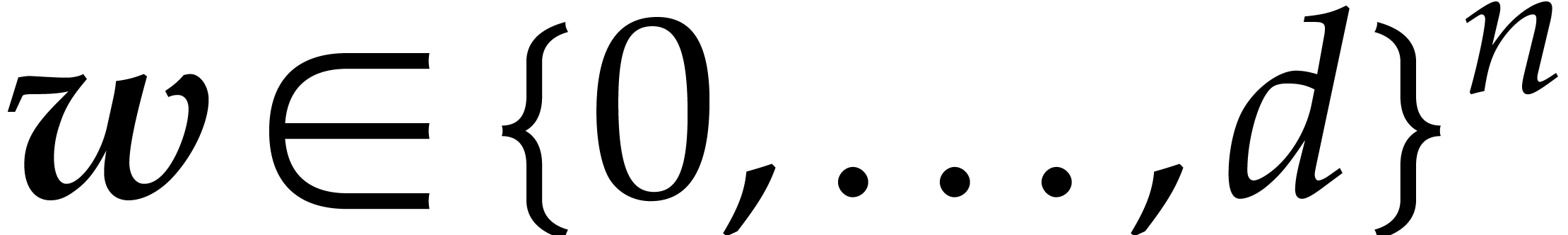 for which
for which 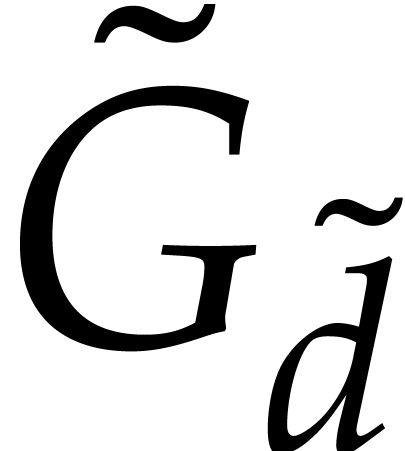 contains a unique term. Let
contains a unique term. Let  be an element of the support
be an element of the support  of
of  for which
for which 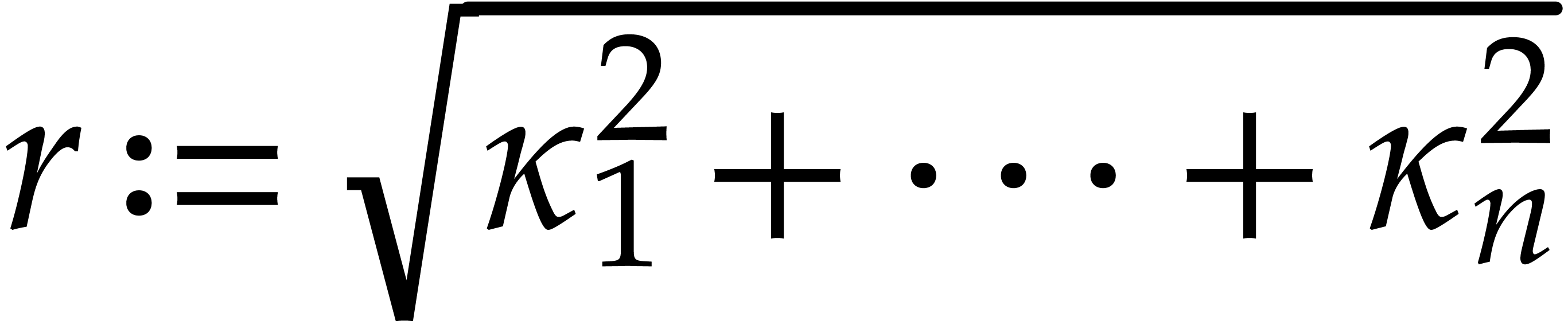 is maximal. Then
is maximal. Then  is included in the ball with center
is included in the ball with center  and radius
and radius
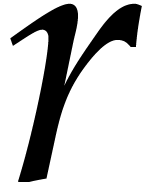 , so the tangent space to
this ball at
, so the tangent space to
this ball at  intersects
intersects  only at
only at  . Taking
. Taking  to be the normal vector to this tangent space, it follows
that
to be the normal vector to this tangent space, it follows
that 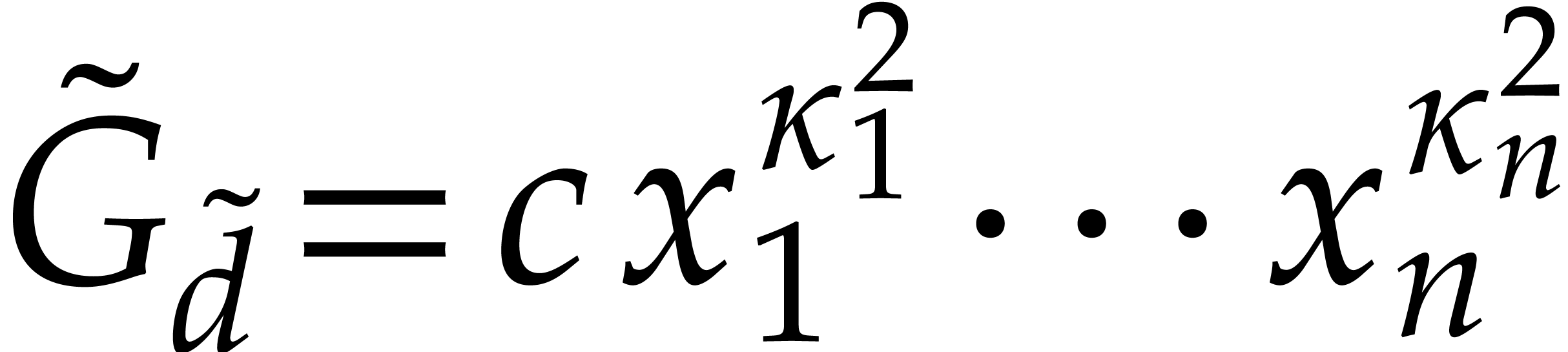 for some
for some 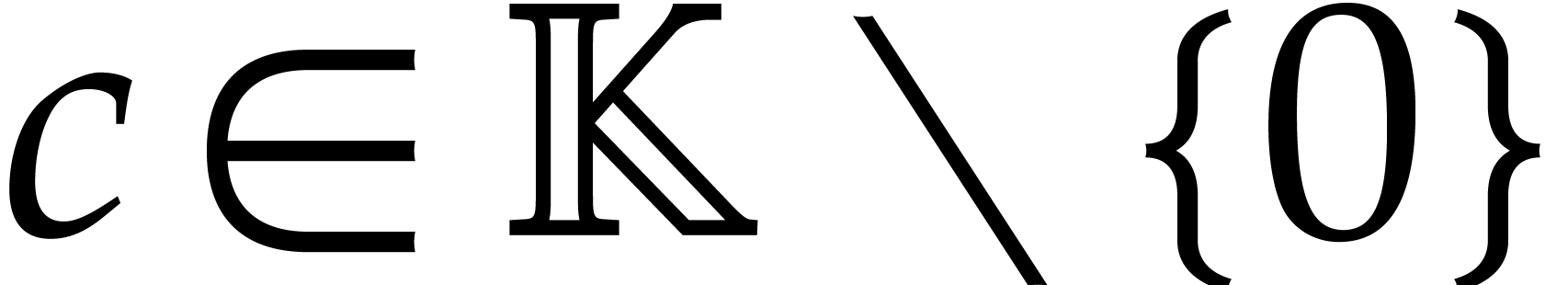 .
.
A. Arnold, M. Giesbrecht, and D. S. Roche. Faster sparse multivariate polynomial interpolation of straight-line programs. J. Symbolic Comput., 75:4–24, 2016.
A. Cuyt and W.-S. Lee. Sparse interpolation of multivariate rational functions. Theor. Comput. Sci., 412:1445–1456, 2011.
J. de Kleine, M. Monagan, and A. Wittkopf. Algorithms for the non-monic case of the sparse modular gcd algorithm. In Proceedings of the 2005 International Symposium on Symbolic and Algebraic Computation, ISSAC '05, pages 124–131. New York, NY, USA, 2005. ACM.
S. Garg and É. Schost. Interpolation of polynomials given by straight-line programs. Theor. Comput. Sci., 410(27-29):2659–2662, 2009.
J. von zur Gathen and J. Gerhard. Modern computer algebra. Cambridge University Press, New York, 3rd edition, 2013.
D. Grigoriev, M. Karpinski, and M. F. Singer. Computational complexity of sparse rational interpolation. SIAM J. Comput., 23(1):1–11, 1994.
J. van der Hoeven. Probably faster multiplication of sparse polynomials. Technical Report, HAL, 2020. http://hal.archives-ouvertes.fr/hal-02473830.
J. van der Hoeven. The Jolly Writer. Your Guide to GNU TeXmacs. Scypress, 2020.
J. van der Hoeven and G. Lecerf. Sparse polynomial interpolation in practice. ACM Commun. Comput. Algebra, 48(3/4):187–191, 2015.
J. van der Hoeven and G. Lecerf. Sparse polynomial interpolation. Exploring fast heuristic algorithms over finite fields. Technical Report, HAL, 2019. http://hal.archives-ouvertes.fr/hal-02382117.
J. Hu and M. Monagan. A fast parallel sparse polynomial GCD algorithm. J. Symbolic Comput., 2020. https://doi.org/10.1016/j.jsc.2020.06.001.
Q.-L. Huang and X.-S. Gao. Sparse rational function interpolation with finitely many values for the coefficients. In J. Blömer, I. S. Kotsireas, T. Kutsia, and D. E. Simos, editors, Mathematical Aspects of Computer and Information Sciences. 7th International Conference, MACIS 2017, Vienna, Austria, November 15-17, 2017, Proceedings, number 10693 in Theoretical Computer Science and General Issues, pages 227–242. Cham, 2017. Springer International Publishing.
M. Javadi and M. Monagan. Parallel sparse polynomial interpolation over finite fields. In M. Moreno Maza and J.-L. Roch, editors, PASCO '10: Proceedings of the 4th International Workshop on Parallel and Symbolic Computation, pages 160–168. New York, NY, USA, 2010. ACM.
E. Kaltofen and B. M. Trager. Computing with polynomials given by black boxes for their evaluations: greatest common divisors, factorization, separation of numerators and denominators. J. Symbolic Comput., 9(3):301–320, 1990.
S. Lang. Algebra, volume 211 of Graduate Texts in Mathematics. Springer-Verlag, New York, 3rd edition, 2002.
G. Lecerf. On the complexity of the Lickteig–Roy subresultant algorithm. J. Symbolic Comput., 92:243–268, 2019.
D. S. Roche. What can (and can't) we do with sparse polynomials? In C. Arreche, editor, ISSAC '18: Proceedings of the 2018 ACM International Symposium on Symbolic and Algebraic Computation, pages 25–30. New York, NY, USA, 2018. ACM.
R. Zippel. Probabilistic algorithms for sparse polynomials. In Edward W. Ng, editor, Symbolic and Algebraic Computation. EUROSAM '79, An International Symposium on Symbolic and Algebraic Manipulation, Marseille, France, June 1979, volume 72 of Lect. Notes Comput. Sci., pages 216–226. Springer Berlin Heidelberg, 1979.