Making fast multiplication of polynomials
numerically stable |
|
| January 21, 2008 |
|
 . This work has
partially been supported by the ANR Gecko project.
. This work has
partially been supported by the ANR Gecko project.
Consider two polynomials
|
Let 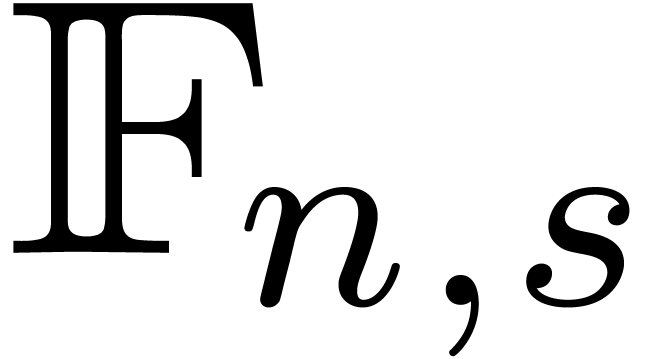 be the set of floating point numbers with an
be the set of floating point numbers with an
 -bit mantissa and an
-bit mantissa and an  -bit exponent. Each non-zero number
-bit exponent. Each non-zero number
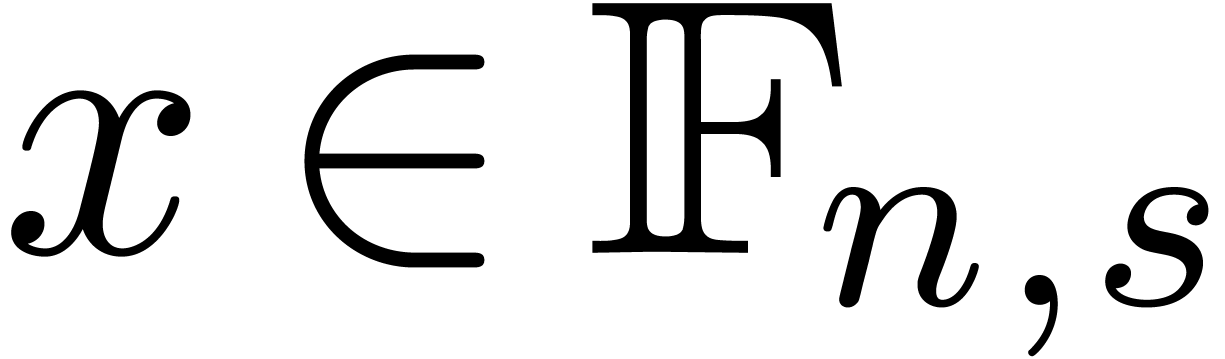 of this kind can be written as
of this kind can be written as 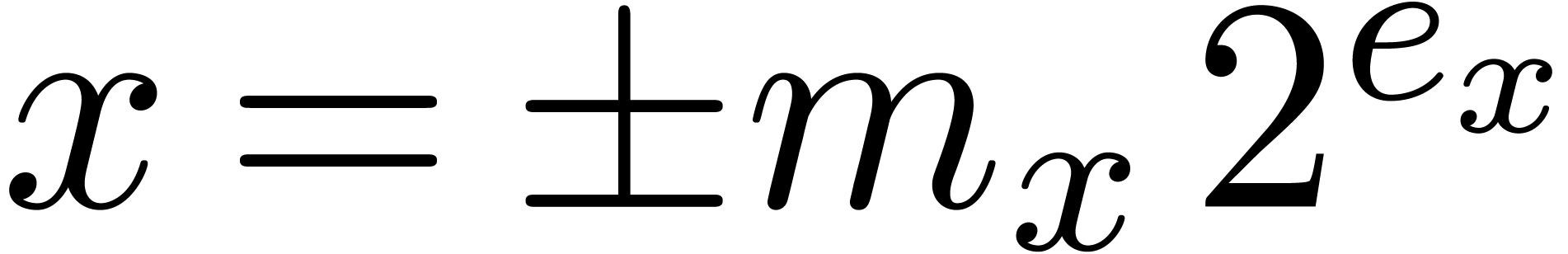 , with
, with
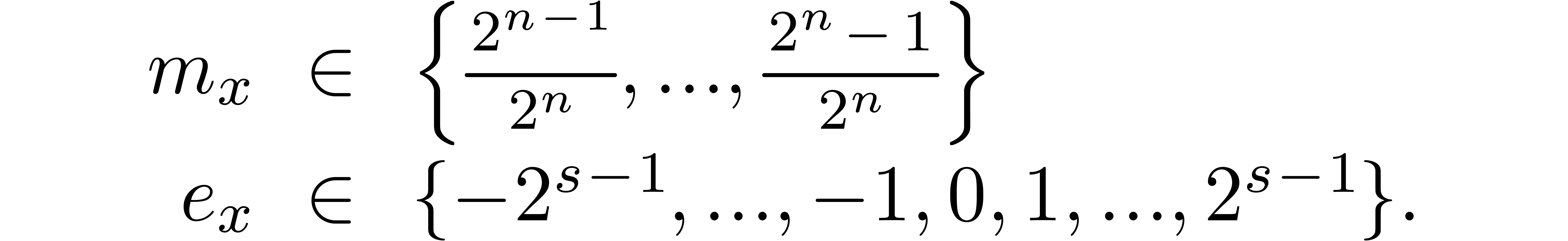
In what follows,  is assumed to be fixed once and
for all. For the sake of simplicity, we will not study overflows and
underflows in detail and instead make the assumption that
is assumed to be fixed once and
for all. For the sake of simplicity, we will not study overflows and
underflows in detail and instead make the assumption that  has been chosen large enough with respect to the input
data. Consider two polynomials
has been chosen large enough with respect to the input
data. Consider two polynomials

with coefficients in  . For
definiteness, we will assume
. For
definiteness, we will assume  ,
,
 ,
, 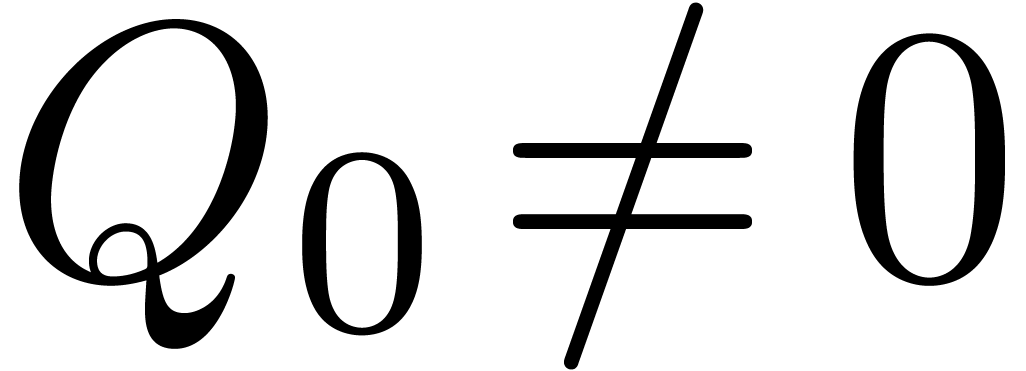 and
and
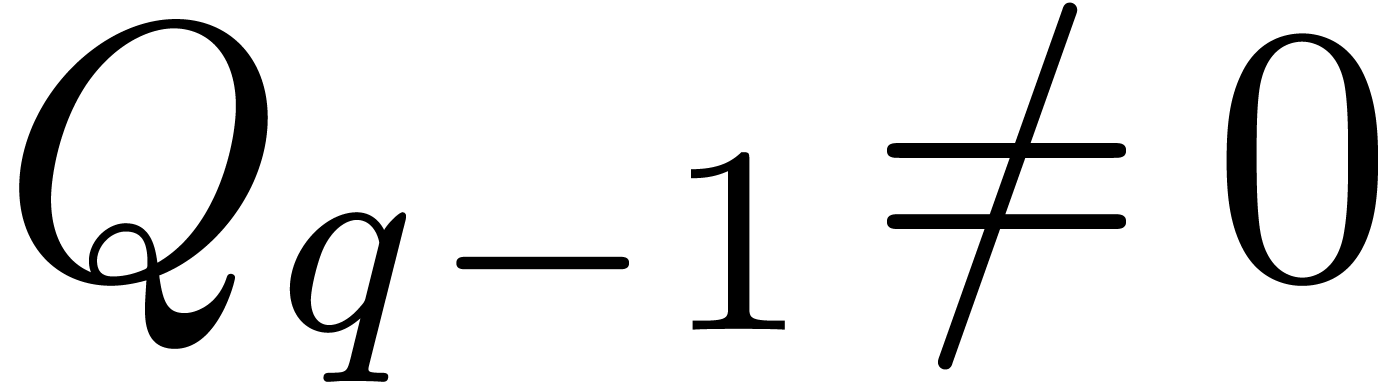 . In this paper, we study the
problem of multiplying
. In this paper, we study the
problem of multiplying  and
and  .
.
Using FFT-multiplication [CT65], the polynomials  and
and  can in principle be multiplied
in time
can in principle be multiplied
in time 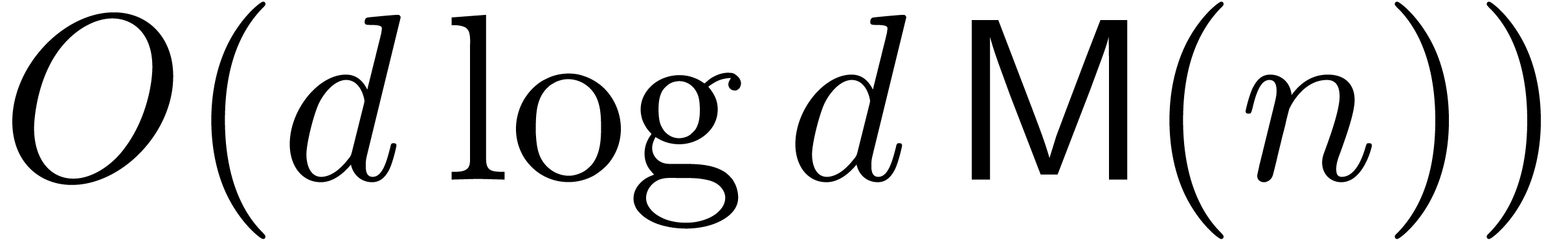 . Here
. Here 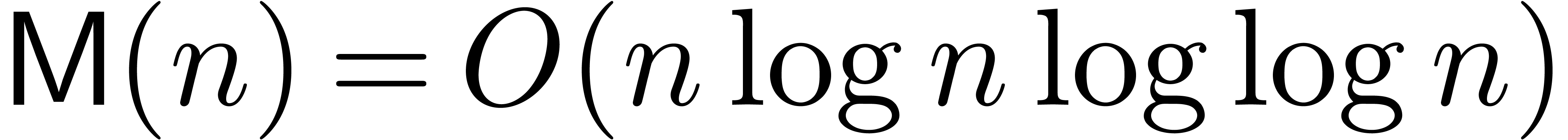 is the complexity of
is the complexity of 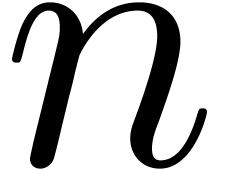 -bit
integer multiplication [SS71] and it can be assumed that
-bit
integer multiplication [SS71] and it can be assumed that
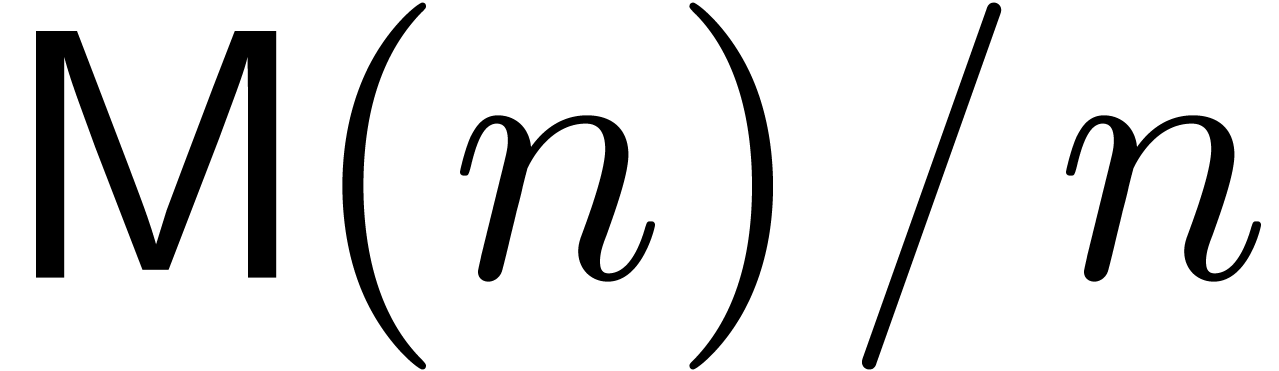 increases with
increases with 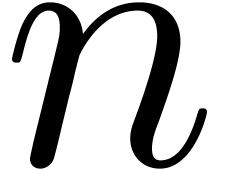 .
Alternatively, one may rewrite
.
Alternatively, one may rewrite  and
and  as “floating point polynomials”, with an
as “floating point polynomials”, with an  -bit integer exponent and
polynomials with
-bit integer exponent and
polynomials with 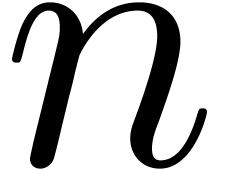 -bit integer
coefficients as mantissas. Using Kronecker's method, we may then
multiply
-bit integer
coefficients as mantissas. Using Kronecker's method, we may then
multiply  and
and  in time
in time
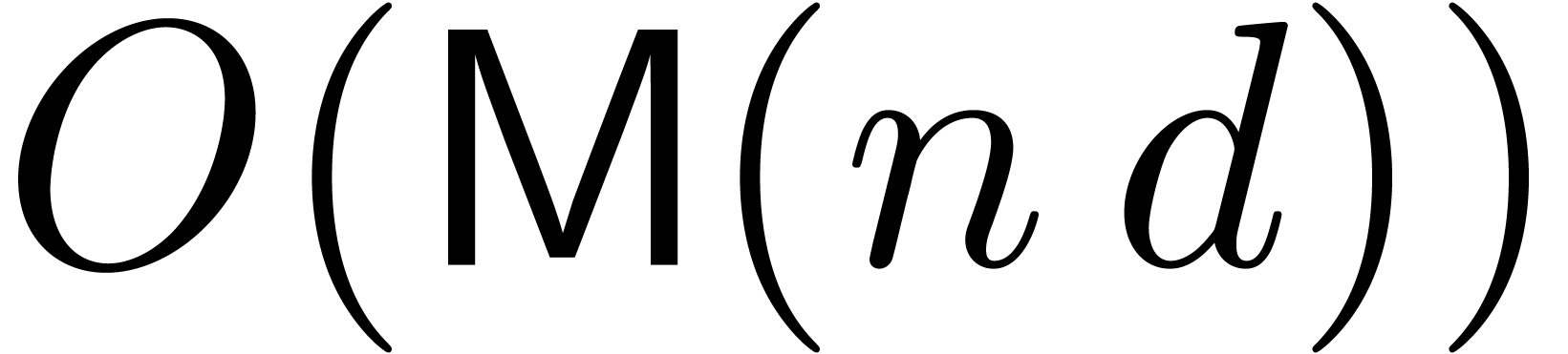 , where
, where 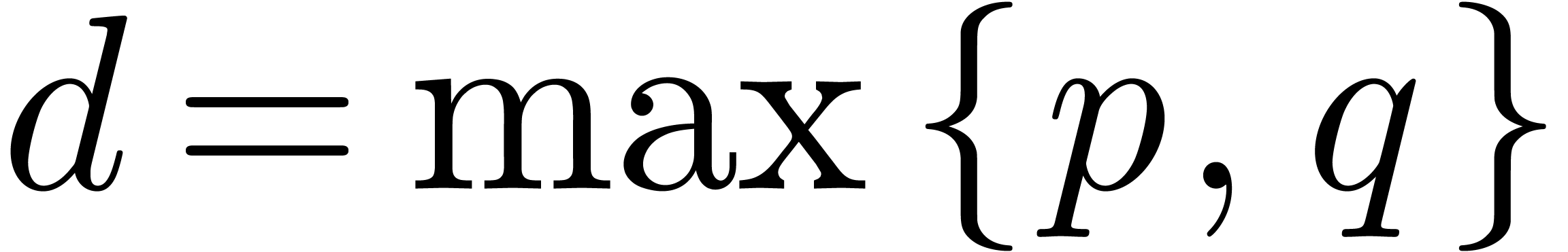 . If
. If 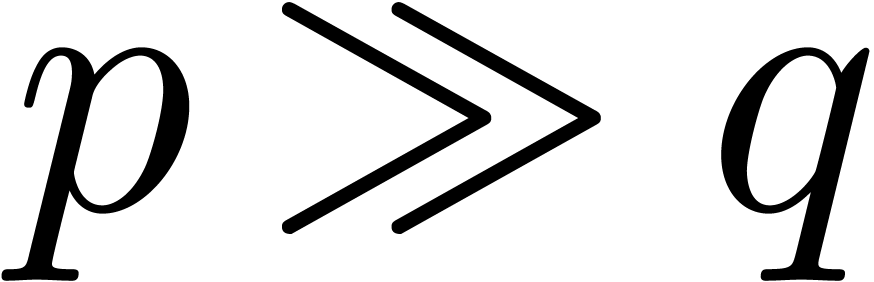 ,
then this complexity can be improved a bit further into
,
then this complexity can be improved a bit further into 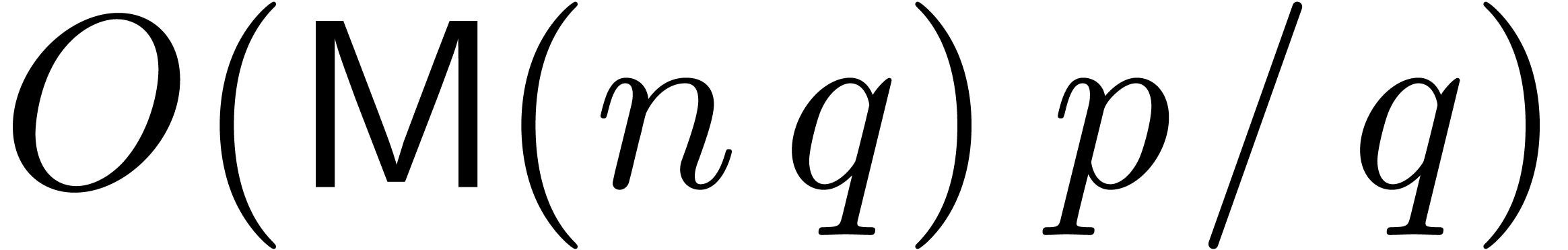 by using
by using 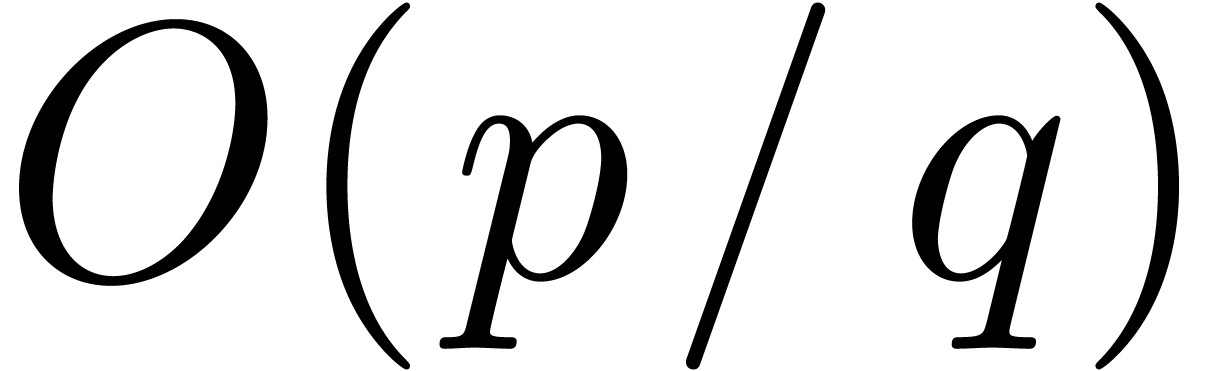 multiplications of degrees
multiplications of degrees  .
.
In the case when the coefficients of  are all of
the same order of magnitude, and similarly for
are all of
the same order of magnitude, and similarly for  , the above algorithms are very efficient and
numerically stable. In section 2, we will give a more
detailed uniform error analysis. Unfortunately, the algorithms are very
unstable if the coefficients of
, the above algorithms are very efficient and
numerically stable. In section 2, we will give a more
detailed uniform error analysis. Unfortunately, the algorithms are very
unstable if the coefficients of  or
or  are not of the same order of magnitude. For instance,
taking
are not of the same order of magnitude. For instance,
taking 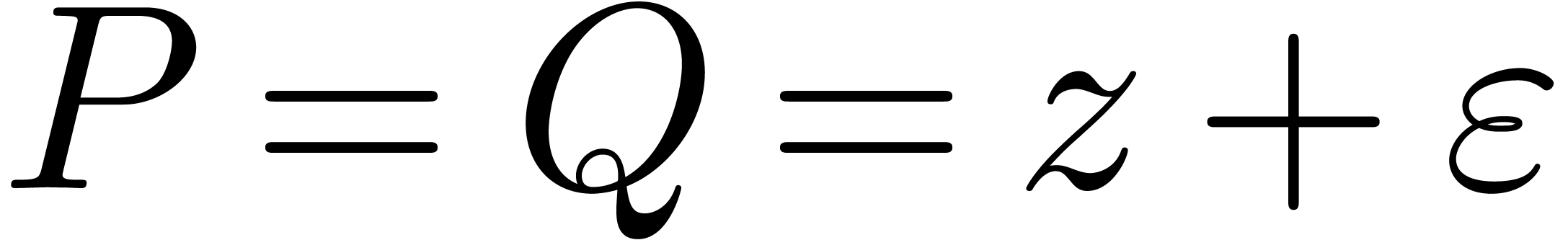 with
with 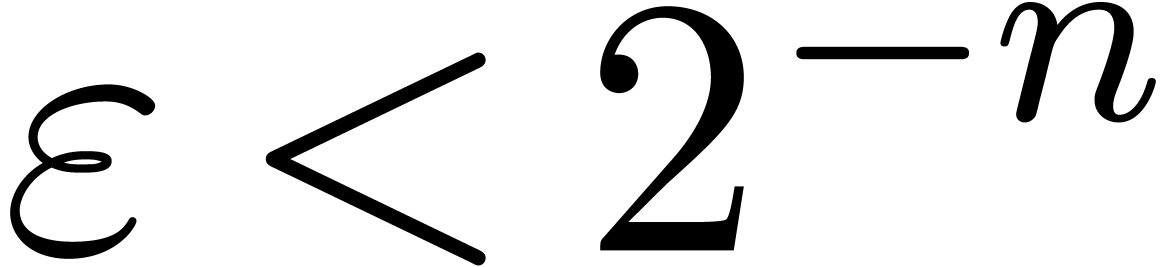 ,
the transformation of
,
the transformation of  and
and  into floating point polynomials
into floating point polynomials 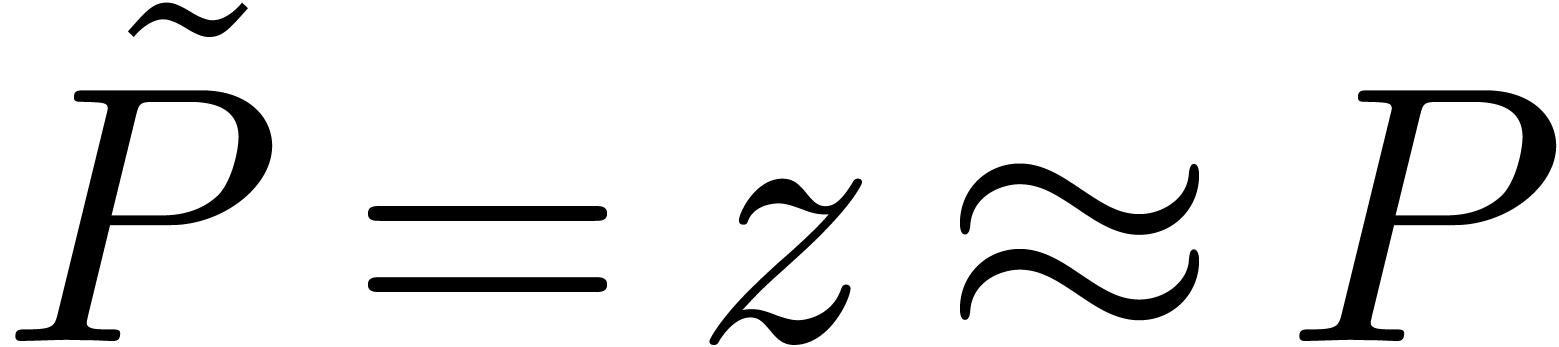 and
and 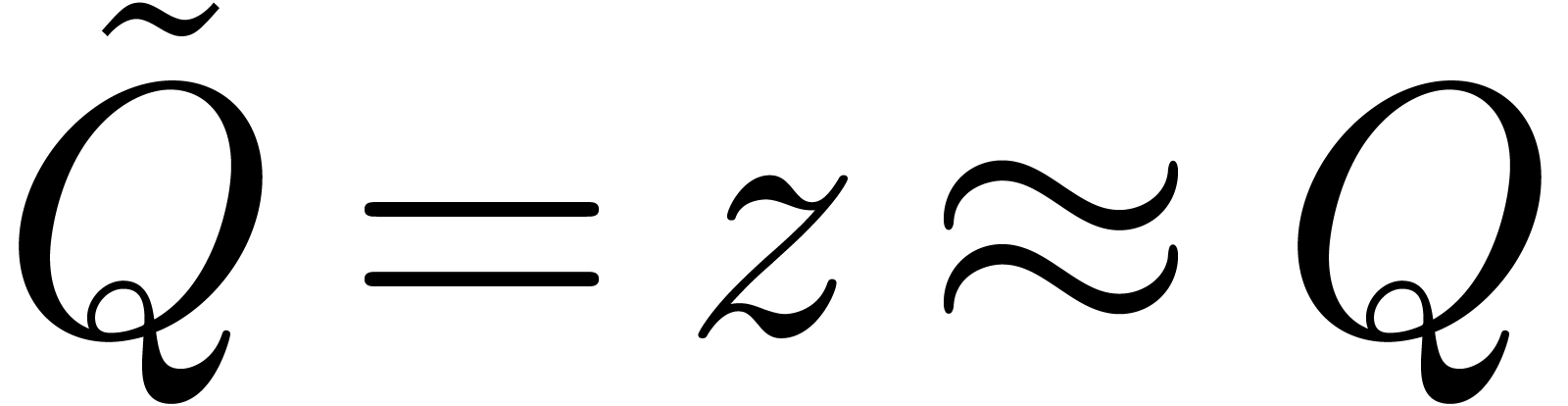 amounts to neglecting the coefficients
amounts to neglecting the coefficients 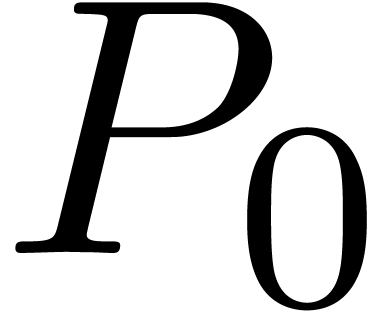 and
and 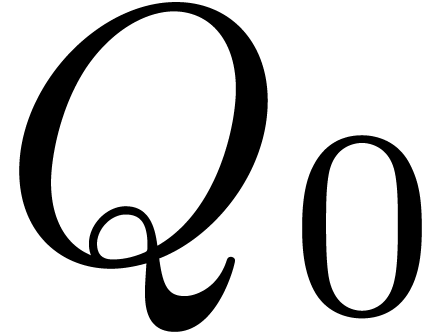 . In particular, when
approximating
. In particular, when
approximating  , only the
leading coefficient
, only the
leading coefficient  of the product will be
computed with a satisfactory accuracy.
of the product will be
computed with a satisfactory accuracy.
A situation which arises often in practice is that the above fast multiplication algorithms can be made numerically stable using a suitable scaling
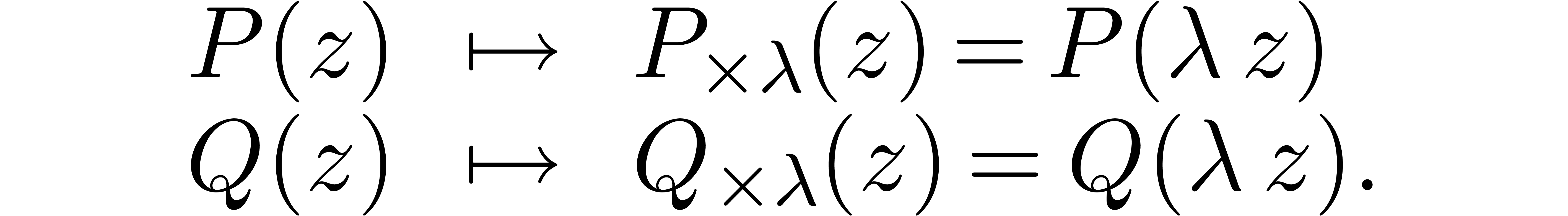
For instance, in the above example when 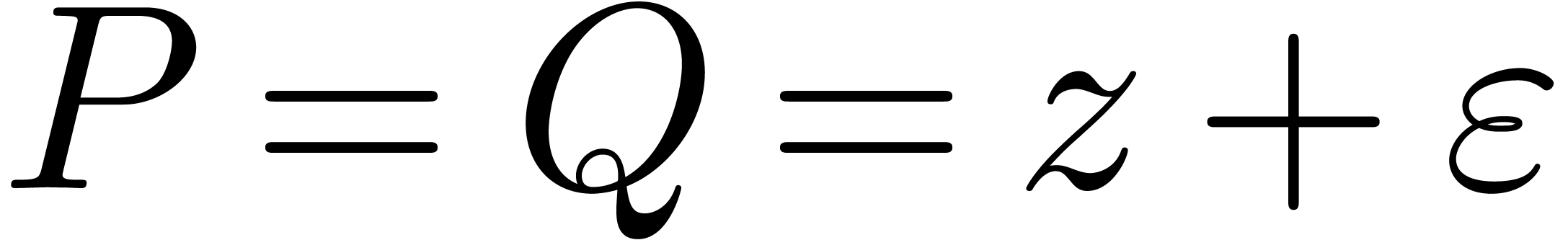 ,
we may multiply
,
we may multiply  and
and  using
using
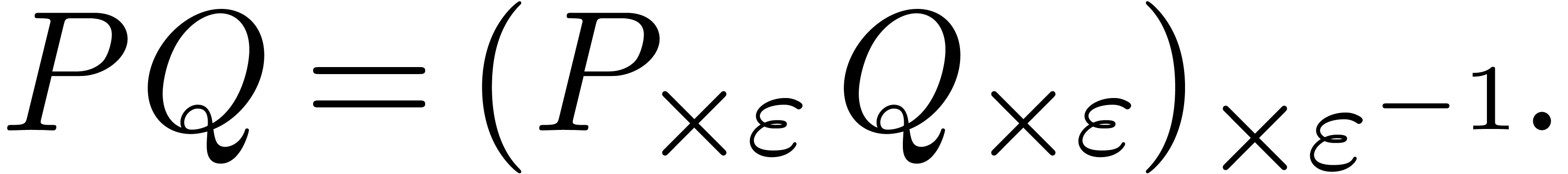
This scaling method is particularly useful in the case when  and
and  are truncations of formal
power series. In section 3, we will briefly explain why and
we refer to [vdH02a, Section 6.2] for a more detailed
analysis.
are truncations of formal
power series. In section 3, we will briefly explain why and
we refer to [vdH02a, Section 6.2] for a more detailed
analysis.
However, fast multiplication with scaling only works in the case when
the coefficients of  have similar orders of
magnitude for a suitable
have similar orders of
magnitude for a suitable  .
Geometrically speaking, this means that the roots of
.
Geometrically speaking, this means that the roots of  all lie in a “not so large” annulus around the circle of
radius
all lie in a “not so large” annulus around the circle of
radius 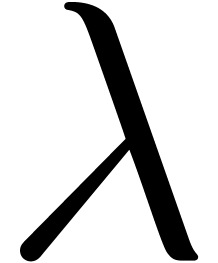 . In practice, this
condition is not always satisfied, which leaves us with the question of
designing a more general multiplication algorithm which is both
asymptotically fast and numerically stable.
. In practice, this
condition is not always satisfied, which leaves us with the question of
designing a more general multiplication algorithm which is both
asymptotically fast and numerically stable.
In its full generality, this problem is ill-posed. For instance, in
cases when cancellation occurs, it is impossible to design an algorithm
which computes all coefficients  with a relative
error bounded by
with a relative
error bounded by 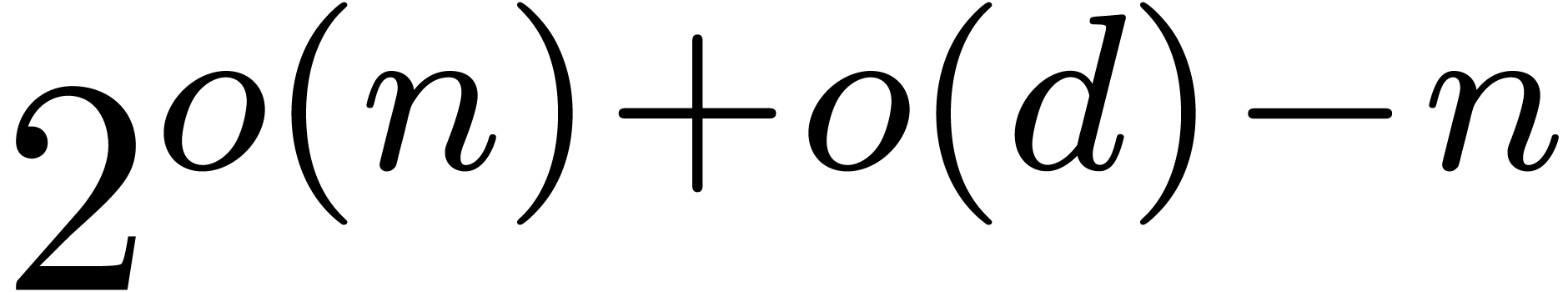 . A simple
example of this situation is the computation of
. A simple
example of this situation is the computation of 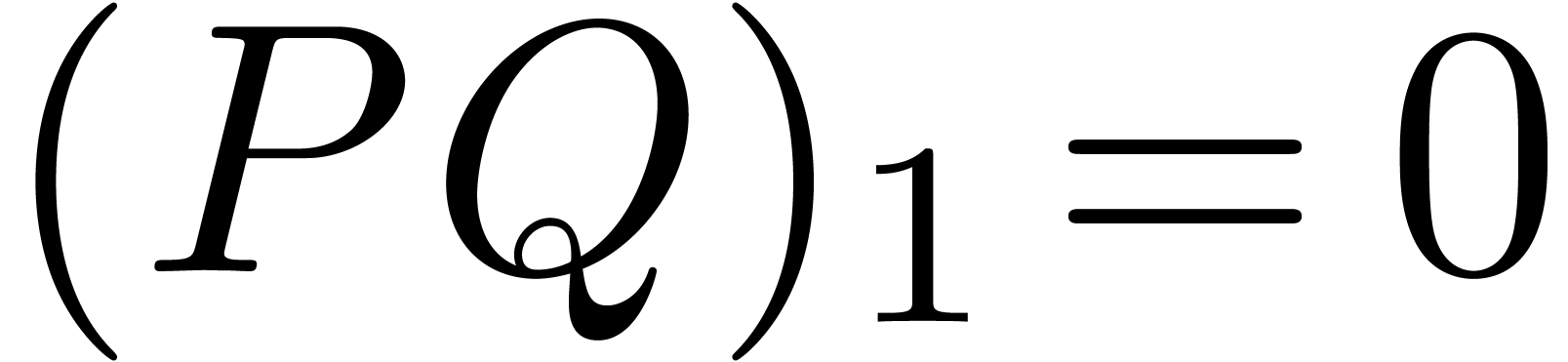 for
for 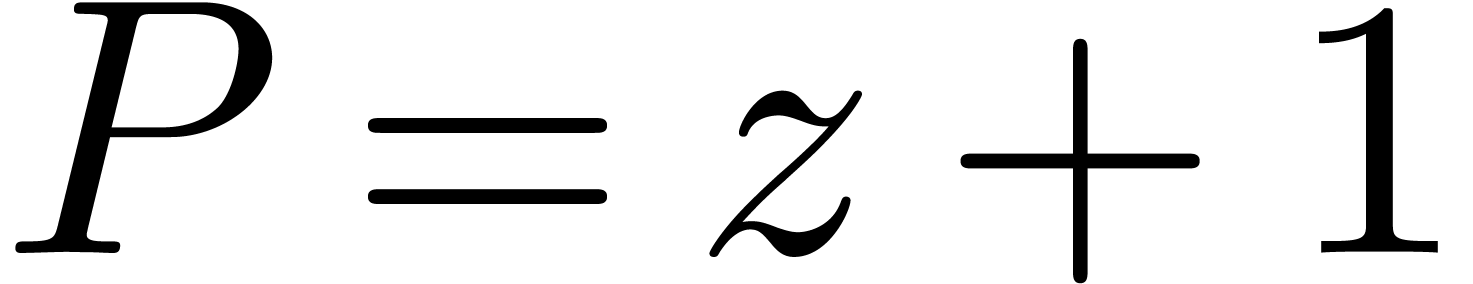 ,
, 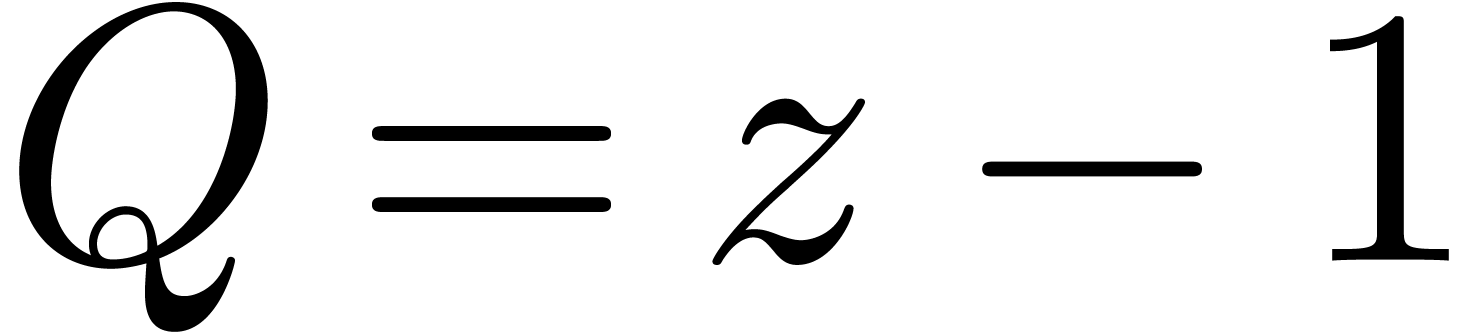 . Nevertheless, such cancellations can only occur
“below” the “numerical Newton polygon” of
. Nevertheless, such cancellations can only occur
“below” the “numerical Newton polygon” of 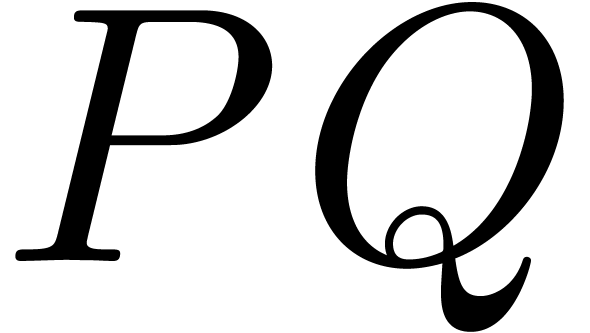 : when using the naive
: when using the naive 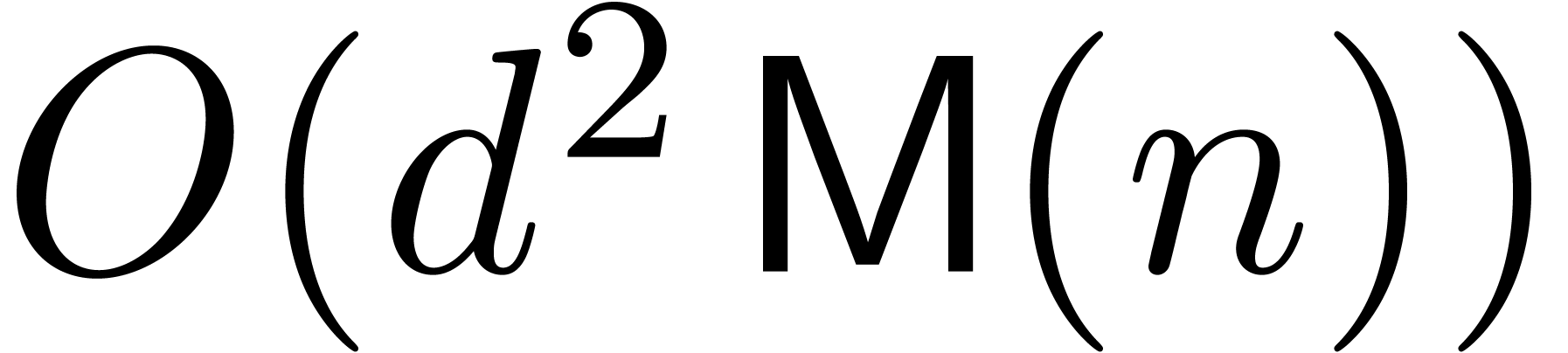 multiplication algorithm, based on the convolution sums
multiplication algorithm, based on the convolution sums
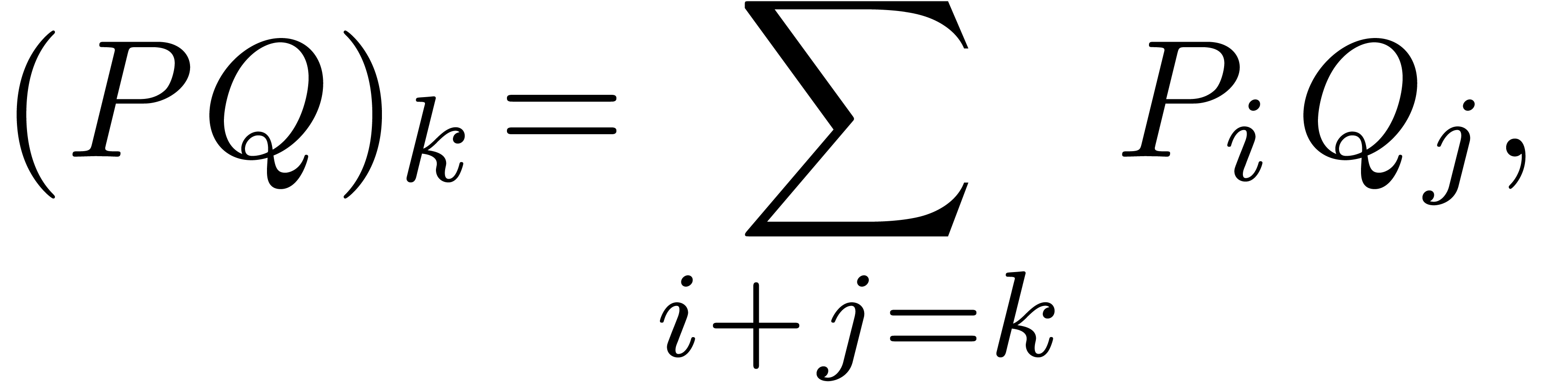
the coefficients  which correspond to vertices of
this Newton polygon are computed accurately, with a relative error
bounded by
which correspond to vertices of
this Newton polygon are computed accurately, with a relative error
bounded by 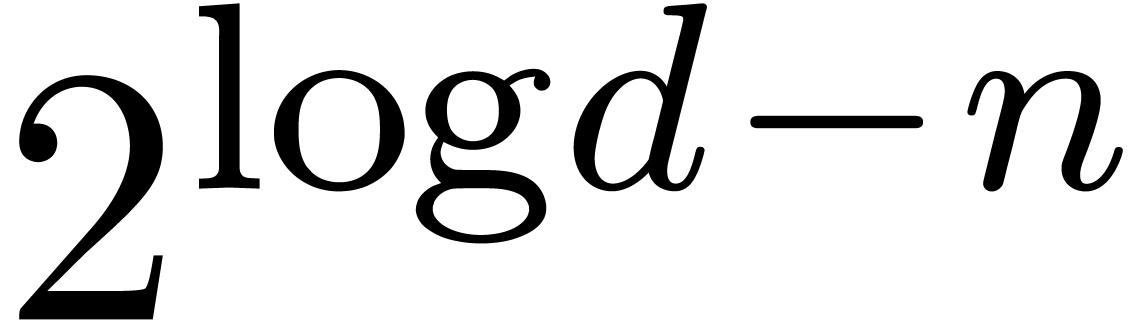 . Numerical Newton
polygons will be defined and discussed in section 4. They
are the natural numeric counterpart of Newton polygons for polynomials
with power series coefficients, based on the analogy between floating
point numbers and (Laurent) series, which goes back to Newton himself.
. Numerical Newton
polygons will be defined and discussed in section 4. They
are the natural numeric counterpart of Newton polygons for polynomials
with power series coefficients, based on the analogy between floating
point numbers and (Laurent) series, which goes back to Newton himself.
A reasonable problem is therefore to compute 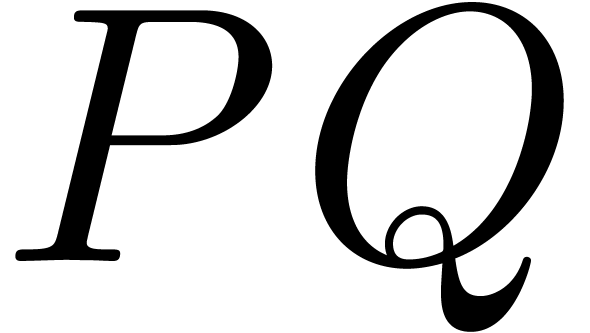 with a similar kind of accuracy as the naive
with a similar kind of accuracy as the naive 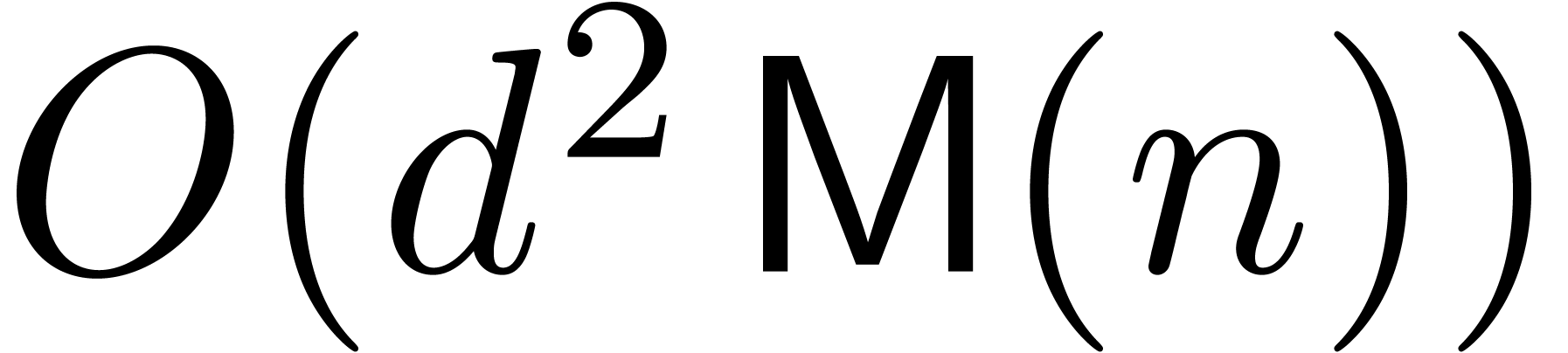 multiplication algorithm does, but faster. This also leads to the
question of formalizing what can be meant by “similar kind of
accuracy”. In section 5, we define the notion of
“relative Newton error”
multiplication algorithm does, but faster. This also leads to the
question of formalizing what can be meant by “similar kind of
accuracy”. In section 5, we define the notion of
“relative Newton error”  for the
computation of
for the
computation of  . We regard
this notion as the natural generalization of the notion of
“relative error”, when numbers are replaced by numerical
polynomials. In section 9, we will state a few interesting
properties of this concept, which provide further evidence for its
usefulness.
. We regard
this notion as the natural generalization of the notion of
“relative error”, when numbers are replaced by numerical
polynomials. In section 9, we will state a few interesting
properties of this concept, which provide further evidence for its
usefulness.
The central part of the paper is devoted to the description of an asymptotically fast multiplication algorithm which has a good numerical stability in terms of the relative Newton error. The main ideas behind the algorithm are the following:
The product 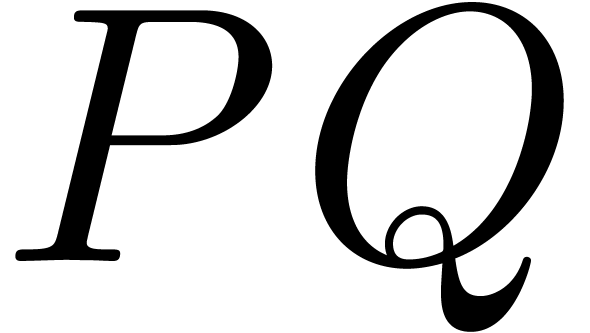 is modeled by a rectangle
is modeled by a rectangle 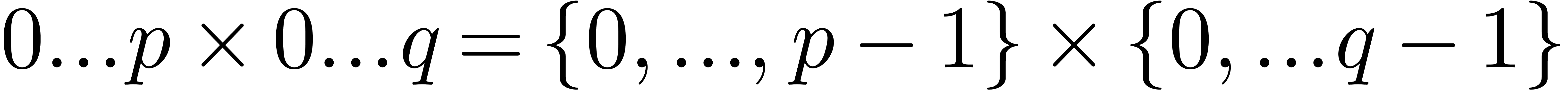 in which each pair
in which each pair 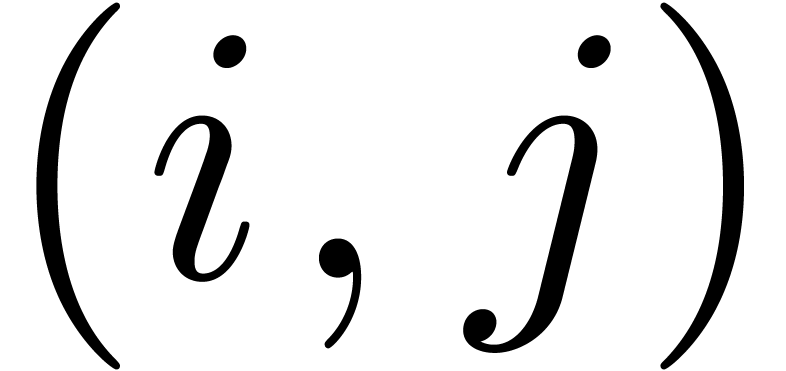 corresponds to the computation of
corresponds to the computation of 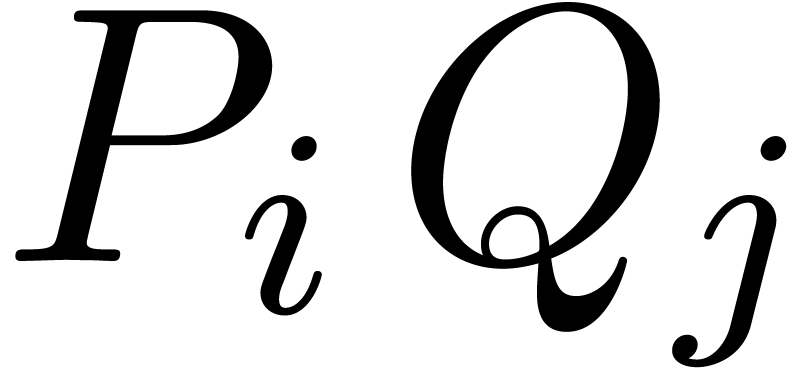 .
.
Only a subregion 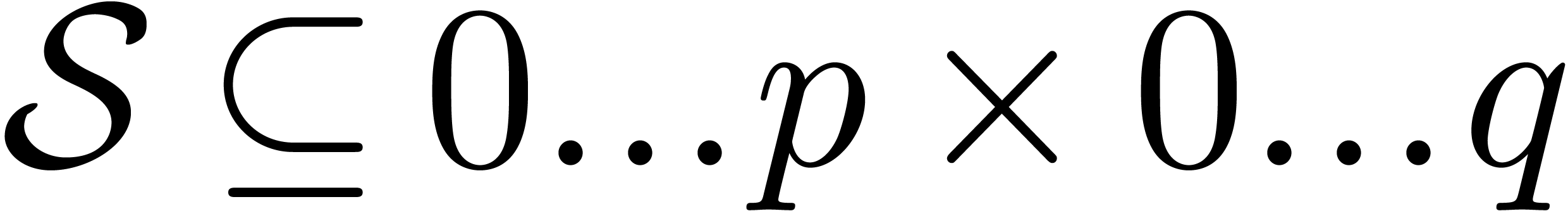 , which
can be determined precisely (section 5), contributes
substantially to the product
, which
can be determined precisely (section 5), contributes
substantially to the product 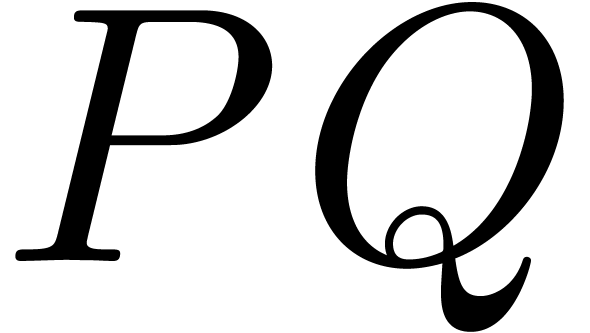 .
The complement can be neglected.
.
The complement can be neglected.
The region  can be covered by a suitable
disjoint union of rectangles
can be covered by a suitable
disjoint union of rectangles  (see sections
6 and 7).
(see sections
6 and 7).
The contribution of each such rectangle  to
to
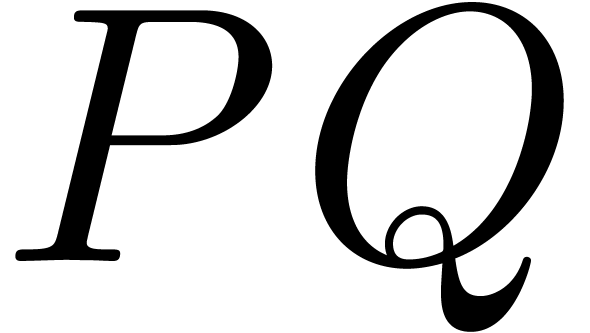 can be computed efficiently using a fast
multiplication algorithm with scaling (section 8).
can be computed efficiently using a fast
multiplication algorithm with scaling (section 8).
The main result of the paper is the following:
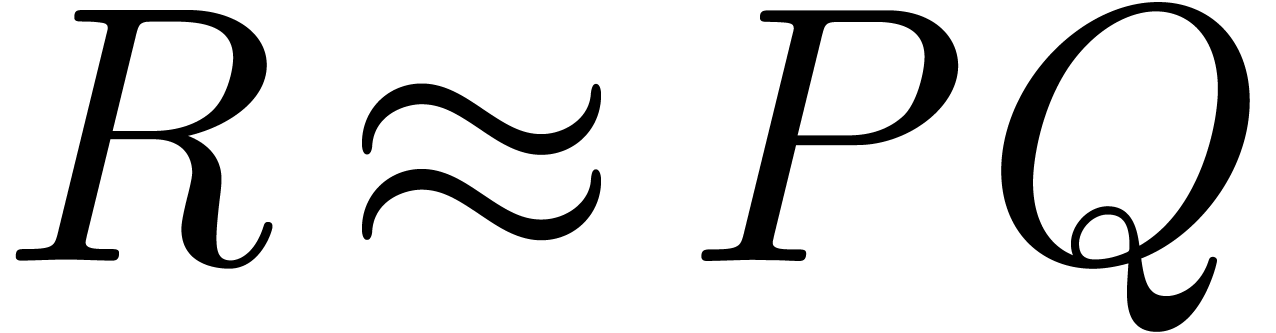 with relative Newton error
with relative Newton error 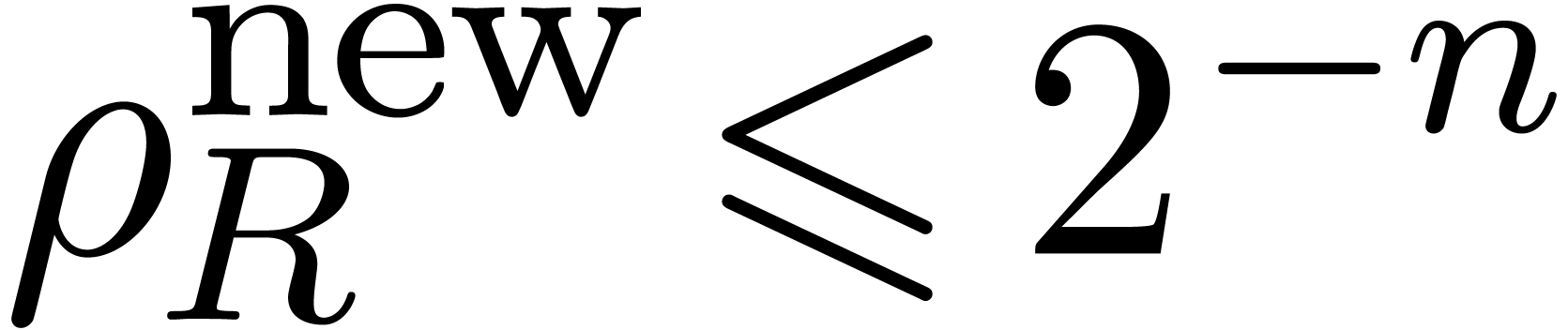 in time
in time 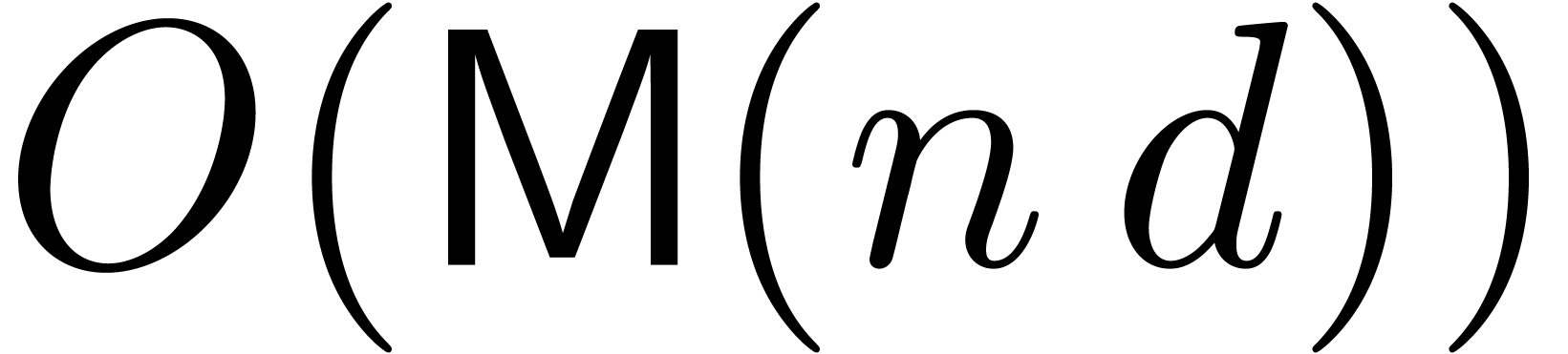 ,
provided that
,
provided that 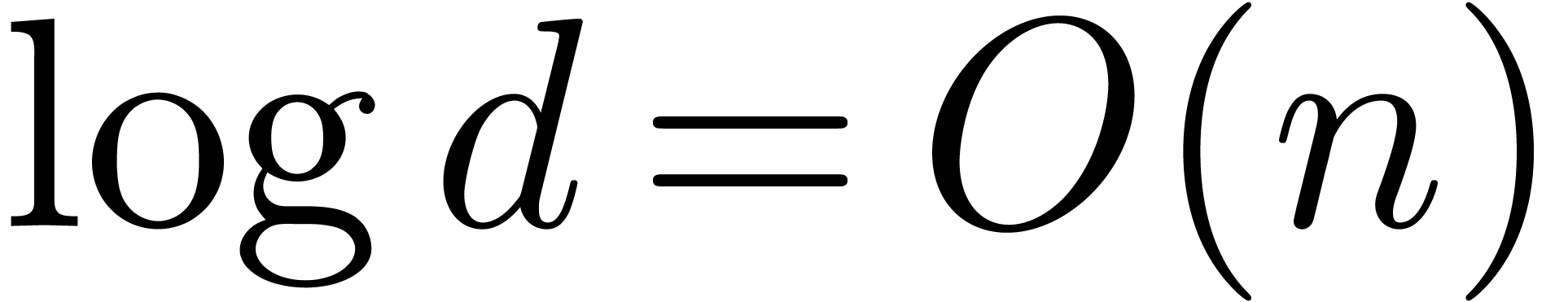 .
.
Let us describe in more detail the second classical multiplication
algorithm mentioned in the introduction, when the coefficients of  are of the same order of magnitude, and similarly for
are of the same order of magnitude, and similarly for
 . We start with the
determination of the maximum exponents
. We start with the
determination of the maximum exponents
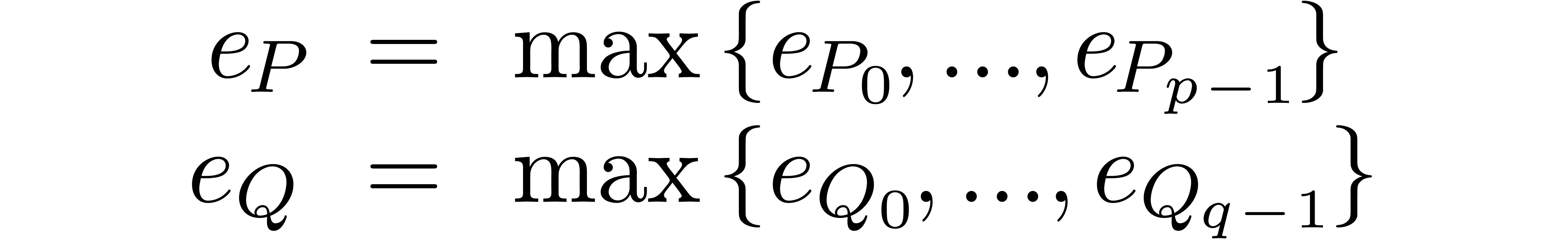
and the approximation of 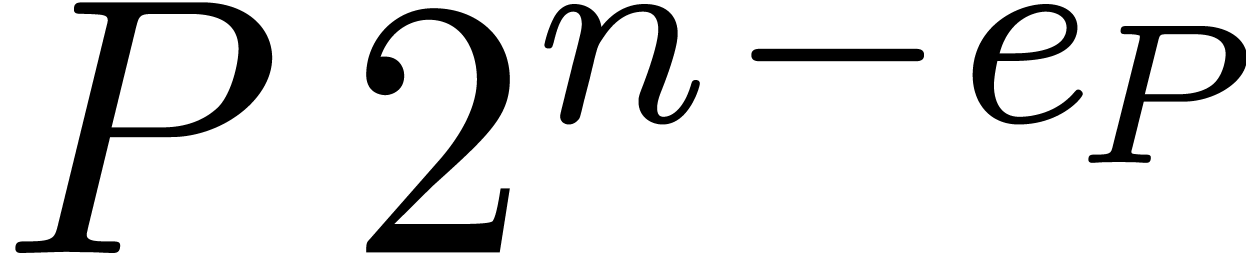 and
and 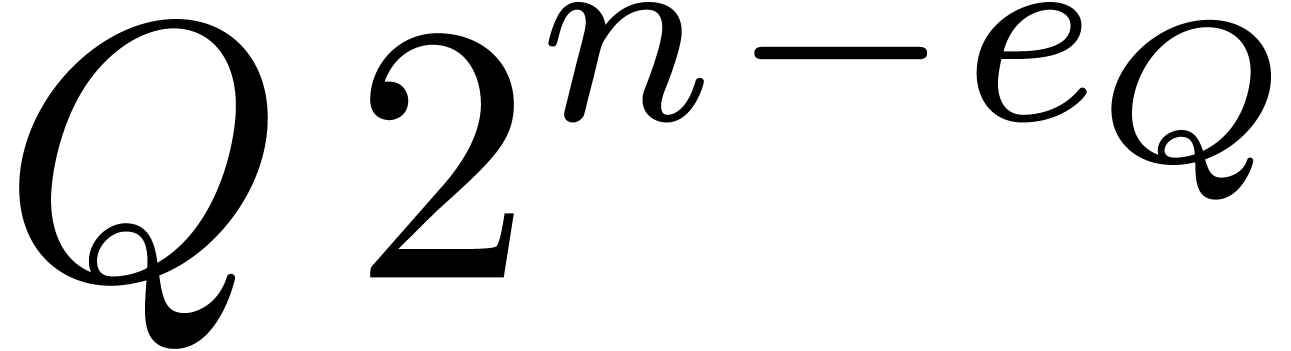 by integer polynomials
by integer polynomials  and
and  whose coefficients have bit-sizes bounded by
whose coefficients have bit-sizes bounded by  . At the second step, we use Kronecker's method for
the multiplication of
. At the second step, we use Kronecker's method for
the multiplication of 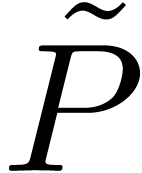 and
and  . Taking
. Taking 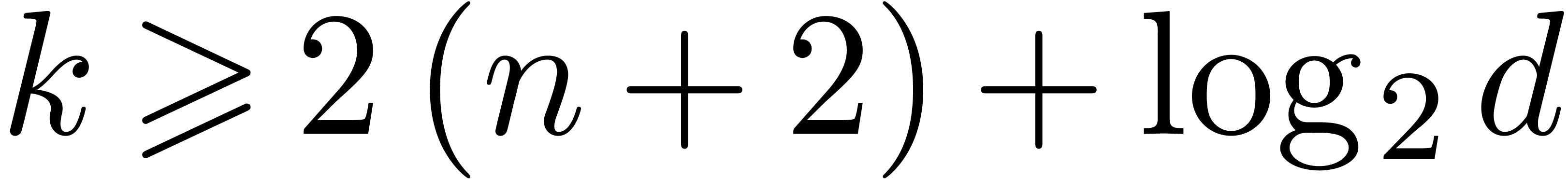 ,
the product
,
the product  can be reconstructed [Kro82,
Sch82] from the product of the integers
can be reconstructed [Kro82,
Sch82] from the product of the integers 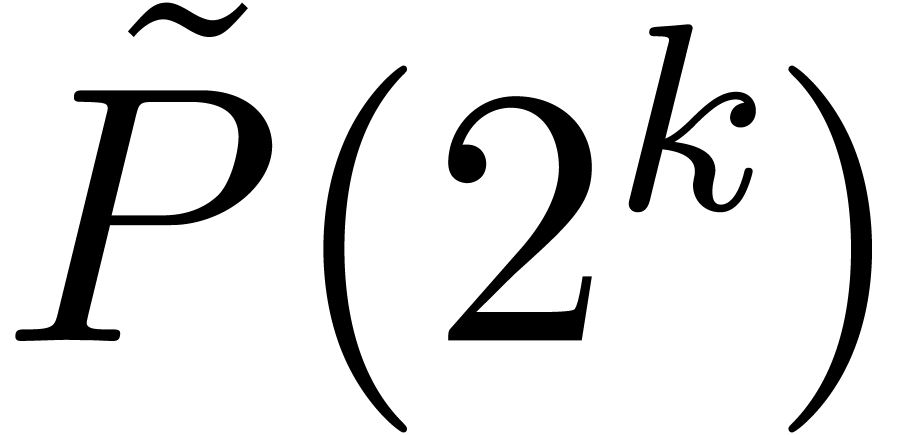 and
and 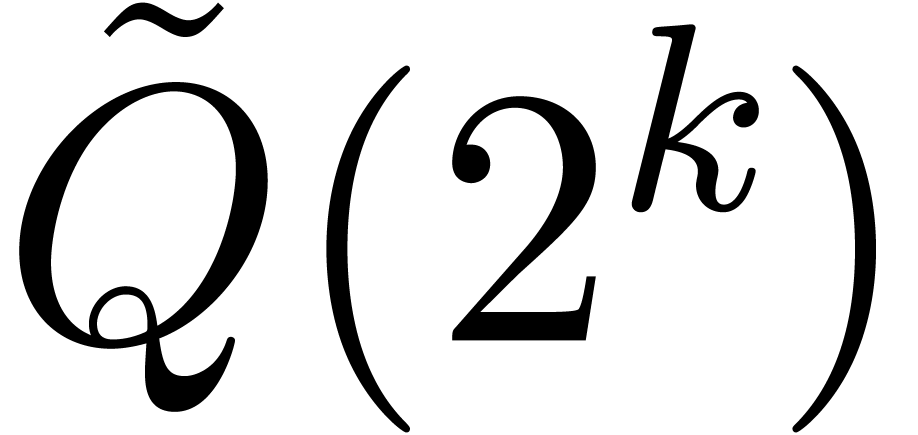 . Assuming that
. Assuming that 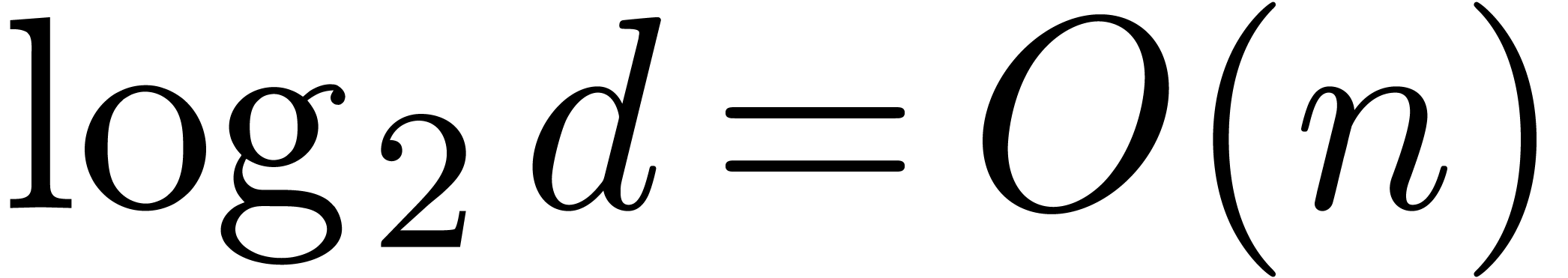 , these integers have sizes
, these integers have sizes 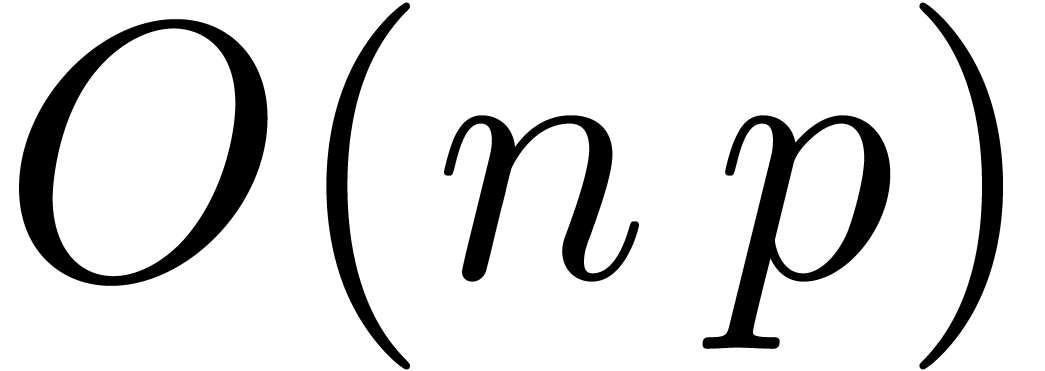 and
and 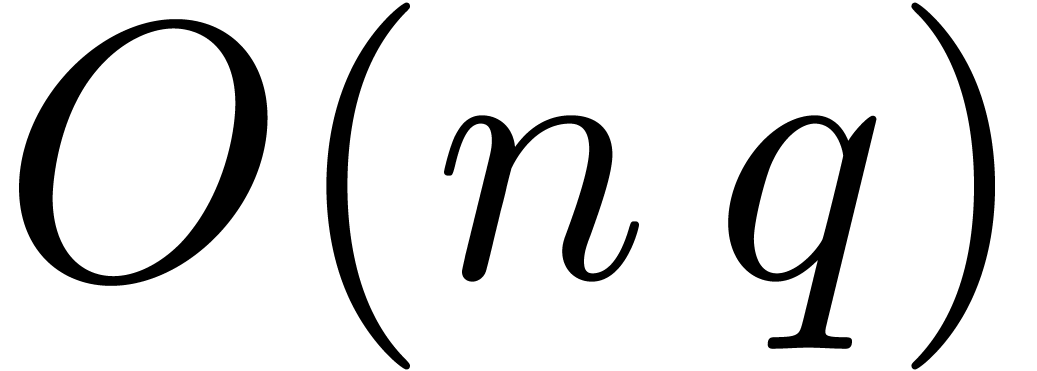 ,
whence can be multiplied in time
,
whence can be multiplied in time 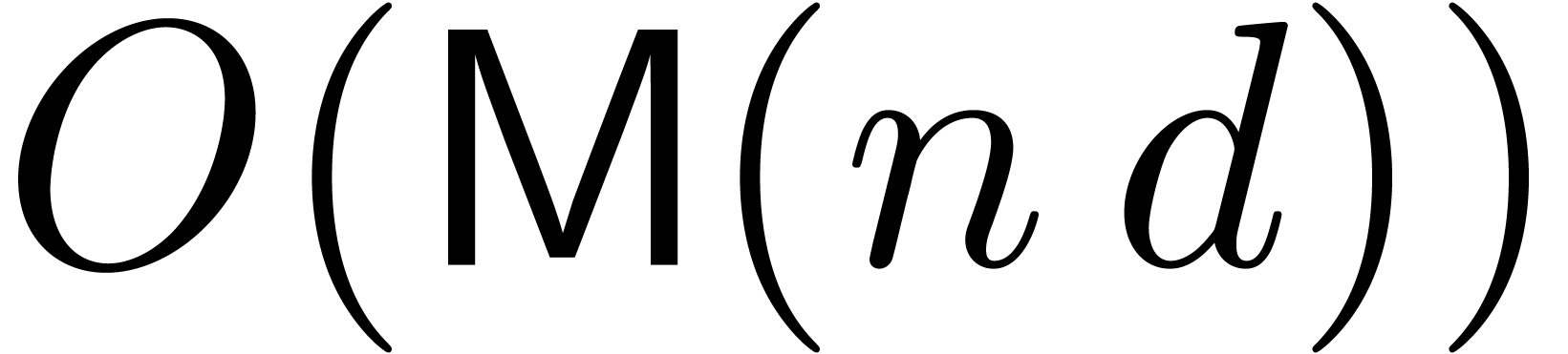 .
We finally obtain an approximation
.
We finally obtain an approximation 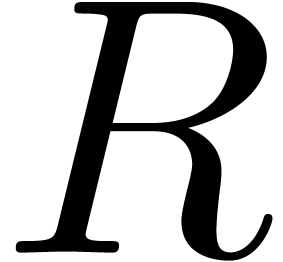 of the
product
of the
product 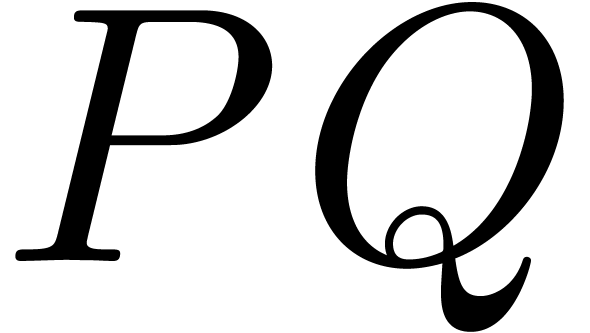 by fitting the coefficients of
by fitting the coefficients of 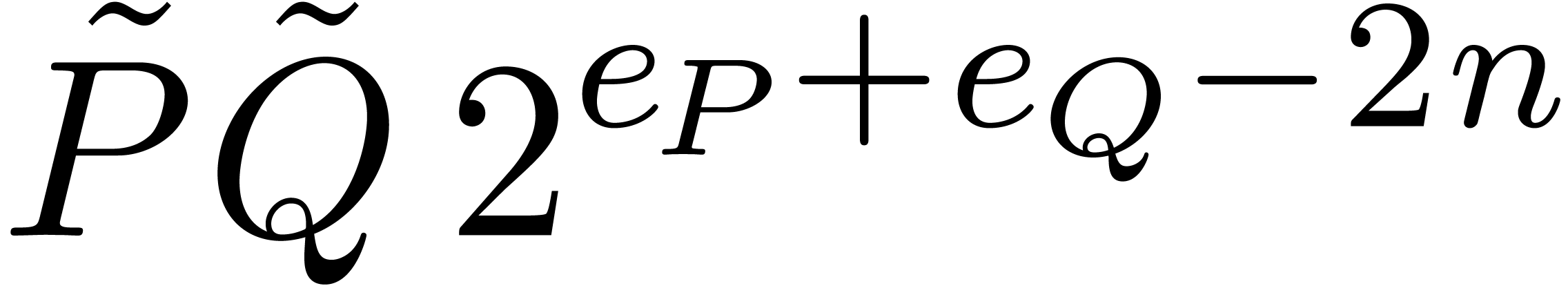 into the nearest available floating point numbers in
into the nearest available floating point numbers in 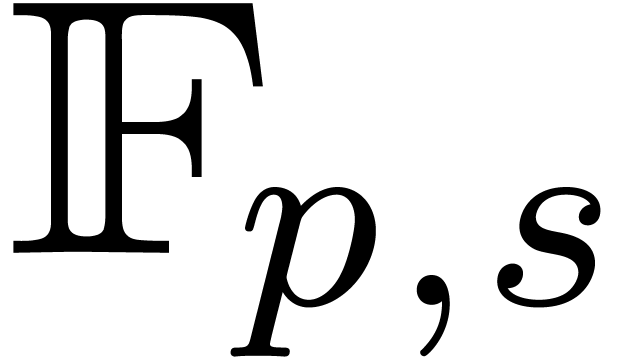 .
.
Let us now analyze the errors induced by the above scheme, where we
recall our assumption that no overflows or underflows occur during our
computations. When computing 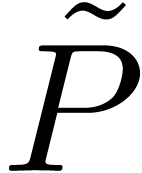 and
and  by rounding to the nearest, we obtain the uniform absolute
error bounds
by rounding to the nearest, we obtain the uniform absolute
error bounds
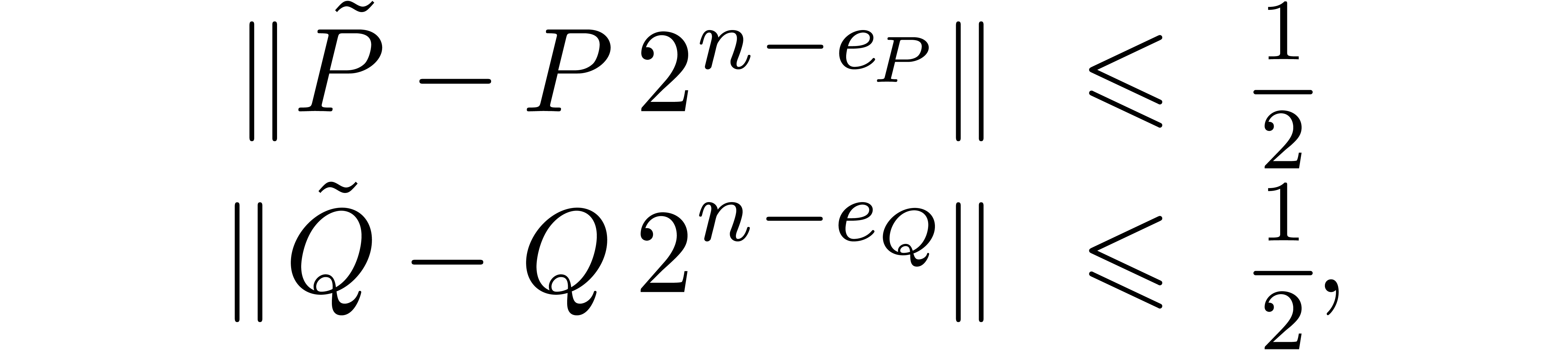
where
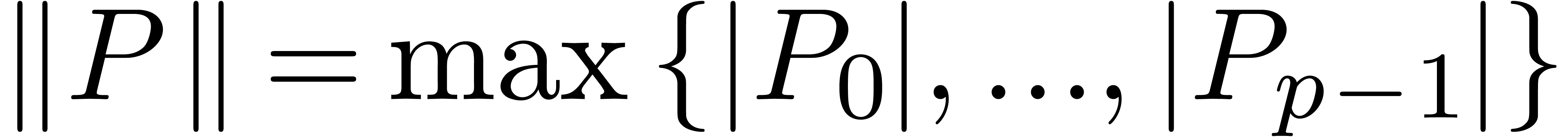
denotes the sup-norm of  if we consider
if we consider  as a vector of coefficients. Consequently,
as a vector of coefficients. Consequently,
On the other hand, we also have the bounds
The second bound follows by considering the FFT transforms of  ,
,  and
and 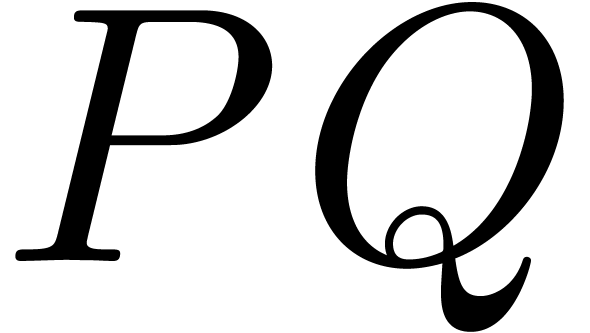 with respect to a
with respect to a 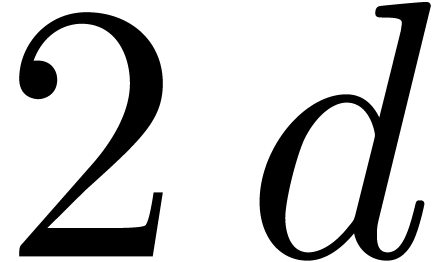 -th
root of unity
-th
root of unity  . Indeed, the
sup-norms of these transforms satisfy
. Indeed, the
sup-norms of these transforms satisfy
whence

When 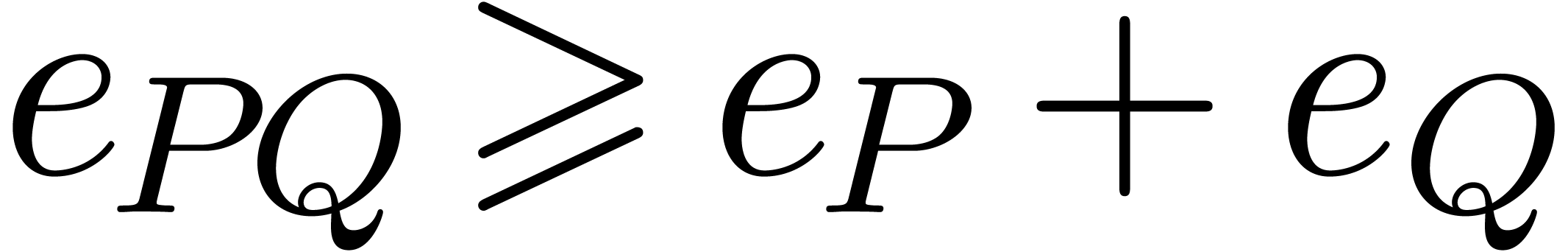 , the combination of (1) and (2) yields the (rough) bound
, the combination of (1) and (2) yields the (rough) bound
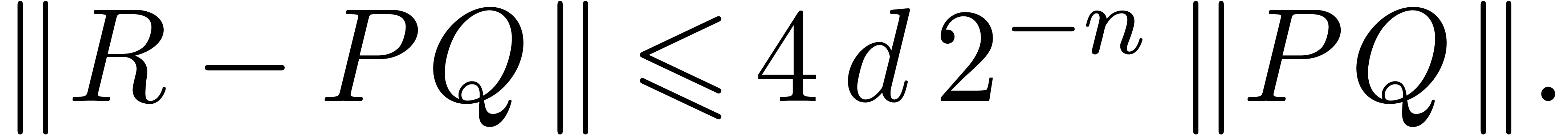
In the case when 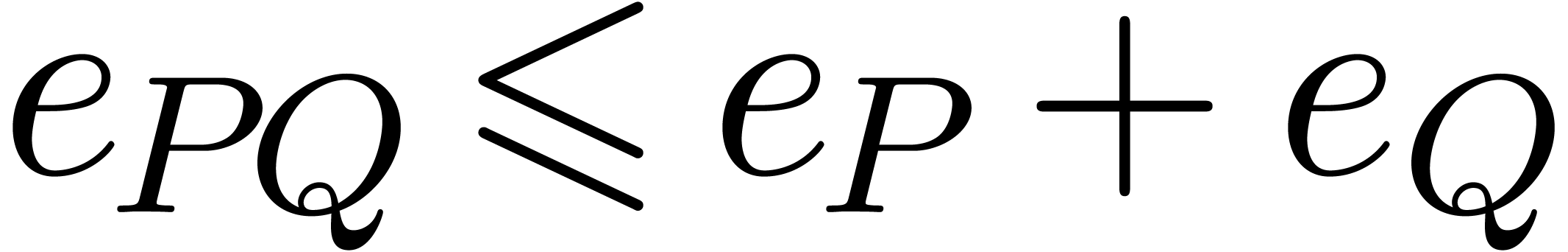 , the
combination of (1) and (3) leads to the same
bound. In all cases, we thus obtain a uniform relative error
bound
, the
combination of (1) and (3) leads to the same
bound. In all cases, we thus obtain a uniform relative error
bound
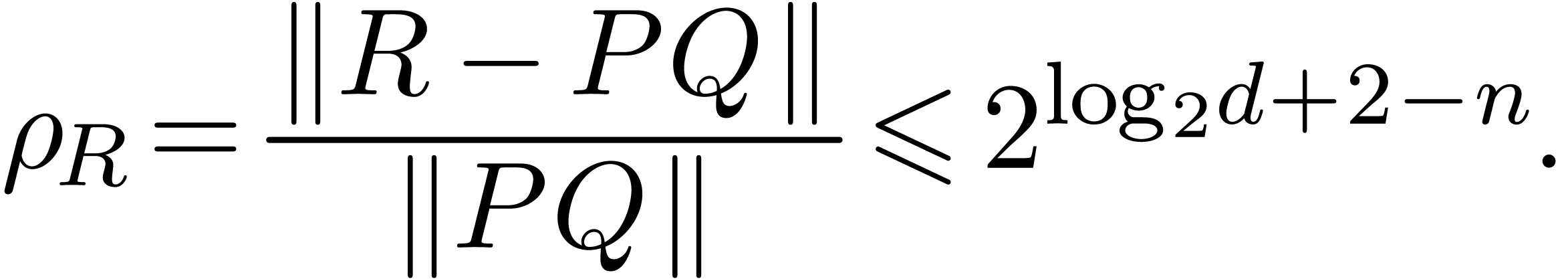 |
(4) |
Remark  , and
rely on FFT multiplication of these polynomials. At the price of
improving
, and
rely on FFT multiplication of these polynomials. At the price of
improving  and
and  . In general, this yields only a
constant speed-up, but in the somewhat exotic case when
. In general, this yields only a
constant speed-up, but in the somewhat exotic case when 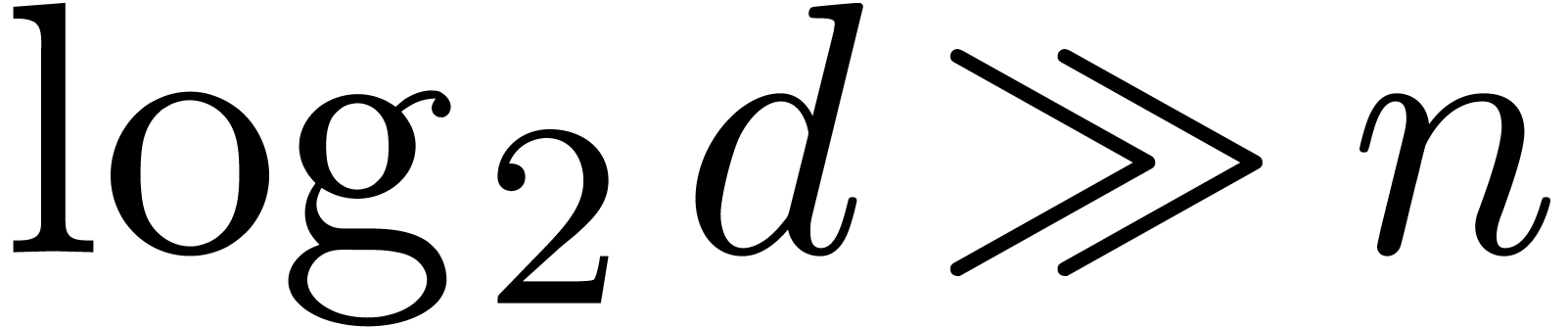 , this method still admits a complexity
, this method still admits a complexity 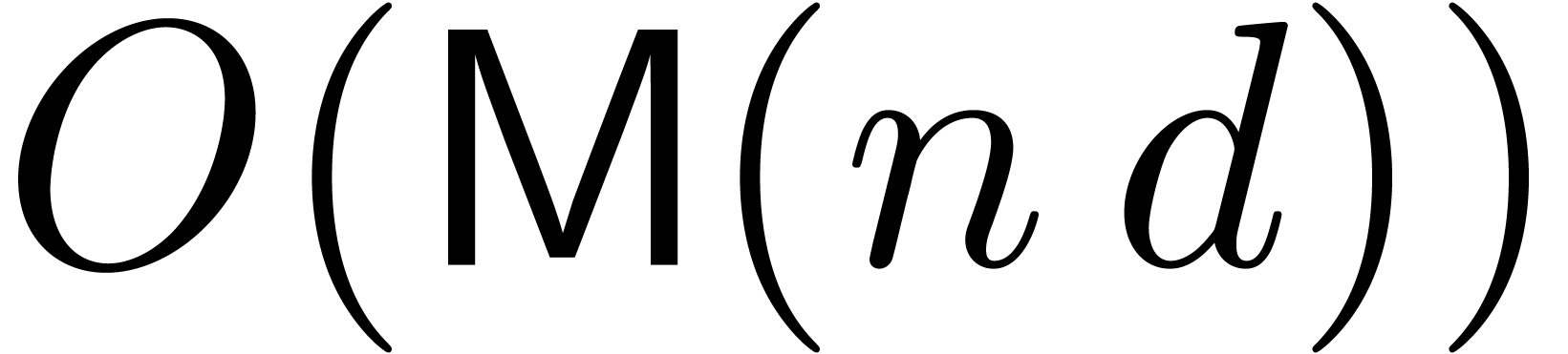 instead of
instead of 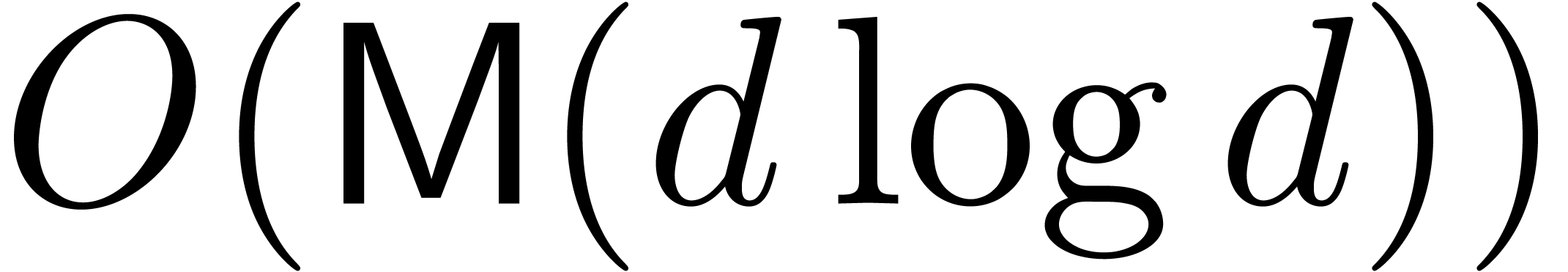 .
.
In the case when the polynomials  and
and  are truncations of formal power series
are truncations of formal power series 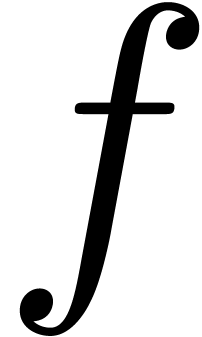 and
and  , the asymptotic
behaviour of the coefficients is usually of the form
, the asymptotic
behaviour of the coefficients is usually of the form
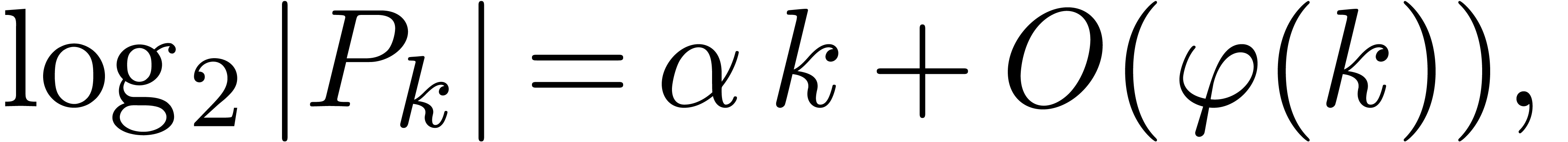 |
(5) |
for some suitable slowly increasing function 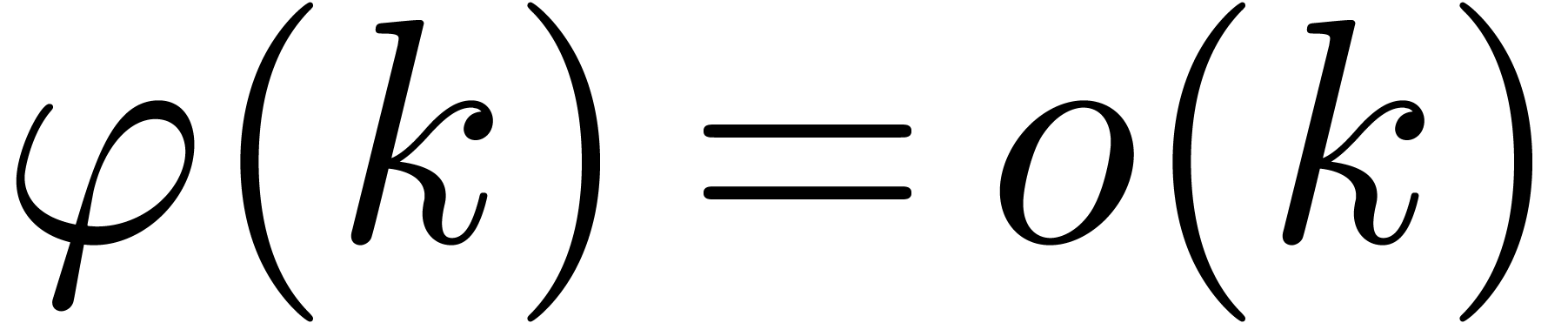 . It is natural to rescale
. It is natural to rescale  by considering the polynomial
by considering the polynomial 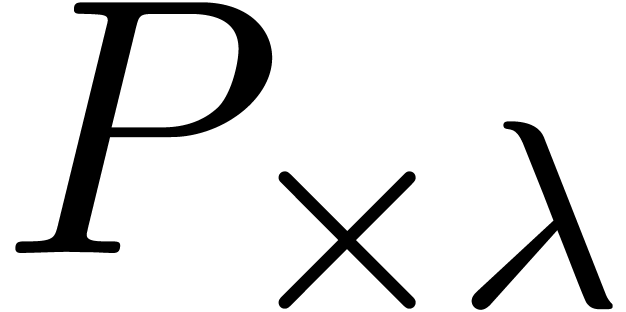
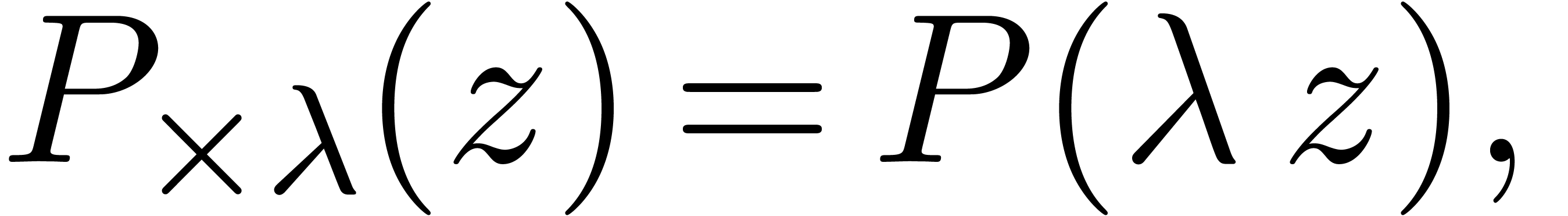
with 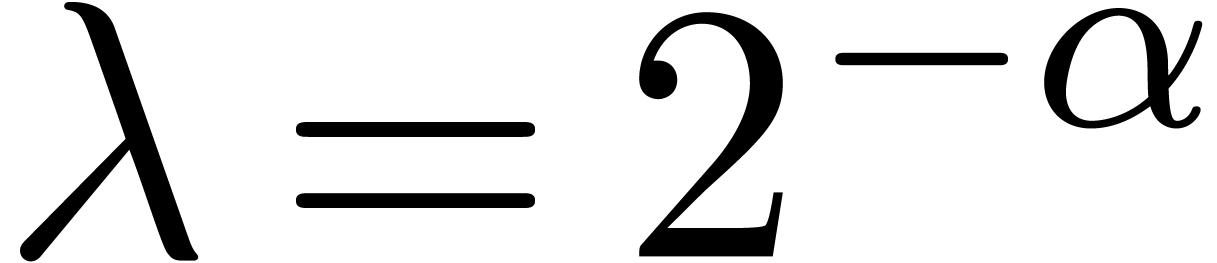 , since its coefficients
, since its coefficients
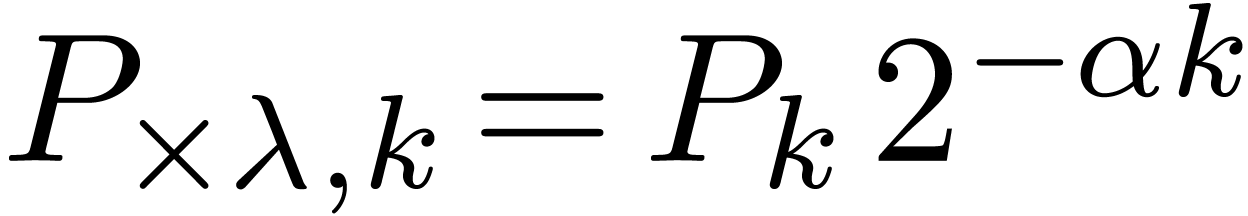 are comparable in magnitude:
are comparable in magnitude:
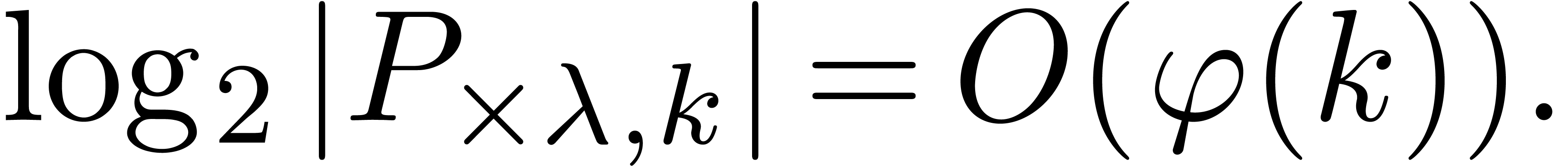
If  has a similar asymptotic behaviour
has a similar asymptotic behaviour
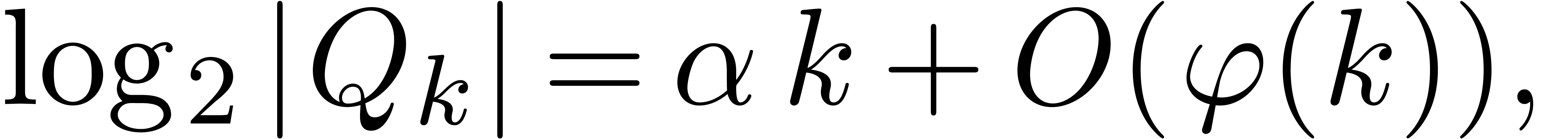 |
(6) |
we may then compute 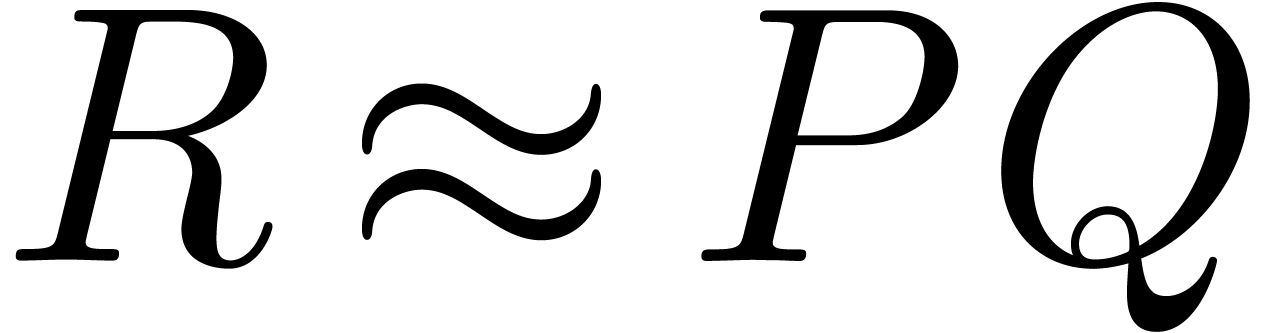 using the formula
using the formula
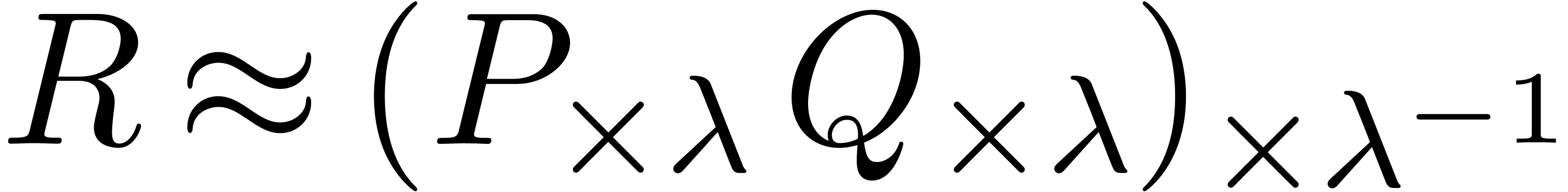
and the algorithm from the previous section for the multiplication of
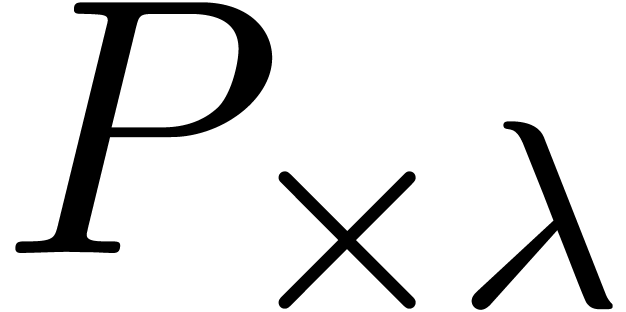 and
and 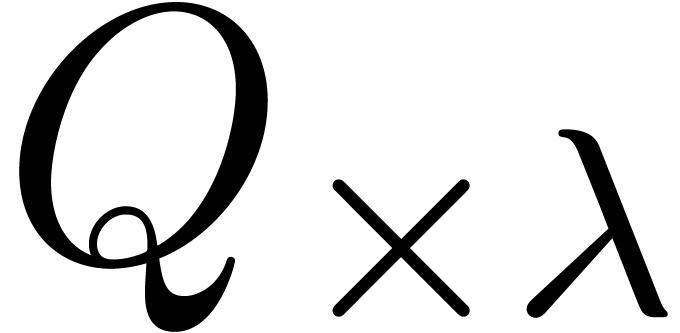 .
.
Now assume that we also have an asymptotic formula
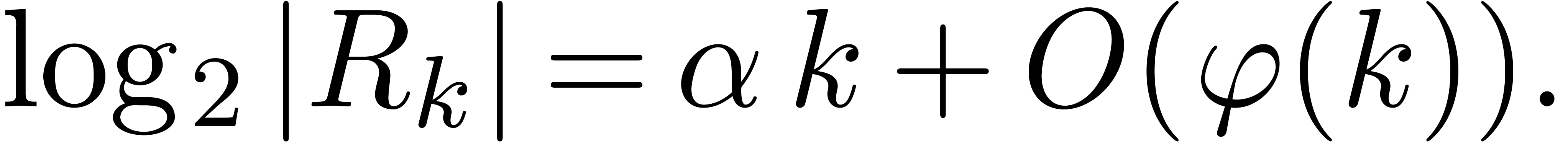
Then it can be shown that the relative error of each individual
coefficient 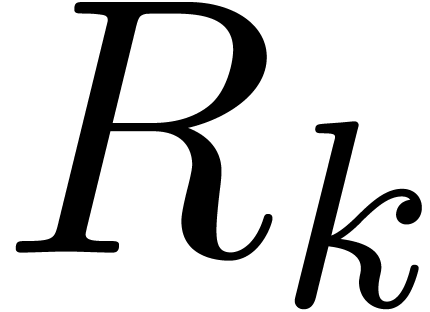 is bounded by
is bounded by
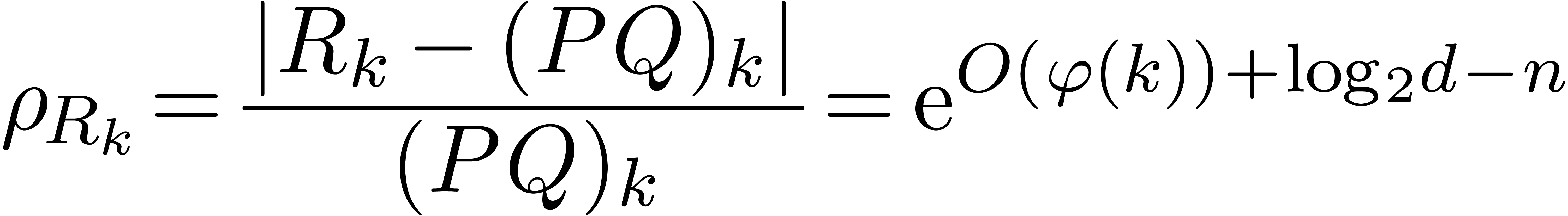 |
(7) |
for all sufficiently large 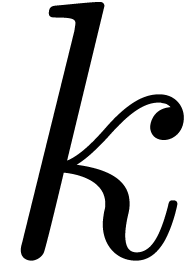 .
In other words, the multiplication method with scaling amounts to a loss
of
.
In other words, the multiplication method with scaling amounts to a loss
of 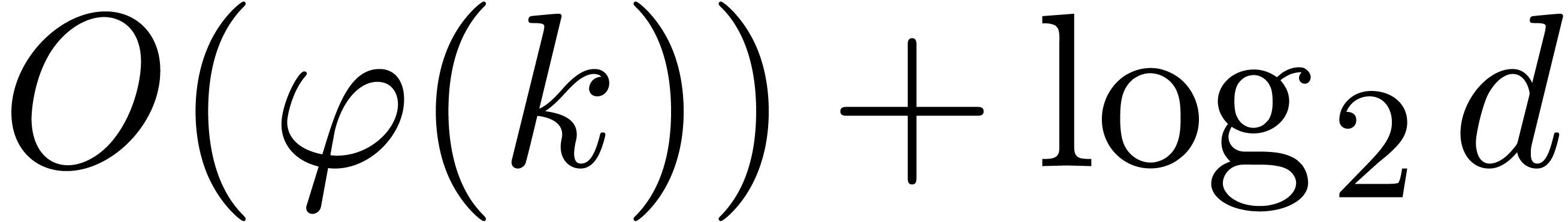 bits of precision. Under the assumption that
bits of precision. Under the assumption that
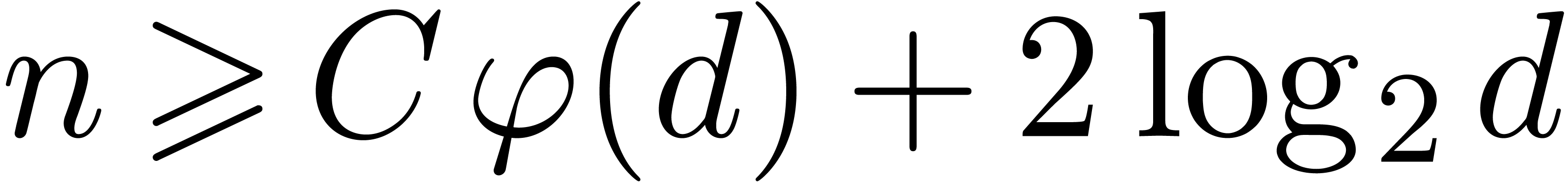 for a sufficiently large constant
for a sufficiently large constant  , we are thus left with at least
, we are thus left with at least 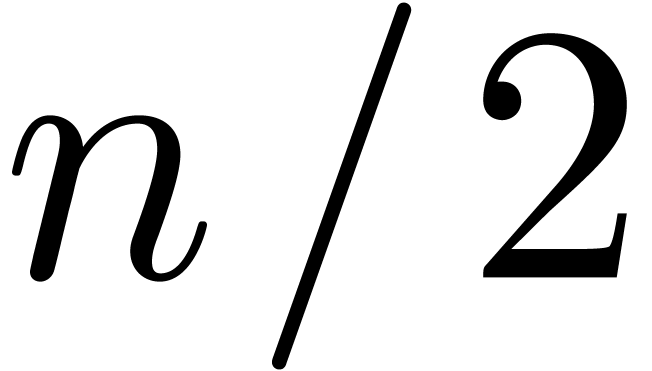 correct leading bits in the mantissa of each coefficient.
The asymptotic behaviour of
correct leading bits in the mantissa of each coefficient.
The asymptotic behaviour of 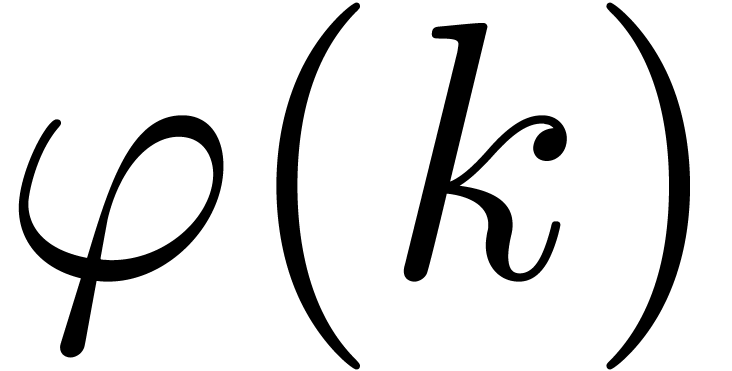 is closely related
to the dominant singularities of
is closely related
to the dominant singularities of 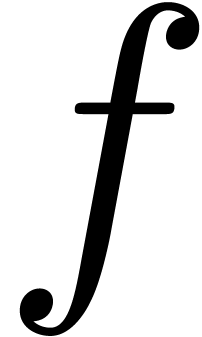 and
and  and for many interesting applications in combinatorics or
physics, one has
and for many interesting applications in combinatorics or
physics, one has 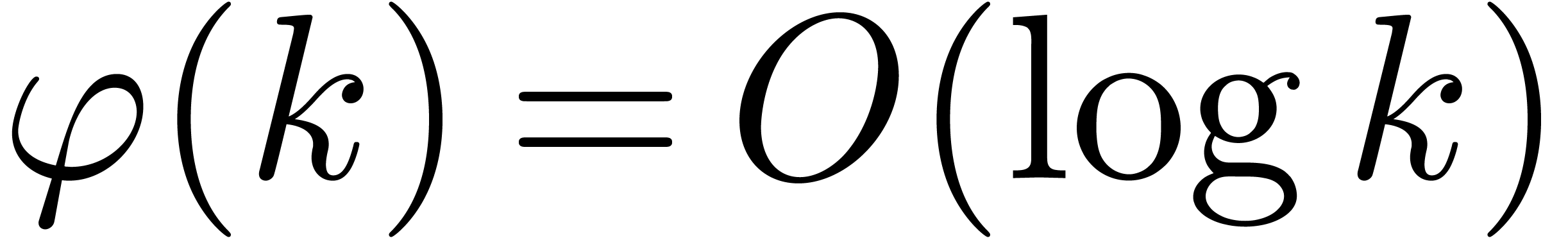 . For more
details, and the application of this technique to the relaxed
computation of formal power series, we refer to [vdH02a,
Section 6.2].
. For more
details, and the application of this technique to the relaxed
computation of formal power series, we refer to [vdH02a,
Section 6.2].
It sometimes happens that only “limsup versions”
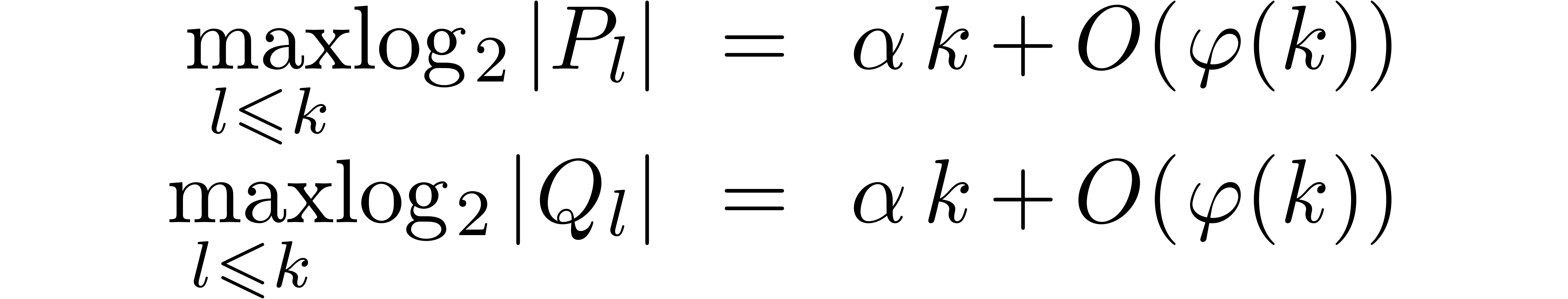
of (5) and (6) are verified. In that case, the individual relative error estimates (7) cease to hold, but we still have the scaled uniform bound
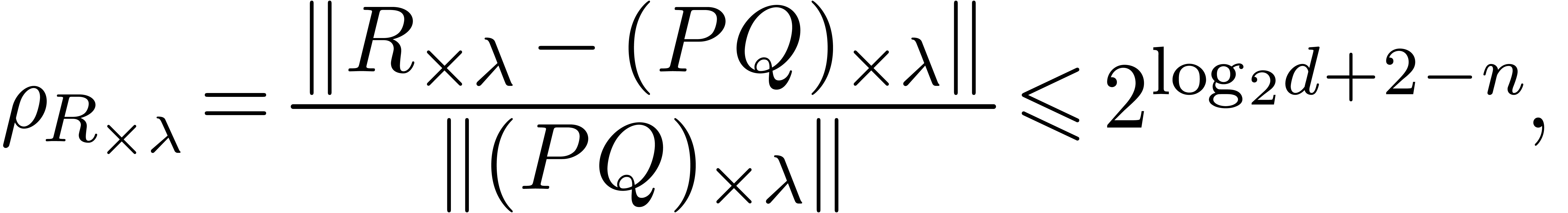 |
(8) |
which is a direct consequence of the corresponding bound (4) in the previous section.
It also frequently occurs that  does not have the
same radius of convergence as
does not have the
same radius of convergence as 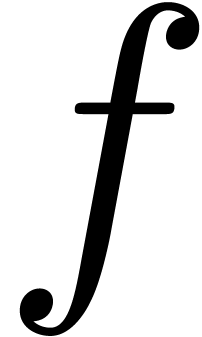 ,
in which case we rather have an asymptotic form
,
in which case we rather have an asymptotic form
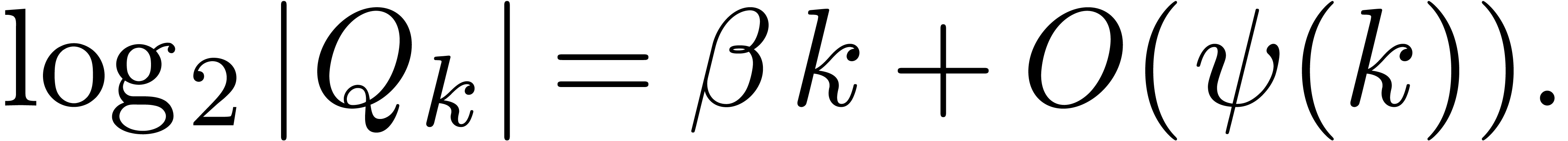
Without loss of generality, we may assume that  . When considering the convolution product
. When considering the convolution product
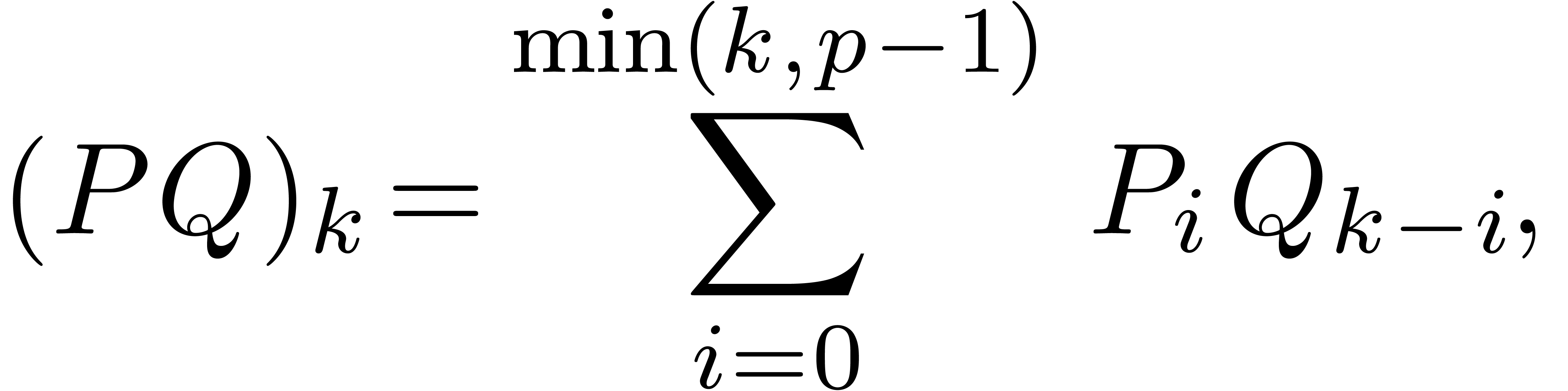 |
(9) |
we observe that the summands 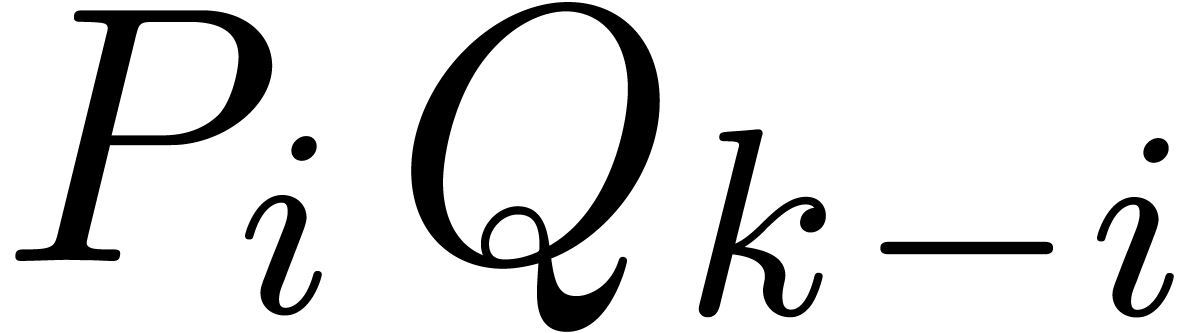 approximately form
a geometric progression. In first approximation, only the last
approximately form
a geometric progression. In first approximation, only the last 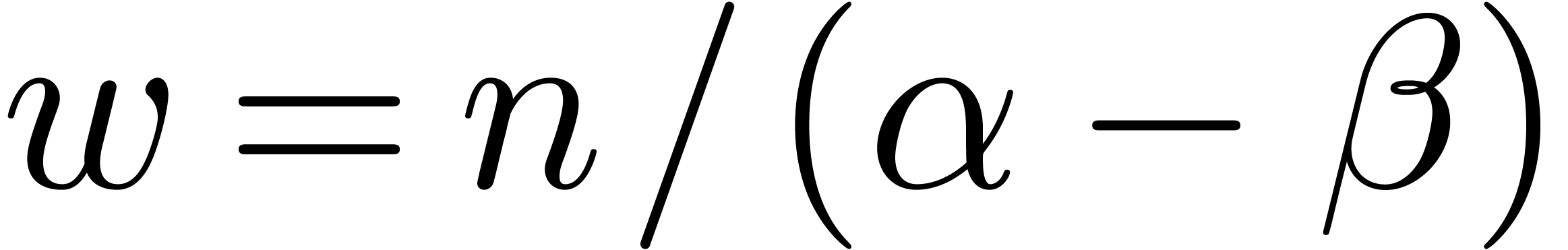 terms therefore contribute to the leading
terms therefore contribute to the leading 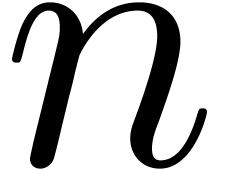 bits of the result (see figure 1). The computation of
bits of the result (see figure 1). The computation of 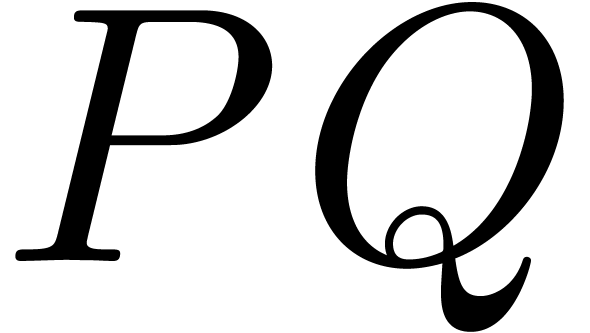 can thus be reduced to the computation of the
products
can thus be reduced to the computation of the
products
using the notation
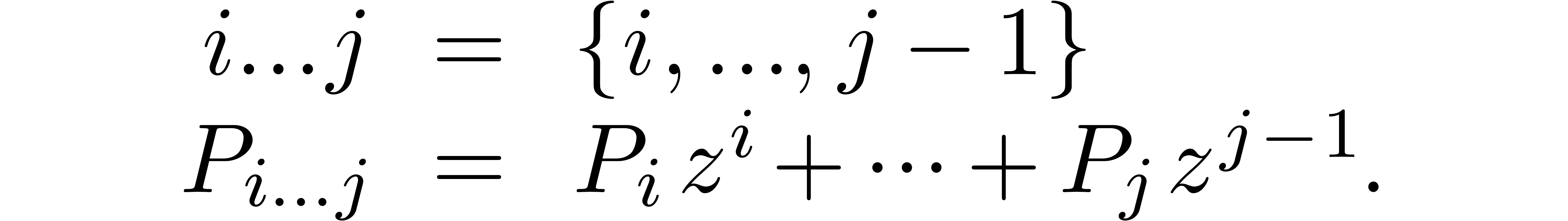
When computing each of these products using the scaling 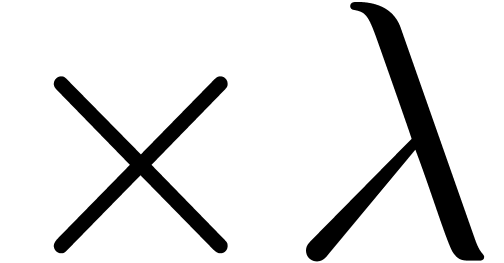 and a doubled precision
and a doubled precision 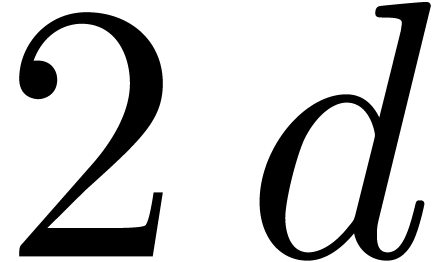 , the
individual coefficients
, the
individual coefficients 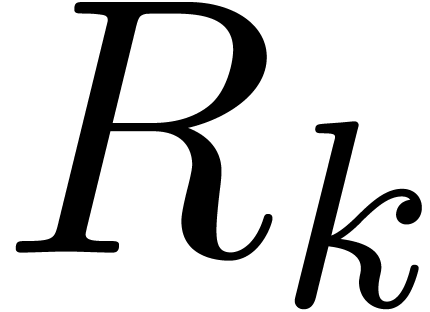 of
of 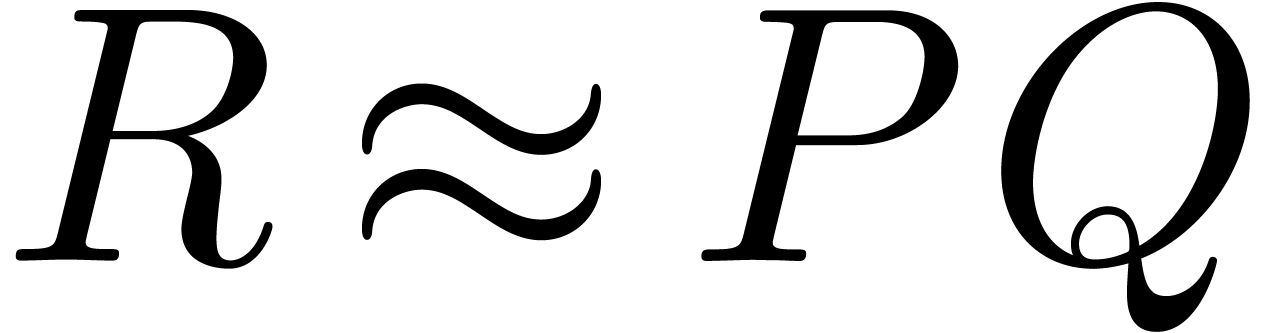 are again obtained with a relative precision of the form
are again obtained with a relative precision of the form 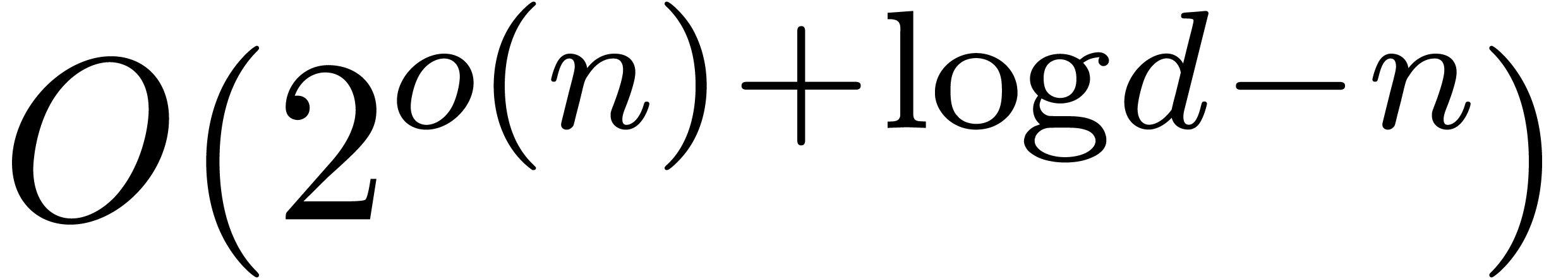 . The total cost of this algorithm is
. The total cost of this algorithm is 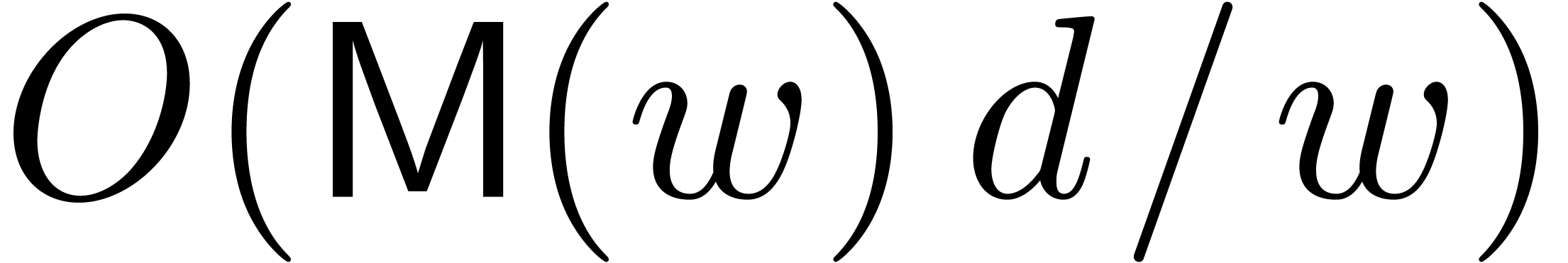 , which reduces to
, which reduces to 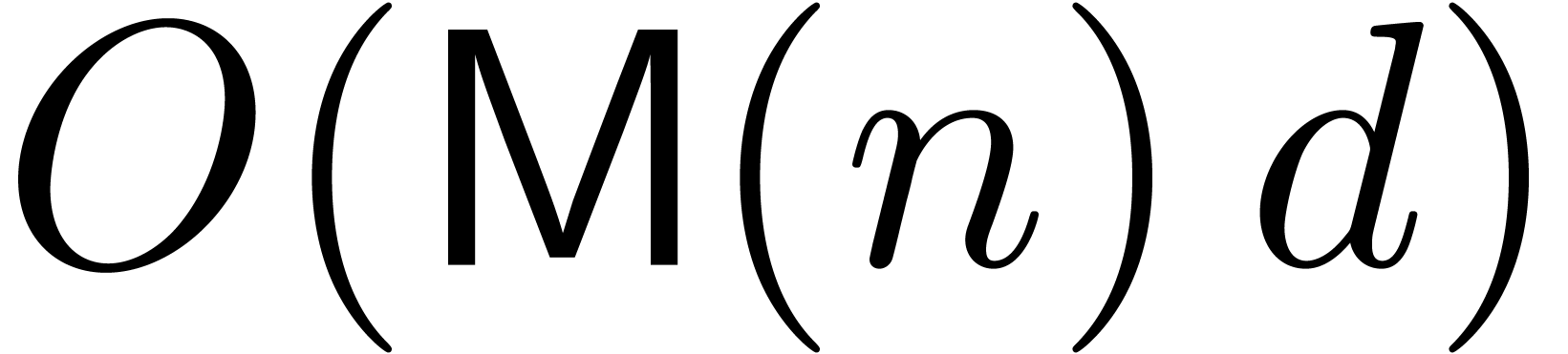 for large
for large 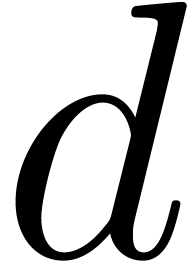 and fixed
and fixed 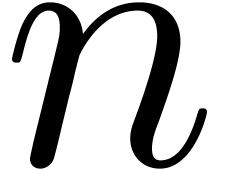 . A generalization of this idea will be analyzed in
more detail in section 7.
. A generalization of this idea will be analyzed in
more detail in section 7.
 |
Roughly speaking, the algorithms from sections 2 and 3 are numerically stable when the roots of  and
and  lie in an annulus around the unit circle
resp. the circle of radius
lie in an annulus around the unit circle
resp. the circle of radius 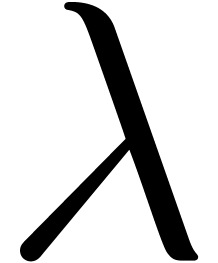 .
When this is no longer the case, one may still try to apply the
algorithm from section 3 for partial products
.
When this is no longer the case, one may still try to apply the
algorithm from section 3 for partial products 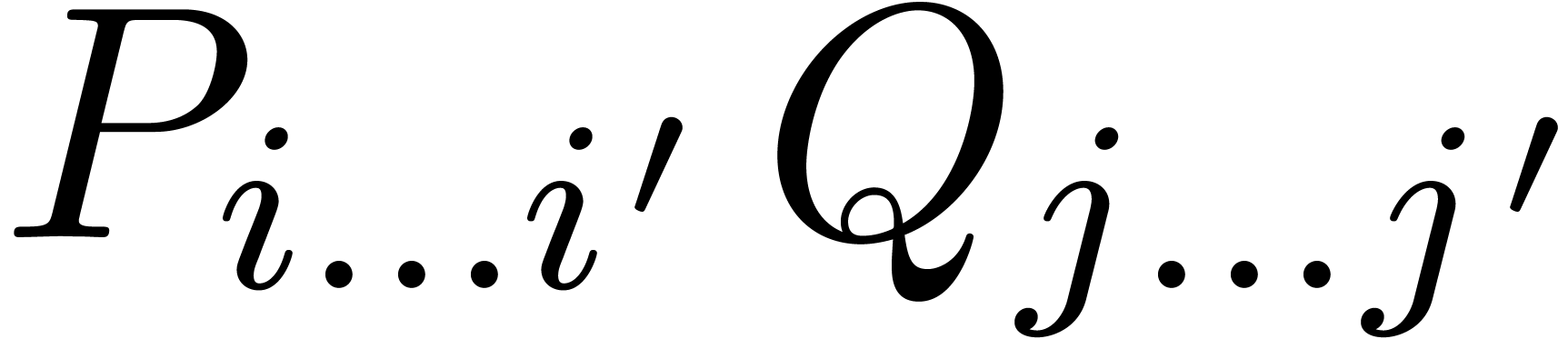 , using scales
, using scales 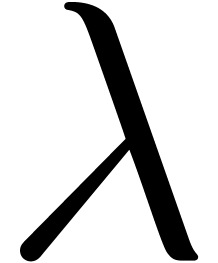 which
vary as a function of
which
vary as a function of  and
and  .
.
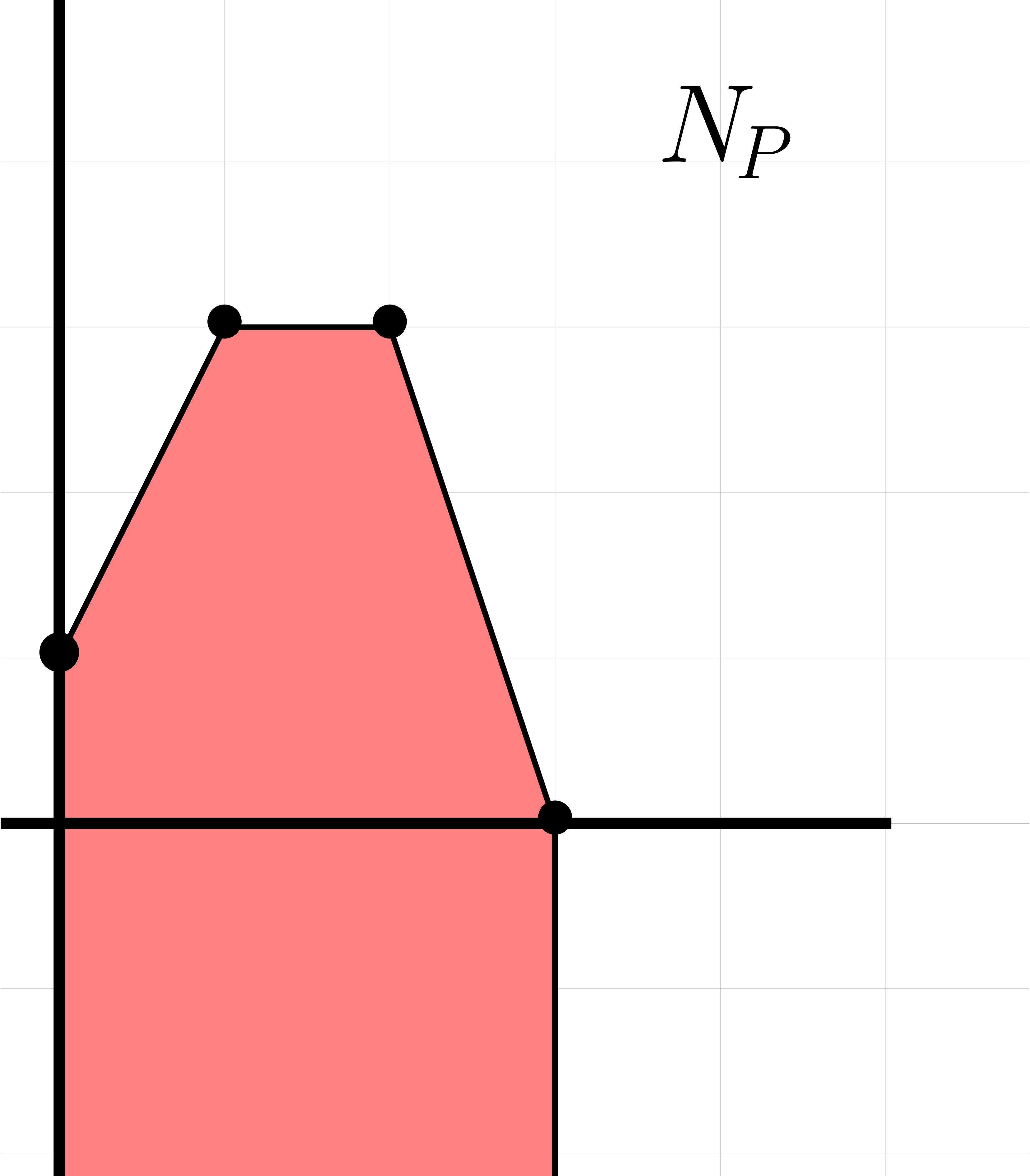
A central concept for doing this is the numeric Newton polygon
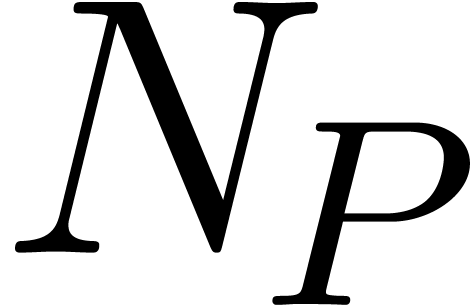 of
of  ,
which is the convex hull of the half-lines
,
which is the convex hull of the half-lines 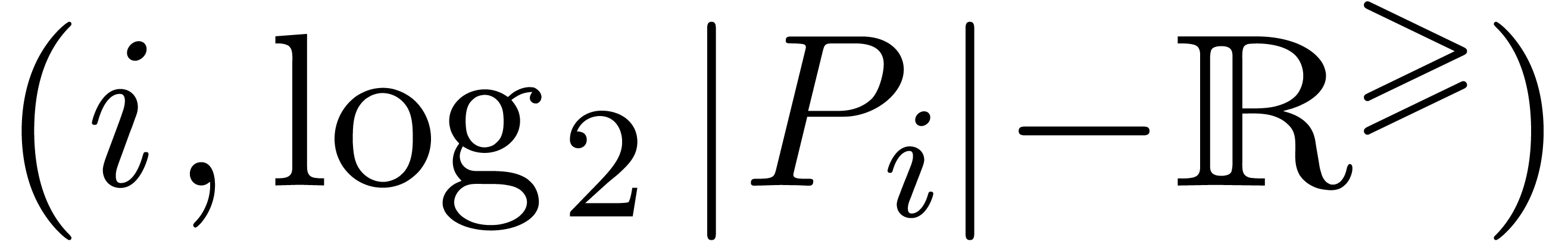 for
all
for
all 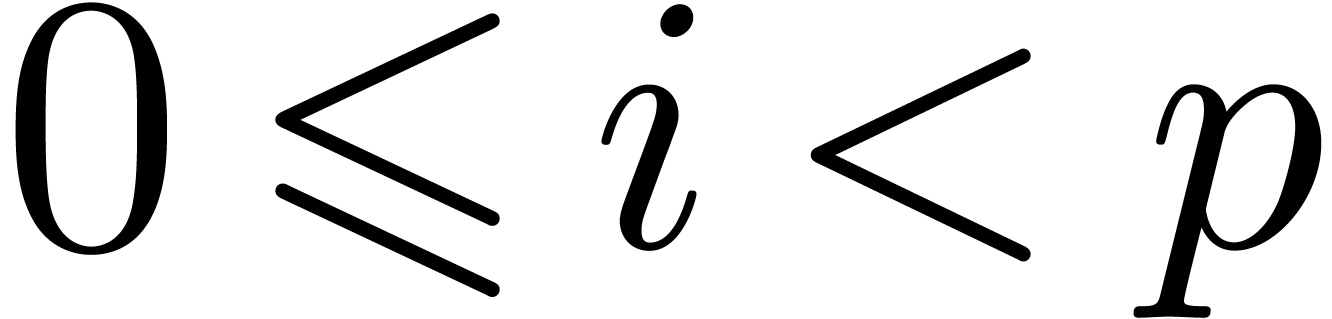 , with the convention
that
, with the convention
that 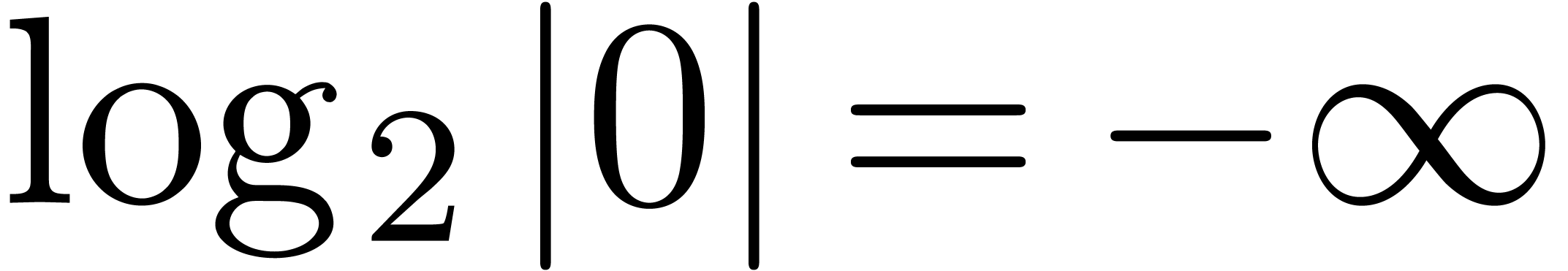 (see figure 2 for two
examples). The numeric Newton polygon
(see figure 2 for two
examples). The numeric Newton polygon 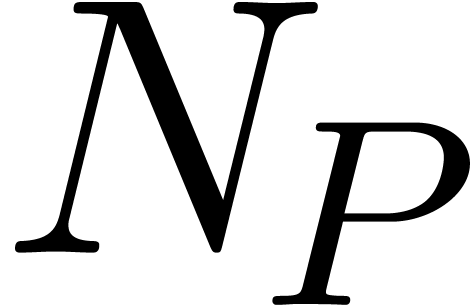 is
characterized by its exponent polynomial
is
characterized by its exponent polynomial
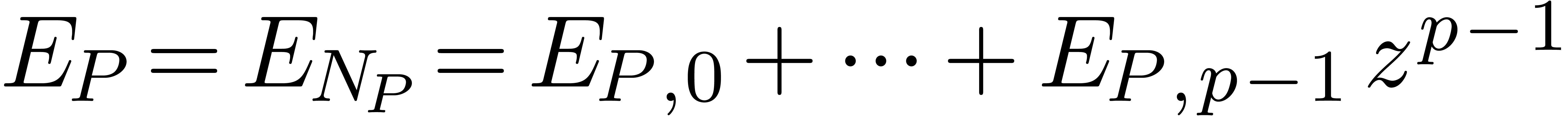
with coefficients
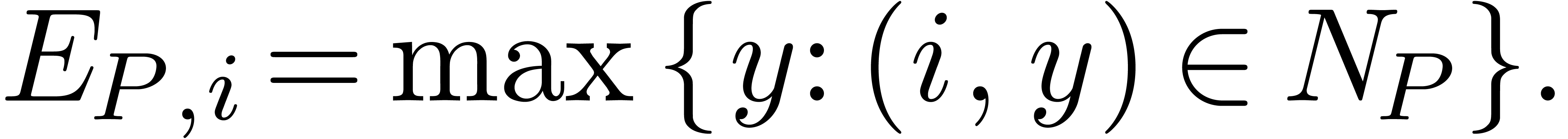
Equivalently, we may characterize  by the first
exponent
by the first
exponent  and the slopes
and the slopes 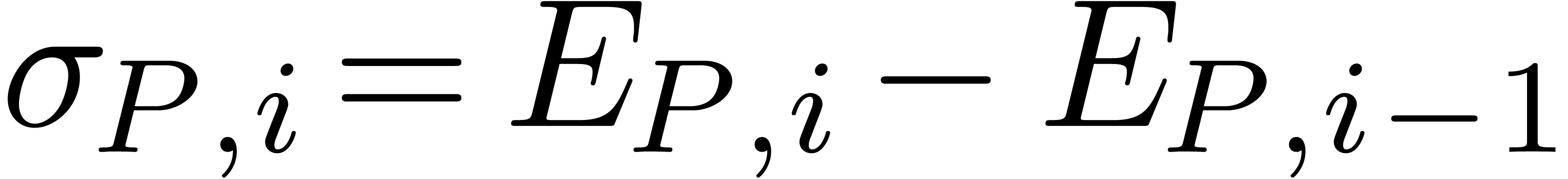 with
with  . Notice that
. Notice that  .
.
It is easy to compute the vertices  ,
,
 of the Newton polynomial of
of the Newton polynomial of 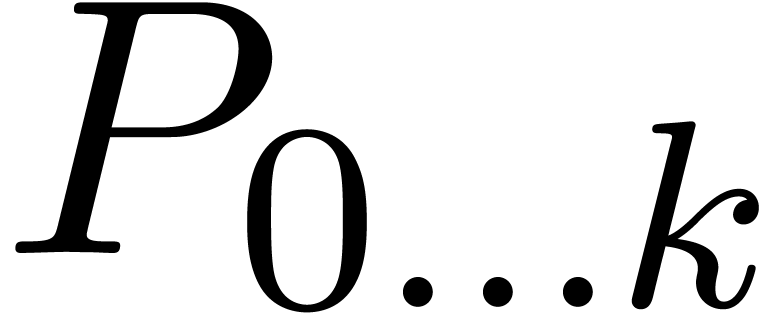 by induction over
by induction over 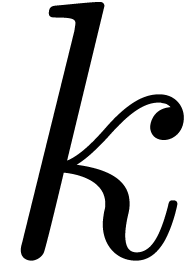 : at each
step, we add
: at each
step, we add  at the right of the sequence and
repeatedly remove the before last pair
at the right of the sequence and
repeatedly remove the before last pair 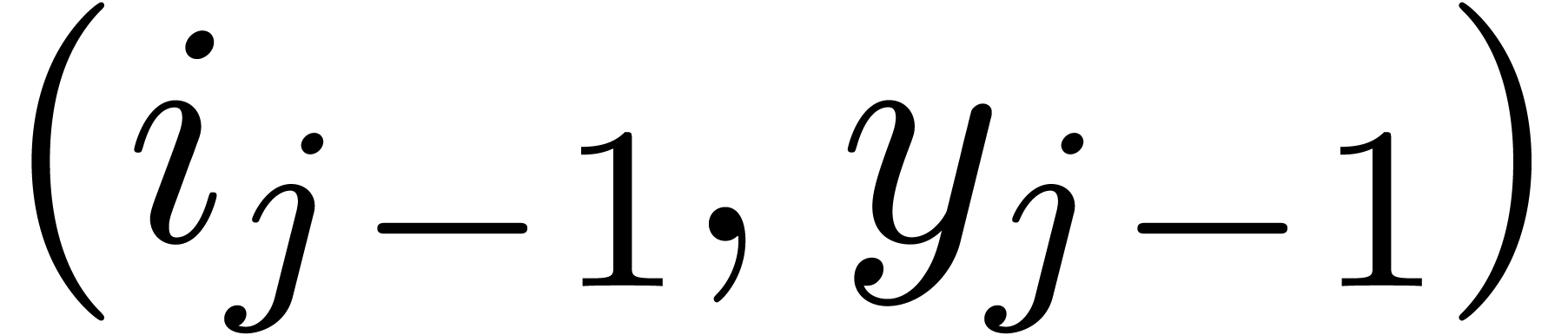 as long
as it lies below the edge from
as long
as it lies below the edge from 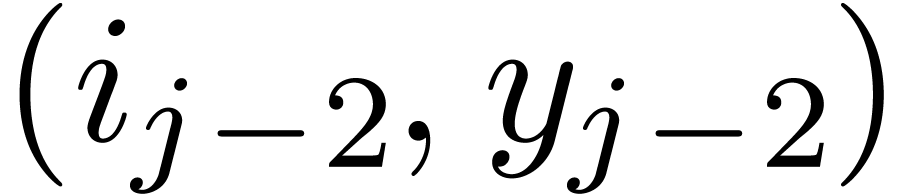 to
to 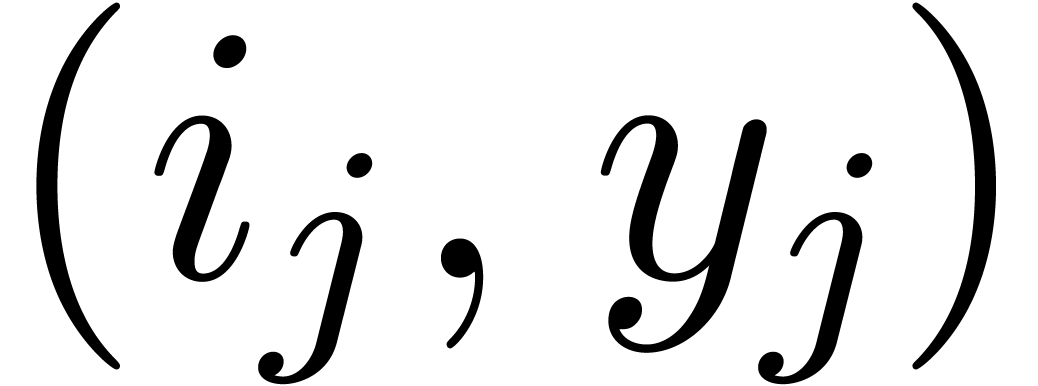 . Using this method, the vertices of
. Using this method, the vertices of  , as well as the numbers
, as well as the numbers  and
and 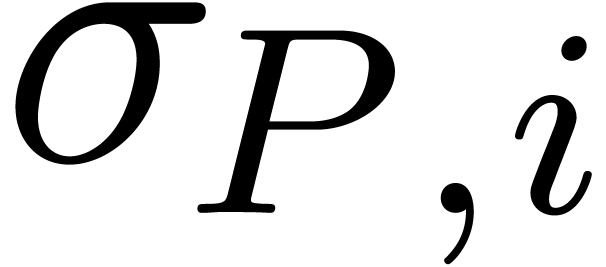 , can be
computed in linear time.
, can be
computed in linear time.
The scaling operation 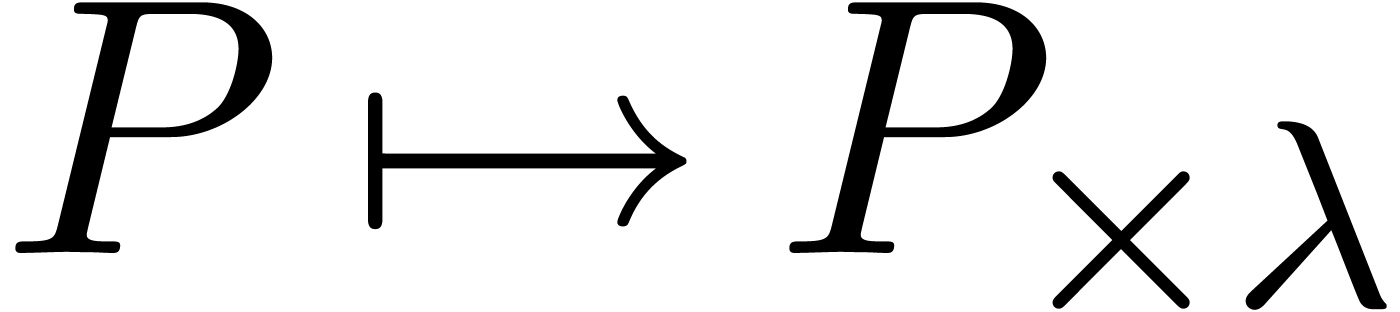 has a simple impact on
exponent polynomials:
has a simple impact on
exponent polynomials:
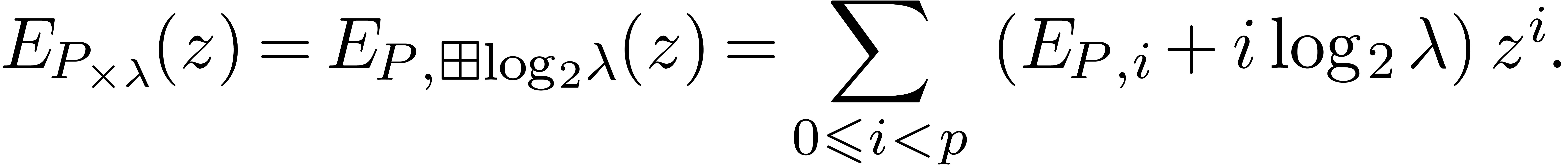
The norms of  and
and 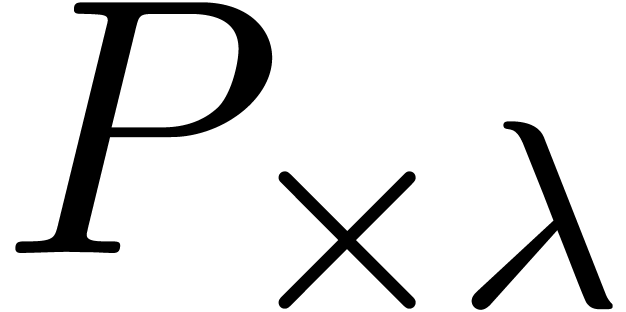 and
their exponent polynomials are related by
and
their exponent polynomials are related by
since the maximum 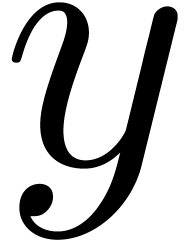 -value of a
convex hull of a set of pairs
-value of a
convex hull of a set of pairs  coincides with the
maximum
coincides with the
maximum  -values of the points
themselves.
-values of the points
themselves.
 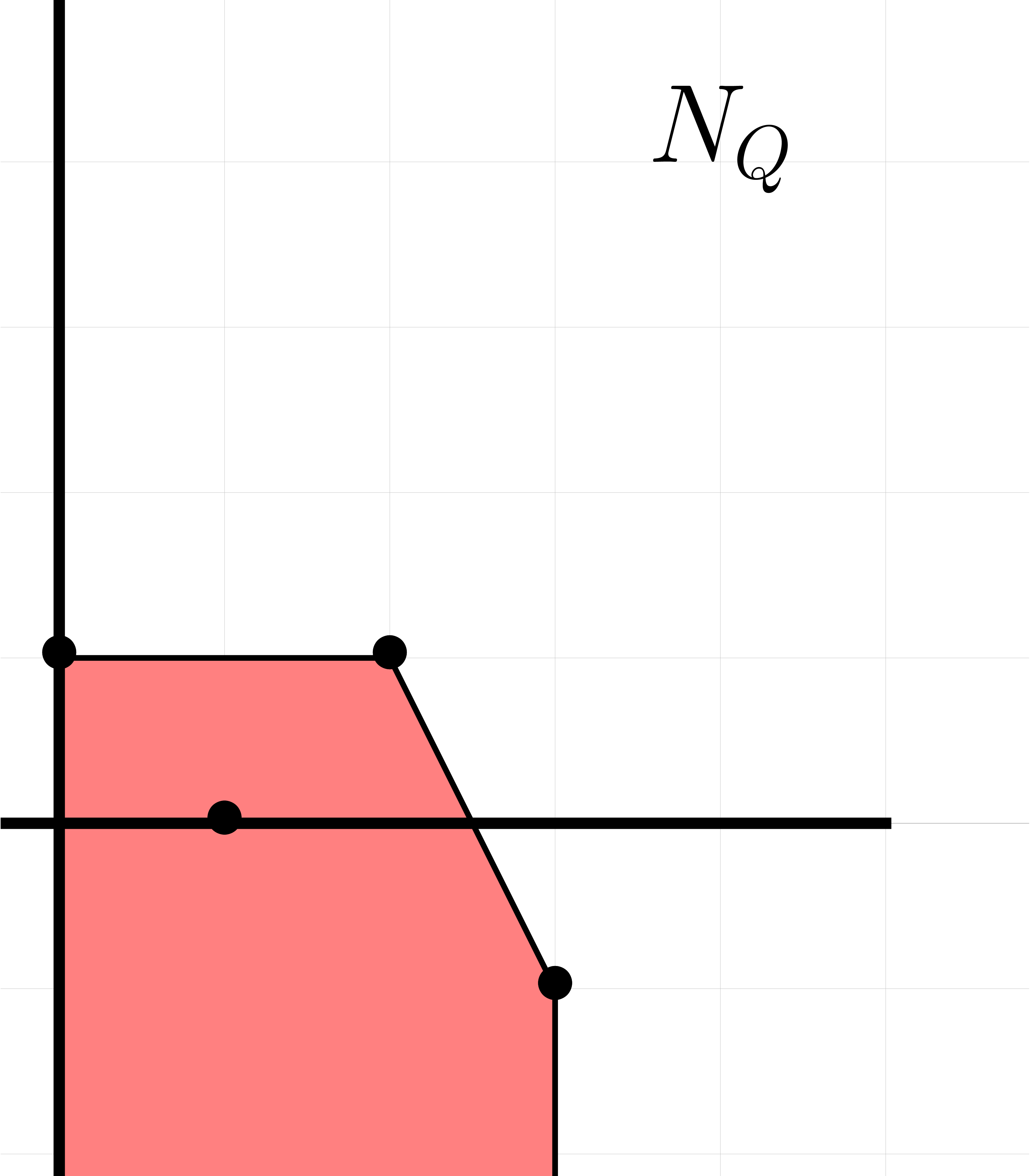 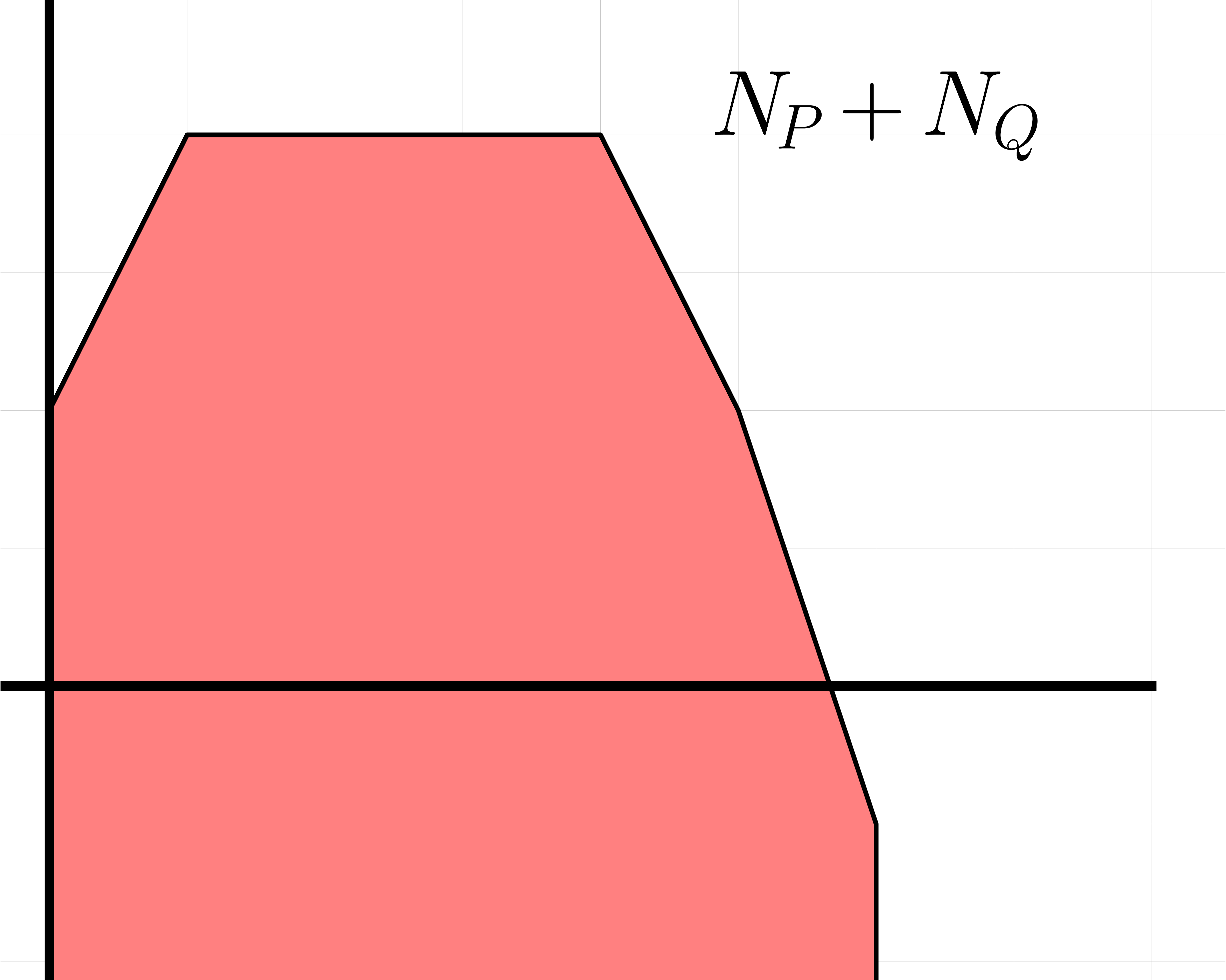 |
Recall that the Minkowski sum of the convex sets 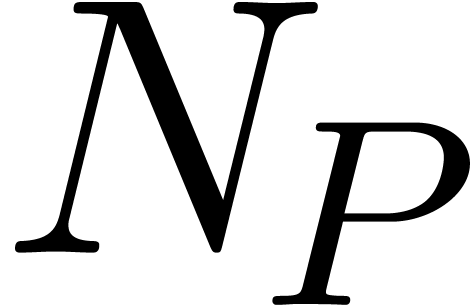 and
and 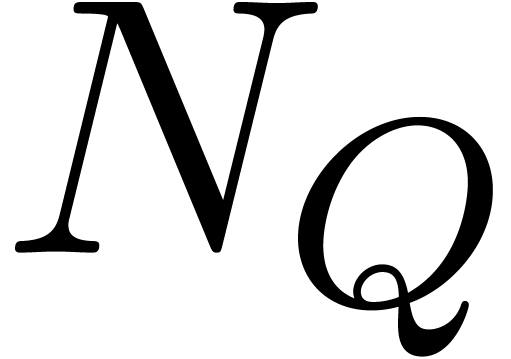 is defined by
is defined by
An example of a Minkowski sum is shown in figure 2. It is
convenient to regard  and
and  as “max-plus polynomials” over the semi-algebra
as “max-plus polynomials” over the semi-algebra 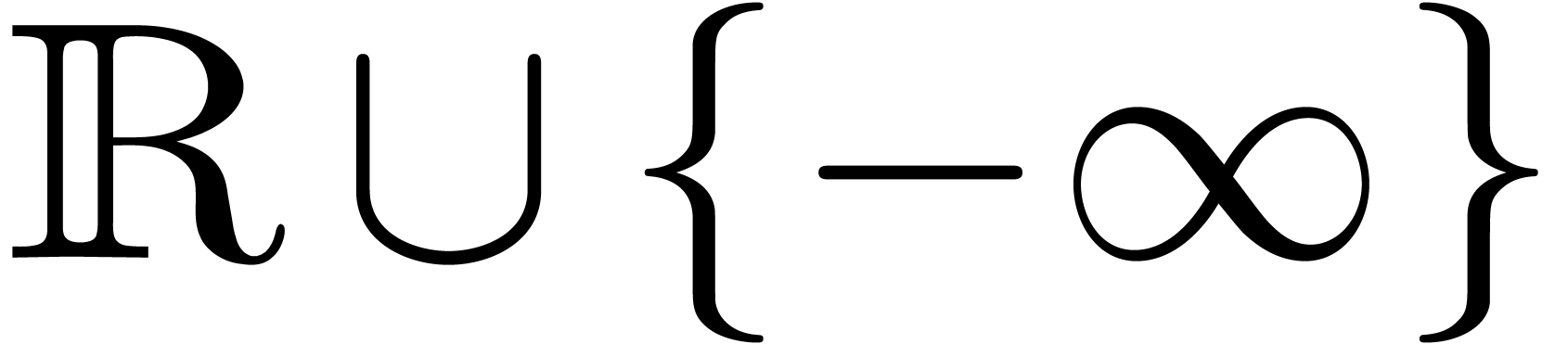 in which multiplication and addition are replaced by
addition and the operator
in which multiplication and addition are replaced by
addition and the operator  .
These polynomials are convex in the sense that its sequences of
coefficients are convex. The exponent polynomial of
.
These polynomials are convex in the sense that its sequences of
coefficients are convex. The exponent polynomial of  may then be reinterpreted as a “product” of polynomials:
may then be reinterpreted as a “product” of polynomials:
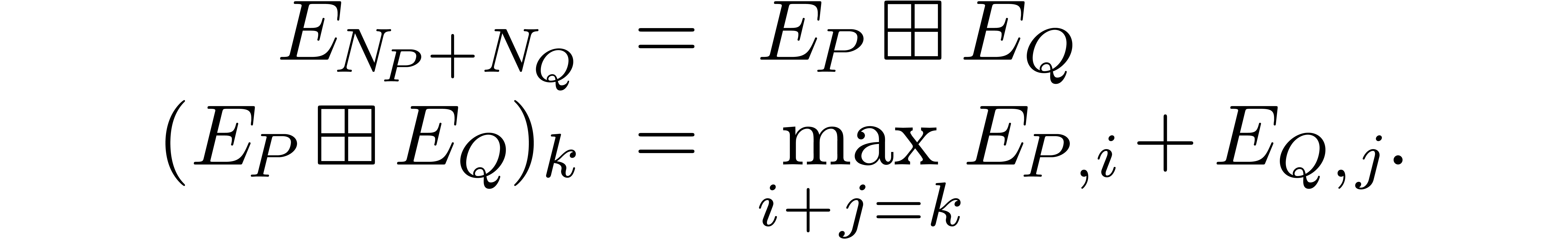
Clearly, 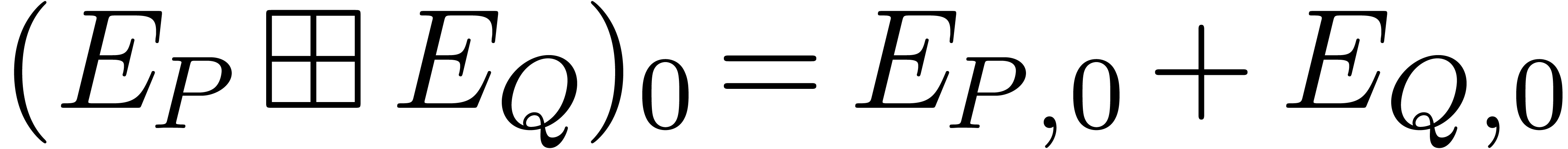 , and it is easily
shown that the slopes of
, and it is easily
shown that the slopes of  are obtained by merging
the ordered lists
are obtained by merging
the ordered lists  and
and  . This provides us with a linear-time algorithm for
the computation of
. This provides us with a linear-time algorithm for
the computation of  as a function of
as a function of  and
and 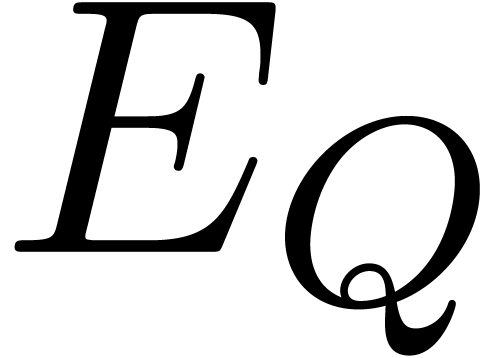 . The
crucial property of
. The
crucial property of  is that it approximates
is that it approximates 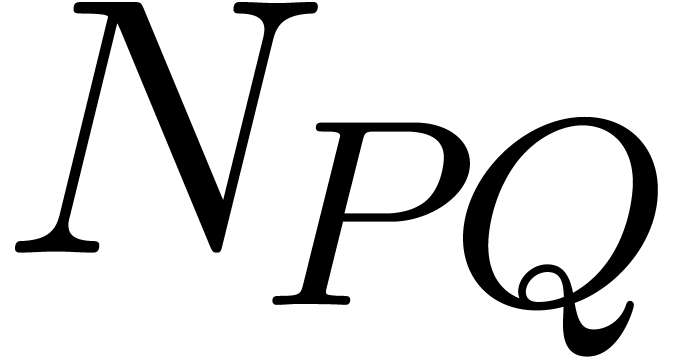 well.
well.
Proof. Let  .
Applying (2) and (3), we have
.
Applying (2) and (3), we have
Using (11) and the fact that 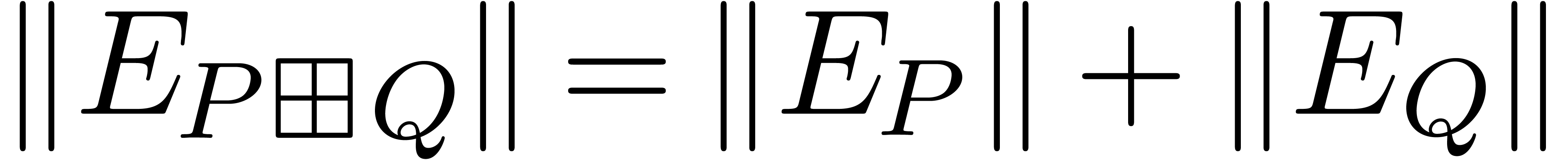 ,
we obtain
,
we obtain
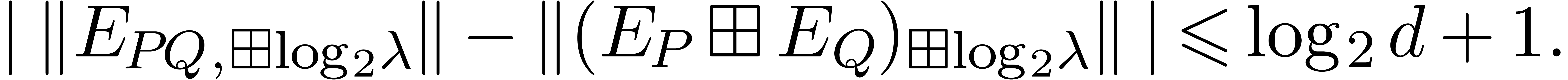
Given arbitrary convex max-plus polynomials  and
and
 with
with 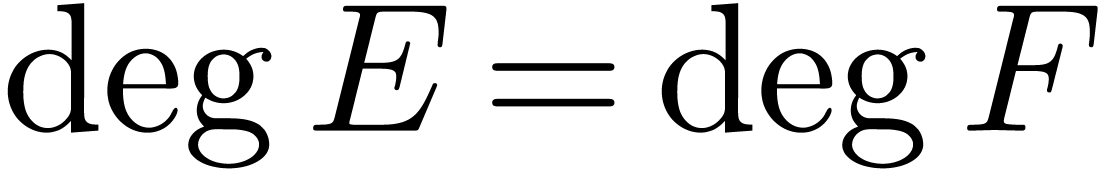 ,
it therefore suffices to show that
,
it therefore suffices to show that
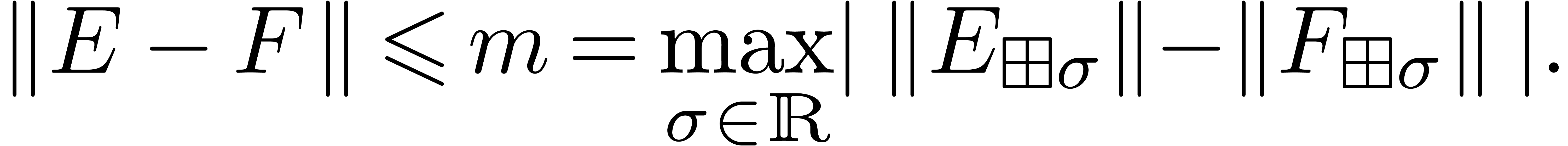
Indeed, for 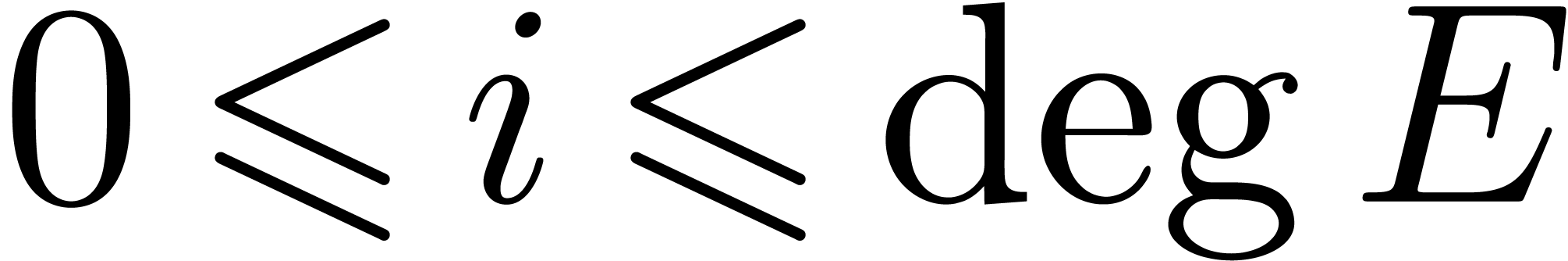 , let
, let  be such that
be such that 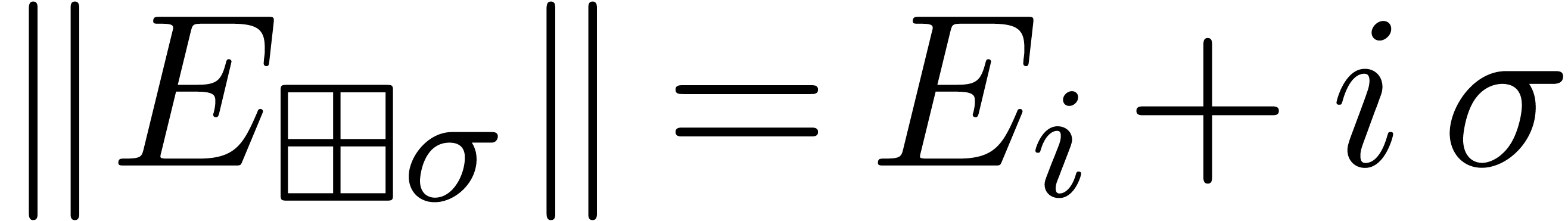 .
Then
.
Then

The relation 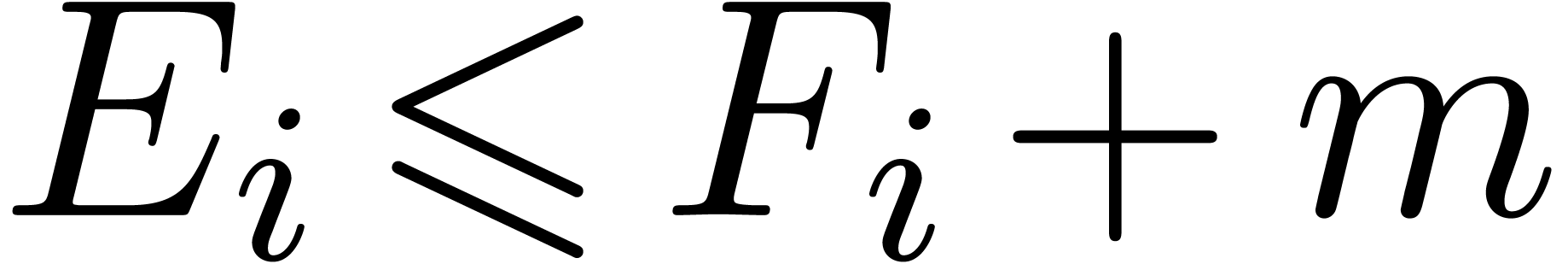 is proved similarly.
is proved similarly.
It is classical that the numeric properties of a polynomial  can be greatly effected by slightly modifying one of its
coefficients. For instance, if
can be greatly effected by slightly modifying one of its
coefficients. For instance, if 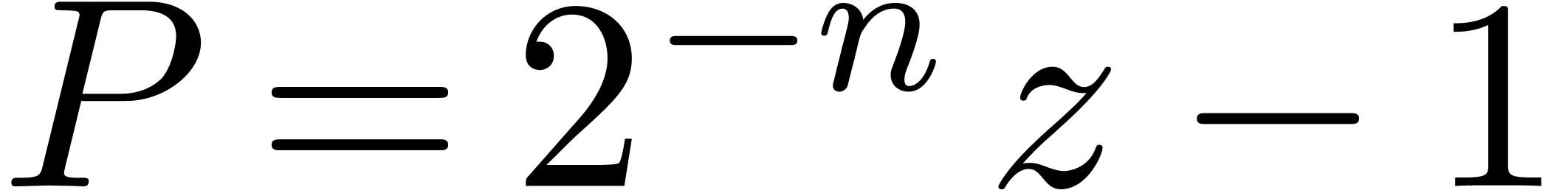 ,
then its root can move from
,
then its root can move from 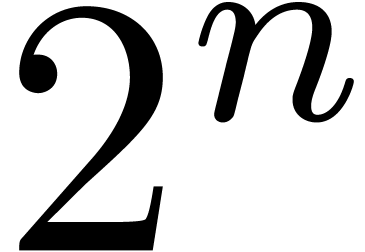 to
to 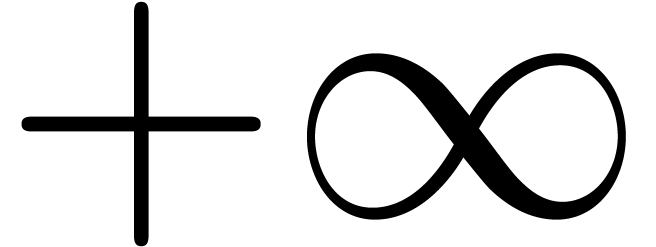 , when modifying its coefficient
, when modifying its coefficient 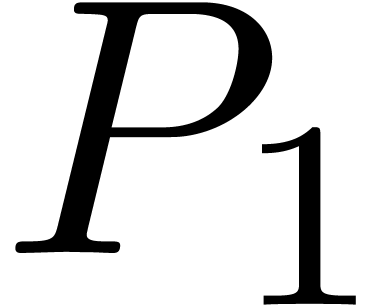 by an amount as small as
by an amount as small as 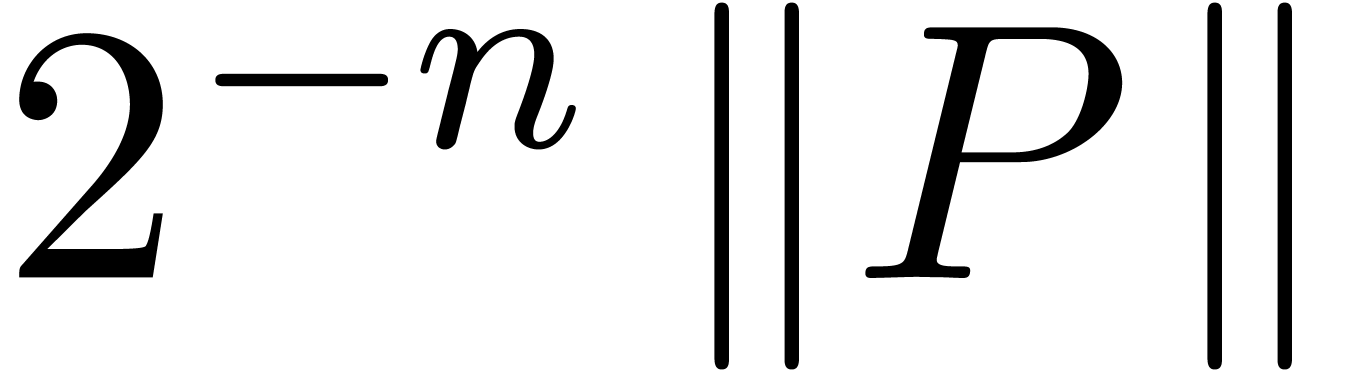 .
Nevertheless, as we will detail in section 9, one may
expect that many of the numeric properties of
.
Nevertheless, as we will detail in section 9, one may
expect that many of the numeric properties of  do
not sensibly change if we modify a coefficient
do
not sensibly change if we modify a coefficient 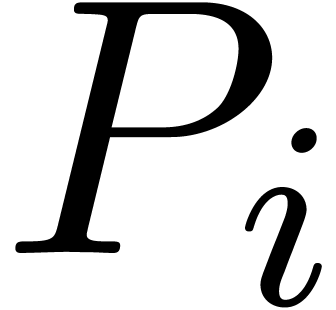 by less than
by less than 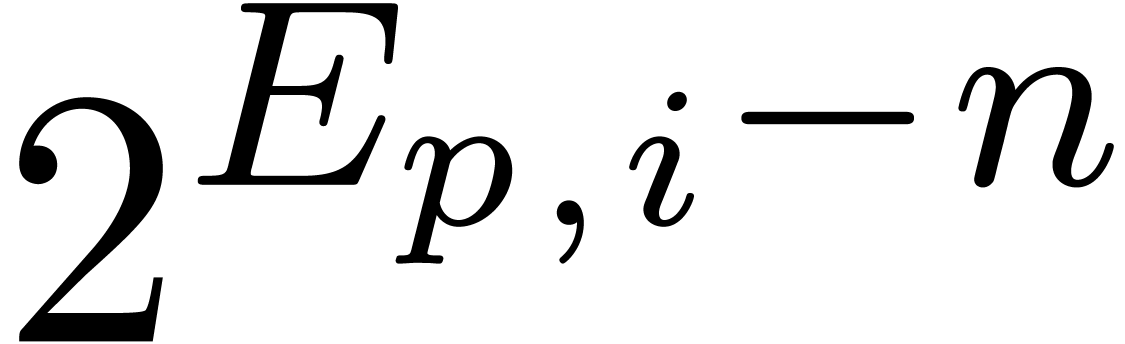 .
.
If the coefficients 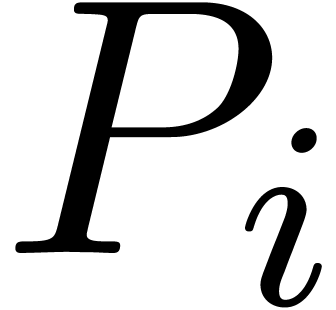 of
of  are known with absolute errors
are known with absolute errors 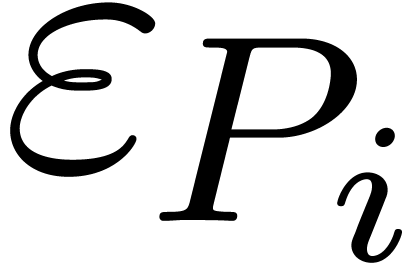 ,
this motivates us to introduce the relative Newton error of
,
this motivates us to introduce the relative Newton error of
 by
by
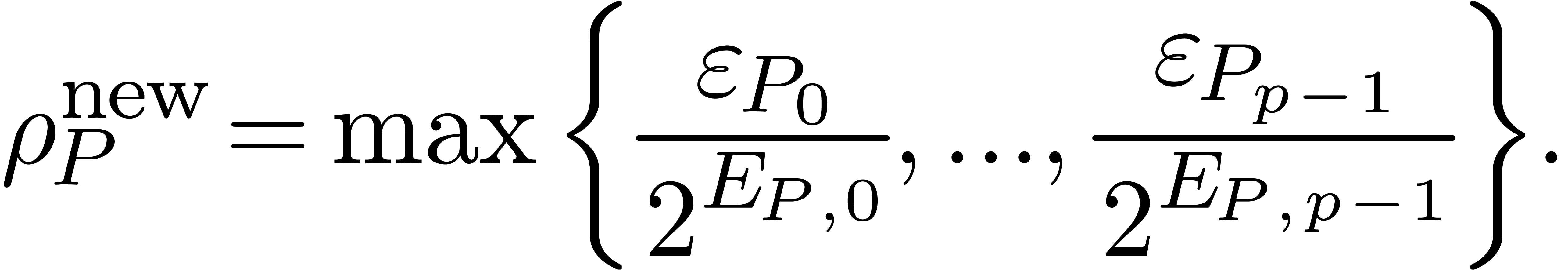
For instance, if  is an approximation of the
product
is an approximation of the
product 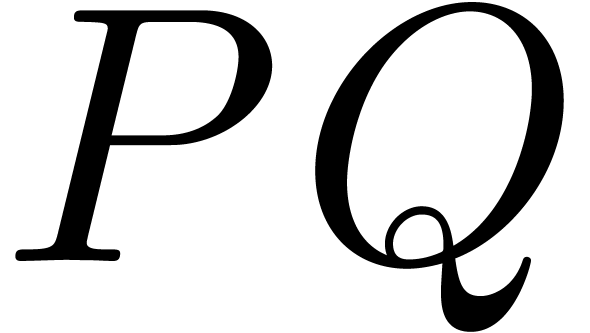 , then its relative
Newton error would typically be given by
, then its relative
Newton error would typically be given by
Alternatively, we may regard  as the minimal
uniform error of the approximations
as the minimal
uniform error of the approximations 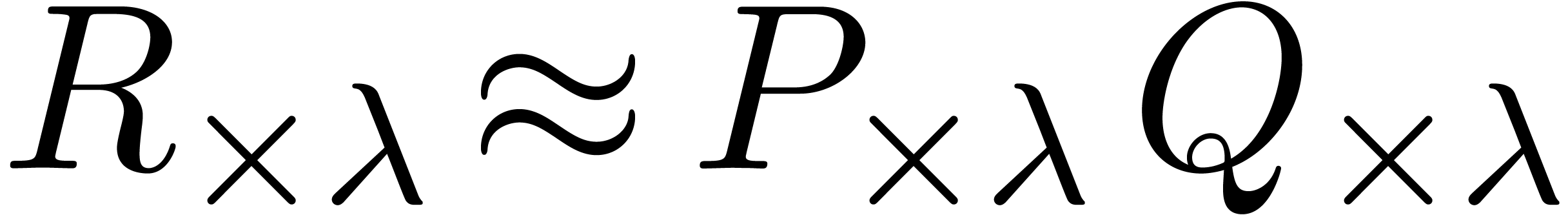 for all
possible scales
for all
possible scales 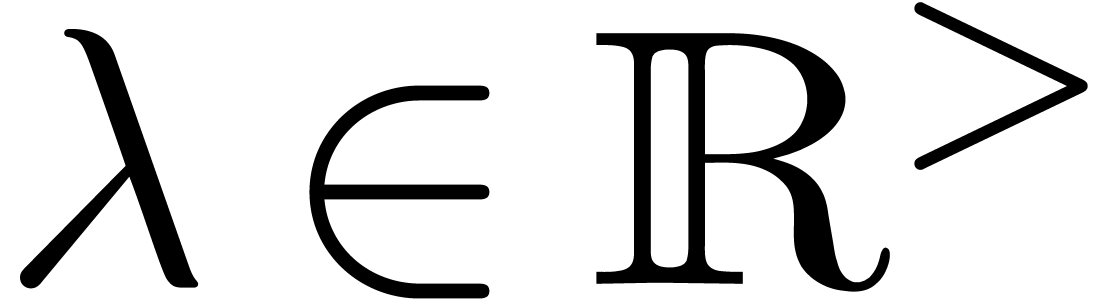 :
:
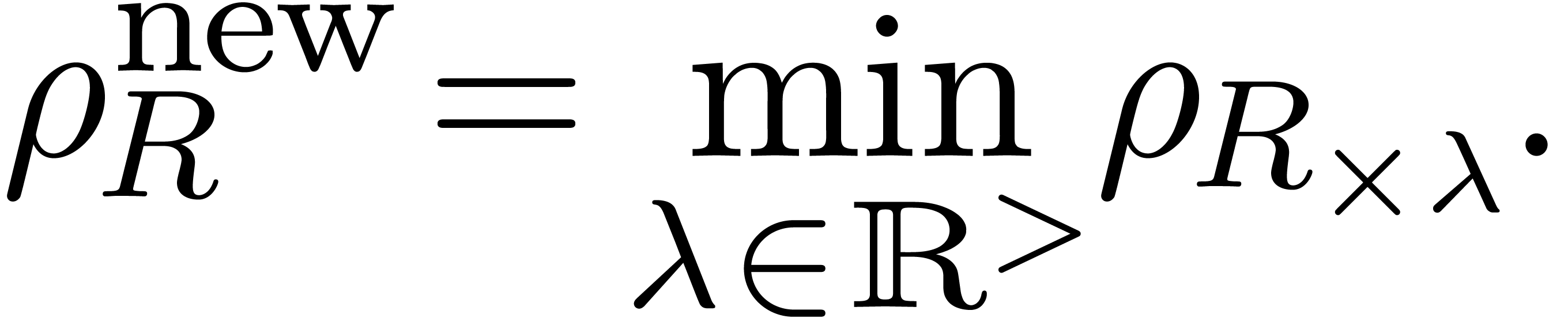
In this section and the subsequent sections, we propose an efficient
algorithm for computing an approximation 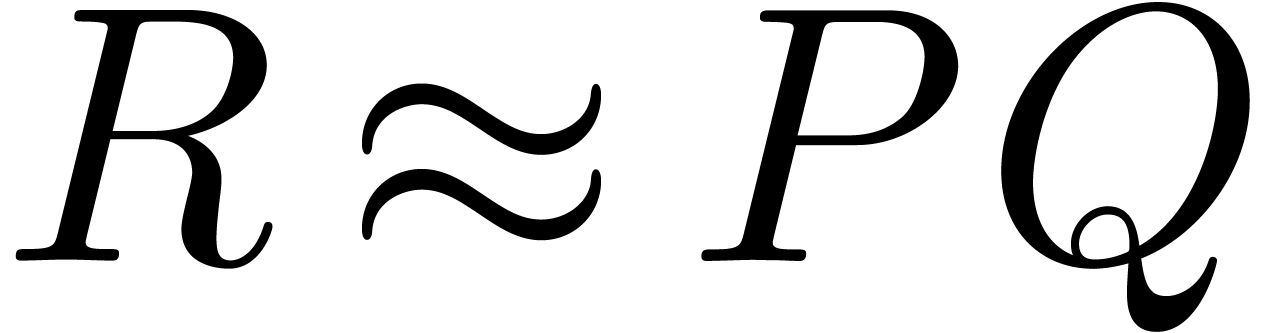 ,
which is numerically stable in the sense that
,
which is numerically stable in the sense that  is
small.
is
small.
The first main idea behind Newton multiplication is that only part of
the products 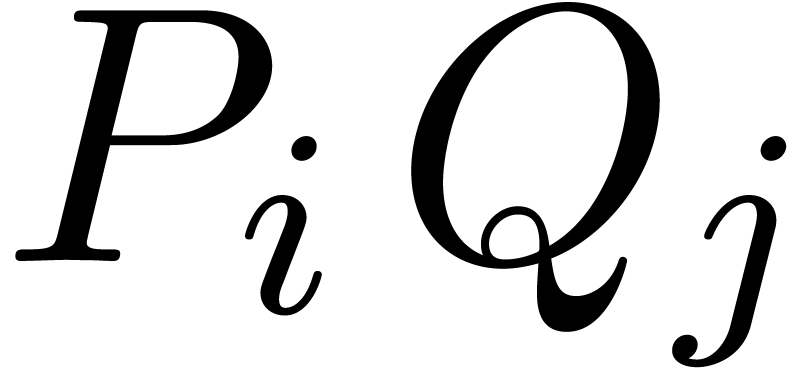 substantially contribute to
substantially contribute to 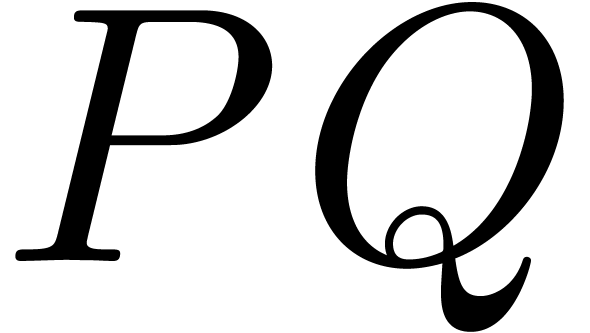 : the pair
: the pair 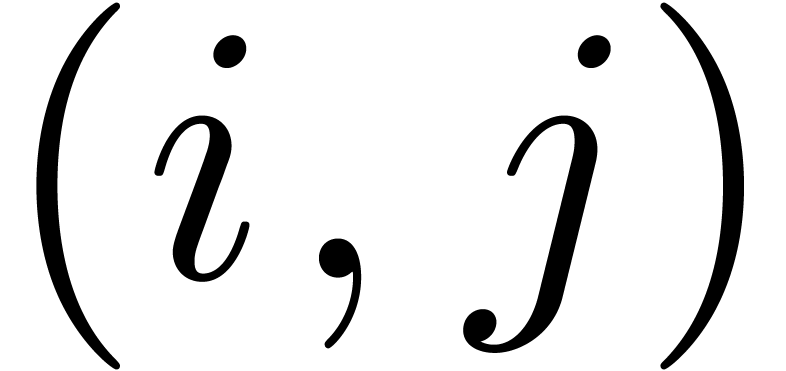 and the corresponding product
and the corresponding product  are said to be
negligible if
are said to be
negligible if

Indeed, when neglecting the sum of all such products in the computation
of  , the corresponding
increase of the relative Newton error is bounded by
, the corresponding
increase of the relative Newton error is bounded by 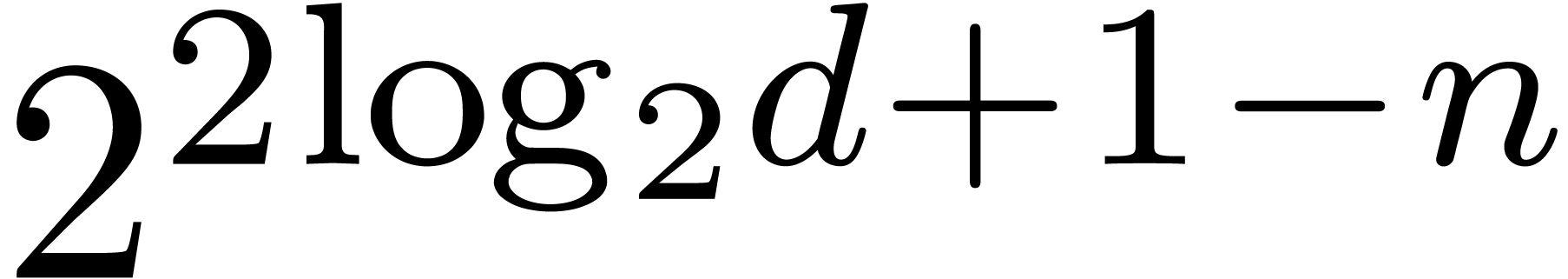 . This follows from proposition 3
and the fact that there are at most
. This follows from proposition 3
and the fact that there are at most 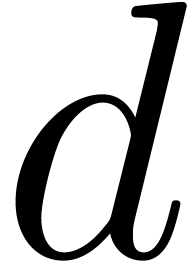 pairs
pairs 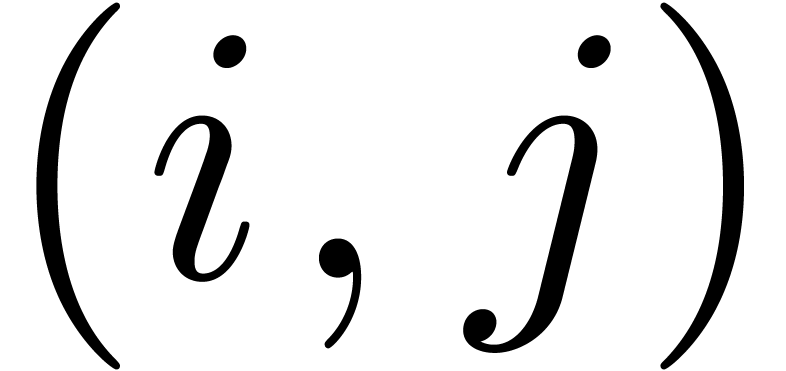 which contribute to a fixed coefficient
which contribute to a fixed coefficient  . The left-hand picture in figure 3
illustrates a typical zone of non-negligible contributions
. The left-hand picture in figure 3
illustrates a typical zone of non-negligible contributions 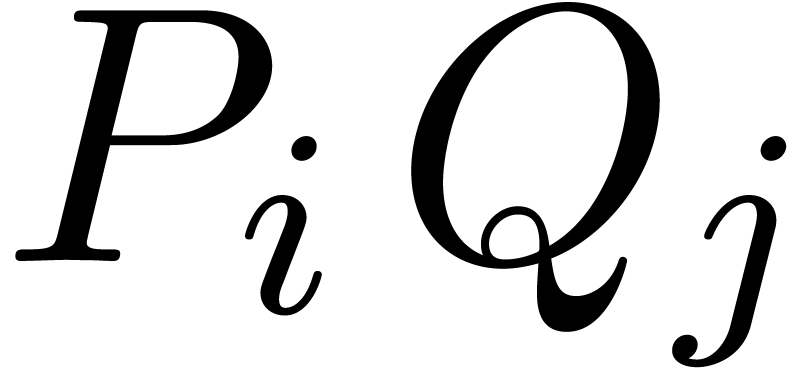 . The lower and upper limits
. The lower and upper limits 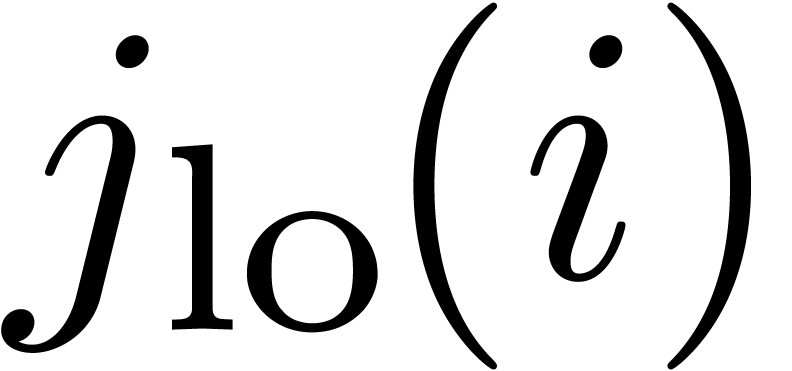 and
and 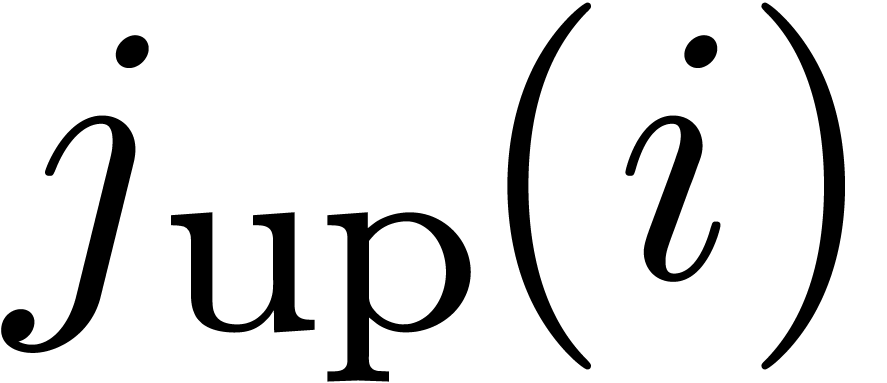 of this zone are increasing functions in
of this zone are increasing functions in
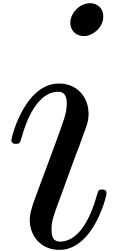 and can therefore be determined in linear time
as a function of
and can therefore be determined in linear time
as a function of  and
and  .
.
A set  of pairs
of pairs 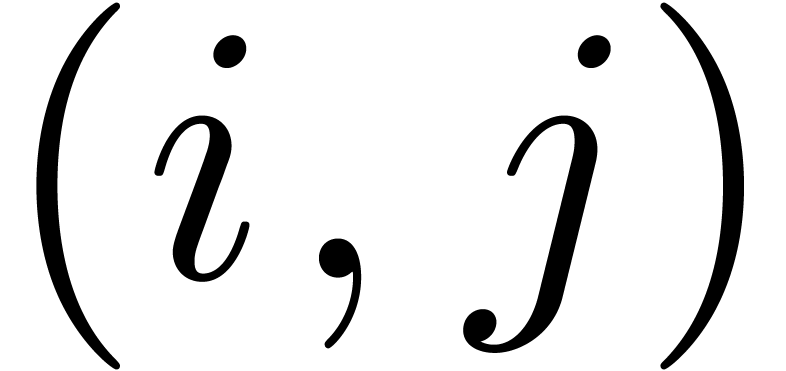 is said
to be negligible if each of its elements is negligible. A partial
product
is said
to be negligible if each of its elements is negligible. A partial
product  is said to be negligible if
is said to be negligible if
 is negligible and admissible if there
exists no proper subrectangle
is negligible and admissible if there
exists no proper subrectangle  of
of  such that
such that 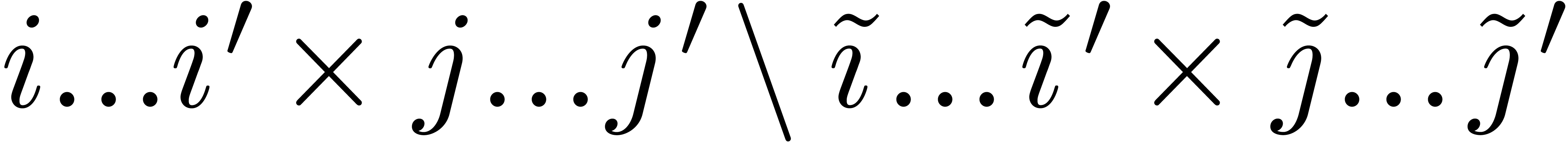 is negligible. Clearly,
any non-negligible partial product
is negligible. Clearly,
any non-negligible partial product 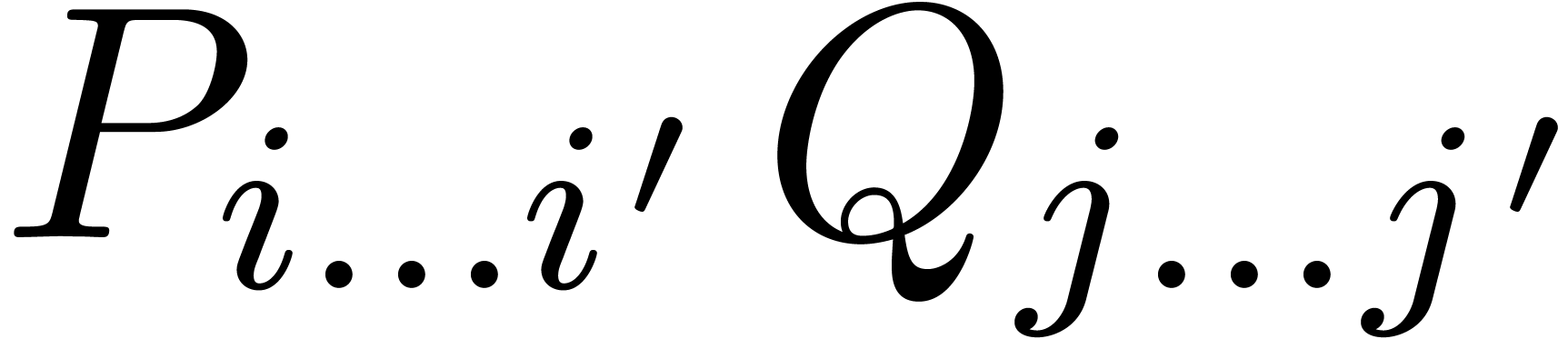 gives rise to
a unique admissible partial product
gives rise to
a unique admissible partial product 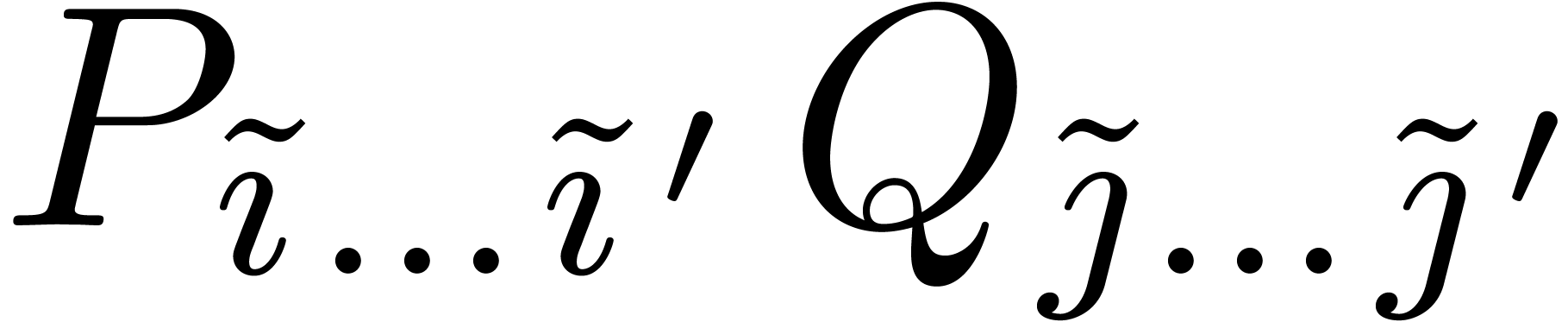 by taking
by taking
 to be the smallest subrectangle whose complement
in
to be the smallest subrectangle whose complement
in  is negligible. Any subdivision
is negligible. Any subdivision
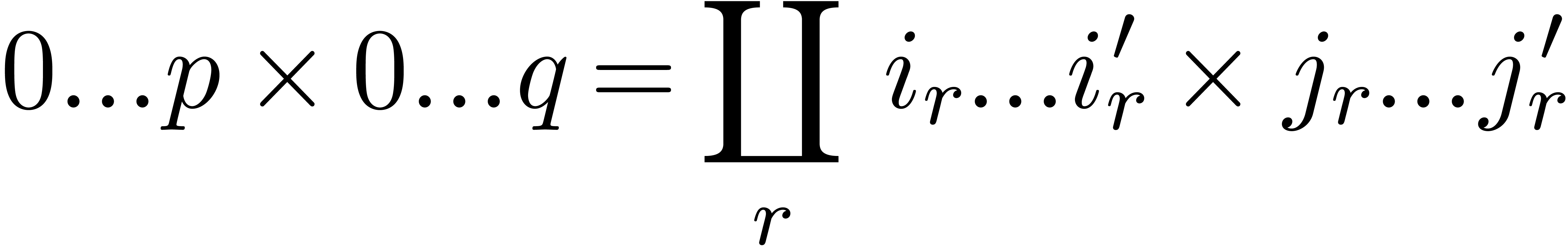 |
(12) |
therefore gives rise to a new disjoint union
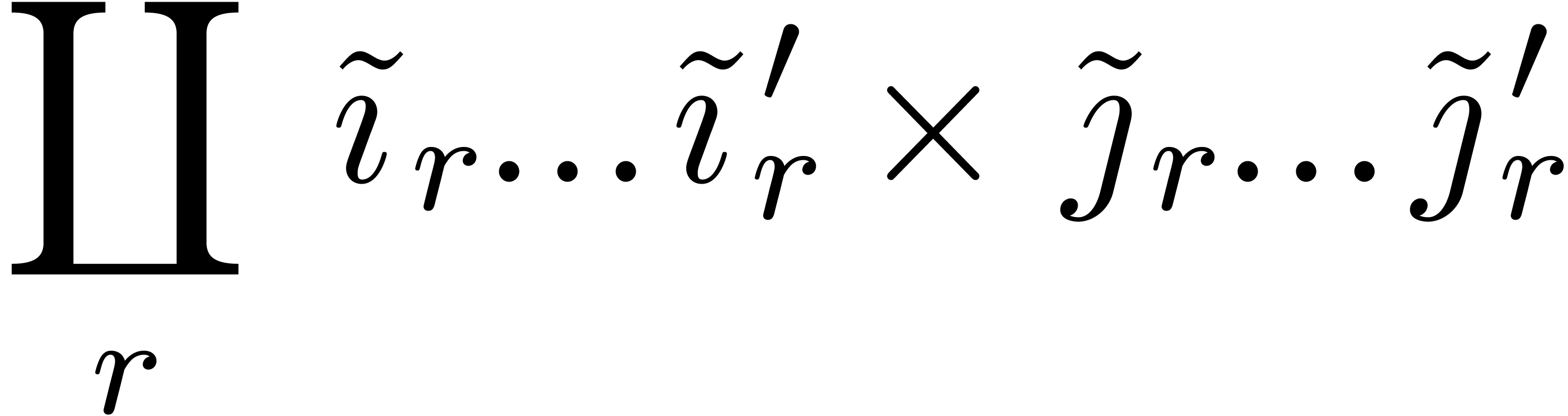 |
(13) |
of admissible subrectangles, whose complement in  is negligible. The second disjoint union will be called the
admissible part of the first one. The right-hand side of figure
3 illustrates the admissible part of a so-called product
subdivision (see section 7 below).
is negligible. The second disjoint union will be called the
admissible part of the first one. The right-hand side of figure
3 illustrates the admissible part of a so-called product
subdivision (see section 7 below).
Our next task is to find a suitable subdivision (12) with
admissible part (13), such that 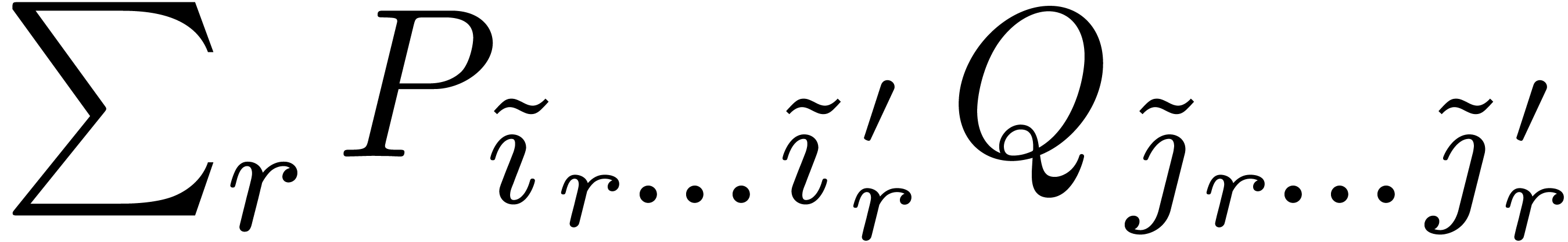 can
be computed both efficiently and in a numerically stable way. The second
main idea behind Newton multiplication is to search for a subdivision
such that the products
can
be computed both efficiently and in a numerically stable way. The second
main idea behind Newton multiplication is to search for a subdivision
such that the products 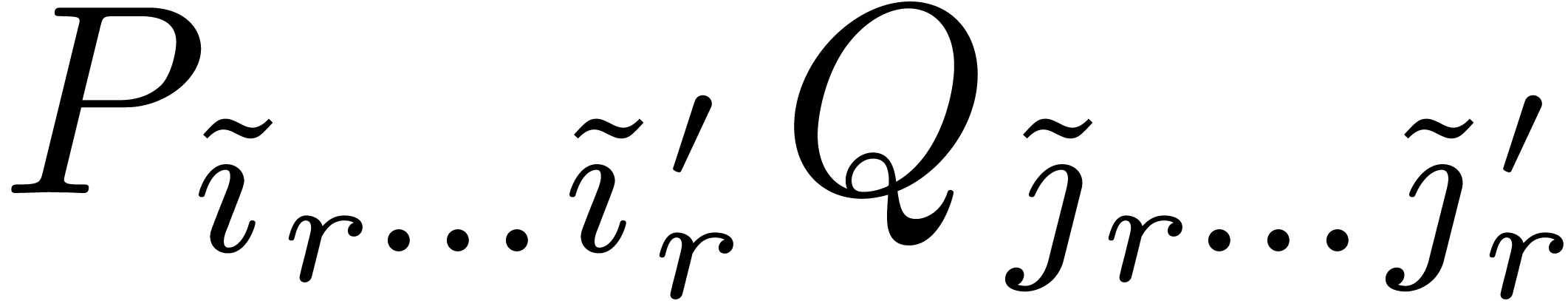 can be performed using
suitable scalings and such that the rectangles
can be performed using
suitable scalings and such that the rectangles  are yet reasonably large. As a first step in this construction, we will
approximate the Newton polygons of
are yet reasonably large. As a first step in this construction, we will
approximate the Newton polygons of  and
and  by simpler ones, merging those edges whose slopes differ
only by a small amount.
by simpler ones, merging those edges whose slopes differ
only by a small amount.
Given a slope 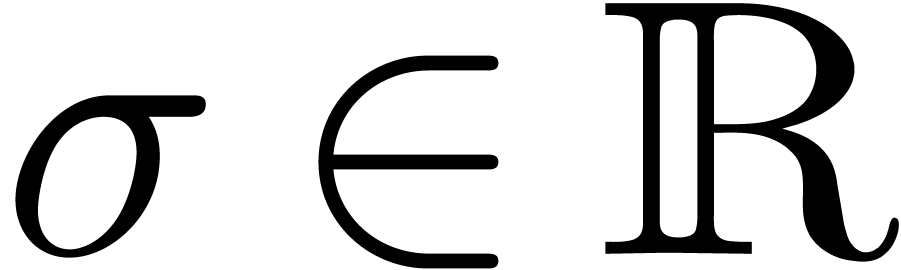 and a convex max-plus polynomial
and a convex max-plus polynomial
 , we define the
, we define the  -discrepancy
-discrepancy 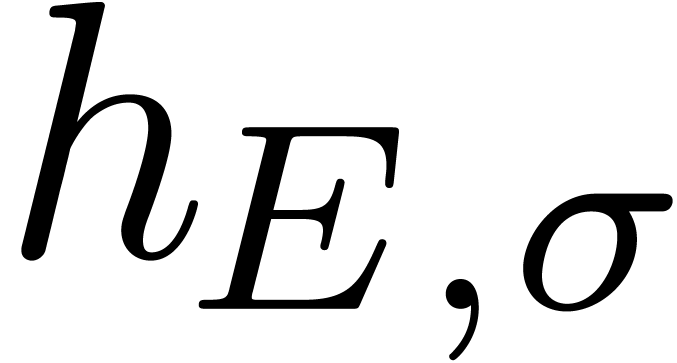 of
of  by
by
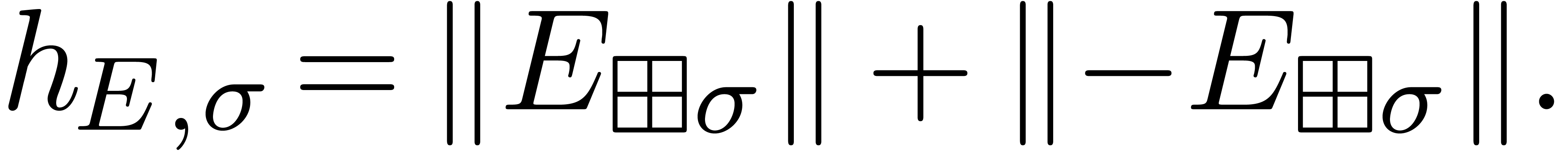
Then the individual exponents 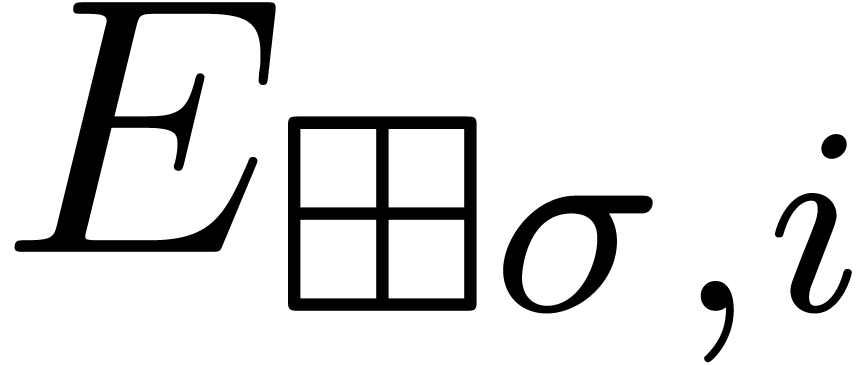 of
of 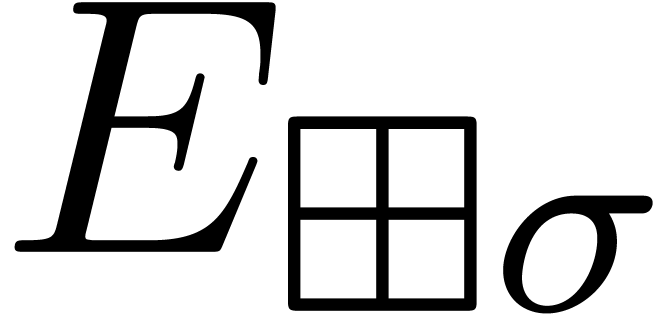 lie in a strip of height
lie in a strip of height 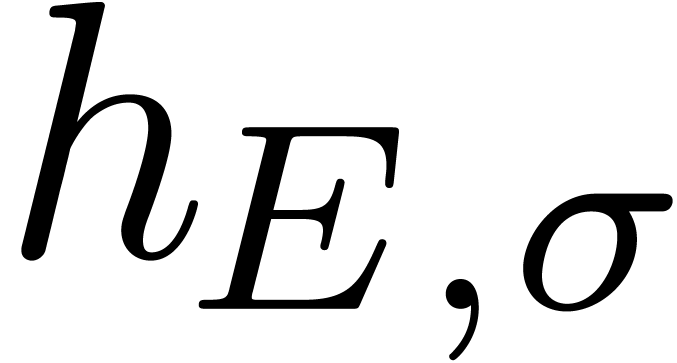 :
:
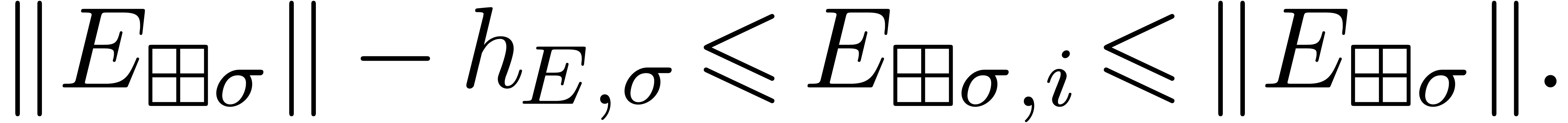 |
(14) |
In the particular case when  equals the main
slope of
equals the main
slope of  ,
,
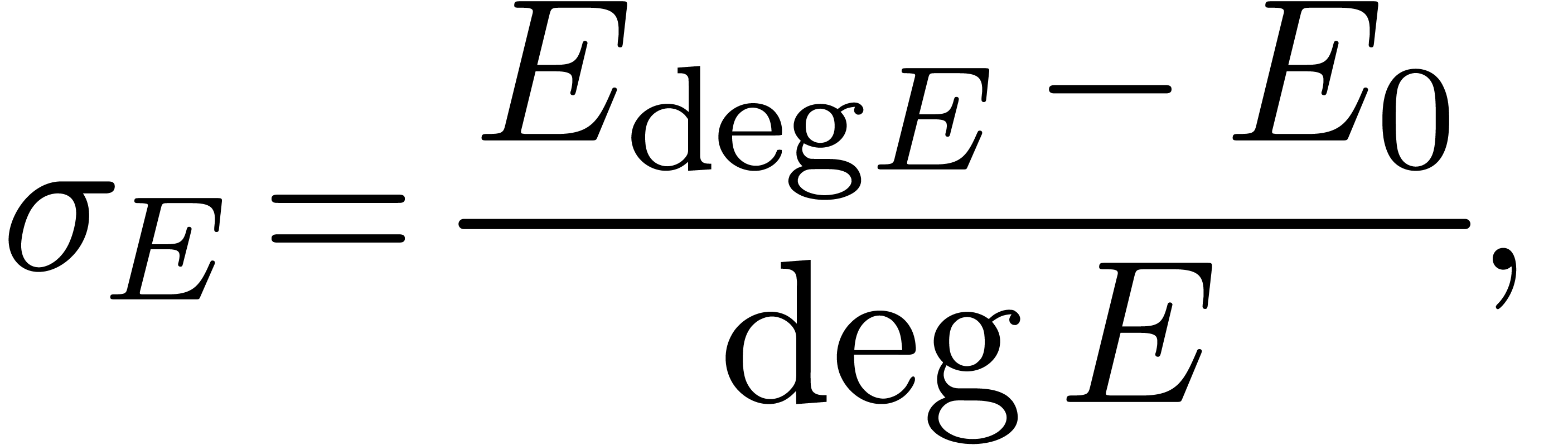
we call 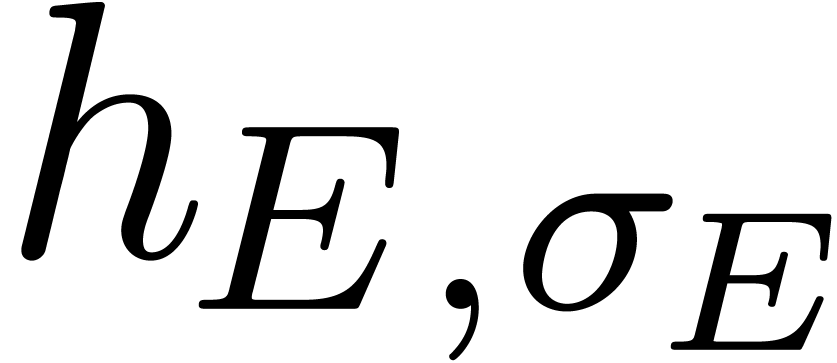 the discrepancy of
the discrepancy of  and also denote it by
and also denote it by 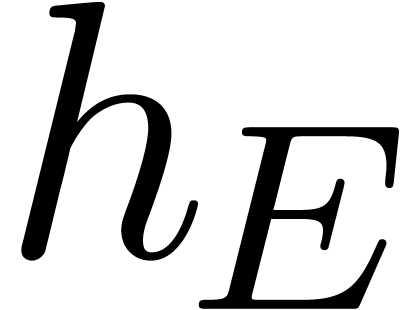 .
For any
.
For any 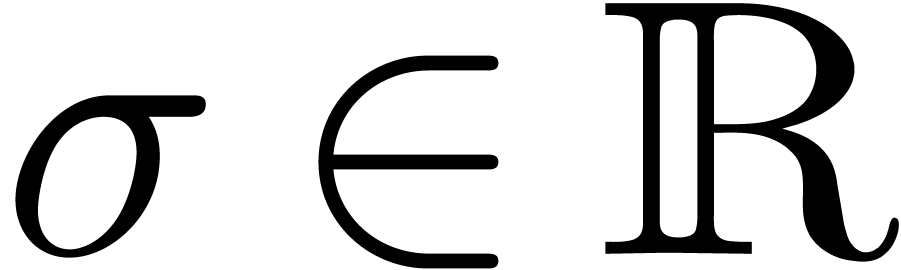 and any second convex max-plus
polynomial
and any second convex max-plus
polynomial  , the convexity of
, the convexity of
 and
and  implies
implies
More generally, one defines the  -discrepancy
-discrepancy
 of
of  on a range
on a range  by
by 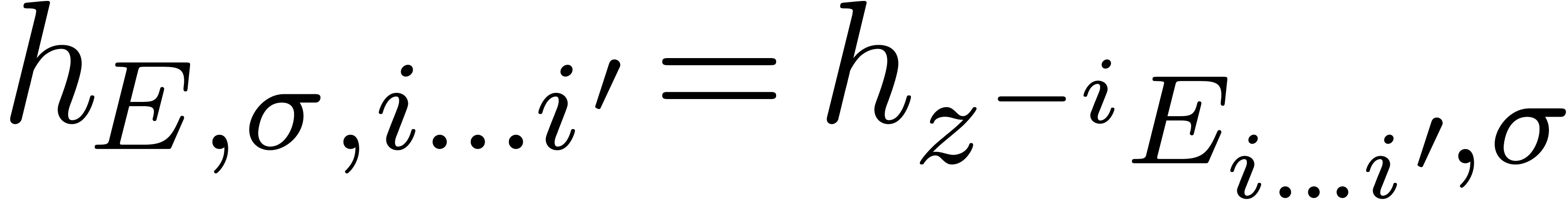 and similarly
and similarly 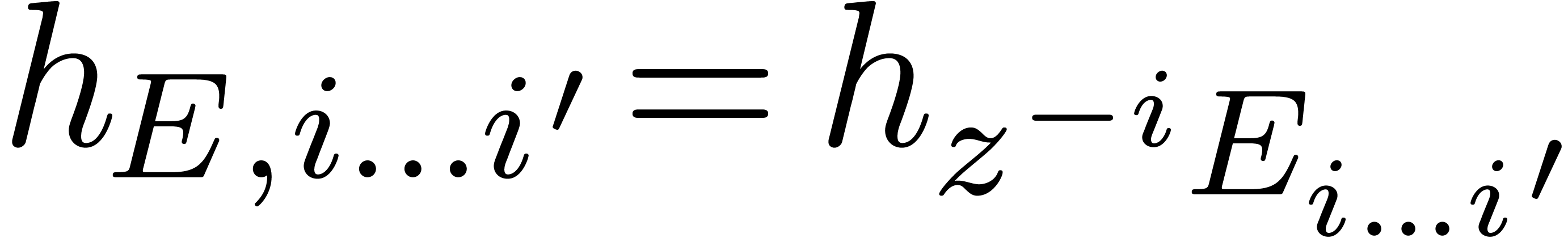 . We have
. We have
for any subdivision of the range 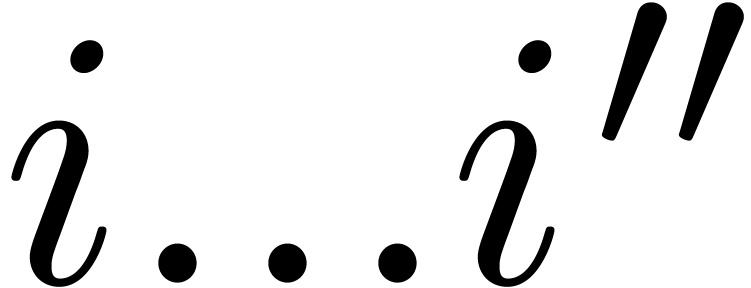 into
into  and
and  .
.
Let us now return to the approximation of the Newton polygon  by a new one with fewer edges. Let
by a new one with fewer edges. Let 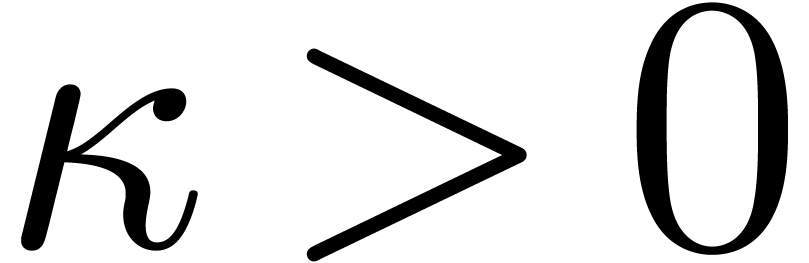 be an arbitrary but fixed constant, such as
be an arbitrary but fixed constant, such as 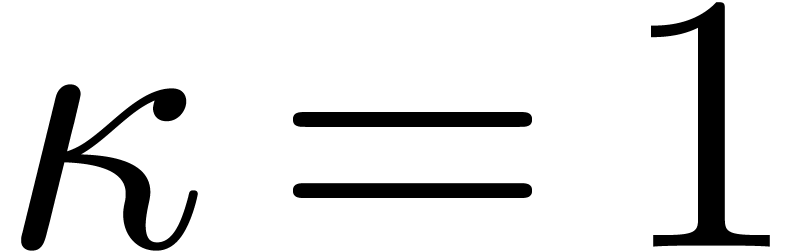 , and denote
, and denote 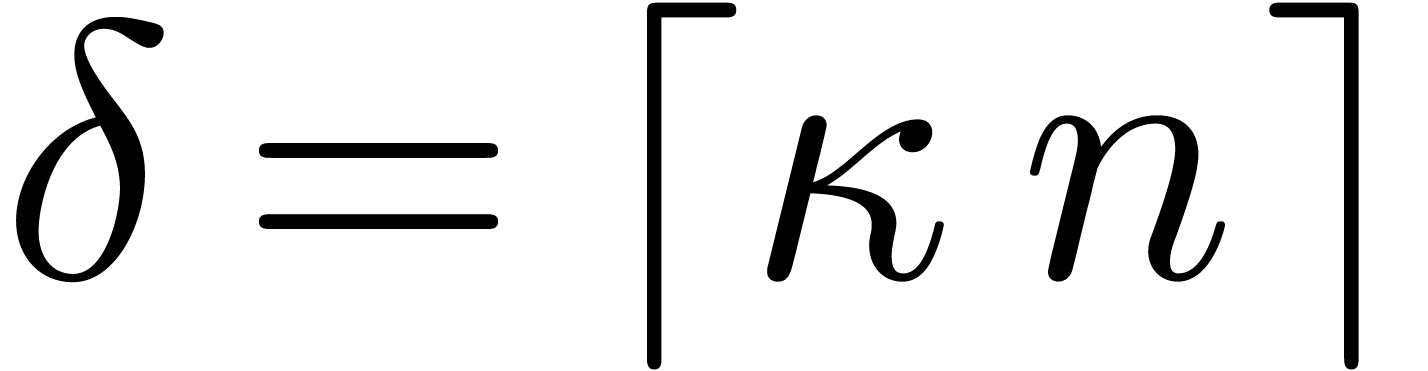 .
We now construct the sequence
.
We now construct the sequence  by taking each
by taking each
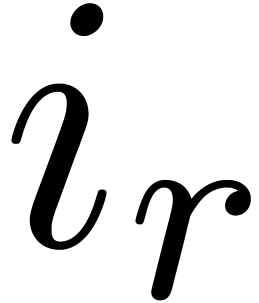 maximal such that
maximal such that 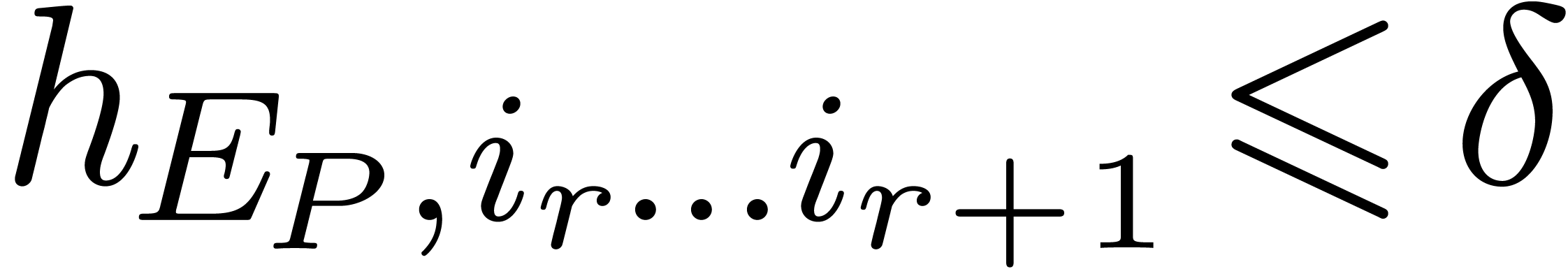 (see
figure 4 below). Using the convexity of
(see
figure 4 below). Using the convexity of  , it is not hard to check that this
construction can be done in linear time using a single traversal of
, it is not hard to check that this
construction can be done in linear time using a single traversal of
 . The edges of
. The edges of  between
between 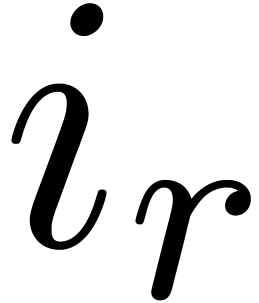 and
and 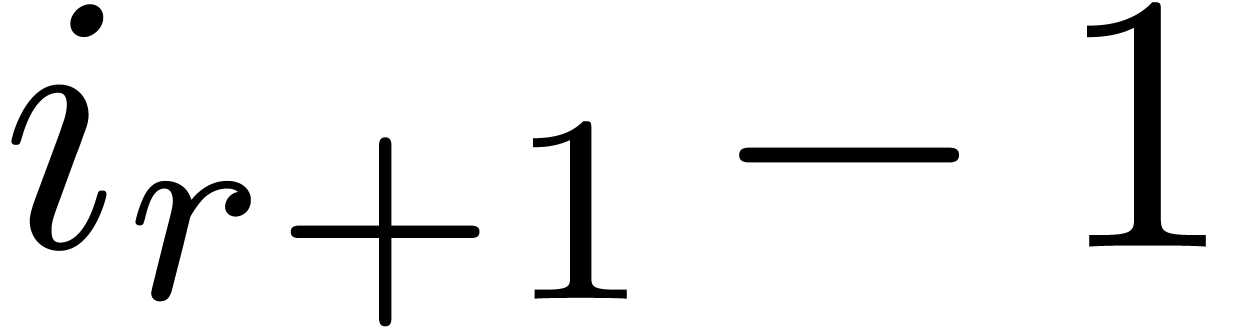 are well-approximated by a single edge from
are well-approximated by a single edge from  to
to
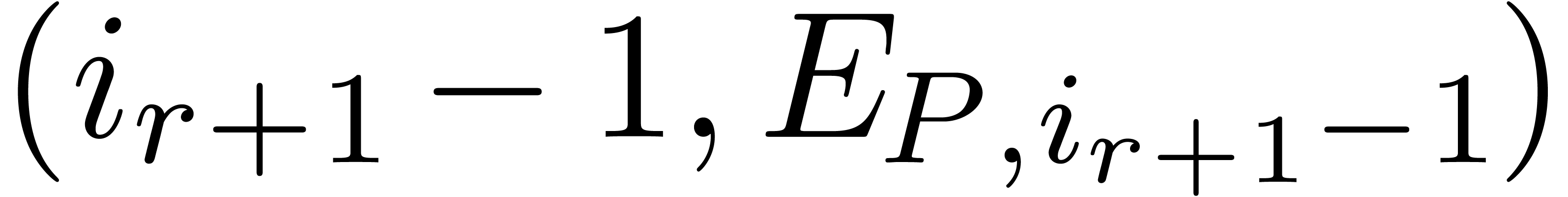 . A similar sequence
. A similar sequence  is constructed for
is constructed for  .
.
A first candidate for the subdivision (12) is the product subdivision:
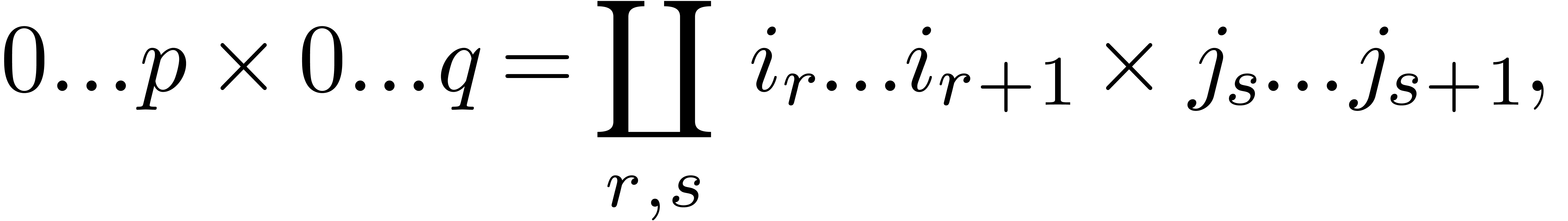 |
(18) |
where the 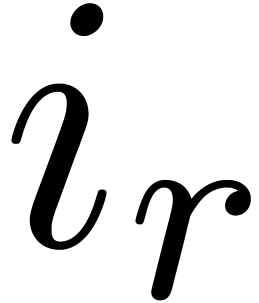 and
and 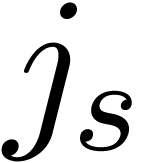 are as in
the previous section. Figure 3 shows an example of a
product subdivision.
are as in
the previous section. Figure 3 shows an example of a
product subdivision.
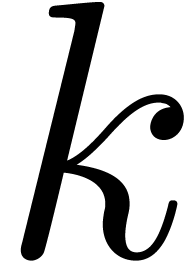 , there exist at most
, there exist at most 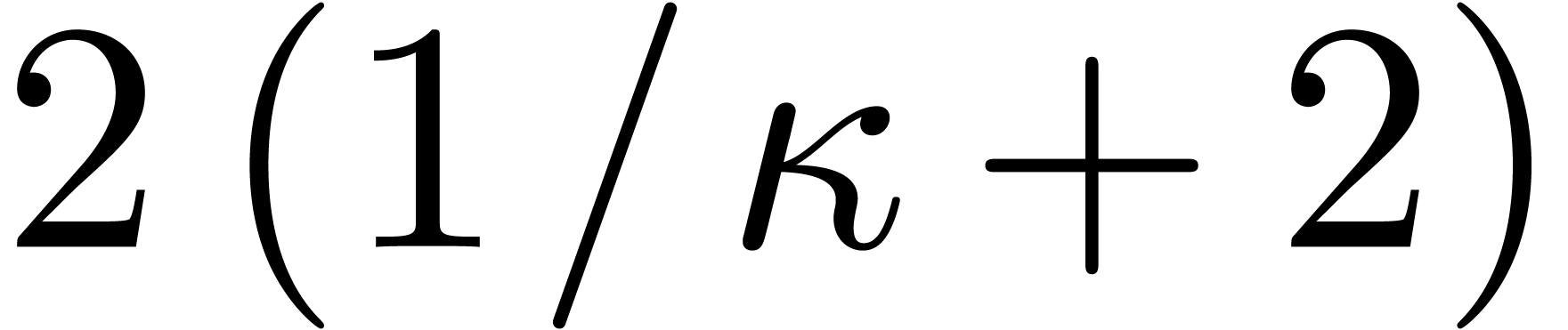 rectangles in the product subdivision, for which
the admissible part contains a pair
rectangles in the product subdivision, for which
the admissible part contains a pair 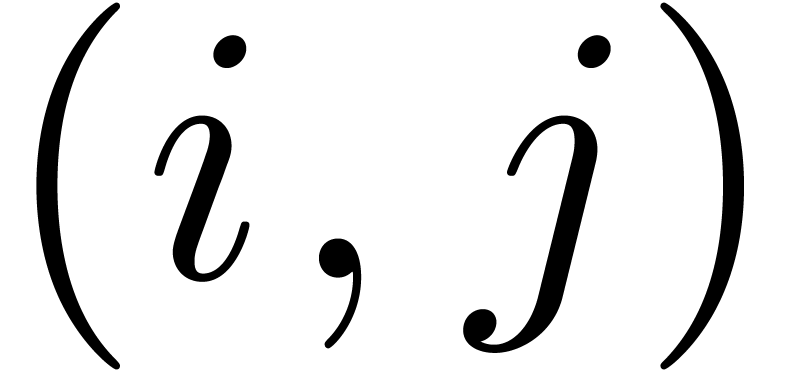 with
with 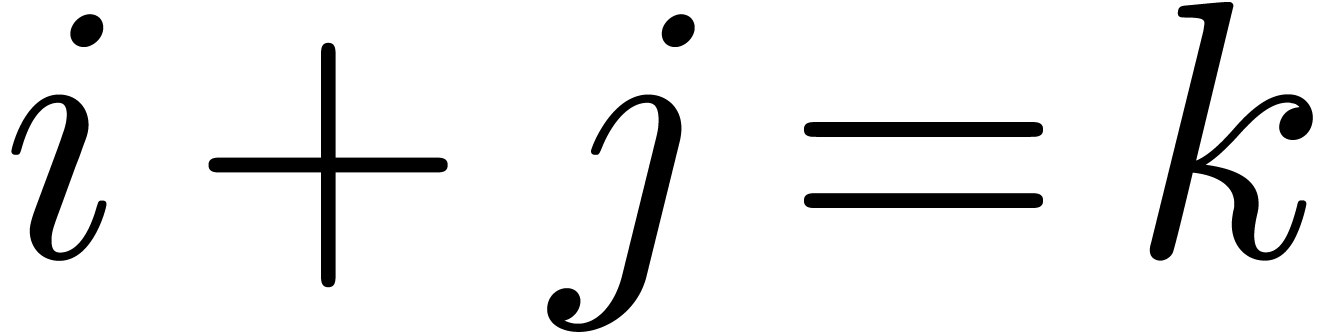 .
.
Proof. Assume the contrary and let  and
and  be the top left and bottom
right rectangles in the product subdivision, for which the admissible
parts contribute to
be the top left and bottom
right rectangles in the product subdivision, for which the admissible
parts contribute to  . We have
. We have
 or
or  .
By symmetry, we may assume
.
By symmetry, we may assume 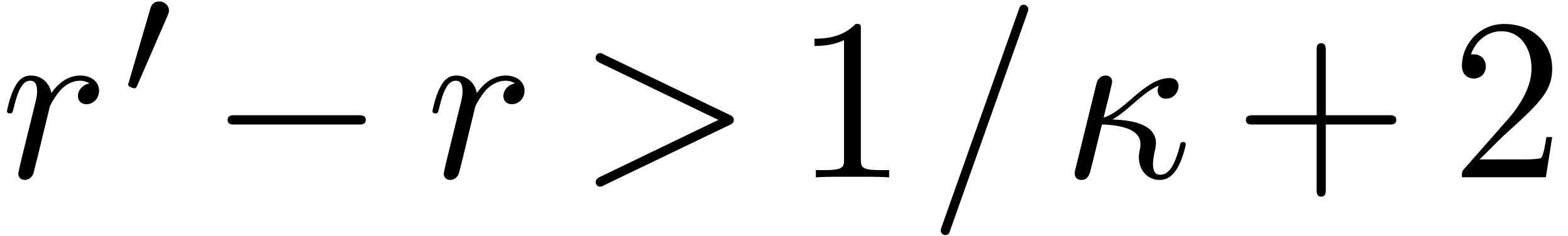 . Now consider the
convex max-plus polynomials
. Now consider the
convex max-plus polynomials
Using (17), we have 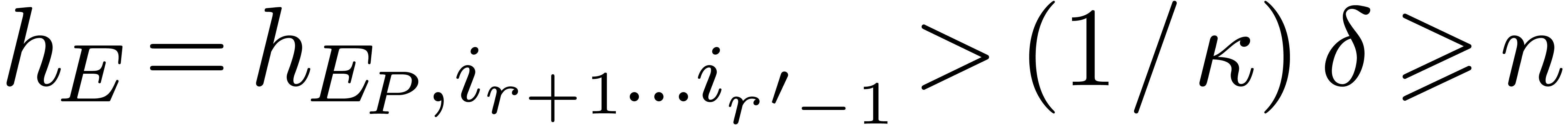 .
From (15) and (16), we thus get
.
From (15) and (16), we thus get
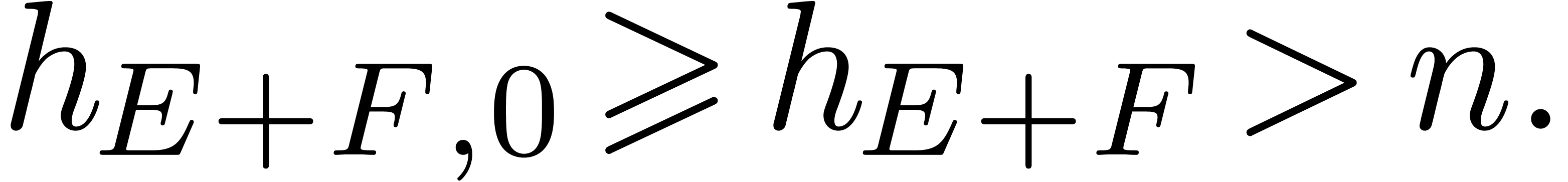
Now  coincides with
coincides with 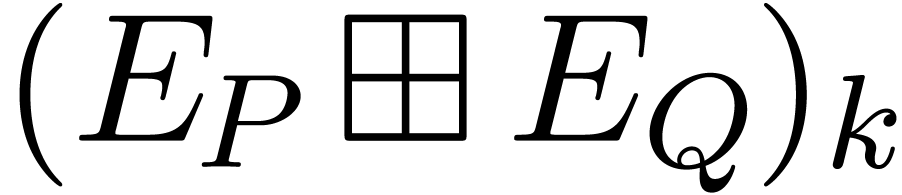 ,
whence there exists an index
,
whence there exists an index 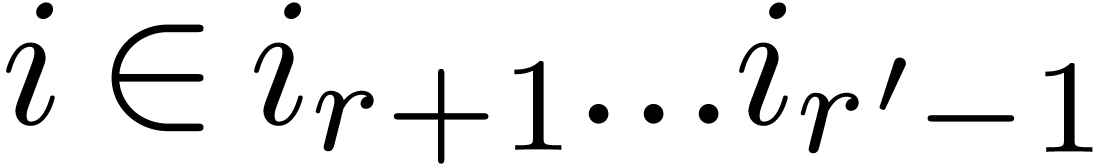 with
with
which means that the pair 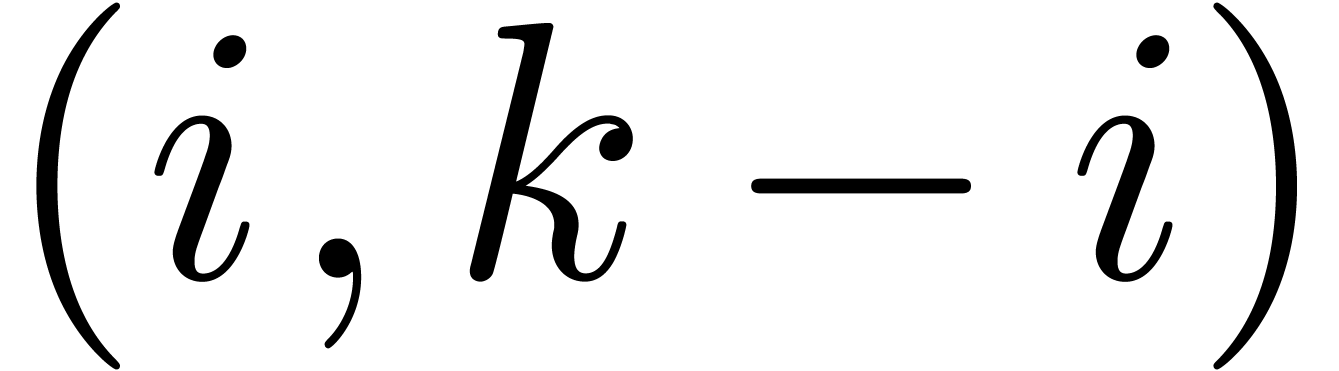 is negligible. But
this is only possible if either
is negligible. But
this is only possible if either 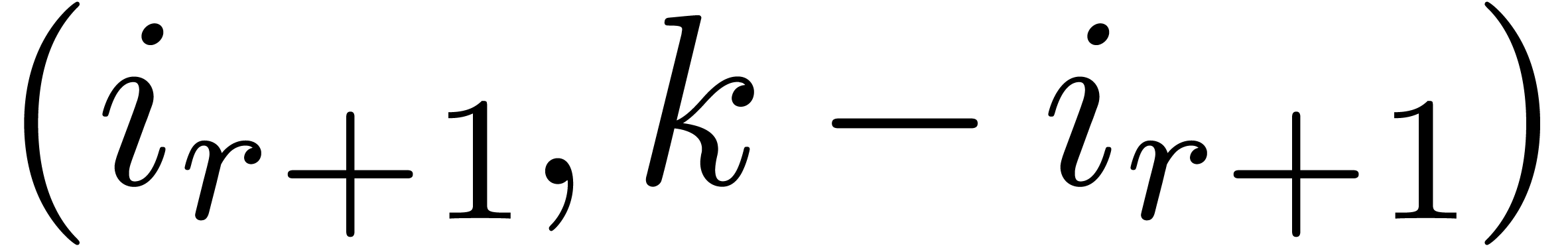 or
or 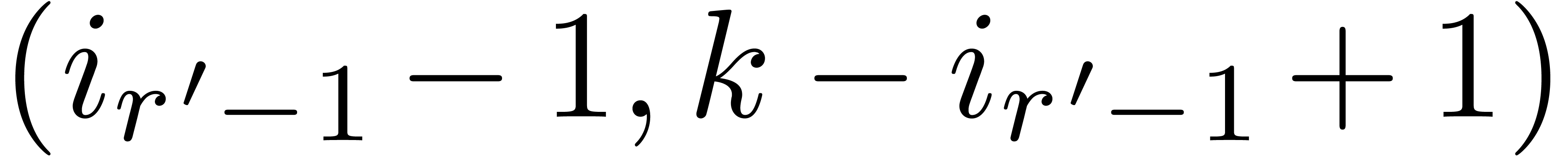 is also negligible. This, in its turn, implies that either
the rectangle
is also negligible. This, in its turn, implies that either
the rectangle  or the rectangle
or the rectangle  is negligible, in contradiction with our hypothesis.
is negligible, in contradiction with our hypothesis.
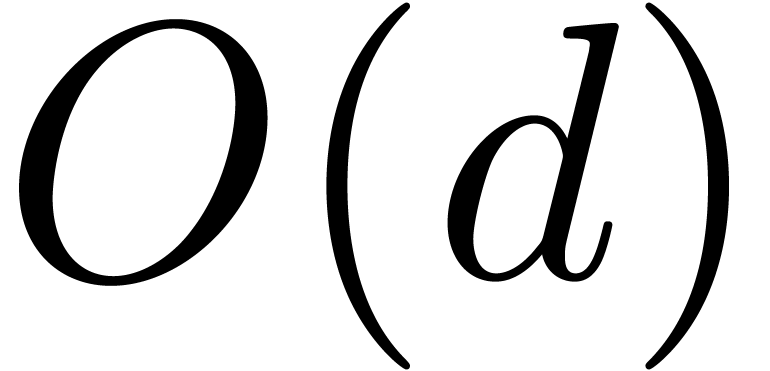 non-negligible
rectangles in the product subdivision, and they can be computed in
linear time.
non-negligible
rectangles in the product subdivision, and they can be computed in
linear time.
Proof. The first assertion follows from the
facts that each diagonal 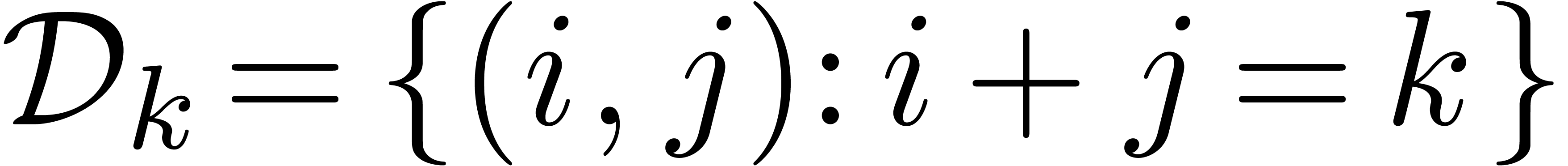 with
with 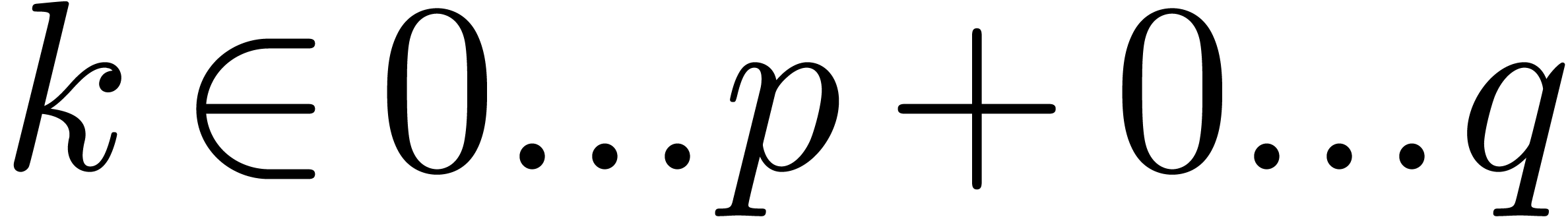 intersects at most
intersects at most 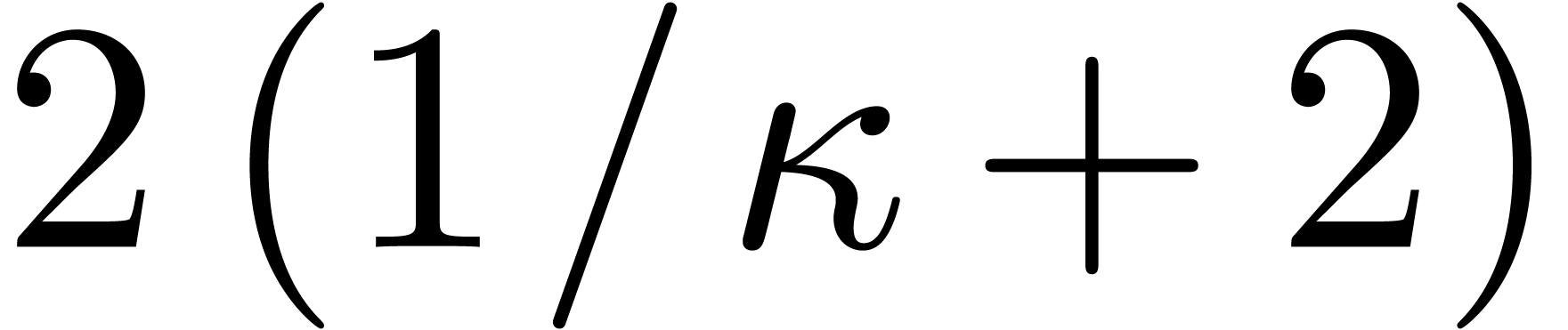 rectangles and that there are
less than
rectangles and that there are
less than 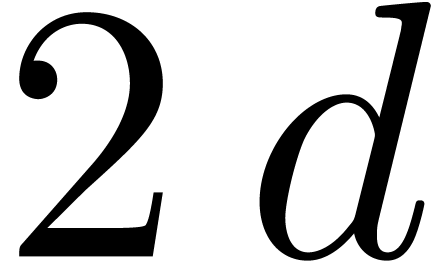 such diagonals. The rectangles can be
computed in time
such diagonals. The rectangles can be
computed in time 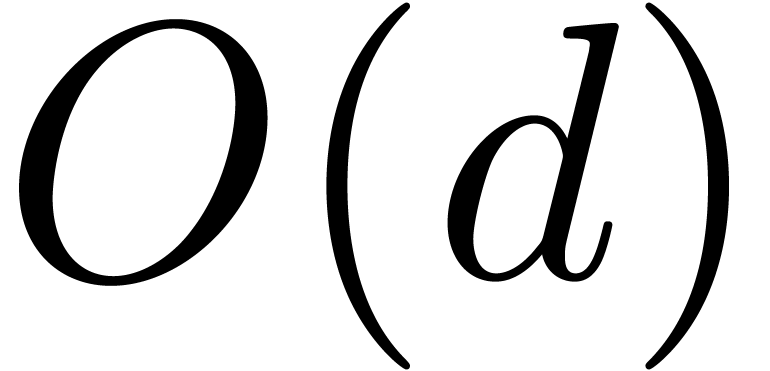 , by
following the lower and upper limits
, by
following the lower and upper limits 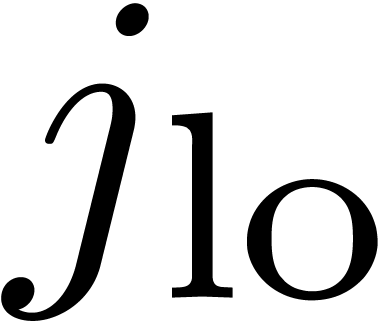 and
and 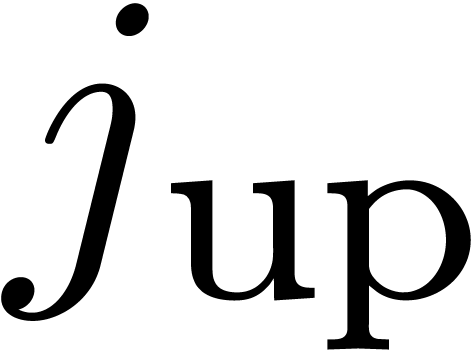 of the zone of non-negligible pairs.
of the zone of non-negligible pairs.
The subdivision we are really after refines (18). More
precisely, consider a non-negligible rectangle  of the form
of the form  . Let
. Let
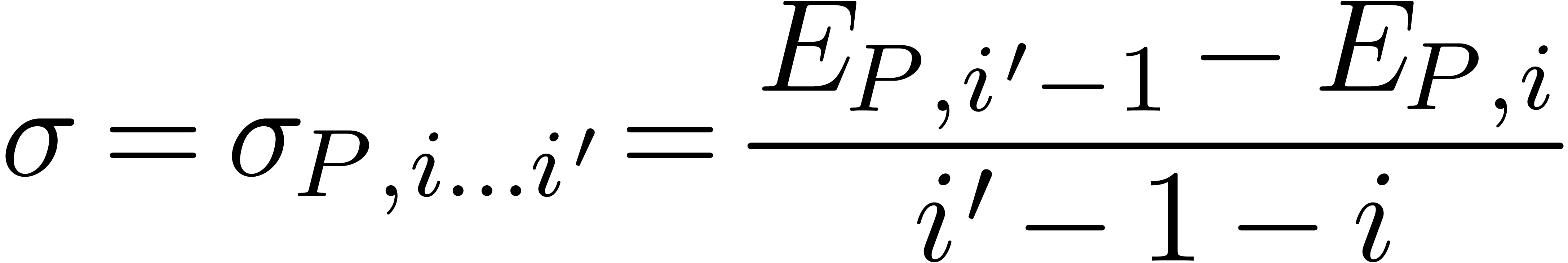
be the slope of  on
on  .
Swapping
.
Swapping  and
and  if
necessary, we may assume without loss of generality that
if
necessary, we may assume without loss of generality that 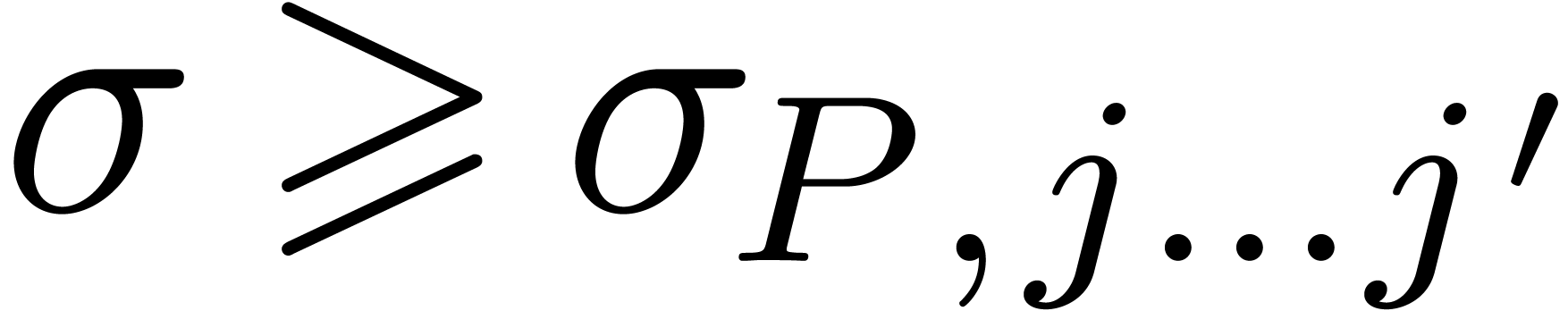 . We now construct the sequence
. We now construct the sequence  , by choosing each
, by choosing each 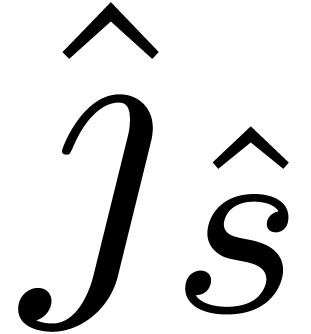 minimal such that
minimal such that 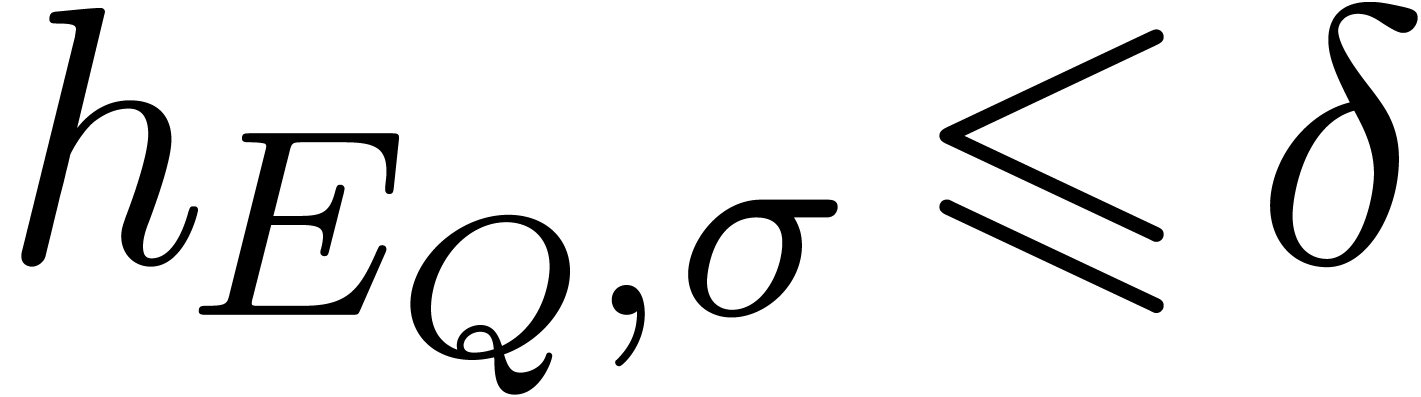 , and
subdivide
, and
subdivide
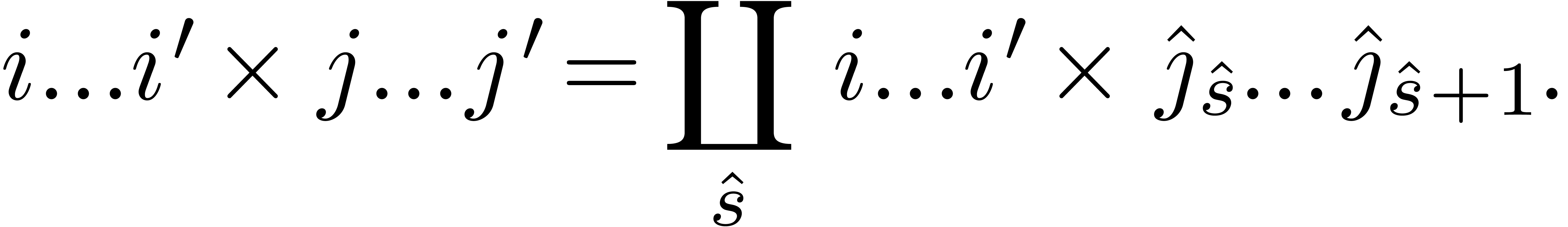 |
(19) |
We may re-interpret figure 1 as an illustration of the
non-negligible pairs inside the rectangle  ,
together with the subdivision (19) and its corresponding
admissible part. Performing the replacement (19) for all
non-negligible rectangles
,
together with the subdivision (19) and its corresponding
admissible part. Performing the replacement (19) for all
non-negligible rectangles  in (18),
while leaving the negligible rectangles untouched, we obtain a finer
subdivision of
in (18),
while leaving the negligible rectangles untouched, we obtain a finer
subdivision of  , which we
call the Newton subdivision.
, which we
call the Newton subdivision.
 , there exist at most
, there exist at most 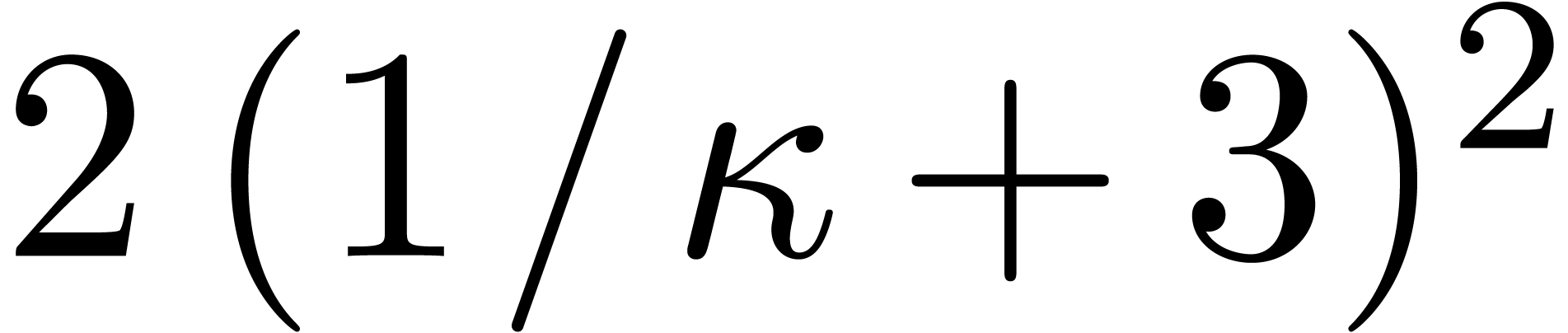 rectangles in the Newton subdivision, for which the
admissible part contains a pair
rectangles in the Newton subdivision, for which the
admissible part contains a pair 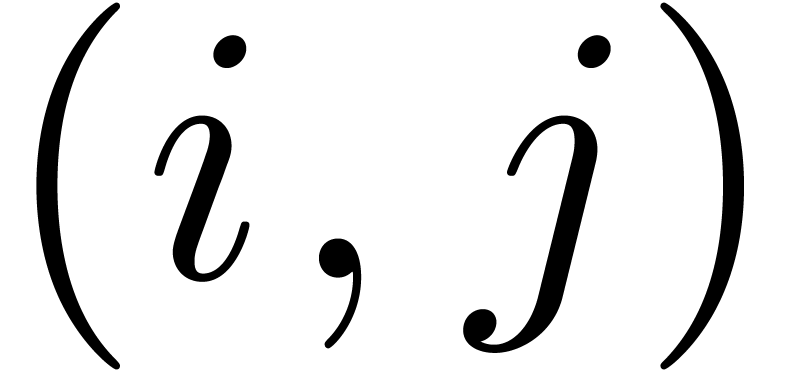 with
with  .
.
Proof. Consider a non-negligible rectangle  in the product subdivision. In view of lemma (4), it suffices to show that there exists at most
in the product subdivision. In view of lemma (4), it suffices to show that there exists at most 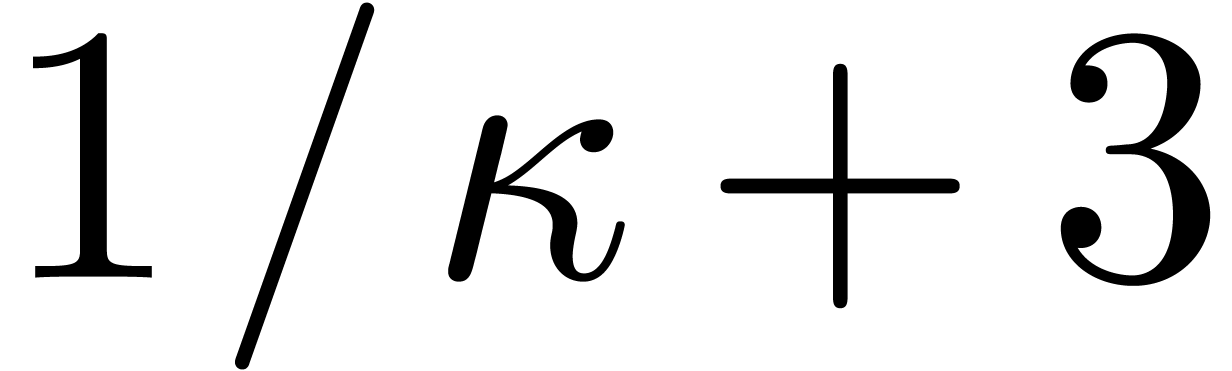 rectangles in the admissible part of its subdivision (19) which contribute to
rectangles in the admissible part of its subdivision (19) which contribute to  .
.
Now assume that  and
and 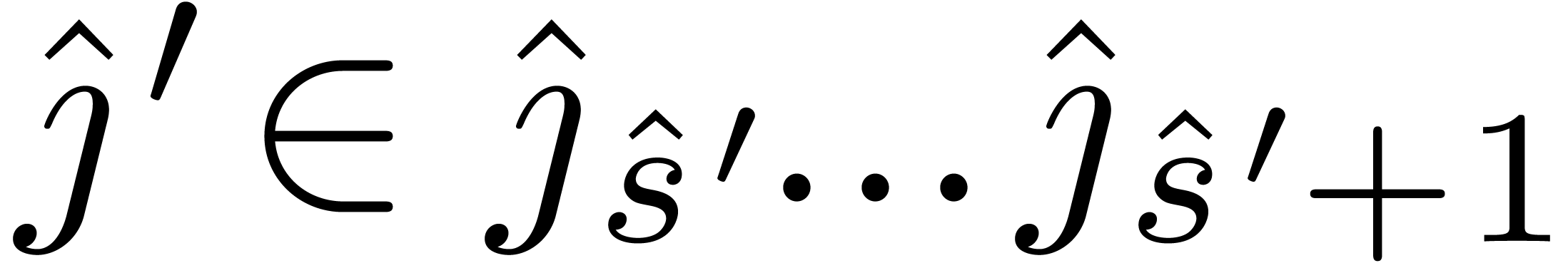 satisfy
satisfy 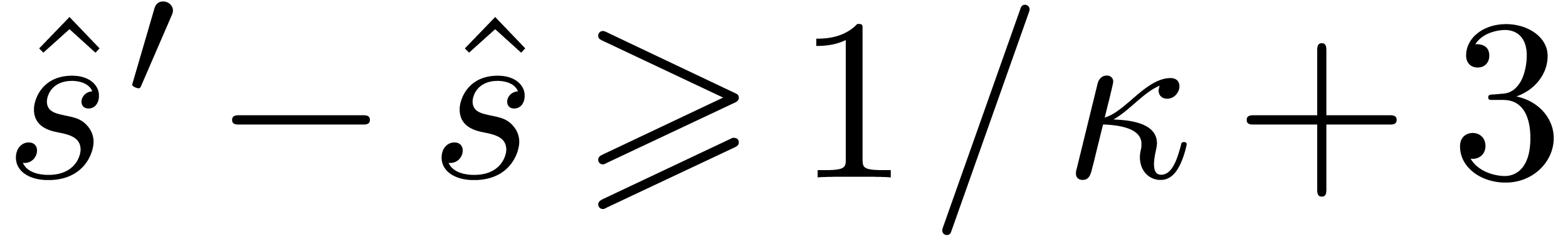 and assume that
and assume that 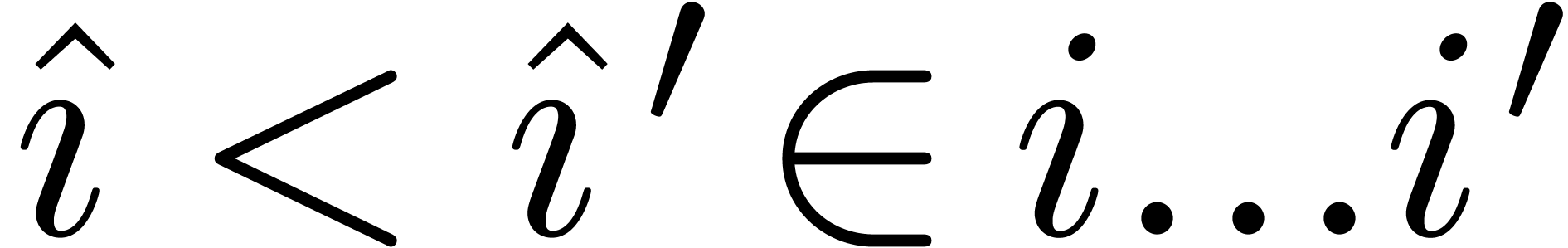 satisfy
satisfy 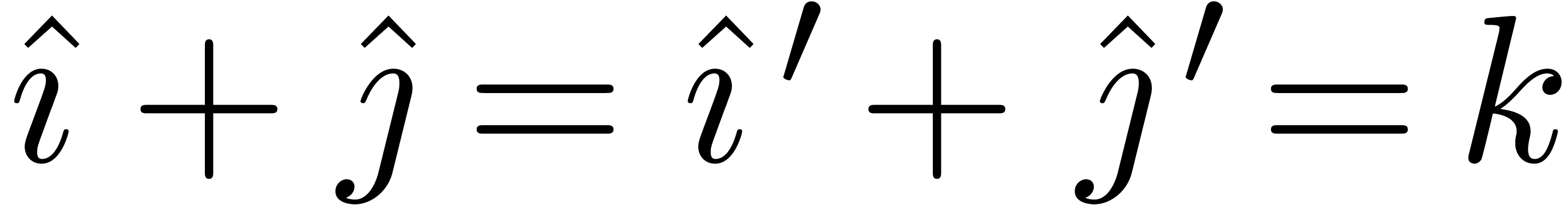 . Setting
. Setting 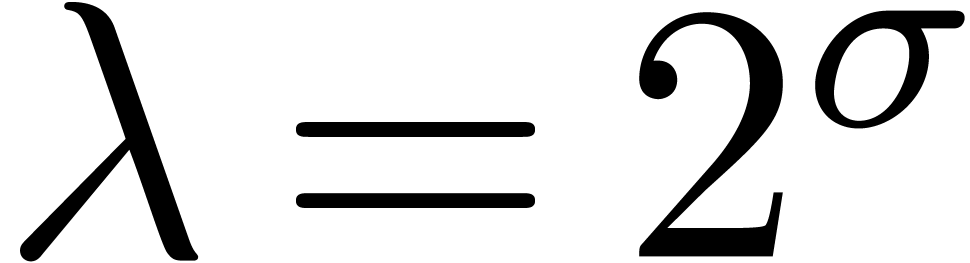 , we then have
, we then have
whence
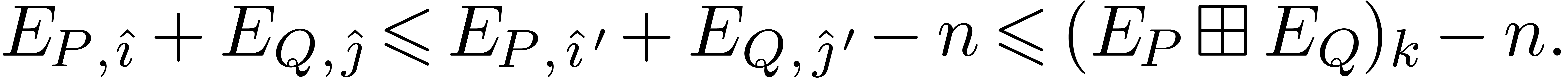
This shows that the pair 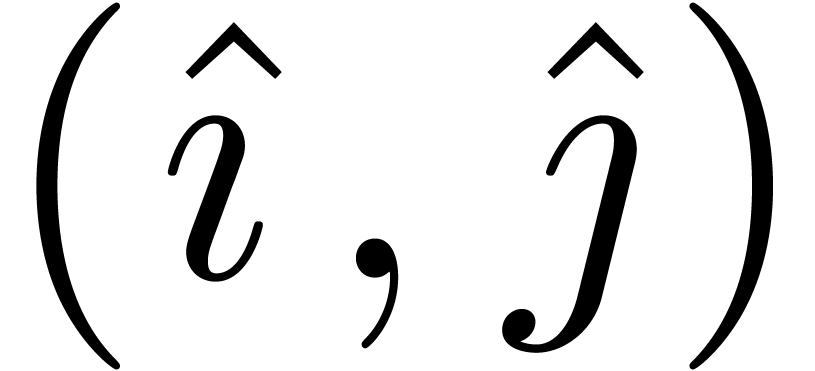 is negligible. We
conclude that the diagonal
is negligible. We
conclude that the diagonal 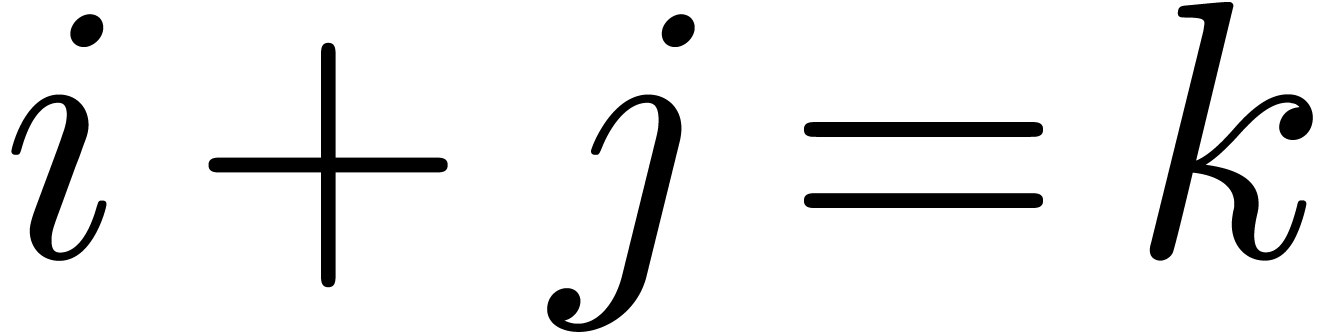 intersects at most
intersects at most
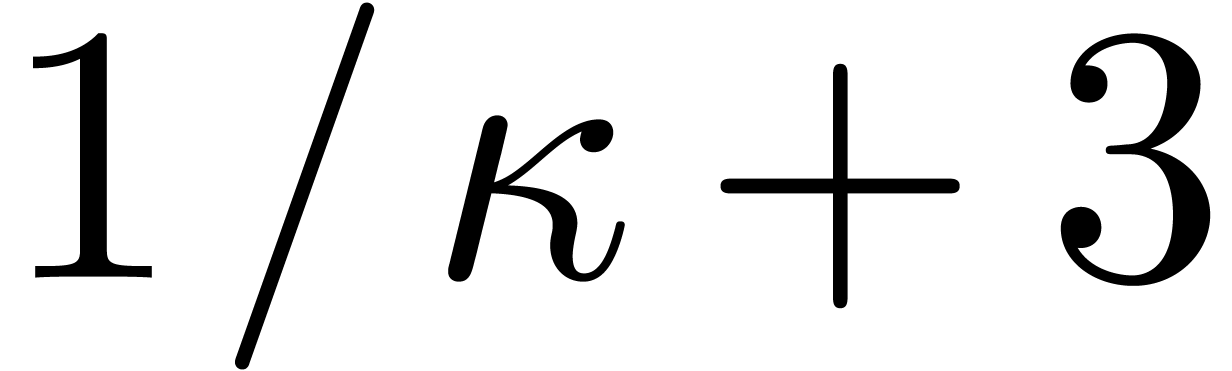 admissible rectangles.
admissible rectangles.
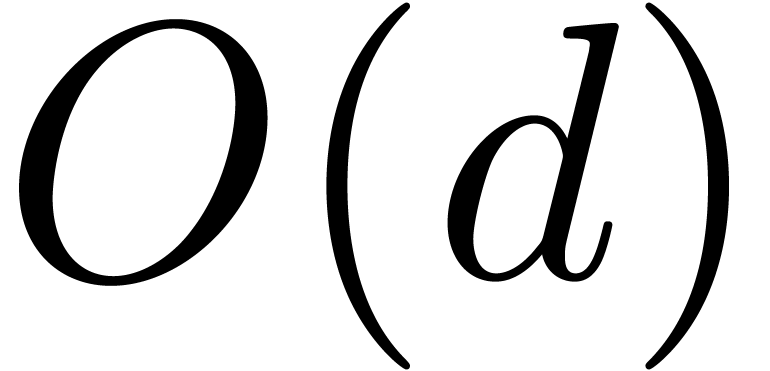 non-negligible
rectangles in the Newton subdivision, and they can be computed in
linear time.
non-negligible
rectangles in the Newton subdivision, and they can be computed in
linear time.
We can now describe our algorithm for computing the product 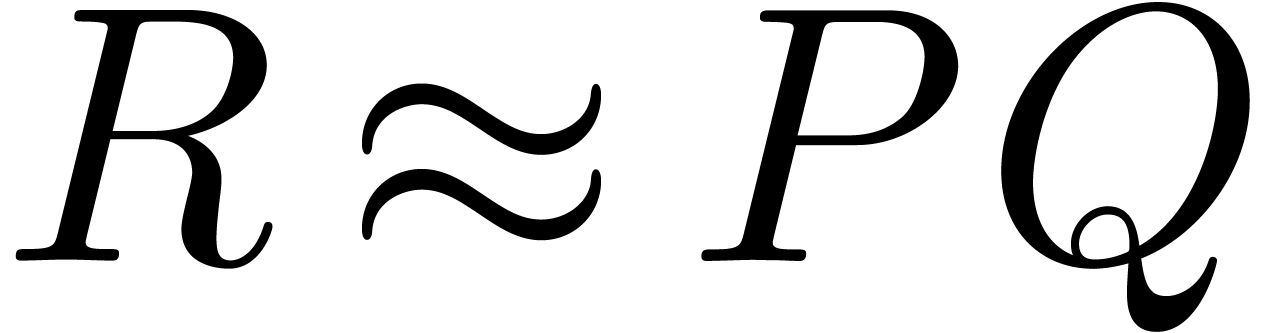 . We start by the computation of the admissible
part of the Newton subdivision. For each rectangle
. We start by the computation of the admissible
part of the Newton subdivision. For each rectangle  in this admissible part, we compute its contribution to
in this admissible part, we compute its contribution to  as follows. By construction, we have
as follows. By construction, we have 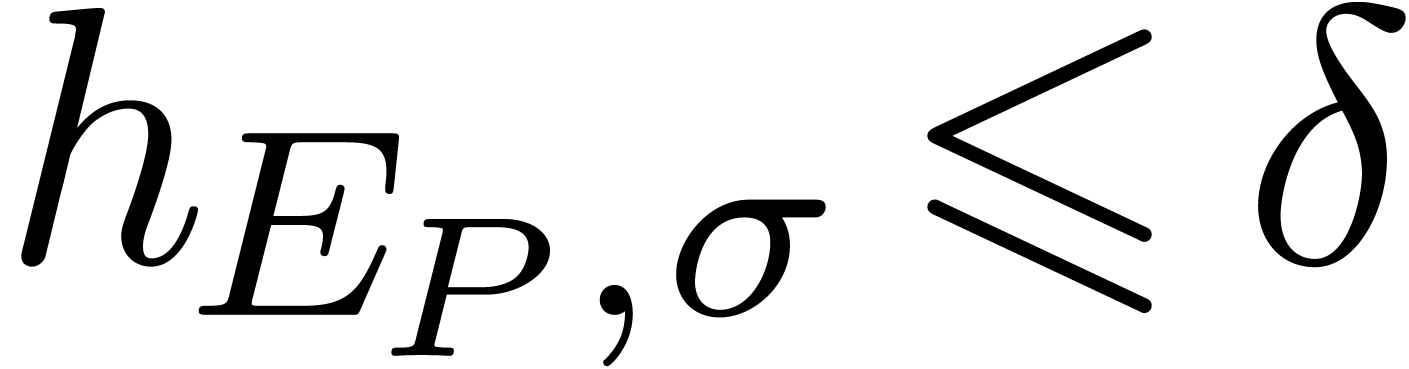 or
or 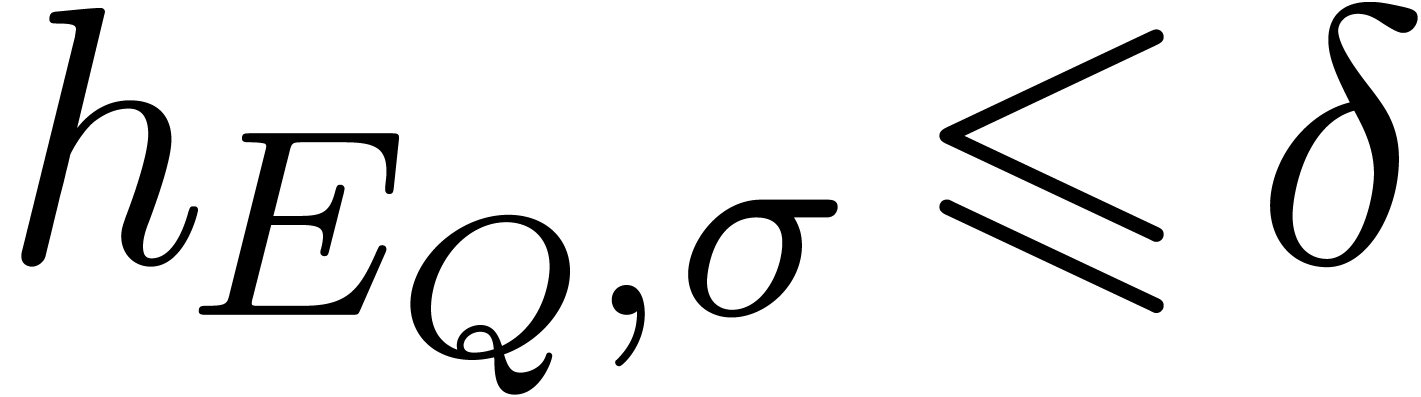 for
for 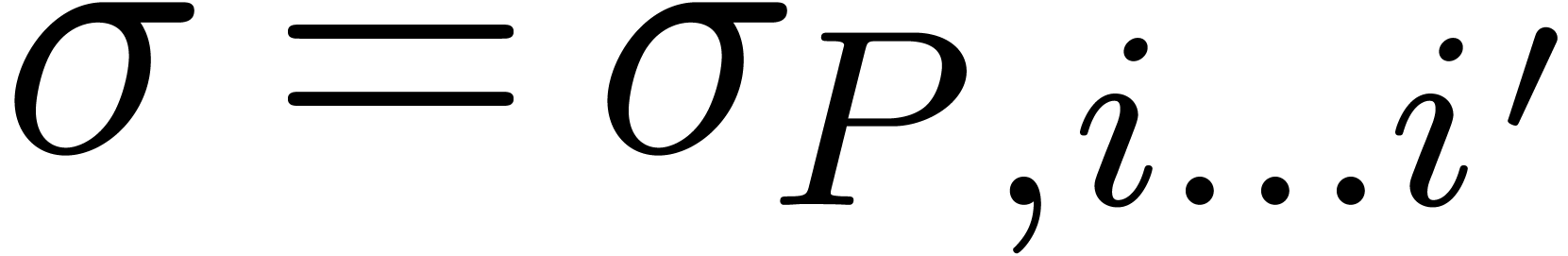 or
or 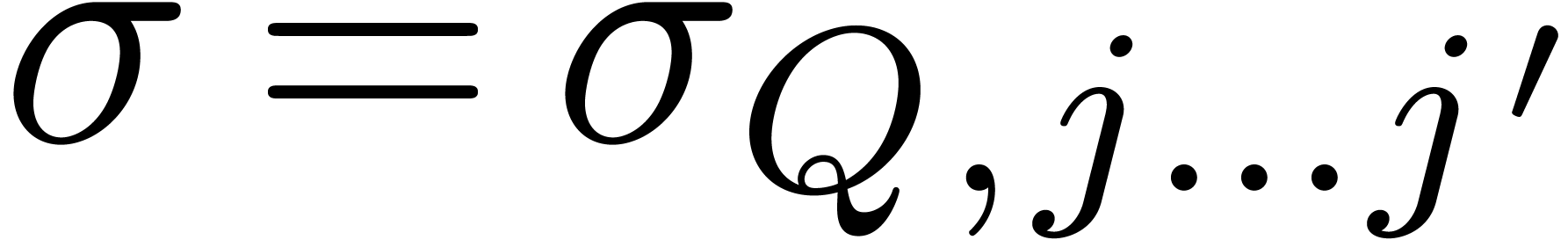 . Setting
. Setting 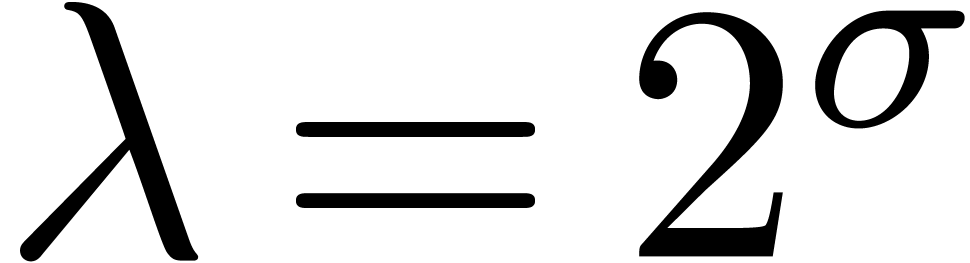 ,
we compute the contribution
,
we compute the contribution 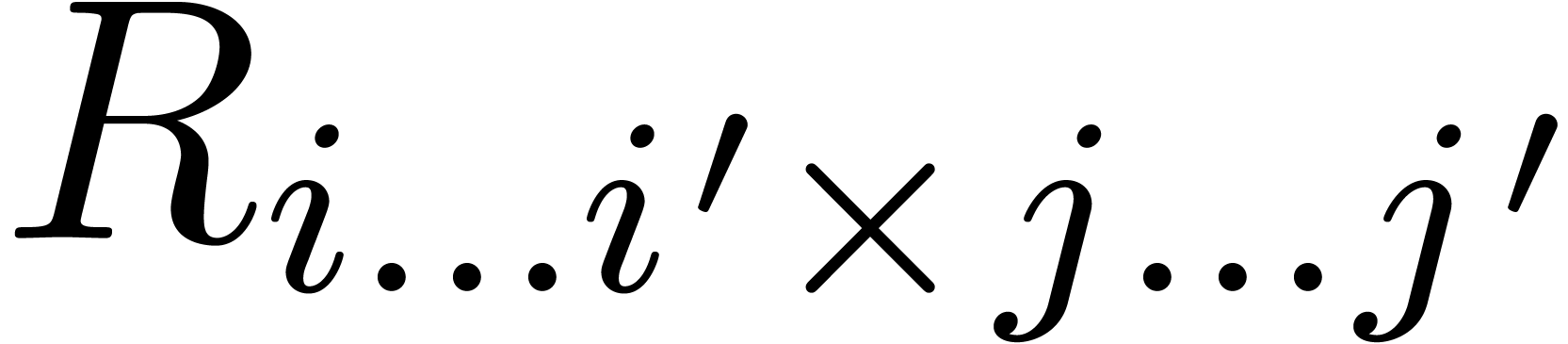 of
of 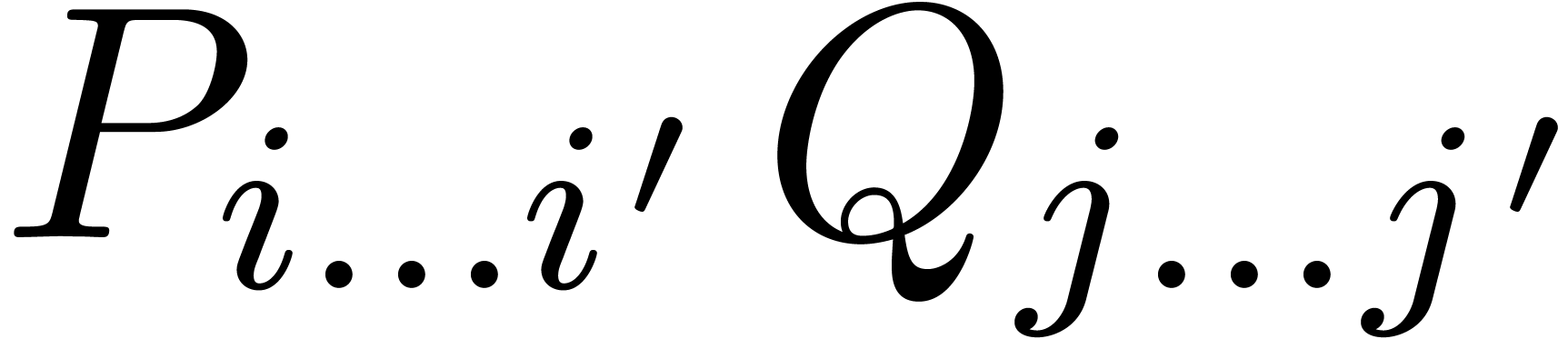 to
to  using the multiplication method with scaling
from section 3,
using the multiplication method with scaling
from section 3,
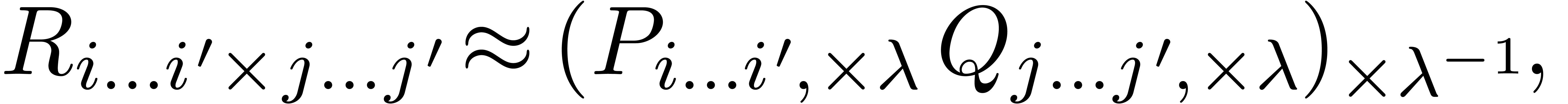 |
(20) |
using a precision of  instead of
instead of  bits. The final result
bits. The final result 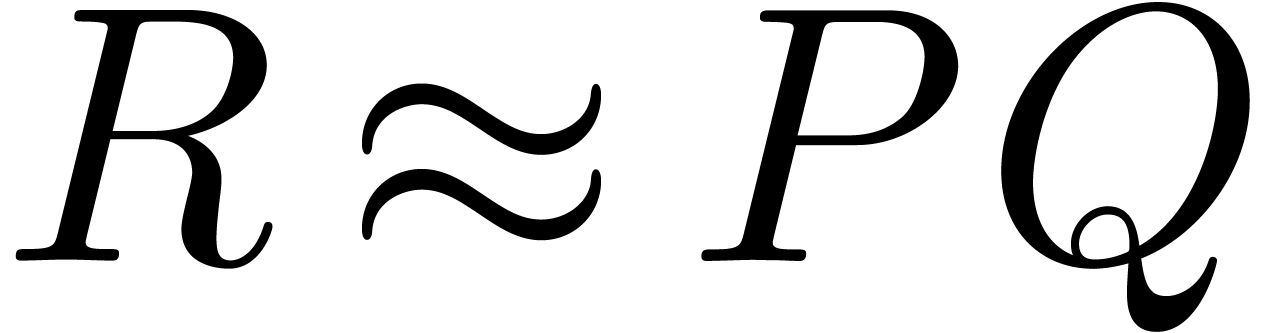 is obtained by summing
all partial products
is obtained by summing
all partial products 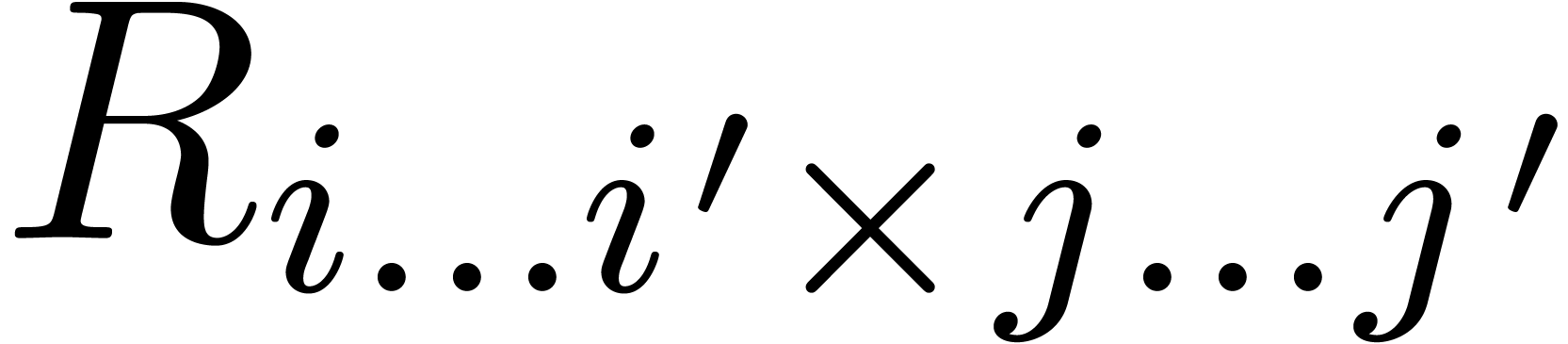 using straightforward
floating point arithmetic. This algorithm leads to the following
refinement of theorem 1.
using straightforward
floating point arithmetic. This algorithm leads to the following
refinement of theorem 1.
 , which computes
, which computes 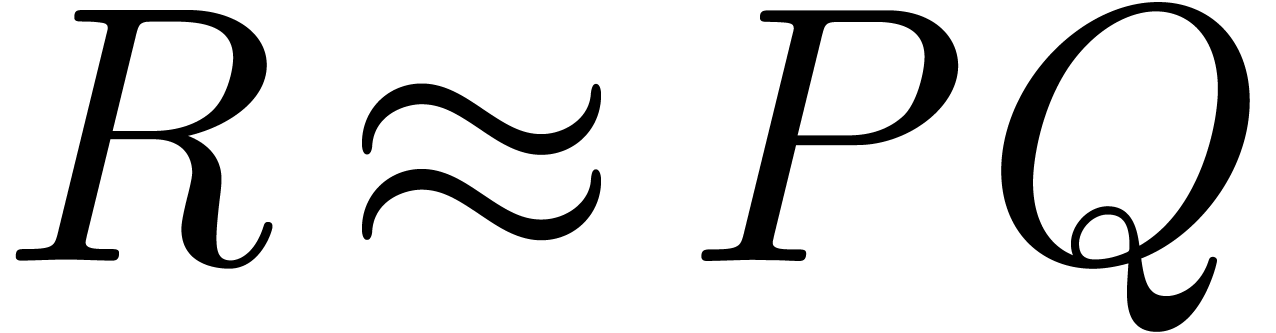 with
relative Newton error
with
relative Newton error
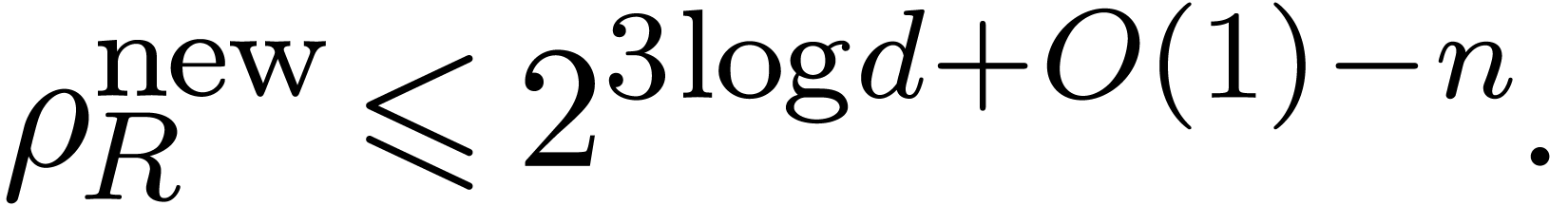 |
(21) |
Proof. We claim that the computation of the
product (20) using a precision of  bits contributes to the relative Newton error of the global product
bits contributes to the relative Newton error of the global product  by an amount which is bounded by
by an amount which is bounded by 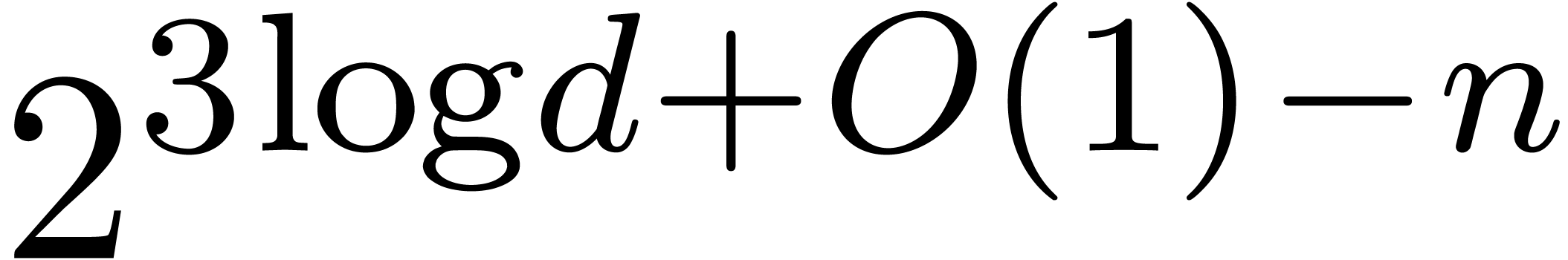 . This clearly implies (21), since
for a fixed coefficient
. This clearly implies (21), since
for a fixed coefficient  in the product, at most
in the product, at most
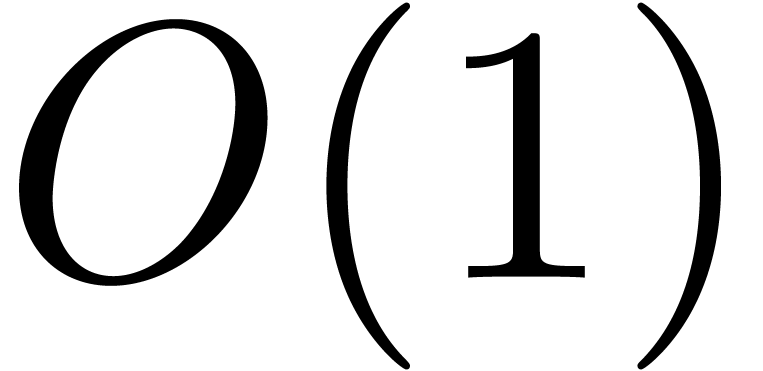 partial products of the form
partial products of the form 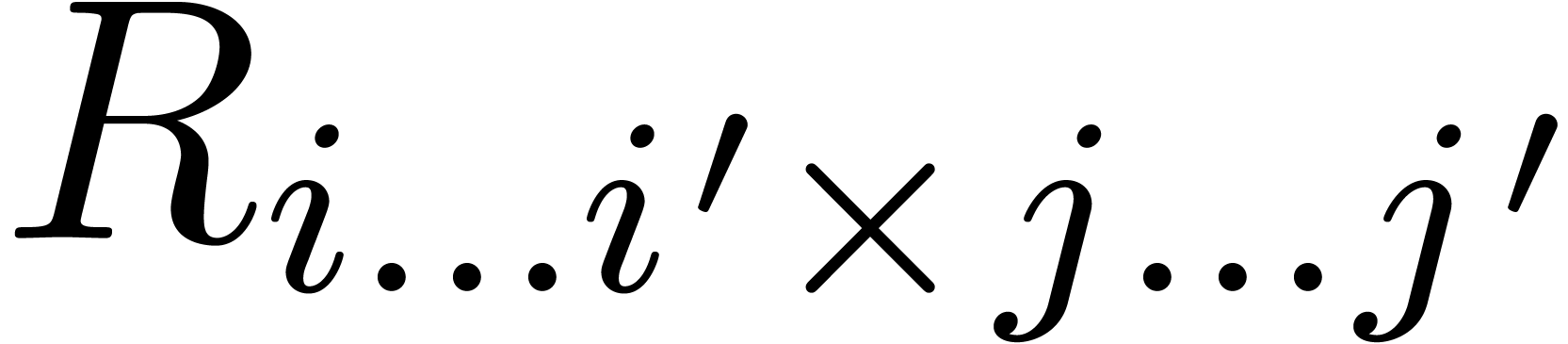 contribute to
contribute to  .
.
Setting 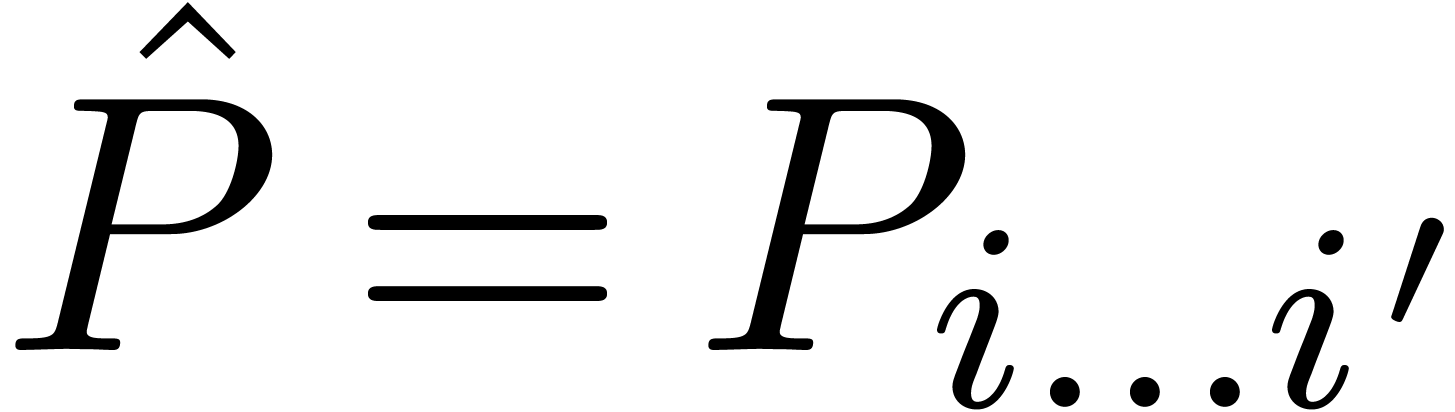 ,
, 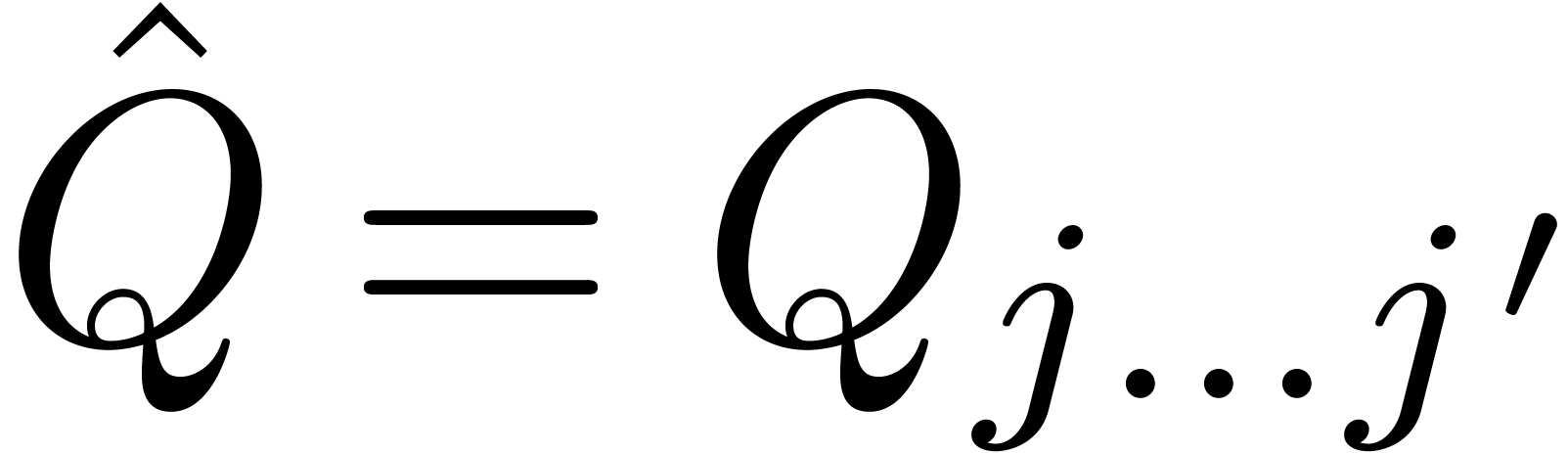 and
and 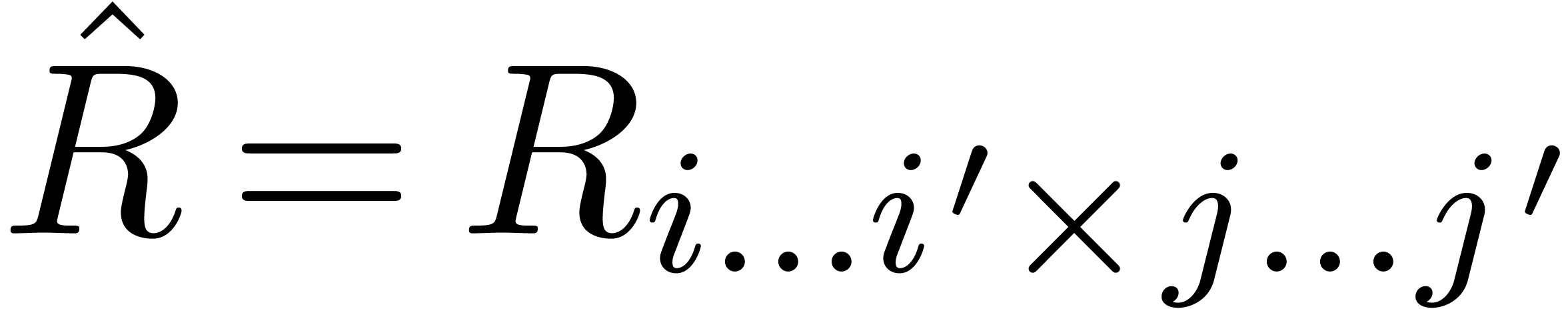 , the bound (8)
yields
, the bound (8)
yields
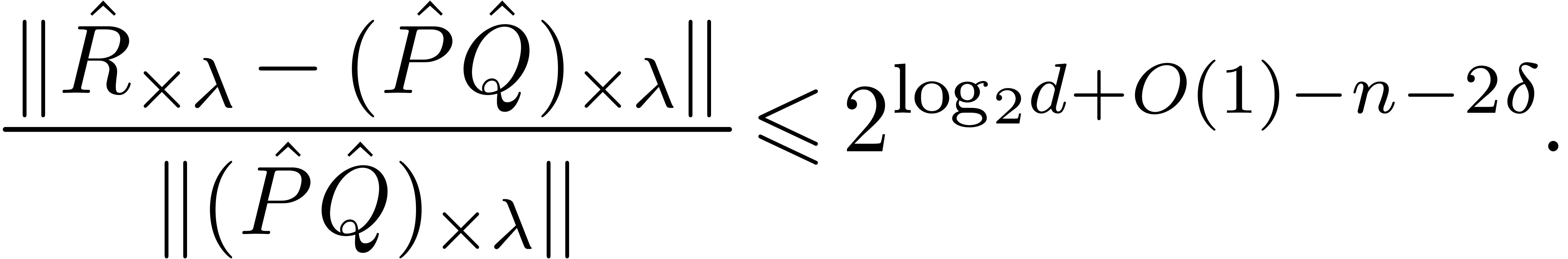
For any 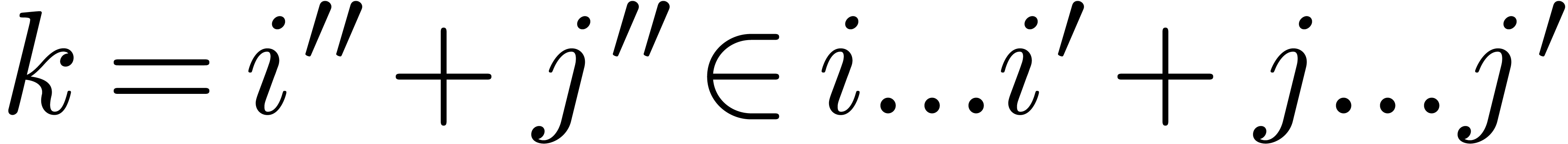 , the bounds (2), (14) and proposition 3 also
imply
, the bounds (2), (14) and proposition 3 also
imply
Combining both estimates, we obtain
This completes the proof of our claim.
The proof of the complexity bound relies on lemma 6. Let
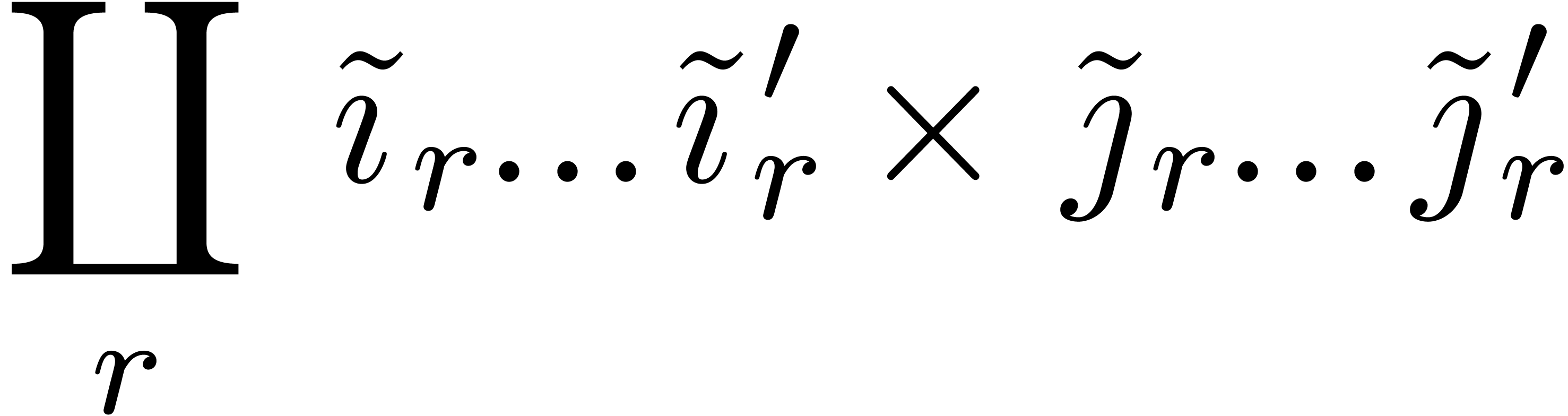
be the admissible part of the Newton subdivision and let 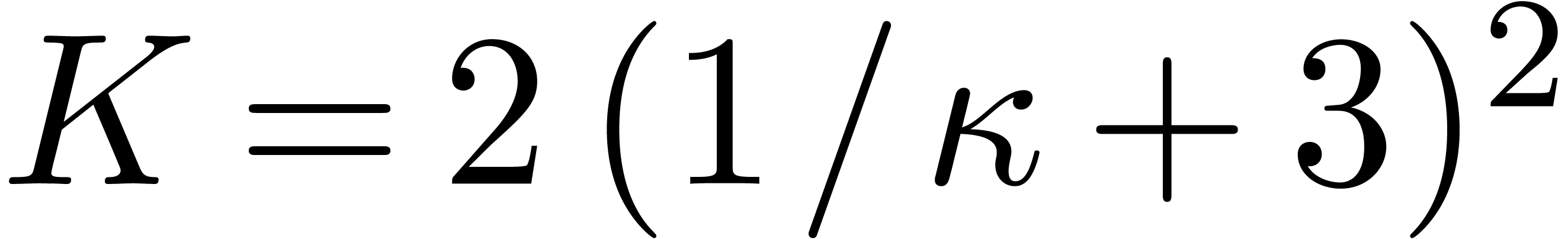 . Consider the total length
. Consider the total length
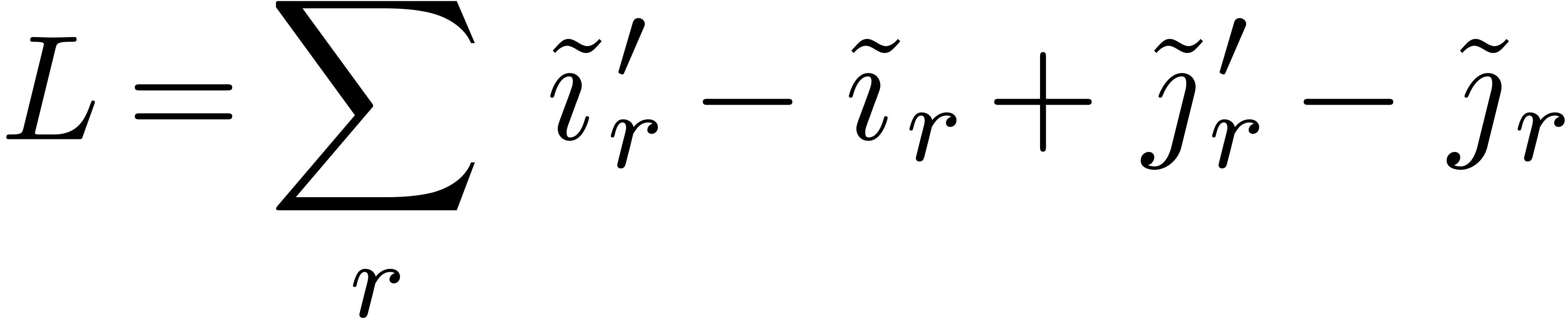
of the left borders and the lower borders of all rectangles  . Since every diagonal hits the union of these
borders in at most
. Since every diagonal hits the union of these
borders in at most 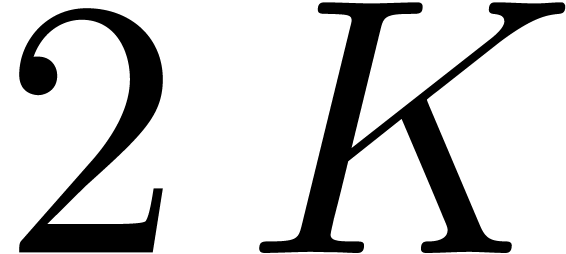 points, we have
points, we have  . The total cost of all multiplications
. The total cost of all multiplications 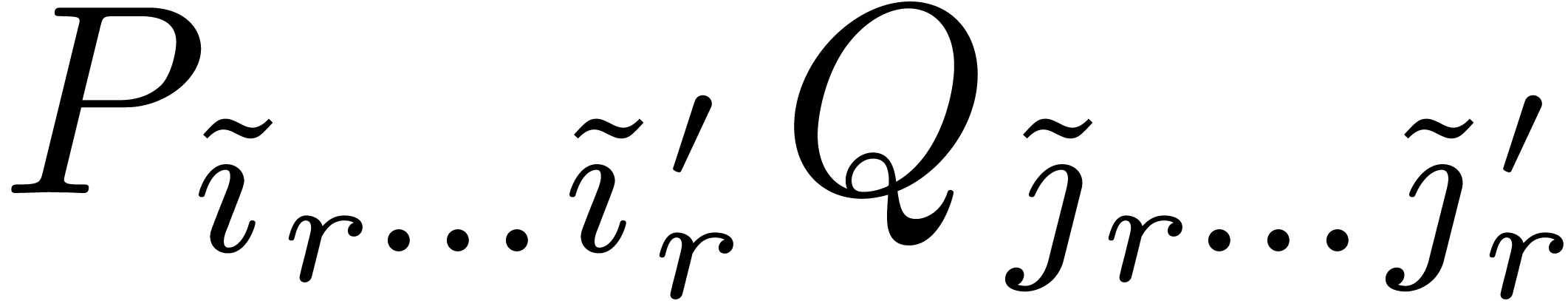 is therefore bounded by
is therefore bounded by
This completes the proof of our theorem.
Remark 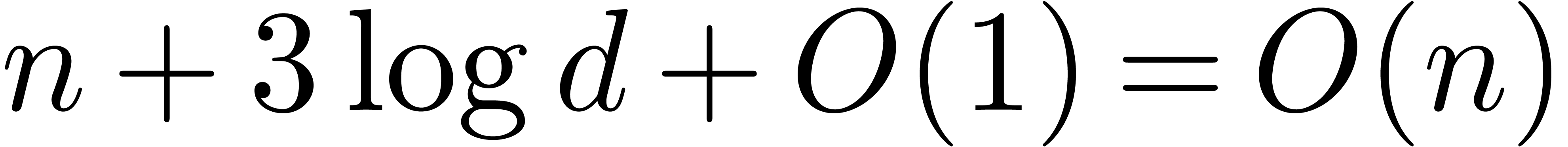 .
.
Now that we have an efficient multiplication which is numerically stable in terms of the relative Newton error, it is interesting to investigate this concept a bit closer. First of all, its name is justified by the property
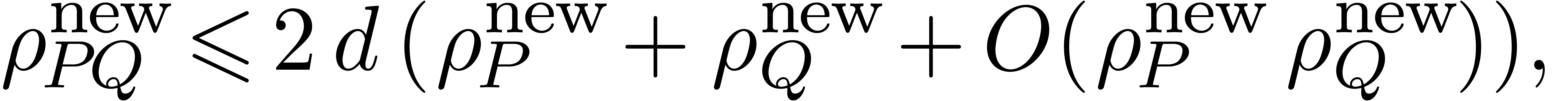
which follows from proposition 3. Some natural numeric
quantities associated to a numeric polynomial  are its coefficients, its roots and its evaluations at points. For our
notion of relative Newton error to be satisfactory, a small relative
Newton error should therefore imply small relative errors for the
coefficients, the roots and evaluations at points.
are its coefficients, its roots and its evaluations at points. For our
notion of relative Newton error to be satisfactory, a small relative
Newton error should therefore imply small relative errors for the
coefficients, the roots and evaluations at points.
Now the example 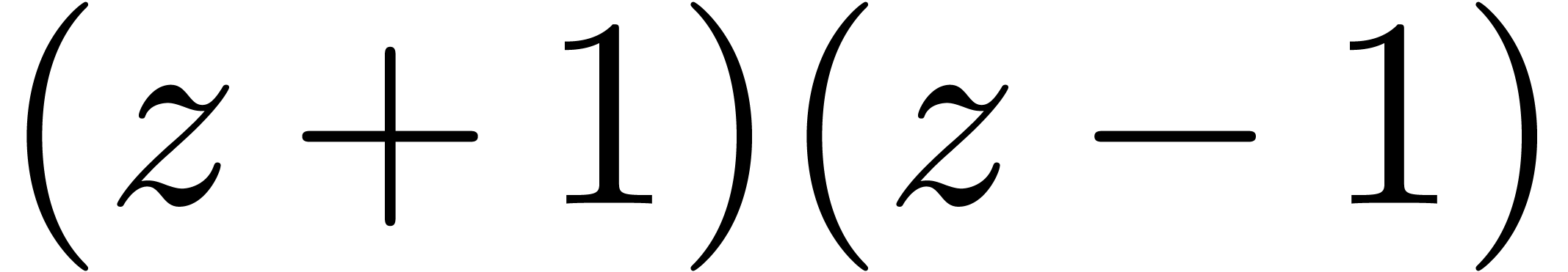 from the introduction shows that
it is impossible to obtain good relative errors for all coefficients.
Nevertheless, given a polynomial
from the introduction shows that
it is impossible to obtain good relative errors for all coefficients.
Nevertheless, given a polynomial  with a small
relative Newton error
with a small
relative Newton error  , we
can at least guarantee small relative errors
, we
can at least guarantee small relative errors 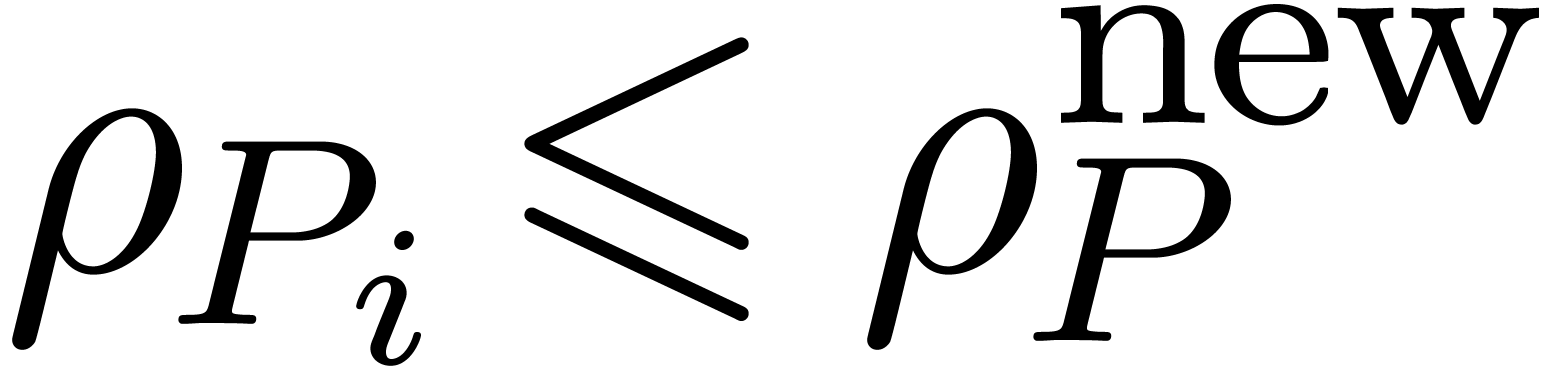 for
those coefficients
for
those coefficients  which correspond to vertices
which correspond to vertices
 of the Newton polygon. For most practical
purposes, we expect this to be sufficient. However, theoretically
speaking, the naive multiplication algorithm of polynomials sometimes
provides better relative errors for other coefficients. This is for
instance the case when squaring a polynomial of the form
of the Newton polygon. For most practical
purposes, we expect this to be sufficient. However, theoretically
speaking, the naive multiplication algorithm of polynomials sometimes
provides better relative errors for other coefficients. This is for
instance the case when squaring a polynomial of the form 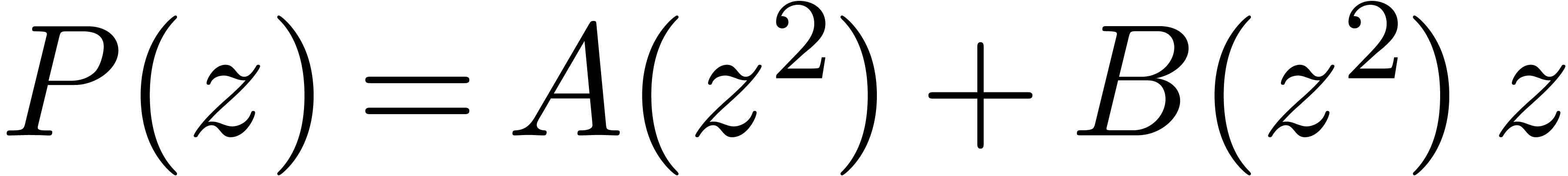 , where
, where  is very small
compared to
is very small
compared to  .
.
For what follows, it will be convenient to redefine  . Let
. Let  denote the set of
roots of
denote the set of
roots of  , ordered by
increasing magnitudes
, ordered by
increasing magnitudes  . By
analogy with the power series setting, the norms
. By
analogy with the power series setting, the norms 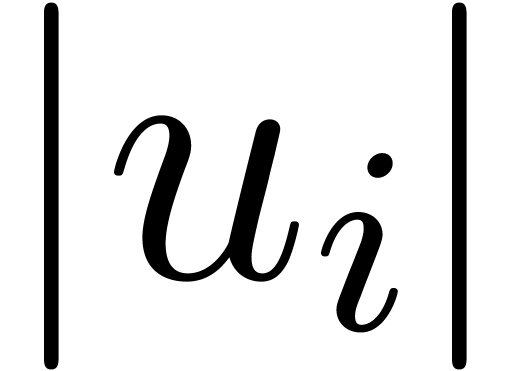 roughly correspond to the slopes
roughly correspond to the slopes 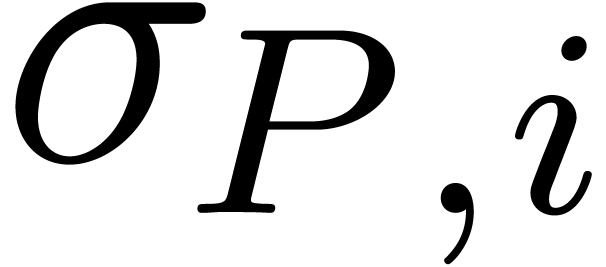 of the Newton
polygon. We expect the existence of a bound
of the Newton
polygon. We expect the existence of a bound
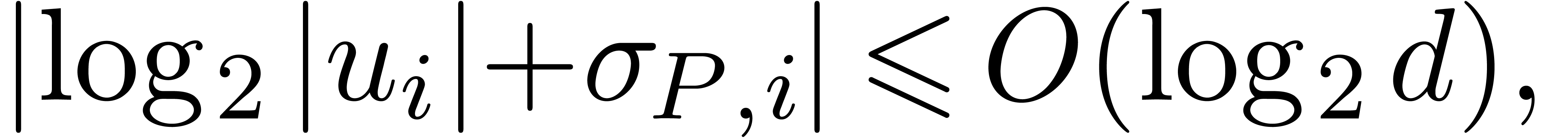
although we have not yet proved this. The worst case arises when  admits a single root of multiplicity
admits a single root of multiplicity 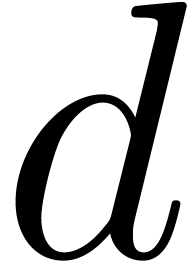 .
.
We define the relative distance 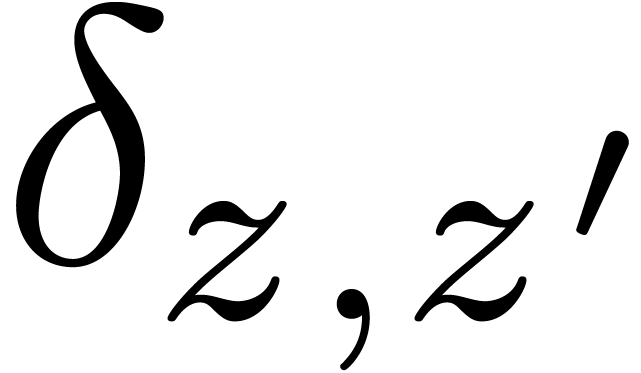 between
between
 (not both zero) by
(not both zero) by
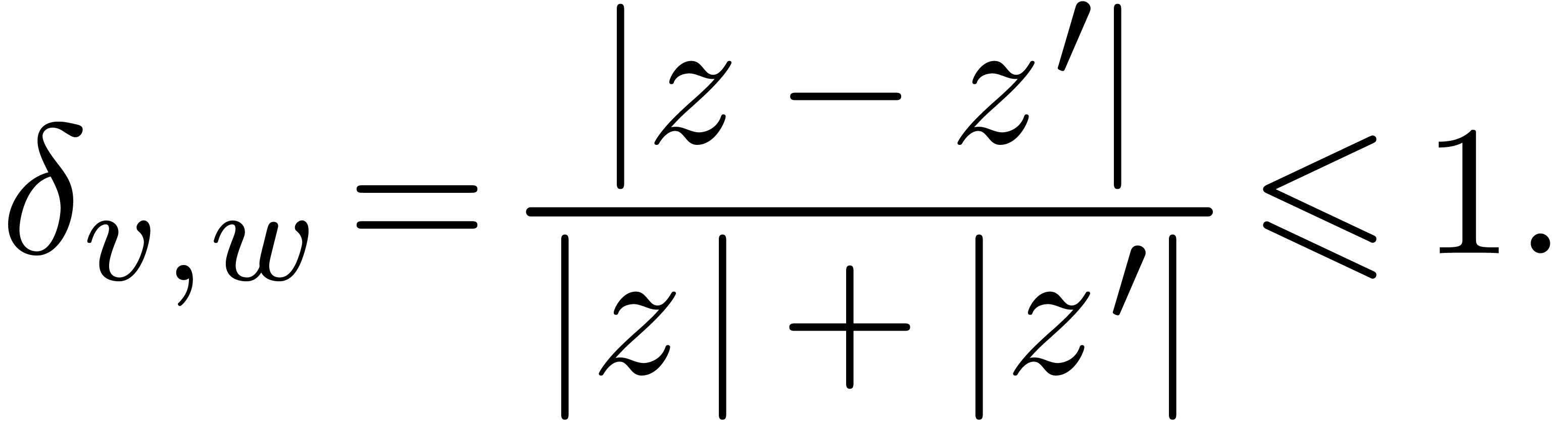
and the relative distance 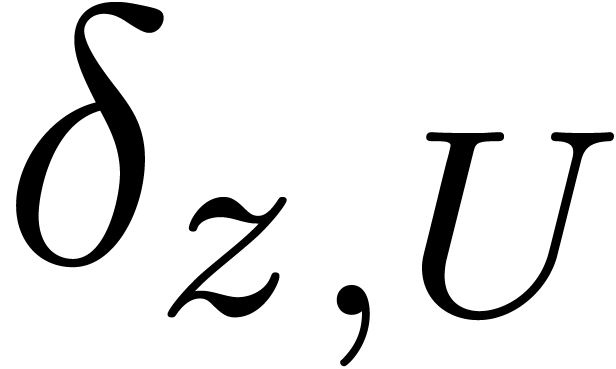 between
between  and
and  , counted
with multiplicities, by
, counted
with multiplicities, by
Clearly, the relative error of the evaluation of  at
at  increases when
increases when  approaches
approaches  . The following
proposition shows that the relative error of
. The following
proposition shows that the relative error of 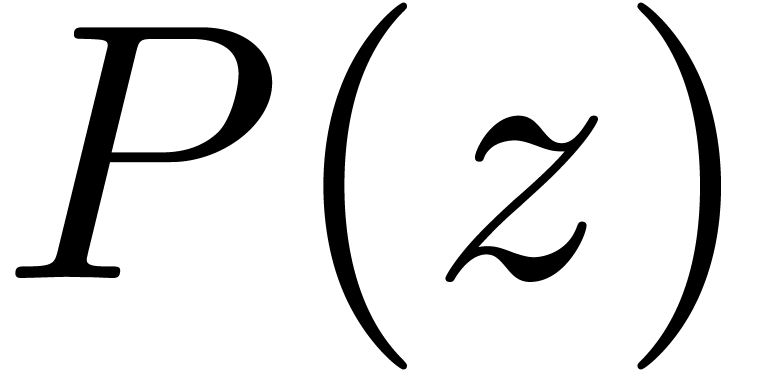 can
be kept small as long as
can
be kept small as long as 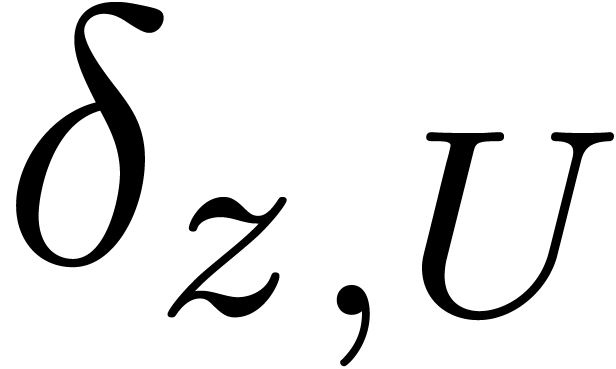 is sufficiently large.
is sufficiently large.
Proof. Modulo a suitable scaling and
multiplication of 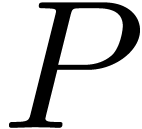 by a constant, we may assume
without loss of generality that
by a constant, we may assume
without loss of generality that 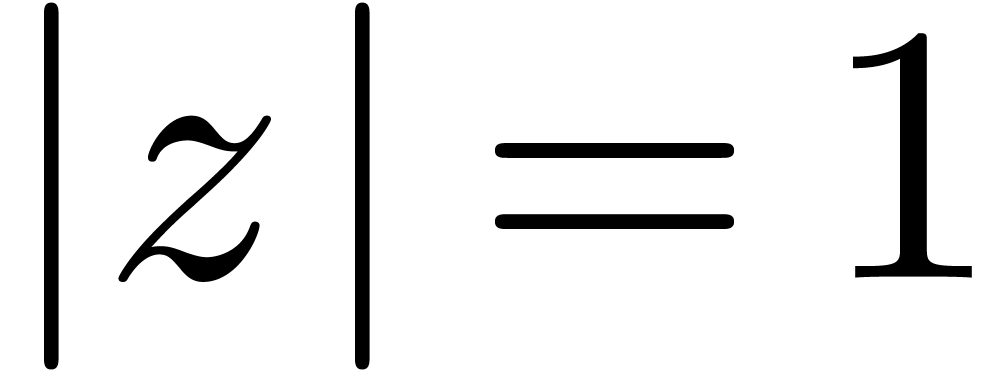 and
and 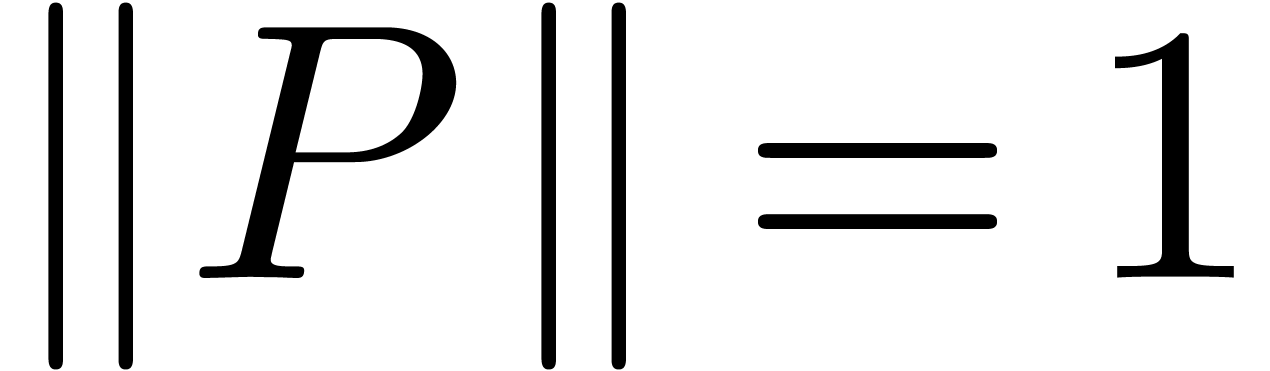 . We claim that
. We claim that 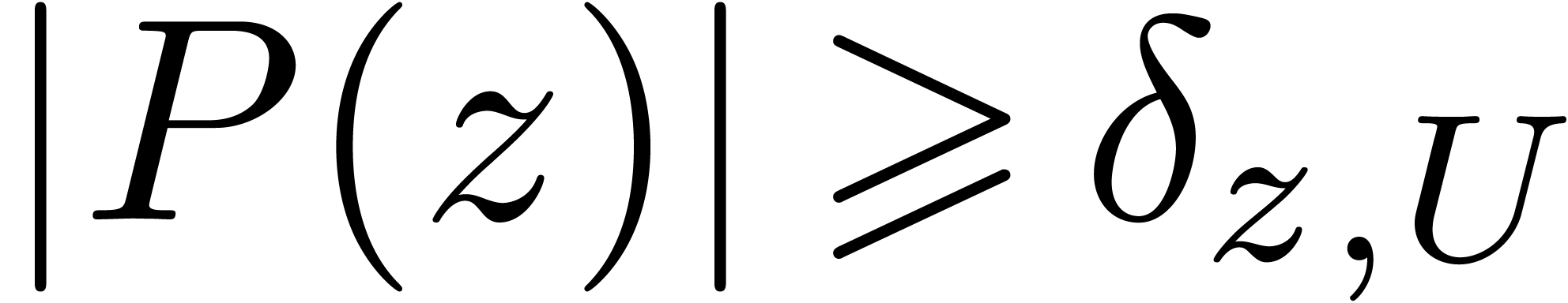 .
Indeed,
.
Indeed,
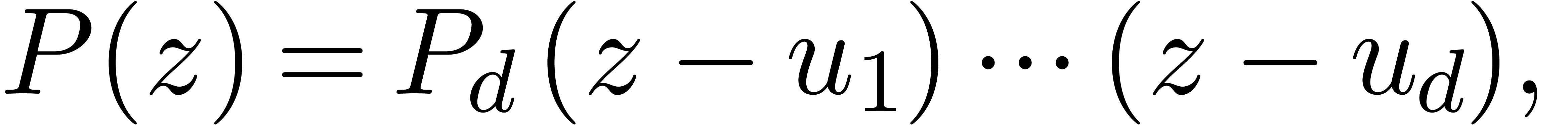
so, considering FFT transforms with respect to a 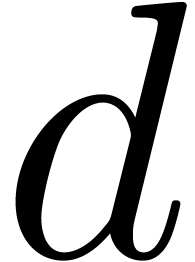 -th root of unity
-th root of unity  ,
we get
,
we get
Since 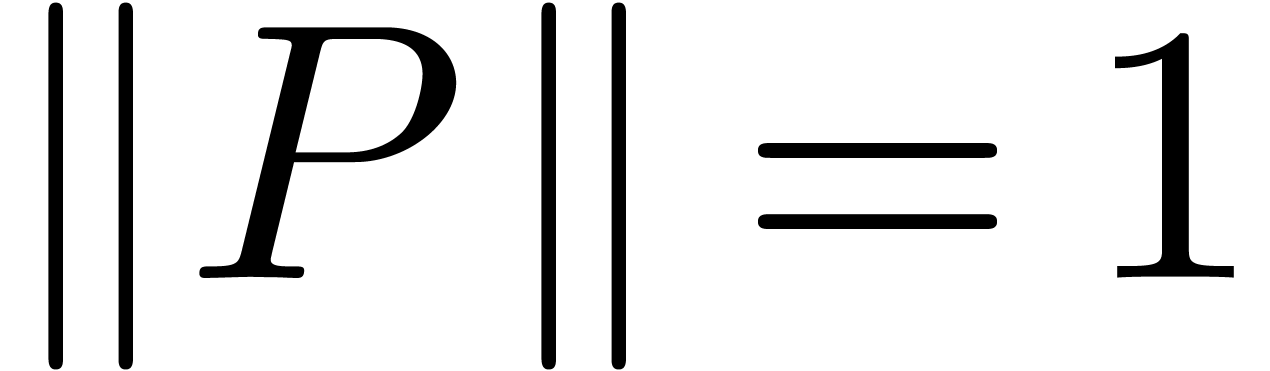 , its coefficients are
known with absolute errors
, its coefficients are
known with absolute errors 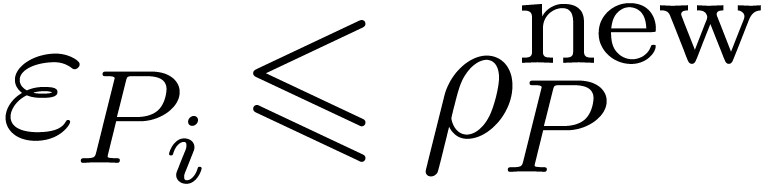 .
We can therefore evaluate
.
We can therefore evaluate 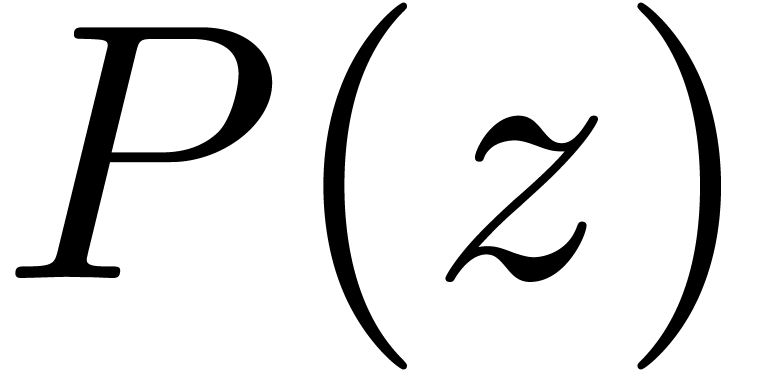 with absolute error
with absolute error
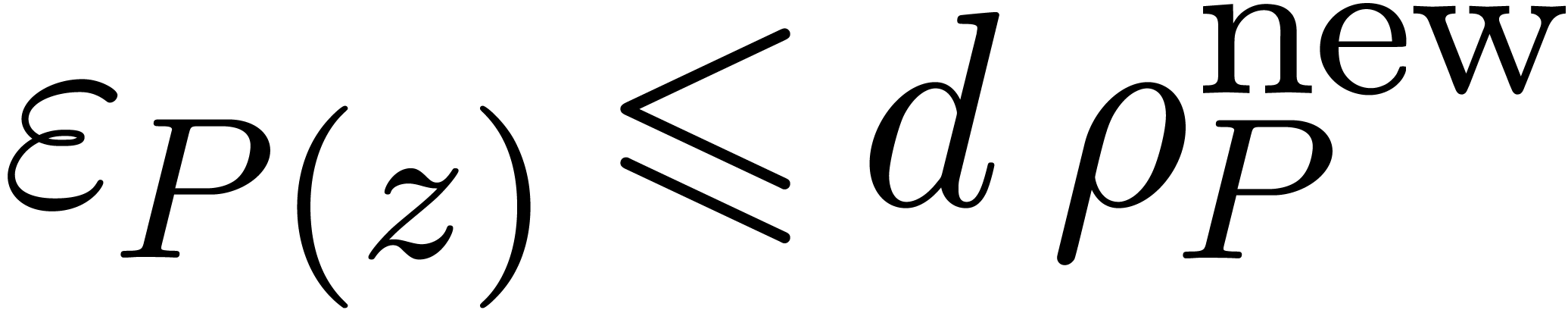 and relative error
and relative error 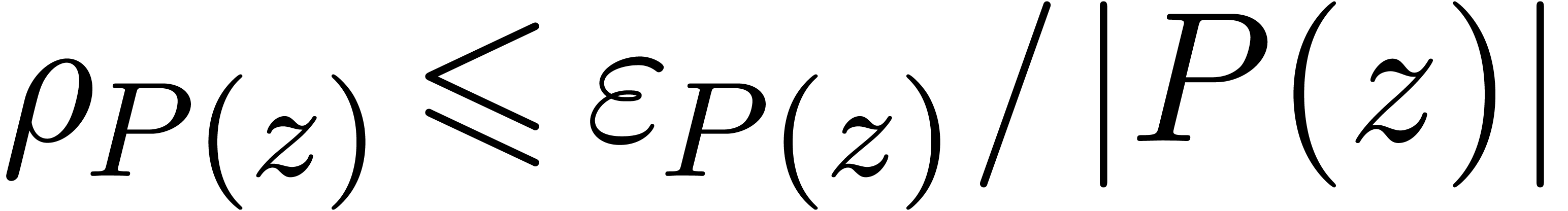 .
.
Let us finally consider the computation of the roots  in the case when
in the case when  is known with relative Newton
error
is known with relative Newton
error  . The worst case again
arises when
. The worst case again
arises when 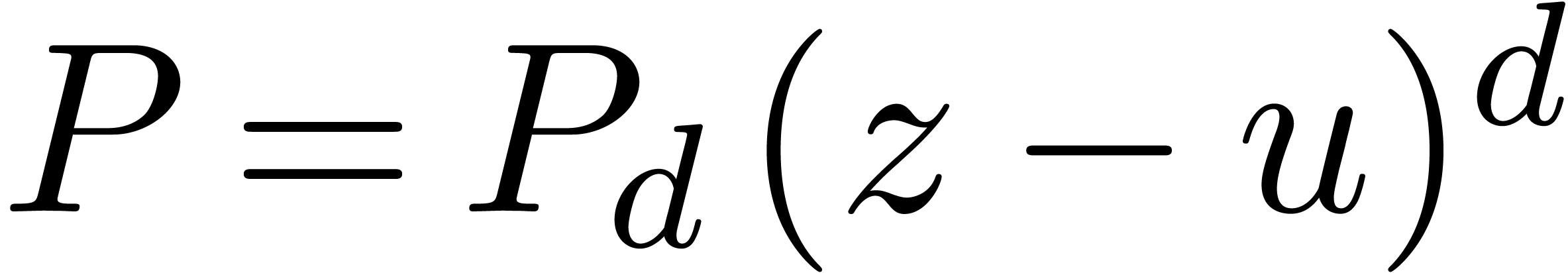 has a single root of multiplicity
has a single root of multiplicity
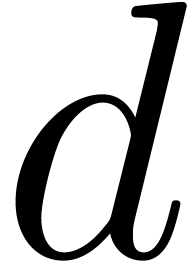 . Indeed, a relative error
. Indeed, a relative error
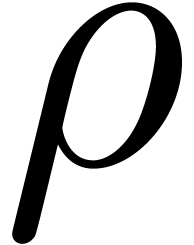 inside
inside 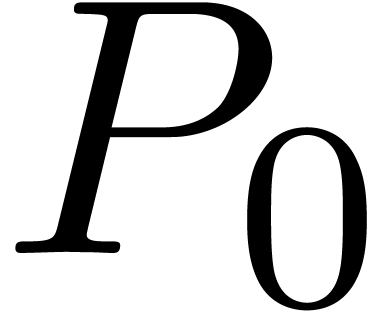 gives rise to a
relative error
gives rise to a
relative error 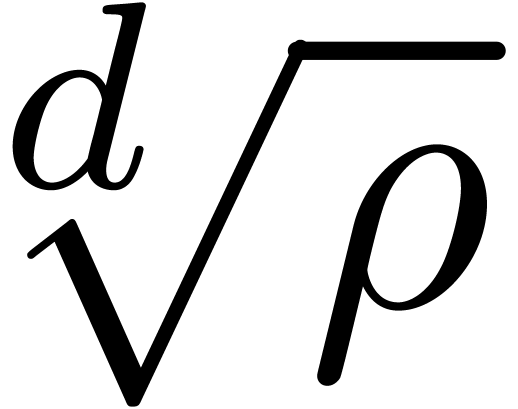 for
for  ,
so that we cannot expect anything better than
,
so that we cannot expect anything better than 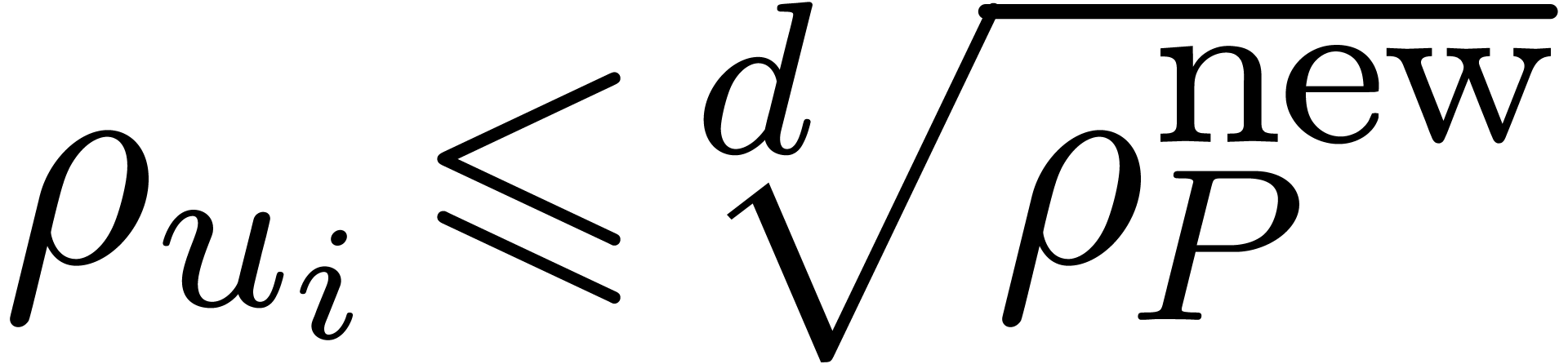 for each
for each 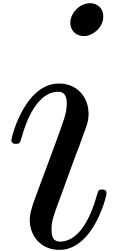 . Nevertheless,
given an isolated root
. Nevertheless,
given an isolated root 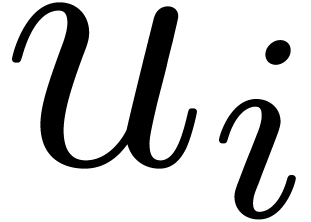 and
and 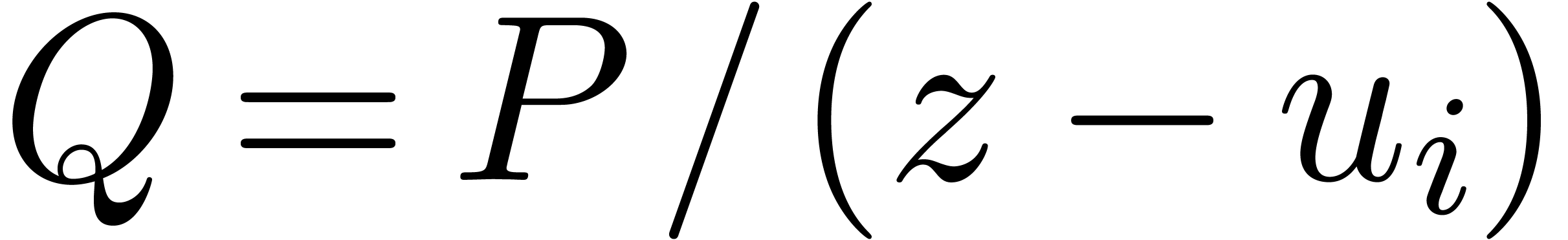 , we have
, we have 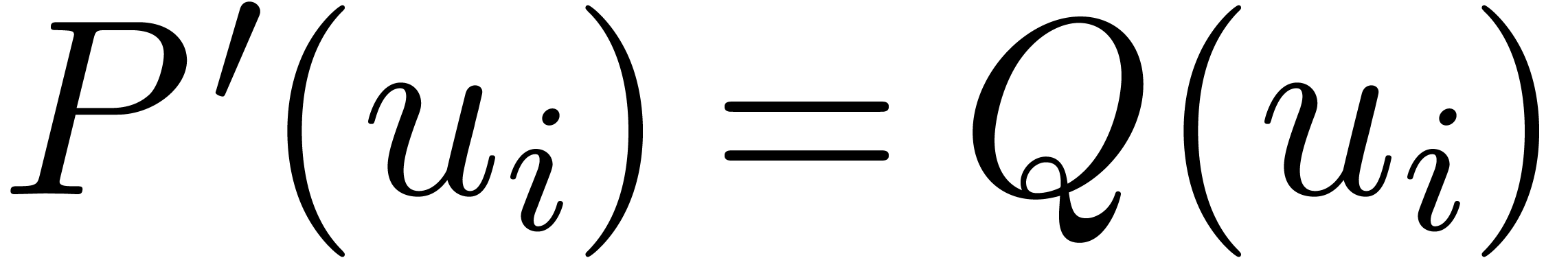 and
and

Using a similar argument as in the proof of proposition 10, it follows that
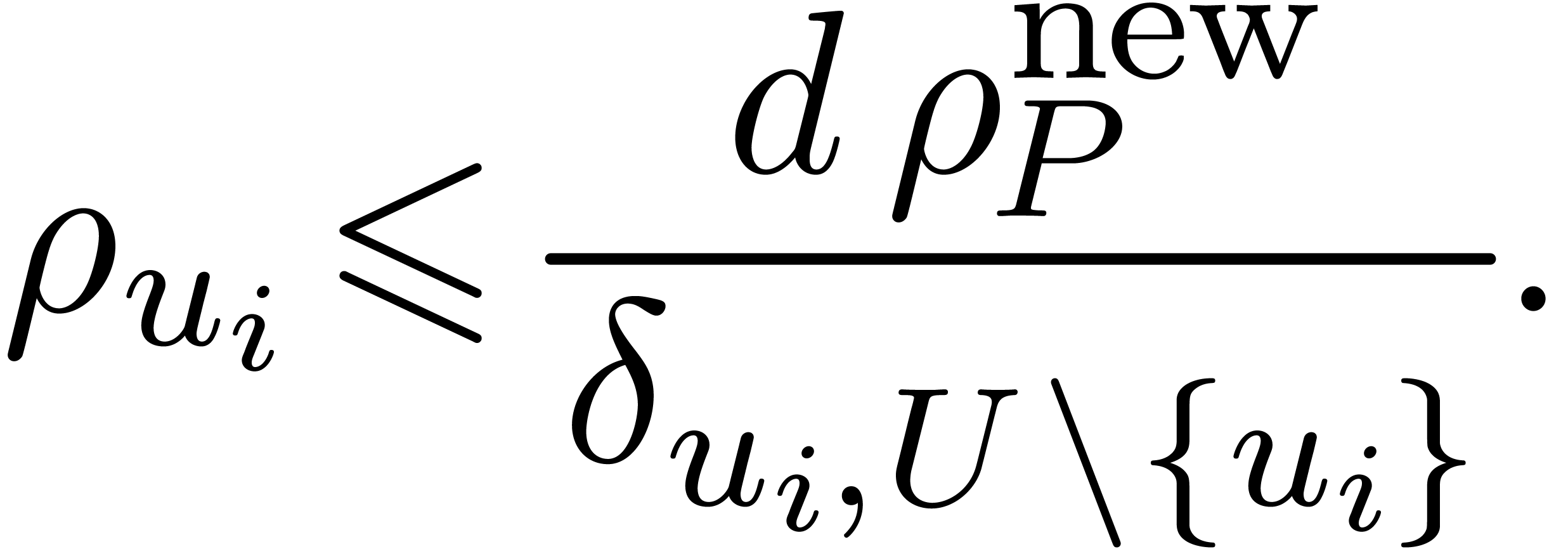
Indeed, after reduction to the case when 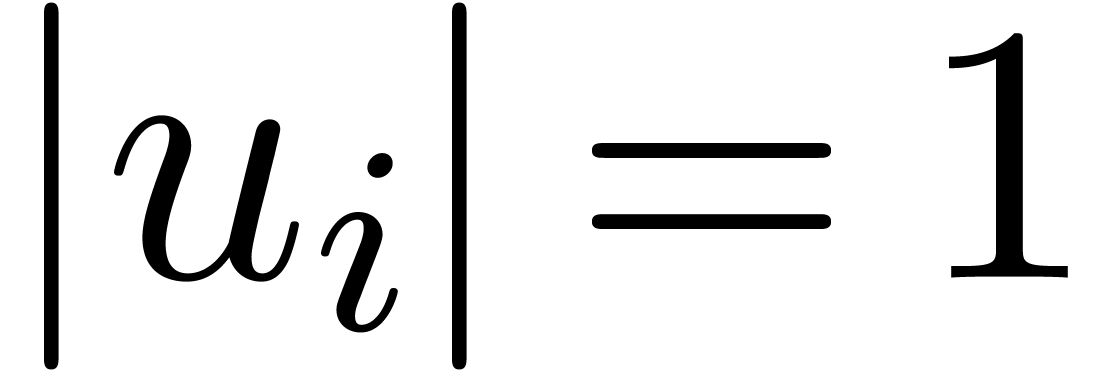 and
and
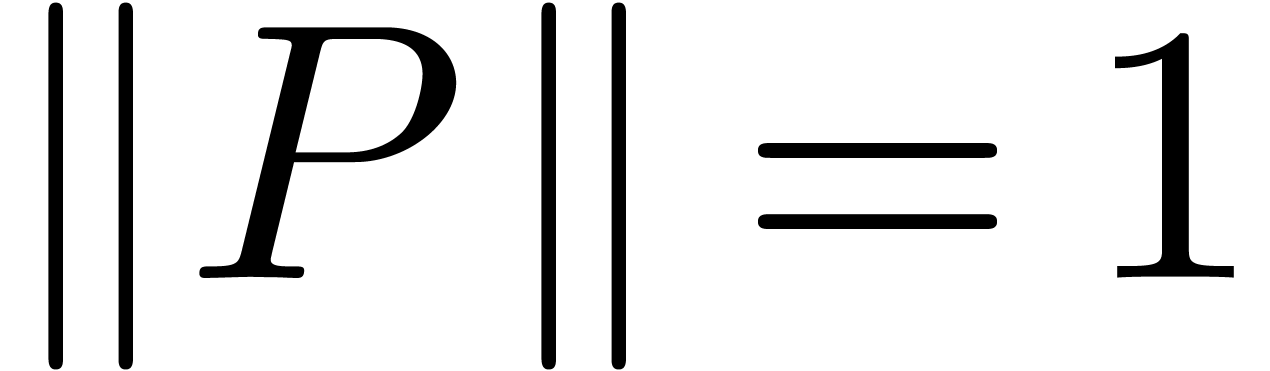 , we combine the facts that
, we combine the facts that
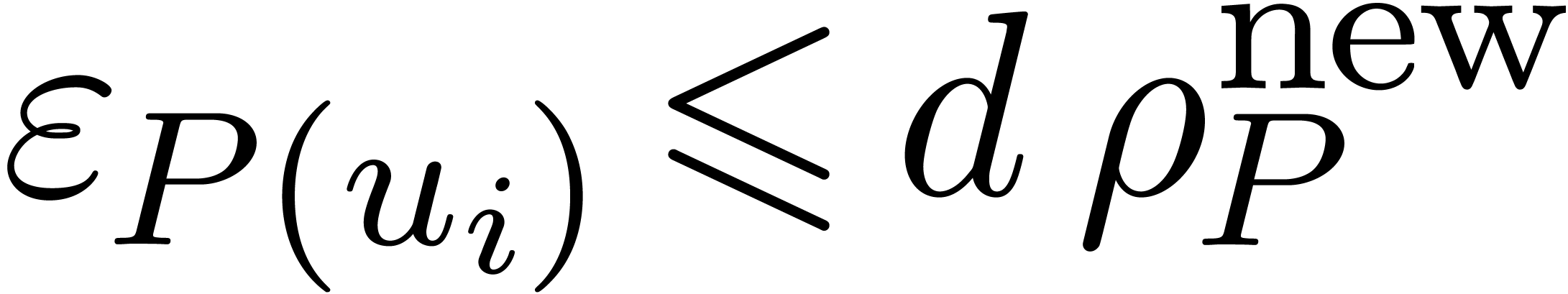 ,
, 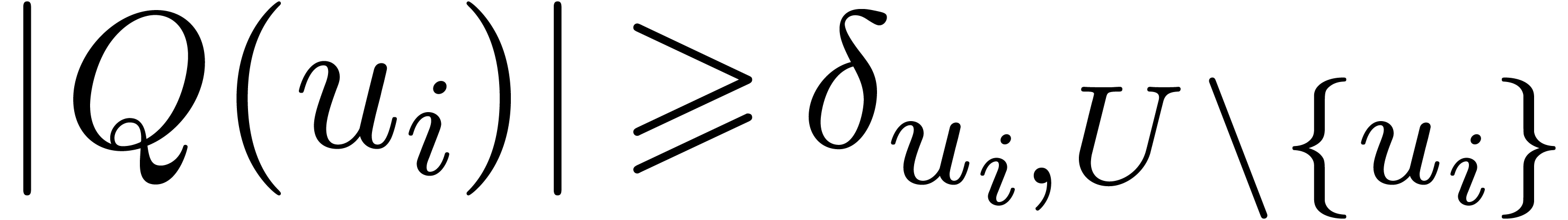 and
and
 .
.
In this paper, we have presented a fast multiplication algorithm for
polynomials over 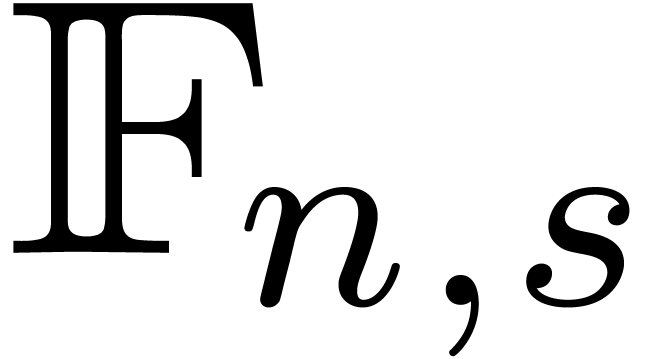 , which is
numerically stable in a wide variety of cases. In order to capture the
increased stability in a precise theorem, we have shown the usefulness
of numeric Newton polygons and the relative Newton error. Even though
our algorithm was presented in the case of real coefficients, it is
straightforward to generalize it to the complex case.
, which is
numerically stable in a wide variety of cases. In order to capture the
increased stability in a precise theorem, we have shown the usefulness
of numeric Newton polygons and the relative Newton error. Even though
our algorithm was presented in the case of real coefficients, it is
straightforward to generalize it to the complex case.
Multiplication being the most fundamental operation on polynomials, it can be hoped that fast and numerically stable algorithms for other operations (division, g.c.d., multi-point evaluation, etc.) can be developed along similar lines. This might for instance have applications to polynomial root finding [Pan96]. Indeed, an operation such as the Graeffe transform can be done both efficiently and accurately using our algorithm.
The multiplication algorithm with scaling from [vdH02a,
Section 6.2] and section 3 has been implemented inside the
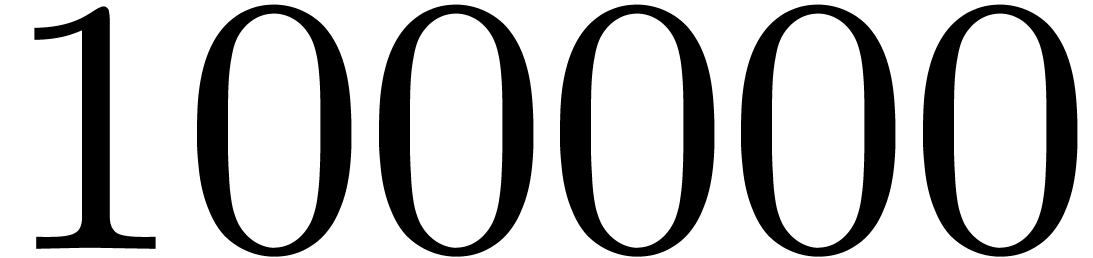 terms
of
terms
of 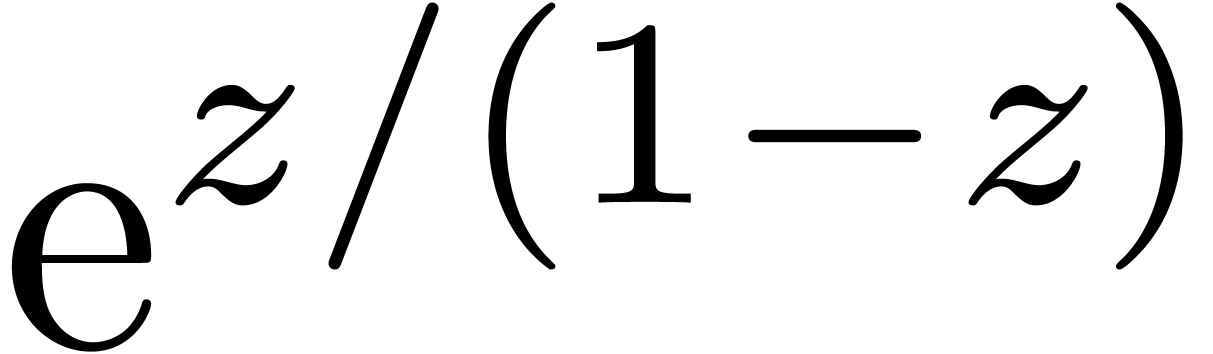 with a
with a 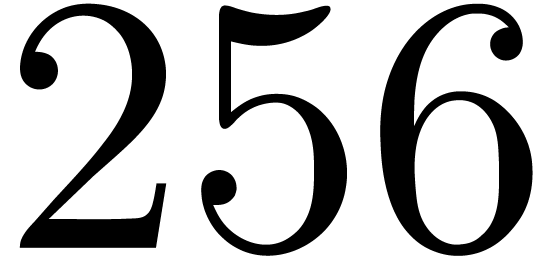 -bit
precision typically takes about one minute. One reason behind this
efficiency stems from the reduction to Kronecker multiplication. Indeed,
multiple precision libraries for floating point numbers, such as
-bit
precision typically takes about one minute. One reason behind this
efficiency stems from the reduction to Kronecker multiplication. Indeed,
multiple precision libraries for floating point numbers, such as
Only a preliminary version of Newton multiplication has been implemented
so far inside
J.W. Cooley and J.W. Tukey. An algorithm for the machine calculation of complex Fourier series. Math. Computat., 19:297–301, 1965.
T. Granlund et al. GMP, the GNU multiple precision arithmetic library.
http://www.swox.com/gmp, 1991.
G. Hanrot, V. Lefèvre, K. Ryde, and P. Zimmermann. MPFR, a C library for multiple-precision floating-point computations with exact rounding. http://www.mpfr.org, 2000.
L. Kronecker. Grundzüge einer arithmetischen Theorie der algebraischen Grössen. Jour. für die reine und ang. Math., 92:1–122, 1882.
Victor Y. Pan. On approximating complex polynomial zeros: Modified quadtree (Weyl's) construction and improved Newton's iteration. Technical Report RR-2894, INRIA Sophia, 1996.
A. Schönhage. Asymptotically fast algorithms for the numerical multiplication and division of polynomials with complex coefficients. In J. Calmet, editor, EUROCAM '82: European Computer Algebra Conference, volume 144 of Lect. Notes Comp. Sci., pages 3–15, Marseille, France, April 1982. Springer.
A. Schönhage and V. Strassen. Schnelle Multiplikation grosser Zahlen. Computing, 7:281–292, 1971.
J. van der Hoeven. Relax, but don't be too lazy. JSC, 34:479–542, 2002.
J. van der Hoeven et al. Mathemagix, 2002. http://www.mathemagix.org.