| Certified Singular Value
Decomposition |
|
|
CNRS, Laboratoire LIX
Campus de l'École Polytechnique
1 rue Honoré d'Estienne d'Orves
Bâtiment Alan Turing CS35003
91120 Palaiseau
France
|
|
Email:
vdhoeven@lix.polytechnique.fr
|
|
|
|
Institut de Mathématiques de Toulouse
Université Paul Sabatier
118 route de Narbonne
31062 Toulouse Cedex 9
France
|
|
Email: yak@mip.ups-tlse.fr
|
|
|
|
In this paper, we present an efficient algorithm for the
certification of numeric singular value decompositions (SVDs) in
the regular case, i.e., in the case when all the singular values
are pairwise distinct. Our algorithm is based on a Newton-like
iteration that can also be used for doubling the precision of an
approximate numerical solution.
|
1.Introduction
Let  be the set of floating point numbers for a
fixed precision and a fixed exponent range. We denote
be the set of floating point numbers for a
fixed precision and a fixed exponent range. We denote  . Consider an
. Consider an  matrix
matrix
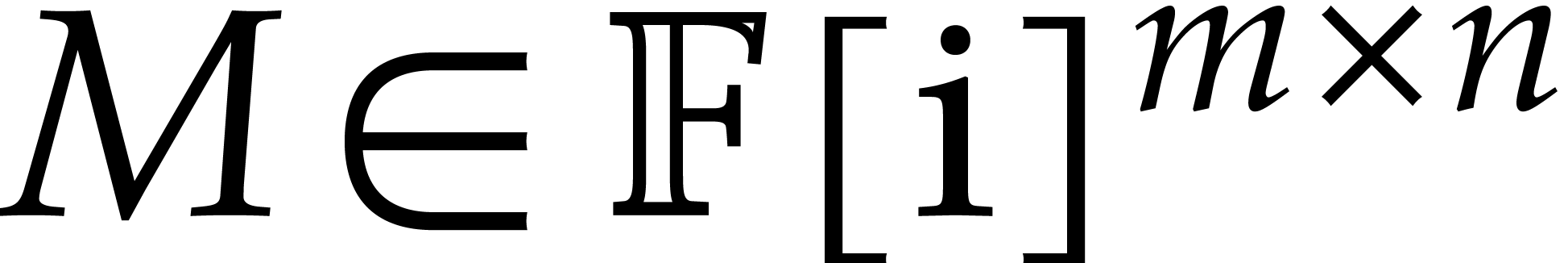 with complex floating entries, where
with complex floating entries, where 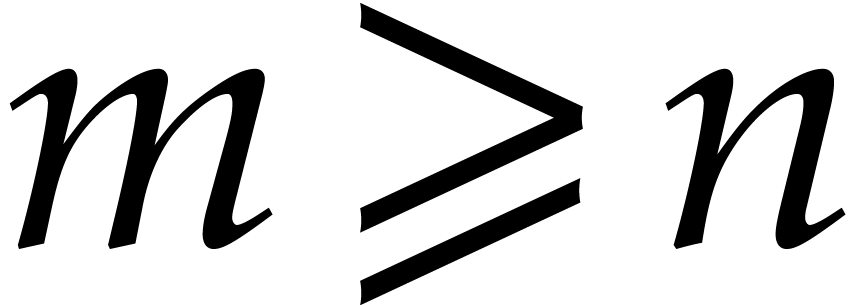 . The problem of computing the
numeric singular value decomposition of
. The problem of computing the
numeric singular value decomposition of 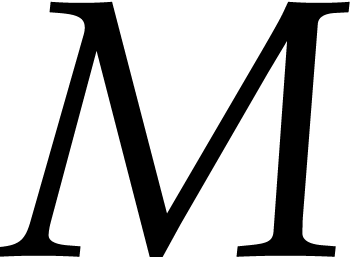 is to compute unitary transformation matrices
is to compute unitary transformation matrices 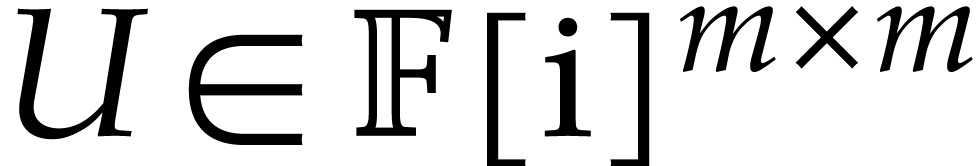 ,
, 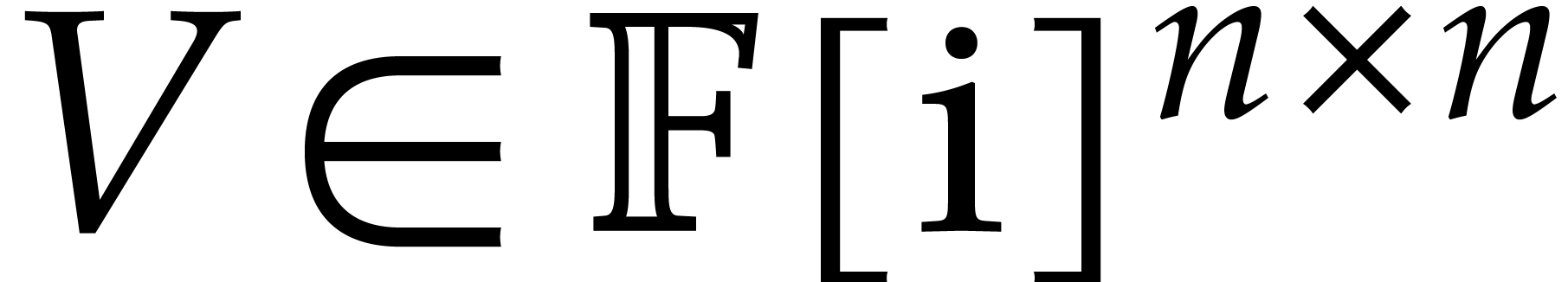 , and a
diagonal matrix
, and a
diagonal matrix 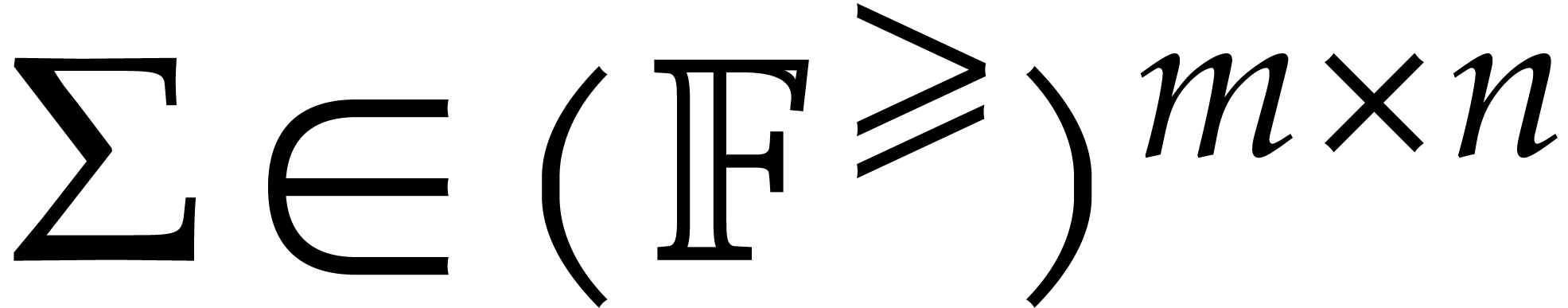 such that
such that
If 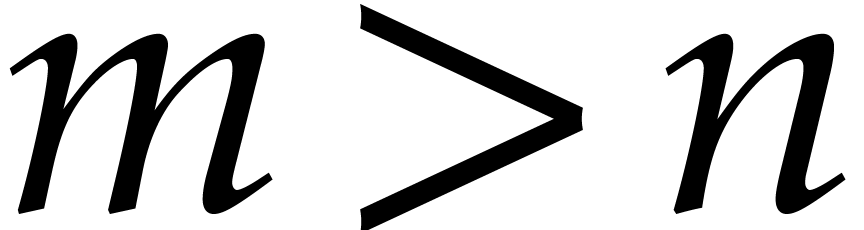 , then
, then 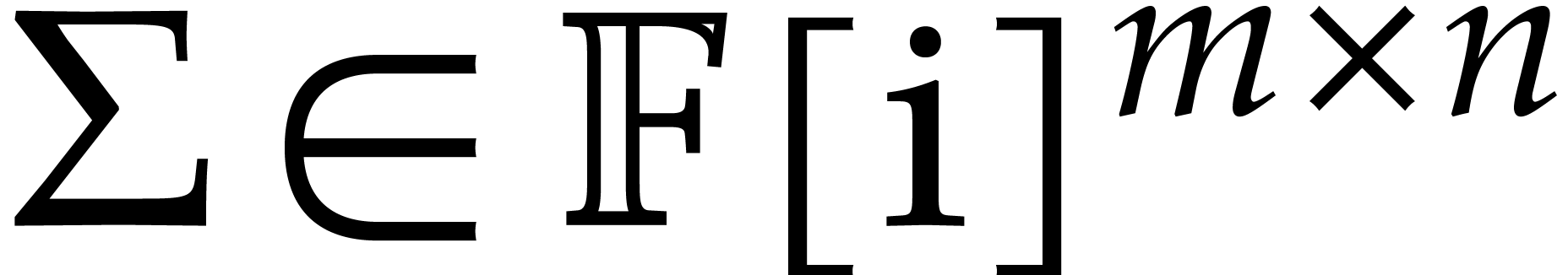 is understood to be “diagonal” if it is of the form
is understood to be “diagonal” if it is of the form
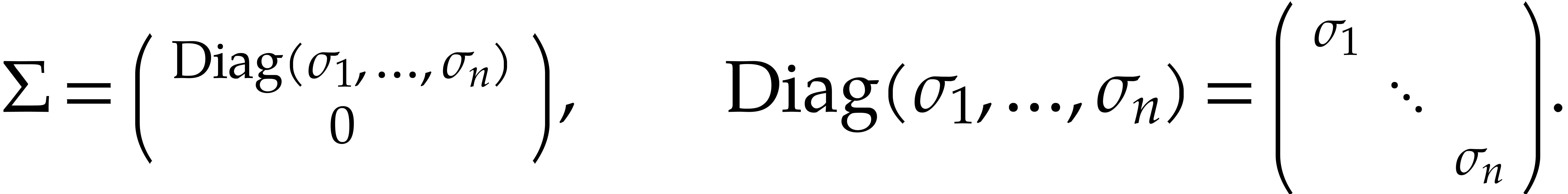
The diagonal entries  of
of  are the approximate singular values of the matrix
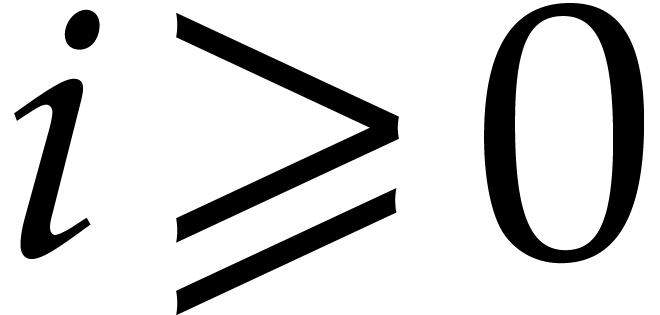
are the approximate singular values of the matrix  and throughout this paper we will assume them to be pairwise distinct
and ordered
and throughout this paper we will assume them to be pairwise distinct
and ordered

There are several well-known algorithms for the computation of numeric
singular value decompositions [8, 4].
Now (1) is only an approximate equality. It is sometimes
important to have a rigorous bound for the distance between an
approximate solution and some exact solution. More precisely, we may ask
for a diagonal matrix  and matrices
and matrices 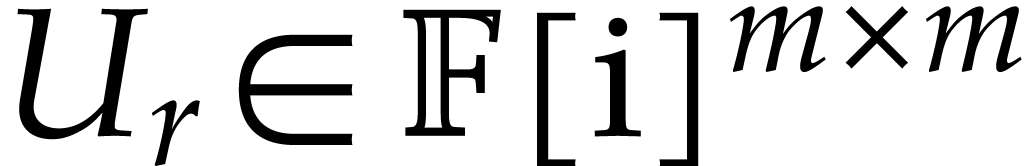 ,
, 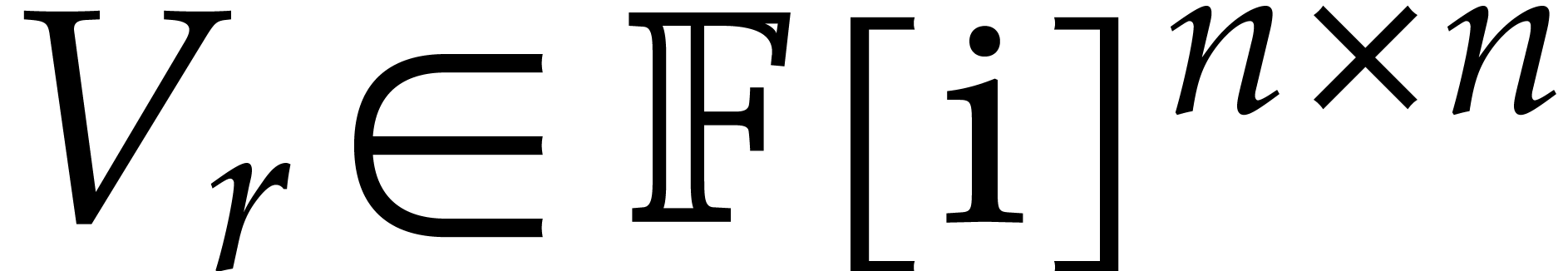 ,
such that there exist unitary matrices
,
such that there exist unitary matrices  ,
,
 , and a diagonal matrix
, and a diagonal matrix  for which
for which
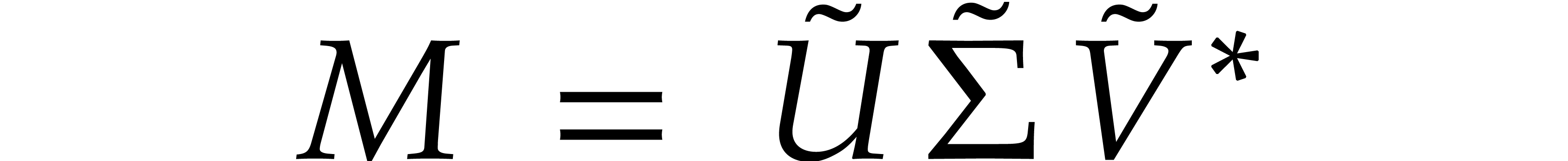
and
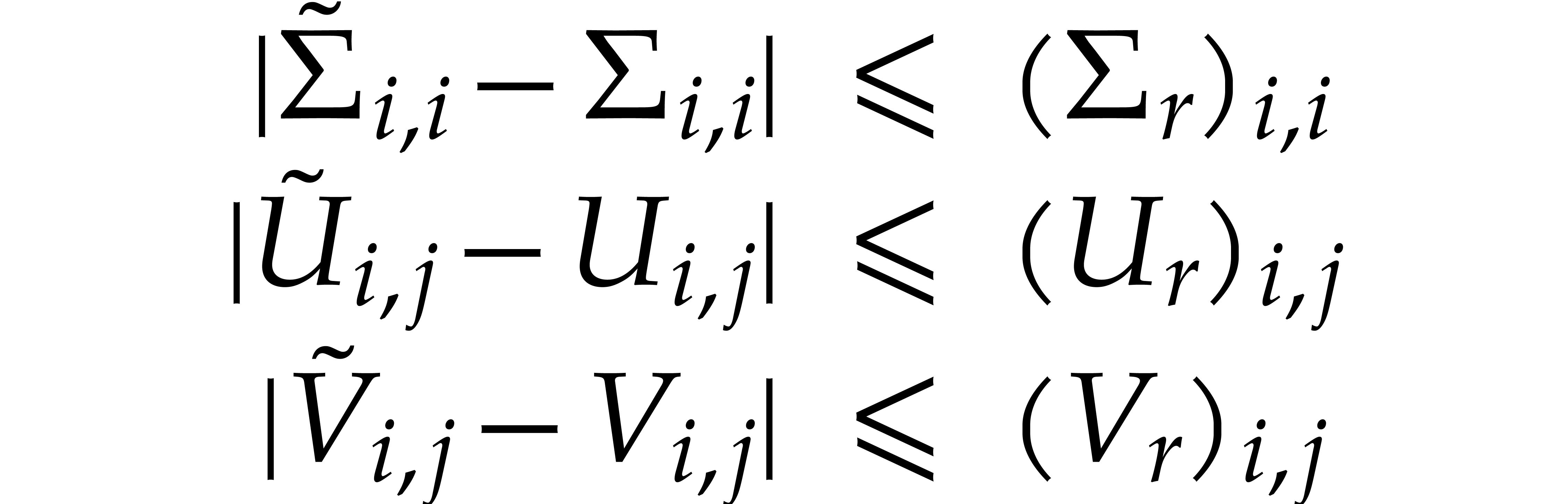
for all 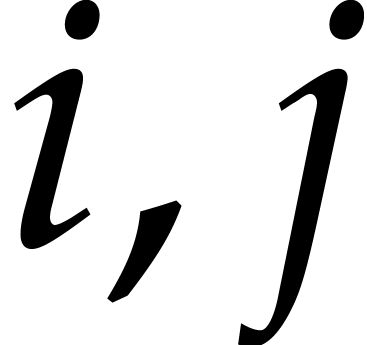 . This task will be
called the certification problem for the given numeric singular
value decomposition (1). The matrices
. This task will be
called the certification problem for the given numeric singular
value decomposition (1). The matrices 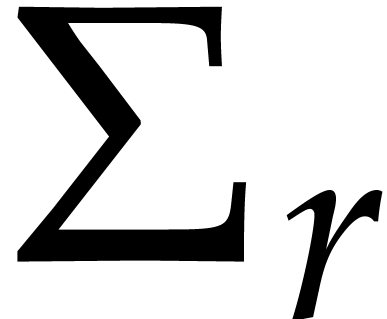 ,
, 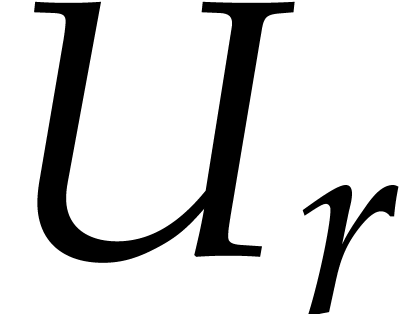 and
and 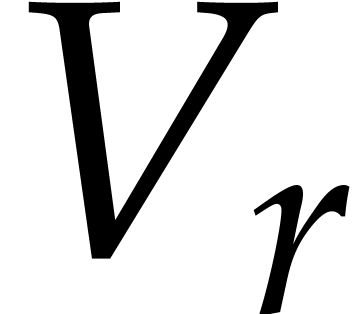 can be thought of as reliable error bounds for the matrices
can be thought of as reliable error bounds for the matrices 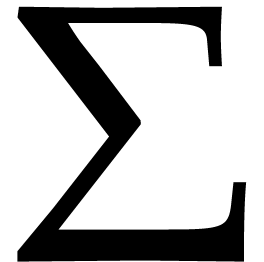 ,
,  and
and  of the numerical solution.
of the numerical solution.
It will be convenient to rely on ball arithmetic [13,
19], which is a systematic technique for this kind of bound
computations. When computing with complex numbers, ball arithmetic is
more accurate than more classical interval arithmetic [22,
1, 23, 18, 21, 24], especially in multiple precision contexts. We will write
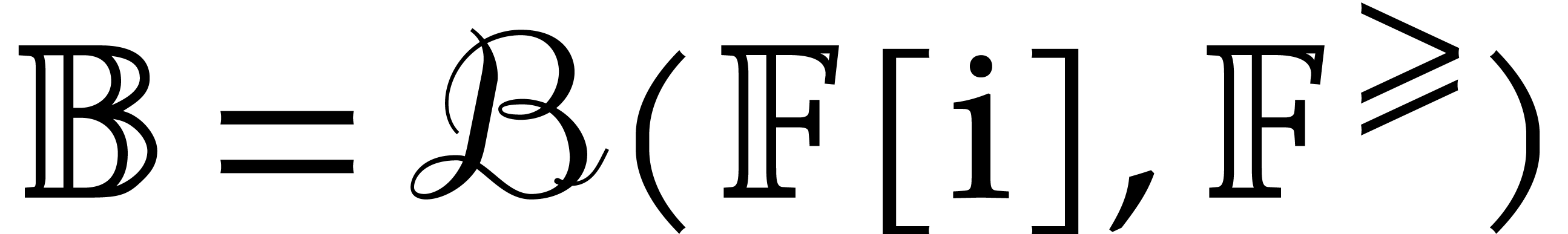 for the set of balls
for the set of balls 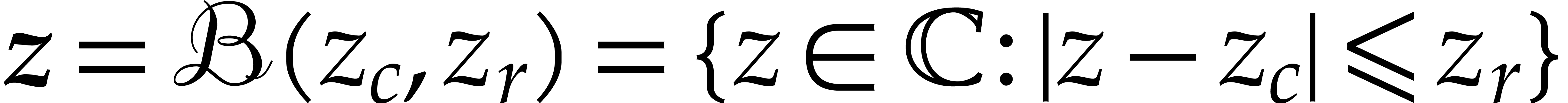 with centers
with centers  in
in 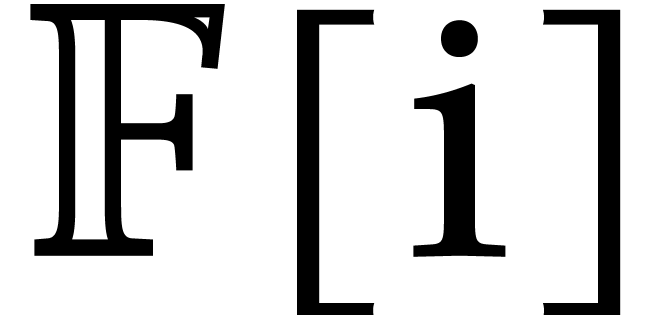 and
radii
and
radii 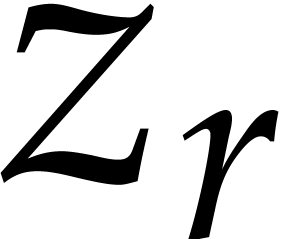 in
in 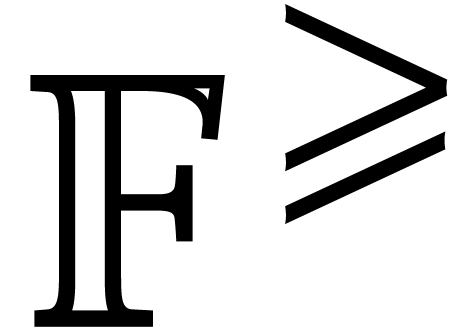 .
In a similar way, we may consider matricial balls
.
In a similar way, we may consider matricial balls 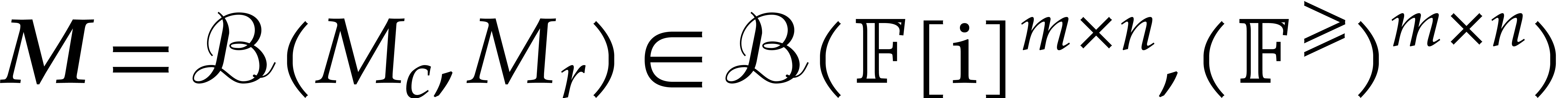 : given a center matrix
: given a center matrix 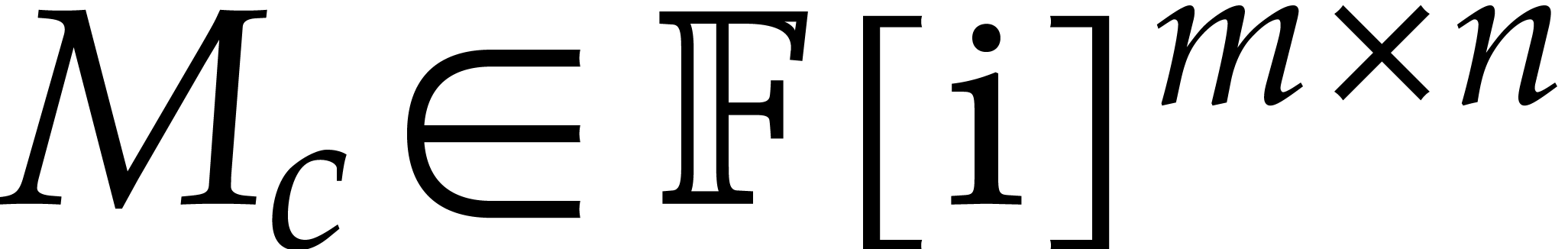 and
a radius matrix
and
a radius matrix  , we have
, we have
Alternatively, we may regard 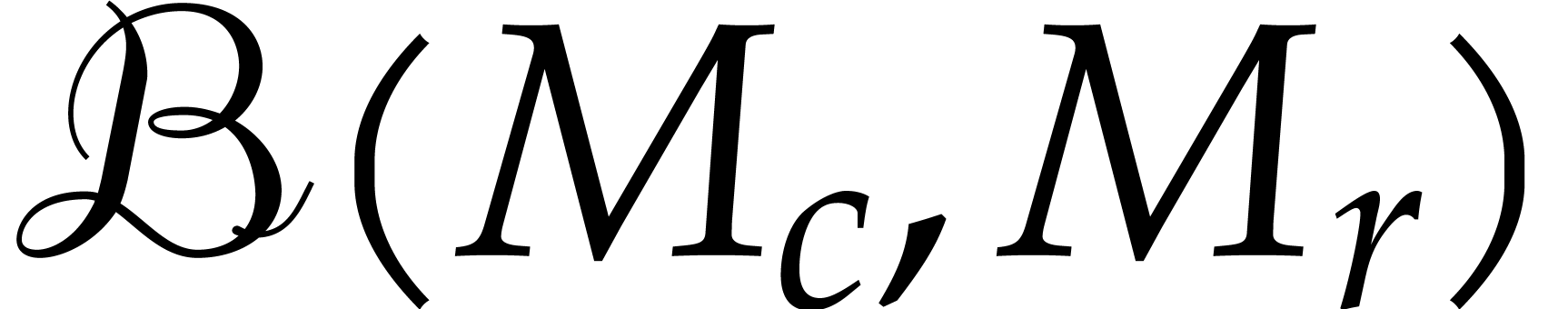 as the set of
matrices in
as the set of
matrices in 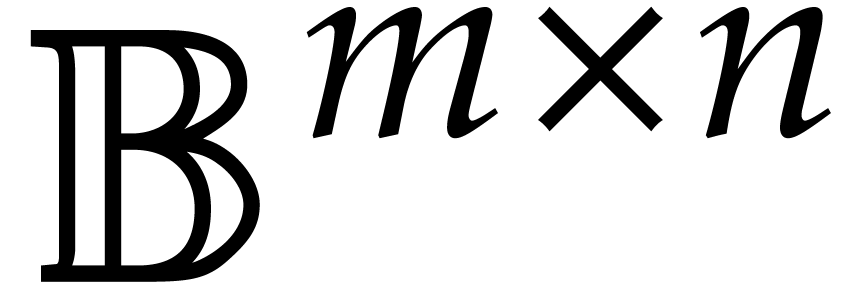 with ball coefficients:
with ball coefficients:

Standard arithmetic operations on balls are carried out in a reliable
way. For instance, if  , then
the computation of the product
, then
the computation of the product  using ball
arithmetic has the property that
using ball
arithmetic has the property that  for any
for any  and
and  .
.
In the language of ball arithmetic, it is natural to allow for small
errors in the input and replace the numeric input 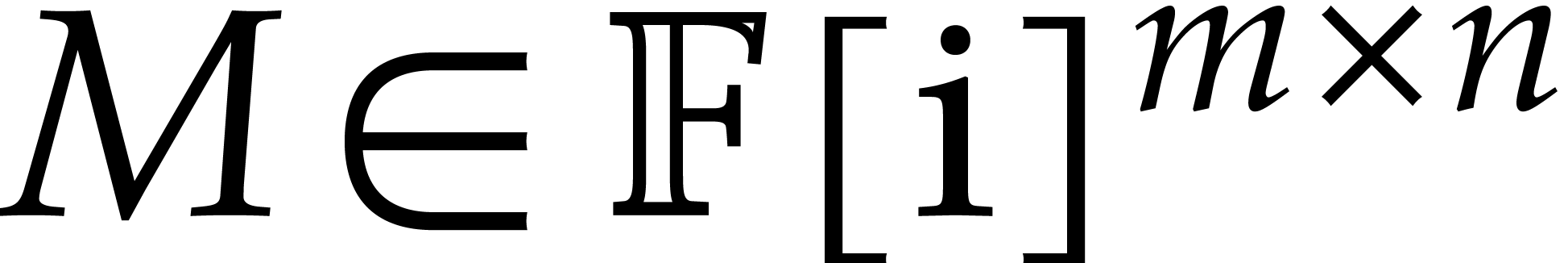 by a ball input
by a ball input 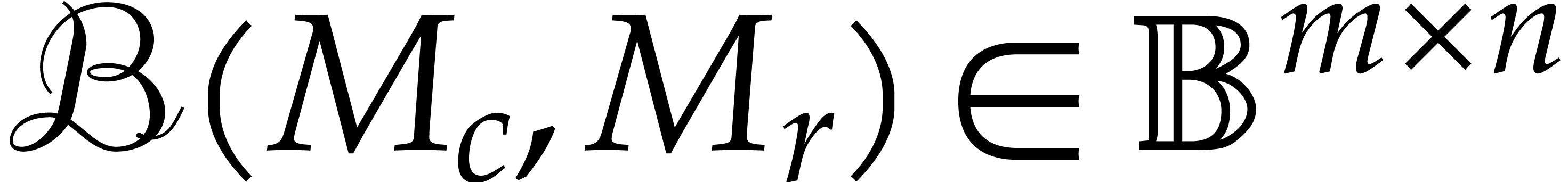 . Then we may
still compute a numeric singular value decomposition of the center
matrix
. Then we may
still compute a numeric singular value decomposition of the center
matrix 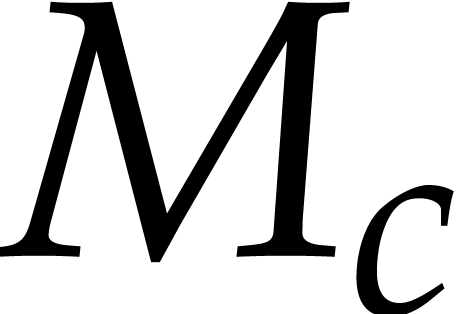 :
:
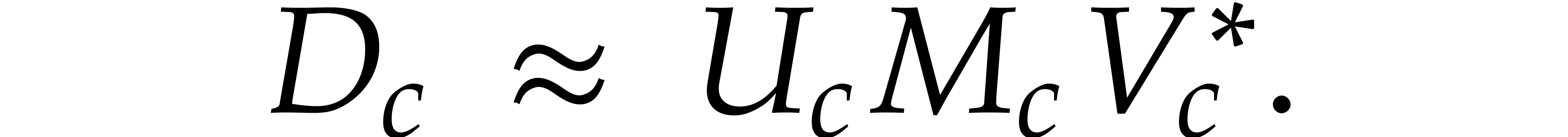 |
(2) |
The generalized certification problem now consists of the
computation of matrices 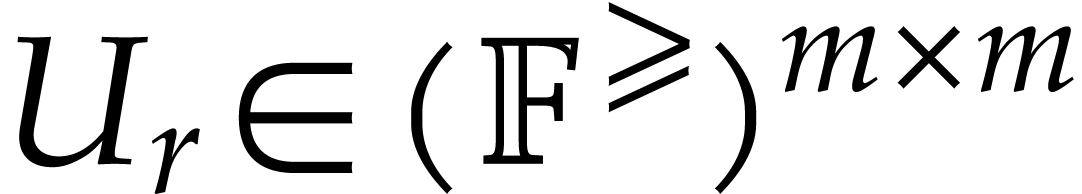 ,
,
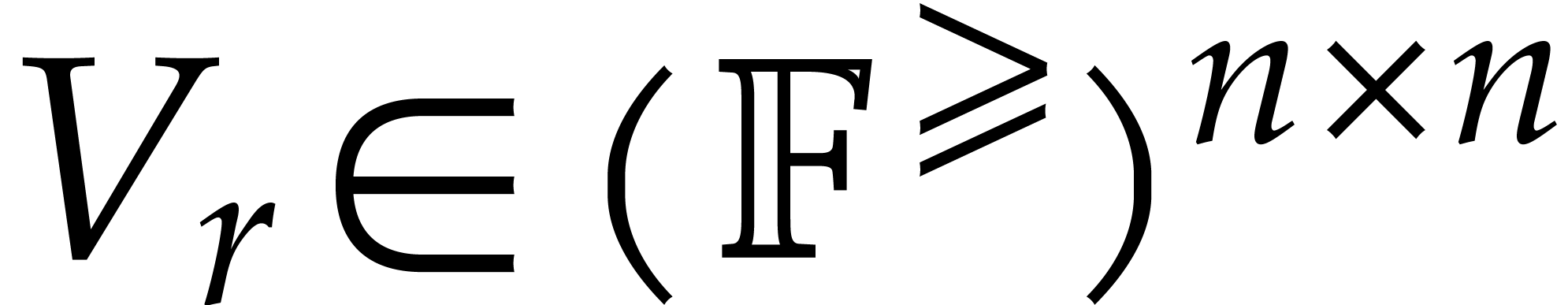 , and a diagonal matrix
, and a diagonal matrix  such that, for every
such that, for every 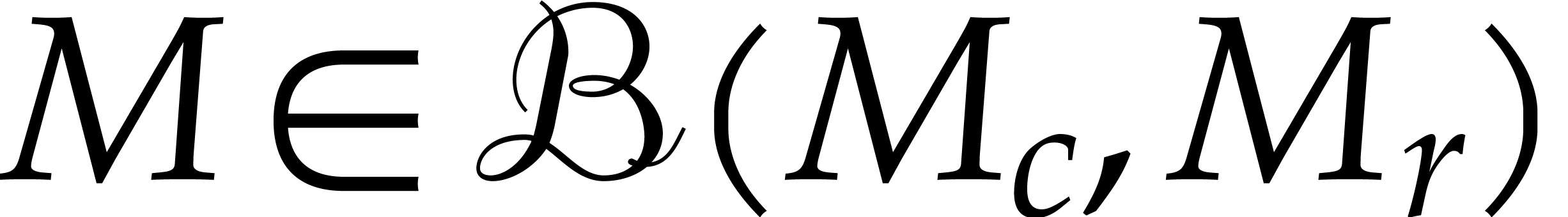 ,
there exist unitary matrices
,
there exist unitary matrices 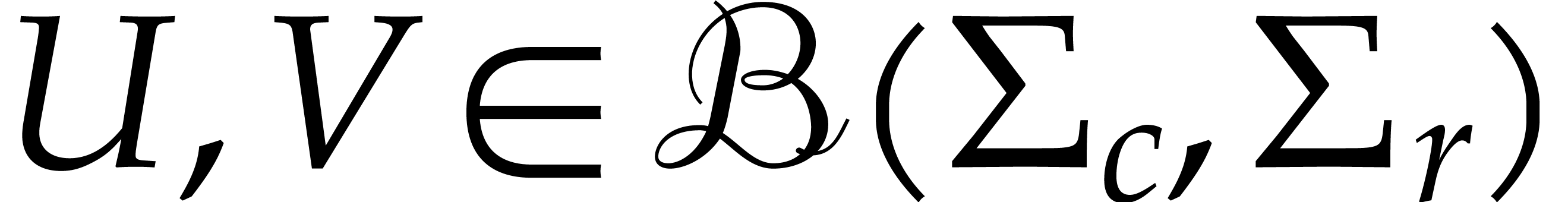 ,
and a diagonal matrix
,
and a diagonal matrix 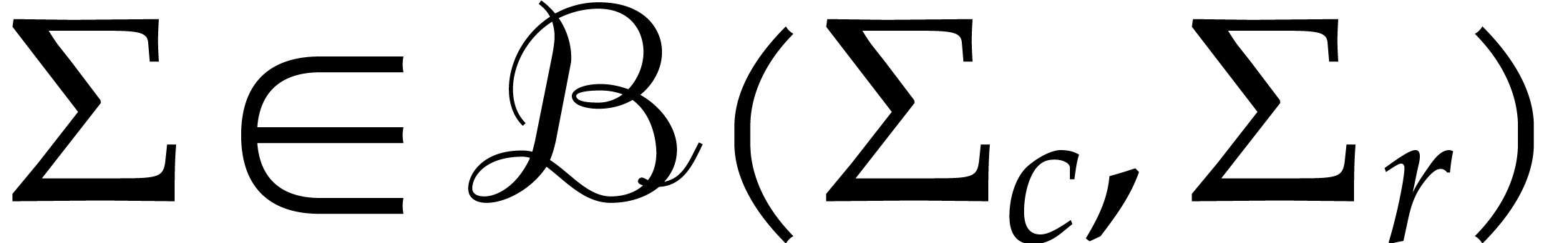 with
with
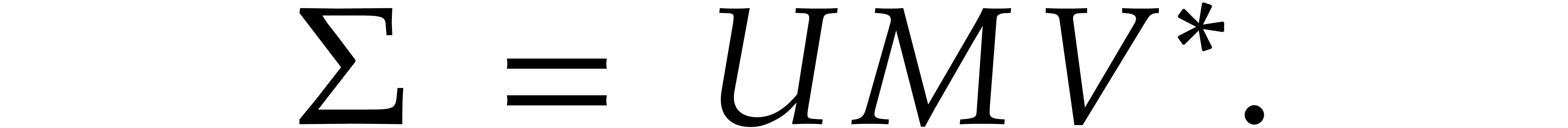
In this paper we propose an efficient solution for this problem in the
case when all singular values are simple. Our algorithm relies on an
efficient Newton iteration that is also useful for doubling the
precision of a given numeric singular value decomposition. The iteration
admits a quadratic convergence and only requires matrix sums and
products of size at most  . In
[13, 15], a similar approach was used for the
certification of eigenvalues and eigenvectors.
. In
[13, 15], a similar approach was used for the
certification of eigenvalues and eigenvectors.
We are not aware of similarly efficient and robust algorithms in the
literature. Jacobi-like methods from Kogbeliantz' SVD algorithm admit
quadratic convergence in the presence of cluster in the Hermitian case
[3], but only linear convergence is achieved in general [5]. Gauss-Newton type methods have also been proposed for the
approximation the regular real SVD in [17, 16].
From the theoretical bit complexity point of view, our algorithm
essentially reduces the certification problem to a constant number of
numeric matrix multiplications. When using a precision of 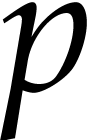 bits for numerical computations, it has recently been
shown [10] that two
bits for numerical computations, it has recently been
shown [10] that two  matrices can be
multiplied in time
matrices can be
multiplied in time
Here 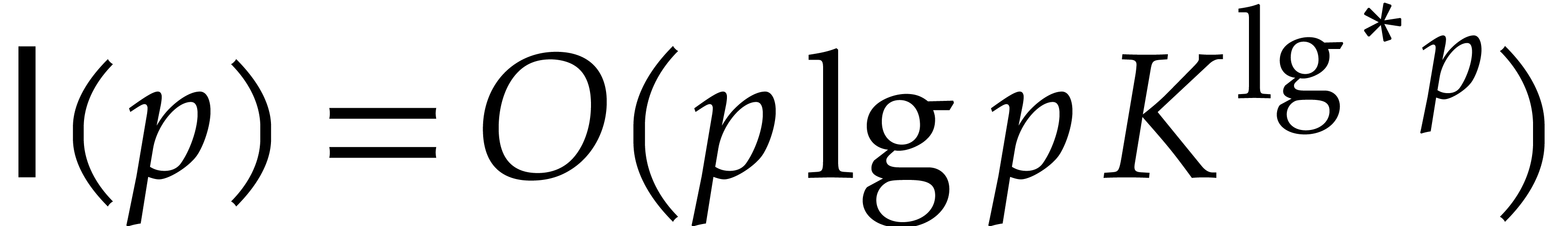 with
with 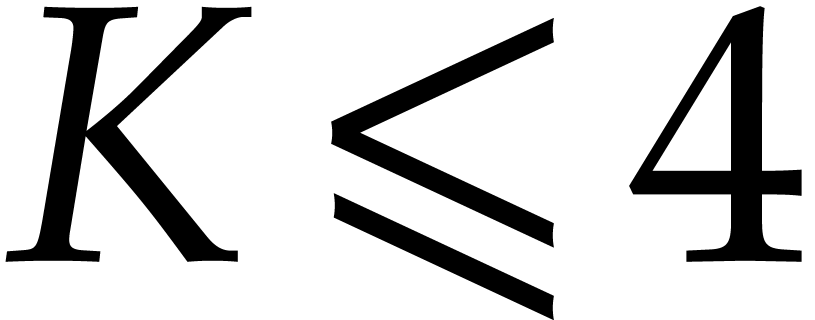 is the cost of
is the cost of
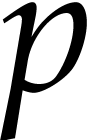 -bit integer multiplication
[11, 9] and
-bit integer multiplication
[11, 9] and  is the
exponent of matrix multiplication [7]. If
is the
exponent of matrix multiplication [7]. If 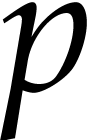 is large enough with respect to the log of the condition number, then
is large enough with respect to the log of the condition number, then
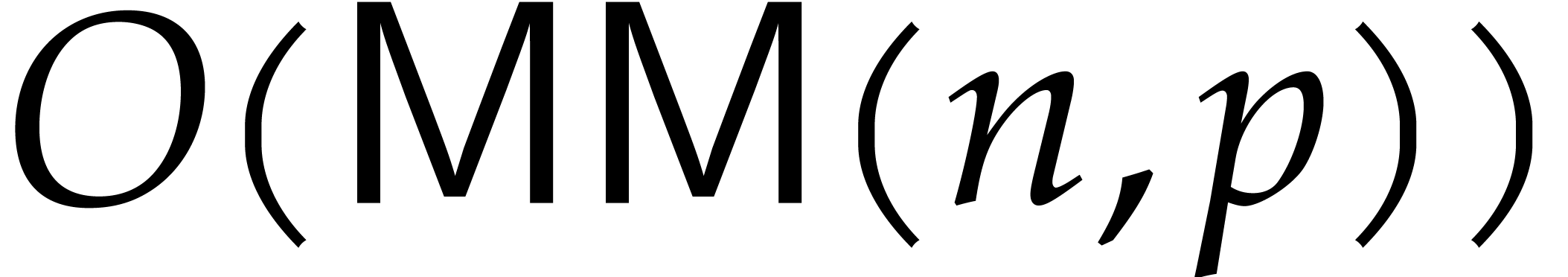 yields an asymptotic bound for the bit
complexity of our certification problem.
yields an asymptotic bound for the bit
complexity of our certification problem.
We have implemented unoptimized versions of the new algorithms in Mathemagix [14] and Matlab.
These toy implementations indeed confirmed the quadratic convergence of
our Newton iteration and the efficiency of the new algorithms. We intend
to report more extensively on implementation issues in a forthcoming
paper.
2.Notations
2.1.Matrix norms
Throughout this paper, we will use the max-norm for vectors and the
corresponding matrix norm. More precisely, given positive integers 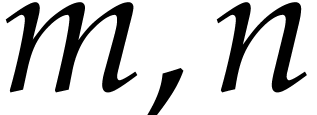 , a vector
, a vector  , and an
, and an  matrix
matrix  , we set
, we set
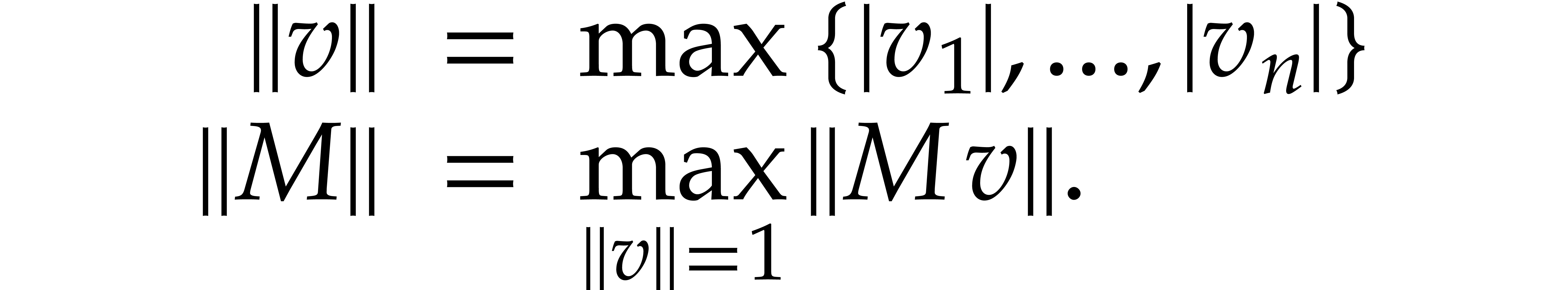
For a second matrix  , we
clearly have
, we
clearly have
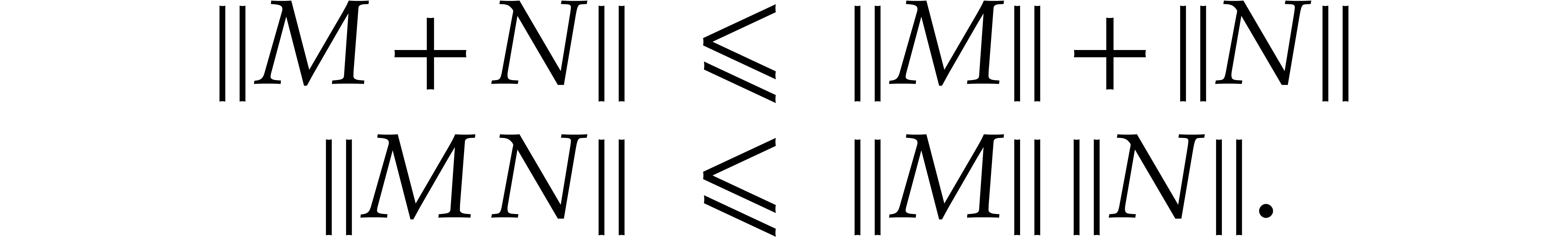
We also define
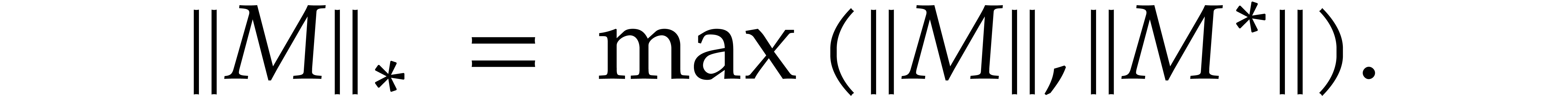 |
(3) |
Explicit machine computation of the matrix norm is easy using the
formula
Given a second matrix  it follows that the
coefficientwise product
it follows that the
coefficientwise product
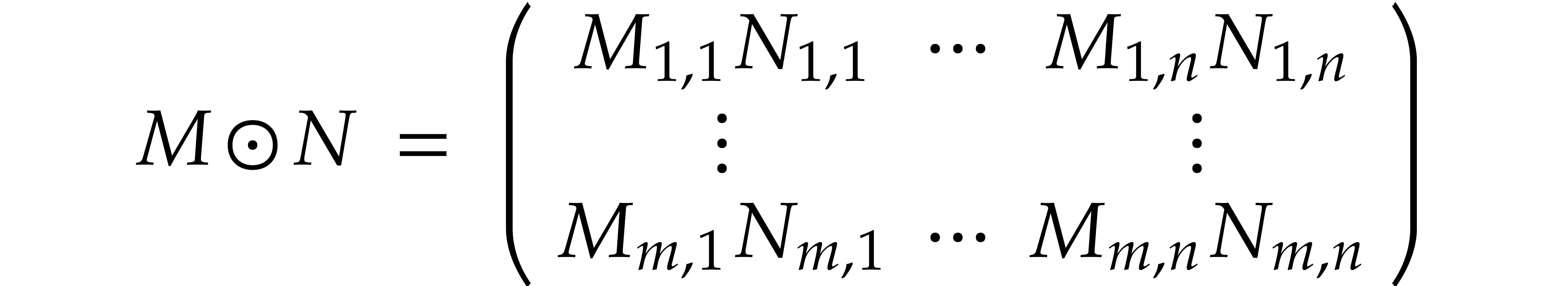
satisfies
In particular, when changing certain entries of a matrix 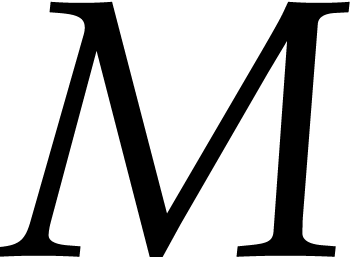 to zero, its matrix norm
to zero, its matrix norm 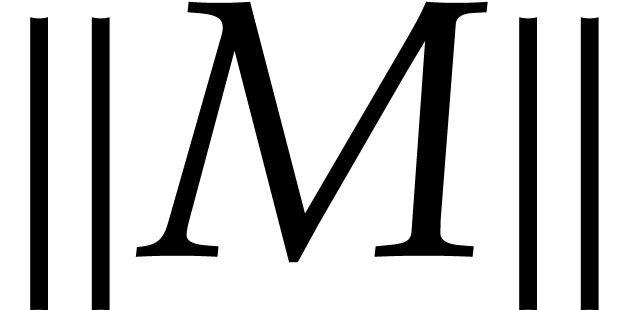 can only
decrease. We will write
can only
decrease. We will write 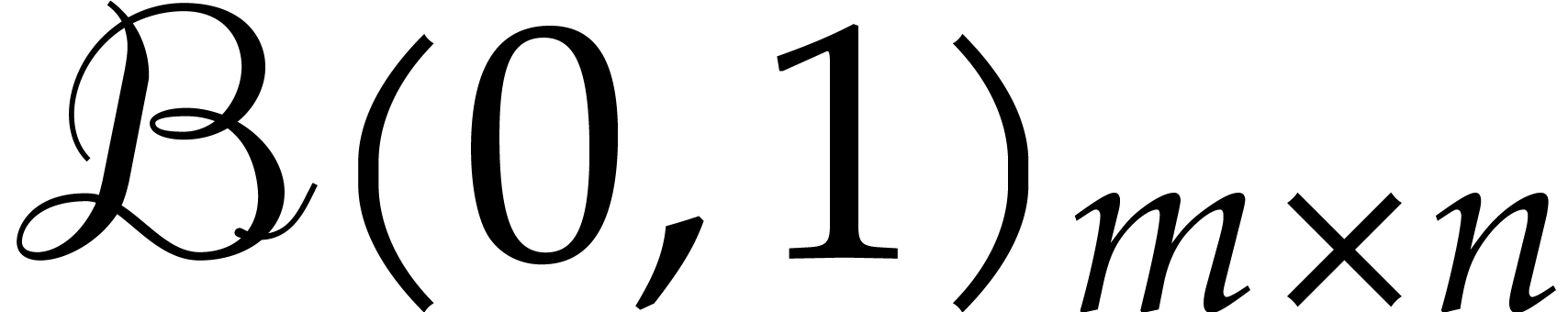 for the
for the  ball matrix whose entries are all unit balls
ball matrix whose entries are all unit balls 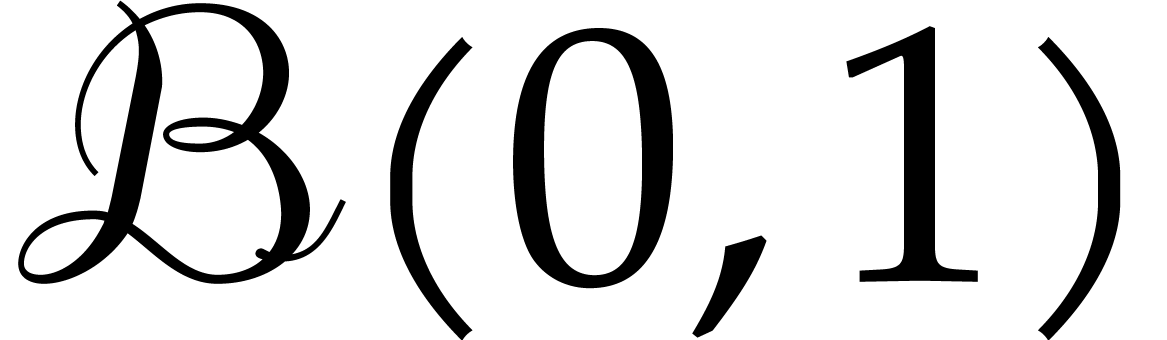 . This matrix has the property that
. This matrix has the property that  for all
for all  matrices
matrices 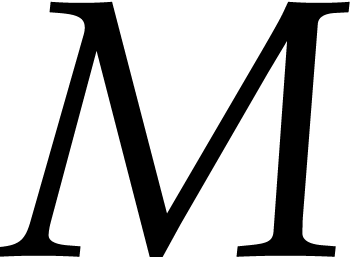 .
.
2.2.Miscellaneous notations
In the sequel we consider two integers 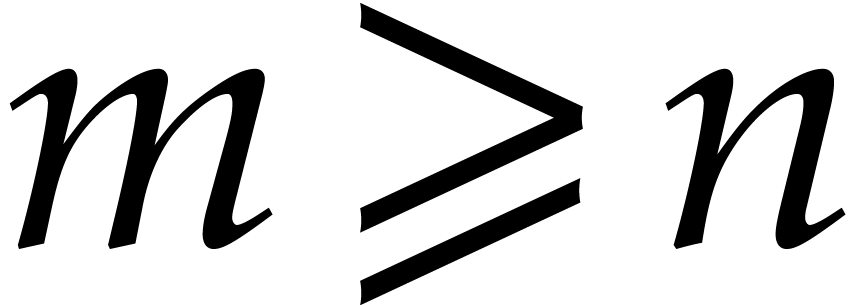 and we
introduce the sets of matrices:
and we
introduce the sets of matrices:
 |
(6) |
and
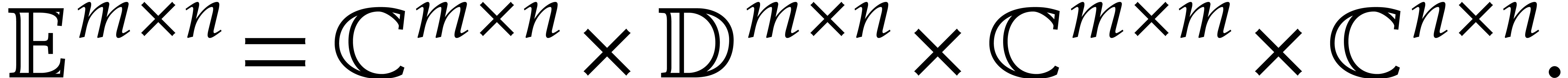
We also write 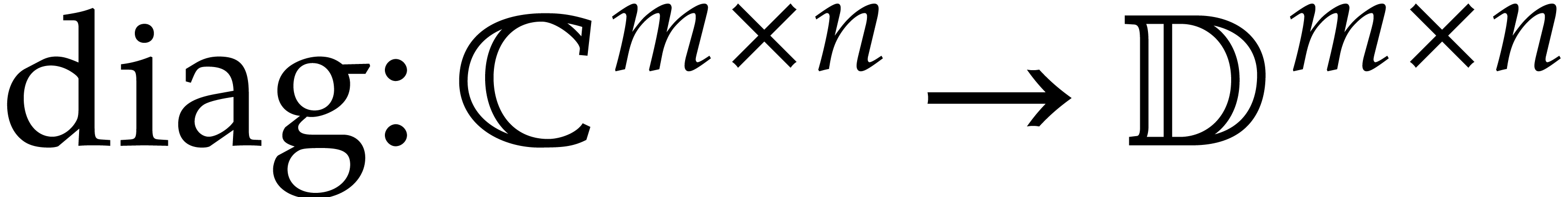 for the natural projection that
replaces all non-diagonal entries by zeros. For any integer
for the natural projection that
replaces all non-diagonal entries by zeros. For any integer 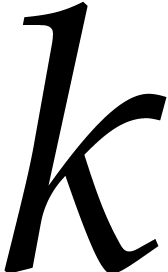 we finally define the map
we finally define the map 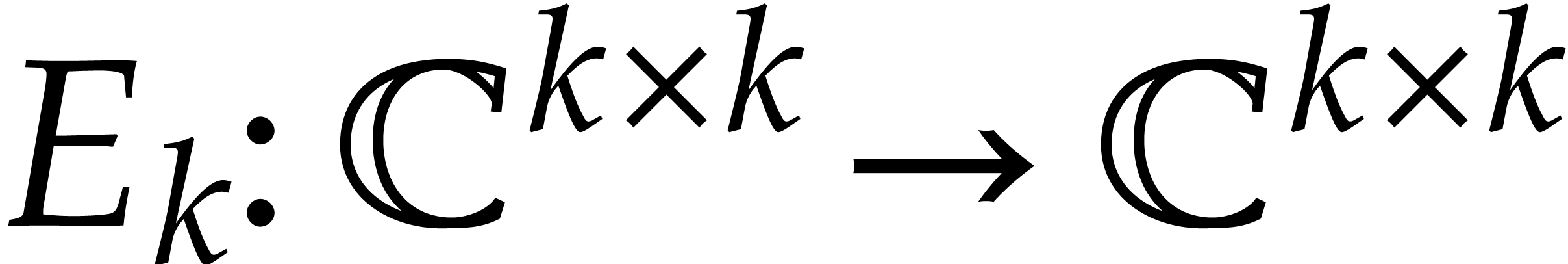 by
by
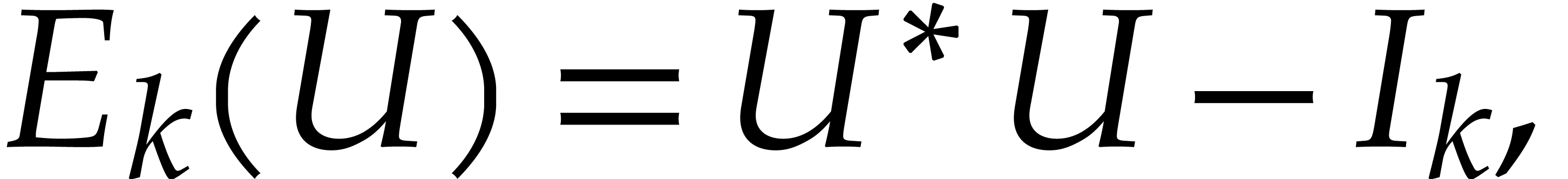
where 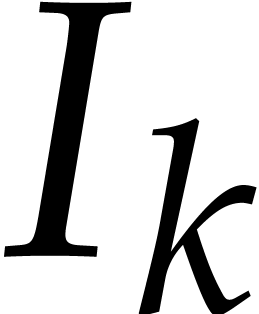 is the identity matrix of size
is the identity matrix of size  .
.
3.Overview of our method
Given  , the triple
, the triple 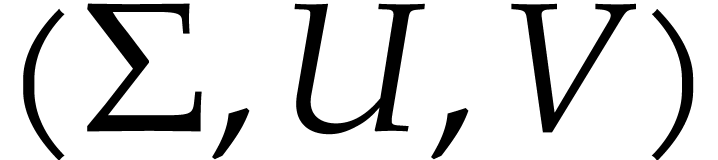 with
with 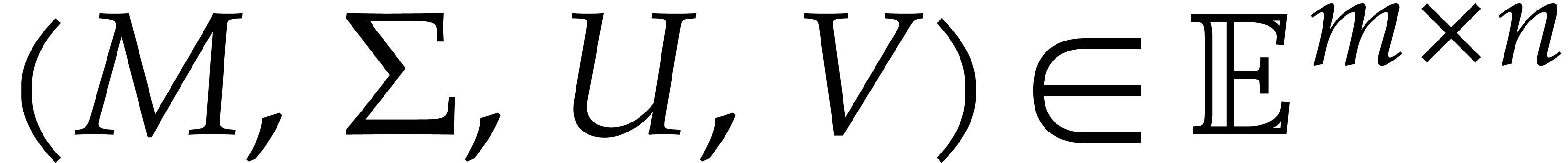 forms an SVD for
forms an SVD for  if and only if it satisfies the following system of
equations:
if and only if it satisfies the following system of
equations:
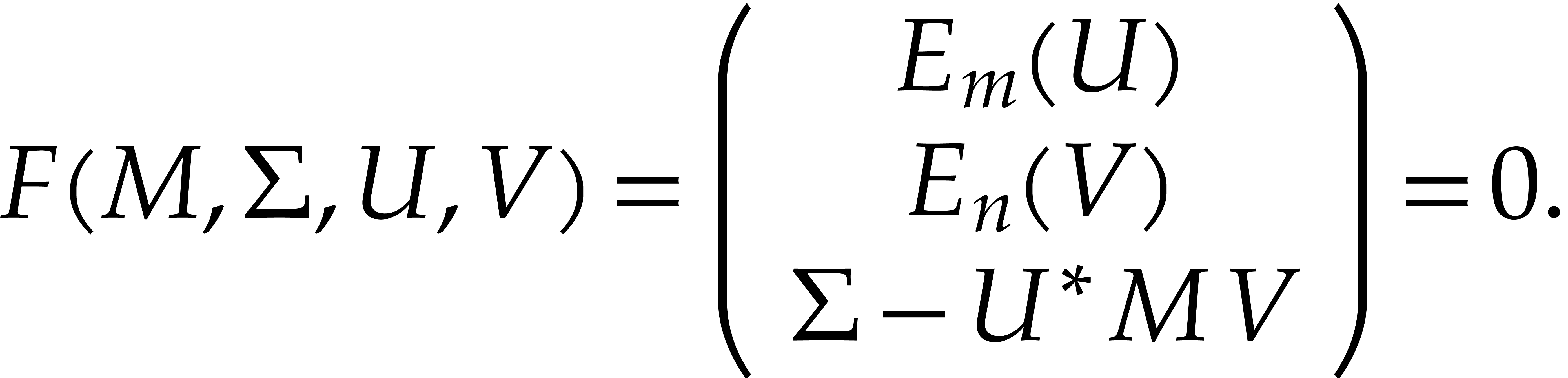 |
(7) |
This is a system of 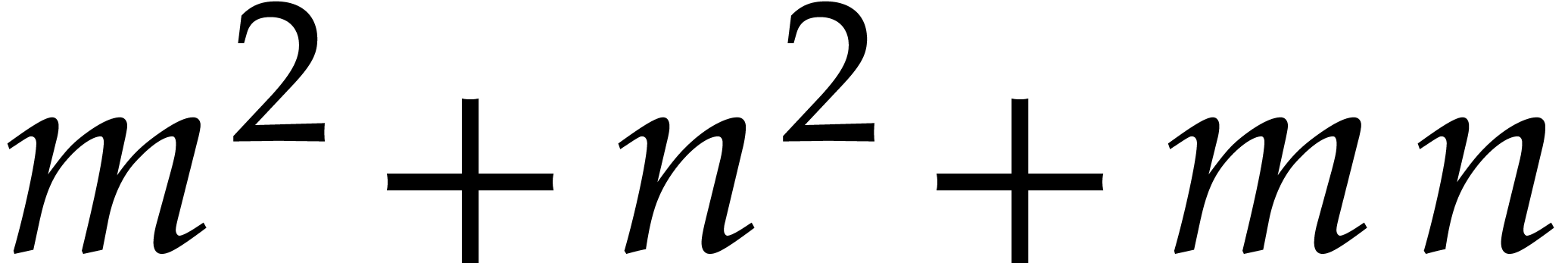 equations with
equations with 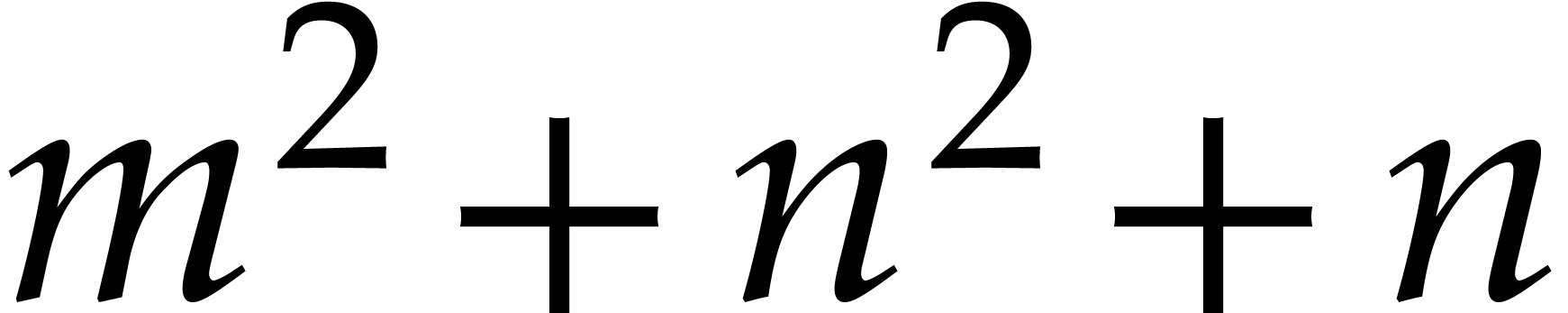 unknowns. Our efficient numerical method for solving this
system will rely on the following principles:
unknowns. Our efficient numerical method for solving this
system will rely on the following principles:
-
For a well-chosen ansatz 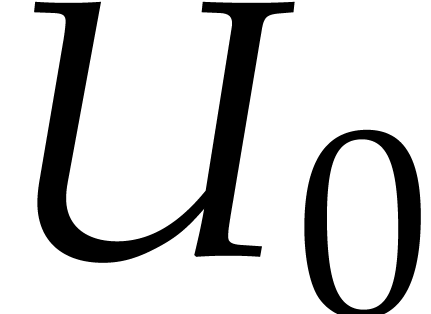 close to
the unitary group
close to
the unitary group  , we
prove that
, we
prove that
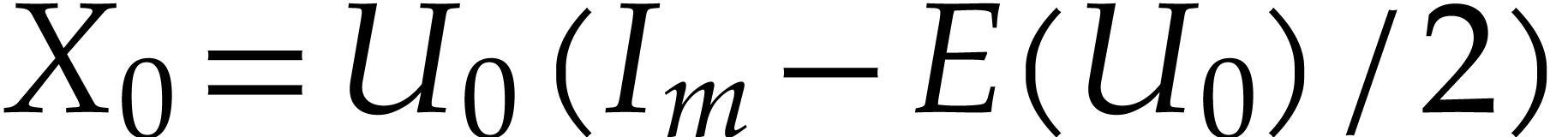
is even closer to the unitary group than 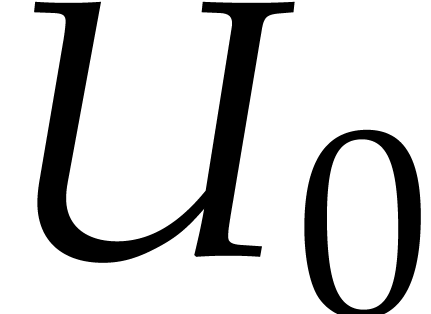 : see section 4. Similarly, for an
ansatz
: see section 4. Similarly, for an
ansatz  close to
close to  , we take
, we take 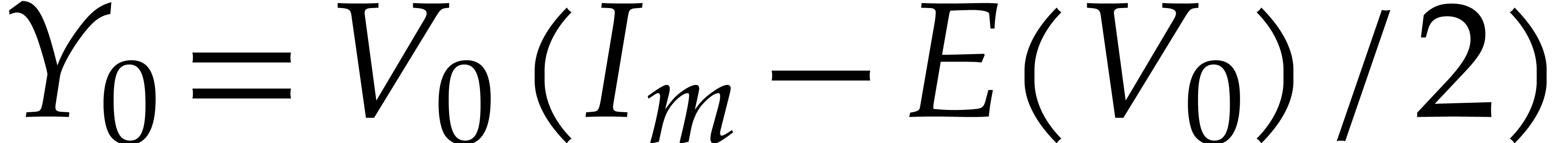
-
From 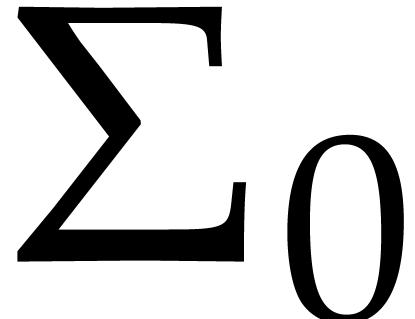 ,
, 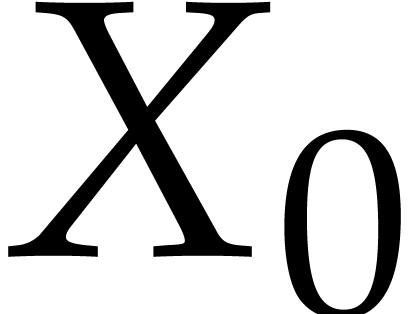 and
and 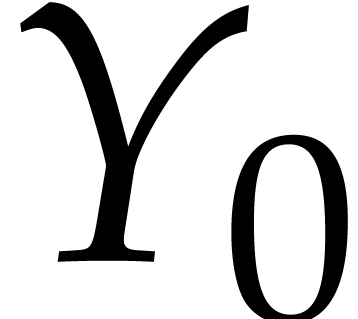 , we prove that is
possible to explicitly compute
, we prove that is
possible to explicitly compute 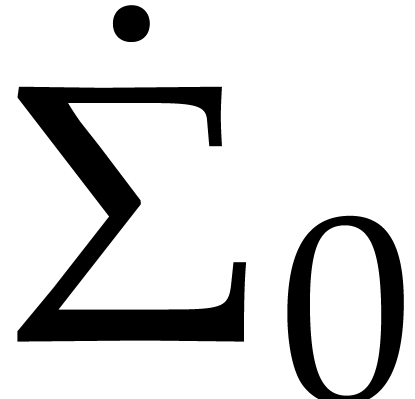 ,
and two skew Hermitian matrices
,
and two skew Hermitian matrices 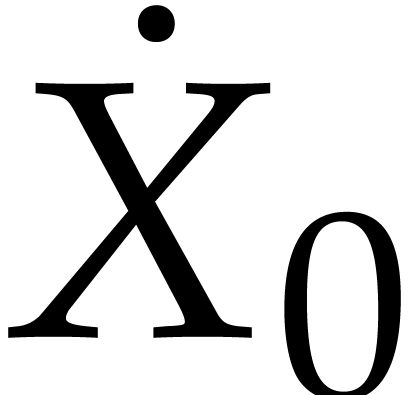 and
and 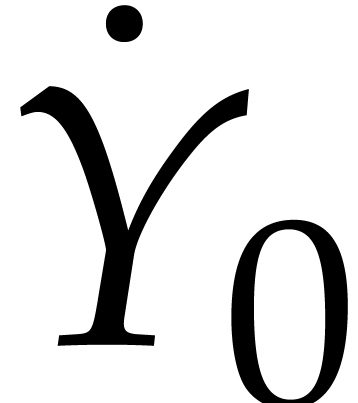 such that
such that
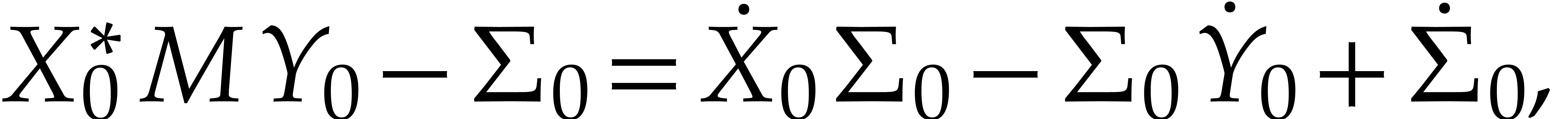
after which 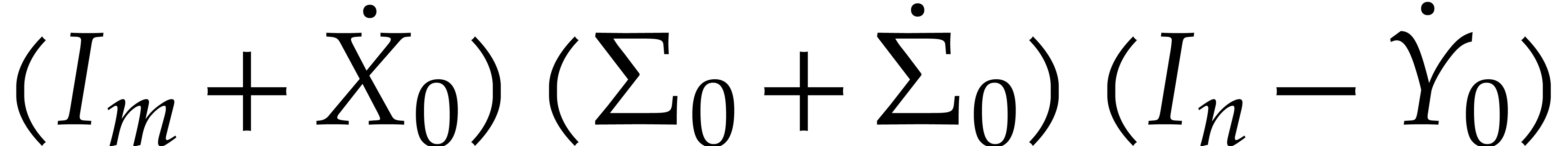 is a first-order approximation
of
is a first-order approximation
of 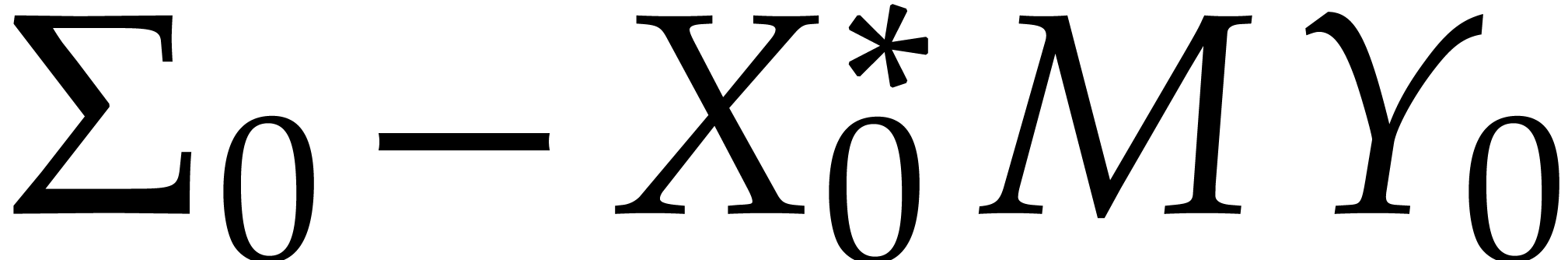 : see section 5.
: see section 5.
-
Let 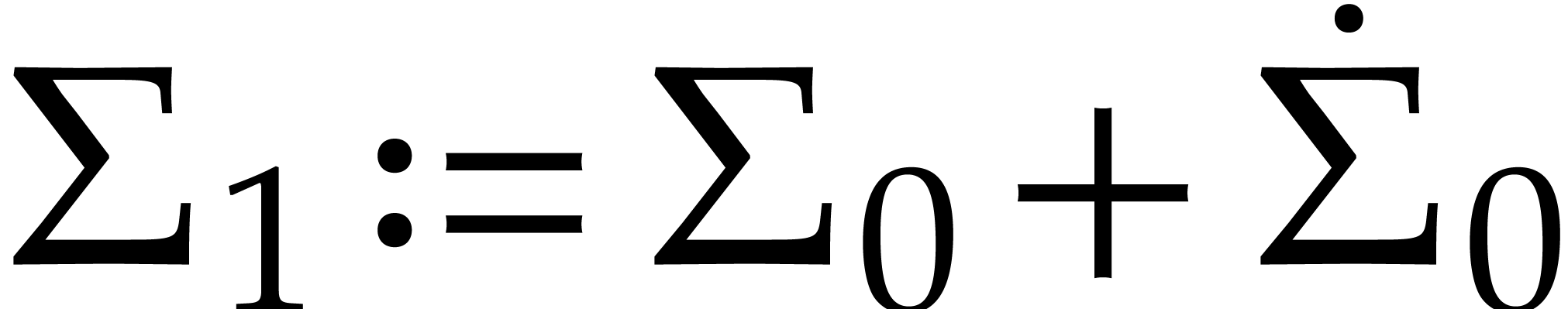 ,
, 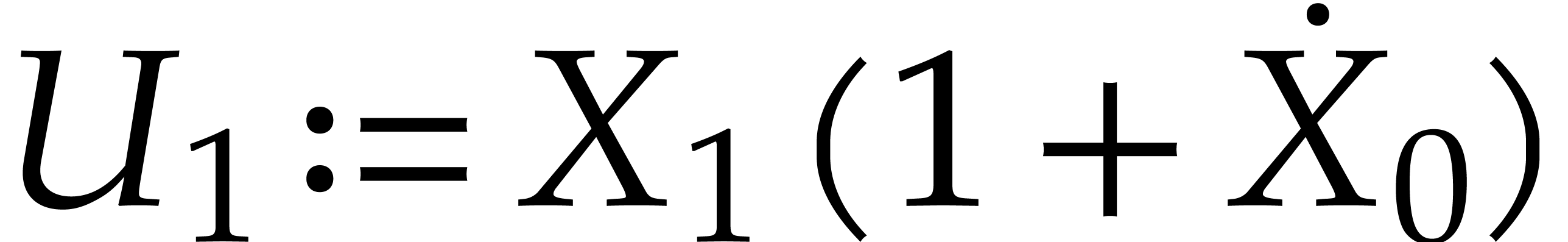 , and
, and 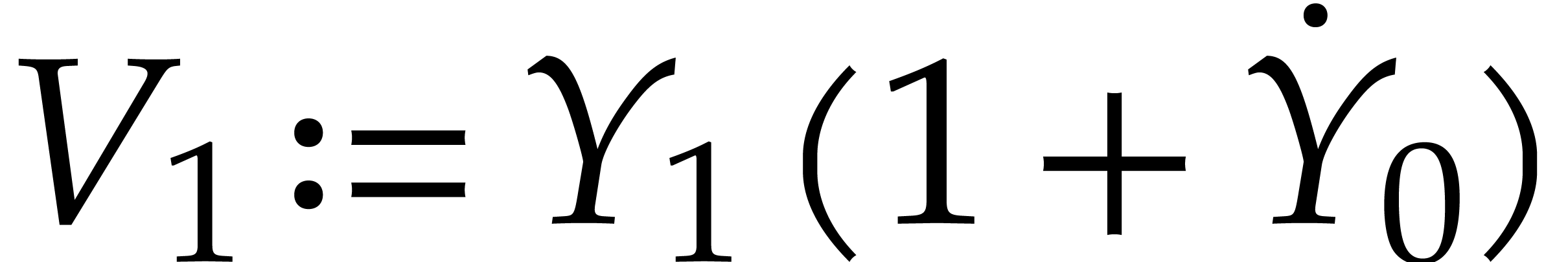 .
If
.
If 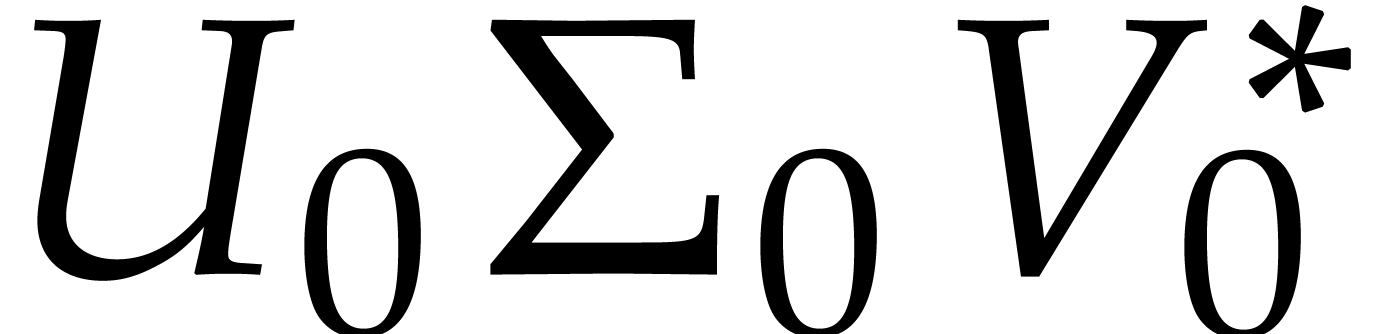 is sufficiently close to
is sufficiently close to 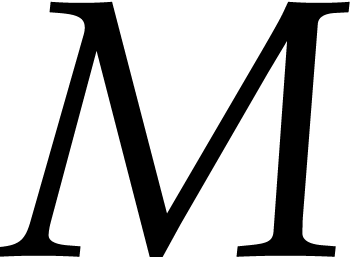 , then we will prove that
, then we will prove that 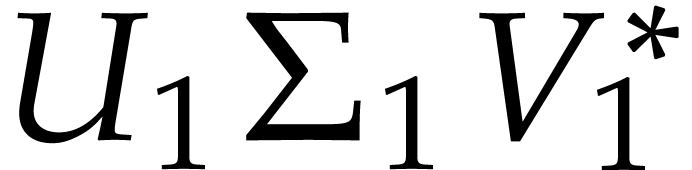 is a better approximation of the matrix
is a better approximation of the matrix 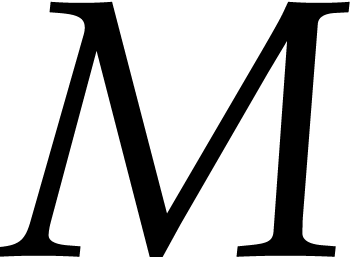 than
than
 :
:
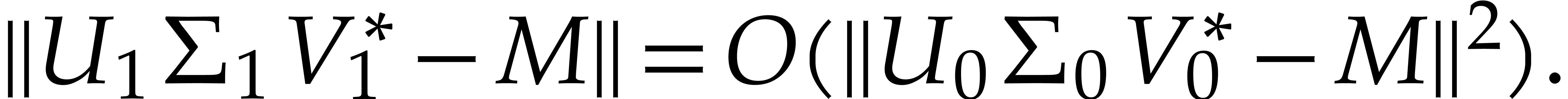
More precisely, given 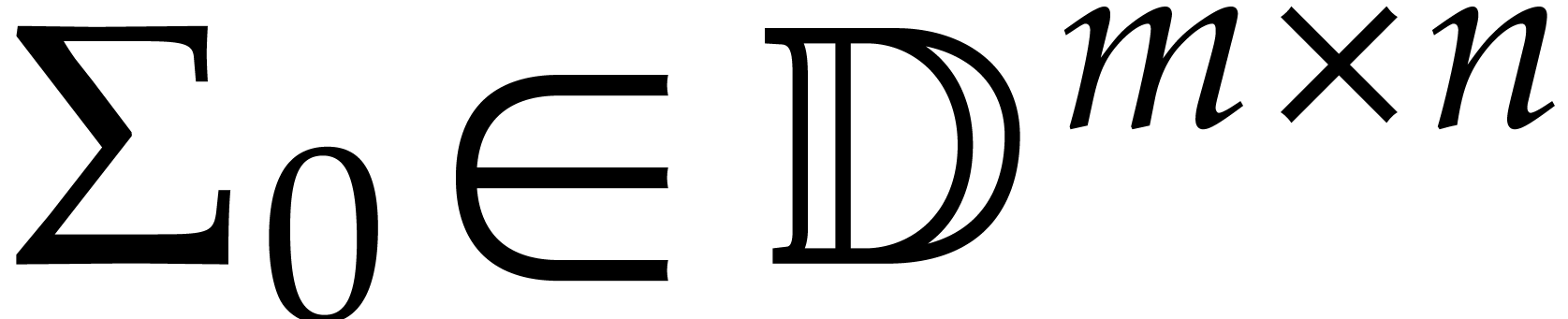 ,
,  , and
, and 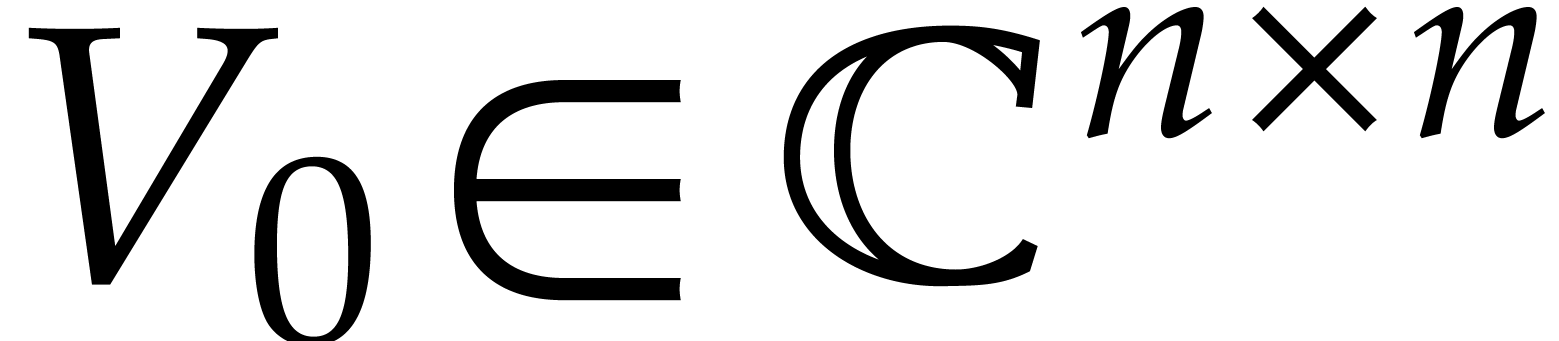 ,
we define the following sequence of matrices
,
we define the following sequence of matrices 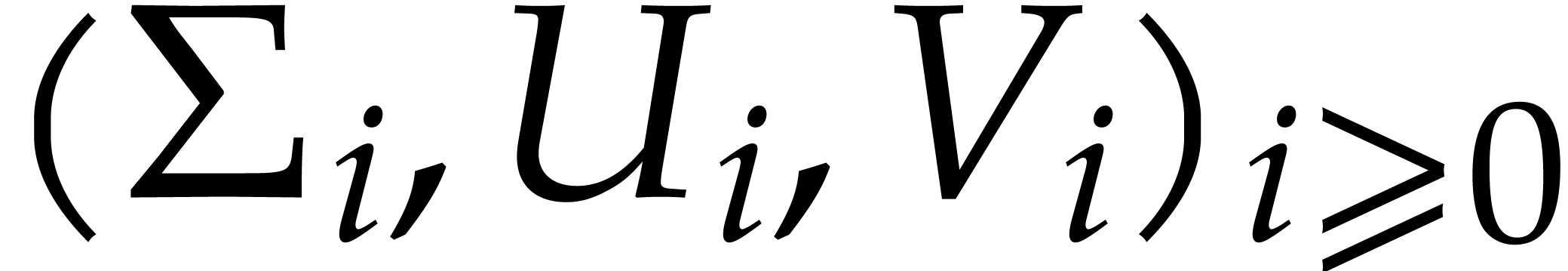
where 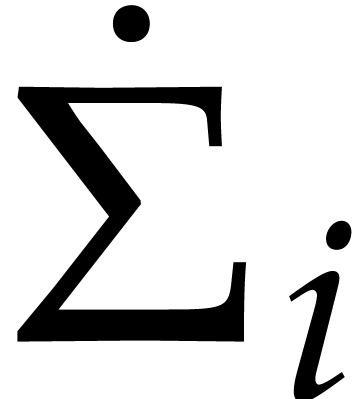 is a diagonal matrix and
is a diagonal matrix and 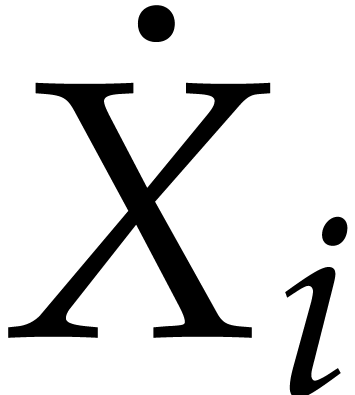 ,
, 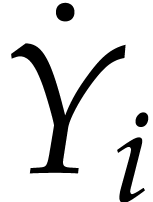 are two skew
Hermitian matrices such that
are two skew
Hermitian matrices such that
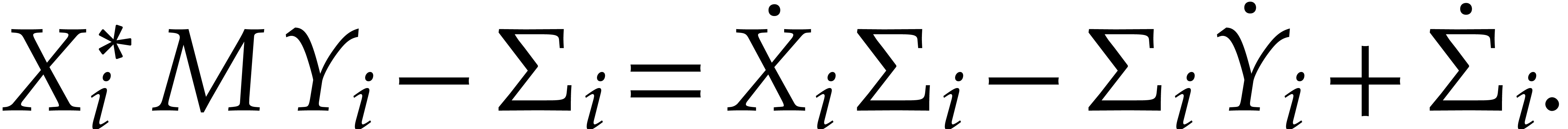 |
(13) |
In order to measure the quality of the ansatz, we define
The main result of the paper is the following theorem that gives
explicit conditions for the quadratic convergence of the sequence 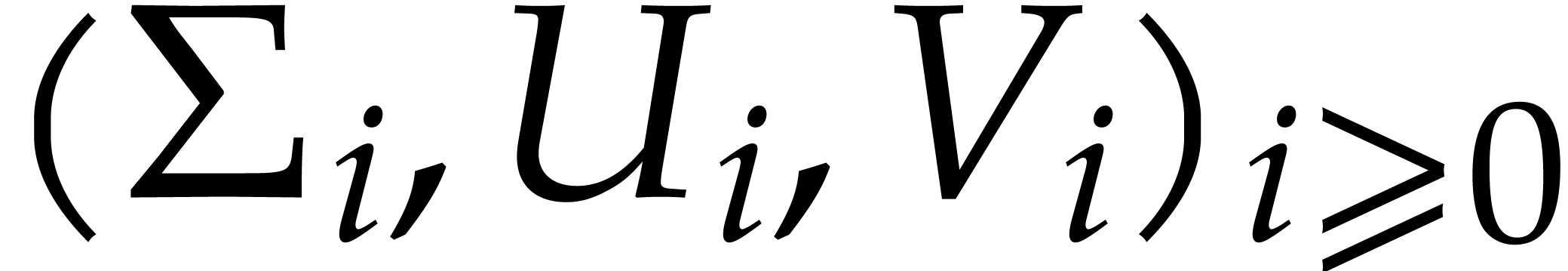 , together with explicit error
bounds.
, together with explicit error
bounds.
The proof of this theorem will be postponed to section 6.
Assuming that the theorem holds, it naturally gives rise to the
following algorithm for certifying an approximate SVD:
Input: an approximate SVD 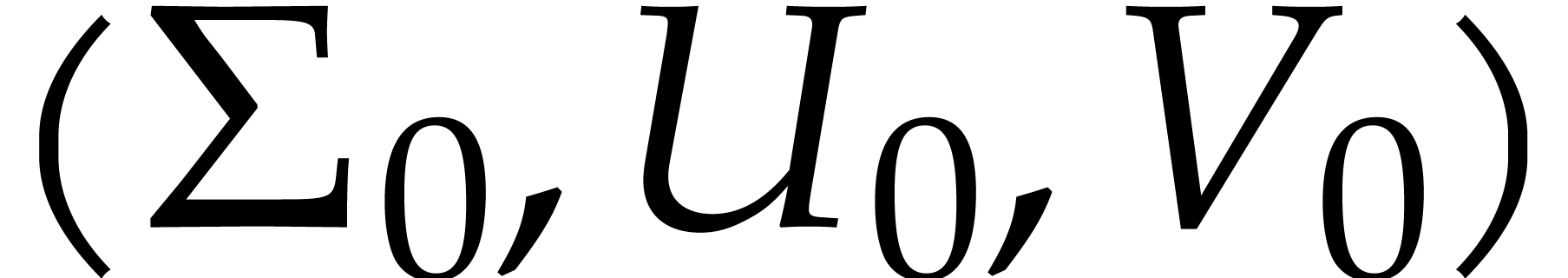 for the center of a ball matrix
for the center of a ball matrix 
Theorem 2.
Algorithm 1 is correct.
Proof. If  ,
then we return matrix balls with infinite radii for which the result is
trivially correct. If
,
then we return matrix balls with infinite radii for which the result is
trivially correct. If 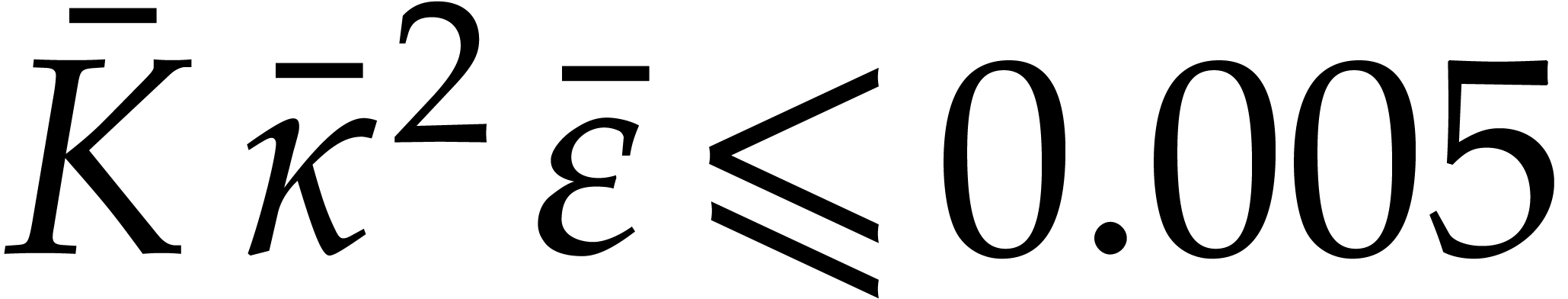 , then
for any
, then
for any  , the actual values
of
, the actual values
of  ,
,  and
and  are bounded by
are bounded by  ,
,
 and
and  ,
so Theorem 1 applies for the ansatz
,
so Theorem 1 applies for the ansatz 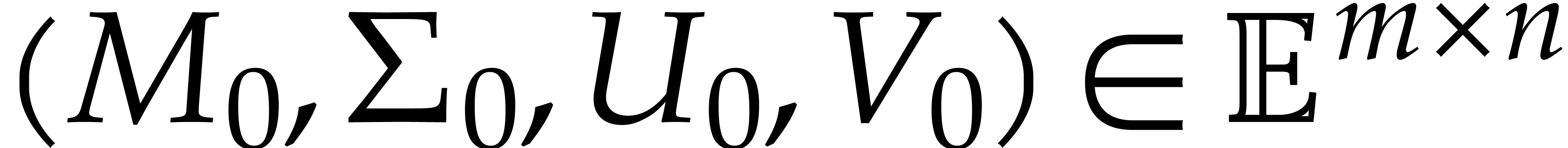 . As a consequence, we obtain an SVD
. As a consequence, we obtain an SVD  for
for 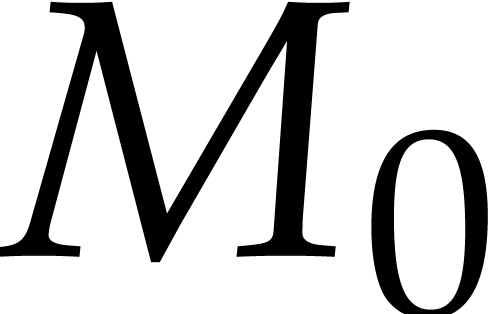 with the property that
with the property that 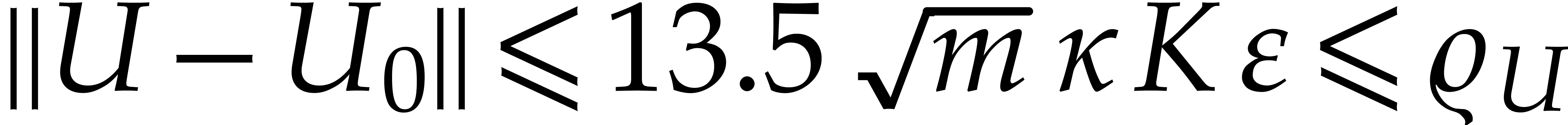 ,
, 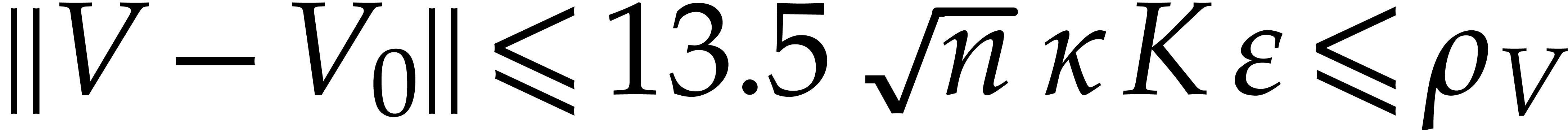 ,
and
,
and 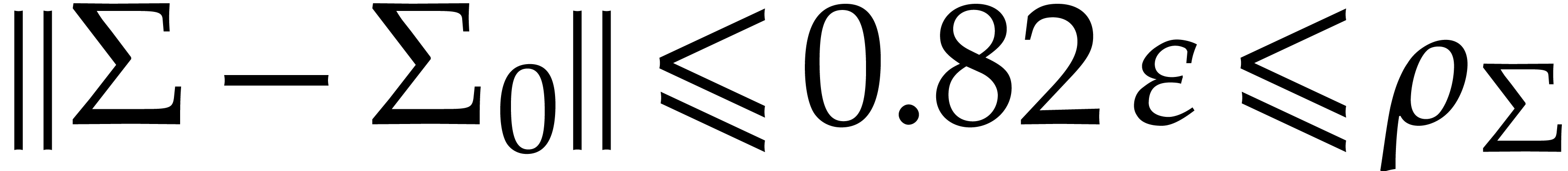 . We conclude that
. We conclude that 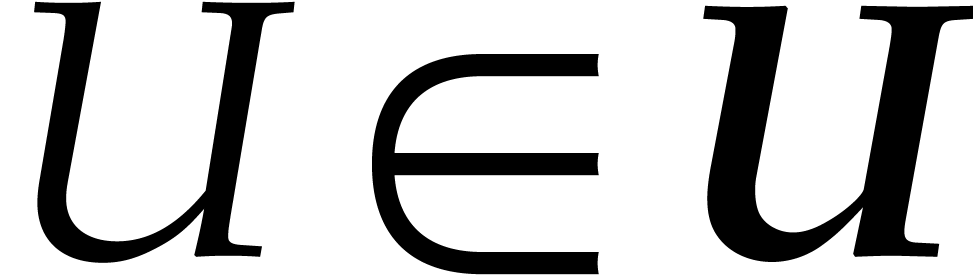 ,
, 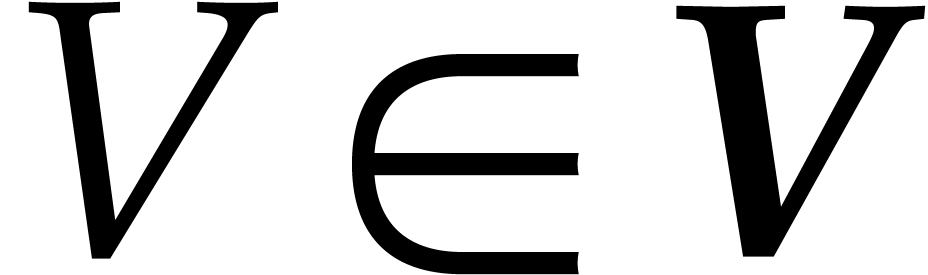 ,
,
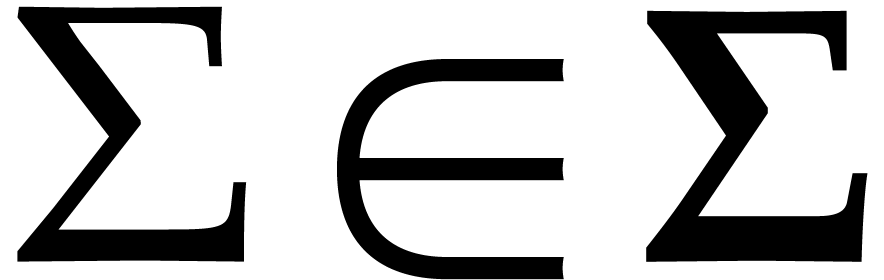 , as desired.
, as desired.
Remark 3. Notice that the
algorithm does not use our Newton iteration in order to improve the
quality of the approximate input SVD (in particular, the output is
worthless whenever  ). The
idea is that Algorithm 1 is only used for the
certification, and not for numerical approximation. The user is free to
use any preferred algorithm for computing the initial approximate SVD.
Of course, our Newton iteration can be of great use to increase the
precision of a rough approximate SVD that was computed by other means.
). The
idea is that Algorithm 1 is only used for the
certification, and not for numerical approximation. The user is free to
use any preferred algorithm for computing the initial approximate SVD.
Of course, our Newton iteration can be of great use to increase the
precision of a rough approximate SVD that was computed by other means.
4.Polar projection
Since we are doing approximate computations, the unitary matrices in an
SVD are not given exactly, so we may wish to estimate the distance
between an approximate unitary matrix and the closest actual unitary
matrix. This is related to the following problem: given an approximately
unitary  matrix
matrix  ,
find a good approximation
,
find a good approximation  for its projection on
the group
for its projection on
the group 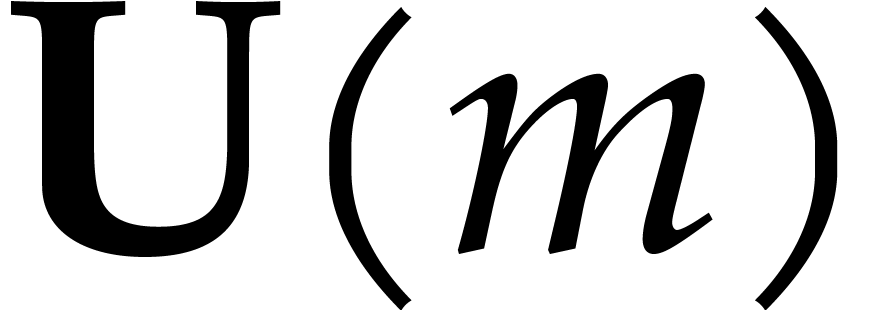 of unitary
of unitary  matrices. We recall a Newton iteration for this problem [20,
2, 12] and provide a detailed analysis of its
(quadratic) convergence.
matrices. We recall a Newton iteration for this problem [20,
2, 12] and provide a detailed analysis of its
(quadratic) convergence.
4.1.The Newton iteration
The tangent space to 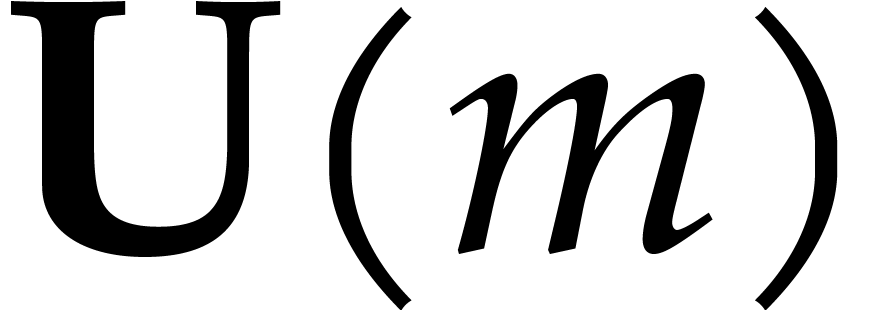 at
at  is
is
 |
(14) |
Consider the Riemannian metric inherited from the embedding space 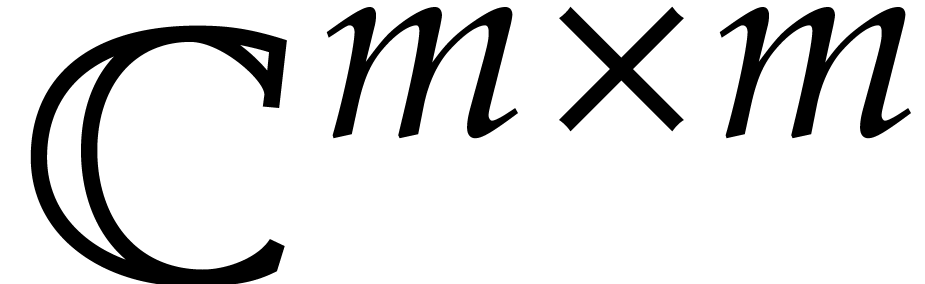
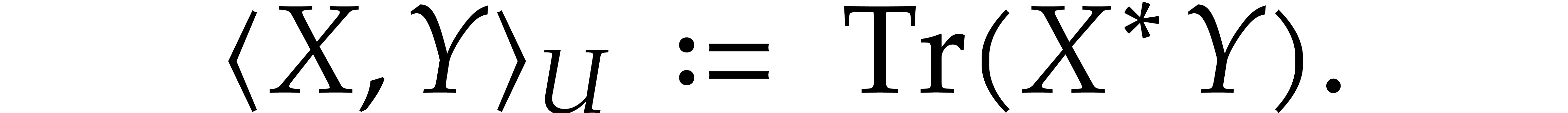
Then the normal space is
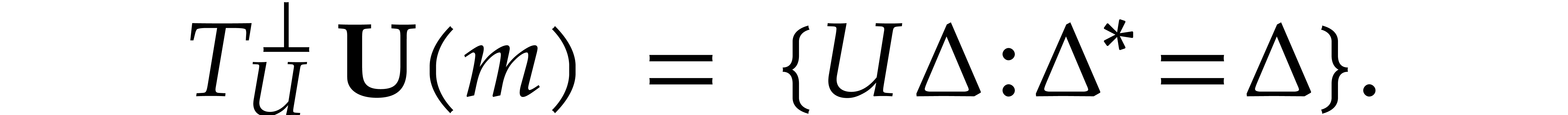
We wish to compute  using an appropriate Newton
iteration. From the characterization of the normal space, it turns out
that it is more convenient to write
using an appropriate Newton
iteration. From the characterization of the normal space, it turns out
that it is more convenient to write 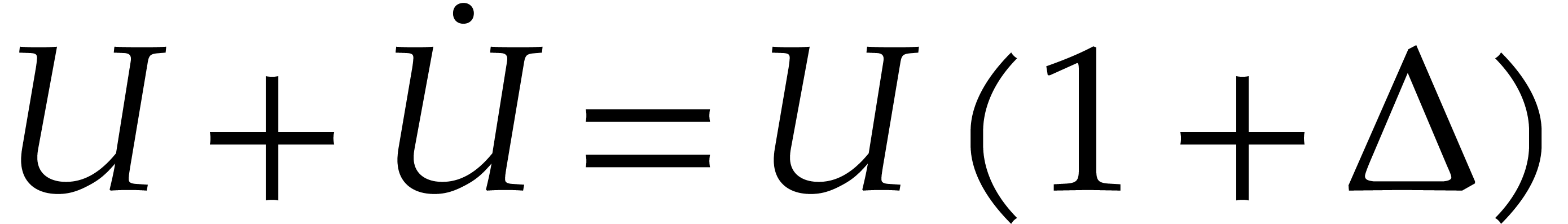 ,
where
,
where  is Hermitian. With
is Hermitian. With 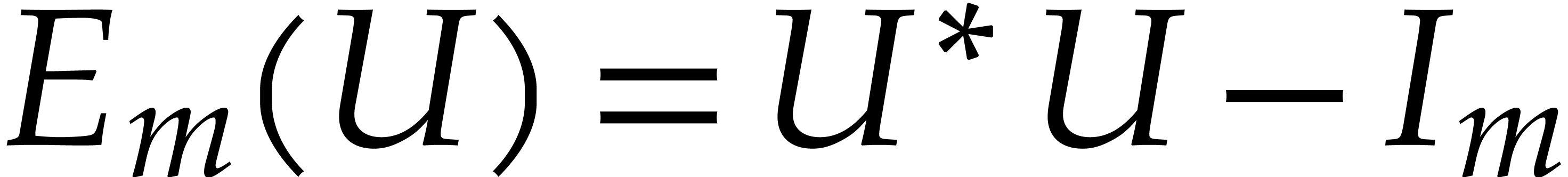 and
and 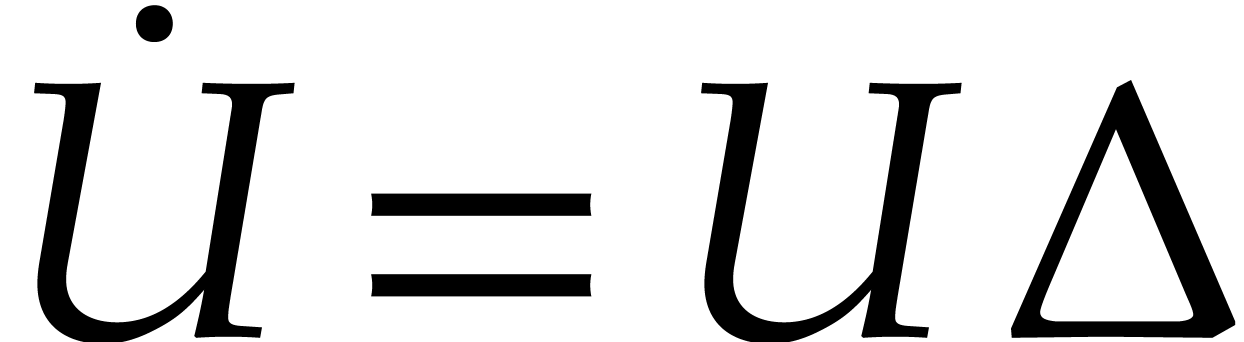 , we have
, we have
Taking
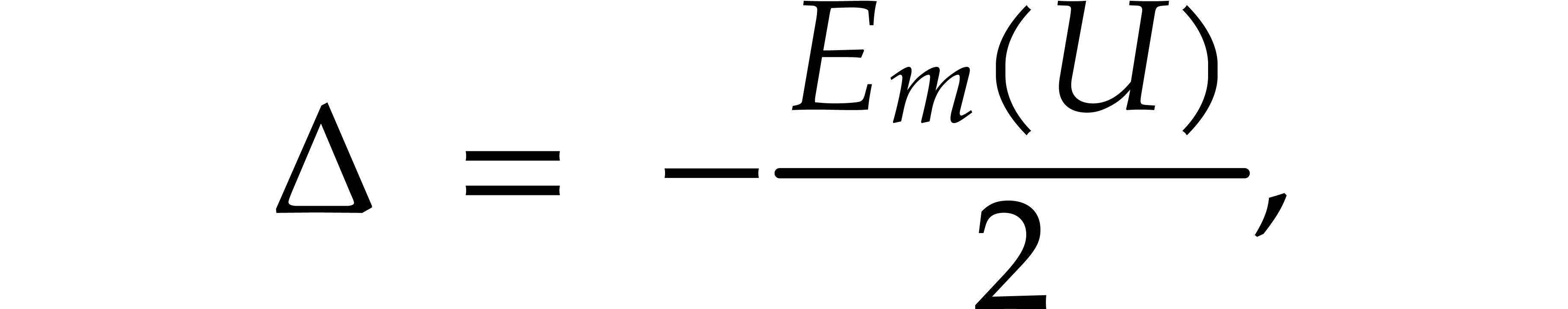 |
(15) |
it follows that
 |
(16) |
We are thus lead to the following Newton iteration that we will further
study below:
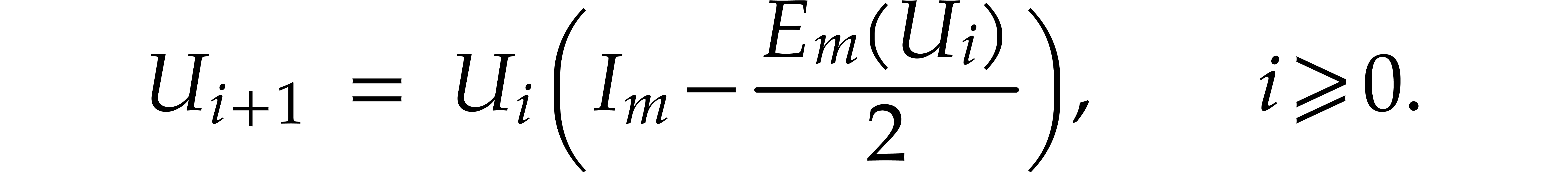 |
(17) |
Remark 4. Another
way to construct the previous iteration is to remark that the derivative
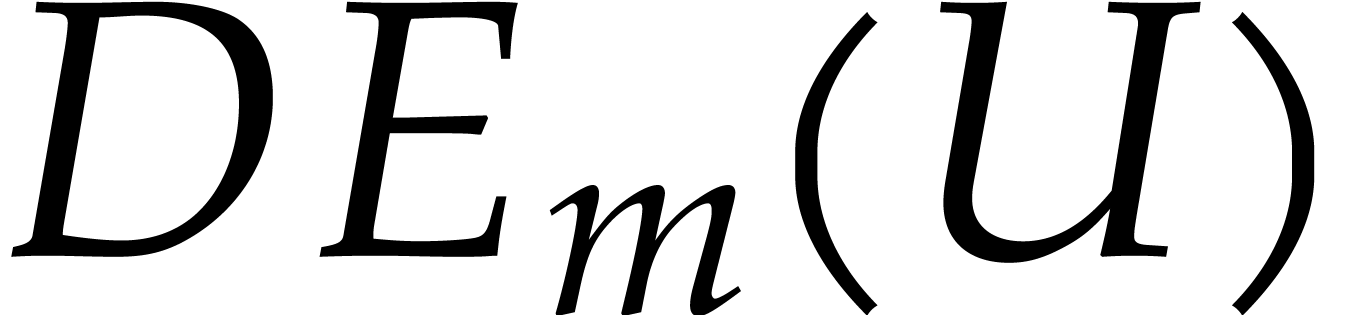 is onto from
is onto from 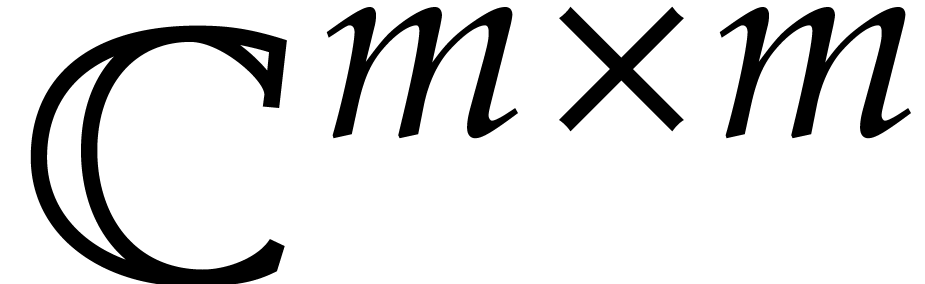 on the
subset
on the
subset  of Hermitian matrices. Then it is easy to
see that for given
of Hermitian matrices. Then it is easy to
see that for given  and
and  , the matrix
, the matrix 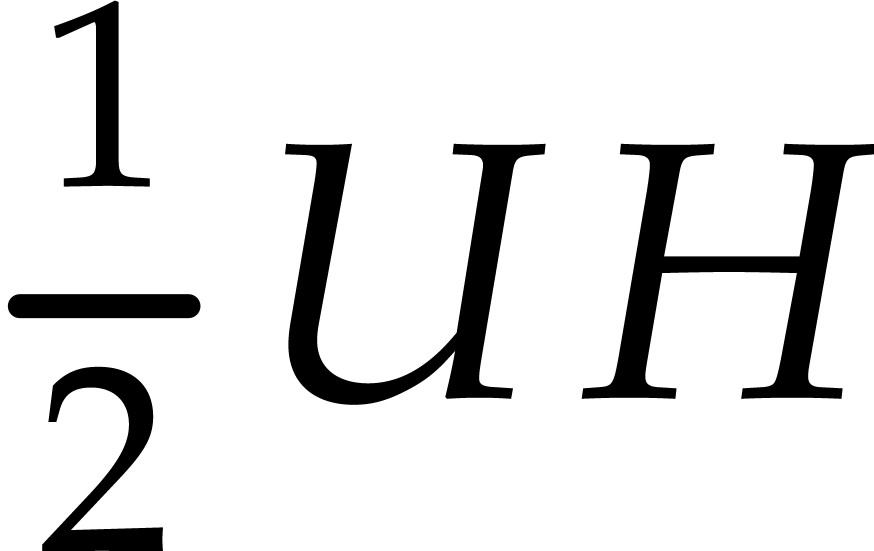 satisfies the
equation
satisfies the
equation 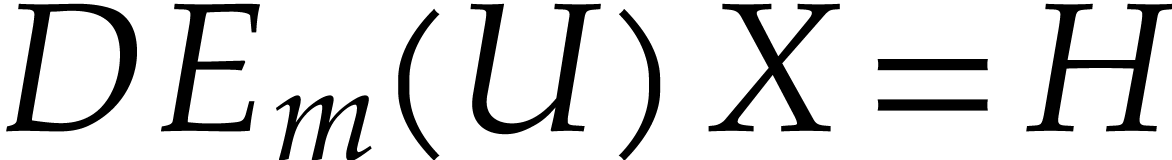 , i.e,
, i.e,
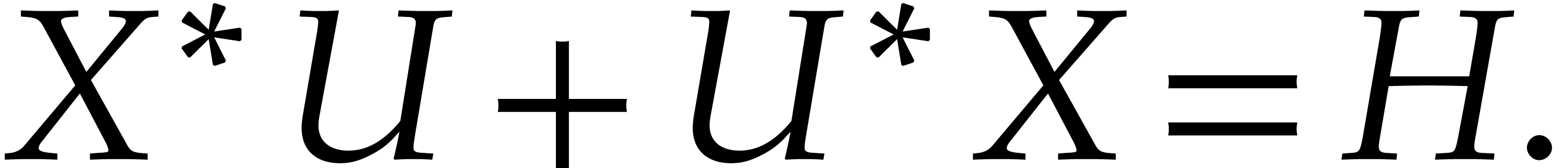
Consequently 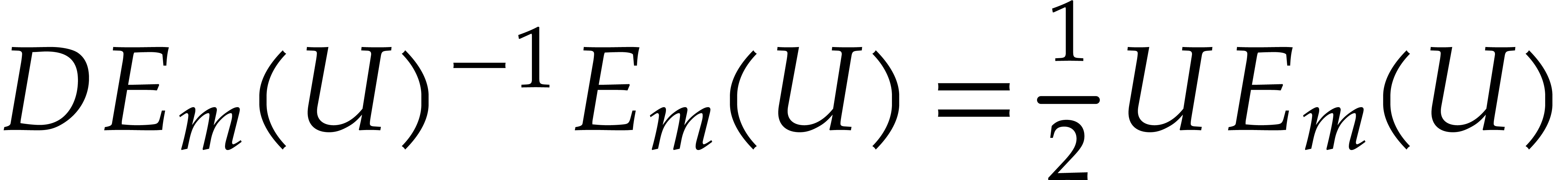 . In this
context the classical Newton operator thus becomes
. In this
context the classical Newton operator thus becomes
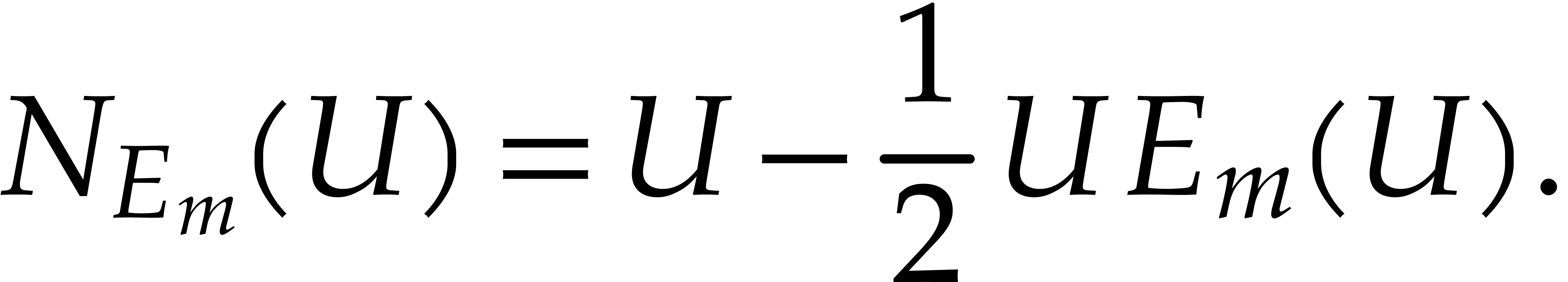
4.2.Error analysis
Proof. The conclusion follows from (16),
since 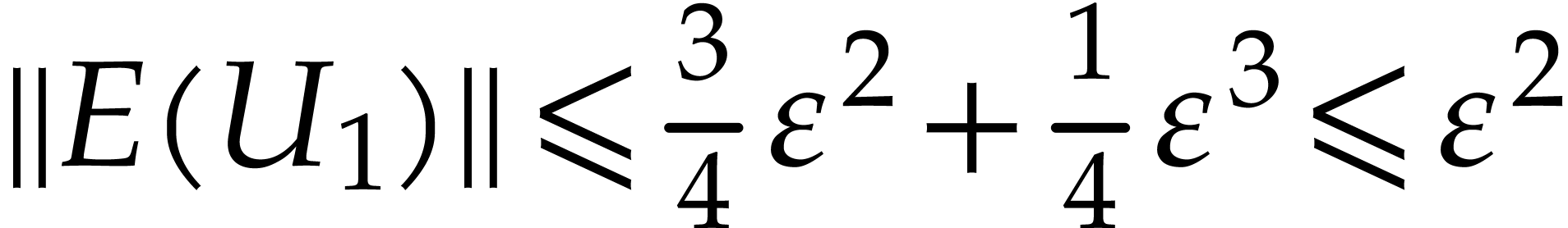 .
.
Proof. Modulo taking 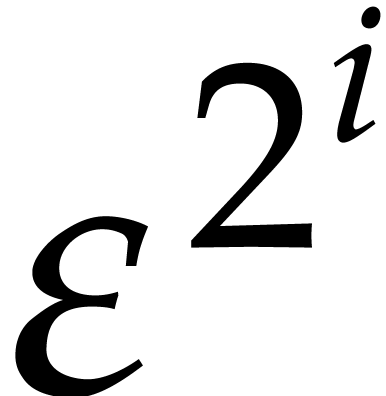 instead of
instead of  , it suffices to
consider the case when
, it suffices to
consider the case when 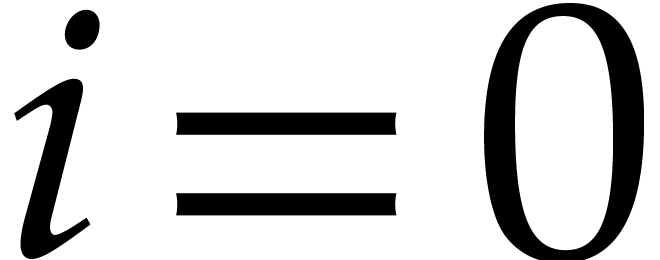 . Now
. Now
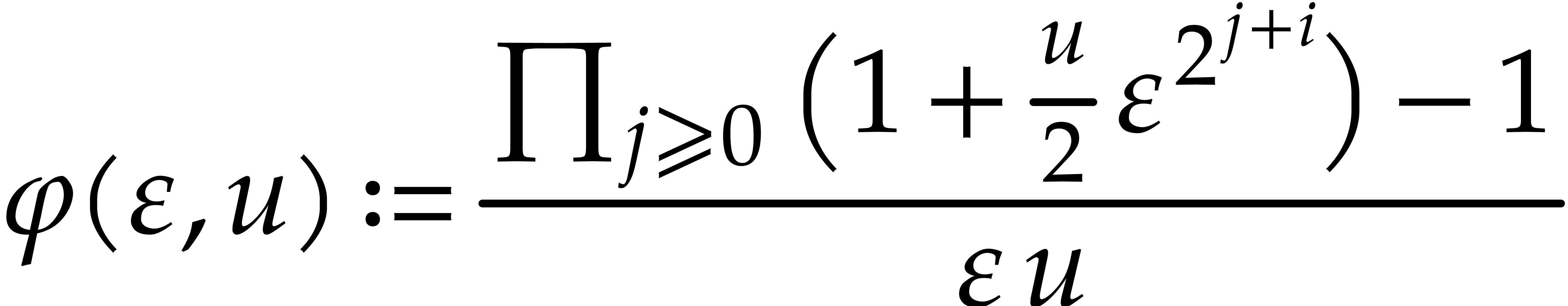
is an increasing function in  and
and 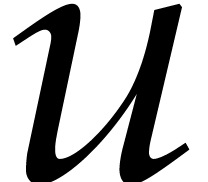 , since its power series expansion in
, since its power series expansion in  and
and 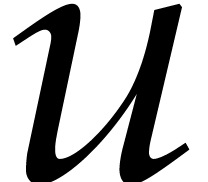 admits only positive
coefficients. Consequently,
admits only positive
coefficients. Consequently, 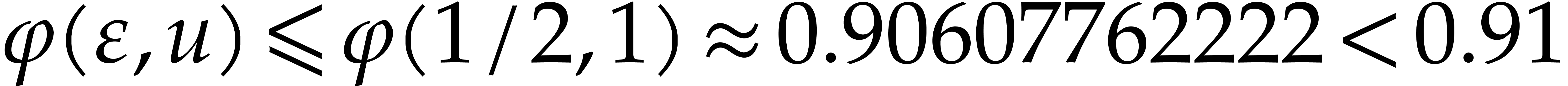 .
.
We recall that any invertible matrix  admits a
unique polar decomposition
admits a
unique polar decomposition
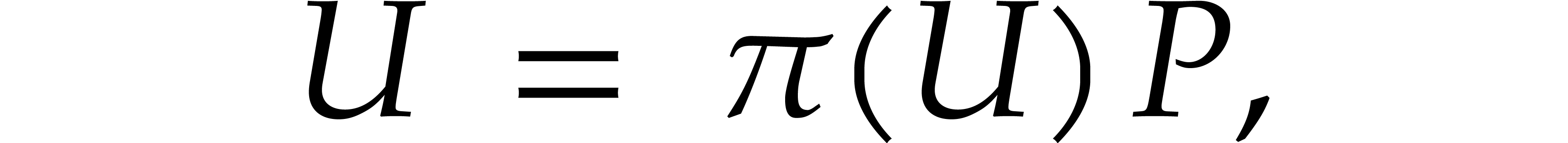
where  and
and  is a
positive-definite Hermitian matrix. We call
is a
positive-definite Hermitian matrix. We call 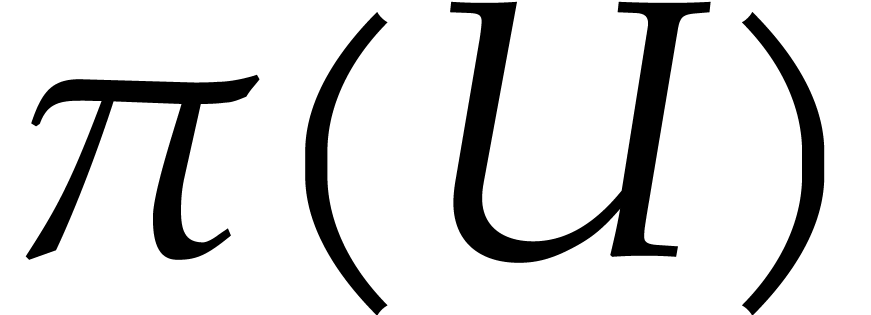 the
polar projection of
the
polar projection of  on
on 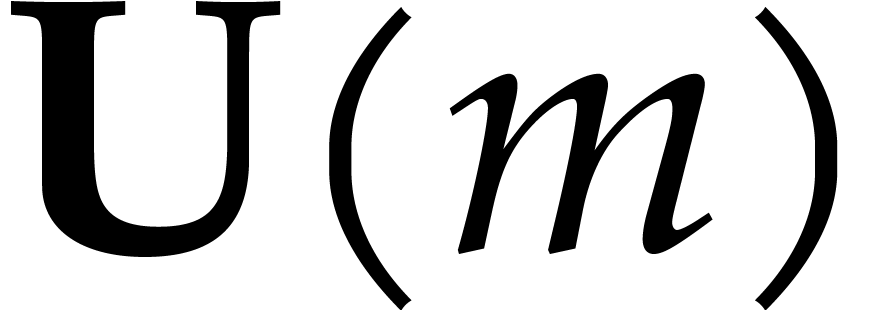 . The matrix
. The matrix  can
uniquely be written as the exponential of another Hermitian matrix. It
is also well known that
can
uniquely be written as the exponential of another Hermitian matrix. It
is also well known that 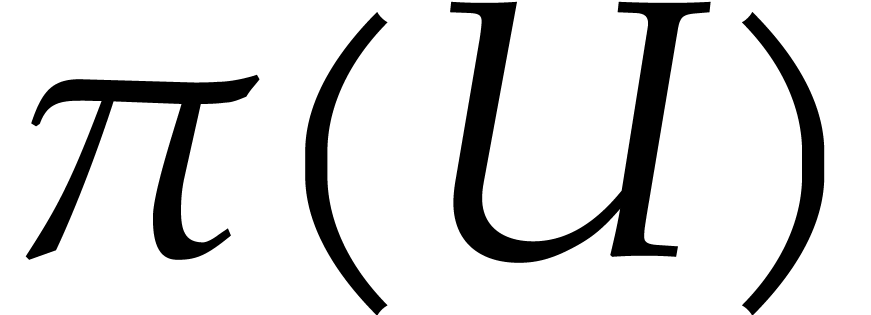 is indeed the closest
element in
is indeed the closest
element in 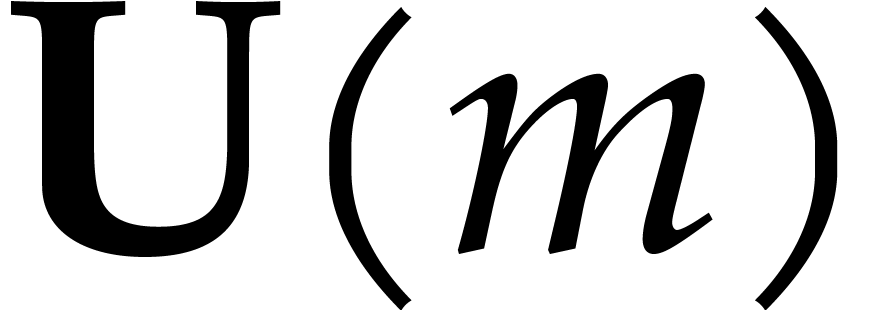 to
to  for the
Riemannian metric [6, Theorem 1].
for the
Riemannian metric [6, Theorem 1].
Proof. The Newton sequence (17)
defined from 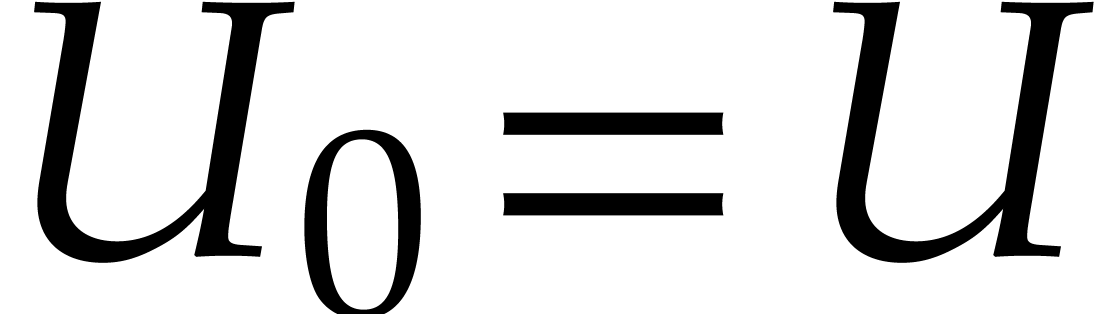 gives
gives
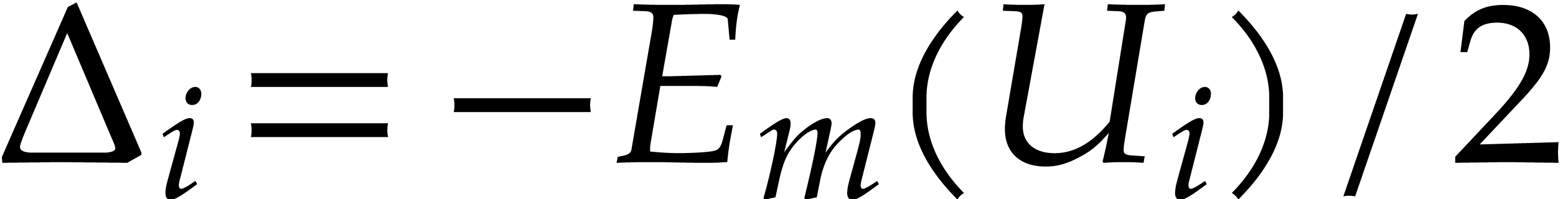
with 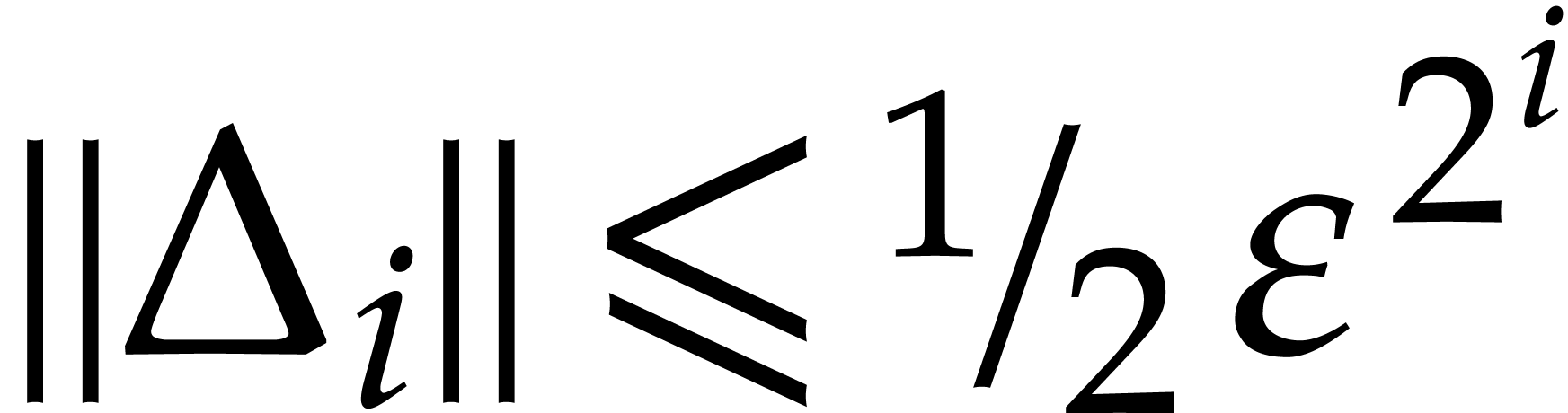 . An obvious induction
using Proposition 5 yields
. An obvious induction
using Proposition 5 yields 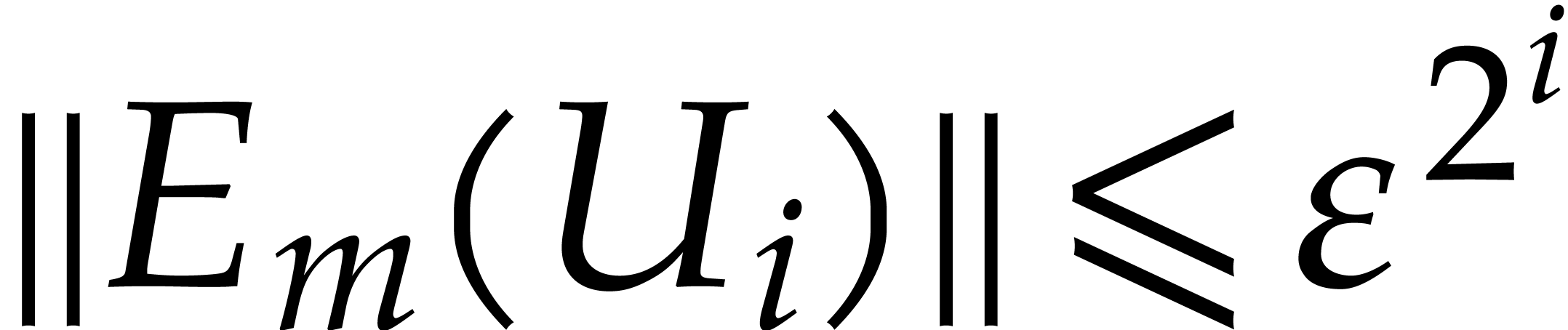 and
and
 . Therefore this sequence
converges to a limit
. Therefore this sequence
converges to a limit  that is given by
that is given by
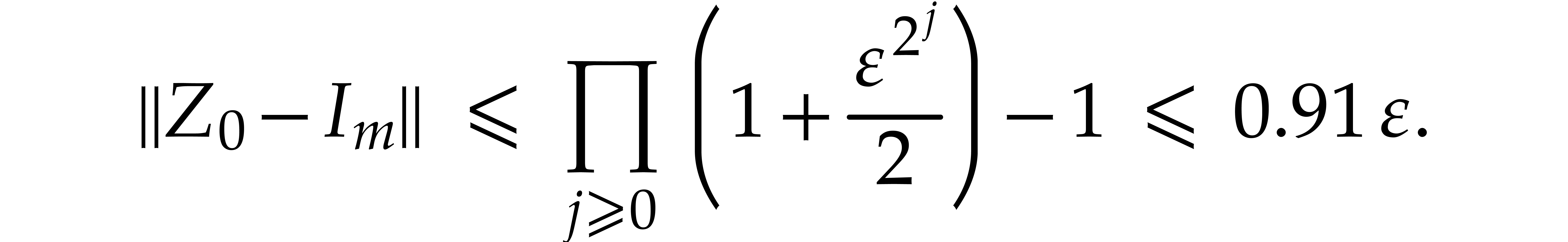
Lemma 6 implies
 |
(20) |
More generally, we have
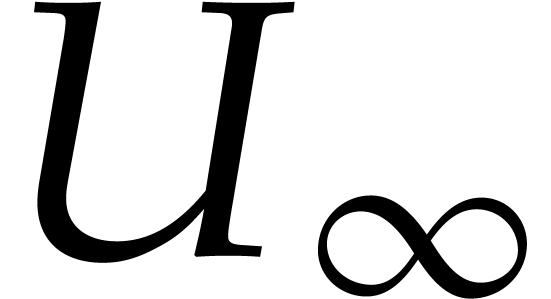
Since  is unitary, we have
is unitary, we have  . Neumann's lemma also implies that
. Neumann's lemma also implies that  is invertible with
is invertible with

By induction on  , it can also
be checked that
, it can also
be checked that  for all
for all 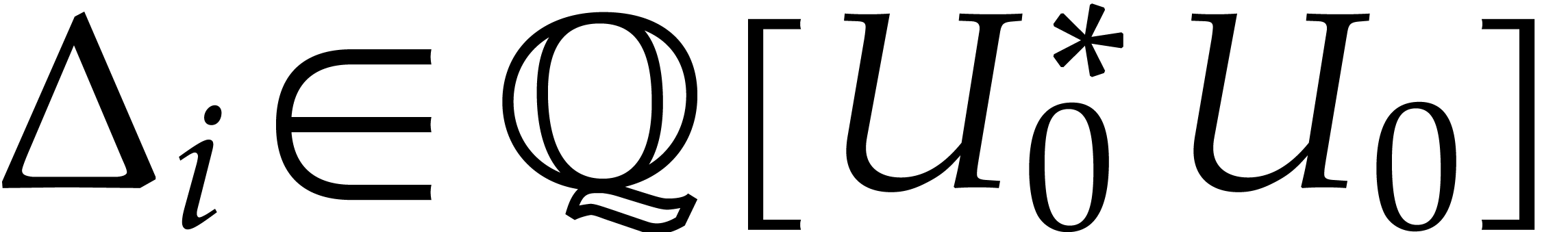 . This means that the
. This means that the 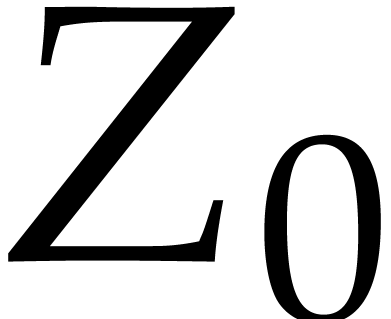 all
commute, whence
all
commute, whence 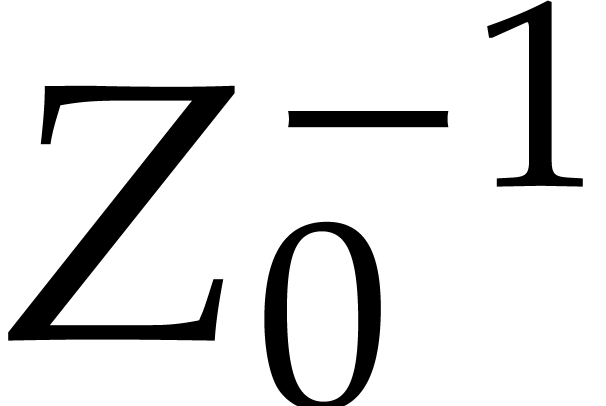 and
and 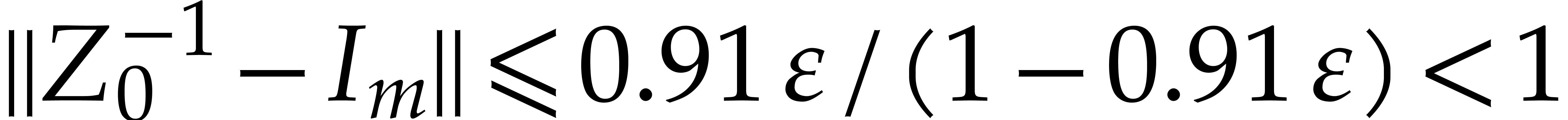 are
actually Hermitian matrices. Since
are
actually Hermitian matrices. Since 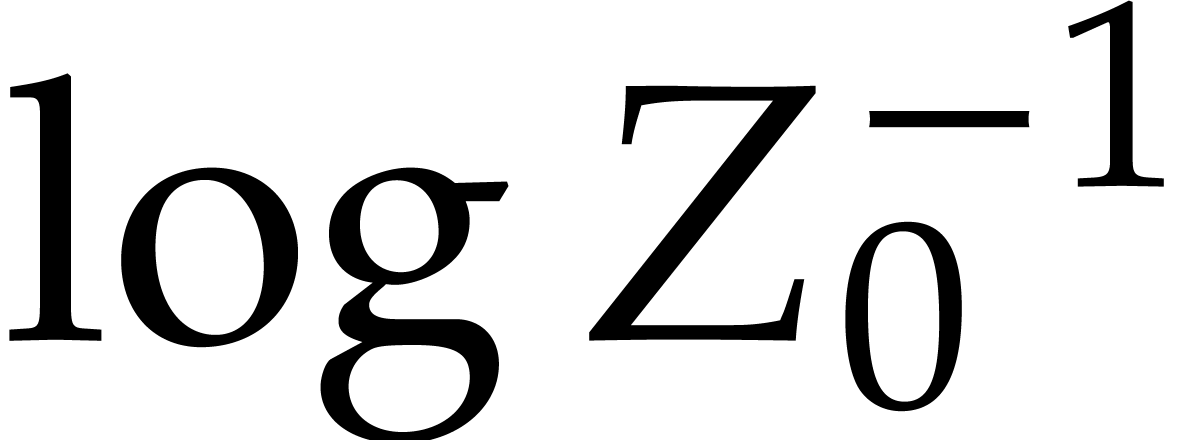 ,
the logarithm
,
the logarithm  is well defined. We conclude that
is well defined. We conclude that
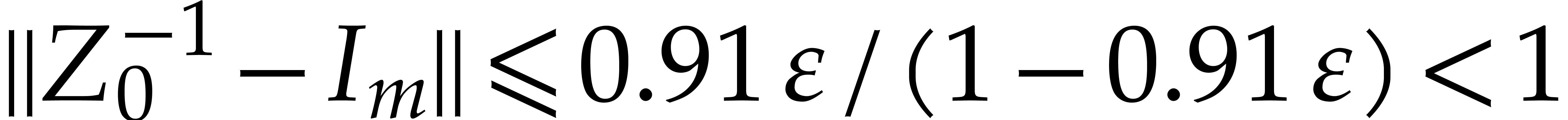 is the exponential of a Hermitian matrix, whence
it is positive-definite.
is the exponential of a Hermitian matrix, whence
it is positive-definite.
5.SVDs for perturbed diagonal
matrices
5.1.Approximate solutions at
order one
Let  be a matrix with diagonal entries
be a matrix with diagonal entries 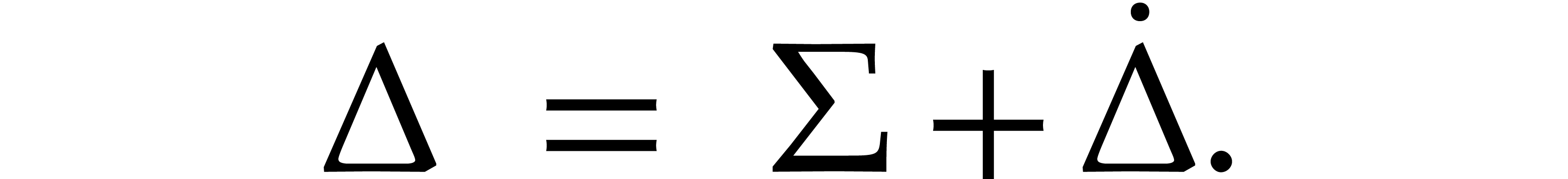 . Consider a perturbation
. Consider a perturbation
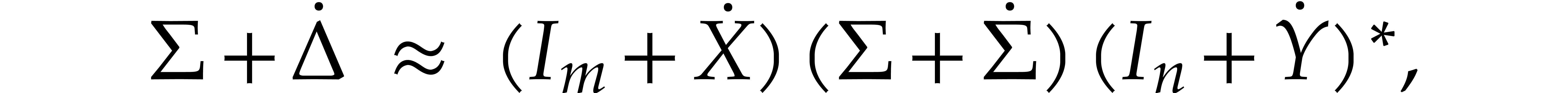
We wish to compute an approximate SVD

where  ,
,  , and
, and 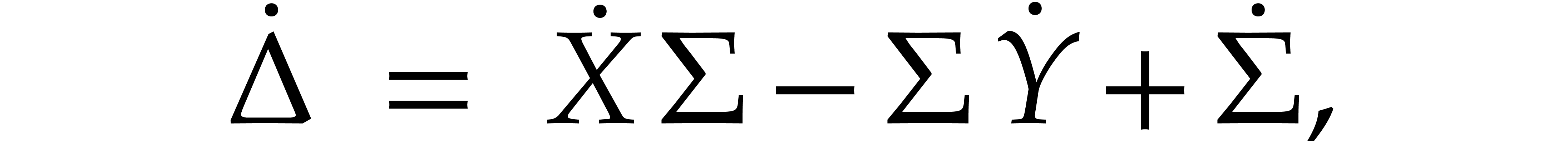 .
Discarding higher order terms, this leads to the linear equation
.
Discarding higher order terms, this leads to the linear equation
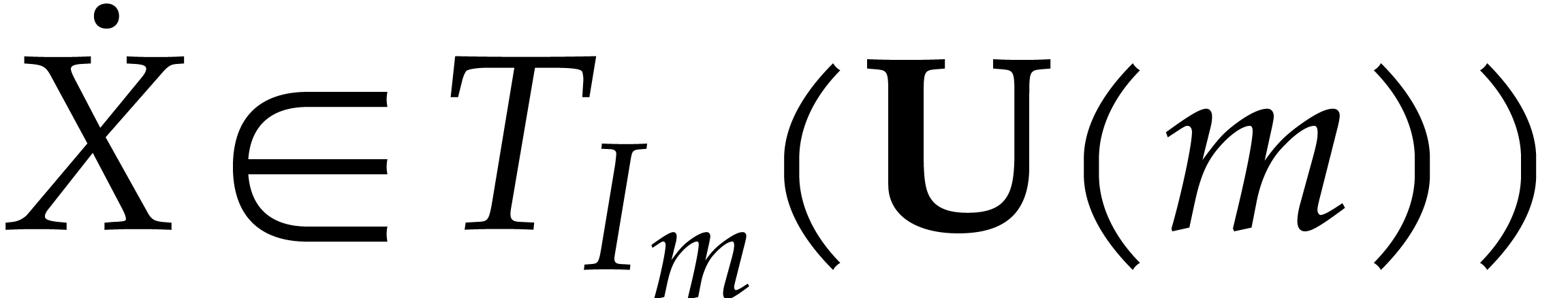
with 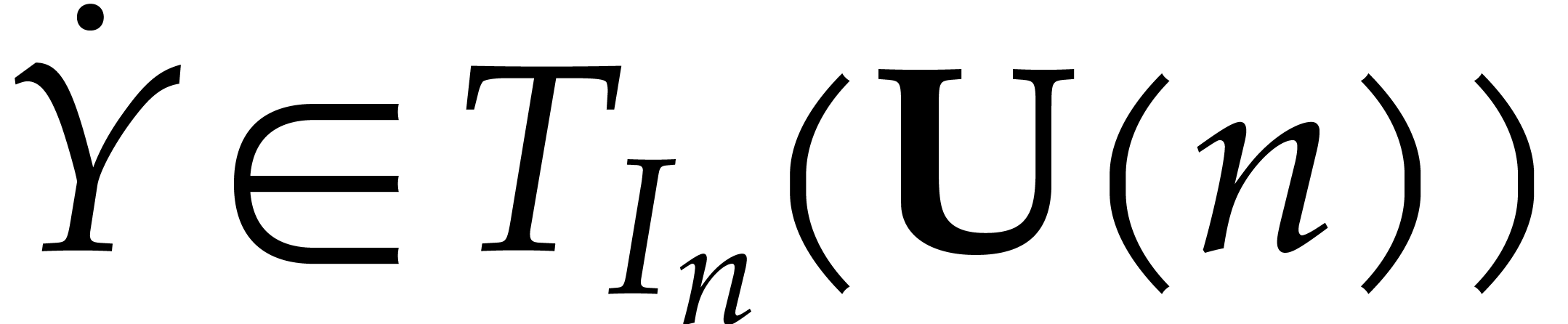 and
and 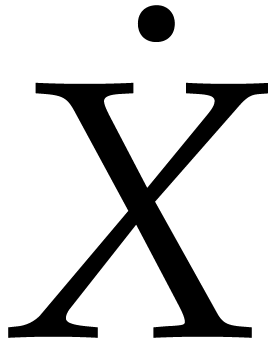 .
In view of (14), this means that
.
In view of (14), this means that 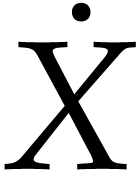 and
and 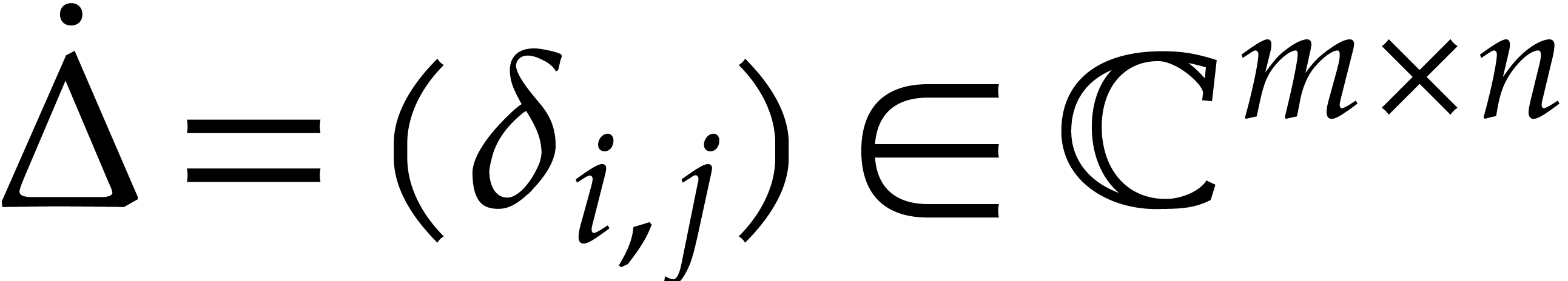 are skew Hermitian. The following
proposition shows how to solve the linear equation explicitly under
these constraints.
are skew Hermitian. The following
proposition shows how to solve the linear equation explicitly under
these constraints.
Proof. Since 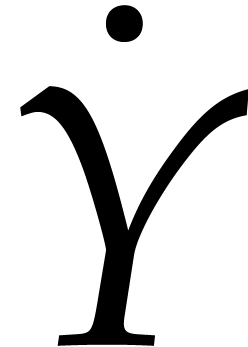 and
and 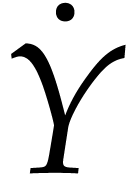 are skew Hermitian, we have
are skew Hermitian, we have  . In view of (21), we thus get
. In view of (21), we thus get

By skew symmetry, for the equation

to hold, it is sufficient to have
The formulas (22) clearly imply (30). The 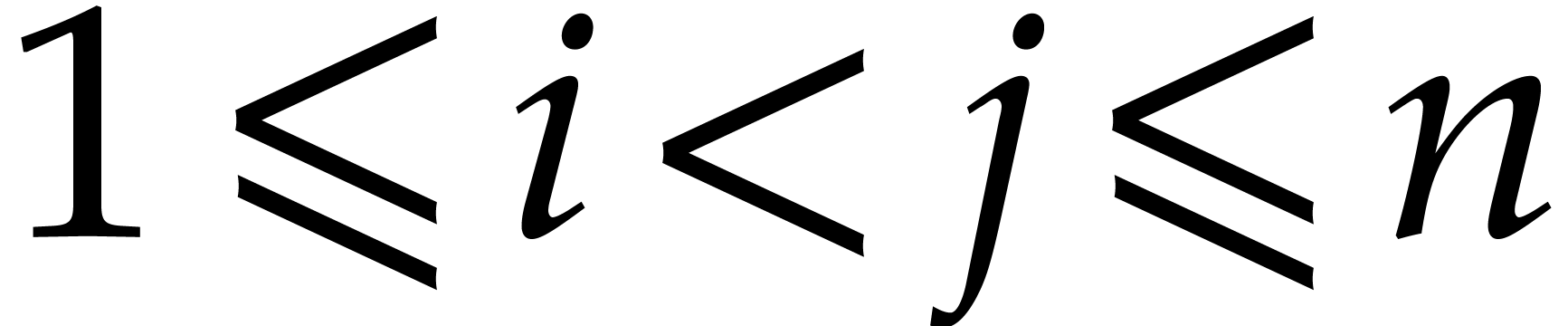 from (27) clearly satisfy (32)
as well. For
from (27) clearly satisfy (32)
as well. For 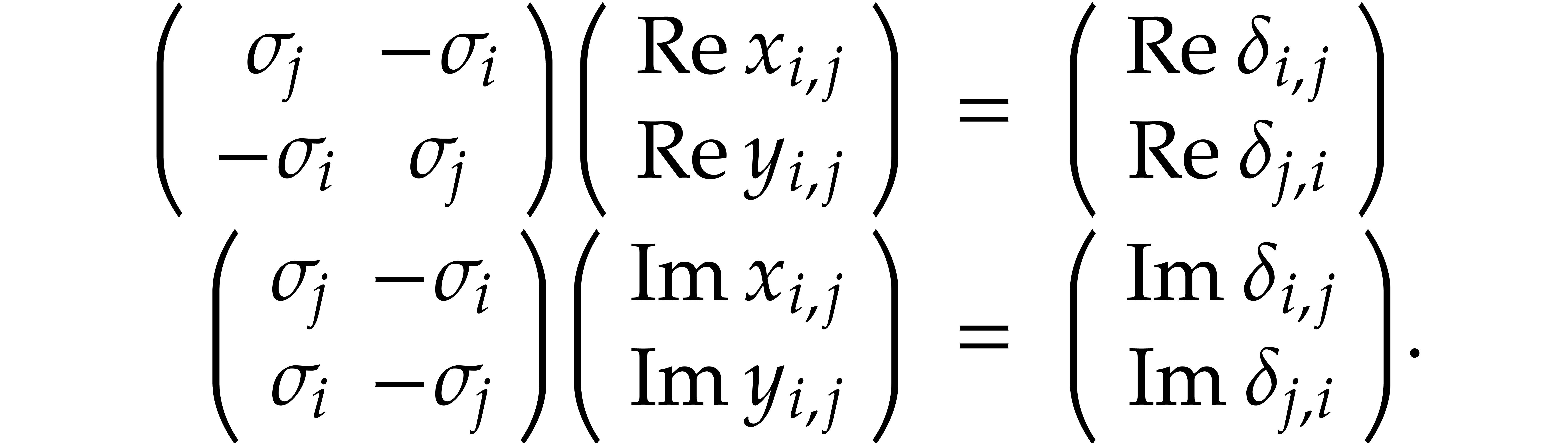 , the formulas
(31) can be rewritten as
, the formulas
(31) can be rewritten as

Since  , the formulas (23–26) indeed provide us with a solution.
The entries
, the formulas (23–26) indeed provide us with a solution.
The entries  with
with  do not
affect the product
do not
affect the product 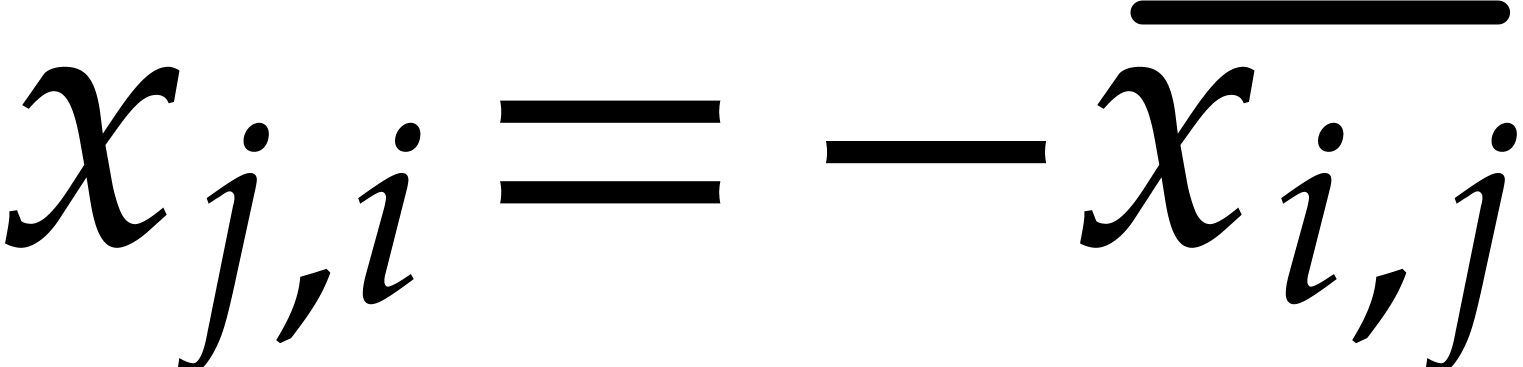 , so they
can be chosen as in (28). In view of the skew symmetry
constraints
, so they
can be chosen as in (28). In view of the skew symmetry
constraints 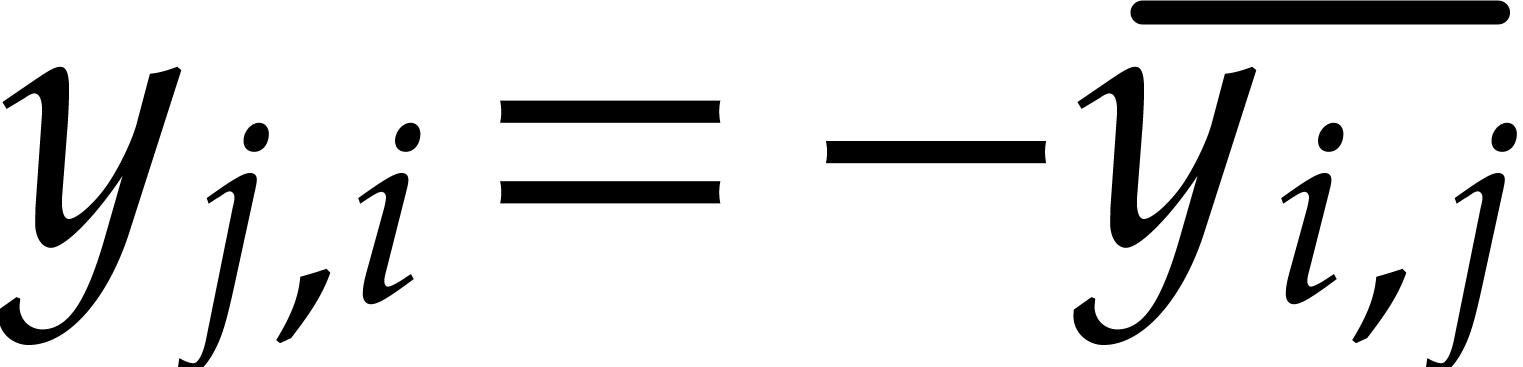 and
and  ,
we notice that the matrices
,
we notice that the matrices  and
and 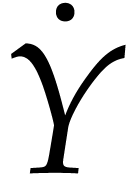 are completely defined.
are completely defined.
5.2.Error analysis
Proposition 9.
Let  .
Assume that
.
Assume that 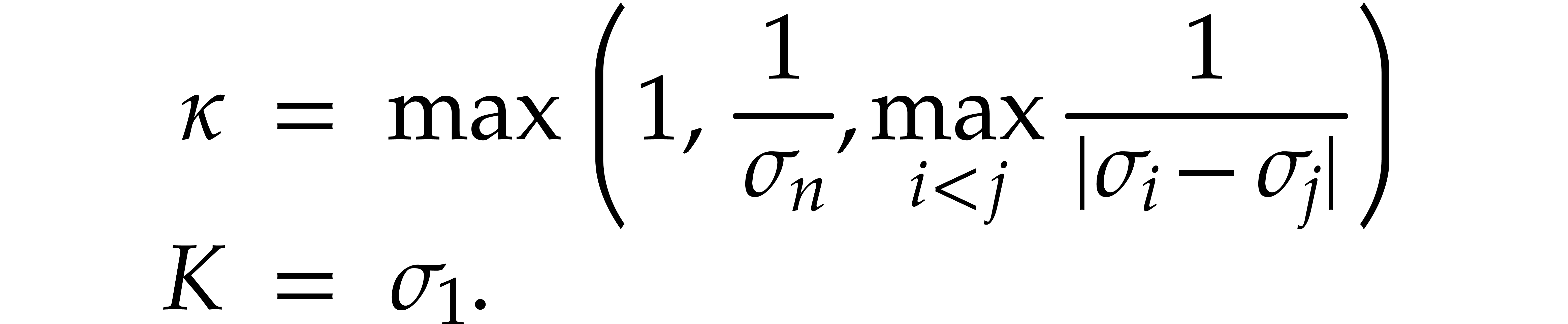 ,
, 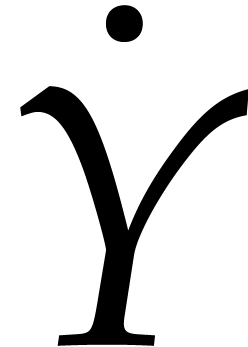 and
and 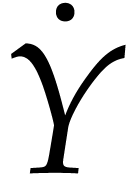 are computed using (21–28). Denote
are computed using (21–28). Denote
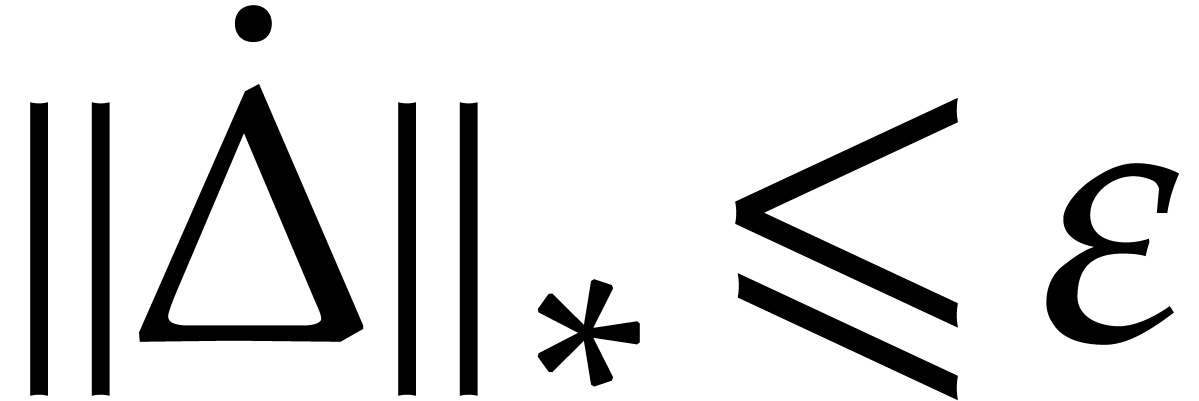
Given  with
with 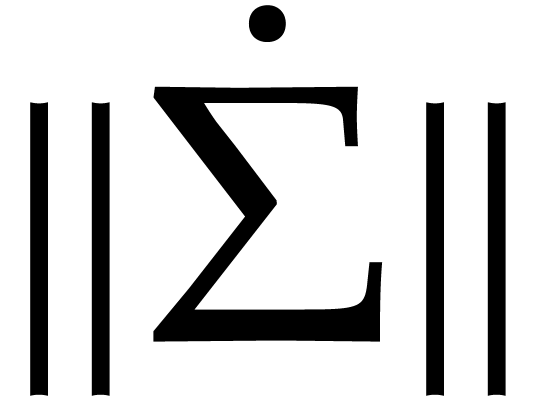 ,
we have
,
we have
Setting
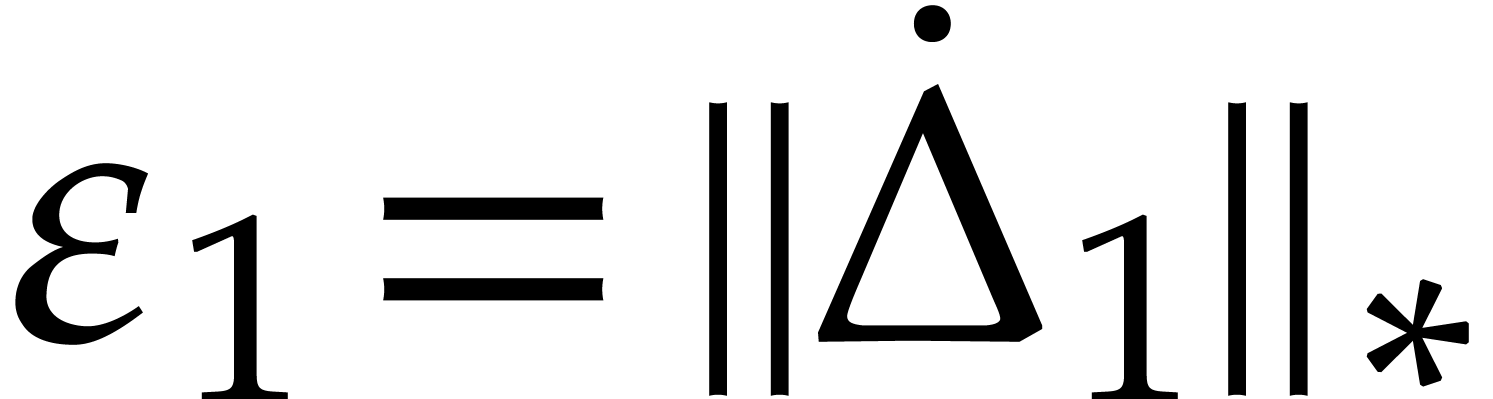
and 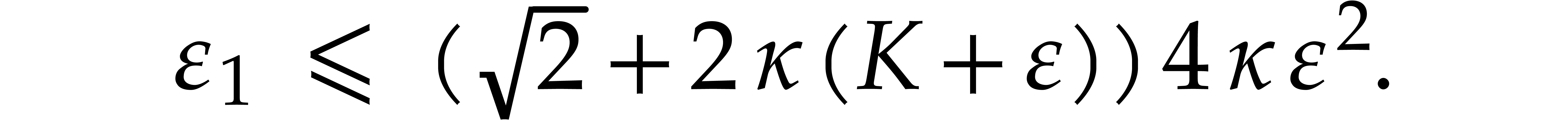 , we also have
, we also have
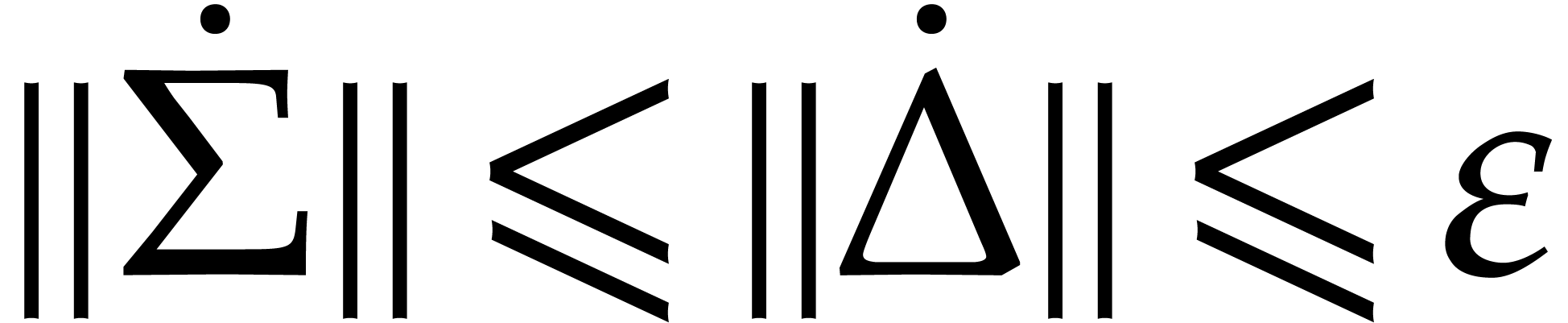
Proof. From the formula (21) we
clearly have 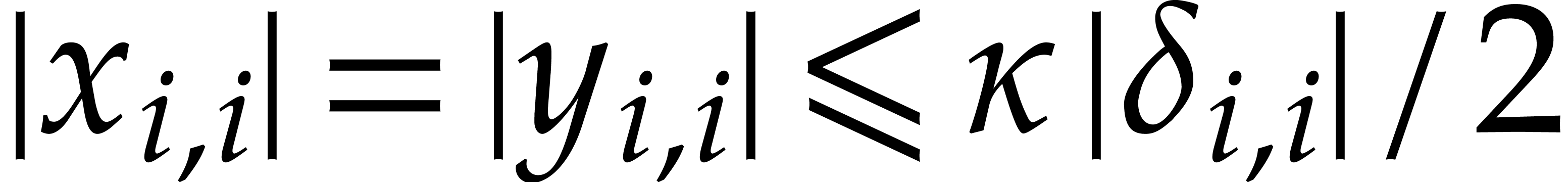 . The formula
(22) implies
. The formula
(22) implies 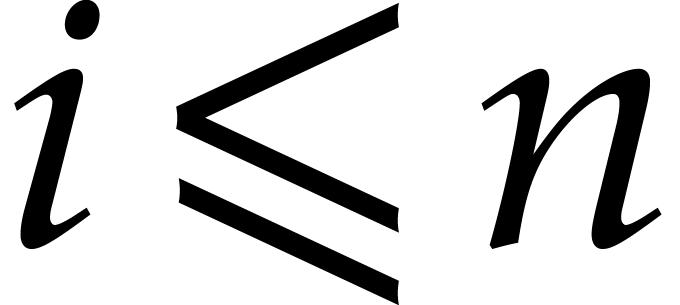 for all
for all 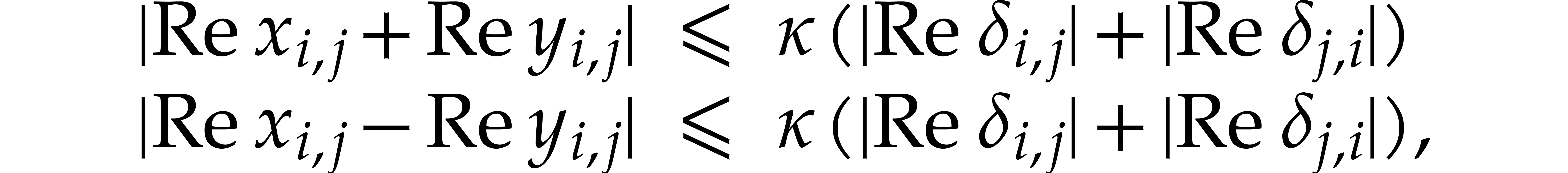 . For
. For 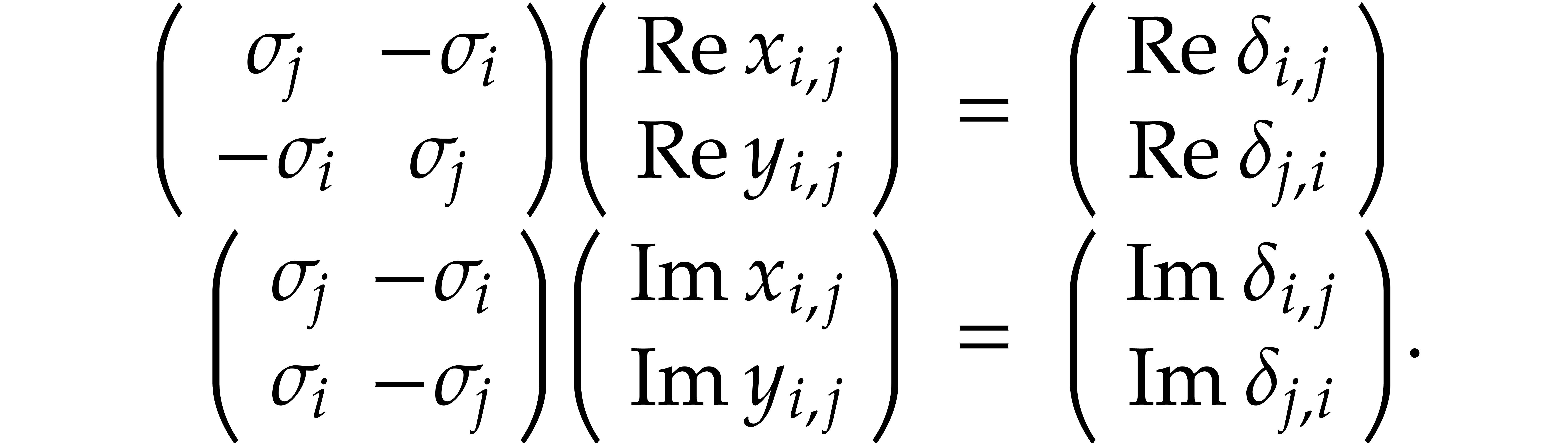 ,
the formulas (23–26) imply
,
the formulas (23–26) imply
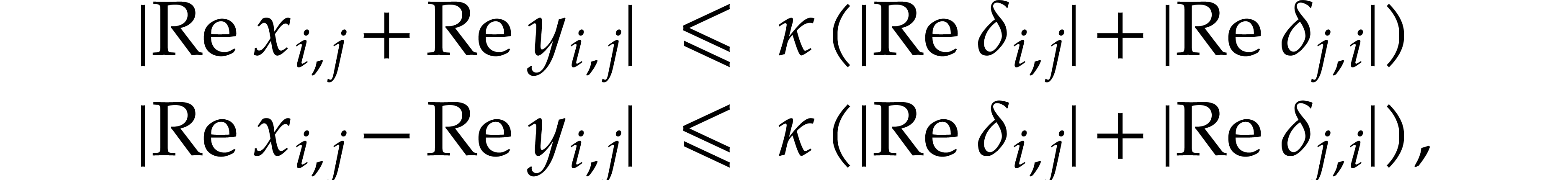
whence
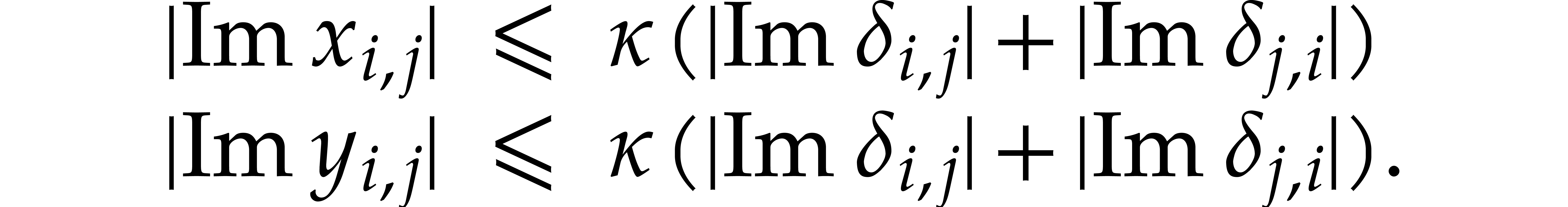
Similarly,

It follows that
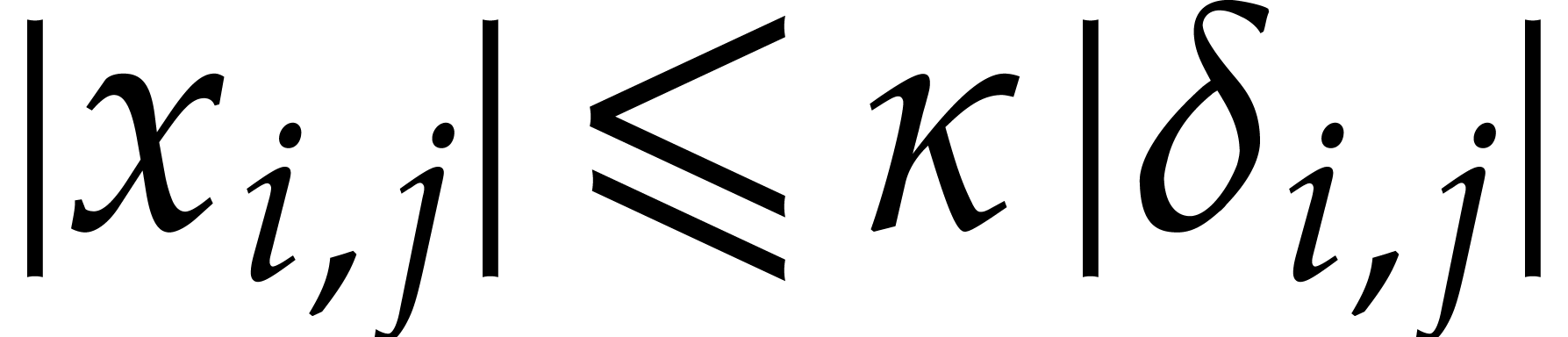
From (27), and using (4), we also deduce that
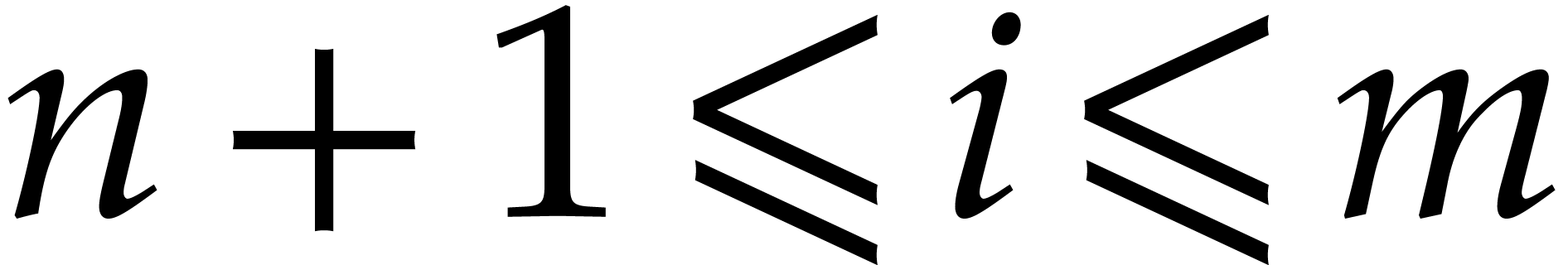 , for
, for 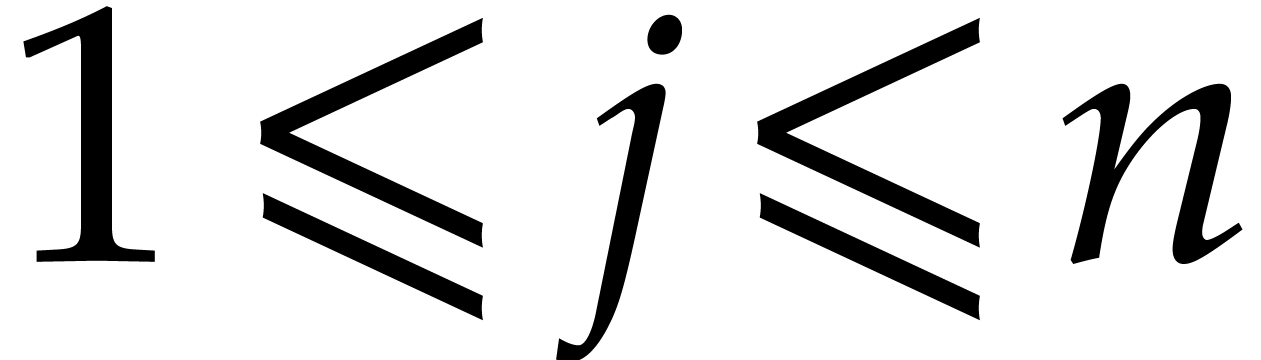 and
and 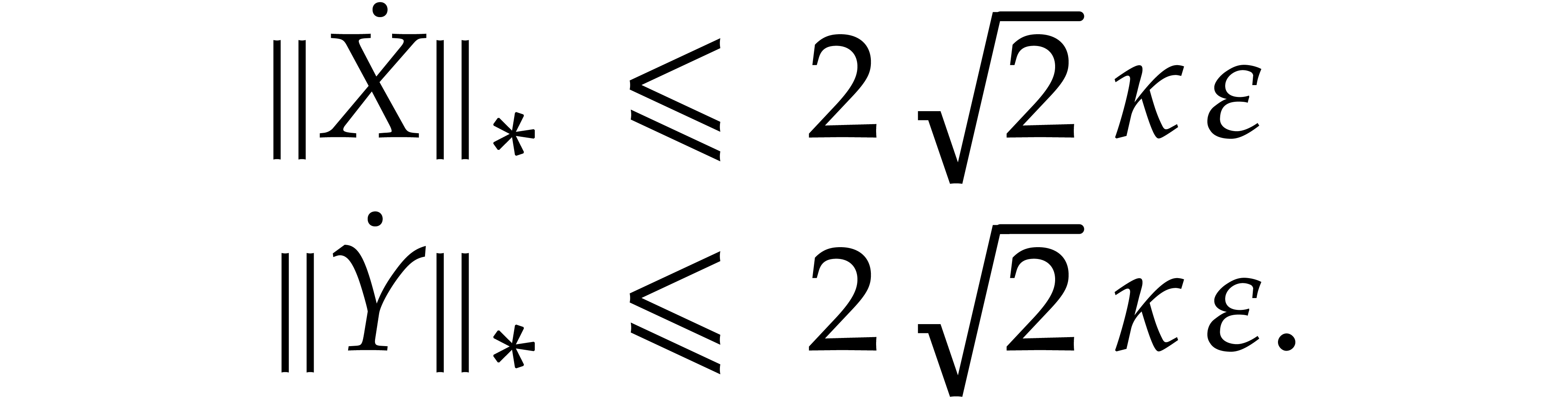 . Combined with the fact
that
. Combined with the fact
that  , we get
, we get
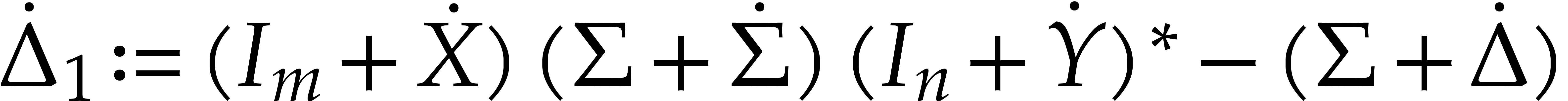
Since 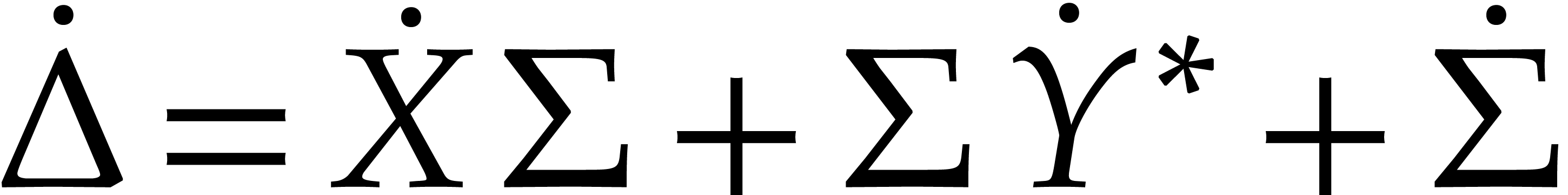 and
and  ,
we now observe that
,
we now observe that
Plugging in the above norm bounds, we deduce that
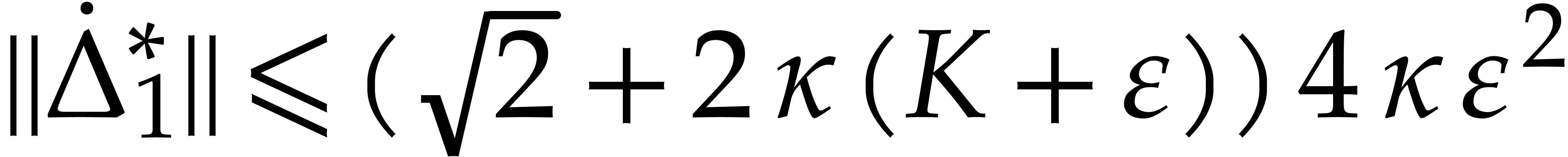
In a similar way, one proves that 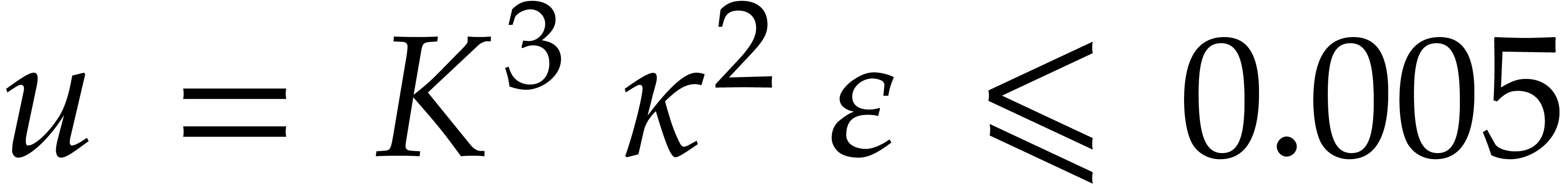 .
.
6.Proof of Theorem 1
Let us denote
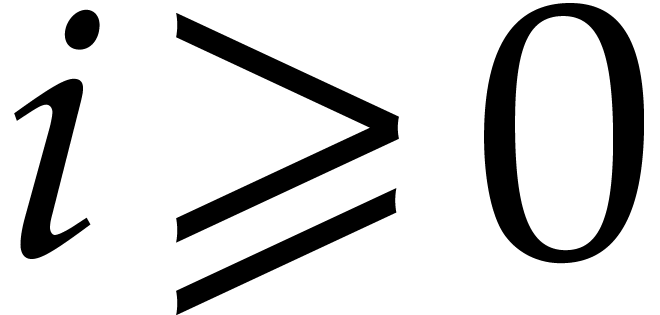
and, for each  ,
,

where 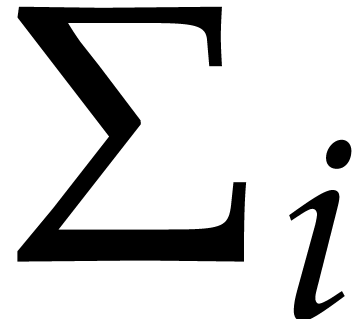 denote the diagonal entries of
denote the diagonal entries of 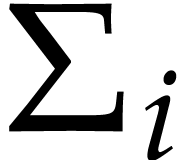 . Let us show by induction on
. Let us show by induction on  that
that
These inequalities clearly hold for 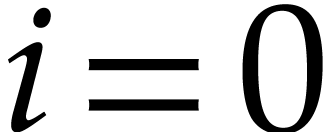 .
Assuming that the induction hypothesis holds for a given
.
Assuming that the induction hypothesis holds for a given  and let us prove it for
and let us prove it for  .
.
By the definition of 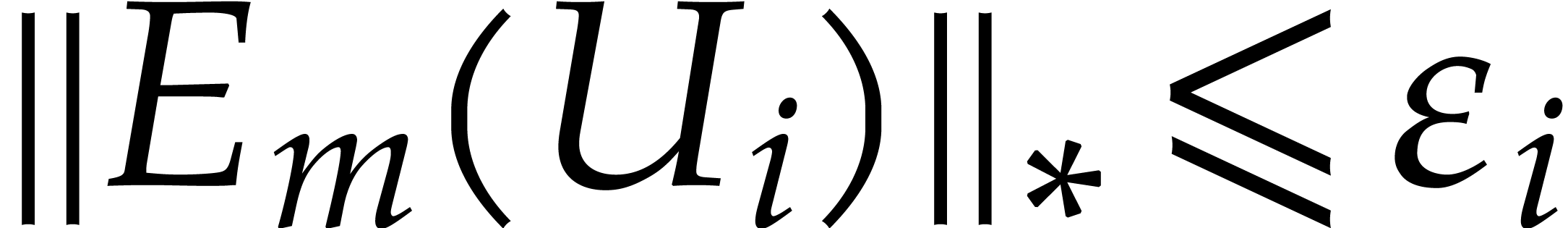 , we
have
, we
have 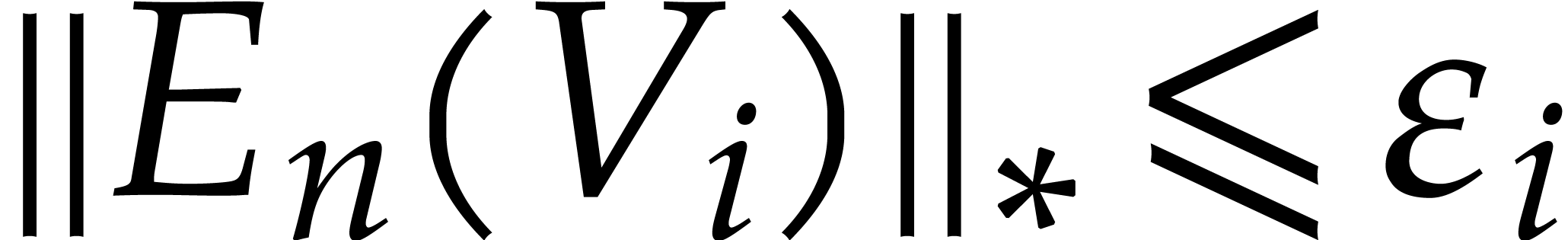 and
and 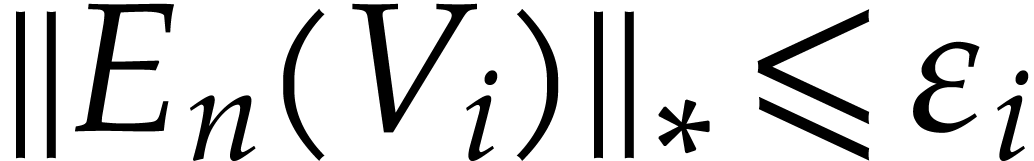 .
Setting
.
Setting
we have
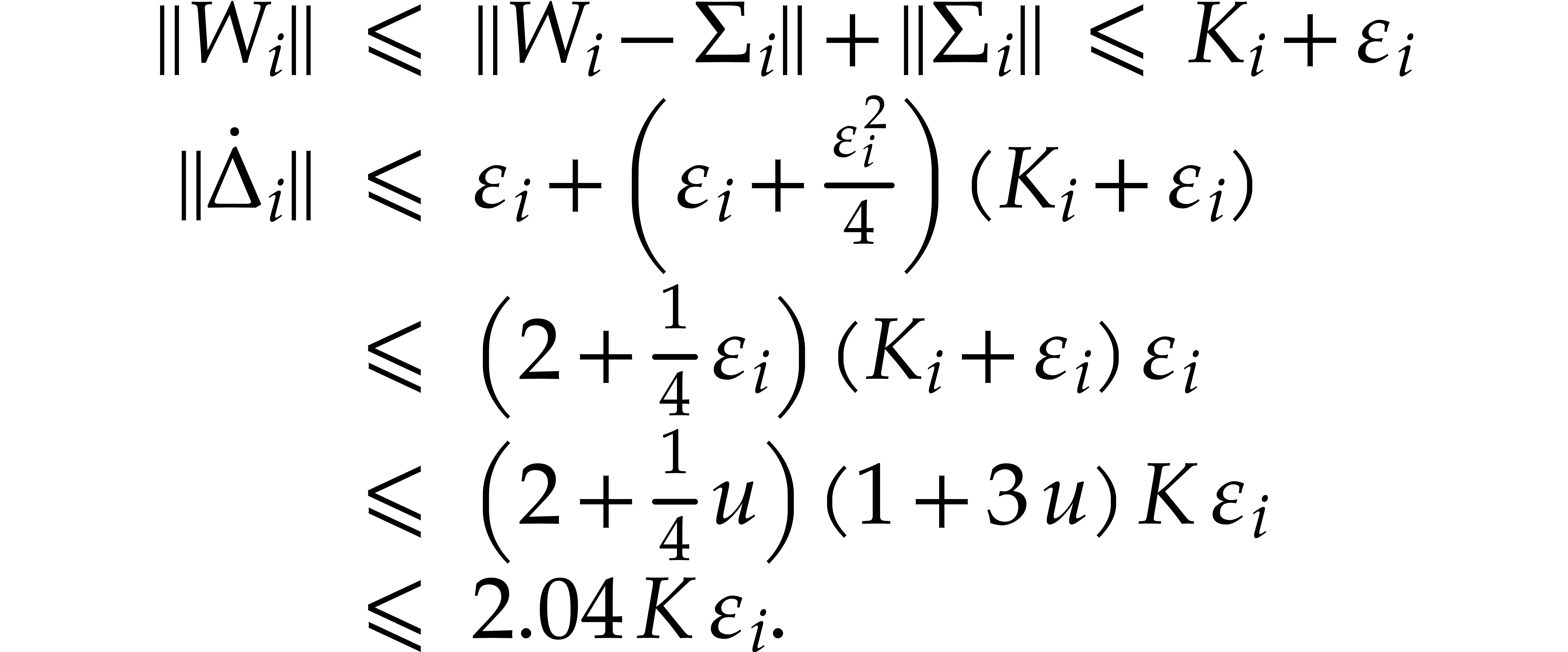
It follows that
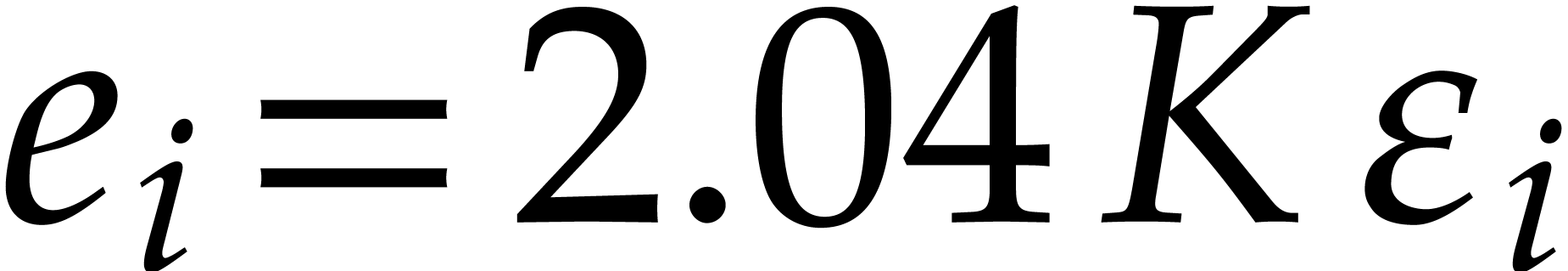
Let 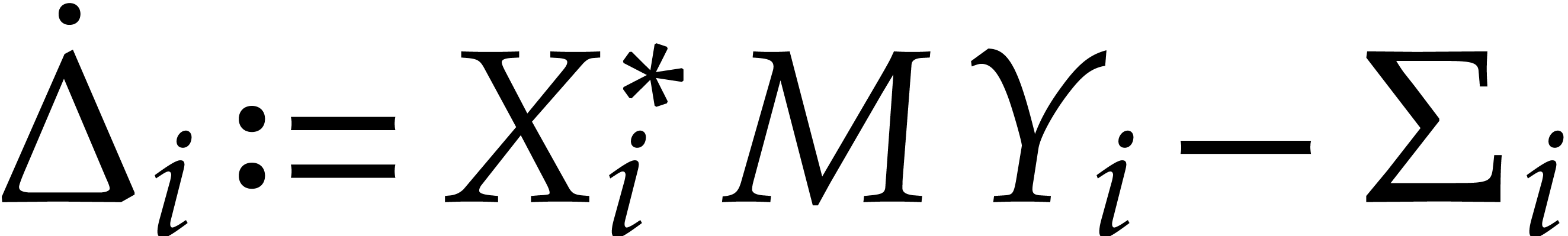 . Applying Proposition 9 to
. Applying Proposition 9 to 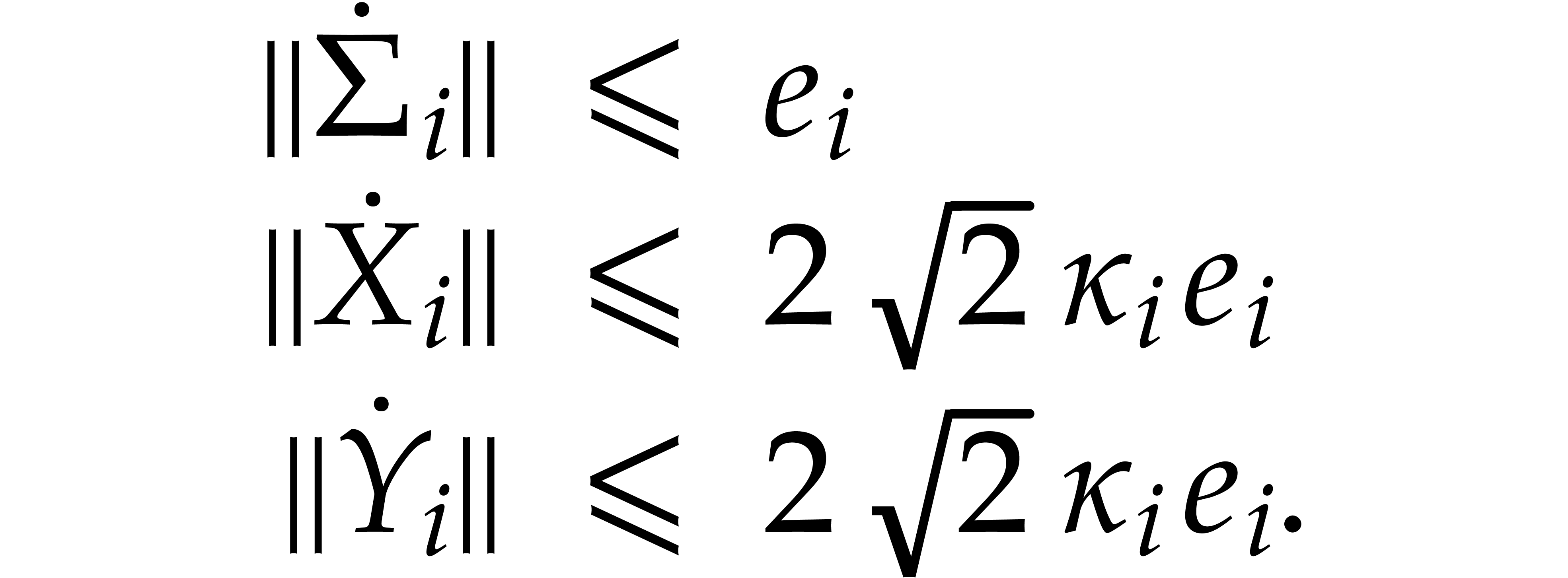 , we get
, we get
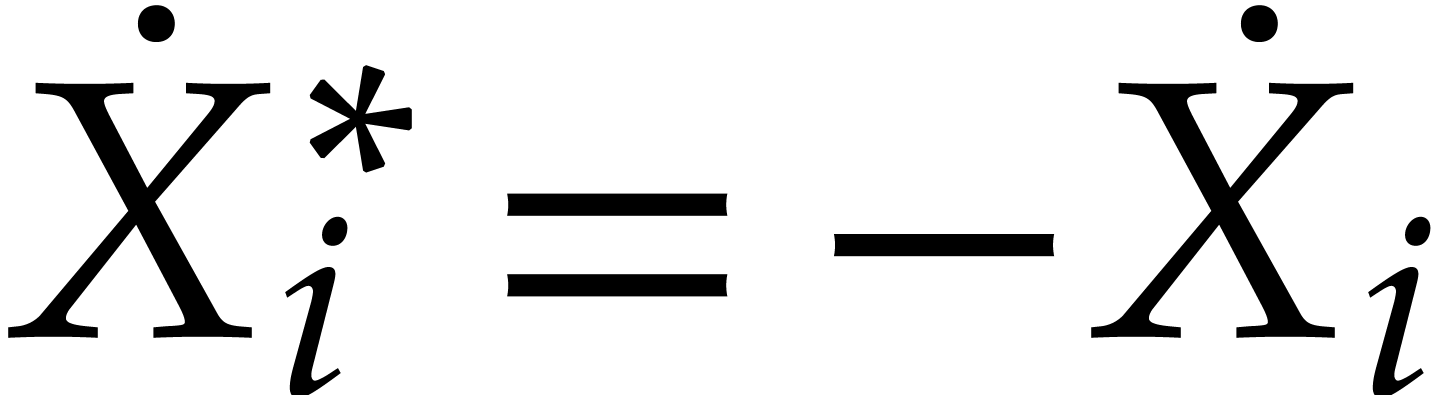
Since  , we have
, we have
Using (18), we obtain
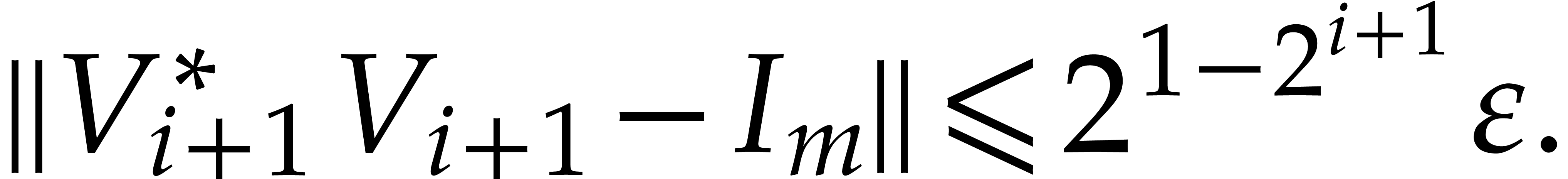
Similarly,
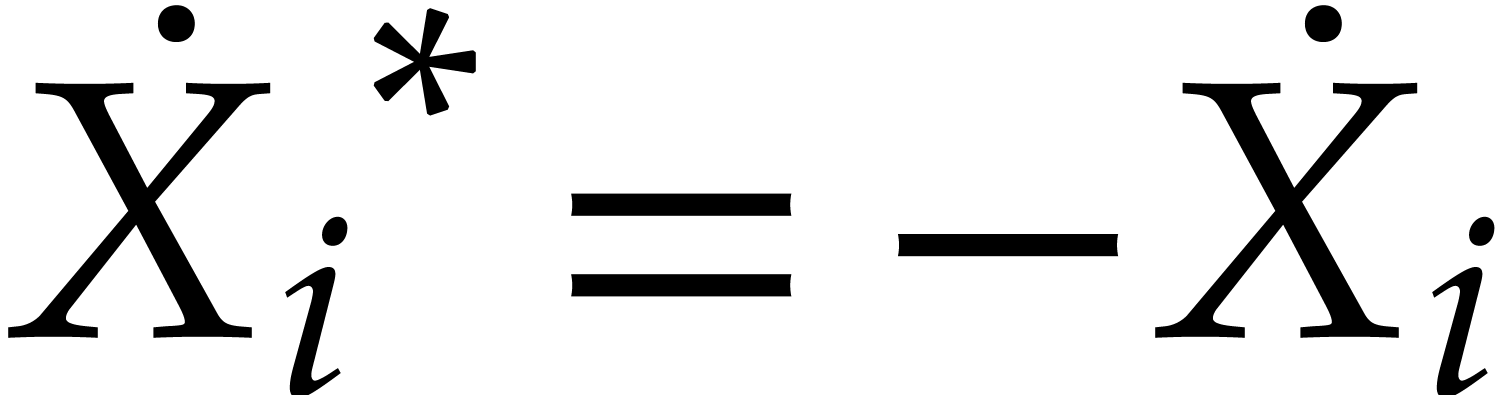
Using  and (13), we next have
and (13), we next have
It follows that
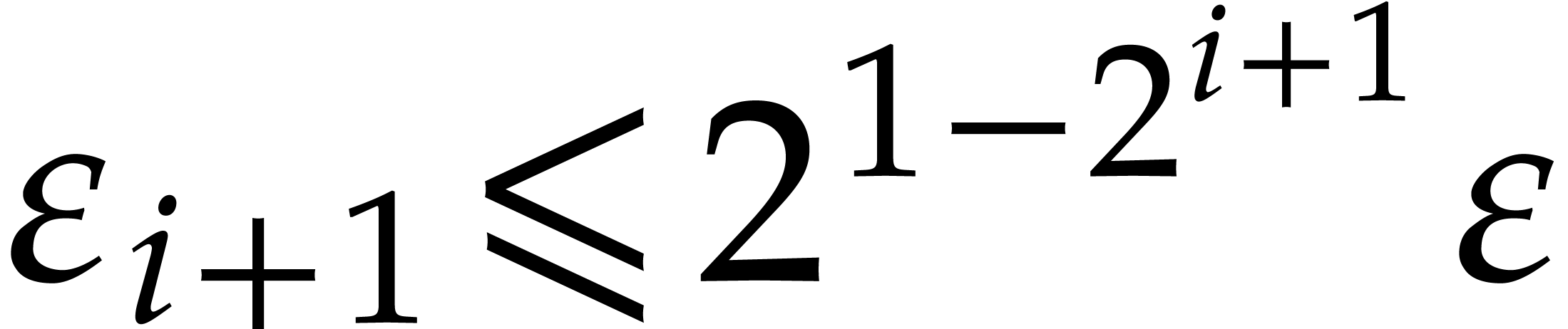
This completes the proof that  .
We also have
.
We also have
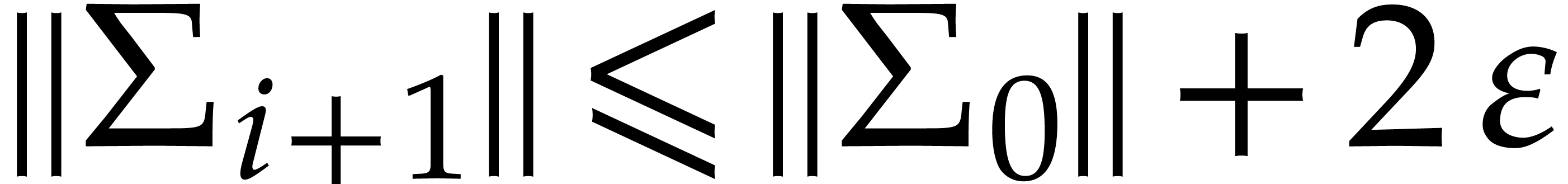
We deduce that 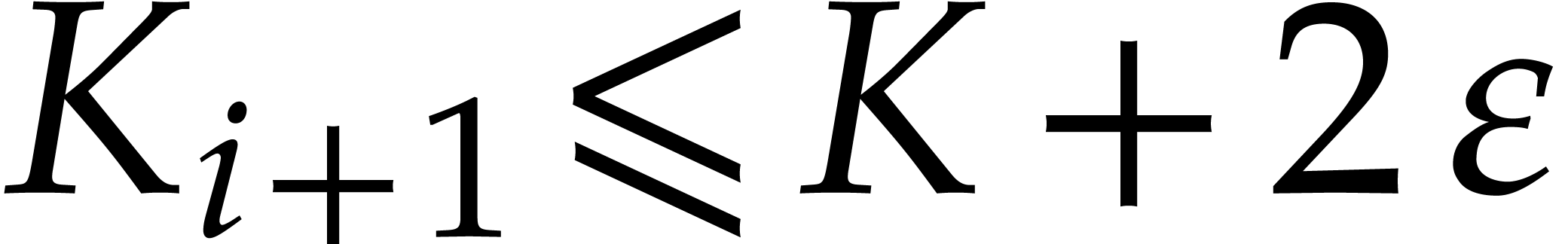 and
and 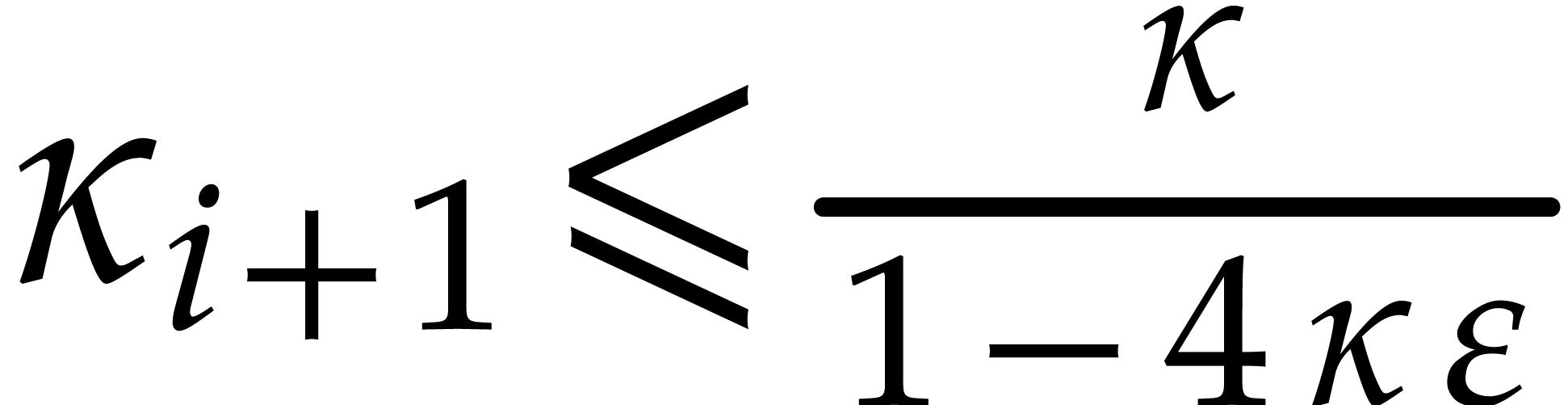 .
Let us finally prove that
.
Let us finally prove that 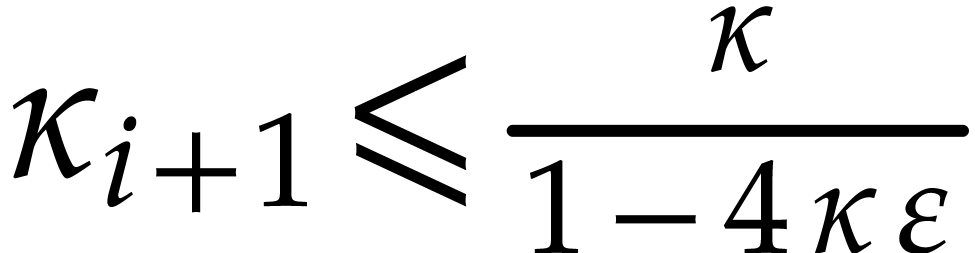 .
From
.
From  , we get
, we get
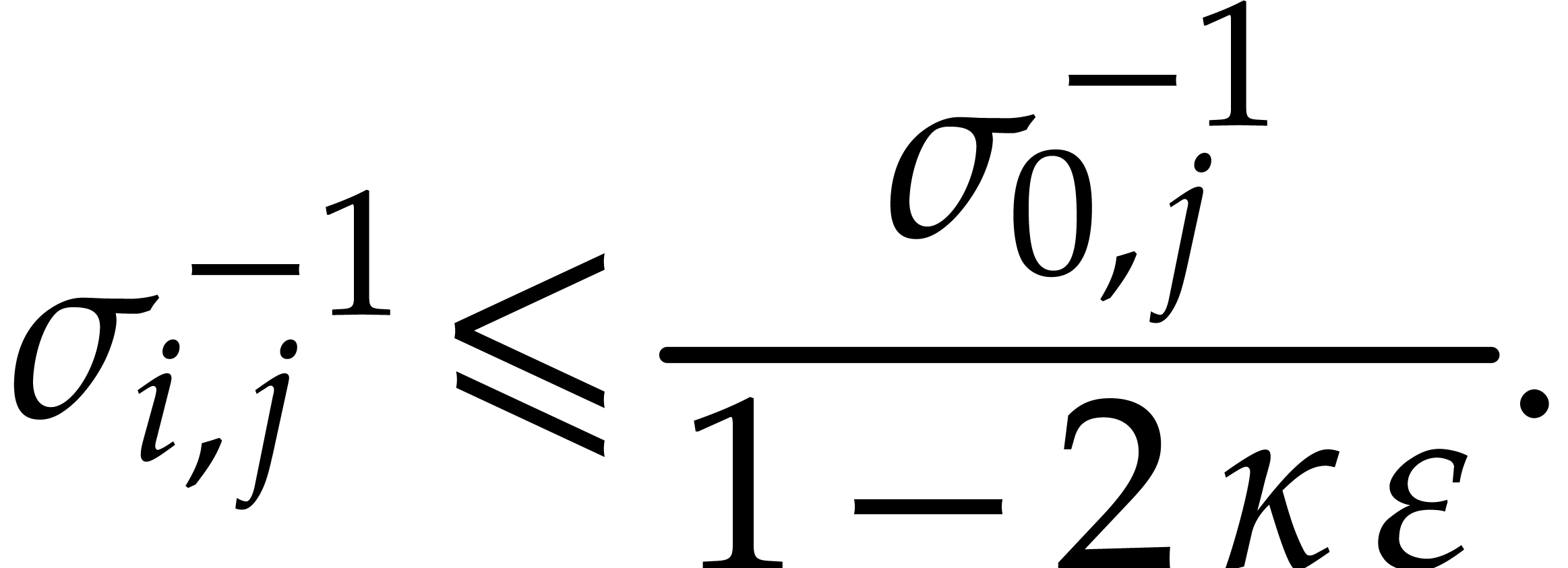
so that
Similarly, using
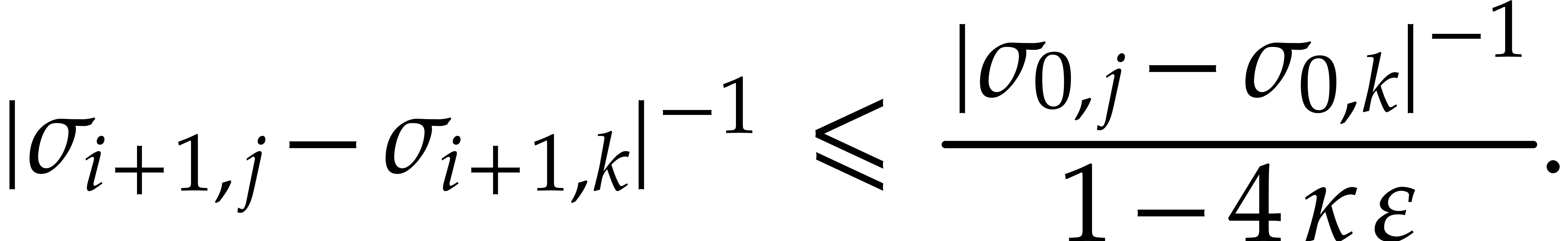
we get
Hence 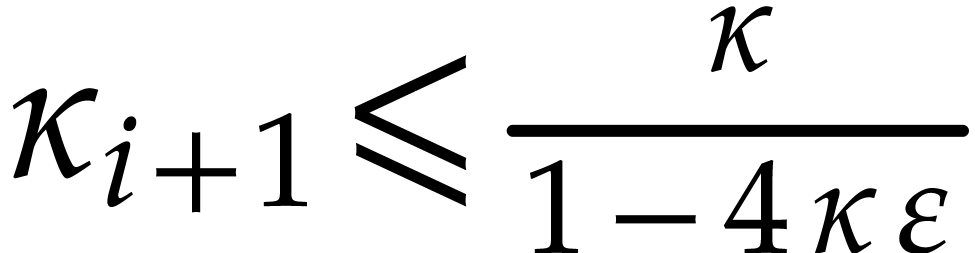 , which completes the
proof of the four induction hypotheses (36–39)
at order
, which completes the
proof of the four induction hypotheses (36–39)
at order  .
.
From the continuity of the maps  ,
,
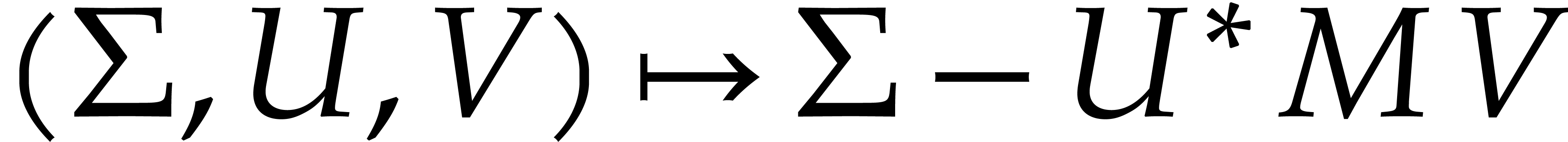 , and
, and 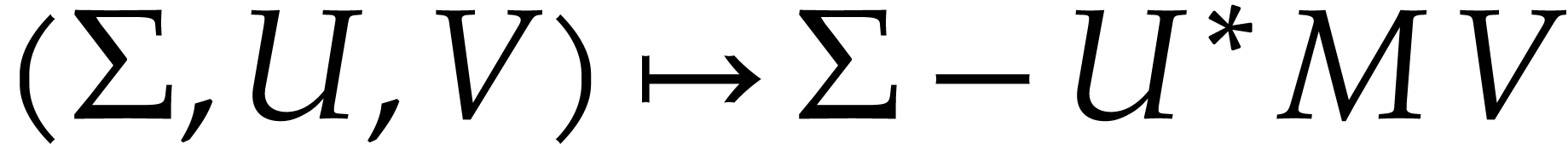 , we deduce that the sequence
, we deduce that the sequence 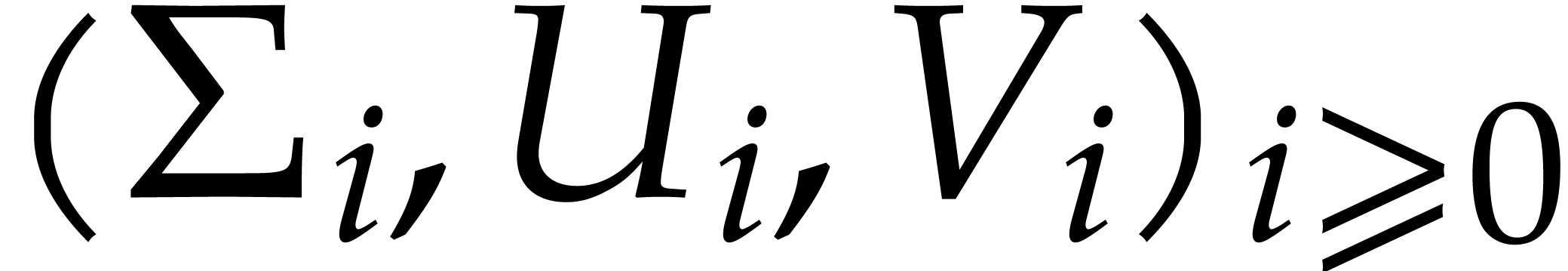 converges. Let
converges. Let  be the limit. By continuity, we
have
be the limit. By continuity, we
have 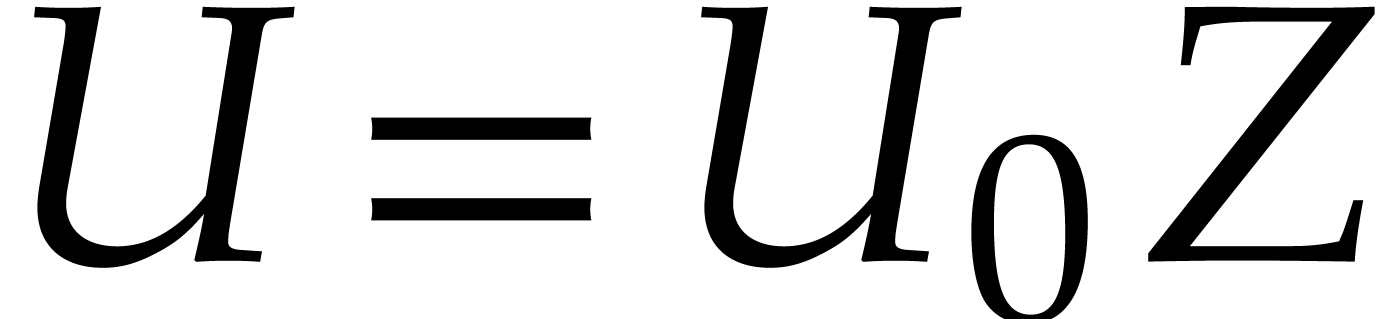 . The unitary matrix
. The unitary matrix
 is of the form
is of the form 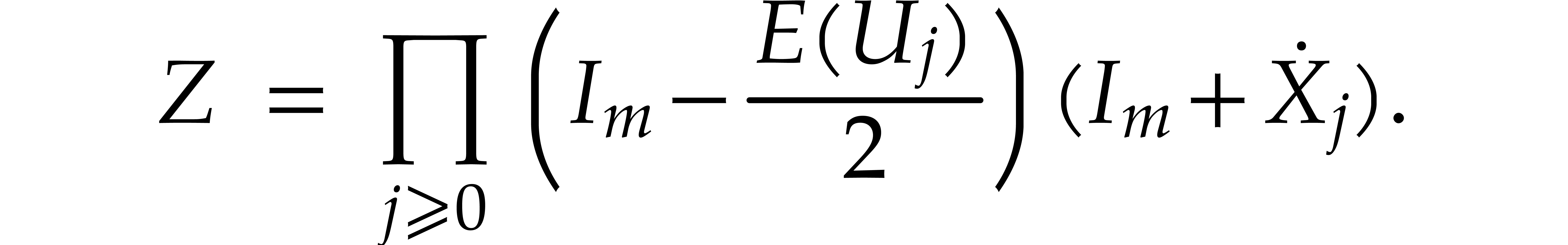 with
with
 |
(40) |
From above we know that
whence
Lemma 6 now implies

This shows that 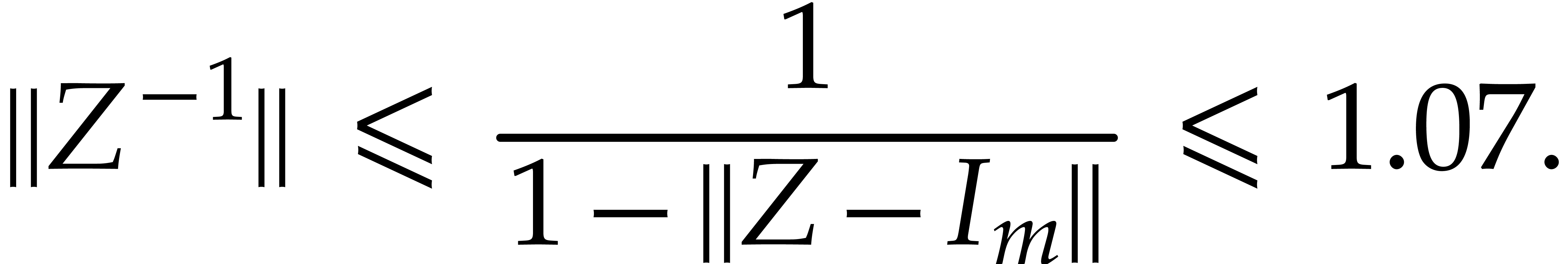 is invertible, with
is invertible, with
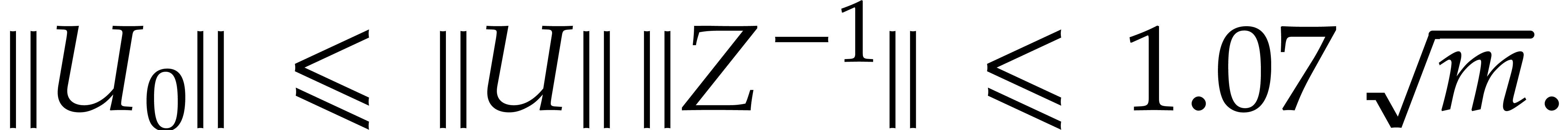
Hence
From the definition of  we also have
we also have
Using Lemma 6, this yields
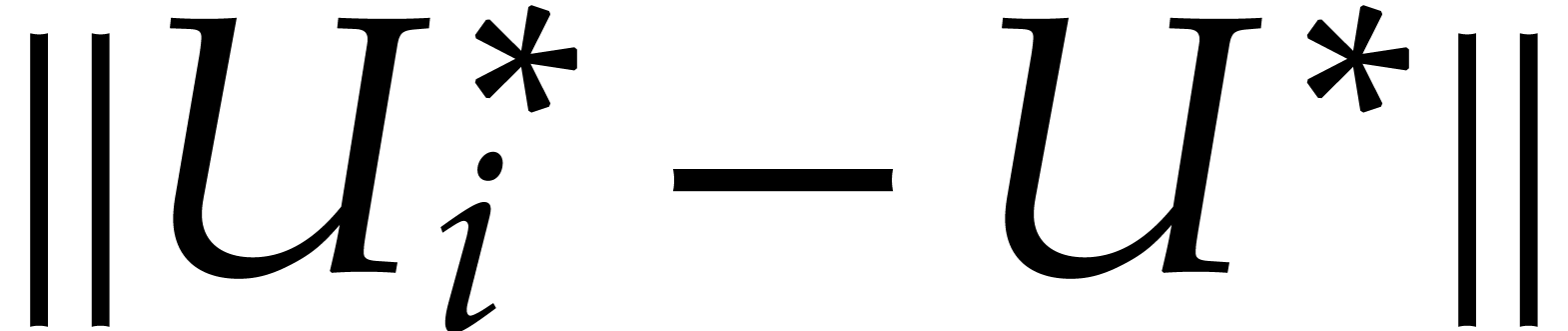
Similar bounds can be computed for 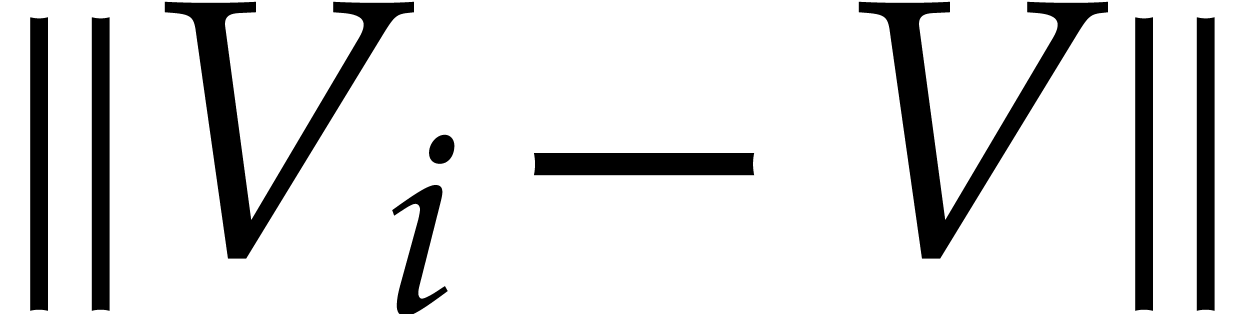 ,
,
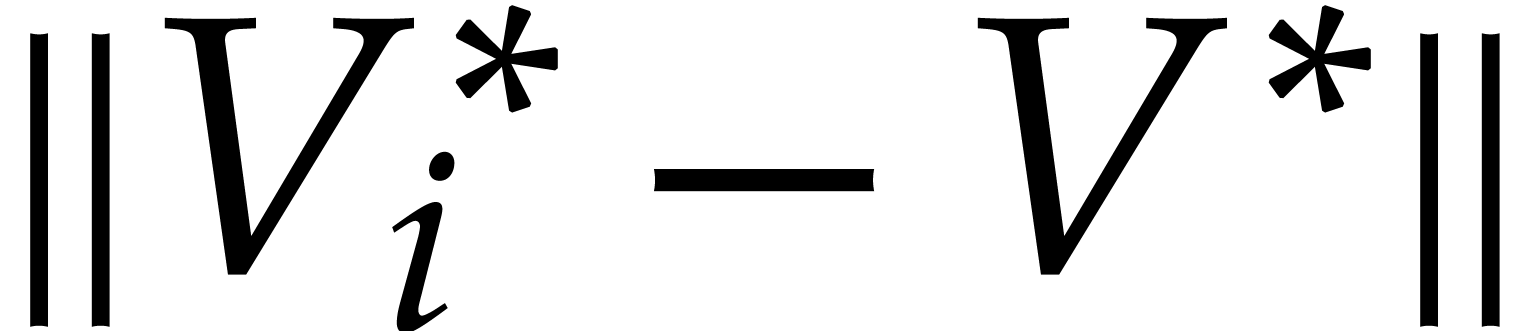 , and
, and 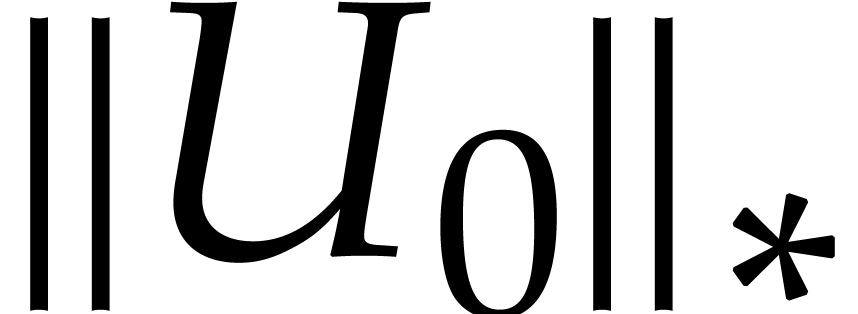 . Altogether, this leads to
. Altogether, this leads to
We finally have
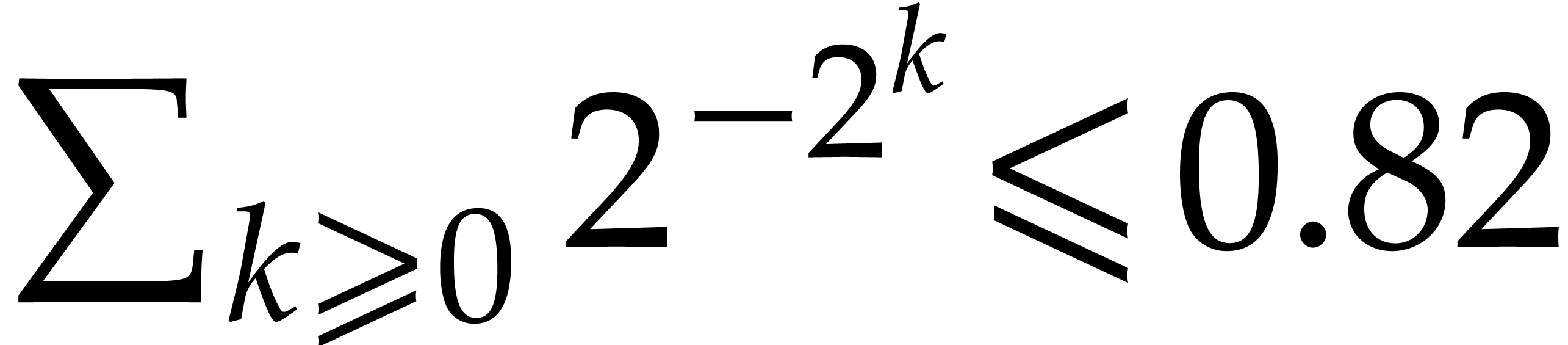
since  . This completes the
proof.
. This completes the
proof.
Bibliography
-
[1]
-
Alefeld, G., and Herzberger, J.
Introduction to interval analysis. Academic Press, New
York, 1983.
-
[2]
-
Björck, Å., and Bowie,
C. An iterative algorithm for computing the best
estimate of an orthogonal matrix. SIAM J. on Num. Analysis
8, 2 (1971), 358–364.
-
[3]
-
Charlier, J.-P., and Van Dooren,
P. On Kogbetliantz's SVD algorithm in the presence of
clusters. Linear Algebra and its Applications 95 (1987),
135–160.
-
[4]
-
Demmel, J. W. Applied
Numerical Linear Algebra, vol. 56. Siam, 1997.
-
[5]
-
Drmac, Z. A global convergence
proof for cyclic Jacobi methods with block rotations. SIAM
journal on matrix analysis and applications 31, 3 (2009),
1329–1350.
-
[6]
-
Fan, K., and Hoffman, A. J.
Some metric inequalities in the space of matrices. Proc. of
the AMS 6, 1 (1955), 111–116.
-
[7]
-
Gall, F. L. Powers of tensors
and fast matrix multiplication. In Proc. ISSAC 2014
(Kobe, Japan, July 2014), pp. 296–303.
-
[8]
-
Golub, G. H., and Loan, F. V.
Matrix Computations. JHU Press, 1996.
-
[9]
-
Harvey, D., and Hoeven, J. v.
d. Faster integer multiplication using short lattice
vectors. Tech. rep., ArXiv, 2018. http://arxiv.org/abs/1802.07932,
to appear in the Proceedings of ANTS 2018.
-
[10]
-
Harvey, D., and Hoeven, J. v.
d. On the complexity of integer matrix multiplication.
JSC 89 (2018), 1–8.
-
[11]
-
Harvey, D., Hoeven, J. v. d., and
Lecerf, G. Even faster integer multiplication.
Journal of Complexity 36 (2016), 1–30.
-
[12]
-
Higham, N. J. Matrix nearness
problems and applications. In Applications of Matrix
Theory (1989), M. J. C. Gover and S. Barnett, Eds., Oxford
University Press, pp. 1–27.
-
[13]
-
Hoeven, J. v. d. Ball
arithmetic. In Logical approaches to Barriers in Computing
and Complexity (February 2010), A. Beckmann, C.
Gaßner, and B. Löwe, Eds., no. 6 in Preprint-Reihe
Mathematik, Ernst-Moritz-Arndt-Universität Greifswald, pp.
179–208. International Workshop.
-
[14]
-
Hoeven, J. v. d., Lecerf, G., Mourrain,
B., et al. Mathemagix, 2002. http://www.mathemagix.org.
-
[15]
-
Hoeven, J. v. d., and Mourrain,
B. Efficient certification of numeric solutions to
eigenproblems. In Proc. MACIS 2017, Vienna, Austria
(Cham, 2017), J. Blömer, I. S. Kotsireas, T. Kutsia, and D.
E. Simos, Eds., Lect. Notes in Computer Science, Springer
International Publishing, pp. 81–94.
-
[16]
-
Janovská, D., Janovsk , V., and Tanabe,
K. An algorithm for computing the analytic singular
value decomposition. World Academy of Science, Engineering
and Technology 47 (2008), 135–140.
, V., and Tanabe,
K. An algorithm for computing the analytic singular
value decomposition. World Academy of Science, Engineering
and Technology 47 (2008), 135–140.
-
[17]
-
Janovsk ,
V., Janovská, D., and Tanabe, K. Computing the
analytic singular value decomposition via a pathfollowing. In
Numerical Mathematics and Advanced Applications.
Springer, 2006, pp. 954–962.
,
V., Janovská, D., and Tanabe, K. Computing the
analytic singular value decomposition via a pathfollowing. In
Numerical Mathematics and Advanced Applications.
Springer, 2006, pp. 954–962.
-
[18]
-
Jaulin, L., Kieffer, M., Didrit, O.,
and Walter, E. Applied interval analysis.
Springer, London, 2001.
-
[19]
-
Johansson, F. Arb: a C library
for ball arithmetic. ACM Commun. Comput. Algebra 47, 3/4
(2014), 166–169.
-
[20]
-
Kovarik, Z. Some iterative
methods for improving orthonormality. SIAM J. on Num.
Analysis 7, 3 (1970), 386–389.
-
[21]
-
Kulisch, U. W. Computer
Arithmetic and Validity. Theory, Implementation, and
Applications. No. 33 in Studies in Mathematics. de Gruyter,
2008.
-
[22]
-
Moore, R. E. Interval
Analysis. Prentice Hall, Englewood Cliffs, N.J., 1966.
-
[23]
-
Neumaier, A. Interval
methods for systems of equations. Cambridge University
Press, Cambridge, 1990.
-
[24]
-
Rump, S. M. INTLAB - INTerval
LABoratory. In Developments in Reliable Computing, T.
Csendes, Ed. Kluwer Academic Publishers, Dordrecht, 1999, pp.
77–104. http://www.ti3.tu-harburg.de/rump/
 be the set of floating point numbers for a
fixed precision and a fixed exponent range. We denote
be the set of floating point numbers for a
fixed precision and a fixed exponent range. We denote  . Consider an
. Consider an  matrix
matrix
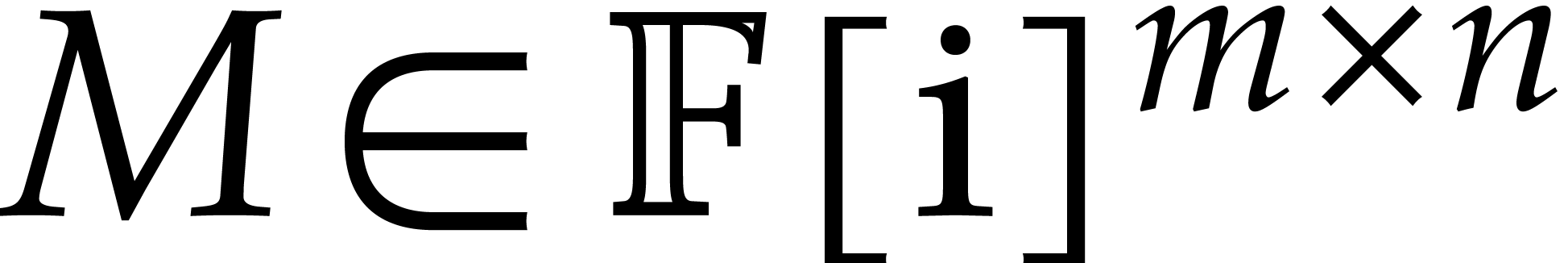 with complex floating entries, where
with complex floating entries, where 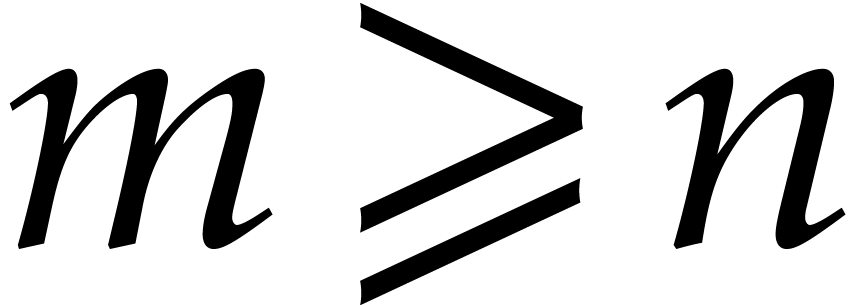 . The problem of computing the
numeric singular value decomposition of
. The problem of computing the
numeric singular value decomposition of  is to compute unitary transformation matrices
is to compute unitary transformation matrices 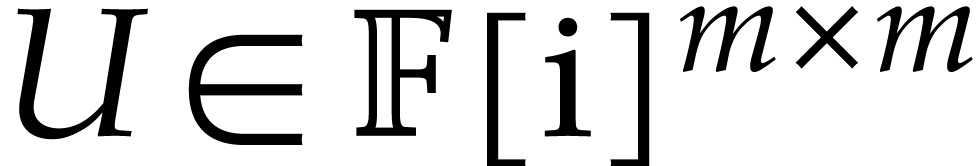 ,
, 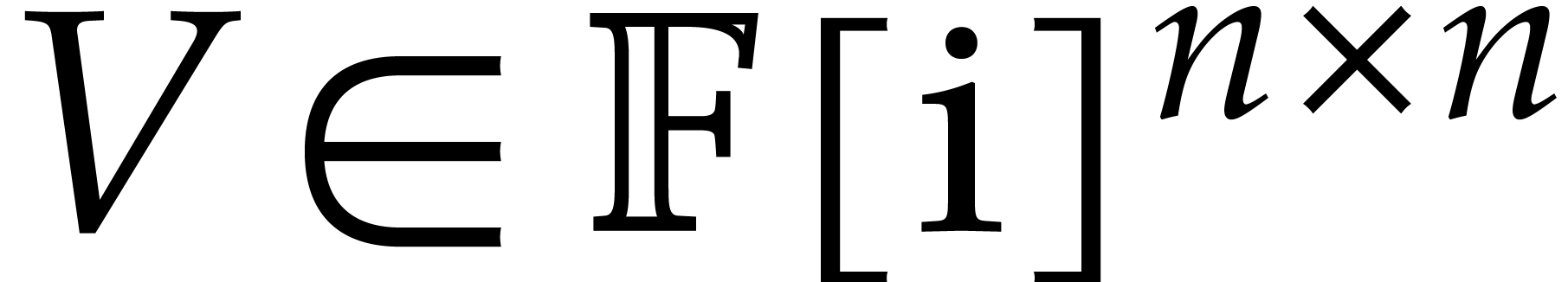 , and a
diagonal matrix
, and a
diagonal matrix 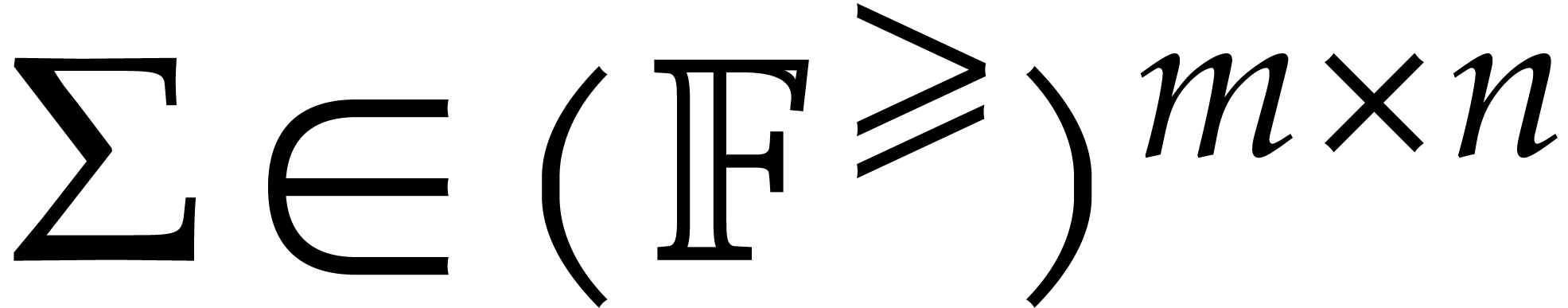 such that
such that
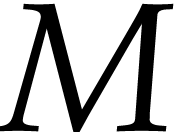


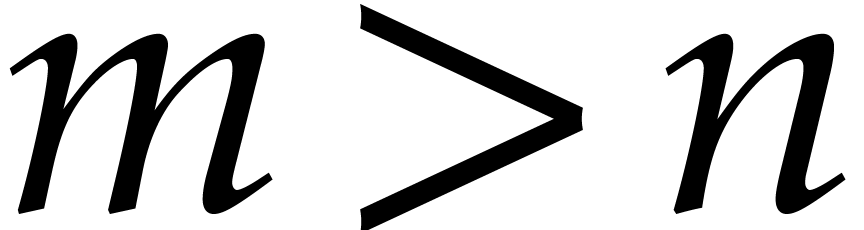 ,
,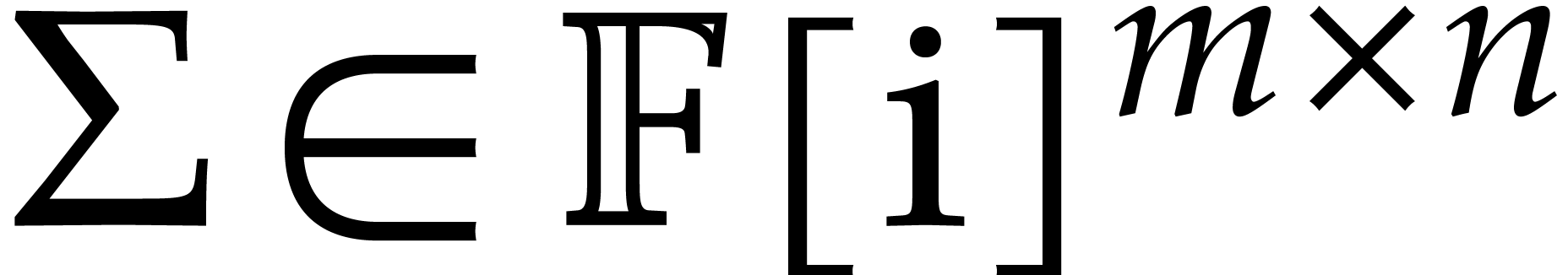 is understood to be “diagonal” if it is of the form
is understood to be “diagonal” if it is of the form
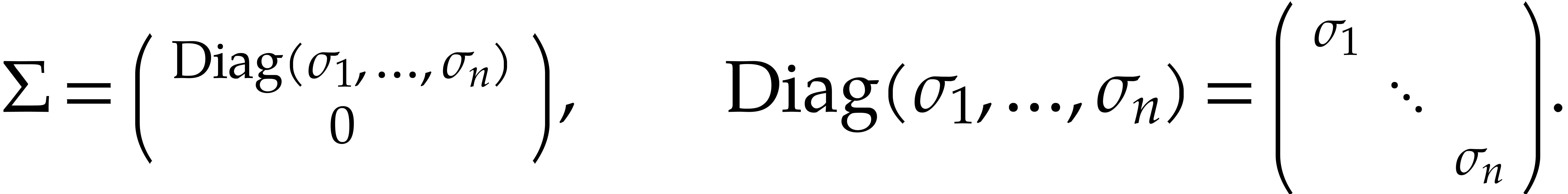
 of
of 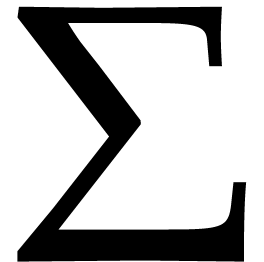 are the approximate singular values of the matrix
are the approximate singular values of the matrix 
 and matrices
and matrices 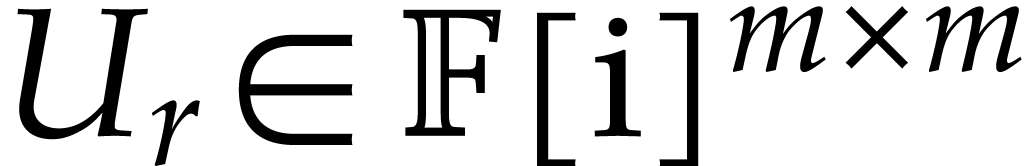 ,
,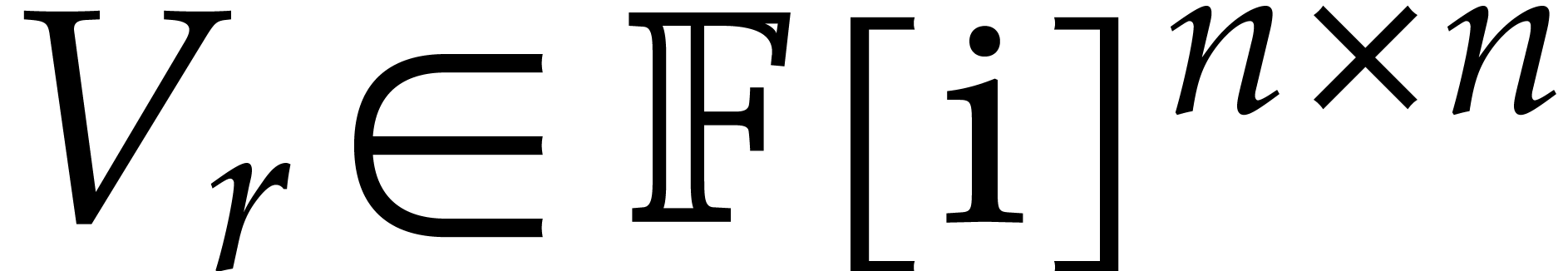 ,
, ,
, ,
, for which
for which
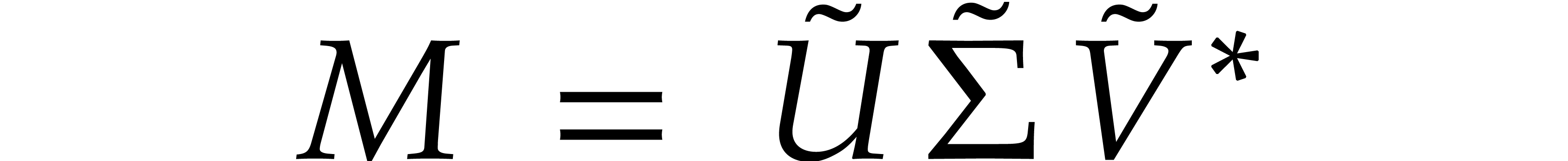
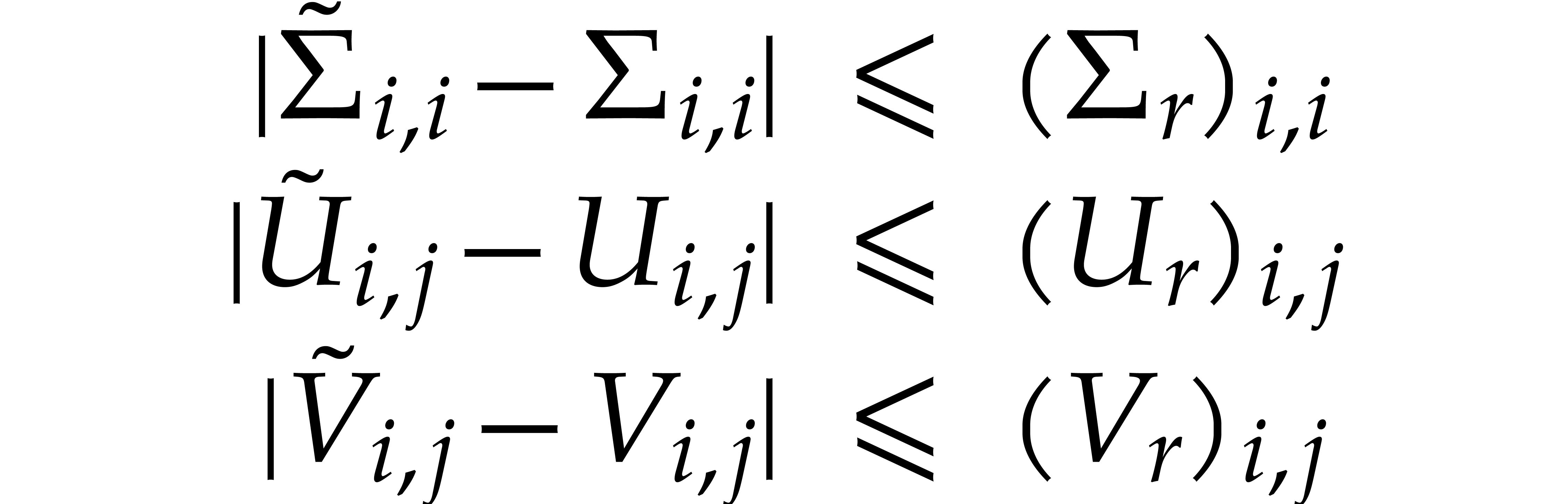
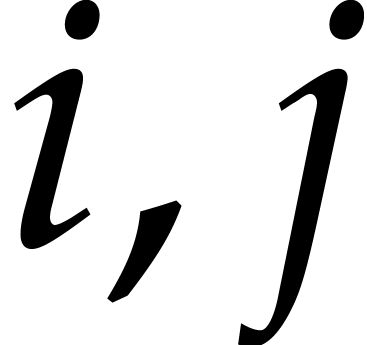 .
.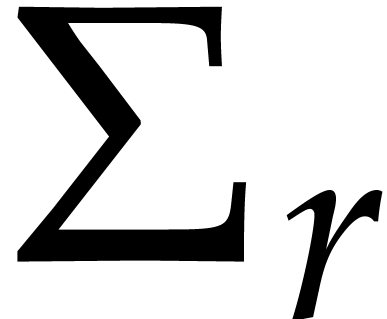 ,
,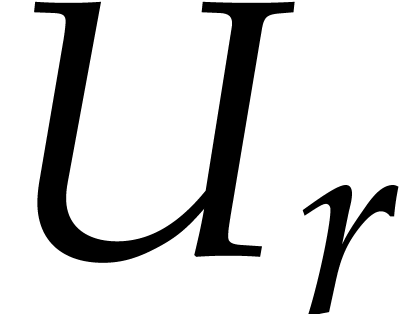 and
and 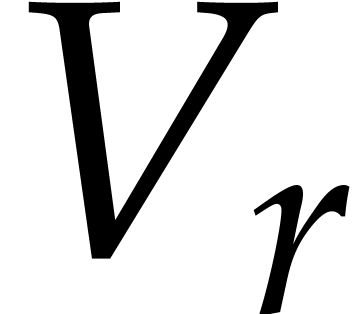 can be thought of as reliable error bounds for the matrices
can be thought of as reliable error bounds for the matrices  and
and  of the numerical solution.
of the numerical solution.
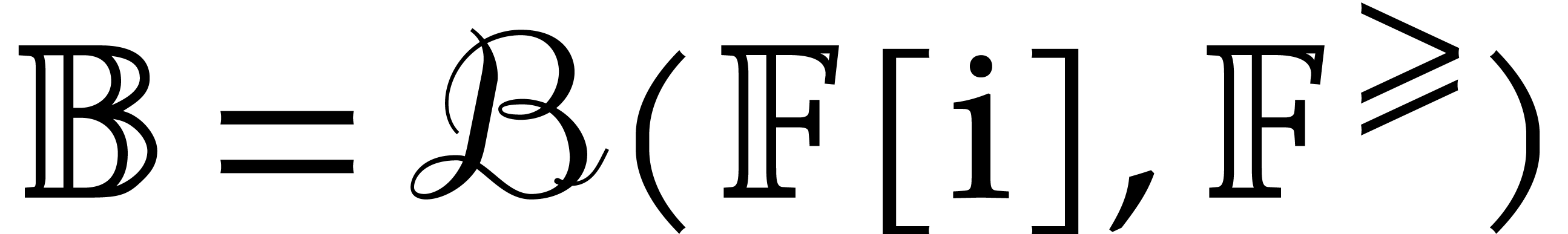 for the set of balls
for the set of balls  with centers
with centers  in
in 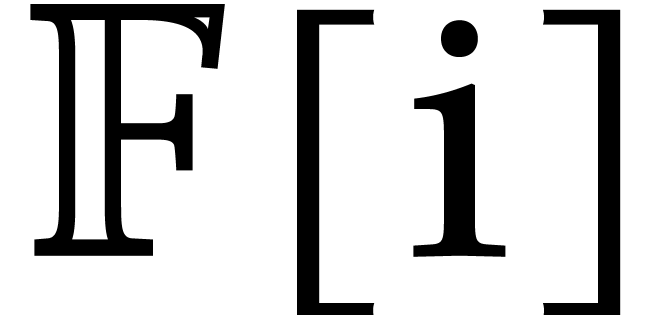 and
radii
and
radii 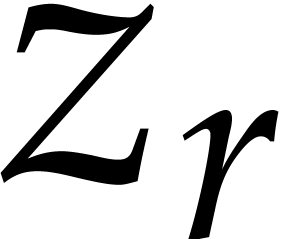 in
in 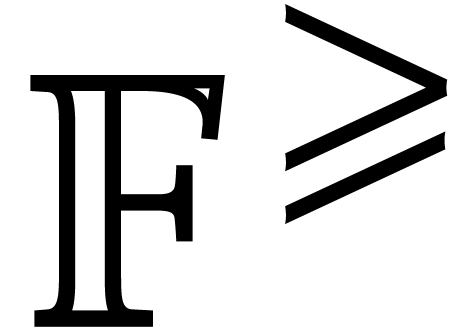 .
. :
: and
a radius matrix
and
a radius matrix  ,
,
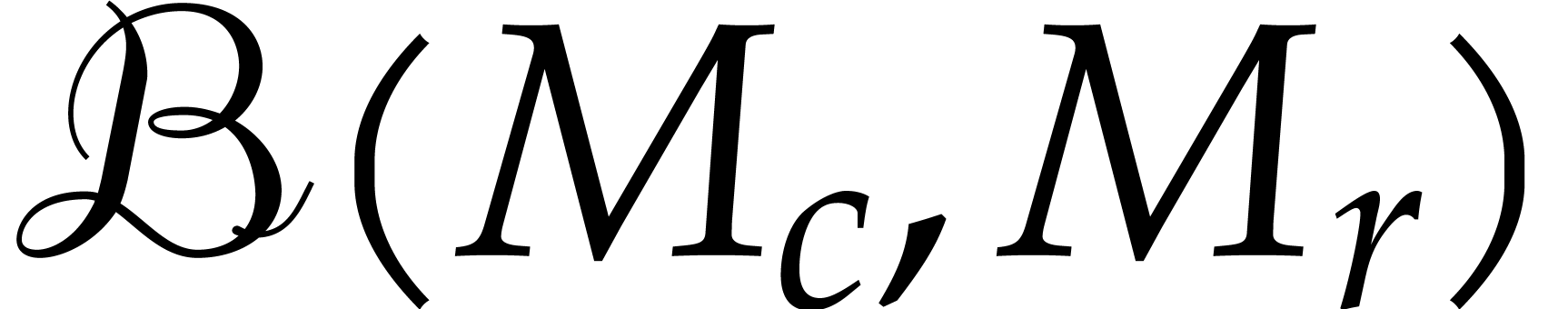 as the set of
matrices in
as the set of
matrices in 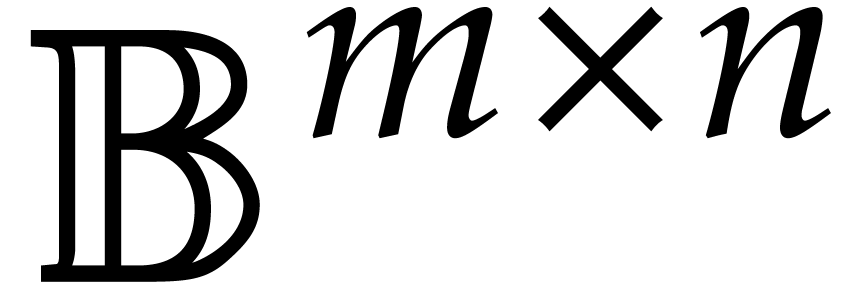 with ball coefficients:
with ball coefficients:

 ,
, using ball
arithmetic has the property that
using ball
arithmetic has the property that  for any
for any  and
and  .
.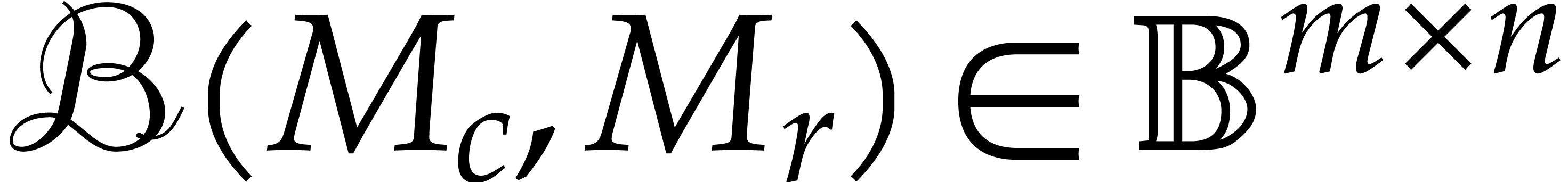 .
.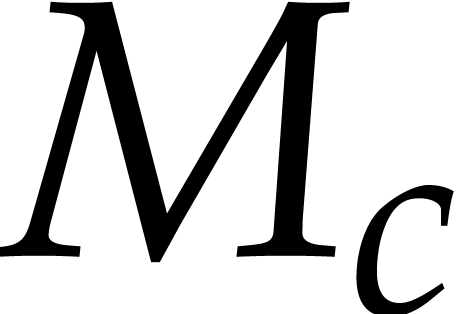 :
: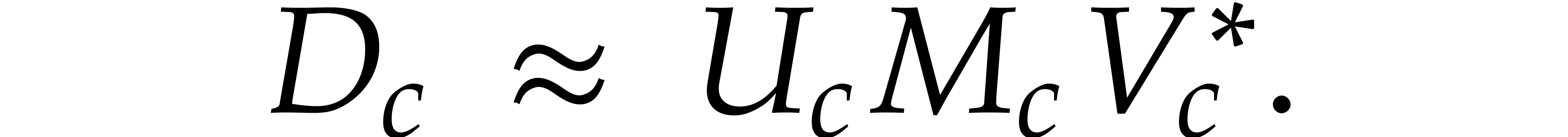
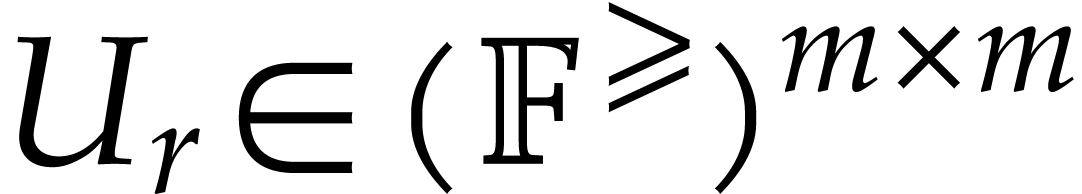 ,
,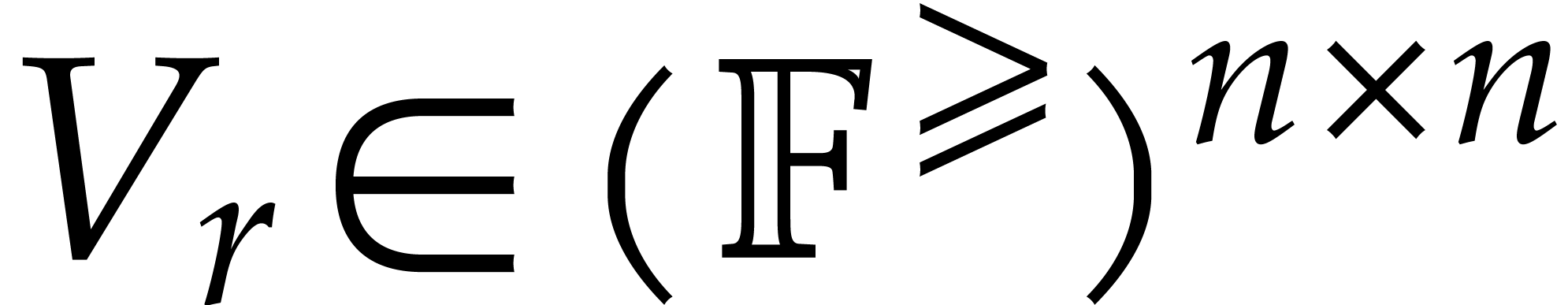 ,
,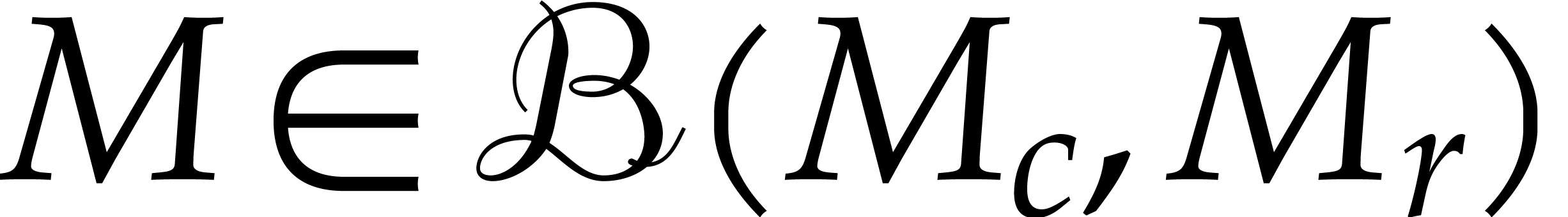 ,
,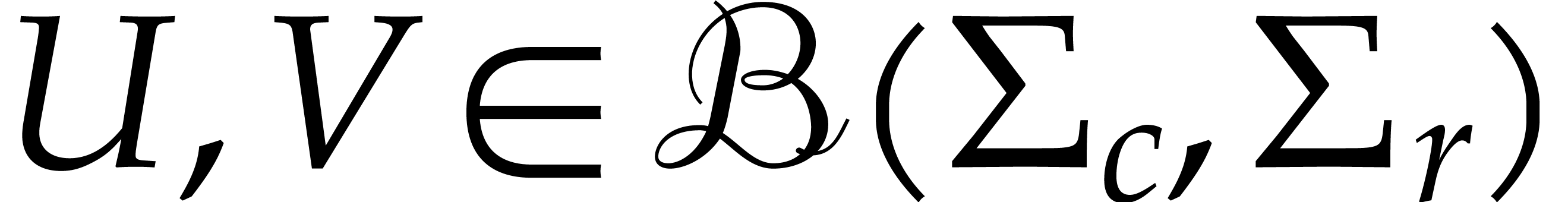 ,
,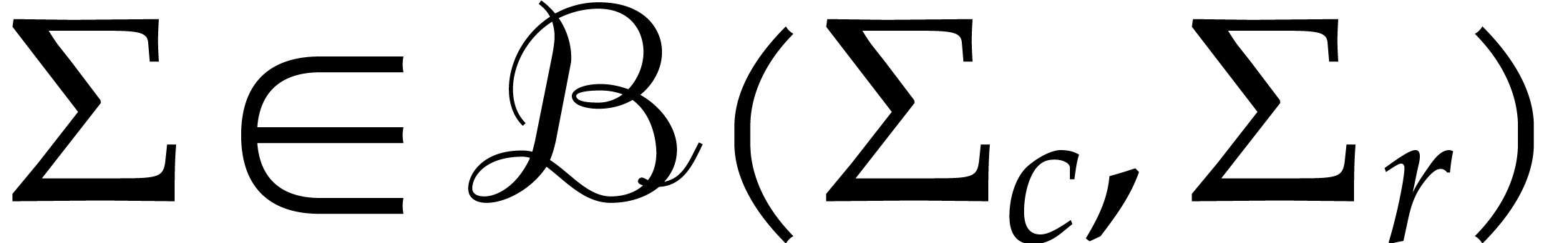 with
with
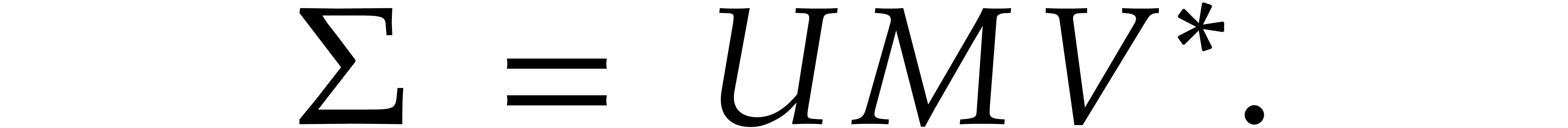
 .
.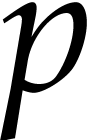 bits for numerical computations, it has recently been
shown [
bits for numerical computations, it has recently been
shown [ matrices can be
multiplied in time
matrices can be
multiplied in time
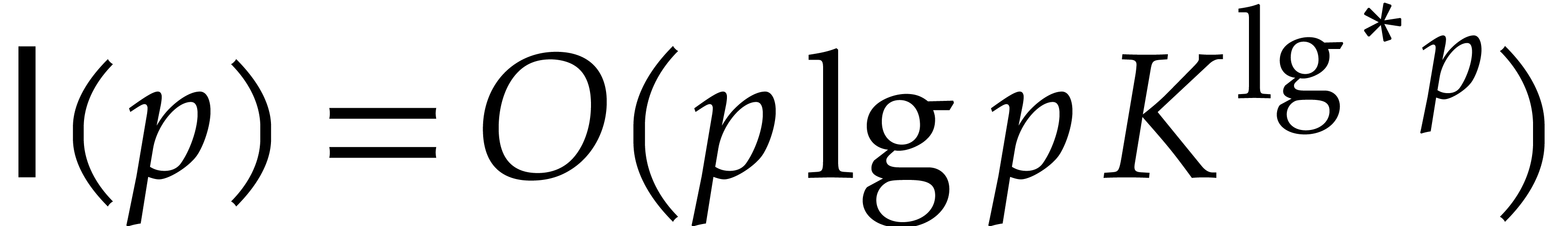 with
with 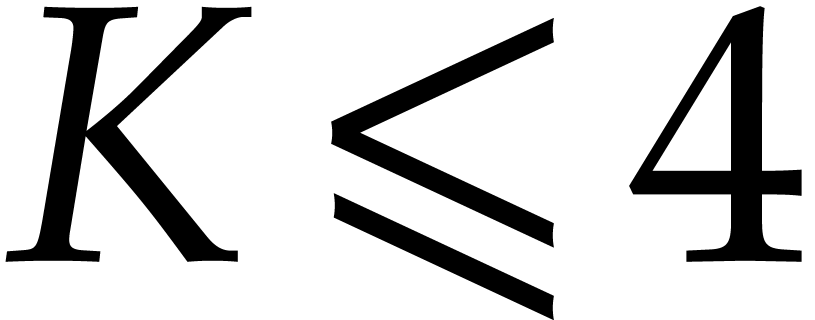 is the cost of
is the cost of
 is the
exponent of matrix multiplication [
is the
exponent of matrix multiplication [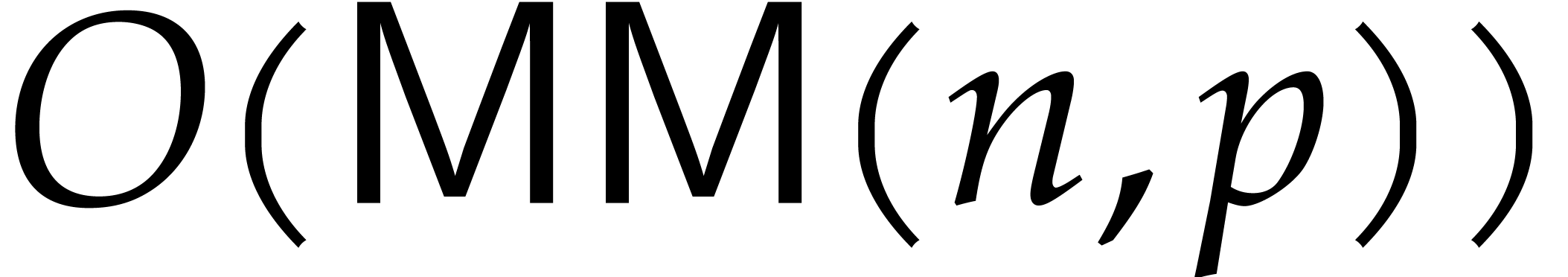 yields an asymptotic bound for the bit
complexity of our certification problem.
yields an asymptotic bound for the bit
complexity of our certification problem.
 ,
, ,
, ,
,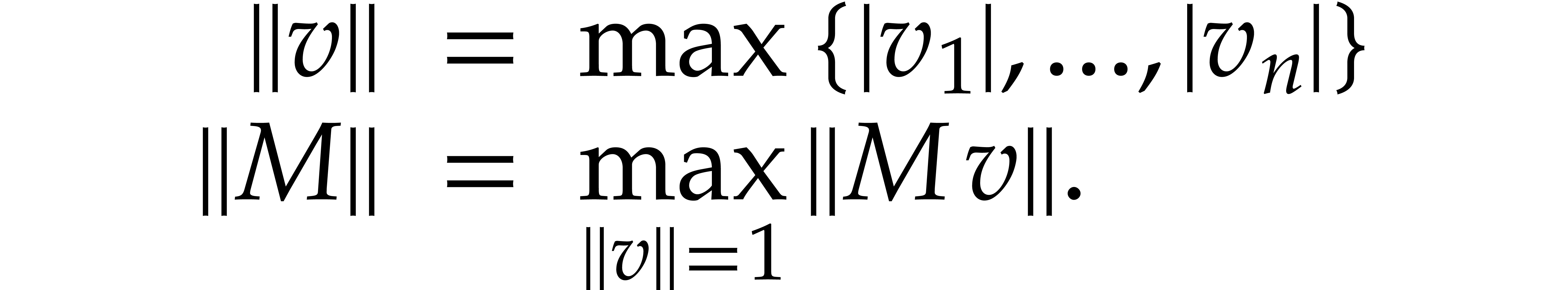
 ,
,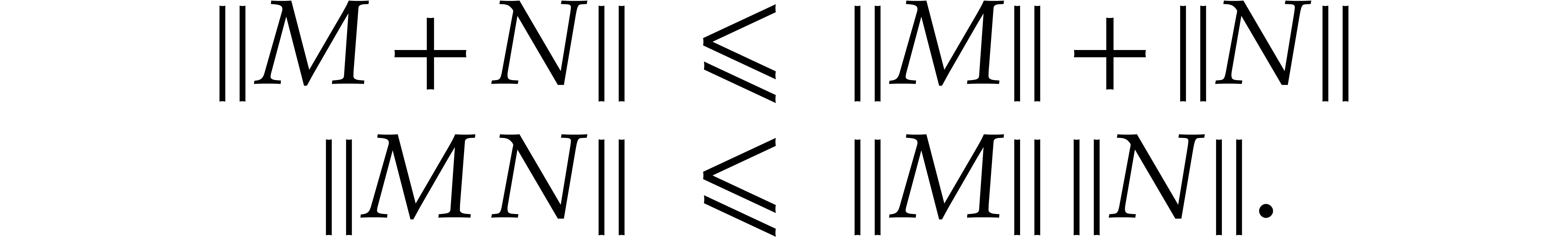
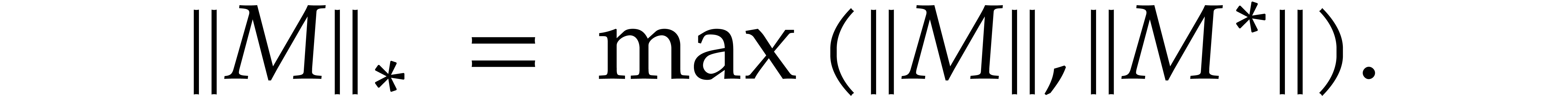
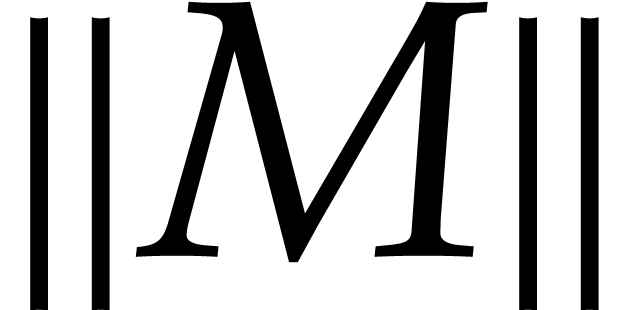

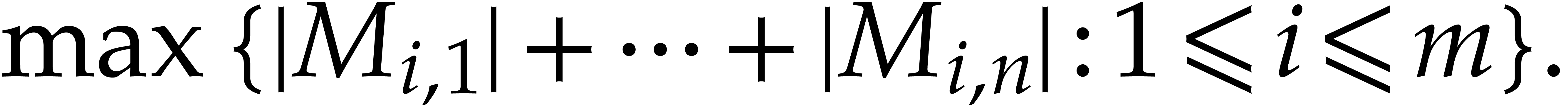
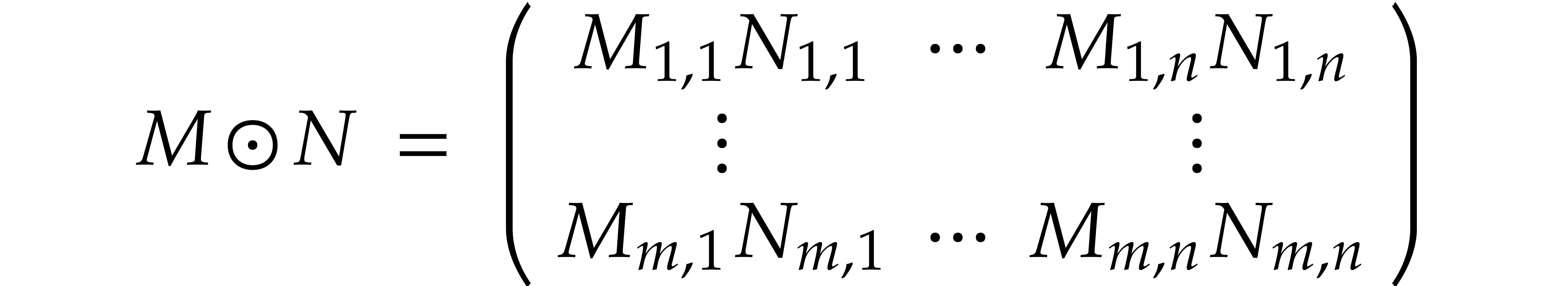

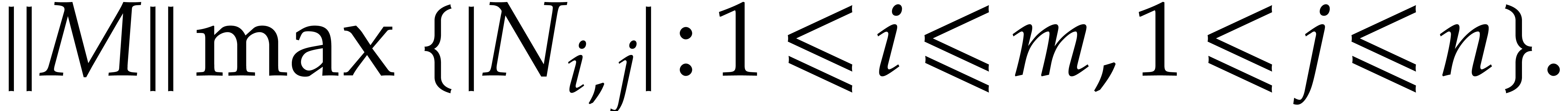
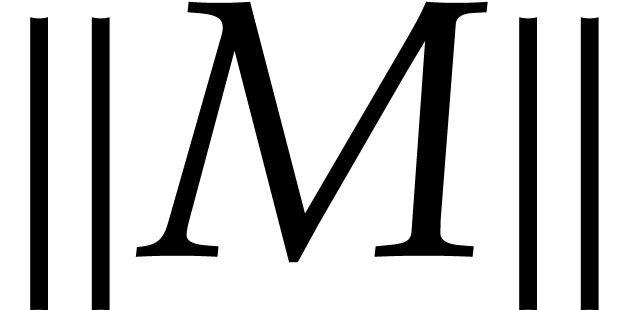 can only
decrease. We will write
can only
decrease. We will write 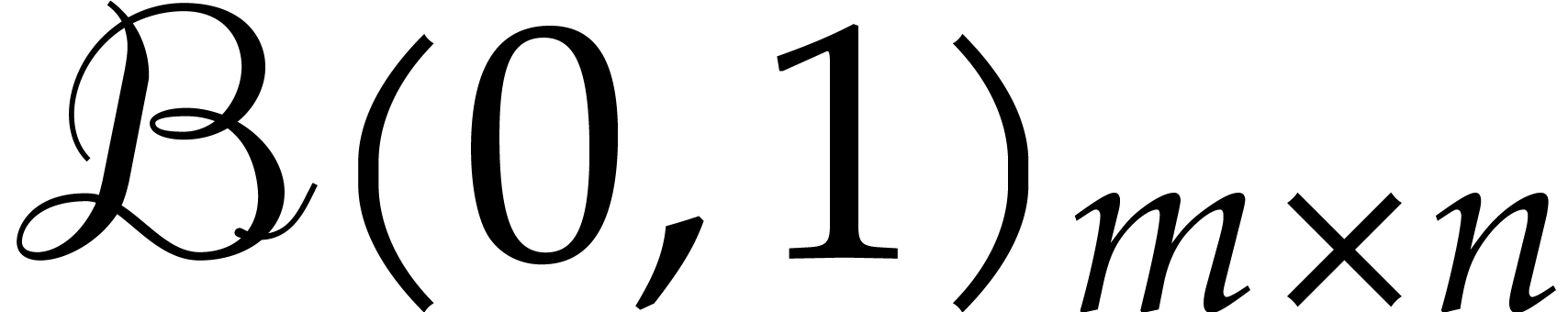 for the
for the 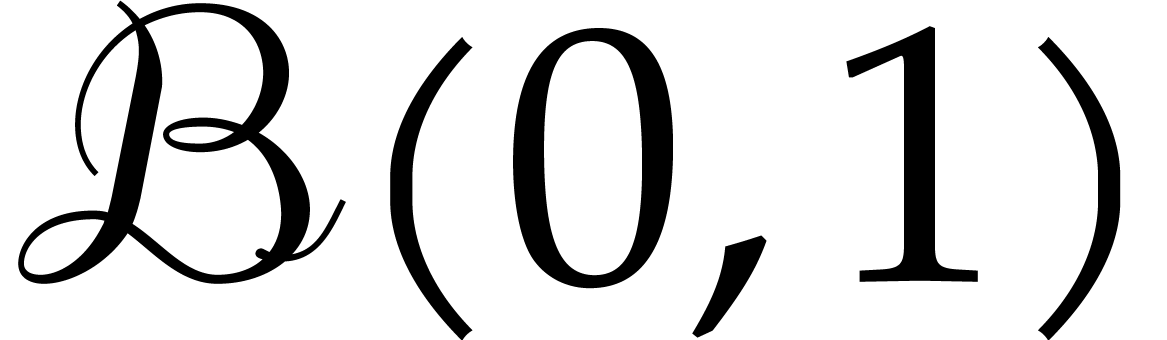 .
. for all
for all 
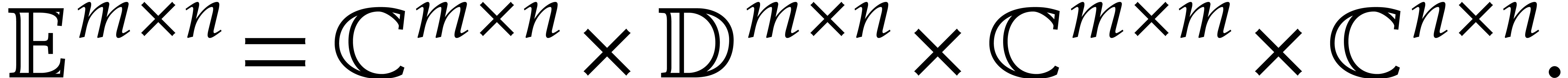
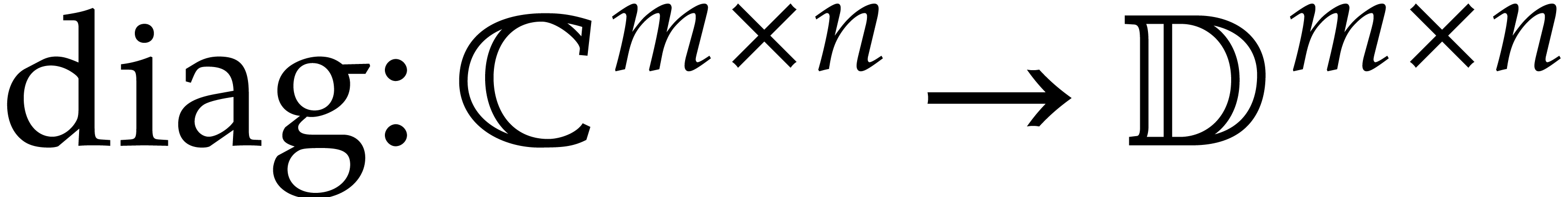 for the natural projection that
replaces all non-diagonal entries by zeros. For any integer
for the natural projection that
replaces all non-diagonal entries by zeros. For any integer  we finally define the map
we finally define the map 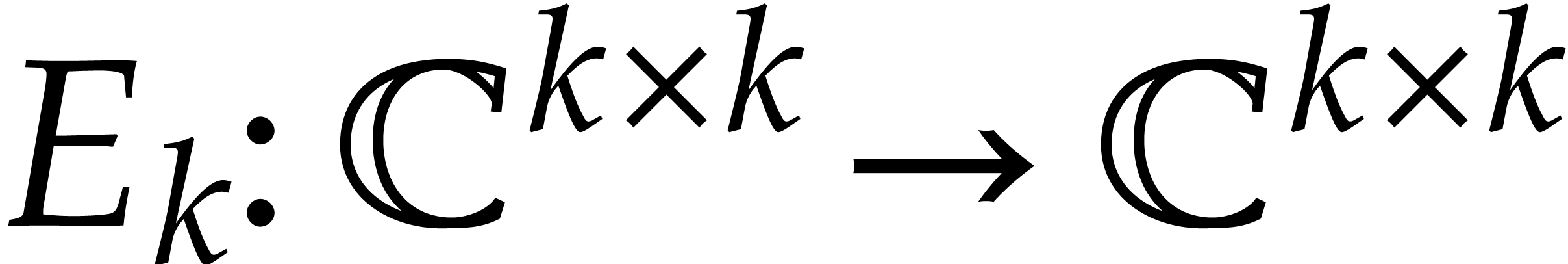 by
by
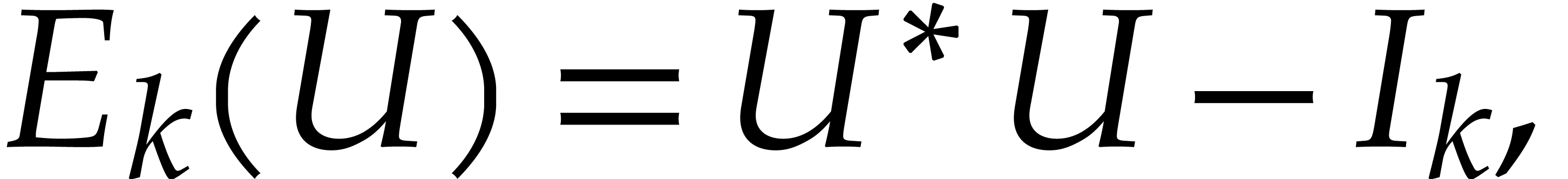
 is the identity matrix of size
is the identity matrix of size  .
.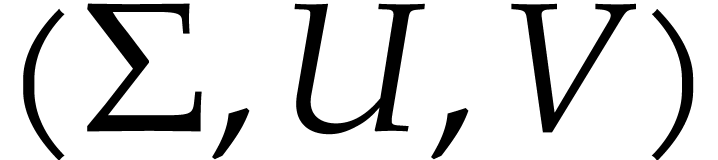 with
with 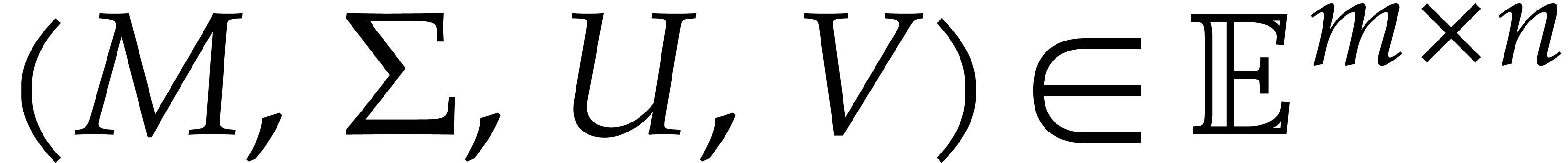 forms an SVD for
forms an SVD for 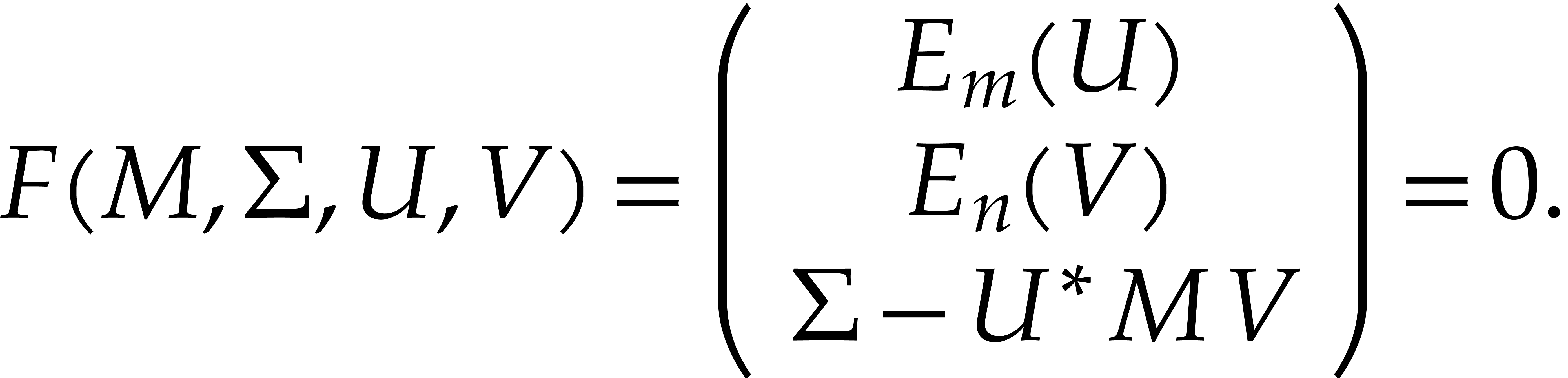
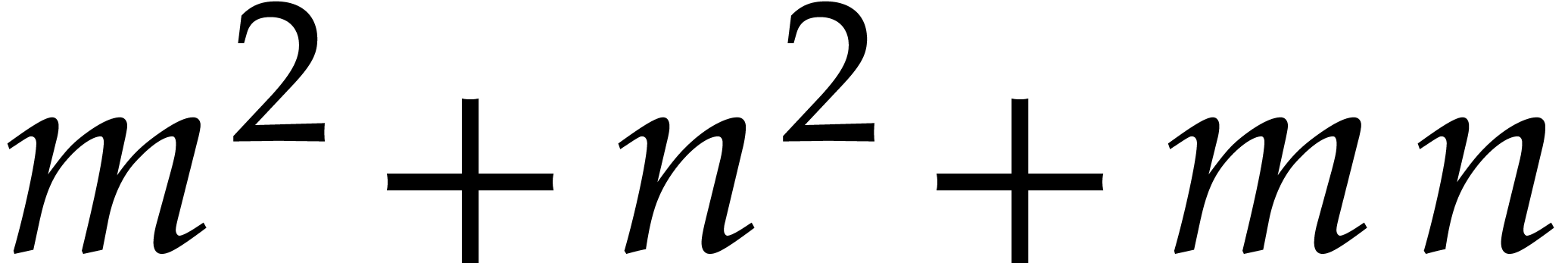 equations with
equations with 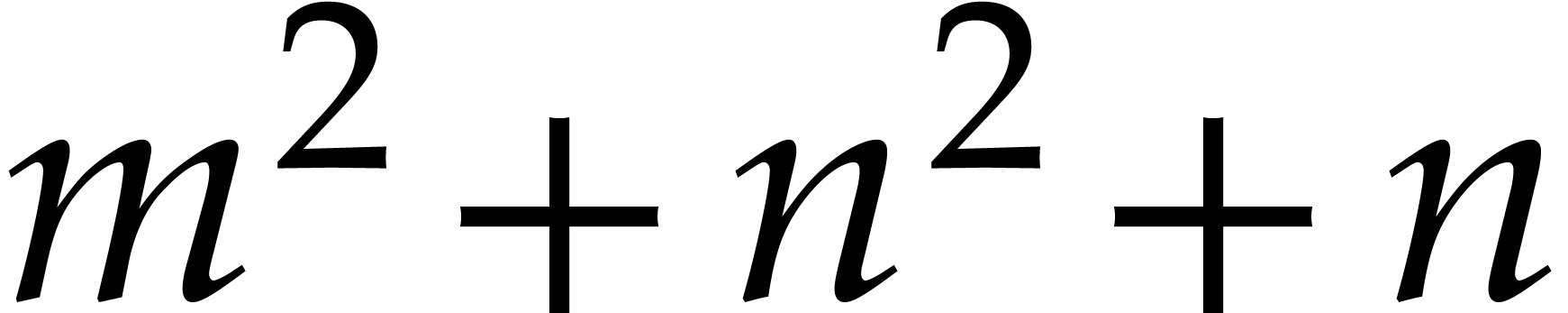 unknowns. Our efficient numerical method for solving this
system will rely on the following principles:
unknowns. Our efficient numerical method for solving this
system will rely on the following principles:
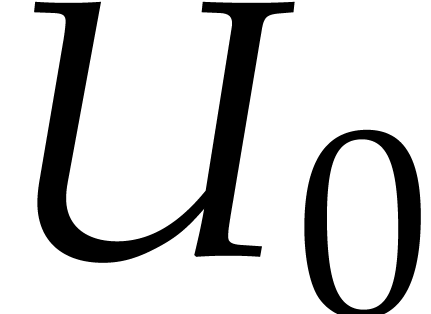 close to
the unitary group
close to
the unitary group  ,
,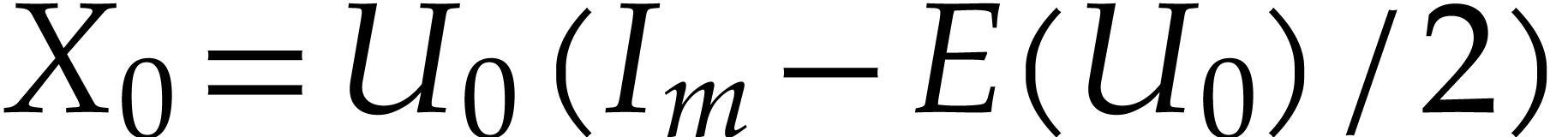
 close to
close to  ,
,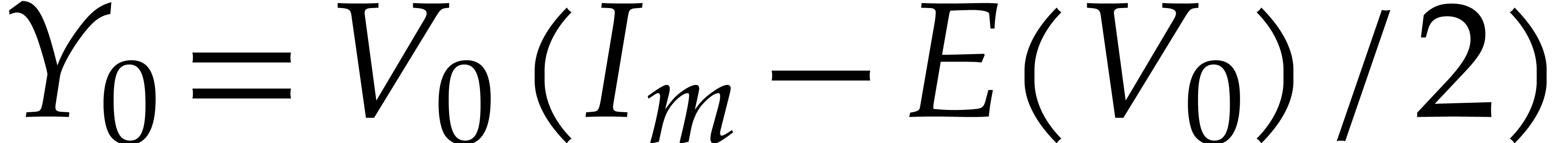
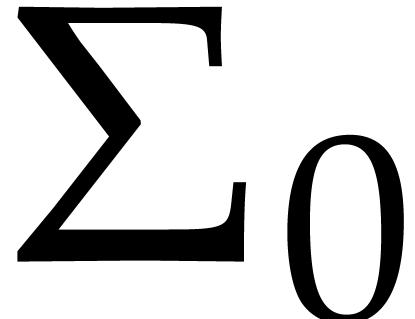 ,
,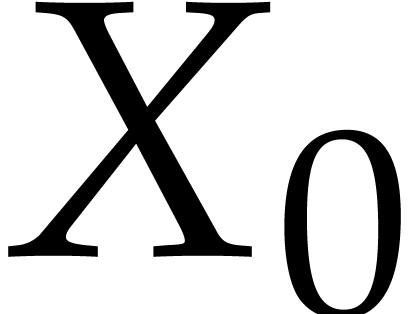 and
and 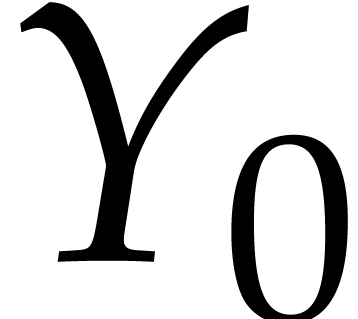 ,
,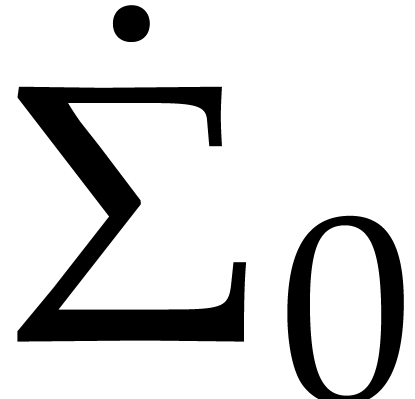 ,
,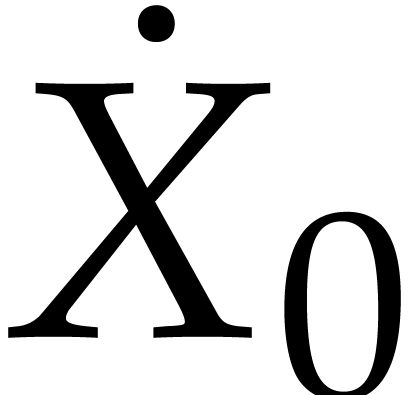 and
and 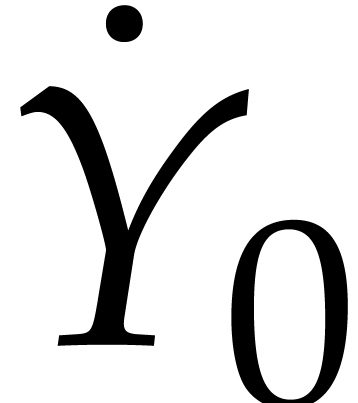 such that
such that
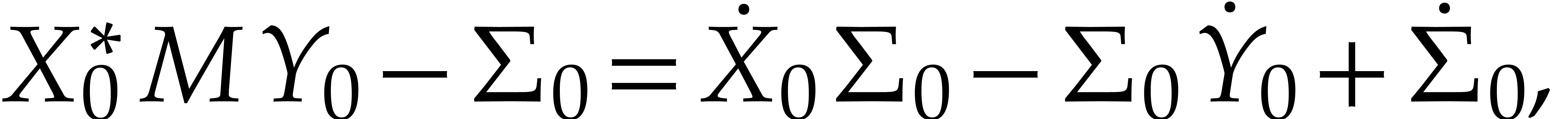
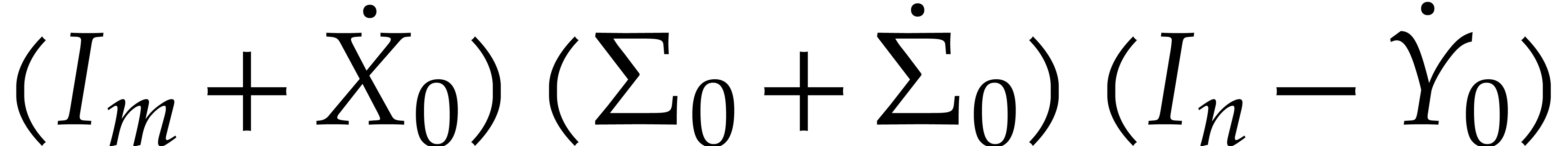 is a first-order approximation
of
is a first-order approximation
of 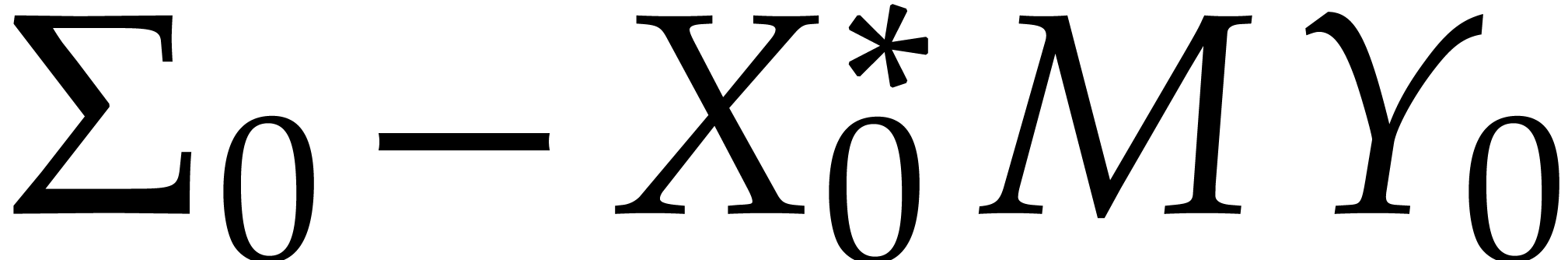 :
: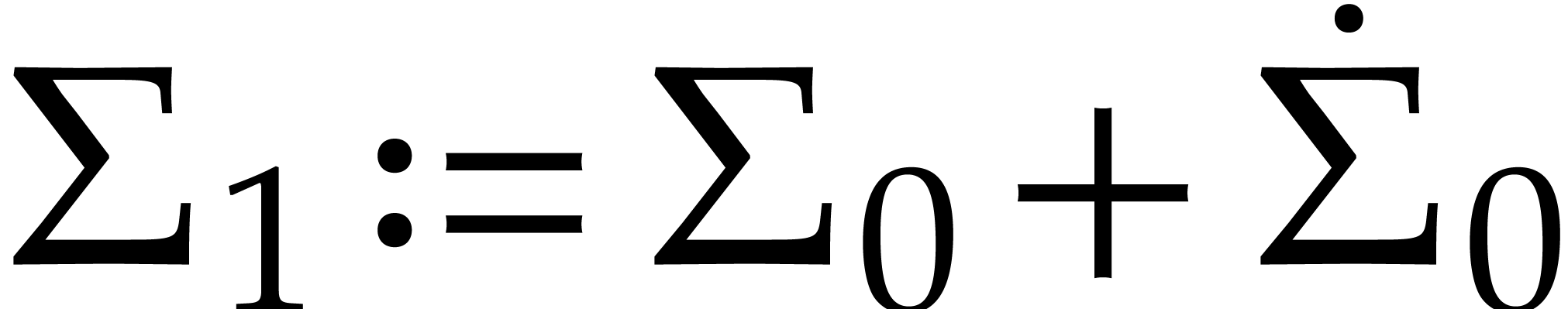 ,
,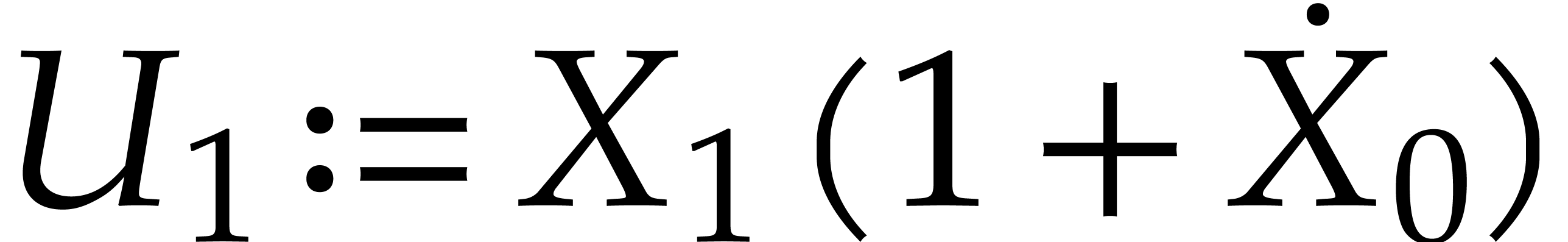 ,
,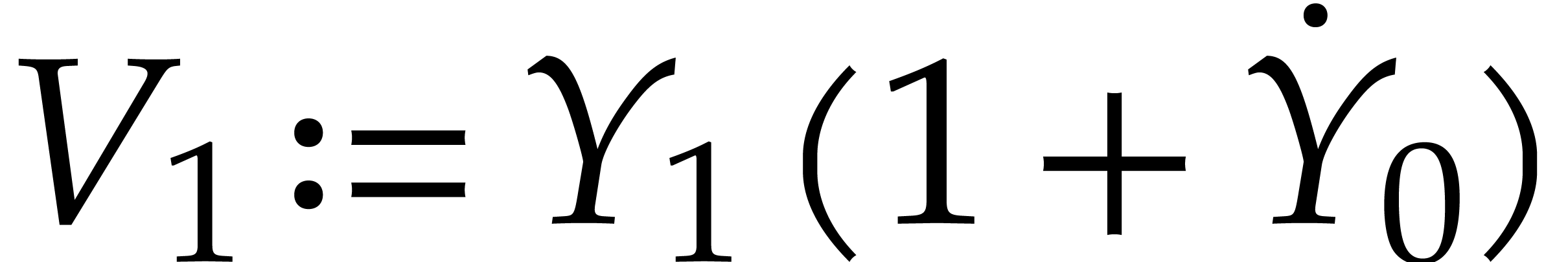 .
. is sufficiently close to
is sufficiently close to 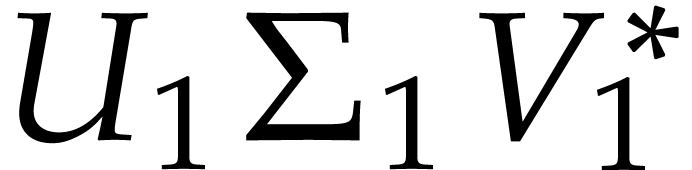 is a better approximation of the matrix
is a better approximation of the matrix 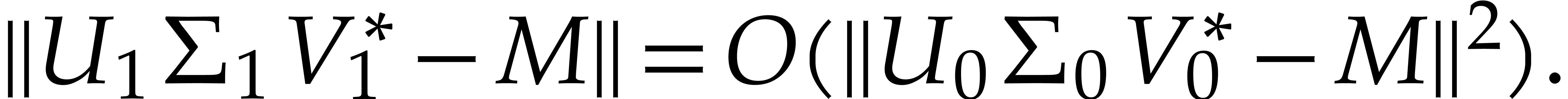
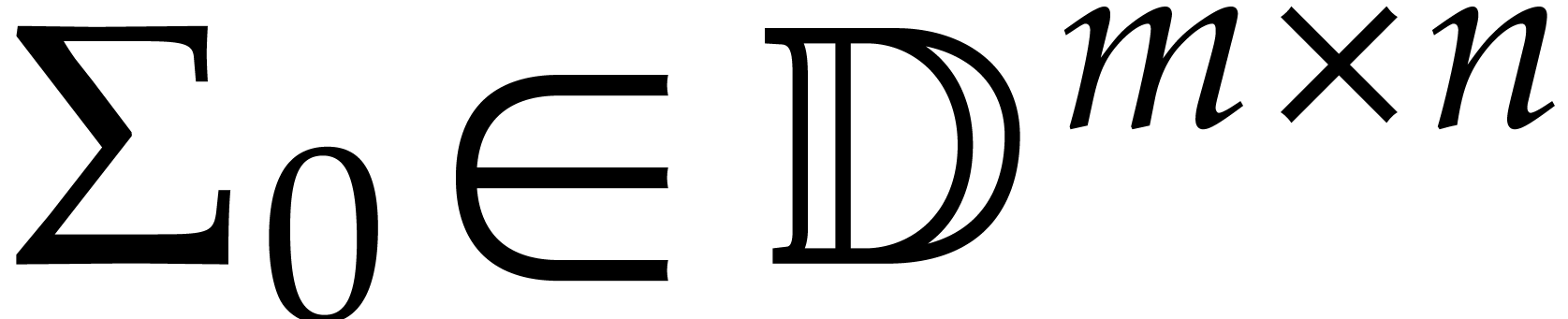 ,
, ,
, ,
,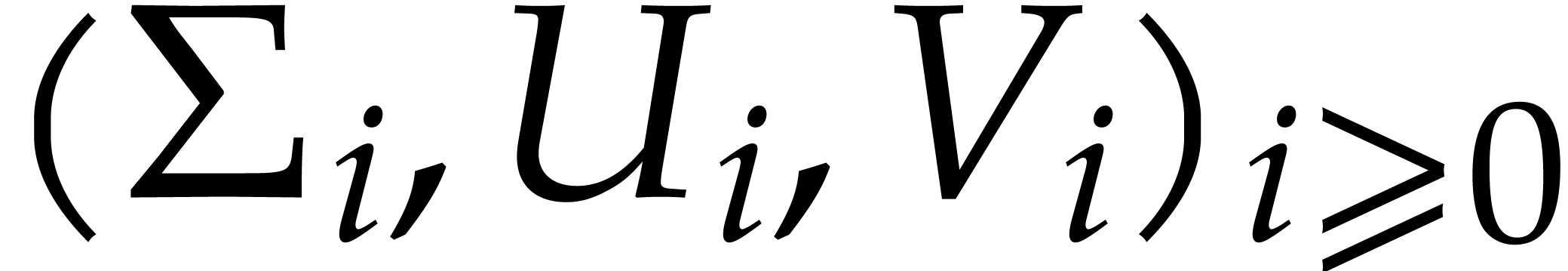
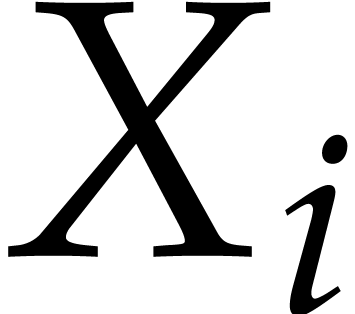
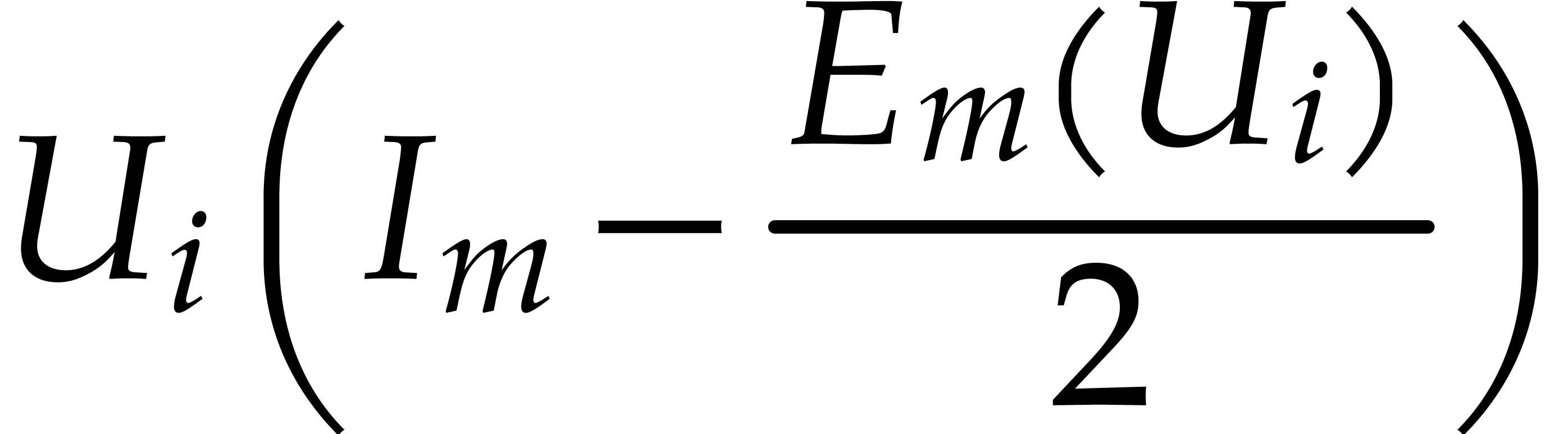
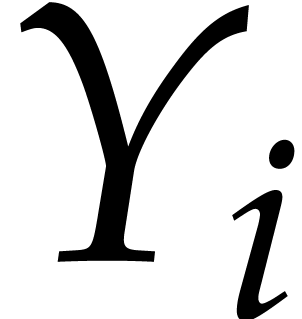
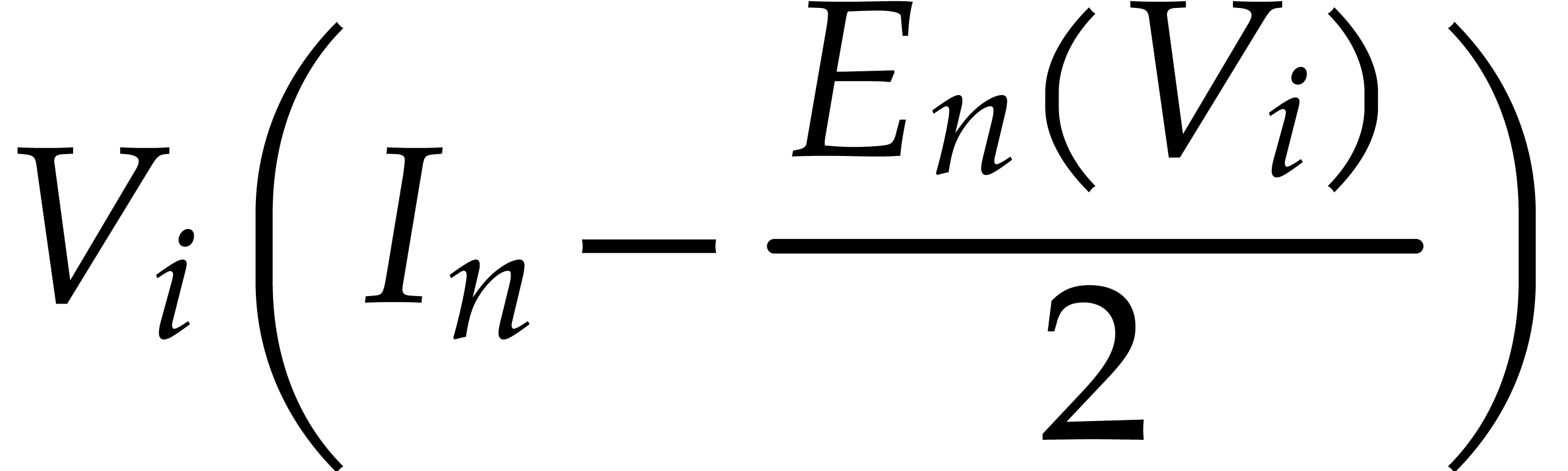
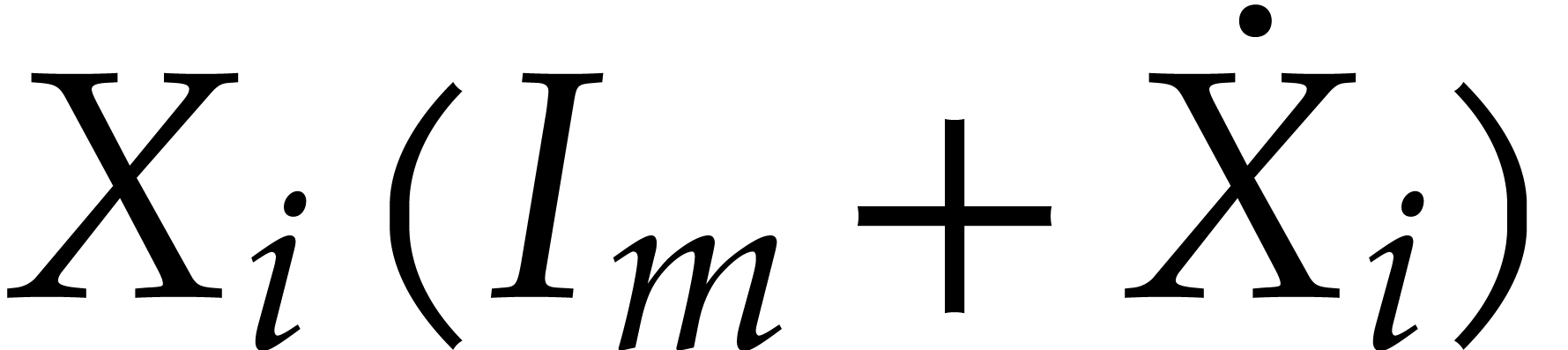
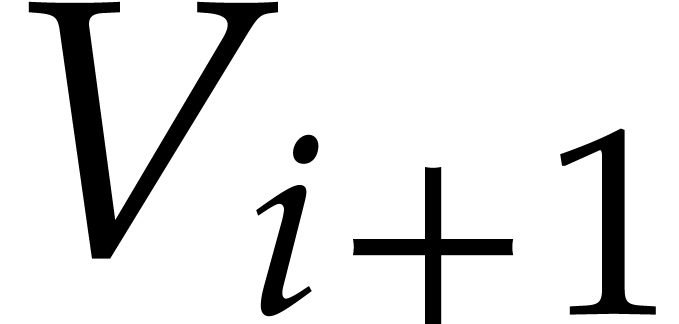
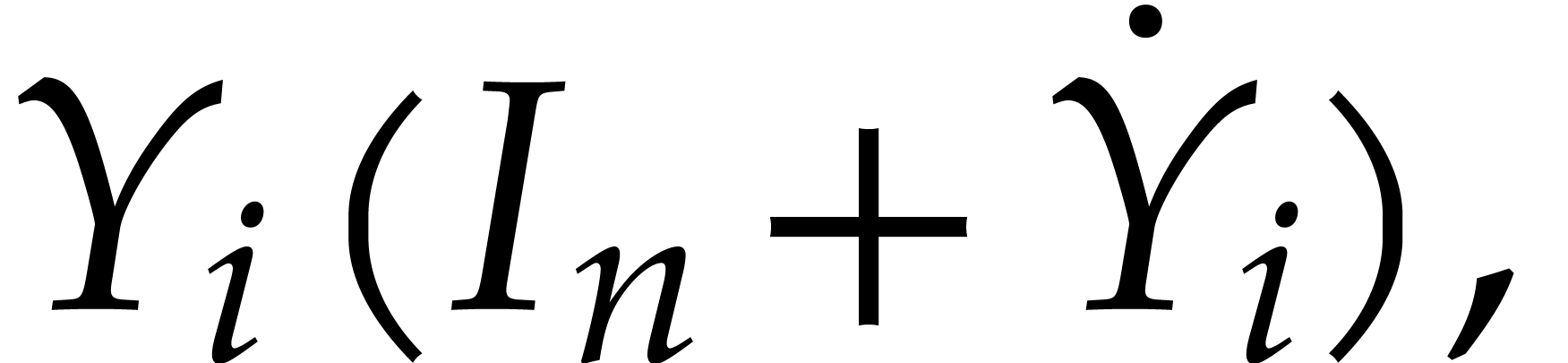
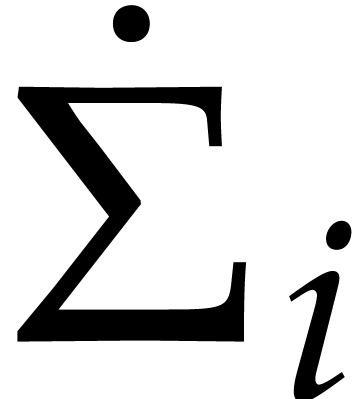 is a diagonal matrix and
is a diagonal matrix and 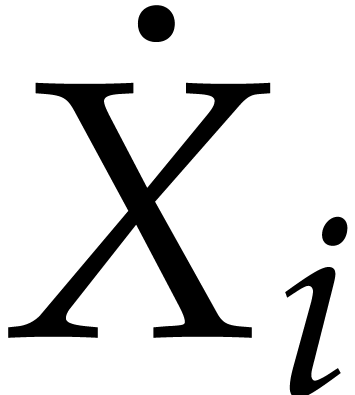 ,
,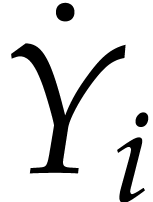 are two skew
Hermitian matrices such that
are two skew
Hermitian matrices such that
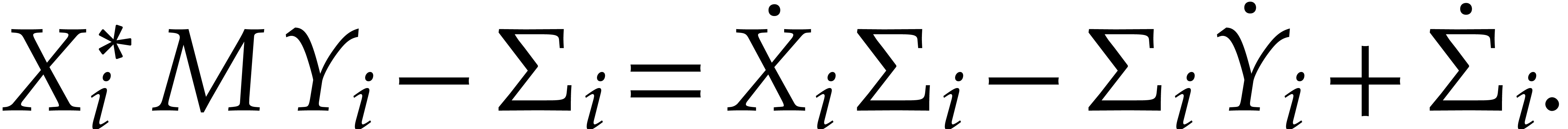
 and
and 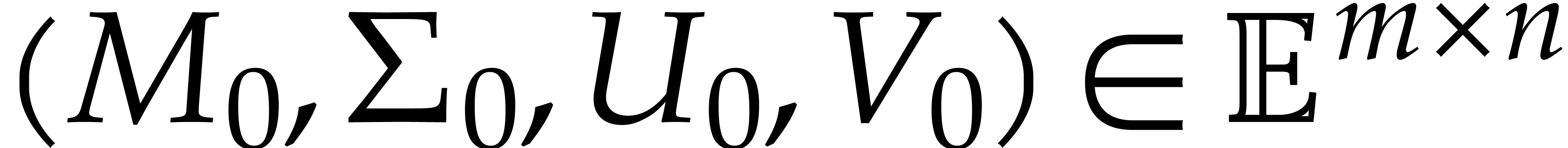 be
such that
be
such that 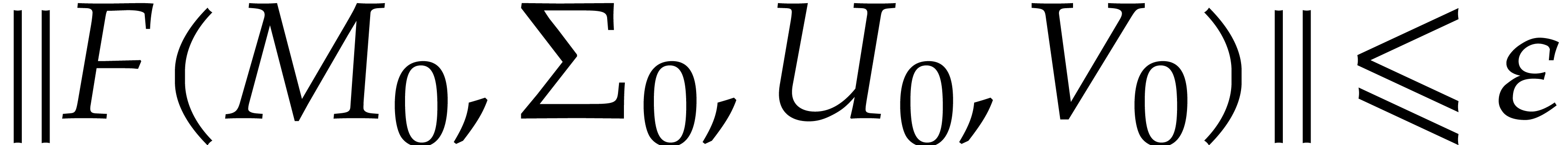 .
.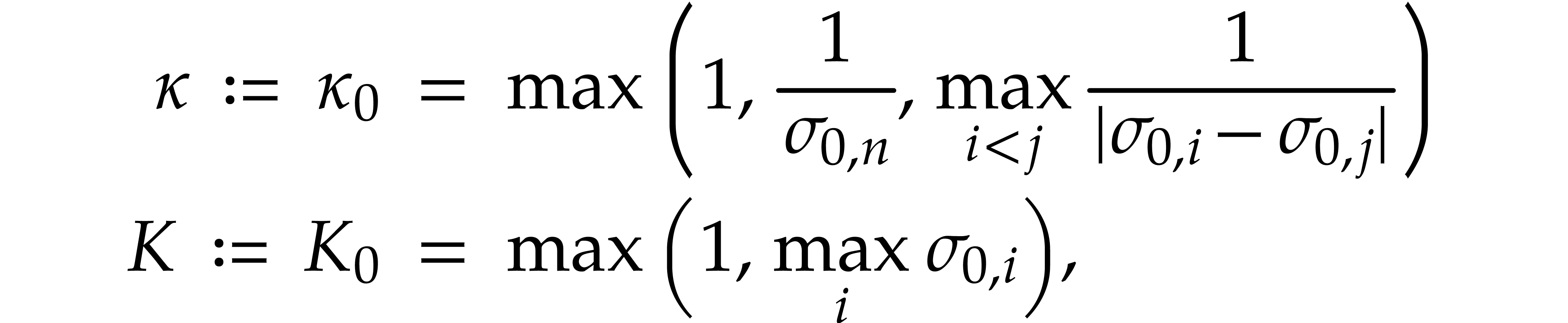
 stand for the diagonal entries of
stand for the diagonal entries of

 of the matrix
of the matrix 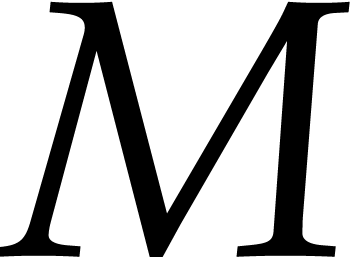 ,
,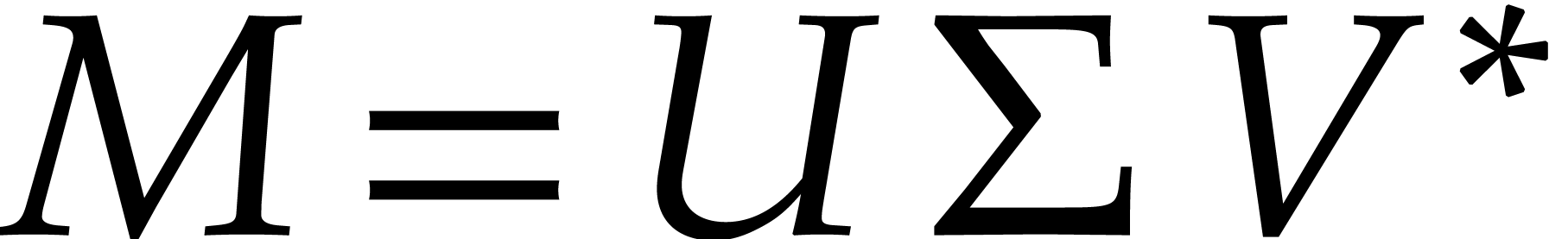 .
. ,
,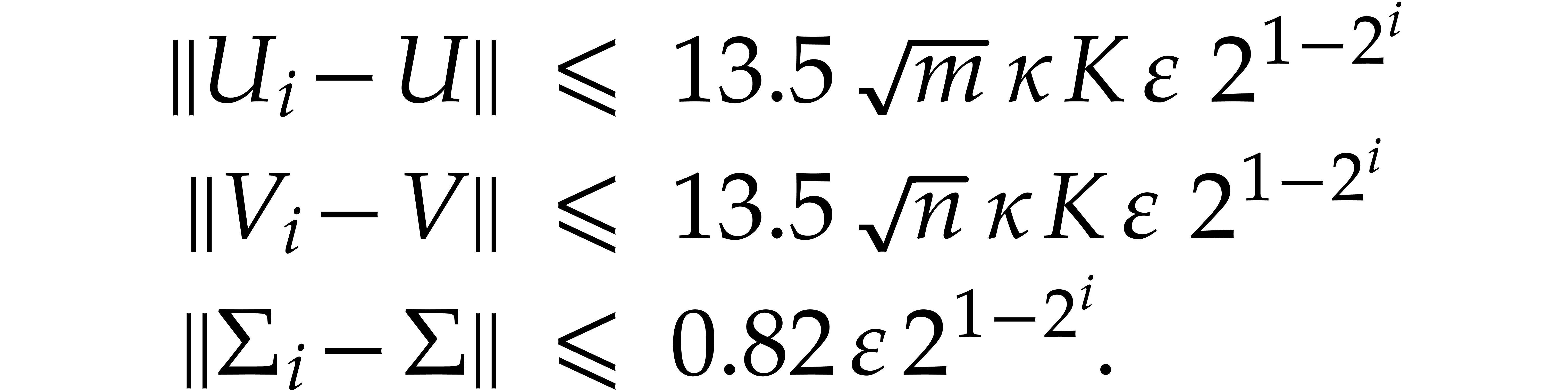
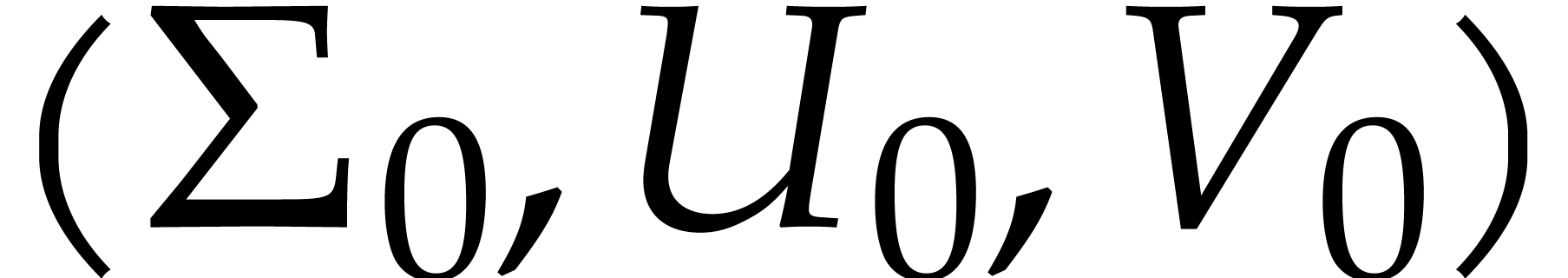 for the center of a ball matrix
for the center of a ball matrix 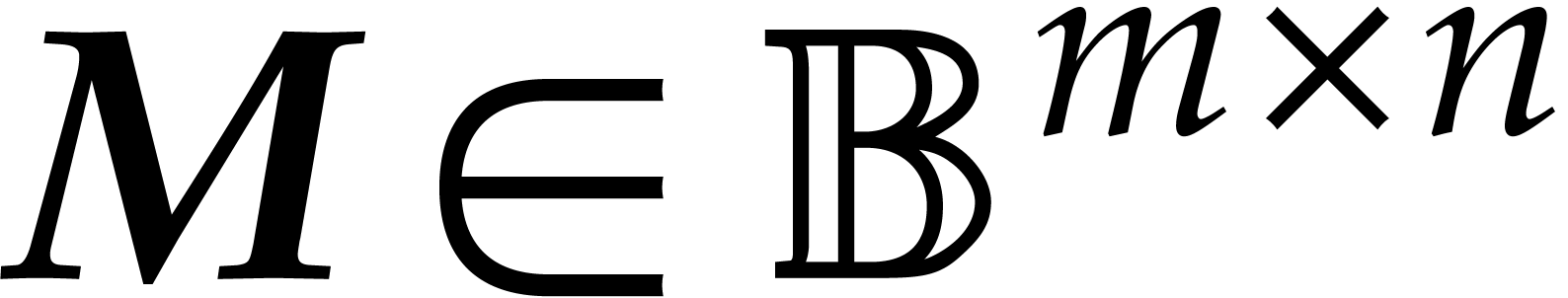
 ,
, and
and 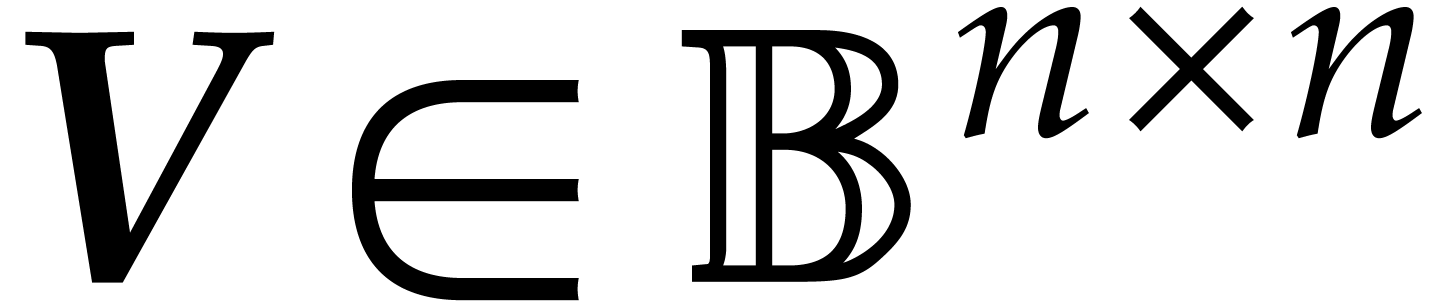 of
of  ,
, ,
,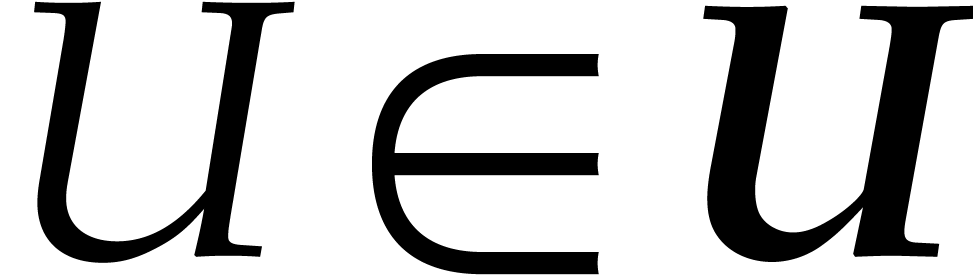 and
and 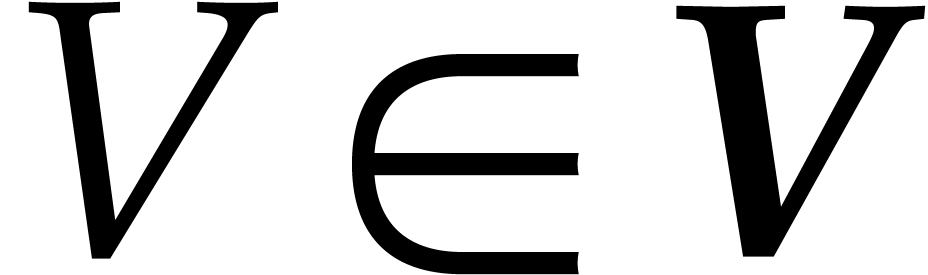 such that
such that 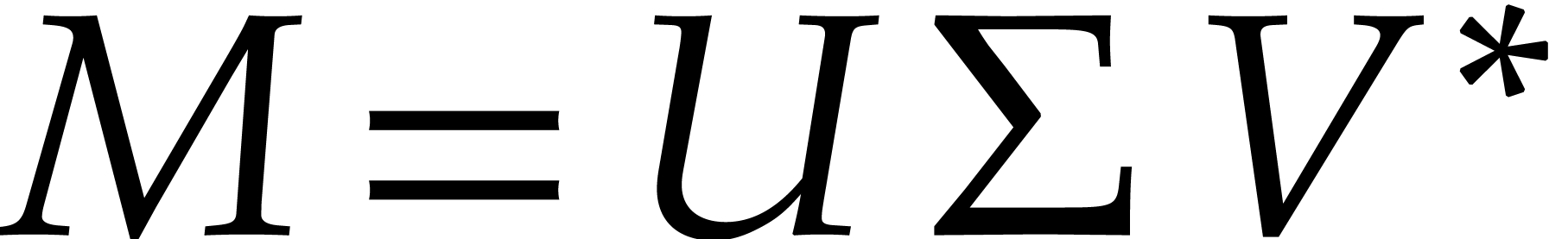 is an exact singular value decomposition of
is an exact singular value decomposition of 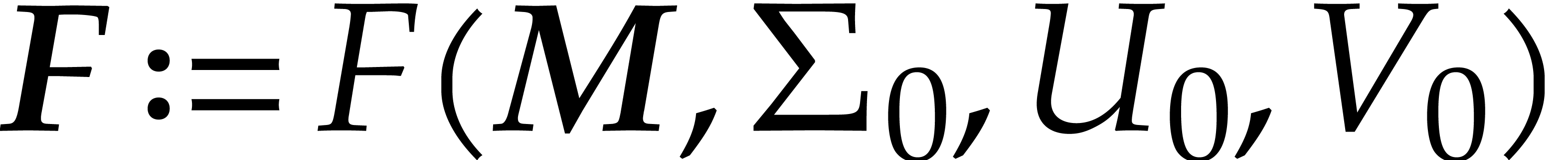 using ball arithmetic
using ball arithmetic
 be an upper bound for
be an upper bound for 
 and
and  be upper
bounds for
be upper
bounds for  and
and  (with
(with  ,
,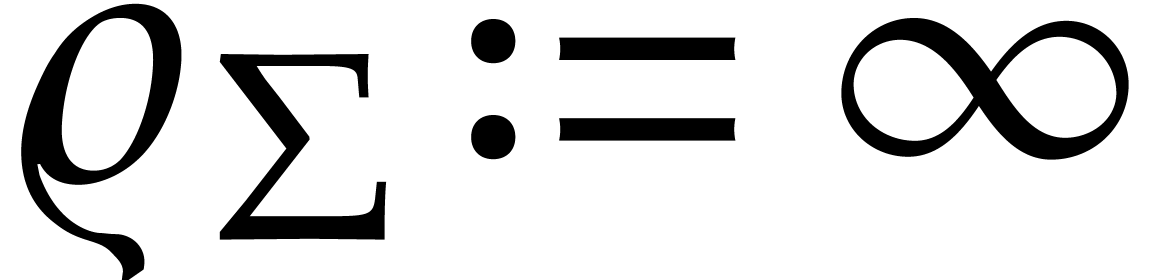 ,
,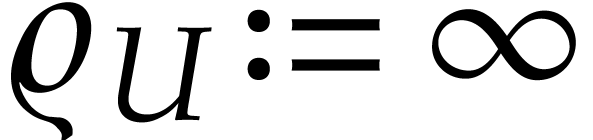 ,
,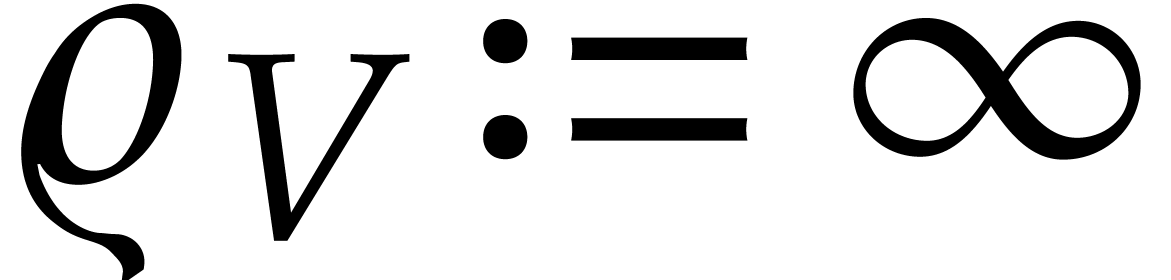
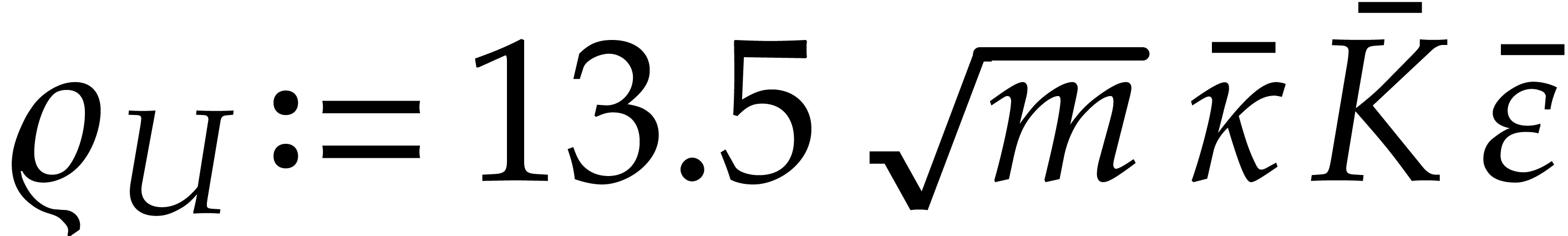 ,
,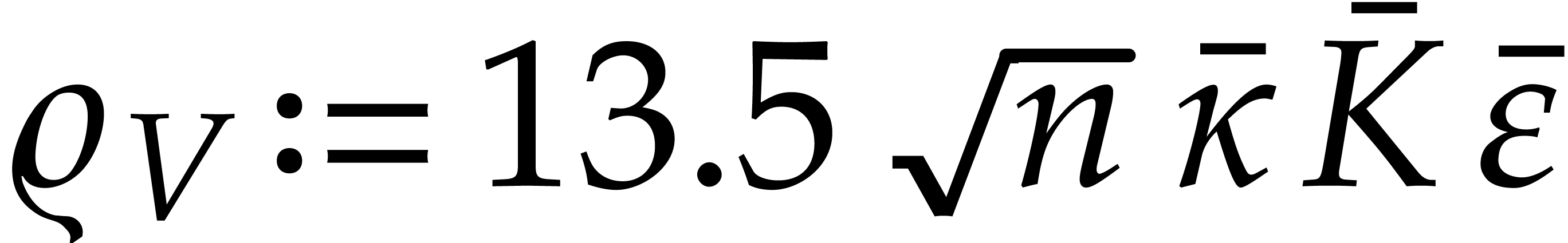 ,
,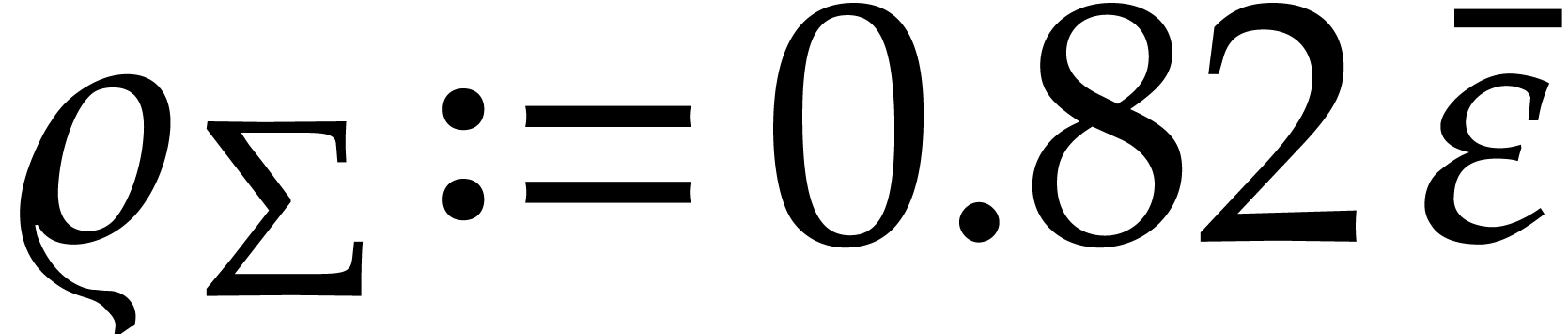 (using upward rounding)
(using upward rounding)
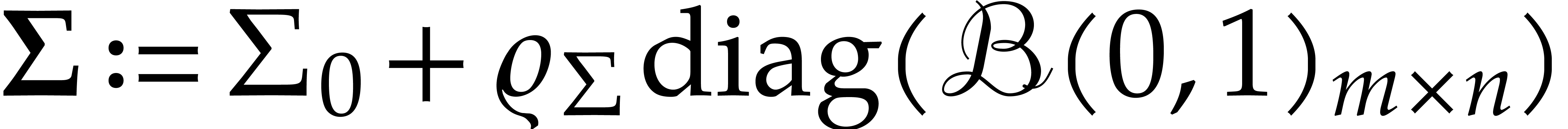

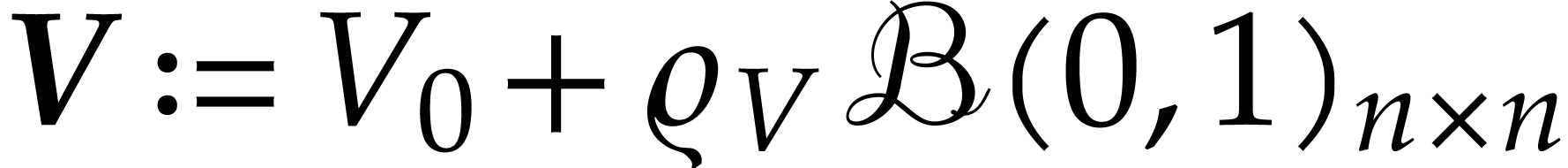

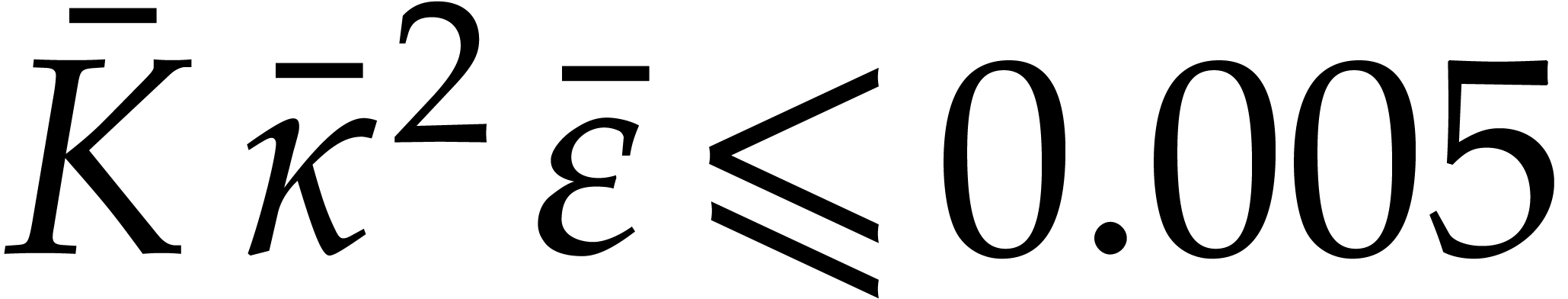 ,
, ,
, ,
, and
and  are bounded by
are bounded by  ,
, and
and  ,
, for
for 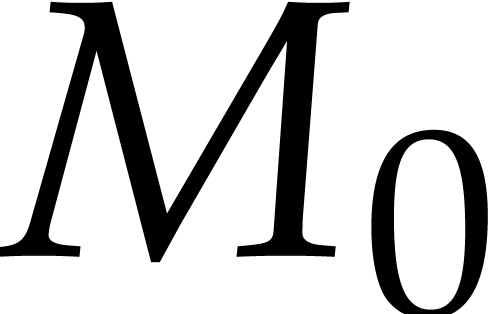 with the property that
with the property that 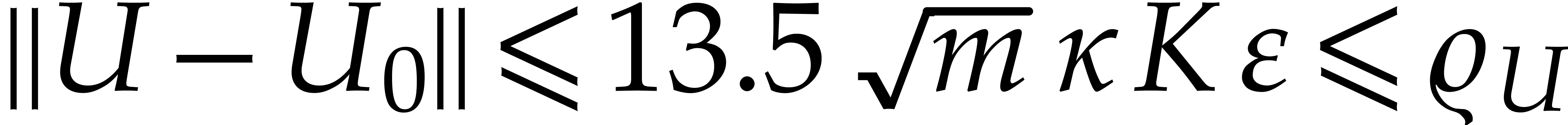 ,
,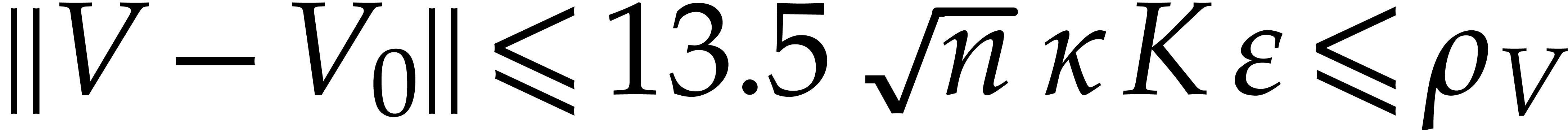 ,
,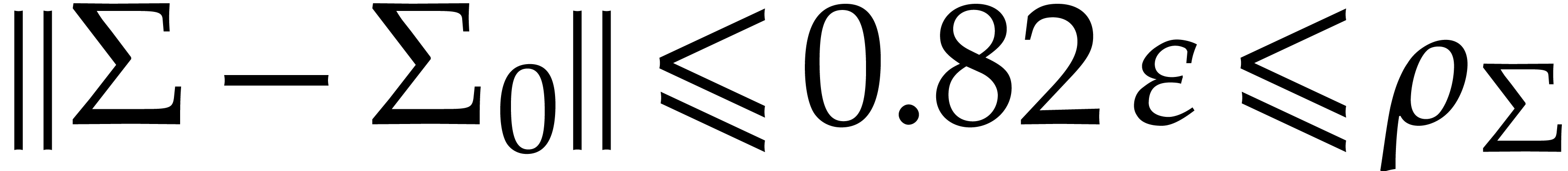 .
.
 for its projection on
the group
for its projection on
the group 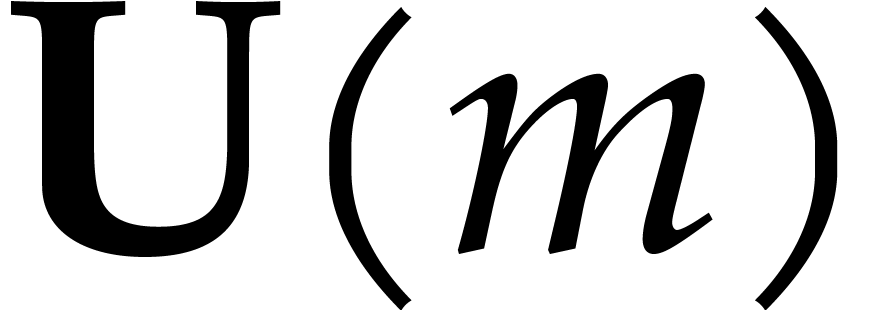 of unitary
of unitary 
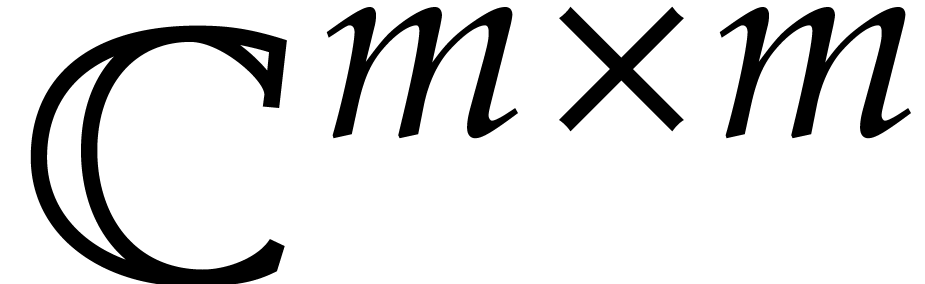
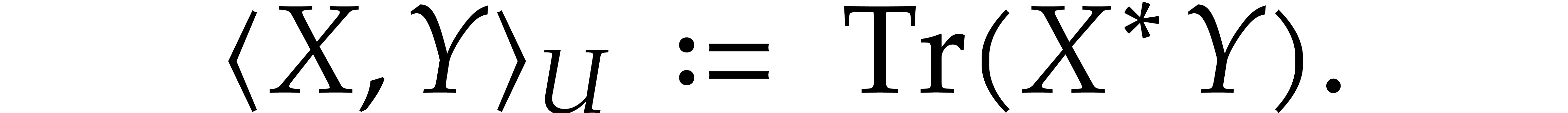
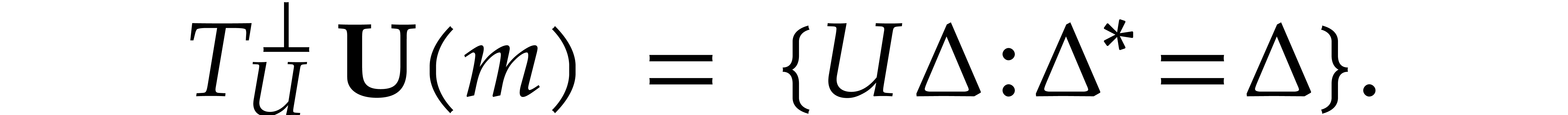
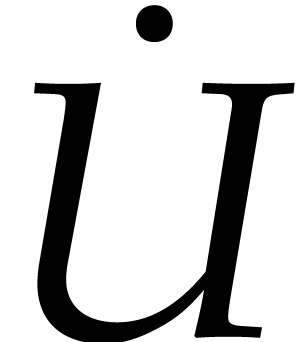 using an appropriate Newton
iteration. From the characterization of the normal space, it turns out
that it is more convenient to write
using an appropriate Newton
iteration. From the characterization of the normal space, it turns out
that it is more convenient to write 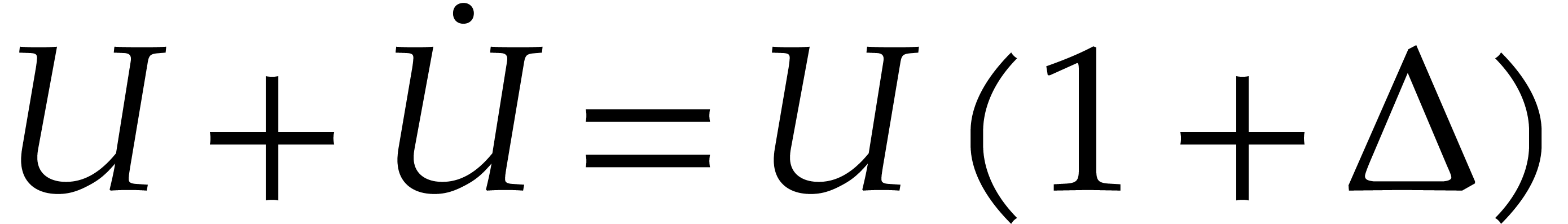 ,
, is Hermitian. With
is Hermitian. With 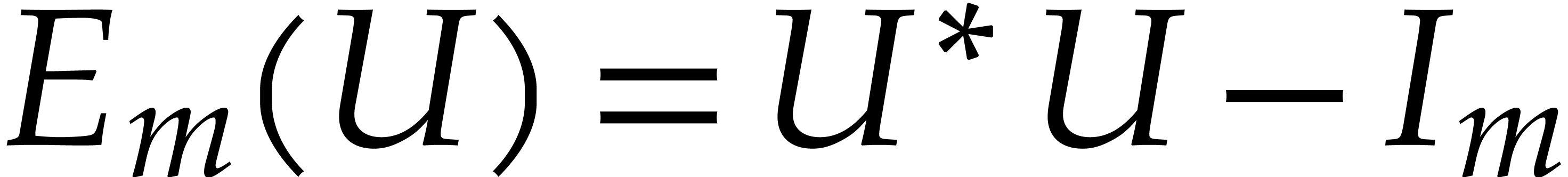 and
and 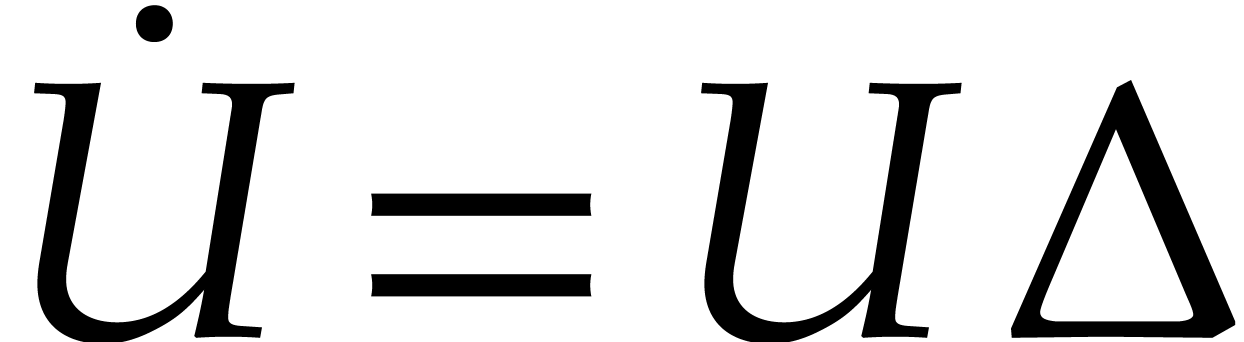 ,
,
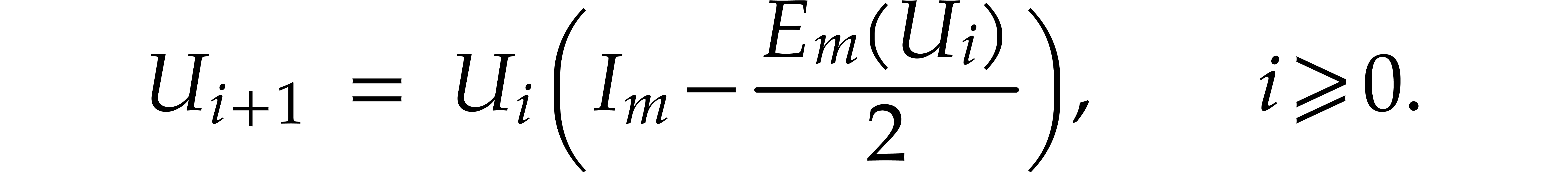
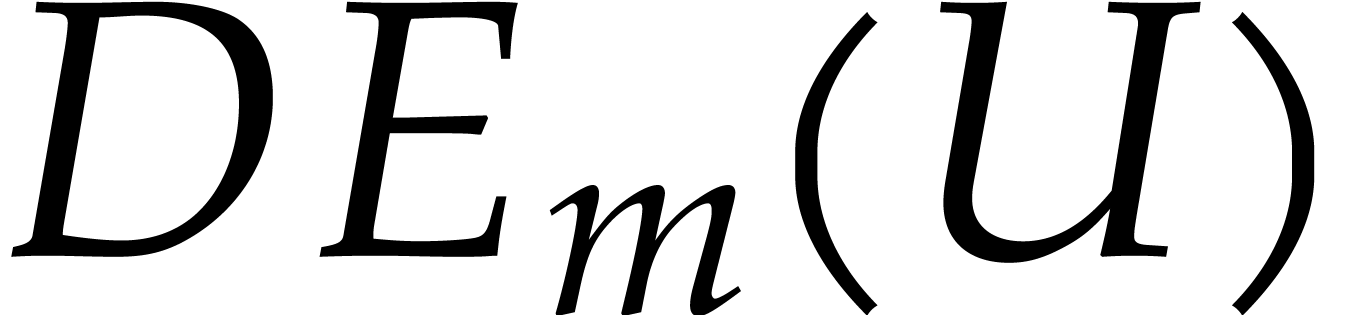 is onto from
is onto from  of Hermitian matrices. Then it is easy to
see that for given
of Hermitian matrices. Then it is easy to
see that for given  and
and  ,
,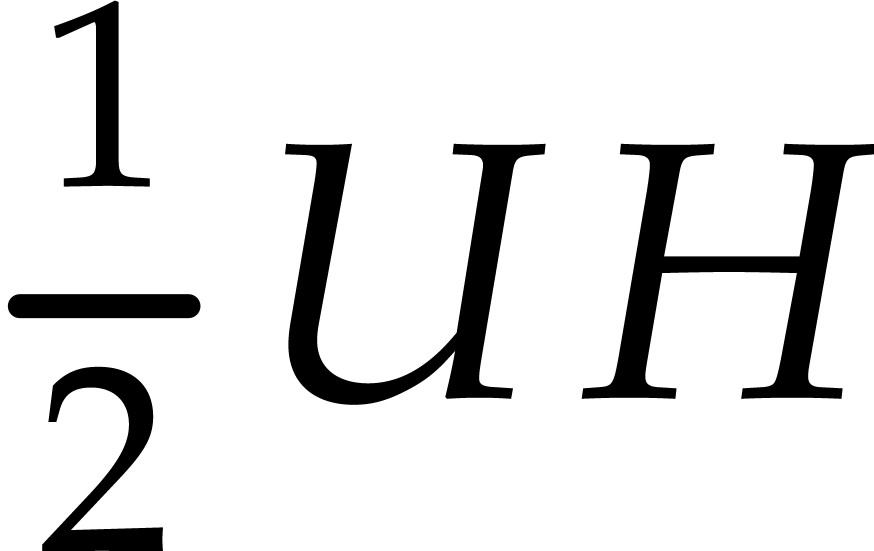 satisfies the
equation
satisfies the
equation 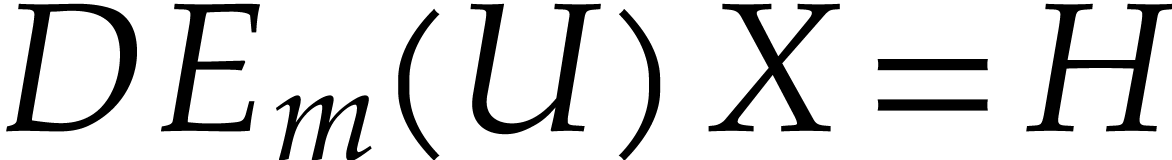 ,
,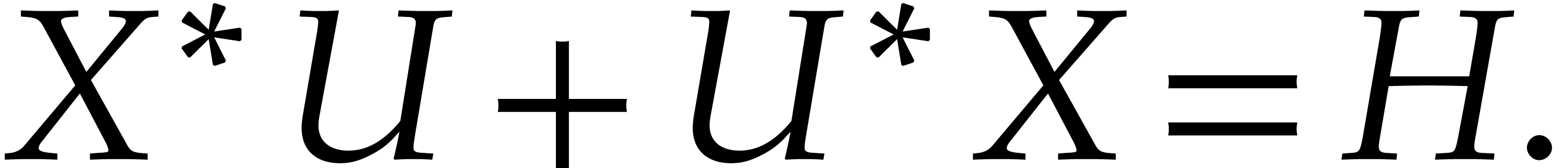
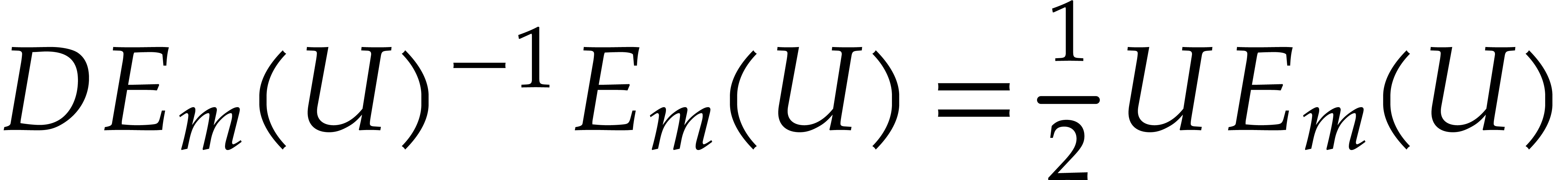 .
.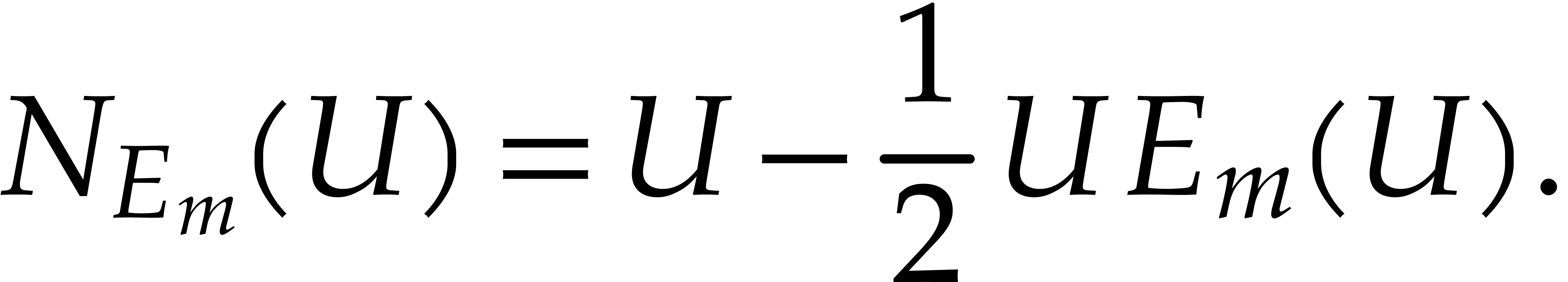
 be an
be an  matrix with
matrix with 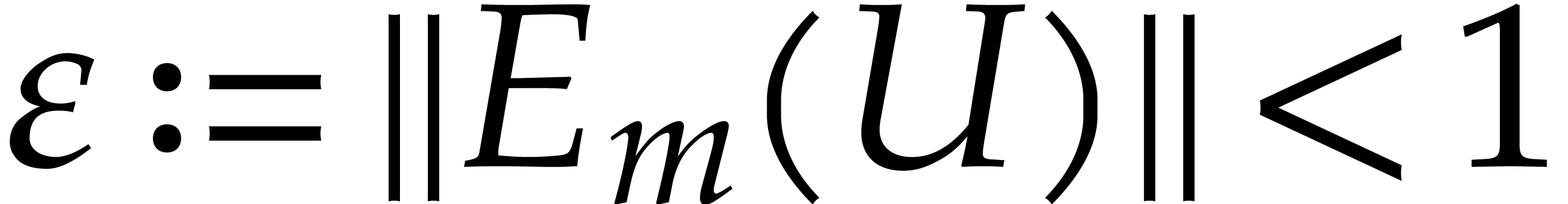 .
.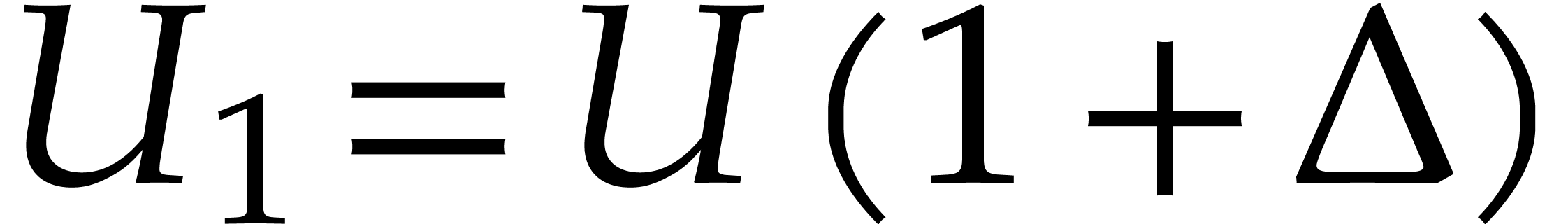 ,
,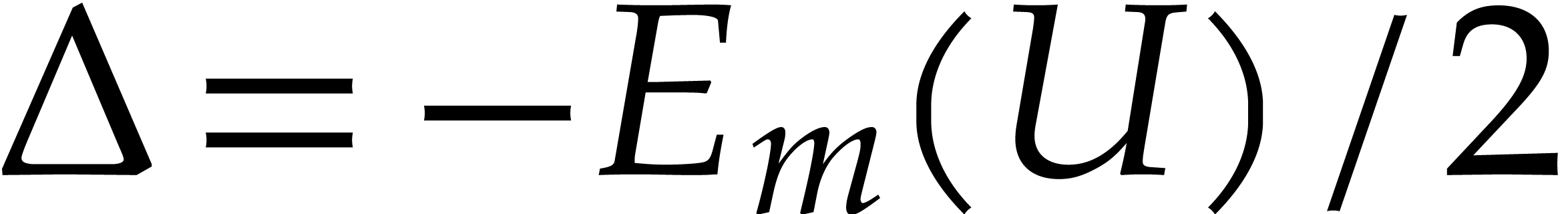 and write
and write 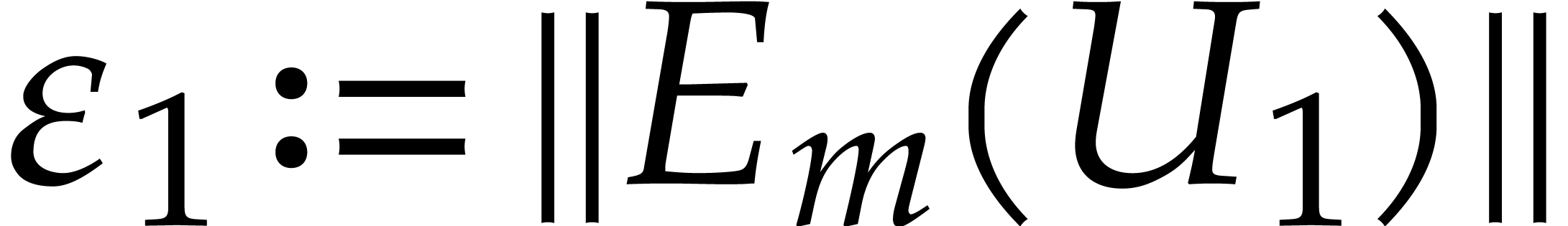 .
.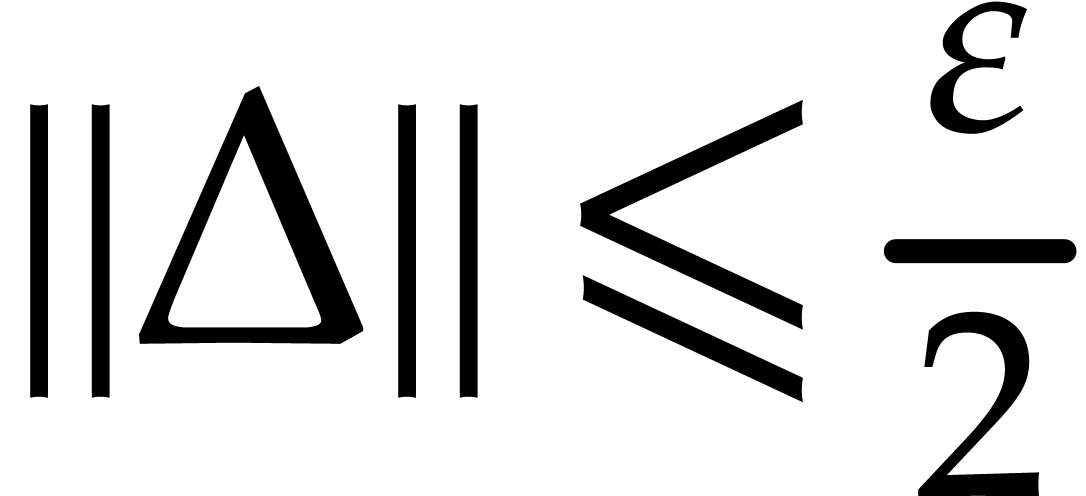 and
and
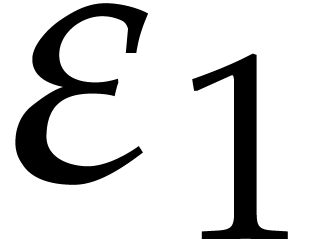
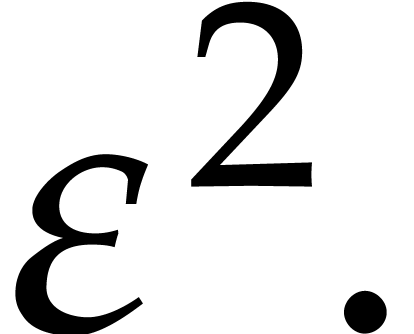
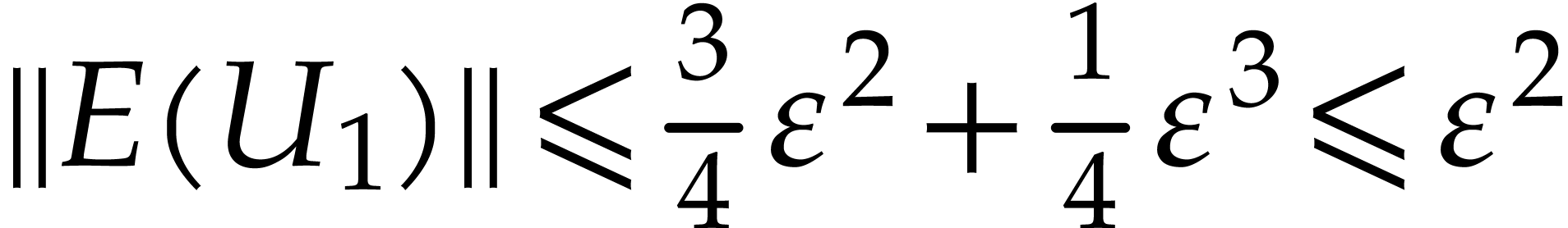 .
.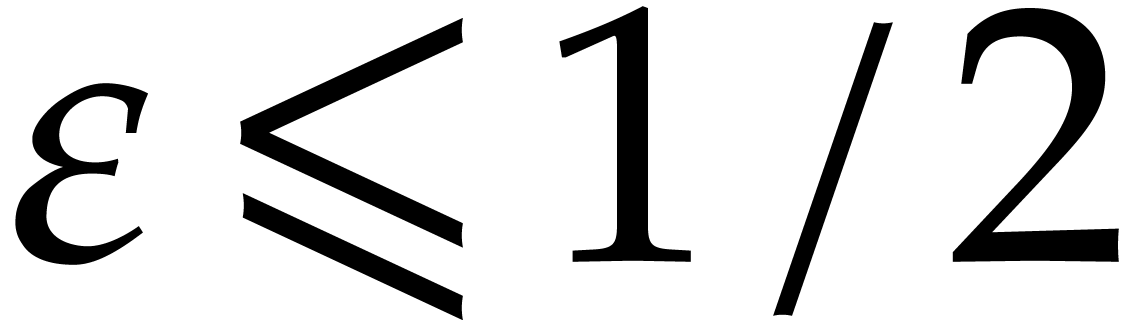 ,
,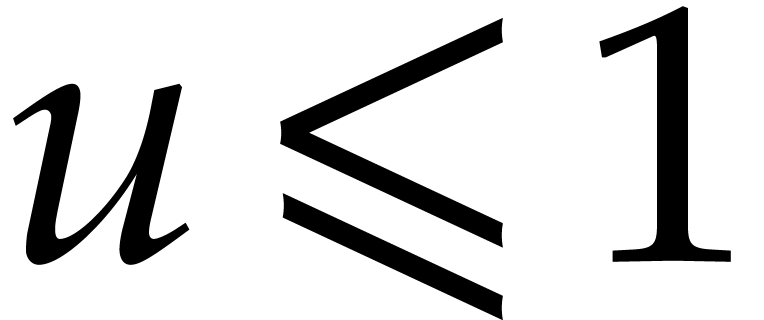 ,
,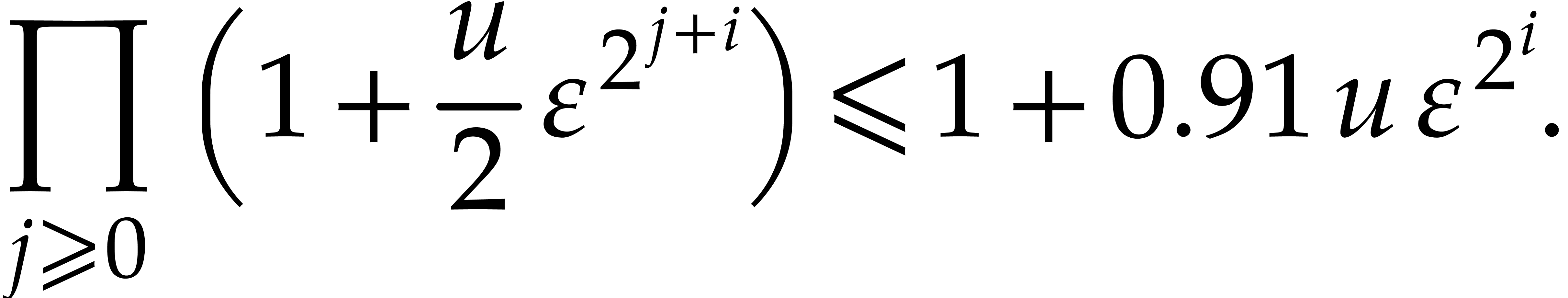
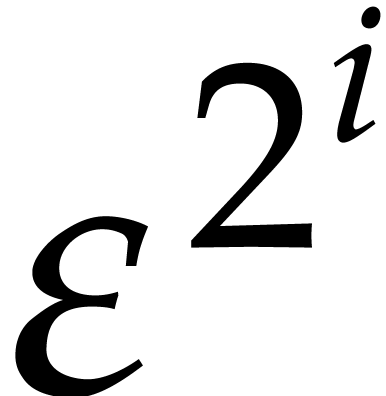 instead of
instead of  .
.
 ,
, .
. admits a
unique polar decomposition
admits a
unique polar decomposition
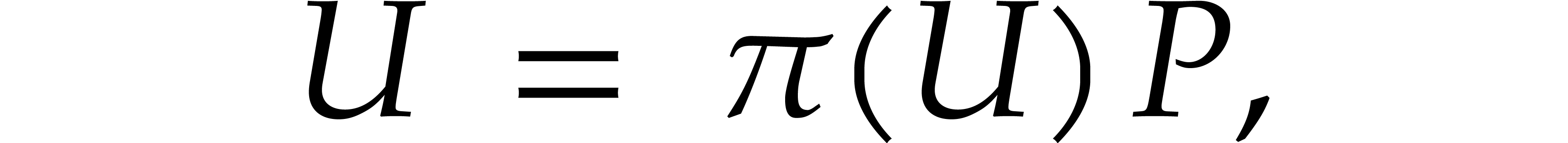
 and
and  is a
positive-definite Hermitian matrix. We call
is a
positive-definite Hermitian matrix. We call 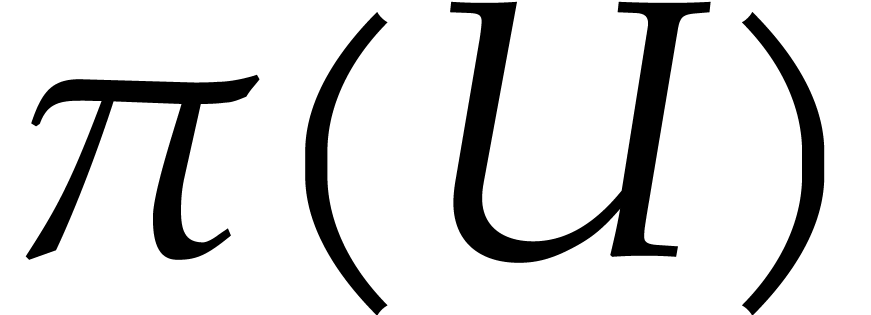 the
polar projection of
the
polar projection of 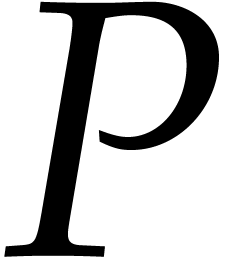 can
uniquely be written as the exponential of another Hermitian matrix. It
is also well known that
can
uniquely be written as the exponential of another Hermitian matrix. It
is also well known that  .
.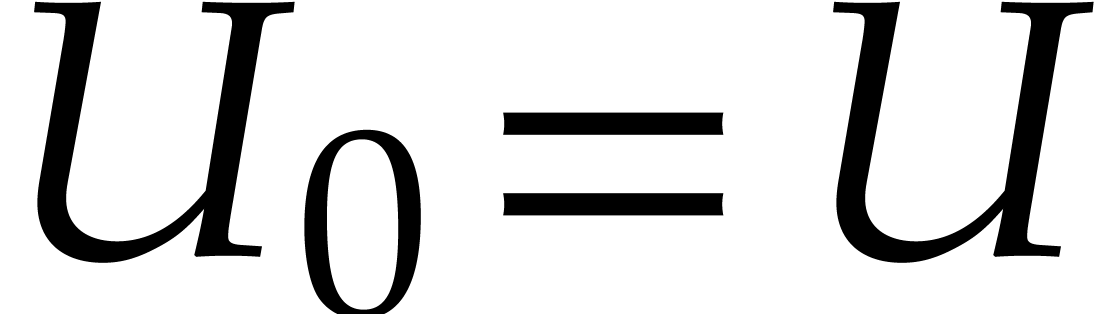 converges
quadratically to the polar projection
converges
quadratically to the polar projection  of
of 
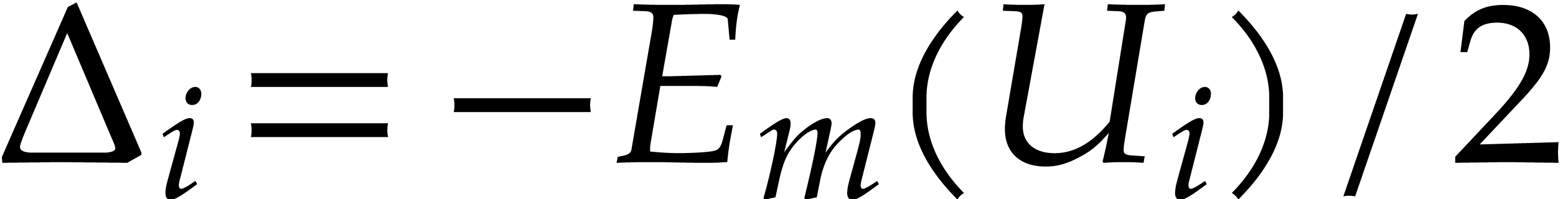
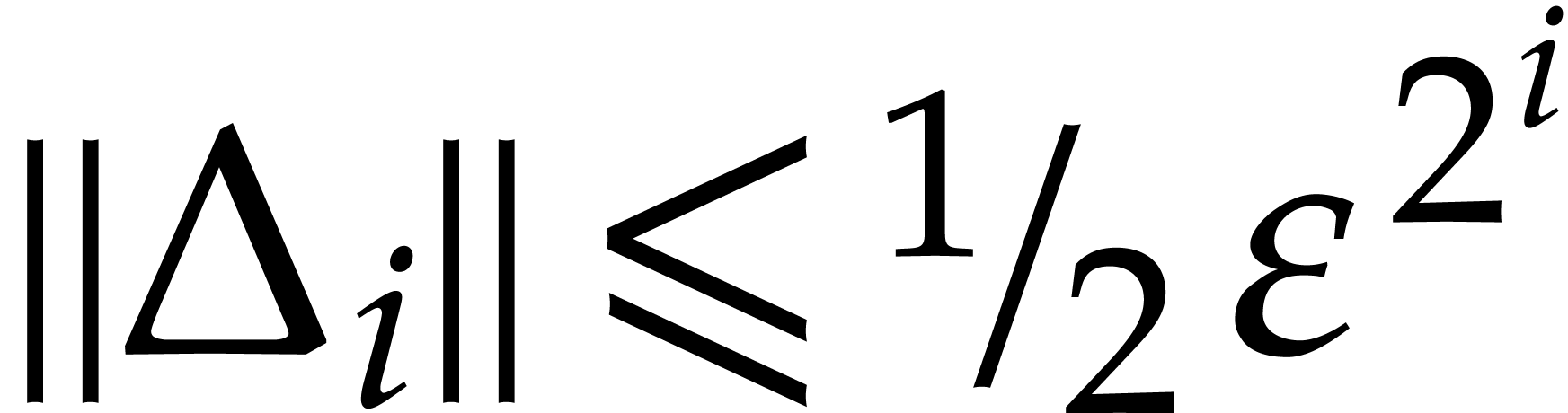 .
.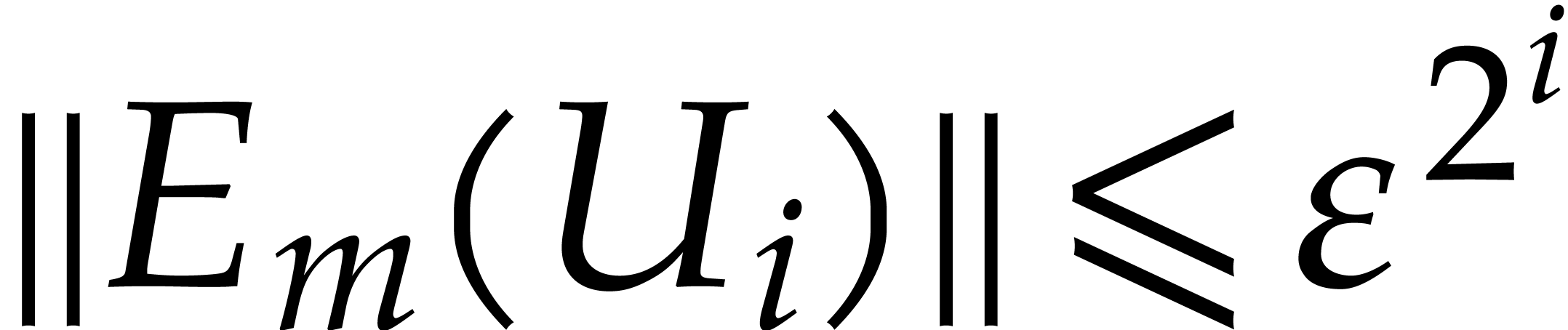 and
and
 .
. that is given by
that is given by
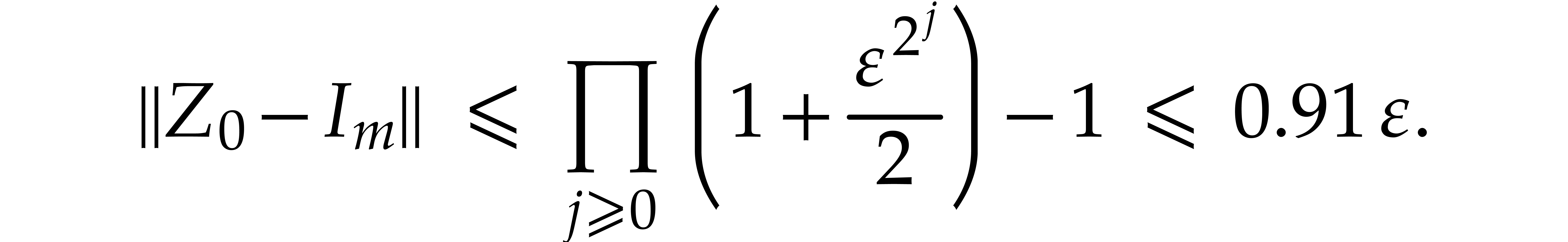
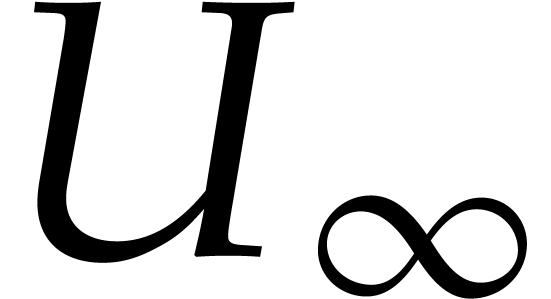
 is unitary, we have
is unitary, we have 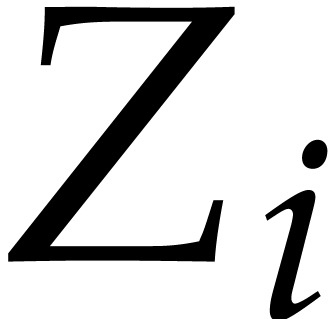 .
. is invertible with
is invertible with

 ,
, for all
for all 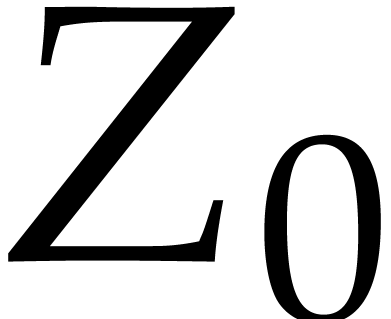 all
commute, whence
all
commute, whence 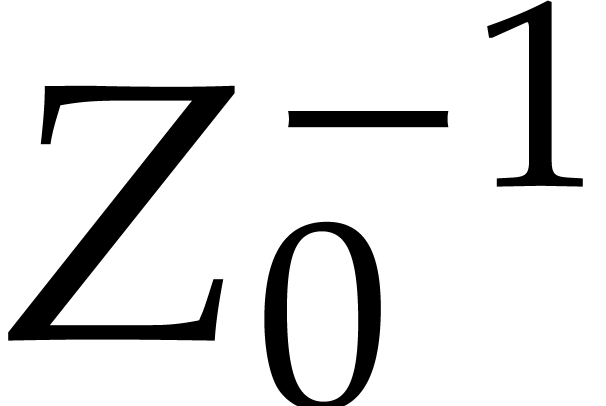 and
and 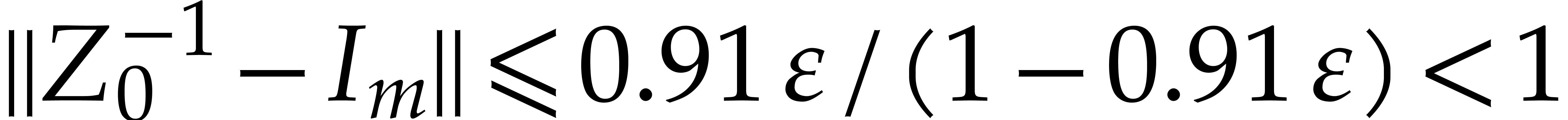 are
actually Hermitian matrices. Since
are
actually Hermitian matrices. Since 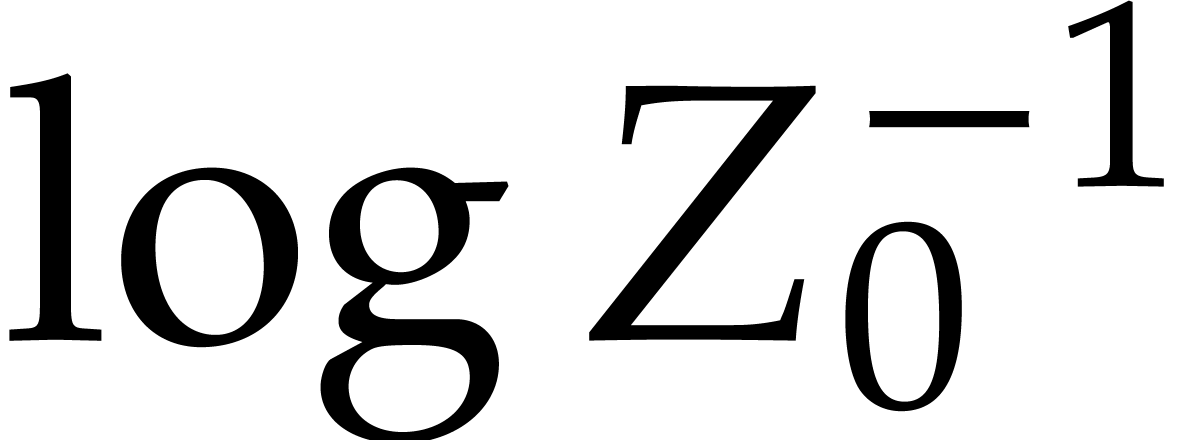 ,
, is well defined. We conclude that
is well defined. We conclude that
 be a matrix with diagonal entries
be a matrix with diagonal entries 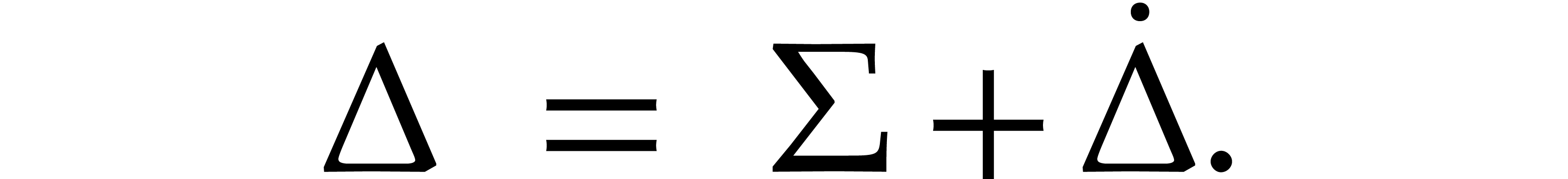 .
.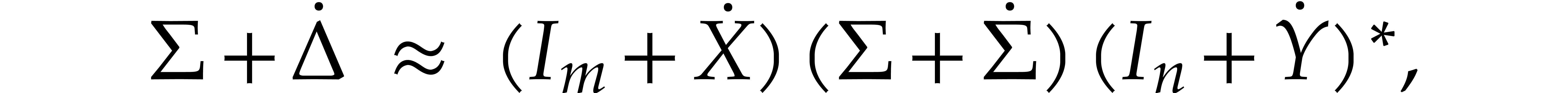

 ,
, ,
,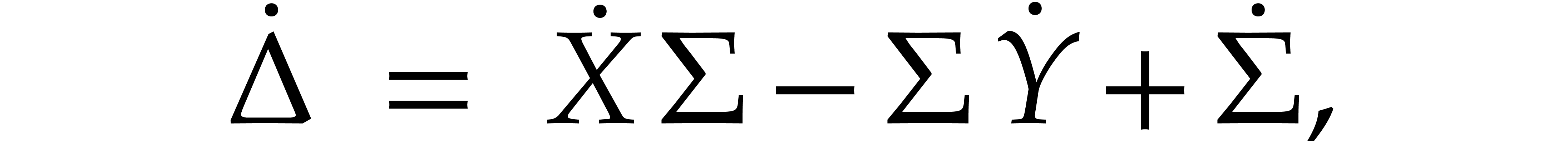 .
.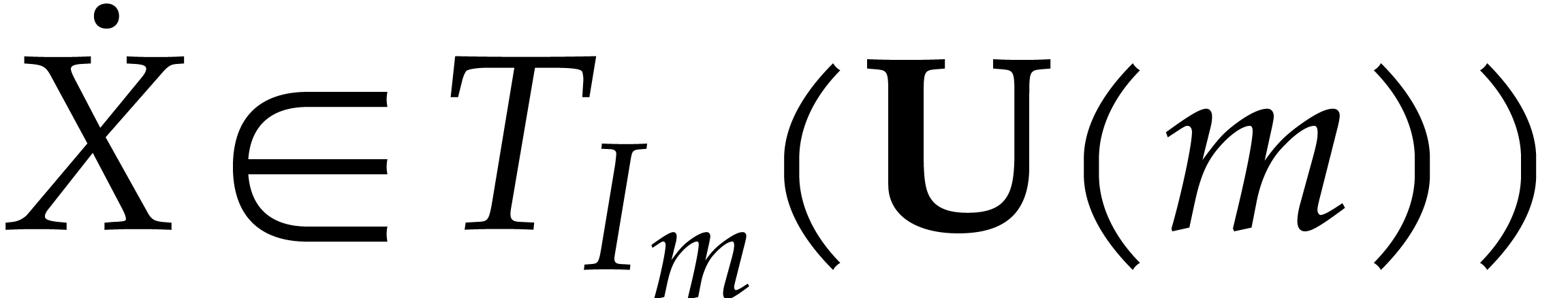
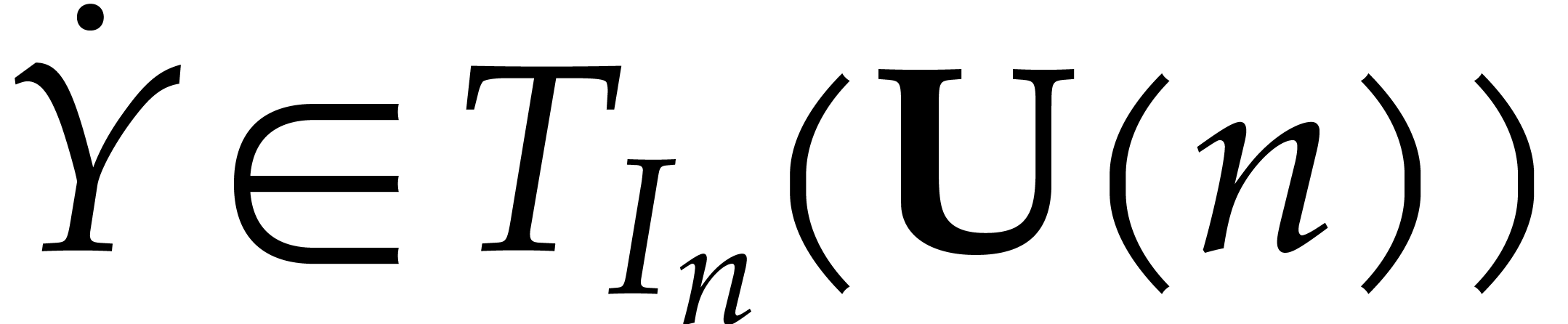 and
and  .
. and
and 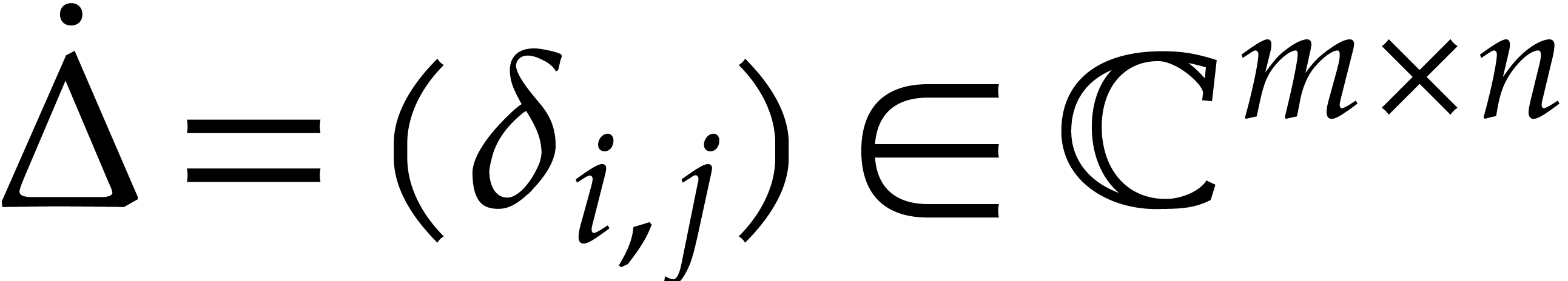 are skew Hermitian. The following
proposition shows how to solve the linear equation explicitly under
these constraints.
are skew Hermitian. The following
proposition shows how to solve the linear equation explicitly under
these constraints.
 .
.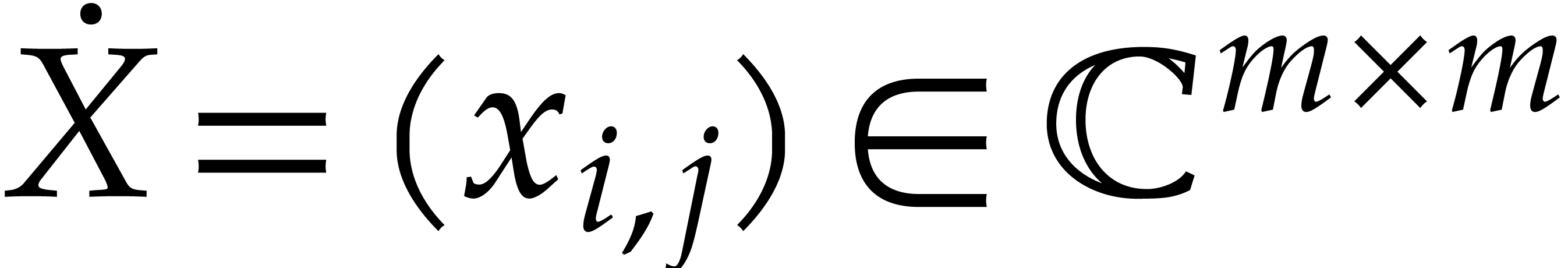 and the two skew Hermitian matrices
and the two skew Hermitian matrices 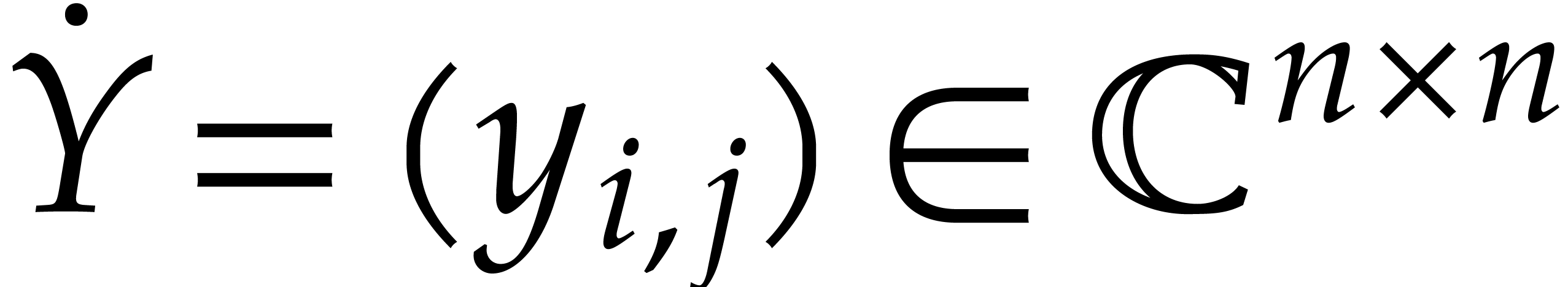 and
and 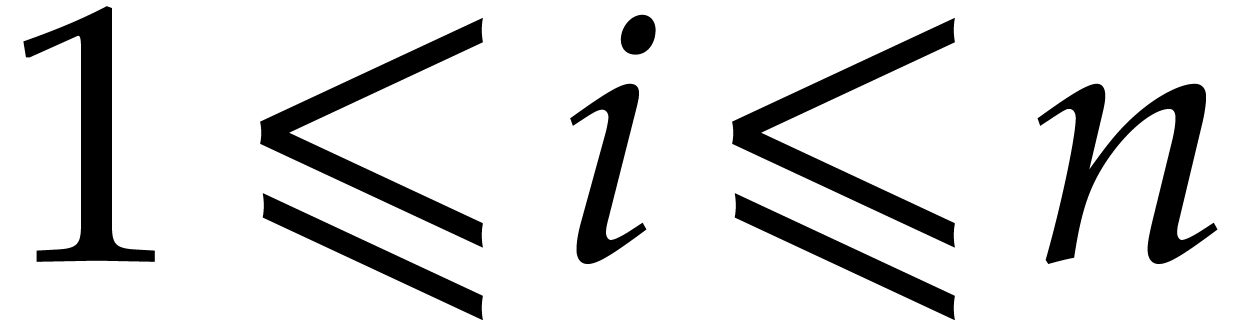 that are defined by the following
formulas:
that are defined by the following
formulas:
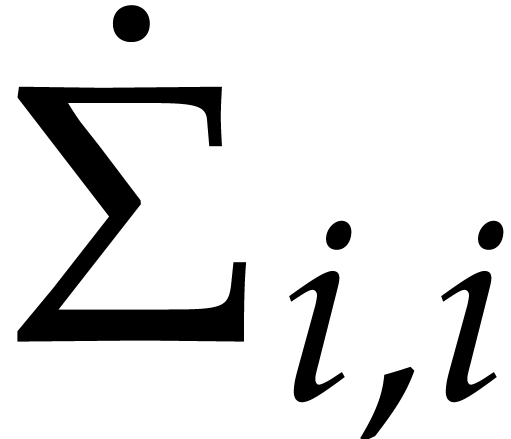 ,
,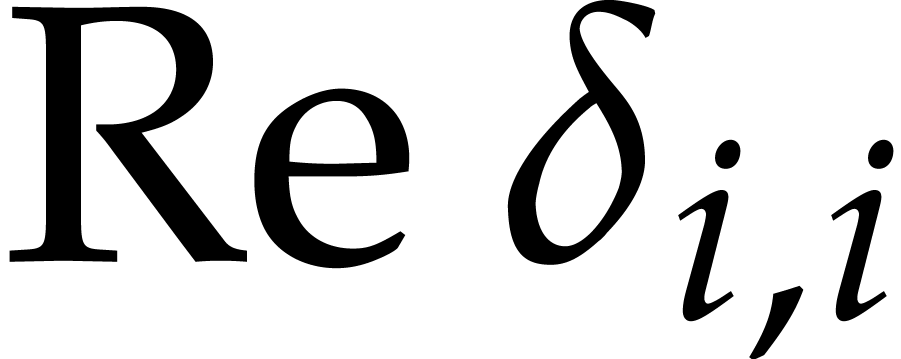
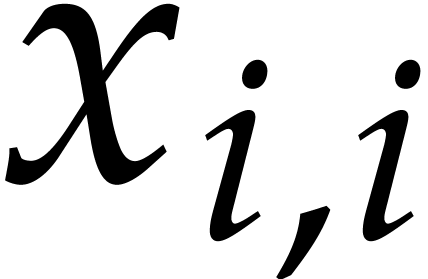
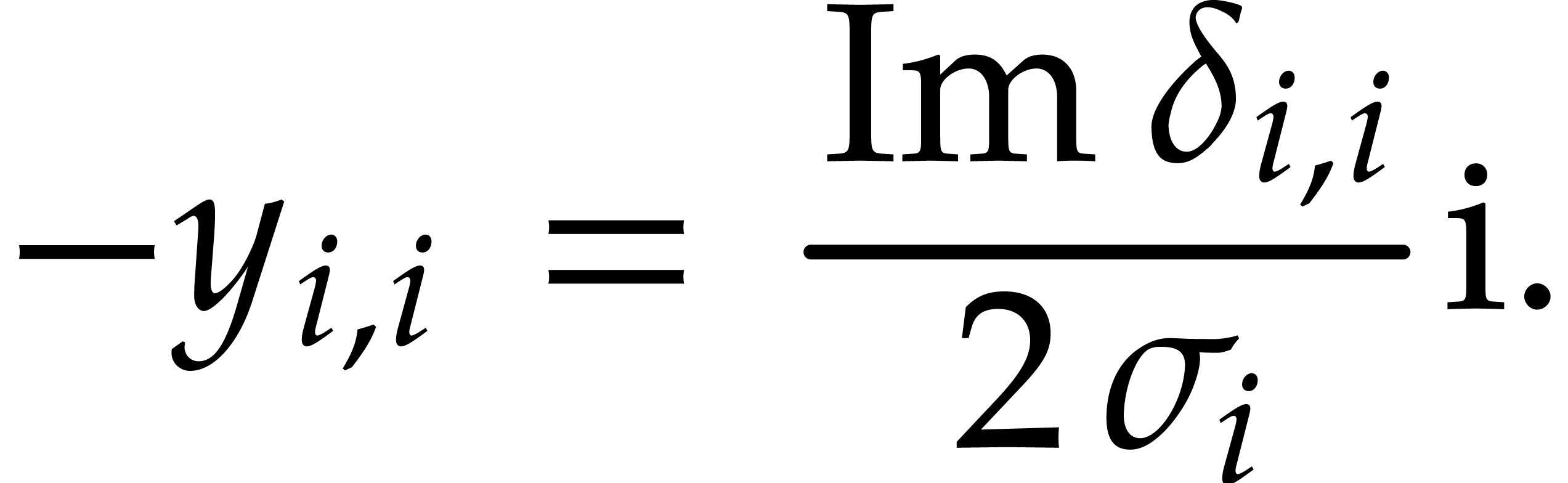
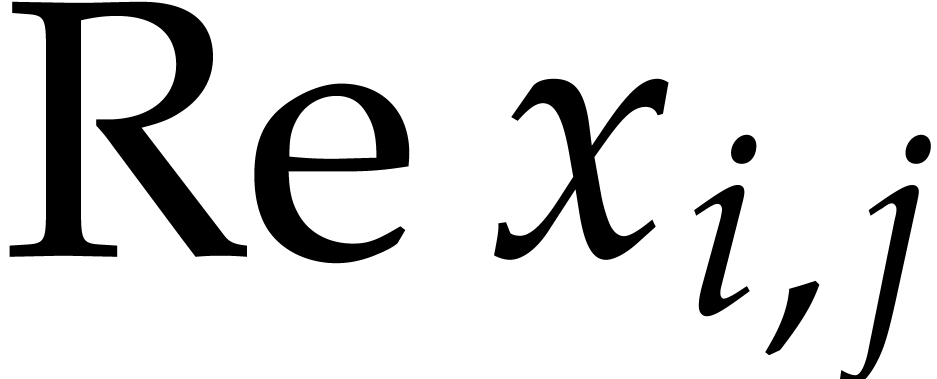 ,
,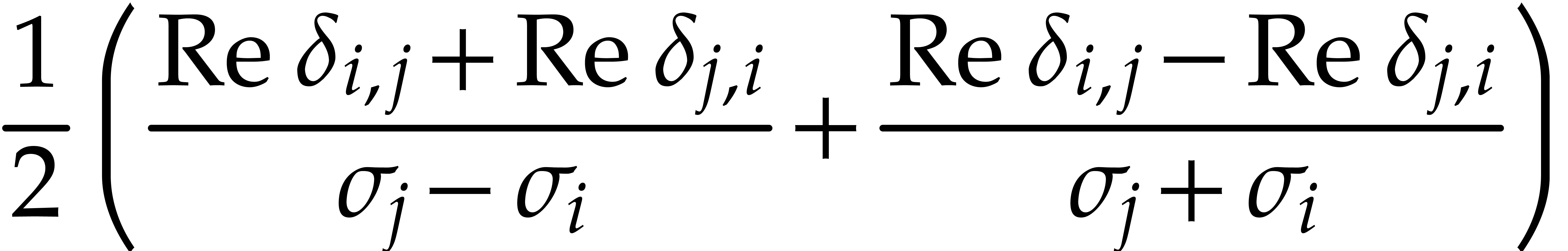
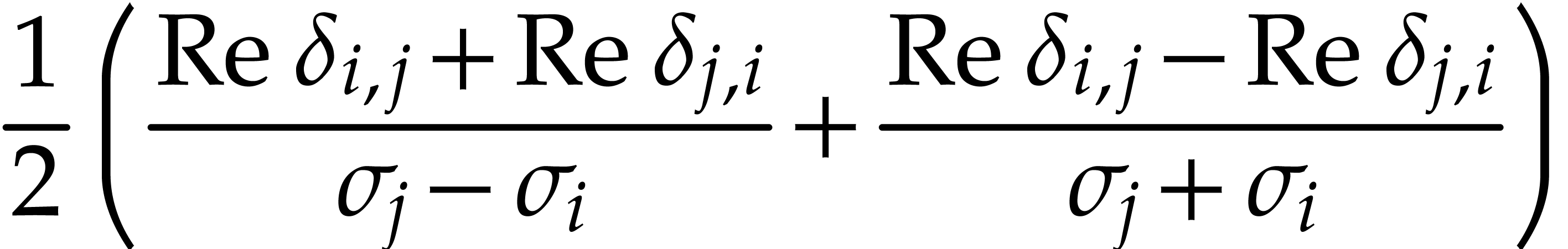
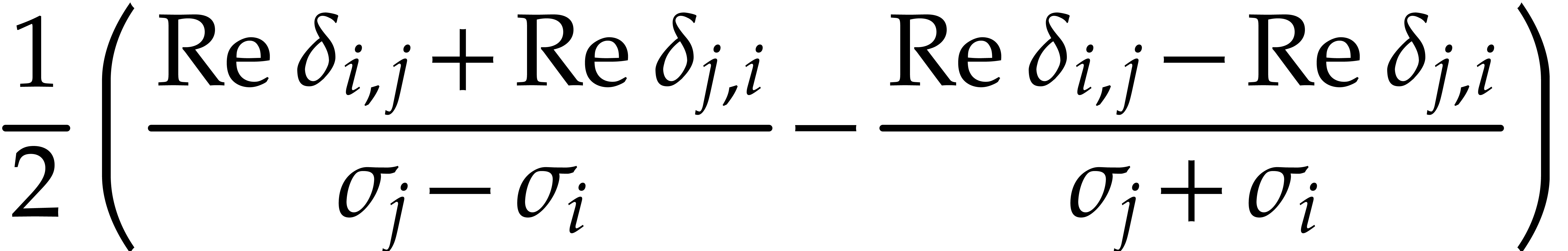
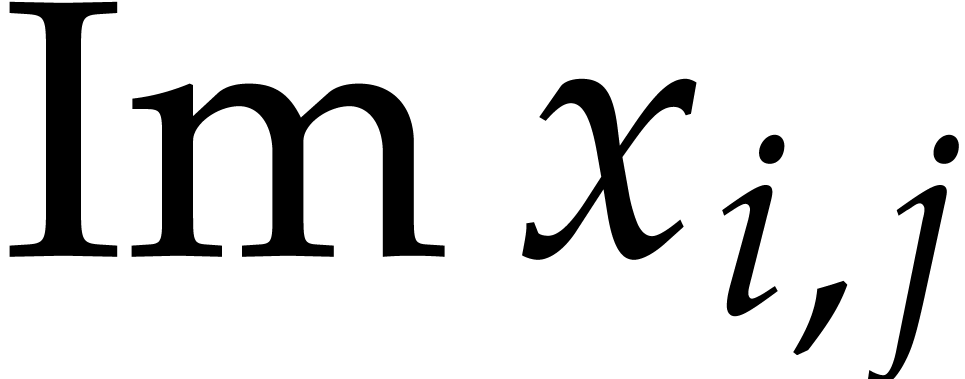
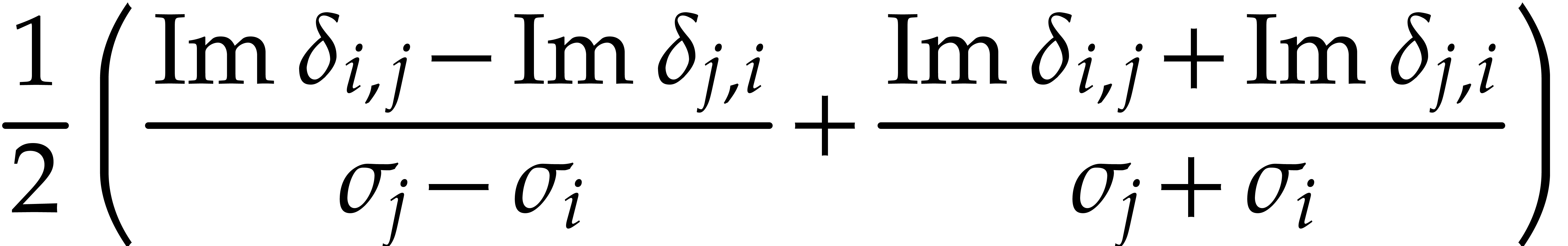
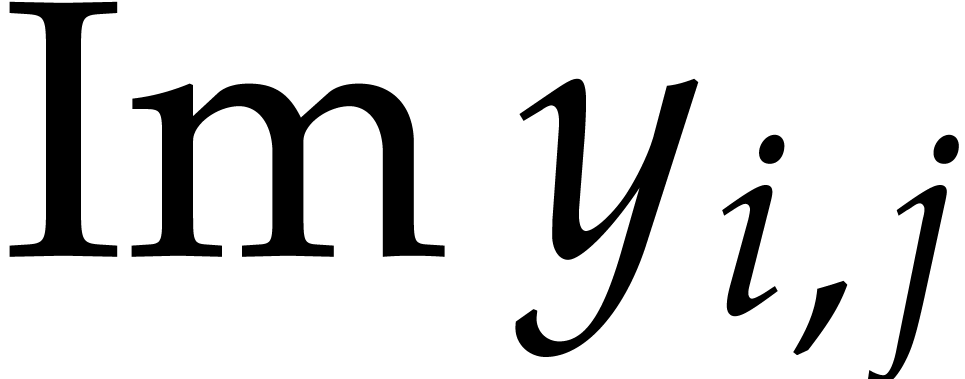
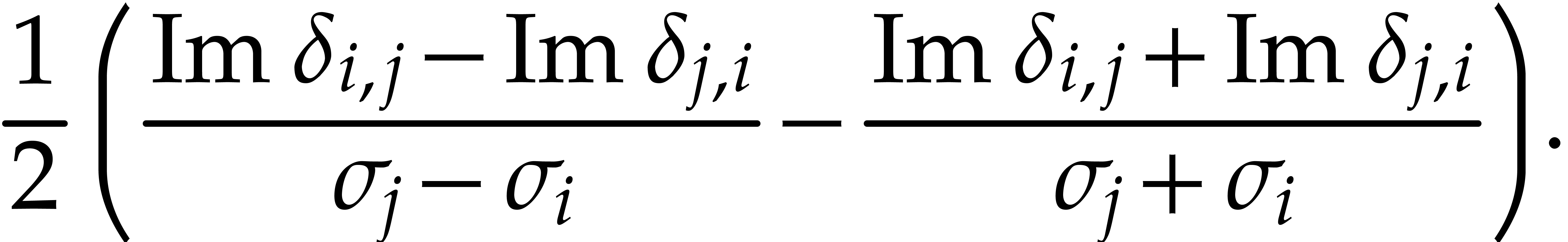
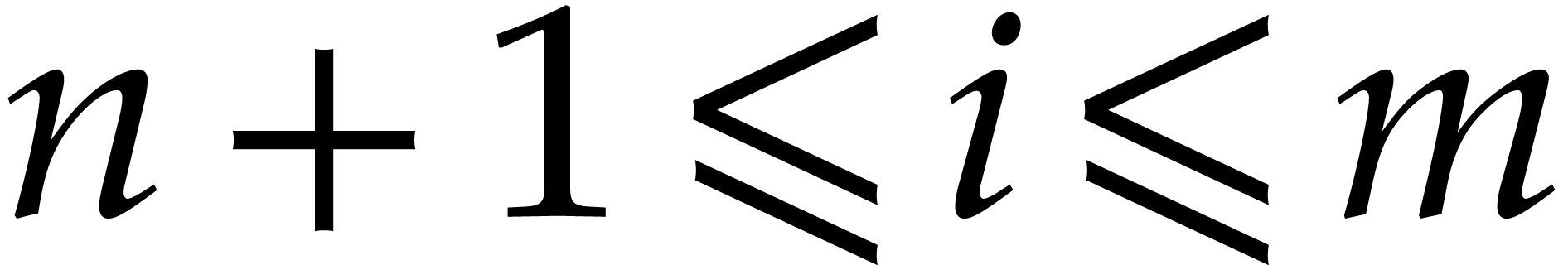
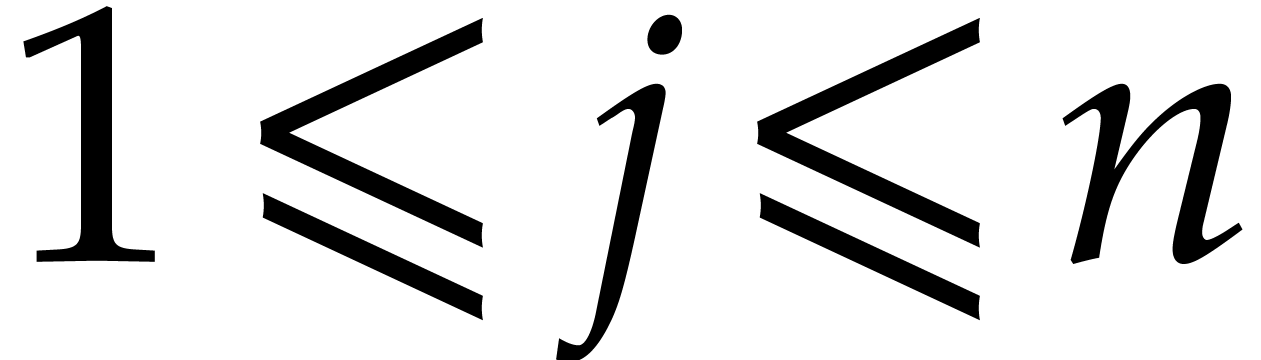 and
and 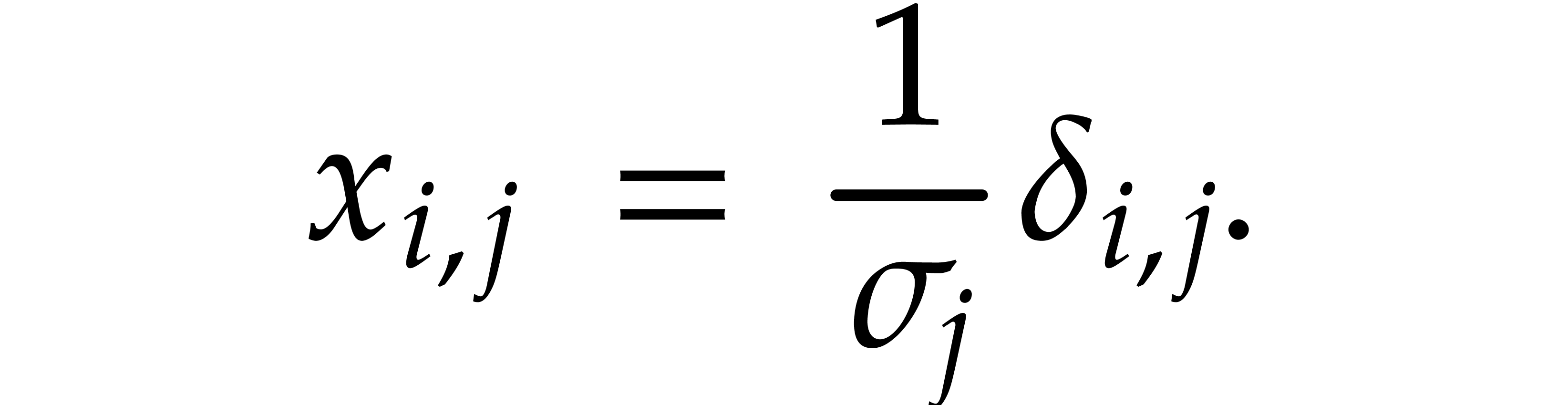 ,
,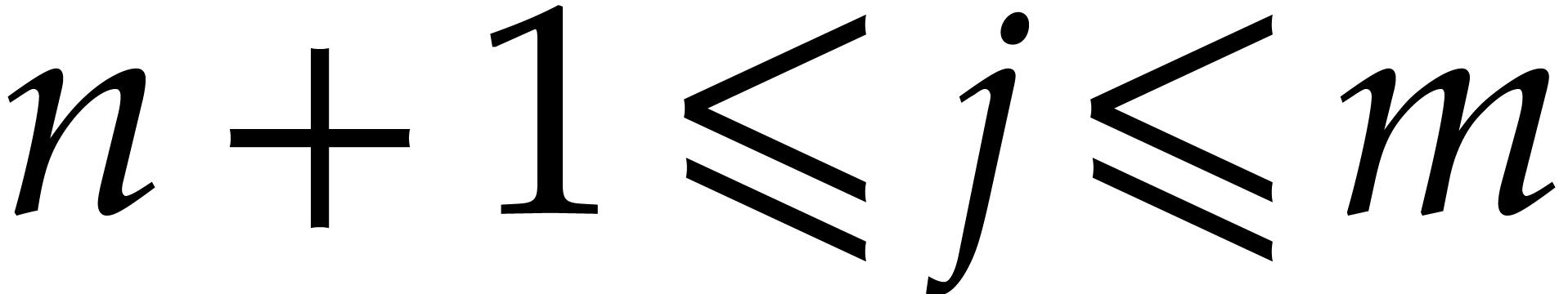
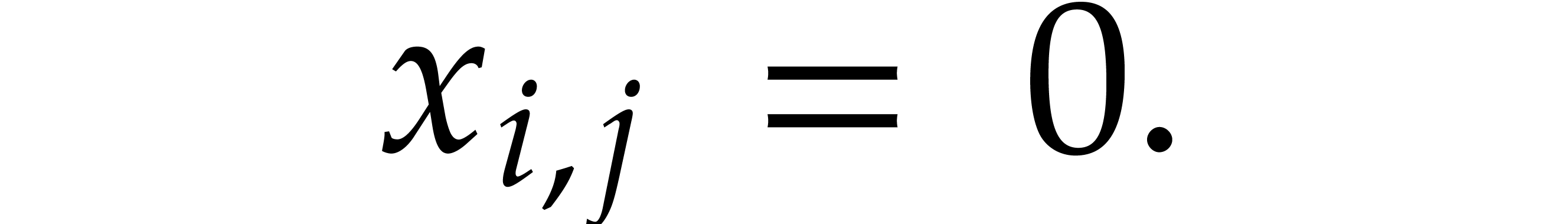 ,
,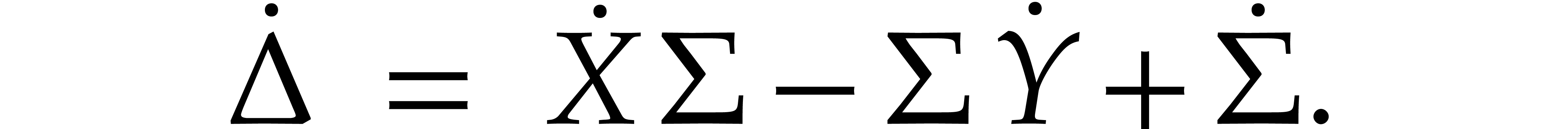
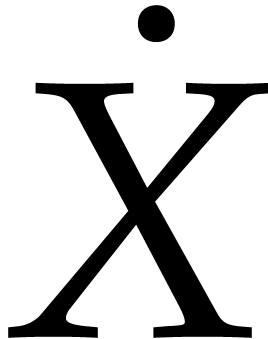
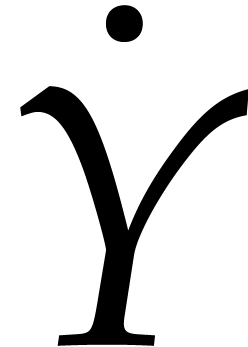 and
and  are skew Hermitian, we have
are skew Hermitian, we have  .
.

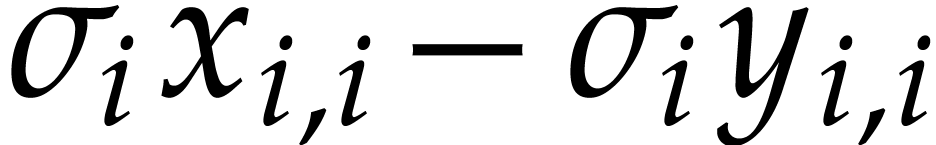

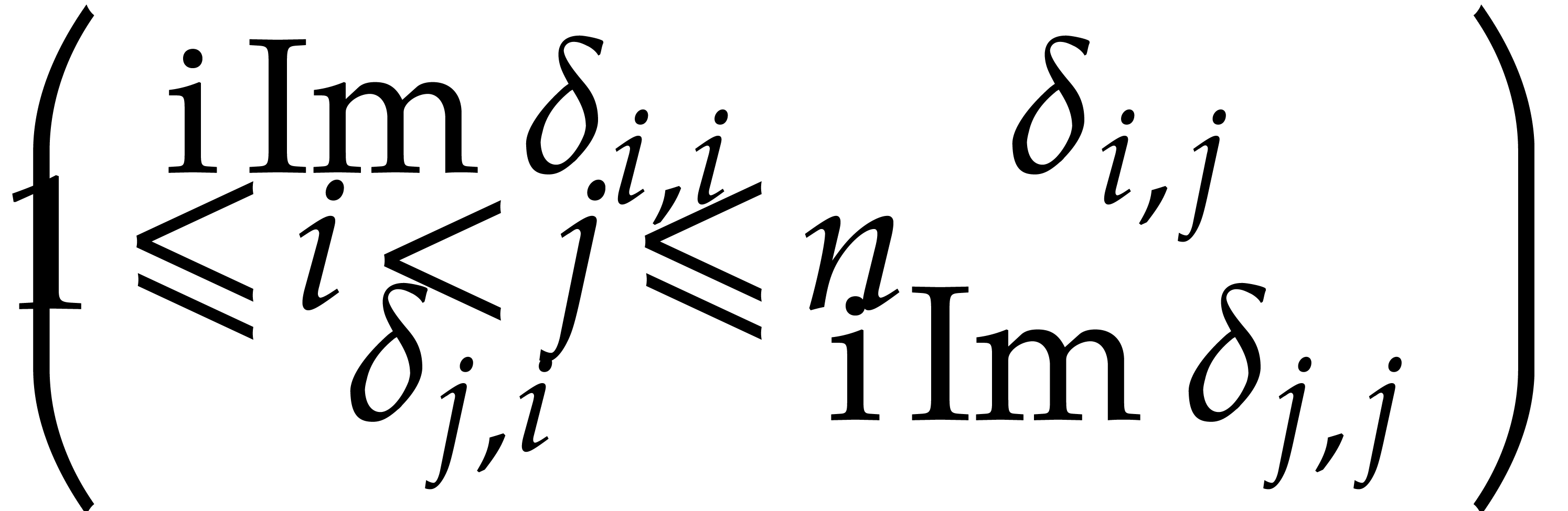
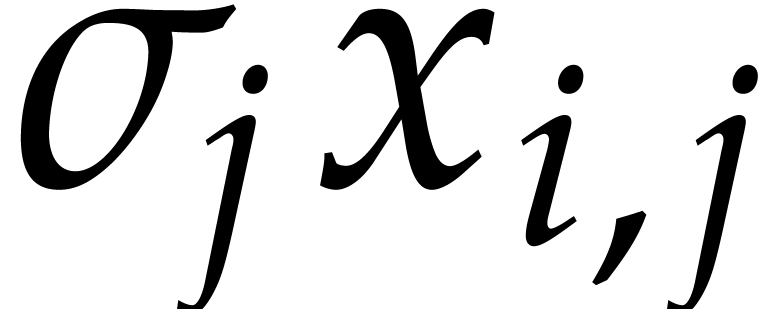
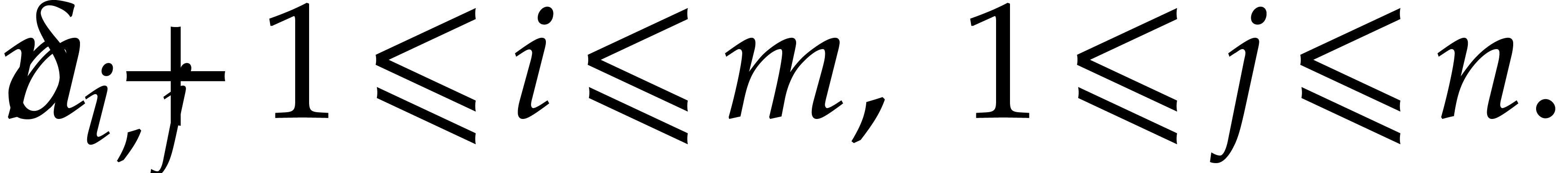
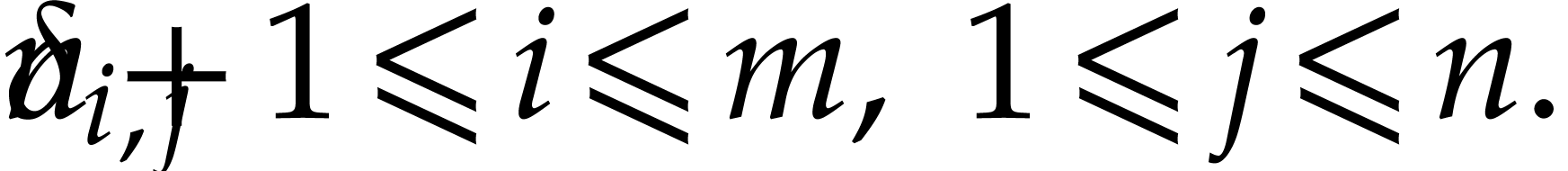
 from (
from (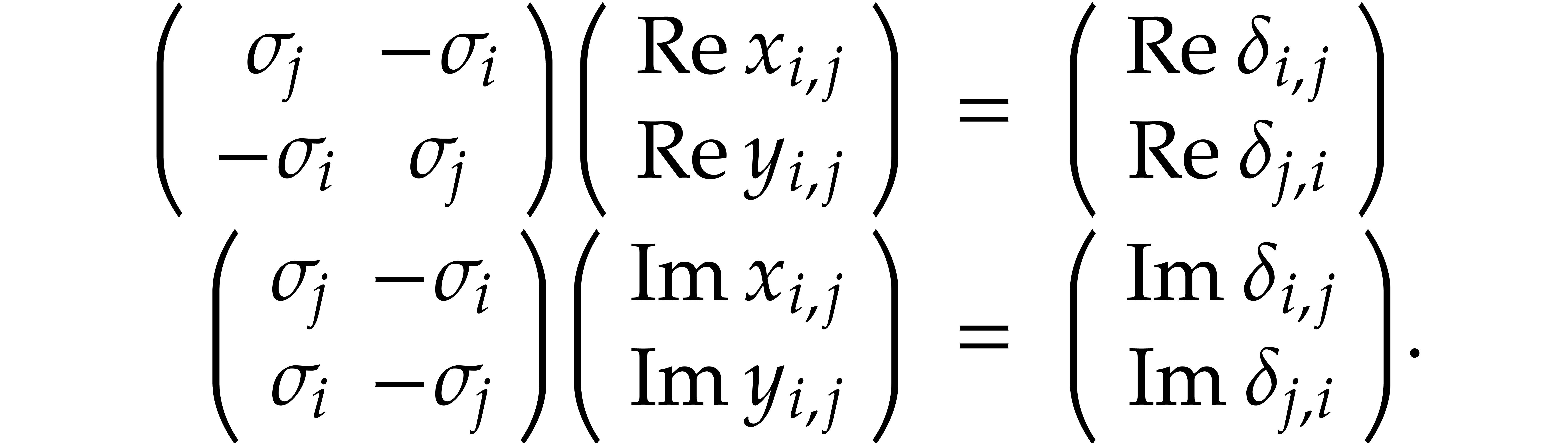 ,
,
 ,
,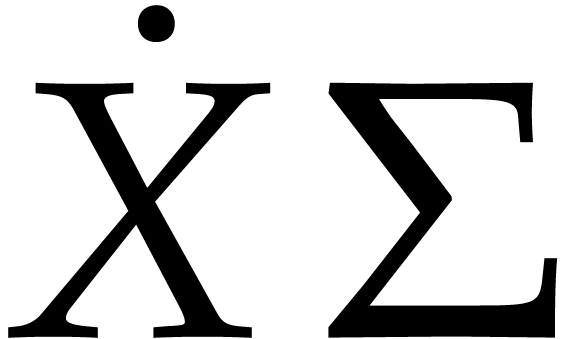 do not
affect the product
do not
affect the product 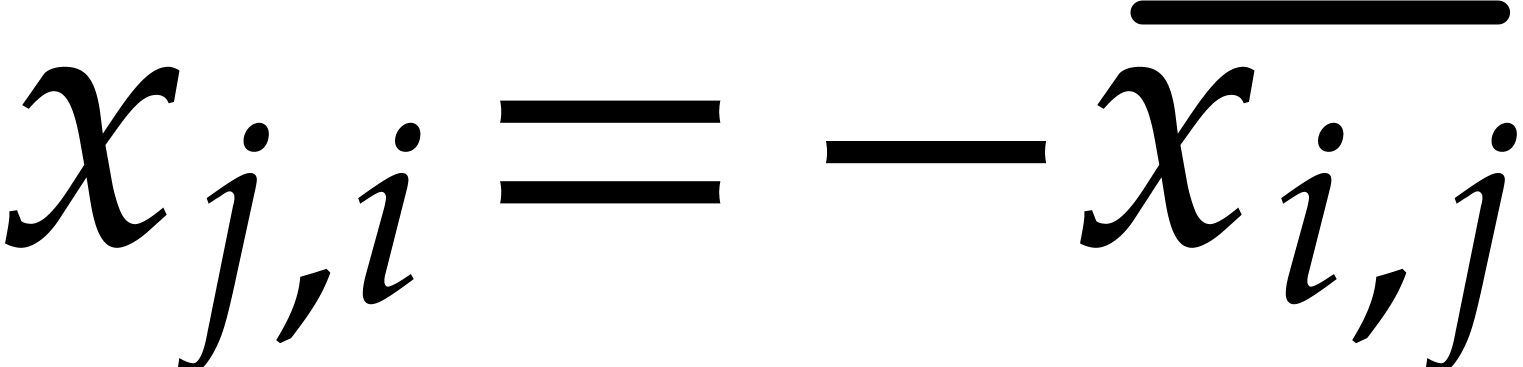 ,
,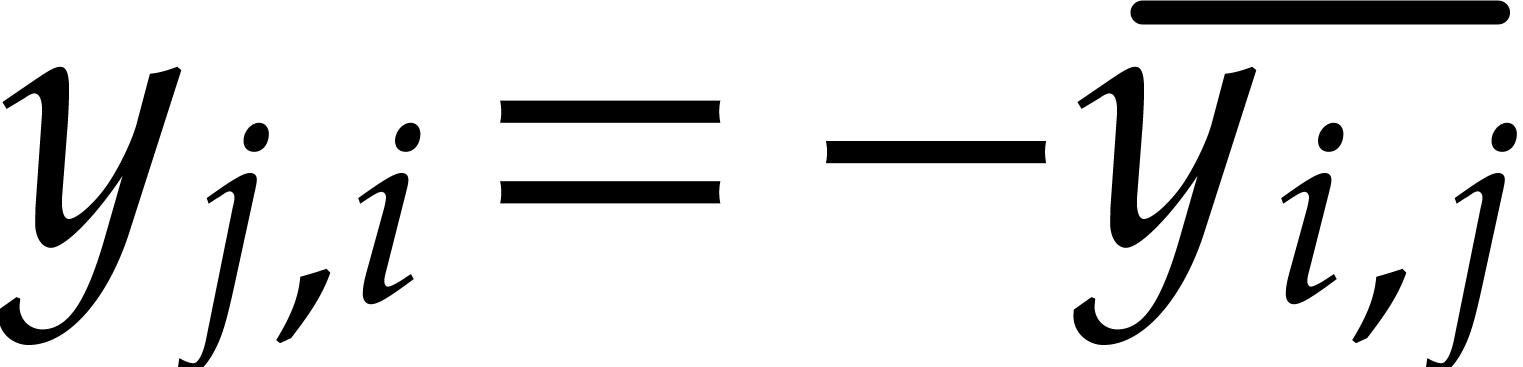 and
and 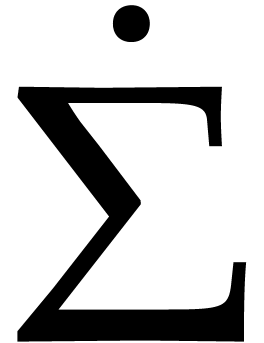 ,
,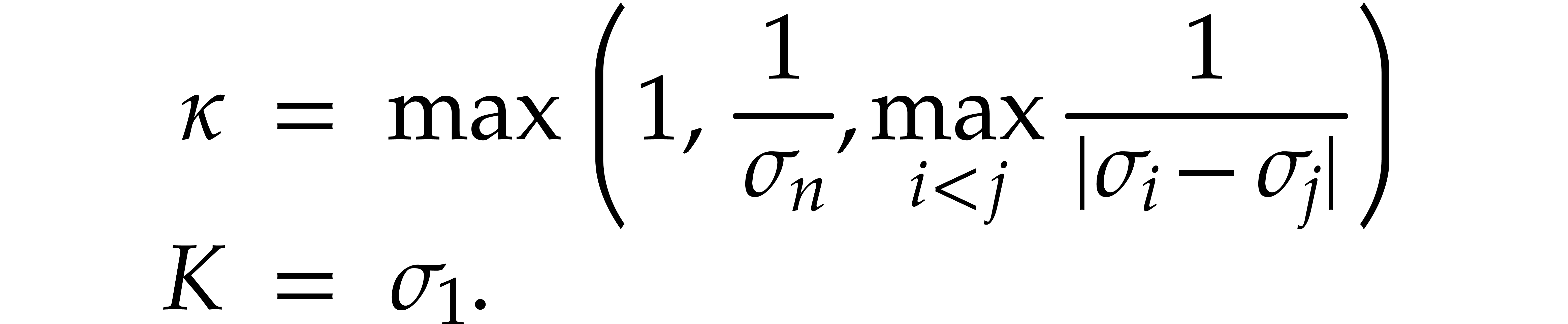 ,
,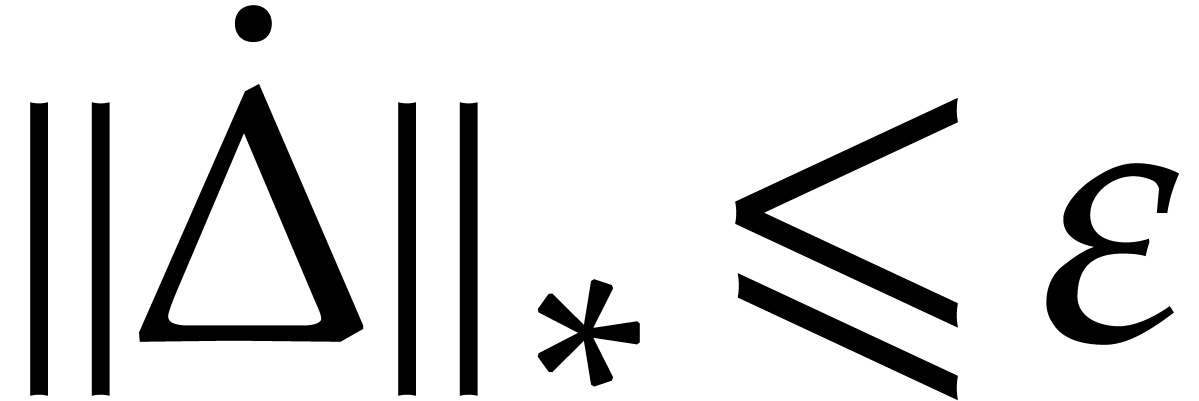
 ,
,
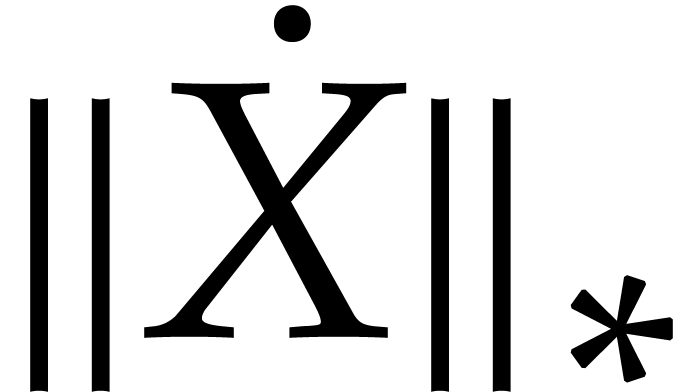
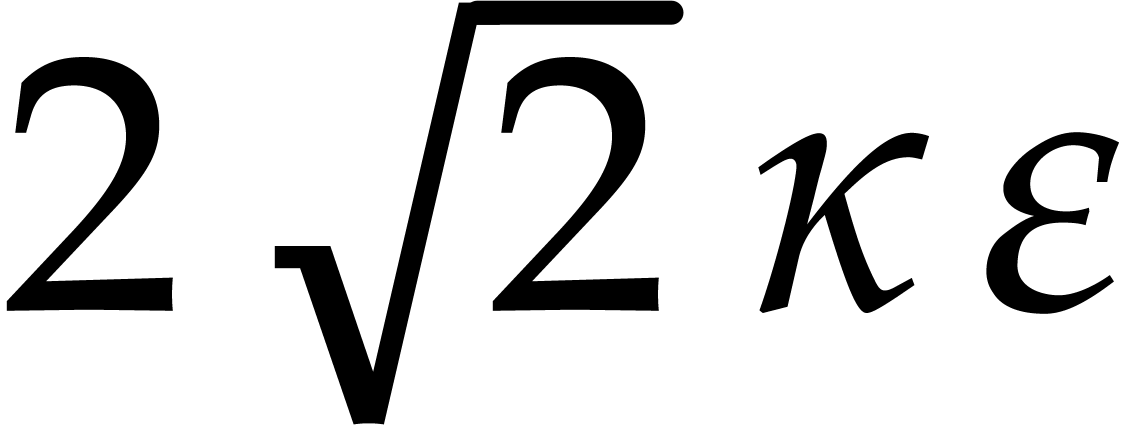
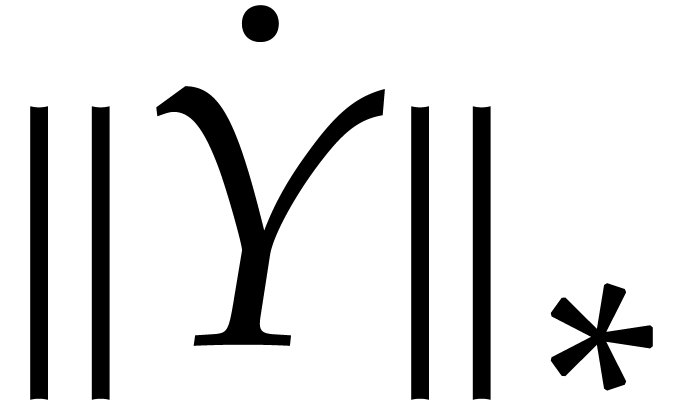
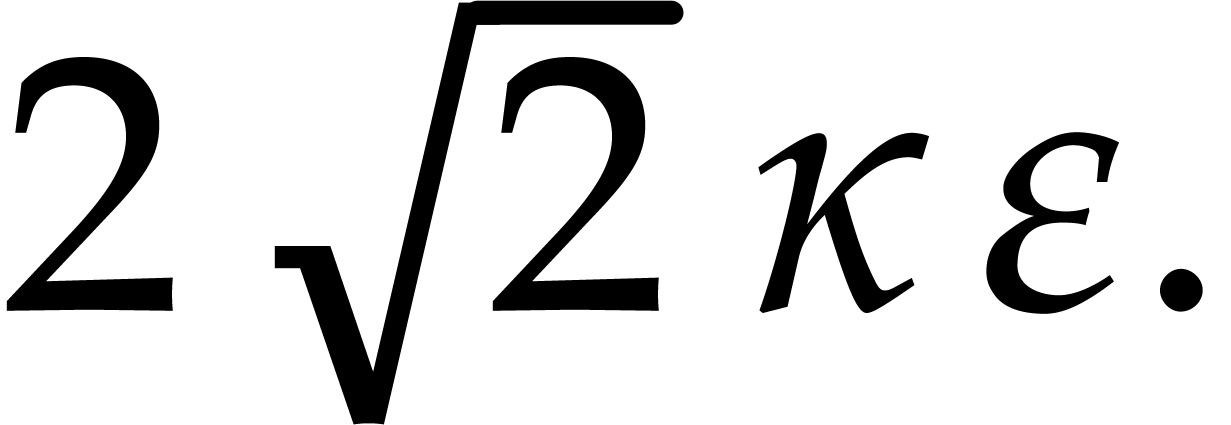
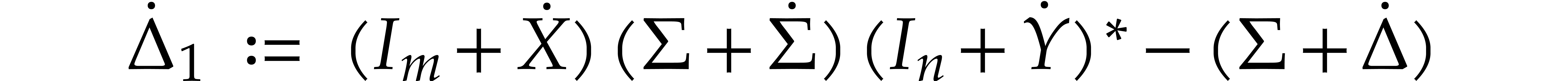
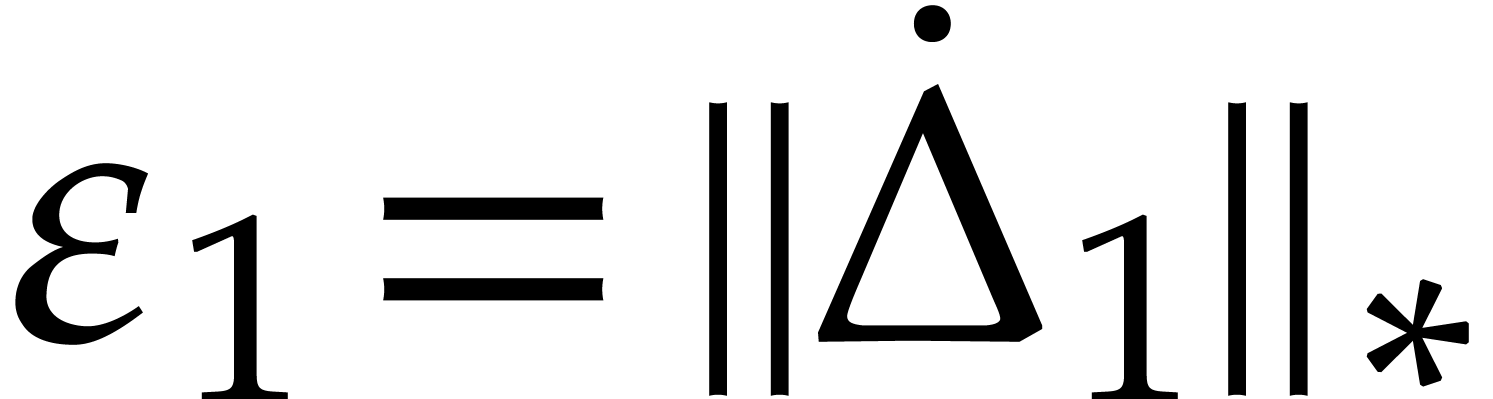
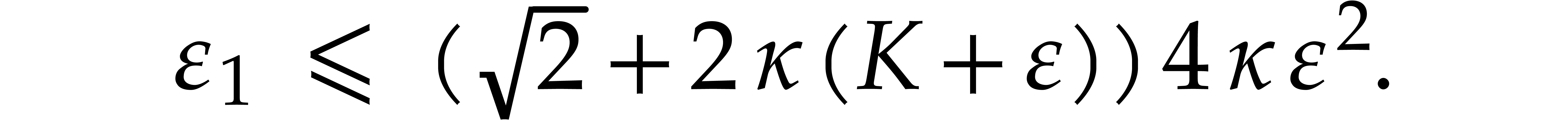 ,
,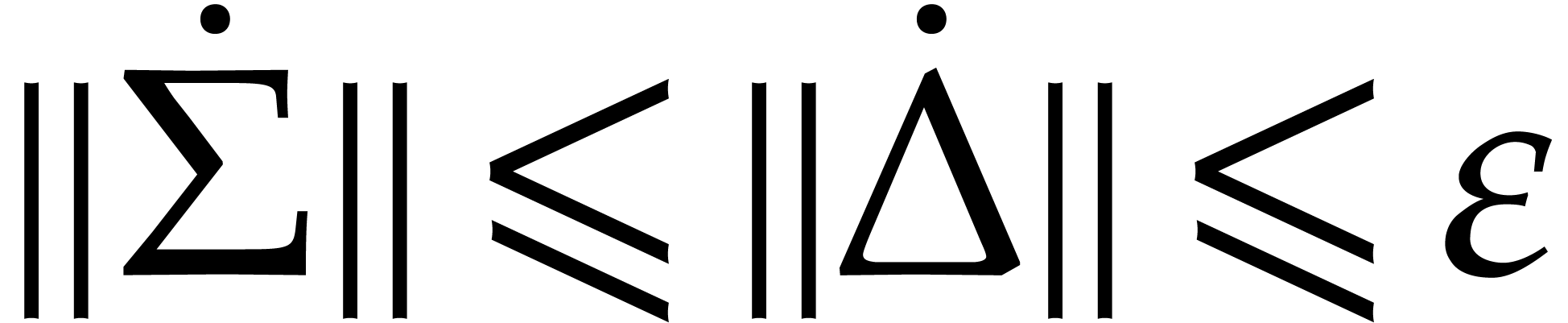
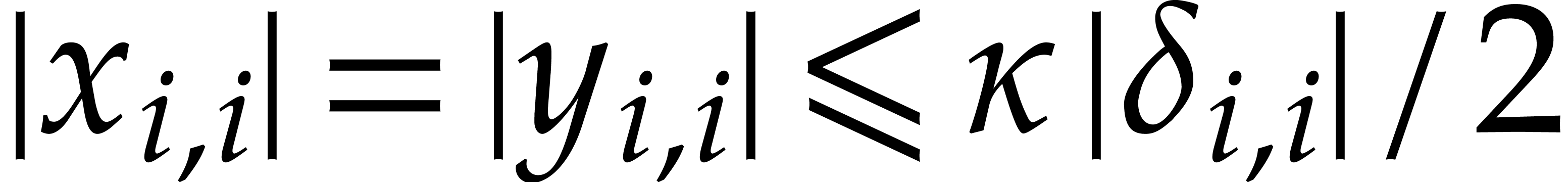 .
. for all
for all 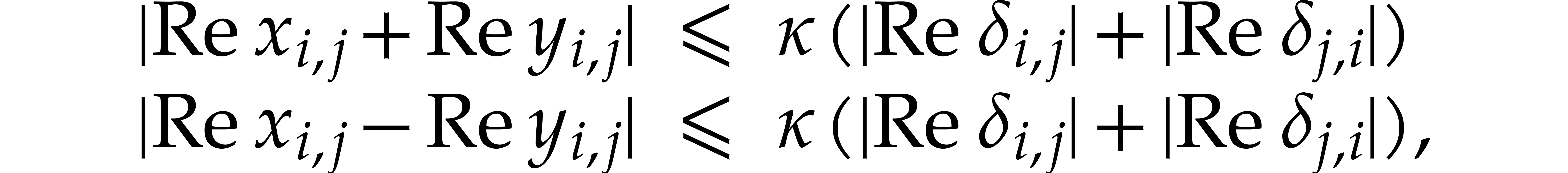 .
.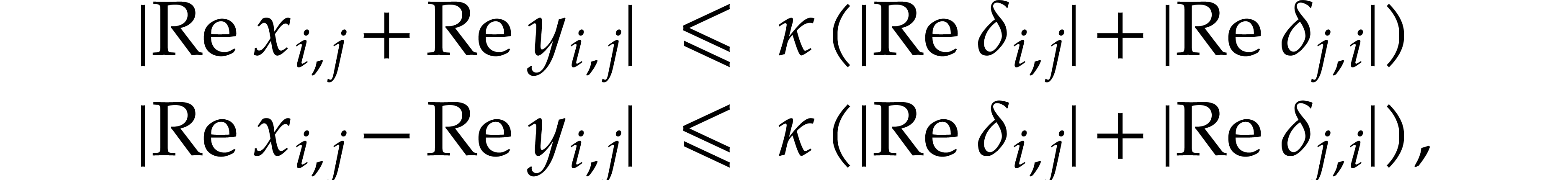
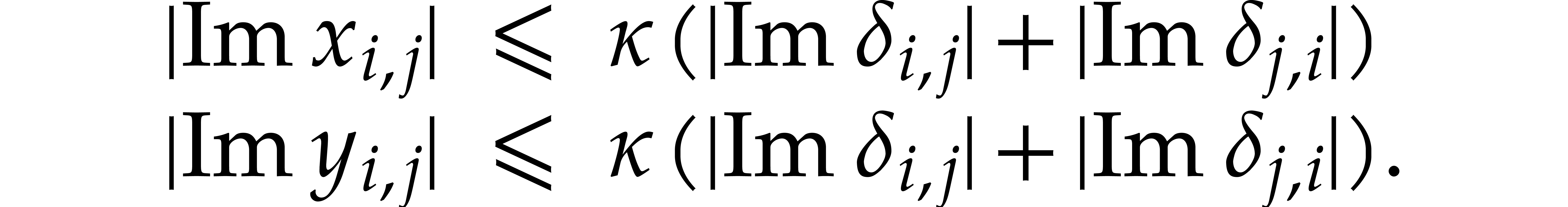

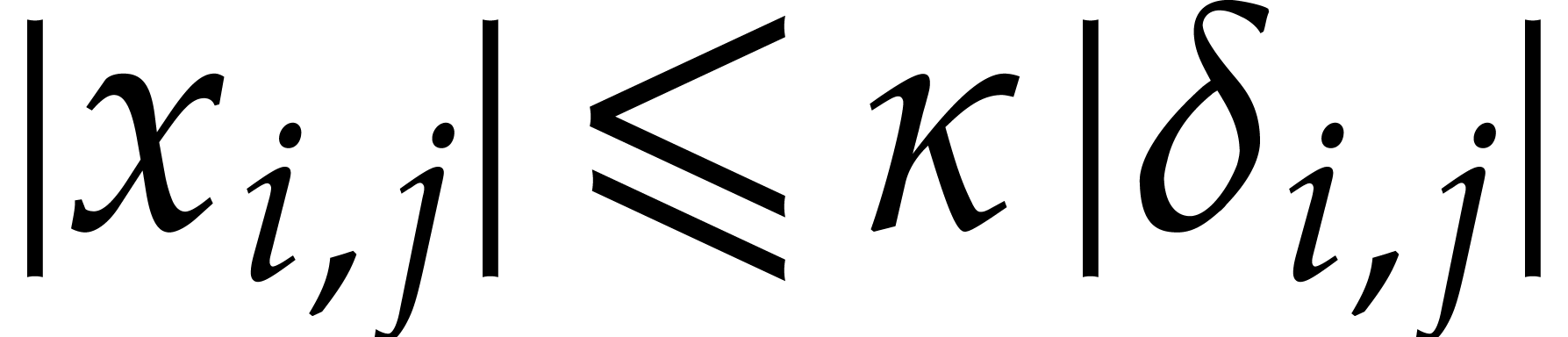
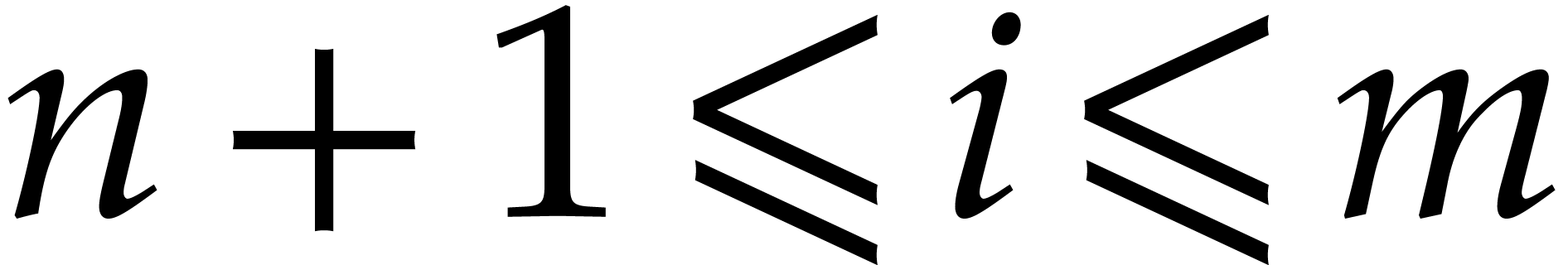 ,
,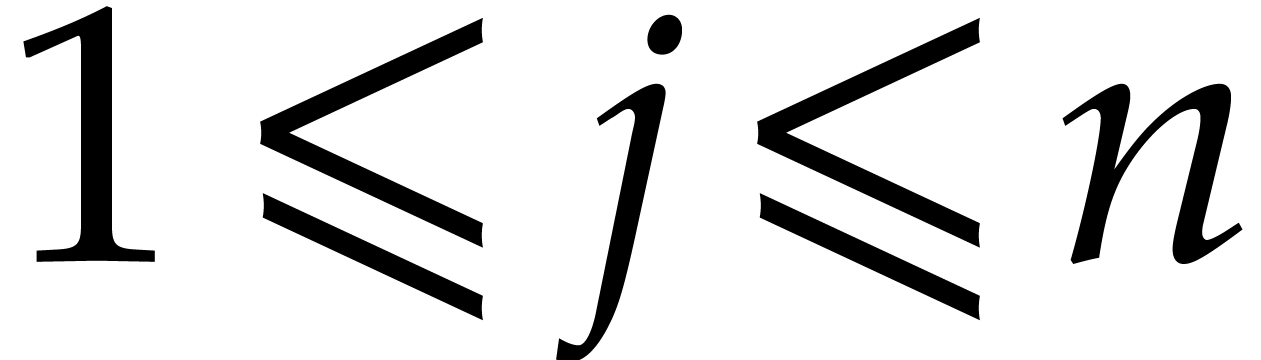 and
and 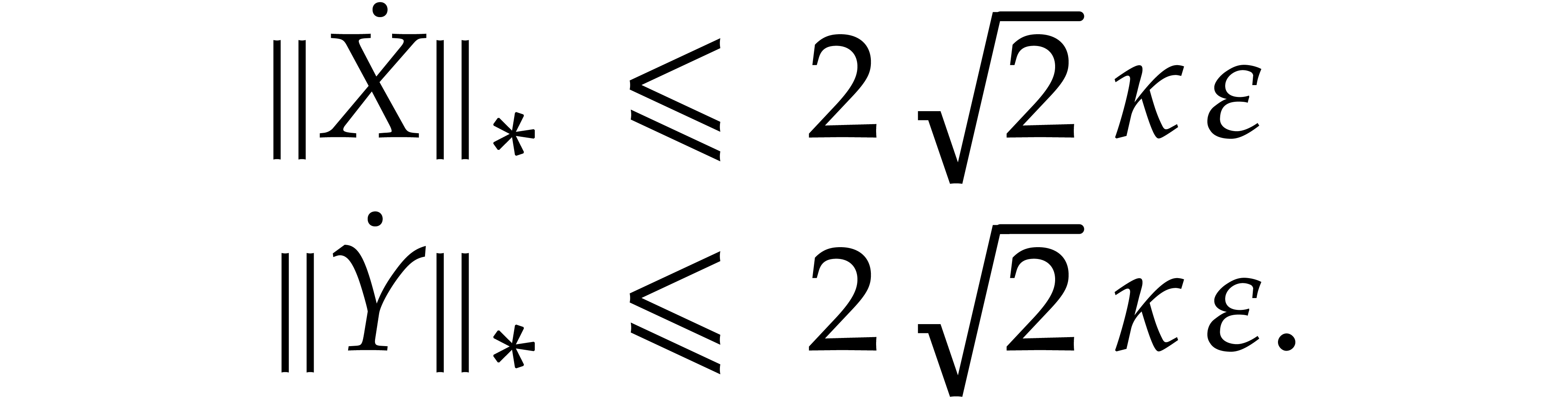 .
.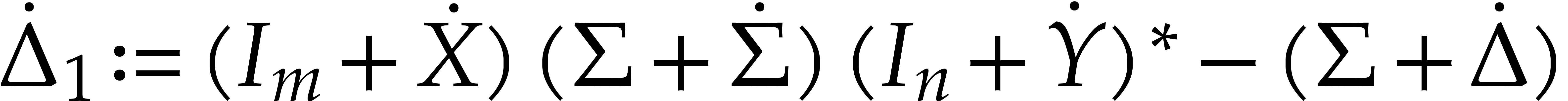
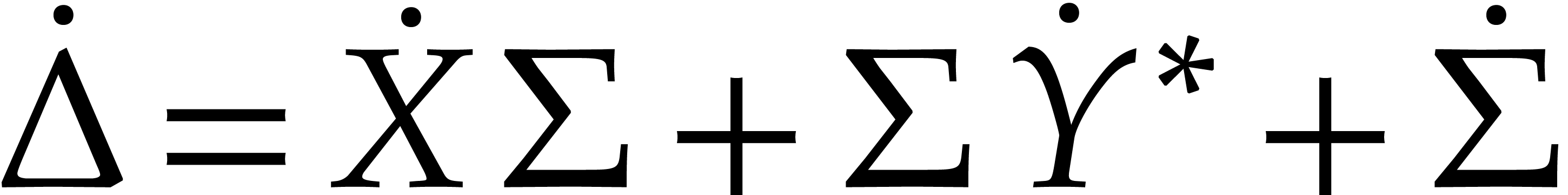 and
and  ,
,
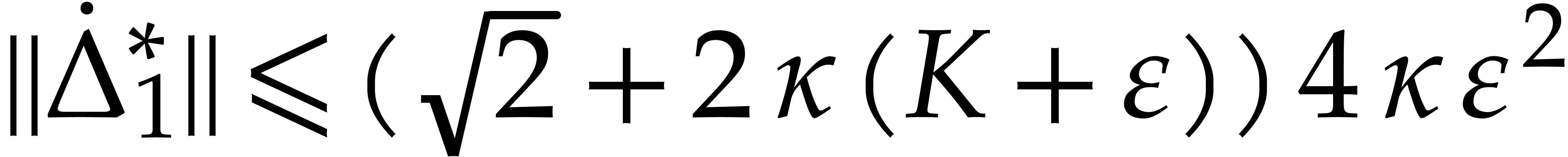
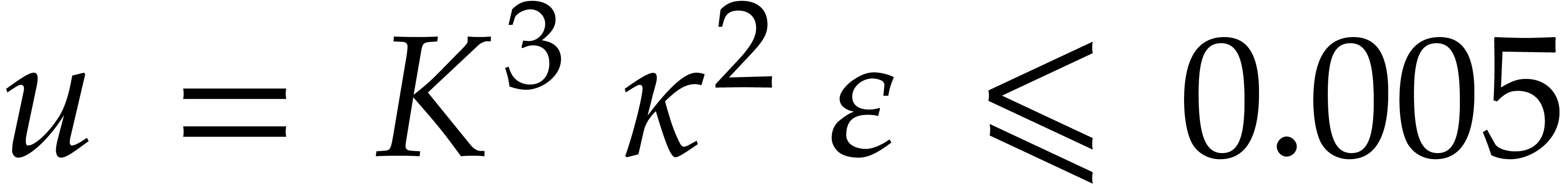 .
.
 ,
,
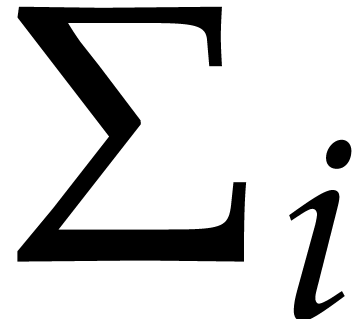 denote the diagonal entries of
denote the diagonal entries of 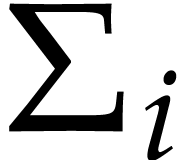 .
. that
that
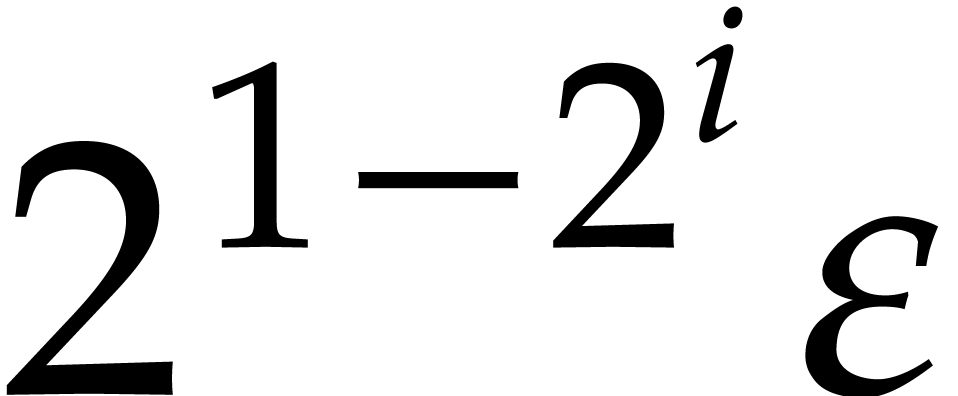
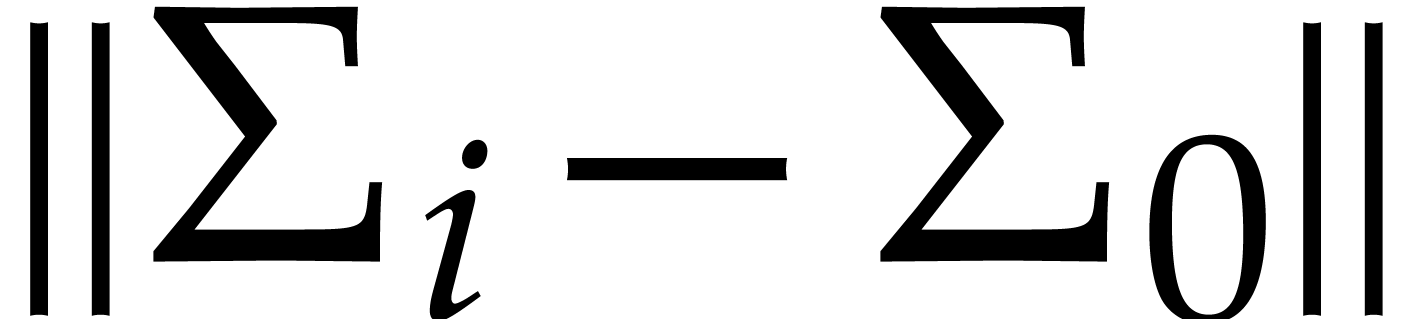
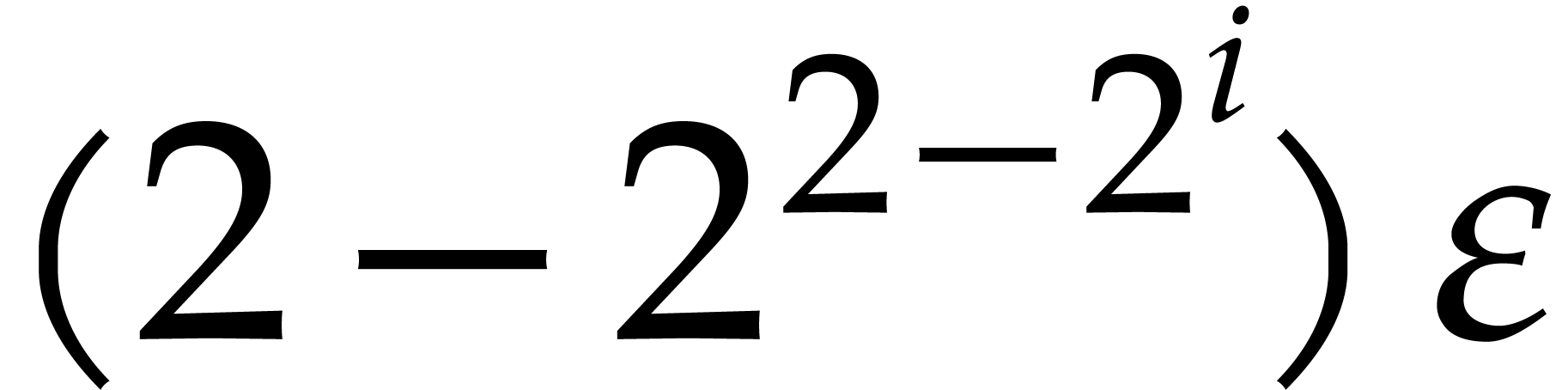
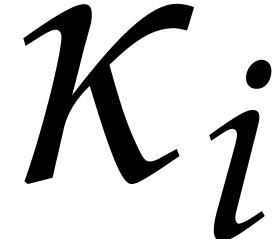
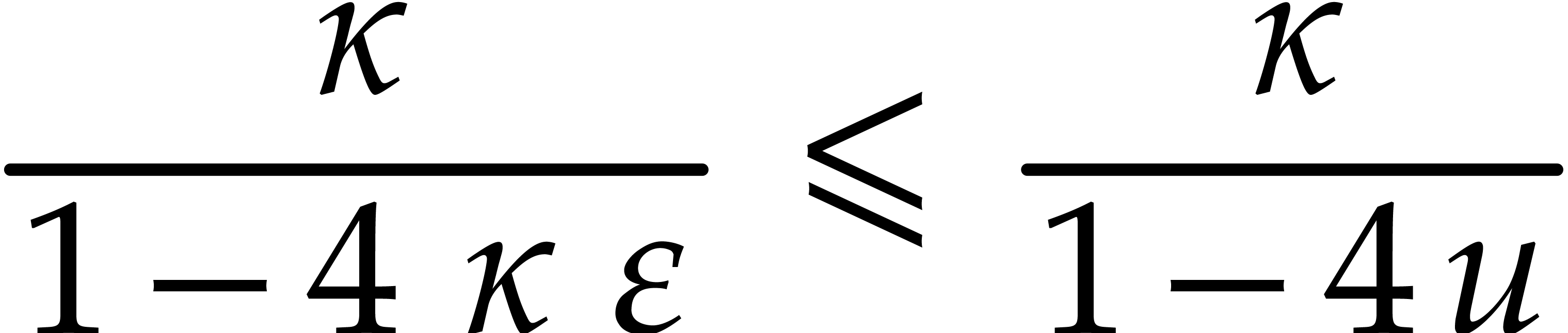
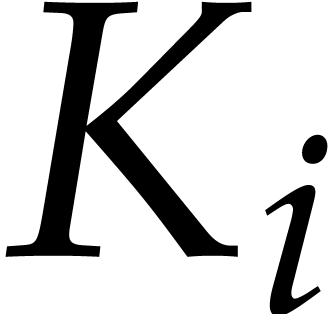
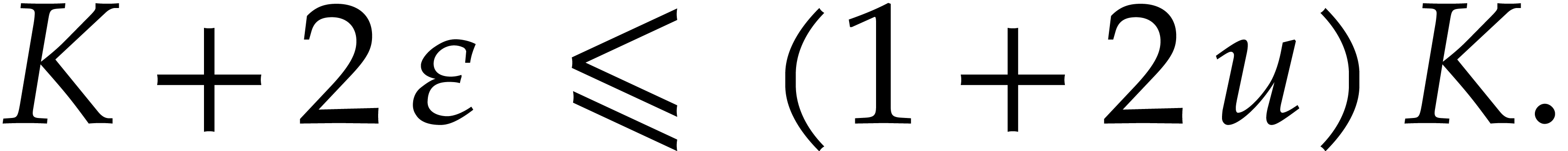
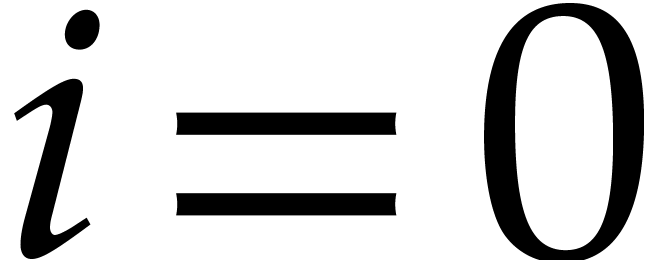
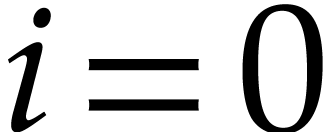 .
. .
.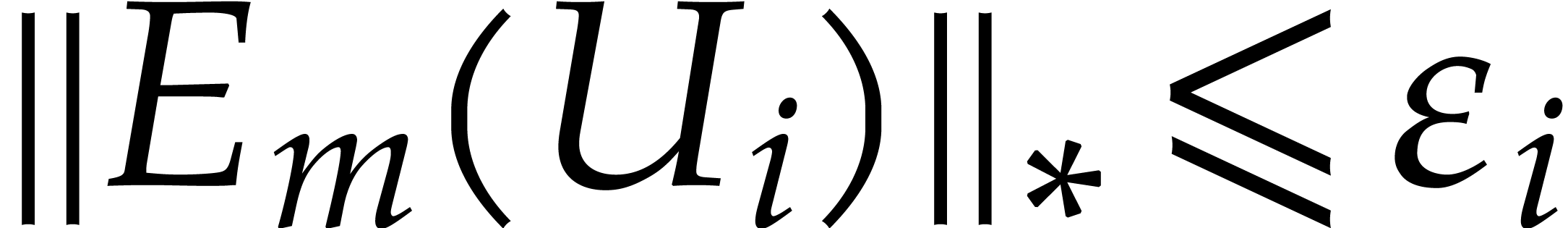 ,
,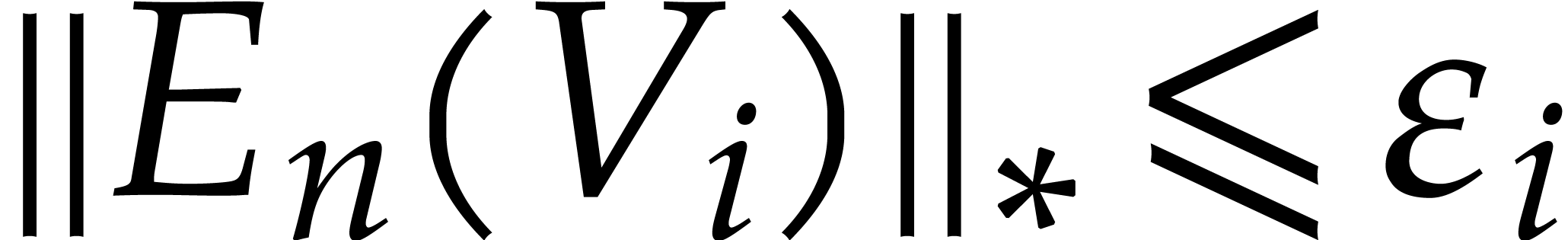 and
and 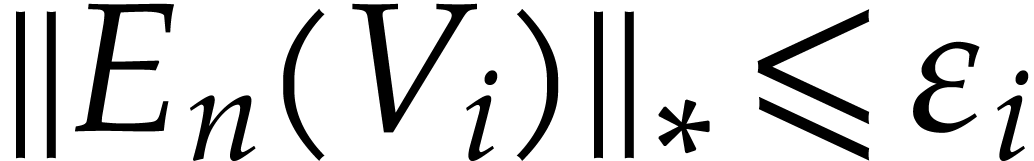 .
.
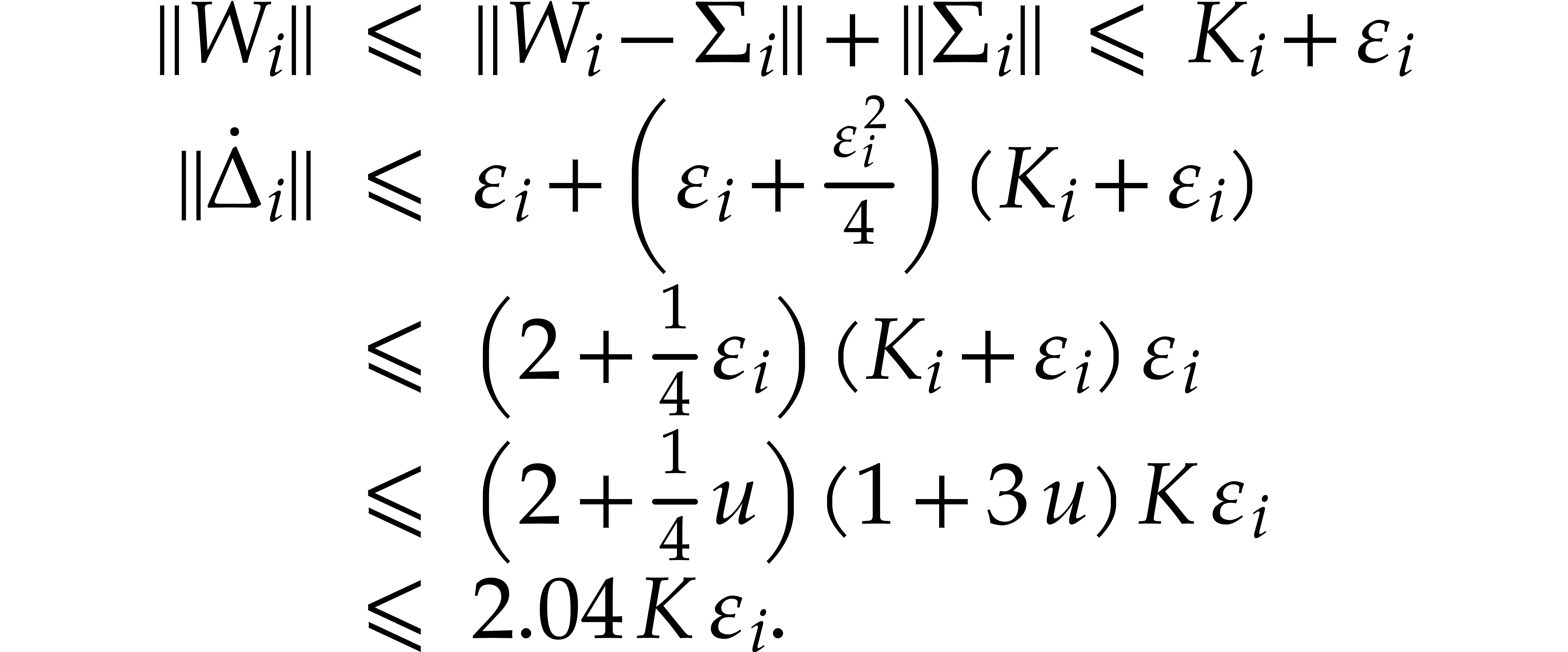
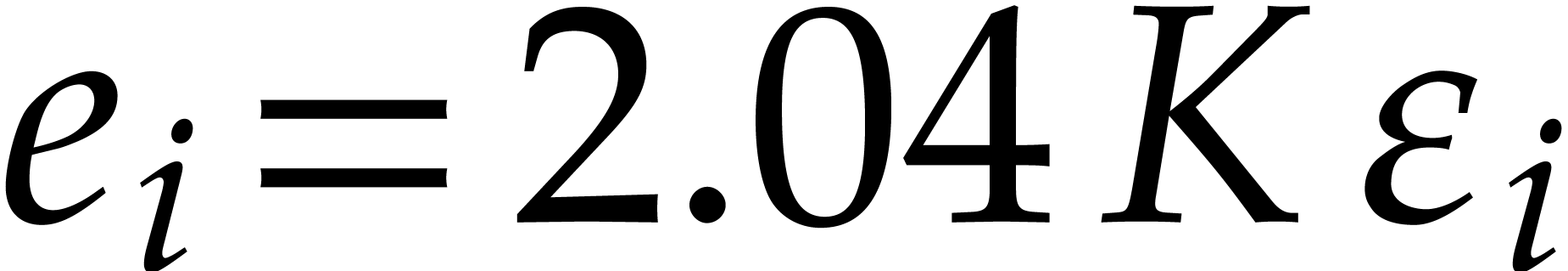
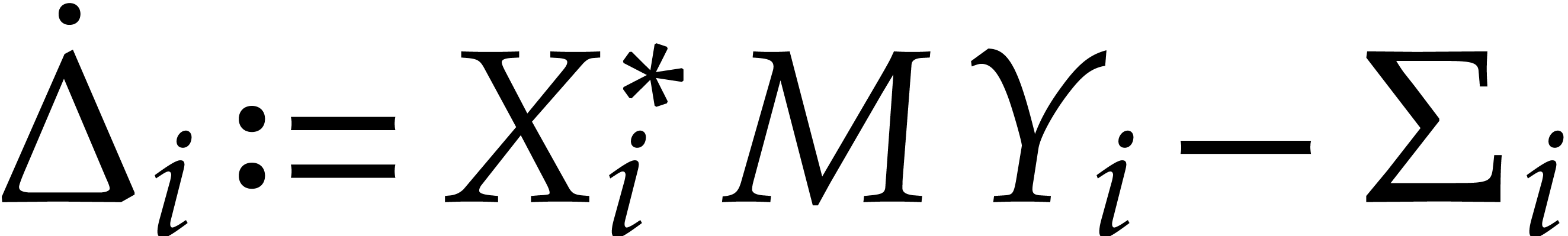 .
.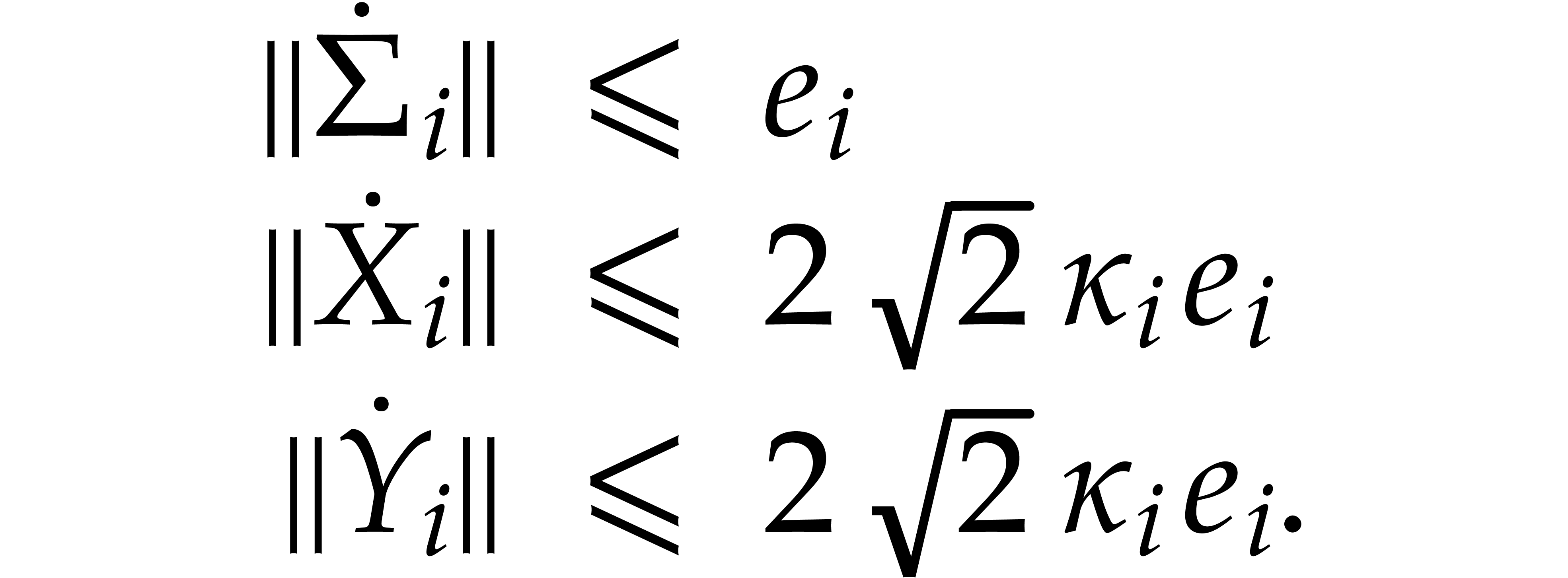 ,
,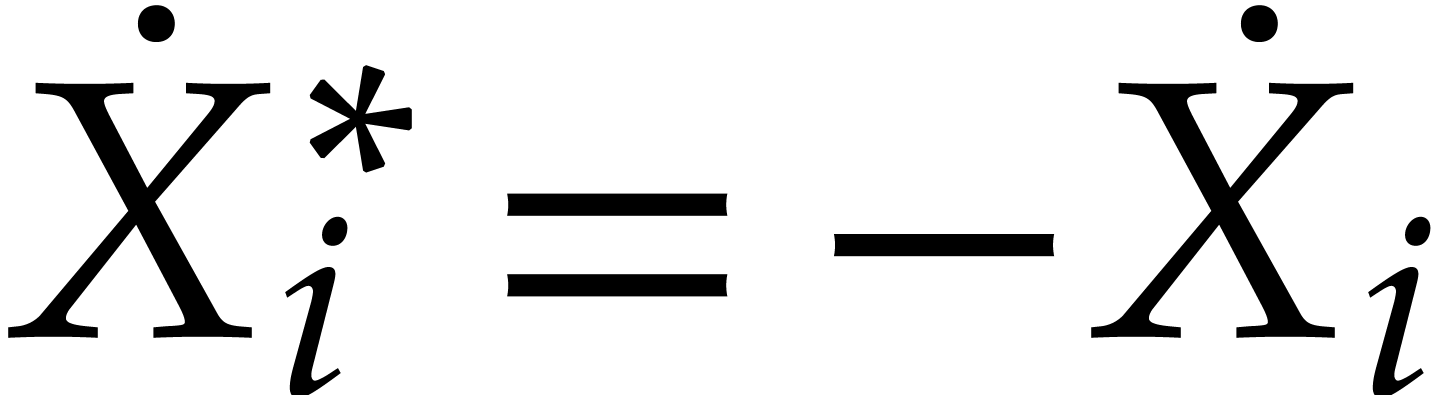
 ,
,
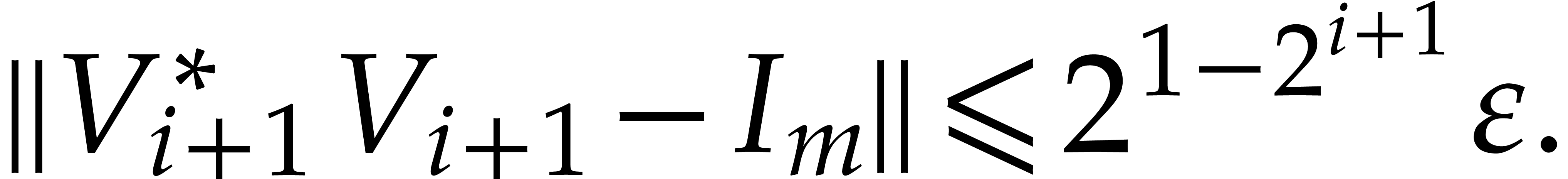
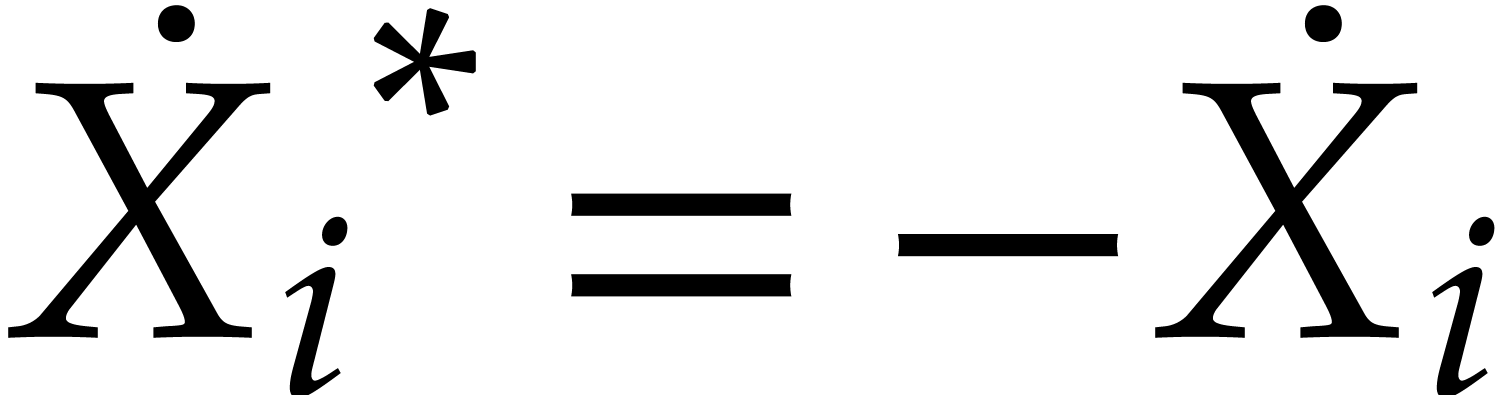
 and (
and (
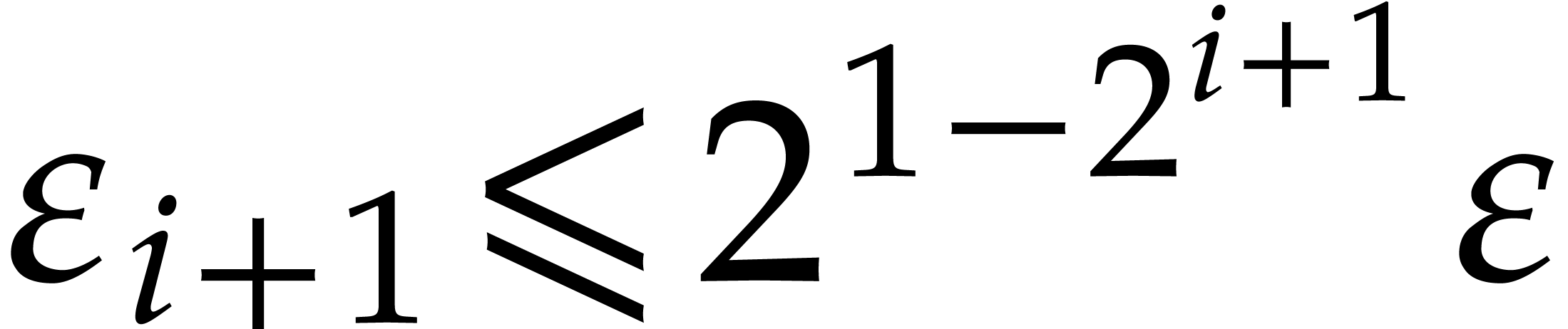
 .
.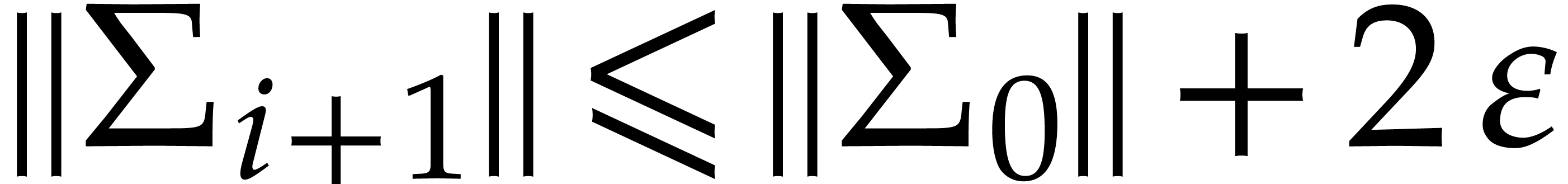
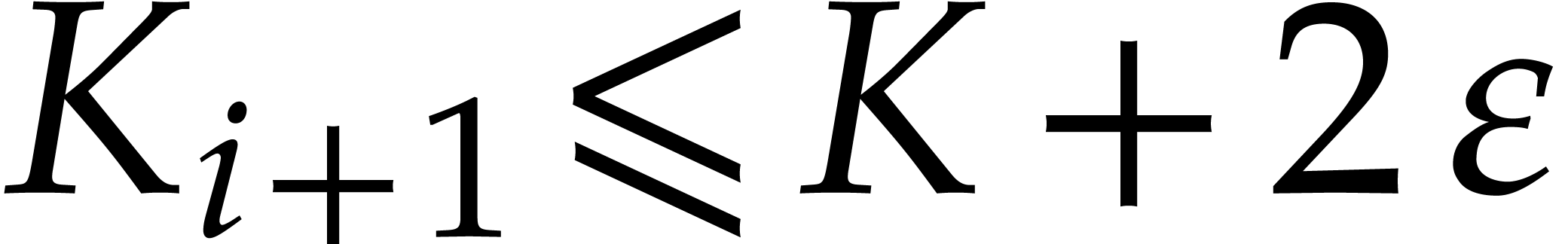 and
and 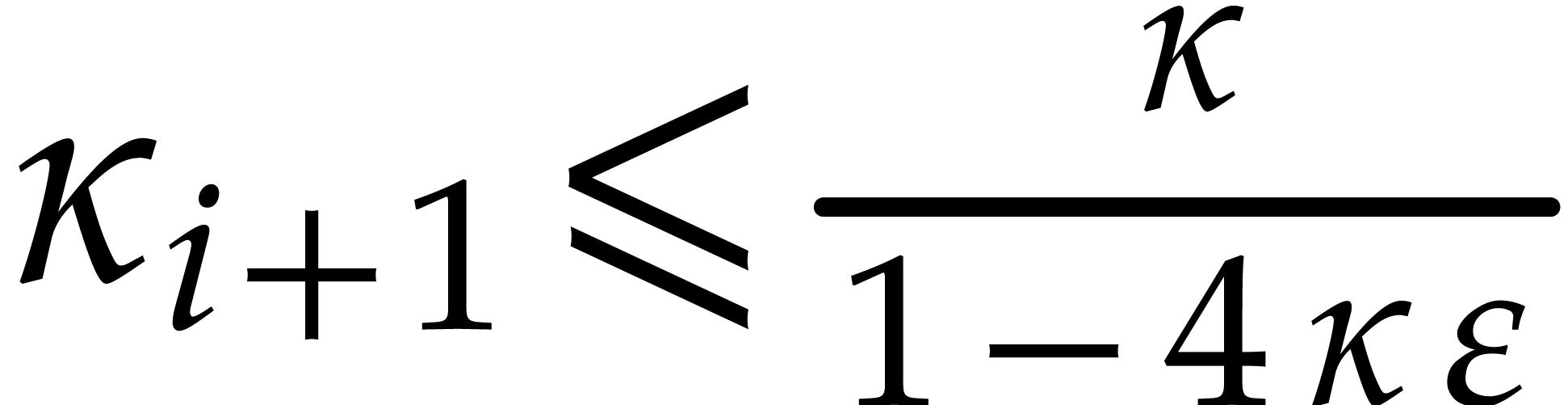 .
.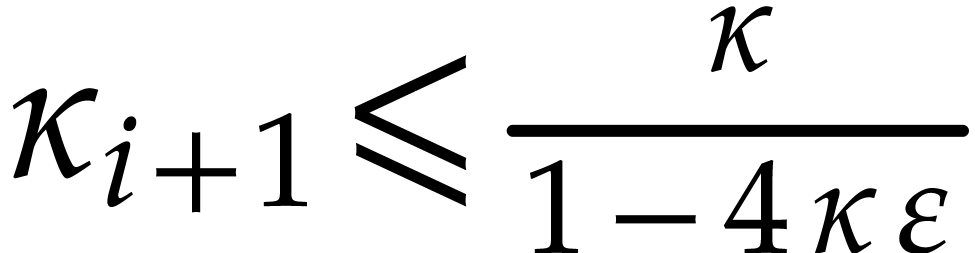 .
. ,
,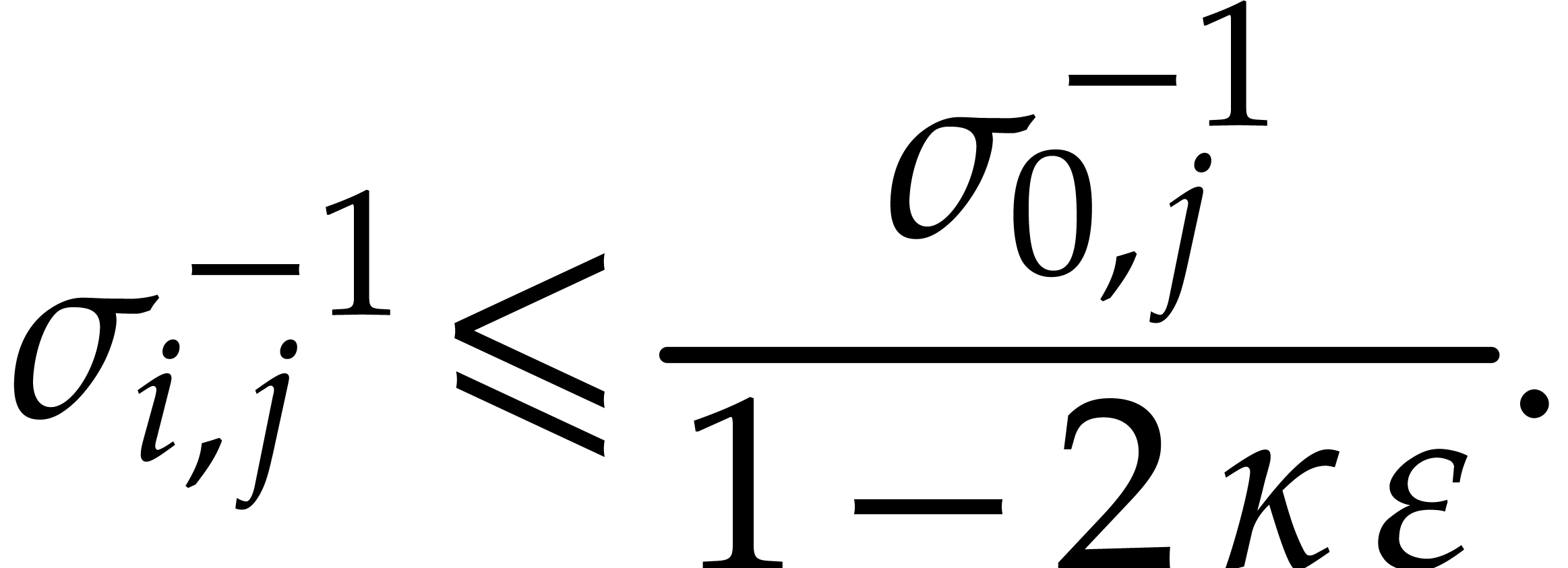
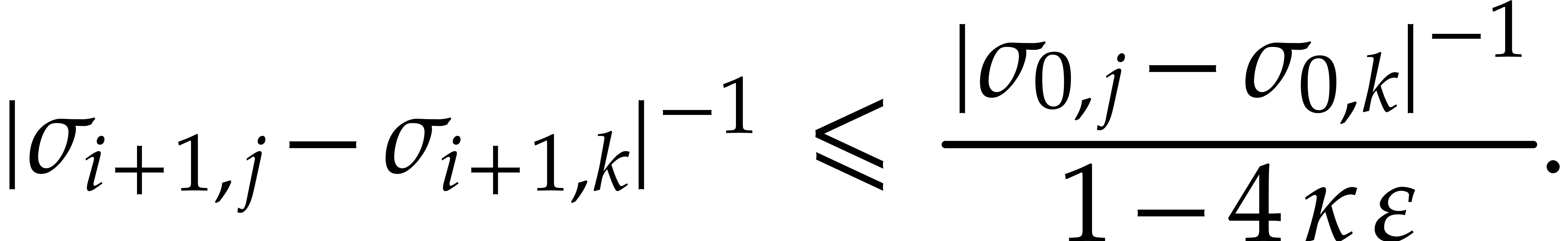
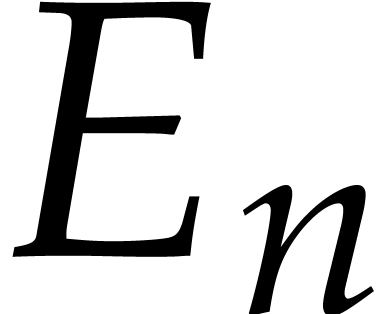 ,
,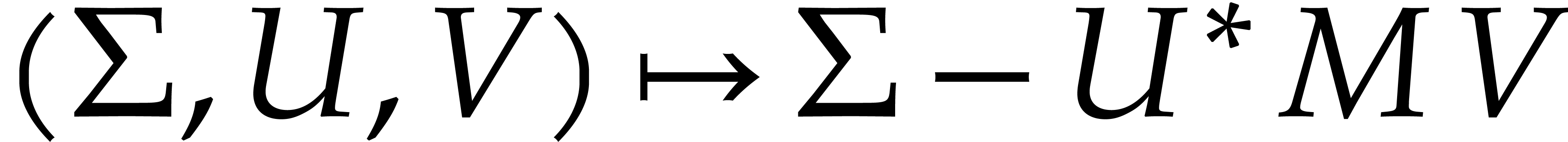 ,
,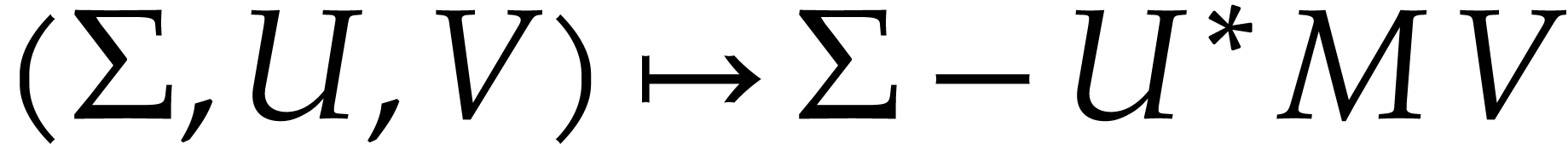 ,
,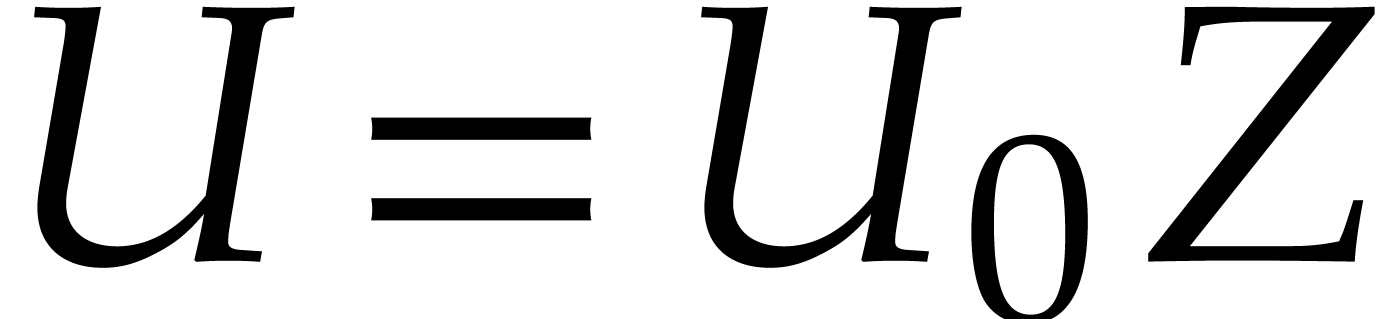 .
.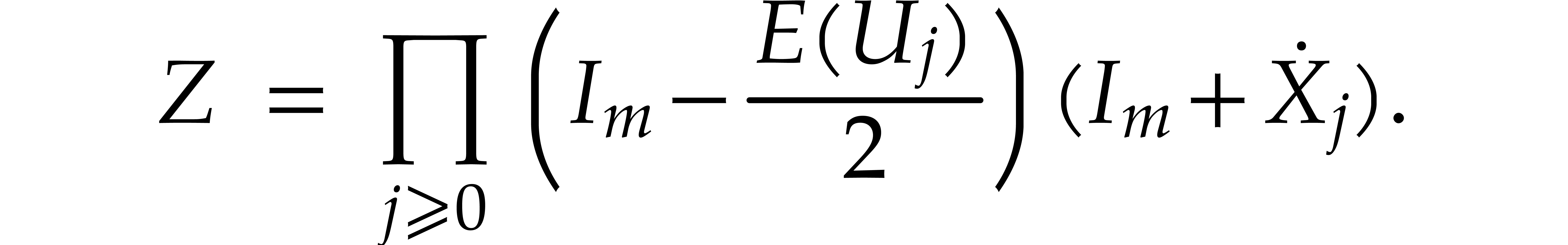 with
with

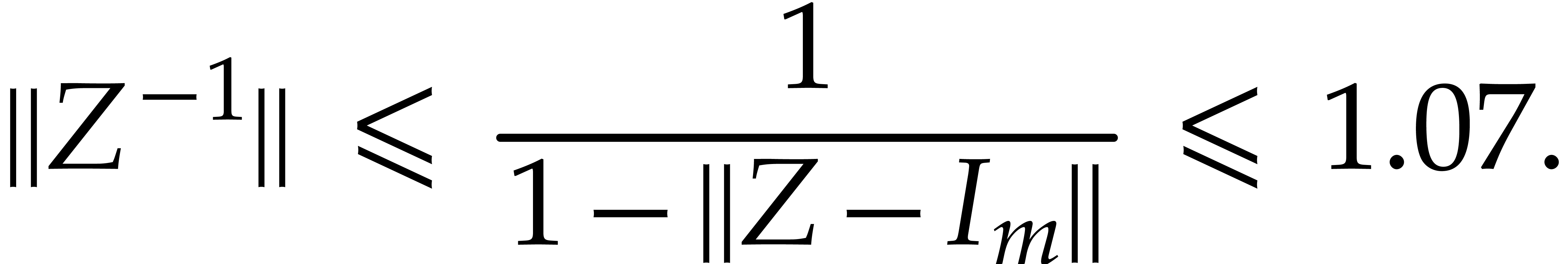 is invertible, with
is invertible, with
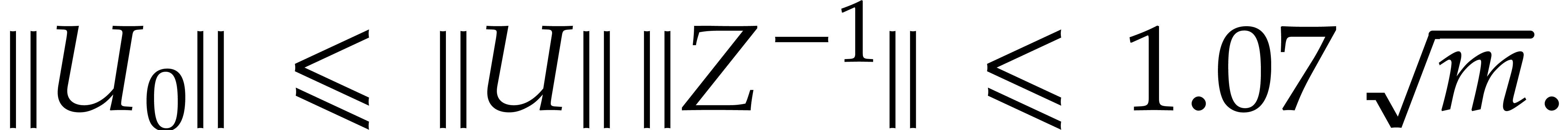
 we also have
we also have
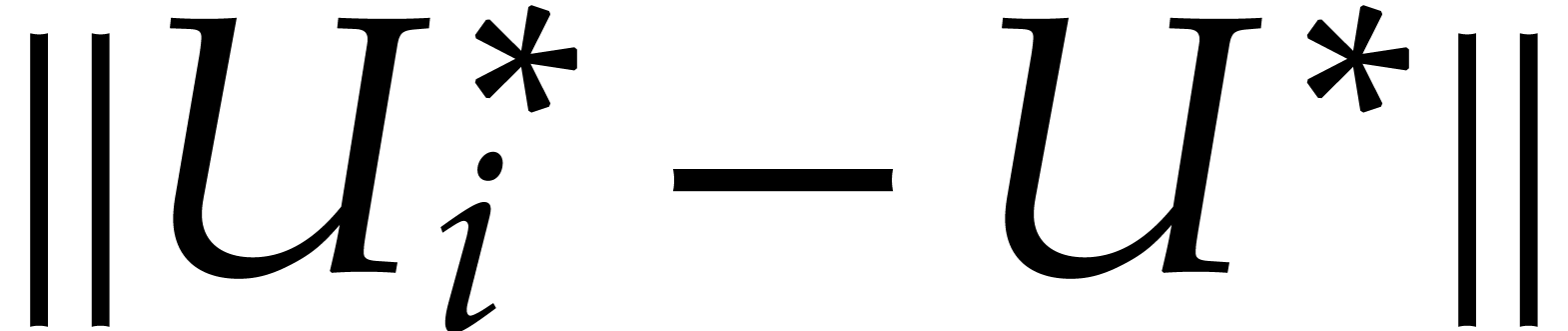
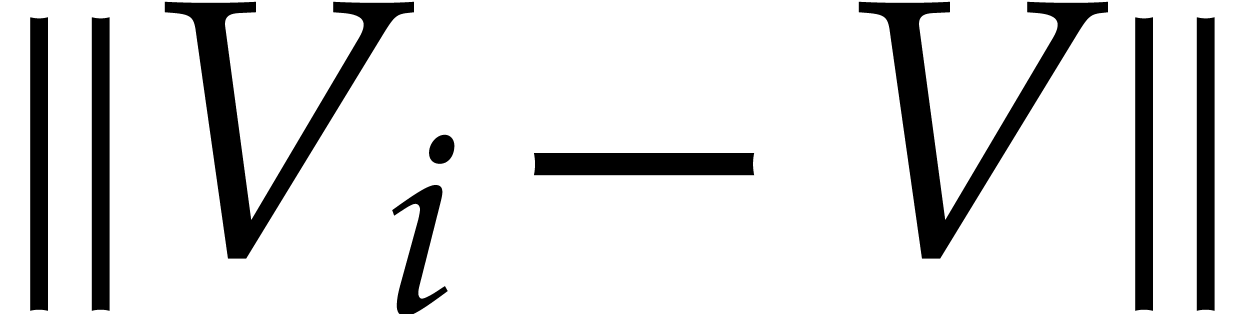 ,
,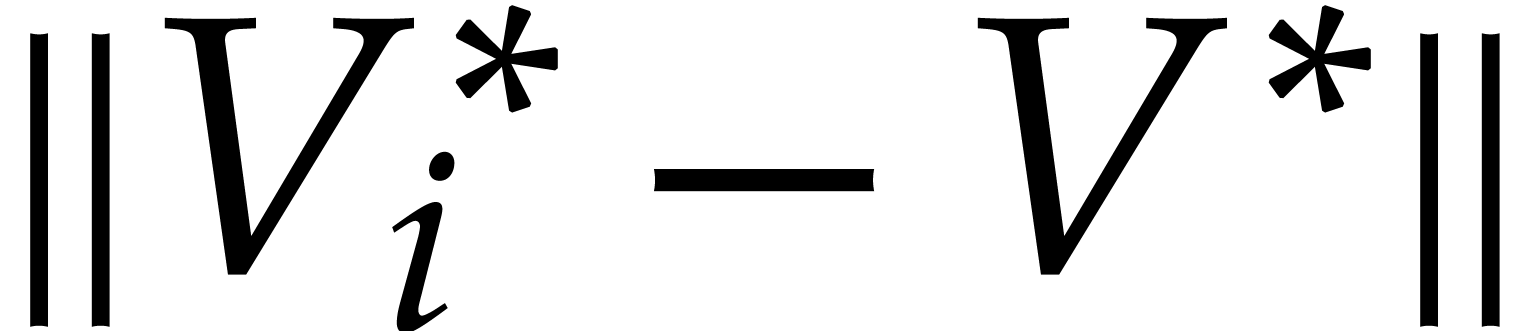 ,
,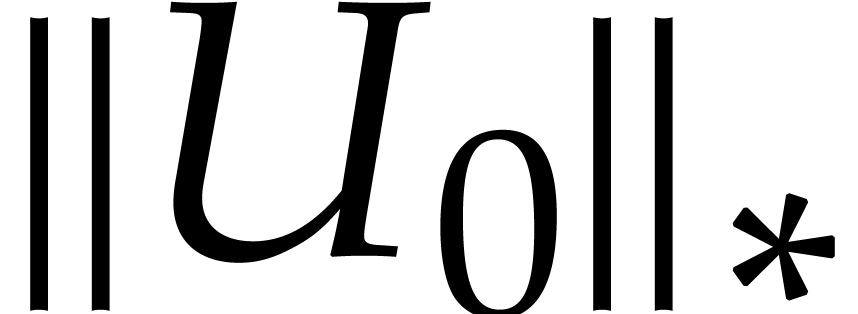 .
.
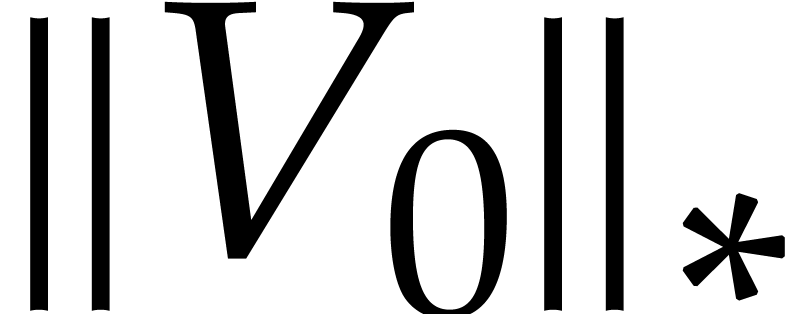

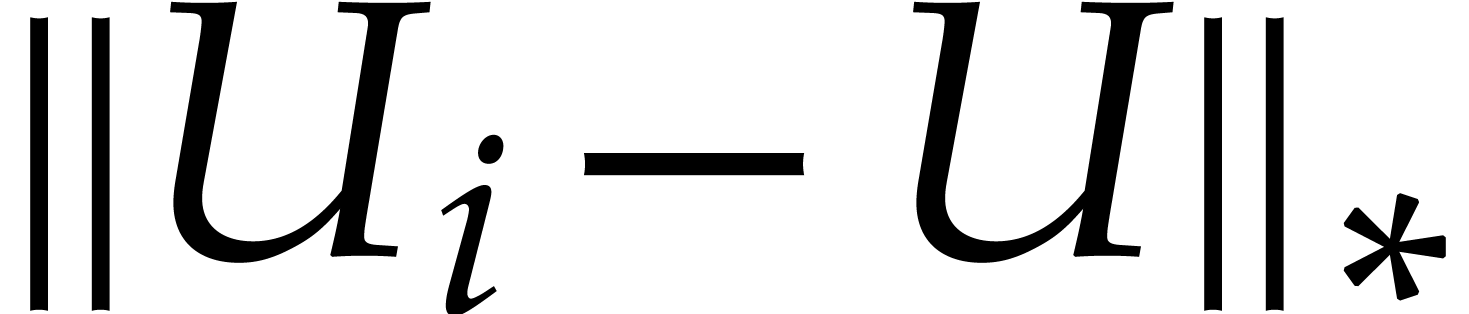
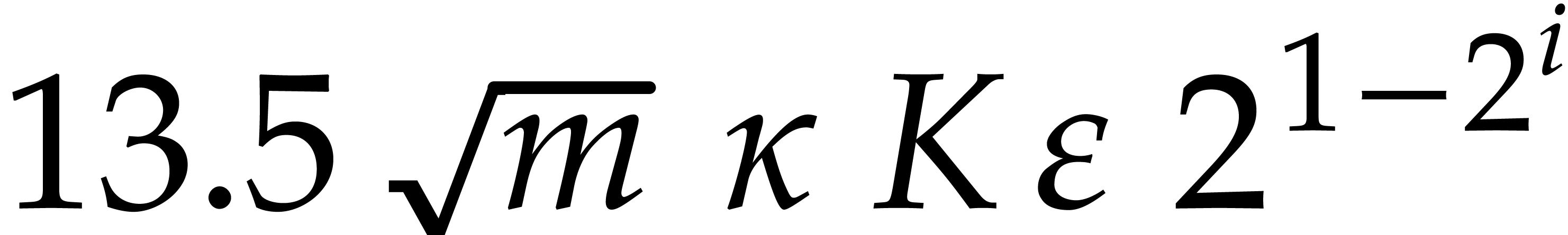
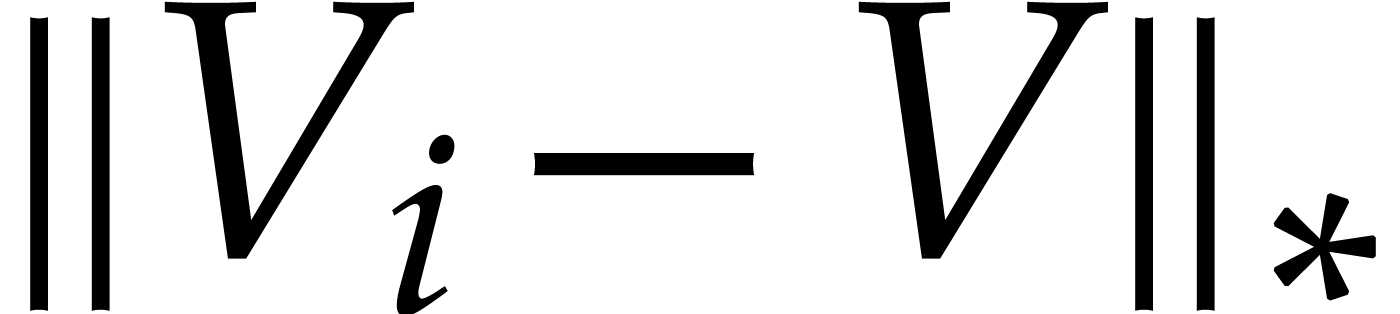
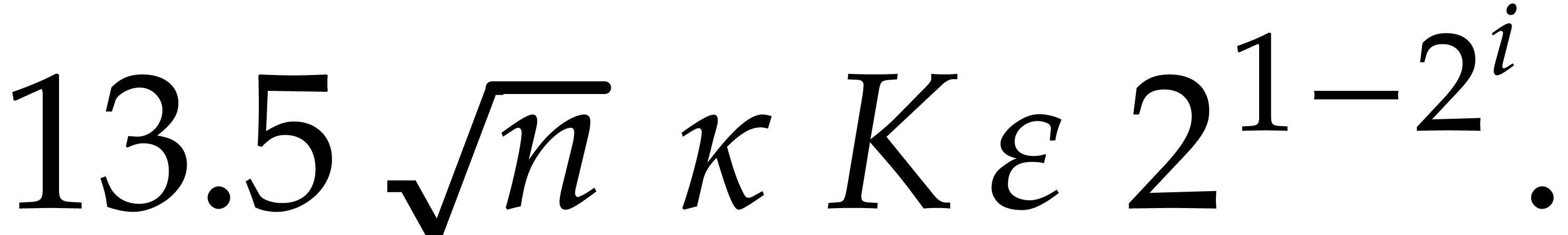
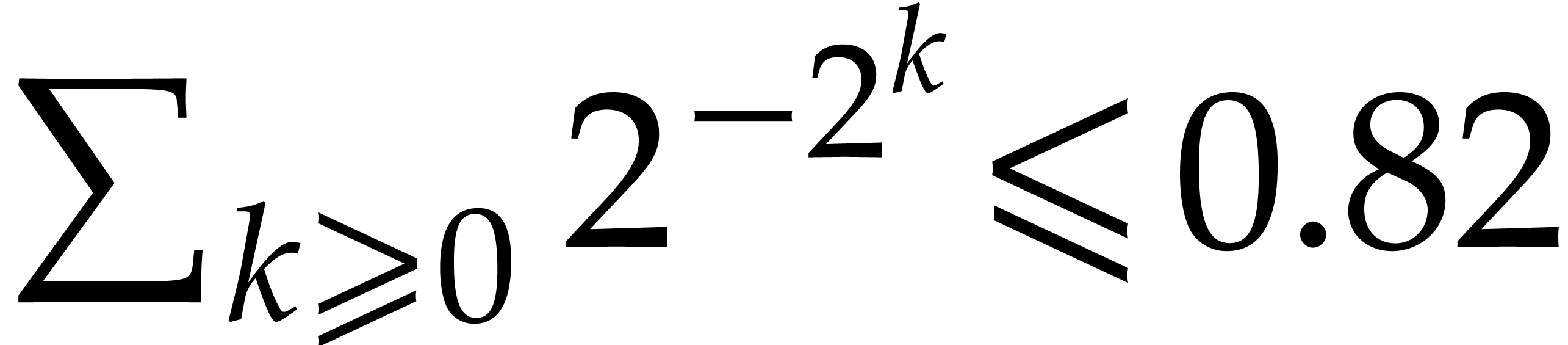
 .
. ,
,