Zero-testing, witness conjectures and
differential diophantine approximation |
|
Dépt. de Mathématiques (bât.
425)
Université Paris-Sud
91405 Orsay
CEDEX
France
|
|
|
Consider a class of constants built up from the rationals
using the field operations and a certain number of transcendental
functions like 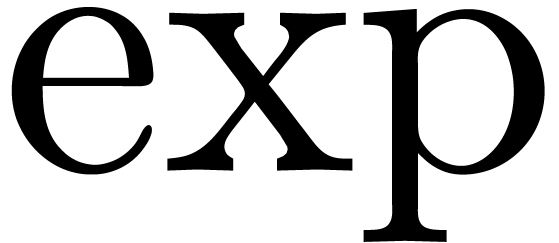 . A central
problem in computer algebra is to test whether such a constant, which
is represented by an expression, is zero.
. A central
problem in computer algebra is to test whether such a constant, which
is represented by an expression, is zero.
The simplest approach to the zero-test problem is to
evaluate the constants up to a certain number of decimal digits.
Modulo certain precautions, we will make it likely that this approach
is actually a valid one. More precisely, one may for instance restrict
oneself to certain subsets of expressions in order to avoid
“high precision fraud”. For such subsets, we will state
witness conjectures, which propose reasonable lower bounds for non
zero constants as a function of the minimal sizes of expressions that
represent them.
Unfortunately, such witness conjectures are extremely
hard to prove, since they are really far reaching generalizations of
results in diophantine approximations. Nevertheless, we will also
discuss their counterparts for formal power series, which are more
accessible.
1Introduction
Zero-testing an important issue in mathematics and more specifically in
computer algebra. Standard mathematical notation provides a way of
representing many transcendental functions. However, trivial cases
apart, this notation gives rise to the following problems:
The first two problems can usually be solved by restricting oneself to
an appropriate setting. Remains the third and most difficult problem,
which is known as the zero-test or zero-equivalence problem, since we
are usually interested in expressions that represent functions in a
ring.
As a reflex, most mathematicians tend to deal with the zero-test problem
by restricting their attention to expressions of a certain form and
proving a structure theorem for such expressions. Some successes of this
approach are the following:
-
Computations in algebraic extensions of a field using Groebner basis
techniques. In this case an element of the algebraic extension is
represented uniquely by its reduction modulo the Groebner basis.
-
The Risch structure theorem [Ris75] allows computations
in differential field extensions by exponentials, logarithms, or
integrals. This technique may be adapted to a few other cases [SSC85].
-
Richardson designed a zero-test for elementary constants (i.e.
constants which may be defined implicitly using rational numbers,
the field operations and exponentiation), which assumes Schanuel's
conjecture [Ric94], [Ax71].
-
More recently, Ecalle has proved several structure theorems for
generalized polylogarithms and zeta functions. One may expect the
design of fast algorithms for dealing with such functions on the
basis of his results.
However, it should be stressed that a structure theorem explicitly
describes all relations which hold for the class of expressions
being considered. Such a theorem is much more powerful than a zero-test
algorithm, which just provides a method to test whether a
particular expression represents zero.
It is therefore recommended to treat the zero-test problem independently
from the problem of establishing a complete structure theorem. Indeed,
we have just stressed that the zero-test problem is less ambitious, so
it may be solved for larger classes of expressions. Secondly, even if a
structure theorem exist, a special purpose zero-test may be more
efficient than a zero-test derived from the theorem, which may be very
complicated.
Now engineers have a very simple solution to the zero-test problem for
constants: evaluate the constant with double precision and test whether
the result vanishes. The advantage of this method, which works most of
the time, is that it is very fast. However, double precision is not
always sufficient to ensure the correctness of the answers. This problem
can not merely be solved by considering quadruple or higher fixed
precisions. Instead, it rises an interesting theoretical question: what
is the required precision of evaluation as a function of the size
of the input expression in the zero-test.
Now there are some well-known examples of small, but non-zero
expressions, like
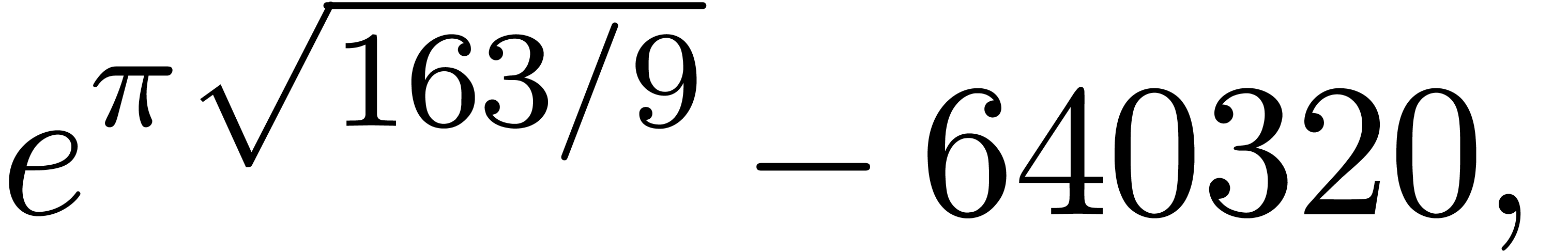 |
(1) |
or
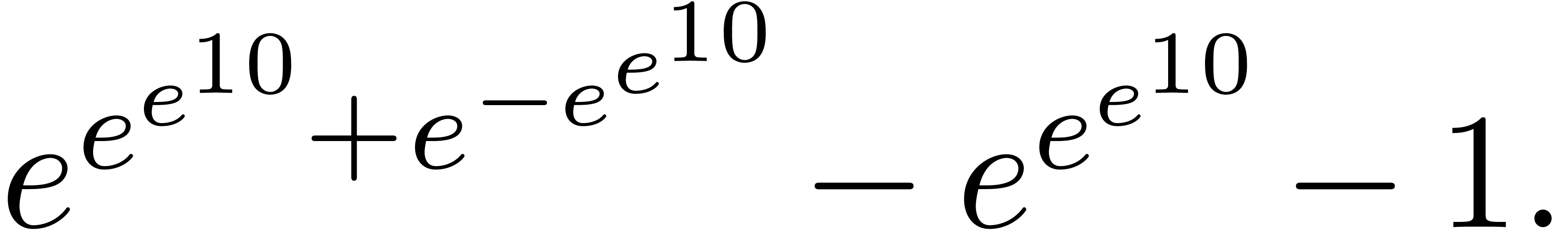 |
(2) |
Essentially, we conjecture that such examples always come down to the
substitution of a very small number in a non-zero power series with high
valuation. This is clear in the second example, but may necessitate some
extra work in other cases. For other nice examples of “high
precision fraud”, we refer to [BB92].
In order to develop reliable zero-tests, we thus have to search for a
setting in which high precision fraud is impossible. In the case of
exp-log constants, one possible approach is to limit the modules of
certain subexpressions. In such a setting an expression like 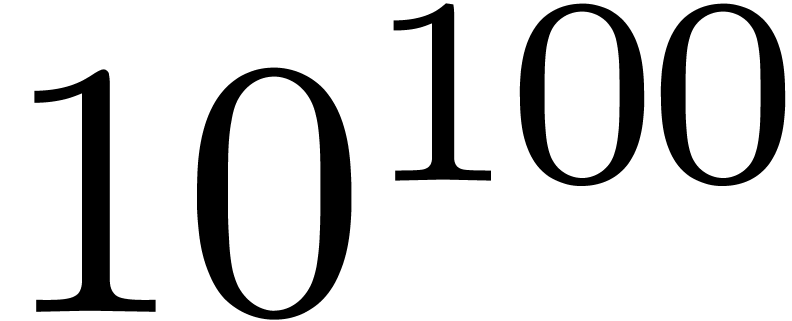 might become invalid and need to be rewritten as
might become invalid and need to be rewritten as  , which increases its size. Then it
is reasonable to expect that there exist bounds from below for the
absolute values of non-zero constants as a function of the sizes of
their representing expressions. Such “witness conjectures”
were first stated in [vdH97, vdH01], and later
by Richardson [Ric01], who has also done some numerical
computations which tend to confirm our expectations.
, which increases its size. Then it
is reasonable to expect that there exist bounds from below for the
absolute values of non-zero constants as a function of the sizes of
their representing expressions. Such “witness conjectures”
were first stated in [vdH97, vdH01], and later
by Richardson [Ric01], who has also done some numerical
computations which tend to confirm our expectations.
In this paper, we study several possible formulations of witness
conjectures and we consider more general transcendental functions,
defined by differential equations and initial conditions. We will also
discuss some analogue conjectures for formal power series, on which we
some progress has already been made [Kho91, SvdH01].
Witness conjectures may be interpreted as far reaching generalizations
of existing conjectures and results in diophantine approximation [Lan71]. Indeed, this theory is concerned with finding good
rational approximations of real numbers  ,
which is equivalent to minimizing
,
which is equivalent to minimizing
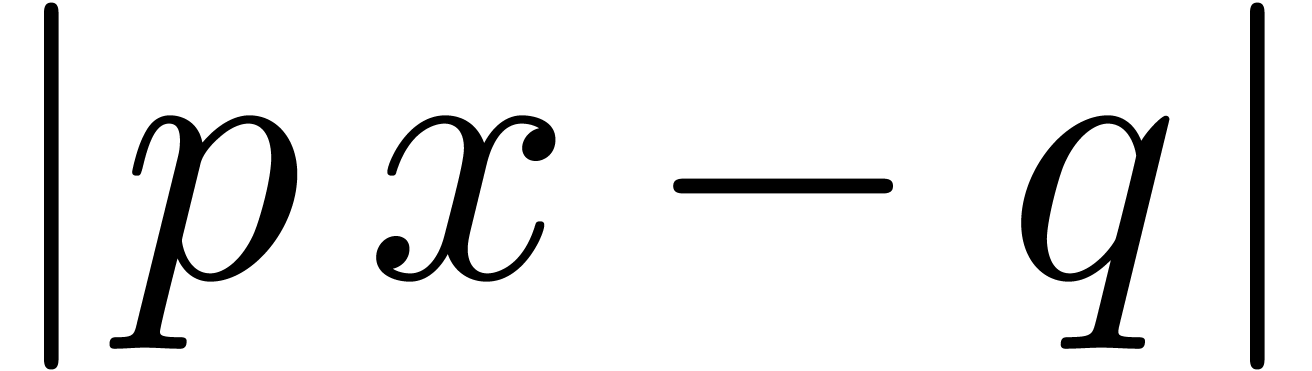
for large 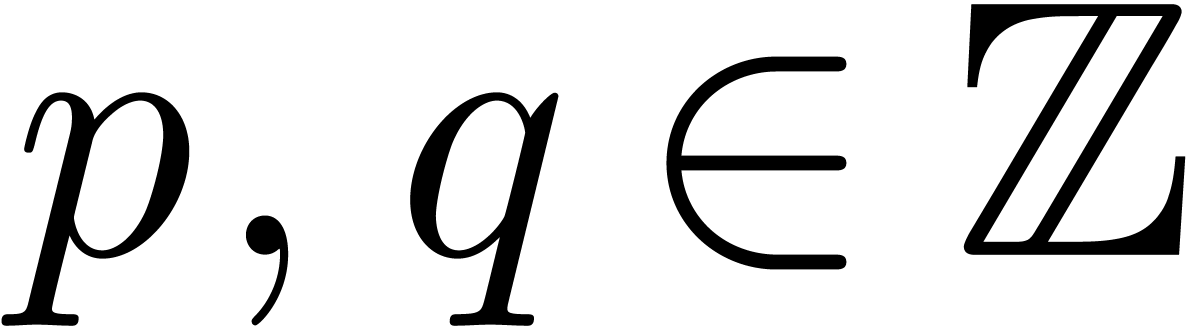 . More generally,
diophantine approximation is concerned with minimizing
. More generally,
diophantine approximation is concerned with minimizing 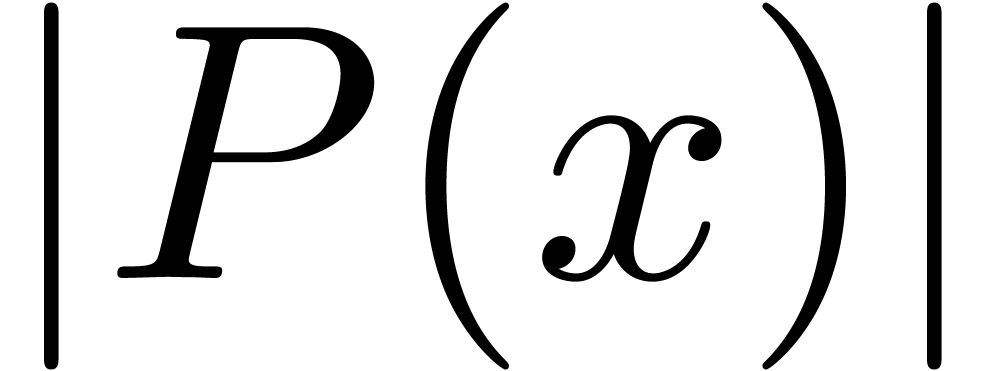 for polynomials
for polynomials 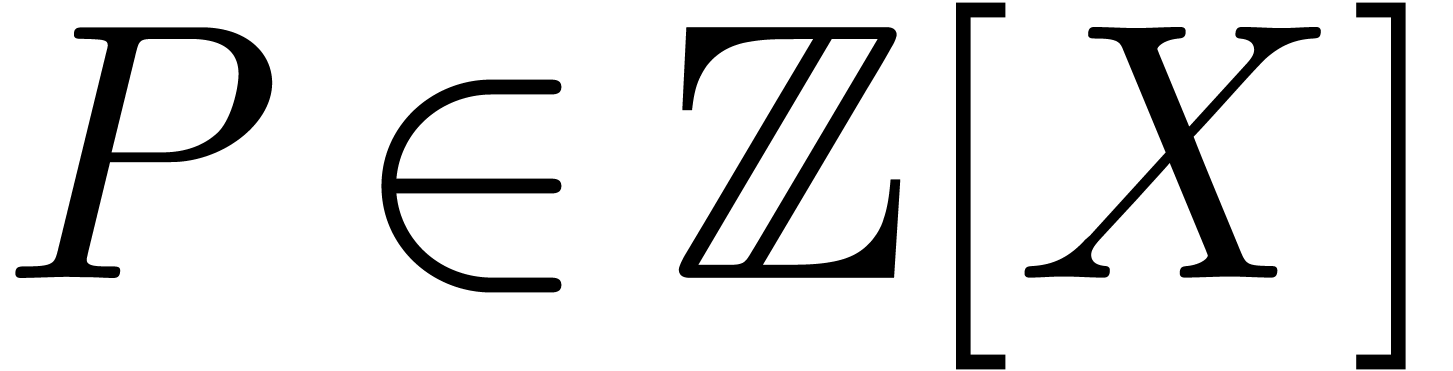 . In our
case, we are interested in even more general expressions, which involve
transcendental functions defined by differential equations and initial
conditions. The theory of minimizing the absolute values of such more
general expressions might therefore be baptized as “differential
diophantine approximation”.
. In our
case, we are interested in even more general expressions, which involve
transcendental functions defined by differential equations and initial
conditions. The theory of minimizing the absolute values of such more
general expressions might therefore be baptized as “differential
diophantine approximation”.
We finally want to stress the interest of our approach for
transcendental number theory. One major problem in this area is that it
is already very hard to just state something like a generalization of
the Schanuel conjecture for more general transcendental functions. The
reason of this difficulty is that this conjecture is a result of the
“structure theorem” approach. In order to state such a
generalization, one thus has to anticipate the structure theorems which
hold in the more general setting. By contrast, our “witness
conjecture” approach directly applies to more general settings and
it is legitimate to hope that some of the tools developed in this
context can also be applied elsewhere.
2Witness conjectures for constants
2.1Exp-log constants
Let  be the set of exp-log constant expressions,
i.e. the expressions formed from
be the set of exp-log constant expressions,
i.e. the expressions formed from 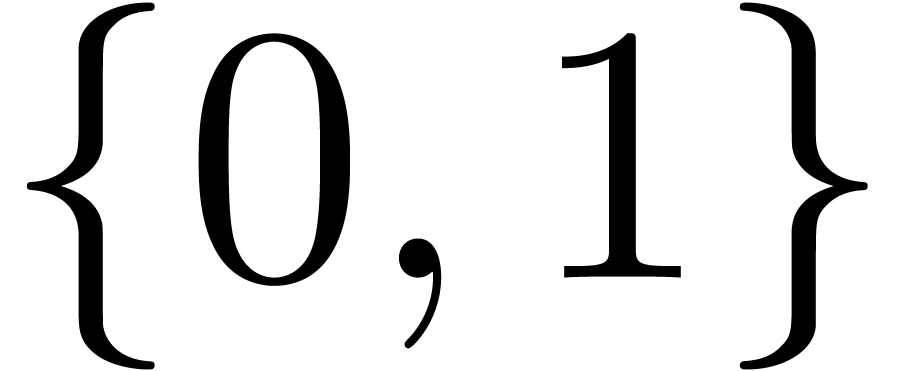 using
using  and
and 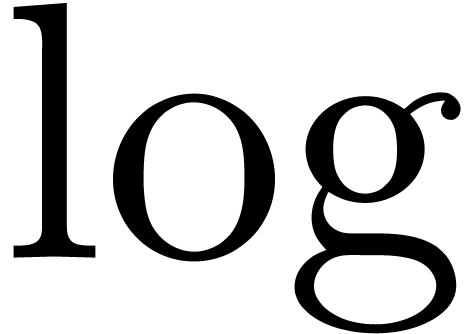 . We will
denote by
. We will
denote by  the set of real numbers which can be
represented by an expression in
the set of real numbers which can be
represented by an expression in  and by
and by  the real number represented by an expression
the real number represented by an expression 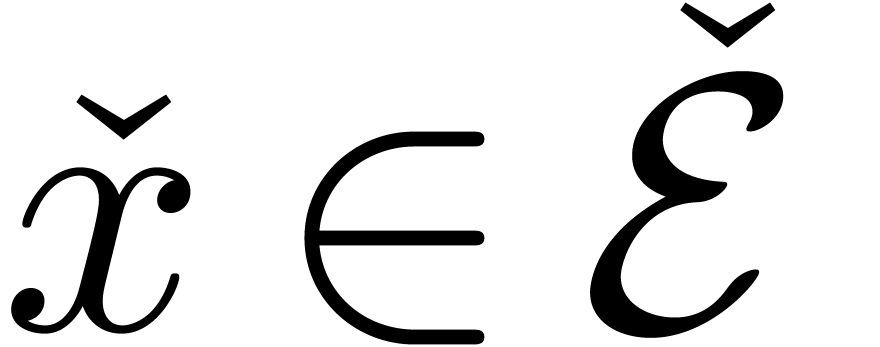 . We will denote by
. We will denote by 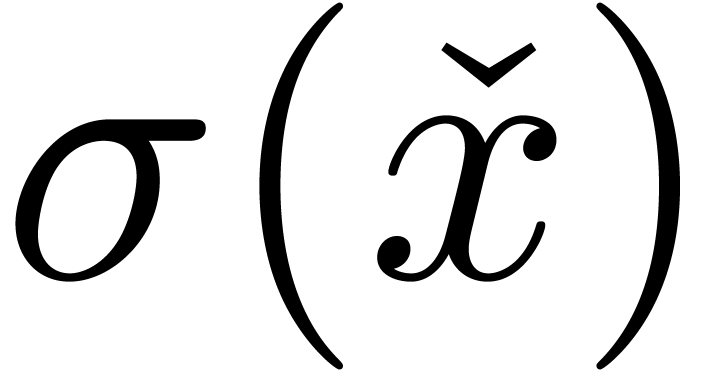 the
size of an expression
the
size of an expression 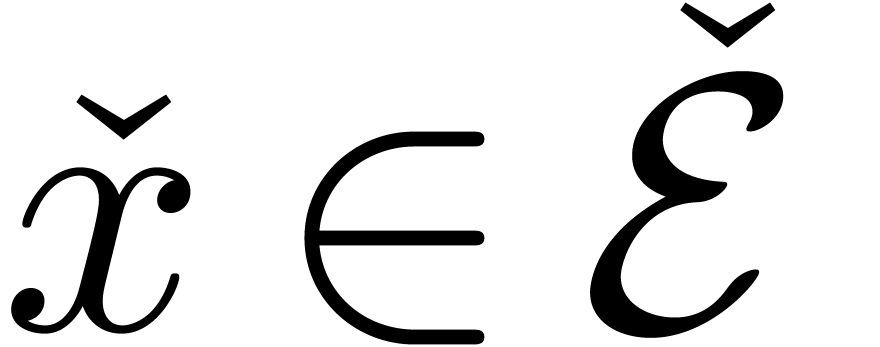 (i.e. the number of nodes
when interpreting the expression as a tree). Given a rational number
(i.e. the number of nodes
when interpreting the expression as a tree). Given a rational number
 , we denote by
, we denote by  the set of all expressions
the set of all expressions 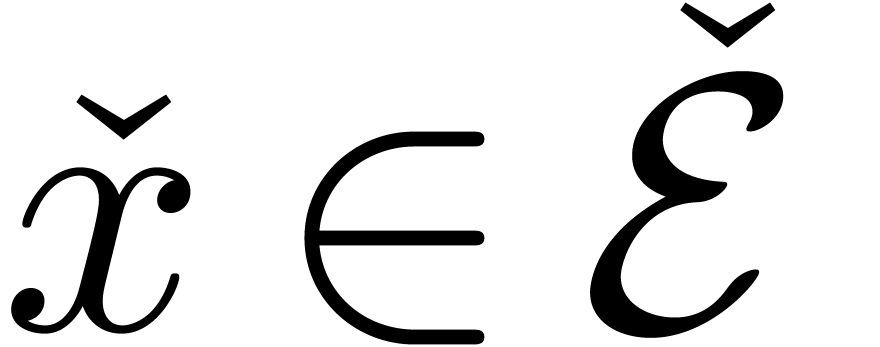 ,
such that
,
such that 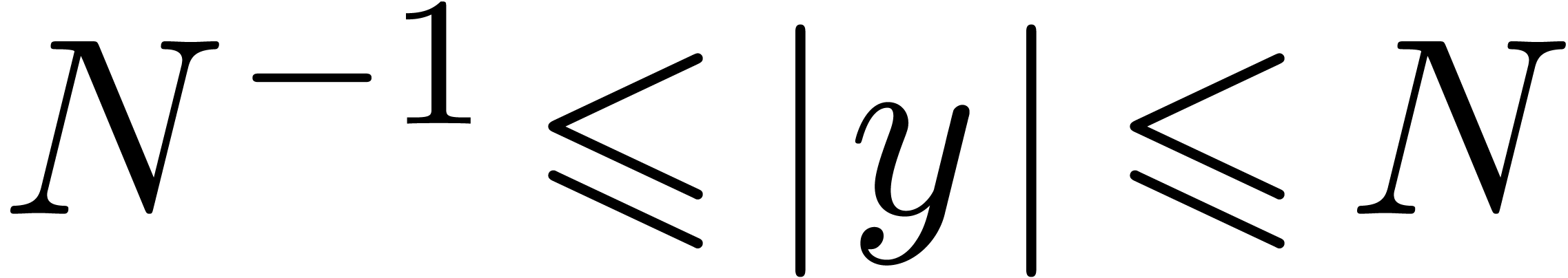 for all subexpressions
for all subexpressions  of
of  . In [vdH97], we stated the first witness conjecture:
. In [vdH97], we stated the first witness conjecture:
Conjecture 1. There
exists a function  of one of the forms
of one of the forms
-
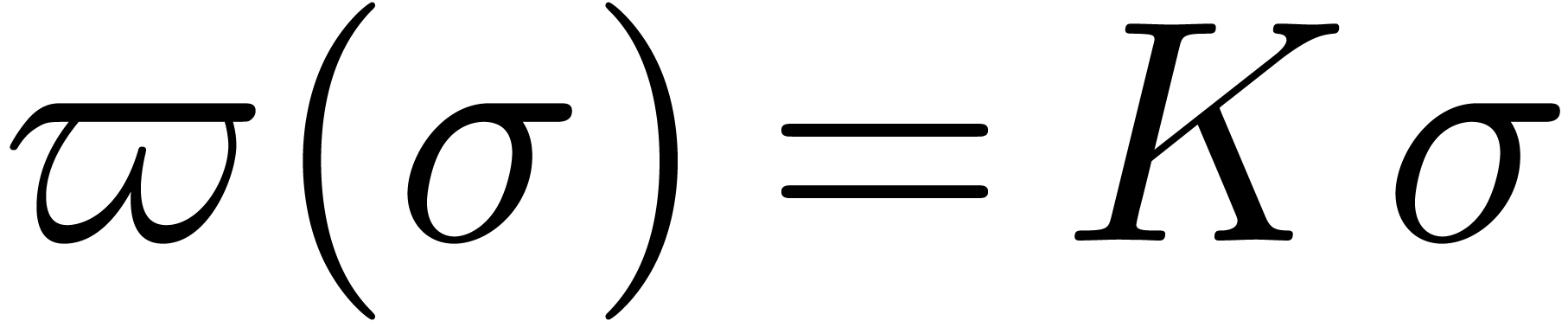 ;
;
-
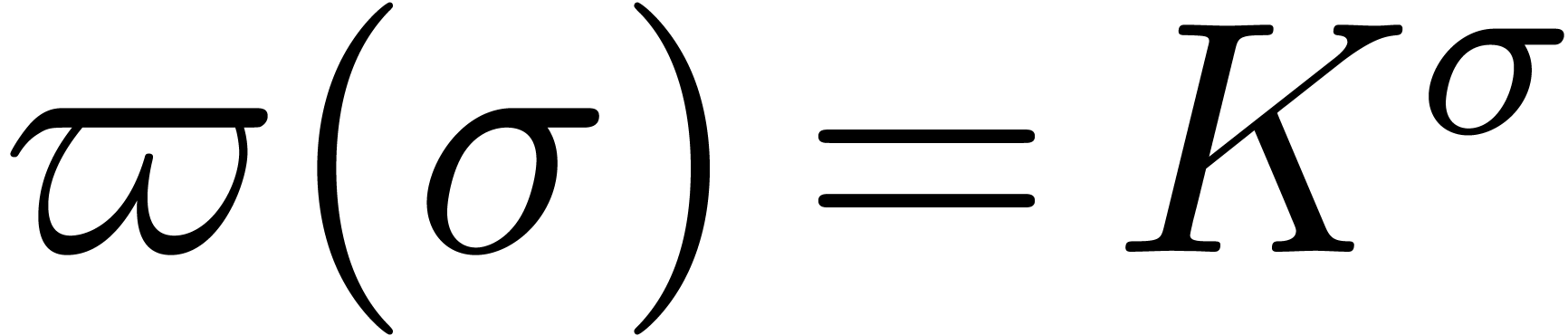 ,
,
where 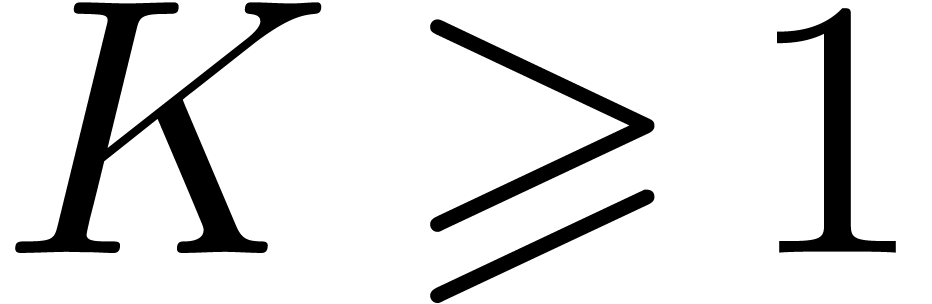 depends on
depends on  , such that
, such that
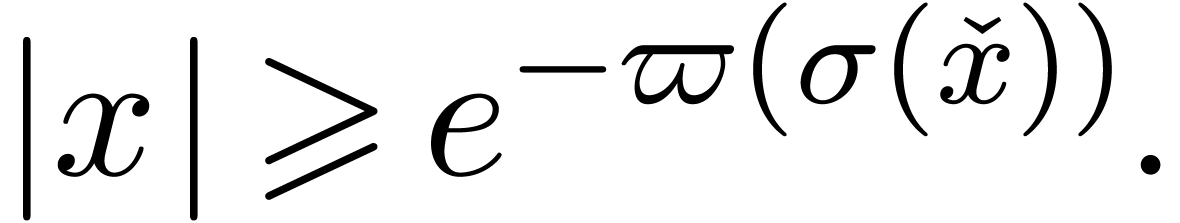 |
(3) |
for all 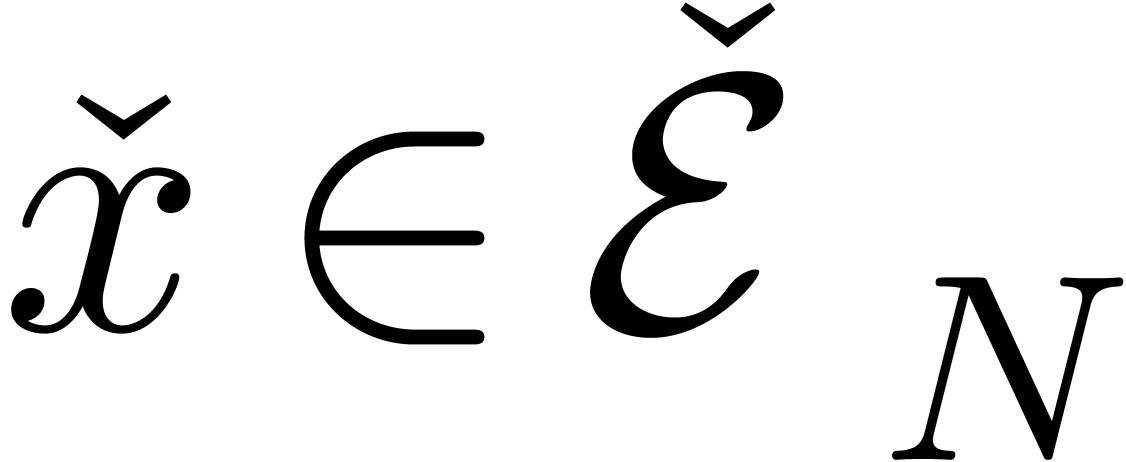 with
with 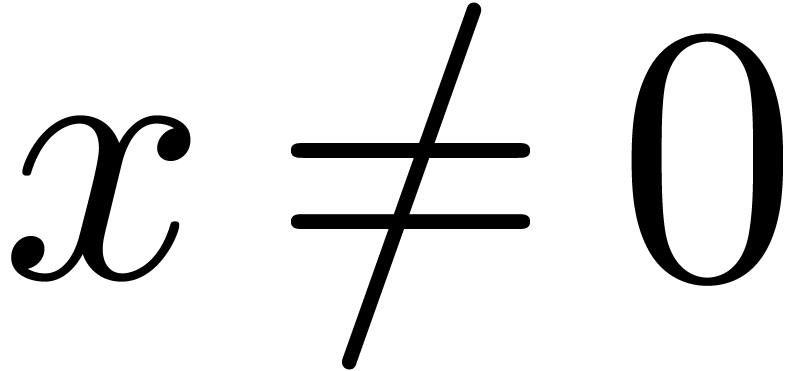 .
.
Actually, we conjectured the b-part and we remarked that the
conjecture might even hold for smaller witness functions  , such as in the a-part. We
will call the a-part a strong witness conjecture and the
b-part a weak witness conjecture. It is also possible to
consider intermediate witness conjecture, by taking
, such as in the a-part. We
will call the a-part a strong witness conjecture and the
b-part a weak witness conjecture. It is also possible to
consider intermediate witness conjecture, by taking 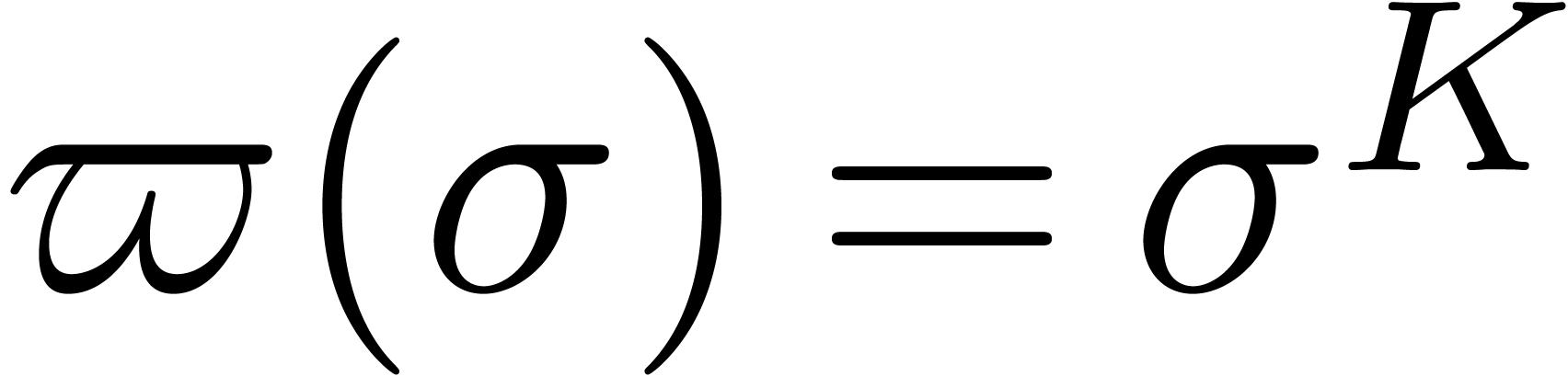 , for instance. In general, we call a weakness
conjecture strong, if
, for instance. In general, we call a weakness
conjecture strong, if  , for
some
, for
some 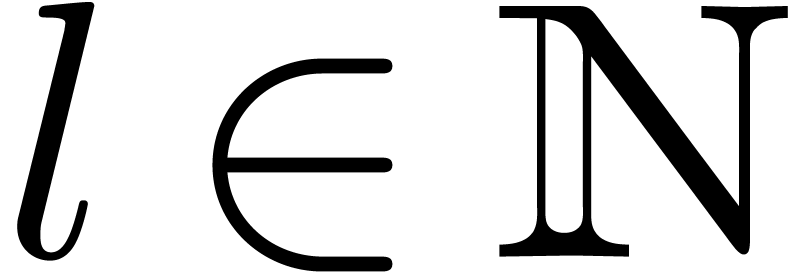 , where
, where  and
and  denote the
denote the  -th
iterates of
-th
iterates of 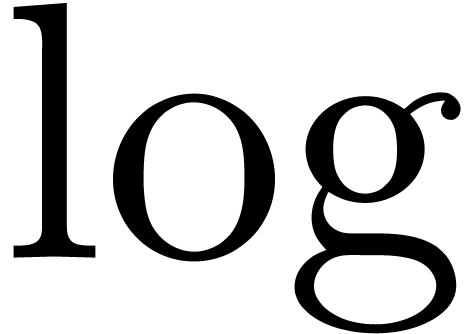 and
and 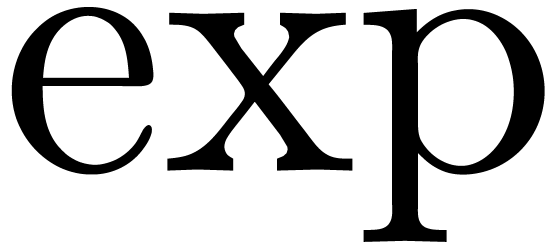 .
In what follows, we will only state strong witness conjectures with
linear witness functions, but it might turn out in the future that other
witness functions are necessary.
.
In what follows, we will only state strong witness conjectures with
linear witness functions, but it might turn out in the future that other
witness functions are necessary.
A slightly different setting was first considered (in a more general
form) in [vdH01]. Given a rational number 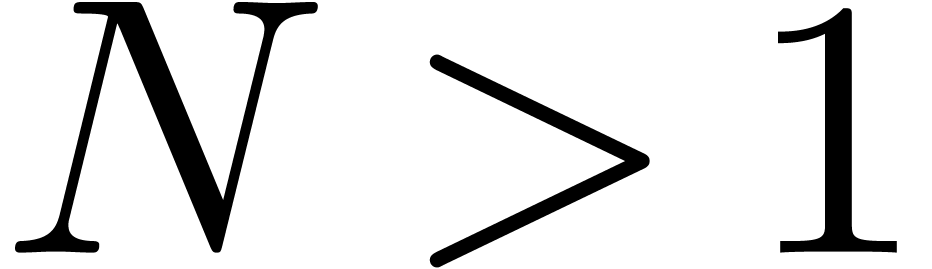 , let
, let 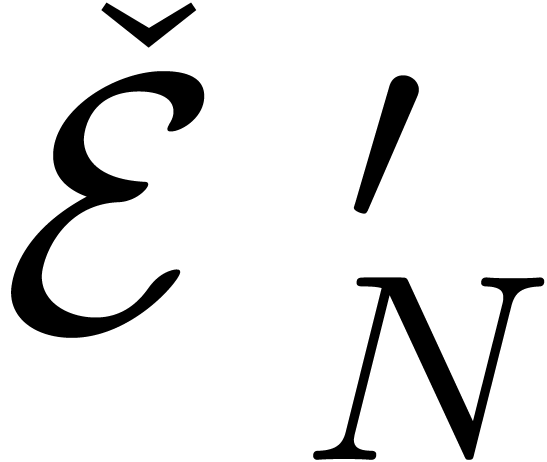 be the class of
all expressions
be the class of
all expressions 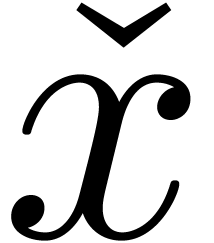 in
in  ,
such that for each subexpression
,
such that for each subexpression  of
of 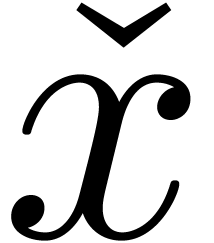 of the form
of the form  we have
we have 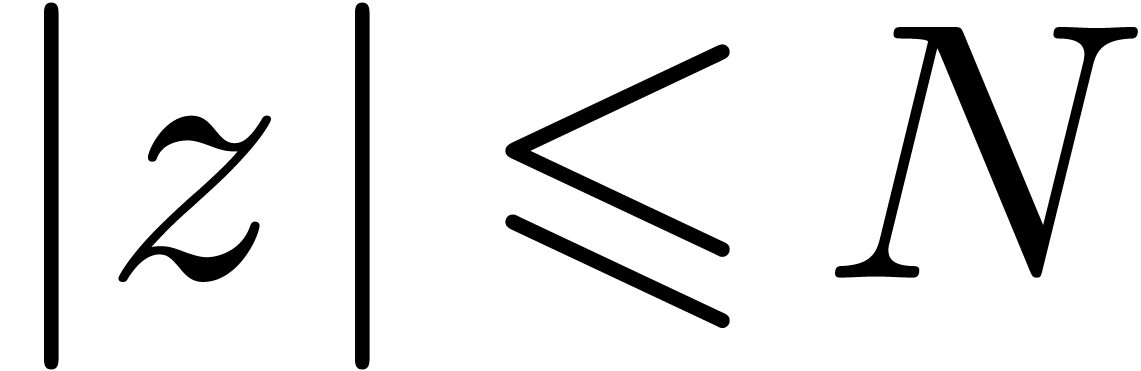 , and such that for each subexpression
, and such that for each subexpression 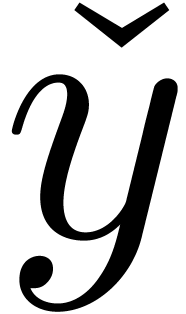 of
of 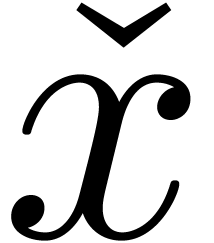 of the form
of the form 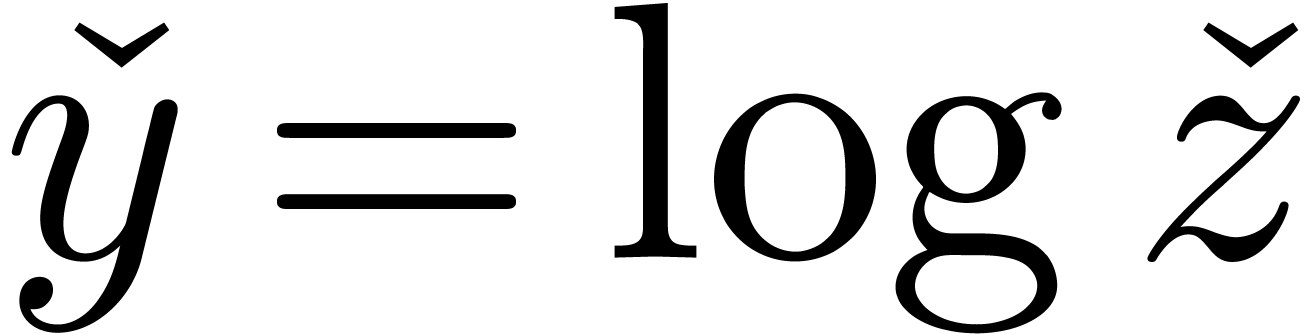 we have
we have 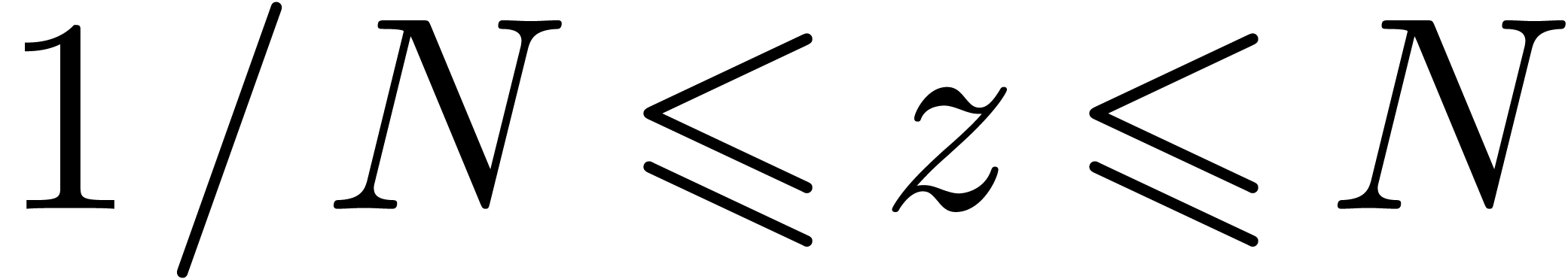 .
.
Conjecture 2. There
exists a witness function of the form 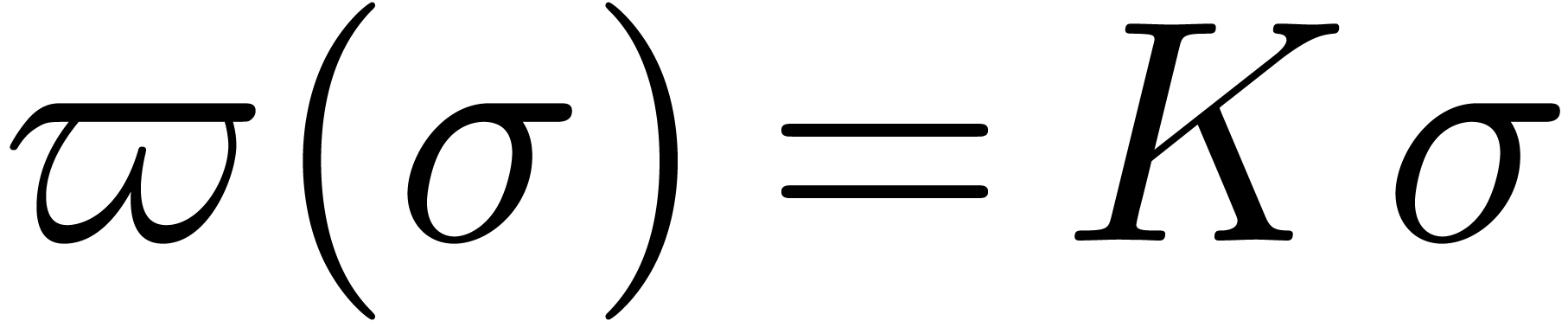 ,
where
,
where 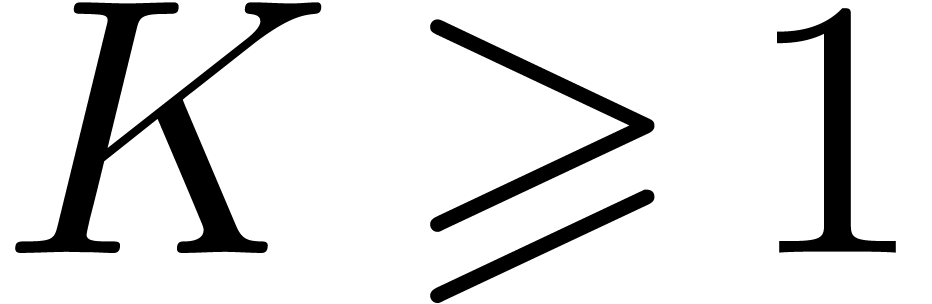 depends on
depends on  ,
and such that for all
,
and such that for all 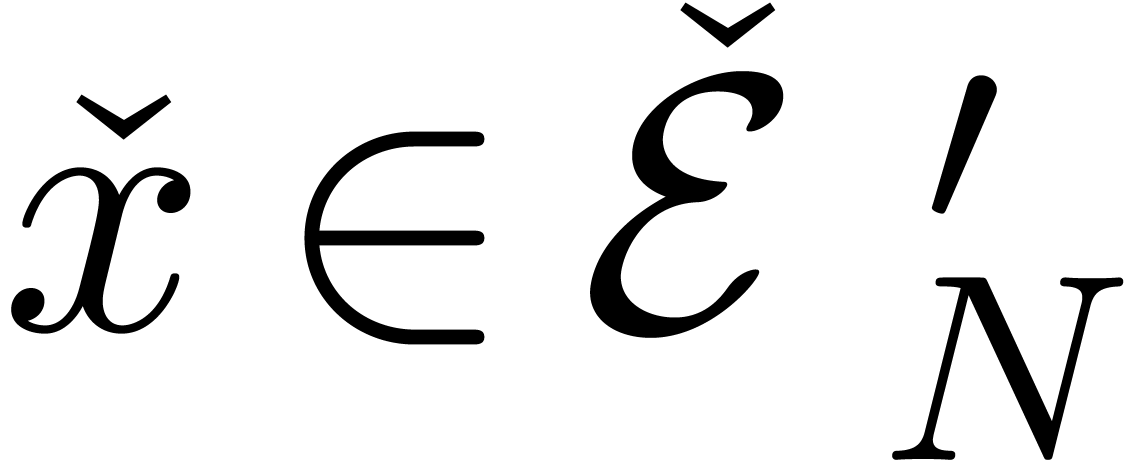 , we
either have
, we
either have 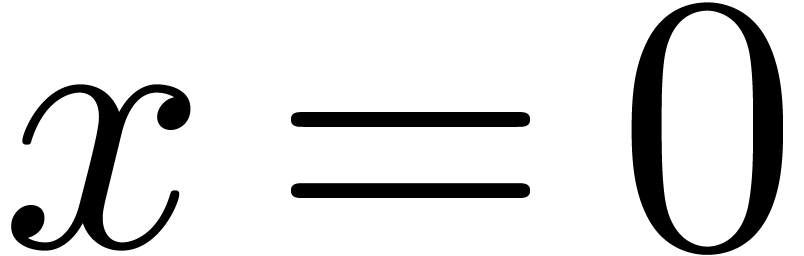 or
or 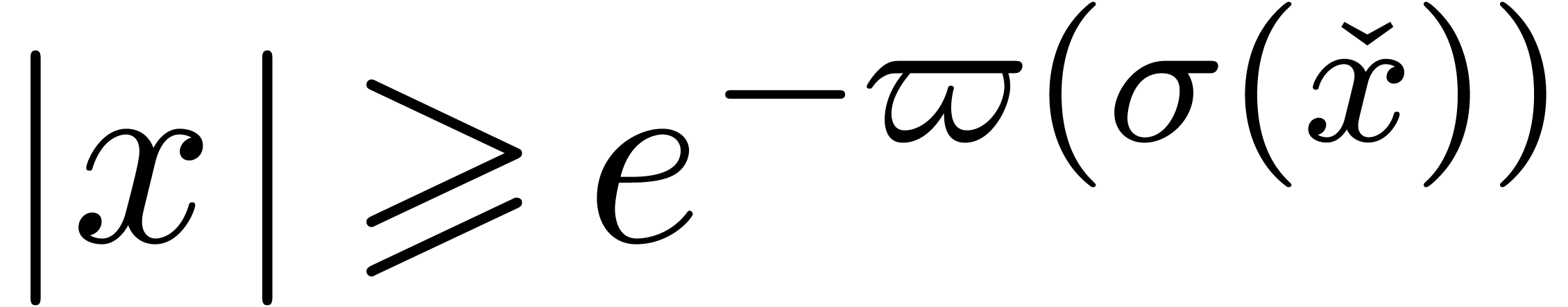 .
.
It should be noticed that this conjecture holds for all  as soon as it holds for a particular
as soon as it holds for a particular 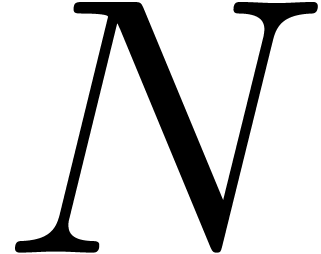 .
Indeed, for
.
Indeed, for 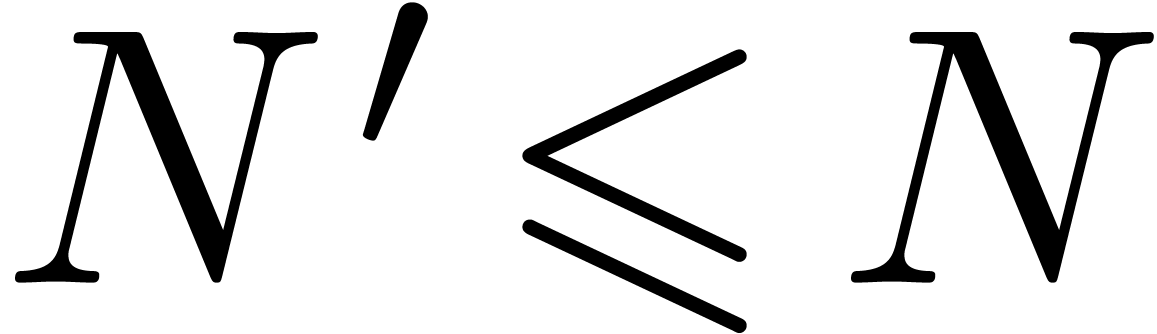 we may take
we may take 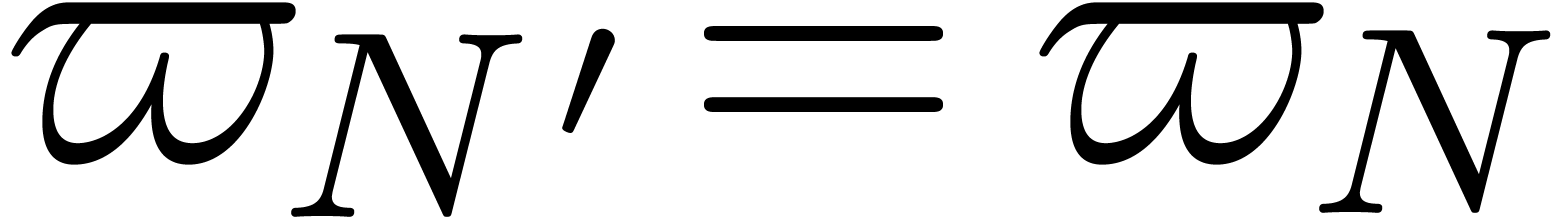 . For
. For 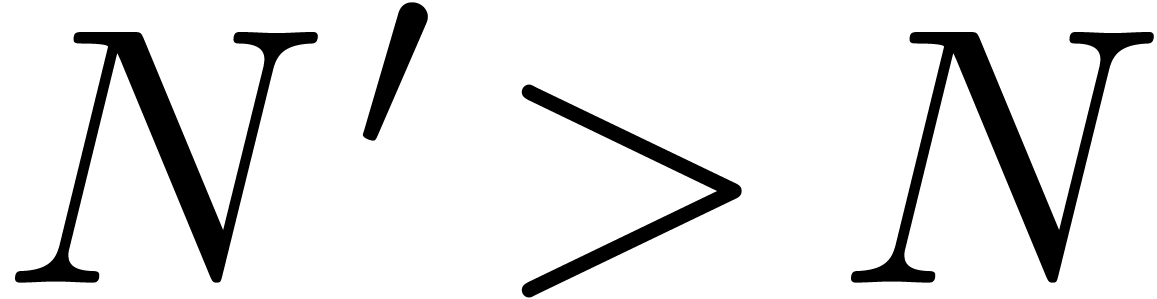 we may take
we may take
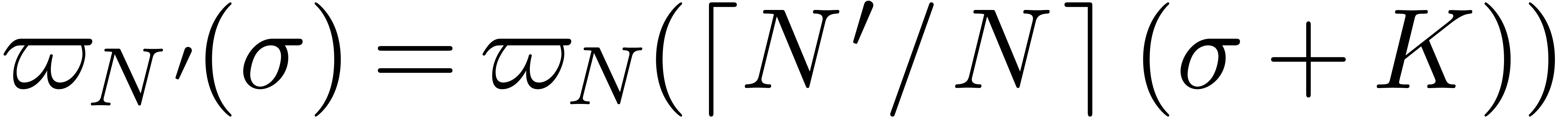 |
(4) |
for some constant  , since any
, since any
 with
with  may be rewritten as
may be rewritten as
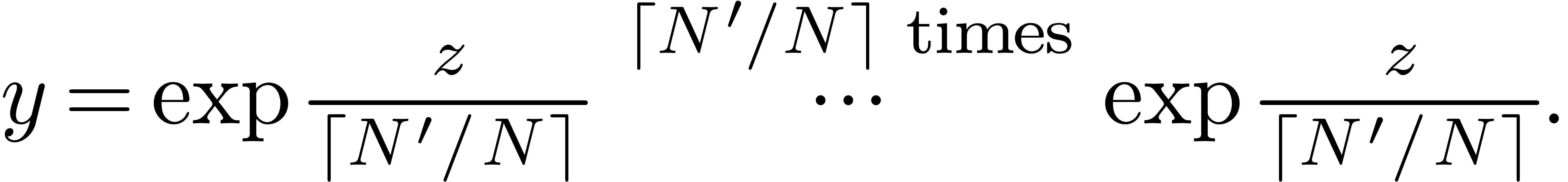
In a similar way, if 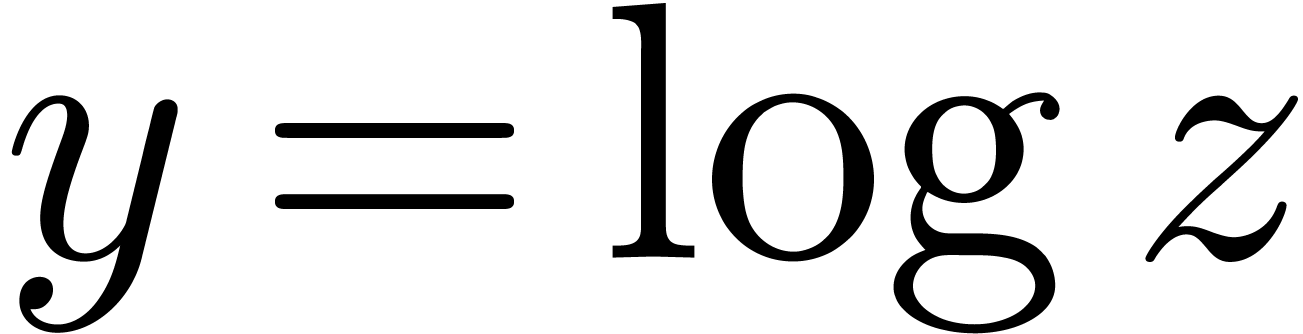 with
with 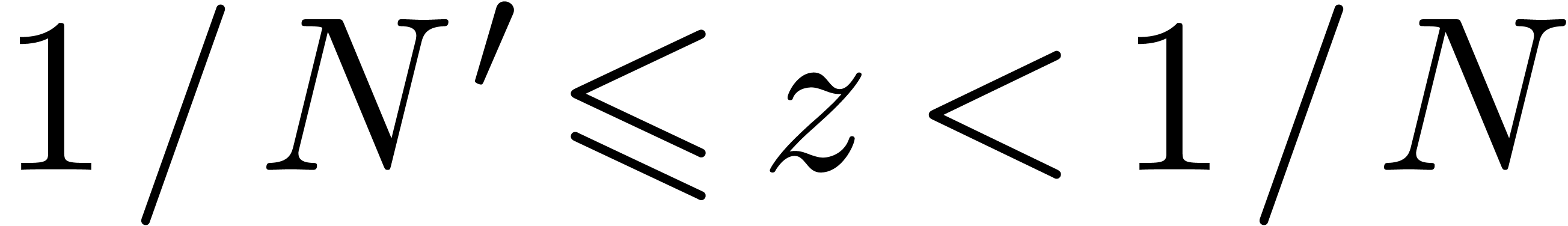 or
or  , then we may decompose
, then we may decompose
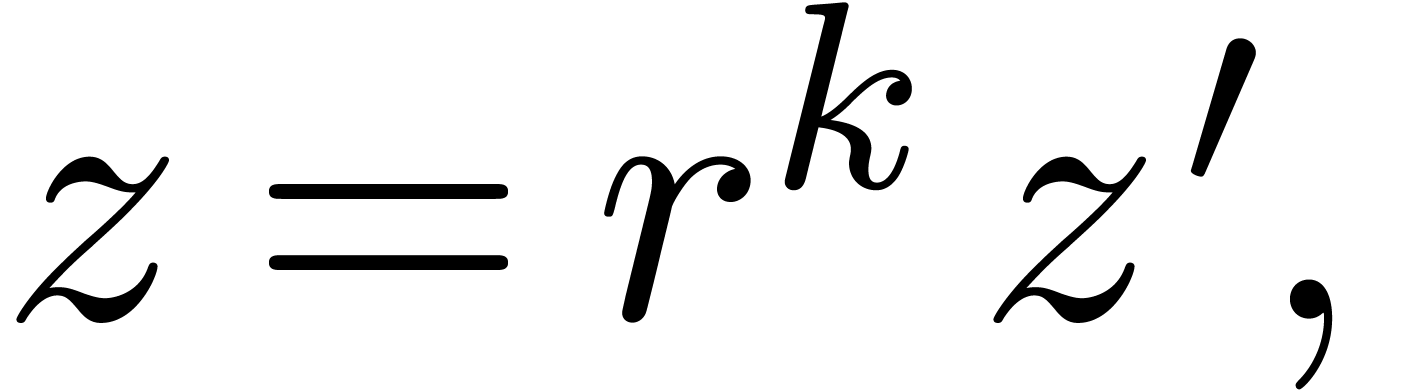 |
(5) |
where 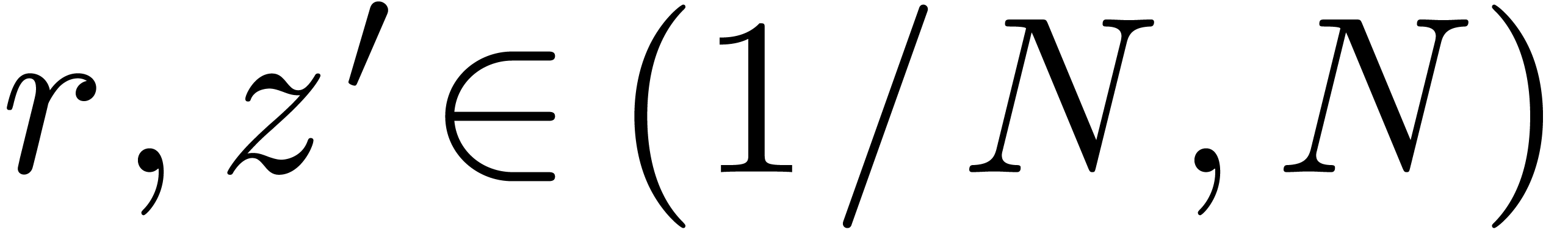 and
and 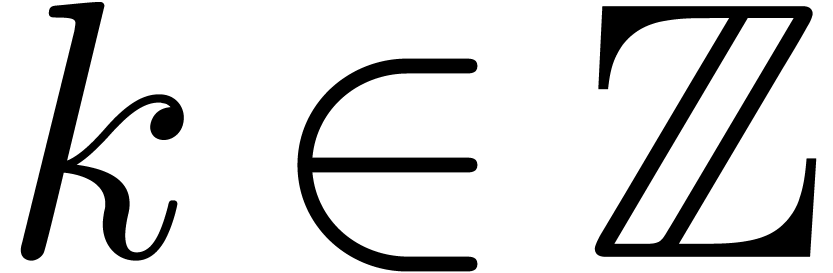 ,
so that
,
so that
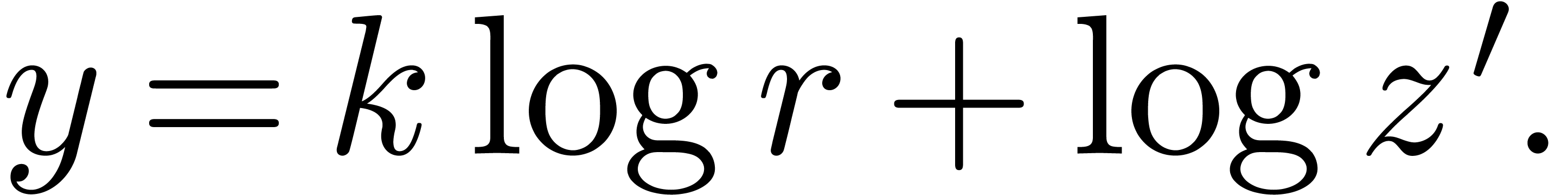
Moreover, by selecting 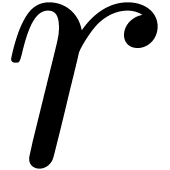 to be a fixed rational
number of small size close to
to be a fixed rational
number of small size close to 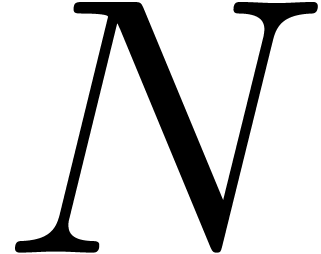 ,
we may bound
,
we may bound 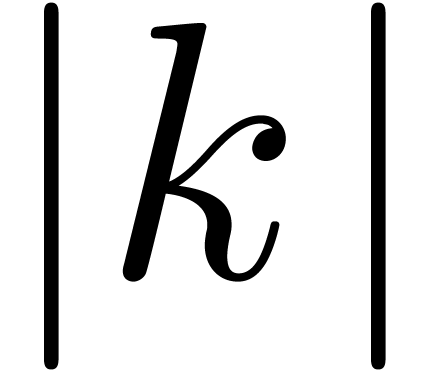 by a fixed constant, which explains
(2.2).
by a fixed constant, which explains
(2.2).
Obviously, conjecture 2.1 is implied by conjecture 2.2.
We do not know at present whether the inverse is also true. Yet another
variant of conjecture 2.2 is obtained by dropping the
requirement on the arguments to logarithms. Using (2.3),
this variant can again be reduced to conjecture 2.2, but
the witness function may change in a non linear way, since  can no longer be bound from above by a fixed constant, but
only by
can no longer be bound from above by a fixed constant, but
only by  .
.
2.2Values of differentially
algebraic functions
In [vdH01], we have generalized the witness conjectures for
exp-log constants to so called “holonomic constants”. Such
constants are formed from the rationals, using the field operations and
holonomic functions (i.e. functions that satisfy a linear differential
equation over 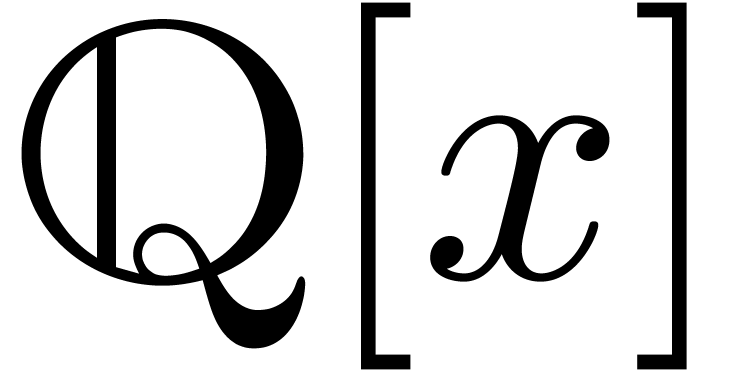 ). The approach
actually easily generalizes to more general constants, which arise as
values of differentially algebraic functions.
). The approach
actually easily generalizes to more general constants, which arise as
values of differentially algebraic functions.
Let 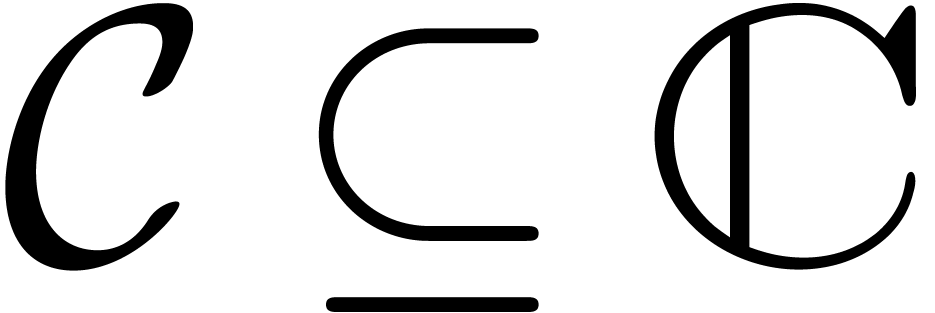 be a certain field of constants and let
be a certain field of constants and let 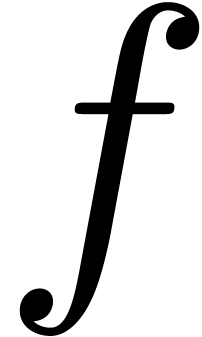 be a function which is analytic in
be a function which is analytic in  . We say that
. We say that 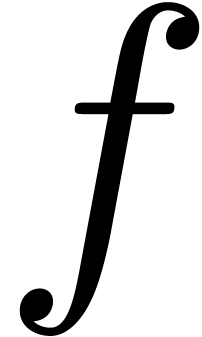 is
differentially algebraic over
is
differentially algebraic over  with initial
conditions in
with initial
conditions in  , if
, if  satisfies a differential equation
satisfies a differential equation
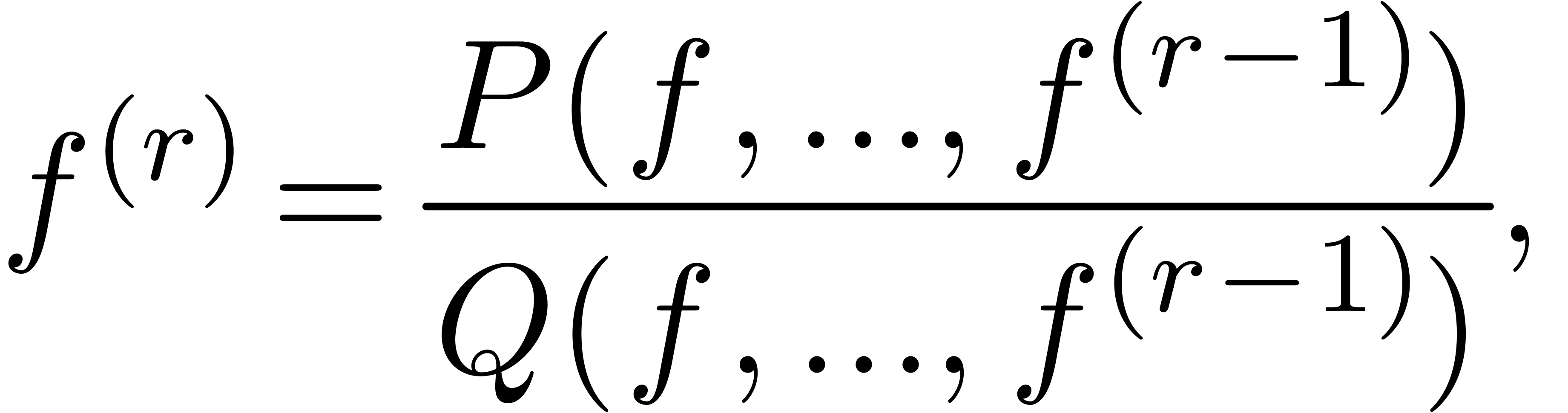
with 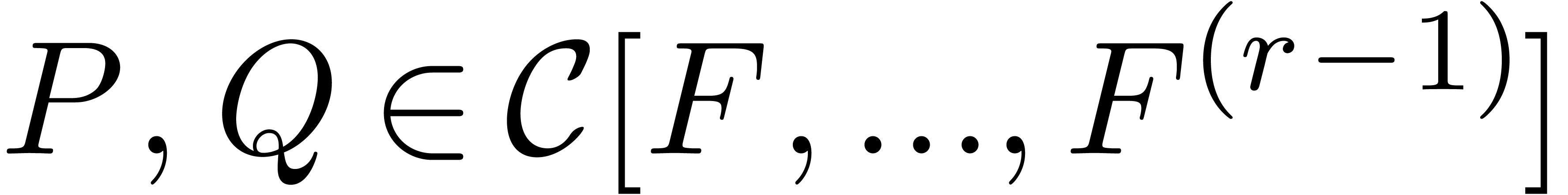 and where
and where 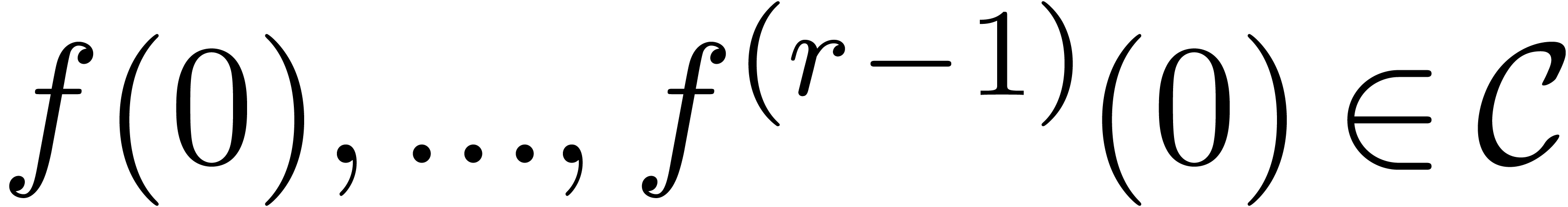 are such
that
are such
that
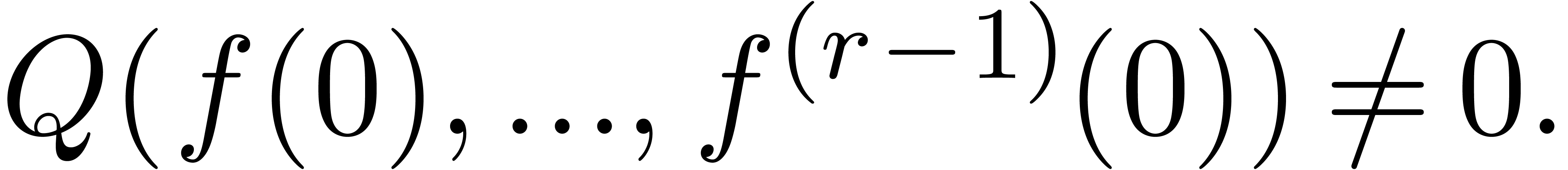
We will consider values of such functions  in
points
in
points 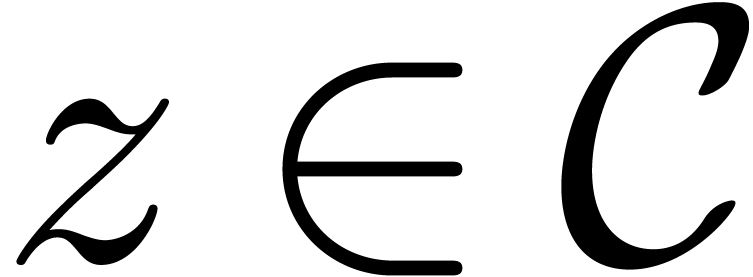 , such that
, such that  is strictly smaller than the radius of convergence
is strictly smaller than the radius of convergence  of
of 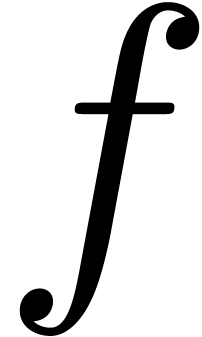 .
.
We may now construct a huge class of constants as follows. We start with
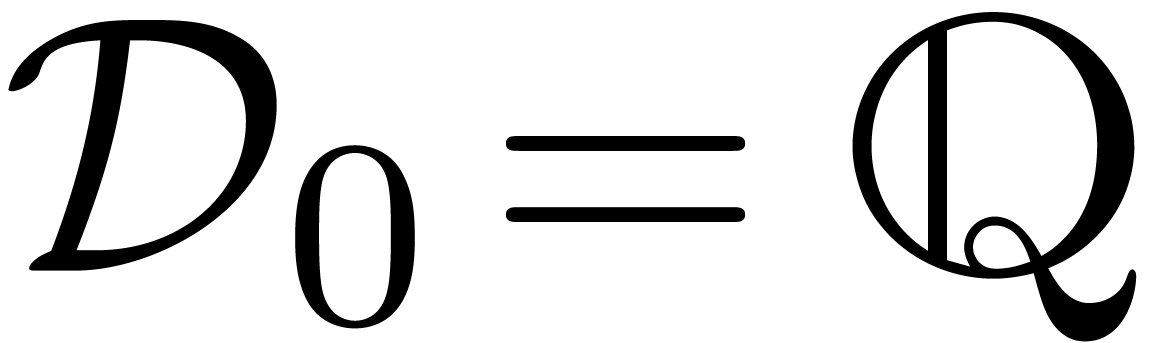 . Assuming that
. Assuming that 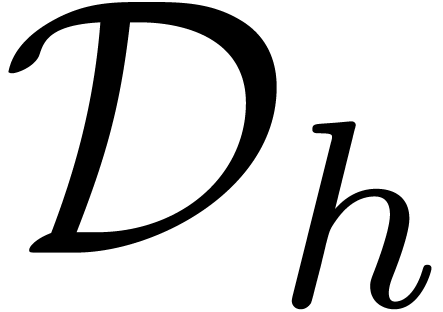 has been constructed, we let
has been constructed, we let 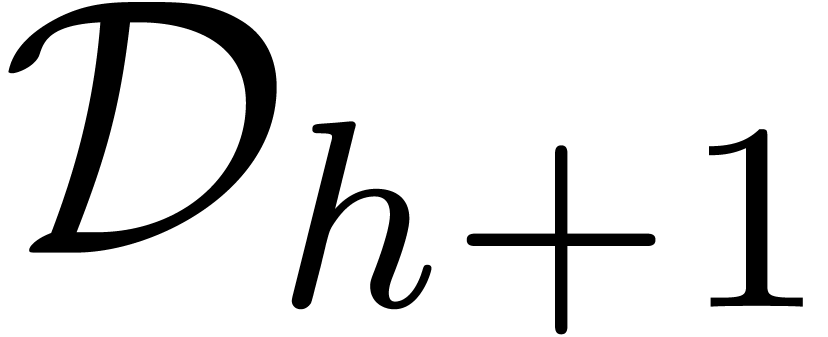 be
the set of all possible values in elements of
be
the set of all possible values in elements of 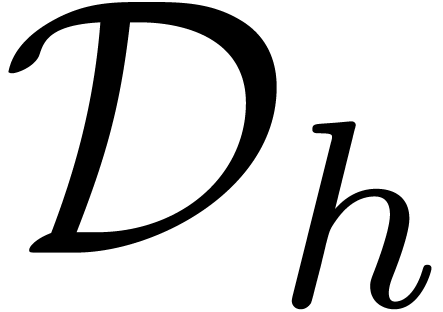 of
differentially algebraic functions over
of
differentially algebraic functions over 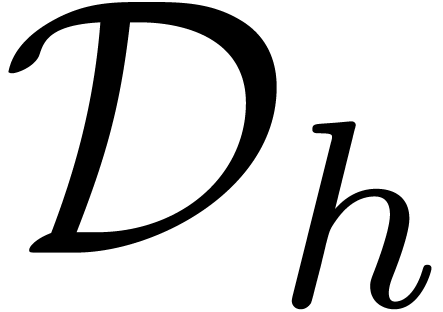 with
initial conditions in
with
initial conditions in 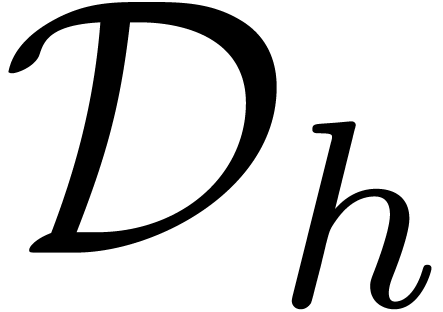 . It
can be shown that each
. It
can be shown that each  is a field, which
contains
is a field, which
contains 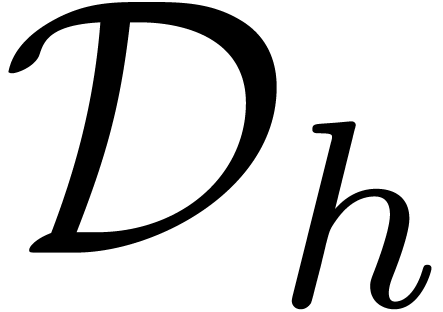 . Finally, we take
. Finally, we take
 . Elements in
. Elements in  may be represented by expressions as follows. Let
may be represented by expressions as follows. Let  be the smallest set of expressions such that
be the smallest set of expressions such that
From the expressiveness point of view, it is not really necessary to
have special expressions for the field operations (if we take 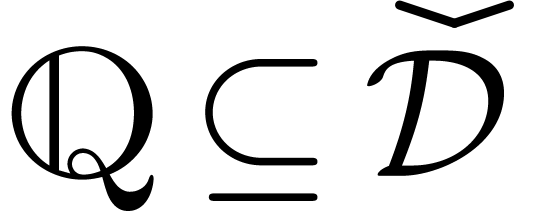 ). However, we do need them in
order to keep the sizes of expressions reasonably small.
). However, we do need them in
order to keep the sizes of expressions reasonably small.
2.3Corrected size functions
In order to state witness conjectures for constants in  , several approaches are possible. One
approach, which will be developed in the section 2.4, is to
restrict ones attention to representations by expressions in
, several approaches are possible. One
approach, which will be developed in the section 2.4, is to
restrict ones attention to representations by expressions in  of a special form, like we did in the case of exp-log
constants.
of a special form, like we did in the case of exp-log
constants.
Another approach, which was introduced in [vdH01], is to
redefine the size of an expression in such a way that expressions like
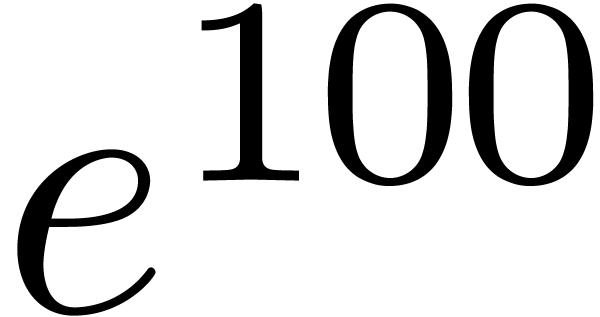 have a large size. In the present setting, this
comes down to defining the “size”
have a large size. In the present setting, this
comes down to defining the “size”  of
an expression
of
an expression 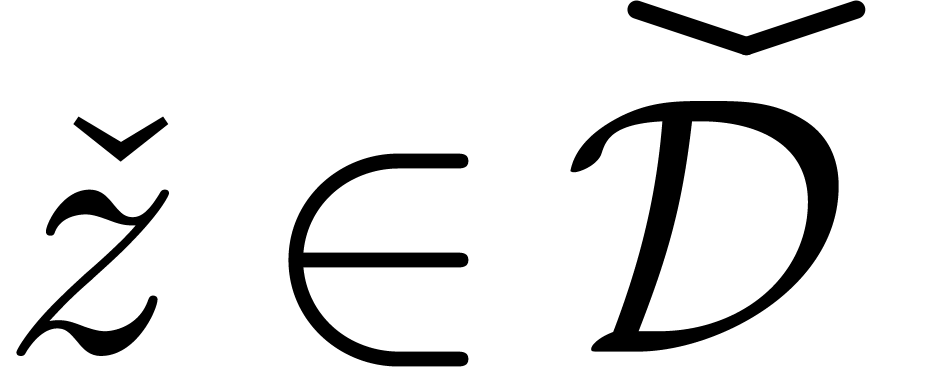 as follows:
as follows:
For example, in the case of the exponential function, we have 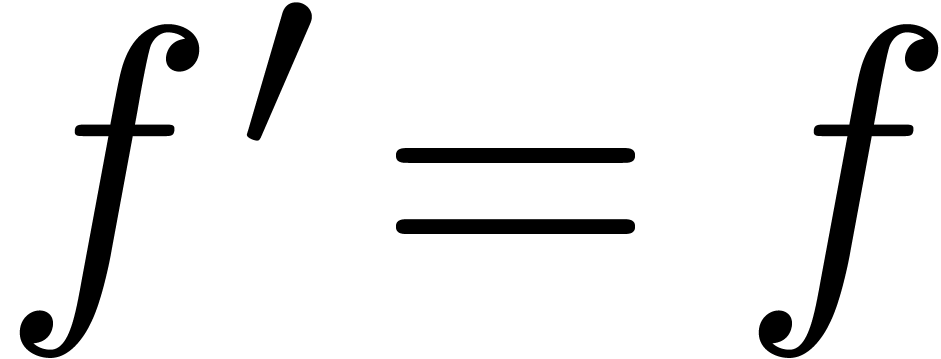 and
and 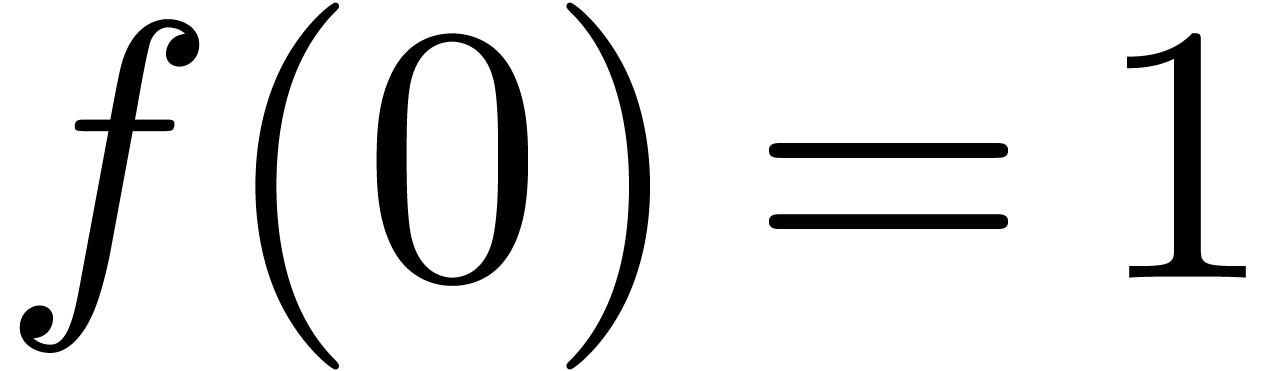 , so that
, so that
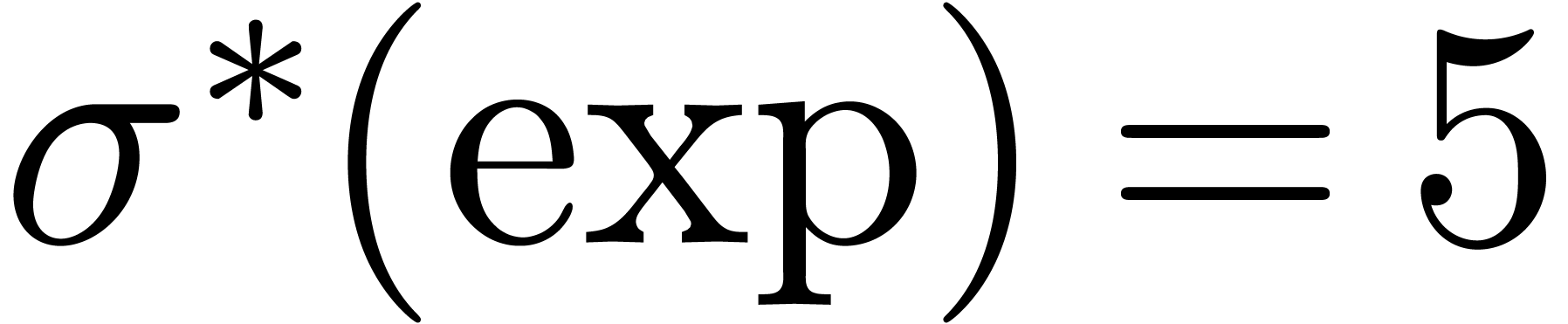 and
and 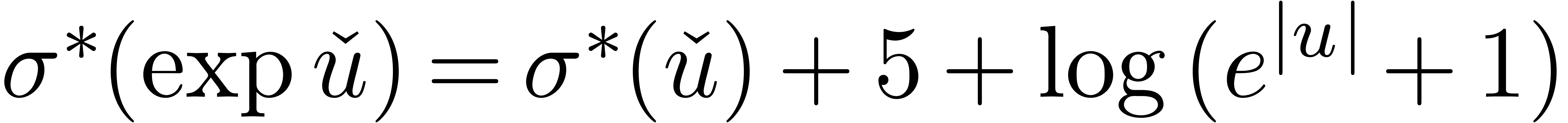 .
Hence,
.
Hence, 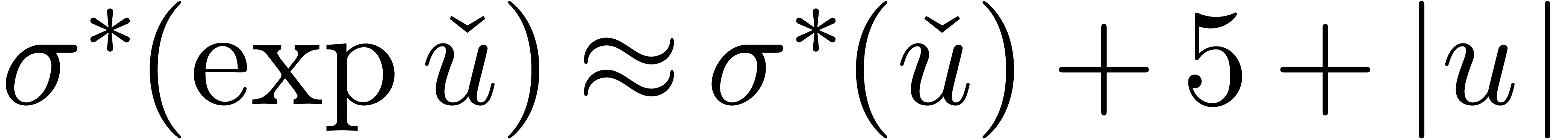 for large
for large  .
Because of the corrective term
.
Because of the corrective term  ,
an expression like
,
an expression like 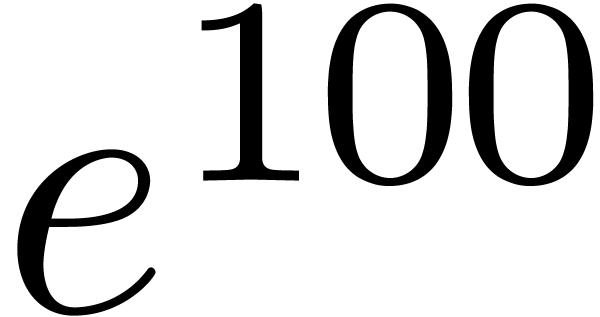 will therefore have a large
size.
will therefore have a large
size.
Conjecture 3. There
exists a witness function 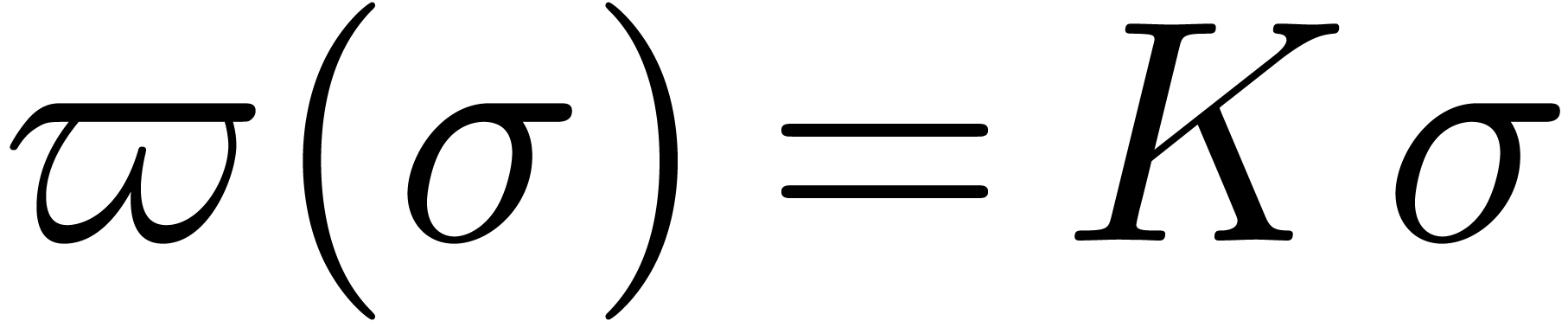 with
with 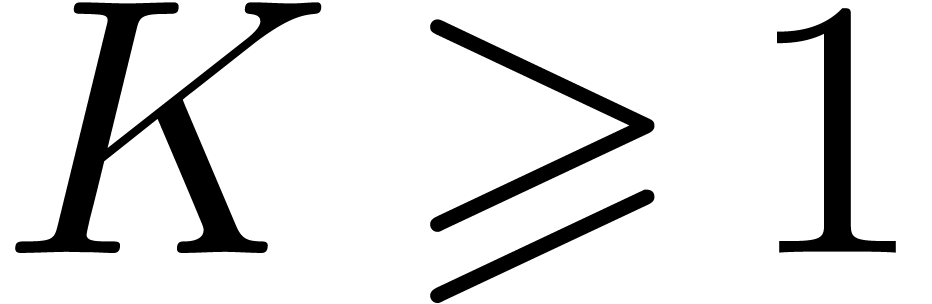 , such that for all
, such that for all 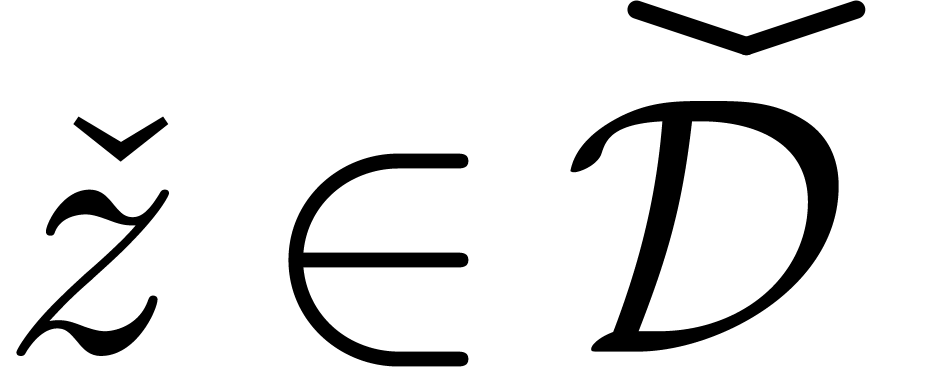 , we either have
, we either have 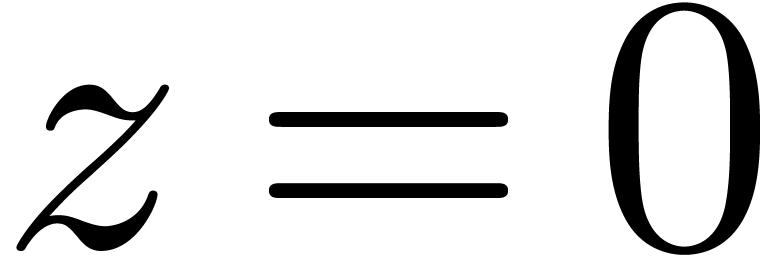 or
or 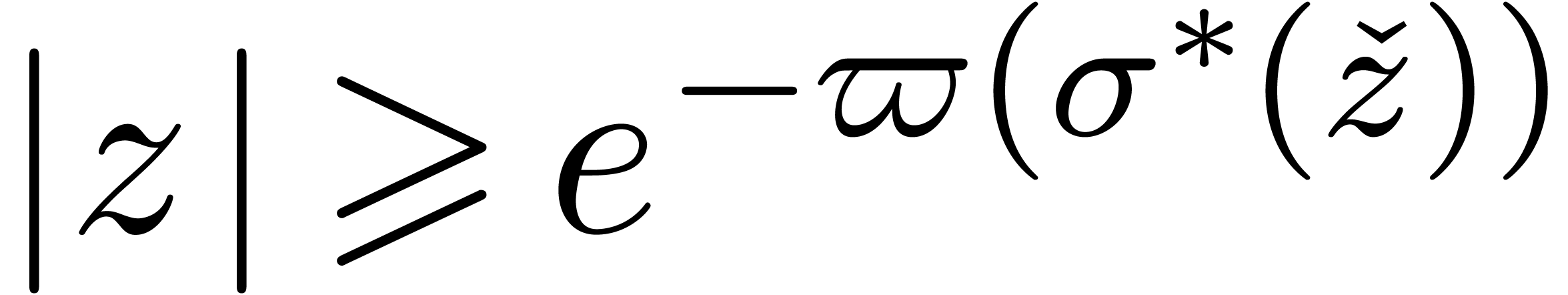 .
.
Remark 4. It is easy to show by
structural induction that we also have the upper bound
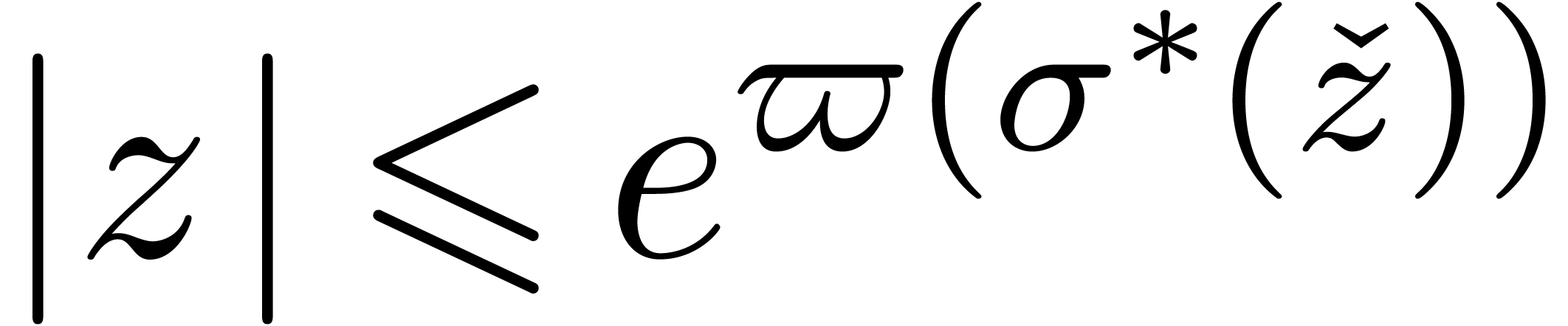
for all 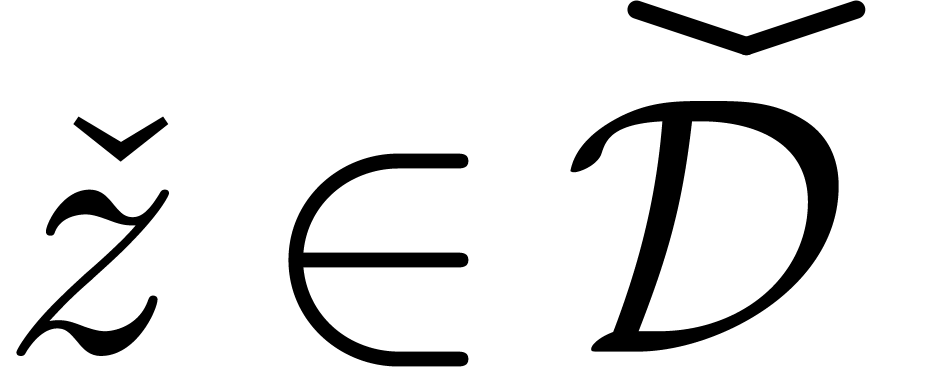 , if the conjecture
holds. Notice also that this bound holds independently from the
conjecture, if we disallow expressions of the form
, if the conjecture
holds. Notice also that this bound holds independently from the
conjecture, if we disallow expressions of the form 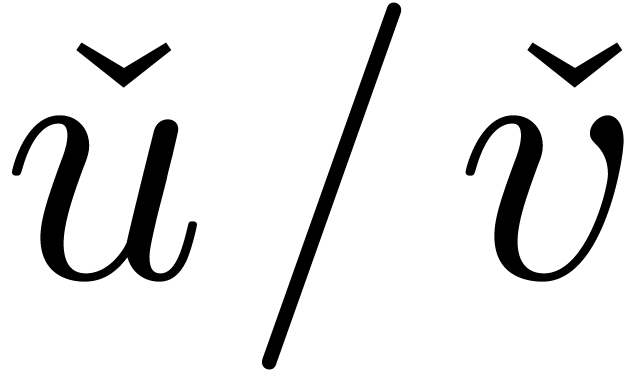 .
.
2.4Admissible expressions
The second approach in order to state witness conjectures for  is to use the usual size function
is to use the usual size function  , which is defined recursively as the corrected size
function
, which is defined recursively as the corrected size
function 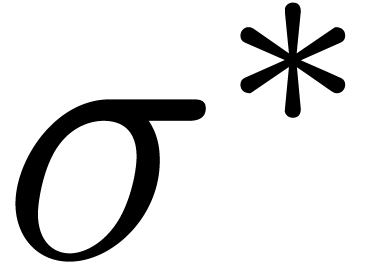 by omitting the corrective term
by omitting the corrective term 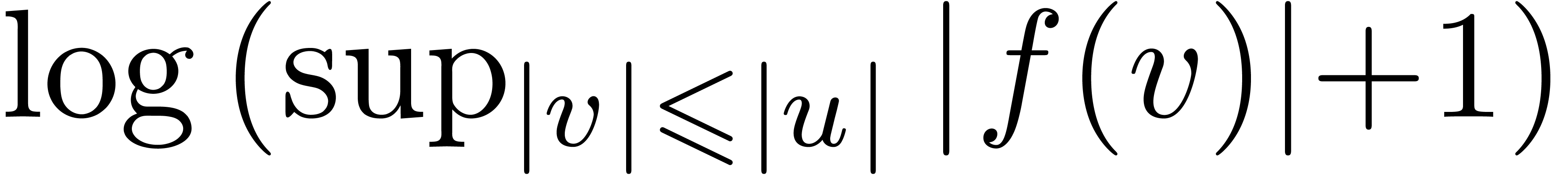 , but to restrict our attention to
a subset of admissible expressions of
, but to restrict our attention to
a subset of admissible expressions of  .
.
Let 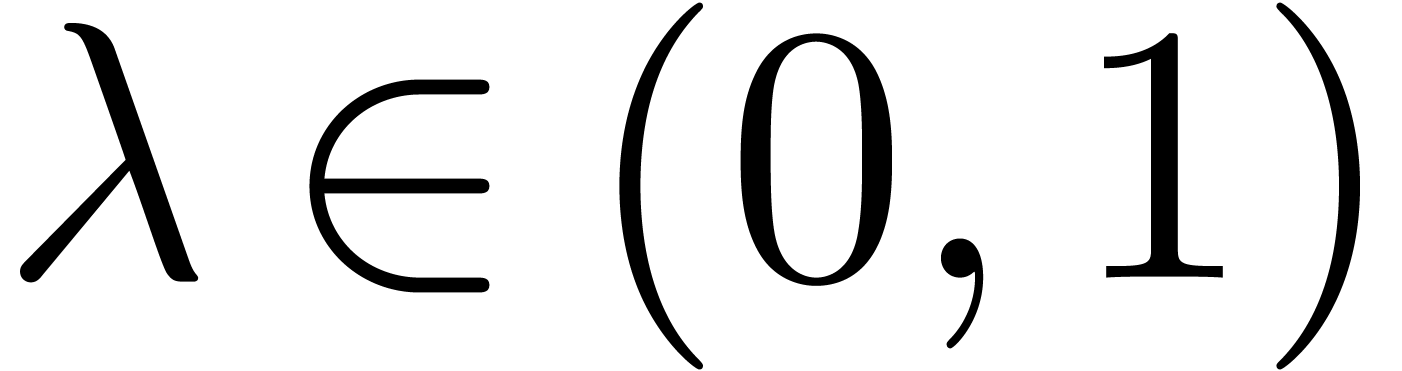 be a rational parameter. We recursively
define the subset
be a rational parameter. We recursively
define the subset 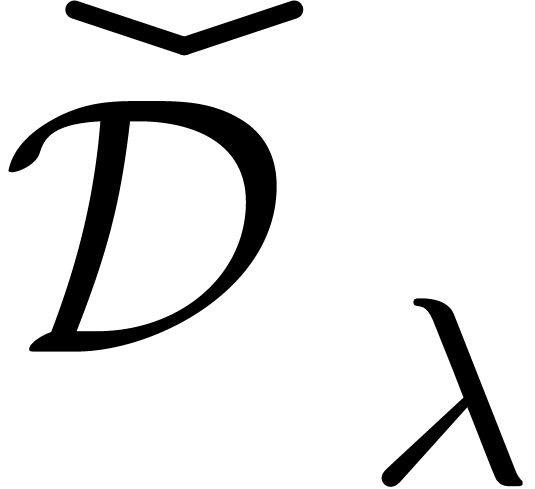 in a similar way as
in a similar way as  , but each time that
, but each time that 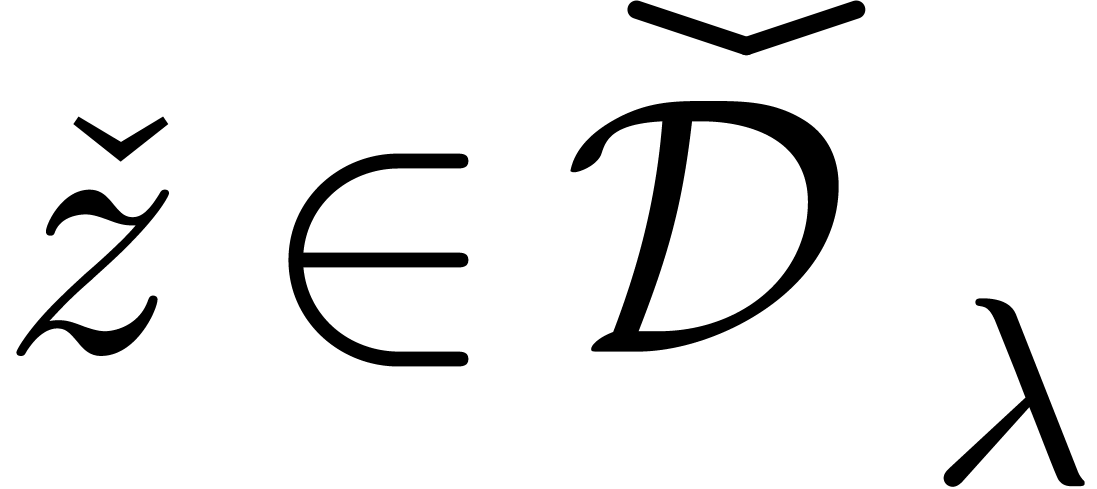 is of the form
is of the form 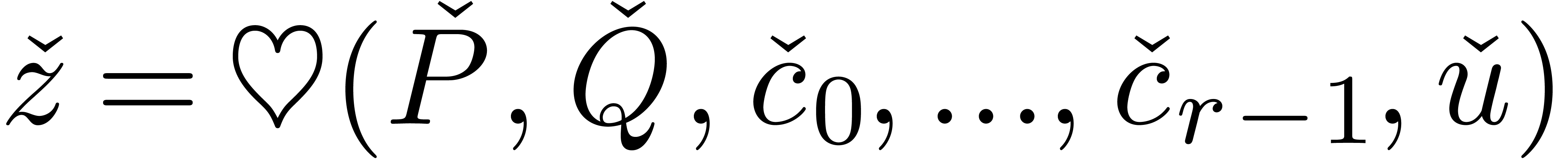 ,
we require that
,
we require that 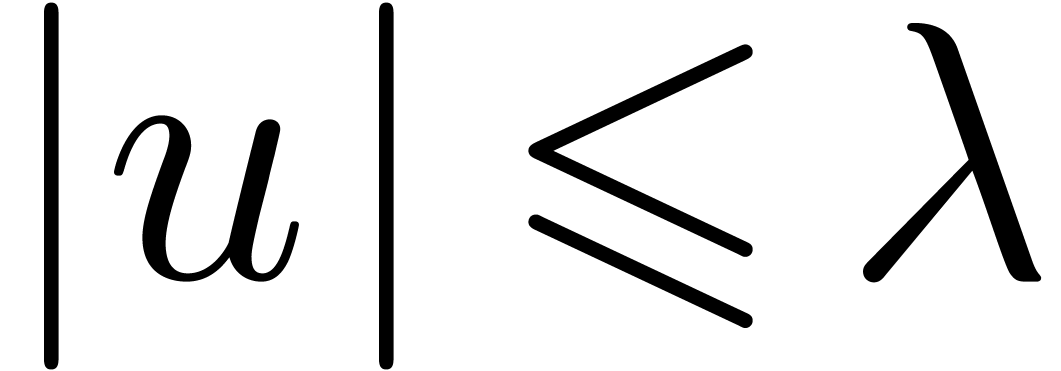 ,
, 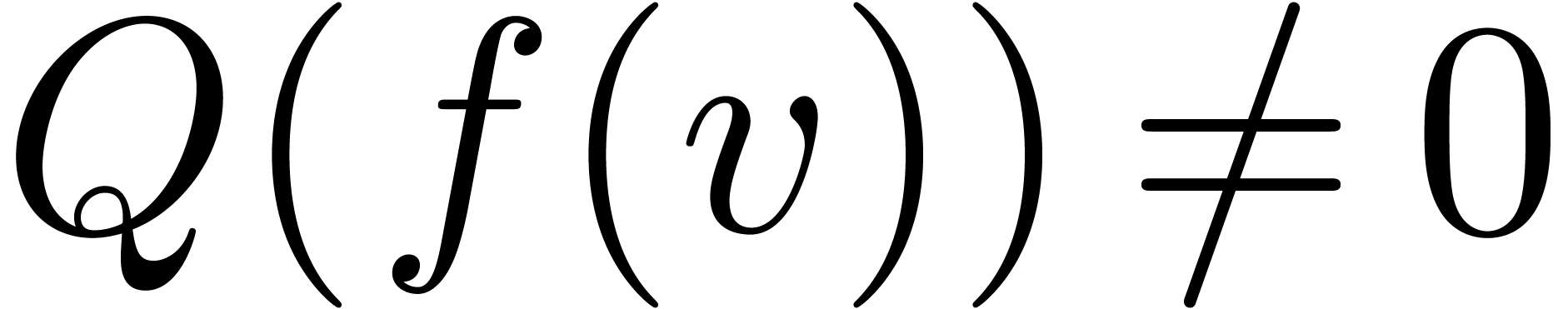 for all
for all 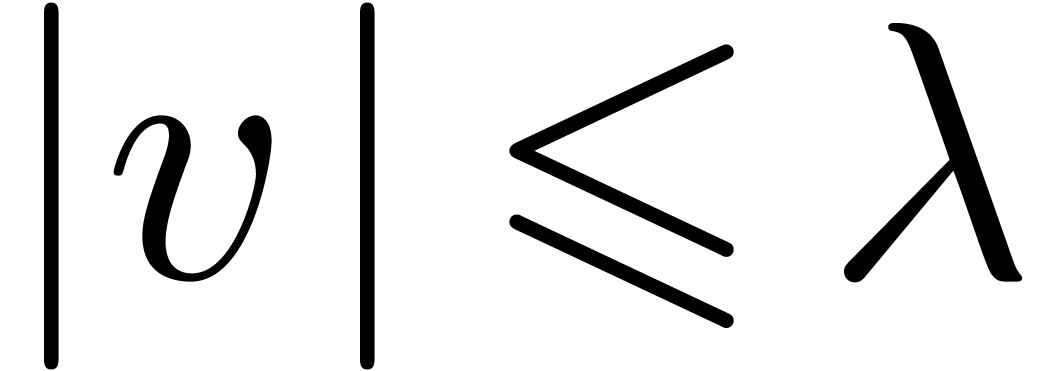 , and
, and
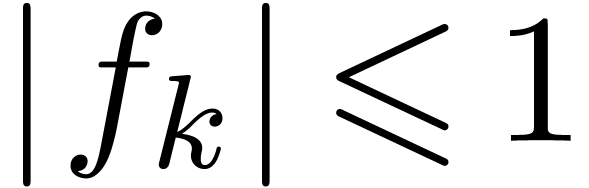 for each Taylor coefficient
for each Taylor coefficient  of
of  . We first claim that each
constant in
. We first claim that each
constant in  may be represented by an expression
in
may be represented by an expression
in  . This follows from the
following two observations:
. This follows from the
following two observations:
We notice that the analytic continuation procedure in the second
observation is very close to rewriting 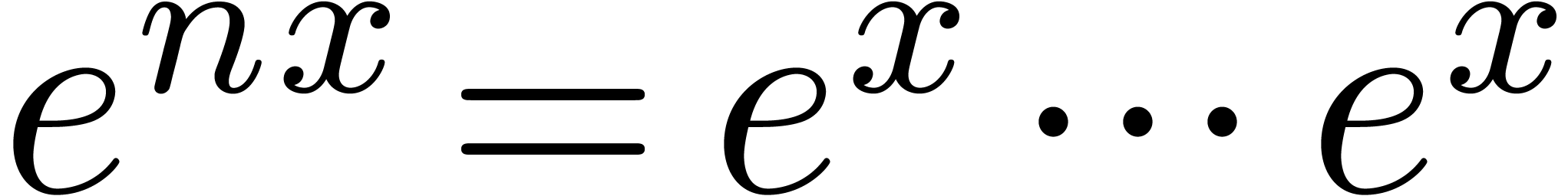 ,
as we did before.
,
as we did before.
Conjecture 5. Let
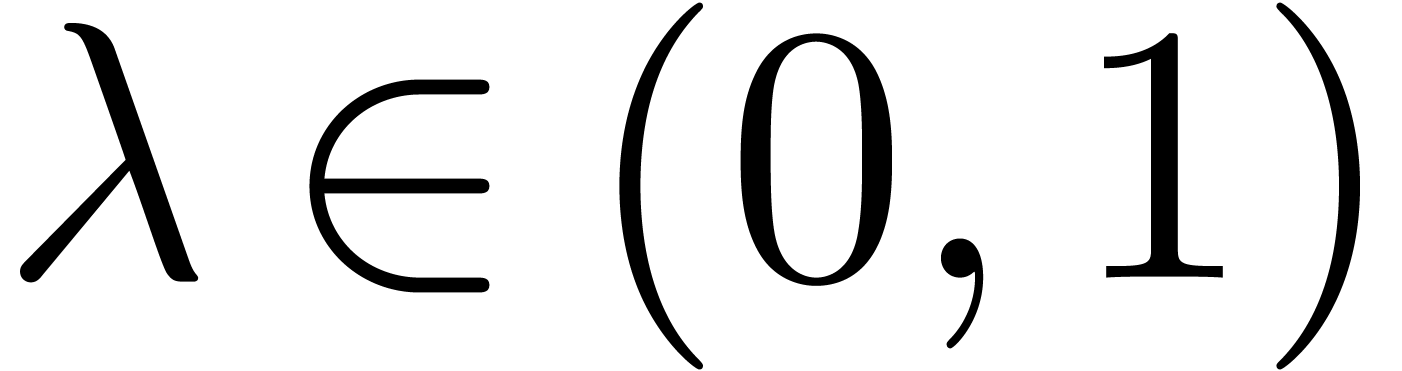 . Then there exists a witness
function
. Then there exists a witness
function 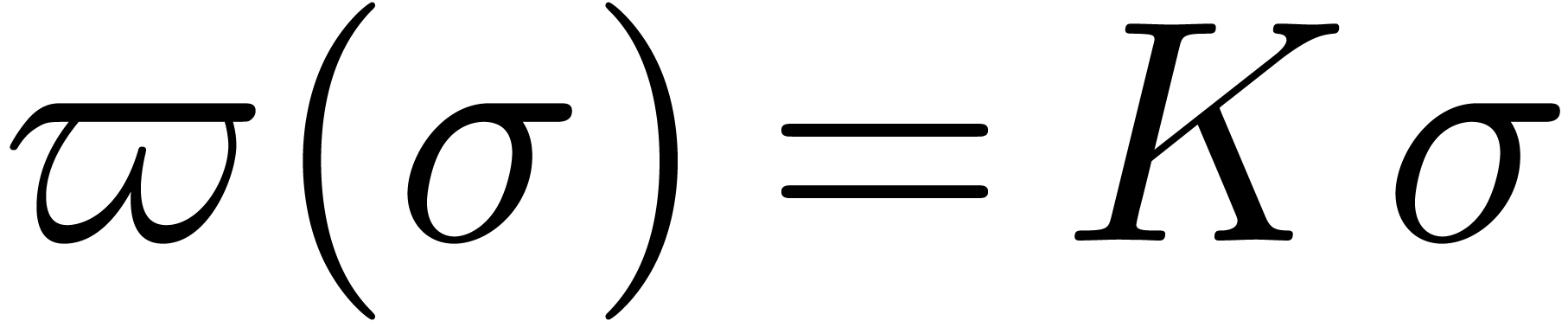 , where
, where 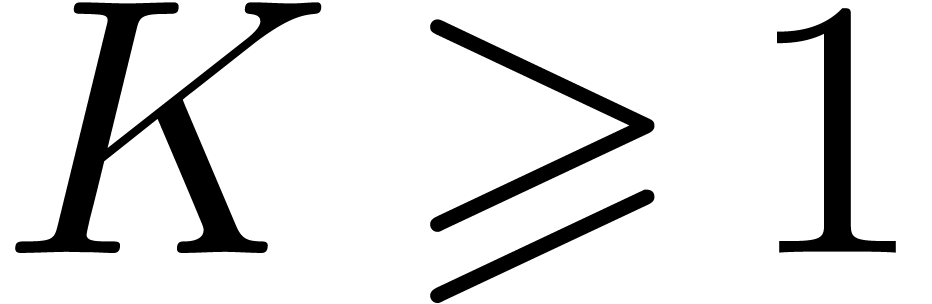 depends on
depends on  ,
and such that for all
,
and such that for all 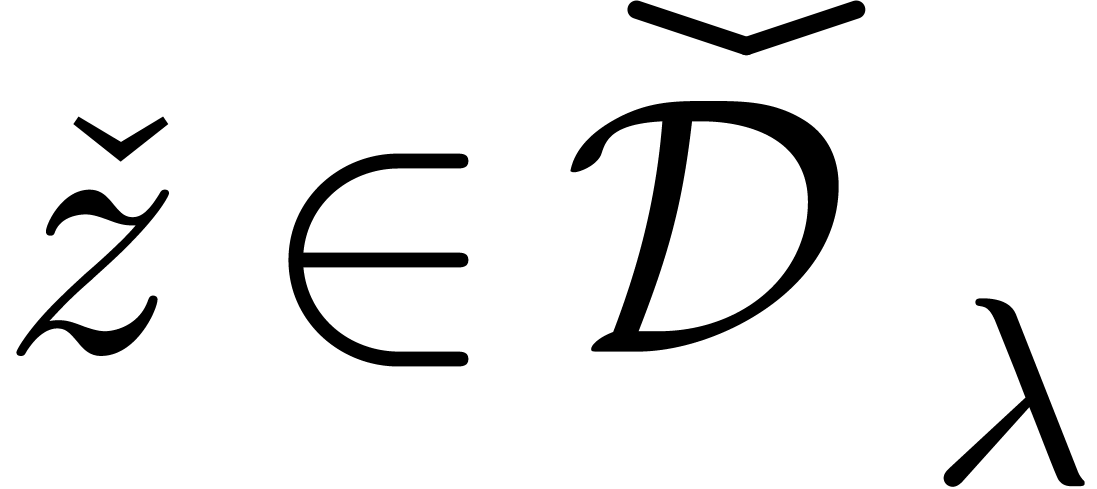 , we
either have
, we
either have  or
or  .
.
Because of the analytic continuation argument, conjecture 3.3
holds for all 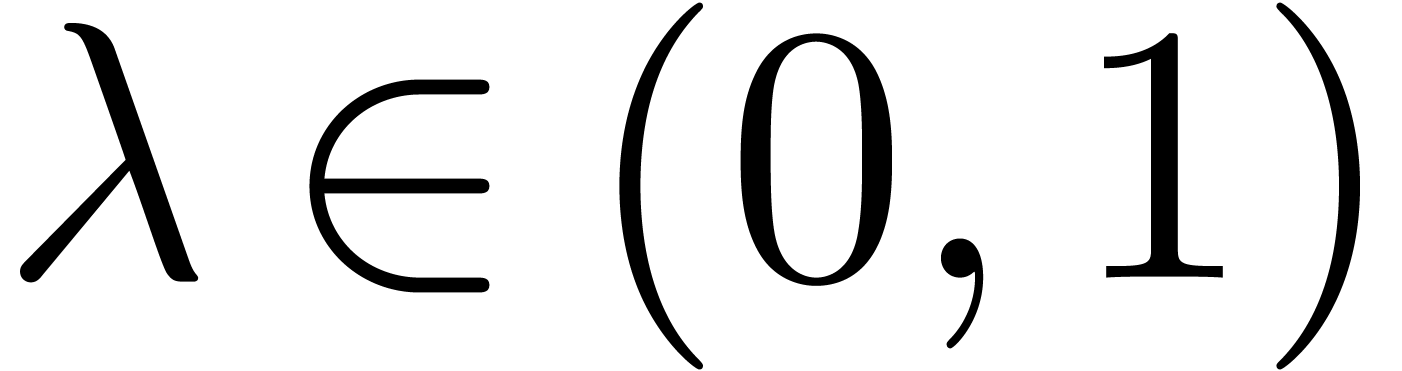 as soon as it holds for a
particular
as soon as it holds for a
particular  . It is not hard
to see that conjecture 2.2 is also implied by conjecture 3.3. Indeed, the coefficients of the Taylor series of
. It is not hard
to see that conjecture 2.2 is also implied by conjecture 3.3. Indeed, the coefficients of the Taylor series of  in
in  are all bounded by
are all bounded by  in module, so if
in module, so if 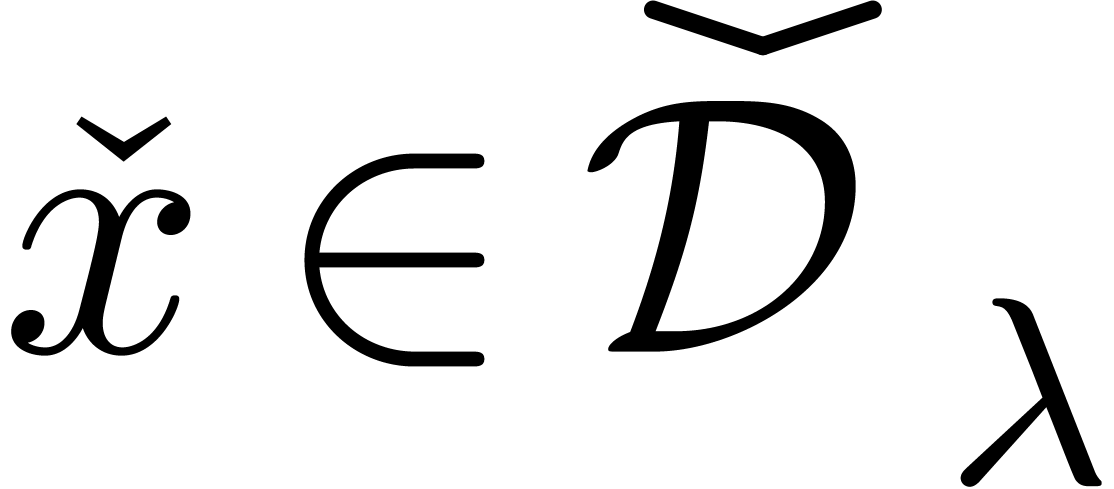 and
and 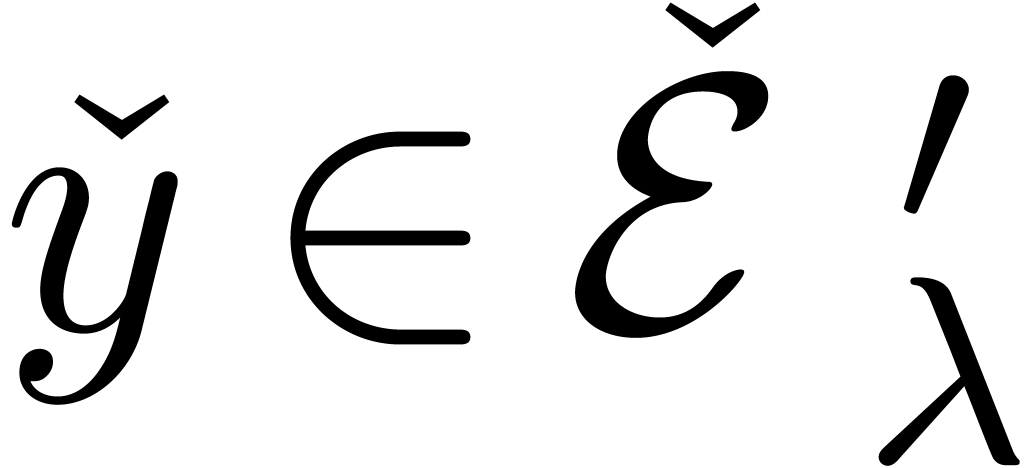 represent the same number
represent the same number  with
with 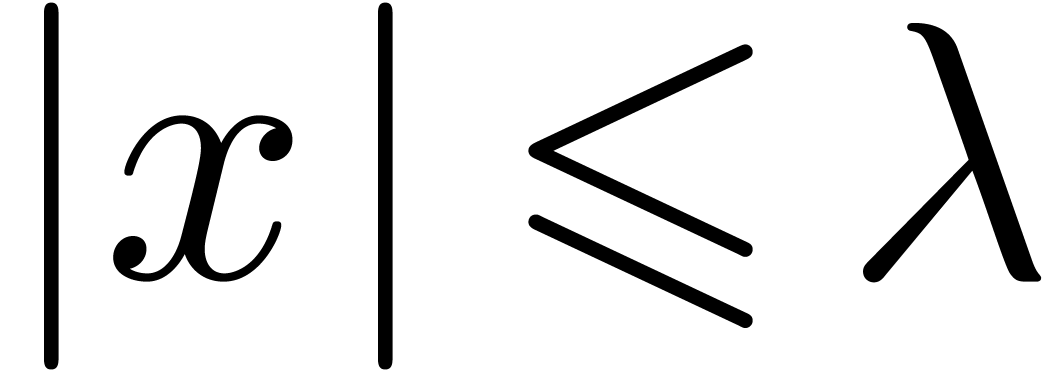 , then
, then 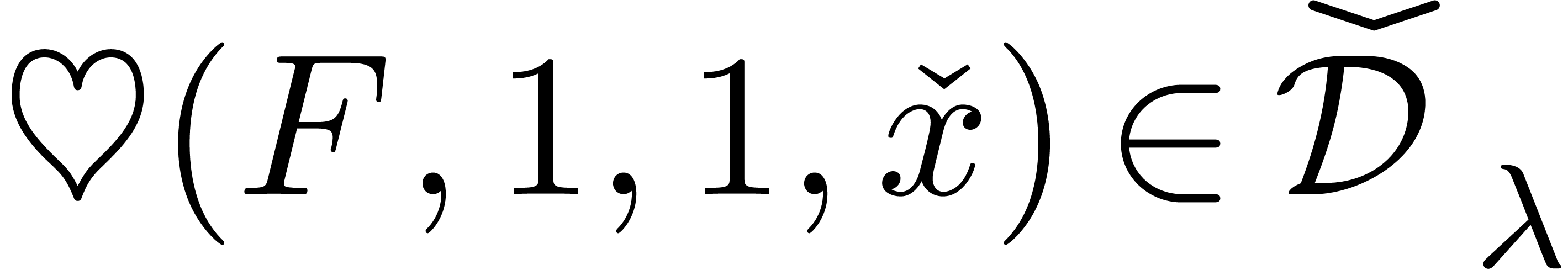 and
and 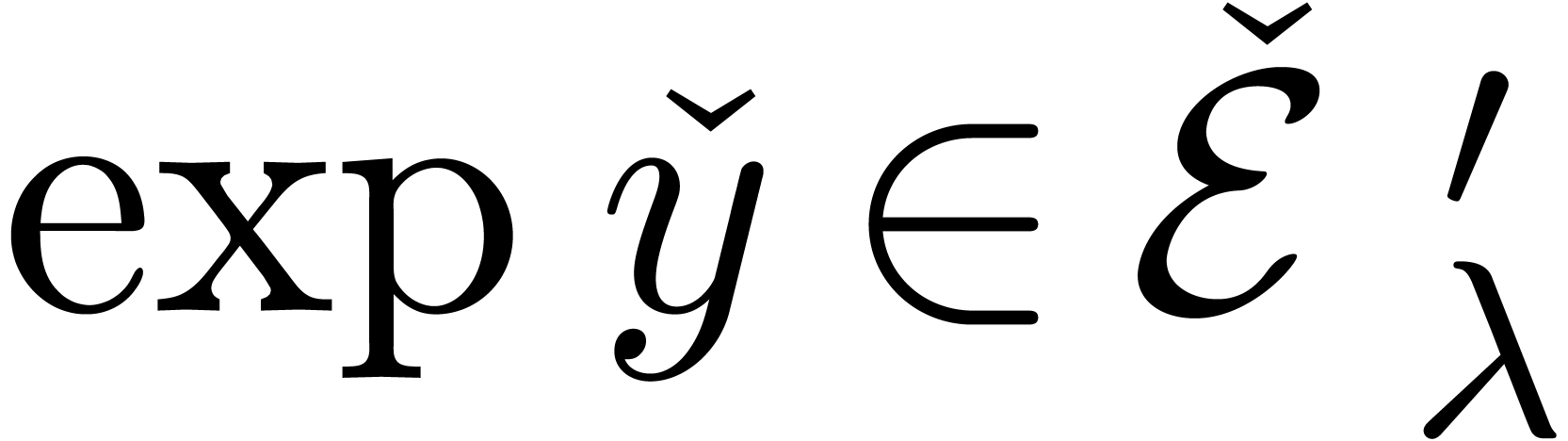 both represent
both represent 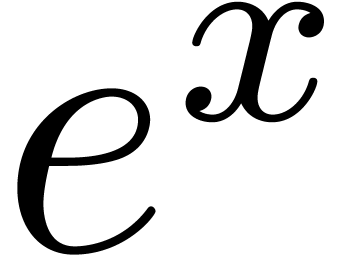 and
we have
and
we have 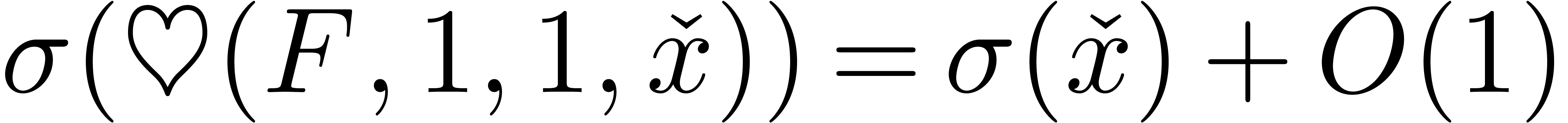 as well as
as well as 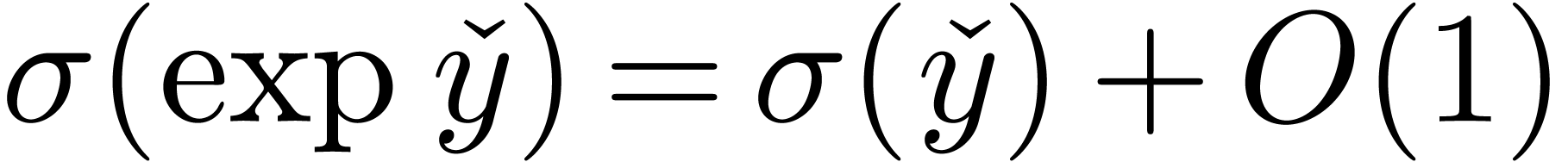 .
Logarithms may be handled in a similar fashion.
.
Logarithms may be handled in a similar fashion.
Let us now show that conjecture 3.3 is implied by
conjecture 2.3. Indeed, an analytic function 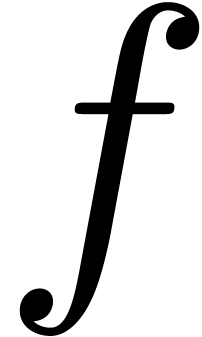 , such that
, such that 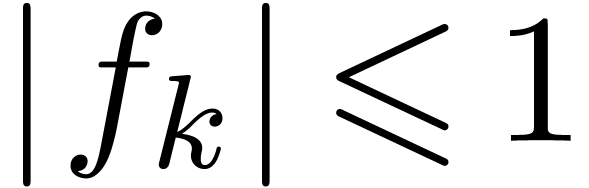 for all
for all
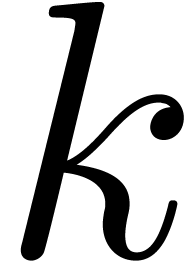 , satisfies the bound
, satisfies the bound
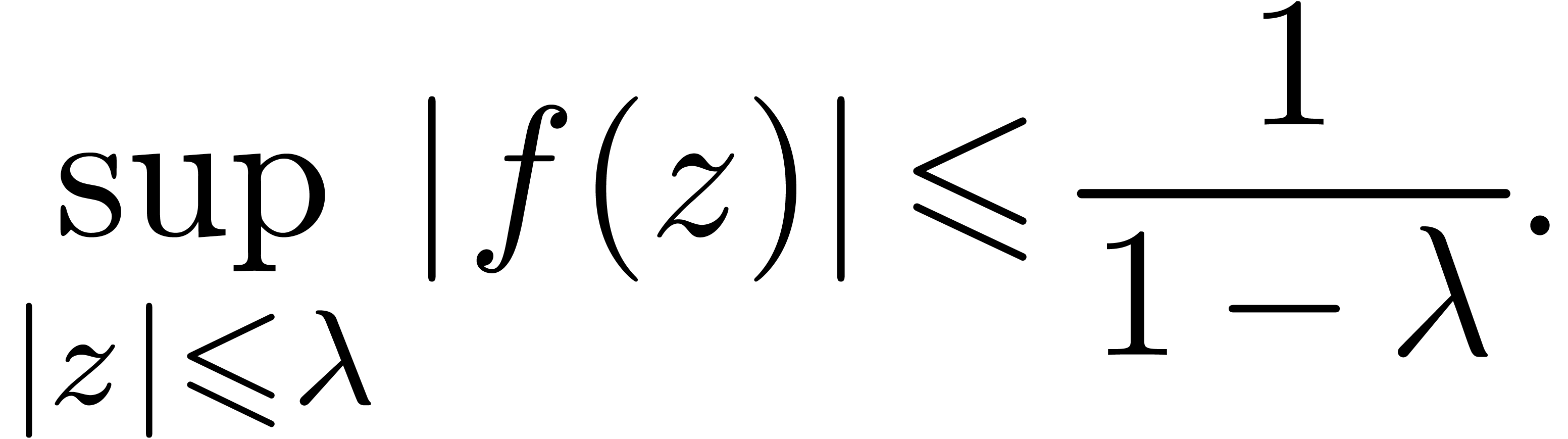
Consequently, the corrective terms in the corrected sizes 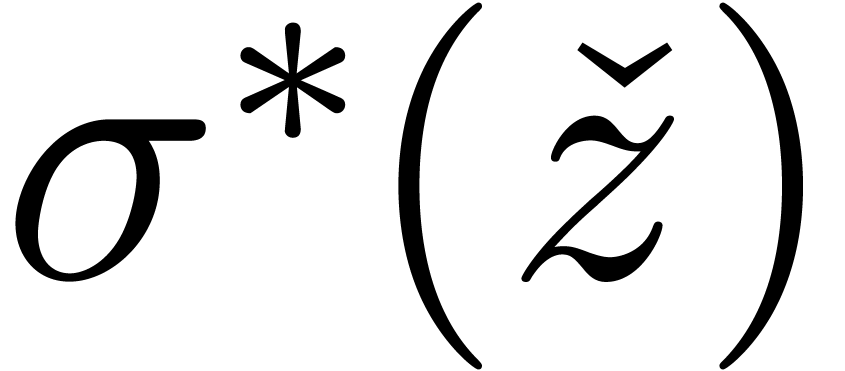 of expressions
of expressions 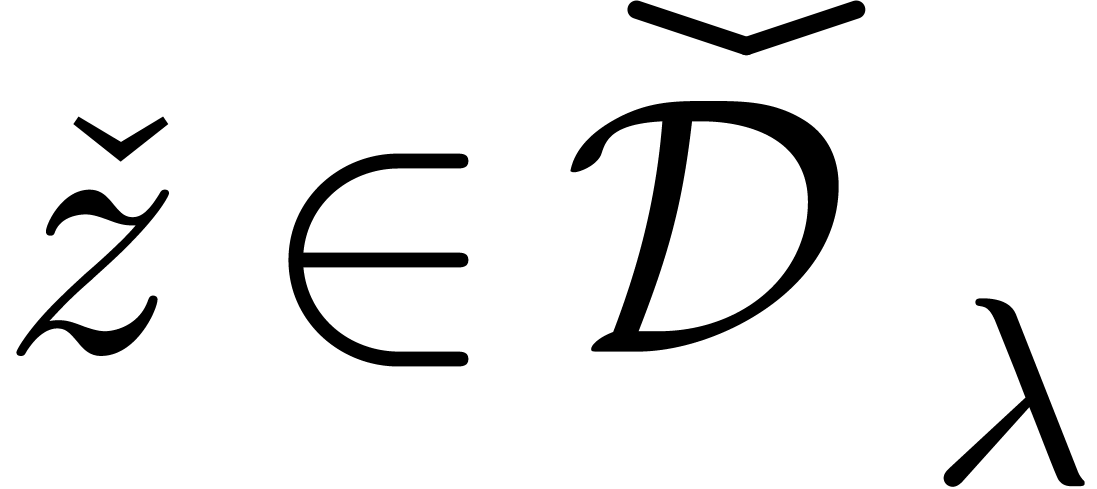 are uniformly
bounded. We conclude that
are uniformly
bounded. We conclude that 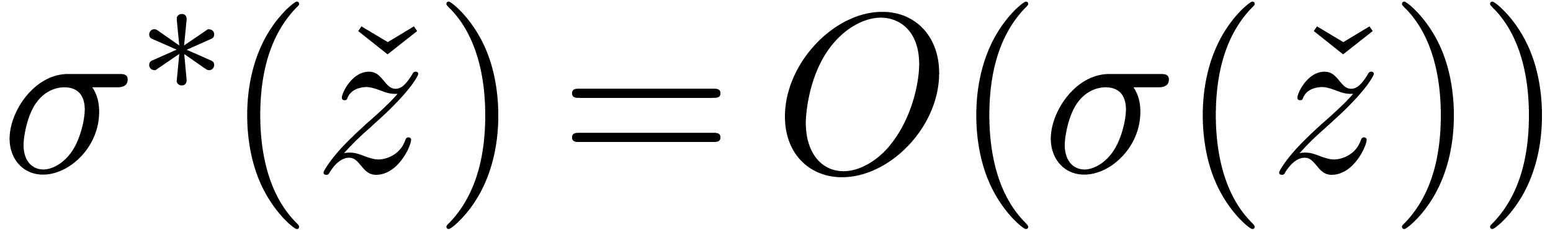 for
for 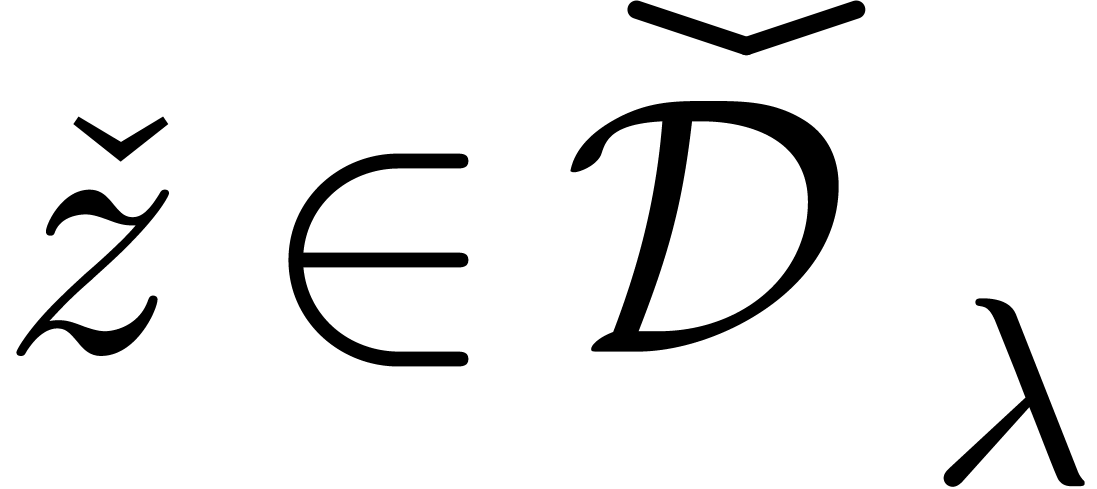 , which implies our claim.
, which implies our claim.
Actually, conjecture 2.3 seems to be slightly stronger than
conjecture 3.3. When using
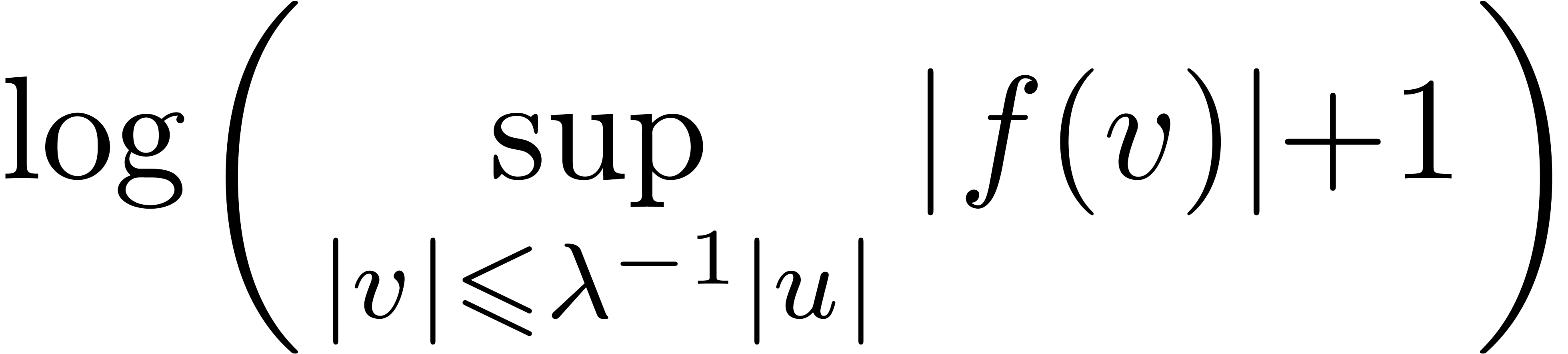
as a corrective term for some rational 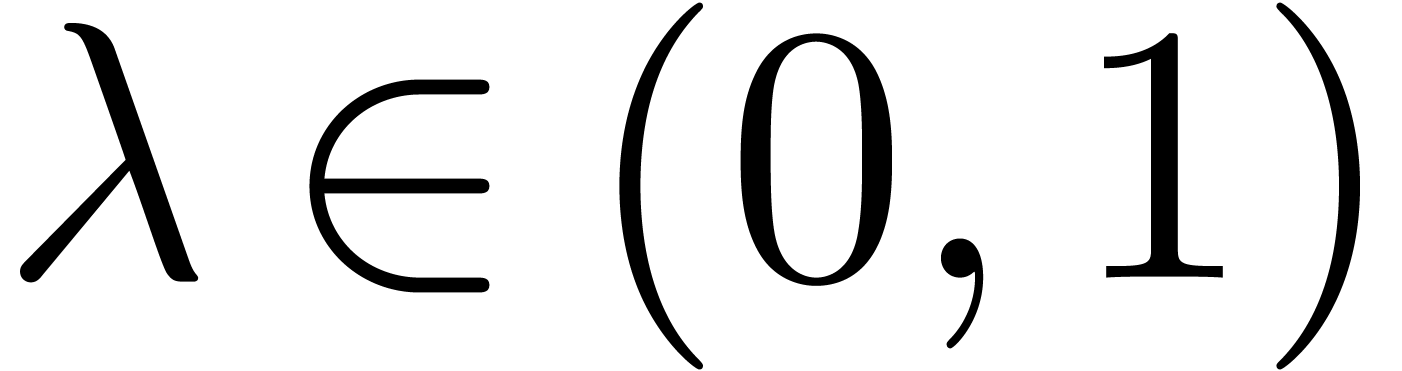 instead
of the usual one, both conjectures are equivalent. Indeed, in this case
we may normalize
instead
of the usual one, both conjectures are equivalent. Indeed, in this case
we may normalize 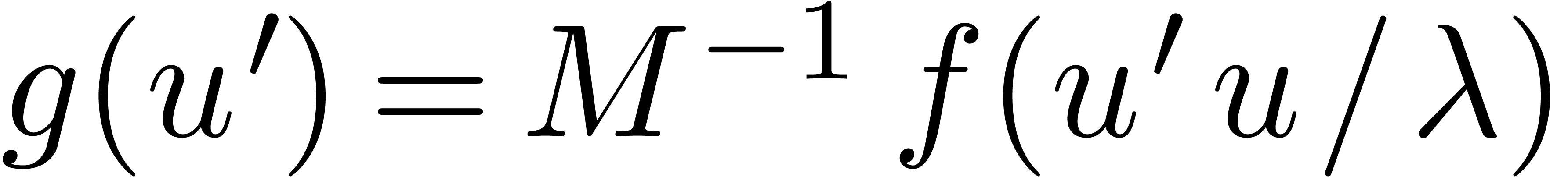 and replace
and replace 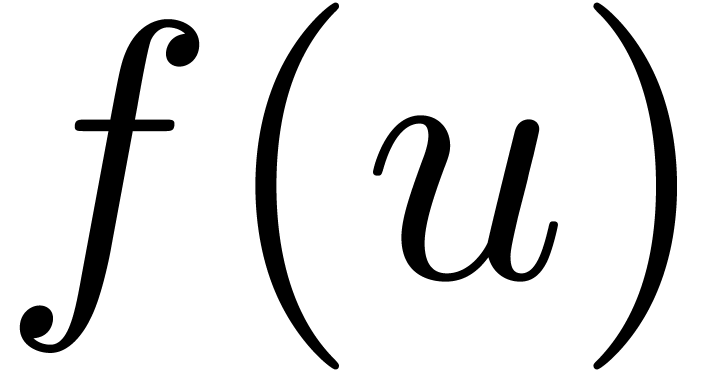 by
by 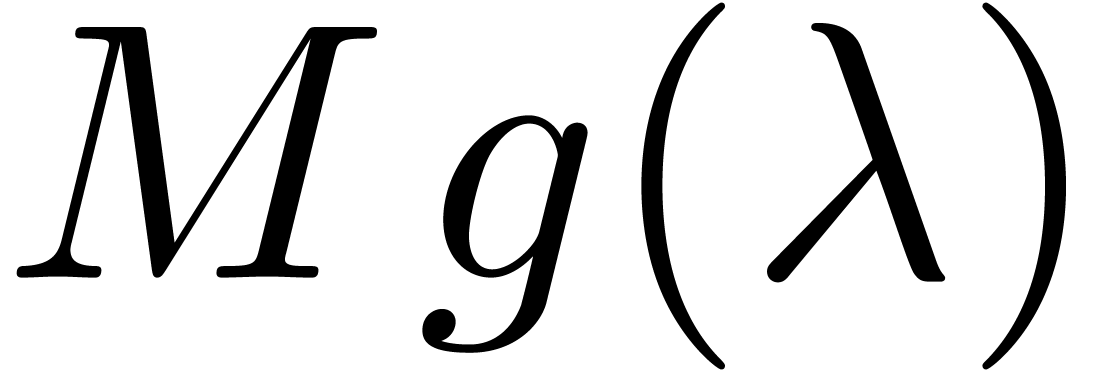 , where
, where 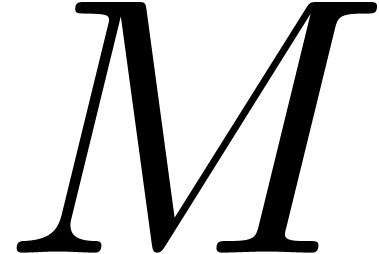 is a good rational upper approximation of
is a good rational upper approximation of 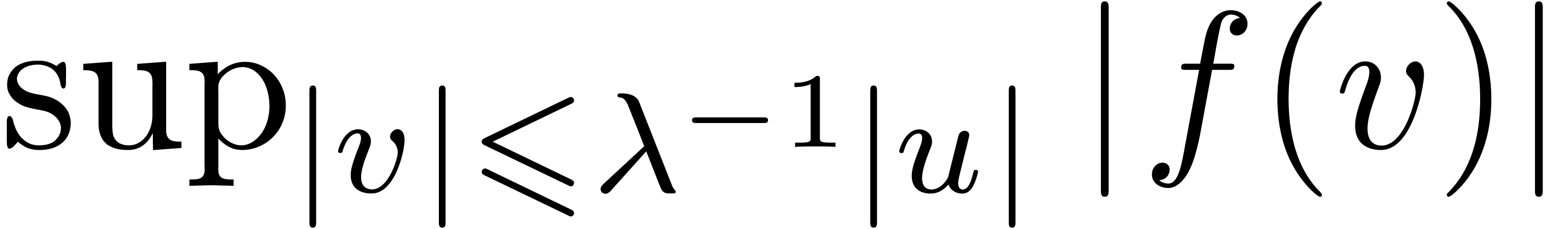 .
Performing this trick recursively in expressions in
.
Performing this trick recursively in expressions in  of corrected size
of corrected size  , we end up
with expressions in
, we end up
with expressions in 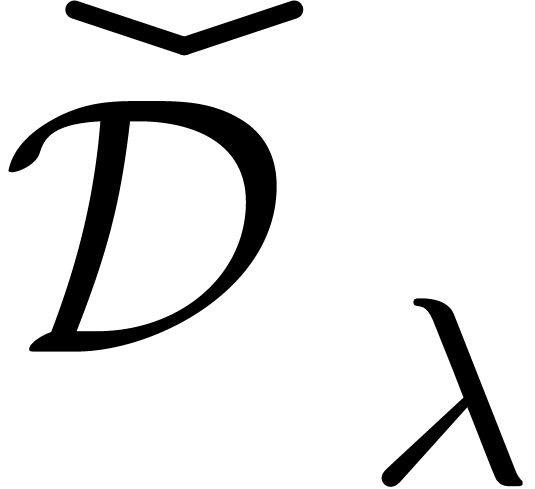 of usual size
of usual size 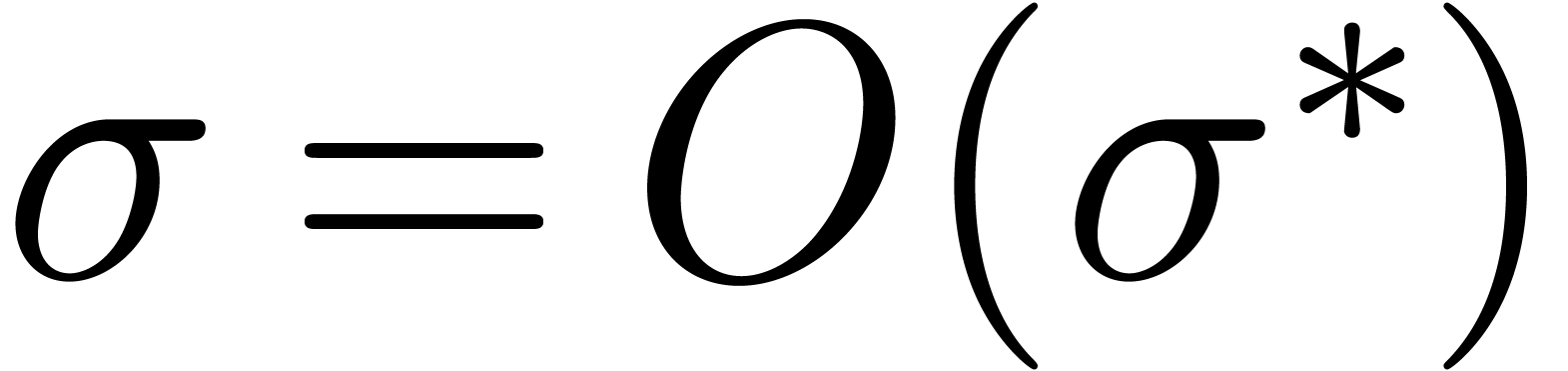 .
.
2.5More general constants
Witness conjectures may also be stated for more general types of
constants, such as
-
Constants that arise as values of solutions to partial differential
equations, whose boundary conditions recursively satisfy partial
differential equations in less variables.
-
Constants that arise during the process of accelero-summation [É92] of divergent solutions to algebraic
differential equations, or as limits of such solutions in singular
points, if these limits exist. This may for instance be done using
the approach from section 2.3, but where the supremum
in the corrective term for 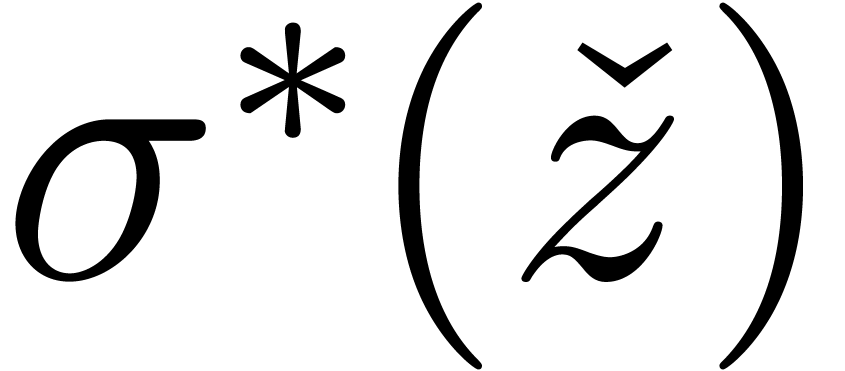 is taken over a
sector instead of a disk.
is taken over a
sector instead of a disk.
-
Constants that arise as values of solutions to more general
functional equations. Of course, one has to be much more careful in
this setting, since it is much easier to construct examples of
high-precision fraud in this setting, by considering equations such
as
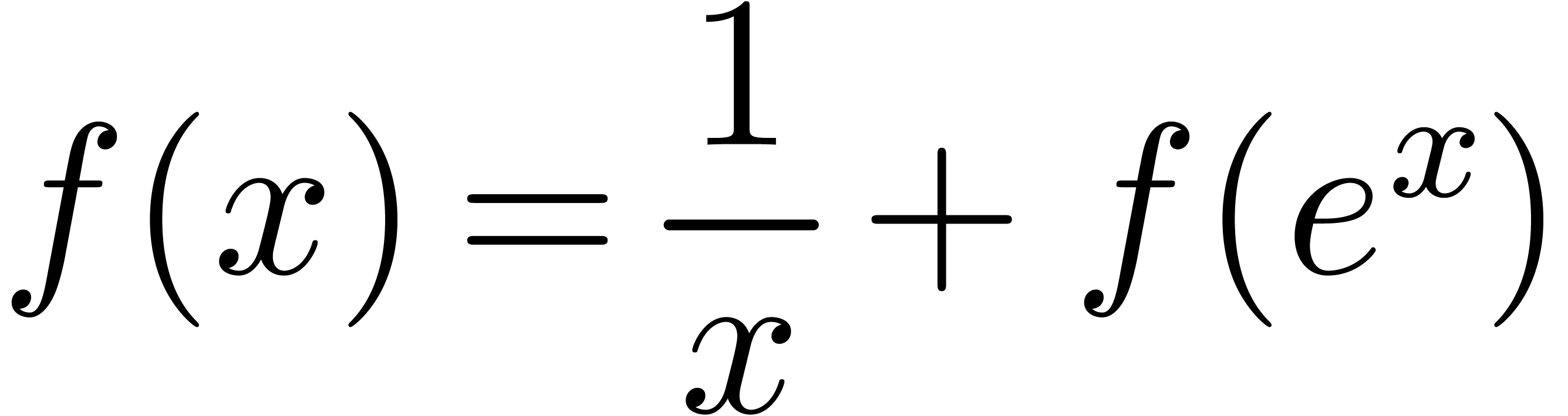
for  .
.
3Witness conjectures for power series
3.1Exp-log series
Consider the ring of formal power series 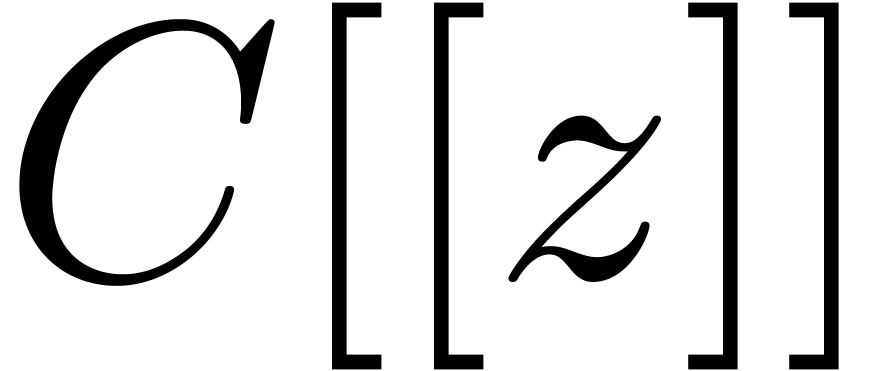 over a
field
over a
field  of characteristic zero. Let
of characteristic zero. Let  be the smallest set of expressions
be the smallest set of expressions 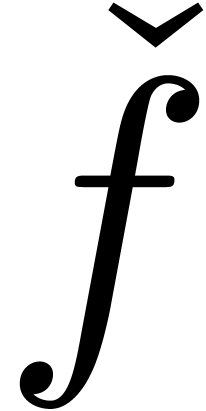 that represent series
that represent series  , such
that
, such
that
The set  of series represented by expressions in
of series represented by expressions in
 is called the set of exp-log series in
is called the set of exp-log series in
 . We will denote by
. We will denote by  the valuation of a series
the valuation of a series  .
.
Conjecture 6. There
exists a constant 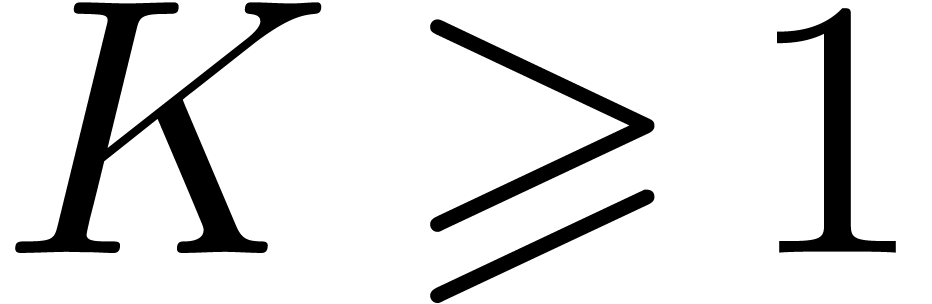 , such that
for all
, such that
for all 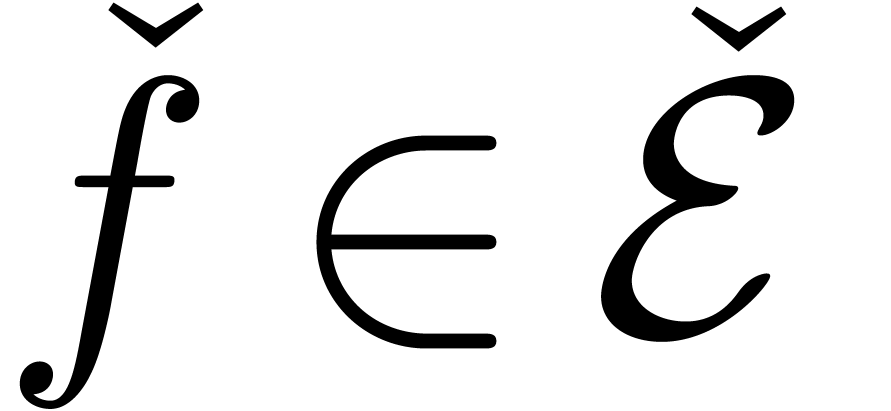 , we either have
, we either have 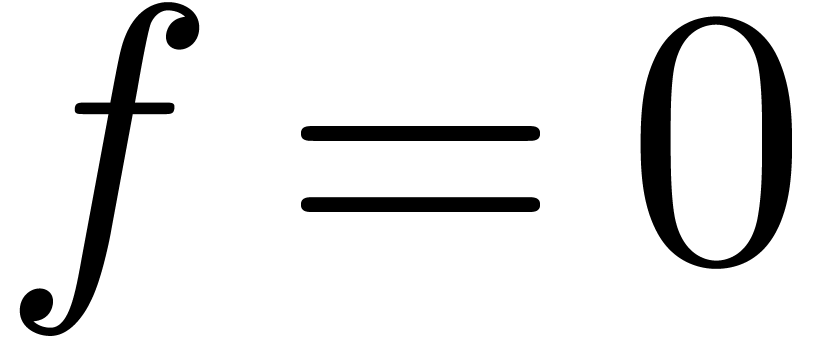 or
or  .
.
We observe that the coefficients of  are
polynomials with rational coefficients in the constants of
are
polynomials with rational coefficients in the constants of  which occur in a representing expression
which occur in a representing expression 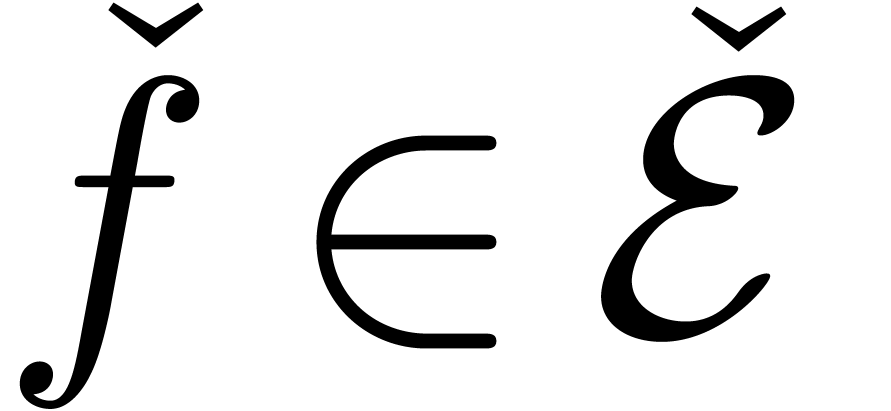 of
of 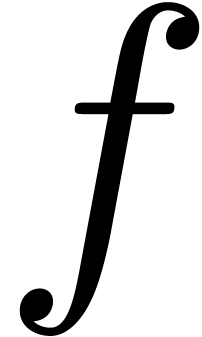 . Consequently, it
suffices to check conjecture 3.1 in the case when
. Consequently, it
suffices to check conjecture 3.1 in the case when  is the field of algebraic numbers.
is the field of algebraic numbers.
Let us now show that conjecture 3.1 is implied by
conjecture 2.2(a) in the case when 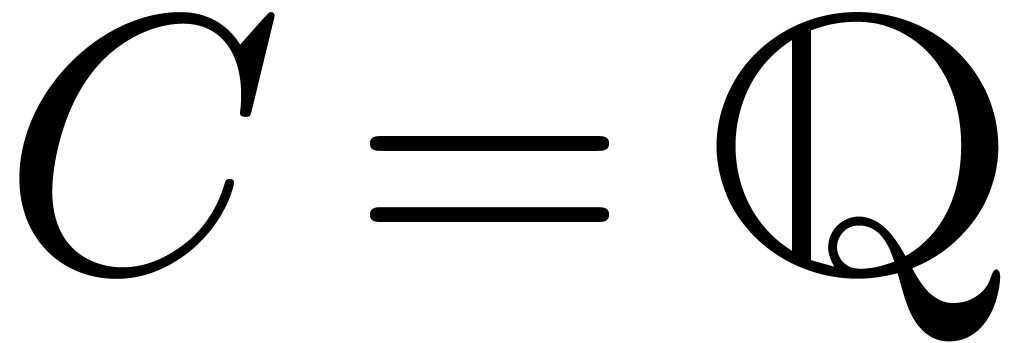 . Indeed, assume that there exists a
counterexample
. Indeed, assume that there exists a
counterexample 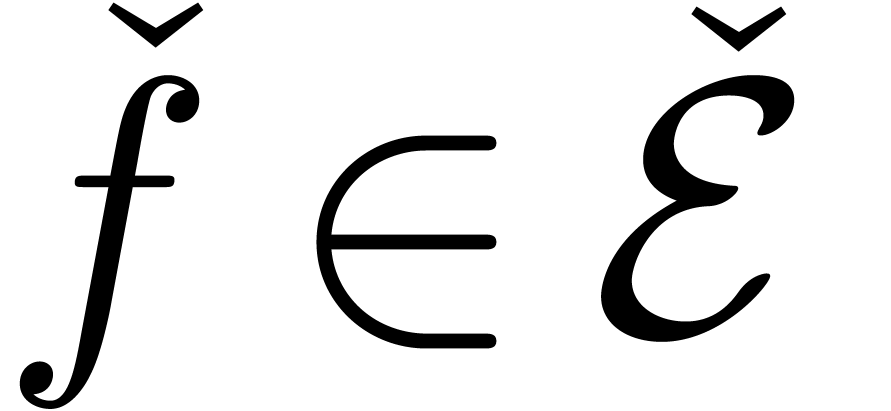 to conjecture 3.1
for each
to conjecture 3.1
for each 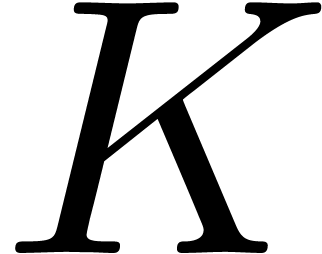 with
with 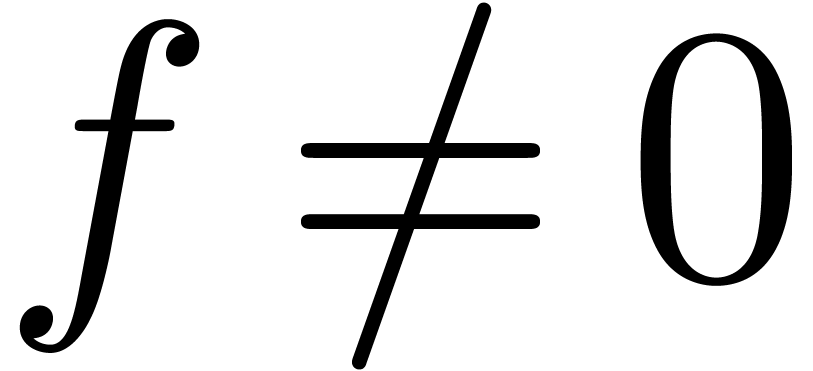 and
and 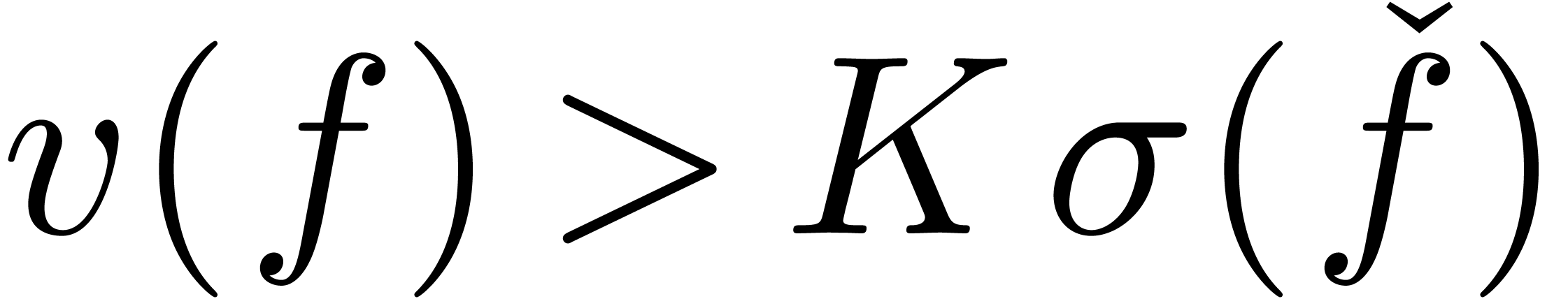 . Then for
. Then for 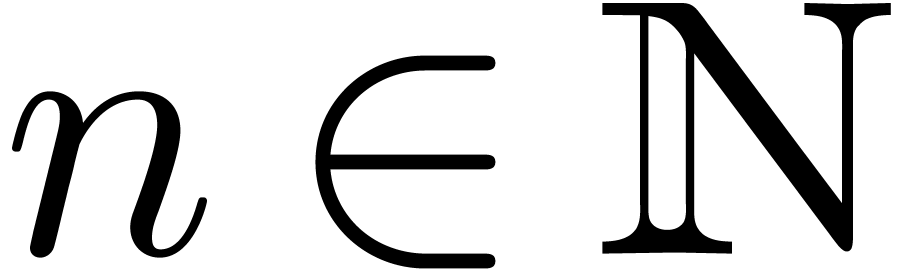 sufficiently large, we may represent
sufficiently large, we may represent 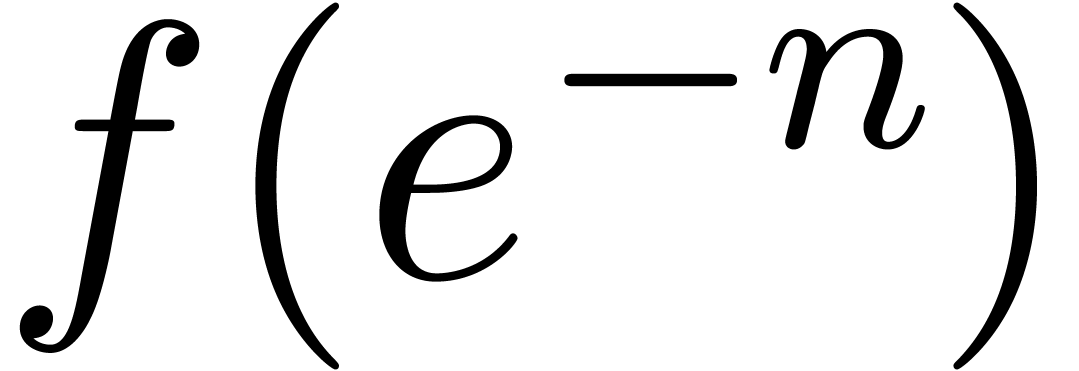 by an
expression in
by an
expression in  whose size is bounded by
whose size is bounded by  . Moreover, since
. Moreover, since  is a counterexample to conjecture 3.1, there exists a
constant
is a counterexample to conjecture 3.1, there exists a
constant 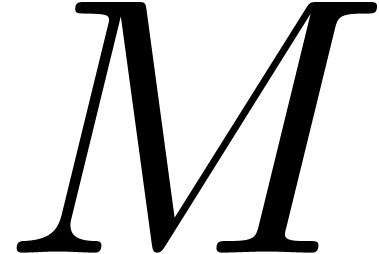 , such that
, such that 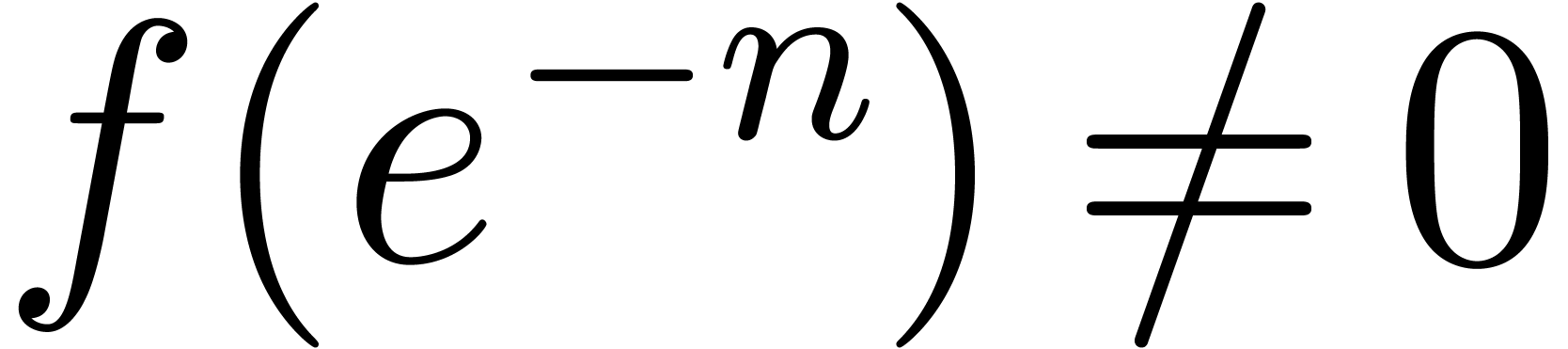 and
and
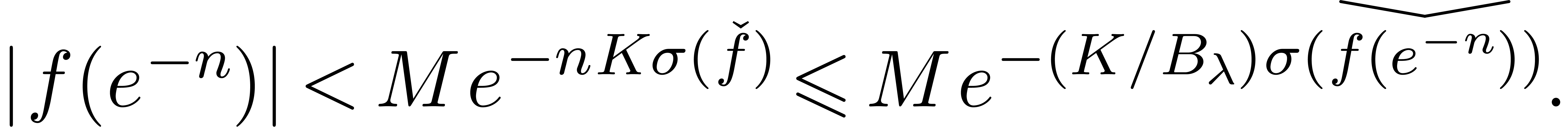
This yields a counterexample to conjecture 2.2(a),
for sufficiently large 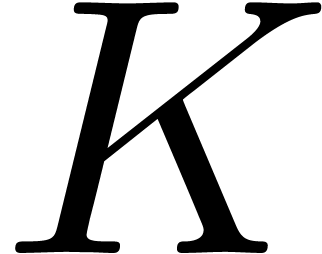 .
.
The above argument suggests that, in order to prove numerical witness
conjectures, it may be good to start proving their power series
equivalents. Although this project seems still to be out of reach for
linear witness functions, we were able to prove the following weak
witness theorem [SvdH01]; this result is based on a careful
complexity analysis of the zero-test algorithm from [Sha89].
Theorem 7. For all
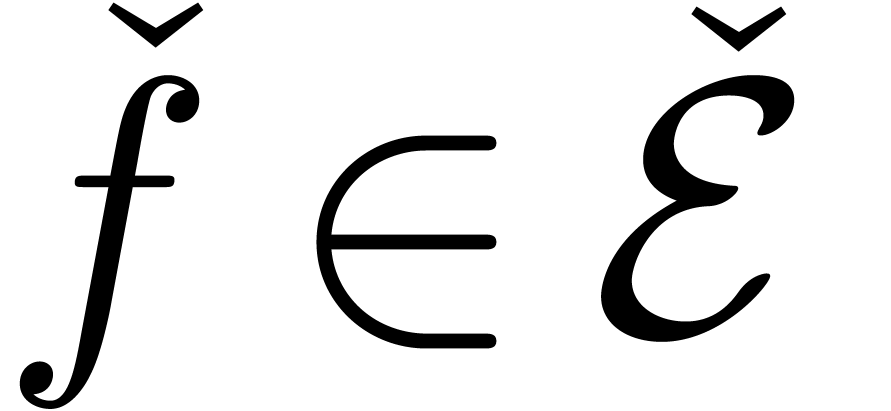 , we either have
, we either have 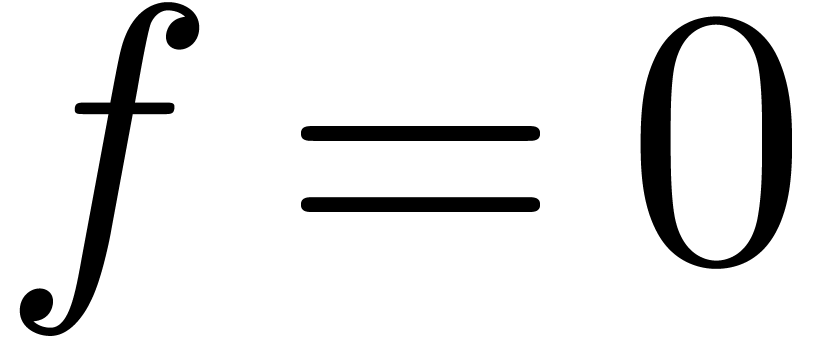 or
or 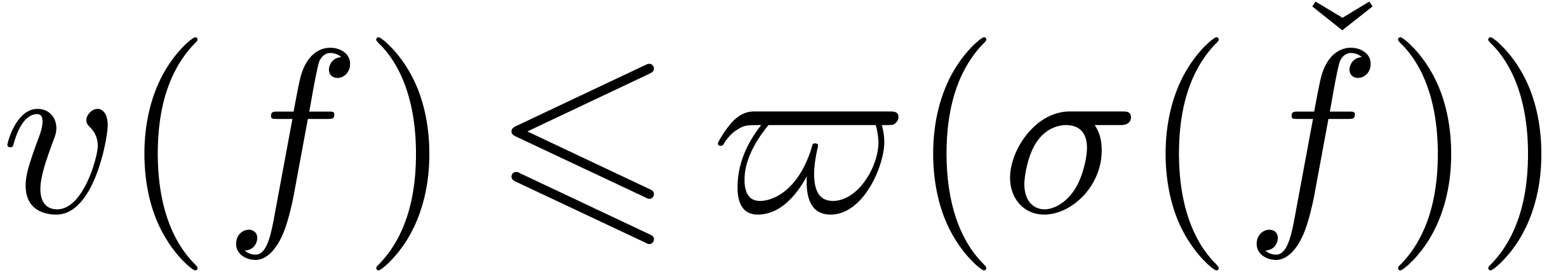 , with
, with 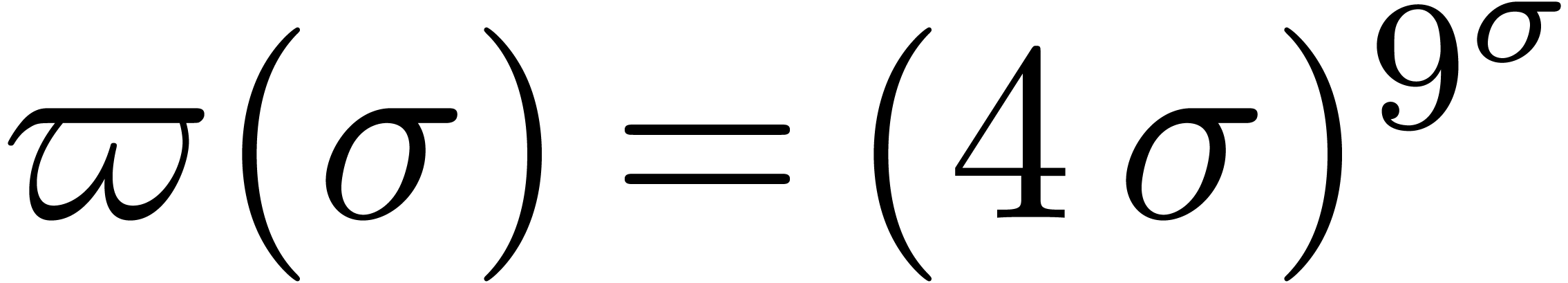 .
.
Recently, we have been made aware of the work of Khovanskii [Kho91],
which seems to imply even better bounds of the form 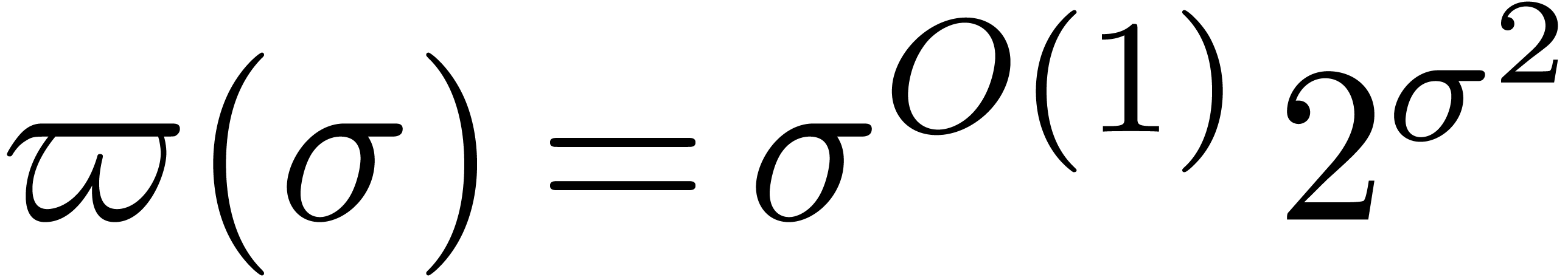 . We are still studying this work and trying to
prove similar bounds with our techniques. Our main reason for doing this
is that the techniques from [SvdH01] are better suited for
generalizations.
. We are still studying this work and trying to
prove similar bounds with our techniques. Our main reason for doing this
is that the techniques from [SvdH01] are better suited for
generalizations.
3.2Differentially algebraic
series
Let 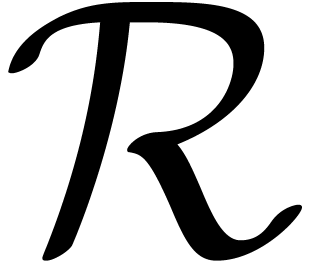 be a differential subring of
be a differential subring of 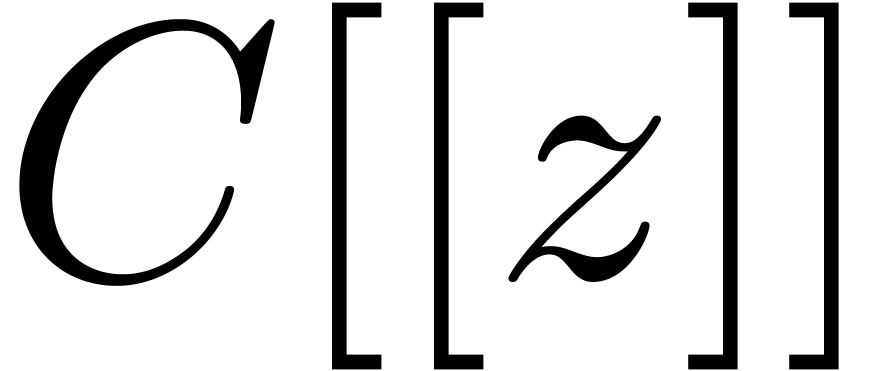 . In analogy with section 2.2, we
define a series
. In analogy with section 2.2, we
define a series  to be differentially algebraic
over
to be differentially algebraic
over 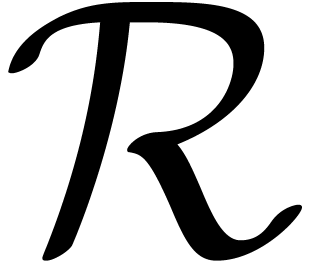 , if
, if  satisfies an algebraic differential equation
satisfies an algebraic differential equation
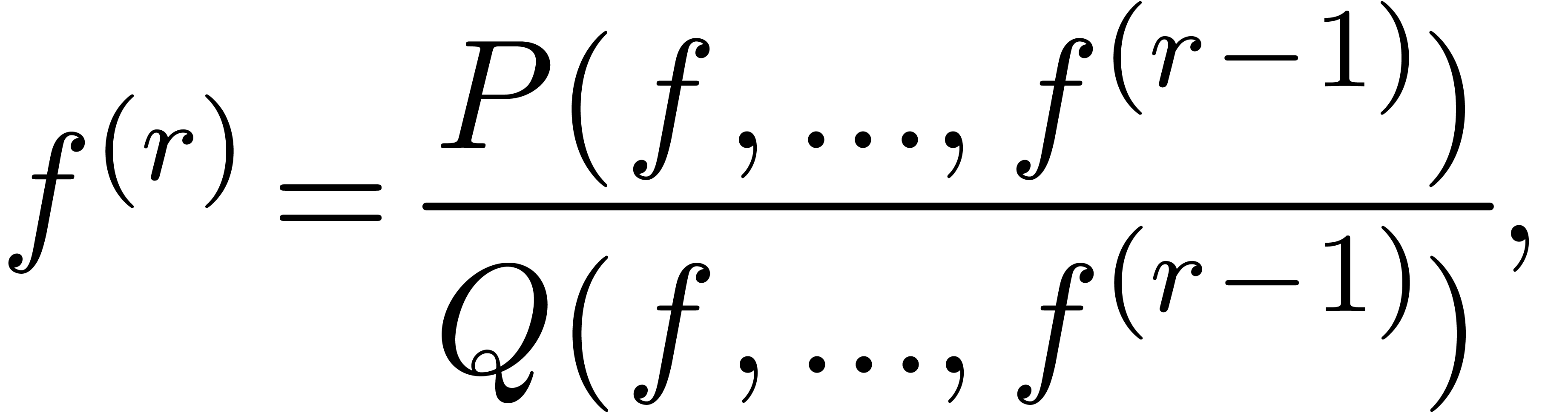 |
(6) |
with 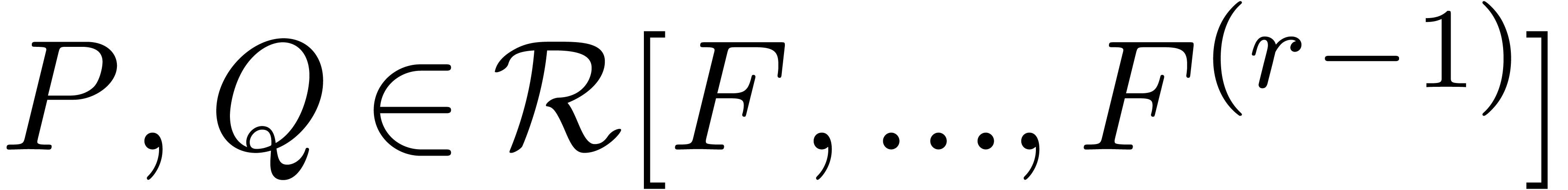 and where
and where 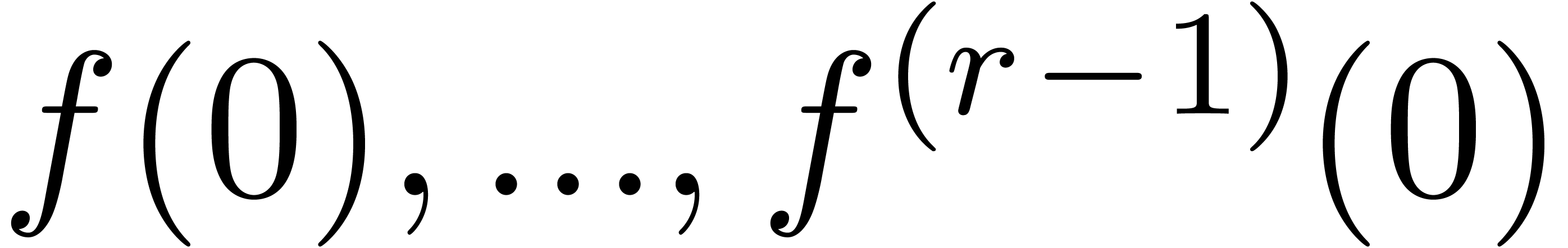 are such
that
are such
that
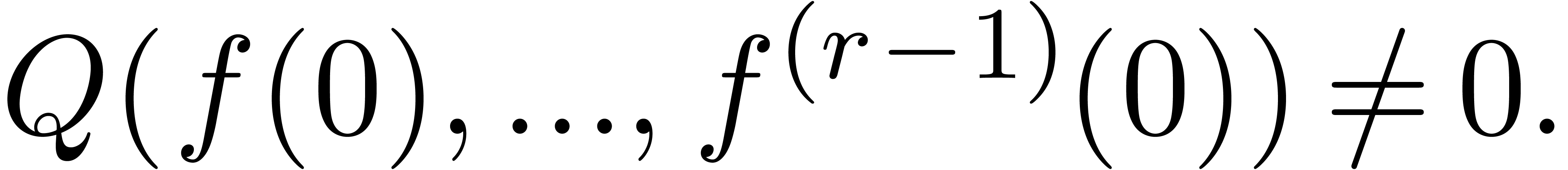
Starting with 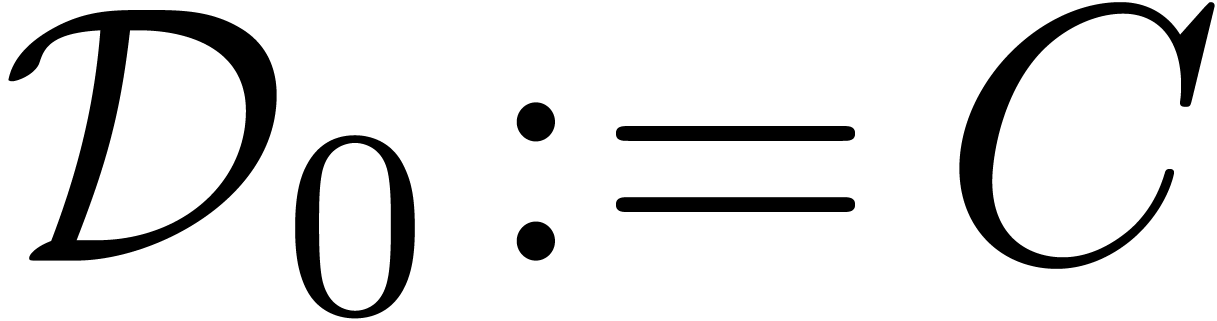 , we may again
recursively construct
, we may again
recursively construct 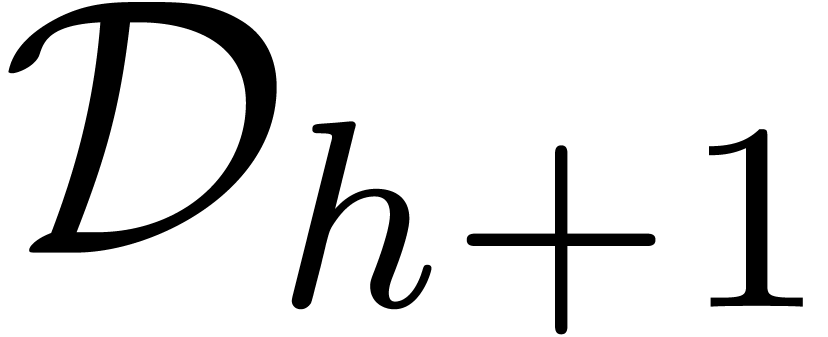 to be the ring of
differentially algebraic power series over
to be the ring of
differentially algebraic power series over 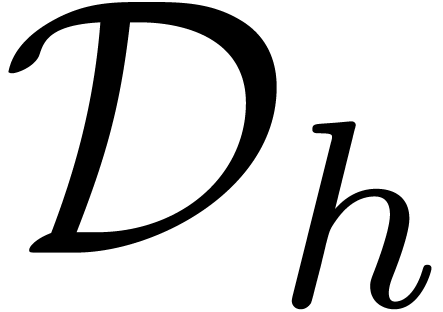 ,
and define
,
and define 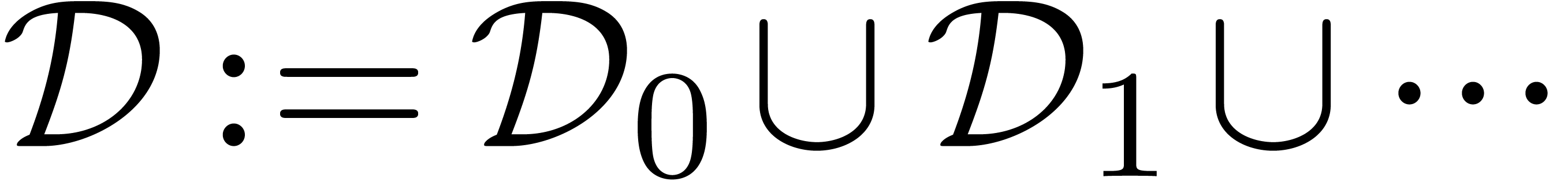 . Power series in
. Power series in
 may be represented in a similar way as in
section 2.2 and we have the following power series analogue
of conjectures 2.3 and 3.3.
may be represented in a similar way as in
section 2.2 and we have the following power series analogue
of conjectures 2.3 and 3.3.
Conjecture 8. There
exists a witness function 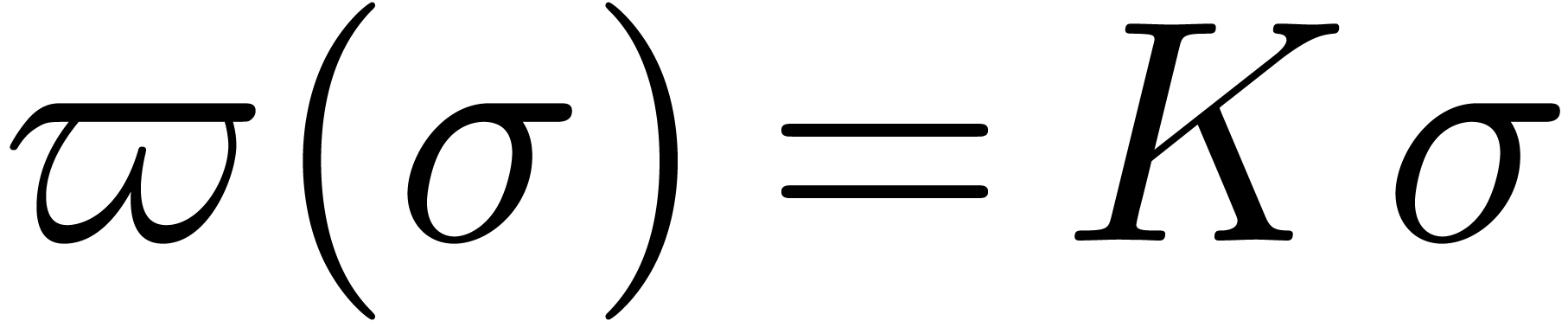 with
with 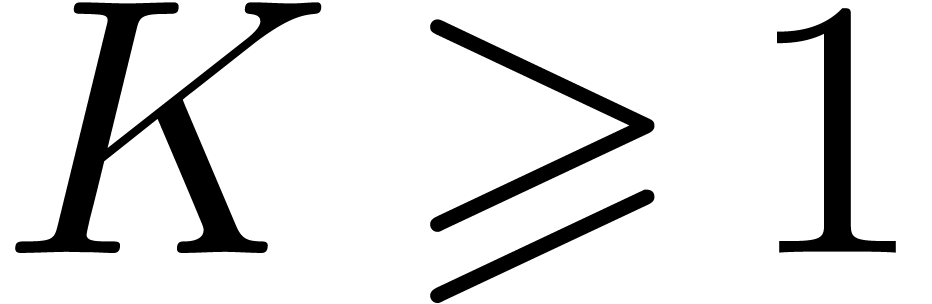 , such that for all
, such that for all 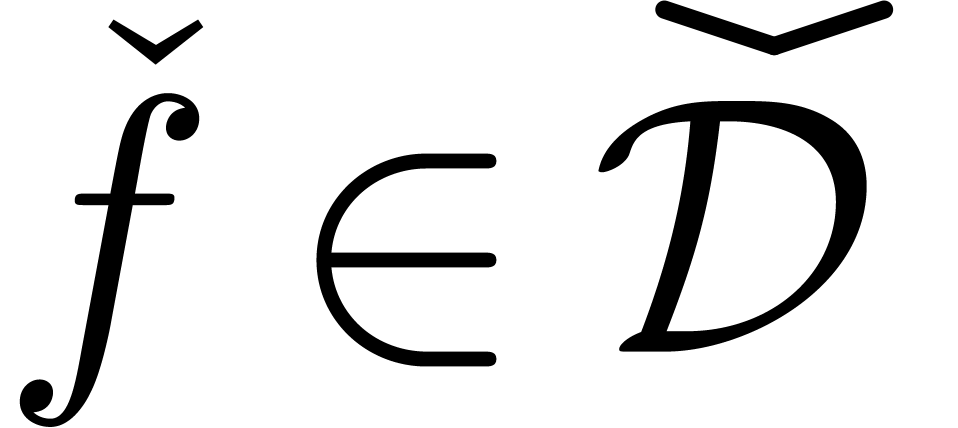 , we either have
, we either have 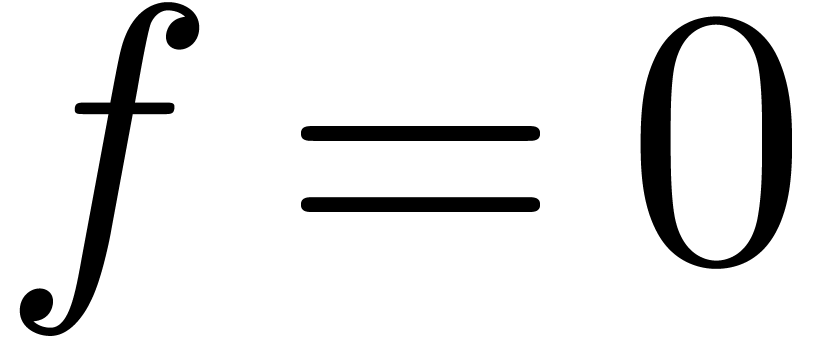 or
or 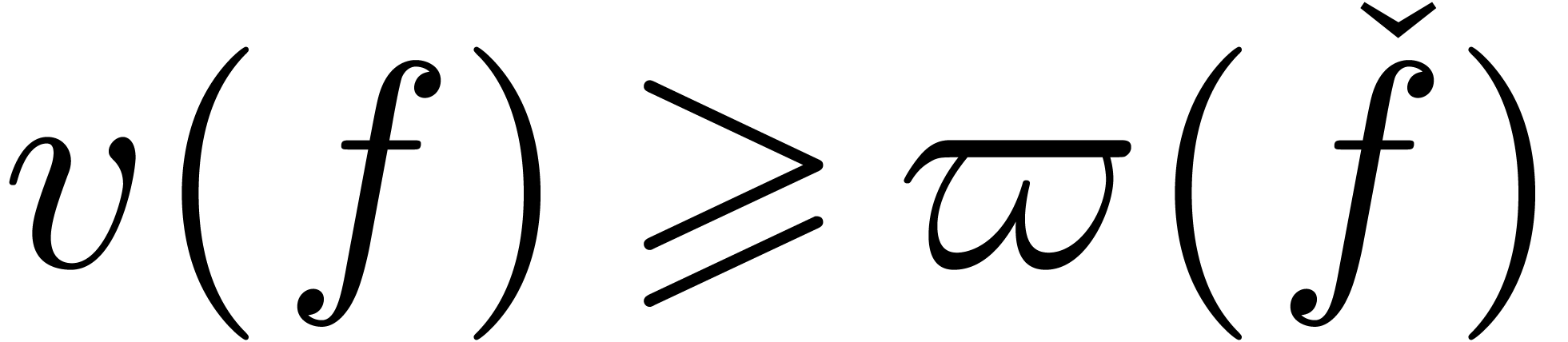 .
.
In [SvdH01], we proved the above conjecture for 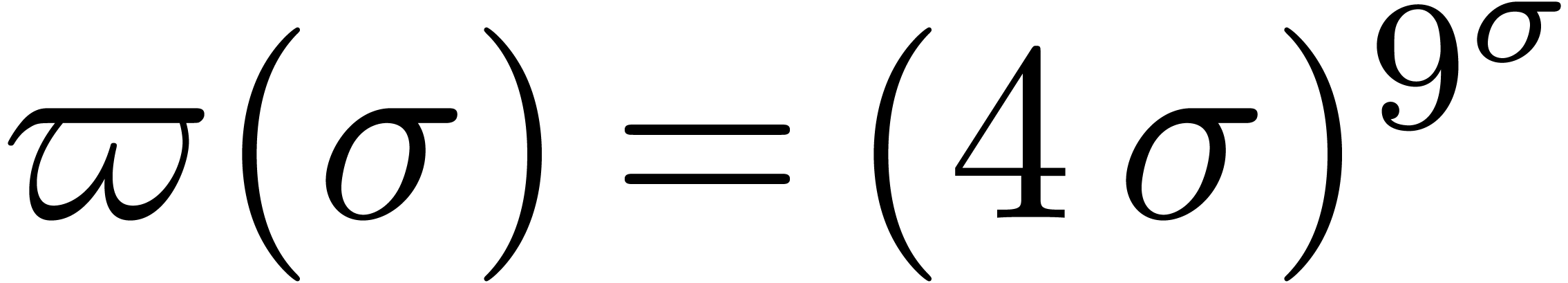 in the case of differential equations (3.1)
of order
in the case of differential equations (3.1)
of order  . We believe to have
found a generalization of this theorem to higher orders, but this still
has to be worked out in detail. In the first order case, better bounds
of the form
. We believe to have
found a generalization of this theorem to higher orders, but this still
has to be worked out in detail. In the first order case, better bounds
of the form 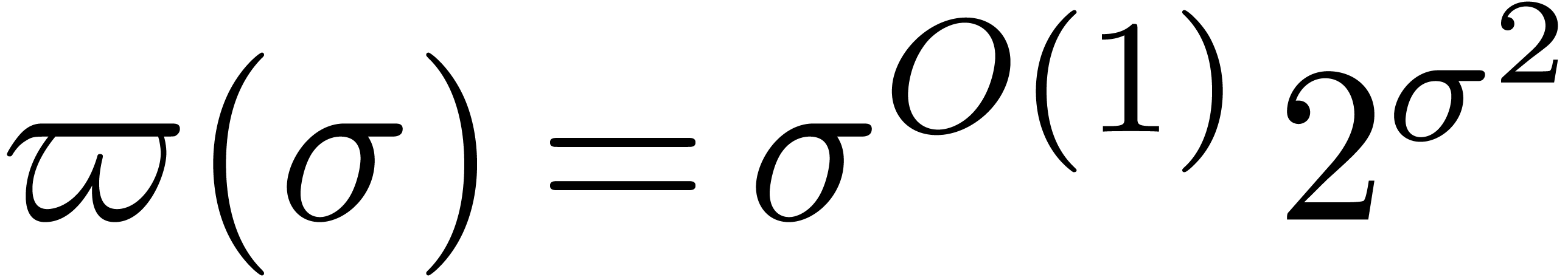 seem to result from [Kho91].
seem to result from [Kho91].
3.3Multivariate series
Actually, there is no reason to restrict ourselves to formal power
series in one variable in sections 3.1 and 3.2,
so that we may very well replace 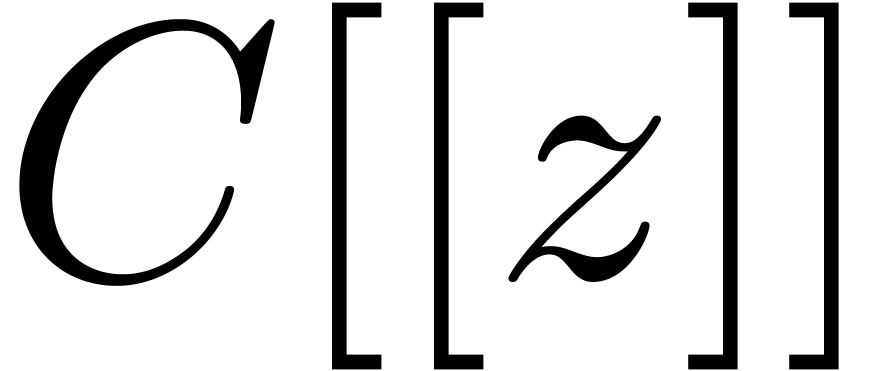 by
by 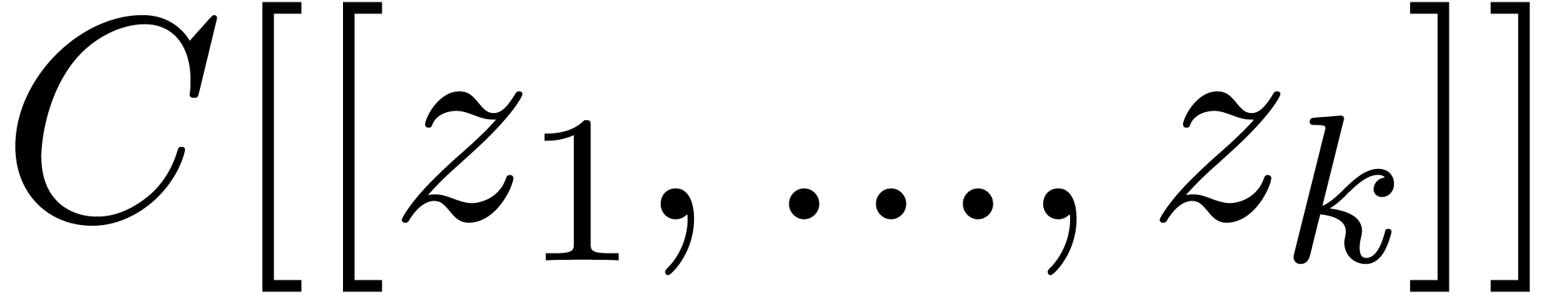 . In the construction of
. In the construction of  , given
, given 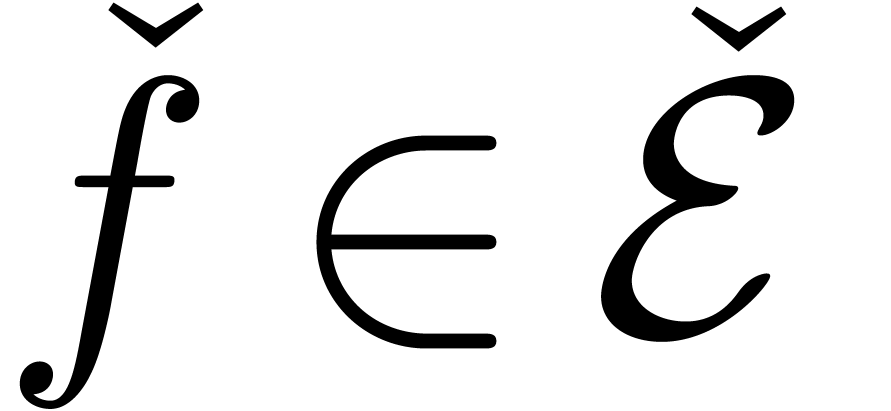 ,
we then have to assume that
,
we then have to assume that 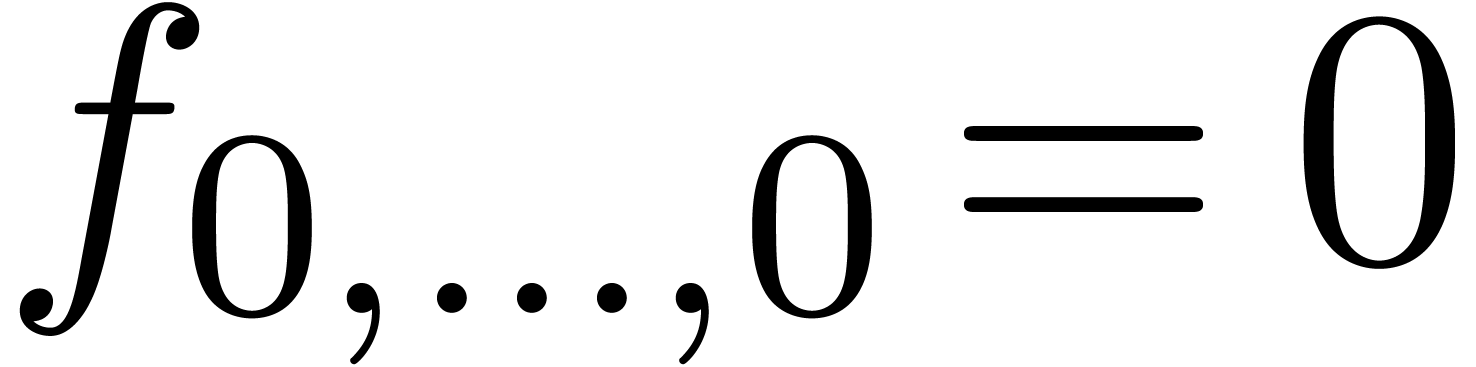 ,
for
,
for 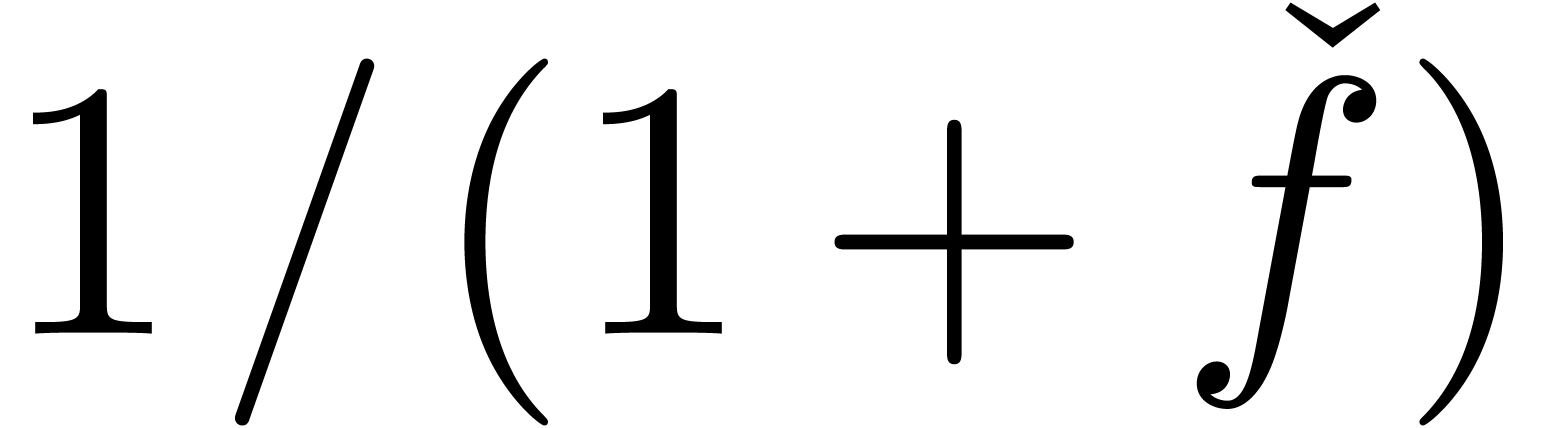 ,
, 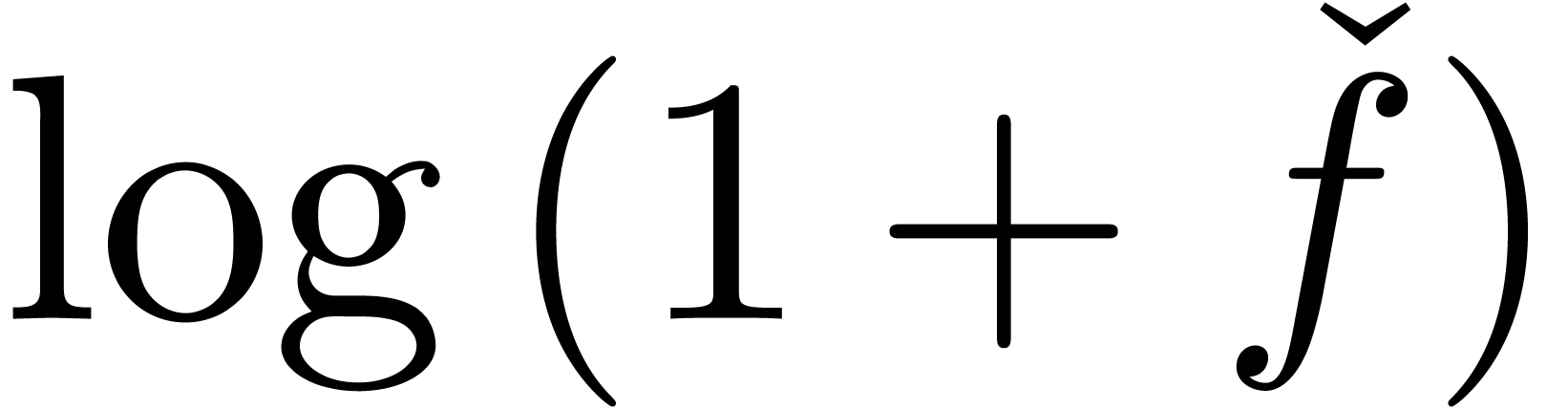 or
or 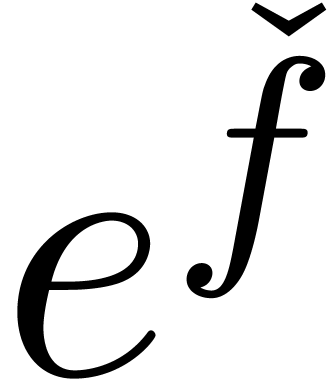 to be in
to be in  .
Similarly, the differential equation (3.1) should be
replaced by a system of partial differential equations
.
Similarly, the differential equation (3.1) should be
replaced by a system of partial differential equations
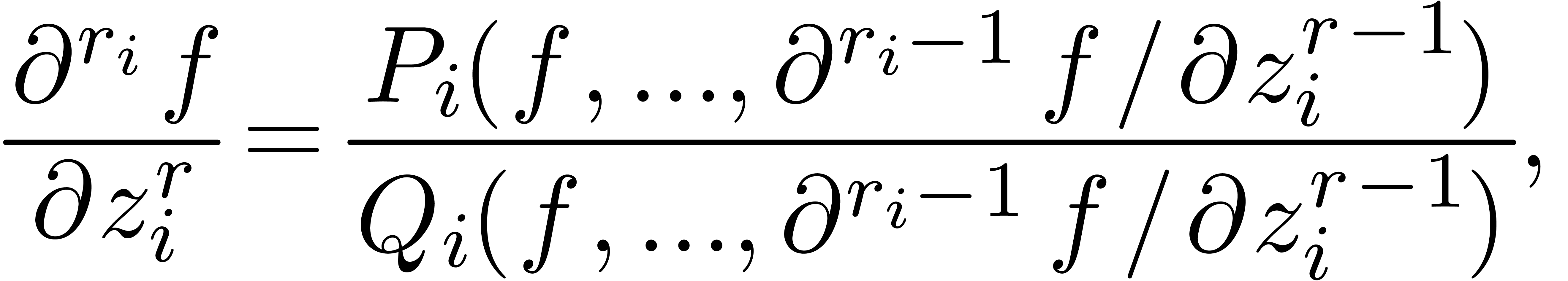 |
(7) |
for 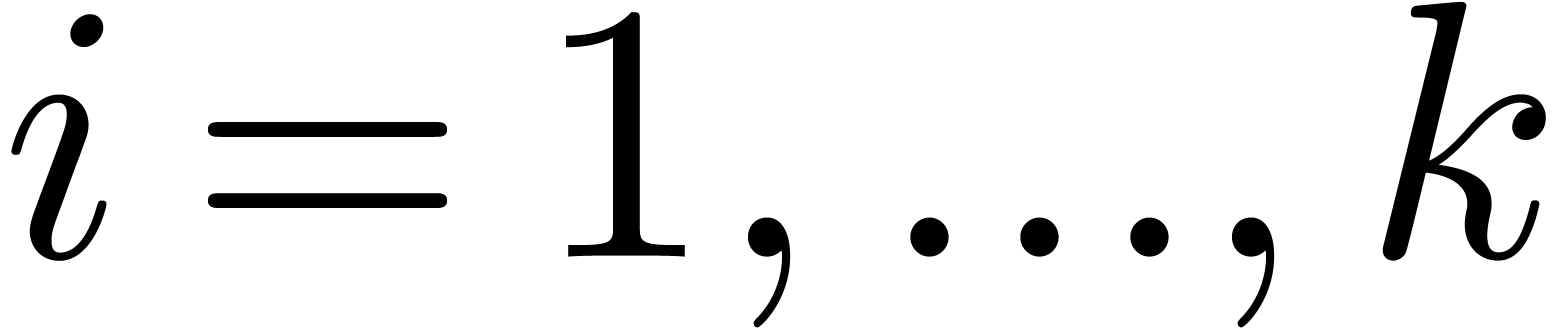 , such that the
polynomials
, such that the
polynomials 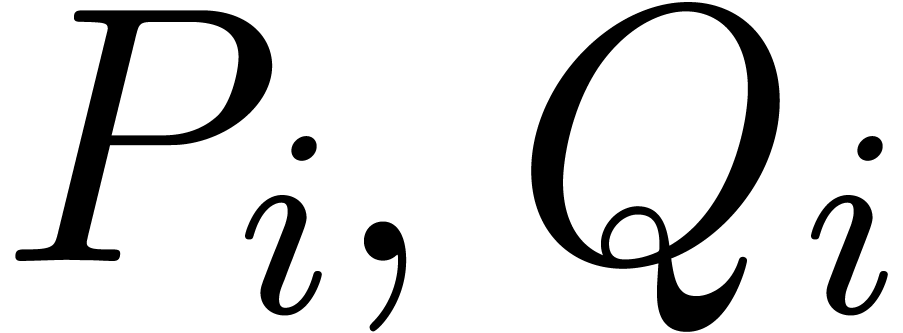 satisfy
satisfy
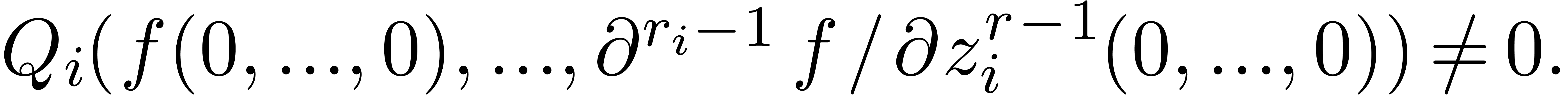
One might also investigate other ways to present the partial
differential equations (3.2), such as coherent autoreduced
systems.
Now given such a multivariate setting, it is interesting to study the
dependence of the witness conjectures on the parameter 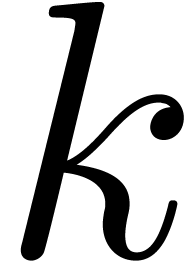 . The following result has been proved in [SvdH01]; better bounds might follow from [Kho91].
. The following result has been proved in [SvdH01]; better bounds might follow from [Kho91].
Theorem 9. For all 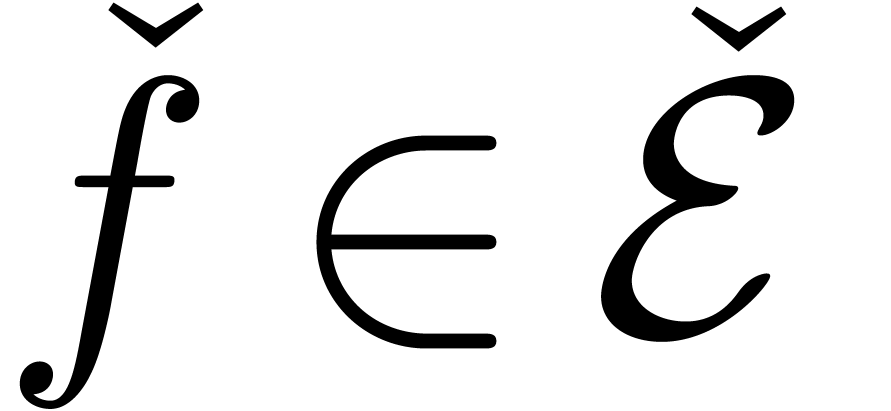 , we either have
, we either have 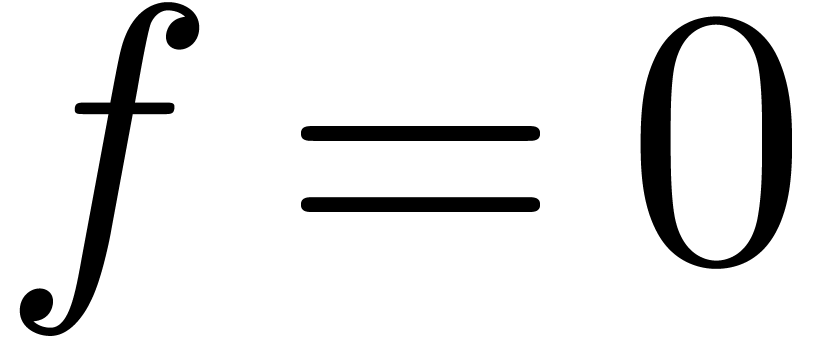 or
or 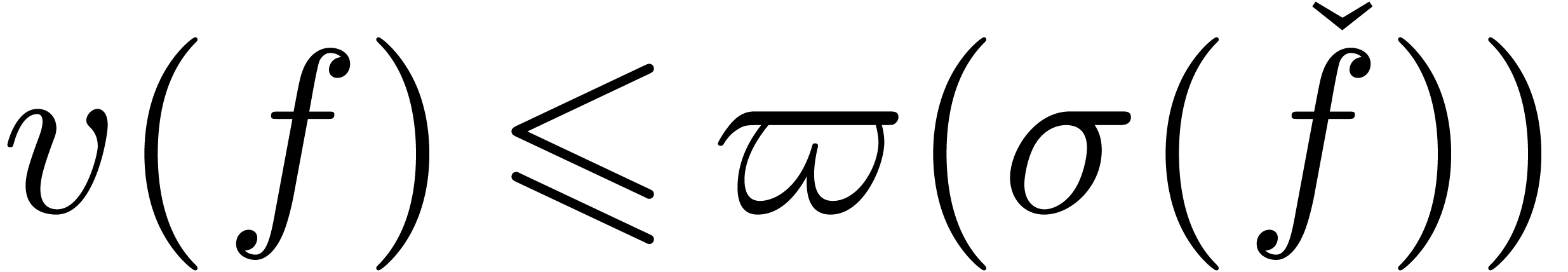 , where
, where 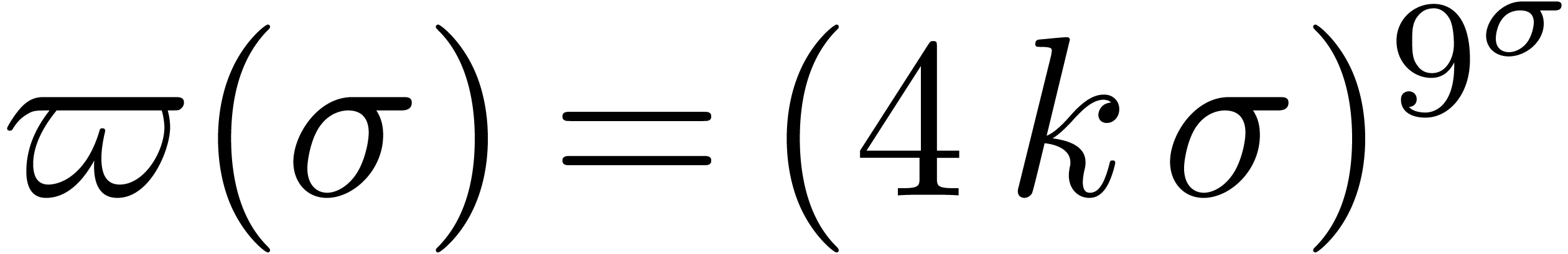 .
.
3.4Finer size parameters
Technically speaking, it turns out that the exponential behavior in 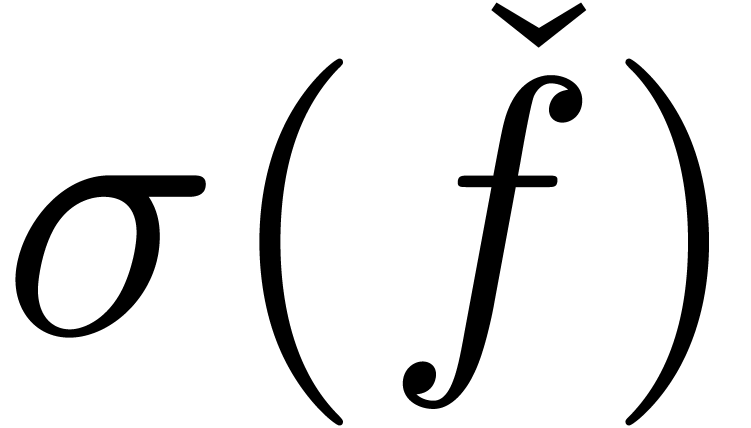 in theorem 3.2 is due to the
“differential part” of
in theorem 3.2 is due to the
“differential part” of 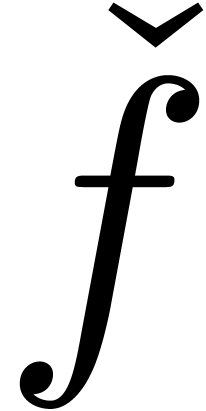 .
More precisely, if we consider a non zero power series
.
More precisely, if we consider a non zero power series 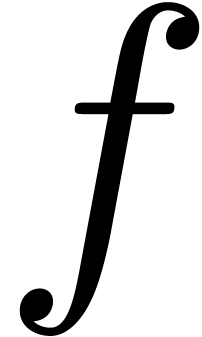 in a fixed polynomial ring
in a fixed polynomial ring 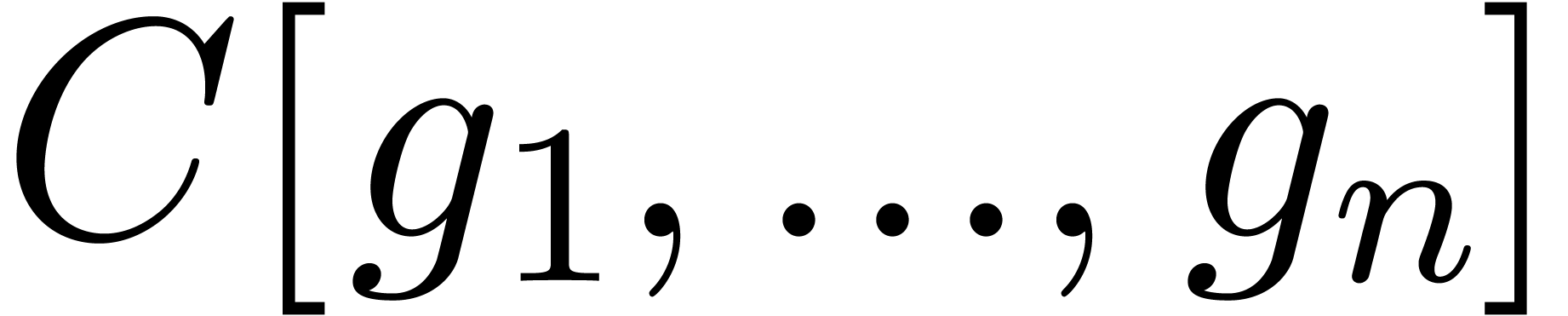 with
with 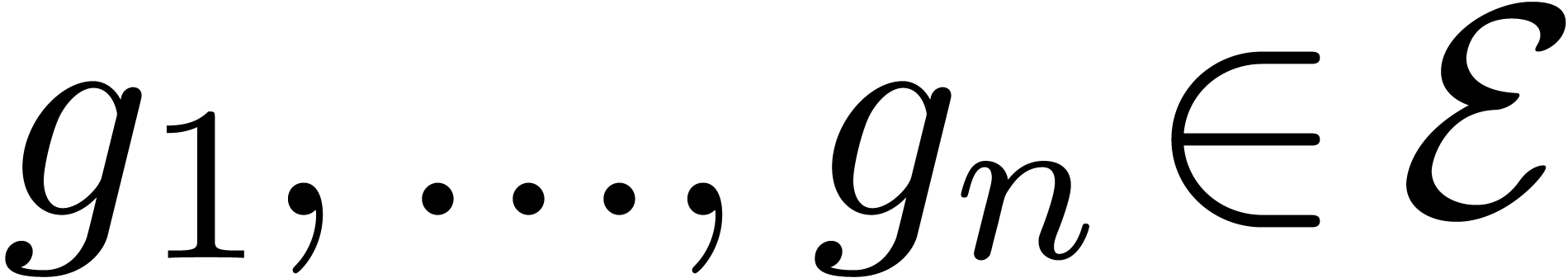 , then there exists a polynomial bound for
, then there exists a polynomial bound for 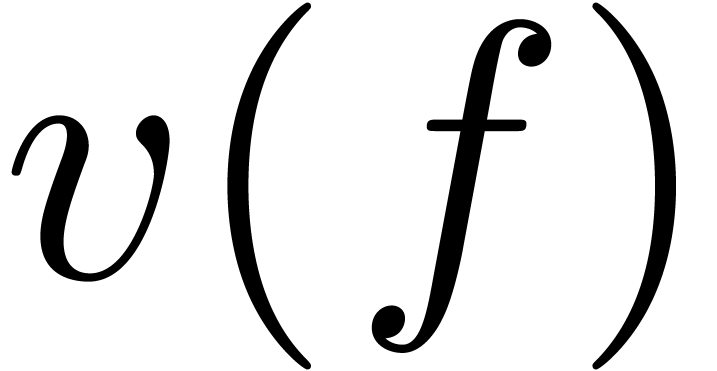 in
in 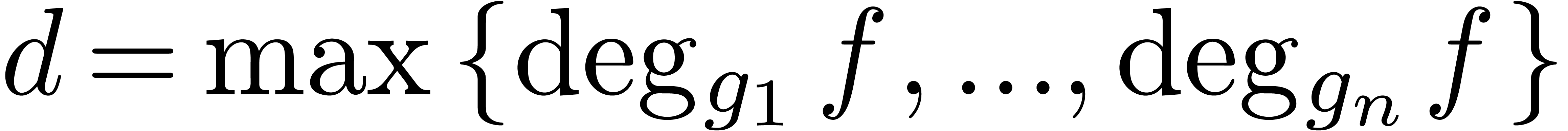 . This
observation seems to generalize to higher order differential power
series.
. This
observation seems to generalize to higher order differential power
series.
As a first step to the proofs of stronger witness conjectures for
differential power series, it may therefore be a good idea to find more
subtle size parameters for expressions in  ,
such as
,
such as 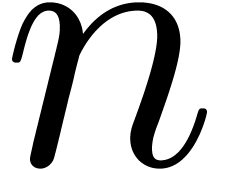 and
and 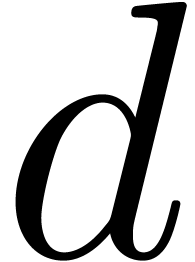 above. It
may also be interesting to consider other interesting classes of power
series, such as rings of the form
above. It
may also be interesting to consider other interesting classes of power
series, such as rings of the form
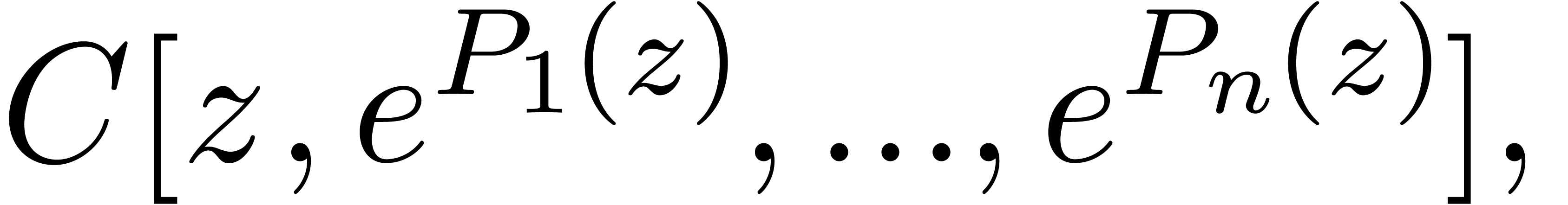
where 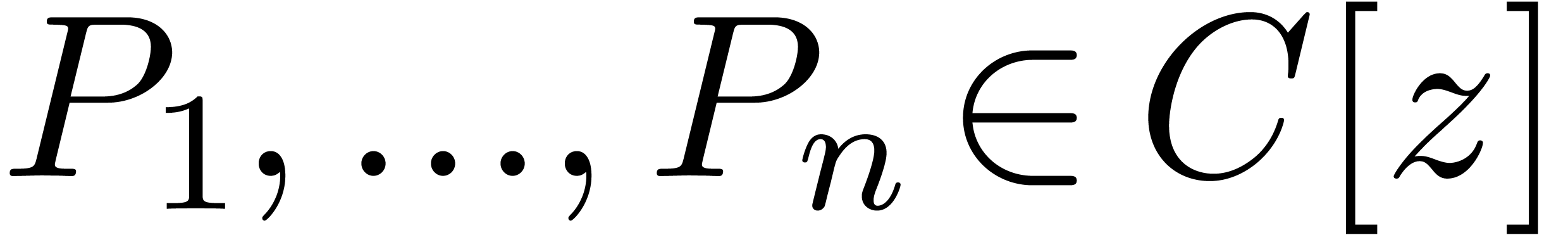 . Can the exponential
bound in
. Can the exponential
bound in 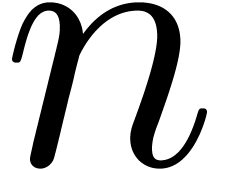 be further improved for such rings?
be further improved for such rings?
It might also be interesting to do some computer algebra experiments for
expressions of a simple form and small size. For instance, one might
consider all expressions formed using  ,
formal parameters
,
formal parameters 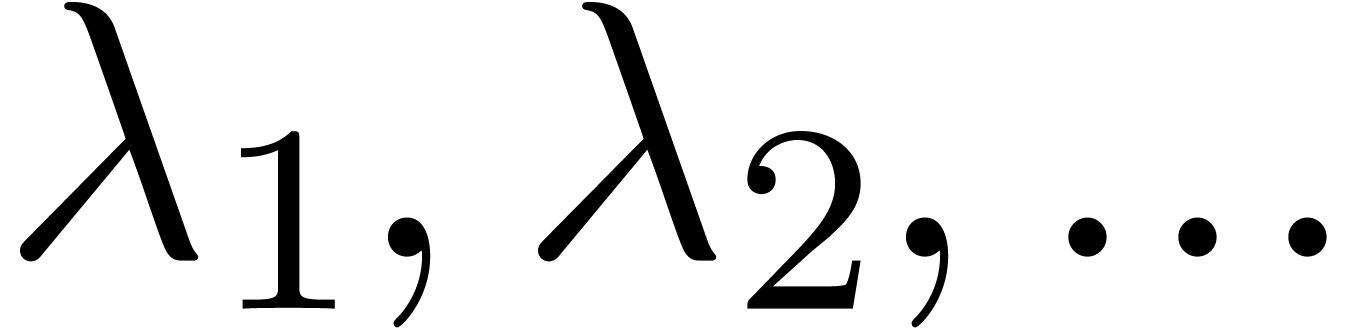 ,
additional, multiplication and exponentiation of infinitesimals. Given a
power series represented by such an expression, one may set the first
,
additional, multiplication and exponentiation of infinitesimals. Given a
power series represented by such an expression, one may set the first
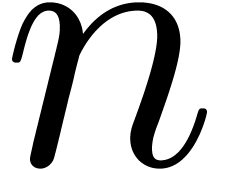 coefficients to zero (this puts constraints on
the parameters
coefficients to zero (this puts constraints on
the parameters 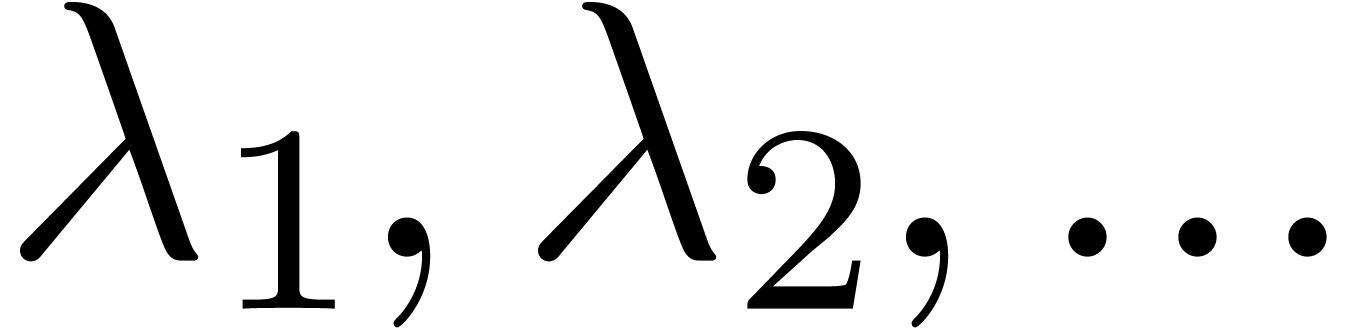 ) and study
the number of remaining free parameters as a function of
) and study
the number of remaining free parameters as a function of 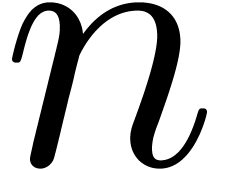 . Doing this for all expressions up to a
certain size, one may collect concrete evidence for the witness
conjectures and determine the “worst case expressions”.
. Doing this for all expressions up to a
certain size, one may collect concrete evidence for the witness
conjectures and determine the “worst case expressions”.
4Differential diophantine approximation
4.1Classical results in diophantine
approximation
Now we have stated different types of witness conjectures, it is
interesting to investigate what is already known on this subject.
Probably, the classical theory of diophantine approximation, which is
concerned with the approximation of a given real number  by rationals, comes closest to our subject. Equivalently, one may ask
how small
by rationals, comes closest to our subject. Equivalently, one may ask
how small 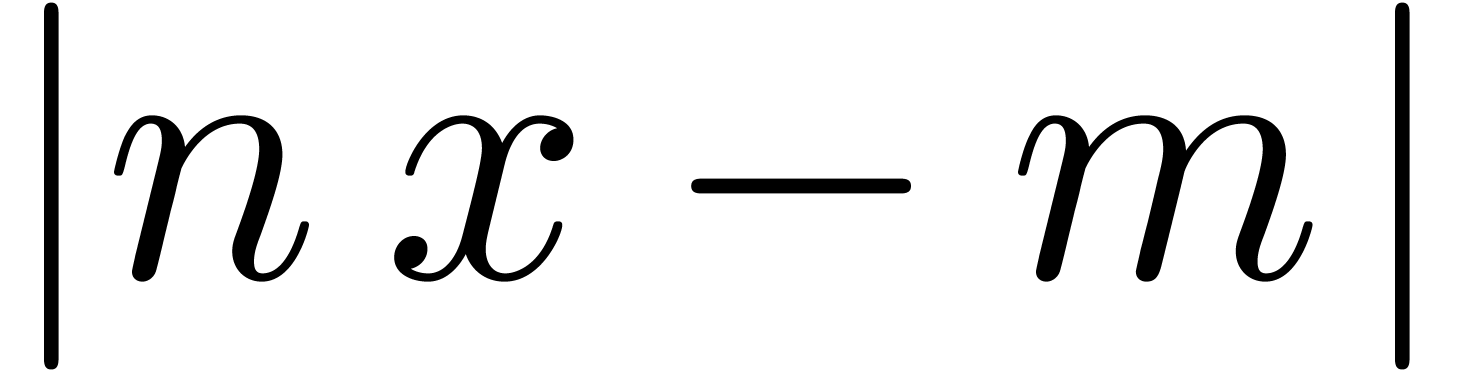 can get for large
can get for large  . More generally, an interesting question is to
know how small
. More generally, an interesting question is to
know how small 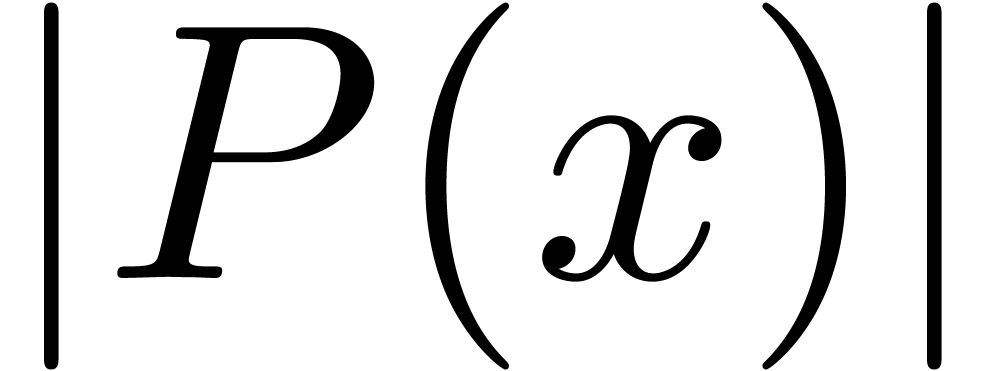 can get as a function of
can get as a function of 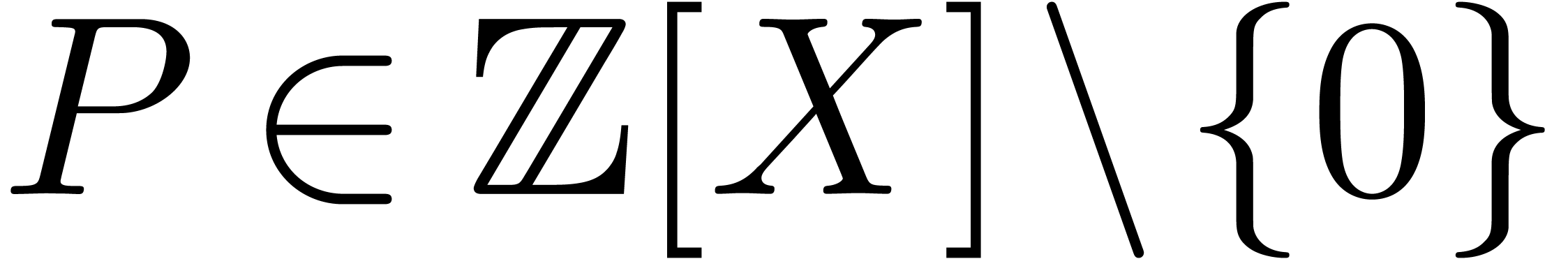 . Even more generally, one may
consider complex numbers
. Even more generally, one may
consider complex numbers  and ask how small
and ask how small 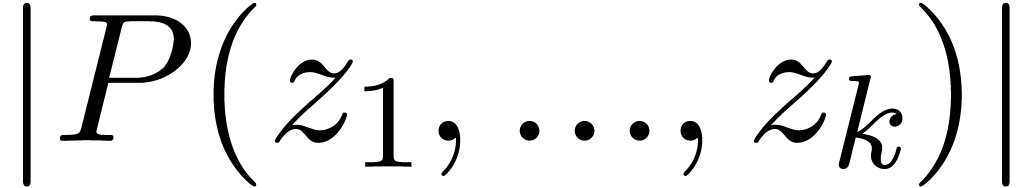 can get as a function of
can get as a function of  .
.
Let us first consider an algebraic number  ,
with
,
with  for some polynomial
for some polynomial  of minimal degree
of minimal degree 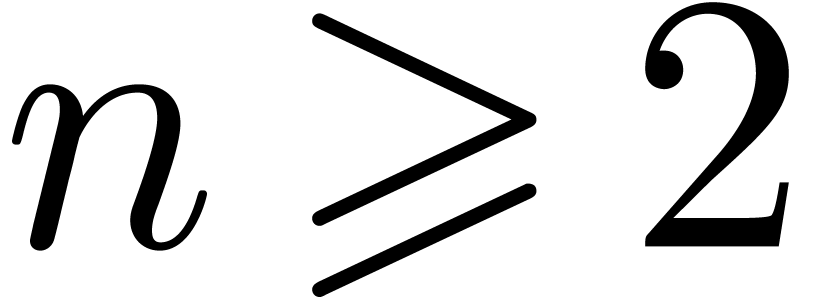 and minimal leading
coefficient
and minimal leading
coefficient 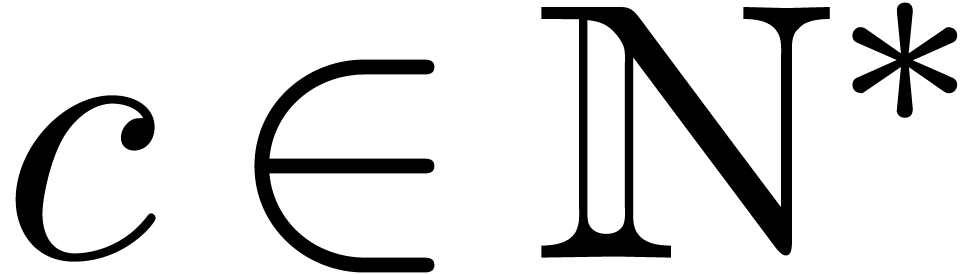 . Let
. Let
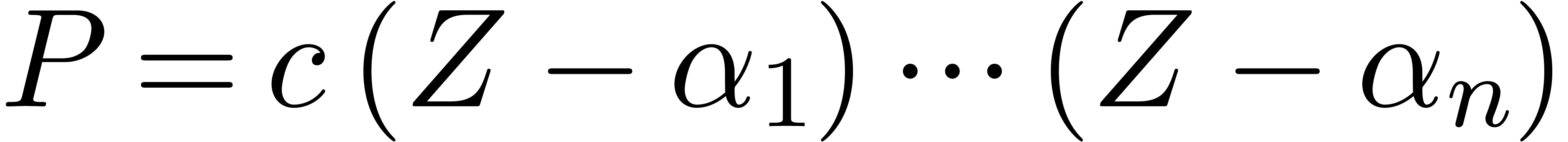
be the factorization of 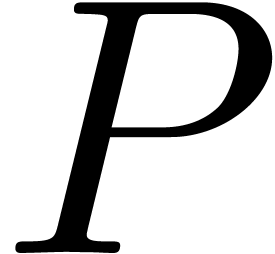 with
with 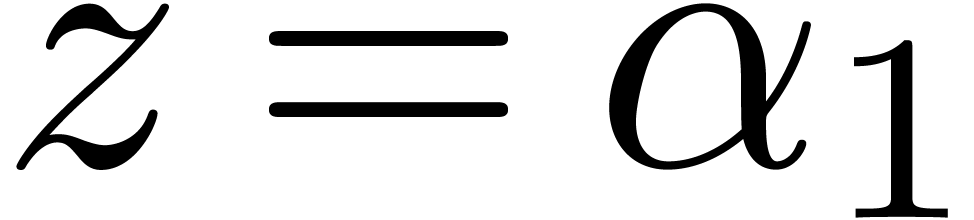 and
and 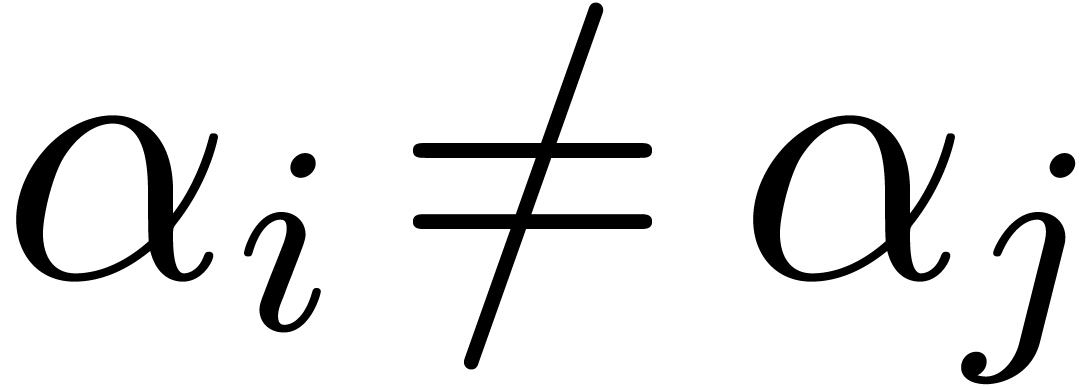 for all
for all 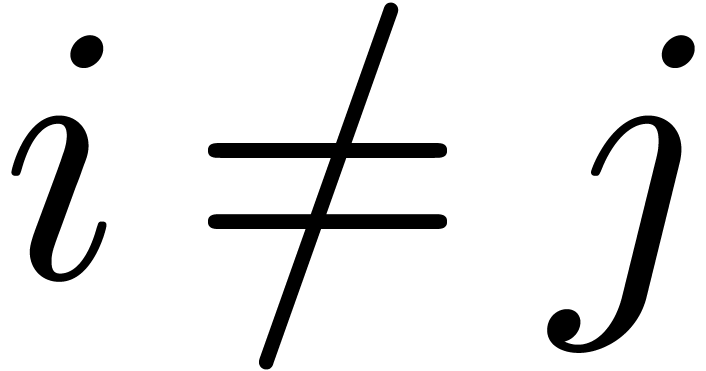 .
Given
.
Given  close to
close to  (say
(say  for all
for all 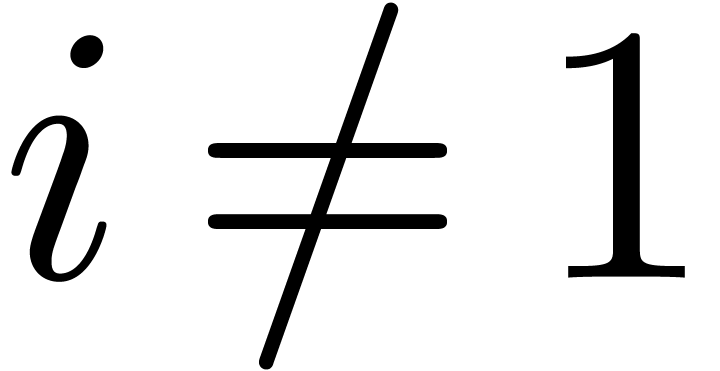 ),
we then have
),
we then have
since 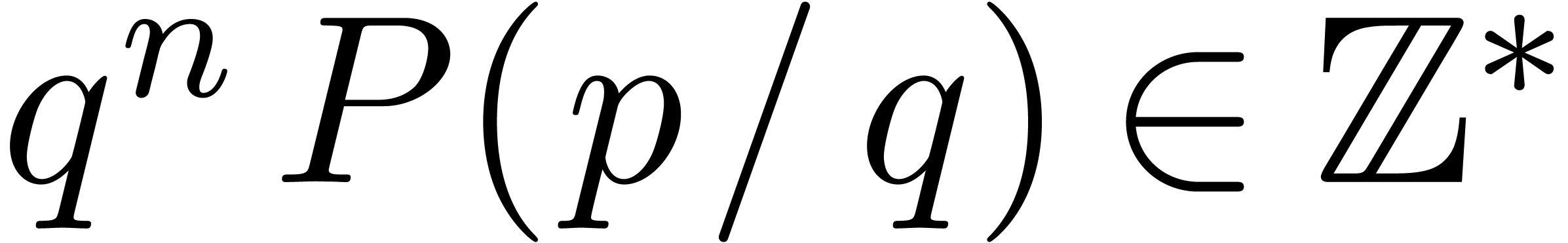 . This bound, which is
due to Liouville, shows that
. This bound, which is
due to Liouville, shows that 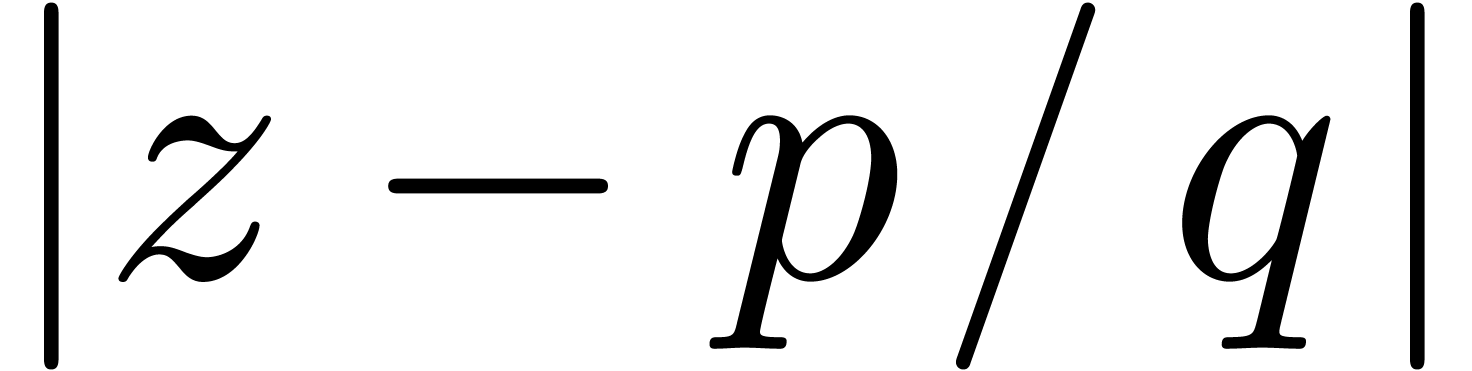 can be bounded from
below by an expression of the form
can be bounded from
below by an expression of the form 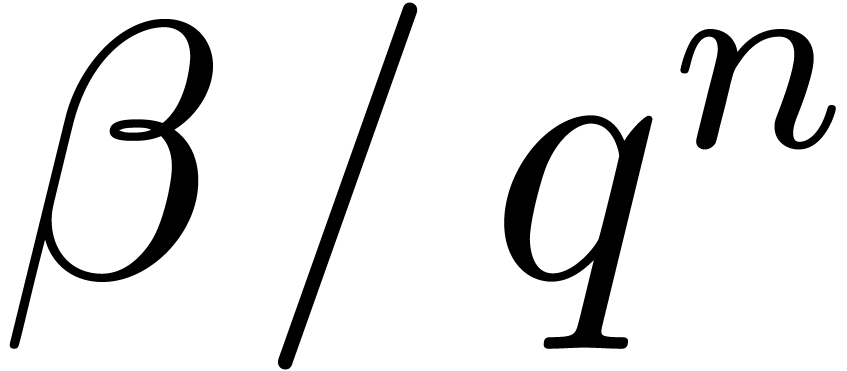 ,
where
,
where  can be expressed as a function of the
polynomial
can be expressed as a function of the
polynomial 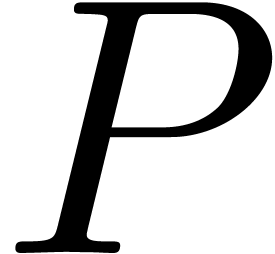 (and actually as a function of its
size). This seems to give some evidence for a strong witness conjecture
for algebraic numbers.
(and actually as a function of its
size). This seems to give some evidence for a strong witness conjecture
for algebraic numbers.
Actually, the above bound can be sharpened in an asymptotical way. Given
a real number  , let
, let  be the distance between
be the distance between  and the
closest point in
and the
closest point in  . The
following theorem is due to Roth [Rot55], based on previous
work by Schneider [Sch36].
. The
following theorem is due to Roth [Rot55], based on previous
work by Schneider [Sch36].
Theorem 10. Given
an algebraic irrational number  and
and  , there are only a finite number of solutions
to the inequality
, there are only a finite number of solutions
to the inequality  , for
, for 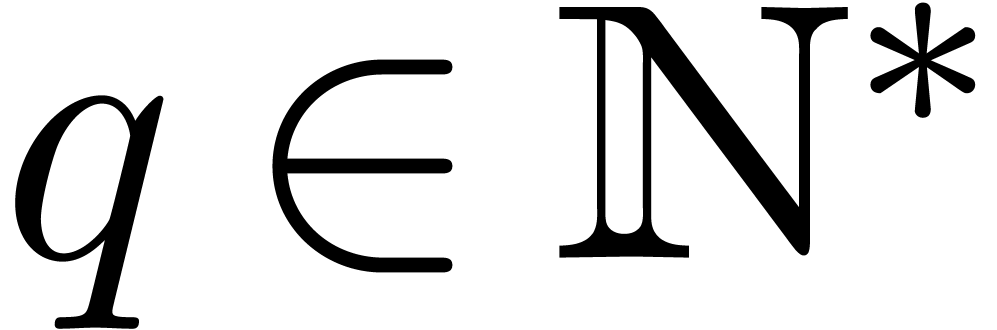 .
.
Unfortunately, asymptotic bounds are not really suited for establishing
witness theorems, because such theorems do not accommodate exceptions,
even if finite in number. Nevertheless, they contribute to the
likeliness of witness conjectures. Another, very general, probabilistic
and asymptotic result is the following [Khi61]:
Theorem 11. Let
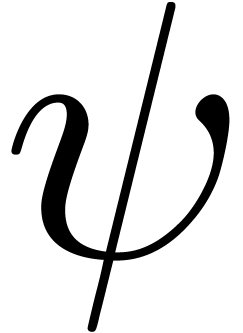 be a positive function, such that
be a positive function, such that 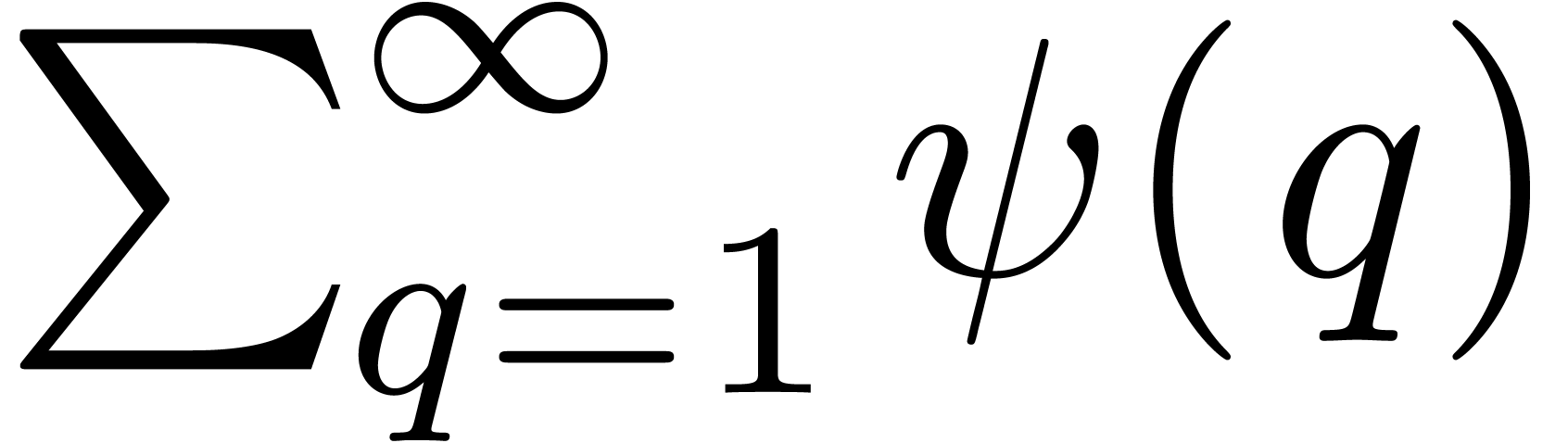 converges. Then for almost all numbers
converges. Then for almost all numbers  (for the Lebesgue measure), the equation
(for the Lebesgue measure), the equation  admits
only a finite number of solutions.
admits
only a finite number of solutions.
We refer to [Lan71] for a more detailed survey on
diophantine approximation and in particular on the diophantine
approximation of transcendental constants like  , logarithms and exponentials of algebraic numbers
and so on. Unfortunately, the scope of the actual theory is very limited
from our point of view, since it lacks effectiveness and no general
results exist for, say, the exp-log constants.
, logarithms and exponentials of algebraic numbers
and so on. Unfortunately, the scope of the actual theory is very limited
from our point of view, since it lacks effectiveness and no general
results exist for, say, the exp-log constants.
4.2Differential diophantine approximation
In the light of witness conjectures, there is no good reason to restrict
oneself to the approximation of transcendental constants by rational or
algebraic numbers. On the contrary, we might consider the approximation
by more general constants, like exp-log constants or differentially
algebraic constants. Equivalently, given complex numbers  and a class of multivariate analytic functions
and a class of multivariate analytic functions  , one might be interested in lower
bounds for
, one might be interested in lower
bounds for  as a function of the size of an
expression which represents
as a function of the size of an
expression which represents 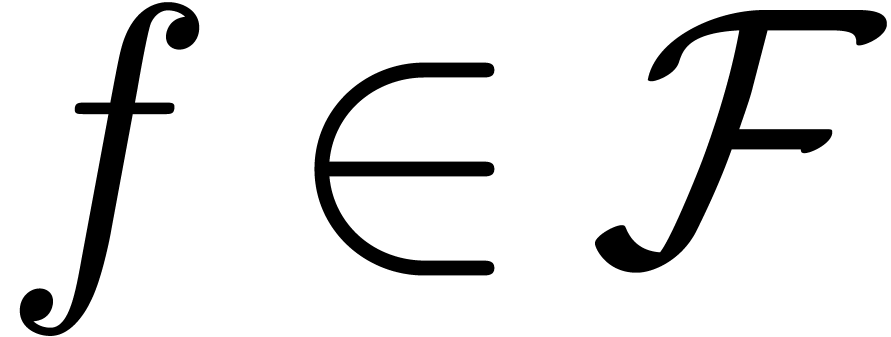 .
.
Several classical questions in diophantine approximations have natural
analogues. For instance, is there an analogue of theorem 4.2?
We expect this to be so, since we will usually only consider countable
sets of constants. Similarly, one may search for analogues of asymptotic
results like theorem 4.1. It would also be interesting to
have effective analogues for continued fraction expansions. By
preference, such expansions should have more structure than the
successive approximations found by, say, the LLL-algorithm [LLL82].
Finally, it is worth it to investigate the power series counterpart of
differential diophantine approximation. In this context, there is a need
for transfer principles back to the numeric setting. Of course, such
transfer principles would also be useful for proving witness conjectures
or designing zero-tests for constants. In the case of zero-tests, one
might for instance wonder how to represent a constant which is suspected
to be zero by the value of a function which can be proved to vanish
globally.
5Applications that rely on witness
conjectures
The main application of witness conjectures is zero-testing. However, it
is not recommended to directly apply the witness conjectures in all
circumstances. For instance, if we want to test whether the expression
(1.2) from the introduction vanishes, then conjecture 2.1 would give a very bad bound for the number of digits that
we need to evaluate. Nevertheless, using asymptotic expansion
techniques, it is easy to detect that (1.2) does not
vanish.
In this section, we briefly discuss two zero-test algorithms which only
indirectly rely on witness conjectures. In both cases, the witness
conjectures enable us to obtain reasonable complexity bounds for such
zero-tests, something which is impossible for algorithms that rely on
structure theorems [Ric94].
We should also mention that it is not necessary to wait for proofs of
the witness conjecture in order to base zero-test algorithms on them.
Indeed, since most general purpose zero-tests implemented so far are
either based on non reliable heuristic or are limited to relatively
small classes of constants, we think that the mere statement of a
precise conjecture already forms a progress, since such a conjecture can
be used as a reliable and efficient heuristic.
5.1Linear combinations of exponentials
In [vdH01], we considered linear combinations of the form
 |
(8) |
where 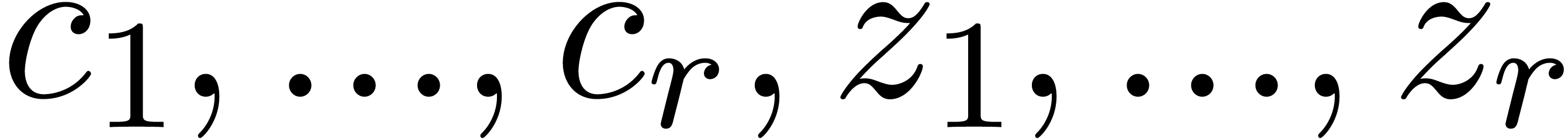 are “holonomic constants”.
Such expressions naturally occur when computing with solutions to linear
differential equations near singularities. We proved a theorem, which
implies the following one for “sufficiently regular” witness
functions
are “holonomic constants”.
Such expressions naturally occur when computing with solutions to linear
differential equations near singularities. We proved a theorem, which
implies the following one for “sufficiently regular” witness
functions  :
:
Theorem 12. Assume
conjecture 2.3. Then we may test whether (5.1) vanishes in a time bounded by
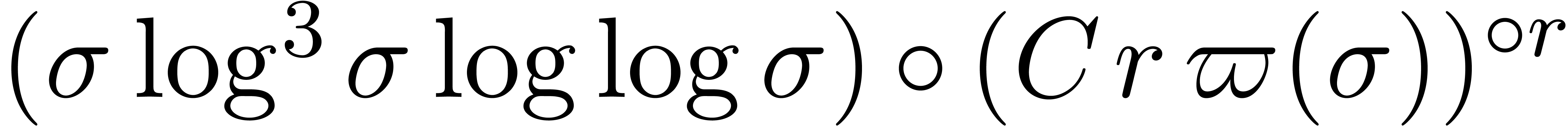
for some constant 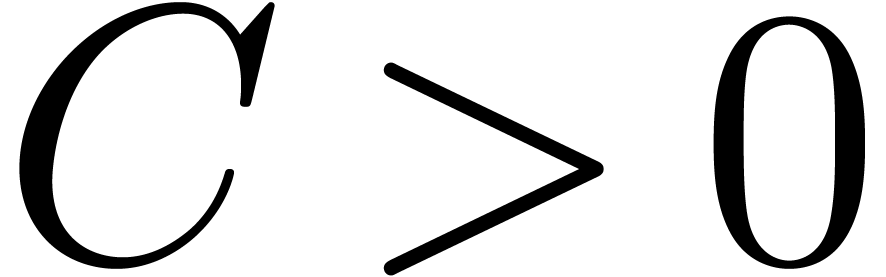 , and
where
, and
where 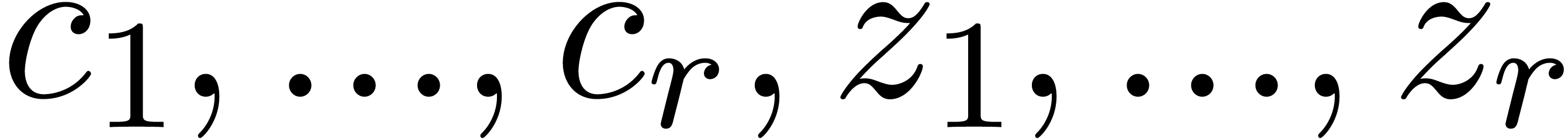 can be represented by expressions of size
can be represented by expressions of size
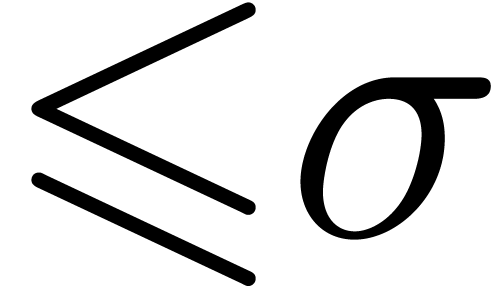 .
.
The following points should be noticed about this result:
-
The left composition with 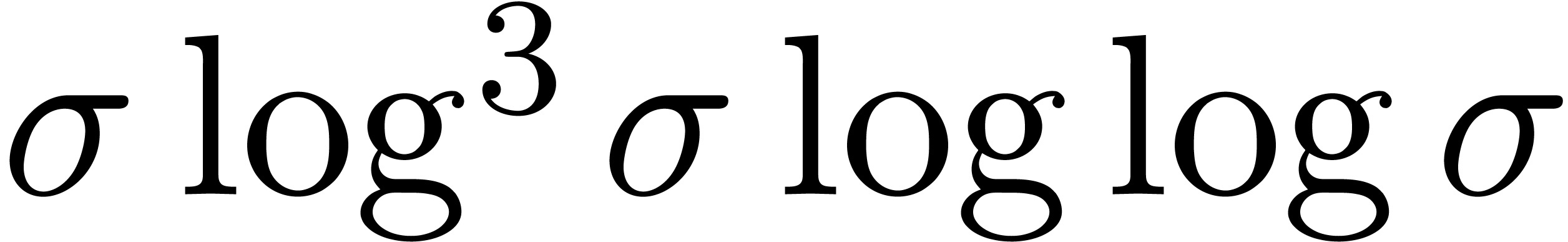 is due to the cost
of the evaluation of (5.1) up to
is due to the cost
of the evaluation of (5.1) up to  digits. If the class of holonomic constants is replaced by a larger
one, such as
digits. If the class of holonomic constants is replaced by a larger
one, such as 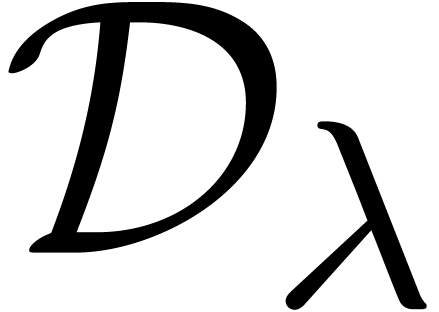 , then one
should rather compose on the left by
, then one
should rather compose on the left by 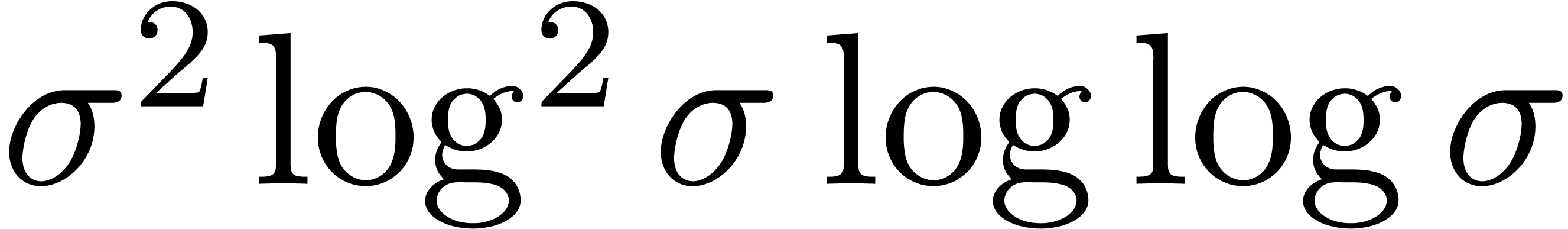 .
.
-
There is a big difference between strong and weak witness
conjectures as to the behavior of the 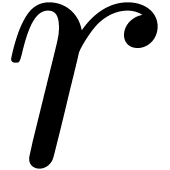 -th
iterate of
-th
iterate of  . Indeed, if
. Indeed, if
 has exponentiality zero in
has exponentiality zero in  , then so has its
, then so has its 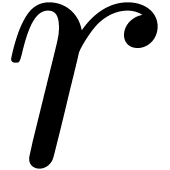 -th iterate (see [vdH97] for a
definition of exponentiality; examples of such functions are
-th iterate (see [vdH97] for a
definition of exponentiality; examples of such functions are 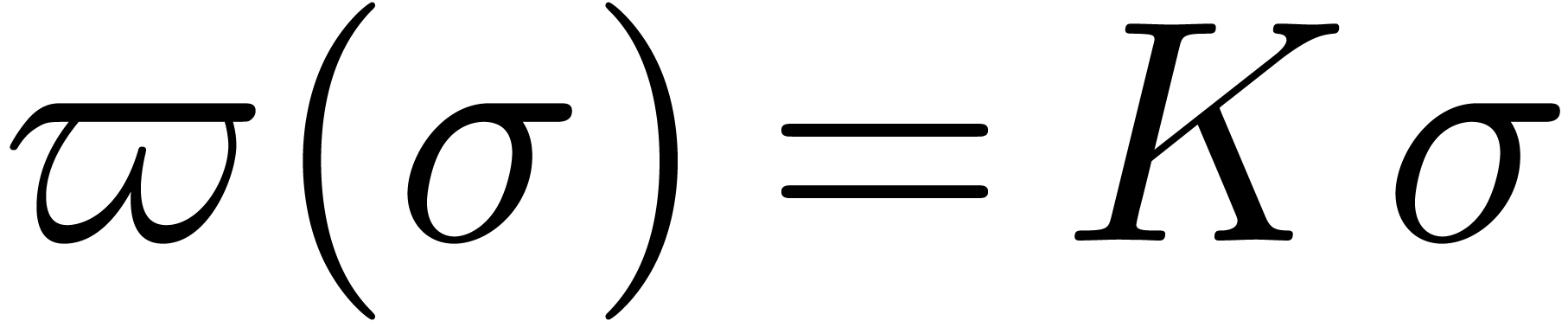 ,
, 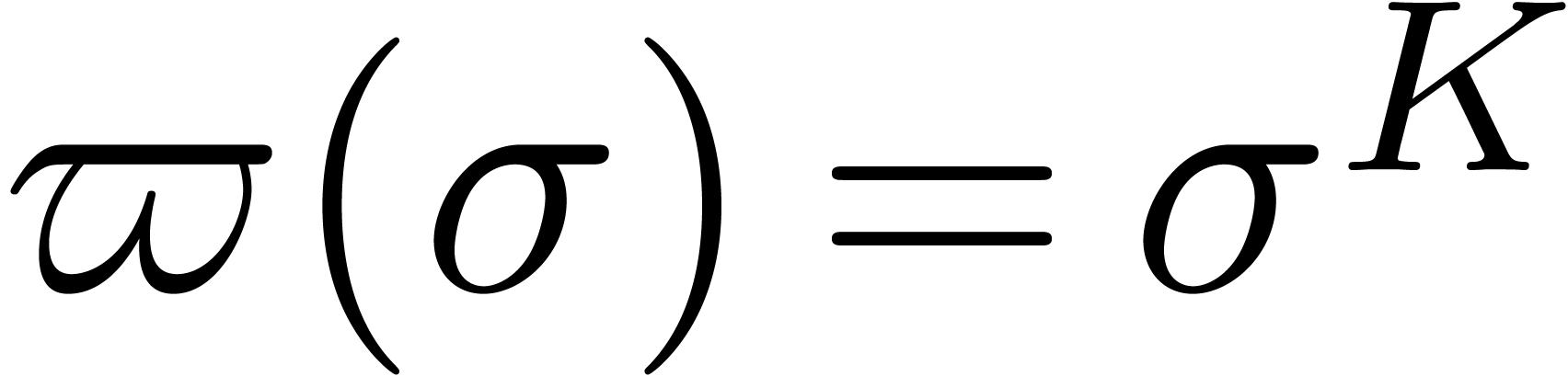 or
or
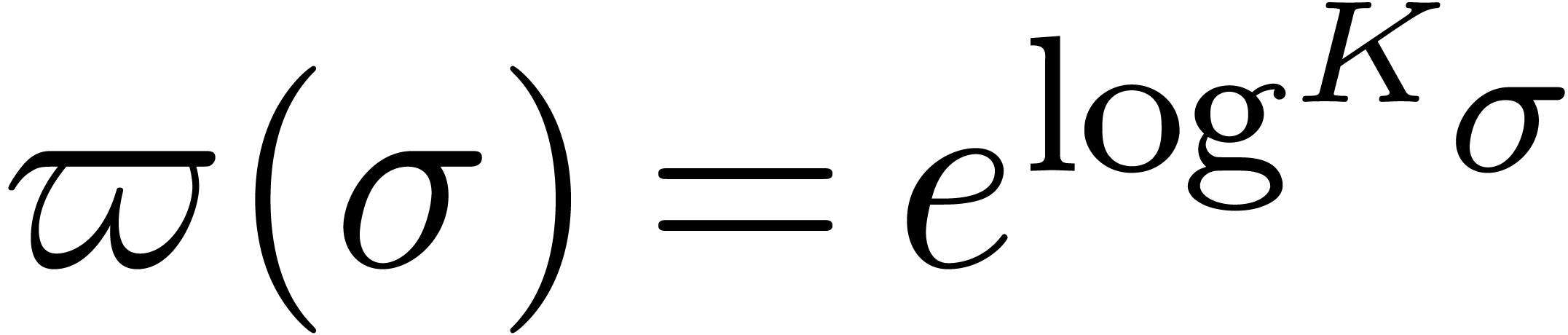 ). Moreover, the growth
of
). Moreover, the growth
of  in
in  is bounded by
an iterated exponential in this case.
is bounded by
an iterated exponential in this case.
On the other hand, as soon as  has
exponentiality
has
exponentiality  , the
, the
 -th iterate of
-th iterate of  has an extremely bad behavior for large
has an extremely bad behavior for large 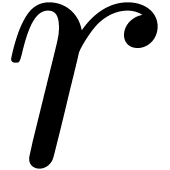 , since it is not longer bounded by any
iterated exponential. It is therefore of the greatest practical
interest to prove witness conjectures for witness functions of
exponentiality
, since it is not longer bounded by any
iterated exponential. It is therefore of the greatest practical
interest to prove witness conjectures for witness functions of
exponentiality 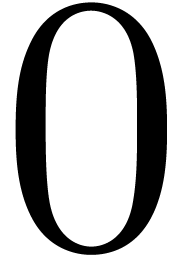 ;
unfortunately, even in the power series setting, the existing
techniques do not allow us to do so.
;
unfortunately, even in the power series setting, the existing
techniques do not allow us to do so.
5.2Exp-log constants
In [vdH95] we described the first efficient zero-test for
real exp-log constants. At the time, we were not able to give any
complexity bound for our algorithm, and this was one of our main
motivation for the statement of witness conjectures.
Using the more powerful asymptotic expansion algorithms from [vdH97],
which rely on Cartesian representations, and the more powerful
zero-tests for multivariate exp-log series from [SvdH01],
we also designed a more efficient zero-test for real exp-log constants
in collaboration with J. Shackell. This algorithm, which will be
detailed in a forthcoming paper, is expected to satisfy a similar
complexity bound as in theorem 5.1 in the sense that it
again involves an iterate of the witness function  .
.
Bibliography
-
[Ax71]
-
J. Ax. On Schanuel's conjecture. Ann. of
Math., 93:252–268, 1971.
-
[BB92]
-
J.M. Borwein and P.B. Borwein. Strange series and
high precision fraud. Mathematical Monthly,
99:622–640, 1992.
-
[É92]
-
J. Écalle. Introduction aux fonctions
analysables et preuve constructive de la conjecture de
Dulac. Hermann, collection: Actualités
mathématiques, 1992.
-
[Khi61]
-
A. Ya. Khinchin. Continued fractions.
Fizmatgiz, Moscow, 1961. English transl., Univ. of Chicago
Press, Chicago, Ill., 1964, MR 28 #5037.
-
[Kho91]
-
A. G. Khovanskii. Fewnomials. American
Mathematical Society, Providence, RI, 1991.
-
[Lan71]
-
S. Lang. Transcendental numbers and diophantine
approximation. Bull. Amer. Math. Soc.,
77/5:635–677, 1971.
-
[LLL82]
-
A.K. Lenstra, H.W. Lenstra, and L. Lovász.
Factoring polynomials with rational coefficients. Math.
Ann., 261:515–534, 1982.
-
[Ric94]
-
D. Richardson. How to recognise zero. J. Symbol.
Comput., 24(6):627–646, 1994.
-
[Ric01]
-
D. Richardson. The uniformity conjecture. In
Lecture Notes in Computer Science, volume 2064, pages
253–272. Springer Verlag, 2001.
-
[Ris75]
-
R.H. Risch. Algebraic properties of elementary
functions in analysis. Amer. Journ. of Math.,
4(101):743–759, 1975.
-
[Rot55]
-
K. Roth. Rational approximations to algebraic
numbers. Mathematika, 2:1–20, 1955. Corrigendum,
168, MR 17, 242.
-
[Sch36]
-
T. Schneider. Über die approximation
algebraischer zahlen. J. Reine Angew. Math.,
175:110–128, 1936.
-
[Sha89]
-
J.R. Shackell. A differential-equations approach to
functional equivalence. In G. Gonnet, editor, ISSAC '89
Proceedings, pages 7–10, Portland, Oregon, 1989.
A.C.M. Press.
-
[SSC85]
-
M.F. Singer, B.D. Saunders, and B.F. Caviness. An
extension of Liouville's theorem on integration in finite terms.
SIAM J. Comp., 14:966–990, 1985.
-
[SvdH01]
-
J.R. Shackell and J. van der Hoeven. Complexity
bounds for zero-test algorithms. Technical Report 2001-63,
Prépublications d'Orsay, 2001.
-
[vdH95]
-
J. van der Hoeven. Automatic numerical expansions. In
J.-C. Bajard, D. Michelucci, J.-M. Moreau, and J.-M.
Müller, editors, Proc. of the conference "Real
numbers and computers", Saint-Étienne, France,
pages 261–274, 1995.
-
[vdH97]
-
J. van der Hoeven. Asymptotique automatique.
PhD thesis, École Polytechnique, Laboratoire
d'Informatique, École Polytechnique, Paris, France, 1997.
-
[vdH01]
-
J. van der Hoeven. Fast evaluation of holonomic
functions near and in singularities. JSC,
31:717–743, 2001.
 . A central
problem in computer algebra is to test whether such a constant, which
is represented by an expression, is zero.
. A central
problem in computer algebra is to test whether such a constant, which
is represented by an expression, is zero.
 ,
,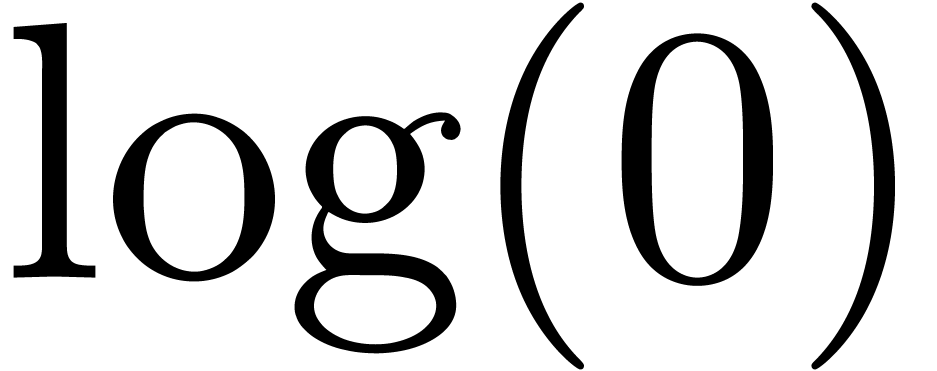 or
or 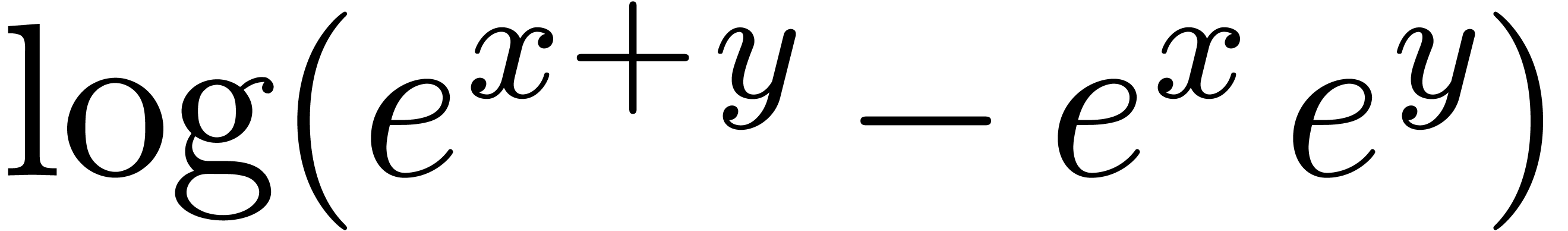 .
.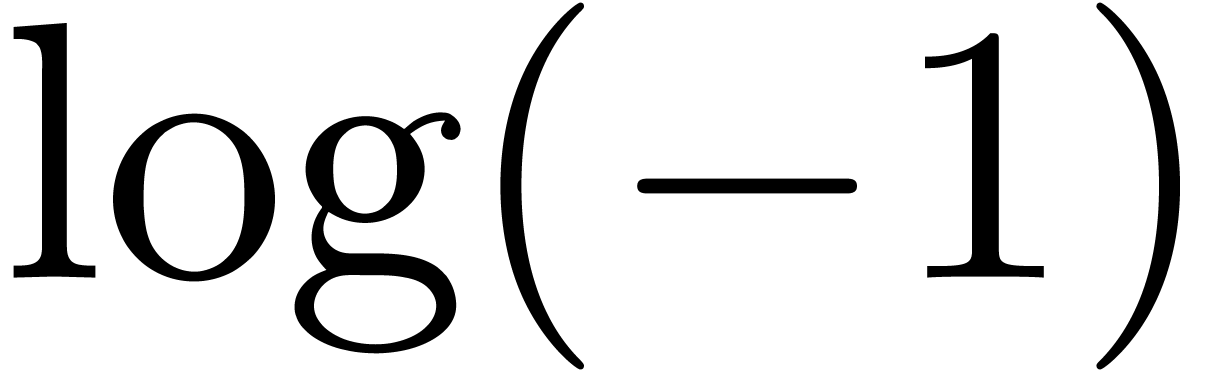 or
or 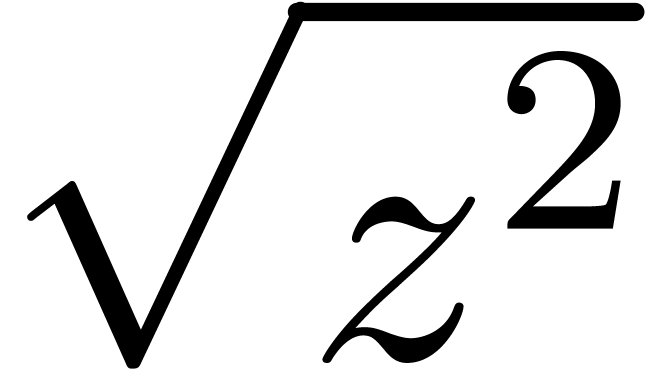 ?
?
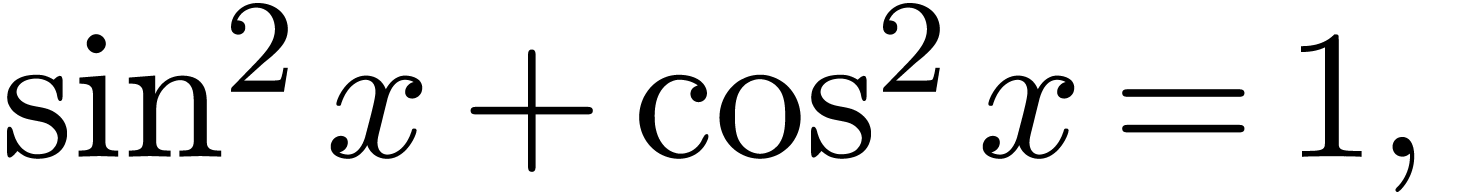
 and
and  are
different as expressions. Similarly,
are
different as expressions. Similarly,
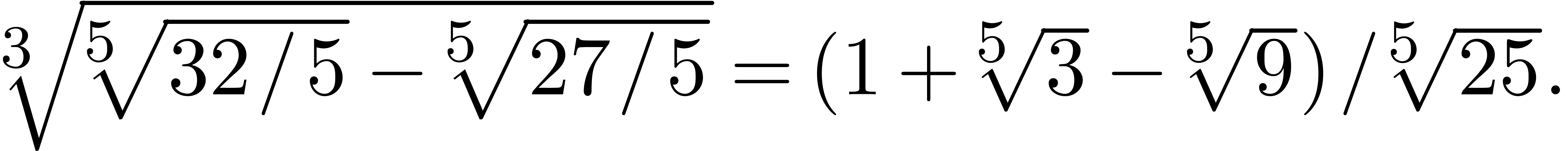
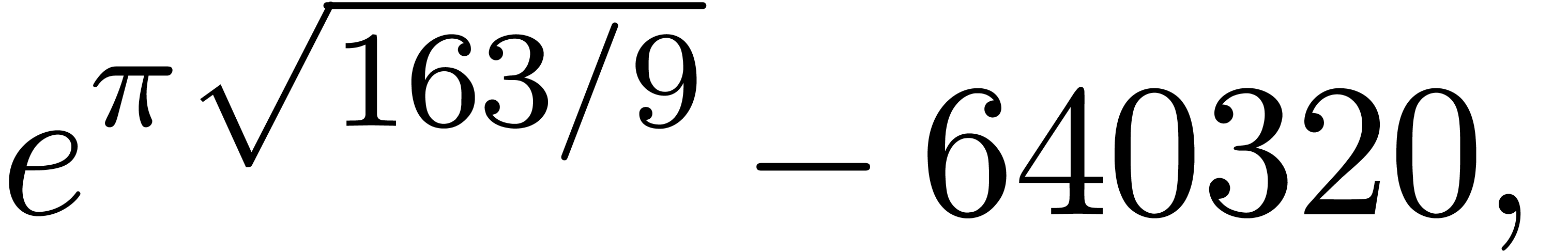
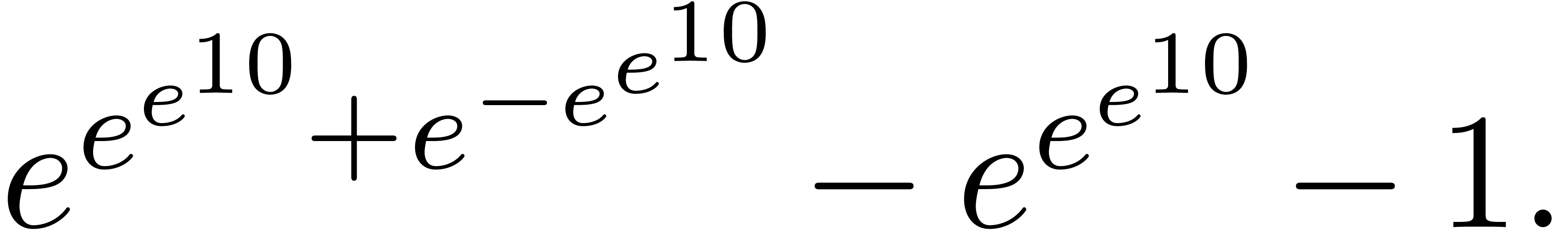
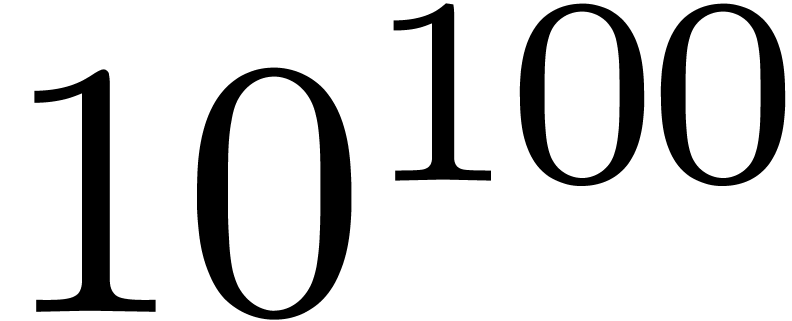 might become invalid and need to be rewritten as
might become invalid and need to be rewritten as  ,
, ,
,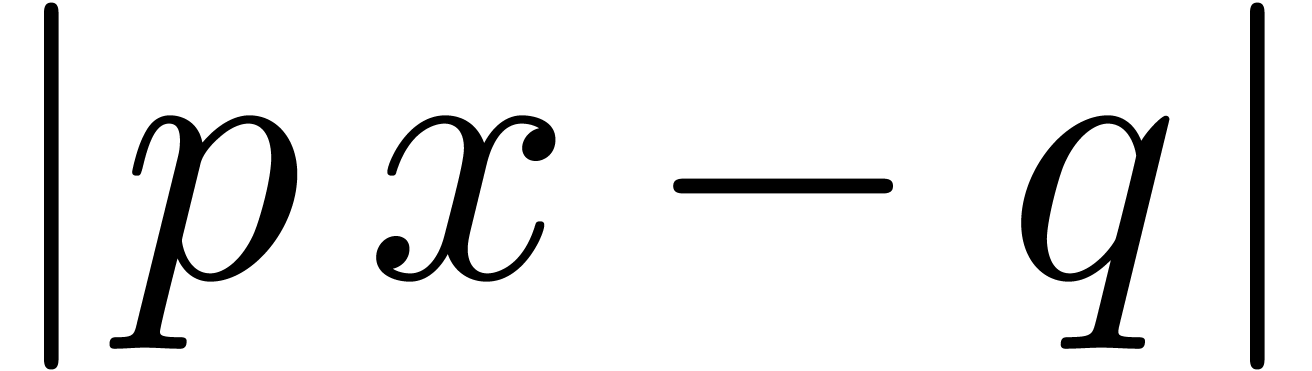
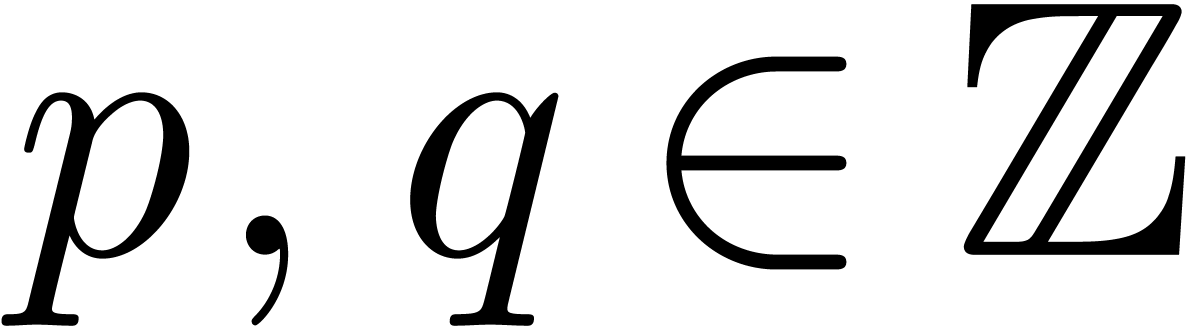 .
.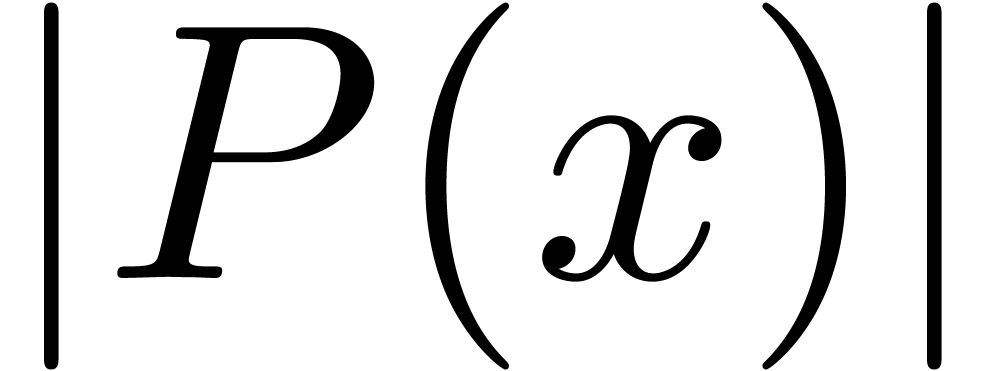 for polynomials
for polynomials 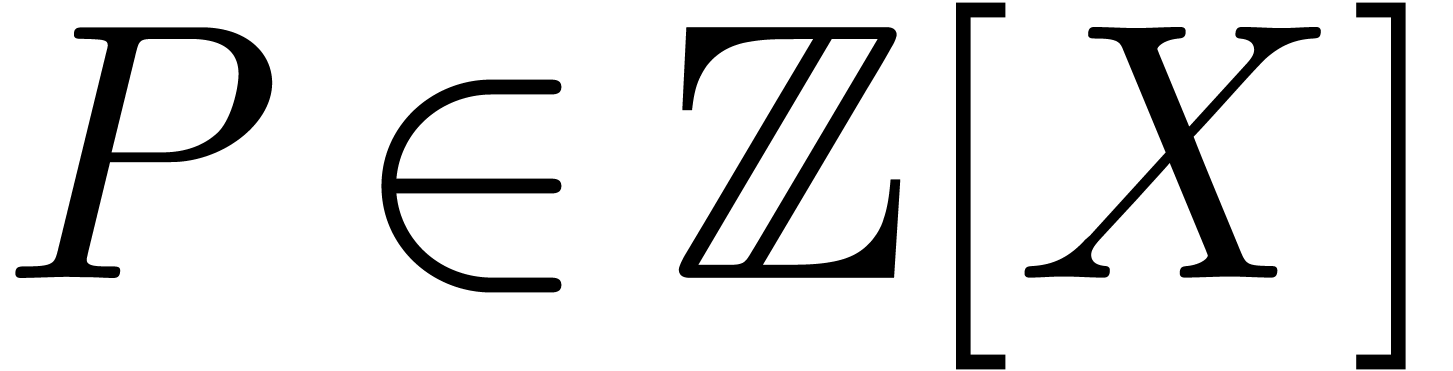 .
. be the set of exp-log constant expressions,
i.e. the expressions formed from
be the set of exp-log constant expressions,
i.e. the expressions formed from  using
using  and
and  .
. the set of real numbers which can be
represented by an expression in
the set of real numbers which can be
represented by an expression in  the real number represented by an expression
the real number represented by an expression 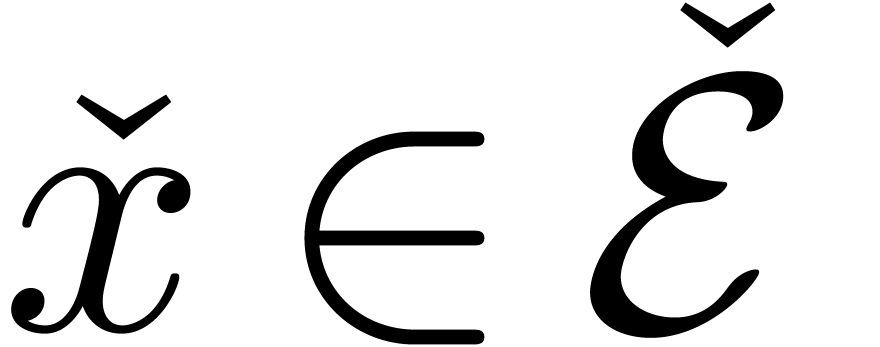 .
.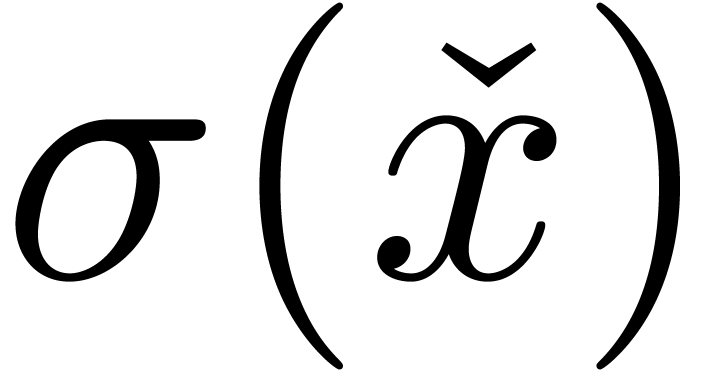 the
size of an expression
the
size of an expression 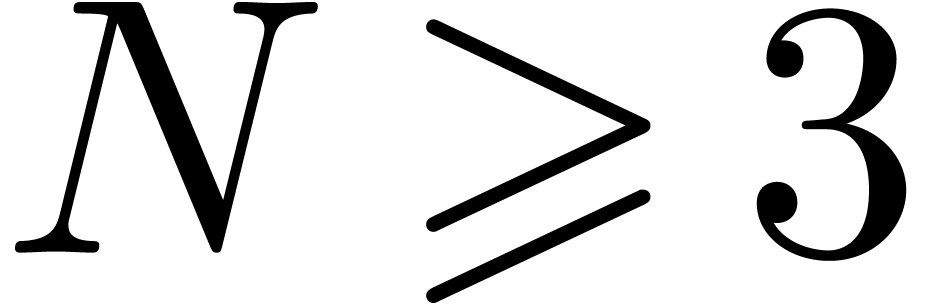 ,
,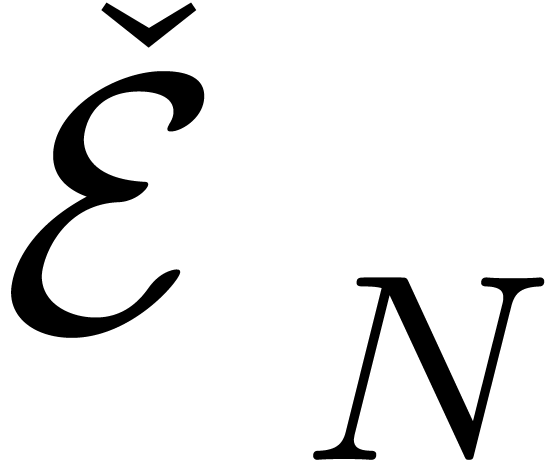 the set of all expressions
the set of all expressions 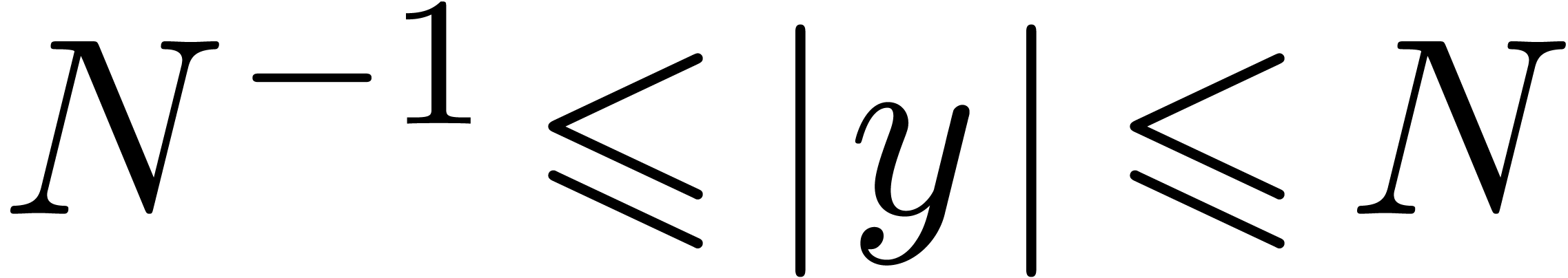 for all subexpressions
for all subexpressions  of
of  .
. of one of the forms
of one of the forms
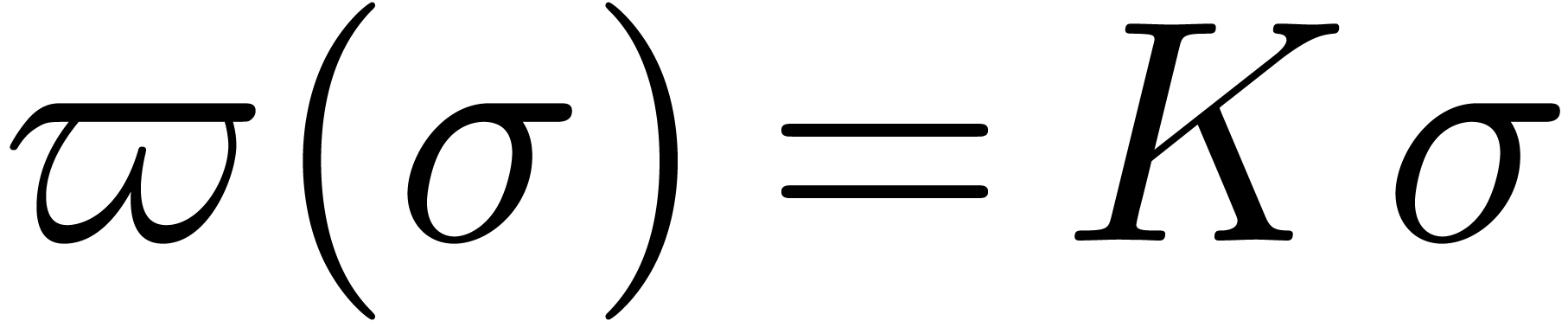 ;
;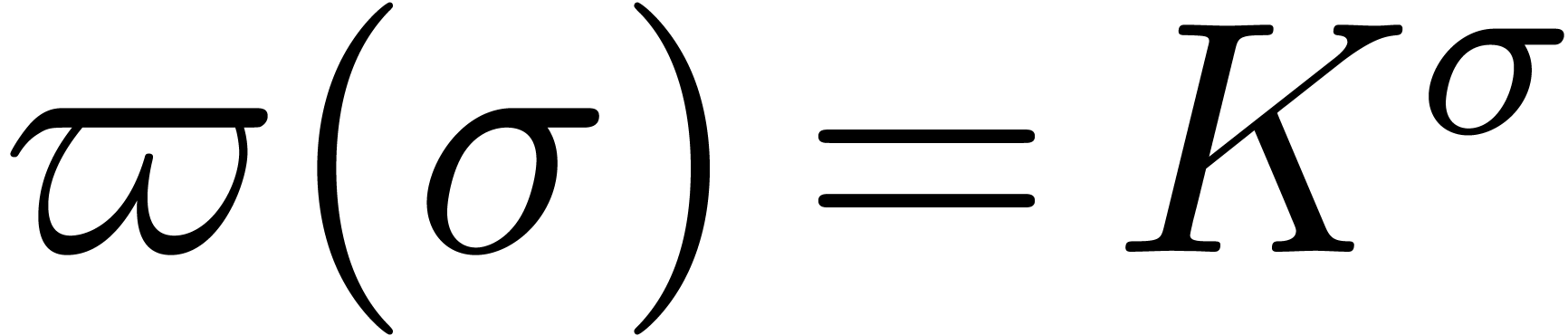 ,
,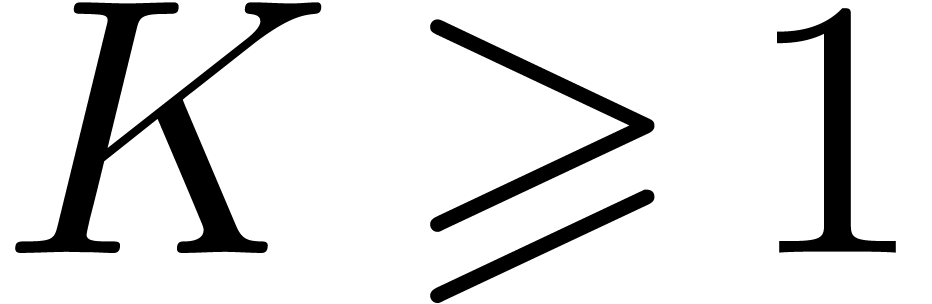 depends on
depends on  ,
,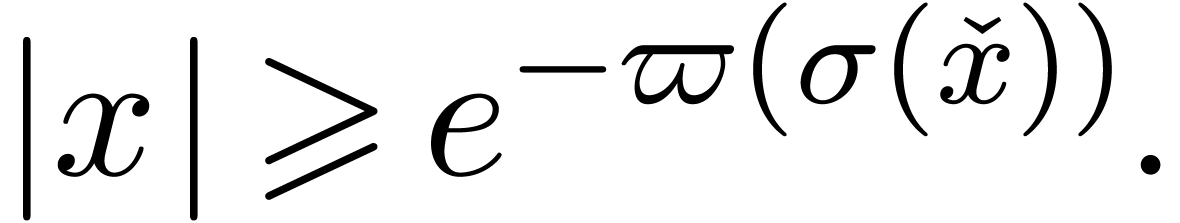
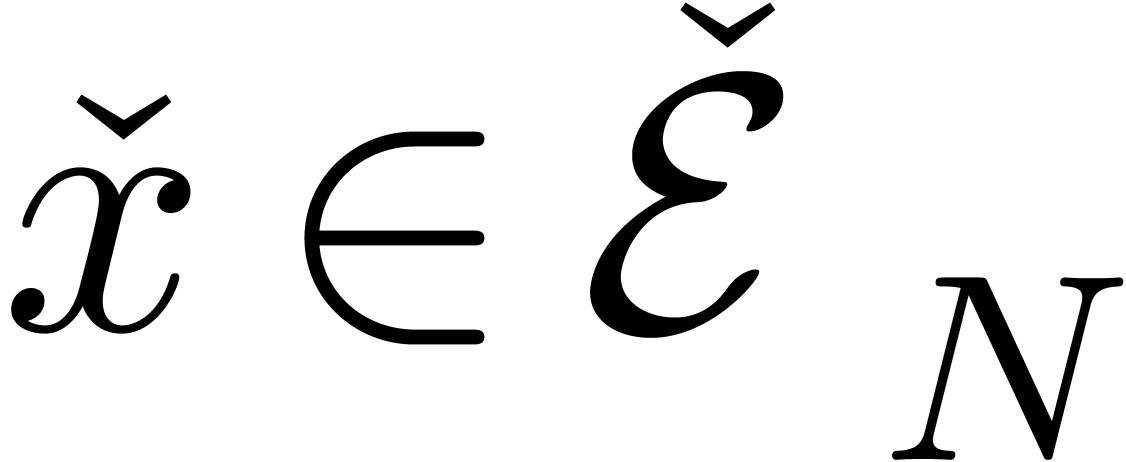 with
with 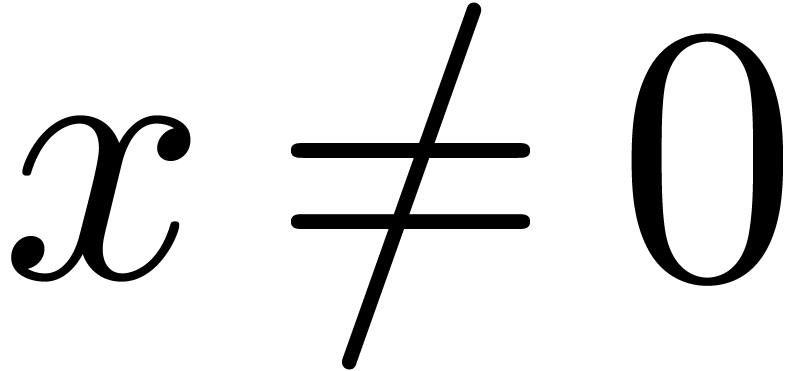 .
. ,
,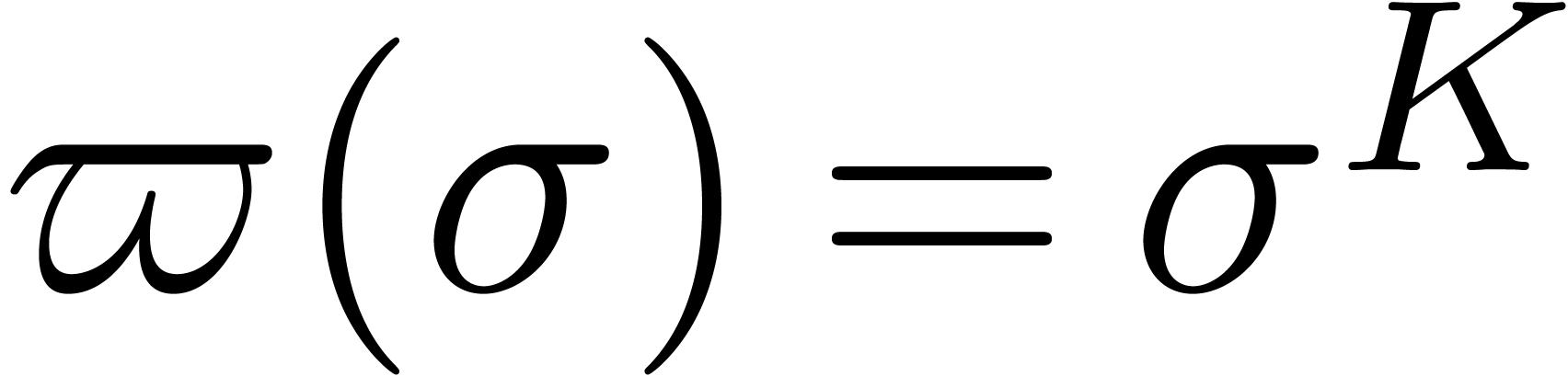 ,
,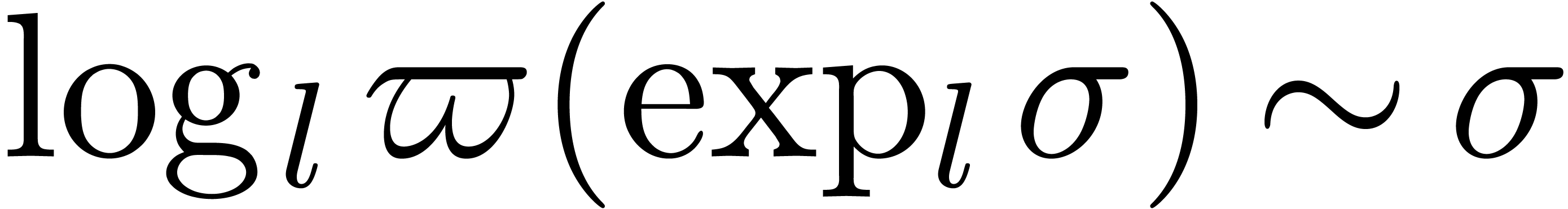 ,
,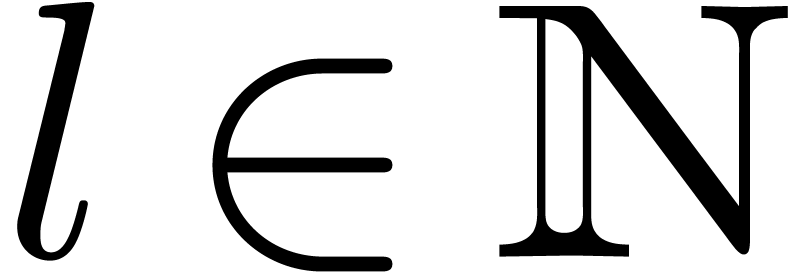 ,
, and
and  denote the
denote the  -th
-th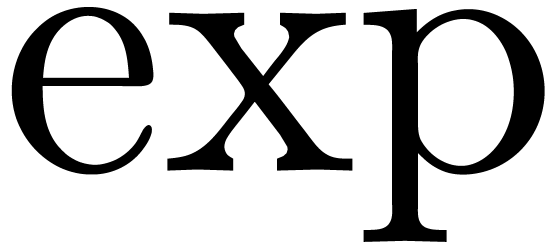 .
.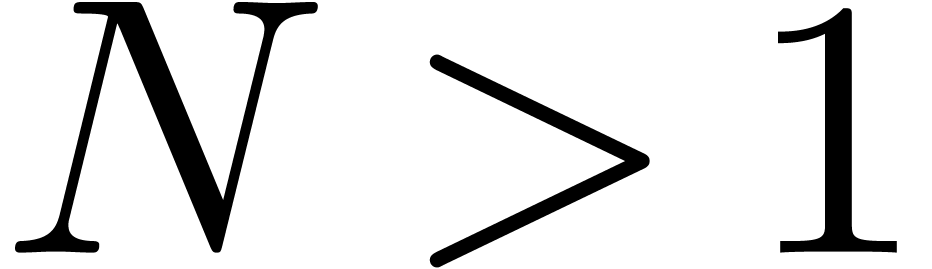 ,
, be the class of
all expressions
be the class of
all expressions  we have
we have  ,
,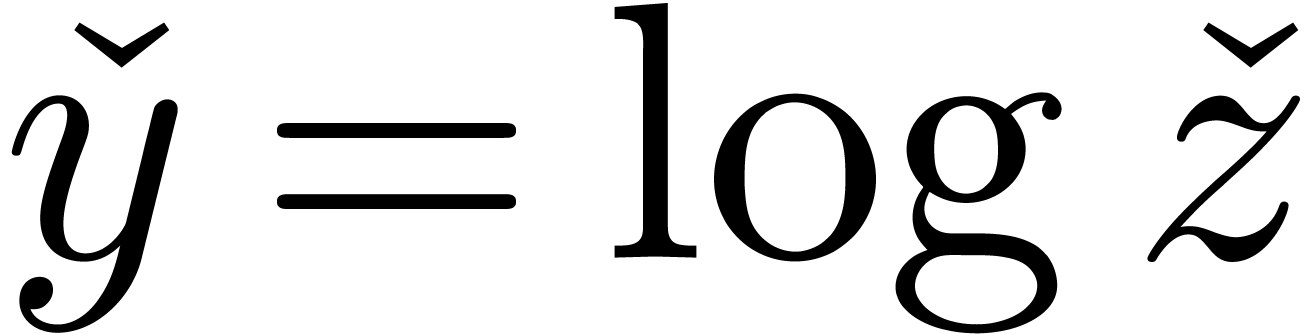 we have
we have 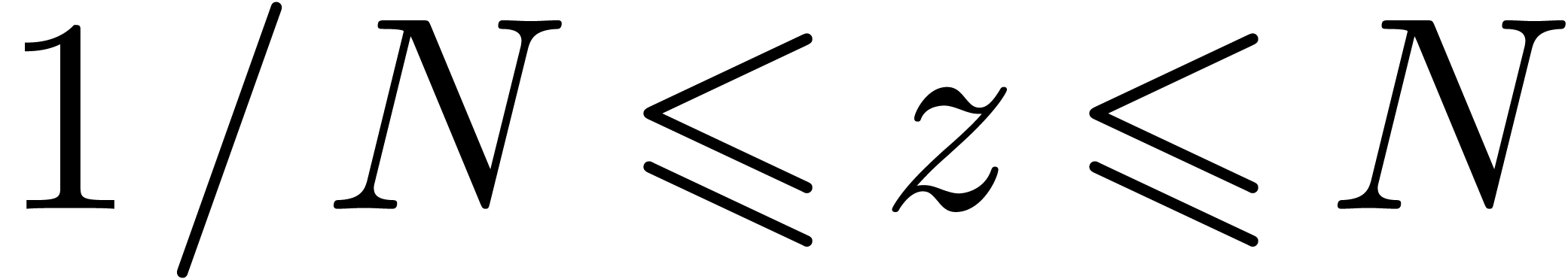 .
.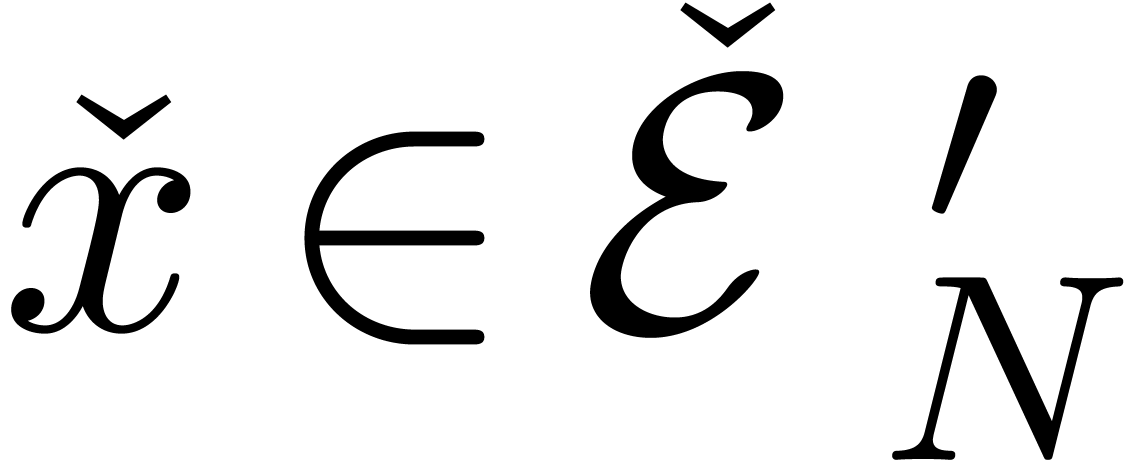 ,
,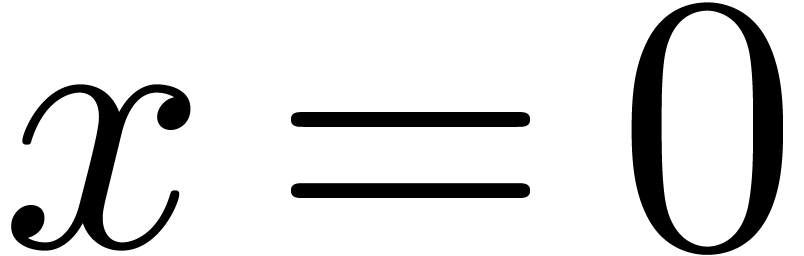 or
or 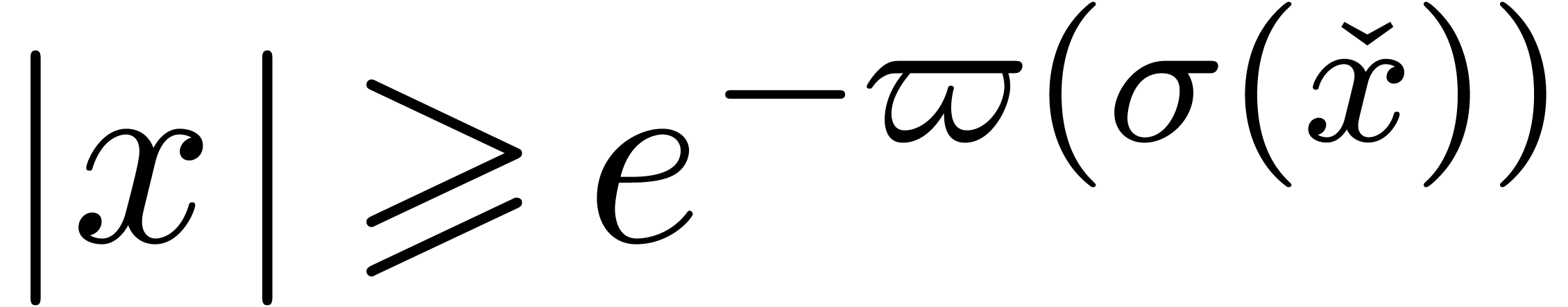 .
.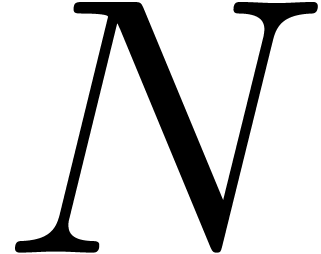 as soon as it holds for a particular
as soon as it holds for a particular  we may take
we may take  .
.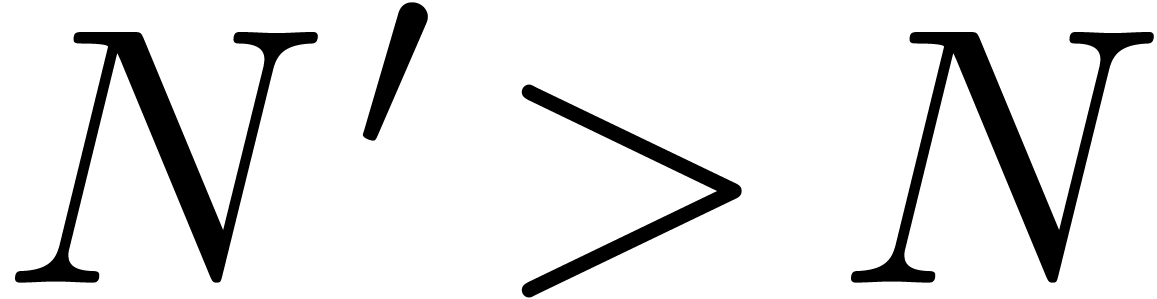 we may take
we may take
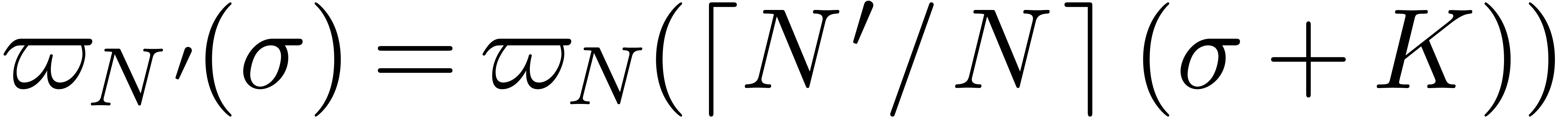
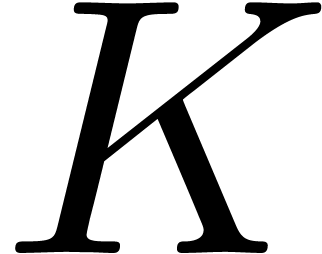 ,
, with
with  may be rewritten as
may be rewritten as
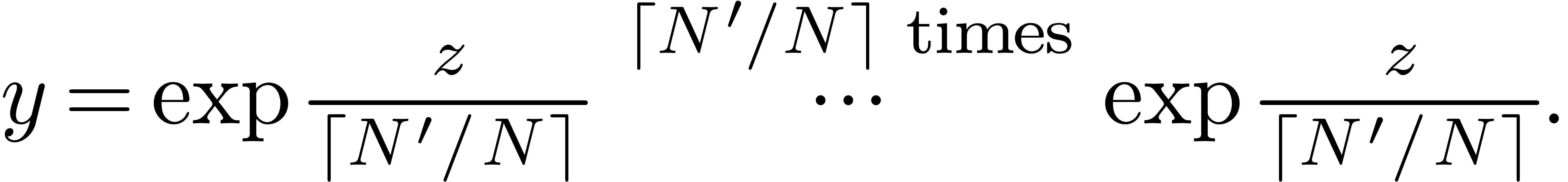
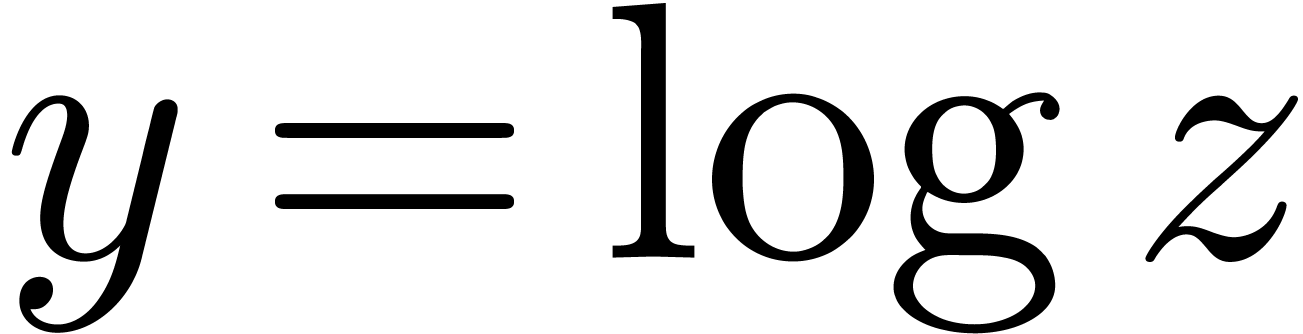 with
with 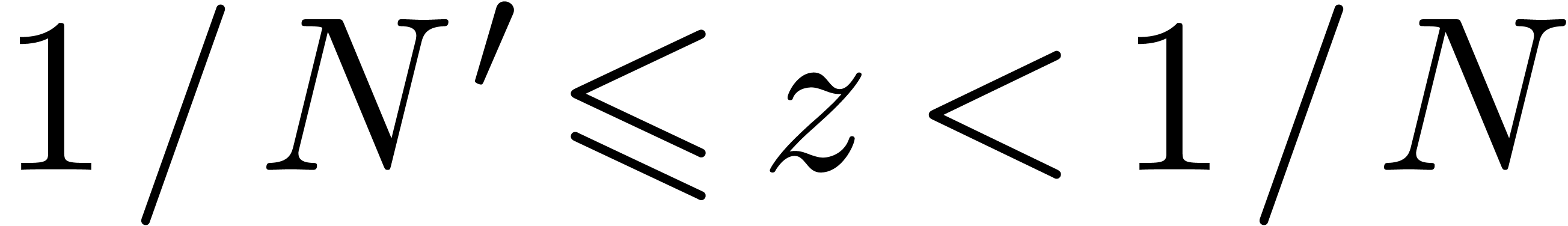 or
or 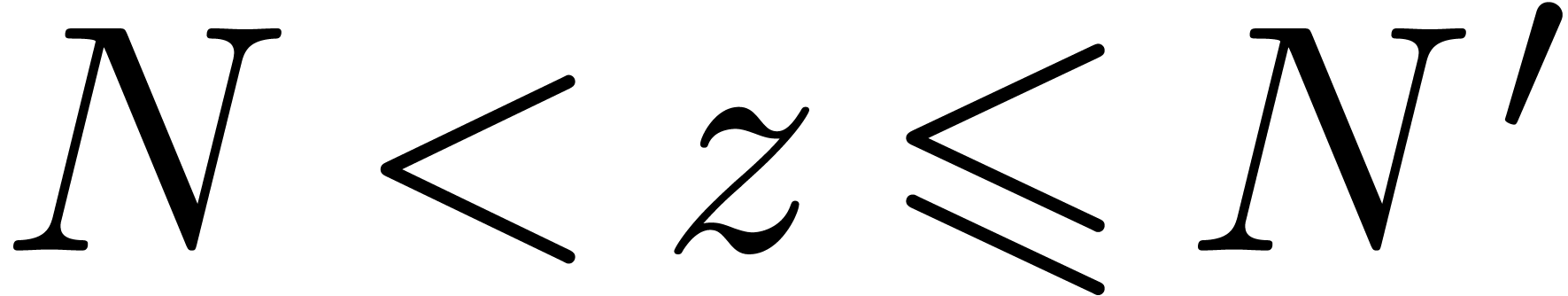 ,
,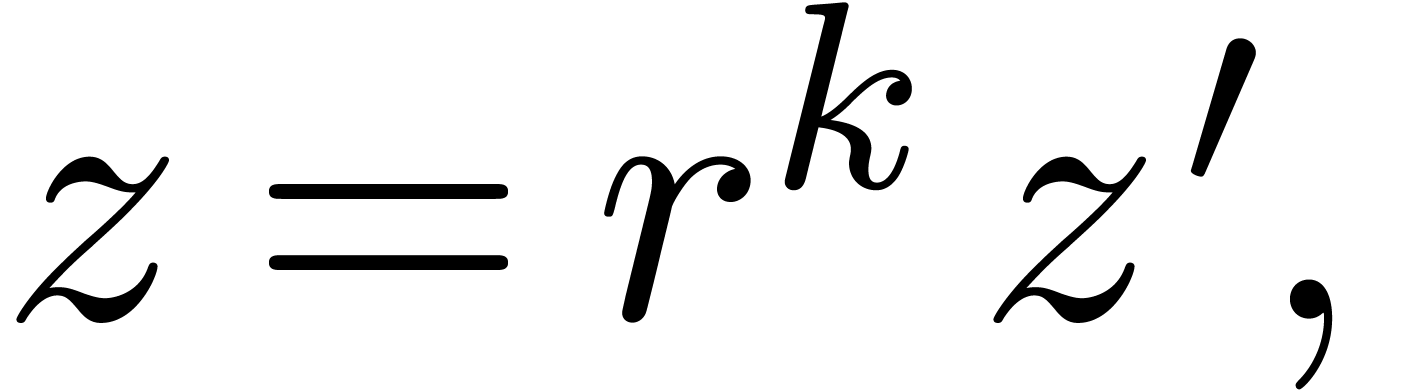
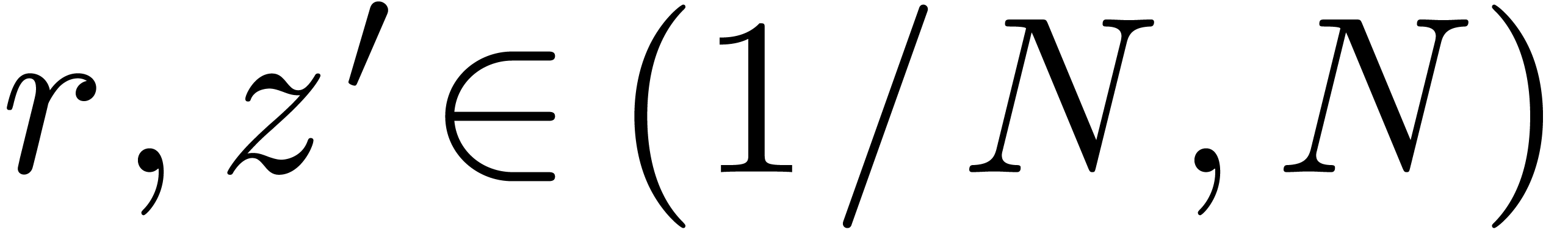 and
and  ,
,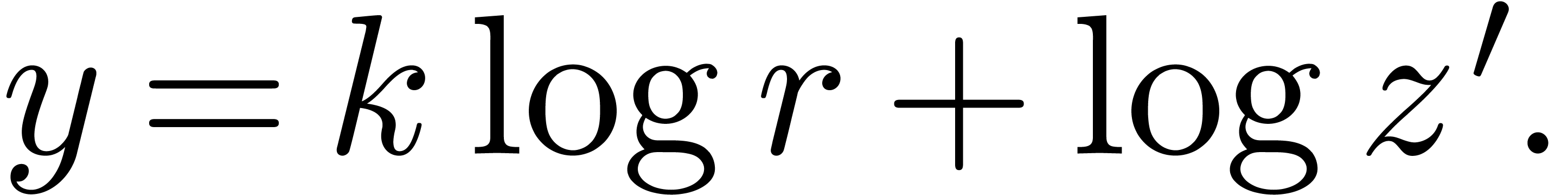
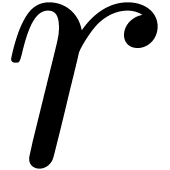 to be a fixed rational
number of small size close to
to be a fixed rational
number of small size close to  by a fixed constant, which explains
(
by a fixed constant, which explains
( .
.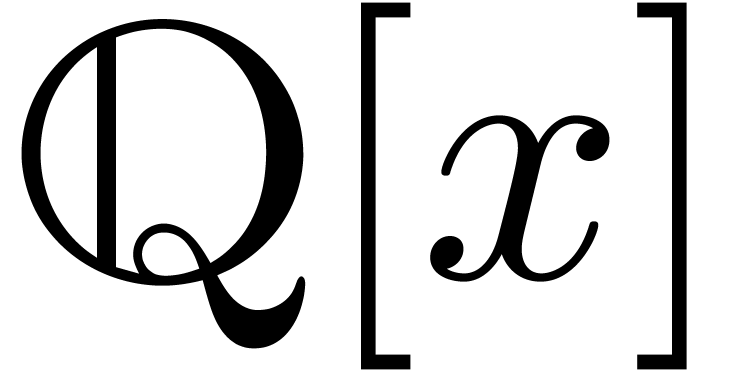 ).
). be a certain field of constants and let
be a certain field of constants and let 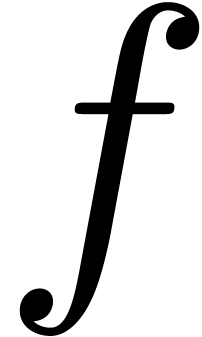 be a function which is analytic in
be a function which is analytic in 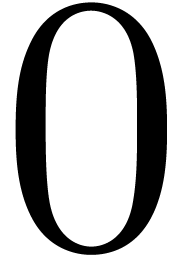 .
.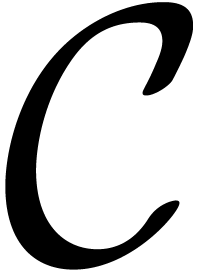 with initial
conditions in
with initial
conditions in 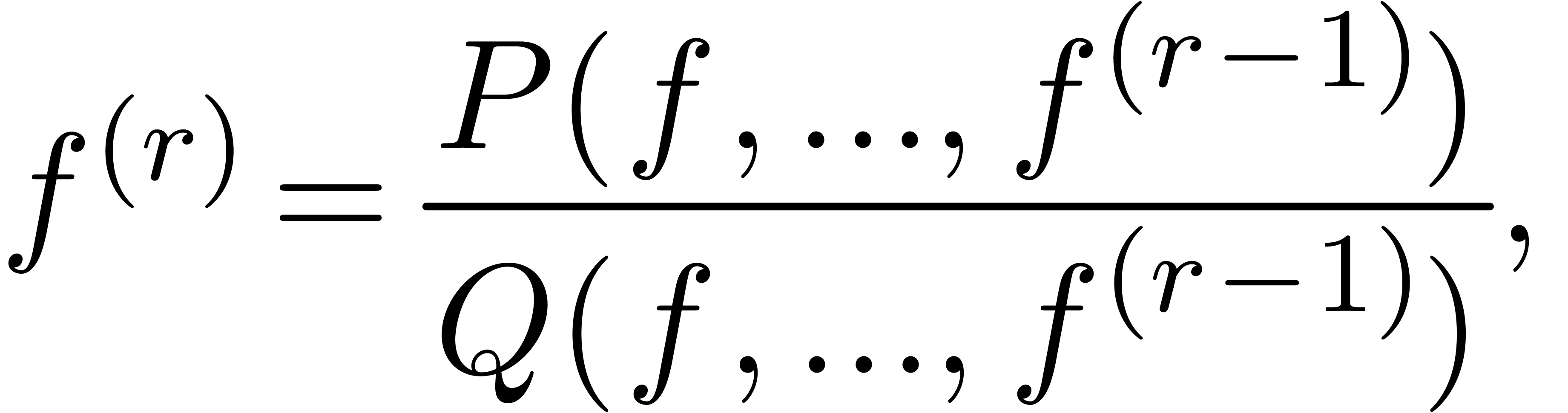
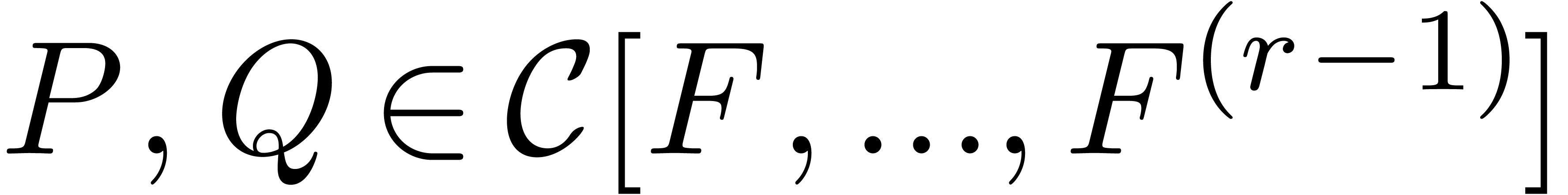 and where
and where 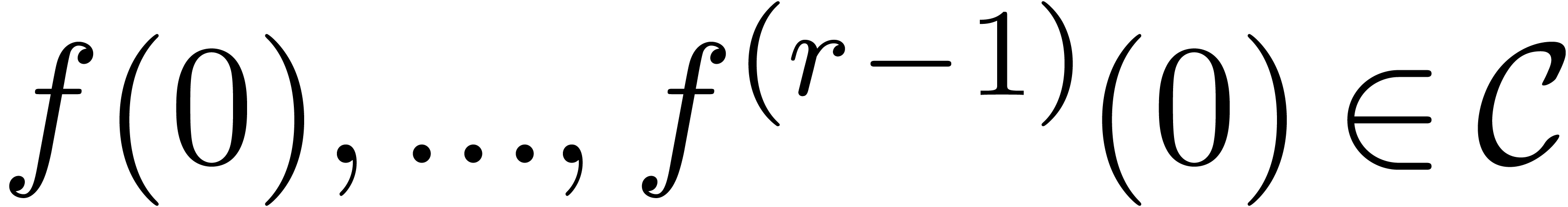 are such
that
are such
that
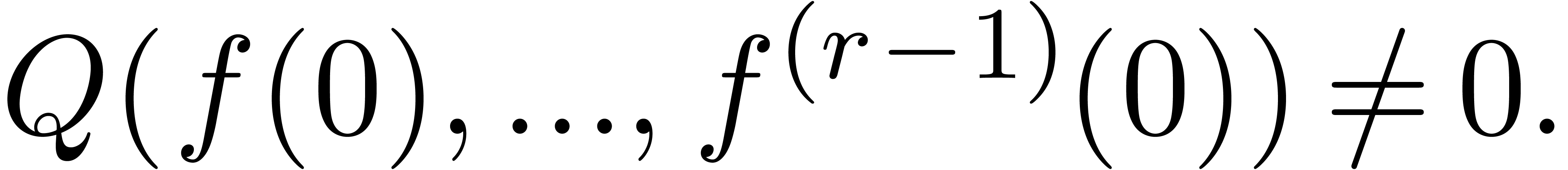
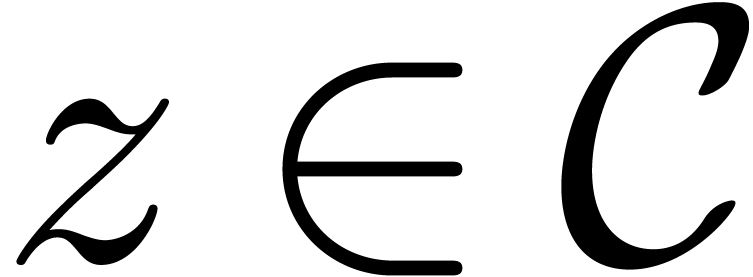 ,
, is strictly smaller than the radius of convergence
is strictly smaller than the radius of convergence  of
of 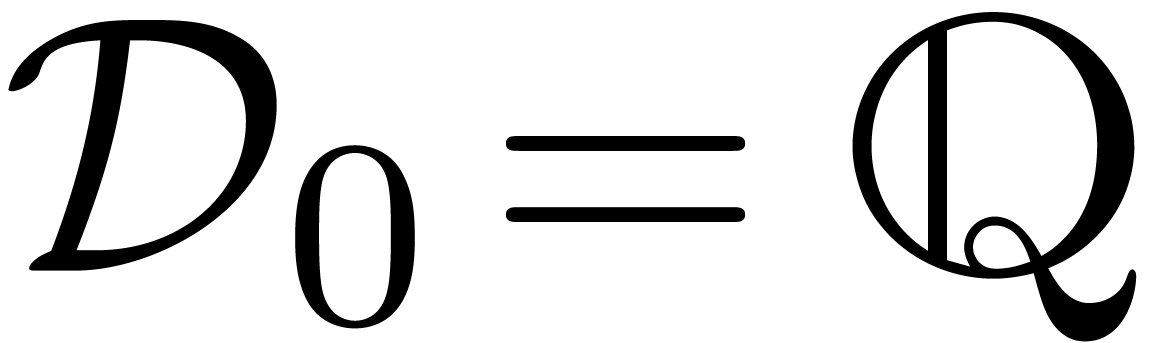 .
.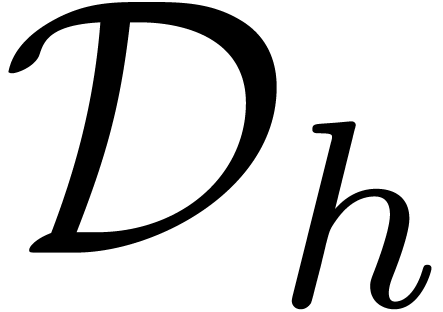 has been constructed, we let
has been constructed, we let 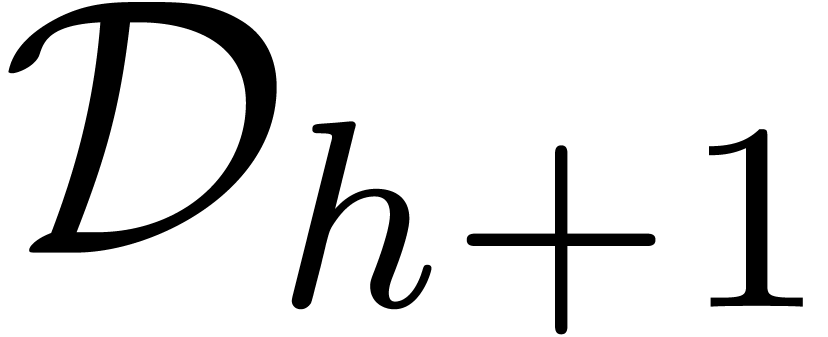 be
the set of all possible values in elements of
be
the set of all possible values in elements of  .
. may be represented by expressions as follows. Let
may be represented by expressions as follows. Let  be the smallest set of expressions such that
be the smallest set of expressions such that
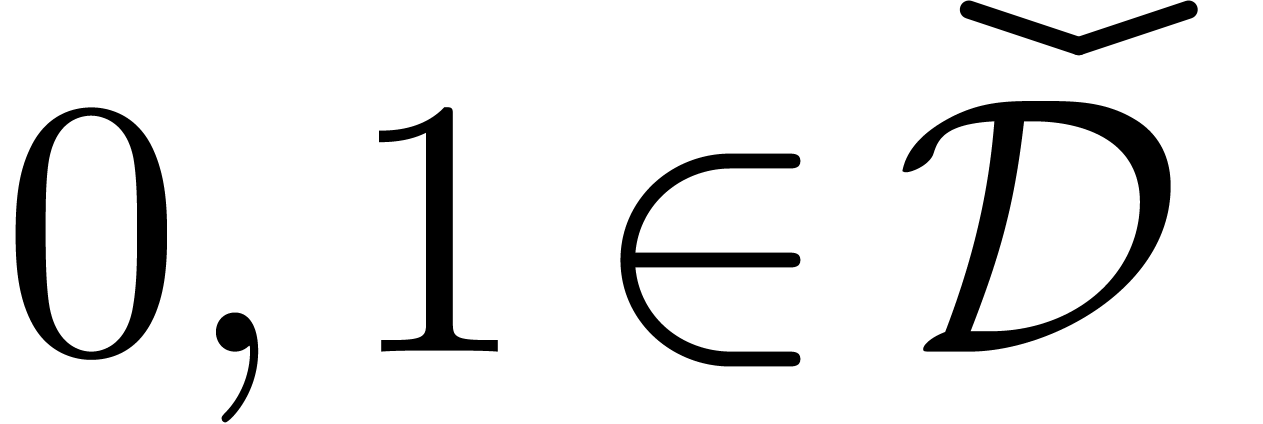 .
.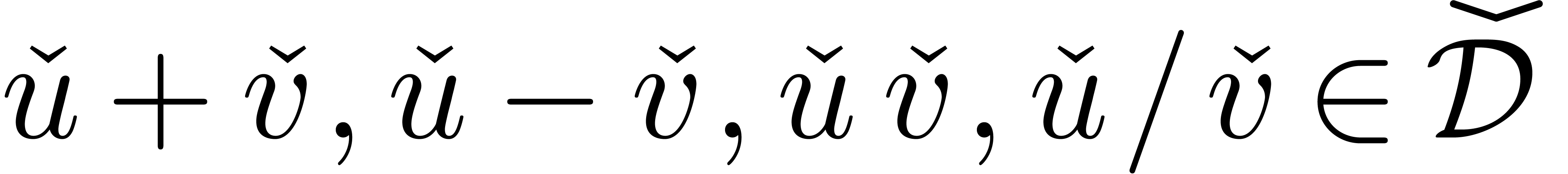 for all
for all 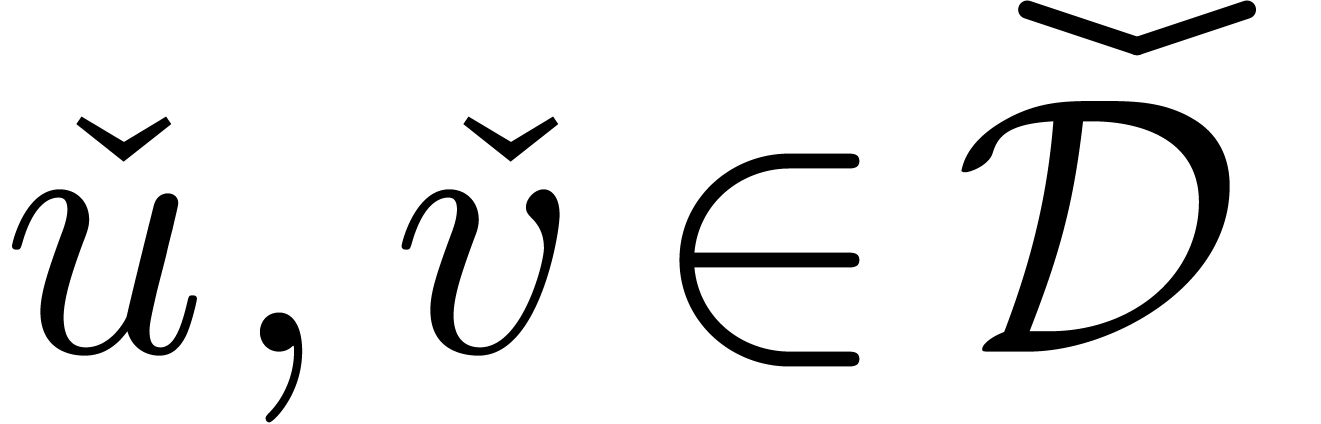 .
.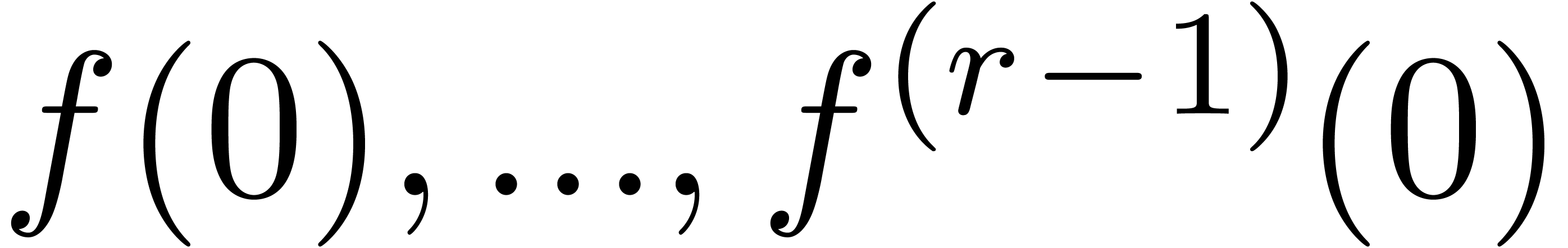 are represented by
are represented by 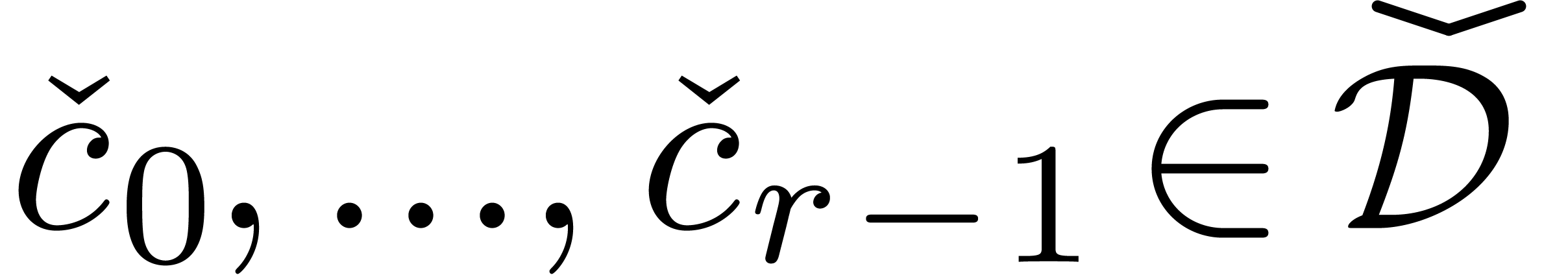 and such that
and such that  and
and  are represented by expressions in
are represented by expressions in 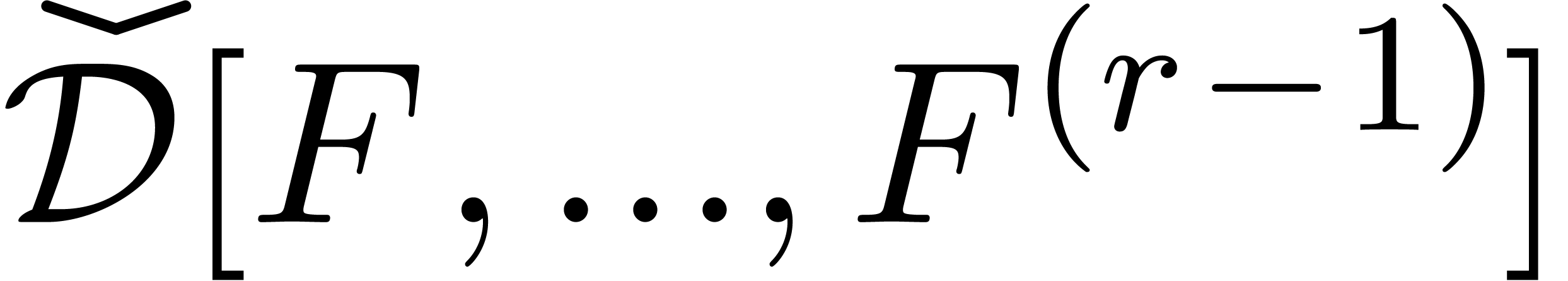 .
.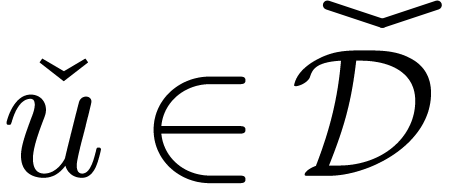 with
with 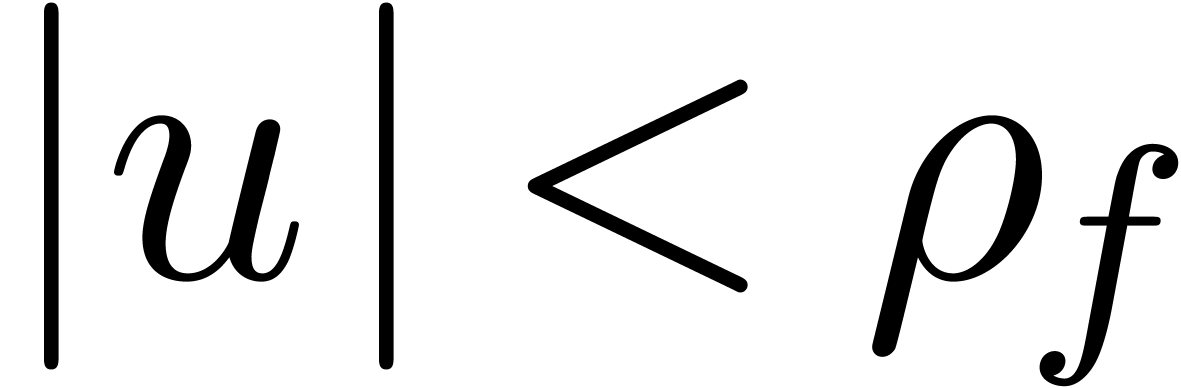 ,
, then represents
then represents  .
.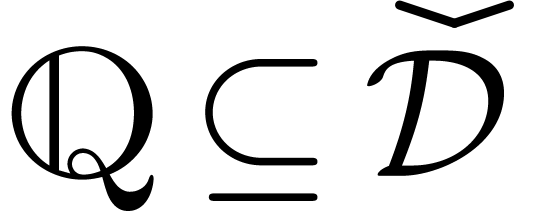 ).
). have a large size. In the present setting, this
comes down to defining the “size”
have a large size. In the present setting, this
comes down to defining the “size”  of
an expression
of
an expression  as follows:
as follows:
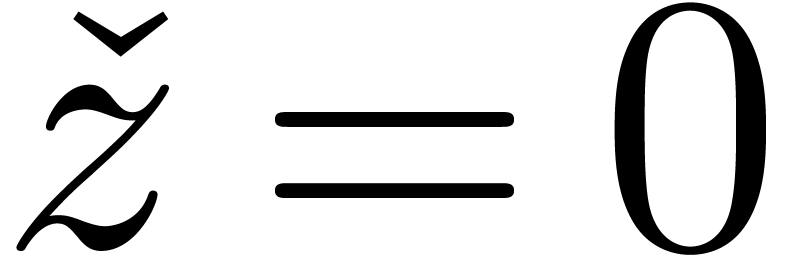 or
or 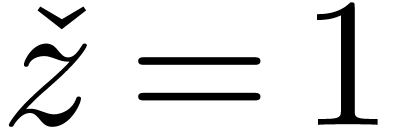 ,
, .
. or
or  ,
,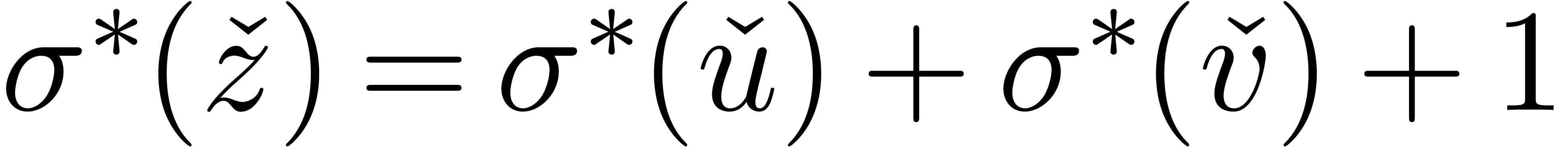 .
.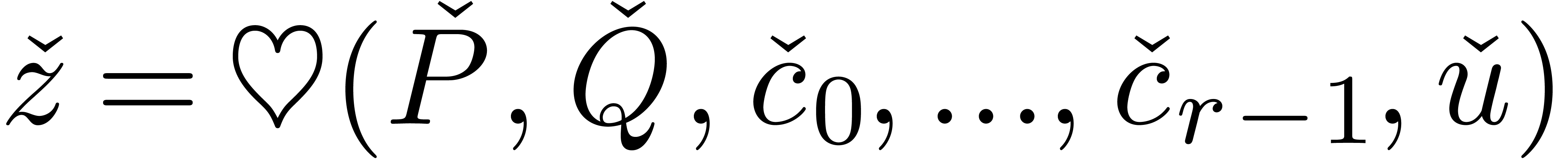 ,
,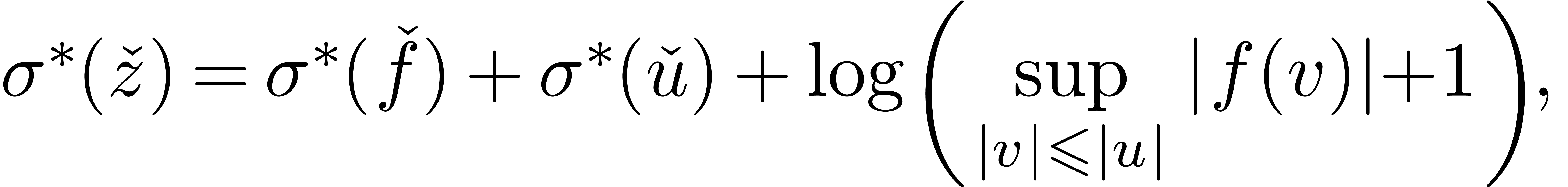
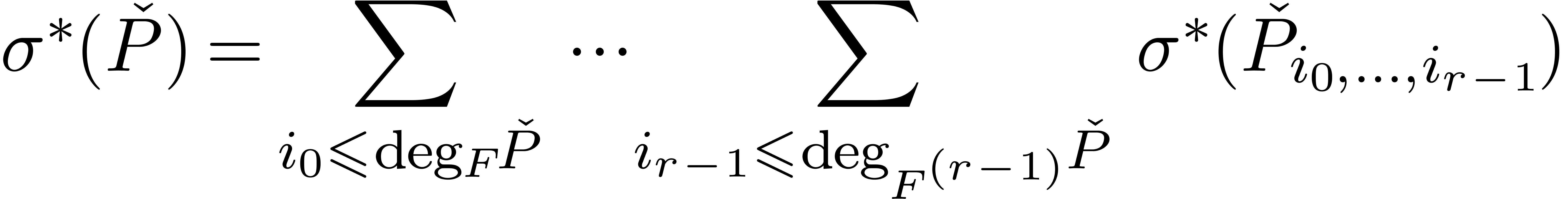
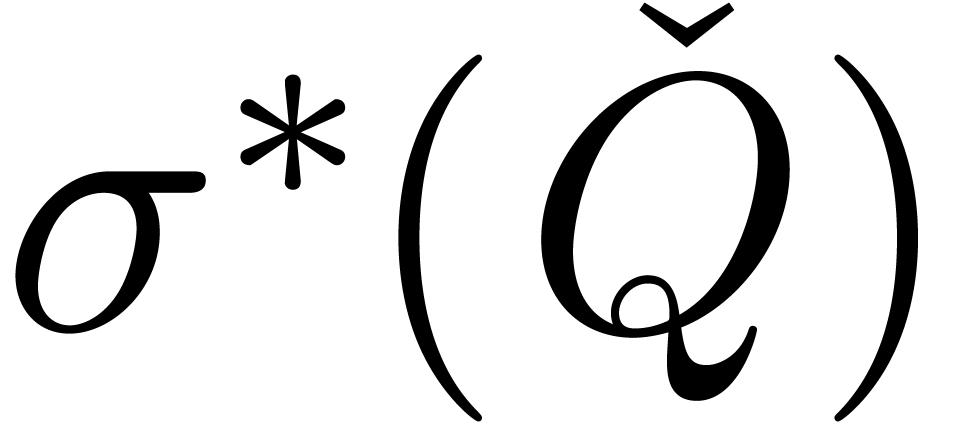 .
.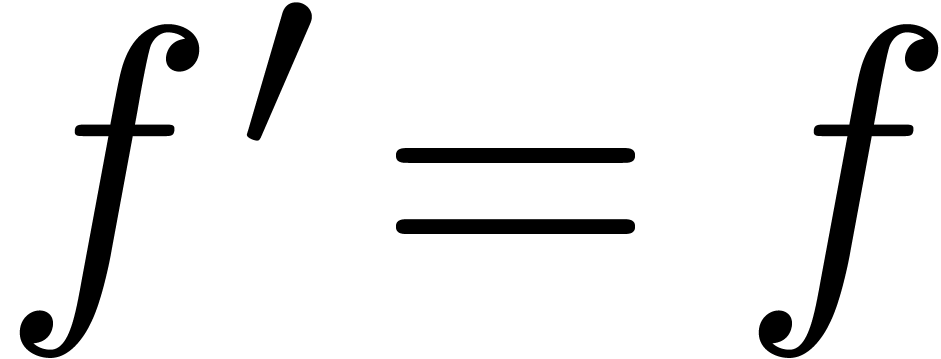 and
and 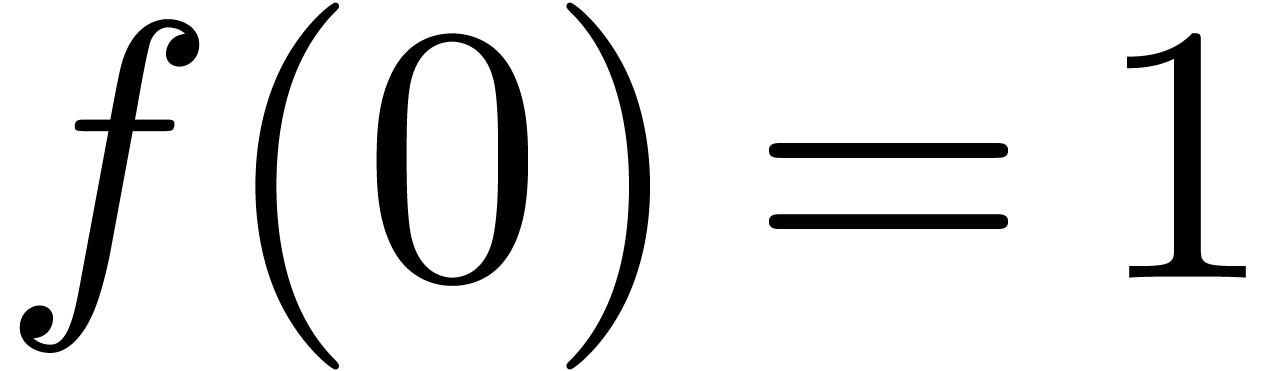 ,
,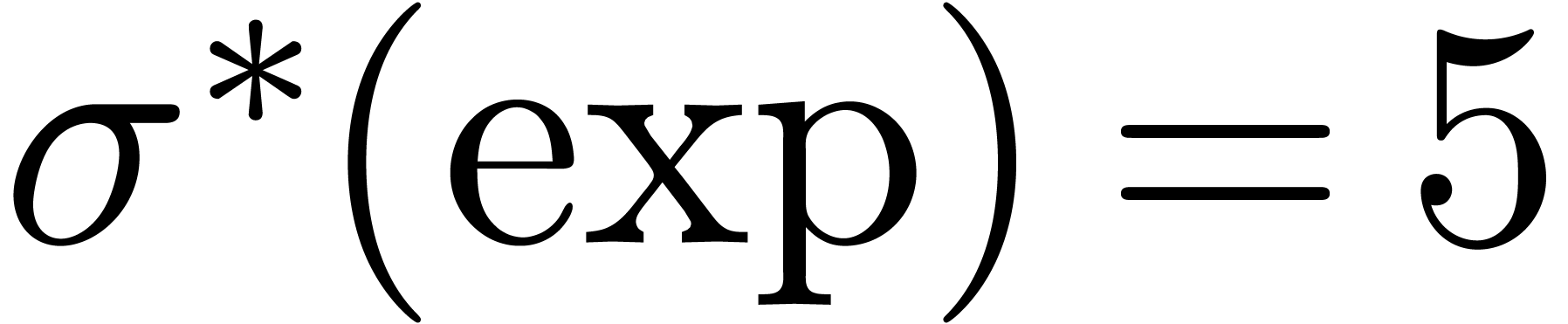 and
and 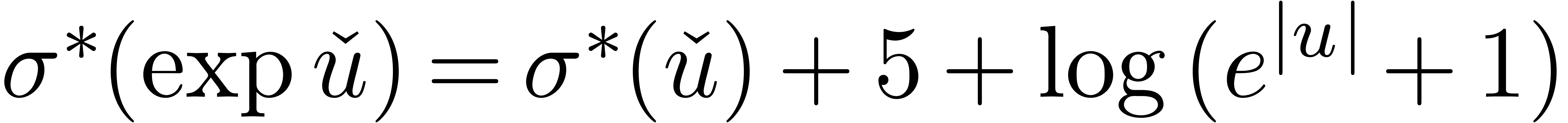 .
. for large
for large  .
. ,
, or
or 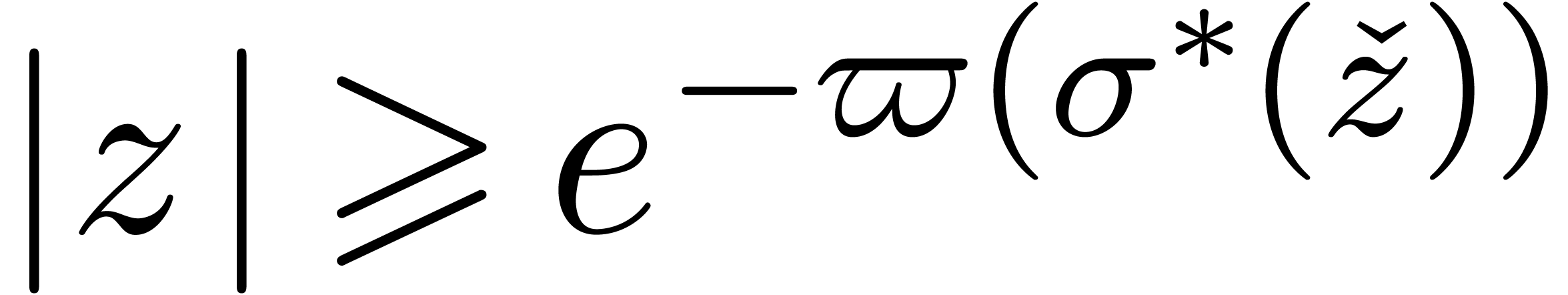 .
.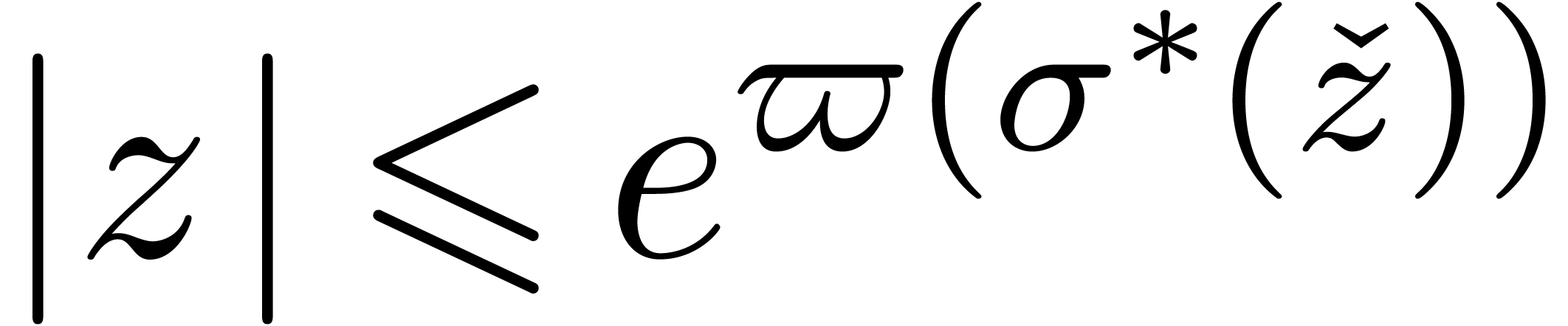
 .
. ,
, by omitting the corrective term
by omitting the corrective term 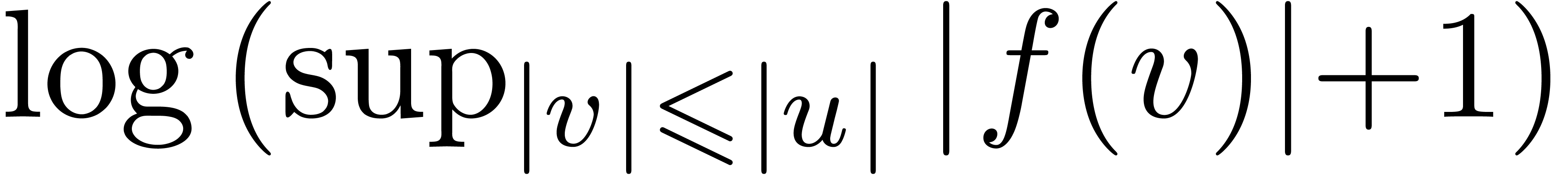 ,
,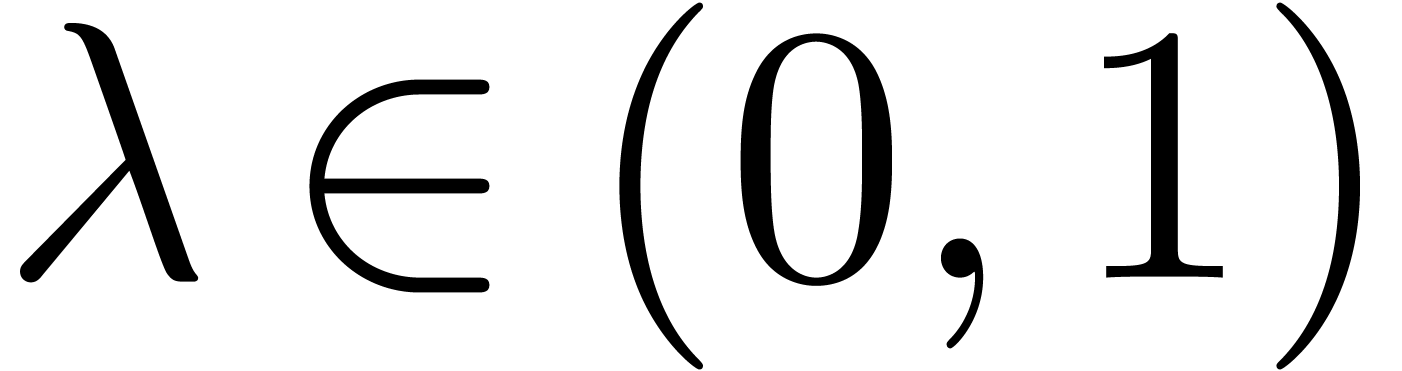 be a rational parameter. We recursively
define the subset
be a rational parameter. We recursively
define the subset  in a similar way as
in a similar way as  is of the form
is of the form  ,
, for all
for all  ,
,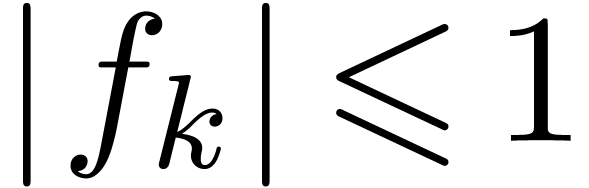 for each Taylor coefficient
for each Taylor coefficient  of
of 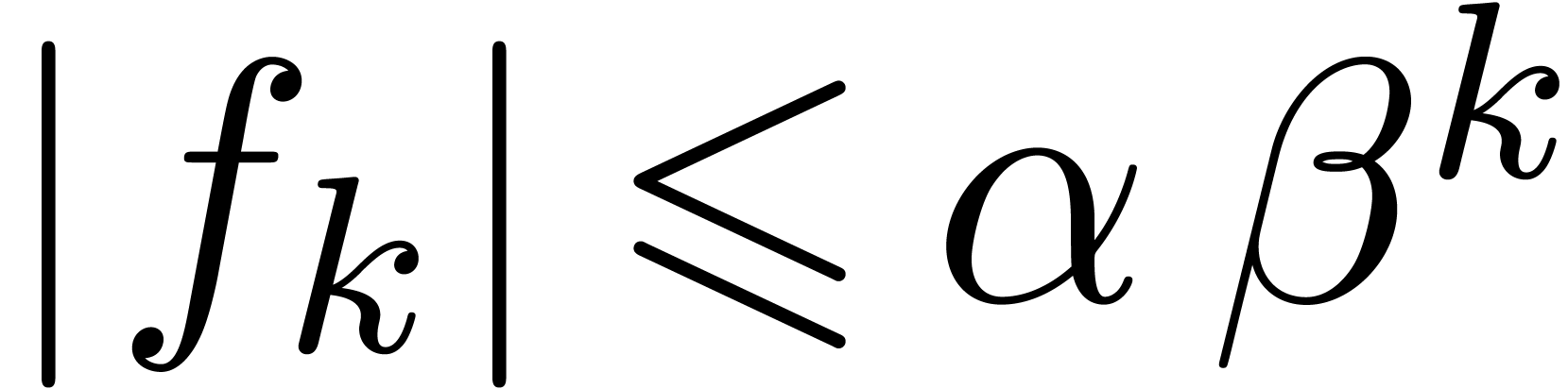 ,
, (and
(and 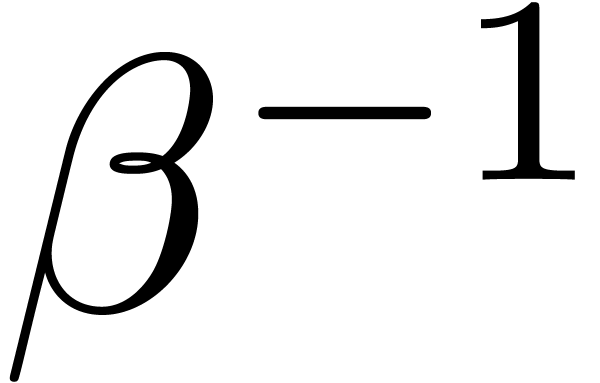 as close to
as close to 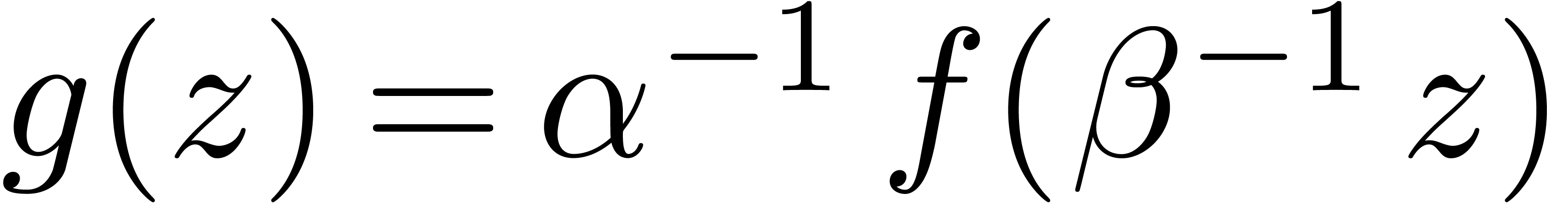 .
.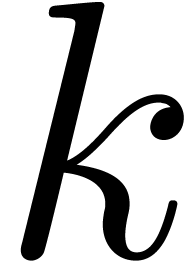 when constructing
constants in
when constructing
constants in  with
with 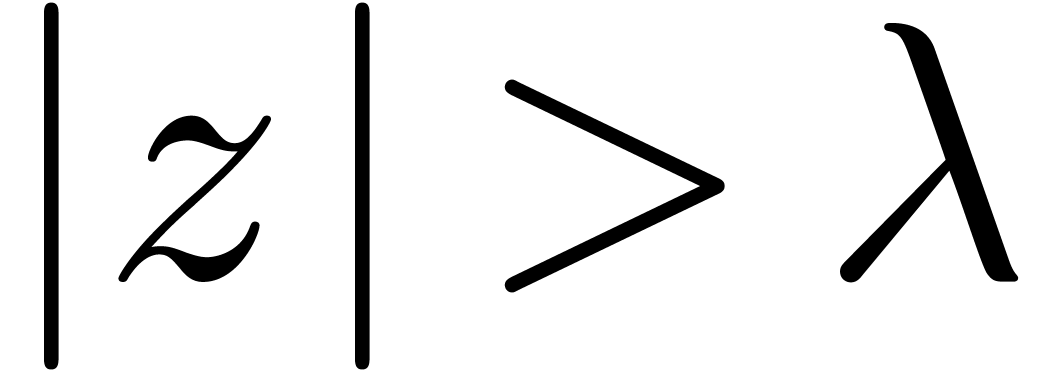 ,
,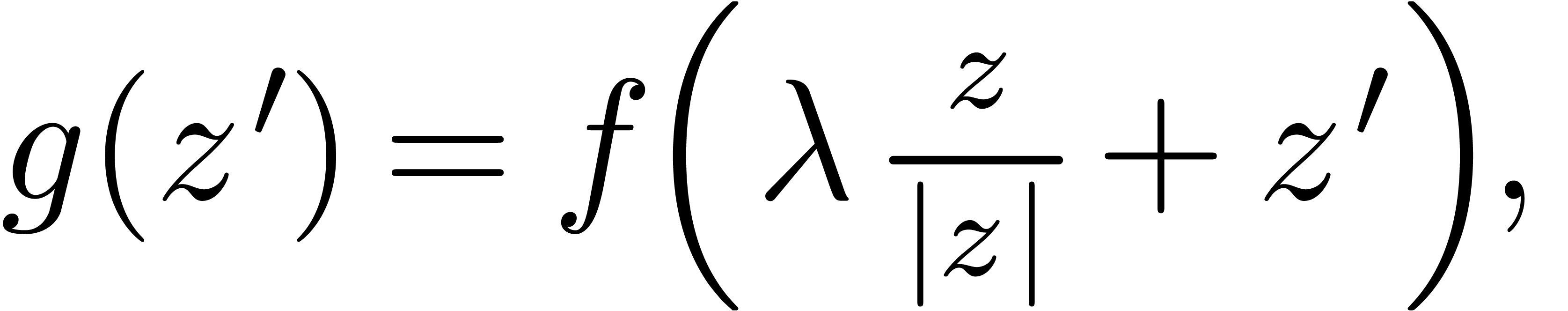
 satisfies a similar algebraic differential
equation as
satisfies a similar algebraic differential
equation as 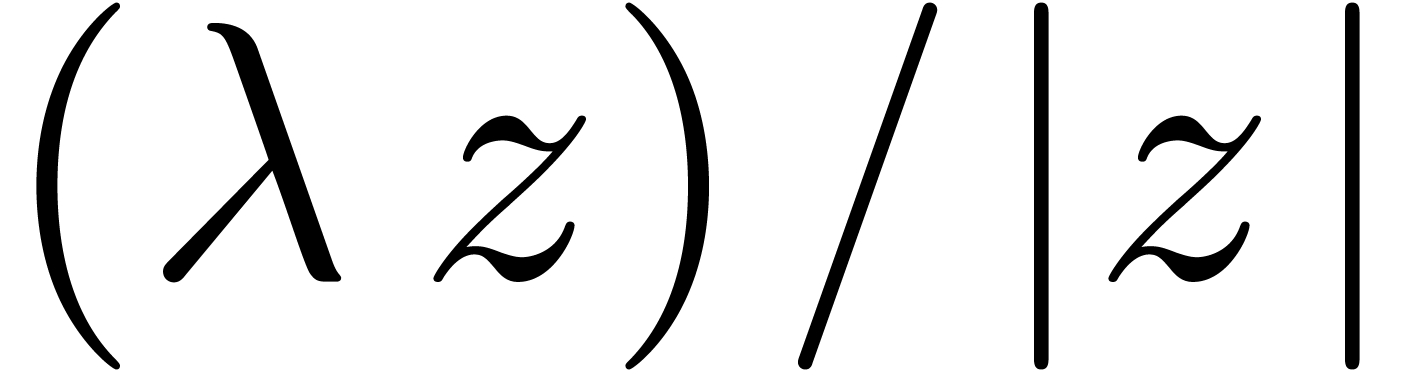 .
. ,
, ,
,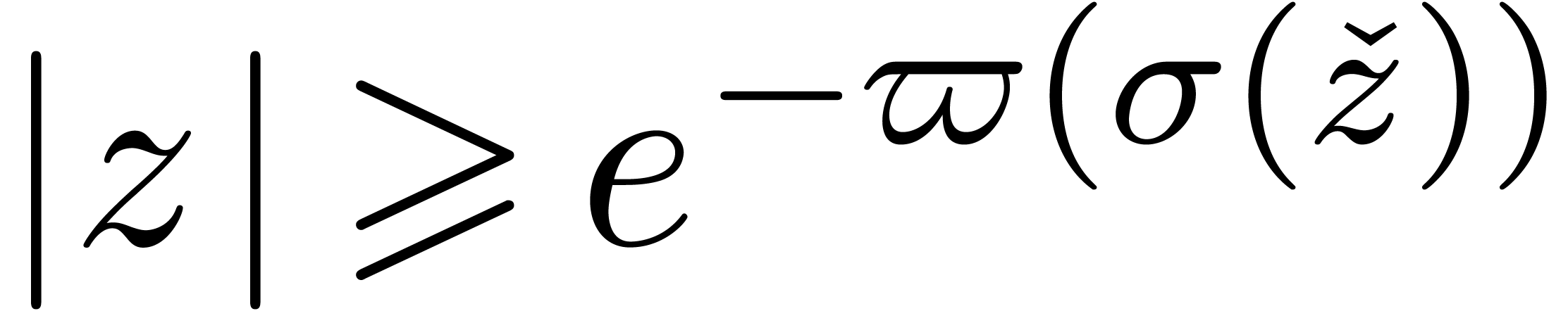 .
. .
. and
and  represent the same number
represent the same number 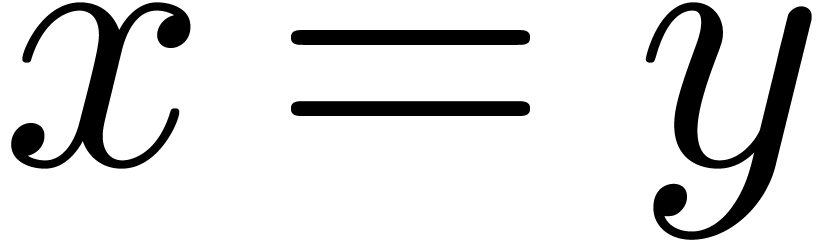 with
with  ,
, and
and  both represent
both represent  and
we have
and
we have 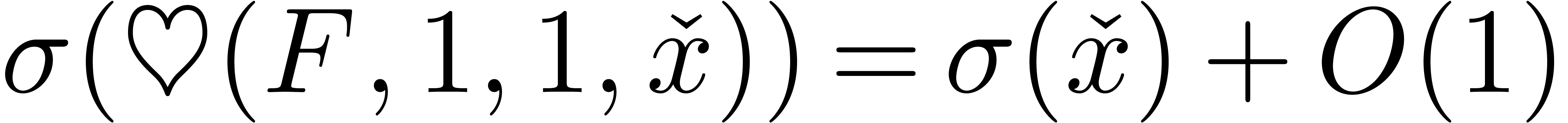 as well as
as well as 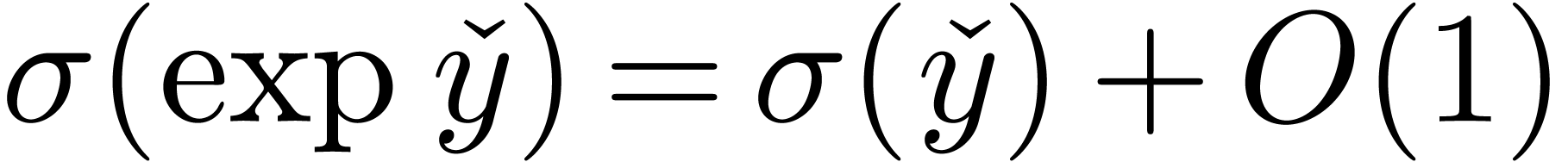 .
.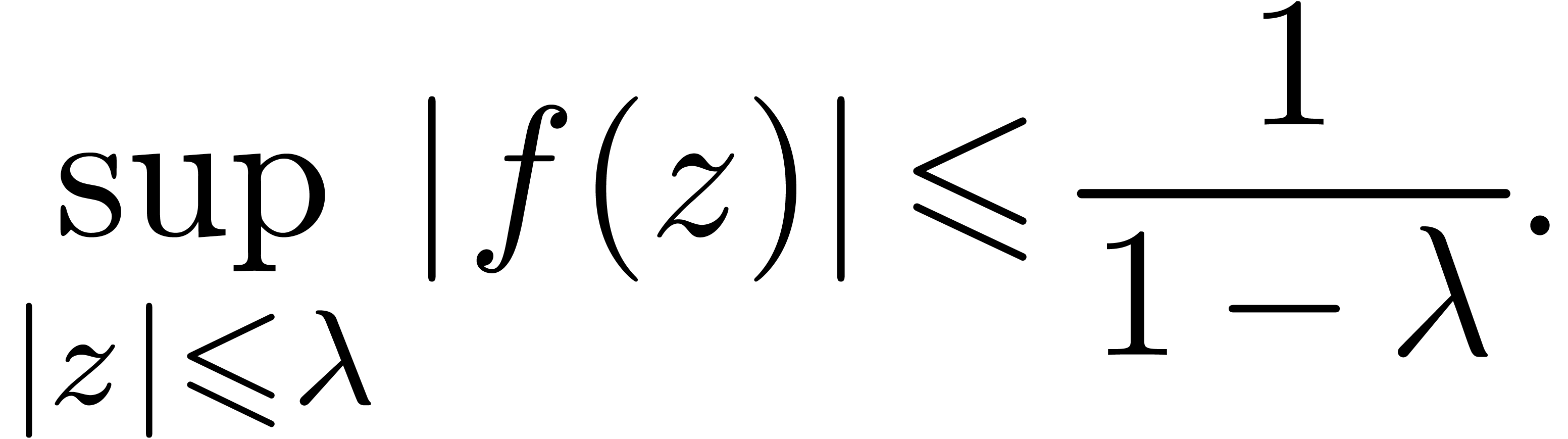
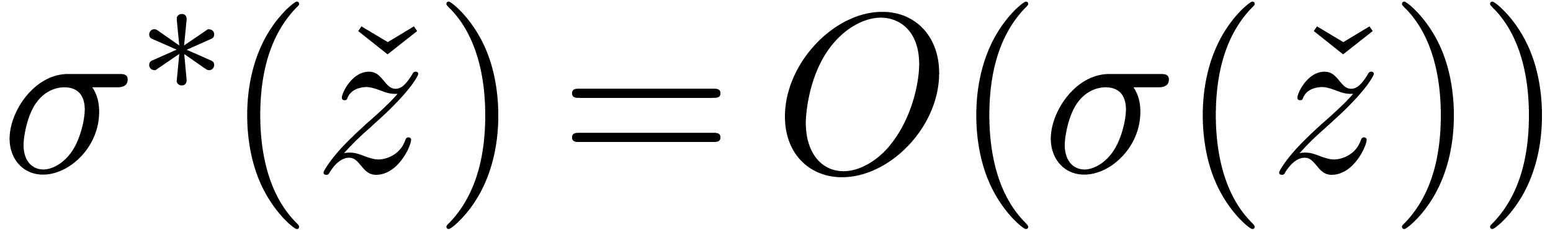 for
for 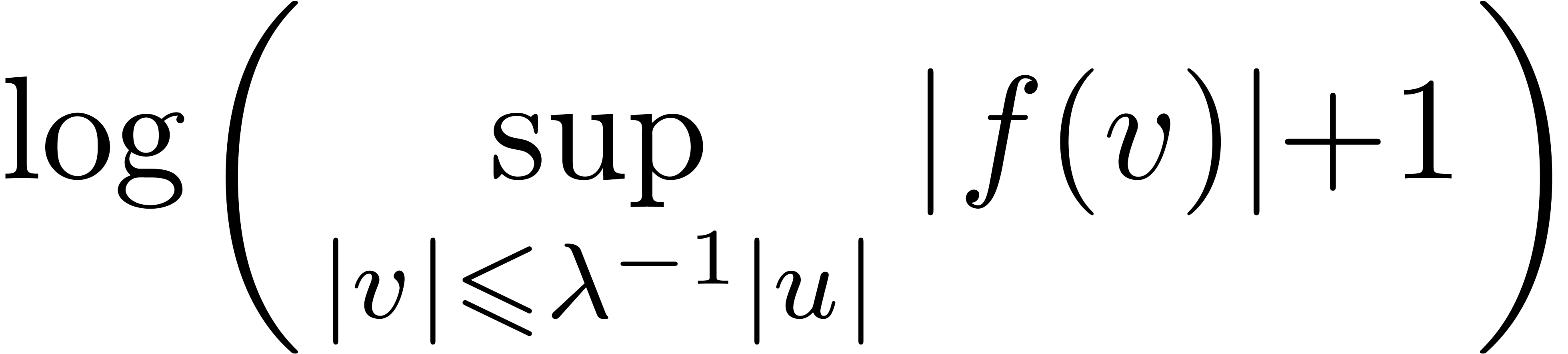
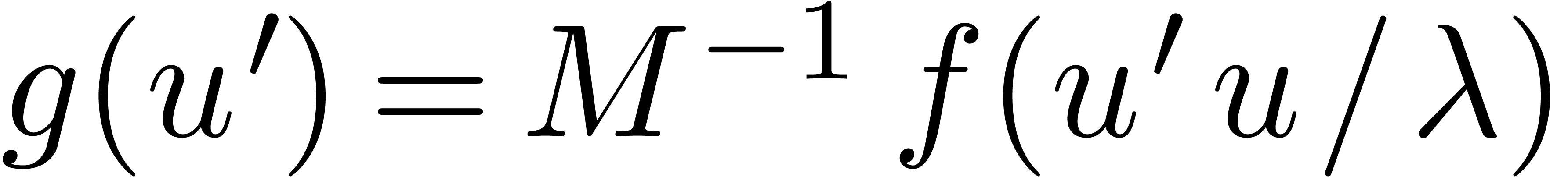 and replace
and replace  by
by  ,
, is a good rational upper approximation of
is a good rational upper approximation of 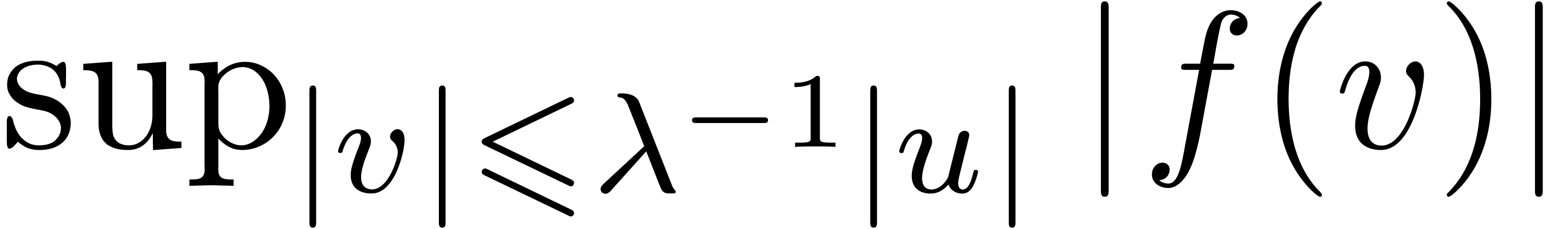 .
.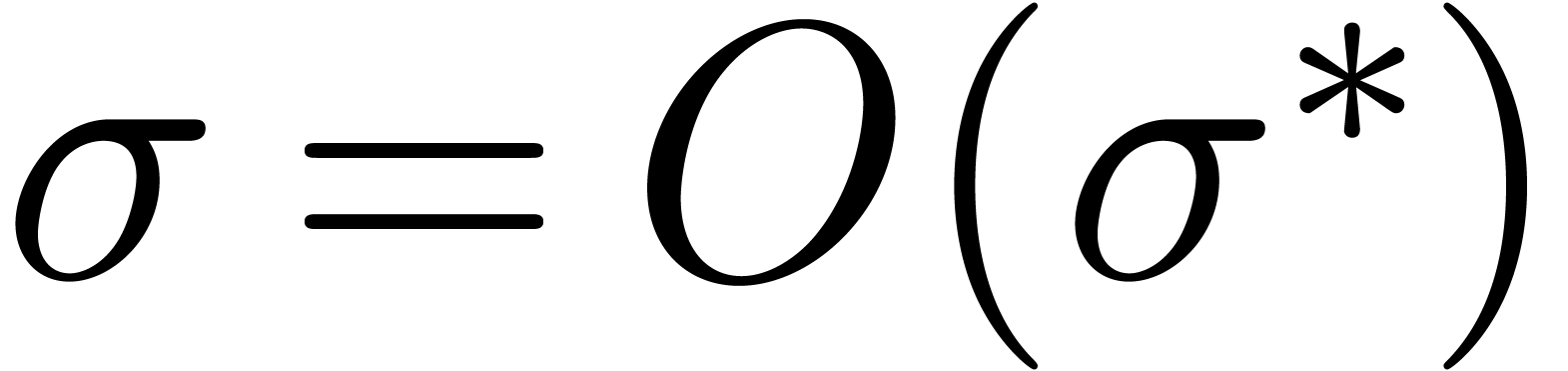 .
.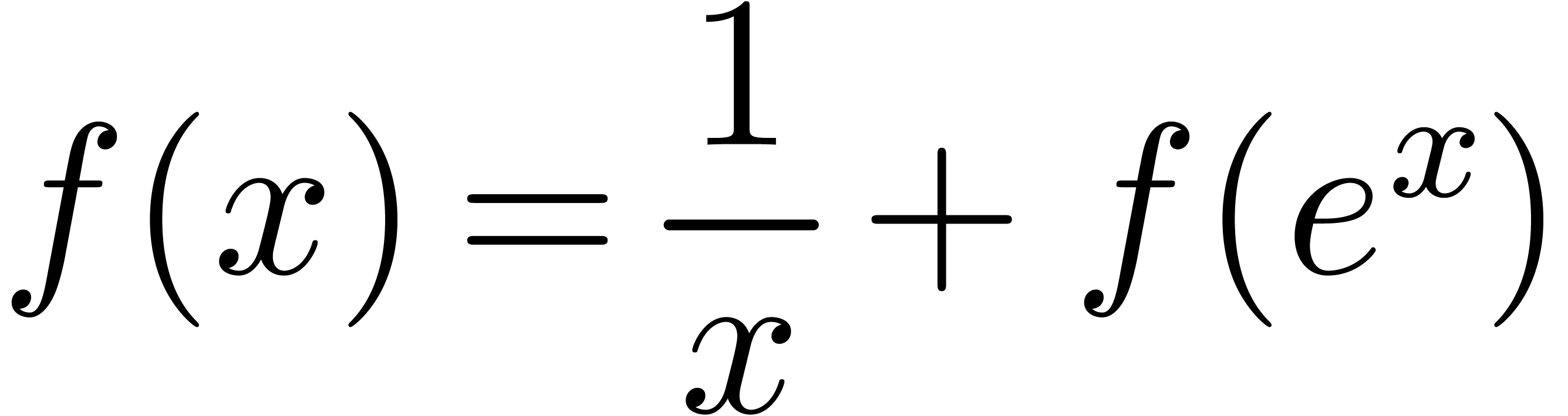
 .
.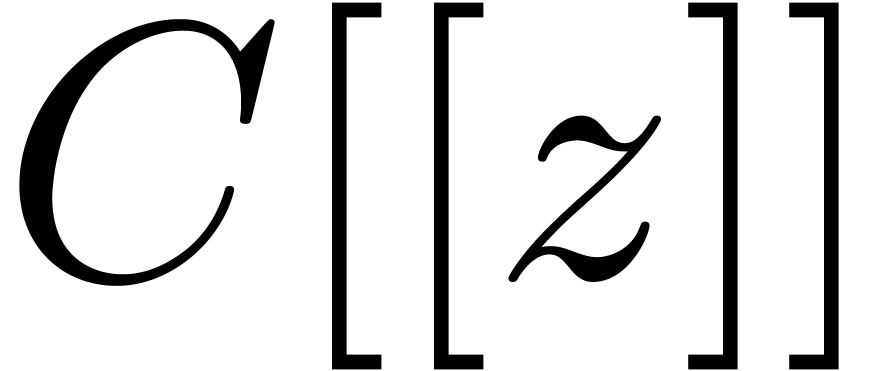 over a
field
over a
field  of characteristic zero. Let
of characteristic zero. Let  that represent series
that represent series  ,
, .
. ,
,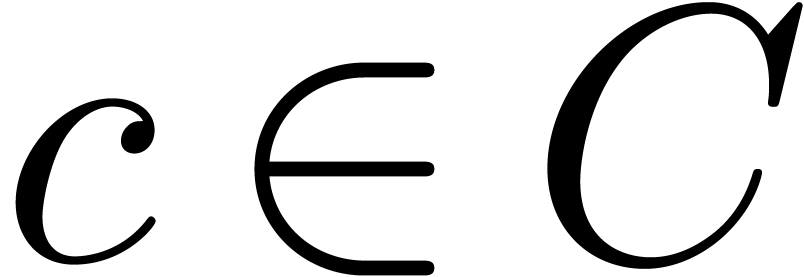 .
.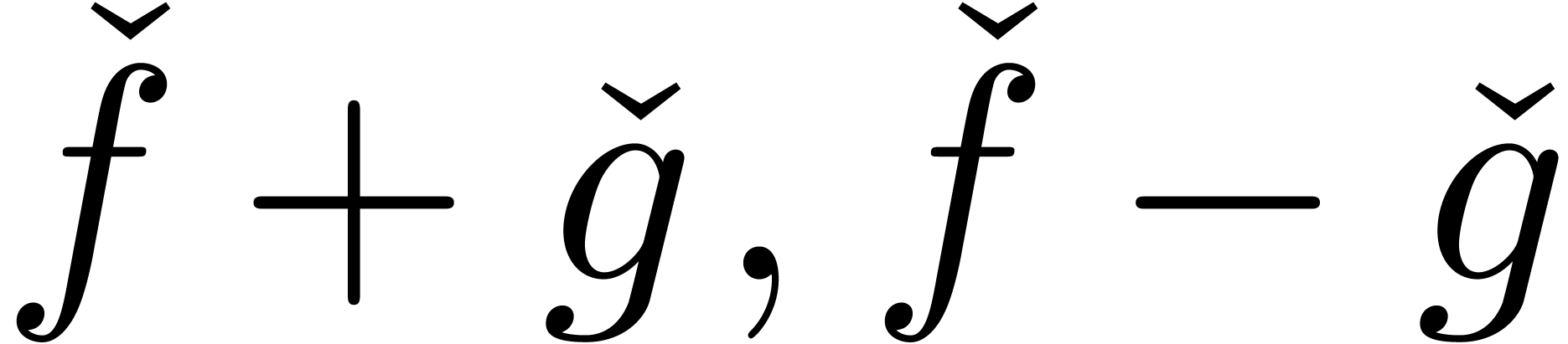 and
and  are in
are in 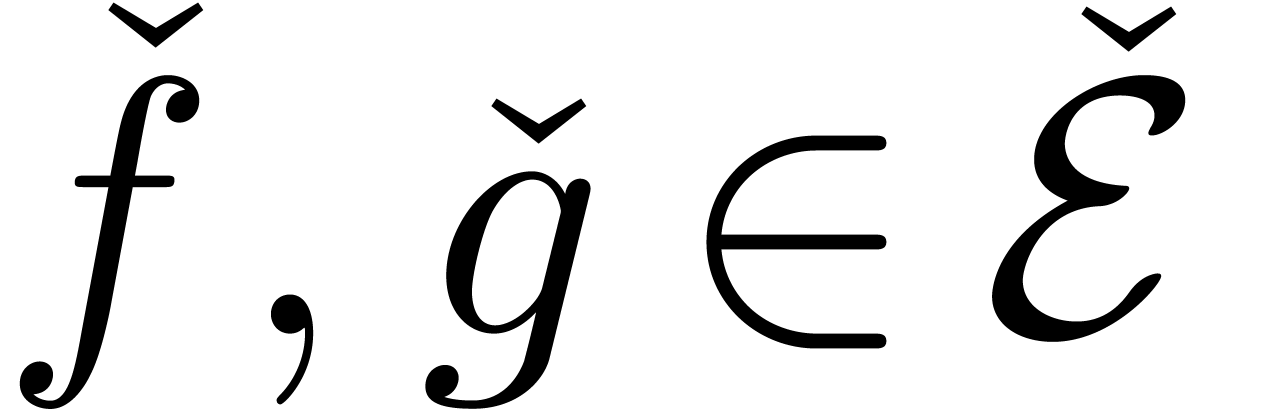 .
.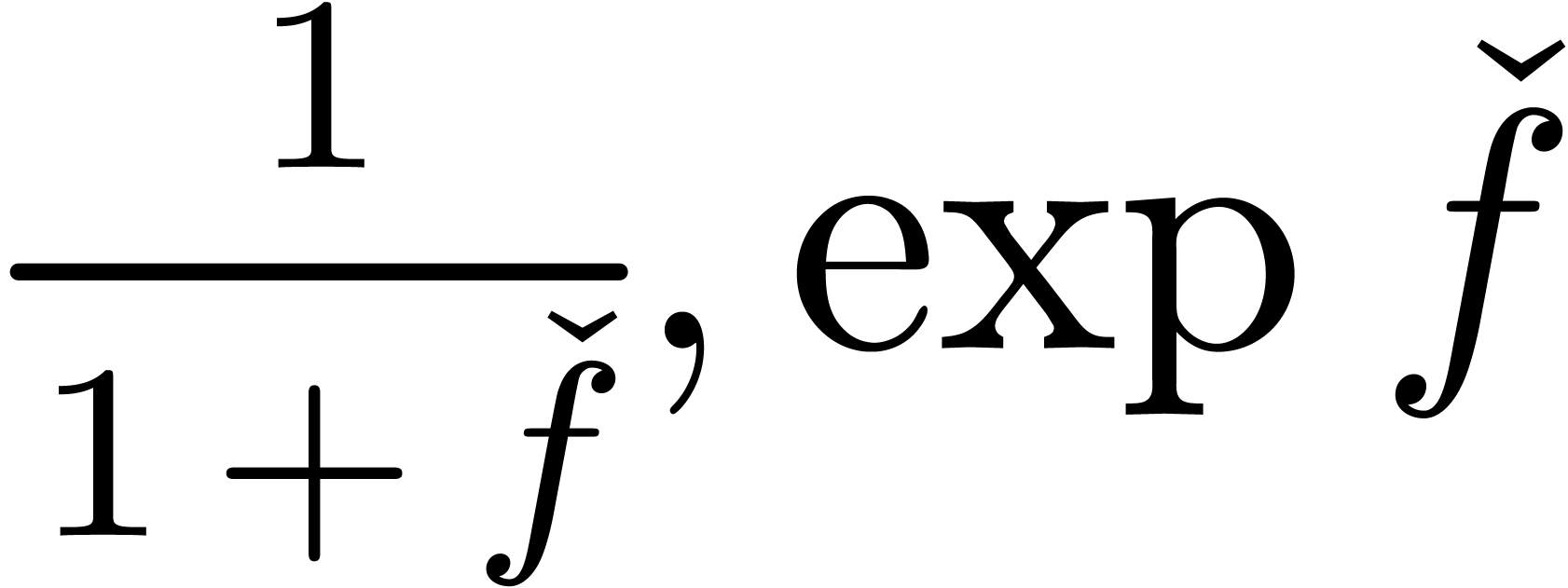 and
and 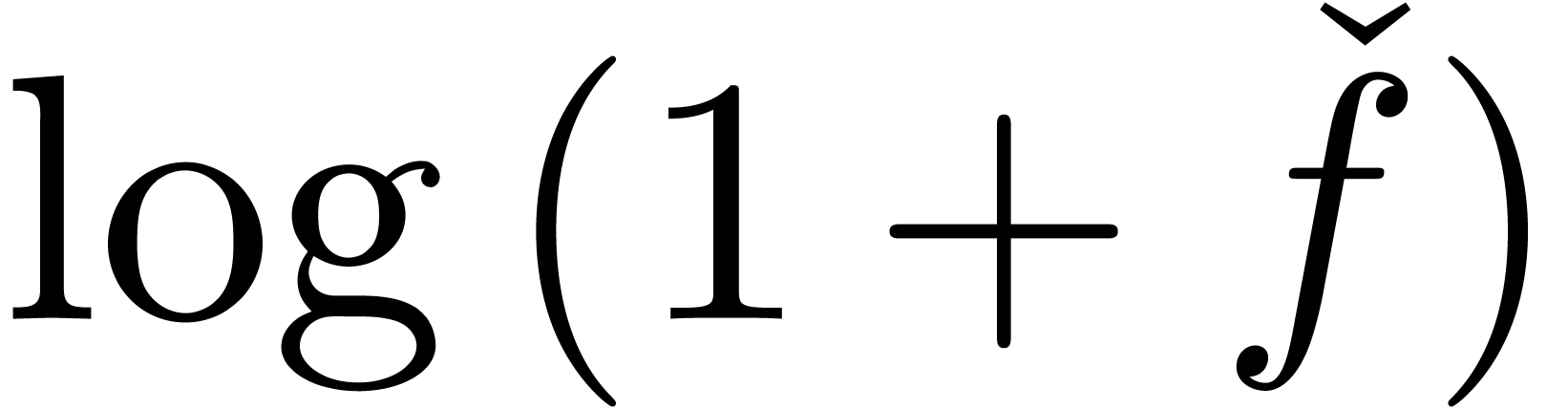 are in
are in 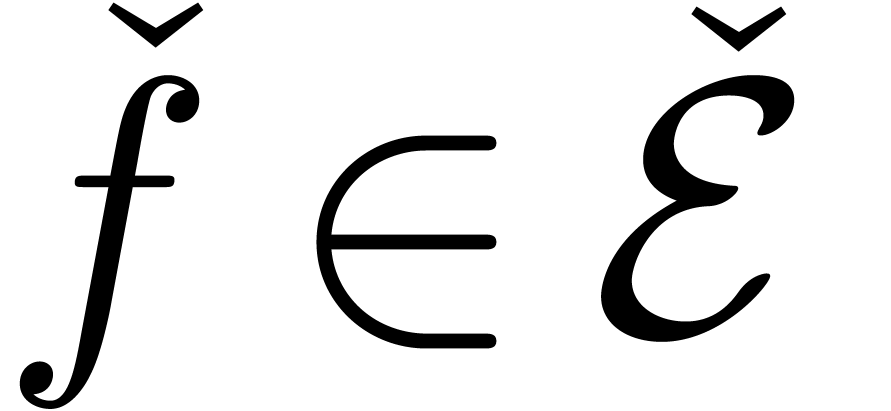 with
with  .
.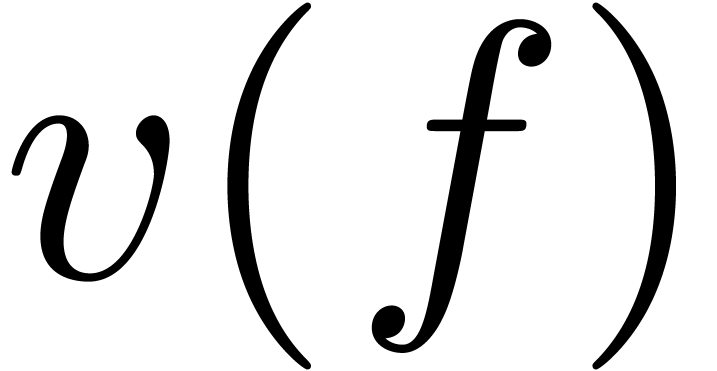 the valuation of a series
the valuation of a series 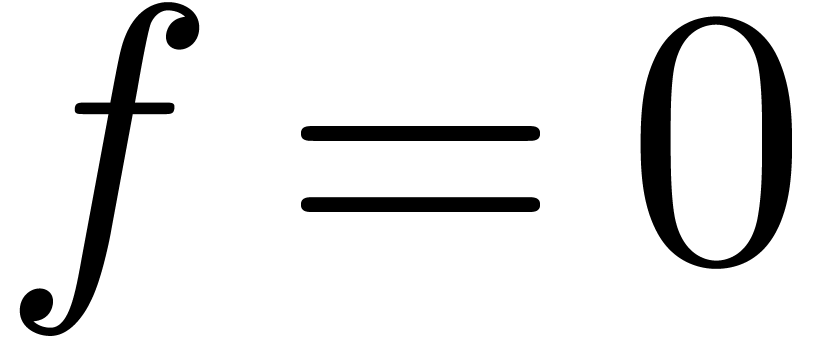 or
or 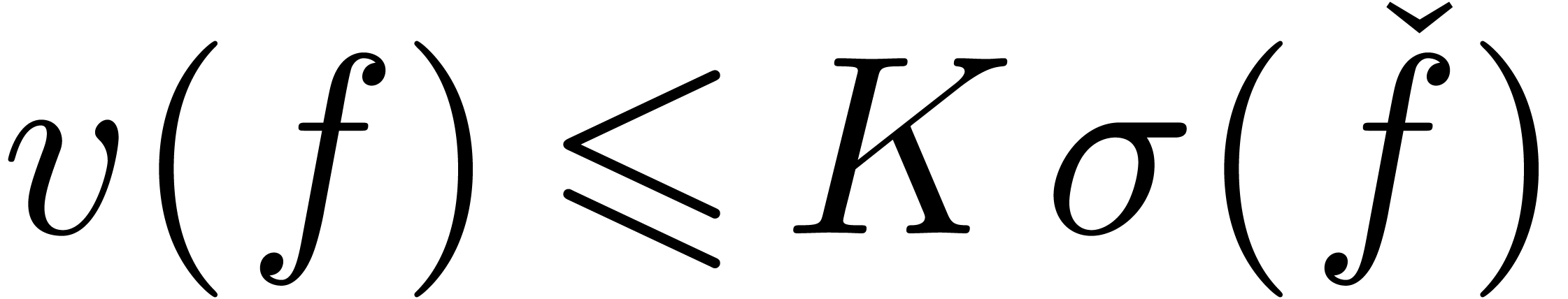 .
. are
polynomials with rational coefficients in the constants of
are
polynomials with rational coefficients in the constants of 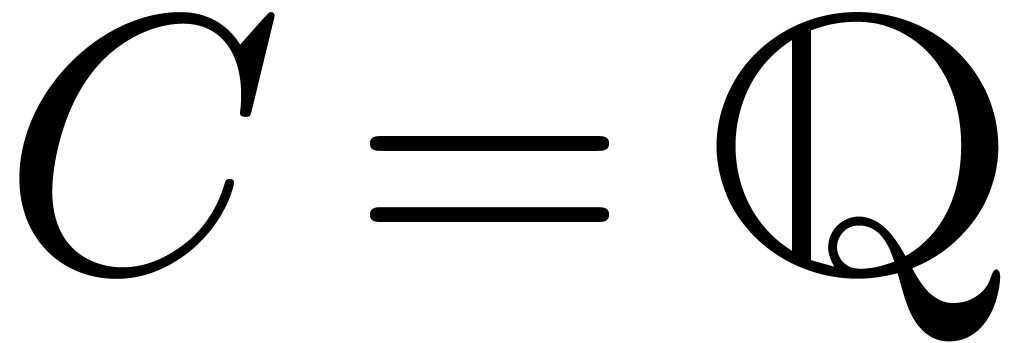 .
.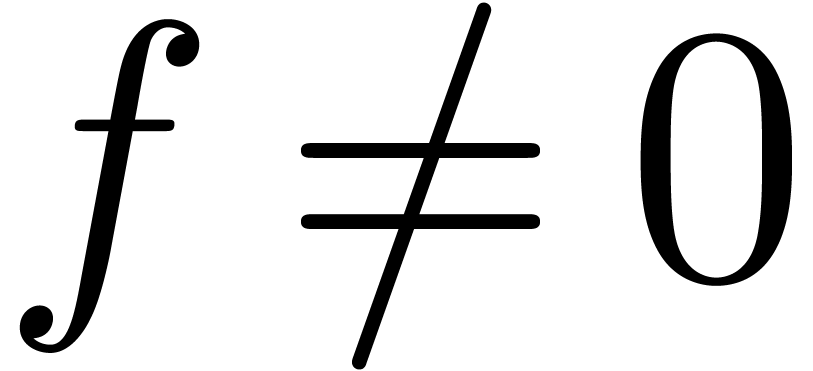 and
and 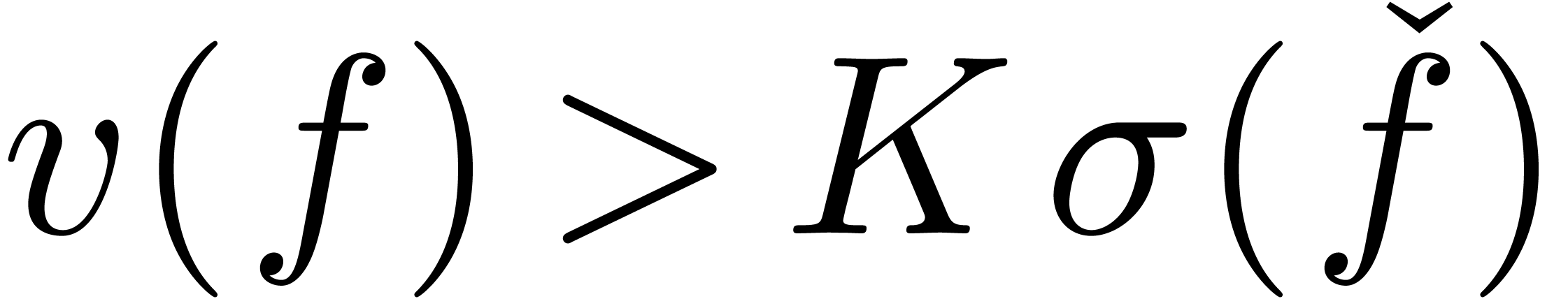 .
. sufficiently large, we may represent
sufficiently large, we may represent 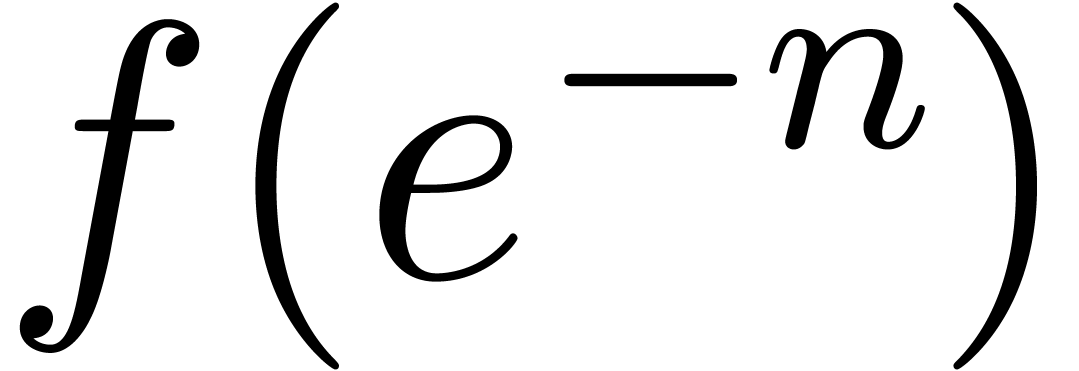 by an
expression in
by an
expression in  whose size is bounded by
whose size is bounded by 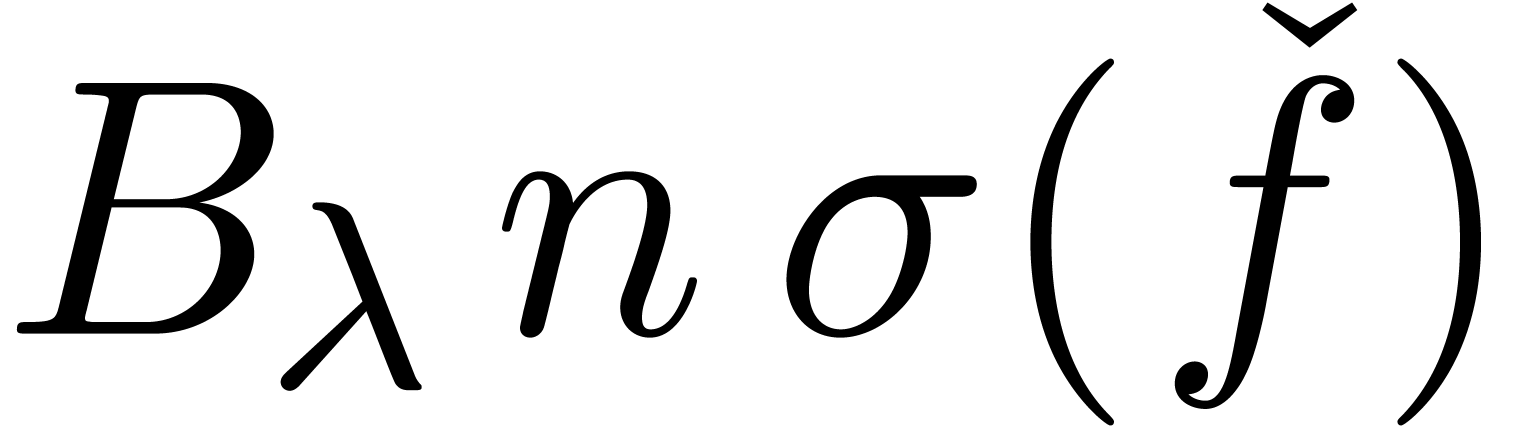 .
. and
and
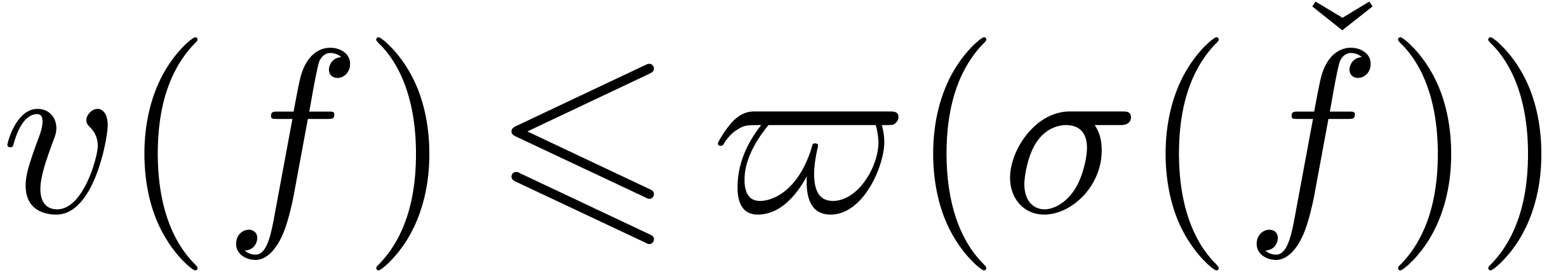 ,
,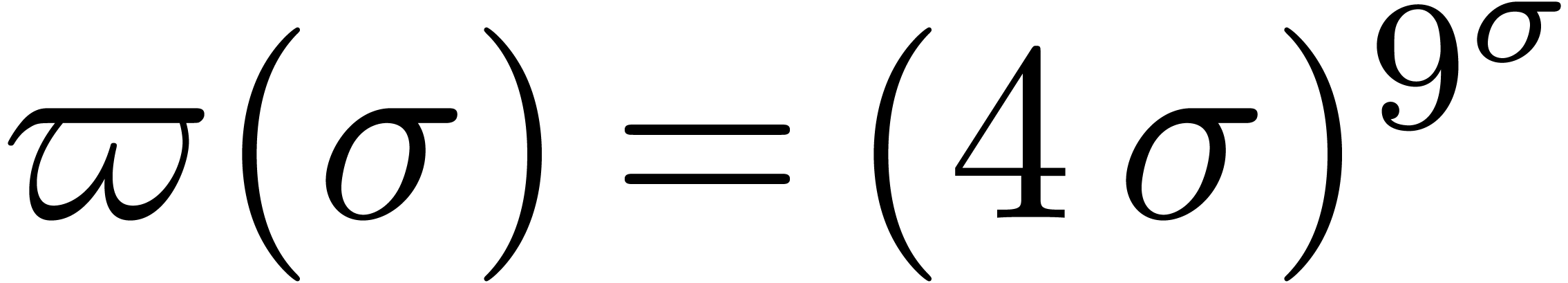 .
.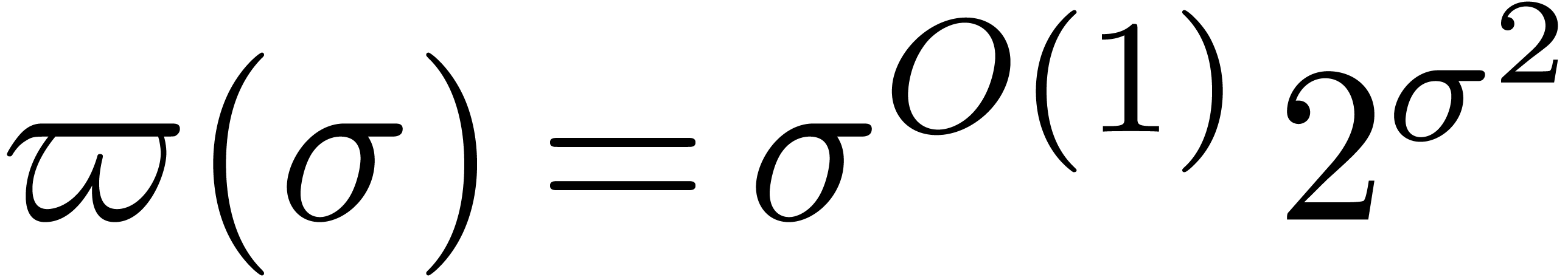 .
. be a differential subring of
be a differential subring of 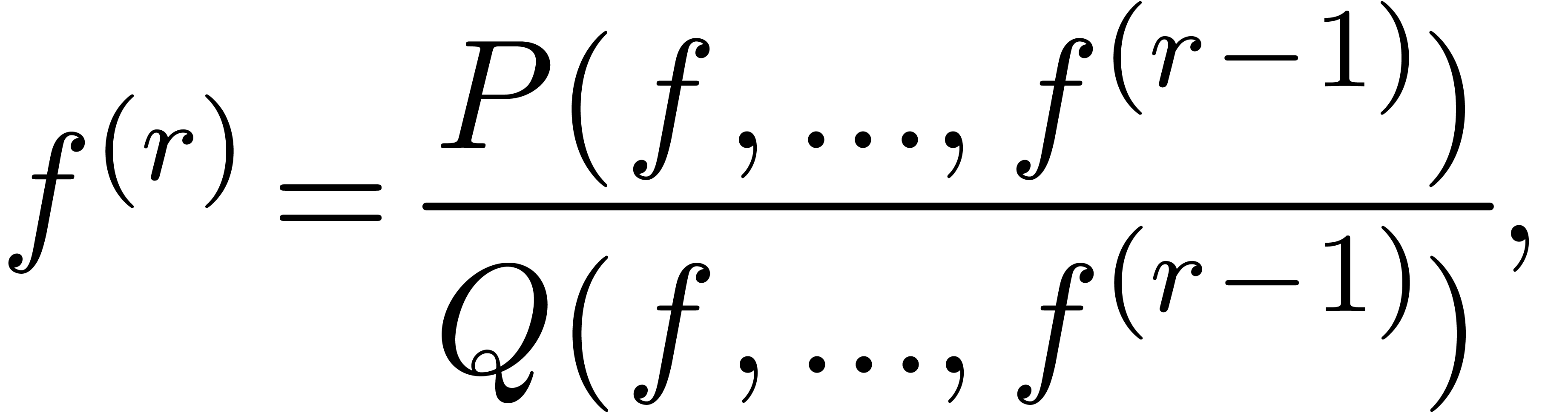
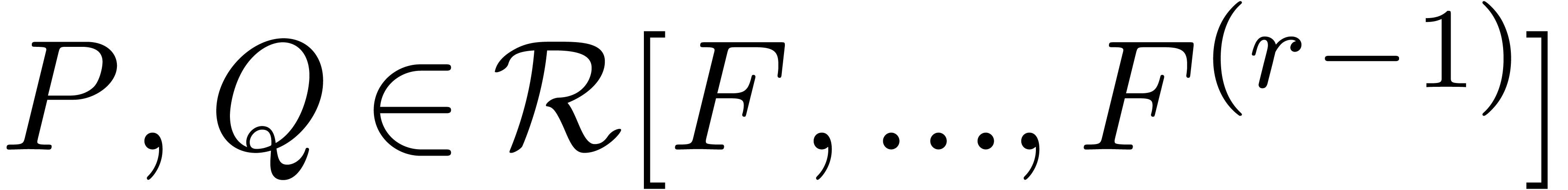 and where
and where  ,
, .
.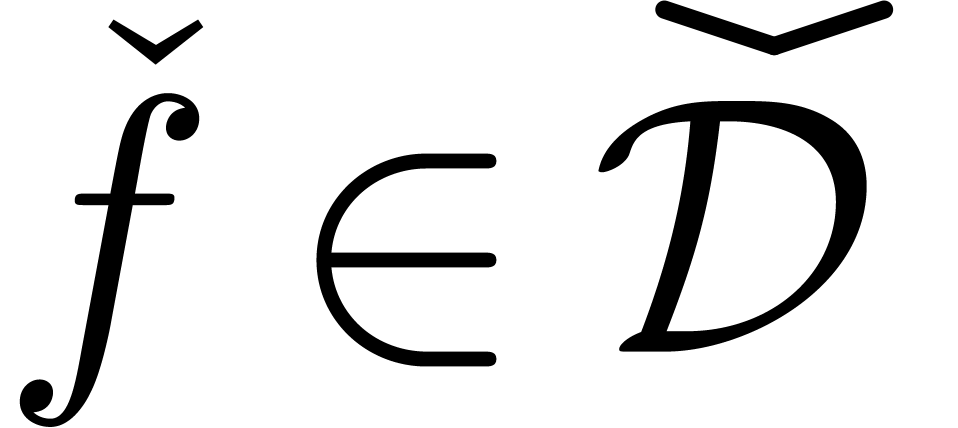 ,
,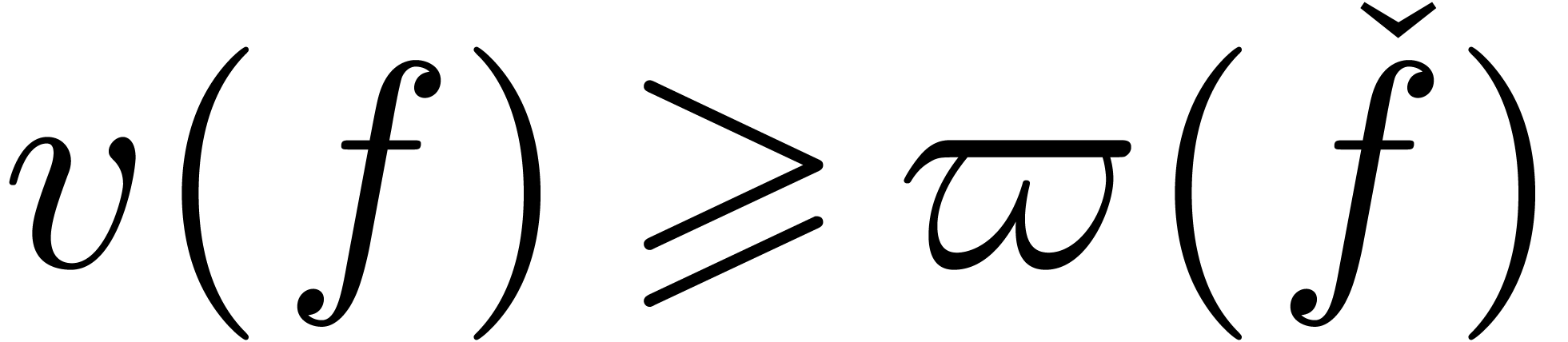 .
. .
.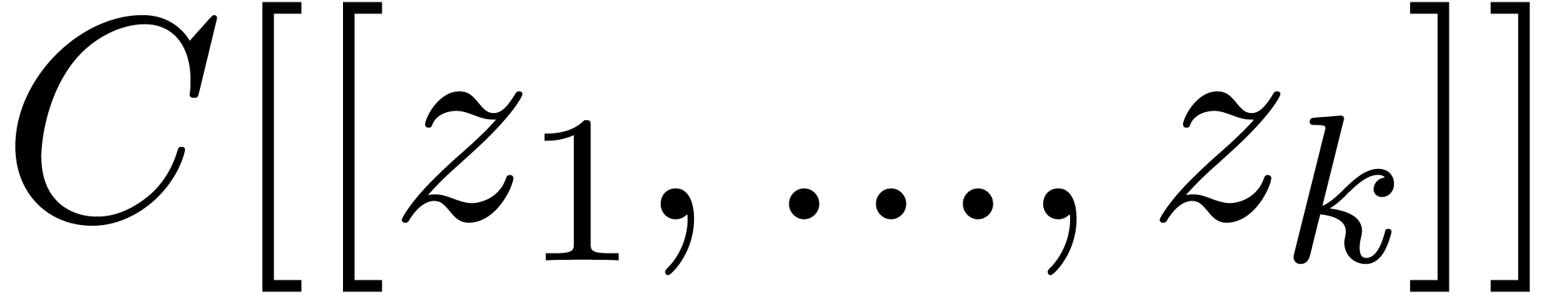 .
.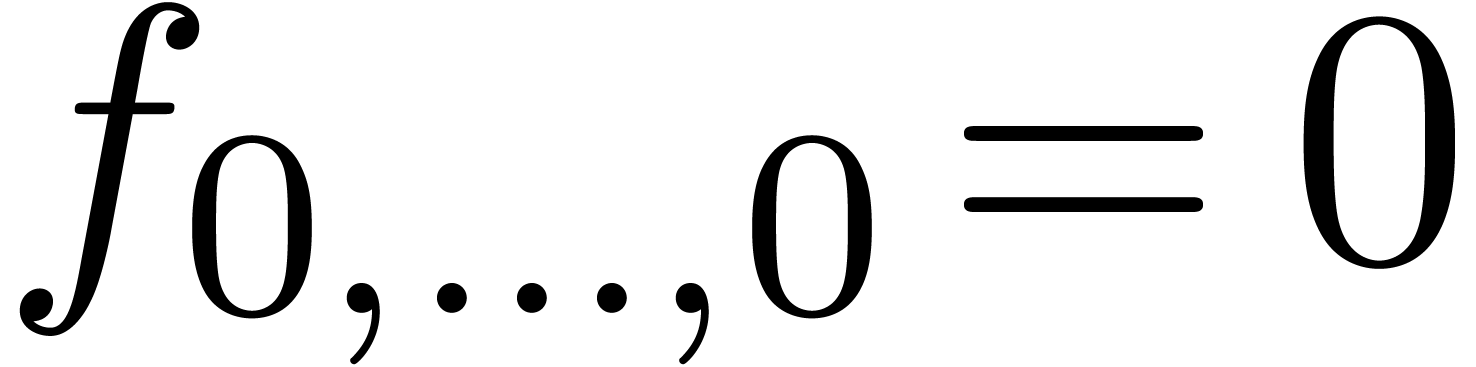 ,
,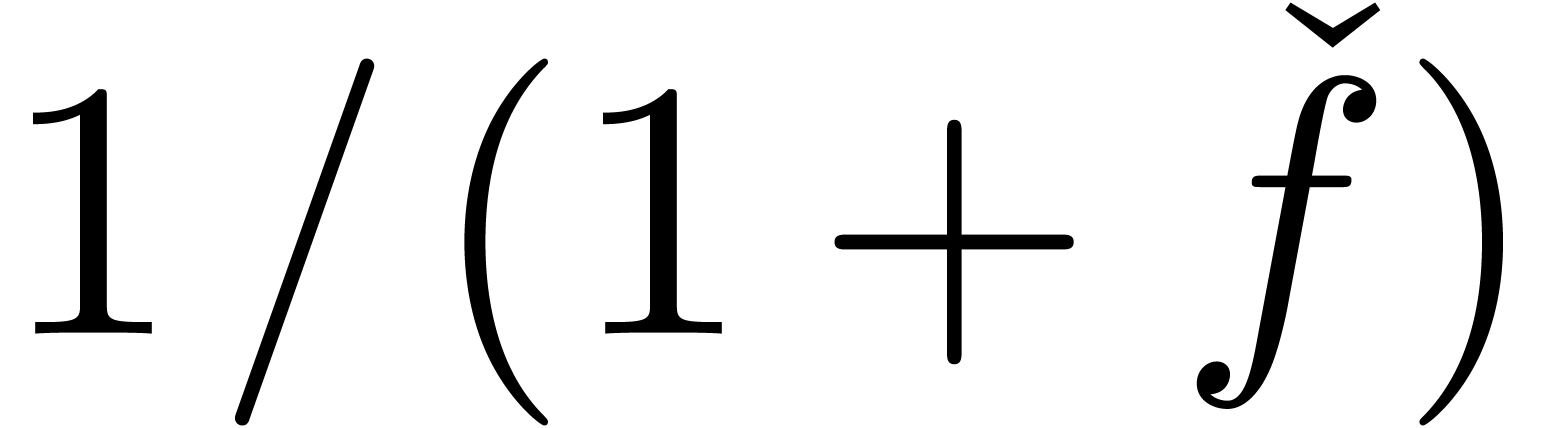 ,
,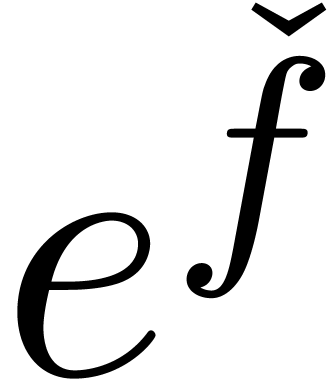 to be in
to be in 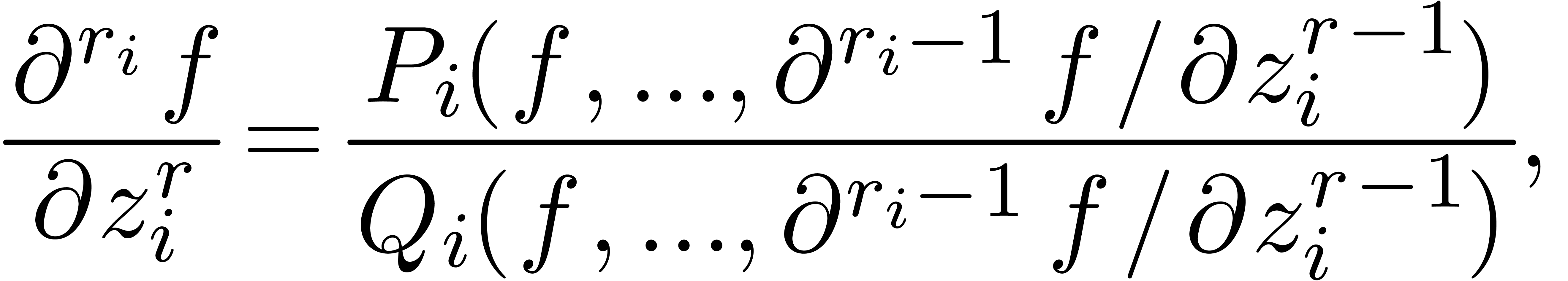
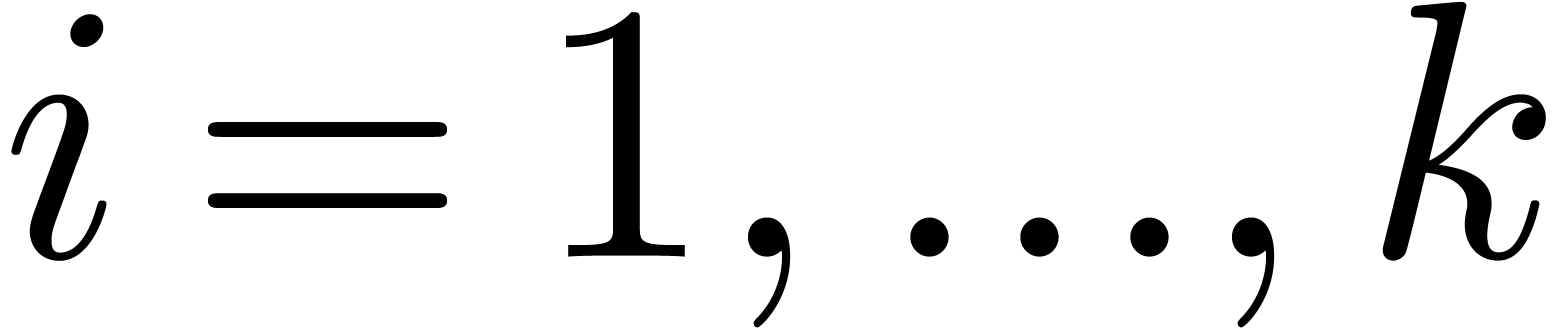 ,
,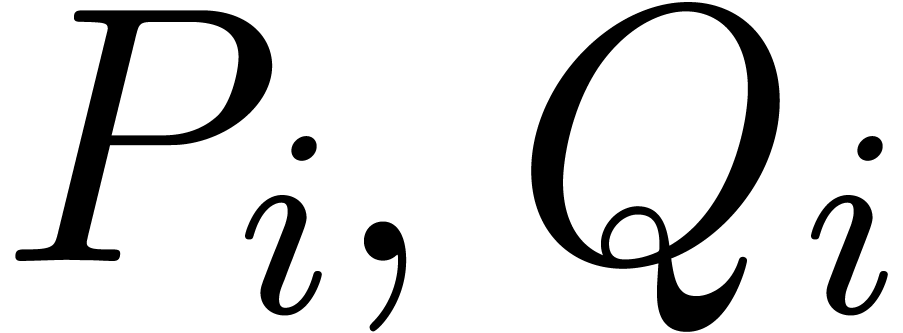 satisfy
satisfy
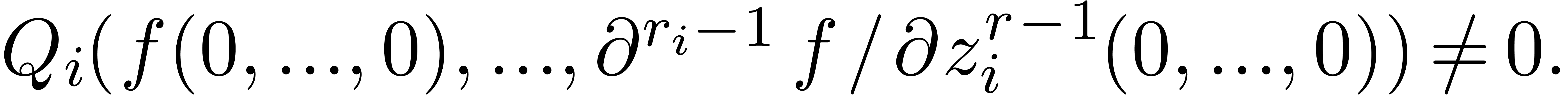
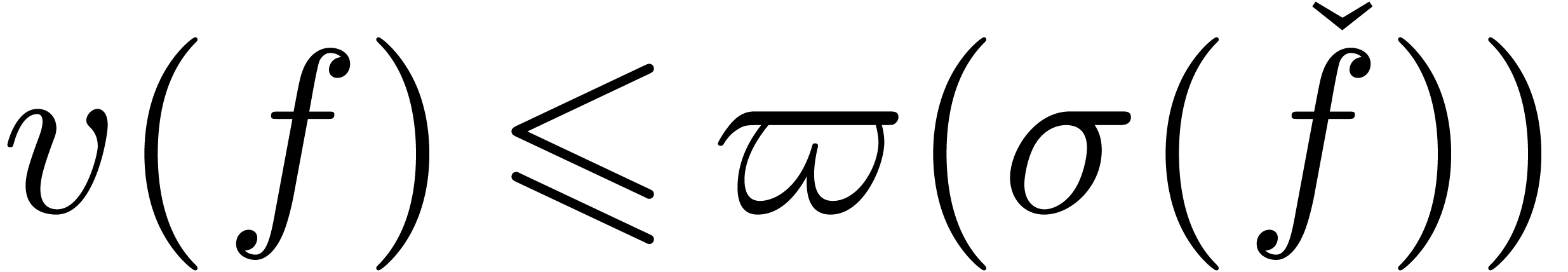 ,
,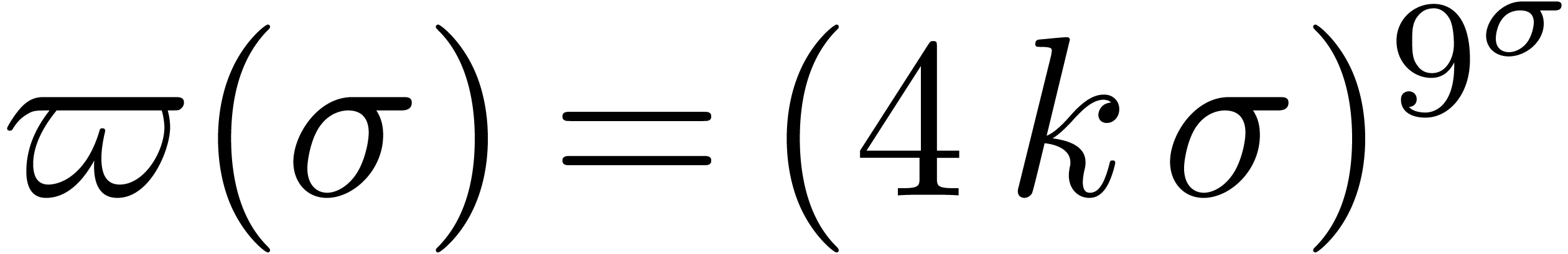 .
.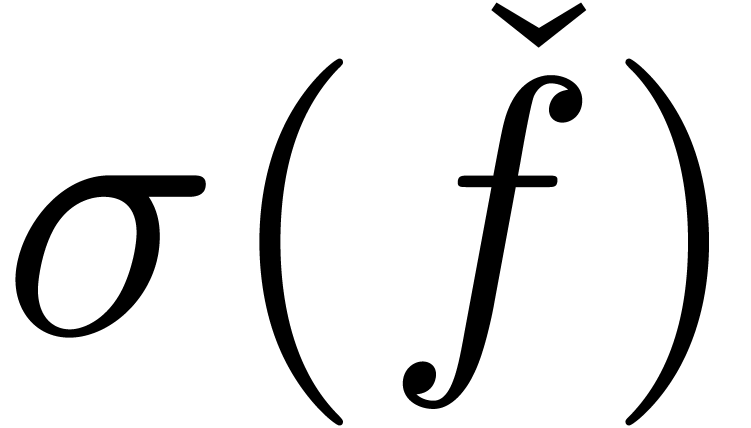 in theorem
in theorem  with
with  ,
,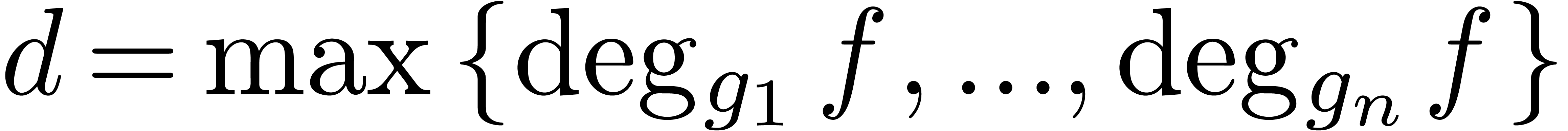 .
.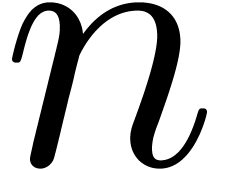 and
and  above. It
may also be interesting to consider other interesting classes of power
series, such as rings of the form
above. It
may also be interesting to consider other interesting classes of power
series, such as rings of the form
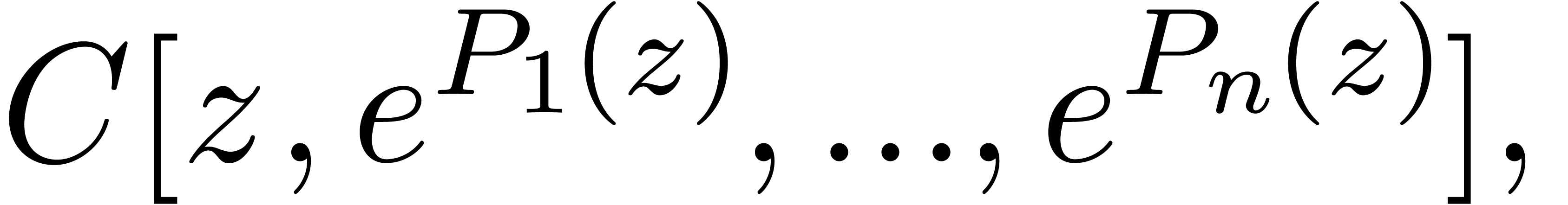
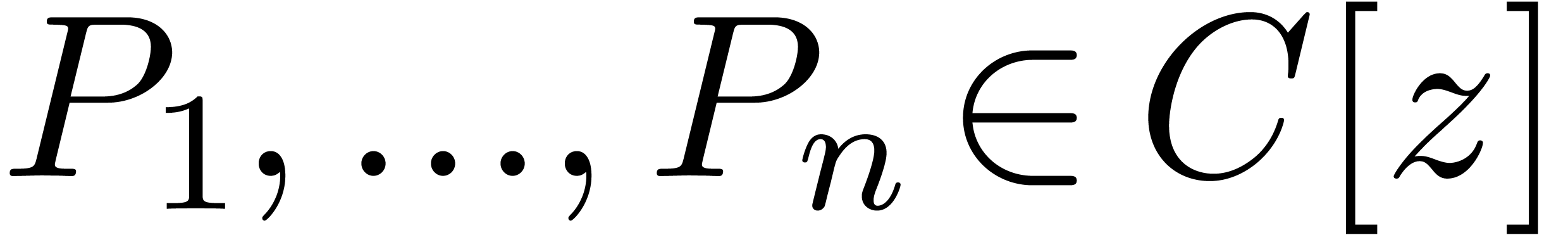 .
.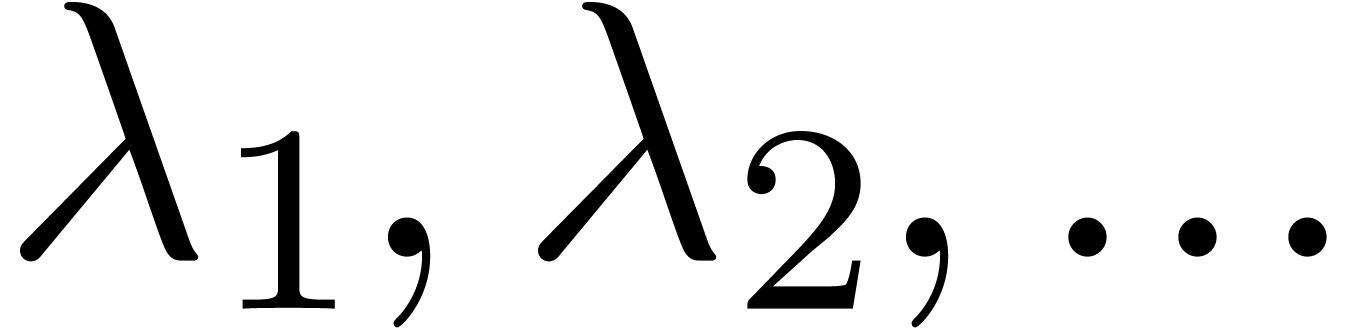 ,
,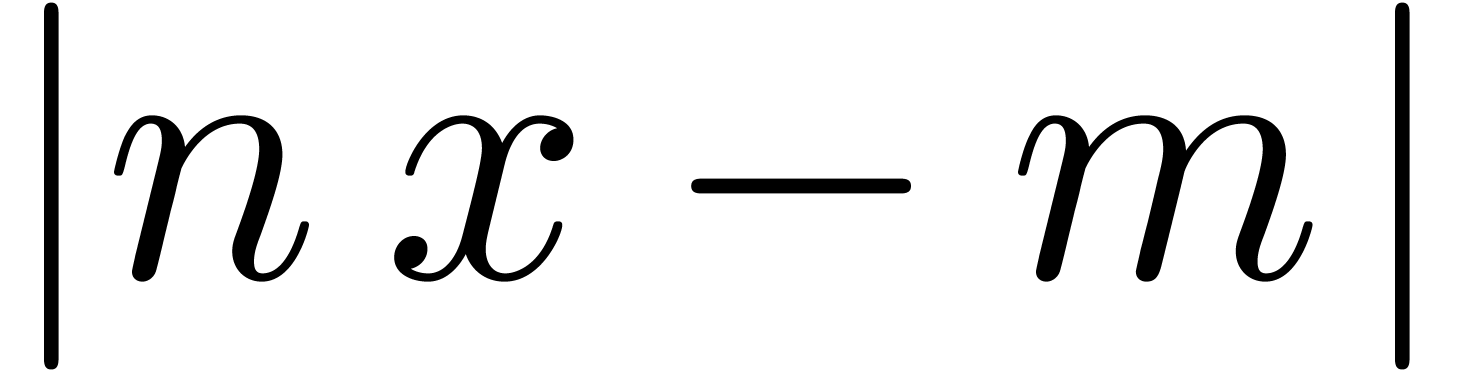 can get for large
can get for large 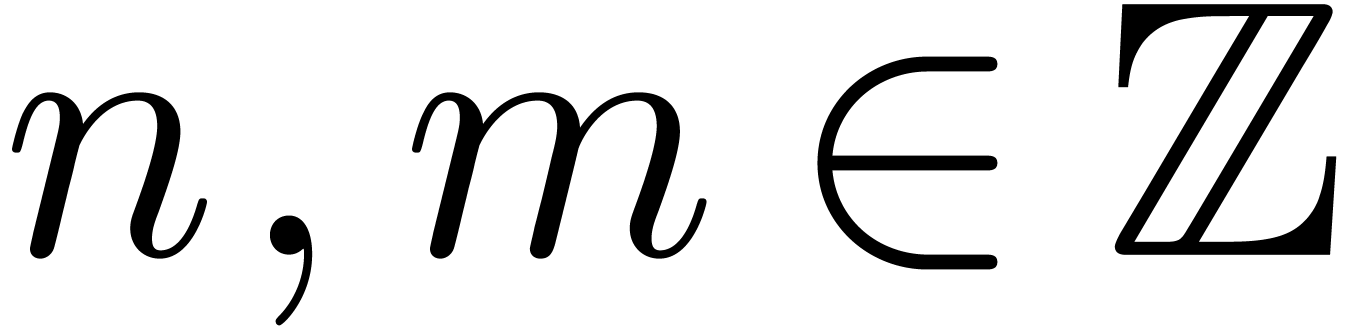 .
.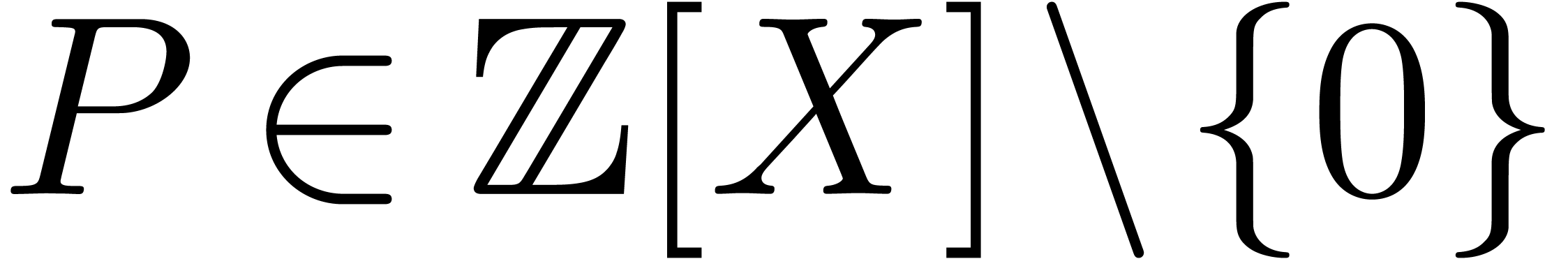 .
. and ask how small
and ask how small 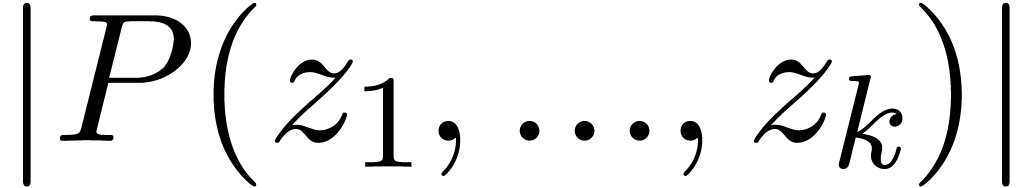 can get as a function of
can get as a function of  .
.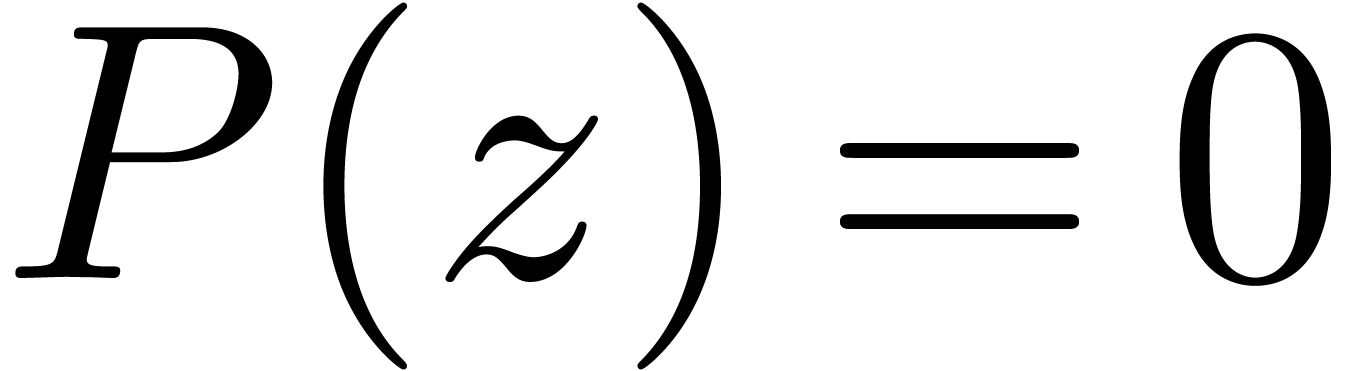 for some polynomial
for some polynomial 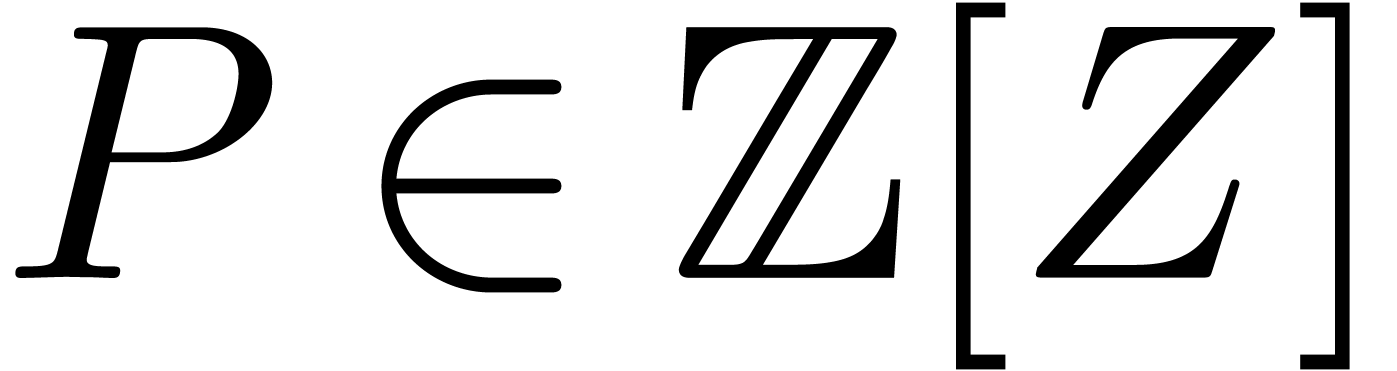 of minimal degree
of minimal degree  and minimal leading
coefficient
and minimal leading
coefficient 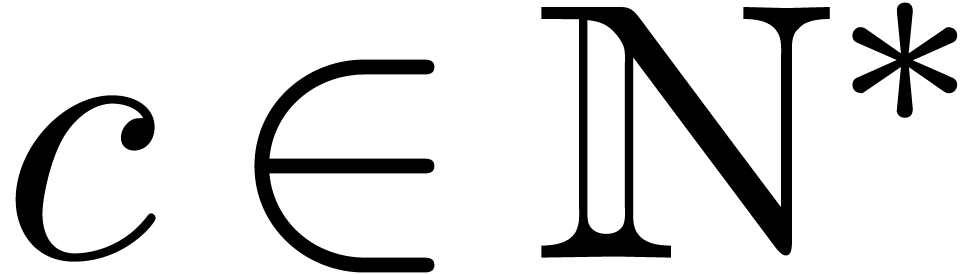 .
.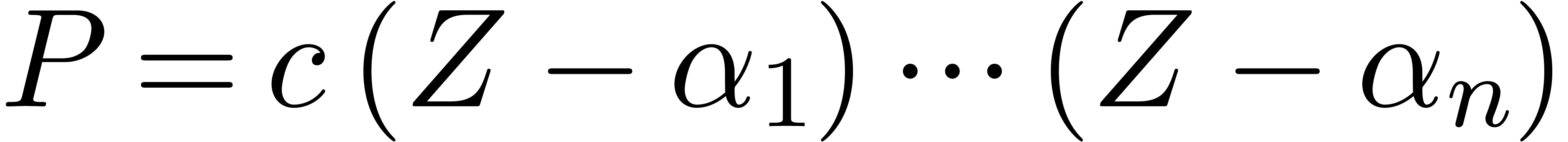
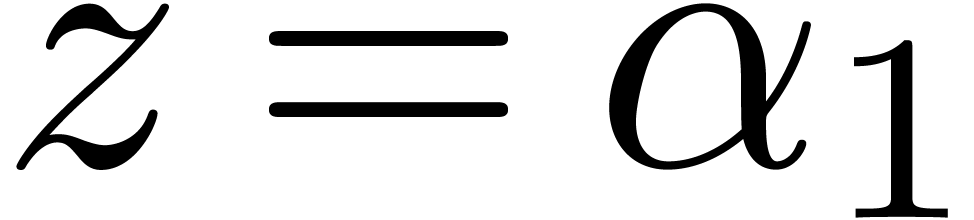 and
and 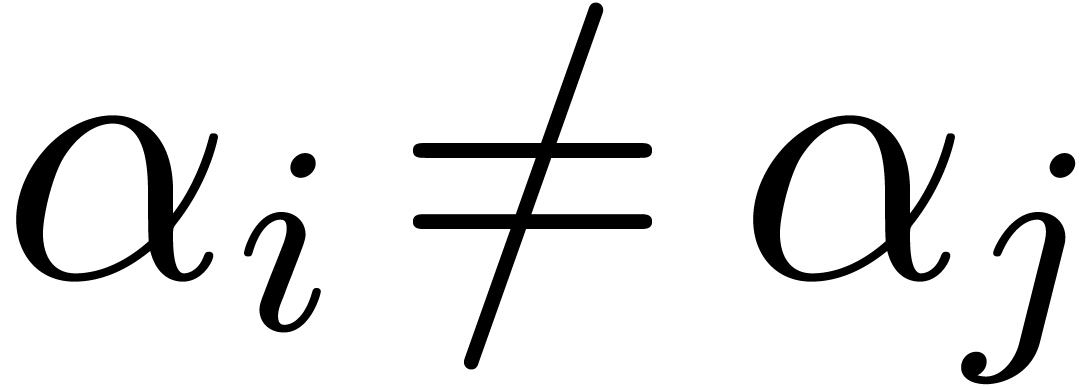 for all
for all 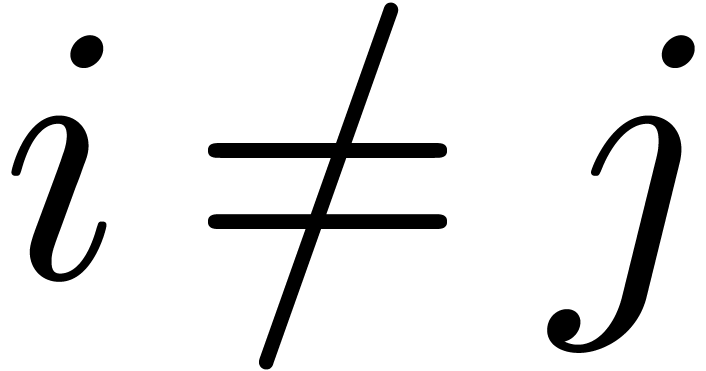 .
. close to
close to  for all
for all 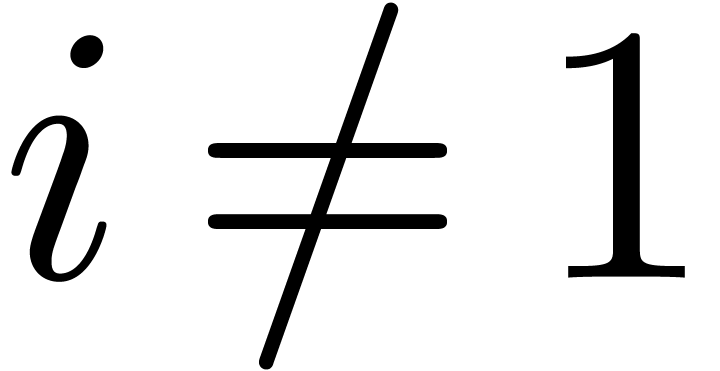 ),
),
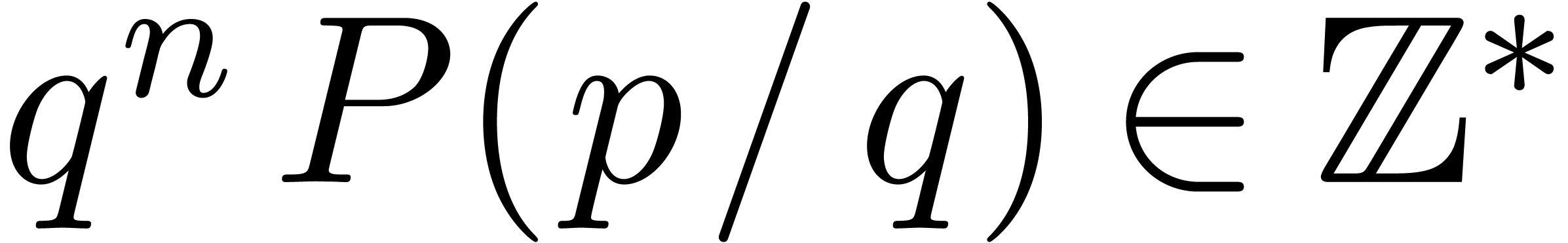 .
.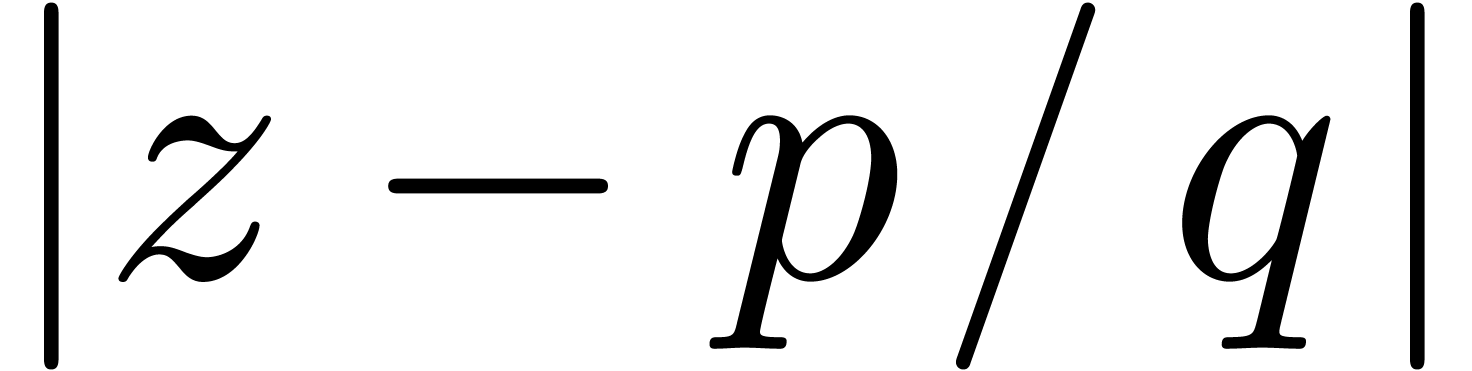 can be bounded from
below by an expression of the form
can be bounded from
below by an expression of the form 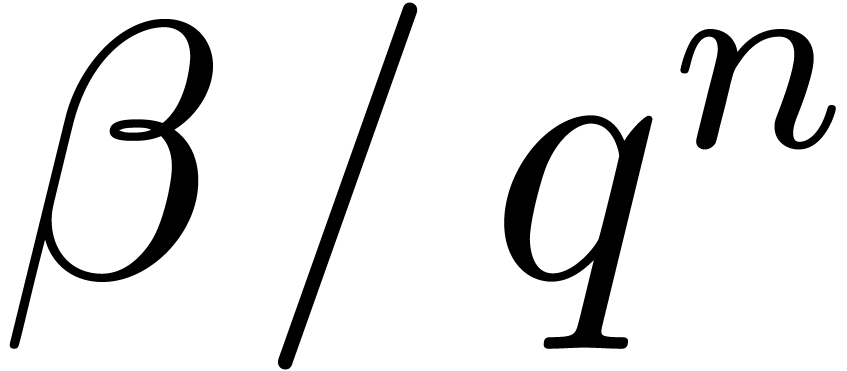 ,
, can be expressed as a function of the
polynomial
can be expressed as a function of the
polynomial  be the distance between
be the distance between  .
. and
and  ,
,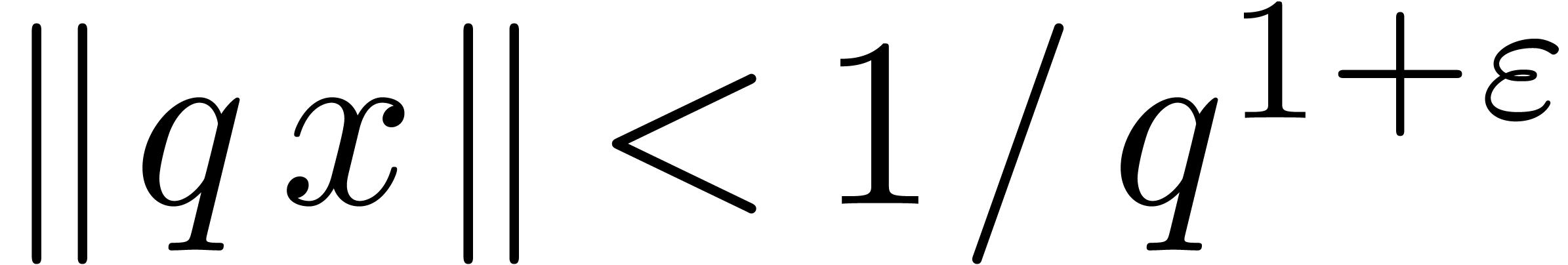 ,
,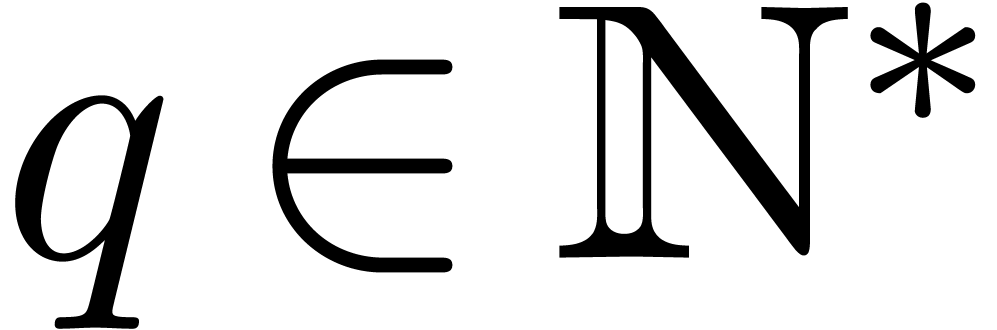 .
.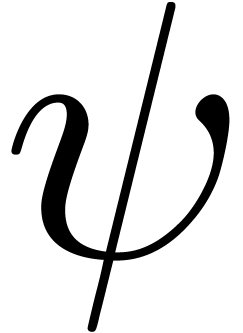 be a positive function, such that
be a positive function, such that 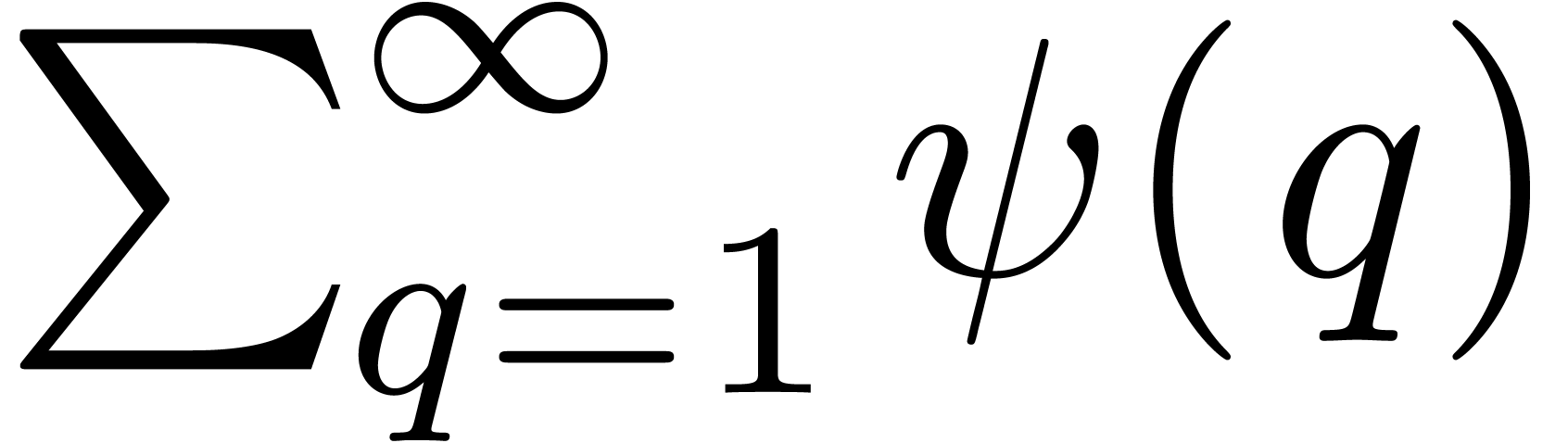 converges. Then for almost all numbers
converges. Then for almost all numbers  admits
only a finite number of solutions.
admits
only a finite number of solutions.
 ,
, ,
, as a function of the size of an
expression which represents
as a function of the size of an
expression which represents 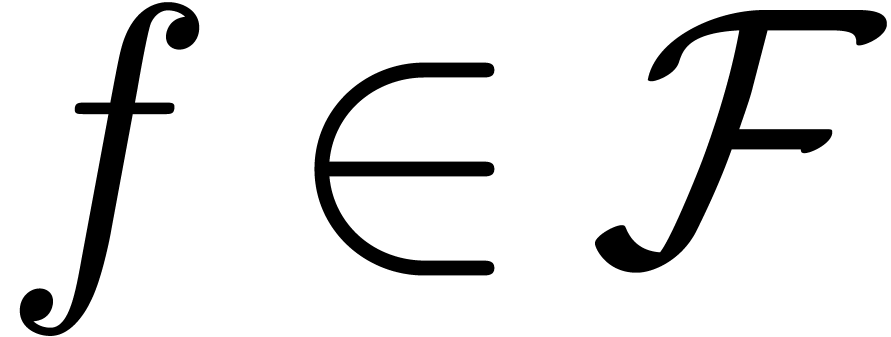 .
.
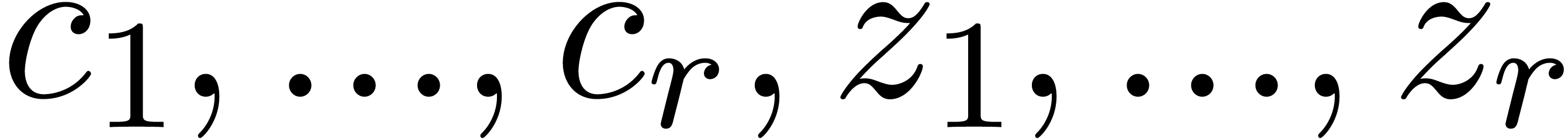 are “holonomic constants”.
Such expressions naturally occur when computing with solutions to linear
differential equations near singularities. We proved a theorem, which
implies the following one for “sufficiently regular” witness
functions
are “holonomic constants”.
Such expressions naturally occur when computing with solutions to linear
differential equations near singularities. We proved a theorem, which
implies the following one for “sufficiently regular” witness
functions 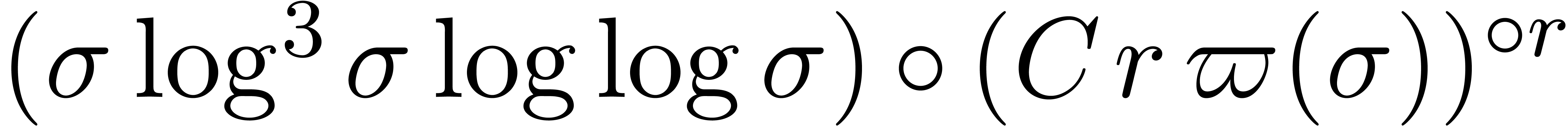
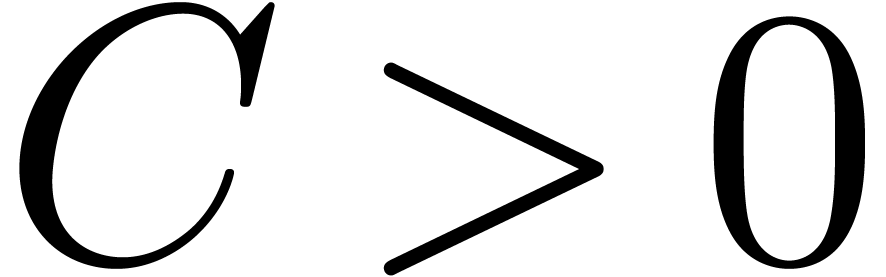 ,
,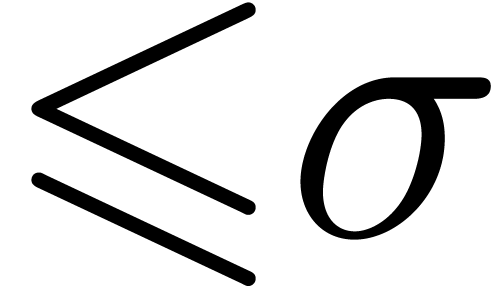 .
.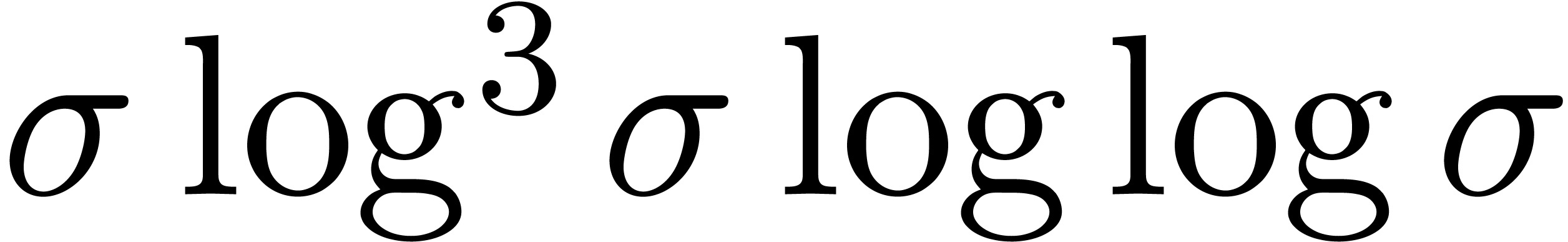 is due to the cost
of the evaluation of (
is due to the cost
of the evaluation of ( digits. If the class of holonomic constants is replaced by a larger
one, such as
digits. If the class of holonomic constants is replaced by a larger
one, such as 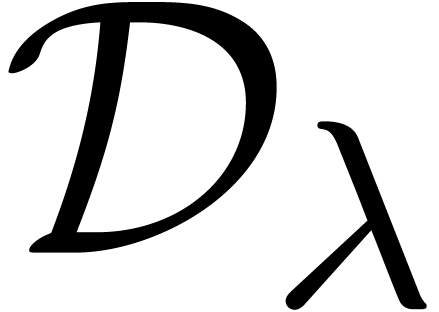 ,
,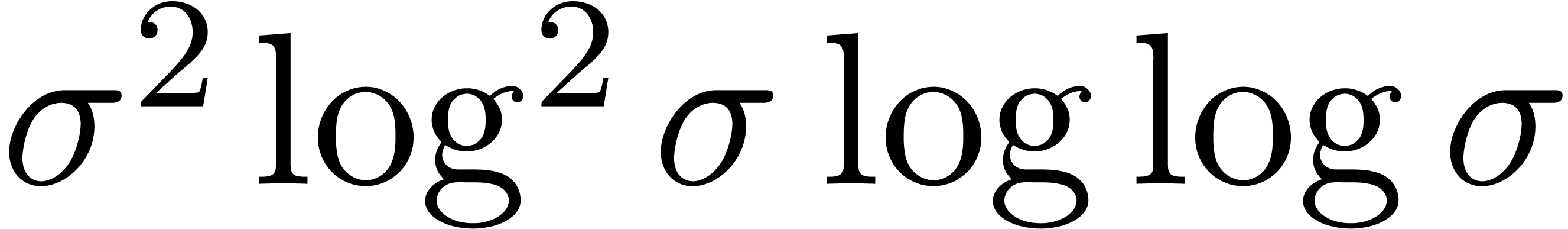 .
. .
.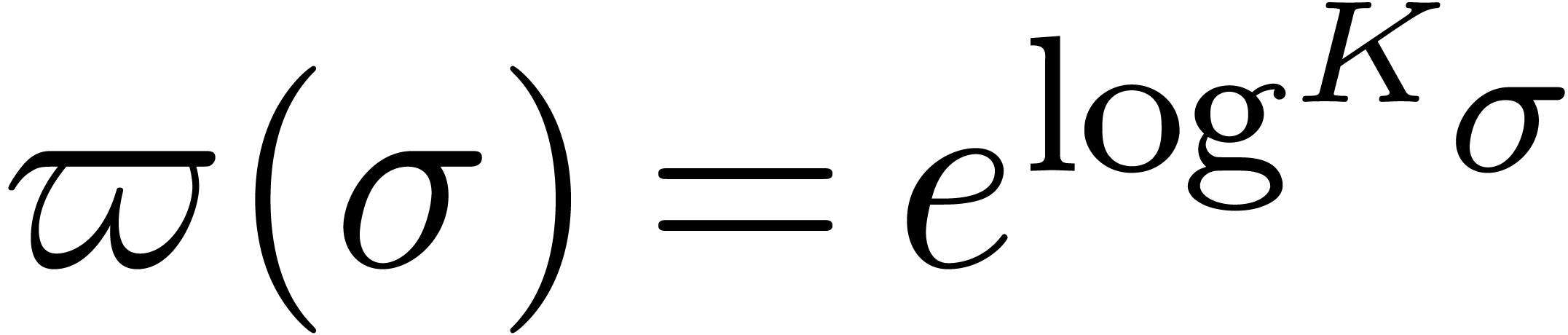 ).
). ,
,