| ON THE COMPLEXITY OF INTEGER MATRIX
MULTIPLICATION |
|
1.Introduction
In this paper we study the complexity of multiplying  matrices whose entries are integers with at most
matrices whose entries are integers with at most 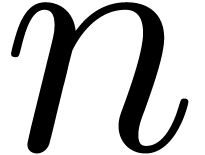 bits. We are particularly interested in the case that
bits. We are particularly interested in the case that 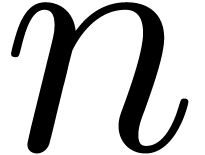 is very large compared to
is very large compared to 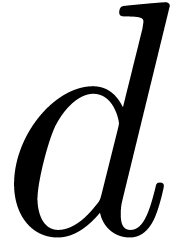 ,
say
,
say 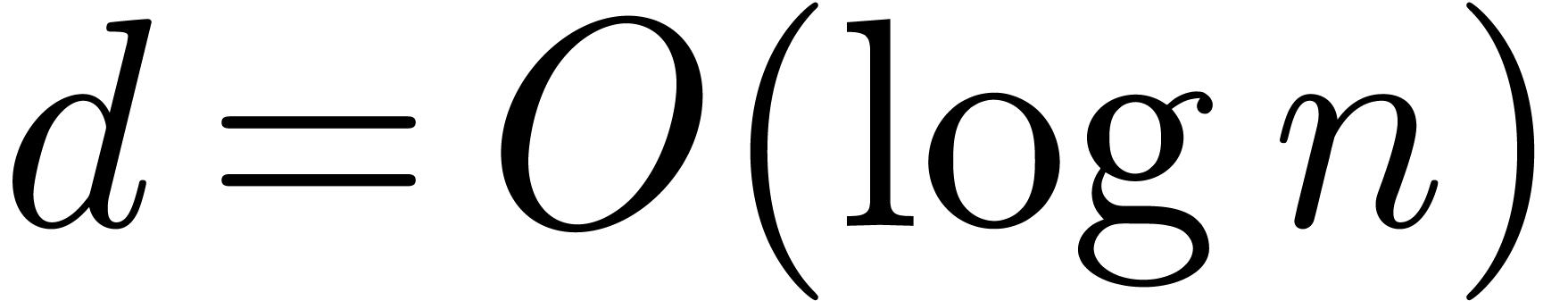 . All complexity bounds
refer to deterministic bit complexity, in the sense of the multi-tape
Turing model [Pap94].
. All complexity bounds
refer to deterministic bit complexity, in the sense of the multi-tape
Turing model [Pap94].
Matrices with large integer coefficients appear naturally in several
areas. One first application is to the efficient high precision
evaluation of so-called holonomic functions (such as exp, log, sin,
Bessel functions, and hypergeometric functions) using a divide and
conquer technique [CC90, HP97, Hoe99,
Hoe01, Hoe07]. Another application concerns
recent algorithms for computing the 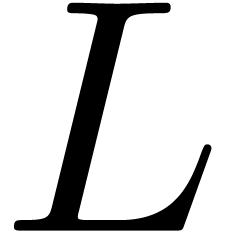 -series
of algebraic curves [Har14, HS14]. The
practical running time in these applications is dominated by the
multiplication of matrices with large integer entries, and it is vital
to have a highly efficient implementation of this fundamental operation.
Typical parameters for these applications are
-series
of algebraic curves [Har14, HS14]. The
practical running time in these applications is dominated by the
multiplication of matrices with large integer entries, and it is vital
to have a highly efficient implementation of this fundamental operation.
Typical parameters for these applications are 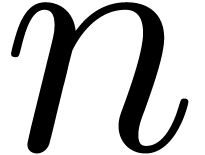 around
around 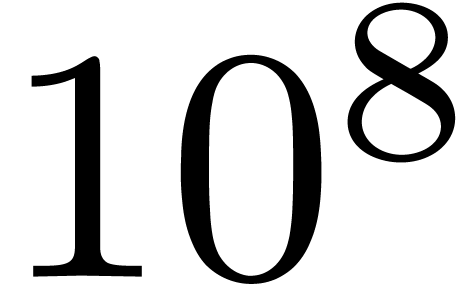 bits, and
bits, and 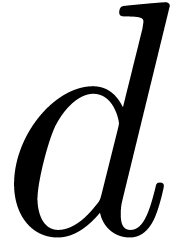 around
10.
around
10.
In this paper, we focus mainly on theoretical bounds. We write 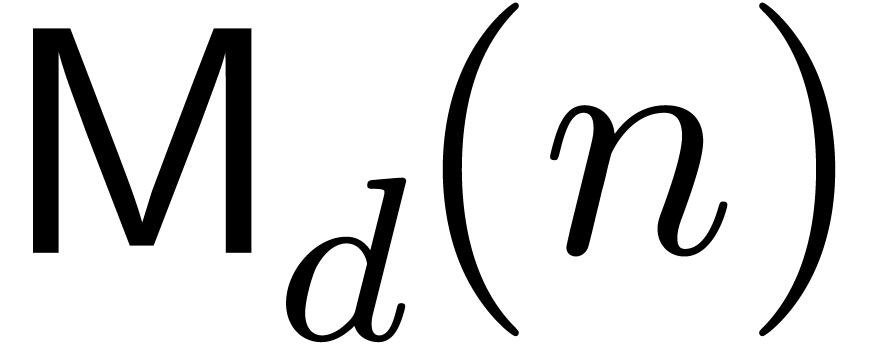 for the cost of the
for the cost of the  matrix
multiplication, and
matrix
multiplication, and 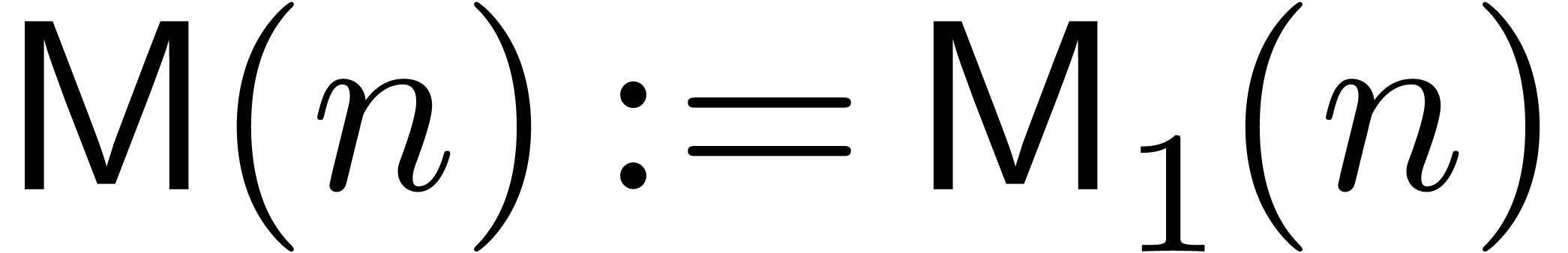 for the cost of multiplying
for the cost of multiplying
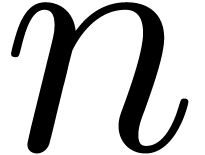 -bit integers. We will also
write
-bit integers. We will also
write 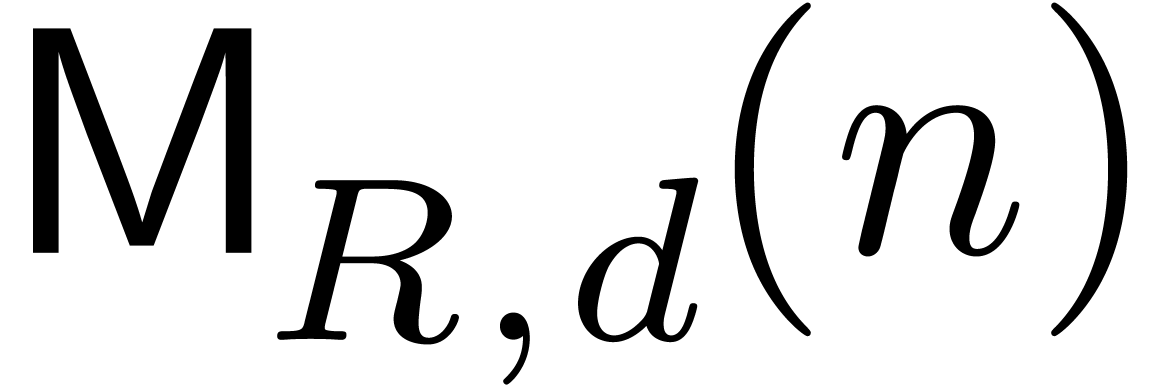 for the algebraic complexity of
multiplying
for the algebraic complexity of
multiplying  matrices whose entries are
polynomials of degrees
matrices whose entries are
polynomials of degrees 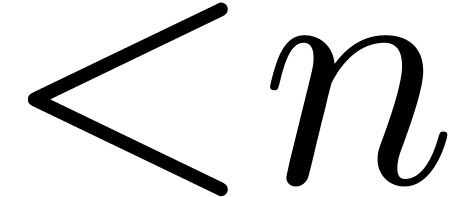 over an abstract
effective ring
over an abstract
effective ring 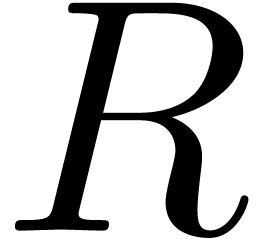 , and
, and  .
.
Schönhage and Strassen [SS71] used fast Fourier
transforms (FFTs) to prove that 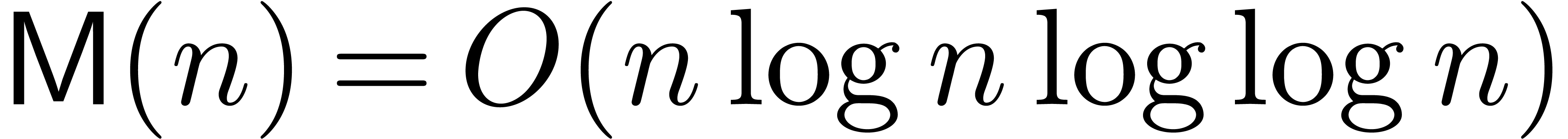 for large
for large 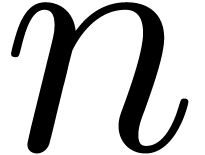 . Fürer [Für09]
improved this to
. Fürer [Für09]
improved this to 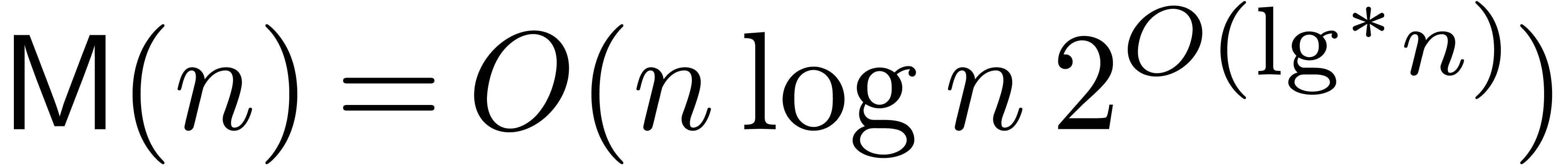 where
where 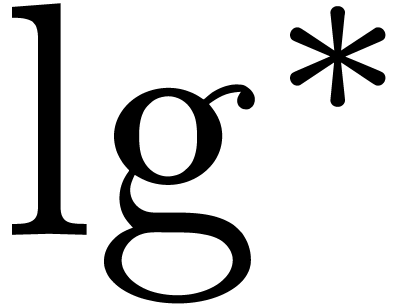 is the iterated logarithm, i.e.,
is the iterated logarithm, i.e.,
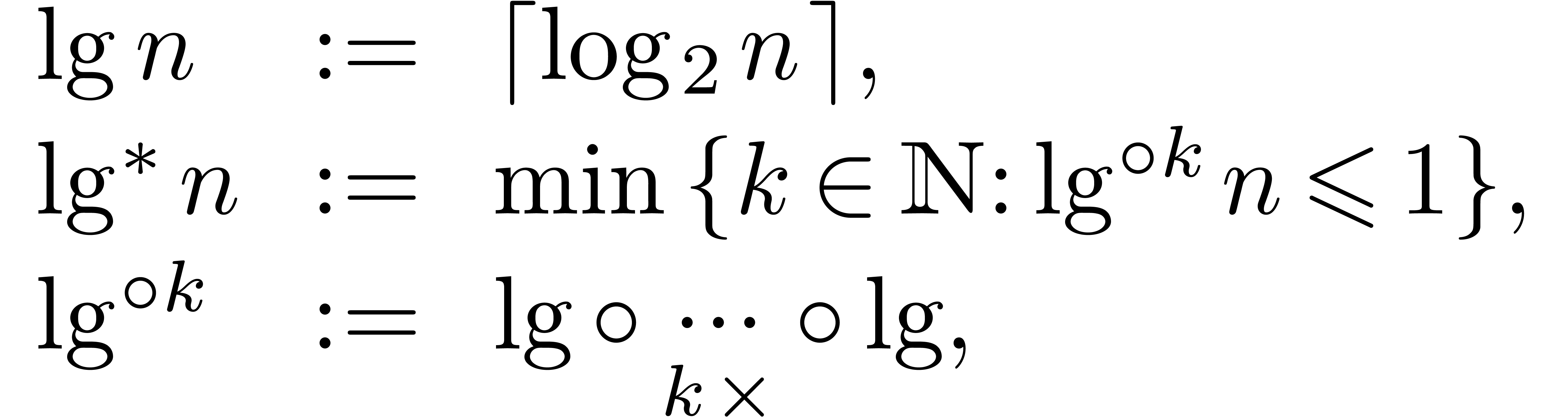
and this was recently sharpened to 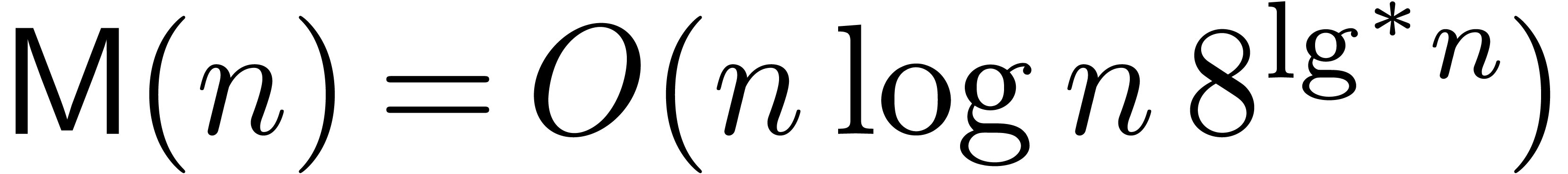 [HHL14a].
The best currently known bound [CK91] for
[HHL14a].
The best currently known bound [CK91] for 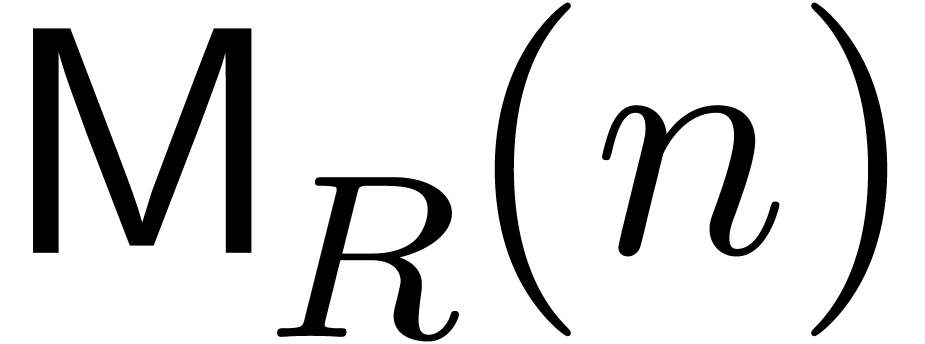 is
is 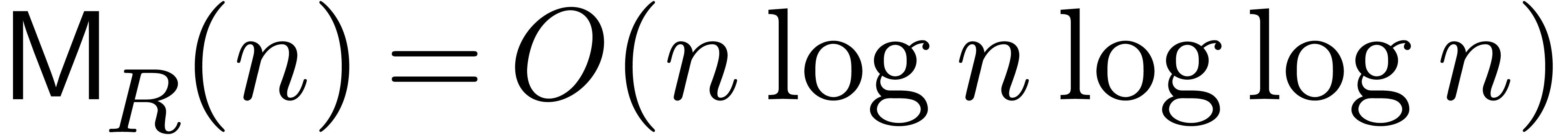 ; if
; if  is a ring of finite characteristic this may be improved to
is a ring of finite characteristic this may be improved to 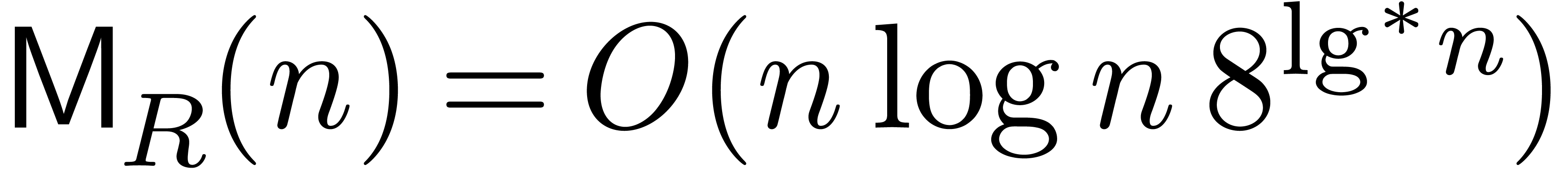 [HHL14b].
[HHL14b].
The algebraic complexity of  matrix
multiplication is usually assumed to be of the form
matrix
multiplication is usually assumed to be of the form 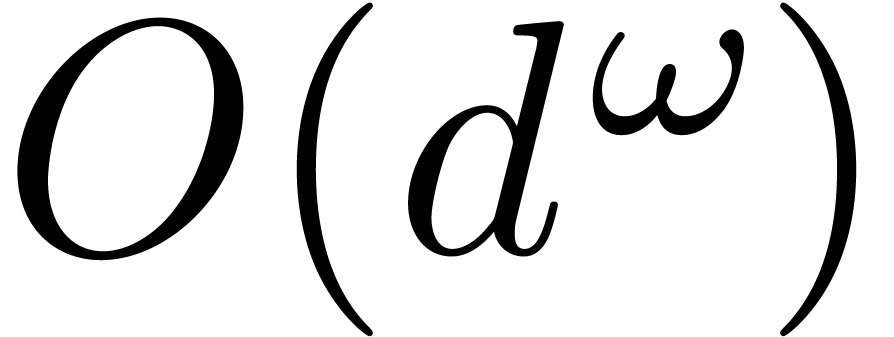 , where
, where  is a so-called
exponent of matrix multiplication [vzGG03, Ch. 12].
Classical matrix multiplication yields
is a so-called
exponent of matrix multiplication [vzGG03, Ch. 12].
Classical matrix multiplication yields 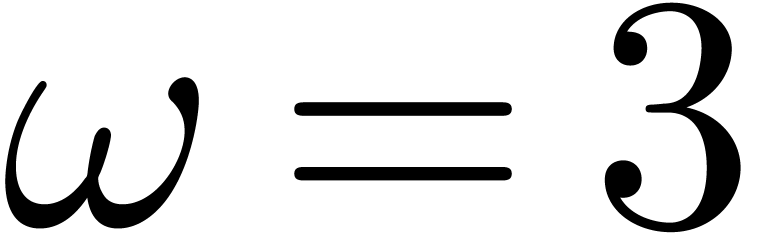 ,
and Strassen's algorithm [Str69] achieves
,
and Strassen's algorithm [Str69] achieves 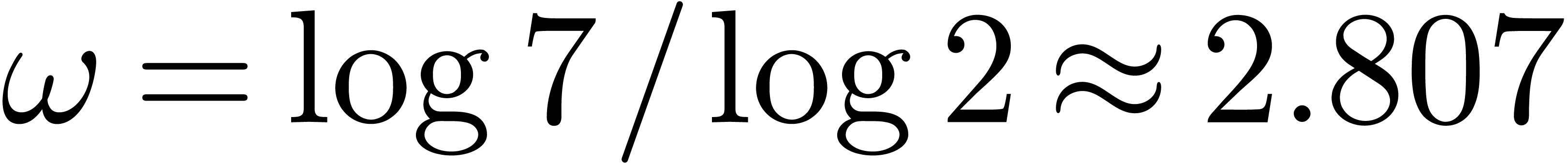 . The best currently known exponent
. The best currently known exponent  was found by Le Gall [Gal14, CW87].
was found by Le Gall [Gal14, CW87].
When working over the integers and taking into account the growth of
coefficients, the general bound for matrix multiplication specialises to
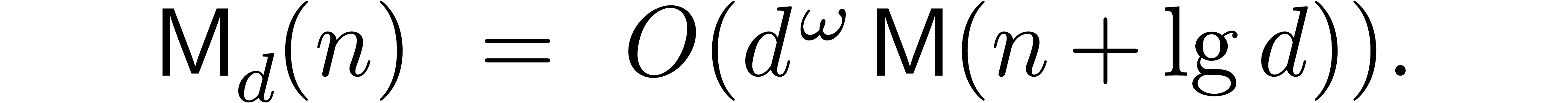
Throughout this paper we will enforce the very mild restriction that
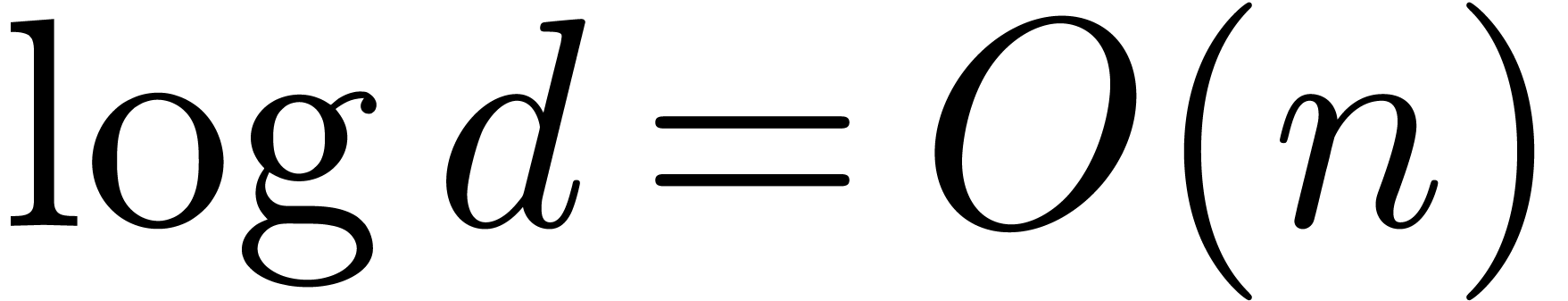 . Under this assumption the
above bound simplifies to
. Under this assumption the
above bound simplifies to
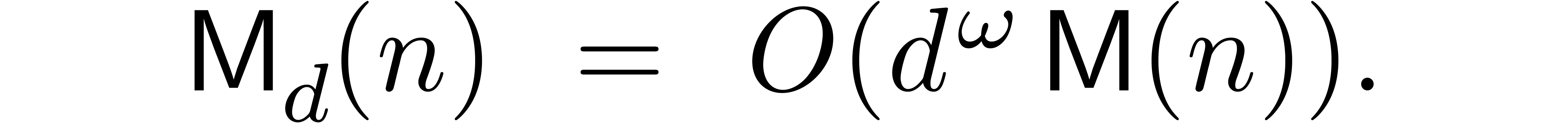
The main result of this paper is the following improvement.
Theorem 1. Assume
that 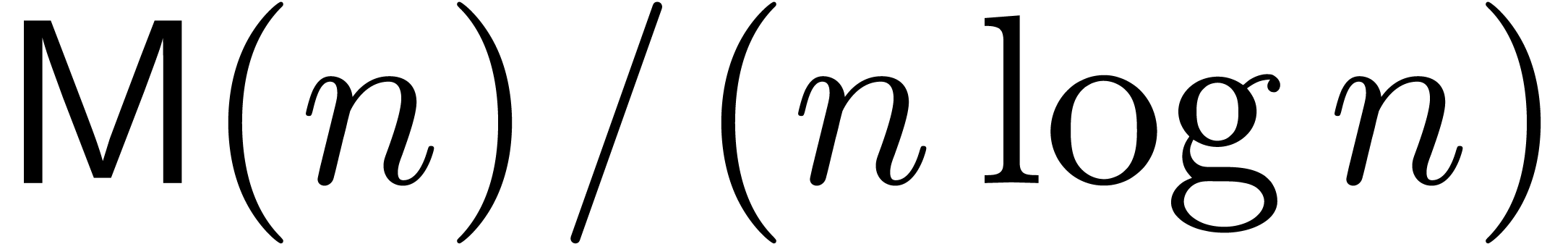 is increasing. Let
is increasing. Let 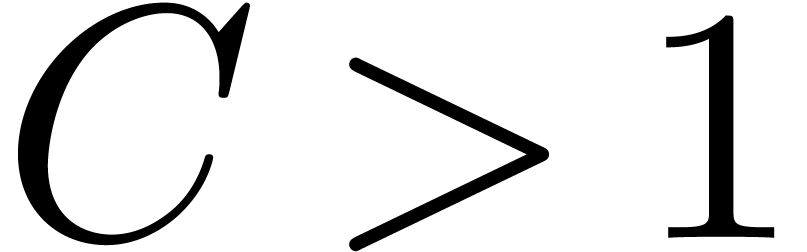 be a constant. Then
be a constant. Then
 |
(1) |
uniformly for all 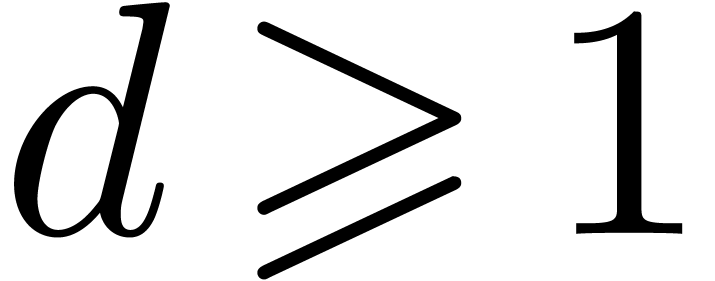 ,
, 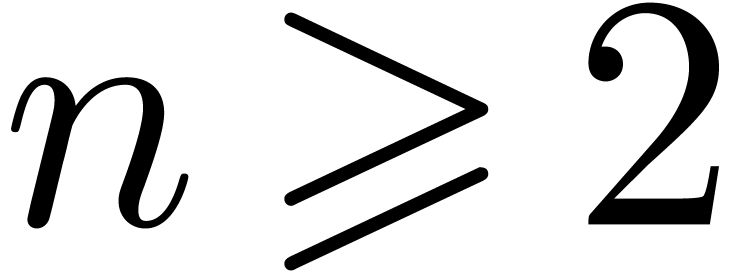 with
with 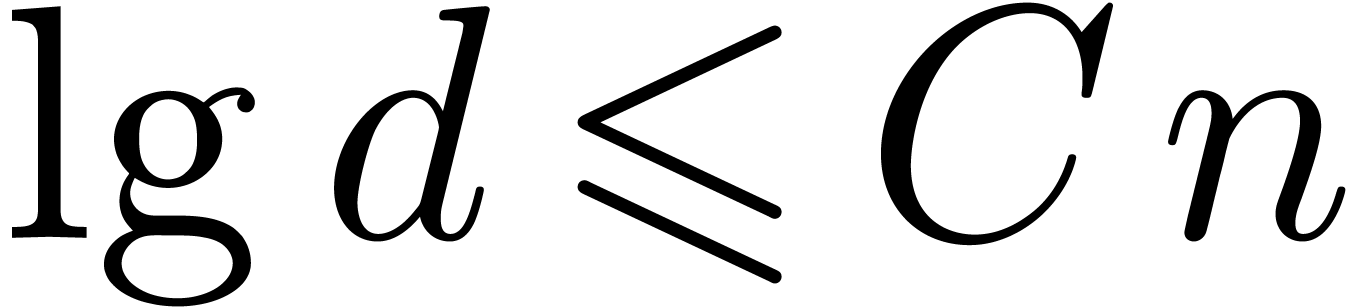 .
.
In particular, if 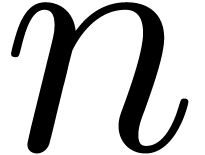 is large compared to
is large compared to 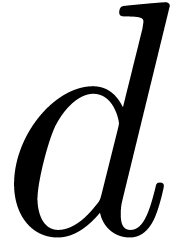 , say
, say 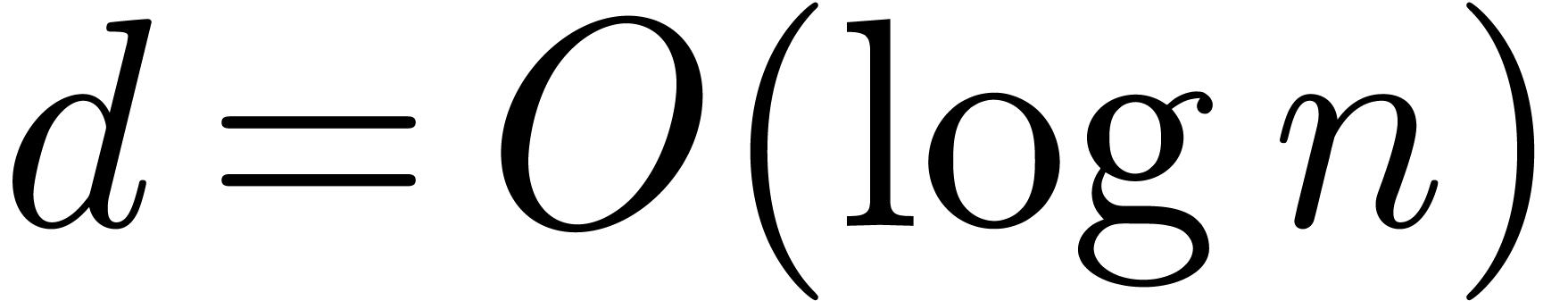 ,
then (1) simplifies to
,
then (1) simplifies to
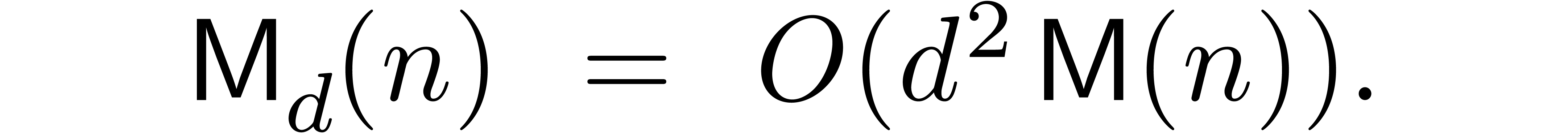 |
(2) |
This bound is essentially optimal (up to constant factors), in the sense
that we cannot expect to do better for  ,
and the bound grows proportionally to the input and output size as a
function of
,
and the bound grows proportionally to the input and output size as a
function of 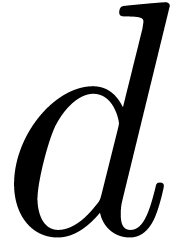 .
.
The new algorithm has its roots in studies of analogous problems in the
algebraic complexity setting. When working over an arbitrary effective
ring 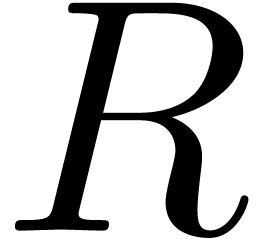 , a classical technique
for multiplying polynomial matrices is to use an
evaluation-interpolation scheme. There are many different
evaluation-interpolation strategies [Hoe10, Sections
2.1–2.3] such as Karatsuba, Toom–Cook, FFT,
Schönhage–Strassen and general multi-point. The efficiency of
a particular evaluation-interpolation strategy can be expressed in terms
of two quantities: the complexity
, a classical technique
for multiplying polynomial matrices is to use an
evaluation-interpolation scheme. There are many different
evaluation-interpolation strategies [Hoe10, Sections
2.1–2.3] such as Karatsuba, Toom–Cook, FFT,
Schönhage–Strassen and general multi-point. The efficiency of
a particular evaluation-interpolation strategy can be expressed in terms
of two quantities: the complexity 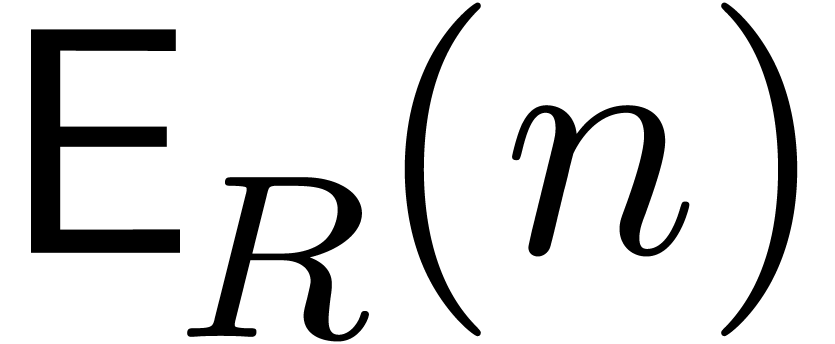 of
evaluation/interpolation and the number
of
evaluation/interpolation and the number 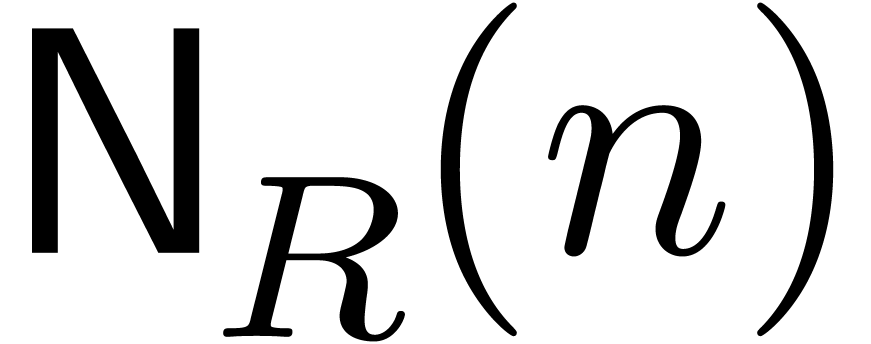 of
evaluation points. In terms of these quantities, we have
of
evaluation points. In terms of these quantities, we have
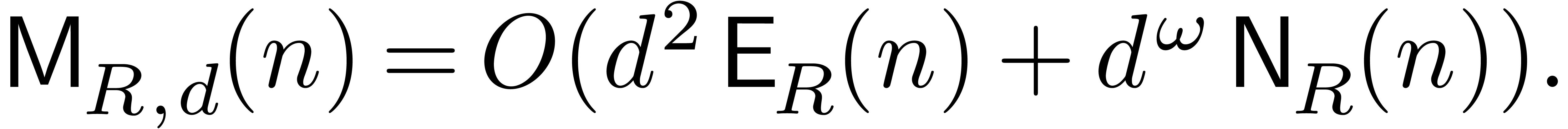 |
(3) |
If 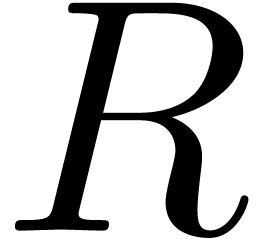 admits many primitive
admits many primitive 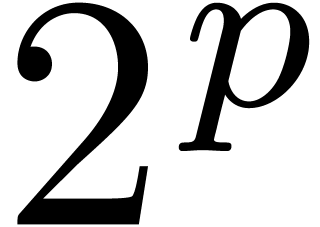 -th roots of unity, then the FFT provides an
efficient evaluation-interpolation strategy that achieves
-th roots of unity, then the FFT provides an
efficient evaluation-interpolation strategy that achieves 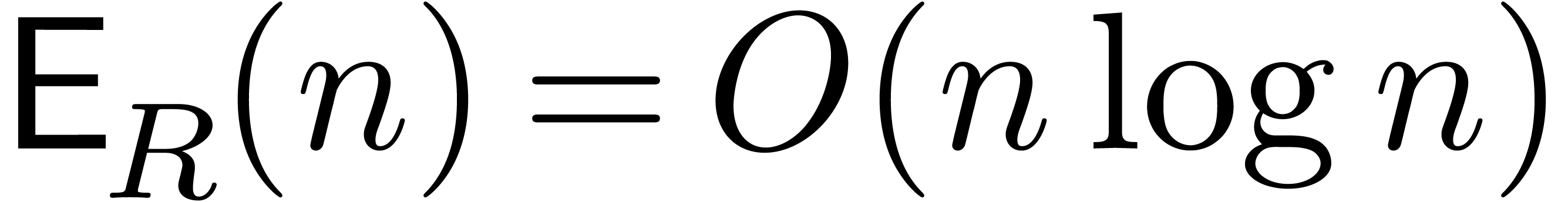 and
and 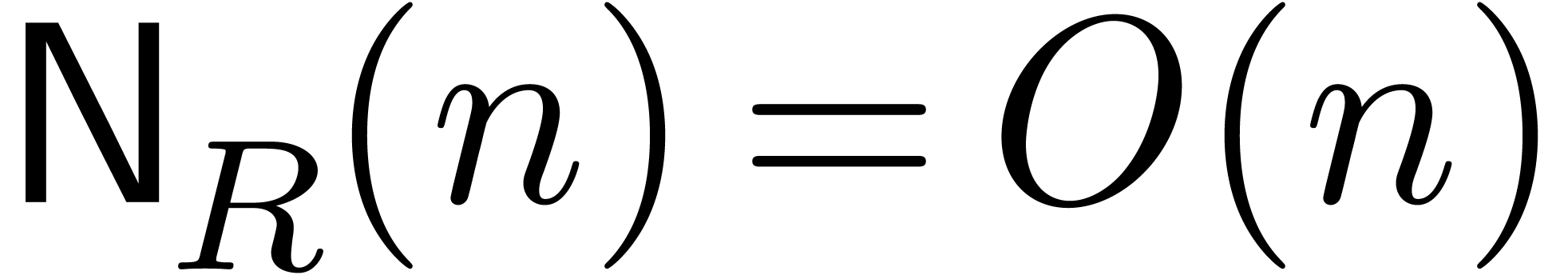 . Moreover,
when using the TFT [Hoe04], one may take
. Moreover,
when using the TFT [Hoe04], one may take 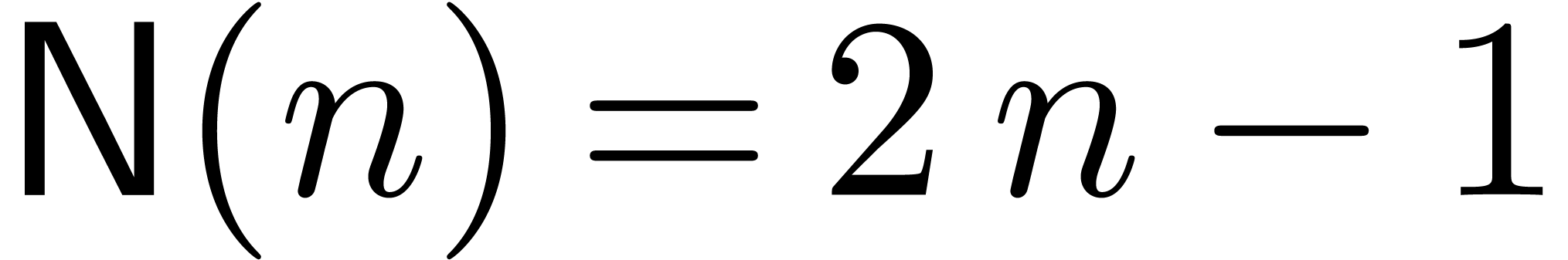 , which is optimal. If
, which is optimal. If 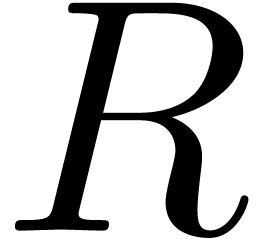 is a field of characteristic zero, or a finite field with sufficiently
many elements, then Bostan and Schost proved [BS05, Thm. 4]
that one may achieve
is a field of characteristic zero, or a finite field with sufficiently
many elements, then Bostan and Schost proved [BS05, Thm. 4]
that one may achieve  and
and 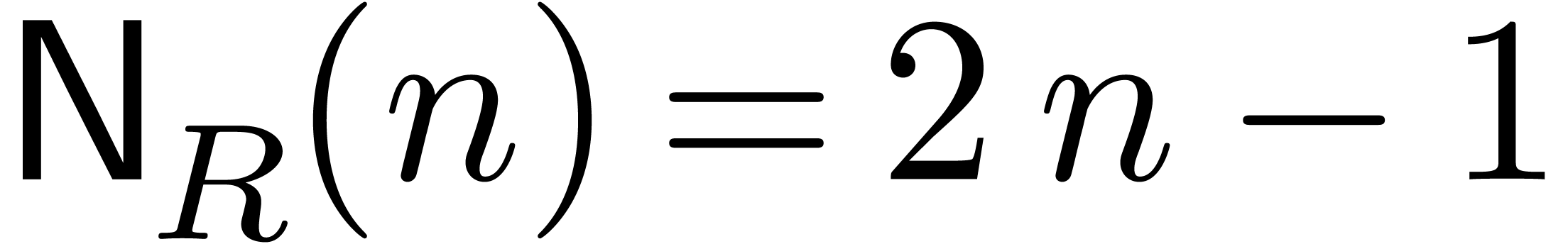 by evaluating at geometric sequences. Thus, in this situation they
obtain
by evaluating at geometric sequences. Thus, in this situation they
obtain
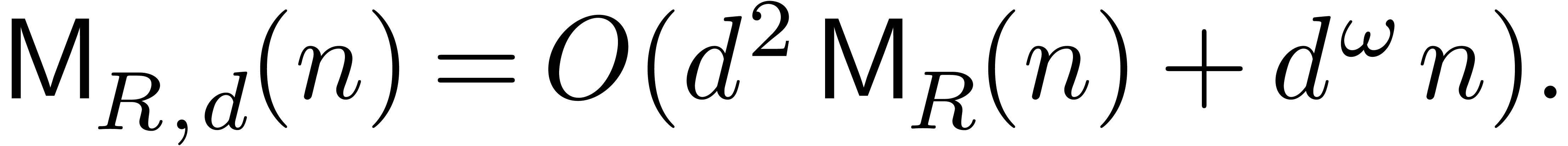 |
(4) |
In the setting of integer coefficients, a popular
evaluation-interpolation strategy is Chinese remaindering with respect
to many small primes of bit length 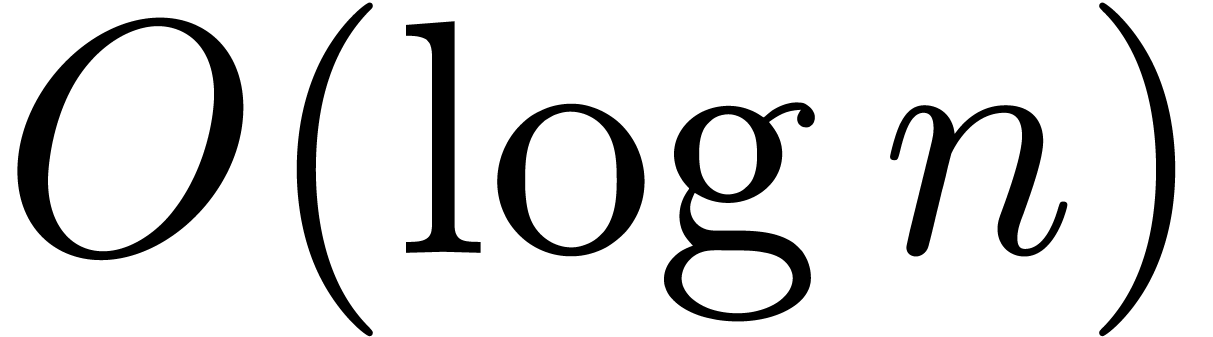 .
Still assuming that
.
Still assuming that 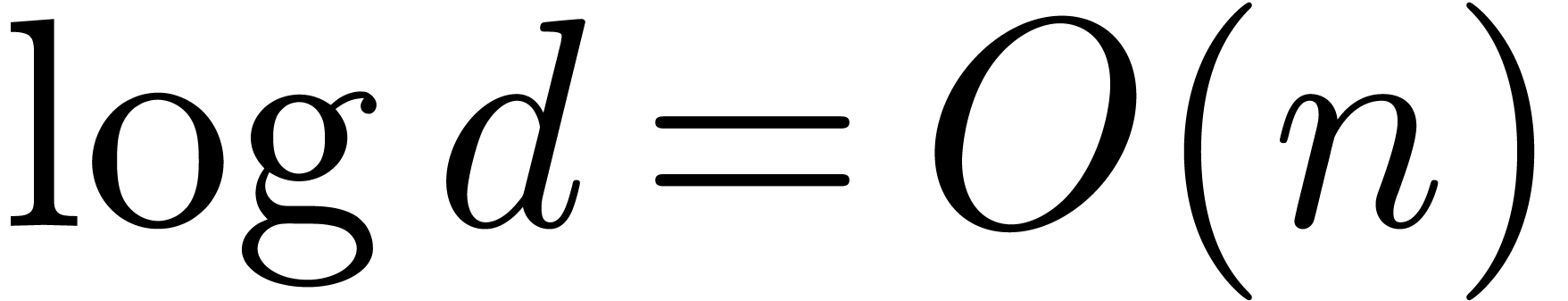 , this
yields the bound (see [Sto00, Lemma 1.7], for instance)
, this
yields the bound (see [Sto00, Lemma 1.7], for instance)
and recursive application of this bound yields
Comparing with the algebraic bound (4),
we notice an extra factor of 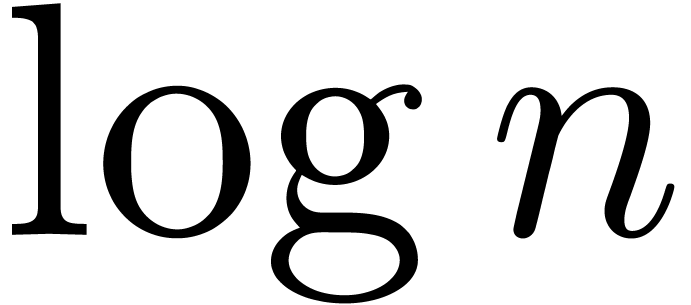 in the first term.
This factor arises from the cost of computing a certain product tree
(and remainder tree) in the Chinese remaindering algorithm.
in the first term.
This factor arises from the cost of computing a certain product tree
(and remainder tree) in the Chinese remaindering algorithm.
A well-known method that attempts to avoid the spurious 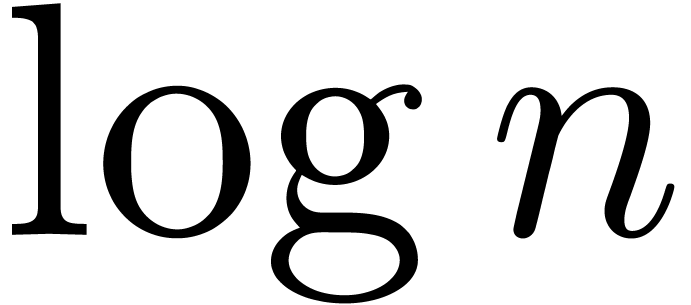 factor is to use FFTs. For example, suppose that we are using the
Schönhage–Strassen integer multiplication algorithm. This
works by cutting up the integers into into chunks of about
factor is to use FFTs. For example, suppose that we are using the
Schönhage–Strassen integer multiplication algorithm. This
works by cutting up the integers into into chunks of about 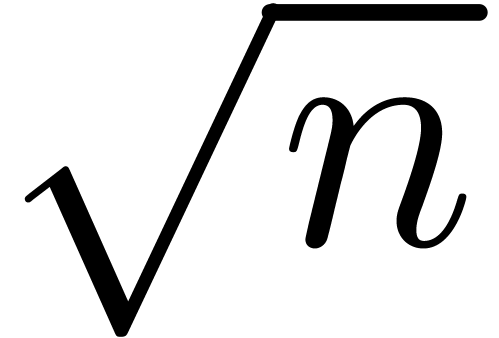 bits, and then performs FFTs over a ring of the form
bits, and then performs FFTs over a ring of the form 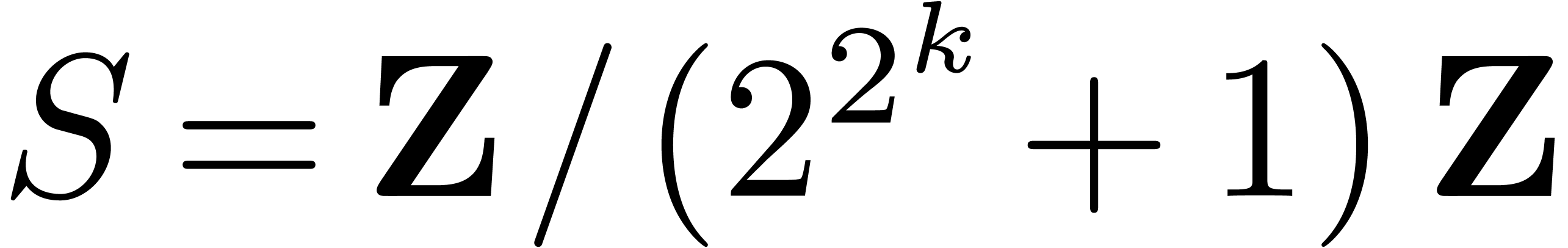 where
where 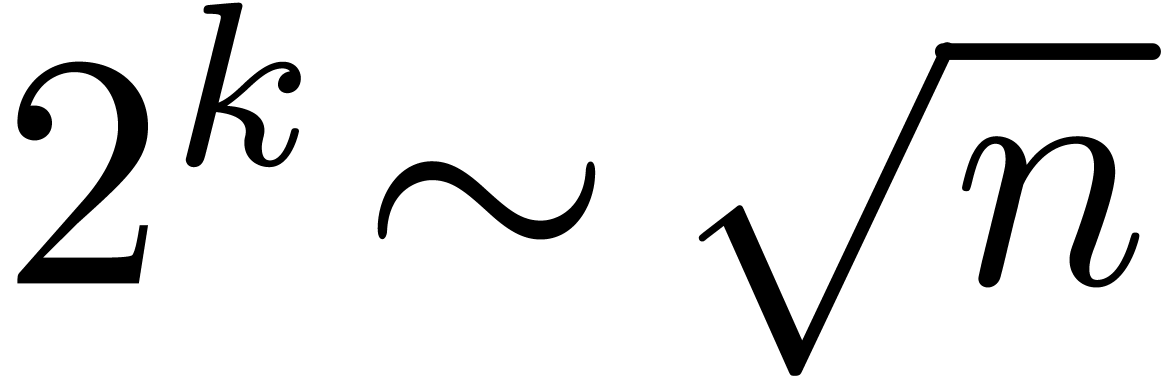 . We
can multiply integer matrices the same way, by cutting up each entry
into chunks of about
. We
can multiply integer matrices the same way, by cutting up each entry
into chunks of about 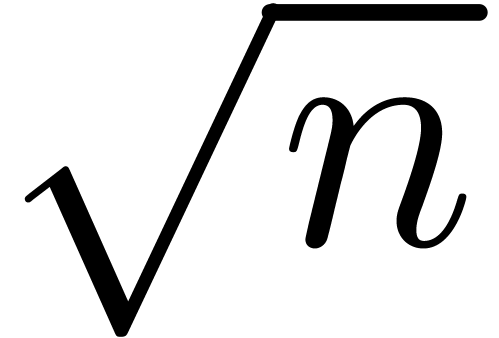 bits, performing FFTs over
bits, performing FFTs over
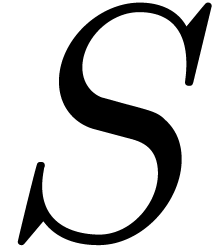 , and then multiplying the
matrices of Fourier coefficients. When
, and then multiplying the
matrices of Fourier coefficients. When 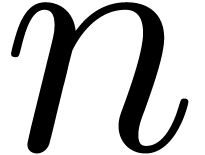 is
much larger than
is
much larger than 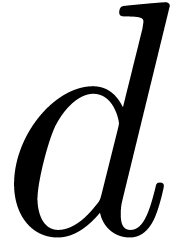 , the latter
step takes negligible time, and the bulk of the time is spent performing
FFTs. Since each matrix entry is only transformed once, this leads to a
bound of the type
, the latter
step takes negligible time, and the bulk of the time is spent performing
FFTs. Since each matrix entry is only transformed once, this leads to a
bound of the type 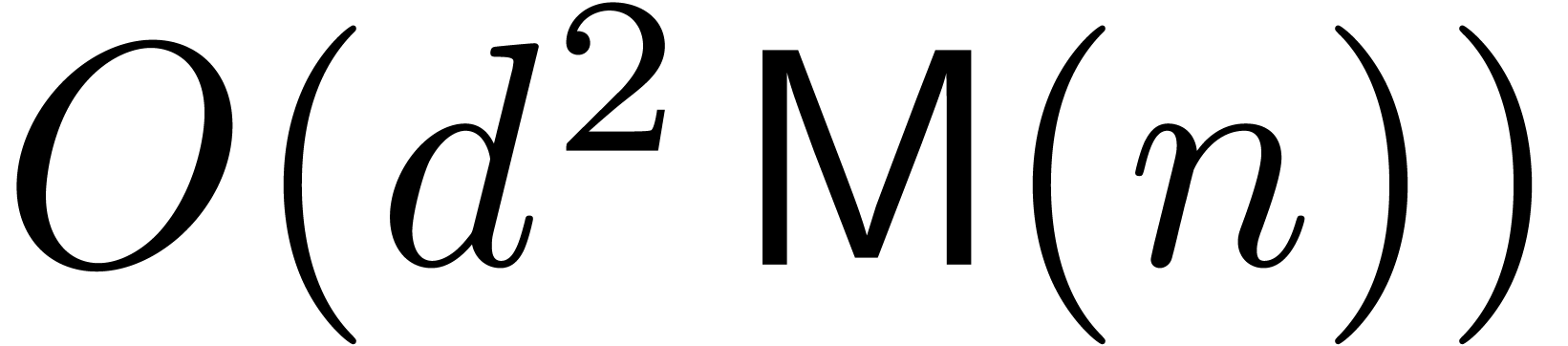 , without
the extraneous
, without
the extraneous 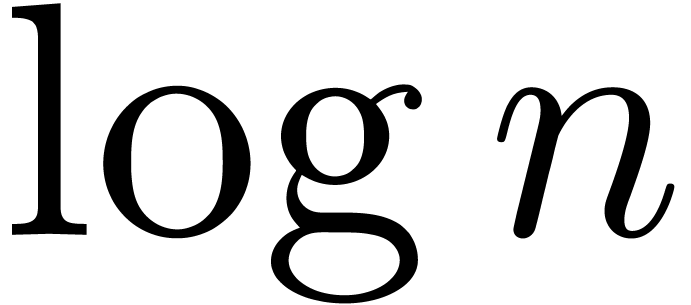 factor. This method is very
efficient in practice; both [HS14] and Mathemagix
[HLM+02, HLQ14] contain implementations based
on number-theoretic transforms (i.e., FFTs modulo word-sized prime
numbers).
factor. This method is very
efficient in practice; both [HS14] and Mathemagix
[HLM+02, HLQ14] contain implementations based
on number-theoretic transforms (i.e., FFTs modulo word-sized prime
numbers).
However, the theoretical question remains as to whether the 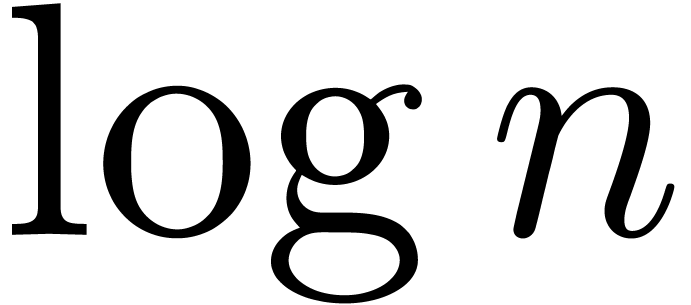 overhead can be removed unconditionally, independently of
the “internal structure” of the currently fastest algorithm
for integer multiplication. Our Theorem 1 shows that this
is indeed the case. More precisely, we reduce integer matrix
multiplication to the multiplication of matrix polynomials over
overhead can be removed unconditionally, independently of
the “internal structure” of the currently fastest algorithm
for integer multiplication. Our Theorem 1 shows that this
is indeed the case. More precisely, we reduce integer matrix
multiplication to the multiplication of matrix polynomials over 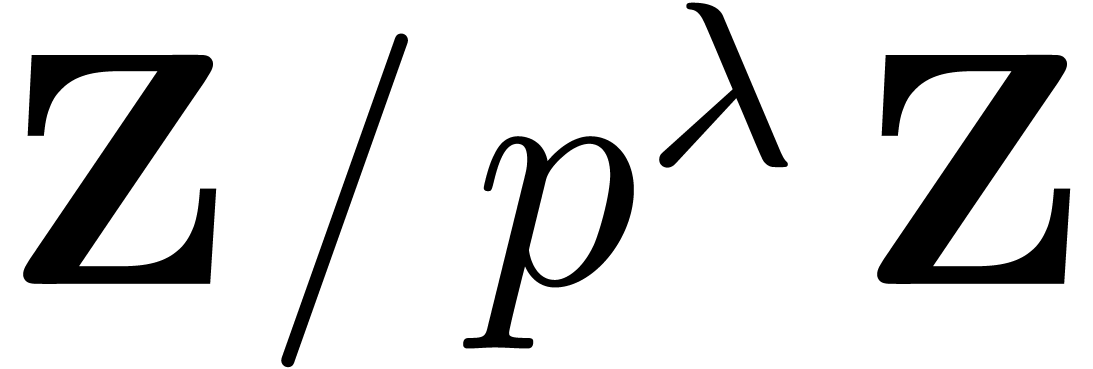 for a suitable prime power
for a suitable prime power 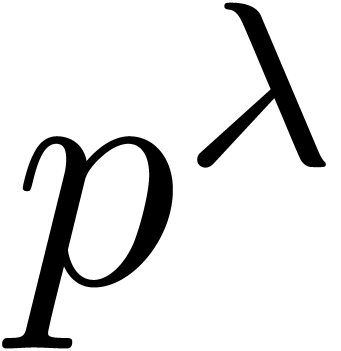 . The multiplication of such polynomials is done
using FFTs. However, instead of using a classical algorithm for
computing the FFT of an individual polynomial, we reduce this problem
back to integer multiplication using Bluestein's trick [Blu70]
and Kronecker substitution [vzGG03, Ch. 8]. This central
idea of the paper will be explained in section 2. In
section 3, we prove our main complexity bound (1).
. The multiplication of such polynomials is done
using FFTs. However, instead of using a classical algorithm for
computing the FFT of an individual polynomial, we reduce this problem
back to integer multiplication using Bluestein's trick [Blu70]
and Kronecker substitution [vzGG03, Ch. 8]. This central
idea of the paper will be explained in section 2. In
section 3, we prove our main complexity bound (1).
We stress that Theorem 1 is a theoretical result, and we do
not recommend our algorithm for practical computations. For any given
FFT-based integer multiplication algorithm, it should always be better,
by a constant factor, to apply the same FFT scheme to the matrix entries
directly, as outlined above. See Remark 6 for further
discussion about the implied big- constant.
constant.
Remark 2. The observation that the
Bluestein–Kronecker combination leads to a particularly efficient
FFT algorithm was announced previously in [HHL14a]. We
mention as a historical remark that the development of the main ideas of
the present paper actually preceded [HHL14a].
2.Bluestein–Kronecker
reduction
We begin with a lemma that converts a certain polynomial evaluation
problem to integer multiplication.
Lemma 3. Assume
that 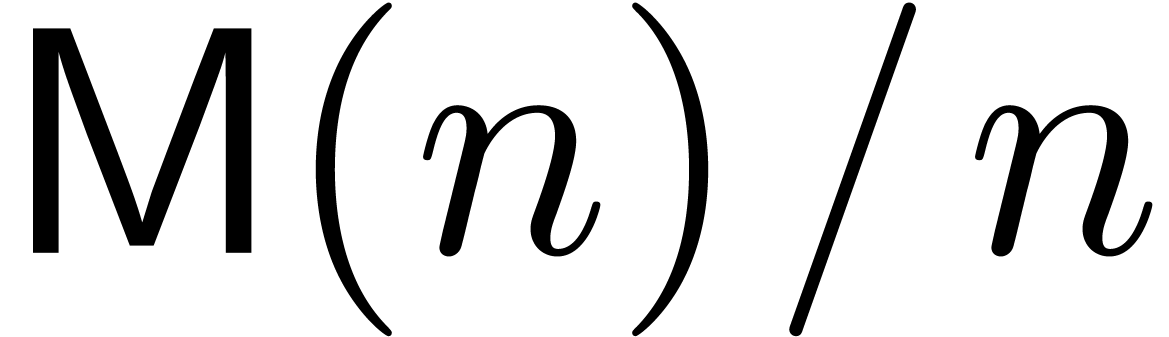 is increasing. Let
is increasing. Let 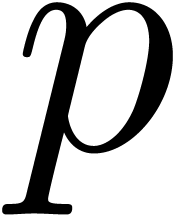 be an odd prime, let
be an odd prime, let 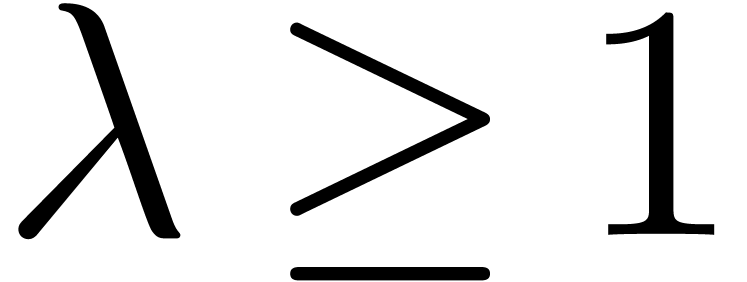 be an integer, and let
be an integer, and let 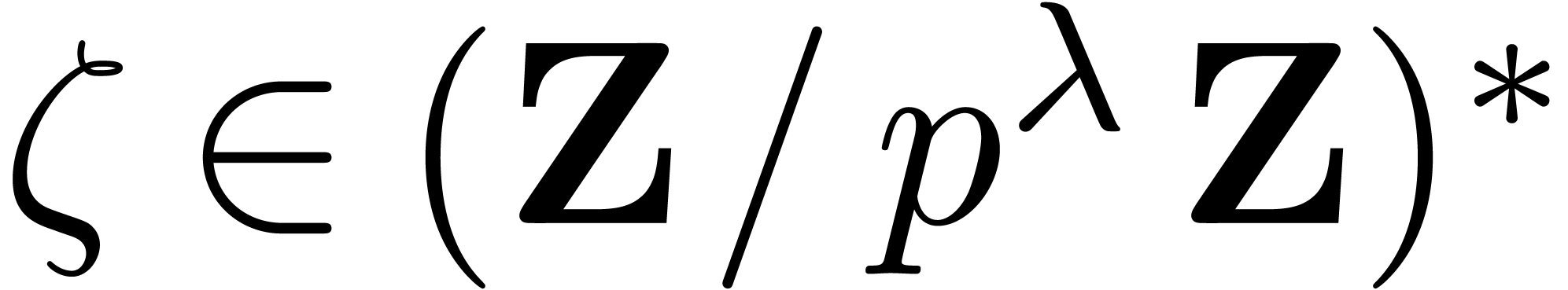 be an element of order
be an element of order 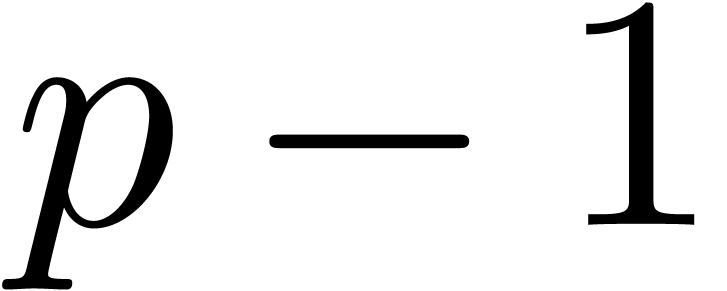 .
Given as input
.
Given as input 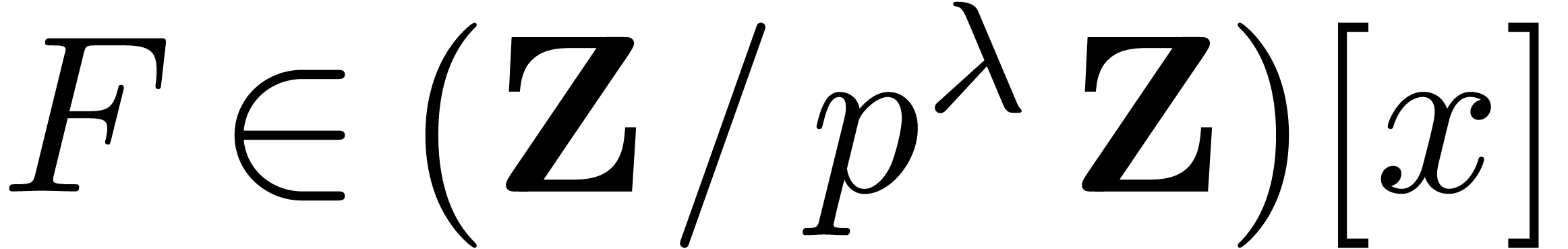 , with
, with  , we may compute
, we may compute 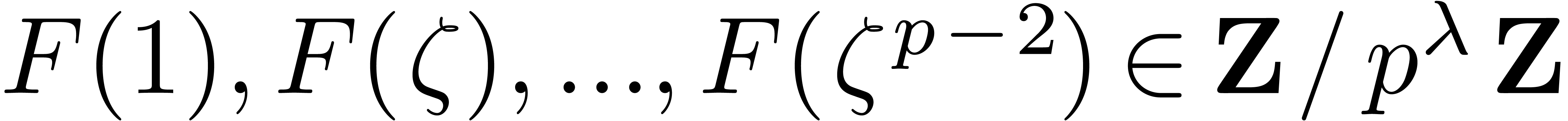 in time
in time
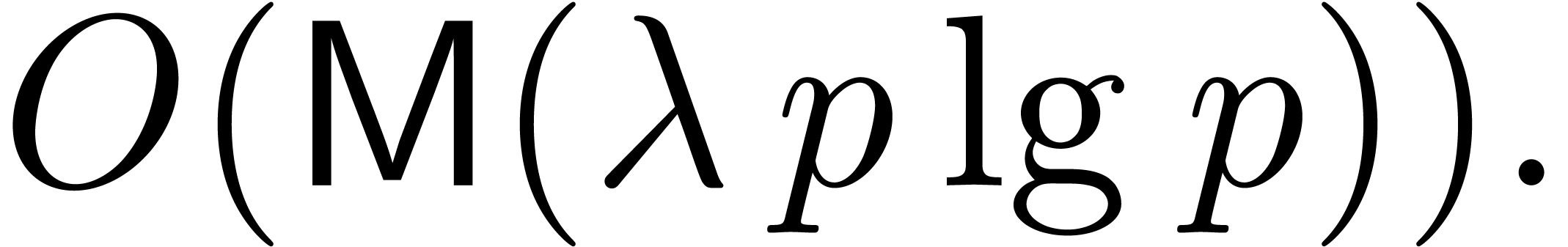
Proof. Let 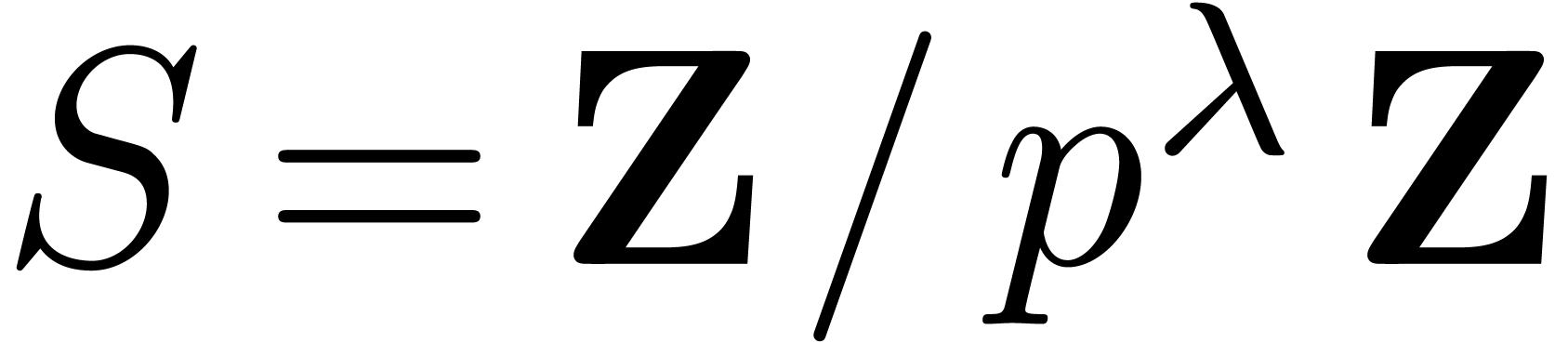 and let
and let 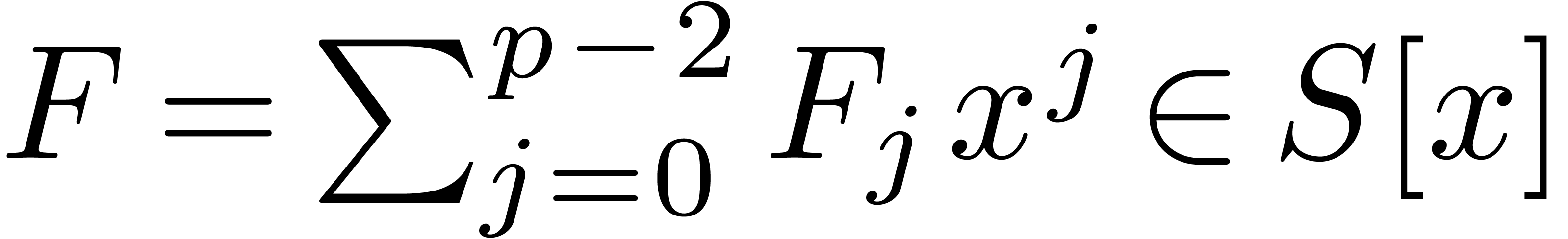 . We first use Bluestein's trick [Blu70]
to convert the evaluation problem to a polynomial multiplication
problem. Namely, from the identity
. We first use Bluestein's trick [Blu70]
to convert the evaluation problem to a polynomial multiplication
problem. Namely, from the identity 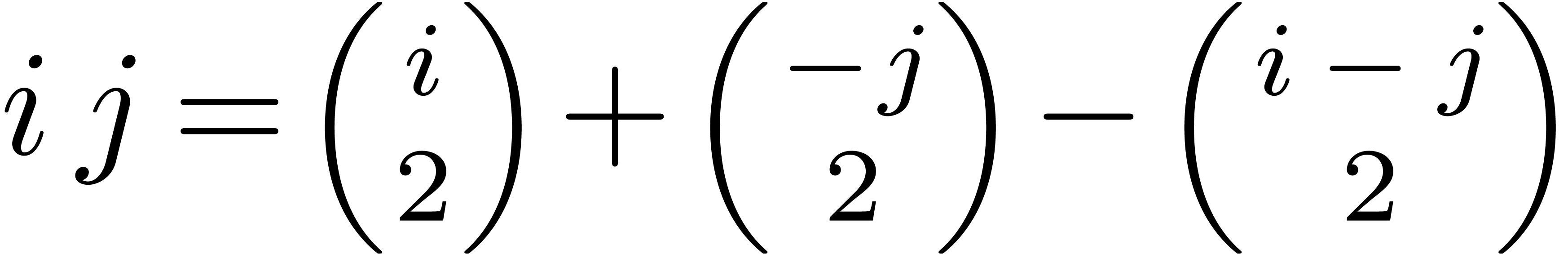 we obtain
we obtain
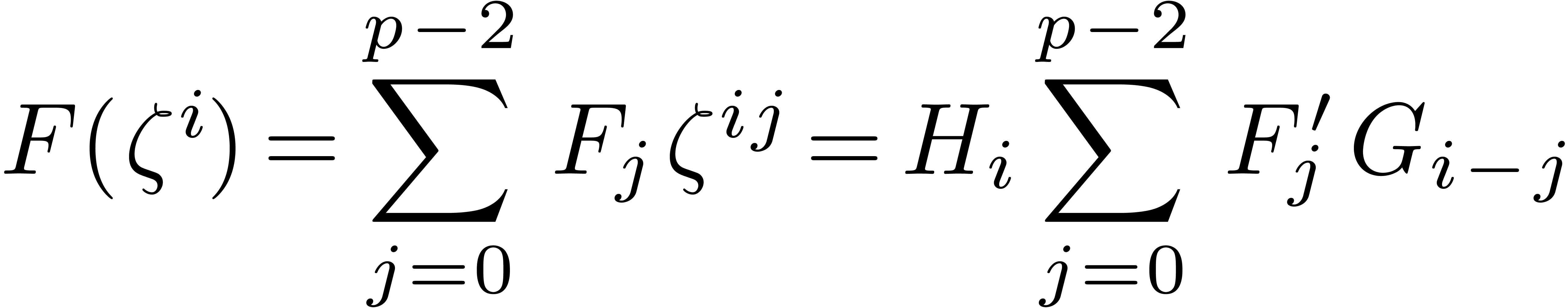 |
(5) |
where
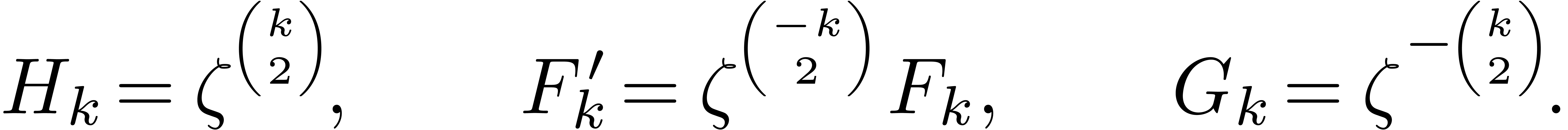
Since 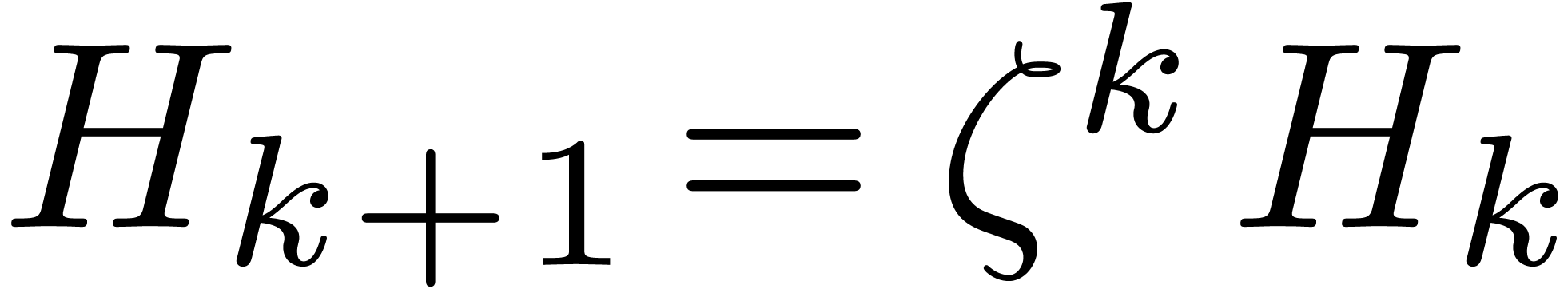 and
and 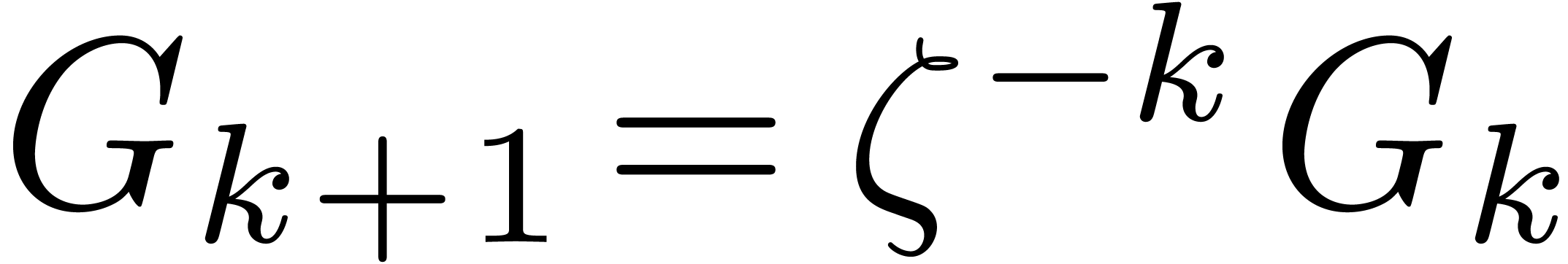 ,
we may easily compute
,
we may easily compute  and
and 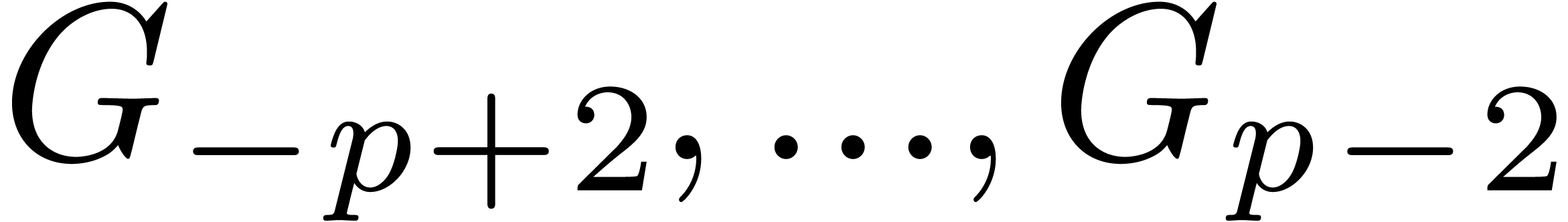 from
from  and
and 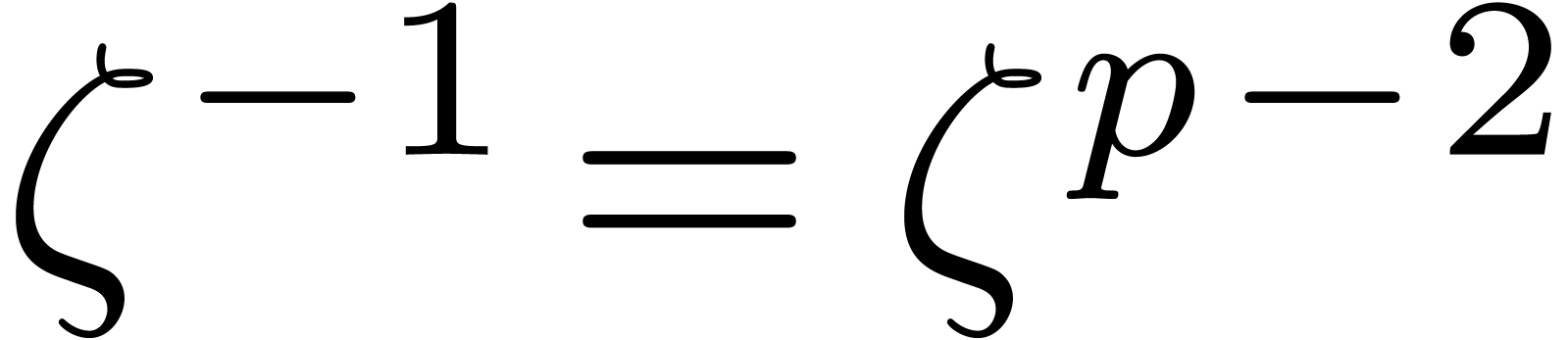 using
using  ring operations in
ring operations in  .
Similarly we may obtain the
.
Similarly we may obtain the  from the
from the 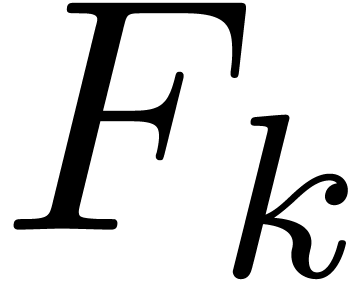 using
using 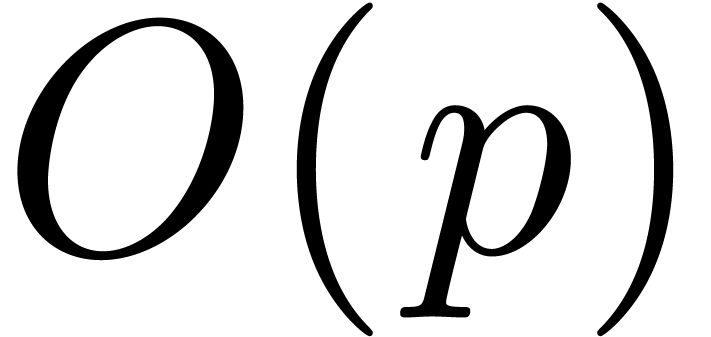 ring operations. The sum
ring operations. The sum
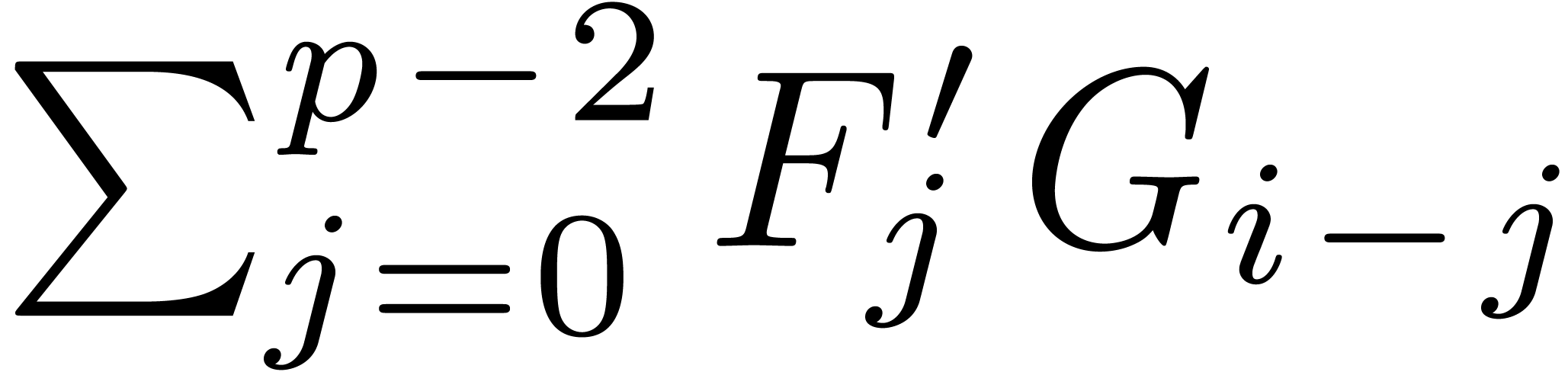 in (5) may be
interpreted as the coefficient of
in (5) may be
interpreted as the coefficient of 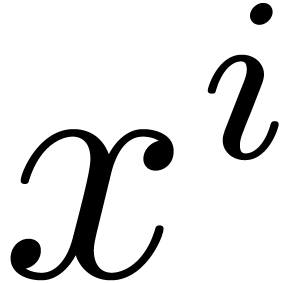 in the product
of the (Laurent) polynomials
in the product
of the (Laurent) polynomials
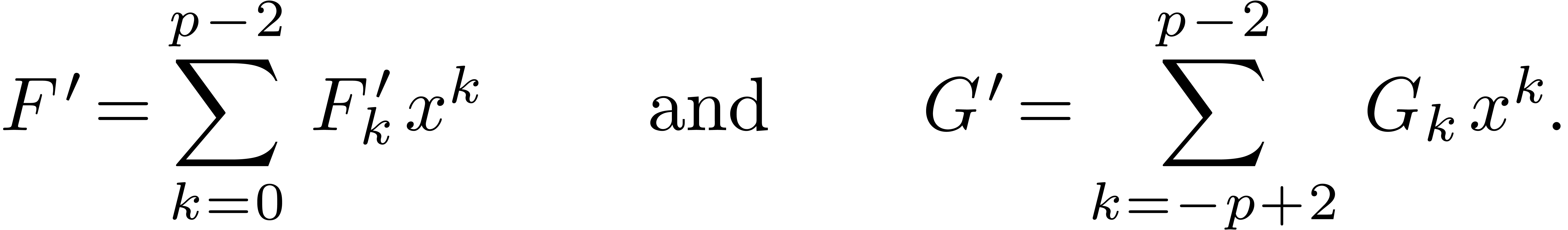
Thus it suffices to compute the product 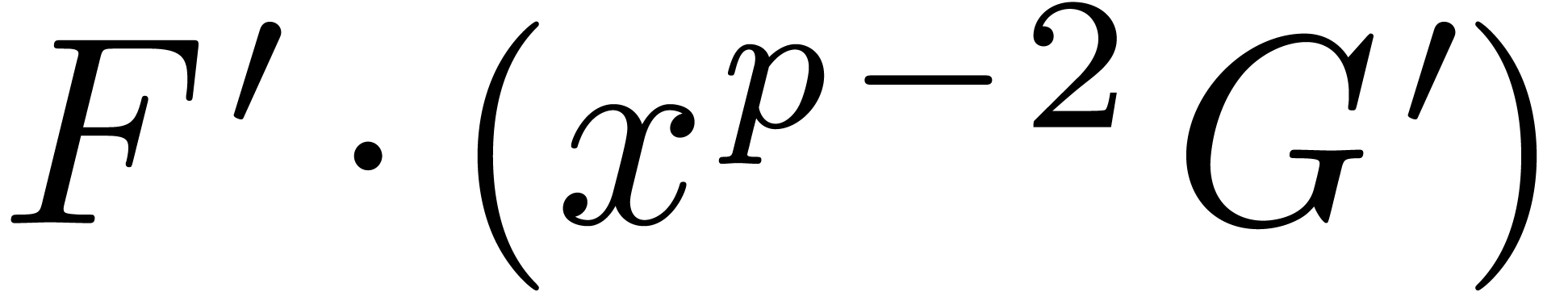 in
in 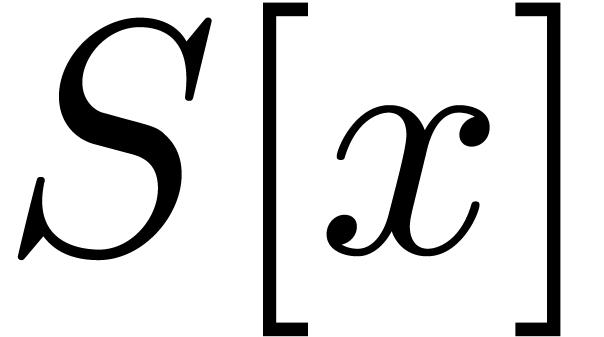 . To compute this product, we lift
the problem to
. To compute this product, we lift
the problem to 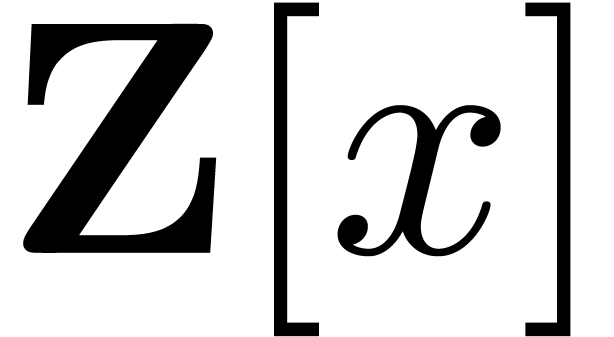 , and use
Kronecker substitution [vzGG03, Ch. 8] to convert to an
integer multiplication problem. The coefficients of
, and use
Kronecker substitution [vzGG03, Ch. 8] to convert to an
integer multiplication problem. The coefficients of 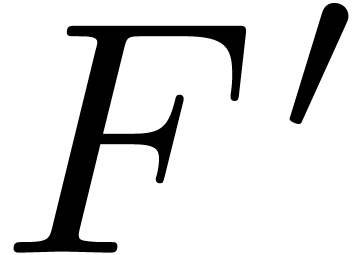 and
and 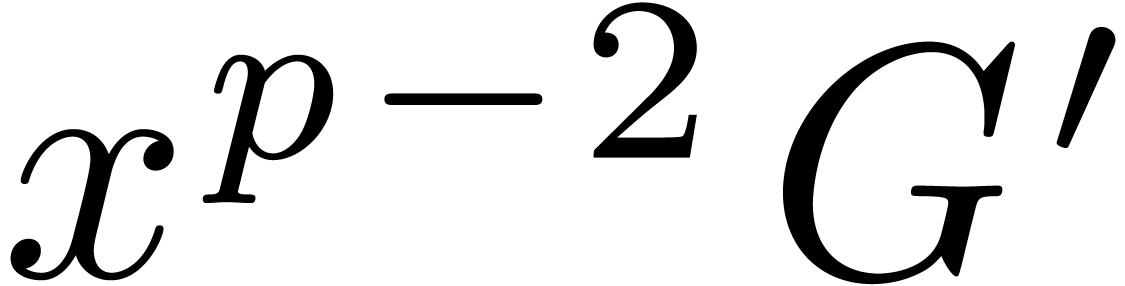 are bounded by
are bounded by  ,
and their degrees by
,
and their degrees by  , so the
coefficients of their product in
, so the
coefficients of their product in 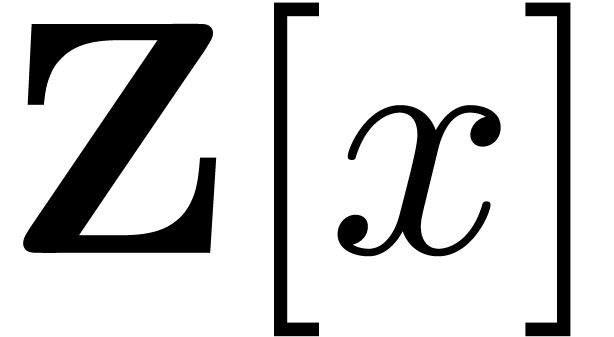 have at most
have at most
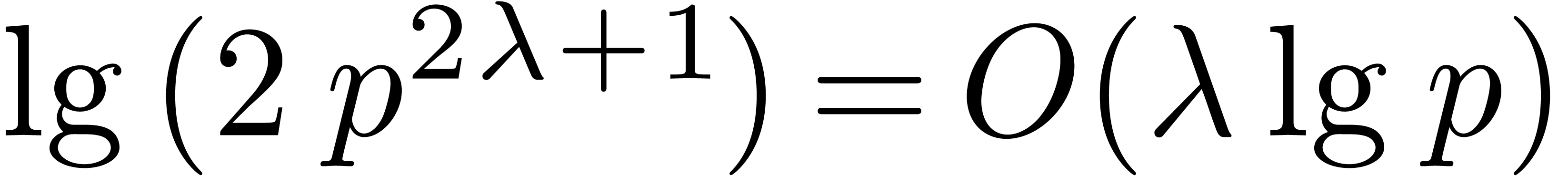 bits. Therefore the integers being multiplied
have at most
bits. Therefore the integers being multiplied
have at most 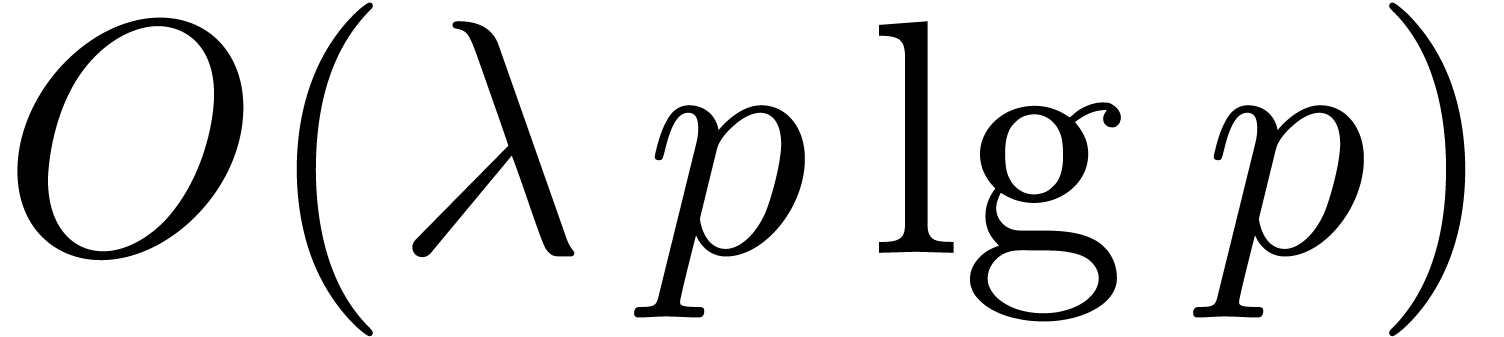 bits, leading to the desired
bits, leading to the desired 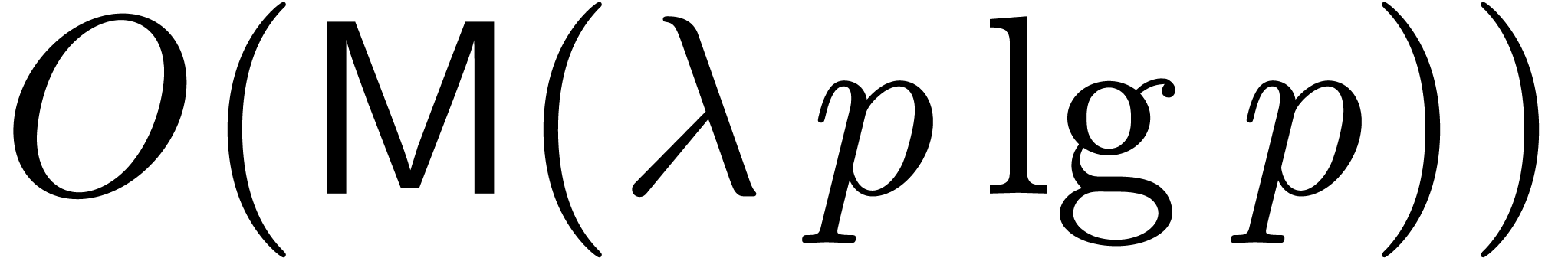 bound. The remaining work consists of
bound. The remaining work consists of 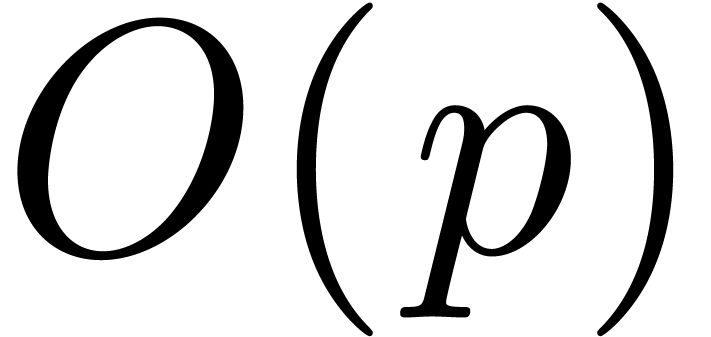 ring operations in
ring operations in  ,
contributing a further
,
contributing a further 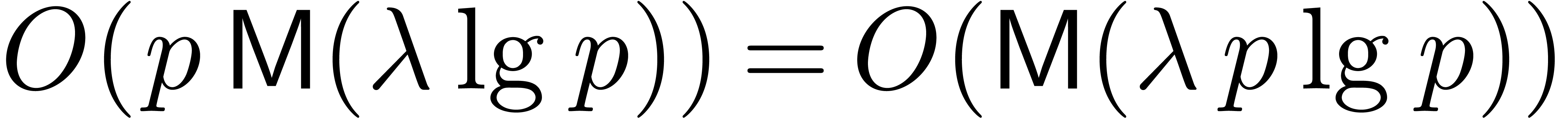 bit operations since
bit operations since 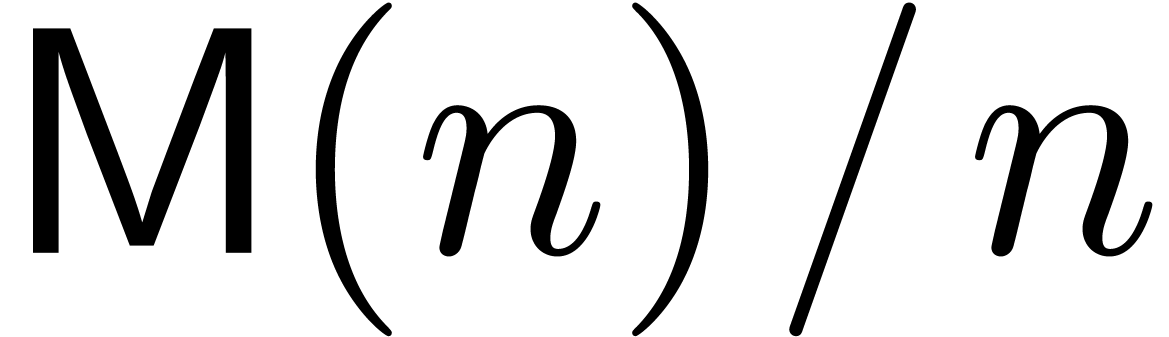 is increasing.
is increasing.
3.Integer matrix
multiplication
Proposition 4. Assume
that 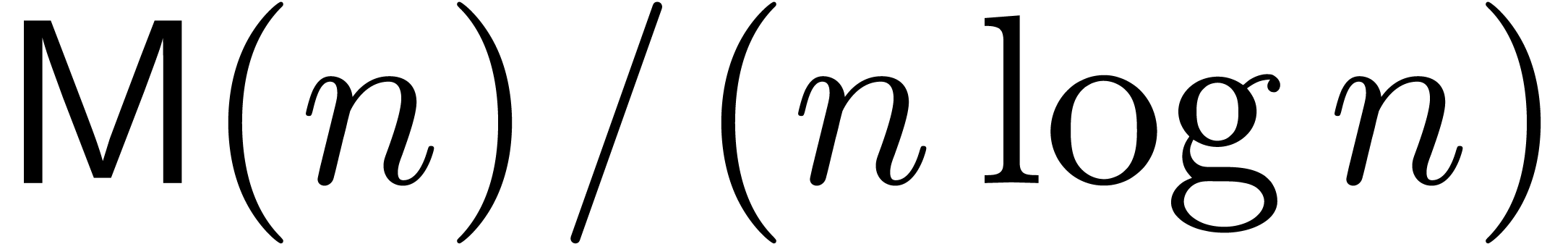 is increasing. Let
is increasing. Let 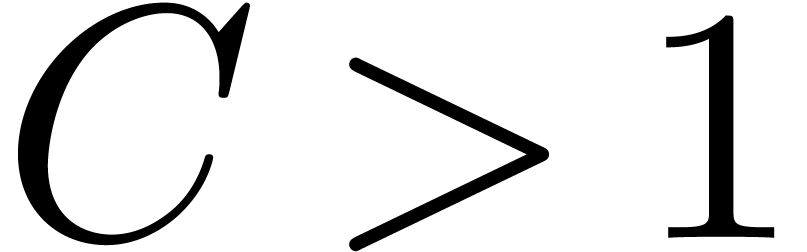 be a constant. Then
be a constant. Then
uniformly for all 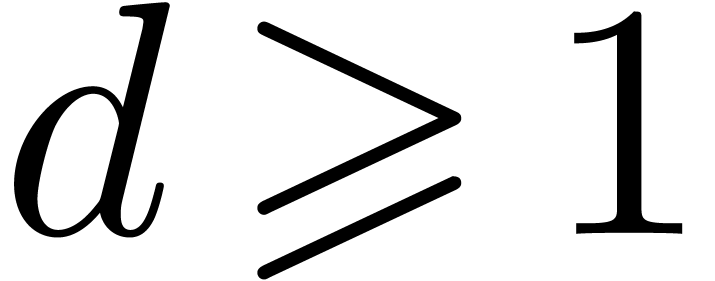 ,
,  with
with  .
.
Proof. The input consists of matrices 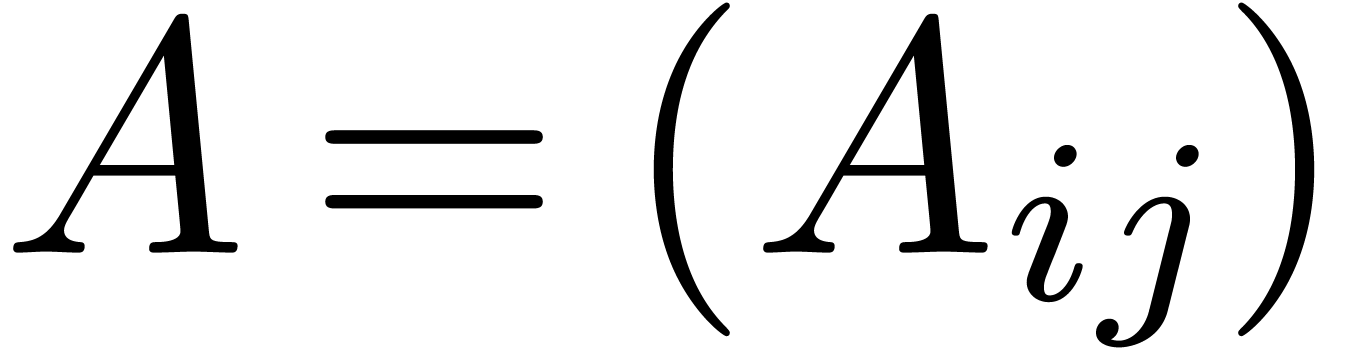 and
and
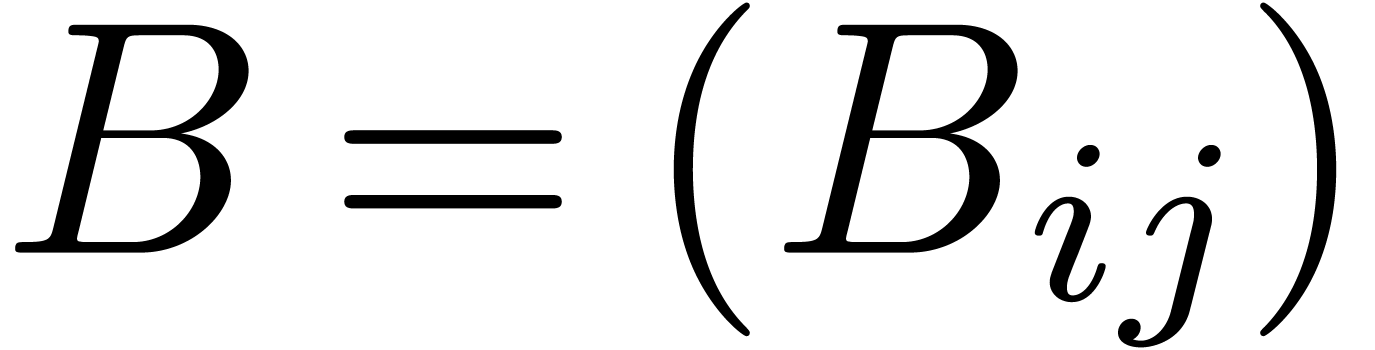 , where
, where 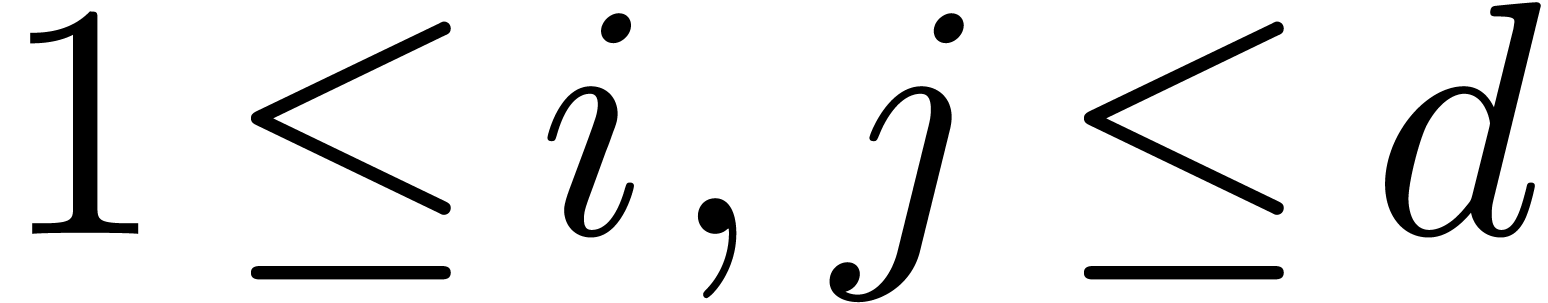 and
and 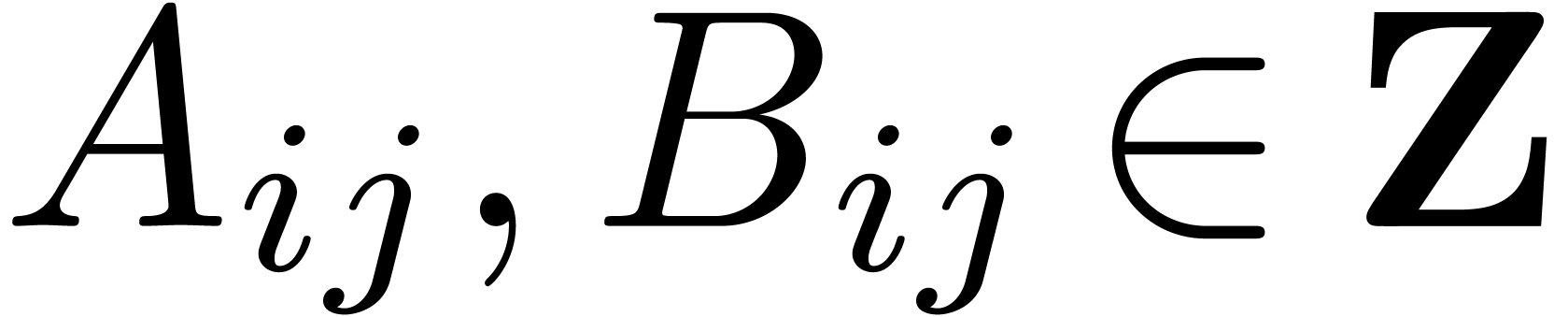 ,
, 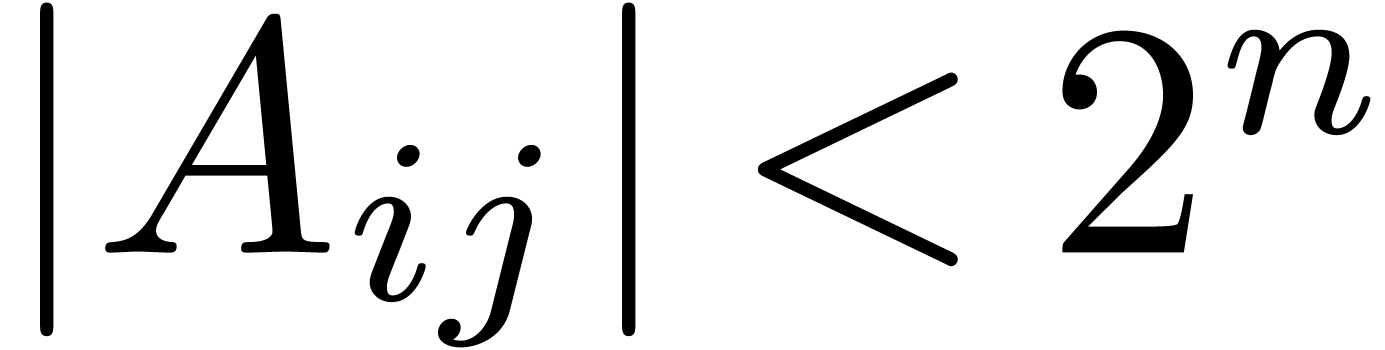 ,
, 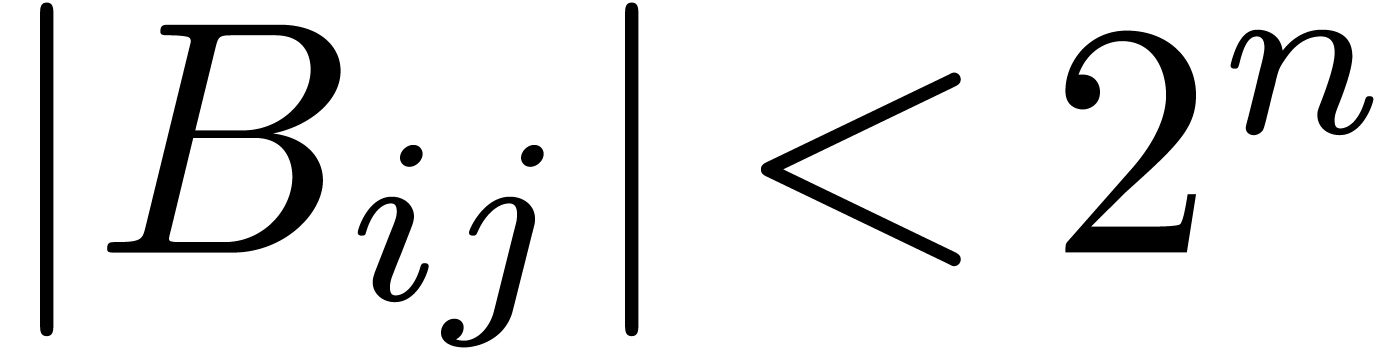 . We
wish to compute the product
. We
wish to compute the product 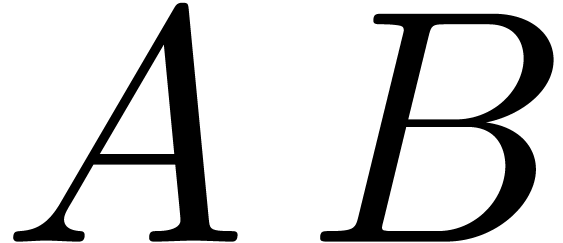 .
.
Let 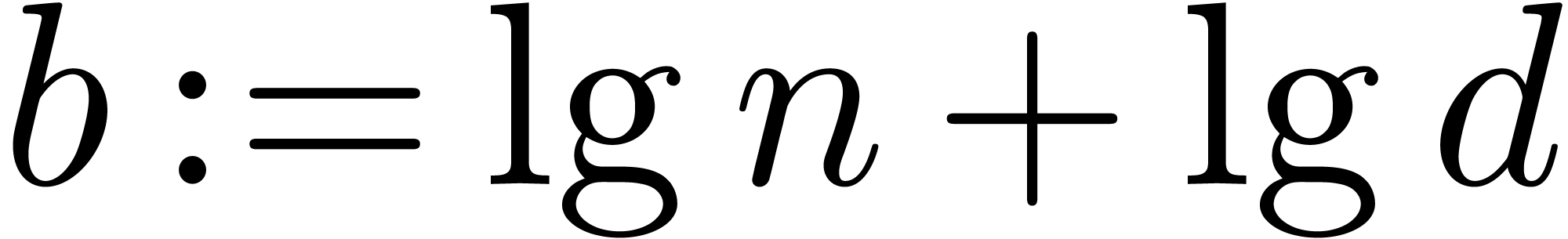 and
and 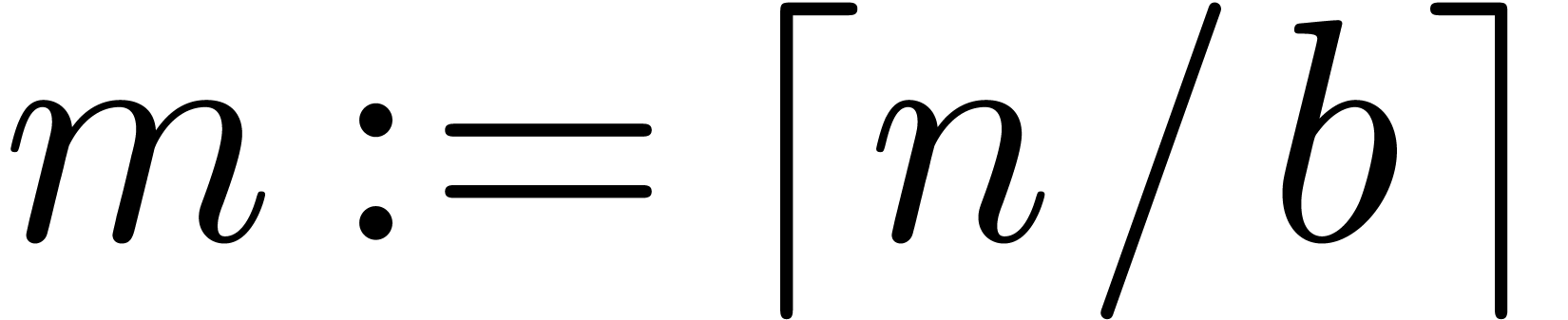 .
Note that
.
Note that 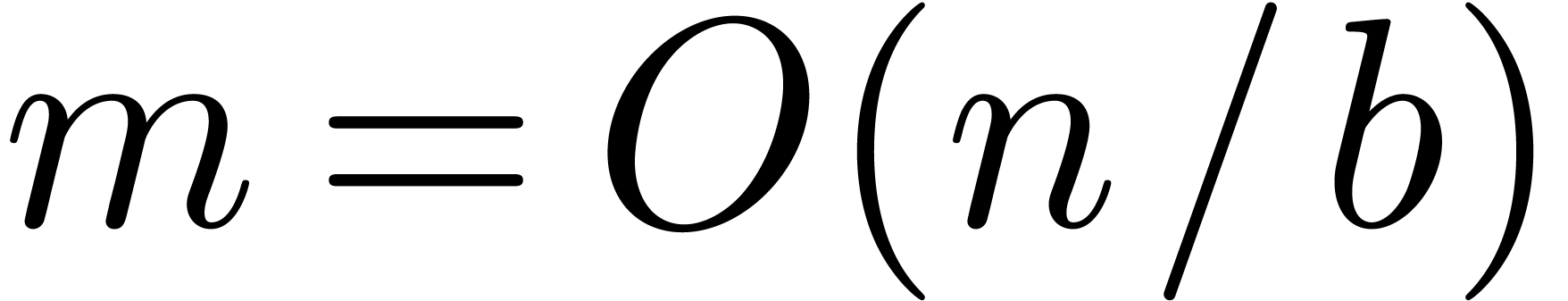 since we assumed that
since we assumed that  . We split the entries
. We split the entries 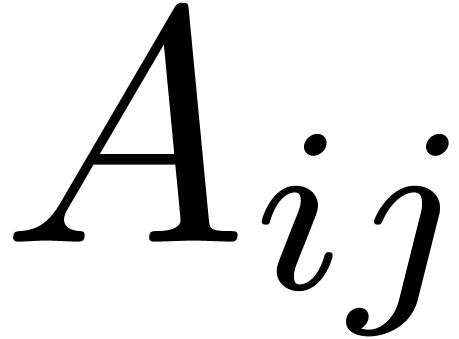 into chunks of
into chunks of 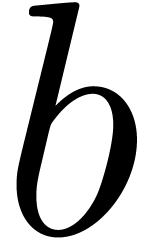 bits, choosing
bits, choosing 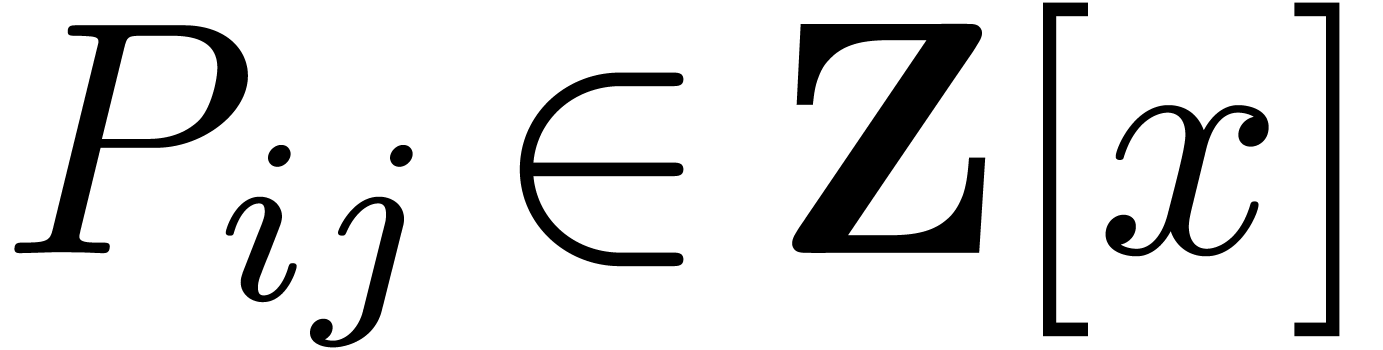 so that
so that 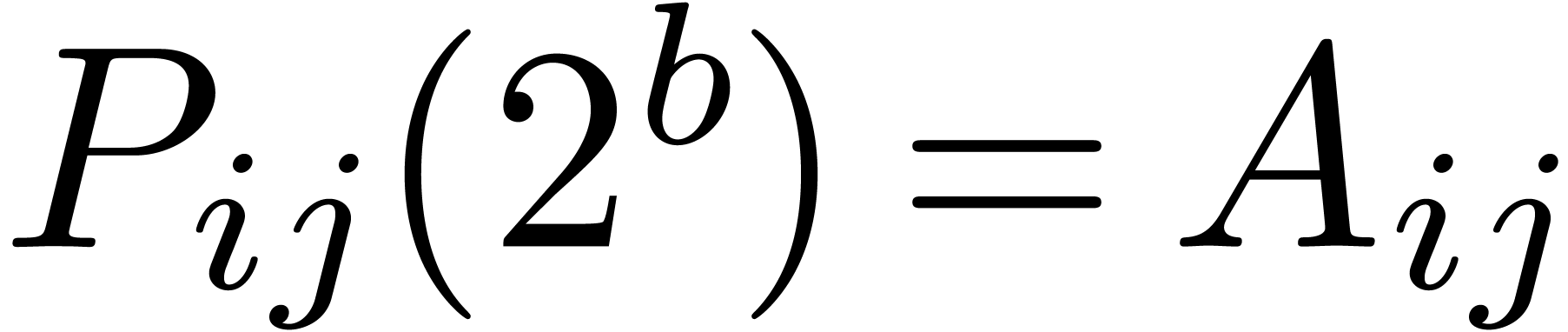 with
with 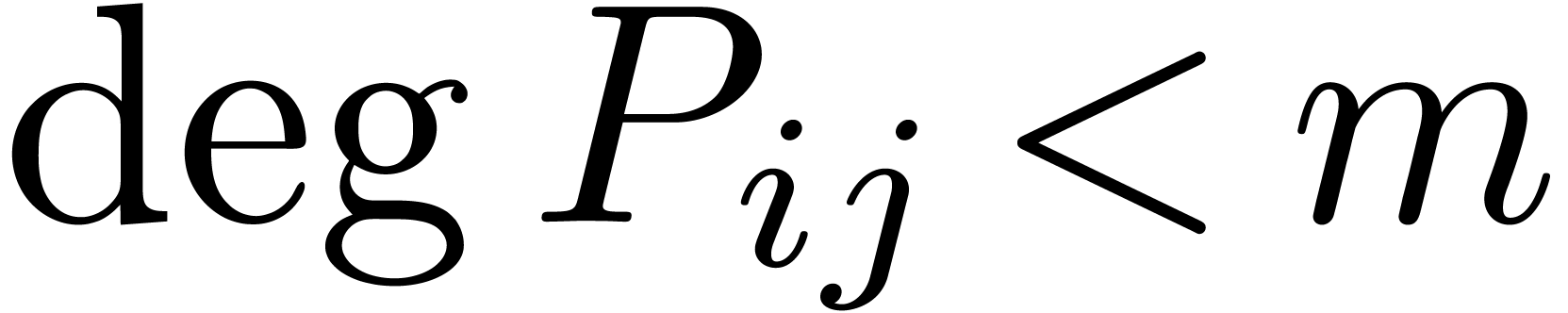 ,
and such that the coefficients of
,
and such that the coefficients of 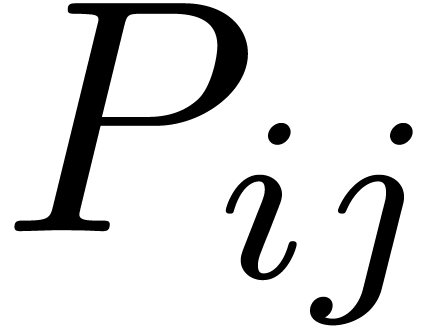 are bounded in
absolute value by
are bounded in
absolute value by 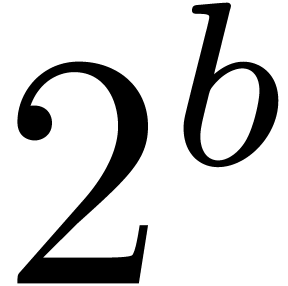 . Similarly
choose
. Similarly
choose 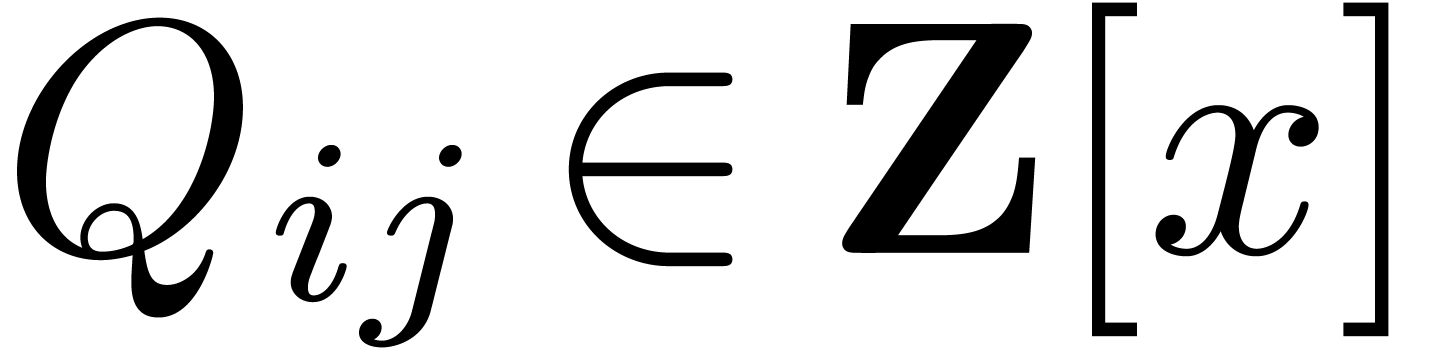 for
for  .
Let
.
Let  and
and 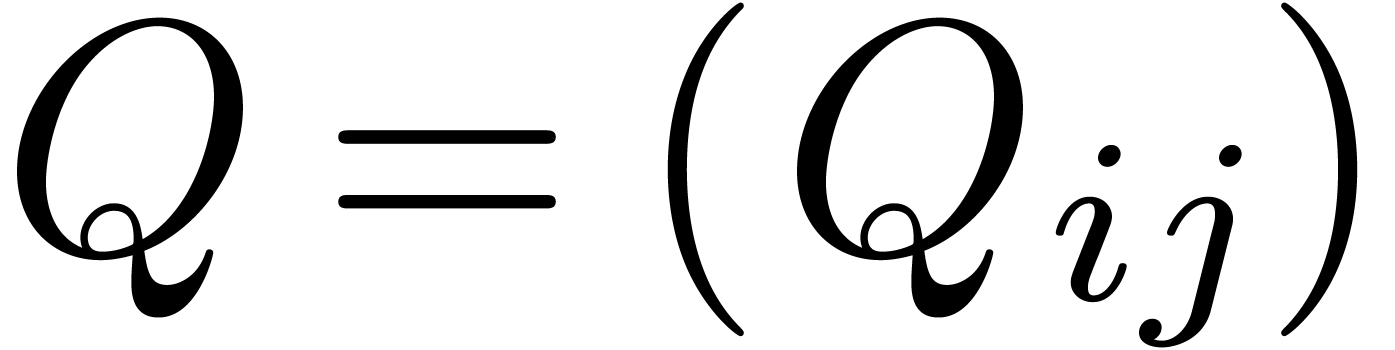 be the
corresponding
be the
corresponding  matrices of polynomials. The
coefficients of the entries of
matrices of polynomials. The
coefficients of the entries of 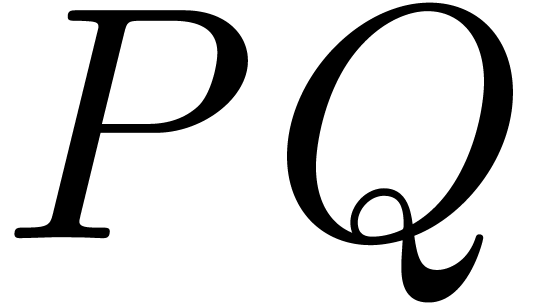 are bounded in
absolute value by
are bounded in
absolute value by 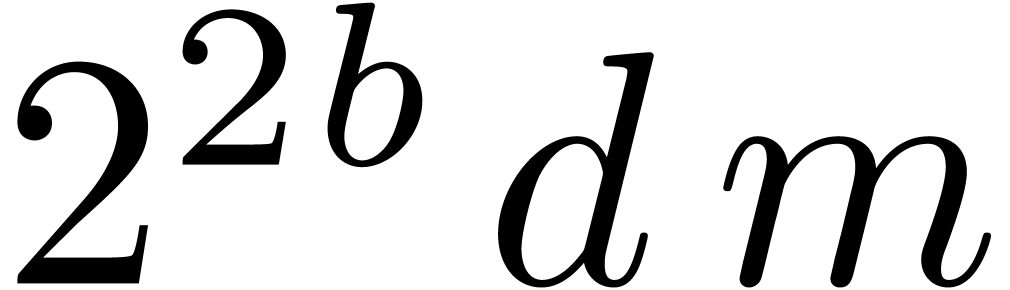 , and thus
have bit size bounded by
, and thus
have bit size bounded by 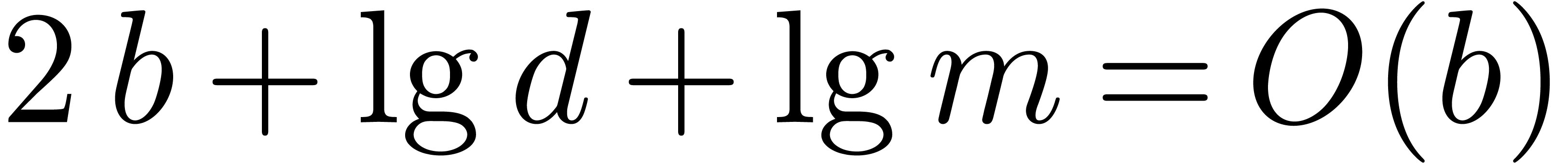 .
The product
.
The product 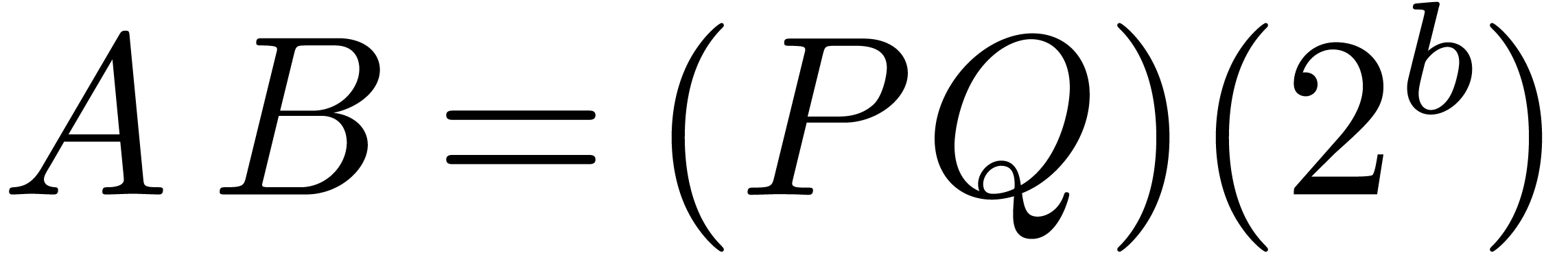 may be deduced from
may be deduced from 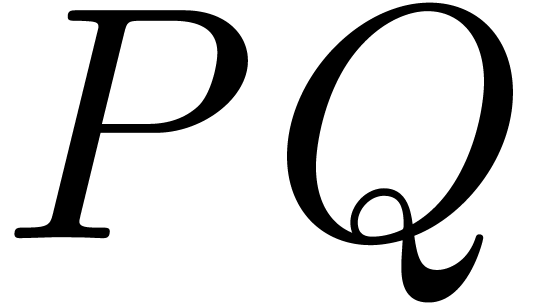 in time
in time 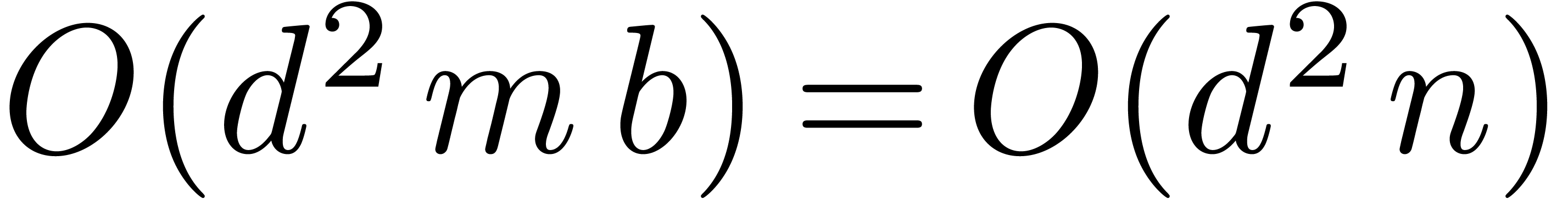 . Thus we have
reduced to the problem of computing
. Thus we have
reduced to the problem of computing 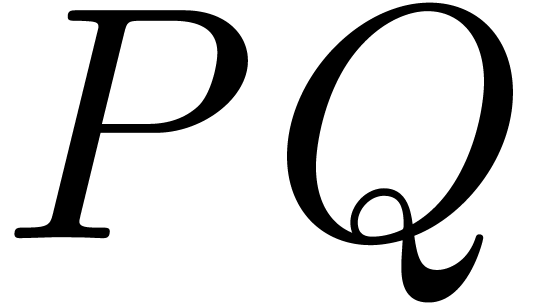 .
.
The degrees of the entries of 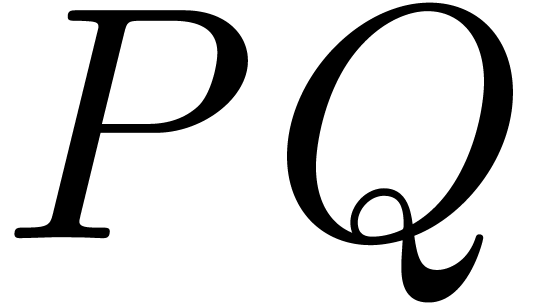 are less than
are less than
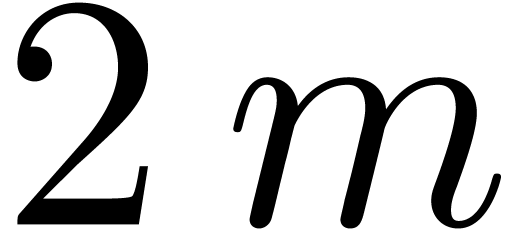 . Let
. Let 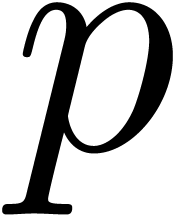 be the least odd prime such that
be the least odd prime such that 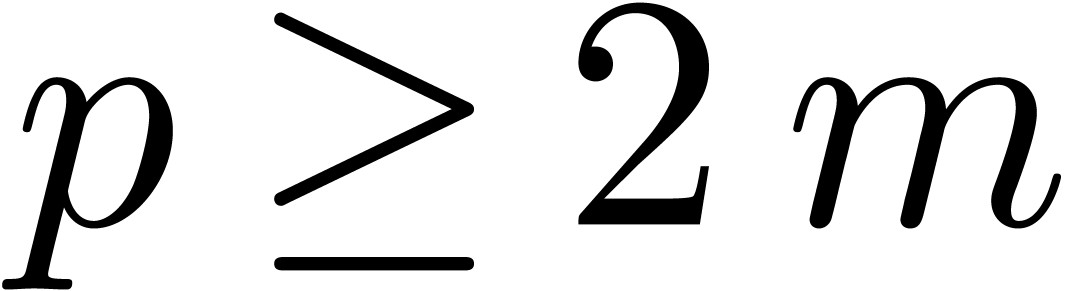 .
By [BHP01] we have
.
By [BHP01] we have 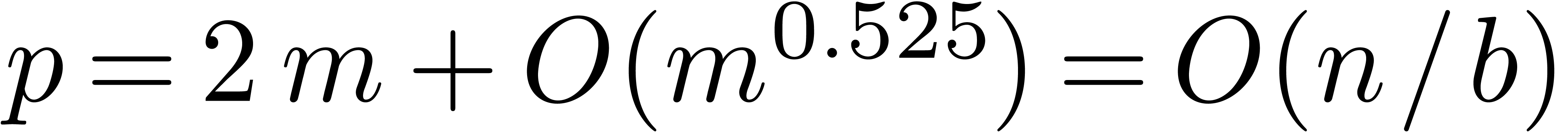 .
We may find
.
We may find 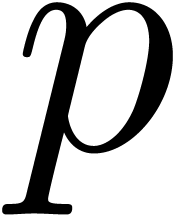 by testing candidates successively;
the cost is
by testing candidates successively;
the cost is 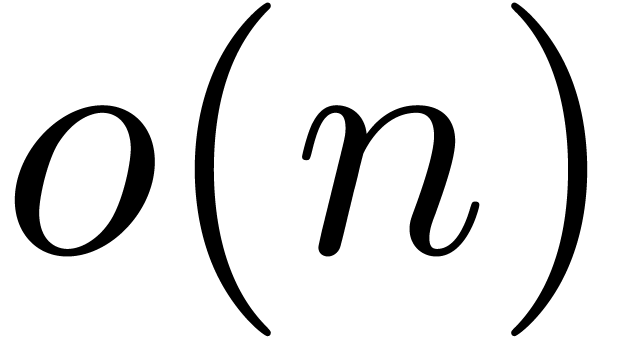 , since each
candidate requires
, since each
candidate requires 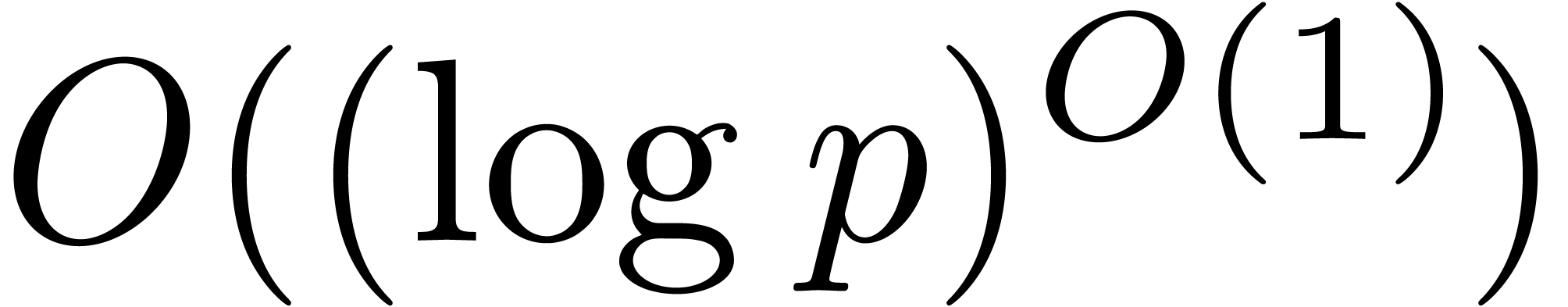 bit operations [AKS04].
bit operations [AKS04].
To compute 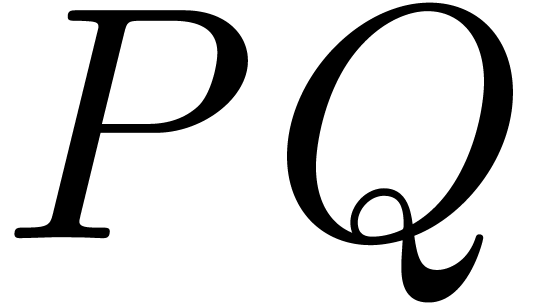 , it suffices to
compute
, it suffices to
compute 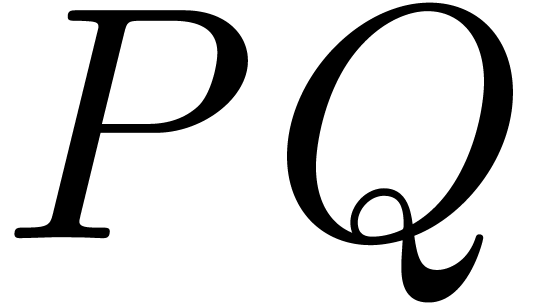 modulo
modulo 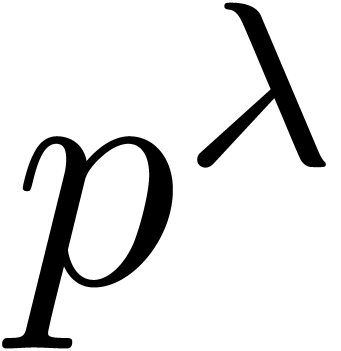 ,
where
,
where 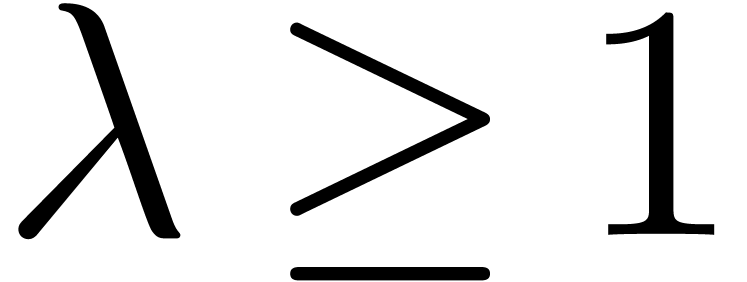 is the least positive integer for which
is the least positive integer for which
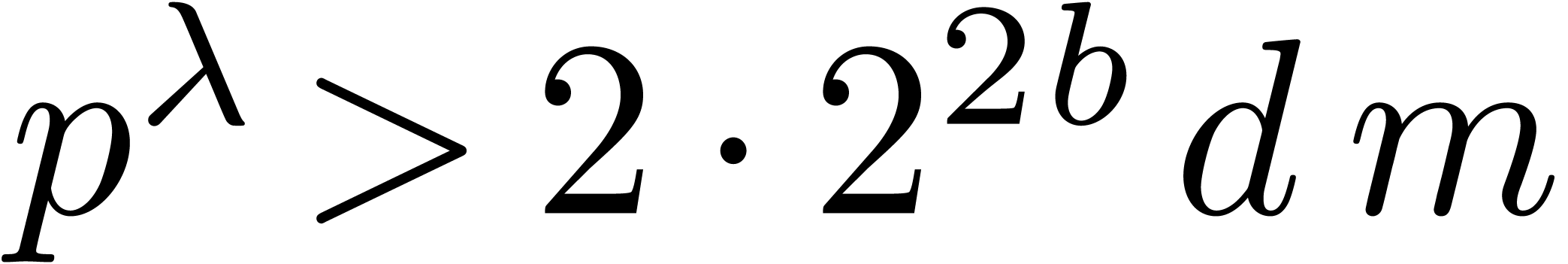 . Since
. Since 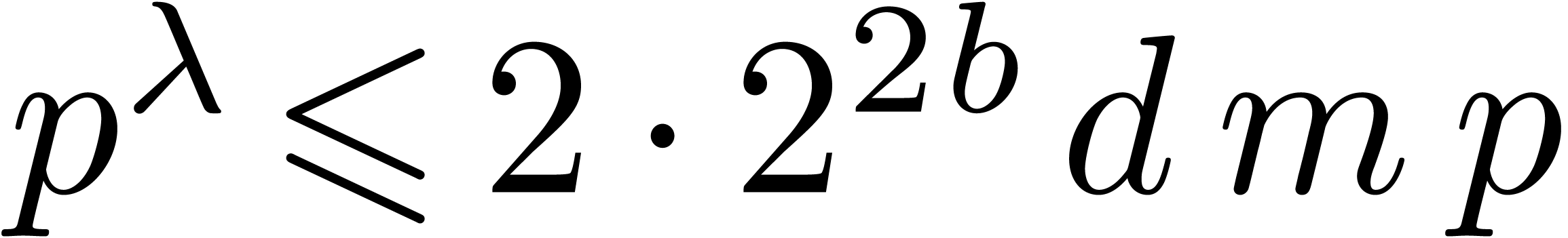 we have
we have 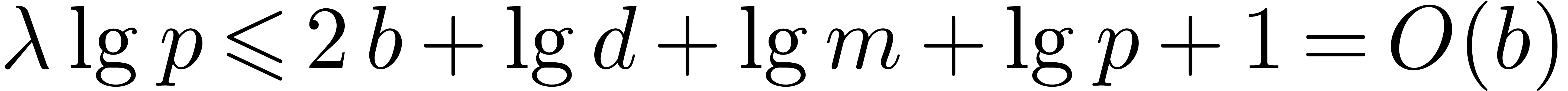 . Our plan is to
compute
. Our plan is to
compute  over
over 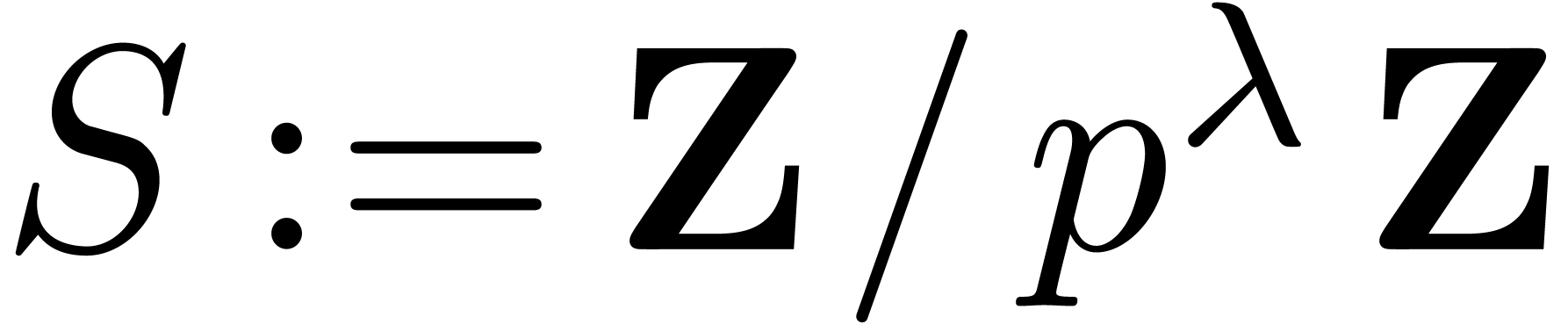 by means of
an evaluation-interpolation scheme, using Lemma 3 for the
evaluations. The lemma requires a precomputed element
by means of
an evaluation-interpolation scheme, using Lemma 3 for the
evaluations. The lemma requires a precomputed element 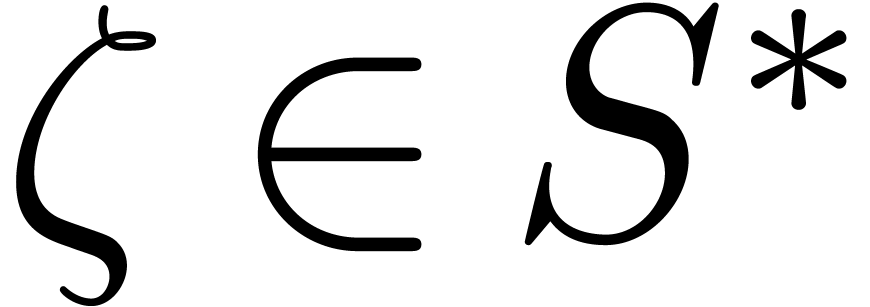 of order
of order 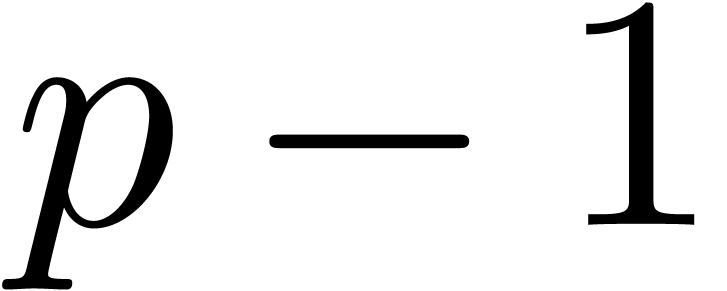 . To find
. To find  , we first compute a generator of
, we first compute a generator of
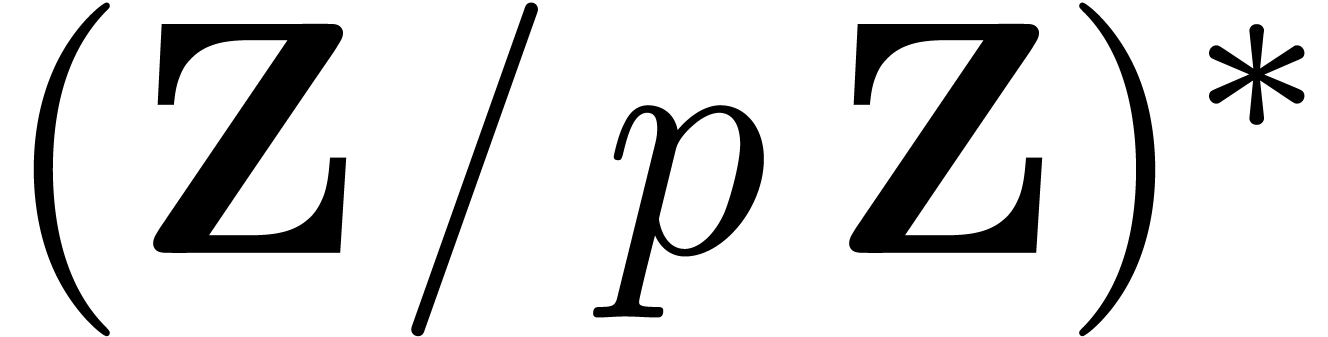 in (deterministic) time
in (deterministic) time 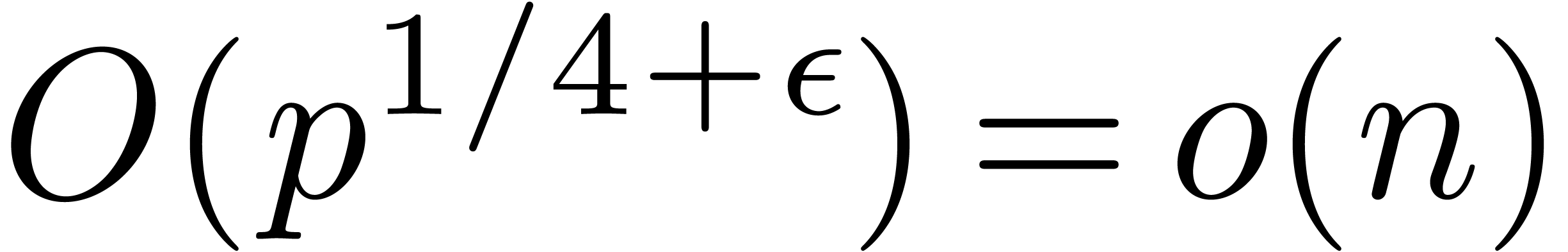 [Shp96], and then lift it to a suitable
[Shp96], and then lift it to a suitable 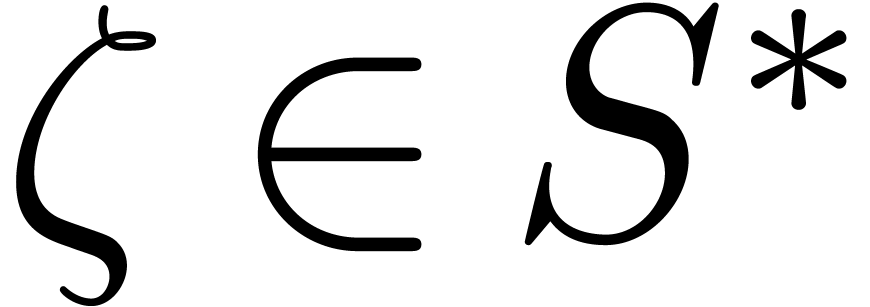 in time
in time 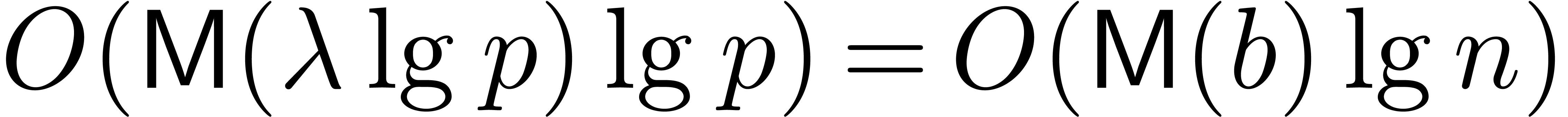 [vzGG03, Ch. 15]. This last
bound lies in
[vzGG03, Ch. 15]. This last
bound lies in 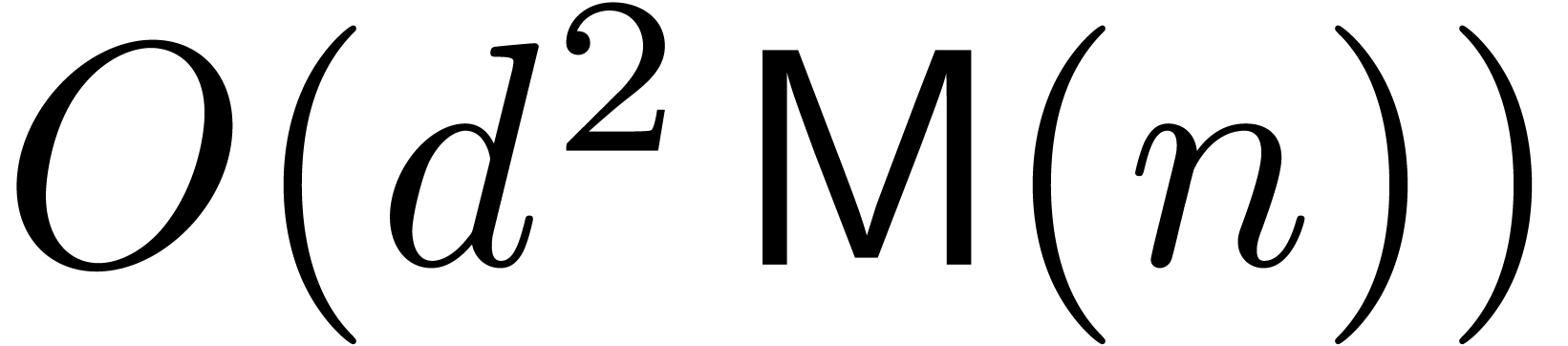 (one may check the cases
(one may check the cases 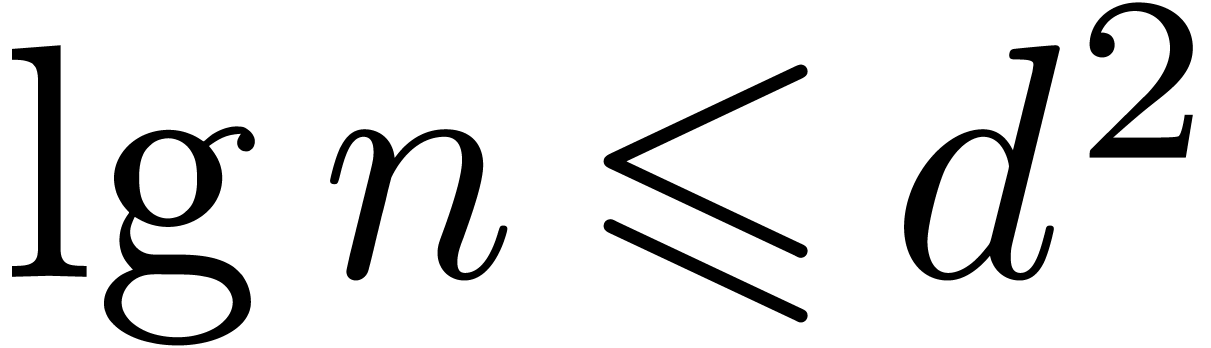 and
and 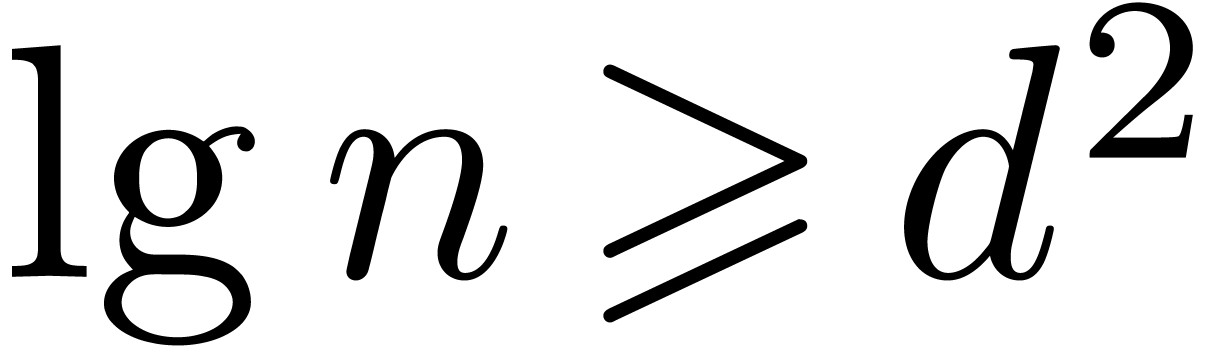 separately).
separately).
Having selected 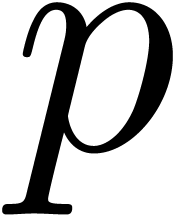 ,
, 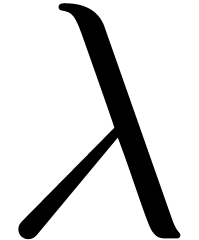 and
and  , we now
apply Lemma 3 to each matrix entry to evaluate
, we now
apply Lemma 3 to each matrix entry to evaluate 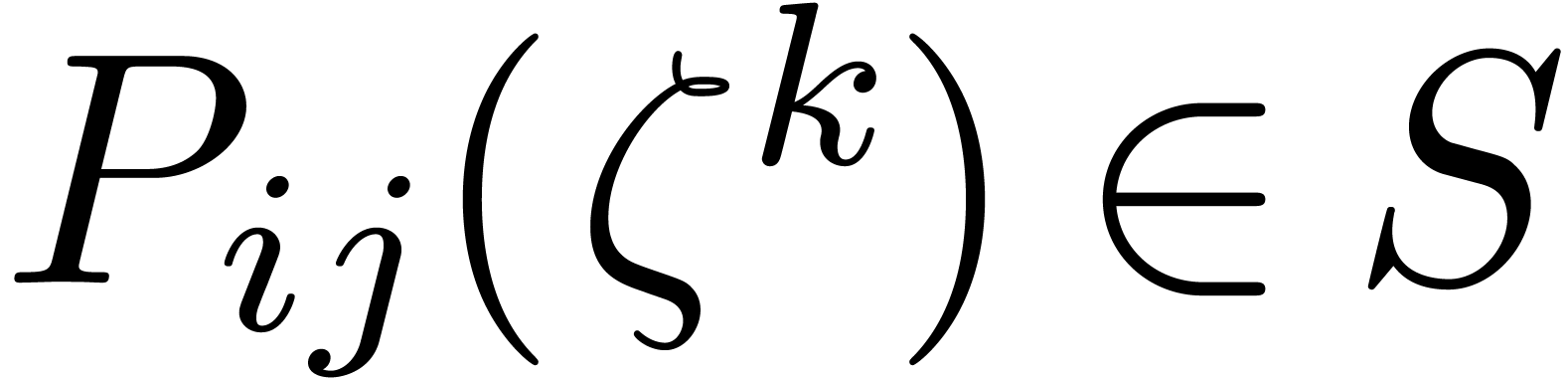 and
and 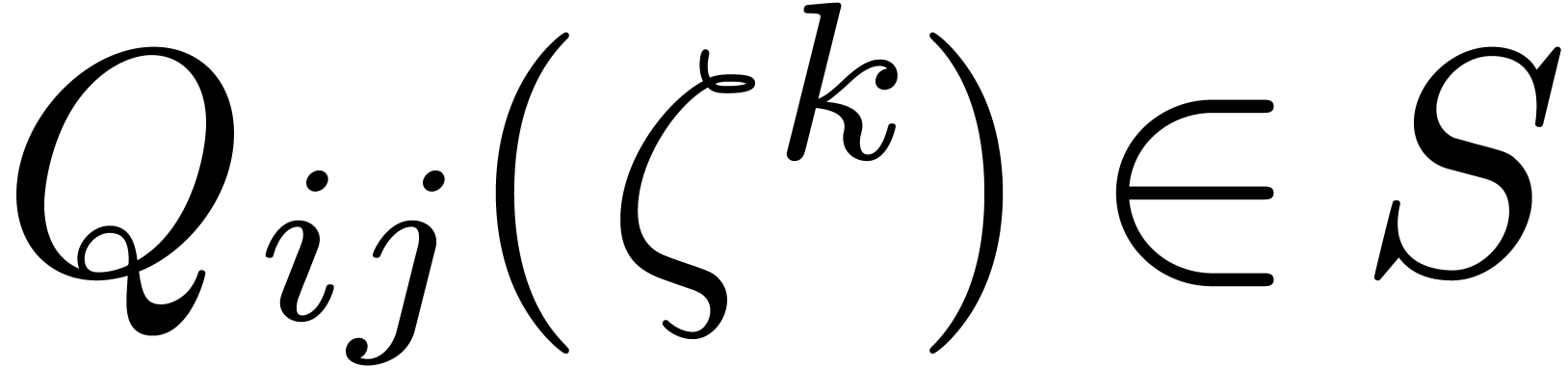 for
for  . This step takes time
. This step takes time 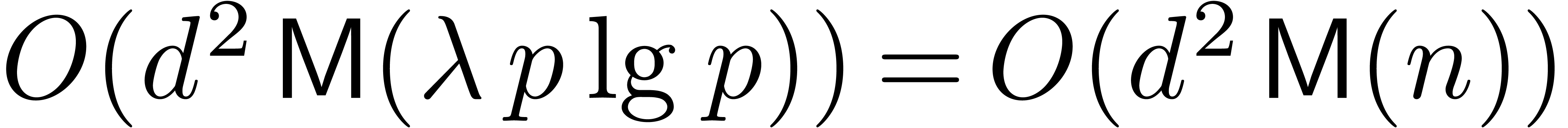 .
Next we perform the pointwise multiplications
.
Next we perform the pointwise multiplications 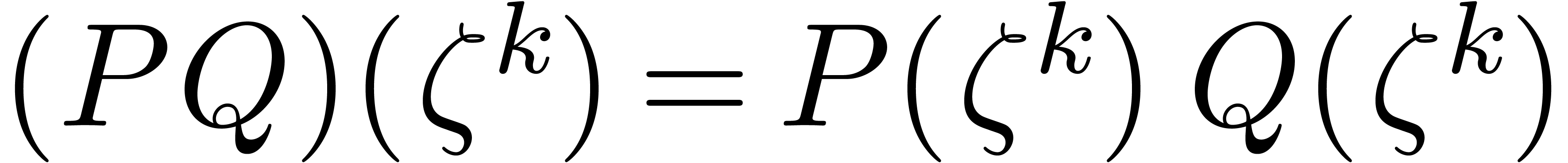 . These are achieved by first lifting to
integer matrix products, and then reducing the results modulo
. These are achieved by first lifting to
integer matrix products, and then reducing the results modulo
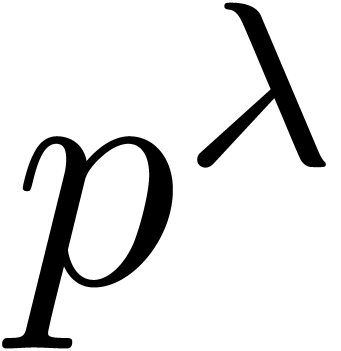 . The integer products cost
. The integer products cost
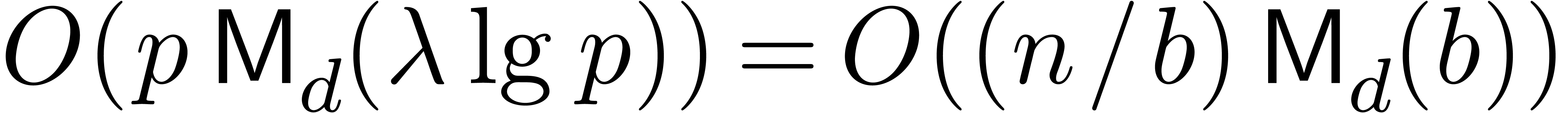 . The bit size of the entries
of the products are bounded by
. The bit size of the entries
of the products are bounded by 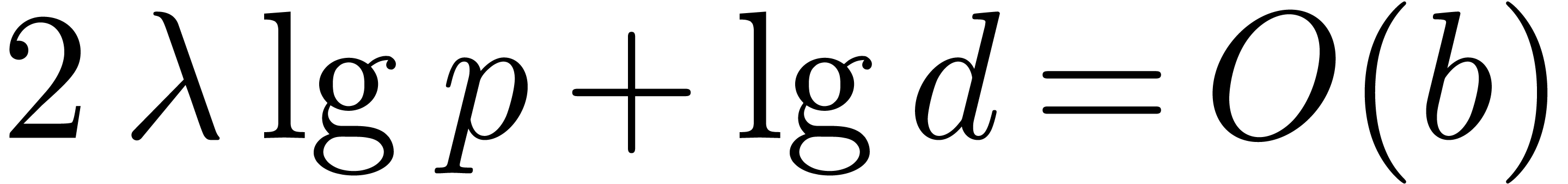 ,
so the reduction step costs
,
so the reduction step costs 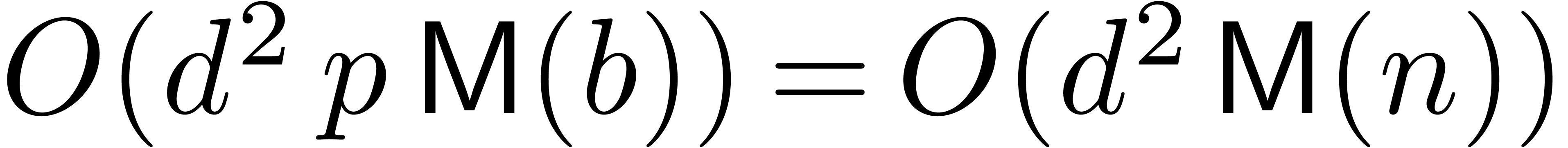 .
Since the evaluation is really a discrete Fourier transform over
.
Since the evaluation is really a discrete Fourier transform over  , the interpolation step is
algebraically the same, with
, the interpolation step is
algebraically the same, with  replaced by
replaced by  . Thus we may recover
. Thus we may recover  using Lemma 3 again, with cost
using Lemma 3 again, with cost 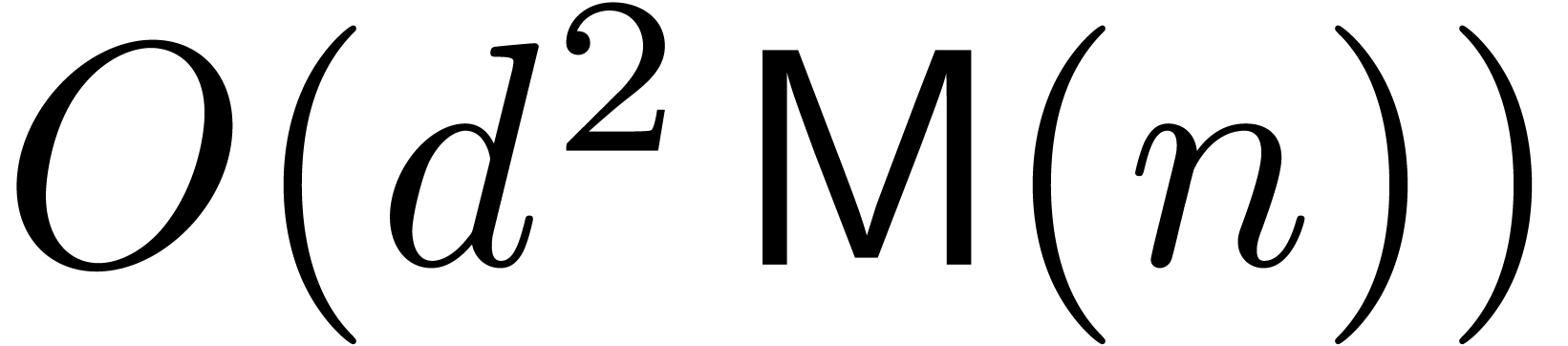 . There is also a final division (scaling) by
. There is also a final division (scaling) by
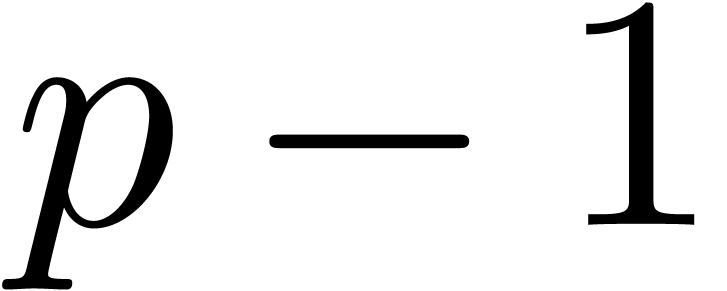 , whose cost is subsumed into
the above.
, whose cost is subsumed into
the above.
In the Turing model, we must also take into account the cost of data
rearrangement. Specifically, in the above algorithm we switch between
“matrix of vectors” and “vector of matrices”
representations of the data. Using the algorithm in the Appendix to [BGS07], this needs only 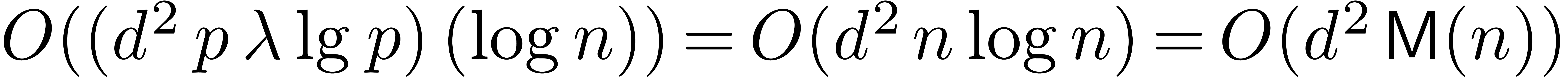 bit
operations, since we assumed that
bit
operations, since we assumed that 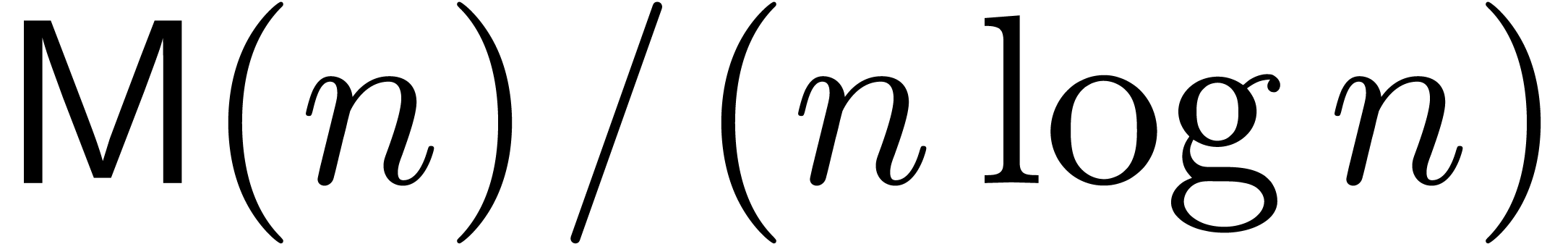 is
increasing.
is
increasing.
Remark 5. We could replace 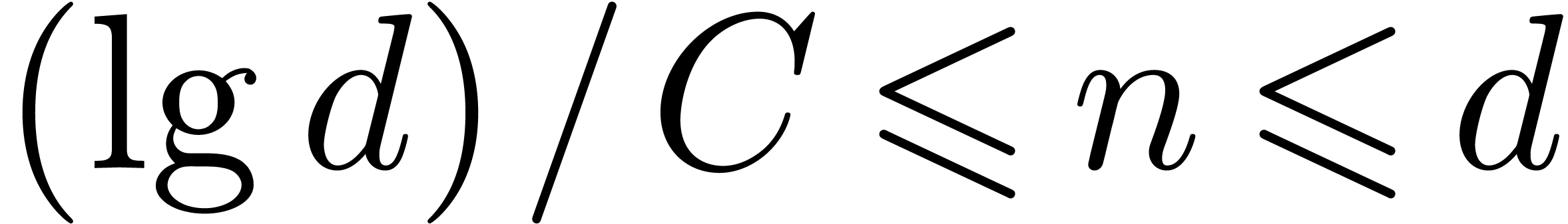 by a “ring” of finite-precision approximations to complex
numbers, and obtain results of the same strength. The latter approach
has the disadvantage that it introduces a tedious floating-point error
analysis.
by a “ring” of finite-precision approximations to complex
numbers, and obtain results of the same strength. The latter approach
has the disadvantage that it introduces a tedious floating-point error
analysis.
Now we may prove the main theorem announced in the introduction.
Proof of Theorem 1. First consider the region 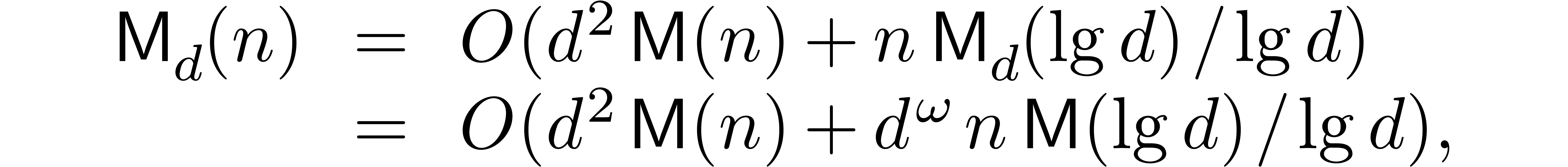 . Proposition 4 yields
. Proposition 4 yields
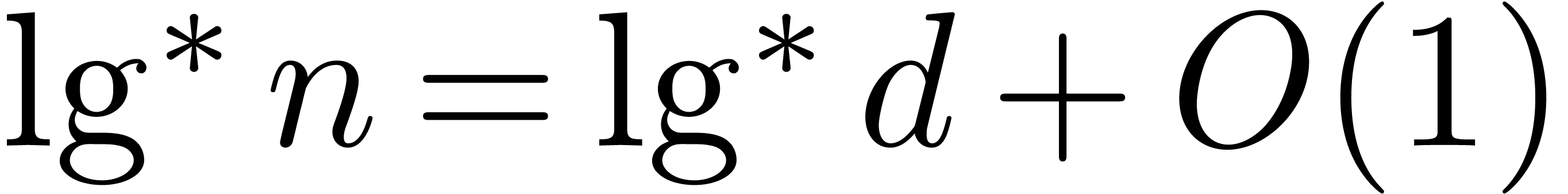
and for such 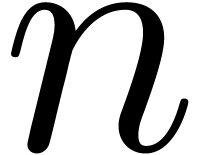 we have
we have  , so the desired bound holds in this region.
, so the desired bound holds in this region.
Now consider the case 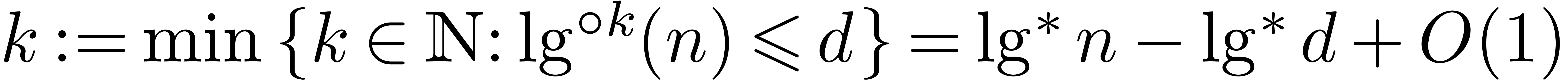 . Let
. Let
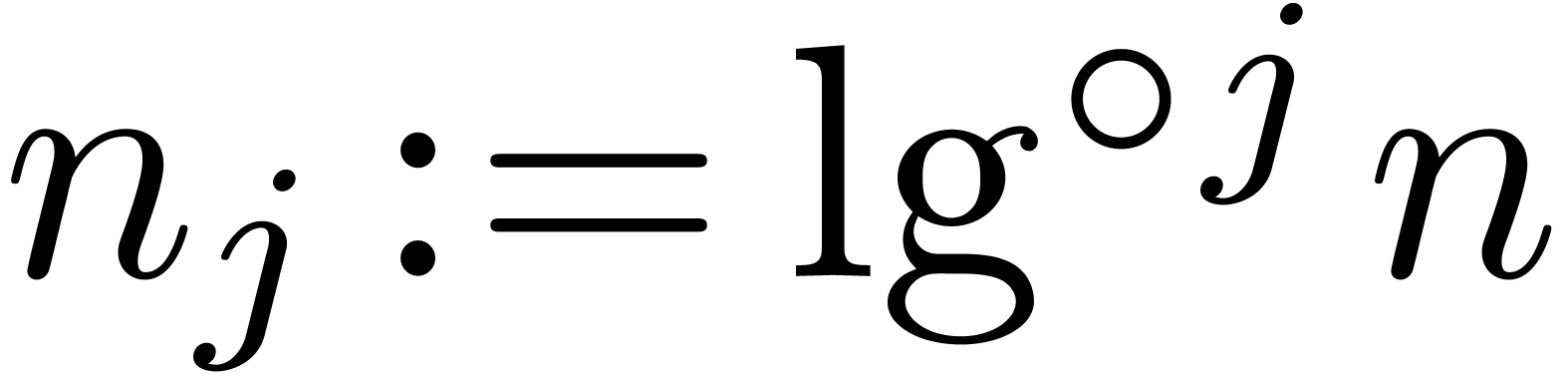 , and let
, and let 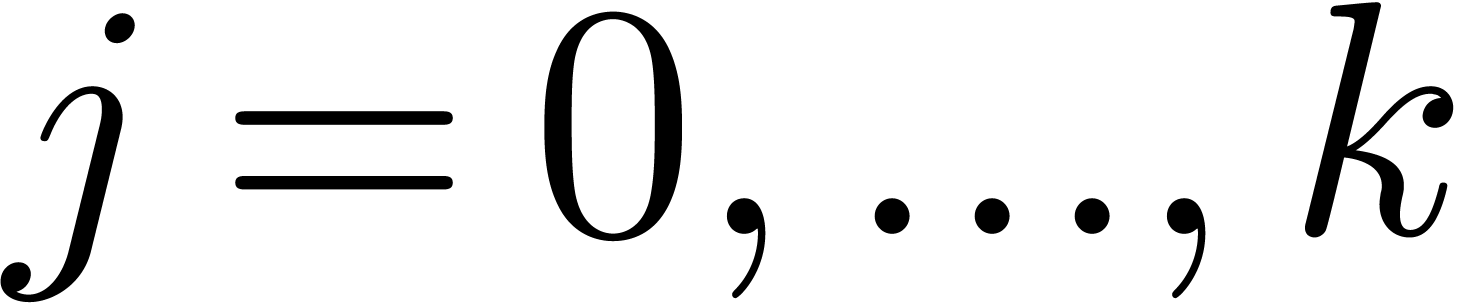 for
for 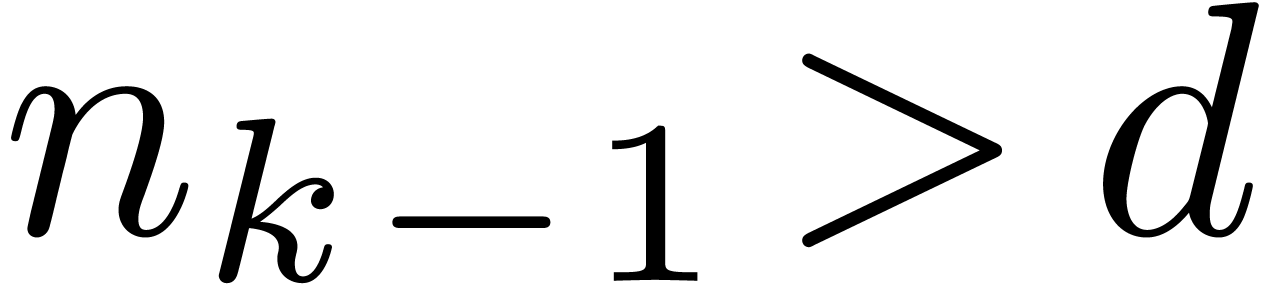 , so that
, so that 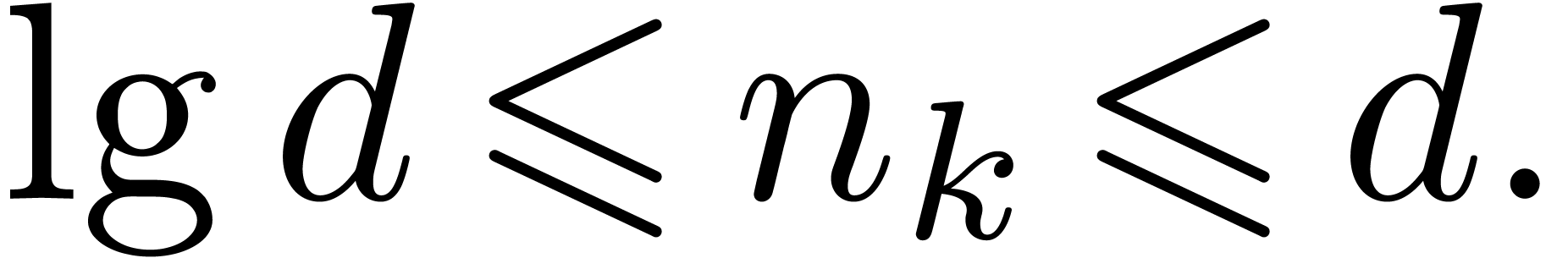 and
and 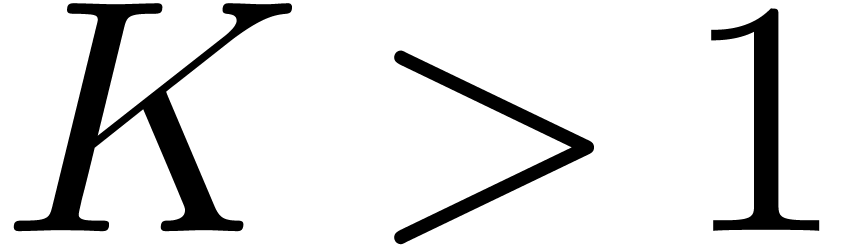 By Proposition 4
there is a constant
By Proposition 4
there is a constant  (depending only on
(depending only on 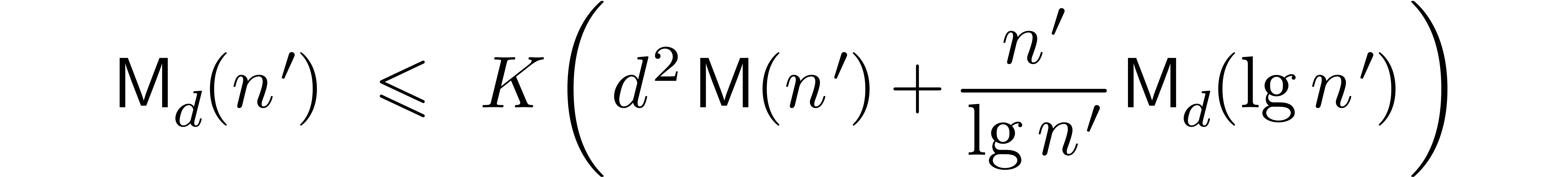 ) such that
) such that
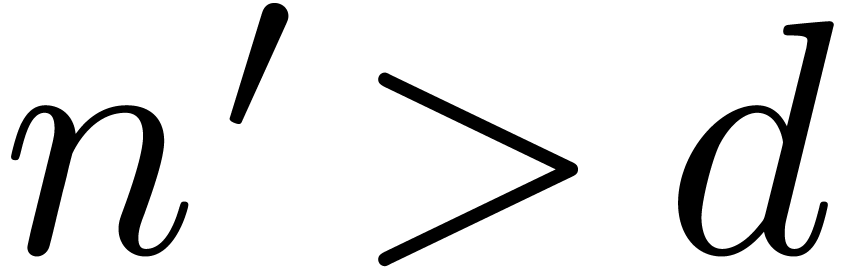
for any 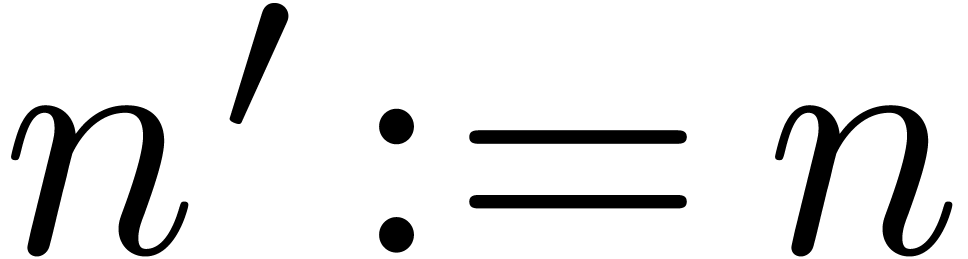 . Starting with
. Starting with 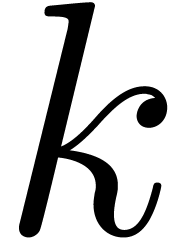 and iterating
and iterating  times yields
times yields
By the argument in the first paragraph, we may apply Proposition 4 once more (and increase  if
necessary) to obtain
if
necessary) to obtain
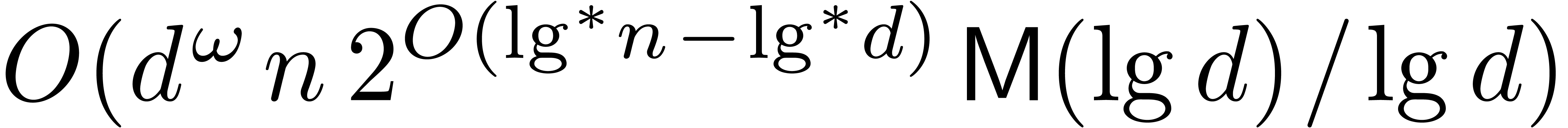
The second term lies in  .
Since
.
Since 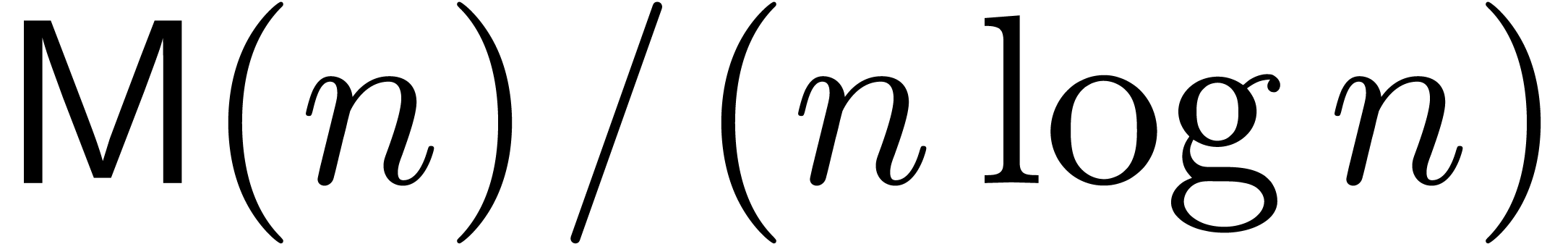 is increasing, the first term is bounded
by
is increasing, the first term is bounded
by


Remark 6. An important question
is to determine the best possible big-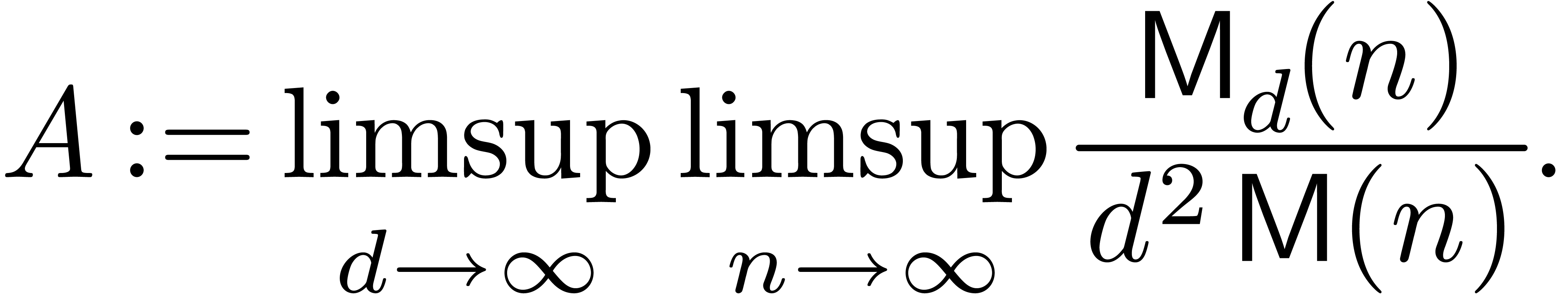 constant
in Theorem 1. For simplicity, consider the case where
constant
in Theorem 1. For simplicity, consider the case where 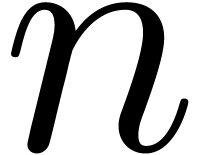 is much larger than
is much larger than 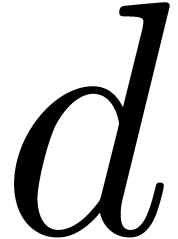 ,
and define
,
and define
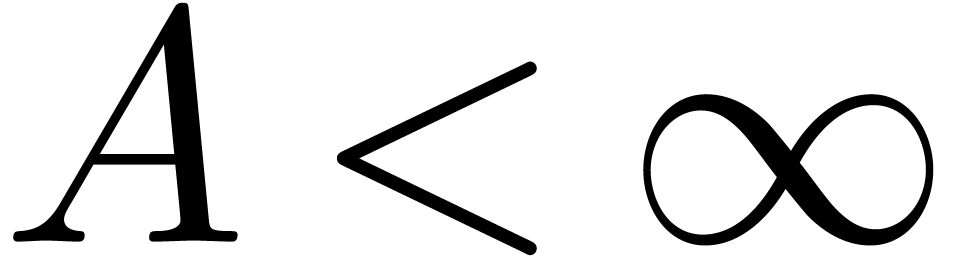
Theorem 1 shows that 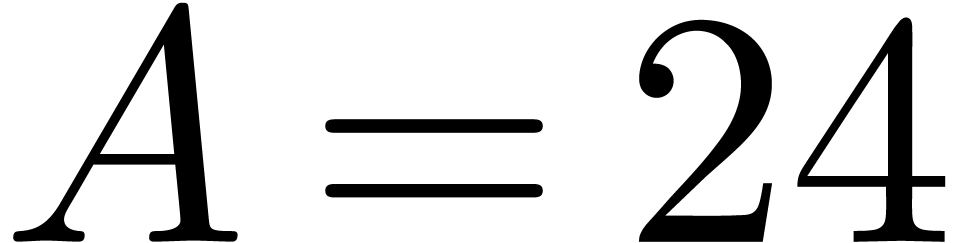 .
.
After some optimisations, it is possible to achieve 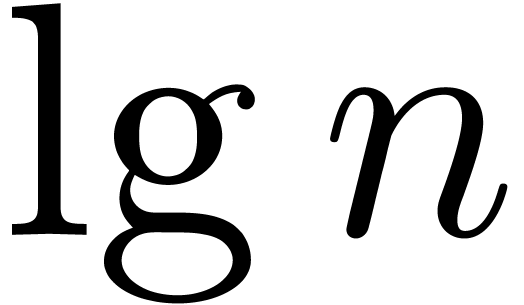 . (We omit the details. The idea is to increase
the chunk size
. (We omit the details. The idea is to increase
the chunk size 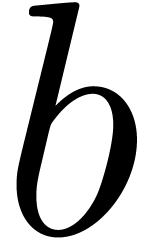 , say from
, say from
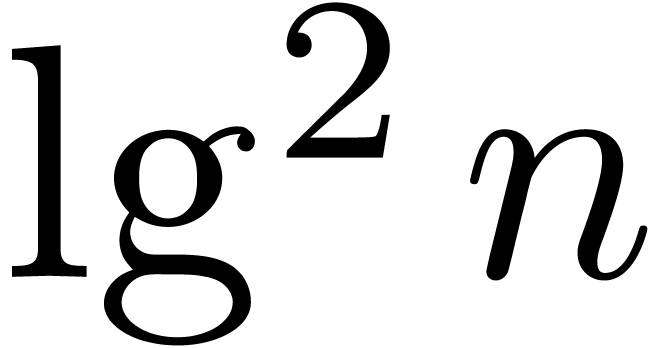 to
to 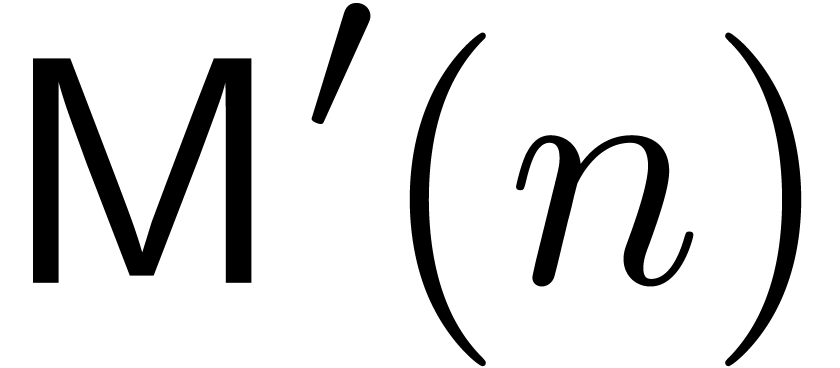 ,
and use the fact that Bluestein's trick actually produces a negacyclic
convolution.)
,
and use the fact that Bluestein's trick actually produces a negacyclic
convolution.)
We can do even better if we change the basic problem slightly. Define
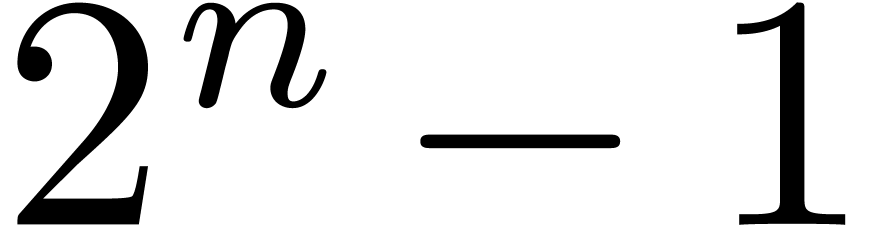 to be the cost of an
to be the cost of an 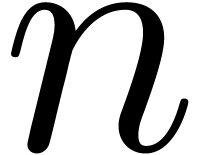 -bit cyclic integer convolution, i.e.,
multiplication modulo
-bit cyclic integer convolution, i.e.,
multiplication modulo 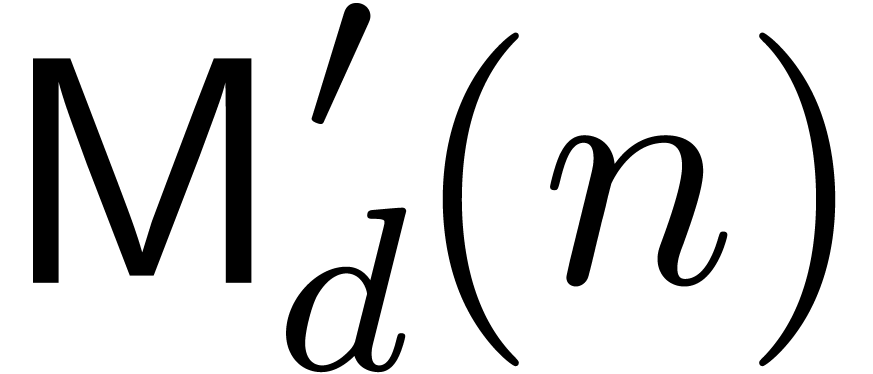 . This
kind of multiplication problem is of interest because all of the fastest
known multiplication algorithms, i.e., based on FFTs, actually compute
convolutions. (In this brief sketch we ignore the difficulty that such
algorithms typically only work for
. This
kind of multiplication problem is of interest because all of the fastest
known multiplication algorithms, i.e., based on FFTs, actually compute
convolutions. (In this brief sketch we ignore the difficulty that such
algorithms typically only work for 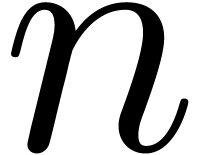 belonging to
some sparse set.) Let
belonging to
some sparse set.) Let  be the cost of the
corresponding
be the cost of the
corresponding  matrix multiplication
(convolution) problem, and let
matrix multiplication
(convolution) problem, and let 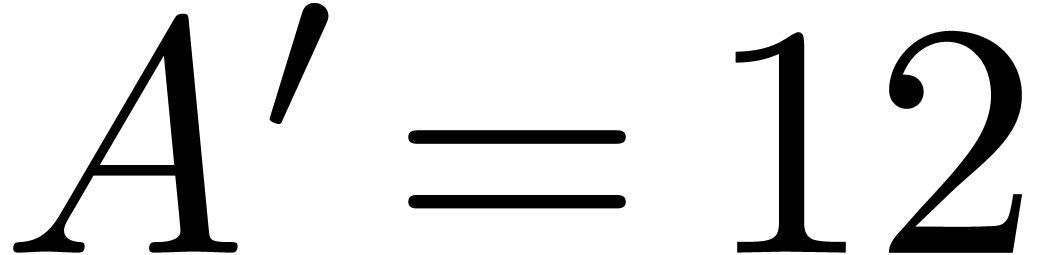 be the
corresponding constant defined as above. Then by mapping the Bluestein
convolution directly to integer convolution, one saves a factor of two,
obtaining
be the
corresponding constant defined as above. Then by mapping the Bluestein
convolution directly to integer convolution, one saves a factor of two,
obtaining 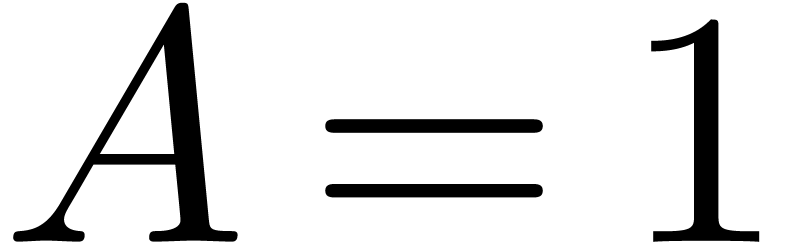 .
.
We conjecture that in fact one can achieve 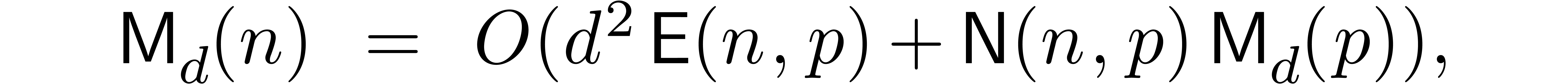 .
This conjecture can be proved for all integer multiplication algorithms
known to the authors, and it is also consistent with measurements of the
performance of the implementation described in [HS14, HLQ14]. The point is that the implementation transforms each
matrix entry exactly once, and the time spent on the small-coefficient
matrix multiplications is negligible if
.
This conjecture can be proved for all integer multiplication algorithms
known to the authors, and it is also consistent with measurements of the
performance of the implementation described in [HS14, HLQ14]. The point is that the implementation transforms each
matrix entry exactly once, and the time spent on the small-coefficient
matrix multiplications is negligible if 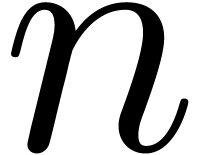 is
large.
is
large.
Remark 7. It is tempting to interpret the
bound in Theorem 1 as an analogue of (3) in
the case of integer coefficients. However, several technical problems
arise if one wants to make this more precise. Indeed, most
“evaluation-interpolation” strategies for integers (apart
from Chinese remaindering) involve cutting the integers into several
chunks, which prevents the evaluation mappings from being algebraic
homomorphisms. Moreover, due to carry management, we have to include an
additional parameter for the target precision of our evaluations. Thus,
in the case of matrix multiplication, we really should be looking for
bounds of the form
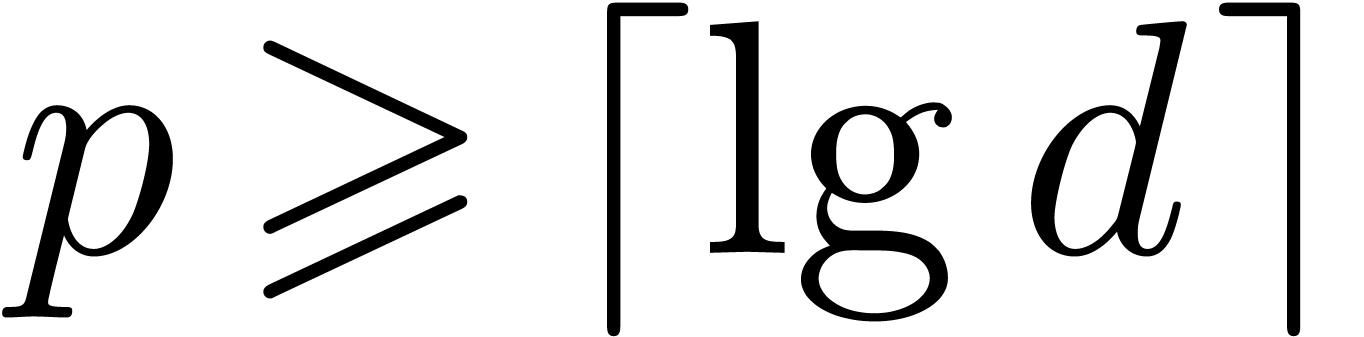
where 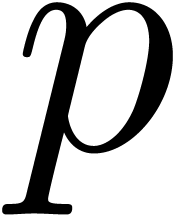 stands for the precision at our evaluation
points and
stands for the precision at our evaluation
points and 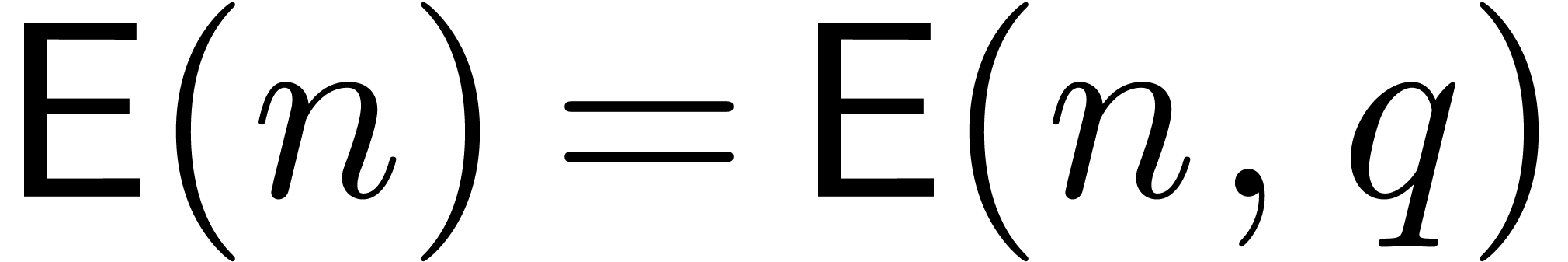 . In terms of
. In terms of 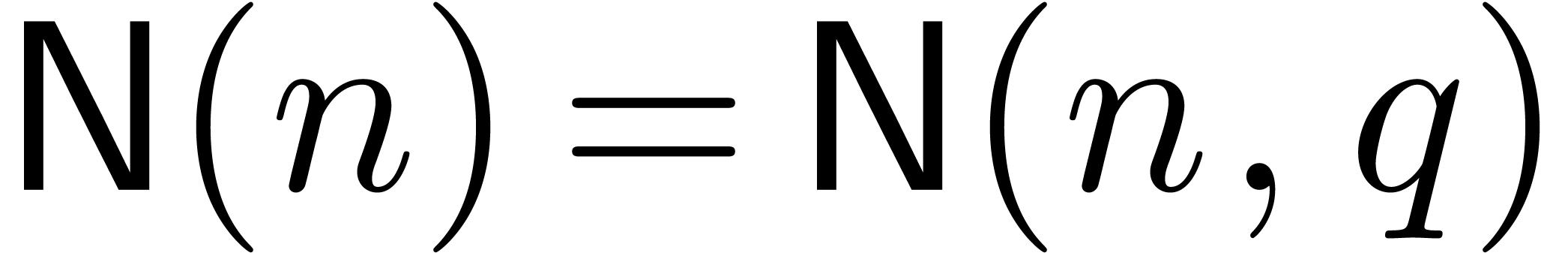 and
and 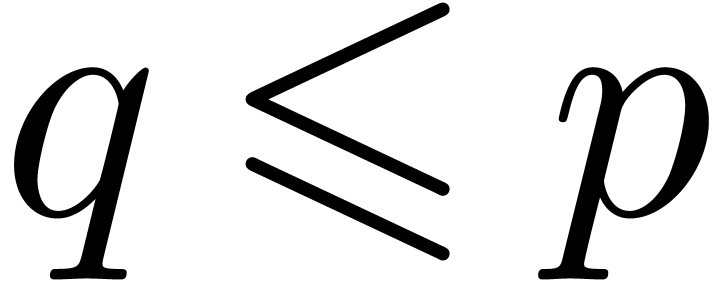 for some small fixed
precision
for some small fixed
precision 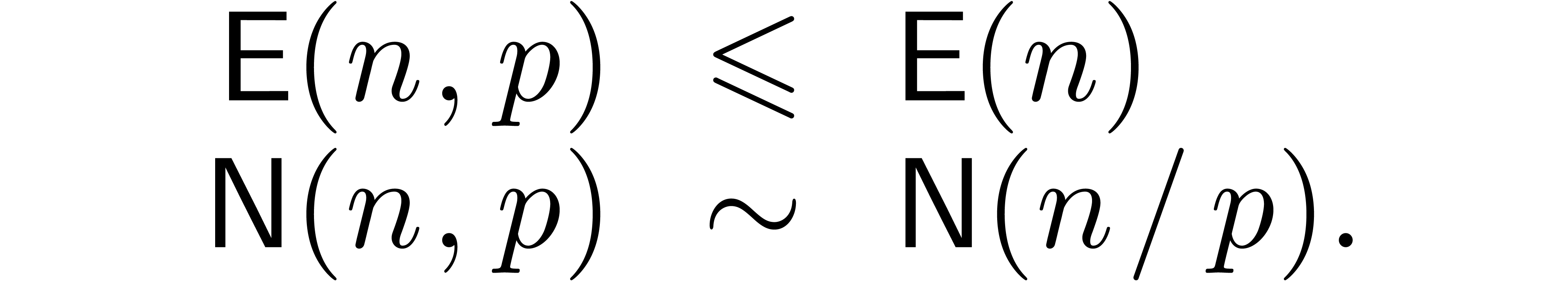 , we have
, we have
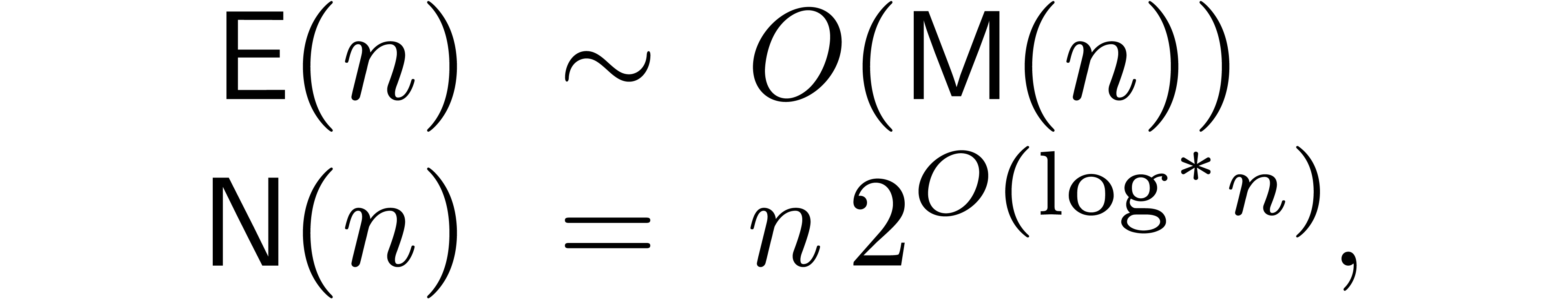
Reformulated in this way, our new evaluation-interpolation strategy
achieves
and it can be applied to several other problems, such as the
multiplication of multivariate polynomials or power series with large
integer coefficients.
Acknowledgments
The authors thank Arne Storjohann for helpful conversations. The first
author was supported by the Australian Research Council, DECRA Grant
DE120101293.
Bibliography
-
[AKS04]
-
Manindra Agrawal, Neeraj Kayal, and Nitin Saxena,
PRIMES is in P, Ann. of Math. (2) 160 (2004),
no. 2, 781–793. MR 2123939 (2006a:11170)
-
[BGS07]
-
Alin Bostan, Pierrick Gaudry, and Éric Schost,
Linear recurrences with polynomial coefficients and
application to integer factorization and Cartier-Manin
operator, SIAM J. Comput. 36 (2007), no. 6,
1777–1806. MR 2299425 (2008a:11156)
-
[BHP01]
-
R. C. Baker, G. Harman, and J. Pintz, The
difference between consecutive primes. II, Proc. London
Math. Soc. (3) 83 (2001), no. 3, 532–562. MR
1851081 (2002f:11125)
-
[Blu70]
-
L. Bluestein, A linear filtering approach to the
computation of discrete fourier transform, Audio and
Electroacoustics, IEEE Transactions on 18 (1970), no. 4,
451–455.
-
[BS05]
-
Alin Bostan and Éric Schost, Polynomial
evaluation and interpolation on special sets of points, J.
Complexity 21 (2005), no. 4, 420–446. MR 2152715
(2006g:12016)
-
[CC90]
-
D.V. Chudnovsky and G.V. Chudnovsky, Computer
algebra in the service of mathematical physics and number theory
(computers in mathematics, stanford, ca, 1986), Lect. Notes
in Pure and Applied Math. (New-York), vol. 125, Dekker, 1990,
pp. 109–232.
-
[CK91]
-
D.G. Cantor and E. Kaltofen, On fast
multiplication of polynomials over arbitrary algebras, Acta
Informatica 28 (1991), 693–701.
-
[CW87]
-
D. Coppersmith and S. Winograd, Matrix
multiplication via arithmetic progressions, Proc. of the
 Annual Symposium on Theory of Computing
(New York City), may 25–27 1987, pp. 1–6.
Annual Symposium on Theory of Computing
(New York City), may 25–27 1987, pp. 1–6.
-
[Für09]
-
Martin Fürer, Faster integer
multiplication, SIAM J. Comput. 39 (2009), no. 3,
979–1005. MR 2538847 (2011b:68296)
-
[Gal14]
-
François Le Gall, Powers of tensors and
fast matrix multiplication, Proc. ISSAC 2014 (Kobe, Japan),
July 23–25 2014, pp. 296–303.
-
[Har14]
-
David Harvey, Counting points on hyperelliptic
curves in average polynomial time, Ann. of Math. (2)
179 (2014), no. 2, 783–803.
-
[HHL14a]
-
David Harvey, Joris van der Hoeven, and
Grégoire Lecerf, Even faster integer
multiplication, preprint http://arxiv.org/abs/1407.3360,
2014.
-
[HHL14b]
-
–-, Faster polynomial multiplication over
finite fields, preprint http://arxiv.org/abs/1407.3361,
2014.
-
[HLM+02]
-
J. van der Hoeven, G. Lecerf, B. Mourrain, et al.,
Mathemagix, 2002, http://www.mathemagix.org.
-
[HLQ14]
-
J. van der Hoeven, G. Lecerf, and G. Quintin,
Modular SIMD arithmetic in Mathemagix, Tech. report,
ArXiv, 2014, http://arxiv.org/abs/1407.3383.
-
[Hoe99]
-
J. van der Hoeven, Fast evaluation of holonomic
functions, TCS 210 (1999), 199–215.
-
[Hoe01]
-
–-, Fast evaluation of holonomic functions
near and in singularities, JSC 31 (2001),
717–743.
-
[Hoe04]
-
–-, The truncated Fourier transform and
applications, Proc. ISSAC 2004 (Univ. of Cantabria,
Santander, Spain) (J. Gutierrez, ed.), July 4–7 2004, pp.
290–296.
-
[Hoe07]
-
–-, Efficient accelero-summation of
holonomic functions, JSC 42 (2007), no. 4,
389–428.
-
[Hoe10]
-
–-, Newton's method and FFT trading,
JSC 45 (2010), no. 8, 857–878.
-
[HP97]
-
B. Haible and T. Papanikolaou, Fast
multiple-precision evaluation of elementary functions,
Tech. Report TI-7/97, Universität Darmstadt, 1997.
-
[HS14]
-
David Harvey and Andrew V. Sutherland, Computing
Hasse–Witt matrices of hyperelliptic curves in average
polynomial time, Algorithmic Number Theory Eleventh
International Symposium (ANTS XI), vol. 17, London Mathematical
Society Journal of Computation and Mathematics, 2014, pp.
257–273.
-
[Pap94]
-
Christos H. Papadimitriou, Computational
complexity, Addison-Wesley Publishing Company, Reading, MA,
1994. MR 1251285 (95f:68082)
-
[Shp96]
-
Igor Shparlinski, On finding primitive roots in
finite fields, Theoret. Comput. Sci. 157 (1996), no.
2, 273–275. MR 1389773 (97a:11203)
-
[SS71]
-
A. Schönhage and V. Strassen, Schnelle
Multiplikation grosser Zahlen, Computing (Arch. Elektron.
Rechnen) 7 (1971), 281–292. MR 0292344 (45 #1431)
-
[Sto00]
-
Arne Storjohann, Algorithms for matrix canonical
forms, Ph.D. thesis, ETH Zürich, 2000, http://dx.doi.org/10.3929/ethz-a-004141007.
-
[Str69]
-
V. Strassen, Gaussian elimination is not
optimal, Numer. Math. 13 (1969), 352–356.
-
[vzGG03]
-
Joachim von zur Gathen and Jürgen Gerhard,
Modern computer algebra, second ed., Cambridge
University Press, Cambridge, 2003. MR 2001757 (2004g:68202)
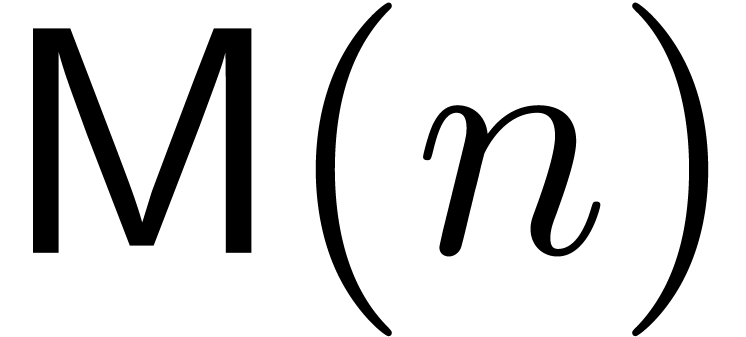 denote the bit complexity of
multiplying
denote the bit complexity of
multiplying 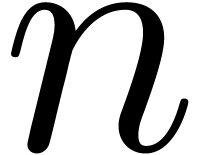 -bit integers,
let
-bit integers,
let 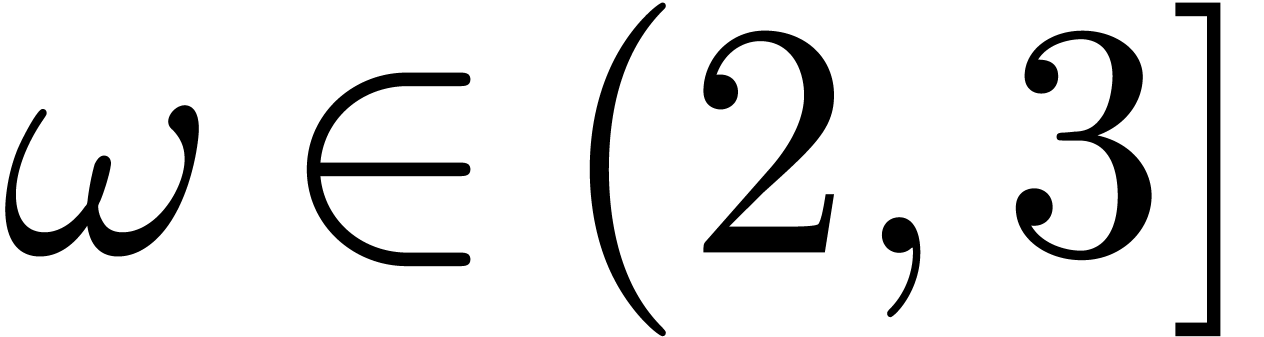 be an exponent for matrix multiplication,
and let
be an exponent for matrix multiplication,
and let 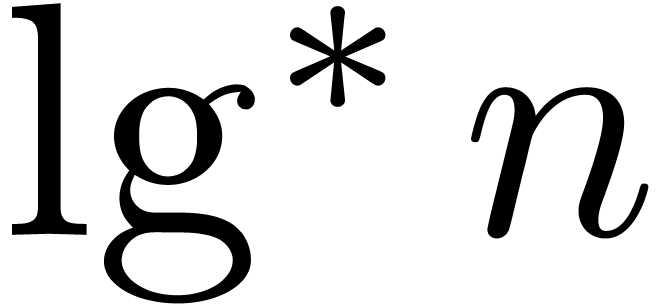 be the iterated logarithm. Assuming
that
be the iterated logarithm. Assuming
that 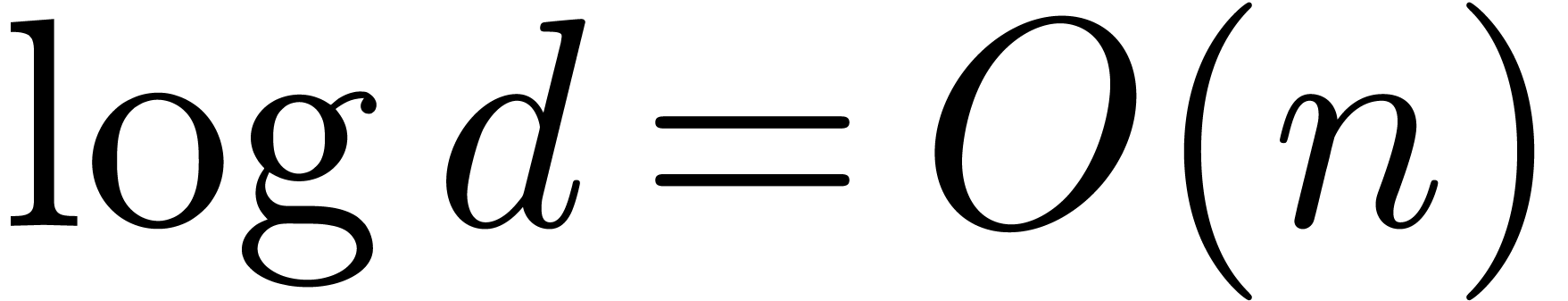 and that
and that 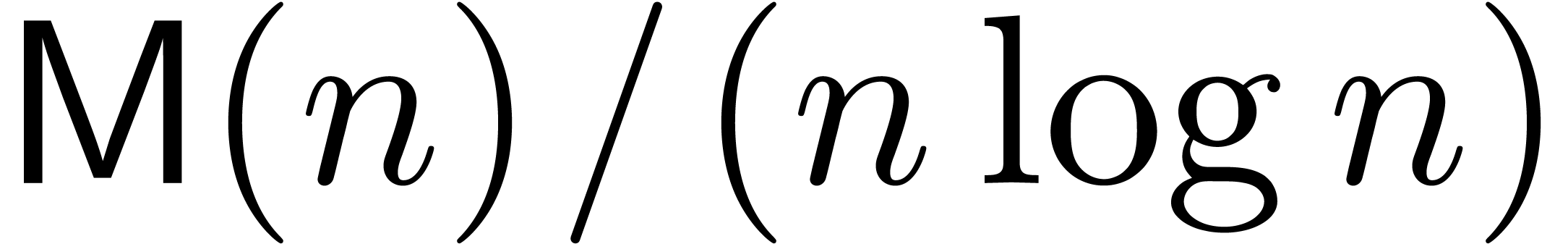 is
increasing, we prove that
is
increasing, we prove that  matrices with
matrices with 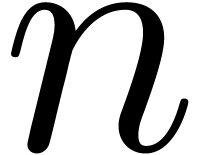 -bit integer entries may be
multiplied in
-bit integer entries may be
multiplied in
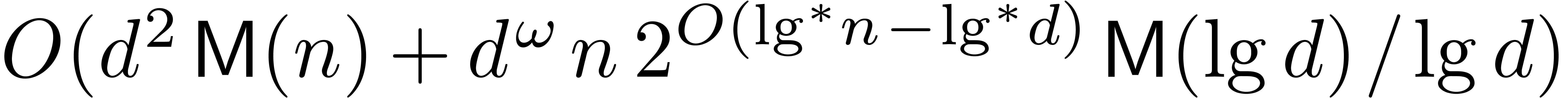
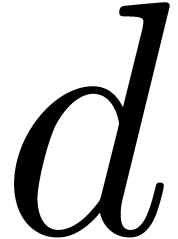 ,
,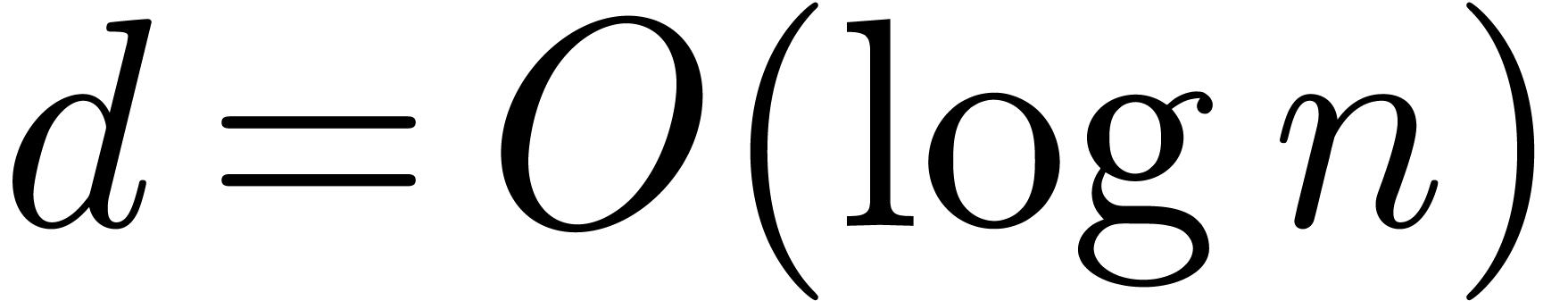 ,
,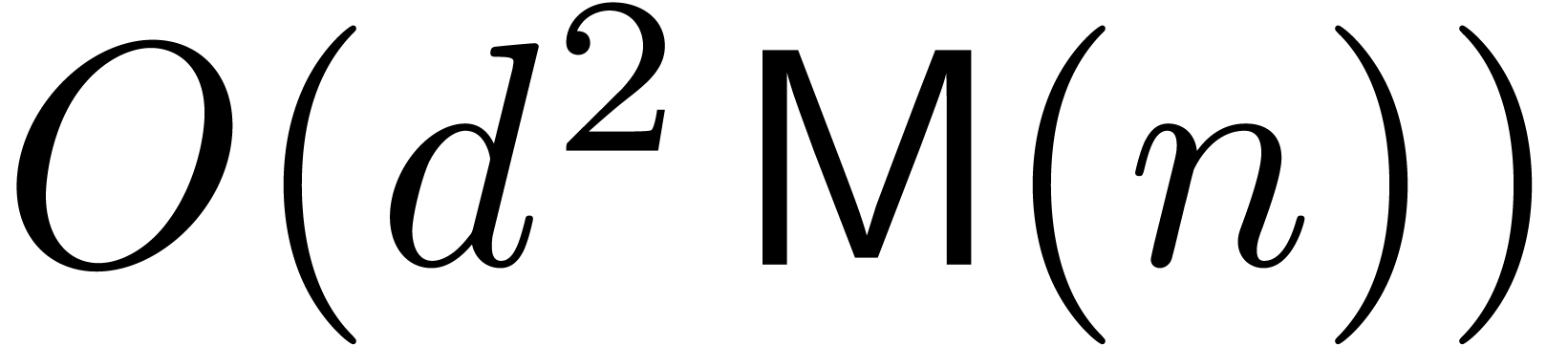 .
. matrices whose entries are integers with at most
matrices whose entries are integers with at most 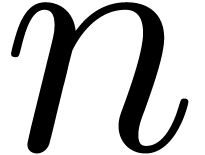 bits. We are particularly interested in the case that
bits. We are particularly interested in the case that 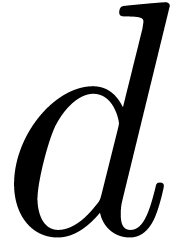 ,
, -series
-series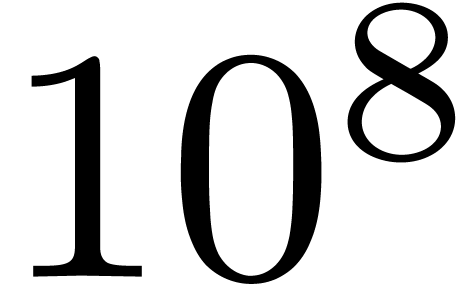 bits, and
bits, and 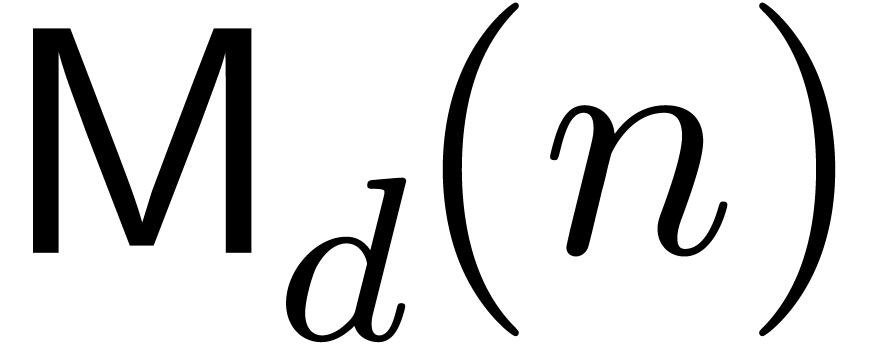 for the cost of the
for the cost of the 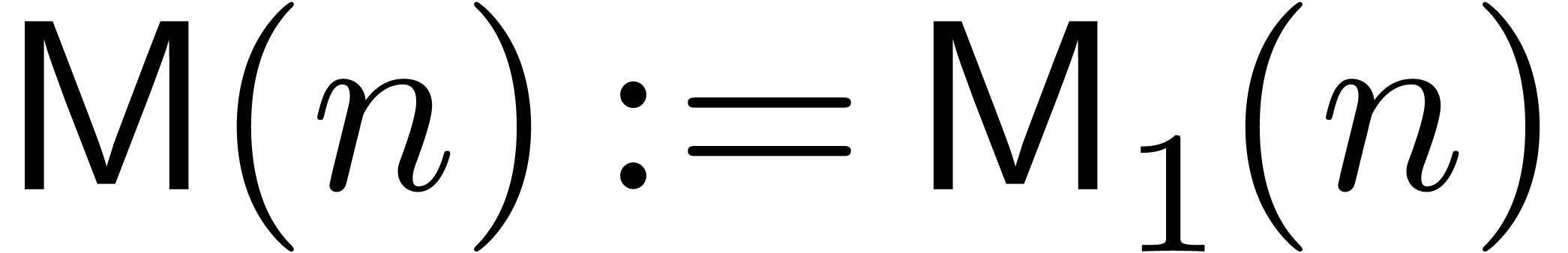 for the cost of multiplying
for the cost of multiplying
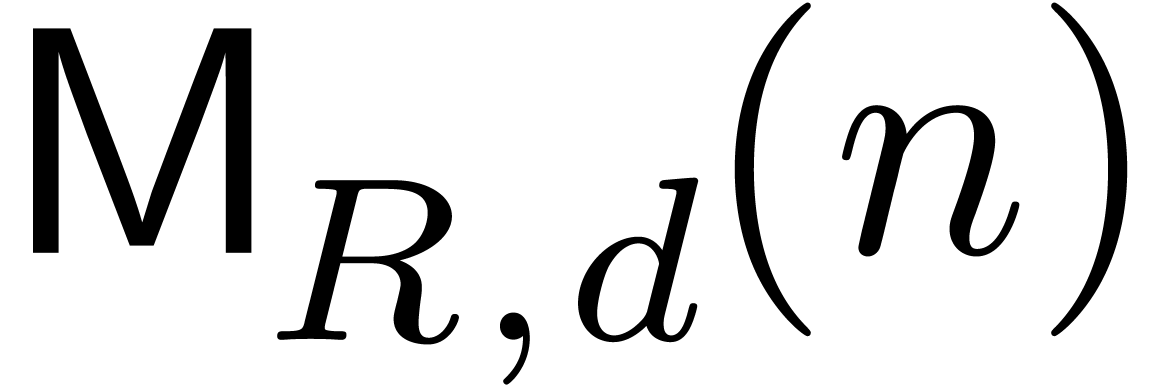 for the algebraic complexity of
multiplying
for the algebraic complexity of
multiplying 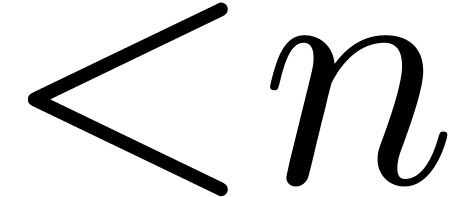 over an abstract
effective ring
over an abstract
effective ring 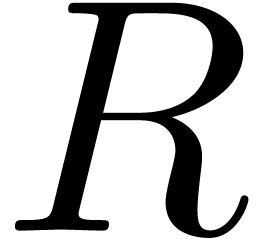 ,
,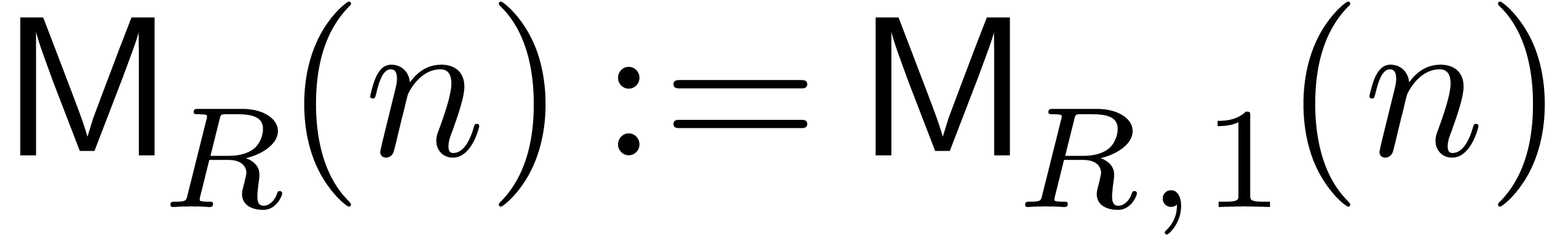 .
.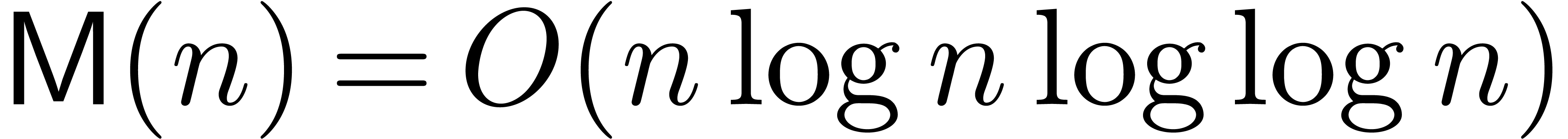 for large
for large 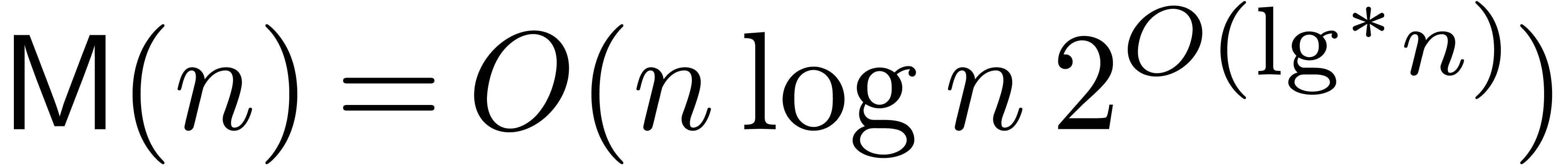 where
where 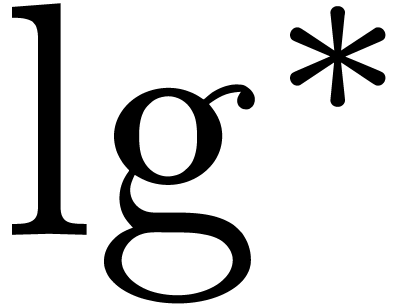 is the iterated logarithm, i.e.,
is the iterated logarithm, i.e.,
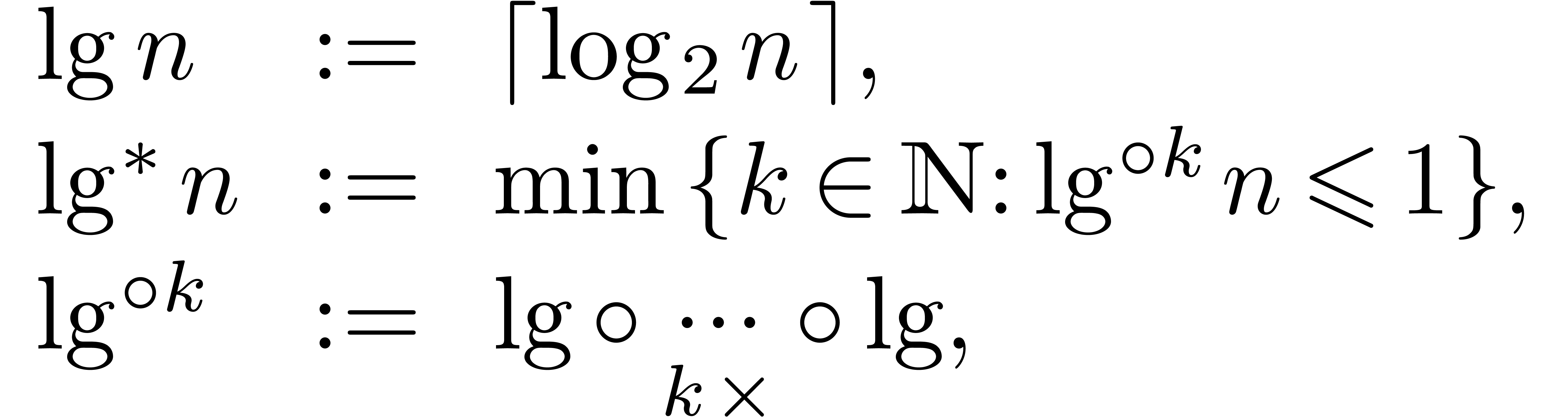
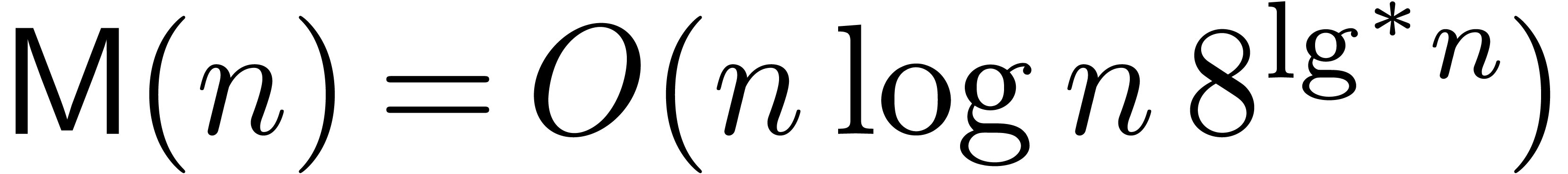 [
[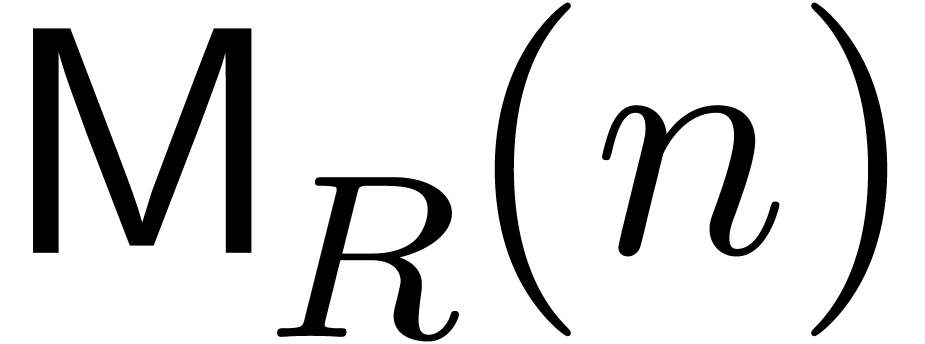 is
is 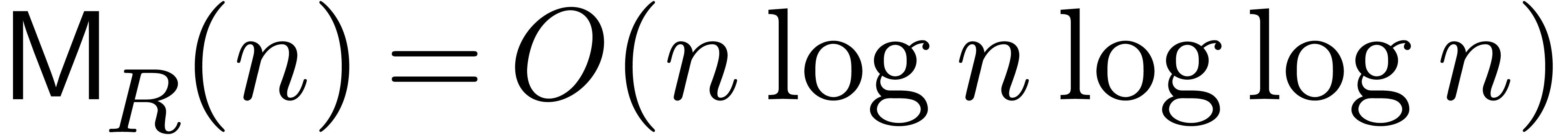 ;
;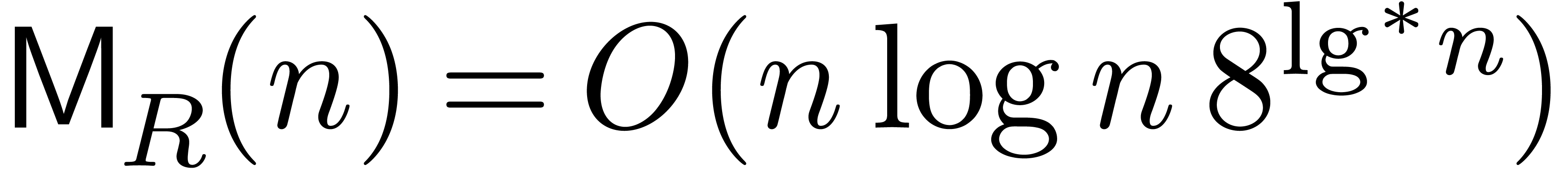 [
[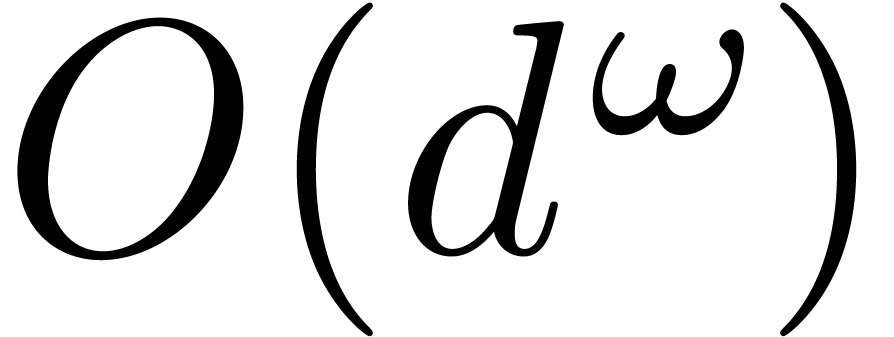 ,
, is a so-called
exponent of matrix multiplication [
is a so-called
exponent of matrix multiplication [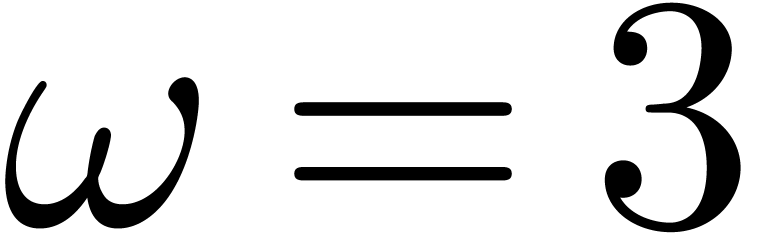 ,
,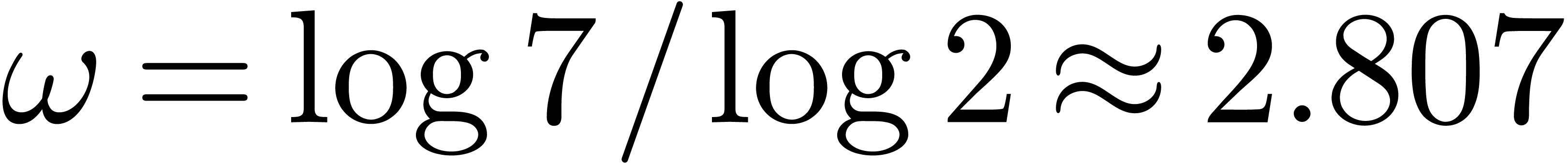 .
. was found by Le Gall [
was found by Le Gall [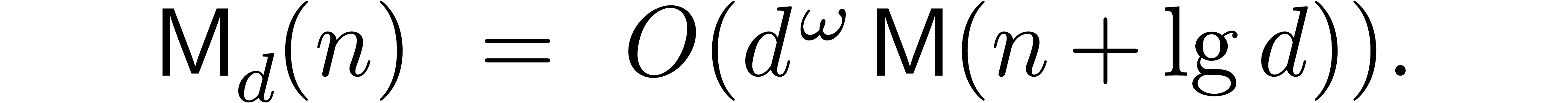
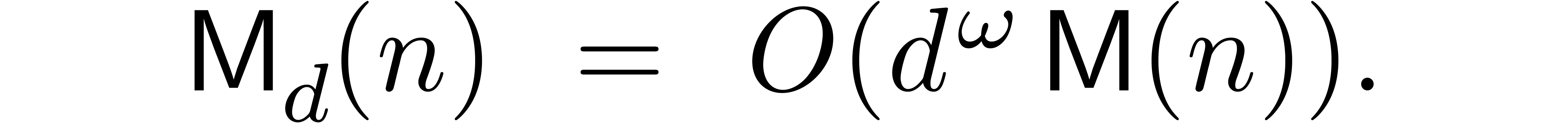
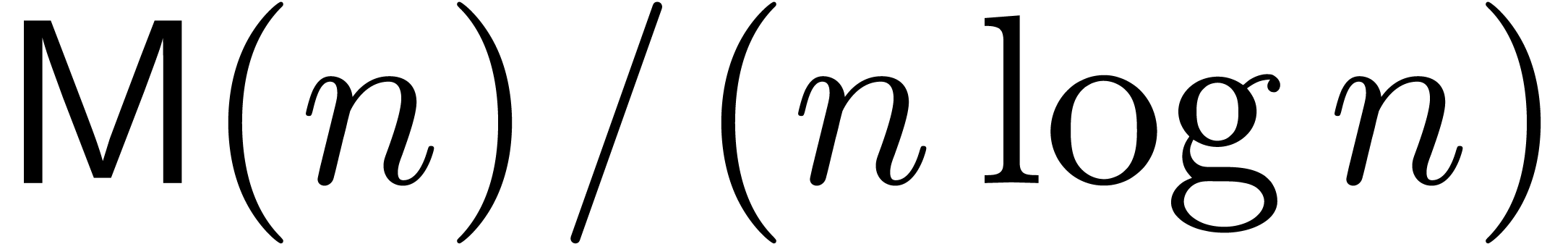 is increasing. Let
is increasing. Let 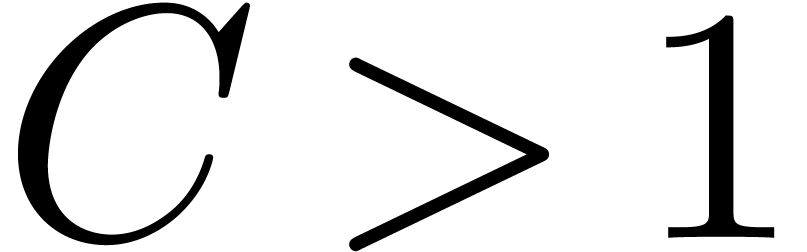 be a constant. Then
be a constant. Then
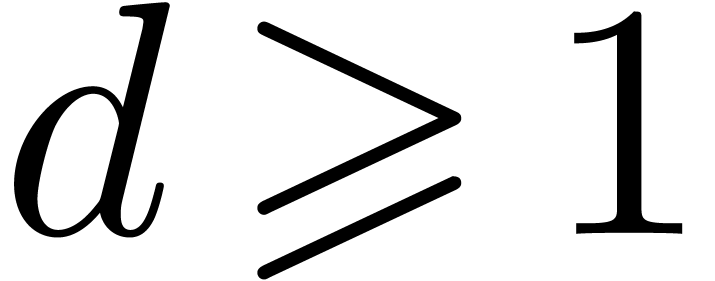 ,
, with
with  .
.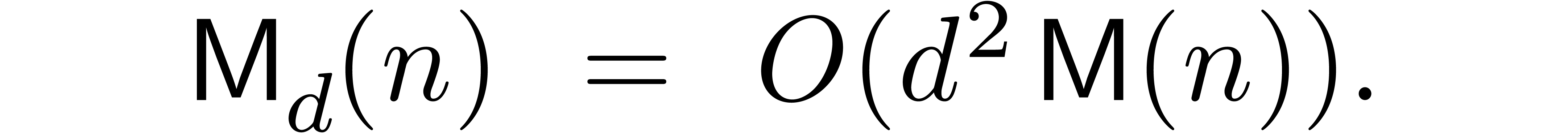
 ,
,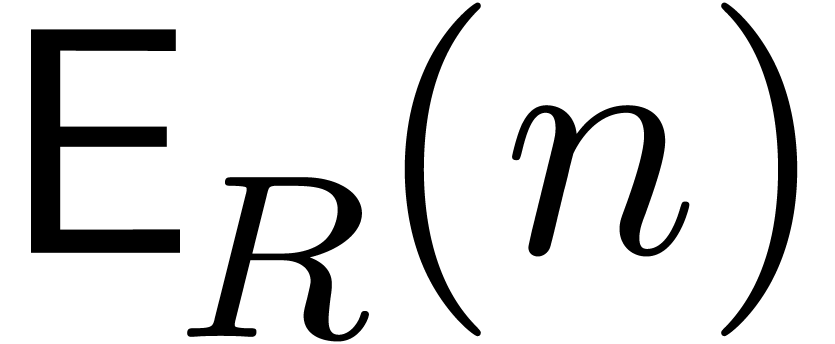 of
evaluation/interpolation and the number
of
evaluation/interpolation and the number 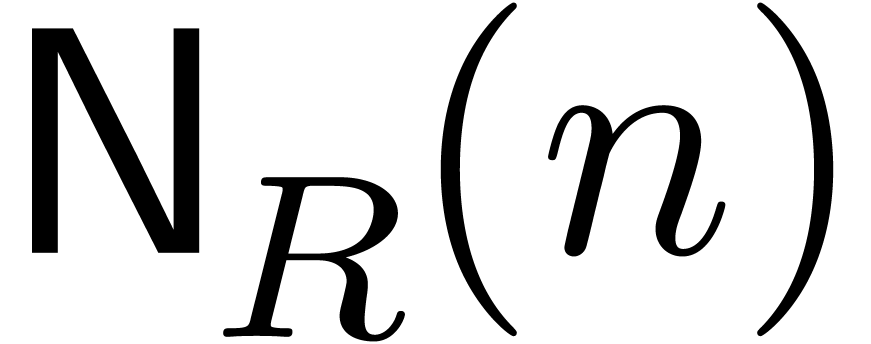 of
evaluation points. In terms of these quantities, we have
of
evaluation points. In terms of these quantities, we have
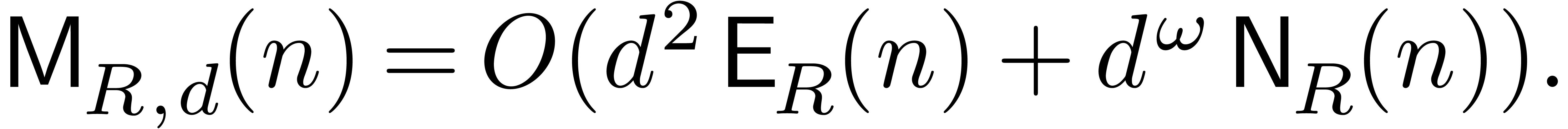
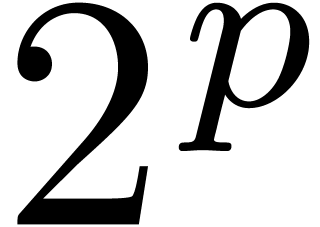 -th
-th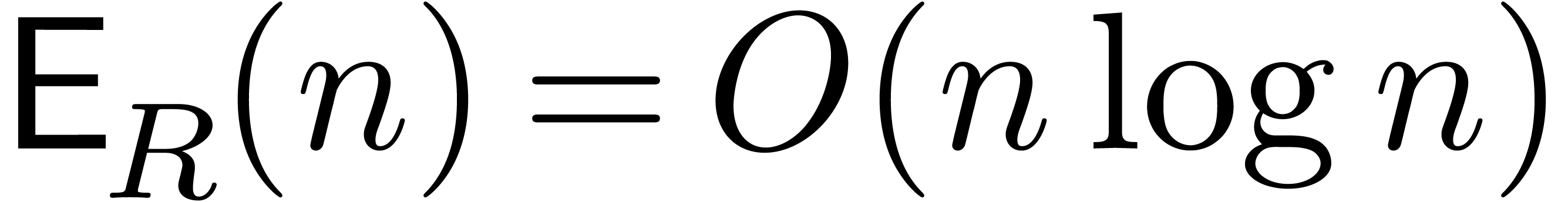 and
and 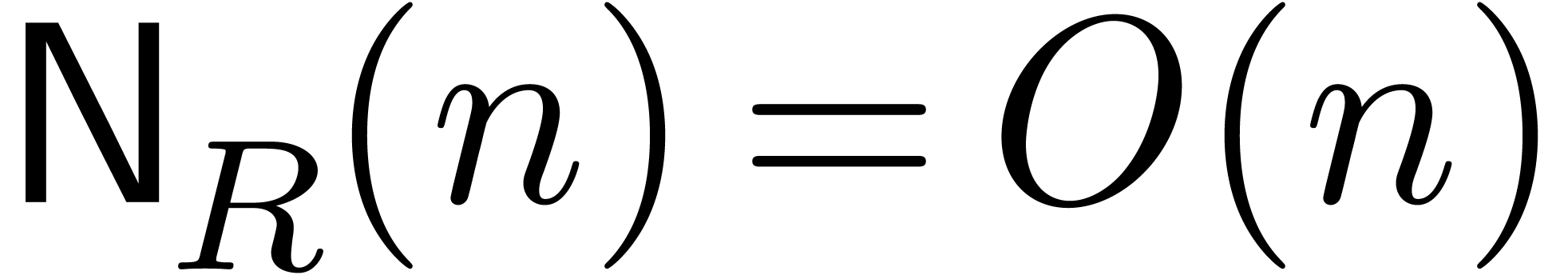 .
.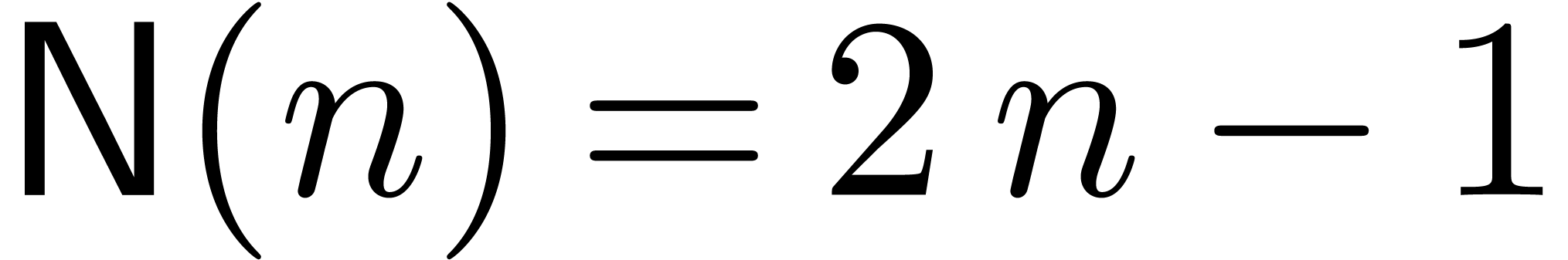 ,
, and
and 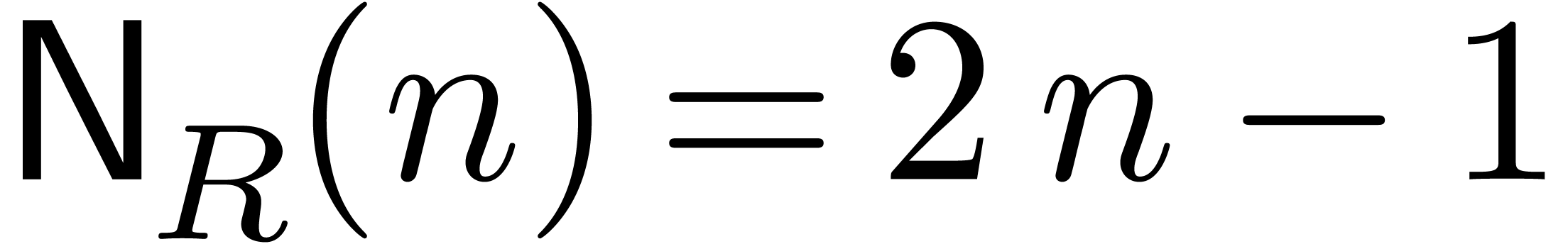 by evaluating at geometric sequences. Thus, in this situation they
obtain
by evaluating at geometric sequences. Thus, in this situation they
obtain
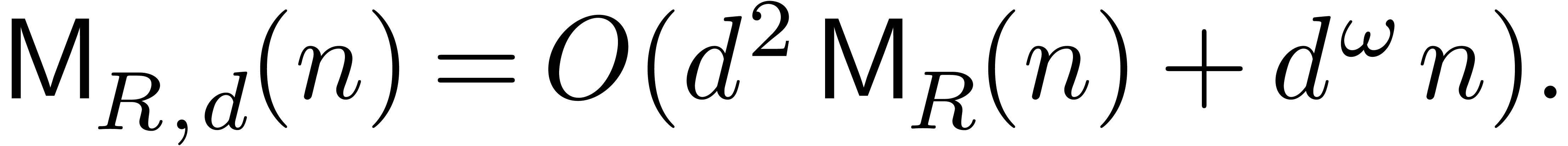
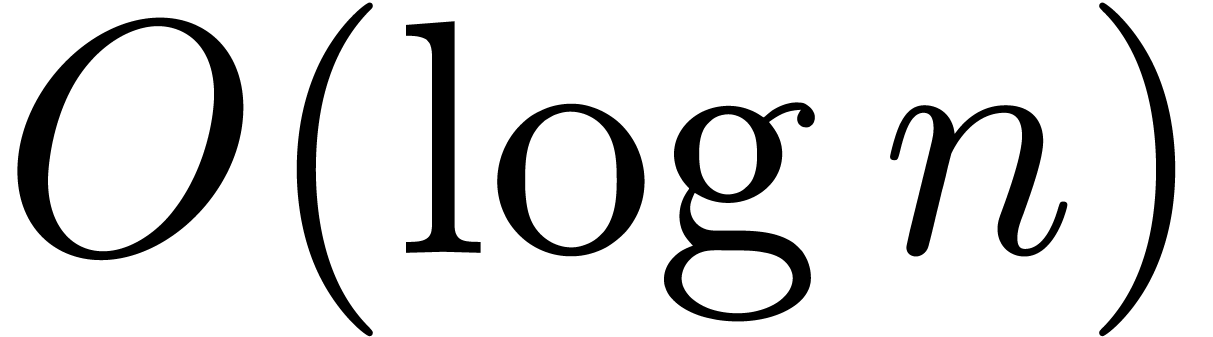 .
.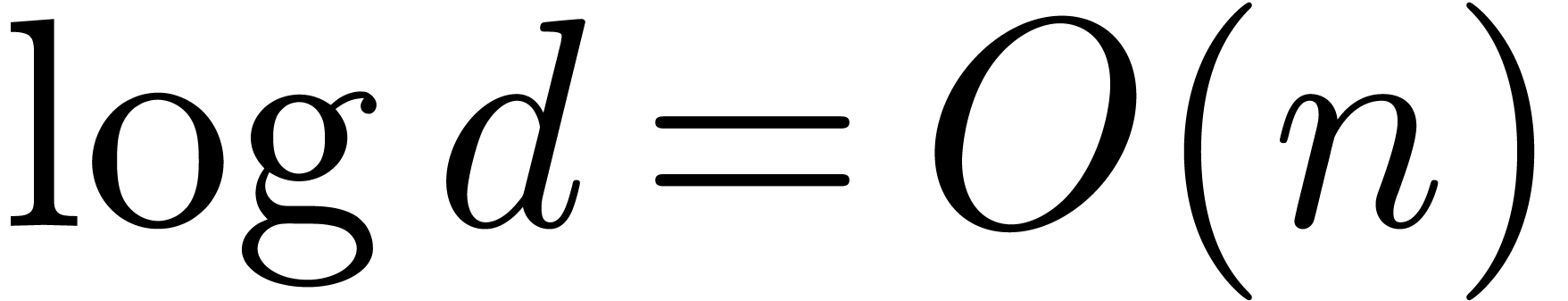 ,
,
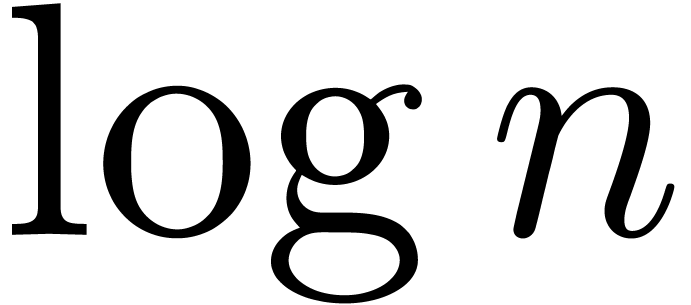 in the first term.
This factor arises from the cost of computing a certain product tree
(and remainder tree) in the Chinese remaindering algorithm.
in the first term.
This factor arises from the cost of computing a certain product tree
(and remainder tree) in the Chinese remaindering algorithm.
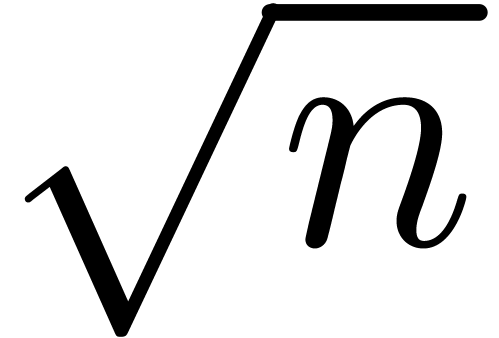 bits, and then performs FFTs over a ring of the form
bits, and then performs FFTs over a ring of the form 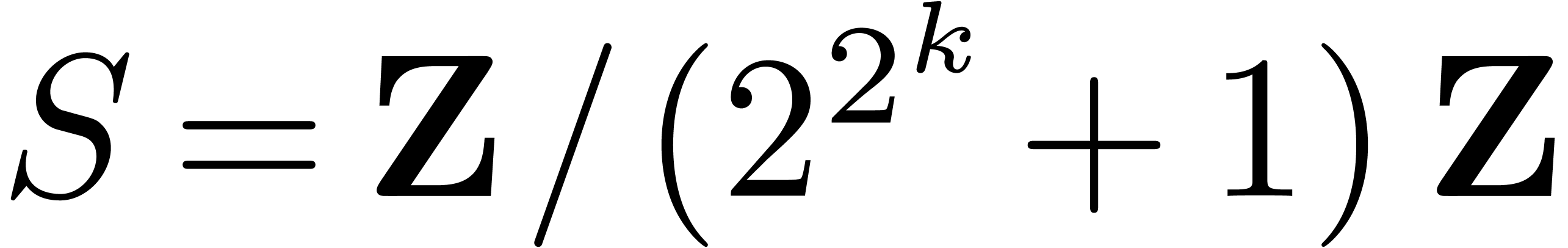 where
where 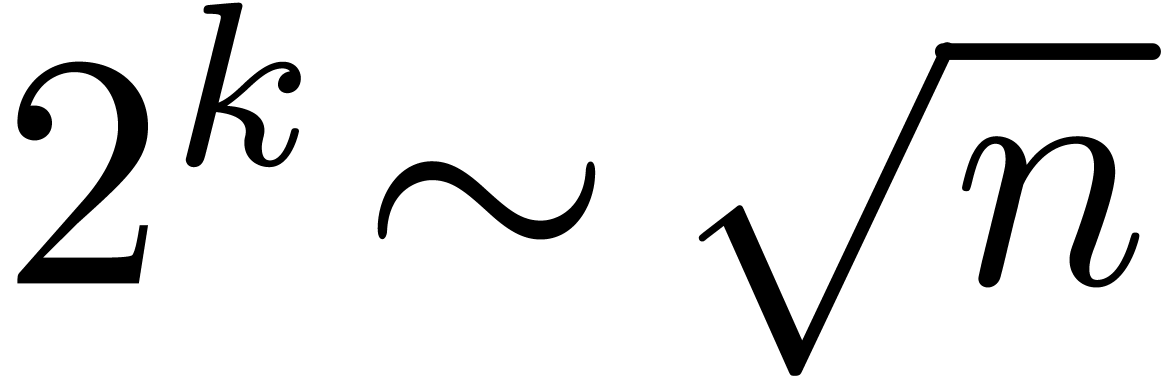 .
. ,
,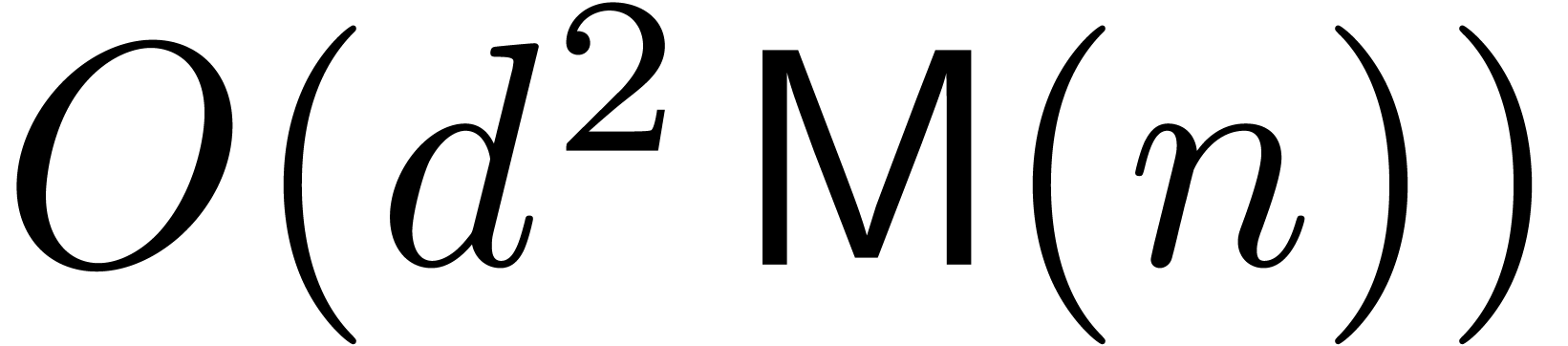 ,
,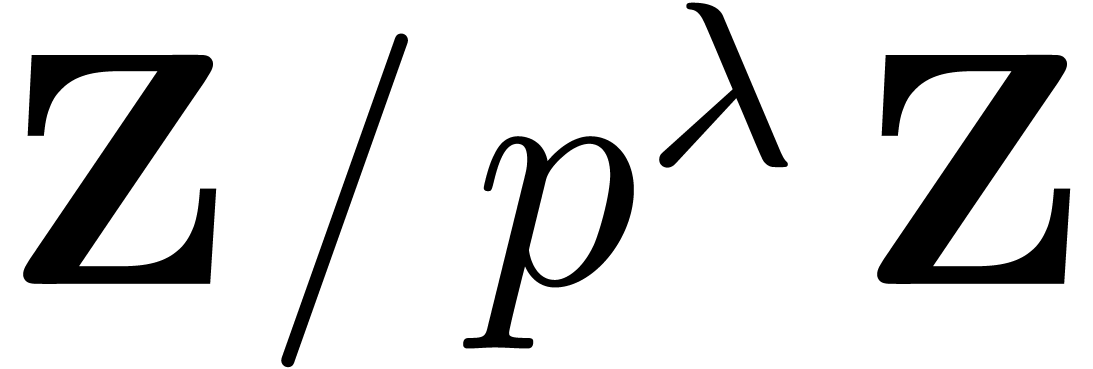 for a suitable prime power
for a suitable prime power 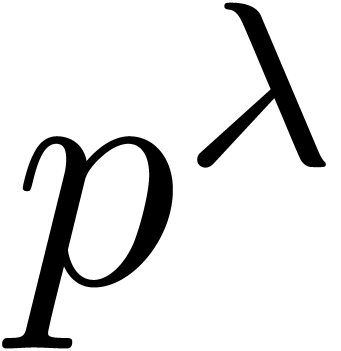 .
. constant.
constant.
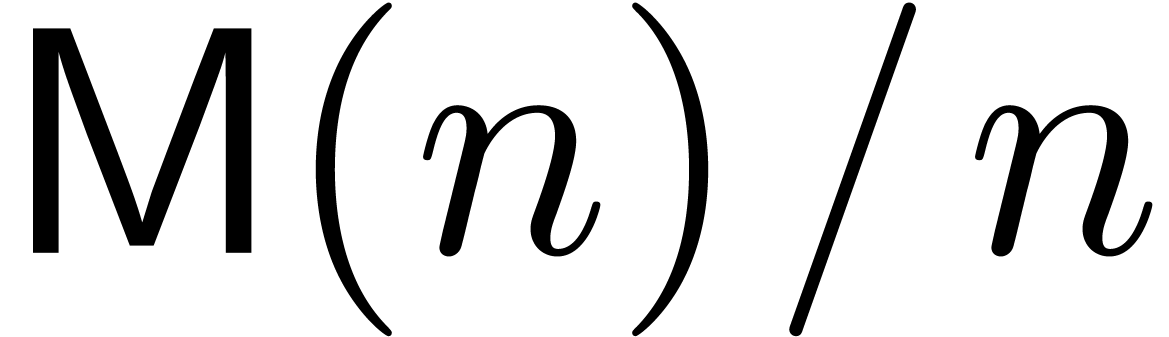 is increasing. Let
is increasing. Let 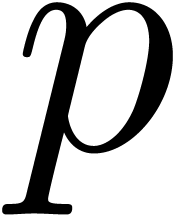 be an odd prime, let
be an odd prime, let 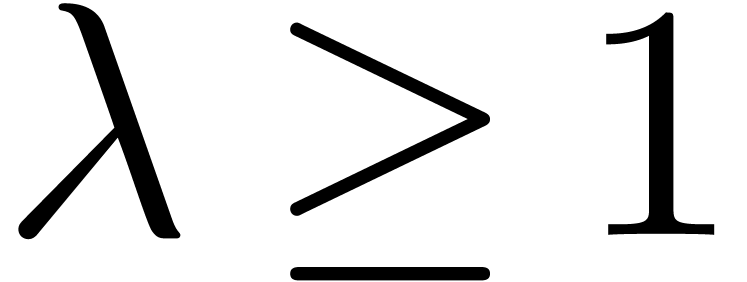 be an integer, and let
be an integer, and let 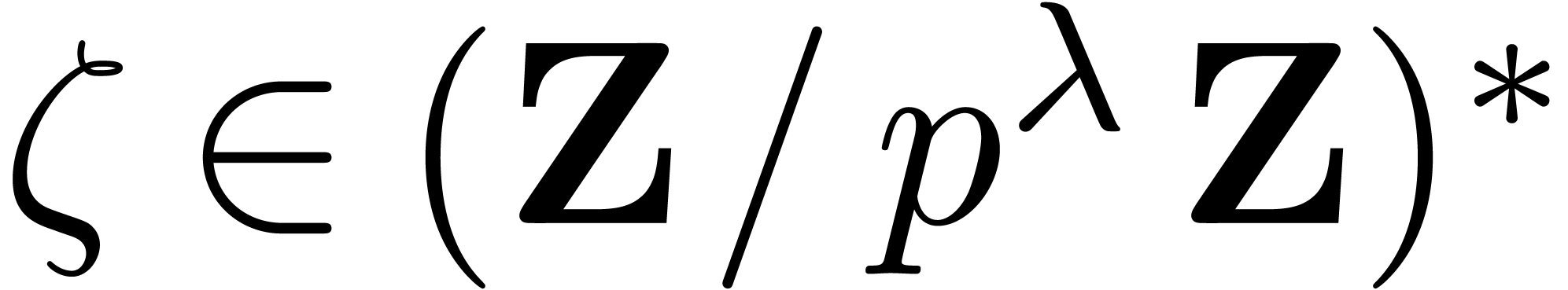 be an element of order
be an element of order 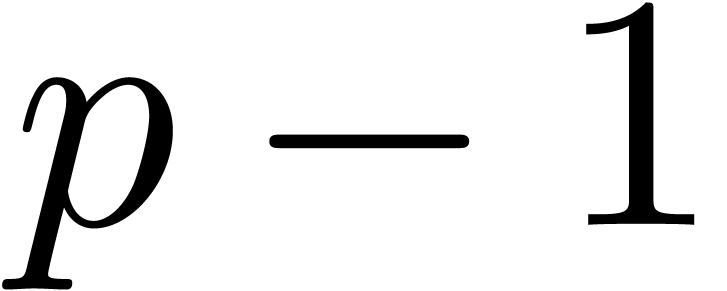 .
.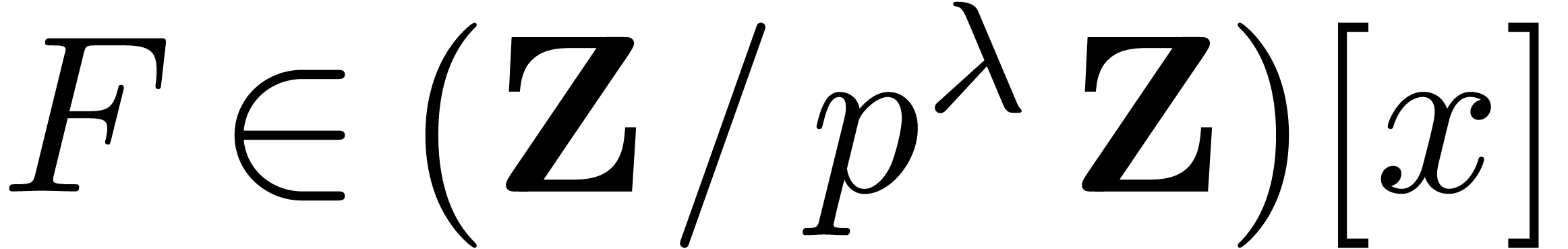 ,
, ,
,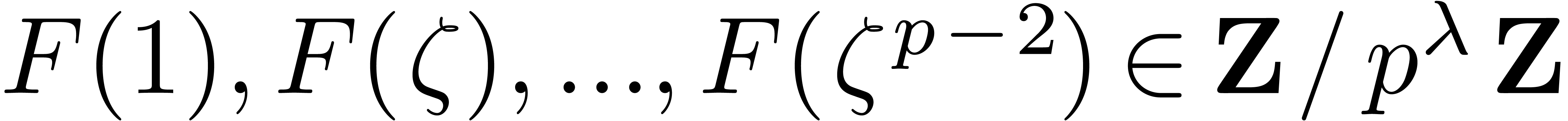 in time
in time
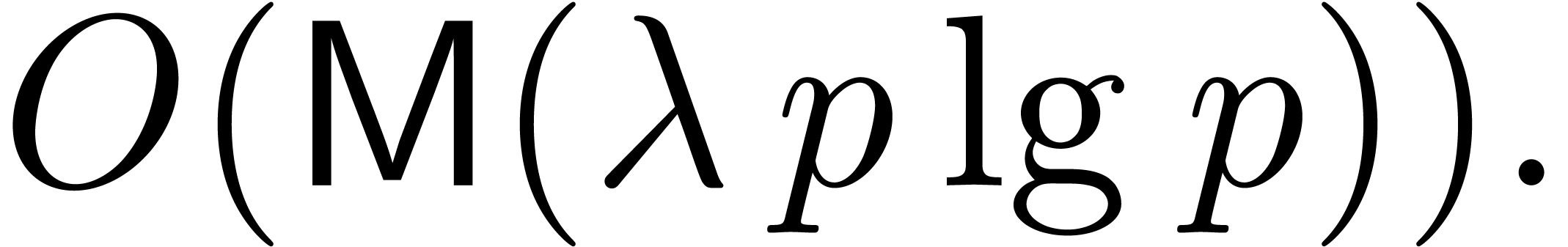
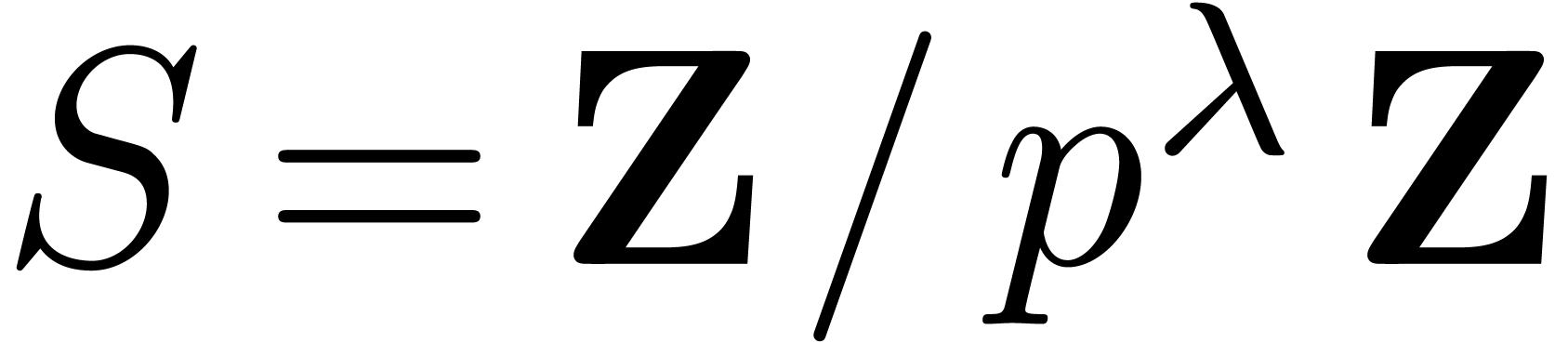 and let
and let 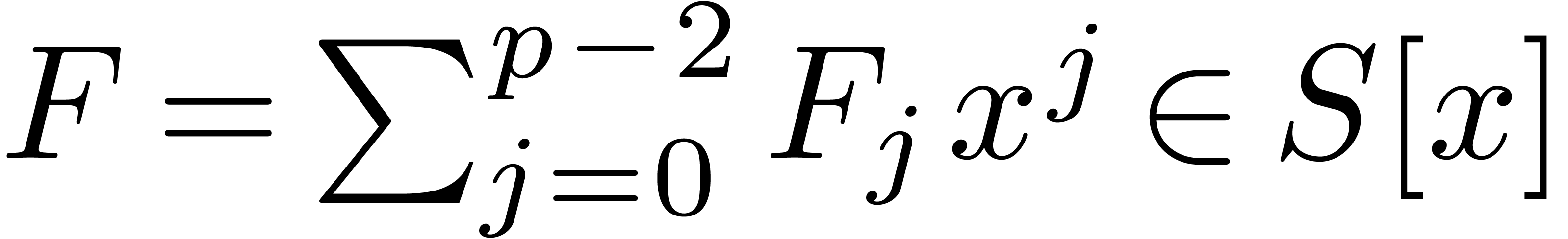 .
.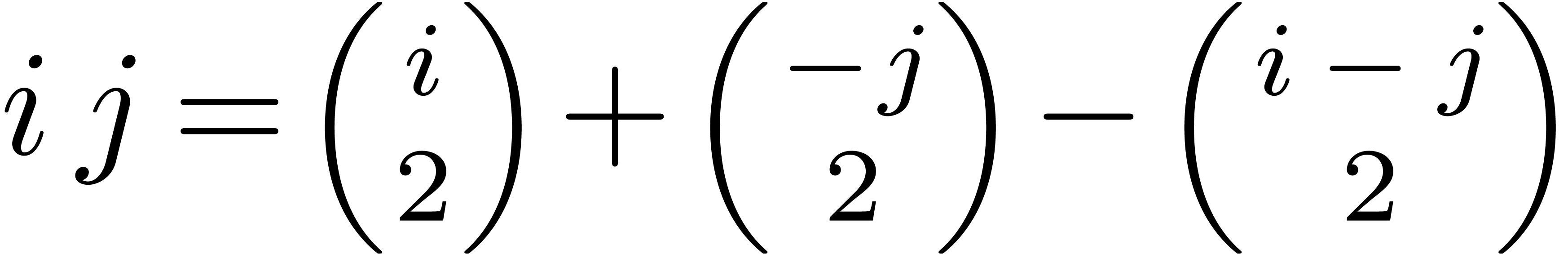 we obtain
we obtain
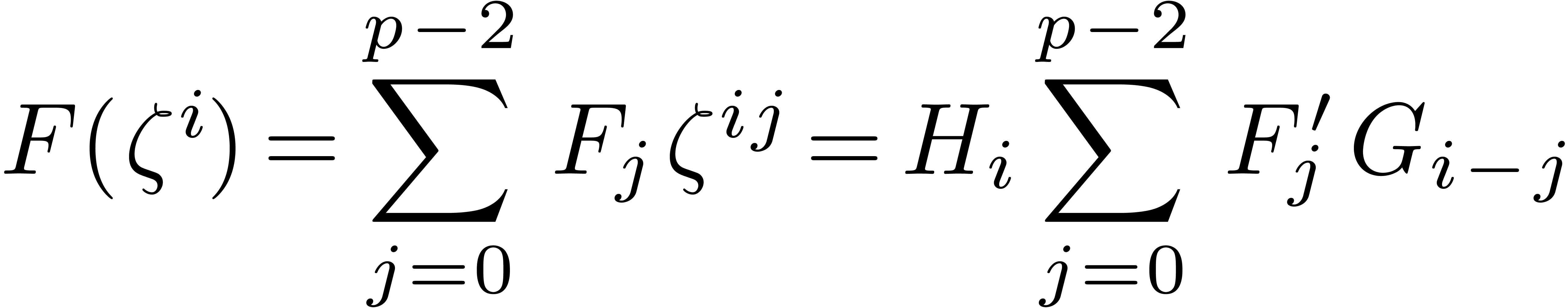
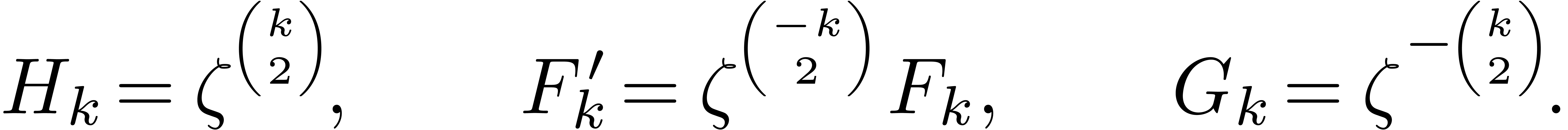
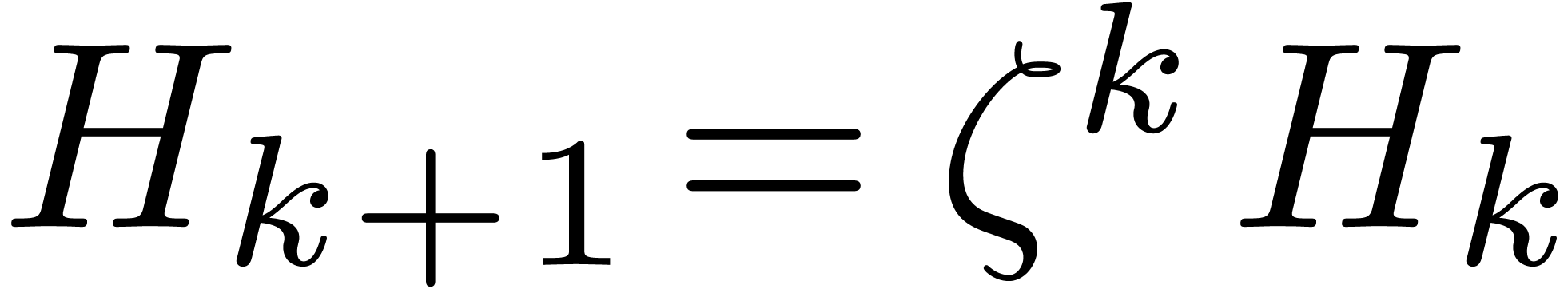 and
and 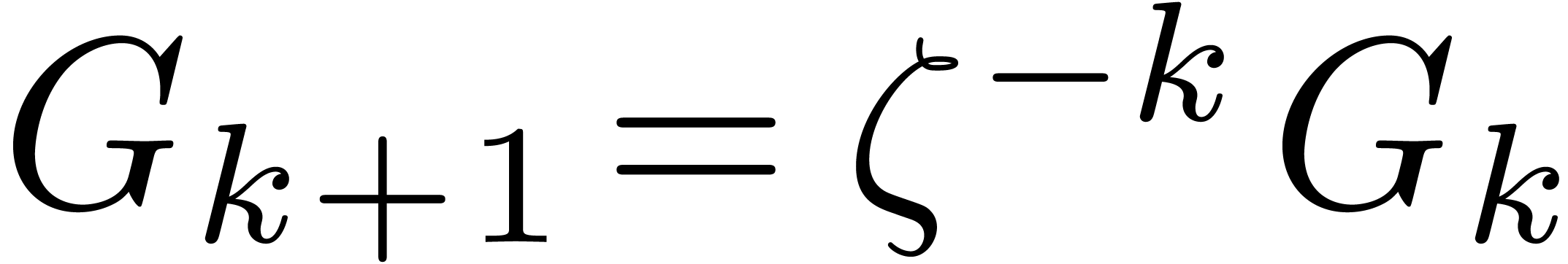 ,
,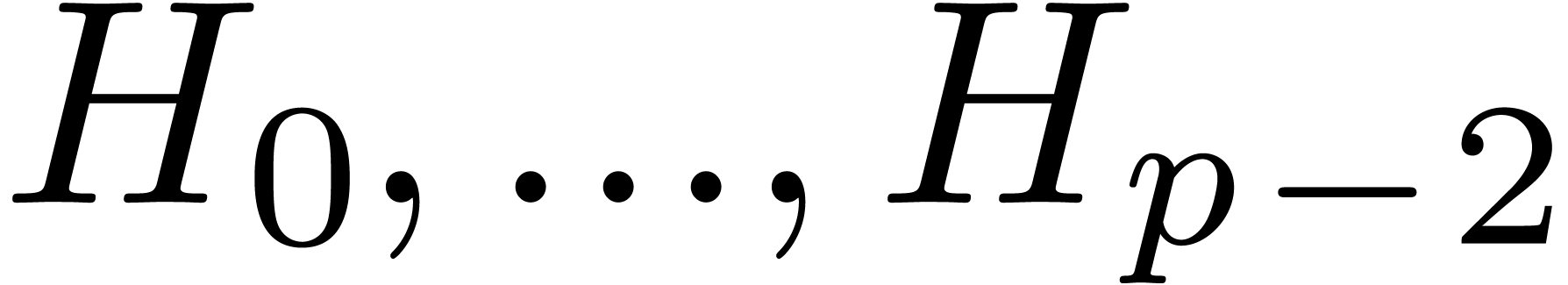 and
and 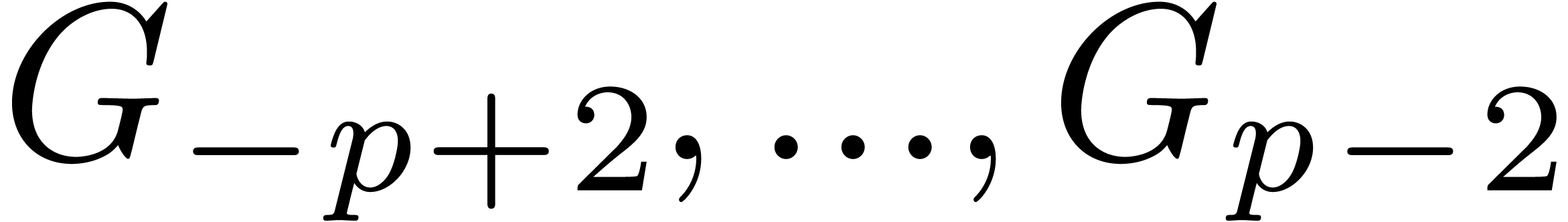 from
from  and
and 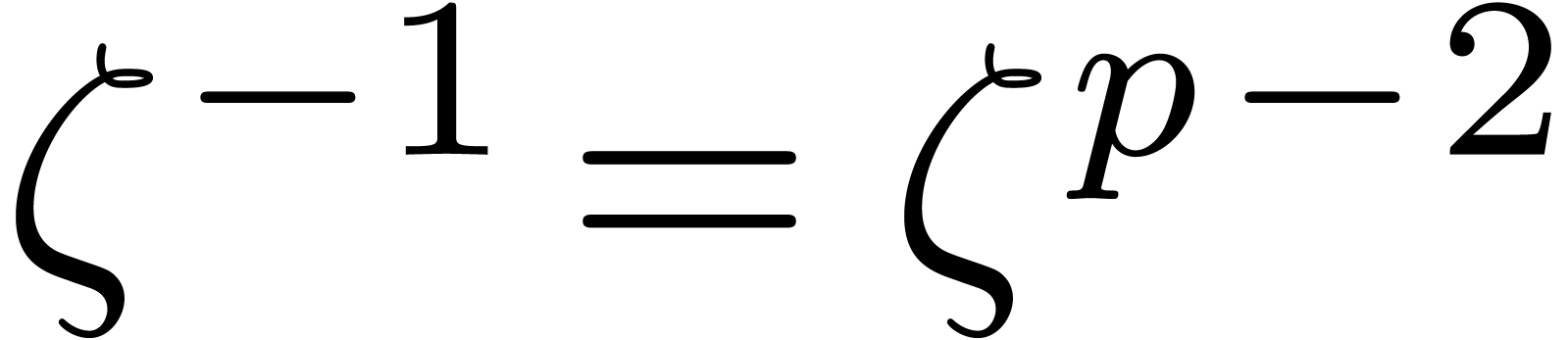 using
using 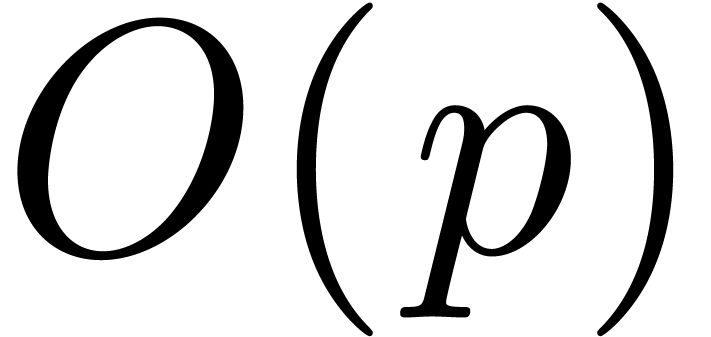 ring operations in
ring operations in 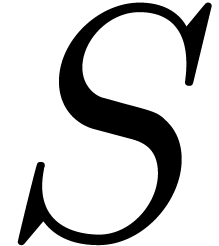 .
. from the
from the 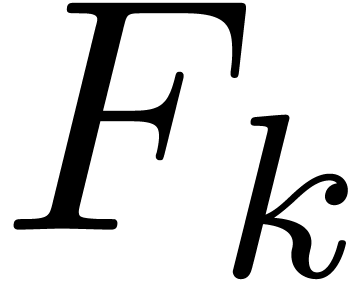 using
using 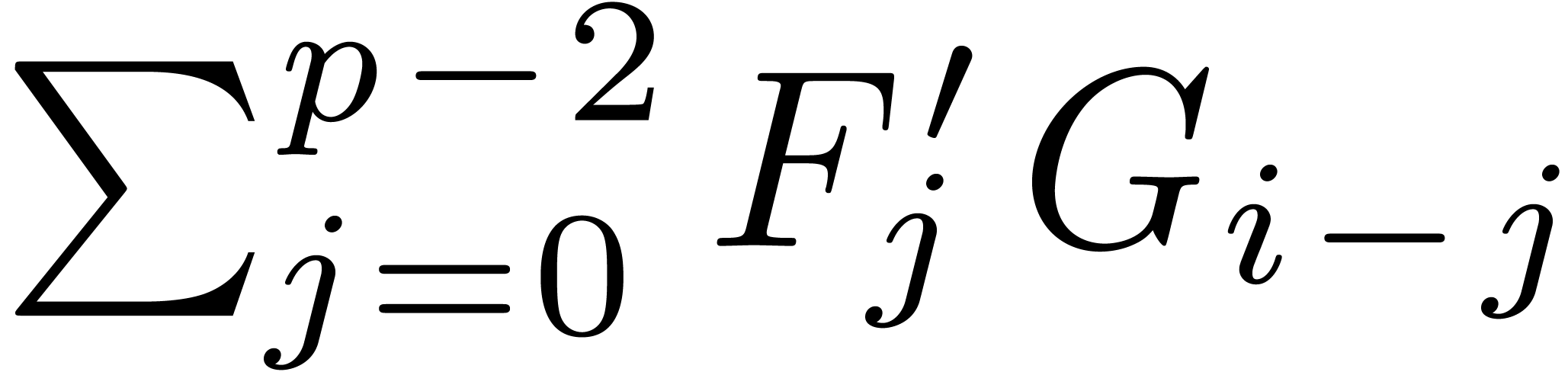 in
in 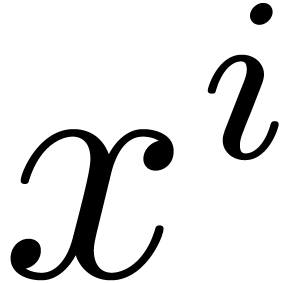 in the product
of the (Laurent) polynomials
in the product
of the (Laurent) polynomials
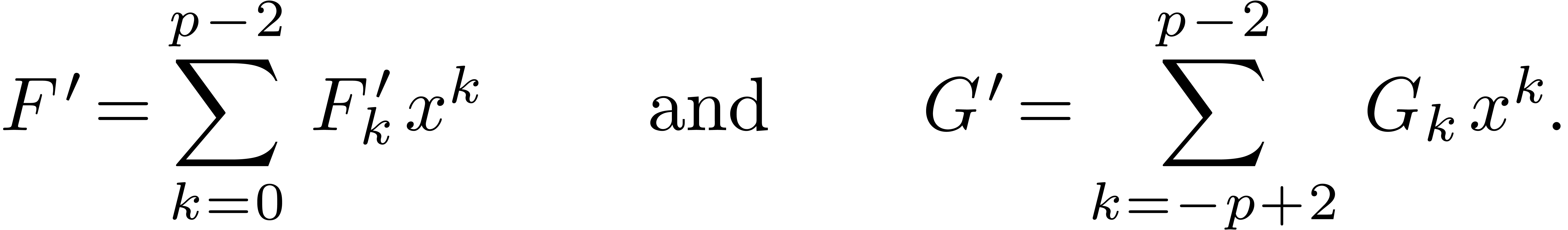
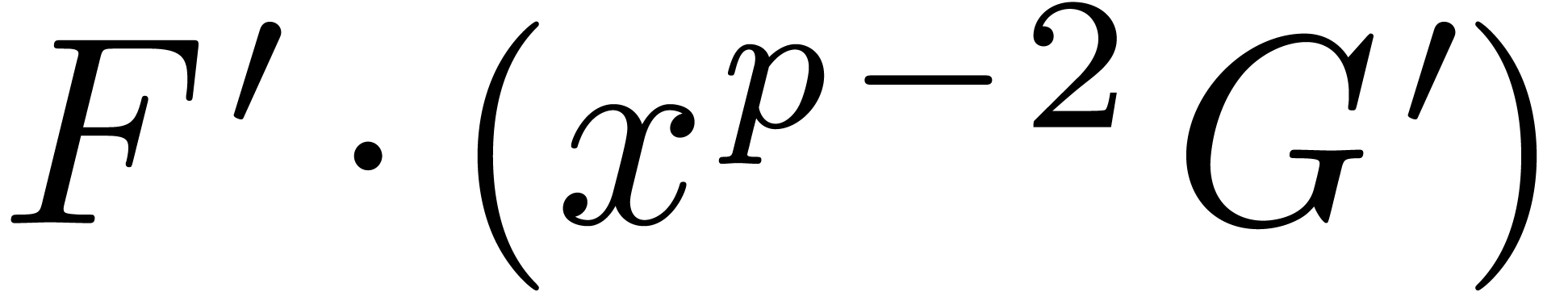 in
in 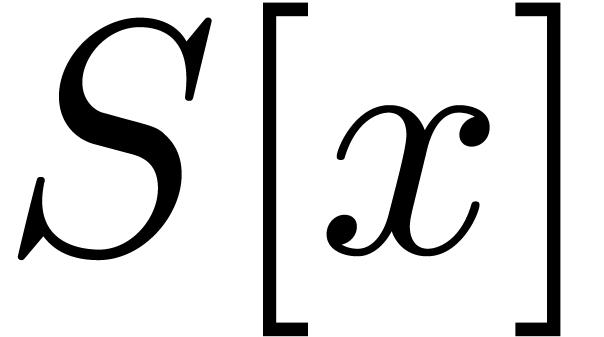 .
.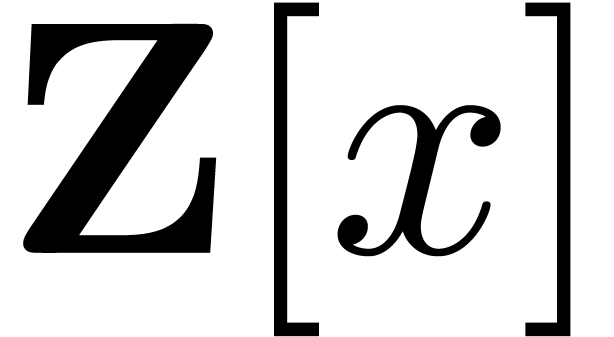 ,
,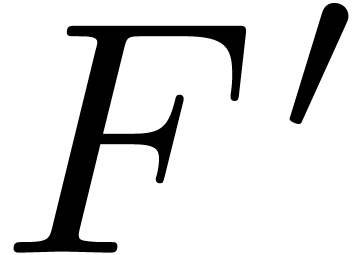 and
and 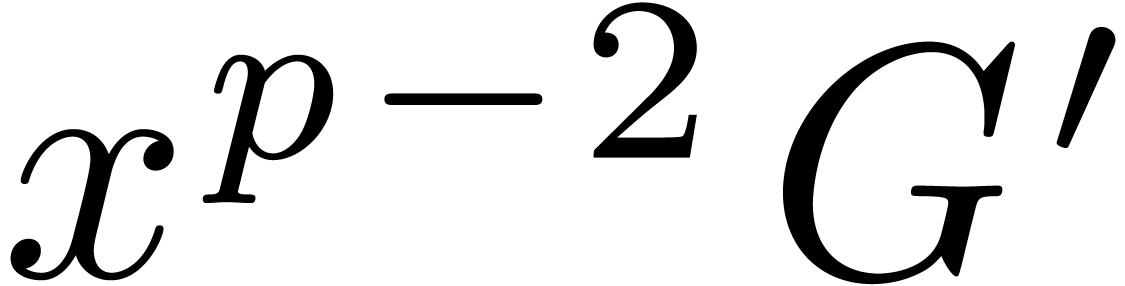 are bounded by
are bounded by 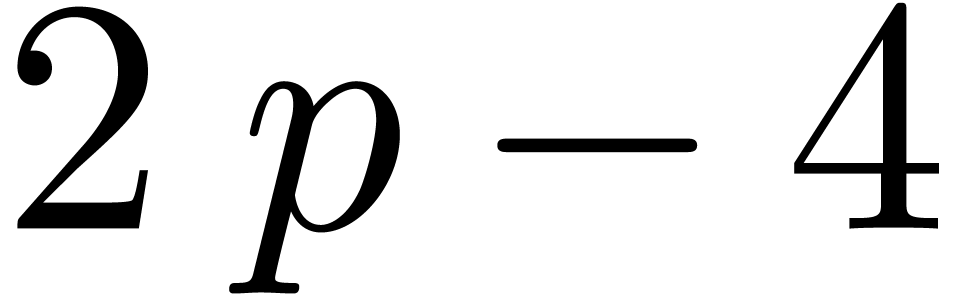 ,
,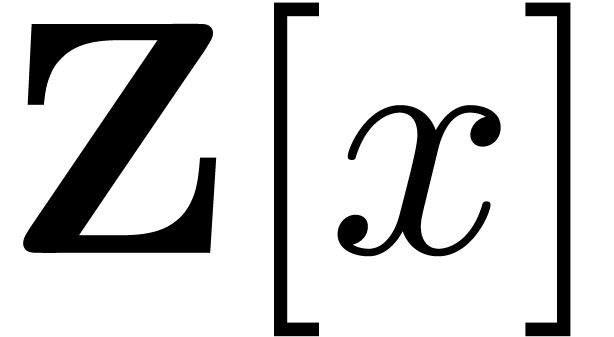 have at most
have at most
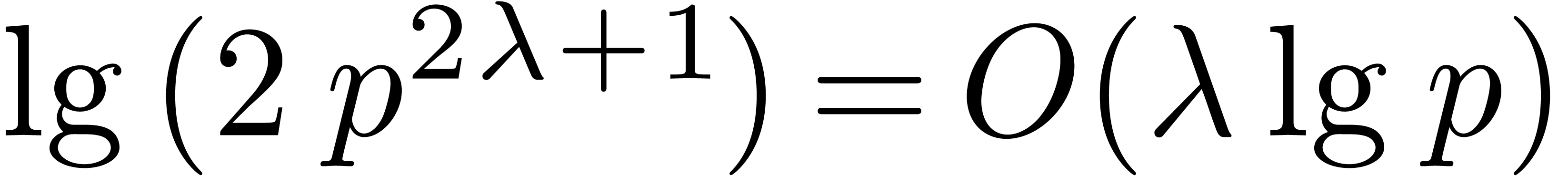 bits. Therefore the integers being multiplied
have at most
bits. Therefore the integers being multiplied
have at most 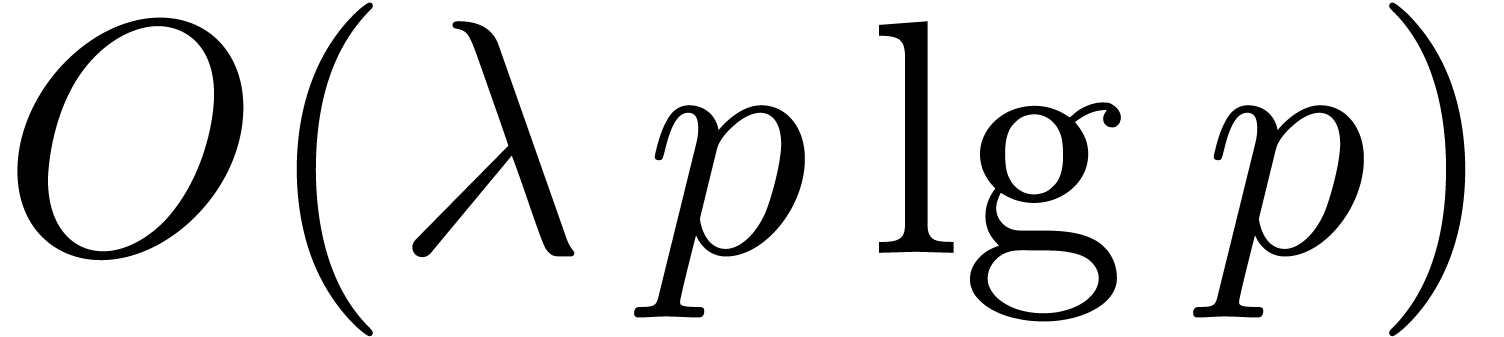 bits, leading to the desired
bits, leading to the desired 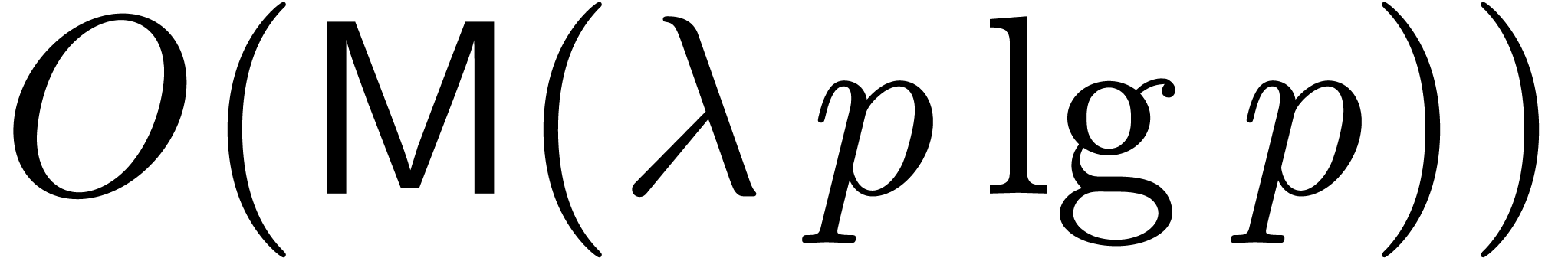 bound. The remaining work consists of
bound. The remaining work consists of 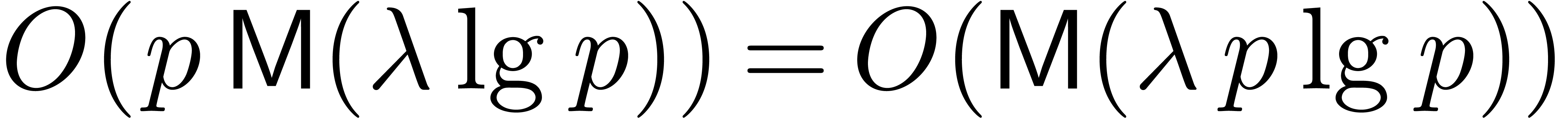 bit operations since
bit operations since 
 and
and
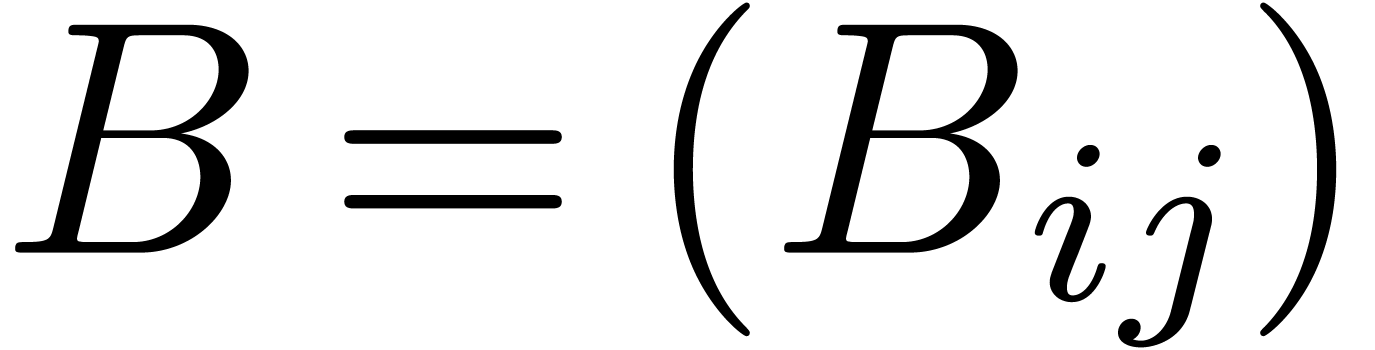 ,
,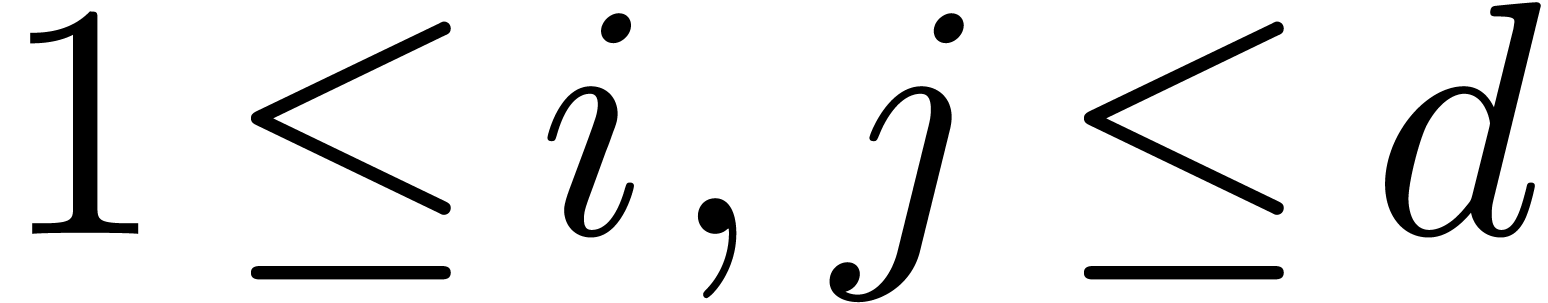 and
and 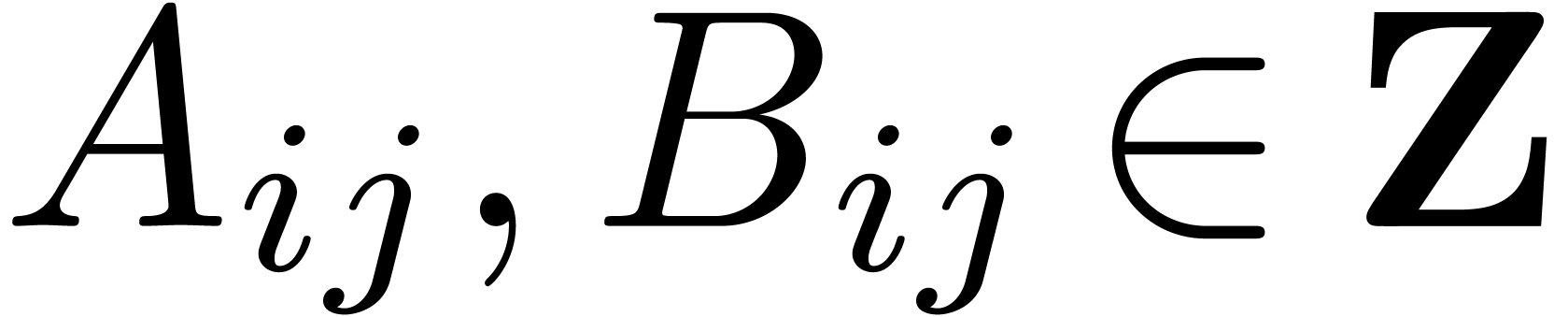 ,
,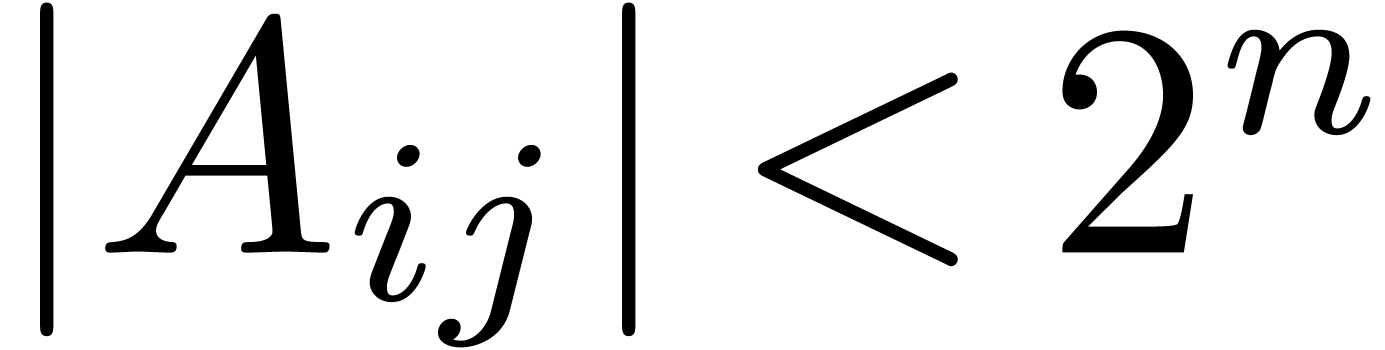 ,
,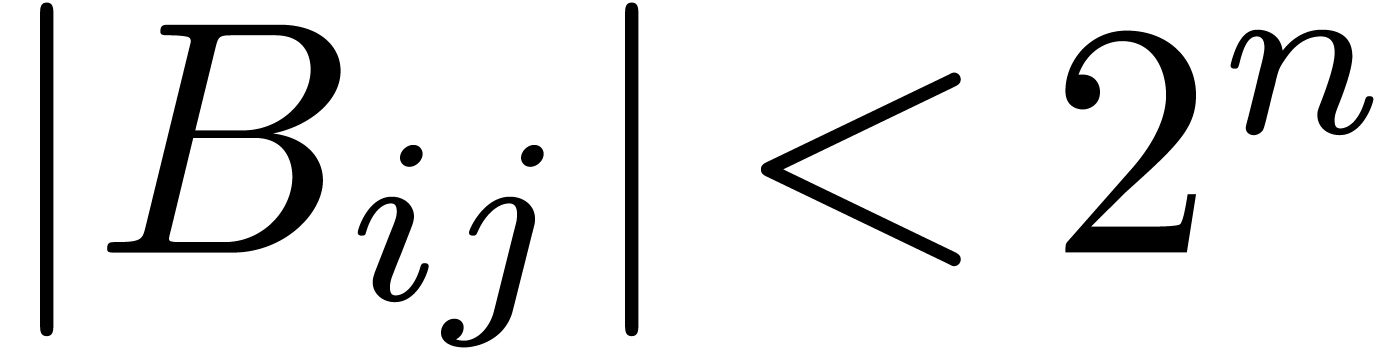 .
.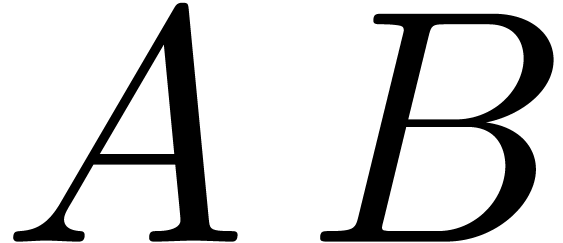 .
.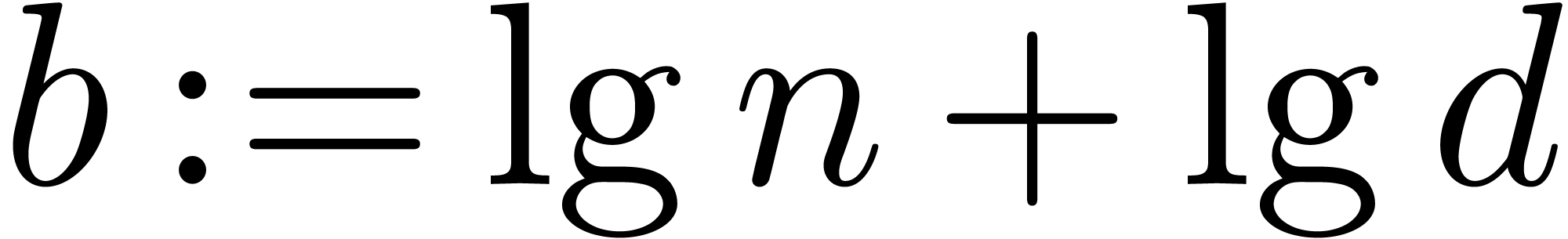 and
and 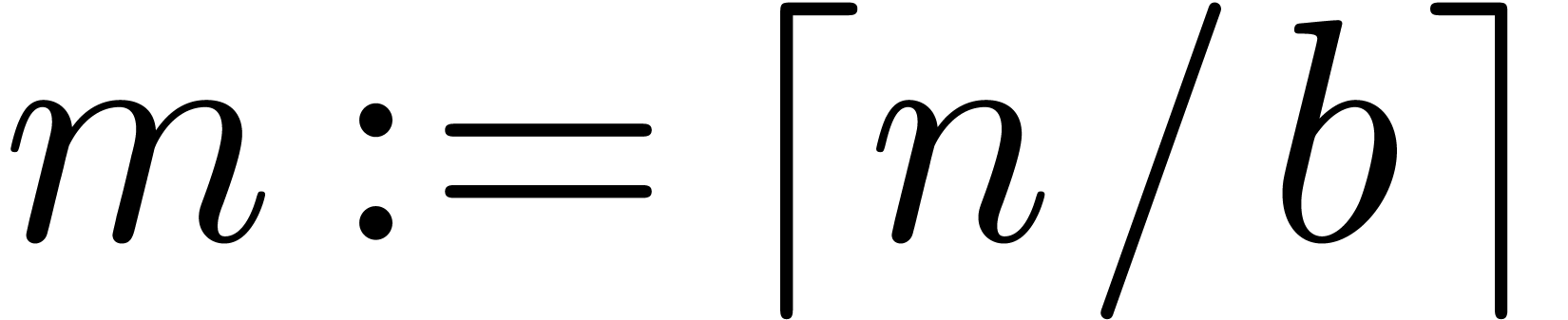 .
.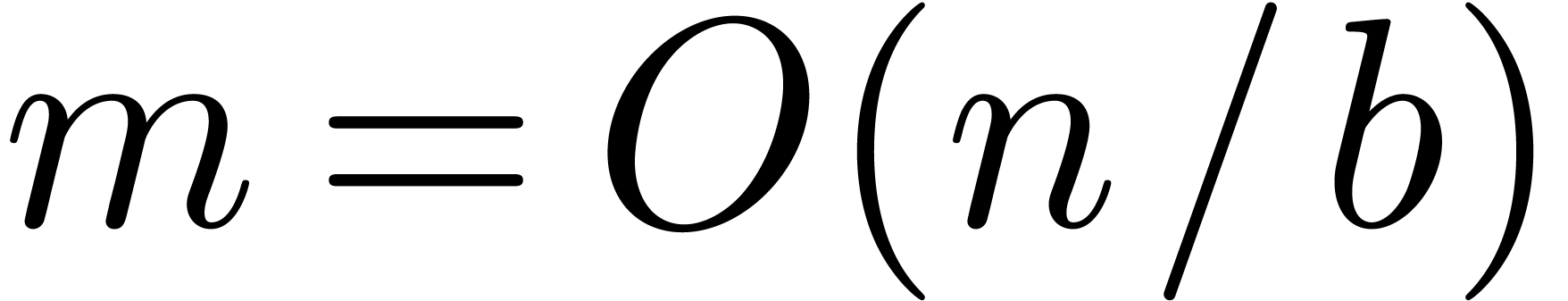 since we assumed that
since we assumed that  .
.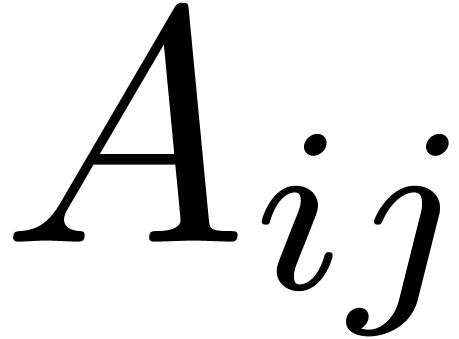 into chunks of
into chunks of 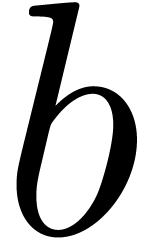 bits, choosing
bits, choosing 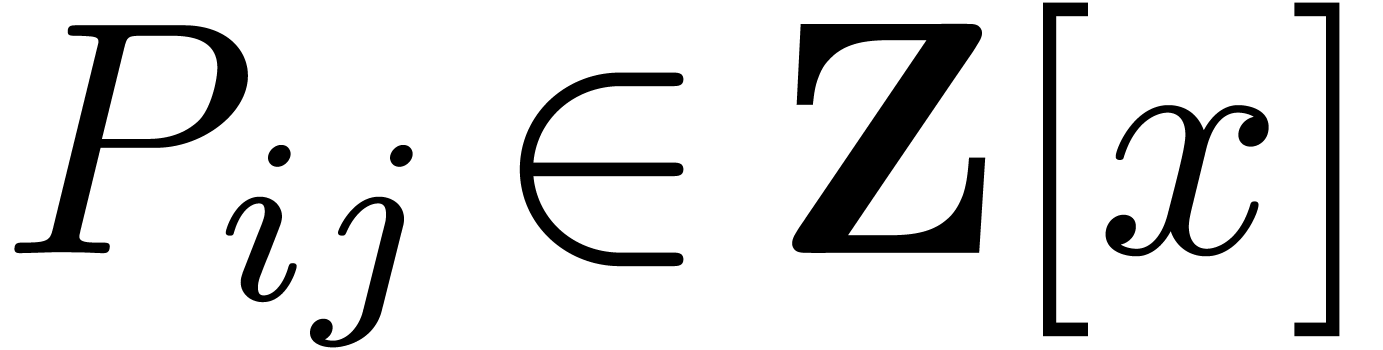 so that
so that 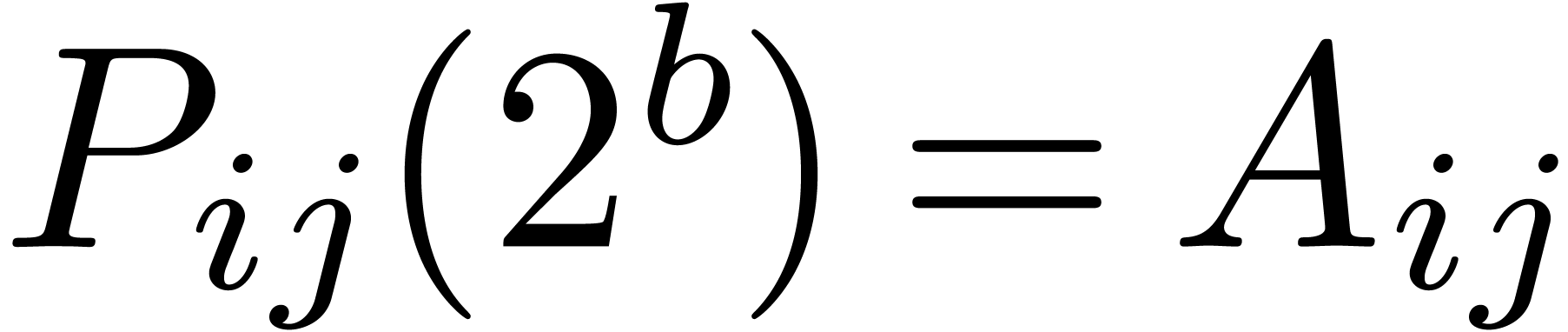 with
with 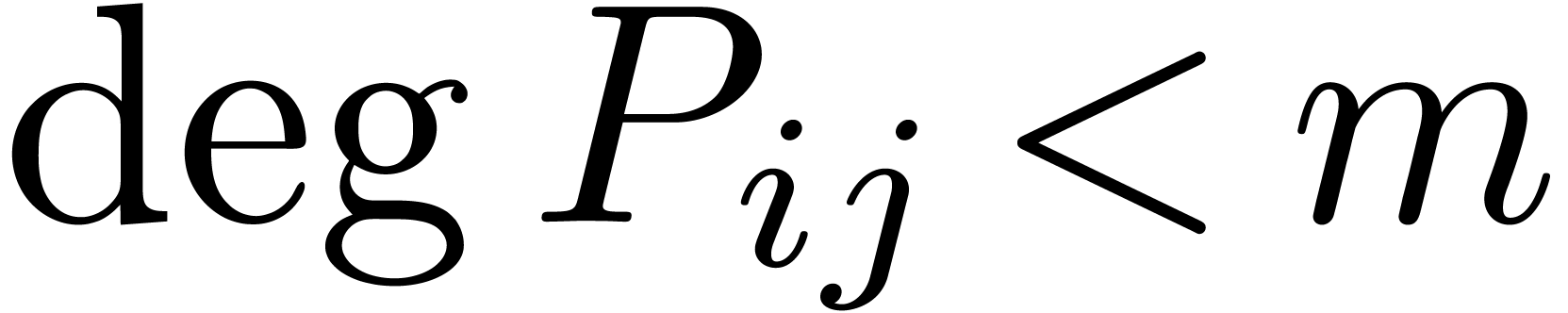 ,
,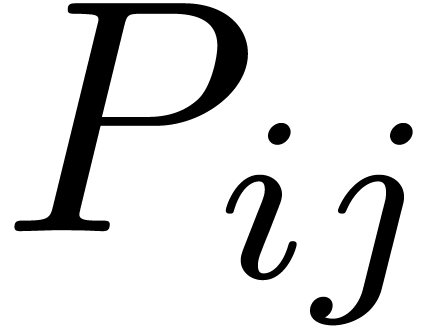 are bounded in
absolute value by
are bounded in
absolute value by 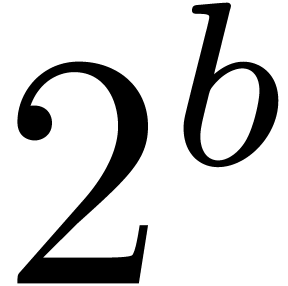 .
.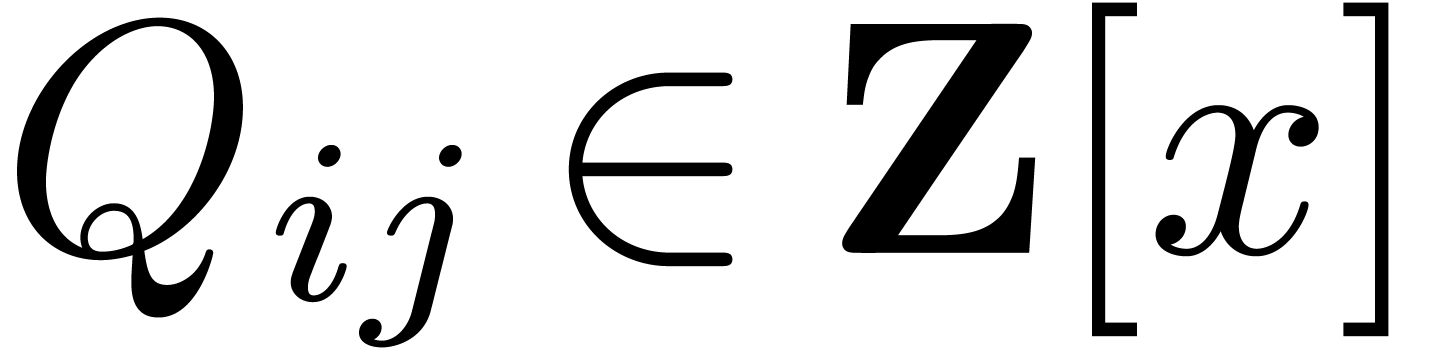 for
for 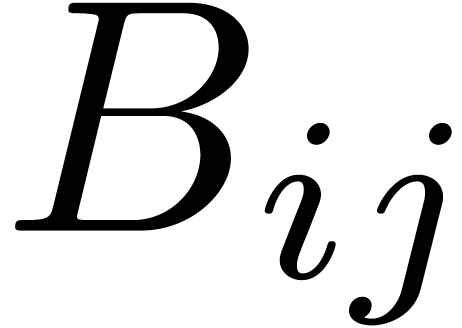 .
.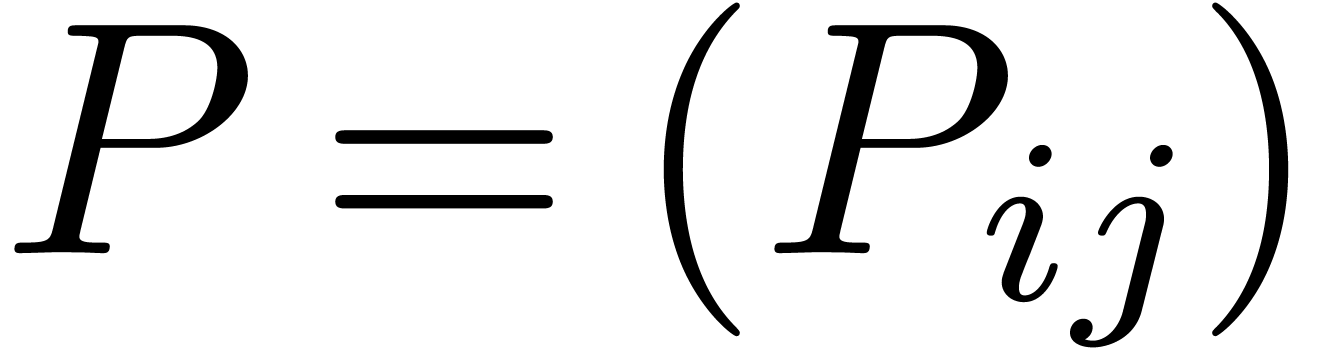 and
and 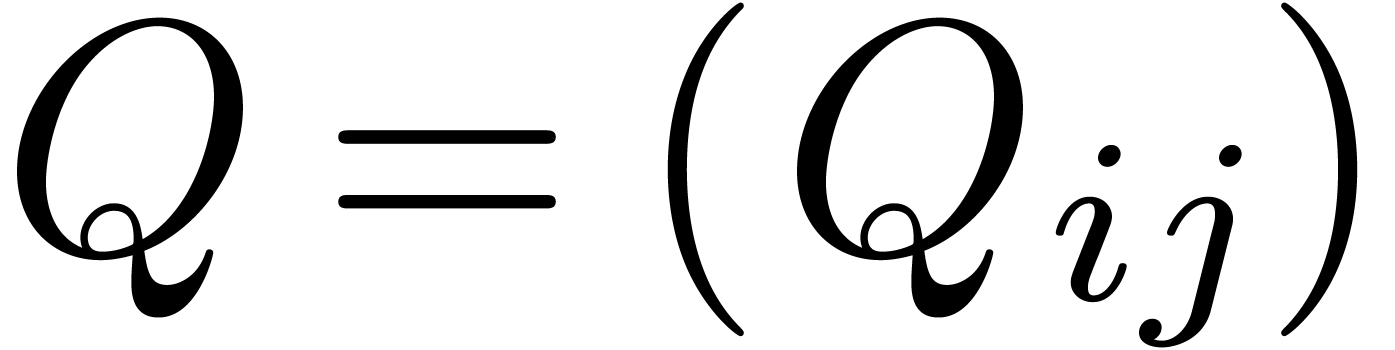 be the
corresponding
be the
corresponding 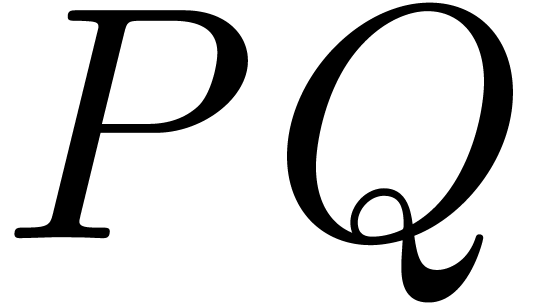 are bounded in
absolute value by
are bounded in
absolute value by 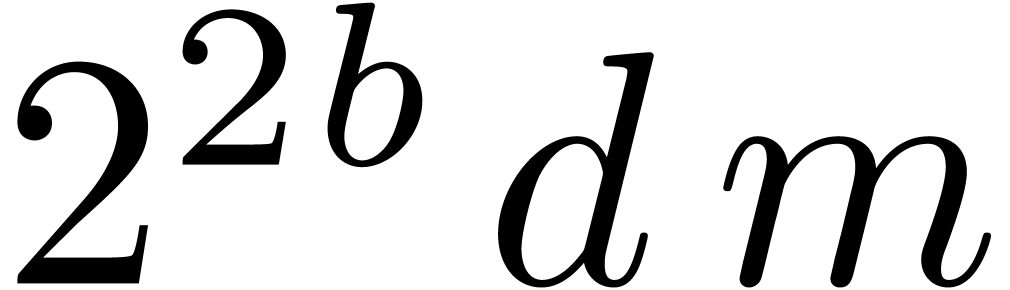 ,
,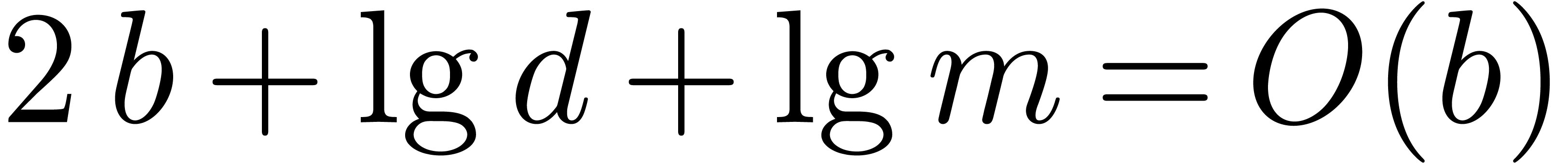 .
.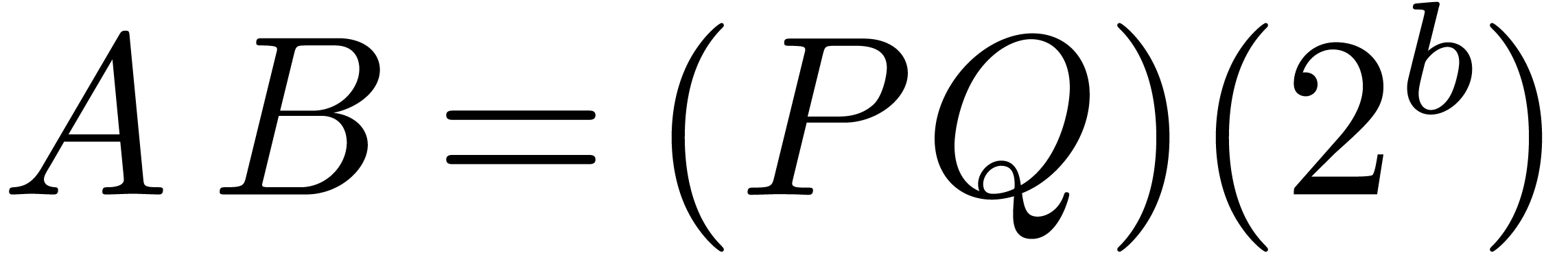 may be deduced from
may be deduced from 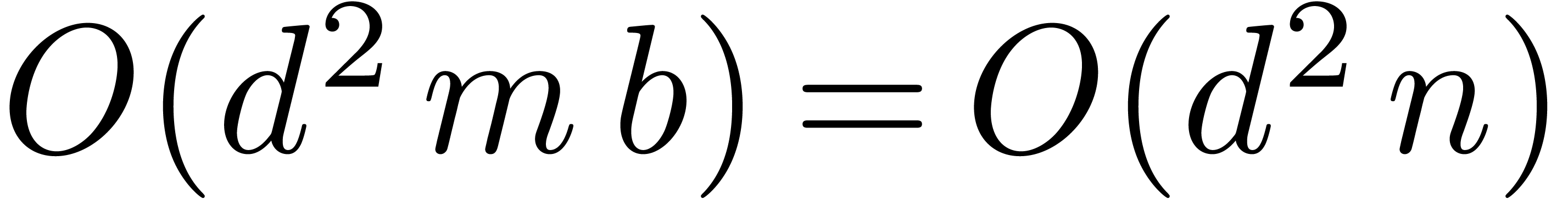 .
.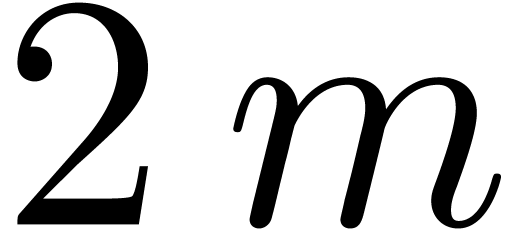 .
.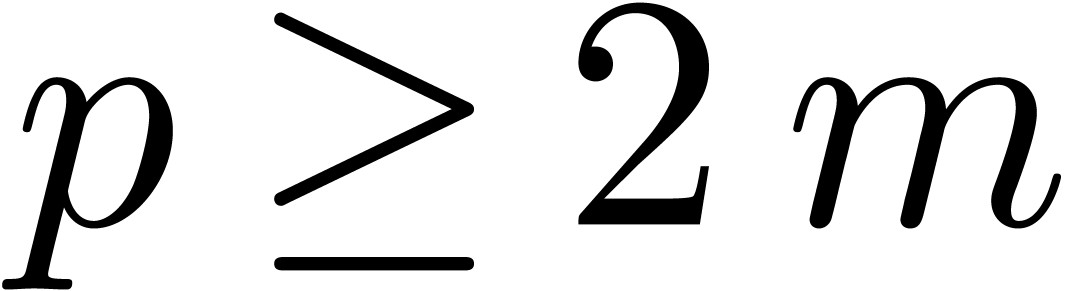 .
.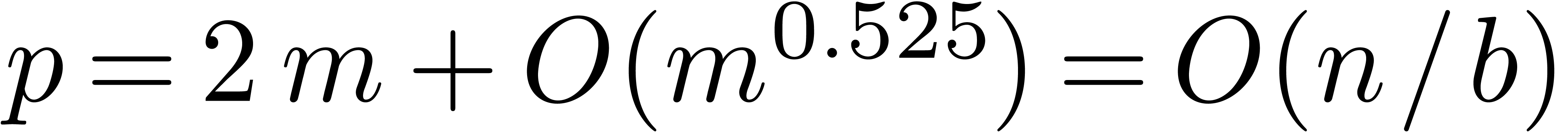 .
.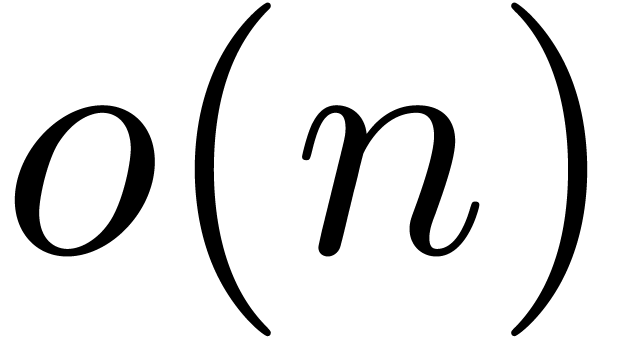 ,
,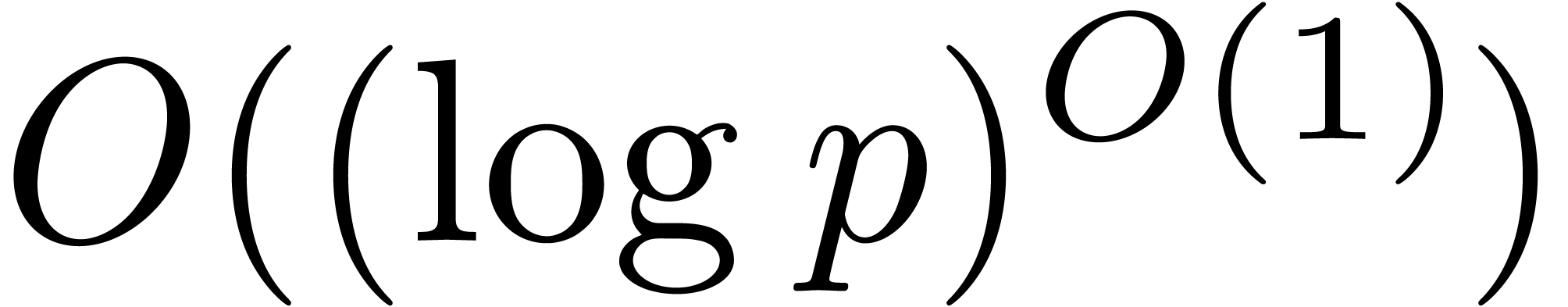 bit operations [
bit operations [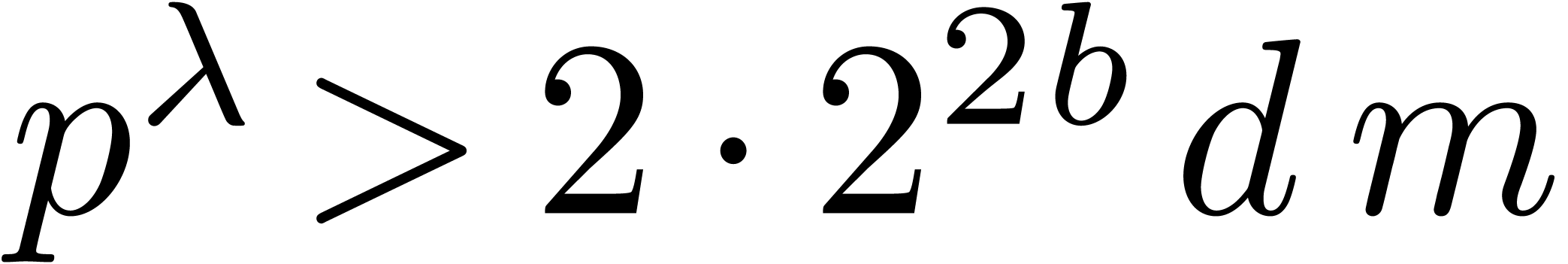 .
.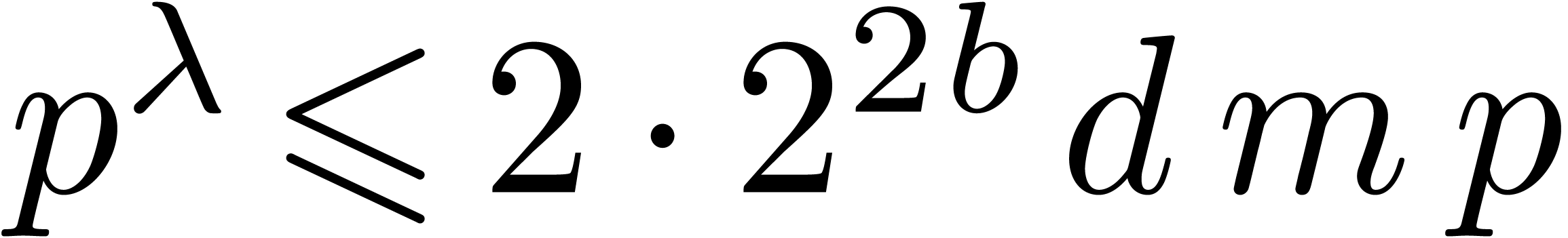 we have
we have 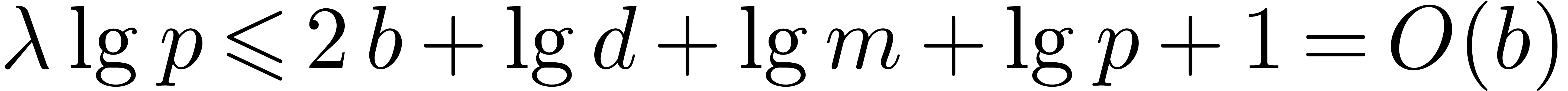 .
.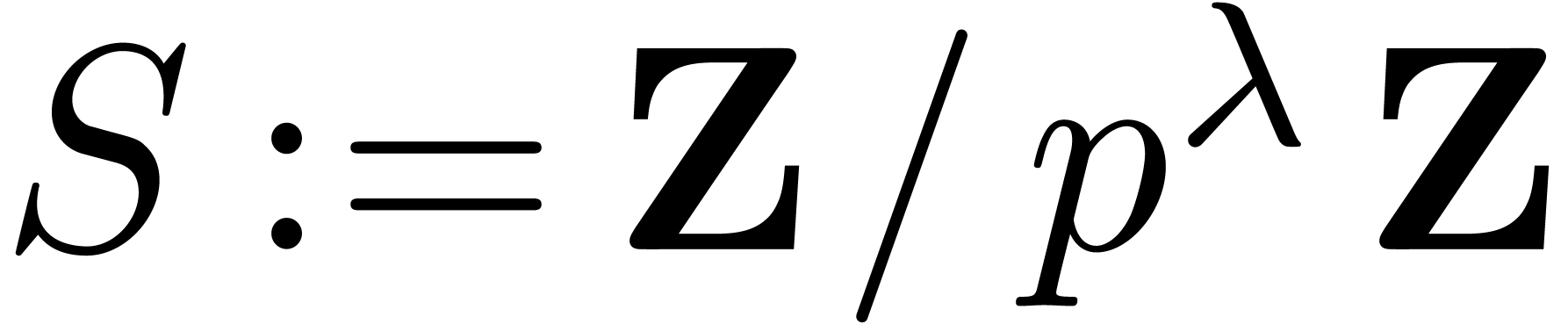 by means of
an evaluation-interpolation scheme, using Lemma
by means of
an evaluation-interpolation scheme, using Lemma 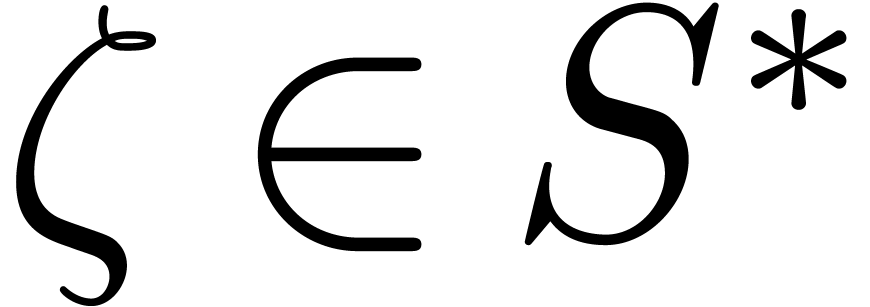 of order
of order 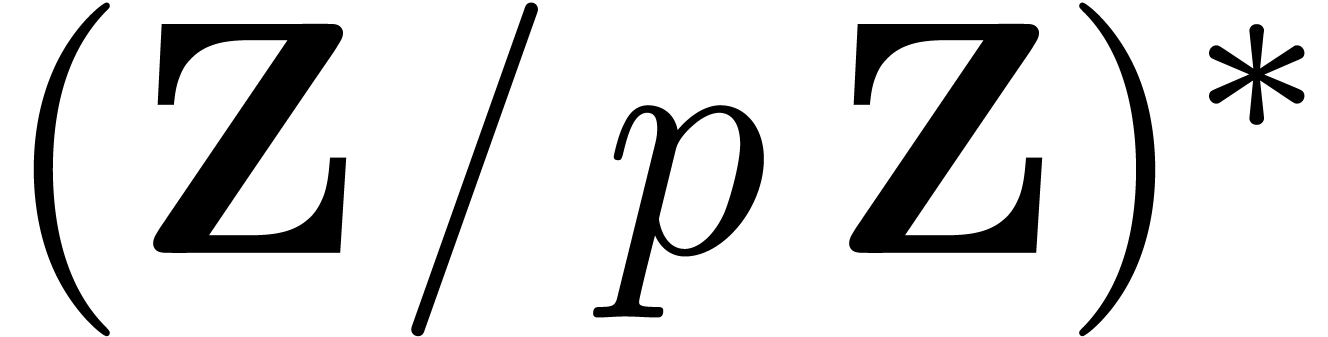 in (deterministic) time
in (deterministic) time 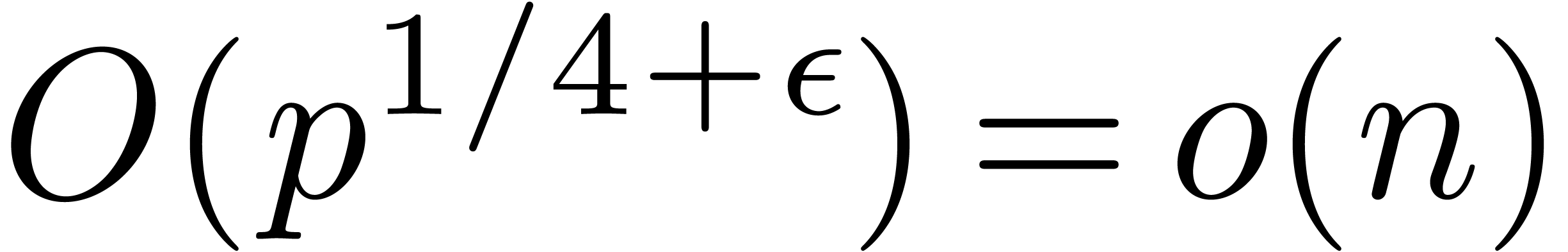 [
[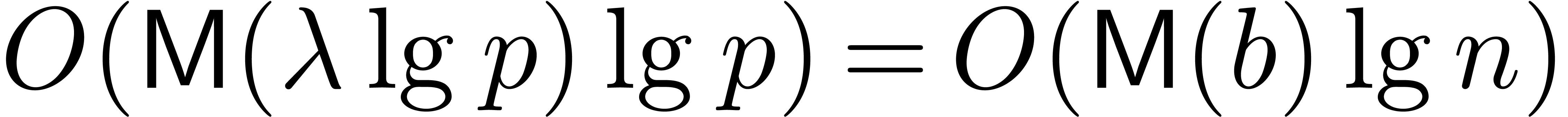 [
[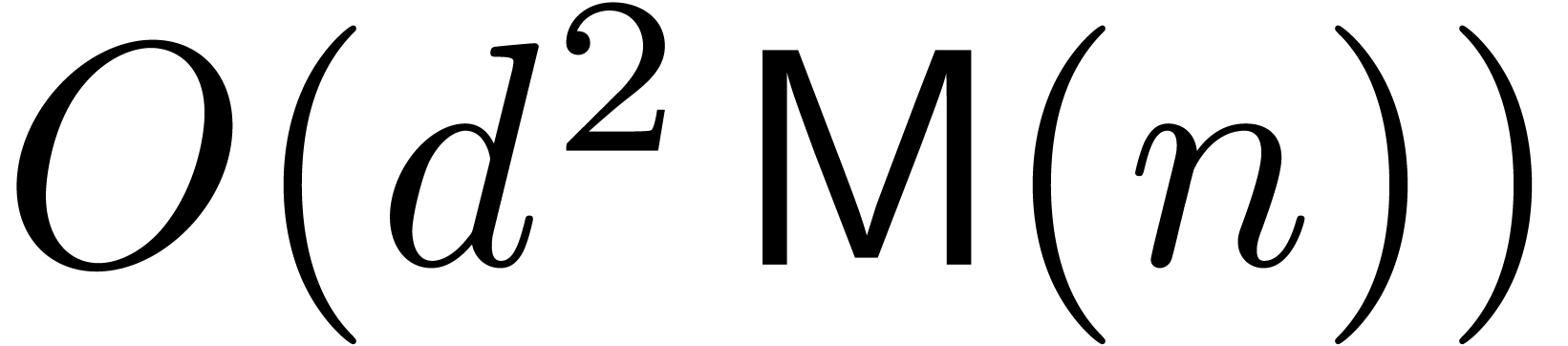 (one may check the cases
(one may check the cases 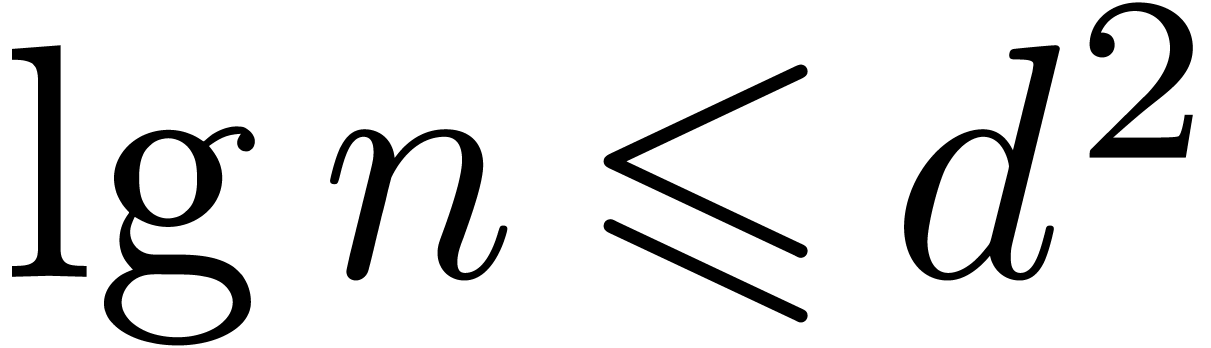 and
and 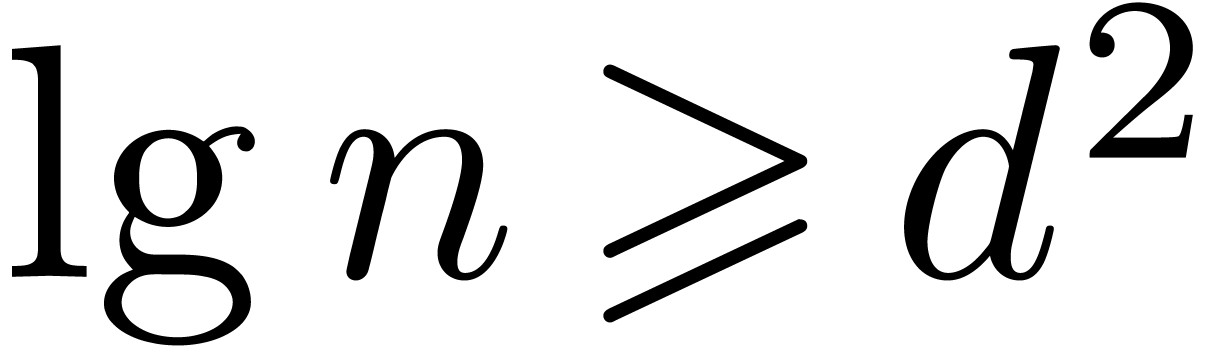 separately).
separately).
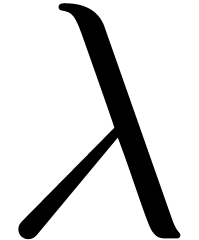 and
and 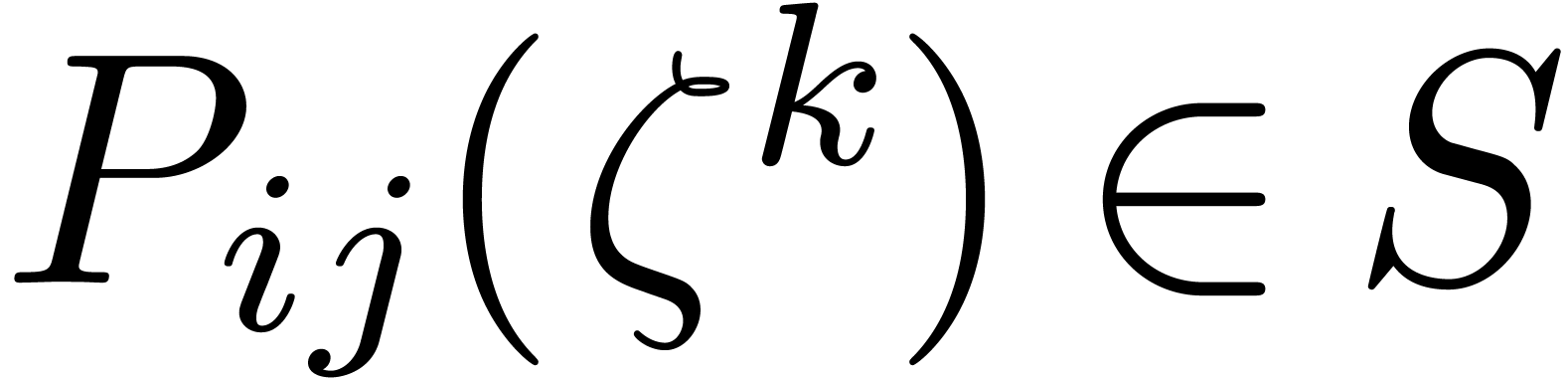 and
and 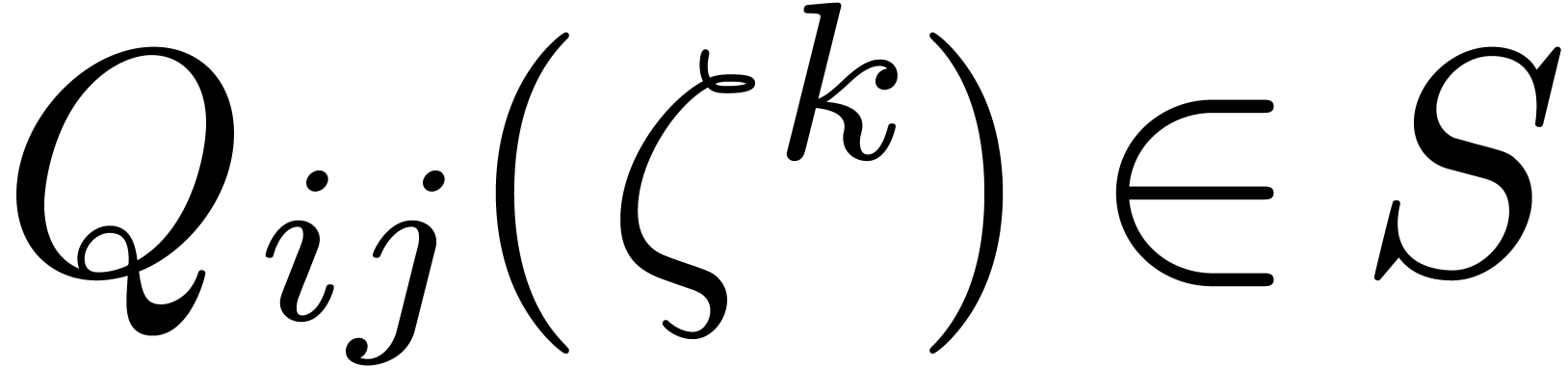 for
for  .
.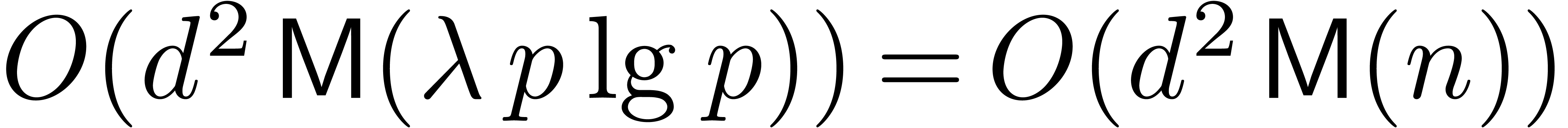 .
.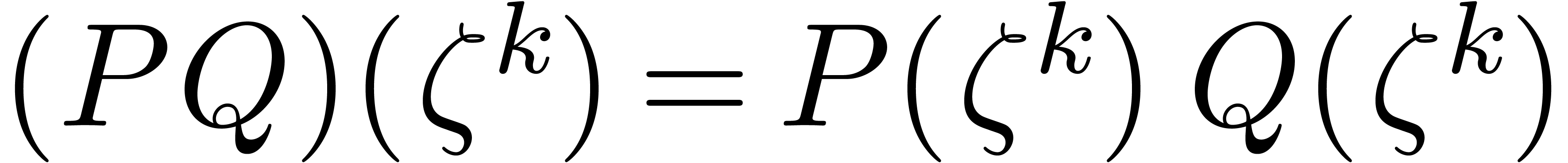 .
.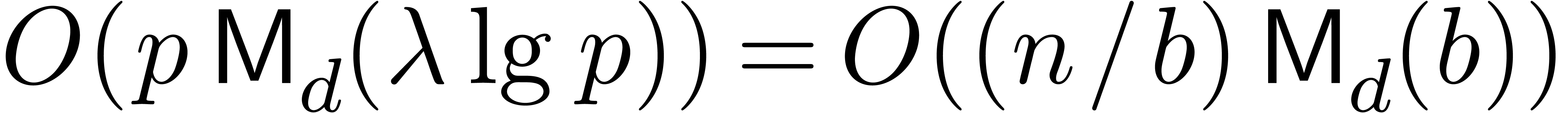 .
.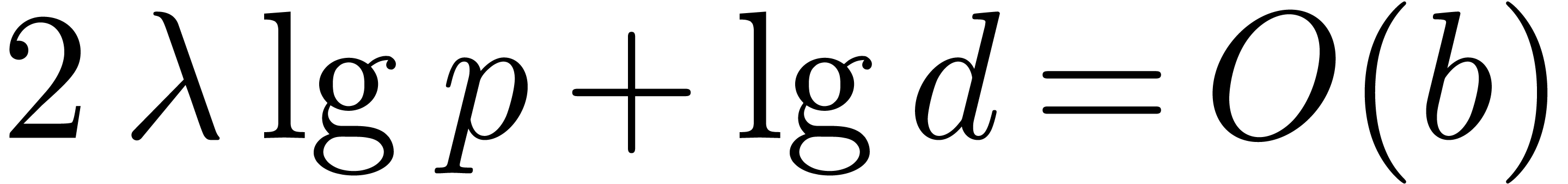 ,
,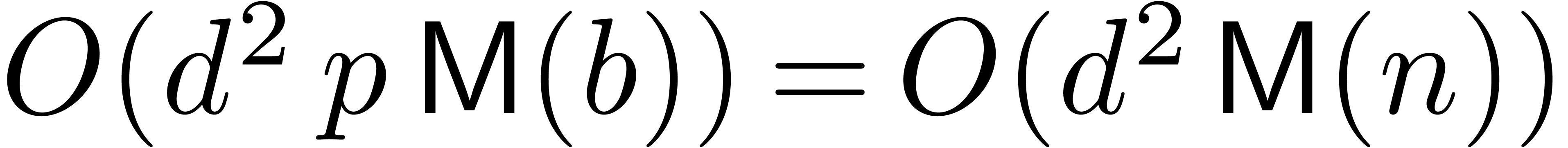 .
. .
. using Lemma
using Lemma 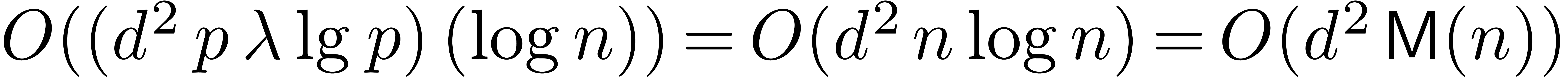 bit
operations, since we assumed that
bit
operations, since we assumed that 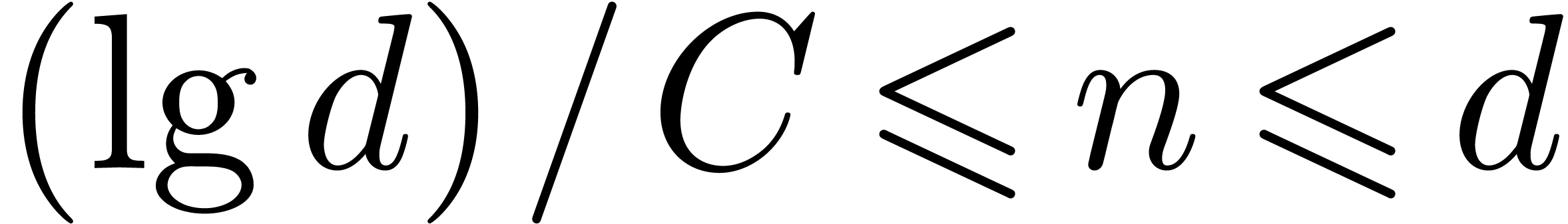 by a “ring” of finite-precision approximations to complex
numbers, and obtain results of the same strength. The latter approach
has the disadvantage that it introduces a tedious floating-point error
analysis.
by a “ring” of finite-precision approximations to complex
numbers, and obtain results of the same strength. The latter approach
has the disadvantage that it introduces a tedious floating-point error
analysis.
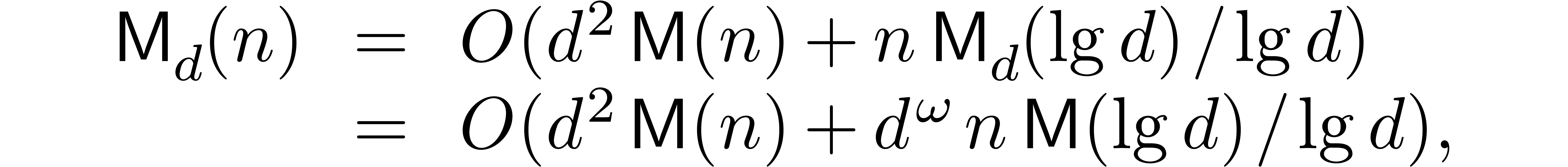 .
.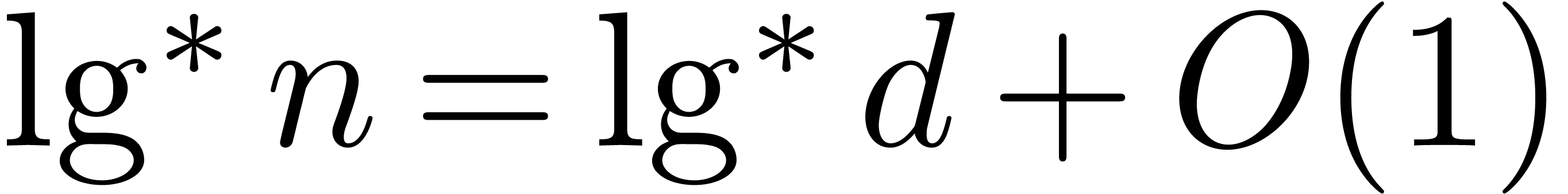
 ,
,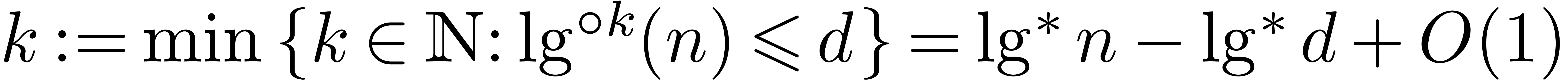 .
.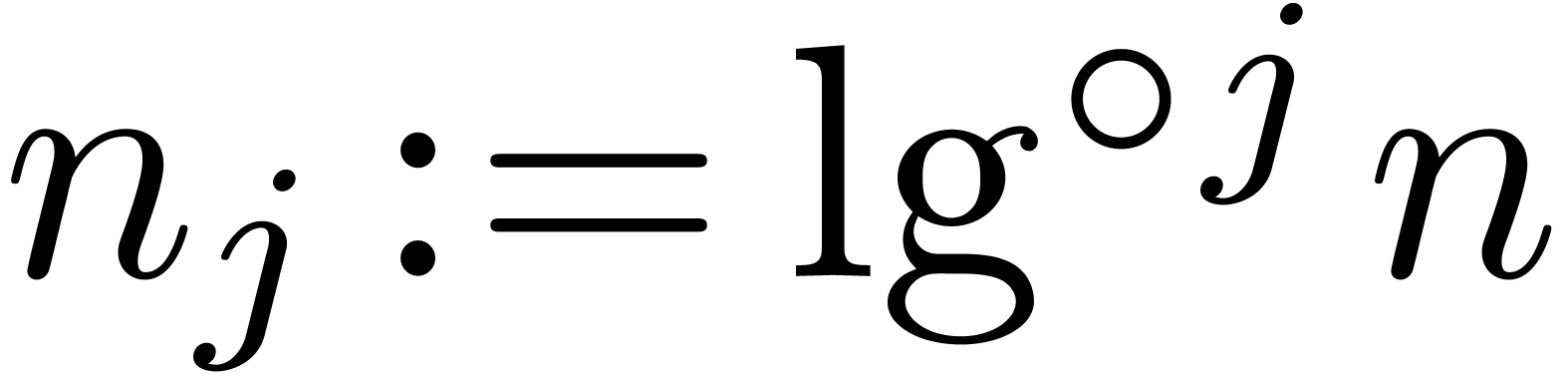 ,
,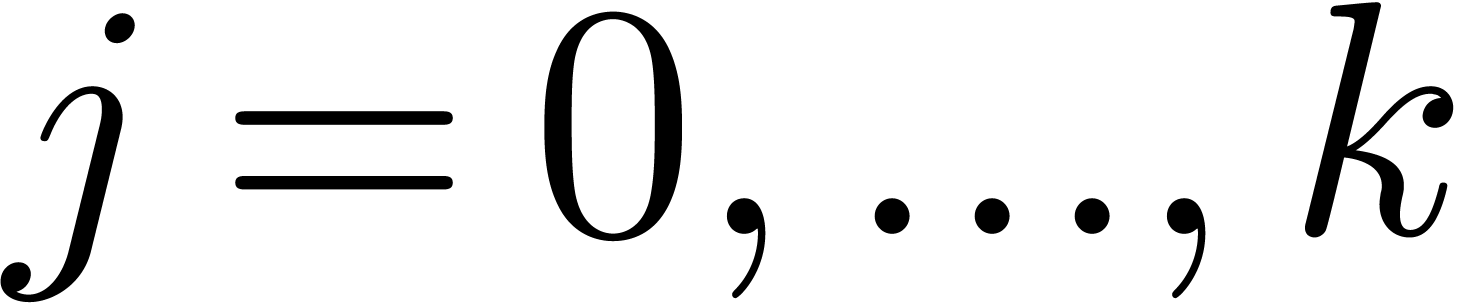 for
for 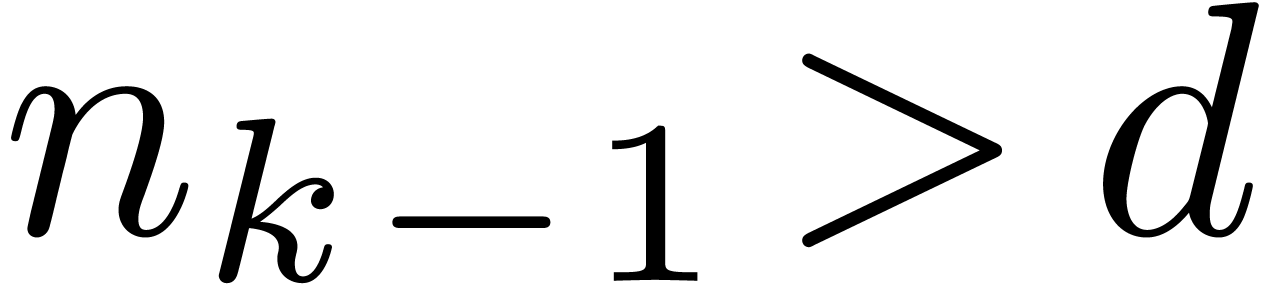 ,
,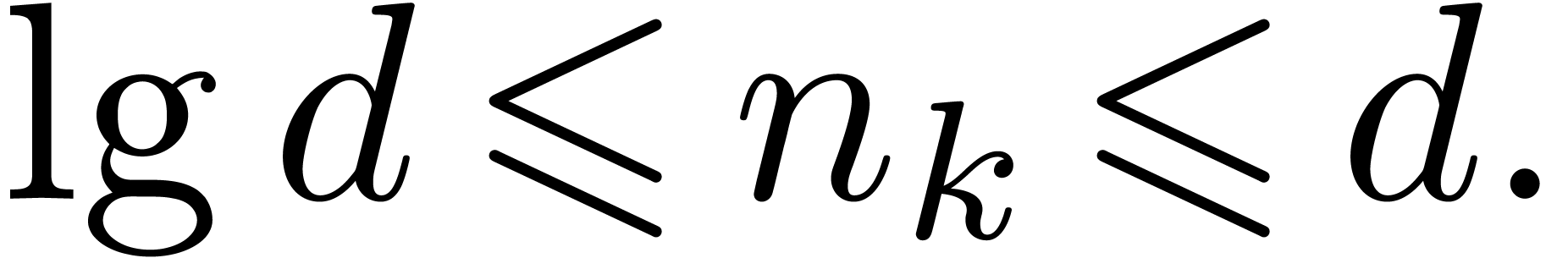 and
and 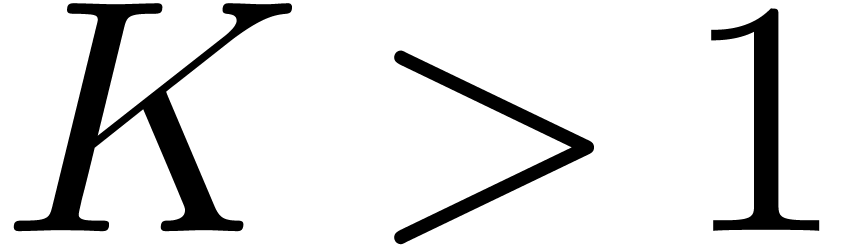 By Proposition
By Proposition  (depending only on
(depending only on 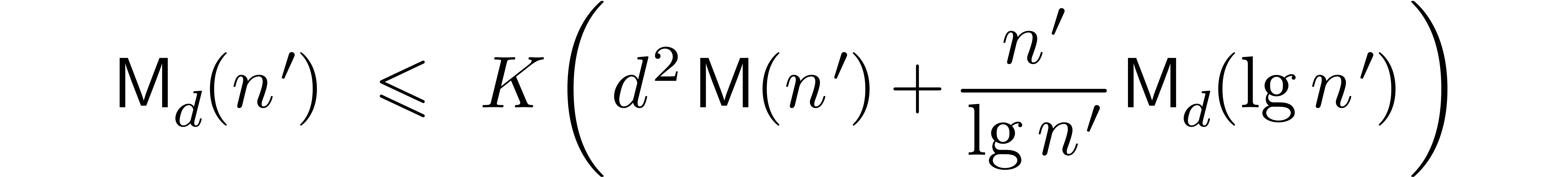 )
)
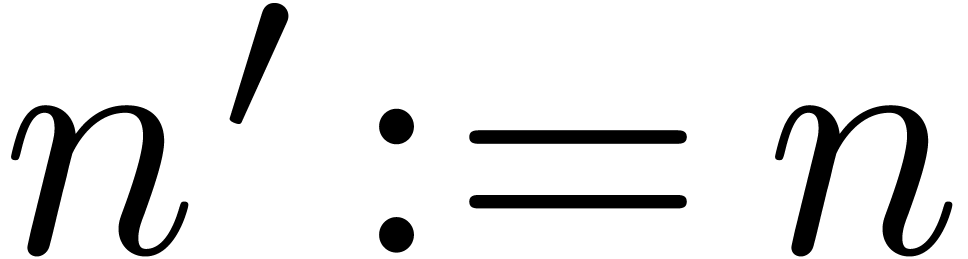 .
.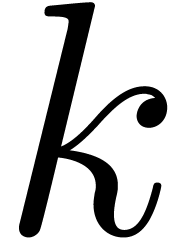 and iterating
and iterating  times yields
times yields
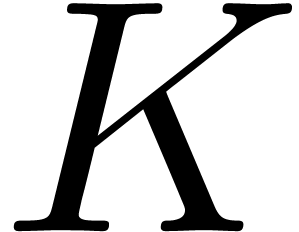
 if
necessary) to obtain
if
necessary) to obtain
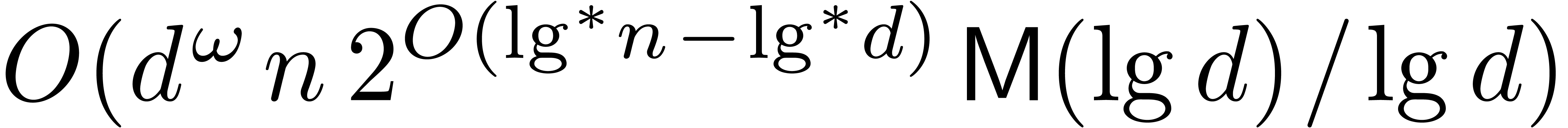
 .
.
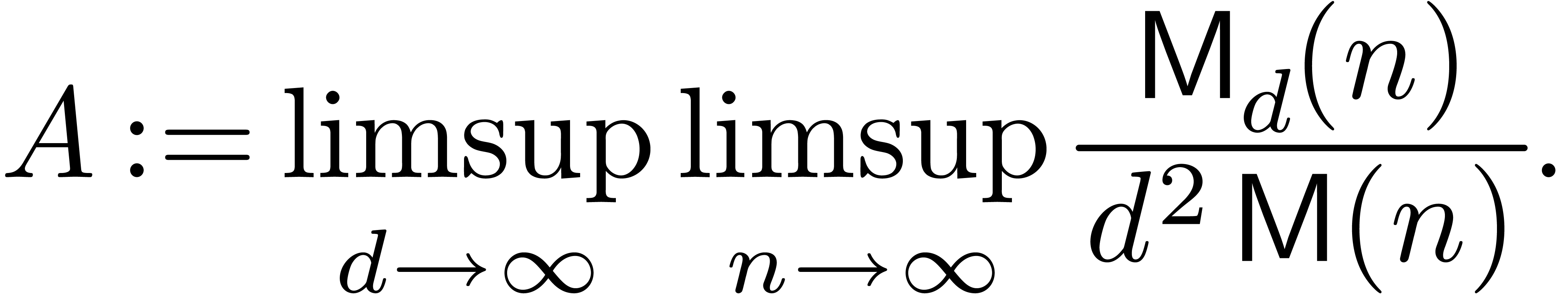 constant
in Theorem
constant
in Theorem 
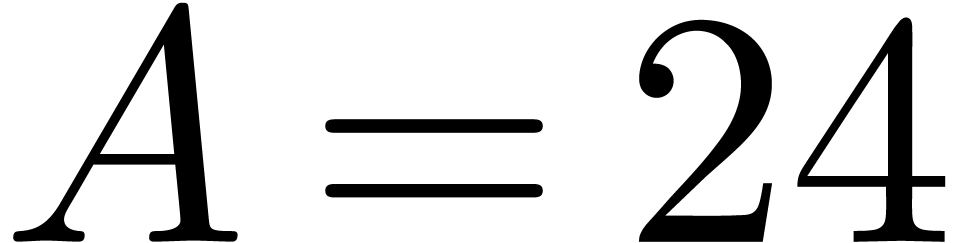 .
.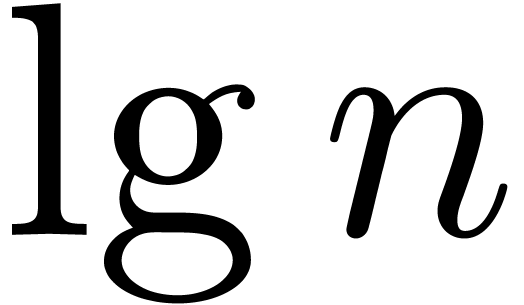 .
.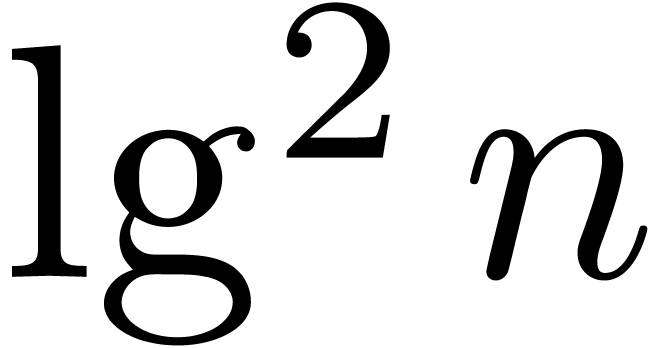 to
to 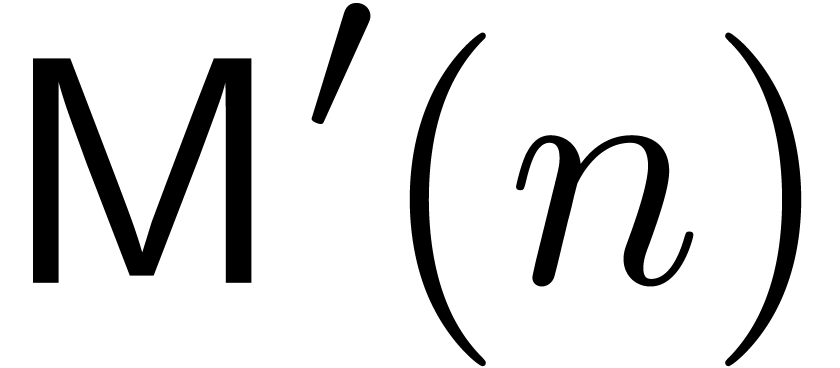 ,
,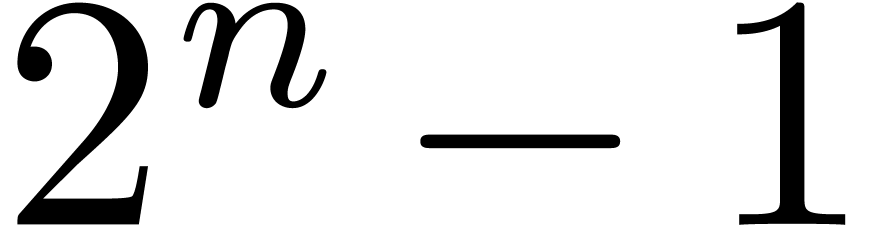 to be the cost of an
to be the cost of an 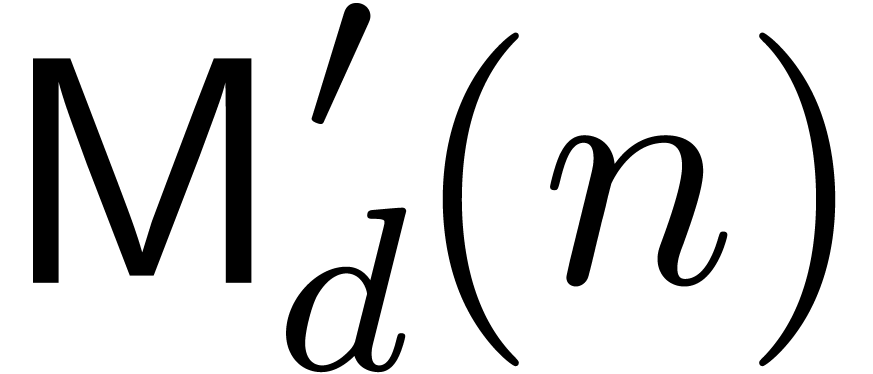 .
. be the cost of the
corresponding
be the cost of the
corresponding 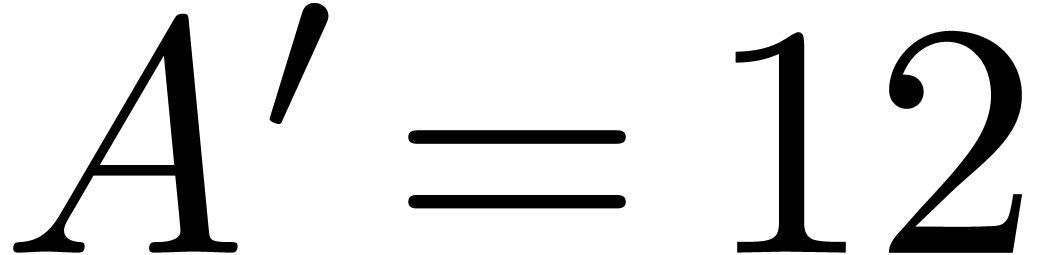 be the
corresponding constant defined as above. Then by mapping the Bluestein
convolution directly to integer convolution, one saves a factor of two,
obtaining
be the
corresponding constant defined as above. Then by mapping the Bluestein
convolution directly to integer convolution, one saves a factor of two,
obtaining 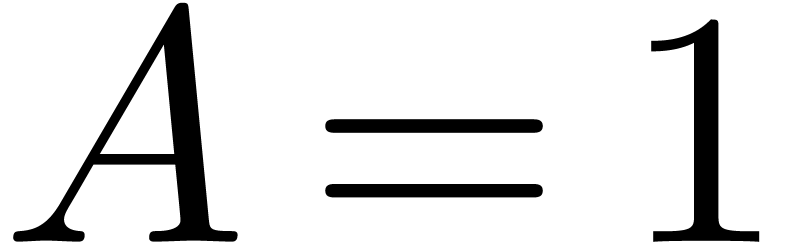 .
.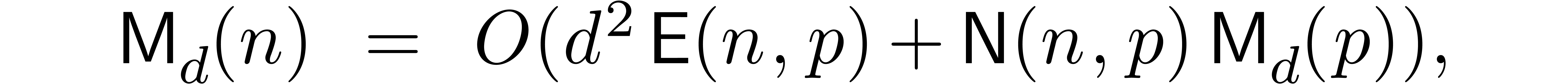 .
.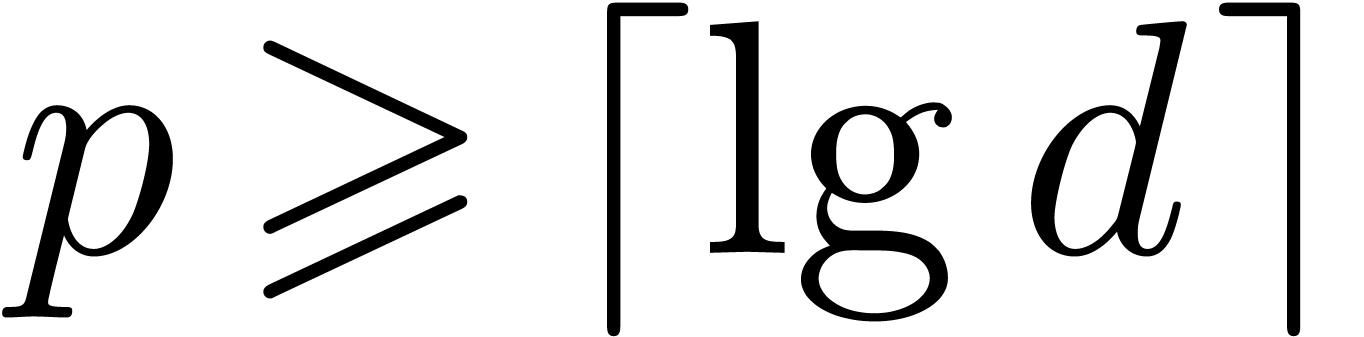
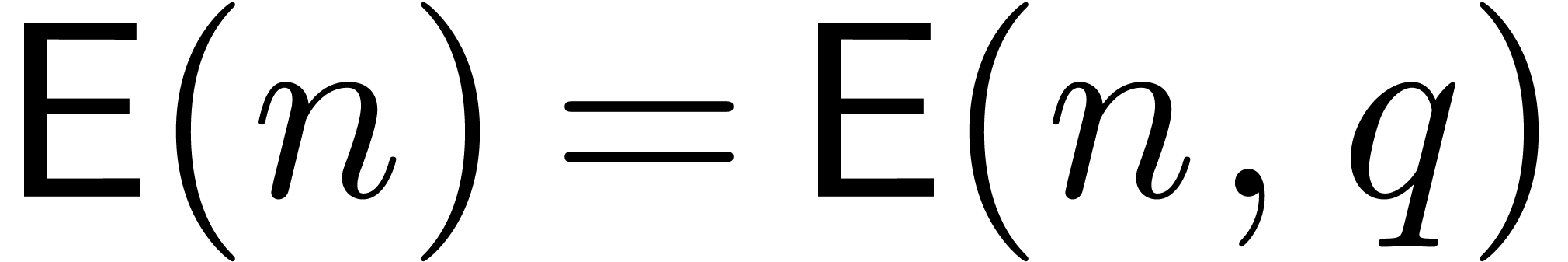 .
.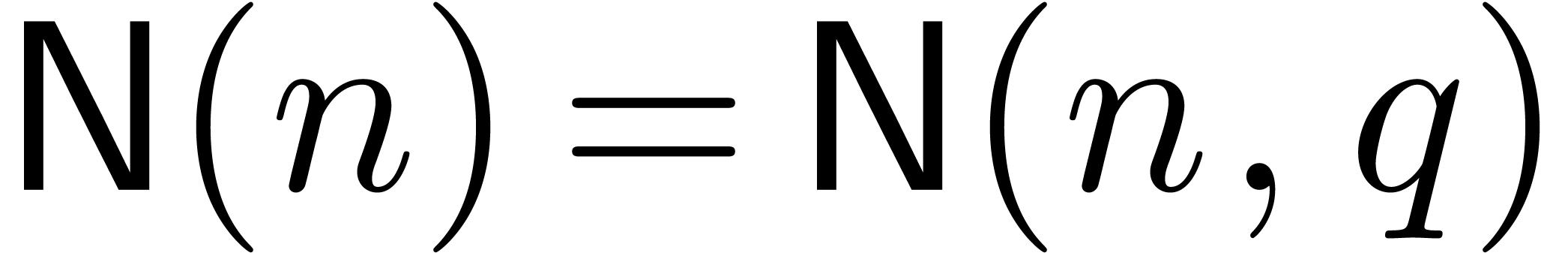 and
and  for some small fixed
precision
for some small fixed
precision 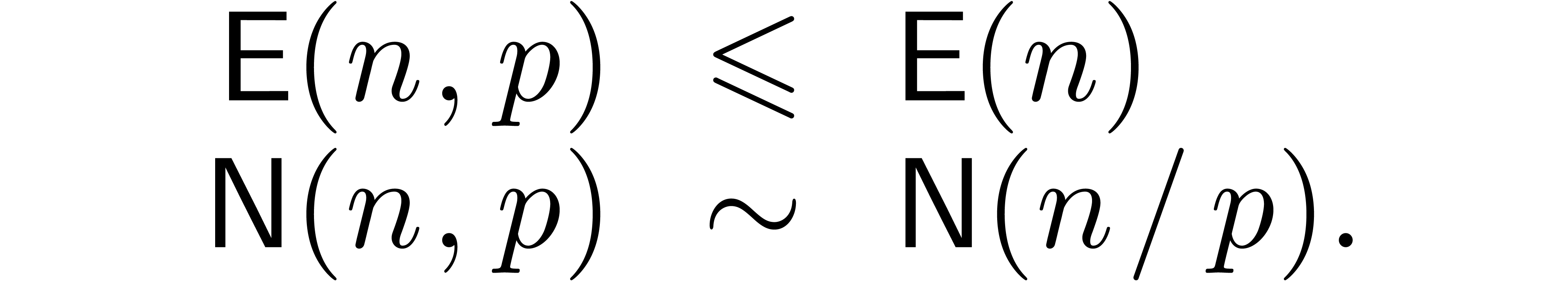 ,
,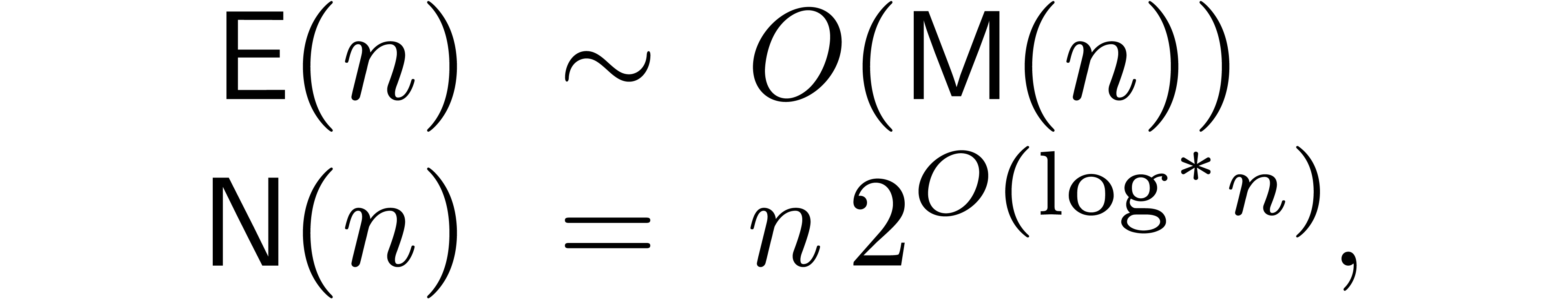
 Annual Symposium on Theory of Computing
(New York City), may 25–27 1987, pp. 1–6.
Annual Symposium on Theory of Computing
(New York City), may 25–27 1987, pp. 1–6.