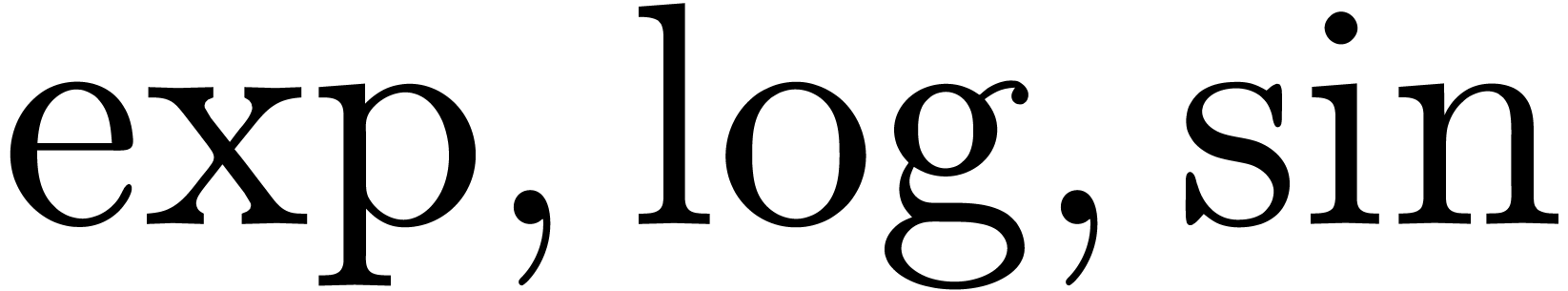A holonomic function is an analytic function, which satisfies a linear differential equation with polynomial coefficients. In particular, the elementary functions 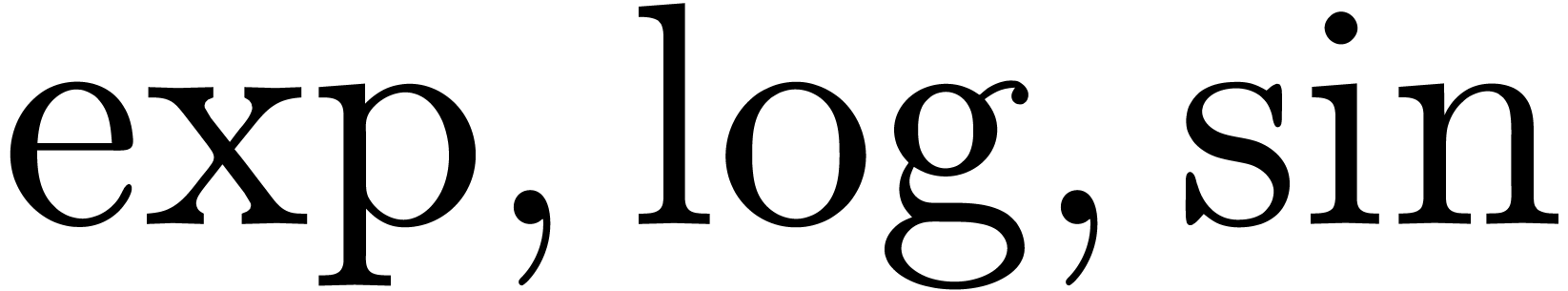, etc. and many special functions like , , Bessel functions, etc. are holonomic functions.

Given a holonomic function 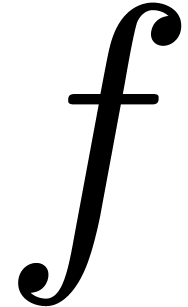(determined by the linear differential equation it satisfies and initial conditions in a non singular point ), we show how to perform arbitrary precision evaluations of 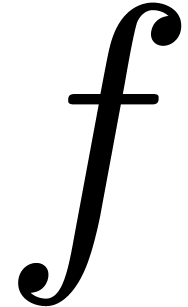at a non singular point on the Riemann surface of 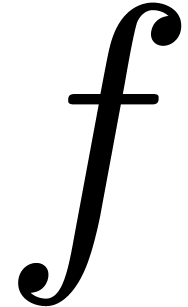, while estimating the error.

Moreover, if the coefficients of the polynomials in the equation for 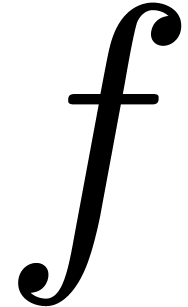are algebraic numbers, then our algorithm is asymptotically very fast: if 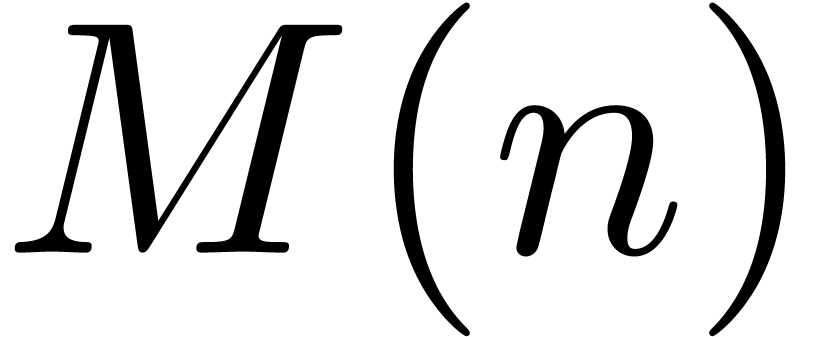is the time needed to multiply two 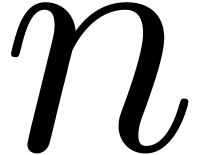digit numbers, then we need a time 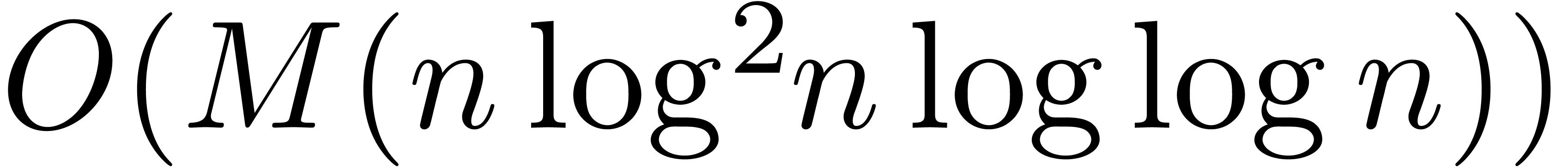to compute 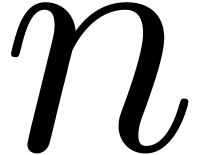digits of .

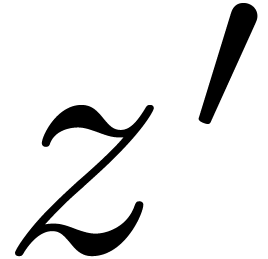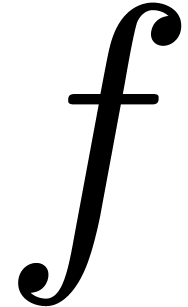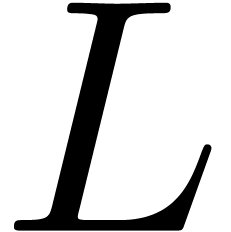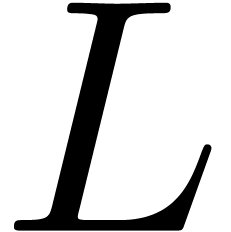The above algorithm becomes inefficient, when approaches a singularity of . We extend our efficient algorithms to the evaluation of holonomic functions near and in singular points where the differential operator is regular (or, slightly more generally, where is quasi-regular — a concept to be introduced below). We will give an application of this extension to the efficient evaluation of polylogarithms and the computation of multiple zeta values.

Occasions: seminar Alpha & Géode at École polytechnique, March 17, 1998; seminar at INRIA Lorraine, March 8, 1998

Documents: slides

Note: the first algorithm for non singular points was essentially a rediscovery of a similar result by the Chudnovky brothers (however, there were a few improvements: a better asymptotic complexity and full control of the error). The extension to the quasi-regular case was only published in 2001 in JSC.