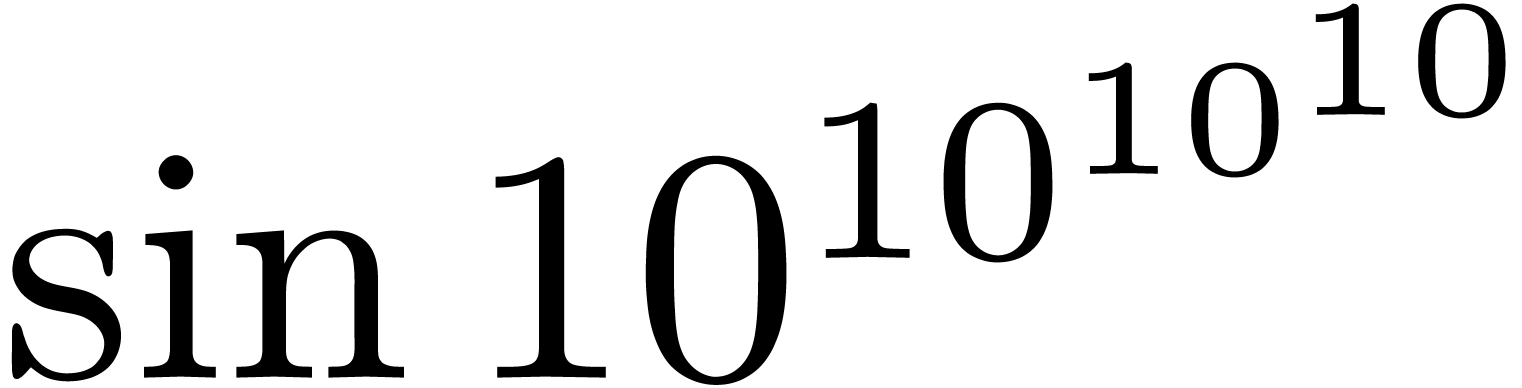To several mathematicians, the undecidability theorem of Gödel came as a shock. Under the influence of this shock, a general opinion has arisen that as soon as one proves a problem to be undecidable, this problem is to hard and in a certain sense, not worth it studying it any longer. In our talk, we want to put into perspective the importance of the concept of undecidability in the sense of Gödel on the hand of our main research topic: the automatic resolution of non linear differential equations.

First of all, many theoretically undecidable problems may be almost decidable in practice in the sense that the undecidable part of the problem is “degenerate”. For instance, the problem of solving algebraic differential equations locally (when stated in a sufficiently general way) is undecidable. Nevertheless, when we write down such an equation at random, we have a large probability that we may solve it by the implicit function theorem.

On the other hand, certain questions which are theoretically decidable may be very hard to decide in practice. For instance, there exists an “algorithm” to compute the sign of 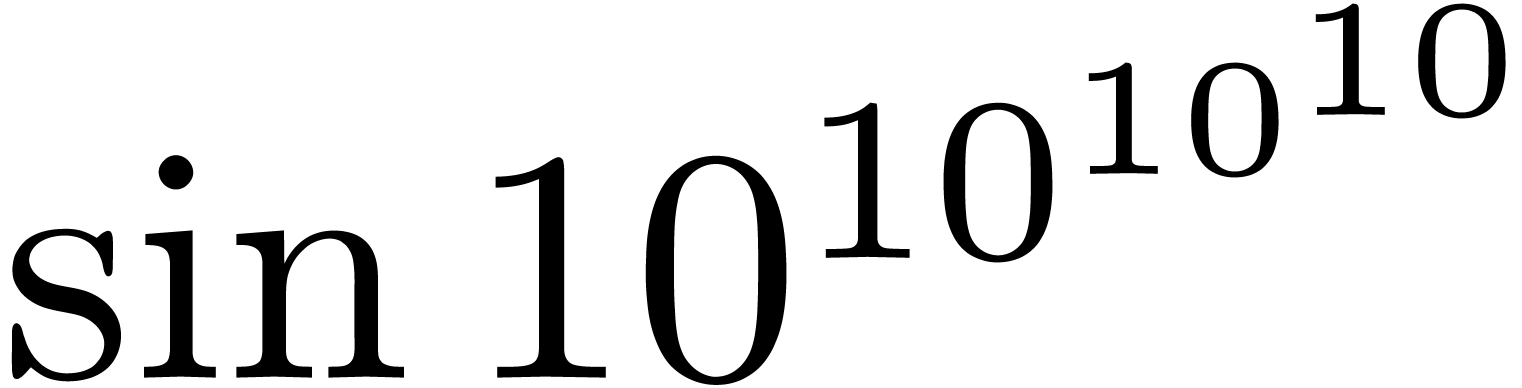, but we would be very happy to own a computer which would actually be able to compute this sign.

The above discussion shows that the classical concept of undecidability is somehow not adapted to practice. Now the important question is how to build a theory of practical decidability? Ideally speaking, we would like to have algorithms for solving differential equations, which are able to detect whether the resolution of a given equation essentially involves a practically undecidable problem and, if not, to actually solve the equation.

In order to make this work, it is important to make a “catalogue” of practically undecidable problems, which may be very different from the undecidable problems we are used to. We will see that in absence of oscillation, we do have practical decidability. In cases of oscillation, we shall discuss the problems of levels of exponentiality, Diophantine approximation, small divisors and a link between “chaos” and resummation theory.

A final interesting aspect of our approach is that it may be necessary to found the theory on a new system of “plausible axioms”. The logical problem we are faced to here is the following: it is highly probable that many mathematical truths can not be proved, because the classical set of mathematical axioms is to weak. For instance, consider the zero-test problem for exp-log constants (i.e. constants built up from the rationals by and ). 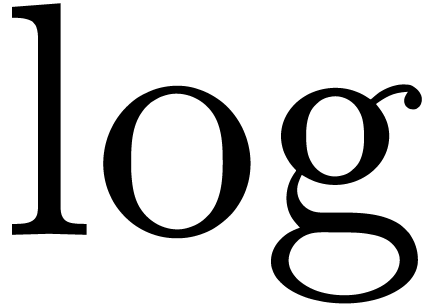Such a zero-test was given by Richardson if Schanuel's conjecture holds. This algorithm has the particularity that it fails on a particular input if and only if this input leads to an explicit counter example. For this reason, Schanuel's conjecture would be a good candidate for a “plausible axiom”, but others will be discussed in our talk.

Occasions: Logic Colloquium, Prague, August 10, 1998

Documents: slides