Abstract
Sparse polynomial interpolation consists in recovering of a sparse
representation of a polynomial 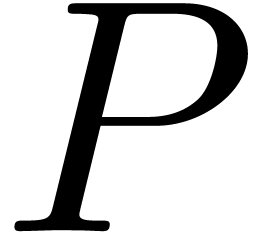 given by a blackbox program which computes values of
given by a blackbox program which computes values of 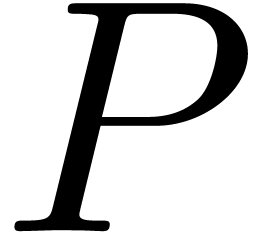 at as many points as necessary. In practice
at as many points as necessary. In practice
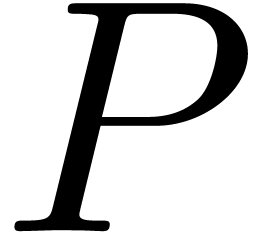 is typically represented by
DAGs (Directed Acyclic Graphs) or SPLs (Straight Line Programs). For
polynomials with at most
is typically represented by
DAGs (Directed Acyclic Graphs) or SPLs (Straight Line Programs). For
polynomials with at most 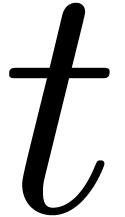 terms over a field
terms over a field  , this
task typically involves
, this
task typically involves 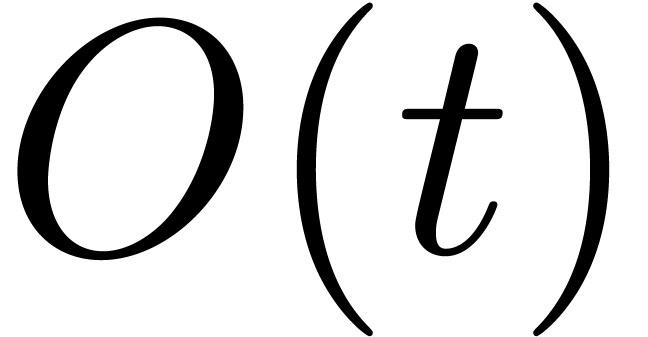 evaluations of
evaluations of  , operations
on integers for discovering the exponents of the nonzero terms of
, operations
on integers for discovering the exponents of the nonzero terms of  , and an additional number of
operations in
, and an additional number of
operations in  that can be
bounded by
that can be
bounded by 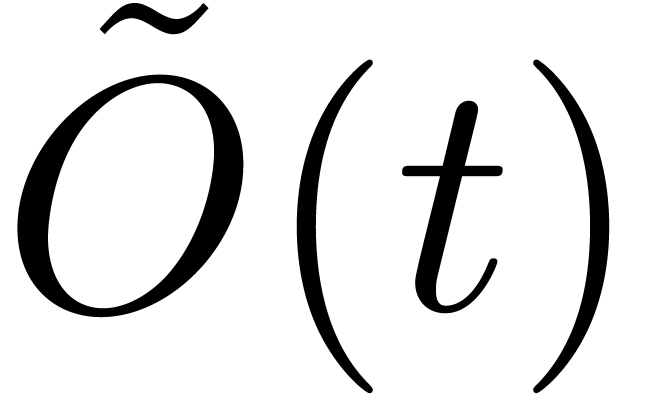 for recovering the coefficients.
for recovering the coefficients.
However, the latter complexity analysis does not take into account the
sizes of coefficients in  and
the expression swell that might occur when evaluating at points with
high height. For practical implementations, it is important to perform
most of the computations over a prime finite field
and
the expression swell that might occur when evaluating at points with
high height. For practical implementations, it is important to perform
most of the computations over a prime finite field 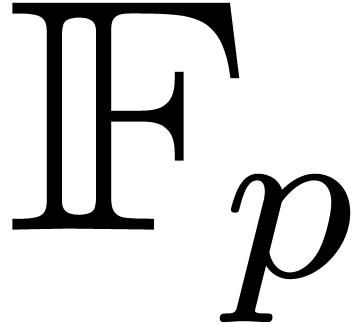 , where
, where 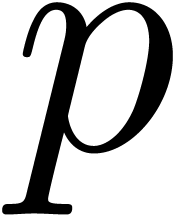 fits into a single machine register. On modern architectures, this
typically means that
fits into a single machine register. On modern architectures, this
typically means that 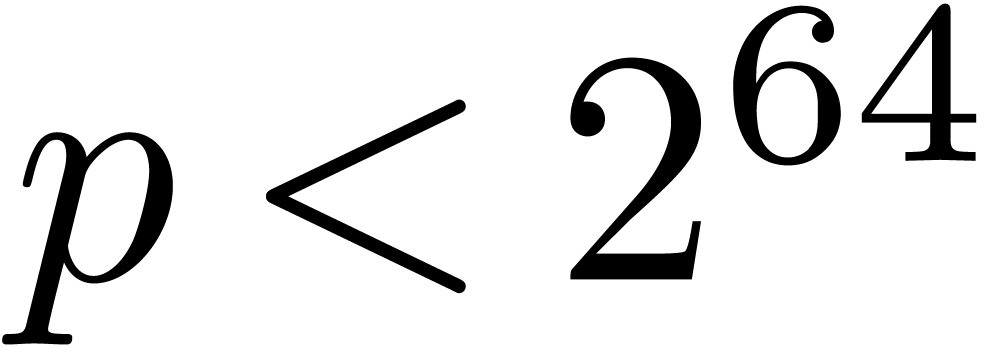 . There
mainly are two approaches which can be used over finite fields: the
“prime number” approach and the “Kronecker
substitution” approach. We present new techniques which can be
used to further enhance and combine these classical approaches.
. There
mainly are two approaches which can be used over finite fields: the
“prime number” approach and the “Kronecker
substitution” approach. We present new techniques which can be
used to further enhance and combine these classical approaches.
We report on our implementations in the multimix
C++ library of the Mathemagix
system. For the sake of conciseness some discussions on the
probabilistic aspects will be informal. Of course, once a candidate for
the sparse representation is found, then the Schwartz-Zippel lemma can
be used to verify it with a low level of failure.
Occasion: Software presentation, ISSAC 2014, Kobe, July
23, 2014
Award: Distinguished software presentation at ISSAC
2014
Coauthor: Grégoire Lecerf
Documents: slideshow, TeXmacs
source
 given by a blackbox program which computes values of
given by a blackbox program which computes values of 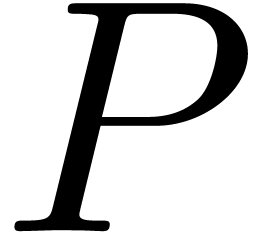 at as many points as necessary. In practice
at as many points as necessary. In practice
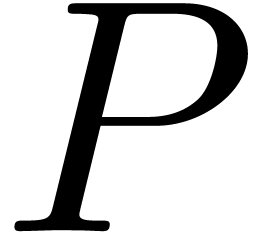 is typically represented by
DAGs (Directed Acyclic Graphs) or SPLs (Straight Line Programs). For
polynomials with at most
is typically represented by
DAGs (Directed Acyclic Graphs) or SPLs (Straight Line Programs). For
polynomials with at most 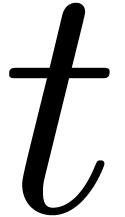 terms over a field
terms over a field  , this
task typically involves
, this
task typically involves 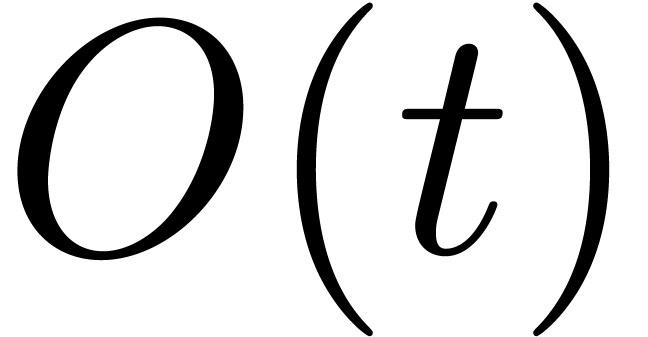 evaluations of
evaluations of 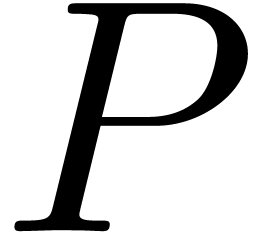 , operations
on integers for discovering the exponents of the nonzero terms of
, operations
on integers for discovering the exponents of the nonzero terms of 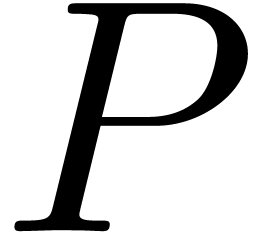 , and an additional number of
operations in
, and an additional number of
operations in  that can be
bounded by
that can be
bounded by 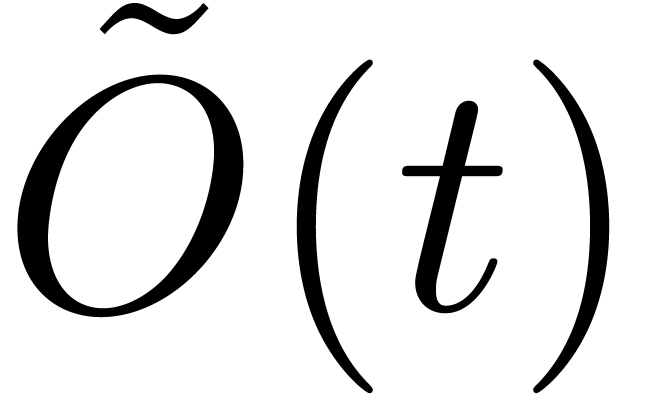 for recovering the coefficients.
for recovering the coefficients.
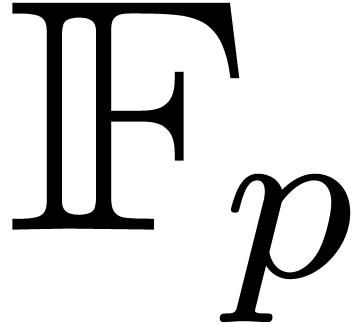 , where
, where 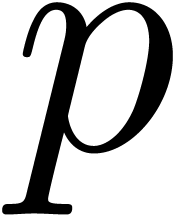 fits into a single machine register. On modern architectures, this
typically means that
fits into a single machine register. On modern architectures, this
typically means that 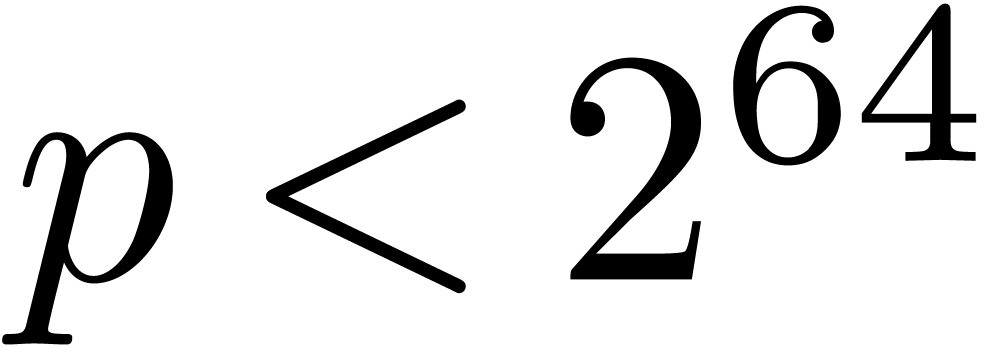 . There
mainly are two approaches which can be used over finite fields: the
“prime number” approach and the “Kronecker
substitution” approach. We present new techniques which can be
used to further enhance and combine these classical approaches.
. There
mainly are two approaches which can be used over finite fields: the
“prime number” approach and the “Kronecker
substitution” approach. We present new techniques which can be
used to further enhance and combine these classical approaches.