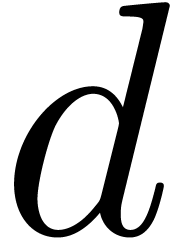,
then, under mild assumptions on the coefficient ring, we show that their
product can be computed with 
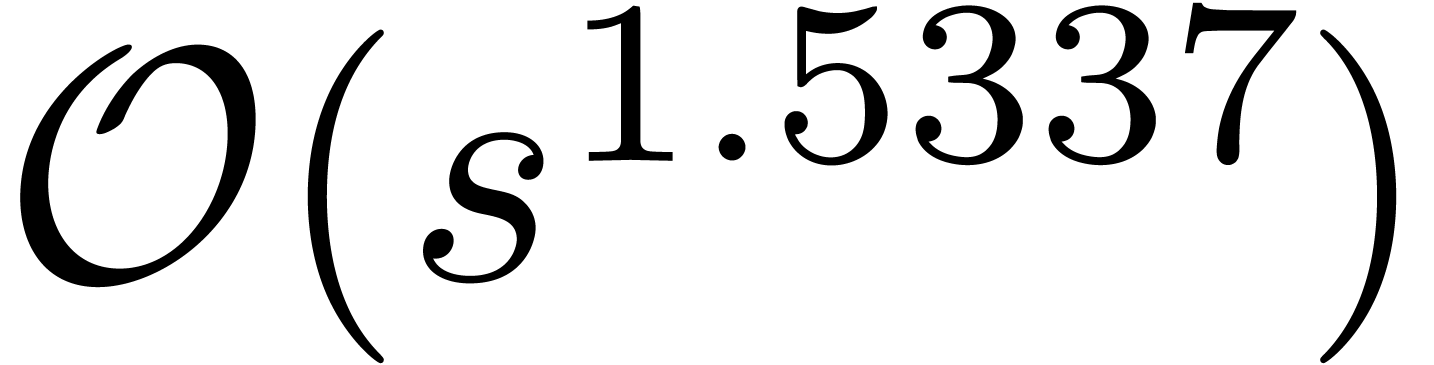ring operations, where 
denotes the number of all the monomials of total degree at most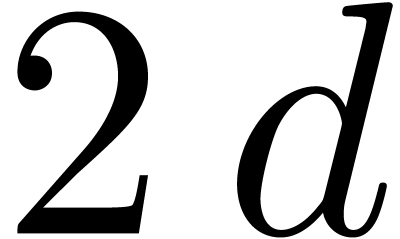 
.
| HomepagePublicationsTalksTeXmacsMathemagix |
In this article, we study the problem of multiplying two multivariate
polynomials which are somewhat but not too sparse, typically like
polynomials with convex supports. We design and analyze an algorithm
which is based on blockwise decomposition of the input polynomials, and
which performs the actual multiplication in an FFT model or some other
more general so called “evaluated model”. If the input
polynomials have total degrees at most ,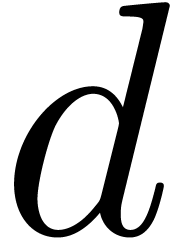
then, under mild assumptions on the coefficient ring, we show that their
product can be computed with
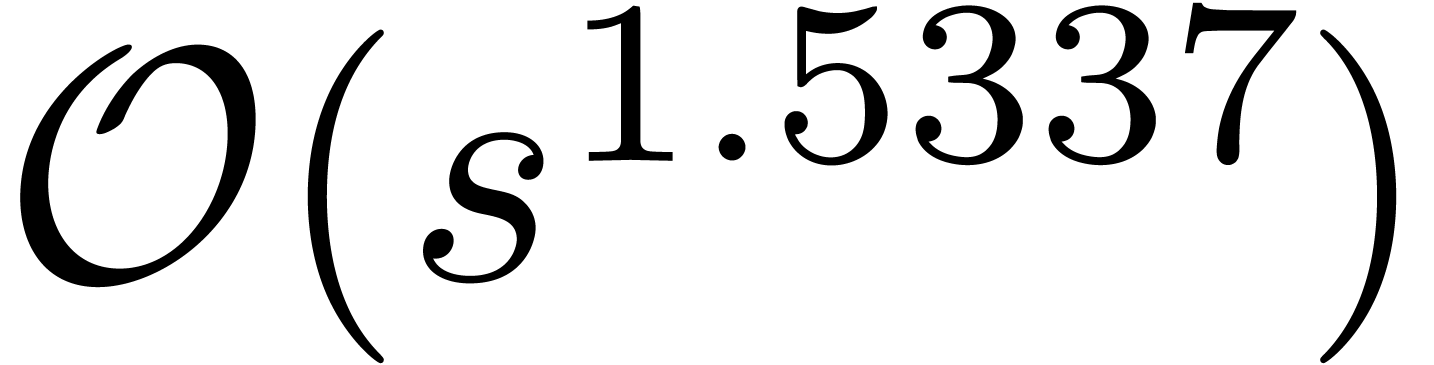ring operations, where
denotes the number of all the monomials of total degree at most .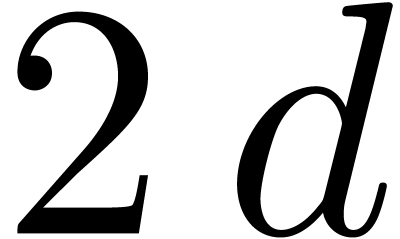
Authors:
Keywords: sparse polynomial multiplication, multivariate power series, evaluation-interpolation, algorithm
A.M.S. subject classification: 68W30, 12-04, 30B10, 42-04