Abstract
We design new deterministic algorithms, based on Graeffe transforms, to
compute all the roots of a polynomial which splits over a finite field
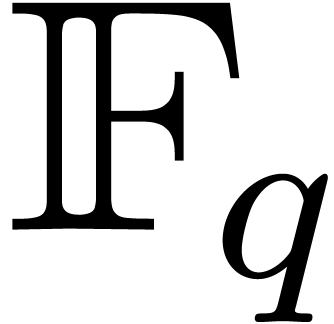 . Our algorithms were
designed to be particularly efficient in the case when the cardinality
. Our algorithms were
designed to be particularly efficient in the case when the cardinality
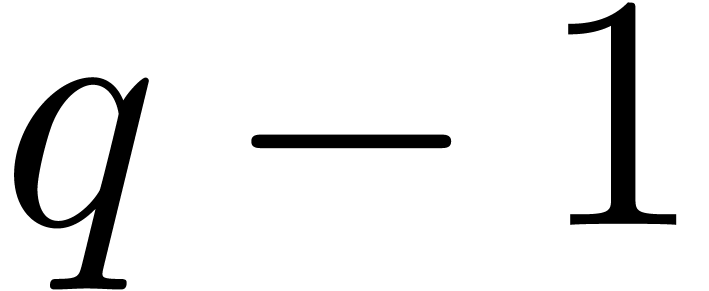 of the multiplicative group
of
of the multiplicative group
of 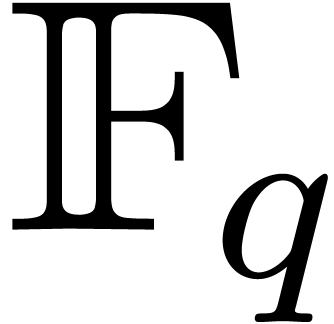 is smooth. Such fields
are often used in practice because they support fast discrete Fourier
transforms. We also present a new nearly optimal algorithm for computing
characteristic polynomials of multiplication endomorphisms in finite
field extensions. This algorithm allows for the efficient computation of
Graeffe transforms of arbitrary orders.
is smooth. Such fields
are often used in practice because they support fast discrete Fourier
transforms. We also present a new nearly optimal algorithm for computing
characteristic polynomials of multiplication endomorphisms in finite
field extensions. This algorithm allows for the efficient computation of
Graeffe transforms of arbitrary orders.
Authors: Bruno Grenet, Joris van der Hoeven, Grégoire
Lecerf
View: Html, TeXmacs, Pdf,
BibTeX
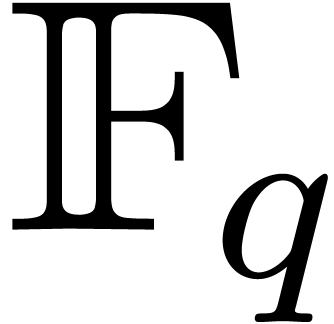 . Our algorithms were
designed to be particularly efficient in the case when the cardinality
. Our algorithms were
designed to be particularly efficient in the case when the cardinality
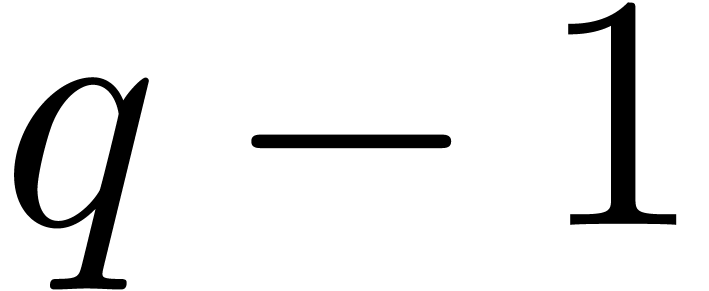 of the multiplicative group
of
of the multiplicative group
of 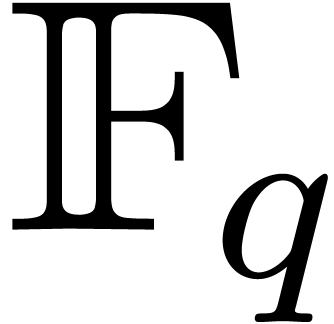 is smooth. Such fields
are often used in practice because they support fast discrete Fourier
transforms. We also present a new nearly optimal algorithm for computing
characteristic polynomials of multiplication endomorphisms in finite
field extensions. This algorithm allows for the efficient computation of
Graeffe transforms of arbitrary orders.
is smooth. Such fields
are often used in practice because they support fast discrete Fourier
transforms. We also present a new nearly optimal algorithm for computing
characteristic polynomials of multiplication endomorphisms in finite
field extensions. This algorithm allows for the efficient computation of
Graeffe transforms of arbitrary orders.