Abstract
Let 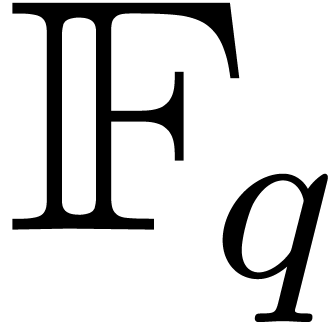 be the finite field with
be the finite field with
 elements and let
elements and let  be a primitive
be a primitive 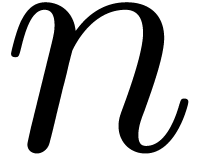 -th root of unity in an extension field
-th root of unity in an extension field 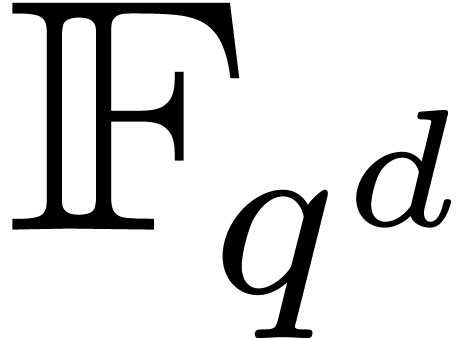 of
of 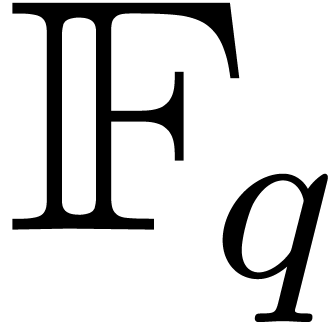 .
Given a polynomial
.
Given a polynomial 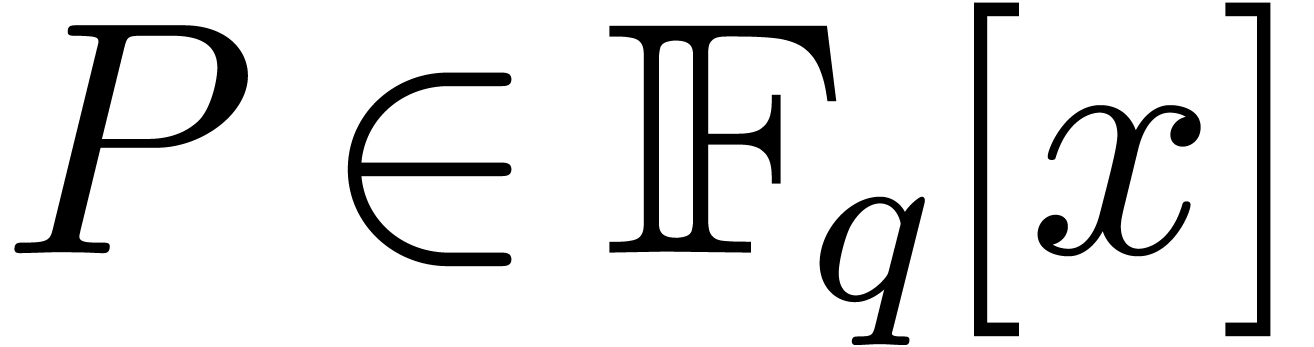 of degree
less than
of degree
less than 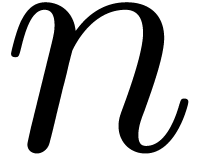 , we will show that
its discrete Fourier transform
, we will show that
its discrete Fourier transform 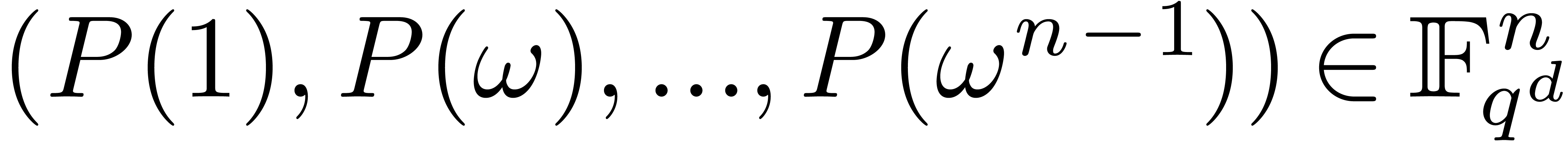 can be computed essentially
can be computed essentially 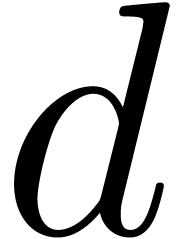 times faster than the discrete Fourier transform of a polynomial
times faster than the discrete Fourier transform of a polynomial 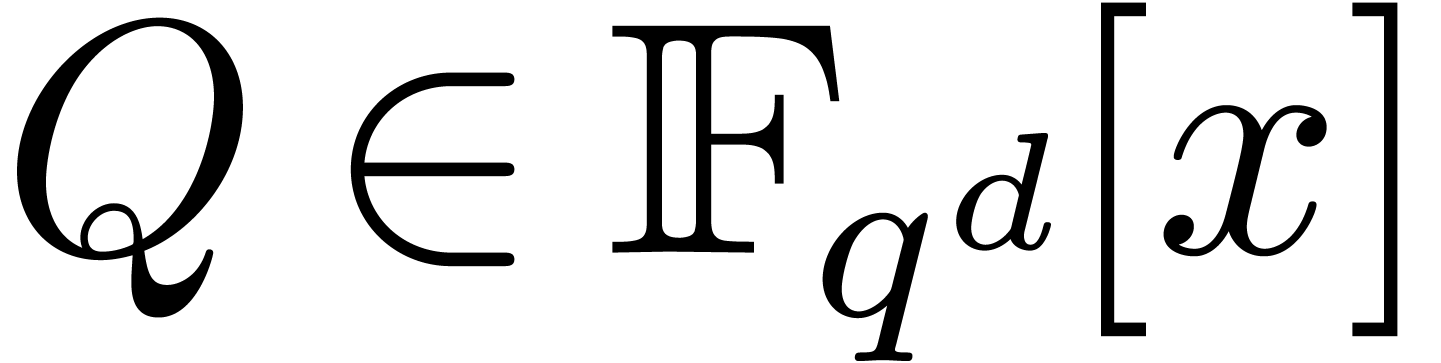 of degree less than
of degree less than 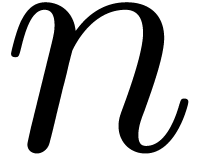 , in many cases. This result is achieved by
exploiting the symmetries provided by the Frobenius automorphism of
, in many cases. This result is achieved by
exploiting the symmetries provided by the Frobenius automorphism of
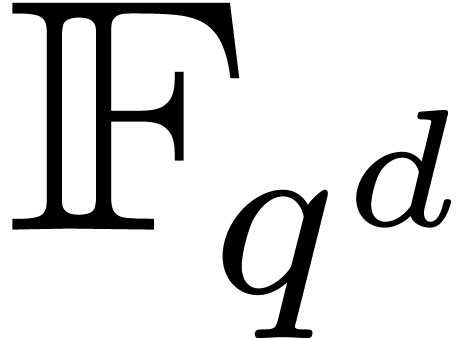 over
over 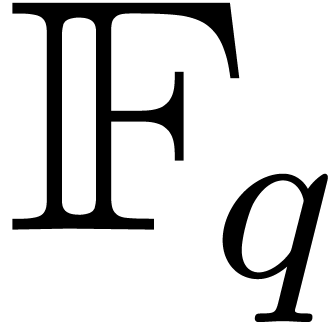 .
.
Authors: Joris van der Hoeven,
Robin Larrieu
Keywords: FFT, finite field, complexity bound,
Frobenius automorphism
View: Html, TeXmacs, Pdf,
BibTeX
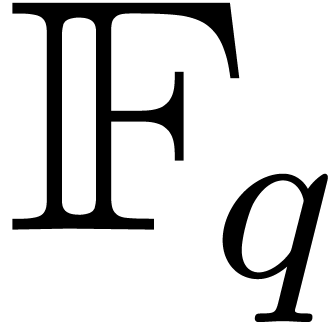 be the finite field with
be the finite field with
 elements and let
elements and let  be a primitive
be a primitive 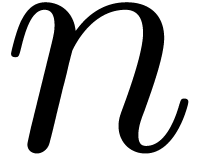 -th root of unity in an extension field
-th root of unity in an extension field 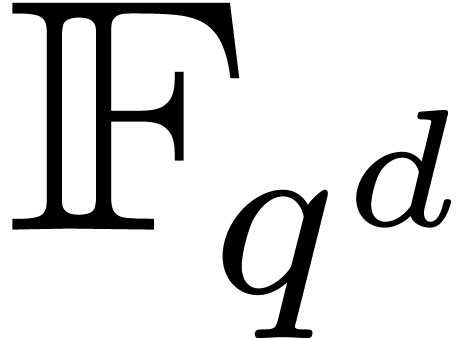 of
of 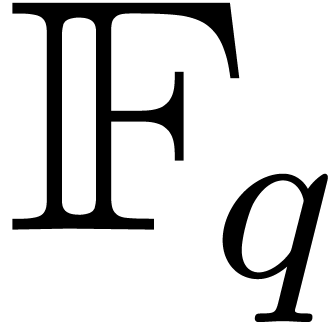 .
Given a polynomial
.
Given a polynomial 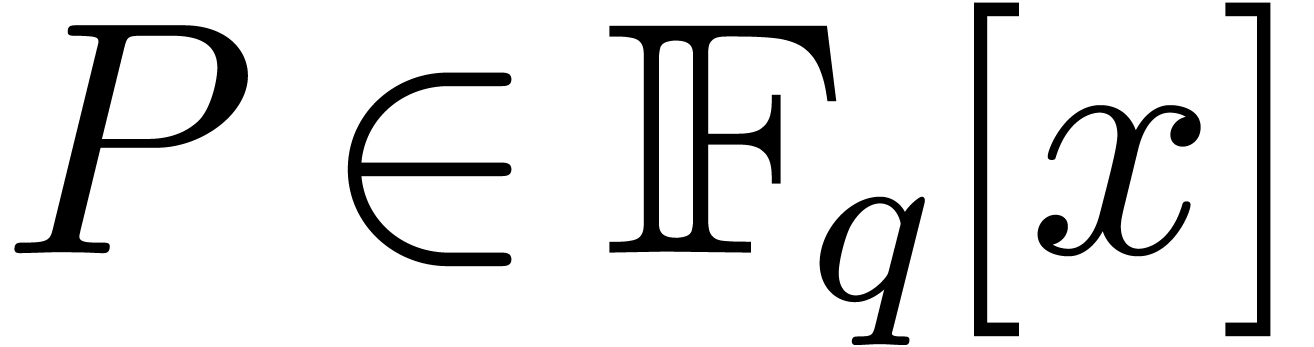 of degree
less than
of degree
less than 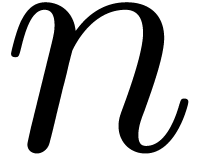 , we will show that
its discrete Fourier transform
, we will show that
its discrete Fourier transform 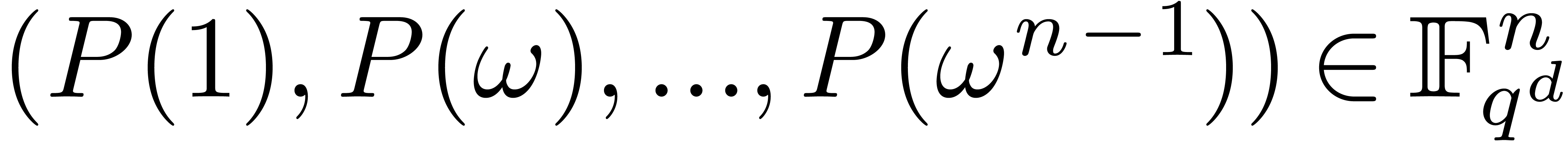 can be computed essentially
can be computed essentially 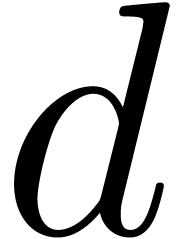 times faster than the discrete Fourier transform of a polynomial
times faster than the discrete Fourier transform of a polynomial 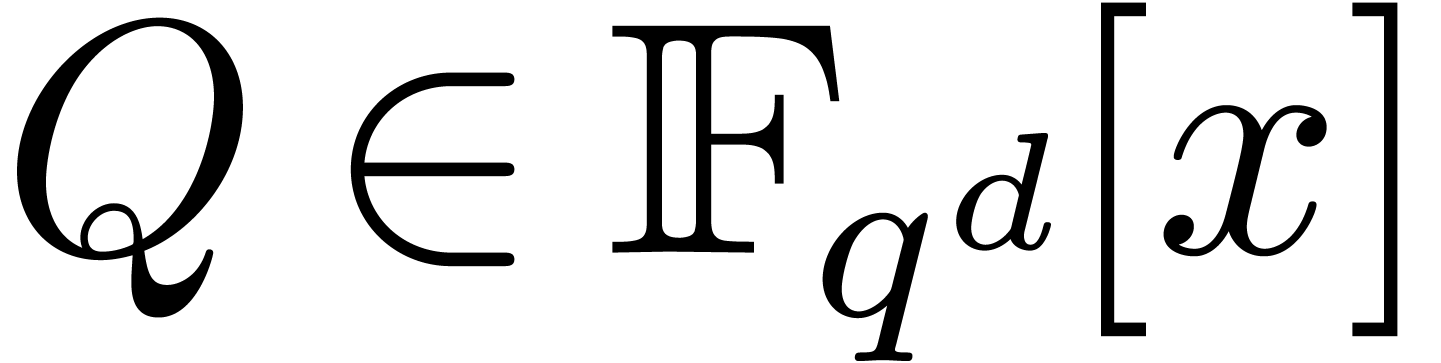 of degree less than
of degree less than 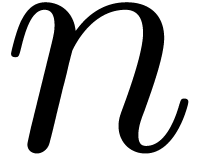 , in many cases. This result is achieved by
exploiting the symmetries provided by the Frobenius automorphism of
, in many cases. This result is achieved by
exploiting the symmetries provided by the Frobenius automorphism of
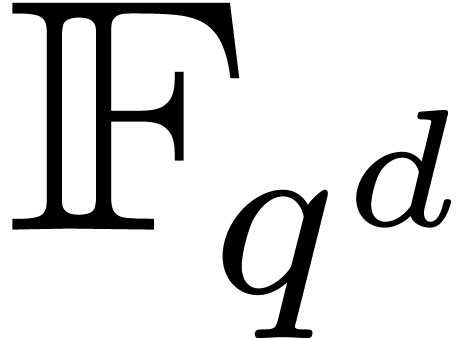 over
over 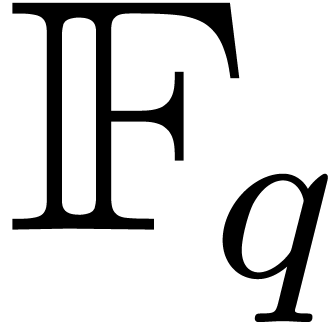 .
.