Abstract
Let 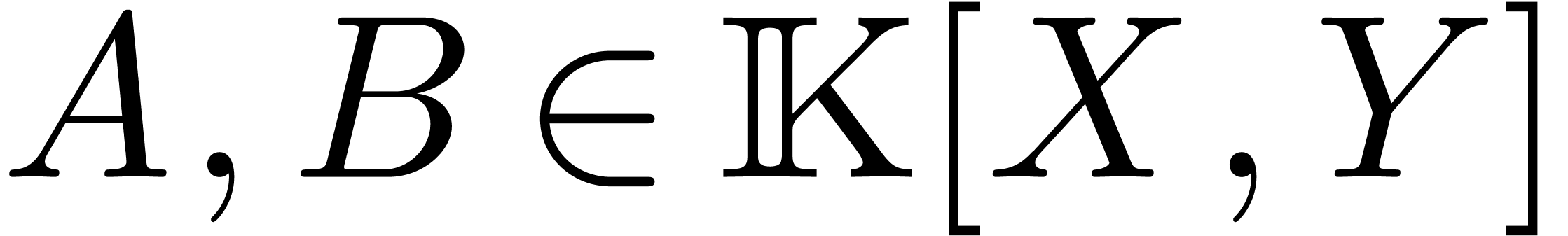 be two bivariate
polynomials over an effective field
be two bivariate
polynomials over an effective field  ,
and let
,
and let  be the reduced
Gröbner basis of the ideal
be the reduced
Gröbner basis of the ideal  generated by
generated by  and
and  with respect to the usual degree
lexicographic order. Assuming
with respect to the usual degree
lexicographic order. Assuming  and
and  sufficiently generic, we
design a quasi-optimal algorithm for the reduction of
sufficiently generic, we
design a quasi-optimal algorithm for the reduction of 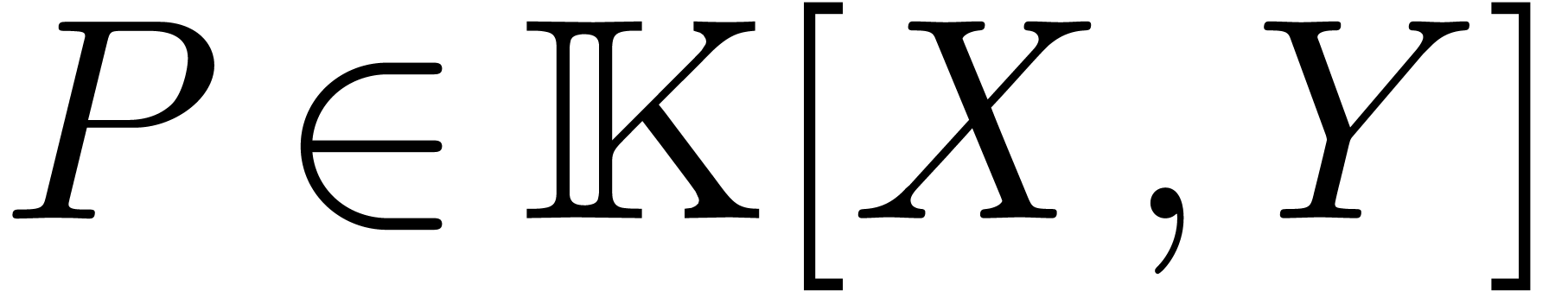 modulo
modulo  ,
where “quasi-optimal” is meant in terms of the size of the
input
,
where “quasi-optimal” is meant in terms of the size of the
input  . Immediate
applications are an ideal membership test and a multiplication algorithm
for the quotient algebra
. Immediate
applications are an ideal membership test and a multiplication algorithm
for the quotient algebra 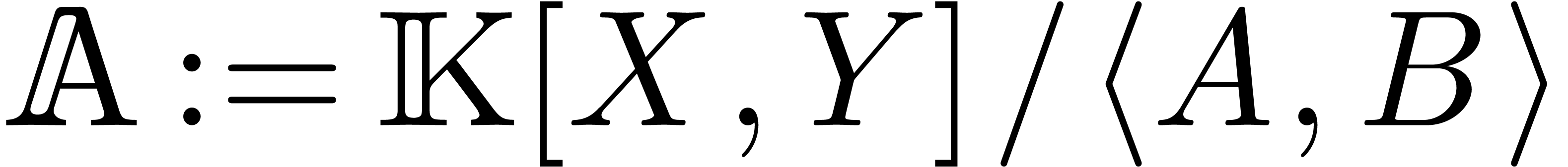 ,
both in quasi-linear time. Moreover, we show that
,
both in quasi-linear time. Moreover, we show that  itself can be computed in quasi-linear time with
respect to the output size.
itself can be computed in quasi-linear time with
respect to the output size.
Authors: Joris van der Hoeven,
Robin Larrieu
Keywords: Gröbner basis, polynomial reduction,
algorithm, complexity
View: Html, TeXmacs, Pdf,
BibTeX
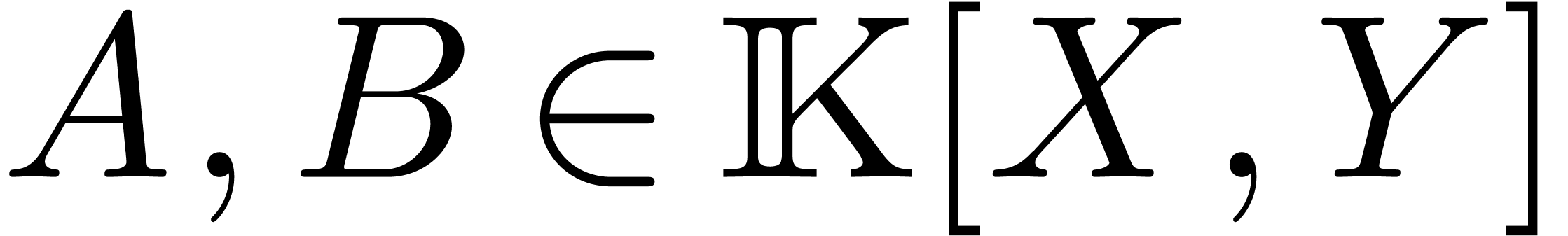 be two bivariate
polynomials over an effective field
be two bivariate
polynomials over an effective field  ,
and let
,
and let  be the reduced
Gröbner basis of the ideal
be the reduced
Gröbner basis of the ideal  generated by
generated by  and
and  with respect to the usual degree
lexicographic order. Assuming
with respect to the usual degree
lexicographic order. Assuming  and
and  sufficiently generic, we
design a quasi-optimal algorithm for the reduction of
sufficiently generic, we
design a quasi-optimal algorithm for the reduction of 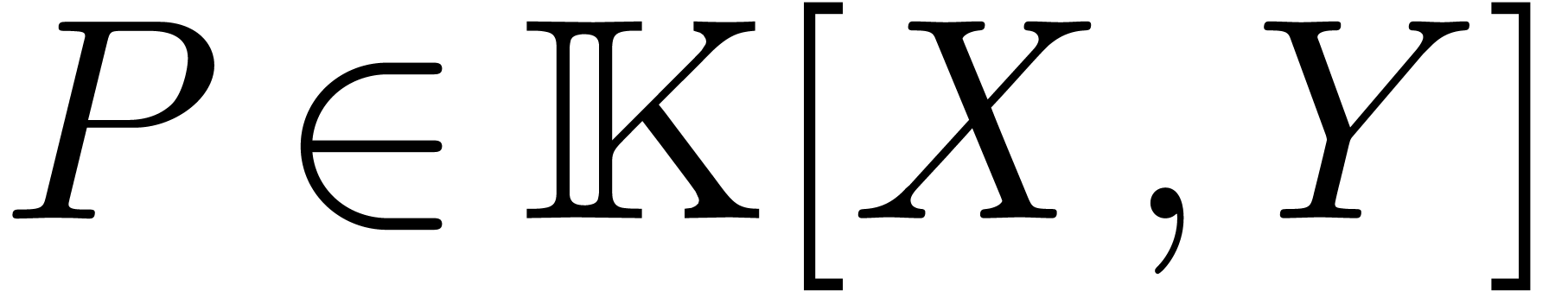 modulo
modulo  ,
where “quasi-optimal” is meant in terms of the size of the
input
,
where “quasi-optimal” is meant in terms of the size of the
input  . Immediate
applications are an ideal membership test and a multiplication algorithm
for the quotient algebra
. Immediate
applications are an ideal membership test and a multiplication algorithm
for the quotient algebra 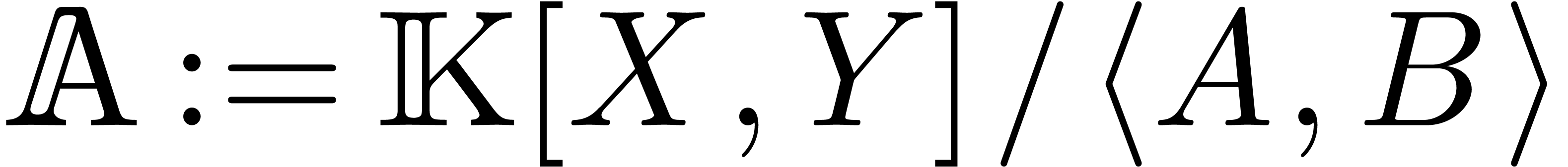 ,
both in quasi-linear time. Moreover, we show that
,
both in quasi-linear time. Moreover, we show that  itself can be computed in quasi-linear time with
respect to the output size.
itself can be computed in quasi-linear time with
respect to the output size.