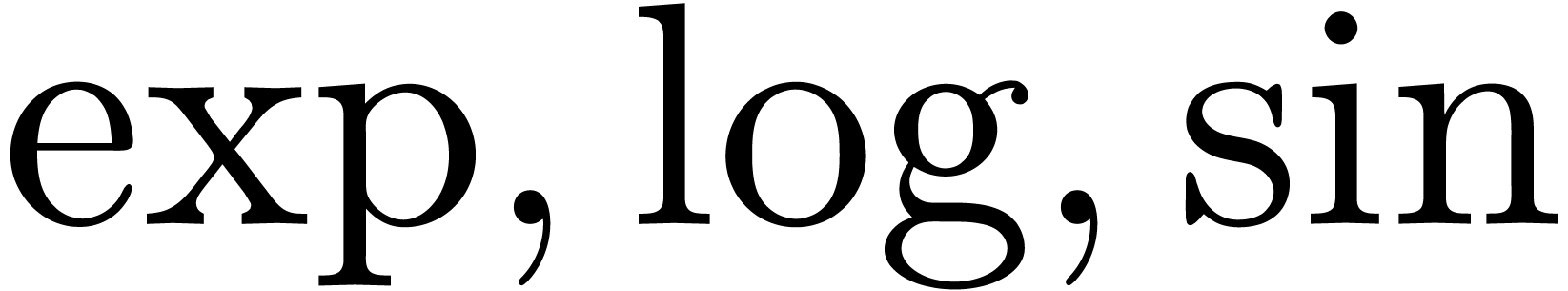, etc.
and many special functions like 
,
, Bessel functions, etc. are
holonomic functions.
| HomepagePublicationsTalksTeXmacsMathemagix |
A holonomic function is an analytic function, which satisfies a linear
differential equation with polynomial coefficients. In particular, the
elementary functions 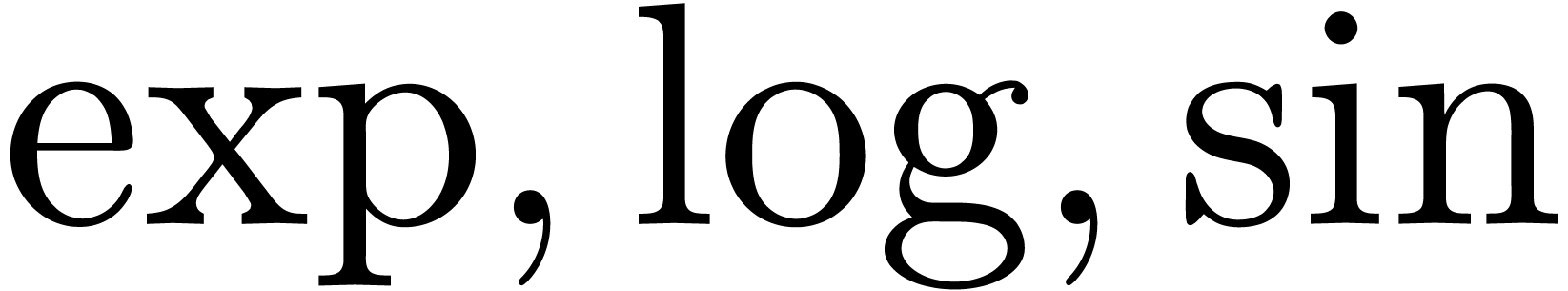, etc.
and many special functions like ,
, Bessel functions, etc. are
holonomic functions.
Given a holonomic function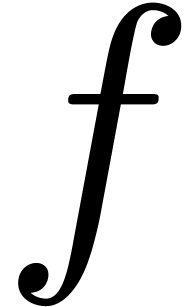 
(determined by the linear differential equation it satisfies and initial
conditions in a non singular point 
),
we show how to perform arbitrary precision evaluations of 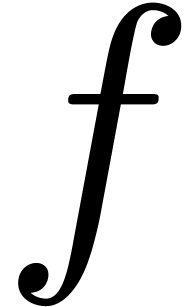at a non singular point 
on the Riemann surface of 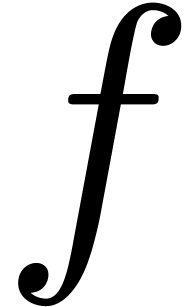, while estimating the error.
Moreover, if the coefficients of the polynomials in the equation for
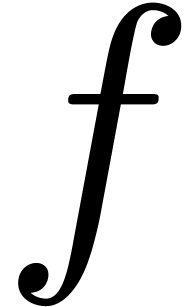are algebraic numbers, then
our algorithm is asymptotically very fast: if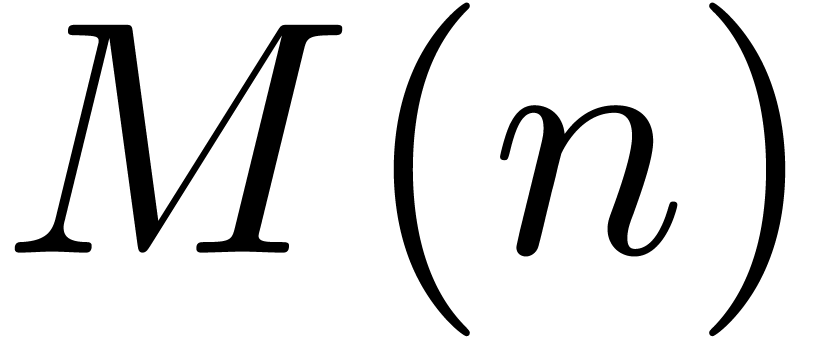 
is the time needed to multiply two 
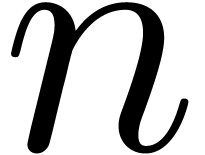digit numbers, then we need a time 
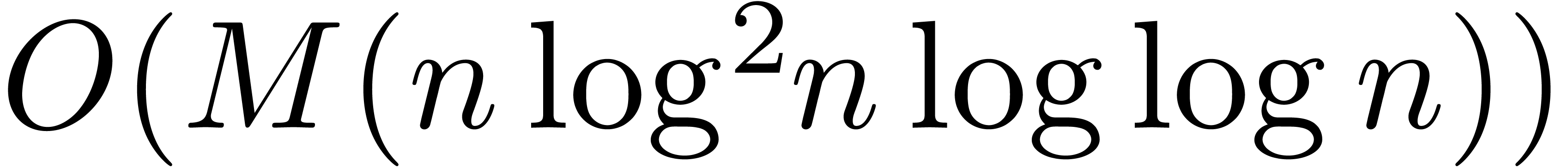to compute 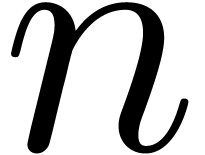digits of 
.
Note: this paper also occurred as appendix C in my PhD. and as a 1996 preprint.