| HomepagePublicationsTalksTeXmacsMathemagix |
Ce papier est essentiellement la troisième chapitre de mon D.E.A. On étudie l'asymptotique des produits de la forme
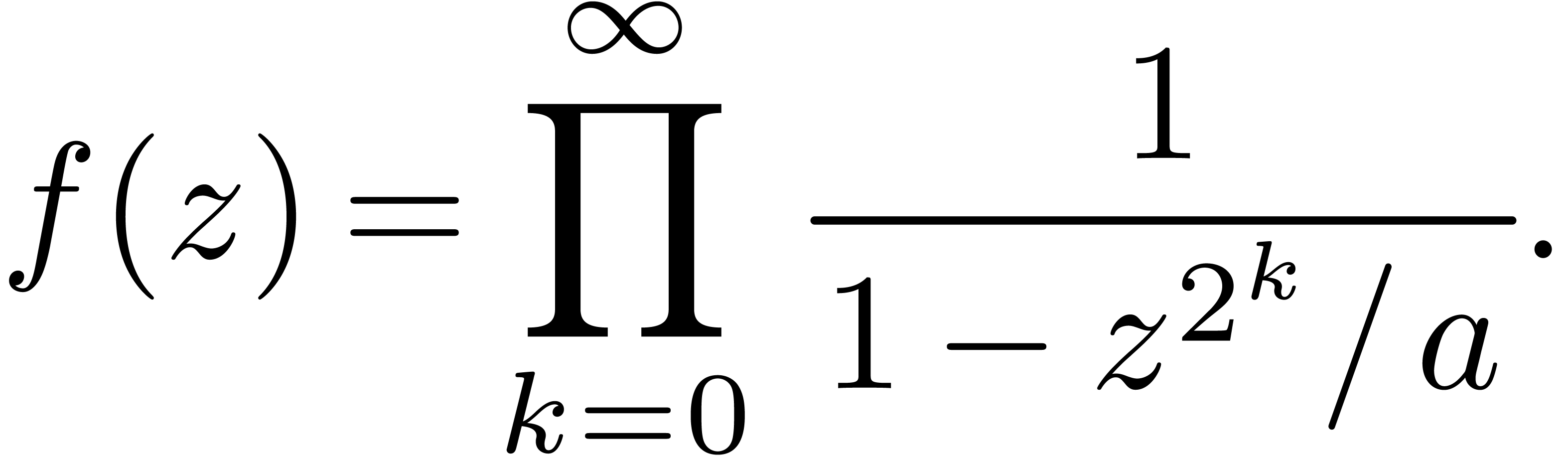
Cette fonction vérifie l'équation mahlérienne suivante:
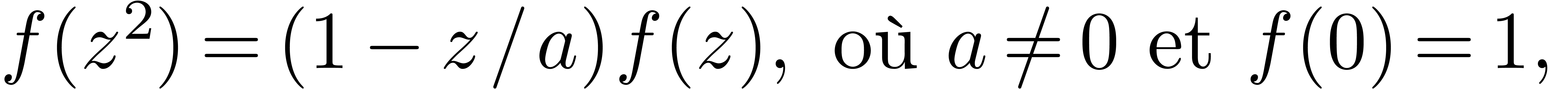
L'étude de cette équation est importante, car toute suite
mahlérienne est produit de convolution de suites
mahlériennes relevant de cette équation et d'une «
suite régulière ». On montre que le comportement du
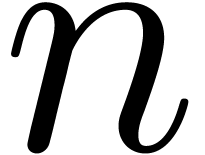 -ième coefficient de
Taylor
-ième coefficient de
Taylor 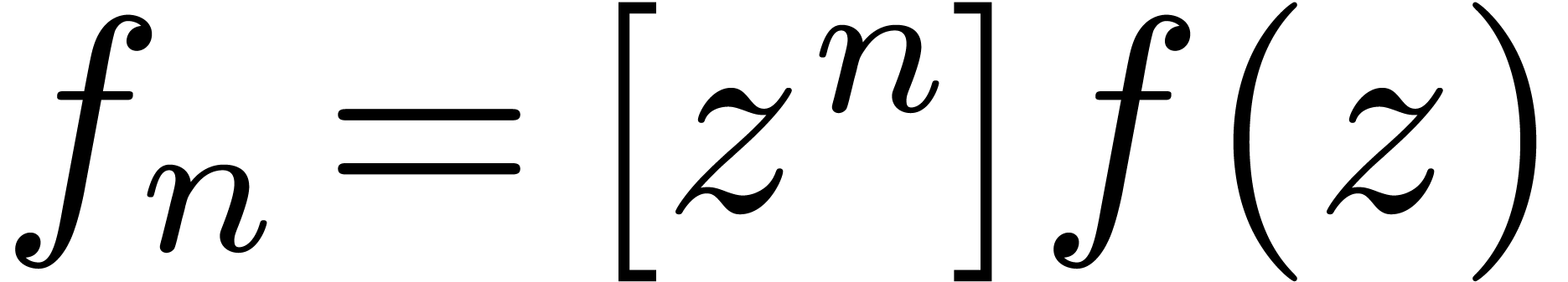 dépend
essentiellement du module de
dépend
essentiellement du module de  .
Si le module de
.
Si le module de  est
inférieur Ě 1, l'analyse des
est
inférieur Ě 1, l'analyse des 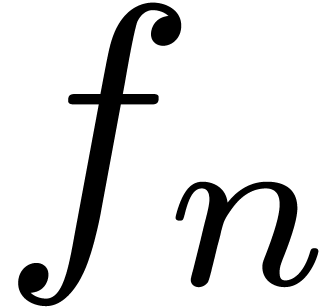 est facile;
est facile; 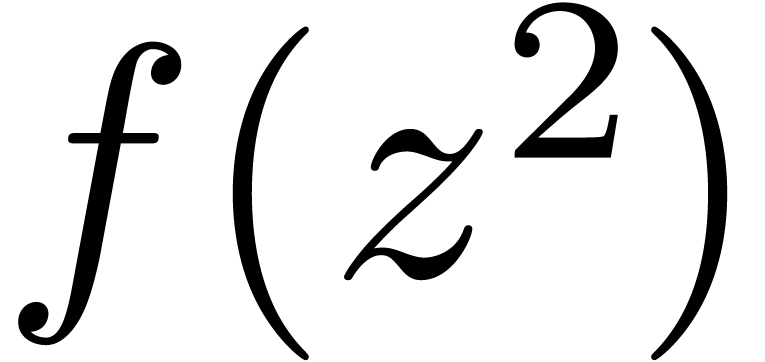 étant
analytique pour
étant
analytique pour 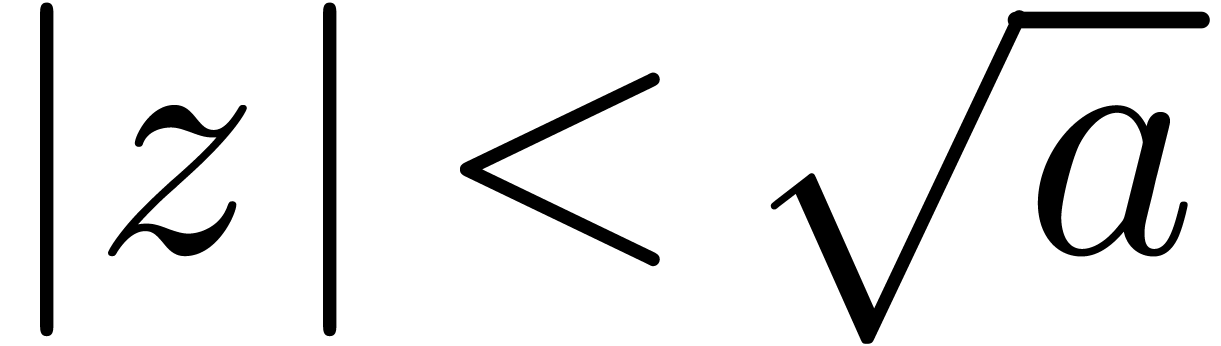 , on a:
, on a:
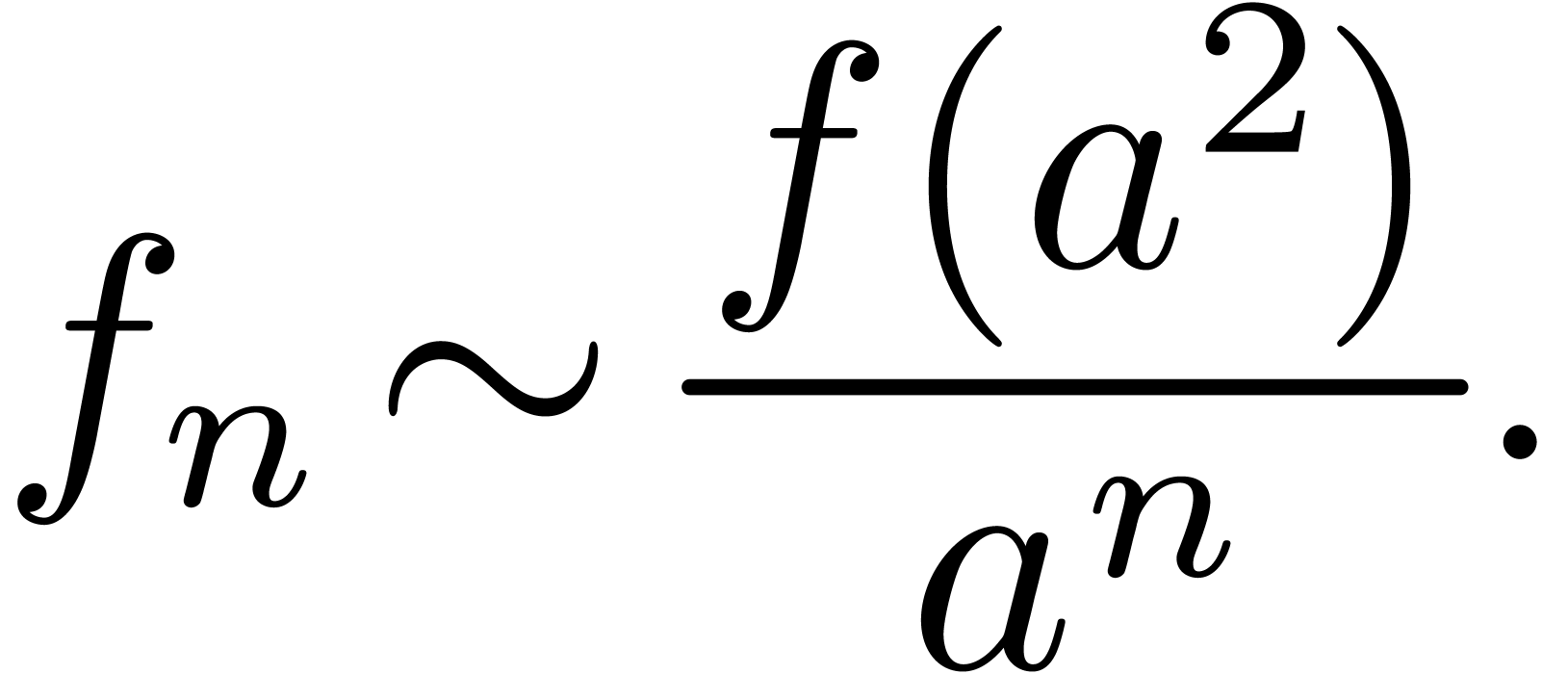
En revanche le cas 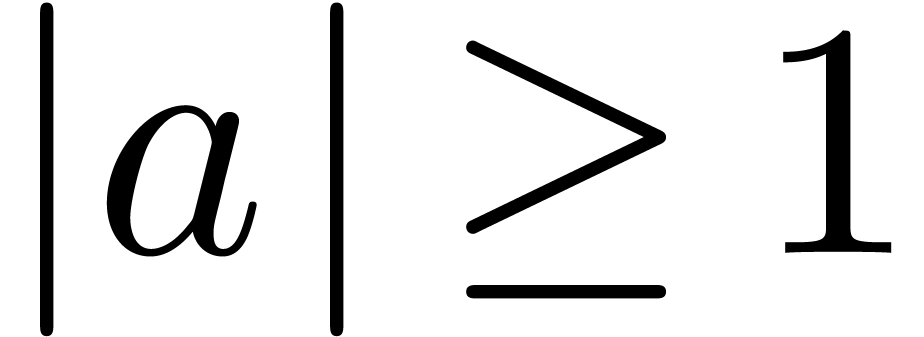 donne
lieu à des comportements très divers. Dans la
quatrième section on montre que pour toute “bonne”
fonction
donne
lieu à des comportements très divers. Dans la
quatrième section on montre que pour toute “bonne”
fonction 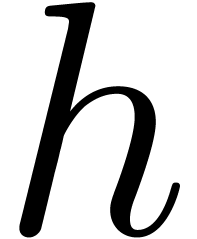 , avec
, avec 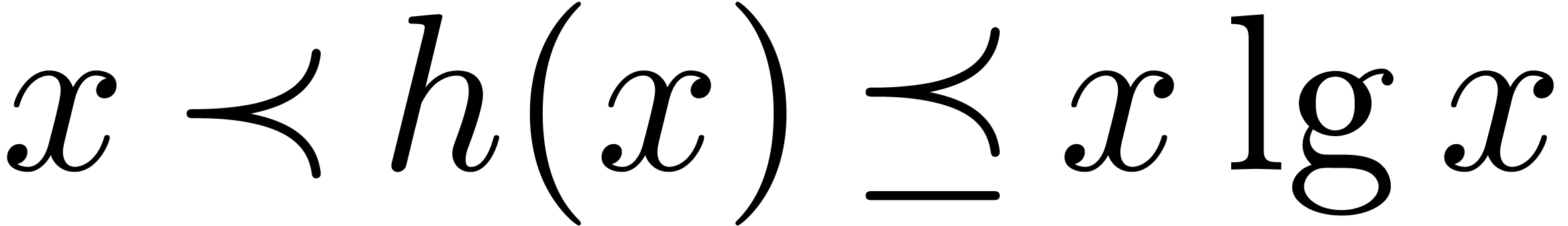 , il existe un
, il existe un  de module 1, tel que
de module 1, tel que 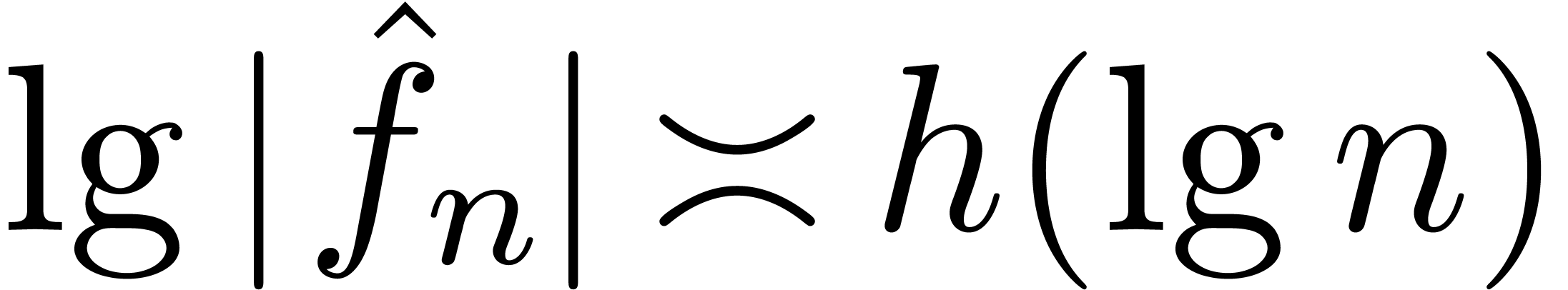 ; ici
; ici
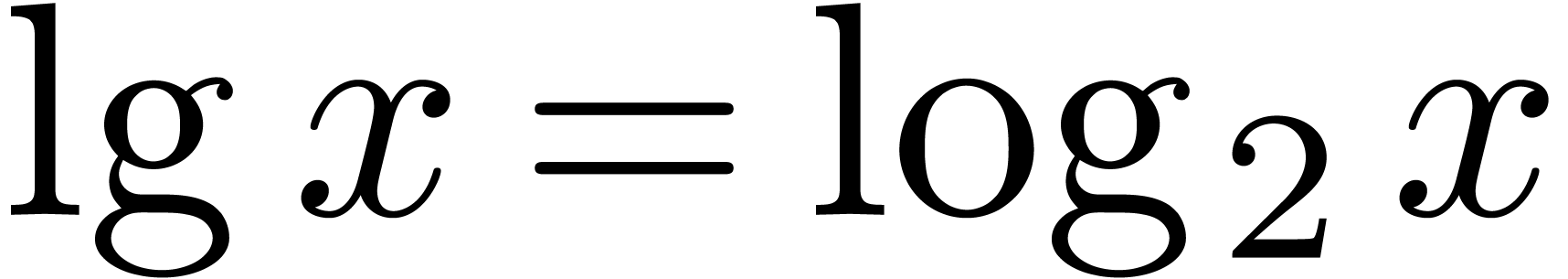 et
et 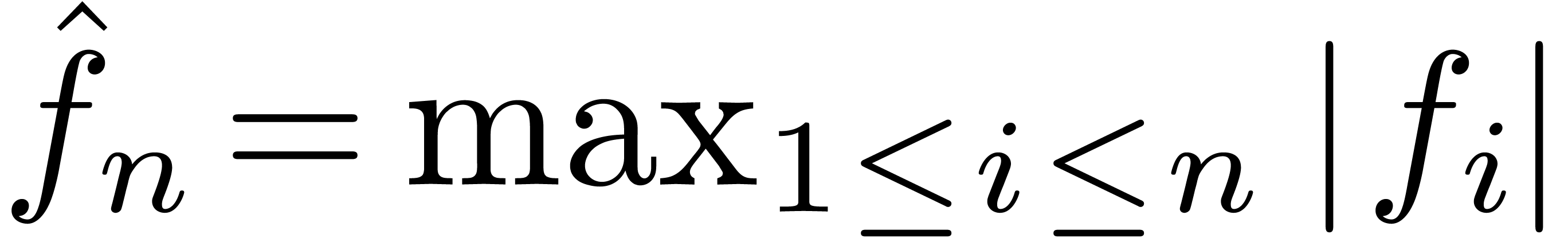 . En fait, le comportement des
. En fait, le comportement des 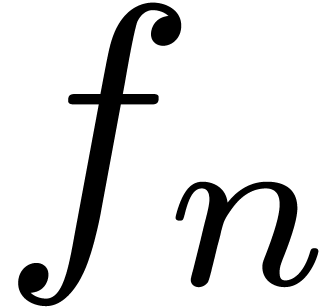 dépend essentiellement du
développement en binaire de
dépend essentiellement du
développement en binaire de 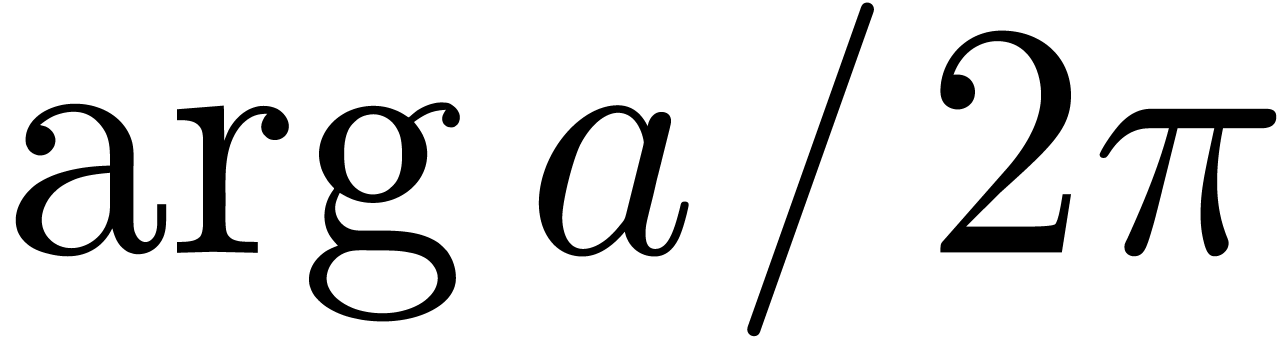 .
Enfin, pour
.
Enfin, pour 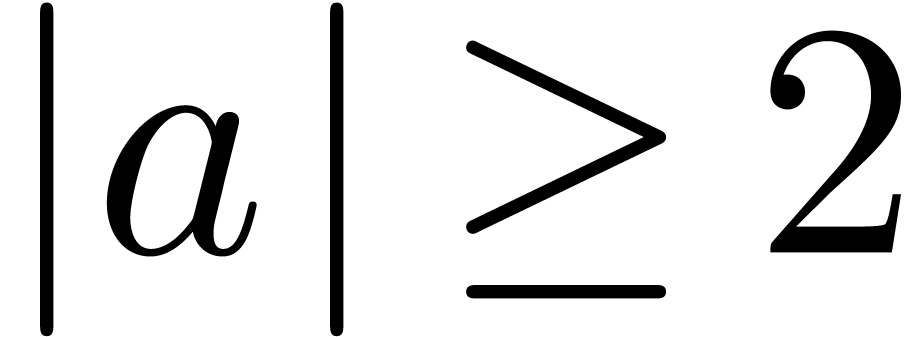 , les
, les 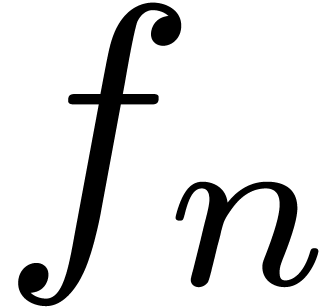 restent bornées, mais se
comportent de façon extrêmement chaotique. Il y a donc peu
de chance que le comportement des
restent bornées, mais se
comportent de façon extrêmement chaotique. Il y a donc peu
de chance que le comportement des 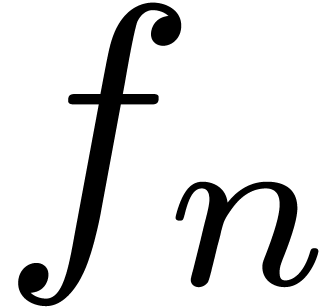 rentre dans une échelle asymptotique habituelle.
rentre dans une échelle asymptotique habituelle.