Abstract
In this paper, we propose efficient new algorithms for multi-dimensional
multi-point evaluation and interpolation on certain subsets of so called
tensor product grids. These point-sets naturally occur in the design of
efficient multiplication algorithms for finite-dimensional 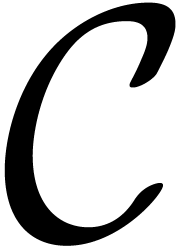 -algebras of the form
-algebras of the form 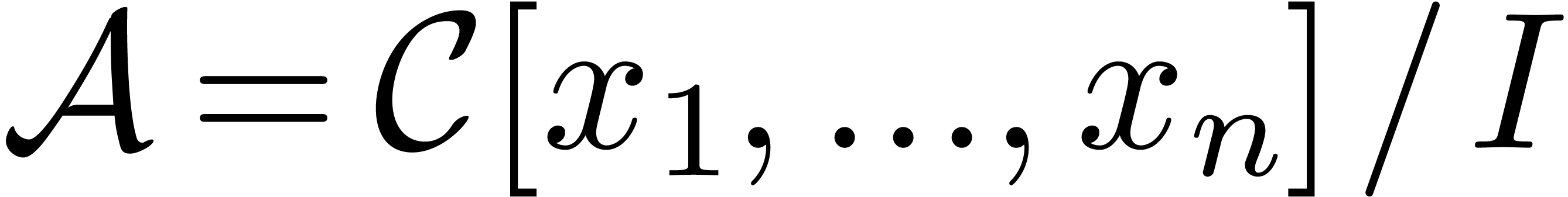 , where
, where 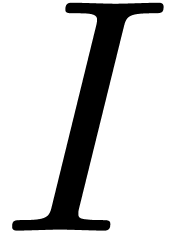 is generated by monomials of the form
is generated by monomials of the form  ;
one particularly important example is the algebra of truncated power
series
;
one particularly important example is the algebra of truncated power
series 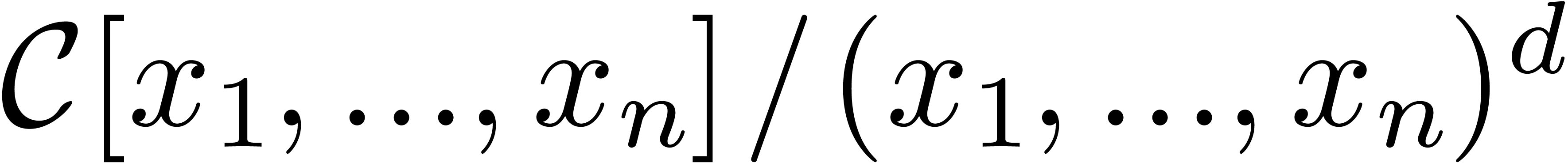 . Similarly to what is
known for multi-point evaluation and interpolation in the univariate
case, our algorithms have quasi-linear time complexity. As a known
consequence, we obtain fast multiplication algorithms for algebras
. Similarly to what is
known for multi-point evaluation and interpolation in the univariate
case, our algorithms have quasi-linear time complexity. As a known
consequence, we obtain fast multiplication algorithms for algebras  of the above form.
of the above form.
Authors: Joris van der Hoeven,
Éric Schost
Keywords: multi-point evaluation, multi-point
interpolation, algorithm, complexity, power series multiplication
A.M.S. subject classification: 12Y05, 68W30, 68W40,
13P10, 65F99
View: Html, TeXmacs, Pdf,
BibTeX
 -algebras of the form
-algebras of the form 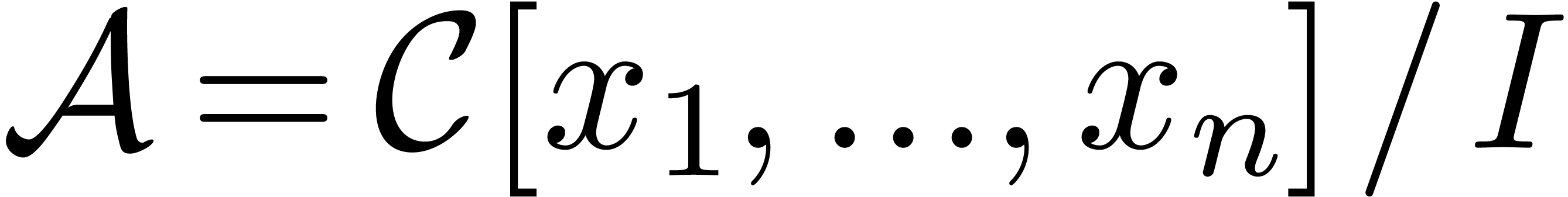 , where
, where 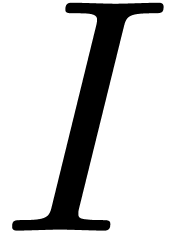 is generated by monomials of the form
is generated by monomials of the form  ;
one particularly important example is the algebra of truncated power
series
;
one particularly important example is the algebra of truncated power
series 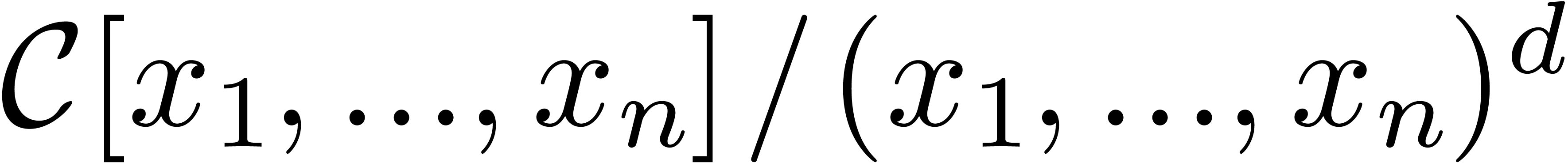 . Similarly to what is
known for multi-point evaluation and interpolation in the univariate
case, our algorithms have quasi-linear time complexity. As a known
consequence, we obtain fast multiplication algorithms for algebras
. Similarly to what is
known for multi-point evaluation and interpolation in the univariate
case, our algorithms have quasi-linear time complexity. As a known
consequence, we obtain fast multiplication algorithms for algebras  of the above form.
of the above form.