Abstract
Given a ring  and a totally
(resp. partially) ordered set of “monomials”
and a totally
(resp. partially) ordered set of “monomials”  , Hahn (resp. Higman) defined the set of power
series
, Hahn (resp. Higman) defined the set of power
series 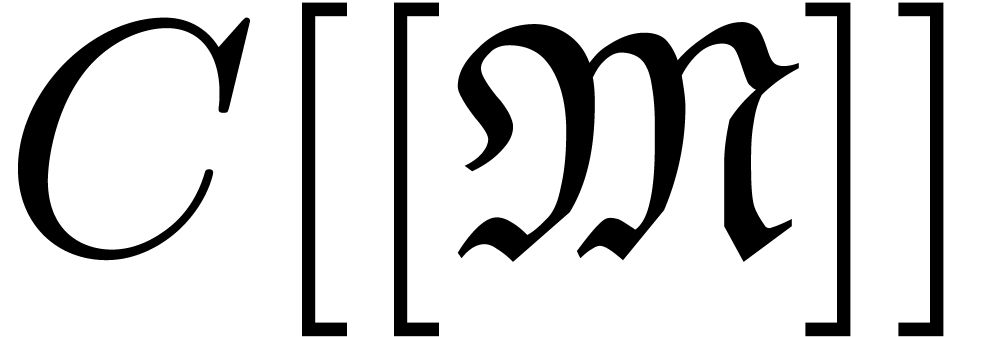 with well-ordered
(resp. Noetherian or well-quasi-ordered) support in
with well-ordered
(resp. Noetherian or well-quasi-ordered) support in  . This set
. This set 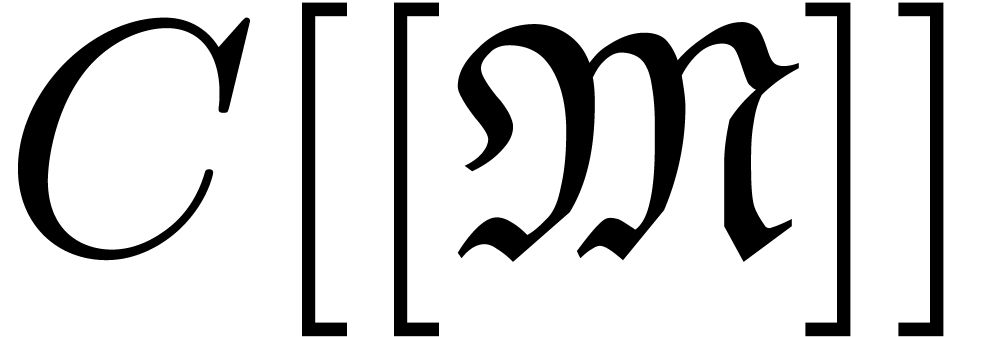 can usually be given a lot of additional structure: if
can usually be given a lot of additional structure: if  is a field and
is a field and  a totally ordered group, then Hahn proved that
a totally ordered group, then Hahn proved that 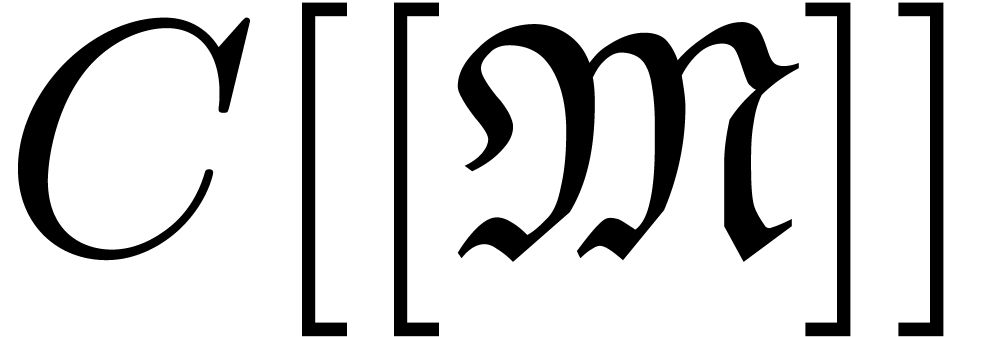 is a field. More recently, we have constructed
fields of “transseries” of the form
is a field. More recently, we have constructed
fields of “transseries” of the form 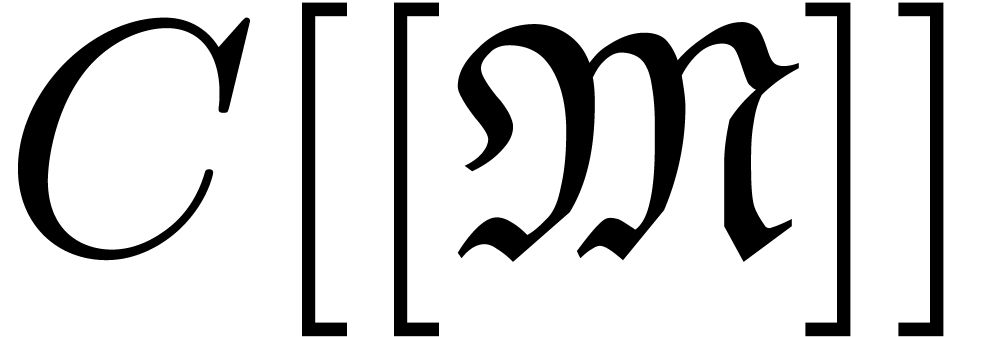 on which we defined natural derivations and
compositions.
on which we defined natural derivations and
compositions.
In this paper we develop an operator theory for generalized power series
of the above form. We first study linear and multilinear operators. We
next isolate a big class of so-called Noetherian operators 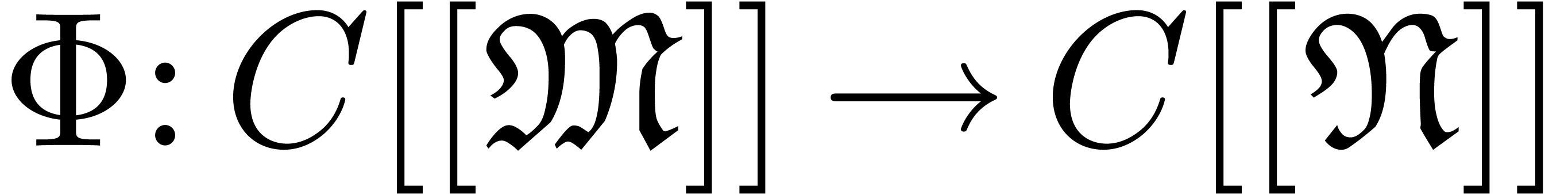 , which include (when defined) summation,
multiplication, differentiation, composition, etc. Our main result is
the proof of an implicit function theorem for Noetherian operators. This
theorem may be used to explicitly solve very general types of functional
equations in generalized power series.
, which include (when defined) summation,
multiplication, differentiation, composition, etc. Our main result is
the proof of an implicit function theorem for Noetherian operators. This
theorem may be used to explicitly solve very general types of functional
equations in generalized power series.
View: Html, TeXmacs, Pdf,
BibTeX
 and a totally
(resp. partially) ordered set of “monomials”
and a totally
(resp. partially) ordered set of “monomials”  , Hahn (resp. Higman) defined the set of power
series
, Hahn (resp. Higman) defined the set of power
series 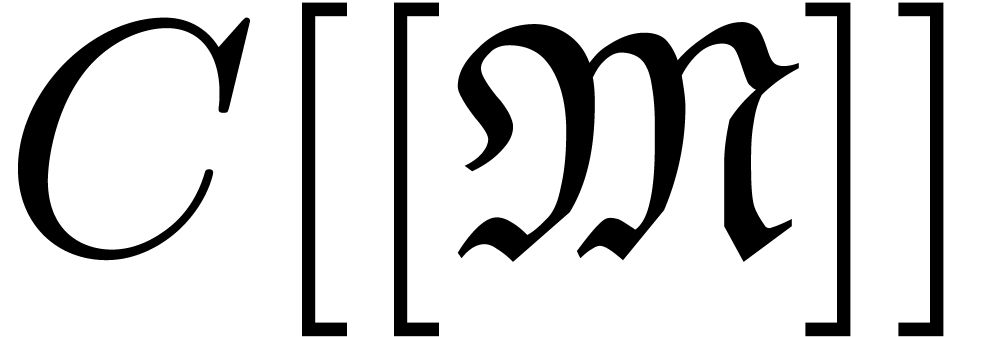 with well-ordered
(resp. Noetherian or well-quasi-ordered) support in
with well-ordered
(resp. Noetherian or well-quasi-ordered) support in  . This set
. This set 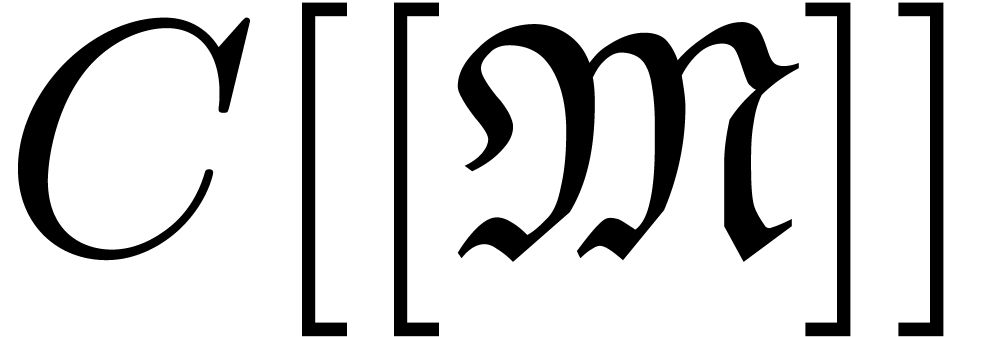 can usually be given a lot of additional structure: if
can usually be given a lot of additional structure: if  is a field and
is a field and  a totally ordered group, then Hahn proved that
a totally ordered group, then Hahn proved that 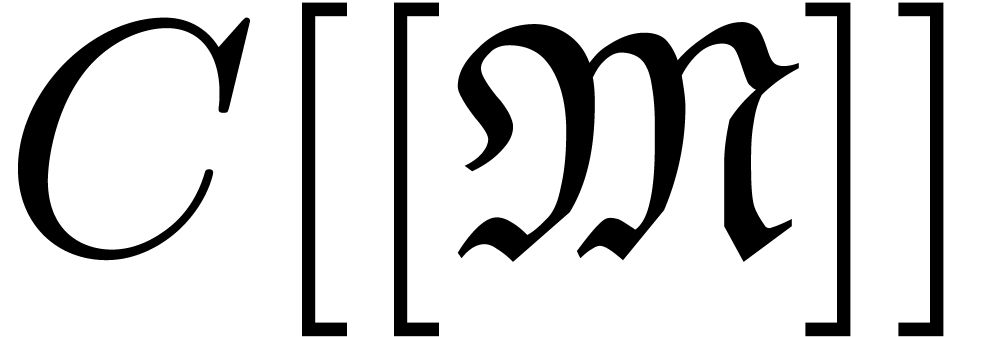 is a field. More recently, we have constructed
fields of “transseries” of the form
is a field. More recently, we have constructed
fields of “transseries” of the form 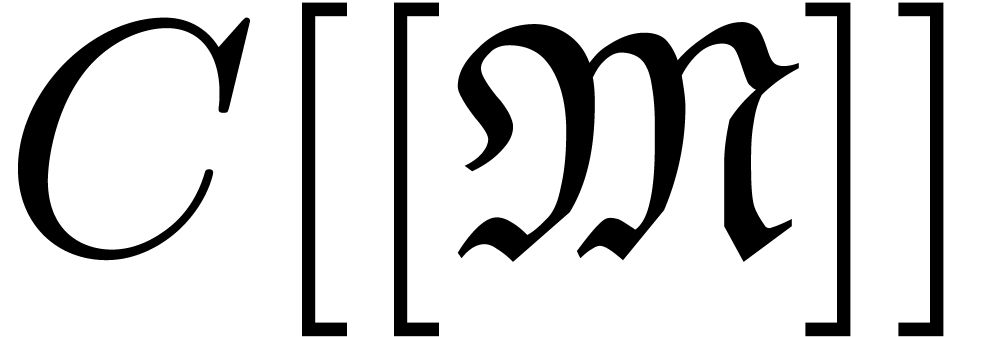 on which we defined natural derivations and
compositions.
on which we defined natural derivations and
compositions.
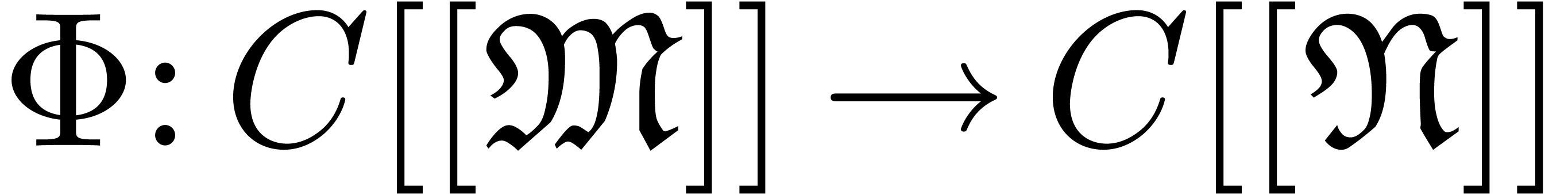 , which include (when defined) summation,
multiplication, differentiation, composition, etc. Our main result is
the proof of an implicit function theorem for Noetherian operators. This
theorem may be used to explicitly solve very general types of functional
equations in generalized power series.
, which include (when defined) summation,
multiplication, differentiation, composition, etc. Our main result is
the proof of an implicit function theorem for Noetherian operators. This
theorem may be used to explicitly solve very general types of functional
equations in generalized power series.