Abstract
Let 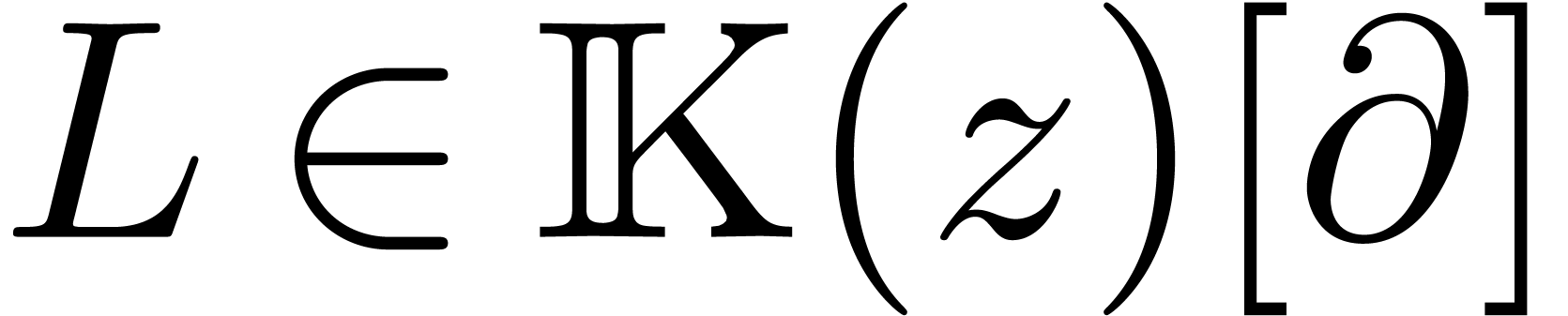 be a linear differential
operator, where
be a linear differential
operator, where  is the field
of algebraic numbers. A holonomic function over
is the field
of algebraic numbers. A holonomic function over  is a solution
is a solution 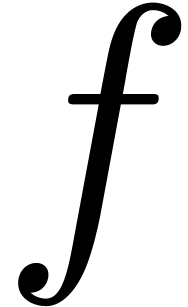 to the equation
to the equation 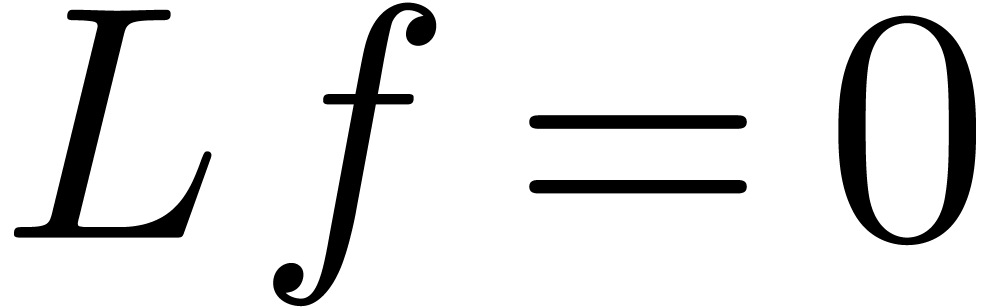 . We will
also assume that
. We will
also assume that 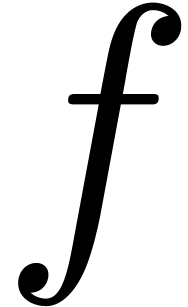 admits
initial conditions in
admits
initial conditions in  at a
non-singular point
at a
non-singular point 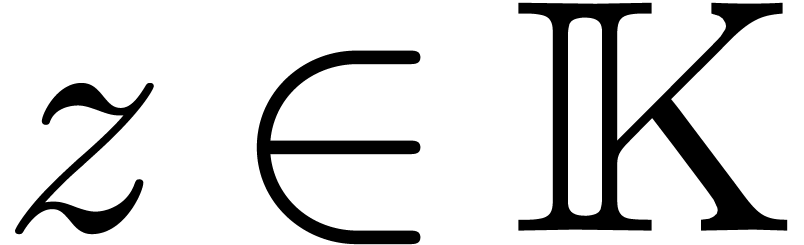 .
.
Given a broken-line path 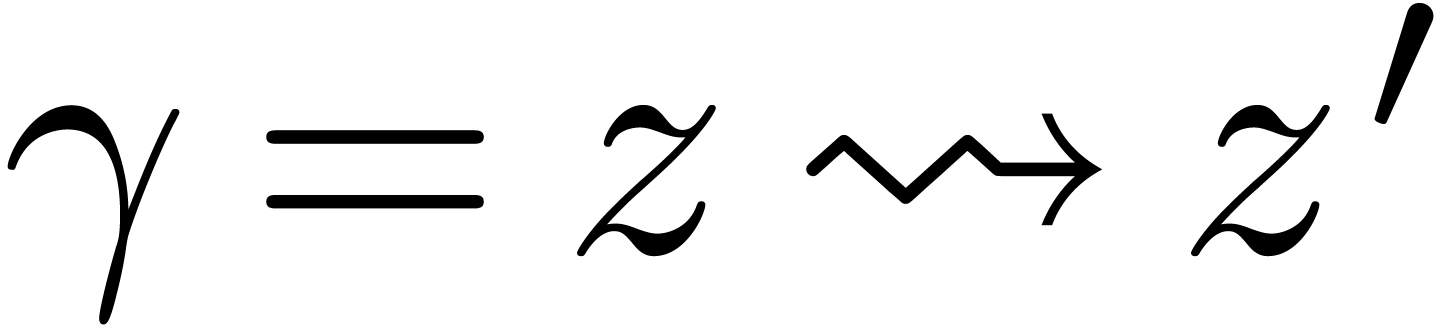 between
between  and
and 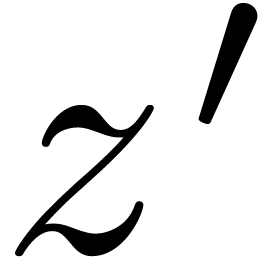 , which avoids the singularities of
, which avoids the singularities of  and with vertices in
and with vertices in  , we have shown in a previous
paper how to compute
, we have shown in a previous
paper how to compute 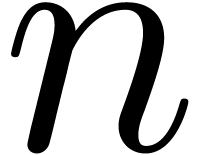 digits of the analytic continuation of
digits of the analytic continuation of 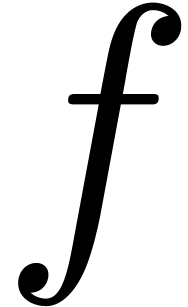 along
along 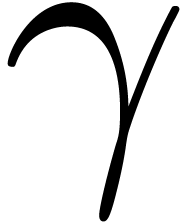 in time
in time 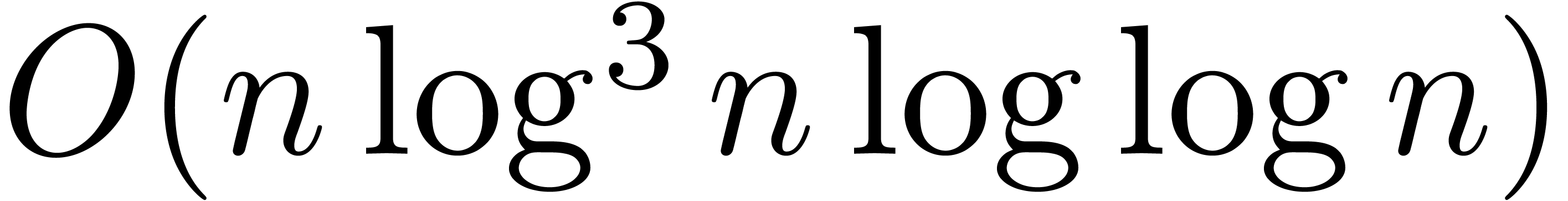 . In a second paper, this result
was generalized to the case when
. In a second paper, this result
was generalized to the case when 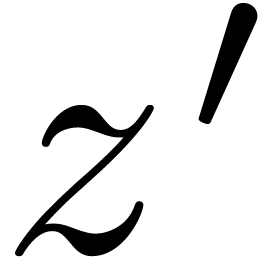 is allowed to be a regular singularity, in which case we compute the
limit of
is allowed to be a regular singularity, in which case we compute the
limit of 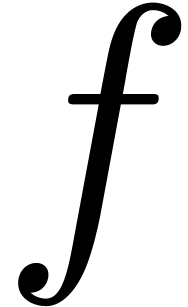 when we approach
the singularity along
when we approach
the singularity along 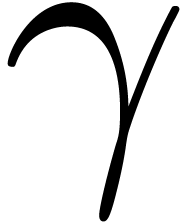 .
.
In the present paper, we treat the remaining case when the end-point of
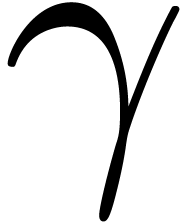 is an irregular singularity.
In fact, we will solve the more general problem to compute
“singular transition matrices” between non standard points
above a singularity and regular points in
is an irregular singularity.
In fact, we will solve the more general problem to compute
“singular transition matrices” between non standard points
above a singularity and regular points in  near the singularity. These non standard points correspond to the choice
of “non-singular directions” in Écalle's
accelero-summation process.
near the singularity. These non standard points correspond to the choice
of “non-singular directions” in Écalle's
accelero-summation process.
We will show that the entries of the singular transition matrices may be
approximated up to 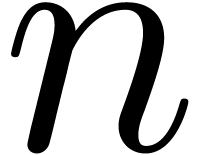 decimal
digits in time
decimal
digits in time 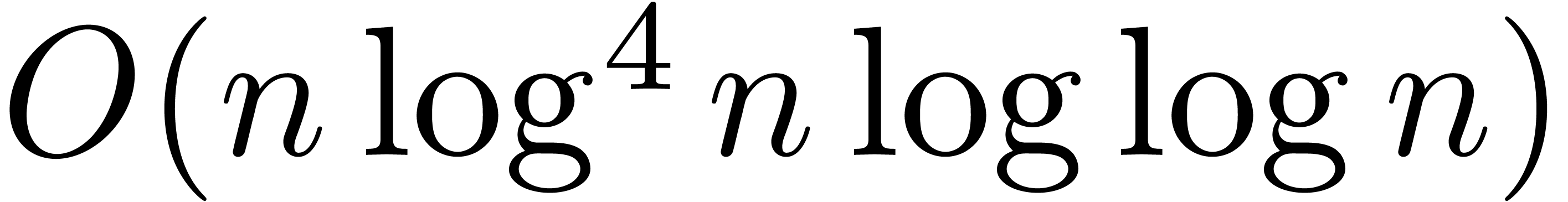 . As a
consequence, the entries of the Stokes matrices for
. As a
consequence, the entries of the Stokes matrices for 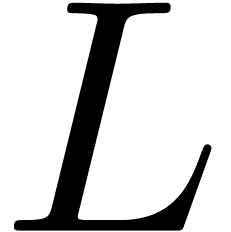 at each singularity may be approximated with
the same time complexity.
at each singularity may be approximated with
the same time complexity.
Keywords: algorithm, holonomic function,
accelero-summation, Stokes matrix
A.M.S. subject classification: 33-04, 30-04, 40-04,
33F05, 33E30, 40G10, 30B40
View: Html, TeXmacs, Pdf,
BibTeX
February 2021: Errata, Corrected
version
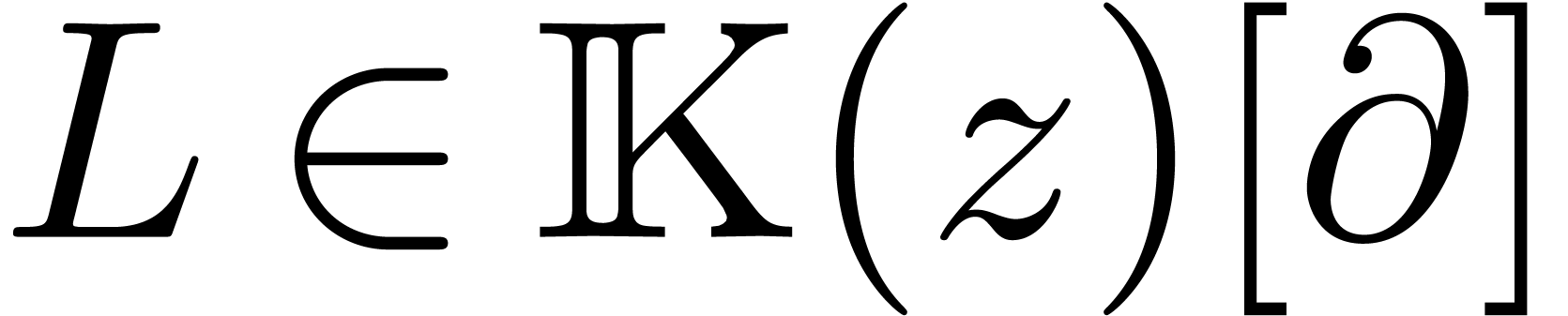 be a linear differential
operator, where
be a linear differential
operator, where  is the field
of algebraic numbers. A holonomic function over
is the field
of algebraic numbers. A holonomic function over  is a solution
is a solution 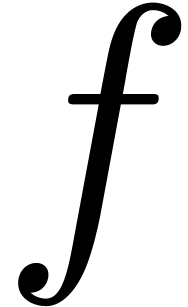 to the equation
to the equation 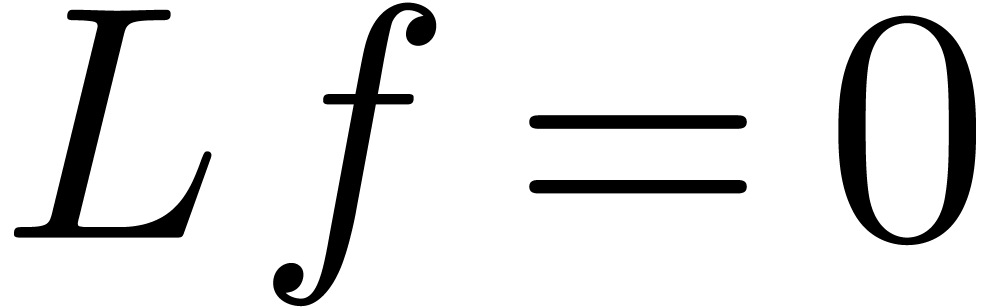 . We will
also assume that
. We will
also assume that 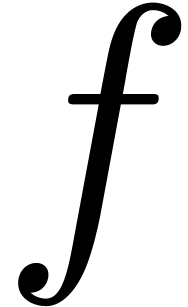 admits
initial conditions in
admits
initial conditions in  at a
non-singular point
at a
non-singular point 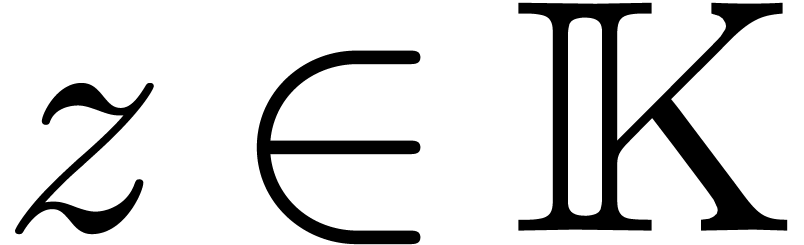 .
.
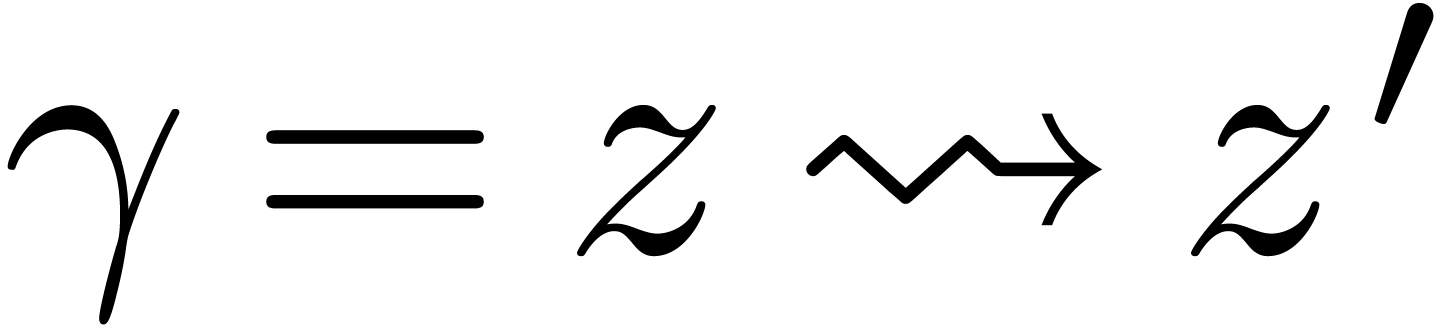 between
between  and
and 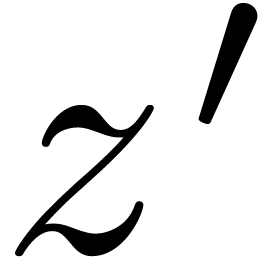 , which avoids the singularities of
, which avoids the singularities of  and with vertices in
and with vertices in  digits of the analytic continuation of
digits of the analytic continuation of 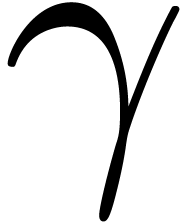 in time
in time 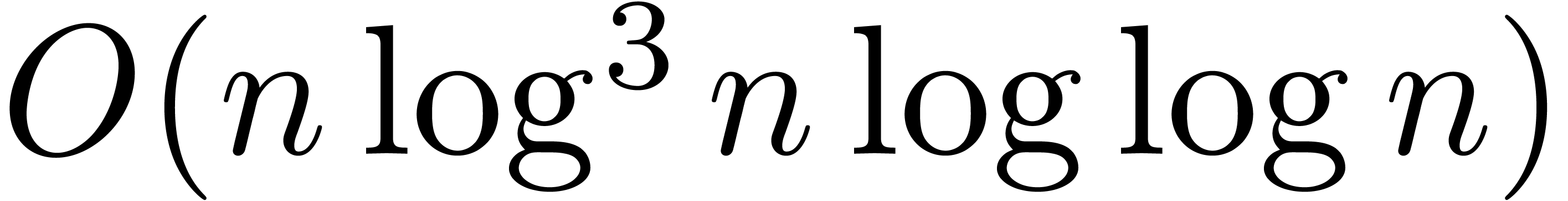 . In a
. In a 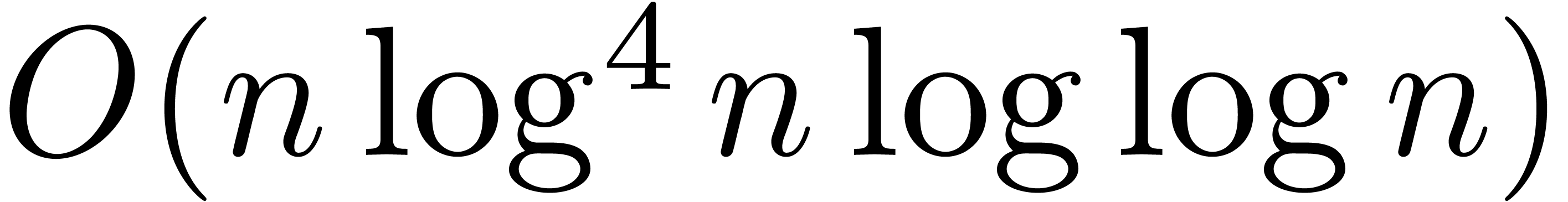 . As a
consequence, the entries of the Stokes matrices for
. As a
consequence, the entries of the Stokes matrices for