Abstract
Consider a finite field 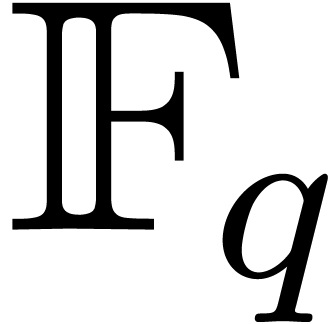 whose multiplicative group has smooth cardinality. We study the problem
of computing all roots of a polynomial that splits over
whose multiplicative group has smooth cardinality. We study the problem
of computing all roots of a polynomial that splits over 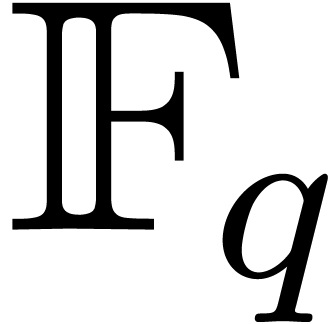 , which was one of the bottlenecks for fast
sparse interpolation in practice. We revisit and slightly improve
existing algorithms and then present new randomized ones based on the
Graeffe transform. We report on our implementation in the Mathemagix
computer algebra system, confirming that our ideas gain by an order of
magnitude in practice.
, which was one of the bottlenecks for fast
sparse interpolation in practice. We revisit and slightly improve
existing algorithms and then present new randomized ones based on the
Graeffe transform. We report on our implementation in the Mathemagix
computer algebra system, confirming that our ideas gain by an order of
magnitude in practice.
Authors: Bruno Grenet, Joris van der Hoeven, Grégoire
Lecerf
View: Html, TeXmacs, Pdf,
BibTeX
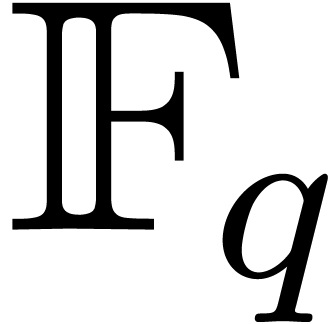 whose multiplicative group has smooth cardinality. We study the problem
of computing all roots of a polynomial that splits over
whose multiplicative group has smooth cardinality. We study the problem
of computing all roots of a polynomial that splits over 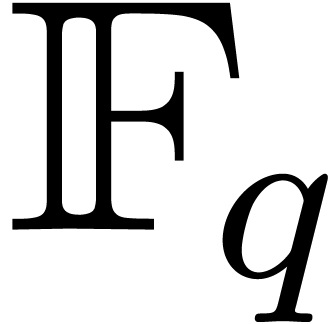 , which was one of the bottlenecks for fast
sparse interpolation in practice. We revisit and slightly improve
existing algorithms and then present new randomized ones based on the
Graeffe transform. We report on our implementation in the
, which was one of the bottlenecks for fast
sparse interpolation in practice. We revisit and slightly improve
existing algorithms and then present new randomized ones based on the
Graeffe transform. We report on our implementation in the