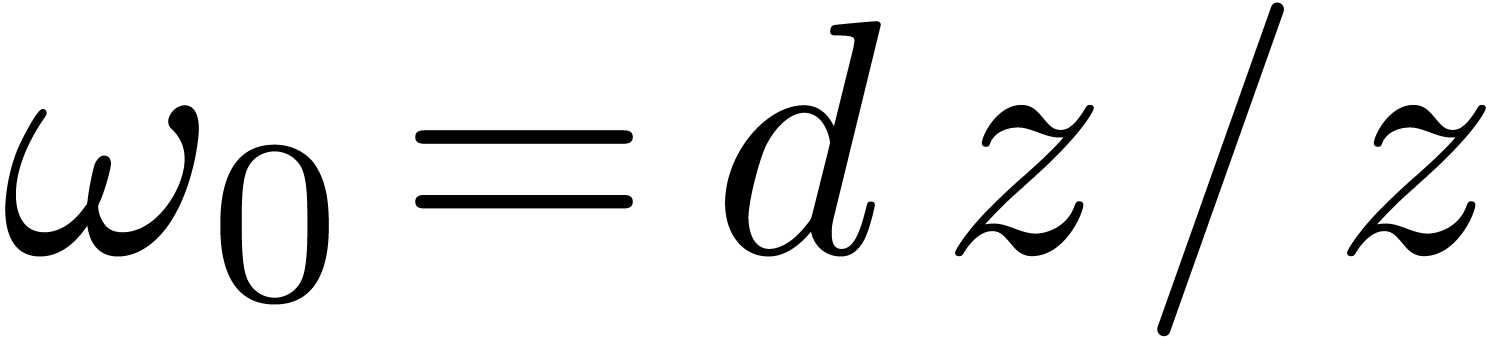 and
and 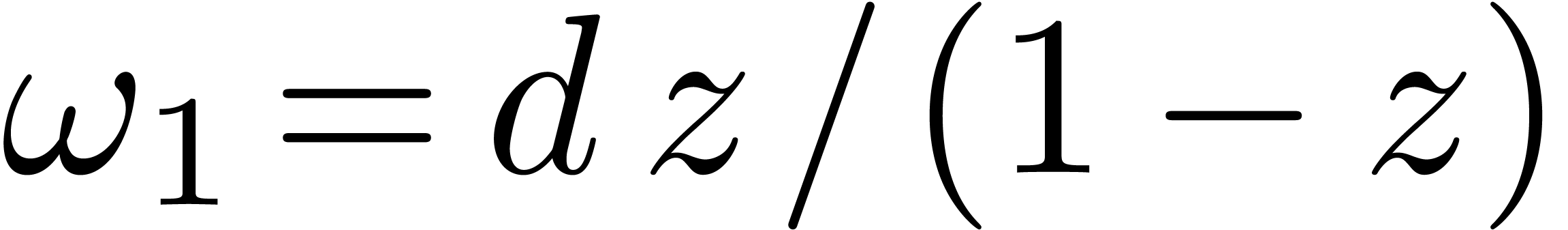 . We prove an algorithm
which computes the monodromy of these special functions. This
algorithm, implemented in
. We prove an algorithm
which computes the monodromy of these special functions. This
algorithm, implemented in | HomepagePublicationsTalksTeXmacsMathemagix |
Generalized polylogarithms are defined as iterated integrals with
respect to the two differential forms 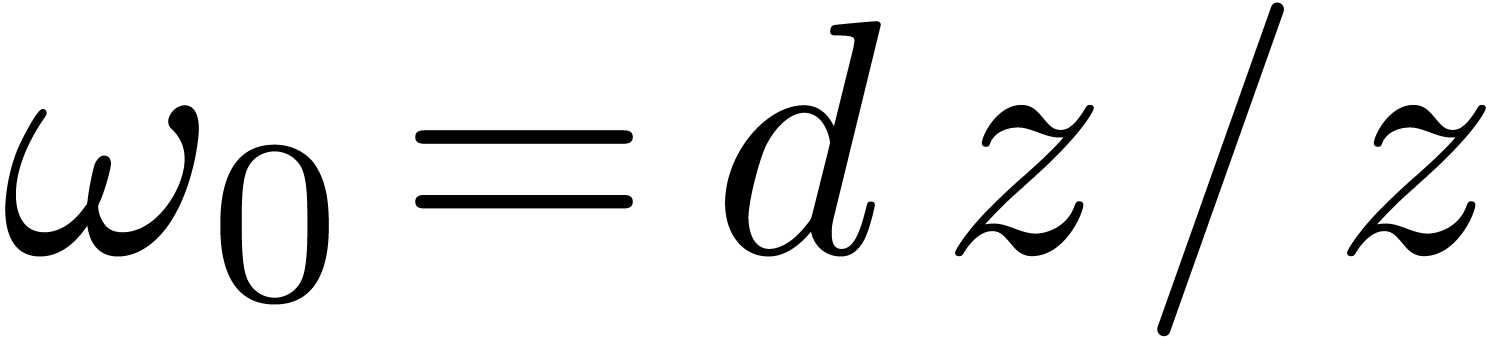 and
and 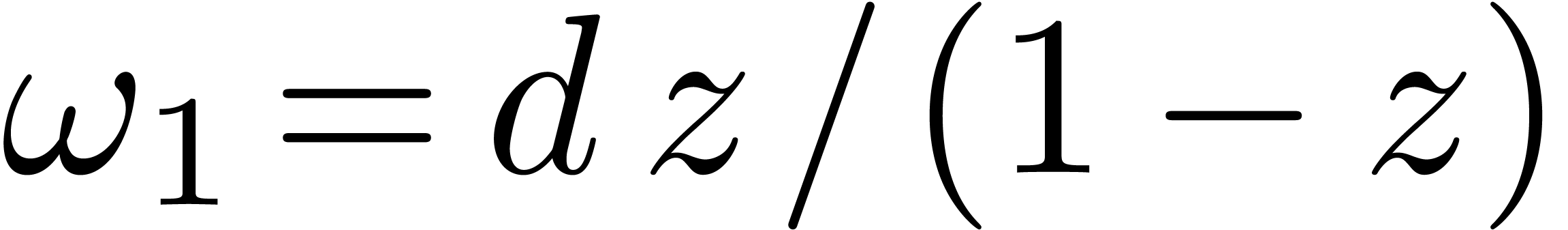 . We prove an algorithm
which computes the monodromy of these special functions. This
algorithm, implemented in
. We prove an algorithm
which computes the monodromy of these special functions. This
algorithm, implemented in
Authors:
Keywords: polylogarithms, multiple zeta values, monodromy, Lyndon words