Abstract
A holonomic function is an analytic function, which satisfies a linear
differential equation 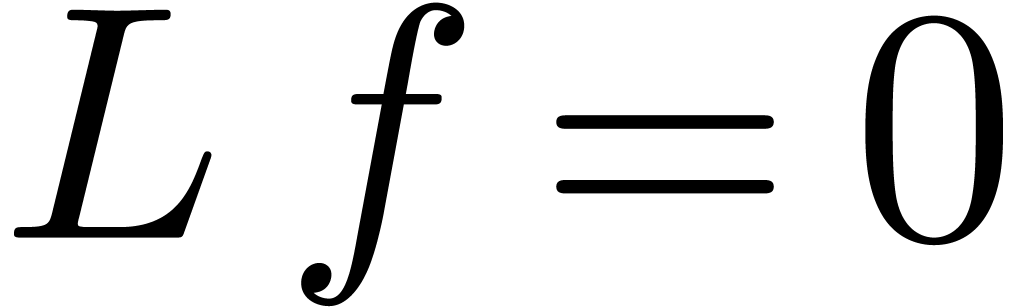 with
polynomial coefficients. In particular, the elementary functions
with
polynomial coefficients. In particular, the elementary functions 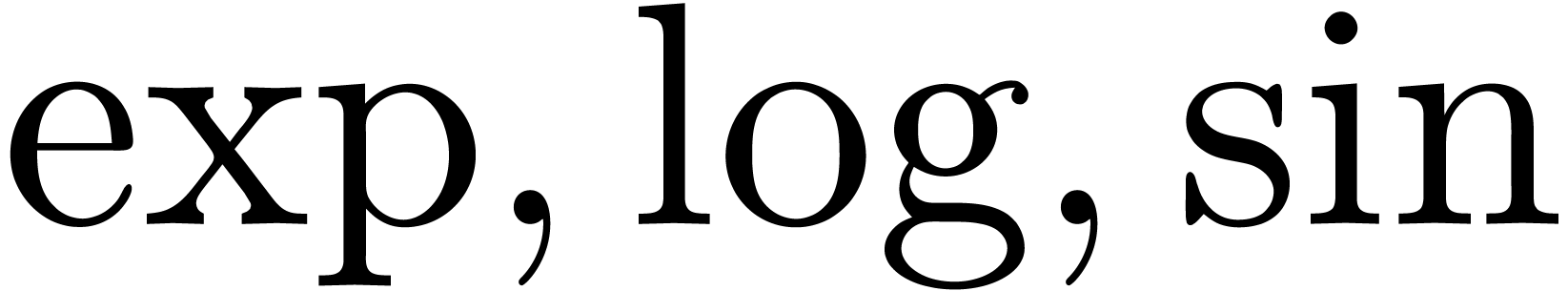 , etc. and many
special functions like
, etc. and many
special functions like  ,
,
 , Bessel functions, etc. are
holonomic functions. In a previous paper, we have given an
asymptoticallyfast algorithm to evaluate a holonomic function
, Bessel functions, etc. are
holonomic functions. In a previous paper, we have given an
asymptoticallyfast algorithm to evaluate a holonomic function 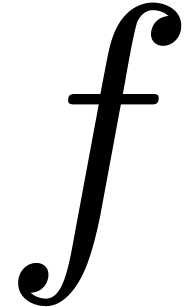 at a non-singular point
at a non-singular point  on the Riemann surface of
on the Riemann surface of 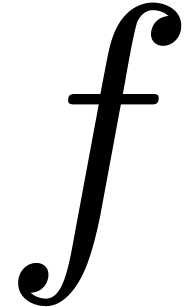 , up to any number of decimal
digits while estimating the error. However, this algorithm becomes
inefficient, when
, up to any number of decimal
digits while estimating the error. However, this algorithm becomes
inefficient, when 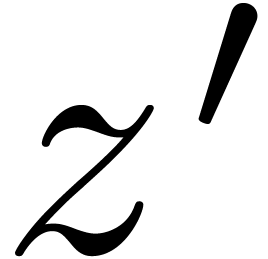 approaches
a singularity of
approaches
a singularity of 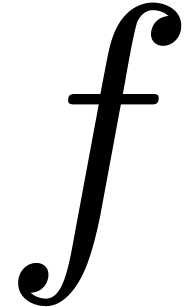 . In this
paper, we obtain efficient algorithms for the evaluation ofholonomic
functions near and in singular points where the differential operator
. In this
paper, we obtain efficient algorithms for the evaluation ofholonomic
functions near and in singular points where the differential operator
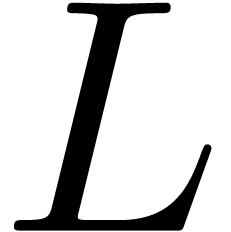 is regular (or, slightly
more generally, where
is regular (or, slightly
more generally, where 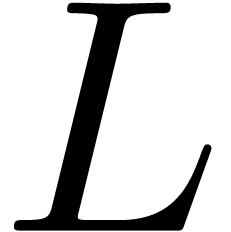 is
quasi-regular — a concept to be introduced below).
is
quasi-regular — a concept to be introduced below).
View: Pdf, BibTeX
Note: the submission process of this paper turned out
to be very long (9 rounds!). Contrary to what is stated in the journal
version, the first submission took place on 1998, March 19.
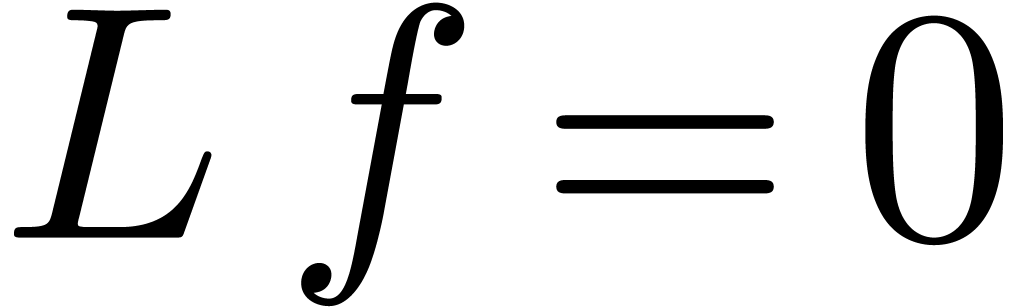 with
polynomial coefficients. In particular, the elementary functions
with
polynomial coefficients. In particular, the elementary functions 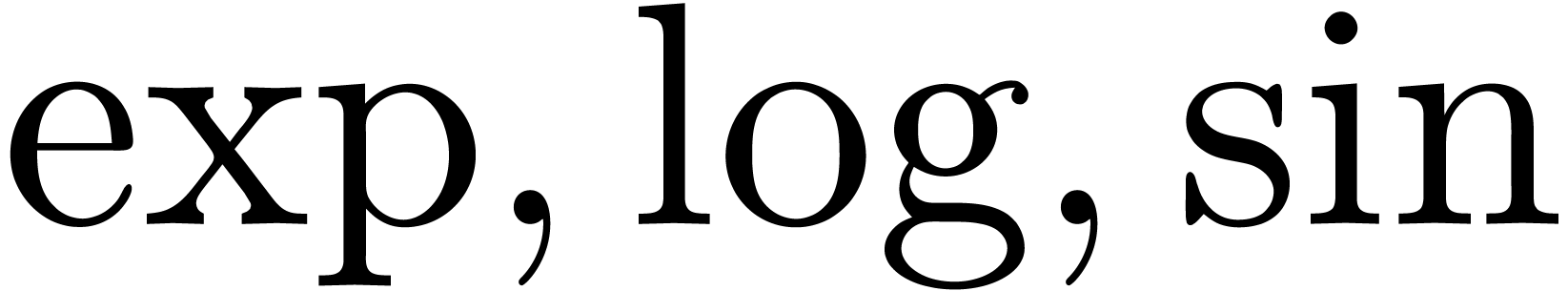 , etc. and many
special functions like
, etc. and many
special functions like  ,
,
 , Bessel functions, etc. are
holonomic functions. In a previous paper, we have given an
asymptoticallyfast algorithm to evaluate a holonomic function
, Bessel functions, etc. are
holonomic functions. In a previous paper, we have given an
asymptoticallyfast algorithm to evaluate a holonomic function 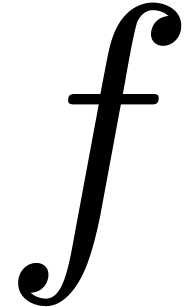 at a non-singular point
at a non-singular point 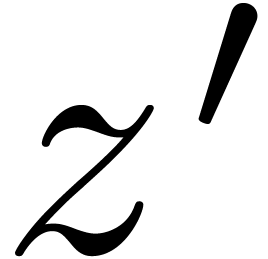 on the Riemann surface of
on the Riemann surface of 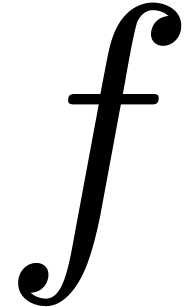 , up to any number of decimal
digits while estimating the error. However, this algorithm becomes
inefficient, when
, up to any number of decimal
digits while estimating the error. However, this algorithm becomes
inefficient, when 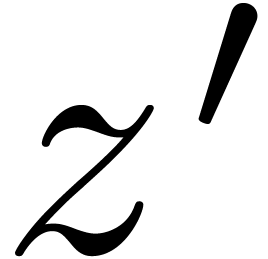 approaches
a singularity of
approaches
a singularity of 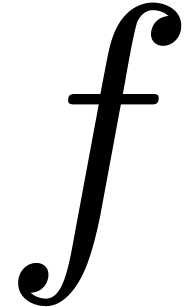 . In this
paper, we obtain efficient algorithms for the evaluation ofholonomic
functions near and in singular points where the differential operator
. In this
paper, we obtain efficient algorithms for the evaluation ofholonomic
functions near and in singular points where the differential operator
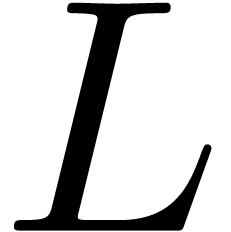 is regular (or, slightly
more generally, where
is regular (or, slightly
more generally, where 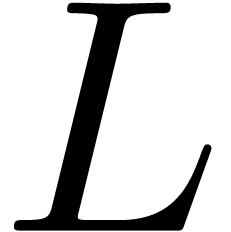 is
quasi-regular — a concept to be introduced below).
is
quasi-regular — a concept to be introduced below).