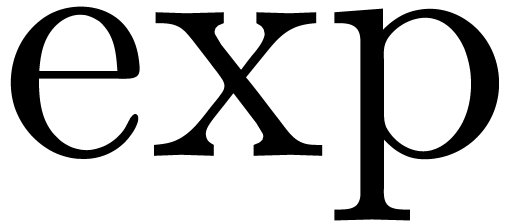Consider a class of constants built up from the rationals using the field operations and a certain number of transcendental functions like 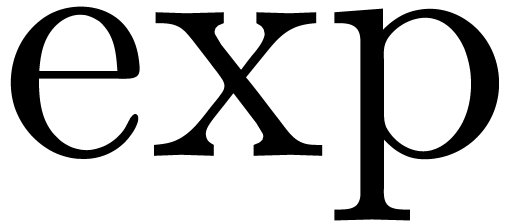. A central problem in computer algebra is to test whether such a constant, which is represented by an expression, is zero.

The simplest approach to the zero-test problem is to evaluate the constants up to a certain number of decimal digits. Modulo certain precautions, we will make it likely that this approach is actually a valid one. More precisely, one may for instance restrict oneself to certain subsets of expressions in order to avoid “high precision fraud”. For such subsets, we will state witness conjectures, which propose reasonable lower bounds for non zero constants as a function of the minimal sizes of expressions that represent them.

Unfortunately, such witness conjectures are extremely hard to prove, since they are really far reaching generalizations of results in diophantine approximations. Nevertheless, we will also discuss their counterparts for formal power series, which are more accessible.

Keywords: witness conjecture, zero test, power series, Diophantine approximation

A.M.S. subject classification: 69W30, 11Y60, 34-04, 35-04, 12H05, 40-04, 13P10

View: Html, TeXmacs, Pdf, BibTeX