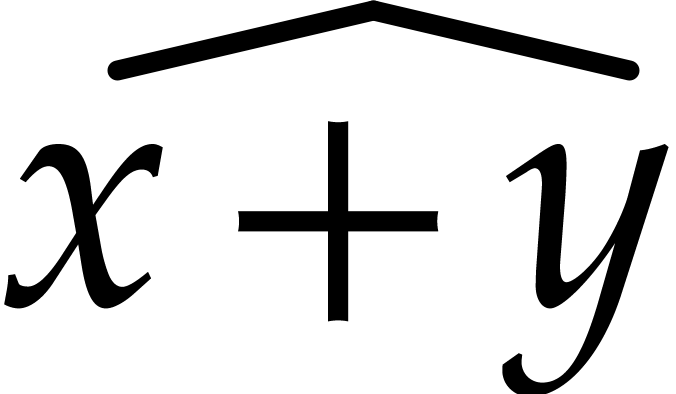
Mathematical formulas
Mathematical formulas
One of the main purposes of TeXmacs is to edit mathematical formulas.
If the cursor is inside a formula (i.e. inside
“math mode”), then the mode sensitive menus and toolbars
provide buttons for entering common mathematical constructs.
Similarly, as will be detailed in this section, the bahaviour of the
keyboard changes so as to allow for the rapid typing of mathematical
symbols. For instance, typing ->
inserts the arrow  .
.
Starting with version 1.0.7.10, TeXmacs also incorporates several features for the “semantic” editing of mathematical formulas, which will be described at the end of this section. When used appropriately, this allows you to write documents in which all formulas are at least correct from a syntactical point of view. A “syntax corrector” is included to assist you with this task. Documents with more semantics are for instance useful when using formulas as inputs for a computer algebra system. Such documents are also less likely to contain “typos”. Other interesting features, such as semantic search and replace, should be developed in the future.
1.Incorporating mathematical formulas into documents
TeXmacs provides three main ways in order to enter a mathematical formulas into the main text:
-
Insert →Mathematics →Inline formula or $ -
This entry corresponds to small inline formulas like
 inside a textual paragraph. Note that
formulas are typeset specially so they do not take too much
vertical space. For example, limits are always displayed on the
right. Limits can be displayed below in formulas with
inside a textual paragraph. Note that
formulas are typeset specially so they do not take too much
vertical space. For example, limits are always displayed on the
right. Limits can be displayed below in formulas with Format →Display style →on . In formulas, display style is off by default. -
Insert →Mathematics →Displayed formula or Alt+$ -
This entry is used for entering bigger displayed equations, like

which are typeset in a paragraph of their own. You may use the shortcut Ctrl+# in order to give the equation a number (or to remove the number of an equation). Also, Ctrl+Tab allows you to switch between inline formulas and displayed equations.
-
Insert →Mathematics →Several equations or Alt+& -
This entry allows you to create an
eqnarray* , a three columns wide table-like environment (see creating tables). This environment is typically used for lists of multiple relations like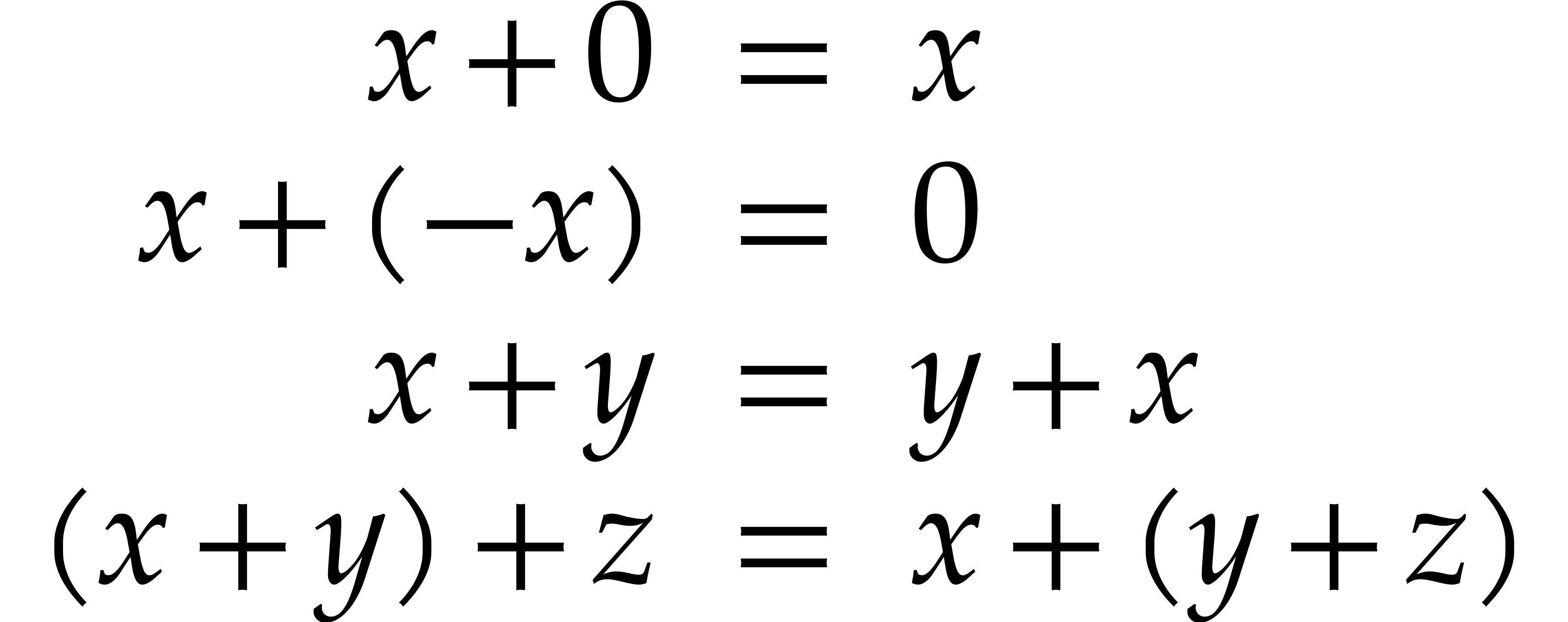
The first column is centered to the right, the second one at the middle and the last one at the left. Another typical use of the
eqnarray* environment is a step by step computation
in which many entries of the left column are left open.
2.Typing mathematical symbols
The Greek characters are obtained in TeXmacs using the Shift+F7-key.
For instance, Shift+F7A yields
 and Shift+F7Shift+G
yields
and Shift+F7Shift+G
yields  . Similarly, F6,
F7, F8 and Shift+F6
can be used in order to type bold, calligraphic, fraktur and
blackboard bold characters. For instance, F8M yields
. Similarly, F6,
F7, F8 and Shift+F6
can be used in order to type bold, calligraphic, fraktur and
blackboard bold characters. For instance, F8M yields  , Shift+F6Shift+R yields
, Shift+F6Shift+R yields  and F6F7Shift+Z yields
and F6F7Shift+Z yields  .
.
Greek characters can also be obtained as “variants” of
Latin characters using the Tab-key. For instance,
PTab yields  .
The Tab-key is also used for obtaining variants of
the Greek letters themselves. For instance, both Shift+F7PTab and PTabTab yield
.
The Tab-key is also used for obtaining variants of
the Greek letters themselves. For instance, both Shift+F7PTab and PTabTab yield  .
An alternative way to enter blackboard bold characters is to type the
same capital twice. For instance, Shift+ZShift+Z yields
.
An alternative way to enter blackboard bold characters is to type the
same capital twice. For instance, Shift+ZShift+Z yields  .
.
Some symbols admit many variants. For instance, <
yields  , <Tab
yields
, <Tab
yields  , <TabTab yields
, <TabTab yields  , <TabTabTab yields
, <TabTabTab yields
 , and so on. You may “cycle back”
among the variants using Shift+Tab. For instance,
<TabTabShift+Tab is equivalent to <Tab.
, and so on. You may “cycle back”
among the variants using Shift+Tab. For instance,
<TabTabShift+Tab is equivalent to <Tab.
Many other mathematical symbols are obtained by “natural”
key-combinations. For instance, ->
yields  , --> yields
, --> yields  and >= yields
and >= yields  . Similarly, |Tab- yields
. Similarly, |Tab- yields
 , |-> yields
, |-> yields  and -><- yields
and -><- yields
 . The following general rules hold in order to
enter mathematical symbols:
. The following general rules hold in order to
enter mathematical symbols:
- Tab
-
is the main key for obtaining variants. For instance, >= yields
 ,
but >=Tab
yields
,
but >=Tab
yields  . Similarly, <TabTab yields
. Similarly, <TabTab yields  ,
<TabTab= yields
,
<TabTab= yields  and <TabTab=Tab yields
and <TabTab=Tab yields  . Also, Shift+PTab yields
. Also, Shift+PTab yields  and ETab
yields the constant
and ETab
yields the constant  .
.
- @
-
is used for putting symbols into circles or boxes. For instance, @+ yields
 and @X
yields
and @X
yields  . Similarly, @Tab+ yields
. Similarly, @Tab+ yields  .
.
- /
-
is used for negations. For instance, =/ yields
 and <=/ yields
and <=/ yields  .
Notice that <=TabTab/
yields
.
Notice that <=TabTab/
yields  , while <=TabTab/Tab yields
, while <=TabTab/Tab yields  .
.
- !
-
is used after arrows in order to force scripts to be placed above or below the arrow. For instance, -->^X yields
 , but -->!^X yields
, but -->!^X yields  .
.
The logical relations  and
and  are obtained using & and %.
The operators
are obtained using & and %.
The operators  and
and  are
natural variants &Tab and
%Tab. Various miscellaneous
symbols can be obtained using the Shift+F5 prefix.
are
natural variants &Tab and
%Tab. Various miscellaneous
symbols can be obtained using the Shift+F5 prefix.
Notice that certain symbols with a different mathematical meaning are
sometimes denoted in a similar way; such symbols are called
homoglyphs. For instance, the vertical bar  can be used as a separator for defining sets
can be used as a separator for defining sets  ,
but also as the binary relation “divides”
,
but also as the binary relation “divides”  .
Often, but not always, homoglyphs admit a different spacing. The most
annoying ambiguity is between invisible multiplication
.
Often, but not always, homoglyphs admit a different spacing. The most
annoying ambiguity is between invisible multiplication  and function application
and function application  , which
are entered using the shortcuts *
resp. Space.
, which
are entered using the shortcuts *
resp. Space.
In order to facilitate certain automated treatments of your documents, such as mathematical syntax checking, we incite authors to pay attention to the homoglyph problem when entering formulas. For more information on this issue and how TeXmacs can assist you to use the appropriate notations, we refer to our section on the semantics of mathematical symbols.
3.Main mathematical constructs
The main mathematical objects are created using the Alt+ prefix as follows:
|
||||||||||||||||||
Primes, subscripts and superscripts are created as follows:
|
|||||||||||||||||||||
Some important mathematical constructs are actually tabular constructs and are documented separately.
4.Typing large delimiters
Brackets inside mathematical formulas should always match: as soon as
you enter an opening bracket “(”, TeXmacs will
automatically insert the matching closing bracket “)”. You
may disable this feature using
Sometimes, you do not want the closing bracket, or you may want to
replace it by another closing bracket. No problem: if your cursor is
just before the closing bracket inside  , then
pressing ] will turn the expression into
, then
pressing ] will turn the expression into  . Alternatively, deletion of a bracket will actually turn
it into an invisible bracket, after which you can replace
it by an arbitrary opening or closing bracket.
. Alternatively, deletion of a bracket will actually turn
it into an invisible bracket, after which you can replace
it by an arbitrary opening or closing bracket.
By default, the sizes of the brackets are adjusted to the expression between the brackets. Small delimiters, which are created using the Alt+-prefix, keep their sizes independently of the enclosed expression. Alternatively, you may use Ctrl+* in order to toggle between large and small delimiters.
For some delimiters, such as  , the opening and
closing delimiters coincide. For instance, entering a vertical bar
| will produce an absolute value. The (small)
bar-separator
, the opening and
closing delimiters coincide. For instance, entering a vertical bar
| will produce an absolute value. The (small)
bar-separator  is obtained using F5|, or as a variant using |Tab. The big bar-separator is entered using Alt+M|. In TeX and LaTeX, such large separators do not exist;
they are used for producing the vertical bars in formulas like
is obtained using F5|, or as a variant using |Tab. The big bar-separator is entered using Alt+M|. In TeX and LaTeX, such large separators do not exist;
they are used for producing the vertical bars in formulas like
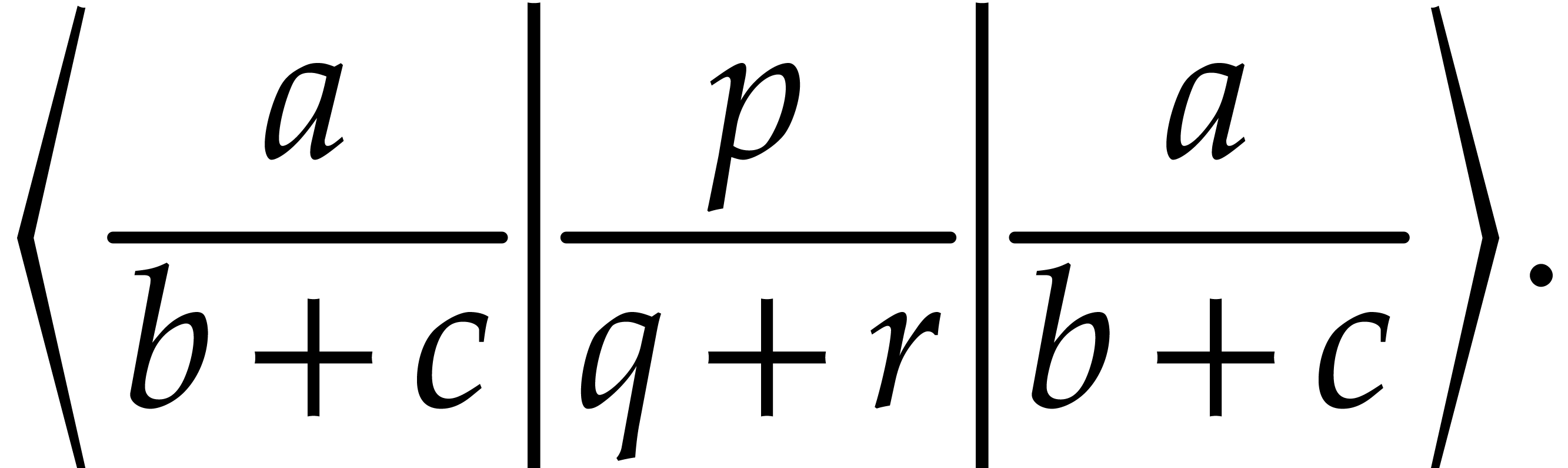
There may be as many middle delimiters between a left and a right delimiter as one wishes. Notice that there are still another number of variants of vertical bars. For instance, the binary relation “divides” is entered using F5|TabTab or |TabTabTabTab.
In TeXmacs, large delimiters may either be “left
delimiters”, “right delimiters” or “middle
delimiters”. By default,  and
and  are left delimiters,
are left delimiters,  and
and  are right delimiters. But there status can be
changed using the Alt+L, Alt+R
and Alt+M key combinations. For instance, Alt+L) produces
are right delimiters. But there status can be
changed using the Alt+L, Alt+R
and Alt+M key combinations. For instance, Alt+L) produces  ,
considered as a large left delimiter.
,
considered as a large left delimiter.
Sometimes you may want large delimiters of a particular size, instead
of self-adjusting ones. This can be achieved by resizing the
expression in between the brackets using the items in
Notice that it is possible to insert a pair of invisible brackets using ?. This is for instance useful in computational contexts, in which formulas should admit a precise, not merely visual semantics. Alternatively, one may put the formula inside a “rigid box” using Meta+Shift+R, which additionally prevents the formula from being hyphenated.
5.Typing big operators
The following key-combinations are used in order to create big symbols:
|
||||||||||||||||||||||||||||
The scopes of big operators are indicated visually, through the light cyan boxes around the tags which contain the cursor.
The big integral signs admit two variants, depending on where you want to place subscripts and superscripts. By default, the scripts are placed as follows:

The alternative rendering “with limits”

is obtained using Shift+F5Shift+LShift+I. Similarly, you may type Shift+F5Shift+LShift+O in order to obtain
 with limits.
with limits.
6.Wide mathematical accents
The table below shows how to type mathematical accents above symbols or entire formulas. Indeed, some of these accents automatically become as wide as the formulas below them.
|
|||||||||||||||||||||||||||||||||||
The same accents may be inserted below the expressions using the Alt+U prefix. For instance, Alt+UShift+BX+Y can be used in order to enter  .
.
7.Semantic editing facilities
Starting with version 1.0.7.10, TeXmacs incorporates several features
for the “semantic” editing of mathematical formulas. When
used appropriately, this allows you to write documents in which all
formulas are at least correct from a syntactical point of view. For
instance, in the formulas  , the computer will
understand that
, the computer will
understand that  is an operator which applies
to the arguments
is an operator which applies
to the arguments  and
and  .
Notice that our “semantics” does not go any further:
TeXmacs is unaware of the mathematical nature of addition.
.
Notice that our “semantics” does not go any further:
TeXmacs is unaware of the mathematical nature of addition.
Semantic editing does require additional efforts from the user, at least a little adaptation. For instance, it is the user's job to enter multiplications using the shortcut * and function applications using Space. Indeed, from the graphical point of view, these operations cannot be distinguished, since they are both printed as invisible whitespace. However, the semantics of these operations is clearly very different.
Although semantically correct documents are usually not very different from informal presentation-oriented documents as far as typesetting is concerned, the additional user effort may pay off for several reasons:
-
Documents with more semantics are for instance useful when using formulas as inputs for a computer algebra system.
-
Syntactically correct documents are less likely to contain “typos” or more intricate mathematical errors.
-
For certain editing operations, such as cut and paste, one may directly select subformulas which are meaningful from the syntactical point of view.
-
It reduces the risk of using non standard notations, which will be difficult to understand for potential readers of your work.
Furthermore, other semantic facilities might be integrated in the future, such as semantic search and replace, or semantic search on the web.
In order to activate the semantic editing facilities, please toggle
The semantic focus is useful for several reasons. First of all, it is displayed in green if the formula is syntactically correct and in red if you made an error. This allows to quickly notice any typos while entering a formula. Secondly, if you have any doubt on the precedence of a mathematical operator or relation, then the semantic focus will inform you on the default interpretation: by putting your cursor right next to your operator, the subexpression to which the operator applies will be highlighted. In the case of an addition, or a more general associative operator, all summands are highlighted.
8.Common errors and syntax correction
By default, the semantic editing mode “understands” most classical mathematical notations. This is achieved through the use of a carefully designed grammar for mainstream mathematics. Obviously, the use of a fixed grammar may cause the following problems:
-
Mathematical formulas frequently contain ad hoc notations. For instance, the formulas might contain some text or meaningful whitespace. Another example of an ad hoc notation is the sign sequence
 . In such
cases, the user should explicitly annotate the
appropriate parts of the formula in order to make them
semantically meaningful.
. In such
cases, the user should explicitly annotate the
appropriate parts of the formula in order to make them
semantically meaningful.
-
The TeXmacs grammar used for the interpretation of mathematical formulas may be incomplete or inadequate for certain situations. It is possible to customize or extend the grammar using the standard TeXmacs macro mechanism. Notations for specific areas may be grouped together in dedicated style packages.
Besides these intrinsically hard to avoid problems, the following common and “easy-to-make” mistakes are a further source of trouble for associating semantics to mathematical formulas:
-
Since TeXmacs is a wysiwyg editor, some of the structure of the document is invisible for the user. For instance, the presence of a mathematical formula
 is indicated
through the use of an italic slant and special spacing. However,
in the formula
is indicated
through the use of an italic slant and special spacing. However,
in the formula  it is easy to type the
closing bracket outside the formula, with no visual difference.
it is easy to type the
closing bracket outside the formula, with no visual difference.
-
Various mathematical notations are visually ambiguous. For instance,
 would usually be understood as
would usually be understood as
 , whereas
, whereas  rather
corresponds to a function application. In the semantic editing
mode, the user is expected to resolve this ambiguity by hand by
entering multiplications using * and spaces
using Space. The multiply/apply ambiguity is
one of the main sources of syntax errors, since many users do not
pay attention to invisible differences. Similarly, the
rather
corresponds to a function application. In the semantic editing
mode, the user is expected to resolve this ambiguity by hand by
entering multiplications using * and spaces
using Space. The multiply/apply ambiguity is
one of the main sources of syntax errors, since many users do not
pay attention to invisible differences. Similarly, the  glyph could be the “logical and” or the
“wedge product”. This “homoglyph” issue
will be addressed in more detail in the section on the semantics
of mathematical symbols.
glyph could be the “logical and” or the
“wedge product”. This “homoglyph” issue
will be addressed in more detail in the section on the semantics
of mathematical symbols.
-
It could be that a text was originally written in LaTeX or an old version of TeXmacs. In that case, the document contains no special indication on matching brackets or the scopes of big operators. For instance, in the formula
 , should we
interpret the second bracket as a closing bracket? This is indeed
the standard french notation for an interval with an open right
end. More generally, all problems that we have mentioned so far
tend to be present simultaneously when trying to associate
semantics to existing documents.
, should we
interpret the second bracket as a closing bracket? This is indeed
the standard french notation for an interval with an open right
end. More generally, all problems that we have mentioned so far
tend to be present simultaneously when trying to associate
semantics to existing documents.
After activation of the semantic editing mode, you may check whether a
formula is correct by positioning your cursor inside it and looking at
the color of the bounding box of the semantic focus: a
green color corresponds to a correct formula and a red color indicates
an error in the formula. Alternatively, assuming that the focus is on
a mathematical formula, you may select
For the second kind of “easy-to-make” errors, TeXmacs
includes an automatic syntax corrector. Assuming that your cursor is
inside a formula, you may use
The precise algorithms which are used for the correction may be
enabled or disabled from
-
Remove superfluous invisible operators -
This algorithm is used in order to remove any superfluous function applications or multiplications. For instance, users who are accustomed to editing ASCII files often type spaces around binary infixes such as addition. Such “function applications” will be removed by this algorithm.
-
Insert missing invisible operators -
In LaTeX, multiplications and function applications are never entered explicitly. When importing a LaTeX document, it is therefore important to detect and insert missing multiplications and function applications.
-
Homoglyph substitutions -
This algorithm may perform some other useful substitutions of symbols by visually similar, but semantically distinct symbols. For instance, the backslash symbol
 is
replaced by the binary set differences infix (as in
is
replaced by the binary set differences infix (as in  ), whenever appropriate.
), whenever appropriate.
From the
After syntax correction, the remaining errors indicate genuine typos at worst or non standard or non supported notations at best. We also notice that “correct” formulas do not necessarily have the intended meaning. In order to check whether the operators indeed apply to the intended arguments, you should keep an eye on the current focus while typing your formulas.
9.Semantics of mathematical symbols
The mathematical symbols in TeXmacs all come with a certain number of
properties which correspond to their intended meaning. For instance,
TeXmacs is aware that  is an infix operator,
whereas ! is rather a postfix, and , a separator.
is an infix operator,
whereas ! is rather a postfix, and , a separator.
TeXmacs has special symbols  ,
,  and
and  for important mathematical constants,
which display differently from the mere characters
for important mathematical constants,
which display differently from the mere characters  ,
,
 and
and  , and which can be
entered using the shortcuts ETabTab, PTabTab and ITabTab. We recommend to systematically use these shortcuts.
, and which can be
entered using the shortcuts ETabTab, PTabTab and ITabTab. We recommend to systematically use these shortcuts.
Inversely, semantically distinct symbols may display in a similar way.
For instance, the comma separator, as in  , is
different from the decimal comma, as in
, is
different from the decimal comma, as in  .
Notice that the two symbols admit different spacing rules.
Semantically distinct symbols which are rendered by the same glyph are
called homoglyphs. Notice that our semantics is purely
syntactic: for instance, the
.
Notice that the two symbols admit different spacing rules.
Semantically distinct symbols which are rendered by the same glyph are
called homoglyphs. Notice that our semantics is purely
syntactic: for instance, the  infix is commonly
used for addition, but sometimes also for the concatenation of
strings. Nevertheless, these two uses do not differ from a syntactical
point of view, since the
infix is commonly
used for addition, but sometimes also for the concatenation of
strings. Nevertheless, these two uses do not differ from a syntactical
point of view, since the  symbol remains a
binary infix with the same precedence with respect to other symbols.
symbol remains a
binary infix with the same precedence with respect to other symbols.
The most confusing homoglyphs are the various invisible symbols supported by TeXmacs:
-
The multiplication, entered by *. Example:
 .
.
-
Function application, entered by Space. Example:
 .
.
-
An invisible separator, entered by ,TabTab. Example: the matrix
 .
.
-
An invisible addition, entered by +TabTabTabTab. Example:
 .
.
-
An invisible symbol, entered by .TabTabTab. Example: the increment
 .
.
-
An invisible bracket (mainly for internal use). A matching pair of invisible brackets is entered using (Tab.
Again it is recommended that authors carefully enter these various
invisible symbols when appropriate. It is particularly important to
distinguish between multiplication and function application, since
there is no 100% safe automatic way to make this distinction (we
already mentioned the formulas  and
and  before).
before).
TeXmacs supports two quite general schemes for entering homoglyphs. On
the one hand, we often rely on the standard variant system. For
instance,  and
and  are
obtained using *Tab and *TabTab. In
table ? we have given the complete list of homoglyphs
supported by TeXmacs.
are
obtained using *Tab and *TabTab. In
table ? we have given the complete list of homoglyphs
supported by TeXmacs.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
10.Customized mathematical semantics
We have done our best to support most of the classical mathematical notations. Nevertheless, the user may sometimes want to define notations with a non standard semantics. Certain areas may also require special notations which are not supported by default.
TeXmacs provides a very simple
For instance, if we enter  as the first
argument and
as the first
argument and  as the second one, then the
as the second one, then the  will be interpreted as a binary relation, exactly
in the same way as
will be interpreted as a binary relation, exactly
in the same way as  . Moreover, the spacing
around
. Moreover, the spacing
around  will be adapted, so as to mimic the
spacing around
will be adapted, so as to mimic the
spacing around  . In this particular example, we
might have obtained the same result by using the
. In this particular example, we
might have obtained the same result by using the  as its second argument. Most standard operator types are available
from
as its second argument. Most standard operator types are available
from
The  .
It is likely that the intended interpretation of
.
It is likely that the intended interpretation of  is
is  and not
and not  . Therefore,
if we often use the constant
. Therefore,
if we often use the constant  , then we might
want to define a macro
, then we might
want to define a macro
<assign|twopii|<macro|<syntax| |
| >>>
>>>
Such macros may be grouped together into a style package with the user's favourite notations. Future versions of TeXmacs might also provide style packages with notations dedicated to specific areas.
Let us finally notice that there are usually several ways for
redefining the semantics of a formula. For instance, an alternative
way to define the macro
<assign|twopii|<macro| >>
>>
where we inserted a pair of invisible brackets around  .
Similarly, in the formula
.
Similarly, in the formula

we may either select the whole formula and give it the semantics of an
ordinary symbol, by pressing Alt+XO.
However, a nicer solution is to only select the subformula  , and give it the semantics of an ordinary symbol. Yet
another example is the sign sequence
, and give it the semantics of an ordinary symbol. Yet
another example is the sign sequence  mentioned
earlier. This sequence can be interpreted correctly by inserting
invisible separators between the different signs using the ,Space shortcut.
mentioned
earlier. This sequence can be interpreted correctly by inserting
invisible separators between the different signs using the ,Space shortcut.


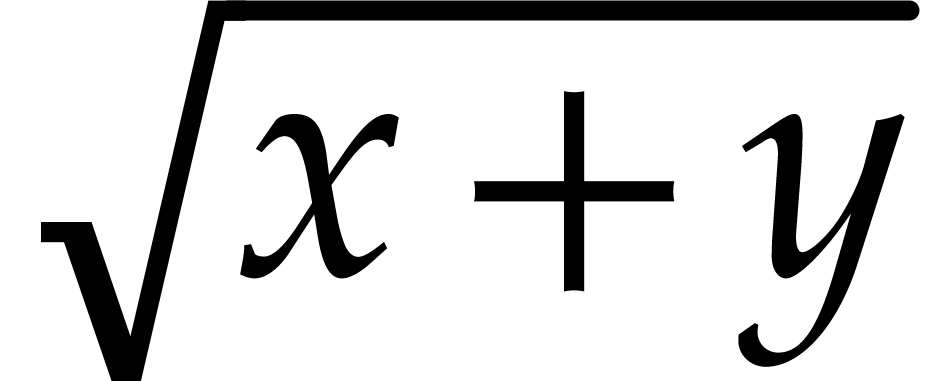
 -th Roots
-th Roots
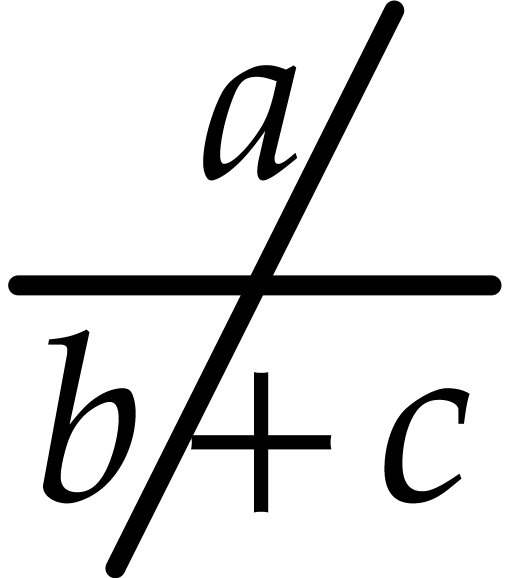
 or
or 

 or
or 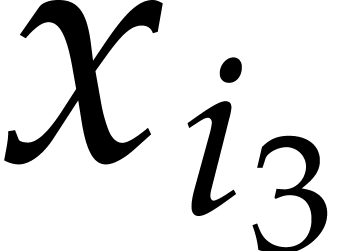
 ,
,  or
or


 or
or