 be an algebraic function defined on
be an algebraic function defined on 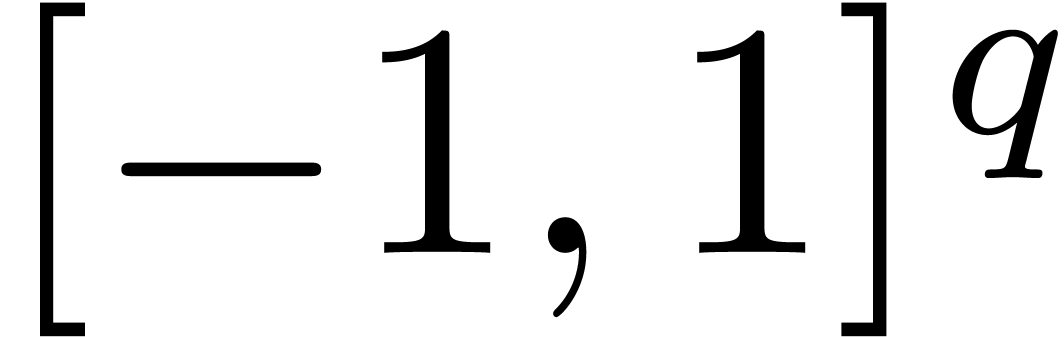 , let
, let  be exp-log functions at infinity in
be exp-log functions at infinity in 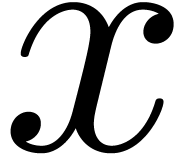 ,
and let
,
and let
| HomepagePublicationsTalksTeXmacsMathemagix |
In the last years, several asymptotic expansion algorithms have appeared, which have the property that they can deal with very general types of singularities, such as singularities arising in the study of algebraic differential equations. However, attention has been restricted so far to functions with “strongly monotonic” asymptotic behaviour: formally speaking, the functions lie in a common Hardy field, or, alternatively, they are determined by transseries.
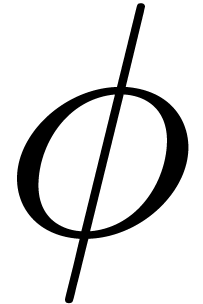
In this article, we make a first step towards the treatment of functions
involving oscillatory behaviour. More precisely, let  be an algebraic function defined on
be an algebraic function defined on 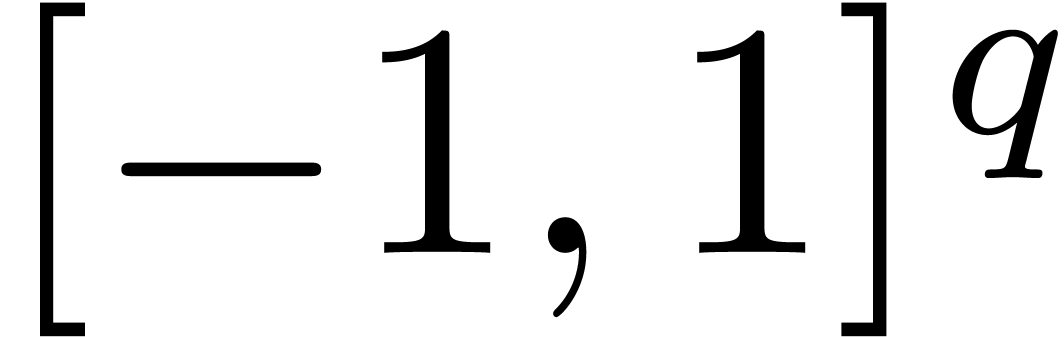 , let
, let  be exp-log functions at infinity in
be exp-log functions at infinity in 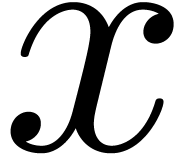 ,
and let
,
and let
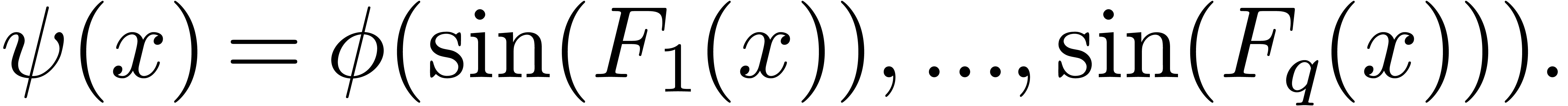
We give a method to compute 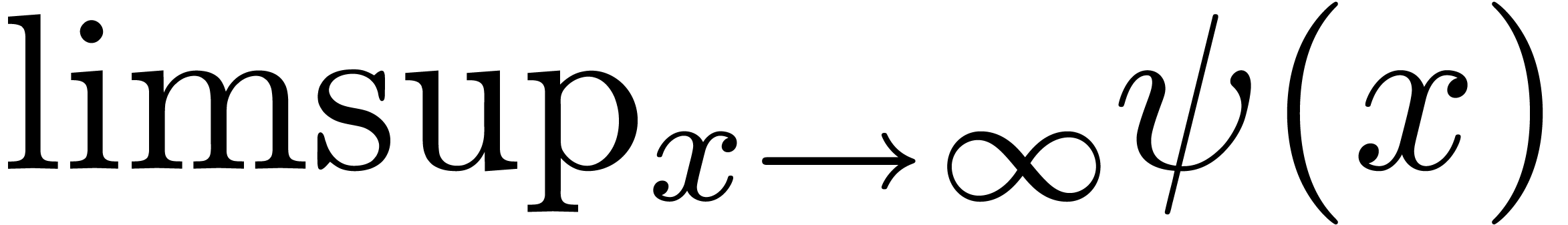 .
Moreover, the techniques we use are stronger than this result might
suggest, and we outline further applications.
.
Moreover, the techniques we use are stronger than this result might
suggest, and we outline further applications.
Conference: MEGA '96, June 6, 1996, Eindhoven, Netherlands
Documents: slides, full paper