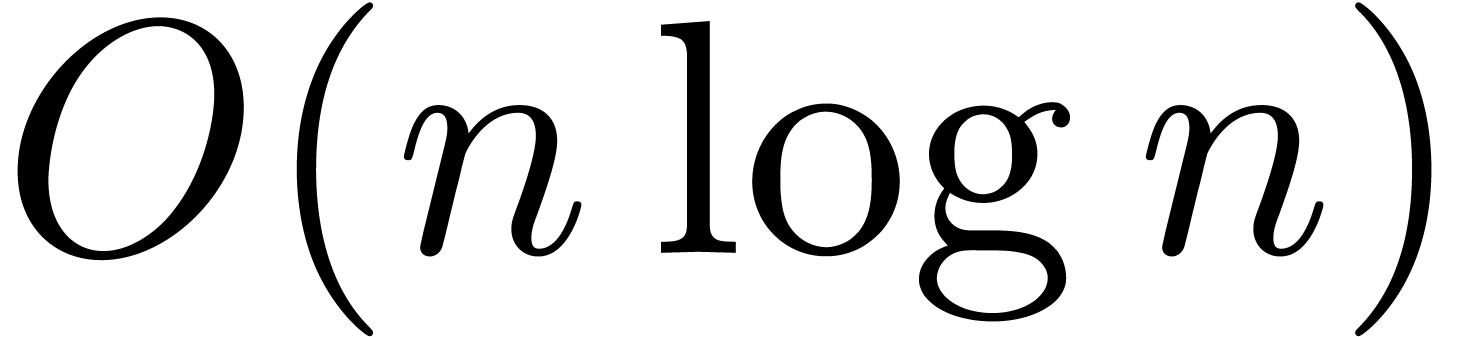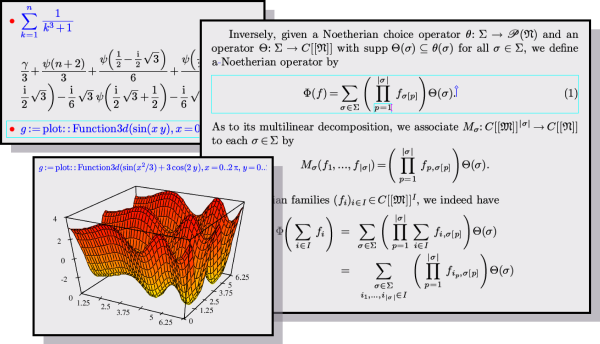
My research interests mainly concern the automation of asymptotic calculus and complex analysis, as well as fast arithmetic. Besides, I am the main developer of the software systems GNU TeXmacs and Mathemagix.

My PhD. thesis and the book Transseries and Real Differential Algebra are devoted to the theory of transseries. The main results concern the asymptotic resolution of differential equations, several closure theorems and embedding theorems into Hardy fields. This work has been further extended in collaboration with Matthias Aschenbrenner and Lou van den Dries. Together, we published the book Asymptotic Differential Algebra and Model Theory of Transseries, in which we prove a quantifier elimination theorem for asymptotic differential algebra.

Another main research topic of mine is the automation of complex analysis and computations with special functions or more general solutions to differential equations. On the one hand, this leads to interesting theoretical questions about computability, zero-testing, singularities, etc. On the other hand, this requires the development and implementation of fast, certified and numerically stable algorithms for multi-precision computations.

The development of fast algorithms for basic mathematical operations has evolved into one of my research topics on its own. In collaboration with David Harvey and Grégoire Lecerf, we improved the best known complexity bounds for integer multiplication and polynomial multiplication over finite fields. Continued work with David Harvey culminated in our O(n log n) bound for integer multiplication. Many special functions fall in, or are related to the class of holonomic functions. I contributed to the development of some particularly efficient algorithms for such functions.

GNU TeXmacs is a free wysiwyw (what you see is what you want) editing platform with special features for scientists. The software aims to provide a unified and user friendly framework for editing structured documents with different types of content (text, graphics, mathematics, interactive content, etc.). The rendering engine uses high-quality typesetting algorithms so as to produce professionally looking documents, which can either be printed out or presented from a laptop.

The software includes a text editor with support for mathematical formulas, a small technical picture editor and a tool for making presentations from a laptop. Moreover, TeXmacs can be used as an interface for many external systems for computer algebra, numerical analysis, statistics, etc. New presentation styles can be written by the user and new features can be added to the editor using the Scheme extension language. A native spreadsheet and tools for collaborative authoring are planned for later.

Mathemagix is a free computer algebra system under development. It consists of the following ingredients:

1. A new high level language, which is imperative, strongly typed, with polymorphim and parametrized types. Mathemagix can also be used as an “extension language”.

2. Efficient standard libraries are available for algebraic and analytic computations: large numbers, polynomials, power series, matrices, analytic functions, transseries, symbolic expressions, etc.

3. GNU TeXmacs can be used as a graphical front-end.