Abstract
In previous work, we have introduced several fast algorithms for relaxed
power series multiplication (also known under the name on-line
multiplication) up to a given order 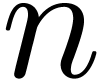 .
The fastest currently known algorithm works over an effective base field
.
The fastest currently known algorithm works over an effective base field
 with sufficiently many
with sufficiently many 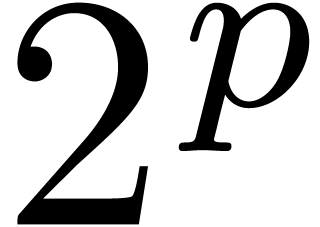 -th roots of unity and has
algebraic time complexity
-th roots of unity and has
algebraic time complexity 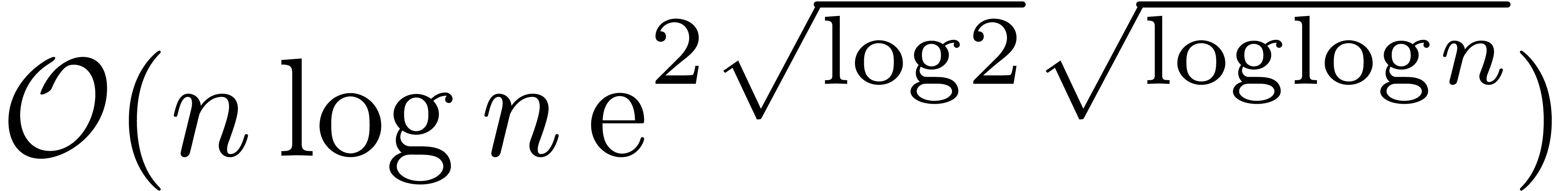 .
In this paper, we will generalize this algorithm to the cases when
.
In this paper, we will generalize this algorithm to the cases when  is replaced by an effective ring
of positive characteristic or by an effective ring of characteristic
zero, which is also torsion-free as a
is replaced by an effective ring
of positive characteristic or by an effective ring of characteristic
zero, which is also torsion-free as a  -module
and comes with an additional algorithm for partial division by integers.
In particular, we may take
-module
and comes with an additional algorithm for partial division by integers.
In particular, we may take  to be any effective field. We will also present an asymptotically faster
algorithm for relaxed multiplication of
to be any effective field. We will also present an asymptotically faster
algorithm for relaxed multiplication of 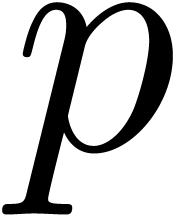 -adic
numbers.
-adic
numbers.
Occasion: ISSAC 2014, Kobe, July 23, 2014
Documents: slideshow, TeXmacs
source
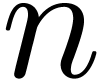 .
The fastest currently known algorithm works over an effective base field
.
The fastest currently known algorithm works over an effective base field
 with sufficiently many
with sufficiently many 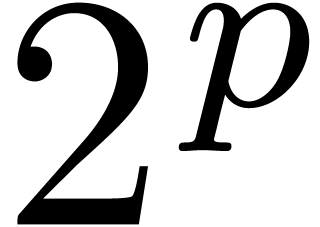 -th roots of unity and has
algebraic time complexity
-th roots of unity and has
algebraic time complexity 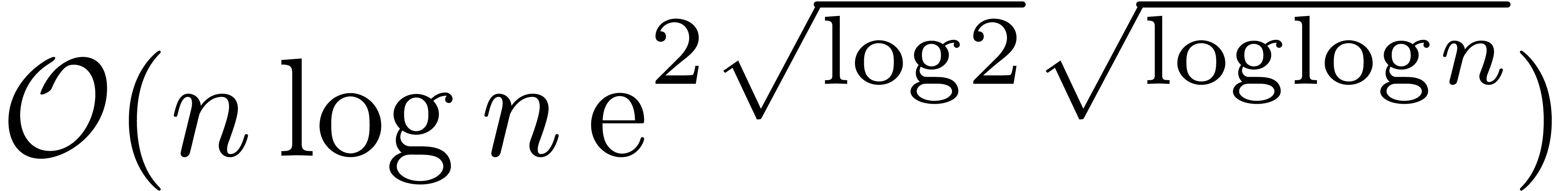 .
In this paper, we will generalize this algorithm to the cases when
.
In this paper, we will generalize this algorithm to the cases when  is replaced by an effective ring
of positive characteristic or by an effective ring of characteristic
zero, which is also torsion-free as a
is replaced by an effective ring
of positive characteristic or by an effective ring of characteristic
zero, which is also torsion-free as a  -module
and comes with an additional algorithm for partial division by integers.
In particular, we may take
-module
and comes with an additional algorithm for partial division by integers.
In particular, we may take  to be any effective field. We will also present an asymptotically faster
algorithm for relaxed multiplication of
to be any effective field. We will also present an asymptotically faster
algorithm for relaxed multiplication of 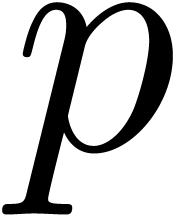 -adic
numbers.
-adic
numbers.