Résumé
At the end of the 19th century two types of mathematical
infinities were introduced: du Bois-Reymond developed a “calculus
of infinities” to deal with the “regular” growth rates
of real functions at infinity, whereas Cantor proposed his theory of
ordinal numbers as a way to count beyond all natural numbers.
Transseries and surreal numbers provide two modern generalizations of
these theories. Transseries are formal objects that cover most regular
growth rates that can be encountered at infinity. Conway's surreal
numbers form the ultimate extension of the field of real numbers with
infinitely large and small quantities and in particular with all
Cantor's ordinal numbers.
Together with Bagayoko, Schmeling, Kaplan, and van den Dries, I have
developed a further (and ultimate) generalization of transseries, called
hyperseries, with the aim of covering all regular
formal growth rates of functions at infinity.
It turns out that there is a remarkable correspondence between surreal
numbers and hyperseries: any surreal number can be written uniquely as
the value of a hyperseries at the first infinite ordinal  . Current work in progress concerns the
definition of a derivation and a composition on hyperseries in an
infinitely large indeterminate
. Current work in progress concerns the
definition of a derivation and a composition on hyperseries in an
infinitely large indeterminate 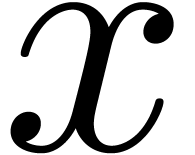 .Via
the above correspondence, this should also lead to a canonical
derivation and composition on the field of surreal numbers.
.Via
the above correspondence, this should also lead to a canonical
derivation and composition on the field of surreal numbers.
Occasion: Mini-workshop on Transseries and Dynamical
Systems, Fields Institute, Toronto, June 1, 2022
Documents: slideshow, TeXmacs
source
 . Current work in progress concerns the
definition of a derivation and a composition on hyperseries in an
infinitely large indeterminate
. Current work in progress concerns the
definition of a derivation and a composition on hyperseries in an
infinitely large indeterminate 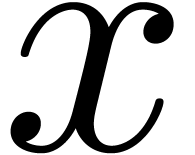 .Via
the above correspondence, this should also lead to a canonical
derivation and composition on the field of surreal numbers.
.Via
the above correspondence, this should also lead to a canonical
derivation and composition on the field of surreal numbers.