We consider a bivariate rational generating function

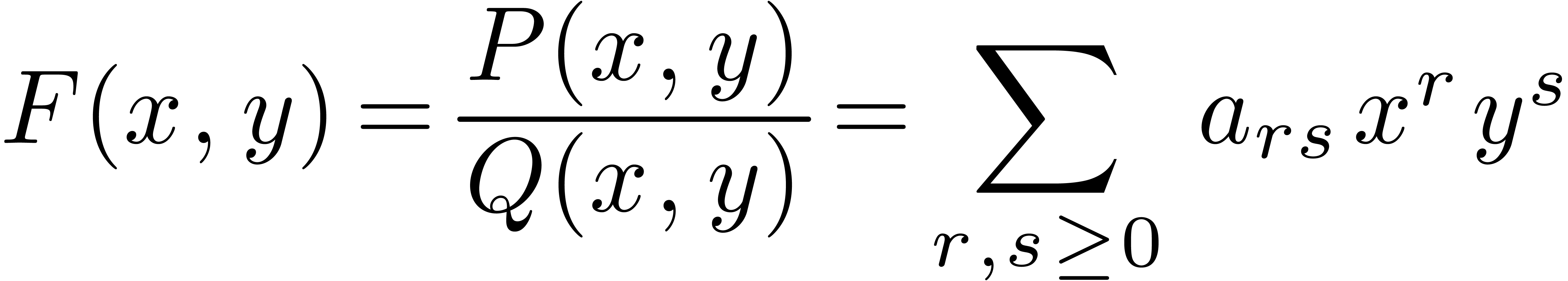
under the assumption that the complex algebraic curve 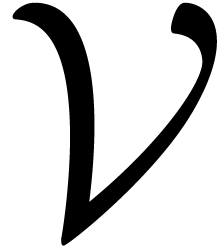on which vanishes is smooth. Formulae for the asymptotics of the coefficients 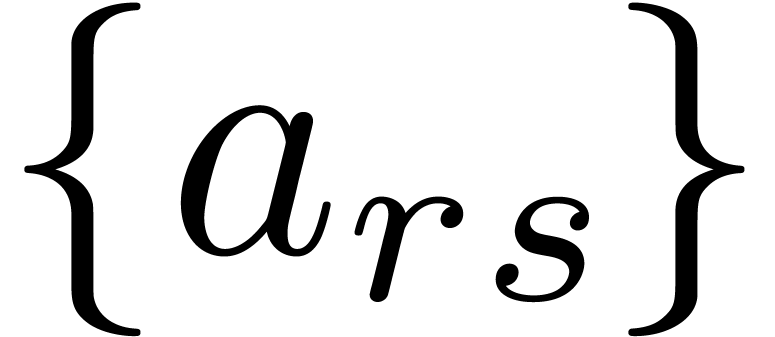are derived in [R. Pemantle and M.C. Wilson. Asymptotics of multivariate sequences]. These formulae are in terms of algebraic and topological invariants of 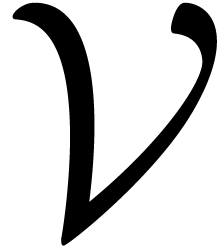, but up to now these invariants could be computed onlyunder a minimality hypothesis, namely that the dominant saddle must lie on the boundary of the domain of convergence. In the present paper, we give an effective method for computing the topological invariants, and hence the asymptotics of 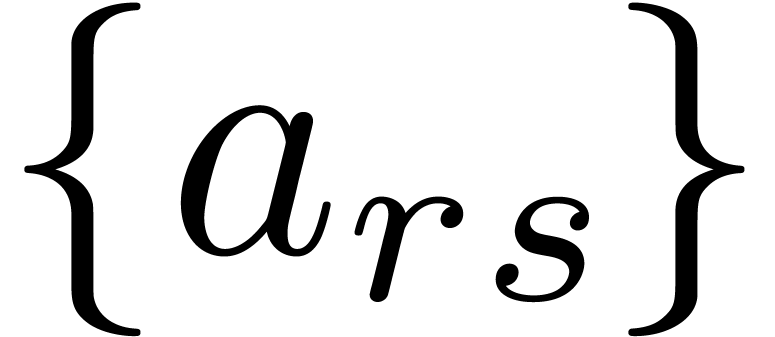, without the minimality assumption. This leads to a theoretically rigorous algorithm, whose implementation is in progress at http://www.mathemagix.org.

Keywords: rational function, generating function, Morse theory, Cauchy integral, Fourier-Laplace integral

A.M.S. subject classification: 05A15

Authors: Tim DeVries, Joris van der Hoeven, Robin Pemantle

View: Pdf, BibTeX