Abstract
The Chinese remainder theorem is a key tool for the design of efficient
multi-modular algorithms. In this paper, we study the case when the
moduli  are fixed and can
even be chosen by the user. Through an appropriate use of the technique
of FFT-trading, we will show that this assumption allows for the gain of
an asymptotic factor
are fixed and can
even be chosen by the user. Through an appropriate use of the technique
of FFT-trading, we will show that this assumption allows for the gain of
an asymptotic factor 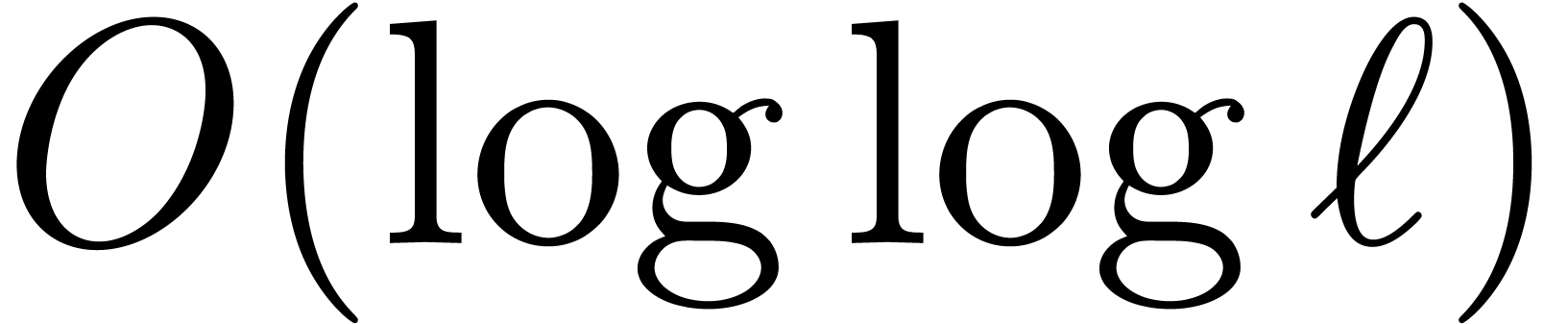 in the
complexity of “Chinese remaindering”. For small
in the
complexity of “Chinese remaindering”. For small  , we will also show how to choose “gentle
moduli” that allow for further gains at the other end. The
multiplication of integer matrices is one typical application where we
expect practical gains for various common matrix dimensions and integer
bitsizes.
, we will also show how to choose “gentle
moduli” that allow for further gains at the other end. The
multiplication of integer matrices is one typical application where we
expect practical gains for various common matrix dimensions and integer
bitsizes.
Keywords: Chinese remainder theorem, algorithm,
complexity, integer matrix multiplication
View: Html, TeXmacs, Pdf,
BibTeX
Note: this paper has partly been published at the MACIS
2017 conference under the title “Fast Chinese
remaindering in practice”
 are fixed and can
even be chosen by the user. Through an appropriate use of the technique
of FFT-trading, we will show that this assumption allows for the gain of
an asymptotic factor
are fixed and can
even be chosen by the user. Through an appropriate use of the technique
of FFT-trading, we will show that this assumption allows for the gain of
an asymptotic factor 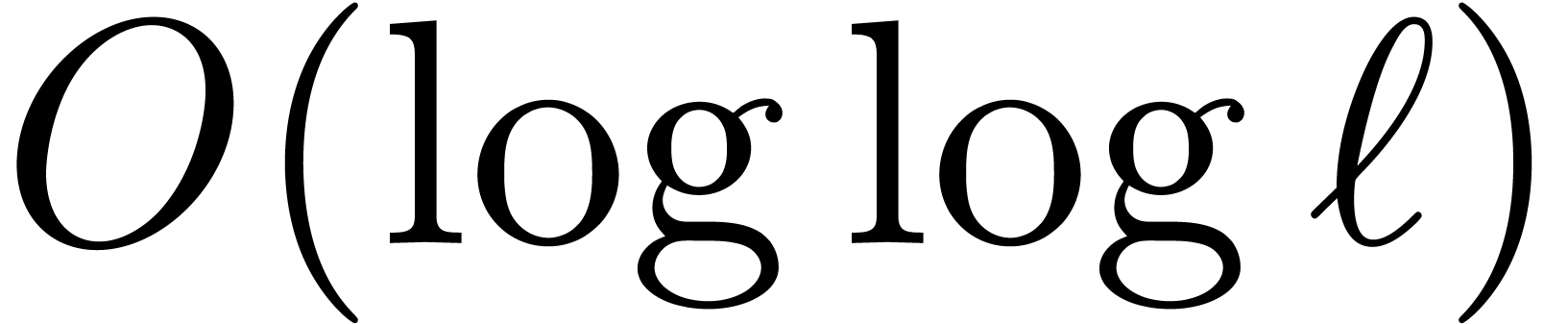 in the
complexity of “Chinese remaindering”. For small
in the
complexity of “Chinese remaindering”. For small  , we will also show how to choose “gentle
moduli” that allow for further gains at the other end. The
multiplication of integer matrices is one typical application where we
expect practical gains for various common matrix dimensions and integer
bitsizes.
, we will also show how to choose “gentle
moduli” that allow for further gains at the other end. The
multiplication of integer matrices is one typical application where we
expect practical gains for various common matrix dimensions and integer
bitsizes.