Abstract
A real number 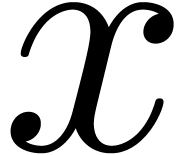 is said to be
effective if there exists an algorithm which, given a required tolerance
is said to be
effective if there exists an algorithm which, given a required tolerance
 , returns a binary
approximation
, returns a binary
approximation  for
for 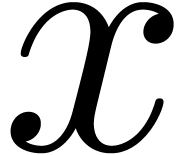 with
with 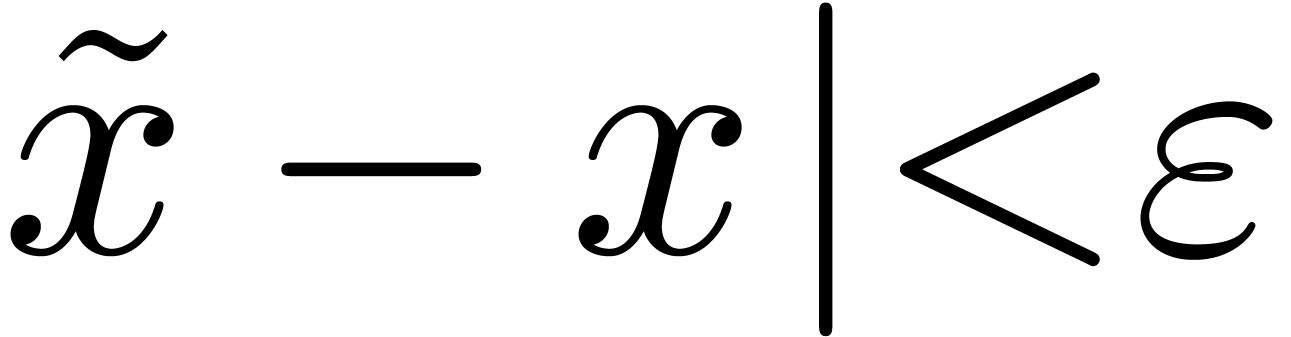 .
Effective real numbers are interesting in areas of numerical analysis
where numerical instability is a major problem.
.
Effective real numbers are interesting in areas of numerical analysis
where numerical instability is a major problem.
One key problem with effective real numbers is to perform intermediate
computations at the smallest precision which is sufficient to guarantee
an exact end-result. In this paper we first review two classical
techniques to achieve this: a priori error estimates and
interval analysis. We next present two new techniques: “relaxed
evaluations” reduce the amount of re-evaluations at larger
precisions and “balanced error estimates” automatically
provide good tolerances for intermediate computations.
Keywords: effective real number, algorithm, interval
analysis, error estimates
A.M.S. subject classification: 68W25, 65G20, 65G40,
26E40
View: Html, TeXmacs, Pdf,
BibTeX
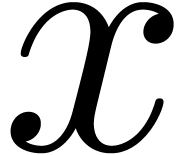 is said to be
effective if there exists an algorithm which, given a required tolerance
is said to be
effective if there exists an algorithm which, given a required tolerance
 , returns a binary
approximation
, returns a binary
approximation  for
for 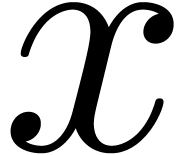 with
with 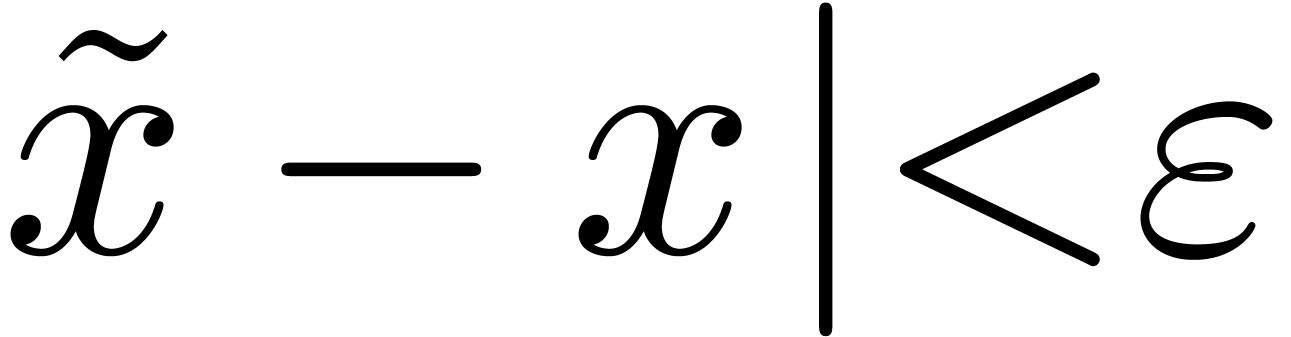 .
Effective real numbers are interesting in areas of numerical analysis
where numerical instability is a major problem.
.
Effective real numbers are interesting in areas of numerical analysis
where numerical instability is a major problem.