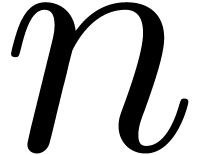-bit integers
may be multiplied in 
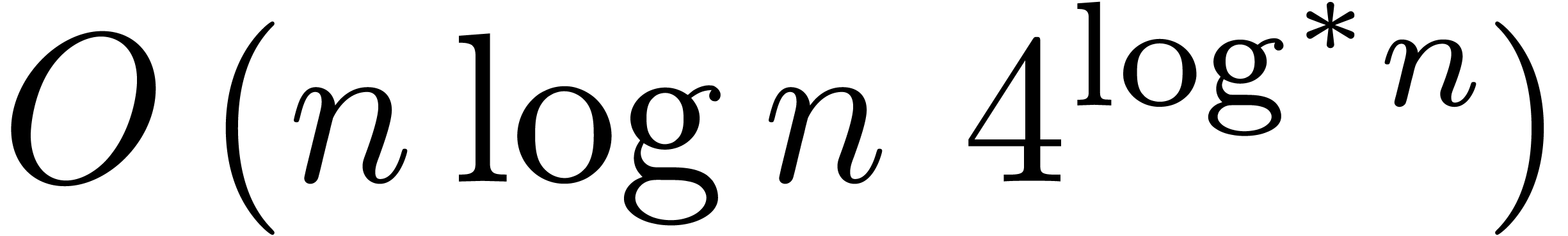bit
operations. This complexity bound had been achieved previously by
several authors, assuming various unproved number-theoretic hypotheses.
Our proof is unconditional, and depends in an essential way on
Minkowski's theorem concerning lattice vectors in symmetric convex sets.