Abstract
Let  be the reduced
Gröbner basis of a zero-dimensional ideal
be the reduced
Gröbner basis of a zero-dimensional ideal 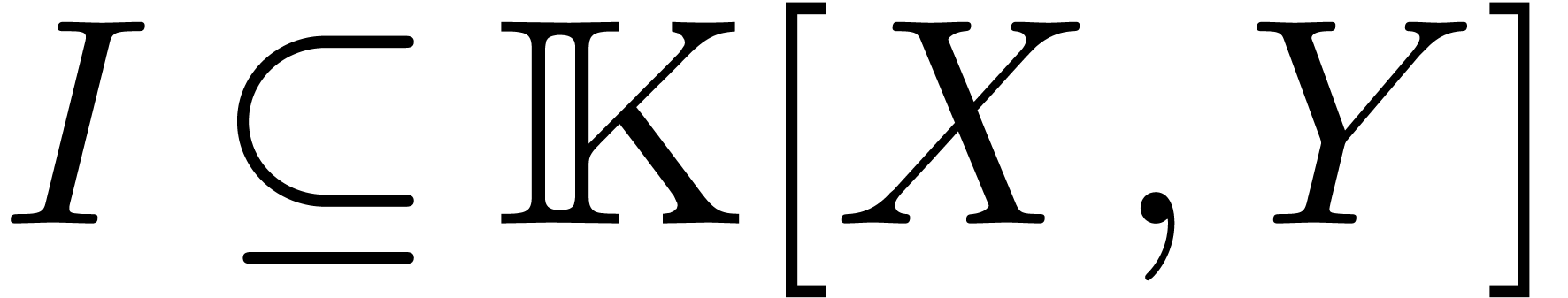 of bivariate polynomials over an effective field
of bivariate polynomials over an effective field
 . Modulo suitable regularity
assumptions on
. Modulo suitable regularity
assumptions on  and suitable
precomputations as a function of
and suitable
precomputations as a function of  ,
we prove the existence of a quasi-optimal algorithm for the reduction of
polynomials in
,
we prove the existence of a quasi-optimal algorithm for the reduction of
polynomials in 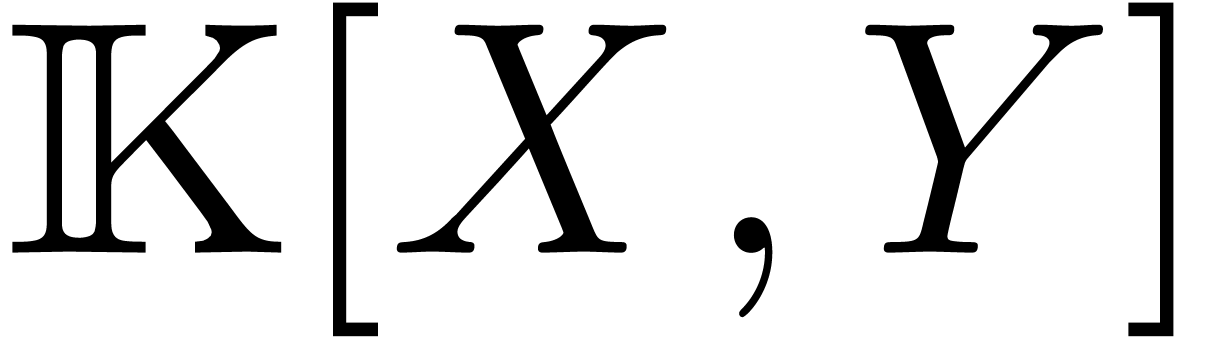 with respect
to
with respect
to  . Applications include
fast algorithms for multiplication in the quotient algebra
. Applications include
fast algorithms for multiplication in the quotient algebra 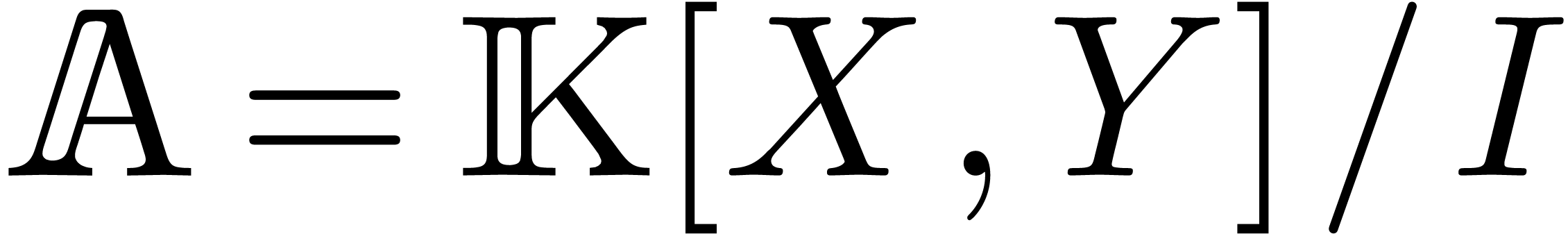 and for conversions due to changes of the term
ordering.
and for conversions due to changes of the term
ordering.
Authors: Joris van der Hoeven,
Robin Larrieu
Keywords: polynomial reduction, algorithm, complexity,
Gröbner basis
View: Html, TeXmacs, Pdf,
BibTeX
 be the reduced
Gröbner basis of a zero-dimensional ideal
be the reduced
Gröbner basis of a zero-dimensional ideal 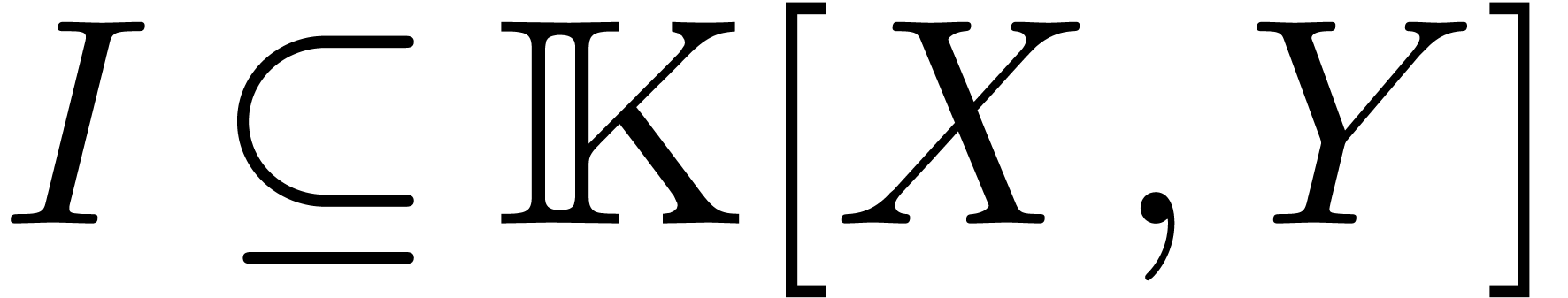 of bivariate polynomials over an effective field
of bivariate polynomials over an effective field
 . Modulo suitable regularity
assumptions on
. Modulo suitable regularity
assumptions on  and suitable
precomputations as a function of
and suitable
precomputations as a function of  ,
we prove the existence of a quasi-optimal algorithm for the reduction of
polynomials in
,
we prove the existence of a quasi-optimal algorithm for the reduction of
polynomials in 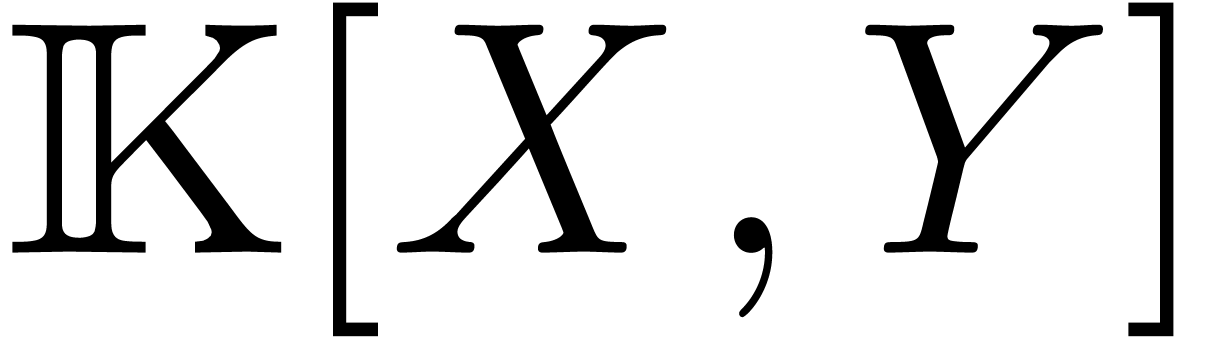 with respect
to
with respect
to  . Applications include
fast algorithms for multiplication in the quotient algebra
. Applications include
fast algorithms for multiplication in the quotient algebra 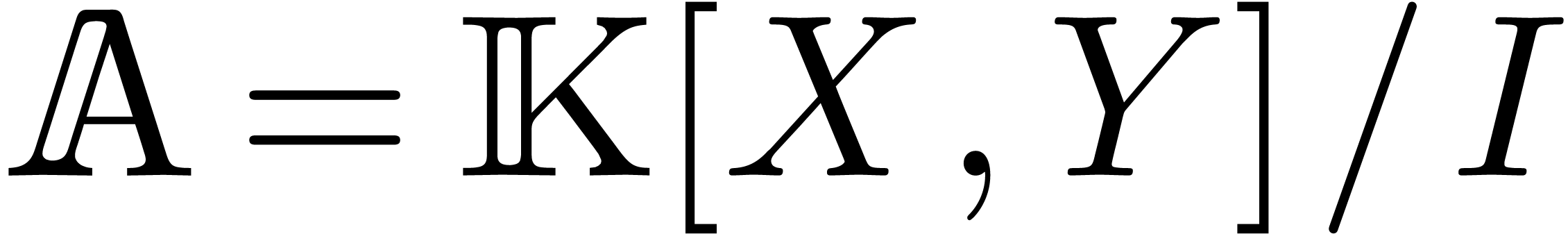 and for conversions due to changes of the term
ordering.
and for conversions due to changes of the term
ordering.