Working in the multitape Turing model, we show how to reduce the problem of matrix transposition to the problem of integer multiplication. If transposing an binary matrix requires 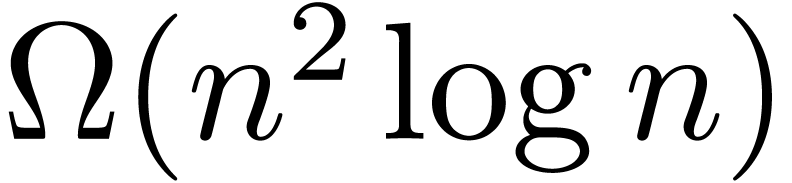steps on a Turing machine, then our reduction implies that multiplying 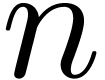-bit integers requires 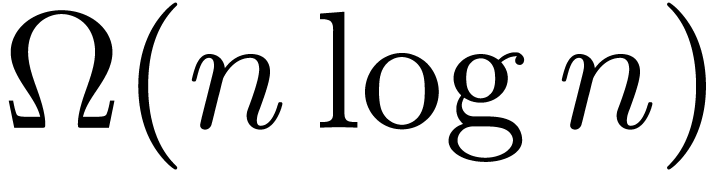steps. In other words, if matrix transposition is as hard as expected, then integer multiplication is also as hard as expected.

Authors: David Harvey, Joris van der Hoeven

View: Pdf, BibTeX