Abstract
In this paper, we describe an algorithm for the
“uniformization” of a multivariate power series. Let  be the field of “grid-based
power series” over a sufficiently large non archimedean
“monomial group” (or value group)
be the field of “grid-based
power series” over a sufficiently large non archimedean
“monomial group” (or value group)  , such as
, such as 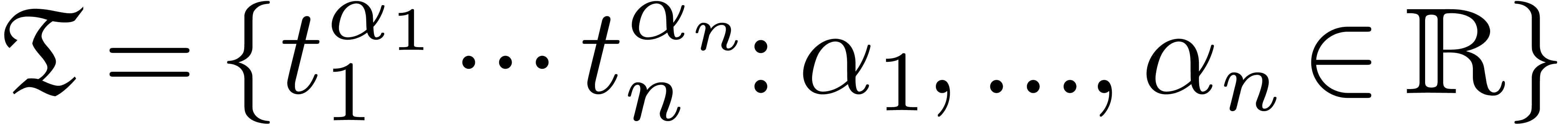 with the lexicographical ordering on
with the lexicographical ordering on  .
We interpret power series
.
We interpret power series 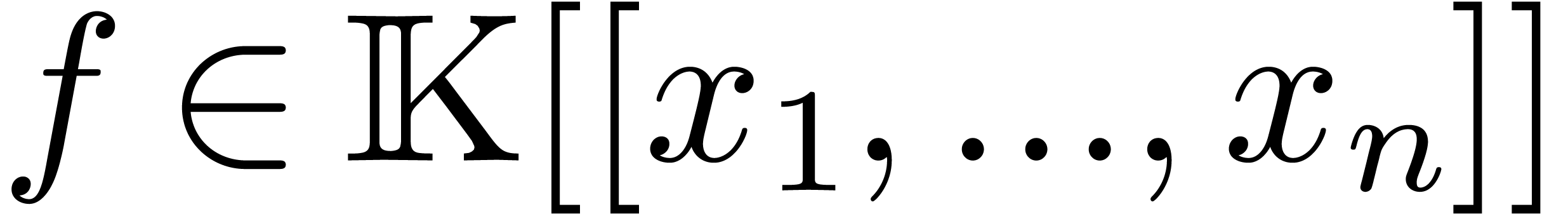 as
functions
as
functions 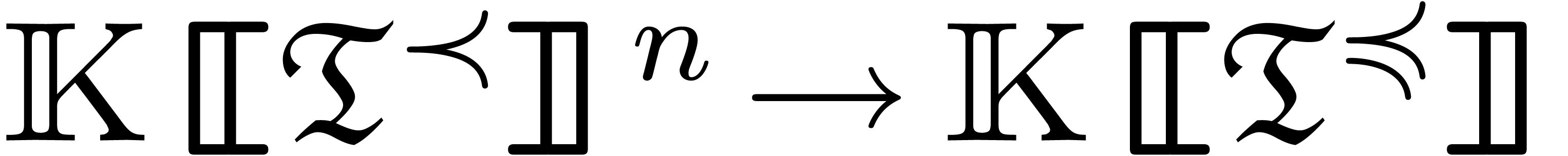 . On certain
“regions”
. On certain
“regions”  of the
space
of the
space 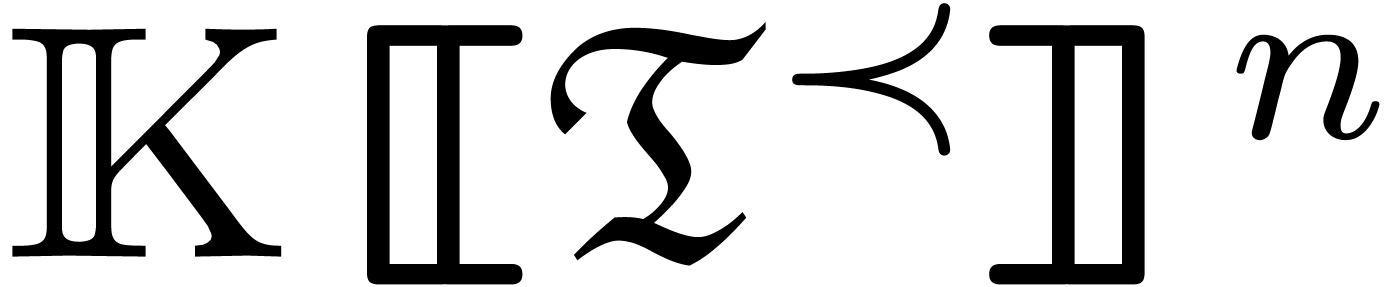 , it may happen that
the valuation of
, it may happen that
the valuation of 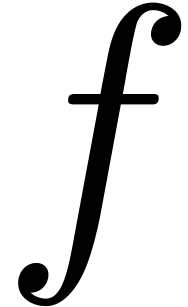 can be read
off from the valuations of the
can be read
off from the valuations of the 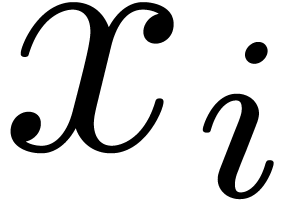 .
In that case,
.
In that case, 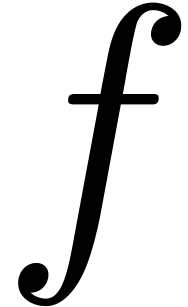 is said to be
“uniform” on
is said to be
“uniform” on  . We
will describe an algorithm for cutting
. We
will describe an algorithm for cutting 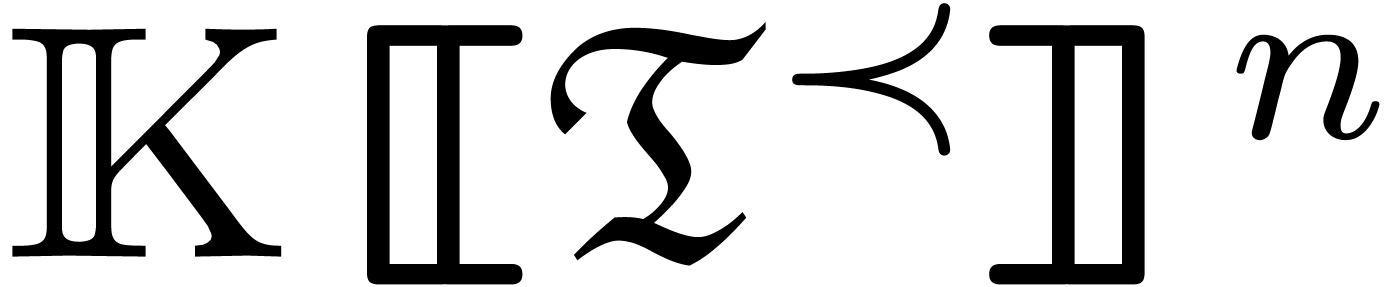 into a finite number of regions, each on which
into a finite number of regions, each on which  is uniform for a suitable change of coordinates,
which preserves the elimination ordering on
is uniform for a suitable change of coordinates,
which preserves the elimination ordering on  . The algorithm can probably be seen as an effective
counterpart of local uniformization in the sense of Zariski, even though
this connection remains to be established in detail.
. The algorithm can probably be seen as an effective
counterpart of local uniformization in the sense of Zariski, even though
this connection remains to be established in detail.
Keywords: algorithm, power series, grid-based power
series, local uniformization, Newton polygon method, desingularization
A.M.S. subject classification: 14B05, 68W30, 14E15
View: Html, TeXmacs, Pdf,
BibTeX
 be the field of “grid-based
power series” over a sufficiently large non archimedean
“monomial group” (or value group)
be the field of “grid-based
power series” over a sufficiently large non archimedean
“monomial group” (or value group)  , such as
, such as 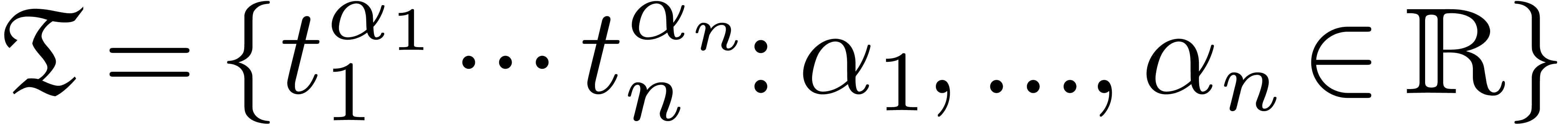 with the lexicographical ordering on
with the lexicographical ordering on  .
We interpret power series
.
We interpret power series 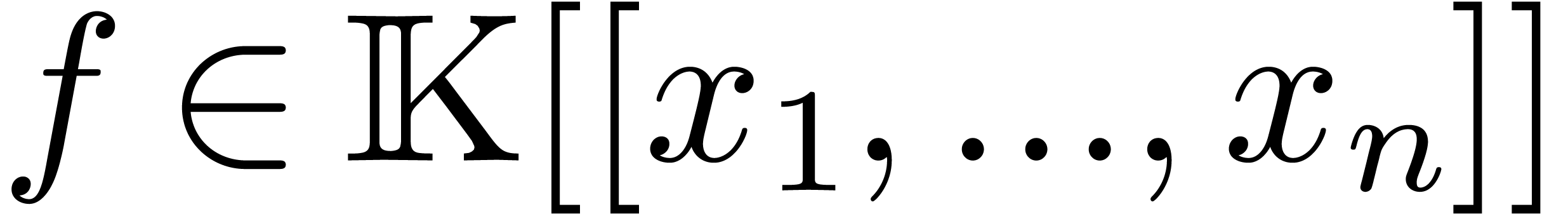 as
functions
as
functions 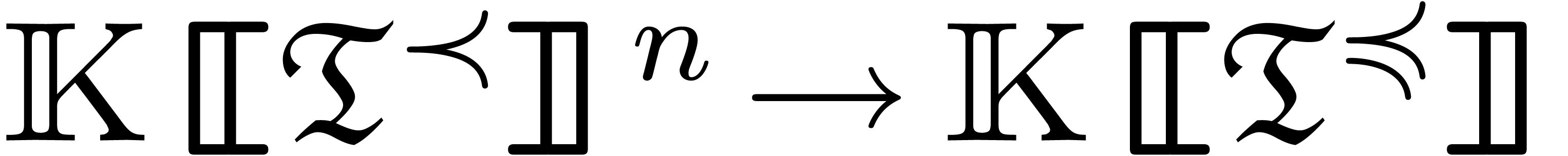 . On certain
“regions”
. On certain
“regions”  of the
space
of the
space 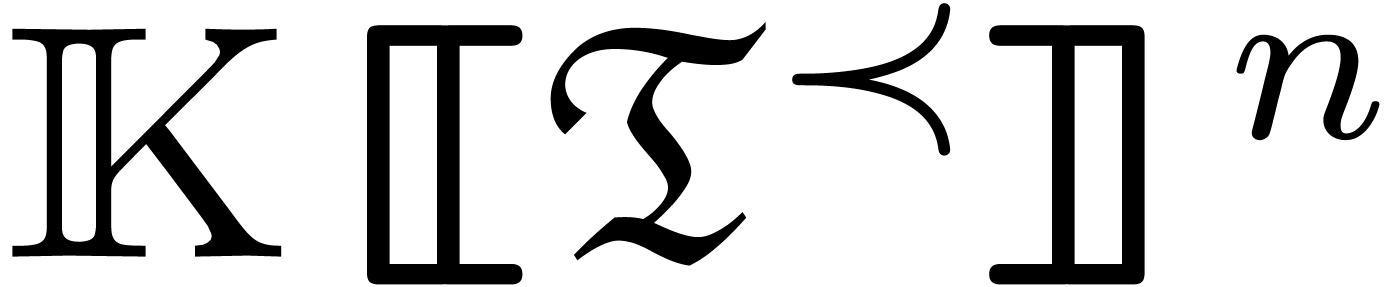 , it may happen that
the valuation of
, it may happen that
the valuation of 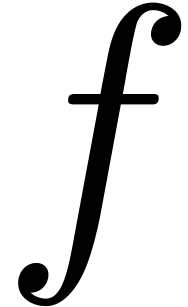 can be read
off from the valuations of the
can be read
off from the valuations of the 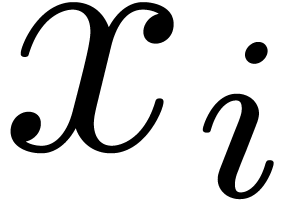 .
In that case,
.
In that case, 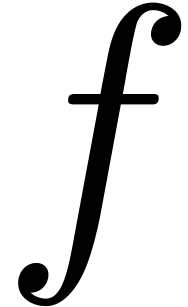 is said to be
“uniform” on
is said to be
“uniform” on 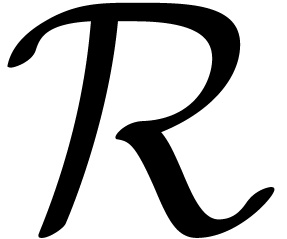 . We
will describe an algorithm for cutting
. We
will describe an algorithm for cutting 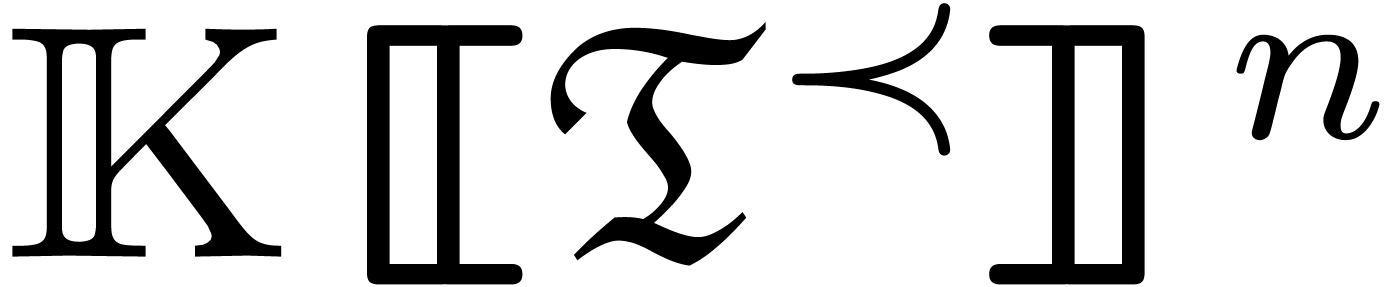 into a finite number of regions, each on which
into a finite number of regions, each on which 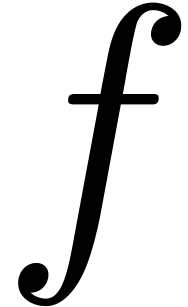 is uniform for a suitable change of coordinates,
which preserves the elimination ordering on
is uniform for a suitable change of coordinates,
which preserves the elimination ordering on  . The algorithm can probably be seen as an effective
counterpart of local uniformization in the sense of Zariski, even though
this connection remains to be established in detail.
. The algorithm can probably be seen as an effective
counterpart of local uniformization in the sense of Zariski, even though
this connection remains to be established in detail.