Abstract
Consider a power series  ,
which is obtained by a precise mathematical construction. For instance,
,
which is obtained by a precise mathematical construction. For instance,
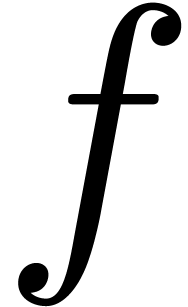 might be the solution to
some differential or functional initial value problem or the diagonal of
the solution to a partial differential equation. In cases when no
suitable method is beforehand for determining the asymptotics of the
coefficients
might be the solution to
some differential or functional initial value problem or the diagonal of
the solution to a partial differential equation. In cases when no
suitable method is beforehand for determining the asymptotics of the
coefficients 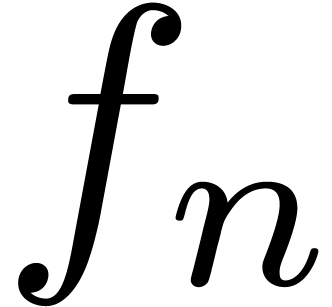 , but when many
such coefficients can be computed with high accuracy, it would be useful
if a plausible asymptotic expansion for
, but when many
such coefficients can be computed with high accuracy, it would be useful
if a plausible asymptotic expansion for 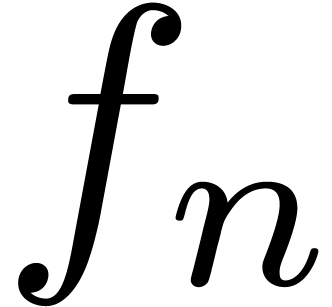 could be guessed automatically.
could be guessed automatically.
In this paper, we will present a general scheme for the design of such
“asymptotic extrapolation algorithms”. Roughly speaking,
using discrete differentiation and techniques from automatic
asymptotics, we strip off the terms of the asymptotic expansion one by
one. The knowledge of more terms of the asymptotic expansion will then
allow us to approximate the coefficients in the expansion with high
accuracy.
Keywords: interpolation, asymptotic expansion,
algorithm, guessing
A.M.S. subject classification: 41A05, 41A60, 65B05,
68W30
View: Html, TeXmacs, Pdf,
BibTeX
 ,
which is obtained by a precise mathematical construction. For instance,
,
which is obtained by a precise mathematical construction. For instance,
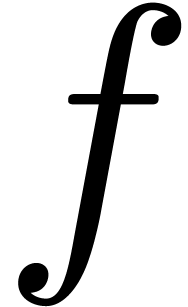 might be the solution to
some differential or functional initial value problem or the diagonal of
the solution to a partial differential equation. In cases when no
suitable method is beforehand for determining the asymptotics of the
coefficients
might be the solution to
some differential or functional initial value problem or the diagonal of
the solution to a partial differential equation. In cases when no
suitable method is beforehand for determining the asymptotics of the
coefficients 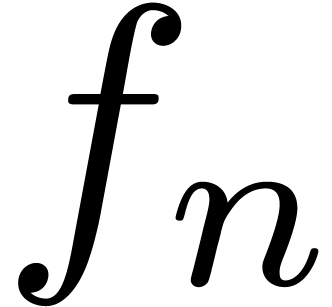 , but when many
such coefficients can be computed with high accuracy, it would be useful
if a plausible asymptotic expansion for
, but when many
such coefficients can be computed with high accuracy, it would be useful
if a plausible asymptotic expansion for 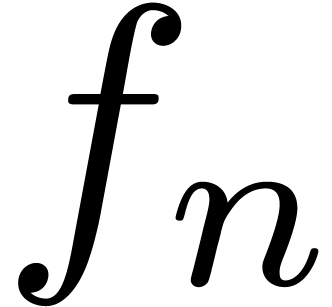 could be guessed automatically.
could be guessed automatically.