Abstract
In previous work, we have introduced several fast algorithms for relaxed
power series multiplication (also known under the name on-line
multiplication) up till a given order 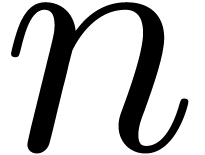 .
The fastest currently known algorithm works over an effective base field
.
The fastest currently known algorithm works over an effective base field
 with sufficiently many
with sufficiently many 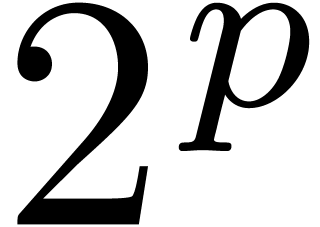 -th roots of unity and has
algebraic time complexity
-th roots of unity and has
algebraic time complexity 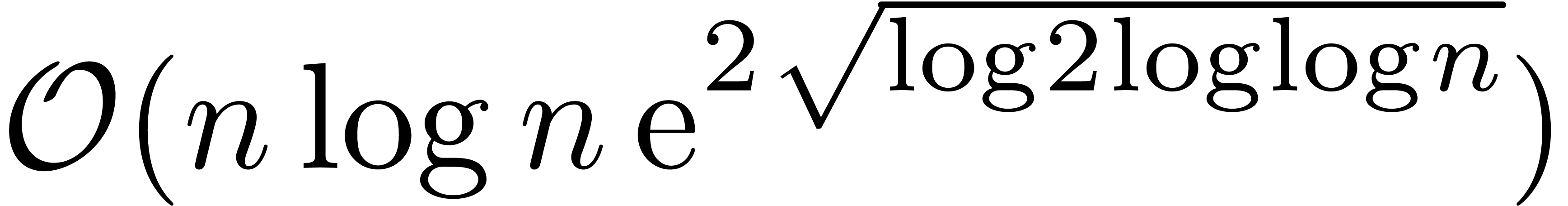 .
In this note, we will generalize this algorithm to the cases when
.
In this note, we will generalize this algorithm to the cases when  is replaced by an effective ring
of positive characteristic or by an effective ring of characteristic
zero, which is also torsion-free as a
is replaced by an effective ring
of positive characteristic or by an effective ring of characteristic
zero, which is also torsion-free as a  -module
and comes with an additional algorithm for partial division by integers.
We will also present an asymptotically faster algorithm for relaxed
multiplication of
-module
and comes with an additional algorithm for partial division by integers.
We will also present an asymptotically faster algorithm for relaxed
multiplication of 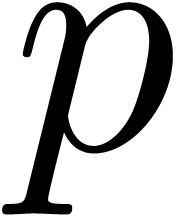 -adic
numbers.
-adic
numbers.
Keywords: power series, multiplication, on-line
algorithm, FFT, computer algebra
A.M.S. subject classification: 68W30, 30B10, 68W25,
33F05, 11Y55, 42-04
View: Html, TeXmacs, Pdf,
BibTeX
Revised version: Html, TeXmacs,
Pdf, BibTeX
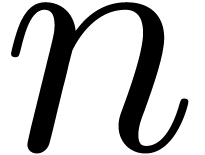 .
The fastest currently known algorithm works over an effective base field
.
The fastest currently known algorithm works over an effective base field
 with sufficiently many
with sufficiently many 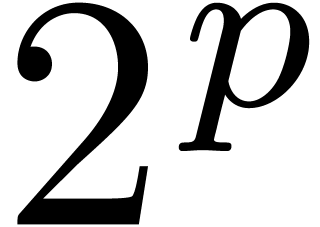 -th roots of unity and has
algebraic time complexity
-th roots of unity and has
algebraic time complexity 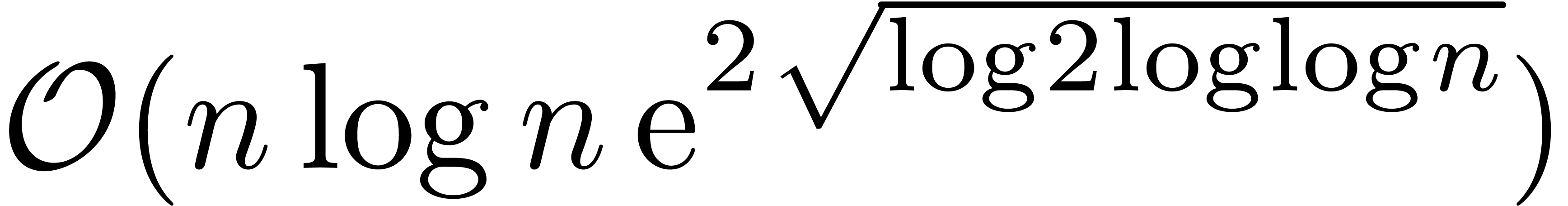 .
In this note, we will generalize this algorithm to the cases when
.
In this note, we will generalize this algorithm to the cases when  is replaced by an effective ring
of positive characteristic or by an effective ring of characteristic
zero, which is also torsion-free as a
is replaced by an effective ring
of positive characteristic or by an effective ring of characteristic
zero, which is also torsion-free as a  -module
and comes with an additional algorithm for partial division by integers.
We will also present an asymptotically faster algorithm for relaxed
multiplication of
-module
and comes with an additional algorithm for partial division by integers.
We will also present an asymptotically faster algorithm for relaxed
multiplication of 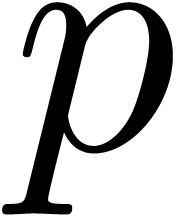 -adic
numbers.
-adic
numbers.