Abstract
Let 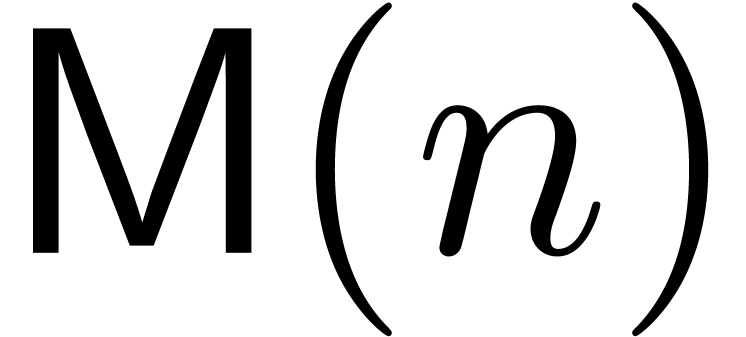 denote the bit
complexity of multiplying
denote the bit
complexity of multiplying 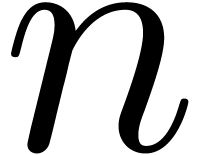 -bit
integers, let
-bit
integers, let 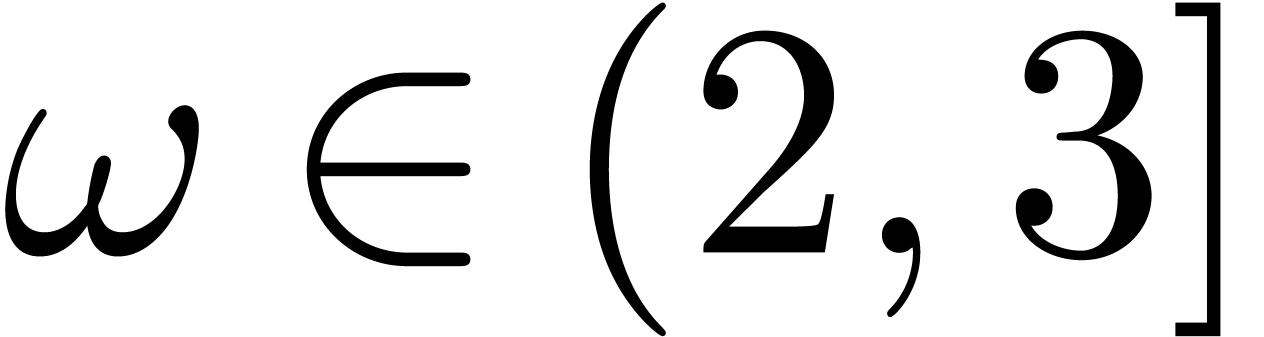 be an exponent
for matrix multiplication, and let
be an exponent
for matrix multiplication, and let 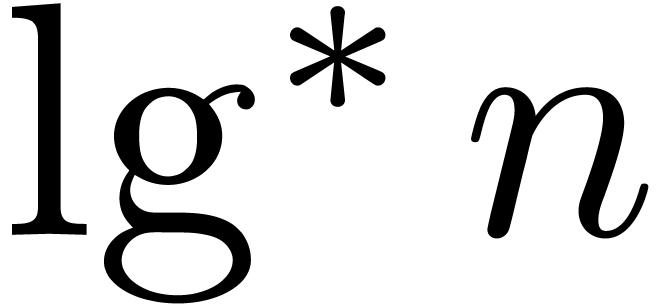 be the iterated logarithm. Assuming that
be the iterated logarithm. Assuming that 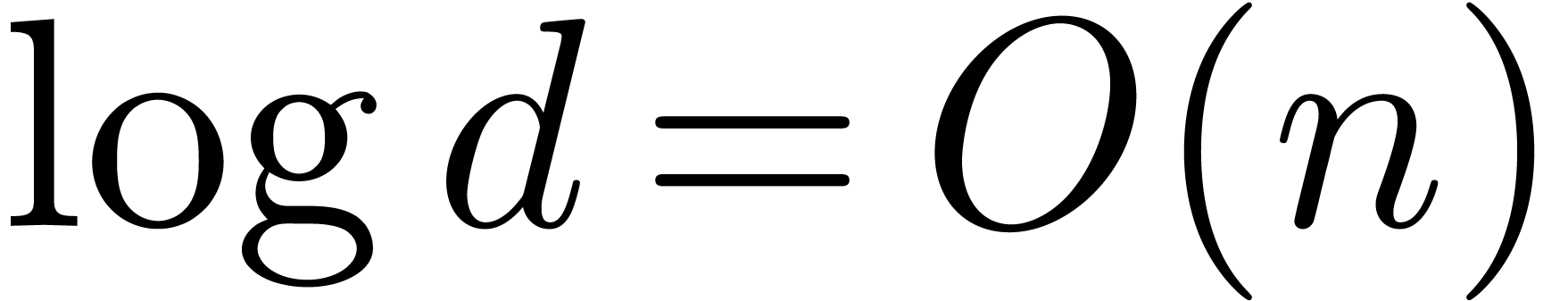 and that
and that 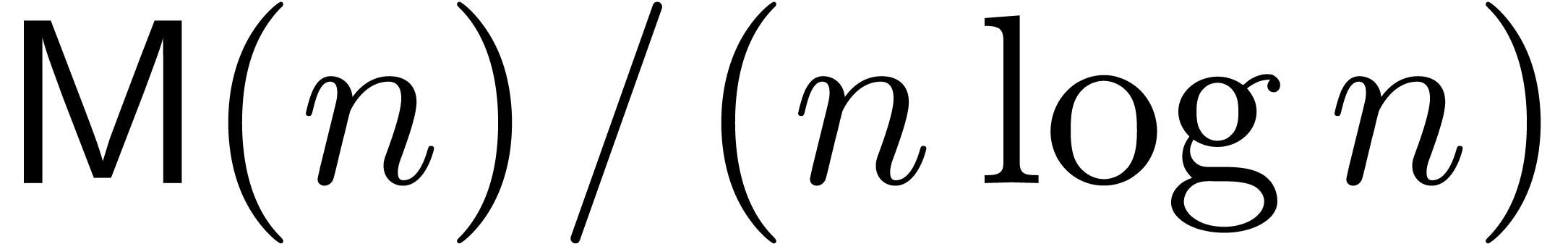 is increasing, we
prove that
is increasing, we
prove that  matrices with
matrices with
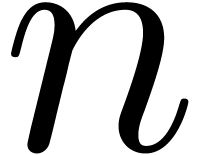 -bit integer entries may be
multiplied in
-bit integer entries may be
multiplied in
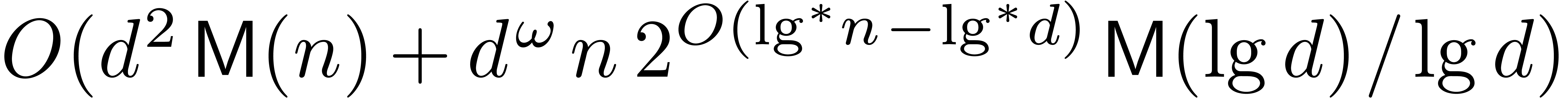
bit operations. In particular, if 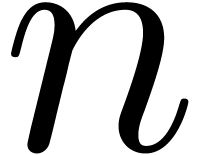 is large compared to
is large compared to 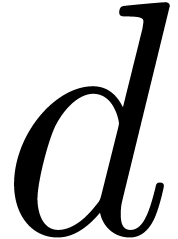 , say
, say
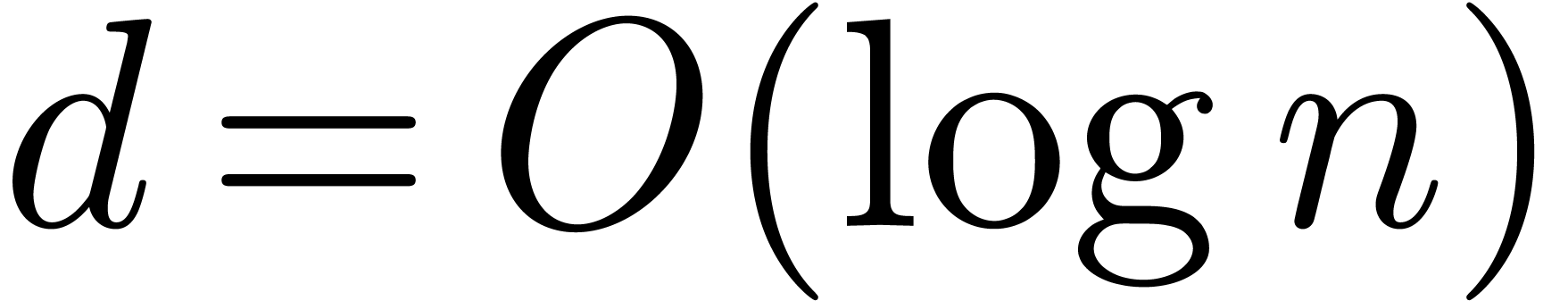 , then the complexity is only
, then the complexity is only
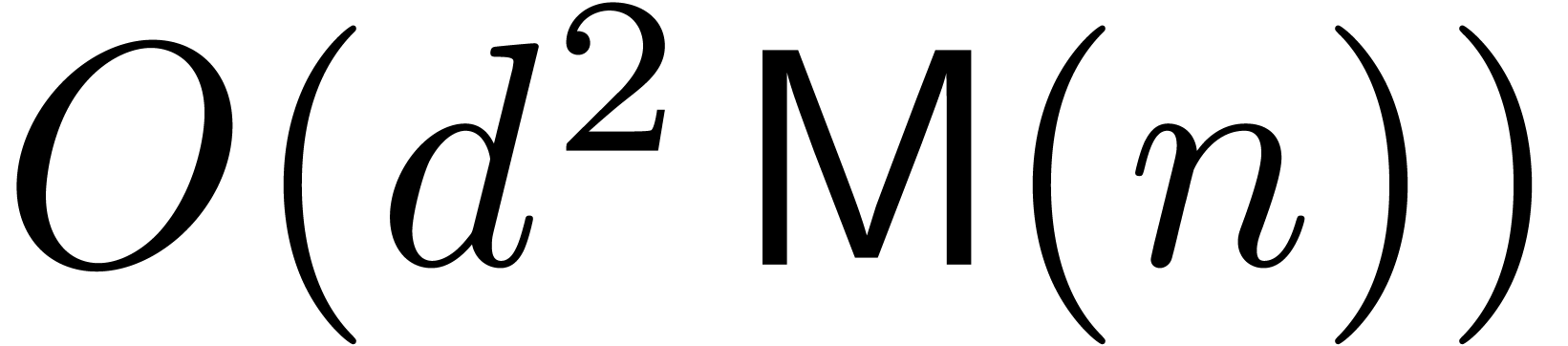 .
.
Authors: David Harvey, Joris van der Hoeven
Keywords: matrix multiplication, complexity, algorithm,
FFT, Bluestein reduction
A.M.S. subject classification: 68W30, 68Q17, 68W40
View: Html, TeXmacs, Pdf,
BibTeX
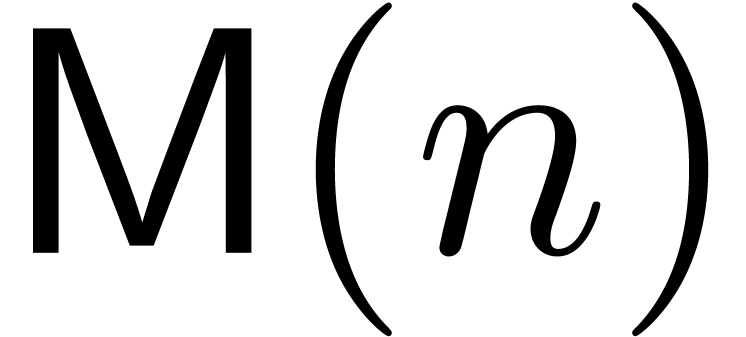 denote the bit
complexity of multiplying
denote the bit
complexity of multiplying 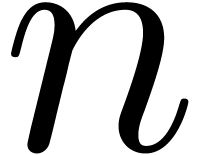 -bit
integers, let
-bit
integers, let 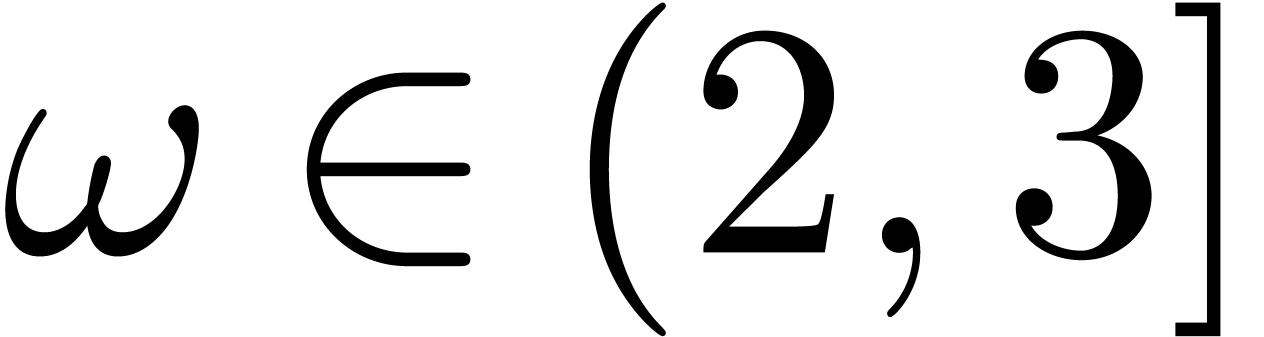 be an exponent
for matrix multiplication, and let
be an exponent
for matrix multiplication, and let 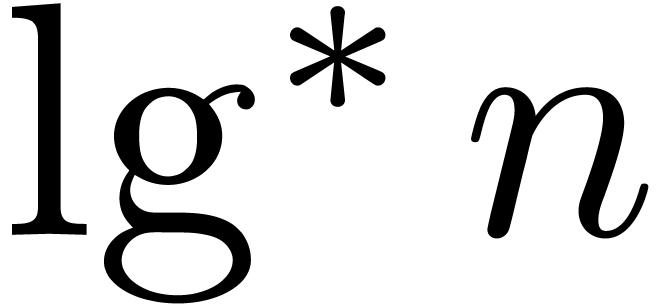 be the iterated logarithm. Assuming that
be the iterated logarithm. Assuming that 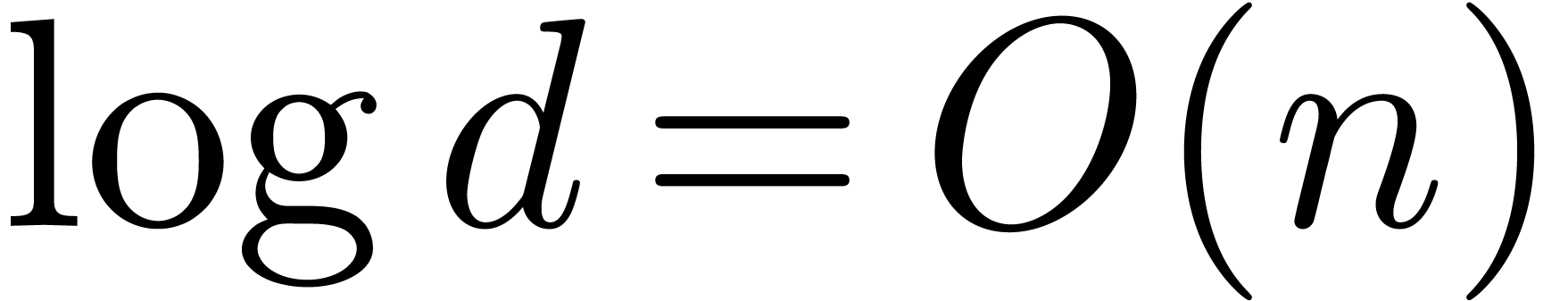 and that
and that 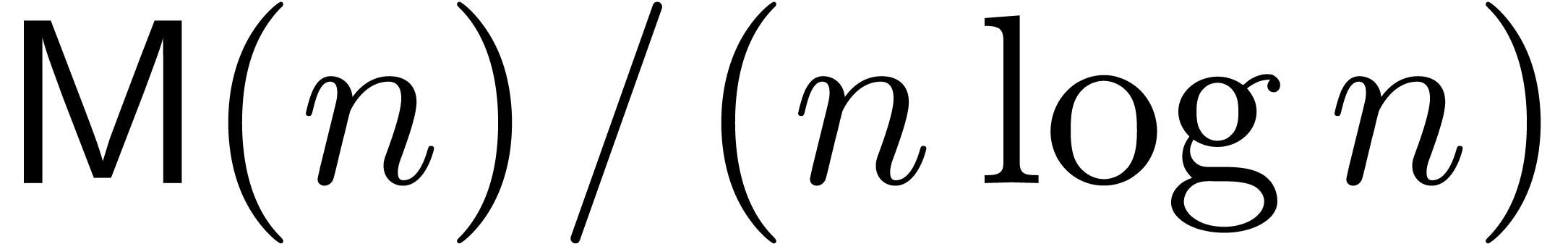 is increasing, we
prove that
is increasing, we
prove that  matrices with
matrices with
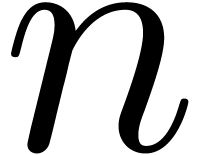 -bit integer entries may be
multiplied in
-bit integer entries may be
multiplied in
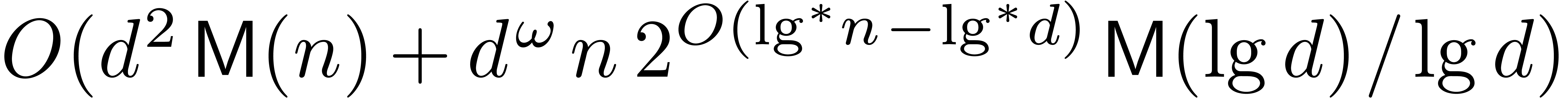
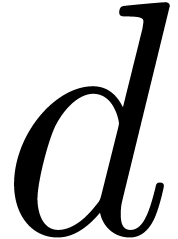 , say
, say
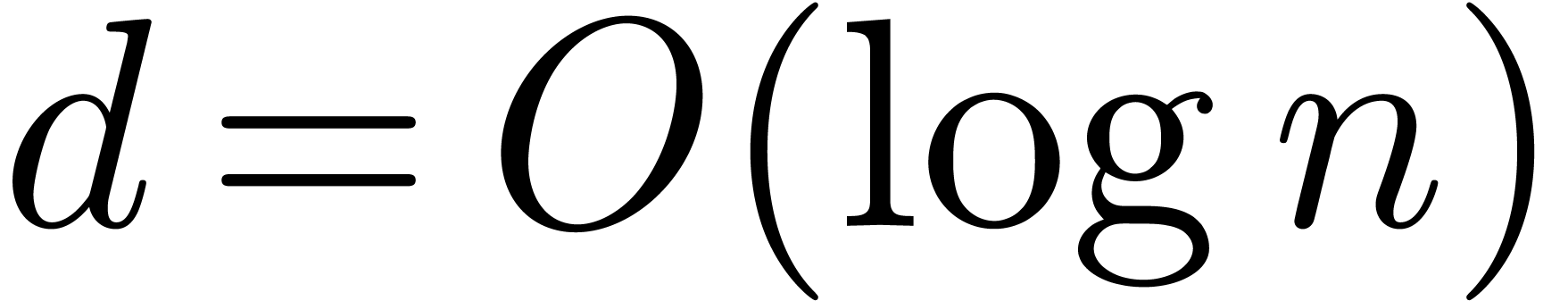 , then the complexity is only
, then the complexity is only
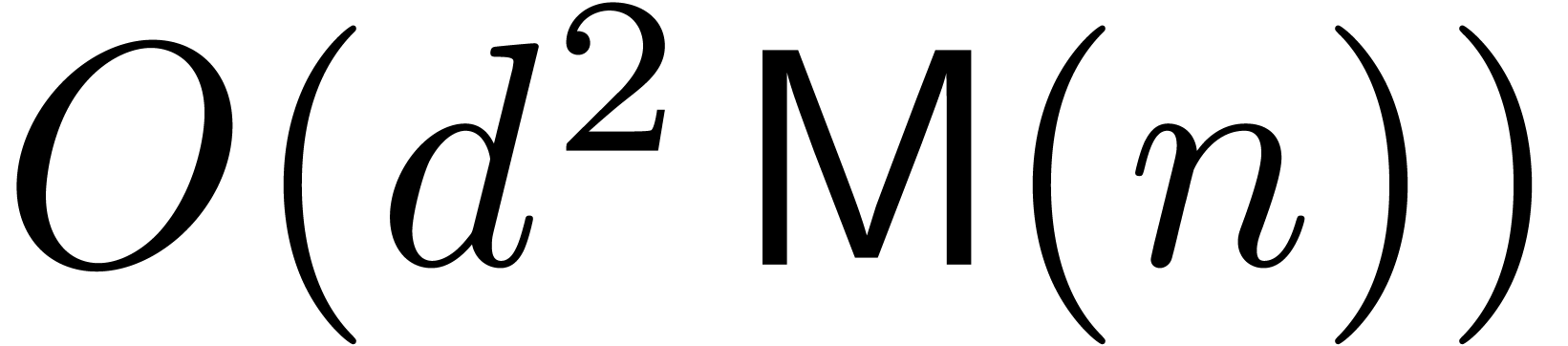 .
.