Abstract
A Hardy 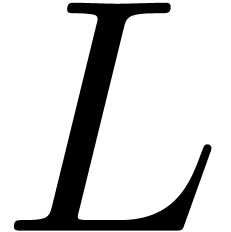 -function is a
function constructed from
-function is a
function constructed from 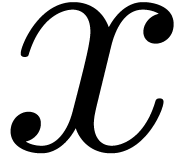 and
and  using the field
operation, exponentiation, logarithm and algebraic functions. Hardy
showed that the germs of
using the field
operation, exponentiation, logarithm and algebraic functions. Hardy
showed that the germs of 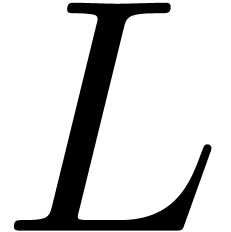 -functions
at infinity form a totally ordered field. He asked the question whether
the functional inverse of
-functions
at infinity form a totally ordered field. He asked the question whether
the functional inverse of 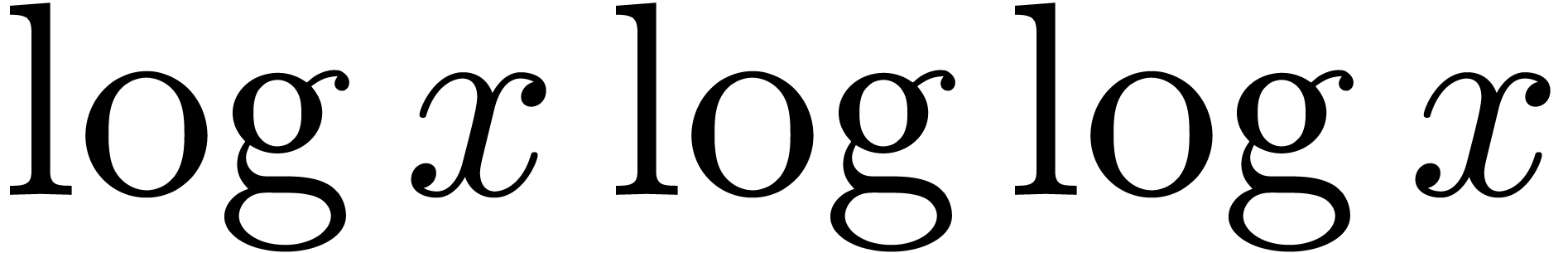 can be expanded with respect to an asymptotic scale of
can be expanded with respect to an asymptotic scale of 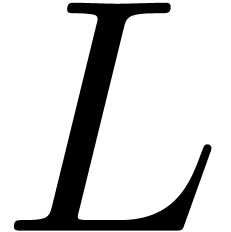 -functions. We will prove that this is not the
case.
-functions. We will prove that this is not the
case.
Occasions: ICM 1998, Berlin, August 24, 1998
Documents: slides
Note: the same result was proved independently by
Marker, Macintyre and van den Dries. A similar result for the functional
inverse of 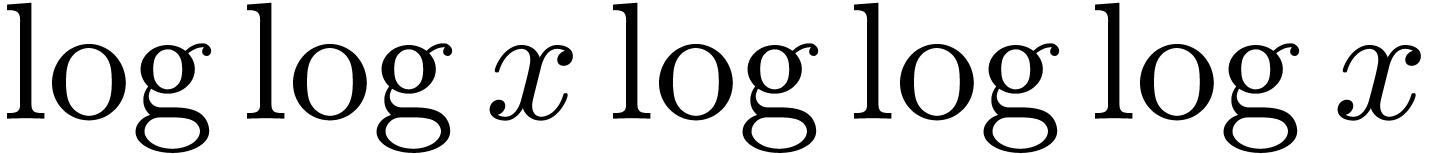 was obtained by
Shackell.
was obtained by
Shackell.
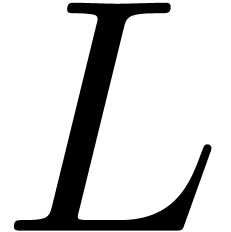 -function is a
function constructed from
-function is a
function constructed from 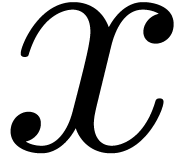 and
and  using the field
operation, exponentiation, logarithm and algebraic functions. Hardy
showed that the germs of
using the field
operation, exponentiation, logarithm and algebraic functions. Hardy
showed that the germs of 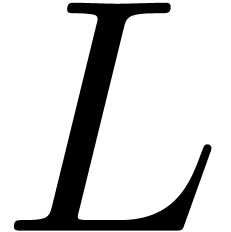 -functions
at infinity form a totally ordered field. He asked the question whether
the functional inverse of
-functions
at infinity form a totally ordered field. He asked the question whether
the functional inverse of 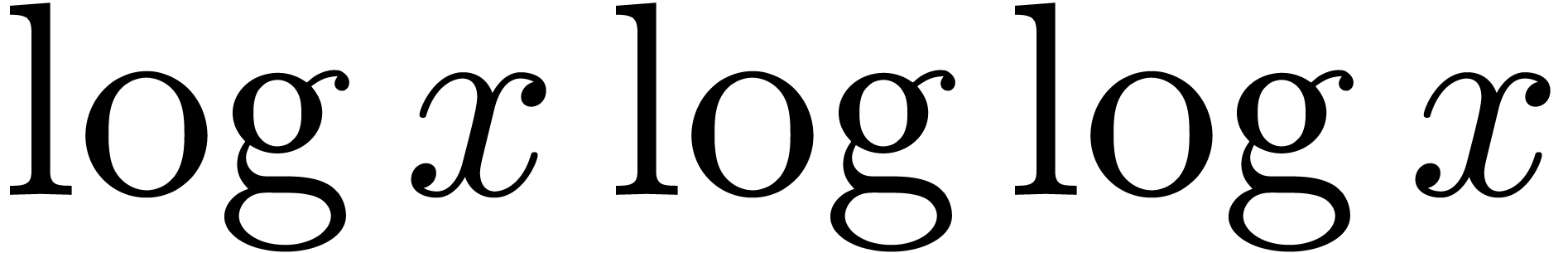 can be expanded with respect to an asymptotic scale of
can be expanded with respect to an asymptotic scale of 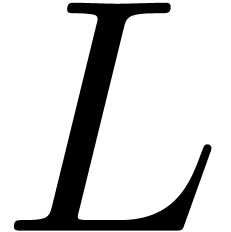 -functions. We will prove that this is not the
case.
-functions. We will prove that this is not the
case.
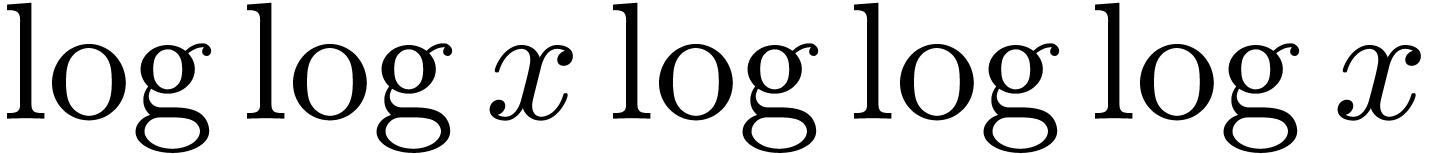 was obtained by
Shackell.
was obtained by
Shackell.