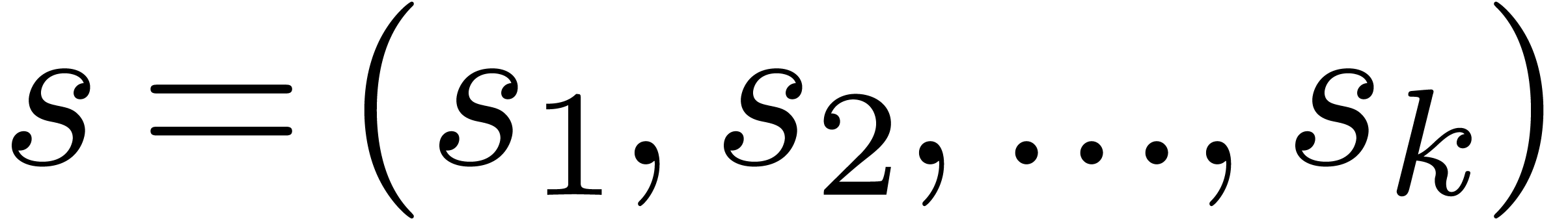For each multi–index 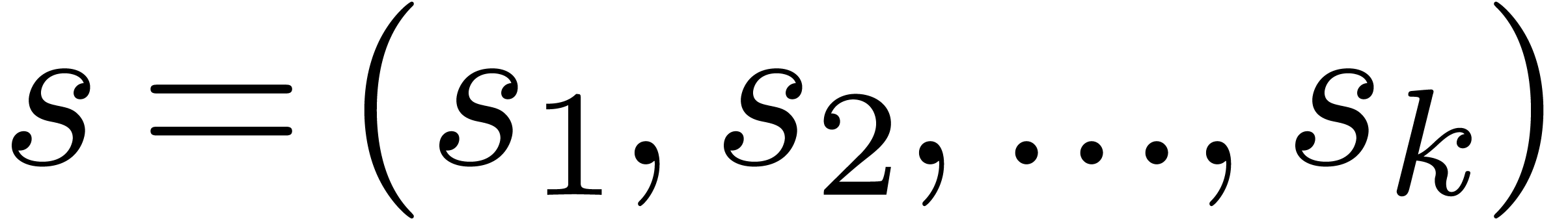of positive integers, one defines the generalized polylogarithms

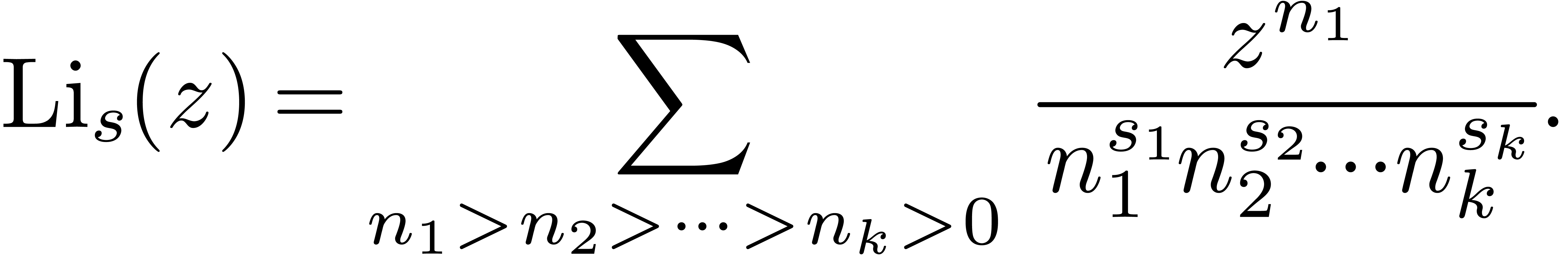(1)

This series in 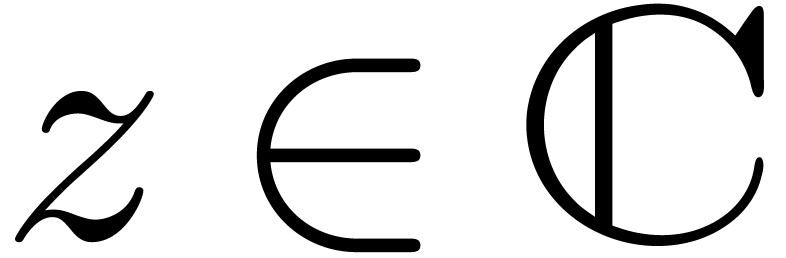converges at the interior of the open unit disk. In , these polylogarithms yield the generalized Riemann function

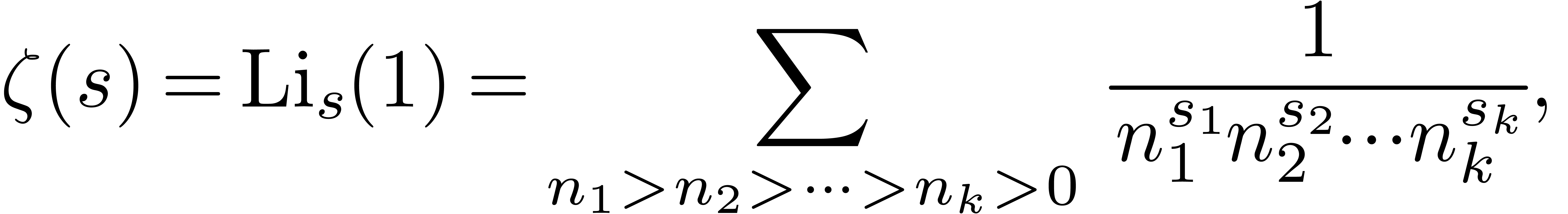(2)

which converges for .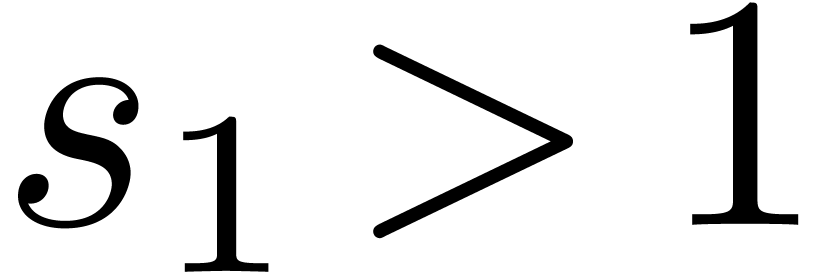

Let 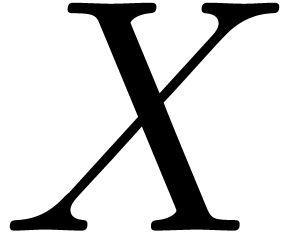be the alphabet on two letters 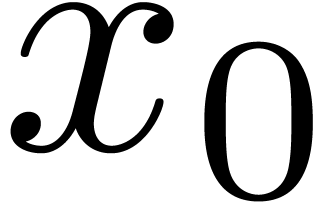and 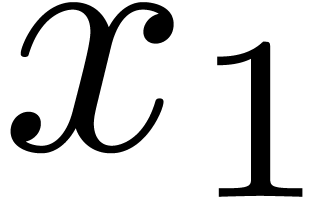. Any multi–index 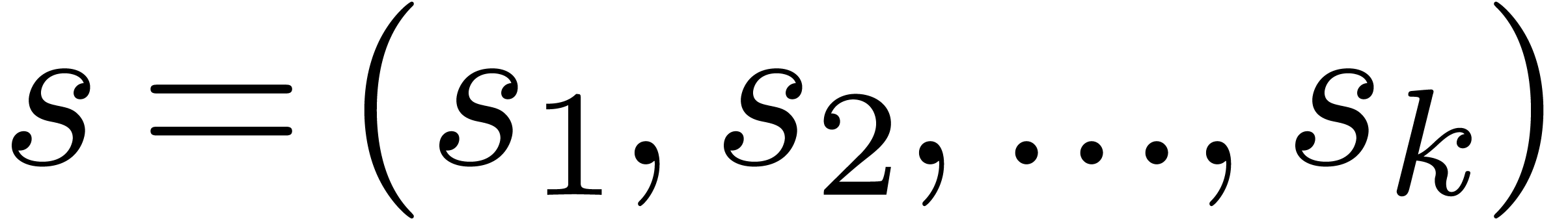can be encoded by a unique word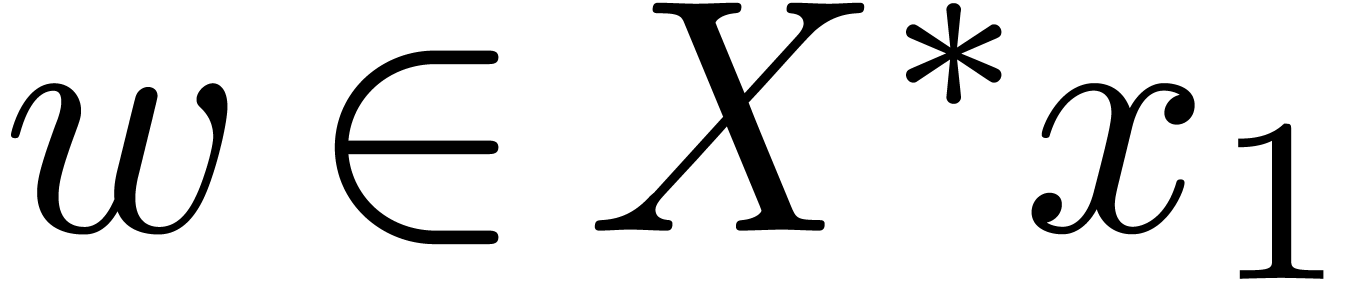

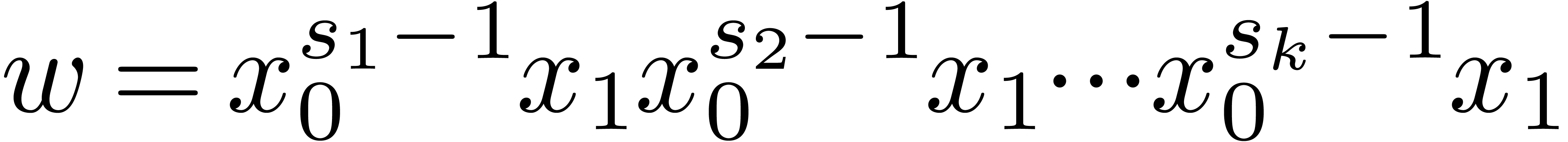(3)

Now each function 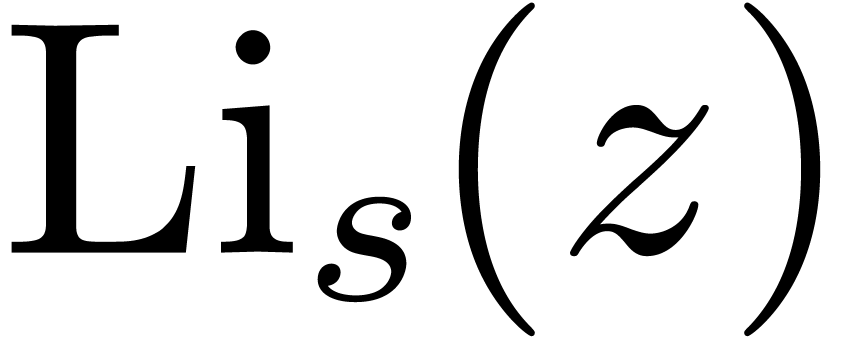, which is also denoted by 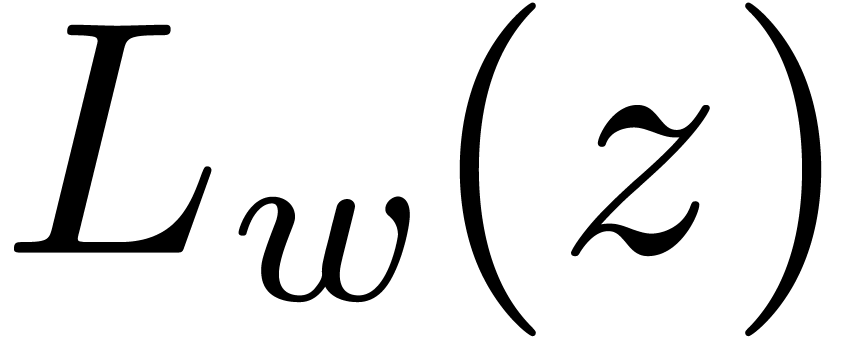, can be obtained by an iterated integral as follows:

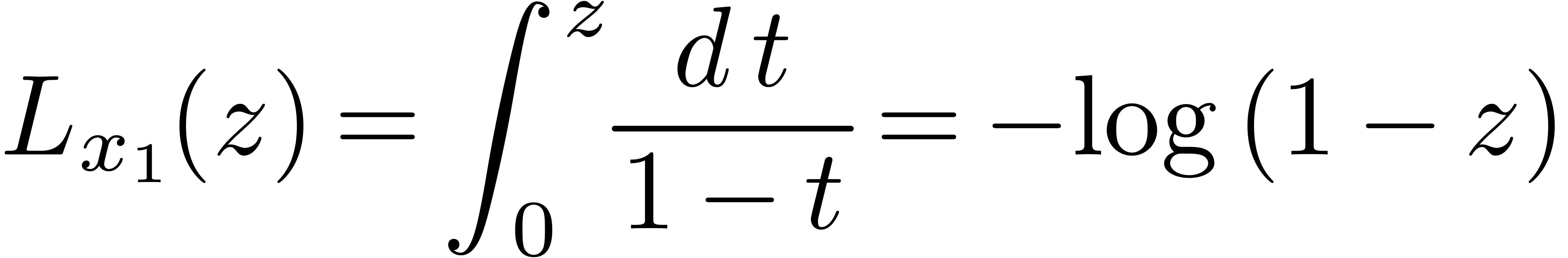
and

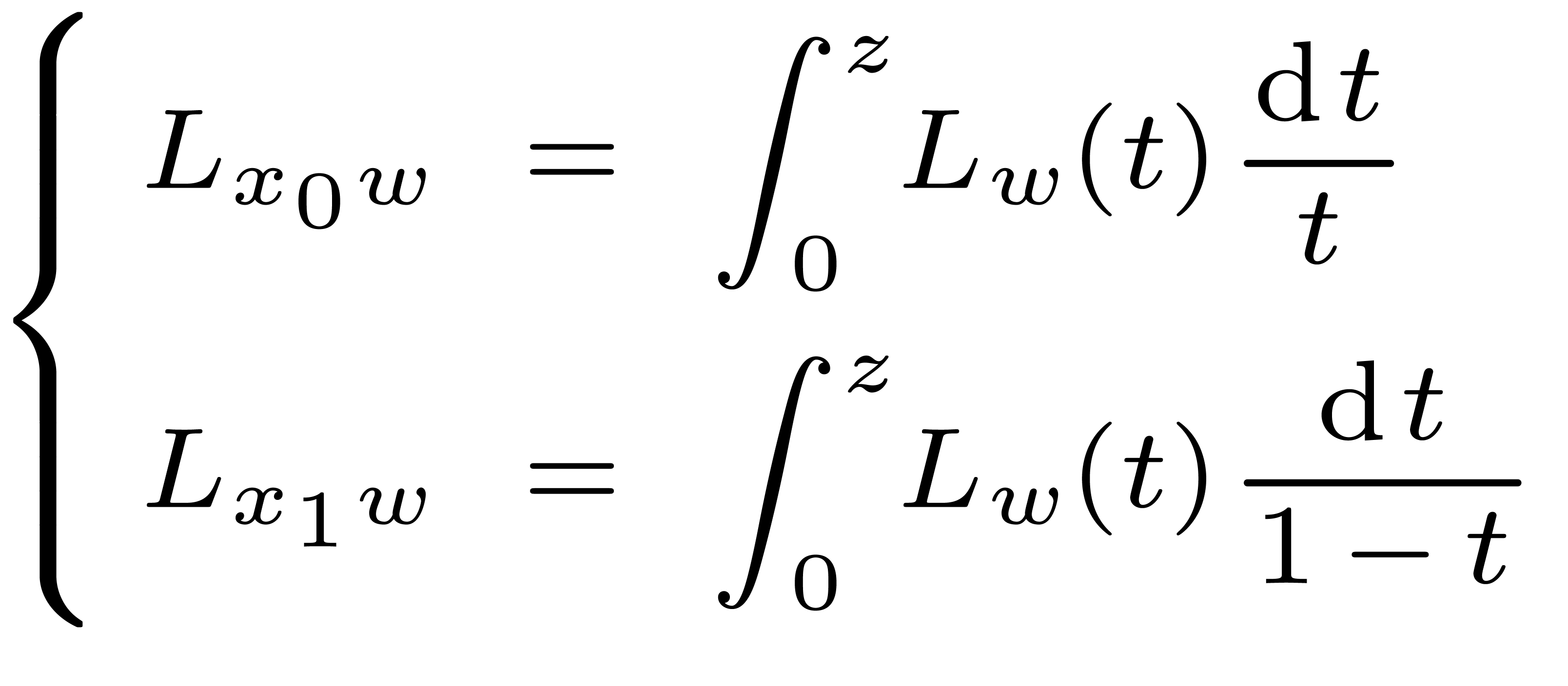(4)

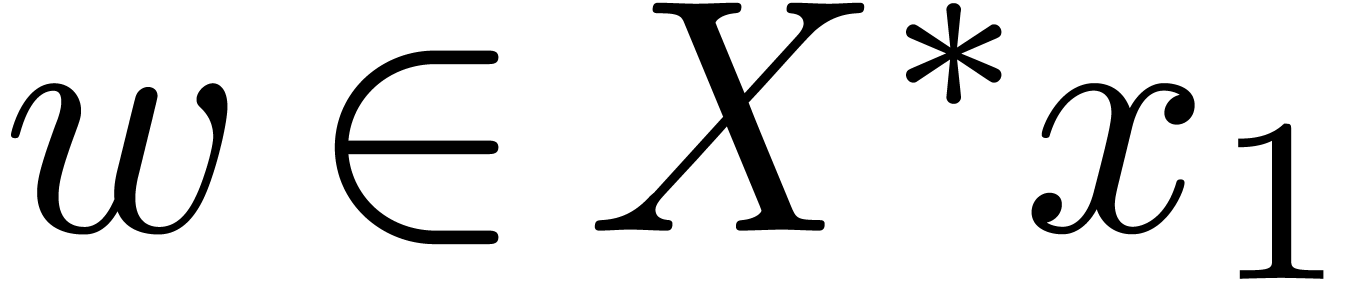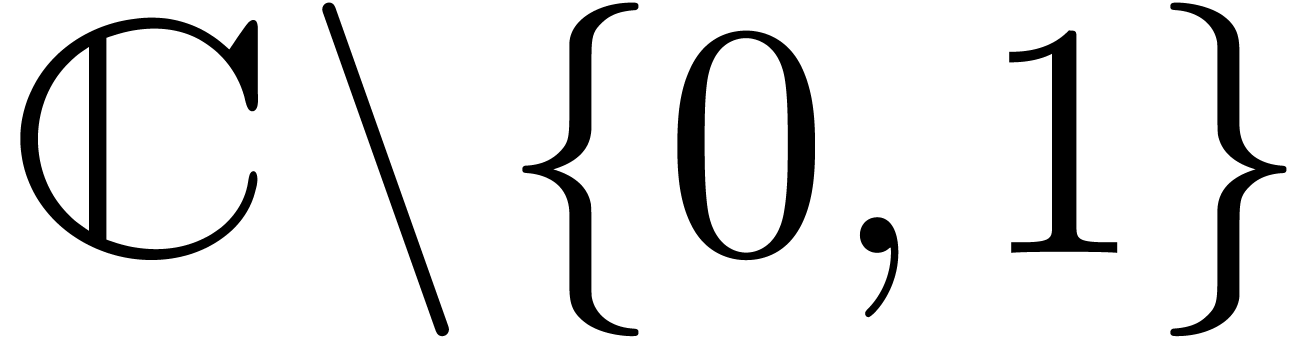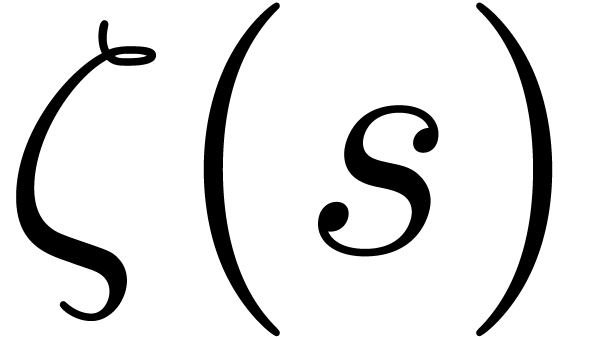for any . These integrals are functions defined on the universal Riemann surface above . The real number is also denoted by 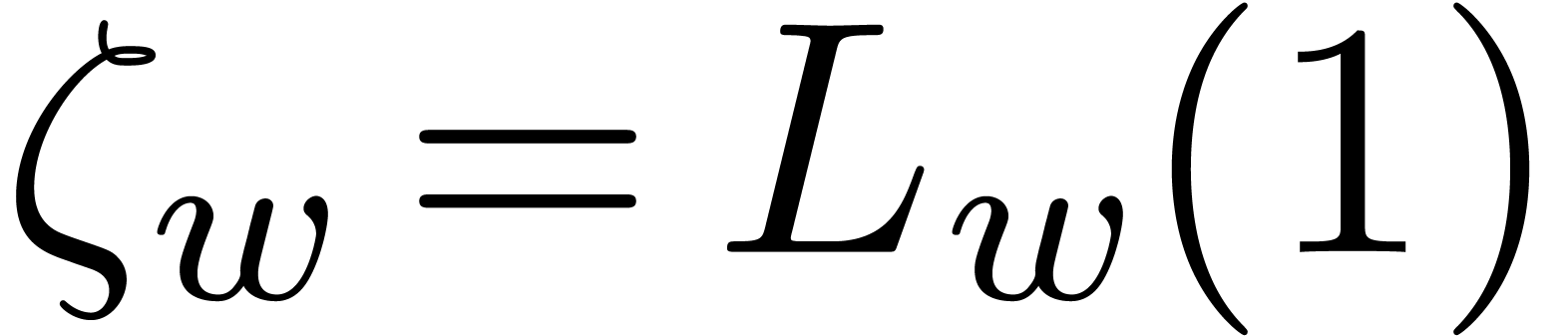for all .

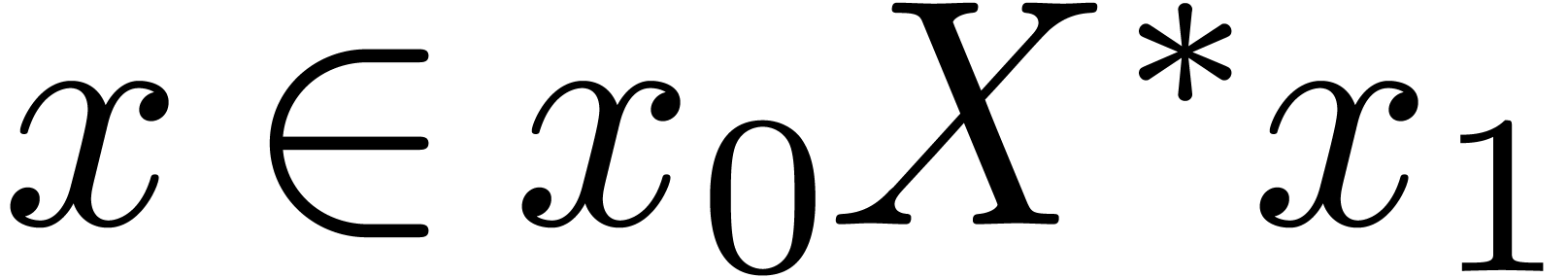It is useful to extend the above definition of 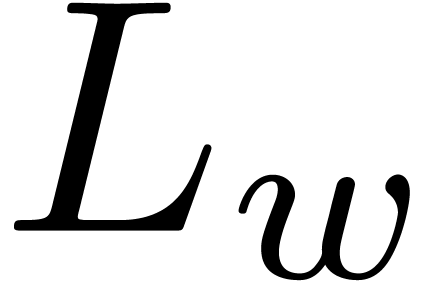to the case when 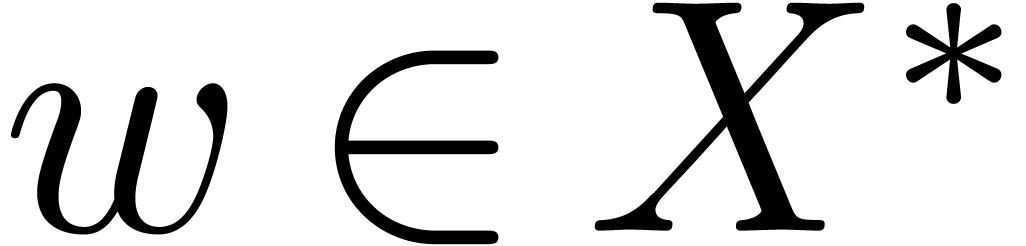. For each 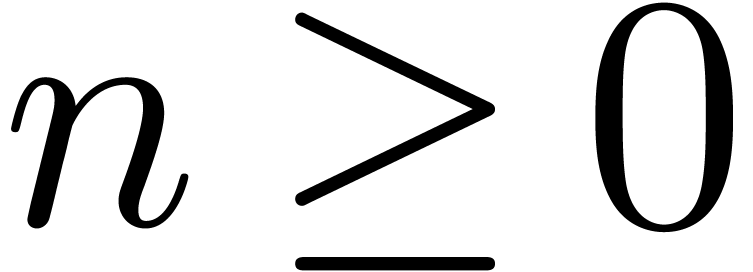, we take

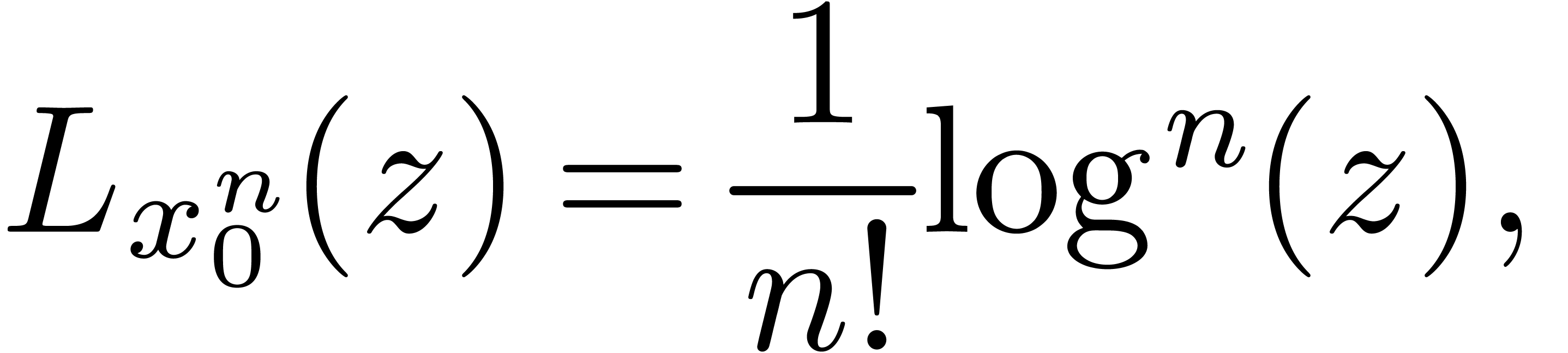(5)

and we extend the definition to 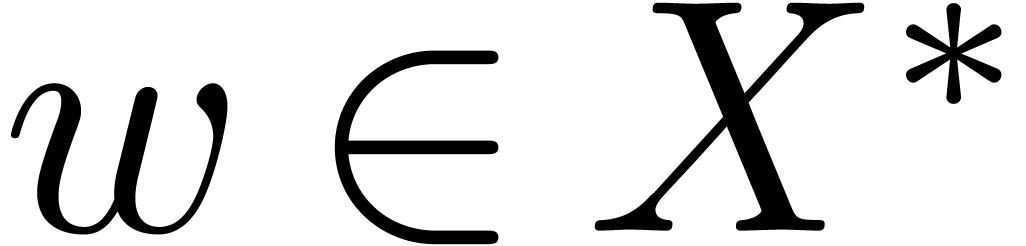using (4). These generalized polylogarithms are again defined on and we will prove the important fact that

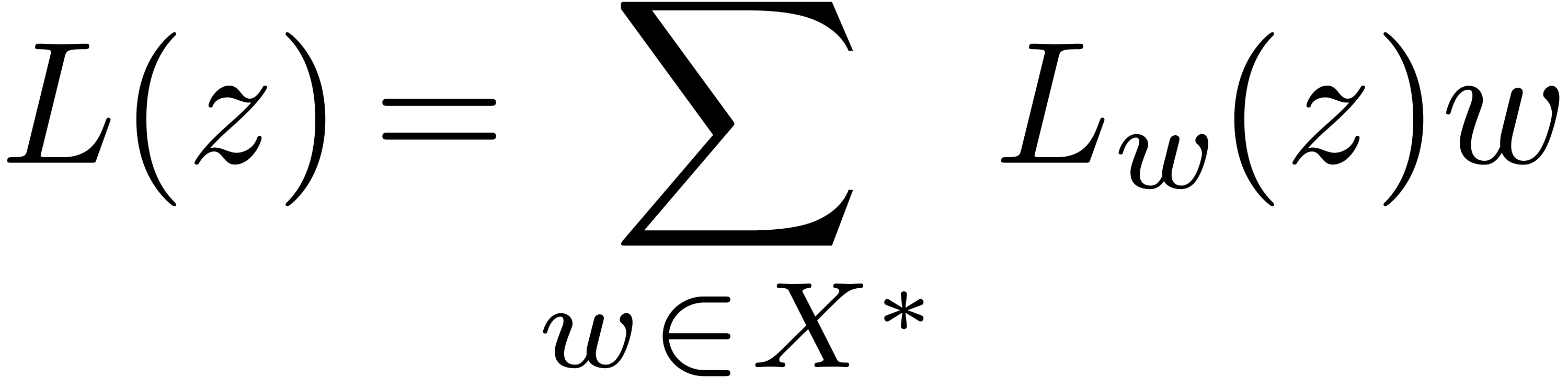(6)

is a Lie exponential for all .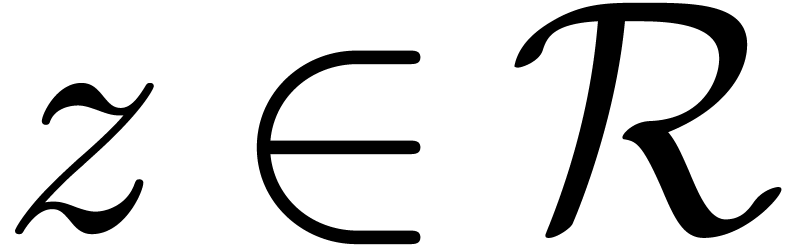

The monodromy of the classical polylogarithms 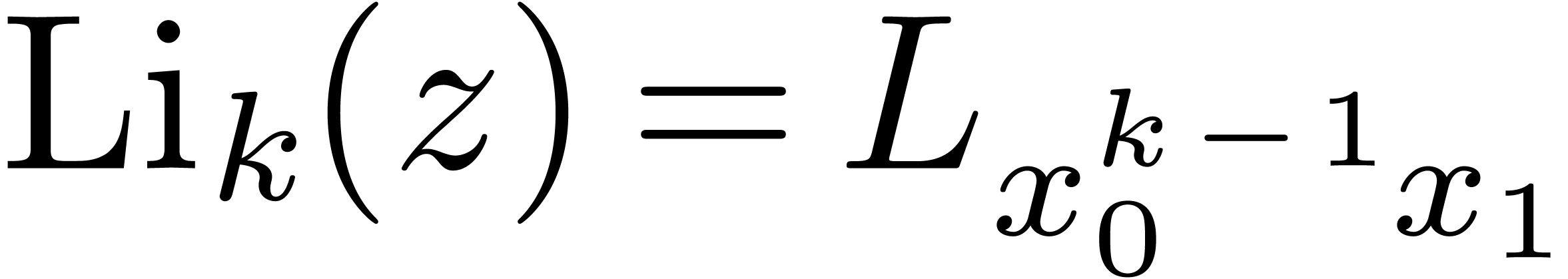, when turning around the point has been computed previously

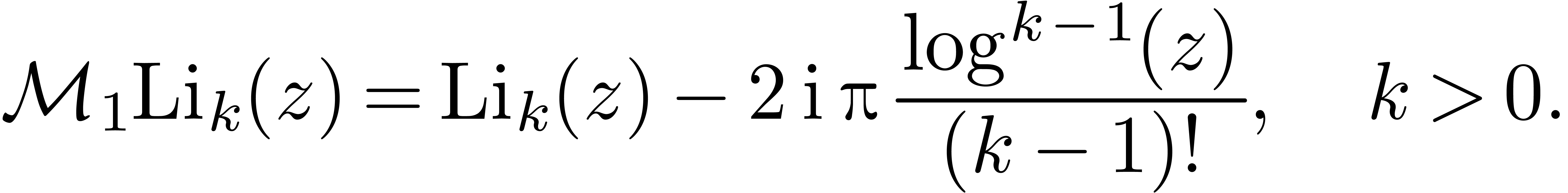(7)

From a theoretical point the monodromy of the series 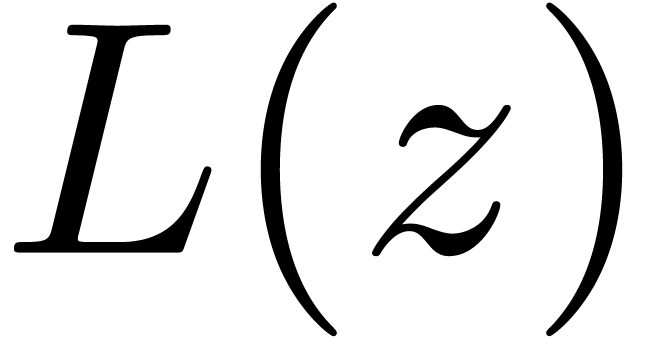can be computed using tools developed by J. Écalle. Notice that the monodromy of 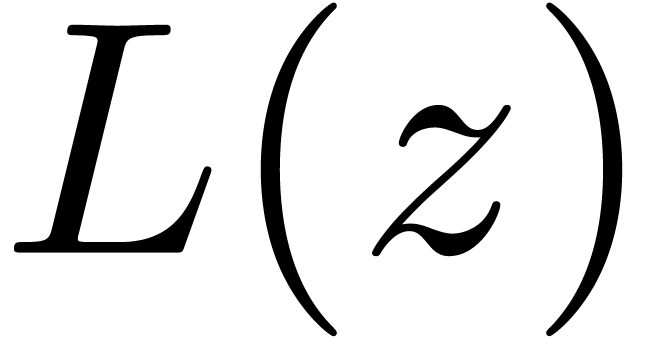in particular yields the monodromy of each 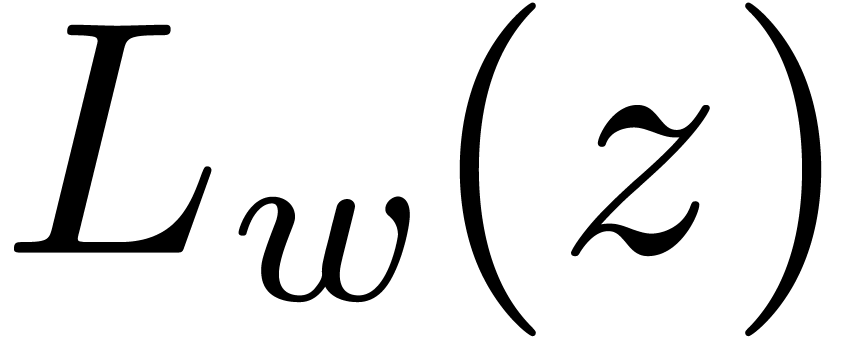for .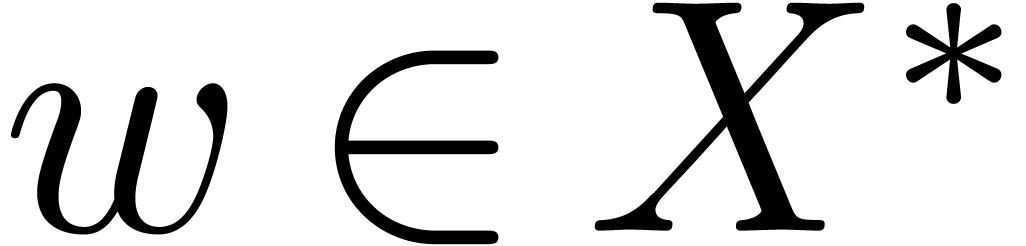

In this paper, we give an explicit method to compute the monodromy. Our algorithm has been implemented in the 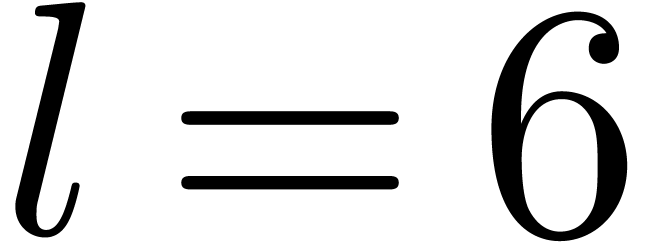Axiom system and we have given the output of the algorithm for in appendix B. Our methods rely on the theory of non commutative power series and the factorization of Lie exponentials. Our formulas for the monodromy of 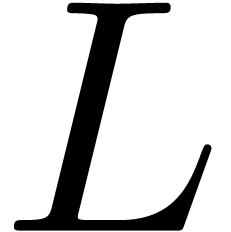involve only convergent 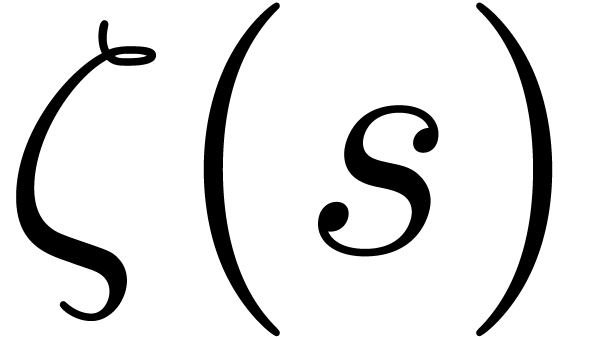defined by (2).

Coauthors: H.N. Minh and M. Petitot

Occasions: ISSAC 1998, Rostock, August 20

Documents: slides