Creative telescoping is a fairly general technique that can be used for proving combinatorial identities. Roughly speaking, it allows for the computation of sums or integrals of the form

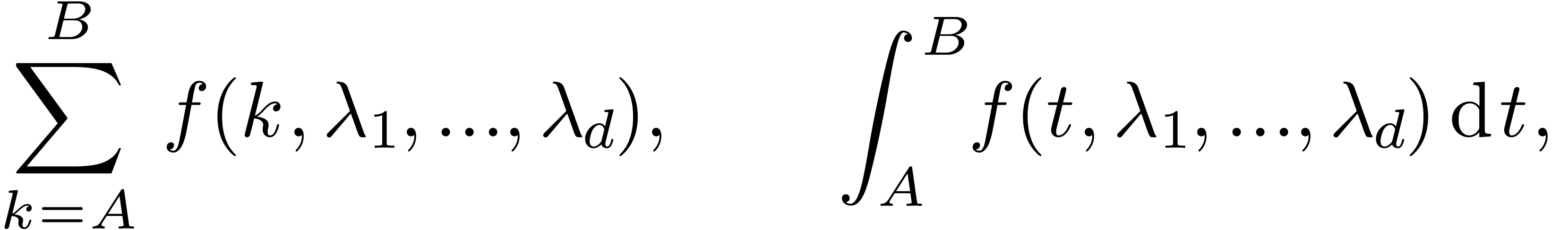
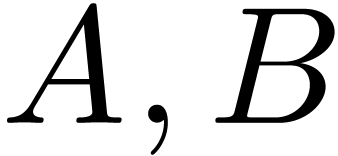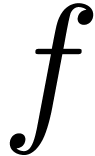where are suitable limits and belongs to a suitable class of D-finite or holonomic functions. The technique was introduced by Doron Zeilberger and it has been generalized and optimized during the last two decades.

One recent approach to creative telescoping is based on so-called “reductions”. This has given rise to a series of efficient algorithms for increasingly general situations and also allowed to gain insight into the complexity of creative telescoping. In my talk, I will briefly review these recent developments and then present an algorithm that works for general (differentially) D-finite functions.

Occasion: Combinatorial Potlatch Conference 2019, Billingham (USA), November 23, 2019

Documents: slideshow, TeXmacs source