 ,
, 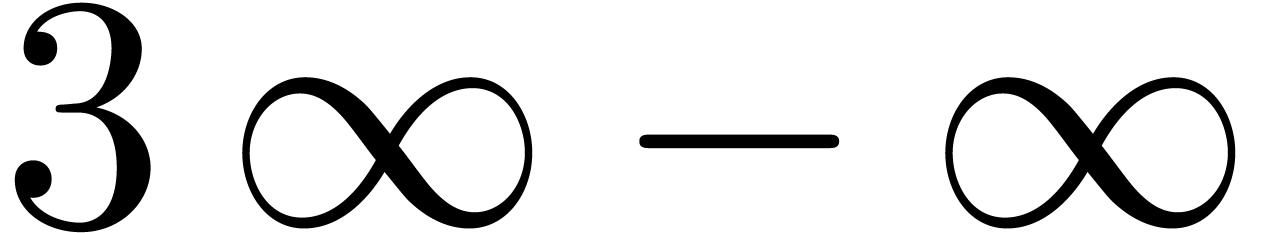 ,
,
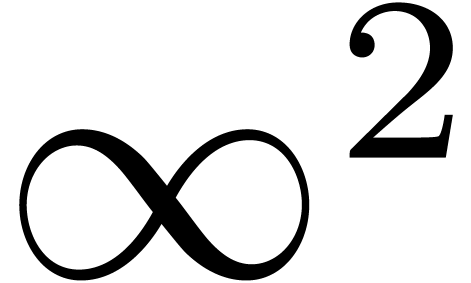 ,
,  ? The mathematical study of this kind of questions
started during the end of the 19th century.
? The mathematical study of this kind of questions
started during the end of the 19th century.
| HomepagePublicationsTalksTeXmacsMathemagix |
Are there infinities that are “larger” than others? If so,
how to carry out computations with infinite quantities, like  ,
, 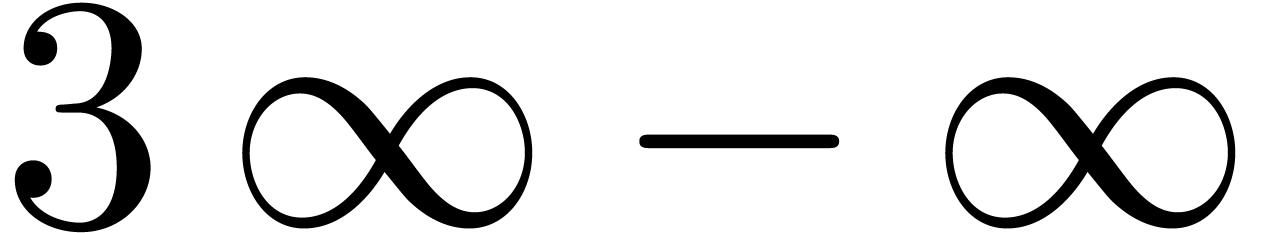 ,
,
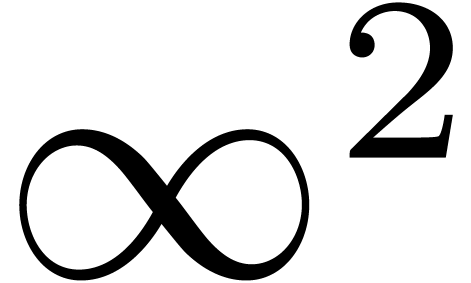 ,
,  ? The mathematical study of this kind of questions
started during the end of the 19th century.
? The mathematical study of this kind of questions
started during the end of the 19th century.
On the one hand, Cantor introduced ordinal and cardinal arithmetic [6, 13], which allowed him to quantify the “size” of an infinite set. Slightly anterior to Cantor's work, but less well known, du Bois-Reymond [9, 10, 11] developed a “calculus of infinities” to deal with growth rates of real functions in one variable, representing their “potential infinity” by an “actual infinite” quantity.
At first sight, Cantor's discrete infinities (generalizing natural numbers) and du Bois Reymond's growth orders (generalizing real numbers) are of a very different nature. We will survey the subsequent developments of these theories and recent progress towards their ultimate unification [2].
Note: Joint work with Matthias
Occasion: ALGOS 2020: ALgebras, Graphs and Ordered Sets, Nancy, August 27
Dedicated to: 75th birthday of Maurice
Documents: slideshow, TeXmacs source
Extended abstract |
Ordinal numbers can be regarded as a generalization of natural numbers, where we are “allowed to count beyond all numbers that we already constructed”:
In Conway's theory of surreal numbers [7, 20],
we may also construct numbers between already known numbers: given two
sets 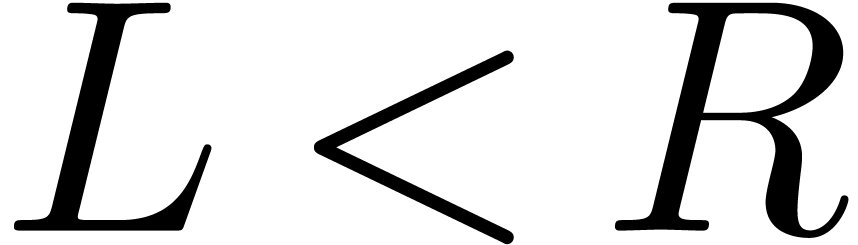 of surreal numbers,
there exists a simplest surreal number
of surreal numbers,
there exists a simplest surreal number 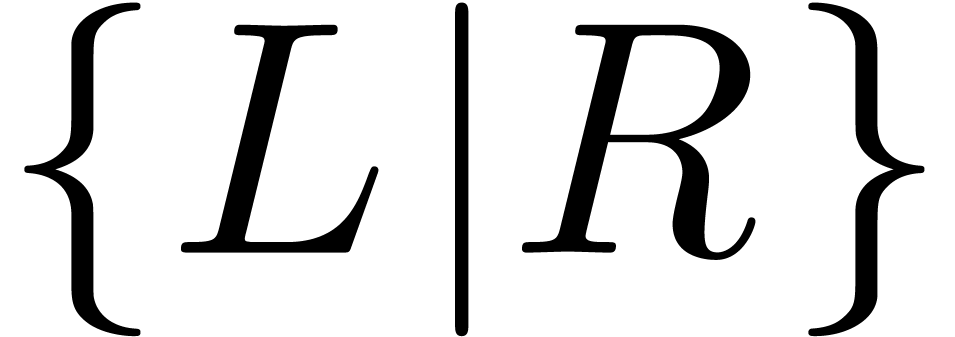 with
with 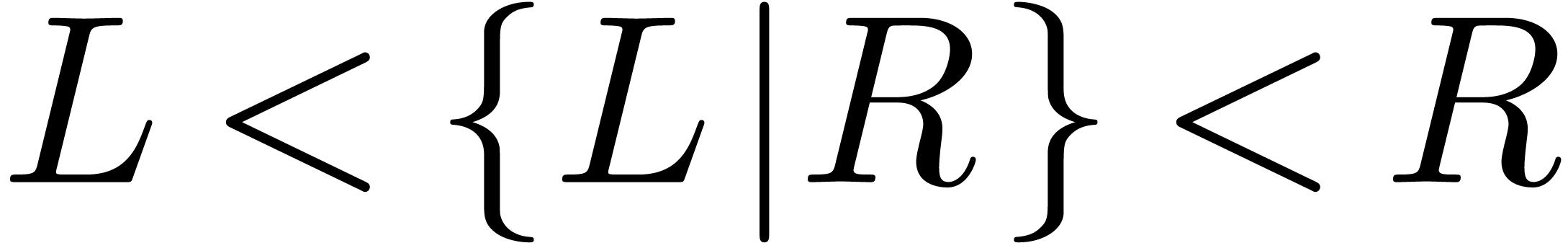 . This theory naturally
extends Cantor's theory of ordinal numbers:
. This theory naturally
extends Cantor's theory of ordinal numbers:

More interestingly, arithmetic operations on surreal numbers can be
defined in a surprisingly elegant way, after which the class  of all surreal numbers turns out
to be a totally ordered real closed field that contains
of all surreal numbers turns out
to be a totally ordered real closed field that contains  . For instance:
. For instance:
An interesting question is which other real calculus operations
“naturally” extend to the surreal numbers. For instance,
Gonshor defined an exponential on  with the same first order properties as the usual exponential [14].
More recently, Berarducci and Mantova showed how to define a derivation
with respect to
with the same first order properties as the usual exponential [14].
More recently, Berarducci and Mantova showed how to define a derivation
with respect to  on
on  [4].
[4].
Du Bois-Reymond's ideas were put on a firm bases by Hausdorff [17] and Hardy [15, 16]. Hardy introduced the set of “logarithmic-exponential functions” such as
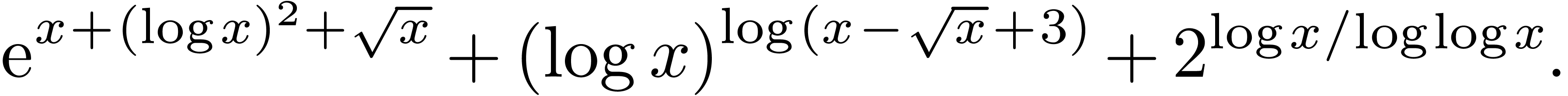
He proved the remarkable fact that the set of germs of such functions at infinity form a real closed differential field. This was later generalized by Bourbaki [5], who defined a Hardy field to be any field of germs at infinity that is stable under differentiation.
Another formal direction of generalization is to consider so-called “transseries”, which are infinite logarithmic-exponential expressions such as
Transseries were introduced independently by Dahn–Göring [8] and Écalle [12], and their theory was further developed in [18, 19, 1]. Again, it turns out that the class of all transseries forms a totally ordered differential field.
We have now seen three types of real closed differential fields with
infinitely large quantities: the surreal numbers, Hardy fields, and the
field of transseries. In each of the three cases, it turns out that the
derivation and the ordering satisfy additional compatibility properties
like 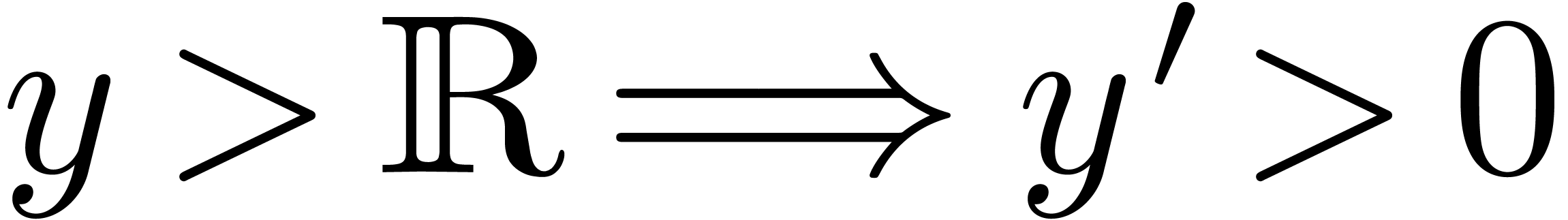 . The notion of an
“H-field” captures the most obvious common first order
properties of this kind.
. The notion of an
“H-field” captures the most obvious common first order
properties of this kind.
The field of transseries  also satisfies several less obvious first order properties such as the
intermediate value theorem [19]: given a differential
polynomial
also satisfies several less obvious first order properties such as the
intermediate value theorem [19]: given a differential
polynomial 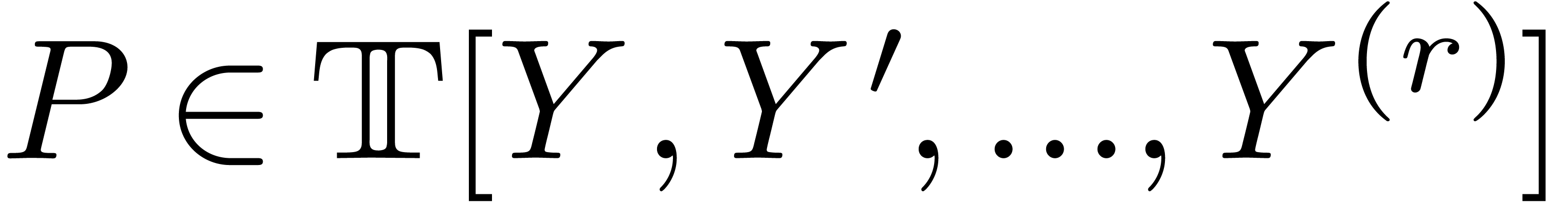 and
and 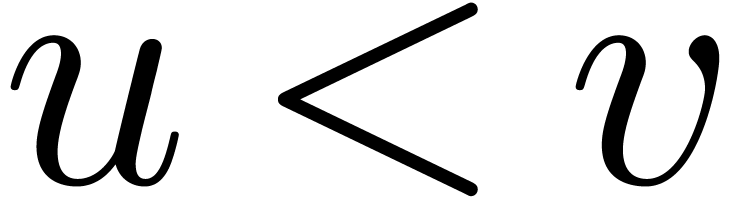 in
in  with
with 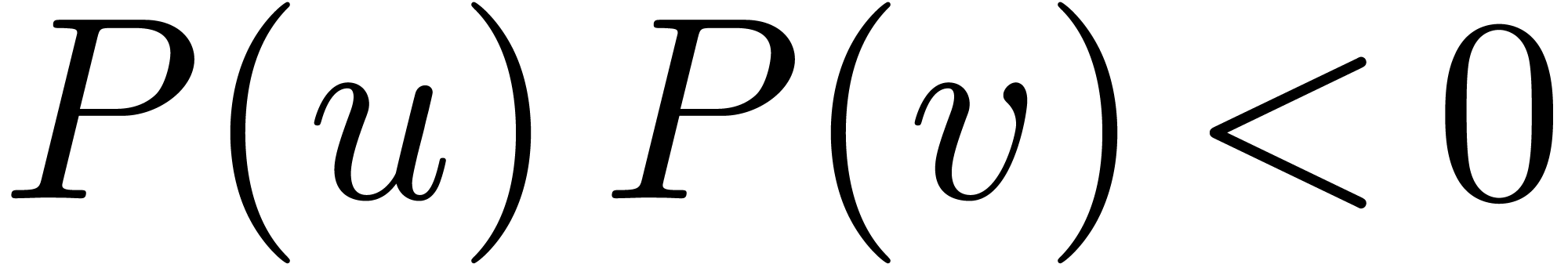 , there exists a
, there exists a 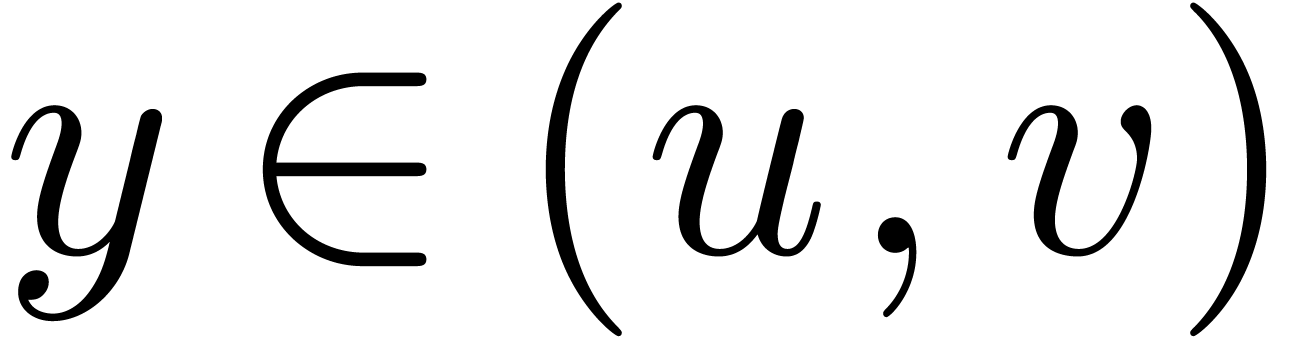 with
with 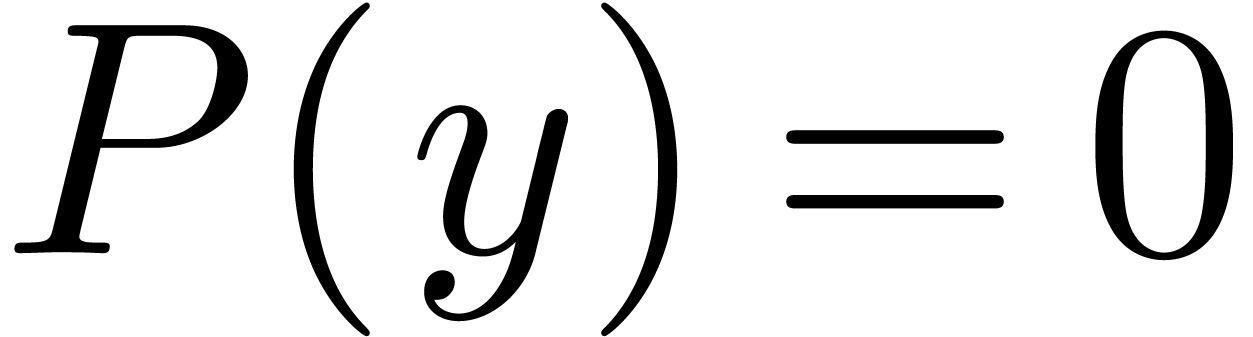 .
An H-field is said to be “H-closed” if it satisfies this and
a few other closure properties. The main result of [1] is
that the elementary theory of
.
An H-field is said to be “H-closed” if it satisfies this and
a few other closure properties. The main result of [1] is
that the elementary theory of  is completely axiomatized by the axioms of H-closed H-fields. Moreover,
we proved a quantifier elimination theorem for a natural expansion of
this theory.
is completely axiomatized by the axioms of H-closed H-fields. Moreover,
we proved a quantifier elimination theorem for a natural expansion of
this theory.
The language of H-fields allows us to make the relations between surreal
numbers, Hardy fields, and transseries more precise. For instance, the
ordered differential field of surreal numbers  is elementary equivalent to
is elementary equivalent to  [3]. We conjecture that the same holds
for all maximal Hardy fields. We also conjecture that there exists a
natural isomorphism between
[3]. We conjecture that the same holds
for all maximal Hardy fields. We also conjecture that there exists a
natural isomorphism between  and a suitable field
and a suitable field  of
“hyperseries”—a generalization of transseries with
functions such as the solution of
of
“hyperseries”—a generalization of transseries with
functions such as the solution of 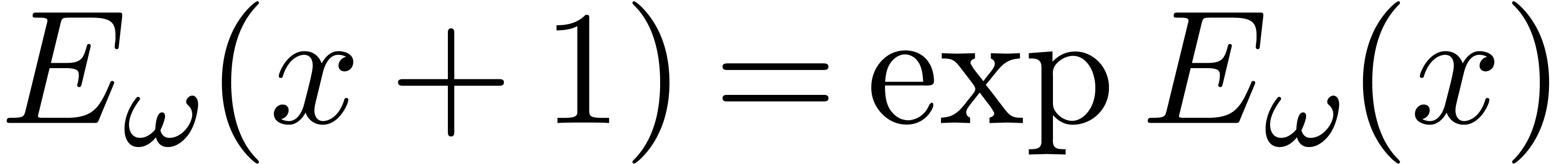 .
We refer to [2] for detailed statements and partial
results.
.
We refer to [2] for detailed statements and partial
results.
M. Aschenbrenner, L. van den Dries, and J. van der Hoeven. Asymptotic Differential Algebra and Model Theory of Transseries. Number 195 in Annals of Mathematics studies. Princeton University Press, 2017.
M. Aschenbrenner, L. van den Dries, and J. van der Hoeven. On numbers, germs, and transseries. In Proc. Int. Cong. of Math. 2018, volume 1, pages 1–24. Rio de Janeiro, 2018.
M. Aschenbrenner, L. van den Dries, and J. van der
Hoeven. The surreal numbers as a universal  -field. J. Eur. Math. Soc.,
21(4):1179–1199, 2019.
-field. J. Eur. Math. Soc.,
21(4):1179–1199, 2019.
A. Berarducci and V. Mantova. Surreal numbers, derivations and transseries. JEMS, 20(2):339–390, 2018.
N. Bourbaki. Fonctions d'une variable réelle. Éléments de Mathématiques (Chap. 5). Hermann, 2-nd edition, 1961.
G. Cantor. Sur les fondements de la théorie des ensembles transfinis. Jacques Gabay, 1899. Reprint from les Mémoires de la Société des Sciences physiques et naturelles de Bordeaux.
B. I. Dahn and P. Göring. Notes on exponential-logarithmic terms. Fundamenta Mathematicae, 127:45–50, 1986.
P. du Bois-Reymond. Sur la grandeur relative des infinis des fonctions. Annali di Matematica Pura ed Applicata (1867-1897), 4(1):338–353, 1870.
P. du Bois-Reymond. Über asymptotische Werte, infinitäre Approximationen und infinitäre Auflösung von Gleichungen. Math. Ann., 8:363–414, 1875.
P. du Bois-Reymond. Über die Paradoxen des Infinitärscalcüls. Math. Ann., 11:149–167, 1877.
J. Écalle. Introduction aux fonctions analysables et preuve constructive de la conjecture de Dulac. Hermann, collection: Actualités mathématiques, 1992.
Ph. Ehrlich. The rise of non-Archimedean mathematics and the roots of a misconception i: the emergence of non-Archimedean systems of magnitudes. Arch. Hist. Exact Sci., 60:1–121, 2006.
H. Gonshor. An Introduction to the Theory of Surreal Numbers. Cambridge Univ. Press, 1986.
G. H. Hardy. Orders of infinity. Cambridge Univ. Press, 1910.
G. H. Hardy. Properties of logarithmico-exponential functions. Proceedings of the London Mathematical Society, 10(2):54–90, 1911.
F. Hausdorff. Grundzüge einer Theorie der geordneten Mengen. Math. Ann., 65:435–505, 1908.
J. van der Hoeven. Automatic asymptotics. PhD thesis, École polytechnique, Palaiseau, France, 1997.
J. van der Hoeven. Transseries and real differential algebra, volume 1888 of Lecture Notes in Mathematics. Springer-Verlag, 2006.
D.E. Knuth. Surreal Numbers: How Two Ex-students Turned on to Pure Mathematics and Found Total Happiness : a Mathematical Novelette. Addison-Wesley Publishing Company, 1974.