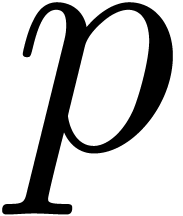 ,
polynomials in
,
polynomials in 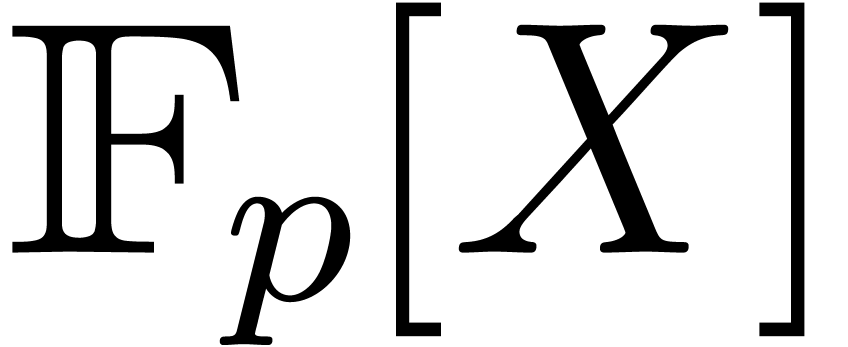 of degree
of degree
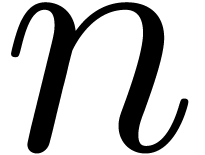 may be multiplied in
may be multiplied in 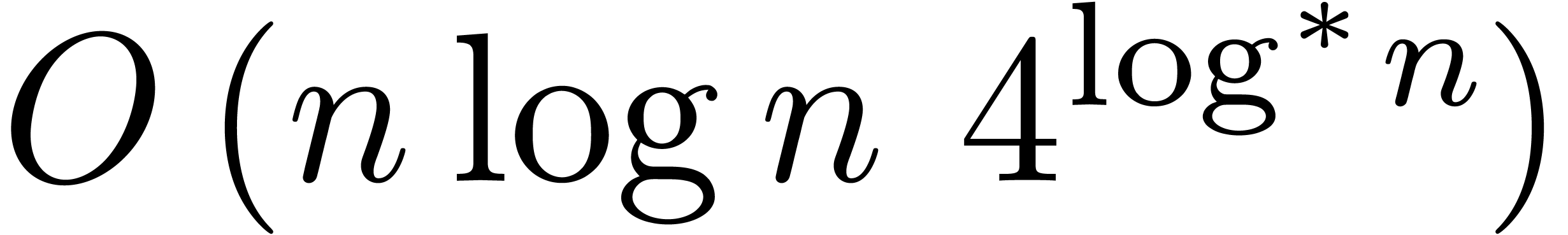 bit operations; the previous best
bound was
bit operations; the previous best
bound was 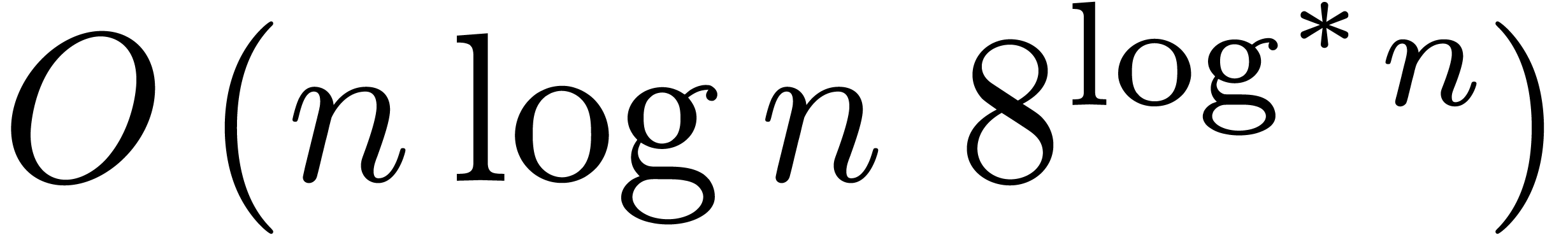 .
.
| HomepagePublicationsTalksTeXmacsMathemagix |
We prove that for a fixed prime 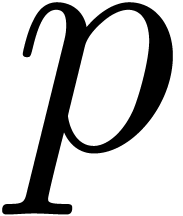 ,
polynomials in
,
polynomials in 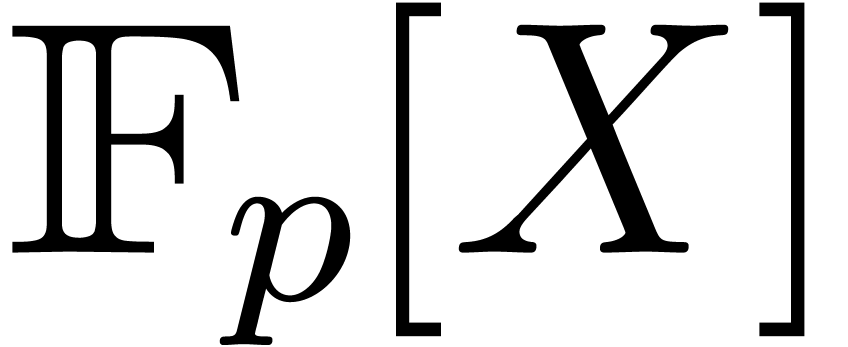 of degree
of degree
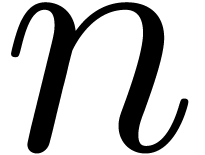 may be multiplied in
may be multiplied in 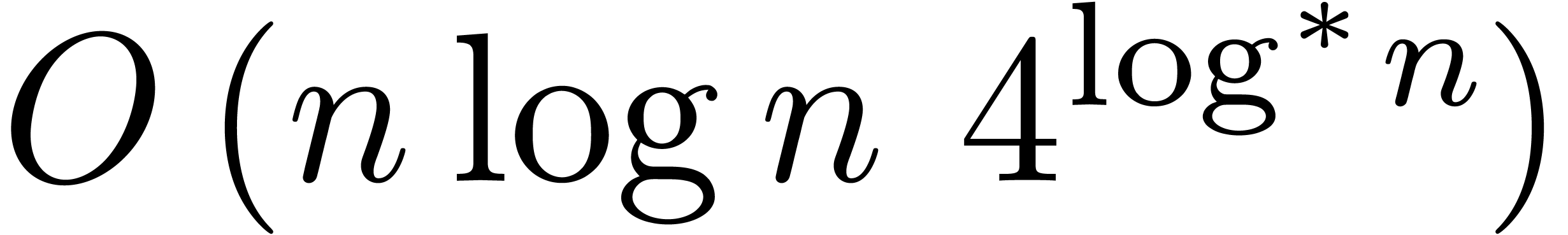 bit operations; the previous best
bound was
bit operations; the previous best
bound was 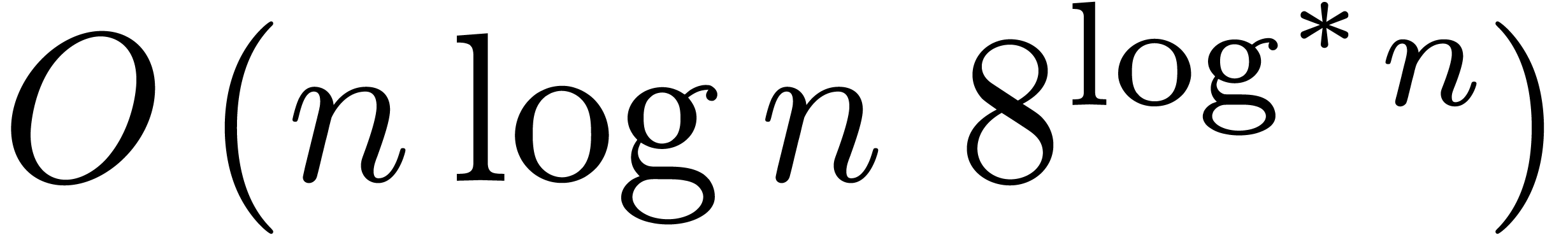 .
.
In the original preprint version, with title “Faster integer and
polynomial multiplication using cyclotomic coefficient rings”, we
also presented an algorithm that computes the product of two 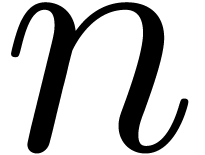 -bit integers in
-bit integers in 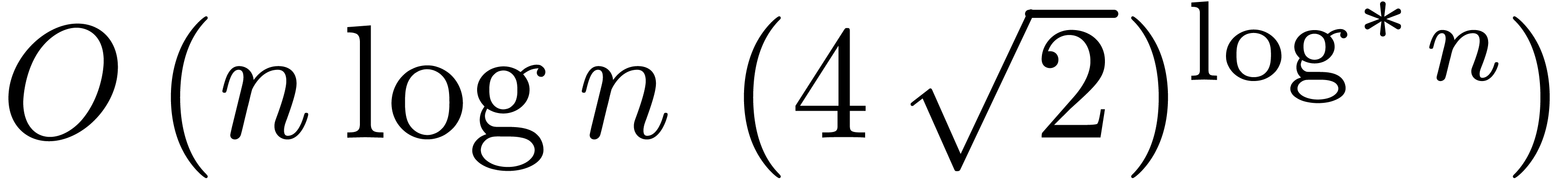 bit operations, thereby improving on the
previously best known bound
bit operations, thereby improving on the
previously best known bound 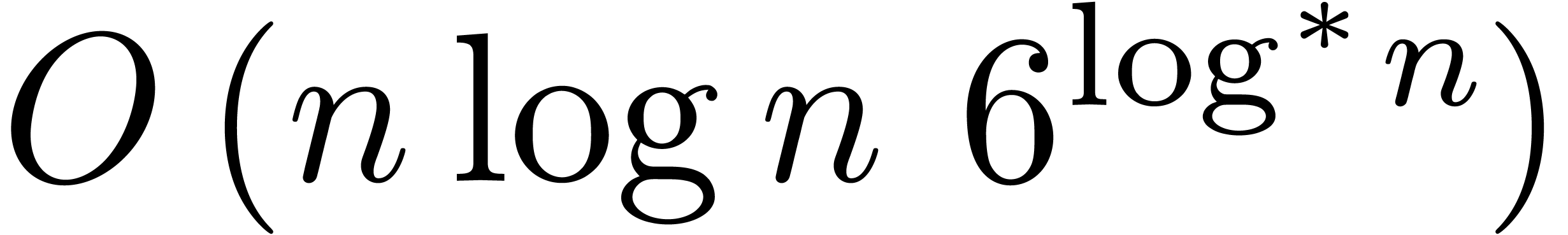 .
This bound was superseded itself by “Faster integer
multiplication using short lattice vectors”.
.
This bound was superseded itself by “Faster integer
multiplication using short lattice vectors”.
Authors:
View: Pdf, BibTeX, Preprint version